1. Introduction
It is well known that classical linear regression model and time series models are most widely used in statistical inference, including medical treatment, education, finance, science, technology and many other fields. Most of the cases, these models are used for single-valued random variables. In the real world, there are plenty of random phenomenas cannot be characterized by single-valued random variables. Taking the price of a stock on a given day for example, it is clearly unreasonable to use a single-valued data to decribe the stock price. If only single-valued data such as stock closing price or opening price are used, the fluctuation information in the process of stock trading is ignored and the resulting analysis results provided to decision-makers are also one-sided. Moreover, people will pay more attention to the data in a certain range, such as the temperature for a given day, instead of knowing the temperature at a certain time of one day, people care more about the maximum and minimum temperature of one day. In economic forecasting, economists mostly give a prediction range of economic growth rate. In the process of medical impact diagnosis, the impact result is usually a two-dimensional plan, and it is not a single value. Therefor, the interval-valued data are more appropriate and valuable in these cases because they provide more information. Thus it is necessary to consider the interval-valued statistical models and statictical inference problems.
Interval-valued random variables are special set-valued random variables. In mid twentith century, Aumann and Debreu first used set-valued mapping when studying economic phenomena. Aumann [
1] gave the integral of set-valued random variables in 1965. Hiai and Umegaki [
6] gave the concept of conditional expectation of set-valued random variables in 1978. Lyashenko [
11,
12] discussed the properties of set-valued random variables in Euclidean space, introduced the definition of set-valued Gaussian random variables, and gave the definition of variance for set-valued random variables. Vitale [
16] studied the properties of
distance. In 2005, Xuhua Yang and Shoumei Li [
17] gave the definitions of variance and covariance for set-valued random variables under the
distance, and obtained excellent properties. In 2008, Blanco et. al. defined the variance and studied the properties of interval valued random variables under a new distance in [
2]. Hess [
5], Papageorgiou [
14,
15], Shoumei Li et. al. [
7,
8,
9] explored the convergence theory of set-valued random variables under different conditions. Molchanov in [
13], Shoumei Li et. al. in [
10] systematically summarized the theory of set-valued random variables. The above research promoted the development of set-valued random variable theory.
For interval-valued statistical models, Billard and Diday [
3] established a linear regression model by using the midpoint of interval-valued random variables in 2000. In 2002, Billard and Diday [
4] established linear regression models by using the two endpoints of interval-valued random variables respectively. In 2008, Lima Neto and de Carvalho [
19] established linear regression models by using the center and radius of interval-valued random variables. In 2010, Lima Neto and de Carvalho [
20] imposed non-negative constraints on the regression coefficients of radius on the basis of [
19]. Wang [
22] in 2012 proposed the complete information method to deal with the interval-valued linear regression model. Souza [
23] introduced the parametrization method to linear regression model in 2017. In 2015, Wang Xun et. al. in [
24] used set-valued theory to study linear regression problems, and gave the least square estimaor and the related properties. All the above research works are about the linear regression models of interval-valued random variables. The research on interval-valued spatial regression models and spatial error models are still blank.
As for the single-valued spatial error model, Anselin gave the maximum likelihood estimation method in [
26] in 1988. Prucha proposed the generalized moment estimation method in [
27] in 1999. In 2020, Yildirim [
25] systematically summarized the methods of parameter estimation of spatial error model and proposed a new parameter estimation method based on likelihood equation. Many scholars have studied the classical linear regression and time series models of interval-valued random variables and achieved wonderful research results. We are considering the interval-valued spatial error models.
This paper attempts to extend the classical spatial error model to interval-valued case. The orginazation of this paper is as follows: in
Section 2, we mainly introduce the notations and basic concepts of interval-valued random theory. In
Section 3, we mainly discuss the interval-valued spatial error model, give the least square estimator of parameter obtain a series of digital characteristics and consistency of parameter estimation; In
Section 4, the effectiveness of the method is illustrated by numerical simulation; In
Section 5, gives an application of the model by studying the relationship between temperature and latitude in major cities of China.
3. Interval-valued spatial error model
Consider the classical spatial error model with the following form, where X is the explanatory variable, Y is the explained variable, is the unknown parameter, error term u, and are single point values, and W is a known space weight matrix, is a spatial autoregressive coefficient parameter,
the error item
,
is an identity matrix. By transforming, model (3.1) becomes,
denoted by
Model (3.2) can be expressed as
Now we extend the above classical single-valued model to interval-valued case.
Definition 3.1 If is the n-dimensional vector of interval-valued observations, is the single point valued design matrix, is a p-dimensional interval-valued parameter vector, then model (3.3), is called interval-valued space error model.
Next, we give the algorithm for multiplication of the matrix and interval values.
Definition 3.2 Let
be the interval in
, the interval value vector
is multiplied by any
dimensional matrix
, the algorithm is defined as follows:
For the general single-valued linear model, the idea of the least squares estimation method is to minimize the sum of the squares of the residuals. We shall use the same mathematical idea here. For interval-valued spatial error model, the least square estimation of interval-valued unknown parameter
is to minimize
under the definition of
distance
where
and
represent the center and radius of interval value
m respectively. The above formula is the quadratic function of
and
, and
, so there is a minimum value.
Next, calculate the partial derivatives of
and
respectively
The regular equation is:
where
. The parameter estimation of the interval-valued spatial error model can be obtained by solving the regular equation. The following is the result about the rank of
.
Lemma 3.3 If , then .
Proof Since
and
it has
The result is proved. □
Based on Lemma 3.3, suppose , then the estimator of interval-valued spatial error model can be obtained by solving the regular equation, which is shown in the following theorem.
Theorem 3.3 Under the condition of Lemma 3.3, the least squares estimation of interval-valued spatial error model is unique, which is denoted as
After obtaining the estimation form of unknown parameter , we then discuss the properties. First, consider the unbiasedness of .
Theorem 3.4 The least squares estimate is an unbiased estimate of .
Proof By Theorem 3.3,
The result is proved. □
For the interval-valued spatial error model, when , the covariance of can be obtained, as shown in the following result.
Theorem 3.5 If , , , then the covariance matrix of is
(2)
,
where
represent the
ith and
jth element of
respectively, and
represent the
ith,
jth rows of matrix
A respectively.
Proof For the
ith and
jth element of
, if
, it has
When
, it has
The result is proved. □
Next we discuss the estimation of error and error variance. We mainly consider the expectation and covariance of interval-valued error estimation.
Theorem 3.6 The error estimator can be obtained from , and its expectation and variance are as follows:
(1)
(2),
where .
Proof
(2) On the other hand,
Then the
ith element of
is
Thus when
,
where
respectively represent the
ith and
jth rows of matrix
A. When
,
The result is proved. □
Next, we consider the estimation of and . Denote .
Theorem 3.7 and are unbiased estimators of and respectively.
Proof Since
is an idempotent matrix, it has
So
Then the estimator of
is gived as
So
Since
is an idempotent matrix, so
Furthermore
The estimator of
is given as
So
The result is proved. □
In the following, we discuss the independence of and .
Theorem 3.8 and are independent, and are independent.
Proof Since
it can be seen that
is the quadratic form of
,
is the linear form of
, and
According to the independence theorem of quadratic form and linear form of normal variables, it is necessary to prove that they are independent of each other, that is, the product of linear part, variance part and quadratic part of normal variables is 0. Then
Similarly,
is the quadratic form of
,
is the linear form of
, and
then
Thus
and
are independent,
and
are independent. □
Theorem 3.9 In the sense of
distance, the sufficient condition for the strong consistentancy of
for estimating
is:
where,
,
Proof According to Theorem 3.4,
is an unbiased estimate of
, namely,
From
it has
Therefore, in the sense of metric, is a strong consistent estimate of . □
4. Numerical simulation
In this part, the parameter estimation process of interval-valued spatial error model is further explored by numerical simulation. Based on the distance of the interval value, mean square error of the estimator is calculated to measure the goodness of the estimation.
Based on Equation 3.3, the interval-valued spatial error model in matrix form is expanded as follows:
where
is the unit matrix of dimension
n,
is the spatial autocorrelation coefficient. and
W as the spatial weight matrix. Using the first-order adjacency method, assuming that
n samples are arranged in one font, the spatial weight matrix can be written as follows:
The true values of the given interval value parameters are
respectively. Then,
where, the error term follows the normal distribution, that is
First, take , the explanatory variable X is generated according to the rules of , and a set of values will be obtained in each simulation experiment.
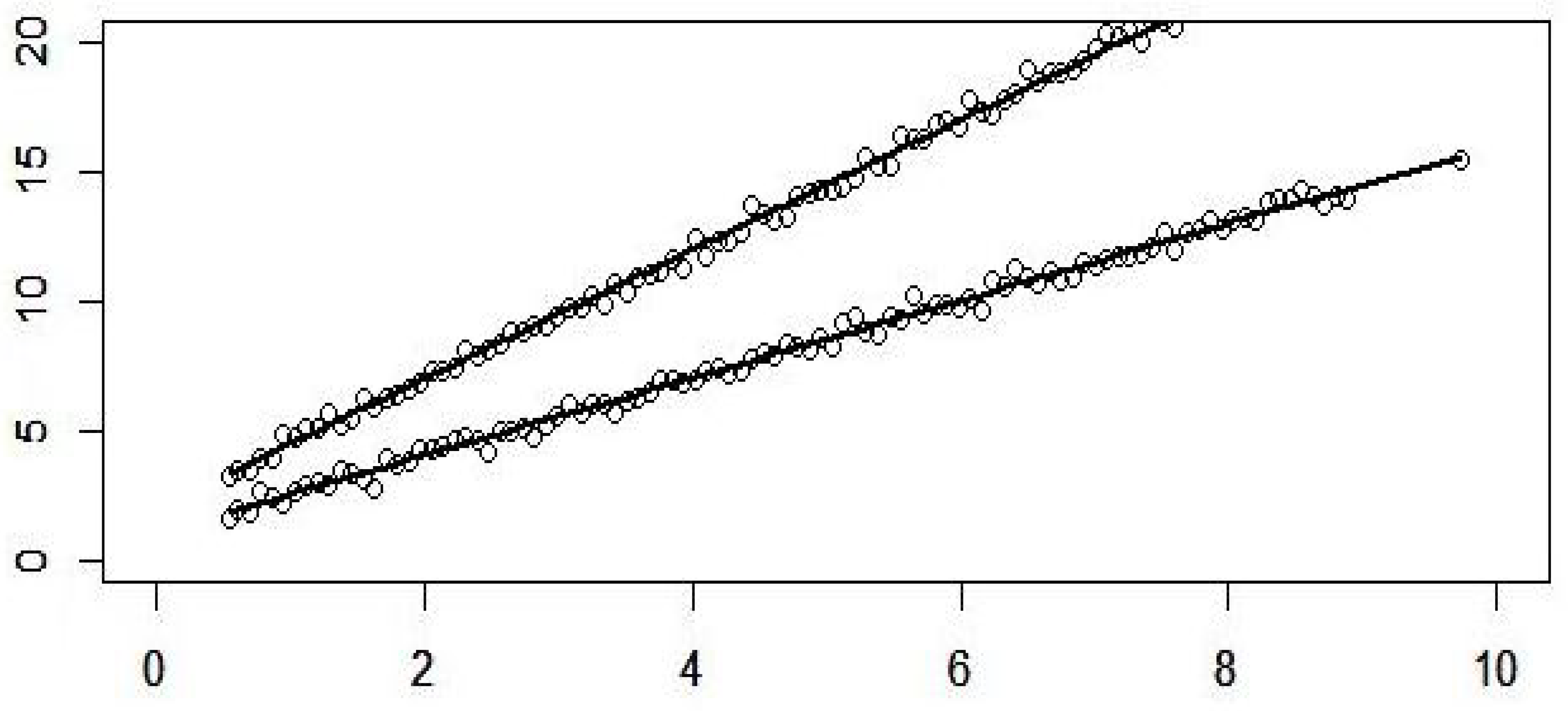
The scatter point in
Figure 1 is the
data generated by a simulation experiment, and the two fitting lines are the corresponding interval value spatial error model function:
Repeat the above process for 500 times to obtain the average value of
as follows:
Next, the mean square error MSE of the parameter estimation obtained by the model is calculated as one of the criteria to measure the goodness of the estimation. The calculation method is based on interval value
distance:
By calculation, the MSE of samples are 0.0165 and 0.0006 respectively.
Similarly, set
, repeat the above simulation process for 500 times respectively, and obtain the average value of
and the sample mean square error MSE respectively. The specific simulation results are summarized in
Table 1 and
Table 2.
It can be seen from the simulation results that when , the obtained parameter estimation is very close to the real value. With the increase of sample size, the obtained estimation is closer to the real value, and the sample mean square error MSE is smaller and smaller.