Prerpints.org logo
Preprint
Article

Spectral Analysis of the Metamaterial Formed by Optimally Shaped Omega Elements on a Silicon Substrate at Oblique Incidence of S- and P-polarized Terahertz Radiation

Altmetrics

Downloads

128

Views

33

Comments

1

A peer-reviewed article of this preprint also exists.

Submitted:

22 December 2023

Posted:

25 December 2023

You are already at the latest version

Alerts
Abstract
The reflection and transmission spectra of a metamaterial formed by omega-shaped elements with pre-calculated optimal parameters on a silicon substrate have been recorded in the terahertz range at oblique incidence for the s- and p- polarizations of the incident wave. The spectra were interpreted within the dipole radiation theory of electromagnetic waves. Both measurement results and analysis provide evidence sup-porting the presence of a pronounced polarization anisotropy impact in the reflection and transmission of the metamaterial. The potential of these materials to be utilized in the development of devices that control the polarization properties of THz radiation across a wide spectral range is examined.
Keywords: 
Subject: Physical Sciences  -   Optics and Photonics

1. Introduction

The advancements of next generation high-speed communication systems, commonly referred to as 6G, and non-contact spectroscopic systems have caused growing attention towards the practical applications of radiation using ever-increasingly high frequencies, such as the terahertz (THz) range. Consequently, there is an increasing focus on the development of techniques and technologies aimed at controlling the properties of THz radiation. The selected spectral range additionally offers favorable prospects for experimental modelling of compact radiation control devices intended for application in other ranges. This is due to the fact that the fabrication of prototypes and models for experimental THz devices does not require highly precise nanoscale technological procedures, which may be essential for devices operating in the optical range. In contrast to radio band devices operating at centimeter wavelengths, the model devices will exhibit relatively compact dimensions.
In recent times, there has been considerable research focused on artificial media with negative values of dielectric permittivity and magnetic permeability (ε < 0 and μ < 0). These media have great potential for manipulating the amplitude, spectral, and angular characteristics of THz radiation. Media that possess a negative value for one of the parameters are commonly referred to as ε-negative or μ-negative, denoted as ENG and MNG accordingly [1,2]. The genuine metamaterial, devoid of any analogues in the environment is recognized as a binegative medium (BNG), which possesses both parameters in the negative. The latter option has the potential to offer the highest degree of flexibility in designing compact devices for controlling radiation parameters with unique functionality [3]. In our perspective, this option is particularly appealing for further investigation. One potential application, among others, for metamaterials is their utilization as polarization converters for electromagnetic waves across various spectral ranges. These polarizers may consist of variously shaped elements, such as helices with different numbers of turns, split rings oriented in different ways, as well as classical or rectangular omega-shaped elements [4,5,6,7,8,9,10,11,12]. The polarizers function predominantly within the microwave and, to a lesser degree, THz frequency ranges.

2. Production of an experimental sample

The authors previously conducted calculations and experimental investigations on omega-elements that possess an optimal shape within the microwave range of 2.55 to 3.8 GHz [13,14]. Omega-particles of this nature demonstrate a harmonious combination of dielectric and magnetic characteristics, rendering them potentially valuable components for metamaterials and metasurfaces. The authors conducted a study in [15,16] to investigate the transition from the microwave to the THz region. That study involved the modelling of a single omega-shaped element and a metasurface composed of these resonators in the field of a THz wave. The present paper describes the findings of an empirical investigation conducted on an omega-shaped element and a metamaterial based on this element, whereby the properties of the latter were optimized specifically for THz radiation. This research focuses on the advancement and examination of the spectral-polarization properties of an omega-structured metamaterial. The constituent elements of this metamaterial are designed to possess equivalent importance in terms of both dielectric permittivity and magnetic permeability. It is demonstrated that the metamaterial based on an array of omega-elements with a pre-calculated optimal shape exhibits polarization-selective properties and can perform the functions of an effective converter of electromagnetic wave polarization in the THz range.
The metamaterial was fabricated using aluminum elements arranged in the shape of the Greek letter Ω, which were positioned in a rectangular array on the surface of a silicon substrate. All elements in the array exhibited the same orientation. Figure 1 displays the omega-shaped element parameters along with a microscopically captured image of the material surface.
The omega-shaped element consists of two main components, namely a split ring resonator (SRR [2]) and a linear dipole that are electrically interconnected to form a single system. A notable distinction from the structure suggested in [3] is the substantial electrical connection observed between the components of the element. This kind of connection can result in the emergence of radiation polarization conversion effects when combined with polarization-dependent spectral filtering. The dimensions of the element determine its resonance properties for both components of the electromagnetic field of THz radiation.
It is noteworthy that the omega-shaped elements constitute a metasurface due to the exceedingly thin nature of their layer. The term "metamaterial" is employed to emphasize the existence of a substrate that is significantly thicker than the omega-shaped element layer.

3. Experiment and discussion of results

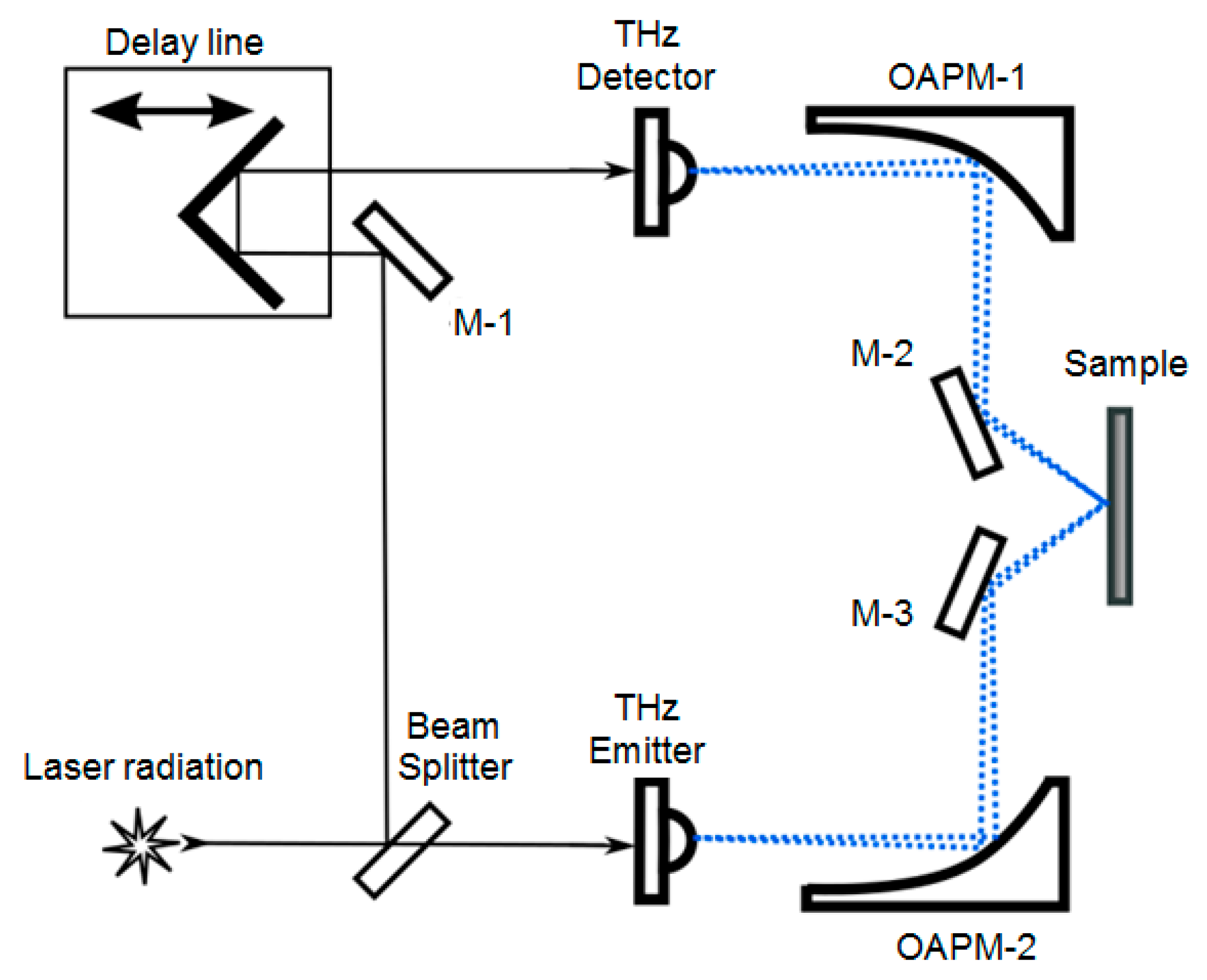
In order to investigate the polarization and spectral properties of a metamaterial formed by omega-shaped elements on a silicon substrate, THz radiation path of a pulse terahertz spectrometer was built accordingly to sketch represented in Figure 2.
The sensitivity to polarization is a significant characteristic shown by photoconductive antennas employed in THz spectrometer sources and radiation receivers. This sensitivity enables the detector to function as a polarization analyzer. In this particular scenario, the orientation of the antennas is such that the electric field vector is aligned with the horizontal plane. This alignment corresponds to the plane of the schematic diagram in Figure 2 and also agrees with the p-polarization of incidence radiation. To convert the alignment to s-polarization, it was made available to rotate the assembly, including mirrors 3-2 and 3-3, along with the sample holder. The radiation will be displaced off the plane. Here, the sample will be positioned beneath the mirrors. As a result, the plane of the metamaterial will be aligned in parallel to the polarization plane of the THz radiation. The polarization of the THz wave in this case is perpendicular to the plane of incidence. A more detailed description of the spectrometer set-up can be found in [17].
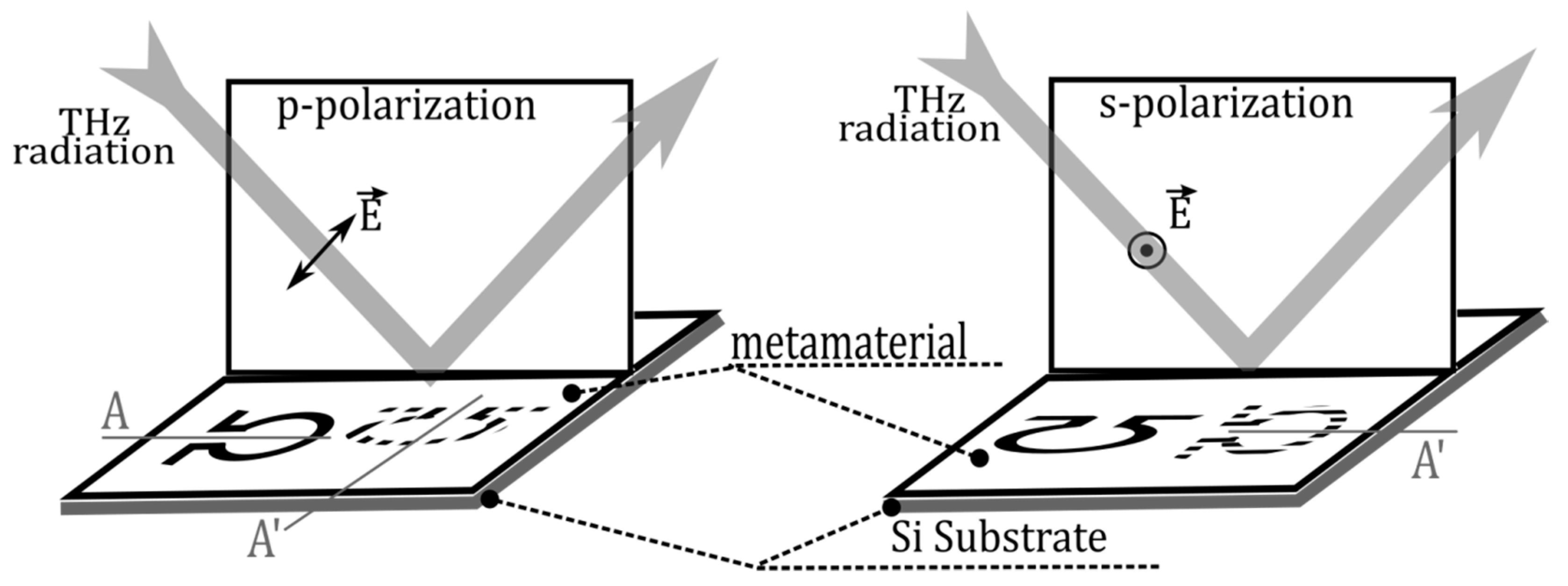
The study focused on examining changes in the spectral composition of THz radiation reflected from a metamaterial. The investigation specifically looked at how these changes were influenced by the orientation of the symmetry axis of the omega-shaped element in relation to the projection of the radiation polarization direction onto the plane of the metamaterial. The system of designations for rotation angles that has been adopted is explained in Figure 3.
The standard representation of the metamaterial in Figure 3 consists of a single omega element. The element represented in the schematic by a dashed line signifies the alteration in the orientation of its symmetry axis A as the metamaterial undergoes rotation around an axis perpendicular to its surface for π/2 to reach the position A’. The measurement of the rotation angle of the symmetry axis of the omega-shaped element is conducted with respect to the electric-field vector of the incident wave. Therefore, the zero value of the angle φ corresponds to the position of the symmetry axis inside the plane of oscillations of the electric vector of THz radiation that is directed towards the sample. At an angle φ of 90 degrees, the symmetry axis of the omega-shaped element is orthogonal to the electric vector of the incident wave, while the "arms" of the omega-shaped element are situated within the plane of oscillations of the electric vector of the incident THz radiation. The designations and nomenclature frequently employed for the components of the electric field vector of the wave are E s and E p . The numerical values within the notations of the dependencies depicted in the schematics presented below are representative of the rotation angles φ expressed in degrees.
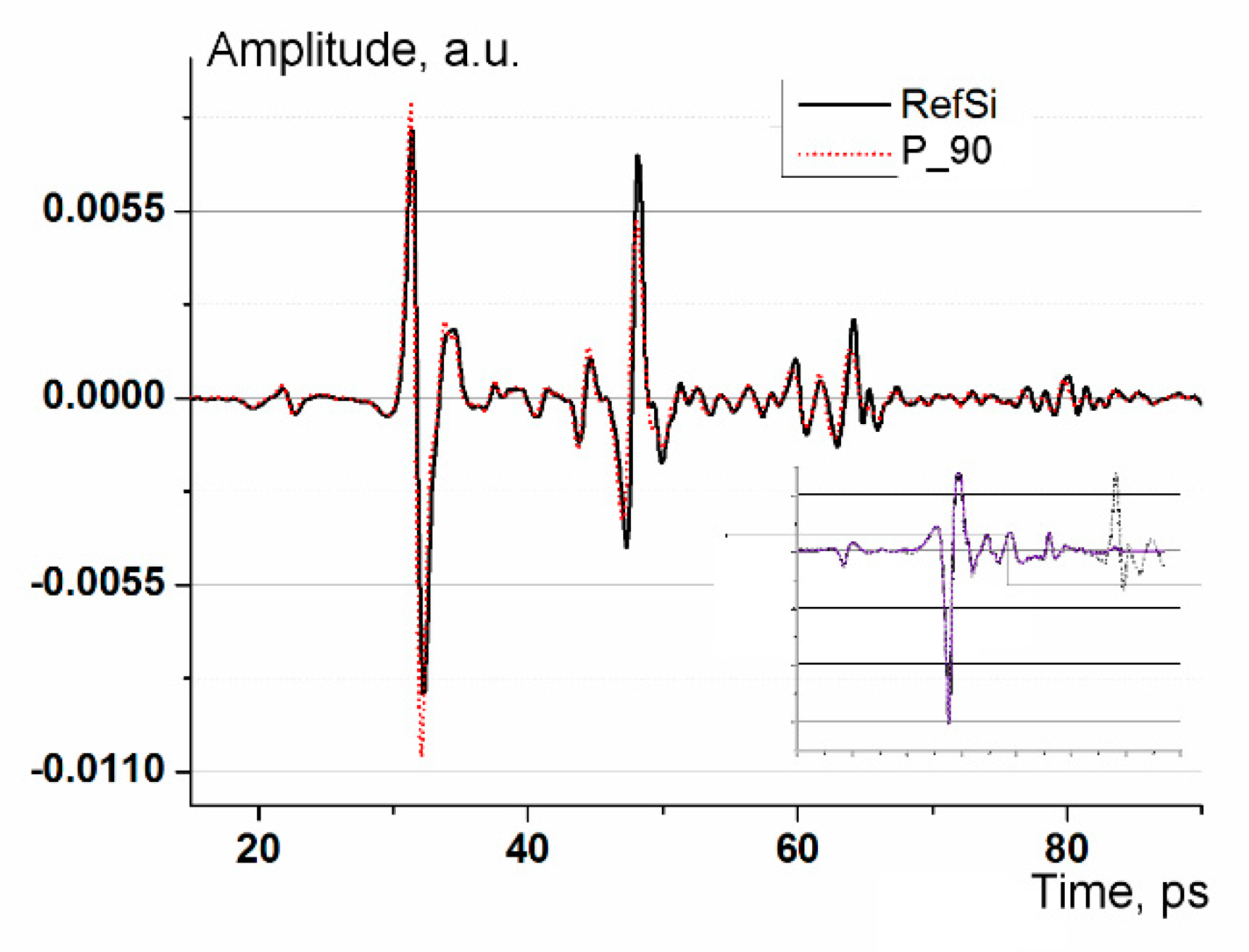
Time-domain spectrometers are conventionally used to perform a point-by-point measurement of the current in a PCA detector, induced by the electrical component of the THz pulse field. The current is proportional to the field strength and recorded as function of delay time. The waveform length was 140 ps, and the delay line scanning step was chosen to be ~0.075 ps. The indicated parameters correspond to a spectral resolution of ~0.008 THz and a frequency range of up to 7.5 THz after the Fourier transform. The excess range width is justified by the possibility to determine more accurately the position of the pulse on the time scale. Accordingly, visual control of the sample positioning is ensured during the waveform recording. Also, it is possible to estimate the average refractive index, as well as to choose parameters for data preprocessing before the Fourier transform. The selected waveform duration and corresponded spectral resolution are sufficient and meet the measurement requirements.
The high transparency and relatively large refractive index of the Si substrate, equal to an average of 3.5, cause the appearance of several echo pulses in the waveform. Echoes are produced by reflections in the plane-parallel silicon layer. As a result, the spectrum after the Fourier transform is distorted by the so-called Fabry-Perot effect [18]. Moreover, components of the transmission spectrum are added to the reflection spectrum. The information about these components is carried by echo pulses passing twice through the metasurface layer. Figure 4 demonstrates an example of the waveform and preprocessing results.
It is notable that the reflectivity of the matrix is higher than that of the Si substrate. Therefore, we used the reflection from the aluminum plate as a reference signal. The weak peak visible on the waveform at 23 ps is caused by the design of the emitter and is compensated in the Fourier transform by a symmetrical analogue that is formed in the detector antenna. To suppress the Fabry-Perot effects, we used the window function proposed in [19].
w j = 6 u 5 − 15 u 4 + 10 u 3           u = 2 j N − 1 , j ∈ 0 … N − 1 2 − 6 u 5 + 15 u 4 − 10 u 3 + 1       u = 2 j + 1 − N N − 1 , j ∈ N − 1 2 … N − 1
This function is smooth and its derivatives are smooth as well. Compared to the common window functions, such as Hann, Hanning, etc., it introduces less attenuation near the peak due to a wider and flatter top. The result of applying the window function is presented in the inset of Figure 4. Here, the solid line shows the result of applying the window function, while the suppressed echo signal is indicated by the dotted line. The resulting spectra retained a small residual modulation, which did not prevent the correct analysis of polarization-dependent spectral changes.
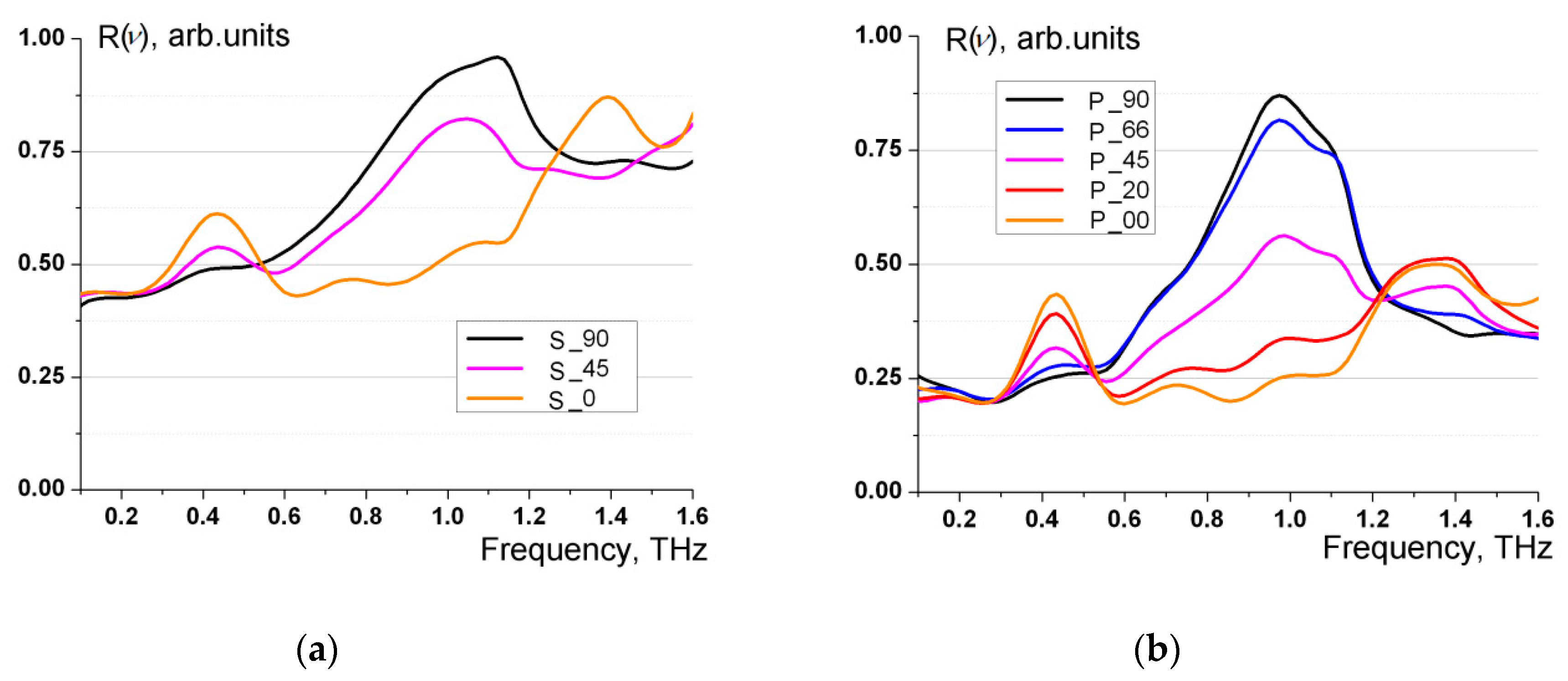
The reflection from a thin aluminum plate, that was fixed in the holder instead of the sample, was used as a reference signal. Figure 5 illustrates families of characteristic reflection spectra.
The acquired experimental outcomes are explicable in light of the theory of dipole radiation of electromagnetic waves [20]. The dipole radiation theory is applicable because the dimensions of each omega-shaped element are considerably smaller than the wavelength of the electromagnetic field. In the dipole approximation, the electric field intensity of the wave emitted by an omega-shaped element has the following form
E → R → , t = μ 0 4 π R p → ¨ , n → n → + 1 c n → , m → ¨ ,
where R → is the radius-vector from the center of the omega-element to the observation point; μ 0 is the vacuum permeability; R is the distance from the center of the omega-element to the observation point; n → is the unit vector of the wave normal; с is the speed of light in vacuum; p → is the dipole moment of the omega-shaped element, m → is the magnetic moment of the omega-shaped element (two dots above the vectors denote the second derivative of these vector quantities).
According to equation (2), it can be deduced that an omega-shaped element exhibits efficient wave radiation when it experiences a substantial induction of electric dipole moment p → and/or magnetic moment m → . The metamaterial under investigation uses omega-shaped elements that possess pre-calculated parameters, which are characterized by the simultaneous excitation of both electric dipole moment and magnetic moment, with the absolute values of both moments satisfying the following relation with a certain degree of accuracy
p = m c .
Therefore, the omega-shaped element can be regarded as a bianisotropic particle exhibiting both electric and magnetic properties.
The omega-shaped element exhibits most effective excitation when its "arms" are aligned with the plane of oscillation of the electric field vector of the incident wave, specifically in the case of φ = 90 ° . Here, the displacement of conduction electrons along the "arms" is accompanied by the appearance of electric current within the coil. Specifically, both the electric dipole moment and magnetic moment are induced simultaneously. The plots of reflection coefficients in Figure 4 for these cases of effective activation of the omega-shaped element at φ = 90 ° are denoted as s_90 and p_90. It can be deduced from Figure 5 that the wave reflection coefficients attain their maximum values precisely in the cases indicated as s_90 and p_90. In the case of s_90, the "arms" of the omega-shaped element are parallel to the incident wave vector E s . In the case involving p_90, the "arms" of the omega-shaped element are situated within the plane of oscillations of the incident wave vector E p . Throughout the experiment, the angle φ between the symmetry axis of the omega-shaped element and the plane of oscillation of the incident wave electric vector takes the values of 90, 66, 45, 20 and 0 degrees. It is possible to consider the component E l of the electric vector of the incident wave parallel to the "arms" of the omega-shaped element, which is equal to E l = E s sin ⁡ φ , E l = E p cos ⁡ α sin ⁡ φ , where α is the incidence angle of the wave on the surface of the metamaterial. As the angle φ decreases, there is a corresponding decrease in the component E l , resulting in an ensuing decrease in the reflection coefficient. Figure 5 illustrates precisely this behavior of reflection coefficients for incident waves with s- and p- polarizations.
Thus, the experimental findings relating to the reflection coefficients, which are displayed in Figure 5, are consistent with the outcomes of the theoretical analysis.
Additionally, the frequency dependence of the reflection coefficients for s- and p- polarization of the incident wave, as depicted in Figure 5, is noteworthy. The resonant nature of the metamaterial reflection spectra can be attributed to the enhanced excitation of each omega-shaped element at a certain frequency, which is related to the geometrical parameters of the omega-shaped element. The resonant excitation of the omega-shaped element occurs when its full length in the straightened state is approximately equal to half the wavelength of the electromagnetic field. Consequently, the resonant frequency satisfies the relation
ν 1 = c 2 L 1 = c 2 2 l + 2 π r .
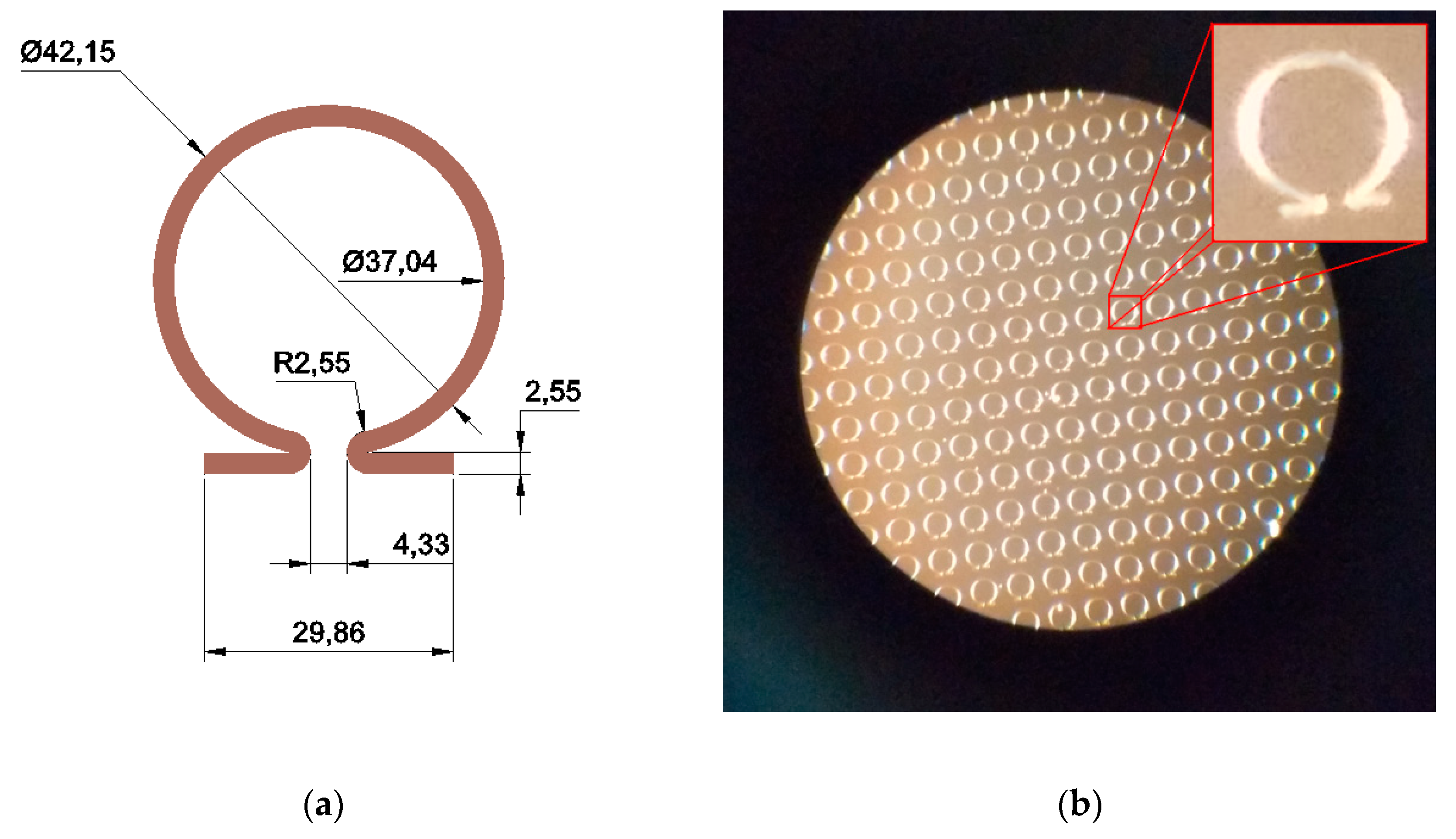
Here, L 1 is the full length of the omega-shaped element in the straightened state, l is the omega-shaped element arm length, r is the coil radius of the omega-shaped element. The metamaterial under investigation uses omega-shaped elements with parameters l =12.8 μm, r =19.8 μm. Therefore, based on equation (4), it can be concluded that the resonance frequency is ν 1 = 1.0 THz, which is approximately equal to the maximum frequency of the reflection coefficients in Figure 5. These coefficients are obtained at the angles between the symmetry axis of the omega-shaped element and the plane of oscillation of the electric vector of the incident wave φ = 90 ° , 66 ° , 45 ° . At these specific angles φ , the omega-shaped elements are activated predominantly by the electric vector of the incident wave, resulting in the fulfilment of relation (4). When the angle between the symmetry axis of the omega-shaped element and the plane of oscillation of the electric vector of the incident wave assumes values of φ = 20 ° , 0 ° , it can be observed that the omega-shaped elements are mostly excited by the magnetic field vector of the incident wave. In this instance, the electric current originates primarily in the coil of the omega-shaped element, with its arms not contributing, which results in another resonant frequency formula
ν 2 = c 2 L 2 = c 4 π r .
By employing formula (4), the resonance frequency is determined to be ν 2 = 1.2 THz. The frequency obtained is roughly equivalent to the frequency of the second maximum of the reflection coefficients shown in Figure 5.
Hence, the frequency dependence of reflection coefficients displayed in Figure 5, including the occurrence of two main maxima, correlates with the findings of the theoretical study.
The incidence angle of radiation on the metamaterial is not accounted for in formulas (4) and (5). Experimental studies performed at normal incidence of THz waves on the metamaterial confirm the presence of two main maxima in the reflection spectra at the same frequency values ν 1 and ν 2 as well as notable polarization anisotropy in the reflection coefficients.
It is essential to consider a significant distinction between the reflected waves at s- and p-polarization of the incident wave, which arises from the different polarization of the reflected radiation. According to equation (2), when a wave with s-polarization is incident on a metamaterial, the resulting reflected radiation is likewise linearly polarized and comprises only an s-component. When the incident wave is p-polarized, the reflected radiation demonstrates an elliptical polarization that closely resembles circular polarization.
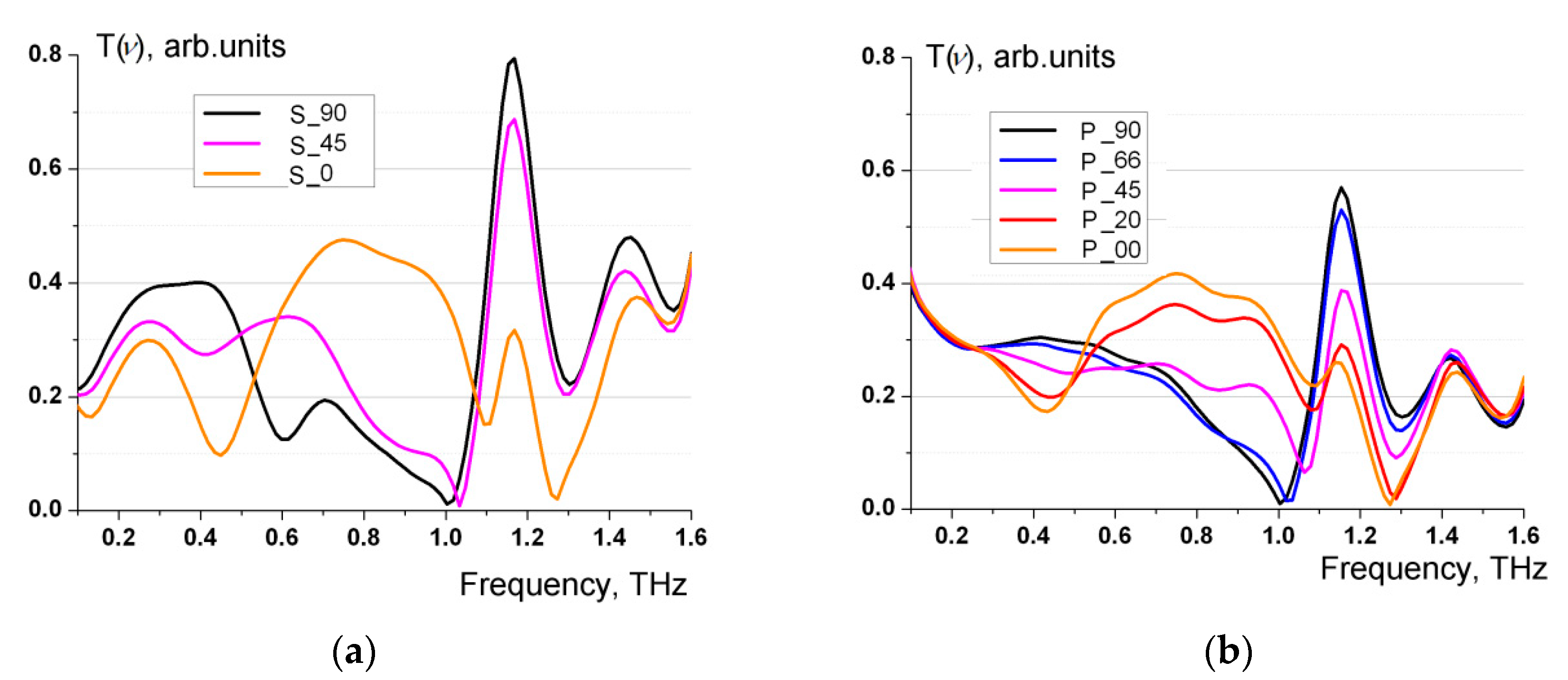
Additionally, an investigation into the transmission of THz radiation through the metamaterial was conducted. Figure 6 illustrate families of characteristic transmission spectra.
When constructing the spectra, standard normalization to the wave intensity in the absence of metamaterial was performed. The transmission spectra T ν exhibit a resonant nature and demonstrate an almost total lack of the transmitted wave in close proximity to the frequency ν 1 for the cases s_90, s_45, p_90, p_66, as well as in the vicinity of the frequency ν 2 for the cases s_0, p_20, p_0. The analysis reveals that the spectra 1 − T ν are close to the frequency dependence R ν of the reflection coefficients presented in Figure 5.

4. Conclusions

The reflection and transmission spectra of a metamaterial formed by omega-shaped elements with pre-calculated optimal parameters on a silicon substrate have been recorded in the terahertz range at oblique incidence for the s- and p- polarizations of the incident wave. The spectra were interpreted within the dipole radiation theory of electromagnetic waves. The obtained measurement findings indicate a significant polarization anisotropy of reflection and transmission of the metamaterial formed by omega elements on a silicon substrate, which can be used to control THz radiation, including broadband radiation.

Author Contributions

Conceptualization, A.V.L. and I.V.S.; methodology, I.V.S, A.L.S. and M.A.P.; investigation, A.L.S., M.A.P., G.V.S., and A.Y.K.; writing—original draft preparation, A.V.L., I.V.S. and S.A.K.; writing—review and editing, A.V.L., I.V.S. and S.A.K.; visualization, A.Y.K.; supervision, A.V.L., I.V.S. and S.A.K.; project administration, A.L.S. All authors have read and agreed to the published version of the manuscript.

Funding

The research was conducted as part of the State Research Program titled “Photonics and Electronics for Innovations”.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

The authors wish to thank Tatyana Lozovskaya, a senior teacher, for their help in translating the article.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

  1. Chen, H. T.; Padilla, W. J.; Zide J., M.; Gossard, A. C.; Taylor, A. J.; Averitt, R. D. Active terahertz metamaterial devices. Nature 2006, 444(7119), 597–600. [Google Scholar] [CrossRef] [PubMed]
  2. Pendry, J. B.; Holden, A. J.; Robbins, D. J.; Stewart, W. J. Magnetism from conductors and enhanced nonlinear phenomena. IEEE transactions on microwave theory and techniques 1999, 47(11), 2075–2084. [Google Scholar] [CrossRef]
  3. Xu, T.; Lin Y., S. Tunable Terahertz Metamaterial Using an Electric Split-Ring Resonator with Polarization-Sensitive Characteristic. Appl. Sci. 2020, 10, 4660–4668. [Google Scholar] [CrossRef]
  4. Cheng, Z.; Cheng, Y. A multi-functional polarization convertor based on chiral metamaterial for terahertz waves. Opt. Comm. 2019, 435, 178–182. [Google Scholar] [CrossRef]
  5. Sun, B.; Yingying, Y. Optical refractive index sensor based on the conjugated bilayer Г-shaped chiral metamaterials. Optik 2019, 182, 587–593. [Google Scholar] [CrossRef]
  6. Yu, Y.; Sun, B. Analysis of giant circular dichroism metamaterial based on conductive coupling. Optik 2019, 182, 1046–1052. [Google Scholar] [CrossRef]
  7. Mirzamohammadi, F.; Nourinia, J.; Ghobadi, C.; Majidzadeh, M. A bi-layered chiral metamaterial with high-performance broadband asymmetric transmission of linearly polarized wave. AEU – Int. Journ. of Electronics and Communications 2019, 98, 58–67. [Google Scholar] [CrossRef]
  8. Cheng, Y.Z.; Nie, Y.; Cheng, Z.Z.; Wang, X.; Gong, R.Z. Asymmetric chiral metamaterial circular polarizer based on twisted split-ring resonator. Appl. Phys. B 2014, 116, 129–134. [Google Scholar] [CrossRef]
  9. Sakellari, I.; Yin, X.; Nesterov, M.L.; Terzaki, K.; Xomalis, A.; Farsari, M. 3D chiral plasmonic metamaterials fabricated by direct laser writing: the twisted omega particle. Adv. Opt. Mater 2017, 5(16), 1700200. [Google Scholar] [CrossRef]
  10. Stojanović, D.B.; Beličev, P. P.; Radovanović, J.; Milanović, V. Numerical parametric study of chiral effects and group delays in Ω element based terahertz metamaterial. Physics Letters A 2019, 383, 1816–1820. [Google Scholar] [CrossRef]
  11. Liu, D. J.; Xiao, Z. Y.; Ma, X. L.; Xu, K. K.; Tang, J. Y.; Wang, Z. H. Broadband asymmetric transmission and polarization conversion of a linearly polarized wave based on chiral metamaterial in terahertz region. Wave Motion 2016, 66, 1–9. [Google Scholar] [CrossRef]
  12. Liu, D. J.; Xiao, Z. Y.; Ma, X. L.; Wang, Z. H. Broadband asymmetric transmission and multi-band 90° polarization rotator of linearly polarized wave based on multi-layered metamaterial. Opt. Commun. 2015, 354, 272–276. [Google Scholar] [CrossRef]
  13. Semchenko, I. V.; Khakhomov, S. A.; Podalov, M. A.; Tretyakov, S. A. Radiation of circularly polarized microwaves by a plane periodic structure of Ω elements. Journal of Communications Technology and Electronics 2007, 52, 1002–1005. [Google Scholar] [CrossRef]
  14. Semchenko, I. V.; Khakhomov, S. A.; Samofalov, A.L.; Podalov, M.A. ; Songsong, Q. The effective optimal parameters of metamaterial on the base of omega-elements, Recent Global Research and Education: Technological Challenges / Ed. by Ryszard Jablonski and Roman Szewczyk, Advances in Intelligent Systems and Computing, Vol. 519, Springer, 2017, 3-9.
  15. Balmakou, A.; Podalov, M.; Khakhomov, S.; Stavenga, D.; Semchenko, I. Ground-plane-less bidirectional terahertz absorber based on omega resonators. Optics letters 2015, 40(9), 2084–2087. [Google Scholar] [CrossRef] [PubMed]
  16. Semchenko, I.; Khakhomov, S.; Samofalov, A.; Podalov, M.; Solodukha, V.; Pyatlitski, A.; Kovalchuk, N. Omega-structured substrate-supported metamaterial for the transformation of wave polarization in THz frequency range. In Recent Advances in Technology Research and Education: Proceedings of the 16th International Conference on Global Research and Education Inter-Academia 2017. Springer, 2018, 660, 72-80.
  17. Khodasevich, M. A.; Lyakhnovich, A. V.; Eriklioglu, H. Chocolate Sample Classification by Principal Component Analysis of Preprocessed Terahertz Transmission Spectra. Journal of Applied Spectroscopy 2022, 89(2), 251–255. [Google Scholar] [CrossRef]
  18. Fastampa, R; Pilozzi, L; Missori, M. Cancellation of Fabry-Perot interference effects in terahertz time-domain spectroscopy of optically thin samples. Physical Review A, 2017, 95, 063831.
  19. Lyon; D.A. The Discrete Fourier Transform, Part 4: Spectral Leakage Journal of Object Technology, vol. 8. no. 7, November - December 2009, 23 – 34.
  20. Landau, L.D.; Lifshitz, E.M. The Classical Theory of Fields, 4 ed.; Publisher: Pergamon, 1975; Volume 2, 402 p.
Preprints 94214 g001
Figure 1. (a) Omega-shaped element parameters for the THz range, denoted in micrometers; (b) a microscopic photograph of the metamaterial, revealing a single element.
Figure 1. (a) Omega-shaped element parameters for the THz range, denoted in micrometers; (b) a microscopic photograph of the metamaterial, revealing a single element.
Preprints 94214 g001
Preprints 94214 g002
Figure 2. Schematic of the THz spectrometer (M-1, M-2 and M-3 are the metal mirrors; OAPM-1, OAPM-2 are the parabolic mirrors).
Figure 2. Schematic of the THz spectrometer (M-1, M-2 and M-3 are the metal mirrors; OAPM-1, OAPM-2 are the parabolic mirrors).
Preprints 94214 g002
Preprints 94214 g003
Figure 3. Orientation of the symmetry axis of omega-shaped elements A and A’ with respect to the polarization of THz radiation with φ angle values of 0° and 90°, accordingly.
Figure 3. Orientation of the symmetry axis of omega-shaped elements A and A’ with respect to the polarization of THz radiation with φ angle values of 0° and 90°, accordingly.
Preprints 94214 g003
Preprints 94214 g004
Figure 4. View of the typical waveform for the metamaterial (P_90) and for the silicon substrate (RefSi). Inset illustrates the application of window function.
Figure 4. View of the typical waveform for the metamaterial (P_90) and for the silicon substrate (RefSi). Inset illustrates the application of window function.
Preprints 94214 g004
Preprints 94214 g005
Figure 5. Reflection spectra of a metamaterial formed by omega-shaped elements on a silicon substrate for s- (a) and p-polarization (b) of the incident wave.
Figure 5. Reflection spectra of a metamaterial formed by omega-shaped elements on a silicon substrate for s- (a) and p-polarization (b) of the incident wave.
Preprints 94214 g005
Preprints 94214 g006
Figure 6. Transmission spectra of a metamaterial formed by omega-shaped elements on a silicon substrate for s-polarization (a) and p-polarization (b) of the incident wave.
Figure 6. Transmission spectra of a metamaterial formed by omega-shaped elements on a silicon substrate for s-polarization (a) and p-polarization (b) of the incident wave.
Preprints 94214 g006
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated