Subdomain Analytical Modeling of a Double-Stator Spoke-Type Permanent-Magnet Vernier Machine

Preprint

Article

Subdomain Analytical Modeling of a Double-Stator Spoke-Type Permanent-Magnet Vernier Machine

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

26 December 2023

Posted:

27 December 2023

You are already at the latest version

Alerts

Abstract

This paper proposes an analytical model of the double-stator spoke-type permanent-magnet vernier machine (DSSTVM) using the subdomain model (SDM), which can be used to calculate the mag-netic field distribution and corresponding electromagnetic parameters of the DSSTVM. The whole field domain is divided into several subdomains according to the magnetic characteristics of each region, within which Laplace's and Poisson's equations are solved accordingly in terms of magnetic vector potential (MVP). Then, the magnetic flux density distribution, back electromotive force (EMF), and electromagnetic torque of the DSSTVM can be obtained correspondingly. Ultimately, finite element analysis (FEA) is adopted to validate the proposed analytical model's effectiveness for quickly predicting the no-load and on-load performances of the DSSTVM.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

1. Introduction

Compared to conventional single-stator electric machines, double-stator machines (DSMs) have the merits of a more compact structure, higher torque/power density, and better fault-tolerant capability [1]. Due to these advantages, DSMs have great potential to be applied in torque-sensitive scenarios, such as wind turbines, ship propulsion motors, robot actuators, etc. [2]. With the development of manufacturing technology, DSMs have recently become a research hot spot, and various types of DSMs have been proposed, including DS flux-switching machines [3,4], DS synchronous machines [5], DS-switched reluctance machines [6], and DS vernier machines. The prominent feature of DSMs is the double-stator structure, where two stators sandwich the rotor at the inner and outer sides. Thus, DSMs can effectively use the magnetic force at both air gaps to produce a large torque.

Among all the DSM topologies, DS vernier machines have the largest torque density due to the use of the magnetic-gearing effect [7,8], but it has a relatively low power factor. A DS vernier machine topology was raised in [9], and the low power factor problem can be solved with the introduction of spoke-type permanent magnets. This motor topology is named a double-stator spoke-type permanent-magnet vernier machine (DSSTVM), and it shows great promise in low-speed direct-drive applications. However, the electromagnetic performance prediction for this DSSTVM is never an easy task.

In general, the difficulties of the DSSTVM's field prediction come in two aspects. The first one is the dual-air-gap structure. The second is plenty of effective spatial harmonics within the DSSTVM to generate such a large output torque. The finite element analysis (FEA) can accurately calculate the electromagnetic field of the electrical machines. However, the FEA model for the DSSTVM should have a very dense mesh to accurately calculate its electromagnetic parameters, which significantly reduces the computation speed.

An alternative to FEA used for the preliminary design of electric machines is the analytical modeling method. Up to now, various analytical modeling methods have been proposed based on different mathematical theories. Three analytical modeling methods have been frequently used for field prediction of various electric machines, namely the conformal mapping method (CMM), magnetic equivalent circuit method (MEC), and subdomain method (SDM). CMM can be used for single-rotor electric machines with two different magnetic potentials [10], and the sliding mesh modeling is very complicated in MEC [11,12]. Thus, neither CMM nor MEC is feasible for the field prediction of DSSTVM. SDM is a semi-analytical modeling method that utilizes the Fourier series expansion to satisfy magnetic field distribution within electric machines [13]. It owns the advantages of high accuracy and fast computation speed, and it's highly suitable for modeling vernier machines where plenty of spatial harmonics exist [14]. However, there is little literature concerning the SDM for DSM. The magnetic field of a consequent-pole DSM is solved using SDM in [15], but the mathematical modeling of open slot structure, split-tooth structure, and spoke-type PMs are not involved.

This paper provides an SDM model for the field prediction of the DSSTVM with a split tooth structure. The modeling deduction is a supplement to [15]. Thereafter, SDM can be completed to be used for magnetic field predictions of DSMs with any topologies and pole-slot combinations. Finally, the proposed SDM model is verified by using FEA software.

2. Machine Geometry and Methodology

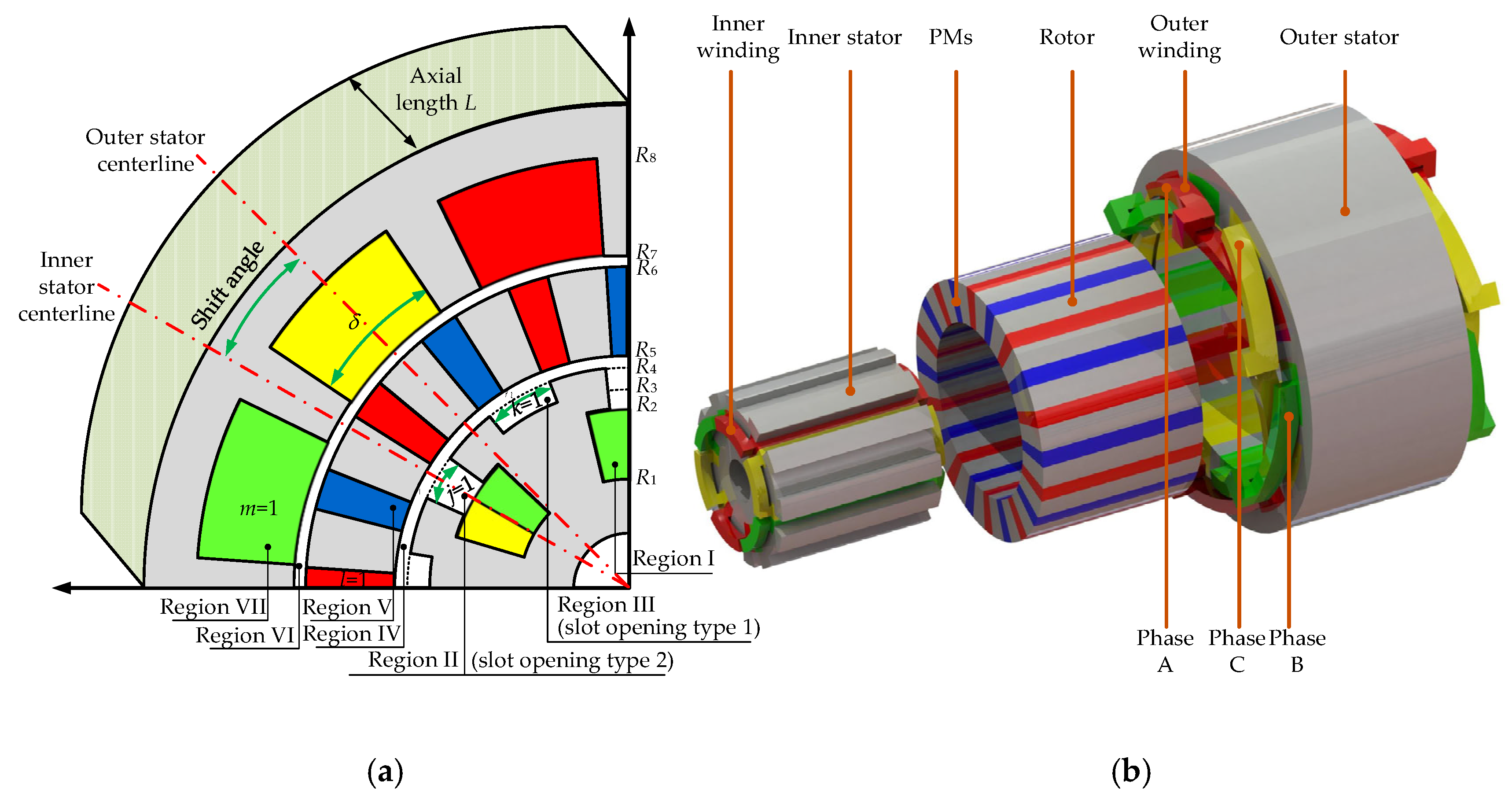
The studied DSSTVM is composed of three components, namely a rotor, an open-slot outer stator, and a split-tooth inner stator, as depicted in Figure 1. In this DSSTVM, its rotor's permanent magnets (PMs) pole pair number, the pole-pair numbers of the inner and outer stators' windings, and the slot numbers of the inner and outer stators are represented by

P_{r}

P_{w}

, and

Z

, respectively. To output a relatively large torque, this DSSTVM should obey the basic flux modulation principle of vernier machines [16]. Hence, the relation among

P_{r}

P_{w}

, and

Z

is governed by

P_{w} = Z - P_{r}

(1)

Besides, the values of geometrical parameters for the studied DSSTVM are provided in Table 1. All the sides of the machine's geometry are parallel to the axes of the polar coordinates to simplify the modeling process. Additionally, a few assumptions are settled before the detailed modeling process: 1) the permeability of silicon steel is regarded as infinite; 2) the axial-direction magnetic field is ignored.

To solve the magnetic field within the DSSTVM, one can first divide the whole field domain into seven subdomains, namely the inner stator slot, slot opening type 1, slot opening type 2, inner air gap, rotor slot, outer air gap, and outer stator slot. Then, the magnetic field distribution within each region should follow Maxwell's equation. By adopting magnetic vector potential (MVP)

A_{z}

in the polar coordinates and considering various materials' properties, one can obtain the general expressions as follows [17]:

\frac{\partial A_{z}}{\partial r^{2}} + \frac{1}{r} \frac{\partial A_{z}}{\partial r} + \frac{1}{r^{2}} \frac{\partial A_{z}}{\partial θ^{2}} = - \frac{μ_{0}}{r} (\frac{\partial (r \cdot M_{θ})}{\partial r} - \frac{\partial M_{r}}{\partial θ}) - μ_{0} J_{z}

(2)

where

M_{r}

and

M_{θ}

are the magnetizations in radial and tangential directions, respectively.

J_{z}

is the current density in the z-direction,

μ_{0}

is the magnetic permeability in vacuum.

Both Region I and VII only contain electrified conductors, so (2) can be transferred into a Poisson's equation where the magnetization term is eliminated. Region V only contains the tangential magnetization, so (2) can be transferred into another Poisson's equation where the radial magnetization term and the current term are eliminated. As for the rest regions, they contain nothing but air, so (2) can be simplified into Laplace's equation.

The general solution of (2) is the sum of particular integral and complementary solution. Using the method of separation of variables, the complementary solution to (2) can be written as:

\begin{array}{l} A_{z} (r, θ) = (A_{0} + B_{0} \ln r) (C_{0} θ + D_{0}) \\ + \sum_{n = 1}^{\infty} (A_{n} r^{n} + B_{n} r^{- n}) (C_{n} \cos n θ + D_{n} \sin n θ) \end{array}

(3)

where

A_{0}

B_{0}

C_{0}

D_{0}

A_{n}

B_{n}

C_{n}

and

D_{n}

are the Fourier coefficients to be determined through boundary conditions satisfaction in Section III. n is the harmonic order in the Fourier series, and the maximum number of harmonics used in the calculation is represented by N. Then, the expression of a particular integral varies with the right side of (2), and it will be discussed case by case in the following section.

Additionally, two notations, namely

P_{w} (u, v)

and

E_{w} (u, v)

, are introduced to simplify the expressions of general solutions [18]:

P_{w} (u, v) = {(\frac{u}{v})}^{w} + {(\frac{v}{u})}^{w}

(4)

E_{w} (u, v) = {(\frac{u}{v})}^{w} - {(\frac{v}{u})}^{w}

(5)

3. Analytical Modeling Process

3.1. Boundary Condition and General Solution Expressions

There are three kinds of boundary conditions within the DSSTVM, namely periodic condition, continuous condition, and Neumann condition [18]: In the air gap region, MVP has a period of 2π; at the interfaces between two regions, MVP

A_{Z}

should be continuous, while the tangential component of the magnetic field intensity H should be continuous. Considering that the permeability of iron cores is regarded as infinite, the tangential component of H should be zero at the interface between the iron core and the region with other materials. With the above continuity rules, the boundary conditions of the DSSTVM will be determined from the innermost region to the outermost one subsequently.

3.1.1. Region I

First, the three sides surrounding the ith slot within Region I are connected to the iron core, where the tangential component of the magnetic field is zero. These features lead to:

\{\begin{matrix} {\frac{\partial A_{I, i}}{\partial r}|}_{r = R_{1}} = 0; θ \in [θ_{i}, θ_{i} + α] \\ {\frac{\partial A_{I, i}}{\partial θ}|}_{θ_{i}} = 0 & {\frac{\partial A_{I, i}}{\partial θ}|}_{θ_{i} + α} = 0; r \in [R_{1}, R_{2}] \end{matrix}

(6)

The remaining upper side of Region I is connected to both the iron core and Region II. For the arc that corresponds to the iron core, the tangential component of the magnetic field is zero, while for the arc that corresponds to Region II, the tangential component of the magnetic field is continuous between Region I and Region II, so we can obtain following boundary condition:

{\frac{\partial A_{I, i}}{\partial r}|}_{r = R_{2}} = \{\begin{array}{l} {\frac{\partial A_{I I, j}}{\partial r}|}_{r = R_{2}} θ \in [θ_{j}, θ_{j} + β_{1}] \\ 0 e l s e w h e r e \end{array} with i = j

(7)

Considering the boundary conditions in (6) and (7), the general solution of MVP and the corresponding Fourier series coefficient in Region I can be expressed as:

\begin{array}{l} A_{I, i} (r, θ) = A_{0}^{i} + \frac{1}{2} μ_{0} J_{i 0} (R_{1}^{2} \ln r - \frac{1}{2} r^{2}) \\ + \sum_{n_{1} = 1}^{\infty} \frac{A_{n_{1}}^{i} α R_{2}}{n_{1} π} \frac{P_{n_{1} π / α} (r, R_{1})}{E_{n_{1} π / α} (R_{2}, R_{1})} \cos (\frac{n_{1} π}{α} (θ - θ_{i})) \\ + \sum_{n_{1} = 1}^{\infty} \begin{array}{l} (\frac{2 α}{n_{1} π} \frac{R_{1}^{2} P_{n_{1} π / α} (r, R_{2}) - R_{2}^{2} P_{n_{1} π / α} (r, R_{1})}{E_{n_{1} π / α} (R_{2}, R_{1})} + r^{2}) \\ \cdot \frac{μ_{0} J_{i n}}{{(n_{1} π / α)}^{2} - 4} \cdot \cos (\frac{n_{1} π}{α} (θ - θ_{i})) \end{array} \end{array}

(8)

where

A_{n_{1}}^{i} = \frac{2}{α} \int_{θ_{j}}^{θ_{j} + β_{1}} {\frac{\partial A_{I I, j}}{\partial r}|}_{r = R_{2}} \cos \frac{n_{1} π}{α} (θ - θ_{i}) d θ

(9)

3.1.2. Region II

Second, for the jth slot of Region II, its two lateral sides are connected to the iron core, while the lower and upper sides are connected to the ith slot of Region I and IV, respectively. Thus, the boundary conditions can be deduced as:

{\frac{\partial A_{I I, j}}{\partial θ}|}_{θ_{j}} = 0; {\frac{\partial A_{I I, j}}{\partial θ}|}_{θ_{j} + β_{1}} = 0 with r \in [R_{2}, R_{4}]

(10)

\begin{matrix} A_{I I, j} (R_{2}, θ) = A_{I, i} (R_{2}, θ) \\ θ \in [θ_{j}, θ_{j} + β_{1}] \end{matrix} ； \begin{matrix} A_{I I, j} (R_{4}, θ) = A_{I V} (R_{4}, θ) \\ θ \in [θ_{j}, θ_{j} + β_{1}] \end{matrix}

(11)

Combining the boundary conditions in (10) and (11), the general solution of MVP and the corresponding Fourier series coefficient in Region II can be given by:

\begin{array}{l} A_{I I, j} (r, θ) = A_{0}^{j} + B_{0}^{j} \ln r \\ + \sum_{n_{2} = 1}^{\infty} (A_{n_{2}}^{j} \frac{E_{n_{2} π / β_{1}} (r, R_{4})}{E_{n_{2} π / β_{1}} (R_{2}, R_{4})} - B_{n_{2}}^{j} \frac{E_{n_{2} π / β_{1}} (r, R_{2})}{E_{n_{2} π / β_{1}} (R_{2}, R_{4})}) \cos (\frac{n_{2} π}{β_{1}} (θ - θ_{j})) \end{array}

(12)

where

A_{0}^{j} + B_{0}^{j} \ln R_{2} = \frac{1}{β_{1}} \int_{θ_{i} + \frac{α - β_{1}}{2}}^{θ_{i} + \frac{α + β_{1}}{2}} A_{I, i} (R_{2}, θ) d θ

(13)

A_{0}^{j} + B_{0}^{j} \ln R_{4} = \frac{1}{β_{1}} \int_{θ_{i} + \frac{α - β_{1}}{2}}^{θ_{i} + \frac{α + β_{1}}{2}} A_{I V} (R_{4}, θ) d θ

(14)

A_{n_{2}}^{j} = \frac{2}{β_{1}} \int_{θ_{j}}^{θ_{j} + β_{1}} A_{I, i} (R_{2}, θ) \cos (\frac{n_{2} π}{β_{1}} (θ - θ_{j})) d θ

(15)

B_{n_{2}}^{j} = \frac{2}{β_{1}} \int_{θ_{j}}^{θ_{j} + β_{1}} A_{I V} (R_{4}, θ) \cos (\frac{n_{2} π}{β_{1}} (θ - θ_{j})) d θ

(16)

3.1.3. Region III

Next, for the kth slot belonging to Region III, its three sides are connected to the iron core, where the tangential component of the magnetic field should be zero. The remaining upper side is connected to Region IV, so the MVPs of Regions III and IV are continuous at the upper side. Hence, the boundary conditions can be represented as:

\{\begin{matrix} {\frac{\partial A_{I I I, k}}{\partial θ}|}_{θ_{k}} = 0 \\ {\frac{\partial A_{I I I, k}}{\partial θ}|}_{θ_{k} + β_{2}} = 0 \end{matrix} ， r \in [R_{3}, R_{4}] ； \begin{matrix} {\frac{\partial A_{I I I, k}}{\partial r}|}_{r = R_{3}} = 0 \\ θ \in [θ_{k}, θ_{k} + β_{2}] \end{matrix}

(17)

A_{I I I, k} (R_{4}, θ) = A_{I V} (R_{4}, θ) with θ \in [θ_{k}, θ_{k} + β_{2}]

(18)

Taking into account the boundary conditions (17) and (18), the general solution of MVP and the corresponding Fourier series coefficient in Region III can be acquired as:

A_{I I I, k} (r, θ) = A_{0}^{k} + \sum_{n_{3} = 1}^{\infty} A_{n_{3}}^{k} \frac{P_{n_{3} π / β_{2}} (r, R_{4})}{P_{n_{3} π / β_{2}} (R_{3}, R_{4})} \cos (\frac{n_{3} π}{β_{2}} (θ - θ_{k}))

(19)

where

A_{n_{3}}^{k} = \frac{2}{β} \int_{θ_{k}}^{θ_{k} + β_{2}} A_{I V} (R_{4}, θ) \cos (\frac{n_{3} π}{β_{2}} (θ - θ_{k})) d θ

(20)

3.1.4. Region IV

Then, the boundary conditions for Region IV are more complicated since Region IV is adjacent to Regions II, III, and V and the iron core. We use the continuity of the tangential component of the magnetic field and handle the boundary condition by introducing piecewise function as follows:

{\frac{\partial A_{I V}}{\partial r}|}_{r = R_{4}} = f_{1} (θ) = \{\begin{array}{l} {\frac{\partial A_{I I, j}}{\partial r}|}_{r = R_{4}} & θ \in [θ_{j}, θ_{j} + β_{1}] \\ {\frac{\partial A_{I I I, k}}{\partial r}|}_{r = R_{4}} θ \in [θ_{k}, θ_{k} + β_{2}] & θ \in [θ_{k}, θ_{k} + β_{2}] \\ 0 & e l s e w h e r e \end{array}

(21)

{\frac{\partial A_{I V}}{\partial r}|}_{r = R_{5}} = f_{2} (θ) = \{\begin{array}{l} {\frac{\partial A_{V, l}}{\partial r}|}_{r = R_{5}} + μ_{0} M_{θ, l} & θ \in [θ_{l}, θ_{l} + γ] \\ 0 & e l s e w h e r e \end{array}

(22)

We take the boundary conditions in (21) and (22) into consideration, so the general solution of MVP and the corresponding Fourier series coefficient in Region IV can be written as:

\begin{array}{l} A_{I V} (r, θ) = A_{0}^{I V} \\ + \sum_{n_{4} = 1}^{\infty} \begin{array}{l} (A_{n_{4}}^{I V} \frac{R_{4}}{n_{4}} \frac{P_{n_{4}} (r, R_{5})}{E_{n_{4}} (R_{4}, R_{5})} + B_{n_{4}}^{I V} \frac{R_{5}}{n_{4}} \frac{P_{n_{4}} (r, R_{4})}{E_{n_{4}} (R_{5}, R_{4})}) \\ \cdot \cos (n θ) \end{array} \\ + \sum_{n_{4} = 1}^{\infty} \begin{array}{l} (C_{n_{4}}^{I V} \frac{R_{4}}{n_{4}} \frac{P_{n_{4}} (r, R_{5})}{E_{n_{4}} (R_{4}, R_{5})} + D_{n_{4}}^{I V} \frac{R_{5}}{n_{4}} \frac{P_{n_{4}} (r, R_{4})}{E_{n_{4}} (R_{5}, R_{4})}) \\ \cdot \sin (n θ) \end{array} \end{array}

(23)

where

A_{n_{4}}^{I V} = \frac{1}{π} \int_{0}^{2 π} f_{1} (θ) \cos (n_{4} θ) d θ; C_{n_{4}}^{I V} = \frac{1}{π} \int_{0}^{2 π} f_{1} (θ) \sin (n_{4} θ) d θ

(24)

B_{n_{4}}^{I V} = \frac{1}{π} \int_{0}^{2 π} f_{2} (θ) \cos (n_{4} θ) d θ; D_{n_{4}}^{I V} = \frac{1}{π} \int_{0}^{2 π} f_{2} (θ) \sin (n_{4} θ) d θ

(25)

3.1.5. Region V

Subsequently, for the lth slot in Region V, its two lateral sides are adjacent to the iron core, and the lower and upper sides are adjacent to Region IV and Region VI, respectively. Hence, its boundary conditions can be written as follows:

{\frac{\partial A_{V, l}}{\partial θ}|}_{θ = θ_{l}} = 0; {\frac{\partial A_{V, l}}{\partial θ}|}_{θ = θ_{l} + γ} = 0 with r \in [R_{5}, R_{6}]

(26)

\begin{matrix} A_{V, l} (R_{5}, θ) = A_{I V} (R_{5}, θ) \\ θ \in [θ_{l}, θ_{l} + γ] \end{matrix}; \begin{matrix} A_{V, l} (R_{6}, θ) = A_{V I} (R_{6}, θ) \\ θ \in [θ_{l}, θ_{l} + γ] \end{matrix}

(27)

Combing the boundary conditions in (26) and (27), the general solution of MVP and the corresponding Fourier series coefficient in Region V can be obtained as:

\begin{array}{l} A_{V, l} (r, θ) = A_{0}^{l} + B_{0}^{l} \ln r - μ_{0} M_{θ, l} r \\ + \sum_{n_{5} = 1}^{\infty} \begin{array}{l} (A_{n_{5}}^{l} \frac{E_{n_{5} π / γ} (r, R_{6})}{E_{n_{5} π / γ} (R_{5}, R_{6})} - B_{n_{5}}^{l} \frac{E_{n_{5} π / γ} (r, R_{5})}{E_{n_{5} π / γ} (R_{5}, R_{6})}) \\ \cdot \cos (\frac{n_{5} π}{γ} (θ - θ_{l})) \end{array} \end{array}

(28)

where

A_{0}^{l} + B_{0}^{l} \ln R_{5} = \frac{1}{γ} \int_{θ_{l}}^{θ_{l} + γ} A_{I V} (R_{5}, θ) d θ

(29)

A_{0}^{l} + B_{0}^{l} \ln R_{6} = \frac{1}{γ} \int_{θ_{l}}^{θ_{l} + γ} A_{V I} (R_{6}, θ) d θ

(30)

A_{n_{5}}^{l} = \frac{2}{γ} \int_{θ_{l}}^{θ_{l} + γ} A_{I V} (R_{5}, θ) \cos (\frac{n_{5} π}{γ} (θ - θ_{l})) d θ

(31)

B_{n_{5}}^{l} = \frac{2}{γ} \int_{θ_{l}}^{θ_{l} + γ} A_{V I} (R_{6}, θ) \cos (\frac{n_{5} π}{γ} (θ - θ_{l})) d θ

(32)

3.1.6. Region VI

Similar to the boundary conditions in Region IV, Region VI is adjacent to Region V and VII. We can write the boundary conditions for Region VI using the piecewise function as follows:

{\frac{\partial A_{V I}}{\partial r}|}_{r = R_{6}} = g_{1} (θ) = \{\begin{array}{l} {\frac{\partial A_{V, l}}{\partial r}|}_{r = R_{6}} + μ_{0} M_{θ, l} & θ \in [θ_{l}, θ_{l} + γ] \\ 0 & e l s e w h e r e \end{array}

(33)

{\frac{\partial A_{V I}}{\partial r}|}_{r = R_{7}} = g_{2} (θ) = \{\begin{array}{l} {\frac{\partial A_{V I I, m}}{\partial r}|}_{r = R_{7}} & θ \in [θ_{m}, θ_{m} + δ] \\ 0 & e l s e w h e r e \end{array}

(34)

Taking into account the boundary conditions (33) and (34), the general solution of MVP and the corresponding Fourier series coefficient in Region VI can be calculated as:

\begin{array}{l} A_{V I} (r, θ) = A_{0}^{V I} + \sum_{n_{6} = 1}^{\infty} \begin{array}{l}  \end{array} (A_{n_{6}}^{V I} \frac{R_{6}}{n_{6}} \frac{P_{n_{6}} (r, R_{7})}{E_{n_{6}} (R_{4}, R_{5})} + B_{n_{6}}^{V I} \frac{R_{7}}{n_{6}} \frac{P_{n_{6}} (r, R_{6})}{E_{n_{6}} (R_{7}, R_{6})}) \cdot \cos (n θ) \\ + \sum_{n_{6} = 1}^{\infty} \begin{array}{l}  \end{array} (C_{n_{6}}^{V I} \frac{R_{6}}{n_{6}} \frac{P_{n_{6}} (r, R_{7})}{E_{n_{6}} (R_{4}, R_{5})} + D_{n_{6}}^{V I} \frac{R_{7}}{n_{6}} \frac{P_{n_{6}} (r, R_{6})}{E_{n_{6}} (R_{7}, R_{6})}) \cdot \sin (n θ) \end{array}

(35)

where

A_{n_{6}}^{V I} = \frac{1}{π} \int_{0}^{2 π} g_{1} (θ) \cos (n_{6} θ) d θ; C_{n_{6}}^{V I} = \frac{1}{π} \int_{0}^{2 π} g_{1} (θ) \sin (n_{6} θ) d θ

(36)

B_{n_{6}}^{V I} = \frac{1}{π} \int_{0}^{2 π} g_{2} (θ) \cos (n_{6} θ) d θ; D_{n_{6}}^{V I} = \frac{1}{π} \int_{0}^{2 π} g_{2} (θ) \sin (n_{6} θ) d θ

(37)

3.1.7. Region VII

Finally, the three sides of the mth slot within Region VII are connected to the iron core, and the remaining lower side is adjacent to Region VI. Therefore, the corresponding boundary conditions can be arranged as:

\{\begin{matrix} {\frac{\partial A_{V I I, m}}{\partial θ}|}_{θ_{m}} = 0 \\ {\frac{\partial A_{V I I, m}}{\partial θ}|}_{θ_{m} + δ} = 0 \end{matrix} ， r \in [R_{7}, R_{8}] ； \begin{matrix} {\frac{\partial A_{V I I, m}}{\partial r}|}_{r = R_{8}} = 0 \\ θ \in [θ_{m}, θ_{m} + δ] \end{matrix}

(38)

where

A_{V I I, m} (R_{7}, θ) = A_{V I} (R_{7}, θ) with θ \in [θ_{m}, θ_{m} + δ]

(39)

Taking account of the boundary conditions (38) and (39) together, the general solution of MVP and the corresponding Fourier series coefficient in Region VI can be written as:

\begin{array}{l} A_{V I I, m} (r, θ) = A_{0}^{m} + \frac{1}{2} μ_{0} J_{m} (R_{8}^{2} \ln r - \frac{1}{2} r^{2}) \\ + \sum_{n_{7} = 1}^{\infty} A_{n_{7}}^{m} \frac{P_{n_{7} π / δ} (r, R_{8})}{P_{n_{7} π / δ} (R_{7}, R_{8})} \cos (\frac{n_{7} π}{δ} (θ - θ_{m})) \end{array}

(40)

where

A_{n_{7}}^{m} = \frac{2}{δ} \int_{θ_{m}}^{θ_{m} + δ} A_{V I} (R_{7}, θ) \cos (\frac{n_{7} π}{δ} (θ - θ_{m})) d θ

(41)

Ultimately, by combining all the Fourier series coefficient expressions of MVPs within the machine domain, we can obtain a system of linear equations with a unique solution. The Fourier series coefficients can be obtained by solving the system of linear equations in numeric computing software, MATLAB, for instance. Subsequently, the magnetic flux density B in all these regions can be acquired according to:

B_{r} = \frac{1}{r} \frac{\partial A_{z}}{\partial θ} and B_{θ} = - \frac{\partial A_{z}}{\partial r}

(42)

where

B_{r}

and

B_{θ}

are the radial and tangential components of magnetic flux density, respectively.

3.2. Postprocessing Electromagnetic Parameters Calculation

The output torque on the rotor of DSSTVM

T_{r}

should be the sum of electromagnetic torques on the inner air gap and outer air gap, namely

T_{i n n e r_g a p}

and

T_{o u t e r_g a p}

. Then, the electromagnetic torque on the air gap can be calculated by using the Maxwell stress tensor, which can be given as follows:

T_{i n n e r_g a p} = \frac{L R_{i n}^{2}}{μ_{0}} \int_{0}^{2 π} B_{I V, r} (R_{i n}, θ) B_{I V, θ} (R_{i n}, θ) d θ

(43)

T_{o u t e r_g a p} = \frac{L R_{o u t}^{2}}{μ_{0}} \int_{0}^{2 π} B_{V I, r} (R_{o u t}, θ) B_{V I, θ} (R_{o u t}, θ) d θ

(44)

T_{r} = T_{i n n e r_g a p} + T_{o u t e r_g a p}

(45)

where

R_{i n}

, and

R_{o u t}

are the radii in the middle of the inner air gap and outer air gap.

As for the flux linkage of each coil, it can be calculated as the area integral of MVP within the slot region. Then, the phase flux can be obtained as the product of the slot connecting matrix and the flux linkage vector. The back electromotive force (EMF) can be acquired as the derivative of phase flux with respect to time. The detailed deduction process can be referred to [19].

4. Finite Element Analysis Validation

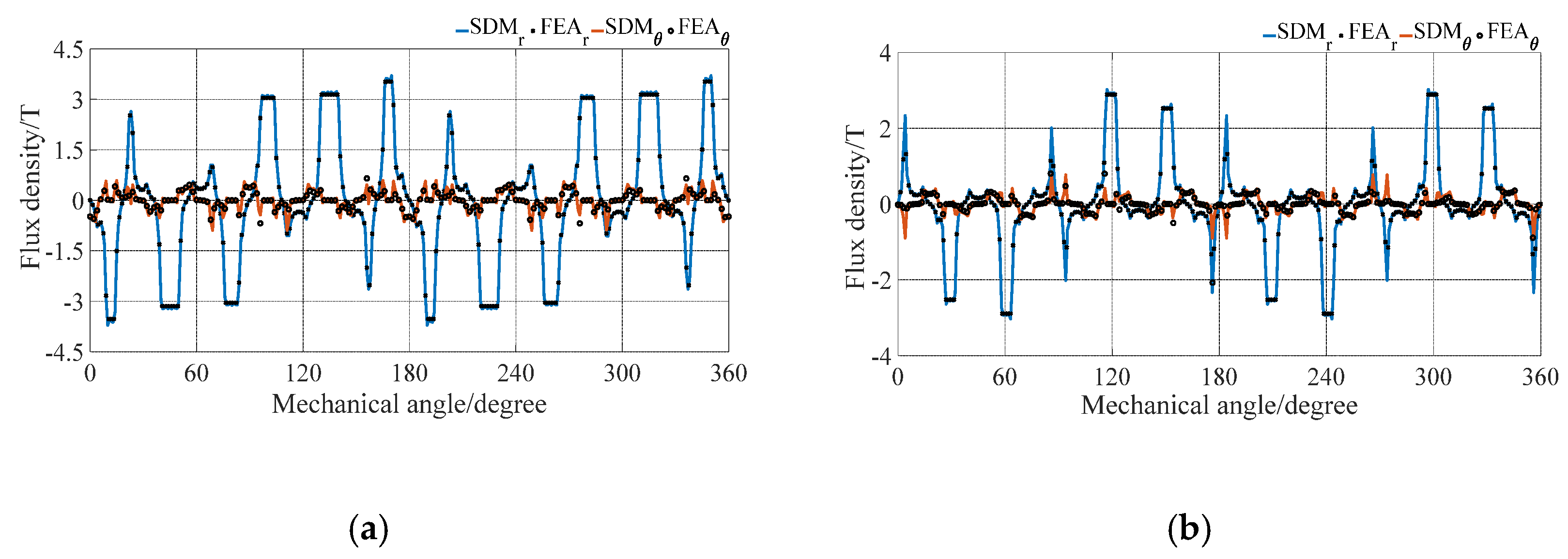
The DSSTVM simulation model is constructed via FEA to verify the effectiveness of the proposed SDM, and the structural parameters of the DSSTVM model are referred to Table 1.. The no-load magnetic flux density and flux line distributions calculated by FEA are depicted in Figure 2. 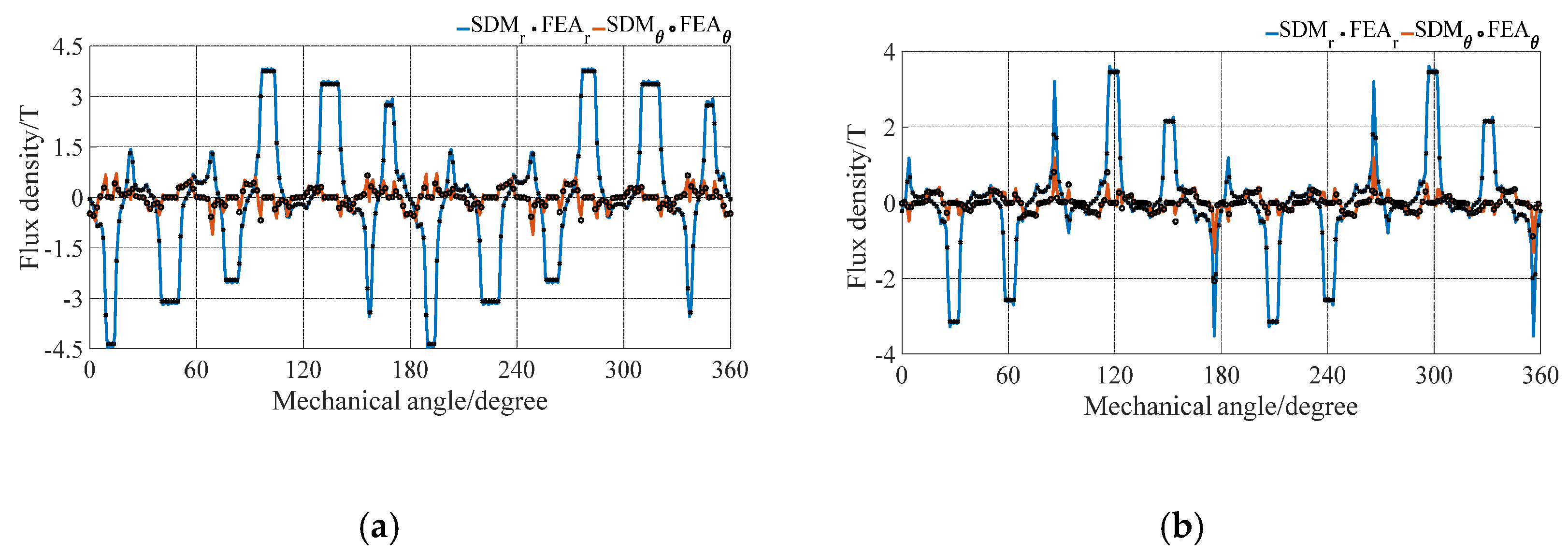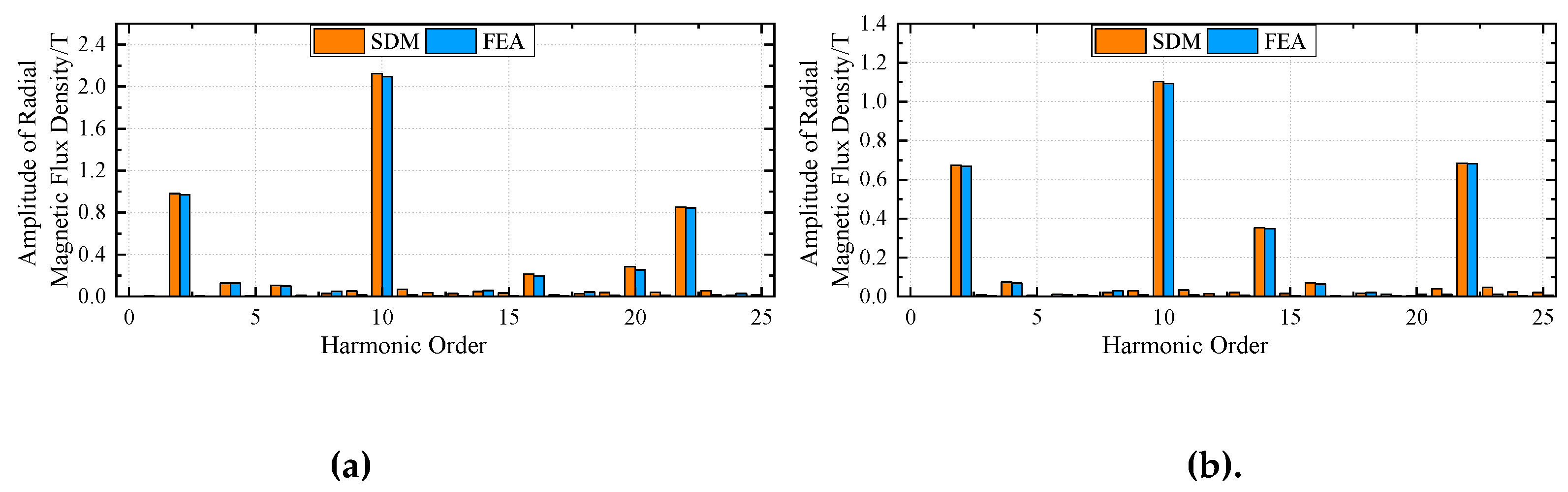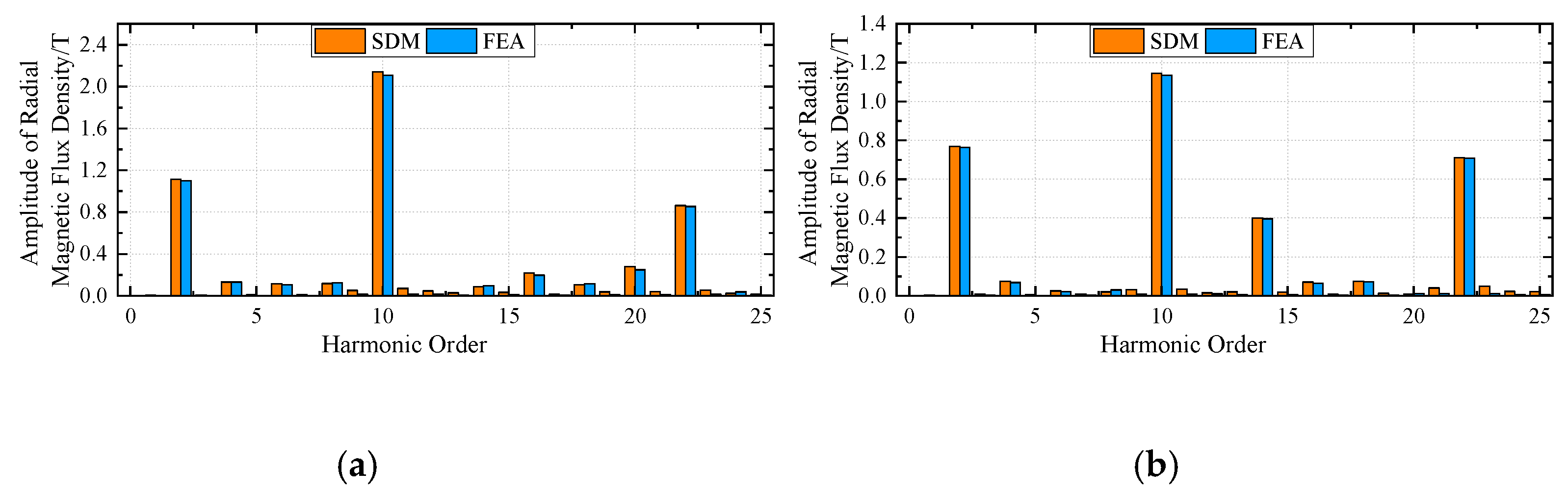The no-load and on-load magnetic flux density distribution comparison between SDM and FEA in the inner and outer air gaps are illustrated in Figure 3 and Figure 5, respectively. The harmonic spectrum of the air gap magnetic flux density in the middle of the inner air gap and outer air gap under no load condition and rated load condition between SDM and FEA are illustrated in Figure 1 and Figure 2, respectively. It can be observed that the proposed SDM has a good agreement with that of FEA in terms of the magnetic flux densities and harmonic spectrum in inner and outer air gaps.

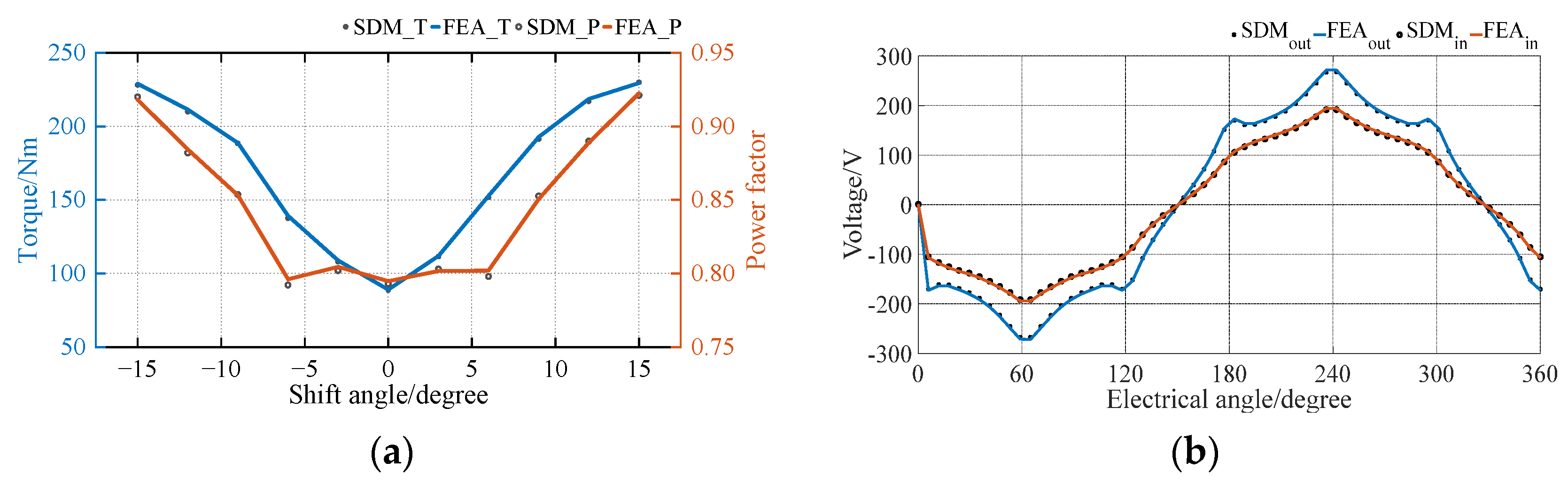
One prominent advantage of using DSSTVM is to reduce the flux leakage, so the output torque and power factor of the machines can be greatly improved. To minimize the flux leakage of the spoke-type PMs on the rotor, one can determine the optimal shift angle between the inner and outer stators via the parameter sweeping method, as depicted in Figure 1. This can also be achieved by using the proposed SDM, and Figure 7 (a) illustrates the variation of the output torque and power factor with the variation of shift angle from 0 to 30 degrees calculated by both SDM and FEA.

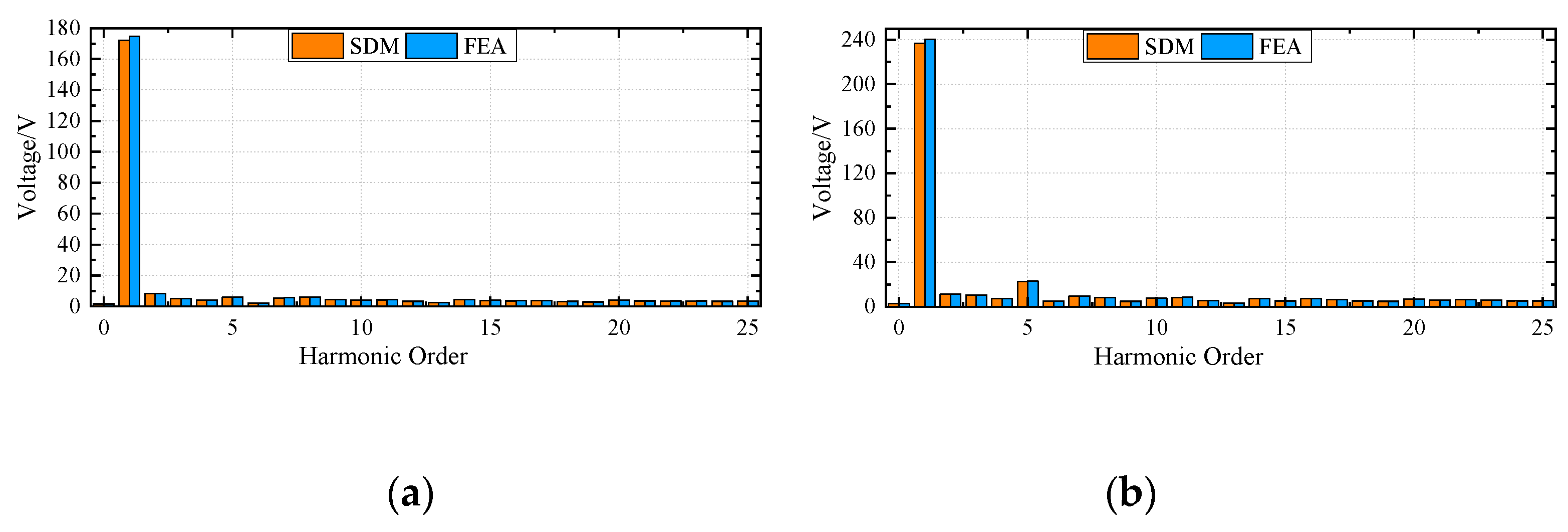
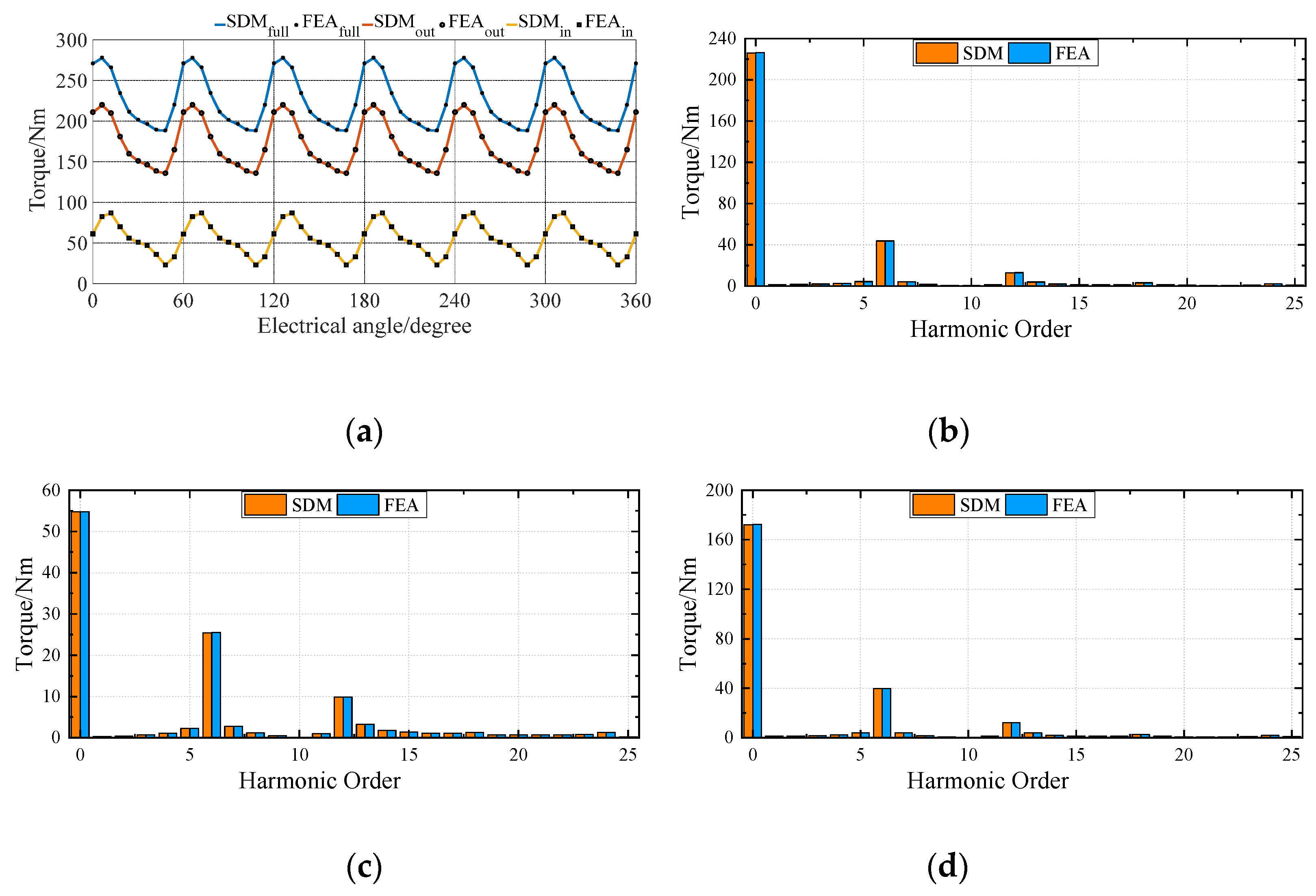
Then, the DSSTVM's no-load back EMF waveforms and output torques with different sets of windings operating can be obtained by using FEA and SDM, as can be seen in Figure 7 (b) and Figure 9 (a), respectively. The harmonic spectrum of the no-load back EMF waveforms in the inner stator and outer stator between SDM and FEA are illustrated in Figure 8 (a) and Figure 8 (b), respectively. The rated load torque harmonic spectrum of the DSSTVM in mode 1 (the inner and outer parts of DSSTVM operate simultaneously to generate the torque), mode 2 (the inner part of DSSTVM operates to generate the torque), and mode 3 (the outer part of DSSTVM operate to generate the torque) between SDM and FEA are illustrated in Figure 9 (b), Figure 9 (c) and Figure 9 (d), respectively. A slight deviation between the two approaches can be observed, where the values of SDM are smaller. This is due to the maximum harmonic limit of the SDM, and the error can be smaller if the calculated maximum harmonic number increases. However, the computation time increases along with the rise of the calculated maximum harmonic number, so we should make a trade-off for different application scenarios.

As for the computation time, it takes the SDM 29 s for a single step, while it takes FEA 47 s. Thus, the computation time of SDM is only 62 % of that of FEA, proving that the SDM is prior to being applied to the initial design stage to determine the slot-pole combinations and parameters' ranges to be optimized for DSSTVM as well as other double-stator machines.

5. Conclusions

This paper presents a high-fidelity analytical method, namely the subdomain model, for calculating the magnetic field distribution and the related electromagnetic parameters in DSSTVM. The magnetic flux density distribution, back EMF, and output torque of the DSSTVM are computed by both the SDM and FEA. Compared to FEA, the proposed SDM can save computation time while maintaining accuracy. The deduction process completes the SDM for double-stator machines with various structures as well as slot-pole combinations. This analytical method can be applied for topology investigation and optimization for double-stator machines.

Author Contributions

Conceptualization, X.S.; methodology, X.S.; software, H.Z.; validation, H.Z.; formal analysis, J.Y.; investigation, J.Y.; resources, X.S.; data curation, H.Z.; writing---original draft preparation, X.S.; writing---review and editing, C.L.; visualization, Z.O.; supervision, H.Z.; project administration, H.Z.; funding acquisition, H.Z. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported in part by the Guangdong Basic and Applied Basic Research Foundation under Project 2022A1515110361 and Guangzhou Science and Technology Bureau under Project SL2022A04J00605 and Project SL2022A03J00086.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

The unknown Fourier series coefficients in MVP expression of each subdomain need to be deduced and calculated for consequent Fourier series coefficients matrices solution. The detailed Fourier series coefficients in the MVP expression of each subdomain can be calculated via the Fourier expansion in each subdomain boundary and applying the adjacent subdomain MVP values or derivative information. Therefore, the detailed Fourier series coefficients in each subdomain of DSVMs can be calculated as follows.

First of all, according to the definition of (4) and (5), the relationship of

P_{w} (u, v)

and

E_{w} (u, v)

are described as follows for later clarity and simplicity in partial derivation.

\frac{\partial P_{w} (u, v)}{\partial u} = E_{w} (u, v)

(46)

\frac{\partial E_{w} (u, v)}{\partial u} = P_{w} (u, v)

(47)

In Region I, considering the boundary condition of Region I and Region II, after substituting (12) into (9), we get:

\begin{array}{l} A_{n_{1}}^{i} = \frac{4 B_{0}^{j}}{n_{1} π R_{2}} \sin (\frac{n_{1} π β_{1}}{2 α}) \cos (\frac{n_{1} π}{2}) \\ + \sum_{n_{2} = 1}^{\infty} (A_{n_{2}}^{j} \frac{P_{n_{2} π / β_{1}} (R_{2}, R_{4})}{E_{n_{2} π / β_{1}} (R_{2}, R_{4})} - B_{n_{2}}^{j} \frac{2}{E_{n_{2} π / β_{1}} (R_{2}, R_{4})}) \cdot \frac{2 n_{2} π}{α β_{1} R_{2}} \cdot F (n_{1}, n_{2}) \end{array}

(48)

In Region II, considering the boundary condition of Region I and Region II, after substituting (8) into (15), considering the boundary condition of Region II and Region IV, after substituting (23) into (16), we get:

\begin{array}{l} A_{n_{2}}^{j} = \sum_{n_{1} = 1}^{\infty} (A_{n_{1}}^{i} \frac{2 α R_{2}}{n_{1} π β_{1}} \frac{P_{n_{1} π / α} (R_{2}, R_{1})}{E_{n_{1} π / α} (R_{2}, R_{1})} \\ - \frac{2 μ_{0} J_{i n}}{β_{1} ({(n_{1} π / α)}^{2} - 4)} (\frac{2 α}{n_{1} π} \frac{R_{1}^{2} \cdot 2 - R_{2}^{2} P_{n_{1} π / α} (R_{2}, R_{1})}{E_{n_{1} π / α} (R_{2}, R_{1})} + R_{2}^{2}) \cdot F (n_{1}, n_{2}) \end{array}

(49)

\begin{array}{l} B_{n_{2}}^{j} = \sum_{n_{4} = 1}^{\infty} (A_{n_{4}}^{I V} \frac{2 R_{4}}{n_{4} β_{1}} \frac{P_{n_{4}} (R_{4}, R_{5})}{E_{n_{4}} (R_{4}, R_{5})} + B_{n_{4}}^{I V} \frac{2 R_{5}}{n_{4} β_{1}} \frac{2}{E_{n_{4}} (R_{5}, R_{4})}) \cdot f_{a} (n_{2}, n_{4}, j) \\ + \sum_{n_{4} = 1}^{\infty} (C_{n_{4}}^{I V} \frac{2 R_{4}}{n_{4} β_{1}} \frac{P_{n_{4}} (R_{4}, R_{5})}{E_{n_{4}} (R_{4}, R_{5})} + D_{n_{4}}^{I V} \frac{2 R_{5}}{n_{4} β_{1}} \frac{2}{E_{n_{4}} (R_{5}, R_{4})}) \cdot g_{a} (n_{2}, n_{4}, j) \end{array}

(50)

In Region III, considering the boundary condition of Region III and Region IV, after substituting (23) into (20), we get:

\begin{array}{l} A_{n_{3}}^{k} = \sum_{n_{4} = 1}^{\infty} (A_{n_{4}}^{I V} \frac{2 R_{4}}{n_{4} β_{1}} \frac{P_{n_{4}} (R_{4}, R_{5})}{E_{n_{4}} (R_{4}, R_{5})} + B_{n}^{I V} \frac{2 R_{5}}{n_{4} β_{1}} \frac{2}{E_{n_{4}} (R_{5}, R_{4})}) \cdot f_{t} (n_{3}, n_{4}, k) \\ + \sum_{n_{4} = 1}^{\infty} (A_{n_{4}}^{I V} \frac{2 R_{4}}{n_{4} β_{1}} \frac{P_{n_{4}} (R_{4}, R_{5})}{E_{n_{4}} (R_{4}, R_{5})} + B_{n}^{I V} \frac{2 R_{5}}{n_{4} β_{1}} \frac{2}{E_{n_{4}} (R_{5}, R_{4})}) \cdot g_{t} (n_{3}, n_{4}, k) \end{array}

(51)

In Region IV, considering the boundary condition of Region IV, Region II, and Region III, after substituting (12), (19) and (21) into (24), considering the boundary condition of Region IV and Region V, after substituting (22) and (28) into (25), we get:

\begin{array}{l} A_{n_{4}}^{I V} = \sum_{j = 1}^{P_{i}} \frac{B_{0}^{j}}{π R_{4}} \cdot r_{j} (n_{4}, j) + \sum_{j = 1}^{P_{i}} \sum_{n_{2} = 1}^{\infty} A_{n_{2}}^{j} \frac{n_{2}}{β_{1} R_{4}} \frac{2}{E_{n_{2} π / β_{1}} (R_{2}, R_{4})} \cdot f_{a} (n_{2}, n_{4}, j) \\ - \sum_{j = 1}^{P_{i}} \sum_{n_{2} = 1}^{\infty} B_{n_{2}}^{j} \frac{n_{2}}{β_{1} R_{4}} \frac{P_{n_{2} π / β_{1}} (R_{4}, R_{2})}{E_{n_{2} π / β_{1}} (R_{2}, R_{4})} \cdot f_{a} (n_{2}, n_{4}, j) \\ + \sum_{k = 1}^{P_{i}} \sum_{n_{3} = 1}^{\infty} A_{n_{3}}^{k} \frac{n_{3}}{β_{2} R_{4}} \frac{E_{n_{3} π / β_{2}} (R_{4}, R_{3})}{P_{n_{3} π / β_{2}} (R_{3}, R_{4})} \cdot f_{t} (n_{3}, n_{4}, k) \end{array}

(52)

\begin{array}{l} C_{n_{4}}^{I V} = \sum_{j = 1}^{P_{i}} \frac{B_{0}^{j}}{π R_{4}} \cdot s_{j} (n_{4}, j) + \sum_{j = 1}^{P_{i}} \sum_{n_{2} = 1}^{\infty} A_{n_{2}}^{j} \frac{n_{2}}{β_{1} R_{4}} \frac{2}{E_{n_{2} π / β_{1}} (R_{2}, R_{4})} \cdot g_{a} (n_{2}, n_{4}, j) \\ - \sum_{j = 1}^{P_{i}} \sum_{n_{2} = 1}^{\infty} B_{n_{2}}^{j} \frac{n_{2}}{β_{1} R_{4}} \frac{P_{n_{2} π / β_{1}} (R_{4}, R_{2})}{E_{n_{2} π / β_{1}} (R_{2}, R_{4})} \cdot g_{a} (n_{2}, n_{4}, j) \\ + \sum_{k = 1}^{P_{i}} \sum_{n_{3} = 1}^{\infty} A_{n_{3}}^{k} \frac{n_{3}}{β_{2} R_{4}} \frac{E_{n_{3} π / β_{2}} (R_{4}, R_{3})}{P_{n_{3} π / β_{2}} (R_{3}, R_{4})} \cdot g_{t} (n_{3}, n_{4}, k) \end{array}

(53)

\begin{array}{l} B_{n_{4}}^{I V} = \sum_{l = 1}^{Q} \frac{B_{0}^{l}}{π R_{5}} \cdot r_{f} (n_{4}, l) + \sum_{l = 1}^{Q} \sum_{n_{5} = 1}^{\infty} A_{n_{5}}^{l} \frac{n_{5}}{γ R_{5}} \frac{P_{n_{5} π / γ} (R_{5}, R_{6})}{E_{n_{5} π / γ} (R_{5}, R_{6})} \cdot f_{f} (n_{5}, n_{4}, l) \\ - \sum_{l = 1}^{Q} \sum_{n_{5} = 1}^{\infty} B_{n_{5}}^{l} \frac{n_{5}}{γ R_{5}} \frac{2}{E_{n_{5} π / γ} (R_{5}, R_{6})} \cdot f_{f} (n_{5}, n_{4}, l) \end{array}

(54)

\begin{array}{l} D_{n_{4}}^{I V} = \sum_{l = 1}^{Q} \frac{B_{0}^{l}}{π R_{5}} \cdot s_{f} (n_{4}, l) + \sum_{l = 1}^{Q} \sum_{n_{5} = 1}^{\infty} A_{n_{5}}^{l} \frac{n_{5}}{γ R_{5}} \frac{P_{n_{5} π / γ} (R_{5}, R_{6})}{E_{n_{5} π / γ} (R_{5}, R_{6})} \cdot g_{f} (n_{5}, n_{4}, l) \\ - \sum_{l = 1}^{Q} \sum_{n_{5} = 1}^{\infty} B_{n_{5}}^{l} \frac{n_{5}}{γ R_{5}} \frac{2}{E_{n_{5} π / γ} (R_{5}, R_{6})} \cdot g_{f} (n_{5}, n_{4}, l) \end{array}

(55)

In Region V, considering the boundary condition of Region V and Region IV, after substituting (23) into (29) and (31), considering the boundary condition of Region V and Region VI, after substituting (35) into (30) and (32), we get:

\begin{array}{l} A_{n_{5}}^{l} = \sum_{n_{4} = 1}^{\infty} (A_{n_{4}}^{I V} \frac{2 R_{4}}{n_{4} γ} \frac{2}{E_{n_{4}} (R_{4}, R_{5})} + B_{n_{4}}^{I V} \frac{2 R_{5}}{n_{4} γ} \frac{P_{n_{4}} (R_{5}, R_{4})}{E_{n_{4}} (R_{5}, R_{4})}) \cdot f_{f} (n_{5}, n_{4}, l) \\ + \sum_{n_{4} = 1}^{\infty} (C_{n_{4}}^{I V} \frac{2 R_{4}}{n_{4} γ} \frac{2}{E_{n_{4}} (R_{4}, R_{5})} + D_{n_{4}}^{I V} \frac{2 R_{5}}{n_{4} γ} \frac{P_{n_{4}} (R_{5}, R_{4})}{E_{n_{4}} (R_{5}, R_{4})}) \cdot g_{f} (n_{5}, n_{4}, l) \end{array}

(56)

\begin{array}{l} B_{n_{5}}^{l} = \sum_{n_{6} = 1}^{\infty} (A_{n_{6}}^{V I} \frac{2 R_{6}}{n_{6} γ} \frac{P_{n_{6}} (R_{6}, R_{7})}{E_{n_{6}} (R_{6}, R_{7})} + B_{n_{6}}^{V I} \frac{2 R_{7}}{n_{6} γ} \frac{2}{E_{n_{6}} (R_{7}, R_{6})}) \cdot f_{f} (n_{5}, n_{6}, l) \\ + \sum_{n_{6} = 1}^{\infty} (C_{n_{6}}^{V I} \frac{2 R_{6}}{n_{6} γ} \frac{P_{n_{6}} (R_{6}, R_{7})}{E_{n_{6}} (R_{6}, R_{7})} + D_{n_{6}}^{V I} \frac{2 R_{7}}{n_{6} γ} \frac{2}{E_{n_{6}} (R_{7}, R_{6})}) \cdot g_{f} (n_{5}, n_{6}, l) \end{array}

(57)

\begin{array}{l} A_{0}^{l} + B_{0}^{l} \ln R_{5} - μ_{0} M_{θ, l} R_{5} = \\ A_{0}^{I V} + \sum_{n_{4} = 1}^{\infty} (A_{n_{4}}^{I V} \frac{R_{4}}{n_{4} γ} \frac{2}{E_{n_{4}} (R_{4}, R_{5})} + B_{n_{4}}^{I V} \frac{R_{5}}{n_{4} γ} \frac{P_{n_{4}} (R_{5}, R_{4})}{E_{n_{4}} (R_{5}, R_{4})}) \cdot r_{f} (n_{4}, l) \\ + \sum_{n_{4} = 1}^{\infty} (C_{n_{4}}^{I V} \frac{R_{4}}{n_{4} γ} \frac{2}{E_{n_{4}} (R_{4}, R_{5})} + D_{n_{4}}^{I V} \frac{R_{5}}{n_{4} γ} \frac{P_{n_{4}} (R_{5}, R_{4})}{E_{n_{4}} (R_{5}, R_{4})}) \cdot s_{f} (n_{4}, l) \end{array}

(58)

\begin{array}{l} A_{0}^{l} + B_{0}^{l} \ln R_{6} - μ_{0} M_{θ, l} R_{6} = \\ A_{0}^{V I} + \sum_{n_{6} = 1}^{\infty} (A_{n_{6}}^{V I} \frac{R_{6}}{n_{6} γ} \frac{P_{n_{6}} (R_{6}, R_{7})}{E_{n_{6}} (R_{6}, R_{7})} + B_{n_{6}}^{V I} \frac{R_{7}}{n_{6} γ} \frac{2}{E_{n_{6}} (R_{7}, R_{6})}) \cdot r_{f} (n_{6}, l) \\ + \sum_{n_{6} = 1}^{\infty} (C_{n_{6}}^{V I} \frac{R_{6}}{n_{6} γ} \frac{P_{n_{6}} (R_{6}, R_{7})}{E_{n_{6}} (R_{6}, R_{7})} + D_{n_{6}}^{V I} \frac{R_{7}}{n_{6} γ} \frac{2}{E_{n_{6}} (R_{7}, R_{6})}) \cdot s_{f} (n_{6}, l) \end{array}

(59)

In Region VI, considering the boundary condition of Region VI and Region V, after substituting (28) and (33) into (36), considering the boundary condition of Region VI and Region VII, after substituting (34) and (40) into (37), we get:

\begin{array}{l} A_{n_{6}}^{V I} = \sum_{l = 1}^{Q} \frac{B_{0}^{l}}{π R_{6}} \cdot r_{f} (n_{6}, l) + \sum_{l = 1}^{Q} \sum_{n_{5} = 1}^{\infty} A_{n_{5}}^{l} \frac{n_{5}}{γ R_{6}} \frac{2}{E_{n_{5} π / γ} (R_{5}, R_{6})} \cdot f_{f} (n_{5}, n_{6}, l) \\ - \sum_{l = 1}^{Q} \sum_{n_{5} = 1}^{\infty} B_{n_{5}}^{l} \frac{n_{5}}{γ R_{6}} \frac{P_{n_{5} π / γ} (R_{6}, R_{5})}{E_{n_{5} π / γ} (R_{5}, R_{6})} \cdot f_{f} (n_{5}, n_{6}, l) \end{array}

(60)

\begin{array}{l} C_{n_{6}}^{V I} = \sum_{l = 1}^{Q} \frac{B_{0}^{l}}{π R_{6}} \cdot s_{f} (n_{6}, l) + \sum_{l = 1}^{Q} \sum_{n_{5} = 1}^{\infty} A_{n_{5}}^{l} \frac{n_{5}}{γ R_{6}} \frac{2}{E_{n_{5} π / γ} (R_{5}, R_{6})} \cdot g_{f} (n_{5}, n_{6}, l) \\ - \sum_{l = 1}^{Q} \sum_{n_{5} = 1}^{\infty} B_{n_{5}}^{l} \frac{n_{5}}{γ R_{6}} \frac{P_{n_{5} π / γ} (R_{6}, R_{5})}{E_{n_{5} π / γ} (R_{5}, R_{6})} \cdot g_{f} (n_{5}, n_{6}, l) \end{array}

(61)

\begin{array}{l} B_{n_{6}}^{V I} = \sum_{m = 1}^{P_{o}} \frac{μ_{0} J_{m}}{2 π} (\frac{R_{8}^{2}}{R_{7}} - R_{7}) \cdot r_{s} (n_{6}, m) \\ + \sum_{m = 1}^{P_{o}} \sum_{n_{7} = 1}^{\infty} A_{n_{7}}^{m} \frac{n_{7}}{δ R_{7}} \frac{E_{n_{7} π / δ} (R_{7}, R_{8})}{P_{n_{7} π / δ} (R_{7}, R_{8})} \cdot f_{s} (n_{7}, n_{6}, m) \end{array}

(62)

\begin{array}{l} D_{n_{6}}^{V I} = \sum_{m = 1}^{P_{o}} \frac{μ_{0} J_{m}}{2 π} (\frac{R_{8}^{2}}{R_{7}} - R_{7}) \cdot s_{s} (n_{6}, m) \\ + \sum_{m = 1}^{P_{o}} \sum_{n_{7} = 1}^{\infty} A_{n_{7}}^{m} \frac{n_{7}}{δ R_{7}} \frac{E_{n_{7} π / δ} (R_{7}, R_{8})}{P_{n_{7} π / δ} (R_{7}, R_{8})} \cdot g_{s} (n_{7}, n_{6}, m) \end{array}

(63)

In Region VII, considering the boundary condition of Region VI and Region VII, after substituting (35) into (41), we get:

\begin{array}{l} A_{n_{7}}^{m} = \sum_{n_{6} = 1}^{\infty} (A_{n_{6}}^{V I} \frac{2 R_{6}}{n_{6} δ} \frac{2}{E_{n} (R_{6}, R_{7})} + B_{n_{6}}^{V I} \frac{2 R_{7}}{n_{6} δ} \frac{P_{n} (R_{7}, R_{6})}{E_{n} (R_{7}, R_{6})}) f_{s} (n_{7}, n_{6}, m) \\ + \sum_{n_{6} = 1}^{\infty} (C_{n_{6}}^{V I} \frac{2 R_{6}}{n_{6} δ} \frac{2}{E_{n} (R_{6}, R_{7})} + D_{n_{6}}^{V I} \frac{2 R_{7}}{n_{6} δ} \frac{P_{n} (R_{7}, R_{6})}{E_{n} (R_{7}, R_{6})}) g_{s} (n_{7}, n_{6}, m) \end{array}

(64)

Appendix B

The integral function

f_{a} (n_{2}, n_{4}, j)

g_{a} (n_{2}, n_{4}, j)

f_{t} (n_{3}, n_{4}, k)

g_{t} (n_{3}, n_{4}, k)

f_{f} (n_{5}, n_{4}, l)

g_{f} (n_{5}, n_{4}, l)

f_{f} (n_{5}, n_{6}, l)

g_{f} (n_{5}, n_{6}, l)

f_{s} (n_{7}, n_{6}, m)

g_{s} (n_{7}, n_{6}, m)

r_{j} (n_{4}, j)

s_{j} (n_{4}, j)

r_{f} (n_{4}, l)

s_{f} (n_{4}, l)

r_{s} (n_{6}, m)

s_{s} (n_{6}, m)

and

F (n_{1}, n_{2})

are expressed as follows for consequent Fourier series coefficients matrices solution.

f_{a} (n_{2}, n_{4}, j) = \int_{θ_{j}}^{θ_{j} + β_{1}} \cos (n_{4} θ) \cos (\frac{n_{2} π}{β_{1}} (θ - θ_{j})) d θ

(65)

g_{a} (n_{2}, n_{4}, j) = \int_{θ_{j}}^{θ_{j} + β_{1}} \sin (n_{4} θ) \cos (\frac{n_{2} π}{β_{1}} (θ - θ_{j})) d θ

(66)

f_{t} (n_{3}, n_{4}, k) = \int_{θ_{k}}^{θ_{k} + β_{2}} \cos (n_{4} θ) \cos (\frac{n_{3} π}{β_{2}} (θ - θ_{k})) d θ

(67)

g_{t} (n_{3}, n_{4}, k) = \int_{θ_{k}}^{θ_{k} + β_{2}} \sin (n_{4} θ) \cos (\frac{n_{3} π}{β_{2}} (θ - θ_{k})) d θ

(68)

f_{f} (n_{5}, n_{4}, l) = \int_{θ_{l}}^{θ_{l} + γ} \cos (n_{4} θ) \cos (\frac{n_{5} π}{γ} (θ - θ_{l})) d θ

(69)

g_{f} (n_{5}, n_{4}, l) = \int_{θ_{l}}^{θ_{l} + γ} \sin (n_{4} θ) \cos (\frac{n_{5} π}{γ} (θ - θ_{l})) d θ

(70)

f_{f} (n_{5}, n_{6}, l) = \int_{θ_{l}}^{θ_{l} + γ} \cos (n_{6} θ) \cos (\frac{n_{5} π}{γ} (θ - θ_{l})) d θ

(71)

g_{f} (n_{5}, n_{6}, l) = \int_{θ_{l}}^{θ_{l} + γ} \sin (n_{6} θ) \cos (\frac{n_{5} π}{γ} (θ - θ_{l})) d θ

(72)

f_{s} (n_{7}, n_{6}, m) = \int_{θ_{m}}^{θ_{m} + δ} \cos (n_{6} θ) \cos (\frac{n_{7} π}{δ} (θ - θ_{m})) d θ

(73)

g_{s} (n_{7}, n_{6}, m) = \int_{θ_{m}}^{θ_{m} + δ} \sin (n_{6} θ) \cos (\frac{n_{7} π}{δ} (θ - θ_{m})) d θ

(74)

r_{j} (n_{4}, j) = \int_{θ_{j}}^{θ_{j} + β_{1}} \cos (n_{4} θ) d θ = \frac{1}{n} [\sin (n_{4} (θ_{j} + β_{1})) - \sin (n_{4} θ_{j})]

(75)

s_{j} (n_{4}, j) = \int_{θ_{j}}^{θ_{j} + β_{1}} \sin (n_{4} θ) d θ = \frac{1}{n} [- \cos (n_{4} (θ_{j} + β_{1})) + \cos (n_{4} θ_{j})]

(76)

r_{f} (n_{4}, l) = \int_{θ_{l}}^{θ_{l} + γ} \cos (n_{4} θ) d θ = \frac{1}{n} [\sin (n_{4} (θ_{l} + γ)) - \sin (n_{4} θ_{l})]

(77)

s_{f} (n_{4}, l) = \int_{θ_{l}}^{θ_{l} + γ} \sin (n_{4} θ) d θ = \frac{1}{n} [- \cos (n_{4} (θ_{l} + γ)) + \cos (n_{4} θ_{l})]

(78)

r_{f} (n_{6}, l) = \int_{θ_{l}}^{θ_{l} + γ} \cos (n_{6} θ) d θ = \frac{1}{n} [\sin (n_{6} (θ_{l} + γ)) - \sin (n_{6} θ_{l})]

(79)

s_{f} (n_{6}, l) = \int_{θ_{l}}^{θ_{l} + γ} \sin (n_{6} θ) d θ = \frac{1}{n} [- \cos (n_{6} (θ_{l} + γ)) + \cos (n_{6} θ_{l})]

(80)

r_{s} (n_{6}, m) = \int_{θ_{m}}^{θ_{m} + δ} \cos (n_{6} θ) d θ = \frac{1}{n} [\sin (n_{6} (θ_{m} + δ)) - \sin (n_{6} θ_{m})]

(81)

s_{s} (n_{6}, m) = \int_{θ_{m}}^{θ_{m} + δ} \sin (n_{6} θ) d θ = \frac{1}{n} [- \cos (n_{6} (θ_{m} + δ)) + \cos (n_{6} θ_{m})]

(82)

F (n_{1}, n_{2}) = \int_{θ_{j}}^{θ_{j} + β_{1}} \cos (\frac{n_{1} π}{α} (θ - θ_{i})) \cos (\frac{n_{2} π}{β_{1}} (θ - θ_{j})) d θ

(83)

Then,

f_{a} (n_{2}, n_{4}, j)

g_{a} (n_{2}, n_{4}, j)

f_{t} (n_{3}, n_{4}, k)

g_{t} (n_{3}, n_{4}, k)

f_{f} (n_{5}, n_{4}, l)

g_{f} (n_{5}, n_{4}, l)

f_{s} (n_{7}, n_{6}, m)

and

g_{s} (n_{7}, n_{6}, m)

can be further simplified as:

f_{a} (n_{2}, n_{4}, j) = \{\begin{cases} \frac{n_{4}^{2} β_{1}^{2} [\sin (n_{4} θ_{j}) + {(- 1)}^{n_{2} + 1} \sin (n_{4} (θ_{j} + β_{1}))]}{n_{2}^{2} π^{2} - n_{4}^{2} β_{1}^{2}}, n_{2} π \neq n_{4} β_{1} \\ \frac{2 n_{4} β_{1} \cos (n_{4} θ_{j}) - \sin (n_{4} θ_{j}) + \sin (n_{4} (θ_{j} + β_{1}))}{4 n_{4}}, n_{2} π = n_{4} β_{1} \end{cases}

(84)

g_{a} (n_{2}, n_{4}, j) = \{\begin{cases} \frac{n_{4}^{2} β_{1}^{2} [- \cos (n_{4} θ_{j}) + {(- 1)}^{n_{2}} \cos (n_{4} (θ_{j} + β_{1}))]}{n_{2}^{2} π^{2} - n_{4}^{2} β_{1}^{2}}, n_{2} π \neq n_{4} β_{1} \\ \frac{2 n_{4} β_{1} \sin (n_{4} θ_{j}) + \cos (n_{4} θ_{j}) - \cos (n_{4} (θ_{j} + β_{1}))}{4 n_{4}}, n_{2} π = n_{4} β_{1} \end{cases}

(85)

f_{t} (n_{3}, n_{4}, k) = \{\begin{cases} \frac{n_{4}^{2} β_{2}^{2} [\sin (n_{4} θ_{k}) + {(- 1)}^{n_{3} + 1} \sin (n_{4} (θ_{k} + β_{2}))]}{n_{3}^{2} π^{2} - n_{4}^{2} β_{2}^{2}}, n_{3} π \neq n_{4} β_{2} \\ \frac{2 n_{4} β_{2} \cos (n_{4} θ_{k}) - \sin (n_{4} θ_{k}) + \sin (n_{4} (θ_{k} + β_{2}))}{4 n_{4}}, n_{3} π = n_{4} β_{2} \end{cases}

(86)

g_{t} (n_{3}, n_{4}, k) = \{\begin{cases} \frac{n_{4}^{2} β_{2}^{2} [- \cos (n_{4} θ_{k}) + {(- 1)}^{n_{3}} \cos (n_{4} (θ_{k} + β_{2}))]}{n_{3}^{2} π^{2} - n_{4}^{2} β_{2}^{2}}, n_{3} π \neq n_{4} β_{2} \\ \frac{2 n_{4} β_{2} \sin (n_{4} θ_{k}) + \cos (n_{4} θ_{k}) - \cos (n_{4} (θ_{k} + β_{2}))}{4 n_{4}}, n_{3} π = n_{4} β_{2} \end{cases}

(87)

f_{f} (n_{5}, n_{4}, l) = \{\begin{cases} \frac{n_{4}^{2} γ^{2} [\sin (n_{4} θ_{l}) + {(- 1)}^{n_{5} + 1} \sin (n_{4} (θ_{l} + γ))]}{n_{5}^{2} π^{2} - n_{4}^{2} γ^{2}}, n_{5} π \neq n_{4} γ \\ \frac{2 n_{4} γ \cos (n_{4} θ_{l}) - \sin (n_{4} θ_{l}) + \sin (n_{4} (θ_{l} + γ))}{4 n_{4}}, n_{5} π = n_{4} γ \end{cases}

(88)

g_{f} (n_{5}, n_{4}, l) = \{\begin{cases} \frac{n_{4}^{2} γ^{2} [- \cos (n_{4} θ_{l}) + {(- 1)}^{n_{5}} \cos (n_{4} (θ_{l} + γ))]}{n_{5}^{2} π^{2} - n_{4}^{2} γ^{2}}, n_{5} π \neq n_{4} γ \\ \frac{2 n_{4} γ \sin (n_{4} θ_{l}) + \cos (n_{4} θ_{l}) - \cos (n_{4} (θ_{l} + γ))}{4 n_{4}}, n_{5} π = n_{4} γ \end{cases}

(89)

f_{f} (n_{5}, n_{6}, l) = \{\begin{cases} \frac{n_{6}^{2} γ^{2} [\sin (n_{6} θ_{l}) + {(- 1)}^{n_{5} + 1} \sin (n_{6} (θ_{l} + γ))]}{n_{5}^{2} π^{2} - n_{6}^{2} γ^{2}}, n_{5} π \neq n_{6} γ \\ \frac{2 n_{6} γ \cos (n_{6} θ_{l}) - \sin (n_{6} θ_{l}) + \sin (n_{6} (θ_{l} + γ))}{4 n_{6}}, n_{5} π = n_{6} γ \end{cases}

(90)

g_{f} (n_{5}, n_{6}, l) = \{\begin{cases} \frac{n_{6}^{2} γ^{2} [- \cos (n_{6} θ_{l}) + {(- 1)}^{n_{5}} \cos (n_{6} (θ_{l} + γ))]}{n_{5}^{2} π^{2} - n_{6}^{2} γ^{2}}, n_{5} π \neq n_{6} γ \\ \frac{2 n_{6} γ \sin (n_{6} θ_{l}) + \cos (n_{6} θ_{l}) - \cos (n_{6} (θ_{l} + γ))}{4 n_{6}}, n_{5} π = n_{6} γ \end{cases}

(91)

f_{s} (n_{7}, n_{6}, m) = \{\begin{cases} \frac{n_{6}^{2} δ^{2} [\sin (n_{6} θ_{m}) + {(- 1)}^{n_{7} + 1} \sin (n_{6} (θ_{m} + δ))]}{n_{7}^{2} π^{2} - n_{6}^{2} δ^{2}}, n_{7} π \neq n_{6} δ \\ \frac{2 n_{6} δ \cos (n_{6} θ_{m}) - \sin (n_{6} θ_{m}) + \sin (n_{6} (θ_{m} + δ))}{4 n_{6}}, n_{7} π = n_{6} δ \end{cases}

(92)

g_{s} (n_{7}, n_{6}, m) = \{\begin{cases} \frac{n_{6}^{2} δ^{2} [- \cos (n_{6} θ_{m}) + {(- 1)}^{n_{7}} \cos (n_{6} (θ_{m} + δ))]}{n_{7}^{2} π^{2} - n_{6}^{2} δ^{2}}, n_{7} π \neq n_{6} δ \\ \frac{2 n_{6} δ \sin (n_{6} θ_{m}) + \cos (n_{6} θ_{m}) - \cos (n_{6} (θ_{m} + δ))}{4 n_{6}}, n_{7} π = n_{6} δ \end{cases}

(93)

F (n_{1}, n_{2})

can be further simplified as:

F (n_{1}, n_{2}) = \{\begin{cases} \frac{\frac{n_{1} π}{α} [{(- 1)}^{n_{2}} \sin (\frac{n_{1} π (α + β_{1})}{2 α}) - \sin (\frac{n_{1} π (α - β_{1})}{2 α})]}{{(\frac{n_{1} π}{α})}^{2} - {(\frac{n_{2} π}{β_{1}})}^{2}}, \frac{n_{1} π}{α} \neq \frac{n_{2} π}{β_{1}} \\ \frac{β_{1}}{2} \cos (\frac{n_{2} π}{2 β_{1}} (β_{1} - α)), \frac{n_{1} π}{α} = \frac{n_{2} π}{β_{1}} \end{cases}

(94)

References

S. Niu, K. T. Chau, J. Z. Jiang and C. Liu, "Design and Control of a New Double-Stator Cup-Rotor Permanent-Magnet Machine for Wind Power Generation," in IEEE Transactions on Magnetics, vol. 43, no. 6, pp. 2501-2503, June 2007. [CrossRef]
W. Gul, Q. Gao and W. Lenwari, "Optimal Design of a 5-MW Double-Stator Single-Rotor PMSG for Offshore Direct Drive Wind Turbines," in IEEE Transactions on Industry Applications, vol. 56, no. 1, pp. 216-225, Jan.-Feb. 2020. [CrossRef]
D. Fan, L. Quan, X. Zhu, Z. Xiang and H. Que, "Airgap-Harmonic-Based Multilevel Design and Optimization of a Double-Stator Flux-Modulated Permanent-Magnet Motor," in IEEE Transactions on Indus-trial Electronics, vol. 68, no. 11, pp. 10534-10545, Nov. 2021. [CrossRef]
J. Yu, C. Liu, Z. Song and H. Zhao, "Permeance and Inductance Modeling of a Double-Stator Hybrid-Excited Flux-Switching Permanent-Magnet Machine," in IEEE Transactions on Transportation Electrification, vol. 6, no. 3, pp. 1134-1145, Sept. 2020. [CrossRef]
P. Asef, R. B. Perpiñà, S. Moazami and A. C. Lapthorn, "Rotor Shape Multi-Level Design Optimization for Double-Stator Permanent Magnet Synchronous Motors," in IEEE Transactions on Energy Conversion, vol. 34, no. 3, pp. 1223-1231, Sept. 2019. [CrossRef]
C. Röth, F. Milde, D. Trebbels, J. Schmidt and M. Doppelbauer, "A Stator With Offset Segments and a Double Stator Design for the Reduction of Torque Ripple of a Switched Reluctance Motor," in IEEE Transactions on Energy Conversion, vol. 37, no. 2, pp. 1233-1240, June 2022. [CrossRef]
A. Toba and T. A. Lipo, "Generic Torque-Maximizing Design Methodology of Surface Permanent-Magnet Vernier Machine," in IEEE Transactions on Industry Applications, vol. 36, no. 6, pp. 1539-1546, Nov.-Dec. 2000. [CrossRef]
H. Zhao, C. Liu, Z. Song and W. Wang, "Exact Modeling and Multiobjective Optimization of Vernier Machines," in IEEE Transactions on Industrial Electronics, vol. 68, no. 12, pp. 11740-11751, Dec. 2021. [CrossRef]
D. Li, R. Qu and T. A. Lipo, "High-Power-Factor Vernier Permanent-Magnet Machines," in IEEE Transactions on Industry Applications, vol. 50, no. 6, pp. 3664-3674, Nov.-Dec. 2014. [CrossRef]
K. Boughrara, R. Ibtiouen, D. Z̆arko, O. Touhami and A. Rezzoug, "Magnetic Field Analysis of External Rotor Permanent-Magnet Synchronous Motors Using Conformal Mapping," in IEEE Transactions on Magnetics, vol. 46, no. 9, pp. 3684-3693, Sept. 2010. [CrossRef]
A. Hemeida et al., "A Simple and Efficient Quasi-3D Magnetic Equivalent Circuit for Surface Axial Flux Permanent Magnet Synchronous Machines," in IEEE Transactions on Industrial Electronics, vol. 66, no. 11, pp. 8318-8333, Nov. 2019. [CrossRef]
H. Zhao, K. T. Chau, T. Yang, Z. Song and C. Liu, "A Novel Quasi-3D Analytical Model for Axial Flux Motors Considering Magnetic Saturation," in IEEE Transactions on Energy Conversion, vol. 37, no. 2, pp. 1358-1368, June 2022. [CrossRef]
H. Zhao, C. Liu, Z. Song and W. Wang, "Analytical Modeling of a Double-Rotor Multiwinding Machine for Hybrid Aircraft Propulsion," in IEEE Transactions on Transportation Electrification, vol. 6, no. 4, pp. 1537-1550, Dec. 2020. [CrossRef]
Y. Oner, Z. Q. Zhu, L. J. Wu, X. Ge, H. Zhan and J. T. Chen, "Analytical on-Load Subdomain Field Model of Permanent-Magnet Vernier Machines," in IEEE Transactions on Industrial Electronics, vol. 63, no. 7, pp. 4105-4117, July 2016. [CrossRef]
L. Wu, M. Zhu, D. Wang and Y. Fang, "A Subdomain Model for Open-Circuit Field Prediction in Dual-Stator Consequent-Pole Permanent Magnet Machines," in IEEE Transactions on Magnetics, vol. 55, no. 8, pp. 1-12, Aug. 2019. [CrossRef]
M. Cheng, P. Han and W. Hua, "General Airgap Field Modulation Theory for Electrical Machines," in IEEE Transactions on Industrial Electronics, vol. 64, no. 8, pp. 6063-6074, Aug. 2017.
B. L. J. Gysen, K. J. Meessen, J. J. H. Paulides and E. A. Lomonova, "General Formulation of the Electromagnetic Field Distribution in Machines and Devices Using Fourier Analysis," in IEEE Transactions on Magnetics, vol. 46, no. 1, pp. 39-52, Jan. 2010. [CrossRef]
T. Lubin, S. Mezani and A. Rezzoug, "2-D Exact Analytical Model for Surface-Mounted Permanent-Magnet Motors with Semi-Closed Slots," in IEEE Transactions on Magnetics, vol. 47, no. 2, pp. 479-492, Feb. 2011. [CrossRef]
H. Zhao, C. Liu, Z. Song, S. Liu, and T. Lubin, "Analytical Model for Magnetic-Geared Double-Rotor Machines and Its d–q-Axis Determination," IET Electric Power Appl., vol. 14, no. 2, pp. 175–183, Feb. 2020.

Figure 1. DSSTVM topology. (a) Subdomain division parameters and shift angle definition in the studied DSSTVM; (b) 3D scheme and winding configuration of the studied DSSTVM.

Figure 2. Magnetic field distribution of the studied DSSTVM calculated by the FEA. (a) No-load condition; (b) On-load condition.

Figure 3. No-load magnetic flux density distribution of the studied DSSTVM. (a) Radial and tangential component in the middle of the inner air gap; (b) Radial and tangential component in the middle of the outer air gap.

Figure 4. No load magnetic flux density distribution of the studied DSSTVM. (a) Harmonic spectrum of the radial component in the middle of the inner air gap; (b) Harmonic spectrum of the radial component in the middle of the outer air gap.

Figure 5. Rated load magnetic flux density distribution of the studied DSSTVM. (a) Radial and tangential component in the middle of the inner air gap; (b) Radial and tangential component in the middle of the outer air gap.

Figure 6. Rated load magnetic flux density distribution of the studied DSSTVM. (a) Harmonic spectrum of the radial component in the middle of the inner air gap; (b) Harmonic spectrum of the radial component in the middle of the outer air gap.

Figure 7. Torque and power factor optimization of the studied DSSTVM. (a) Torque and power factor change with the variation of shift angle; (b) No-load back EMF waveforms.

Figure 8. Harmonic spectrum of no-load back EMF waveforms of the studied DSSTVM. (a) Inner stator; (b) Outer stator.

Figure 9. Rated load torque and harmonic spectrum of the studied DSSTVM. (a) Torque wave-forms of three different modes (mode 1, mode 2 and model 3, respectively); (b) Harmonic spectrum of the torque wave-form of mode 1; (c) Harmonic spectrum of the torque wave-form of mode 2; (d) Harmonic spectrum of the torque wave-form of mode 3.

Table 1. Geometrical Parameters of The Studied DSSTVM.

Symbol	Value	Symbol	Value
R₁	24.8 mm	α	π/6 rad
R₂	41 mm	β₁	π/9 rad
R₃	45.3 mm	β₂	π/10 rad
R₄	50.3 mm	δ	37π/300 rad
R₅	50.9 mm	P_r	10
R₆	66 mm	P_w	2
R₇	75.2 mm	Z	12
N	200	J_z	6 A/mm²
L	100

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Subdomain Analytical Modeling of a Double-Stator Spoke-Type Permanent-Magnet Vernier Machine

Abstract

1. Introduction

2. Machine Geometry and Methodology

3. Analytical Modeling Process

3.1. Boundary Condition and General Solution Expressions

3.1.1. Region I

3.1.2. Region II

3.1.3. Region III

3.1.4. Region IV

3.1.5. Region V

3.1.6. Region VI

3.1.7. Region VII

3.2. Postprocessing Electromagnetic Parameters Calculation

4. Finite Element Analysis Validation

5. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Conflicts of Interest

Appendix A

Appendix B

References

MDPI Initiatives

Important Links

Subscribe