1. Introduction
The surging demand for ubiquitous electricity is catalyzing innovations in wireless power transfer (WPT) to overcome the constraints of wired charging interfaces, such as frequent plugging and unplugging of charging ports and ageing of wire connections[
1]. While WPT commercialization for low-power electronic devices, such as toothbrushes, mobile phones, electric bicycles, etc, is accelerating, efficiency and universality remain limiting factors restricting its broader adoption [
2,
3,
4,
5].
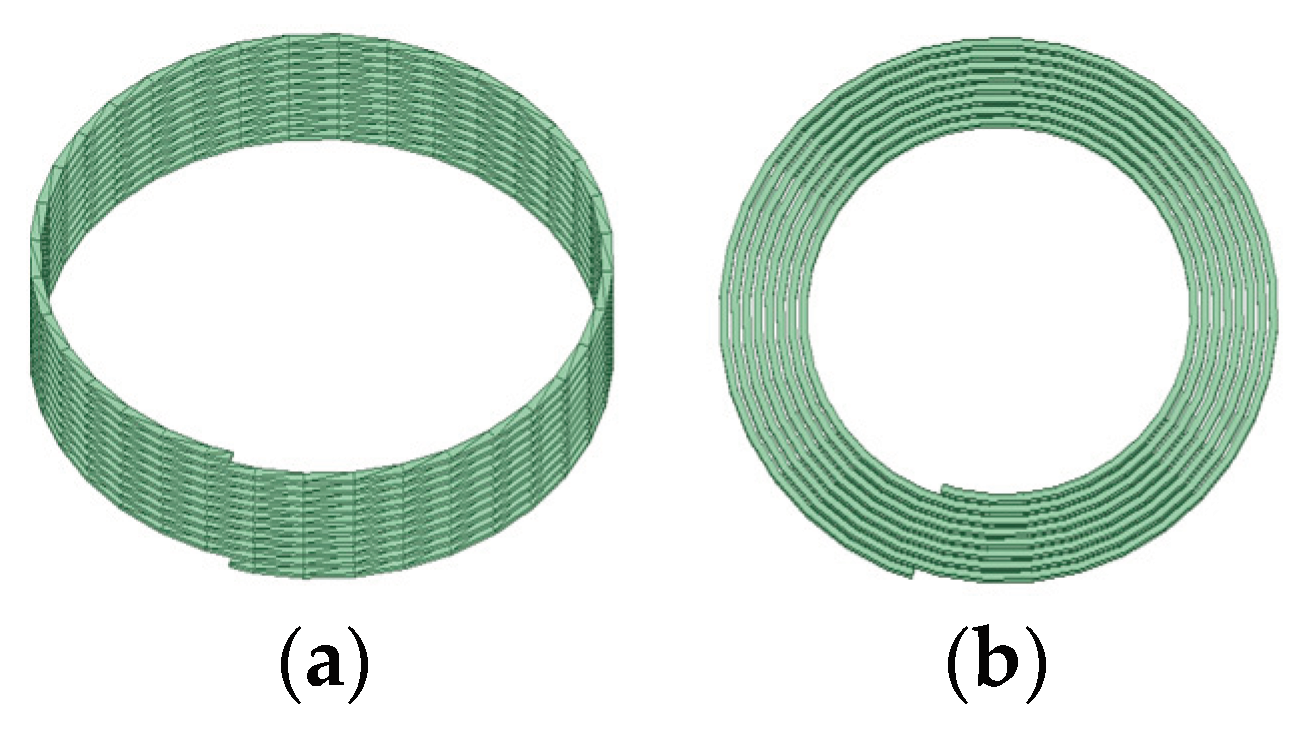
WPT coils have two typical solutions, namely the spatial spiral and the planar spiral structure. Although planar geometries pose inherent efficiency challenges relative to spatial coils, it achieve better size and weight reductions through PCB integration.
Figure 1 shows two types of coil structures.
The skin effect of enamelled wire is more pronounced under high-frequency conditions[
6]. The skin effect refers to the uneven distribution of current inside a conductor when an alternating current or alternating electromagnetic field is present[
7]. The current is concentrated in a thin layer on the surface of the conductor; the closer it is to the surface of the conductor, the higher the current density, and the smaller the actual current inside the conductor[
8]. As a result, the resistance of the conductor is higher, increasing its loss power[
9].
Under high-frequency conditions, the proximity effect of the Leeds line is more pronounced. The proximity effect refers to the uneven distribution of current on the cross-section of a conductor when subjected to high AC voltage.
However, the skin and proximity effects of PCB coils in the same environment have small impacts and small sizes, and PCB coils exhibit good stability, making them a good choice for application in mobile electronic devices[
10,
11].
2. Analysis of the Compensation Network and Coil Parameters
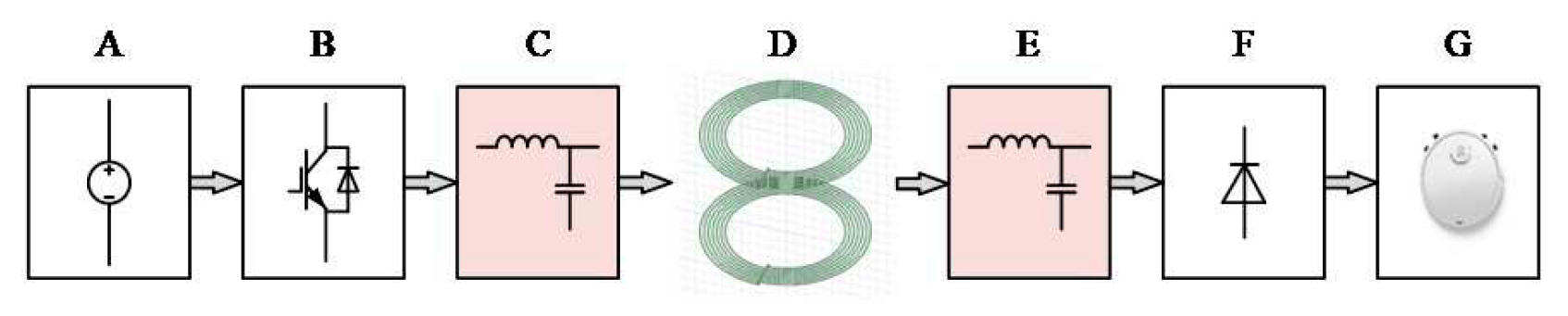
The structure of the wireless power transmission system is depicted in
Figure 2. A represents a DC power supply. B is the inverter circuit. C and E are compensation networks[
12]. D is a mutual inductance coil, which is a device for power transmission. F is a rectifier circuit. G is the electrical equipment.
A magnetic coupling structure is used to transmit power through alternating magnetic fields in high-frequency resonant circuits. The alternating magnetic field can be divided into near and far regions, with magnetic induction being the main source in the near region and radiation being the main source in the far region[
13]. Energy is emitted outwards in the form of electromagnetic waves.
2.1. Coupling Coil Circuit Model
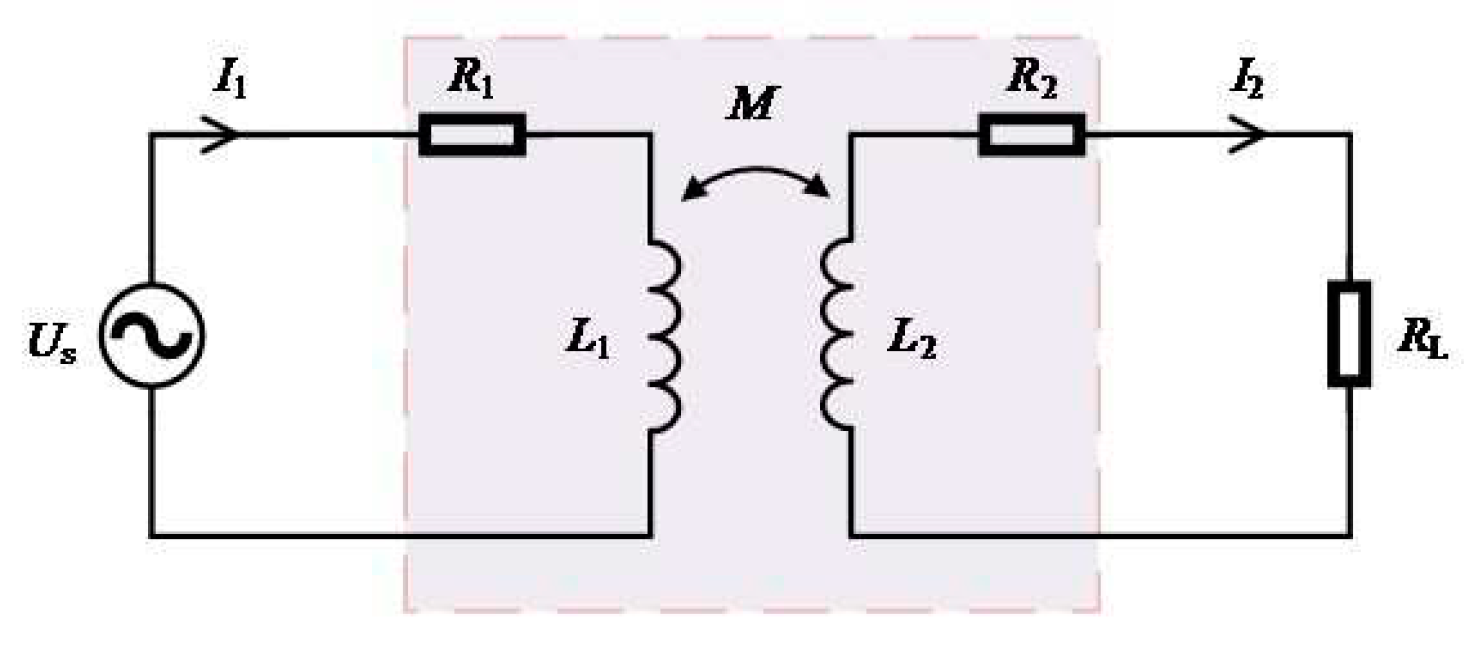
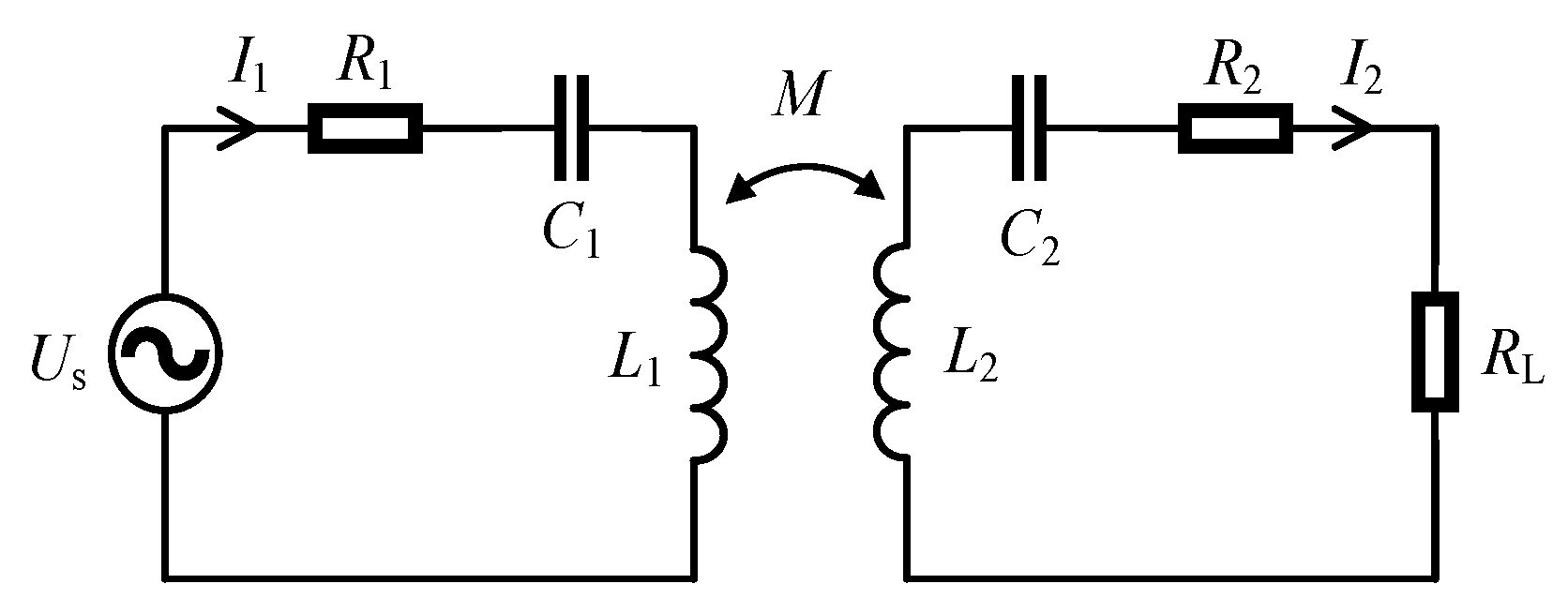
The mutual inductance circuit model of the coupling coil is shown in
Figure 3.
US is the AC power supply at the transmitting coil, and
I1 and
I2 are the currents of the transmitting and receiving circuits,
L1 and
L2 are the self-inductances of the transmitting and receiving coils, and
R1 and
R2 are the coil resistances of the transmitting and receiving coils, respectively. Mutual inductance
M is used to represent the degree of coupling between the two coils[
14].
The total impedance expression of the receiving end circuit is shown in equation (1), where
ω denotes the working angular frequency[
15].
Reflection impedance is the influence of the receiving end circuit on the transmitting end circuit and is expressed in equation (2).
The real and imaginary parts reflecting impedance are shown in equations (3) and (4).
Wireless power transmission is a device similar to a transformer, but unlike a transformer, the distance between the transmitting and receiving of infinite power transmission is relatively large. Increasing the magnetic leakage will increase the reactive power of the system and thus the energy loss of the system. Therefore, the transmission efficiency must be improved by adding compensation capacitors to both ends.
2.2. Compensation Circuit
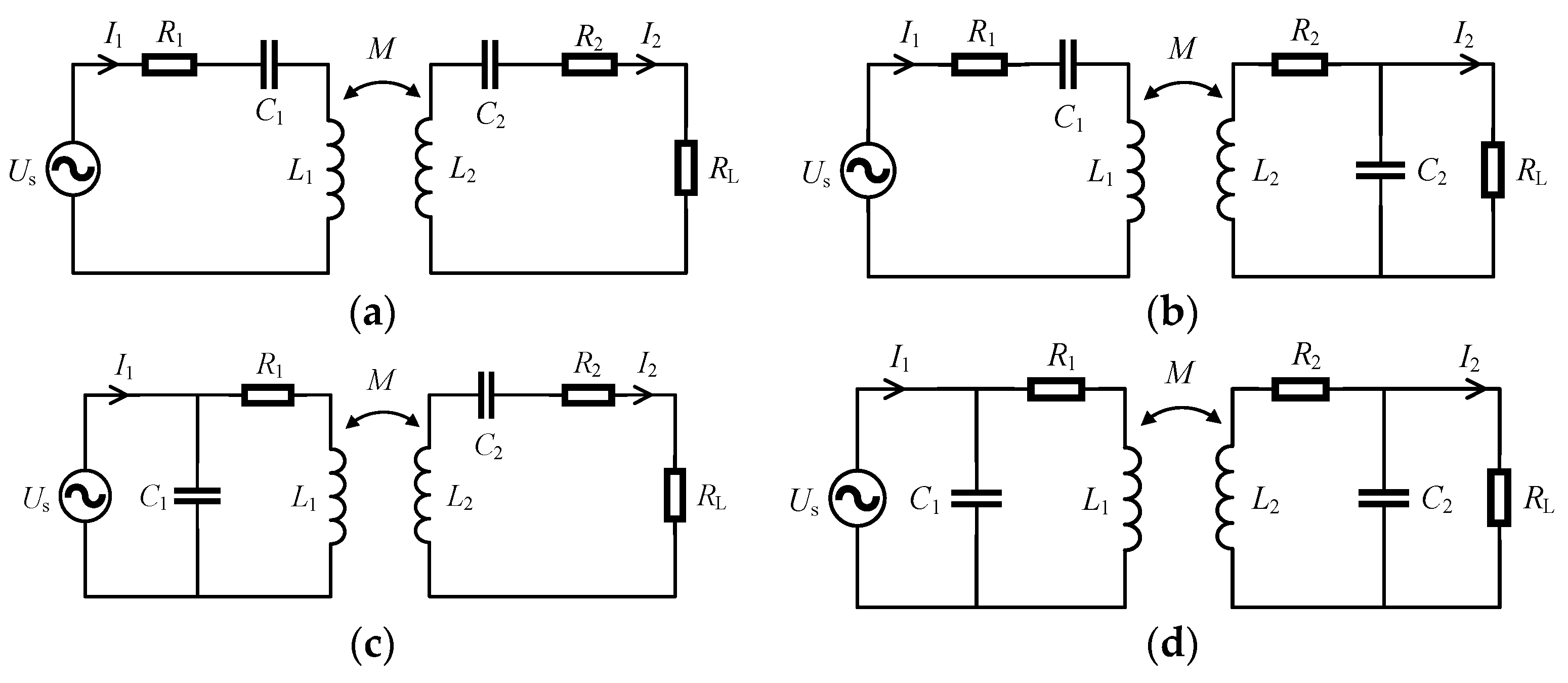
The reactive power compensation of the circuit is usually constructed by increasing the compensation capacitance. Because the position of the compensation capacitor in the circuit differs, its effect also differs. According to the position of the compensation capacitor, it can categorized as series and parallel, and the receiver and transmitter can also choose whether to add to it. Therefore, the capacitor can be divided into single-sided transmitters in series and parallel transmitters[
16]. The receiver is connected in series and in parallel. Bilateral compensation can be divided into series series (SS), series parallel (SP), parallel series (PS) and parallel parallel (PP). Several circuit diagrams of bilateral compensation are shown in
Figure 4.
Next, we analyse the bilateral compensation circuit. When compensating capacitors are added to the receiving circuit, Z
s1 and Z
r1 are used to represent the total impedance of the receiving circuit and the reflected impedance of the transmitting circuit. R
r1 and X
r1 are used to represent the reflected impedance and reactance at the transmitting circuit[
17]. When the compensating capacitor at the receiving is connected in series to the circuit, the total impedance and reflection impedance at the receiving transmitter can be represented by equations (5) and (6).
The reflection impedance R
r1 and reflection reactance X
r1 of the transmitting circuit are represented by equations (7) and (8), respectively.
The above two equations illustrate that when the parameters are connected as in equation (9), the reactance is reflected as zero. At this time, the receiving compensation circuit is in a resonant working state.
Similarly, using the same algorithm, when the compensating capacitors of the receiving circuit are connected in parallel, the total impedance, reflection impedance, reflection resistance, and reflection reactance of the receiving end are shown in equations (10), (11), (12), and (13), respectively:
By incorporating the equation for resonance, the reflection resistance and reflection impedance of the receiver with the compensation capacitor can be obtained. The parameters are defined in
Table 1.
When compensating capacitors are connected in parallel, the reflected impedance is not zero and is related to the coil mutual inductance and self-inductance of the receiving end coil, and the reflected impedance is capacitive. In contrast, when the capacitors are connected in series, the reflected impedance is resistive. Therefore, to compensate for the reactive power, capacitors should be connected in series at the receiving end for compensation.
This same method can be used to calculate the parameter values when the transmitter is connected in series. The input impedance at this point is expressed by equation (14). Additionally, the data in
Table 1 illustrates that when the receiving end is a compensation capacitor connected in series, the input impedance is expressed by equation (15).
Equation (15) illustrates that the input impedance always has an imaginary part; therefore, reactive power is always present. When equation (16) is satisfied, the transmitting end is in a resonant state; it should simultaneously meet the resonance formula of the receiving end. This is used to ensure that the entire circuit of the system is in a resonant state[
16].
The size of the series compensation capacitor at the starting emitter can be calculated as:
The capacitance values are calculated under the other three conditions while ensuring that the circuit operates in a resonant state. The compensation capacitance values for different compensation methods are shown in
Table 2.
The compensation capacitance values of the PS and PP compensation methods are related to the load resistance value. To ensure that the circuit operates in a resonant state, these two compensation methods are not suitable for this study. When the compensation method is SP, the compensation capacitance value is related to the mutual inductance of the coil. When the position of the coil changes, the mutual inductance also changes accordingly, causing the resonance state to change. When the compensation method is SS, the compensation capacitance value is only related to the coil self-inductance and frequency, making this value easy to fix. Therefore, in this article, the SS compensation method is adopted to optimize the coil parameters. The coupling coil mutual inductance circuit model of the SS compensation method is shown in
Figure 5.
The total impedance of the receiving end circuit and the total impedance of the transmitting end circuit are calculated using the equation for resonance mentioned above. Equations (18) and (19) are given as follows.
The current
I1 at the transmitting end is shown in equation (20).
The current
I2 of the receiving end circuit is calculated according to equation (1), as shown in equation (21).
By calculating the current, the power
Pout and energy transmission efficiency
η of the receiving circuit can be obtained, as shown in equations (22) and (23), respectively.
The transmission efficiency of the coil is related to the system's operating frequency, load resistance, coil mutual inductance, and coil resistance. To further improve the efficiency of the method, this study is primarily focused on changing the coil structure parameters.
3. Optimization of PCB Coil Structure Parameters
Coupling coils are primarily planar spiral coils and spatial spiral coils. Space spiral coils, often used for equipment with a cylindrical shape, are installed on vertical structures in the equipment and occupy large spaces. Flat spiral coils, used in most electronic and electrical equipment, are installed on flat structures in equipment and occupy small spaces. Planer spiral coils are more suitable for the PCB coil structure studied in this article[
17].
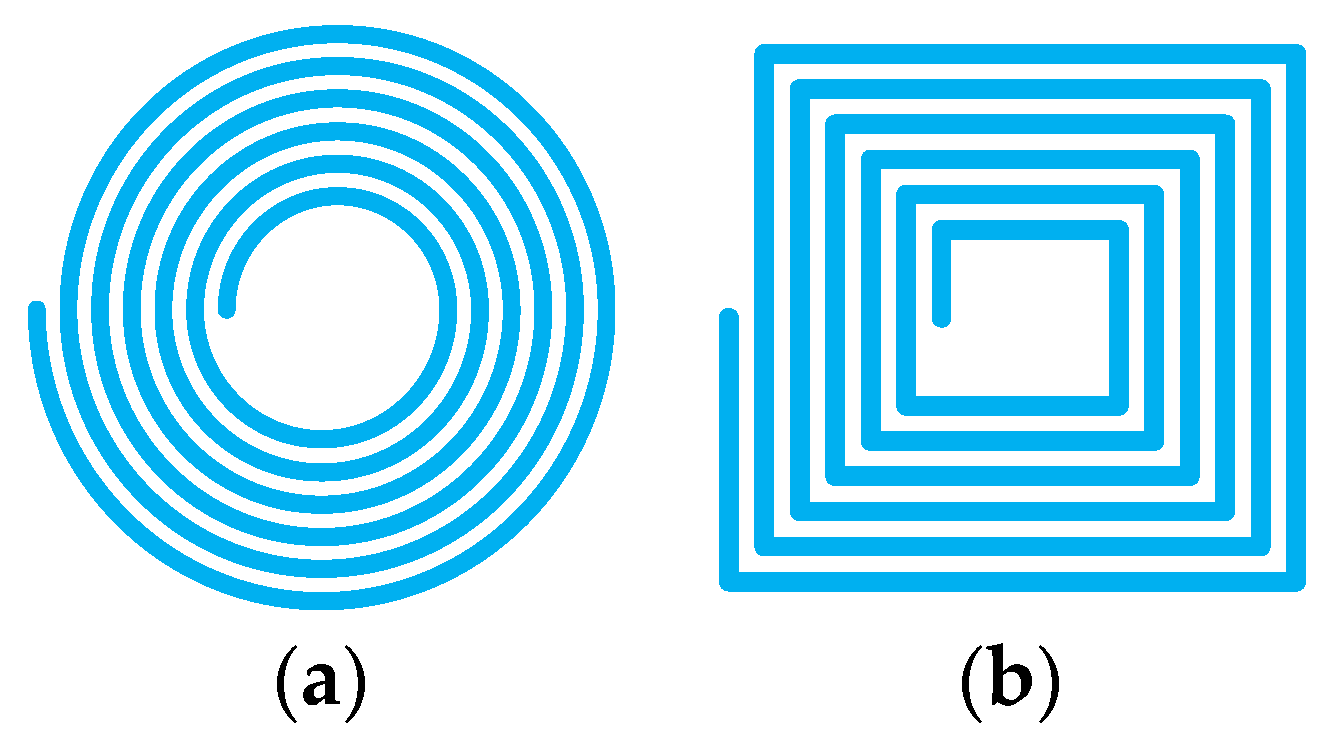
The flat coil is primarily circular or rectangular in shape, as shown in
Figure 6.
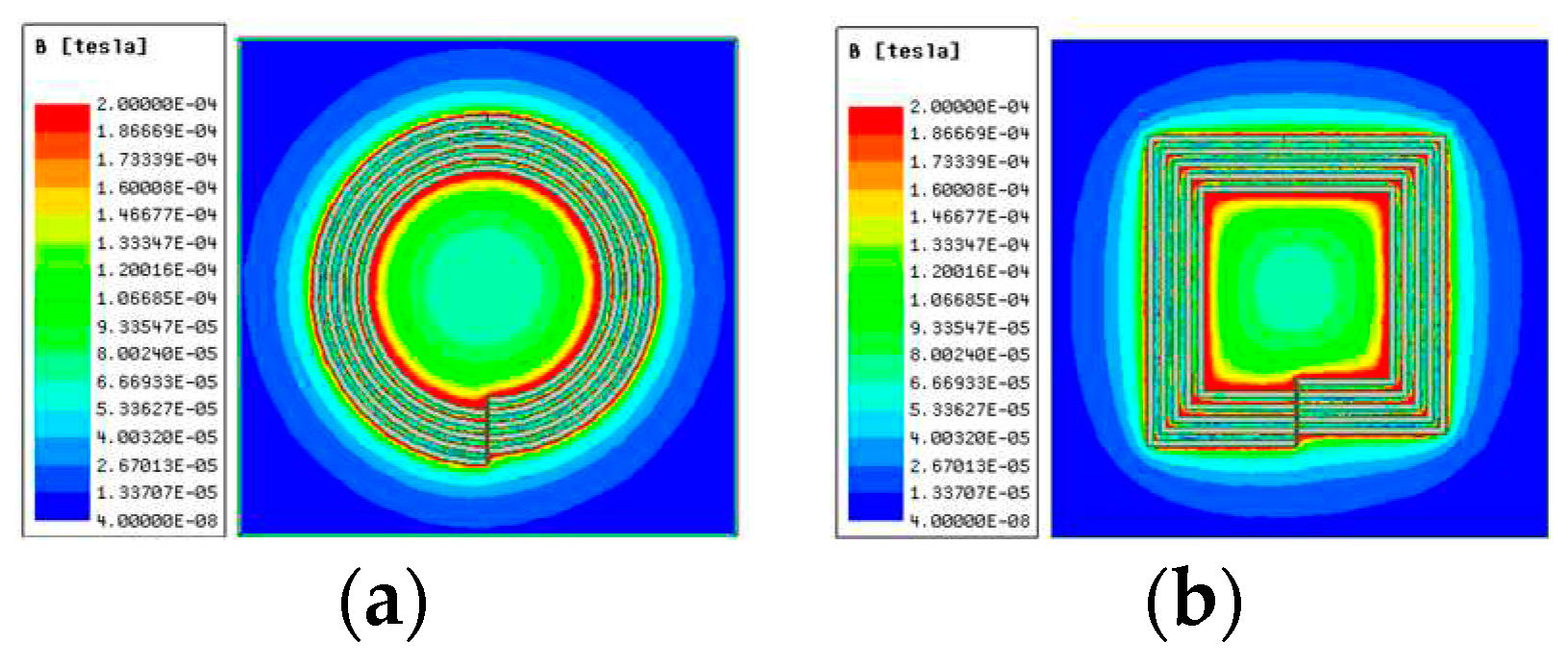
To compare the advantages and disadvantages of circular planar coils and rectangular planar coils, 3D simulation models of multiturn circular planar coils and rectangular planar coils are established in the finite element simulation software Maxwell. To avoid errors during comparison, the area size, wire diameter, number of turns, and turn spacing of the two coils are set to be consistent when the coil model is established. The simulated magnetic field cloud map obtained through simulation analysis is shown in
Figure 7.
The parameters of the circular and rectangular planar coils and the simulation results of the coil shapes are shown in
Table 3.
The inductance value of the circular coil is slightly higher than that of the rectangular coil. The resistance of the circular coil is smaller than that of a rectangular coil, the magnetic field distribution is more uniform, and the convergence is better. Therefore, planar circular coils are ideal for most infinite power transmissions.
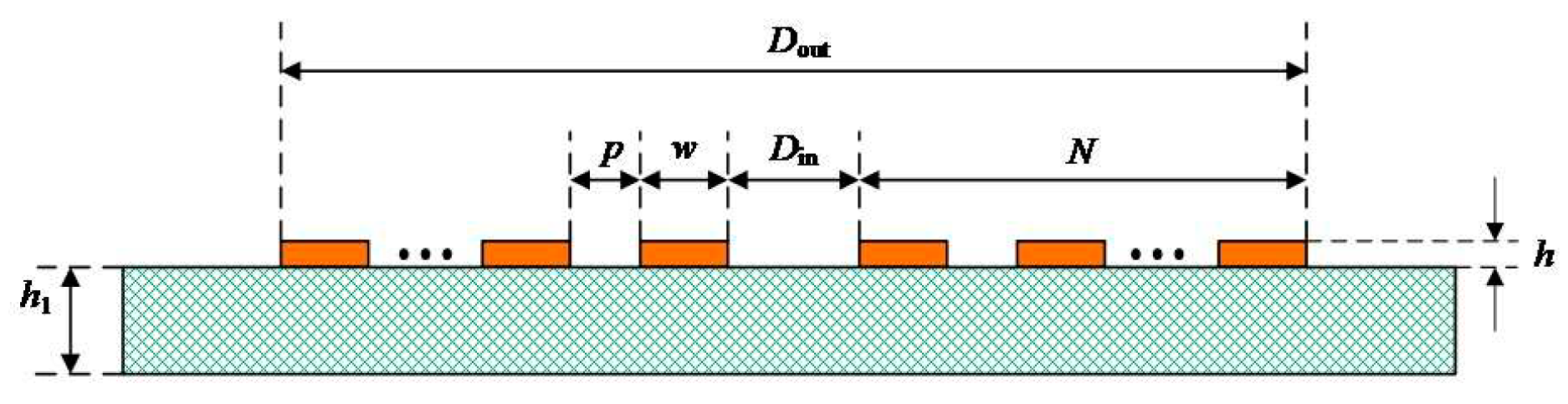
The cross-section of the circular coil designed through PCB is shown in
Figure 8.
N is the number of coil turns,
Dout is the outer diameter of the coil,
Din is the inner diameter of the coil,
P is the coil turn spacing,
w is the coil wire width,
h is the thickness of the copper wire laid on the PCB, and
h1 is the thickness of the PCB.
The formula for calculating the depth of skin effect of wires made of copper material at different temperatures[
18] is presented in equation (24).
The wire diameter length of the PCB coil is:
The average wire diameter of the coil is:
The defined coil filling coefficient is:
The DC resistance of the coil is expressed as:
The AC resistance of the coil under high-frequency conditions is expressed as:
Incorporating the DC resistance expression into (29) yields:
where σ is the conductivity of the coil wire, and d is the depth of the wire skin effect.
The resistance of a coil when high-frequency AC power is incorporated is related to the wire diameter length, coil thickness, and skin effect depth of the coil. Therefore, simulation research must be conducted on the structural parameters of the coil, and the impacts of changes in coil structural parameters on the coil resistance must be examined.
The inductance of a PCB planar circular coil is expressed as:
Before the coil parameters are examined, the quality factor
Q and coupling coefficient
k are introduced:
Substituting (32) and (33) into (23) yields:
Simplifying (34) yields equation (35).
The first partial derivative of
RL in equation (35) is zero , and the second order partial derivative is less than zero . The following can be concluded:
Q1Q2k2 is defined as the strong coupling coefficient[
19] of the coil. Equation (36) reveals that the larger the strong coupling coefficient is, the higher the transmission efficiency of the coil. Previous analysis has shown that the design of the coil must consider the degree of coupling between the coils in addition to its quality factor. The quality factor and the coupling coefficient of the coil correlates with the strong coupling coefficient. Therefore, maximizing the strong coupling coefficient has become a research goal.
The structural parameters of the receiving and transmitting ends of the PCB coil studied in this article are the same, and
Q1 and
Q2 are also the same. The efficiency of the coil can be simplified as:
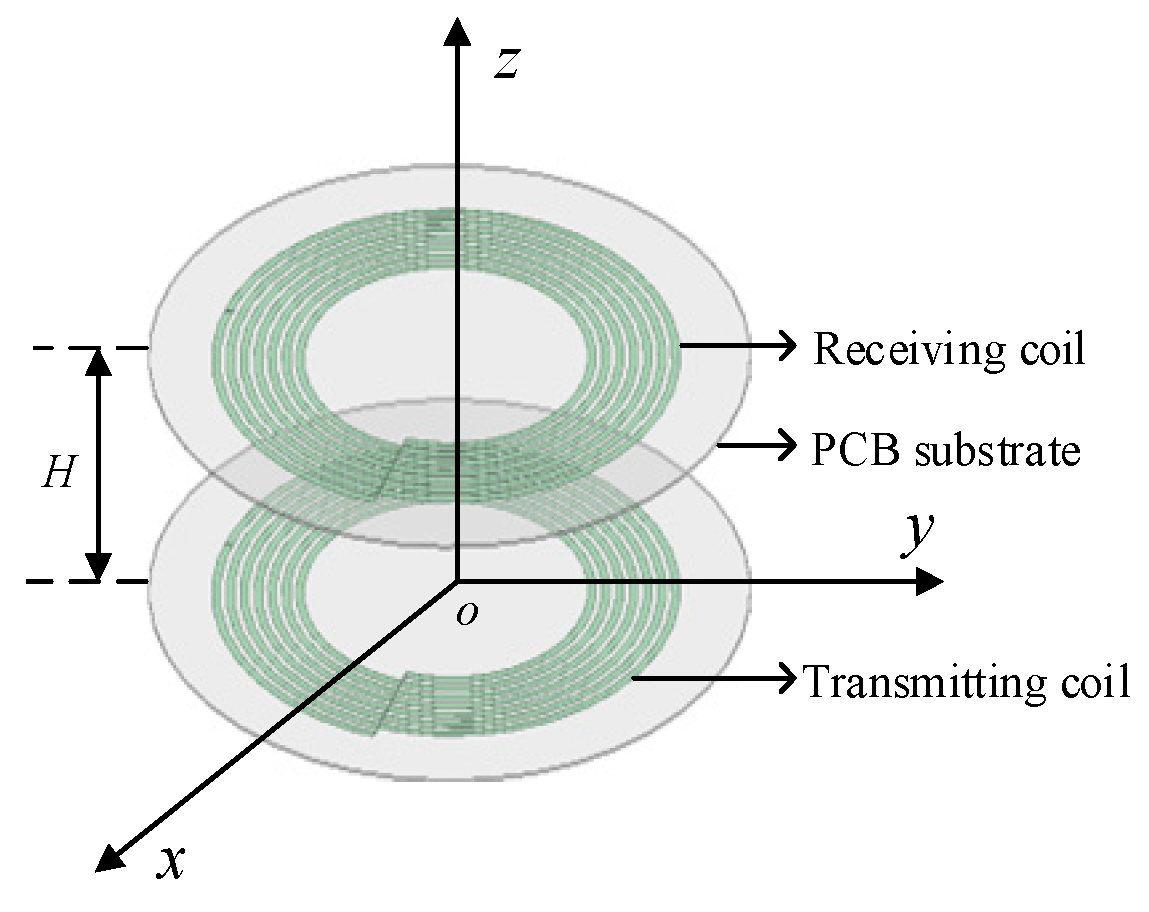
A simulation model is formed with two coils placed in parallel and coaxially with a distance H of 4.5 cm, as shown in
Figure 9.
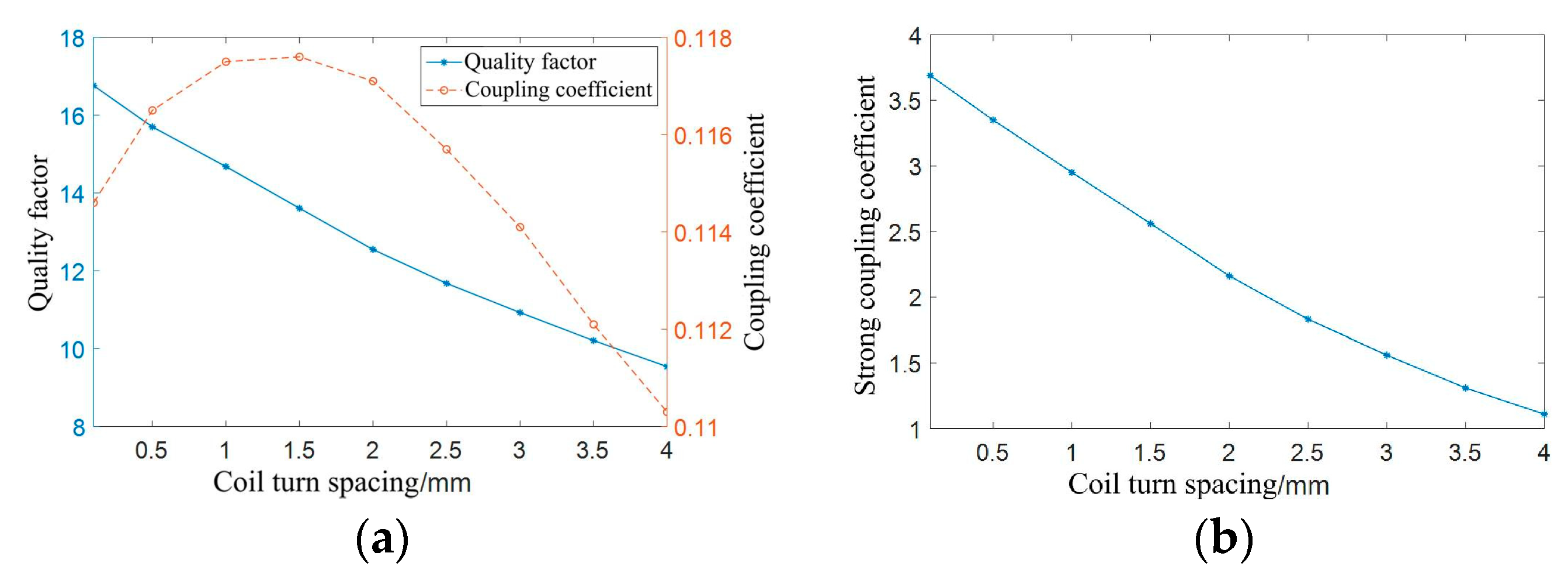
3.1. Coil turn spacing
The outer diameter of the fixed coil is set as 9 cm, the coil thickness is set to 0.07 mm, the coil line width is set as 2 mm, the coil turns are set as 7 turns, and the frequency is set as 100 kHz. The coil turn spacing changes from 0.5 mm to 4 mm in steps of 0.5 mm, and a simulation with a coil turn spacing of 0.2 mm is conducted. The simulation results are shown in
Figure 10.
Figure 10 (a) illustrates that as the pitch between the coils increases, the quality factor of the coils decreases, and the coupling coefficient between coils first increases and then decreases, exhibiting a maximum coupling coefficient.
Figure 10 (b) shows the simulation data curve of the strong coupling coefficient of the coil. The strong coupling coefficient curve shows a decreasing trend. Considering the requirements of the PCB manufacturing process, the coil turn spacing is set as 0.2 mm in this article.
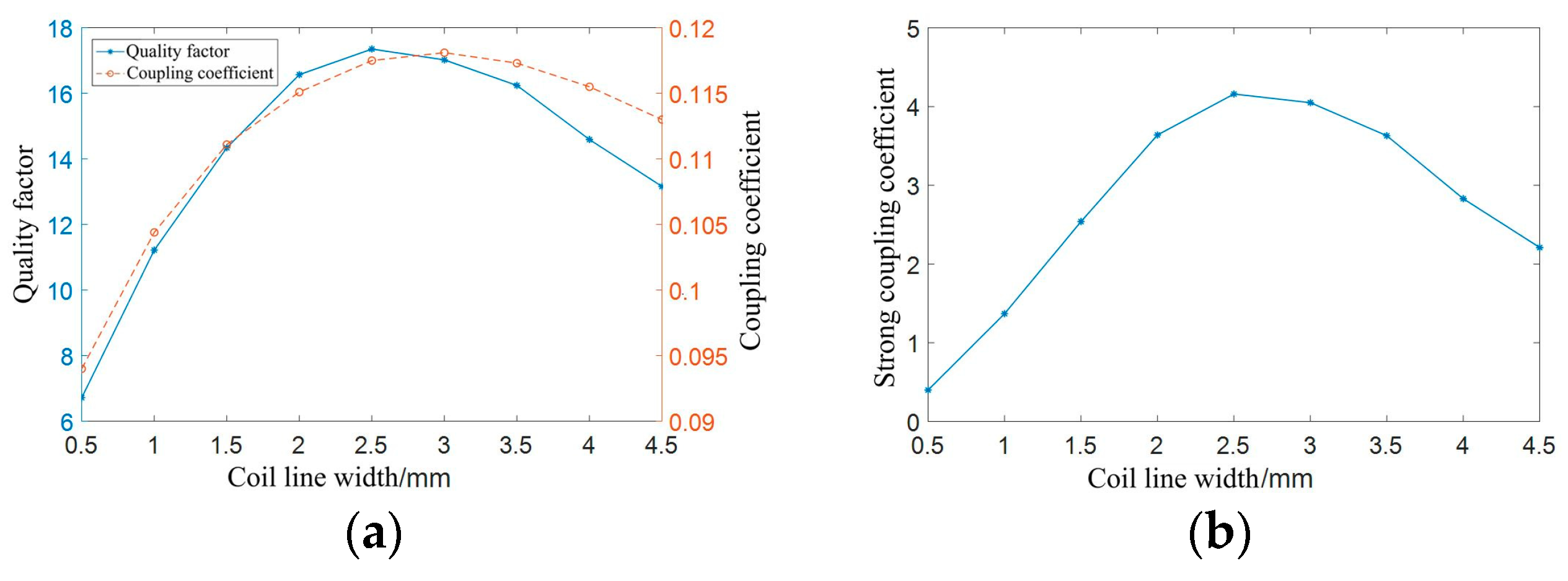
3.2. Coil line width
The outer diameter of the fixed coil is set as 9 cm, the coil thickness is set as 0.07 mm, the coil turn spacing is set as 0.2 mm, the coil turns are set as 7 turns, the frequency is set as 100 kHz, and the coil line width changes from 0.5 mm to 4.5 mm in steps of 0.5 mm. The simulation results are shown in
Figure 11.
Figure 11 (a) illustrates that as the coil width increases, the quality factor of the coil first increases and then decreases. The maximum value occurs when the coil width is 2.5 mm, and the coupling coefficient between coils first increases and then decreases.
Figure 11 (b) shows the simulation data curve of the strong coupling coefficient of the coil. The strong coupling coefficient first increases and then decreases. In this figure, the maximum value occurs the coil width is 2.5 mm. Because the simulated curve in
Figure 11 is based on the order of magnitude of the coil line width changing in steps of 0.5 mm, to clarify whether the strong coupling coefficient of the coil is maximized at a line width of 2.5 mm or at a certain line width near 2.5 mm, the simulation values for the line width from 2.4 mm to 2.9 mm in steps of 0.1 mm are shown in
Table 4.
Table 4 shows that the maximum value of the strong coupling coefficient of the coil is achieved when the line width is 2.8 mm, which differs slightly from the maximum value of the strong coupling coefficient in
Figure 11 (b). Therefore, the coil line width is set as 2.8 mm in this article.
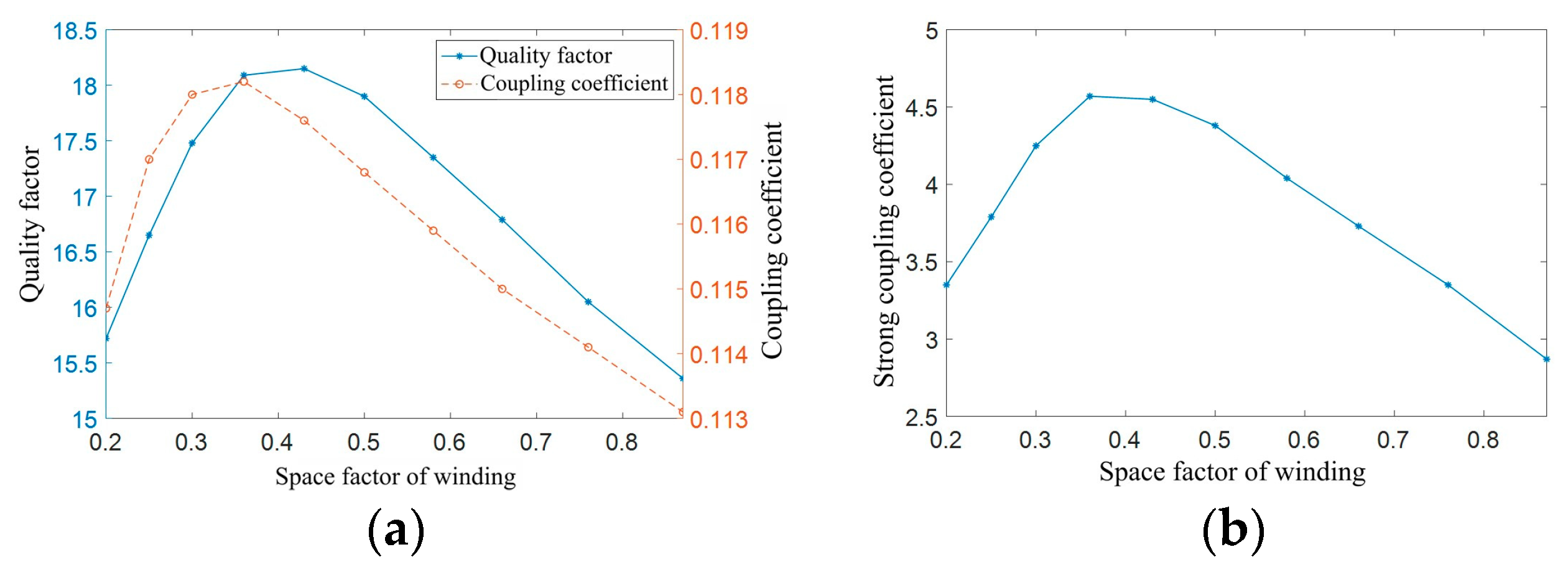
3.3. Coil turns
The outer diameter of the fixed coil is set as 9 cm, the coil thickness is set to 0.07 mm, the coil turn spacing is set as 0.2 mm, the coil line width is set as 2.8 mm, and the frequency is set as 100 kHz. The number of coil turns changes from 5 to 14 in steps of 1. The corresponding relationship between the coil filling coefficient and the number of turns and the inner diameter of the coil is shown in
Table 5.
The simulation data obtained by simulating different turns of the coil are shown in
Figure 12.
Figure 12 (b) depicts a simulation data curve of the strong coupling coefficient of the coil. The strong coupling coefficient first increases and then decreases. The filling coefficient of the coil is 0.36, which means that the strong coupling coefficient reaches its maximum when the number of coil turns is equal to 8. Therefore, the number of coil turns is set as 8 in this paper.
Previous research has shown that regardless of the outer diameter of the coil, after setting the coil line width and turn spacing, the inner diameter of the coil and the optimal number of turns of the coil can be determined using the formula for the coil filling coefficient and the optimal value of the coil filling coefficient[
20].
4. Research on the Offset Characteristics of Pcb Coils
The deviation of the coil significantly impacts the coupling coefficient between coils, which in turn affects the strong coupling coefficient of the coil. After the coil is offset, the magnetic field weakens, decreasing the coupling degree between the transmitting end coil and the receiving end coil and decreasing the coupling coefficient between the coils. To reduce the adverse effects of coil offset, a double-layer PCB coil, which lays coils on both the top and bottom layers of the PCB board, is designed in this paper[
21].
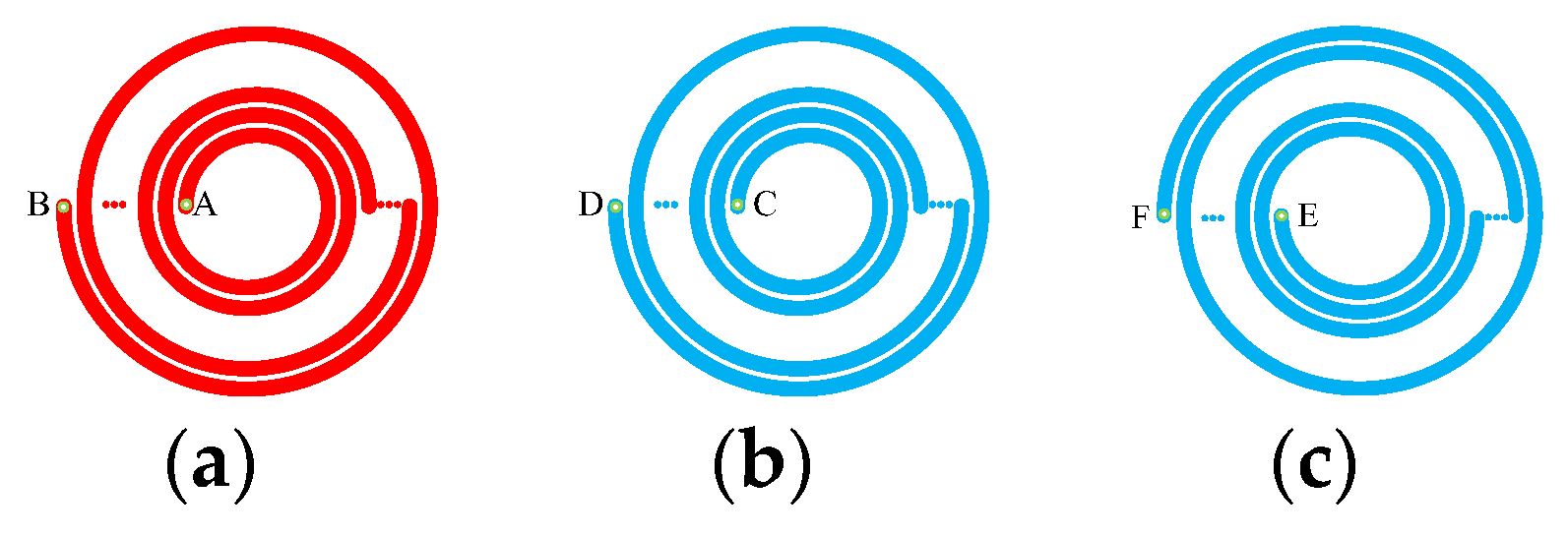
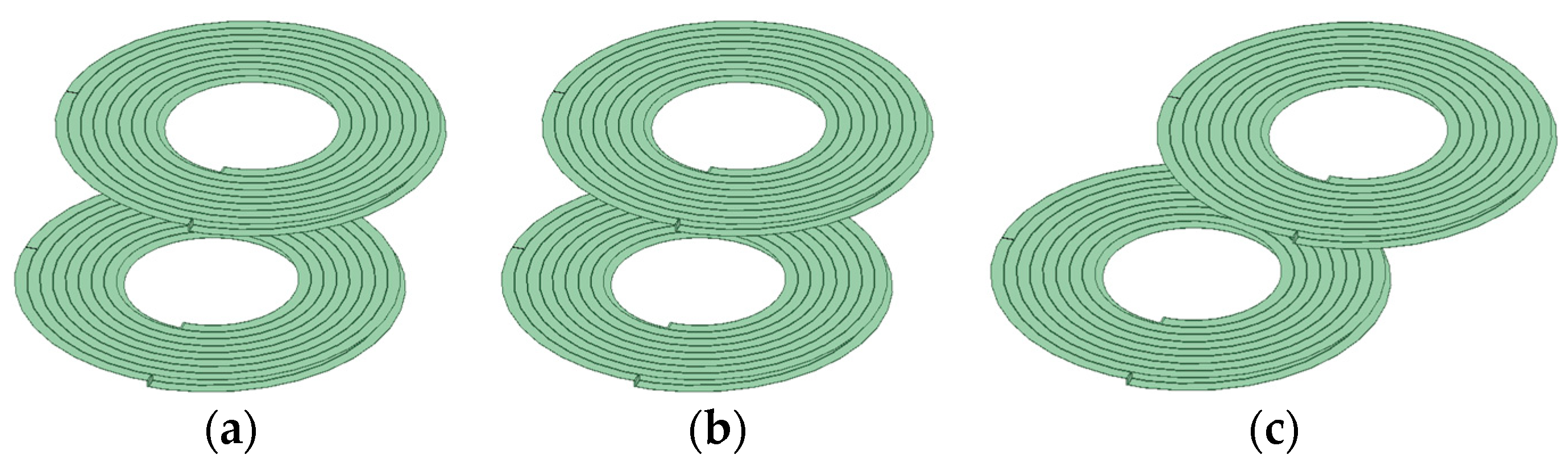
Figure 13 depicts a top view of the top and bottom layers of a double-layer PCB coil. Two design methods for the bottom layers of the coil are proposed. The current directions of the top and bottom layers of the coil are the same. A, B, C, D, E, and F in the figure represent the interface between the coil and the external connection.
Figure 13 (a) is the top view of the coil,
Figure 13 (b) is the top view of the coil bottom in Scheme 1, and
Figure 13 (c) is the top view of the coil bottom in Scheme 2. The bottom layer of the coil adopts Scheme 1, where interface C of the bottom layer coil is connected to interface A of the top layer, and interfaces B and D are connected to external circuits. When the bottom layer of the coil adopts Scheme 2, interface E of the bottom layer coil is connected to interface A of the top layer, and interfaces B and F are connected to external circuits.
To simulate the offset phenomenon in real scenarios, four simulation studies were conducted: coaxial parallel offset, coaxial nonparallel offset, different axis parallel offset, and different axis nonparallel offset. We next explore whether the transmission efficiency of this structure is better than that of single-layer PCB coils.
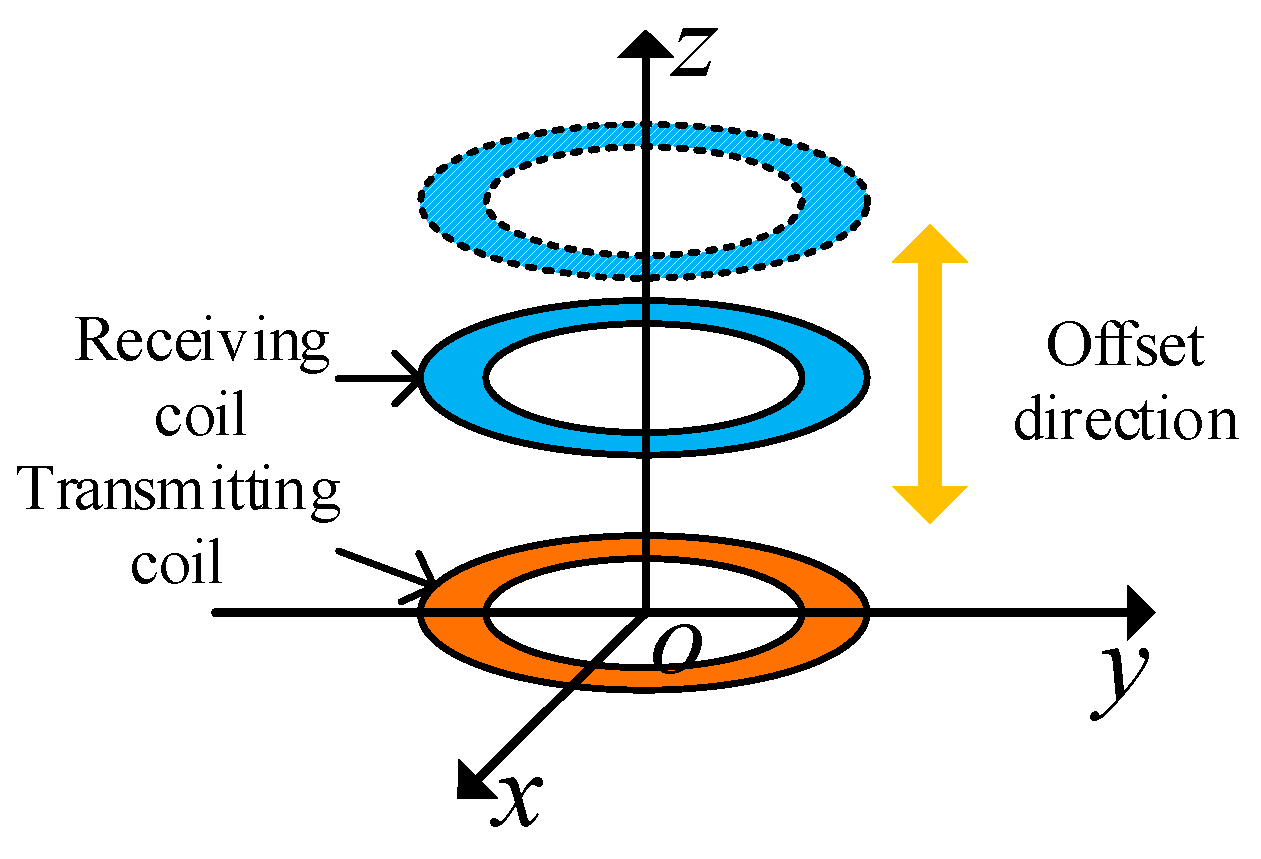
4.1. Coaxial parallel offset
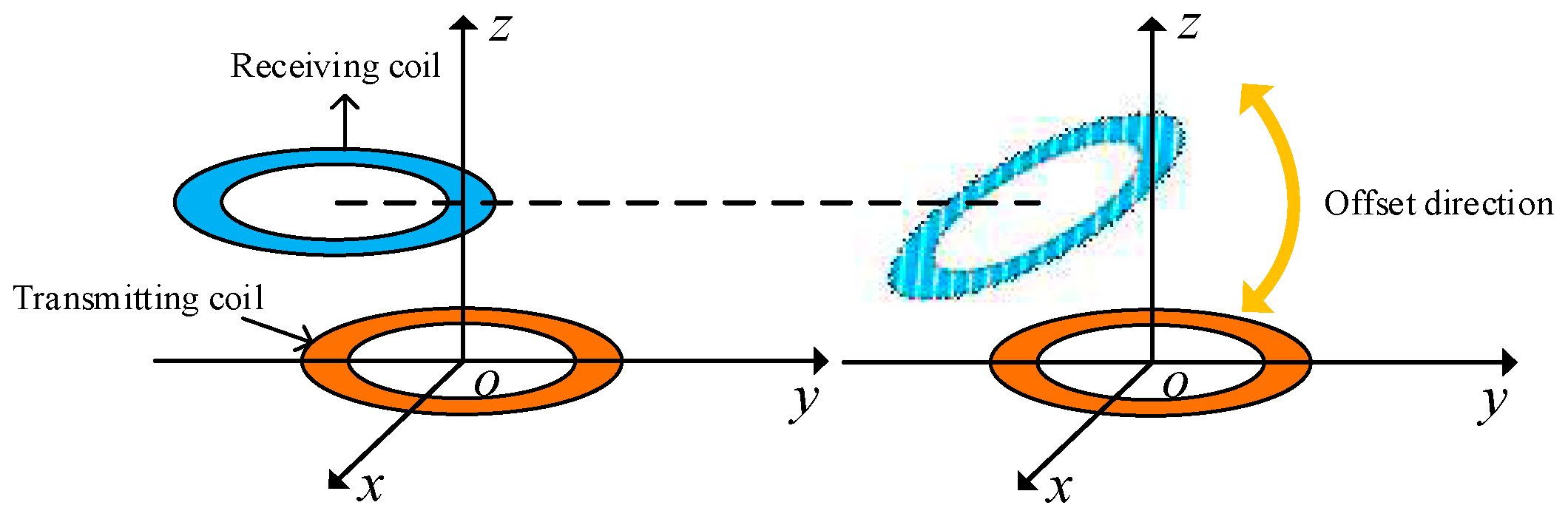
First, the coaxial parallel offset of the coil is studied.
Figure 14 is a schematic diagram of the coaxial parallel offset of the coil. The centre of the transmitting coil is fixed at the coordinate origin, and the transmitting and receiving coils in the figure remain coaxial and fixed.
When coaxial parallel offset simulation analysis is conducted on the coil, the outer diameter of the coil is fixed at 9 cm, the coil thickness is set as 0.07 mm, the coil turn spacing is set as 0.2 mm, the coil line width is set as 2.8 mm, the number of coil turns is set as 8, the operating frequency is set as 100 kHz, and the offset distance of the coil changes from 1 cm to 7 cm.
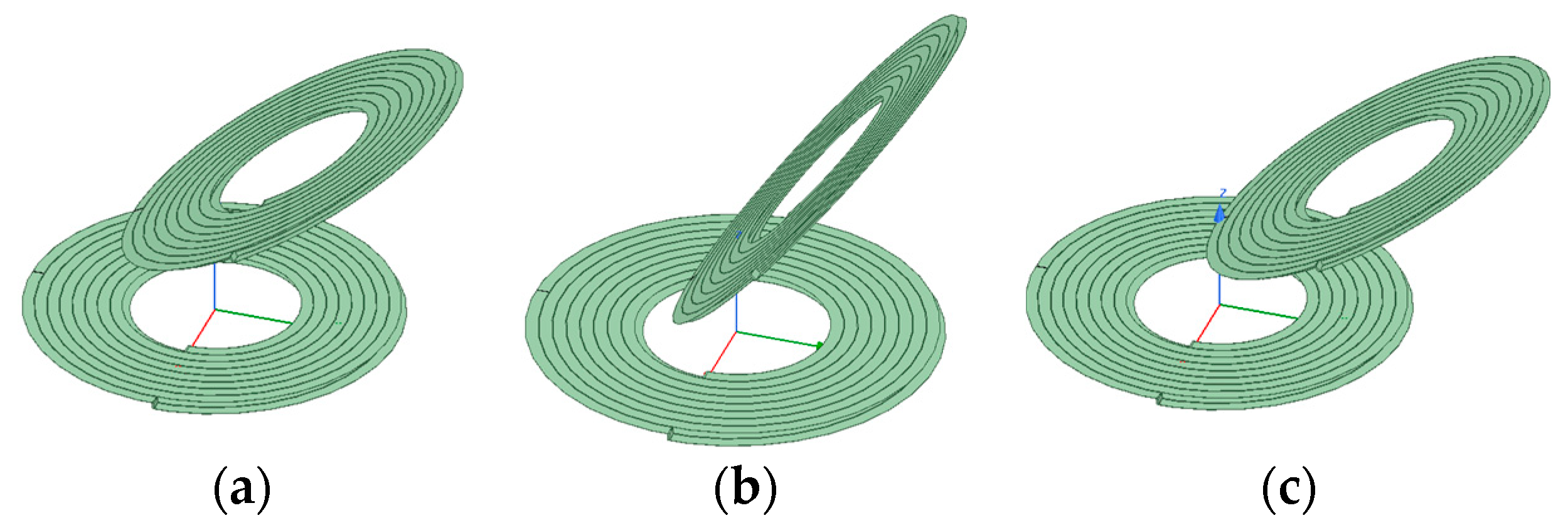
Figure 15 depicts a partial model diagram of the simulation of the coaxial parallel offset of the coil.
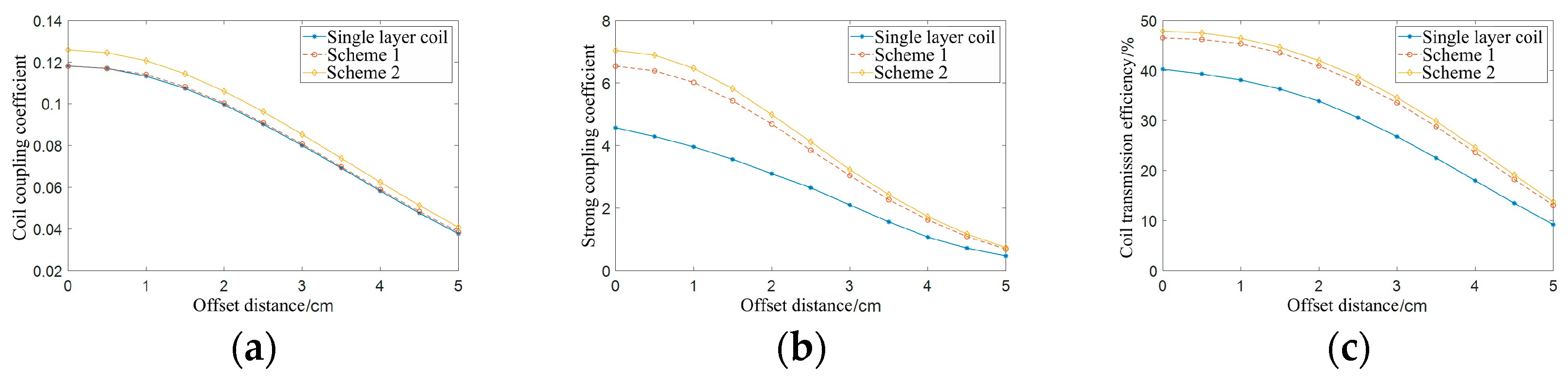
Table 6 provides the simulation values of the quality factor, self-inductance, and resistance of the single-layer coil, Scheme 1, and Scheme 2 coils. The simulation data of the single-layer coil, Scheme 1, and Scheme 2 double-layer coils are depicted in
Figure 16.
Table 6 shows that the quality factor of the double layer coil in Scheme 1 is higher than that of the other two types of coils, and the coil resistance is the smallest among the three types of coils. The self-inductance value of the double-layer coil in Scheme 2 is significantly higher than that of the other two types of coils, and the coil quality factor is higher than that of the single-layer coil; however, its resistance is significantly higher.
Figure 16 (c) depicts a simulation data graph of the transmission efficiency of three types of coils. As the offset distance increases, the transmission efficiency of the coil decreases. For Scheme 2, the transmission efficiency of the double-layer coil is higher than that of the other two types of coils. At the offset distance of the coil radius, the transmission efficiency is 48%, which is approximately 8% higher than that of the single-layer coil at the same distance.
4.2. Coaxial nonparallel offset
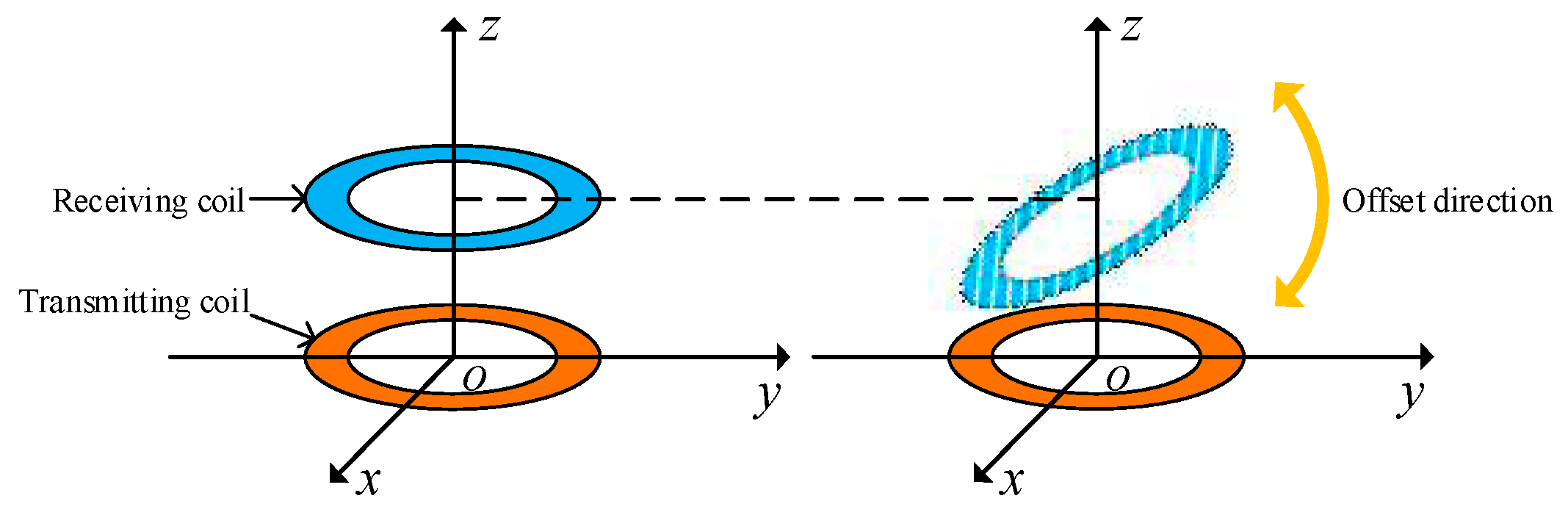
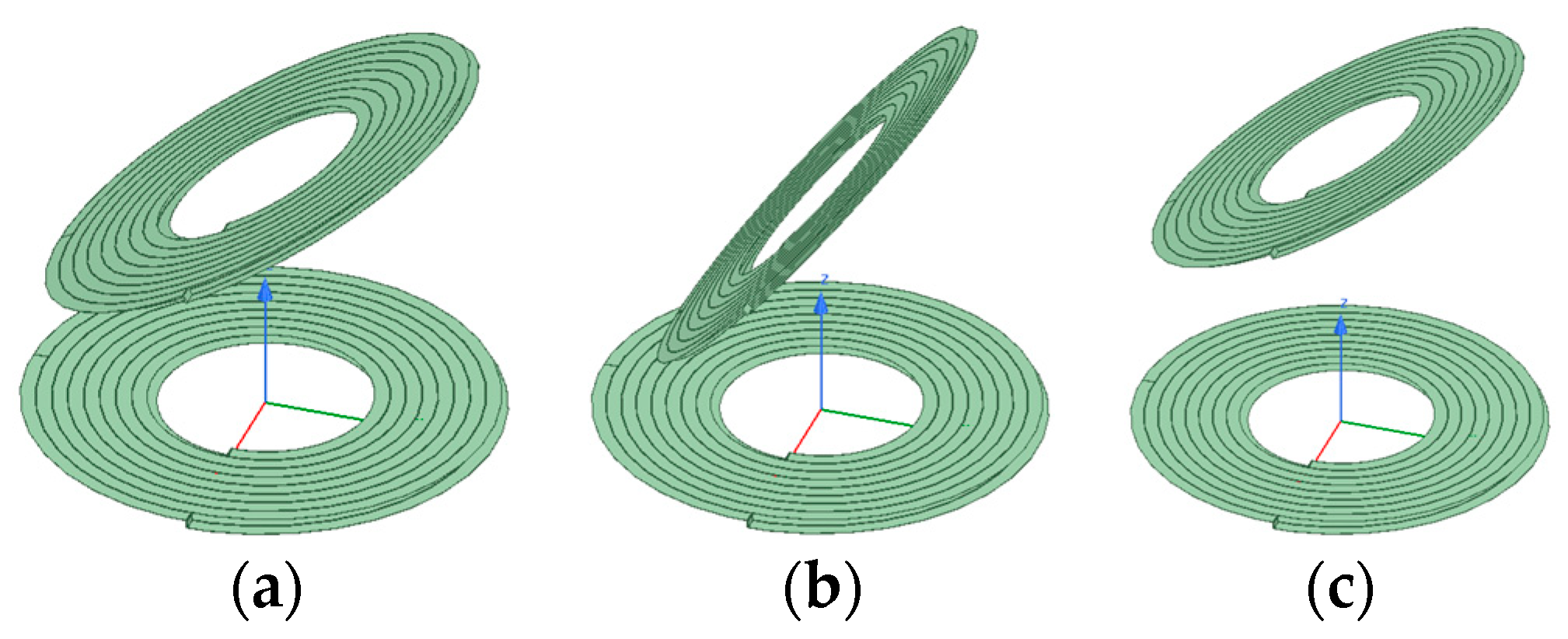
Figure 17 depicts a schematic diagram of the coaxial nonparallel offset of the coil. The centre of the transmitting end coil is fixed at the coordinate origin, and the transmitting end and receiving end coils in the figure remain coaxial and fixed. The receiving end coil undergoes an angular offset in the z-axis direction.
When simulation analysis is conducted on the coaxial nonparallel offset of the coil, the basic simulation parameters of the coil are consistent with those of the coaxial parallel offset, with a working frequency of 100 kHz. The offset angle of the coil changes from 0 degrees to 80 degrees, and the offset distance changes from 4.5 cm to 7 cm. During the simulation, the coil is assumed to be offset in the positive direction of the z-axis.
Figure 18 depicts a partial model diagram of the coil coaxial nonparallel offset simulation. The simulation data of the single-layer coil, and the Scheme 1 and Scheme 2 double-layer coils are shown in
Figure 19.
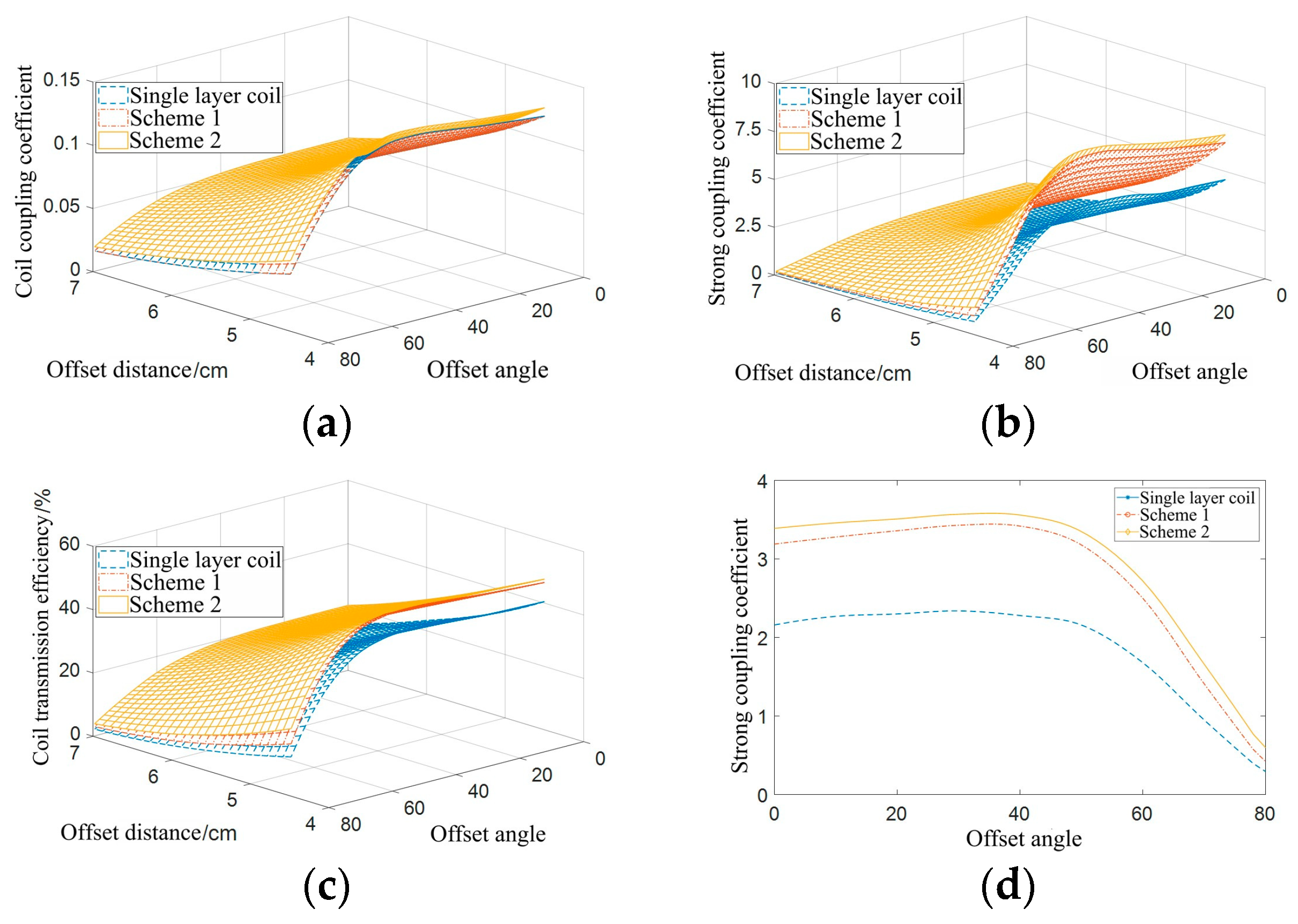
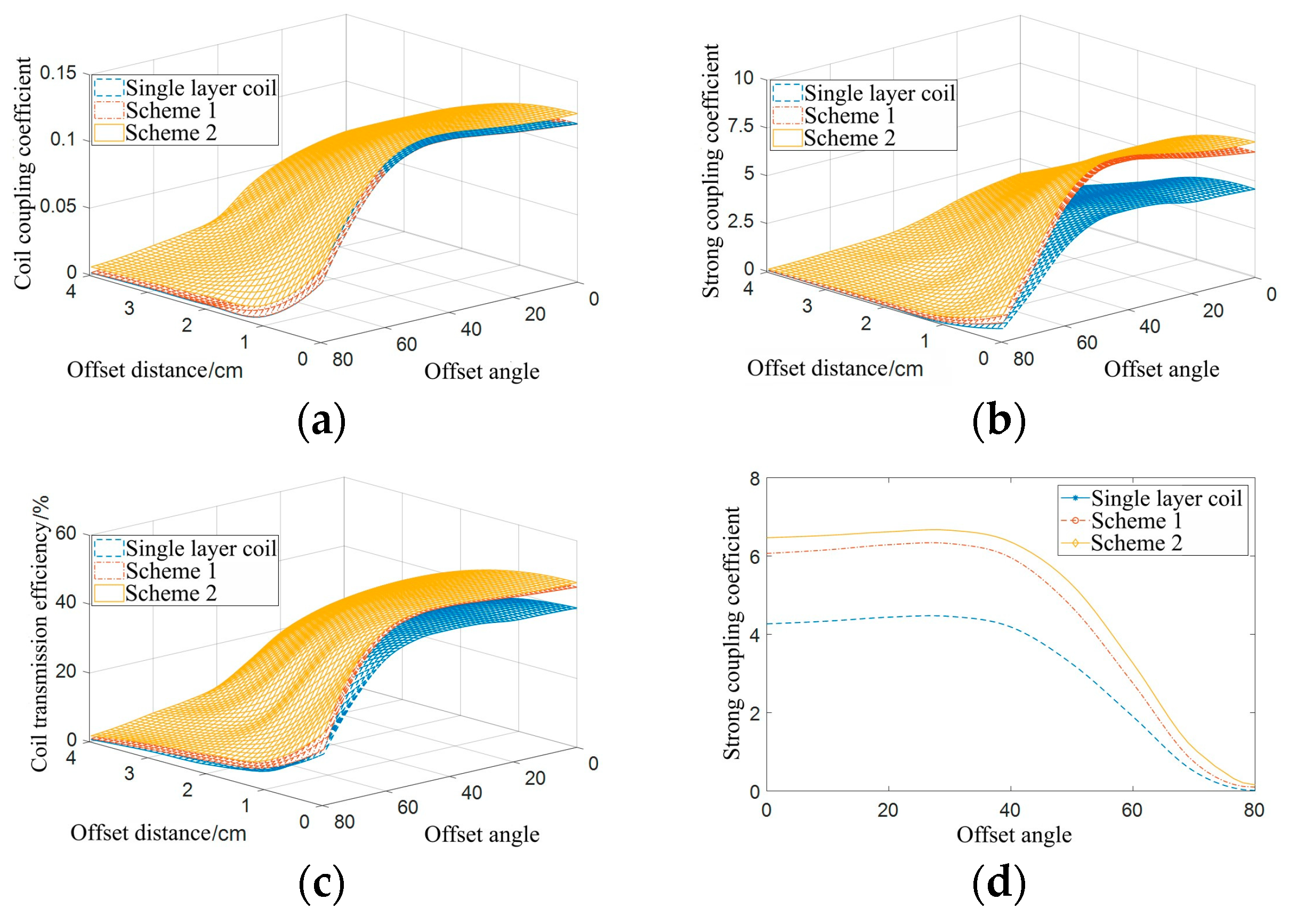
The coupling coefficients of the single-layer coil and the double-layer coil in Scheme 1 are basically identical. At the same offset angle, the coupling coefficients and strong coupling coefficients of the double-layer coil in Scheme 2 are greater than those of the other two coils, and the strong coupling coefficient of the single-layer coil is the smallest. The transmission efficiency of the double-layer coil in Scheme 2 is higher than that of the other two coil structures.
Figure 19 (d) shows the data comparison curve of the strong coupling coefficient under different offset angles when the coil offset distance is 5.5 cm. Scheme 2 has the largest strong coupling coefficient, while Scheme 1 has a slightly smaller strong coupling coefficient than Scheme 2. The single-layer coil has the smallest strong coupling coefficient. These results indicate that Scheme 2 has a stronger anti-offset ability than the other two coils.
4.3. Parallel offset of different axes
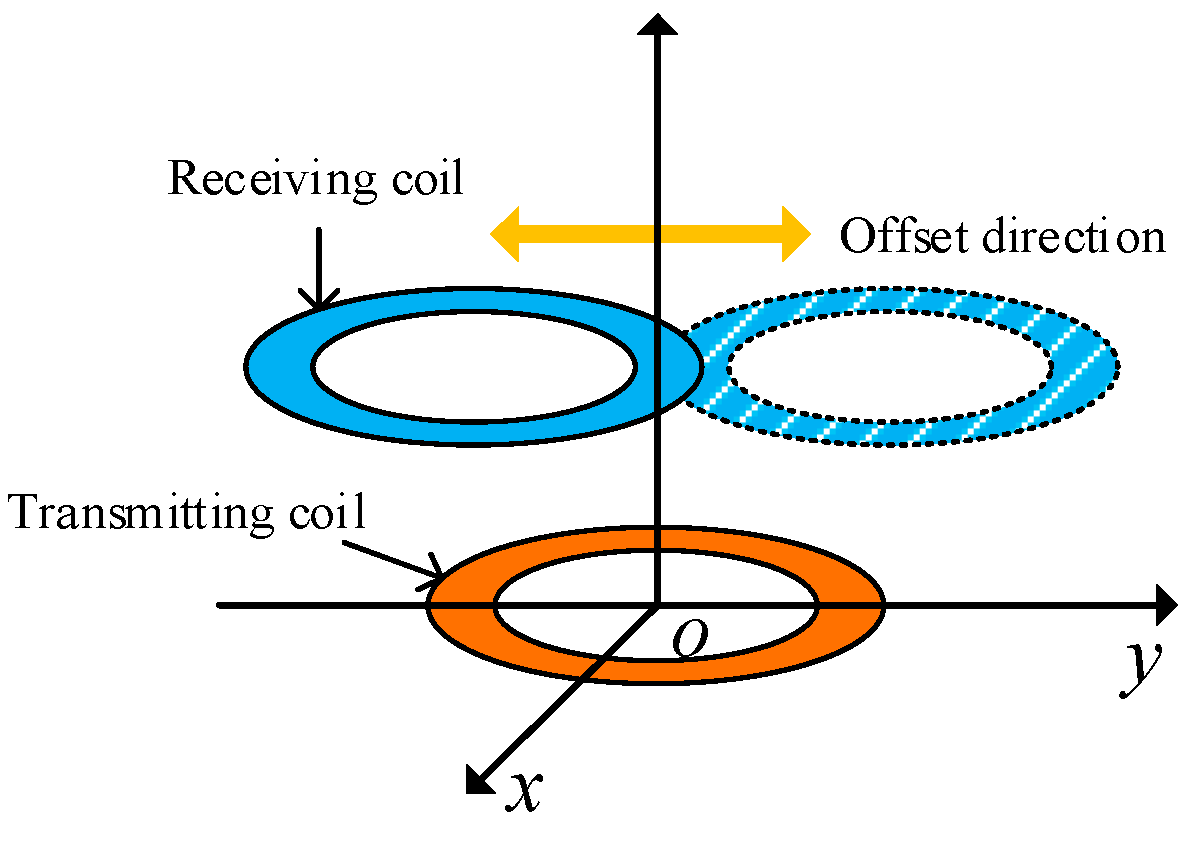
Figure 20 depicts a schematic diagram of the parallel offset of different axes of the coil. The centre of the transmitting end coil is fixed at the coordinate origin. The transmitting end and receiving end coils in the figure have different axes, and the receiving end coil experiences parallel offset in the horizontal direction. The centre of the coil is assumed to remain on the y-axis when the receiving end coil is offset.
When simulation analysis is conducted on the parallel offset of different axes of the coil, the basic simulation parameters of the coil are consistent with those of the coaxial parallel offset. The operating frequency is set as 100 kHz, and the vertical distance between the two coils is fixed at 4.5 mm. During simulation, the lower coil is assumed to be offset in the positive y-axis direction and the offset distance of the coil is assumed to change from 0 to 5 cm.
Figure 21 depicts a partial model diagram of the simulation of the coaxial nonparallel offset of the coil. The simulation data of the single-layer coil and Scheme 1 and Scheme 2 double-layer coils are shown in
Figure 22.
Figure 22 (c) depicts a simulation data graph of the transmission efficiency of three types of coils. As the offset distance increases, the transmission efficiency of the coils decreases. The transmission efficiency of the double-layer coils in Scheme 2 is higher than that of the other two coils at the same offset distance.
4.4. Different axes are not parallel offset
Figure 23 depicts a schematic diagram of the nonparallel offset of different axes of the coil. The centre of the transmitting end coil is fixed at the coordinate origin. The transmitting end and receiving end coils in the figure have different axes, and the receiving end coil is offset in the y-axis direction with an angle. The centre of the coil is assumed to remain on the y-axis when the receiving end coil is offset.
When simulation analysis is conducted on the nonparallel offset of different axes of the coil, the basic simulation parameters of the coil are consistent with those of the coaxial parallel offset, with a working frequency of 100 kHz, a fixed vertical distance of 4.5 mm between the two coils, a variation in the offset angle of the coil from 0 degrees to 80 degrees, and a variation in the horizontal offset distance from 0 to 4 cm. During the simulation, the coil is assumed to be offset in the positive direction of the y-axis.
Figure 24 depicts a partial model diagram of the simulation of different axis nonparallel offsets of the coil. The simulation data of the single-layer coil and Scheme 1 and Scheme 2 double-layer coils are shown in
Figure 25.
Figure 25 (a) is a simulation data graph of three types of coil coupling coefficients,
Figure 25 (b) is a simulation data graph of three types of coil strong coupling coefficients, and
Figure 25 (c) is a simulation data graph of three types of coil transmission efficiency. Figures (a), (b), and (c) illustrate that when the deviation angle is approximately 0 to 30 degrees, the coupling coefficient, strong coupling coefficient, and coil transmission efficiency remain basically unchanged, and a slight increasing trend is exhibited. After the angle deviation is beyond 30 degrees, excessive angle deviation occurs, and the magnetic field relationship between coils weakens, the coupling coefficient, strong coupling coefficient, and coil transmission efficiency begin decreasing, and the decreasing trend accelerates[
22]. The coupling coefficients of the single-layer coil and the double-layer coil in Scheme 1 are basically the same. At the same offset angle, the coupling coefficient and strong coupling coefficient of the double-layer coil in Scheme 2 are greater than those of the other two coils, and the strong coupling coefficient of the single-layer coil is the smallest. The transmission efficiency of the double-layer coil in Scheme 2 is higher than that of the other two coil structures. As the offset distance increases, the coupling coefficient, strong coupling coefficient, and transmission efficiency of the coil gradually decrease[
23,
24,
25].
Figure 25 (d) shows the data comparison curve of the strong coupling coefficient under different offset angles when the coil offset distance is 1 cm. Scheme 2 has the largest strong coupling coefficient, while Scheme 1 has a slightly smaller strong coupling coefficient than Scheme 2. The single-layer coil has the smallest strong coupling coefficient, indicating that Scheme 2's double-layer coil has a stronger anti-offset ability than the other two coil structures.
These results indicate that the anti-offset characteristics of the coil structure in Scheme 2 are better than those of the Scheme 1 and single-layer coils, and the wireless power transmission efficiency is better than that of single-layer PCB coils.
Figure 1.
Two types of coil structures. (a) Spatial spiral structure. (b) Planar spiral structure.
Figure 1.
Two types of coil structures. (a) Spatial spiral structure. (b) Planar spiral structure.
Figure 2.
Structure diagram of the wireless power transfer system.
Figure 2.
Structure diagram of the wireless power transfer system.
Figure 3.
Coupled coil mutual inductance circuit model.
Figure 3.
Coupled coil mutual inductance circuit model.
Figure 4.
Circuit figure of the bilateral compensation method . (a) SS type compensation. (b) SP type compensation. (c) PS type compensation. (d) PP type compensation.
Figure 4.
Circuit figure of the bilateral compensation method . (a) SS type compensation. (b) SP type compensation. (c) PS type compensation. (d) PP type compensation.
Figure 5.
Coupling coil mutual inductance circuit model of the SS compensation method.
Figure 5.
Coupling coil mutual inductance circuit model of the SS compensation method.
Figure 6.
Flat coils with different shapes. (a) Circular plane spiral coil. (b) Rectangular plane spiral coil.
Figure 6.
Flat coils with different shapes. (a) Circular plane spiral coil. (b) Rectangular plane spiral coil.
Figure 7.
Magnetic field nephogram of plane coils with different shapes. (a) Circular plane spiral coil. (b) Rectangular plane spiral coil.
Figure 7.
Magnetic field nephogram of plane coils with different shapes. (a) Circular plane spiral coil. (b) Rectangular plane spiral coil.
Figure 8.
Sectional figure of the PCB plane circular coil.
Figure 8.
Sectional figure of the PCB plane circular coil.
Figure 9.
Three-dimensional simulation model of the coil.
Figure 9.
Three-dimensional simulation model of the coil.
Figure 10.
Simulation results of different coil turn spacings. (a) Coil quality factor and coupling coefficient. (b) Strong coupling coefficient of coil.
Figure 10.
Simulation results of different coil turn spacings. (a) Coil quality factor and coupling coefficient. (b) Strong coupling coefficient of coil.
Figure 11.
Simulation results of different coil turn spacings. (a) Coil quality factor and coupling coefficient. (b) Strong coupling coefficient of coil.
Figure 11.
Simulation results of different coil turn spacings. (a) Coil quality factor and coupling coefficient. (b) Strong coupling coefficient of coil.
Figure 12.
Simulation data of different coil turns. (a) Coil quality factor and coupling coefficient. (b) Strong coupling coefficient of coil.
Figure 12.
Simulation data of different coil turns. (a) Coil quality factor and coupling coefficient. (b) Strong coupling coefficient of coil.
Figure 13.
Top view of the double-layer PCB coil. (a) Top view of the coil top layer. (b) Top view of the coil bottom layer in Scheme 1. (c) Top view of the coil bottom layer in Scheme 2.
Figure 13.
Top view of the double-layer PCB coil. (a) Top view of the coil top layer. (b) Top view of the coil bottom layer in Scheme 1. (c) Top view of the coil bottom layer in Scheme 2.
Figure 14.
Model figure of coil coaxial parallel offset.
Figure 14.
Model figure of coil coaxial parallel offset.
Figure 15.
Schematic figure of coil coaxial parallel offset.(a) Offset 3 cm. (b) Offset 5 cm. (c) Offset 7 cm.
Figure 15.
Schematic figure of coil coaxial parallel offset.(a) Offset 3 cm. (b) Offset 5 cm. (c) Offset 7 cm.
Figure 16.
Simulation data of coil coaxial parallel offset. (a) Coil coupling coefficient. (b) Coil strong coupling coefficient. (c) Coil transmission efficiency.
Figure 16.
Simulation data of coil coaxial parallel offset. (a) Coil coupling coefficient. (b) Coil strong coupling coefficient. (c) Coil transmission efficiency.
Figure 17.
Schematic figure of coil coaxial nonparallel offset.
Figure 17.
Schematic figure of coil coaxial nonparallel offset.
Figure 18.
Model figure of coil coaxial nonparallel offset. (a) Offset 5 cm, offset 30 degrees. (b) Offset 5 cm, offset 60 degrees. (c) Offset 7 cm, offset 30 degrees.
Figure 18.
Model figure of coil coaxial nonparallel offset. (a) Offset 5 cm, offset 30 degrees. (b) Offset 5 cm, offset 60 degrees. (c) Offset 7 cm, offset 30 degrees.
Figure 19.
Simulation results of coil coaxial nonparallel offset. (a) Coil coupling coefficient. (b) Coil strong coupling coefficient. (c) Coil transmission efficiency. (d) Comparison of strong coupling coefficients at different offset angles under the condition of an offset distance of 5.5 cm.
Figure 19.
Simulation results of coil coaxial nonparallel offset. (a) Coil coupling coefficient. (b) Coil strong coupling coefficient. (c) Coil transmission efficiency. (d) Comparison of strong coupling coefficients at different offset angles under the condition of an offset distance of 5.5 cm.
Figure 20.
Schematic figure of coil different axes parallel offset.
Figure 20.
Schematic figure of coil different axes parallel offset.
Figure 21.
Model figure of coil different axes parallel offset. (a) Offset 1 cm. (b) Offset 2.5 cm. (c) Offset 4 cm.
Figure 21.
Model figure of coil different axes parallel offset. (a) Offset 1 cm. (b) Offset 2.5 cm. (c) Offset 4 cm.
Figure 22.
Simulation data of coils with different parallel offset axes. (a) Coil coupling coefficient. (b) Coil strong coupling coefficient. (c) Coil transmission efficiency.
Figure 22.
Simulation data of coils with different parallel offset axes. (a) Coil coupling coefficient. (b) Coil strong coupling coefficient. (c) Coil transmission efficiency.
Figure 23.
Schematic figure of coil different axes parallel offset.
Figure 23.
Schematic figure of coil different axes parallel offset.
Figure 24.
Model figure of coil different axes nonparallel offset. (a) Offset 2 cm, angle 30 degrees. (b) Offset 2 cm, angle 60 degrees. (c) Offset 4 cm, angle 30 degrees.
Figure 24.
Model figure of coil different axes nonparallel offset. (a) Offset 2 cm, angle 30 degrees. (b) Offset 2 cm, angle 60 degrees. (c) Offset 4 cm, angle 30 degrees.
Figure 25.
Simulation data of coils with different nonparallel offset axes. (a) Coil coupling coefficient. (b) Coil strong coupling coefficient. (c) Coil transmission efficiency. (d) Comparison of strong coupling coefficients at different offset angles under the condition of a 1 cm offset distance.
Figure 25.
Simulation data of coils with different nonparallel offset axes. (a) Coil coupling coefficient. (b) Coil strong coupling coefficient. (c) Coil transmission efficiency. (d) Comparison of strong coupling coefficients at different offset angles under the condition of a 1 cm offset distance.
Figure 26.
Physical figure of a single-layer coil. (a) Coil 1. (b) Coil 2. (c) Coil 3. (d) Coil 4. (e) Coil 5. (f) Coil 6. (g) Coil 7. (h) Coil 8. (h) Coil 9.
Figure 26.
Physical figure of a single-layer coil. (a) Coil 1. (b) Coil 2. (c) Coil 3. (d) Coil 4. (e) Coil 5. (f) Coil 6. (g) Coil 7. (h) Coil 8. (h) Coil 9.
Figure 28.
Experimental platform for coil parameter measurement. (a) Self-inductance measurement. (b) Mutual inductance measurement.
Figure 28.
Experimental platform for coil parameter measurement. (a) Self-inductance measurement. (b) Mutual inductance measurement.
Figure 29.
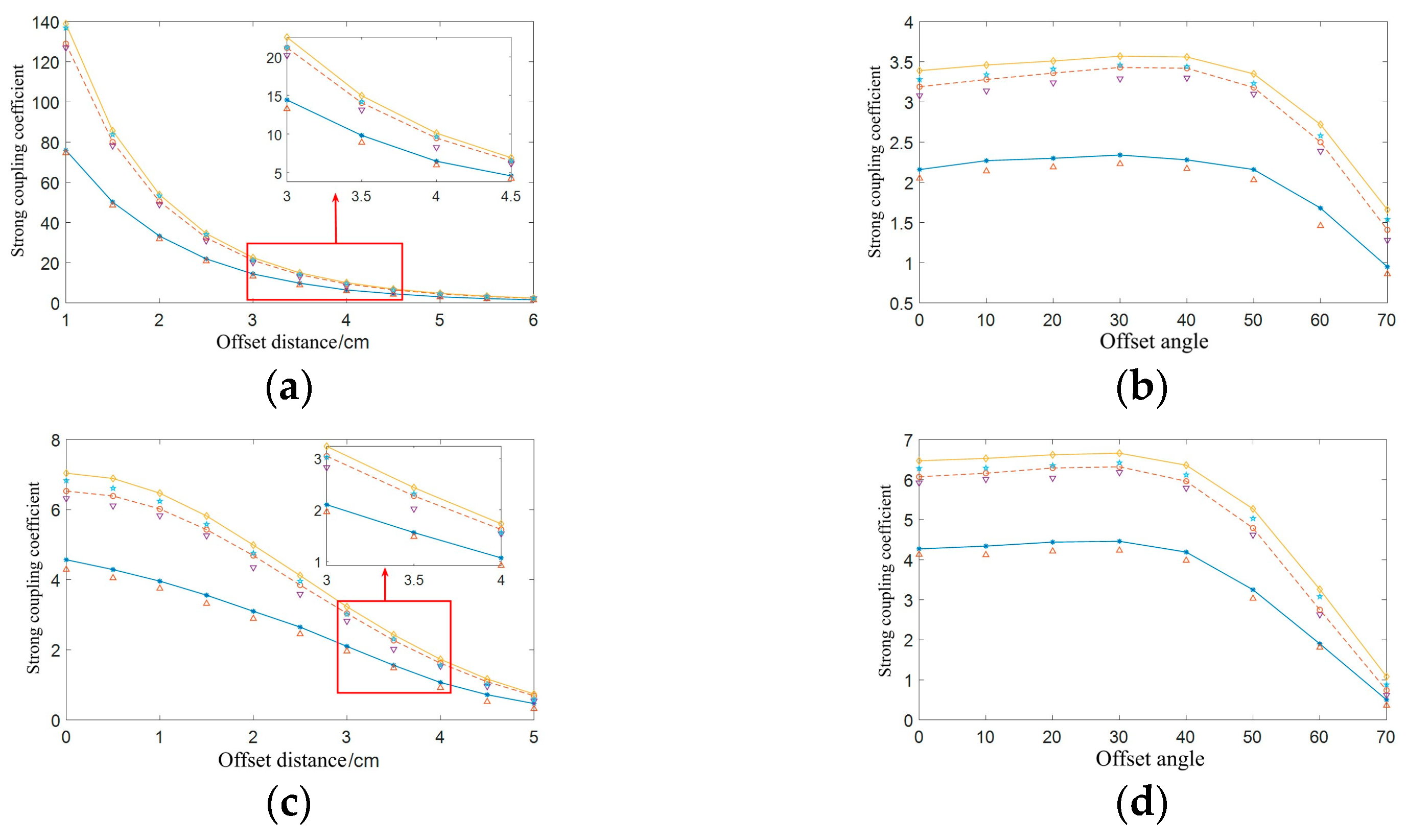
Simulation data and measurement calculation data of the strong coupling coefficient for coil offset. (a) Coaxial parallel offset. (b) Coaxial nonparallel offset. (c) Parallel offset of different axes. (d) Different axes are not parallel offset.
Figure 29.
Simulation data and measurement calculation data of the strong coupling coefficient for coil offset. (a) Coaxial parallel offset. (b) Coaxial nonparallel offset. (c) Parallel offset of different axes. (d) Different axes are not parallel offset.
Figure 30.
Wireless power transfer system experimental platform.
Figure 30.
Wireless power transfer system experimental platform.
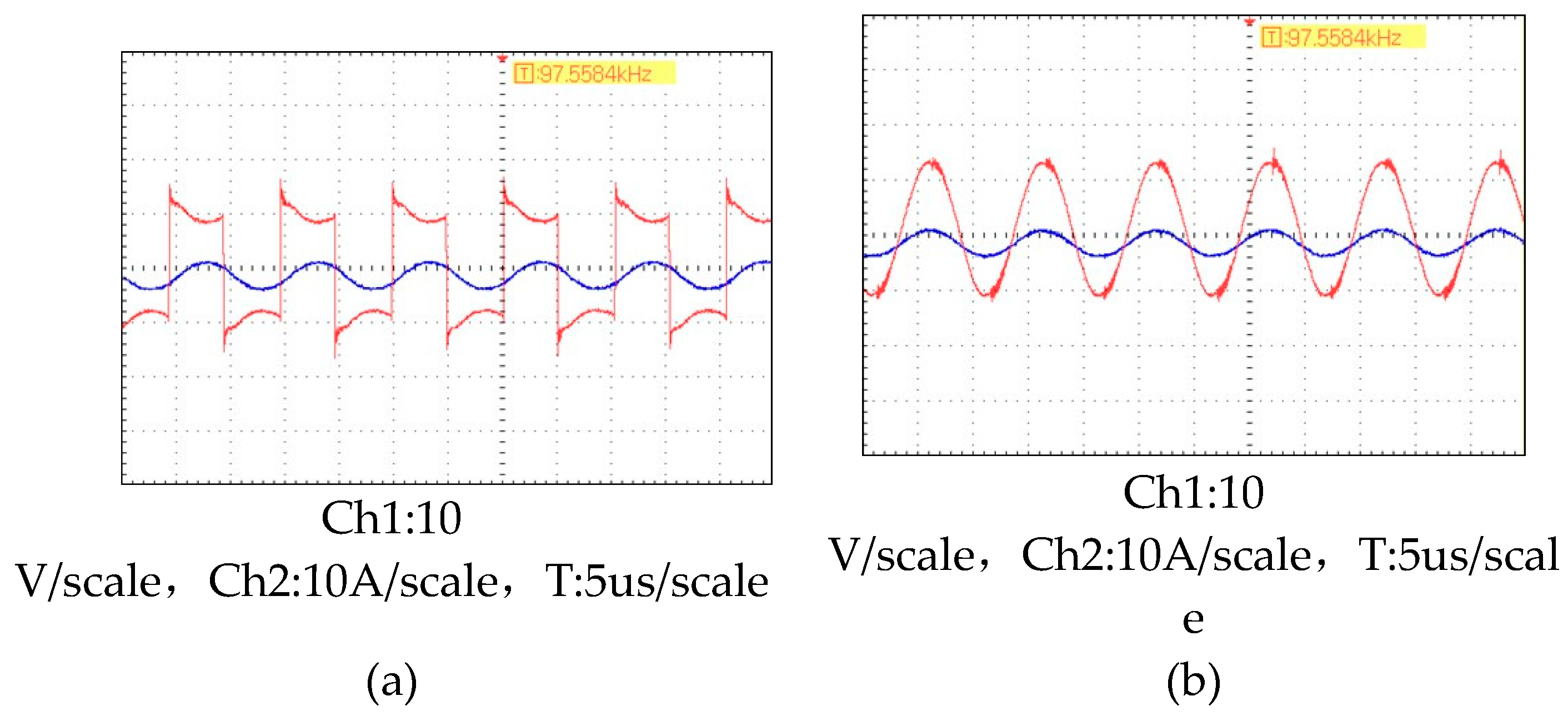
Figure 31.
Oscilloscope-measured waveform. (a) Voltage and current waveforms at the transmitting end (b) Load voltage and current waveform at the receiving end.
Figure 31.
Oscilloscope-measured waveform. (a) Voltage and current waveforms at the transmitting end (b) Load voltage and current waveform at the receiving end.
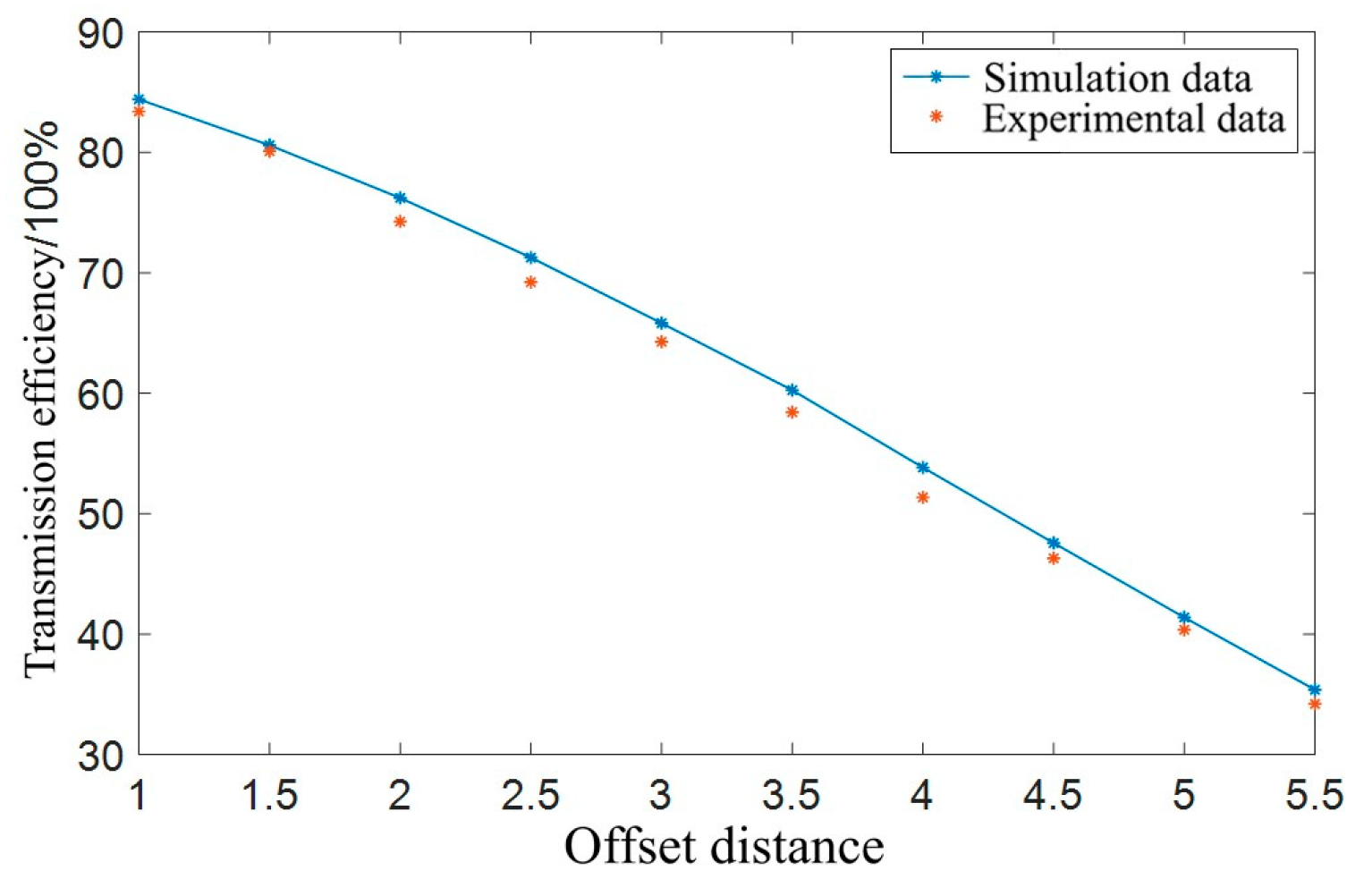
Figure 32.
Simulation and experimental data on coil transmission efficiency.
Figure 32.
Simulation and experimental data on coil transmission efficiency.
Table 1.
Reflecting resistance and reflecting reactance at the receiving end.
Table 1.
Reflecting resistance and reflecting reactance at the receiving end.
| Receiving capacitance compensation method |
Capacitor in Series |
Capacitor in Parallel |
| Reflective resistance Rr
|
|
|
| Reflective reactance X |
0 |
|
Table 2.
Different compensation methods for the capacitor value.
Table 2.
Different compensation methods for the capacitor value.
| Compensation method |
Transmitting end compensation capacitor C1
|
Receiving end compensation capacitor C2
|
| SS |
|
|
| SP |
|
|
| PS |
|
|
| PP |
|
|
Table 3.
Parameters of coils with different shapes.
Table 3.
Parameters of coils with different shapes.
| Coil shape |
Outside diameter (cm) |
Area(cm2) |
Inductance (uH) |
Resistance (mΩ) |
| Circular |
11.26 |
99.58 |
3.72 |
363 |
| Rectangle |
10 |
100 |
3.58 |
393 |
Table 4.
Parameters of coils with different line widths.
Table 4.
Parameters of coils with different line widths.
| Line width (mm) |
2.4 |
2.5 |
2.6 |
2.7 |
2.8 |
2.9 |
| Quality factor |
17.22 |
17.31 |
17.37 |
17.42 |
17.47 |
17.38 |
| Coupling coefficient |
0.1167 |
0.1171 |
0.1175 |
0.1178 |
0.1180 |
0.1181 |
| Strong coupling coefficient |
4.04 |
4.11 |
4.17 |
4.21 |
4.25 |
4.21 |
Table 5.
Relation between coil filling coefficient and turns and inner diameter.
Table 5.
Relation between coil filling coefficient and turns and inner diameter.
| Fill factor |
0.20 |
0.25 |
0.30 |
0.36 |
0.43 |
0.50 |
0.58 |
0.66 |
0.76 |
0.87 |
| Coil turns |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
| Inside diameter (mm) |
60.2 |
54.2 |
48.2 |
42.2 |
36.2 |
30.2 |
24.2 |
18.2 |
12.2 |
6.2 |
Table 6.
Simulation data of the coil quality factor, self-inductance, and resistance.
Table 6.
Simulation data of the coil quality factor, self-inductance, and resistance.
| Coil type |
Quality factor |
Self-inductance (uH) |
Resistance (mΩ) |
| Single layer coil |
18.09 |
5.12 |
178 |
| Scheme 1 |
21.62 |
5.13 |
149 |
| Scheme 2 |
21.08 |
20.61 |
614 |
Table 7.
Parameters of the coil structure.
Table 7.
Parameters of the coil structure.
| Coil number |
thickness (mm) |
pitch of turn (mm) |
Line width (mm) |
Number of turns |
Number of layers |
| 1 |
0.035 |
0.5 |
2 |
7 |
1 |
| 2 |
0.07 |
0.2 |
2 |
7 |
1 |
| 3 |
0.07 |
0.5 |
2 |
7 |
1 |
| 4 |
0.07 |
1 |
2 |
7 |
1 |
| 5 |
0.07 |
0.2 |
2.7 |
7 |
1 |
| 6 |
0.07 |
0.2 |
2.8 |
7 |
1 |
| 7 |
0.07 |
0.2 |
2.9 |
7 |
1 |
| 8 |
0.07 |
0.2 |
2.8 |
8 |
1 |
| 9 |
0.07 |
0.2 |
2.8 |
9 |
1 |
| 10 |
0.07 |
0.2 |
2.8 |
8 |
2 |
| 11 |
0.07 |
0.2 |
2.8 |
8 |
2 |
Table 8.
Simulation and measured calculation values of the coil strong coupling coefficient.
Table 8.
Simulation and measured calculation values of the coil strong coupling coefficient.
| Coil number |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| Simulation value |
0.92 |
3.63 |
3.36 |
2.98 |
4.21 |
4.25 |
4.21 |
4.57 |
4.55 |
| Measurement calculation value |
0.86 |
3.39 |
3.10 |
2.74 |
3.90 |
4.93 |
3.89 |
4.23 |
4.20 |
Table 9.
Simulated and measured values of the coil quality factor, self-inductance, and resistance.
Table 9.
Simulated and measured values of the coil quality factor, self-inductance, and resistance.
| Parameter |
Single layer coil |
Scheme 1 coil |
Scheme 2 coil |
| Quality factor simulation value |
18.09 |
21.61 |
21.08 |
| Quality factor measurement value |
17.44 |
20.81 |
20.33 |
| Self-perception simulation value (uH) |
5.12 |
5.13 |
20.61 |
| Self-inductance measurement value (uH) |
5.25 |
5.27 |
20.85 |
| Resistance simulation value (mΩ) |
178 |
152 |
623 |
| Resistance measurement value (mΩ) |
189 |
159 |
644 |
Table 10.
Experimental system parameter.
Table 10.
Experimental system parameter.
| System parameter |
Value |
| Operating Frequency |
98 kHz |
| Transmitting and receiving end coil self-sensing |
20.85 uH |
| Transmitting and receiving terminal coil resistance |
0.64 Ω |
| Compensation capacitance at the transmitting and receiving ends |
126 nF |
| Input voltage at the transmitting end |
12 V |
| Receiving end load resistance |
5 Ω |