Prerpints.org logo
Preprint
Article

Modeling of Electrochemical SOFC- Based Sensors

This version is not peer-reviewed.

Submitted:

02 January 2024

Posted:

03 January 2024

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract
Electrochemical sensors have been used for many decades. Yet, modeling of such sensors used in electrolysis mode is poorly documented, especially in the case parallel action of multiple gases. Those ones are of great interest since they constitute the first brick to bring information on natures and concentrations of a gaseous mixture composition thanks to grey box modeling of sensors array for example. Based on Butler Volmer’s equations, a model assuming parallel reactions at gold cathode has been introduced in this article and confronted to experimental results. Establishment of the model is based on the extraction of 3 variables: the charge transfer coefficient “α”, the reaction order γ, and the reaction constant rate k0. Tests performed without pollutants and with different concentrations of oxygen could be nicely fitted by the model. Then, the influence of polarization current on the 3 variables of the model has been evaluated showing a clear influence on the constant rate and the reaction order. Also, increasing the polarization current enabled us to get selectivity to oxidant gases. Similarly, the effect of the oxygen concentration was evaluated. Results showed that, in this case, the charge transfer coefficients “α” obtained for oxidant gases is quite different that the ones obtained in the polarization current varying conditions. Therefore, the model will be interesting in situations where polarization current and oxygen content are not varied together. Variation of polarization current can be quite interesting to get increased information for multivariate analysis purpose in constant oxygen content situations. Besides, other parameters have are required for applications in which the oxygen content is bound to change like exhaust gases or combustion.
Keywords: 
Subject: 
Chemistry and Materials Science  -   Electrochemistry

1. Introduction

Nowadays, air pollution has become a major society issue. With the increased development of motorized vehicles, polluting and even toxic gases are being released in alarming concentrations into the atmosphere with all known consequences [1,2]. With the apparition of the concerns about the impact of human activity on global warming, European legislations have started to impose more and more drastic emission limits through the European emission standards (euro 6D currently). The standards concern both particulate matter and polluting gases emitted from motorized vehicles. In a close future, industries, and particularly those having combustion furnaces will also be impacted by the European pollution standards. Controlling the concentration of emitted gases and particles has, therefore, become a major issue in automotive industry and new sensors responding to the requirements of the harsh environment present in exhausts have emerged. In response to those requirements, electrochemical sensors based on solid-state ceramic electrolyte are an ideal candidate for these applications [3,4].
However, just like gas sensors based on other transducing principles (electrical, mechanical, colorimetric and optical), a lack of selectivity compels electro-chemical sensors’ users to find different methods to extract the analyte’s nature and concentration. One of the methods currently used consists in modifying the composition of the sensor. This can be achieved by adding a selective sensitive layer that responds to one target gas [5,6,7,8] or by integrating a filter that will prevent the access to the sensor’s reaction sites to certain gases similarly to the work reported by Gao et al. [9]. It should be noted that in the case of electro-chemical sensors, the sensitive layers are the electrodes themselves. As a result, both anode and cathode can be tuned [10,11,12].
Another method used to achieve good selectivity consists of using sensor arrays. This technique may be used as an alternative to the first one. In this case, no modification of the sensor’s composition is made but signal treatment based on multivariate analysis enables the extraction of the analytes’ nature and concentration due to increased size of data collected by the different sensors of the array [13,14]. These arrays can use different sensors based one transducing principle, or can group sensors with different transducing principles (arrays of MOX sensors [15,16,17], arrays of electrochemical sensors [18,19]…).
Unfortunately, none of the previously reported methods was able to achieve satisfying results. As a result, both techniques still need improvement to minimize gas identification errors and reach lower limits of detection. One potential improvement that can be made lies within the use of knowledge models describing the physical behavior of the sensor instead of the black-box models currently used in multivariate analysis of sensors’ data.
Therefore, better knowledge of the electrochemical sensor’s working principle, especially when exposed to gas mixtures, is crucial. This implies the establishment of predicting analytical and/or digital models describing the sensor’s behavior under different operating conditions. For all sensors, transduction is based on the modification of an output electrical characteristic induced by a physico-chemical change in the sensor’s surrounding environment. Different models describing electrochemical sensors have thus been reported in the literature. Their aim is to achieve selectivity, similarly to work that has been reported for other transducing principles, such as cantilever based sensors [22]. The reported electrochemical models are limited to null current potentiometry based measurement. In this case, models used to describe the operation of the sensor are often based on Nernst model (thermodynamic equilibrium) or on the mixed potential theory [23,24,25]. However, only few of them describe the sensor’s kinetics behavior when used in electrolysis mode (imposed current potentiometry).
This paper reports two analytical models of an electrochemical sensor. The sensor’s electrical response is linked to the electrochemical reaction occurring at both cathode and anode. Therefore, it will both give information on the analyte’s concentration and on the redox behavior of the species involved in the reaction. The models proposed in this work describe the response of an electrochemical sensor used in electrolysis mode. In Section 2, the architecture of the electrochemical sensor used in this study is described in details. Section 3 explains the two models proposed, the first is a kinetics model while the second is an electrochemical and electrical associated model. These models describe the response of an electrochemical sensor used in electrolysis mode. They result from the association of the Butler-Volmer equations [26] and an equivalent electrical circuit. Section 4 compares these models to different experimental curves to test their robustness. For this purpose, a Matlab code was developed to extract the models’ kinetic parameter. Section 5 concludes this article and highlights the advantages of the adopted approach for the selective detection of gases.

2. Materials and Methods

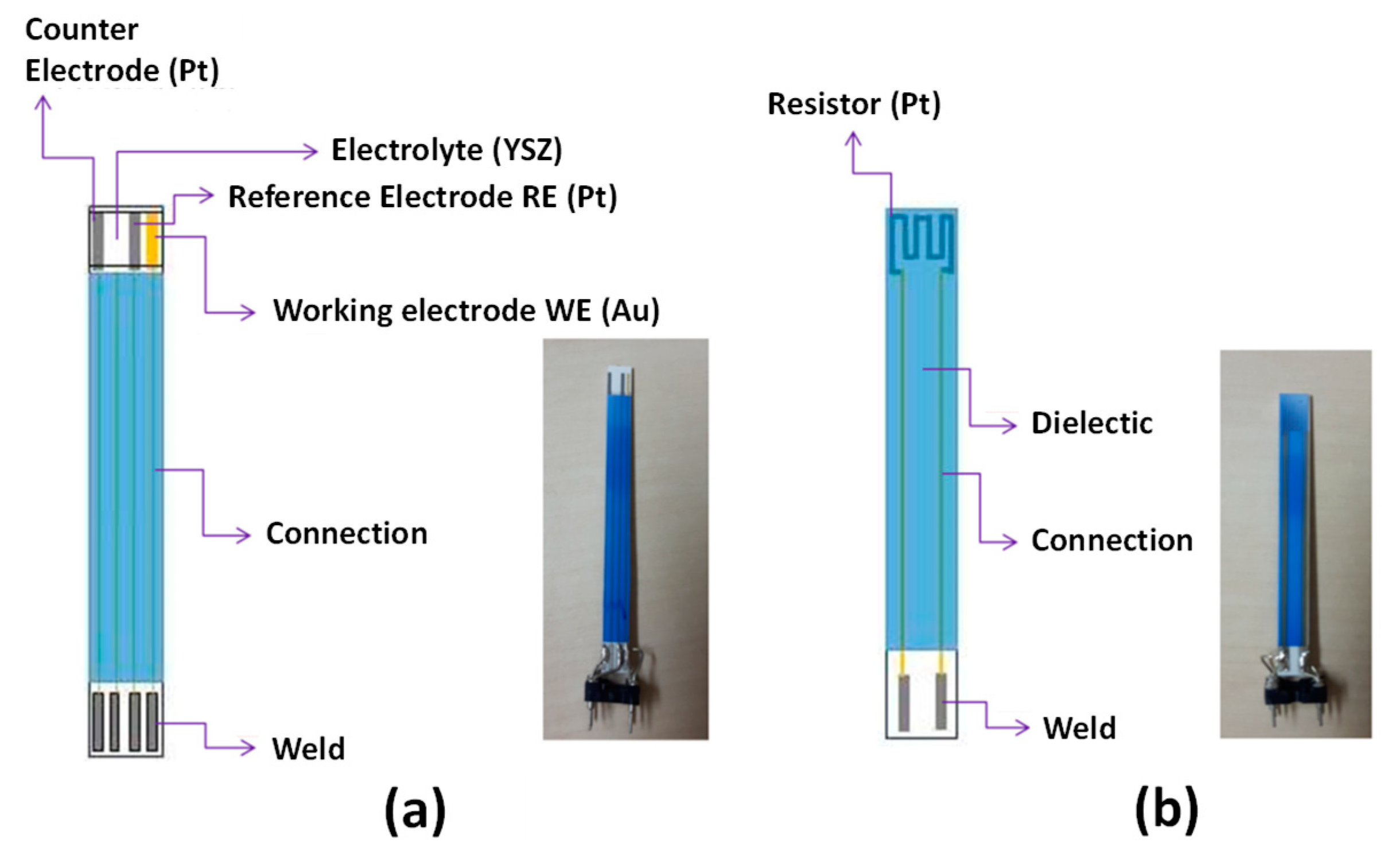
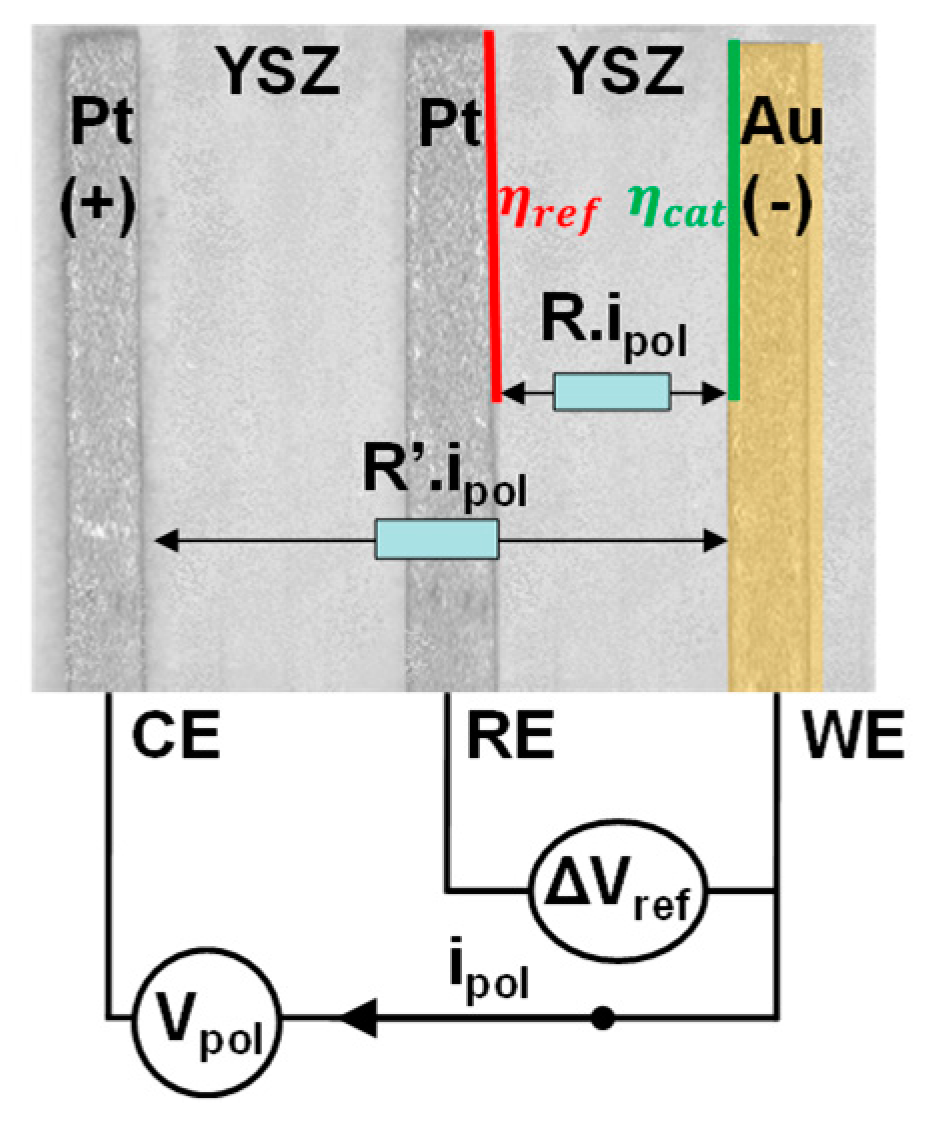
2.1. Sensor’s Physical and Electro-Chemical Description

The considered system is an electrochemical planar sensor. On its “sensing side”, the sensor is composed of an YSZ layer screen-printed onto a 5cm x 0.5cm alumina substrate and three metallic electrodes screen-printed onto the YSZ layer (Figure 1). A platinum resistance on the “heating side” of the alumina substrate enables to heat the YSZ layer by Joule effect to a temperature at which the ionic conductivity of the solid electrolyte becomes reasonable. Besides, the same platinum heater is used to monitor the temperature. On both side, a dielectric layer (blue color on Figure 1) guaranties electronic isolations of electrodes’ or resistance’s wirings. In this work, the sensor was used in electrolysis mode, i.e. a current was applied between working and counter electrodes. Low currents (0-70 nA) were applied between the working gold electrode (WE) negatively polarized as a cathode, and the platinum counter electrode (CE) playing an anode’s role. The sensor response ( Δ V r e f ) was measured as the potential difference between the reference platinum electrode (RE) and (WE). Several sensors were tested in this work. Sensitivity and selectivity of those sensors to NOX were investigated in a test bench in the temperature range 450-550°C for atmospheres containing O2 (1-12vol.%), H2O (1.5% absolute humidity) and N2. Alternatively, various polluting gas injections are performed: NO (0-1000ppm), NO2 (0-1000ppm), CO (0-1000ppm) and NH3 (0-20ppm). Analyte detection tests were carried out in a gas line test bench developed in the laboratory. More details about the test bench and experimental facilities can be found in [27,28,29].
As mentioned earlier, the sensor is operated in its electrolysis galvanostatic mode, i.e. a constant current I is applied between WE and CE and a potential difference Δ V r e f is measured between WE and RE : Δ V r e f = V R E − V W E (Figure 2). The measured voltage is given by the following equation [28]:
Δ V r e f ≈ R . I + Δ V 0 − η c a t
Where Δ V 0 is the output voltage measured between WE and RE when no current is applied between the electrodes ( η c a t is considered null at I=0), η c a t is the cathodic over-potential and R is the electrolyte resistance. The overpotential is linked to an additional quantity of energy required (compared to the one expected thermodynamically) by a reaction to occur over an electrode. Therefore, it is closely linked to the reaction kinetics over the considered electrode. In our case, platinum which is a well-known oxidation catalyst [30,31] is used as the anode. Consequence will be a quite overpotential η r e f for the platinum anode compared to the gold cathode. Then, η r e f will be neglected in this study. Extraction of the overpotential η c a t requires the determination of Δ V 0 and R. The first parameter is the measured Δ V r e f signal when the polarization current is null. It is measured for each gas concentration that will be used in electrolysis mode. R is obtained from the electrolyte impedance measurement at 100Hz thanks an electronic circuit developed at the laboratory.
The over-potential η is linked to the energy that has to be brought to the gas / electrode / electrolyte interface to enable the current flow. This parameter has been for us of interest for many years [28] since it best reflects the effects of the gas on the sensors’ response. Since the sensor is of electro-chemical nature, the current flow is made possible by the redox reactions happening at both electrodes. It should be noted that the current has an ionic nature (O2- ions) in the electrolyte and an electronic nature in the external circuit linking the electrodes. The transition between one form of current to the other is guaranteed by the redox reactions. At the triple phase boundaries, the current form is changed from ionic to electronic at the anode (Pt electrode here) and inversely at the cathode (Au electrode here). This change implies an energy supply, which can be electrically interpreted as a potential evolution. Therefore, the over-potential can be seen as the voltage across an interface resistance (the capacitive component of the interface being linked to the transient state (adsorption) [32] and the double layer phenomena unaddressed in this paper):
η I = R i n t e r f a c e . I + η 0
η 0 is the over-potential value at I=0 ( η 0 is considered null like mentioned earlier). The gaseous composition of the surrounding atmosphere will have a strong impact on the value of R i n t e r f a c e . Depending on the present gases, an evolution of the over-potential is experimentally observed. An increase of the absolute value of over-potential is noticed when a reducing gas is added to the atmosphere and a decrease of this last one is observed when the sensor’s atmosphere is modified by addition of an oxidizing gas.
The model developed in this works aims to give a prediction η m o d of the over-potential η e x p experimentally determined. Many parameters like the temperature, the oxygen and polluting gas concentrations or the imposed current were modulated to test the model’s robustness. From this, it will be deduced that the oxidizing analytes will have a “positive” action on the current flow (decrease of the resistance interface : R i n t e r f a c e ) whereas reducing gases will have the opposite effect.
The global kinetics of a reaction relies on three phenomena, each guided by their own kinetics: the ionic or gaseous species transport to the electrodes, the molecules’ adsorption and the charge transfer at triple phase boundaries (points of contact of electrolyte, electrode and gaseous phase). For the polarization currents chosen in this work, the high oxygen concentration and the constant flow rate of 60L/h are supposed to prevent kinetics limitation by diffusion transport. Even though including adsorption models would have enabled us to get information on the transitory phases (polarization current change) and possible drift occurring, we chose not to consider the adsorption kinetics models to limit the number of undetermined parameters. For these reasons, the physics included in the developed model to fit the experimental results are those considering kinetics limited by charge transfer.
In many kinetics approaches, reactions are considered elemental and a first order is chosen for the kinetic study [33,34]. Sometimes, the reaction order can rely on the operational conditions (especially in the case of gases) and can be a function of temperature for example. A proper evaluation of the reaction order requires exposing the sensor to different concentrations of the reactant gases while varying the experimental conditions like the temperature to check their effect on the reaction order. Then, the current (I) can be linearly linked to both the reductant and oxidant concentrations (by convention, the oxidation current is positive and the reduction current is negative) :
I = n F S k + C r e d γ − k − C o x γ
Where k + and k − are respectively the oxidation rate constant and the reduction rate constant, C r e d and C o x are respectively the reductant and oxidant concentration at the electrode / electrolyte interface, γ the reaction order, S the electrode surface, F the Faraday constant and n the number of electrons exchanged during the redox reaction. It can be demonstrated that [35]:
k + = k 0 . e x p 1 − α . n F . E − E 0 R T
k − = k 0 . e x p − α . n F . E − E 0 R T
Where k 0 is the intrinsic standard rate constant,   E the electrode potential, E 0 the standard potential of the redox couple involved (for example, E0 (O2/O2-)=1.12V vs SHE), E the electrode potential and α the cathodic charge transfer coefficient. Here, we assume that the sum of cathodic and anodic charge transfer coefficients is equal to 1. As a result, ( 1 − α ) represents the anodic charge transfer coefficient.
When the global current I is null, the cathodic and anodic currents are equal. We define by current exchange: I 0 the value of this anodic or cathodic current from equations (3), (4), (5) :
I 0 = n F S . k 0 . e x p 1 − α . n F . E e q − E 0 R T . C r e d * γ
I 0 = n F S . k 0 . e x p − α . n F . E e q − E 0 R T . C o x * γ
C o x * and C r e d * are respectively the gas concentration in the atmosphere close to the sensor and the reductant concentration inside electrolyte (O2- ion). Here, we suppose that the electric current is low enough and that the mass transfer by convection (gas flow) is fast enough so that the species concentration far from the electrode remain similar to the one near the electrode (diffusion is not the limiting step). This implies that C o x * = C o x   and C r e d * = C r e d   .
E e q is the electrode potential at equilibrium that can be expressed by Nernst law:
E e q = E 0 + R . T n . F . l n a o x a r e d
a o x   and a r e d   are respectively the activity of the gas in the atmosphere near the sensor (for the gaseous analytes) and the reductant activity of the adsorbed analyte (here the O2- ions) considered equal to 1 since O2- are present in solid phase in the electrolyte matrix.
a o x = p o x p ° = x p t o t p °
Where p o x is the partial pressure of the oxidant gas, p ° the reference pressure (1bar), p t o t the total pressure of the gas mixture (in our case, it is the atmospheric pressure) and x the molar fraction of the oxidant gas. Since, in our case, the total pressure is the atmospheric pressure, which about 1bar, a o x is assimilated to x . Then, taking into account the expression of the over-potential: η = E − E e q and all equations previously mentioned, the current (I) can be given by:
I = I 0 . e x p n F η R T 1 − α − e x p n F η R T − α
From this equation, approximations can be performed to extract over-potential:
  • If η is very low, the current value can be approximated by a first order Taylor series expansion :
    η ≈ I . R T I 0 . n F
  • f η > 100 m V and η < 0 (As it will be seen later, for our tested polarization currents and gaseous compositions, overpotential at gold cathode has been measured between -1.1V and -0.1V) :
    η ≈ − R T α n F l n I I 0
    By association of equation (7) to (12), the following expression can be formulated:
    η ≈ − R T α n F l n I n F S . k 0 . e x p − α . n F . E e q − E 0 R T . C o x   γ
Used gases have been considered as ideal gases. Then, using the Ideal Gas Law and equation (8), the last expression can be reformulated by:
η ≈ − R T α n F l n I . R T γ n F S . k 0 . x γ − α . p a t m   γ

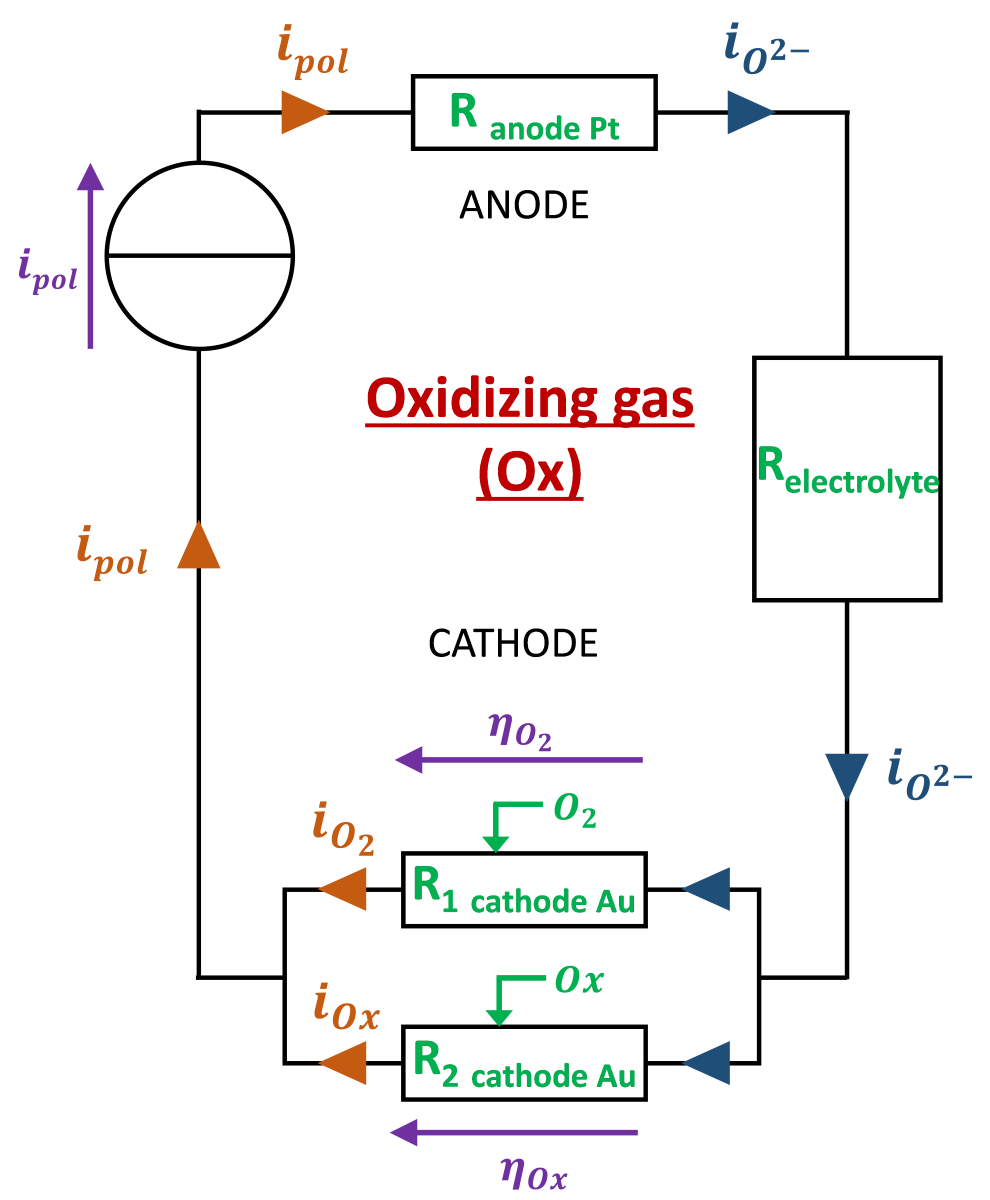
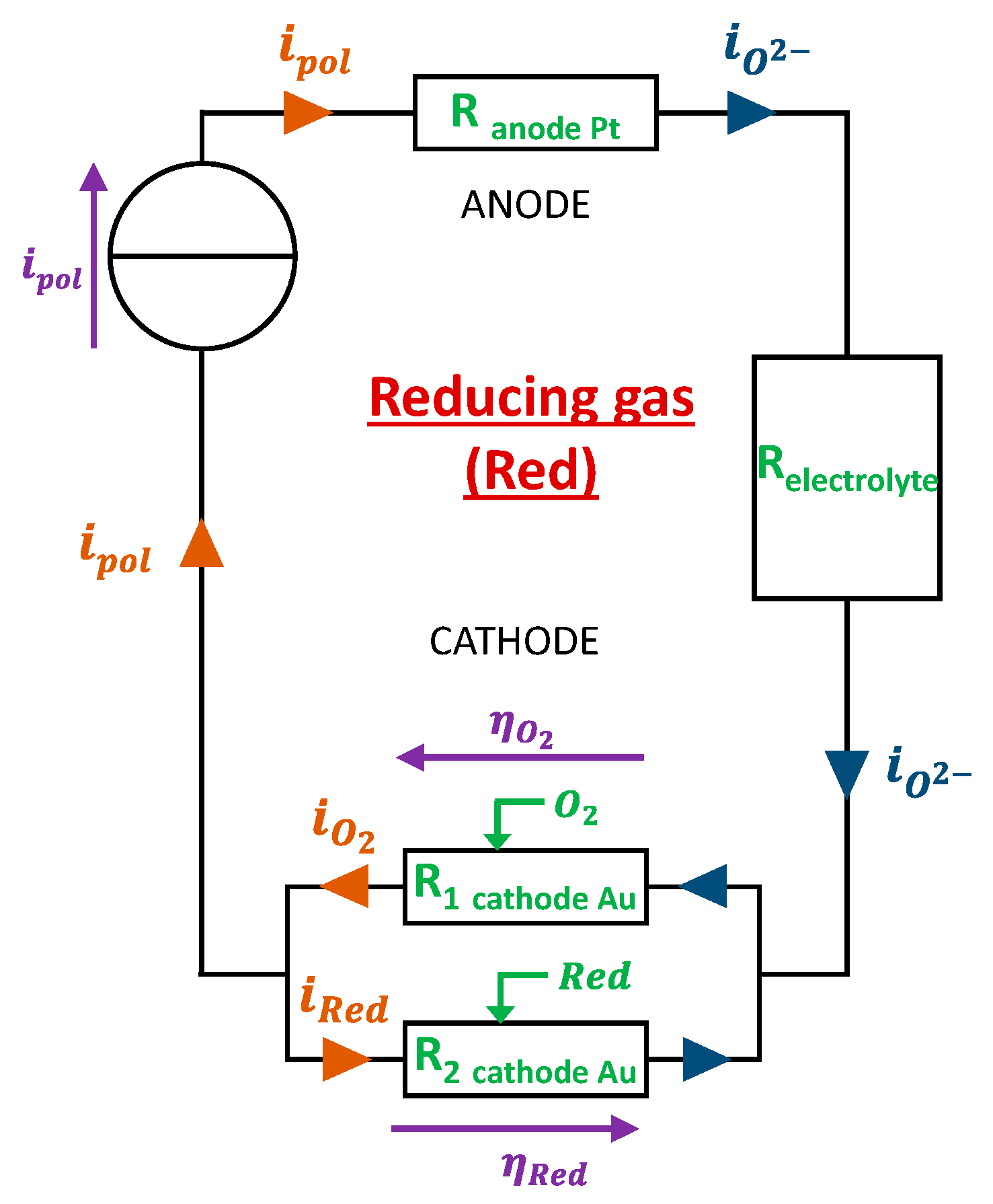
2.2. Electrochemical and Associated Electrical Models

According to the gaseous environment, different reactions will occur at the anode and the cathode. For the electrochemical model, we can distinguish three cases:
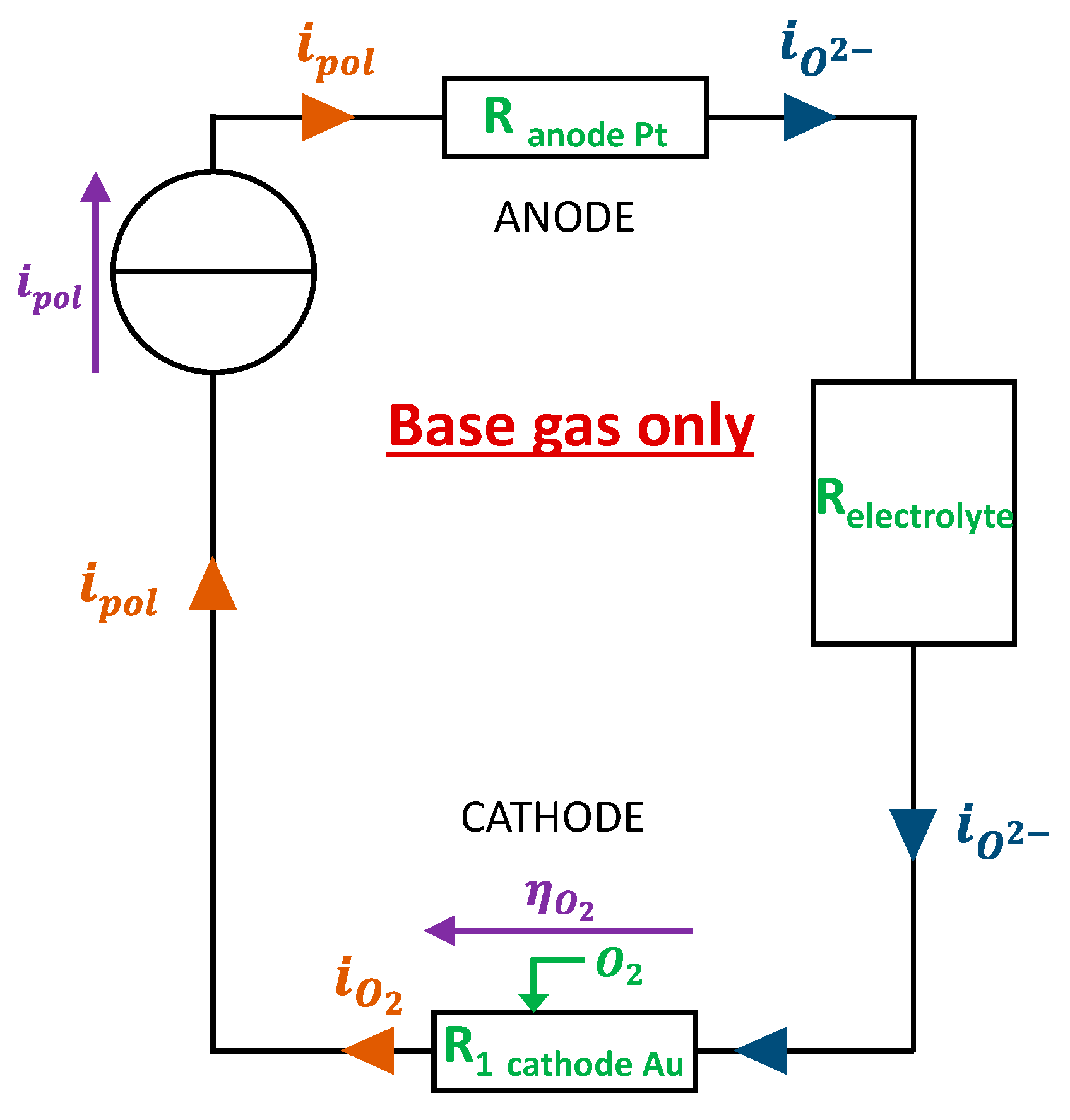
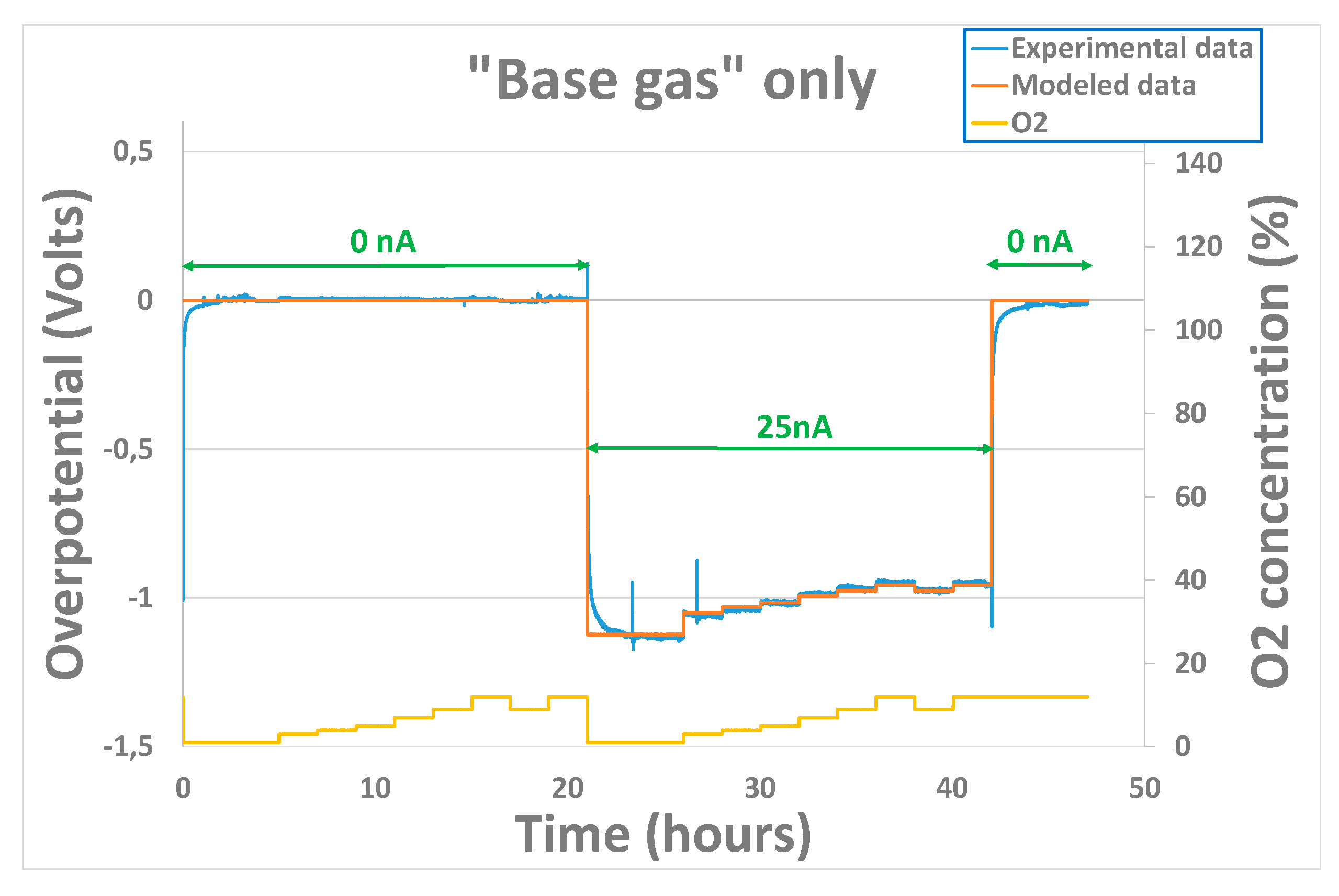
  • Model 1 : “Base gas” case
In the “base gas” case, the atmosphere around the sensor is composed of O2 (0.5 - 12vol.%), H2O (1.0% absolute humidity) and N2. In this case, the reactions taking place are the following ones:
-
at the cathode : O 2 + 4 e − → 2 O 2 −
-
at the anode : 2 O 2 − → O 2 + 4 e −
The electrical modeling reliant with the electrochemical description is proposed in Figure 3. At the cathode, adsorbed O2 molecules are dissociated and thanks to the electrons brought by the generator are converted to O2- ions transporting charges in a ionic form through the electrolyte to the anode.
The modeled over-potential under base gas can expressed by the following equation:
η m o d = − R . T α b a s e . n 1 . F . l n i p o l . R . T γ b a s e S . k 0 b a s e . n . F . x ( O 2 ) γ b a s e − α b a s e . P a t m γ b a s e
Where the electrode surface S = 3.68   m m 2 , a ( O 2 ) is the activity of dioxygen, n = 4 is the number of electrons exchanged in the reduction reaction of O2. The modeled overpotential evolution according to time during exposure of the sensor to base gas (varying O2 concentration) will, in the following part, be fitted to the experimental overpotential curve thanks to α b a s e , k 0 b a s e , γ b a s e parameters.
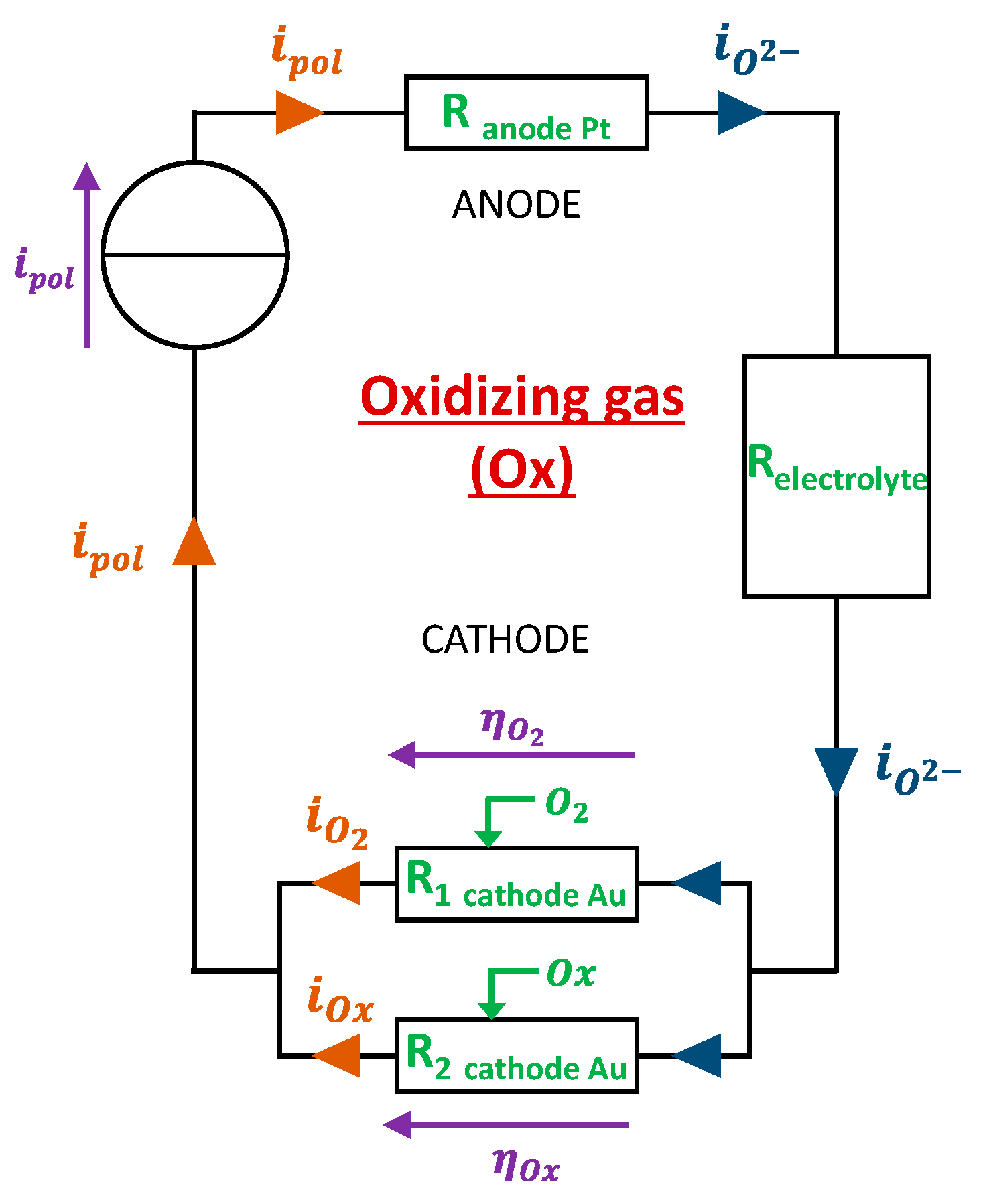
  • Model 2 : Presence of an oxidizing gas (NO2, NO)
When an oxidizing gas (NO2 or NO) is added to the “base gas”, the following reactions are expected:
-
at the cathode : O 2 + 4 e − → 2 O 2 −
N O 2 + 4 e − → 1 2 N 2 + 2 O 2 −
o r
N O + 2 e − → 1 2 N 2 + O 2 −
-
at the cathode : 2 O 2 − → O 2 + 4 e −
The current flow when an oxidizing gas is present is facilitated by the contribution of NO2 and NO bringing more O2- which are the current carrying ions. The consequence is the reduction of the gold cathode / gas / electrolyte interface resistance and the reduction of the cathode’s overpotential. This can be electrically modeled by the scheme in Figure 4.
It can be deduced that, compared to the “base gas” case, when an oxidizing gas is present, the imposed polarization current i p o l is sustained not only by the O 2 reaction at the interface but also by the polluting oxidant gas reduction: i p o l = i O 2 + i O x . Moreover, according to Kirchhoff law, the overpotentials η O 2 and η O x should be equal. Then, the problem is to determine the quantity of current that will be sustained by O2 and the quantity that will be sustained by the oxidant gas. This requires another equation linking i O 2 and i O x to have a system with 2 equations and 2 unknowns.
An hypothesis that gave the better modeling results consists in considering that the ratio of current sustained respectively by O2 and the oxidant gas is the same as the ratio of exchange currents obtained when the global current is null:
i O 2 i O x = I 0   ( O 2 ) I 0   ( O x )
I 0   ( O 2 ) and I 0   ( O x ) can be calculated respectively according to α b a s e , k 0 b a s e , γ b a s e (relative to reduction reaction of O2) and α g a s , k g a s , γ g a s (relative to reduction reaction of oxidant gas).
Finally, when an oxidant is added to the base gas, cathodic overpotential is changed to the following value:
η m o d = − R . T α g a s . n 1 . F . l n i O x . R . T γ g a s S . k 0 g a s . n . F . a ( O 2 ) γ g a s − α g a s . P a t m γ g a s
Where n   is the number of electrons exchanged in the reduction reaction of the oxidant gas considered. The modeled overpotential evolution according to time during exposure of the sensor to sequences during which the sensor will alternatively be exposed to base gas (varying O2 concentration or not) and oxidant gases (fixed concentrations or varying ones) will, in the following part, be fitted to the experimental overpotential curve thanks to α b a s e , k 0 b a s e , γ b a s e and α g a s , k 0 g a s , γ g a s parameters
  • Model 3 : Presence of a reducing gas (NH3, CO)
When the sensor is exposed oxidant gases in galvanostatic mode (constant i p o l ) like it was done in our case, the absolute value of the overpotential is seen to decrease. This is explained by the fact that the reduction of the oxidant gas decrease the interface resistance by providing O2- ions. Regarding exposure of the sensor to reducing gases, we experimentally observed a tendency of the overpotential to maintain constant or slightly increase (in absolute value). To explain this behavior, we propose a mechanism in which the reducing gases will react with O2- ions produced by the reduction of O2 at the cathode. The model associated to this reaction mechanism is described hereafter for two reducing gases (CO and NH3):
-
at the cathode : O 2 + 4 e − → 2 O 2 −
C O + O 2 − → C O 2 + 2 e −
o r
N H 3 + 5 2 O 2 − → N O + 3 2 H 2 O + 5 e −
-
at the anode : 2 O 2 − → O 2 + 4 e −
This model assumes that the presence of CO or NH3 tends to decrease the quantity of 𝑂2- ions. Thus, the the current flow will be made more difficult due to the decrease of the number of available charge carriers. This will therefore increase the gold cathode / gas / electrolyte interface resistance and the cathode’s overpotential.
Preprints 95211 g005
Figure 5. Electrical design of the electrode for model 3.a: addition of a reducing gas reacting with O2-.
Figure 5. Electrical design of the electrode for model 3.a: addition of a reducing gas reacting with O2-.
Preprints 95211 g005
When a reducing gas is present, the imposed polarization current i p o l is sustained only by the O 2 reaction at the interface. Moreover, a part of the current that comes from O 2 reduction reaction is used to oxidize the present reducing gas: i p o l = i O 2 − i r e d . The consequence is the increase of the cathodic overpotential compared to “base gas” case. Finally, the addition of a reductant to the base gas will change the cathodic overpotential in accordance with expression (17). Nevertheless, in this case, expression of i O x will be replaced by: i r e d = i O 2 − i p o l .

2.3. Multivariate Fitting Methods

As mentioned previously, experimental sensor response curves were obtained by modifying analytes concentrations or polarization current. From those raw response curves, experimental overpotential according to time could be extracted from equation (1) (Figure 6).
MATLAB algorithms were developed, based on the previously mentioned laws, in order to check, if there are sets of parameters (α, γ , k0, ...) allowing a good correspondence between the experimental and the modeled data. This corresponds to a three-parameter non-linear multivariate fitting problem. For convenience, vector gathering the three parameters was noted: p = α γ k 0 . 3 methods were chosen and tested to solve this problem: the Least Squares method, the Newton-Gauss method and the Levenberg-Marquardt method. For each one, an iterative algorithm was developed with Matlab to extract the vector p values allowing the lowest difference between the experimental and modeled data. Then, a comparison of their fitting performance was performed through the RMSE (Root Mean Square Error). Besides, during the implementation of the different methods, it was noticed that the Newton-Gauss and Levenberg-Marquardt methods were very sensitive to the initialization conditions. This is why, in the completed versions of the code, a fitting with the method of least squares was first performed. Then, the parameters obtained were used as input parameters for the two other methods. The values of the parameters displayed in this work are those of the method that gives the best fit, i.e. the smallest RMSE.

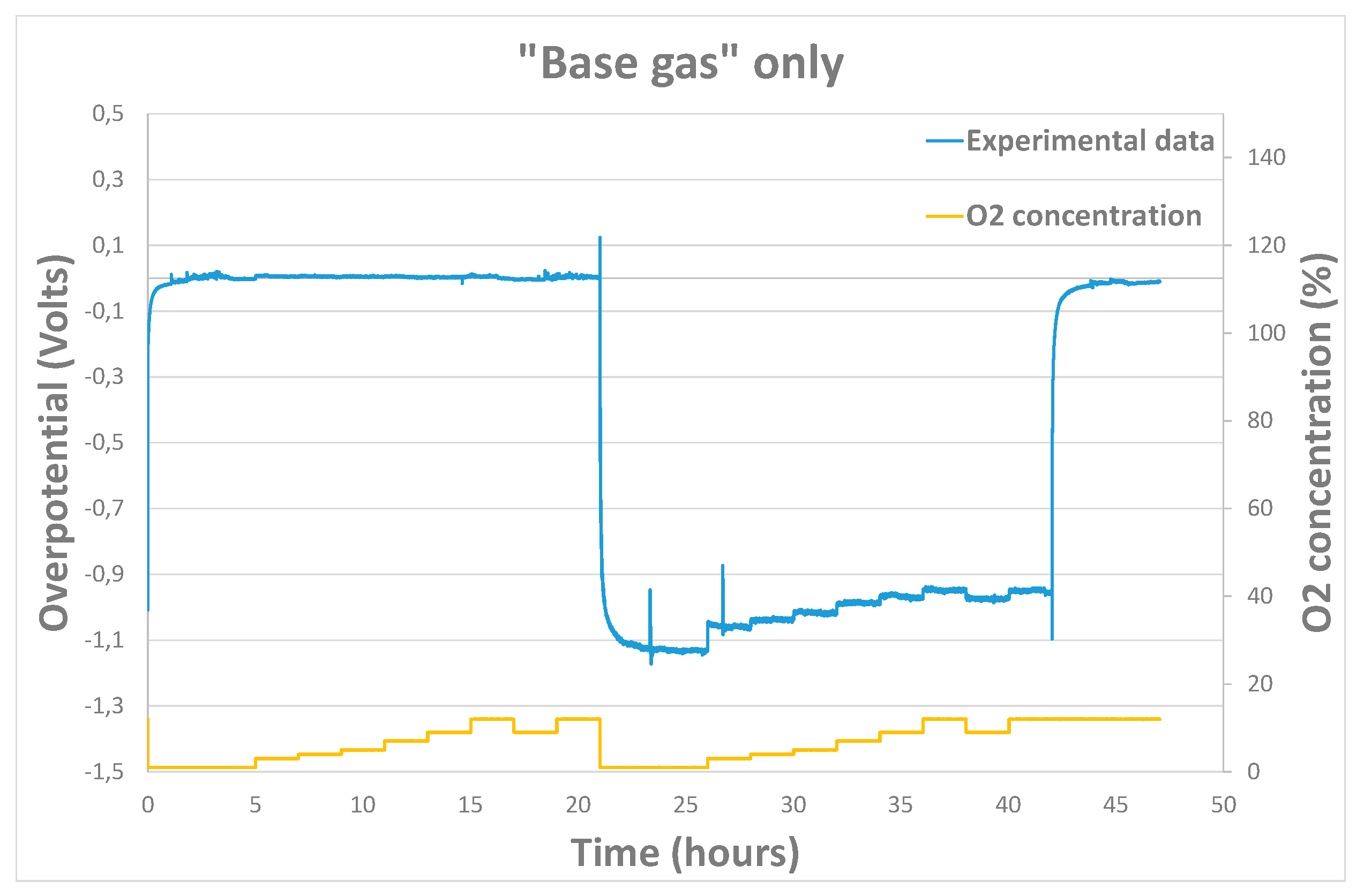
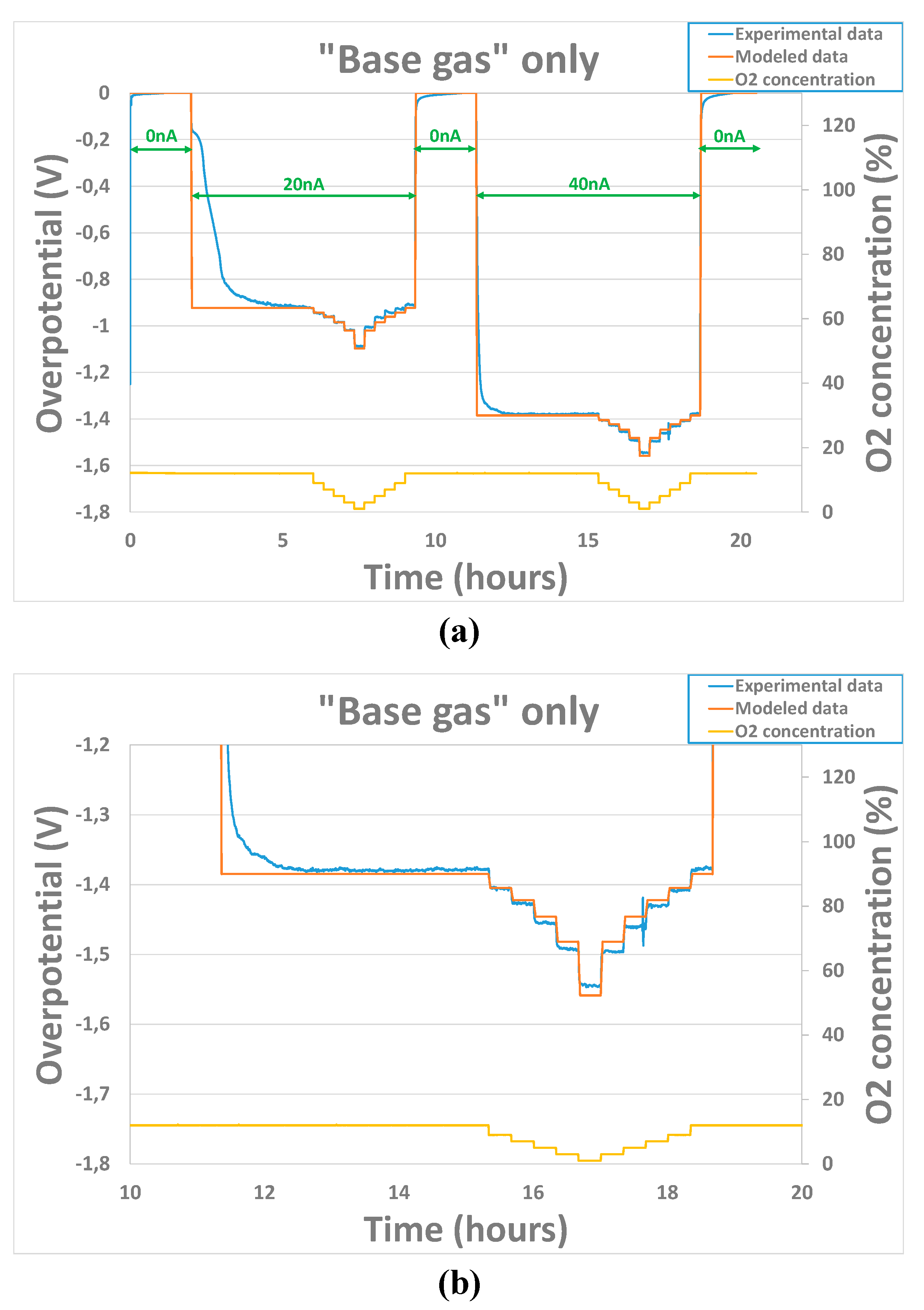
3. Results & Discussions

3.1. “Base Gas” Alone Case
Results, shown here, were obtained for 2 sensors heated at temperatures from 450°C to 550°C and exposed to base gas only, with different oxygen concentrations going from 1% to 12%. Polarization cycle includes steps of 2 hours with 0nA polarization current and steps of 7 hours with either 20nA or 40nA polarization current. The overpotential (calculated from Eq. 1) linked to the gold electrode is null when i p o l = 0 n A . Then, after application of a 20nA or 40nA polarization current, an important evolution of the overpotential is observed (example at 500°C in Figure 7). When i p o l is brought back to 0nA, the overpotential goes back to a value close to 0V the same way. The α b a s e coefficient is the only parameter that can increase the difference of overpotential value between a sensor exposed at the same O2 concentration for two values of polarization current. The γ b a s e will mainly have an effect on the difference of overpotential value between a sensor exposed at different O2 concentrations for the same value of polarization current. The k 0 b a s e value will have an overall effect on the overpotential signal that will be entirely shifted up or down according to k 0 b a s e value.
Parameters enabling the best fitting results are listed in Table 1 for the two sensors tested. For α b a s e and γ b a s e , it seems that there is no influence of temperature whereas for k 0 b a s e , the tendency is clearly an increase of this parameter according to the temperature. k 0 being a reduction constant rate, it seems logical according to Arrhenius law that its value is increased when the temperature is raised.
Since those parameters are strongly correlated to the kinetics of the reactions occurring at the triple phase boundaries around the gold cathode, the electrode history and to the “chemical state” of this last one at the beginning of the experiment (species that remains sorbed, chemical availability of the triple phase boundaries..) will play a non-negligible role in the sensor behavior. Therefore, another test was performed on a sensor coming from another batch of production. Overpotential evolution results, shown on Figure 8 were obtained for the sensor heated at 500°C and exposed to base gas only, with different oxygen concentrations varying from 1% to 12%. No polarization current was applied from the beginning to 21h. Then, after application of a 25nA polarization current, an important decrease of the overpotential is observed in the same way as previously. After 42h, polarization is brought back to 0nA and the overpotential goes back, as previously, to a value close to 0V. Initial values (before fitting operation) of the k 0 b a s e , α b a s e and γ b a s e parameters were those obtained with sensor 1 at 500°C. After fitting, parameter values obtained were coherent with the one obtained previously : k 0 b a s e = 3,7   .   10 − 9 , α b a s e = 0,025 and γ b a s e = 0,13 .
For all the tests performed, the variations of experimental overpotential with O2 concentration are well reproduced by modeled data. Nevertheless, it can be noticed that for polarization current transitions from 0 to 20 / 25 / 40nA or from 20 / 25 / 40nA to 0nA, fitting error performed is much higher. This can be explained by the fact that, liked mentioned earlier, the capacitive part of the phenomenon has not been taken into account in the model. Physically, this capacitance can be linked to the oxygen species adsorbed at the interface electrode-electrolyte-air. In fact, a modification of the polarization current will induce a modification of the sorption equilibrium of O2 molecules. As it can be seen on Figure 7 and Figure 8, the time required to reach the new equilibrium conditions (steady state) is quite long: 2 hours. This can be explained partly by the important volume of the cells in which the sensors are placed during the exposition but mainly by the sorption kinetics, i.e the kinetics linked to the creation / destruction of bonds between O2 molecules and triples phase boundaries around the gold electrode.

3.2. Introduction of Pollutant Gases together with “Base Gas”

While introducing pollutant gases, the variability in the operating conditions becomes important (polarization current, temperature, concentration of oxygen, concentration of pollutant gases)… This section will be divided in two parts and will involve tests operated on different conditions on 3 other sensors. In the first part, the effect of polarization voltage on the sensors’ output will be studied according to the concentration of pollutant gases (both reductant and oxidant) at a fixed temperature of 500°C. The third part will be dedicated to the fitting of sensors’ output curves in which the polarization current and temperature are remained constant (25nA and 450°C respectively) and the concentration of pollutant gases will be varied together with the concentration of oxygen. Moreover, in each case, initialization of the “base gas” parameters will be done according to the results obtained in section 3.1.

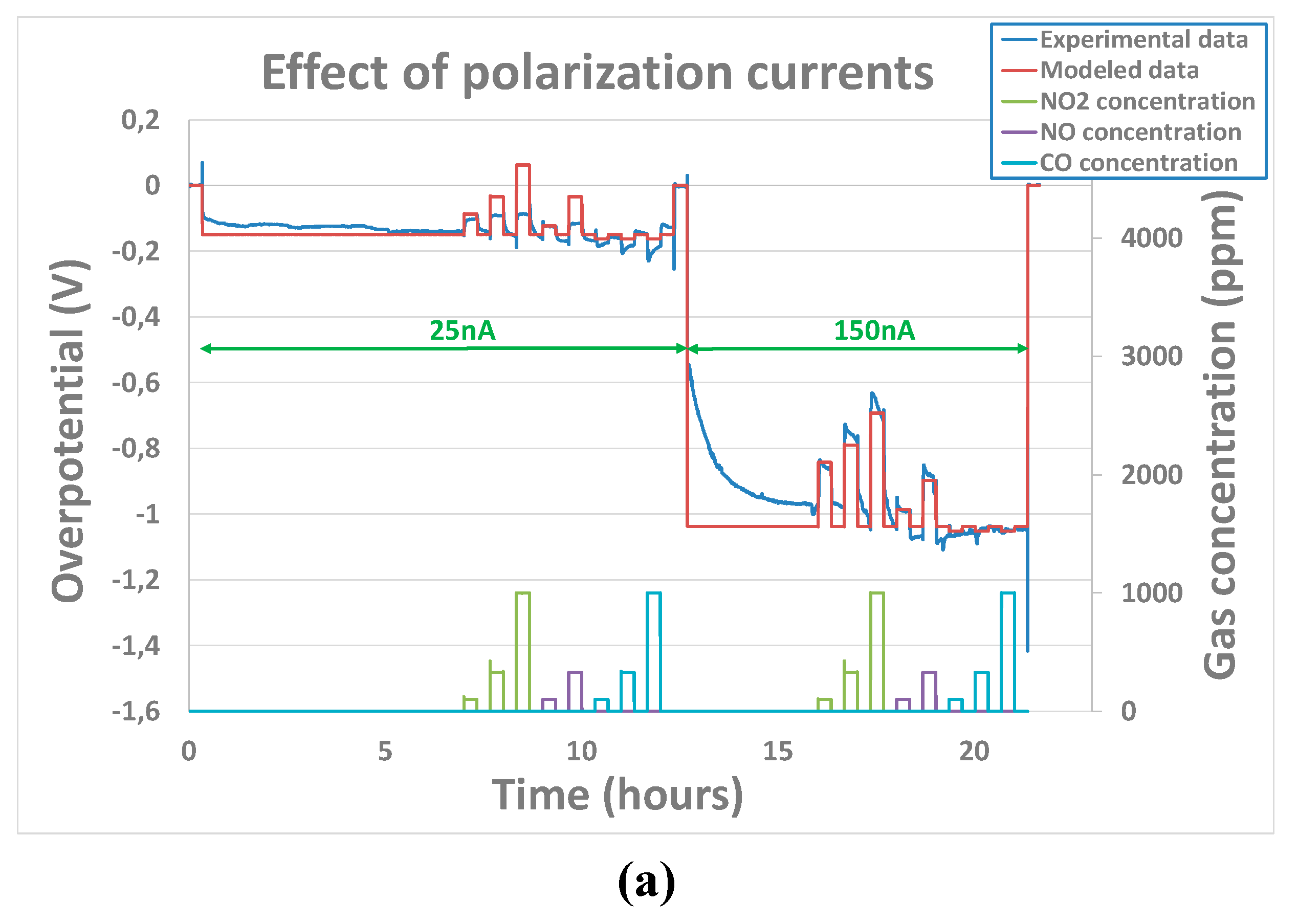
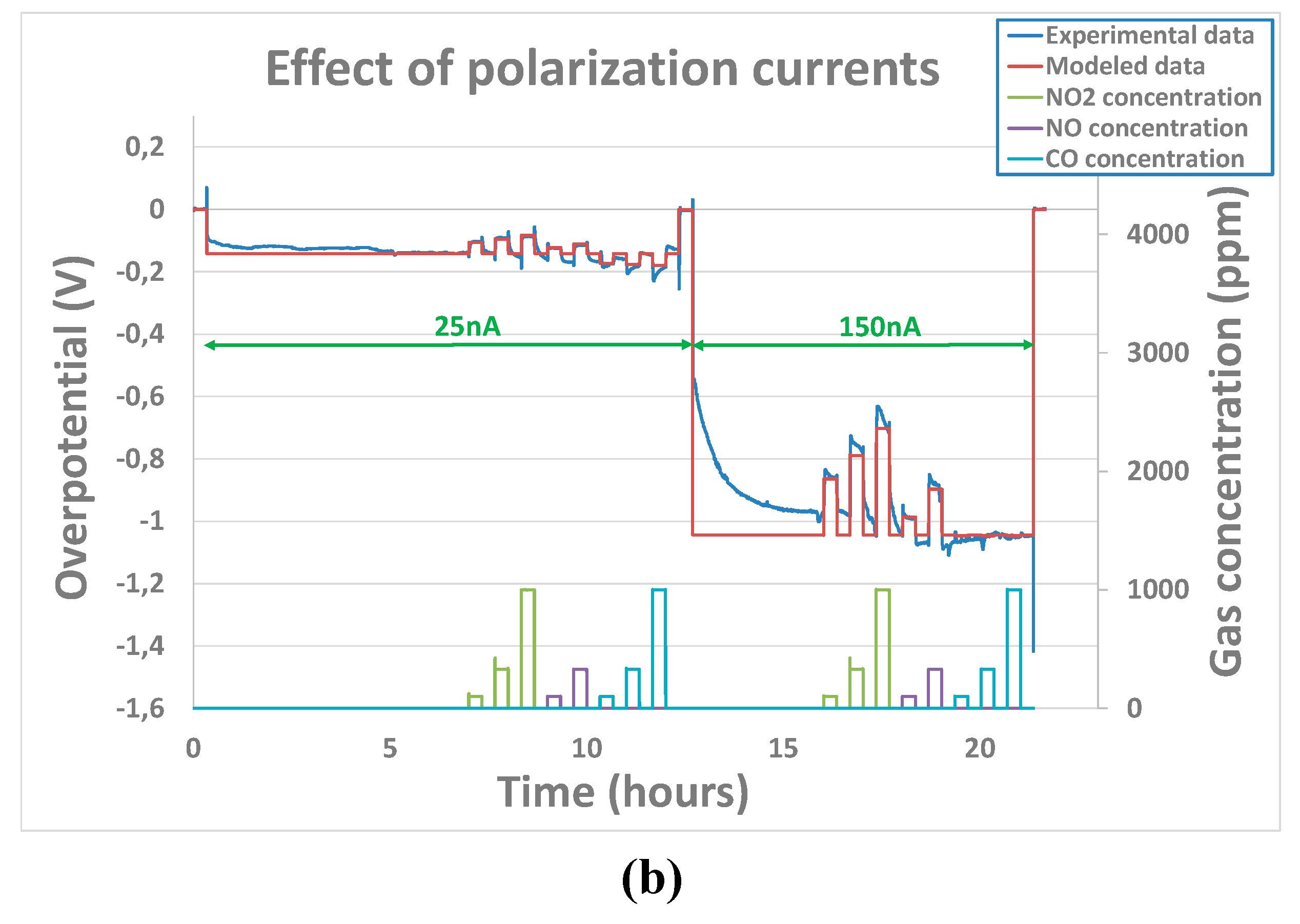
3.2.1. Effect of Polarization Current

Changing the polarization current can be interesting since measurements performed at different levels of polarization currents could bring a bigger quantity of information exploitable in a view to reach selective detection. Tests have been performed for polarization current of 20nA, 50nA, 150nA (to reach overpotential values between 0V and -1.5V) on two sensors. Concerning the operating conditions, O2 concentration has been set at 12% while pollutant analytes concentrations (NO, NO2, CO) have been varied from 100ppm to 1000ppm.
In contrast to the case with base gas only, for which no clear influence of polarization was observed, the couple k 0 g a s , γ g a s seems to be different according to polarization voltage for the tested pollutant analytes. This means that, the polarization voltage influences order or reactions and constant rates. Indeed, as it can be seen from example of Figure 9) a), the parameters that have been adjusted for the polarization current of 150nA are not relevant for a polarization voltage of 25nA. Indeed, they do not enable a correct fitting of the sensor’s output when the analytes concentrations are varied. Besides, the charge transfer coefficient α b a s e which is, by definition, not supposed to vary with polarization current, has been considered fixed for one analyte. A correct fitting of the experimental curve (Figure 9) b) ) was obtained while allowing couple k 0 g a s , γ g a s to vary according to the polarization current. Parameters’ fitting results obtained for the three tested sensors at polarization currents of 25nA, 50nA and 150nA have been summarized in Table 2 for NO2, NO and CO analytes.
From Table 2, a clear distinction between oxidant gases (NO and NO2) parameters and the reductant gas (CO) can be established. It seems that constant rates k 0 g a s and reaction order γ g a s of oxidant gases are clearly influenced the polarization current. Overall, an increase of the constant rate and the reaction order has been noticed in the case of oxidant gases. In the case of the tested reductant gas CO, the opposite behavior has been observed. Indeed, when the current reaches 50nA, the reaction rate become so low that no overpotential variation is observed which is in line with the observations made by Viricelle et al. on equivalent sensors [28] showing that distinction could be made between oxidant and reducing gases variating the polarization current. Therefore, in the case of CO analyte, it was not possible to extract constant rate, charge transfer coefficient or reaction rate.

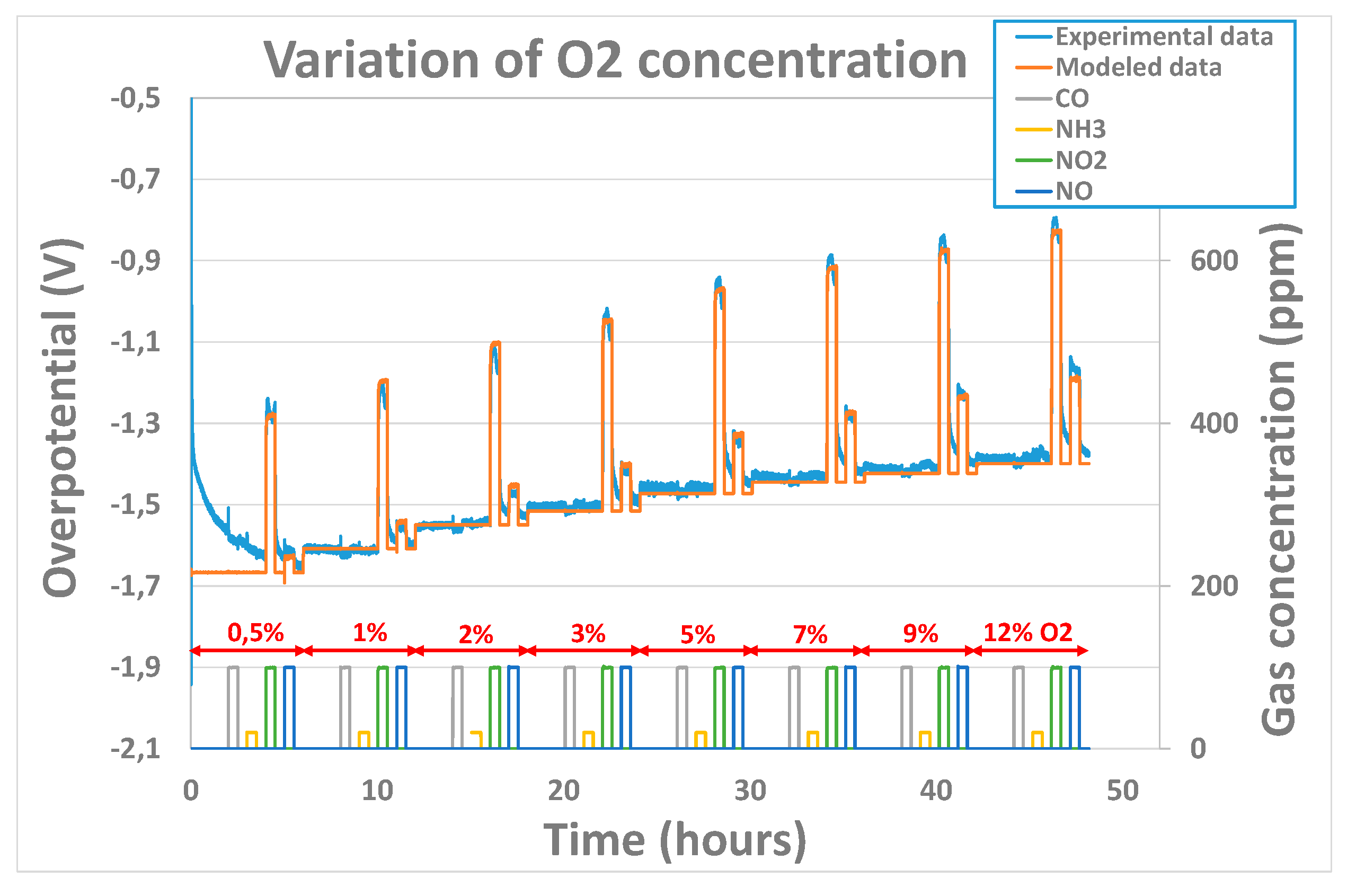
3.2.1. Effect of Oxygen Concentration

When used in the open-air conditions, the oxygen concentration is not supposed to vary. However, for some applications, like process control in the chemical industry for example, it can be interesting to validate the model in conditions where the oxygen concentration is not fixed. The robustness of the model was evaluated at 450°C in conditions where the polarization current is kept constant (25nA) and the concentration of oxygen is varied from 0.5% to 12% while pollutant concentrations of 100ppm for NO2, NO and CO and 20ppm for NH3 were introduced periodically and for each O2 concentration value. The fitting results obtained were good as can be observed on Figure 10. Yet, in this case, the fitting parameters extracted (Table 3) for the pollutant gases are more dispersed for the tested sensors than the ones extracted in Table 2 especially for α g a s coefficient of oxidant gases (NO and NO2’s). Values from 0.003 to 0.015 for α N O 2 and from 0.003 to 0.05 for α N O were obtained. Indeed, those ones vary a lot from one sensor to another and are not comparable with the ones observed in previous part whereas the constant rates k 0 g a s and γ g a s obtained are in the same range of order as the ones observed in previous part. Besides, extracted values for NO and NO2’s cathodic charge transfer coefficient are significantly lower than the ones obtained in previous part. This means that the model is not able to describe the evolution of the overpotential of a sensor for which both the oxygen concentration and the polarization current is varied. The cathodic charge transfer coefficient is linked to the velocity at which the electrons are transferred at triple point boundaries, i.e. to the reaction rate. A lower value of charge transfer coefficient will result in a poor correlation between the electrode potential and the reaction rate. Therefore, it is strongly linked to the surface state of the gold electrode (species adsorbed, roughness…) which can vary a lot from one sensor to another and according the history of one sensor. Then, one hypothesis which can explain the great variability of α N O and α N O 2 between different sensors while changing the O2 concentration is the fact that the ratio of adsorbed NO2 molecules compared adsorbed O2 molecules can be quite different from one sensor to another.
Concerning the reducing gases, results obtained are consistent with the ones obtained in previous part. More, it seems that the reaction rate, in the case of NH3, is so low that, as for last part, the 3 parameters could not be clearly be extracted.

4. Conclusions

An analytic model of electrochemical YSZ based sensor used in polarization mode and exposed to different gaseous mixtures was performed. The model, based on Butler-Volmer equations, was developed and compared to experimental results obtained under different conditions. It relies on two parallel reactions occurring at gold cathode. The first one is the reduction of O2 and the second one either the reduction of an oxidizing gas (NO or NO2) or the reaction between a reducing gas and O2- anions resulting from the reduction of O2. In a view to test the robustness of the model in conditions in which it could be used, the influence of the polarization current and oxygen concentration was studied. Main results concerning the influence of polarization current is that the constant rate of pollutant oxidant gases and their reaction order rely on its value while for reducing gases, an increase of polarization current will decrease the reaction rate in a way that over 50nA, the overpotential response is brought to zero for those reducing gases. Besides, extracted α g a s parameters from modeling of tests performed under increasing concentration of oxygen were more dispersed and different from the ones obtained with a constant concentration of oxygen and a polarization current variating. This means that the model is not suitable for use under experimental conditions where both oxygen concentration and polarization current are varied. The other conclusion for the modeling tests under different concentration of oxygen was that the extracted parameters were not exportable from one sensor to another, especially concerning the value of the cathodic charge transfer parameter.
Next target for the developed model is to use it in multivariate analysis to reach the objective of both selective and quantitative detection. For that purpose, we need to make sure that the modeling parameters extracted for one sensor in particular experimental condition (temperature, polarization current) remain constant over time. Therefore, reproducibility tests should be performed and eventually a study of the influence of sensor ageing on the modeling parameters. Finally, based on the model, prediction of a simple gaseous composition composed of a base gas and one of the pollutant gas tested in this work is aimed.

Author Contributions

Conceptualization, R.L.; methodology and investigation, R.L., M.R., and J.-P.V.; validation, R.L., M.R., R.A. and J.-P.V.; data curation, R.L.; writing—original draft preparation, R.L.; writing—review and editing, R.L., M.R., R.A., and J.-P.V.; supervision, R.L., M.R., and J.-P.V.; All authors have read and agreed to the published version of the manuscript

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Acknowledgments

The authors would like to acknowledge the Mines Saint-Etienne and UMR 5307 LGF for the financial support to this research.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. J. Hansen, L. Nazarenko, Soot climate forcing via snow and ice albedos, Proceedings of the National Academy of Sciences of the United States of America 2004, 101, n°2, p423-428, (2004).
  2. EEA report, 2013, National emissions reported to the Convention on Long-range Transboundary Air Pollution (LRTAP Convention) (http://www.eea.europa.eu).
  3. J.W. Fergus, Sensing mechanism of non-equilibrium solid-electrolyte-based chemical sensors, Journal of Solid State Electrochemistry 2011, 15, p971–984. [CrossRef]
  4. H. Ryu, D. Thompson, Y. Huang, B. Li, Y. Lei, Electrochemical sensors for nitrogen species: A review, Sensors and Actuators Reports 2020, 2, Issue 1, 100022. [CrossRef]
  5. Y. Tang, X. Xu, H. Du, H. Zhu, D. Li, D. Ao, Y. Guo, Y. Fu, X Zu, Cellulose nano-crystals as a sensitive and selective layer for high performance surface acoustic wave HCl gas sensors, Sensors and Actuators A: Physical 2020, 301, 111792. [CrossRef]
  6. S-H. Hsiao, J-X. Wu, H-I. Chen, High-selectivity NOx sensors based on an Au/InGaP Schottky diode functionalized with self-assembled monolayer of alkanedithiols, Sensors and Actuators B: Chemical 2020, 305, 127269. [CrossRef]
  7. P.A. Pushpanjali, J.G. Manjunatha, M.T. Srinivas, Highly sensitive platform utilizing poly(l-methionine) layered carbon nanotube paste sensor for the determination of voltaren, FlatChem 2020, 24, 100207. [CrossRef]
  8. K. Staszek, A. Szkudlarek, M. Kawa, A. Rydosz, Microwave system with sensor utilizing GO-based gas-sensitive layer and its application to acetone detection, Sensors and Actuators B: Chemical 2019, 297, 126699. [CrossRef]
  9. J. Gao, J-P. Viricelle, P. Breuil, C. Pijolat, P.Vernoux, A. Boreave, A. Giroir-Fendler, Improvement of the NOx selectivity for a planar YSZ, Sensors and Actuators B 2011, 154, p 106-110. [CrossRef]
  10. Axin Liang, B. Huipeng Hou, C. Shanshan Tang, D. Liquan Sun, E. Aiqin Luo, An advanced molecularly imprinted electrochemical sensor for the highly sensitive and selective detection and determination of Human IgG, Bioelectrochemistry 2021, 137, 107671. [CrossRef]
  11. Q. Wang, X. Xiao, X. Hu, L. Huang, T. Li, M. Yang, Molecularly imprinted electrochemical sensor for ascorbic acid determination based on MXene modified electrode, Materials Letters 2021, 285, 129158. [CrossRef]
  12. [12] K.A. Alamry, M.A. Hussein, J-W. Choi, W.A. El-Said, Non-enzymatic electrochemical sensor to detect γ-aminobutyric acid with ligand-based on graphene oxide modified gold electrode, Journal of Electroanalytical Chemistry 2020, 879, 114789. [CrossRef]
  13. B.S.O. Alsaedi, C.M. McGraw, T.M. Schaerf, P.W. Dillingham, Multivariate limit of detection for non-linear sensor arrays, Chemometrics and Intelligent Laboratory Systems 2020, 201, article 104016. [CrossRef]
  14. L.M.M. Ferro, S.G. Lemos, M. Ferreira, F. Trivinho-Strixino, Use of multivariate analysis on Fabry-Pérot interference spectra of nanoporous anodic alumina (NAA) for optical sensors purposes, Sensors and Actuators B: Chemical 2017, 248, p718-723. [CrossRef]
  15. L. Song, L. Yang, Z. Wang, D. Liu, L. Luo, X. Zhu, Y. Xi, Z. Yang, N. Han, F. Wang, Y. Chen, One-step electrospun SnO2/MOx heterostructured nanomaterials for highly selective gas sensor array integration, Sensors and Actuators B: Chemical 2019, 283, p793-801. 283.
  16. Yousefi-Darani, M. Babor, O. Paquet-Durand, B. Hitzmann, Model-based calibration of a gas sensor array for on-line monitoring of ethanol concentration in Saccharomyces cerevisiae batch cultivation, Biosystems Engineering 2020, 198, p.198-209.
  17. J. Chu, W. Li, X. Yang, Y. Wu, D. Wang, A. Yang, H. Yuan, X. Wang, Y. Li, M. Rong, Identification of gas mixtures via sensor array combining with neural networks, Sensors and Actuators B: Chemical 2020, 329, 129090. [CrossRef]
  18. V. Singh, Quantum dot decorated multi-walled carbon nanotube modified electrochemical sensor array for single drop insulin detection, Materials Letters 2019, 254, p.415-418. [CrossRef]
  19. D.D. Gornall, S.D. Collyer, S.P.J. Higson, Investigations into the use of screen-printed carbon electrodes as templates for electrochemical sensors and sonochemically fabricated microelectrode arrays, Sensors and Actuators B: Chemical 2009, 141, Issue 2, p.581-591. [CrossRef]
  20. J. Guo, G. Fang, S. Wang, J. Wang, Quartz crystal microbalance sensor based on 11-mercaptoundecanoic acid self-assembly and amidated nano-titanium film for selective and ultrafast detection of phosphoproteins in food, Food Chemistry 2020, 344, 128656. [CrossRef]
  21. S. Sri Surya Srikanth, B. Rajesh Kumar, V. Suresh, V. Jyothi, I. Sreenivasa Rao, G. Aswani Kumar, Design of MEMS Cantilever Sensors for Identification of VOCs Using IntelliSuite, Materials Today: Proceedings 2020, 22, Part 4, p.3162-3170. [CrossRef]
  22. L. Iglesias, M.T. Boudjiet, I. Dufour, Discrimination and concentration measurement of different binary gas mixtures with a simple resonator through viscosity and mass density, Sensors and Actuators B: Chemical 2019, 285, p.487-494. [CrossRef]
  23. T. Ritter, J. Lattus, G. Hagen, R. Moos, On the influence of the NOx equilibrium reaction on mixed potential sensor signals: A comparison between FE modelling and experimental data, Sensors and Actuators B: Chemical 2019, 296, p. 126627.
  24. T. Liu, H. Guan, T. Wang, X. Liang, F. Liu, C. Zhang, G. Lu, Mixed potential type acetone sensor based on GDC used for breath analysis, Sensors and Actuators B: Chemical 2021, 326, 128846. [CrossRef]
  25. Eric L. Brosha, Rangachary Mukundan, David R. Brown, Fernando H. Garzon, J.H. Visser, Development of ceramic mixed potential sensors for automotive applications, Solid State Ionics 2002, 148, Issues 1–2, p.61-69. [CrossRef]
  26. A.J. Bard, L.R. Faulkner, Electrochemical Methods. Fundamentals and Applications, 2nd ed., John Wiley & Sons, Inc. : Hoboken, New Jersey, United States, 2001 p. 92-105.
  27. Romanytsia, J-P. Viricelle, P. Vernoux, C. Pijolat, Application of advanced morphology Au–X (X=YSZ, ZrO2) composites as sensing electrode for solid state mixed-potential exhaust NOx sensor, Sensors and Actuators B: Chemical 2015, 207, Part A, p.391-397. [CrossRef]
  28. J-P. Viricelle, P. Vernoux, J. Gao, I. Romanytsia, P. Breuil, NO2-selective electrochemical sensors for Diesel exhausts, EUROSENSORS 2016, Budapest, Procedia Engineering 2016, 168, p.7-10. [CrossRef]
  29. J-P. Viricelle, P Vernoux, C. Pijolat, P. Breuil, Capteur NOx à filtre catalytique et polarisation, Patent FR3037655 (B1) 2017-07-28 , US US2018188202 (A1) 2018-07-05; Canada CA2989484 (A1) 2016-12-22;; WO2016202997 (A1) 2016-12-22.
  30. J. Cui, Z. Hao, Y. Wang, L. Xue, H. Xue, L. Tu, L. Hao, M. Tian, J. Guo, D. Zhao, G. Kevin Li, H. Ding, Mechanism of ozone-assisted catalytic oxidation of isopropanol over single-atom platinum catalysts at ambient temperature, Chemical Engineering Journal 2022, 446, Part 2, p.136989. [CrossRef]
  31. H. Wei, T. Wei, L. Li, T. Zhang, F. Seidi, Y. Jin, H. Xiao, Morphological effect of ceria-supported platinum catalyst on low-temperature ethylene oxidation, Applied Catalysis B: Environmental 2023, 324, p.122242. [CrossRef]
  32. C. Krause, V.M. Mirsky, and K.D. Heckmann, Capacitive Detection of Surfactant Adsorption on Hydrophobized Gold Electrodes, Langmuir 1996, 12 (25), p.6059-6064. [CrossRef]
  33. Y. Shi and N. Cai, A general mechanistic model of solid oxide fuel cells, Tsinghua Science and Technology 2006, 11(6), p.701-711. [CrossRef]
  34. M. Aliramezani, C.R. Koch, M. Secanell, R.E. Hayes, R. Patrick, An electrochemical model of an amperometric NOx sensor, Sensors and Actuators B: Chemical 2019, 290, p.302-311. [CrossRef]
  35. V. S. Bagotzky, Fundamentals of electrochemistry, 2nd ed.; John Wiley & Sons, Inc. : Hoboken, New Jersey, United States, 2006.
Preprints 95211 g001
Figure 1. a) Sensing side of the NOX sensor , b) Heating side of the NOX sensor.
Figure 1. a) Sensing side of the NOX sensor , b) Heating side of the NOX sensor.
Preprints 95211 g001
Preprints 95211 g002
Figure 2. E.F.M measurement of a polarized voltage.
Figure 2. E.F.M measurement of a polarized voltage.
Preprints 95211 g002
Preprints 95211 g003
Figure 3. Electrical design of the electrode for model 1: base gas only.
Figure 3. Electrical design of the electrode for model 1: base gas only.
Preprints 95211 g003
Preprints 95211 g004
Figure 4. Electrical design of the electrode for model 2: addition of an oxidizing gas.
Figure 4. Electrical design of the electrode for model 2: addition of an oxidizing gas.
Preprints 95211 g004
Preprints 95211 g006
Figure 6. Example of response curve obtained experimentally under base gas modifying O2 concentration.
Figure 6. Example of response curve obtained experimentally under base gas modifying O2 concentration.
Preprints 95211 g006
Preprints 95211 g007
Figure 7. a) Experimental and modeled overpotential evolution according to gaseous environment (base gas – O2 variation from 1 to 12% at 500°C) and polarization current sequence (0nA - 20nA - 0nA – 40nA – 0nA) at 500°C b) Zoomed view of the second part with polarization current of 40nA.
Figure 7. a) Experimental and modeled overpotential evolution according to gaseous environment (base gas – O2 variation from 1 to 12% at 500°C) and polarization current sequence (0nA - 20nA - 0nA – 40nA – 0nA) at 500°C b) Zoomed view of the second part with polarization current of 40nA.
Preprints 95211 g007
Preprints 95211 g008
Figure 8. Experimental and modeled overpotential evolution according to gaseous environment (base gas – O2 variation from 1 to 12%) and polarization current sequence (0nA – 25nA - 0nA) at 500°C.
Figure 8. Experimental and modeled overpotential evolution according to gaseous environment (base gas – O2 variation from 1 to 12%) and polarization current sequence (0nA – 25nA - 0nA) at 500°C.
Preprints 95211 g008
Preprints 95211 g009aPreprints 95211 g009b
Figure 9. Experimental and modeled overpotential evolution according to gaseous environment (12% O2 + gas concentrations between 100 and 1000ppm) and polarization current sequence (0nA - 25nA – 150nA - 0nA) at 500°C - a)with assumption that k 0 g a s , γ g a s don’t change while changing the polarization current b) with assumption that k 0 g a s , γ g a s can change while changing the polarization current.
Figure 9. Experimental and modeled overpotential evolution according to gaseous environment (12% O2 + gas concentrations between 100 and 1000ppm) and polarization current sequence (0nA - 25nA – 150nA - 0nA) at 500°C - a)with assumption that k 0 g a s , γ g a s don’t change while changing the polarization current b) with assumption that k 0 g a s , γ g a s can change while changing the polarization current.
Preprints 95211 g009aPreprints 95211 g009b
Preprints 95211 g010
Figure 10. Experimental and modeled overpotential evolution according to gaseous environment (base gas, CO, NH3, NO, NO2) and oxygen concentrations (0.5%, 1%, 2%, 3%, 5%, 7%, 9%, 12%) at 450°C.
Figure 10. Experimental and modeled overpotential evolution according to gaseous environment (base gas, CO, NH3, NO, NO2) and oxygen concentrations (0.5%, 1%, 2%, 3%, 5%, 7%, 9%, 12%) at 450°C.
Preprints 95211 g010
Table 1. k 0 b a s e , α b a s e and γ b a s e extracted values for temperatures between 450 and 550°C.
Table 1. k 0 b a s e , α b a s e and γ b a s e extracted values for temperatures between 450 and 550°C.
Sensor Temperature (°C) k 0 b a s e × 10 − 9 α b a s e γ b a s e
1 450 3.2 0.026 0.09
500 11 0.025 0.13
550 25 0.027 0.13
2 450 3.5 0.025 0.10
500 5.5 0.034 0.10
550 14.8 0.027 0.09
Table 2. k 0 b a s e , α b a s e  and γ b a s e extracted values for the polarization currents tested at 500°C.
Table 2. k 0 b a s e , α b a s e  and γ b a s e extracted values for the polarization currents tested at 500°C.
Gas Polarization current (nA) k 0 b a s e α b a s e γ b a s e
Base gas 25 - 50 - 150 [5 – 12].10-9 0.03 – 0.04 0.1 – 0.15
N O 2 25 [3 – 5].10-9 0.03 - 0.04 0.25 - 0.3
50 [3 – 7].10-8 0.03 - 0.04 0.4 - 0.6
150 [3 - 13].10-8 0.03 - 0.04 0.4 - 0.7
N O 25 [4 – 8].10-9 0.06 – 0.08 0.5
50 [7 – 17].10-8 0.06 – 0.08 0.5 - 0.7
150 [12 - 40].10-8 0.06 – 0.08 0.5 - 0.8
C O 25 [7 – 25].10-9 0.03 - 0.04 0.09
50 < 10-10 Not assessable Not assessable
150 < 10-10 Not assessable Not assessable
Table 3. Extracted parameters while varying the oxygen concentration.
Table 3. Extracted parameters while varying the oxygen concentration.
Gas k 0 b a s e α b a s e γ b a s e
Base gas [ 1.5 − 3.5 ]   .   10 − 9   0.02 – 0.035 0.09 - 0.16
Oxidant gas NO2 [ 6 − 10 ]   .   10 − 8 0.0014 – 0.015 0.3 - 0.4
NO [ 5 − 47 ]   .   10 − 8 0.003 – 0.05 0.4 – 0.5
Reductant gas CO [ 2 − 7 ]   .   10 − 9   0.02 – 0.035 0.09 - 0.16
NH3 < 10-10 Not assessable Not assessable
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated