1. Introduction
Modern cosmology is a dynamic nexus of theoretical and experimental endeavors, continually evolving to surmount novel challenges. The discipline necessitates systematic reconstruction to harmonize theory with emerging observational data at each juncture. A watershed moment in this ongoing narrative unfolded with the revelation of supernova dimming, a phenomenon that revealed the limitations of the Friedmann-Lemaitre-Robertson-Walker metric (herein Friedmann metric). The cosmological constant was introduced to align the theoretical predictions with empirical insights (Riess et al., 1998) to address this dissonance.
Contemporary surveys and astronomical observations reveal galaxies exhibiting an escalating recession from our vantage point. At the heart of current cosmological discourse lies the pivotal conundrum of elucidating the structure formation and galactic evolution juxtaposed against the backdrop of the accelerated expansion in the late-time universe. The Friedmann model, rooted in the cosmological principle, has admirably explained the universe's evolution in concordance with empirical observations. Yet, the enigma of dark energy, the impetus behind cosmic acceleration, remains an intractable challenge within the ambit of contemporary physical cosmology.
Various attempts to explain cosmic acceleration lean on constructs such as the cosmological constant or regimes dominated by dark energy. Nevertheless, the elusive origins of dark energy, coupled with the cosmological constant's conundrums, pose formidable puzzles. Compounding these challenges is the potential violation of the cosmological principle when homogeneity or isotropy falters in galaxy structure formation (Melia & Shevchuk, 2012).
As three-dimensional redshift surveys delve deeper into the cosmos, revealing structures bereft of a transition to homogeneity, questions proliferate regarding the steadfastness of the cosmological principle. The identification of large quasar groups (LQG) further catalyzes the debate, suggesting an inherent inhomogeneity incompatible with prevailing cosmological paradigms (Clowes et al., 2013; Pandey & Sarkar, 2016). Such revelations underscore the need for a profound cosmological reassessment.
While two-dimensional projections appear consonant with isotropy and homogeneity, three-dimensional catalogues unveil an intricate tapestry of inhomogeneous galactic distributions. Divergent findings regarding the transition to homogeneity confound attempts at a unified perspective (Labini, 2011; Meszaros, 2019). The advent of the Vera Rubin Observatory promises a transformative ten-year vista, poised to capture the entire visible night sky and delve into the cosmic intricacies, armed with a 3.6 Gigapixel camera (Brough et al., 2020).
The juxtaposition of these observations challenges the conventional tenets of cosmic homogeneity and isotropy. The implications extend beyond mere academic discourse, with potential ramifications for understanding cosmic acceleration and the need for an additional dark energy component (Ellis, 2011). Motivated by these considerations, this study seeks to unravel the intricacies of the cosmos, probing the validity of the cosmological principle and explaining the universe's structure formation, evolution, and late-time accelerated expansion.
However, these ambitious objectives hinge upon an indispensable prerequisite—an abundance of accurate and expansive cosmological data. Despite the burgeoning corpus of observational data, limitations persist, necessitating a cautious interpretation of the current cosmological model's completeness and accuracy (Paris et al., 2017). The yawning gap between observational data and theoretical aspirations prompts an introspective evaluation of the present cosmological paradigm.
In light of the disquieting revelations from three-dimensional catalogues, a pervasive unease pervades the current cosmological model's standing. In an attempt to bridge this gap, we propose a modified Friedmann model calibrated to the distribution of luminous matter in the universe. This paper delineates our quest to ascertain the validity of the prevailing cosmological model, offering a lens through which to scrutinize its shortcomings and potential incompleteness. As we embark on this analytical odyssey, guided by the framework of cold dark matter cosmologies, our gaze extends beyond the current cosmological dogma, contemplating the far-reaching implications of a modified redshift approach.
The ensuing sections of this paper are structured to unfold as follows:
Section 2 introduces pertinent models relevant to our discourse, while
Section 3 illuminates our analytical findings.
Section 4 engages in the simulation and discussion of these findings, and the paper culminates in
Section 5 with definitive conclusions.
2. Background Model Formulation
2.1. Parametric Model
The parametric model proposed by Bassett et al. in 2015 introduces modifications to the traditional redshift paradigm, seeking to refine our understanding of cosmic dynamics. This model involves the introduction of parameters that capture modifications in the redshift-space, allowing for a more nuanced interpretation of observational data. The model addresses nuanced aspects of cosmic phenomena by incorporating specific parameters, providing a more detailed and accurate representation of redshift-related observations.
2.2. Non-parametric Model
The non-parametric model, as formulated by Wojtak and Prada in 2017, takes a distinct approach by avoiding predefined parameters, allowing for greater flexibility in modeling cosmic phenomena. Unlike parametric models, the non-parametric model refrains from imposing fixed parameters, enabling a more adaptive and data-driven analysis of redshift-related phenomena.
This model is precious in scenarios where the underlying dynamics are complex and not easily encapsulated by predefined parameters. It provides a more versatile tool for interpreting observational data.
The above two models proposed by Bassett et al., (2015) and Wojtak & Prada (2017) and used in this paper contribute to the diverse toolkit in cosmology, offering different perspectives on how redshift modifications can enhance our understanding of the universe. While the parametric model introduces specific parameters to capture nuances, the non-parametric model embraces a more flexible and adaptive approach, catering to the intricacies of cosmic dynamics.
2.3. The Friedmann Model
Consider the Einstein field equations in the form:
Here, is the Einstein tensor, which is computed from the metric tensor , is the Ricci tensor, is the Ricci scalar, λ is the cosmological constant representing the dark energy component, is the energy-momentum tensor characterizing matter distribution and β = where G is the gravitational constant and is the speed of light.
Consider also the Friedmann-Lemaitre-Robertson-Walker spacetime metric for a universe that is filled with homogeneous and isotropic matter:
Here, being the scale factor of the universe representing the time-dependent evolution of spatial part of the metric on surfaces of constant time , and , determines the geometry of these spatial sections as non-flat and flat, respectively.
Derivations involving equations (1) and (2) yield two Friedmann equations for describing the relativistic dynamics and evolution of the universe (see details of calculations in Langa et al., 2017), expressed as:
and
Here, the single and double overhead dots denote the first and second derivatives with respect to time t, respectively; is the space curvature geometry with values or ; and is the pressure while is the density of the universe both expressed as functions of time .
Equations (3) and (4) have been demonstrated (Langa et al., 2017; Wamalwa, 2016) to yield:
The left-hand-side of this equation represents the rate of change of total energy in the universe. In the matter-dominated cosmology, where the main energy density is in cold, non-relativistic matter behaving like dust (i.e.,
), equation (5) simplifies to
Equation (6) indicates that the total mass contained in the universe remains constant, aligning with the relativistic theory of matter and fields (Noether’s theorem), where there is no preferred direction for the motion of matter to maintain isotropy.
Equation (6) can be reformulated as (Langa et al., 2017; Wamalwa, 2016):
Equation (7) represents the time taken for a light photon to travel at a distance =), describing a matter-dominated Friedmann Universe. Friedmann equations (3) and (4) in the form of equation (7) will later be employed in this paper to derive the light intensity-modified redshift and number density-modified redshift relations.
2.4. Modified Redshift Model
In this work, we undertake an examination of a modified redshift relation to scrutinize the nascent evolution, structure formation, and characteristics of dark matter and dark energy within a matter-dominated Friedmann universe. Our methodology involves the incorporation of a modified version of the standard redshift relation, as introduced by Tian in 2017, into the Friedmann equations. The model (Tian, 2017) is succinctly delineated as follows:
The conventional correlation between cosmological redshift and the cosmic scale factor for light photons is expressed as
hereafter referred to as the standard redshift relation. Should we posit that unknown quantum effects exert a discernible influence on the frequency of light photons during their cosmological propagation; the aforementioned relation can be altered to
It is discernible from the modified redshift equation that when = , the equation reverts to its standard form. Consequently, the modified equation, being more generalized, is anticipated to yield more comprehensive results upon the appropriate specification of . This augmentation transcends classical experimental tests aimed at discerning between the metric and non-metric origins of the cosmological redshift. Consequently, we address the inquiry of whether the phenomenologically modified redshift relation model aligns with theoretical analytical outcomes within the λCDM cosmological model and, if not, endeavor to discern its implications. This modification is grounded in the premise that photons, central to the early development of quantum theory, must exhibit quantum effects during their spatial propagation.
We shall proceed to fit the derived Friedmann equations using parameteric equation ( Bassett et al., 2015):
where
and
are arbitrary parameters and non-parametric (Wojtak & Prada , 2017) modified redshift functions
where
is a freely varying function of
. The parameter values in these models are constrained through standard observational datasets to deduce the optimal present values of cosmological parameters for a comprehensive analysis of the behavior of physical parameters. Notably, these models, grounded in the redshift-scale factor-remapping concept, exhibit consistency with contemporary astronomical observations (Wojtak & Prada, 2017). We introduce slight variations in parameter values and endeavor to elucidate the late-time accelerated expansion of the universe across both light intensity and number density measurement channels. The overarching aim is to assess the compatibility of the general outcomes with ongoing and prospective cosmological observations.
Furthermore, we posit a theoretical model in the form
The utilization of a model incorporating a free parameter, denoted as ε, unfolds a compelling framework (equation (12)). As ε approaches unity, the model seamlessly converges with a well-established expression, wherein z/ε approximates z. Importantly, this model accommodates scenarios where both z is less than z/ε and z surpasses z/ε. The versatility of this model, in conjunction with other aforementioned models, renders it a promising tool for scrutinizing cosmic structures. Furthermore, its application serves as a stringent test for the consistency of the standard λCDM model.
These models, when integrated into the Friedmann equations, offer a nuanced perspective on relativistic dynamics and structure formation within a matter-dominated Friedmann universe. However, the amalgamation of the Friedmann equation with modified redshift mapping may initially appear incongruous. This apparent incongruity stems from the inherent limitation of assuming the accuracy of the Friedmann metric across all scales and the correctness of General Relativity, at least on large-length scales.
The inconsistency in this amalgamation can be attributed to either the inadequacy of the Friedmann metric in capturing the first derivatives of the actual metric of the universe ( Green & Wald, 2014) or the potential violation of the General Relativity framework, particularly when photons traverse along null geodesic lines. Notably, the inadequacies of the Friedmann metric may be pronounced in scenarios involving cosmic acceleration.
In the realm of cosmic acceleration, models devoid of dark energy, and dominated by matter, assume special significance. In these models, the modified redshift, determined through observation, plays a pivotal role in accounting for cosmic acceleration. This underscores the need for a comprehensive exploration of these models to refine our understanding of the universe and reconcile discrepancies in existing frameworks.
3. Analytical Solutions
3.1. Light intensityModified Redshift
To establish a functional relationship between light intensity,
emanating from an astronomical object and the modified redshift
, let
be the time when a star or galaxy emits a light ray that travels towards an observer located at the origin of our coordinate system. The light reaches the observer at time,
. Thus, the emitted light commences at
and travels towards the origin, ultimately arriving at
. Suppose that at time
, ((
)), an observer measures the brightness,
of that light which he receives at that given redshift. The light emitted in the time interval
will transverse the observer in the time interval
. During this process, the number of photons is conserved as the radiation traverses through the universe. Nevertheless, each of this photon is red-shifted relative to the emitted increasing wavelength of their spectrum leading to a decrease in their energy by a factor
This means that the energy that passes through our spherical ball of radius
during the interval
is the same as the product of
and the energy emitted during the interval (
. We can therefore, express light intensity,
which is dependent on luminosity,
of luminous matter in the universe as
where
denotes the surface area of the sphere of radius,
at time
.
For light-like events or null geodesics (i.e.,
) in equation (2):
Together with equation (7)
, it is easy to show that:
where we have applied the principle of reversibility of light and assumed that
is positive and
is negative.
Calculations based on equation (15) for three cases of curvature of the universe i.e., for flat (
and non-flat (
universes gives
Here, we have applied the equation = 0 together with the modified redshift relation in equation (9).
For the case of a unit sphere, we set = 1; so that is the separation distance between stars or galaxies in the universe at the present observational time and is the distance between stars or galaxies in the universe after emission of light photons (the late-time value of the cosmological scale factor after emission of light photons).
The three curvature cases in equation (17) can be compacted to one solid equation as
Defining:
and considering that the cosmic time
depends on the evolution of the function
, we therefore consider
as a function of
such that equation (18) can be simplified as
The function in the modified redshift equation (18) is a more general form of the redshift than in the standard case i.e., when . The results are also bound to be more general and may deviate from the standard redshift predictions.
Equation (15) can be simplified and integrated from time,
of emission to time,
of observation and from the coordinate radius
to
as:
Integration of equation (22) involving application of fundamental theorem of integral calculus, modified redshift relation = = , and surface area of the sphere,
=
gives:
Application of equation (21) in equation (23) gives the first analytical result
If we drop
λ, then the corresponding formula for
without dark energy reduces to
with
3.2. Number Density-Modified Redshift
Assuming that our astronomical objects (stars or galaxies) under considerations are distributed uniformly in the universe such that we can count the number of stars or galaxies we observe in a given redshift interval. Taking as the number of stars or galaxies per unit volume of space with metric by and volume element of the hyper-sphere surface as , the number of stars between coordinates and is .
Differentiation of equation (18) with respect to
in view of equations (19) and (20) gives:
The number of galaxies enclosed between coordinate hyper-spheres in a given redshift interval is given as
so that substituting equations (18) and (21) into equation (26), we get the first analytical result
If we drop
, then the corresponding formula of
without dark energy reduces to
where
Equations (25) and (29) form two relativistic analytical modified Friedmann equations for describing dynamics and evolution of our universe.
The evolution of light intensity and number density of galaxies or stars as functions of redshift is given respectively by (see Langa et al., 2017)
and
where
Equations (30) and (31) encapsulate the relativistic dynamic Friedmann analytical solutions, elucidating the dynamics and evolution of the universe within the standard λCDM model. However, in the subsequent evolution of the universe simulated for phenomenological models, the consideration of vacuum energy becomes superfluous. The observed value of cosmological constant is conspicuously minuscule and diverges significantly from theoretical predictions—approximately 122 orders of magnitude smaller than the value anticipated by quantum field theory.
To circumvent this incongruity, a cosmic methodology has been employed, one that effectively nullifies the contribution of quantum vacuum energy to gravity (λ=0). This deliberate exclusion of vacuum energy serves as a foundation for studying the early evolution, structure formation, and large-scale distribution of the universe. Our computer simulations, grounded in this novel approach, afford us the opportunity to delve into the properties of dark matter and dark energy, offering insights into their roles in shaping the universe.
By embracing this alternative perspective, we aim to unravel the intricacies of the universe's early epochs, comprehend the mechanisms driving structure formation, and gain a nuanced understanding of the distribution of cosmic structures on expansive scales. This departure from the conventional treatment of vacuum energy in our simulations reflects a commitment to exploring novel avenues in cosmological research, where theoretical predictions and observed values are reconciled through innovative methodologies.
4. Numerical Solutions
This section embarks on the simulation of predictions derived from the analytical solutions of two cosmological models, namely the standard λCDM universe and the modified CDM Friedmann model. The equations governing light intensity and number density as functions of redshift are explicitly articulated for both models – equations (30) and (31) for the λCDM universe, and equations (25) and (29) for the modified CDM model. Through these simulations, we seek to elucidate the impact of cosmic accelerated expansion on galaxy formation, distinguishing between the effects attributed to modified redshift and those arising from the cosmological constant, λ. The overarching goal is to underscore the robust theoretical underpinning of cosmic acceleration, irrespective of the ongoing debates surrounding the mysteries of dark matter and dark energy.
The simulated results presented herein align consistently with cosmological observations, thereby bolstering our comprehension of the accelerated expansion of the universe and contributing insights into lingering challenges in physical cosmology.
Parameter values employed in these simulations are meticulously chosen, with constraints derived from cosmological observational data. Variations in parameters, achieved through a nuanced adjustment in the MATLAB application, shed light on the kind of universe expected from our model. Notably, parameters such as ε=α₁ and γ=α₂=(1,0) exhibit no discernible modification of the redshift, rendering the standard and modified model curves indistinguishable. However, it is emphasized that only sufficiently small parameter values permit the formation of a universe conducive to hosting observers. Larger positive values induce rapid expansion, hindering the formation of gravitational structures, while large negative values precipitate a swift collapse, also precluding galaxy formation. The subtle variation of parameters serves the dual purpose of exploring additional statistically significant features of cosmic structures and revealing the resilience of the model under slight perturbations.
The MATLAB codes employed in these simulations adhere to constants such as redshift spanning from z = 0 to z = 5, density of the universe ranging from ρ(to) = 3e−27 kgm−3 to ρ(to) = 8.78e−25 kgm−3, speed of light c = 3 × 108 m/s, cosmic scale factor R(to) = 9e25 m (modifiable as needed), gravitational constant G = 6.67 × 10−11 m³ kg⁻¹ s⁻², and the geometric curvature of the universe, where κ = 0 signifies a flat universe, κ = +1 designates a closed universe, and κ = -1 represents an open universe. Parameter values reconstructed from observational data are incorporated into the modified redshift models and are slightly varied for comparison under consistent matter density and curvature of the universe. All values employed in the codes adhere to existing statistical data.
Figure (4.1.1) displays the simulation results for the evolution of light intensity in the λCDM model, based on equation (30), while Figures (4.1.2) – (4.1.4) portray simulation outcomes for the evolution of light intensity within modified models, grounded in equation (25). These visual representations offer a nuanced understanding of the intricate dynamics governing the evolution of cosmic structures under distinct cosmological paradigms.
4.1. Light Intensity-Redshift Graphs
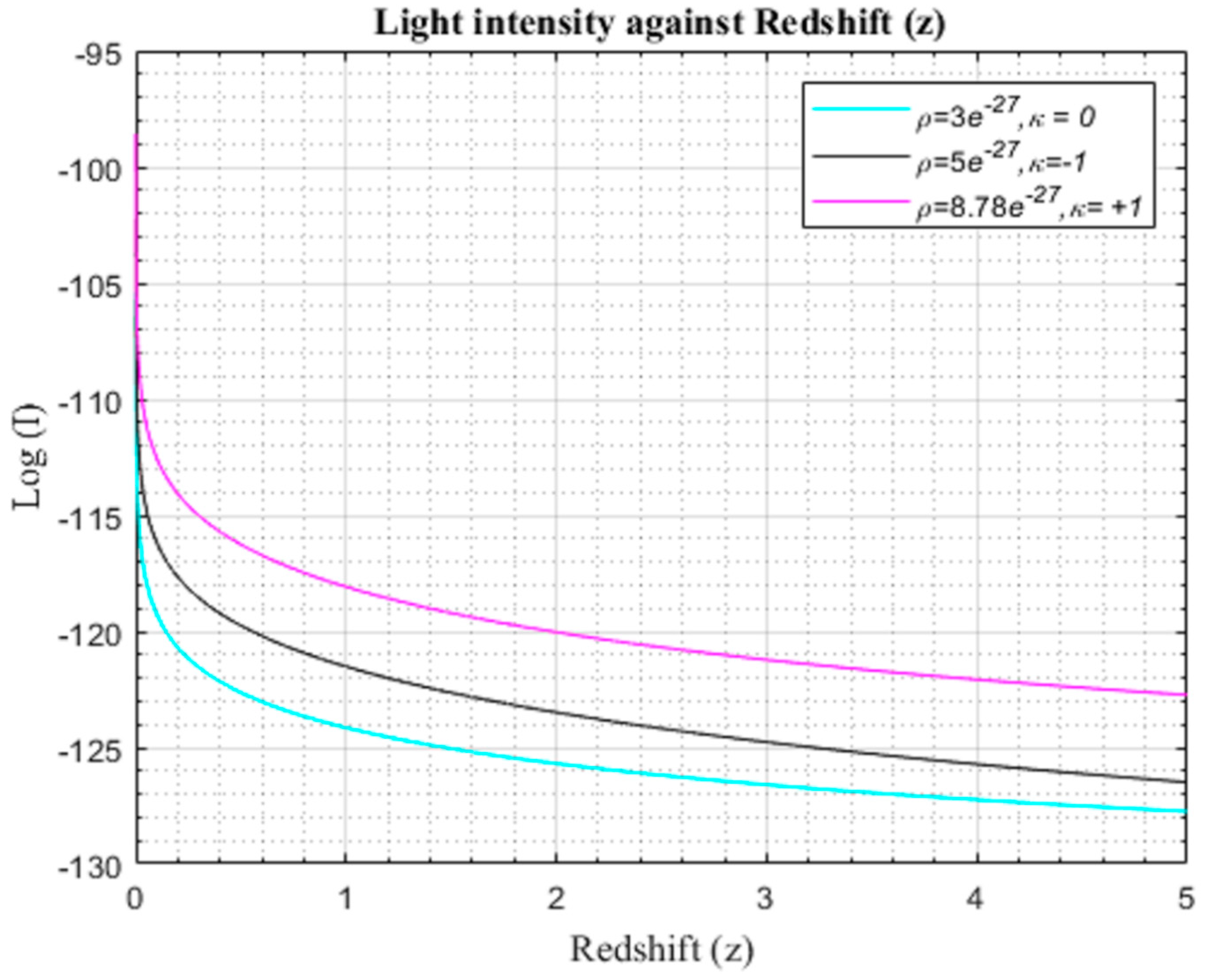
Figure 4.1.1.
Simulation result for log (I) against redshift for to for the λCDM model.
Figure 4.1.1.
Simulation result for log (I) against redshift for to for the λCDM model.
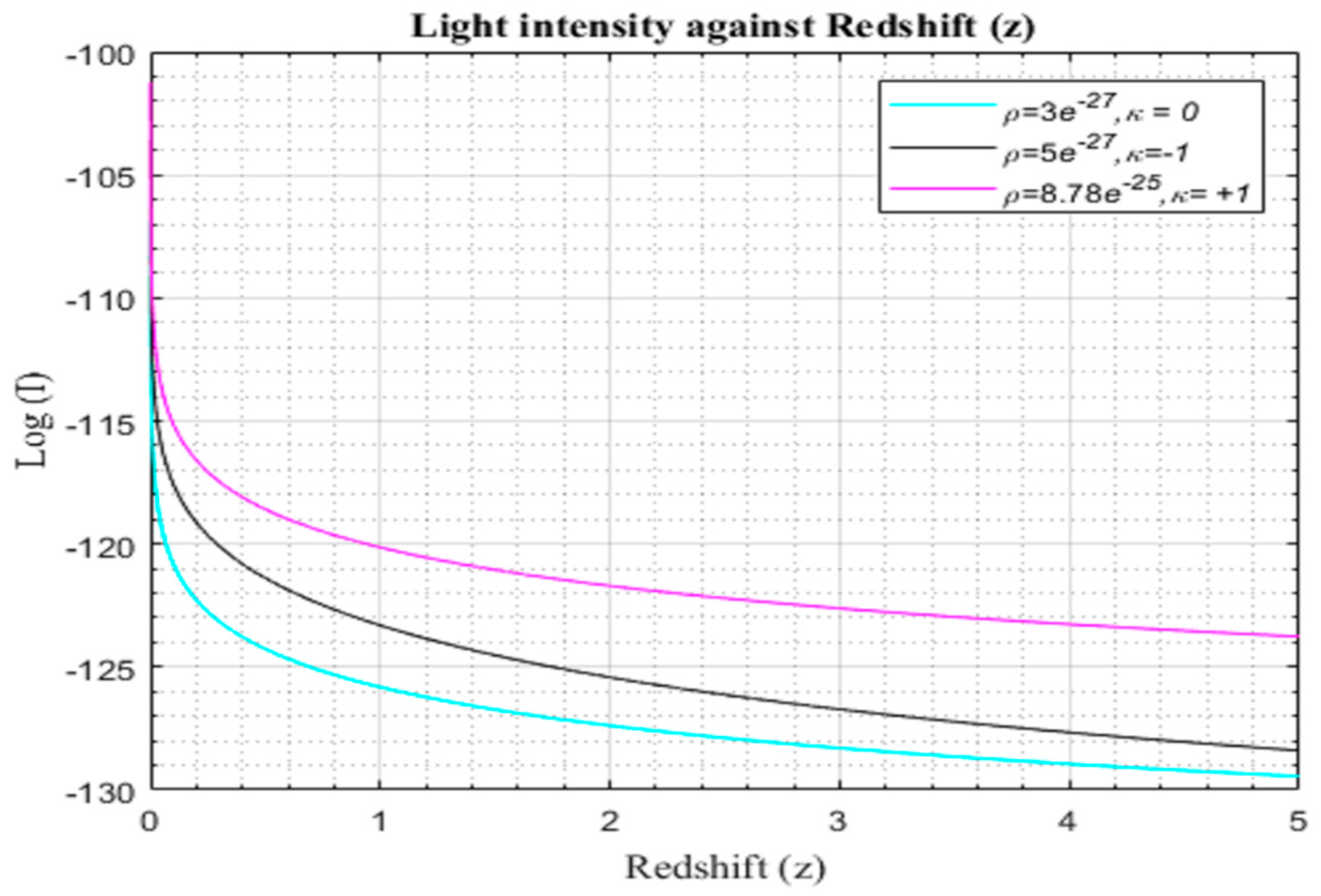
Figure 4.1.2.
Simulation result for log (I) against redshift with and for to for the modified CDM model.
Figure 4.1.2.
Simulation result for log (I) against redshift with and for to for the modified CDM model.
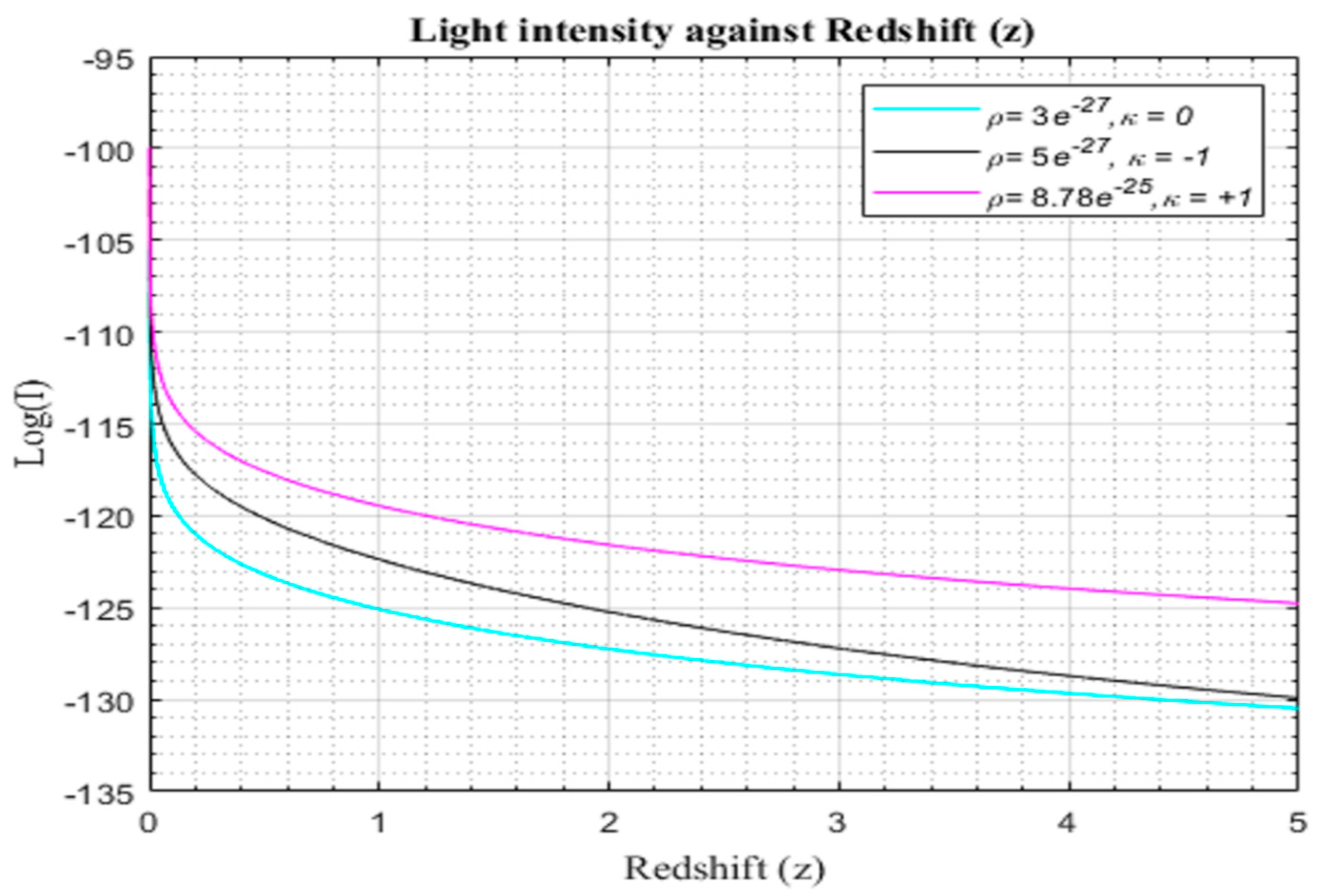
Figure 4.1.3.
Simulation result for log (I) against redshift =, where is a free function of with for to for the modified CDM model.
Figure 4.1.3.
Simulation result for log (I) against redshift =, where is a free function of with for to for the modified CDM model.
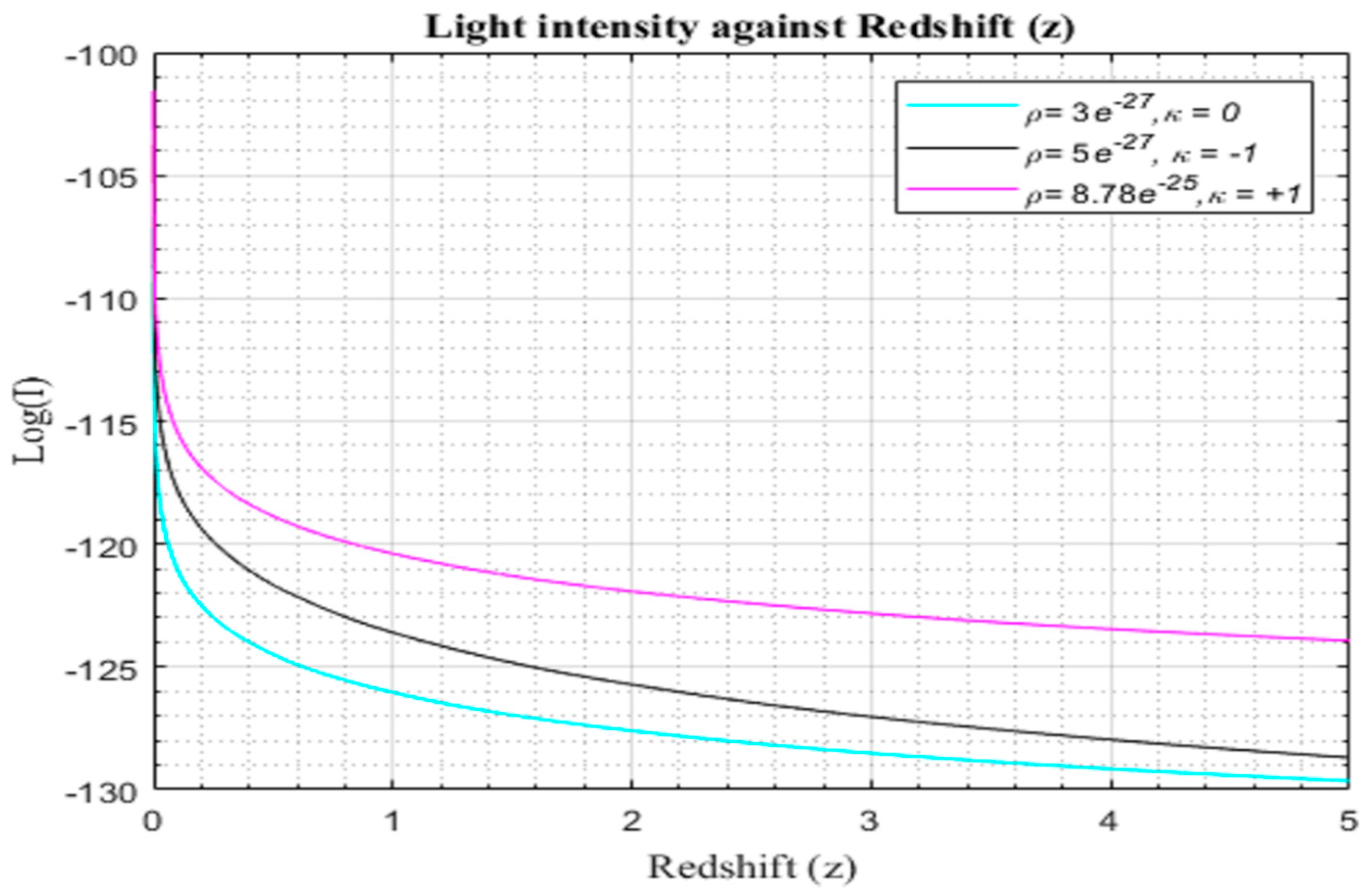
Figure 4.1.4.
Simulation result for log (I) against redshift with for to for the modified CDM model.
Figure 4.1.4.
Simulation result for log (I) against redshift with for to for the modified CDM model.
4.2. Number Density-Redshift Graphs
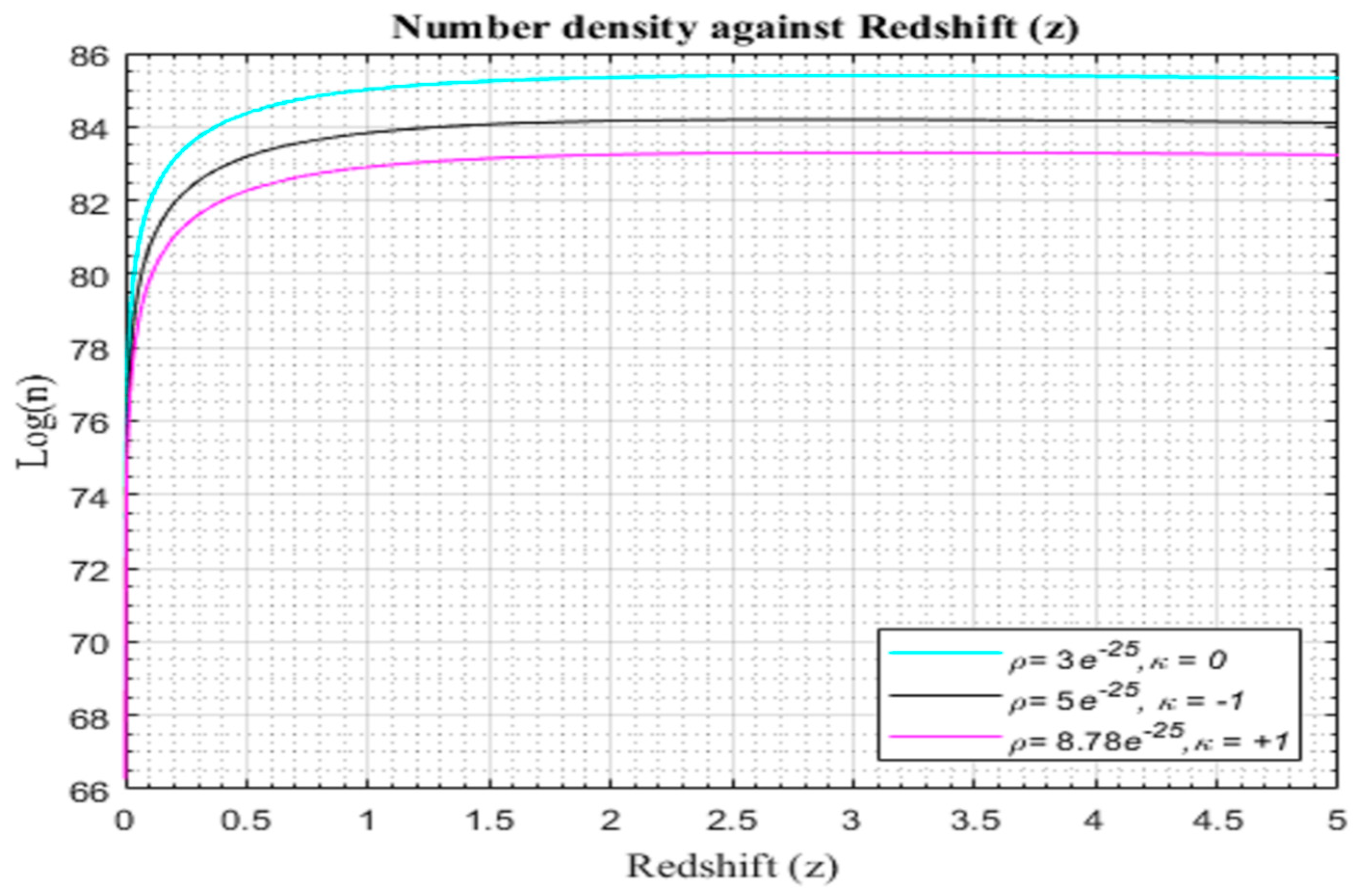
Figures (4.2.1) show simulation result of number density of galaxy formation with dark energy in the λCDM model based on equation (31) while Figures (4.2.2) – (4.2.4) show simulation result of number density of galaxy formation with modified CDM model based on equation (31).
Figure 4.2.1.
Simulation result for log (n) against redshift for to for the λCDM model.
Figure 4.2.1.
Simulation result for log (n) against redshift for to for the λCDM model.
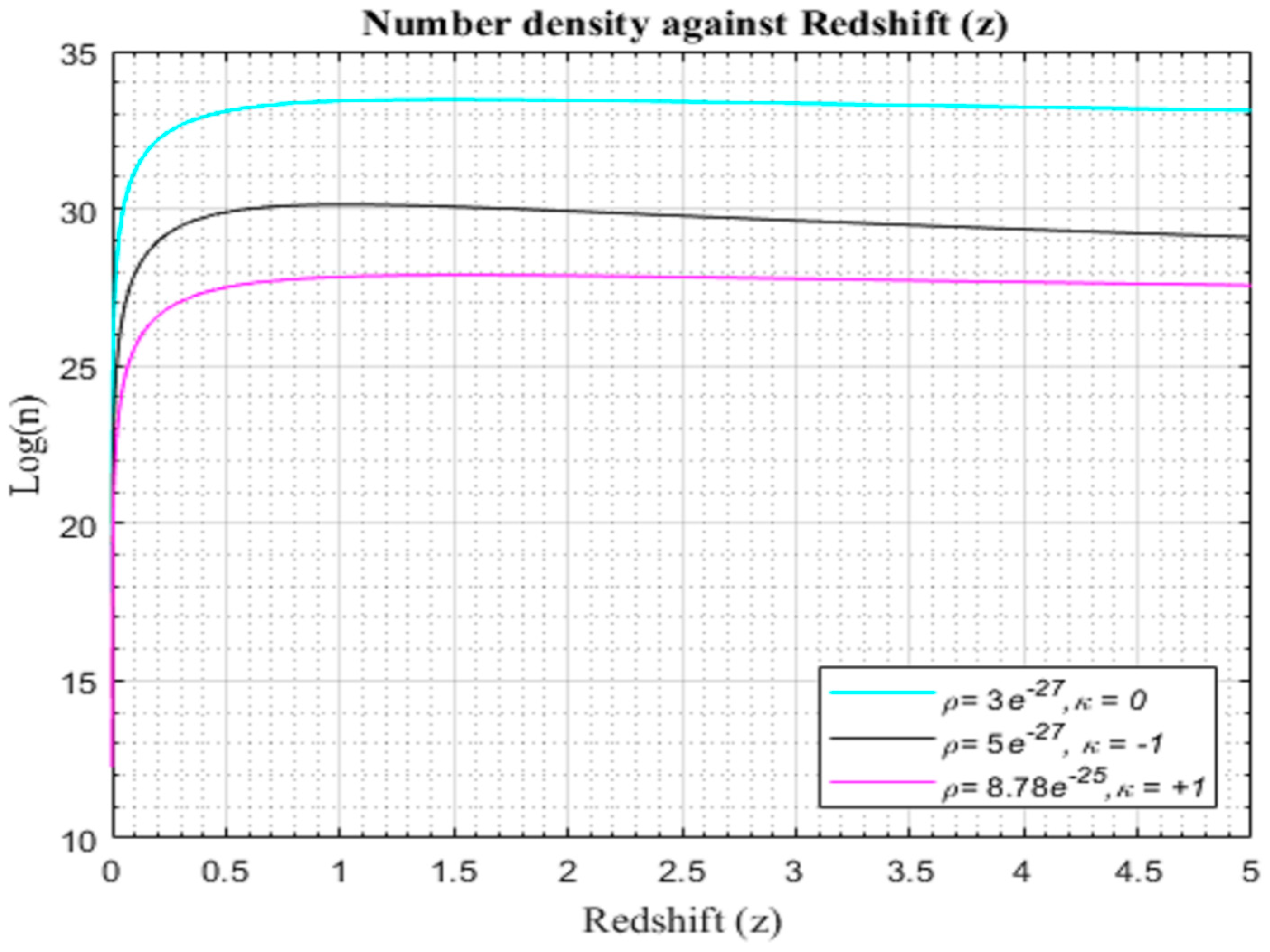
Figure 4.2.2.
Simulation result for log (n) against redshift with and for to for the modified CDM model.
Figure 4.2.2.
Simulation result for log (n) against redshift with and for to for the modified CDM model.
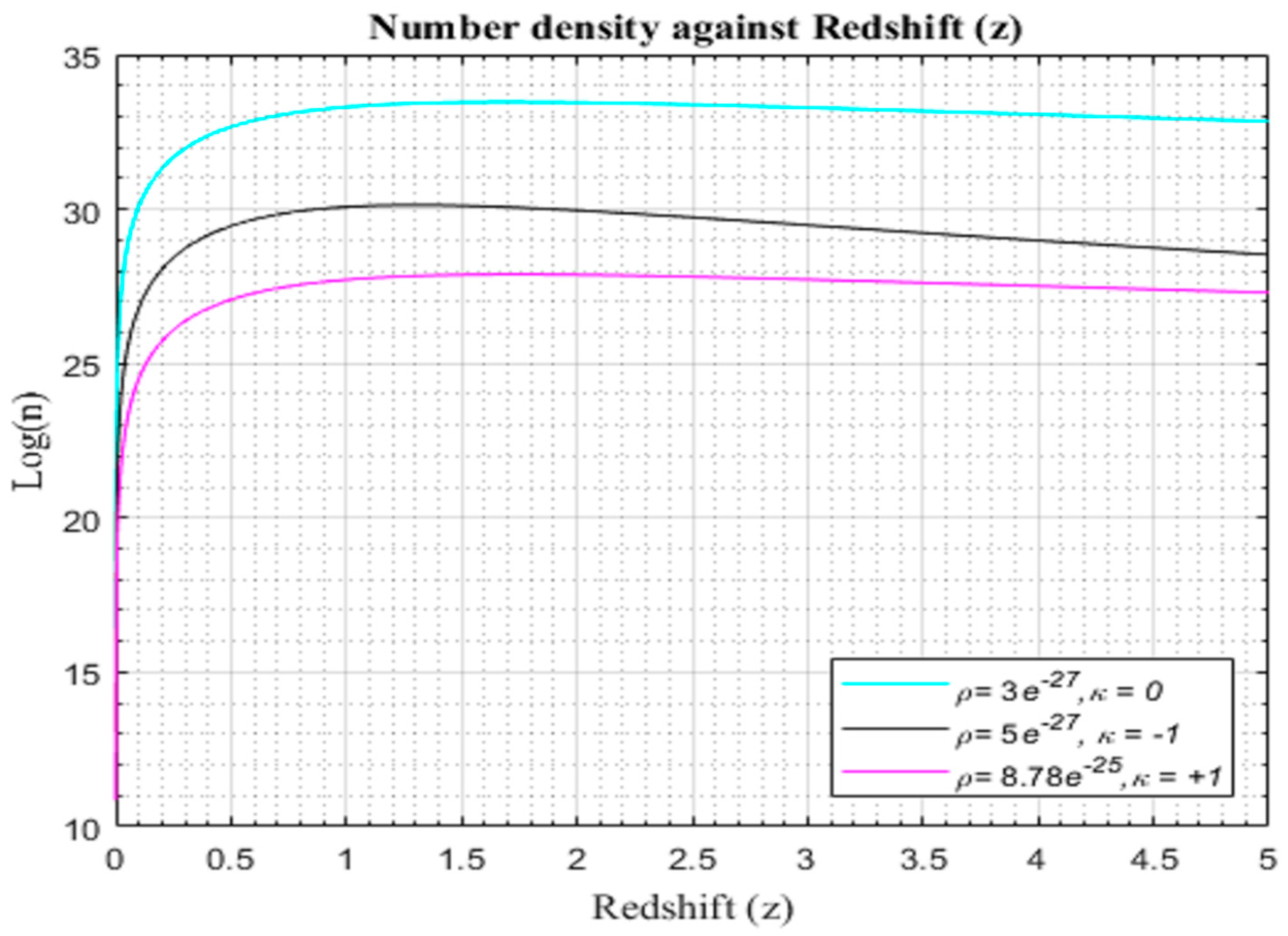
Figure 4.2.3.
Simulation result for log (n) against redshift = , where is a free function of with for to for the modified CDM model.
Figure 4.2.3.
Simulation result for log (n) against redshift = , where is a free function of with for to for the modified CDM model.
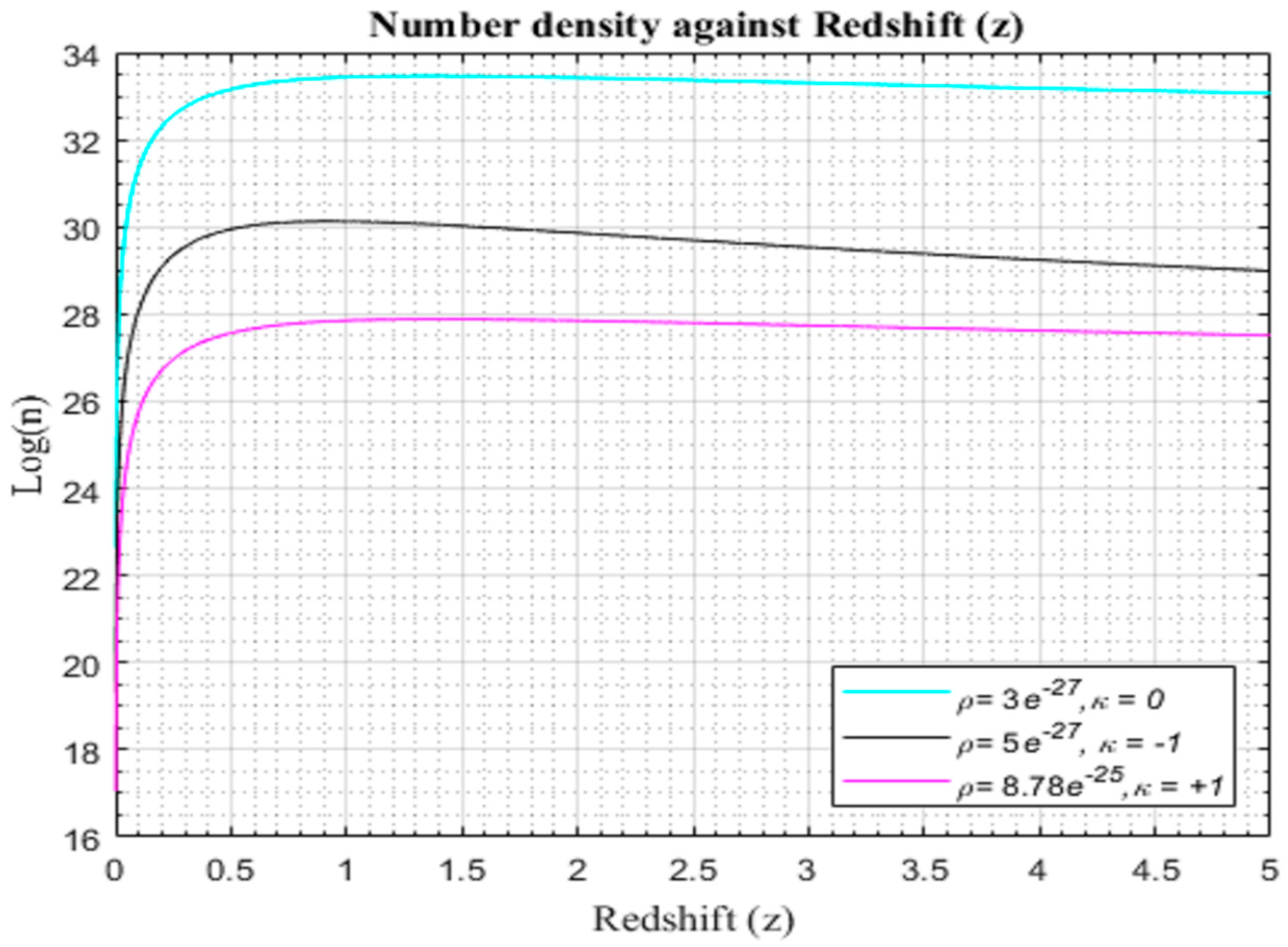
Figure 4.2.4.
Simulation result for log (n) against redshift with for to for the modified CDM model.
Figure 4.2.4.
Simulation result for log (n) against redshift with for to for the modified CDM model.
5. Discussion
5.1. Light Intensity of Galaxy Distribution
The light intensity from galaxies manifest a discernible pattern in the range of redshifts delineated in Figures (4.1.2)–(4.1.4), characterized by an exponential attenuation without discernible bounds. Intriguingly, the profiles of the modified light curves mirror this decay, aligning remarkably with the λCDM reference curves. This congruence in behavior persists irrespective of the underlying geometry of the universe, suggesting a level of universality in the light intensity dynamics.
A notable departure emerges when scrutinizing the temporal evolution of these light intensity functions. The modified model exhibits a trajectory distinct from the λCDM model, deviating notably at early epochs and extending into the future. This temporal bifurcation concurs with the theoretical propositions put forth by Langa et al. in 2017, thereby reinforcing the credibility of the modified model's departure from the conventional cosmic trajectories.
It is crucial to underscore that, despite sharing identical initial conditions at the epoch of the earliest universe (z=0), the λCDM model and the modified model diverge notably in the later stages of evolution (z>0). A nuanced analysis of the high-redshift galaxies in the modified model reveals an additional dimming effect when compared to their counterparts in the
CDM model. This disparity in light intensity attenuation serves as a crucial indicator of the accelerated expansion of the universe within the modified model, a phenomenon vividly elucidated in figures (4.1.2)-(4.1.4) when compared with figure (4.1.1).
This discernible extra dimming of high-redshift galaxies in the modified model not only underscores the dynamical distinctions between the λCDM model and the proposed modification but also serves as a compelling observational validation of the hypothesized acceleration in the expansion of the universe. Such findings contribute substantially to the ongoing discourse on cosmological models, offering nuanced insights into the intricacies of cosmic evolution. The theoretical underpinnings presented by Langa et al. (2017) further fortify the scientific rationale behind these observed divergences and accentuate the need for continued exploration into the nuanced interplay between theoretical frameworks and empirical observations
5.2. Number Density of Galaxy Formation
In examining the early stages of our universes, characterized by the initial burst of galaxy or star formation, a remarkable uniformity is observed among our models. The accelerating expansion of space, a key determinant in rendering any future accretion negligible, serves as a unifying factor at these nascent cosmic epochs. The indistinguishability of each model at early times, therefore, lays the foundation for understanding the subsequent divergences in their evolutionary trajectories.
The historical divergence among our models becomes conspicuous in the late stages, primarily attributable to the onset of dark matter-powered accelerating expansion. A noteworthy consequence of this divergence is the elimination of the coincidence problem. In scenarios where λ equals zero equates the era of matter growth that propels the cosmic accelerating force responsible for the late-time spatial acceleration. In the modified case, departure from the standard λCDM model transpires throughout all cosmic epochs. A pivotal outcome of this departure is the unmistakable manifestation of a matter density transition, marking a significant achievement in this research.
Examining Figures (4.2.2)–(4.2.4), the number density of galaxy formation exhibits a rapid rise, culminating around z≈1.8, followed by a gradual decline. Structural growth attains its zenith from approximately z≈0 to z≈1, a period coinciding with the maximum expansion rate of cosmic structures formed at z~0.9. The model we propose undergoes a phase of deceleration in the early evolution of the universe, transitioning into an acceleration phase in later times. This critical transition from early deceleration to late-time acceleration is pivotal, as the decelerating phase is imperative for structure formation, while the freeze-out of large-scale structure growth signifies the onset of dominant accelerating cosmic expansion.
As galaxies disperse due to the expanding universe, the processes of accretion and merging decelerate significantly. Consequently, there is a substantial reduction in the efficiency of the galaxy formation rate, and the total number density is predominantly dictated by contributions from the peak, stabilizing into a plateau around z≈2. The observationally reconstructed modified redshift models, propelled by dark matter dynamics, seamlessly account for all observable signatures of cosmic acceleration.
It is noteworthy that variations in parameter values, even by an order of magnitude, exert only a minor influence on the galaxy formation history and the efficiency of the universe. Furthermore, minimal adjustments to parameter values are required from those initially reconstructed from cosmological data to align with current observations. The role of cosmological constant in shaping the structure formation in the universe appears less impactful in curtailing late-time structure formation rate efficiency compared to the observed values in modified models, as elucidated in Figure (4.2.1) and Figures (4.2.2-4.2.4). Figures (4.2.2)–(4.2.4) underscore that the universe, largely, has already produced the majority of its eventual structures, contributing only marginally to future developments.
5.3. Comparing the ΛCDM and the Modified CDM Cosmological Models
In this section, our primary focus resides in the comparative analysis of the properties inherent to two cosmological models i.e., the λCDM model and the modified CDM model.
As we delve into the vast reaches of cosmic time, a salient characteristic emerges within the standard λCDM model. Here, the expansion of the universe tends asymptotically towards a constant value, portraying a distinctive trajectory. Conversely, the modified CDM model, in contrast, exhibits a more gradual descent subsequent to its zenith. This nuanced behavior leads to a discernible decrease in the number density conducive to galaxy formation, particularly as the temporal evolution progresses into the later epochs.
A critical divergence manifests in the expansion histories of universes characterized by the presence or absence of dark energy, as encapsulated by the λCDM model. This dissimilarity begets disparate growth patterns in density perturbations, especially when projected into the future temporal landscape. Notably, our model, while exhibiting statistical scaling behavior akin to λCDM during the early universe's evolutionary phase, diverges markedly as time unfolds.
The graphical representations elucidate a pronounced gap between the trajectories delineated by the
CDM and modified CDM models. This conspicuous separation serves as an empirical indicator of the influence exerted by dark matter, instigating an accelerated expansion. Despite this disparity, a commonality emerges as both cosmologies evidence the culmination of galaxy formation in the early universe.
It is imperative to acknowledge that, as temporal progression unfolds, the universe undergoes a transformative shift. During this process, the contribution of cosmic acceleration assumes paramount significance. Simultaneously, the influence of dark matter imparts a suppressive effect on the overarching structure formation, influencing the destiny of galaxies as the cosmic narrative advances into the future.
In summation, while our model aligns statistically with the λCDM paradigm during the nascent stages of the universe's evolution, a distinctive trajectory unfolds as temporal currents carry us towards the future. The interplay of dark matter and cosmic acceleration, as evidenced by the observed trajectories, serves as a testament to the multifaceted dynamics governing the complex tapestry of cosmological evolution.
5.4. Transition from Decelerating to Accelerating Expanding Universe
In this section, our primary focus revolves around discerning the suppression point within the structure amplitude, a crucial facet of our simulation on the number density of galaxies. This investigation serves as a valuable guide in anticipating the transition points between deceleration and acceleration in our modified cosmological model.
A critical examination of figures (4.2.2)-(4.2.4) unveils a notable trend in the formation of galaxies. At the inception of the universe, galaxies manifested at an accelerated pace, experiencing a stellar or galactic burst around redshift z≈1, reaching its pinnacle at z~1.5 for a flat universe and z~2 for non-flat universes. Intriguingly, there appears to be a distinct phase of universe expansion within the redshift transition range. Beyond this threshold, the development of galaxy structures becomes inconsequential, contributing minimally to the future evolution of the universe. This point signifies the commencement of cosmic acceleration, aligning seamlessly with the observations of distant spiral galaxies exhibiting a gradual decline or near constancy in galaxy formation over time (Bentabol et al., 2022).
The evolutionary trajectory of the universe unfolds from a deceleration expansion phase after its zenith, transitioning into an accelerating expanding universe. Notably, the universe undergoes a range of redshift transitions, as evidenced by the seminal work of Riess et al. (1998), wherein the mass-energy content of the universe transits from matter domination to an accelerating expansion-dominated state. The persistence of the accelerated expansion necessitates overcoming gravitational attraction forces exerted by the cosmological fluid, primarily composed of ordinary matter.
Within the framework of our model, the shift from deceleration to acceleration expansion materializes at a finite redshift. The exact values of the lower and upper bounds hinge upon the density parameter for ordinary matter and the geometry of the universe. Our findings indicate that a transition from matter domination to acceleration expansion is plausible only if the energy effects propelling the universe into acceleration commence in an epoch preceding z > 1.8. However, to pinpoint the accurate redshift transition point, model parameters necessitate calibration against cosmological data. This methodology aligns with Aydiner's work in 2022, wherein a plausible temporal transition between a matter-dominated universe and a dark energy-dominated universe is predicted, underscoring the relevance of fitting model parameters to observational data for precision and reliability in cosmological predictions.
5.5. Meaning of our results
The investigation into the evolution and distribution of the number density of galaxies has yielded intriguing results, as various modified models consistently predict an accelerating expanding universe. Despite nuanced variations in their underlying mechanisms, these models converge on the same analytical outcome regarding the magnitude of observed structure formation in comparison with the widely accepted λCDM model.
A noteworthy disparity emerges when examining the trajectories of different structures formed by the λCDM and modified CDM models. This variance suggests the existence of dark matter playing a pivotal role in steering the late-time acceleration of the expanding universe. Figures (4.2.2)-(4.2.4) encapsulate the crux of our findings, revealing that the modified redshift relation aligns with a positive cosmological constant within a λCDM model. Notably, this alignment with the standard relationship between cosmological redshift and cosmic scale factor for light photons implies that the introduction of a cosmological constant in our background model results in an excess of dark energy, causing a gradual flattening of the profile of structure formation amplitude.
The interplay between the total light intensity of galaxies or stars and the total number of galaxies or stars formed becomes apparent. Distinct histories unfold for late-type and early-type galaxies, with varying trajectories in light intensity and number density throughout their formation and evolution. Surprisingly, our results challenge the conventional wisdom necessitating the introduction of a cosmological constant or other form of dark energy, characterized by peculiar negative pressure, to elucidate the observed accelerating expansion of the universe. The notion of suppressing structure amplitudes emerges as a pertinent condition for the viability of our dark-matter-dominated cosmological model.
The well-established and almost model-independent theoretical fact of the late-time universe's accelerated expansion appears impervious to ongoing debates surrounding the enigma of the cosmological constant. Despite differences in the rate of structural growth, the impact of accelerated expansion due to modified redshift becomes significant only after the majority of structures have been formed. Subsequently, this leads to a decrease in the total number density of galaxies formed. Remarkably, reconstructed modified redshift models successfully account for all observational signatures of cosmic acceleration.
Intriguingly, simulations devoid of dark energy predict a crossover in the cosmic galaxy formation rate, transitioning from deceleration to acceleration. These findings underscore the complexity of cosmic dynamics and highlight the intricate interplay between various factors influencing the evolution of our expansive universe.
6. Summary and Conclusion
The present astronomical inquiry stands as a diligent effort to scrutinize the fundamental tenets of cosmology, specifically addressing the homogeneity and isotropy assumptions inherent in the concordance model. Extensive research has already been dedicated to testing spatial isotropy through a spectrum of techniques and probes. Nevertheless, the homogeneity hypothesis presents a formidable challenge, prompting a focused investigation.
This study extends the groundwork laid by prior research on the λCDM concordance model. The impetus is derived from an intrinsic modification of the standard redshift, offering a novel interpretation of Friedmann equations. This reinterpretation is grounded in a phenomenologically modified redshift model, deliberately devoid of dark energy.
The Modified Standard Redshift, as introduced in this study, serves as a nuanced instrument for characterizing the distribution of luminous matter within the cosmic framework. Emphasizing the Friedmann model, the investigation is particularly attuned to the growth rate of cosmic structures. This parameter emerges as a discerning factor, poised to differentiate between the General Relativity-backed λCDM concordance model and alternative scenarios rooted in the modified Friedmann model. The overarching goal is to establish a framework for discerning between competing cosmological models.
Three distinct phenomenologically modified redshift models, namely parametric (Bassett et al., 2015) and non-parametric (Wojtak & Prada, 2017) models, are systematically explored within the context of a matter-dominated Friedmann universe. The analytical prowess of this study is demonstrated through the rigorous solution of relativistic dynamic Friedmann equations. These solutions, in turn, shed light on the light intensity and number density of galaxies, delineating their evolution as functions of the modified redshift.
The early consideration of dark energy within the framework is a methodological choice, enabling subsequent analyses to nullify its impact. This is achieved by setting the cosmological constant to zero for dark matter-powered phenomenological models. This calibration ensures alignment with empirical cosmological observations, thus fortifying the study's empirical foundation.
Simulation exercises are then meticulously executed utilizing MATLAB applications. The simulation spans the redshift range from 0 to 5, revealing intriguing dynamics. Notably, augmented values of the modified model parameters are correlated with a precipitous decline in the redshift, signifying an earlier onset of cosmic expansion acceleration. The simulation unfolds a distinctive picture of galaxy formation, characterized by a pronounced burst around redshift z ≈ 1, peaking at z ≈ 1.8, followed by a gradual tapering. Furthermore, simulations without dark energy unveil a phase crossover point in the cosmic galaxy formation rate, marking the transition from deceleration to accelerating expansion at redshifts around z ~ 1.5 for flat universe and z ~ 2 for both open and closed universes.
A critical observation emerges concerning the differential impact of cosmological constant on structure formation. The study posits that the cosmological constant within the λCDM concordance model exhibits a less pronounced effect on late-time structure formation efficiency compared to the modified model. This nuanced disparity underscores the heightened explanatory power of the modified model, wherein the deceleration of universe expansion beyond z > 2 is attributed to dark matter-powered cosmic acceleration rather than the effect of the cosmological constant.
The study concludes with a resolute stance against the necessity of introducing the cosmological constant into the modified model. The latter, characterized by a positive cosmological constant in the context of the λCDM concordance model, obviates the need for cosmological constant, thereby precluding excessive dark energy and mitigating the exigency for fine-tuning at an implausibly minute accuracy. The inexorable acceleration of the late-time universe is posited as a well-established and nearly model-independent theoretical fact, impervious to the ongoing debates regarding the nature of the cosmological constant.
The observational fidelity of the reconstructed modified models stands as a testament to their comprehensive accommodation of all discernible signatures of cosmic acceleration. The call for future inquiry echoes a commitment to expanding the parameter space and delving deeper into the intricacies of cosmological models. This scholarly endeavor, rooted in analysis and empirical calibration, contributes to the ongoing discourse on the dynamic evolution of our universe.
Acknowledgements
We are grateful to the department of Physics, Masinde Muliro University of Science and Technology for material support of this research work.
References
- Bassett et al. (2015). A Tale of Two Redshift. arXiv:1312.2593v1[astro-ph. Co], 1-9. [CrossRef]
- Amendola & Palladino. (1999). The Scale of Homogeneity in the Las Campanas Redshift Survey. The Astrophysical Journal, L1-L4. [CrossRef]
- Aydiner. (2022). The Late Time Transition of Universe and the Hybrid Scale Factor. The Europena Physical Journal, 82-39. [CrossRef]
- Brough et al. (2020). The Vera Rubin Observatory Legacy Survey of Space and Time and the Low Surface Brightness Universe. ArXiv: 2001. 11067v1 [Astro-Ph], 1-7. [CrossRef]
- Clowes et al. (2013). A structure in the early Universe at z= 1.3 that exceeds the homogeneity scale of the R-W concordance cosmology. Monthly Notices of the Royal Astronomical Society, 2910-2916. [CrossRef]
- Conn et al. (2013). The Three Dimensional Structure of the M31 Satellite System; Strong Evidence for an Inhomogeneous Distribution of Satellites. The Astrophysical Journal, 120. [CrossRef]
- deGrijs. (2012). Advancing the Physics of Cosmic Distances: Conference Summary. ArXiv: 1209. 6529v1 [Astro- Ph], 1-10. [CrossRef]
- Ellis. (2011). Inhomogeneity effects in Cosmology. Class.Quant.Grav. 28 (2011) 164001, 1-29. [CrossRef]
- Gomez. (2011). On Friedmann-Lemaitre-Robertson-Walker cosmologies in non-standard gravity. ArXiv: 1104. 0813v1, 193. [CrossRef]
- Huang. (2020). Supernova Magnitude Evolution and PAge Approximation. The Astrophysical Journal, 892:L28. [CrossRef]
- Labini. (2011). Inhomogeneities in the universe. arXiv: 1103. 5974v2 [astro-ph. CO], 1-30. [CrossRef]
- Labini et al. (1998). Scale-invariance of galaxy clustering. arXiv:astro-ph/9711073v1, 1-232. [CrossRef]
- Langa et al. (2017). Relativistic Dynamics in a matter-Dominated Friedmann Universes. Journal of Astrophysics and Astronomy, 1-10. [CrossRef]
- Meszaros. (2019). An Oppositeness in the Cosmology: Distribution of the Gamma-Ray Bursts and the Cosmological Principle. ArXiv: 1912. 07523 [Astro- ph], 1-6. [CrossRef]
- Pandey & Sarkar. (2016). Probing large scale homogeneity and periodicity in the LRG distribution using Shannon entropy. Monthly Notices of the Royal Astronomical Society, 1519-1528. [CrossRef]
- Paris et al. (2017). The Sloan Digital Sky Survey Quasar Catalog: Twelfth data release. The Astrophysical Journal, 1-25. [CrossRef]
- Ribeiro, & Miguelote. (1998). Fractals and the Distribution of Galaxies. Brazilian Journal of Physics, 1-29. [CrossRef]
- Riess et al. (1998). Observational evidence from supernovae for an accelerating universe and a cosmological constant. The Astronomical Journal, 1009-1038. [CrossRef]
- Salcido et al. (2018). The impact of dark energy on galaxy formation. What does the future of the Universe hold? Roya Astronomical Society, 3744-3759. [CrossRef]
- Secrest et al. (2020). A Test of the Cosmological Principle with Quasars. The Astrophysical Journal, 1-9. [CrossRef]
- Tian. (2017). The relation between cosmological redshift and scale factor for photons. The Astrophysical Journal, 1538-4357. [CrossRef]
- Wamalwa. (2016). On the Friedmann Cosmology. International Journal of Pure and Applied Mathematics, 107. [CrossRef]
- Werner & Schermelleh-Engel. (2010). Deciding Between Competing Models: Chi-Square Difference Tests. The Astrophysical Journal, 1-3.
- Wojtak & Prada. (2017). Redshift remapping and cosmic acceleration in dark-matter-dominated cosmological models. Monthly Notices of the Royal Astronomical Society, 4493-4511. [CrossRef]
- York et al. (2000). The Sloan Digital Sky Survey: Technical Summary. The Astronomical Journal, 1199-1204. [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).