Prerpints.org logo
Preprint
Article

Digital Miniature Cathode Ray Magnetometer

Altmetrics

Downloads

97

Views

24

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

02 January 2024

Posted:

04 January 2024

You are already at the latest version

Alerts
Abstract
In this study, we introduce the concept and construction of an innovative Digital Miniature Cathode Ray Magnetometer designed for the precise detection of magnetic fields. This device addresses several limitations inherent to magnetic probes such as D.C. offset, nonlinearity, temperature drift, sensor aging, and the need for frequent recalibration, while capable of oper-ating in a wide range of magnetic fields. The core principle of this device involves the utilization of a charged particle beam as the sensitivity medium. The system leverages the interaction of an electron beam with a scintillator material, which, then, emits visible light that is captured by an imager. The emitted scintillation light is captured by a CMOS sensor. This sensor not only rec-ords the scintillation light but also accurately determines the position of the electron beam, providing invaluable spatial information crucial for magnetic field mapping. The key innova-tion lies in the combination of electron beam projection, CMOS imager scintillation-based de-tection and digital image signal processing. By employing this synergy, the magnetometer achieves remarkable accuracy, sensitivity and dynamic range. The precise position registration enabled by the CMOS sensor further enhances the device's utility in capturing complex magnetic field patterns, allowing for 2D field mapping. In this work, the optimization of the probe's per-formance is tailored for applications related to the characterization of insertion devices in light sources, including undulators.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

The beginnings of magnetic measuring technology date back to 1820 when Hans Christian Oersted observed the deflection of a compass needle by an electric current, confirming the link between electricity and magnetism. Over the bicentennial evolution of this science, various sensors and techniques, such as Hall probes, SQUIDs (Superconducting Quantum Interference Device), Fluxgates, GMRs (Giant Magnetoresistance), Fluxmeters, NMRs (Nuclear Magnetic Resonance), SSWs (Single Stretched Wire), and others, have emerged for characterizing magnetic systems. In modern applications, the accurate measurement of magnetic fields plays a pivotal role in the construction, testing, and certification of advanced magnetic devices. This process frequently involves the utilization of various sensor types to comprehensively characterize components like undulators.
Despite the wide array of available technologies, limitations persist, prompting the need for innovation. Parameters like accuracy, field range, temperature of operation, spatial resolution, size, sensitivity, noise density, and bandwidth present a complex compromise, where in one characteristic a sensor can excel while on another perform poorly making direct comparisons between sensors challenging. For instance, SQUIDs excel in detecting faint fields but demand cryogenic temperatures to operate [1]. In this context, a magnetometer capable of exceling in multiple parameters is an important addition.
Measurement technologies, such as Hall sensors, wire-based methods, and sensing coils, each have their strengths and limitations. Hall sensors, while widely used, suffer from issues like D.C. offset and temperature drift, requiring frequent recalibration [2]. Wire-based methods, like the SSW and pulsed wire techniques, offer simplicity but lack spatial resolution [3]. Sensing coils, fixed or rotating, provide good performance but may have limited spatial resolution and can be deployed only to characterize magnetic fields on simple geometries.
The fundamental operation of this magnetic probe centers on the generation of a low-energy electron beam, emanating from a miniature electron gun. This particle beam subsequently engages with a target scintillator screen, inducing illumination upon impact. The illuminated screen is then captured by a CMOS sensor seamlessly integrated with a Digital Imaging Processing unit. In the event of the electron beams trajectory being altered by a magnetic field, this deviation is promptly detected by the imager. Subsequently, the Digital Signal Processing algorithm takes charge, executing calculations essential for deducing both the magnitude and orientation of the magnetic field.
The novel magnetometer introduced in this study overcomes numerous limitations inherent to existing systems. It excels in sensitivity, accuracy, spatial resolution, and repeatability, addressing key challenges present in current technologies. Specifically engineered to navigate complex geometries and operate across a broad temperature spectrum, including cryogenic environments without the need of calibration, this probe is particular useful for the characterization of light source undulators, wigglers, and magnets. Due to its excellent sensitivity, this magnetometer can be very useful to biomedical systems. Its diagnostic potential can play a crucial role in medical equipment for treatment and diagnostics, encompassing magnetocardiography, magnetoneurography, magnetoencephalography, and magnetomyography [4]. Moreover, this magnetometer can find practical application in the construction of medical devices, contributing to the characterization of Gantry systems for radiotherapy, and characterization of MRI magnets.
In this study, particular emphasis will be devoted for the application in characterizing insertion devices for light sources, notably undulators. The intricate nature of insertion devices, which play a pivotal role in generating synchrotron radiation within light sources, demands a sophisticated and precise approach in their characterization, which this magnetometer proposes to address. We will comprehensively explore the construction, and characterization of prototypes that have undergone testing to date. We begin by providing a detailed description of the system, including a thorough examination of the calculations and rationale behind the engineering of this device. Subsequently, we analyze current results and simulations pertaining to the system. Finally, we conclude by discussing the future plans and capabilities envisioned for this system.

2. Construction and Materials

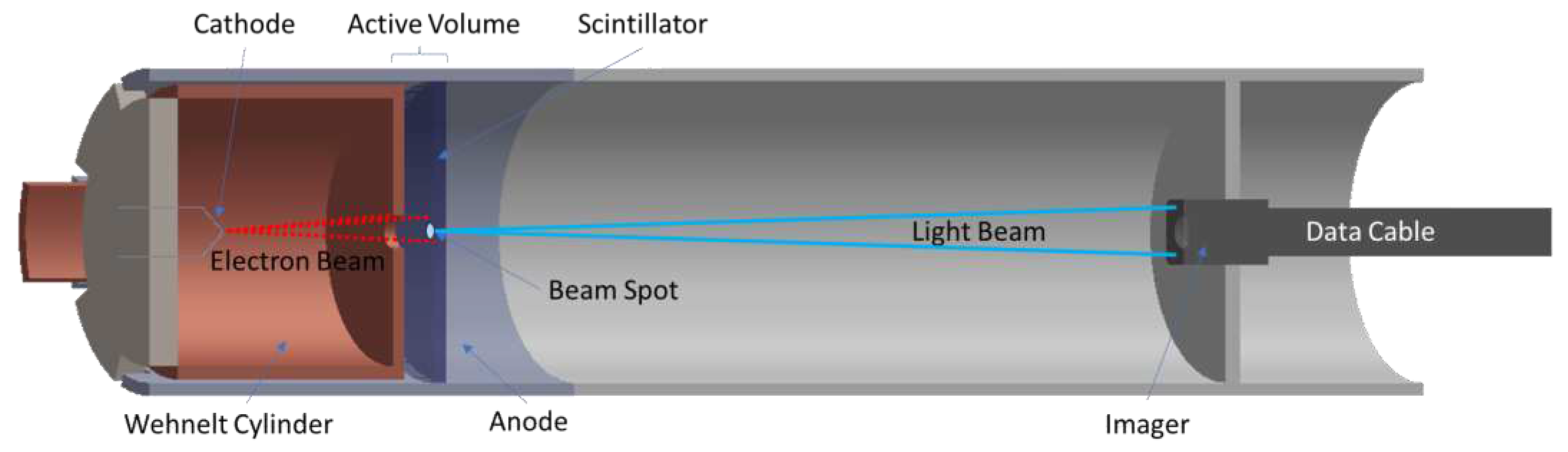
The magnetic probe investigated in this study incorporates a compact micro-Cathode Ray Tube (mCRT) [5] seamlessly integrated with a CMOS (Complementary Metal-Oxide Semiconductor) imager. Within this device, the mCRT's electron gun propels a low-energy electron beam towards the imaging system, positioned perpendicular to the beam at the opposite end of the cathode. The system is contained by an evacuated ceramic tube operating at around 10-7 torr, with its overall composition described by Figure 1.
The cathode, serving as the electron emitter, is fashioned from either Tungsten (W) or Lanthanum Hexaboride (LaB6). Both materials were employed in the prototypes tested in this work, with LaB6 providing higher brightness and a slightly narrower energy spread, albeit at a significantly higher cost. When Tungsten cathodes were used, the probe exhibited erratic behavior for fields exceeding 1T due to the deflection of the tungsten wire. While a more robust tungsten-based cathode is conceivable, it has not yet been implemented in this probe. All high magnetic field tests were conducted using Lanthanum Hexaboride [6].
Preprints 95300 g002
Figure 2. The electron gun assembly contains three basic elements; (a) the electron emitter, (b) the Wehnelt cylinder, and (c) the anode.
Figure 2. The electron gun assembly contains three basic elements; (a) the electron emitter, (b) the Wehnelt cylinder, and (c) the anode.
Preprints 95300 g002
The electrons generated at the cathode are accelerated from within the Wehnelt cylinder to the anode, with the beam collimated and focused by the cylinder assembly. The cylinder is set to a voltage between 0V and -50V, adjustable for optimal beam focus. The distance between the cylinder aperture and the electron emitter plays a crucial role in determining the brightness and collimation of the beam. Proximity to the orifice enhances brightness but diminishes collimation, during tests the cathode was positioned within a range of 200µm to 800µm of the cylinder aperture.
The anode, a thin metal ring situated for different prototypes at various distances from the Wehnelt cylinder, was tested with positive voltages ranging from 200V to 2000V, the acceleration field. The applied voltage to the anode determines the final energy of the electrons before their collision with the scintillator. Higher voltages extend the magnetic dynamic range of the probe but compromise sensitivity. The field strength can be dynamically adjustable based on the users’ requirements for sensitive and magnetic field range.
The electrons traversing the space in between the cylinder and the anode assembly are the ones employed for sensing the magnetic field, interacting with the scintillator composed of a layer of silver-activated zinc sulfide phosphor (ZnS:Ag). This space is the active volume of the probe, and it determines the probe's spatial resolution. During this study, the active length of the probe was tested between 400µm to 10000µm.
When interacting with the scintillator, electrons create a beam spot with photon emission at 450nm [7]. These photons are collected either by a CMOS camera at a defined distance determined by the camera's focal point or by a CMOS sensor without optical lenses directly attached to the scintillator. While the former generally yields superior magnetic sensitivity due to better pixel resolution, attaching a CMOS sensor directly to probes with a diameter smaller than 5mm presents challenges for existing Commercial off-the-shelf CMOS sensors [8]. When no lenses system is required, the scintillator is either deposited on a glass disc or directly onto the CMOS sensor.
Preprints 95300 g003
Figure 3. (a) 1mm×1mm CMOS sensor with lens assembly, and (b) CMOS sensor directed coupled to scintillator.
Figure 3. (a) 1mm×1mm CMOS sensor with lens assembly, and (b) CMOS sensor directed coupled to scintillator.
Preprints 95300 g003
The image, captured by the CMOS sensor, is subsequently transmitted to a computer via differential lines for digital signal processing. Currently, a computer functions as the digital signal processor unit, and computes the magnetic field based on the position and shape of the beam spot. Any deviation in the beam spot from its rest position is translated into a magnetic field measurement. To enhance magnetic resolution, the signal processing algorithm conducts centroid localization, considering both the illuminated pixel position and its intensity. Signal processing may also encompass averaging several frames of the beam spot to enhance sensitivity, albeit at the expense of speed. The centroid localization is performed via k-means algorithm to determine a pixel cluster within an unlabeled multidimensional dataset [9]. In this context, the image inputted to the k-means clustering algorithm comprises the hits registered on the CMOS detector. Given that the source utilized is a Gaussian with a tens of microns spatial spread, most particles deposit charge in a primary cluster. However, scattering of particles due to the beam interacting with the scintillator and Wehnelt cylinder leads some electrons to deposit charges away from the central cluster. The center of the cluster is determined as the statistical mean of all points belonging to a specific cluster. This process is iterated multiple times or until the center of the group shows insignificant changes between iterations [10].

3. Performance and Optimization

The continuous evolution of this magnetometer involves a series of incremental improvements aimed at enhancing its overall performance. In this section we will describe the current state of the probe, providing detailed insights into its performance metrics and the parameters currently undergoing optimization.
Preprints 95300 g004
Figure 4. Depiction of a typical magnetic probe undergoing testing.
Figure 4. Depiction of a typical magnetic probe undergoing testing.
Preprints 95300 g004
The optimization of the probe is primarily guided by its designated application, in this case the focus is on the characterization of undulators for insertion devices [11]. This specific application demands probes with a compact diameter ranging from 3mm to 5mm, spatial resolution of 500μm or less, and a wide magnetic field range, capable of measuring up to 3 T, all while maintaining a magnetic sensitivity of 25μT. Additionally, it is crucial for the probe to swiftly traverse through undulators, allowing for rapid characterization with a targeted minimum linear speed of 10mm/s with 40 measurement per second [12,13,14,15].
In addressing the challenges associated with a small diameter, as illustrated in Figure 3, two strategies have been implemented. For smaller diameters where space prohibits direct sensor attachment to the scintillator, an alternative approach is adopted where a micro camera with a lens system is deployed. Conversely, when the diameter allows, a scintillator can be directly deposited onto the sensor. It has been determined that the imager can effectively incorporate pixels as large as 10μm x 10μm while still yielding 25μT resolution.
The current performance of the 5mm diameter probe, as showcased in Table 1. Despite the outer diameter being 5.00 mm, the active area of the rectangular CMOS sensor utilized has a maximum length of 4.5mm [16]. While the maximum magnetic field for this application is easily attainable with the existing prototypes, the field sensitivity remains a crucial factor, currently falling short by a factor of ten from the targeted performance. Thus, ongoing improvements are imperative for this particular application.
The accelerating electric field is a very important factor for the performance of this probe and it’s mainly defined by the difference of electric potential between the cathode and the anode. Presently, the optimal voltage for a probe featuring a channel length ranging from 350μm to 500μm stands at 250V for the requirements of this application. There are two main limitations for this parameter; higher values can cause electric arc due to the probe reduced dimensions limiting the maximum voltage to 2000V, and lower values are limited by the scintillator cross section with this particular scintillator reducing its efficiency exponentially under 200V. For this application the accelerating electric field could not be too high in order to preserve high sensitivity while maintaining the desired dynamic range.
The LaB6 cathode maintains a minimum stable current of approximately 10nA, equivalent to 6.25×1010 electrons per second. Less than 10% of these electrons successfully traverse the collimating orifice with the actual percentage depending on the position of the cathode. The spatial distribution beyond the orifice and at the scintillator/phosphor plane approximates a 2D Gaussian with a standard deviation of 20 micrometers. The beam electrons, depending on the operating voltage, possess energy levels ranging from 200 to 2,000 eV. Considering a 250V accelerating potential, each electron generates 2-3 scintillation photons, but only about ~5% of these photons lead to a signal (an ionization e-h pair) in the CMOS sensor [16]. We can currently reach 1 micrometer position resolution that yields 250µT for a 600µm long channel as illustrated by Table 1, with measurements of the beam position within 25ms time intervals. In such intervals, in theory over 10 million ionization electrons could be measured, in practice it saturates the sensor and have to be dimmed by a filter.
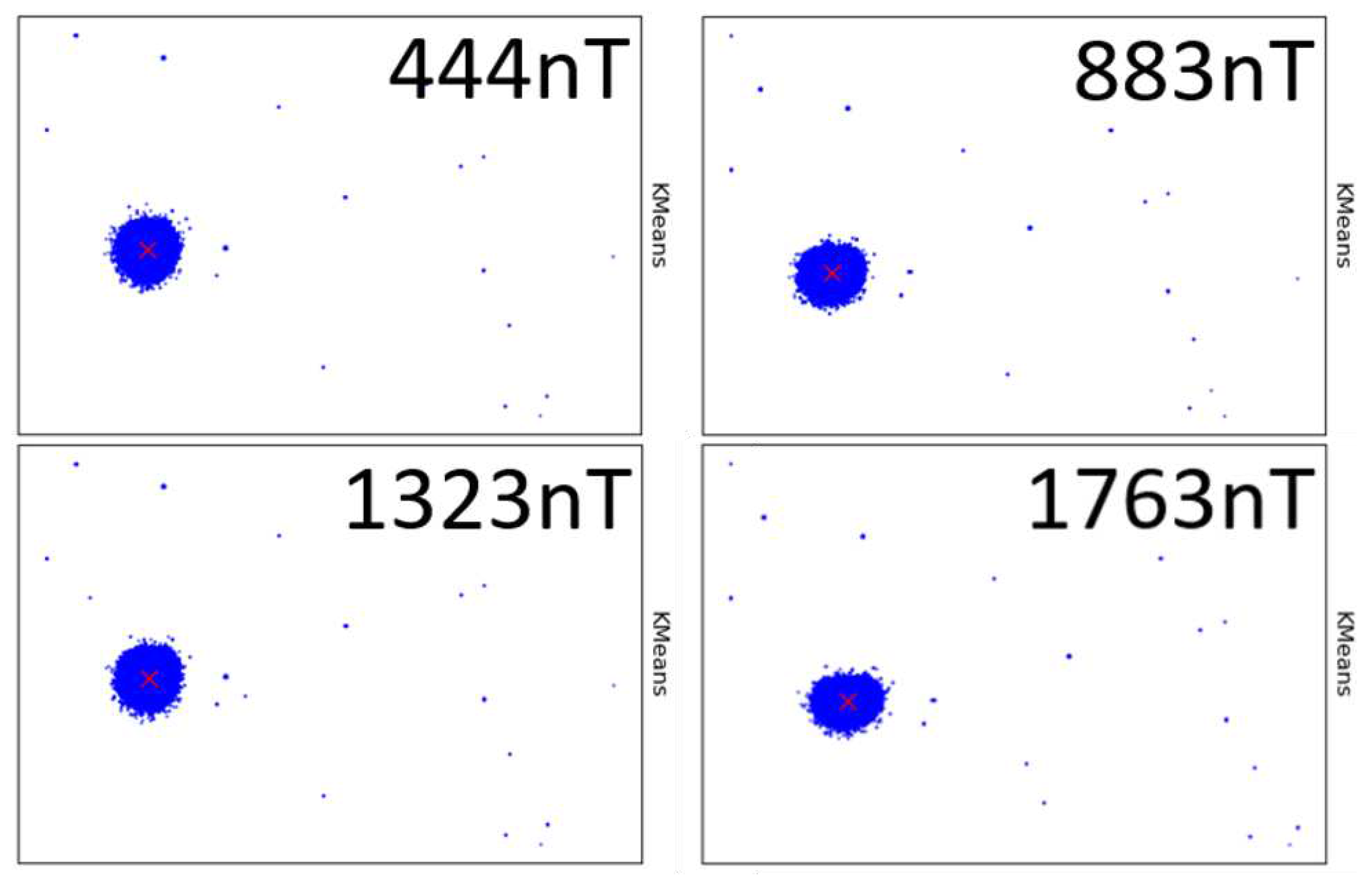
Probes with longer active channel, designed for applications demanding heightened sensitivity but with reduced dynamic range, are currently undergoing testing. Figure 5 displays the performance obtained from a 10mm long probe capable of reaching 50 nT field sensitivity. The figure portrays the typical pattern captured by the imager, highlighting the presence of rogue pixels attributed to electron scattering. Additionally, the image underscores that a beam spot cluster can consist of hundreds of pixels.
It is noteworthy that employing relatively large beam spots contributes to enhancing the probe's sensitivity by offering more statistical data for centroid calculations. However, a trade-off is evident, as larger pixel clusters, mirroring the beam spot's size, result in a reduction of the probe's dynamic range. This occurs when the beam spot reaches the sensor boundary earlier in instances of large pixel clusters.
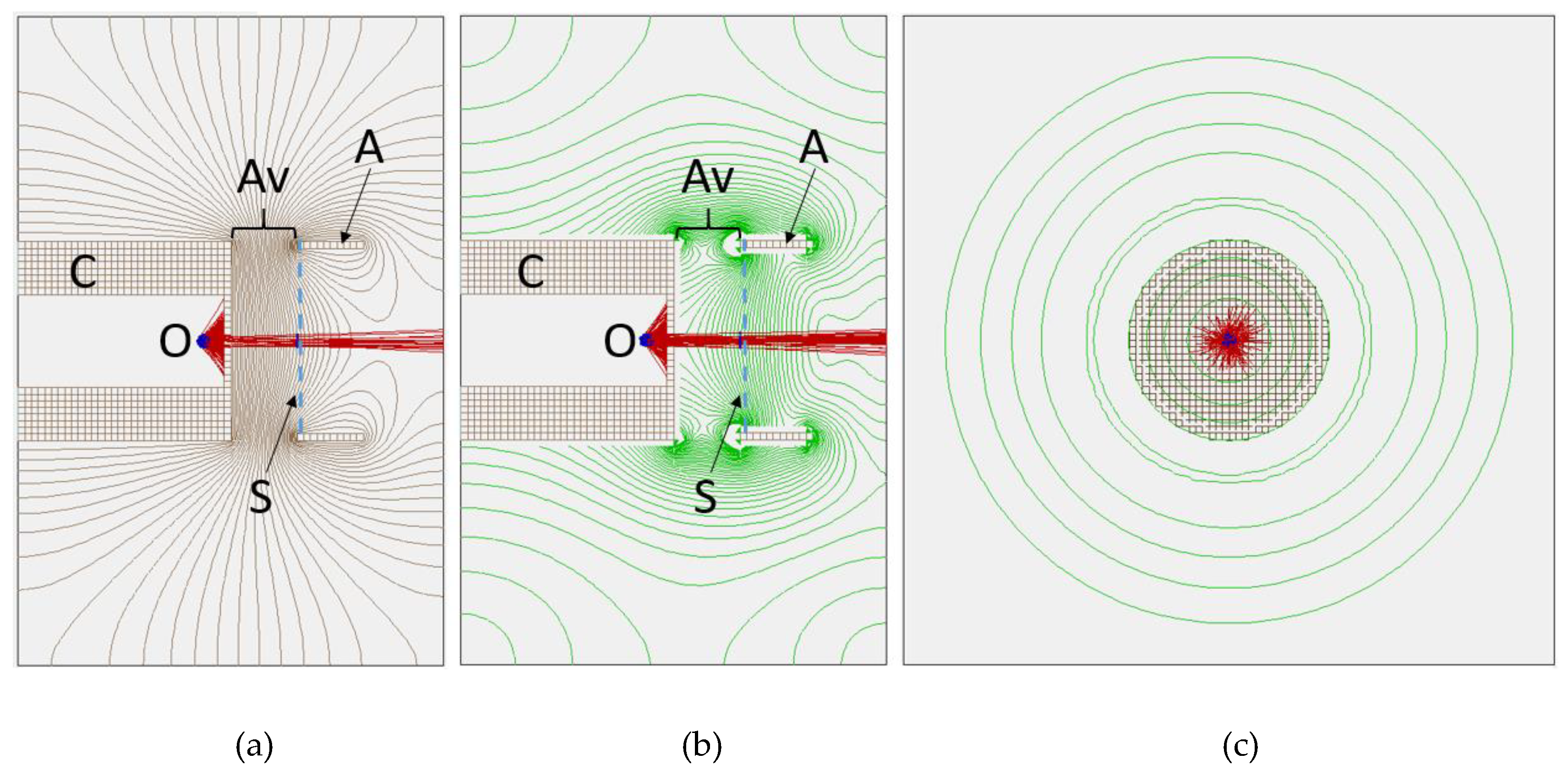
Another important optimization implemented in this probe is the distance between the electron emitter and the Wehnelt cylinder. This important parameter optimizes the beam divergence and its brightness. For this probe the tip of the LaB6 emitter was located at 400um from the Wehnelt cylinder with a 150um aperture. This provided the best trade-off between brightness and divergence. The transmitted brightness is determined by the percentage of electrons generated by the cathode that successfully traverse the cylinder aperture before converted into light by the scintillator.
These values, were derived from simulation and confirmed by measurements within a 20% margin of error, obtained by assessing the number of photons emitted by the scintillator. Figure 6 shown electrostatic simulations that helped to optimize the relative position of the electron emitter. For this application the Wehnelt cylinder was kept at zero electric potential.
This probe demonstrates versatility by functioning in a cold environment, with prototype versions capable of operating while immersed in liquid nitrogen. The primary factor influencing performance is the CMOS cameras. Notably, some CMOS cameras exhibit enhanced performance when directly operated in liquid nitrogen due to reduced dark current caused by the low temperature [17]. Cold operation is facilitated by the internal hot cathode, which functions as a heater, maintaining the probe's internals at a temperature warmer than the surrounding environment. This configuration effectively creates a reverse cryostat, akin to the operation of numerous cryogenic cameras [18]. No performance degradation was observed when operating at 77K other than an increase in the cathode current due to the reduction on its internal resistance resulting from the cold environment.
While the probe operates effectively in cryogenic liquid, its prolonged functioning in such an environment, along with its resilience to multiple thermal cycles, remains uncertain.

4. Discussion

Previously, we established that the performance of the magnetic probe is intricately linked to trade-offs among key parameters, encompassing accuracy, spatial resolution, temperature range, and sensitivity. The optimization of these parameters becomes particularly crucial when tailoring the probe for specific applications. In the context of our focus application, the primary hurdle lies in achieving the targeted sensitivity while maintaining the desired dynamic range.
To address this challenge, an array of proactive strategies is actively being pursued. These strategies include the implementation of advanced signal processing techniques, exploration of alternative scintillator types, and the integration of electrostatic deflecting plates. The collective objective of these endeavors is to elevate the sensitivity of the prototype and align it with the specified target of 25µT.
The primary challenge arises from the minimal detectable displacement of the electron beam by the imager. Factors contributing to this measurement error include the suboptimal scintillator material for detecting low-energy electrons, which currently limits the usable energy range. We are actively exploring alternative scintillating materials capable of operating effectively with lower energy electrons [17].
However, the utilization of lower-energy electrons introduces a new challenge, it further reduces the dynamic range of the probe due to excessive beam deflection. To address this issue, our strategy involves the integration of deflecting electrostatic rings [18,19]. This approach aims to counteract magnetic deflection, ensuring efficacy with lower-energy electrons while simultaneously achieving the targeted dynamic range and sensitivity. This is achieved by a feedback system that is constantly compensating the magnetic field.
Another solution we are pursuing is to enhance sensitivity via the replacement of the monolithic scintillator. The current scintillator exhibits excessive light bleeding, which compromises the capacity of the signal processing algorithm in resolving the centroid. To address this, a pixelated scintillator is in development. With a sensor featuring 5x5 micrometers pixels, the light spreads over 100 pixels, translating to ~100,000 ionization electrons. This surpasses the typical pixel charge capacity (well depth), necessitating light attenuation, ideally around 1-10% transparency. A semi-transparent deposited thin film can easily achieve this requirement.
In this system, the position resolution primarily hinges on the beam width at the phosphor plane (larger than the light guides and sensor pixels) and the quantity of measured ionization electron quanta. With a presumed 95% light attenuation, we anticipate measuring approximately half a million ionization electrons. This would result in a resolution of around 20μm/sqrt(5×106), theoretically making it possible to determine the beam spot center within 0.03μm within a 25ms time interval. Achieving this level of resolution allows our current 800μm probe, as presented in Table 1, to exhibit a sensitivity of 0.5µT, while the 400μm probe demonstrates a sensitivity of 20 µT, within the applicable range for this particular application. Determining the beam position involves centroid calculation of pixels with collected charge above a noise threshold. Sensor noise is not a significant limitation, given that the collected charges in illuminated pixels far exceed typical sensor noise. The primary systematic error is expected from the square light guides and sensor pixels.
The centroid finding algorithm can be refined through simulations and/or direct measurements in a known varying magnetic field. At present, this critical function is executed by a conventional computer, where the emphasis lies on sustaining real-time operation, thus necessitating a streamlined algorithm that avoids computationally intensive processes. A pivotal shift is underway as we migrate from a computer-based infrastructure to a Field Programmable Gate Array (FPGA) device. By leveraging FPGA's parallel processing power, we anticipate a profound boost in computational efficiency, paving the way for more intricate and resource-demanding image processing algorithms[20].
One of the main changes on the algorithm is the increased use of averaging within each image frame. This strategic upgrade not only enhances the efficiency of the image processing algorithm but also aligns with our objective of advancing the overall capabilities of the probe for more sophisticated and nuanced magnetic field measurements. In a single frame, the probe can capture a cluster of many pixels enabling the determination of the beam's position and, consequently, the incident magnetic field. Averaging an 'n' number of pixels per frame, leads to an enhanced signal-to-noise ratio. The frame image processing addresses random noise, assuming that cluster noise is genuinely random. This approach ensures that fluctuations (noise) in the image gradually smooth out as more pixels are averaged. Generally, the magnitude of fluctuations diminishes by the square root of the number of averaged pixels. The relationship between performance improvement and the number of samples can be expressed by
S N R n = n   × S N R i
with SNRn being the average signal-to-noise ratio, n the number of pixels being averaged, and SNRi initial signal-to-noise ratio (SNRi). It is possible that this strategy alone will get the performance of this probe to the desired sensitivity while maintaining the speed requirements of 40 frames per second, with each frame being a magnetic measurement the algorithm has to take 25 milliseconds to converge for each measurement.
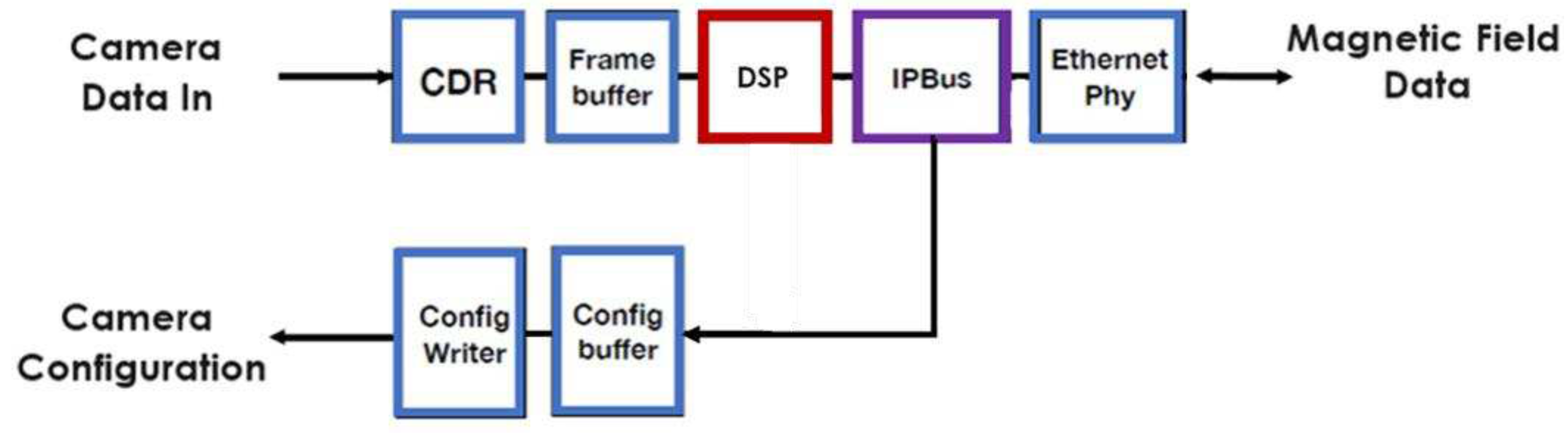
The FPGA implementation of the full system will allow this magnetic probe to be a stand-alone system. As illustrated by Figure 7, data originated from the probe arrives from the CMOS camera in a single LVDS (Low Voltage Differential Signal) line, and it is immediately decoded by the CDR (Clock and Data Recovery) block and is then formatted in a frame. The framed data is then handled to the DSP block where the magnetic field is calculated from the raw pixel data and forward to the IPBus, a straightforward control protocol based on packets for reading and modifying memory-mapped resources within the FPGA. The IPBus then makes the information available for broadcast in to the Ethernet Phy. External commands can also be received via Ethernet to configure the camera via the configuration blocks “config writer”, and “config buffer”.
The combination of these strategies is expected to enhance the probe's magnetic sensitivity sufficiently for our target application.

5. Conclusions

The examination of the Digital Miniature Cathode Ray Magnetometer prototype in this research underscores the viability of this emerging technology, showcasing its potential for optimization across a diverse array of applications. While the current emphasis is on characterizing undulators, the prototype's sensitivity parameters require additional refinement to meet the more extreme cases this specific application.
In addition to the immediate enhancements discussed in this work, our future vision involves implementing further improvements in the longer term. Specifically, we propose the development of a custom-made CMOS imager tailored for direct detection of electrons, leveraging the experience we have accumulated so far.
Another noteworthy advancement is the ongoing development of a prototype featuring an optical fiber bundle. This fiber bundle, comprising 3µm fibers, will replace the conventional detector and be strategically positioned at the current probe's imager location. In this configuration, the electron beam will illuminate a scintillator affixed to the optical fiber bundle. The resulting optical pattern will be transmitted to the imager affixed to the far end of the bundle. Subsequently, a signal processing algorithm will be applied to compute the centroid of the beam. It is important to note that, when compared to an imager integrated inside the probe as presented in this article, the fiber bundle has limitations, particularly in terms of lower resolution due to the restricted number of fibers. Nevertheless, the fiber bundle offers increased robustness, enabling operation in high radiation settings and at deep cryogenic such as liquid helium—conditions challenging for traditional image sensors.
In a broader context, this research significantly contributes to the progression of magnetic measurement technology. Its potential implications extend beyond the targeted application, encompassing scientific, medical, and industrial fields. The findings suggest that the innovative features of this magnetometer hold promise for advancing various domains, making it a valuable asset in the ongoing evolution of measurement technologies.

References

  1. J. Kawai, M.Miyamoto, M.Kawabata, M.Nosé, Y.Haruta and G. Uehara, "Characterization and demonstration results of a SQUID magnetometer system developed for geomagnetic field measurements," Superconductor Science and Technology, IOP Publishing Ltd, vol. 30, no. 8. [CrossRef]
  2. E. Ramsden, "Hall-Effect Sensors: Theory and Application," Elsevier, 2011.
  3. A. Temnykh, Y.Levashov and Z.Wolf, "A study of undulator magnets characterization using the vibrating wire technique," Nuclear Instruments and Methods in Physics Research, vol. 622, no. 3, p. 650–656, 2010. [CrossRef]
  4. K. Zhu and A. Kiourti, "A Review of Magnetic Field Emissions From the Human Body: Sources, Sensors, and Uses," IEEE Open Journal of Antennas and Propagation, vol. 3, pp. pp. 732-744, 2022. [CrossRef]
  5. T. R. H. Wheeler and M. G. Clark, "CRT technology," Springer, pp. 221-256, 1992.
  6. P.B.Sewell, "General Guidelines For Operating ES-423R LaB6 Cathodes," Kimball Physics Inc, 1991.
  7. W. M. Yen, S. Shionoya and H. Yamamoto, Phosphor Handbook, Second Edition, Boca Raton, FL: CRC Press, Taylor & Francis Group, 2007.
  8. A. Hoffman, M. Loose and V. Suntharalingam, "CMOS detector technology," Experim. Astron, vol. 19, no. 1-3, pp. 111-134, 2006. [CrossRef]
  9. S. Na, L. Xumin and G. Yong, "Research on k-means Clustering Algorithm: An Improved k-means Clustering Algorithm," Third International Symposium on Intelligent Information Technology and Security Informatics, China, pp. 63-67, 2010. [CrossRef]
  10. A. W. Chen, J. Luo and K. J. Parker, "Image segmentation via adaptive K-mean clustering and knowledge-based morphological operations with biomedical applications," IEEE Transactions on Image Processing, vol. 7, no. 12, pp. 1673-1683, 1998. [CrossRef]
  11. J.E.Baader, S.Abeghyan, D. C. S.Casalbuoni, B. Marchetti, M.Yakopov, H.J.Eckoldt, A.Hauberg, S.Lederer, L.Lilje, T.Wohlenberg, R.Zimmermann and A. Grau, "SUNDAE2 at EuXFEL: A Test Stand to Characterize the Magnetic Field of Superconducting Undulators," in 13th International Particle Accelerator Conference, Thailand, 2022.
  12. J.Wei, X. Y.Li, Z.Chen and X. X.Zhang, "Development and magnetic field measurement of a 0.5-m-long superconducting undulator at IHEP," Journal of Synchrotron Radiation, vol. 29, no. 4, pp. 997-1003, 2022. [CrossRef]
  13. M.Calvi, C.Camenzuli, R.Ganter, N.Sammut and T.Schmidt, " Magnetic assessment and modelling of the Aramis undulator beamline," Journal of Synchrotron Radiation, vol. 25, no. 3, pp. 686-705, 2018. [CrossRef]
  14. S.Gerstl, C.Boffo, S.Casalbuoni, T.Gerhard, N.Glamann, A.Grau, T.Holubek, D. d. Jauregui, M.Turenne and R.Voutta, "First Characterization of a Superconducting Undulator Mockup with the CASPER II Magnetic Measurement System," 2023.
  15. T.Tanaka and T. R.Tsuru, "Magnetic characterization for cryogenic permanent-magnet undulators: a first result," Journal of Synchrotron Radiation, vol. 14, no. 5, pp. 416-20, 2007. [CrossRef]
  16. J. R. J. e. al., "Scientific charge-coupled devices," Opt. Eng., vol. 26, no. 8, 1987.
  17. T. Yanagida, "Inorganic scintillating materials and scintillation detectors," Proc. Jpn. Acad, vol. 94, no. 2, p. 75–97, 2018. [CrossRef]
  18. S. Bheesette and M. Turqueti, "Simulation Studies for an Electron Gun Based Magnetic Probe," IEEE Transactions on Nuclear Science, vol. 70, no. 3, pp. 177-188, 2023.
  19. A. Baumgärtel, R. T. Smith and S. Maher, "Accurately predicting electron beam deflections in fringing fields of a solenoid," vol. 10, no. 1, p. 1–13, 2020. [CrossRef]
  20. Y. Li, Q. Yao, B. Tian and W. Xu, "Fast double-parallel image processing based on FPGA," in 2011 IEEE International Conference on Vehicular Electronics and Safety, China, 2011.
  21. F. Siddiqui, S. Amiri, U. Minhas, T. Deng, R. Woods, K. Rafferty and D. Crookes, "FPGA-Based Processor Acceleration for Image Processing Applications," J. Imaging, vol. 5, no. 16, 2019. [CrossRef]
  22. N. McConkey, N. Spooner, M. Thiesse, M. Wallbank and T. Warburton, "Cryogenic CMOS cameras for high voltage monitoring in liquid argon," Journal of Instrumentation, vol. 12, 2017. [CrossRef]
Preprints 95300 g001
Figure 1. This figure illustrates the basic design of the magnetic probe that is devided in two basic blocks; the electron accelerator on the left, and the imager in the right. The electron beam originated in the cathode (dashed line), is accelerated towards the scintillator and the resulting beam spot is imaged by the CMOS camera.
Figure 1. This figure illustrates the basic design of the magnetic probe that is devided in two basic blocks; the electron accelerator on the left, and the imager in the right. The electron beam originated in the cathode (dashed line), is accelerated towards the scintillator and the resulting beam spot is imaged by the CMOS camera.
Preprints 95300 g001
Preprints 95300 g005
Figure 5. Four frames at different magnetic field for a probe with an active channel of 10mm. The centroids marked in each cluster were calculated using k-means.
Figure 5. Four frames at different magnetic field for a probe with an active channel of 10mm. The centroids marked in each cluster were calculated using k-means.
Preprints 95300 g005
Preprints 95300 g006
Figure 6. Illustrates the electrostatic simulation of the probe, with key elements designated as follows: "O" denotes the origin of the electron beam, "S" represents the scintillator, "C" signifies the Wehlnet cylinder, "A" denotes the anode, and "Av" encompasses the active volume of the probe spanning the distance between the anode and the Wehlnet cylinder, set to 600 μm. In detail, (a) portrays the vertical cross-section of the electric field equipotential, (b) presents the vertical cross-section of the gradient lines, and (c) illustrates the horizontal cross-section of the gradient lines. The interactions between electrons originating at the cathode, are depicted in blue, and the scintillator are highlighted, with the electron beam shown in red.
Figure 6. Illustrates the electrostatic simulation of the probe, with key elements designated as follows: "O" denotes the origin of the electron beam, "S" represents the scintillator, "C" signifies the Wehlnet cylinder, "A" denotes the anode, and "Av" encompasses the active volume of the probe spanning the distance between the anode and the Wehlnet cylinder, set to 600 μm. In detail, (a) portrays the vertical cross-section of the electric field equipotential, (b) presents the vertical cross-section of the gradient lines, and (c) illustrates the horizontal cross-section of the gradient lines. The interactions between electrons originating at the cathode, are depicted in blue, and the scintillator are highlighted, with the electron beam shown in red.
Preprints 95300 g006
Preprints 95300 g007
Figure 7. The block diagram depicts the implementation of the probe as a system-on-a-chip within the FPGA.
Figure 7. The block diagram depicts the implementation of the probe as a system-on-a-chip within the FPGA.
Preprints 95300 g007
Table 1. The results below show the current performance of a 5 mm diameter probe, with 250V electrostatic acceleration
Table 1. The results below show the current performance of a 5 mm diameter probe, with 250V electrostatic acceleration
Spatial Resolution(µm) Field Sensitivity (µT) Maximum Field (T)
400 600 3.00*
600 250 1.33
800 150 0.75
* This is particular value was reached by simulation and confirmed by extrapolating test results. We currently have the capability to test articles only up to 1.5T.
Table 2. The results below show the electron beam divergence and electron transmission rate dependence on the electron emitter distance from the Wehnelt cylinder aperture to the cathode. The cylinder potential was set to zero, and the acceleration field to 250V.
Table 2. The results below show the electron beam divergence and electron transmission rate dependence on the electron emitter distance from the Wehnelt cylinder aperture to the cathode. The cylinder potential was set to zero, and the acceleration field to 250V.
Distance (µm) Transmitted brightness (%) Divergence Angle (°)
200
400		 7.4
3.0		 2.2
1.7
600 1.9 1.4
800 0.9 1.0
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated