Preprint
Article
Dissipative Chaotic Itinerancy and the Dirichlet Eta Function
Altmetrics
Downloads
126
Views
860
Comments
1
This version is not peer-reviewed
Submitted:
05 January 2024
Posted:
08 January 2024
You are already at the latest version
Alerts
Abstract
This work presents a new type of chaotic dynamical system originated from Dirichlet Eta function. Although the exposition describes only a bidimensional instance, it is certainly possible to construct higher dimensional such models. The novelty resides in the multitude of interesting characteristics concentrated in only one kind of dynamical system, mainly because of its simple abstract definition - it provokes dissipative, chaotic and itinerant behavior, and its paths typically display nonrecurring quasi-attractors and associate regions of ruin. In addition, it is discrete and nonautonomous, being additively driven by a simple real vector sequence. Also, the defining formulas have parameters which permit to activate bifurcatory effects, mainly related to setting the number of quasi-attractors and overall geometric complexity and diversity. In this fashion, it holds a certain similarity with classical itinerant chaotic systems, but it is a completely different object. One of its parameters is very influential and may be intuitively compared to a type of "potential energy", capable of changing the duration of sojourns etc. In this fashion, there is a potential opportunity to employ artificial inference techniques for designing specific structures on paths. Of course, the other parameters are also relevant, but not necessarily in the control of the number of quasi-attractors and the permanence periods near them. It is important to state that the described system was found during a previous investigation about certain features of the Riemann hypothesis, using the Dirichlet Eta function instead of the Riemann Zeta function - the components of the system under study here were part of certain series whose convergence had to be established, and that scenario produced this very positive side effect. The text also suggests an atypical, but important, potential application in philosophy: the representation of the Hindu concepts of Samsara and Moksha.
Keywords:
Subject: Computer Science and Mathematics - Mathematics
1. Introduction
The concept of chaotic itinerancy is strongly associated to models of neural activity, driving the cortex in sequences of quasi-attractors, which are regions of convergent and divergent flows, featuring irregular (chaotic) activity outside them - they are usually associated to perceptions, thoughts and memories, the chaos between them with searches, and itinerancy with sequences of thoughts, speech and writing activities.
The first known reference to chaotic itinerancy in the scientific literature occurred in the late 1980’s, and the concept itself was defined as a chaotic transition dynamics resulting from weak instability of Milnor-type attractors [30].
Until the1980’s, complex high-dimensional dynamical systems attracted much attention in various fields, such as physics, mathematics, biology and so on. Accordingly, many complex phenomena were modeled based on such systems in optical turbulence, for instance [16].
Independently, similar transitory phenomena were identified in neural network models of associative memory [29], in which not only a single association of a certain memory, but also a successive association of memories were realized. The underlying states associated to transitions were considered to be Milnor attractors [22] whose basins of attraction have positive Lebesgue measures, opening the possibility of leaving them after a sojourn period. Many researchers discussed the universality of this kind of transitory behavior - the most relevant topics were the successive transitions among quasi-attractors [13,31], the stability of the states changes via transitions, the drastic change of local dimensionality during the transitions and so on. In this context, local dimensionality can be calculated by instantaneous Lyapunov exponents defined by the eigenvalues of Jacobian matrix at each point of the trajectories.
Therefore, many authors started calling the phenomenon characterized by those features "chaotic itinerancy", in which nearby regions of quasi-attractors were named "attractor ruins", as these regions in phase space are not occupied by classic attractors, but contain trajectories which can be nearly stationary, as if a conventional attractor were there.
A Milnor attractor is considered to be an adequate model for describing a quasi-attractor because, even under minimal perturbations, trajectories escape from attractors sooner or later, as it can include a region or a set with neutral stability. This destabilized state of the attractor results in an attractor ruin. In this fashion, complete convergence to an attractor fails and the continuing presence of a collapsing gradient leads to the appearance of the effect of real nonlinearity even in a neighborhood of the attractor.
As the transitory phenomena observed in the brain include chaotic changes, the interpretation in terms of chaotic itinerancy depends basicaly on the presence of stationary motion nearby an ordered state, which is assured by the existence of attractor ruins. In [9] it is proposed a concept similar to chaotic itinerancy - the dynamic functional binding of information processing based on metastability to represent both a particular information processing to each cortical local area and overall integration of local information processing.
In certain types of dynamical systems, such as the ones modeled by differential equations, the number of dimensions may be fundamental to produce more complex global dynamical behavior. Usually, systems with less than 3 dimensions have two types of attractors: fixed points and limit cycles. On the other hand, systems with 3 dimensions have produced chaotic attractors.
It is now clear that chaotic itinerancy is able to model some transitory dynamics among quasi-attractors, and it is possible to describe several kinds of states in terms of the concept of attractors in dynamical systems. In this fashion, steady states are represented by fixed points, periodic motions by limit cycles, irregular configurations by strange attractors and so on. However, the analysis of certain kinds of transitory behavior could be facilitated by a new type of dynamical concept, similar to chaotic itinerancy, presenting the ability to precisely describe sequences of transitions finalized by stable or even asymptotically stable paths, for example. This is so because although the concept of chaotic itinerancy expresses the transitions between quasi-attractors, such areas of transitory permanence do not contain asymptotically stable subsets. It is clear that the cited notion of quasi-attractor is similar to the concept proposed by Milnor in [22]. But, if a Milnor attractor is abandoned, trajectories may converge to another one, getting indefinitely constrained near it, unless additional perturbations occur, and an "attractor ruin" allows the evolving path to get far from thecurrent attraction region.
The system described in the present work has similar characteristics to the ones above described and includes a final (asymptotically) stable region. Besides, it is nonautonomous and dissipative, as will be amply shown below. In addition, the orbits near intermediate quasi-attractors have a unique behavior, given the regularity of the arrival and departure from the corresponding most internal points, as will be seen in what follows.
A very interesting potential application in the human sciences and philosophy would be the representation of the Hindu philosophical concepts of Samsara and Moksha, the former associated to a set of quasi-attractors and the latter to the unique and final region of higher evolutionary level, where evolution continues, approaching a specific point.
In very general terms, Hindu scriptures state that Samsara is the very long cycle of physical birth and rebirth, while Moksha is associated to the individual liberation from Samsara [21].
By observing the outputs of the new system, it is possible to note that the very initial parts of paths display disordered activity, previously the appearance of quasi-attractors - condition compatible with the suggested application. Besides, the interpretation of transition segments between quasi-attractors as sojourns outside physical dimensions would be very reasonable and intuitive.
2. Theoretical Aspects and Fundamental Definitions
As the Dirichlet Eta function and associated vector field gave origin to the dynamical system here studied, nothing more natural than to start with their definitions.
The expression for Eta (in the open right half-plane) in terms of the complex variable s is:
As said above, the study is restricted to the open subset - please, refer to Figure 1. In general lines, the underlying idea in this work is to face the eta function as a mapping, associating to each element of A one vector in , that is to say, a 2-dimensional vector field usually referred to as the field associated to [18], namely, , using the same designation for both entities. This viewpoint gives rise to the autonomous system
which will serve as the basis for the definition of the new system.
2.1. The Dirichlet Eta Function and Its Associated Vector Field
As established in [26], by identifying and , the Dirichlet Eta function can be put in the following form
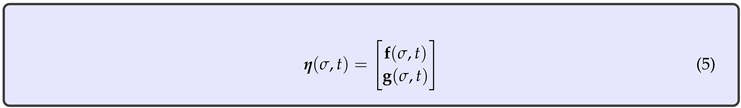 and seen as a vector field whose components are its real and imaginary parts, restricted to and .
and seen as a vector field whose components are its real and imaginary parts, restricted to and .Being holomorphic, its components are and have partial derivatives of all orders. In addition, it satisfies Cauchy-Riemann equations [18].
The total differentials of f and g are
and considering that
it results in
2.2. The Expression for the Poincaré Index
The Poincaré index of an equilibrium point of V, , is defined to be the index of a closed curve C which surrounds only this specific point, not existing equilibria on the closed curve.
2.3. Detailed Description of Parameters and Formulas Leading to the New Dynamical System
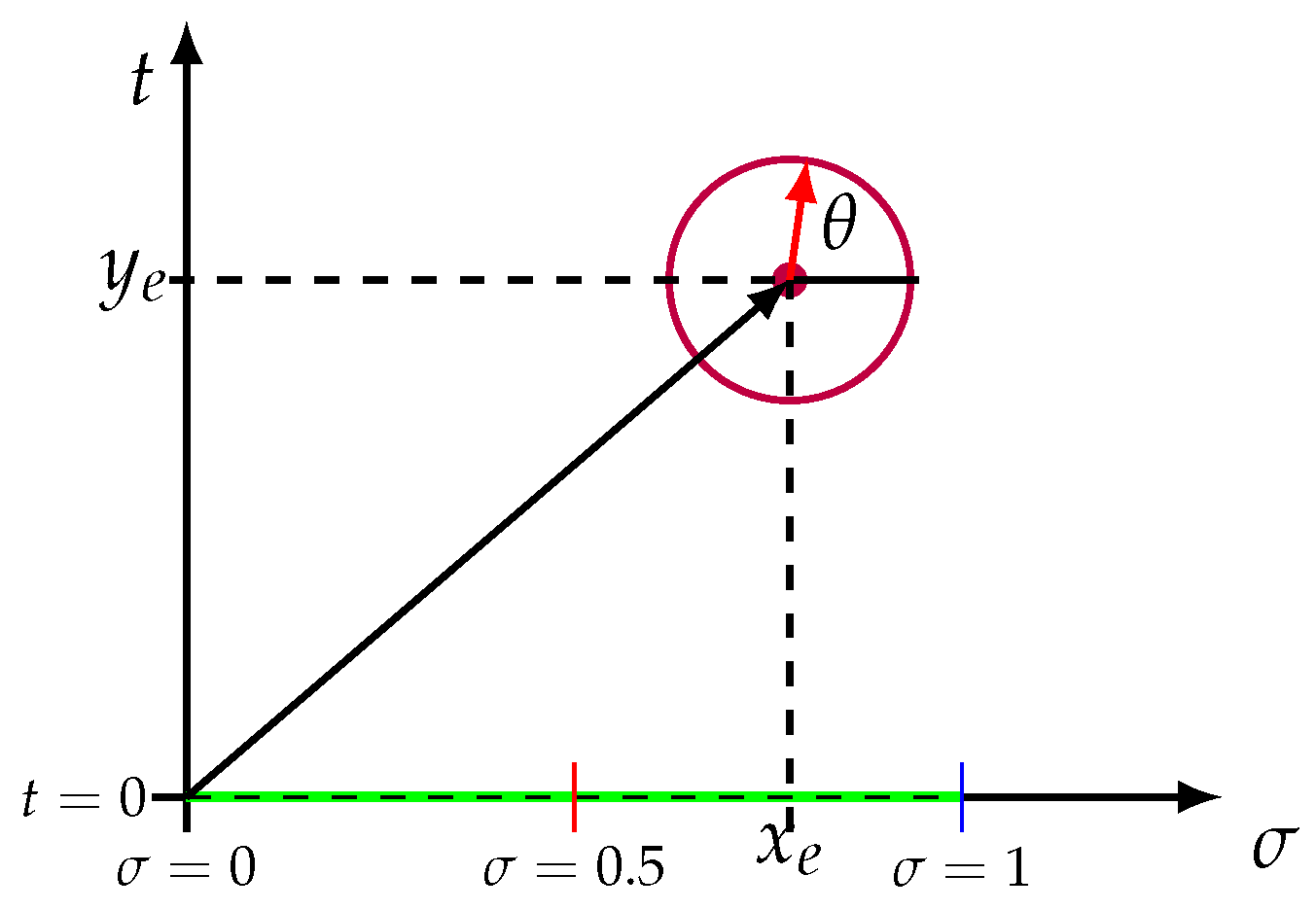
In [26] it was assumed that there is a nontrivial and isolated zero of the function, located outside the critical line (and inside the open and simply connected region ) - the basic idea was to arrive at a contradiction, demonstrating that the initial assumption is false. In addition, the curve C was a circle with center at , radius R, and parameterized by the angle , indicated in Figure 2. In this fashion, the parameters and nomenclature are:
where .
2.4. Coordinates Change
At this point, a global change of variables is about to reveal the final expression used to obtain the Poincaré index, this time including and other parameters. For details, please see [26]. After several simplifications, the following expression arises:
where
In order to investigate the convergence of the series (20) and (21)
some well-known tests were used, Dirichlet’s (page 152 of [19]) and direct calculations, for instance.
For expression (19), define
Dirichlet’s test states that, if is monotonic and converges to 0, and is bounded for all N, (expression (20) ) converges.
It happens that all conditions are satisfied, as demonstrated in [26], but from now on the expression for is one central element for the definition of the new system under study, taking into account that it is the first coordinate function for the input of the device.
Relatively to (21), the same reasoning applies and the definitions are:
Again, all conditions are satisfied, as detailed in [26], but, as above, the expression for this describes the second coordinate function for the input of the device.
Finally, the expressions for the inputs of the system are
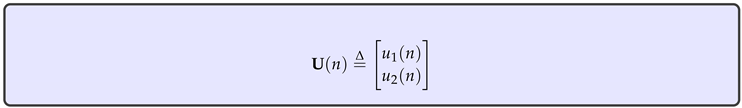
, a more precise notation would be
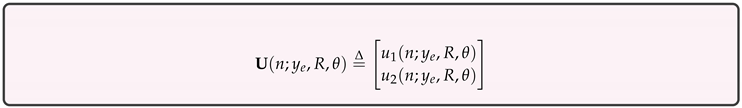 mainly because parameters like have a strong bifurcatory potential in the present setting. Please, note that the meaning of in [26] is totally unrelated to the present exposition - here they will play the role of geometric and dynamical modellers.
mainly because parameters like have a strong bifurcatory potential in the present setting. Please, note that the meaning of in [26] is totally unrelated to the present exposition - here they will play the role of geometric and dynamical modellers.However, the simpler notation will be kept.
3. Equations of the New System
Let us define the 2-dimensional system as

An elementary but interesting observation is that the Euclidean norm of is 1, that is, all inputs are taken from the standard unitary circle in .
Another way to express the same formula is
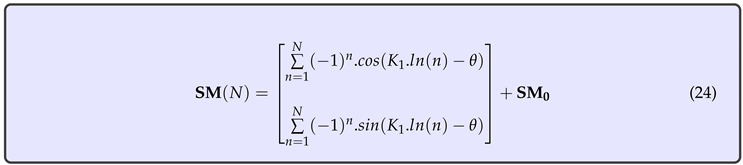
In view of the results of the previous section, it follows that the paths of are always contained in bounded regions of the Euclidean plane.
4. Simulations
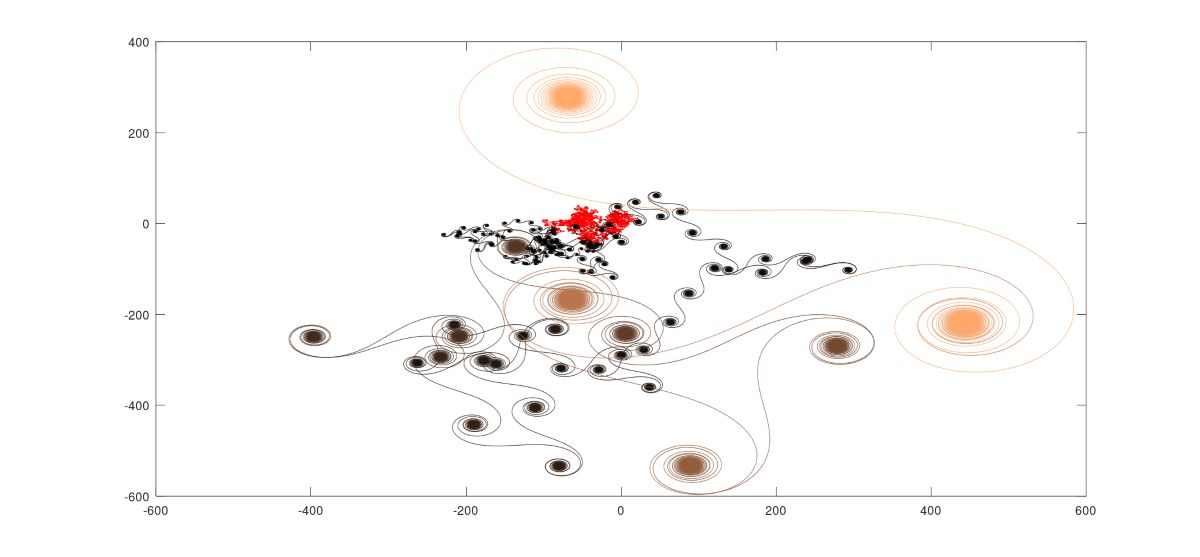
In this section, several configurations will be generated by varying values of parameters of the model, and the respective results will be commented. The emphasis will be on due to its great bifurcatory potential, relatively to changing the number and position of quasi- attractors. For example, the initial condition translates the whole path in , but does not change geometric or dynamical aspects. The colors in the paths indicate the several phases (red appears in initial stages, copperish regions signal final stages). All paths display a final phase represented by a unique and dense spiral-like structure. In the very beginning, there is a somewhat disordered evolution, followed by sojourns near several quasi-attractors.
4.1. Example 1: - 10000 Iterations
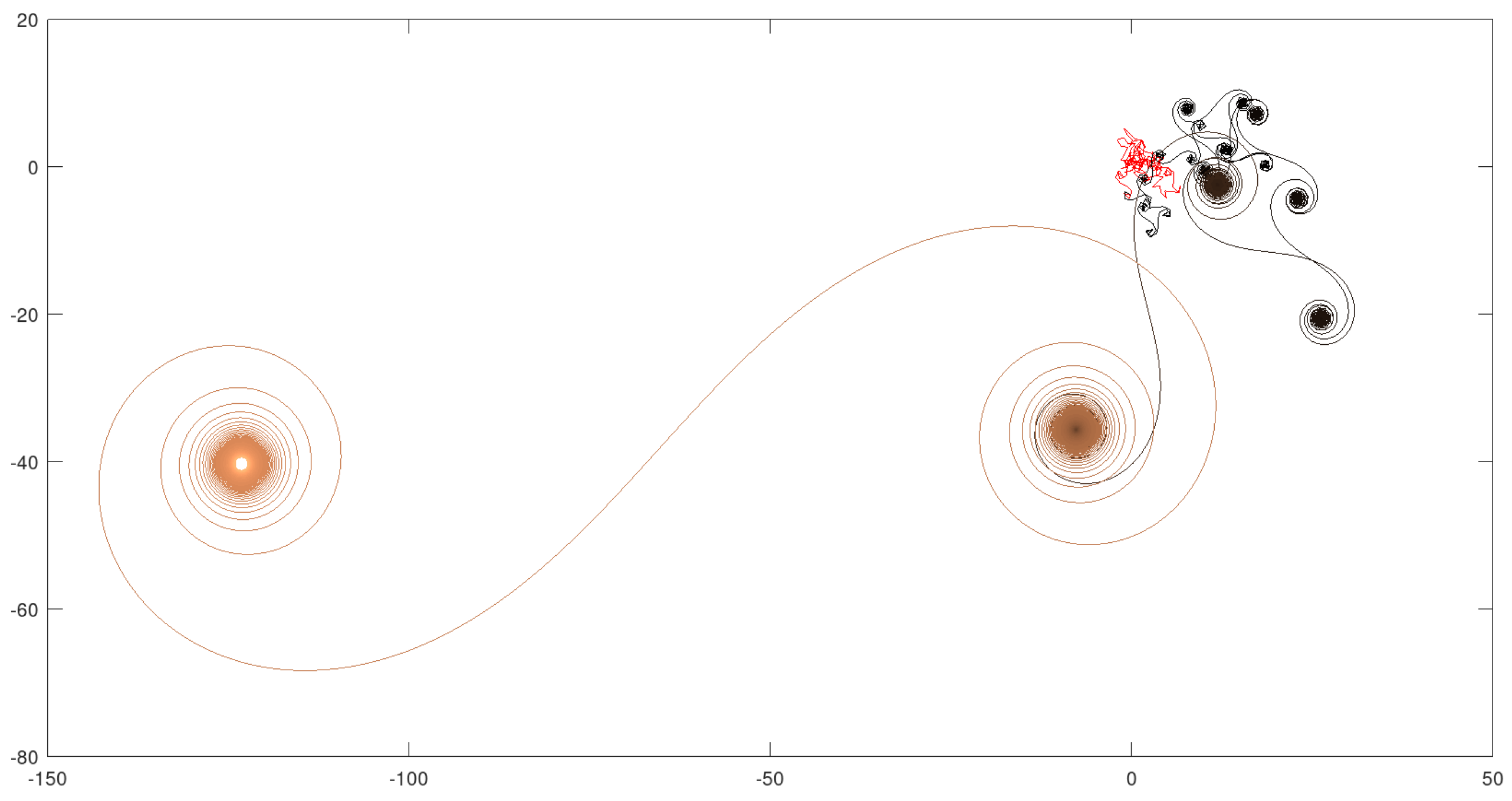
In this example the value for may be considered intermediate, resulting in few visits to quasi-attractors and a fast evolution until reaching the final stabilization and progressive approach to a specific equilibrium point. The initial disordered phase is also very short. The estimated Hausdorff dimension of the curve in Figure 4 is 1.31591.
Figure 3.
Coordinate functions for the state of .
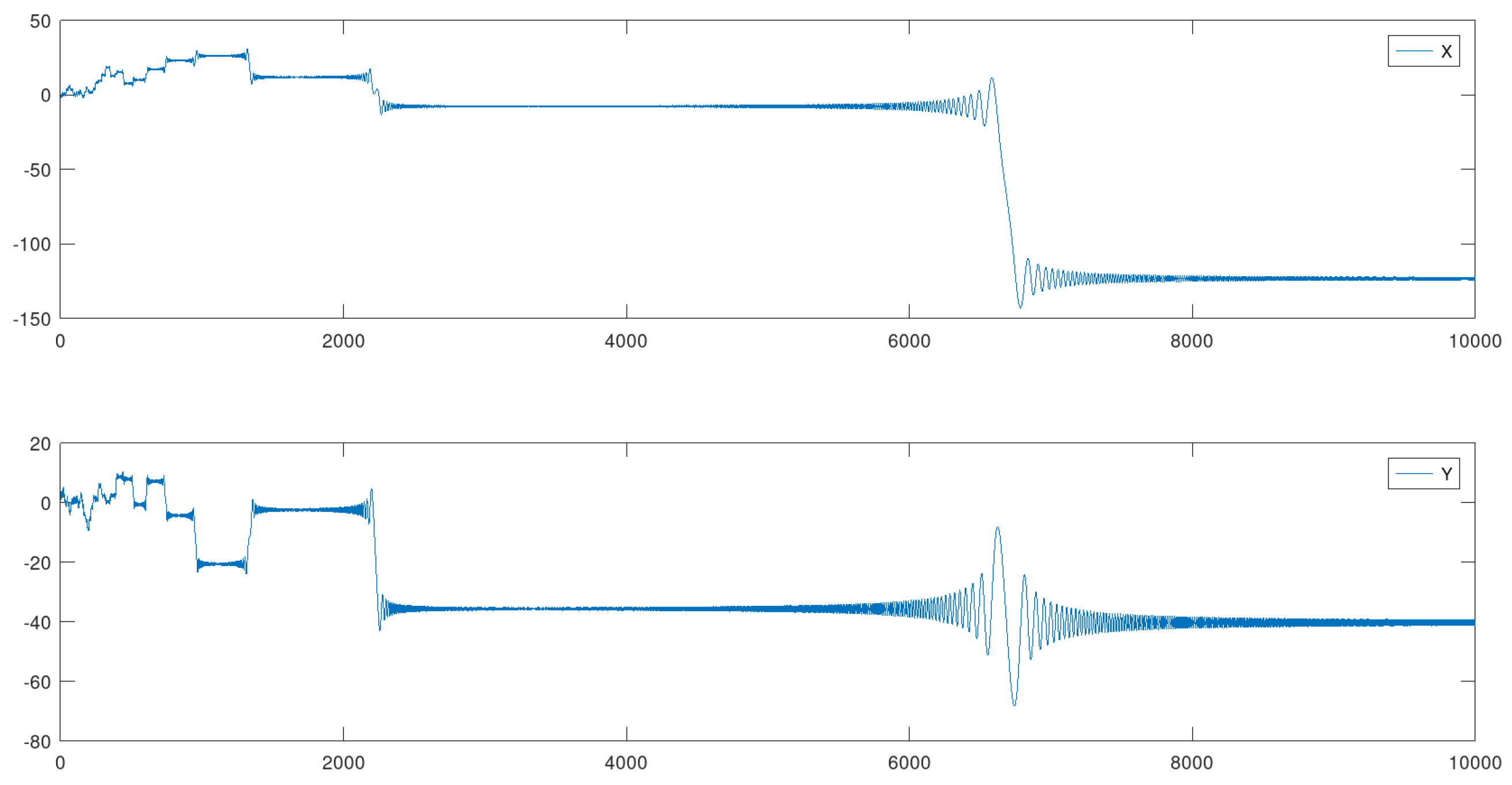
Figure 4.
Complete 2-dimensional graph.
4.2. Example 2: - 90000 Iterations
In this example the value for is somewhat greater than the previous one, but not enough to provoke a big qualitative change, although it is possible to note a certain densification in most quasi-attractors. The initial disordered phase was also enlarged, and the diameter of the whole set was substantially increased. The estimated Hausdorff dimension of the curve in Figure 6 is 1.32921.
Figure 5.
Coordinate functions for the state of .
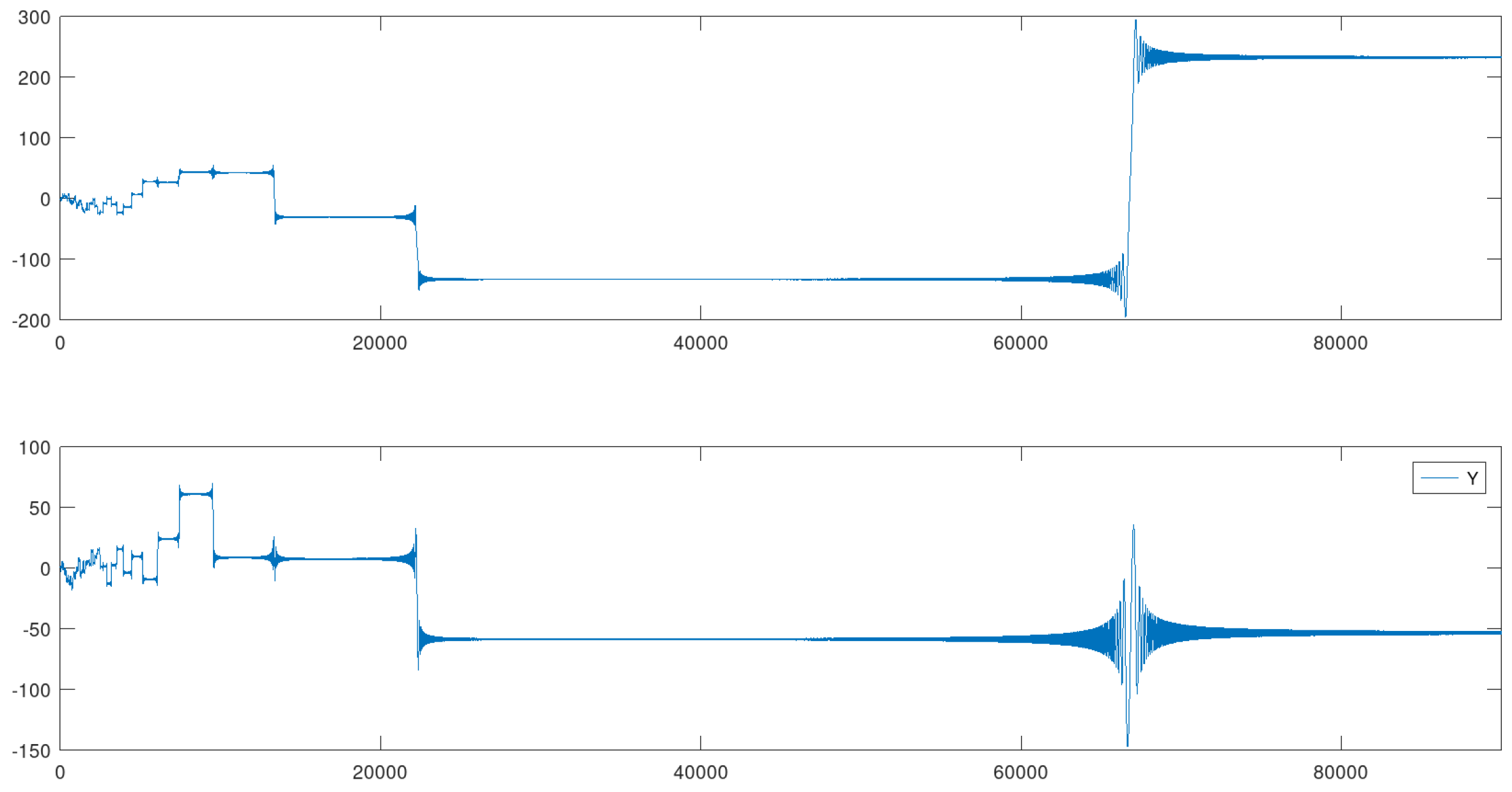
Figure 6.
Complete 2-dimensional graph.
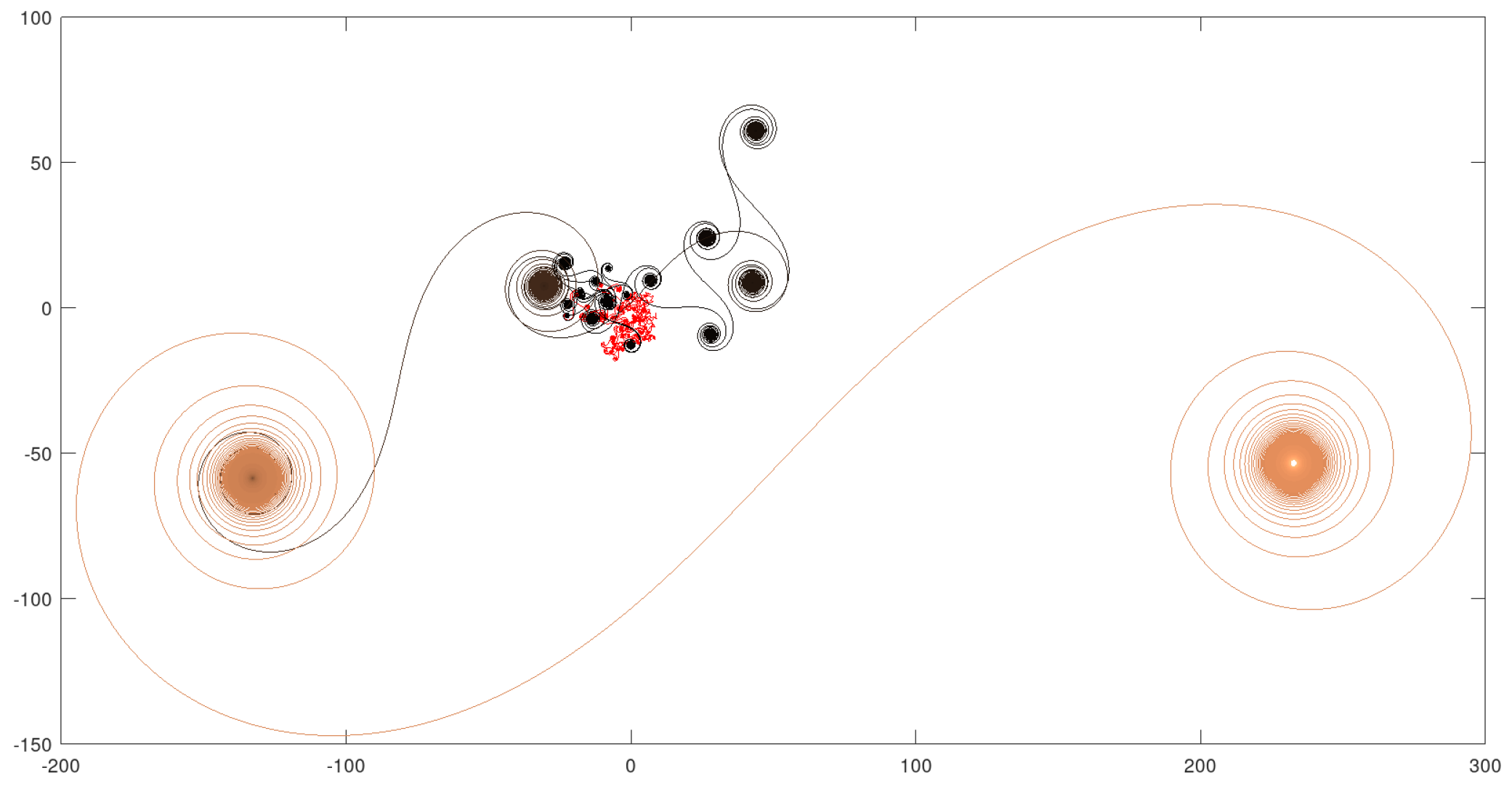
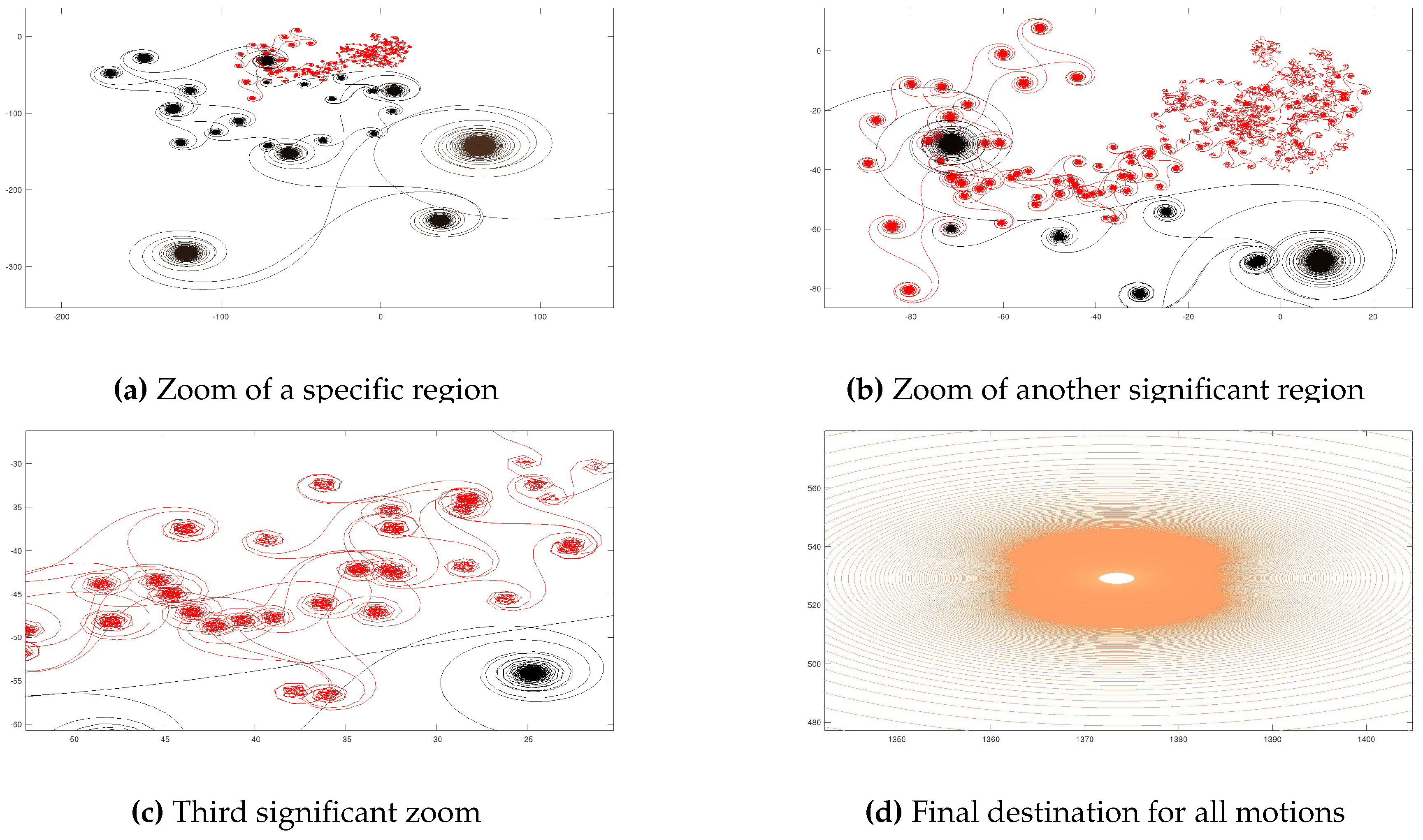
4.3. Example 3: - 800000 Iterations
Here, the value of was sufficient to make a more complex path and provide a reasonable qualitative change, in number and complexity of quasi-attractors’ combinations. The initial disordered phase was also greatly enlarged, and the diameter of the whole set was also substantially increased. The complementary views make it possible a better examination of the path. The estimated Hausdorff dimension of the curve in Figure 8 is 1.32188.
Figure 7.
Coordinate functions for the state of .
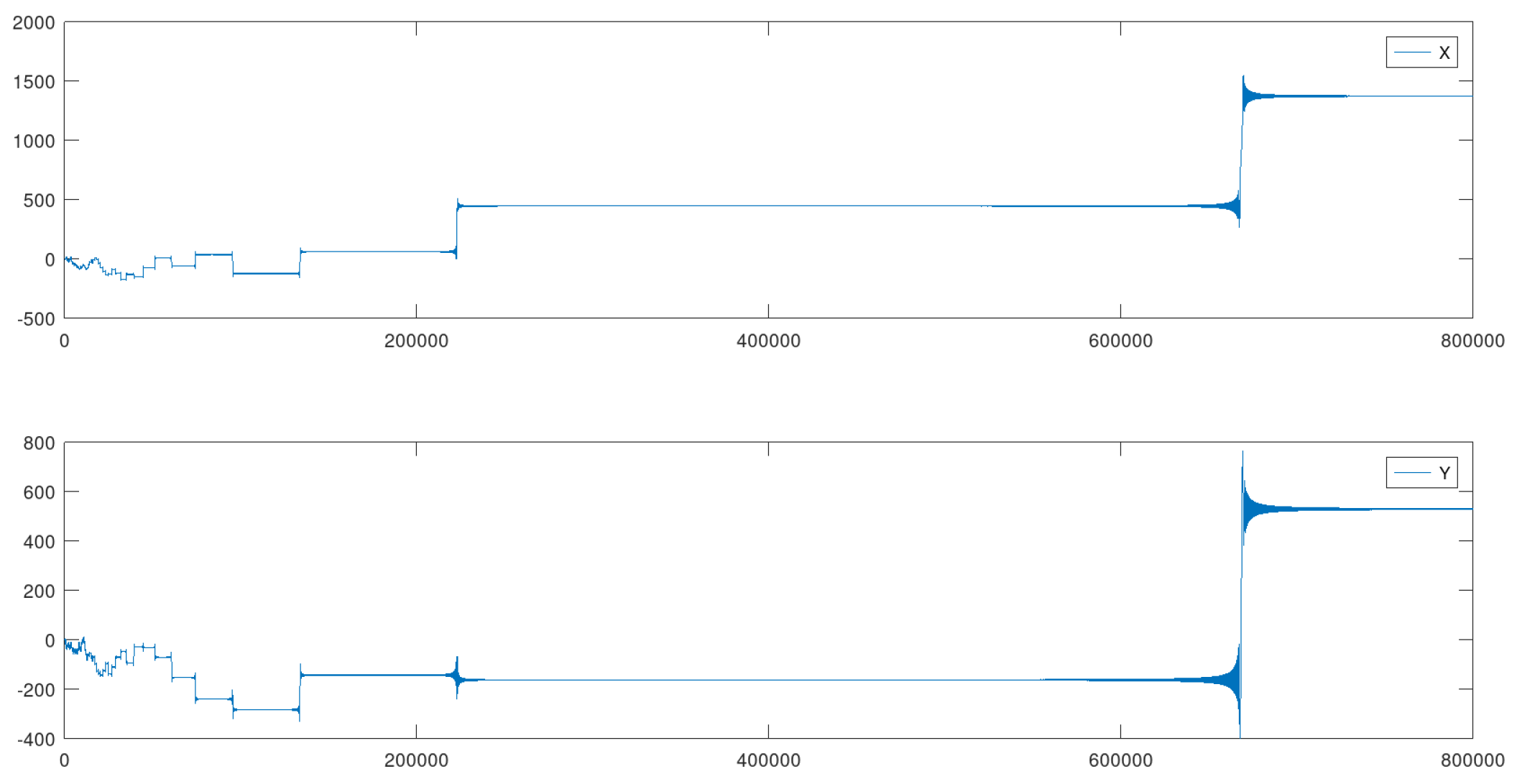
Figure 8.
Complete 2-dimensional graph.
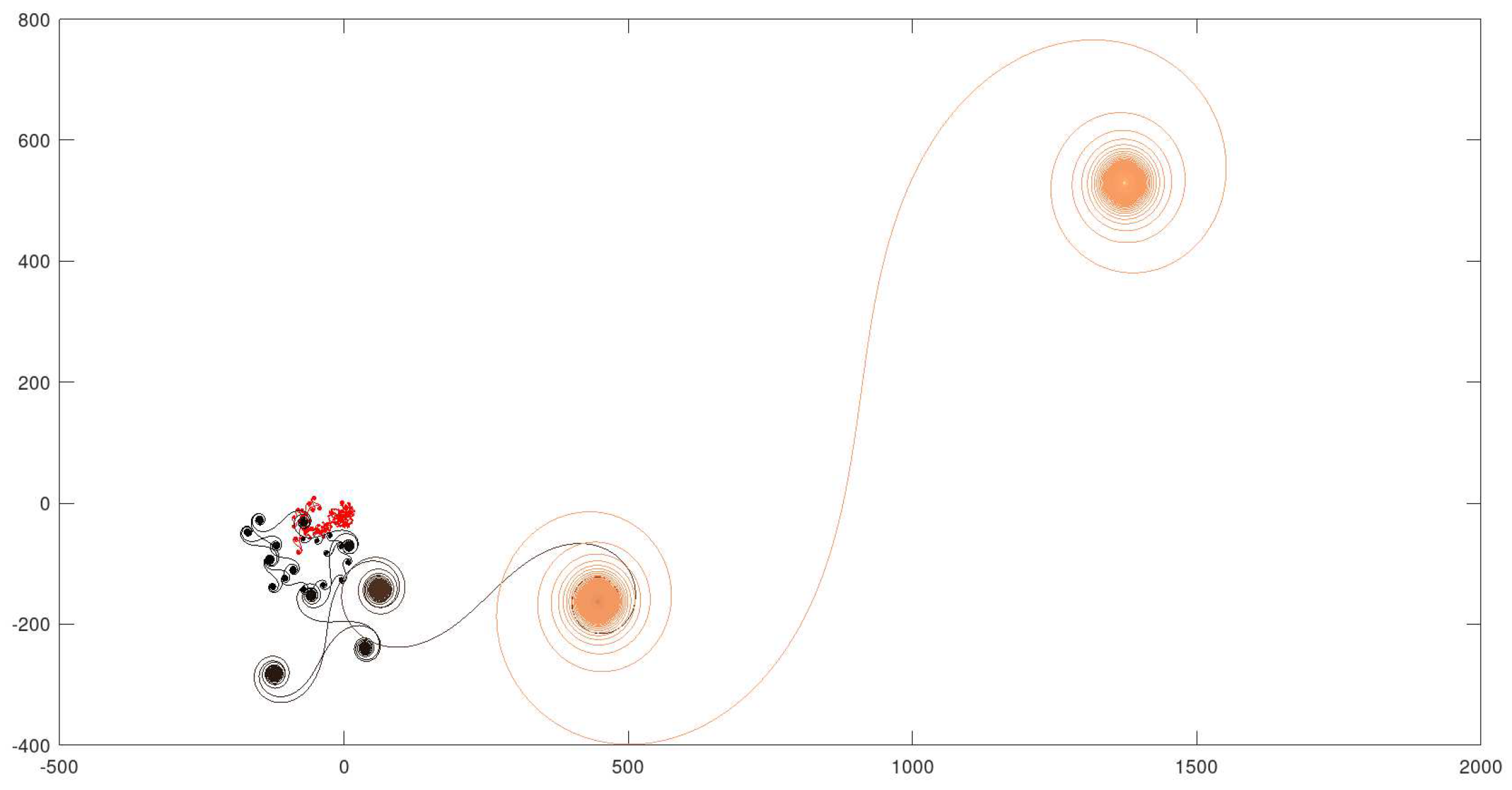
Figure 9.
Several amplified views of significant subsets.
4.4. Example 4: - 1400000 Iterations
Here again, the rise in the value of triggered an even more complex path, providing a reasonable increase in the number of quasi-attractors. The complementary graphs make it possible to obtain a better examination of the path. The estimated Hausdorff dimension of the curve in Figure 11 is 1.51213.
Figure 10.
Coordinate functions of .

Figure 11.
Full path of .
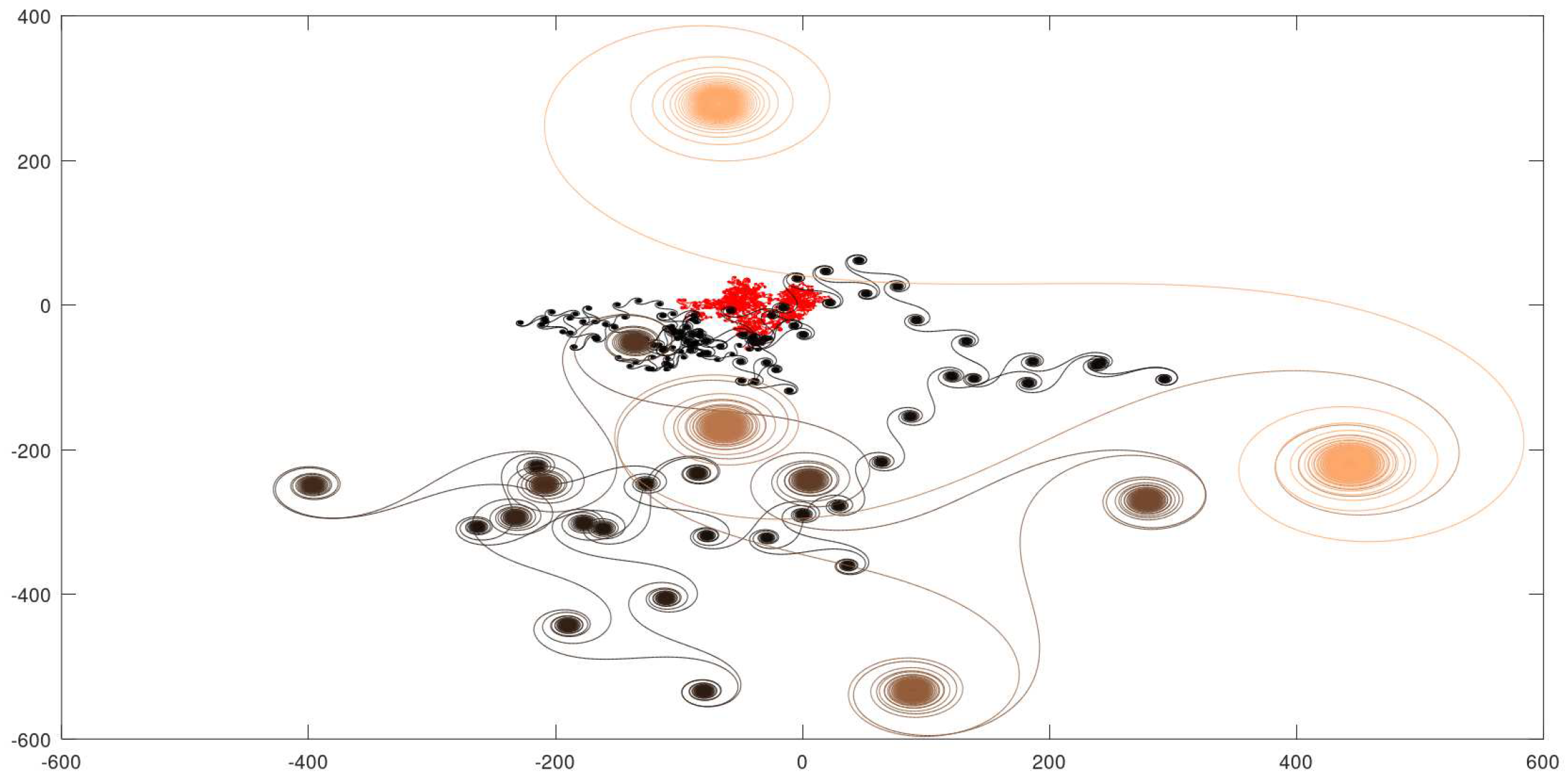
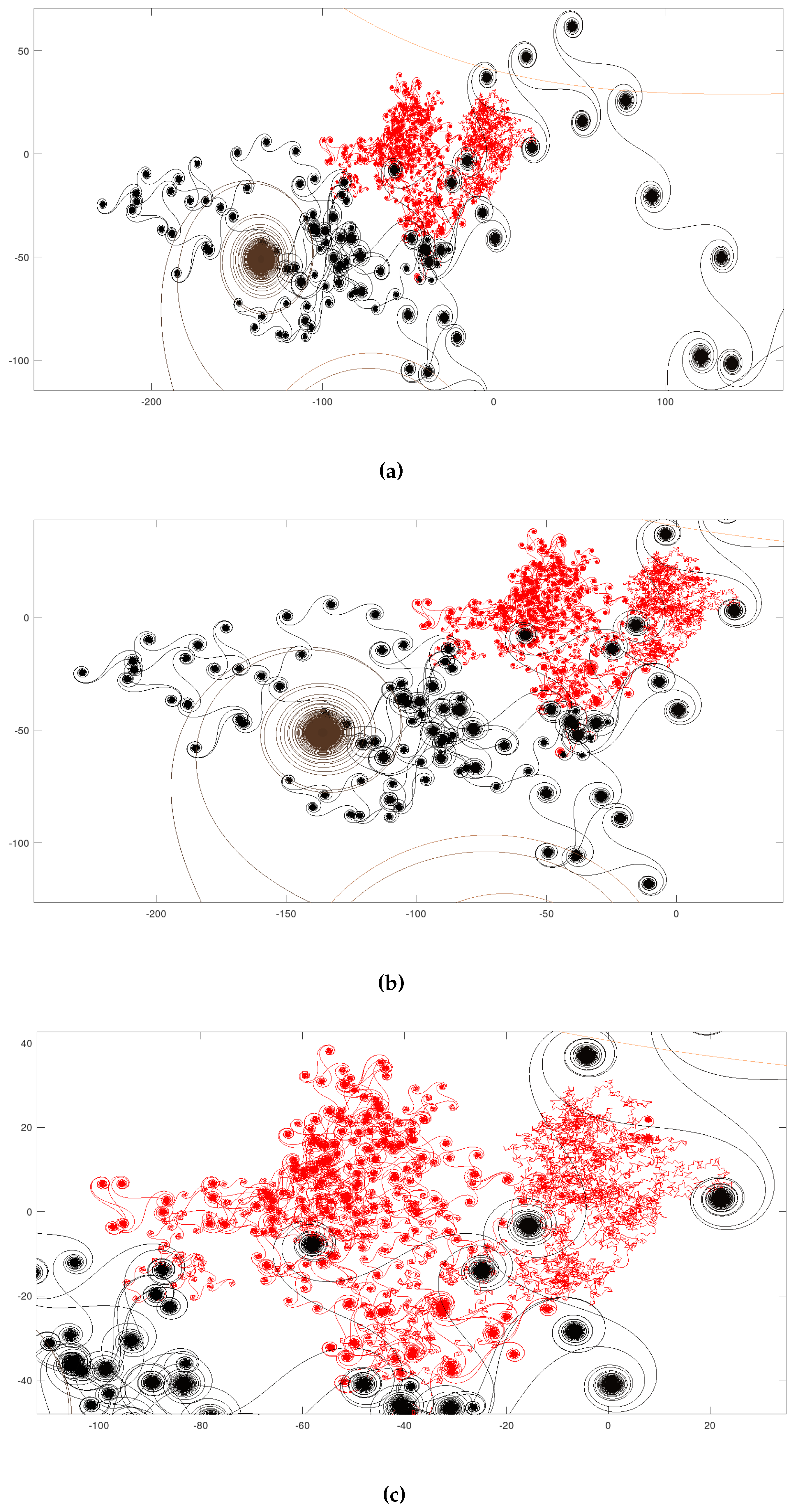
Figure 12.
Several amplified views.
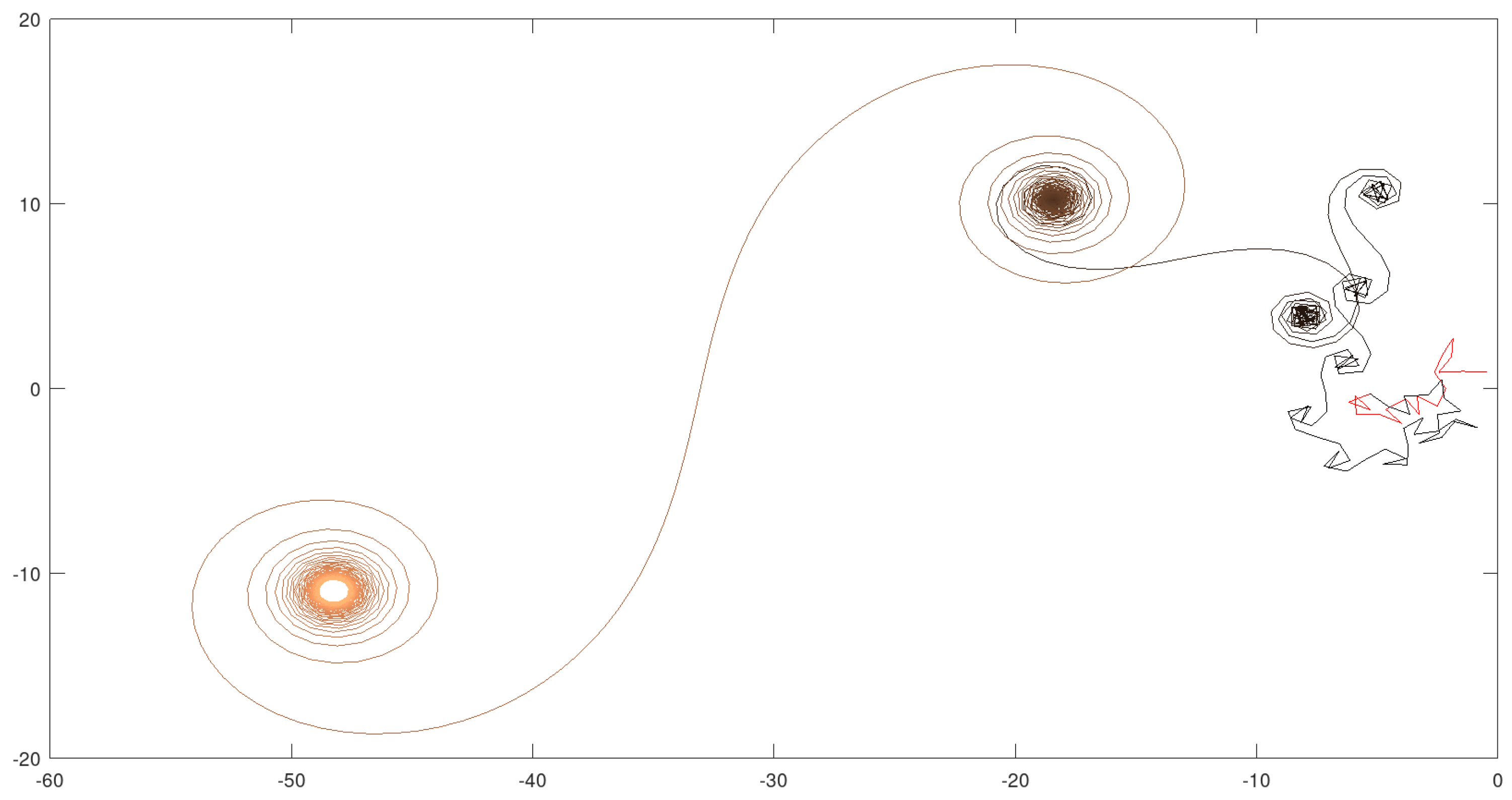
4.5. Example 5: - 1200 Iterations
In this case the value for was abruptly reduced, inducing a substantial reduction in the complexity of the global scenario. Anyway, all phases are present: disordered, visits to quasi-attractors and final restriction to a bounded region. The estimated Hausdorff dimension of the curve in Figure 14 is 1.23883.
Figure 13.
Coordinate functions of .
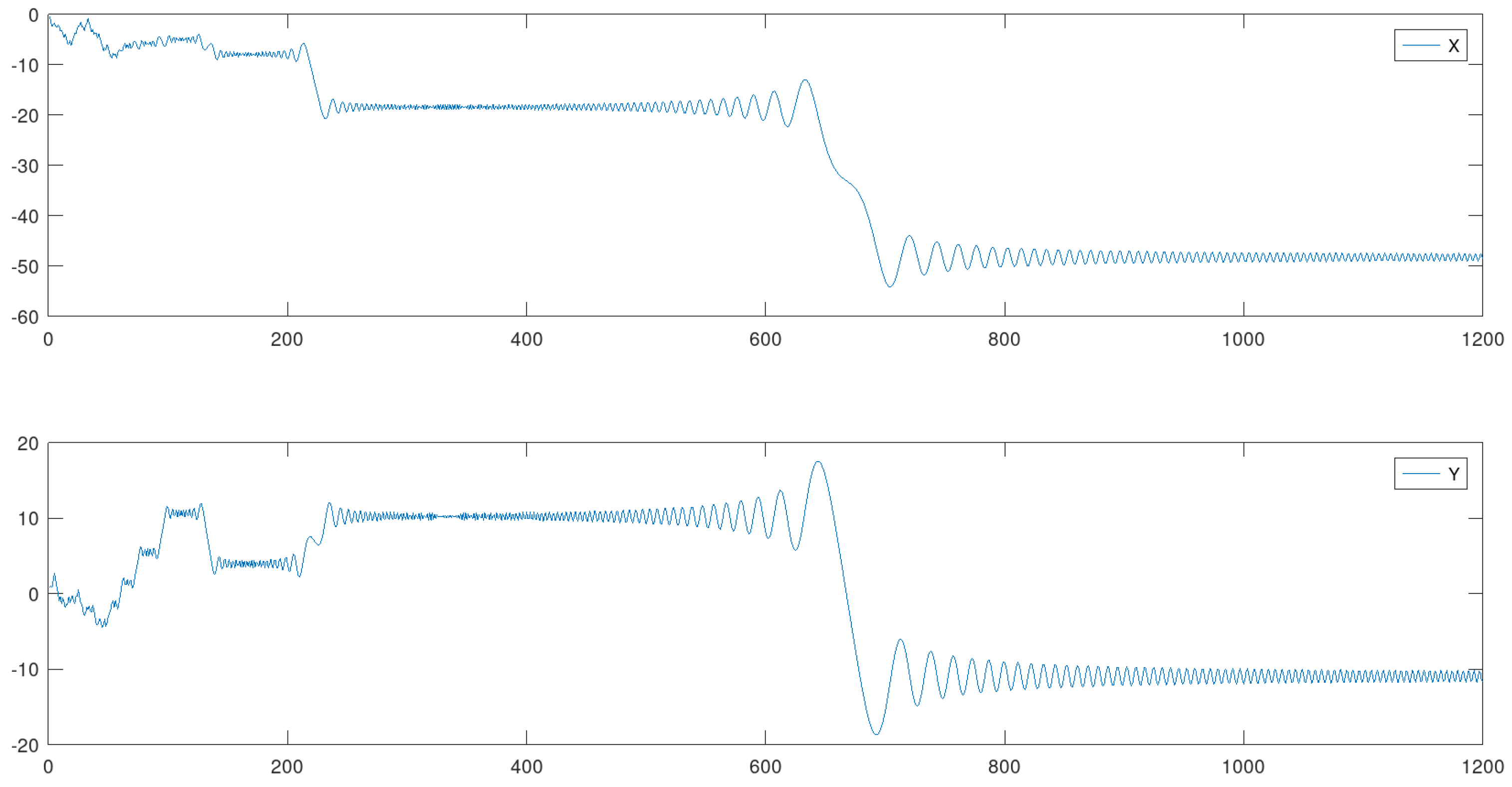
Figure 14.
Path of .
4.6. Example 6: - 11000000 Iterations
The final example brings the most complex path with the highest value for among all created in the article. Below, amplified images show that a very large number of quasi-attractors were created in various size levels, reinforcing the perception that is directly connected to geometric and dynamical complexity. The estimated Hausdorff dimension of the curve in Figure 16 is 1.40825.
Figure 15.
Coordinate functions of .
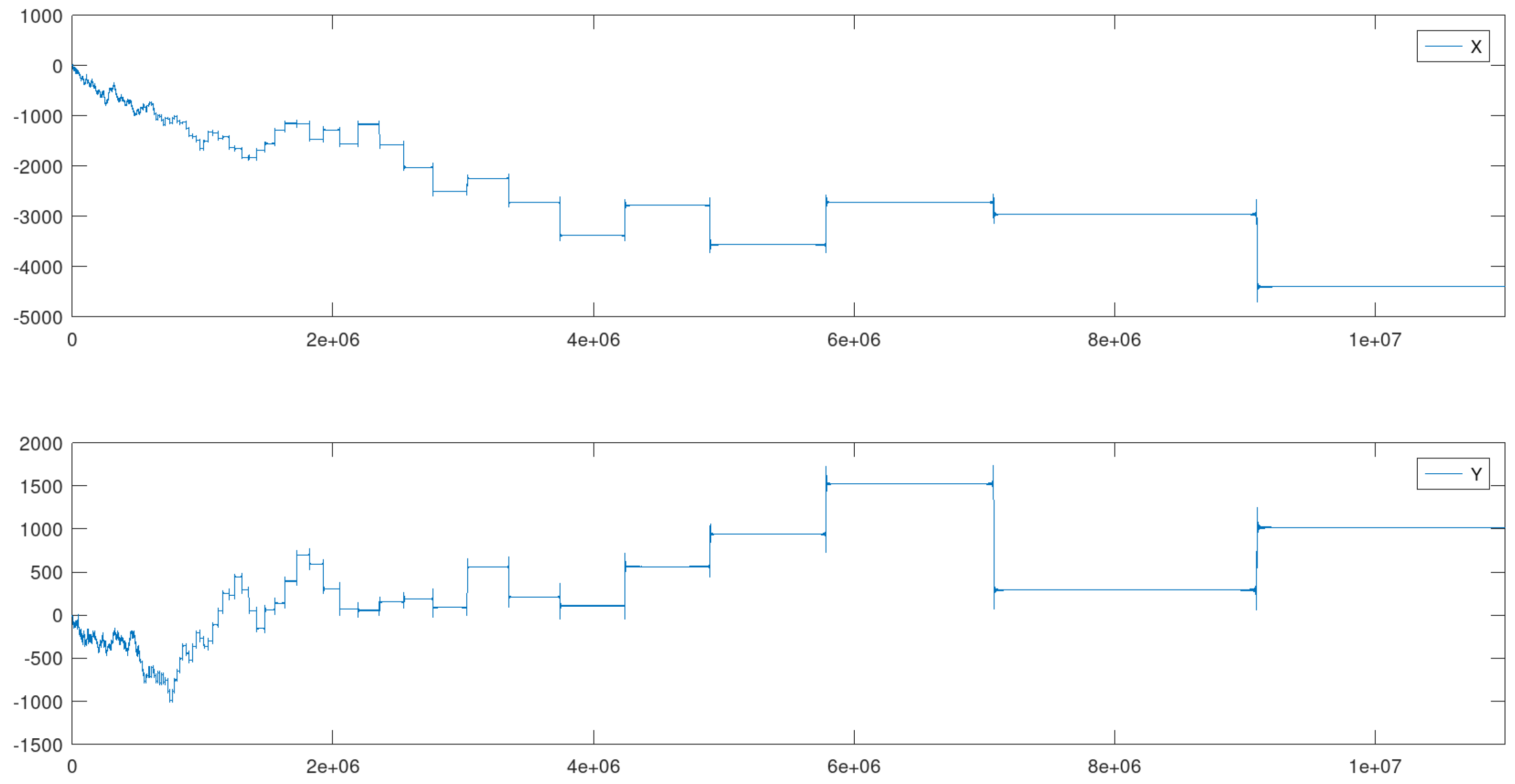
Figure 16.
Path of .
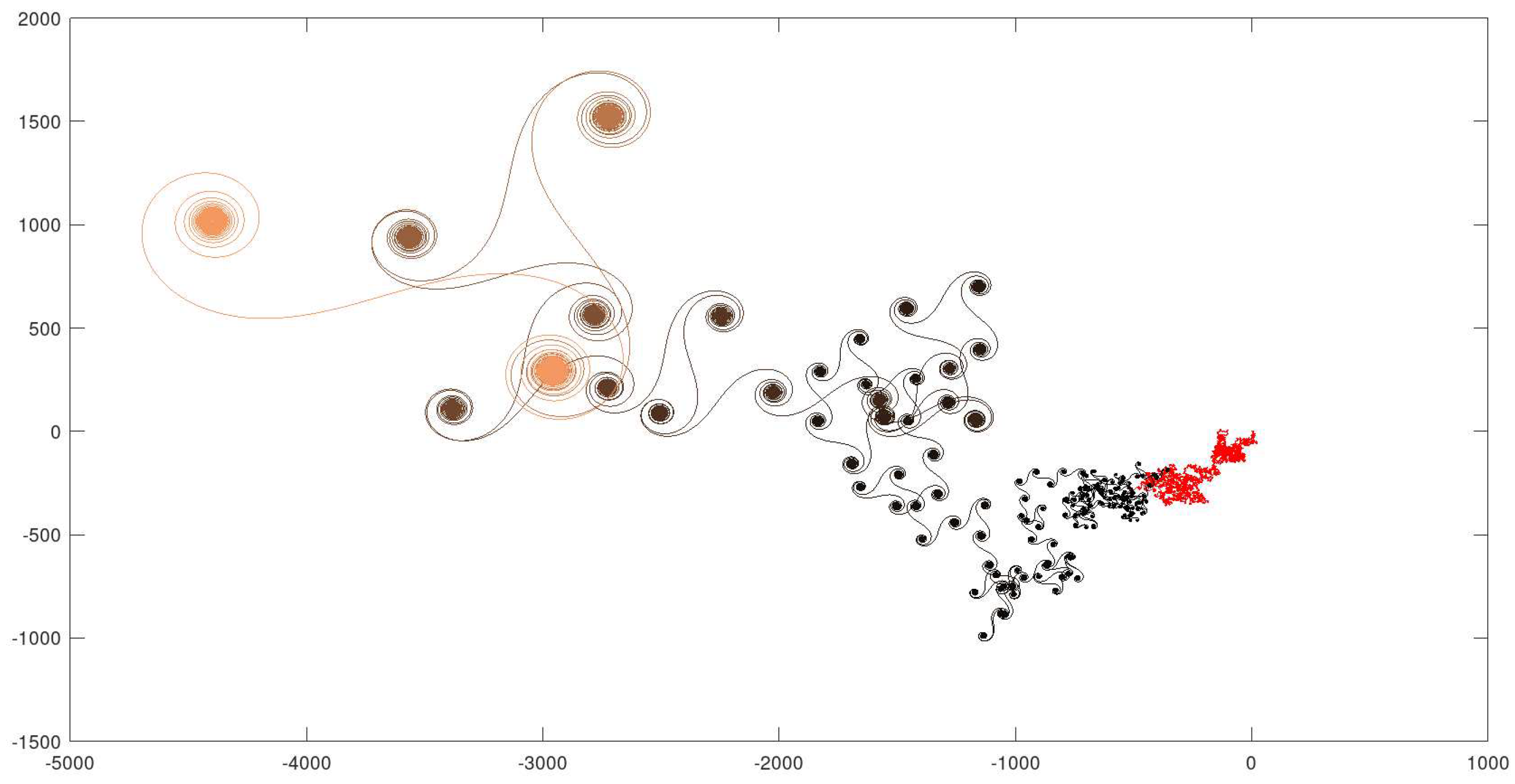
Figure 17.
Several zooms of sub-regions.
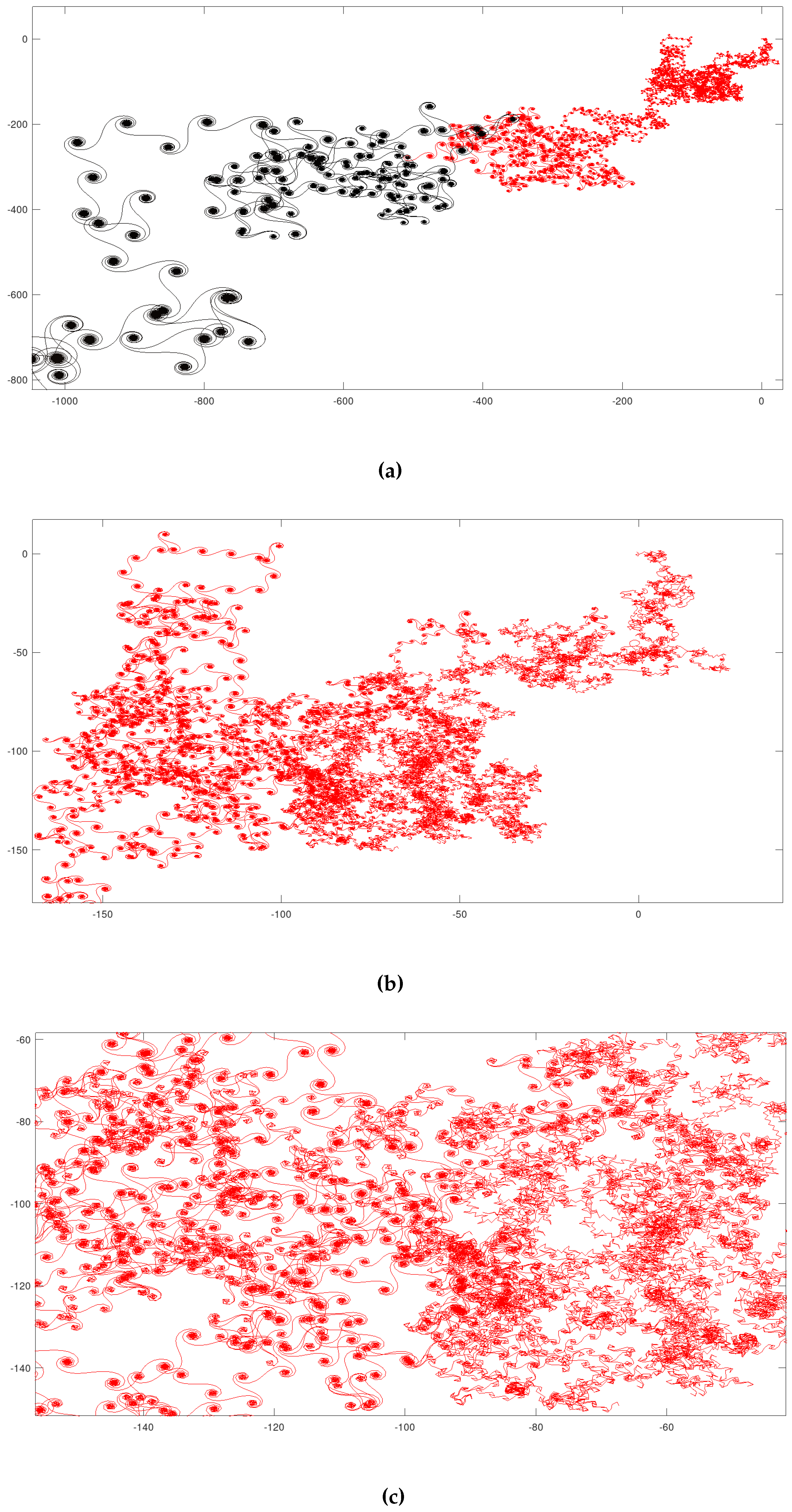
4.7. Source Code Used in the Tests
In order to assist readers in additional experiments, a very simple Octave script is listed below.
| Listing 1. Example Octave script. |
 |
5. Conclusions
The paper presented a new type of chaotic dynamical system originated from Dirichlet Eta function. The described system has many characteristics, typically dispersed in diverse types of devices, in only one kind of dynamical element, showing dissipative, chaotic and itinerant behavior. In addition, generated paths feature nonrecurring quasi-attractors and respective regions of ruin. Being discrete and nonautonomous, it is additively driven by a simple real vector input sequence.
In all cases, paths are eventually "attracted" to an asymptotically stable and limited region.
Another very relevant aspect is that its defining formulas contain parameters capable of activating bifurcatory effects, mainly related to setting the number of quasi-attractors and overall geometric complexity and diversity. In this sense, it bears a certain resemblance to classical itinerant chaotic systems, although completely different.
The most influential parameter could be interpreted as a type of condensed or potential energy, capable of strongly interfere in sojourns nearby quasi-attractors etc. Therefore, there is room to employ artificial inference/global learning techniques and automatically design tailored paths.
The text also cites an atypical, but important, potential application in philosophy: the representation of the Hindu concepts of Samsara and Moksha - the former associated to a set of quasi-attractors and the latter to the unique and final asymptotically stable region, where evolution continues, approaching a specific point. The very initial parts of paths display disordered activity, just before the appearance of quasi-attractors - another indication for the application at hand. It is also possible to interpret the transition segments between quasi-attractors as periods of permanence outside physical dimensions.
References
- ALEKSANDROV, Alexander G. The Poincaré index and its applications. Universe, v. 8, n. 4, p. 223, 2022.
- A. A. Andronov, E. A. Leontovich, I. I. Gordon and A. G. Maier, Qualitative Theory of Second-Order Dynamic Systems. Halsted Press, New York, 1973.
- A. A. Andronov, E. A. Leontovich, I. I. Gordon and A. G. Maier, Theory of Bifurcations of Dynamical Systems on a Plane. Wiley, New York, 1973.
- N. ARWASHAN, THE RIEMANN HYPOTHESIS AND THE DISTRIBUTION OF PRIME NUMBERS, Nova Science Publisher Inc, 2021.
- V. I. Arnold, Mathematical Methods of Classical Mechanics, Springer, New York, 1989.
- V. I. Arnold, Geometrical Methods in the Theory of Ordinary Differential Equations, Springer, New York, 1983.
- D. K. Arrowsmith and C. M. Place, Ordinary Differential Equations. A Qualitative Approach with Applications. Chapman & Hall, London, 1982.
- F. Brauer, J. A. Nohel, The Qualitative Theory of Ordinary Differential Equations: An Introduction. Courier Corporation, New York,1989.
- S.Bressler, J. Kelso. Cortical coordination dynamics and cognition. Trends in Cogn Sci 5: 26-36, 2001.
- J. Derbyshire, Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York, Penguin, 2004.
- Edwards, H. M. Riemann’s Zeta Function. New York: Dover, 2001.
- J. Guckenheimer and P. Holmes, Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields, Springer, New York, 2013.
- H. Haken. Beyond attractor neural networks for pattern recognition. Nonlinear Phenomena in Complex Systems 9: 163-172, 2006.
- J. K. Hale, Ordinary Differential Equations. Robert E. Krieger Publishing Co. Inc., New York,1980.
- P. Hartman, Ordinary Differential Equations. John Wiley & Sons, New York, 1964.
- K Ikeda, K. Otsuka, K. Matsumoto. Maxwell-Bloch turbulence. Prog. Theor. Phys. Suppl. 99: 295-324, 1989.
- K. Knopp, Theory and Application of Infinite Series, Dover, 1990.
- S. Lang, Complex Analysis, 4th ed., Springer-Verlag, 1999.
- C. H. C. Little, K. L. Teo, B. van Brunt, Real Analysis via Sequences and Series, Springer, New York, 2015.
- R. Marangell, Index Theory Lecture Notes, University of Sydney, 2017.
- D. McKenzie, Samsara: An Exploration of the Hidden Forces that Shape and Bind Us, Mantra Books, 2022.
- J. Milnor. On the concept of attractor. Comm Math Phys 99: 177-195, 1985.
- M. Mureşan, A Concrete Approach to Classical Analysis, Springer-Verlag, New York, 2009.
- Z. Nitecki, Differentiable Dynamics - An Introduction to the Orbit Structure of Diffeomorphisms. The MIT Press, New York, 1971.
- H. Oliveira, Existence of Zeros for Holomorphic Complex Functions: A Dynamical Systems Approach. Preprints 2023, 2023090357. [CrossRef]
- H. Oliveira, A Modest Contribution to the Riemann Hypothesis Using the Poincaré Index. Preprints 2023, 2023090513. [CrossRef]
- L. Perko, Differential Equations and Dynamical Systems. Springer Science & Business Media, New York, 2001.
- E. C. Titchmarsh.. The Theory of the Riemann Zeta Function, 2nd edition, Oxford University Press, 1986.
- I. Tsuda I, E. Korner E, H. Shimizu. Memory dynamics in asynchronous neural networks. Prog Theor Phys 78:51-71, 1987.
- I. Tsuda. The plausibility of a chaotic brain theory, The Behavioral and Brain Sciences 24 (4), 2002.
- I. Tsuda. Toward an interpretation of dynamic neural activity in terms of chaotic dynamical systems. Behav. Brain Sci. 24: 793-847, 2001.
- I. Tsuda., T. Umemura. Chaotic itinerancy generated by coupling of Milnor attractors. Chaos 13: 926-936, 2003.
- S. Wiggins. An introduction to applied nonlinear dynamical systems and chaos 2nd ed., Springer, 2003.
Figure 1.
Part of open critical strip and critical line.
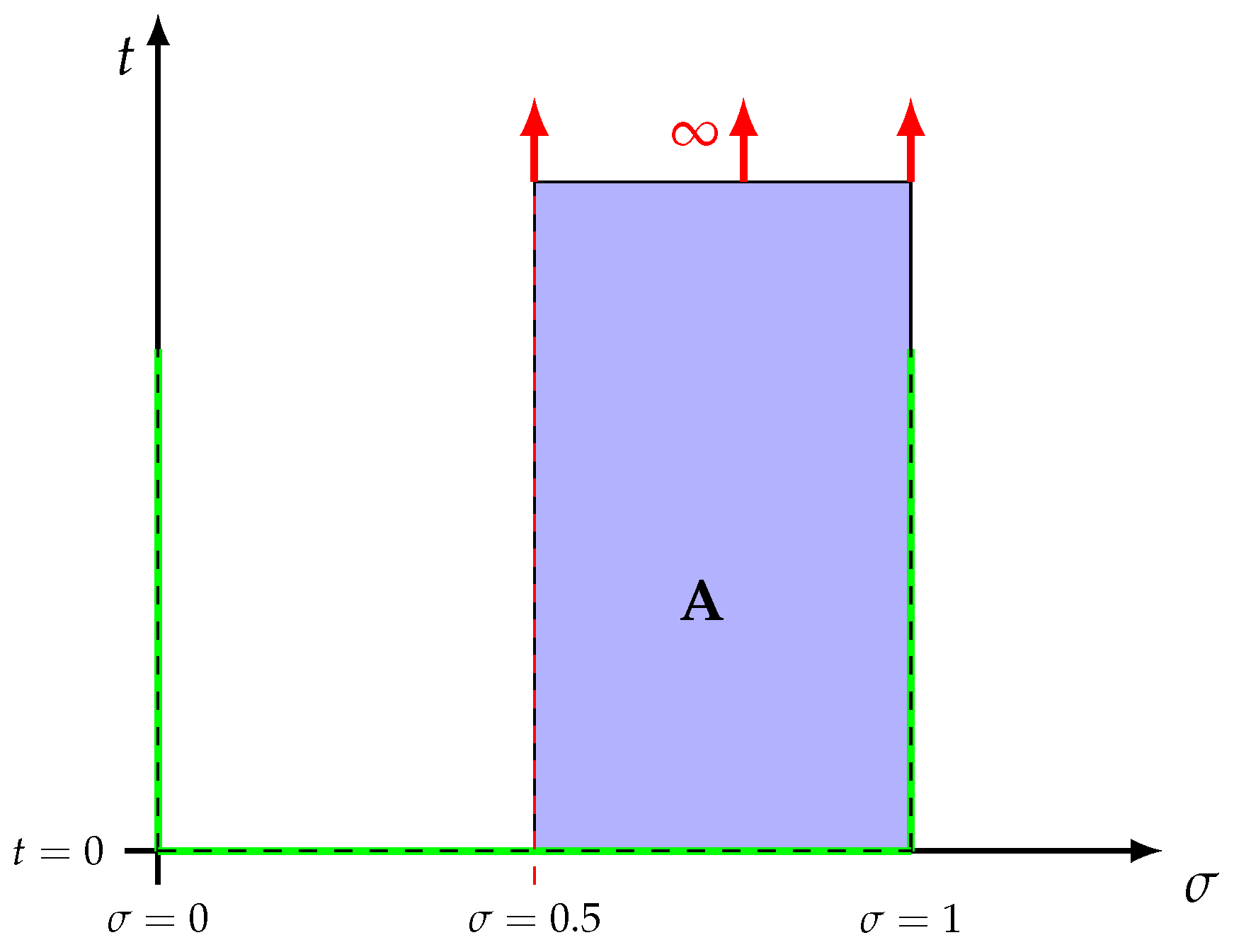
Figure 2.
Geometric setting of the problem
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated




