Prerpints.org logo
Preprint
Article

Predictive Model to Evaluate Water and Nutrient Uptake in Vertically Grown Lettuce under Mediterranean Greenhouse Conditions

Altmetrics

Downloads

170

Views

95

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

29 December 2023

Posted:

04 January 2024

You are already at the latest version

Alerts
Abstract
Agriculture is the main driver of depletion resources worldwide, and its duty is to ensure food security within a rapidly increasing demographic and urbanization, so it is important to transition to sustainable production systems. Vertical crops (VCs) can reduce the pressure on conventional agriculture because they save water and nutrients and increase crop yield. Therefore, this study aimed to validate a proposed predictive model (PM) to simulate water and nutrient uptake in vertical crops under greenhouse conditions. Based on the Penman-Monteith equation, PM estimates transpiration, while nutrient uptake was estimated using the Carmassi-Sonneveld submodel. PM was experimentally evaluated for vertically grown lettuce under Mediterranean greenhouse conditions, during spring 2023. The irrigation technique was a closed-loop fertigation circuit. The experimental consisted of testing two densities (50 and 80 plants·m-2), where each unit of the experiment unit was divided into three heights (low, medium, and upper). It performed ANOVA with a value of p < 0.05 and R2 to assess PM performance. The results suggest a high degree of PM, since R2 ranged from 0.7 to 0.9 for the uptake of water and nutrients. Both densities had a yield between 17-20 times higher than conventional lettuce production and significant savings in water, between 85-88%. In this sense, PM has great potential to intelligently manage VC fertigation, saving water and nutrients, which represents an advance towards reaching SDG 6 and SDG 12, within the 2030 Agenda.
Keywords: 
Subject: Biology and Life Sciences  -   Horticulture

1. Introduction

Rapid demographic growth will cause the world’s population to reach 10 billion people by 2050, and 7 out of 10 people will live in cities [1,2]. To ensure food security, agrifood systems must be able to increase production by around 3 billion tons [3,4], and reduce losses by around 30% to achieve SDG 12 of the 2030 Agenda [5]. Likewise, there is a profound concern about the depletion of resources and climate change and its relationship with agricultural activity [6]. Agriculture accounts for 37% of the land surface [7], consumes 74% of freshwater withdrawals [8], and produces 31% of greenhouse gas emissions [9]. Today, agriculture has become one of the main drivers of land degradation, water shortages, and climate change [5]. Therefore, it is important to face these world hazards and challenges through sustainable strategies that include stopping arable land expansion, increasing crop yields, reducing waste food and land degradation, and protecting biodiversity [10]. Closed-loop fertigation systems (CLFS) for soilless crops allow improving the efficiency of water and fertilizer use, but require adequate knowledge of the behavior of the system to optimize the process with benefits for crop growth and development [11,12].
An innovative and sustainable alternative to food production in urban and peri-urban areas is vertical crops (VC) [13,14,15], which can reduce the high pressure of conventional agriculture. Vertical crops require short production cycles, between 60 and 90 days, and can produce year-round, increasing the efficiency of arable land efficiency between 4 and 10 times [12], reducing 60% of transport costs and carbon footprint, reducing food waste by up to 30% [16], and saving water between 90 and 95% through accurate and efficient irrigation strategies [17,18,19]. These systems have great potential to reduce the use of water and fertilizers and are competitive and feasible with yields of close to 500 t·ha-1 per year [20]. Currently, VCs are carried out in buildings, basements, warehouses, growth chambers, containers known as Vertical Farms (VF), greenhouses, or even in an open field, and allow the production of a wide variety of fresh and nutritious foods such as fruits, verdures, herbs, cereals, mushrooms, and flowers with high profits [15,18,21,22]. In greenhouses, VC consume 40% less energy than VF or plant factories (PF) because they increase the energy demand by around 42% just for LED lighting [23]. In addition, they reduce crop water needs between 20 and 40% [24], and increase the yield 5-8 times regarding to conventional agriculture [25]. Therefore, vertical crop production in greenhouses can increase yield even more without the need for more energy for radiation supply [25].
Modeling closed-loop fertigation systems (CLFS) for soilless culture such as used in vertical farms allows us to understand the behavior of the system and, at the same time, improve its control and optimization [26]. A model that describes crop growth in a CLFS greenhouse must be capable of simulating water and nutrient uptake by the crop as a function of its concentration and distribution on the substrate. Moreover, it must consider the accumulation of salts and the effects of salinity on crop production [26,27], which after a specific threshold can reduce the yield of crops [28].
Greenhouse crop models about salt accumulation in CLFS, such as the Giuffrida model, show a simplified management of crop fertigation based on two rules. Replace all the nutrient solution when the initial electrical conductivity reaches a threshold or eliminate a fraction of the nutrient solution (approximately 65%) when sodium reaches a specific concentration, both strategies mean lower water consumption between 51-61% compared to open growing systems [29]. The model proposed by Silberbush & Ben-Asher is more complete but at the same time more complex. This includes the expected concentration of all nutritive ions (NO3-, NH4+, K+, H2PO4-, Ca2+, Mg2+, SO42-) and non-nutritive ions (Na+ and Cl-) within a hydroponic channel. It assumes that water losses are due solely to the transpiration process and solute depletion to root absorption. In addition, it simulates plant growth parameters such as root length density and leaf area index (LAI) [30]. Unlike before, the conceptual model proposed by Carmassi et al. is simpler and simulates changes in the recirculating nutrient solution for CLFS for ion concentration and electrical conductivity (EC) with respect to sodium (Na+) variations. This model is derived by a balance equation for the uptake of nutrients from crops and the equation proposed by Sonneveld et al. for estimating EC as a function of the sum of cation concentration that is useful for estimating Na+ concentration [31,32,33]. This model is also applied to calculate leaching requirements in semi-closed systems for a soilless crop such as rockwool tomatoes. The conceptual and mechanistic nutrients uptake submodel is based on an apparent ion uptake concentration and not on a real ion uptake concentration of ions; and the empirical water uptake submodel is a function of LAI and radiation intercepted by the plant, calculated through the canopy light extinction coefficient [34,35]. These mathematical and agronomic bases set up useful tools to establish an optimum algorithm to manage fertigation in closed loop hydroponics since allowing prediction of amount of replacing nutrient solution along time and adjustment of nutrient concentration in nutrient solution, which means a best decision support system for automatic function of fertigation in greenhouse closed hydroponics systems [36].
Lettuce (Lactuca sativa L.) belongs to the Asteraceae family and is a crop commonly eaten as salads around the world due to its high nutritional value and medicinal properties. It is a rich source of polyphenols, carotenoids, fiber, antioxidant compounds such as vitamin C, and minerals such as Ca, P, among others. It is classified as one of the most relevant leaf vegetables on the economic level and one of the products of the IV-Gamma (minimally processed vegetables and fruits) with a greater demand world-wide [37,38,39]. Currently, net lettuce production around the world is approximately 27 million tons, whose main producers are China, the United States, India, and Spain [40]. This vegetable can be used as a model plant in VC due to its rapid growth, short production cycle, and small size [41]
Despite the efforts and scientific studies carried out in recent years around VC, it is important to encourage more R&D activities to determine the feasibility of this crop system at the economic, social, and environmental level [17,20,42]. It is possible to use a predictive model to improve the management and refreshment needs of the recirculating nutrient solution to make better performance and productivity in a closed vertical farming system.
Therefore, this research project aimed to prove the validity of a predictive model of water and nutrients uptake in a closed-loop fertigation system established within a vertical crop under greenhouse conditions, allowing the establishment of additional sustainable fertigation strategies through fewer resources used with high yields in greenhouse horticulture.

2. Materials and Methods

2.1. Predictive Model of Water and Nutrients Uptake

Two submodels working together compose this proposed predictive model (PM): water uptake submodel (WUS) and nutrients concentration submodel (NCS). PM is adapted for vertical crops under greenhouse conditions.

2.1.1. Water Uptake Submodel

The water uptake submodel (WUS) was derived from the Penman-Monteith equation established as the FAO standard method to measure crop evapotranspiration. This version was modified by the American Society of Civil Engineers (ASCE) to calculate the reference crop evapotranspiration (ETo) in hourly periods (mm·h-1). The model run according to two different factors that consider daytime and nighttime hours [43,44], as follows:
ETo = [0.408Δ(Rn – G) + 37u2γ(es - ea)·(T + 273)-1]·[Δ + γ(1 + u2Cd)]-1
where: Δ (KPa·C°-1) is the slope of the relationship of saturation vapour pressure with temperature. Rn and G (MJ·m-2·h-1) are net radiation at the crop surface and the soil heat flux at the soil surface, respectively. γ (KPa·C°-1) is the psychrometric constant. u2 (m·s-1) is the mean hourly wind velocity. (es-ea) (KPa) represents the VPD of the air. T (°C) is the mean hourly air temperature and Cd (s·m-1) is the day and night factor: Cd = 0.24 for hours of the day and Cd = 0.96 for hours of the night.
Two modifications were conducted to adapt the Equation 1 to the reference crop evapotranspiration on vertical crops in the greenhouse (ETo′). The term G was assumed to be zero because the soil does not exist in this type of system. Rn was calculated as the product between solar radiation (Rs) outside and the transmissivity coefficient (α) associated with the characteristics of the greenhouse film. In addition, the crop coefficient used to calculate the standard evapotranspiration (ETc) was equal to the basal crop coefficient (Kcb) to consider only the transpiration (Tr) process. Finally, a new factor (Φ) was included that considers the relationship between the density of the vertical crop (a) and its equivalent in a standard horizontal density (b), so the results (a·b-1). In this way, the proposed Tr predictive model is the following:
ETc’ = ΦKcbETo’
Tr ≈ AETc’
where: ETo′ (mm·h-1 = L·m-2·h-1) is the crop reference evapotranspiration for vertical crops in the greenhouse. Kcb (-) is the basal crop coefficient, whose is calibrated by the PM. Φ is the density index. ETc’ (L·m-2·h-1) is the crop evapotranspiration under standard conditions for vertical crops in the greenhouse. A (m-2) is the land surface of the vertical crop, and Tr (L·h-1) is the hourly crop transpiration for vertical crops under greenhouse conditions.

2.1.2. Nutrient Concentration Submodel

The nutrient concentration submodel (NCS) is based on a simple model of ion concentration variations proposed by Carmassi et al. in 2003 for closed-loop hydroponic systems, which is a function of crop transpiration and other fertigation parameters [32,33,45]. The concentration (expressed as mM) of the nutritive ions can be calculated with Equation 4, while the non-nutritive ions can be computed with Equation 5 as follows:
[I]t+1 = [I]t + TrV-1([I]R – [I]U)
[I]t+1 = ([I]t - [I]Rp-1)exp(-pTrV-1) + [I]Rp-1
where: [I]t+1 is the concentration of ion I at time t+1. [I]t is the concentration of ion I at time t. [I]R is the recharge concentration of ion I at time t+1, [I]U (mM) is the crop uptake concentration (CUC) of ion I that stays constant over time. V (L) is the volume of the nutrient solution tank. p (-) is a coefficient that depends on the sensibility of a the crop in front of specific ion, and ranges from 0.01-0.3 [31].
This submodel includes the electrical conductivity as a function of the sum of cations in the nutrient solution (Equation 6), proposed by Sonneveld & Van der Wees in 1990, as shown below [31]
EC = 0.19 + 0.095[C+]
where: EC (dS·m-1) is the electrical conductivity and [C+] (meq·L-1) is the sum of cations concentration in the nutrient solution (NH4+, K+, Ca+2, Mg+2, and Na+).

2.2. Modelling Process

The simulation time was 24 days, which started at 7 day and finished at 31 days after transplanting (crop time).
The WUS submodel worked with initial Kcb values equal to 0.15 for the initial crop stage and 0.9 for the midseason and final crop stages, which were later calibrated. The durations of the crop stages were as follows: 0 days for the initial stage because the transplantation was carried out 19 days after the sowing, 30 days for the development stage, 15 days for the mid-season stage, and 0 days for the late season because the harvesting was done before this stage started [43,46]. The standard horizontal density (11 plants·m-2) was calculated from a distance be-tween plants and furrows of 0.3 m. Adjustment of WUS to measured data was carried out through a nonlinear least squares process using the generalized reduced gradient (GRG) method that tries to minimize a target value [45,47]. For this, the Microsoft Excel© Solver tool [48], and mean absolute error (MAE) as target value, whose variable cells during the simulation process were Kcb values.
The NCS submodel used as initial values for crop uptake concentrations [I]u in (mM), as follows: 5.73 K+, 3.20 Mg+2, 9.06 Ca+2 and 0.97 NH4+ [49]. Likewise, it used an initial sensibility coefficient p equal to 0.2 for Na+ [33]. Both these values and initial concentrations in the nutrient solution calculated were calibrated by PM through Solver tool as well, where target value was the total sum of mean absolute error of each cation.

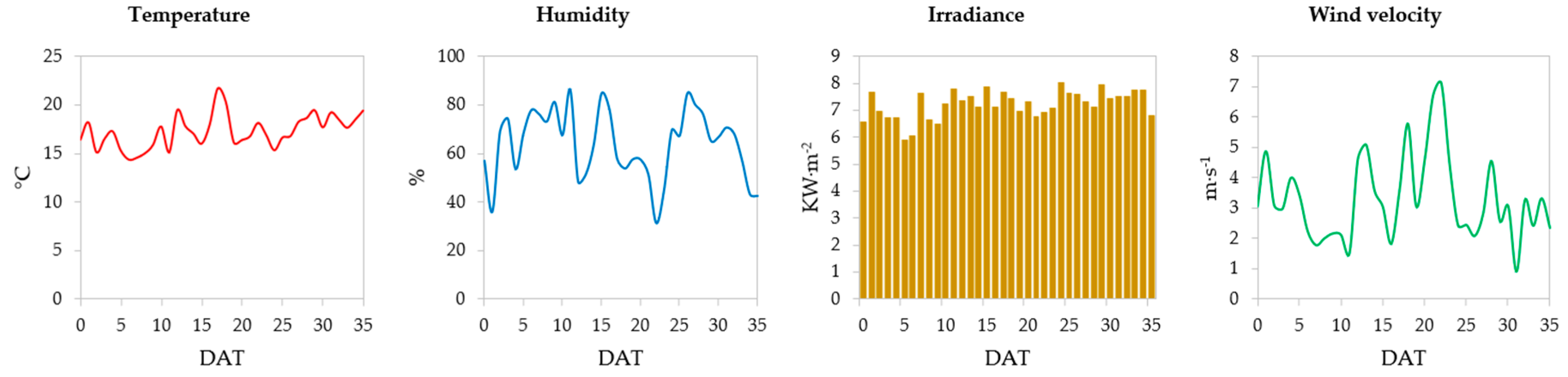
2.3. Location, Climatic Conditions, and Time Experiment

The experiment was conducted in a tunnel-type medium technology greenhouse (TG) of the Almeria University close to the Mediterranean Sea (La Cañada de San Urbano, Almería, Spain; 36° 46′ 37.8″ N, 2° 24′ 20.1″ W) with northwest-southeast orientation. The TG had a surface of 51 m2, 6.3 m wide, 8.1 m long, 3.5 m height up to the ridge, with polycarbonate side, front, and back walls. The roof cover material was polyethylene low density 720 gauge with radiometric properties in front of UV radiation and whitened with lime. Ventilation was natural and consisted of a longitudinal window mechanic with axis on the roof (zenithal ventilation), 8.1 m in length, with an opening of 94% and totally covered with anti-aphid mesh of 50 x 25 threads per inch. Inside a mobile black shade screen to a height of 2.5 m. The transmissivity coefficient (α) of the film cover was 0.2, indirectly measured relating the measurements outside of TG by a pyranometer of an automatic climate station (ACS) and the measurements inside of TG by a luxometer, Sekonic C-7000, the conversion factor used was 1 lx = 118 W·m-2 [50].
Within TG, three Elitech RC-51H sensor dataloggers (DT) were strategically placed in the vertical crop, which registered temperature (°C) and relative humidity (%) each 30 minutes at a height of 1.2 m. ACS was a greenhouse climate control system installed by Atenix Electronics & Automatics S.L. and placed 15 m from TG, and 4.5 m height. This device had sensors to measure irradiance (W·m-2), temperature (°C), humidity (%), and wind velocity (km·h-1), whose data also registered each 30 minutes.
The climate database used by the predictive model was based on information from ACS and DT devices. Data were complemented with the European Commission Photovoltaic Geographical Information System (PVGIS) [51], and the Almería airport automatic meteorological station (36° 50′ 47″ N, 2° 21′ 25″ W) of the State Meteorological Agency (AEMET) [52]. The outside wind velocity measurements were transformed into the inside greenhouse velocity measurements with a linear model of Wang, proposed for this type of greenhouse [53]. The average climate conditions of Almería belong to a hot semi-arid climate according to Köppen’s classification with an average month temperature of 19 °C, an average month relative humidity of 65%, an annual precipitation equal to 200 mm with 25 rain days and an annual insolation of 2,800 hours [54]
Figure 1 shows outside environmental conditions during the time experiment, spring season 2023 (transplant March 15, harvest April 19). The average temperature for 35 days was 17.3 °C and ranged from 21.7 to 14.4 °C. The diary humidity had an average value of 63.6% and ranged from 31.1 to 86.1%. The average irradiance was 7.2 KW·m-2 and ranged from 5.9 to 8.0 KW·m-2. The diary average wind speed was 3.3 m·s-1 and ranged from 0.9 to 7.1 m·s-1.

2.4. Plant Material

The vegetable used was baby lettuce cv. Gatsby supplied by the house seeds Gautier Semences. Lettuce seeds sown on 24 February 2023, on a substrate composed of a mixture of peat moss and vermiculite, were transplanted 20 days after sowing (15 March) in the first hours of day, in polystyrene foam (3 x 3 cm). At DAT 0, lettuce plants were 15.5 ± 0.2 cm in height, stem diameter 4.86 ± 0.11 mm, root length 18.4 ± 1.2 cm and had average eight leaves. The harvest process was carried out 35 days after transplantation (DAT) in the morning (19 April).

2.5. Experimental Design and Vertical Crop Set-Up

Two different experimental designs were implemented. The first (ED1) aimed to evaluate the performance of the predictive model by measuring water and nutrient uptake on the vertical crop, and the second (ED2) aimed to assess the effects on physiological and development crop parameters under these environmental and system conditions.

2.5.1. Experimental Design 1 (ED1)

The experimental unit was a vertical crop tower type (VCT) of 2.25 m height arrangement in a row of 6 m length (Figure 2-a), elevated 0.25 m over the ground and mounted over a collection drainage pipe (250 mm Ø), both components were supported by a structure of anodized aluminum resting on ground. Each vertical crop was made up of cylindrical units or towers designated as columns (CLs). In turn, 15 individuals GrowPipes® (GP) units (Figure 2-b) formed each column. Each GP has 15 cm height and 7.5 cm diameter; moreover, divided inside into two cavities by an inner septum and features a hole in one of the sides, which supports a plant by an integrated water collecting slide. The setup of multiple GP was conducted placing one on the other, opposing the holes for the plants 180 °, while the vertical distance between plants was 30 cm (Figure 2-c).
The performance of the predictive model was assessed under different conditions through ED1, which consisted of a completely randomised design to compare two crop densities (CDs). The two crop densities were obtained by modifying the distance between CLs. Low density (LD) comprise 20 CLs placed each 0.3 m including 300 plants at 50 plants·m-2. High density (HD) consists of 32 CLs placed each 0.19 m, including 480 plants at 80 plants·m-2. Each with three replicates. The distance between two consecutive rows of vertical crops was 1 m. Furthermore, days after transplantation (DAT) and replications (RP) were included as variation sources to increase the accuracy of the experiment.

2.5.2. Experimental Design 2 (ED2)

The developmental crop response to the system was evaluated with the ED2 experiment, which consisted of a nested or hierarchical design in which the relative plant position (PP) of plant relative to the ground was nested in the CD. The PP nest factor had three levels: Low (L), where plants were located between 0.25-1.0 m; Medium (M) between 1.0-1.75 m, and Upper (U) between 1.75-2.5 m above ground. In this way, the experimental unit VCT was divided into these three levels (Figure 3-d). Thus, the vertical crop LD had 100 plants per level and HD vertical crop had 180 plants per level. Likewise, RP was included as variation sources again to increase the accuracy of the experiment.
Lettuce plants at the U level received 100% indoor radiation (57 W·m-2 = 260 µmol·m-2·s-1), M level 36% (21 W·m-2 = 96 µmol·m-2·s-1) and L level 24% (14 W·m-2 = 64 µmol·m-2·s-1). The conversion factor used to transform sunlight, since the units of irradiance to units of photons, was 1 µmol·m-2·s-1 = 0.219 W·m-2 [55]. The U level had an average value of sunlight photons 4% higher than ideal photosynthetically active radiation (PAR) for lettuce, established at 250 µmol·m-2·s-1 [56].

2.6. Management of Fertigation System

Fertilizers and the water dosage mechanism consisted of a closed-loop fertigation system (CLFS) with irrigation drip type. Below each experimental unit at ground level was located a 250 mm diameter PVC collection drainpipe, 6.26 m long, with 250 L capacity, whose purpose was to collect all drains from the vertical crop and, in turn worked as a nutrient solution tank (NST) of the fertigation system. Each NST had an automatic water replenishment mechanism composed of a plastic buoy, which allowed filtered water from the reserve tank (RT) to maintain the same level in the NST during the time experiment. Each RT had a capacity of 100 L connected to NST by a 6 mm diameter polyurethane hose. The input of filtered water into RT came from a reverse osmosis system (ROS) Mega Grow 1000. The water output had a pH of 7 and an electrical conductivity (EC) of 0.52 dS·m-1, with these ion concentrations in (mM): 0.50 HCO3-, 0.13 NO3-, 0.01 NH4+, 0.86 PO4-3, 0.01 K+, 0.11 Ca2+, 0.73 Mg2+, 1.78 Na+, 0.49 SO42- and 1.85 Cl-.
Automatic supply and adjustment of fertilizers and pH inside NST was conducted by a pH and EC hydroponic controller (HP) (Prosystem Aqua Europe S.L. model 04001), through three peristaltic pumps, two for fertilizers and one for pH. The nutrient solution in NST was pumped up to an irrigation lateral (IL) 20 mm diameter, placed over the VCT using a Monzana MZPP27 peripheral pump of 550 W, coupled to the filter system whose filtering material was balls of polypropylene. Each column had two flow-regulated drippers (Rivulis Supertit) with a flow rate of 2.2 L·h-1 flow rate, which supplied water through a 6 mm diameter microtube connected with irrigation pickets. The vertical crop LD had an IL with 40 drippers separated 15 cm, and the vertical crop HD 64 drippers separated 9.4 cm.
The fertigation frequency was established using an analogic Coati irrigation timer. Irrigation programming consisted of irrigate each 15 minutes between 10:00 to 16:00, and each 45 minutes for the rest of the day. The nutrient solution was calculated using the Nutrient Solutions Calculator developed by Incrocci et al. [58]. The ion concentrations of macronutrients in (mM) and micronutrients in (µM) of the calculated nutrient solution (NS) were: 15.0 NO3-, 1.0 NH4+, 2.0 H2PO4-, 10.0 K+, 4.5 Ca2+, 1.0 Mg2+, 2.6 SO42-, 1.78 Na+, 1.85 Cl-, 40 Fe, 5 Mn, 1 Zn, 1 Cu, 30 B, and 1 Mo. The NS was concentrated 100 times to prepare concentrated nutrient solutions (CNS) A and B. In tank A, Ca (NO3)2, and micronutrients were dissolved, while tank B, contained MgSO4, NH4H2PO4, KNO3, KH2PO4 and K2SO4. The pH was regulated with HNO3 nitric acid, as a result, NS EC was to 2.45 dS·m-1 and pH 5.5. Three intervals for the management of the nutrient solution (fertigation phases) were defined: the EC target was set at 2.45 dS·m-1 between 0-6 DAT to acclimatize lettuce crop, then increased to 3.3 dS·m-1 between 7-31 DAT (simulation time), and finally not provided for the remaining time.

2.7. Response Variables

For ED1, water uptake and nutrients concentration on NST were considered as response variables. The sampling process consisted of taking 21 samples from NST in the morning (9:00) between 6-30 DAT. The diary water uptake (DWU) was measured as the volume in liters of water needed to recharge NST at the original level through a plastic bucket calibrated to 1 L accuracy. Diary variation in ion concentration in NST was measured. For that samples were taken in containers of 50 ml, which maintained in a refrigerator 4 °C until their measurement at the final experiment time. Specifically, the concentrations of nutritive cations (NH4+, K+, Ca+2, and Mg+2) and non-nutritive cations (Na+) were measured in mM, using a portable ion-selective electrode meter (ISE) Imacimus® IC-5 with a precision of 0.01 mM.
The sampling in ED2 was 35 DAT collecting 16 plants per each level of PP factor. Leaf number (LN) and productivity parameters were determined. Productivity (g·plant-1) was measured as fresh weight (FW) for the root, shoot (leaves + stem) and harvested head with an analytical balance with 0.01 g precision. The root / shoot ratio (R/S), calculated for FW as Shoot·Root-1). Fresh weight of the heads was extrapolated to express yield as t·ha-1. To determine the dry mass, the fresh mass samples were dried (in a 631 Plus forced convection oven model) at 70 °C for 48 h to obtain dry weight (DW) of shoot and root. Water content of plants was expressed as percentage of (FW-DW)·FW-1. Shoot biomass index (SBI) calculates as shoot FW·LN-1 (in g·leaf-1).

2.8. Statistical Analysis

Data from both statistical designs (ED1, ED2) were analyzed with IBM SPSS Statistics v.28 software (IBM®, Armonk, NY, USA), using an analysis of variance ANOVA with statistical significance (p-value < 0.05) and Tukey test for the comparison of mean values in ED2. The fit goodness (accuracy) of PM was measured by statistics metrics for assessing performance of prognostic models: coefficient of determination R2, mean absolute error (MAE), mean square error (MSE) and root mean square error (RMSE) [59,60,61,62]

3. Results and Discussion

3.1. Statistical Performance of the Predictive Model

Table 1 shows that PM had a better fit for water uptake, NH4+ and K+ concentrations for both densities, whose R2 ranged from 0.826 to 0.920, so these variables can be called “good fit variables”, while Mg+2 and Na+ concentrations, R2, ranged from 0.707 to 0.748, thus allowing the so-called “acceptable fit variables”. For the Ca+2 concentration, the PM could not explain its variation for both densities, a fact that will be discussed later. Comparing the two densities, found that NH4+, K+ and Mg+2 had a better R2 in the LD system than in HD, while quite the opposite for water uptake and Na+ concentration, whose R2 values were better in HD.
Regarding the other metrics (MAE, MSE and RMSE), all cation concentrations had higher values in HD than in LD, being higher for K+ and Ca+2 concentrations, so PM was less accurate in denser vertical crops. MAE was less than 0.267 mM for all cations, except for K+ and Ca+2 concentrations, whose value ranged from 0.728 to 0.996 mM. The same occurred for RMSE, whose value was lower than 0.337 mM for the concentrations of NH4+ Mg+2 and Na+ concentrations and ranged from 0.882 to 1.224 mM for the rest of the cations. However, with respect to water uptake, PM was less accurate in LD, with a MAE 40% higher and RMSE 31% higher than HD. Overall was, PM had a mean absolute error lower than 2 L·day-1.
Although EC is not estimated by PM, because this is a fixed parameter along the time established by the user for the simulation process, its value was 3.3 dS·m-1 (EC target) between 7-31 DAT simulation time. The mean absolute error (MAE), mean square error (MSE) and root mean square error (RMSE) of the measured data with respect to the EC fixed in PM were calculated. Therefore, in Table 1, it is shown that LD had an average error 41% higher than the vertical crop HD with respect to the MAE and RMSE statistic metrics, but for both densities the maximum error threshold was lower than 0.341 dS·m-1, meant a 10% of the EC target value.

3.2. Water Uptake and Cation Concentrations

Table 2 shows the ANOVA for all response variables: water uptake and cation (NH4+, K+, Ca+2, Mg+2 and Na+) concentrations, for both densities in vertical crop. The CD together with DAT significantly affected all variables, even if their interaction was influential. Although not all-variable responses presented statistically significant differences between replications, as expected. Similarly, the values of the HD vertical crop for all response variables were significantly higher than LD. In the case of water uptake, results were agreed on expected outputs because HD crop had 60% more plants than the LD. However, for all nutritive cation concentrations, it was expected that LD consumes less than HD vertical crop, in other words, the average cation concentration in LD was higher than HD vertical crop, as a result of a smaller difference between initial and final concentration of each cation, but it did not happen. In the same way, this reasoning is applicable for no-nutritive cation as Na+, because despite this being accumulated in the NST, the crop consumes little quantities over time. This fact can be explained later by analyzing how the crop was affected by the system and the climate conditions through the ED2 response variables. In addition, the management parameters of the nutrient solution as pH and EC also were shown in Table 2, which ones were significantly influenced by crop density, LD had an EC statistically lower than HD, while quite the opposite occurred for the pH parameter.

3.2.1. Water Uptake

The graphs shown in Fig. 3 show that the PM overestimated quite the real water consumption using the initial values of Kcb. Since forecast a water consumption roughly 105 L for LD (Fig. 3a) and 168 L for HD (Fig. 3b), at 31 DAT, while the PM adjusted with does Kcb values calibrated not exceed the 30 L consumed per day for both densities. LD got the following calibrated Kcb values, 0.01 for initial stage, and 0.21 for the midseason and late stages, meaning a decrease between 77 and 100%; while HD had Kcb equal to 0.04 for the initial stage and 0.14 for midseason and late stages, so the basal crop coefficient reduced between 74 and 85%. In this way, based on the modeling process deduces that the crop basal coefficients are lower in vertical crops than in conventional agriculture.
According to Fig. 3c, the adjusted PM forecasted a diary water consumption for the vertical LD crop between 5 L and 24 L, at 7 and 31 DAT, respectively, while in Fig. 3d, it shows that the diary water consumed by HD ranged from 10 to 25 L (7-31 DAT). As a result, the compound diary growth rate (CDGR) was 6.4% for LD and 3.9% for HD, so the model established that LD consumed water faster. The adjusted PM had a good fit in both densities, since R2 was 0.826 for LD and 0.858 for HD, being a better performance better in HD because its R2 was higher than linear regression.
HD consumed significantly more water than LD crop density, since had an average diary consumption of 15 L (4 L less than HD), whose average consumption was 19 L per day (Table 2). Therefore, the average consumption per plant was 50 ml·d-1 for LD, higher than 40 ml·d-1 for the HD system. For the same time interval, the PM adjusted, estimated an average diary consumption of 12 L for LD and 20 L for HD, but with the same average consumption per plant, rough 40 ml·d-1, this is a proof that PM assumes that all plants are healthy and with the same irrigation conditions. When comparing the results with the water uptake for lettuce crop in conventional agriculture, whose diary consumption per plant is around 334 ml·d-1 [63]. Vertical crops were found to significantly save water, as the LD system reduced plant uptake by 284 ml, which represents 85% savings, lower than the HD system, since the water reduction was roughly 294 ml, which is equal to an 88% savings. Even, compared to horizontal hydroponic lettuce, whose average consumption is approximately 94 ml·plant-1·day-1 [63], vertical crops are better because the LD system saves 44 ml, equal to 47% savings, and the HD system 54 ml, 57% savings. In these ranges, water savings are close to those reported for vertical farms as plant factories, which are capable of saving water by more than 95% than conventional crop methods [63,64].
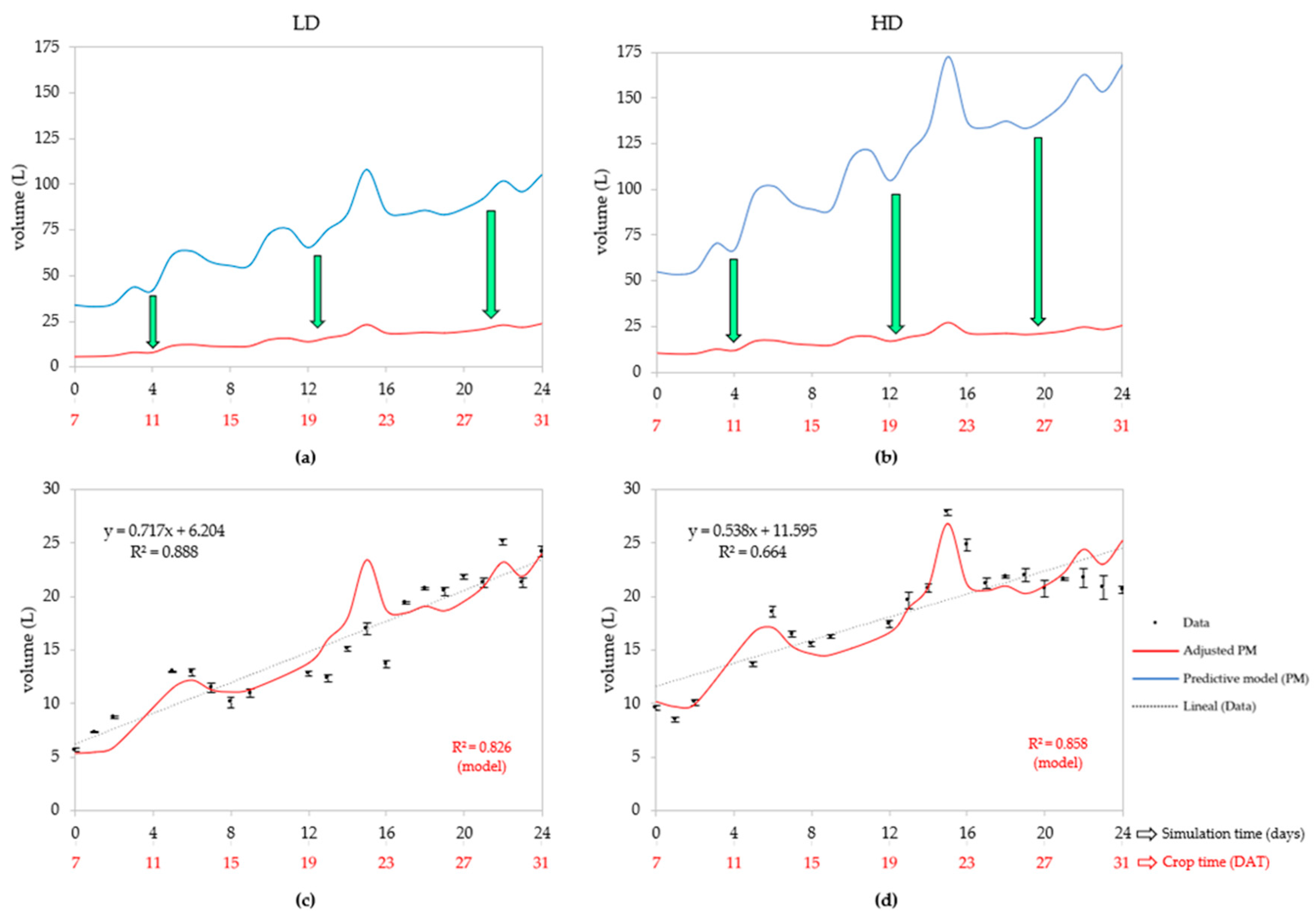
Preprints 94921 g003
Figure 3. Lettuce water uptake days after transplantation (DAT) of the adjusted predictive model, for low (a and c) and high density (b and d), respectively. In: (a,b) graphs with predictive model run with initial and adjusted parameters. In (c,d) graphs of adjusted model with linear regression of the data and R2.
Figure 3. Lettuce water uptake days after transplantation (DAT) of the adjusted predictive model, for low (a and c) and high density (b and d), respectively. In: (a,b) graphs with predictive model run with initial and adjusted parameters. In (c,d) graphs of adjusted model with linear regression of the data and R2.
Preprints 94921 g003

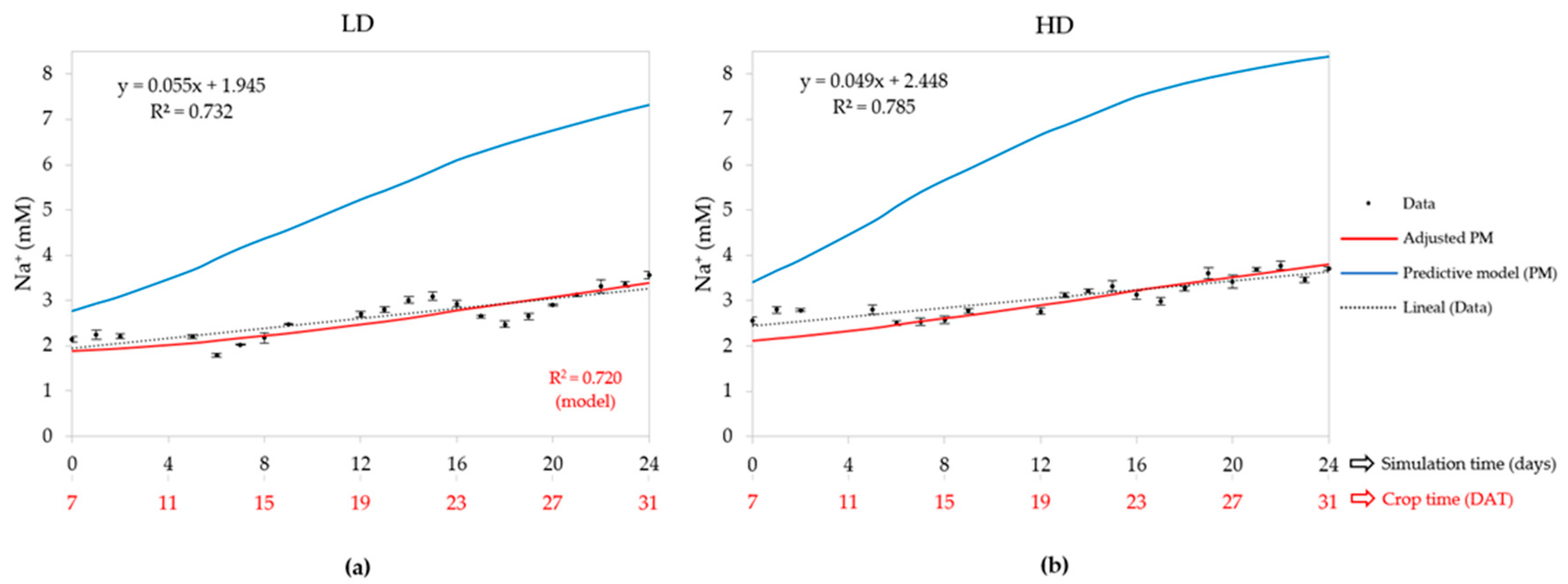
3.2.2. Sodium Concentration (Na+)

The initial Na+ concentration used by the PM at 0 DAT was 1.78 mM for both densities, according to the quality of the irrigation water. The initial value of the sensibility coefficient p was 0.2, later calibrated was equal to 0.27 for LD and 0.29 for HD, so within the range (0.01-0.3) reported by Carmassi et al. [33,45].
In Figure 4, the blue graph shows that the predictive model run with the initial values overestimated the data. The red graph, corresponding to the adjusted PM, shows that Na+ concentration at 7 DAT was 1.88 mM for LD and the 2.11 mM for HD, and the final values were 3.39 and 3.80 mM, respectively. This establishes a difference of 1.51 mM for LD and 1.69 mM for HD, despite that, the CDGR values for both densities were equal to 2.5%, so based on PM deduces that Na+ was accumulated in the same ratio independent of density. In both densities, adjusted PM presented a high correlation with measured data, since R2 was 0.720 for LD and 0.743 for HD, but no greater than linear regression, indicating that it could be feasible and simpler to use a straight line instead of an exponential function just as PM works for non-nutritive ions.
The sensibility coefficients were calibrated together with the average Na+ concentration by the model fitted between 7-31 DAT, 2.60 mM for LD and 2.99 mM for HD. For this, we estimate that the Na+ crop uptake concentration (CUC) by the lettuce crop was 0.71 mM for LD and 0.87 mM for HD, values close to 1 mM, a value reported for the formulation of the nutrient solution for the lettuce crop [66,67]. Furthermore, the measured data indicate that the average Na+ concentration for the vertical HD crop during the experimental calibration time was 3.09 mM, significantly higher than the LD system, whose value was 2.66 mM (Table 2). This indicates that CD of the vertical crop significantly affected this variable, suggesting increased accumulation of Na+ in the denser systems. In comparison, the average concentrations from the data and the adjusted model found that during 24 days of simulation time there was a relative error range of 2-3%. The CUC based on the measured data was 0.72 mM for LD and 0.90 mM for HD.

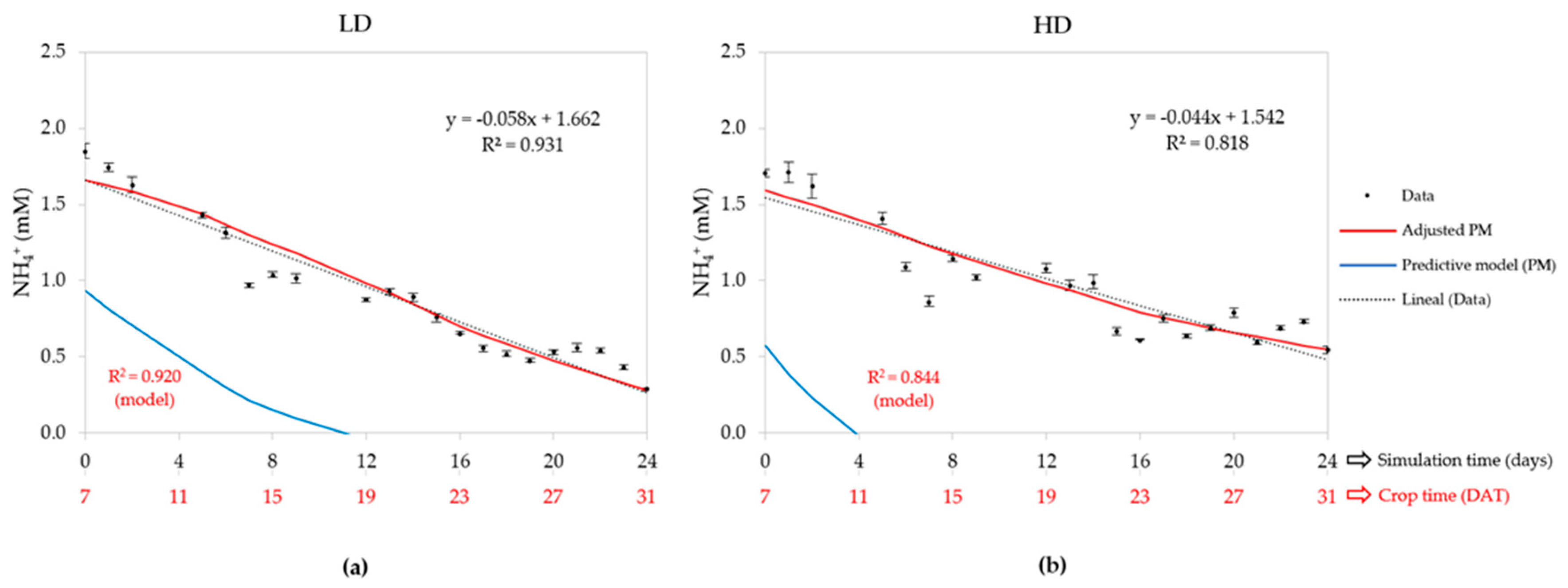
3.2.3. Ammonium Concentration (NH4+)

Figure 5, show the graph of the PM run with initial values does not adjust to the data, while the PM run with parameters adjusted accordingly. The adjusted model used initial concentrations (0 DAT) calibrated at 0.45 for LD and 0.49 mM for HD. These values differ more than twice with respect to the initial concentration of NH4+ in the NST, set at 1 mM.
If we analyze the model adjusted between 7-31 DAT, we found that initial concentration was 1.66 mM for LD and 1.59 mM for HD, and their corresponding final values were 0.28 and 0.55 mM, so results differences of 1.38 and 1.05 mM, respectively. Both values are close to 1 mM reported in the nutrient solution for lettuce [68,69]. As a result, the compound diary decrease rate (CDDR) was 7% for LD and 4% for HD. So one deduces that LD consumed this cation almost to double the velocity than HD. Overall. The adjusted PM suited well with the measured data because R2 was 0.920 for LD and 0.844 for HD, and linear regression had an R2 higher than LD.
The average NH4+ concentration for CD between 7 and 31 DAT was 0.91 mM, significantly lower in LD than in HD, whose value was 0.97 mM (Table 2). If we compare these values with the average concentrations of the model adjusted, 0.92 mM for LD and 0.97 mM for HD, we find a maximum relative error of 1%. The calibrated crop uptake concentration (CUC) values were 1.72 mM for LD and 1.12 mM for HD. These differs maximum 77% from 0.97 mM reported for tomatoes and sweet peppers [49,70]

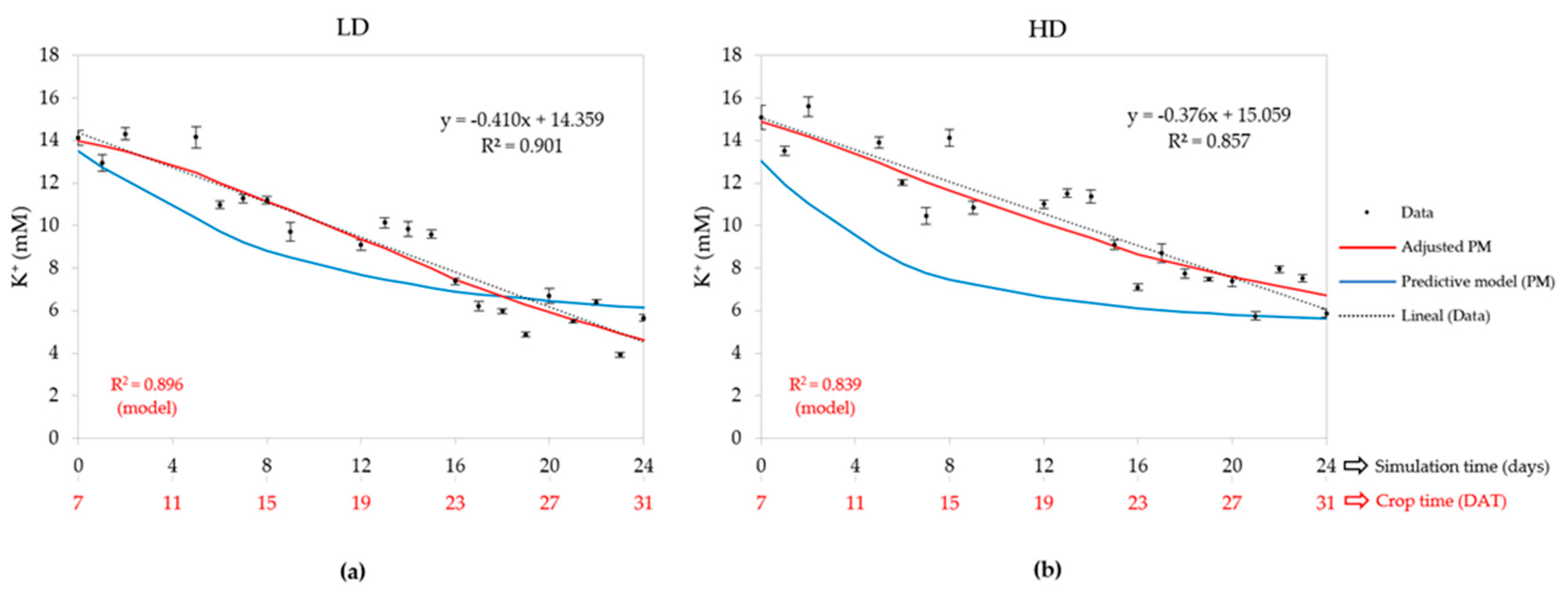
3.2.4. Potassium Concentration (K+)

Figure 6 shows that the model run with initial values did not adjust to data (blue graph). The adjusted model worked with an initial K+ concentration (0 DAT) calibrated of 3.56 mM for LD and 4.15 mM for HD, both values differ more than double regarding the initial concentration in the NST, whose value was 10 mM. The initial concentration predicted by the adjusted model at 7 DAT was 13.99 mM for LD and 14.90 mM for HD, with their corresponding final concentrations (31 DAT) equal to 4.60 and 6.72 mM. As a result of differences of 9.39 and 8.18 mM were obtained, both values differ between 4-10% with respect to K+ value reported in the nutrient solution for horizontal hydroponic lettuce, 8.5 mM [71]. CDDR was 4.5% for LD and 3.3% for HD, so the conclusion is that LD consumed K+ faster. The performance of the adjusted model was good because R2 in both densities was 0.896 and 0.839, for LD and HD, respectively. Linear regression in both cases had a R2 higher.
The average K+ concentration between 7-31 DAT for LD was 9.05 mM, significantly lower than that of the HD system, whose value was 10.19 mM (Table 2). Compares these values with average concentrations of the adjusted model, 8.93 mM for LD and 10.05 mM for HD, it finds a relative error lower than 2%. The CUC values calibrated by model were 11.71 and 8.79 mM for LD and HD, respectively, which compared to literature, whose value reported is 6.6 mM for cucumber [49], result in a differ between 33-77%.

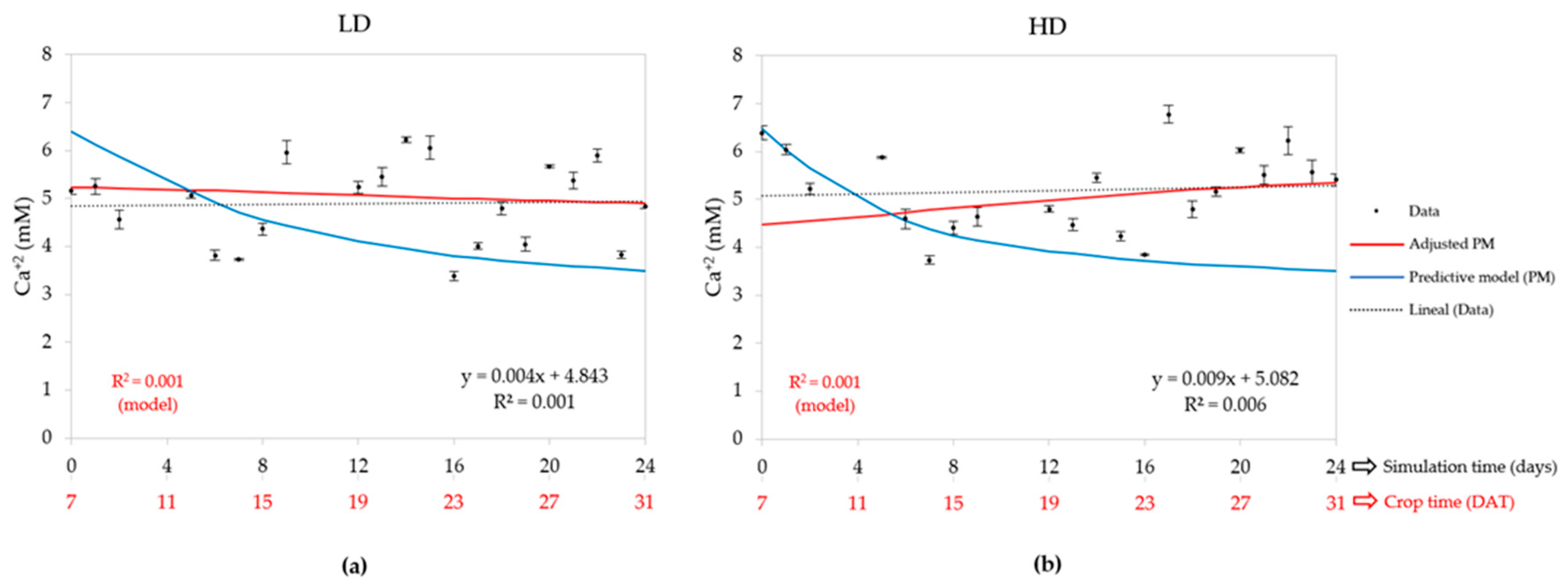
3.2.5. Calcium Concentration (Ca2+)

According to Table 2, there were statistically significant differences between the LD and HD systems, so CD was influential in Ca2+ concentration in the NST. The average value for LD was 4.89 mM and 5.20 mM for HD. Figure 7 shows that the PM (blue graph) run with initial values follows a decrease tendency but without any adjustment over the data. Whereas the adjusted model (red graph) does not follow a decrease trend for HD and presents a light decrease tendency for LD, a strange behavior that does not correspond to normal nutrient consumption. In contrast, in the case of HD it seems that Ca2+ concentration increases along crop time, resulting in accumulation in the NST. The linear regression shows this unusual behavior because the slope of the straight line is positive for both densities, an indication that Ca2+ concentration is increasing over time. Just like the PM run with initial data, the adjusted PM had no correlation with the data because R2 were 0.001, because the measured data are very disperse. The CUC calibrated by the model were negative values or small, 0.41 mM for LD and -0.95 mM for HD. This unusual behavior can be explained as a system response to two reasons: low velocity uptake by the crop and the crop uptake concentration was lower than the concentration replenishment in the NST by the pH and EC controller; as a result, there was accumulation. Consequently, lettuce plants expressed a physiological disorder known as tip burn, the cause could have been a deficient ventilation within the greenhouse [72].

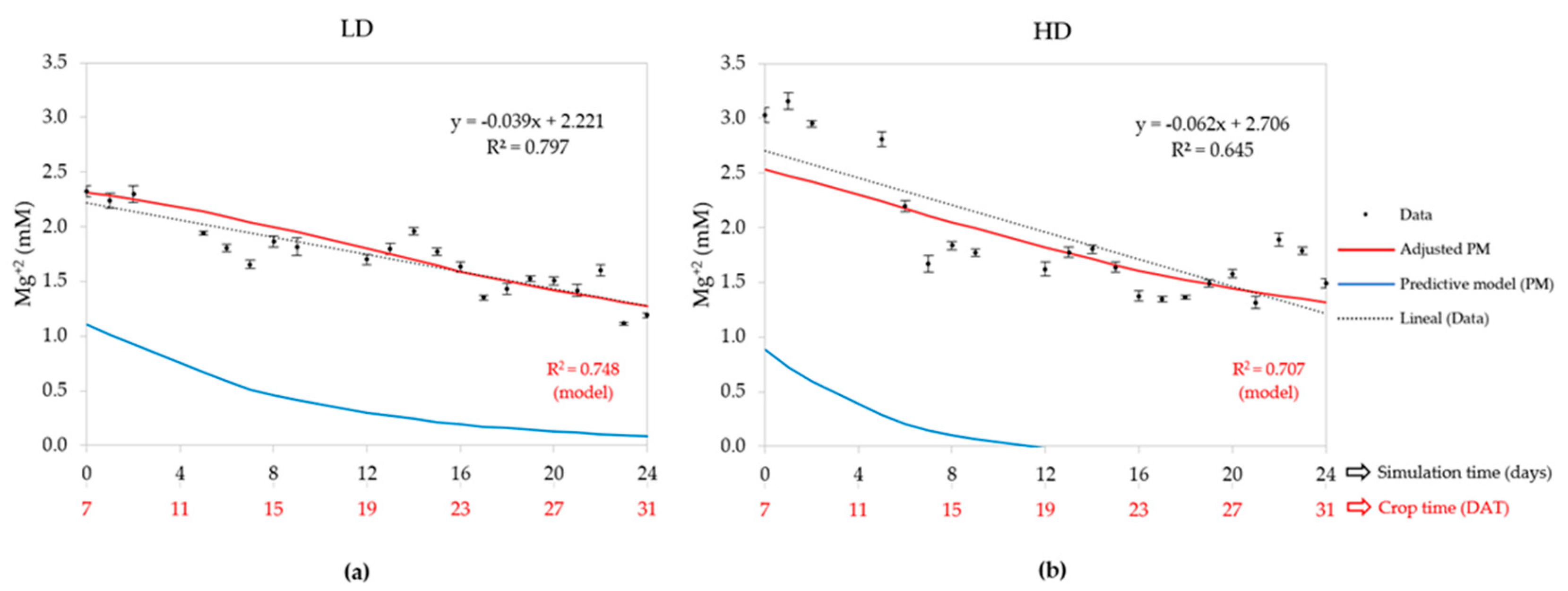
3.2.6. Magnesium Concentration (Mg2+)

Figure 8 shows a no correlation to the PM data (blue graph) running with the initial values. The adjusted model used initial concentrations (0 DAT) calibrated at 0.54 and 0.66 mM for LD and HD, respectively. These values differ between 56-64% in terms of the initial concentration of NST, whose value was 1.50 mM. At 7 DAT, the adjusted model predicted a magnesium concentration of 2.31 mM for LD and 2.53 mM for HD, and final concentrations (31 DAT) of 1.28 and 1.32 mM, respectively. This resulted in differences of 1.04 mM for LD and 1.21 mM for HD, both values are within the range values reported for hydroponic lettuce (0.7-1.40 mM) [66,73]. CDDR was 2.4% for LD and 2.7% for HD, so based on the model it is deduced that HD consumed this cation faster. In relation to the adjusted PM performance, this was a good fit to data because R2 for LD and HD were 0.748 and 0.707, respectively, being LD higher than HD. Linear regression only had an R2 higher than the model for the LD crop density.
The average magnesium concentration for LD between 7-31 DAT was 1.71 mM, significantly lower than that of the HD system, whose value was 1.90 mM (Table 2). Comparing these values with the average concentrations of the adjusted model, 1.75 and 1.81 mM for LD and HD, results in relative error ranges 2-5%. The CUC calibrated by model were 1.29 mM for LD and 1.30 mM for HD, which when comparing them to the literature, whose value is 0.9 mM for tomato [49], determines a difference of 44%.

3.3. Crop Behavoir: Physiological and Production Parameters

Table 3 shows the mean values and statistical significance of lettuce crop behaviour in vertical cropping systems with two planting densities (CD) nested at three levels of plant positioning (PP). Replicas of the experimental design did not show significant differences, so they can be considered homogeneous. All variables are affected by PP in the crop column and by CD (except for water content).
The increase in CD results in a reduction in the individual fresh and dry biomass of each plant (46-47 % in the shoot and 60-61% in the root), which means a reduction in the R/S ratio of 22- 13%, but does not affect the water content of the plant. The rate of accumulation of shoot biomass (SBI) decreases by more than half in high CD and by 40% with decreasing PP. On the other hand, the number of leaves developed per plant increases by 10% with higher CDs and by 33% with decreasing PP. This increase is progressive with the decrease in PP and is more pronounced for LD (up to 40%) than for HD (up to 25%). The fresh weight of the aerial part (shoot) and the shoot biomass index (SBI) show significant interactions between CD and PP. The behaviour of leaf development and shoot fresh weight is responsible for the significant interaction of CDxPP for shoot FW and SBI, while these reductions are progressive for HD, and they are only visible between the top level and the rest of the column for BD.
According to Table 3, the shoot and root fresh biomass of lettuce plants for LD whose respective mean values were 148.6 and 14.6 g, were between 55-67% higher than the FW values of shoot FW reported for lettuce grown in horizontal hydroponic greenhouses (HHG), and between 41-66% higher than values of the roots of HHG, whose respective ranges of literature are 88.8-96.1 g for the shoot and 8.78-11.5 for root FW [74], while the HD system had a FW soot FW between 9-16% lower than lettuce in HHG, and a FW of the root between 33-49% lower than HHG. If we compare these values with data reported for lettuce in open field systems (OFS), which range between 5.32-9.07 g for shoot and 0.24-0.84 g for root FW [75], founds that both crop densities in vertical crops had on average a shoot FW between 11-21 times higher than OFS and a root FW between 11-27 times higher than OFS.
Regarding of mean values of these variables for PP levels within the LD system, which vary between 136.3-172.7 g for shoot and 12.8-18.1 g for root FW. These results found a major similarity to reported by Kerbiriou et al. for lettuce in HHG (152-167 g, shoot and 11.2-11.8 g root FW) [76], and by Gavhane et al. for lettuce in vertical hydroponic systems (VHS) (150-200 g, shoot and 9-15 g, root FW) [77]. However, within the HD system, mean values presented lower values, even below the threshold of 127 g for shoot and 11 g for root FW, reaching values of 43.5 g for the shoot and 3.4 g for root on the lower level, close to the values reported for lettuce in HHG by Voutsinos et al. (58.1 g, shoot and 5.4 g, root FW) [41], or the values reported for lettuce in aeroponics and substrate (37.8-50.9 g, shoot and 3.9-11.5 g, root FW [74]. The mean values of the FW of the shoot for LD, and its values for each PP level, were higher than the range reported for a plant factory with artificial lighting (PFAL) 64.9-123.3 g [41], while in the case of the HD vertical crop, they were within the range of the literature except the levels mean value of the U and L levels, that was higher and lower, respectively. Regarding the root FW, the literature reported a range between 9.4-17.8 g [41] for a PFAL, this range includes all mean values except the average value for HD and the levels of mean of the M and L in HD, that were lower; and the mean of the U level in LD, which was higher.
The root-shoot ratio for both LD and HD, whose respective mean values were 0.09 and 0.07, were on average between 18-36% lower than the range reported for lettuce in HHG (0.10-0.12) [74,78], but equal to the 0.09 value reported by Voutsinos et al. [40,41], in the case of LD. Compared to the VHS, whose range is 0.06-0.08 [78], [81], LD was 13% higher than maximum limit of the range, and HD was within the range, but at the same time, LD was a 36% lower than 0.14 reported for a PFAL [41], while HD had a mean equal to half of this. For both densities, the mean values were within the range reported for lettuce in OFS, 0.03-0.13 [75]. In relation to mean values of PP levels for LD, these were closer to values reported for lettuce in HHG and in turn within the OFS values, while for HD, were closer to the VHS values.
None of the mean values of the shoot DW were within the range reported for lettuce in HHG (4.12-4.86 g) [41,74], but if within the range reported for the VHS and PFAL systems (4.00-8.77 g) [41,77], except the mean value of HD and the HD, and mean values of M and L levels of the HD, since they were lower than bottom limit of the range. The root DW of the LD and the U level in LD were higher than the top limit of the range reported for lettuce in HHG, 0.54-0.82 g [74,76]. The mean of the M and L levels in LD, together with the mean of the U level in HD within the literature range. The rest values were lower. However, compared to the VHS and PFAL systems, 0.3-0.7 g [41,77], the LD and its mean values of each PP level were higher, while the average value of the HD and its mean for U level were within the range; and the rest values were lower.
All mean values of water content were within the general range published for the lettuce crop (90-99%) [79], being the more common value [80]. Likewise, they were close to the values informed for lettuce in HHG (94-95%) [74,81,82], and for the VHS systems (97%) [77].
The lettuce productivity (extrapolated to t·ha-1) differs significantly between systems (Table 3). LD systems are 13% more productive than HD systems, and their average head weight is 45% higher. Plants in the upper levels produce, on average, 94 t·ha-1, 32% more than those in the middle and 44% more than those in the lower levels. However, there is a significant interaction between CD and PP for harvesting. Analysis of this interaction significantly differentiates the behaviour of both systems. First, the harvest in the LD system is more uniform than in HD, both for the production per unit area (t·ha-1) and for the average weight of the heads (shoot FW). At 35 DAT, all heads collected in LD reach marketable weights (>120g), while only those collected at the upper level for HD reach it. Second, the differences for PP are linearly descending for the HD (-57% for the medium and -65% for lower level), while there are only differences between the upper level and the rest for the LD (-20%). Finally, the highest yields are obtained at the upper level of HD (110 t·ha-1 with 127 g·head-1) followed by the upper level of LD (86 t·ha with 173 g·head-1).
The LD system had a mean of 74.3 t·ha-1, 61% higher than the top limit of the range reported for lettuce in HHG (12-46 t·ha-1) [63,74,81,83], roughly 20 times more than yield of the OFS systems, 3.73 t·ha-1, noted by Barbosa et al. [63], 55% higher than the value published by Orsini et al. for urban agriculture, 48 t·ha-1 [16], 2 times higher than value described by Voutsinos et al. for a PFAL (19-37 t·ha-1) [41], but 20% lower than bottom limit of the range reported for VHS (93-125 t·ha-1) [77], which requires high energy imput. While the yield of the vertical crop HD was 40% higher than that of lettuce in HHG, 17 times higher than that of that of the OFS, 34% higher than urban agriculture, 74% higher than that of a PFAL, but 31% lower than the VHS. The average value of the low level in HD was within the range for lettuce in HHG, the medium level was closer to the value reported to urban agriculture since it differed only 20%, the mean value of the upper level in HD was within the VHS range, and the mean values of the PP levels in LD were closer to the VHS range since differ between 7-27%.
The behaviour of production at the lower levels allows us to assume that both systems can be used to obtain continuous harvests year-round (with different sowing and harvesting time schedules) in vertical systems in a Mediterranean climate. In other words, a stepped harvest, to minimize the effect of shadow casting on the plants further down and achieve more sustainable horticultural production and greater efficiency in water and nutrient resources..

4. Conclusions

The predictive model is capable of forecasting the water uptake and cation concentrations in the nutrient solution tank of a closed-loop hydroponic circuit for vertical crops under greenhouse conditions, with better performance for the water uptake, the ammonium and potassium cations, followed by the sodium and magnesium cations. At the same time, is more accurate in less dense vertical crops. Moreover, the simulation process suggests new basal crop coefficients and crop uptake concentrations for vertical crops in these climate conditions that can be used as a reference point to design highly efficient fertigation strategies over the water and fertilizer resources. Nevertheless, the model has potential improvement points, on one hand, the addition of nutritive and non-nutritive anions, and also the regulation of the proportions among all ions to avoid issues about disequilibrium that will affect the product.
Vertical crops under greenhouse conditions are more competitive to conventional agriculture and even horizontal hydroponics systems, due to their more yield and development of aboveground biomass, but at the same time are limited by the shade projection of the highest levels, so it is important to establish parameters for predict and carry out a stepped harvest year-round, being the net radiation, the canopy light extinction coefficient and leaf area index, key parameters with high potential to better simulate better the plant conditions in vertical crops and its relationship with the water and nutrients uptake.

Author Contributions

Writing original draught preparation, MFLM; review and editing paper, MFQC and JMGP; execution of experiment and methodology, MFLM and CB; statistical analysis and analysis of results and prepare all figures and tables, MFLM and MCSS; analyzing of model performance, MFLM and CAGM; agronomy interpretation of results, MFLM and MCSS; supervision and project administration, MFQC and JMGP All authors have read and agreed to the published version of the manuscript.

Funding

Research project TRFE-I-2021/013 “Closed Vertical Crop System in Cascade (GroVert)” PPI 2021 of Almeria University (UAL) and research project CPP2021-008801 “Production and validation of multifunctional nanoparticles for more efficient and sustainable precision agriculture” funded by “Plan Estatal de Investigación Cientifica, Técnica y de Innovación 2021-2023”.

Data Availability Statement

Data are available in Almería University repository; Collection: Datasets - Research Objects Dept. Agronomy: http://hdl.handle.net/10835/14861.

Acknowledgements

The research groups RNM 151 PAIDI-UAL and UASLP-CA-236 developed the research project. Likewise, supported by AUIP and CONACYT.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. UUNN World Population Prospects 2019; 2019. ISBN 9789211483161.
  2. World Bank. Population estimates and projections | DataBank Available online:. Available online: https://databank.worldbank.org/source/population-estimates-and-projections (accessed on 18 December 2023).
  3. FAO The future of food and agriculture–Trends and challenges. Annu. Rep. 2017, 1–180.
  4. Calicioglu, O.; Flammini, A.; Bracco, S.; Bellù, L.; Sims, R. The future challenges of food and agriculture: An integrated analysis of trends and solutions. Sustain. 2019, 11. [Google Scholar] [CrossRef]
  5. FAO The State of the World’s Land and Water Resources for Food and Agriculture – Systems at breaking point, Syntesis report 2021. 2021; 63. [CrossRef]
  6. Feng, T.; Xiong, R.; Huan, P. Productive use of natural resources in agriculture: The main policy lessons. Resour. Policy 2023, 85, 103793. [Google Scholar] [CrossRef]
  7. FAO Land statistics and indicators 2000–2021. FAOSTAT Anal. Br. Ser. 2023, 71, 14. [CrossRef]
  8. FAO AQUASTAT Dissemination Platform. Available online: https://data.apps.fao.org/aquastat/?lang=en (accessed on 18 December 2023).
  9. FAO Greenhouse gas emissions from agrifood systems Global, regional and country trends, 2000-2020. FAOSTAT Anal. Br. Ser. 2022, 50, 1–12.
  10. Foley, J.A.; Ramankutty, N.; Brauman, K.A.; Cassidy, E.S.; Gerber, J.S.; Johnston, M.; Mueller, N.D.; O’Connell, C.; Ray, D.K.; West, P.C.; et al. Solutions for a cultivated planet. Nature 2011, 478, 337–342. [Google Scholar] [CrossRef] [PubMed]
  11. Sambo, P.; Nicoletto, C.; Giro, A.; Pii, Y.; Valentinuzzi, F.; Mimmo, T.; Lugli, P.; Orzes, G.; Mazzetto, F.; Astolfi, S.; et al. Hydroponic Solutions for Soilless Production Systems: Issues and Opportunities in a Smart Agriculture Perspective. Front. Plant Sci. 2019, 10, 923. [Google Scholar] [CrossRef] [PubMed]
  12. Fussy, A.; Papenbrock, J. An Overview of Soil and Soilless Cultivation Techniques—Chances, Challenges and the Neglected Question of Sustainability. Plants 2022, 11. [Google Scholar] [CrossRef]
  13. Sushma Devi, N.; Hatibarua, P.; Bijaya Devi, N.; Jamja, T.; Tagi, N.; Tabing, R. Urban Horticulture for Sustainable Food Production and Food Security. Eco. Env. Cons. 2022, 28, 324–335. [Google Scholar] [CrossRef]
  14. Orsini, F.; Pennisi, G.; Michelon, N.; Minelli, A.; Bazzocchi, G.; Sanyé-Mengual, E.; Gianquinto, G. Features and Functions of Multifunctional Urban Agriculture in the Global North: A Review. Front. Sustain. Food Syst. 2020, 4. [Google Scholar] [CrossRef]
  15. van Delden, S.H.; SharathKumar, M.; Butturini, M.; Graamans, L.J.A.A.; Heuvelink, E.; Kacira, M.; Kaiser, E.; Klamer, R.S.; Klerkx, L.; Kootstra, G.; et al. Current status and future challenges in implementing and upscaling vertical farming systems. Nat. Food 2021, 2, 944–956. [Google Scholar] [CrossRef] [PubMed]
  16. Orsini, F.; Kahane, R.; Nono-Womdim, R.; Gianquinto, G. Urban agriculture in the developing world: A review. Agron. Sustain. Dev. 2013, 33, 695–720. [Google Scholar] [CrossRef]
  17. Al-Kodmany, K. The vertical farm: A review of developments and implications for the vertical city. Buildings 2018, 8. [Google Scholar] [CrossRef]
  18. Supraja, M.L. Opportunities and challenges of vertical farming. Int. J. Res. Trends Innov. 2022, 7, 1071–1074. [Google Scholar]
  19. Van Gerrewey, T.; Boon, N.; Geelen, D. Vertical farming: The only way is up? Agronomy 2022, 12. [Google Scholar] [CrossRef]
  20. Beacham, A.M.; Vickers, L.H.; Monaghan, J.M. Vertical farming: a summary of approaches to growing skywards. J. Hortic. Sci. Biotechnol. 2019, 94, 277–283. [Google Scholar] [CrossRef]
  21. Oh, S.; Lu, C. Vertical farming - smart urban agriculture for enhancing resilience and sustainability in food security. J. Hortic. Sci. Biotechnol. 2023, 98, 133–140. [Google Scholar] [CrossRef]
  22. Kabir, M.S.N.; Reza, M.N.; Chowdhury, M.; Ali, M.; Samsuzzaman; Ali, M.R.; Lee, K.Y.; Chung, S. Technological Trends and Engineering Issues on Vertical Farms: A Review. Horticulturae 2023, 9, 1229. [Google Scholar] [CrossRef]
  23. Graamans, L.; Baeza, E.; van den Dobbelsteen, A.; Tsafaras, I.; Stanghellini, C. Plant factories versus greenhouses: Comparison of resource use efficiency. Agric. Syst. 2018, 160, 31–43. [Google Scholar] [CrossRef]
  24. Nikolaou, G.; Neocleous, D.; Katsoulas, N.; Kittas, C. Irrigation of Greenhouse Crops. Hortic. 2019, 5, 7. [Google Scholar] [CrossRef]
  25. Avgoustaki, D.D.; Xydis, G. Plant factories in the water-food-energy Nexus era: a systematic bibliographical review. Food Secur. 2020, 12, 253–268. [Google Scholar] [CrossRef]
  26. Voogt, W.; Bar-Yosef, B. Water and nutrient management and crops response to nutrient solution recycling in soilless growing systems in greenhouses; Second Edi.; Elsevier B.V., 2019. ISBN 9780444636966.
  27. Heuvelink, E.; Bakker, M.; Stanghellini, C. Salinity effects on fruit yield in vegetable crops: A simulation study. Acta Hortic. 2003, 609, 133–140. [Google Scholar] [CrossRef]
  28. Stanghellini, C.; Kempkes, F.; Pardossi, A.; Incrocci, L. Closed Water Loop in Greenhouses: Effect of Water Quality and Value of Produce. Acta Hortic. 2005, 691, 233–242. [Google Scholar] [CrossRef]
  29. Giuffrida, F.; Lipari, V.; Leonardi, C. A simplified management of closed soilless cultivation systems. Acta Hortic. 2003, 614, 155–160. [Google Scholar] [CrossRef]
  30. Silberbush, M.; Ben-Asher, J. Simulation study of nutrient uptake by plants from soilless cultures as affected by salinity buildup and transpiration. Plant Soil 2001, 233, 59–69. [Google Scholar] [CrossRef]
  31. Sonneveld, C.; Voogt, W.; Spaans, L. A universal algorithm for calculation of nutrient solutions. Acta Hortic. 1999, 481, 331–339. [Google Scholar] [CrossRef]
  32. Carmassi, G.; Incrocci, L.; Maggini, R.; Malorgio, F.; Tognoni, F.; Pardossi, A. Modeling Salinity Build-Up in Recirculating Nutrient Solution Culture. J. Plant Nutr. 2005, 28, 431–445. [Google Scholar] [CrossRef]
  33. Carmassi, G.; Incrocci, L.; Malorgio, M.; Tognoni, F.; Pardossi, A. A simple model for salt accumulation in closed-loop hydroponics. Acta Hortic. 2003, 614, 149–154. [Google Scholar] [CrossRef]
  34. Carmassi, G.; Incrocci, L.; Maggini, R.; Malorgio, F.; Tognoni, F.; Pardossi, A. An aggregated model for water requirements of greenhouse tomato grown in closed rockwool culture with saline water. Agric. Water Manag. 2007, 88, 73–82. [Google Scholar] [CrossRef]
  35. Incrocci, L.; Massa, D.; Carmassi, G.; Pulizzi, R.; Maggini, R.; Pardossi, A.; Bibbiani, C. SIMULHYDRO, a simple tool for predicting water use and water use efficiency in tomato closed-loop soilless cultivations. Acta Hortic. 2008, 801 PART 2, 1005–1011. [Google Scholar] [CrossRef]
  36. Son, J.-E.; Ahn, T.I.; Moon, T. Advances in nutrient management modelling and nutrient concentration prediction for soilless culture systems. In Advances in horticultural soilless culture; Burleigh Dodds Science Publishing: London, UK, 2021; pp. 277–301. ISBN 9781003048206. [Google Scholar]
  37. Noumedem, J.A.K.; Djeussi, D.E.; Hritcu, L.; Mihasan, M.; Kuete, V. Lactuca sativa. In Medicinal Spices and Vegetables from Africa; Elsevier, 2017; pp. 437–449.
  38. Shatilov, M. V; Razin, A.F.; Ivanova, M.I. Analysis of the world lettuce market. IOP Conf. Ser. Earth Environ. Sci. 2019, 395, 012053. [Google Scholar] [CrossRef]
  39. Yang, X.; Gil, M.I.; Yang, Q.; Tomás-Barberán, F.A. Bioactive compounds in lettuce: Highlighting the benefits to human health and impacts of preharvest and postharvest practices. Compr. Rev. Food Sci. Food Saf. 2022, 21, 4–45. [Google Scholar] [CrossRef]
  40. FAO FAOSTAT. Crops and livestock products. Available online: https://www.fao.org/faostat/en/#data/QCL (accessed on 18 December 2023).
  41. Voutsinos, O.; Mastoraki, M.; Ntatsi, G.; Liakopoulos, G.; Savvas, D. Comparative Assessment of Hydroponic Lettuce Production Either under Artificial Lighting, or in a Mediterranean Greenhouse during Wintertime. Agriculture 2021, 11, 503. [Google Scholar] [CrossRef]
  42. Asseng, S.; Guarin, J.R.; Raman, M.; Monje, O.; Kiss, G.; Despommier, D.D.; Meggers, F.M.; Gauthier, P.P.G. Wheat yield potential in controlled-environment vertical farms. Proc. Natl. Acad. Sci. 2020, 117, 19131–19135. [Google Scholar] [CrossRef] [PubMed]
  43. Pereira, L.S.; Allen, R.G.; Smith, M.; Raes, D. Crop evapotranspiration estimation with FAO56: Past and future. Agric. Water Manag. 2015, 147, 4–20. [Google Scholar] [CrossRef]
  44. Walter, I.A.; Allen, R.G.; Elliott, R.; Jensen, M.E.; Itenfisu, D.; Mecham, B.; Howell, T.A.; Snyder, R.; Brown, P.; Echings, S.; et al. ASCE’s Standardized Reference Evapotranspiration Equation. In Proceedings of the Watershed Management and Operations Management 2000; American Society of Civil Engineers: Reston, VA, 2001; pp. 1–11. [Google Scholar]
  45. Carmassi, G.; Maggini, R.; Incrocci, L. Modelling ion concentration in the culture solution of closed-loop hydroponics. Acta Hortic. 2004, 654, 251–256. [Google Scholar] [CrossRef]
  46. Allen, R.G.; Pereira, L.S.; Raes, D.; Martin Smith, S. Crop evapotranspiration - Guidelines for computing crop water requirements.; FAO Irrigation and drainage. Paper 56, 1998. ISBN 92-5-104219-5.
  47. Chapra, E.C.; Canale, R.P.; Valle Sotelo, J.C. Numerical methods for engineers.; Fifth.; McGraw-Hill Companies, Inc., 2006. ISBN 0-07-291873-X.
  48. Fylstra, D.; Lasdon, L.; Watson, J.; Waren, A. Design and Use of the Microsoft Excel Solver. Interfaces (Providence). 1998, 28, 29–55. [Google Scholar] [CrossRef]
  49. Sonneveld, C. Effects of salinity on substrate grown vegetables and ornamentals in greenhouse horticulture; Wageningen, 2004. ISBN 9058081907.
  50. Michael, P.R.; Johnston, D.E.; Moreno, W. A conversion guide: solar irradiance and lux illuminance. J. Meas. Eng. 2020, 8, 153–166. [Google Scholar] [CrossRef]
  51. EU. European Commission Photovoltaic Geographical Information System (PVGIS). Solar radiation. Available online: https://re.jrc.ec.europa.eu/pvg_tools/en/ (accessed on 18 December 2023).
  52. EU Meteostat Station Identifiers “Almeria aeropuerto”. Available online: https://meteostat.net/en/station/08487?t=2023-05-05/2023-05-12 (accessed on 18 December 2023).
  53. Wang, S. Air speed profiles in a naturally ventilated greenhouse with a tomato crop. Agric. For. Meteorol. 1999, 96, 181–188. [Google Scholar] [CrossRef]
  54. AEMET (Agencia Estatal de Meteorología) Valores climatológicos normales, Almería Aeropuerto. Available online: https://www.aemet.es/es/serviciosclimaticos/datosclimatologicos/valoresclimatologicos?l=6325O&k=undefined (accessed on 18 December 2023).
  55. Franklin, J. Plant Growth Chamber Handbook.; Langhans, R.W., Tibbits, T.W., Eds.; SR-99; Cambridge University Press: Iowa State University. Agriculture and Home Economics Experiment Station, 1997. [Google Scholar]
  56. Ahmed, H.A.; Yu-Xin, T.; Qi-Chang, Y. Optimal control of environmental conditions affecting lettuce plant growth in a controlled environment with artificial lighting: A review. South African J. Bot. 2020, 130, 75–89. [Google Scholar] [CrossRef]
  57. Bussotti, F.; Kalaji, M.H.; Desotgiu, R.; Pollastrini, M.; Loboda, T.; Bosa, K. Misurare la vitalità delle piante per mezzo della fluorescenza della clorofilla; Bussotti, F., et al., Eds.; Strumenti per la didattica e la ricerca; 1st ed.; Firenze University Press: Firenze, 2012; Vol. 137, ISBN 978-88-6655-215-4. [Google Scholar]
  58. Pardossi, A.; Carmassi, G.; Diara, C.; Incrocci, L.; Maggini, R.; Massa, D. Fertigation and substrate management in closed soilless culture; Pisa, Italy, 2011; Vol. 1.
  59. Chicco, D.; Warrens, M.J.; Jurman, G. The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation. PeerJ Comput. Sci. 2021, 7, 1–24. [Google Scholar] [CrossRef] [PubMed]
  60. Hai, T.; Sharafati, A.; Mohammed, A.; Salih, S.Q.; Deo, R.C.; Al-Ansari, N.; Yaseen, Z.M. Global Solar Radiation Estimation and Climatic Variability Analysis Using Extreme Learning Machine Based Predictive Model. IEEE Access 2020, 8, 12026–12042. [Google Scholar] [CrossRef]
  61. Yang, J.M.; Yang, J.Y.; Liu, S.; Hoogenboom, G. An evaluation of the statistical methods for testing the performance of crop models with observed data. Agric. Syst. 2014, 127, 81–89. [Google Scholar] [CrossRef]
  62. Saxena, A.; Celaya, J.; Balaban, E.; Goebel, K.; Saha, B.; Saha, S.; Schwabacher, M. Metrics for evaluating performance of prognostic techniques. 2008 Int. Conf. Progn. Heal. Manag. PHM 2008 2008. [Google Scholar] [CrossRef]
  63. Barbosa, G.L.; Almeida Gadelha, F.D.; Kublik, N.; Proctor, A.; Reichelm, L.; Weissinger, E.; Wohlleb, G.M.; Halden, R.U. Comparison of land, water, and energy requirements of lettuce grown using hydroponic vs. Conventional agricultural methods. Int. J. Environ. Res. Public Health 2015, 12, 6879–6891. [Google Scholar] [CrossRef]
  64. Kozai, T. Why LED Lighting for Urban Agriculture. In LED Lighting for Urban Agriculture; Springer Singapore: Singapore, 2016; pp. 3–18. [Google Scholar]
  65. Kozai, T.; Niu, G. Role of the plant factory with artificial lighting (PFAL) in urban areas; Elsevier Inc., 2019. ISBN 9780128166918.
  66. Formisano, L.; Ciriello, M.; Cirillo, V.; Pannico, A.; El-Nakhel, C.; Cristofano, F.; Duri, L.G.; Giordano, M.; Rouphael, Y.; De Pascale, S. Divergent Leaf Morpho-Physiological and Anatomical Adaptations of Four Lettuce Cultivars in Response to Different Greenhouse Irradiance Levels in Early Summer Season. Plants 2021, 10, 1179. [Google Scholar] [CrossRef]
  67. Cristofano, F.; El-Nakhel, C.; Colla, G.; Cardarelli, M.; Pii, Y.; Lucini, L.; Rouphael, Y. Tracking the Biostimulatory Effect of Fractions from a Commercial Plant Protein Hydrolysate in Greenhouse-Grown Lettuce. Antioxidants 2023, 12. [Google Scholar] [CrossRef]
  68. Carillo, P.; De Micco, V.; Ciriello, M.; Formisano, L.; El-Nakhel, C.; Giordano, M.; Colla, G.; Rouphael, Y. Morpho-Anatomical, Physiological, and Mineral Composition Responses Induced by a Vegetal-Based Biostimulant at Three Rates of Foliar Application in Greenhouse Lettuce. Plants 2022, 11, 2030. [Google Scholar] [CrossRef] [PubMed]
  69. Buturi, C.V.; Sabatino, L.; Mauro, R.P.; Navarro-León, E.; Blasco, B.; Leonardi, C.; Giuffrida, F. Iron Biofortification of Greenhouse Soilless Lettuce: An Effective Agronomic Tool to Improve the Dietary Mineral Intake. Agronomy 2022, 12, 1793. [Google Scholar] [CrossRef]
  70. Söylemez, S. The impact of different growth media and ammonium-nitrate ratio on yield and nitrate accumulation in lettuce (Lactuca sativa var. longifolia). Not. Bot. Horti Agrobot. Cluj-Napoca 2021, 49, 1–14. [Google Scholar] [CrossRef]
  71. Lycoskoufis, I.; Kavga, A.; Koubouris, G.; Karamousantas, D. Ultraviolet Radiation Management in Greenhouse to Improve Red Lettuce Quality and Yield. Agriculture 2022, 12, 1620. [Google Scholar] [CrossRef]
  72. Hamidon, M.H.; Ahamed, T. Detection of Tip-Burn Stress on Lettuce Grown in an Indoor Environment Using Deep Learning Algorithms. Sensors 2022, 22. [Google Scholar] [CrossRef] [PubMed]
  73. Hernández, E.; Timmons, M.B.; Mattson, N.S. Quality, Yield, and Biomass Efficacy of Several Hydroponic Lettuce (Lactuca sativa L.) Cultivars in Response to High Pressure Sodium Lights or Light Emitting Diodes for Greenhouse Supplemental Lighting. Horticulturae 2020, 6, 7. [Google Scholar] [CrossRef]
  74. Li, Q.; Li, X.; Tang, B.; Gu, M. Growth responses and root characteristics of lettuce grown in Aeroponics, Hydroponics, and Substrate Culture. Horticulturae 2018, 4. [Google Scholar] [CrossRef]
  75. Neumann, G.; Bott, S.; Ohler, M.A.; Mock, H.P.; Lippmann, R.; Grosch, R.; Smalla, K. Root exudation and root development of lettuce (lactuca sativa l. Cv. Tizian) as affected by different soils. Front. Microbiol. 2014, 5, 1–6. [Google Scholar] [CrossRef]
  76. Kerbiriou, P.J.; Stomph, T.J.; Van Der Putten, P.E.L.; Lammerts Van Bueren, E.T.; Struik, P.C. Shoot growth, root growth and resource capture under limiting water and N supply for two cultivars of lettuce (Lactuca sativa L.). Plant Soil 2013, 371, 281–297. [Google Scholar] [CrossRef]
  77. Gavhane, K.P.; Hasan, M.; Singh, D.K.; Kumar, S.N.; Sahoo, R.N.; Alam, W. Determination of optimal daily light integral (DLI) for indoor cultivation of iceberg lettuce in an indigenous vertical hydroponic system. Sci. Rep. 2023, 13, 1–15. [Google Scholar] [CrossRef]
  78. Vetrano, F.; Moncada, A.; Miceli, A. Use of gibberellic acid to increase the salt tolerance of leaf lettuce and rocket grown in a floating system. Agronomy 2020, 10. [Google Scholar] [CrossRef]
  79. Popkin, B.M.; D’Anci, K.E.; Rosenberg, I.H. Water, hydration, and health. Nutr. Rev. 2010, 68, 439–458. [Google Scholar] [CrossRef]
  80. Murray, J.J.; Basset, G.; Sandoya, G. Nutritional Benefits of Lettuce Consumed at Recommended Portion Sizes. EDIS 2021, 2021, 1–8. [Google Scholar] [CrossRef]
  81. Travieso, L.L.; Leon, A.P.; Logegaray, V.R.; Frezza, D.; Chiesa, A. Loose Leaf Lettuce Quality Grown in Two Production Systems. Eur. Sci. Journal, ESJ 2016, 12, 55. [Google Scholar] [CrossRef]
  82. Gang, M.S.; Kim, H.J.; Kim, D.W. Estimation of Greenhouse Lettuce Growth Indices Based on a Two-Stage CNN Using RGB-D Images. Sensors 2022, 22, 1–17. [Google Scholar] [CrossRef] [PubMed]
  83. Ahmed, Z.F.R.; Alnuaimi, A.K.H.; Askri, A.; Tzortzakis, N. Evaluation of Lettuce (Lactuca sativa L.) Production under Hydroponic System: Nutrient Solution Derived from Fish Waste vs. Inorganic Nutrient Solution. Horticulturae 2021, 7, 292. [Google Scholar] [CrossRef]
Preprints 94921 g001
Figure 1. External environmental conditions with diary frequency for the day after transplantation (DAT): temperature (°C), humidity (%), irradiance (KW·m-2) and wind velocity (m·s-1).
Figure 1. External environmental conditions with diary frequency for the day after transplantation (DAT): temperature (°C), humidity (%), irradiance (KW·m-2) and wind velocity (m·s-1).
Preprints 94921 g001
Preprints 94921 g002
Figure 2. Montage of vertical crops according to the experimental designs: (a) experimental unit and ED1 CD levels of ED1; (b) GrowPipes® unit; (c) assembly of GP units; and (d) levels of nested factor P in ED2 (d).
Figure 2. Montage of vertical crops according to the experimental designs: (a) experimental unit and ED1 CD levels of ED1; (b) GrowPipes® unit; (c) assembly of GP units; and (d) levels of nested factor P in ED2 (d).
Preprints 94921 g002
Preprints 94921 g004
Figure 4. Days after transplant (DAT) concentration of Na+ in the nutrient solution tank (NST) at (a) low density (LD) and (b) high density (HD); also contains measured data, predictive model (PM), adjusted PM and linear regression of measured data with their equation and R2.
Figure 4. Days after transplant (DAT) concentration of Na+ in the nutrient solution tank (NST) at (a) low density (LD) and (b) high density (HD); also contains measured data, predictive model (PM), adjusted PM and linear regression of measured data with their equation and R2.
Preprints 94921 g004
Preprints 94921 g005
Figure 5. Days after transplant (DAT) concentration of NH4+ in the nutrien solution tank (NST): (a) low density (LD) and (b) high density (HD); also contains measured data, predictive model (PM), PM adjusted, and a linear regression of the measured data with their equation and R2.
Figure 5. Days after transplant (DAT) concentration of NH4+ in the nutrien solution tank (NST): (a) low density (LD) and (b) high density (HD); also contains measured data, predictive model (PM), PM adjusted, and a linear regression of the measured data with their equation and R2.
Preprints 94921 g005
Preprints 94921 g006
Figure 6. Days after transplantation (DAT) K+ concentration in nutrient solution tank (NST): (a) low density (LD) and (b) high density (HD); also contains measured data, predictive model (PM), adjusted PM, and linear regression of measured data with their equation and R2.
Figure 6. Days after transplantation (DAT) K+ concentration in nutrient solution tank (NST): (a) low density (LD) and (b) high density (HD); also contains measured data, predictive model (PM), adjusted PM, and linear regression of measured data with their equation and R2.
Preprints 94921 g006
Preprints 94921 g007
Figure 7. Days after transplantation (DAT) Calcium concentration in nutrient solution tank (NST): (a) low density (LD) and (b) high density (HD); also contains measured data, predictive model (PM), adjusted PM, and a linear regression of measured data with their equation and R2.
Figure 7. Days after transplantation (DAT) Calcium concentration in nutrient solution tank (NST): (a) low density (LD) and (b) high density (HD); also contains measured data, predictive model (PM), adjusted PM, and a linear regression of measured data with their equation and R2.
Preprints 94921 g007
Preprints 94921 g008
Figure 8. Days after transplantation (DAT) Magnesium concentration in nutrient solution tank: (a) low density (LD), (b) high density (HD); also contains measured data, predictive model (PM), adjusted PM, and a linear regression of measured data with their equation and R2.
Figure 8. Days after transplantation (DAT) Magnesium concentration in nutrient solution tank: (a) low density (LD), (b) high density (HD); also contains measured data, predictive model (PM), adjusted PM, and a linear regression of measured data with their equation and R2.
Preprints 94921 g008
Table 1. Statistical performance metrics of PM in front of water uptake and cation concentrations for low and high density vertical crops.
Table 1. Statistical performance metrics of PM in front of water uptake and cation concentrations for low and high density vertical crops.
Density Statistic Water uptake EC Cation concentrations (mM)
(plants·m-2) metric (L·day-1) (dS·m-1) NH4+ K+ Ca+2 Mg+2 Na+
LD (50) R2 0.826 - 0.920 0.896 0.001 0.748 0.720
MAE 1.895 0.341 0.098 0.854 0.728 0.146 0.235
MSE 5.939 0.177 0.016 1.075 0.778 0.032 0.074
RMSE 2.437 0.420 0.128 1.037 0.882 0.178 0.272
HD (80) R2 0.858 - 0.844 0.839 0.001 0.707 0.743
MAE 1.354 0.243 0.112 0.996 0.732 0.267 0.222
MSE 3.482 0.087 0.021 1.498 0.831 0.114 0.084
RMSE 1.866 0.295 0.144 1.224 0.912 0.337 0.290
R2 (-): coefficient of determination; MAE: Mean Absolute Error; MSE: Mean Square Error; RMSE: Root Mean Square Error. MAE and RMSE are in L·day-1 for water uptake, mM for cation concentrations, and dS·m-1 for EC. MSE is in the same units, but in the second power.
Table 2. Water uptake, pH, EC and cation concentration for crop density (CD): high density (HD) and low density (LD) in the nutrient solution tank (NST) of vertical crop.
Table 2. Water uptake, pH, EC and cation concentration for crop density (CD): high density (HD) and low density (LD) in the nutrient solution tank (NST) of vertical crop.
Sources of Water uptake pH EC Cation concentration (mM)
variation (L·day-1) (dS·m-1) NH4+ K+ Ca2+ Mg2+ Na+
CD (plants·m-2) * * * * * * * *
LD (50) 15a 5.67b 3.25a 0.91a 9.05a 4.89a 1.71a 2.66a
HD (80) 19b 5.27a 3.53b 0.97b 10.19b 5.20b 1.90b 3.09b
DAT * * * * * * * *
CD x DAT * * * * * * * *
RP ns ns ns ns ns ns ns ns
Mean values of three replicates. CD: crop density, DAT: days after transplanting. Asterisks denote statistical significance according to ANOVA with p-value < 0.05; ns means not significant. Different letters among treatments indicate Tukey test significant difference at p < 0.05.
Table 3. Fresh and dry weight, yield, and related parameter behavior at 35 DAT for vertical lettuce crop growth with different crop density (CD) and plant position (PP).
Table 3. Fresh and dry weight, yield, and related parameter behavior at 35 DAT for vertical lettuce crop growth with different crop density (CD) and plant position (PP).
Variation Sources Fresh Weight Dry Weight Leaf (nº) SBI
(g·leaf-1)
Shoot Root Yield Shoot Root Water
(g) (g) R/S (t·ha-1) (g) (g) (%)
CD (plants·m-2) * * * * * * ns * *
PP * * * * * * * * *
LD (50) 148.6b 14.6b 0.09b 74.3b 5.8b 0.9b 96.0 20.2a 7.53b
Upper 172.7b 18.1b 0.10b 86.4b 7.4b 1.2b 95.5 16.8a 5.7a
Medium 135.4a 13.5a 0.09b 67.7a 4.9a 0.8a 96.2 20.2b 8.2b
Low 137.5a 12.1a 0.08a 68.7a 5.1a 0.8a 96.2 23.6c 8.7b
HD (80) 80.6a 5.9a 0.07a 64.5a 3.1a 0.4a 95.9 22.4b 3.48a
Upper 126.5c 10.8c 0.08b 101.2c 5.0c 0.7c 95.6a 20.1a 5.0c
Medium 71.9b 4.3b 0.06a 57.5b 2.7b 0.2b 95.9ab 21.9b 3.2b
Low 43.6a 2.5a 0.06a 34.8a 1.5a 0.1a 96.4b 25.3c 2.1a
CD x PP * ns ns * ns ns ns ns *
RP ns ns ns ns ns ns ns ns ns
Mean values of three replicates. For each parameter, different letters among treatments indicate significant difference at p < 0.05. CD: crop density (plants·m-2); PP: Plant Position; DAT: days after transplanting; RP: Replications. Asterisks denote statistical significance according to ANOVA with p-value < 0.05; ns means not significant.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated