Study on SR-Crossbar RF MEMS Switch Matrix Port Configuration Scheme with Optimized Consistency

Preprint

Article

Study on SR-Crossbar RF MEMS Switch Matrix Port Configuration Scheme with Optimized Consistency

Altmetrics

Downloads

Views

Comments

This version is not peer-reviewed

Submitted:

04 January 2024

Posted:

05 January 2024

You are already at the latest version

Alerts

Abstract

The performance consistency of an RF MEMS switch matrix is a crucial metric, which directly impacts its operational lifespan. An improved crossbar-based RF MEMS switch matrix topology, the SR-Crossbar, was investigated in this article. An optimized port configuration scheme was proposed for the RF MEMS switch matrix. Both the utilization probability of individual switch nodes and path lengths in the switch matrix achieve best consistency simultaneously under the proposed port configuration scheme. One significant advantage of this scheme lies in that it only adjusts positions of input and output ports, with topology and individual switch nodes kept unchanged. This grants it a high level of generality and feasibility, and also introduces an additional degree of freedom for optimizations. The article also constructed a universal utilization probability function of single nodes, and formulated an optimization objective function for the SR-Crossbar RF MEMS switch matrix, which provides a convenient approach to directly solving the optimized port configuration scheme for practical applications.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

1. Introduction

As RF systems continue to evolve towards high integration, multifunctionality, and reconfigurability, RF switch matrices play an increasingly vital role in them. Especially in compact systems, where RF switch matrices must meet the demands of high performance and good reliability, while maintaining a compact size. RF MEMS switches, characterized by low power consumption, low loss, high linearity, high isolation, and small size, are thus becoming the ideal solution in such systems [1].

However, the short lifespan of RF MEMS switch units significantly hinders their further development and application [2]. This issue also applies to matrices composed of RF MEMS switch units. Additionally, due to the presence of multiple switch units in RF paths in the matrix, there is an accumulative effect on path loss, amplifying the performance discrepancies of the switch units within the paths. Consequently, using the switch matrix may lead to a situation where, although the degradation of individual switch unit performance is within an acceptable range, the accumulative losses in the matrix paths result in a substantial increase in overall performance degradation. The disparities in performance between paths are also greatly amplified, potentially exceeding acceptable limits, which ultimately leads to the failure of the switch matrix. These issues present a new challenge in the design of RF switch matrices.

An RF switch matrix is designed to route RF signals by selectively connecting different RF paths. Each RF path contains multiple RF switches, and there are variations in both the length and structure of each path. For an RF switch matrix, it is desirable not only to maintain good performance at a specific moment, but also to ensure that the performance and its consistency do not undergo significant changes during matrix usage. In other words, the RF performance consistency of the switch matrix manifests in two different aspects:

Static Consistency: This is determined by the fixed, static design, such as the design of individual switch units and topology of the matrix. It primarily manifests in the uniformity of path lengths and structures. This type of consistency does not change during the usage of the switch matrix. In this article, we define it as static consistency.
Dynamic Consistency: This is determined by the performance degradation during usage of the switch matrix. It mainly manifests in the uniformity of performance degradation of switch units, which is related to the frequency of usage for switch units. In this article, we define it as dynamic consistency.

Possessing excellent static and dynamic consistency ensures that the RF MEMS switch matrix maintains outstanding performance throughout its operational life, thus prolonging its lifespan.

Previous research efforts have primarily focused on improving the static consistency of switch matrices. Enhancing static consistency can be achieved through methods such as increasing reliability of switch units and optimizing the topology of switch matrices. For switch units, static consistency is directly related to unit reliability. Optimization approaches include material selection, restoring mechanism design, electrical protection mechanism implementation, fluid filling and so on [2,3,4,5]. In the paper [6], an analysis of contact materials and contact damage mechanisms for RF MEMS switches was conducted to improve the reliability of switch units. The mechanically coupled structure designed in the paper [7] applies additional restoring force to the switch, resulting in enhanced anti-adhesion capability compared to traditional switches. Additionally, applying protection to switch contacts is an effective measure. In the paper [8], a pre-contact mechanism was designed such that protective contacts absorb initial contact force, which reduces degradation on the main contact and enhancing the thermal switching reliability of switch units.

Regarding topology, common structures include various variants of Benes and crossbar structures. The paper [9] designed an RF MEMS switch matrix with a Benes structure, which exhibited superior path uniformity and modular design capability. However, this switch matrix structure suffers from a lack of compactness. Crossbar structures, advantageous for large-scale matrices due to their compactness and ease of expansion. The paper [10] designed and fabricated a switch matrix with a crossbar structure, which was compact and easy to expand. However, a major drawback of the crossbar structure is its subpar static consistency among different RF paths, particularly evident at higher orders of switch matrices [11]. Addressing this, an L-shaped matrix structure was proposed in paper [12]. This structure retains the compactness and expandability advantages of crossbar, but with less favorable port layouts for chip fabrication and integration.

Combining the advantages of the aforementioned switch matrix topologies, the paper [13] designed the SR-Crossbar topology. This topology significantly reduces the number of switch units used in the switch matrix, thereby enhancing the overall reliability and RF performance of the switch matrix. Additionally, due to the reduction of switch units in the paths, the static consistency of each path is also improved.

These studies have conducted extensive research from various aspects, greatly enhancing the reliability of RF MEMS switch units. Additionally, by employing different designs of switch matrix topologies, they have improved the overall matrix performance. While these studies have evidently improved the matrix static consistency, research on dynamic consistency of RF MEMS switch matrices is relatively rare. Given that dynamic consistency optimization can be conducted without modifying switch units or matrix topology thus keeping the optimized static consistency, it can significantly enhance the overall consistency of the switch matrix.

This article begins by focusing on dynamic consistency, to optimize the overall consistency in RF MEMS switch matrices with SR-Crossbar topology. While maintaining the switch units and matrix topology unchanged, the optimization to improve consistency of switch matrix is achieved only by adjusting input and output ports configuration scheme.

2. Modelling and Analysis

In RF MEMS switch matrices, crossbar topology is simple and easily scalable, which makes it one of the most commonly used network topologies. For switch matrices based on the crossbar topology, input and output ports are typically distributed along two adjacent sides of the matrix. Signals entering through input ports into corresponding rows/columns, are routed via turning nodes to output columns/rows, and then exit through output ports. These nodes, composed of switch units, can work at different states to route signals in various directions. From this working principle, it can be inferred that, in scenarios where inputs and outputs are randomly interconnected without being blocked, the units near the input and output ports are more likely to be utilized, while those farther away have a lower probability of utilization. Over time, this leads to more significant performance degradation in units near the ports, which reduces the dynamic consistency of the entire switch matrix. 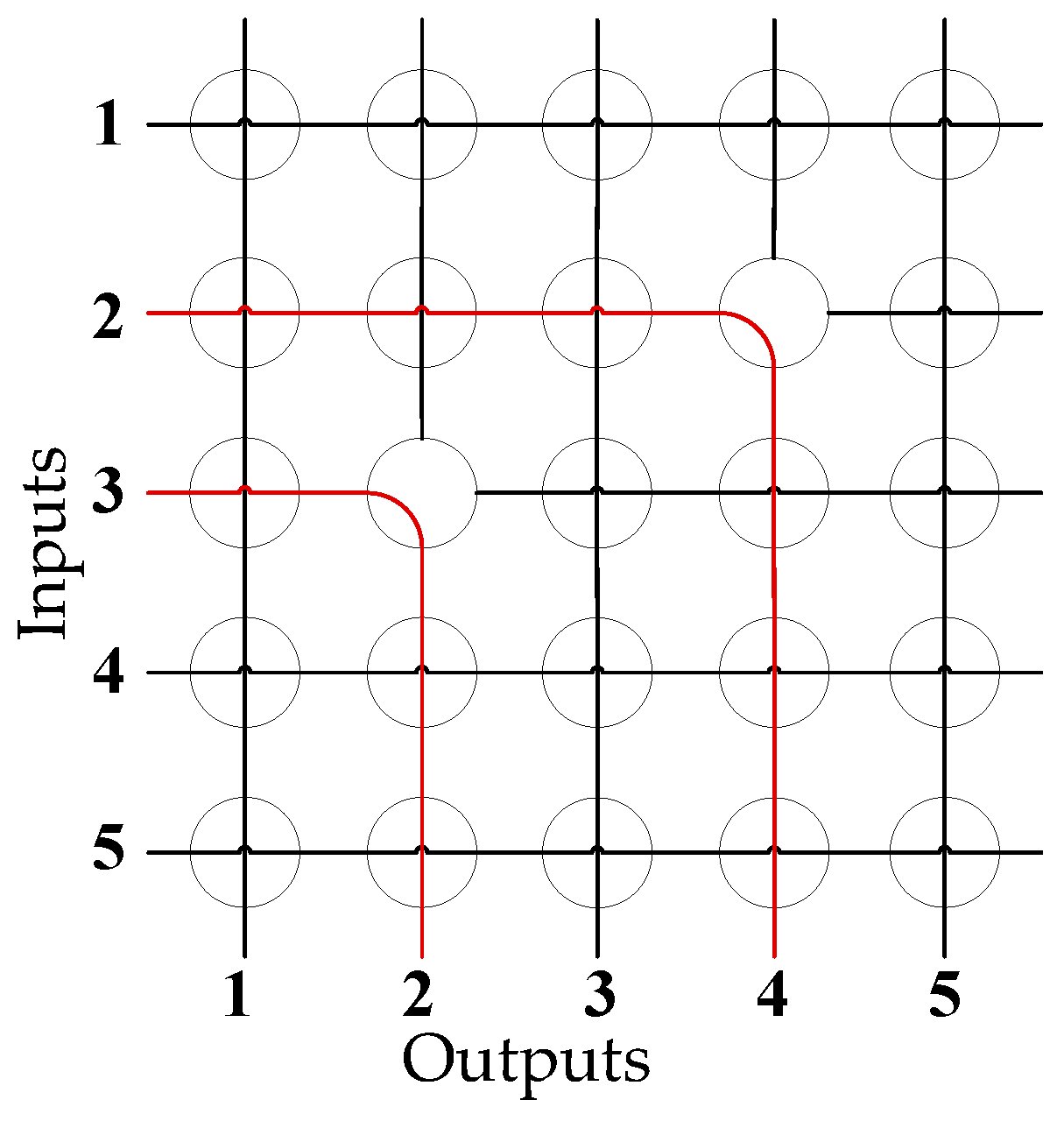Figure 1 shows a crossbar switch matrix.

Therefore, the key to optimizing the dynamic consistency of the switch matrix lies in ensuring that the probability of each switch unit being utilized is as uniform as possible in the matrix. Meanwhile, by just modifying the configuration of input and output ports while keeping switch unit and matrix topology unchanged to optimize overall matrix consistency, this approach offers additional degree of freedom to improve the overall lifespan of switch matrices. Thus, this port configuration optimization approach is broadly applicable to crossbar-based switch matrices, independent of the switch unit types composing the matrix, which makes the approach highly versatile.

The SR-Crossbar structure proposed in paper [13] improves the overall reliability and performance of RF switch matrices by reducing the number of switch units in a crossbar matrix. This article builds upon this foundation to further research, optimizing input and output port configurations to enhance dynamic consistency.

As analyzed above, for the SR-Crossbar switch matrix with random non-blocking interconnections between inputs and outputs, the switch units near the inputs and outputs generally have a higher probability of being utilized, while the switch units far from the ports have a lower probability of being utilized. Therefore, this leads to more severe performance degradation in units near the ports, creating significant inconsistencies in the performance of the entire switch matrix. Thus, accurately establishing a utilization probability model for the matrix nodes is key to analyzing and optimizing port configuration schemes.

In the following context, we will provide a detailed analysis of the probability of each node being utilized in an SR-Crossbar switch matrix with random non-blocking interconnections between any input and output ports.

Assuming an SR-Crossbar RF MEMS switch matrix with

M

rows and

N

columns, we conducted an analysis on the switch matrix node located at

(m, n)

. Here,

M

N

m

, and

n

satisfy the following conditions:

M, N \in Z, M, N \geq 2

m = 1,2, 3, \dots, M

and

n = 1,2, 3, \dots, N

For any RF MEMS switch matrix based on a crossbar topology, there exists a critical node in each established path between input and output ports. This node directs signal from input row/column to output column/row. In this article, we refer to this node as the “Turning Node” denoted as TN. For example, in Figure 1, nodes (3,2) and (2,4) are both Turning Nodes (TNs).

As per the non-blocking characteristic of the crossbar matrix topology, at any given time, there is only one working TN in the same row and same column. Additionally, given that the input and output ports are fixed in practical applications, a TN uniquely corresponds to an RF signal path, with other nodes in the path considered as regular nodes. This allows a clear analysis of the relationship between each regular node and TNs in the switch matrix.

Let

a

represents the number of TNs in the same row as

(m, n)

, in which case node

(m, n)

will be utilized by the path corresponding to the TN. Similarly, let

b

represents the number of TNs on the same column as

(m, n)

, in which case node

(m, n)

will be utilized by the path corresponding to the TN. For example, in Figure 1, selecting either node (3,3), (3,4) or (3,5) in third row or selecting either node (1,2) or (2,2) in second column as TN will utilize node (3,2). Thus

a

and

b

of node (3,2) equal to 3 and 2, respectively.

In a crossbar-based including SR-Crossbar RF MEMS switch matrix, where ports are traditionally configured, without losing generality, one can assume that the input ports are on the left side and output ports are on the bottom side. Therefore, it can be derived that:

a = N - n, b = m - 1,

(1)

Here we consider the case where the number of input and output ports in the switch matrix are equal, i.e.,

M = N

, which is the case for most non-blocking switch matrices.

For a fully configured switch matrix, there are a total of

M

TNs, with each TN determining one signal path. Based on the non-blocking nature of the crossbar topologies, it is known that within the same row and column of the matrix, there is one only one TN. Therefore, the interconnectivity between the ports of the switch matrix can be uniquely determined by the positions of all TNs. Thus, analyzing all possible interconnections between input and output ports can be simplified to analyzing the TN positions of all paths. In one single RF signal path, there’s only one TN and other nodes are considered as normal nodes. As a result, different distributions of TNs correspond to different utilization scenarios for the nodes on the paths.

Hence, generating a specific port configuration can be simplified to choose

M

TNs’ locations according to requirements and within regulation of non-block crossbar topology.

For the node

(m, n)

, the probability of its utilization can be divided into four parts:

The TNs which will utilize node $(m, n)$ only exist in the same row, of which the probability is calculated as follows:

P_{1} = a \times \frac{(M - 2)!}{(M - 2 - b)!} \times (M - 1 - b)! \times {(M!)}^{- 1} \begin{matrix} = a \times (M - 2)! \times (M - 1 - b) \times {(M!)}^{- 1} \end{matrix}

(2)

Here, let

a

be Factor One,

(M - 2)! / (M - 2 - b)!

be the Factor Two,

(M - 1 - b)!

be the Factor Three, and

{(M!)}^{- 1}

be Factor Four. The probability can be deducted by analyzing the locations

M

TNs. The analysis and calculation process for

P_{1}

is as follows:

(1): First, select $a$ TNs in the same row that will utilize node $(m, n)$ as the TN. This gives the Factor One.
(2): Second, starting from the first row one by one until $b$ -th row to choose TNs. Since the TN utilizing node $(m, n)$ can only be in the $n$ -th row with node $(m, n)$ , nodes in column $n$ cannot be selected as TNs in this step. The total number of TN selection schemes is $(M - 2)! / (M - 2 - b)!$ , resulting in Factor Two.
(3): Third, starting from the $(b + 1)$ -th row until the $M$ -th row to choose TNs. The first two steps have already completed the selection of $b + 1$ TNs. The remaining $(M - 1 - b)$ TNs have a total selection scheme of $(M - 1 - b)!$ , resulting in Factor Three.
(4): Finally, the total number of random TN selection schemes for the non-blocking interconnection scheme, is $M!$ . This serves as the denominator in Factor Four.

2.: The TNs which will utilize node $(m, n)$ only exist in the same column, of which the probability is calculated as follows:

Similar to case above, and given that

M = N

, we have:

P_{2} = b \times (M - 2)! \times (M - 1 - a) \times {(M!)}^{- 1},

(3)

3.: The TNs which will utilize node $(m, n)$ exist in the same row and same column at the same time, of which the probability is calculated as follows:

P_{3} = a \times b \times (M - 2)! \times {(M!)}^{- 1},

(4)

Similarly:

(1): First, select $a$ TNs in the same row that will utilize node $(m, n)$ as the TN. This gives Factor One.
(2): Second, select $b$ TNs in the same column that will utilize node $(m, n)$ as the TN. This gives Factor Two.
(3): The remaining $(M - 2)$ TNs have a total number of selection scheme $(M - 2)!$ . This gives Factor Three.
(4): The total number of TN selection schemes is $M!$ . This serves as the denominator of Factor Four.

4.: Node $(m, n)$ is the TN, and the probability is calculated as follows:

P_{4} = 1 \times (M - 1)! \times {(M!)}^{- 1},

(5)

(1): First, select node $(m, n)$ itself as the first TN, thus the number of selections is 1. This gives Factor One.
(2): The remaining $(M - 1)$ TNs have a total selection scheme of $(M - 1)!$ . This gives Factor Two.
(3): The total number of TN selection schemes is $M!$ . This serves as the denominator of Factor Three. Therefore, the total probability is:

\begin{matrix} P (m, n) & = P_{1} + P_{2} + P_{3} + P_{4} \\ = \frac{(M - 1) (a + b + 1) - a b}{M (M - 1)} \\ = \frac{a + b + 1}{M} - \frac{a b}{M (M - 1)} \end{matrix}

(6)

Let’s consider the probability distribution of each node in a specific traditional port-configured crossbar matrix. We assume that both the number of input and output ports are 16, i.e.,

M = N = 16

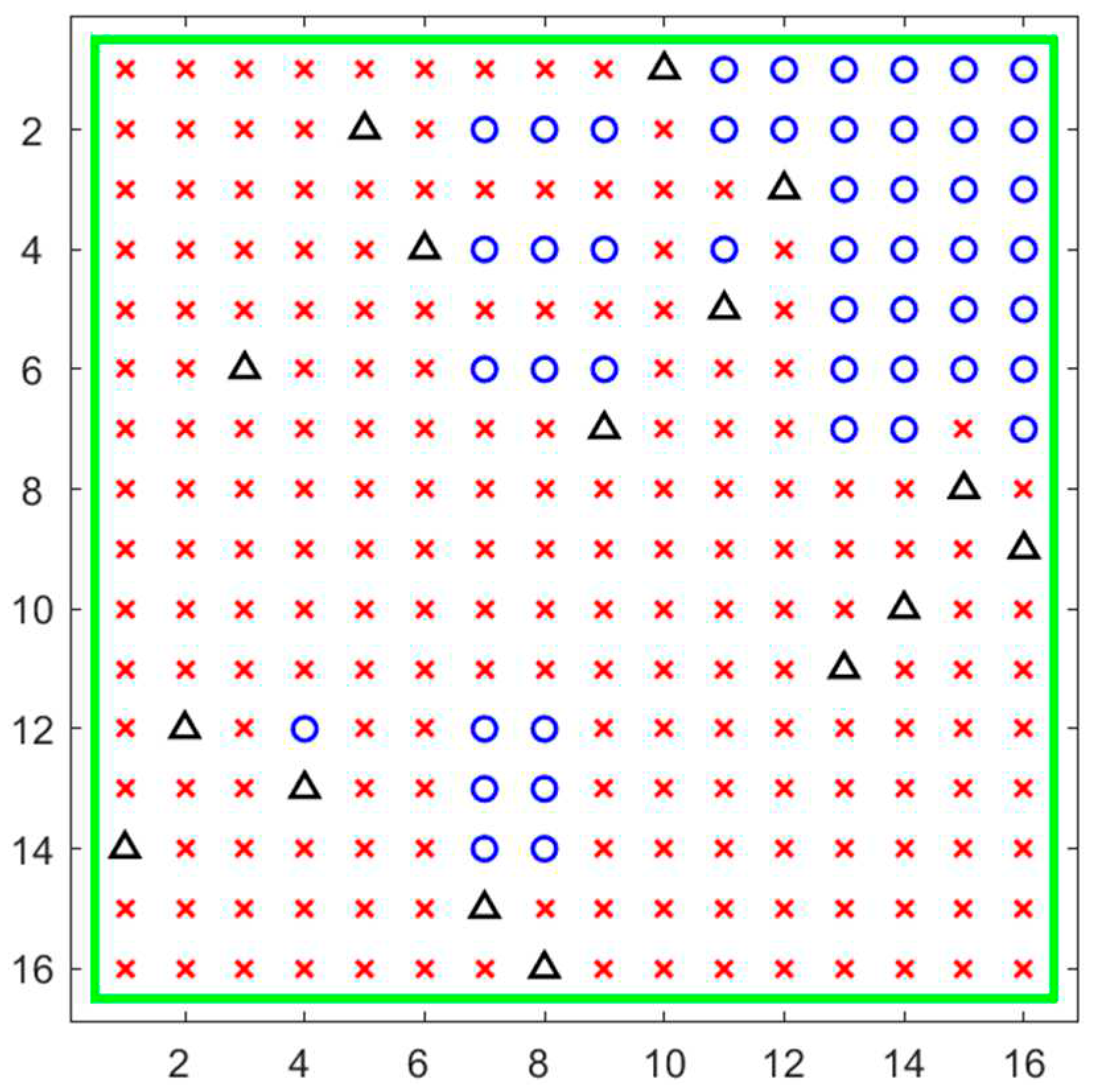
. Here, without loss of generality, we assume that the inputs are on the left side and the outputs are on the bottom side. Here we generate a set of port configuration scheme, i.e., a combination of different TN locations in the matrix, the randomly generated configuration is shown in Figure 2:

As shown in Figure 2, the numbers on the left and bottom are indices of rows and columns, respectively. The input ports are on the left and the output ports are on the bottom. The black triangles represent locations of random generated TNs. It can also be observed that there is one and only one TN in the same row or column. The corresponding RF path starts from the left signal input, turns after passing through TN, and outputs to the output port below it. The red crosses indicate the nodes in the matrix that are utilized in this configuration. The blue circles denote the nodes that are currently unutilized, which are redundant ones. In different configuration schemes, the locations of TNs vary, leading to differences in the occupied and redundant nodes within the matrix.

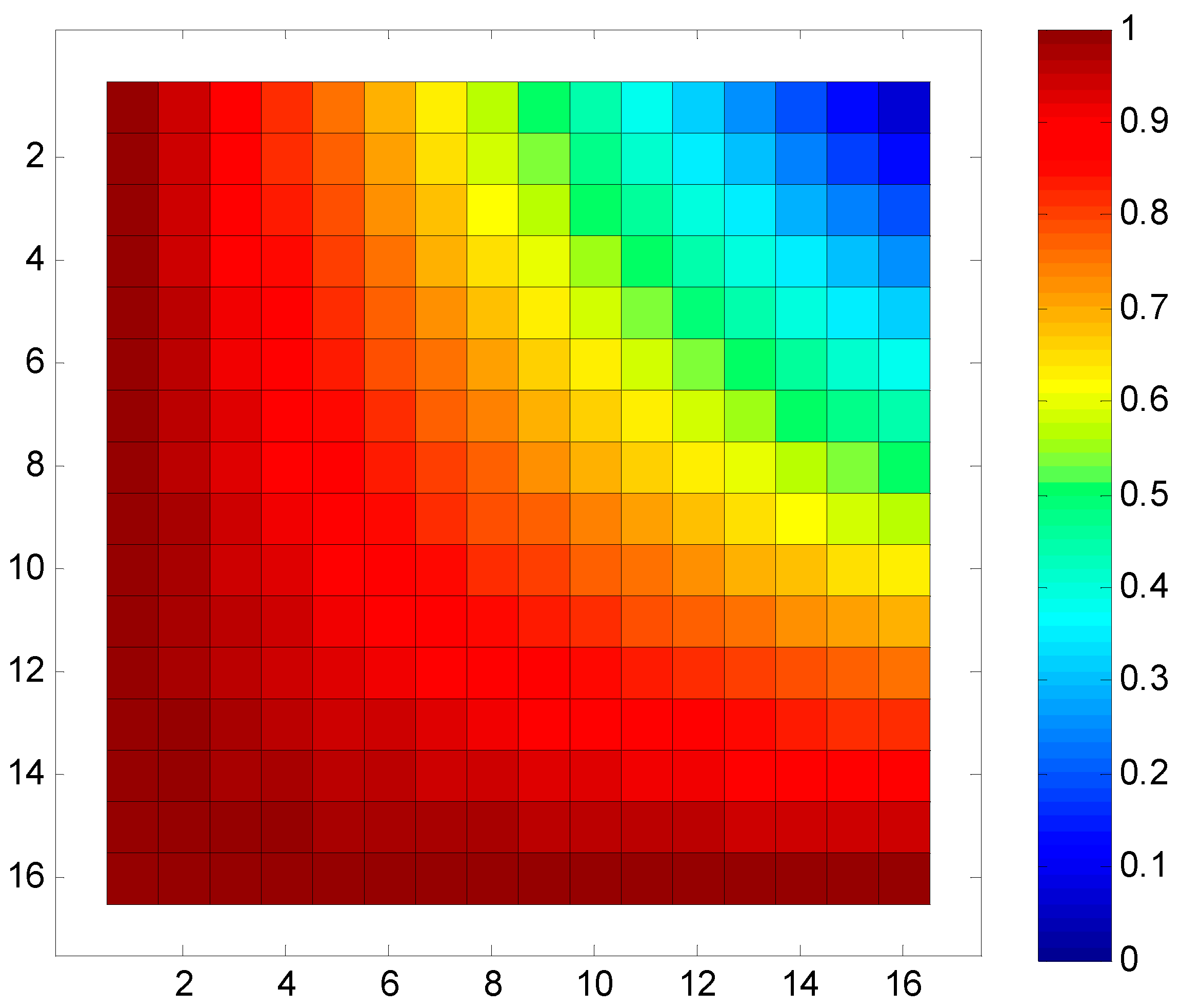
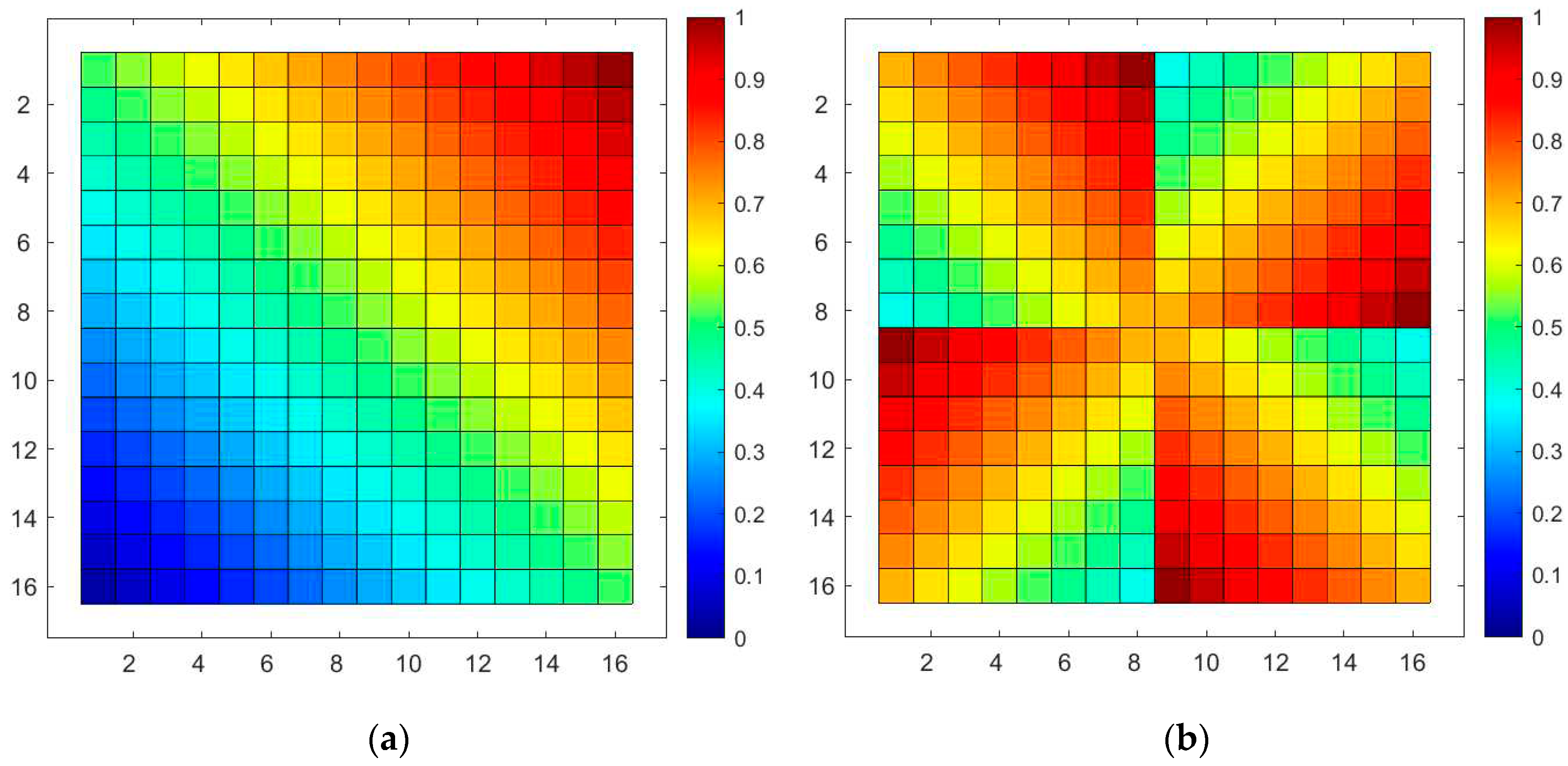
Based on Equation (6), we can derive the probability of each node’s utilization in a 16x16 SR-Crossbar RF MEMS switch matrix when any input and output port are all connected in a non-blocking manner.

Figure 3. Node utilization probability of a 16×16 SR-Crossbar switch matrix.

In the aforementioned switch matrix, the minimum probability of utilization for each node is 0.0625, the maximum is 1, and the standard deviation is 0.2226. The consistency of node utilization probabilities is relatively poor. As previously analyzed, it’s evident that nodes closer to the input and output ports have higher utilization probabilities, while those farther away have lower probabilities. We aim to optimize the ports to achieve a more balanced utilization probability for these nodes, thereby enhancing the dynamic consistency of the switch matrix.

Now that we have obtained the probabilities of each node being utilized in the SR-Crossbar switch matrix under random non-blocking interconnection of ports, in order to achieve optimal dynamic consistency of the matrix, we need to make the probability of utilization for each node varies as least as possible.

3. Optimization

Based on the basic characteristics of SR-Crossbar topology, we have conducted an analysis to obtain the utilization probabilities of each node in the crossbar switch matrix, its utilization probabilities of nodes follow Equation (6). However, the values of parameters

a

and

b

for different input and output port configurations are different. Therefore, determining the port configuration scheme that leads to higher consistency in utilization probabilities for each node in the matrix, can be simplified to finding the values of

a

and

b

corresponding to different port configuration schemes.

Due to the fact that the SR-Crossbar topology is composed from the basic building blocks through sequential rotation, the SR-Crossbar RF MEMS switch matrix possesses rotational symmetry. Therefore, without loss of generality, we can assume that all input ports are on the rows of the switch matrix, and all output ports are on the columns. Thus, determining the entire port configuration scheme for the switch matrix can be simplified to deciding whether each row’s input ports are on the left or right side, and whether each column’s output ports are on the top or bottom side.

Meanwhile, regardless of the port configuration scheme, for a non-blocking SR-Crossbar switch matrix with equal numbers of input and output ports, there are a total of

M (M = N)

turning nodes (TNs). Each TN determines one input-output RF signal path. Additionally, according to the characteristics of a non-blocking topology, each row and each column in the matrix has exactly one and only one TN. In this scenario, for each path in the switch matrix, there are four possible directions of signal flow: left-down (LD), right-down (RD), left-up (LU), and right-up (RU).

Therefore, the expressions for

a

and

b

in Formula 6 for the utilization probability of each node are as follows:

a = \{\begin{matrix} N - n, Type LD \\ n - 1, Type RD \\ N - n, Type LU \\ n - 1, Type RU \end{matrix}, b = \{\begin{matrix} m - 1, Type LD \\ m - 1, Type RD \\ M - m, Type LU \\ M - m, Type RU \end{matrix},

(7)

The key to establishing the optimization model is obtaining the probability function for the utilization of each node in the matrix. However, discussing the values of

a

and

b

in different cases makes it difficult to establish a simplified and analytical function.

Therefore, we rewrite the above equation to:

a = {(- 1)}^{x_{m}} \cdot n - {(- N)}^{x_{m}}, b = {(- 1)}^{y_{n}} \cdot m - {(- M)}^{y_{n}},

(8)

Here,

x_{m}

and

y_{n}

can take values of 0 or 1, where

x_{m} = 0

1

represents the input port on the right or left side respectively, and

y_{n} = 0

1

represents the output port on the bottom or top side respectively. The Equation (1) in the previous context corresponds to a specific case where

x_{m} = 1

and

y_{n} = 0

In order to achieve the highest consistency in utilization probabilities for each node, we aim to find a set of values for

x_{m}

and

y_{n}

that minimize the standard deviation of

P (m, n)

, hence we have the objective function, which is

m i n {σ}

. Here

σ = \sqrt{\frac{1}{M N} \sum_{m, n} {(P (m, n) - μ)}^{2}},

(9)

In which

μ = \frac{1}{M N} \sum_{m, n} P (m, n),

(10)

Here, we have established the port configuration optimization model along with its objective function. For a specific switch matrix, we simply need to substitute the given values of the switch ports, i.e., the values of

M

and

N

as mentioned in the previous text to Equations (6) and (8)–(10), to obtain the optimal solution.

For example, in the case of a 16x16 matrix, which means

M = N = 16

, and utilizing a PSO (Particle Swarm Optimization) algorithm to solve for

m i n {σ}

, we obtain the optimal solution as:

X = [x_{m}] = [1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0] Y = [y_{n}] = [0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1]

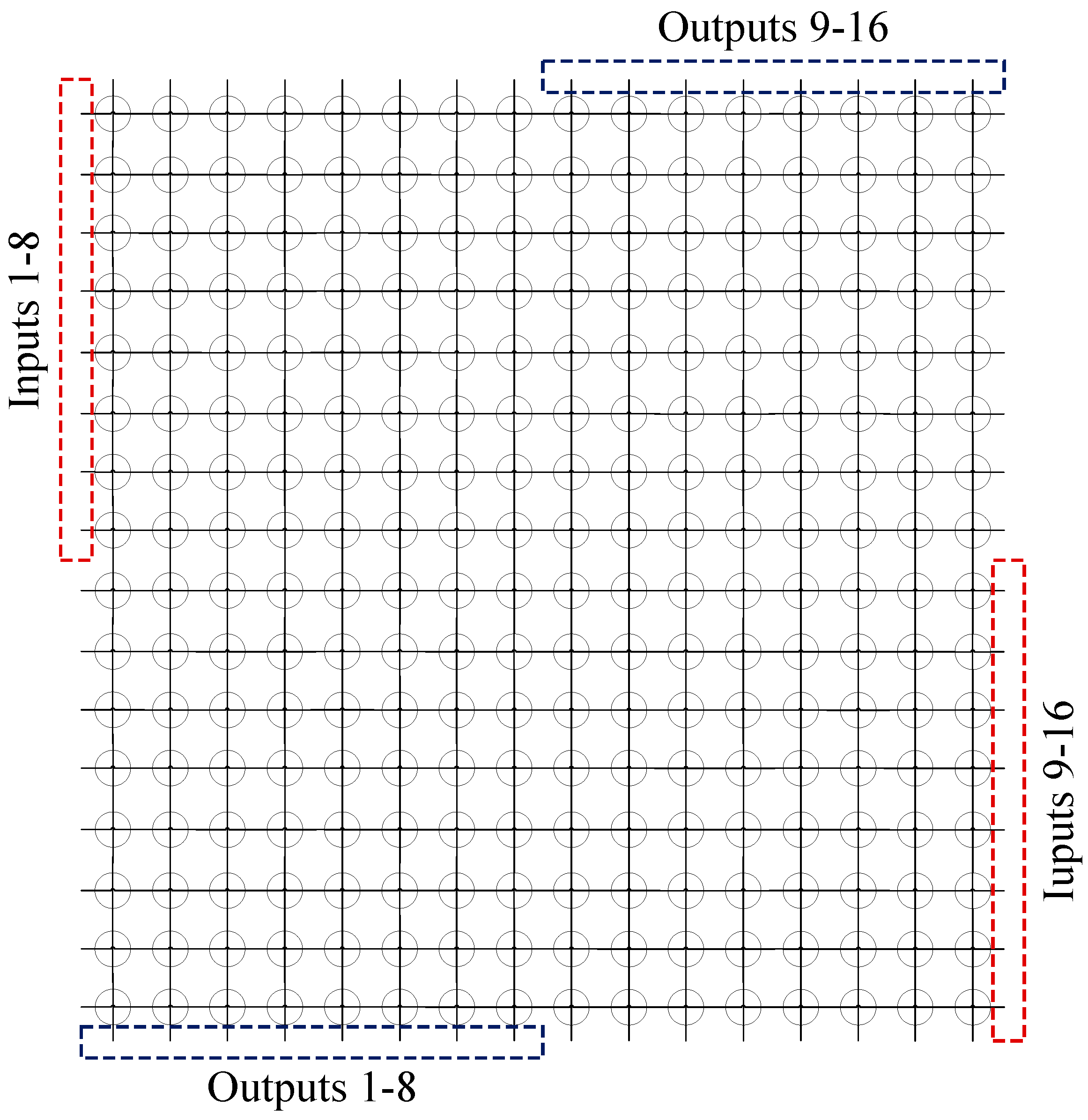
At this point, the simplified schematic diagram of the switch matrix port configuration is as shown in the following Figure 4:

Figure 4. Optimized port configuration scheme of a 16×16 SR-Crossbar switch matrix.

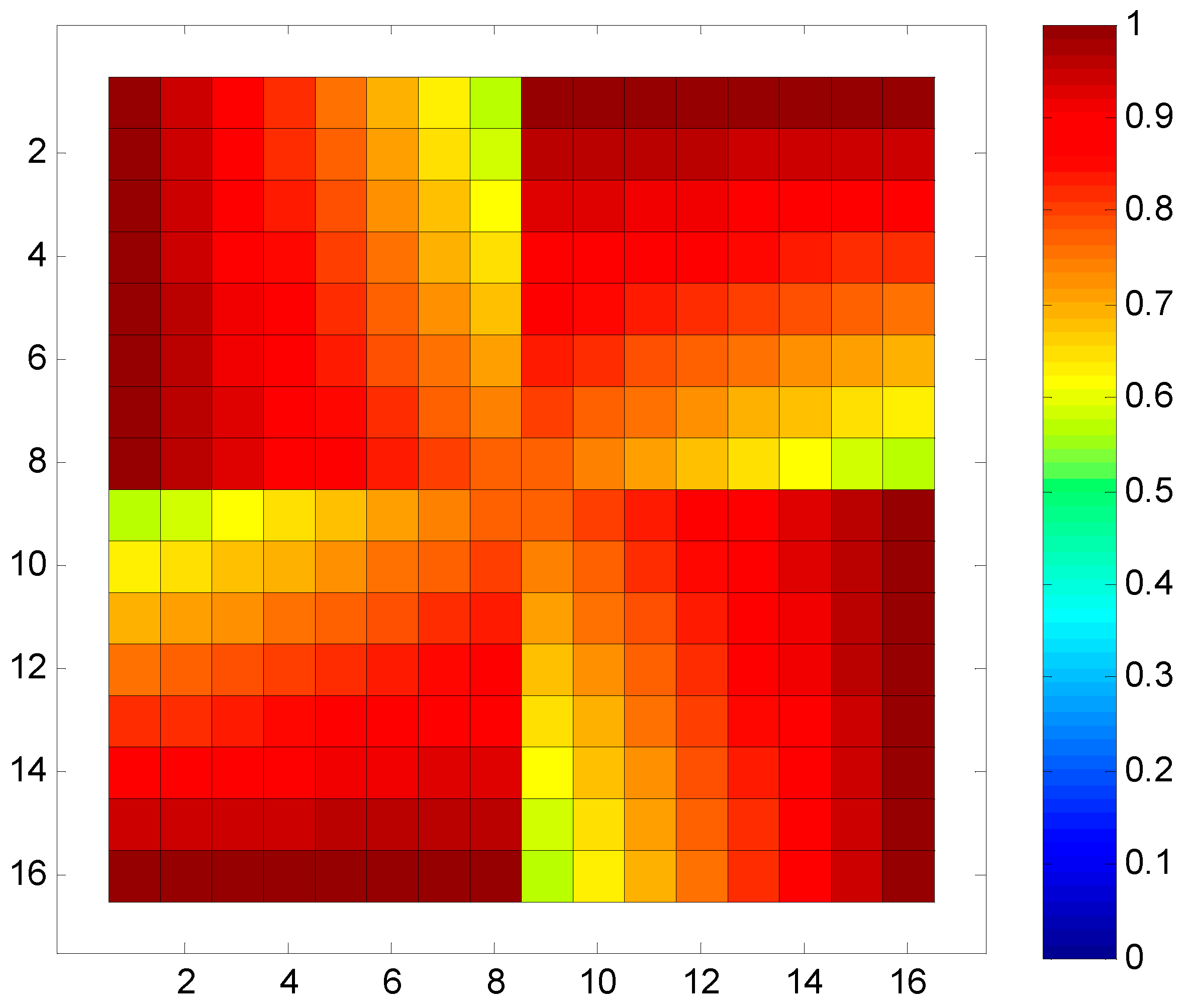
Figure 5. Optimized node utilization probability of a 16×16 SR-Crossbar switch matrix.

The probability distribution of each node is shown in Figure 5. It is evident from the figure that utilization probability distribution of each node in the entire switch matrix is more uniform compared to the traditional port configuration scheme in Figure 3. The minimum and maximum probabilities of node utilization are 0.5625 and 1 respectively, with a standard deviation of 0.1171. The standard deviation has significantly reduced compared to the original matrix. As a result, the overall utilization probability of nodes in the switch matrix is more balanced, leading to a significant improvement in the dynamic consistency of the entire switch matrix.

The previous analysis focused on SR-Crossbar RF MEMS switch matrix, obtaining the utilization probability for each node. Meanwhile, a detailed port configuration optimization was conducted for the SR-Crossbar structure. An optimization model was established, providing an objective function to maximize the consistency of node utilization probability. A specific switch matrix, a 16-input 16-output SR-Crossbar RF MEMS switch matrix, was compared between the traditional port configuration scheme and the optimized port configuration scheme. The results showed that the optimized port configuration scheme reduced the standard deviation of node utilization probability by 47.4% compared to the traditional scheme, greatly improving the dynamic consistency of the SR-Crossbar-type RF MEMS switch matrix.

As analyzed earlier, the consistency of the switch matrix includes both dynamic and static aspects. Optimizing the consistency of RF signal path lengths is one of the most effective methods for static consistency.

Similar to the previous method, we aim to find an optimal port configuration scheme that minimizes the differences in lengths of each path in the SR-Crossbar switch matrix.

We employ a similar analytical process as described above. However, in contrast to the utilization probability for each node discussed earlier, our focus here is on the length of RF signal paths, which refers to the number of nodes utilized in each path.

The length of the path with the node

(m, n)

as the turning point TN is denoted as

L (m, n)

, and can be expressed as:

L (m, n) = (N - a) + (M - b) - 1,

(11)

where

a

and

b

are defined the same as in Equation (8). Similarly, we aim to minimize the standard deviation of

L (m, n)

for all combinations of

m

and

n

, with the objective function min{σ’}.

σ^{'} = \sqrt{\frac{1}{M N} \sum_{m, n} {(L (m, n) - μ^{'})}^{2}},

(12)

In which

μ^{'} = \frac{1}{M N} \sum_{m, n} L (m, n),

(13)

The obtained set of

x_{m}

and

y_{n}

is interesting. The optimized solution, with the objective of minimizing the probability standard deviation, is the same as it is in the former context:

X = [x_{m}] = [1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0] Y = [y_{n}] = [0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1]

For better visualization, we normalize the path lengths by divide each path length by the maximum value among them all. The normalized path lengths in traditional and optimized port configuration SR-Crossbar switch matrices are shown in Figure 6a and Figure 6b, respectively.

In the traditional port configuration scheme, the minimum and maximum lengths of each path in the matrix are 1 and 31, respectively. The standard deviation is 6.5320. In the optimized scheme, the minimum and maximum lengths of each path are 9 and 23, respectively, with a standard deviation of 3.2467. The standard deviation is reduced by 50.3% compared to the traditional port configuration scheme.

Multiple optimized port configuration schemes for SR-Crossbars with different input and output numbers are calculated. For the same matrix, whether aiming for the best consistency in node utilization probability or path length, the results of the optimization are the same. Therefore, for these SR-Crossbar RF MEMS switch matrices, the optimal port configuration scheme calculated in the manner proposed in this article will significantly enhance both the dynamic and static consistency of the matrix. This provides two benefits for the switch matrix: better consistency in the performance degradation of each switch unit, which maximizes the lifespan and stability; and for each conducting path in the switch matrix, the RF performance varies less, resulting in better channel consistency.

The optimization above demonstrated the case of a

16 \times 16

switch matrix for simplicity. In reality, when the dimensions of the switch matrix are higher, improving its consistency becomes even more important. The proposed port optimization scheme in this article can optimize the lifespan and overall performance of the switch matrix by simply optimizing the port positions, while keeping the topology of the switch matrix and the switch units remain unchanged. Hence the proposed optimization has significant practical value and high feasibility.

4. Conclusions

The performance consistency of RF MEMS switch matrices is an important indicator. This article proposes the concepts of dynamic and static consistency of the matrix. Starting from optimizing the dynamic consistency of the RF MEMS switch matrix with an SR-Crossbar structure, the article conducts detailed research on its port configuration scheme. Utilization probability for each node in the matrix and the optimization objective function to achieve the best consistency of node utilization probability are given. By using the method proposed in the article, the best port configuration scheme for a specific

16 \times 16

matrix is obtained. Compared to the traditional port configuration scheme, the standard deviation of node utilization probability is reduced by 47.4%, significantly optimizing the dynamic consistency of the matrix. Furthermore, this port configuration scheme also applies to achieving the highest static consistency, with which RF signal path variation is minimized. The standard deviation of path lengths is reduced by 50.3% compared to the traditional port configuration scheme, thus static consistency is also significantly optimized. Moreover, a major advantage of the port configuration optimization scheme proposed in the article is that it can achieve optimization by simply adjusting positions of input and output ports while keeping the topology of the switch matrix and the switch units unchanged. It has evident universality and operability, providing additional degrees of freedom for optimizing matrix consistency.

Author Contributions

conceptualization, W.S. and W.Z.; methodology, W.Z. and B.Y.; validation, W.Z.; writing—original draft preparation, W.Z.; writing—review and editing, W.S.; supervision, W.S.; project administration, W.S. All authors have read and agreed to the published version of the manuscript.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data used to support the finds of this research are available from the corresponding author upon request.

Conflicts of Interest

The authors declare no conflicts of interest.

References

Iannacci, J. RF-MEMS: an enabling technology for modern wireless systems bearing a market potential still not fully displayed. Microsystem Technologies 2015, 21, 2039–2052. [Google Scholar] [CrossRef]
Ma, L.; Soin, N.; Daut, M.H.M.; Hatta, S.F.W.M. Comprehensive Study on RF-MEMS Switches Used for 5G Scenario. IEEE Access 2019, 7, 107506–107522. [Google Scholar] [CrossRef]
Iannacci, J. Expectations versus actual market of RF-MEMS: analysis and explanation of a repeatedly fluctuating scenario. In RF-MEMS Technology for High-Performance Passives (2nd Edition), IOP Publishing: 2022.
Zorpette, G. RF MEMS deliver the “ideal switch”: After two decades of development, MEMS-based RF switches are finally finding real-world uses. IEEE Spectrum 2020, 57, 8–9. [Google Scholar] [CrossRef]
Zhu, H.; Cui, W.; Li, Y.; Song, M. Design and Analysis of a Fluid-Filled RF MEMS Switch. Sensors 2023, 23, 2692. [Google Scholar] [CrossRef] [PubMed]
Basu, A.; Adams, G.G.; McGruer, N.E. A review of micro-contact physics, materials, and failure mechanisms in direct-contact RF MEMS switches. Journal of Micromechanics and Microengineering 2016, 26, 104004. [Google Scholar] [CrossRef]
Kim, C.H. Mechanically Coupled Low-Voltage Electrostatic Resistive RF Multithrow Switch. IEEE Transactions on Industrial Electronics 2012, 59, 1114–1122. [Google Scholar] [CrossRef]
Liu, Y.; Bey, Y.; Liu, X. Extension of the Hot-Switching Reliability of RF-MEMS Switches Using a Series Contact Protection Technique. IEEE Transactions on Microwave Theory and Techniques 2016, 64, 3151–3162. [Google Scholar] [CrossRef]
Di Nardo, S.; Farinelli, P.; Kim, T.; Marcelli, R.; Margesin, B.; Paola, E.; Pochesci, D.; Vietzorreck, L.; Vitulli, F. Design of RF MEMS based switch matrix for space applications. Advances in Radio Science 2013, 11, 143–152. [Google Scholar] [CrossRef]
Fomani, A.A.; Mansour, R.R. Monolithically Integrated Multiport RF MEMS Switch Matrices. Microwave Theory and Techniques. IEEE Transactions on 2009, 57, 3434–3441. [Google Scholar]
Daneshmand, M.; Mansour, R.R. RF MEMS Satellite Switch Matrices. Microwave Magazine, IEEE 2011, 12, 92–109. [Google Scholar] [CrossRef]
King Yuk, C.; Daneshmand, M.; Mansour, R.R.; Ramer, R. Scalable RF MEMS Switch Matrices: Methodology and Design. Microwave Theory and Techniques, IEEE Transactions on 2009, 57, 1612–1621. [Google Scholar] [CrossRef]
Zhou, W.; Sheng, W.; Cui, J.; Han, Y.; Ma, X.; Zhang, R. SR-Crossbar topology for large-scale RF MEMS switch matrices. In IET Microwaves, Antennas & Propagation; Institution of Engineering and Technology: 2019; Volume 13, pp. 231–238.

Figure 1. A crossbar switch matrix with input 2 to output 4 and input 3 to output 2 connected.

Figure 2. A random port configuration scheme of a 16×16 SR-Crossbar switch matrix.

Figure 6. Normalized path lengths before and after port configuration optimization of SR-Crossbar switch matrix: (a) Normalized path lengths in traditional port configuration of SR-Crossbar switch matrix; (b) Normalized path lengths in optimized port configuration of SR-Crossbar switch matrix.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Study on SR-Crossbar RF MEMS Switch Matrix Port Configuration Scheme with Optimized Consistency

Abstract

1. Introduction

2. Modelling and Analysis

3. Optimization

4. Conclusions

Author Contributions

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe