New Tanimoto Similarity and Distance Measures for Pythagorean Fuzzy Sets With Applications

1. Introduction

Decision-making is a common behavior. Ideally, the data required for decision-making would be precise and comprehensive; unfortunately, in reality, the majority of the information we have for decision-making is either uncertain or incomplete, implying the presence of uncertainty [1,2]. Uncertainty is the primary factor impeding correct decision-making, and it has become increasingly pervasive in various fields because of the complexity of practical issuses and the natural bounds of understanding. This ambiguity always manifests itself randomly and in uncertain manners, which leads to the difficulties of accurate depiction and decision-making process. Therefore, how to accurately describe uncertainty has become a paramount challenge [3,4]. Currently, numerous innovative theories and techniques have been suggested for depicting uncertainty in real-world scenarios, including fuzzy sets [5], Intuitionistic fuzzy sets (IFSs) [6], evidence theory [7,8], rough sets [9,10,11] and R-numbers [12]. Among the array of theories, the IFSs stands out for its proficiency in capturing ambiguity and indeterminacy through the delineation of membership and nonmembership intervals for elements. This distinctive characteristic has rendered IFSs an indispensable instrument across various disciplines for grappling with uncertainties [13,14,15]. However, in some cases, the condition that the sum of the membership degree and nonmembership degree required by the International Federations must be less than or equal to 1 may be violated. Inspired by this, Yager [16] first introduced Pythagorean fuzzy sets (PFSs) as an evolution of IFSs in 2013. The hallmark of this model is its employment of the Pythagorean membership function, which introduces a degree of hesitation into the parameters of IFSs, including their membership degree, nonmembership degree and indeterminacy degree. PFSs stipulate that the sum of squares of membership and nonmembership is not more than 1, making it more effective in representing uncertain information. Subsequently, Zhang and Xu [17] introduced the concept of Pythagorean fuzzy numbers (PFNs) and subsequently proposed the PF-TOPSIS method for multi-attribute decision-making (MADM) problems. Wei and Gao [18,19] developed the Pythagorean fuzzy interactive aggregation operator based on arithmetic and topological measures. As a means of simplifying supplier selection, Li [20] proposed a fuzzy Hamy mean operator. Gao [21] proposed a Pythagorean fuzzy Hamacher priority aggregation operator for MADM based on existing priority aggregation operators [22]. Wei and Lu [23] developed a Pythagorean fuzzy Maclaurin symmetric mean operator, which enabled the capture of relationships between multiple parameters.

A similarity measure is a mathematical function that assesses the degree of resemblance between two objects. In the context of fuzzy sets, similarity measures are of utmost importance in solving clustering, classification and decision-making problems [24,25,26]. At present, various similarity measures have been proposed for Pythagorean fuzzy sets:

• Wei [27] proposed some similarity measures between PFSs based on cosine function. To address the problem of MADM, Garg [28] developed a PFSs-based correlation measure and Wang [29] proposed a generalized Dice similarity measure. Zhang [30] introduced exponential functions and proposed several new similarity measures for Pythagorean fuzzy sets. Li [31] proposed a new similarity measure for PFSs based on spherical arc distance from a geometric perspective and constructed a MADM method in a Pythagorean fuzzy environment. Hussian and Yang [32] proposed new similarity measures for PFSs based on the Hausdorff measures and applied them to solve MADM problems. Li and Lu [33] proposed new similarity measures by extending the Hamming distance and Hausdorff distance. Zeng, Li and Yin [34] developed a novel similarity measure for PFSs and applied it to analyzing decision makers’ preferences. Zhang [35] presented a similarity measure and proposed a method for approximately calculating experts’ weights when their weights are entirely unknown. In addition, for more similarity measures for PFSs, please refer to the papers[36,37,38].

The concept of a similarity measure is used to express the degree of resemblance between individuals, while a distance measure represents the degree of divergence between individuals:

• Hussian and Yang [32] developed a measure to calculate the distance between PFSs using the Hasudorff measures. Li and Lu [33] proposed some novel distance while Xu [17] proposed a Hamming distance measure. Moreover, Ren, Xu and Gou [39] proposed a novel distance measure that builds upon the Euclidean distance model. Chen [40] has developed a novel method based on VIKOR for multi-criteria decision-making tasks involving Pythagorean fuzzy information. Simultaneously, Li and Zeng [41] proposed multiple distance measures after considering the four parameters of PFSs. Zeng, Li and Yin [34] proposed a series of modified distance measures by taking into account the importance of incorporating ambiguity into the equation. In addition, Chen [42] defined a novel generalized distance measure and devised a distance-based compromise method for decision analysis based on multiple criteria. There are more existing distance measures for PFSs [43,44,45].

In many cases, similarity and distance measures are used interchangeably, with distance being seen as the inverse of similarity, and vice versa. In practical applications, for distance calculations, the shortest distance is observed between the closest observation points, while for similarity calculations, the highest level of similarity is observed between the closest observation points.

Currently, the utilization of PFSs is exceedingly well-received [46,47,48,49,50,51,52], yet the existing similarity and distance measures may yield counter-intuitive outcomes in certain situations. Therefore, the exploration and utilization of similarity and distance measures for PFSs is a highly valuable area of inquiry. This paper proposes several novel similarity measures and distance measures for PFSs, inspired by Tanimoto similarity [53]. Our examples illustrate the properties of these measures. As well, a pair of models is also proposed for using these measures in patterns recognition, medical diagnosis, and MADM issues in Pythagorean fuzzy environments. As part of our experiment, we compared our proposed measures with a number of existing ones. In addition to overcoming numerous counter-intuitive scenarios in existing measures, our measures provide more differentiated measurement results when distinguishing between PFSs. These qualities exemplify the superior nature of our proposed measures.

The main contributions of this paper are as follows:

(1) We propose several similarity and distance measures for PFSs based on the Tanimoto similarity measure and prove their basic properties;

(2) Two models based on the Tanimoto measures are proposed and applied to pattern recognition, medical diagnosis and MADM problems to verify their effectiveness;

(3) Several experiments demonstrate that the proposed measures overcome counter-intuitive limitations of existing measures for PFSs and tend to produce more significant results when distinguishing PFSs.

Section 2 provides a brief review of the basic ideas and mathematical foundations of fuzzy sets. Several new similarity and distance measures for fuzzy sets are introduced in Section 3 and their mathematical properties are established. Section 4 presents two models based on the proposed measures to address pattern recognition, medical diagnosis and MADM problems, respectively. Section 5 draws conclusions and provides future research directions.

2. Preliminaries

In this section, some basic concepts related to fuzzy sets, Tanimoto measure and several existing measures for PFSs will be given.

2.1. Intuitionistic Fuzzy Sets

Definition 1 

([6]). We utilize the symbol Z to denote a finite set. An Intuitionistic fuzzy set I is given by:

$$I=\left\{〈z,{\rho }_I\left(z\right),{\sigma }_I\left(z\right)〉:z\in Z\right\}$$

(1)

where ${\rho }_I\left(z\right):Z\to [0,1]$ signifies the membership degree of z, and ${\sigma }_I\left(z\right):Z\to [0,1]$ expresses the nonmembership degree of z. $\forall z$, ${\rho }_I\left(z\right)$ and ${\sigma }_I\left(z\right)$ satisfy:

$$0\le {\rho }_I\left(z\right)+{\sigma }_I\left(z\right)\le 1$$

(2)

$\forall z$, the indeterminacy degree of z is:

$${\theta }_I\left(z\right)=1-{\rho }_I\left(z\right)-{\sigma }_I\left(z\right)$$

(3)

2.2. Pythagorean fuzzy sets

Definition 2 

([16] ). The Pythagorean fuzzy set P is defined as:

$$P=\left\{〈z,{\rho }_P\left(z\right),{\sigma }_P\left(z\right)〉:z\in Z\right\}$$

(4)

where ${\rho }_P\left(z\right):Z\to [0,1]$ and ${\sigma }_P\left(z\right):Z\to [0,1]$ denote, respectively, the membership degree and nonmembership degree of z. $\forall z$, ${\rho }_P\left(z\right)$ and ${\sigma }_P\left(z\right)$ satisfy:

$$0\le {\rho }_P^2\left(z\right)+{\sigma }_P^2\left(z\right)\le 1$$

(5)

$\forall z$, the indeterminacy degree of z is:

$${\theta }_P\left(z\right)=\sqrt[]{1-{\rho }_P^2\left(z\right)-{\sigma }_P^2\left(z\right)}$$

(6)

Table 1 presents a number of classic measures between PFSs.

2.3. Tanimoto measure

Definition 3 

([53]). For two probability sets $A=\{a_1,a_2,\dots ,a_n\}$ and $B=\{b_1,b_2,\dots ,b_n\}$, the Tanimoto measure can be defined as:

$$T(A,B)=\frac{\sum _{i=1}^n{a}_i{b}_i}{\sum _{i=1}^n{a}_i^2+\sum _{i=1}^n{b}_i^2-\sum _{i=1}^n{a}_i{b}_i}$$

(7)

3. Some novel tanimoto similarity and distance measures for PFSs

This section presents the Pythagorean fuzzy version of the Tanimoto measure, which includes both similarity and distance measures. Furthermore, we demonstrate several outstanding properties satisfied by the proposed measures. Comparative experiments with existing measures are conducted to verify their effectiveness and superiority.

3.1. Novel similarity measures

Definition 4. 

For two PFSs, $F=\{(z,[{\rho }_F(z_i,),{\sigma }_F\left(z_i\right)]):z_i\in Z\}$ and $G=\{(z,[{\rho }_G(z_i,),{\sigma }_G\left(z_i\right)]):z_i\in Z\}$, where $Z=\{z_1,z_2,\dots ,z_n\}$, the Tanimoto similarity measure for them can be given by:

$$T_{PFS}(F,G)=\frac{\sum _{i=1}^n({\rho }_F^2\left(z_i\right){\rho }_G^2\left(z_i\right)+{\sigma }_F^2\left(z_i\right){\sigma }_G^2\left(z_i\right))}{\sum _{i=1}^n({\rho }_F^4\left(z_i\right)+{\rho }_G^4\left(z_i\right)-{\rho }_F^2\left(z_i\right){\rho }_G^2\left(z_i\right))+\sum _{i=1}^n({\sigma }_F^4\left(z_i\right)+{\sigma }_G^4\left(z_i\right)-{\sigma }_F^2\left(z_i\right){\sigma }_G^2\left(z_i\right))}$$

(8)

Theorem 1. 

For any two PFSs F and G, the $T_{PFS}(F,G)$ satisfies:

1. 

$0\le T_{PFS}(F,G)\le 1$;

2. 

$T_{PFS}(F,G)=T_{PFS}(G,F)$;

3. 

$T_{PFS}(F,G)=1$, if $F=G({\rho }_F\left(z_i\right)={\rho }_G\left(z_i\right),{\sigma }_F\left(z_i\right)={\sigma }_G\left(z_i\right))$.

Proof of Theorem 1. 

• Considering the ith item of the summation in Equation 8:

  $$T_{PFS}(F,G)=\frac{{\rho }_F^2\left(z_i\right){\rho }_G^2\left(z_i\right)+{\sigma }_F^2\left(z_i\right){\sigma }_G^2\left(z_i\right)}{{\rho }_F^4\left(z_i\right)+{\rho }_G^4\left(z_i\right)-{\rho }_F^2\left(z_i\right){\rho }_G^2\left(z_i\right)+{\sigma }_F^4\left(z_i\right)+{\sigma }_G^4\left(z_i\right)-{\sigma }_F^2\left(z_i\right){\sigma }_G^2\left(z_i\right)}$$

  (9)
  According to $0\le \rho \left(z_i\right)\le 1$ and $0\le \sigma \left(z_i\right)\le 1$, we can get ${\rho }_F^2\left(z_i\right){\rho }_G^2\left(z_i\right)+{\sigma }_F^2\left(z_i\right){\sigma }_G^2\left(z_i\right)\ge 0$. According to the inequality $a^2+b^2\ge 2ab$, ${\rho }_F^4\left(z_i\right)+{\rho }_G^4\left(z_i\right)+{\sigma }_F^4\left(z_i\right)+{\sigma }_G^4\left(z_i\right)-{\rho }_F^2\left(z_i\right){\rho }_G^2\left(z_i\right)-{\sigma }_F^2\left(z_i\right){\sigma }_G^2\left(z_i\right)\ge {\rho }_F^2\left(z_i\right){\rho }_G^2\left(z_i\right)+{\sigma }_F^2\left(z_i\right){\sigma }_G^2\left(z_i\right)$. Therefore, $0\le T_{PFS}(F,G)\le 1$. From the Equation 8, the sumation of n terms is $0\le T_{PFS}(F,G)\le 1$.
• $$\begin{array}{cc}\hfill T_{PFS}(F,G)& =\frac{\sum _{i=1}^n({\rho }_F^2\left(z_i\right){\rho }_G^2\left(z_i\right)+{\sigma }_F^2\left(z_i\right){\sigma }_G^2\left(z_i\right))}{(\sum _{i=1}^n({\rho }_F^4\left(z_i\right)+{\rho }_G^4\left(z_i\right)-{\rho }_F^2\left(z_i\right){\rho }_G^2\left(z_i\right))+\sum _{i=1}^n({\sigma }_F^4\left(z_i\right)+{\sigma }_G^4\left(z_i\right)-{\sigma }_F^2\left(z_i\right){\sigma }_G^2\left(z_i\right))}\hfill \\ & =\frac{\sum _{i=1}^n({\rho }_G^2\left(z_i\right){\rho }_F^2\left(z_i\right)+{\sigma }_G^2\left(z_i\right){\sigma }_F^2\left(z_i\right))}{(\sum _{i=1}^n({\rho }_G^4\left(z_i\right)+{\rho }_F^4\left(z_i\right)-{\rho }_G^2\left(z_i\right){\rho }_F^2\left(z_i\right))+\sum _{i=1}^n({\sigma }_G^4\left(z_i\right)+{\sigma }_F^4\left(z_i\right)-{\sigma }_G^2\left(z_i\right){\sigma }_F^2\left(z_i\right))}\hfill \\ & =T_{PFS}(G,F)\hfill \end{array}$$
• When F = G, there are ${\rho }_F\left(z_i\right)={\rho }_G\left(z_i\right),({\sigma }_F\left(z_i\right)={\sigma }_G\left(z_i\right)$, for $i=1,2,\dots n$. So, there is

  $$\begin{array}{cc}\hfill T_{PFS}(F,G)& =\frac{\sum _{i=1}^n({\rho }_F^2\left(z_i\right){\rho }_F^2\left(z_i\right)+{\sigma }_F^2\left(z_i\right){\sigma }_F^2\left(z_i\right))}{(\sum _{i=1}^n({\rho }_F^4\left(z_i\right)+{\rho }_F^4\left(z_i\right)-{\rho }_F^2\left(z_i\right){\rho }_F^2\left(z_i\right))+\sum _{i=1}^n({\sigma }_F^4\left(z_i\right)+{\sigma }_F^4\left(z_i\right)-{\sigma }_F^2\left(z_i\right){\sigma }_F^2\left(z_i\right))}\hfill \\ & =\frac{\sum _{i=1}^n({\rho }_F^2\left(z_i\right){\rho }_F^2\left(z_i\right)+{\sigma }_F^2\left(z_i\right){\sigma }_F^2\left(z_i\right))}{\sum _{i=1}^n({\rho }_F^2\left(z_i\right){\rho }_F^2\left(z_i\right)+{\sigma }_F^2\left(z_i\right){\sigma }_F^2\left(z_i\right)}\hfill \\ & =1\hfill \end{array}$$

Therefore, we have finished the proofs.    □

If we consider the weights of $z_i$, a weighted Tanimoto similarity measure between PFSs F and G is proposed as fllows:

Definition 5. 

For $z_i\in Z$, take the weight ${\omega }_i$. The weighted Tanimoto measure $T_{PFS}^{\omega }(F,G)$ is described as:

$$T_{PFS}^{\omega }(F,G)=\frac{\sum _{i=1}^n{\omega }_{\mathrm{i}}^4({\rho }_F^2\left(z_i\right){\rho }_G^2\left(z_i\right)+{\sigma }_F^2\left(z_i\right){\sigma }_G^2\left(z_i\right))}{\sum _{i=1}^n{\omega }_{\mathrm{i}}^4({\rho }_F^4\left(z_i\right)+{\rho }_G^4\left(z_i\right)-{\rho }_F^2\left(z_i\right){\rho }_G^2\left(z_i\right))+\sum _{i=1}^n{\omega }_{\mathrm{i}}^4({\sigma }_F^4\left(z_i\right)+{\sigma }_G^4\left(z_i\right)-{\sigma }_F^2\left(z_i\right){\sigma }_G^2\left(z_i\right))}$$

(10)

Similar to the Proof of Theorem 1, we can get:

Theorem 2. 

For any two PFSs F and G, the $T_{PFS}^{\omega }(F,G)$ satisfies:

1. 

$0\le T_{PFS}^{\omega }(F,G)\le 1$;

2. 

$T_{PFS}^{\omega }(F,G)=T_{PFS}^{\omega }(G,F)$;

3. 

$T_{PFS}^{\omega }(F,G)=1$, if $F=G({\rho }_F\left(z_i\right)={\rho }_G\left(z_i\right),{\sigma }_F\left(z_i\right)={\sigma }_G\left(z_i\right))$.

For $z_i\in Z$, taking the indeterminacy degree ${\theta }_i$, we can get:

$$\begin{array}{c}\hfill T_{PFS}^{\theta }(F,G)=\frac{\sum _{i=1}^n({\rho }_F^2\left(z_i\right){\rho }_G^2\left(z_i\right)+{\sigma }_F^2\left(z_i\right){\sigma }_G^2\left(z_i\right)+{\theta }_F^2\left(z_i\right){\theta }_G^2\left(z_i\right))}{\sum _{i=1}^n({\rho }_F^4\left(z_i\right)+{\rho }_G^4\left(z_i\right)-{\rho }_F^2\left(z_i\right){\rho }_G^2\left(z_i\right))+\sum _{i=1}^n({\sigma }_F^4\left(z_i\right)+{\sigma }_G^4\left(z_i\right)-{\sigma }_F^2\left(z_i\right){\sigma }_G^2\left(z_i\right))+\sum _{i=1}^n({\theta }_F^4\left(z_i\right)+{\theta }_G^4\left(z_i\right)-{\theta }_F^2\left(z_i\right){\theta }_G^2\left(z_i\right))}\end{array}$$

(11)

$$\begin{array}{c}\hfill T_{PFS}^{\omega \theta }(F,G)=\frac{\sum _{i=1}^n{\omega }_{\mathrm{i}}^4({\rho }_F^2\left(z_i\right){\rho }_G^2\left(z_i\right)+{\sigma }_F^2\left(z_i\right){\sigma }_G^2\left(z_i\right)+{\theta }_F^2\left(z_i\right){\theta }_G^2\left(z_i\right))}{\sum _{i=1}^n{\omega }_{\mathrm{i}}^4({\rho }_F^4\left(z_i\right)+{\rho }_G^4\left(z_i\right)-{\rho }_F^2\left(z_i\right){\rho }_G^2\left(z_i\right))+\sum _{i=1}^n{\omega }_{\mathrm{i}}^4({\sigma }_F^4\left(z_i\right)+{\sigma }_G^4\left(z_i\right)-{\sigma }_F^2\left(z_i\right){\sigma }_G^2\left(z_i\right))+\sum _{i=1}^n{\omega }_{\mathrm{i}}^4({\theta }_F^4\left(z_i\right)+{\theta }_G^4\left(z_i\right)-{\theta }_F^2\left(z_i\right){\theta }_G^2\left(z_i\right))}\end{array}$$

(12)

3.2. Novel distance measures

Definition 6. 

For two PFSs, $F=\{(z,[{\rho }_F(z_i,),{\sigma }_F\left(z_i\right)]):z_i\in Z\}$ and $G=\{(z,[{\rho }_G(z_i,),{\sigma }_G\left(z_i\right)]):z_i\in Z\}$, where $Z=\{z_1,z_2,\dots ,z_n\}$, the Tanimoto distance measure for them can be given by:

$$D{T}_{PFS}(F,G)=1-T_{PFS}(F,G)$$

(13)

The larger the $D{T}_{PFS}(F,G)$ is, the greater the difference between two PFSs.

Theorem 3. 

For any two PFSs F and G, the $D{T}_{PFS}(F,G)$ satisfies the conditions:

1. 

$0\le D{T}_{PFS}(F,G)\le 1$;

2. 

$D{T}_{PFS}(F,G)=D{T}_{PFS}(G,F)$;

3. 

$D{T}_{PFS}(F,G)=0$, if $F=G({\rho }_F\left(z_i\right)={\rho }_G\left(z_i\right),{\sigma }_F\left(z_i\right)={\sigma }_G\left(z_i\right))$.

If we consider the weights of $z_i$, a weighted Tanimoto distance measure between PFSs F and G is proposed as fllows:

Definition 7. 

For $z_i\in Z$, take the weight ${\omega }_i$. The weighted Tanimoto measure $D{T}_{PFS}^{\omega }(F,G)$ is described as:

$$D{T}_{PFS}^{\omega }(F,G)=1-T_{PFS}^{\omega }(F,G)$$

(14)

Theorem 4. 

For any two PFSs F and G, the $D{T}_{PFS}^{\omega }(F,G)$ satisfies the conditions:

1. 

$0\le D{T}_{PFS}^{\omega }(F,G)\le 1$;

2. 

$D{T}_{PFS}^{\omega }(F,G)=D{T}_{PFS}^{\omega }(G,F)$;

3. 

$D{T}_{PFS}^{\omega }(F,G)=0$, if $F=G({\rho }_F\left(z_i\right)={\rho }_G\left(z_i\right),{\sigma }_F\left(z_i\right)={\sigma }_G\left(z_i\right))$.

Taking the the indeterminacy degree into consideration, then:

$$\begin{array}{c}\hfill D{T}_{PFS}^{\theta }(F,G)=1-T_{PFS}^{\theta }(F,G)\end{array}$$

(15)

$$\begin{array}{c}\hfill D{T}_{PFS}^{\omega \theta }(F,G)=1-T_{PFS}^{\omega \theta }(F,G)\end{array}$$

(16)

3.3. Numerical experiments

Example 1. 

Let $F_1,F_2,F_3$ be three PFSs in $Z=\{z_1,z_2\}$, which are expressed as:

$$\begin{array}{c}{F}_1=\{〈z_1,0.4,0.3〉,〈z_2,0.5,0.2〉\}\hfill \\ F_2=\{〈z_1,0.4,0.3〉,〈z_2,0.5,0.2〉\}\hfill \\ F_3=\{〈z_1,0.7,0.5〉,〈z_2,0.3,0.4〉\}\hfill \end{array}$$

Based on the equations presented before, the Tanimoto measures have been computed and shown in Table 2 and Table 3.

Taking the weights $\omega =\{0.3,0.7\}$, the weighted Tanimoto measures between PFSs $F_1,F_2$, and $F_3$ are shown in Table 4 and Table 5.

According to the results above, it is discernible that when $F_1=F_2$, the Tanimoto measures between $F_{1}and{F}_2$ , $T_{PFS}(F_1,F_2)=1$ and $D{T}_{PFS}(F_1,F_2)=0$, which satisfies the Property 3 in Definition 4 and Property 3 in Definition 6. Besides, $T_{PFS}(F_1,F_3)=T_{PFS}(F_3,F_1)$ and $D{T}_{PFS}(F_1,F_3)=D{T}_{PFS}(F_3,F_1)$, which satisfy the Property 2 in Definition 4 and Property 2 in Definition 6.

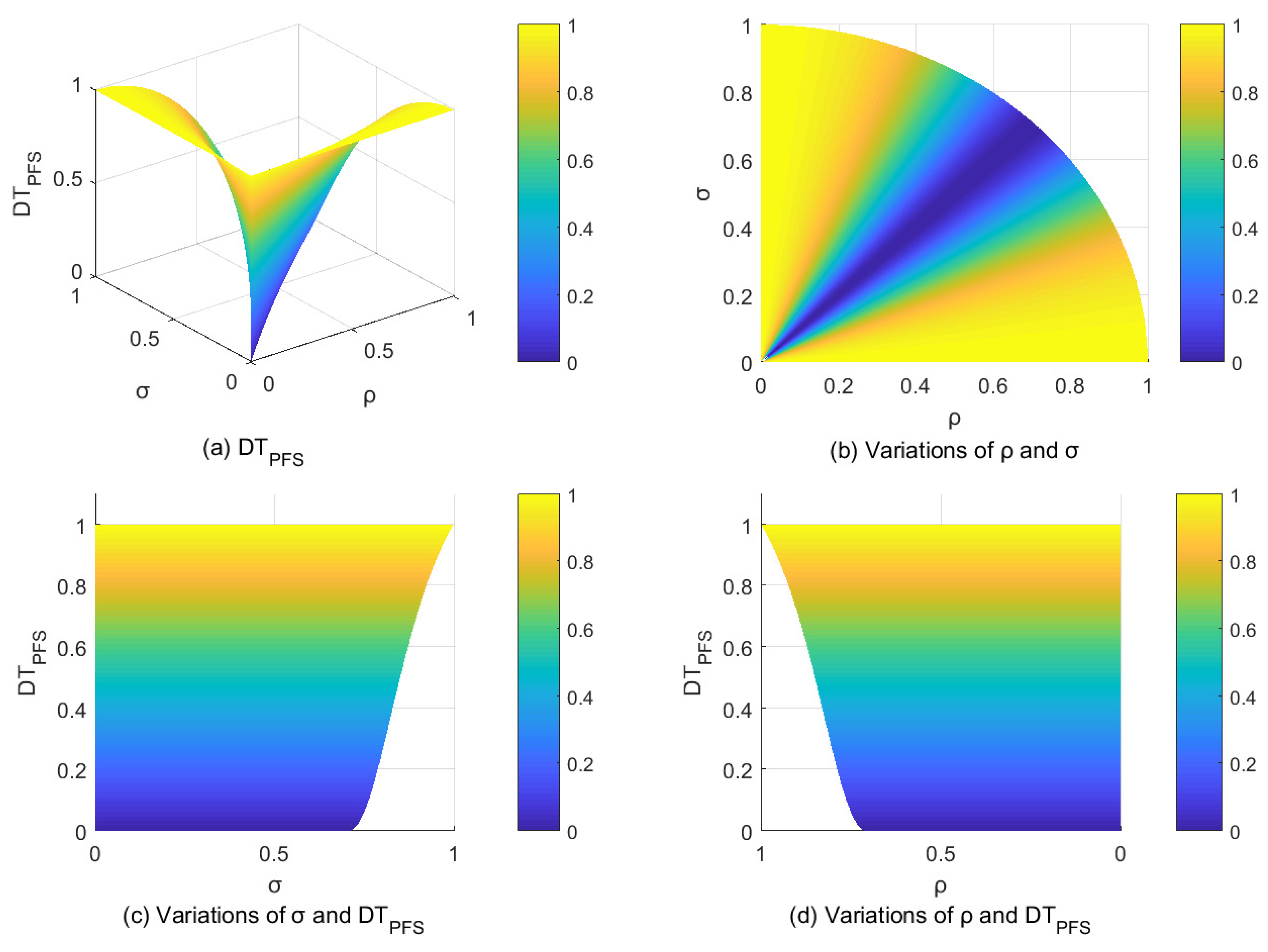
Example 2. 

$F_1$ and $F_2$ are two PFSs in z, where

$$F_1=\left\{〈\mathrm{z},\rho ,\sigma 〉\right\},F_2=\left\{〈\mathrm{z},\sigma ,\rho 〉\right\}$$

. In this example, Figure 1 illustrates the distribution of the proposed similarity measure under changes in both membership degree and nonmembership degree. As shown in Figure 1 (c) and Figure 1 (d), with variations in ρ and σ, the value of $T_{PFS}$ remains within the range of $[0,1]$. Additionally, when ρ equals σ, the similarity measure between $F_1$ and $F_2$ achieves its maximum value of 1, and when ρ equals 1 and σ equals 0 or when ρ equals 0 and σ equals 1, it reaches its minimum value of 0. This confirms that the Tanimoto measure satisfies Property 1 as defined in Definition 4.

Example 3. 

F and G are two PFSs under different cases in $Z=\{z_1,z_2\}$ and shown in Table 6.

As Table 6 indicates, the F of $Case$ 1 is equivalent to the F of $Case$ 2, while their Gs differ. Hence, the similarity between F and G in $Case$ 1 ought to differ from that of F and G in $Case$ 2. Similar observations hold for other cases. Table 7 presents the outcomes of employing diverse similarity measures to assess the similarity between F and G across different cases. In each case group, we employed distinct colors to highlight the counter-intuitive outcomes generated by each measure. Specifically, red denotes counter-intuitive results obtained in $Case$ 1 and 2, blue represents those in $Case$ 3 and 4, and green indicates the counter-intuitive results observed in $Case$ 5 and 6. Notably, most similarity measures yield counter-intuitive measure outcomes. Specifically, $S{M}_{PFS}^2$, $D_{PFS}$, $G_{PFS}$, $C_{PFS}^1$ and $C_{PFS}^2$ produce counter-intuitive outcomes on $Case$ 1 and $Case$ 2; $S{M}_{PFS}^2$, $D_{PFS}$ and $G_{PFS}$ yield counter-intuitive outcomes on $Case$ 3 and $Case$ 4; and, $S{M}_{PFS}^1$, $G_{PFS}$, $C_{PFS}^1$ and $C_{PFS}^2$ yield counter-intuitive outcomes on $Case$ 5 and $Case$ 6. However, the proposed Tanimoto similarity measures perform correctly in all cases, demonstrating the superiority of our measures.

Example 4. 

Similar to Example 3, we apply the proposed Tanimoto distance measures to the counter-intuitive cases of existing distance measures. As shown in Table 8, F and G are two PFSs under different cases, and Table 9 presents the measurement results. In each case group, we use different colors to highlight the counter-intuitive results generated by each measures. Specifically, $D{H}_{PFS}$ produce counter-intuitive outcomes on $Case$ 1 and $Case$ 2; $D{E}_{PFS}$ yield counter-intuitive outcomes on $Case$ 3 and $Case$ 4; and, $D{H}_{PFS}$ and $D{E}_{PFS}$ yield counter-intuitive outcomes on $Case$ 5 and $Case$ 6. However, the proposed Tanimoto distance measures perform correctly in all cases, demonstrating the superiority of our measures.

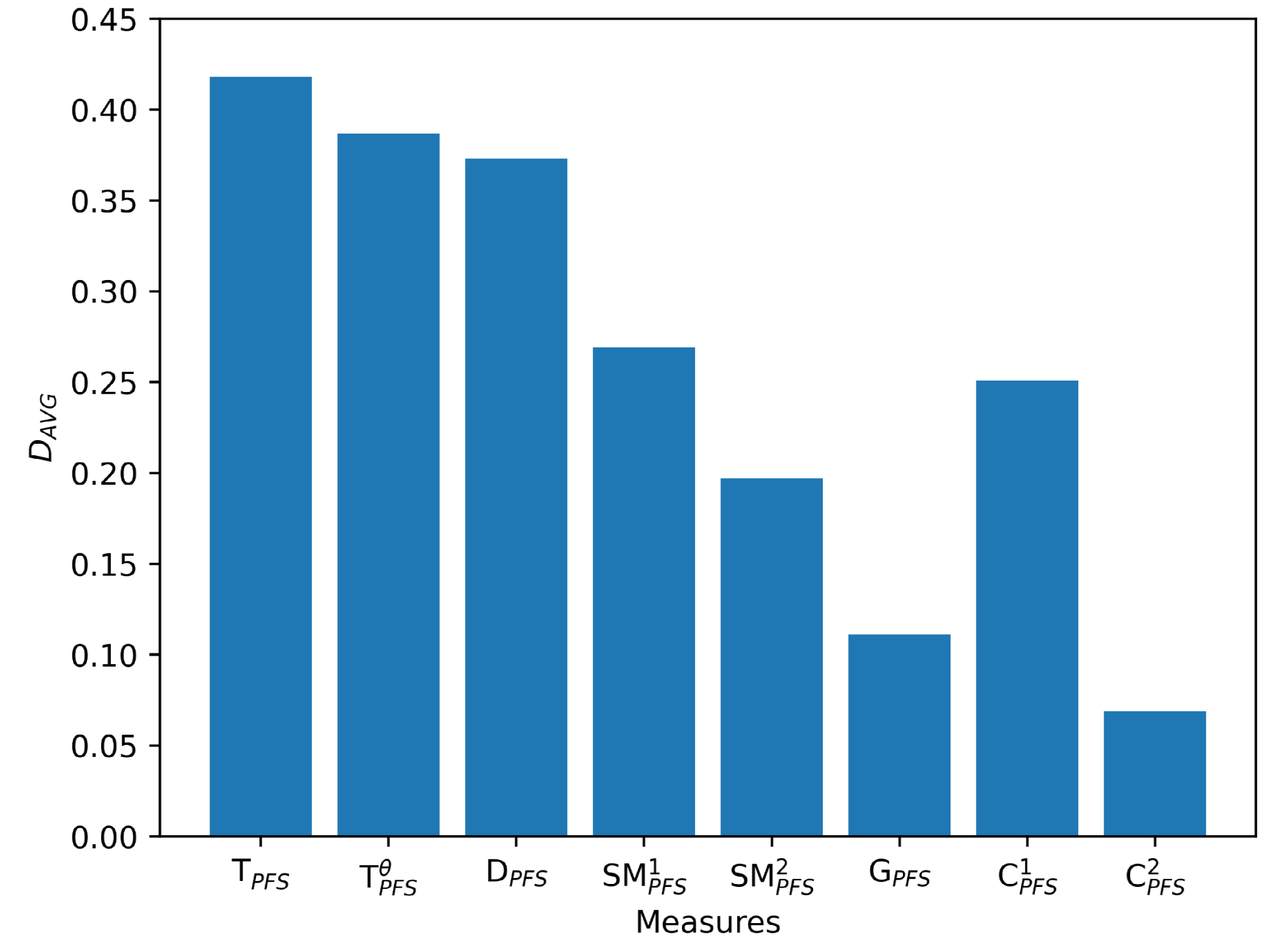
Example 5. 

A, B and C are three random PFSs. We employ the proposed similarity measure to assess their similarity and subtract the minimum value from the maximum Tanimoto similarity value to obtain $D_{value}$. We have conducted 100 such experiments and computed the average of the final results to get the average distance between the maximum and minimum values of similarity results in these 100 experiments ($D_{AVG}=\frac{D_{value}}{100}$). Similarly, we will compare $D_{AVG}$s obtained using other measures, as shown in Figure 3.

The findings in Figure 3 suggest that the Tanimoto similarity measure exhibits the maximum $D_{AVG}$, indicating that the proposed similarity measure tends to assign more differentiated similarity values when distinguishing between different fuzzy sets. This attribute endows it with greater discriminatory power to discern different levels of similarity and enhances its performance in distinguishing PFSs with high similarity. A wider range of similarity values assigned to different PFSs may enhance the credibility of PFSs classification and foster more confident decision-making. On the other hand, $C_{PFS}^2$ has the smallest $D_{AVG}$, which means that it is more likely to classify highly similar PFSs into the same category or exhibit more hesitation in selecting between different samples. This characteristic will be detrimental to high-precision decision-making. These results indicate that our proposed measures are superior to the existing measures. These characteristics will be further validated in the subsequent examples.

4. Applications

In this section, we introduce two models that utilize the proposed measures in pattern recognition, medical diagnosis and MADM problems. Furthermore, we conducted a series of experiments and compared our models with existing measures to demonstrate their effectiveness and superiority.

4.1. A model for pattern recognition and medical diagnosis

There are some known patterns $F=\{F_1,F_2,\dots ,F_n\}$, denoted by PFSs $F_i=\{〈z_l,{\rho }_{F_i},{\sigma }_{F_i}〉:z_l\in Z\}(i=1,2,\dots ,n)$ represented by a finite universe of discourse $Z=\{z_1,z_2,\dots ,z_k\}$. There are some samples of unknown categories $S=\{S_1,S_2,\dots ,S_m\}$ , denoted by $S_j=\{〈z_l,{\rho }_{S_j},{\sigma }_{S_j}〉:z_l\in Z\}(j=1,2,\dots ,m)$. Our goal is to classify $S_j$ into the given patterns $F_i$. The recognition process is described in detail below:

Step 1

Calculate the Tanimoto similarity(or distance) between $S_j$ and $F_i$.

Step 2

Obtain the maximum Tanimoto similarity $sm\left(F_o,S_j\right)$ using equation 17 or the minimum Tanimoto distance $d\left(F_o,S_j\right)$ using equation 18:

$$sm\left(F_o,S_j\right)=max\left\{T_{PFS}(F_i,S_j)\right\}$$

(17)

$$d\left(F_o,S_j\right)=min\left\{D{T}_{PFS}(F_i,S_j)\right\}$$

(18)

Step 3

If any pattern $F_o$ has the highest Tanimoto similarity between $S_i$, then, $S_i$ and $F_o$ belong to the same category:

$$o=argmax\left\{sm\left(F_o,S_j\right)\right\},S_j\to F_o$$

(19)

If distance measure is used as the standard of measure, then the following form would be applied:

$$o=argmin\left\{d\left(F_o,S_j\right)\right\},S_j\to F_o$$

(20)

The pseudo code description of the model is as Algorithm 1.

Algorithm 1 Algorithm for pattern recognition and medical diagnosis

Example 6. 

This example is centered on the recognition of patterns. It leverages PFSs for the delineation of three instances whose categories have been confirmed, denoted as $F=\{F_1,F_2,F_3\}$, as well as a solitary sample from an as yet unrecognized category, labeled S. The parameters $z_i(i=1,2,3,4,5)$ that govern these samples are detailed in Table 10.

In order to ascertain the categorical ascription of the unknown sample S, we employed the Tanimoto similarity measures as delineated in our methodological framework:

Step 1

Calculate the Tanimoto similarity(or distance) between $S_j$ and $F_i$, the results are presented in Table 11 and Table 12.

Step 2

According to the equation 17 and equation 18, the maximum similarity and minimum distance are shown as below:

$$sm\left(F_2,S\right)=0.804$$

$$d\left(F_2,S\right)=0.196$$

Step 3

According to the principle of maximum similarity and minimum distance, the pattern recognition result of S are as follows:

$$S\to F_2$$

Furthermore, the measurement results derived from the extant methods are detailed in Table 13.

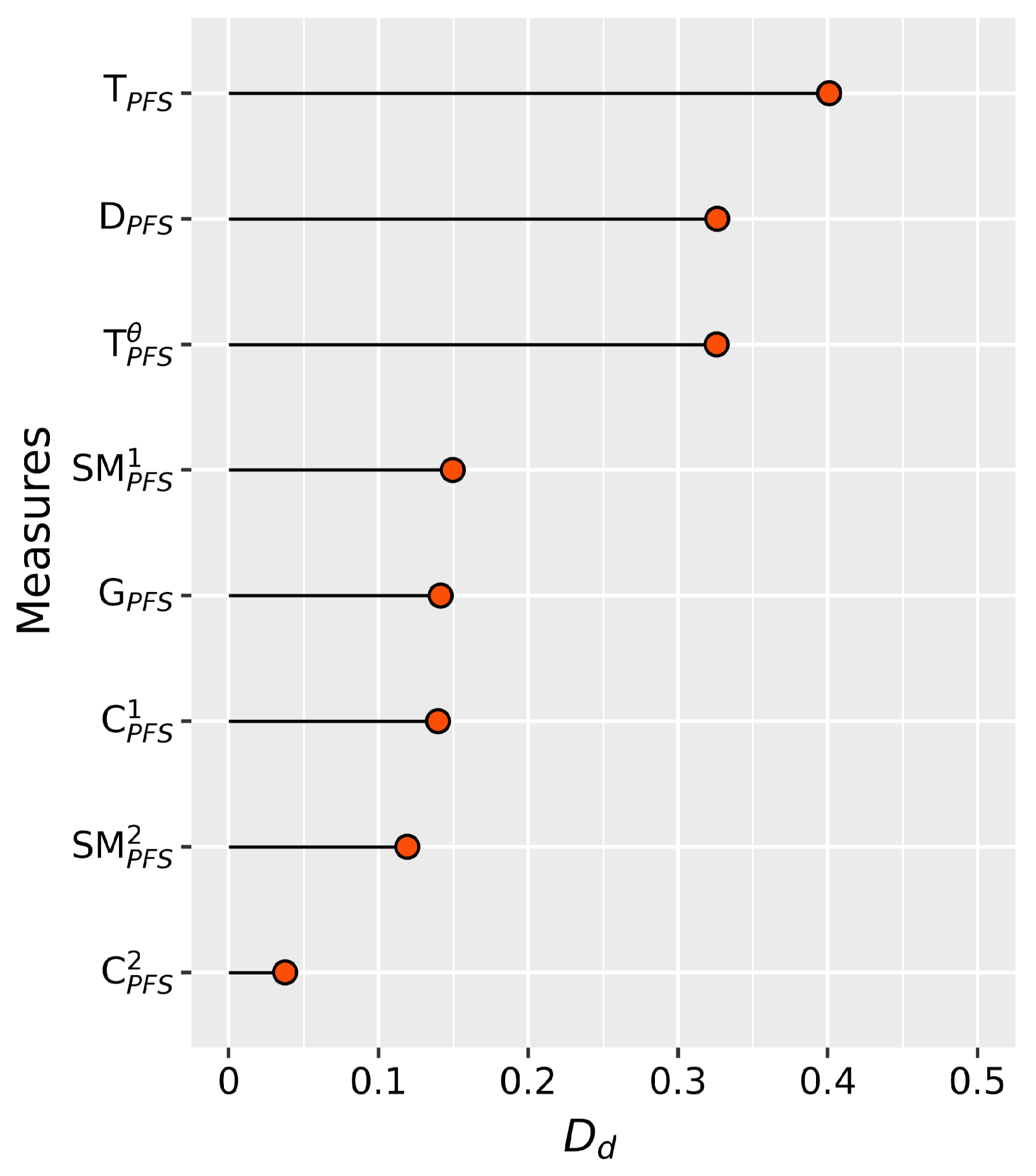
Utilizing the data shown in Table 13, we can identify that S and $F_2$ demonstrate the highest degree of similarity. This finding is consistently confirmed across the Tanimoto similarity measures before, validating the effectiveness of the proposed similarity measures. It is noteworthy that the similarity scores derived from the Tanimoto measures exhibit significant variability. We computed the Tanimoto similarity values for all PFSs with respect to S and subtracted the second highest value from the maximum one, denoted as $D_d$, and a similar analysis was conducted for other measures, as depicted in Figure 4. We can find that the Tanimoto similarity measure yields the highest $D_d$ and ranks third in terms of indeterminacy. The similarity scores between S and $F_2$ as determined by our proposed metrics are substantially different from those between S and other PFSs. Consequently, we can assert with confidence that $F_2$ is a more suitable pattern. However, the similarity scores between S and the known samples derived from other measures are more closely aligned. Hence, relying on these measures for decision-making may result in greater hesitation. These findings align with the conclusions drawn in Example 5, suggesting that our proposed measures are superior in distinguishing between samples.

Example 7. 

In this example, the aim is to recognize mineral categories through pattern recognition. Specifically, we consider six common mixtures of minerals that are represented by PFSs $F_i(i=1,2,3,4,5,6)$, with each mixture consisting of six fundamental minerals which collectively form the universe of discourse $z_i(i=1,2,3,4,5,6)$. Our primary goal is to employ the proposed measure in order to determine the category to which an unknown mixed mineral S pertains. Table 14 displays the known PFSs and the unidentified mineral S, whereas Table 15 summarizes the resulting outcomes.

Table 15 displays the similarity measures for mineral S and $F_4$, with the Tanimoto measure producing the highest similarity score. This result confirms that mineral S belongs to $F_4$, which is consistent with findings from other studies that have used various similarity measures. Likewise, Figure 5 illustrates the $D_d$ among different measures, and the Tanimoto similarity measures rank the first and the second among the measures shown in the figure.

Example 8 

([55]). Assuming the presence of four patients, namely Ragu, Mathi, Velu and Karthi, denoted by $I=\{I_1,I_2,I_3,I_4\}$, and exhibiting symptoms including Headache, Acidity, Burning eyes, Back pain and Depression, represented as $Z=\{Z_1,Z_2,Z_3,Z_4,Z_5\}$. The set of possible diagnoses is denoted by $D=\{D_1,D_2,D_3,D_4,D_5\}$, and includes: $D_1$: Stress; $D_2$: Ulcer; $D_3$: Vision problem; $D_4$: Spinal problem; $D_5$: Blood pressure. The Pythagorean fuzzy relation $I\to Z$ is expressed by PFS, as shown in Table 16, while the Pythagorean fuzzy relation $Z\to D$ is represented by PFSs and listed in Table 17. Every entry in both tables is defined by the PFS, with the values indicating membership degree and nonmembership degree, respectively. The proposed similarity and distance measures are employed to evaluate the similarity and distance between each patient and potential diagnosis. Based on the principle of maximum similarity or minimum distance, each patient is diagnosed accordingly. Table 18 and Table 19 present the similarity measure outcomes and distance measure outcomes of each patient I towards each diagnosis D, alongside the ultimate diagnosis results.

Based on the findings presented in Table 18 and Table 19, it is observed that $I_1$ exhibits the highest Tanimoto similarity measure and the lowest Tanimoto distance measure towards $D_1$; $I_2$ displays the highest Tanimoto similarity measure and the lowest Tanimoto distance measure towards $D_4$; $I_3$ demonstrates the highest Tanimoto similarity measure and the lowest Tanimoto distance measure towards $D_3$; and $I_4$ showcases the highest Tanimoto similarity measure and the lowest Tanimoto distance measure towards $D_1$. Thus, we can conclude that Ragu is diagnosed with stress, Mathi with spinal problems, Velu with vision problems and Karthi with stress.

In order to validate the effectiveness of our proposed measures, a comparison was conducted against other methods, and the outcomes have been summarized in Table 20. It is observed from Table 20 that our proposed measures provide diagnostic outcomes that are consistent with those obtained using methods proposed by Xiao and Ding [55], Zhou [56] and Deng [57]. The experimental results lend support to the practicability of our proposed similarity and distance measures.

4.2. The model for MADM

Suppose that $I=\{I_1,I_2,\dots ,I_m\}$ is a discrete set of alternatives, and $A=\{A_1,A_2,\dots ,A_n\}$ is the set of attributes, $\omega =\{{\omega }_1,{\omega }_2,\dots ,{\omega }_n\}$ is the weighting vector of the attribute $A_j(j=1,2,\dots ,n)$, where $\omega >0$, $\sum _{j=1}^n{w}_j=1$. $T=\left\{t_1,t_2,\dots ,t_n\right\}$ is the experts evaluate, representing the type of each attribute, where 1 represents the benefit type and 0 represents the cost type. Suppose that $R={({\rho }_{ij},{\sigma }_{ij})}_{m\times n}$ is the Pythagorean fuzzy matrix, where ${\rho }_{ij}$ indicates the degree that the alternative $I_i$ satisfies the attribute $A_j$ and ${\sigma }_{ij}$ indicates the degree that the alternative $I_i$ does not satisfy the attribute $A_j$, ${\rho }_{ij}\subset [0,1]$, ${\sigma }_{ij}\subset [0,1]$, ${\left({\rho }_{ij}\right)}^2+{\left({\sigma }_{ij}\right)}^2\le 1$, $i=1,2,\dots ,m$, $j=1,2,\dots ,n$. The proposed model is described below:

Step 1

Defining the Pythagorean fuzzy positive ideal solution $I^{+}$:

$$({\rho }^{+},{\sigma }^{+})=(({\rho }_1^{+},{\sigma }_1^{+}),({\rho }_2^{+},{\sigma }_2^{+}),\dots ,({\rho }_n^{+},{\sigma }_n^{+}))=((1,0),(1,0),\dots ,(1,0))$$

(21)

The equation for correction is as follows:

$$I^{+}=\left(\left({\rho }_j,{\sigma }_j\right)\right)\left\{\begin{array}{c}\begin{array}{cc}\left({\rho }_j,{\sigma }_j\right)& for{t}_j=1\end{array}\\ \begin{array}{cc}\left({\sigma }_j,{\rho }_j\right)& for{t}_j=0\end{array}\end{array}\right.$$

(22)

Step 2

Calculating the weighted Tanimoto similarity measure between $I_i(i=1,2,\dots ,m)$ and $I^{+}$ as follows:

$$T_{PFS}^{\omega }(I_{\mathrm{i}},I^{+})=\frac{\sum _{i=1}^n{\omega }_{\mathrm{i}}^4({\rho }_{ij}^2{\left({\rho }_j^{+}\right)}^2+{\sigma }_{ij}^2{\left({\sigma }_j^{+}\right)}^2)}{(\sum _{i=1}^n{\omega }_{\mathrm{i}}^4({\rho }_{ij}^4+{\left({\rho }_j^{+}\right)}^4-{\rho }_{ij}^2{\left({\rho }_j^{+}\right)}^2)+\sum _{i=1}^n{\omega }_{\mathrm{i}}^4({\sigma }_{ij}^4+{\left({\sigma }_j^{+}\right)}^4-{\sigma }_{ij}^2{\left({\sigma }_j^{+}\right)}^2))}$$

(23)

If the standard of measure is distance, then additional distance measures must be calculated in the following way:

$$D{T}_{PFS}^{\omega }(I_i,I^{+})=1-T_{PFS}^{\omega }(I_i,I^{+})$$

(24)

Step 3

Obtain the maximum Tanimoto similarity $sm\left(I_o,I^{+}\right)$ using equation 25 or the minimum Tanimoto distance $d\left(I_o,I^{+}\right)$ using equation 26:

$$sm\left(I_o,I^{+}\right)=max\left\{T_{PFS}(I_i,I^{+})\right\}$$

(25)

$$d\left(I_o,I^{+}\right)=min\left\{D{T}_{PFS}(I_i,I^{+})\right\}$$

(26)

Step 4

If any alternative $I_o$ has the highest Tanimoto similarity between $I^{+}$, then, $I_o$ is the most important alternative:

$$o=argmax\left\{sm\left(I_o,I^{+}\right)\right\},I_o\to Result$$

(27)

If distance measure is used as the standard of measure, then the following form would be applied:

$$o=argmin\left\{d\left(I_o,I^{+}\right)\right\},I_o\to Result$$

(28)

The pseudo code description of the model is as Algorithm 2.

Algorithm 1 Algorithm for MADM

Example 9. 

A company is planning to purchase a batch of computers, with six alternative model schemes $I_{\mathrm{i}}(i=1,2,3,4,5,6)$ to choose from, and has selected five attributes as selection criteria, including the materials used, reputation, response time, service life and price $A_j(j=1,2,3,4,5)$. The weights of these attributes are denoted by ${\omega }_j(j=1,2,3,4,5)$, where $\omega =(0.2,0.4,0.1,0.1,0.2)$. After expert evaluation, all attribute types are provided: $T=\left\{1,1,0,1,0\right\}$. Forming a Pythagorean fuzzy decision matrix $R_{6\times 5}$:

$$R_{6\times 5}=\left[\begin{array}{ccccc}\left(0.287,0.955\right)& \left(0.846,0.123\right)& \left(0.622,0.776\right)& \left(0.214,0.791\right)& \left(0.808,0.524\right)\\ \left(0.232,0.364\right)& \left(0.940,0.241\right)& \left(0.564,0.366\right)& \left(0.019,0.805\right)& \left(0.207,0.834\right)\\ \left(0.081,0.645\right)& \left(0.026,0.584\right)& \left(0.801,0.266\right)& \left(0.870,0.030\right)& \left(0.598,0.554\right)\\ \left(0.565,0.459\right)& \left(0.759,0.416\right)& \left(0.860,0.093\right)& \left(0.480,0.145\right)& \left(0.622,0.743\right)\\ \left(0.130,0.768\right)& \left(0.613,0.584\right)& \left(0.114,0.653\right)& \left(0.048,0.531\right)& \left(0.050,0.440\right)\\ \left(0.210,0.300\right)& \left(0.634,0.176\right)& \left(0.146,0.919\right)& \left(0.323,0.702\right)& \left(0.812,0.575\right)\end{array}\right]$$

We will utilize the proposed MADM model to select the most appropriate solution.

Step 1

Defining the Pythagorean fuzzy positive ideal solution $I^{+}$. As we want the response time and price to be as low as possible, these two attributes are defined as cost types and set to $\left(0,1\right)$:

$$\begin{array}{cc}\hfill ({\rho }^{+},{\sigma }^{+})& =(({\rho }_1^{+},{\sigma }_1^{+}),({\rho }_2^{+},{\sigma }_2^{+}),({\rho }_3^{+},{\sigma }_3^{+}),({\rho }_4^{+},{\sigma }_4^{+}),({\rho }_5^{+},{\sigma }_5^{+}))\hfill \\ & =\left(\right(1,0),(1,0),(0,1),(1,0),(0,1\left)\right).\hfill \end{array}$$

Step 2

Calculating the weighted Tanimoto measure between $I_i(i=1,2,\dots ,6)$ and $I^{+}$ as Table 21 and Table 22.

Step 3

According to the equation 25 and equation 26, the maximum similarity and minimum distance are shown as below:

$$\begin{array}{c}sm\left(I_2,I^{+}\right)=0.913\\ d\left(I_2,I^{+}\right)=0.087\end{array}$$

Step 4

According to the equation 27 and equation 28, the most suitable computer type is $I_2$.

Furthermore, we have obtained congruent outcomes by employing the MADM models proposed by Wang [29] and Zhang [30], respectively, which proves the effectiveness of the proposed model. The corresponding calculation outcomes have been delineated in Table 23 and Table 24, respectively. The parameter α is a positive constant and $U^{+}$ represents the positive ideal solution, which are calculated using Wang’s method.

5. Conclusions

In this study, we propose a set of innovative similarity and distance measures for PFSs, drawing inspiration from the Tanimoto coefficient. The experiment demonstrated that the proposed measures possess two outstanding characteristics: (1) avoiding numerous counter-intuitive outcomes caused by existing measures; and (2) providing more differentiated measurement results when distinguishing between different PFSs. Therefore, decision-making based on this measure can yield more confident results. Compared to some existing PFSs measures, the proposed measures are more effective and superior. We also designed two decision models based on the proposed measures and applied them to problems such as pattern recognition, medical diagnosis and multi-attribute decision-making to demonstrate their effectiveness. Future research will apply the various measures proposed to a wider range of scenario problems to confirm the potential of our measures and PFSs.