Prerpints.org logo
Preprint
Article

Comparison of Different Machine Learning Methods to Reconstruct Daily Evapotranspiration Estimated by Thermal-Infrared Remote Sensing

Altmetrics

Downloads

127

Views

57

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

08 January 2024

Posted:

09 January 2024

You are already at the latest version

Alerts
Abstract
Remote sensing-based models usually have difficulty in generating spatio-temporally continuous terrestrial evapotranspiration (ET) due to cloud cover and model failures. To overcome this problem, machine learning methods have been widely used to reconstruct ET. However, studies comparing and evaluating the accuracy and effectiveness of reconstruction among different machine learning methods remain scarce. In this study, four popular machine learning methods (deep forest, deep neural network, random forest, extreme gradient boosting) were used to reconstruct the ET product, addressing gaps resulting from cloud cover and model failure. The ET reconstructed by four methods were evaluated and compared in Heihe River Basin. The results showed that four methods performed well in the Heihe River Basin, but the RF method was particularly robust. It not only performed well compared with ground measurement (R = 0.73), but also reconstructed ET throughout the basin. Validation based on ground measurement showed that DNN and XGB models performed well (R > 0.70). However, few gaps still existed in the desert after reconstruction, especially for the XGB model. The DF model filled these gaps throughout the basin, but the model had lower consistency compared with ground measurement (R = 0.66) and yielded many low values. The results of this study suggested that machine learning methods had considerable potential in reconstruction of ET at regional scale.
Keywords: 
Subject: Environmental and Earth Sciences  -   Remote Sensing

1. Introduction

Terrestrial Evapotranspiration (ET) is a crucial component of land-atmosphere hydrology, energy and material cycle [1,2]. Accurate and reliable estimation of regional ET is important for basin hydrology, agricultural water management and drought monitoring [3]. Currently, the ground measurement systems including eddy covariance (EC) system and large-aperture scintillometer (LAS) are commonly used to measure ET under different vegetation types [4,5]. These measurement techniques, however, can only provide valid measurement at meters to ~100 meters scale, difficulty in larger scales [4]. Therefore, the ground-based observations are usually used to validate ET products based on remote sensing. By contrast, remote sensing techniques provide the ability to easily monitor large-scale geographical information according to satellites, and thus become a commonly used way to detect ET.
However, remote sensing techniques can only detect surface parameters related to ET, rather than directly observe ET. In order to acquire reliable ET over larger scales, many remote sensing-based ET simulation models have been proposed which can be used to acquire ET over larger scales [6,7,8,9,10,11,12,13]. Among these models, thermal infrared-based models are widely used to estimate regional ET based on thermal infrared-based land surface temperature (LST) [14,15,16]. Two source energy balance (TSEB) model is one of the most widely applied, which has a more reasonable physical mechanism compared to single source models [6]. It has been shown that the TSEB model can more accurately simulate the energy exchanges between the atmosphere, soil and vegetation, and is more adaptable under different vegetation types and climatic regions [17,18,19]. However, the TSEB model relies on inputting thermal infrared-based surface temperature as boundary constrain. This often leads to model invalidation in regions where surface temperatures are influenced by solid clouds, thus limiting practical applications of the model [12,20,21,22]. Moreover, due to the mechanism of TSEB model, it may still produce gaps in areas shrouded by solid clouds with low radiation, even when land surface temperatures are available [23].
Hence, exploring reliable methods for spatio-temporal reconstruction of TSEB estimated ET is significant to agricultural water management and hydrological applications [20,23]. In response to these challenges, various machine learning methods, such as random forest (RF) [24], deep forest (DF) [25], deep neural network (DNN) [23] and extreme gradient boosting (XGBoost) [26], have provided viable solutions for the reconstruction of ET. These methods have been applied to estimate or reconstruct the surface parameters from remote sensing data in previous studies [27,28,29,30,31]. The conventional approach usually entailed the initial training of a model at site scale, and then expanding the model to a larger regional scale using remote sensing and other data [32,33,34]. However, although such well-trained models typically performed well at the site scale, unevenly distributed and limited sites could not adequately represent heterogeneous surface [33]. Hence, some relevant research has used the effective target parameters obtained from model as input samples for training machine learning methods, which are used to fill the gaps in the model estimation by combining the spatio-temporal continuous impact factors [23,31]. This innovative methodology ensures that machine learning methods not only fill in the gaps, but also guarantee the accuracy and reliability of the models. However, few studies used this way to reconstruct ET. And, whether different machine learning methods perform differently when combined with physical models also needs to be investigated.
The purposes of this paper are to reconstruct the gaps after TSEB model-estimated ET in Heihe River Basin by using four machine learning methods (RF, DF, DNN, XGBoost), and to compare the accuracy and effectiveness of the different methods. In the following sections, we delve into the methodology of combining TSEB model with machine learning for ET estimation along with reconstruction, and comprehensively compare the accuracy and effectiveness of the different machine learning methods coupled TSEB model at different spatial scales.

2. Materials and Methods

2.1. Study Area and EC sites

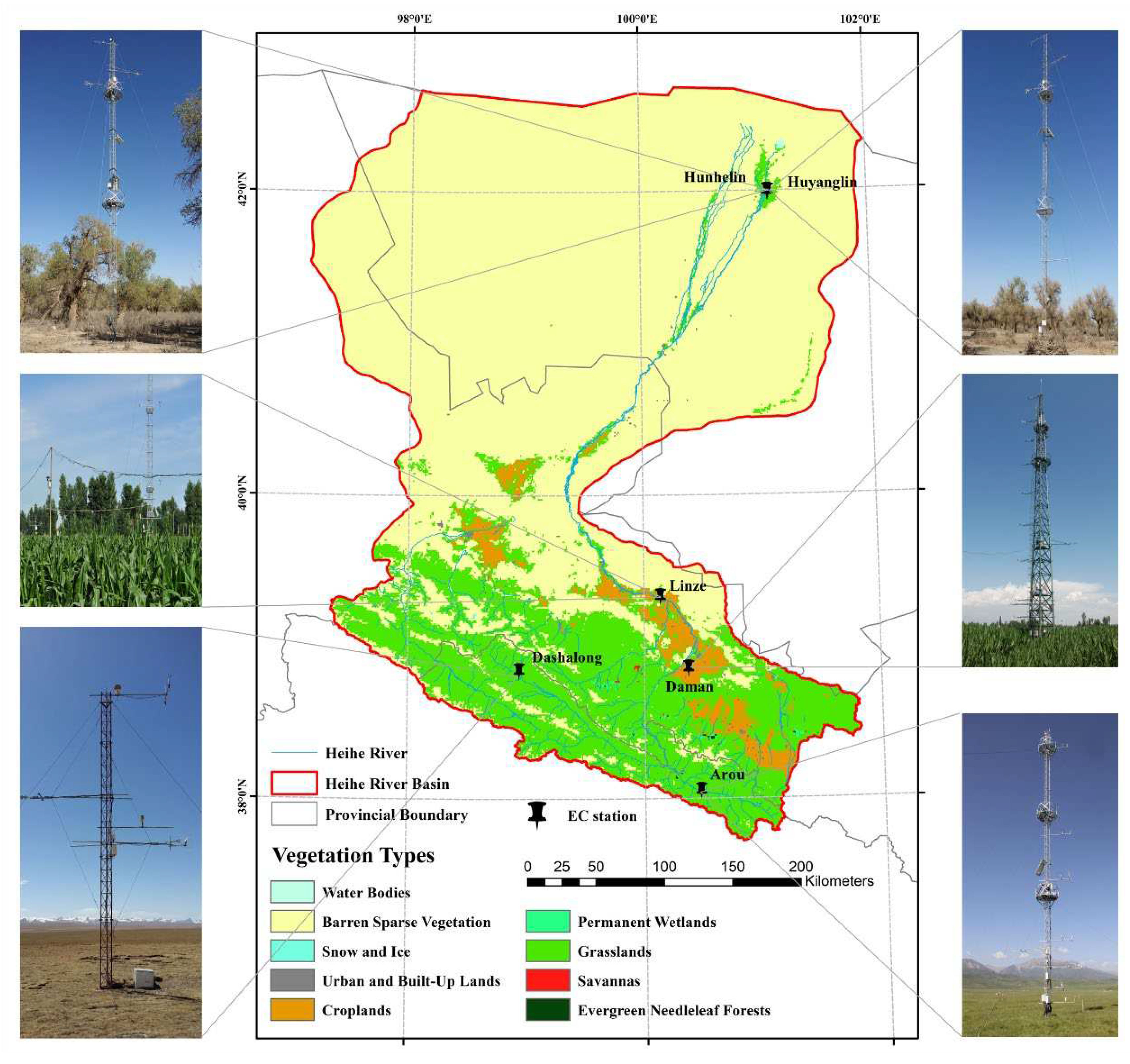
The study area is Heihe River Basin located in the middle of the Hexi corridor, which is the second largest inland basin in northwest China, covering approximately 1,432,000 km2 [35,36]. According to the hydrological characteristics, the basin can be divided into upstream, midstream and downstream. The Heihe River Basin is characterized by widespread desert, sporadic grassland and cropland, and riparian forest in the downstream regions, and widespread grassland, riparian ecosystems, wetland, and cropland (cultivated with crops such as maize, wheat, and vegetables) in the upstream and midstream (Figure 1) [35,36]. This area is in arid and semi-arid regions and has a typical temperate continental climate, with mean annual temperature of 6.0~8.0 °C , mean annual precipitation of 100~250 mm, and a mean annual evapotranspiration of 1200~1800 mm.
The Heihe Watershed Allied Telemetry Experimental Research (HiWATER) had been conducted in this area for better understanding hydrological, ecological and other land surface processes, accumulating numerous surface observation data [36]. Six EC stations from 2011 to 2016 with relatively homogeneous surface were collected to validate the accuracy of estimated and reconstructed daily ET in this study (Table 1). These sites include one wetland EC station (Dashalong) [37], one grassland EC station (Arou) [37], two cropland EC stations (Daman and Linze) [5,37,38], and two forest EC stations (Huyanglin and Hunhelin) (Figure 1) [37].
Original EC measurement data was stored as the average latent heat flux per 30 minutes (48 data per day). In this study, the daily ET measurements were aggregated from 8:00 to 19:00 when less than 25% of the observations were absent. All ground measurement data can be acquired from the National Tibetan Plateau Data Center (TPDC).

2.2. Multisource data

In this study, TSEB model needs to input surface boundary parameters for constrain surface heat fluxes, including LST, leaf area index (LAI) and land cover type (LC). These parameters can be acquired through remote sensing technique. Among them, the LST dataset utilized a fusion product that combines Global Land Data Assimilation System (GLDAS) and Terra MODIS LST [39]. This fusion product was based on the time series decomposition model of LST, reconstructing the gaps in MODIS LST, with a spatial and temporal resolution of 1 km and daily [39]. The LAI dataset collected from the Global LAnd Surface Satellite (GLASS) LAI dataset with a spatial and temporal resolution of 500 m and 8-day [40]. In order to ensure consistency with other data in temporal resolution, the LAI is temporally linearly smoothed to daily scale. Besides, the Albedo dataset was used to the reconstruction of daily ET, which is also collected from GLASS and similarly processed. The land cover type map based on International Geosphere-Biosphere Programme (IGBP) classification system can be acquired from MCD12Q1 Version 6.1 data product [41]. Considering the influence of topography on ET, digital elevation model (DEM) was collected to reconstruct ET in this study.
The ERA5-land dataset, with a spatial and temporal resolution of 0.1° and 1 h, was selected for driving TSEB model and reconstructing gaps, because of its high quality[42]. Considering the TSEB model and reconstruction, six meteorological variables in ERA5-land were selected, including air temperature (TA), wind speed (WS), surface pressure (SP), relative humidity (RH), surface solar radiation downward (SSRD) and surface thermal radiation downward (STRD). Each meteorological parameter was processed as instantaneous values at 14:00 for driving TSEB model, and daily average value for reconstruction.
Due to different sources, there are considerable variations in the spatial resolution of these parameters. Therefore, the spatial resolution of all datasets was unified to 0.01° by bilinear interpolation.

2.3. Methods

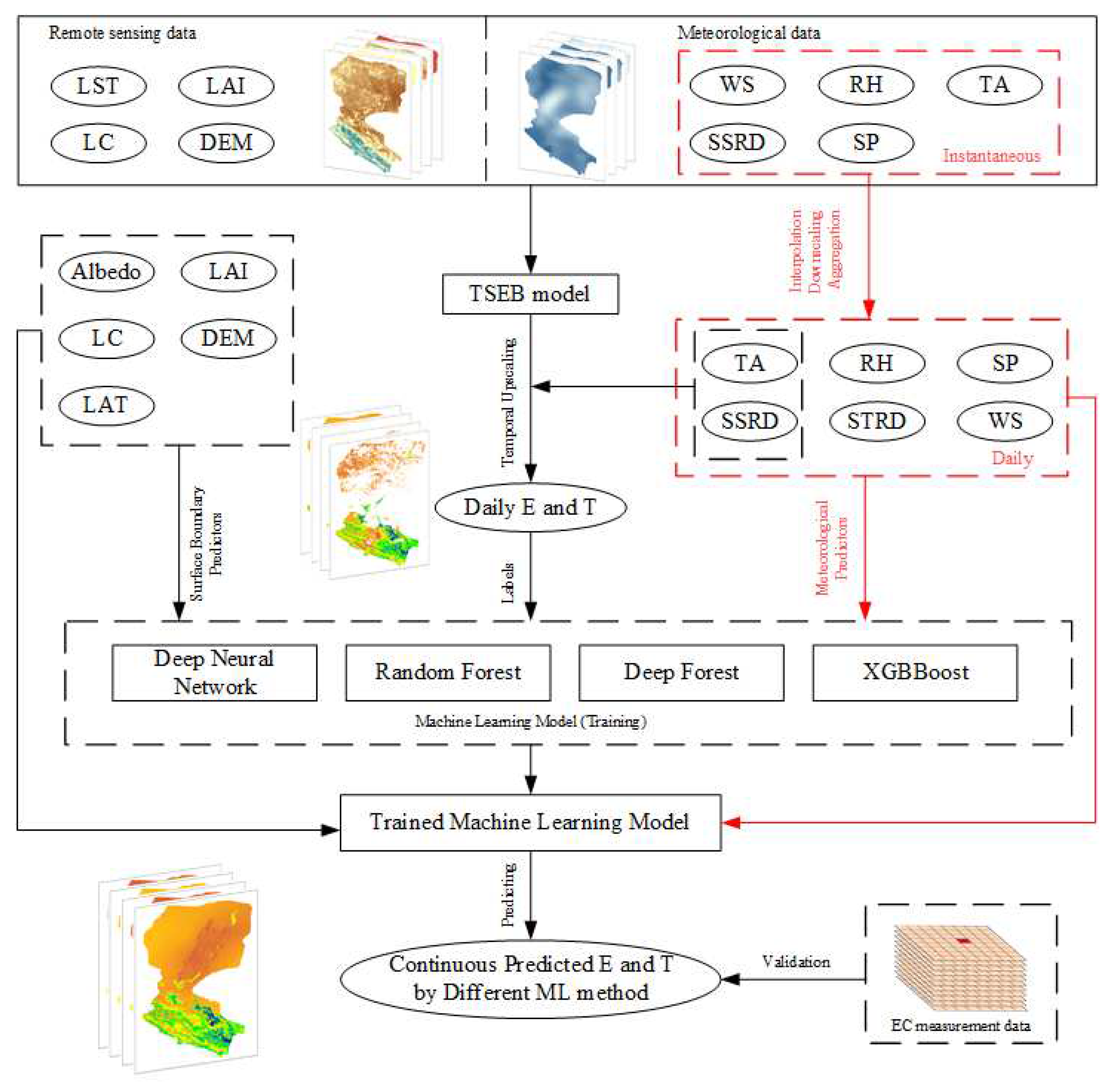
The flowchart for generating spatio-temporal continuous daily ET by the TSEB model and machine learning methods is shown in Figure 2. After pre-processing of remote sensing and meteorological data is finished, the spatio-temporal discontinuous daily ET was first generated by the TSEB model using remote sensing and instantaneous meteorological data. To reconstruct the gaps in TSEB simulation, four machine learning methods (RF, DNN, DF, XGBoost) were trained and then employed to reconstruct the above gaps in this study. At last, the reconstructed daily ET using different machine learning methods was validated and compared at site and basin scales.

2.3.1. Description of the TSEB model

The TSEB model, proposed by Norman in 1995 [6], is a physically-based two-source energy balance model used in remote sensing and hydrological studies. The TSEB model can be used to estimate surface energy fluxes at different scales, and considers two separate energy components: the soil and the vegetation. It can be applied to accurately estimate the radiative and turbulent energy exchange between canopy, soil and atmosphere under different vegetation types and climatic areas, and has demonstrated robust performances [43,44]. Moreover, the TSEB model is easy to combine with remote sensing, enabling estimation of evapotranspiration with high spatio-temporal resolution [45]. In this study, the TSEB model was initially utilized to estimate the latent fluxes from the canopy and soil at 14:00, and then temporally upscaled to daily scale by evaporative fraction constant (ConEF) method. Details of TSEB model and ConEF method can be found in relevant articles [21,46,47].

2.3.2. Machine Learning Methods for Filling the Gaps

The TSEB model did not always estimate valid ET and its component T and E, due to the cloud cover and the mechanism of TSEB [23]. Machine learning methods can be used to explore and establish complex nonlinear relationships between multiple variables [23,30]. In this study, four machine learning methods (RF, DF, DNN, XGBoost) were employed to reconstruct gaps after TSEB estimation in the Heihe River basin. Considering the influence of various factors on ET, surface parameters including LAI, Albedo, LC, and meteorological variables including Ta, RH, RH, SSRD, STRD, WS were used to train the machine learning methods. 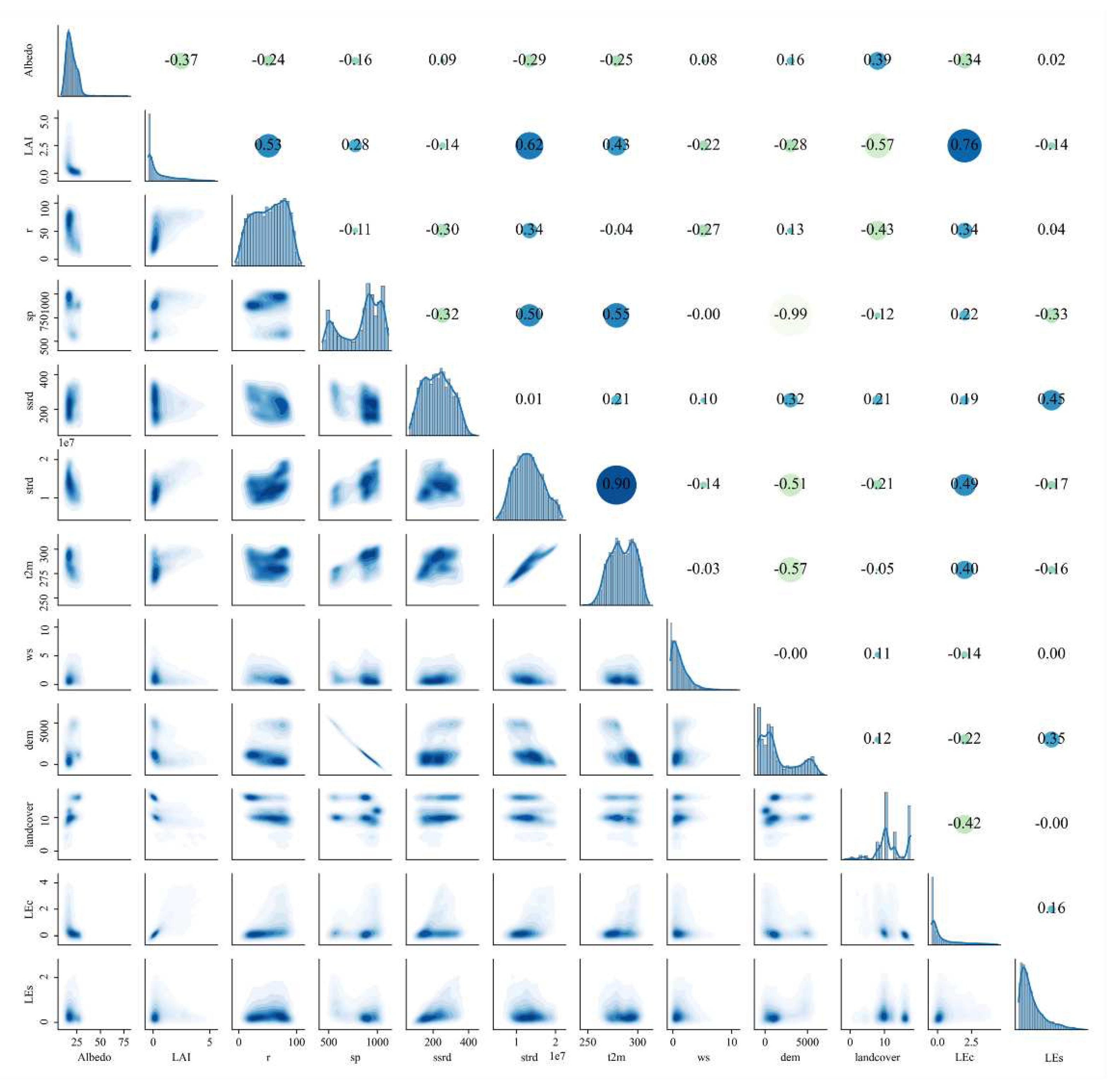Besides, the DEM and latitude (LAT) were also employed to further constrain and train machine learning methods in order to depict the influence of terrain and latitudinal zonation on ET [23]. The pearson product-moment correlation coefficient matrix is an important tool for exploring linear correlations between variables [48]. In order to judge whether the choice of variables is reasonable, the results of the correlation analysis of this study are shown in Figure 3. All the variables showed different correlation with T and E.
The trained models combining spatio-temporally continuous parameters were subsequently applied to reconstruct gaps, respectively. The relationship of ET and impact factors can be expressed as follow:
E , T = f R F , D F , D N N , X G B A l b e d o , L A I , D E M , L C , l a t , R H , S P , S S R D , S T R D , T A , W S
where the f represents the nonlinear relationship between the E , T and impact factors, the subscript represents different machine learning methods. It should be noted that, in order to improve the stability, accelerate the convergence, and avoid gradient vanishing or exploding, the inputs of the training parameters were normalized initially.

2.4. Site-scale Validation

Based on the EC flux data, the daily ET generated by different machine learning methods were compared with the ground measurement, to validate the accuracy of them, respectively. In this study, the correlation coefficient (R), Bias (unit: mm day-1) and root mean square error (RMSE, unit: mm day-1) were selected as quantitative indicators to evaluate the accuracy of generated ET, and the expression as follows:
R = ∑ i = 1 n E T E i − E T E ¯ E T O B i − E T O B ¯ ∑ i = 1 n E T E i − E T E ¯ 2 ∑ i = 1 n E T O B i − E T O B ¯ 2
R M S E = 1 n ∑ i = 1 n E T E i − E T O B i 2
B a i s = 1 n ∑ i = 1 n E T E i − E T O B i
Where the E T E and E T O B represent the generated and observed daily ET, respectively, the subscript i denotes the ith sample, the symbols of E T E ¯ and E T O B ¯ denotes the mean of generated and observed daily ET, and n represents the sample size. A larger R and smaller RMSE and Bias indicate better performance, furthermore the bias can reflect the overall overestimation and underestimation.

2.5. Uncertainty Evaluation at Regional Scale

Since site-scale validation is not representative of accuracy in the whole basin, the three-cornered hat (TCH) method was employed for cross-validation between daily ET reconstructed by different machine learning methods. The generalized TCH method can be employed to estimate the relative uncertainty of the ET time series from different reconstruction methods without any ground measurement. The details of the generalized TCH method are described below.
The time series of daily ET can be decomposed into two parts: the true value and error:
X i = X t + ε i , ∀ i = 1 , 2 , ⋯ , N
where all variables are time series, the X i represent i th time series of reconstructed daily ET, the X t is the truth value series, the ε i represents the error term of ith time series, N is the number of datasets involved in the calculation. In this study, N is 4. In order to calculate the relative uncertainty of each reconstructed ET result, the true value series ( X t ) needs to be known. But most of the true values are difficult to observe. Therefore, the TCH method defined the difference between series and reference series ( X N ) as follows:
Y i , N = X i − X N = ε i − ε N , i = 1 , 2 , ⋯ , N − 1
Where Y is a matrix with N − 1 time series. Since the choice of X N is theoretically insensitive in TCH method, therefore, it can be randomly selected. DNN reconstructed daily ET was selected as X N in this study. The covariance matrix of Y can be obtained using S = c o v ( Y ) . The unknown N × N covariance matrix of the individual noise R is related to S as:
S = J · R · J T
J = Z − a T
where Z is a ( N − 1 ) × ( N − 1 ) identity matrix, a is 1   1 ⋯ 1 ( 1 × ( N − 1 ) ) . Because the number of unknown elements is larger than the number of equations, The above equation cannot be solved. In order to solve these equations. The constrained minimization problem was proposed by Galindo and Palacio [49] based on the Kuhn-Tucker theorem. Finally, the matrix R is obtained by minimizing the objective function. The uncertainty of the time series ( X i ) is the square root of the diagonal elements of the R matrix, and the relative uncertainty is defined as the ratio of the uncertainty to the mean value of each uncertainty.

3. Results

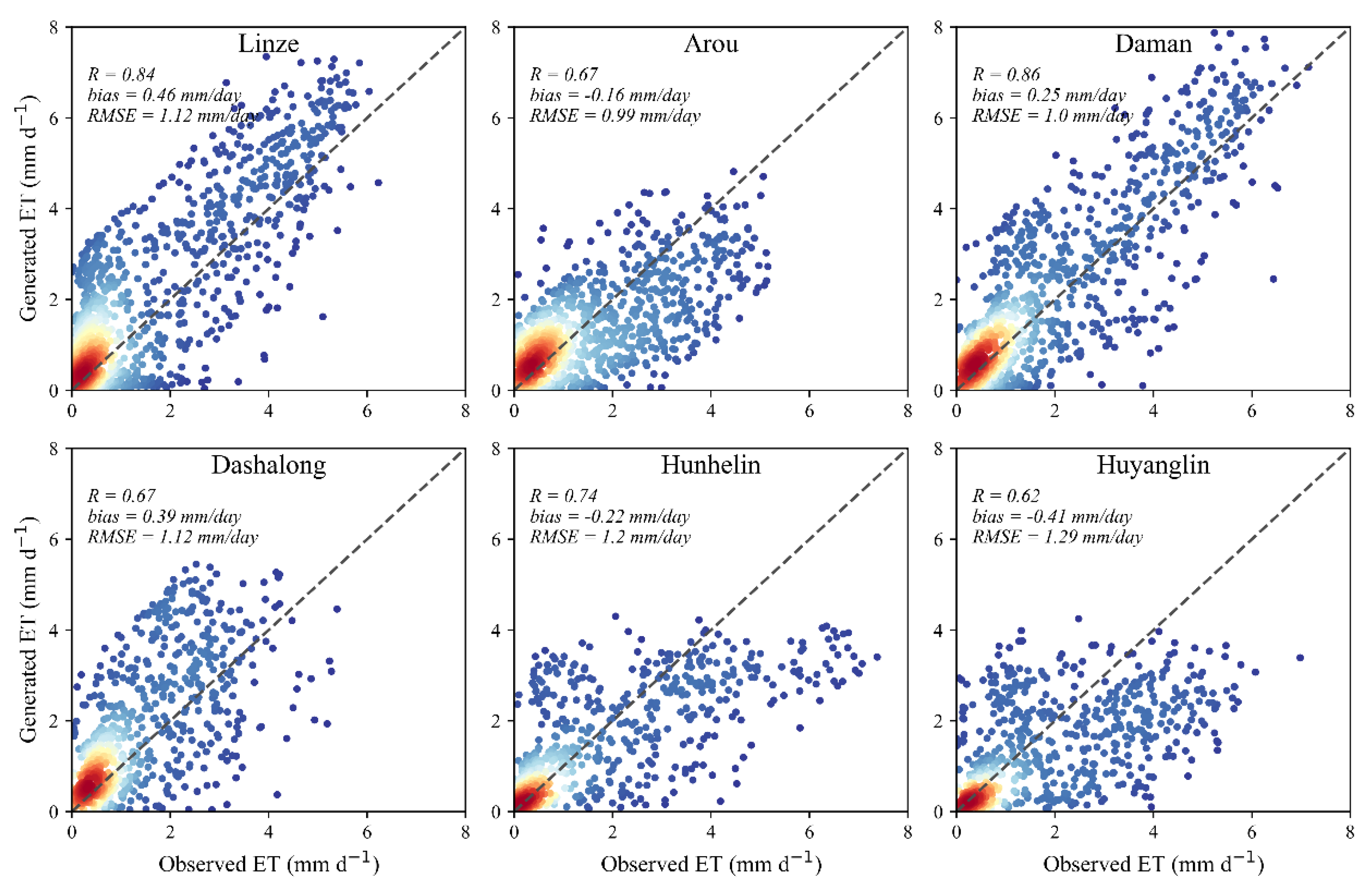
3.1. Validation of reconstructed daily ET

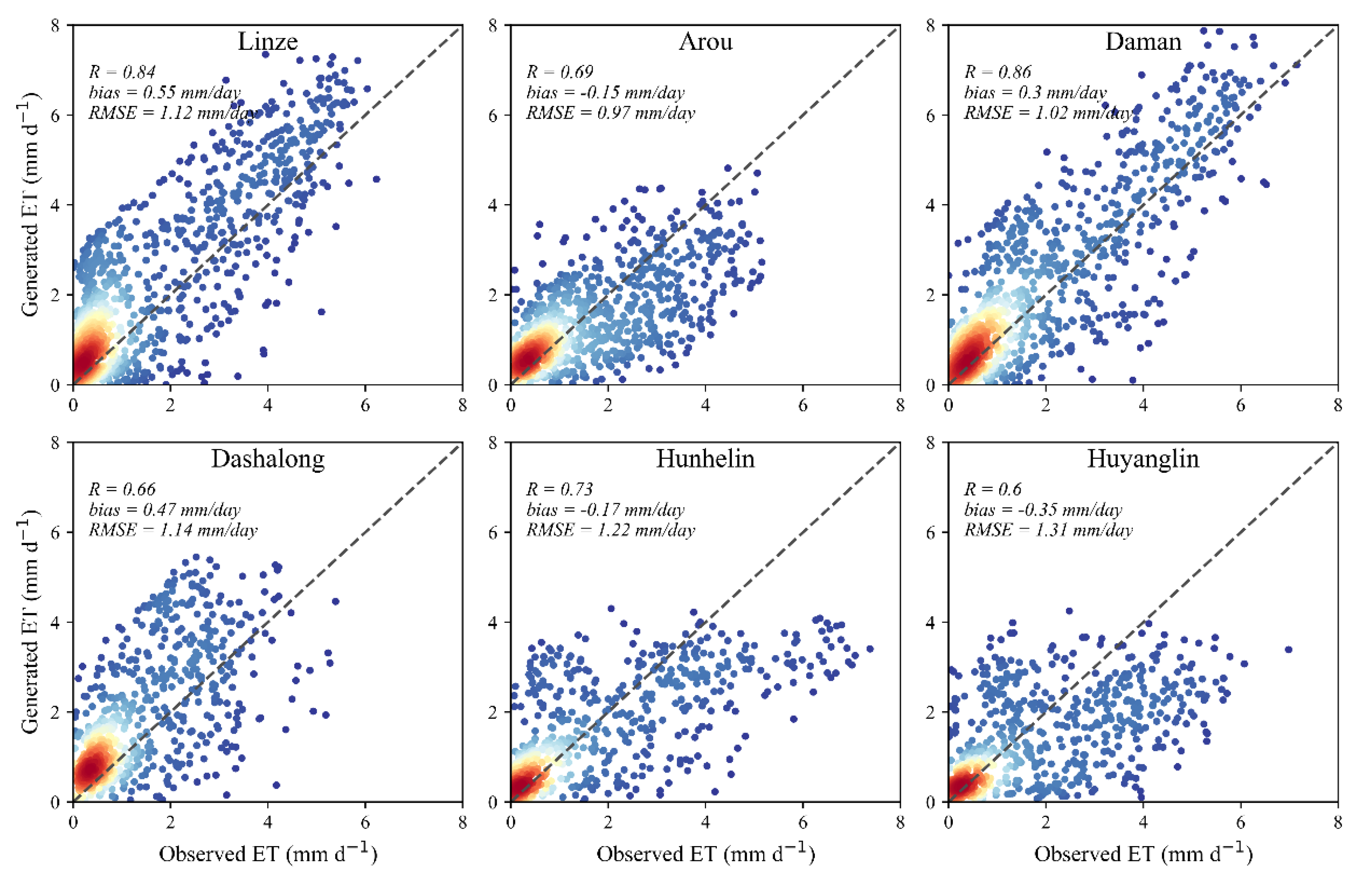
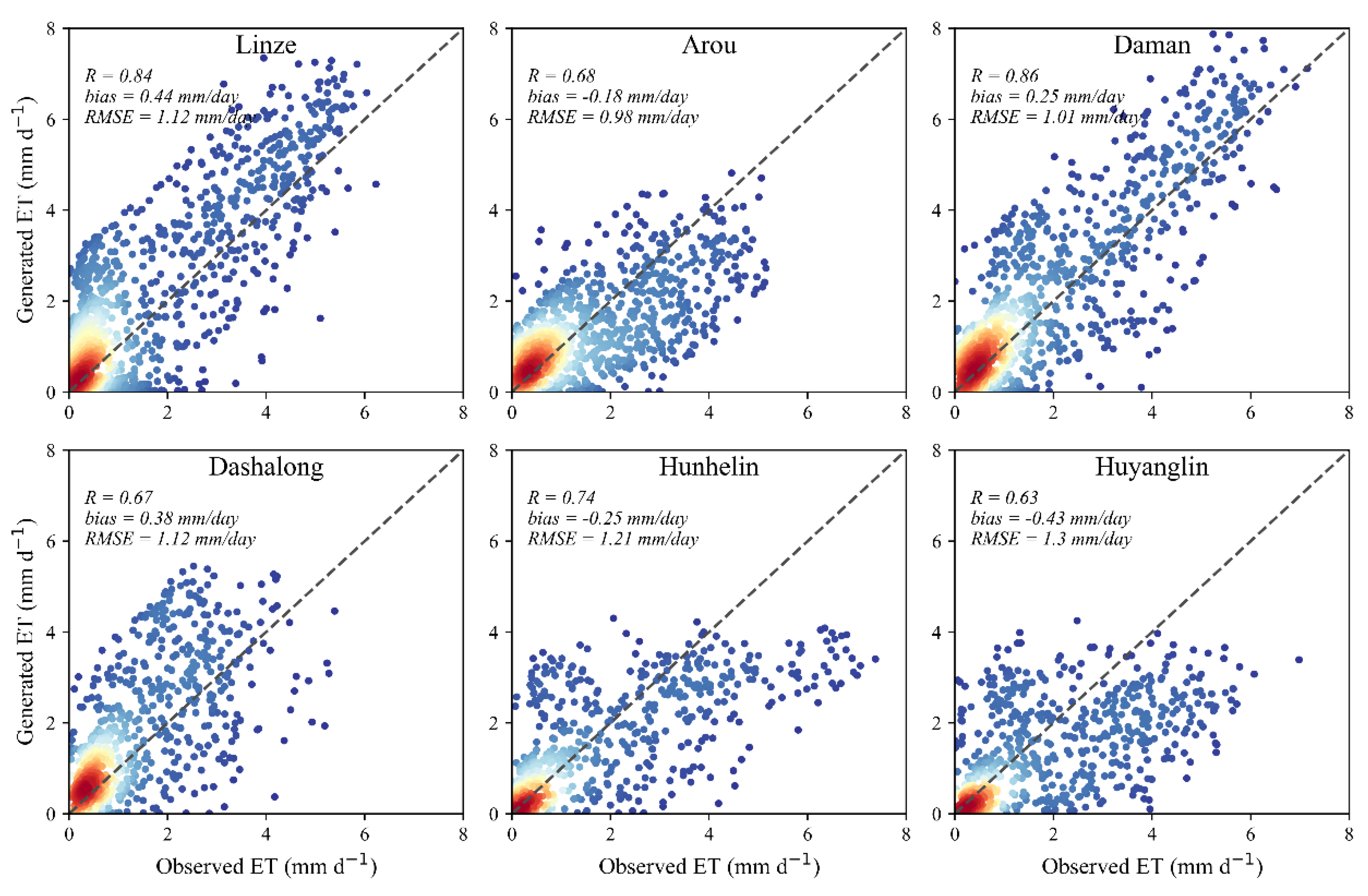
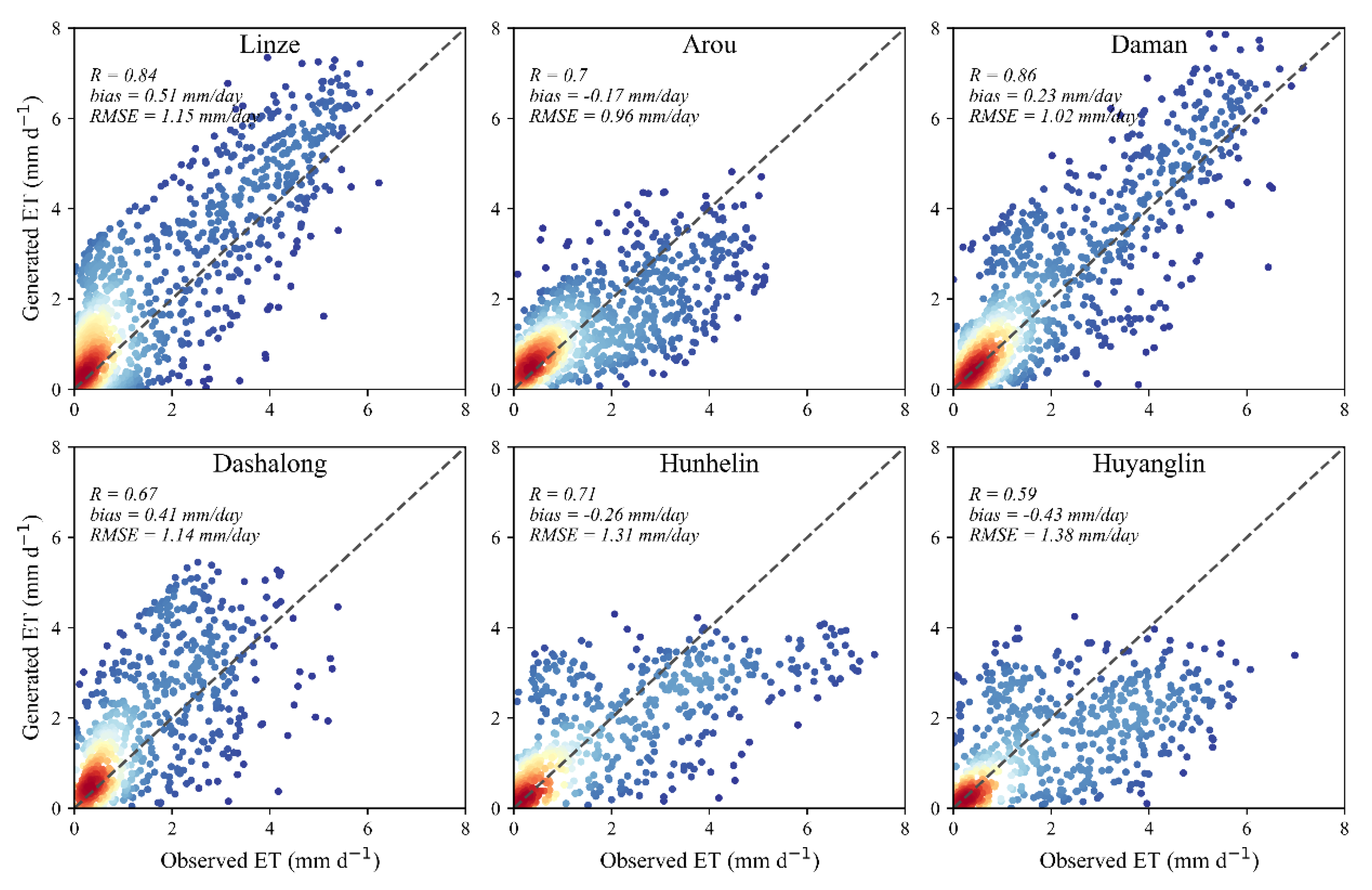
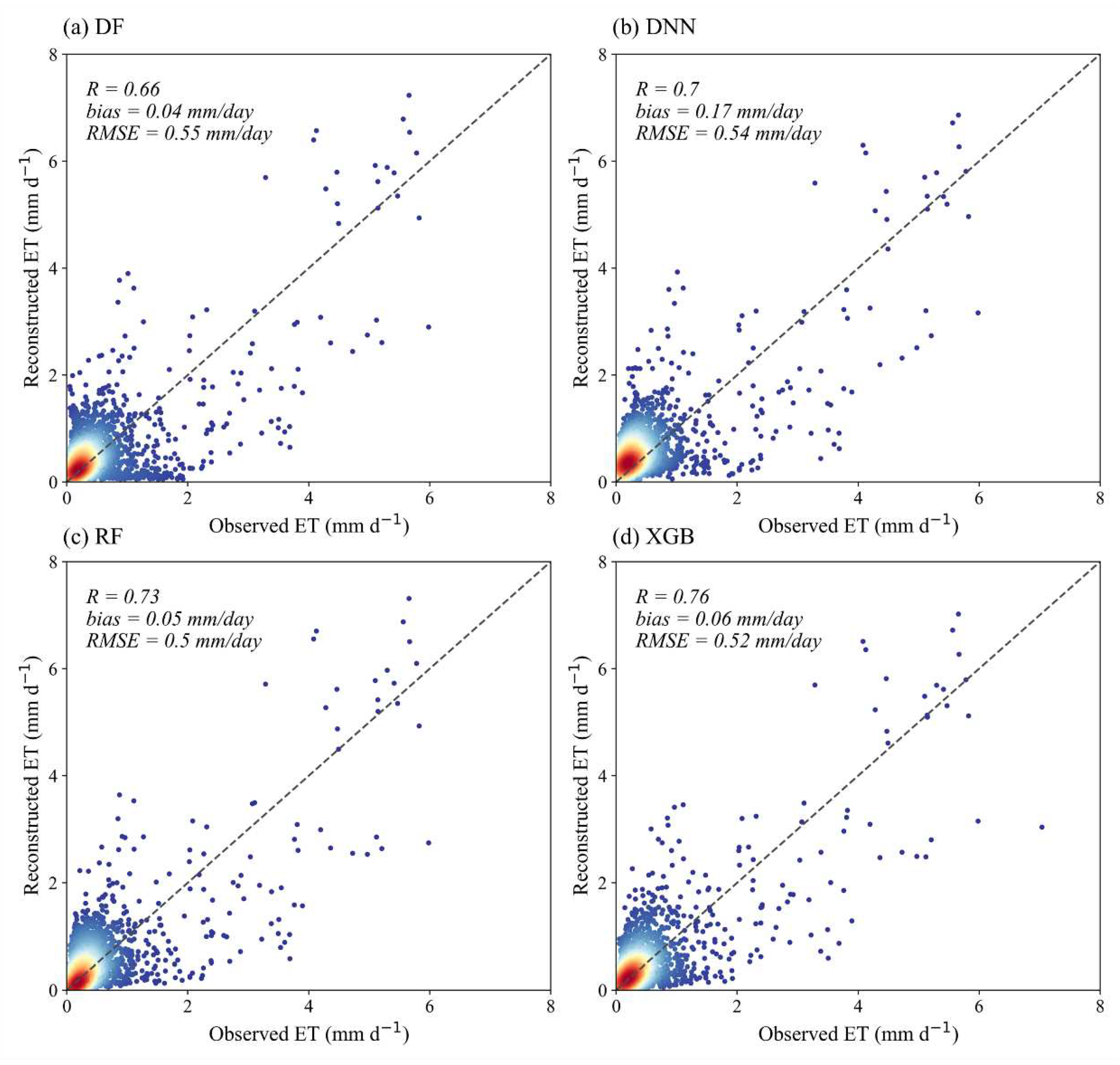
Figure 4, Figure 5, Figure 6 and Figure 7 showed the daily ET reconstructed by different machine learning methods compared to ground measurement at the six EC sites. Overall, considering all samples, four machine learning methods demonstrated great and similar performances with an average R of 0.74, bias between 0.08 and 0.11 mm day-1, and RMSE between 1.11 and 1.15 mm day-1. However, when only the reconstructed samples are considered, the discrepancies between different machine learning methods were reflected (Figure 8). Apparently, most points are clustered in the range where ET less than 2 mm day-1. This phenomenon can be attributed to the lower ET are usually accompanied by lower solar radiation. Under these conditions, LST may not be available and the TSEB model is more likely to fail. As the ET increases, the distribution of points tends to disperse. Despite these discrepancies, the reconstructed ET by different machine learning methods usually showed reasonable accuracy. Among them, the daily ET reconstructed by XGB model had the highest performance with a R, Bias and RMSE of 0.76, 0.06 mm day-1 and 0.52 mm day-1, followed by the DNN and RF models. On the contrary, the DF model showed slightly worse performance with R, bias and RMSE of 0.66, 0.04 mm day-1 and 0.55 mm day-1, respectively, and the reconstruction had greater scatter in the lower value range.

3.2. Relative uncertainty at the basin scale

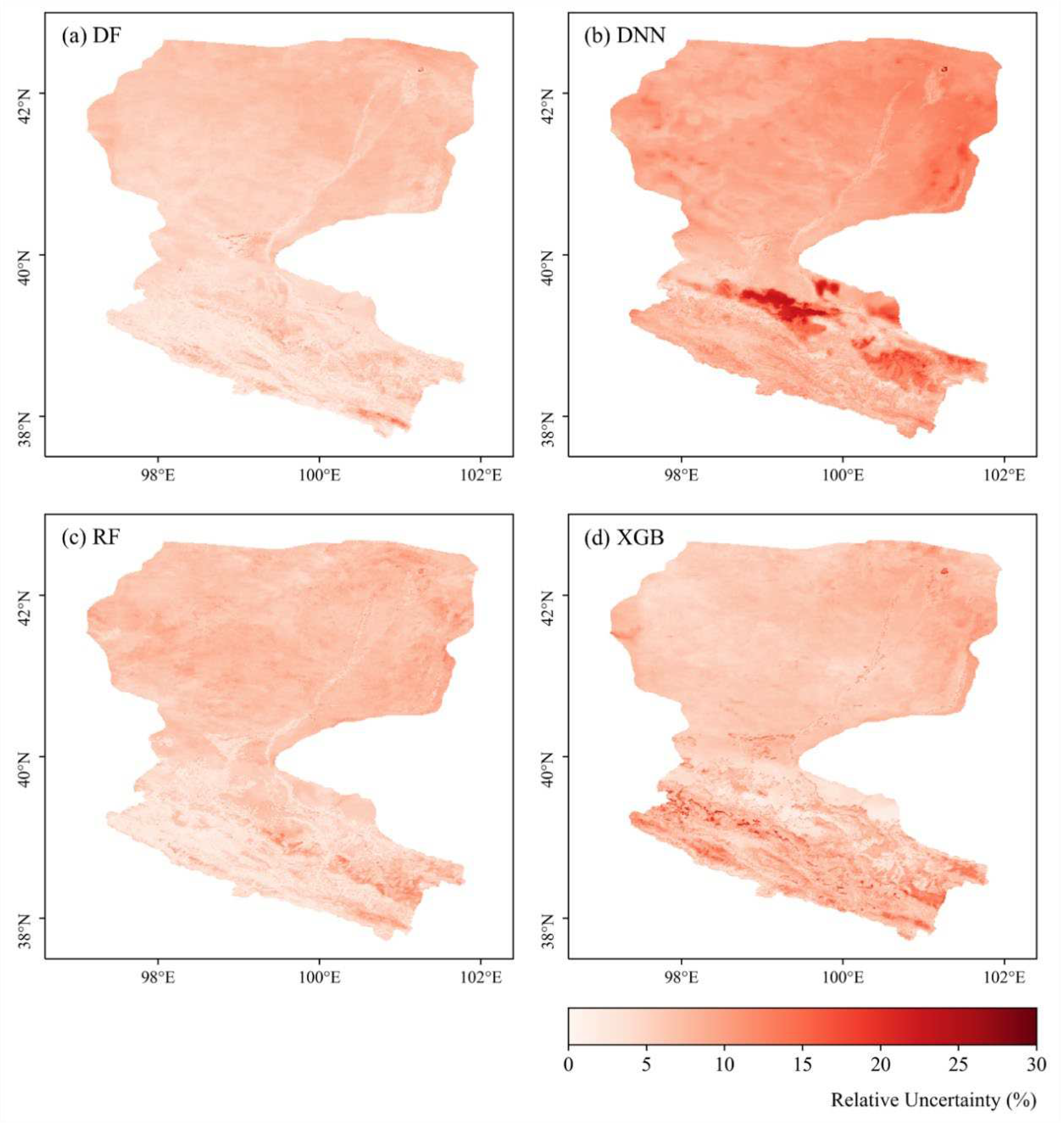
Direct validation at the site scale does not adequately represent spatial performance. Due to the difficulty of obtaining direct observations at large scales, the TCH method was employed to calculate the relative uncertainty of different machine learning methods in this study. The spatial distributions of relative uncertainty of daily ET reconstructed by different models were shown in Figure 9. Overall, the reconstruction results of all four methods have low relative uncertainty in whole Basin, with average relative uncertainty of 5.36%, 9.35%, 5.95%, and 6.44% for DF, DNN, RF, and XGB, respectively. However, the DNN model had overall high relative uncertainty, especially in the deserts at the junction between the midstream and upstream (>20%). Meanwhile, the relative uncertainty of XGB reconstructed daily ET showed a patchy distribution in the Heihe River region. This may be related to the gaps that remained in these regions after XGB model reconstruction. The DF and RF models, on the other hand, have analogical distribution of uncertainty across the basin, without significant high values. This could mean that DF and RF are more robust on large regional scales.

3.3. Spatial distribution of reconstructed ET

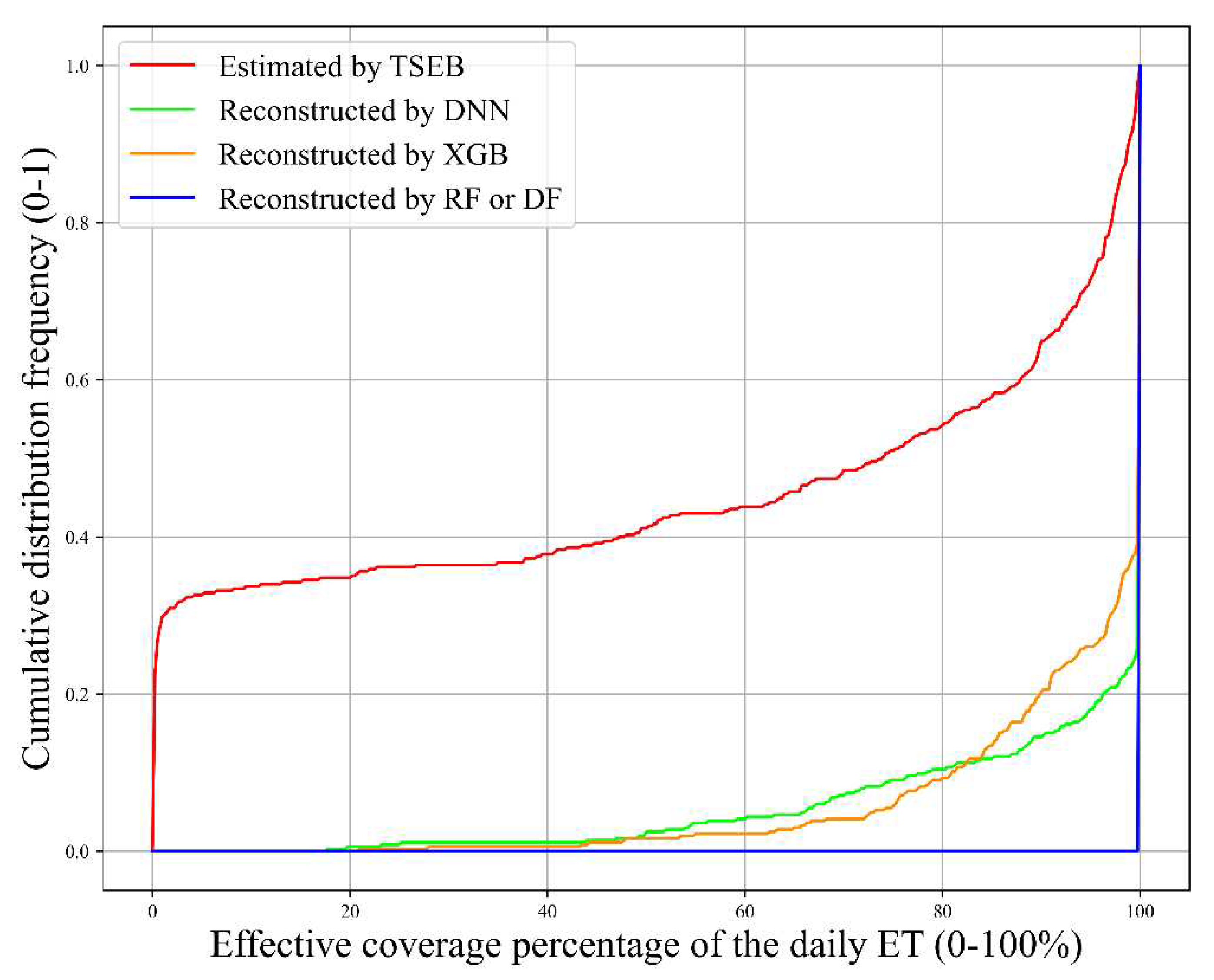
Figure 10 showed cumulative distribution frequency curves vs. effective coverage percentage of the TSEB estimated and different machine learning methods reconstructed daily ET. The areas of the curve with the X-axis in the figure can represent the missing amounts. It indicated that The RF and DF completely reconstructed the gaps after the TSEB estimation after TSEB estimation, but there remained few gaps when reconstructed by the DNN and XGB. 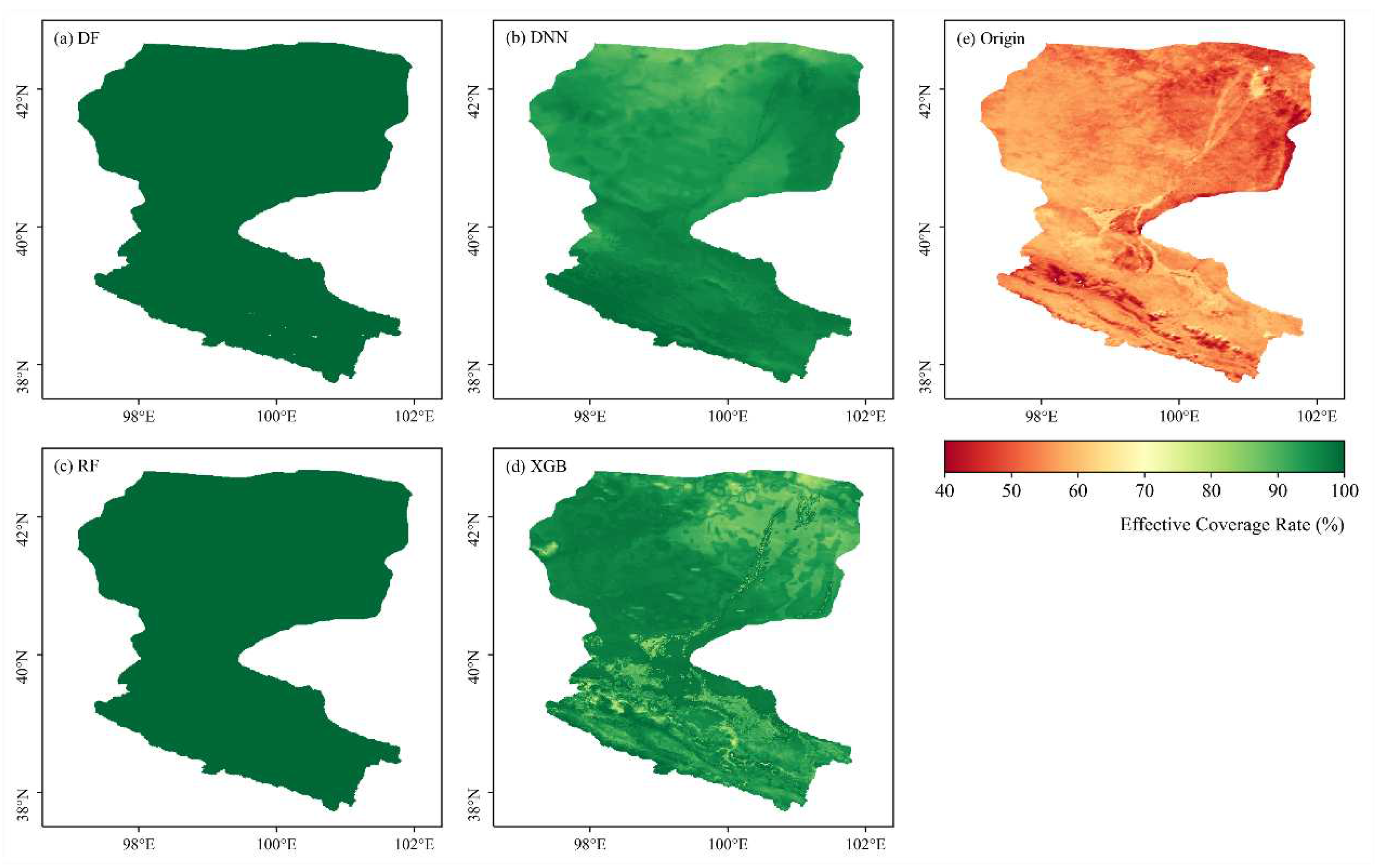In order to further understand the reconstruction effectiveness of different machine learning methods, the spatial pattern of effective coverage rate of daily ET (ratio of the number of days having valid ET against the total days) estimated by different machine learning methods and original TSEB model was shown in Figure 11. The coverage of TSEB model-estimated ET in deserts is lower than in other regions, regardless of the region of the basin. During this period, the average effective coverage rates of daily ET after the reconstruction with DF, DNN, RF and XGB were improved from 54.8% to 100%, 94.8%, 100% and 94.5%, respectively, for the original TSEB model (Figure 10 and Figure 11). The DNN model exhibited a low coverage rate in the downstream desert regions, while the low coverage rate after the XGB model reconstruction is sporadically distributed throughout the basin.
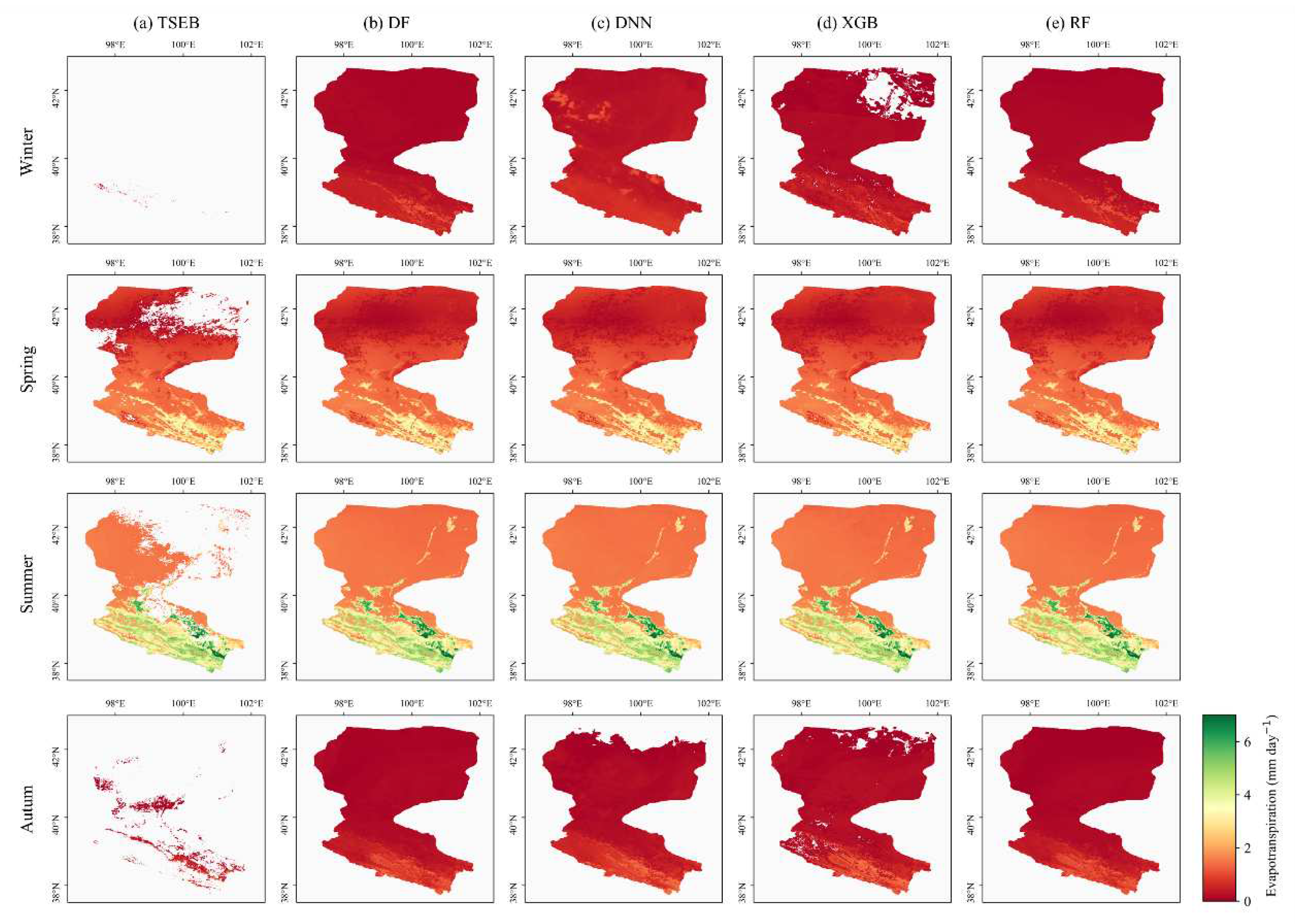
Figure 12 showed the spatial patterns of the TSEB model-estimated and different machine learning methods reconstructed daily ET in different seasons. The daily ET varies significantly from season to season. The daily ET is lowest in the winter, approaching zero in desert areas. It begun to increase in the spring, was highest in the summer, and begun to decrease again in the autumn. Besides, the ET were higher in those areas with dense vegetation cover, such as grassland, cropland and wetland, than in desert with sparse vegetation cover. In terms of spatial effectiveness, the TSEB model-estimated ET showed significant gaps in all seasons. Combined with Figure 10, observing the reconstruction results by different machine learning methods, the DF and RF methods completely reconstructed the daily ET in all seasons, but the DNN and XGB methods showed some localized gaps in winter and autumn. Most of these gaps are usually more apparent in the desert region of the downstream. Furthermore, the XGB model showed more patchy gaps in the upstream and midstream regions.

4. Discussion

4.1. Coupling of TSEB model and machine learning methods

In this study, the TSEB model-estimated ET was reconstructed by using different machine learning methods and multi-source remote sensing data. The results showed that although most of the reconstructed daily ET values are concentrated in the lower range, these low values of daily ET still have an important influence in the hydrological effects of the basin [50]. In addition, the high values of ET in this study also showed reasonable consistency compared to the ground measurement. In previous studies, machine learning methods were mainly widely used to upscale daily ET using ground measurement [34,51]. While this approach may be able to generate spatio-temporally continuous ET in regional scale, it lacks a reasonable physical explanation [30]. Subsequent studies have employed machine learning methods for reconstruction in regional scale where LST information is invalid [23]. In such studies, researchers trained machine learning methods using the valid outputs of physical models as labels. The models trained by this way not only have the support of the physical theory, but also can provide accurate ET estimates without LST information [52]. However, previous studies found that the TSEB model and machine learning methods may not yield valid results due to low solar shortwave radiation, even when the LST information is available [23]. The reasons for this phenomenon may be the limitations of the TSEB model itself under low available energy conditions and extreme meteorological conditions [14]. Therefore, this study also explored whether different machine learning methods perform reasonably well in such regions.

4.2. Importance of input parameters

The selection of appropriate input variables is crucial before deep learning model training [48]. In the theory of TSEB, ET is constrained not only by surface parameters but also by various meteorological driving factors [14]. Based on this, in this study, Albedo and LC were chosen to represent the effect of land surface character, LAI represents the effect of vegetation, and WS, TA, RH, SP, SSRD, and STRD represent the effect of atmosphere. Also, considering the latitudinal zonation of ET and topography, DEM and LAT were chosen as the key input parameters [23].
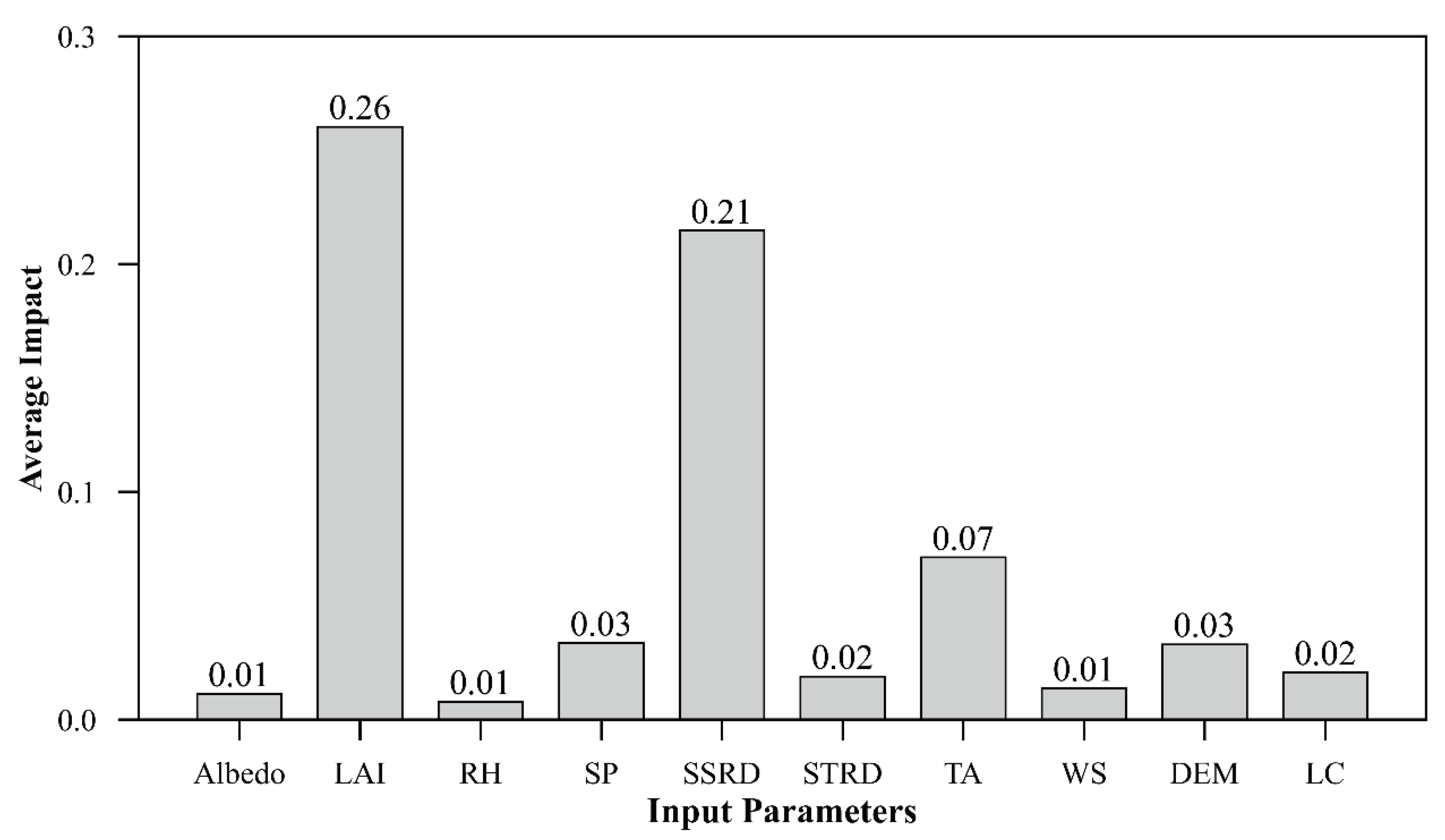
To quantify the contribution of each factor to daily ET, the SHapley Additive exPlanations (SHAP) method was employed to analyze the contribution of each parameter to ET. The absolute mean of SHAP value indicates the average influence of each parameter on model predictions, and serves as a metric for measuring its importance [53]. The importance of all parameters is shown in Figure 13. The LAI and surface solar radiation downward were found to play the most significant roles, with average impacts of 0.21 and 0.26, respectively. These results align with the understanding that LAI is a key determinant of energy partitioning and vegetation transpiration, while SSRD represents the primary energy source driving ET. Other parameters also exhibited significant average impact. This highlights their influence on the water exchange between the surface and the atmosphere.
Besides, this study was conducted at a spatial resolution of 0.01°. Given that multiple variables are required for the TSEB model and machine learning methods, we combined input parameters from multiple sources and unified their spatial and temporal resolution to 0.01° and daily by bilinear interpolation. However, this approach to data processing may raise some issues. For instance, the meteorological factors provided by ERA5-land dataset originally had a spatial resolution of 0.1°, and we downscale it to 0.01° by bilinear interpolation. However, extreme meteorological conditions and advection are prevalent in the Heihe River Basin, which may result in the ERA5-land data with 0.1° resolution failing to accurately reflect the actual meteorological conditions due to smoothing effects during the downscale [54]. Similarly, the GLASS LAI dataset suffers from comparable problem. The temporal resolution of GLASS LAI is 8-day. In this study, the LAI data were smoothed to daily by a linear smoothing method. This may have little effect in natural vegetation conditions, but it may not accurately capture sharp changes in LAI caused by crop harvesting in cropland. Currently, spatial representation of remotely sensing remains a major challenge. It is expected that more reliable datasets can be developed in future studies, to further develop the application of remote sensing in the estimation of surface parameters.

4.3. Comparison of different machine learning methods for reconstruction.

To reconstruct the TSEB model-estimated ET, four different machine learning methods were used in this study. Although we anticipated a complete reconstruction of the ET over the whole Heihe River Basin, the XGB and DNN models remained gaps after reconstruction. Despite the high reconstruction accuracy of the XGB and the DNN models compared to ground measurement (R>0.7), these gaps indicated that they still have potential for improvement in reconstruction of regional ET. The gaps of the DNN model are uniformly distributed in the desert region downstream of the Heihe River Basin, while the gaps of the XGB model showed a patchy distribution throughout the Heihe River Basin. This phenomenon suggested that the DNN model may have a more robust performance than the XGB model over the whole basin, even though the accuracy of both the two models in comparison with the ground measurement is comparable. The DF model is a development of the RF model, which has a higher potential in theory. Moreover, the DF model is insensitive to the parameter settings [25,29]. However, we found that although the DF model completely reconstructed the daily ET in whole basin, the DF model has the lowest R value (R = 0.66) compared with ground measurement. Besides, the DF model produced numerous low values of daily ET that did not match observations. These issues suggested that the DF model may have limitations in reconstruction of surface parameters. Summarizing the above comparison, among the four machine learning methods in this study, the RF model has the most robust performance. The RF model not only accomplished the reconstruction of daily ET in the Heihe River Basin, but also performed well in comparison with the ground measurement. Moreover, the RF model had the highest efficiency among the four methods.
In addition, each machine learning method has many parameters to support normal operation. Therefore, the performance of these models may vary significantly with parameter changes [55,56]. However, the focus of this study was to compare their performances in the reconstruction of daily ET. Therefore, the original parameters were not intentionally adjusted here.

5. Conclusions

This study initially drove TSEB to estimate ET in the Heihe River Basin. Subsequently, daily ET was reconstructed using four different machine learning methods (DF, DNN, RF, XGB). At last, the performances of the reconstructed ET from the four machine learning methods were evaluated and compared at different scales. The results showed that the four methods all performed well in the Heihe River Basin. The RF model not only demonstrated high prediction accuracy (R = 0.73), but also effectively reconstructed regional ET across all vegetation types, being a more robust model overall. The DNN and XGB models achieved high accuracy compared with ground measurement (R > 0.70). However, the reconstructed daily ET remained gaps in the desert region, especially in the XGB model, which has patchy distributed gaps. The DF model successfully reconstructed daily ET across the whole basin, but it performed poorly (R = 0.66) compared with ground measurement. Moreover, the DF model produced many unreasonable low values. This means that models of decision tree-coupled deep learning structures may not be suitable for such researches. The exploration of this study may provide more references for scholars to estimate or reconstruct ET.

Author Contributions

This paper is a collaborative work by all of the authors. Conceptualization, G.Z., L.S; Data curation, G.Z.; Formal analysis, G.Z.; Methodology, G.Z. and L.S.; Supervision, S.T., L.S., L.Z and G.Z.; Writing (original draft), G.Z.; Writing (review and editing), G.Z., L.S., S.T., and L.Z. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the National Natural Science Foundation of China (42071298) and the Anhui Province’s University Science Project for Distinguished Young Scholars (022AH030025).

Data Availability Statement

We gratefully acknowledge all people participation in EC measurements and sharing the measured data on platform of National Tibetan Plateau Data Center (https://data.tpdc.ac.cn/).

Acknowledgments

Here, I would like to thank Professor Song Lisheng for his guidance, Tao Sino for his suggestions on revising the paper, and Zhao Long for his valuable comments and discussions.

Conflicts of Interest

The authors declare that they have no conflict of interest to disclose.

References

  1. Jung, M.; Reichstein, M.; Ciais, P.; Seneviratne, S.I.; Sheffield, J.; Goulden, M.L.; Bonan, G.; Cescatti, A.; Chen, J.Q.; de Jeu, R.; et al. Recent decline in the global land evapotranspiration trend due to limited moisture supply. Nature 2010, 467, 951-954. [CrossRef]
  2. Seneviratne, S.I.; Corti, T.; Davin, E.L.; Hirschi, M.; Jaeger, E.B.; Lehner, I.; Orlowsky, B.; Teuling, A.J. Investigating soil moisture-climate interactions in a changing climate: A review. Earth-Sci Rev 2010, 99, 125-161. [CrossRef]
  3. Chen, H.; Huang, J.H.J.; McBean, E.; Singh, V.P. Evaluation of alternative two-source remote sensing models in partitioning of land evapotranspiration. Journal of Hydrology 2021, 597, 126029. [CrossRef]
  4. Wang, K.C.; Dickinson, R.E. A Review of Global Terrestrial Evapotranspiration: Observation, Modeling, Climatology, and Climatic Variability. Rev Geophys 2012, 50, RG2005. [CrossRef]
  5. Liu, S.M.; Xu, Z.W.; Song, L.S.; Zhao, Q.Y.; Ge, Y.; Xu, T.R.; Ma, Y.F.; Zhu, Z.L.; Jia, Z.Z.; Zhang, F. Upscaling evapotranspiration measurements from multi-site to the satellite pixel scale over heterogeneous land surfaces. Agr Forest Meteorol 2016, 230, 97-113. [CrossRef]
  6. Norman, J.M.; Kustas, W.P.; Humes, K.S. Source Approach for Estimating Soil and Vegetation Energy Fluxes in Observations of Directional Radiometric Surface-Temperature. Agr Forest Meteorol 1995, 77, 263-293. [CrossRef]
  7. Norman, J.M.; Kustas, W.P.; Prueger, J.H.; Diak, G.R. Surface flux estimation using radiometric temperature: A dual temperature-difference method to minimize measurement errors. Water Resour Res 2000, 36, 2263-2274. [CrossRef]
  8. Penman, H.L. Natural Evaporation from Open Water, Bare Soil and Grass. Proc R Soc Lon Ser-A 1948, 193, 120-&, doi:DOI 10.1098/rspa.1948.0037.
  9. Leuning, R.; Zhang, Y.Q.; Rajaud, A.; Cleugh, H.; Tu, K. A simple surface conductance model to estimate regional evaporation using MODIS leaf area index and the Penman-Monteith equation. Water Resour Res 2008, 44, W10419. [CrossRef]
  10. Zhang, Y.Q.; Leuning, R.; Hutley, L.B.; Beringer, J.; McHugh, I.; Walker, J.P. Using long-term water balances to parameterize surface conductances and calculate evaporation at 0.05 degrees spatial resolution. Water Resour Res 2010, 46, W05512. [CrossRef]
  11. Bastiaanssen, W.G.M.; Menenti, M.; Feddes, R.A.; Holtslag, A.A.M. A remote sensing surface energy balance algorithm for land (SEBAL) - 1. Formulation. Journal of Hydrology 1998, 212, 198-212, doi:Doi 10.1016/S0022-1694(98)00253-4.
  12. Chen, J.M.; Liu, J. Evolution of evapotranspiration models using thermal and shortwave remote sensing data. Remote Sensing of Environment 2020, 237, 111594. [CrossRef]
  13. Song, L.S.; Ding, Z.H.; Kustas, W.P.; Xu, Y.H.; Zhao, G.; Liu, S.M.; Ma, M.G.; Xue, K.J.; Bai, Y.; Xu, Z.W. Applications of a thermal-based two-source energy balance model coupled to surface soil moisture. Remote Sensing of Environment 2022, 271, 112923. [CrossRef]
  14. Song, L.S.; Kustas, W.P.; Liu, S.M.; Colaizzi, P.D.; Nieto, H.; Xu, Z.W.; Ma, Y.F.; Li, M.S.; Xu, T.R.; Agam, N.; et al. Applications of a thermal-based two-source energy balance model using Priestley-Taylor approach for surface temperature partitioning under advective conditions. Journal of Hydrology 2016, 540, 574-587. [CrossRef]
  15. Xu, Y.H.; Song, L.S.; Kustas, W.P.; Xue, K.J.; Liu, S.M.; Ma, M.G.; Xu, T.R.; Zhao, L. Application of the two-source energy balance model with microwave-derived soil moisture in a semi-arid agricultural region. Int J Appl Earth Obs 2022, 112, 102879. [CrossRef]
  16. Knipper, K.; Yang, Y.; Anderson, M.; Bambach, N.; Kustas, W.; McElrone, A.; Gao, F.; Alsina, M.M. Decreased latency in landsat-derived land surface temperature products: A case for near-real-time evapotranspiration estimation in California. Agr Water Manage 2023, 283, 108316. [CrossRef]
  17. Li, Y.; Huang, C.L.; Kustas, W.P.; Nieto, H.; Sun, L.; Hou, J.L. Evapotranspiration Partitioning at Field Scales Using TSEB and Multi-Satellite Data Fusion in The Middle Reaches of Heihe River Basin, Northwest China. Remote Sensing 2020, 12, 3223. [CrossRef]
  18. Guzinski, R.; Nieto, H.; Sandholt, I.; Karamitilios, G. Modelling High-Resolution Actual Evapotranspiration through Sentinel-2 and Sentinel-3 Data Fusion. Remote Sensing 2020, 12, 1433. [CrossRef]
  19. Feng, J.J.; Wang, W.Z.; Che, T.; Xu, F.A. Performance of the improved two-source energy balance model for estimating evapotranspiration over the heterogeneous surface. Agr Water Manage 2023, 278, 108159. [CrossRef]
  20. Song, L.S.; Bateni, S.M.; Xu, Y.H.; Xu, T.R.; He, X.L.; Ki, S.J.; Liu, S.M.; Ma, M.G.; Yang, Y. Reconstruction of remotely sensed daily evapotranspiration data in cloudy-sky conditions. Agr Water Manage 2021, 255, 107000. [CrossRef]
  21. Xu, T.; Liu, S.; Xu, L.; Chen, Y.; Jia, Z.; Xu, Z.; Nielson, J. Temporal Upscaling and Reconstruction of Thermal Remotely Sensed Instantaneous Evapotranspiration. Remote Sensing 2015, 7, 3400-3425. [CrossRef]
  22. Jiang, Y.Z.; Tang, R.L.; Li, Z.L. Reconstruction of daily evapotranspiration under cloudy sky constrained by soil water budget balance. Journal of Hydrology 2022, 605, 127288. [CrossRef]
  23. Cui, Y.K.; Song, L.S.; Fan, W.J. Generation of spatio-temporally continuous evapotranspiration and its components by coupling a two-source energy balance model and a deep neural network over the Heihe River Basin. Journal of Hydrology 2021, 597, 126176. [CrossRef]
  24. Breiman, L. Random forests. Mach Learn 2001, 45, 5-32, doi:Doi 10.1023/A:1010933404324.
  25. Zhou, Z.H.; Feng, J. Deep forest. Natl Sci Rev 2019, 6, 74-86. [CrossRef]
  26. Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. ACM 2016.
  27. Agrawal, Y.; Kumar, M.; Ananthakrishnan, S.; Kumarapuram, G. Evapotranspiration Modeling Using Different Tree Based Ensembled Machine Learning Algorithm. Water Resour Manag 2022, 36, 1025-1042. [CrossRef]
  28. Chatterjee, S.; Kandiah, R.; Watts, D.; Sritharan, S.; Osterberg, J. Estimating Completely Remote Sensing-Based Evapotranspiration for Salt Cedar (Tamarix ramosissima), in the Southwestern United States, Using Machine Learning Algorithms. Remote Sensing 2023, 15, 5021. [CrossRef]
  29. Li, M.Y.; Yang, Q.Q.; Yuan, Q.Q.; Zhu, L.Y. Estimation of high spatial resolution ground-level ozone concentrations based on Landsat 8 TIR bands with deep forest model. Chemosphere 2022, 301, 134817. [CrossRef]
  30. Yuan, Q.Q.; Shen, H.F.; Li, T.W.; Li, Z.W.; Li, S.W.; Jiang, Y.; Xu, H.Z.; Tan, W.W.; Yang, Q.Q.; Wang, J.W.; et al. Deep learning in environmental remote sensing: Achievements and challenges. Remote Sensing of Environment 2020, 241, 111716. [CrossRef]
  31. Duan, S.B.; Lian, Y.H.; Zhao, E.Y.; Chen, H.; Han, W.J.; Wu, Z.H. A Novel Approach to All-Weather LST Estimation Using XGBoost Model and Multisource Data. Ieee T Geosci Remote 2023, 61, 5004614. [CrossRef]
  32. Yu, T.; Zhang, Q.; Sun, R. Comparison of Machine Learning Methods to Up-Scale Gross Primary Production. Remote Sensing 2021, 13, 2448. [CrossRef]
  33. Li, Q.L.; Shi, G.S.; Shangguan, W.; Nourani, V.; Li, J.D.; Li, L.; Huang, F.N.; Zhang, Y.; Wang, C.Y.; Wang, D.G.; et al. A 1 km daily soil moisture dataset over China using in situ measurement and machine learning. Earth System Science Data 2022, 14, 5267-5286. [CrossRef]
  34. Xu, T.R.; Guo, Z.X.; Liu, S.M.; He, X.L.; Meng, Y.F.Y.; Xu, Z.W.; Xia, Y.L.; Xiao, J.F.; Zhang, Y.; Ma, Y.F.; et al. Evaluating Diffferent Machine Learning Methods for Upscaling Evapotranspiration from Flux Towers to the Regional Scale. J Geophys Res-Atmos 2018, 123, 8674-8690. [CrossRef]
  35. Cheng, G.D.; Li, X.; Zhao, W.Z.; Xu, Z.M.; Feng, Q.; Xiao, S.C.; Xiao, H.L. Integrated study of the water-ecosystem-economy in the Heihe River Basin. Natl Sci Rev 2014, 1, 413-428. [CrossRef]
  36. Li, X.; Cheng, G.D.; Liu, S.M.; Xiao, Q.; Ma, M.G.; Jin, R.; Che, T.; Liu, Q.H.; Wang, W.Z.; Qi, Y.; et al. Heihe Watershed Allied Telemetry Experimental Research (HiWATER): Scientific Objectives and Experimental Design. B Am Meteorol Soc 2013, 94, 1145-1160. [CrossRef]
  37. Liu, S.M.; Li, X.; Xu, Z.W.; Che, T.; Xiao, Q.; Ma, M.G.; Liu, Q.H.; Jin, R.; Guo, J.W.; Wang, L.X.; et al. The Heihe Integrated Observatory Network: A Basin-Scale Land Surface Processes Observatory in China. Vadose Zone J 2018, 17, 180072. [CrossRef]
  38. Ji, X.B.; Zhao, W.Z.; Jin, B.W.; Zhao, L.W.; Zhao, W.Y.; Du, Z.Y.; Chen, Z.; Zhang, L.M. A dataset of water, heat, and carbon fluxes of an oasis agroecosystem in the middle areas of the Hexi Corridor (2012–2015). China Scientific Data 2023, 8. [CrossRef]
  39. Zhang, X.D.; Zhou, J.; Liang, S.L.; Wang, D.D. A practical reanalysis data and thermal infrared remote sensing data merging (RTM) method for reconstruction of a 1-km all-weather land surface temperature. Remote Sensing of Environment 2021, 260, 112437. [CrossRef]
  40. Liang, S.L.; Zhao, X.; Liu, S.H.; Yuan, W.P.; Cheng, X.; Xiao, Z.Q.; Zhang, X.T.; Liu, Q.; Cheng, J.; Tang, H.R.; et al. A long-term Global LAnd Surface Satellite (GLASS) data-set for environmental studies. Int J Digit Earth 2013, 6, 5-33. [CrossRef]
  41. Sulla-Menashe, D.; Gray, J.M.; Abercrombie, S.P.; Friedl, M.A. Hierarchical mapping of annual global land cover 2001 to present: The MODIS Collection 6 Land Cover product. Remote Sensing of Environment 2019, 222, 183-194. [CrossRef]
  42. Muñoz-Sabater, J.; Dutra, E.; Agustí-Panareda, A.; Albergel, C.; Arduini, G.; Balsamo, G.; Boussetta, S.; Choulga, M.; Harrigan, S.; Hersbach, H.; et al. ERA5-Land: a state-of-the-art global reanalysis dataset for land applications. Earth System Science Data 2021, 13, 4349-4383. [CrossRef]
  43. Kustas, W.P.; Norman, J.M. A two-source energy balance approach using directional radiometric temperature observations for sparse canopy covered surfaces. Agron J 2000, 92, 847-854, doi:DOI 10.2134/agronj2000.925847x.
  44. Burchard-Levine, V.; Nieto, H.; Riano, D.; Kustas, W.P.; Migliavacca, M.; El-Madany, T.S.; Nelson, J.A.; Andreu, A.; Carrara, A.; Beringer, J.; et al. A remote sensing-based three-source energy balance model to improve global estimations of evapotranspiration in semi-arid tree-grass ecosystems. Global Change Biol 2022, 28, 1493-1515. [CrossRef]
  45. Jaafar, H.H.; Mourad, R.M.; Kustas, W.P.; Anderson, M.C. A Global Implementation of Single- and Dual-Source Surface Energy Balance Models for Estimating Actual Evapotranspiration at 30-m Resolution Using Google Earth Engine. Water Resour Res 2022, 58, e2022WR032800. [CrossRef]
  46. Kustas, W.P.; Alfieri, J.G.; Nieto, H.; Wilson, T.G.; Gao, F.; Anderson, M.C. Utility of the two-source energy balance (TSEB) model in vine and interrow flux partitioning over the growing season. Irrigation Sci 2019, 37, 375-388. [CrossRef]
  47. Cammalleri, C.; Anderson, M.C.; Kustas, A.P. Upscaling of evapotranspiration fluxes from instantaneous to daytime scales for thermal remote sensing applications. Hydrol Earth Syst Sc 2014, 18, 1885-1894. [CrossRef]
  48. Qin, Z.L.; Zhou, X.Y.; Li, M.Y.; Tong, Y.X.; Luo, H.X. Landslide Susceptibility Mapping Based on Resampling Method and FR-CNN: A Case Study of Changdu. Land-Basel 2023, 12, 1213. [CrossRef]
  49. Galindo, F.J.; Palacio, J. Estimating the Instabilities of N Correlated Clocks. 1999.
  50. Xue, B.L.; Wang, L.; Li, X.P.; Yang, K.; Chen, D.L.; Sun, L.T. Evaluation of evapotranspiration estimates for two river basins on the Tibetan Plateau by a water balance method. Journal of Hydrology 2013, 492, 290-297. [CrossRef]
  51. Zhang, C.Y.; Brodylo, D.; Rahman, M.; Rahman, M.A.; Douglas, T.A.; Comas, X. Using an object-based machine learning ensemble approach to upscale evapotranspiration measured from eddy covariance towers in a subtropical wetland. Sci Total Environ 2022, 831, 154969. [CrossRef]
  52. Liang, X.G.; Song, C.Q.; Liu, K.; Chen, T.; Fan, C.Y. Reconstructing Centennial-Scale Water Level of Large Pan-Arctic Lakes Using Machine Learning Methods. J Earth Sci-China 2023, 34, 1218-1230. [CrossRef]
  53. Lundberg, S.; Lee, S.I. A Unified Approach to Interpreting Model Predictions. In Proceedings of the Nips, 2017.
  54. Gao, H.R.; Zhang, Z.J.; Zhang, W.C.; Chen, H.; Xi, M.J. Spatial Downscaling Based on Spectrum Analysis for Soil Freeze/Thaw Status Retrieved From Passive Microwave. Ieee T Geosci Remote 2022, 60, 4300211. [CrossRef]
  55. Oliveira, A.L.I.; Braga, P.L.; Lima, R.M.F.; Cornélio, M.L. GA-based method for feature selection and parameters optimization for machine learning regression applied to software effort estimation. Inform Software Tech 2010, 52, 1155-1166. [CrossRef]
  56. Zuo, X.; Guo, H.; Shi, S.Y.; Zhang, X.C. Comparison of Six Machine Learning Methods for Estimating PM2.5 Concentration Using the Himawari-8 Aerosol Optical Depth. J Indian Soc Remote 2020, 48, 1277-1287. [CrossRef]
Preprints 95744 g001
Figure 1. Study area and vegetation type map in Heihe River Basin, and the location of EC sites in the upstream, midstream and downstream, along with the landscape around the EC sites.
Figure 1. Study area and vegetation type map in Heihe River Basin, and the location of EC sites in the upstream, midstream and downstream, along with the landscape around the EC sites.
Preprints 95744 g001
Preprints 95744 g002
Figure 2. Flowchart of the estimation and reconstruction of the daily T and E based on TSEB and four machine learning methods. Note that: the EC measurement data is used only for accuracy verification.
Figure 2. Flowchart of the estimation and reconstruction of the daily T and E based on TSEB and four machine learning methods. Note that: the EC measurement data is used only for accuracy verification.
Preprints 95744 g002
Preprints 95744 g003
Figure 3. Pearson correlation coefficient matrix of all parameters.
Figure 3. Pearson correlation coefficient matrix of all parameters.
Preprints 95744 g003
Preprints 95744 g004
Figure 4. Validation of all generated daily ET using DF at six EC sites. The dashed line is 1:1 line.
Figure 4. Validation of all generated daily ET using DF at six EC sites. The dashed line is 1:1 line.
Preprints 95744 g004
Preprints 95744 g005
Figure 5. Validation of all generated daily ET using DNN at six EC sites.
Figure 5. Validation of all generated daily ET using DNN at six EC sites.
Preprints 95744 g005
Preprints 95744 g006
Figure 6. Validation of all generated daily ET using RF at six EC sites.
Figure 6. Validation of all generated daily ET using RF at six EC sites.
Preprints 95744 g006
Preprints 95744 g007
Figure 7. Validation of all generated daily ET using XGB at six EC sites.
Figure 7. Validation of all generated daily ET using XGB at six EC sites.
Preprints 95744 g007
Preprints 95744 g008
Figure 8. Validation of reconstructed daily ET by (a) DF, (b) DNN, (c) RF, (d) XGB at EC sites.
Figure 8. Validation of reconstructed daily ET by (a) DF, (b) DNN, (c) RF, (d) XGB at EC sites.
Preprints 95744 g008
Preprints 95744 g009
Figure 9. Spatial distribution of relative uncertainties of daily ET reconstructed by four machine learning methods over the Heihe River Basin.
Figure 9. Spatial distribution of relative uncertainties of daily ET reconstructed by four machine learning methods over the Heihe River Basin.
Preprints 95744 g009
Preprints 95744 g010
Figure 10. Plot of cumulative distribution frequency curves vs. effective coverage percentage of the daily ET. The area of the curve with the X-axis in the figure can represent the missing amount. The blue line in figure indicates that the coverage of daily ET reconstructed by RF or DF is always 100%.
Figure 10. Plot of cumulative distribution frequency curves vs. effective coverage percentage of the daily ET. The area of the curve with the X-axis in the figure can represent the missing amount. The blue line in figure indicates that the coverage of daily ET reconstructed by RF or DF is always 100%.
Preprints 95744 g010
Preprints 95744 g011
Figure 11. Temporal coverage of ET estimated from different machine learning methods (a-d) and original TSEB models (e) in 2016.
Figure 11. Temporal coverage of ET estimated from different machine learning methods (a-d) and original TSEB models (e) in 2016.
Preprints 95744 g011
Preprints 95744 g012
Figure 12. Spatial patterns of (a) TSEB estimated daily ET, and daily ET reconstructed by (b) DF, (c) DNN, (d) XGB and (e) RF in different seasons. The white areas represent missing.
Figure 12. Spatial patterns of (a) TSEB estimated daily ET, and daily ET reconstructed by (b) DF, (c) DNN, (d) XGB and (e) RF in different seasons. The white areas represent missing.
Preprints 95744 g012
Preprints 95744 g013
Figure 13. Average impact values of input parameters calculated by SHAP method.
Figure 13. Average impact values of input parameters calculated by SHAP method.
Preprints 95744 g013
Table 1. Information of the EC measurement stations. MF (mixed forest), DBF (deciduous broadleaved forest), GRA (grassland), CRO (cropland).
Table 1. Information of the EC measurement stations. MF (mixed forest), DBF (deciduous broadleaved forest), GRA (grassland), CRO (cropland).
Station Longitude (°) Latitude
(°)		 Elevation (m) Vegetation Types Time Range
Hunhelin 101.1335 41.9903 874 MF 2013-2016
Arou 100.4643 38.0473 3033 GRA 2013-2016
Daman 100.3722 38.8555 1556 GRO 2013-2016
Linze 100.1408 39.3272 1370 CRO 2012-2015
Dashalong 98.9406 38.8399 3739 WET 2013-2016
Huyanglin 101.1236 41.9928 876 DBF 2013-2015
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated