Prerpints.org logo
Preprint
Article

The Delta-Homotopy Perturbation Method

Altmetrics

Downloads

165

Views

54

Comments

0

This version is not peer-reviewed

Submitted:

06 January 2024

Posted:

09 January 2024

You are already at the latest version

Alerts
Abstract
Homotopy perturbation and analysis methods have been widely used to obtain both approximate and exact so- lutions to nonlinear problems. In general, these two methods are based on the Taylor series with respect to an embedding parameter. Many researchers have compared the two methods and raised more concerns on the homo- topy perturbation method (HPM) because the homotopy analysis method (HAM) contains a convergence-control parameter ~: For this reason, in this article, a more general form of HPM is introduced as the -homotopy per- turbation method (-HPM), which contains a control parameter : The introduction of parameter  in this new modi cation gives a better way to adjust and control the convergence region and the rate of the series solution. We con rm through the given examples in this study that the HPM is a special case of the -HPM. The error and convergence analysis of this proposed method are also presented
Keywords: 
Subject: Computer Science and Mathematics  -   Computational Mathematics

1. Introduction

The notion of homotopy, which is based on the introduction of a parameter p that varies from zero to one, has been used by many researchers to solve nonlinear problems in science and engineering. The problem simplifies to a somewhat trivial problem when p = 0 , which is usually linear and whose solution can be found relatively easily. A family of solutions are obtained when p is incremented to one, which approaches the desired solution as p tends to one.
In 1992, Liao used the basic concept of homotopy to develop a general analytical method called homotopy analysis method (HAM) [43,44]. Liao reiterated the method by inserting an auxiliary parameter ℏ, beside another auxiliary function in his problem formulation. This parameter ℏ can be employed in controlling the convergence of solution series obtained as the power series in p . The HAM has been implemented on a wide class of boundary and initial value problems [1,2,3,10,11,12,19,27,28,45,46,47,48,49,50,51,58,60]. The further search of expanding the convergence region led to a modification of HAM called q-HAM, proposed by El-Tawil and Huseen [17]. The q-HAM have been successful employed to various problems in science and engineering [6,7,8,17,18,35,36,37,38,39,40,41,55,56,57]. On the contrary, He [29] later explained that it was not necessary to use the auxiliary parameter ℏ and proposed another analytical method called the homotopy perturbation method (HPM). This method has gained the attention of researchers and have been used to solve linear and nonlinear problems [16,21,22,23,24,25,29,30,31,32,33,59,62]. However some issues of HPM have been published in [1,53,61,63]. To overcome these issues, an improved modification of HPM called the parameterized homotopy perturbation method (PHPM) was proposed in [4,5]. However, the new modification proposed in this study can be seen as a good refinement of existing numerical methods and can be used to study nonlinear models that describe natural phenomena.
In this paper, we propose a more general form of HPM namely, δ -homotopy perturbation method, ( δ -HPM) which guarantees a convergent series solution. The introduction of a parameter δ in this modification help in adjusting and controlling the convergence region and the convergence rate of solution series. The examples provided in this paper confirm that when the approximation solutions obtained by using HPM is divergent, we can achieve a convergent series solution simply by selecting an appropriate value of δ from the so-called δ -curve where the horizontal line test is employed to attain the intervals containing the optimal values.
This paper is organized as follows: In Section 2, we present the fundamental idea of the proposed method, the error analysis and convergence theorem. The numerical examples, numerical comparison, absolute errors in tabular form and δ -curves of each example are presented in Section 3. Finally, Section 4 gives the conclusion.

2. Analysis of the proposed algorithm

2.1. Fundamental idea of the δ -HPM

Here, we present the basic idea of δ -HPM. We refer the readers to He’s works [29,30,31,32,33,34] for a good understanding of HPM where more developments can be found. To describe the proposed method, consider the nonlinear differential equation
F ( y ( x , t ) ) − g ( x , t ) = 0 , x , t ∈ Ω ,
subject to some boundary conditions
B y , ∂ y ∂ n = 0 , x , t ∈ ∂ Ω .
Here, y ( x , t ) is an unknown function of x and t , F represents the differential operator, B signifies boundary operator, g ( x , t ) is a known analytic function, ∂ Ω is the boundary of the domain Ω , and ∂ y ∂ n is the differentiation in the direction normal to ∂ Ω . The operator F in Eq. (1) can be written in the form F = M + N , where M and N are respectively linear and nonlinear operators. Thus Eq. (1) is reformulated as
M ( y ( x , t ) ) + N ( y ( x , t ) ) − g ( x , t ) = 0 .
In the view of He’s homotopy construction in [31], we formulate the homotopy G ( w ( x , t ; p ) , p ) as:
G ( w ( x , t ; p ) , p ) = 1 − p δ M ( w ( x , t ; p ) ) − M ( y 0 ( x , t ) ) + p F ( w ( x , t ; p ) ) − g ( x , t ) = 0 .
Equivalently,
M ( w ( x , t ; p ) ) − M ( y 0 ( x , t ) ) = p δ M ( w ( x , t ; p ) ) − M ( y 0 ( x , t ) ) − p M ( w ( x , t ; p ) ) + N ( w ( x , t ; p ) ) − g ( x , t ) = p 1 δ − 1 M ( w ( x , t ; p ) ) − p δ M ( y 0 ( x , t ) ) − p N ( w ( x , t ; p ) ) − g ( x , t ) .
The embedding parameter p varies from zero to a nonzero parameter δ , y 0 ( x , t ) is the initial approximation of Eq. (1) satisfying the boundary conditions Eq. (2). From Eq. (4) with p = 0 and p = δ , we obtain the following:
M ( w ( x , t ; 0 ) ) − M ( y 0 ( x , t ) ) = 0 , F ( w ( x , t ; δ ) ) − g ( x , t ) = 0 .
The variation of p from zero to δ corresponds to precisely that of w ( x , t ; p ) from y 0 ( x , t ) to the solution y ( x , t ) . This process is called in topology, deformation process. Now, we make the critical assumption that the solution of Eq. (4) can be expressed as a power series in p given as
w ( x , t ; p ) = ∑ r = 0 ∞ w r ( x , t ) p r .
By setting p = δ , the solution of Eq. (1) can be obtained as
y ( x , t ) = lim p → δ w ( x , t ; p ) = ∑ r = 0 ∞ Y r ( x , t ; δ ) = ∑ r = 0 ∞ w r ( x , t ) δ r .
Remark. 
It should be noted that the special case with δ = 1 is the standard HPM.

2.2. Convergence and error analysis

Theorem 1. 
Let Y m ( x , t ; δ ) and y ( x , t ) be defined in Banach space B [42]. Then the series solution defined in Eq. (7) as
∑ r = 0 ∞ Y r ( x , t ; δ ) = ∑ r = 0 ∞ w r ( x , t ) δ r ,
is convergent for a prescribed value of δ , if
Y r + 1 ≤ β | δ | Y r , ∀ Y 0 ∈ B ,
for some β such that 0 < β < | δ | .
Proof. 
We first define a sequence of partial sums { P m } m = 0 ∞ as follows
P 0 = w 0 , P 1 = w 0 + w 1 δ , P 2 = w 0 + w 1 δ + w 2 δ 2 , ⋮ P m = w 0 + w 1 δ + w 2 δ 2 + ⋯ + w m δ m .
Then, we show that { P m } m = 0 ∞ is a Cauchy sequence in the Banach space B . Thus, for a nonzero parameter δ , we have
P m + 1 − P m = Y m + 1 ≤ β | δ | Y m ≤ β | δ | 2 Y m − 1 ≤ ⋯ ≤ β | δ | m + 1 Y 0 .
For every m , n ∈ N with m ≥ n , and applying the triangle inequality, we obtain
P m − P n = ( P m − P m − 1 ) + ( P m − 1 − P m − 2 ) + ⋯ + ( P n + 1 − P n ) ≤ P m − P m − 1 + P m − 1 − P m − 2 + ⋯ + P n + 1 − P n ≤ β | δ | m Y 0 + β | δ | m − 1 Y 0 + ⋯ + β | δ | n + 1 Y 0 ≤ β | δ | n + 1 β | δ | m − n − 1 + β | δ | m − n − 2 + ⋯ + β | δ | + 1 Y 0 ≤ β | δ | n + 1 1 − β | δ | m − n 1 − β | δ | Y 0 .
Since 0 < β < | δ | , we have 1 − β | δ | m − n < 1 . Hence, Eq. (13) implies
P m − P n ≤ β | δ | n + 1 1 − β | δ | Y 0 .
Considering that Y 0 < ∞ , we have
lim m → ∞ P m − P n = 0 .
Therefore, { P m } m = 0 ∞ is a Cauchy sequence in the Banach space B and every Cauchy sequence is a convergent sequence. Accordingly, the series solution defined in Eq. (7) is convergent.   □
Theorem 2. 
Suppose that the truncated series
∑ r = 0 Λ Y r ( x , t ; δ ) = ∑ r = 0 Λ w r ( x , t ) δ r ,
is utilized as an approximate solution of 1. Then the maximum absolute truncation error is projected as
y ( x , t ) − ∑ r = 0 Λ Y r ( x , t ; δ ) ≤ β | δ | Λ + 1 1 − β | δ | Y 0 .
Proof. 
This follows from inequality 13 in Theorem 1. In particular, for m ≥ Λ , we have
P m − P Λ ≤ β | δ | Λ + 1 1 − β | δ | m − Λ 1 − β | δ | Y 0 .
As m → ∞ , for a prescribed value of δ , P m → y ( x , t ) and 1 − β | δ | m − Λ < 1 . Hence,
y ( x , t ) − ∑ r = 0 Λ Y r ( x , t ; δ ) ≤ β | δ | Λ + 1 | δ | | δ | − β Y 0 ,
where Y 0 = w 0 = y 0 . This completes the proof.  □

3. Numerical examples

Example 1. 
Consider the partial differential equation [24,53]
∂ y ∂ t + ∂ y ∂ x = 2 ∂ 3 y ∂ x 2 ∂ t , x ∈ R , t > 0 ,
with the initial condition
y ( x , 0 ) = e − x .
The exact solution is
y ( x , t ) = e − x − t .
In order to solve Eq. (20) with initial condition Eq. (21), we construct the following homotopy:
1 − p δ ∂ w ∂ t − ∂ y 0 ∂ t + p ∂ w ∂ t + ∂ w ∂ x − 2 ∂ 3 w ∂ x 2 ∂ t = 0 .
Equivalently,
∂ w ∂ t − ∂ y 0 ∂ t = p δ ∂ w ∂ t − ∂ y 0 ∂ t − p ∂ w ∂ t + ∂ w ∂ x − 2 ∂ 3 w ∂ x 2 ∂ t .
Substituting Eq. (7) into Eq. (24) and setting the identical powers of p equal to each other, we obtain
p ( 0 ) : ∂ w 0 ∂ t − ∂ y 0 ∂ t = 0 , p ( 1 ) : ∂ w 1 ∂ t = 1 δ − 1 ∂ w 0 ∂ t − 1 δ ∂ y 0 ∂ t − ∂ w 0 ∂ x + 2 ∂ 3 w 0 ∂ x 2 ∂ t , w 1 ( x , 0 ) = 0 , p ( 2 ) : ∂ w 2 ∂ t = 1 δ − 1 ∂ w 1 ∂ t − ∂ w 1 ∂ x + 2 ∂ 3 w 1 ∂ x 2 ∂ t , w 2 ( x , 0 ) = 0 , ⋮ p ( r ) : ∂ w r ∂ t = 1 δ − 1 ∂ w r − 1 ∂ t − ∂ w r − 1 ∂ x + 2 ∂ 3 w r − 1 ∂ x 2 ∂ t , w r ( x , 0 ) = 0 , r = 2 , 3 , 4 , ⋯ .
For simplicity we take w 0 ( x , t ) = y 0 ( x , t ) = e − x and we obtain the following recurrence relations:
w 1 ( x , t ) = ∫ 0 t − ∂ w 0 ( x , ξ ) ∂ x + 2 ∂ 3 w 0 ( x , ξ ) ∂ x 2 ∂ ξ d ξ , w r ( x , t ) = ∫ 0 t 1 δ − 1 ∂ w r − 1 ( x , ξ ) ∂ ξ − ∂ w r − 1 ( x , ξ ) ∂ x + 2 ∂ 3 w r − 1 ( x , ξ ) ∂ x 2 ∂ ξ d ξ , r = 2 , 3 , 4 , ⋯ .
The components of the δ -HPM solution are obtained from Eq. (26) as follows:
w 0 ( x , t ) = e − x , w 1 ( x , t ) = t e − x , w 2 ( x , t ) = t e − x 2 δ δ t + 2 δ + 2 , w 3 ( x , t ) = t e − x 6 δ 2 δ 2 t 2 + 6 δ 2 t + 6 δ 2 + 6 δ t + 12 δ + 6 , w 4 ( x , t ) = t e − x 24 δ 3 ( δ 3 t 3 + 12 δ 3 t 2 + 36 δ 3 t + 24 δ 3 + 12 δ 2 t 2 + 72 δ 2 t + 72 δ 2 + 36 δ t + 72 δ + 24 ) , w 5 ( x , t ) = t e − x 120 δ 4 ( δ 4 t 4 + 20 δ 4 t 3 + 120 δ 4 t 2 + 240 δ 4 t + 120 δ 4 + 20 δ 3 t 3 + 240 δ 3 t 2 + 720 δ 3 t + 480 δ 3 + 120 δ 2 t 2 + 720 δ 2 t + 720 δ 2 + 240 δ t + 480 δ + 120 ) , w 6 ( x , t ) = t e − x 720 δ 5 ( δ 5 t 5 + 30 δ 5 t 4 + 300 δ 5 t 3 + 1200 δ 5 t 2 + 1800 δ 5 t + 720 δ 5 + 30 δ 4 t 4 + 600 δ 4 t 3 + 3600 δ 4 t 3 + 7200 δ 4 t + 3600 δ 4 + 300 δ 3 t 3 + 3600 δ 3 t 2 + 10800 δ 3 t + 7200 δ 3 + 1200 δ 2 t 2 + 7200 δ 2 t + 7200 δ 2 + 1800 δ t + 3600 δ + 720 ) , ⋮
The ( Λ + 1 ) term approximate solution for problem (20)-(21) is
Y Λ ( x , t ; δ ) = ∑ r = 0 Λ w r ( x , t ) δ r = w 0 + w 1 δ + w 2 δ 2 + w 3 δ 3 + ⋯ + w Λ δ Λ .
Setting δ = 1 in Eq. (28) with reference to Eq. (27), we have
Y 6 ( x , t ; 1 ) = e − x 720 t 6 + 66 t 5 + 1470 t 4 + 13320 t 3 + 46440 t 2 + 45360 t + 720 ,
which is precisely same solution obtained by Ganji et al. [24] using HPM. As a consequence, the HPM solution is undoubtedly a special case of the δ -HPM solution with δ = 1 . Liang et al. [53] shows that for a given x ≥ 0 , the HPM solution Eq. (29) increases monotonously to infinity as t increases and very quickly the relative error increases monotonously. Indeed, one can easily verify that the HPM solution series is divergent for every t and x except at t = 0 , nevertheless corresponds to y ( x , 0 ) = e − x , the given initial condition. In a nutshell, the radius of convergence of the series solution Eq. (29) by HPM is zero. The use of HPM in this example might produce a divergent approximations. But it is important to obtain a convergent series solution. For this reason, we introduce the parameter δ to ensure the convergence of the solution series by δ -HPM. In this example we demonstrated that, if the approximations given by the standard HPM is divergent, one can still achieve a convergent solution series simply by choosing a suitable δ value from the δ -curve. In other words, to select an appropriate δ that guarantees a convergent series solution, we first plot the δ -curve of 16 t h order approximate solution, as shown in Figure 1, and use the line segment nearly parallel to the horizontal axis as a valid region of δ .  Table 1 shows that the 16 t h order approximate solution series obtained by the standard HPM is divergent for every t and x except at t = 0 and the absolute error monotonously increases very quickly. However, the 16 t h order approximate solution series obtained by δ -HPM with δ = − 1 is in good agreement with the exact solution. Furthermore, it is easily seen from Eq. (27) that the δ -HPM solutions with δ = − 1 yields
Y 1 ( x , t ; − 1 ) = e − x ( 1 − t ) , Y 2 ( x , t ; − 1 ) = e − x 1 − t + t 2 2 ! , Y 3 ( x , t ; − 1 ) = e − x 1 − t + t 2 2 ! − t 3 3 ! , Y 4 ( x , t ; − 1 ) = e − x 1 − t + t 2 2 ! − t 3 3 ! + t 4 4 ! , Y 5 ( x , t ; − 1 ) = e − x 1 − t + t 2 2 ! − t 3 3 ! + t 4 4 ! − t 5 5 ! , Y 6 ( x , t ; − 1 ) = e − x 1 − t + t 2 2 ! − t 3 3 ! + t 4 4 ! − t 5 5 ! + t 6 6 ! , ⋮ Y Λ ( x , t ; − 1 ) = e − x ∑ r = 0 Λ ( − t ) r r ! .
Thus,
y ( x , t ) = e − x lim Λ → ∞ ∑ r = 0 Λ ( − t ) r r ! = e − x − t ,
which is obviously the exact solution. Therefore, the convergence-control parameter δ in this new modification equips us with a convenient way to guarantee the convergence of series solution.
Example 2. 
Consider the nonlinear partial differential Burger’s equation [26]
∂ y ∂ t + y ∂ y ∂ x = ∂ 2 y ∂ x 2 , ( x , t ) ∈ R × 0 , 1 2 ,
with the initial condition
y ( x , 0 ) = 2 x .
This equation characterizes various phenomena, for instance, a mathematical model of turbulence and the approximation theory of the flow through a shock wave traveling in a viscous fluid [13]. The exact solution is
y ( x , t ) = 2 x 2 t + 1 .
In order to solve Eq. (32) with initial condition Eq. (33), we construct the following homotopy:
1 − p δ ∂ w ∂ t − ∂ y 0 ∂ t + p ∂ w ∂ t + w ∂ w ∂ x − ∂ 2 w ∂ x 2 = 0 .
Equivalently,
∂ w ∂ t − ∂ y 0 ∂ t = p δ ∂ w ∂ t − ∂ y 0 ∂ t − p ∂ w ∂ t + w ∂ w ∂ x − ∂ 2 w ∂ x 2 .
Substituting Eq. (7) into Eq. (36) and setting the identical powers of p equal to each other, we obtain
p ( 0 ) : ∂ w 0 ∂ t − ∂ y 0 ∂ t = 0 , p ( 1 ) : ∂ w 1 ∂ t = 1 δ − 1 ∂ w 0 ∂ t − 1 δ ∂ y 0 ∂ t − w 0 ∂ w 0 ∂ x + ∂ 2 w 0 ∂ x 2 , w 1 ( x , 0 ) = 0 , p ( 2 ) : ∂ w 2 ∂ t = 1 δ − 1 ∂ w 1 ∂ t − w 0 ∂ w 1 ∂ x − w 1 ∂ w 0 ∂ x + ∂ 2 w 1 ∂ x 2 , w 2 ( x , 0 ) = 0 , ⋮ p ( r ) : ∂ w r ∂ t = 1 δ − 1 ∂ w r − 1 ∂ t − ∑ m = 0 r − 1 w m ∂ w r − m − 1 ∂ x − ∂ 2 w r − 1 ∂ x 2 , w r ( x , 0 ) = 0 , r = 2 , 3 , 4 , ⋯ .
Case 1. 
For simplicity we take w 0 ( x , t ) = y 0 ( x , t ) = 2 x ( 1 + t ) and we obtained the following recurrent relation
w 1 ( x , t ) = ∫ 0 t − ∂ w 0 ( x , ξ ) ∂ ξ − w 0 ( x , ξ ) ∂ w 0 ( x , ξ ) ∂ x + ∂ 2 w 0 ( x , ξ ) ∂ x 2 d ξ , w r ( x , t ) = ∫ 0 t 1 δ − 1 ∂ w r − 1 ( x , ξ ) ∂ ξ + ∑ m = 0 r − 1 w m ∂ w r − m − 1 ( x , ξ ) ∂ x − ∂ 2 w r − 1 ( x , ξ ) ∂ x 2 d ξ , r = 2 , 3 , 4 , ⋯ .
The components of the δ-HPM solution are obtain from Eq. (38) as follows:
w 0 ( x , t ) = 2 x ( 1 + t ) , w 1 ( x , t ) = − 6 x t − 4 x t 2 − 4 3 x t 3 , w 2 ( x , t ) = 6 ( δ − 1 ) δ x t + 4 ( 4 δ − 1 ) δ x t 2 + 4 ( 11 δ − 1 ) 3 δ x t 3 + 16 3 x t 4 + 16 15 x t 5 , w 3 ( x , t ) = − 6 ( δ − 1 ) 2 δ 2 x t − 4 ( 7 δ 2 − 8 δ + 1 ) δ 2 x t 2 − 4 ( 42 δ 2 − 22 δ + 1 ) 3 δ 2 x t 3 − 16 ( 9 δ − 2 ) 3 δ x t 4 − 32 ( 11 δ − 1 ) 15 δ x t 5 − 272 45 x t 6 − 272 315 x t 7 , ⋮
The ( Λ + 1 ) term approximate solution for problem (32)-(33) is
Y Λ ( x , t ; δ ) = ∑ r = 0 Λ w r ( x , t ) δ r = w 0 + w 1 δ + w 2 δ 2 + w 3 δ 3 + ⋯ + w Λ δ Λ .
Setting δ = 1 in Eq. (40) with reference to Eq. (39), we have
Y 3 ( x , t ; 1 ) = 2 x − 4 x t + 8 x t 2 − 16 x t 3 − 32 x t 4 − 304 15 x t 5 − 272 45 x t 6 − 272 315 x t 7 .
Case 2. 
Alternatively, by taking w 0 ( x , t ) = y 0 ( x , t ) = 2 x , then from Eq. (38), we obtain the following
w 0 ( x , t ) = 2 x , w 1 ( x , t ) = − 4 x t , w 2 ( x , t ) = 4 x t ( δ + 2 δ t − 1 ) δ , w 3 ( x , t ) = − 4 x t ( δ + 2 δ t − 1 ) 2 δ 2 , ⋮ w r ( x , t ) = ( − 1 ) r 4 x t ( δ + 2 δ t − 1 ) r − 1 δ r − 1 , r = 1 , 2 , 3 , ⋯ .
The ( Λ + 1 ) term approximate solution for problem (32)-(33) is
Y Λ ( x , t ; δ ) = ∑ r = 0 Λ w r ( x , t ) δ r = 2 x + ∑ r = 1 Λ ( − 1 ) r 4 x t δ ( δ + 2 δ t − 1 ) r − 1 .
Setting δ = 1 in Eq. (43) with reference to Eq. (42), we have
Y Λ ( x , t ; 1 ) = 2 x ∑ r = 0 Λ ( − 1 ) r ( 2 t ) r .
which is in agreement with the solution obtained using HPTM [14]. Furthermore, from Eq. (44), we have the exact solution as
y ( x , t ) = 2 x lim Λ → ∞ ∑ r = 0 Λ ( − 1 ) r ( 2 t ) r = 2 x 2 t + 1 .
Remark 2. 
It should be noted in case 2 that
lim m → ∞ w m + 1 w m = δ + 2 δ t − 1 < 1 .
Thus, in agreement with Theorem 1 and holds for the values of − 1 2 < t < 2 − δ 2 δ . For example, δ = 1 , holds for the values of − 1 2 < t < 1 2 .
Remark 3. 
From Table 2, we can observe that it is better to seek other values for δ besides 1. For example, δ = 0.80 gives a better approximation when compared with δ = 1 . Thus, δ-HPM is more general and reliable than HPM.
Example 3. 
Consider Bratu’s first boundary value problem [9,20,64]
d 2 y d x 2 + λ e y = 0 , 0 ≤ x ≤ 1 ,
with the boundary conditions
y ( 0 ) = 0 , y ( 0 ) = 1 .
This problem comes originally from a simplification of the solid fuel ignition model in thermal combustion theory. The exact solution of Eq. (47) and Eq. (48) is
y ( x ) = − 2 ln cosh θ 2 x − 1 2 cosh ( θ 4 ) ,
where θ satisfies θ = 2 λ cosh ( θ 4 ) .
In order to solve Eq. (47) with the boundary condition Eq. (48), we expand e y into a Taylor series as
e y = ∑ r = 0 ∞ y r r ! = 1 + y + y 2 2 + y 3 6 + ⋯ ,
Now, we construct the following homotopy:
1 − p δ d 2 w d x 2 − d 2 y 0 d x 2 + p d 2 w d x 2 + λ + λ w + λ 2 w 2 + λ 6 w 3 = 0 .
Equivalently,
d 2 w d x 2 − d 2 y 0 d x 2 = p δ d 2 w d x 2 − d 2 y 0 d x 2 − p d 2 w d x 2 + λ + λ w + λ 2 w 2 + λ 6 w 3 .
Substituting Eq. (7) into Eq. (52) and setting the identical powers of p equal to each other, we obtain
p ( 0 ) : d 2 w 0 d x 2 − d 2 y 0 d x 2 = 0 , w 0 ( 0 ) = 0 , w 0 ( 1 ) = 0 , p ( 1 ) : d 2 w 1 d x 2 = 1 δ − 1 d 2 w 0 ∂ x 2 − 1 δ d 2 y 0 d x 2 − λ − λ w 0 − λ 2 w 0 2 − λ 6 w 0 3 , w 1 ( 0 ) = 0 , w 1 ( 1 ) = 0 , p ( 2 ) : d 2 w 2 d x 2 = 1 δ − 1 d 2 w 1 d x 2 − λ w 1 − λ w 0 w 1 − λ 2 w 0 2 w 1 , w 2 ( 0 ) = 0 , w 2 ( 1 ) = 0 , ⋮ p ( r ) : d 2 w r d x 2 = 1 δ − 1 d 2 w r − 1 d x 2 − λ w r − 1 − λ 2 ∑ m = 0 r − 1 w m w r − m − 1 − λ 6 ∑ m = 0 r − 1 ∑ k = 0 m w k w m − k w r − m − 1 , w r ( 0 ) = 0 , w r ( 1 ) = 0 , r = 2 , 3 , 4 , ⋯ .
Considering d 2 w 0 d x 2 − d 2 y 0 d x 2 = 0 with boundary conditions w 0 ( 0 ) = 0 and w 0 ( 1 ) = 0 , we have w 0 ( x ) = y 0 ( x ) = 0 . From Eq. (53), we obtain the following recurrence relations
w 1 ( x ) = ∫ 0 x ∫ 0 x − λ d ξ d ξ + C 1 x + C 1 ′ , w 1 ( 0 ) = 0 , w 1 ( 1 ) = 0 , w r ( x ) = ∫ 0 x ∫ 0 x { 1 δ − 1 d 2 w r − 1 ( ξ ) d ξ 2 − λ w r − 1 ( ξ ) − λ 2 ∑ m = 0 r − 1 w m ( ξ ) w r − m − 1 ( ξ ) − λ 6 ∑ m = 0 r − 1 ∑ k = 0 m w k ( ξ ) w m − k ( ξ ) w r − m − 1 ( ξ ) } d ξ d ξ + C r x + C r ′ , w r ( 0 ) = 0 , w r ( 1 ) = 0 , r = 2 , 3 , ⋯ ,
where C 1 , C 1 ′ , C r , and C r ′ are the integration constants to be determined. The components of the δ -HPM solution are obtained from Eq. (54) as follows:
w 0 ( x ) = 0 , w 1 ( x ) = λ 2 x − x 2 , w 2 ( x ) = λ x 2 24 δ λ δ x 2 − 2 λ δ x + 12 δ − 12 + λ x 24 δ λ δ − 12 δ + 12 , w 3 ( x ) = λ x 2 1440 δ 2 ( − 8 λ 2 δ 2 x 4 + 24 λ 2 δ 2 x 3 − 15 λ 2 δ 2 x 2 − 10 λ 2 δ 2 x − 120 λ δ 2 x 2 + 240 λ δ 2 x + 120 λ δ x 2 − 240 λ δ x − 720 δ 2 + 1440 δ − 720 ) + λ x 1440 δ 2 9 λ 2 δ 2 − 120 λ δ 2 + 120 λ δ + 720 δ 2 − 1440 δ + 720 w 4 ( x ) = λ x 20160 δ 3 ( 23 δ 3 λ 3 − 378 δ 3 λ 2 + 2520 δ 3 λ − 10080 δ 3 + 378 δ 2 λ 2 − 5040 δ 2 λ + 30240 δ 2 + 2520 δ λ − 30240 δ + 10080 ) + λ x 2 20160 δ 3 ( 2520 δ ( λ x 2 − 2 λ x + 12 ) − 42 δ 2 ( 8 λ 2 x 4 − 24 λ 2 x 3 + 15 λ ( λ + 8 ) x 2 + 10 ( λ − 24 ) λ x + 720 ) − 10080 ) + δ 3 ( 17 λ 3 x 6 − 68 λ 3 x 5 + 7 λ 2 ( 11 λ + 48 ) x 4 + 7 ( λ − 144 ) λ 2 x 3 − 35 λ λ 2 − 18 λ − 72 x 2 − 21 λ ( λ 2 − 20 λ + 240 ) x + 10080 ) ) ⋮
The ( Λ + 1 ) term approximate solution for the boundary value problem (47)-(48) is
Y Λ ( x ; δ ) = ∑ r = 0 Λ w r ( x ) δ r = w 0 + w 1 δ + w 2 δ 2 + w 3 δ 3 + ⋯ + w Λ δ λ .
Setting δ = 1 in Eq. (56) with reference to Eq. (55), we have
Y 4 ( x ; 1 ) = λ 2 x − x 2 + λ 2 24 x 4 − 2 x 3 + x + λ 3 1440 − 8 x 6 + 24 x 5 − 15 x 4 − 10 x 3 + 9 x + λ 4 20160 17 x 8 − 68 x 7 + 77 x 6 + 7 x 5 − 35 x 4 − 21 x 3 + 23 x ,
which is precisely the same solution obtained by Feng et al. [20] using HPM.
Remark 4. 
From Table 3, we can observe that the result with the present modification called δ-HPM is more accurate than the result of HPM (δ-HPM with δ = 1 ) and PIA [9]. PIA represents perturbation–iteration algorithms.
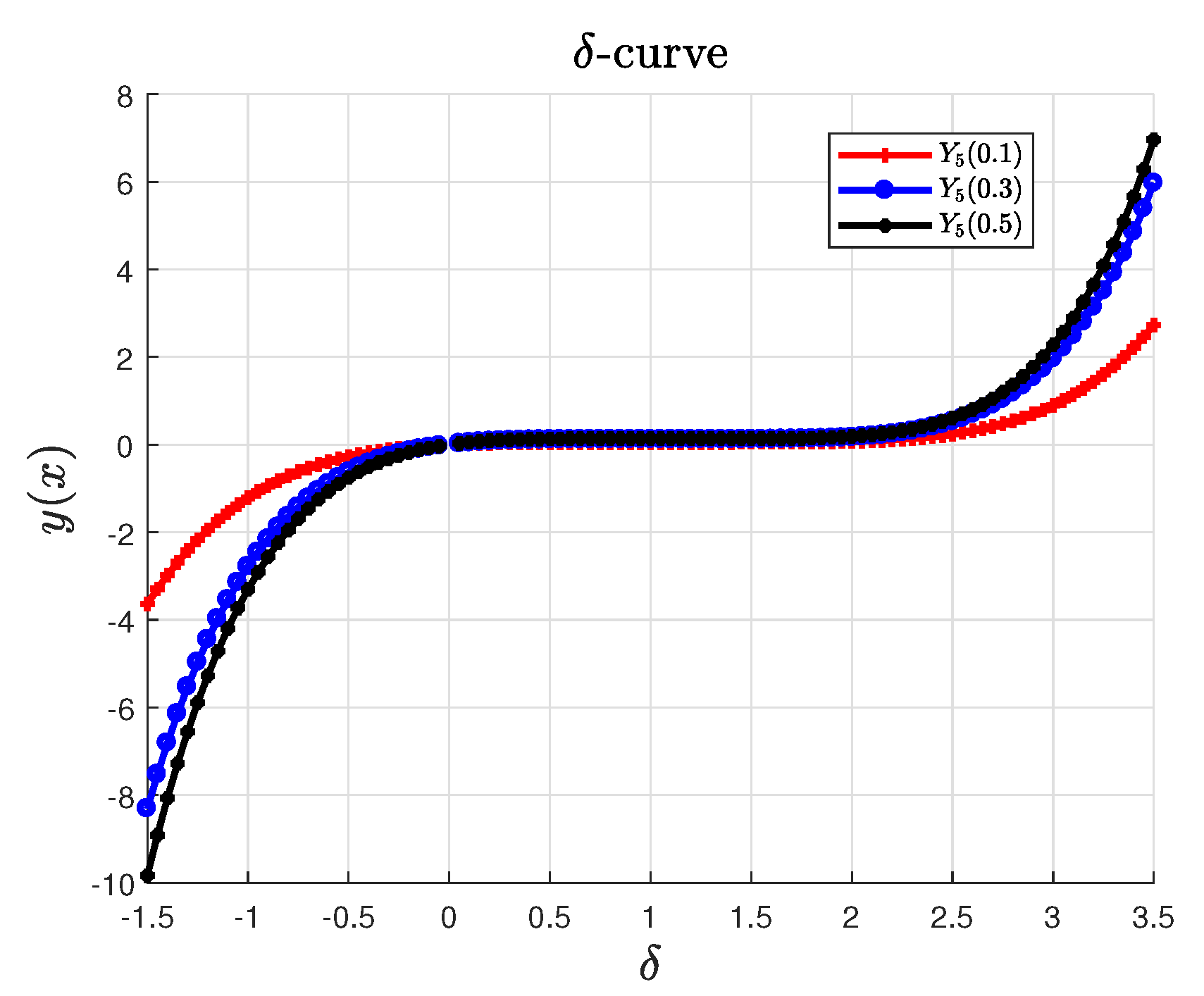
Preprints 95691 g003
Figure 3. The δ -curve of Y 5 ( x ) solution with different x for Example 3
Figure 3. The δ -curve of Y 5 ( x ) solution with different x for Example 3
Preprints 95691 g003

4. Concluding remarks

In this present paper, we introduced a generalization of the homotopy perturbation method, (HPM) proposed by He [29]. We call the generalization the δ-homotopy perturbation method (δ-HPM). We compared the δ-HPM and the HPM through some models arising from engineering and physics. It is verified in these examples that HPM is actually a special case of δ-HPM for δ = 1. As stated by Liao [52], “the homotopy perturbation method had to use a good enough initial guess,” but this is not the case for δ-HPM because of the use of the δ-curve that provides us some range for δ that guarantee a convergent series solution. The parameter δ provides us the flexibility to adjust and control the convergence region including the rate of series solution. Hence, by using δ-HPM, one can overcome a divergent result produced by HPM. A high level of accuracy reveals the complete efficiency and reliability of the proposed method.

References

  1. Abbasbandy, S.: The application of homotopy analysis method to nonlinear equations arising in heat transfer. Physics Letters A 360, 109-113 (2006). [CrossRef]
  2. Abbasbandy, S., Shirzadi, A.: Homotopy analysis method for multiple solutions of the fractional Sturm-Liouville problems, Numerical Algorithms 54, 521-532 (2010). [CrossRef]
  3. Abbasbandy, S., Ashtiani, M., Babolian, E.: Analytic solution of the SharmaTasso-Olver equation by homotopy analysis method. Zeitschrift für Naturforschung 65(4), 285-290 (2014). [CrossRef]
  4. Adamu, M.Y., Ogenyi, P.: Parameterized Homotopy Perturbation Method, Nonlinear Science Letters A 8(2), 240-243 (2017).
  5. Adamu, M.Y., Ogenyi, P.: New approach to parameterized homotopy perturbation method. Therm. Sci. 22, 1815–1870 (2018). [CrossRef]
  6. Akinyemi, L., Iyiola, O.S., Akpan, U.: Iterative methods for solving fourth- and sixth-order time-fractional Cahn-Hillard equation. Math. Meth. Appl. Sci. 1–25 (2020). [CrossRef]
  7. Akinyemi, L.: q-Homotopy analysis method for solving the seventh-order time-fractional Lax’s Korteweg–de Vries and Sawada-Kotera equations. Comp. Appl. Math. 38(4), 1-22 (2019).
  8. Akinyemi, L., Iyiola, O. S.: Analytical Study of (3+1)-Dimensional Fractional-Reaction Diffusion Trimolecular Models. International J. Appl. Comput. Math. 7(3), 1-24 (2021). [CrossRef]
  9. Aksoy, Y., Pakdemirli, M.: New perturbation-iteration solutions for Bratu-type equations. Comput. Math. Appl. 59(8), 2802–2808 (2010). [CrossRef]
  10. Ayub, M., Rasheed, A., Hayat, T.: Exact flow of a third grade fluid past a porous plate using homotopy analysis method. Inter. J. Eng. Sci. 41, 2091-2103 (2003). [CrossRef]
  11. Bataineh, A.S., Noorani, M.S.M., Hashim, I.: Homotopy analysis method for singular IVPs of Emden-Fowler type. Communications in Nonlinear Science and Numerical Simulation 14, 1121-1131 (2009). [CrossRef]
  12. Bataineh, A.S., Noorani, M.S.M., Hashim, I.: Solving systems of ODEs by homotopy analysis method, Communications in Nonlinear Science and Numerical Simulation 13, 2060-2070 (2008).
  13. Benton Edward, R.: Some new exact, viscous, nonsteady solutions of burgers’ equation. Phys. Fluids 9, 1247–1248 (1966).
  14. Biazar, J., Ghazvini, H.: Convergence of the homotopy perturbation method for partial differential equations. Nonlinear Analysis Real World Applications 10(5), 2633–2640 (2009). [CrossRef]
  15. Crane, L.: Flow past a stretching plate. Z. Angew. Math. Phys. 21, 645–647 (1970). [CrossRef]
  16. Elbeleze, A.A., Kılıçman, A. Taib, B.M.: Note on the convergence analysis of homotopy perturbation method for fractional partial differential equations. Abstract and Applied Analysis, 2014, 1-8 (2014).
  17. El-Tawil, M.A., Huseen, S.N.: The q-Homotopy Analysis Method (qHAM). Inter. J. Appl. math. mech. 8(15), 51-75 (2012).
  18. El-Tawil, M.A, Huseen, S.N.: On Convergence of The q-Homotopy Analysis Method, Int. J. Contemp. Math. Sciences 8(10), 481-497 (2013). [CrossRef]
  19. Fadravi, H.H., Nik, H.S., Buzhabadi, R.: Homotopy Analysis Method for Solving Foam Drainage Equation with Space- and Time Fractional Derivatives. Int. J. Differ. Equ. 2011(12), 1-12 (2011). 2011. [CrossRef]
  20. Feng, X., He, Y., Meng, J.: Application of homotopy perturbation method to the Bratu-type equations. Topol. Meth. Nonli. Anal 31(2), 243–252 (2008). [CrossRef]
  21. Ganji, D.D., Rajabi, A.: Assessment of homotopy-perturbation and perturbation methods in heat radiation equations. International Communications in Heat and Mass Transfer 33, 391-400 (2006).
  22. Ganji, D.D., Rafei, M.: Solitary wave solutions for a generalized HirotaSatsuma coupled KdV equation by homotopy perturbation method. Physics Letters A 356, 131-137 (2006). [CrossRef]
  23. Ganji, D.D., Afrouzi, G.A., Hosseinzadeh, H., Talarposhti, R.A.: Application of Homotopy perturbation method to the second kind of nonlinear integral equations. Phy. Letters A 371, 20-25 (2007). [CrossRef]
  24. Ganji, D.D., Tari, H., Bakhshi Jooybari, M.: Variational iteration method and homotopy perturbation method for nonlinear evolution equations. Comput. Math. Appl. 54, 1018-1027 (2007). [CrossRef]
  25. Ganji, D.D., Sadighi, A.: Application of He’s Homotopy-perturbation Method to Nonlinear Coupled Systems of Reaction-diffusion Equations, International Journal of Nonlinear Sciences and Numerical Simulation 7(4), 411-418 (2011).
  26. Gorguis, A.: A comparison between Cole-Hopf transformation and the decomposition method for solving Burgers equations. Appl. Math. Comput. 173, 126–136 (2006).
  27. Hashim, I. Abdulaziz, O., Momani, S.: Homotopy analysis method for fractional IVPs, Communications in Nonlinear Science and Numerical Simulation 14, 674–684 (2009).
  28. Hayat, T., Khan, M., Asghar, S.: Homotopy analysis of MHD flows of an Oldroyd 8-constant fluid. Acta Mechanica 168(3-4), 213-232 (2004). [CrossRef]
  29. He, J.H.: Homotopy perturbation technique. Comput. Methods Appl. Mech. Eng. 178(3-4), 257-262 (1999). [CrossRef]
  30. He, J.H.: A coupling method of homotopy technique and perturbation technique for nonlinear problems. Int. J. Nonlinear. Mech. 35(1), 37-43 (2000).
  31. He J.H.: Homotopy Perturbation Method: A New Nonlinear Analytical Technique, Appl. Math. Comput. 135, 73–79, (2003).
  32. He, J.H.: Limit cycle and bifurcation of nonlinear problems. Chaos Soliton. Fract. 26, 827-833 (2005). [CrossRef]
  33. He, J.H.: Homotopy perturbation method for bifurcation of nonlinear problems. Int. J. Nonlinear. Sci. Numer. Simul. 6(2), 207-208 (2005). [CrossRef]
  34. He, J.H.: Recent development of the homotopy perturbation method Topol. Methods. Non linear Anal. 31, 205-209 (2008).
  35. Huseen, S.N., Grace, S,R.: Approximate Solutions of Nonlinear Partial Differential Equations by Modified q-Homotopy Analysis Method (mq-HAM). J. Appl. Math. 2013, 1-9 (2013) Article ID 569674.
  36. Huseen, S.N., Grace, S.R., El-Tawil, M.A.: The Optimal q-Homotopy Analysis Method (Oq-HAM). International Journal of Computers and Technology 11(8), 2859-2866 (2013).
  37. Huseen, S.N.: Application of optimal q-homotopy analysis method to second order initial and boundary value problems. Int. J. Sci. Innovative Math. Res. 3, 18–24 (2015). 2015; 3.
  38. Huseen, S.N.: Solving the K(2,2) Equation by Means of the q-Homotopy Analysis Method (q-HAM). International Journal of Innovative Science, Engineering and Technology 2(8), 805-817 (2015).
  39. Huseen, S.N.: Series Solutions of Fractional Initial-Value Problems by qHomotopy Analysis Method. International Journal of Innovative Science, Engineering and Technology 3(1), 27-41 (2016).
  40. Huseen, S.N.: A Numerical Study of One-Dimensional Hyperbolic Telegraph Equation. Journal of Mathematics and System Science 7, 62-72 (2017).
  41. Iyiola, O.S., Ojo, G.O., Audu, J.D.: A Comparison Results of Some Analytical Solutions of Model in Double Phase Flow through Porous Media. Journal of Mathematics and System Science 4, 275-284 (2014).
  42. Lang, S.: Real and Functional Analysis, 3rd edn. Springer, Berlin (1993).
  43. Liao, S.J.: The proposed homotopy analysis technique for the solution of nonlinear problems. Ph.D thesis, Shanghai Jiao, Tong University (1992).
  44. Liao, S.J.: On the homotopy analysis method for nonlinear problems. Appl. Math. Comput. 147(2), 499-513 (2004).
  45. Liao, S.J.: An approximate solution technique which does not depend upon small parameters: a special example. Int. J. Non-linear Mech. 30, 371-380 (1995).
  46. Liao, S.J.: Homotopy analysis method and its applications in mathematics. J. Basic Sci Eng. 5(2), 111-125 (1997).
  47. Liao, S.J.: An explicit, totally analytic approximation of Blasius viscous flow problem. Int. J. Non-Linear Mech. 34, 759-778 (1999).
  48. Liao, S.J.: A uniformly valid analytic solution of 2D viscous flow past a semi infinite flat plate. J Fluid Mech. 385, 101-128 (1999).
  49. Liao, S.J., Campo, A.: Analytic solutions of the temperature distribution in Blasius viscous flow problems J. Fluid Mech. 453, 411-425 (2002).
  50. Liao, S.J., Tan Y.: A general approach to obtain series solutions of nonlinear differential equations. Stud. Appl. Math. 119, 297-354 (20. [CrossRef]
  51. Liao, S.J.: A general approach to get series solution of non-similarity boundary-layer flows. Commun. Nonlinear. Sci. Numer. Simulat. 14, 2144-2159 (2009).
  52. Liao, S.J.: Comparison between the homotopy analysis method and homotopy perturbation method. Appl. Math. Comput. 169, 1186-1194 (2005). [CrossRef]
  53. Liang, S., Jeffrey, D.J.: Comparison of homotopy analysis method and homotopy perturbation method through an evolution equation. communications in nonlinear science and numerical simulation 14(12), 4057-4064 (2009). [CrossRef]
  54. Magyari, E., Keller, B.: Exact solutions for self-similar boundary-layer flows induced by permeable stretching walls. Eur. J. Mech. B Fluids 19, 109–122 (2000). [CrossRef]
  55. Şenol, M., Iyiola, O.S., Daei Kasmaei, H., Akinyemi, L.: Efficient analytical techniques for solving time-fractional nonlinear coupled Jaulent-Miodek system with energy-dependent Schrödinger potential. Adv. Differ. Equ. 2019, 1-21 (2019). [CrossRef]
  56. Şenol, M., Akinyemi, L., Ata, A., Iyiola, O. S.: Approximate and generalized solutions of conformable type Coudrey-Dodd-Gibbon-Sawada-Kotera equation. International Journal of Modern Physics B, 35(02), 2150021 (2021).
  57. Srivastava, H.M., Kumar, D., Singh, J.: An efficient analytical technique for fractional model of vibration equation. Appl. Math. Model. 45, 192-204 (2017). [CrossRef]
  58. Turkyilmazoglu, M.: Convergence accelerating in the homotopy analysis method: a new approach. Adv. Appl. Math. Mech. 10, 1-24 (2019). [CrossRef]
  59. Turkyilmazoglu, M.: Is homotopy perturbation method the traditional Taylor series expansion. Hacet. J. Math. Stat. 44, 651-657 (2015). [CrossRef]
  60. Turkyilmazoglu, M.: An effective approach for approximate analytical solutions of the damped Duffing equation. Phys. Scr, 86, 1-6 (2012). [CrossRef]
  61. Turkyilmazoglu, M.: Some issues on HPM and HAM methods: A convergence scheme Mathematical and Computer Modelling 53(9–10), 1929-1936 (2011).
  62. Turkyilmazoglu, M.: Convergence of the homotopy perturbation method. Int. J. Nonli. Sci. Numer. Simul. 12, 9–14 (2011).
  63. VanGorder, R.A., Vajravelu, K.: Analytic and numerical solutions to the Lane–Emden equation. Phys. Lett. A 372, 6060-6065 (2008). [CrossRef]
  64. Wazwaz, A.M.: Adomian decomposition method for a reliable treatment of the Bratu-type equations. Appl. Math. Comput. 166(3), 652-663 (2005). [CrossRef]
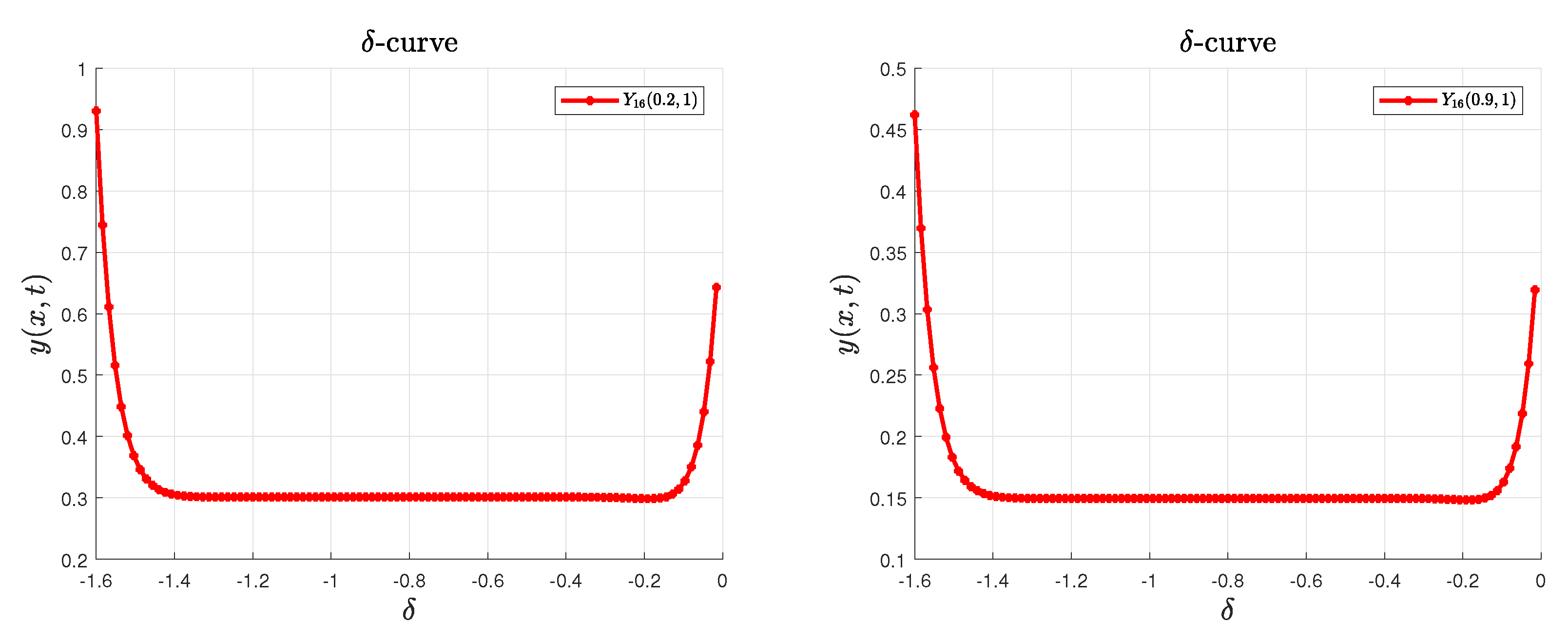
Preprints 95691 g001
Figure 1. The δ -curve of Y 16 ( x , t ) solution with different x at t = 1 for Example 1
Figure 1. The δ -curve of Y 16 ( x , t ) solution with different x at t = 1 for Example 1
Preprints 95691 g001
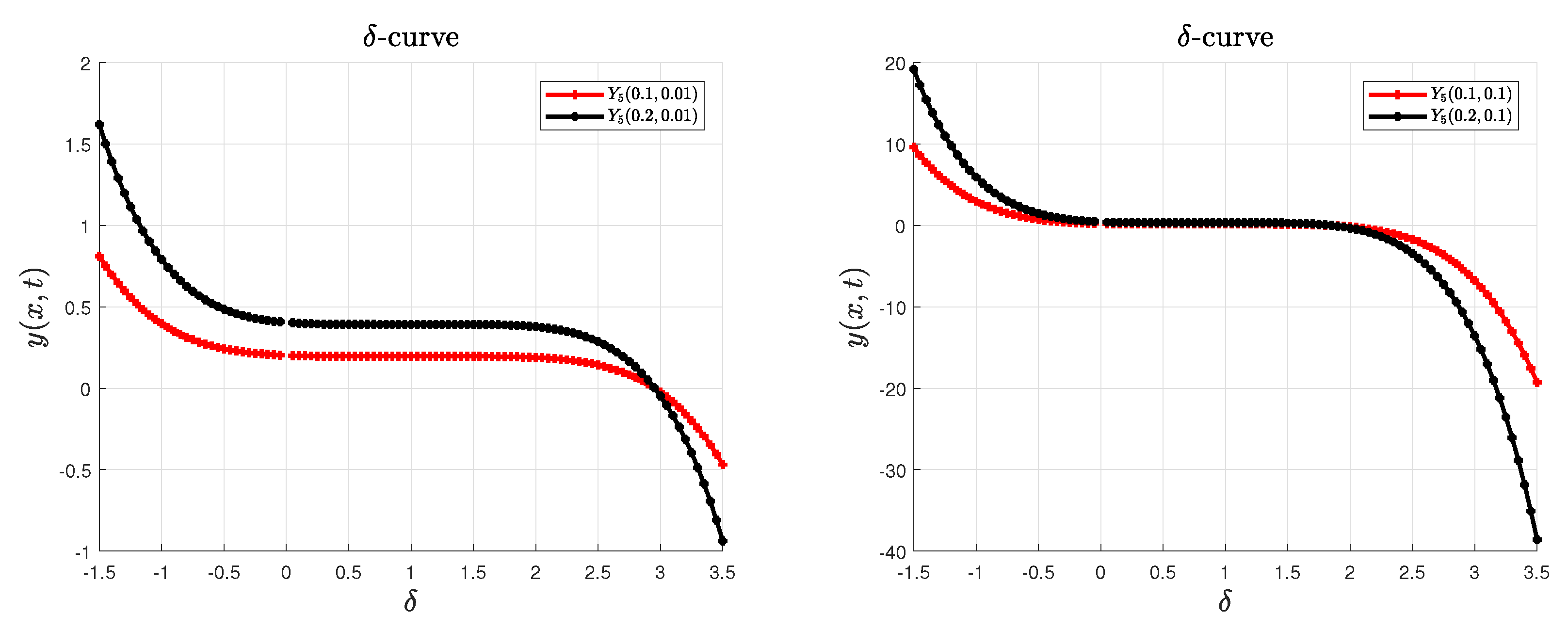
Preprints 95691 g002
Figure 2. The δ -curve of Y 5 ( x , t ) solution with different x and t for Example 2 case 1
Figure 2. The δ -curve of Y 5 ( x , t ) solution with different x and t for Example 2 case 1
Preprints 95691 g002
Table 1. The comparative study of Y 16 of δ -HPM, HPM and the exact solution for Example 1
Table 1. The comparative study of Y 16 of δ -HPM, HPM and the exact solution for Example 1
δ -HPM ( δ = − 1 ) HPM ( δ = 1 )
x t Exact Approx. Absolute error Approx. Absolute error
0 0.1353352832 0.1353352832 0 0.1353352832 0
0.1 0.1224564283 0.1224564283 1.221245 × 10 − 15 1.2332686540 × 10 03 1.233146 × 10 03
2 0.2 0.1108031584 0.1108031584 7.063794 × 10 − 15 3.3171025221 × 10 03 3.316992 × 10 03
0.3 0.1002588437 0.1002588437 9.157952 × 10 − 14 6.5260426500 × 10 03 6.525942 × 10 03
0.4 0.0907179533 0.0907179533 6.301903 × 10 − 14 1.1189446548 × 10 04 1.118936 × 10 04
0.5 0.0820849986 0.0820849986 2.581269 × 10 − 15 1.7699263871 × 10 04 1.769918 × 10 04
0 0.0024787522 0.0024787522 0 0.0024787522 0
0.1 0.0022428677 0.0022428677 2.081668 × 10 − 17 2.2588103319 × 10 01 2.258586 × 10 01
6 0.2 0.0020294306 0.0020294306 1.301043 × 10 − 16 6.0754851951 × 10 01 6.075282 × 10 01
0.3 0.0018363048 0.0018363048 1.677261 × 10 − 15 1.1952864055 × 10 02 1.195268 × 10 02
0.4 0.0016615573 0.0016615573 1.155760 × 10 − 15 2.0494186234 × 10 02 2.049402 × 10 02
0.5 0.0015034392 0.0015034392 4.683753 × 10 − 17 3.2417332565 × 10 02 3.241718 × 10 02
Table 2. The comparative study of Y 5 of δ -HPM, HPM and the exact solution for Example 2 case 1
Table 2. The comparative study of Y 5 of δ -HPM, HPM and the exact solution for Example 2 case 1
δ -HPM ( δ = 0.80 ) HPM ( δ = 1 )
x t Exact Approx. Absolute error Approx. Absolute error
0.08 0.0172413793 0.0172416459 2.665546 × 10 − 7 0.0172404940 8.852999 × 10 − 7
0.10 0.0166666667 0.0166670364 3.697086 × 10 − 7 0.0166632809 3.385753 × 10 − 6
0.12 0.0161290323 0.0161295280 4.957343 × 10 − 7 0.0161188868 1.014542 × 10 − 5
0.01 0.14 0.0156250000 0.0156256389 6.389195 × 10 − 7 0.0155993038 2.569623 × 10 − 5
0.16 0.0151515152 0.0151522465 7.313646 × 10 − 7 0.0150939574 5.755779 × 10 − 5
0.18 0.0147058824 0.0147063985 5.161891 × 10 − 7 0.0145884896 1.173927 × 10 − 4
0.20 0.0142857143 0.0142850695 6.447537 × 10 − 7 0.0140633199 2.223944 × 10 − 4
0.08 0.0862068966 0.0862082293 1.332773 × 10 − 6 0.0862024701 4.426500 × 10 − 6
0.10 0.0833333333 0.0833351819 1.848543 × 10 − 6 0.0833164046 1.692877 × 10 − 5
0.12 0.0806451613 0.0806476400 2.478671 × 10 − 6 0.0805944342 5.072708 × 10 − 5
0.05 0.14 0.0781250000 0.0781281946 3.194597 × 10 − 6 0.0779965188 1.284812 × 10 − 4
0.16 0.0757575758 0.0757612326 3.656823 × 10 − 6 0.0754697868 2.877889 × 10 − 4
0.18 0.0735294118 0.0735319927 2.580946 × 10 − 6 0.0729424482 5.869635 × 10 − 4
0.20 0.0714285714 0.0714253477 3.223769 × 10 − 6 0.0703165993 1.111972 × 10 − 3
Table 3. The comparative study of Y 3 , Y 5 of δ -HPM, HPM, PIA [9] and the exact solution with λ = 1 for Example 3
Table 3. The comparative study of Y 3 , Y 5 of δ -HPM, HPM, PIA [9] and the exact solution with λ = 1 for Example 3
Approx. Approx. Approx.
x Exact Y 5 ( δ = 1.15 ) Y 5 ( δ = 1 ) Y 3 ( δ = 1.125 ) Y 3 ( δ = 1 ) PIA ( 1 , 1 ) [9] PIA ( 1 , 2 ) [9]
0.1 0.04985 0.04985 0.04984 0.04985 0.04970 0.04949 0.04983
0.2 0.08919 0.08919 0.08918 0.08918 0.08892 0.08851 0.08915
0.3 0.11761 0.11761 0.11759 0.11759 0.11723 0.11665 0.11756
0.4 0.13479 0.13479 0.13477 0.13476 0.13434 0.13365 0.13473
0.5 0.14054 0.14054 0.14052 0.14051 0.14006 0.13934 0.14048
0.6 0.13479 0.13479 0.13477 0.13476 0.13434 0.13365 0.13473
0.7 0.11761 0.11761 0.11759 0.11759 0.11723 0.11665 0.11756
0.8 0.08919 0.08919 0.08918 0.08918 0.08892 0.08851 0.08915
0.9 0.04985 0.04985 0.04984 0.04985 0.04970 0.04949 0.04983
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated