Prerpints.org logo
Preprint
Article

Robustness of Corner-Supported Modular Steel Buildings with Core Walls

Altmetrics

Downloads

100

Views

57

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

10 January 2024

Posted:

10 January 2024

You are already at the latest version

Alerts
Abstract
This paper studies the dynamic response of corner supported modular steel buildings with a core wall system, under progressive collapse scenarios, associated with corner module removals. Since using secondary systems such as concrete core in mid- to high-rise buildings is currently una-voidable, understanding their impact on load transfer between modules during collapse scenarios becomes essential. The designated buildings with four-, eight- and twelve-story were modelled using the macro-model based finite element method in Abaqus. Also, three different locations are considered for the concrete shear core within the building plan, leading to nine various case scenarios. Each vertical and horizontal inter-module connection was modelled by one axial and two shear springs with predefined nonlinear force-displacement behaviour. The local and global buckling, which plays an essential role in the building's stability, was considered to obtain accurate results. Finally, parametric studies on the building response were carried out, including the intra-module connection rigidity and inter-module connection stiffness. The results demonstrated that the core wall could maintain the robustness of modular steel building through two mechanisms dependent on its location within the plan. Also, preventing plastic hinges from forming in beams could be introduced as an anti-collapse mechanism in the corner module removal scenarios
Keywords: 
Subject: Engineering  -   Civil Engineering

1. Introduction

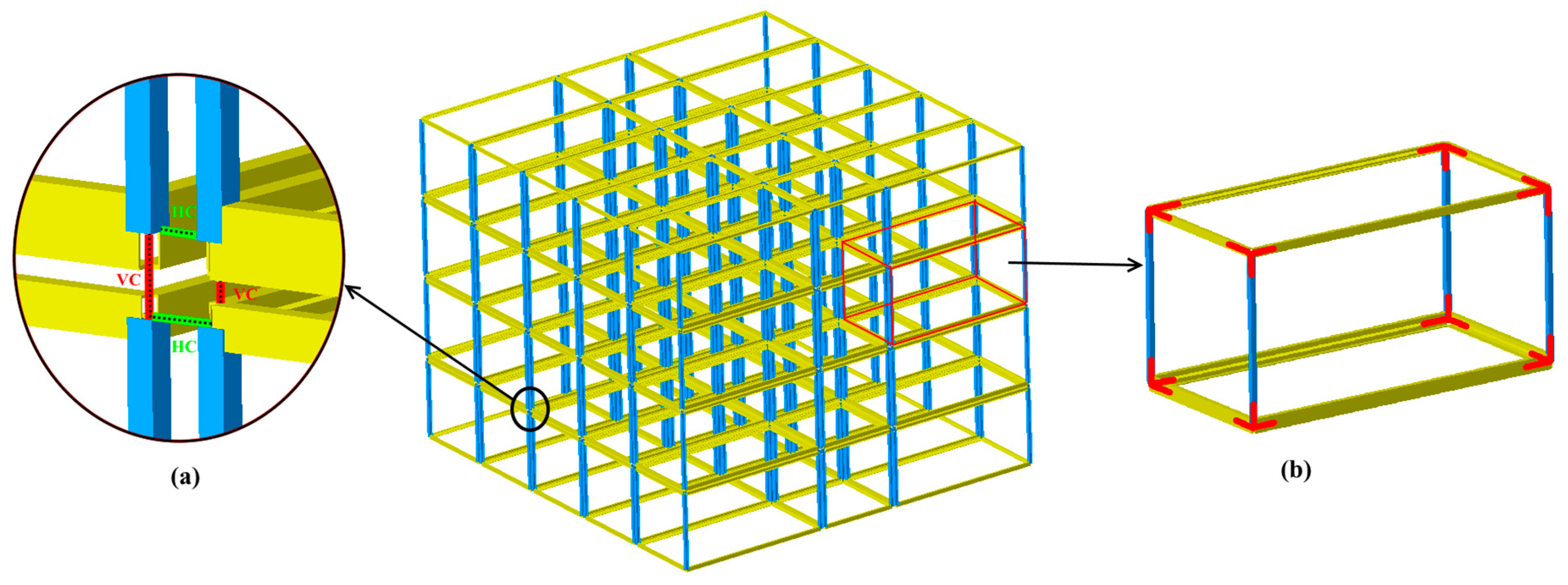
The Modular steel buildings (MSBs) are construction systems made of repeating pieces known as prefabricated prefinished modules. This system has quickly gained popularity in many countries as it offers several benefits, including fast-track construction, off-site construction, cost-effectiveness, less site waste, and lower environmental impact [1,2,3]. Corner-supported modular building shown in Figure 1 is one type of MSB in which each module is tied at its corners by horizontal connections (HC) as well as vertical connections (VC), which are called inter-module connections (see Figure 1(a)) and having intra-module connections, Figure 1(b). The interconnection with corner posts is the sole component responsible for transferring loads from one module to another.
A typical structural layout for modular structures is comprised of stacked modules to carry gravity loads and a core system to mainly resist lateral loads [4]. This paper presents the impact of a core system on the collapse capacity of the MSB against corner module loss scenarios by adopting the results of 9 different cases.
The inter-module connections act as the linking elements between modules for load distribution and efficient load transfer to the foundation. Since these connections play a key role in the stability of the entire building [5], most of the research studies from the literature have been focused on the structural performance or constructional challenges [6,7,8]. Lacy et al. [6,9] studied the stiffness of bolted connections and showed that rotational stiffness has a modest impact on global structural responses. It was concluded that simplified modelling of inter-module connections could accurately predict overall building response under gravity and lateral demands [10]. Peng et al. [11] developed a tenon inter-module connection using spring elements in Abaqus, which significantly lowered the computational expenses. Feng et al. [12] studied the seismic performance of four types of inter-module connection for modular box buildings, and the results showed that none satisfied Chinese code limitations such as inter-story drifts. Similarly, Peng et al. [13] showed that a 12-story MSBs cannot meet the drift requirements against service wind loads.
Some notions have been put forward in recent research to overcome the former shortcomings, ranging from developing innovative inter-modular connections [14,15,16] as well as precast concrete core wall systems [17,18,19] to various module layouts [20,21].Therefore, a secondary system such as a core wall system is essential in mid- to high-rise MSB [22]. Chua et al. [18] and Yee [23] investigated the lateral performance of a high-rise MSB with a central concrete core. Bi et al. [19] also, studied the lateral performance of a multi-story MSB with two concrete cores under wind loads, as a case study located in China.
From the MSBs collapse perspective, several research has been undertaken. Luo et al. (2019) studied the steel-frame progressive collapse by assuming that all connections are rigid [24]. However, actual connection behaviours would also be necessary to understand the extent of damage in the aftermath of a blast or fire events. Alembagheri et al. [25,26] and Sharafi et al. [27] investigated the collapse capacity of rigid modular buildings in the macro model context in which the connections were modelled by translational axial and shear nonlinear springs. Also, their early work on the progressive collapse of a flexible six-story modular steel frame revealed that the global column buckling dominates the progressive collapse response of the building [28]. The behaviour of semi-rigid joints is one of the issues that should be addressed in simplified numerical methods [29,30]. Thai et al. [31] performed a parametric study on the progressive collapse of 12-story braced MSB. The results showed that the robustness of modular buildings is significantly increased by bracing system, as it decreases effective length of columns. Likewise, it was indicated that the MSB‘s ability to withstand collapse can be improved by up to 50% when wall panels are tied in each module [32].
As using alternative lateral force resisting systems in mid- to high-rise MSBs to meet drift requirements is unavoidable, a comprehensive study on their role in collapse scenarios is essential. In the current literature, it is mostly done based on the progressive collapse of modular steel buildings without considering the contribution of the secondary systems such as shear wall (core) or bracing systems. This paper studies the dynamic response of corner-supported modular steel buildings incorporating a core wall system when subjected to progressive collapse scenarios, with a focus on recognizing the role of secondary systems. The primary aim of the current study is to provide insight into the impact of these systems on load redistribution and the structural robustness of the building during the loss of a corner module. For this purpose, 9 modular building cases are considered with four, eight and twelve-story and three different locations on the plan, for a core wall system. The inter-module connections are modelled using the macro-model-based finite element method. The guideline based on the alternative path method is used to study the collapse response of modular buildings, and the corner modules are considered a missing vertical load-bearing component. Then a parametric analysis is conducted to examine the effect of inter-module connection stiffness, intra-module joint rigidity, and plastic hinges on the MSBs robustness.

2. Gravity-induced progressive collapse

All buildings contain critical components that, if lost under extreme conditions such as blast, might cause the entire structure to collapse. The Alternative Load Path (ALP) method has been developed to address this issue. The ALP method is threat-independent, upon which a critical component of a building is removed, and then the ability of the building to survive the loss scenario is investigated [33–38]. If the other components are capable of resisting the redistributed loads, the building is deemed to be robust; otherwise, it may result in a cascading failure and progressive collapse unless an essential element design or segmentation is introduced [39]. The probable ALPs due to the corner module loss are shown in Figure 2.

3. Simulated modular building

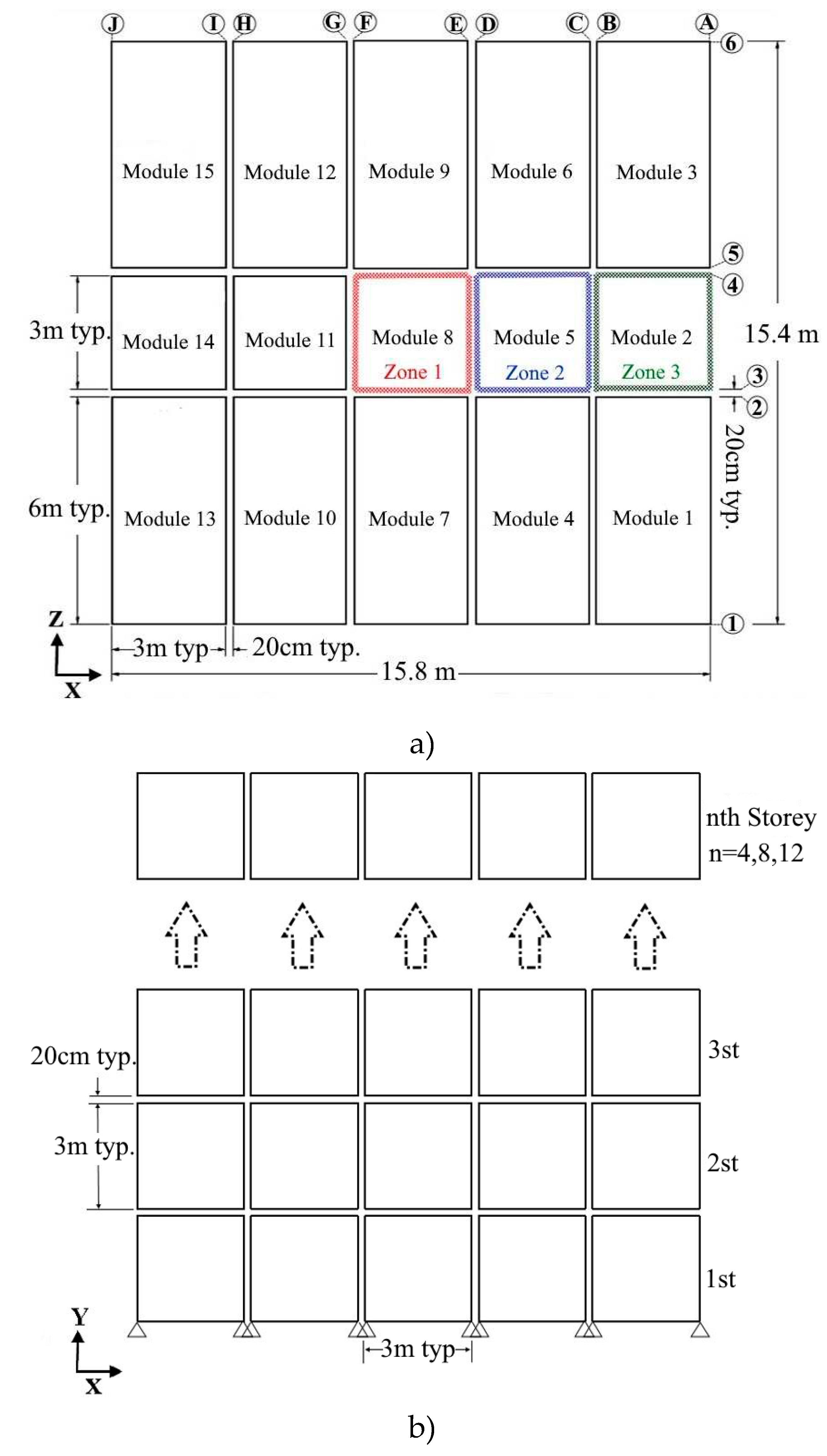
A typical plan shown in Figure 3(a) is chosen to study the robustness of modular buildings with core. There are 15 modules in three rows, with the middle module considered a corridor. In this study, shear walls are in three zones: zone (1), zone (2), and zone (3). There are two types of modules; the first has a 6m length, 3m width, 3m height, and a total mass of 20 tones. The other has a 3m length, 3m width, 3m height, and a total mass of 10 tones. It should be noted that the mass of each module is calculated by adopting dead loads plus 25% of live loads specified by GSA guidelines [37]. The horizontal and vertical clearances between neighbouring modules are 0.2m, as depicted in Figure 3(b). Three building heights are considered in this study.
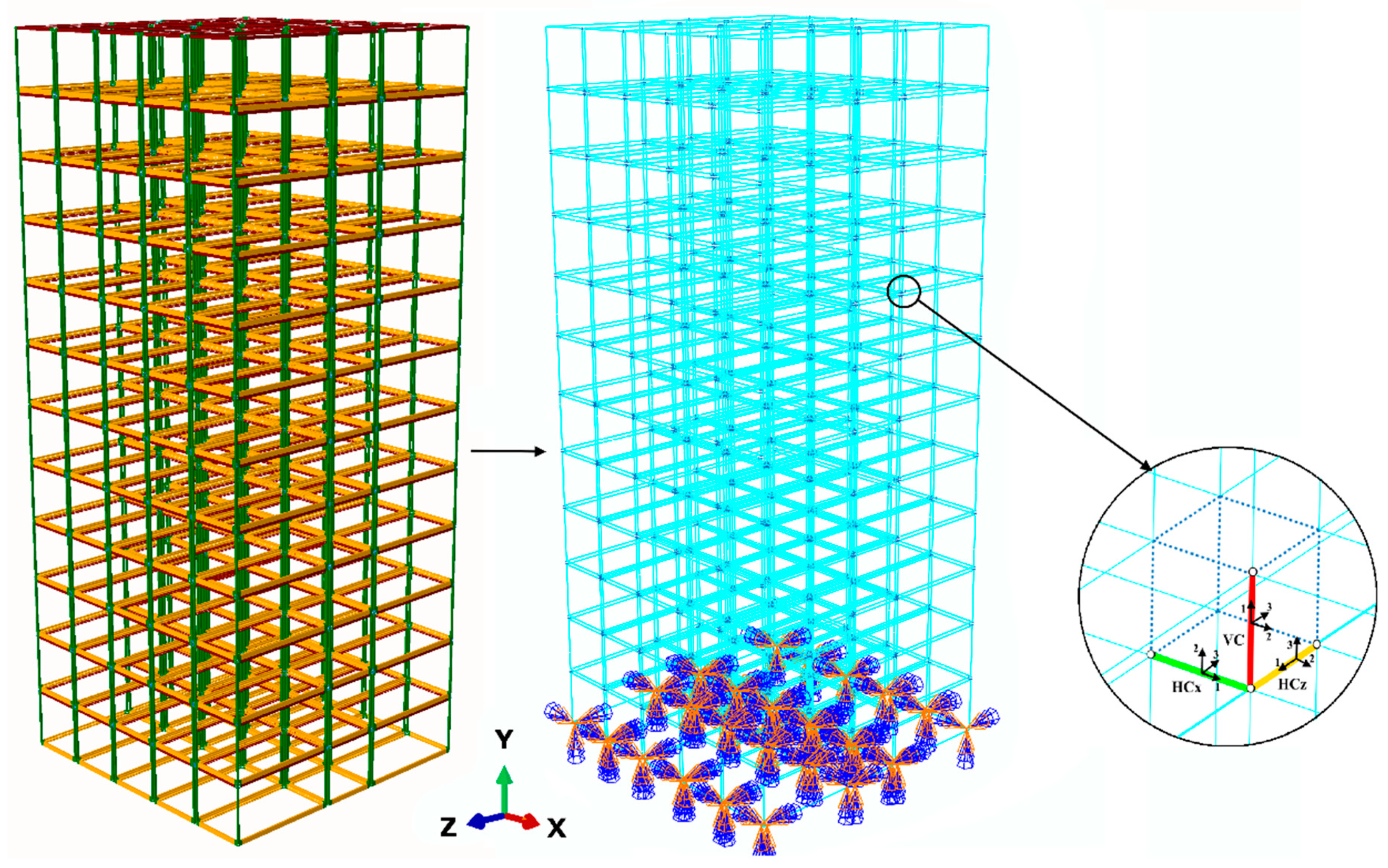
All buildings were designed in accordance with the requirements of AS1170 and AS4100 [40]. The design resulted in SHS 100×100×9 for columns, 180UB for floor beams, and 150UB for ceiling beams. The steel material for columns was assumed as a tri-linear elastoplastic [41] model with an initial yielding stress of 350 MPa, an ultimate strength of 490 MPa at a plastic strain of 0.02. For beams, however, steel is treated as an elastic material because plastic hinges are regarded at their ends. Further, a density of 7800 kg/m3, Young’s modulus of 200 GPa, and Poisson’s ratio of 0.25 were considered for steel material. A thickness of 250 mm was adopted for the concrete core wall with elastic material behaviour and the concrete density, Young’s modulus, and Poisson’s ratio were, respectively, assumed to be 2400 kg/m3, 30 GPa, and 0.3. The finite element (FE) mesh discretization developed in the Abaqus program is shown in Figure 4. All beams and columns were modelled using 2-node linear beam in space (B31) elements and the core wall was simulated using 4-node doubly curved thin shell elements with reduced integration, hourglass control, and finite membrane strain (S4R). A tie constraint was adopted to link shell nodes to the adjacent beam nodes. A clamped restraint was adopted to fix column nodes to the ground.
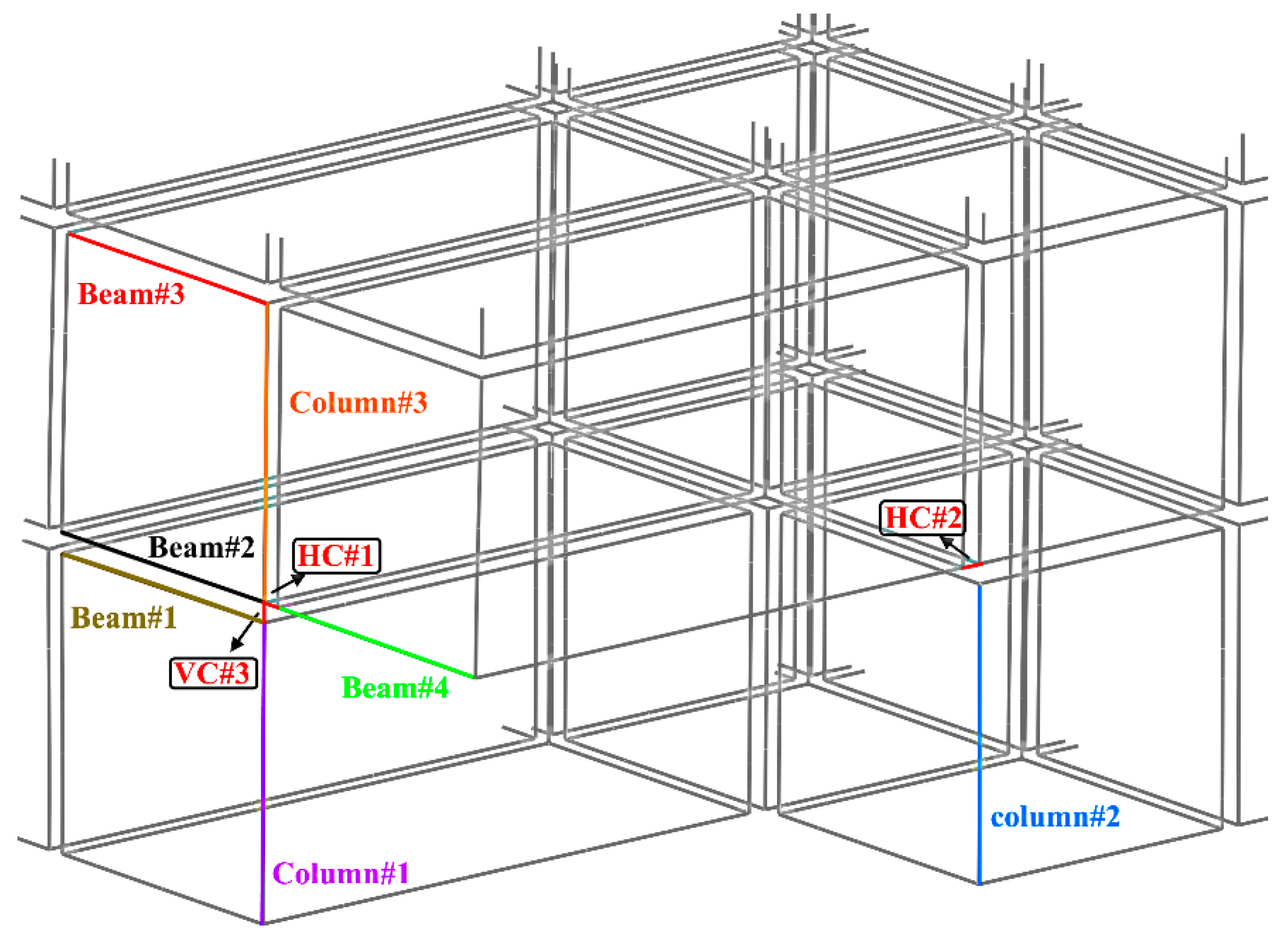
This study had two types of connections: inter-module and intra-module connections. Adjacent Modules were connected to each other via inter-module connections including 6M24 class 10.9 bolts, simplified with two horizontal connectors (HCx, HCz) and one vertical connector (VC), depicted in Figure 4.
A Cartesian connector element, available as a built-in connection in Abaqus, was defined with force-displacement relations proposed in [6], as shown in Figure 5. The Cartesian connection type connects two nodes where the response in three local connection directions is defined. It was assumed that vertical and horizontal connections were eliminated from the model after reaching their failure points as listed in Table 1. Note that the rotational stiffness of inter-module connections was neglected based on previous research [25] because the load-bearing mechanism in MSBs is primarily governed by shear transfer.
Intra-module connections, referred as beam-column connections within a module, were assumed to be rigid. However, concentrated plastic hinges were assigned to both ends of the beam element to consider the effects of local buckling. The hinges were modelled as rotational springs with a symmetric quadrilinear moment rotation relationship for positive and negative rotations. The capacity of these hinges was based on the theoretical moment-curvature (M-ɵ) relationships of the cross-sections using the ASCE41-17 provision [42].
The nonlinear dynamic analysis was performed using the implicit dynamic solver in Abaqus [43]. At first, an Eigenvalue buckling analysis was performed and buckling mode shapes were determined and imposed as an initial state to the model. This analyses that predict the collapse mechanism was performed using the subspace iteration method to extract the buckling modes. This analysis provides buckling eigenvalues and buckling modes which are used in the post-buckling analysis by determining the initial geometric imperfection. Next, the gravity loads including modules’ dead and live loads, were applied gradually through the quasi-static step. The corner module was eventually removed from the model within 0.0001 seconds, and the dynamic response of the remaining model was monitored until it reached the equilibrium state.
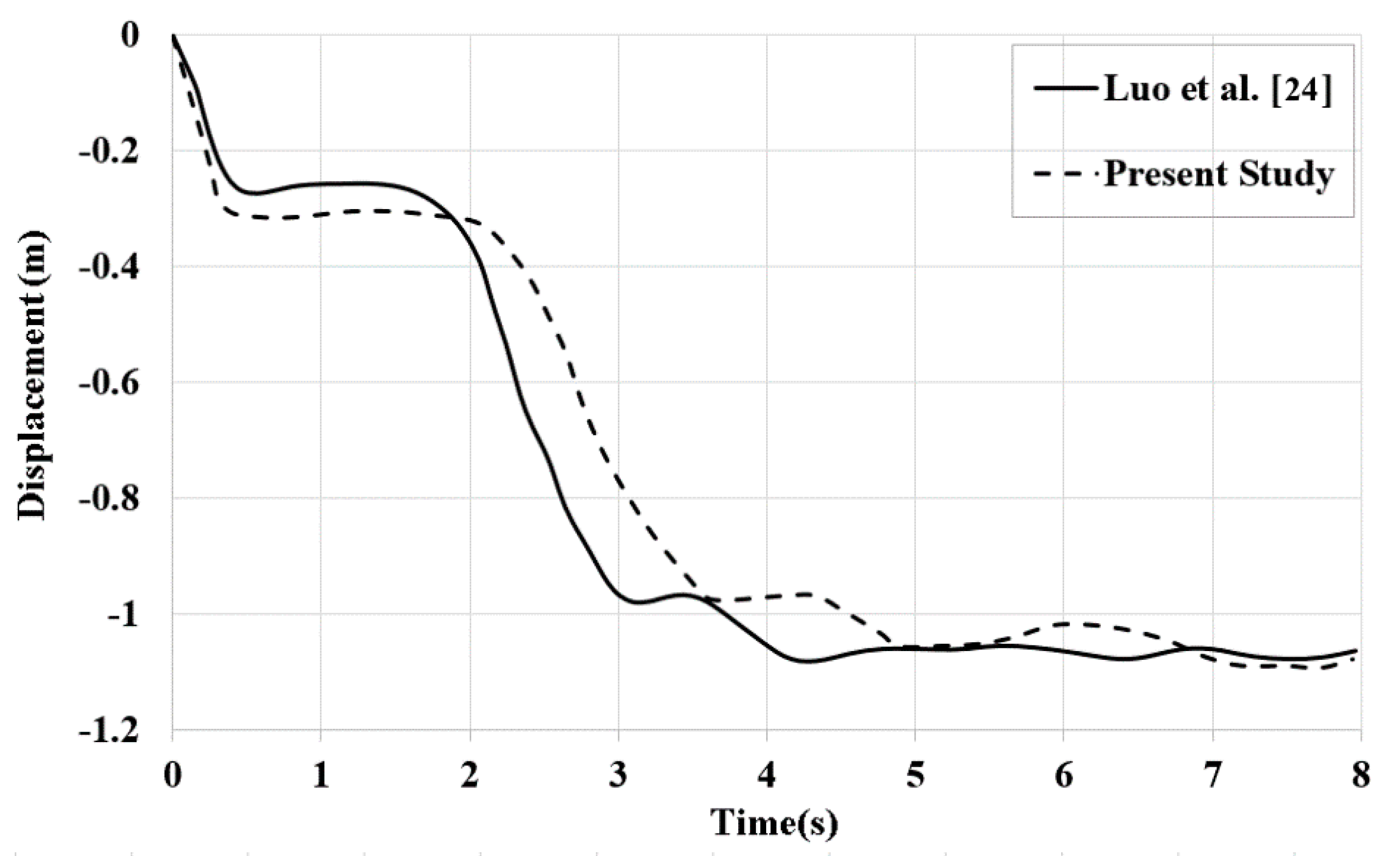
Due to the limited availability of experimental tests specifically addressing the dynamic collapse of modular buildings, the validation of the numerical modelling procedure presented in this study relies on the utilization of previously published numerical models. To achieve this, we developed a steel modular building, which had been previously examined by Luo et al. [50], employing the methodology described in this paper. As shown in Figure 6, there is an acceptable agreement between The developed model that had been verified in our previous research [25] with the original model of Luo et al [24].

4. Response under module loss scenario

The dynamic responses of different cases, reported in Table 2, are presented and compared in this section, to evaluate the core wall role in the building's robustness. To that end, the response history of corner roof displacements, the maximum stress of the shear wall, plastic hinges distribution, and internal forces in critical members in Figure 7 are reported. Also, maximum dynamic to static response ratio: DSR = rmax,dyn/rstatic; the dynamic increase factor: DIF = rmax,dyn/rfinal; demand-capacity ratio: DCR and some design implications are addressed in this section. rstatic is considered as a force at the end of Quasi-static gravity step and rmax,dyn is the maximum element force after corner modules removal.
4.1. 4-storey
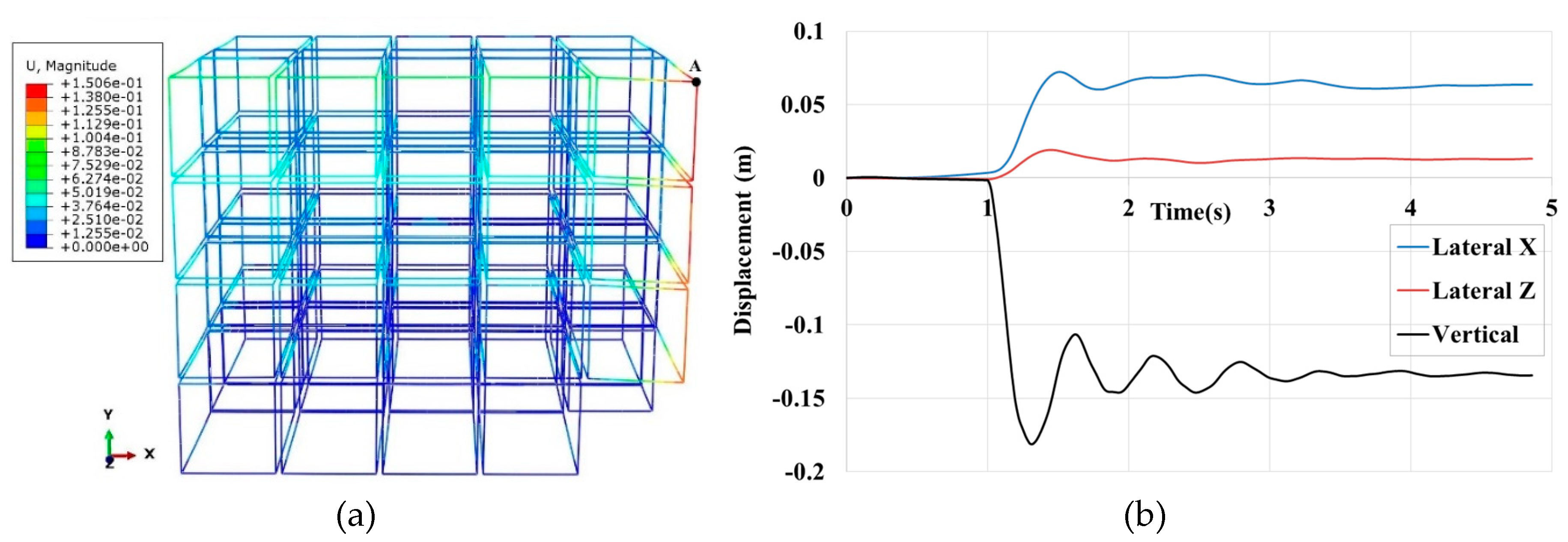
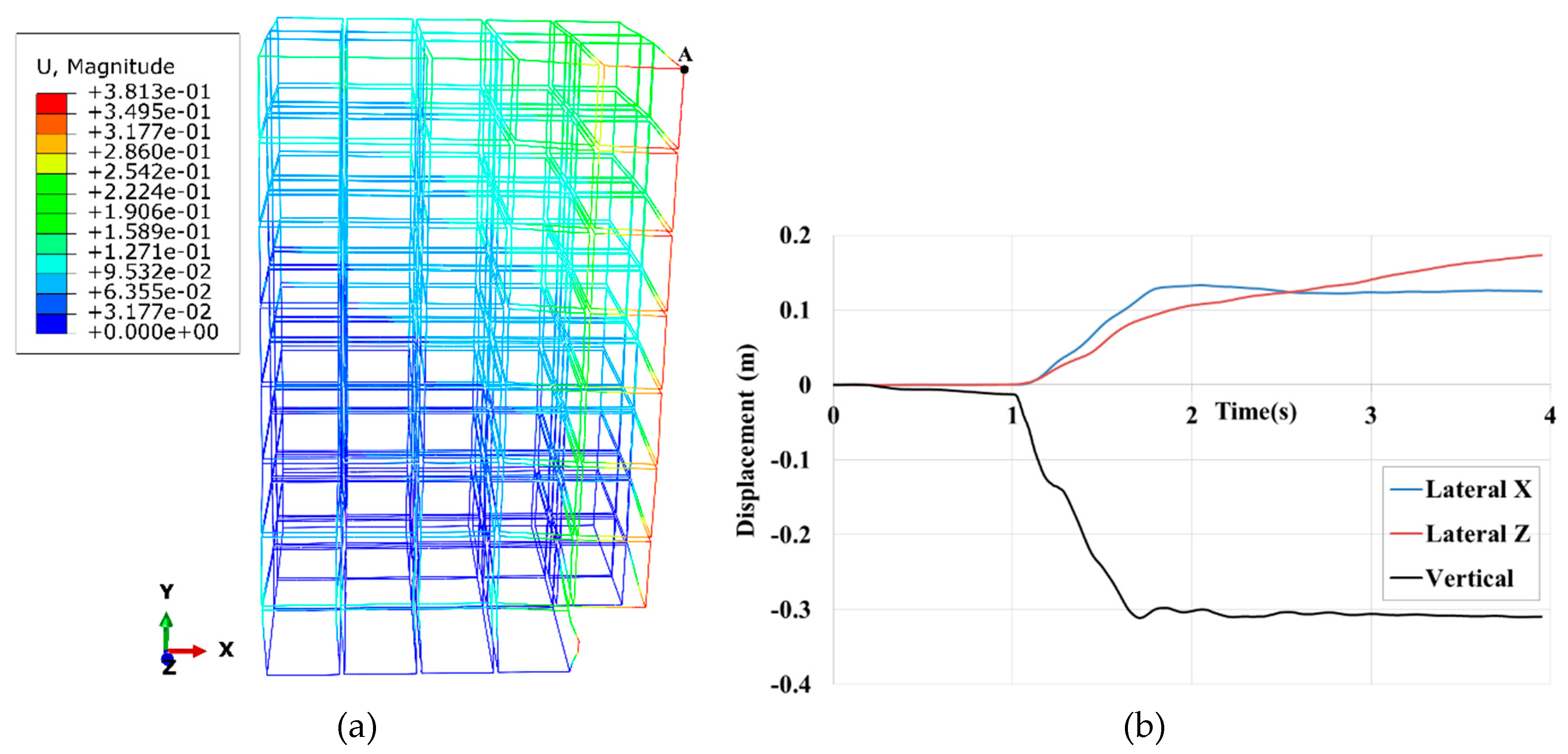
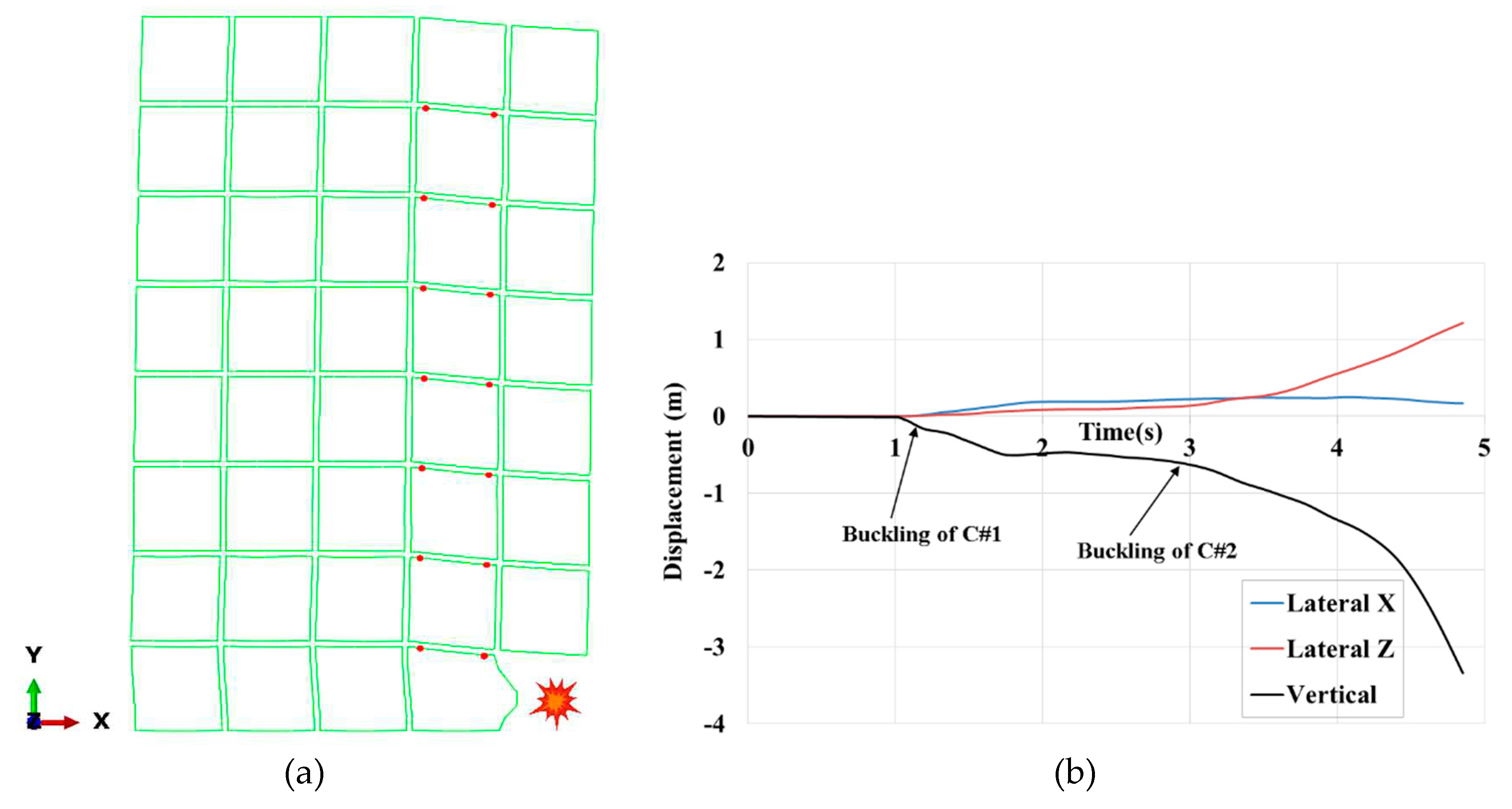
In the first case, the structure was robust after the corner module sudden removal because no column buckling occurred. The time history of lateral and vertical displacements of the roof corner, labelled A is shown in Figure 8(a). The maximum vertical and lateral displacements are about 18cm and 7cm, respectively.
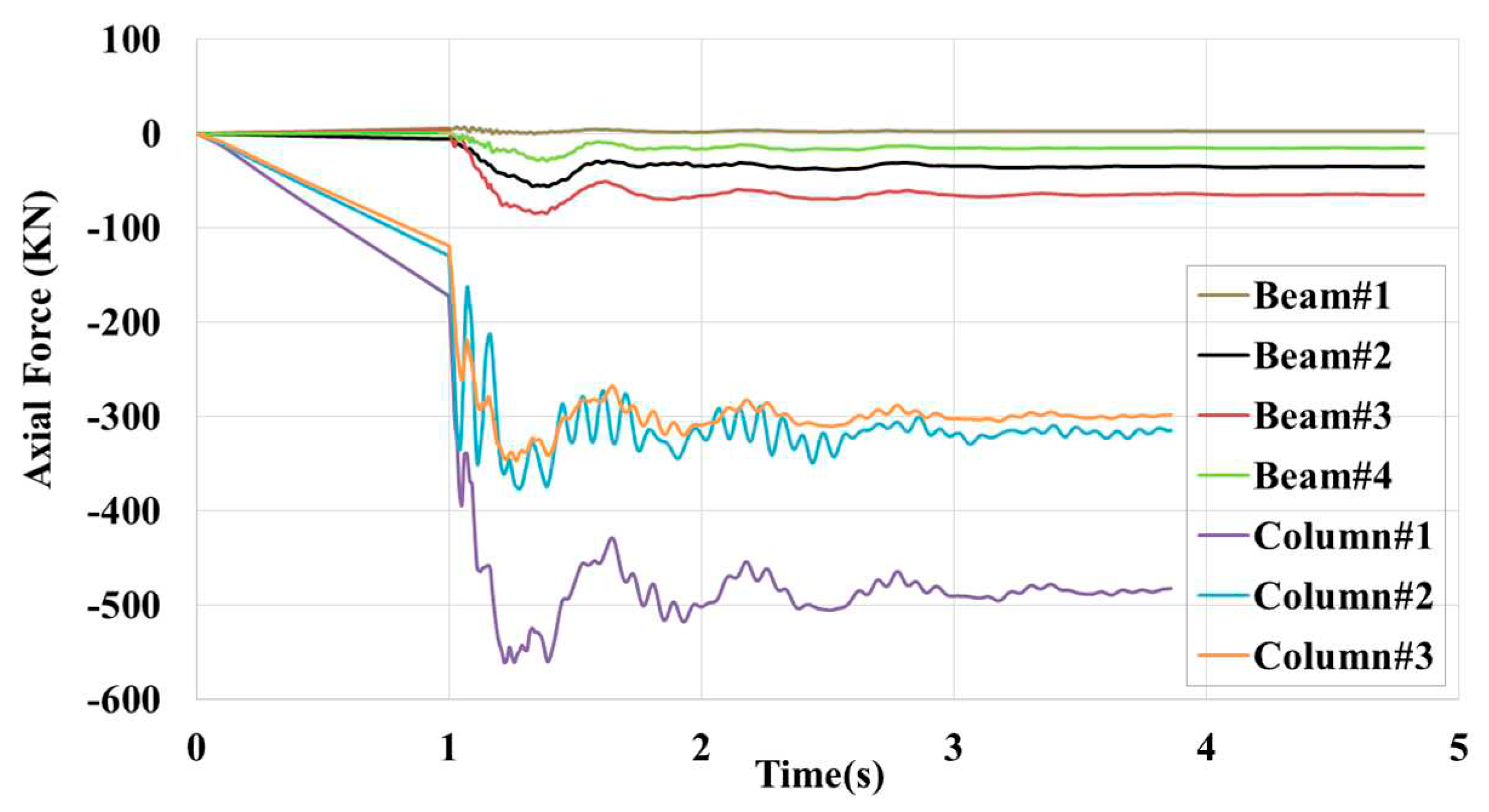
In this case, Column#1 carried the highest load, about 560kN, with a corresponding DSR=3.25 and DIF=1.15. The critical buckling load of columns was about 860kN. In the corner module removal scenario, Column#1 has a key role in the stability of the entire building because, as shown in Figure 9, substantial load distribution occurs. The time history of axial load in beams shows that they are in compression and Beam#3 has the highest value. Additionally, it was observed that, despite the employing of plastic hinges in the finite element model of the MSBs, no plastic hinges formed. This aligns with the findings of the previous study [28], which discussed that in the scenario of corner module removal in low-rise MSBs, the formation of plastic hinges can be disregarded as global column buckling is the dominant behaviour.
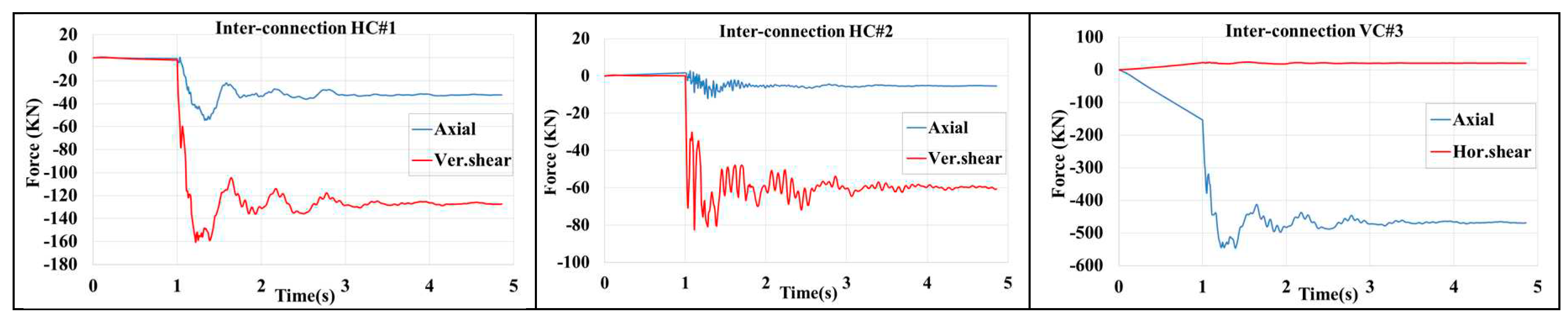
After removing the corner module, no inter-module connection failure is observed (see Figure 10). As mentioned above the failure values for inter module connections are summarized in the Table 1. The compressive force in VC#3 is similar to Column#1. HC#1 carries the highest shear force corresponding to DCR=160/2000=0.08, indicating that the redistributed load flows mainly in the X direction rather than Y.
4.2. 8-storey
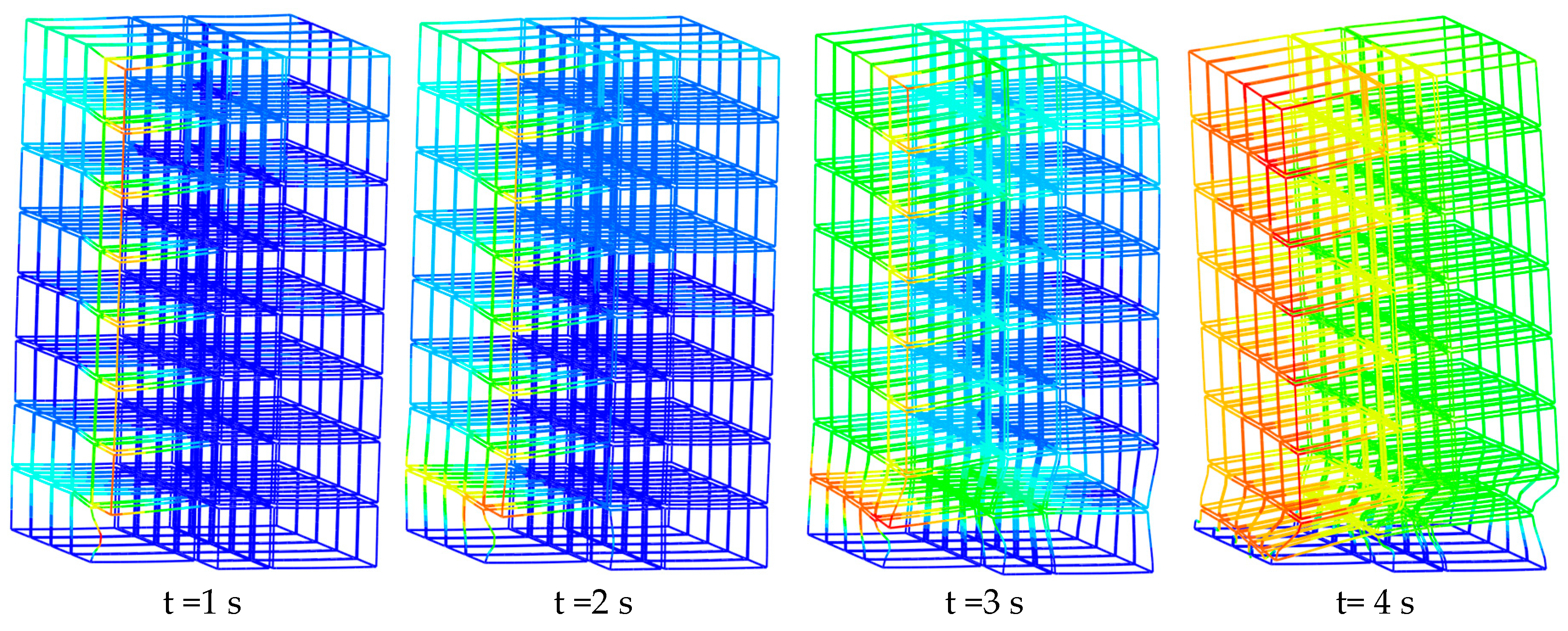
In the second case, the eight-story MSB was inadequate to maintain its robustness and collapsed. The collapse sequence of case no.2 is shown in Figure 11. In the previous case, it was displayed that Colum#1 is very prone to buckling because of substantial load redistribution. Accordingly, in case no.2, the collapse was triggered by the buckling of Column#1 located close to the removed module and was accompanied with the buckling of column#2 after a while. 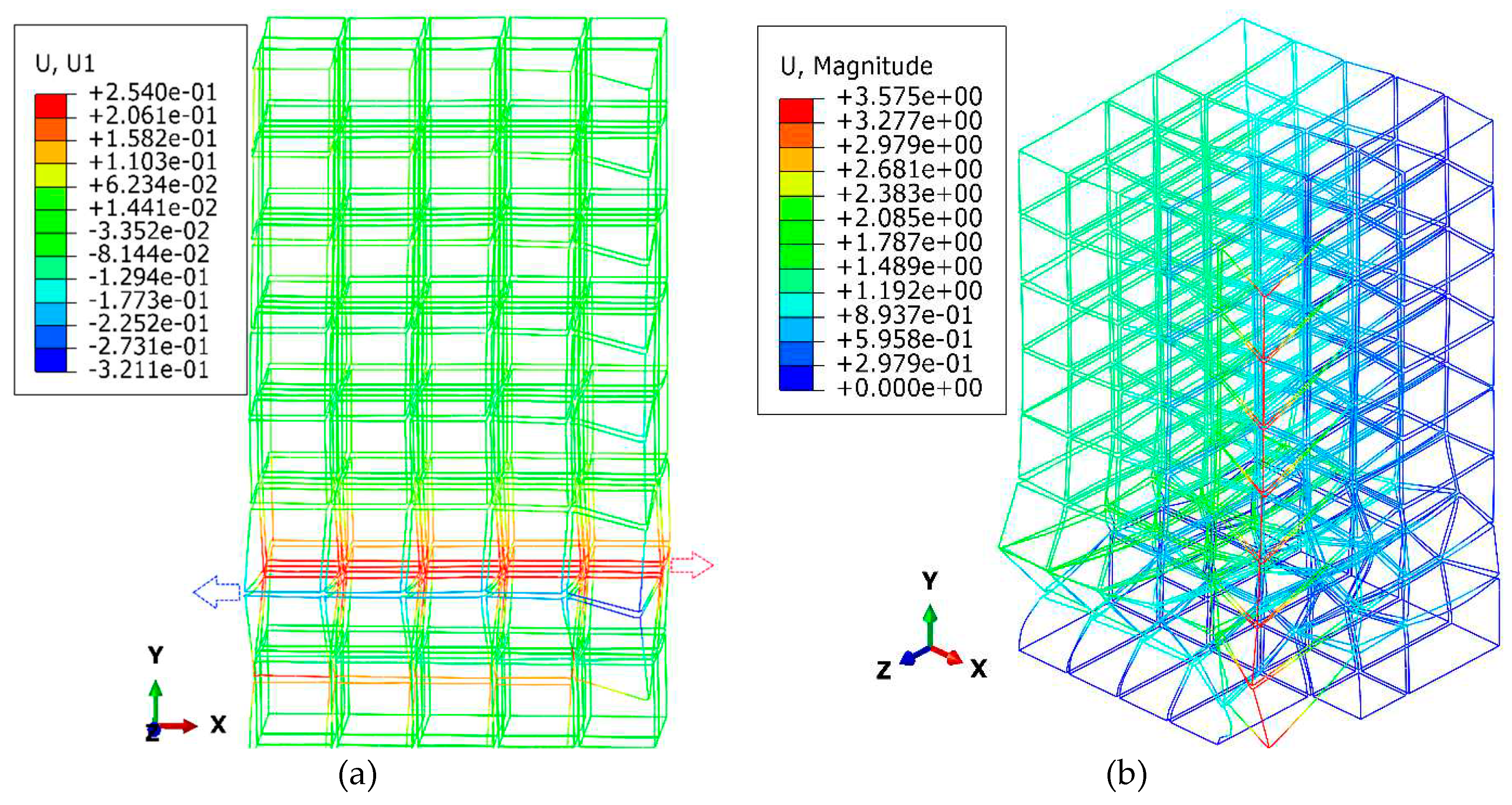As depicted in Figure 12(b), after a second of removing the corner modules, the maximum vertical and lateral displacements are about 49cm and 20cm, respectively. Then, due to successive buckling of columns in the front row, the building tends to overturn around the X-axis.
The initial plastic hinges, which play an essential role in the robustness of the buildings, are shown in Figure 12(a). The hinges are formed in the ceiling beams of the modules right close to the removed one because the rotation of these beams resulting from unsymmetrical deflection is more pronounced than those above the removed modules. After removing the corner modules, the main part of the gravity load tolerated by the removed columns is transferred to the column no.1. Moreover, the plastic hinge formation in the beams connected to the column no.1 increase the effective length factor, K, so that exacerbates the situation of the partially buckled column. The K-factors determining the effective length of columns in corner-supported steel modular buildings are investigated by Farajian et al. [44–46], with consideration for both sway and non-sway frames.
To explore the impact of the core wall on the collapse behaviour of MSB against corner module removal, the core wall system was installed in three zones (case no: 3-5), and their responses were compared with the bare frame (case no.2).
It was shown that the core wall located at the centre of the building (case no.3) arrested the collapse of the building under the corner module loss scenario. The lateral displacements in cases no.2 & 3 were approximately equal when the building was in a stable state. Despite the buckling of column#1 and significant vertical displacement of about 520 mm depicted in Figure 13(a), the building maintains its robustness under dynamic loads. The time history of lateral and vertical displacements of the roof corner is shown in Figure 13(b). The distribution of the first plastic hinges is the same as in case no.2.
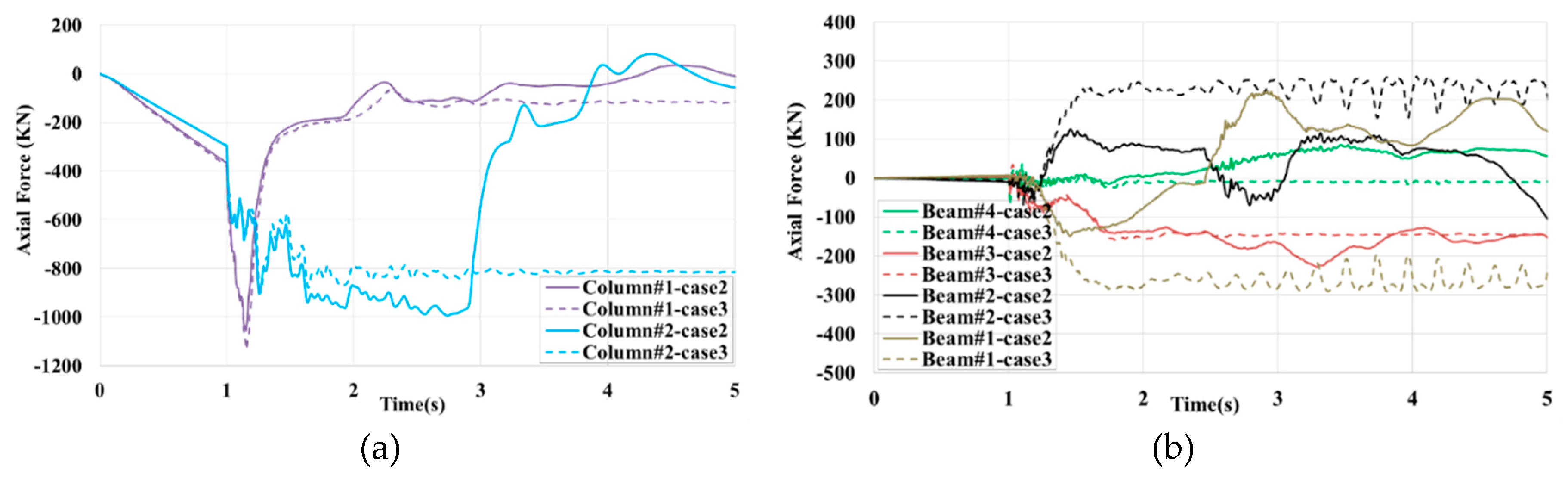
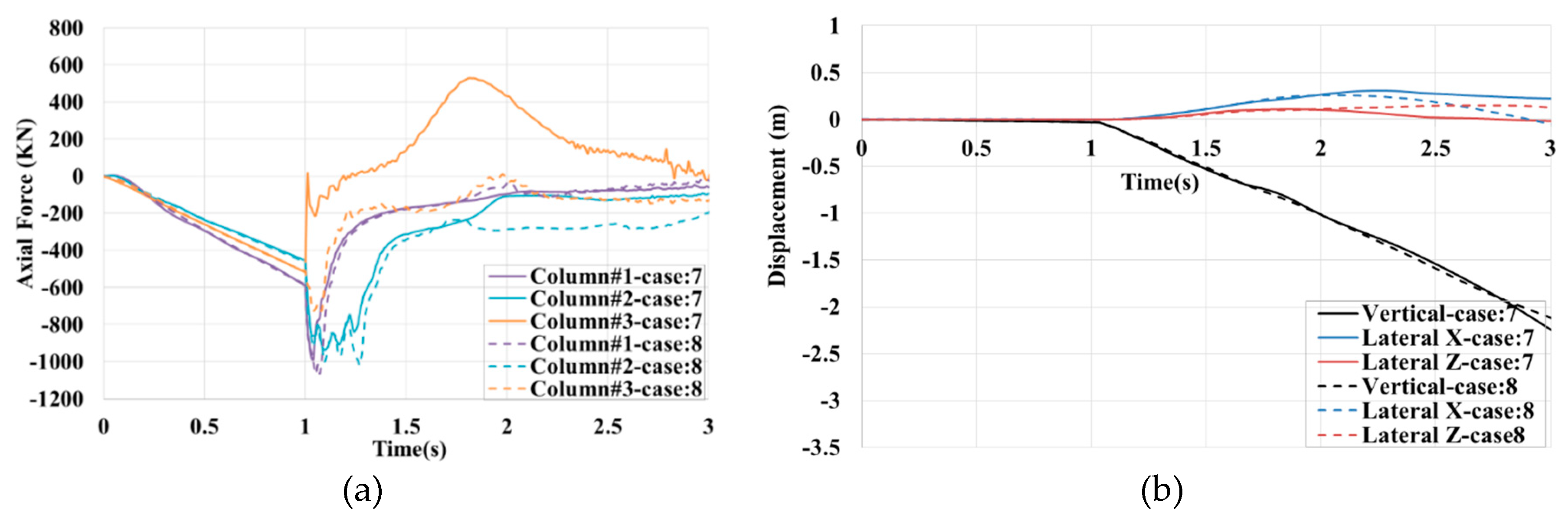
The time history of axial forces in several beams and columns in case no.2 and case no.3 is compared in Figure 14. In case no.2 the DSR of column#1 and column#2 are 2.87kN and 3.34kN, respectively. The highest load redistribution in column#2 for case no.3 and case no.2 is about 867kN and 993kN, respectively. In case no.3, where the core wall was cantered, beams experienced more fluctuation in their axial load immediately after module removal. The axial force in Beam#1 and Beam 2 was the opposite of each other. As Beam#2 was linked to HC#1 had to bear tensile load while Beam#1 suffered compressive load. In case no.3, after the buckling of Column#1 occurred, twice as many loads were redistributed in these beams compared to case no.2. It showed that the concrete core led to better load sharing through the beams in the vicinity of removed modules. Thus, the less axial load is redistributed to Column#2, as shown in Figure 14(a). The maximum redistributed load in Column#2 is reduced by 12% compared with case no.2. In both cases no.2 and no.3, Column#1 carried a load of about 1100kN, which was higher than the buckling capacity.
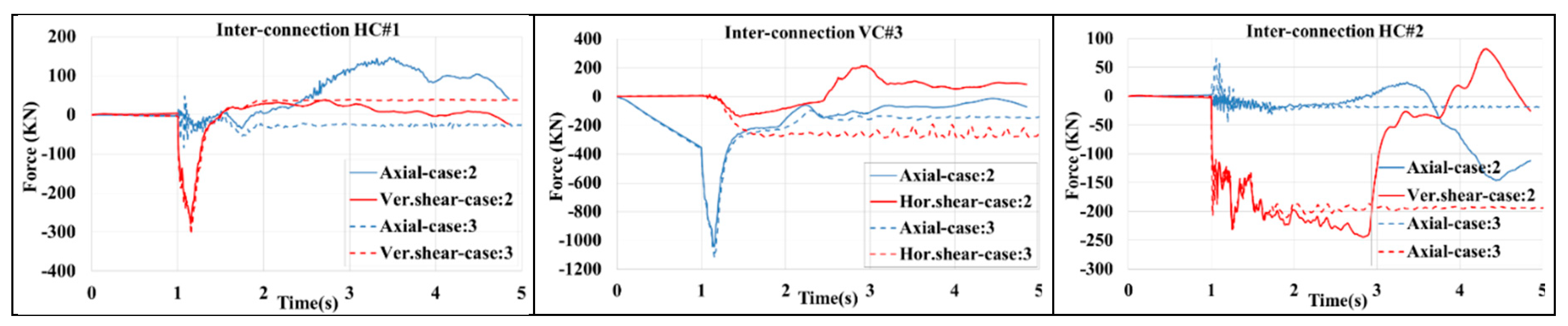
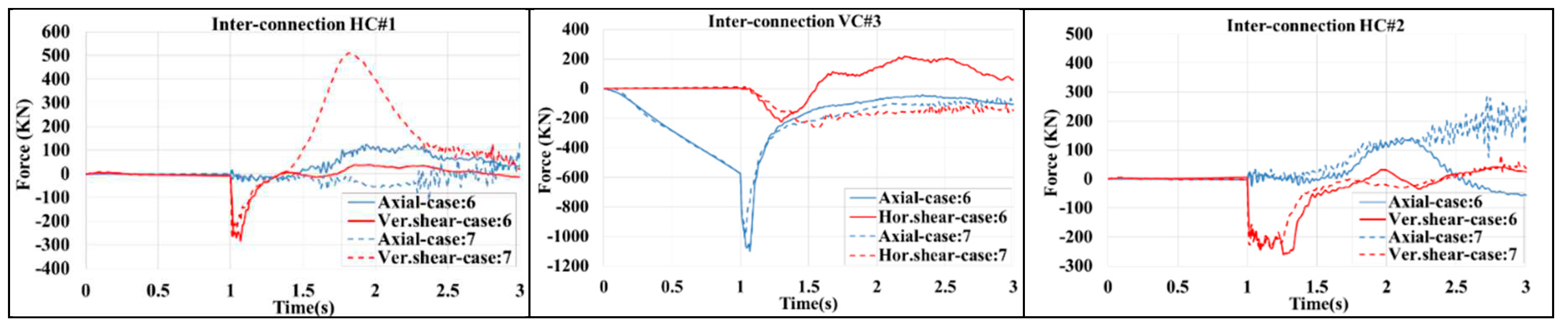
Regarding inter-module connections, shown in Figure 15, when column#2 buckles in case no.2 the load-bearing capacity of HC#2 tends to zero. Despite the high deformation of the building, no inter-module connection failure was observed because the dynamic redistribution in inter-module connections, especially HC#1, which was considered the most critical connection, was much lower than failure values. In both cases, The HC#1 maximum shear force was about 300kN with a DCR of 300/2000=0.15. The highest force redistribution through the inter-module connections was the axial force in VC#3, approximately equal to the buckling load in Column#1.
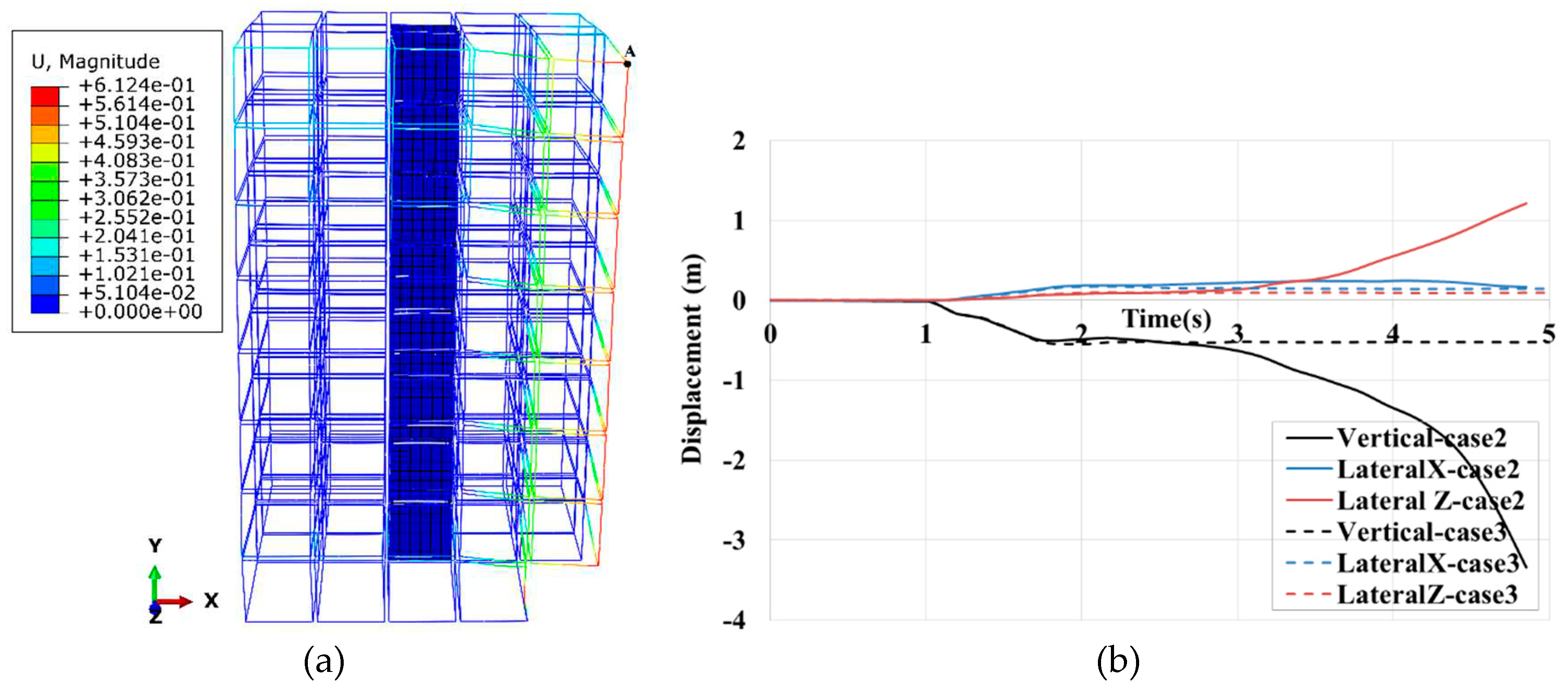
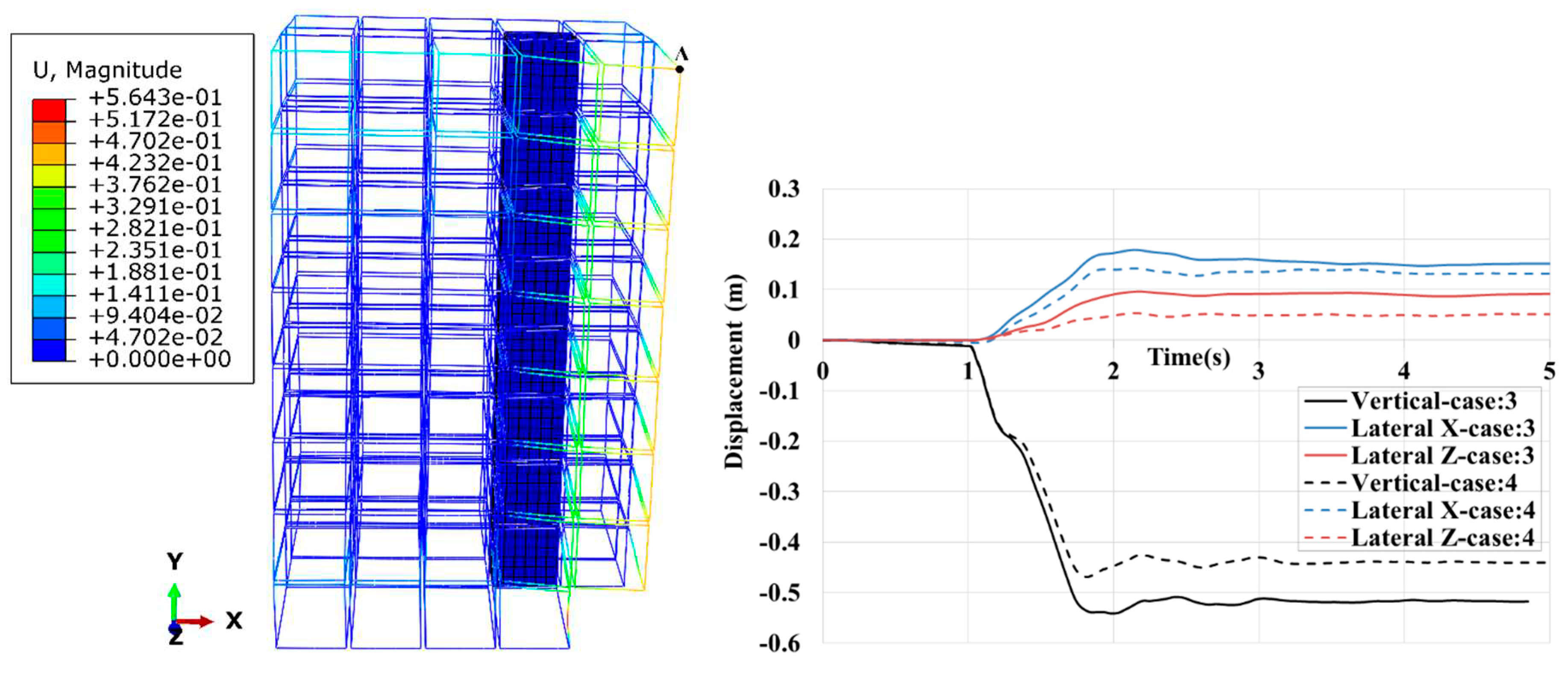
In the following, the outcomes of cases no. 4 & 5 are compared with case no.3. The results of case no.4 and case no.5 in terms of displacements, axial forces, and inter-module connection forces are very close to each other. However, the axial force in column#2 of case no.5 attached to shear walls was reduced by about 50% compared with case no.4. Contrary to case no.3, when the core wall was directly connected to the removal zone through inter-module connections, the shear wall reduced horizontal displacements, as observed in Figure 16(b). The lateral Z displacement in case no.4 is about 50% lesser than in case no.3.
Figure 17 presents the time history of axial forces in the columns is virtually the same; however, the redistributed load for column#2 in case no.4 is a bit higher than in case no.3. Although the shear core did not reduce the redistributed load in column#2, the vertical displacement that the building undergoes is a little lesser than in case no.3. This is because of decreasing the horizontal displacements provided by the stiff core wall, connected directly to the modules above the missing modules. In fact, as illustrated, the horizontal displacements can accelerate the column’s buckling, and restraining them helps the building stay robust.
It can be seen from Figure 18; that the tensile envelope contours are mostly appeared on the walls that are parallel to the X-direction. The maximum tensile stress is about 2.7 MPa, which is lower than the ultimate tensile strength of concrete. The majority of the envelope contour is located in the walls of the first four stories of MSB. Moreover, the bracing effect on these walls can be seen. Therefore, walls with less thickness or braces should be considered for upper levels. On the other hand, The Maximum compressive stress is just limited to the vicinity of columns.

4.3. 12-storey

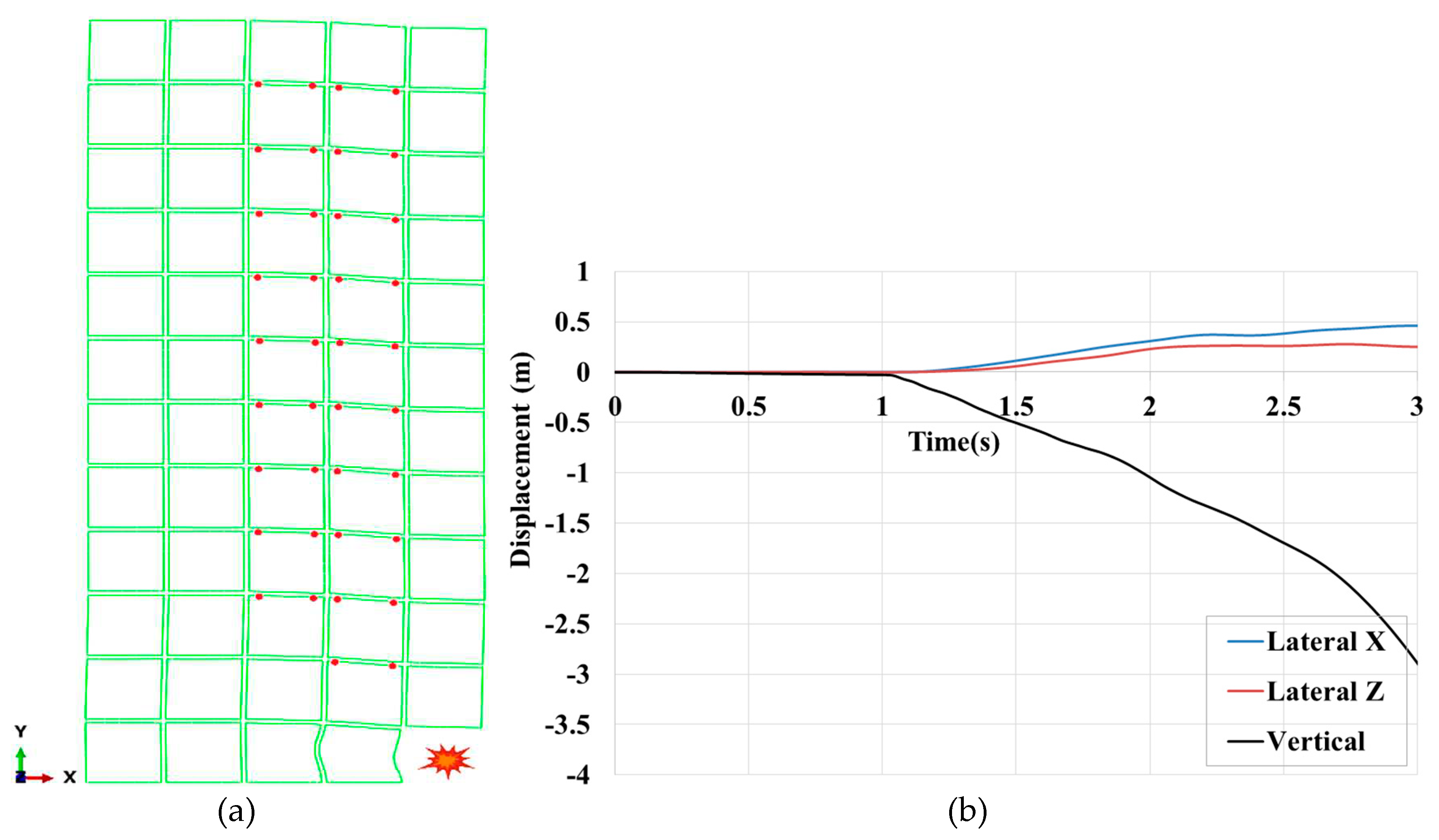
In the sixth case, the 12-story MSB, considered as a high-rise building, collapses two seconds after removing the corner module. The collapse sequence of this case is shown in Figure 19. Analogous to the 8-storey MSB, the collapse initiates with the buckling of columns #1 & #2 but continues with the buckling of the rest of the columns at the first and second storey simultaneously. In Figure 19(b), after 0.5 seconds of removing the corner modules, the maximum vertical and lateral displacements are about 500 mm and 110mm, respectively. Then due to further column buckling at the front row, the building tends to overturn about the X-axis.
As shown in Figure 20(a), the first set of plastic hinges formed in 0.6 seconds after the sudden removal of corner modules at the first elevation. Unlike the 8-story MSB, no hinges are observed at the first storey immediately after module removal. In addition, the hinges are extended to the center modules at the first elevation demonstrating more beams participated in load bearing.
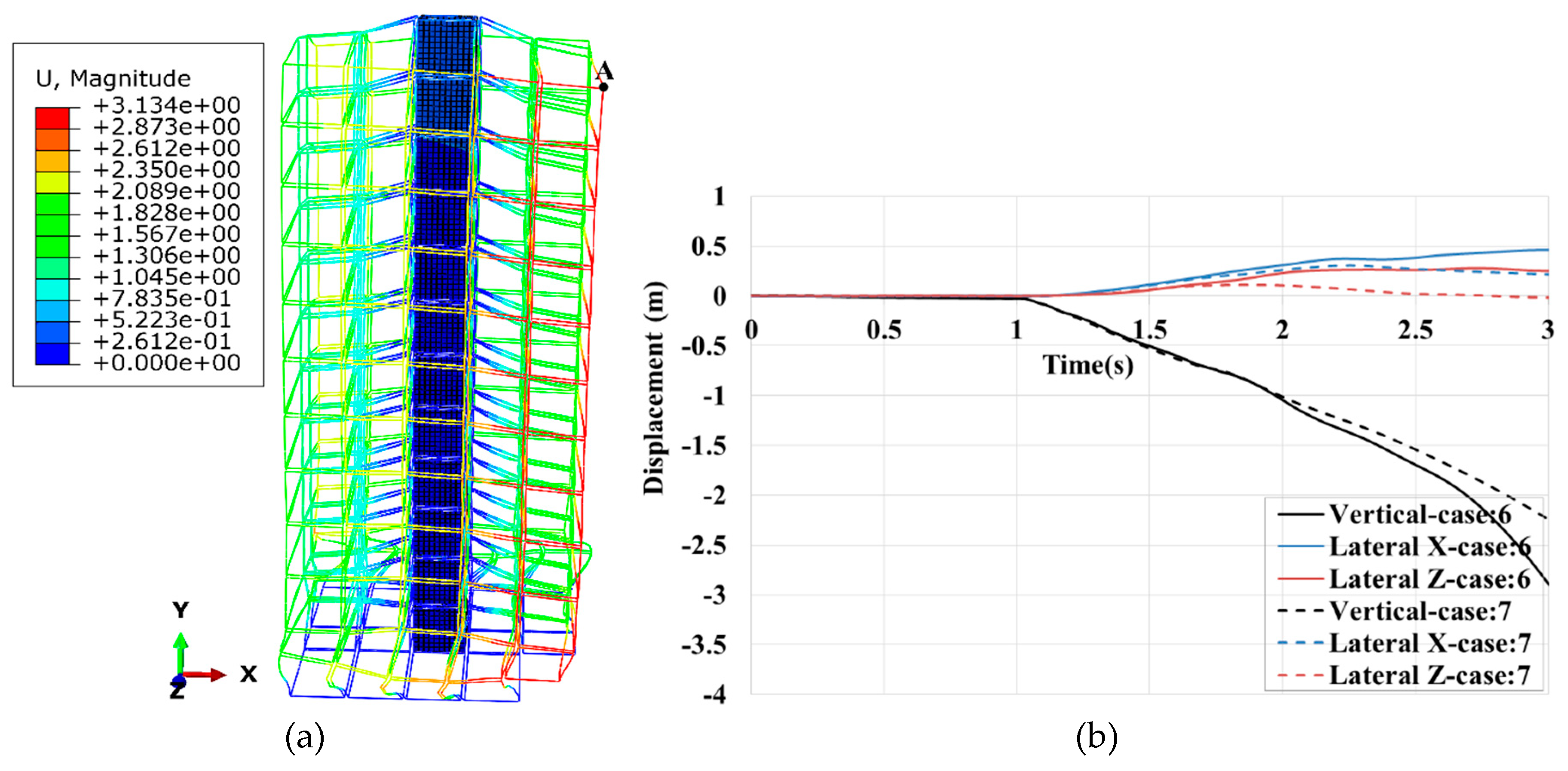
In the following, the effect of the shear wall (case no:7-9) on the collapse behaviour of a 12-storey MSB is studied. It is shown that the core wall system located at the center of the building (case no.7) does not prevent the building from collapsing. The time history of lateral and vertical displacements of the roof corner is shown in Figure 21(b). The maximum lateral displacements at the beginning are about zero, eventually reaching about 500 mm. Similar to case no.6 (bare frame), the slope of the vertical displacement is constant because columns at the first and second floor buckle successively. The distribution of the first set of plastic hinges is the same as in case no.6.
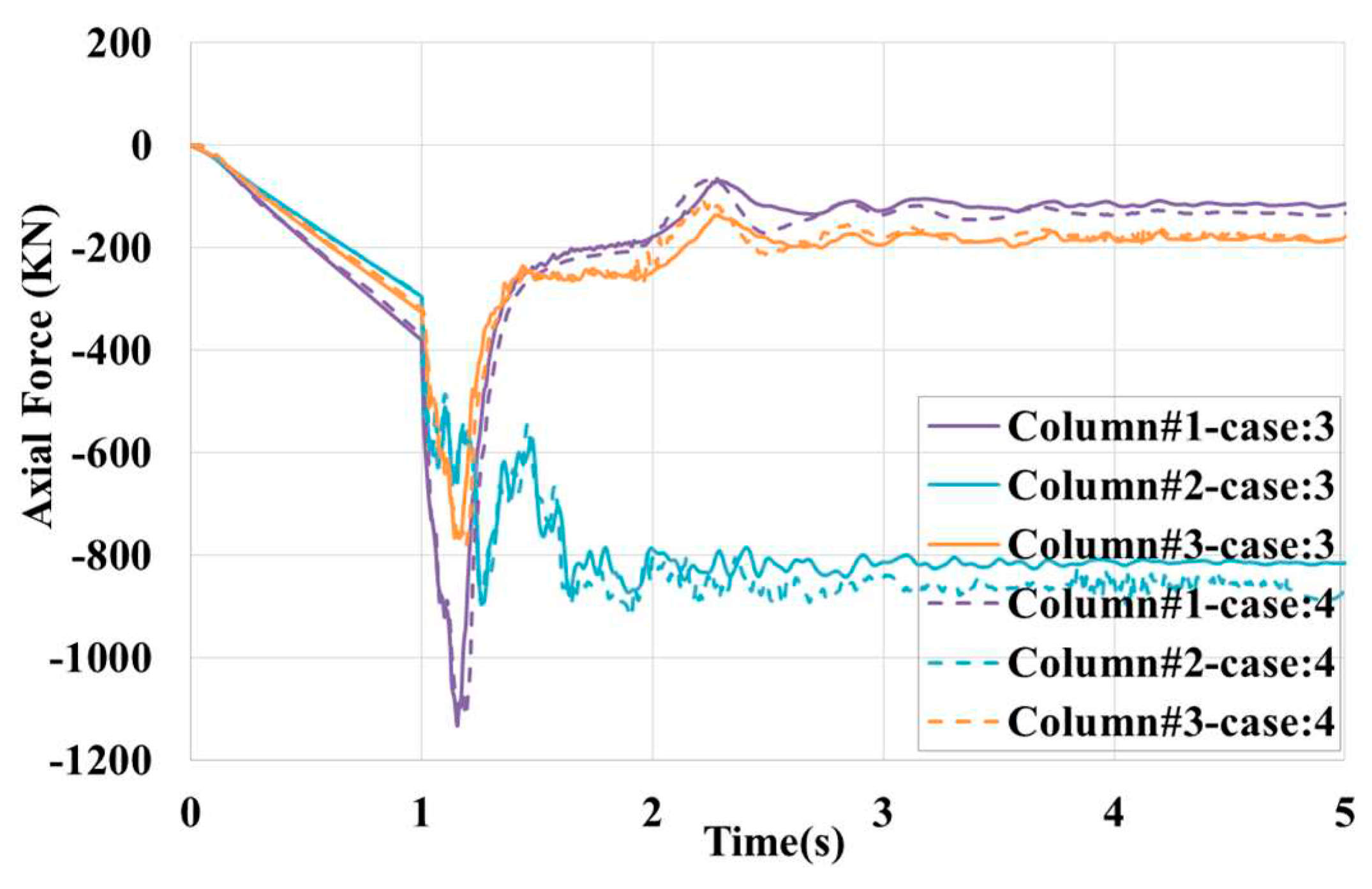
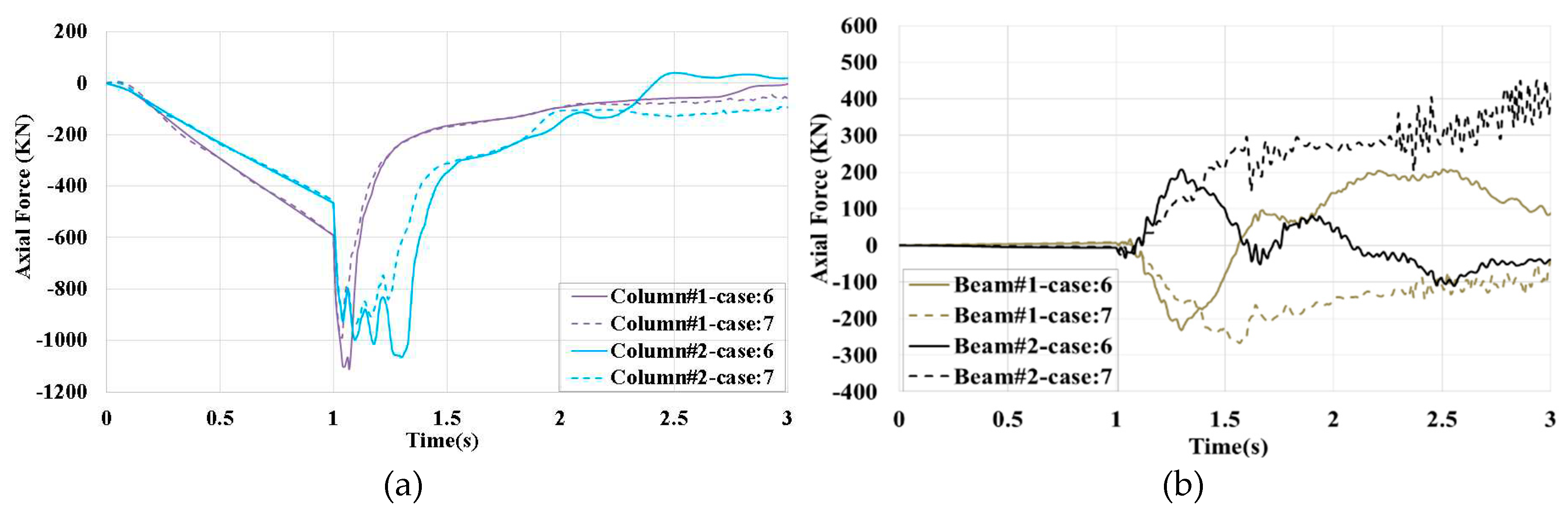
The time history of axial forces in several beams and columns in case no.6 and case no.7 is compared in Figure 22. Like the previous cases, a part of the loads is redistributed by an additional load path, owing to the core wall, in beams #1 and #2. In both cases, the redistributed load in Column#2 and Column#1 is more than the critical buckling load, which is about 860kN, as shown in Figure 22(a). In case no.6, Column#1 tolerates the highest load of about 1051kN with the corresponding DSR =1071/465=2.3.
As shown in Figure 23, there is still a high level of strength reserve capacity in the inter-module connections. VC#3 suffers the maximum compressive force with corresponding DCR=1071/1700=0.63. In case no.7, the shear force in HC#1 increases to 500kN due to the buckling of a column close to Column#3 on the second floor.
As the result of case no.8 and case no.9 was approximately identical, case no.8 is compared with case no.7. The results, depicted in Figure 24, in terms of displacements, axial forces, and inter-module connection forces are very close. In these cases, neither alternative loading paths due to the shear core nor limiting the lateral displacements help the building's robustness.
In terms of the concrete core’s stress pattern, like the 8-storey MSB, most envelope contour is located at the first half-height of the 12-storey MSB. The Maximum compressive stress is localized in the vicinity of columns, and The Maximum tensile stress is found in floor and ceiling beams. The maximum tensile stress is about 3.44 MPa, near the ultimate tensile strength of concrete, and the maximum compressive stress is about 12 MPa, which is much lower than its capacity.
In summary, the final state of each case against the corner module loss scenario is presented in Table 3. In case no: 6-9, because many columns start buckling at the same time, the core wall cannot safeguard the building stability via improving load sharing or reducing lateral displacements.

5. Parametric investigation

A parametric study is conducted to explore the effects of the inter-module connection's behaviour and the rigidity of intra-module connections on the overall response of the building, and their results are presented. The former section indicated that the ultimate capacity of the initial design of inter-module connections is much higher than the corresponding demand. Therefore, the effects of the weakened connections in terms of stiffness and strength on the overall response of the building are studied. In addition, the effect of the rigidity of the beam-to-column connection on the collapse capacity of the building, which is yet to be identified, is investigated.

5.1. Inter-module connection: stiffness and strength change

The horizontal and vertical springs are softened, as described in Figure 25 [25], to study the impact of stiffness and strength reduction on the robustness of MSB. In this process, the force at each displacement is decreased, whereas the corresponding displacement remains constant. The effects of the HCs and VCs are studied separately.
The HCs and VCs springs are softened for 50% and 90%; then, the results are compared to the baseline models (case no.2 and case no.6). Starting with the 8-storey MSB, no inter-module connection failure is observed when the horizontal or vertical springs are softened by 50%. Therefore, as depicted in Figure 26, the vertical displacements and redistributed loads in critical connections are approximately the same as in the base model. On the other hand, the situation for 90% softening is different because of the failure of several inter-module connections. In the model where the vertical connections are 90% softened, the collapse will happen sooner because of the failure of VC#3; As shown in Figure 27(a), its value reaches zero 0.5 s after corner module removal. As shown in Figure 28(a), the failure propagates to the upper stories and side modules. The early-stage failures that take 2 s are limited to the fourth row of modules.
When the horizontal connections are 90% softened, failure of the inter-module connections leads to a delay in the collapse of the whole building for 12 seconds. The reason is that after buckling Column#1, bridging of the remaining load to column#2 is postponed because of the failure of several HC connections shown in Figure 28(b). Then two columns in the second storey, determined in this figure, start to buckle. After 12s, the collapse will happen because of the buckling of column#2 and the numerous columns of the first and second stories. This shows that the building used a higher resistance capacity against buckling and collapse. In addition, unlike the past study where the modules were solid, the successive failure of inter-module connections is not started by losing HC#1.
To recap, softening horizontal connections can convey the redistributed loads from critical columns to other members. Moreover, identifying the first inter-module connection prone to failure in critical situations helps the designers prevent damage propagation to other modules.
In 12-storey MSB, like the 8-storey model, no inter-module connection fails when they are softened by 50%. Consequently, as depicted in Figure 29, the vertical displacements and redistributed loads in critical connections also have the same values as the base model. In 90% HCs, softening the premature failure in inter-module connections is not limited to HCx of the first row. Several HCz of the first and second stories, connecting the first-row modules to the corridor modules failed. Since the base columns must bear more loads in 12-storey buildings than in the 8-storey building, more than just one column starts to buckle immediately after module loss. Thus, the failure of inter-module connections cannot change the situation as it does in the 8-storey building. It should be noted that the first inter-module connection that begins to fail for both 90% HCs and 90% VCs is the same as an 8-storey building.

5.2. Intra-module connection: pin/rigid, plastic hinges and anti-collapse remediation

To investigate the impact of plastic hinge formation on the robustness of MSB, the 8-storey MSB (case no.2) is envisaged precluding local buckling. Figure 30 shows that this assumption conservatively ensures the building's robustness. It should be noted that this assumption for the building with fewer stories, such as case 1 and the one in the former study [23] with less likelihood of plastic hinge formation, can substantially improve computational runtime.
To study the effect of fully pinned intra-module connections on the robustness of the eight-story building, all semi-rigid beam-column connections turn into pinned ones. In the pinned model, since there is a less restraint at both ends of columns, the second and third storey columns become easily distorted after a sudden removal of the corner modules. In Figure 31, at the time frame of 0.5s after module removal, the first and second-row columns in the second and third storey drift oppositely. This results in the buckling of the base columns and the collapse of the whole building. The maximum horizontal displacement of the building has occurred at the level where a module is removed. In contrast, the maximum displacement in the semi-rigid model happened at the roof level.
In the pinned model, more kinetic energy dissipates due to more building deformation. In Figure 32, the redistributed load in VC#3 and Column#1 decreased considerably from 1042 kN to 710 kN. It can be concluded that enhancing the flexibility of the building is beneficial in terms of column buckling unless it will not lead to excessive relative displacements in columns of the lower stories.
Figure 33 compares the time history of vertical displacement of the pinned and semi-rigid twelve-story model. Like the 8-storey, the pinned model has not had enough redundancy, losing its robustness due to high deflection and successive buckling of columns.

Conclusion

The research was focused on studying the role of the concrete core wall in the robustness of MSBs against immediate corner module removal. The verified numerical finite element macro model of the building is simulated by incorporating material and geometric nonlinearities. The inter-module connections are modelled with nonlinear simplified springs, and the intra-module connections are assumed rigid. The dynamic responses, including lateral displacements, inter-module connection forces, and beam and column's internal forces, are reported for MSBs with different stories and shear core wall positions. In the end, parametric studies were undertaken, including stiffness softening of inter-module connections and intra-module rigidity. The main findings from this study are summarized as follows:
  • Unlike low-rise traditional steel buildings, 4-storey MSBs are robust against corner module removal. No columns buckle at the base level, and no plastic hinges appear in structural members. In addition, in the corner module removal scenario, Inter-module connections showed a significant safety factor in all cases, so no inter-module failure was observed.
  • In 12-MSBs, where many columns collapse simultaneously, the core wall has a minimal impact on robustness because there might not be enough time for load sharing. However, 8-MSBs benefited from the core wall system and maintained their robustness. The core wall helps the robustness of MSBs in two ways: The first is enhancing load sharing when the core is located at the centre (zone 1). The second is reducing lateral displacements, provided that the core wall is directly connected to the modules above the missing module (zone 2 or 3).
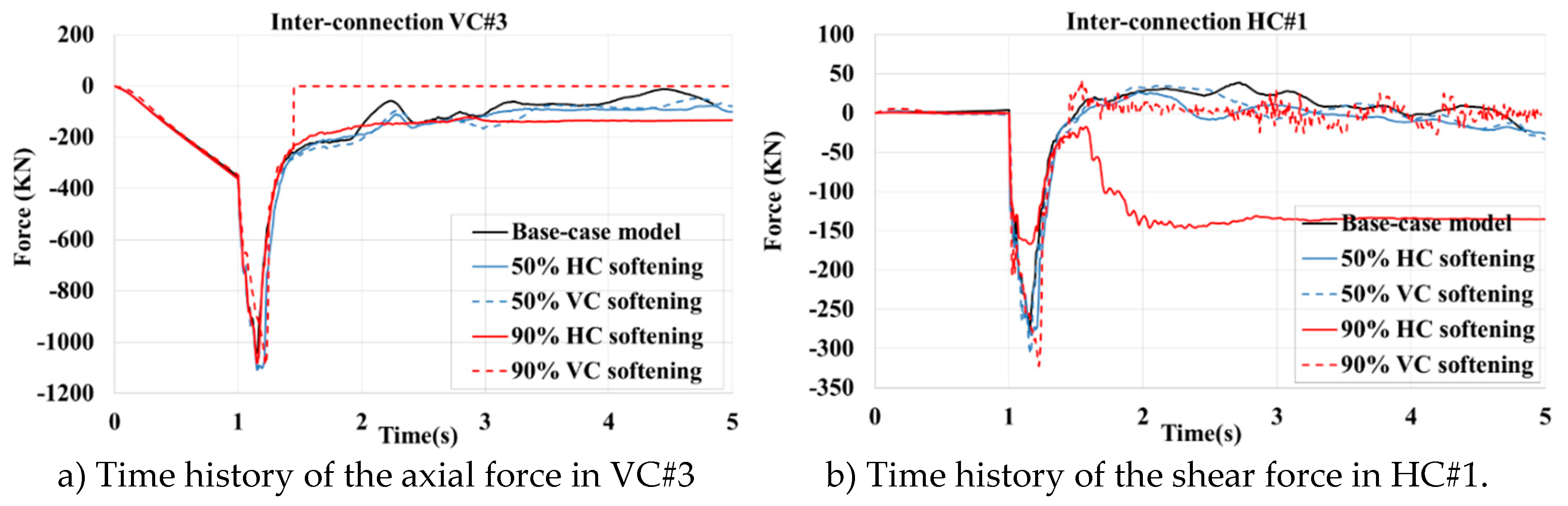
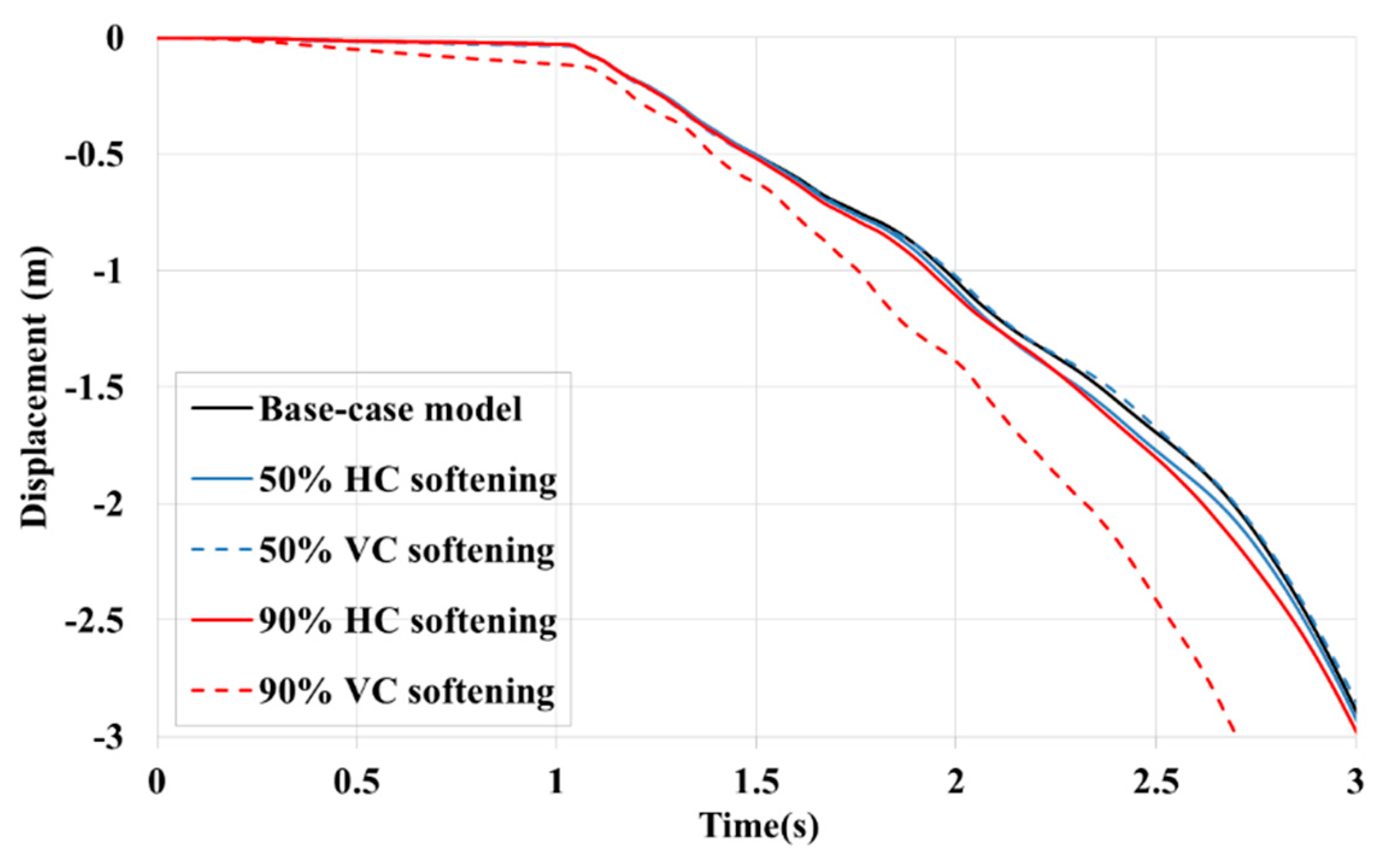
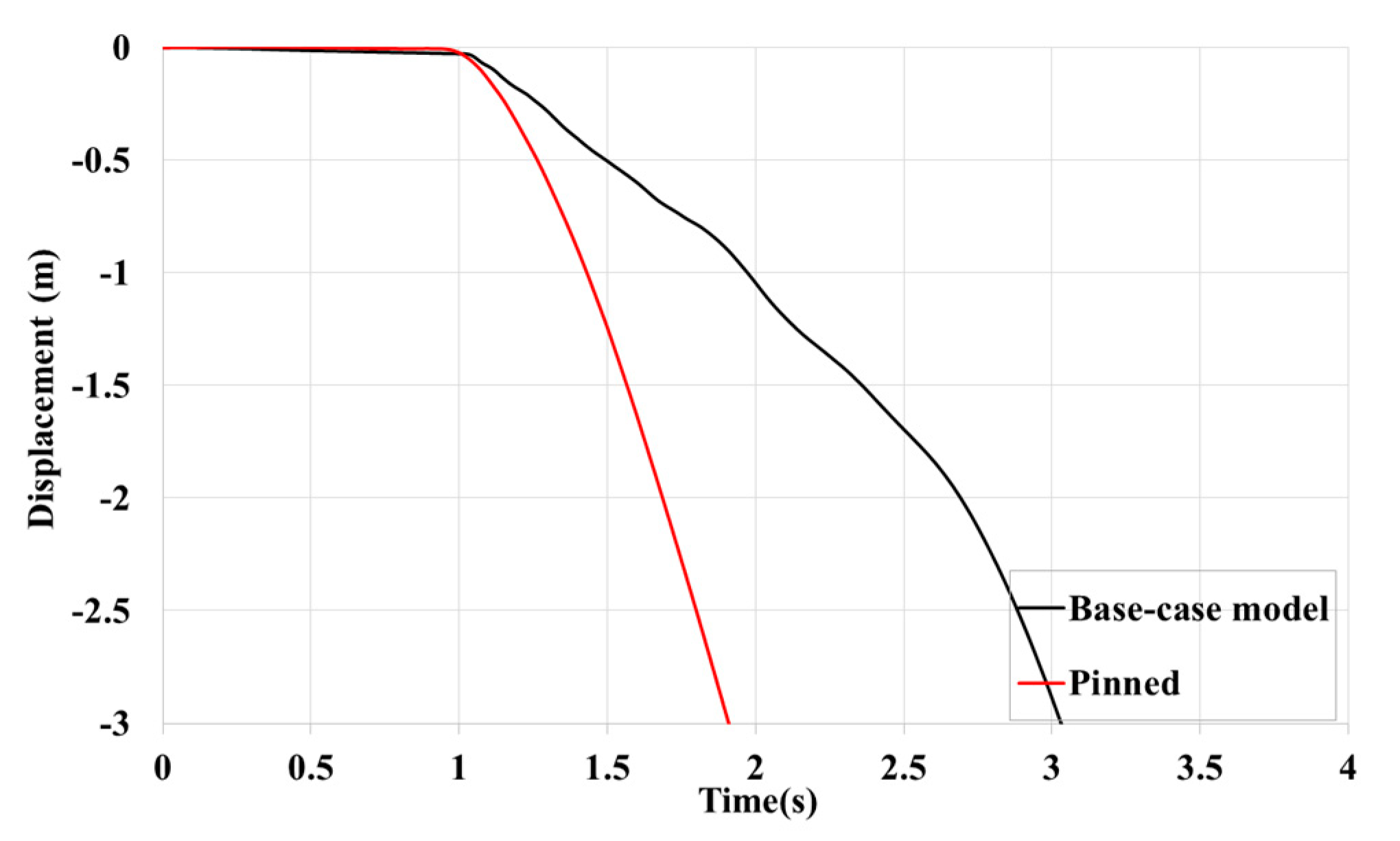
  • Softening Horizontal inter-module connections can worsen or improve the performance of the remaining modules against gravity-induced progressive collapse. In an 8-storey modular building, 50 % and 90% of softening in HCs accelerated and delayed the progressive collapse respectively by increasing flexibility. However, they were accompanied by many connection failures that led to the collapse of the whole building. Therefore, choosing an optimized inter-module connection stiffness is essential for the robustness of MSBs.
  • Preventing plastic hinges from forming can be considered as an anti-collapse mechanism. It turned the unstable bare-frame 8-storey MSB against the corner module removal scenario into a robust one.
  • In the corner-module removal scenario, the early set of plastic hinges formed in the ceiling beams of the first elevation (in the X-direction), which means structural members in this region have higher participation in carrying redistributed loads.
The progressive collapse of steel modular buildings with a shear core is simulated numerically using the finite element software Abaqus. Load redistribution and progressive collapse response of modular steel buildings (MSBs) with a typical layout under corner module loss scenario are investigated. Various modular building cases with three different heights and core wall locations are considered. Moreover, a parametric analysis is conducted to assess the impact of inter-module connection stiffness, intra-module connection rigidity, and plastic hinges on the robustness of the MSB under gravity loading.
The research can be expanded to include other types of layouts and configurations such as different module sizes, geometries, material properties and collapse scenarios. Furthermore, the assumed instantaneous removal time, representing a blast scenario, can be adjusted to a longer duration, which is more representative of a fire scenario.

Author Contributions

Conceptualization, R.H., P.S., M.A.; methodology, R.H and M.A.; software, R.H.; validation, R.H; formal analysis, R.H.; investigation, R.H.; writing—original draft preparation, R.H.; writing—review and editing, K.K. and P.S; supervision, P.S.; project administration, P.S.

Conflicts of Interest

Declare conflicts of interest or state “The authors declare no conflict of interest.” The authors declare no conflict of interest.

References

  1. Lawson, M.; Ogden, R.; Goodier, C.I. Design in modular construction. vol. 476. CRC Press Boca Raton, FL; 2014.
  2. Ferdous, W.; Bai, Y.; Ngo, T.D.; Manalo, A.; Mendis, P. New advancements, challenges and opportunities of multi-storey modular buildings – A state-of-the-art review. Eng. Struct. 2019. [CrossRef]
  3. Thai, H.T.; Ngo, T.; Uy, B. A review on modular construction for high-rise buildings. Structures 2020, 28, 1265–1290. [Google Scholar] [CrossRef]
  4. Ye, Z.; Giriunas, K.; Sezen, H.; Wu, G.; Feng, D.C. State-of-the-art review and investigation of structural stability in multi-story modular buildings. J. Build. Eng. 2021. [CrossRef]
  5. Gunawardena, T.; Ngo, T.; Mendis, P. Behaviour of multi-storey prefabricated modular buildings under seismic loads. Earthq. Struct 2016, 11, 1061–1076. [Google Scholar] [CrossRef]
  6. Lacey, A.W.; Chen, W.; Hao, H.; Bi, K. Review of bolted inter-module connections in modular steel buildings. J. Build. Eng. 2019. [CrossRef]
  7. Corfar, D.-A.; Tsavdaridis, K.D. A comprehensive review and classification of inter-module connections for hot-rolled steel modular building systems. J. Build. Eng. 2022, 50, 104006. [Google Scholar] [CrossRef]
  8. Rajanayagam, H.; Poologanathan, K.; Gatheeshgar, P.; Varelis, G.E.; Sherlock, P.; Nagaratnam, B.; Hackney, P. A-State- Of-The-Art review on modular building connections. Structures, vol. 34, Elsevier; 2021, p. 1903–22.
  9. Lacey, A.W.; Chen, W.; Hao, H.; Bi, K. Effect of inter-module connection stiffness on structural response of a modular steel building subjected to wind and earthquake load. Eng. Struct. 2020. [Google Scholar] [CrossRef]
  10. Rajanayagam, H.; Gunawardena, T.; Mendis, P.; Poologanathan, K.; Gatheeshgar, P.; Dissanayake, M.; Corradi, M. Evaluation of inter-modular connection behaviour under lateral loads: An experimental and numerical study. J. Constr. Steel Res. 2022, 194, 107335. [Google Scholar] [CrossRef]
  11. Peng, J.; Hou, C.; Shen, L. Lateral resistance of multi-story modular buildings using tenon-connected inter-module connections. J. Constr. Steel Res. 2021. [Google Scholar] [CrossRef]
  12. Feng, R.; Shen, L.; Yun, Q. Seismic performance of multi-story modular box buildings. J. Constr. Steel Res. 2020. [Google Scholar] [CrossRef]
  13. Peng, J.; Hou, C.; Shen, L. Numerical analysis of corner-supported composite modular buildings under wind actions. J. Constr. Steel Res. 2021, 187, 106942. [Google Scholar] [CrossRef]
  14. Sendanayake, S. V.; Thambiratnam, D.P.; Perera, N.; Chan, T.; Aghdamy, S. Seismic mitigation of steel modular building structures through innovative inter-modular connections. Heliyon 2019. [Google Scholar] [CrossRef]
  15. Sendanayake, S. V.; Thambiratnam, D.P.; Perera, N.J.; Chan, T.H.T.; Aghdamy, S. Enhancing the lateral performance of modular buildings through innovative inter-modular connections. Structures 2021. [Google Scholar] [CrossRef]
  16. Jing, J.; Charles Clifton, G.; Roy, K.; Lim, J.B.P. Performance of a novel slider device in multi-storey cold-formed steel modular buildings under seismic loading. Structures 2020. [Google Scholar] [CrossRef]
  17. Wang, Z.; Pan, W.; Zhang, Z. High-rise modular buildings with innovative precast concrete shear walls as a lateral force resisting system. Structures 2020, 26, 39–53. [Google Scholar] [CrossRef]
  18. Chua, Y.S.; Liew, J.Y.R.; Pang, S.D. Modelling of connections and lateral behavior of high-rise modular steel buildings. J. Constr. Steel Res. 2020. [Google Scholar] [CrossRef]
  19. Bi, J.; Zong, L.; Si, Q.; Ding, Y.; Lou, N.; Huang, Y. Field measurement and numerical analysis on wind-induced performance of modular structure with concrete cores. Eng. Struct. 2020. [Google Scholar] [CrossRef]
  20. Shi, F.; Wang, H.; Zong, L.; Ding, Y.; Su, J. Seismic behavior of high-rise modular steel constructions with various module layouts. J. Build. Eng. 2020. [Google Scholar] [CrossRef]
  21. Lawson, R.M.; Richards, J. Modular design for high-rise buildings. Proc Inst Civ Eng Build 2010, 163, 151–164. [Google Scholar] [CrossRef]
  22. Deng, E.F.; Zong, L.; Ding, Y.; Zhang, Z.; Zhang, J.F.; Shi, F.W.; Cai, L.M.; Gao, S.C. Seismic performance of mid-to-high rise modular steel construction - A critical review. Thin-Walled Struct. 2020. [Google Scholar] [CrossRef]
  23. Yee, S.S.; Kong, K.H.; Liew, J.Y.R.; Dai, Z. Response Behaviour of High-Rise Modular Building under Wind and Seismic Loads. ce/papers 2021, 4, 1747–1756. [Google Scholar] [CrossRef]
  24. Luo, F.J.; Bai, Y.; Hou, J.; Huang, Y. Progressive collapse analysis and structural robustness of steel-framed modular buildings. Eng. Fail. Anal. 2019. [Google Scholar] [CrossRef]
  25. Alembagheri, M.; Sharafi, P.; Hajirezaei, R.; Tao, Z. Anti-collapse resistance mechanisms in corner-supported modular steel buildings. J. Constr. Steel Res. 2020. [Google Scholar] [CrossRef]
  26. Alembagheri, M.; Sharafi, P.; Hajirezaei, R.; Samali, B. Collapse capacity of modular steel buildings subject to module loss scenarios: The role of inter-module connections. Eng. Struct. 2020, 210. [Google Scholar] [CrossRef]
  27. Sharafi, P.; Alembagheri, M.; Kildashti, K.; Ganji, H.T. Gravity-Induced Progressive Collapse Response of Precast Corner-Supported Modular Buildings. J. Archit. Eng. 2021. [Google Scholar] [CrossRef]
  28. Alembagheri, M.; Sharafi, P.; Tao, Z.; Hajirezaei, R.; Kildashti, K. Robustness of multistory corner-supported modular steel frames against progressive collapse. Struct. Des. Tall Spec. Build. 2021, 30, e1896. [Google Scholar] [CrossRef]
  29. Chen, Z.; Khan, K.; Khan, A.; Javed, K.; Liu, J. Exploration of the multidirectional stability and response of prefabricated volumetric modular steel structures. J. Constr. Steel Res. 2021, 184, 106826. [Google Scholar] [CrossRef]
  30. Peng, J.; Hou, C.; Shen, L. Progressive collapse analysis of corner-supported composite modular buildings. J. Build. Eng. 2022, 48, 103977. [Google Scholar] [CrossRef]
  31. Thai, H.T.; Ho, Q.V.; Li, W.; Ngo, T. Progressive collapse and robustness of modular high-rise buildings. Struct. Infrastruct. Eng. 2021. [Google Scholar] [CrossRef]
  32. Zhang, J.-Z.; Yam, M.C.H.; Li, G.-Q.; Wang, Y.-Z. Anti-collapse behavior of modular steel buildings with corrugated panels. J. Constr. Steel Res. 2022, 193, 107279. [Google Scholar] [CrossRef]
  33. Board, A.B.C. National construction code (NCC). Counc Aust Gov 2016.
  34. 2014, C. 392: Code for anti-collapse design of building structures 2014.
  35. UFC-DoD, U.F.C. Design of Buildings to Resist Progressive Collapse, the US Department of Defense. 2005.
  36. Building CC on, Codes F, Canada NRC of, Code NRC of CAC on the NB. National building code of Canada. Associate Committee on the National Building Code, National Research Council; 1965.
  37. Administration), G.S.A. (General S. Alternate path analysis & design guidelines for progressive collapse resistance. Gen. Serv. Adm.
  38. Eurocode 1. Actions on structures–Part 1–7: General actions–Accidental actions. Br Stand London 2006.
  39. Adam, J.M.; Parisi, F.; Sagaseta, J.; Lu, X. Research and practice on progressive collapse and robustness of building structures in the 21st century. Eng. Struct. 2018. [CrossRef]
  40. Standard A. Structural design actions-Part 4: Earthquake actions in Australia (AS 1170.4-2007). SAI Glob Limited NSW 2001, Aust 2007.
  41. Yun, X.; Gardner, L. Stress-strain curves for hot-rolled steels. J. Constr. Steel Res. 2017. [Google Scholar] [CrossRef]
  42. Seismic Evaluation and Retrofit of Existing Buildings. 2014. [CrossRef]
  43. Simulia. Abaqus 6.11 Theory Manual. Provid RI, USA DS SIMULIA Corp 2017.
  44. Farajian, M.; Sharafi, P.; Alembagheri, M.; Kildashti, K.; Bigdeli, A. Effects of bolted connections’ properties on natural dynamic characteristics of corner-supported modular steel buildings. InStructures 2022 Nov 1 (Vol.45, pp. 1491-1515). Elsevier.
  45. Farajian, M.; Sharafi, P.; Eslamnia, H.; Kildashti, K.; Bai, Y. Classification of inter-modular connections for stiffness and strength in sway corner-supported steel modular frames. J. Constr. Steel Res. 2022, 197, 107458. [Google Scholar] [CrossRef]
  46. Farajian, M.; Sharafi, P.; Eslamnia, H.; Bai, Y.; Samali, B. Classification system for inter-modular connections in non-sway corner-supported steel modular buildings. InStructures 2023 Mar 1 (Vol. 49, pp. 807-825). Elsevier.
Preprints 96001 g001
Figure 1. A typical view of MSB with: (a) inter-module connection; (b) intra-module connection.
Figure 1. A typical view of MSB with: (a) inter-module connection; (b) intra-module connection.
Preprints 96001 g001
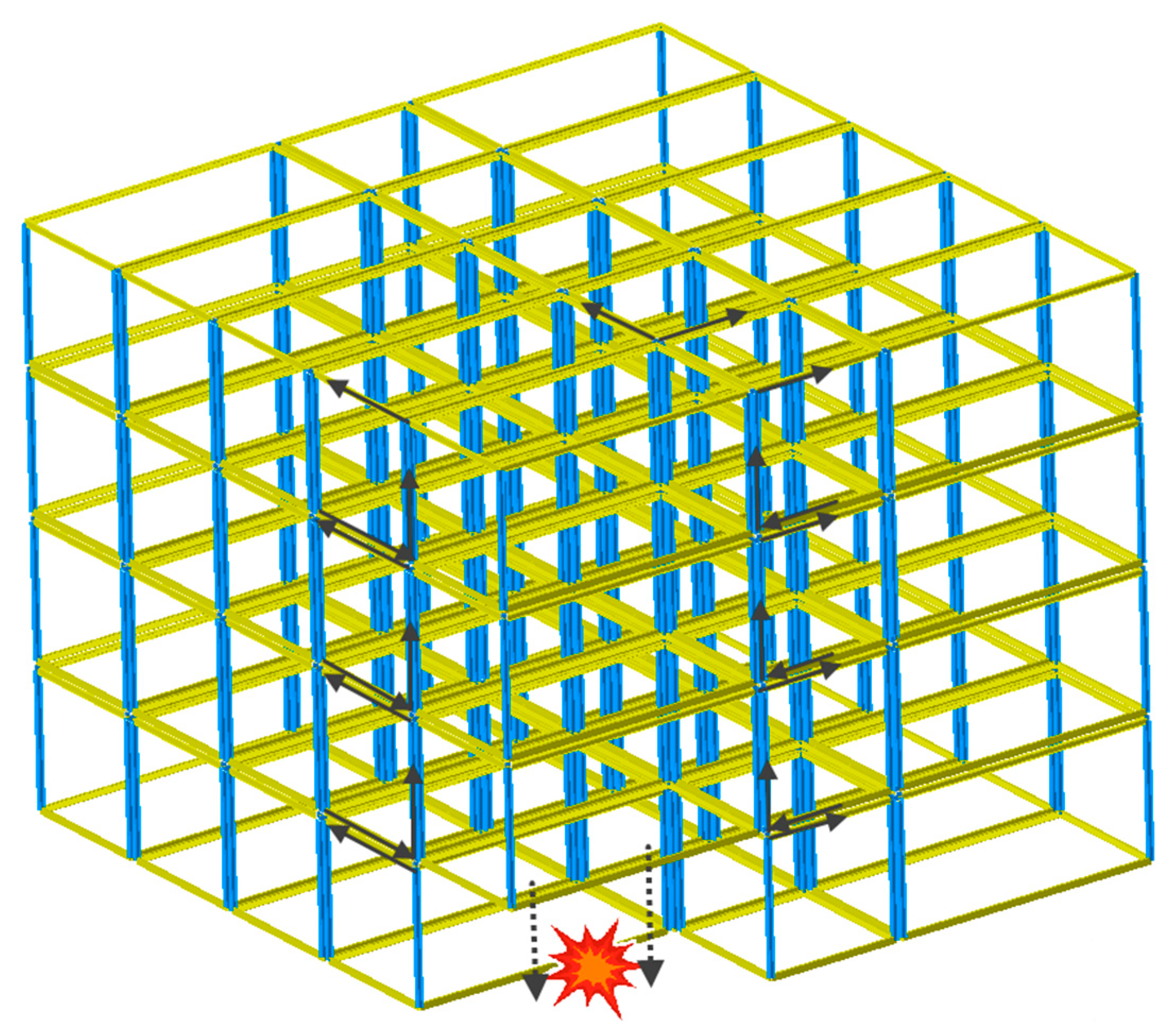
Preprints 96001 g002
Figure 2. ALPs in an MSB under corner module loss scenario.
Figure 2. ALPs in an MSB under corner module loss scenario.
Preprints 96001 g002
Preprints 96001 g003
Figure 3. (a) Typical building plan; (b) Typical elevation view.
Figure 3. (a) Typical building plan; (b) Typical elevation view.
Preprints 96001 g003
Preprints 96001 g004
Figure 4. 3D finite element model of the building.
Figure 4. 3D finite element model of the building.
Preprints 96001 g004
Preprints 96001 g005
Figure 5. 3D finite element model of the building.
Figure 5. 3D finite element model of the building.
Preprints 96001 g005
Preprints 96001 g006
Figure 6. Comparison of dynamic displacement: the present study's results with those reported by Luo et al. [24].
Figure 6. Comparison of dynamic displacement: the present study's results with those reported by Luo et al. [24].
Preprints 96001 g006
Preprints 96001 g007
Figure 7. Typical critical connections and elements.
Figure 7. Typical critical connections and elements.
Preprints 96001 g007
Preprints 96001 g008
Figure 8. (a) The final equilibrium position of the structure after corner module removal. (b) Time history of global displacements of the roof corner above the missing module, designated by A.
Figure 8. (a) The final equilibrium position of the structure after corner module removal. (b) Time history of global displacements of the roof corner above the missing module, designated by A.
Preprints 96001 g008
Preprints 96001 g009
Figure 9. Time history of axial forces in some beams and columns close to the missing module.
Figure 9. Time history of axial forces in some beams and columns close to the missing module.
Preprints 96001 g009
Preprints 96001 g010
Figure 10. Time history of the axial and shear forces in some critical HCs and VCs.
Figure 10. Time history of the axial and shear forces in some critical HCs and VCs.
Preprints 96001 g010
Preprints 96001 g011
Figure 11. Deformation of the case no.2 in different time frames after sudden removal of corner module.
Figure 11. Deformation of the case no.2 in different time frames after sudden removal of corner module.
Preprints 96001 g011
Preprints 96001 g012
Figure 12. (a) Distribution of plastic hinges at elevation:1, in 0.4s after the sudden removal of corner module. (b) Time history of global displacements of the roof corner above the missing module.
Figure 12. (a) Distribution of plastic hinges at elevation:1, in 0.4s after the sudden removal of corner module. (b) Time history of global displacements of the roof corner above the missing module.
Preprints 96001 g012
Preprints 96001 g013
Figure 13. (a) The final equilibrium position of the structure after corner module removal. (b) Time history of global displacements of the roof corner above the missing module, designated by A.
Figure 13. (a) The final equilibrium position of the structure after corner module removal. (b) Time history of global displacements of the roof corner above the missing module, designated by A.
Preprints 96001 g013
Preprints 96001 g014
Figure 14. Time history of axial forces in some (a) columns and (b) beams, close to the missing module.
Figure 14. Time history of axial forces in some (a) columns and (b) beams, close to the missing module.
Preprints 96001 g014
Preprints 96001 g015
Figure 15. Time history of the axial and shear forces in some critical HCs and VCs.
Figure 15. Time history of the axial and shear forces in some critical HCs and VCs.
Preprints 96001 g015
Preprints 96001 g016
Figure 16. (a) The final equilibrium position of the structure after corner module removal. (b) Time history of global displacements of the roof corner above the missing module, designated by A.
Figure 16. (a) The final equilibrium position of the structure after corner module removal. (b) Time history of global displacements of the roof corner above the missing module, designated by A.
Preprints 96001 g016
Preprints 96001 g017
Figure 17. Time history of axial forces in some columns.
Figure 17. Time history of axial forces in some columns.
Preprints 96001 g017
Preprints 96001 g018
Figure 18. Envelope contours of: (a) maximum principal (tensile) and (b) minimum principal (compressive) stress of the shear core located at zone 1.
Figure 18. Envelope contours of: (a) maximum principal (tensile) and (b) minimum principal (compressive) stress of the shear core located at zone 1.
Preprints 96001 g018
Preprints 96001 g019
Figure 19. Deformation of the case no.6 in different time frames after the sudden removal of the corner module.
Figure 19. Deformation of the case no.6 in different time frames after the sudden removal of the corner module.
Preprints 96001 g019
Preprints 96001 g020
Figure 20. (a) Distribution of plastic hinges at elevation (1), in 0.6s after sudden removal of corner module. (b) Time history of global displacements of the roof corner above the missing module.
Figure 20. (a) Distribution of plastic hinges at elevation (1), in 0.6s after sudden removal of corner module. (b) Time history of global displacements of the roof corner above the missing module.
Preprints 96001 g020
Preprints 96001 g021
Figure 21. (a) The collapse mode of the structure after corner module removal. (b) Time history of global displacements of the roof corner above the missing module, designated by A.
Figure 21. (a) The collapse mode of the structure after corner module removal. (b) Time history of global displacements of the roof corner above the missing module, designated by A.
Preprints 96001 g021
Preprints 96001 g022
Figure 22. Time history of axial forces in some a) columns and b) beams, close to the missing module.
Figure 22. Time history of axial forces in some a) columns and b) beams, close to the missing module.
Preprints 96001 g022
Preprints 96001 g023
Figure 23. Time history of the axial and shear forces in some critical HCs and VCs.
Figure 23. Time history of the axial and shear forces in some critical HCs and VCs.
Preprints 96001 g023
Preprints 96001 g024
Figure 24. (a) Time history of axial forces in some columns. (b) Time history of global displacements of the roof corner above the missing module, designated by A.
Figure 24. (a) Time history of axial forces in some columns. (b) Time history of global displacements of the roof corner above the missing module, designated by A.
Preprints 96001 g024
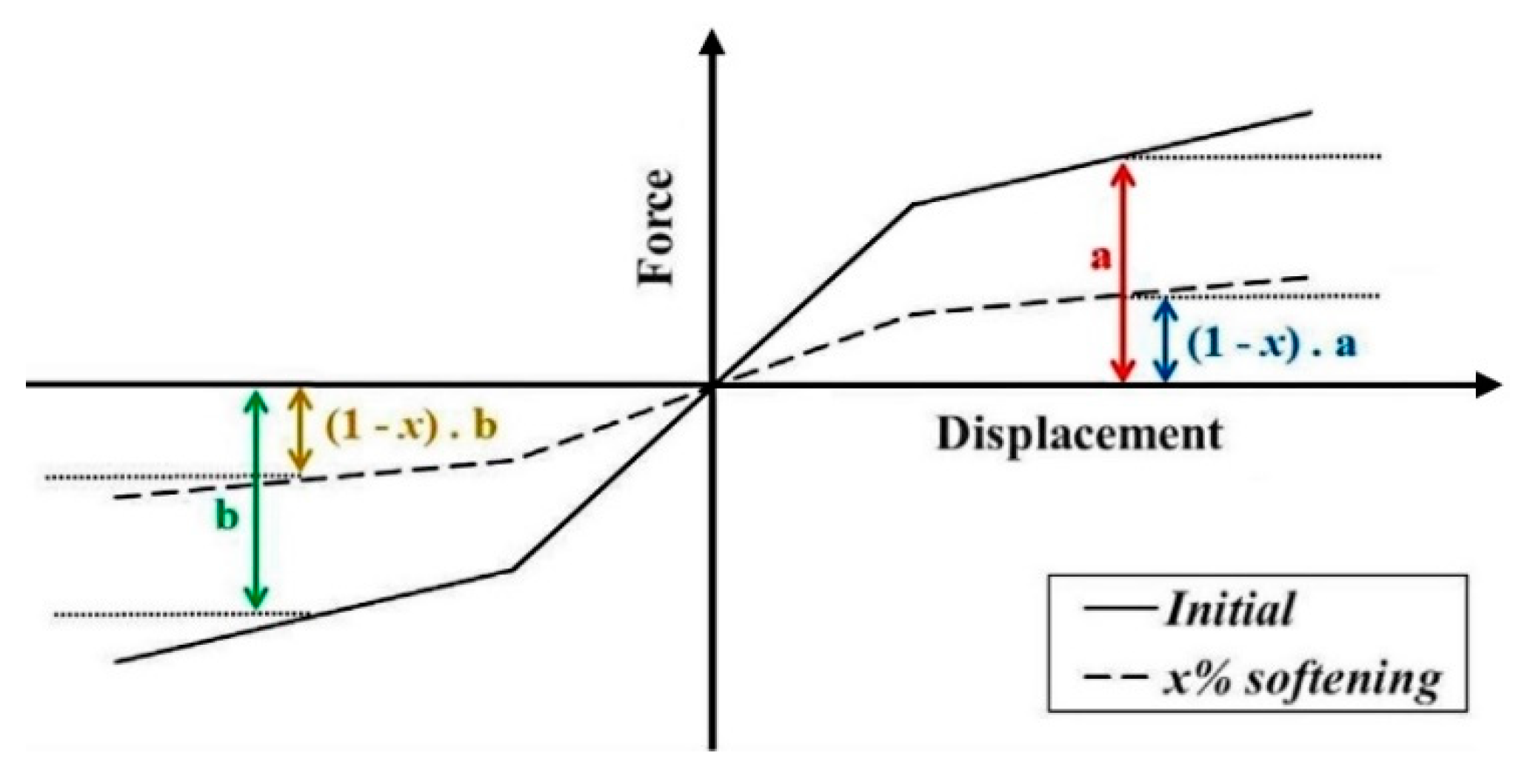
Preprints 96001 g025
Figure 25. Softening of a typical connection’s spring.
Figure 25. Softening of a typical connection’s spring.
Preprints 96001 g025
Preprints 96001 g026
Figure 26. Time history of vertical displacements of the roof corner above the missing module, designated by A.
Figure 26. Time history of vertical displacements of the roof corner above the missing module, designated by A.
Preprints 96001 g026
Preprints 96001 g027
Figure 27. Comparison of the responses of the base case-model, and 50% and %90 softened springs.
Figure 27. Comparison of the responses of the base case-model, and 50% and %90 softened springs.
Preprints 96001 g027
Preprints 96001 g028
Figure 28. Sequence of the early set of inter-module connection failure for (a) 90% VC softening; (b) 90% HC softening.
Figure 28. Sequence of the early set of inter-module connection failure for (a) 90% VC softening; (b) 90% HC softening.
Preprints 96001 g028
Preprints 96001 g029
Figure 29. Time history of vertical displacements of the roof corner above the missing module, designated by A.
Figure 29. Time history of vertical displacements of the roof corner above the missing module, designated by A.
Preprints 96001 g029
Preprints 96001 g030
Figure 30. (a) The final equilibrium position of the structure after corner module removal. (b) Time history of global displacements of the roof corner above the missing module, designated by A.
Figure 30. (a) The final equilibrium position of the structure after corner module removal. (b) Time history of global displacements of the roof corner above the missing module, designated by A.
Preprints 96001 g030
Preprints 96001 g031
Figure 31. (a) The position of the structure at a) 0.5s and (b) 2s after corner module removal.
Figure 31. (a) The position of the structure at a) 0.5s and (b) 2s after corner module removal.
Preprints 96001 g031
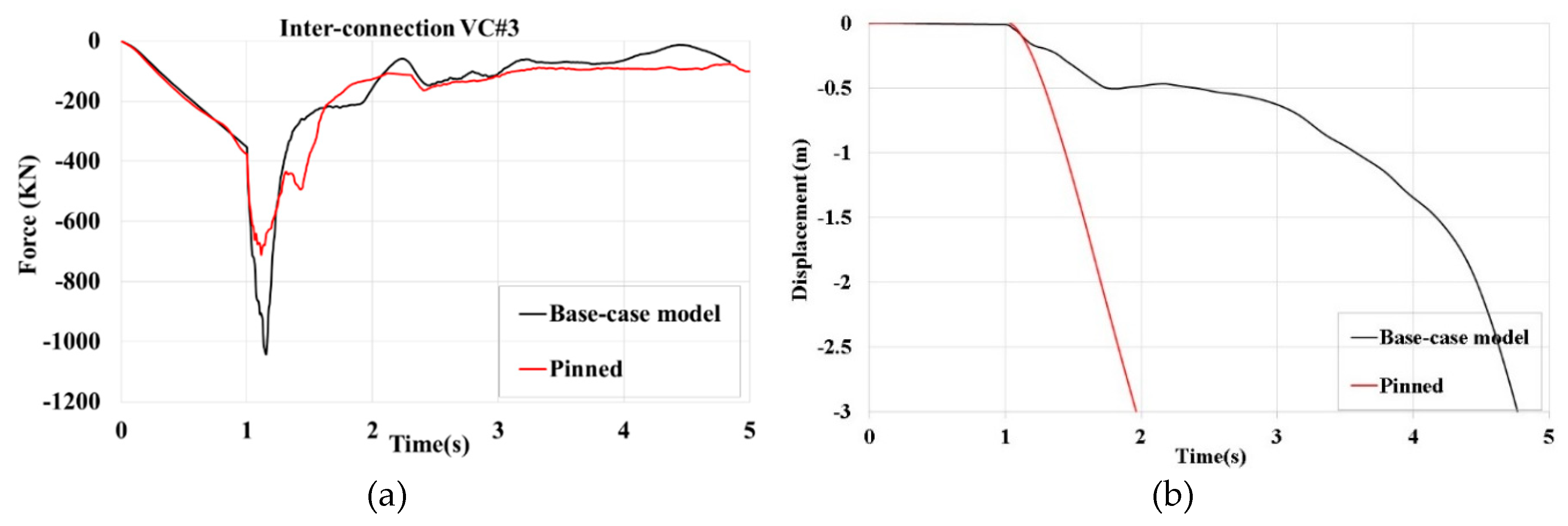
Preprints 96001 g032
Figure 32. (a) Time history of axial forces in VC#3. (b) Time history of global displacements of the roof corner above the missing module, designated by A.
Figure 32. (a) Time history of axial forces in VC#3. (b) Time history of global displacements of the roof corner above the missing module, designated by A.
Preprints 96001 g032
Preprints 96001 g033
Figure 33. Time history of global displacements of the roof corner above the missing module, designated by A.
Figure 33. Time history of global displacements of the roof corner above the missing module, designated by A.
Preprints 96001 g033
Table 1. Failure limits of inter-module connections.
Table 1. Failure limits of inter-module connections.
Connection Axial failure force Shear failure force
Vertical (VC) 1700 KN 2000 KN
Horizontal (HC) 1200 KN 2000 KN
Table 2. Overview of collapse analysis cases and corresponding building configurations.
Table 2. Overview of collapse analysis cases and corresponding building configurations.
Case No. Story No. Building frame types
1 4 Bare frame (4s)
2 8 Bare frame (8s)
3 8 Bare frame + shear core at zone 1 (8 sw1)
4 8 Bare frame + shear core at zone 2 (8 sw2)
5 8 Bare frame + shear core at zone 3 (8 sw3)
6 12 Bare frame (12s)
7 12 Bare frame + shear core at zone 1 (12 sw1)
8 12 Bare frame + shear core at zone 2 (12 sw2)
9 12 Bare frame + shear core at zone 3 (12 sw3)
Table 3. Summary of building's stability results.
Table 3. Summary of building's stability results.
Cases Stability State Main Reasons
1) 4s stable No column buckling
2) 8s collapsed Buckling C#1 and C#2
3) 8 sw1 stable Less redistributed load in C#2
4) 8 sw2 stable Less lateral displacements
5) 8 sw3 stable C#2 constrained with concrete core
6) 12s collapsed Several columns buckling
7) 12 sw1 collapsed Several columns buckling
8) 12 sw2 collapsed Several columns buckling
9) 12 sw3 collapsed Several columns buckling
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated