Electrohydrodynamic (In)stability of Microfluidic Channel Flows: Analytical Expressions in the Limit of Small Reynolds Number

Preprint

Article

Electrohydrodynamic (In)stability of Microfluidic Channel Flows: Analytical Expressions in the Limit of Small Reynolds Number

Altmetrics

Downloads

112

Views

Comments

A peer-reviewed article of this preprint also exists.

Goran Goranovic^*

Mads Peter Sørensen,

Henrik Bruus,Morten Brøns

Goran Goranovic^*

Mads Peter Sørensen,

Henrik Bruus,Morten Brøns

This version is not peer-reviewed

Submitted:

11 January 2024

Posted:

12 January 2024

You are already at the latest version

Alerts

Abstract

We study electrohydrodynamic (EHD) linear (in)stability of microfluidic channel flows, i.e. the stability of interface between two-shearing viscous (perfect) dielectrics exposed to an electric field in large aspect ratio microchannels. We then apply our results to particular microfluidic systems known as electroosmotic (EO) pumps. Our results are detailed analytical expressions for the growth rate of two-dimensional EHD modes in Couette-Poiseuille flows in the limit of small Reynolds number ($R$); the expansions to both zeroth- and first-order-$R$ are considered. The growth rates are complicated functions of viscosity-, height-, density- and dielectric-constant ratio, as well as of wavenumbers and voltages, and to our knowledge have not been presented before in literature. To make the results more useful, e.g., for voltage-control EO pump operations, we also derive equations for the impending voltages of the neutral stability curves that divide stable from unstable regions in voltage-wavenumber stability diagrams. The voltage equations and the stability diagrams are given for all wavenumbers. We finally outline the flow regimes in which our first-order-$R$ voltage corrections could potentially be experimentally measured. Our work gives the insight into the coupling mechanism between electric field and shear flow in parallel-planes channel flows, correcting an erroneous attempt from literature. Our general analysis enables us also to refine the renowned instability mechanism due to viscosity stratification, i.e., the case of pure shear instability, when the first-order-$R$ voltage correction equals zero.

Keywords:

Subject: Physical Sciences - Fluids and Plasmas Physics

1. Introduction

When exposed to an electric (E) field, an interface between two stationary superposed dielectric fluids can become unstable, forming periodic undulations that can further grow and deform [1,2,3,4,5]. The well-studied phenomenon, known as electrohydrodynamic (EHD) instability, depends on the nature of dielectrics (perfect dielectrics without free surface charge [6], or leaky dielectrics [7]), the direction of E-fields (normal [2] vs. tangential [8]) and is generally function of (the ratios of) the fluids’ conductivities, dielectric constants, densities and heights, as well as applied voltages. The seminal work on EHD stability, both experimental and theoretical, was done on macroscopic scale (≳ 10 cm), [1].

When two superposed fluids are in motion, as e.g. in parallel-plane channel flows, things are more complicated since instabilities arise even in the absence of the E-fields, [9,10,11,12,13], and in fact for arbitrary small Reynolds numbers [14]. When E-fields are present, the stability of the growth modes is changed as the fields in general couple to flow, see e.g., [15]. The EHD instability of two shearing (perfect) dielectrics in channel flow has been studied in [16], but as we show, not correctly analyzed. A correct (theoretical) approach of EHD instability of two shearing (leaky) dielectrics in channel flows is done in [17], where the unstable modes with largest growth rate are solved numerically, and then explored systematically over a selected range of parameters; however, the analysis is applied to microfluidic channels and these are typically much longer than wider and higher, so two flowing immiscible dielectrics will generally arrange themselves interspersed between rather than on top of each other, as they try to minimize the free interface energy and thus the contact, [18,19].

The shearing flows having two superposed fluids in microfludic channels require a special configuration, namely that of low-aspect ratio rectangular channels (height much smaller than width, Figure 1(a)) in conjunction with electroosmotic (EO) flow - an application known as EO pump [20,21,22]. The pump has the combined EO/pressure-driven (Couette–Poiseuille) flow profile, rather than the pure pressure-driven (Poiseuille) flow analyzed in [17], and that will affect the stability. Furthermore, numerical studies tend to obscure the nature of the instability. An analytical (closed-form) approach with general parametric expressions, that we use, is preferred over a numerical investigation if one is to study the mechanism of instability. Lastly, we find it more useful to study the onset of instability i.e., the impending voltages that define neutral stability curves (dividing stability diagrams into stable and unstable regions) under various pump operations, rather than to investigate the largest growth mode(s). The modes will definitely be constrained by finite size of microfluidic channels and may even be excluded altogether from the system. With typical dimensions of 1-100

μ

m and typical velocities of 1 mm/s, the systems we are concerned with are in the small Reynolds number regime.

1.1. Structure of the Article

In this comprehensive article we systematically explore the mechanism of EHD (in)stability of two shearing perfect dielectric fluids in a parallel-plane microfluidic Couette–Poiseuille flow, and apply it to EO pumps. The governing equations and the boundary conditions for velocity/pressure and E-fields (E-potentials) are those of two-dimensional flow (the flow between two-infinite planes - an approximation), and are nondimensionalized suitable to microfluidic regime (Section 2). We linearize them first with respect to small interface displacement,

ζ

, considering two-dimensional disturbances (these suffice for the stabiliy analysis), obtaining the zeroth- and the first-order approximations in

ζ

(Section 3).

The perturbed flow to first-order in

ζ

is still two-dimensional allowing us to make use of the stream functions. These identically satisfy the continuity equations and enable transformation of the Navier–Stokes second-degree partial-differential equations for velocity and pressure into the corresponding Orr–Sommerfeld fourth-degree ordinary-differential equations solely for the stream functions (Section 3.3). In the non-linear boundary conditions, Section 3.5, the balance of normal stresses contains the coupling of electric fields with the flow.

We then make another linearization, i.e. expand the stream functions, E-potentials and the phase velocity of the disturbances in small Reynolds number. This is used then to expand and solve the governing Orr–Sommerfeld equations for each fluid and the accompanying boundary conditions to zeroth- (Section 4) and first-order in R (Section 5). Our analysis leads to sets of complicated eigenvalue problems to each order in R for the phase velocity of (un)stable modes. The imaginary part of the phase velocity - a complicated function of all flow/E-field nondimensional parameters as well as wavenumbers - determines the growth rate of the disturbances for all wavenumbers. The analytical expressions for the phase velocity to zeroth- and first-order in R are our main results.

The EHD instability occurs for normal E-fields and already in the zeroth-R expansion (independent of viscosity or zeroth-

ζ

velocity). The (equation for) impending voltages for all wavenumbers, plotted in the corresponding stability diagram, is another of our results (Section 4.3). Unlike the zeroth-R voltages, the impending voltages to first-order R depend on the viscosity and zeroth-

ζ

velocity due to the coupling between the E-fields and shearing flows (Section 5.2). The stability diagram thus gets modified for each flow regime, but the first-order-R voltages are very small and would likely be hard to measure. Our zeroth- and first-order-R expansions correct the erroneous expansions attempted in [16]. We also revisit and refine the instability due to viscosity stratification at small R, [14], which is a special case obtained to first order in R when no E-fields are present (pure shear, Section 5.1).

The analytical expressions for the phase velocity and the voltage to first-order-R are extremely cumbersome and could not be made possible without a symbolic manipulation of computer-algebra software such as Mathematica (similarly observed in [23]). The compressed closed form for the phase velocity, separated into smaller pieces, is in the Appendix C.

The article is long, but it is necessary to showcase the formalism to enable validation of (partial) results.

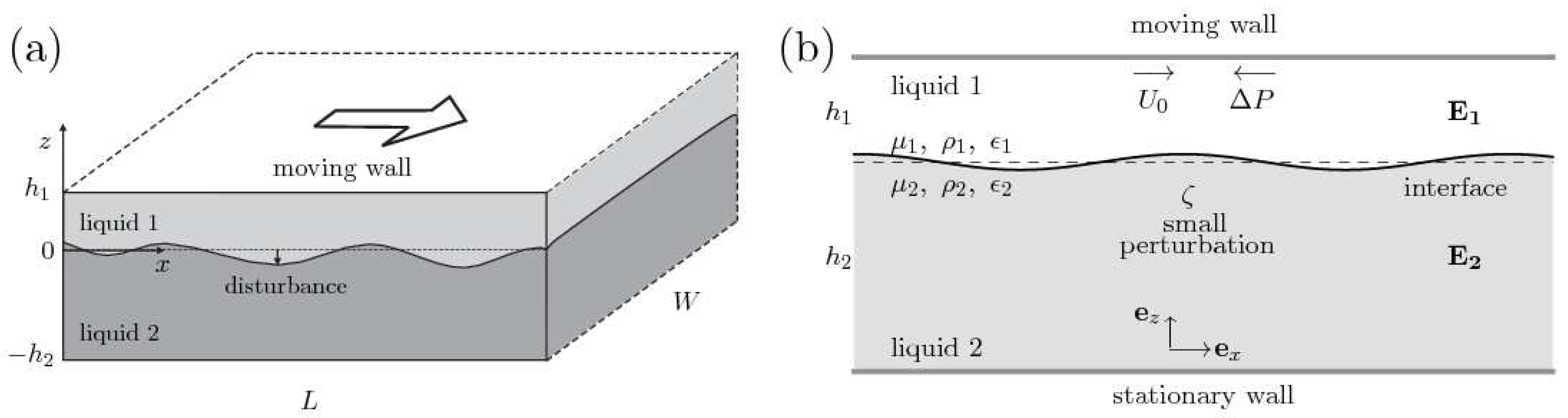
2. Problem Formulation

2.1. General Equations of Motion

Our problem is sketched in Figure 1: the low-aspect ratio configuration of a microfluidc EO pump is approximated by the flow of two viscous dielectrics placed between two parallel infinite planes and exposed to a normal or tangential E-field. The velocity profile is the superposition of the Couette and the (adverse) Poiseuille flow profiles, see Figure 2a.

The equation of motion for a single, isotropic, incompressible, Newtonian fluid placed in an electric field, is given by

ρ D_{t} U = - \nabla P + μ \nabla^{2} U + F_{e},

(1)

where

ρ

is the density, P the pressure,

μ

the dynamical viscosity,

U

the velocity field and

F_{e}^{}

the electric body force.

D_{t}^{}

is the convective derivative

D_{t} = \partial_{t}^{} + U \cdot \nabla .

(2)

The complete electric body force

F_{e}^{}

on an isothermal fluid at temperature T can be expressed as [24]

F_{e}^{} = \frac{1}{2} \nabla [E^{2} ρ {(\partial_{ρ}^{} ϵ)}_{T}] - \frac{1}{2} E^{2} \nabla ϵ + ρ_{e}^{} E,

(3)

where

ϵ

is the dielectric constant and

ρ_{e}^{}

is the charge density. The three contributions on the right-hand side in Equation (3) are due to isotropic deformations (electrostriction), variations of the (relative) dielectric constant, and free charges within the fluid, respectively. In case of a homogeneous, perfect dielectric, (

ϵ =

const.,

ρ_{e}^{} = 0

), we see from Equation (3) that there is no electric body force in the bulk of the fluid. However, a net electric stress will appear on the boundary between two dissimilar dielectrics. This stress can conveniently be expressed as the divergence

F_{e}^{} = \nabla \cdot T^{M}

(4)

of the Maxwell stress tensor

T^{M}

given by

T_{i k}^{M} = - \frac{1}{2} ϵ [1 - \frac{ρ}{ϵ} {(\partial_{ρ}^{} ϵ)}_{T}] E^{2} δ_{i k}^{} + ϵ E_{i}^{} E_{k}^{} .

(5)

This describes the coupling of the electric field at the interface of the two dielectrics. In the case of incompressible fluids, the deformation term in Equations (3) and (5) can be absorbed into a redefined pressure.

Additional equations include the continuity equation for incompressible liquids,

\nabla \cdot U = 0,

(6)

and the Maxwell equations for electric fields, which in the absence of free charges and radiation effects reduce to the quasistatic approximation [25]

\begin{matrix} \nabla \cdot (ϵ E) & = 0, \end{matrix}

(7a)

\begin{matrix} \nabla \times E & = 0 . \end{matrix}

(7b)

From Equation (7b) we can introduce an electrical potential

Φ

E = - \nabla Φ,

(8)

which together with Equation (7a) and a constant

ϵ

yields the Laplace equation

\nabla^{2} Φ = 0 .

(9)

2.2. General Boundary Conditions

To ease later referencing we discuss here the general boundary conditions of our problem. While the perturbation analysis will be introduced in Section 3, we keep in mind that the velocity field

U (x, y, z, t) = (U, V, W)

and the electric field

E

are sums of a zeroth-order field, superscript (0), and a small perturbation, superscript (1), e.g.,

U = U^{(0)} + U^{(1)}

Let us first consider a deformable interface between two dielectrics, Figure 1(b). When unperturbed, the interface is described by the equation

z = 0

. Upon a two-dimensional disturbance the surface is described by

z = ζ (x, t),

(10)

where

ζ

is the vertical displacement from the equilibrium position

z = 0

. We consider only small values of

ζ

. Any deformed surface is characterized by a unit normal vector

n

which for small deformations becomes

n = (- \partial_{x}^{} ζ, 1) .

(11)

We denote the change in any function

f (x, z, t)

across the interface by

[[f]]

\begin{matrix} [[f]] & \equiv f (x, ζ^{-}, t) - f (x, ζ^{+}, t) \\ = {(f_{2}^{} - f_{1}^{})}_{z = ζ} . \end{matrix}

(12)

The interface conditions include the continuity of velocities and tangential stresses, as well as the continuity of tangential electric fields and normal dielectric displacements [26,27]; they also include the discontinuity of normal stresses at the interface caused by the surface tension. At the interface

z = ζ

we write

\begin{matrix} [[U]] = [[V]] = [[W]] = 0, \end{matrix}

(13a)

\begin{matrix} W_{1}^{} = W_{2}^{} = (\partial_{t}^{} + U \partial_{x}^{}) ζ, \end{matrix}

(13b)

\begin{matrix} n \times [[E]] = 0 \Rightarrow [[Φ]] = 0, \end{matrix}

(13c)

\begin{matrix} n \cdot [[ϵ E]] = n \cdot [[ϵ \nabla Φ]] = 0, \end{matrix}

(13d)

\begin{matrix} [[- P]] n_{i}^{} + [[τ_{i k}^{} + T_{i k}^{M}]] n_{k}^{} = γ \partial_{x}^{2} ζ n_{i}^{}, \end{matrix}

(13e)

where

τ_{i k}^{}

is the viscous stress,

γ

the surface tension, and

\partial_{x}^{2} ζ

describes the surface curvature for small deformations in Equation (13e). Equation (13b) expresses the kinematic boundary condition which conserves the motion of the interface points. Equation (13c) is expressed in the simplest form applicable also to unperturbed normal fields.

For the unperturbed velocity field

U^{(0)}

the boundary conditions at the microchannel walls are,

\begin{matrix} U_{1}^{(0)} & = U_{0}^{} e_{x}^{}, & z & = + h_{1}^{} \end{matrix}

(14a)

\begin{matrix} U_{2}^{(0)} & = 0, & z & = - h_{2}^{}, \end{matrix}

(14b)

while for the perturbation

U^{(1)}

no-slip applies,

\begin{matrix} U_{1}^{(1)} & = 0, & z & = + h_{1}^{} \end{matrix}

(15a)

\begin{matrix} U_{2}^{(1)} & = 0, & z & = - h_{2}^{} . \end{matrix}

(15b)

In case of a normal electric field, it is assumed that the rigid walls are perfectly conducting electrodes kept at a potential difference

V_{0}^{}

and in direct contact with the liquids. The two electrodes are large enough so that the fringing fields close to the edges are not important. The unperturbed potential

Φ^{(0)}

thus satisfies the boundary conditions

\begin{matrix} Φ_{1}^{(0)} & = V_{0}^{}, & z & = + h_{1}^{} \end{matrix}

(16a)

\begin{matrix} Φ_{2}^{(0)} & = 0, & z & = - h_{2}^{}, \end{matrix}

(16b)

while the small perturbation

Φ^{(1)}

obeys

\begin{matrix} Φ_{1}^{(1)} & = 0, & z & = + h_{1}^{} \end{matrix}

(17a)

\begin{matrix} Φ_{2}^{(1)} & = 0, & z & = - h_{2}^{}, \end{matrix}

(17b)

In case of an imposed tangential electric field we assume that the liquids are placed between two insulating walls in a uniform horizontal field produced by two large electrodes spaced far apart at

x = \pm \infty

. The uniform-field assumption is particularly valid in the microfluidic case, where the distance between the confining planes is very small. At the insulating rigid wall boundaries the Neumann conditions apply for the E-potentials

\begin{matrix} \partial_{z}^{} Φ_{1}^{(1)} & = 0, & z & = + h_{1}^{}, \end{matrix}

(18a)

\begin{matrix} \partial_{z}^{} Φ_{2}^{(1)} & = 0, & z & = - h_{2}^{} . \end{matrix}

(18b)

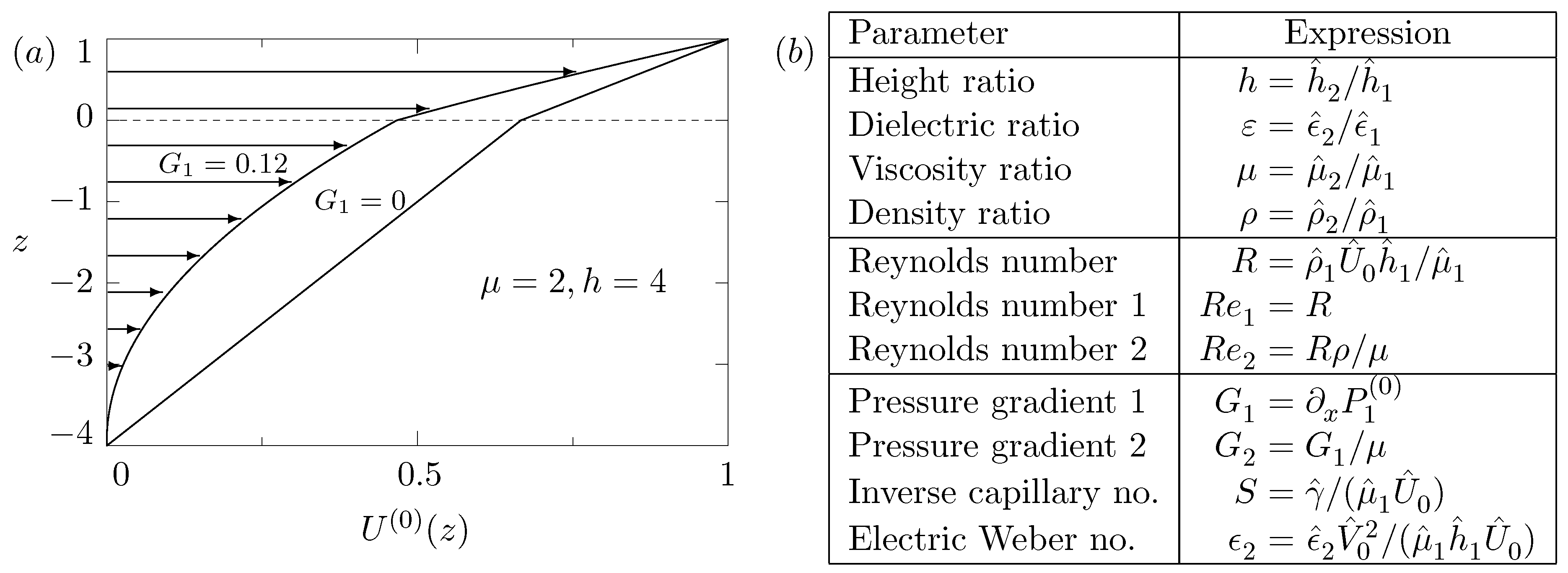
2.3. Two-Dimensional Flow and Nondimensional Equations

The symmetry of our problem with an interfacial wave, see Figure 1(b), implies a y-independent two-dimensional flow,

\hat{U} (x, z, t) = \hat{U} (x, z, t) e_{x}^{} + \hat{W} (x, z, t) e_{z}^{}

, where the direction of the travelling interfacial wave coincides with

e_{x}^{}

. By virtue of Squire’s theorem in uniform and stratified fluids it suffices to consider stability of two-dimensional disturbances [28,29]. Note that physical variables in this section are marked by hats. For each fluid

i = 1, 2

we have

\begin{matrix} {\hat{ρ}}_{i}^{} {\hat{D}}_{t}^{} {\hat{U}}_{i}^{} & = - {\hat{\partial}}_{x}^{} {\hat{P}}_{i}^{} + {\hat{μ}}_{i}^{} {\hat{\nabla}}_{s}^{2} {\hat{U}}_{i}^{}, \end{matrix}

(19a)

\begin{matrix} {\hat{ρ}}_{i}^{} {\hat{D}}_{t}^{} {\hat{W}}_{i}^{} & = - {\hat{\partial}}_{z}^{} {\hat{P}}_{i}^{} + {\hat{μ}}_{i}^{} {\hat{\nabla}}_{s}^{2} {\hat{W}}_{i}^{}, \end{matrix}

(19b)

where

{\hat{D}}_{t}^{} = {\hat{\partial}}_{t}^{} + \hat{U} {\hat{\partial}}_{x}^{} + \hat{W} {\hat{\partial}}_{z}^{}

and

{\hat{\nabla}}_{s}^{2} = {\hat{\partial}}_{x}^{2} + {\hat{\partial}}_{z}^{2}

. As mentioned earlier, the electric terms do not enter the bulk equations, but only the interface conditions. The continuity equation becomes

{\hat{\partial}}_{x}^{} {\hat{U}}_{i}^{} + {\hat{\partial}}_{z}^{} {\hat{W}}_{i}^{} = 0,

(19c)

and the Maxwell equations reduce to

{\hat{\nabla}}_{s}^{2} {\hat{Φ}}_{i} = 0 .

(19d)

We now introduce the nondimensional variables (no hats):

\begin{matrix} (U_{i}^{}, W_{i}^{}) & = & \frac{1}{{\hat{U}}_{0}^{}} ({\hat{U}}_{i}^{}, {\hat{W}}_{i}^{}), & (x, z) & = & \frac{1}{{\hat{h}}_{1}^{}} (\hat{x}, \hat{z}), \end{matrix}

(20a)

\begin{matrix} P_{i}^{} & = & \frac{{\hat{h}}_{1}^{}}{{\hat{μ}}_{i}^{} {\hat{U}}_{0}^{}} {\hat{P}}_{i}^{}, & t & = & \frac{{\hat{U}}_{0}^{}}{{\hat{h}}_{1}^{}} \hat{t}, \end{matrix}

(20b)

\begin{matrix} ϵ_{i}^{} E_{i}^{2} & = & \frac{{\hat{h}}_{1}^{}}{{\hat{μ}}_{1}^{} {\hat{U}}_{0}^{}} {\hat{ϵ}}_{i}^{} {\hat{E}}_{i}^{2}, & Φ_{i}^{} & = & \frac{1}{{\hat{V}}_{0}^{}} {\hat{Φ}}_{i}^{} . \end{matrix}

(20c)

We have chosen the length scale as in [14] but adapted a pressure scale relating to microfluidics due to the small Reynolds numbers. Note that the pressure scales in the two layers differ from each other in Equation (20b), so that the governing Equations (24a)-(24d) appear symmetric for both layers. We also introduce the four other relevant parameters, also listed in Figure 2(b),

h = \frac{{\hat{h}}_{2}^{}}{{\hat{h}}_{1}^{}}, μ = \frac{{\hat{μ}}_{2}^{}}{{\hat{μ}}_{1}^{}}, ρ = \frac{{\hat{ρ}}_{2}^{}}{{\hat{ρ}}_{1}^{}}, ε = \frac{{\hat{ϵ}}_{2}^{}}{{\hat{ϵ}}_{1}^{}},

(21)

and the Reynolds numbers corresponding to the two fluid regions

\begin{matrix} R e_{1}^{} & \equiv R = \frac{{\hat{ρ}}_{1}^{} {\hat{U}}_{0}^{} {\hat{h}}_{1}^{}}{{\hat{μ}}_{1}^{}}, \end{matrix}

(22)

\begin{matrix} R e_{2}^{} & = \frac{{\hat{ρ}}_{2}^{} {\hat{U}}_{0}^{} {\hat{h}}_{1}^{}}{{\hat{μ}}_{2}^{}} = \frac{ρ}{μ} R . \end{matrix}

(23)

In the nondimensional form Equations (19a)–(19d) are

\begin{matrix} R e_{i}^{} D_{t} U_{i} & = - \partial_{x} P_{i} + \nabla_{s}^{2} U_{i}, \end{matrix}

(24a)

\begin{matrix} R e_{i}^{} D_{t} W_{i} & = - \partial_{z} P_{i} + \nabla_{s}^{2} W_{i}, \end{matrix}

(24b)

\begin{matrix} \partial_{x}^{} U_{i}^{} + \partial_{z}^{} W_{i}^{} & = 0, \end{matrix}

(24c)

\begin{matrix} \nabla_{s}^{2} Φ_{i}^{} & = 0 . \end{matrix}

(24d)

3. Linearization in the Interface Displacement $ζ$

We now apply standard linearization theory to Equations (24a)–(24d) as in [30]. In a two-dimensional flow, we consider a harmonic displacement

ζ

given by

ζ (x, t) = ζ_{0}^{} exp [i k (x - c t)],

(25)

where

ζ_{0}^{}

is the amplitude,

k = 2 π / λ

the wavenumber and c the complex phase velocity of the disturbance. Any field f (the velocity

U

, the pressure P, the electric field

E

, the potential

Φ

, and the normal vector

n

) is then written as

f = f^{(0)} + f^{(1)}

(26)

where

f^{(0)}

represents the unperturbed steady-state solution, while

f^{(1)}

is a small perturbation. Putting the perturbed fields f into the governing equations and invoking boundary and interface conditions, the steady-state solutions cancels out, and by only maintaining terms up to linear order in

f^{(1)}

we arrive at linearized equations that govern the perturbations. In compliance with the linearization, the fields at the interface

z = ζ

are also expanded up to first order in

ζ

as follows:

f (ζ) = f^{(0)} (0) + ζ \partial_{z} f^{(0)} (0) + f^{(1)} (0) .

(27)

The first-order solutions are further expressed in terms of normal modes, Equation (25)

f^{(1)} (x, z, t) = f^{(1)} (z) exp [i k (x - c t)] .

(28)

When the normal modes are inserted back into the linearized equations, the problem is transformed into an eigenvalue problem for the complex phase velocity

c = c_{r}^{} + i c_{i}^{}

. It is seen from Equation (28) that

f^{(1)} (x, z, t) \propto exp [- i k c_{r}^{} t] exp [k c_{i}^{} t],

(29)

which means that instability (the exponential growth in time) happens for

c_{i}^{} > 0

. The neutral stability condition

c_{i}^{} = 0

divides the stable from the unstable regions.

3.1. Velocity Field to Zeroth Order in $ζ$

The zeroth-order flow is a steady-state, parallel flow

U = U^{(0)} e_{z}

, with the velocity

U_{0}^{} = 1

at the upper boundary, Figure 1(b). The left-hand sides in Equations (24a) and (24b) drop out and we solve

\partial_{z}^{2} U_{i}^{(0)} = \partial_{x}^{} P_{i}^{(0)} \equiv G_{i}^{},

(30)

where the pressure gradient

G_{i}^{}

is constant due to the translation invariance.

The boundary and interface conditions obtained from Equations (13c)–(14) with

n^{(0)} = e_{z}

are

\begin{matrix} U_{1}^{(0)} (1) = 1, \end{matrix}

(31a)

\begin{matrix} U_{2}^{(0)} (- h) = 0, \end{matrix}

(31b)

\begin{matrix} [[U^{(0)} (0)]] = 0, \end{matrix}

(31c)

\begin{matrix} [[μ \partial_{z}^{} U^{(0)} (0)]] = 0, \end{matrix}

(31d)

\begin{matrix} - & [[P^{(0)}]] + [[\frac{ϵ}{2} ({E_{N}^{(0)}}^{2} - {E_{T}^{(0)}}^{2})]] = 0 . \end{matrix}

(31e)

Note that the electric term in Equation (31d) vanished since the continuity of the electric tangential stresses is trivially satisfied. Furthermore, the zeroth-order electric fields set up a constant equilibrium pressure, Equation (31e). The well-known solution of the above zeroth-order system is

U_{i}^{(0)} = \frac{1}{2} G_{i}^{} z^{2} + a_{i}^{} z + b,

(32)

with

\begin{matrix} G_{1}^{} & = & \partial_{x}^{} P_{1}^{(0)} = \frac{{\hat{h}}_{1}^{2}}{{\hat{μ}}_{1}^{} {\hat{U}}_{0}^{}} \hat{G}, & G_{2}^{} & = & \frac{G_{1}^{}}{μ}, \end{matrix}

(33a)

\begin{matrix} a_{1}^{} & = & \frac{μ - \frac{1}{2} G_{1}^{} (μ - h^{2})}{μ + h}, & a_{2}^{} & = & \frac{a_{1}^{}}{μ}, \end{matrix}

(33b)

\begin{matrix} b & = & \frac{h}{μ + h} [1 - \frac{1}{2} G_{1}^{} (1 + h)] . \end{matrix}

(33c)

where

\hat{G} = {\hat{\partial}}_{x}^{} {\hat{P}}^{(0)}

is a constant physical pressure gradient. Two zeroth-order flow profiles are shown in Figure 2.

3.2. Electric Potentials to Zeroth Order in $ζ$

Now, turning to externally applied electric fields, we first consider the normal electric field between two metallic electrodes kept at a constant potential difference. The condition of a constant normal E-field in the region i

E_{i}^{(0)} = E_{i, N}^{(0)} e_{z},

(34)

which together with Equation (24d) yields

Φ_{i, N}^{(0)} = - E_{i, N}^{(0)} z + C_{i}^{} .

(35)

The constants

C_{i}^{}

are determined from the boundary conditions

\begin{matrix} Φ_{1, N}^{(0)} (1) = 1, \end{matrix}

(36a)

\begin{matrix} Φ_{1, N}^{(0)} (- h) = 0, \end{matrix}

(36b)

\begin{matrix} [[Φ_{N}^{(0)} (0)]] = 0, \end{matrix}

(36c)

\begin{matrix} [[ϵ \partial_{z}^{} Φ_{N}^{(0)} (0)]] = 0 . \end{matrix}

(36d)

We find

\begin{matrix} Φ_{1, N}^{(0)} & = \frac{ε z + h}{ε + h}, \end{matrix}

(37a)

\begin{matrix} Φ_{2, N}^{(0)} & = \frac{z + h}{ε + h}, \end{matrix}

(37b)

and

\begin{matrix} E_{1, N}^{(0)} & = - \frac{ε}{ε + h}, \end{matrix}

(37c)

\begin{matrix} E_{2, N}^{(0)} & = - \frac{1}{ε + h}, \end{matrix}

(37d)

where h and

ε

are given by Equation (21) and Figure 2(b).

In case of a constant tangential E-field in the x-direction, Equation (13) yields

\begin{matrix} E_{1, T}^{(0)} & = E_{2, T}^{(0)} = E_{0}^{} e_{x}, \end{matrix}

(38a)

\begin{matrix} Φ_{1, T}^{(0)} & = Φ_{2, T}^{(0)} = - E_{0}^{} x . \end{matrix}

(38b)

In order to simplify the notation we skip the N and T subscripts and introduce the curly brackets

\begin{matrix} Φ_{1}^{(0)} & = \{\begin{matrix} \frac{ε z + h}{ε + h} \\ - E_{0}^{} x \end{matrix}\}, \end{matrix}

(39a)

\begin{matrix} Φ_{2}^{(0)} & = \{\begin{matrix} \frac{z + h}{ε + h} \\ - E_{0}^{} x \end{matrix}\}, \end{matrix}

(39b)

where the upper and lower parts within the brackets pertain to the case of the normal and tangential E-field, respectively.

3.3. Velocity Field to First Order in $ζ$

Introducing the interface deformation

ζ

, the velocity and pressure fields up to the linear order become

\begin{matrix} U & = [U^{(0)} (z) + U^{(1)} (x, z, t)] e_{x} + W^{(1)} (x, z, t) e_{z}, \end{matrix}

(40a)

\begin{matrix} P & = P^{(0)} + P^{(1)} (x, z, t) . \end{matrix}

(40b)

For the upper liquid Equations (24a)–(24c) yield

\begin{matrix} R (\partial_{t}^{} U_{1}^{(1)} + U_{1}^{(0)} \partial_{x}^{} U_{1}^{(1)} + W_{1}^{(1)} \partial_{z}^{} U_{1}^{(0)}) & = - \partial_{x}^{} P_{1}^{(1)} + \nabla_{s}^{2} U_{1}^{(1)}, \end{matrix}

(41a)

\begin{matrix} R (\partial_{t}^{} W_{1}^{(1)} + U_{1}^{(0)} \partial_{x}^{} W_{1}^{(1)}) & = - \partial_{z}^{} P_{1}^{(1)} + \nabla_{s}^{2} W_{1}^{(1)}, \end{matrix}

(41b)

\begin{matrix} \partial_{x}^{} U_{1}^{(1)} + \partial_{z}^{} W_{1}^{(1)} & = 0 . \end{matrix}

(41c)

Equation (41c) allows the use of a stream function

Ψ

(U_{1}^{(1)}, W_{1}^{(1)}) = (\partial_{z}^{} Ψ_{1}^{}, - \partial_{x}^{} Ψ_{1}^{}) .

(42)

Expanding

Ψ_{1}^{}

and

P_{1}^{(1)}

into the normal modes

(Ψ_{1}^{}, P_{1}^{(1)}) = (ψ_{1}^{} (z), p_{1}^{(1)} (z)) exp [i k (x - c t)],

(43)

and using Equation (42), Equations (41a) and (41b) become

\begin{matrix} i k R [(U_{1}^{(0)} - c) \partial_{z}^{} ψ_{1}^{} - \partial_{z}^{} U_{1}^{(0)} ψ_{1}^{}] & = - i k p_{1}^{(1)} + (\partial_{z}^{3} ψ_{1}^{} - k^{2} \partial_{z}^{} ψ_{1}^{}), \end{matrix}

(44a)

\begin{matrix} k^{2} R (c - U_{1}^{(0)}) ψ_{1}^{} & = \partial_{z}^{} p_{1}^{(1)} + i k (\partial_{z}^{2} ψ_{1}^{} - k^{2} ψ_{1}^{}) . \end{matrix}

(44b)

After eliminating

p_{1}^{(1)}

, Equations (44a) and (44b) yield the known Orr–Sommerfeld equation for the upper liquid

\begin{matrix} ψ_{1}^{''''} - 2 k^{2} ψ_{1}^{''} + k^{4} ψ_{1}^{} & = i k R [(U_{1}^{(0)} - c) (ψ_{1}^{''} - k^{2} ψ_{1}) - {U_{1}^{(0)}}^{''} ψ_{1}^{}], \end{matrix}

(45)

where we have introduced primes for

d / d z

since both

U_{1}^{(0)}

and

ψ_{1}^{}

are functions of z only. In the same manner, using the stream function

Ψ_{2}^{}

we get for the lower liquid

\begin{matrix} ψ_{2}^{''''} - 2 k^{2} ψ_{2}^{''} + k^{4} ψ_{2}^{} & = i \frac{ρ}{μ} k R [(U_{2}^{(0)} - c) (ψ_{2}^{''} - k^{2} ψ_{2}) - {U_{2}^{(0)}}^{''} ψ_{2}^{}] . \end{matrix}

(46)

3.4. Electric Potentials to First Order in $ζ$

To first order the total potential is

Φ = Φ^{(0)} + Φ^{(1)} (x, z, t) .

(47)

Since both

Φ

and

Φ^{(0)}

satisfy the Laplace Equation (24d), it follows

\nabla_{s}^{2} Φ^{(1)} = 0,

(48)

for which the general solution in terms of the normal modes are

\begin{matrix} Φ_{1}^{(1)}, Φ_{2}^{(1)} & \propto \{\begin{matrix} exp [\pm k z] exp [i k (x - c t)] \\ exp [\pm k z] exp [i k (x - c t)] \end{matrix}\} . \end{matrix}

(49)

The boundary and interface conditions for the normal E-field include Equations (13c) and (13d) on the interface and Equation (17) on the rigid electrodes. The linearized conditions are

\begin{matrix} Φ_{1}^{(1)} (1) = 0, \end{matrix}

(50a)

\begin{matrix} Φ_{2}^{(1)} (- h) = 0, \end{matrix}

(50b)

\begin{matrix} [[ζ \partial_{z}^{} Φ^{(0)} (0) + Φ^{(1)} (0)]] = 0, \end{matrix}

(50c)

\begin{matrix} [[ϵ \partial_{z}^{} Φ^{(1)} (0)]] = 0 . \end{matrix}

(50d)

In a similar manner, we have Equation (18) together with the linearized Equations (13c) and (13d) for a tangential field

\begin{matrix} \partial_{z}^{} Φ_{1}^{(1)} (1) = 0, \end{matrix}

(51a)

\begin{matrix} \partial_{z}^{} Φ_{2}^{(1)} (- h) = 0, \end{matrix}

(51b)

\begin{matrix} [[Φ^{(1)} (0)]] = 0, \end{matrix}

(51c)

\begin{matrix} [[ϵ \partial_{z}^{} Φ^{(1)} (0) + i k ζ ϵ E_{0}^{}]] = 0 . \end{matrix}

(51d)

Solving the above system we arrive at the first-order potentials in the regions 1 and 2

\begin{matrix} Φ_{1}^{(1)} & = \{\begin{matrix} - ζ \frac{ε (1 - ε)}{ε + h} \frac{sinh [k (z - 1)]}{cosh [k] (ε tanh [k] + tanh [k h])} \\ - i ζ E_{0}^{} (1 - ε) \frac{cosh [k (z - 1)]}{cosh [k] (ε tanh [k h] + tanh [k])} \end{matrix}\}, \end{matrix}

(52a)

\begin{matrix} Φ_{2}^{(1)} & = \{\begin{matrix} - ζ \frac{1 - ε}{ε + h} \frac{sinh [k (z + h)]}{cosh [k h] (ε tanh [k] + tanh [k h])} \\ - i ζ E_{0}^{} (1 - ε) \frac{cosh [k (z + h)]}{cosh [k h] (ε tanh [k h] + tanh [k])} \end{matrix}\}, \end{matrix}

(52b)

from which the first-order electric fields and stresses are calculated. Note how the voltages’ phases differ, as normal and tangential E-fields affect the interface differently.

3.5. Boundary Conditions

The flow equations Equations (45) and (46) are subject to the following eight linearized boundary and interface conditions, BC1-BC8, expressed in terms of the stream function

Ψ

, Equation (42).

• BC1-BC4: no-slip conditions at the rigid boundaries

\begin{matrix} ψ_{1}^{} (1) & = 0, & ψ_{1}^{'} (1) & = 0, \end{matrix}

(53)

\begin{matrix} ψ_{2}^{} (- h) & = 0, & ψ_{2}^{'} (- h) & = 0, \end{matrix}

(54)

where as before primes denote

d / d z

• BC5: continuity of W at the interface

ψ_{1}^{} (0) = ψ_{2}^{} (0),

(55)

• BC6: continuity of U at the interface

ψ_{1}^{'} (0) - ψ_{2}^{'} (0) = \frac{ψ_{1}^{} (0)}{\tilde{c}} (1 - μ) a_{2}^{},

(56)

where

μ

and

a_{2}^{}

are given in Equations (21) and (33b), respectively, and

\tilde{c} = c - U^{(0)} (0) = c - b

. This result is obtained as follows: the linearized kinematic condition

W^{(1)} (0) = (\partial_{t}^{} + U^{(0)} (0) \partial_{x}^{}) ζ

(57a)

yields

ζ = \frac{ψ_{1}^{} (0)}{\tilde{c}} exp [i k (x - c t)] .

(57b)

We note that if

\tilde{c} = 0

a second-order expansion of the kinematic condition is required to avoid problems involving division by

\tilde{c}

. Now, Equation (57b) together with the linearized Equation (13a) for U

[[\partial_{z}^{} U^{(0)} (0) ζ + U^{(1)} (0)]] = 0,

(57c)

results in Equation (56).

• BC7: continuity of tangential stresses at the interface

ψ_{1}^{''} (0) + k^{2} ψ_{1}^{} (0) = μ (ψ_{2}^{''} (0) + k^{2} ψ_{2}^{} (0)),

(58)

where use is made of the fact that at the interface of two perfect dielectrics tangential electric stresses are always continuous

[[T_{T k}^{M_{}}]] n_{k}^{} = [[ϵ E_{T}^{} E_{N}^{}]] = E_{T}^{} [[ϵ E_{N}^{}]] = 0,

(59a)

due to Equations (13c) and (13d). The remaining tangential viscous stresses of Equation (13e) give

[[μ (\partial_{z}^{2} U^{(0)} ζ + \partial_{z}^{} U^{(1)} (0) + \partial_{x}^{} W^{(1)} (0))]] = 0,

(59b)

which becomes Equation (58).

• BC8: balance of normal stresses

\begin{matrix} i k (k^{2} S + T_{el}^{}) \frac{ψ_{1}^{} (0)}{\tilde{c}} & = μ (ψ_{2}^{'''} (0) - 3 k^{2} ψ_{2}^{'} (0)) + i ρ k R (\tilde{c} ψ_{2}^{'} (0) + a_{2}^{} ψ_{2} (0)) \\ - (ψ_{1}^{'''} (0) - 3 k^{2} ψ_{1}^{'} (0)) - i k R (\tilde{c} ψ_{1}^{'} (0) + a_{1}^{} ψ_{1} (0)), \end{matrix}

(60)

which is found by linearizing Equation (13e) and making use of Equation (44a). In Equation (60)

ρ

is the density ratio of Equation (21), and the nondimensional number S

S = \frac{\hat{γ}}{{\hat{μ}}_{1}^{} {\hat{U}}_{0}^{}},

(61)

is the inverse of the capillary number and gives the normal-stress contribution due to the surface tension

\hat{γ}

T_{el}

is given by

T_{el} = \{\begin{matrix} - k \frac{{\hat{ϵ}}_{2}^{} {\hat{V}}_{0}^{2}}{{\hat{μ}}_{1}^{} {\hat{h}}_{1}^{} {\hat{U}}_{0}^{}} \frac{{(1 - ε)}^{2}}{{(h + ε)}^{2}} \frac{1}{ε tanh [k] + tanh [k h]} \\ + k \frac{{\hat{ϵ}}_{1}^{} {\hat{E}}_{0}^{2} {\hat{h}}_{1}^{}}{{\hat{μ}}_{1}^{} {\hat{U}}_{0}^{}} {(1 - ε)}^{2} \frac{1}{ε tanh [k h] + tanh [k]}, \end{matrix}\},

(62)

and gives the normal-stress contributions of the applied electric fields which are found using Equations (5), (39a), (39b), (52a) and (52b),

\begin{matrix} [[T_{N k}^{M_{}}]] n_{k}^{} & = \{\begin{matrix} [[ϵ \partial_{z}^{} Φ^{(0)} (0) \partial_{z}^{} Φ^{(1)} (0)]] \\ E_{0}^{} [[- ϵ \partial_{x}^{} Φ^{(1)} (0)]] \end{matrix}\} \end{matrix}

(63a)

\begin{matrix} = \{\begin{matrix} - k ϵ_{2}^{} \frac{{(1 - ε)}^{2}}{{(h + ε)}^{2}} \frac{1}{ε tanh [k] + tanh [k h]} ζ \\ + k ϵ_{1}^{} E_{0}^{2} {(1 - ε)}^{2} \frac{1}{ε tanh [k h] + tanh [k]} ζ \end{matrix}\} . \end{matrix}

(63b)

Note that the effective nondimensional values of

ϵ_{2}^{}

in case of the normal E-field, and of

ϵ_{1}^{} E_{0}^{2}

in case of the tangential E-field, in dimensional units correspond to

{\hat{ϵ}}_{2}^{} {\hat{V}}_{0}^{2} / ({\hat{μ}}_{1}^{} {\hat{h}}_{1}^{} {\hat{U}}_{0}^{})

and

{\hat{ϵ}}_{1}^{} {\hat{E}}_{0}^{2} {\hat{h}}_{1}^{} / ({\hat{μ}}_{1}^{} {\hat{U}}_{0}^{})

, respectively. Equations (62) and (63a) were derived here for our bounded system, but recover known results when (one of the) boundaries effectively go to infinity (

k h ≫ 1, k ≫ 1

It is seen from Equations (62) and (63a) that a normal E-field gives a negative first-order stress contribution, whereas a tangential E-field gives a positive first-order stress contribution (the known result). The interface will thus be affected differently by the two types of electric fields. We will further investigate only effects of the destabilizing, normal E-field.

4. Perturbation Expansion in the Reynolds Number R to Zeroth Order

Equations (45) and (46) together with the eight boundary and interface conditions from the previous section present the system of differential equations, which we solve in the limit of small Reynolds number R and arbitrary wavenumber k. We apply the following perturbation expansion in R of the stream function

ψ

, the phase velocity c and the potential (voltage) V,

\begin{matrix} ψ & = ψ^{[0]} + R ψ^{[1]} + R^{2} ψ^{[2]} + \dots, \end{matrix}

(64)

\begin{matrix} c & = c^{[0]} + R c^{[1]} + R^{2} c^{[2]} + \dots, \end{matrix}

(65)

\begin{matrix} V & = V^{[0]} + R V^{[1]} + R^{2} V^{[2]} + \dots, \end{matrix}

(66)

where square brackets distinguish it from the previous linearization in

ζ

marked by round parentheses. With these expansions, the zeroth-order equations in R become

\begin{matrix} {ψ_{1}^{{[0]}_{}}}^{''''} - 2 k^{2} {ψ_{1}^{{[0]}_{}}}^{''} + k^{4} ψ_{1}^{[0]} & = 0 \end{matrix}

(67a)

\begin{matrix} {ψ_{2}^{{[0]}_{}}}^{''''} - 2 k^{2} {ψ_{2}^{{[0]}_{}}}^{''} + k^{4} ψ_{2}^{[0]} & = 0, \end{matrix}

(67b)

with the boundary and interface conditions

\begin{matrix} ψ_{1}^{[0]} (1) = 0; {ψ_{1}^{[0]}}^{'} (1) = 0, \end{matrix}

(68a)

\begin{matrix} ψ_{2}^{[0]} (- h) = 0; {ψ_{2}^{[0]}}^{'} (- h) = 0, \end{matrix}

(68b)

\begin{matrix} ψ_{1}^{[0]} (0) - ψ_{2}^{[0]} (0) = 0, \end{matrix}

(68c)

\begin{matrix} {ψ_{1}^{[0]}}^{'} (0) - {ψ_{2}^{[0]}}^{'} (0) = \frac{ψ_{1}^{[0]} (0)}{{\tilde{c}}^{[0]}} (1 - μ) a_{2}^{}, \end{matrix}

(68d)

\begin{matrix} {ψ_{1}^{[0]}}^{''} (0) + k^{2} ψ_{1}^{[0]} (0) = μ ({ψ_{2}^{[0]}}^{''} (0) + k^{2} ψ_{2}^{[0]} (0)), \end{matrix}

(68e)

\begin{matrix} i k S_{k}^{*} \frac{ψ_{1}^{[0]} (0)}{{\tilde{c}}^{[0]}} = μ [{ψ_{2}^{[0]}}^{'''} (0) - 3 k^{2} {ψ_{2}^{[0]}}^{'} (0)] - [{ψ_{1}^{[0]}}^{'''} (0) - 3 k^{2} {ψ_{1}^{[0]}}^{'} (0)], \end{matrix}

(68f)

where

\begin{matrix} {\tilde{c}}^{[0]} & = c^{[0]} - b, \end{matrix}

(68g)

\begin{matrix} S_{k}^{*} & \equiv k^{2} S + T_{el}^{} . \end{matrix}

(68h)

Strictly speaking, the above zeroth-order approximation is valid for R arbitrary close to but not equal to zero. The reason for this is the rescaling involving division by

{\hat{μ}}_{1}^{} {\hat{U}}_{0}^{}

, see Equations (61) and (62). General solutions of Equations (67a) and (67b) can be written as

\begin{matrix} ψ_{1}^{[0]} = & sinh [k (z - 1)] + B_{1}^{} cosh [k (z - 1)] \\ + C_{1}^{} z sinh [k (z - 1)] + D_{1}^{} z cosh [k (z - 1)], \end{matrix}

(69a)

\begin{matrix} ψ_{2}^{[0]} = & A_{2}^{} sinh [k (z + h)] + B_{2}^{} cosh [k (z + h)] \\ + C_{2}^{} z sinh [k (z + h)] + D_{2}^{} z cosh [k (z + h)] . \end{matrix}

(69b)

Note that

A_{2}^{}

generally differs from unity in order to satisfy the boundary conditions, Equations (68d) and (68f). By putting the above solutions into Equations (68a)–(68f) we arrive at fairly complicated expressions for the coefficients

A_{2}^{}, B_{1, 2}^{}, C_{1, 2}^{}, D_{1, 2}^{}

(given in the Appendix A for the special case

S_{k}^{*} = 0

, for later use). The important result is the expression of the phase velocity

{\tilde{c}}^{[0]}

that determines the stability, Equation (29). We get

{\tilde{c}}^{[0]} = {\tilde{c}}_{r}^{[0]} + i {\tilde{c}}_{i}^{[0]},

(70a)

where

\begin{matrix} {\tilde{c}}_{r}^{[0]} & = 8 a_{2}^{} k^{3} μ (μ - 1) [- 2 k h (1 + h) + h^{2} sinh [2 k] + sinh [2 k h]] D^{- 1}, \\ {\tilde{c}}_{i}^{[0]} & = S_{k}^{*} (4 k μ h cosh [2 k] + 4 k cosh [2 k h] + (2 + 4 k^{2} h^{2}) sinh [2 k] - 4 k [1 + h (μ + 2 k^{2} μ + 2 k^{2} h)] \end{matrix}

(70b)

\begin{matrix} + (2 μ + 4 k^{2} μ) sinh [2 k h] - (μ + 1) sinh [2 k (h + 1)] + (μ - 1) sinh [2 k (1 - h)]) D^{- 1}, \end{matrix}

(70c)

\begin{matrix} D & = 2 k^{2} (2 (μ^{2} - 1) (2 k^{2} h^{2} + 1) cosh [2 k] + {(μ - 1)}^{2} cosh [2 k (h - 1)] \\ - 2 (2 k^{2} + 1) (μ^{2} - 1) cosh [2 k h] + {(μ + 1)}^{2} cosh [2 k (h + 1)] \\ - 2 [1 + μ^{2} + 2 k^{2} (1 + μ^{2} + 4 μ h + h^{2} [1 + μ^{2} + 2 k^{2} {(μ - 1)}^{2}])]) . \end{matrix}

(70d)

In Equation (70c),

{\tilde{c}}_{i}^{[0]}

that governs the growth rate of the waves is independent of

ρ

and

G_{1}^{}

(nondimensional pressure gradient), but depends on k,

μ

, h and importantly on the electric fields through

S_{k}^{*}

. In Figure 3, graphs of

{\tilde{c}}_{i}^{[0]}

are shown for three values of

μ

. It is seen that the k-regions of instability, for which

{\tilde{c}}_{i}^{[0]} > 0

, are independent of the viscosity ratio. Note that in microfluidics

ϵ_{2}^{} \sim 1 - 100

, and that we used a much larger

ϵ_{2}^{}

value to emphasize the main features in a single graph. We now explore this and other electrohydrodynamic aspects of Equations (70b) and (70c) in terms of k,

μ

, h and

T_{el}

, with the emphasis on microfluidics.

4.1. Limit of Vanishingly Small Wavenumbers

In the limit of small wavenumbers

k \to 0

{\tilde{c}}_{r}^{{[0]}_{}}

and

{\tilde{c}}_{i}^{[0]}

from Equations (70b) and (70c) become

\begin{matrix} lim_{k \to 0} {\tilde{c}}_{r}^{[0]} & = \frac{2 a_{2}^{} μ h^{2} (μ - 1) (h + 1)}{μ^{2} + h^{4} + 2 μ h (2 + 3 h + 2 h^{2})} \\ = \frac{h^{2} (μ - 1) (h + 1) [G_{1}^{} h^{2} + (2 - G_{1}^{}) μ]}{(μ + h) [μ^{2} + h^{4} + 2 μ h (2 + 3 h + 2 h^{2})]}, \end{matrix}

(71a)

\begin{matrix} lim_{k \to 0} {\tilde{c}}_{i}^{[0]} & = 0 . \end{matrix}

(71b)

The above two limits mean that our

{\tilde{c}}^{[0]} (= {\tilde{c}}_{r}^{[0]} + i {\tilde{c}}_{i}^{[0]})

{\tilde{c}}_{r}^{[0]}

for

k \to 0

; this is identical to the

{\tilde{c}}^{[0]}

obtained for

k \to 0

in [14] and [20], so it follows that we correctly recover the small-k limit from literature. On the other hand, our result differs from the

{\tilde{c}}^{[0]}

given in [16], page 75, also obtained in the approximation to zeroth order in R. There,

{\tilde{c}}^{[0]} = 0

for

k \to 0

thus not recovering results from [14], making the further calculations and conclusions invalid.

We also note that in [14], page 344, it is stated that Equation (71a) must change the sign but not the magnitude upon the simultaneous exchanges

μ \to 1 / μ

and

h \to 1 / h

. This, however, is true only in two special cases (i)

G_{1}^{} = 0

(pure Couette flow, considered in [14]), arbitrary

μ

and h, (ii)

h = \sqrt{μ}

, arbitrary

G_{1}^{}

4.2. Limit of Large Wavenumbers

Next, we consider the limit of very large wavenumbers, i.e., very short wavelengths. For a given

h > 0

(and a fixed electric field), the leading terms give

\begin{matrix} {\tilde{c}}_{r}^{[0]} & \propto \frac{k sinh [2 k h]}{cosh [2 k (h + 1)]} = k exp (- 2 k), for k \to \infty \end{matrix}

(72)

\begin{matrix} {\tilde{c}}_{i}^{[0]} & = \frac{- S_{k}^{*} (μ + 1) sinh [2 k (h + 1)]}{2 k^{2} {(μ + 1)}^{2} cosh [2 k (h + 1)]} \\ = - \frac{S}{2 (μ + 1)}, for k \to \infty \end{matrix}

(73)

where, as expected, only the contribution of the surface tension remains for very large k. Reverting to the phase velocity c, we get in this limit

c^{[0]} = b + i {\tilde{c}}^{[0]} = b - \frac{i S}{2 (μ + 1)},

(74)

where b is given in Equation (33c).

Equation (73) shows that in the limit

k \to \infty

the short waves are damped within the expansion to zeroth order in R. From Equations (29), (61) and (73) the physical rate of damping for very large wavenumbers is

\frac{k}{{\hat{h}}_{1}^{}} c_{i}^{[0]} {\hat{U}}_{0}^{} = - \frac{\hat{k} \hat{γ}}{2 ({\hat{μ}}_{1}^{} + {\hat{μ}}_{2}^{})},

(75)

which decreases with the increase in viscosities, see the trend in Figure 3. Shorter waves thus become relatively less stable (less damped) if either of the layers becomes more viscous - an example of destabilizing role of viscosity as similarly observed by [31].

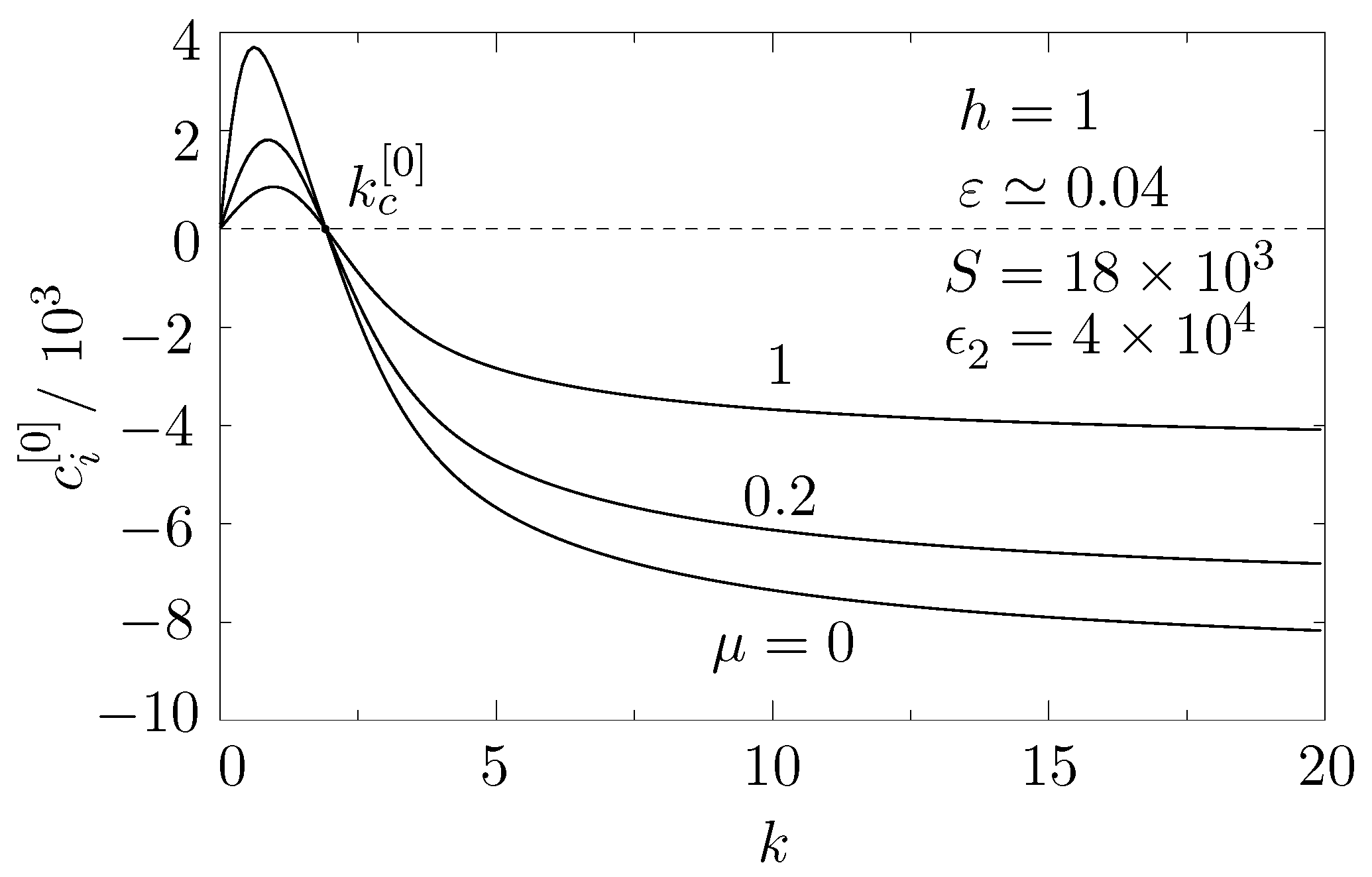
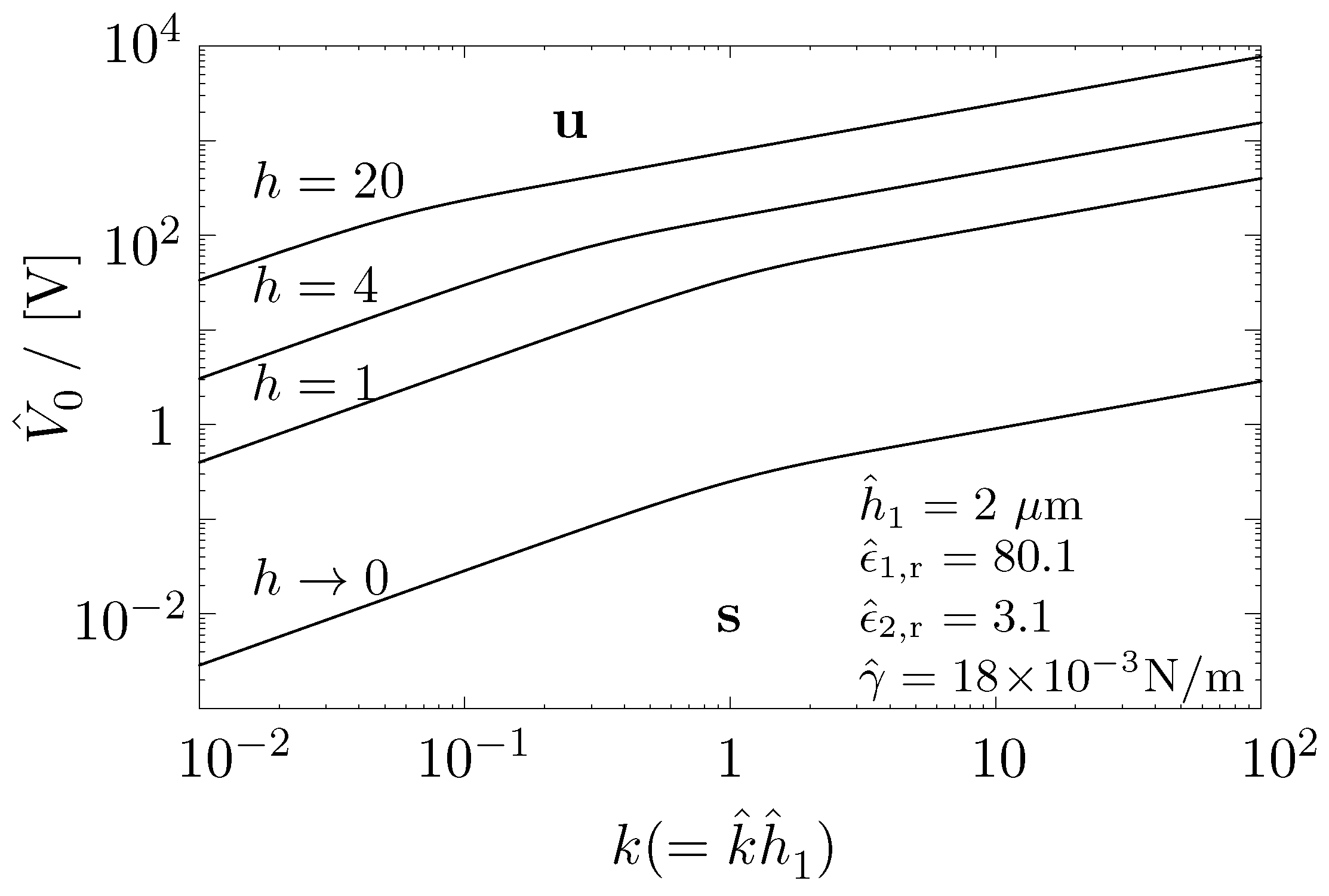
4.3. Onset of EHD Instability to Zeroth Order in R

The two terms in

S_{k}^{*}

from Equation (68h) are each proportional to the square of the phase velocity of the corresponding surface waves - the capillary and the EHD waves - whose interplay can destabilize the system.

S_{k}^{*}

enters explicitly the expression for

{\tilde{c}}_{i}^{[0]}

in Equation (70c) and in fact determines its sign; the condition

S_{k}^{*} = 0,

(76)

is a neutral stability condition in the expansion to zeroth order in R.

With no electric field applied,

c_{i}^{[0]} \leq 0

for all k and the system is never unstable. In order to induce the instability

S_{k}^{*}

must become negative. From Equations (62), (68h) and (76) it is seen that only a normal electric field, with a negative stress contribution, can destabilize a system of two perfect dielectric liquids. Using the nondimensional units, the condition for onset of the EHD instability caused by a normal electric field is given by

ϵ_{2}^{} = \frac{k S {(ε + h)}^{2}}{{(ε - 1)}^{2}} (ε tanh [k] + tanh [k h]),

(77)

where

ϵ_{2}^{} / S

is the electric Weber number proportional to the square of the applied electric field. Equation (77) is identical to inviscid results from literature, more precisely combines in a single equation the findings separately obtained in different limits, [1]:

ϵ_{2}^{} \propto k^{2}

for

k, k h ≪ 1

and

ϵ_{2}^{} \propto k

for

k, k h ≫ 1

. Note that the EHD instability is not possible in case

ε = 1

since no interfacial electric stresses exist for a single dielectric.

Reverting Equation (77) to the physical (dimensional) variables we get for the impending voltage

{\hat{V}}_{inst}^{[0]} = \frac{ε {\hat{h}}_{1}^{} + {\hat{h}}_{2}^{}}{∣ ε - 1 ∣} {[\frac{\hat{γ} \hat{k}}{{\hat{ϵ}}_{2}^{}} (ε tanh [\hat{k} {\hat{h}}_{1}^{}] + tanh [\hat{k} {\hat{h}}_{2}^{}])]}^{\frac{1}{2}} .

(78)

The significance of Equation (78) is that

{\hat{V}}_{inst}^{[0]}

is independent of both

{\hat{U}}_{0}^{}

and

μ

. In other words in the limit

R \to 0

the onset of the EHD instability for two moving, viscous, dielectric fluids coincides with the result for two static, inviscid dielectrics [1,22].

After its hyperbolic tangents are expanded in the limits of small and large wavenumbers, Equation (78) gives respectively

\begin{matrix} {\hat{V}}_{inst}^{[0]} (\hat{k} {\hat{h}}_{1}^{}, \hat{k} {\hat{h}}_{2}^{} ≪ 1) & = \frac{{(ε {\hat{h}}_{1}^{} + {\hat{h}}_{2}^{})}^{\frac{3}{2}}}{∣ ε - 1 ∣} {(\frac{\hat{γ}}{{\hat{ϵ}}_{2}^{}})}^{\frac{1}{2}} \hat{k}, \end{matrix}

(79)

\begin{matrix} {\hat{V}}_{inst}^{[0]} (\hat{k} {\hat{h}}_{1}^{}, \hat{k} {\hat{h}}_{2}^{} ≫ 1) & = \frac{(ε {\hat{h}}_{1}^{} + {\hat{h}}_{2}^{})}{∣ ε - 1 ∣} {[\frac{(ε + 1) \hat{γ}}{{\hat{ϵ}}_{2}^{}}]}^{\frac{1}{2}} {\hat{k}}^{\frac{1}{2}} . \end{matrix}

(80)

The voltages in Equations (79) and (80) increase with

\hat{k}

; thus, for a given

{\hat{V}}_{inst}^{[0]}

, a critical wavenumber

k_{c}^{[0]}

, independent of

μ

ρ

and

G_{1}^{}

, is determined so that all

k < k_{c}^{[0]}

are unstable, see Figure 3. A system can be operated (or designed) to exclude those unstable wavenumbers. For a given size, the maximal operating voltage then needs to make the smallest allowed wavenumber in the system - largest allowed wavelength - to coincide with

k_{c}^{[0]}

i.e. neutrally stable.

We now make an estimate of finite-size constraints. For a large finite 2D surface (

\hat{L} > \hat{W}

), the smallest allowed wavenumber (estimated from inviscid theory) is

{\hat{k}}_{c}^{} = {\hat{k}}_{x}^{} = π / \hat{L}

, where

\hat{L}

is the longer dimension. When

\hat{L} ≫ {\hat{h}}_{1}^{}, {\hat{h}}_{2}^{}

, we can apply Equation (79). Using the two-liquid pump parameters from [20],

\hat{L} = 280 μ

{\hat{h}}_{1}^{} = 2 μ

{\hat{h}}_{2}^{} = 8 μ

ε ≃ 0.04

{\hat{ϵ}}_{2 r}^{} = 3.1

\hat{γ} = 18 \times 10^{- 3} {Nm}^{- 1}

, we get for the impending voltage

{\hat{V}}_{inst}^{[0]} = 6.85

In the limits

ε ≪ \min {1, h}

and

ε ≫ \max {1, h}

the instability voltages of Equations (79) and (80) depend only on the parameters of the dielectric with smaller permitivity. If

\hat{h}

is the layer thickness of the "weaker" dielectric, the voltages scale in both cases with

{\hat{h}}^{3 / 2}

and

{\hat{h}}^{}

in the limits of small and large wavenumbers, respectively. Incidentally, the same results appear in the case of a perfect conductor and a perfect dielectric, where also no electric shear stresses exist at the interface, [8]. This allows to use our results in the corresponding limits to asses a system with a highly-conducting and a nonconducting fluid such as water and oil.

In the limit

ε ≪ 1

{\hat{h}}_{2}^{} \to 0^{+}

, the electric field in the dielectric no. 2 with the smaller permittivity becomes enormous, Equation (37d). For the wavenumber

π / \hat{L}

from the pump example, we apply Equation (79) to get the impending voltage

{\hat{V}}_{inst}^{[0]} = 6.4

mV.

All of the above points are summarized in the stability diagram for the water-oil system, Figure 4, where plots are shown of the neutral stability line separating stable (

s

) and unstable (

u

) regions in the

{\hat{V}}_{inst}^{[0]}

–

k (= \hat{k} {\hat{h}}_{1}^{})

plane. Four different height ratios h are featured and a fixed set of

{\hat{h}}_{1}^{}

\hat{γ}

{\hat{ϵ}}_{1}^{}

and

{\hat{ϵ}}_{2}^{}

. Note how the impending voltage

{\hat{V}}_{inst}^{[0]}

in accordance with Equation (78) is seen to scale as k and

k^{1 / 2}

in the limit of small and large wavenumbers, respectively. Note also that the lines in the stability diagram are in fact the loci of the critical wavenumbers

k_{c}^{[0]}

of Figure 3.

5. Perturbation Expansion in the Reynolds Number R to first order

We now proceed with the expansion to first order in R using Equations (64)-(66). It suffices to consider a system brought to the neutral stability within the zeroth order in R, Equation (76). This is achieved when the applied voltage is equal to the critical impending voltage

{\hat{V}}_{inst}^{[0]}

, determining the

k_{c}^{[0]}

. In other words, we are at the neutral stability lines of Figure 4 (the case

S = T_{el}^{} = 0

, valid for all k, is of purely theoretical significance and can be analyzed as a special case).

A slight increase in the Reynolds number then induces a change in the velocities, also at the interface, Equation (56), giving rise to a small change in the phase velocity of the neutrally-stable perturbations,

c^{[1]}

; a small change in voltage,

V^{[1]}

, is needed to counteract the change and bring the system to neutral stability to first order in R. Note that only the normal stress condition, Equation (60), is affected by (the change in) voltage.

One thus solves the eigenvalue problem for

c^{[1]}

from the newly expanded equations and boundary conditions. The first-order corrections for the impending voltages,

V^{[1]}

, are found from the first-order-R neutral stability condition

c_{i}^{[1]} (V^{[1]}) = 0

The first-order-R equations are

\begin{matrix} {ψ_{1}^{[1]}}^{''''} - 2 k^{2} {ψ_{1}^{[1]}}^{''} + k^{4} ψ_{1}^{[1]} \\ = i k [(U_{1}^{(0)} - c^{[0]}) ({ψ_{1}^{[0]}}^{''} - k^{2} ψ_{1}^{[0]}) - {U_{1}^{(0)}}^{''} ψ_{1}^{[0]}], \end{matrix}

(81)

\begin{matrix} {ψ_{2}^{[1]}}^{''''} - 2 k^{2} {ψ_{2}^{[1]}}^{''} + k^{4} ψ_{2}^{[1]} \\ = i \frac{ρ}{μ} k [(U_{2}^{(0)} - c^{[0]}) ({ψ_{2}^{[0]}}^{''} - k^{2} ψ_{2}^{[0]}) - {U_{2}^{(0)}}^{''} ψ_{1}^{[0]}], \end{matrix}

(82)

where we expanded the zeroth-order-R Equations (67a) and (67b) with the RHS of the full Equations (45) and (46) (note that the RHS are in fact the first-order-R contributions).

U_{1}^{(0)}

and

U_{2}^{(0)}

are unperturbed (zeroth-order-

ζ

) velocities, given in Equation (32).

The first-order-R boundary and interface conditions are

\begin{matrix} ψ_{1}^{[1]} (1) = 0, {ψ_{1}^{[1]}}^{'} (1) = 0, \end{matrix}

(83)

\begin{matrix} ψ_{2}^{[1]} (- h) = 0, {ψ_{2}^{[1]}}^{'} (- h) = 0, \end{matrix}

(84)

\begin{matrix} ψ_{1}^{[1]} (0) - ψ_{2}^{[1]} (0) = 0, \end{matrix}

(85)

\begin{matrix} {ψ_{1}^{[1]}}^{'} (0) - {ψ_{2}^{[1]}}^{'} (0) = (\frac{ψ_{1}^{[1]} (0)}{{\tilde{c}}^{[0]}} - \frac{ψ_{1}^{[0]} (0) {\tilde{c}}^{[1]}}{{({\tilde{c}}^{[0]})}^{2}}) (1 - μ) a_{2}^{}, \end{matrix}

(86)

\begin{matrix} {ψ_{1}^{[1]}}^{''} (0) + k^{2} ψ_{1}^{[1]} (0) = μ ({ψ_{2}^{[1]}}^{''} (0) + k^{2} ψ_{2}^{[1]} (0)), \\ i k 2 T_{el, N}^{[0]} V^{[1]} \frac{ψ_{1}^{[0]} (0)}{{\tilde{c}}^{[0]}} = μ ({ψ_{2}^{[1]}}^{'''} (0) - 3 k^{2} {ψ_{2}^{[1]}}^{'} (0)) + i ρ k ({\tilde{c}}^{[0]} {ψ_{2}^{[0]}}^{'} (0) + a_{2}^{} ψ_{2}^{[0]} (0)) \end{matrix}

(87)

\begin{matrix} - ({ψ_{1}^{[1]}}^{'''} (0) - 3 k^{2} {ψ_{1}^{[1]}}^{'} (0)) - i k ({\tilde{c}}^{[0]} {ψ_{1}^{[0]}}^{'} (0) + a_{1}^{} ψ_{1}^{[0]} (0)) . \end{matrix}

(88)

In Equation (86) both

ψ

and c were expanded. Since

\tilde{c}

differs from c by a constant factor, Equation (68g), we see from Equation (65) that

{\tilde{c}}^{[1]} = c^{[1]} (= {(\partial c / \partial R)}_{R = 0})

. Furthermore,

{\tilde{c}}^{[0]} = {\tilde{c}}_{r}^{[0]}

in Equations (86) and (88), since

{\tilde{c}}_{i}^{[0]} = 0

at the neutral stability to zeroth-R, Equation (70a).

LHS of Equation (88), where the voltage change

V^{[1]}

enters, is obtained by calculating

{(\partial S_{k}^{*} / \partial R)}_{R = 0} = {(\partial T_{el} / \partial R)}_{R = 0} = {(\partial T_{el} / \partial V \cdot \partial V / \partial R)}_{R = 0}

, where

T_{el} = T_{el, N}^{[0]}

is the zeroth-order-R Maxwell’s stress tensor for a normal E-field, the upper part of Equation (62). Note that in dimensional units

V^{[1]} = {\hat{V}}^{[1]} / {\hat{V}}_{0}^{[0]}

The overall solution of Equation (81) or Equation (82) has the form

ψ^{[1]} = ψ_{H}^{[1]} + ψ_{P}^{[1]},

(89)

where

ψ_{H}^{[1]}

is a general solution of the homogeneous equation, and

ψ_{P}^{[1]}

is a particular solution of the inhomogeneous equation. We write the solutions of the two homogeneous equations

\begin{matrix} ψ_{1, H}^{[1]} & = Δ B_{1}^{} cosh [k (z - 1)] \\ + Δ C_{1}^{} z sinh [k (z - 1)] + Δ D_{1}^{} z cosh [k (z - 1)], \end{matrix}

(90)

\begin{matrix} ψ_{2, H}^{[1]} & = Δ A_{2}^{} sinh [k (z + h)] + Δ B_{2}^{} cosh [k (z + h)] \\ + Δ C_{2}^{} z sinh [k (z + h)] + Δ D_{2}^{} z cosh [k (z + h)], \end{matrix}

(91)

where coefficients

Δ A_{2}^{}, Δ B_{1, 2}^{}, Δ C_{1, 2}^{}

and

Δ D_{1, 2}^{}

give the small changes to the corresponding zeroth-order coefficients in Equations (69a) and (69b). Note that

Δ A_{1}^{} = 0

, since we chose to normalize the entire solution

ψ_{1}^{}

with respect to

A_{1}^{}

, as it was done with

ψ_{1}^{[0]}

, Equation (69a). However,

Δ A_{2}^{} \neq 0

, since

A_{2}^{} \neq 0

in Equation (69b), in order to satisfy the boundary and interface conditions Equations (83)–(88).

The particular solutions of Equations (81) and (82) have the form, [14]

\begin{matrix} ψ_{1, P}^{[1]} & = i k z^{2} [sinh [k (z - 1)] P_{1}^{} (z) + cosh [k (z - 1)] Q_{1}^{} (z)], \end{matrix}

(92)

\begin{matrix} ψ_{2, P}^{[1]} & = i k z^{2} [sinh [k (z + h)] P_{2}^{} (z) + cosh [k (z + h)] Q_{2}^{} (z)], \end{matrix}

(93)

where

P_{1, 2}^{} (z)

and

Q_{1, 2}^{} (z)

are the second degree polynomials fully written in the Appendix B.

Inserting the complete solution

ψ^{[1]}

into Equations (83)–(88) we obtain the system

\begin{matrix} Δ B_{1}^{} + Δ D_{1}^{} + i k L_{1}^{} = 0, \end{matrix}

(94)

\begin{matrix} k Δ C_{1}^{} + Δ D_{1}^{} + i k L_{2}^{} = 0, \end{matrix}

(95)

\begin{matrix} Δ B_{2}^{} - h Δ D_{2}^{} + i k \frac{ρ}{μ} L_{3}^{} = 0, \end{matrix}

(96)

\begin{matrix} k Δ A_{2}^{} - k h Δ c_{2}^{} + Δ D_{2}^{} + i k \frac{ρ}{μ} L_{4}^{} = 0, \end{matrix}

(97)

\begin{matrix} cosh [k] Δ B_{1}^{} - cosh [k h] Δ B_{2}^{} - sinh [k h] Δ A_{2}^{} = 0, \end{matrix}

(98)

\begin{matrix} k sinh [k] Δ B_{1}^{} + sinh [k] Δ C_{1}^{} - cosh [k] Δ D_{1}^{} \\ + k cosh [k h] Δ A_{2}^{} + k sinh [k h] Δ B_{2}^{} + sinh [k h] Δ C_{2}^{} \\ + cosh [k h] Δ D_{2}^{} + a_{2}^{} (1 - μ) \frac{{\tilde{c}}_{r}^{[0]} cosh [k] Δ B_{1}^{} - c^{[1]} L_{6}^{}}{{({\tilde{c}}_{r}^{[0]})}^{2}} = 0, \end{matrix}

(99)

\begin{matrix} k cosh [k] Δ B_{1}^{} + cosh [k] Δ C_{1}^{} - sinh [k] Δ D_{1}^{} \\ - k μ sinh [k h] Δ A_{2}^{} - k μ cosh [k h] Δ B_{2}^{} - μ cosh [k h] Δ C_{2}^{} \\ - μ sinh [k h] Δ D_{2}^{} + i L_{7}^{} = 0, \end{matrix}

(100)

\begin{matrix} 2 k^{3} sinh [k] Δ B_{1}^{} + 2 k^{3} μ cosh [k h] Δ A_{2}^{} \\ + 2 k^{3} μ sinh [k h] Δ B_{2}^{} - i k L_{8}^{} = 0, \end{matrix}

(101)

where

L_{1}^{}

L_{8}^{}

are short labels. The system of Equations (94)-(101) can finally be solved for the nontrivial eigenvalue

c^{[1]} (k, μ, h, ρ, G_{1}^{}, V^{[1]})

. The analytical expression for

c^{[1]}

and the expanded

L_{1}^{}

L_{8}^{}

(

L_{8}^{}

contains

V^{[1]}

) are given in the Appendix C.

5.1. Pure shear stress instability to first order in R

It follows from Equation (A13)

c^{[1]} = i c_{i}^{[1]} = i C (k, μ, h, ρ, G_{1}^{}, V^{[1]}),

(102)

where

C

is a very complicated real function of the flow parameters k,

μ

, h,

ρ

G_{1}^{}

and of voltage

V^{[1]}

. The phase velocity

c^{[1]}

is thus a purely imaginary number and the first-order-R instability happens for

c_{i}^{[1]} = C > 0

One can investigate the vast parameter space of Equation (102), but we focus here on a handful of features. We first consider pure shear instability, i.e., the case without a voltage correction,

V^{[1]} = 0

In Figure 5(a) shown is

R c_{i}^{[1]} (k)

, the total change in the phase velocity c per Equation (65), for two sets of parameters

(R, μ, h, ρ, G_{1}^{}, V^{[1]})

, differing in h:

(2 \times 10^{- 3}, 2, 4, 1, 0, 0)

and

(2 \times 10^{- 3}, 2, 1 / 4, 1, 0, 0)

. For

h = 4

there is a critical wavenumber

k_{c}^{[1]}

for which the system is at the neutral stability to first order in R, analogous to

k_{c}^{[0]}

of Figure 3, but the trends in the two figures are opposite: in Figure 5(a) the small wavenumbers,

k < k_{c}^{[1]}

, are stable and the large ones,

k > k_{c}^{[1]}

, unstable. For

h = 1 / 4

, a configuration with a thinner bottom liquid, the system is unstable for all k.

We further notice the orders-of-magnitude smaller values of the first-order corrections. We remember that typical values of

c_{i}^{[0]}

in microfluidics are on the order of 1 (

\sim 10^{3}

times smaller than those in Figure 3, used to showcase the trends). Hence,

R c_{i}^{[1]} / c_{i}^{[0]} \sim 10^{- 7}

. It is perhaps surprising that the shear instability occurs at all. This is the famed Yih’s instability due to viscosity stratification first studied in the limit of small k, [14]. We have performed here the analysis for small R, confirming Yih’s findings as a special case (re-visit Section 4.1): by inspecting Equation (A13), noticing the common factor

{\tilde{c}}_{r}^{[0]}

, and Equation (70b) for

{\tilde{c}}_{r}^{[0]}

, we find the proportionality

c_{i}^{[1]} \sim a_{2}^{} (μ - 1),

(103)

where

a_{2}^{}

is the pressure-gradient dependent factor in the zero-order-

ζ

flow, Equation (33b), and

μ

is the viscosity ratio. It immediately follows from Equation (103) that the condition

μ = 1

(two equal viscosities) is the neutral stability condition to first-order in R, i.e.,

c_{i}^{[1]} (μ = 1) = 0

for all k, and there is no instability; since Yih considered pure Couette flow (

G_{1}^{} = 0

) for which

a_{2}^{} \neq 0

, the instability

c_{i}^{[1]} > 0

is indeed induced for a viscous stratification

μ \neq 1

However, in our more general Couette–Poiseuille flow, the neutral stability for all k happens also when

a_{2}^{} = 0

, which occurs for a non-zero forward pressure gradient

G_{1}^{} < 0

and the value

μ = - G_{1}^{} / (2 - G_{1}^{}) h^{2}

(e.g., for

G_{1}^{} = - 1

and

h = 4

μ = 5 . \dot{3}

yields the neutral stability for all k). This is the case when the compounded zero-order-

ζ

velocity becomes the smooth (unbroken) parabola, Equation (32). Hence, the viscosity stratification is not the sufficient condition - the generalized mechanism of the instability is the discontinuity in the slope (kink) of the zero-order-

ζ

velocity. The criterion does not pertain though to the single

k_{c}^{[1]}

that is independently neutrally stable to first order in R, as determined by the complicated bracketed term in Equation (A13).

We make a final remark. We have just seen that

c_{i}^{[1]}

is identically zero for all wavenumbers for

μ = 1

a_{2}^{} = 0

, on the account of

{\tilde{c}}_{r}^{[0]}

being then zero. At the same time we are already at the zeroth-order-R neutral stability for which

{\tilde{c}}_{i}^{[0]} = 0

. Hence,

{\tilde{c}}_{0}^{} = 0

, Equation (70a), and the denominator of Equation (57b) becomes zero making the disturbance infinite. In such cases we must employ second order expansion of the kinematic condition, as already noted. Nevertheless, a minute change from

μ = 1

and

a_{2}^{} = 0

brings forth the instability as discussed.

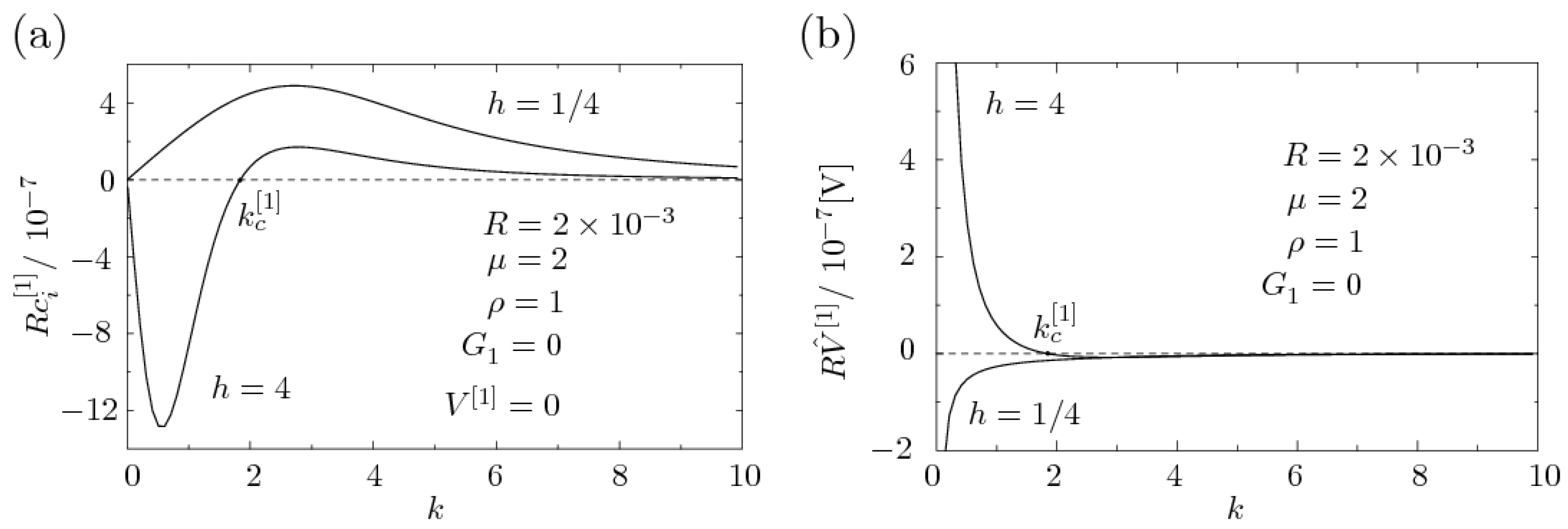
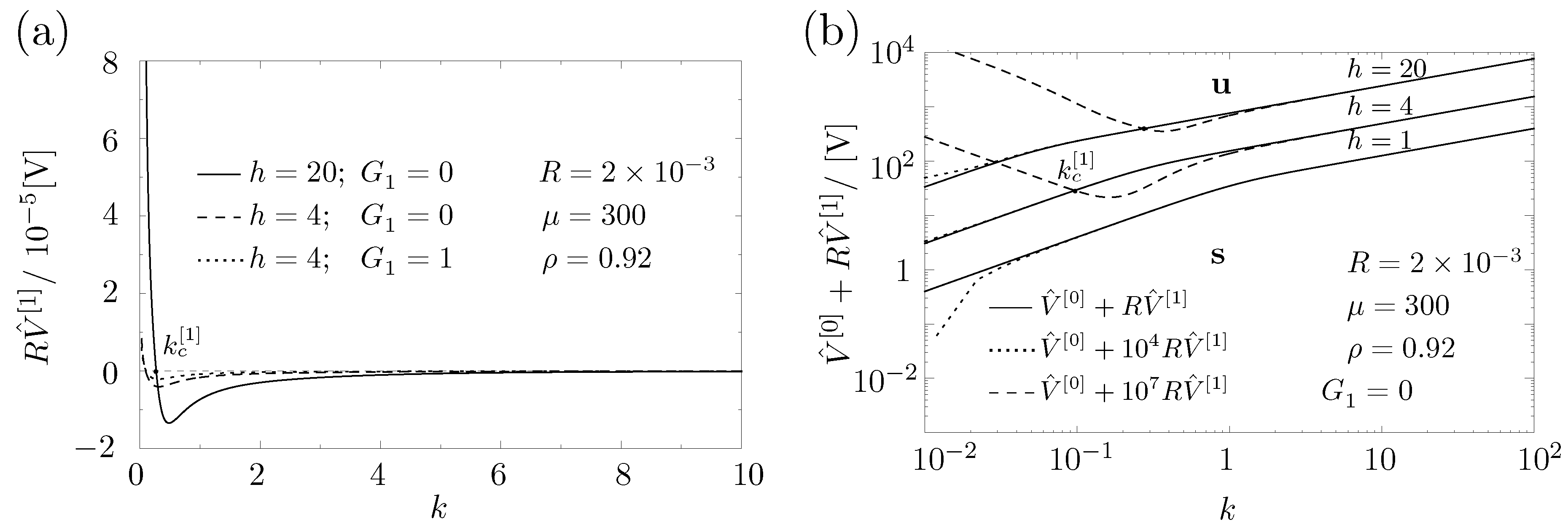
5.2. Onset of EHD Instability to First Order in R

As earlier mentioned, our main interest is the voltage correction

V^{[1]}

that brings the system to neutral stability to first-order in R, i.e., how much the voltage

V^{[0]}

needs to change to compensate for the unstable growth of

c^{[1]}

due to the shear flow at small R. The first-order change is found by solving

c^{[1]} (k, μ, h, ρ, G_{1}^{}, V^{[1]}) = 0,

(104)

for

V^{[1]}

. The analytical solution for

V^{[1]}

is too complicated for display; we use the closed form of

c^{[1]}

, Equation (A13), and work from there to obtain

V^{[1]}

To bring the system to first-order-R neutral EHD stability, we expect the stable regions of

c_{i}^{[1]}

, i.e., those wavenumbers for which

k < k_{c}^{[1]}

, to be destabilized by an increasing voltage

V^{[1]}

(of normal E-field), whereas the unstable regions

k > k_{c}^{[1]}

to be stabilized by a decreasing voltage.

This is indeed the case. Figure 5(b) shows the first-order-R voltage corrections

R {\hat{V}}^{[1]}

vs. k, corresponding to the two cases of Figure 5(a). For

h = 4

, the voltage increases sharply for very stable small wavenumbers,

k < k_{c}^{[1]}

, to destabilize them, but decreases for

k > k_{c}^{[1]}

(the correction is negative), to dampen the growth of unstable ones. Note that

k_{c}^{[1]} (= 1.836)

is the same in the two panels as it should be, since

c_{i}^{[1]} (k_{c}^{[1]}) = {\hat{V}}^{[1]} (k_{c}^{[1]}) = 0

. For

h = 1 / 4

, the voltage correction is negative for all k, in accordance with the all-positive growth rates of the

c_{i}^{[1]} (k)

in panel (a).

Note that we depicted the overall change in the physical voltage,

R {\hat{V}}^{[1]}

, in Volts, in order to get the feel for the actual experimental change to first order in R. Technically,

ϵ_{2}^{}

in the term

T_{el, N}^{[0]} V^{[1]}

of Equation (88) has been expressed as

{\hat{ϵ}}_{2}^{} {\hat{V}}_{inst}^{[0]} {\hat{V}}^{[1]} / ({\hat{μ}}_{1}^{} {\hat{h}}_{1}^{} {\hat{U}}_{0}^{}

), where

{\hat{V}}_{inst}^{[0]}

is the impending voltage of Equation (78). Like with

c^{[1]}

, the first-order-R voltage corrections are six-seven orders of magnitude smaller compared to zeroth-order-R values, making them challenging if not impossible to measure.

We emphasize that the first-order-R corrections are found from the coupled EHD system of Equations (94)-(101). The overall coupling of the first-order E-field and the shear flow means that the phase velocities

c_{i}^{[1]}

of the pure shear relative to those of the coupled EHD cases will have different extremal points in general. The maximal voltage corrections

{\hat{V}}^{[1]}

in the panel (b) thus do not coincide with the maximal

c_{i}^{[1]}

of (a).

Unlike the impending

{\hat{V}}_{inst}^{[0]}

voltages, the

R {\hat{V}}^{[1]}

corrections depend on the flow parameters

μ, ρ, G_{1}^{}

and R. This is shown in Figure 6(a), where three graphs are featured for different parameters of the EO pump of Section 4.3. The pump drags a viscous oil by a thin layer of water:

μ = 300, ρ = 0.92

;

h = 4, 20

Comparing Figure 6(a) with Figure 5(b) we first notice that the magnitudes of

R {\hat{V}}^{[1]}

are 100 times larger in Figure 6(a) due to larger damping/growth rates around

k_{c}^{[1]}

, with more pronounced local minima. Second,

k_{c}^{[1]}

is shifted to the left enlarging the range of unstable wavenumbers (i.e., the area of negative voltage corrections). Stability is thus complicated function of parameters: the increase in

μ

relatively destabilizes the system for

h > 1

by shifting

k_{c}^{[1]}

to the left, and by making the negative voltage corrections for

k > k_{c}^{[1]}

larger; but at the same time it makes the positive voltage corrections for

k < k_{c}^{[1]}

also larger, the indication that already stable wavenumbers for

μ = 2

became even more stable for

μ = 300

From Figure 6(a) alone, increase in h stabilizes the system by shifting

k_{c}^{[1]}

to the right, but, like the increase in

μ

, enhances the magnitudes of the voltage corrections from both sides of

k_{c}^{[1]}

. Increase in adverse pressure (

G_{1}^{} > 0

) shifts

k_{c}^{[1]}

to the right, but dampens the magnitude of the voltage corrections on the two sides.

The voltage corrections

R {\hat{V}}^{[1]}

for the largest wavenumber

\hat{k} = π / \hat{L}

allowed in the pump (

\hat{L} = 280 μ

m, Section 4.3), are

69 \times 10^{- 5}

1.2 \times 10^{- 5}

V, and

1.1 \times 10^{- 5}

V for the three cases

(h = 20, G_{1}^{} = 0), (h = 4, G_{1}^{} = 0), (h = 4, G_{1}^{} = 1)

, respectively. Interestingly, if the driving velocity could be increased by a factor 10 to

U_{0}^{} = 1

cm/s (and correspondingly

R = 0.02

), the voltage corrections

R {\hat{V}}^{[1]}

grow by another factor 100 and come into the experimentally feasible mV range: 69 mV, 1.2 mV and 1.1 mV, respectively.

Finally, the overall trends are best seen in the updated neutral stability diagram: in Figure 6(b), the overall voltage

{\hat{V}}_{tot}^{} = {\hat{V}}^{[0]} + R {\hat{V}}^{[1]}

vs. k is shown on log-log scale for a set of parameters for the EO pump. The actual small changes relative to those of Figure 4 are too small to be seen (full line), and the magnification of

R {\hat{V}}^{[1]}

by a factor

10^{4}

(dotted line) and

10^{7}

(dashed line) is imposed to resolve the trends. The lines thus express the (magnified) neutral stability curves up to first order in R, i.e. the curves for which

c_{i}^{[0]} = c_{i}^{[1]} = 0

For

h = 4

and

h = 20

we see how stable regions, i.e., positive voltage corrections, increase with height, protruding into unstable domains for

k < k_{c}^{[1]}

. For

k > k_{c}^{[1]}

the voltage corrections are negative, and so the unstable domain bulges into the stable one.

For

h = 1

the stable regions are overall diminished (the voltage correction is always negative), as the system is unstable for all k, like

h = 1 / 4

of Figure 5. We finally remind that the neutral stability diagrams differ for different flow regimes.

This ends our comprehensive EHD stability analysis to first order in R.

6. Conclusions

Of many findings in our comprehensive article on the EHD stability of two superposed viscous dielectric liquids in a parallel flow in a microfluidic channel, we select a few.

We have derived in the flow problem analytical, closed-form solutions for the growth rates (the complex-numbered phase velocities) of 2D disturbances and for the accompanying impending voltages, up to first order in small Reynolds number R. Our approach gives a deeper mechanistic insight into the very complicated interplay of various physical parameters.

Only voltages creating E-fields normal to the interface of the dielectrics destabilize it. The zero-order-R impending voltages,

{\hat{V}}_{inst}^{[0]}

, for two shearing viscous dielectrics do not depend on the viscosities, velocities or densities, i.e. are the same as in inviscid, still configurations. The voltages are function of dielectric constants (ratios), depths ratios, surface tension and wavenumbers.

The first-order-R corrections,

R {\hat{V}}^{[1]}

, depend on the mentioned flow parameters, as well as on wavenumbers, but turn up to be very small - the cases investigated are up to seven orders of magnitudes smaller than the

{\hat{V}}_{inst}^{[0]}

values. The results are best sumarized in the voltage-wavenumber neutral stability diagrams which delimit stable from unstable regions, and differ for different flow regimes.

Although the voltage terms

R {\hat{V}}^{[1]}

are small, adjusting the flow parameters can make it feasible to experimentally detect them. As shown, enlarging the Reynolds number, still within the perturbation limits, leads to the first-order voltage corrections in mV range. If R is enhanced even more, the neglected gravity must be taken into account.

We note that the parallel-plane microfluidic channel flow is accomplished in special configurations of the so-called electroosmotic pumps with low aspect ratio channels. The parallel plane flow enables considerations of 2D disturbances and thus the application of analytic methods yielding closed form solutions. Our neutral stability diagrams for the pump show different trends for impending voltages for small and large wavenumbers, both in the zero-order-R and the first-order-R approximations.

There are three major approximations in the article. The first one is the negligence of gravity, justified in microfluidics as the ratio of gravitational to surface tension force, the Bond number, is

B o \sim 10^{- 4} ≪ 1

The second approximation is that we consider the flow between two infinite planes and its 2D disturbances. The finite devices, with a finite width in the y-direction, generally require consideration of 3D disturbances. As this cannot be done in closed form, we decided not to pursue it to avoid burdening our already detailed article. Instead, we made some reasonable estimates for the constraints on wavenumbers imposed by the finite size of the EO pump, using the fact that in microfluidics the EHD onset can be tuned to the smallest wavenumber allowed in the system. Besides, the infinite plane approximation is reasonably well suited to large 2D surfaces of the microfluidic systems considered.

Third, we consider idealized flow with two perfect dielectrics for which only the normal electric stresses exist at the interface, as the tangential stresses are identically satisfied. Incidentally, the same stress conditions are present in the configuration with a perfect conductor and a perfect dielectric, and our analysis ought to be applicable there with a minute correction of setting the E-field in the conductor to zero. More realistic leaky dielectrics would involve net tangential electric stresses at the interface in addition to the viscous ones, which would thus affect the stability of modes and already to zeroth order in R. With the updated boundary conditions, our methodology can be entirely reused for leaky dielectrics.

In spite of the small Reynolds number regime studied, we did not resort to Stokes equation, but have used the full Navier–Stokes equations that for 2D flow transform into the Orr–Sommerfeld equations. These are much more involved to solve. The Reynolds number was defined with respect to the unperturbed height of the upper liquid. Whereas increasing R by one or even two orders of magnitude does not seem to invalidate our analysis and conclusions, we did not consider if some effective Reynolds number, scaled to a very small wavenumber, could become so large and dominant as to violate the expansion.

Finally, our analysis provides new insight with respect to existing literature. We correct the EHD stability study of [16] by providing the fully correct and extremely complicated analytical expressions to both order in small Reynolds number. And we refine and further expand on the seminal study of Yih and his instability due to viscosity stratification [14]; namely, Yih studied the two-fluid shear instability in a Couette flow at small k. Our special case to first order in R whithout electric fields generalizes Yih’s work to any small Reynolds numbers and a more general flow profile. We find that the pure shear instability arises in fact due to discontinuity in the slope (kink) of the unperturbed (zeroth-order-

ζ

) velocity, which becomes transparent in a Couette–Poiseuille flow. Instability due to viscosity stratification becomes thus just a necessary condition. Our EHD voltage corrections to first order in R are then a viable proof of the elusive instability proposed by Yih more than 50 years ago.

Conflicts of Interest

Authors declare no conflicts of interest.

Appendix A. Coefficients for $Ψ_{1}^{[0]}$ and $Ψ_{2}^{[0]}$

The coefficients

A_{2}^{}, B_{1, 2}^{}, C_{1, 2}^{}

and

D_{1, 2}^{}

from Equations (69a) and (69b) for the case of the neutral stability to zeroth-order-R, i.e., for

S_{k}^{*} \equiv k^{2} S + T_{el}^{} = 0

\begin{matrix} B_{1}^{} & = ([μ + 2 k^{2} h^{2} (μ - 1) + μ cosh [2 k h]] sinh [k] - [2 k h (h + 1) - sinh [2 k h]] cosh [k]) N^{- 1} \end{matrix}

(A1)

\begin{matrix} C_{1}^{} & = [(- k [μ + 2 h + 2 k^{2} h^{2} (μ - 1) + μ cosh [2 k h]] + sinh [2 k h]) cosh [k] \\ + (μ + 2 k^{2} h + 2 k^{2} μ h^{2} + μ cosh [2 k h] - k sinh [2 k h]) sinh [k]] {(k N)}^{- 1} \end{matrix}

(A2)

\begin{matrix} D_{1}^{} & = - B_{1}^{} \end{matrix}

(A3)

\begin{matrix} A_{2}^{} & = [(2 μ + h^{2} [2 k^{2} (μ - 1) - 1] - h^{2} cosh [2 k]) cosh [k h] \\ + 2 h μ (k + k h - h cosh [k] sinh [k]) sinh [k h]] {(μ N)}^{- 1} \end{matrix}

(A4)

\begin{matrix} B_{2}^{} & = h (μ [- 2 k (h + 1) + h sinh [2 k]] cosh [k h] \\ + h [1 - 2 k^{2} (μ - 1) + cosh [2 k]] sinh [k h]) {(μ N)}^{- 1} \end{matrix}

(A5)

\begin{matrix} C_{2}^{} & = ([2 k^{3} h (μ - 1) - k (h + 2 μ) - k h cosh [2 k] + μ sinh [2 k]] cosh [k h] \\ + [1 + 2 k^{2} (h μ + 1) + cosh [2 k] - k h μ sinh [2 k]] sinh [k h]) {(k μ N)}^{- 1} \end{matrix}

(A6)

\begin{matrix} D_{2}^{} & = h^{- 1} B_{2}^{} \end{matrix}

(A7)

\begin{matrix} N & = (μ + 2 h^{2} [k^{2} (μ - 1) - 1] + μ cosh [2 k h]) cosh [k] - [2 k h (h + 1) - sinh [2 k h]] sinh [k] \end{matrix}

(A8)

Appendix B. Coefficients for $Ψ_{1, P}^{[1]}$ and $Ψ_{2, P}^{[1]}$

The polynomials

P_{1, 2}^{} (z)

and

Q_{1, 2}^{} (z)

from Equations (92) and (93). The capital letters are the coefficients from Appendix A.

\begin{matrix} P_{1}^{} (z) & = p_{01}^{} + p_{11}^{} z + p_{21}^{} z^{2} \\ = \frac{5 D_{1}^{} G_{1}^{} - 2 (2 a_{1}^{} C_{1}^{} + G_{1}^{}) k - 4 D_{1}^{} {\tilde{c}}_{r}^{[0]} k^{2}}{16 k^{3}} + \frac{2 a_{1}^{} D_{1}^{} k - 3 C_{1}^{} G_{1}^{}}{24 k^{2}} z + \frac{D_{1}^{} G_{1}^{}}{48 k} z^{2}, \end{matrix}

(A9)

\begin{matrix} Q_{1}^{} (z) & = q_{01}^{} + q_{11}^{} z + q_{21}^{} z^{2} \\ = \frac{5 C_{1}^{} G_{1}^{} - 2 (2 a_{1}^{} D_{1}^{} + B_{1}^{} G_{1}^{}) k - 4 C_{1}^{} {\tilde{c}}_{r}^{[0]} k^{2}}{16 k^{3}} + \frac{2 a_{1}^{} C_{1}^{} k - 3 D_{1}^{} G_{1}^{}}{24 k^{2}} z + \frac{C_{1}^{} G_{1}^{}}{48 k} z^{2}, \end{matrix}

(A10)

\begin{matrix} P_{2}^{} (z) & = p_{02}^{} + p_{12}^{} z + p_{22}^{} z^{2} \\ = \frac{ρ}{μ} (\frac{5 D_{2}^{} G_{2}^{} - 2 (2 a_{2}^{} C_{2}^{} + A_{2}^{} G_{2}^{}) k - 4 D_{2}^{} {\tilde{c}}_{r}^{[0]} k^{2}}{16 k^{3}} + \frac{2 a_{2}^{} D_{2}^{} k - 3 C_{2}^{} G_{2}^{}}{24 k^{2}} z + \frac{D_{2}^{} G_{2}^{}}{48 k} z^{2}), \end{matrix}

(A11)

\begin{matrix} Q_{2}^{} (z) & = q_{02}^{} + q_{12}^{} z + q_{22}^{} z^{2} \\ = \frac{ρ}{μ} (\frac{5 C_{2}^{} G_{2}^{} - 2 (2 a_{2}^{} D_{2}^{} + B_{2}^{} G_{2}^{}) k - 4 C_{2}^{} {\tilde{c}}_{r}^{[0]} k^{2}}{16 k^{3}} + \frac{2 a_{2}^{} C_{2}^{} k - 3 D_{2}^{} G_{2}^{}}{24 k^{2}} z + \frac{C_{2}^{} G_{2}^{}}{48 k} z^{2}) . \end{matrix}

(A12)

Appendix C. Phase Velocity c^[1]

The full expression

c^{[1]}

(

= {\tilde{c}}^{[1]}

) for the case of the neutral stability to zeroth-order-R, i.e., for

S_{k}^{*} = 0

. The auxiliary expressions

L_{1}^{} - L_{8}^{}

include the coefficients from the Appendix A and Appendix B, see below.

\begin{matrix} c^{[1]} = i c_{i}^{[1]} = i {\tilde{c}}_{r}^{[0]} (k^{4} [2 a_{2}^{} h^{2} μ (μ - 1) (L_{1}^{} - L_{2}^{}) + {\tilde{c}}_{r}^{[0]} (4 h (h + 1) μ L_{2}^{} \\ - L_{1}^{} [1 + 4 h μ + μ^{2} + 2 k^{2} h^{2} {(μ - 1)}^{2}])] \\ - k^{4} (μ - 1) [2 a_{2}^{} h^{2} μ (L_{2}^{} - L_{1}^{}) + {\tilde{c}}_{r}^{[0]} (μ + 1) L_{1}^{} (1 + 2 k^{2} h^{2})] cosh [2 k] \\ + {\tilde{c}}_{r}^{[0]} k [L_{8}^{} + 2 h μ L_{8}^{} + 2 k^{2} (L_{7}^{} - 2 h^{2} [k^{2} (μ - 1) + μ] L_{7}^{} + h (h + μ) L_{8}^{})] sinh [k] \\ + 4 {\tilde{c}}_{r}^{[0]} k^{3} ρ [μ (k^{2} + 1) L_{3}^{} + h (k^{2} [L_{3}^{} + (μ - 1) L_{4}^{}] + μ L_{4}^{})] sinh [k] cosh [k h] \\ - k^{3} (μ - 1) [- 2 a_{2}^{} k^{2} h^{2} μ L_{1}^{} + {\tilde{c}}_{r}^{[0]} (2 k^{2} h^{2} + 1) (μ + 1) (L_{1}^{} - L_{2}^{})] sinh [2 k] \\ + {\tilde{c}}_{r}^{[0]} k [- k^{3} (μ^{2} + 1) L_{1}^{} cosh [2 k] - (2 k^{2} L_{7}^{} + L_{8}^{}) sinh [k]] cosh [2 k h] \\ - {\tilde{c}}_{r}^{[0]} k^{3} [k (μ^{2} - 1) L_{1}^{} + (μ^{2} + 1) (L_{1}^{} - L_{2}^{}) sinh [2 k]] cosh [2 k h] \\ + 4 {\tilde{c}}_{r}^{[0]} k^{4} ρ [L_{3}^{} + L_{4}^{} + (L_{4}^{} + [k^{2} (μ - 1) + μ] L_{3}^{})] sinh [k] sinh [k h] \\ - {\tilde{c}}_{r}^{[0]} μ [2 k^{3} (L_{1}^{} - L_{2}^{}) cosh [2 k] + (k^{2} + 1) L_{8}^{} sinh [k]] sinh [2 k h] \\ - 2 a_{2}^{} k^{2} h μ (μ - 1) (L_{8}^{} - 2 k^{2} h L_{7}^{}) cosh [k] \\ + {\tilde{c}}_{r}^{[0]} [- 4 k^{4} h (h + 1) μ L_{7}^{} + L_{8}^{} (1 + k^{2} [1 + 2 h (k^{2} h - k^{2} h μ + h + μ)])] cosh [k] \\ + 4 k^{4} ρ ({\tilde{c}}_{r}^{[0]} [(h + 1) μ L_{4}^{} + L_{3}^{} (k^{2} h - k^{2} h μ + h + μ)] - a_{2}^{} μ (μ - 1) (L_{3}^{} + h L_{4}^{})) cosh [k] cosh [k n] \\ - {\tilde{c}}_{r}^{[0]} (k^{2} + 1) L_{8}^{} cosh [k] cosh [2 k h] \\ + 4 k^{3} ρ ({\tilde{c}}_{r}^{[0]} [h (k^{2} - k^{2} μ + 1) L_{4}^{} + (k^{2} + k^{2} h μ + 1) L_{3}^{}] - a_{2}^{} k^{2} h μ (μ - 1) L_{3}^{}) cosh [k] sinh [k h] \\ - k μ (2 {\tilde{c}}_{r}^{[0]} k^{2} L_{7}^{} + a_{2}^{} L_{8}^{} + {\tilde{c}}_{r}^{[0]} L_{8}^{} - a_{2}^{} μ L_{8}^{} + 4 {\tilde{c}}_{r}^{[0]} k^{3} L_{1}^{} sinh [k]) cosh [k] sinh [2 k h]) D_{2}^{- 1}, \end{matrix}

(A13)

\begin{matrix} D_{2}^{} & = 2 a_{2}^{} k^{3} μ (μ - 1) L_{6}^{} ([2 k^{2} h^{2} μ - 2 (k^{2} + 1) h^{2} + μ \\ + μ cosh [2 k h]] cosh [k] [- 2 k h (h + 1) + sinh [2 k h]] sinh [k]) \end{matrix}

(A14)

\begin{matrix} L_{1}^{} & = q_{01}^{} + q_{11}^{} + q_{21}^{} \end{matrix}

(A15)

\begin{matrix} L_{2}^{} & = 2 q_{01}^{} + 3 q_{11}^{} + 4 q_{21}^{} + k (p_{01}^{} + p_{11}^{} + p_{21}^{}) \end{matrix}

(A16)

\begin{matrix} L_{3}^{} & = h^{2} (q_{02}^{} - h q_{12}^{} + h^{2} q_{22}^{}) \end{matrix}

(A17)

\begin{matrix} L_{4}^{} & = - 2 h q_{02}^{} + 3 h^{2} q_{12}^{} - 4 h^{3} q_{22}^{} + k h^{2} (p_{02}^{} - h p_{12}^{} + h^{2} p_{22}^{}) \end{matrix}

(A18)

\begin{matrix} L_{6}^{} & = B_{1}^{} cosh [k] - sinh [k] \end{matrix}

(A19)

\begin{matrix} L_{7}^{} & = q_{01}^{} cosh [k] - ρ q_{02}^{} cosh [k h] - p_{01}^{} sinh [k] - ρ p_{02}^{} sinh [k h] \end{matrix}

(A20)

\begin{matrix} L_{8}^{} & = \frac{1}{{\tilde{c}}_{r}^{[0]}} [({\tilde{c}}_{r}^{[0]} [a_{1}^{} (ρ - 1) B_{1}^{} - 6 (k p_{01}^{} + q_{11}^{}) + {\tilde{c}}_{r}^{[0]} (ρ - 1) (k + D_{1}^{})] - 2 B_{1}^{} T_{el, N}^{[0]} V^{[1]}) cosh [k] \\ + ({\tilde{c}}_{r}^{[0]} [a_{1}^{} + 6 (p_{11}^{} + k q_{01}^{}) - {\tilde{c}}_{r}^{[0]} (ρ - 1) (C_{1}^{} + k B_{1}^{}) - a_{1}^{} ρ] + 2 T_{el, N}^{[0]} V^{[1]}) sinh [k] \\ + 6 {\tilde{c}}_{r}^{[0]} ρ (k p_{02}^{} + q_{12}^{}) cosh [k h] + 6 {\tilde{c}}_{r}^{[0]} ρ (p_{12}^{} + k q_{02}^{}) sinh [k h]] \end{matrix}

(A21)

References

Melcher, J. R. 1963 Field-coupled surface waves: a comparative study of surface-coupled electrohydrodynamic and magnetohydrodynamic waves. Cambridge (MA): M.I.T. Press.
Melcher, J. R. & Smith Jr., C. V. 1969 Electrohydrodynamic charge relaxation and interfacial perpendicular-field instability. Phys. Fluids 12, 778.
Melcher, J. R. & Taylor, G. I 1969 Electrohydrodynamics: a review of the role of interfacial shear stresses. Annu. Rev. Fluid Mech. 1, 111.
Kath, G. S. & Hoburg, J. F. 1977 Interfacial EHD instability in normal electric fields. Phys. Fluids 20, 912.
Castellanos A. & González A. 1992 Interfacial electrohydrodynamic instability: the Kath and Hoburg model revisited. Phys. Fluids A 4, 1307.
Mohammed, A. A. & Elshehawey, E. F. 1983 Nonlinear electrohydrodynamic Rayleigh-Taylor instability. Part 1. A perpendicular field in the absence of surface charges. J. Fluid. Mech. 129, 473.
Saville, D. A. 1997 Electrohydrodynamics: The Taylor-Melcher Leaky dielectric Model. Annu. Rev. Fluid Mech. 29, 27.
Melcher, J. R. & Schwarz Jr., W. J. 1968 Interfacial relaxation overstability in a tangential electric field. Phys. Fluids 11, 2604.
Hooper, A. P. & Boyd, W. G. C.1983 Shear-flow instability at the interface between two viscous fluids. J. Fluid Mech. 128, 507-528.
Joseph, D. D. & Renardy, Y. 1993 Fundamentals of Two-fluid Dynamics, Part I: Mathematical Theory and Applications. New York: Springer-Verlag.
Pozrikidis, C. 1997 Instability of two-layer creeping flow in a channel with parallel-sided walls. J. Fluid Mech. 351, 139.
Yiang, W. Y., Helenbrook, B. & Lin, S. P. 2004 Inertialess instability of a two-layer liquid film flow Phys. Fluid 16, 652.
Yiantsios, S. & Higgins, B. G. 1988 Linear stability of plane Poiseuille flow of two superposed fluids Phys. Fluid 31, 3225-3238.
Yih, C.-S. 1967 Instability due to viscosity stratification. J. Fluid Mech. 27, 337-352.
Eldabe, N. T. M 1987 Electrohydrodynamic stability of two superposed elasticoviscous liquids in plane Couette flow J. Math. Phys. 28, 2791-2800.
Mohammed, A. A., Elshehawey, E. F. & El-Sayed, M. F. 1995 Electrohydrodynamic stability of two superposed viscous fluids. J. Coll. Interf. Sci. 169, 65.
Ozen, O., Aubry, N., Papageorgiu, D. T. & Petropoulos, P. G. 2006 Electrohydrodynamic linear stability of two immiscible fluids in channel flow. Electrochimica Acta 51, 5316-5323.
Jensen, M. J. , Goranović, G., & Bruus, H. 2004 The clogging pressure of bubbles in hydrophilic channel contractions J. Micromech. Microeng. 14, 876-883.
Bruus, H. 2005 Theoretical Microfluidics Oxford University Press.
Brask, A. , Goranović, G., Jensen, M. J. & Bruus, H. 2005 A novel electro-osmotic pump design for nonconducting liquids: theoretical analysis of flow rate-pressure characteristics and stability. J. Micromech. Microeng. 15, 883.
Goranović, G., Sørensen, M. P., Brøns, M. & Bruus, H. 2004 Electrohydrodynamic stability of two-phase microflows. Proc. μTAS 2004, Malmö, Sweden 1, 617.
Goranović, G. 2003 Electrohydrodynamic aspects of two fluid microfluidic systems: theory and simulation, Ph.D. Thesis, Technical University of Denmark, Kongens Lyngby: DTU Tryk, http://www.nanotech.dtu.dk/microfluidics.
Mestel, A. J. 1994 Electrohydrodynamic stability of a slightly viscous jet. J. Fluid Mech. 274, 93.
Landau, L. D. & Lifshitz, E. M. 2004 Electrodynamics of continuous media Course in Theoretical Physics, Volume 8 2nd edn., Landau and Lifshitz, Course of Theoretical Physics, vol. 8. Oxford: Butterworth–Heinemann.
Haus, H. A. & Melcher, J. R. 1989 Electromagnetic fields and energy. Englewood Cliffs (NJ): Prentice Hall.
Landau, L. D. & Lifshitz, E. M. 1987 Fluid Mechanics, 2nd edn., Landau and Lifshitz, Course of Theoretical Physics, vol. 6. Oxford: Butterworth–Heinemann.
Jackson, J. D. 1975 Classical Electrodynamics 2nd ed. New York: John Wiley and Sons.
Squire, H. B. 1933 On the stability for three-dimensional disturbances of viscous fluid flow between parallel walls. Proc. Roy. Soc. A 142, 621.
Yih, C.-S. 1955 Stability of two-dimensional parallel flows for three-dimensional disturbances. Quart. Appl. Math. 12 434.
Nayfeh, A. 1973 Perturbation methods. New York: John Wiley and Sons.
Yih, C.-S. 1963 Stability of liquid flow down an inclined plane. Phys. Fluid 6, 321.

Figure 1. (a) A rectangular microchannel of height

h_{1}^{} + h_{2}^{}

, length L and width W. We consider the low aspect ratio channels for which

h_{1}^{} + h_{2}^{} ≪ W < L

. The two main approximations are: negligible gravity and two-dimensional parallel flows, characteristic of microfluidic electroosmotic pumps [20]. (b) Panel (a) is approximated to two streaming viscous dielectrics confined between two infinite, microscopically spaced plates. The liquids differ in mass density, viscosity and dielectric constants, and occupy different depths of the microchannel. The liquids are in addition exposed to an electric field.

U_{0}

is a slip (driving) velocity at the wall, countering an adverse pressure

Δ P

Figure 1. (a) A rectangular microchannel of height

h_{1}^{} + h_{2}^{}

, length L and width W. We consider the low aspect ratio channels for which

h_{1}^{} + h_{2}^{} ≪ W < L

U_{0}

is a slip (driving) velocity at the wall, countering an adverse pressure

Δ P

Figure 2. (a) The zeroth-order flow profiles at fixed

μ = 2

and

h = 4

for a pure Couette flow,

G_{1}^{} = 0

, and an adverse pressure

G_{1}^{} = 0.12

marked by arrows. (b) A list of parameters used in the analysis.

Figure 2. (a) The zeroth-order flow profiles at fixed

μ = 2

and

h = 4

for a pure Couette flow,

G_{1}^{} = 0

, and an adverse pressure

G_{1}^{} = 0.12

marked by arrows. (b) A list of parameters used in the analysis.

Figure 3. For a normal E-field, the imaginary phase velocity

{\tilde{c}}_{i}^{[0]}

to zeroth order in R is plotted as function of the wavenumber k, for the viscosity ratio

μ = 0, 0.2, 1

and a fixed set of S,

ϵ_{2}^{}

, h and

ε

. The instability region

0 < k < k_{c}^{[0]}

for which

{\tilde{c}}_{i}^{[0]} > 0

is independent of

μ

, which can be deduced from the impending voltage Equation (78). The increase in

μ

decreases the growth rates of unstable waves for small k, but also decreases the damping rates for large k, i.e., makes the short waves relatively less stable, although it does not cause the actual instability. In the limit

k \to \infty

{\tilde{c}}_{i}^{[0]}

reaches the value

- S / [2 (μ + 1)]

. Note that in microfluidic systems

ϵ_{2}^{} \sim 1

, which makes the positive

{\tilde{c}}_{i}^{[0]} \sim 1

, i.e.

10^{3}

times smaller than depicted; we used a large

ϵ_{2}^{}

to better emphasize the trends.

Figure 3. For a normal E-field, the imaginary phase velocity

{\tilde{c}}_{i}^{[0]}

to zeroth order in R is plotted as function of the wavenumber k, for the viscosity ratio

μ = 0, 0.2, 1

and a fixed set of S,

ϵ_{2}^{}

, h and

ε

. The instability region

0 < k < k_{c}^{[0]}

for which

{\tilde{c}}_{i}^{[0]} > 0

is independent of

μ

, which can be deduced from the impending voltage Equation (78). The increase in

μ

k \to \infty

{\tilde{c}}_{i}^{[0]}

reaches the value

- S / [2 (μ + 1)]

. Note that in microfluidic systems

ϵ_{2}^{} \sim 1

, which makes the positive

{\tilde{c}}_{i}^{[0]} \sim 1

, i.e.

10^{3}

times smaller than depicted; we used a large

ϵ_{2}^{}

to better emphasize the trends.

Figure 4. Plots of the neutral stability line separating stable (

s

) and unstable (

u

) regions in the

{\hat{V}}_{inst}^{[0]}

–

\hat{k} {\hat{h}}_{1}^{}

plane (with log-log axes) for

h = 0, 1, 4, 20

. The increase in h causes lower electric fields and thus increases the stable regions and the impending voltages.

Figure 4. Plots of the neutral stability line separating stable (

s

) and unstable (

u

) regions in the

{\hat{V}}_{inst}^{[0]}

–

\hat{k} {\hat{h}}_{1}^{}

plane (with log-log axes) for

h = 0, 1, 4, 20

. The increase in h causes lower electric fields and thus increases the stable regions and the impending voltages.

Figure 5. (a) The first-order-R correction

R c_{i}^{[1]}

vs. k for the pure shear flow i.e. without the first-order electric field (voltage). Two sets of flow parameters are featured: for

h = 4

, instability happens for

k > k_{c}^{[1]}

, and for

h = 1 / 4

for all k. Note the small magnitudes. Compare with Figure (Figure 3). (b) The physical voltage correction

R {\hat{V}}^{[1]}

vs. k, corresponding to the cases in (a). The voltages counteract the stability trends due to shear to bring the system to neutral stability to first order in R; for

h = 4

, positive values of

{\hat{V}}^{[1]}

are needed to destabilize the stable wavenumbers

k < k_{c}^{[1]}

c_{i}^{[1]}

and vice versa; for

h = 1 / 4

, the voltages are always negative to dampen the modes unstable for all k. The EHD system is coupled, Equations (94)-(101), and in general the extremums of the functions

c_{i}^{[1]}

and

{\hat{V}}^{[1]}

do not coincide. However, the value

k_{c}^{[1]} (= 1.836)

is the same in the two panels as it should be. Note the very small magnitudes.

Figure 5. (a) The first-order-R correction

R c_{i}^{[1]}

vs. k for the pure shear flow i.e. without the first-order electric field (voltage). Two sets of flow parameters are featured: for

h = 4

, instability happens for

k > k_{c}^{[1]}

, and for

h = 1 / 4

for all k. Note the small magnitudes. Compare with Figure (Figure 3). (b) The physical voltage correction

R {\hat{V}}^{[1]}

vs. k, corresponding to the cases in (a). The voltages counteract the stability trends due to shear to bring the system to neutral stability to first order in R; for

h = 4

, positive values of

{\hat{V}}^{[1]}

are needed to destabilize the stable wavenumbers

k < k_{c}^{[1]}

c_{i}^{[1]}

and vice versa; for

h = 1 / 4

, the voltages are always negative to dampen the modes unstable for all k. The EHD system is coupled, Equations (94)-(101), and in general the extremums of the functions

c_{i}^{[1]}

and

{\hat{V}}^{[1]}

do not coincide. However, the value

k_{c}^{[1]} (= 1.836)

is the same in the two panels as it should be. Note the very small magnitudes.

Figure 6. (a) First-order-R physical voltages

R {\hat{V}}^{[1]}

vs. k for there different flow cases for an EO pump. Magnitudes are small, but larger than in Figure 5(b). Increase in h and adverse pressure

G_{1}^{}

increase the stability by shifting

k_{c}^{[1]}

to the right (stable k regions enlarged), but the increase in h enhances the voltage corrections around

k_{c}^{[1]}

, whereas the increase in

G_{1}^{}

dampens them. (b) Neutral stability diagram of the overall impending voltage

{\hat{V}}_{tot}^{} = {\hat{V}}^{[0]} + R {\hat{V}}^{[1]}

vs. k to both orders, for a set of parameters for the EO pump (updated Figure 4). The small first-order magnitudes show up only when enhanced. EHD stability increases with h, as the impending voltages increase with h. For

h = 4

and

h = 20

stable regions protrude into unstable ones for

k < k_{c}^{[1]}

, and withdraw for

k > k_{c}^{[1]}

, compare with Figure 5(b). For

h = 1

the first-order-R voltages are negative for all k, i.e. the system is unstable to first-order-R shear, like

h = 1 / 4

in Figure 5(a). The stability diagrams differ for different flow parameters.

Figure 6. (a) First-order-R physical voltages

R {\hat{V}}^{[1]}

vs. k for there different flow cases for an EO pump. Magnitudes are small, but larger than in Figure 5(b). Increase in h and adverse pressure

G_{1}^{}

increase the stability by shifting

k_{c}^{[1]}

to the right (stable k regions enlarged), but the increase in h enhances the voltage corrections around

k_{c}^{[1]}

, whereas the increase in

G_{1}^{}

dampens them. (b) Neutral stability diagram of the overall impending voltage

{\hat{V}}_{tot}^{} = {\hat{V}}^{[0]} + R {\hat{V}}^{[1]}

h = 4

and

h = 20

stable regions protrude into unstable ones for

k < k_{c}^{[1]}

, and withdraw for

k > k_{c}^{[1]}

, compare with Figure 5(b). For

h = 1

the first-order-R voltages are negative for all k, i.e. the system is unstable to first-order-R shear, like

h = 1 / 4

in Figure 5(a). The stability diagrams differ for different flow parameters.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Electrohydrodynamic (In)stability of Microfluidic Channel Flows: Analytical Expressions in the Limit of Small Reynolds Number

Abstract

1. Introduction

1.1. Structure of the Article

2. Problem Formulation

2.1. General Equations of Motion

2.2. General Boundary Conditions

2.3. Two-Dimensional Flow and Nondimensional Equations

3. Linearization in the Interface Displacement ζ

3.1. Velocity Field to Zeroth Order in ζ

3.2. Electric Potentials to Zeroth Order in ζ

3.3. Velocity Field to First Order in ζ

3.4. Electric Potentials to First Order in ζ

3.5. Boundary Conditions

4. Perturbation Expansion in the Reynolds Number R to Zeroth Order

4.1. Limit of Vanishingly Small Wavenumbers

4.2. Limit of Large Wavenumbers

4.3. Onset of EHD Instability to Zeroth Order in R

5. Perturbation Expansion in the Reynolds Number R to first order

5.1. Pure shear stress instability to first order in R

5.2. Onset of EHD Instability to First Order in R

6. Conclusions

Conflicts of Interest

Appendix A. Coefficients for Ψ 1 [ 0 ] and Ψ 2 [ 0 ]

Appendix B. Coefficients for Ψ 1 , P [ 1 ] and Ψ 2 , P [ 1 ]

Appendix C. Phase Velocity c[1]

References

MDPI Initiatives

Important Links

Subscribe

3. Linearization in the Interface Displacement $ζ$

3.1. Velocity Field to Zeroth Order in $ζ$

3.2. Electric Potentials to Zeroth Order in $ζ$

3.3. Velocity Field to First Order in $ζ$

3.4. Electric Potentials to First Order in $ζ$

Appendix A. Coefficients for $Ψ_{1}^{[0]}$ and $Ψ_{2}^{[0]}$

Appendix B. Coefficients for $Ψ_{1, P}^{[1]}$ and $Ψ_{2, P}^{[1]}$

Appendix C. Phase Velocity c^[1]