Prerpints.org logo
Preprint
Article

Influence of Laser Treatment on the Thermoelectric Properties of Bismuth Antimony Telluride Material

Altmetrics

Downloads

109

Views

61

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

11 January 2024

Posted:

12 January 2024

You are already at the latest version

Alerts
Abstract
In this study, the effect of laser processing (LP) on the thermoelectric (TE) properties of bismuth antimony telluride (BST) alloy pellets is investigated. The stoichiometric alloy used is Bi0.4Sb1.6Te3.0, which was prepared by mechanical alloying techniques (MA) and hot pressed (HP) into pellets under optimal pressing and temperature conditions. An innovative approach to HP was also developed to enhance the yield of BST samples per HP process while maintaining the TE profiles of the samples within a variance of less than 1%. The LP process was executed by employing a metal 3D printer, with a thorough analysis of beam parameters. Notably, the laser power (P) was held constant at 25 W, along with a fixed hatching distance (HD) of 50 μm, while the parameter adjusted was the laser's scanning speed (SS), which spanned from [600 - 1800] mm/s in increments of 200 mm/s. Examination via scanning electron microscopy (SEM) revealed two material states: melted and sintered. The melted state formed the surface crust of "canyon" patterns that were held on the surface of the samples, and which both size and quantity were altered with changes in SS. For thermoelectric characterization, two distinct shapes of LP samples were produced: rectangular (for electrical properties) and disk (for thermal properties). The results demonstrated that the electrical properties are profoundly influenced by SS, with the electrical conductivity peak at SS value of 1600 mm/s, while the Seebeck coefficient reaches a minimum at the same value. Consequently, within the temperature range of interest, a notable 12% increase in electrical conductivity and a 9% decrease in the Seebeck coefficient were observed compared to the non-LP material state. Overall, the ZT value experience an 6.9% decline within the same temperature interval.
Keywords: 
Subject: Chemistry and Materials Science  -   Materials Science and Technology

1. Introduction

Advances in thermoelectric materials have undergone a transformative journey, marked by breakthroughs that continue to reshape energy conversion technologies. Researchers have delved into the intricate realm of material properties, harnessing novel concepts to enhance the efficiency of converting heat differentials into usable electricity [1]. Through intricate material engineering, advancements in nanostructuring, and tailored band engineering, scientists have succeeded in boosting thermoelectric performance, effectively increasing the energy conversion efficiency [2]. The exploration of diverse materials, including organic compounds, inorganic semiconductors, and hybrid systems, has expanded the scope of viable thermoelectric candidates. Additionally, the integration of computational simulations and data-driven approaches has revolutionized material discovery and optimization, expediting the identification of materials with desirable thermoelectric properties [3]. These collective innovations hold tremendous potential in addressing pressing energy challenges, ushering in a new era of sustainable power generation, waste heat recovery, and efficient thermal management across various industrial sectors.
Laser texturing is a revolutionary method of treating materials to improve their various properties (mechanical, electrical, tribological, etc.) [4], and it has the potential to be highly promising in the field of thermoelectric materials. This is a sophisticated materials processing technique that involves utilizing laser beams to create controlled and precisely engineered microstructures on the surface of various materials [5,6,7,8,9,10,11]. Localized alterations in the surface morphology of a material can be created by altering laser parameters such as power, scan speed, trajectory strategy, hatch distance, and spot size. Each of these parameters has its own impact scale on the material’s processed surface. The resulting textured surface can exhibit remarkable improvements in mechanical [12,13,14,15,16], tribological [17,18,19,20,21,22,23], and optical [24,25,26,27,28] properties. For instance, in automotive applications, laser surface texturing of engine components can reduce friction and wear by enhancing oil retention and promoting effective lubrication in the textured regions [29,30,31]. In the realm of renewable energy, laser-textured solar absorbers can achieve enhanced light absorption and reduced reflection, boosting the overall efficiency of solar energy harvesting [32,33]. This technique also offers versatile means to process biomaterials for specific functionalities, contributing to advancements in both scientific research and medical applications [34,35,36,37].
The present status of TE materials displays conversion efficiencies spanning between 5% and 20%, a range that holds potential for augmentation through the implementation of suitable alloying, doping, and nanostructuring techniques [38]. The effectiveness of a thermoelectric (TE) material is anticipated by means of the dimensionless thermoelectric figure of merit, ZT [39]. This metric is directly linked to the material’s physical properties and is derived from the equation ZT = (σS2/κ) T, where S stands for the Seebeck coefficient, σ denotes the electrical conductivity, k represents the thermal conductivity and T is the temperature. In the scenario of an exemplary TE material (characterized by a high Seebeck coefficient and electrical conductivity, coupled with a low thermal conductivity), the ZT value ought to exceed one, ensuring an efficiency larger than 10%. Bismuth antimony telluride (BST) alloy stands as a notable and extensively studied thermoelectric material due to its exceptional capacity for converting heat differentials into electrical energy, and vice versa [40]. Since the early findings, the performance of these materials has consistently improved due to a variety of influencing variables [41,42,43] and the thermoelectric dimensionless figure of merit ZT has risen from around 0.5 to far above unity [44,45,46,47,48].
The current research presents a robust approach to the emerging domain of laser textured thermoelectric materials and a hybrid processing methodology within the additive manufacturing field. In this context, "hybrid" denotes the use of precise tools to treat the outer layers of the material instead of the entire bulk material. Additionally, the findings reported in this study not only demonstrate how this technique can modify and enhance the properties of thermoelectric materials but also offer insights and guidance for future research endeavors. Laser processing affords a remarkable level of accuracy and control, enabling the targeted treatment of specific areas on a material’s surface, including surface texturing or roughness reduction. This precision is invaluable for tailoring the characteristics of a thermoelectric device or material according to specific requirements. A prime example of this precision lies in optimizing the interface between thermoelectric materials and electrical contacts. By refining the roughness of both surfaces, contact resistance can be further minimized [49], leading to an overall enhancement in the performance of thermoelectric device

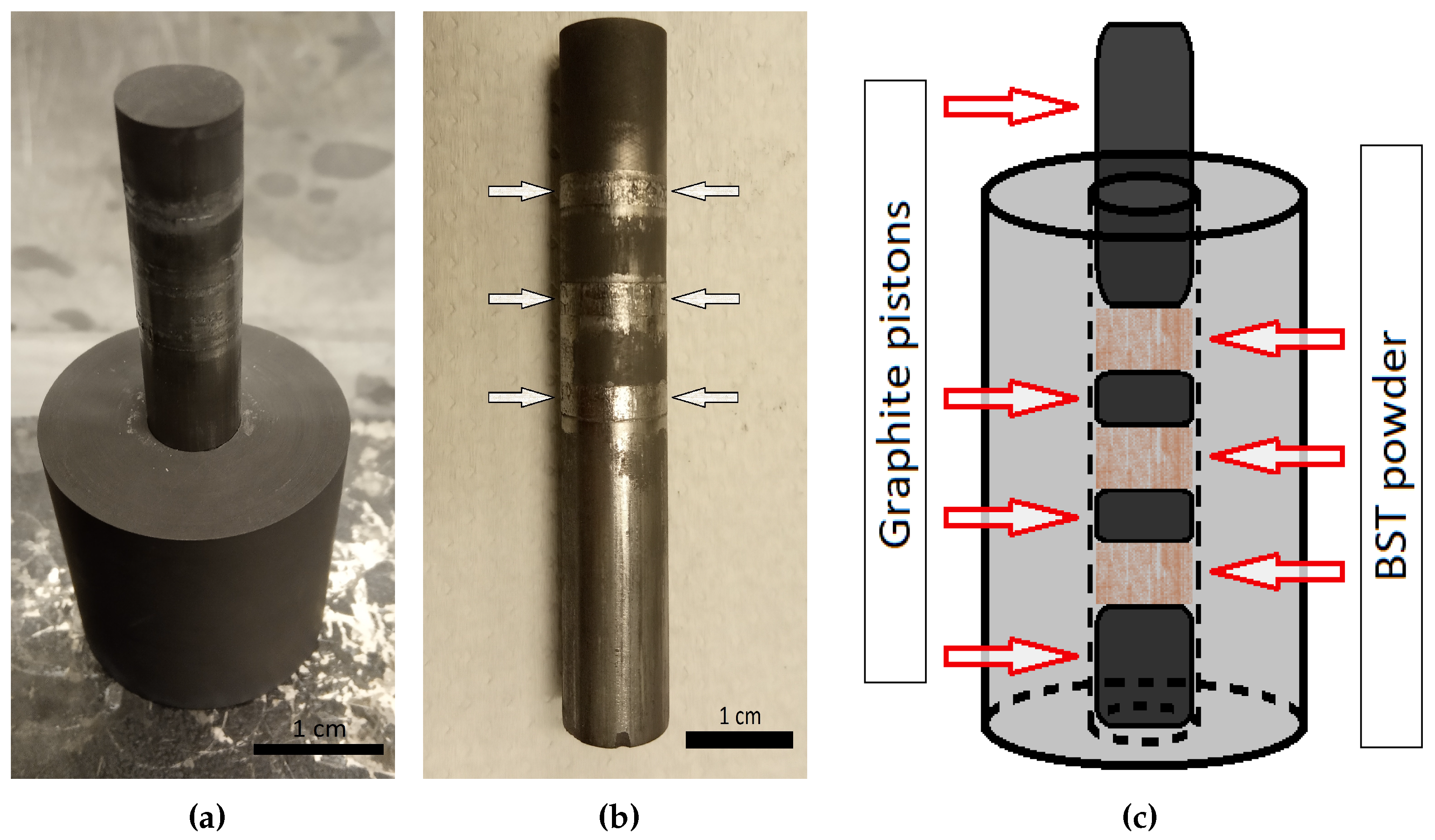
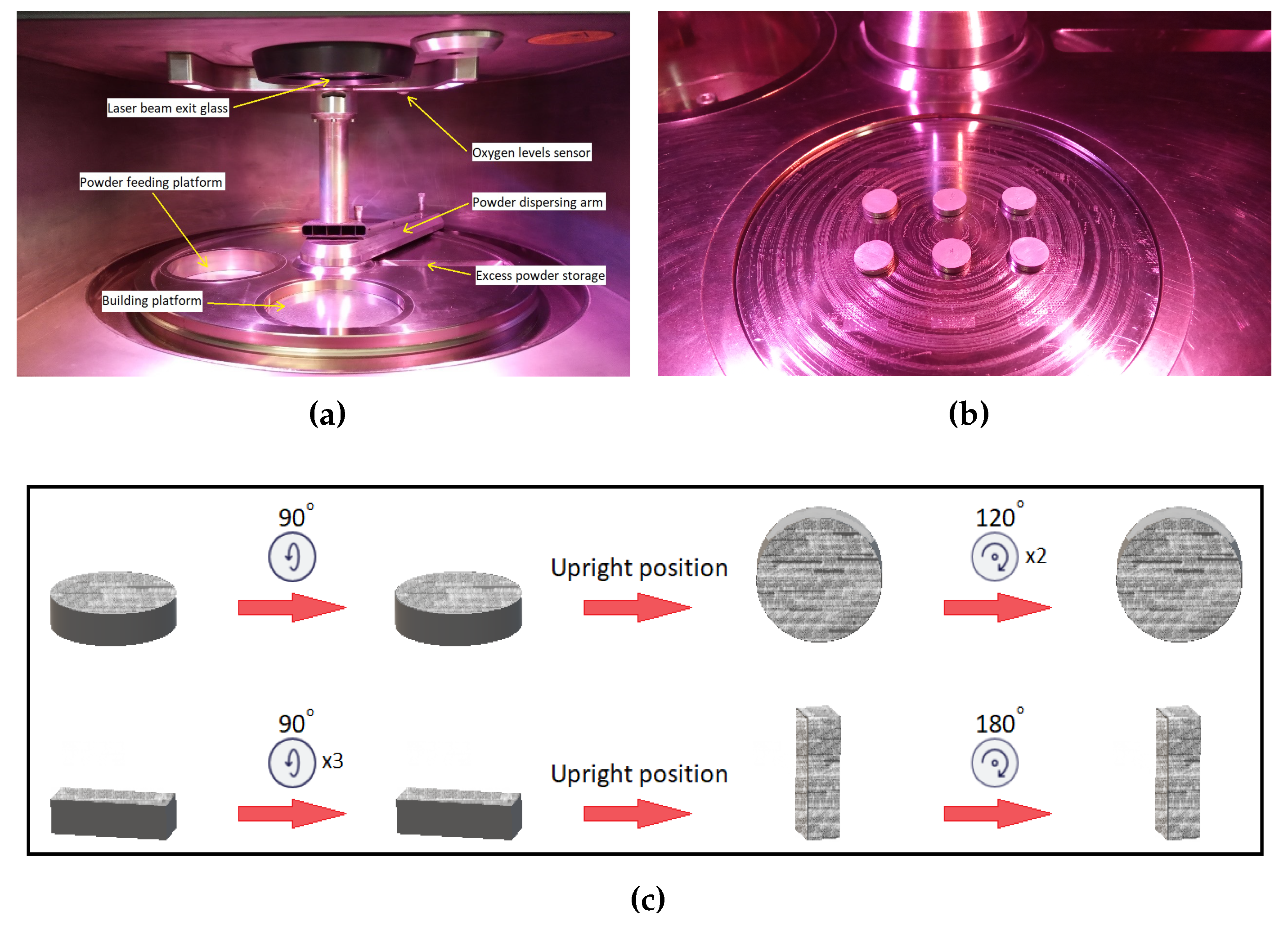
2. Experimental procedures

In this study a large number of HP pellet samples were required to be created in order to examine various aspects and parameters of the LP technique on the TE properties of the BST samples. As a result, the preparation of BST powder was based on the conditions used in our previous work [50], in which significant quantities of BST powder were produced in a short period of time using optimal MA settings and techniques. The HP process was also modified to scale up the pellets preparation and meet the requirements of the LP technique. As is well known, during the HP procedure, a calculated amount of powder is placed into a cylindrical graphite matrix, coupled with two graphite pistons. The matrix is then placed in the HP machine, which heats and mechanically presses the powder. Depending on the temperature and mechanical pressing parameters used, the procedure can take anywhere from several hours to many hours, yielding a single pellet sample. A modified technique was used in this case. Four graphite pistons were utilized instead of two. Two of them had the standard length and one side protruded from the matrix, while the other two pistons, with a shorter length, were placed inside the graphite matrix and the inner space was partitioned into three sections filled with BST powder. Using this process, instead of a single pellet, three pellets were created per HP.
Figure 1 presents the graphite matrix setup with the triplet of the BST samples. The inner diameter of the matrix was 10 mm, and the samples were approximately 2.5 mm thick. According to the schematic (Figure 1c), the bottom and top pellets were symmetrical to the centre pellet, as well as the graphite matrix. The powder loading technique was carried out within an argon-filled glovebox as follows: The bottom piston was initially placed in the graphite matrix with a piece of graphite foil on it. The first round of powder was then loaded with another piece of graphite foil atop it. The second piston was loaded in the same manner as the first, followed by the second round of BST powder, and the matrix was complete once all pistons were in place. The last piston was the longest and protruded far enough to make contact with the larger pistons of the HP machine.
Figure 2 shows the graphs of the thermal and electrical properties of the triplet of BST pellets. The names in the legend were chosen based on how the graphite matrix is placed inside the HP machine. As can be seen in all three plots, there is no significant difference in the property values of the three samples. More particularly, the deviation of the values for the temperature range of interest ([325-350] K was less than 3% for all three properties. The same can be said for their densities (Bottom = 6.094 g/cm3, Middle = 6.105 g/cm3, Top = 6.068 g/cm3), which were measured using the Archimedes method in isopropyl alcohol with deviation of less than 1%. The values shown are from a single round of HP. During the experiments for this work, multiple rounds of HP were done, and the findings of these values were similar.
The ORLAS CREATOR metal 3D printer, equipped with a Yb crystal fiber laser with a maximum output power of 250 W in continuous monochromatic wave (1070 nm wavelength), was used to LP the prepared BST samples. The technique included, among other things, preparing and aligning the printing platform made of stainless steel, as well as aligning the samples so that the laser beam could scan their surface with the correct angle and area, repeatedly. This was accomplished by first marking the surface of the printing platform before placing the pellet samples (Figure 3a), and then precisely locating the samples on the markers (Figure 3b). There were a total of twelve markers on the platform, with six of them being disk-shaped (LP samples prepared for thermal properties measurements) and the other six being rectangular-shaped (LP samples prepared for electrical properties measurements). In terms of laser beam parameters, the laser beam power was kept constant at 25 W, the lowest power feasible provided by the manufacturer, the hatching distance was 50 µm and the scan speed (SS) was adjusted between [600 - 1800] mm/s with as step of 200 mm/s. Because the impact intensity of the laser power parameter on the processed samples is high, keeping the laser power constant at the machine’s lower limit and altering the SS, protected the samples from being rapidly melted, distorted, or shuttered during the process. However, even with this laser power output, some of the samples were shuttered at low SS (high surface energy absorption) during the procedure. Finally, the thermoelectric properties of all samples were evaluated using a Netzsch LFA 457 laser flash apparatus (thermal properties) and a ZEM-3 series ULVAC-Riko system (electrical properties) in the temperature range [300 - 500] K.

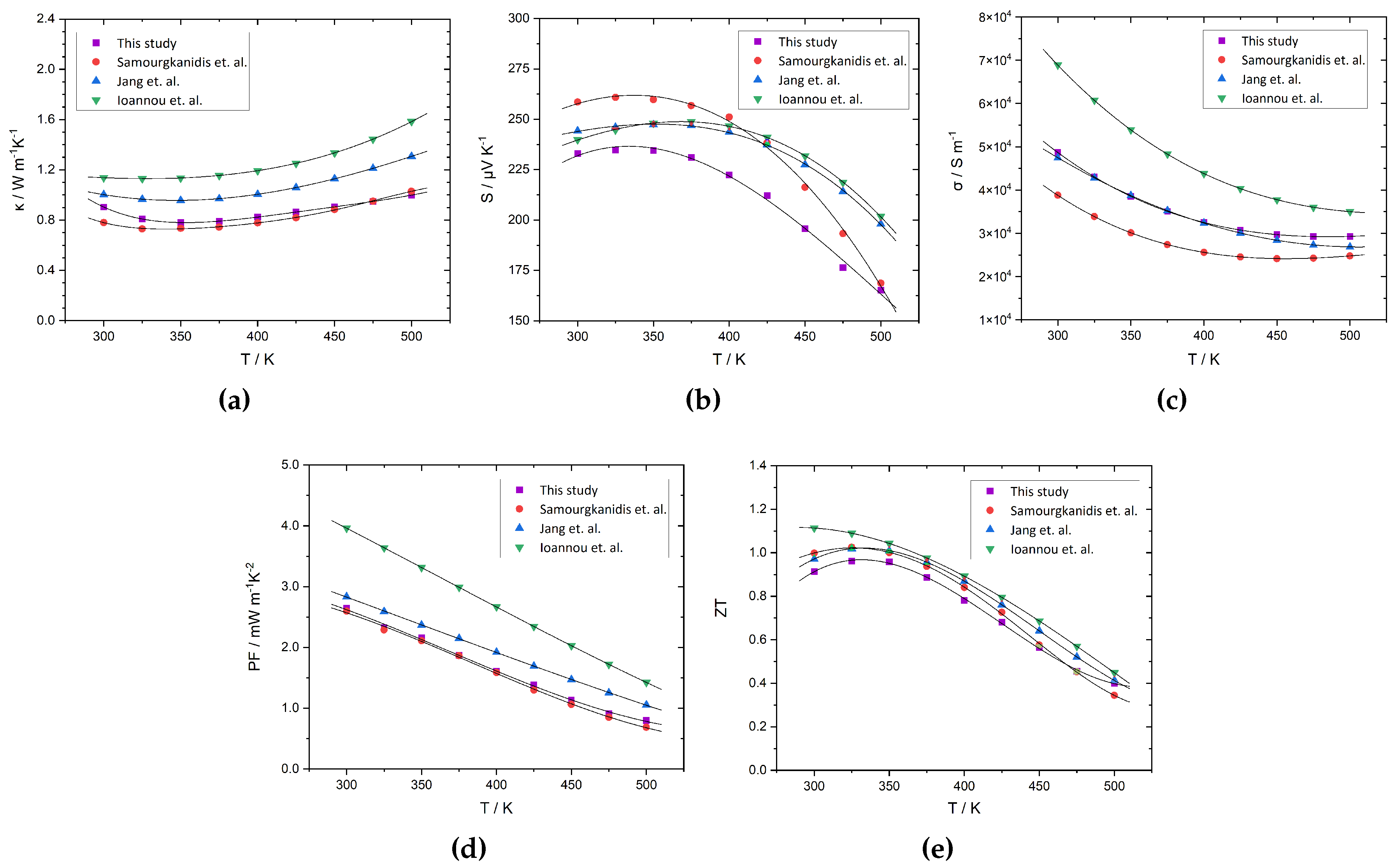
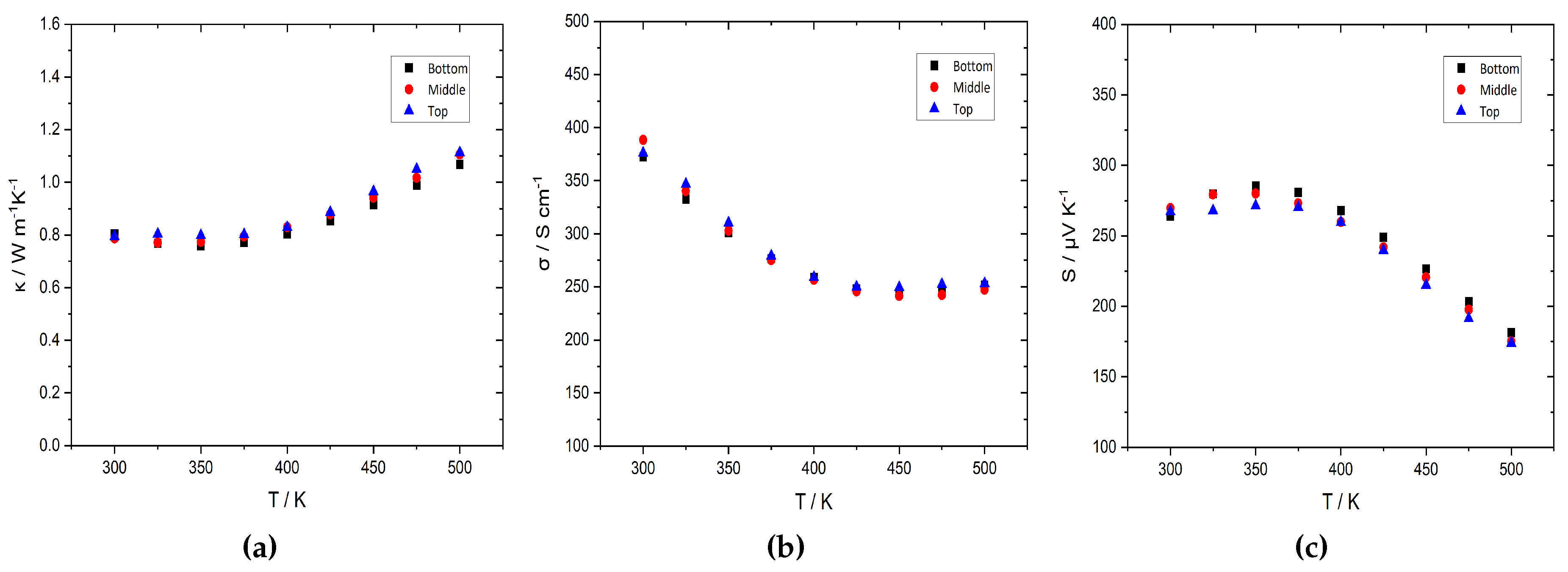
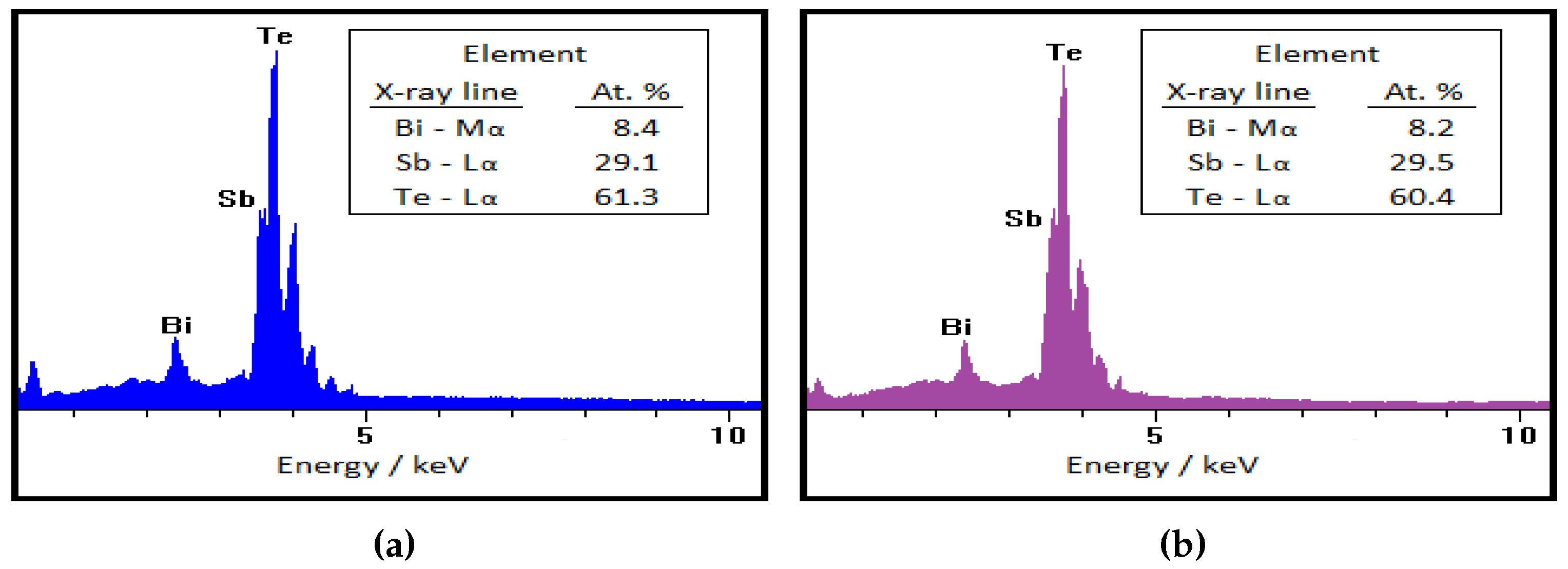
3. Results and discussion

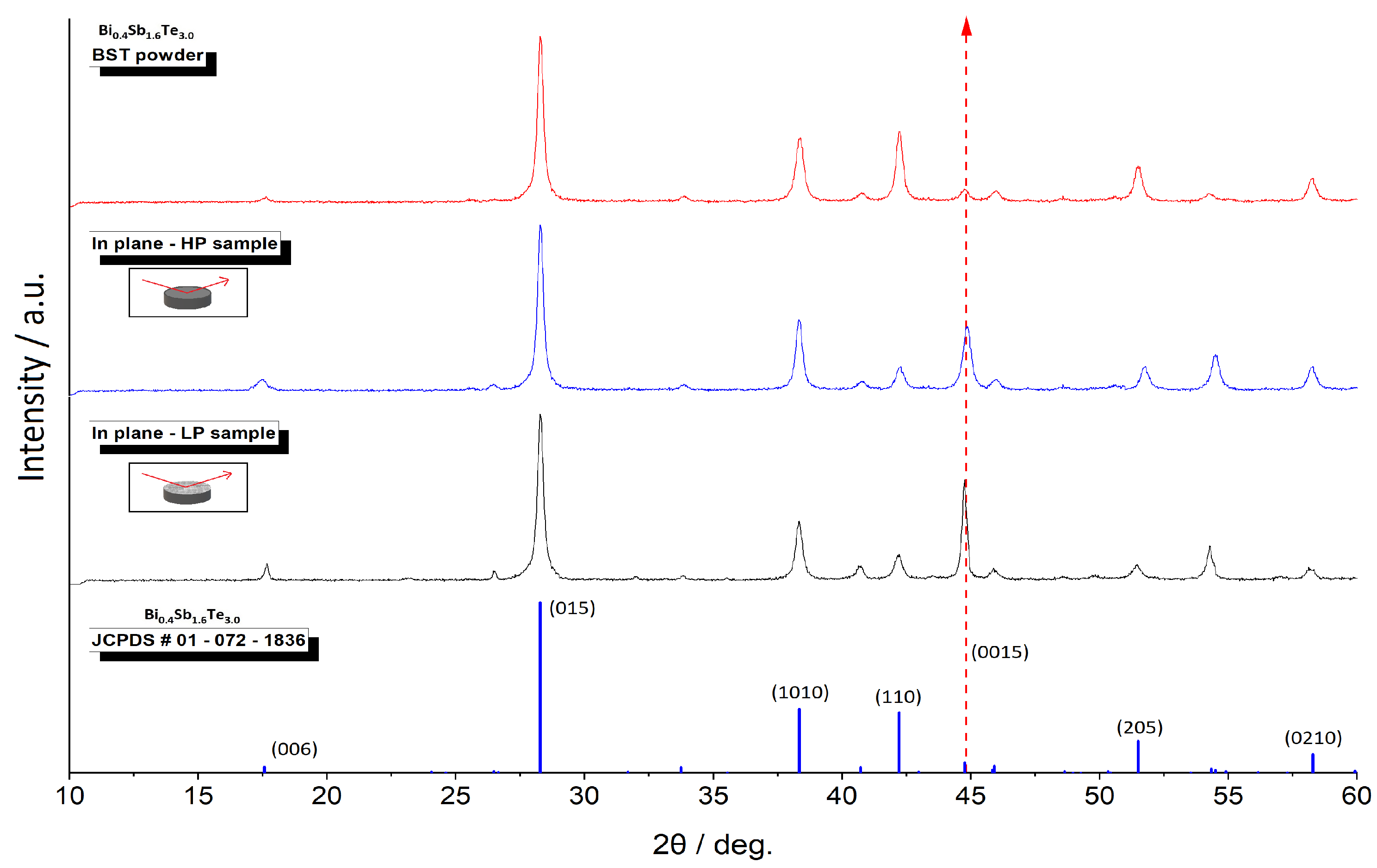
3.1. Laser processing

All BST samples in this study were LP using the ORLAS Creator metal 3D printer. Figure 4a presents the interior chamber of the printer where the samples were processed.
This figure displays the printer’s basic operation: The powder stored on the powder feeding platform is uniformly distributed on the building platform by the powder dispersion arm, and any excess is stored for later recycling. The laser beam, as it emerges from the glass, sequentially melts the powder layer by layer, thereby creating the printed structure. All procedures take place in an argon atmosphere, which is controlled by an oxygen sensor on the chamber’s top side. In our case, the BST samples were placed on the building platform (Figure 4b) and their positions were aligned using the markers produced on the platform (as described in Section 2). To process all sides of the samples, the following approach was implemented (Figure 4c): The disk pellets were first processed on one side and the building platform was then withdrawn from the printer in order to flip all samples and process the opposite side. Following completion of the cross section areas, the disk pellets were put upright and processed on the perimetrical side. The task was carried out 3 times by turning the samples 120 degrees clockwise. In the case of the rectangular BST samples, similar technique was followed. Here, because all sides were flat and the samples did not fall or turn, the processing was easier.
Figure 5a and Figure 5f show LP BST samples with SS values ranging from [800 - 1800] mm/s and a step of 200 mm/s, and Figure 5g presents schematically the laser scanning strategy that was implemented. Based on our prior experience with other materials, the double pass strategies provided smoother, less porous layers [51,52]. The samples displayed here have only been processed once. According to this figure, the surface of the sample melts and solidifies throughout the LP procedure, resulting in randomly dispersed "canyon" form patterns. As the SS grows, the number of these "canyons" increases but their size decreases, resulting in considerably smoother surfaces.
Figure 6a and Figure 6b show SEM images of the BST samples with SS = 600 mm/s and SS = 1600 mm/s (SS1600), respectively. The change in the number and size of the "canyons" as the SS increases is more obvious here. More specifically, from the standpoint of surface energy this behavior can be expected since SS is inversely related to energy (E = P / (SS * HD) where P is the laser beam power, SS the scan speed and HD the hatch distance). As a result, higher energy levels deform the surface of the sample on a bigger scale by causing larger melted "canyons", as can be seen in Figure 6a. A magnified image of the surface of the SS1600 sample presented in Figure 6c. The deformation of the melted surface is considerably clearer here, with pores of varying size and shape being randomly scattered. At this point it has to be mentioned that, during the LP procedure a considerably number of samples were shuttered (thermal shocked) as they were parameterized (the disk pellet shown in Figure 5a was cracked from the first round of the LP cycles). Specifically, the disk pellet samples with SS values less than 1000 mm/s were shuttered at some time during the LP cycles shown in Figure 4c, whereas the rectangular samples were shuttered in SS values less than 1200 mm/s. This was tested twice with a new set of BST samples to see if they shutter randomly or not. As a result, a complete set of samples (disk and rectangular pellets) that "survived" the LP procedure and could be thermoelectrically characterized, had SS values higher than 1200 mm/s.
Figure 7a presents a rectangular BST sample that was LP with the following parameters: SS = 1600 mm/s, P = 25 W, HD = 50 µm, as well as sliced pieces of its disk pellet. These samples were cut before processing using a low RPM diamond wheel cutter, revealing the difference between treated and untreated surfaces. Figure 4c schematically displays the LP cycles that were followed for the current shape. Figure 7c and Figure 7d show SEM images of the same sample’s shuttered cross section after the first LP cycle, revealing the processed and unprocessed surfaces, respectively. The surface processed image (Figure 7c) distinguishes between the sintered (right side of the image) and melted (left side of the image) phases of the material, with the border between them clearly visible. The same border can be seen in Figure 7b, which is the magnified area of the red inset in Figure 7c. The mechanics of the material’s surface melting, as well as the size of its effect, are better conveyed in these images. Specifically, the energy absorbed by the material in the form of heat melts the sintered particles, resulting in a bulk crust with a certain average thickness. This crust forms the walls of the "canyons" seen before. The size of the walls reduces as the absorbed energy drops, while their number increases. This increase on the surface area of the walls, resulting in a homogeneous channel of melted material on the surface of the samples. These channels of different material states primarily impact the electrical properties of the sample, which will be discussed in the next part.
Figure 8 showcases the X-ray diffraction profiles of the BST powder employed, along with its associated JCPDS diagram, and highlights the in-plane orientation of both the HP and LP samples. Here the SS1600 LP sample was examined. The X-ray diffraction analyses were performed over an angular span of 10-60 degrees, utilizing an angular step size of 0.02 degrees and a scan rate of 1 degree per minute. Operating conditions included an acceleration voltage of 30 kV and a beam current of 15 mA, generating Cu-Kα radiation (λ = 1.5406 Å). Upon comparing the patterns, it becomes evident that the intensity of the (0015) peak is notably greater in the in-plane direction, particularly in the LP sample where it appears significantly higher. Given that the LP state involves a molten crust on the sample’s surface, the orientation of (0015) is more favorable compared to the sintered state. Furthermore, in the LP sample, there is a noticeable enhancement in the sharpness of various X-ray peaks compared to the HP sample. Additionally, the qualitative and quantitative alterations in the chemical composition of the SS1600 sample pre- and post-laser processing are observable through the energy-dispersive X-ray spectroscopy (EDXS) analysis presented in Figure 9. The analysis reveals the evident presence of all three elements in the alloy, accompanied by their respective radiated energies and percentage atomic values as detailed in the inset. The outcomes suggest that there is no discernible alteration in the chemical state of the alloy following the LP procedure.

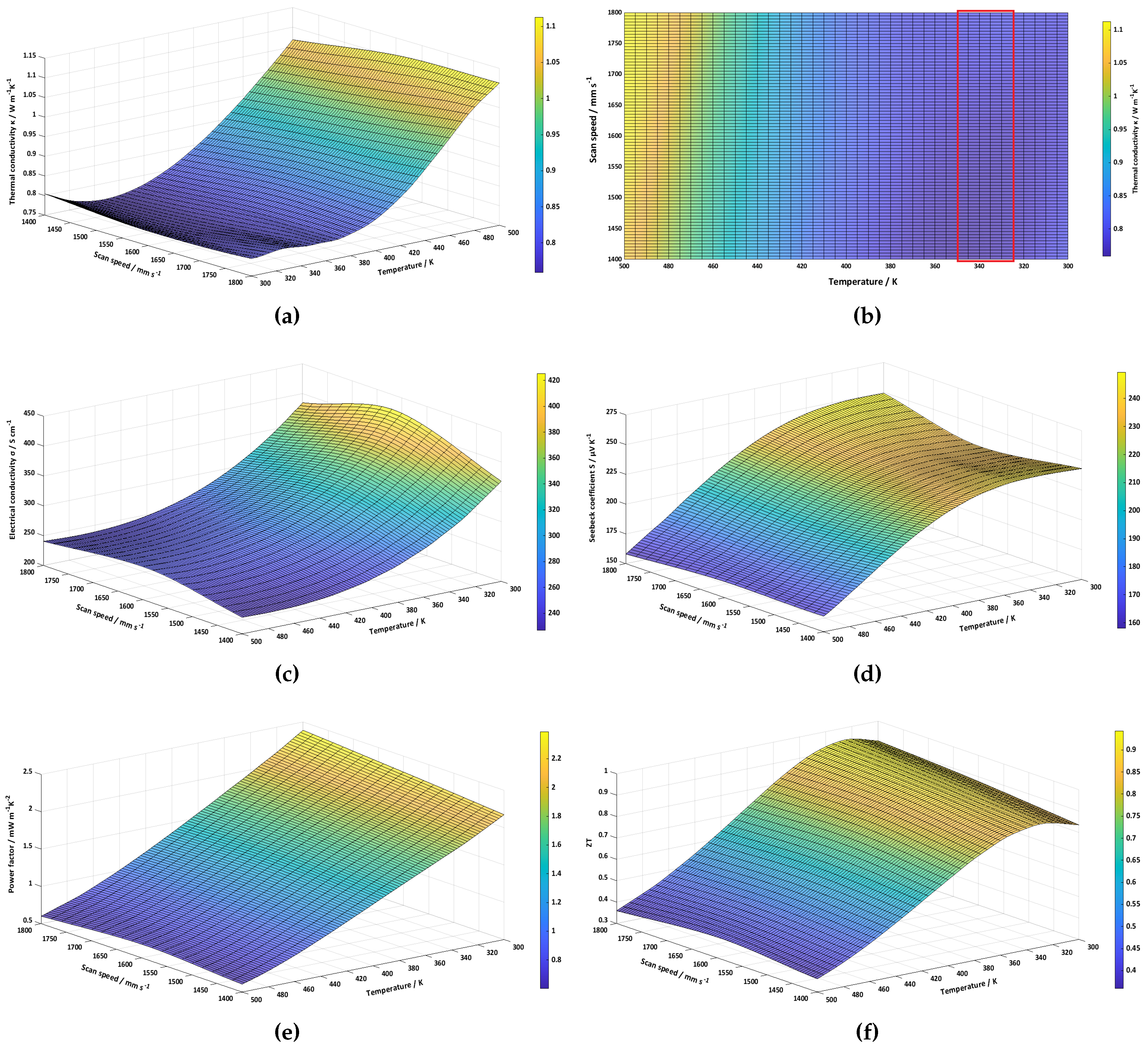
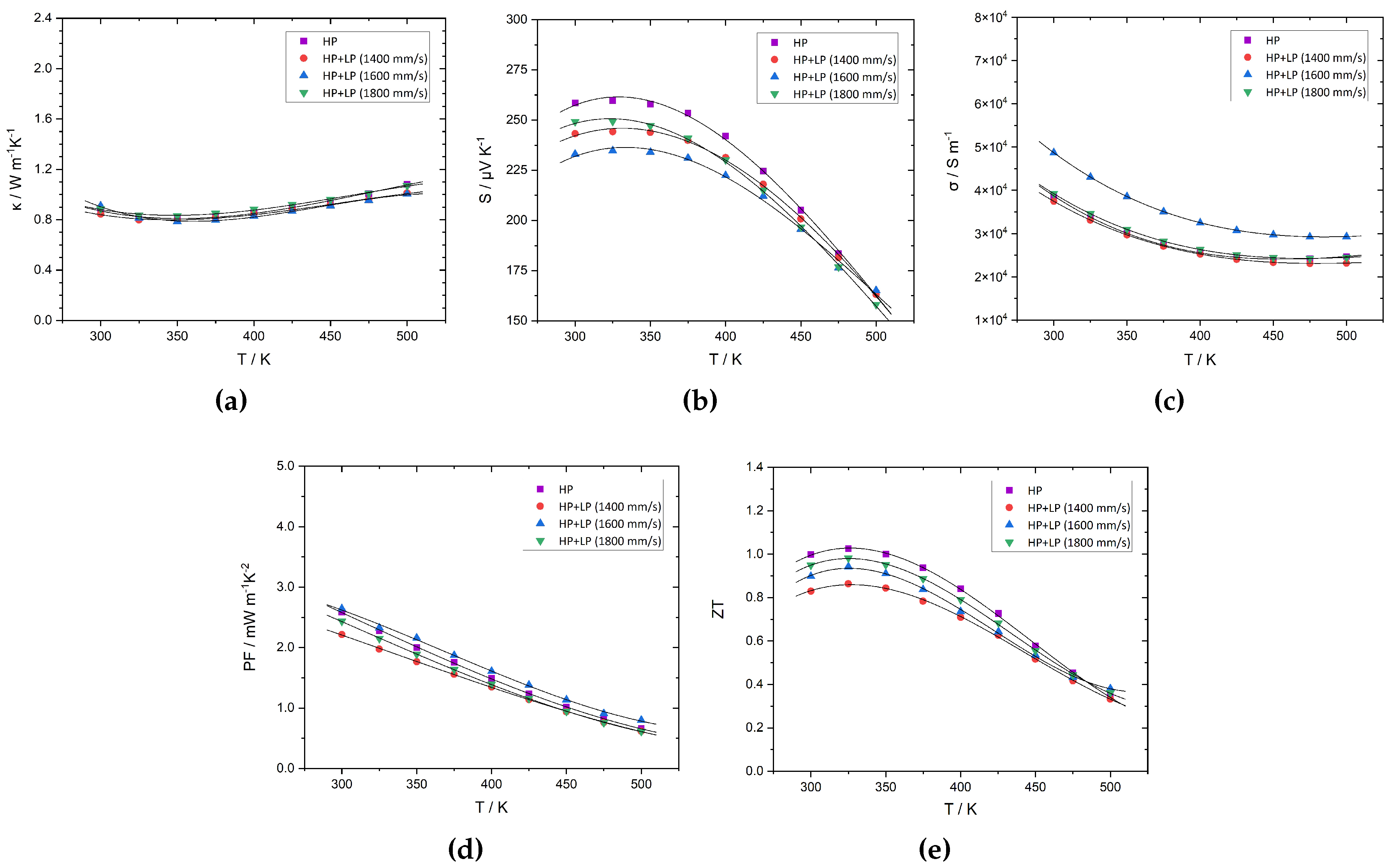
3.2. Thermoelectric characterization

The TE characterization was carried out by electrically characterizing the rectangular shape samples and thermally characterizing the disk-shaped samples. Figure 10 presents 3D color-maps of TE characteristics as a function of temperature and SS. Here, the temperature range is [300-500] K and the SS range is [1400 - 1600] mm/s, and the legend on the right side of each graph colorizes the values of each TE property. Starting with the property of thermal conductivity, as shown in Figure 10a, there is a minimum for all values of SS in the temperature area of [325-350] K, which is also the material’s interest temperature range. At the same time, the values of thermal conductivity in this area (red inset) appear to be mainly steady versus SS, as shown in Figure 10b, which is the XY view of Figure 10a. In particular, the average minimum value of thermal conductivity versus SS in this area is κ = 0.77 Wm−1K−1, with a 1.8% variation.
In terms of electrical conductivity, however, it is clear from Figure 10c that the LP procedure has a considerable impact. More specifically, there is a peak close to the SS = 1600 mm/s in practically all temperature ranges, with higher values at lower temperatures. This maximum has a value of σ = 425 Scm−1 in the temperature range of interest. The Seebeck coefficient, on the other hand, exhibits exactly the opposite trend, which was to be expected considering that increases in electrical conductivity often impact the Seebeck coefficient in the opposite direction due to increases in the thermal conductivity of electrons. According to Figure 10d, a minima for the Seebeck coefficient with an approximately average value of S = 233 µVK−1 occurs near to the SS value of 1600 mm/s within the temperature range of interest, which, however, continuously expands up to 375 K before starting down streaming. The power factor 3D graph is presented in Figure 10e, which is the product of electrical conductivity and the Seebeck coefficient via the equation PF = σS2. According to this graph, the PF appears to rise approximately linearly as the SS increases, with an average slope of Savg = ( 6 ± 1 ) · 10 − 4 mW m−1K−2 / mm s−1 within the temperature range of interest. This represents a notably gradual increase, reflecting the limited influence of SS on PF, which is intricately connected to the opposing behaviors of the two electrical parameters: electrical conductivity and Seebeck coefficient. The same holds for the figure of merit ZT, shown in Figure 10f, which is correlate to the other properties via the relationship ZT = PF/µ. Here, the slope was determined using the highest ZT values and is ZTslope = ( 1.37 ± 0.07 ) · 10 − 4 1 / mm s−1.
Figure 11 displays the comparative analysis of the TE properties. It contrasts the LP samples at SS values of 1400 mm/s, 1600 mm/s, and 1800 mm/s with the untreated state (HP sample), which acts as the reference. Regarding thermal conductivity (Figure 11a), the results indicate that the influence of laser processing is minimal, with deviations less than 0.5%. However, in terms of electrical properties, particularly for the SS1600 sample, the impact is significant. Specifically, the SS1600 sample exhibits an average increase of 12% in electrical conductivity (Figure 11c) and a 9% reduction in Seebeck coefficient (Figure 11b) within the relevant temperature range, leading to an average 6.9% decrease in ZT value (Figure 11e). Additionally, as shown in Figure 10c, increasing the SS values tends to converge the ZT maximum values to the unprocessed maximum value (ZT = 1.02). This is something that is expected, since as previously stated, increasing SS values reduces total energy absorbed, resulting in smoother but less thick melted layers.
Figure 12 illustrates the discussion of the obtained results for the SS1600 LP sample in relation to the existing literature. The outcomes concerning TE properties are juxtaposed with our prior research [50] and other investigations [46,48] conducted on the same BST alloy. Commencing with the thermal conductivity property denoted by κ in Figure 12a, its values fluctuate between [0.7 - 1.0] Wm−1K−1 and reach an absolute minimum of κ m i n = 0.78 Wm−1K−1 within the temperature span of [325 K - 350 K]. This minimum closely resembles the value obtained in our prior research and stands as the lowest among the comparisons with the other two studies. The Seebeck coefficient, as illustrated in Figure 12b, demonstrates its peak value across the same temperature range, reaching its maximum value at Smax = 235 μ V K−1. followed by a steady rapid decline, and in comparison to all three studies it consistently exhibits the lowest values. However, the electrical conductivity σ , depicted in Figure 12c, exhibits higher values in comparison to our prior research and nearly matches the values found in the study conducted by Jang et al. The data indicates a steady convergence of its values towards the minimum value of σ m i n = 2.92 x 104 S/m. The power factor of the specimen is derived by combining the Seebeck coefficient and electrical conductivity values using the equation PF = S 2 σ . As portrayed by the curve in Figure 12d, there is a continual decrease observed as a function of temperature, without any discernible peaks or valleys, maintaining consistency across all three studies. These values remain unchanged in comparison to our previous research and are notably the lowest among the other two studies.
Ultimately, the figure of merit ZT is depicted in Figure 12e, computed via the equation ZT = T*PF/ κ . Observing the curve, a definitive peak with a value of ZT = 0.95 emerges around the temperature of T = 330 K, signifying the optimal operating temperature for the thermoelectric material. In contrast to all three studies, the ZT closely aligns with the curves as they traverse the overall range. Compared to our earlier research, it exhibits a decrease of 6.9%.

4. Conclusions

The impact of laser processing (LP) on the thermoelectric (TE) characteristics of bismuth antimony telluride (BST) alloy (Bi0.4Sb1.6Te3.0) is discussed in the current work. A significant number of unprocessed BST samples were produced using mechanical alloying and hot pressing techniques (HP). Furthermore, a unique HP approach was developed in order to increase the number of BST samples produced per HP process, displaying thermoelectric profile data with variations of less than 1%. The LP was carried out using a metal 3D printer, and the beam parameters were extensively analyzed. The laser power parameter, in particular, was kept constant at 25 W, as was the hatching distance, at 50 µm. What changed was the laser’s scanning speed (SS), which ranged from [600 - 1800] mm/s with a 200 mm/s step. The laser processing of the BST samples showed surface "canyon" shape patterns, the size and quantity of which varied as the SS shifted. Scanning electron microscopy (SEM) images revealed two states of the material, one melted and one sintered, with the melted state forming the crust of the walls of the "canyon" shape patterns. Two different shapes of LP samples were produced for TE characterization, a rectangular shape (for electrical properties) and a disk shape (for thermal properties). The results shown that the electrical properties are most affected in respect to the SS, with the electrical conductivity exhibiting a maximum at the SS value of 1600 mm/s and the Seebeck coefficient exhibiting a minimum at the same value. In particular, an average 12% increase in electrical conductivity and a 9% drop in Seebeck coefficient occurred in the temperature range of interest ([325-350] K), compared to the unprocessed state of the material, with the ZT value decreasing by 6.9% in the same temperature range. The future trajectory of this preliminary research encompasses investigations into these hybrid state materials within TE module devices, as well as the bonding of the LP legs with the device’s intermediate thermal and electrical insulating material. In addition, corrosion experiments on the connection of the legs with the intermediate material will be conducted.

Author Contributions

Conceptualization, G.S.; methodology, G.S.; software, G.S.; validation G.S.; formal analysis, G.S.; investigation, G.S.; resources, T.K.; data curation, G.S.; writing—original draft preparation, G.S.; writing—review and editing, G.S.; visualization, G.S.; supervision, T.K.; project administration, T.K.; funding acquisition, T.K. All authors have read and agreed to the published version of the manuscript.

Funding

This work was funded by the University of Cyprus (internal project ADD-THERM).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data available on request from the authors.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Liu, W.; Hu, J.; Zhang, S.; Deng, M.; Han, C.G.; Liu, Y. New trends, strategies and opportunities in thermoelectric materials: a perspective. Materials Today Physics 2017, 1, 50–60. [Google Scholar] [CrossRef]
  2. Wei, J.; Yang, L.; Ma, Z.; Song, P.; Zhang, M.; Ma, J.; Yang, F.; Wang, X. Review of current high-ZT thermoelectric materials. Journal of Materials Science 2020, 55, 12642–12704. [Google Scholar] [CrossRef]
  3. Wang, T.; Zhang, C.; Snoussi, H.; Zhang, G. Machine learning approaches for thermoelectric materials research. Advanced Functional Materials 2020, 30, 1906041. [Google Scholar] [CrossRef]
  4. Wahab, J.; Ghazali, M.; Yusoff, W.; Sajuri, Z. Enhancing material performance through laser surface texturing: A review. Transactions of the IMF 2016, 94, 193–198. [Google Scholar] [CrossRef]
  5. Nayak, B.; Gupta, M.; Kolasinski, K. Formation of nano-textured conical microstructures in titanium metal surface by femtosecond laser irradiation. Applied Physics A 2008, 90, 399–402. [Google Scholar] [CrossRef]
  6. Neves, D.; Diniz, A.E.; Lima, M.S.F. Microstructural analyses and wear behavior of the cemented carbide tools after laser surface treatment and PVD coating. Applied Surface Science 2013, 282, 680–688. [Google Scholar] [CrossRef]
  7. Razi, S.; Madanipour, K.; Mollabashi, M. Laser surface texturing of 316L stainless steel in air and water: A method for increasing hydrophilicity via direct creation of microstructures. Optics & Laser Technology 2016, 80, 237–246. [Google Scholar]
  8. Zhou, J.; Shen, H.; Pan, Y.; Ding, X. Experimental study on laser microstructures using long pulse. Optics and Lasers in Engineering 2016, 78, 113–120. [Google Scholar] [CrossRef]
  9. Wang, Q.; Zhou, W. Direct fabrication of cone array microstructure on monocrystalline silicon surface by femtosecond laser texturing. Optical Materials 2017, 72, 508–512. [Google Scholar] [CrossRef]
  10. Liu, Y.; Su, J.; Tan, C.; Feng, Z.; Zhang, H.; Wu, L.; Chen, B.; Song, X. Effect of laser texturing on mechanical strength and microstructural properties of hot-pressing joining of carbon fiber reinforced plastic to Ti6Al4V. Journal of Manufacturing Processes 2021, 65, 30–41. [Google Scholar] [CrossRef]
  11. Long, J.; Chu, P.; Li, Y.; Lin, J.; Cao, Z.; Xu, M.; Ren, Q.; Xie, X. Dual-scale porous/grooved microstructures prepared by nanosecond laser surface texturing for high-performance vapor chambers. Journal of Manufacturing Processes 2022, 73, 914–923. [Google Scholar] [CrossRef]
  12. Yu, X.; He, S.; Cai, R. Frictional characteristics of mechanical seals with a laser-textured seal face. Journal of Materials Processing Technology 2002, 129, 463–466. [Google Scholar] [CrossRef]
  13. Bai, S.; Peng, X.; Li, Y.; Sheng, S. A hydrodynamic laser surface-textured gas mechanical face seal. Tribology Letters 2010, 38, 187–194. [Google Scholar] [CrossRef]
  14. Wang, T.; Huang, W.; Liu, X.; Li, Y.; Wang, Y. Experimental study of two-phase mechanical face seals with laser surface texturing. Tribology International 2014, 72, 90–97. [Google Scholar] [CrossRef]
  15. Boinovich, L.B.; Modin, E.B.; Sayfutdinova, A.R.; Emelyanenko, K.A.; Vasiliev, A.L.; Emelyanenko, A.M. Combination of functional nanoengineering and nanosecond laser texturing for design of superhydrophobic aluminum alloy with exceptional mechanical and chemical properties. ACS nano 2017, 11, 10113–10123. [Google Scholar] [CrossRef]
  16. Pereira, R.; Moura, C.; Henriques, B.; Chevalier, J.; Silva, F.; Fredel, M. Influence of laser texturing on surface features, mechanical properties and low-temperature degradation behavior of 3Y-TZP. Ceramics International 2020, 46, 3502–3512. [Google Scholar] [CrossRef]
  17. Etsion, I. Improving tribological performance of mechanical components by laser surface texturing. Tribology letters 2004, 17, 733–737. [Google Scholar] [CrossRef]
  18. Vilhena, L.; Podgornik, B.; Vižintin, J.; Možina, J. Influence of texturing parameters and contact conditions on tribological behaviour of laser textured surfaces. Meccanica 2011, 46, 567–575. [Google Scholar] [CrossRef]
  19. Qiu, Y.; Khonsari, M. Experimental investigation of tribological performance of laser textured stainless steel rings. Tribology International 2011, 44, 635–644. [Google Scholar] [CrossRef]
  20. Bathe, R.; Sai Krishna, V.; Nikumb, S.; Padmanabham, G. Laser surface texturing of gray cast iron for improving tribological behavior. Applied Physics A 2014, 117, 117–123. [Google Scholar] [CrossRef]
  21. Zhang, N.; Yang, F.; Jiang, F.; Liu, G. Study of the effect of surface laser texture on tribological properties of cemented carbide materials. Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture 2020, 234, 993–1006. [Google Scholar] [CrossRef]
  22. Wang, H.; Ma, Y.; Bai, Z.; Liu, J.; Huo, L.; Wang, Q. Evaluation of tribological performance for laser textured surfaces with diverse wettabilities under water/oil lubrication environments. Colloids and Surfaces A: Physicochemical and Engineering Aspects 2022, 645, 128949. [Google Scholar] [CrossRef]
  23. Soltani-Kordshuli, F.; Miller, C.; Harris, N.; Zou, M. Laser surface texturing of both thin polytetrafluoroethylene coatings and stainless steel substrates for improving tribological properties. Polymer Testing 2023, 117, 107852. [Google Scholar] [CrossRef]
  24. Dobrzański, L.; Drygała, A.; Gołombek, K.; Panek, P.; Bielańska, E.; Zięba, P. Laser surface treatment of multicrystalline silicon for enhancing optical properties. journal of materials processing technology 2008, 201, 291–296. [Google Scholar] [CrossRef]
  25. Iyengar, V.V.; Nayak, B.K.; Gupta, M.C. Ultralow reflectance metal surfaces by ultrafast laser texturing. Applied optics 2010, 49, 5983–5988. [Google Scholar] [CrossRef]
  26. Sani, E.; Sciti, D.; Silvestroni, L.; Bellucci, A.; Orlando, S.; Trucchi, D.M. Tailoring optical properties of surfaces in wide spectral ranges by multi-scale femtosecond-laser texturing: A case-study for TaB2 ceramics. Optical Materials 2020, 109, 110347. [Google Scholar] [CrossRef]
  27. Sharma, A.; Marla, D. Understanding the effects of picosecond laser texturing of silicon solar cells on optical and electrical properties. International Journal of Materials Engineering Innovation 2022, 13, 23–32. [Google Scholar] [CrossRef]
  28. Bouchard, F.; Soldera, M.; Lasagni, A.F. PMMA Optical Diffusers with Hierarchical Surface Structures Imprinted by Hot Embossing of Laser-Textured Stainless Steel. Advanced Optical Materials 2023, 11, 2202091. [Google Scholar] [CrossRef]
  29. Ryk, G.; Kligerman, Y.; Etsion, I. Experimental investigation of laser surface texturing for reciprocating automotive components. Tribology Transactions 2002, 45, 444–449. [Google Scholar] [CrossRef]
  30. Tomanik, E.; Profito, F.J.; Zachariadis, D.C. Modelling the hydrodynamic support of cylinder bore and piston rings with laser textured surfaces. Tribology international 2013, 59, 90–96. [Google Scholar] [CrossRef]
  31. Profito, F.J.; Vlădescu, S.C.; Reddyhoff, T.; Dini, D. Transient experimental and modelling studies of laser-textured micro-grooved surfaces with a focus on piston-ring cylinder liner contacts. Tribology International 2017, 113, 125–136. [Google Scholar] [CrossRef]
  32. Abdullah, M.; Alghoul, M.; Naser, H.; Asim, N.; Ahmadi, S.; Yatim, B.; Sopian, K. Research and development efforts on texturization to reduce the optical losses at front surface of silicon solar cell. Renewable and Sustainable Energy Reviews 2016, 66, 380–398. [Google Scholar] [CrossRef]
  33. Abbott, M.; Cotter, J. Optical and electrical properties of laser texturing for high-efficiency solar cells. Progress in Photovoltaics: Research and Applications 2006, 14, 225–235. [Google Scholar] [CrossRef]
  34. Paital, S.R.; Dahotre, N.B. Laser surface treatment for porous and textured Ca–P bio-ceramic coating on Ti–6Al–4V. Biomedical Materials 2007, 2, 274. [Google Scholar] [CrossRef] [PubMed]
  35. Bush, J.R.; Nayak, B.K.; Nair, L.S.; Gupta, M.C.; Laurencin, C.T. Improved bio-implant using ultrafast laser induced self-assembled nanotexture in titanium. Journal of Biomedical Materials Research Part B: Applied Biomaterials 2011, 97, 299–305. [Google Scholar] [CrossRef] [PubMed]
  36. Kumari, R.; Scharnweber, T.; Pfleging, W.; Besser, H.; Majumdar, J.D. Laser surface textured titanium alloy (Ti–6Al–4V)–Part II–Studies on bio-compatibility. Applied Surface Science 2015, 357, 750–758. [Google Scholar] [CrossRef]
  37. Pratap, T.; Patra, K. Mechanical micro-texturing of Ti-6Al-4V surfaces for improved wettability and bio-tribological performances. Surface and Coatings Technology 2018, 349, 71–81. [Google Scholar] [CrossRef]
  38. Kumar, A.; Bano, S.; Govind, B.; Bhardwaj, A.; Bhatt, K.; Misra, D. A review on fundamentals, design and optimization to high ZT of thermoelectric materials for application to thermoelectric technology. Journal of Electronic Materials 2021, 50, 6037–6059. [Google Scholar] [CrossRef]
  39. Ioffe, A.F.; Stil’Bans, L.; Iordanishvili, E.; Stavitskaya, T.; Gelbtuch, A.; Vineyard, G. Semiconductor thermoelements and thermoelectric cooling. Physics Today 1959, 12, 42–42. [Google Scholar] [CrossRef]
  40. Goldsmid, H.J. Bismuth telluride and its alloys as materials for thermoelectric generation. Materials 2014, 7, 2577–2592. [Google Scholar] [CrossRef]
  41. Zhao, P.; Yu, F.; Wang, B.; Zhao, H.; Chen, C.; Wang, D.; Ying, P.; Wu, Y.; Li, P.; Zhang, B.; et al. Porous bismuth antimony telluride alloys with excellent thermoelectric and mechanical properties. Journal of Materials Chemistry A 2021, 9, 4990–4999. [Google Scholar] [CrossRef]
  42. El-Makaty, F.M.; Ahmed, H.K.; Youssef, K.M. The effect of different nanofiller materials on the thermoelectric behavior of bismuth telluride. Materials & Design 2021, 209, 109974. [Google Scholar]
  43. Saberi, Y.; Sajjadi, S.A. A comprehensive review on the effects of doping process on the thermoelectric properties of Bi2Te3 based alloys. Journal of Alloys and Compounds 2022, 904, 163918. [Google Scholar] [CrossRef]
  44. Poudel, B.; Hao, Q.; Ma, Y.; Lan, Y.; Minnich, A.; Yu, B.; Yan, X.; Wang, D.; Muto, A.; Vashaee, D.; et al. High-thermoelectric performance of nanostructured bismuth antimony telluride bulk alloys. Science 2008, 320, 634–638. [Google Scholar] [CrossRef]
  45. Shin, W.H.; Ahn, K.; Jeong, M.; Yoon, J.S.; Song, J.M.; Lee, S.; Seo, W.S.; Lim, Y.S. Enhanced thermoelectric performance of reduced graphene oxide incorporated bismuth-antimony-telluride by lattice thermal conductivity reduction. Journal of Alloys and Compounds 2017, 718, 342–348. [Google Scholar] [CrossRef]
  46. Jang, K.W.; Kim, H.J.; Jung, W.J.; Kim, I.H. Charge transport and thermoelectric properties of p-type Bi 2-x Sb x Te 3 prepared by mechanical alloying and hot pressing. Korean Journal of Metals and Materials 2018, 56, 66–71. [Google Scholar]
  47. Symeou, E.; Nicolaou, C.; Delimitis, A.; Androulakis, J.; Kyratsi, T.; Giapintzakis, J. High thermoelectric performance of Bi2-xSbxTe3 bulk alloys prepared from non-nanostructured starting powders. Journal of Solid State Chemistry 2019, 270, 388–397. [Google Scholar] [CrossRef]
  48. Ioannou, I.; Ioannou, P.S.; Kyratsi, T.; Giapintzakis, J. Low-cost preparation of highly-efficient thermoelectric BixSb2-xTe3 nanostructured powders via mechanical alloying. Journal of Solid State Chemistry 2023, 319, 123823. [Google Scholar] [CrossRef]
  49. Yu, Y.; Zhu, W.; Wang, Y.; Zhu, P.; Peng, K.; Deng, Y. Towards high integration and power density: Zigzag-type thin-film thermoelectric generator assisted by rapid pulse laser patterning technique. Applied Energy 2020, 275, 115404. [Google Scholar] [CrossRef]
  50. Samourgkanidis, G.; Kyratsi, T. Continuous and Intermittent Planetary Ball Milling Effects on the Alloying of a Bismuth Antimony Telluride Powder Mixture. Inorganics 2023, 11, 221. [Google Scholar] [CrossRef]
  51. Stylianou, R.; Evangelou, A.; Loizou, A.; Kim, D.; Wharton, J.; Koutsokeras, L.; Constantinides, G.; Delimitis, A.; Kyratsi, T. Laser powder bed fusion of 316 L stainless steel with 2 wt% nanosized SiO2 additives: Powder processing and consolidation. Powder Technology 2023, 427, 118714. [Google Scholar] [CrossRef]
  52. Evangelou, A.; Stylianou, R.; Loizou, A.; Kim, D.; Liang, A.; Reed, P.; Constantinides, G.; Kyratsi, T. Effects of process parameters and scan strategy on the microstructure and density of stainless steel 316L produced via laser powder bed fusion. Journal of Alloys and Metallurgical Systems 2023, 3, 100027. [Google Scholar] [CrossRef]
Preprints 96157 g001
Figure 1. (a) Graphite matrix after the HP processing, (b) The arrows indicate the triplet of the BST disk pellets, and (c) Schematic of the setup.
Figure 1. (a) Graphite matrix after the HP processing, (b) The arrows indicate the triplet of the BST disk pellets, and (c) Schematic of the setup.
Preprints 96157 g001
Preprints 96157 g002
Figure 2. Thermal and electrical properties of the triplet BST samples: (a) Thermal conductivity, (b) Electrical conductivity, and (c) Seebeck coefficient.
Figure 2. Thermal and electrical properties of the triplet BST samples: (a) Thermal conductivity, (b) Electrical conductivity, and (c) Seebeck coefficient.
Preprints 96157 g002
Preprints 96157 g003
Figure 3. (a) The printing platform with laser-curved marks on its surface, (b) BST pellets aligned on the disk-shaped markers.
Figure 3. (a) The printing platform with laser-curved marks on its surface, (b) BST pellets aligned on the disk-shaped markers.
Preprints 96157 g003
Preprints 96157 g004
Figure 4. (a) Interior chamber of the metal 3D printer, (b) The building platform, along with the aligned BST samples, placed within the chamber, and (c) Sample positioning in order to LP all surfaces.
Figure 4. (a) Interior chamber of the metal 3D printer, (b) The building platform, along with the aligned BST samples, placed within the chamber, and (c) Sample positioning in order to LP all surfaces.
Preprints 96157 g004
Preprints 96157 g005
Figure 5. Surface laser processed BST disk pellet samples: (a) SS = 800 mm/s. This sample cracked during the first LP cycle, (b) SS = 1000 mm/s, (c) SS = 1200 mm/s, (d) SS = 1400 mm/s, (e) SS = 1600 mm/s, (f) SS = 1800 mm/s, and (g) Laser scanning strategy implemented to all LP samples.
Figure 5. Surface laser processed BST disk pellet samples: (a) SS = 800 mm/s. This sample cracked during the first LP cycle, (b) SS = 1000 mm/s, (c) SS = 1200 mm/s, (d) SS = 1400 mm/s, (e) SS = 1600 mm/s, (f) SS = 1800 mm/s, and (g) Laser scanning strategy implemented to all LP samples.
Preprints 96157 g005
Preprints 96157 g006
Figure 6. SEM images of the BST pellet samples: (a) SS = 600 mm/s, (b) SS = 1600 mm/s, and (c) The SS1600 sample surface, magnified.
Figure 6. SEM images of the BST pellet samples: (a) SS = 600 mm/s, (b) SS = 1600 mm/s, and (c) The SS1600 sample surface, magnified.
Preprints 96157 g006
Preprints 96157 g007
Figure 7. (a) A processed rectangular-shape BST sample sliced from a disk pellet, (b) Magnified area of Figure 7c, (c) SEM image of a shuttered cross section of the processed sample in Figure 7a, and (d) The unprocessed side of the same sample.
Figure 7. (a) A processed rectangular-shape BST sample sliced from a disk pellet, (b) Magnified area of Figure 7c, (c) SEM image of a shuttered cross section of the processed sample in Figure 7a, and (d) The unprocessed side of the same sample.
Preprints 96157 g007
Preprints 96157 g008
Figure 8. The X-ray diffraction pattern of the BST material, together with the respective JCPDS diagram, illustrates the patterns for the SS1600 sample shown in Figure 7a. These patterns were acquired from the in-plane direction, both before (HP) and after (LP) the laser processing.
Figure 8. The X-ray diffraction pattern of the BST material, together with the respective JCPDS diagram, illustrates the patterns for the SS1600 sample shown in Figure 7a. These patterns were acquired from the in-plane direction, both before (HP) and after (LP) the laser processing.
Preprints 96157 g008
Preprints 96157 g009
Figure 9. EDXS spectrum of the SS1600 sample, (a) before and (b) after the laser processing.
Figure 9. EDXS spectrum of the SS1600 sample, (a) before and (b) after the laser processing.
Preprints 96157 g009
Preprints 96157 g010
Figure 10. 3D color-maps of the TE properties: (a) Thermal conductivity, (b) X-Y view of thermal conductivity, (c) Electrical conductivity, (d) Seebeck coefficient, (e) Power factor, and (f) Figure of merit ZT.
Figure 10. 3D color-maps of the TE properties: (a) Thermal conductivity, (b) X-Y view of thermal conductivity, (c) Electrical conductivity, (d) Seebeck coefficient, (e) Power factor, and (f) Figure of merit ZT.
Preprints 96157 g010
Preprints 96157 g011
Figure 11. Comparison TE results: (a) Thermal conductivity, (b) Seebeck coefficient, (c) Electrical conductivity, (d) Power factor and (e) Figure of merit.
Figure 11. Comparison TE results: (a) Thermal conductivity, (b) Seebeck coefficient, (c) Electrical conductivity, (d) Power factor and (e) Figure of merit.
Preprints 96157 g011
Preprints 96157 g012
Figure 12. Thermoelectric properties of the SS1600 LP sample compared to the literature (Samourgkanidis et. al. [50], Ioannou et. al. [48] and Jang et. al. [46]): (a) Thermal conductivity, (b) Seebeck coefficient, (c) Electrical conductivity, (d) Power factor and (e) Figure of merit.
Figure 12. Thermoelectric properties of the SS1600 LP sample compared to the literature (Samourgkanidis et. al. [50], Ioannou et. al. [48] and Jang et. al. [46]): (a) Thermal conductivity, (b) Seebeck coefficient, (c) Electrical conductivity, (d) Power factor and (e) Figure of merit.
Preprints 96157 g012
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated