Prerpints.org logo
Preprint
Article

Extended Guided Filter: Simultaneous Noise Suppression and Details Enhancement

Altmetrics

Downloads

90

Views

28

Comments

0

This version is not peer-reviewed

Submitted:

11 January 2024

Posted:

12 January 2024

You are already at the latest version

Alerts
Abstract
Guided image filter implicitly balances noise and details based on local variance, achieving noise suppression while preserving prominent edges. However, we have observed limitations in using variance to distinguish between noise and image details, resulting in the suppression of fine structures alongside noise. Furthermore, the goal of enhancing image details, which is crucial in image filtering, has not been adequately addressed in edge-preserving filter design. In this paper, we approach image filtering as a problem of spectral energy reconfiguration, where the gain of each spectral band is adaptively regulated to achieve simultaneous noise suppression and detail enhancement. Instead of relying on variance, we employ a linear noise estimator to obtain the Signal-to-Noise Ratio (SNR) measurement necessary for dynamic gain regulation. Similar to the guided image filter, we determine the filter coefficients by solving the closed-form solution of the optimizer. We demonstrate that the proposed extended guided filter effectively integrates information from multiple spectral bands locally, allowing for the joint enhancement of meaningful details while simultaneously smoothing noise.
Keywords: 
Subject: Computer Science and Mathematics  -   Signal Processing

1. Introduction

purpose of filtering is to emphasize informative details of interest in the data. Image filtering is widely used in the field of image processing and computer vision for a broad spectrum of applications, such as image denoising[1,2,3,4], smoothing [5,6,7], image fusion [8] and feature extraction [9,10,11], etc. Observed from the frequency domain perspective, spatially invariant filters, e.g. Gaussian averaging filter, give a modulation scheme to the frequency spectrum of the input image, allowing the energy of specific frequencies to pass while suppressing that of certain frequencies. This leads to a global tradeoff between the signal energy and the noise energy. However, meaningful details and noise of natural images always share certain frequencies. As an result, unfortunately, those linear and spatially invariant filters often inevitably damage the meaningful details of an image to a certain extent.
To alleviate this, nonlinear methods such as anisotropic diffusion[5,12,13,14,15], bilateral filter[4,16,17,18,19], WLS filter[20,21] and guided image filter (GIF)[3,22,23,24] have been proposed. They take local content into consideration and can effectively prevent edge pixels from being damaged in denoising. Featuring the advantages of both simple framework and high performance, GIF has established itself as an exemplar for edge-preserving filtering. When the guiding image is the input itself, GIF implicitly measures local noise level based on variance, and thus determines the local combination coefficients between the original image and a constant valued image accordingly.
However, there are two issues of GIF that deserve further improvement. First, we noted that variance, a second-order statistic employed in GIF, is limited in its ability to discriminate between noise and details, and tends to cause tiny structures to be suppressed along with noise. Specifically, the variance of an area with meaningful details in an image is often indistinguishable from the variance of noise (see Figure 2), which is why the edge-preserving filters such as GIF can only preserve significant edges but lose many meaningful details. Second, the focus of GIF and those edge-preserving filters [3,4,14] is on how to smooth the image without destroying the edges rather than enhancing details [25]. Actually, details enhancement is considered as one of the important goals of image filtering besides denoising [26]. Meaningful details carry rich information and should be further emphasized in filtering for the purpose of achieving better image contrast.
In this paper, we propose an extended guided filter (EGF), see Figure 1, primarily motivated by two considerations: Firstly, we regard image filtering as a spectral energy reconfiguration problem, and adaptively regulate the gain of each spectral band to achieve simultaneous noise suppression and detail enhancement locally. Secondly, instead of using variance, we employ a linear noise estimator in the closed-form optimization, to obtain the online SNR measurement required for the dynamical regulation of the signal energy and the noise energy.

2. The Methodology

2.1. The definition of the extended guided filter (EGF)

We assume that filtering is a local recombination of the energy at different spectrum bands of the input image. Therefore, image filter can be regarded as a local linear model, which transform the maps, provided by performing spectrum-selectively filtering on the input, to the output.
A set of spatial filters b 1 ,..., b n , b n + 1 are given targeting different spectral bands of the input image p. A n+1 dimensional functional space is spanned by those filter bases, S n + 1 = span ( b 1 , . . . , b n , b n + 1 ) . Each point of the space, ∑ k = 1 n + 1 a k b k , represents a combined filter. Tensor u is yielded to contain a series of maps u 1 ,..., u n , u n + 1 from p, by performing convolution u k = p ⊗ b k . The task of EGF is to seek locally in the space for such combined filters that meets certain constraints by means of optimization. The output of EGF is denoted as g. locally, g l , the output of an area Ω l centered at pixel l, is defined as a linear combination of those n + 1 corresponding patches u k l ,The guided image filter is an effective method for balancing noise and preserving details based on local variance, achieving noise suppression while retaining prominent edges. However, we have observed limitations in using variance alone to distinguish between noise and image details, resulting in the suppression of fine structures alongside noise. Furthermore, the goal of enhancing image details, which is crucial in image filtering, has not been adequately addressed in edge-preserving filter design. In this study, we approach image filtering as a problem of spectral energy reconfiguration, where the gain of each spectral band is adaptively regulated to achieve simultaneous noise suppression and detail enhancement. Instead of relying on variance, we employ a linear noise estimator to obtain the Signal-to-Noise Ratio (SNR) measurement necessary for dynamic gain regulation. Similar to the guided image filter, we determine the filter coefficients by solving the closed-form solution of the optimizer. Our experiments demonstrate that the proposed extended guided filter effectively integrates information from multiple spectral bands at a local level, allowing for the joint enhancement of meaningful details while simultaneously smoothing noise. g l = ( ∑ k = 1 n + 1 a k l b k l ) ⊗ p l = ∑ k = 1 n + 1 a k l u k l . Without losing the generality, we set b n + 1 = 1 . The coefficients a l are solved by optimization under the following constrains.
E ( a l ) = ∑ Ω l ( ( p l − g l ) 2 + ∑ k = 1 n ( α k ( a k l ) 2 ) + γ ∑ Ω l σ 2 ( g l ) .
The first term of (1) is set to control the error between output and the input. The second term is the coefficient regularizer with hyperparameters α . Besides, the online noise estimation is introduced as the last term with hyperparameter γ in (1), to regulate the energy allocation of the signal and the noise. σ is a linear estimator of noise level, and thus ∑ Ω l σ 2 ( g l ) = ∑ Ω l ( ∑ k = 1 n a k l σ ( u k l ) ) 2 . Please refer to Section 2.3 for details.
arg min a l E ( a l ) could be solved by finding the solution to the linear equations defined by ∂ E ∂ a k l = 0 , and
a 1 : n l = [ diag ( α ) + C ( u l ) + γ G ( σ ( u l ) ] − 1 Cov ( p l , u l ) a n + 1 l = ∑ l p Ω l − ∑ k = 1 n ( a k l ∑ l u k l Ω l ) .
Where Cov ( p l , u l ) = ( Cov ( p l , u 1 l ) , ⋯ , Cov ( p l , u n l ) ) T ,   C ( u l ) is the covariance matrix of u l
C ( u l ) = Cov ( u 1 l , u 1 l ) ⋯ Cov ( u 1 l , u n l ) ⋮ ⋱ ⋮ Cov ( u n l , u 1 l ) ⋯ Cov ( u n l , u n l ) ,
and G ( σ ( u l ) ) is the Gramian matrix of σ ( u l )
G ( σ ( u l ) ) = 〈 σ ( u 1 l ) , σ ( u 1 l ) 〉 ⋯ 〈 σ ( u 1 l ) , σ ( u n l ) 〉 ⋮ ⋱ ⋮ 〈 σ ( u n l ) , σ ( u 1 l ) 〉 ⋯ 〈 σ ( u n l ) , σ ( u n l ) 〉 .
For the entire image, if it is processed in a non-overlapping manner, artifacts will appear at each patch boundary. To avoid this, we adopt the solution in [3], where patch centered at each pixel are reconstruct overlappingly with an interval of one pixel. As a result, each location l, will be covered by Ω l windows and therefore correspond to Ω l sets of reconstruction coefficients. Here, their mean values are directly used as the reconstruction coefficients of the current pixel. The mean value μ ( a k ) of a k is defined as μ ( a k ) = B F ( a k ) , where B F ( . ) is the mean filter with O(n) time complexity proposed by[3]. The EGF filtering result g is given by g = ∑ k = 1 n + 1 μ ( a k ) . * u k .

2.2. Selection of filter bases

In order to construct the functional space S n + 1 , filters are selected as the bases of the space. The following factors are considered in the selection process: 1) in order to allow multi-band information integration during filtering, the bases should contain both the low-pass filters and the high-pass filters 2) filters with relatively simple forms are favorable; 3) both the full spectrum pass filter and the DC component pass filter should be included; 4) filters in consideration are expected to be diverse so that they can be complementary.
Filters can either be defined in spatial domain or equivalently be defined in frequency domain. For the sake of simplicity, we choose filters { B i } with Gaussian form as the space bases in this paper. The spatial domain form b i of B i is gvien by Fourier Transform. Among these Gaussian bases, we suppose that B 1 is a full-band pass filter and B n + 1 is a DC component pass filter, respectively. Accordingly, u 1 = p ⊗ b 1 equals the original image p, and u n + 1 is a constant valued image. The rest of the bases are band-pass filters.
With the bases, the weights for the linear combination for each local area of the image are obtained according to (2). Thus, the linear combination of these bases yields complicated modulation filters in frequency domain. Interestingly, when n = 1 , the form of the combined filter is a 1 l * p + a 2 l , which happens to be the linear model adopted by GIF [3].
In this paper, a low-pass filter and a high-pass filter with empirical parameters are chosen as two bases in addition to the full-pass and DC filters that employed in [3]. It is worth noting that, filters collected from Gabor filter bank [27,28] are also encouranged to employe as bases. One can even learn a set of filter bases in a data-driven way.

2.3. Linear noise estimation for dynamic filtering

In order to regulate the power of signal and noise adaptively and optimally, it is necessary to measure the noise level online at any position of the input. Assuming a noise estimator σ , it gives the results σ ( x l ) for a patch x l of a local region Ω l centered at the pixel l. Obviously, such an estimator is expected to have the same properties at any image locations. Therefore, the simplest form of such a noise estimator must be a linear & spatially invariant (LSI) system, with the kernel h, and the system output is h ⊗ x l . The final noise estimation is given by λ ∑ Ω l σ 2 ( x l ) = λ ∥ h ⊗ x l ∥ F 2 , here ∥ . ∥ F 2 is Frobenius-norm, and λ denote the normalization coefficient.
Interestingly, the authors of [29] have derived a noise estimator kernel
h = 1 , − 2 , 1 ; − 2 , 4 , − 2 ; 1 , − 2 , 1 ,
namely Immerkær estimator, which satisfies all those constraints mentioned above. Immerkær estimator has a simple form and high computational efficiency. In addition, it is a LSI system, and thus could be optimized in a closed-form mannner. Therefore, it is adopted in this paper for online noise estimation.

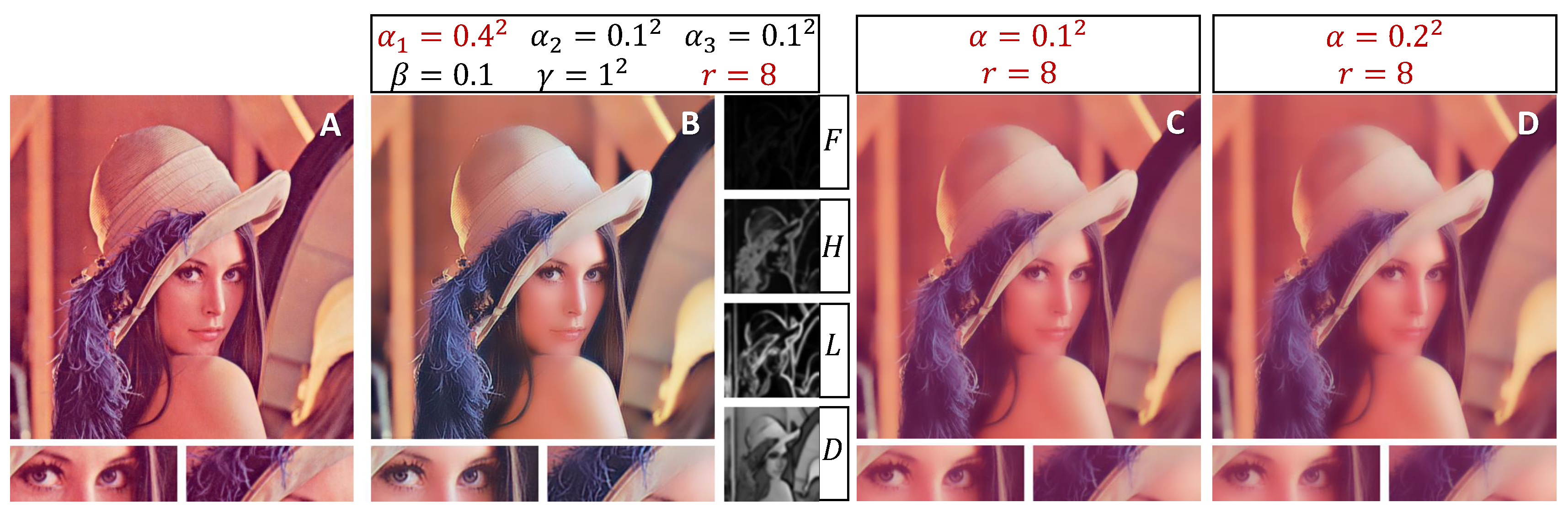
2.4. Image smoothing and details enhancement

In (2), increasing α k is equivalent to increasing the value of the k t h diagonal element of the matrix
[ diag ( α ) + C ( u l ) + γ G ( σ ( u l ) ] .
Such a hyperparameter in the regularization term α k ( a k l ) 2 of (1) is set to punish a k l , the weight of u l k . This super parameter setting provides a choice of which frequency bands we want to enhance or suppress. In addition to tunning the weights channel-wisely, the values of { a k l } could be increased/decreased uniformly to control the degree to which the input image is smoothed.
The meaningful area of an image always contains rich details and thus is dominated by the high frequencies energy. In EGF, these details are expected to be enhanced adaptively. It is assumed that u k l is provided by performing filtering on p k l with a high-pass bases from S n + 1 , and thus informative details of p k l are mainly included in u k l . u k l tends to be assigned a larger weight under the constraints, as the details (e.g. edges, textures, etc.) of u k l are correlative with the content that in p k l , yielding a larger value of Cov ( p k l , u k l ) in (2).
C and G in (1) affect the output from the two aspects of the variance and noise level, respectively. With γ > 0 , the noise penalty term adaptively affect the adjustment of a k . Assuming the noise level of u k l is enlarged, the inner product of σ ( u k l ) and itself increases, thereby raising the value of the k-th diagonal element of the matrix of (5), which is equivalent to enlarging the penalty of the noisy channel u k .
In addition to adaptive balancing between detail enhancement and denoising, EGF can also facilitate balance denoising and edge preservation. Supposing p l is a flat area of the input, Cov ( p l , u ) approaches zero, and as a results a 1 : n l become closer to zeros as well. According to the equation (2), a n + 1 l , the weight of the DC components, will be maximized. This means that the flat area will be strongly smoothed. If p l is an area with rich edges or textures, the covariances between p l and these maps in { u k l } are of of higher values. Thus, the values of a 1 : n l solved are large, and the value of a n + 1 l is close to zero. Therefore p l is reconstructed by those maps selected from { u k l } instead of the DC component.

3. Experimental results and analysis

We first investigate the ability of EGF to enhance meaningful details during smoothing in both 1D and 2D cases, and then compare the performances of the EGF and GIF. In this paper, n is set to be 3, so S n + 1 is a 4D space. As discussed in Section 2.2, b 1 is the impulse function, and therefore u 1 is just the input image. b 4 is the DC pass filter, so u 4 is a constant valued image. b 2 is set to be a high-pass filter, specifically using ∇ 2 f 0.75 , the 2 n d order difference of the Gaussian f with a variance of 0.75; b 3 as a low-pass Gaussian filter, f 3 .

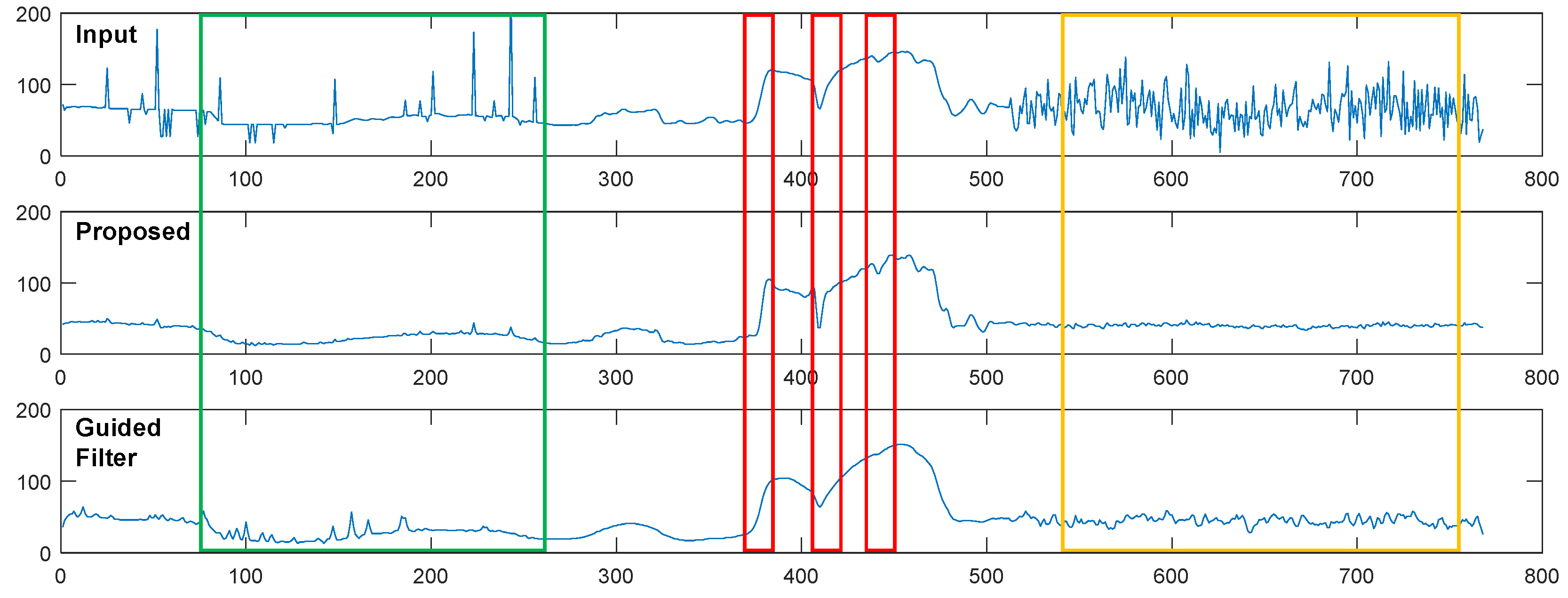
3.1. 1D case

Figure 3 shows the comparison of EGF and GIF on a 1D signal. The 1 s t row is the input which has salt & pepper noise (green square) and Gaussian white noise (yellow square) added to the left and right, respectively. The 2 n d and 3 r d rows are the filtering results of EGF and GIF, respectively. GIF can achieve denoising while preserving dominant edges ( 3 r d row). However, the details of these edges are suppressed to a certain extent. In contrast, the proposed EGF not only preserves these edges, but also enhances the details (red boxes). For Gaussian noise, both GIF and EGF achieve acceptable suppression, but the GIF has not suppressed them out thoroughly. In this case, if the regularization parameter of GIF is increased, the noise could be better suppressed, but at the same time, it will cause more damage to the edge. There is a similar result for salt & pepper noise. EGF is capable of suppressing both types of noise well, while keeping meaningful details to be enhanced. This advantage is achieved by using online noise level estimates and adaptive multi-spectrum bands integration.

3.2. 2D case

Figure 4 shows the filtering results of EGF on Lenna image. To investigate the ability of denoisng and details enhancement of EGF, frequency domain analysis is performed by comparing before and after spectral of three image patches. The enhancement spectrum is defined as ( l o g A { F ( g ) } l o g A { F ( p ) } ) · ( l o g A { F ( g ) } > l o g A { F ( p ) } ) , where A { F ( · ) } is the Fourier amplitude of the input. And suppression spectrum is defined in a similar way.
Patches in red and blue boxes have meaningful details that are expected to be enhanced during filtering for higher contrast. After EGF filtering, the details such as Lenna’s hair and eyes, as well as the brim of the hat, are sharpened and appear more clearly. From the analysis of the enhancement spectrum, One can find that the mid-range frequencies and some high-frequencies of these two image patches, corresponding to meaningful details, have been significantly enhanced.
Patch in green box is flat and has some degree of noise (see its log spectrum). After EGF filtering, the low-frequencies is enhanced (see its enhancement spectrum), while some mid-high frequencies are suppressed. In spatial domain, it indicates that the region has been further smoothed.

3.3. Comparison of EGF with GIF

Figure 5 shows the results of EGF and GIF on the input, with two zoomed patches of higher magnification placed under each result for comparison of details. To depict the filtering process of EGF, four weight maps, corresponding to b 1 ,..., b 4 , are attached to 2 n d col., namely F, H, L, and D, respectively. Since we set α 1 larger than that of other coefficients, EGF will suppress a 1 most, the coefficient of u 1 , thereby forcing u 2 ,..., u 4 to play a greater role in reconstructing the input. u 2 contains more informative details, while u 3 and u 4 contain less noise. The edges of the image are mainly reconstructed by high-frequencies ( u 2 ) and low-frequencies ( u 3 ), whereas the flat area mainly by DC components ( u 4 ). Since a high-pass filter is included as a basis in S n + 1 , EGF is capable to actively enhance the meaningful details, which is the main difference from traditional edge preserving filters. The risk that the enhancement of the high-frequencies may amplify the noise do exists in EGF, and the problem is alleviated through adding a regular term of online noise level evaluation.
GIF is a special case of the proposed EGF (n = 1) . The local combined filter of GIF is optimized within a 2D functional S 2 , where the two bases are all-pass and DC pass, respectively. GIF seeks for a tradeoff locally between the input and a constant valued image ( H & L in Figure 6 are alwanys zero(blank)). Results illustrate GIF is capable to maintain the significant edges in smoothing, but fails at actively enhancing them and keep tiny details from being blurred.
Due to the introduction of regular terms for online noise level estimation, EGF is able to dynamically balance smoothing and detail enhancement according to noise conditions. In the first and the second rows of the Figure 6, different degrees of additive white Gaussian noise were added to the lower right part of each image. EGF(ours) can achieve adaptive noise suppression and detail enhancement. Observing their four weight maps, the noisy area of the image is mainly reconstructed by the energy of the low-frequency part ( L & D ), and the information of the high-frequency part (H) is almost abandoned. The results suggest that EGF adaptively integrates the energy of different frequency bands according to the noise level. For GIF, however, the intensity of smoothing is determined by the variance of the current patch. If the area, corrupted by noise, has larger variance, it will not be sufficiently smoothed. In this case, if we increase the regularization coefficient α to force smooth heavily, more details of the image will be blurred along with noise (see last column of Figure 6). Tests were also conducted on heavy noisy images (see part B of Figure 6). It can be found that EGF keeps more details from being smoothed in filtering.
In imaging environments with low illumination, darker areas in the scene often exhibit stronger noise, which is due to the low signal-to-noise ratio in low illumination regions (as shown in the input image in Figure 7, where darker areas are contaminated by stronger noise). In other words, in low-light scenes, if there is significant variation in brightness across different areas, the spatial distribution of noise intensity in the resulting image also varies. Therefore, it is necessary to design appropriate algorithms to mitigate noise while minimizing disruption to texture regions. Such algorithms can be implemented in post-processing image enhancement software or in the Image Signal Processor (ISP) chip within the camera. However, denoising spatially non-uniform noisy images is a challenging task. For the GIF algorithm, the only adjustable parameter is α 1 . As shown in the figure, we attempted to gradually adjust α 1 from 0.05 2 to 0.2 2 . However, we found that the GIF algorithm cannot achieve a good balance between denoising and preserving weak textures. In other words, when a stronger noise suppression is desired, it inevitably results in severe disruption (filtering out) of weak texture areas in the image. This is primarily due to the GIF algorithm’s reliance solely on variance to evaluate local image information. Since noise areas and texture areas may have similar variances, noise needs to be filtered out while weak textures need to be preserved. In contrast, our proposed EGF algorithm introduces local noise estimation and benefits from the filtering framework presented in this paper, thereby demonstrating a certain capability to differentiate between noise and texture areas and to adaptively process these areas separately.
Next, we further conducted quantitative analysis. For the aforementioned images, we considered extracting noise patches and text patches from the images and conducted a comparative quantitative analysis. We computed the Average Gradient Response (AGR) for these two patches before and after filtering by considering the average gradient response level. We used the Laplacian operator to convolve the aforementioned two areas and calculated the mean value of the convolution response amplitude to represent the average gradient response level. As shown in Table 1, the AGR of the noise area and the text area in the original input image are 59.90 % and 10.45 % , respectively, indicating a high noise level in the noise area. Filtering using the GIF algorithm shows that as α 1 increases, the noise level in the noise area can be reduced from 22.17 % to 80.97 % . However, as α 1 increases, the text area is also significantly suppressed, with suppression rates exceeding 45 % and reaching as high as 88.71 % . Moreover, regardless of the choice of α 1 we cannot achieve good noise suppression while preserving texture areas from severe disruption. In contrast, our proposed EGF algorithm can achieve a noise suppression of 83.02 % while causing only 29.57 % suppression in the texture area.

4. Conclusion

In this paper, we present a new paradigm of image filter design. In this paradigm, filters that corresponding to different spectrum bands are employed as the bases to form a functional space where the optimal locally based filter is solved based on optimization. By introducing noise estimation as regular terms, the filter achieves joint functions of both smoothing and detail enhancement. In addition to Gaussian filter used in this paper, other forms of filter could also be adopted as the bases. There are two problems worthy of further investigation. One is to consider the selection of the bases of the functional subspace as an optimization problem as well as solving the optimal bases; the other is to find a more favorable prior knowledge about a "good" map as a regular term.

Author Contributions

Conceptualization, J.L. and Zp.S.; methodology, J.L.; software, J.L.; validation, J.L., and Zp.S.; writing—original draft preparation, J.L.; writing—review and editing, Zp.S. All authors have read and agreed to the published version of the manuscript.

Funding

This work is supported by the National Natural Science Foundation of China under Grant 61973311.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Kong, X.Y.; Liu, L.; Qian, Y.S. Low-light image enhancement via poisson noise aware retinex model. IEEE Signal Processing Letters 2021, 28, 1540–1544. [Google Scholar] [CrossRef]
  2. Luo, W. An efficient detail-preserving approach for removing impulse noise in images. IEEE signal processing letters 2006, 13, 413–416. [Google Scholar] [CrossRef]
  3. He, K.; Sun, J.; Tang, X. Guided Image Filtering. IEEE Transactions on Pattern Analysis and Machine Intelligence 2013, 35, 1397–1409. [Google Scholar] [CrossRef] [PubMed]
  4. Tomasi, C.; Manduchi, R. Bilateral filtering for gray and color images. Sixth International Conference on Computer Vision (IEEE Cat. No.98CH36271), 1998, pp. 839–846.
  5. Barash, D. Fundamental relationship between bilateral filtering, adaptive smoothing, and the nonlinear diffusion equation. IEEE Transactions on Pattern Analysis and Machine Intelligence 2002, 24, 844–847. [Google Scholar] [CrossRef]
  6. Min, D.; Choi, S.; Lu, J.; Ham, B.; Sohn, K.; Do, M.N. Fast global image smoothing based on weighted least squares. IEEE Transactions on Image Processing 2014, 23, 5638–5653. [Google Scholar] [CrossRef] [PubMed]
  7. Kim, Y.; Min, D.; Ham, B.; Sohn, K. Fast Domain Decomposition for Global Image Smoothing. IEEE Transactions on Image Processing 2017, 26, 4079–4091. [Google Scholar] [CrossRef]
  8. Li, S.; Kang, X.; Hu, J. Image Fusion With Guided Filtering. IEEE Transactions on Image Processing 2013, 22, 2864–2875. [Google Scholar] [PubMed]
  9. Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. International Journal of Computer Vision 2004, 60, 91–110. [Google Scholar] [CrossRef]
  10. Dalal, N.; Triggs, B. Histograms of oriented gradients for human detection. 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), 2005, Vol. 1, pp. 886–893.
  11. Sun, Y.; Ni, R.; Zhao, Y. ET: Edge-Enhanced Transformer for Image Splicing Detection. IEEE Signal Processing Letters 2022, 29, 1232–1236. [Google Scholar] [CrossRef]
  12. Nitzberg, M.; Shiota, T. Nonlinear image filtering with edge and corner enhancement. IEEE Transactions on Pattern Analysis & Machine Intelligence 1992, 14, 826–833. [Google Scholar]
  13. Weickert, J. A review of nonlinear diffusion filtering. International conference on scale-space theories in computer vision. Springer, 1997, pp. 1–28.
  14. Perona, P.; Malik, J. Scale-space and edge detection using anisotropic diffusion. IEEE Transactions on Pattern Analysis and Machine Intelligence 1990, 12, 629–639. [Google Scholar] [CrossRef]
  15. Krissian, K.; Aja-Fernandez, S. Noise-Driven Anisotropic Diffusion Filtering of MRI. IEEE Transactions on Image Processing 2009, 18, 2265–2274. [Google Scholar] [CrossRef] [PubMed]
  16. Chen, B.H.; Tseng, Y.S.; Yin, J.L. Gaussian-adaptive bilateral filter. IEEE Signal Processing Letters 2020, 27, 1670–1674. [Google Scholar] [CrossRef]
  17. Zhang, B.; Allebach, J.P. Adaptive bilateral filter for sharpness enhancement and noise removal. IEEE transactions on Image Processing 2008, 17, 664–678. [Google Scholar] [CrossRef] [PubMed]
  18. Ghosh, S.; Nair, P.; Chaudhury, K.N. Optimized Fourier bilateral filtering. IEEE Signal Processing Letters 2018, 25, 1555–1559. [Google Scholar] [CrossRef]
  19. Elad, M. On the origin of the bilateral filter and ways to improve it. IEEE Transactions on image processing 2002, 11, 1141–1151. [Google Scholar] [CrossRef] [PubMed]
  20. FarbmanZeev.; FattalRaanan.; LischinskiDani.; SzeliskiRichard. Edge-preserving decompositions for multi-scale tone and detail manipulation. ACM Transactions on Graphics, 2008.
  21. Liu, W.; Chen, X.; Shen, C.; Liu, Z.; Yang, J. Semi-global weighted least squares in image filtering. Proceedings of the IEEE International conference on computer vision, 2017, pp. 5861–5869.
  22. He, K.; Sun, J.; Tang, X. Guided image filtering. European conference on computer vision. Springer, 2010, pp. 1–14.
  23. Li, Z.; Zheng, J.; Zhu, Z.; Yao, W.; Wu, S. Weighted guided image filtering. IEEE Transactions on Image Processing 2015, 24, 120–129. [Google Scholar] [PubMed]
  24. Lu, Z.; Long, B.; Li, K.; Lu, F. Effective guided image filtering for contrast enhancement. IEEE Signal Processing Letters 2018, 25, 1585–1589. [Google Scholar] [CrossRef]
  25. Hao, S.; Pan, D.; Guo, Y.; Hong, R.; Wang, M. Image detail enhancement with spatially guided filters. Signal Processing 2016, 120, 789–796. [Google Scholar] [CrossRef]
  26. Kou, F.; Chen, W.; Li, Z.; Wen, C. Content adaptive image detail enhancement. IEEE Signal Processing Letters 2014, 22, 211–215. [Google Scholar] [CrossRef]
  27. Daugman, J.G. Uncertainty relation for resolution in space, spatial frequency, and orientation optimized by two-dimensional visual cortical filters. JOSA A 1985, 2, 1160–1169. [Google Scholar] [CrossRef] [PubMed]
  28. Mehrotra, R.; Namuduri, K.R.; Ranganathan, N. Gabor filter-based edge detection. Pattern recognition 1992, 25, 1479–1494. [Google Scholar] [CrossRef]
  29. Immerkær, J. Fast Noise Variance Estimation. Computer Vision and Image Understanding 1996, 64, 300–302. [Google Scholar] [CrossRef]
Preprints 96091 g001
Figure 1. The proposed extended guided filter (EGF) suppresses image noise and enhances details simultaneously and adaptively. Input image (left) is a slightly blurred image, with Gaussian noise and salt & pepper noise added to the left and right regions, respectively. Benefiting from the adaptive spectral power reconfiguration and dynamic noise estimation, EGF can enhance the meaningful details in the image under the constraint of maxmizing SNR, and suppress the noise that featuring random properties, thereby resulting in an enhanced image with high contrast, rich details, and low noise level.
Figure 1. The proposed extended guided filter (EGF) suppresses image noise and enhances details simultaneously and adaptively. Input image (left) is a slightly blurred image, with Gaussian noise and salt & pepper noise added to the left and right regions, respectively. Benefiting from the adaptive spectral power reconfiguration and dynamic noise estimation, EGF can enhance the meaningful details in the image under the constraint of maxmizing SNR, and suppress the noise that featuring random properties, thereby resulting in an enhanced image with high contrast, rich details, and low noise level.
Preprints 96091 g001
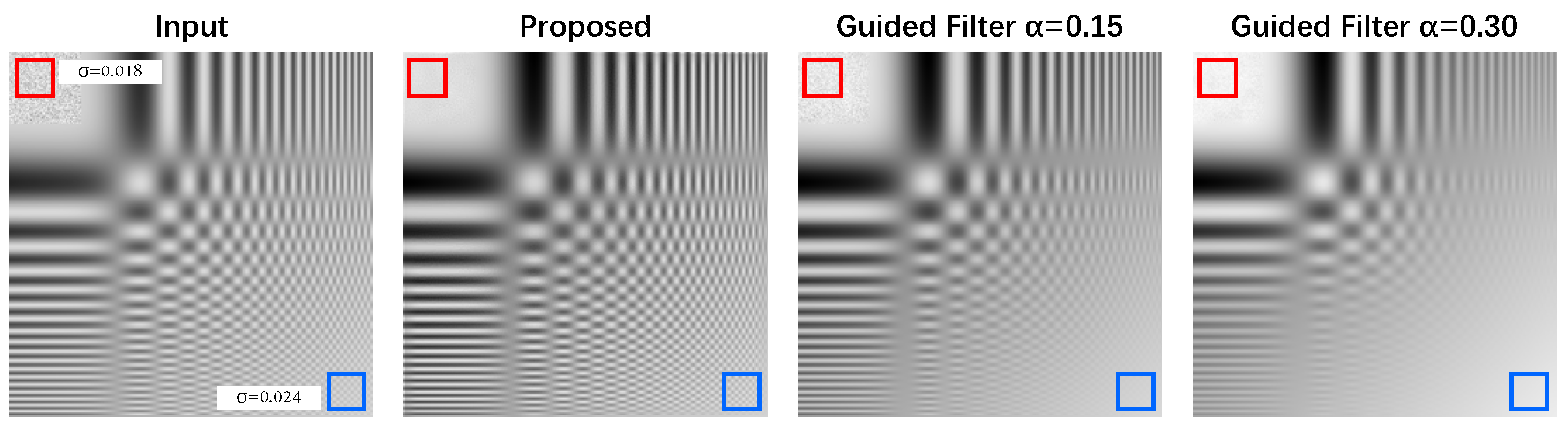
Preprints 96091 g002
Figure 2. Variance is not an effective measure to distinguish noise from meaningful image detail, so GIF loses a lot of image texture (blue square) while suppressing noise. From left to right are the input image with Gaussian noise added in the upper left corner (red square), the filtering result of the proposed method, the GIF filtering result (smaller regularization parameter) and the GIF filtering result (larger regularization parameter). Benefiting from the introduction of noise measure, the proposed method is capable of enhancing image details while denoising. For GIF, since the variance difference between noise and detail is not large enough, simultaneous noise suppression and detail preservation cannot be achieved in filtering.
Figure 2. Variance is not an effective measure to distinguish noise from meaningful image detail, so GIF loses a lot of image texture (blue square) while suppressing noise. From left to right are the input image with Gaussian noise added in the upper left corner (red square), the filtering result of the proposed method, the GIF filtering result (smaller regularization parameter) and the GIF filtering result (larger regularization parameter). Benefiting from the introduction of noise measure, the proposed method is capable of enhancing image details while denoising. For GIF, since the variance difference between noise and detail is not large enough, simultaneous noise suppression and detail preservation cannot be achieved in filtering.
Preprints 96091 g002
Preprints 96091 g003
Figure 3. Comparison results of EGF and GIF on 1D signal.
Figure 3. Comparison results of EGF and GIF on 1D signal.
Preprints 96091 g003
Preprints 96091 g004
Figure 4. Filtering results of EGF on image. From left to right are the input image, the filtering results of EGF, and the frequency domain comparative analysis before and after filtering on the three image patches.
Figure 4. Filtering results of EGF on image. From left to right are the input image, the filtering results of EGF, and the frequency domain comparative analysis before and after filtering on the three image patches.
Preprints 96091 g004
Preprints 96091 g005
Figure 5. Comparison of EGF with GIF. 2 n d col. shows the EGF results of the input images in the 1 s t col., 3 r d and 4 t h col. are the results of GIF
Figure 5. Comparison of EGF with GIF. 2 n d col. shows the EGF results of the input images in the 1 s t col., 3 r d and 4 t h col. are the results of GIF
Preprints 96091 g005
Preprints 96091 g006
Figure 6. Comparison of denoising of EGF and GIF (zoom in for better viewing).
Figure 6. Comparison of denoising of EGF and GIF (zoom in for better viewing).
Preprints 96091 g006
Preprints 96091 g007
Figure 7. Comparison of the ability to simultaneously perserve texture and suppress noise.
Figure 7. Comparison of the ability to simultaneously perserve texture and suppress noise.
Preprints 96091 g007
Table 1. Average Gradient Responses (AGR) for noise patch and texture patch provided by EGF and GIF.
Table 1. Average Gradient Responses (AGR) for noise patch and texture patch provided by EGF and GIF.
Input EGF GIF 0.05 2 GIF 0.10 2 GIF 0.15 2 GIF 0.20 2
Noisy patch 0.5990 0.1017
(-83.02%)		 0.4662
(-22.17%)		 0.2823
(-52.87%)		 0.1735
(-71.04%)		 0.1140
(-80.97%)
Texture patch 0.1045 0.0736
(-29.57%)		 0.0569
(-45.55%)		 0.0263
(-74.83%)		 0.0159
(-84.78%)		 0.0118
(-88.71%)
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated