Prerpints.org logo
Preprint
Article

Multifractal Aspects of Earth's Climate History

Altmetrics

Downloads

72

Views

35

Comments

0

This version is not peer-reviewed

Submitted:

11 January 2024

Posted:

12 January 2024

You are already at the latest version

Alerts
Abstract
Abstract: Earth’s Phanerozoic history is marked by about 100 major events (“golden spikes”) indicating the beginnings of new stages in the Geologic Time Scale (GTS). Stage boundaries signify major deterministic events that are relatively well-known and can be correlated worldwide, mostly on the basis of appearances or disappearances of fossil species. The latest stage (Anthropocene) is human-made and currently involves rapid (approximately linear) increase in average atmospheric temperature. The main cause of Earth’s past and current temperature increases is addition of CO2 to the atmosphere. There is continuous exchange of greenhouse gases between atmosphere and oceans, which (per unit of volume) contain 50 to 60 times as much CO2 as the atmosphere. Abundance of new very precise worldwide observations is allowing multifractal modeling of weather and climate during the latest Quaternary stages during which some variables like temperature of the atmosphere and frequency of forest fires can be described by using the Pareto-lognormal frequency distribution model with parameters that are subject to continuous (deterministic) changes, similar to those in the earlier Phanerozoic.
Keywords: 
Subject: Environmental and Earth Sciences  -   Geophysics and Geology

1. Introduction

During its 4.5-billion-year long history, Earth has gone trough many different types of climates [1,2]. During the Phanerozoic that commenced 542 million years ago, there were about a hundred worldwide events resulting in the geological stage boundaries of the International Geologic Timescale (GTS) [3,4]. These stage boundaries can be correlated worldwide across different continents. Most of them have been marked by “golden spikes” driven into the ground at places where the local geology is exceptionally well-known. It is likely that many stage boundaries signify “extreme events” (cf. Cheng [5]). It can be assumed that some earlier stage boundaries to some extents were created in ways similar to that taking place at the commencement of the Anthropocene. Unfortunately, earlier Phanerozoic stage boundaries cannot be dated with sufficient precision to allow similar non-linear modeling.
In addition to the golden spikes, there are numerous other events (“silver spikes” [6], particularly volcanic ash beds) that were probably worldwide but can only rarely be correlated across larger regions. Ash beds generally contain dateable zircons. The obvious manifestation of Earth climate is weather that is chaotic. Recently, it has been pointed out that weather also contains a component called “macro-weather” that is only moderately chaotic [7,8]. The possibility of extrapolation of multifractal results derived for the latest Quaternary stages to earlier Phanerozoic stages is limited, mainly because of relatively great uncertainties associated with volcanic ash layer age determinations.

2. Role of CO2 in the Anthropocene Atmosphere

Stage boundaries are defined on the basis of first or last appearances of fossils in the worldwide stratigraphic record. Some of them involved changes in CO2 concentration value of the atmosphere and oceans. As originally pointed out by Arrhenius [9], Earth’s past and current temperature increases are primarily caused by CO2 concentration increases in the atmosphere. They are the reason of the current emergence of the Anthropocene as a new stage that, according to several authors, commenced in 1784 [10]. Other greenhouse gases including methane also play a role in atmospheric temperature increases but their contribution is minor [11]. Although methane as a greenhouse gas is more effective than CO2, its concentration values are very small (measured in parts per billion instead of in parts per million).
Human-made addition of greenhouse gases to the Earth’s atmosphere commenced about 12,000 years ago with the appearance of domesticated crops and animals with newly developed tool technologies ([12], Table 2.1, p. 6) and continue to be established worldwide at a much faster rate. Figure 1 in “The Global Climate in 2015-2019” report of the World Meteorological Organization [13] shows that the Earth’s average annual temperature (currently about 14oC) since 1990 is increasing by about 0.02o. If this trend were to continue, Earth’s atmospheric temperature would become about 2o higher by the end of this century. But, in terms of the Earth’s climate history, we are currently living with temperatures well below mean temperatures of the geologic past. Although current average temperature is much smaller than it was during the Earth’s geologic past, the current temperature increase is abnormally strong as argued convincingly in the annual reports of the International Panel on Climate Change (IPCC).

3. Devonian Stage Boundaries and Volcanic Ash Beds

Devonian Earth temperature changes were similar to those in the latest Quaternary allowing some comparison between current and past geological climate and weather. Berner [14] provided a method to construct a Phanerozoic CO2 curve. The latest version of his GEOCARB model curve [15] indicates relatively steep decrease in atmospheric temperature during the Devonian about 14o C, similar as it is to-day (also see discussion on pp. 68-70 in [1]).
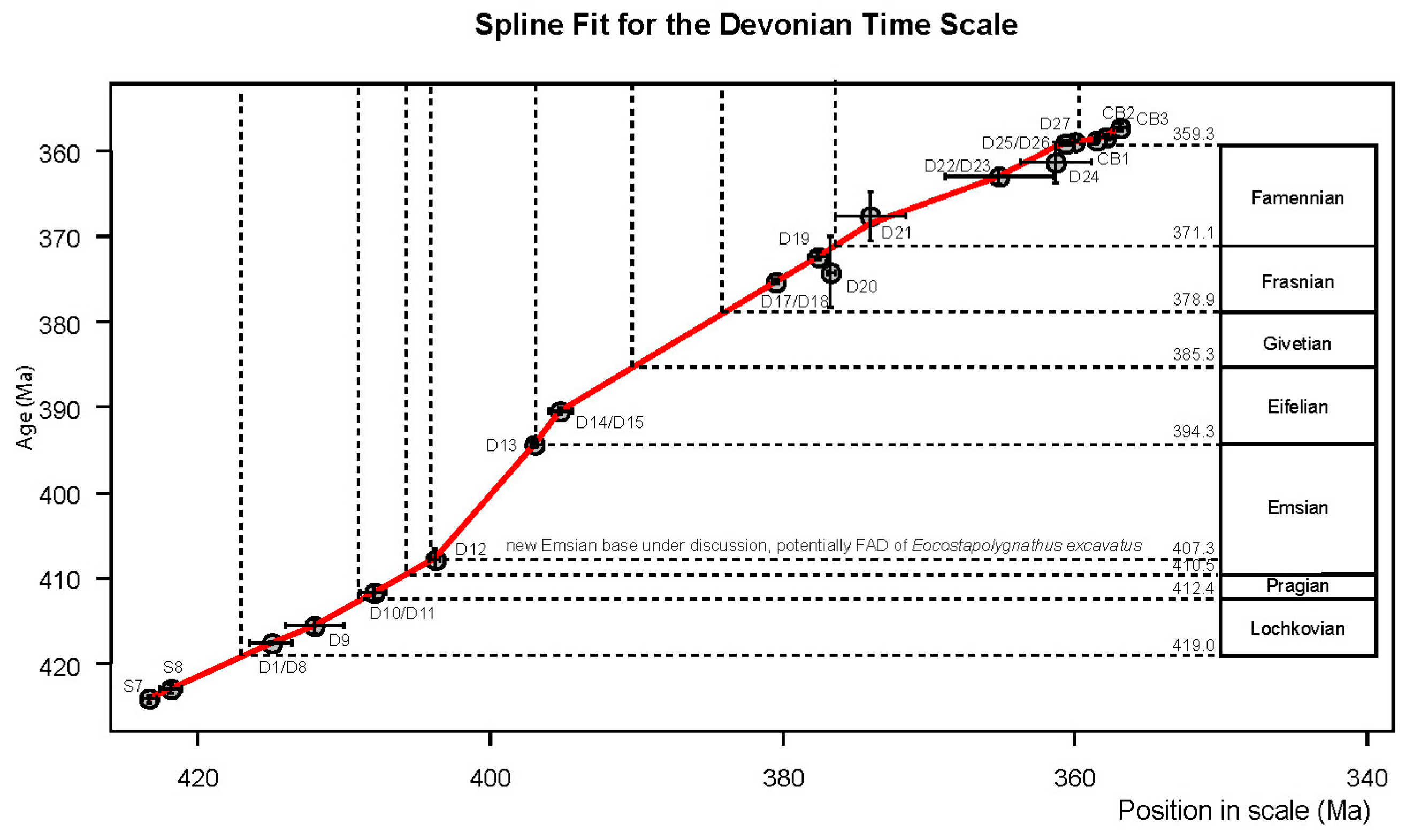
Figure 1 (from [16]) is a two-way graphic plot showing age determinations used to obtain the Devonian time scale. In total, there are 19 data points representing age determinations or averages of two or more radio-isotopic age determinations (on zircons from volcanic ash layers) for calculation of the stage boundaries listed in Appendix 2 of GTS2020 [3] with only 14 data points for the Devonian itself because 3 Carboniferous and 2 Silurian data points were included in order to stabilize the spline-curve fitting at the Epoch boundaries. Several Devonian data points in Figure 1 are averages of two or more measurements on the same ash layer. In total 27 separate age determinations were used.
As explained in more detail elsewhere [17], three sources of uncertainty were considered for estimating the Devonian stage boundary ages on the right side of Figure 1 Two of these are age determination error and chronographic uncertainty plotted in the vertical and horizontal directions for the 19 original data points. The third source of uncertainty considered is due to uneven distribution of ash layers along the geologic time axis.
It is unlikely that relatively many ash layers were preserved. For example, the Devonian lasted approximately 59.7 million years (Myr). Taking the age difference between oldest and youngest published Devonian age determinations, average time interval between known ash layers becomes about (408.42-358.89)/13 = 4.8 Myr. The four latest Anthropocene eruptions producing worldwide ash layers (Tambora: 1835; Krakatau: 1883; El Chicon: 1982 and Mount Pinatubo: 1991; cf. [18]) were, on average, (1991-1835)/3 = 0.000032 Myr apart. Although time intervals between ash layer producing volcanic eruptions during the Anthropocene and the Devonian probably were not equal to one another, the difference between these two time-intervals is so large that it can be assumed that only relatively few worldwide Devonian ash layers were preserved at one or more locations. The best-preserved Devonian ash layer (cf. [19] used for GTS2020 has as many as seven distinct age determinations from the Helderberg Group with outcrops extending from the Catskill Mountains in New York State to Smoke Hole, Virginia.
During most of the Phanerozoic, from base of Ordovician (486.9 Ma) to top of Permian (251.9 Ma), the width of the 95% confidence interval remains approximately constant ranging from a minimum of 0.3 Ma for base of Carboniferous to a maximum of 1.6 Ma for base of Silurian [3,4].
Table 1 shows the GSSPs of the seven Devonian stages. Every GSSP Marker represents a First Appearance Datum of a fossil species. The data in this table have been extracted from Tables 22.1 and 22.31 in Becker et al. [16]. The base of the Famennian is co-defined by the Last Appearance Datum (LAD) of Palmatolepis bogartensis. The Frasnian-Famennian boundary at one time was thought to be the result of extraterrestrial impact of a bolide accompanied by the creation of an iridium anomaly [20]. However, this hypothesis was later discarded as a possible cause. It is not listed in a table of the Earth’s largest impact craters compiled by Earle [21] that includes six such events for the Phanerozoic of which only one led to the definition of a stage boundary: the Chicxulub event that 66.0 million years ago created a 150 km wide crater on the Yucatan Peninsula. The extraterrestrial nature of this event at the Cretaceous-Paleogene boundary was originally discovered because of the occurrence of a worldwide iridium anomaly at this epoch boundary [22].
Although the information in Table 1 represents a best consensus conclusion, it is noted that other conclusions regarding the origin of stage boundaries remain in existence. For example, alternative explanations for the Frasnian-Famennian boundary event include the hypothesis that it was triggered by glaciation and deglaciation or due to sudden warming because of CO2 increase associated with volcanism [23]. Three CO2 increases that probably created mass extinctions have been listed by Esmeray-Senlet [18].
Table 1. Global Boundary Stratotype Sections and Points (GSSPs) of the seven Devonian stages. Every Marker represents a FAD (First Appearance Datum) of a fossil species.; 2σ represents uncertainty.
Table 1. Global Boundary Stratotype Sections and Points (GSSPs) of the seven Devonian stages. Every Marker represents a FAD (First Appearance Datum) of a fossil species.; 2σ represents uncertainty.
Age/Stage AGE (Ma) 2σ GSSP Markers
(Carboniferous) 359.3 0.5 Siphonodella suicata
Famennian 371.1 1.1 Paimatotapia subpertobata
Frasnian 378.9 1.3 Arcyrodella rotnodiloba pristina
Givetian 385.3 1.2 Polignatinus hemiansatus
Eifelian 394.3 1.1 Polignatinus partitus
Emsian 410.5 1.1 Eocostapolygnatinus kitabicus
Pragian 412.4 1.3 Eocostapolygnatinus irregularis

4. Predictability and Randomness

Weather is a chaotic realization of climate that changes gradationally in the course of geologic time. This section and those that follow contain general considerations on how the Earth’s climate should be approached statistically using methods primarily developed in the field of mathematical geoscience. Temperature will be the primary variable of application.
A basic geoscientific prediction problem was considered by Krige as early as 1948 [24]. It consisted of predicting in advance the average gold head of value of panels some distance ahead of mining panels with known gold concentration values. As discussed in more detail elsewhere [25], ordinary linear regression (later also called “kriging”) provided the best prediction results. A similar method is commonly used by meteorologists for prediction of Earth’s future temperature and other parameters. There is, however, the following fundamental difference in the use of regression analysis in these two types of applications.
Krige’s original plots include several for frequencies of average gold concentration values for panel faces that were 30 ft. apart in a Witwatersrand gold mine. The same unit (panel gold content) was used along the two axes of a plot taken for example that shows a contour ellipse for most gold values that, approximately, satisfy a 3-paramer lognormal frequency distribution [24]. Krige’s original regression line on this plot was used for prediction purposes but it deviates strongly from the principal axis of the contour ellipse. The parameters of this axis were estimated by two different methods [25] that, approximately, provided the same answer, The first of these methods consisted of solving Kummell’s equation for linear relationship between two random variables [26]. This method became more widely known as “Deming regression”. The second method was to construct the so-called reduced major axis (RMA) that is scale independent [25]. The latter method will be used for temperature prediction problem later in this paper.
The meteorological prediction problem considered in this paper is more complex that ordinary “kriging” because time-dependent sources of uncertainty have to be considered. Whereas Krige’s gold concentration values satisfy a single lognormal-type frequency distribution model, atmospheric temperature values are to be averaged over specific time intervals during which the average was subject to change. The resulting temperature frequency distributions are heterogeneous mixtures of relatively many single-year average temperature frequency distributions that are probably of the same type but have different means and variances.

5. Worldwide and Large-Area Temperature-Frequency Distribution Modeling

The annual IPCP reports use precise average atmosphere temperature data for a network of fairly large cells (cf. [12] for a simplified discussion). As mentioned before, annual average temperature increase for the entire Earth currently is about 0.02oC.
Stott et al. [28] have considered human contribution to the European heatwave of 2003 that was probably the hottest since at least 1500. Their circum-Mediterranean study area (HadCM3) is bounded by 10oW and 40oE and 30-50o N. Current annual average temperature increase in this region is about 0.05 oC. In the year 2100, its mean temperature would reach about 18 oC. It will be shown for a much smaller continental area (the Netherlands) that its projected 2100 temperature is about the same.
Average temperature increase on the continents significantly exceeds that above the oceans, across which the average regional values are also significantly different but less than on the continents. Above some parts of the oceans there is regional decrease in annual temperature because of absorption of CO2 into the surface water [2].
The current 0.05 C annual increase for the HadCM3 study area is in accordance with a temperature trend line for annual temperatures for the 1900 to 2020 period shown for the Netherlands only on the website www.knmi.nl/kennis-en-datacentrum/achtergrond/gehormoniseerde-reeks-maandtemperatuur-de-Bilt for temperature trend analysis. This website as well as https//www.knminl/klimaat are maintained by the Royal Dutch Meteorological Institute (RDMI).
The preceding estimates of the Earth’s temperature in the year 2100 are small in comparison with Earth’s temperatures in the geological past. However, the current Anthropocene change is unusually rapid and resulting in relatively many chaotic weather conditions. Statistical modeling of weather and climate is obviously of great importance.
The statistical approach taken in this paper differs from methods commonly applied to daily (and yearly) temperature data. The following example (Figure 2, Figure 3 and Figure 4) was derived from the etmgeg_210 file downloaded in August 2023 from the website https//www.knminl/klimaat mentioned above. This notepad file contains daily temperature data for the years from 1951 to 2015 only. Table 2 shows statistics based on the etmgeg_210 file.
Table 2. Comparison of Reduced Major Axis (RMA) with Least Square (LS) coefficients for temperature data extracted from etmgag_210-Notepad file downloaded from the internet.
Table 2. Comparison of Reduced Major Axis (RMA) with Least Square (LS) coefficients for temperature data extracted from etmgag_210-Notepad file downloaded from the internet.
Average Annual Warmest Days Coldest Days
N 109 65 66
RMA Constant -6.015 -2.384 -12.314
RMA Slope 0.048 0.110 0.038
LS Constant -7.712 -5.729 -11.632
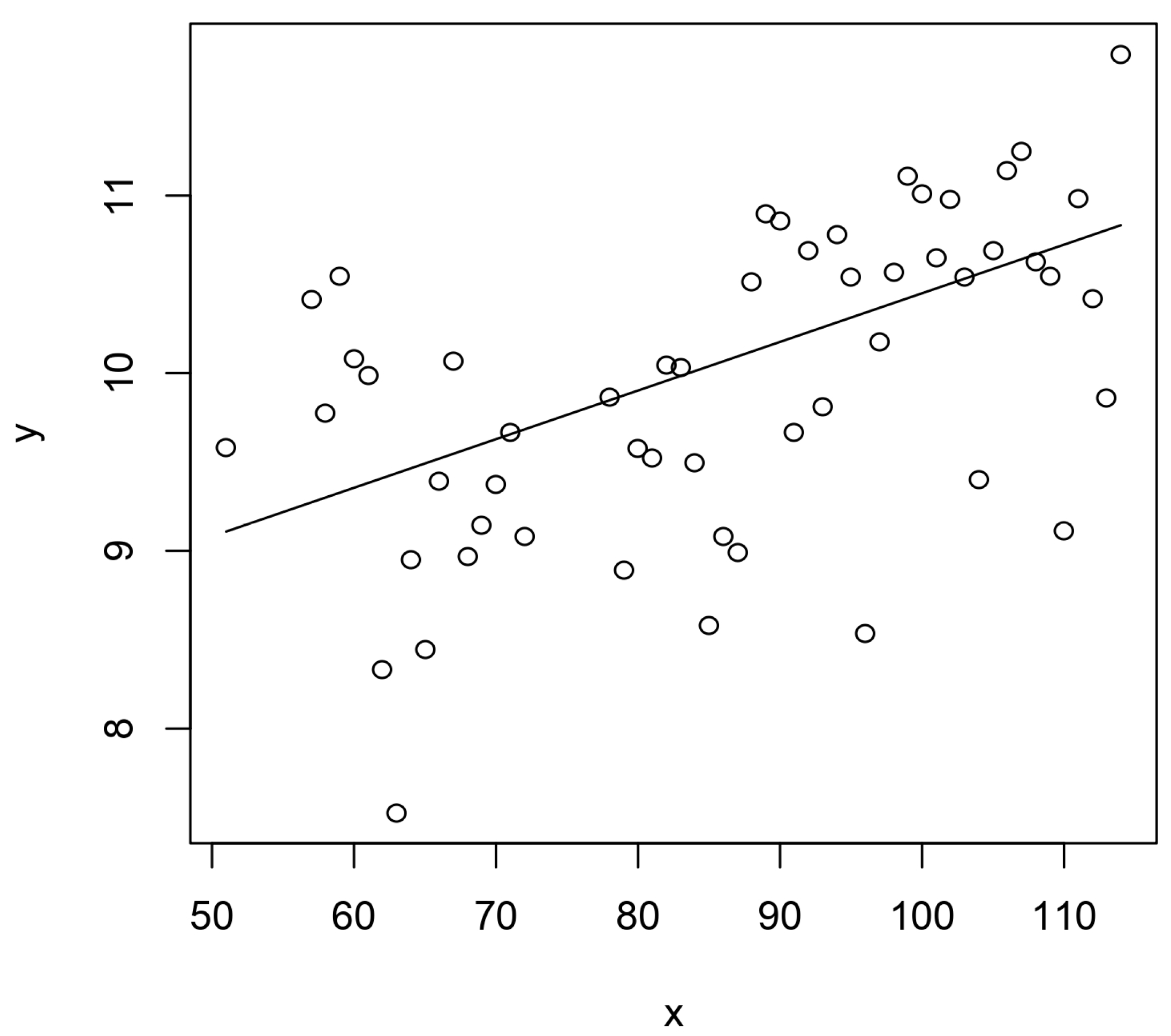
The two statistical techniques applied to etmgeg_210 are ordinary bilinear regression (earliest form of “kriging”) and construction of the RMA (cf. Section 3). In Table 2 the slopes of ordinary regression lines and RMAs are compared with one another for the three types of annual temperature averages shown in Figure 2, Figure 3 and Figure 4.
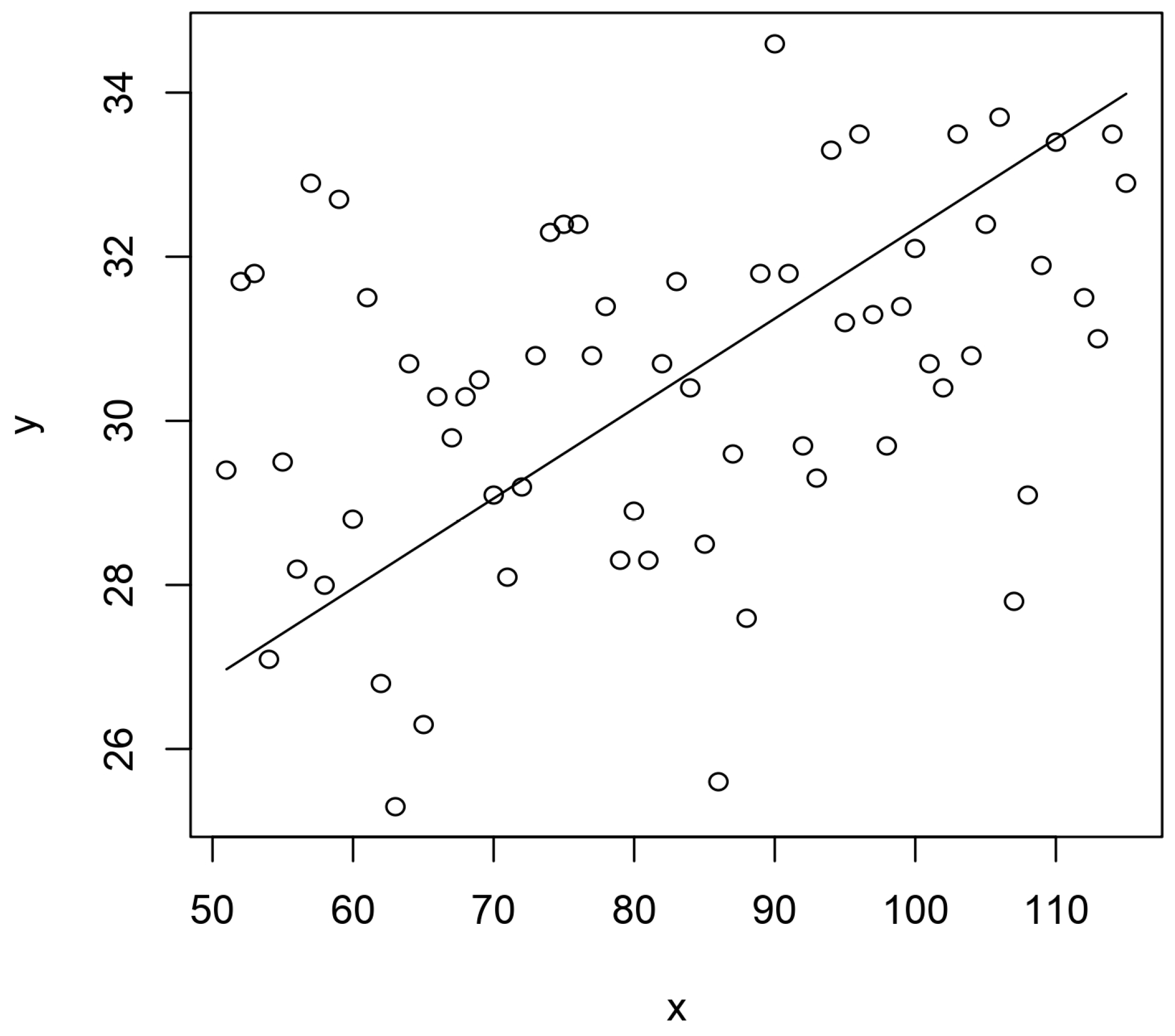
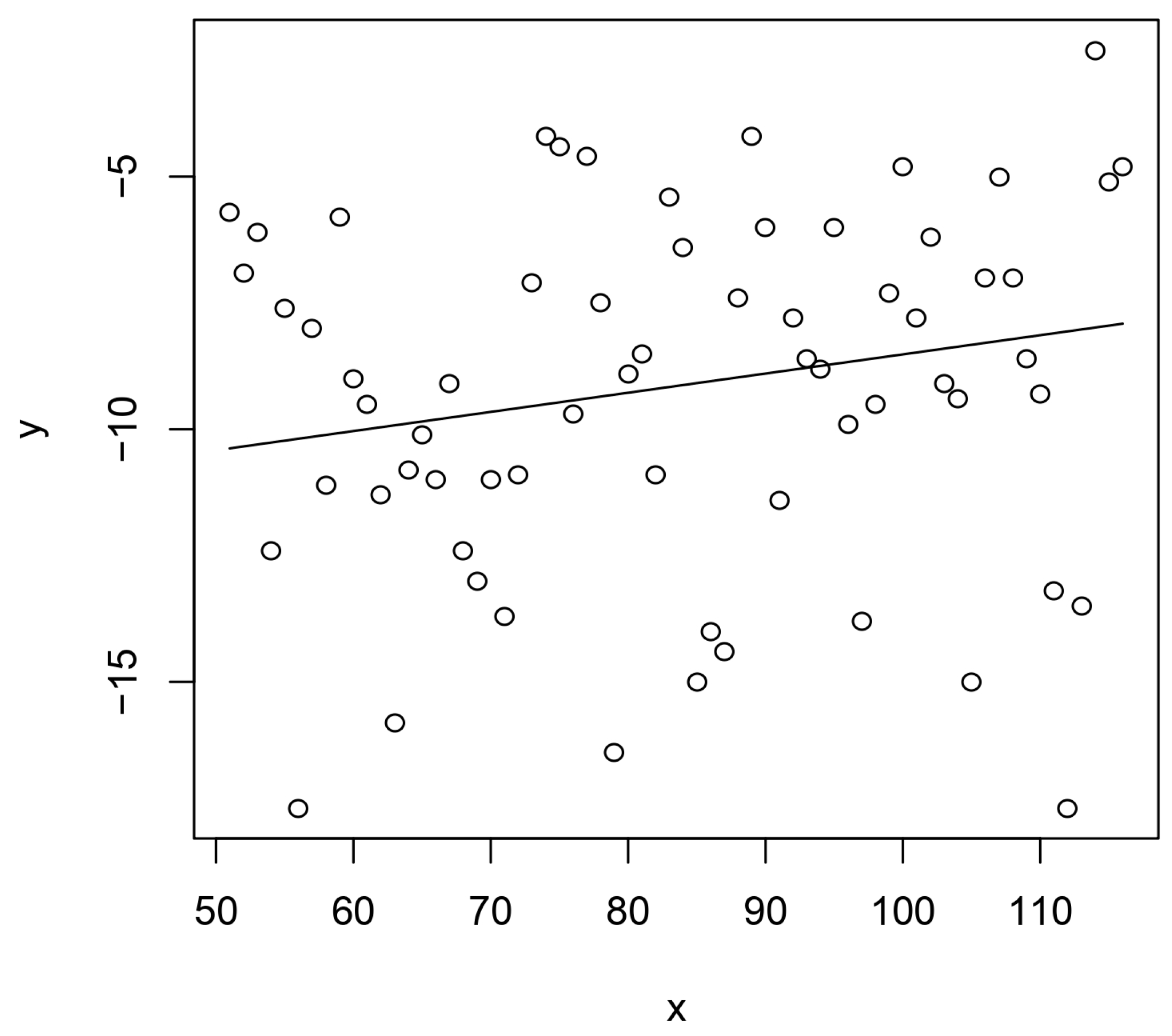
The RMA line shown in Figure 2 coincides approximately with the corresponding segment of the trend pattern produced by RDMI temperature trend analysis and is probably more accurate than the regression line in this application. Figure 3 and Figure 4 show the RMAs for annual maximum and minimum temperatures.
Hottest and coldest days per year are stochastically independent of one another for consecutive years because they are separated from one another by winters or summer s. During any single year, consecutive hottest and coldest days are relatively strongly autocorrelated. For some kinds of statistical analysis as applied by Stott et al. [28], it is useful to work with average temperatures for several consecutive days. This stabilizes the temperature values used but reduces their variances. The RMA’s shown in Figure 3 and Figure 4 are useful because they indicate the spreads of hottest and coldest days in the Netherlands that can be expected if current warming trends would be maintained in the future.
The previously mentioned website https//www.knminl/klimaat contains other interesting information as well. Figure 1 in an article on weather extremes in the Netherlands by Peter Siegmund (for the period from 1960 to 2019) shows annual estimated trend (in oC/60) for the separate 365 (or 366) days per year ranked from coldest to hottest. For nearly the entire year the trend pattern is sub-horizontal fluctuating between about 0.03 and 0.05 oC/60. However, there are two sharp peaks up to about 0.07 and 0.08 oC/60 restricted to the first and last 5 days of the year. In the next sections of this paper, it will be shown that patterns of this type are in accordance with multifractal modeling using a modified version of a multifractal Pareto-lognormal frequency distribution model for world and regional annual temperatures.
Preprints 96158 g002
Figure 2. Average annual temperatures in the Netherlands from 1951 to 2015 as calculated from the etmgag_210-Notepad file downloaded from the internet; x – Year – 1900; y – Temperature (oC). Solid line is Reduced Major Axis (RMA) fitted to data points shown as circles. From 1980 onward the line approximately coincides with 5 October, 2023 KNMI trendline of De Bilt on https//www.knminl/klimaat.
Figure 2. Average annual temperatures in the Netherlands from 1951 to 2015 as calculated from the etmgag_210-Notepad file downloaded from the internet; x – Year – 1900; y – Temperature (oC). Solid line is Reduced Major Axis (RMA) fitted to data points shown as circles. From 1980 onward the line approximately coincides with 5 October, 2023 KNMI trendline of De Bilt on https//www.knminl/klimaat.
Preprints 96158 g002
Preprints 96158 g003
Figure 3. Maximum annual temperatures in the Netherlands from 1951 to 2015 with RMA. x – Year – 1900; y – Temperature (oC).
Figure 3. Maximum annual temperatures in the Netherlands from 1951 to 2015 with RMA. x – Year – 1900; y – Temperature (oC).
Preprints 96158 g003
Preprints 96158 g004
Figure 4. Minimum annual temperatures in the Netherlands from 1951 to 2015 with RMA. x – Year – 1900; y – Temperature (oC).
Figure 4. Minimum annual temperatures in the Netherlands from 1951 to 2015 with RMA. x – Year – 1900; y – Temperature (oC).
Preprints 96158 g004

6. Multifractal Modeling

As mentioned in the Introduction, Anthropocene weather and climate are, to a large extent, characterized by multifractal processes that are difficult to study by traditional methods of time series analysis. Spectral analysis offers a unique tool to establish multifractality. Precise temperature proxy data are available for the last 5 stages of the Quaternary. They come from drilling ice sheets on Greenland and in Antarctica [26]. These data also form the basis of the approach to weather, macroweather and climate advocated by Lovejoy and Schertzer [7,8].
It is well-known that the power spectrum offers a good method to study periodic phenomena. A sine-curve in the time series domain projects as a single point in the spectrum. If real-world phenomena such as the 11- and 22-yeat sunspot cycles are not exactly sinusoidal, such deviations from the sine curve show up as peaks and harmonics on the spectrum. It is less well-known that many types of moving averages for time series become horizontal lines on the spectrum.
Multifractal phenomena become straight lines on the spectrum with a distinct angle of dip commonly written as β that provide a measure of degree of chaos; e.g. the composite spectrum of the GPS (Global Positioning Data) summit ice-core δ18O (a temperature proxy) data (see Figure 1.9 in [7]) show βw ≈ 2, βmw ≈ 0.2 and βc ≈ 1.4, where the subscripts w, mw and c denote weather, macroweather and climate, respectively. This example from Greenland applies to the last 91,000 years. It shows that indicates that both weather and climate are chaotic but accompanied by the fairly stable macroweather.
A comprehensive review of applications of multifractality to recent weather has been provided by Dubrulle [27]/ An application of spectral analysis to recent extreme weather and climate-related events was given by Stott et al. [28]. Undoubtedly, multifractal processes took place frequently during the Earth’s history. Direct evidence of the occurrence of such processes has only rarely been preserved in the geologic record. Korvin [29] has listed relatively many examples of fractals and multifractals that occurred in the distant past including the formation of Early Cretaceous sand banks in the Lloydminster area of Alberta. Another relatively widespread example of Phanerozoic multifractal activity is the so-called Bouma sequence resulting from turbidity currents [30]. However, only Anthropocene multifractality can be explored in great detail, although spectral analysis of Late Quaternary ice-cores in Greenland and Antarctica shows earlier multifractality [1].

7. Pareto-Lognormal Distributions

DaCamara et al. [31] have pointed out that current radiative power released by vegetation fires satisfies a doubly truncated central lognormal frequency distribution with separate Pareto tails instead of lognormal tails for the largest and the smallest values. This multifractal statistical model can be applied to other Earth-temperature related variables including average temperature across different areas above the continents and the oceans.
The Pareto-lognormal size-frequency distribution model is based on the so-called double Pareto-lognormal model originally developed by Reed and Jorgensen [32,33] with cumulative distribution function:
F log ⁡ x ≈ Φ log ⁡ x − μ σ − 1 α + β β ∙ x − α A α , μ , σ Φ log ⁡ x − μ − α σ 2 σ + α ∙ x β A − β , μ , σ Φ c log ⁡ x − μ + β σ 2 σ
where A (ϑ, σ, μ) = exp (ϑ μ + ϑ2σ2/2). This model is characterized by a central lognormal distribution Φ log ⁡ x − μ μ   in which the upper and lower tails are replaced by Pareto distributions with Pareto coefficients equal to α and β, respectively. It has had various applications in the economic and actuarial sciences [34]. One of the properties of the model is that β > 1 [33].
DaCamara et al. [31] attempted to apply the preceding approach to statistical modeling of radiative power released by vegetation fires but discovered that β < 1 instead of β > 1. These authors based their statistical analysis on their global scale FRP (Fire Radiative Power) database extracted from NASA’s Fire Information Resource Management System (FIRMS). Three samples obtained resulted in tens of millions FRP estimates covering a 19-year period. (2002-2021). This study period was further partitioned into 10-year and 9-year subperiods. Excellent fits were obtained for lognormal frequency distributions fitted to the central parts of the series and for two different Pareto distributions fitted to their tail ends.
The (β < 1) problem had been encountered before in that the original Reed double Pareto-lognormal model could not be applied to worldwide and Canadian metal ore size-frequency data, although these metal size- frequency distributions also were shown to have a central lognormal distribution with Pareto tails [35,36,37]. In all applications to metal size-frequency distributions the upper Pareto tail parameter was found to be less than 1 so that the original Reed model [32] could not be applied.
Both normal (or “Gaussian”) and Pareto frequency distributions are “stable” end products resulting from various combinations of random variables that are not necessarily normal nor Pareto-type. This property is better known for the central lognormal because the Pareto applies to relatively rare events only. The relationship between explicitly lognormal and normal distributions is that the normal is a limiting form of the lognormal reached when the logarithmic variance approaches zero. Most applications of the Pareto distributions are to the largest values of variables such as income and town size. Similar considerations apply to the smallest values of many other types of variables. In the following application of the Pareto-lognormal, model, the lower Pareto tail parameter is defined as κ < 1. The following generalization of Reed’s double Pareto-lognormal was originally developed for amounts of metal in worldwide and Canadian mineral deposits [35,36,37]. This mode can be applied to average annual temperatures for large regions as well.
The cumulative frequency distribution for the modified Pareto-lognormal distribution F(x) = F(log x) can be written as
F log ⁡ x ≈ Φ log ⁡ x − μ σ + H ( log ⁡ x − μ ) ∙ B 1 log ⁡ x ∙ ( log ⁡ x − μ ) − α + H μ − log ⁡ x ∙ B 2 log ⁡ x ∙ ( μ − log ⁡ x ) − κ
where Φ log ⁡ x − μ μ   represents the central lognormal (logs base 10). H (…) is the Heaviside function that applies to two filtered Pareto distributions, for positive and negative values of (log x - µ), respectively; it signifies that values at the other side of µ are set equal to zero when this equation is applied to either the upper tail or the lower tail of the Pareto-lognormal distribution. The bridge functions B1(log x) and B2(log x) span relatively short intervals between the central lognormal and the Pareto tail distributions for largest and smallest values, respectively. They satisfy lim x → ∞ ⁡ B 1 log ⁡ x = lim x → 0 ⁡ B 2 log ⁡ x = 1 and lim x → 0 ⁡ B 1 log ⁡ x = lim x → ∞ ⁡ B 2 log ⁡ x = 0 . The exponents in ( log ⁡ x − μ ) − α − 1 and ( μ − log ⁡ x ) − κ − 1 reflect the fact that the Pareto probability density functions in the tails remain linear on a plot with logarithmic scales for both frequency and deposit size, but have steeper dips than in the corresponding plot for the cumulative frequency distribution. In applications to amounts of metal contained in ore deposits, both bridge functions were assumed to be linear and could be defined by two parameters that can be estimated [36,37].

8. Summary and Concluding Remarks

Earth’s Phanerozoic climate history was summarized in the first part of this paper. It is mainly characterized by major deterministic events that resulted in the stage boundaries of the worldwide geologic time scale. Other Phanerozoic events many of which were probably worldwide include the relatively many ash layers that contain dateable zircons. Currently, Earth is being subjected to relatively rapid temperature increases because of abnormally rapid addition of greenhouse gases to the atmosphere. Current weather and climate have both multifractal and deterministic Anthropocene heating trend properties. Because worldwide or regional temperature time series do not have constant mean and variance, it is not possible to fit a single double-sided Pareto lognormal frequency distribution.
Nevertheless, the resulting heterogeneous frequency distributions remain approximately Pareto-lognormal. As discussed elsewhere, the sum of a uniform and a normal frequency distribution [24], is a mixture of normal Ф-distributions with means that increase (or decrease) linearly (and with corresponding variances that change non-linearly) approximately satisfies another normal Ф-distribution. Similar minor alterations of shape probably affected the Pareto tails of the Pareto-lognormal in DaCamara et al.’s applications in which number of years for averaging was sufficiently small. Such condition is probably not satisfied for the examples resulting in Figure 2, Figure 3 and Figure 4 in this paper for which the time series spans 65 years.
As discussed at the end of Section 5, lumping ranked daily temperature-data for the Netherlands over a 60-year time interval resulted in a yearly flat frequency pattern for most days but with sharp peaks at for the relatively few hottest and coldest days of the year. Such pattern departs from near-lognormality of the central part of the overall annual daily temperature frequency distribution but would fit in with the existence of Pareto tails. Admittedly, the examples given in this paper of probable and possible universal double tail Pareto-lognormal frequency distributions that are worldwide and for continental subregions remain largely speculative at this point in time but the approach constitutes a topic worthy of further research.
Earth’s temperature history during the Quaternary was compared with that of the Devonian near the beginning of this paper. It is likely that the Anthropocene multifractality that can be studied in detail also existed during the Earth’s Phanerozoic past but fossilized remains of multifractality are rare and studying them is also handicapped by limited precision of existing age determination methods.

Acknowledgments

Thanks are due to Prof. Felix Gradstein, Emeritus, Natural History Mu-seum, University of Oslo, for discussions and helpful comments.

References

  1. Cronin, T. H. Paleoclimates, Columbia University Press: New York, US, 2009.
  2. Ruddiman, W. F. Earth’s Climate, W.H. Freeman, New York, US, 2001.
  3. Gradstein, F.M. , Ogg, J.G., Schmitz, M.E., Ogg, G.M., Eds., Geologic Time Scale 2020. Elsevier, Amsterdam, 2 volumes, 2020.
  4. Gradstein, F.M. , Agterberg, F.P. Application of Supersplining to the Mesozoic and Paleozoic Geologic Time Scale. Mathematical Geosciences 2022, 54, 1207–1226. [Google Scholar] [CrossRef]
  5. Cheng, Q. Quantitative simulation and prediction of extreme geological events. SCIENCE CHINA Earth Sciences, 2022, 1012-1029.
  6. Agterberg, F.P. , Da Silva, A-C., Gradstein, F.M. Geomathematical and statistical procedures, Gradstein, F.M., Ogg, J.G., Schmitz, M.E., Ogg, G.M., Eds., Geologic Time Scale 2020. Elsevier, Amsterdam, 2 volumes, 2020, 401-424.
  7. Lovejoy, S. , Schertzer, D. The Weather and Climate: Emergent Laws and Multifractal Cascades. Cambridge University Press, 2018.
  8. Lovejoy, S. Weather, Macroweather and the Climate. Oxford University Press, 2019.
  9. Arrhenius, S. On the influence of carbonic acid in the air upon the temperature of the ground. Philosophical Magazine and Journal of Science 1896, 41, 237–276. [Google Scholar] [CrossRef]
  10. Zalaslewicz, J. , Waters, C. , Williams, M. The Anthropocene, Gradstein, F.M., Ogg, J.G., Schmitz, M.E., Ogg, G.M., Eds., Geologic Time Scale 2020., v. 2, Elsevier, Amsterdam 2020, 2, 1257–1280. [Google Scholar]
  11. Ruddiman, W.F. Plows, Plagues, and Petroleum – How Humans took Control of Climate. Princeton University Press, 201berozooic 6.
  12. Easterbrook, S.M. Computing the Climate. Cambridge University Press, 2023.
  13. World Meteorological Organization. The Global Climate in 2015-2019. WMO, Geneva 2020.
  14. Berner, R.A. Atmospheric carbon dioxide levels over Phanerozoic time. Science 1990, 249, 1382–1386. [Google Scholar] [CrossRef] [PubMed]
  15. Berner, R. A Khotavala, Z. GEOCARB III. A revised model for Phanerozoic CO2 over Phanerozoic time. American Journal of Science 2001, 301, 182–204. [Google Scholar] [CrossRef]
  16. Becker, R.T., Marshall, J.F.A., Da Silva, A.‐C. The Devonian Period. Gradstein, F.M., Ogg, J.G., Schmitz, M.E., Ogg, G.M., Eds., Geologic Time Scale 2020., Elsevier, Amsterdam 2020, 2, 713–810.
  17. Agterberg, F.P. Da Silva, A-C., Gradstein, F.M. Geomathematical and statistical procedures. Gradstein, F.M., Ogg, J.G., Schmitz, M.E., Ogg, G.M., Eds., Geologic Time Scale 2020., Elsevier, Amsterdam 2020, 1, 401–424.
  18. Esmeray-Senlet, S. Three major mass extinctions and evolutionary radiations in their aftermath. Gradstein, F.M. Geomathematical and statistical procedures. Gradstein, F.M., Ogg, J.G., Schmitz, M.E., Ogg, G.M., Eds., Geologic Time Scale 2020., Elsevier, Amsterdam 2020, 1, 125–137.
  19. Husson, J.N. , Schoene, B., Bluber, S., Maloof, A.C. Chemostratigraphic and U-Pb geochronologic constraints on carbon cycling Silurian-Devonian boundary. Earth and Planetary Science Letters 2020, 436, 108–120. [Google Scholar] [CrossRef]
  20. McLaren, DJ. Bolides and biostratigraphy. Geol. Soc. of America Bulletin 1983, 94, 313–324. [Google Scholar] [CrossRef]
  21. Earle, S. A brief History of the Earth’s Climate. New Society Publishers, Gabriola Island, B.C., Canada, 2023.
  22. Hildebrand, A. Penfield, G.T, King, D.A., Pilkington, M., Canargo, A., Stein, Z., Jacobson, B., Boynton, W.V. Chicxulub Crater: a possible Cretaceous/Tertiary boundary impact crater on the Yucatan Peninsula, Mexico. Geology 1991 19, 867-871.
  23. Krige, D.G. Economic aspects of stoping through unpayable ore. J. S. Afr. Inst. Min. Metall. 1962, 63, 364–374. [Google Scholar]
  24. Agterberg, F.P. Geomathematics – Mathematical background and geoscience applications. Elsevier, Amsterdam, 1974.
  25. Deming, E. Statistical Adjustment of Datai. Wiley, New York, 1943.
  26. Bradley, R.S. Paleoclimatology – Reconstructing Climates of the Quaternary. Elsevier, Amsterdam, 2019.
  27. Dubrulle, B. Multifractality, universality and singularity in turbulence. Fractal and Fractional 2022 6, 613–637.
  28. Stott, P.E. , Stone, D.A., Allen, M.R. Human contribution to the European heatwave of 2003. Nature 2004, 432, 619–614. [Google Scholar] [CrossRef] [PubMed]
  29. Korvin, G. Fractal Models in the Earth Sciences. Elsevier, Amsterdam 1992.
  30. Agterberg, F. Turbulence. In: Daya Sagar, B.S., Cheng, Q., McKinley, J, Agterberg, F., Eds., Encyclopedia of Mathematical Geosciences. Springer, Cham, Switzerland 2023, 2, 1576–1578.
  31. DaCamara, C.C. Libonati, R., Nunes, S.A., de Zea Bermudes, P., Pereira, J.M.C. Global-scale statistical modeling of the radiative power released by vegetation fires using a doubly truncated lognormal body distribution with generalized Pareto tails. Physics A. Statistical Mechanics and its Applications 2021.
  32. Reed, W.J. The Pareto law of incomes – An explanation and an extension. Physica A 2003, 319, 579–597. [Google Scholar] [CrossRef]
  33. Reed, W.J. , Jorgenson, M. The double Pareto-lognormal distribution – A new parametric model for size distributions. Computational Statistics – Theory and Methods 2003, 33, 1733–1753. [Google Scholar] [CrossRef]
  34. Kleiber, C. Kotz, S. Statistical Distributions in Economics and Actuarial Sciences. Wiley, Hoboken, NJ. 2003.
  35. Agterberg, F.P. Pareto-lognormal modeling of known and unknown metal resources. Natural Resources Research 2017, 26, 1–20, (with erratum on p. 21). [Google Scholar] [CrossRef]
  36. Agterberg, F. Multifractal modeling of worldwide and Canadian metal size frequency distributions. Natural Resources Research 2019, 29, 539–550. [Google Scholar] [CrossRef]
  37. Agterberg, F., Cheng, Q. Chaos in geosciences. In: Daya Sagar, B.S., Cheng, Q., McKinley, J, Agterberg, F., Eds., Encyclopedia of Mathematical Geosciences. Springer, Cham, Switzerland 2023, 1, 107–113.
Preprints 96158 g001
Figure 1. Devonian Time Scale according to Becker et al. [18]. Two-way graphic plot of scaled zonation with cubic spline fit. (Reprinted with permission from [3]).
Figure 1. Devonian Time Scale according to Becker et al. [18]. Two-way graphic plot of scaled zonation with cubic spline fit. (Reprinted with permission from [3]).
Preprints 96158 g001
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated