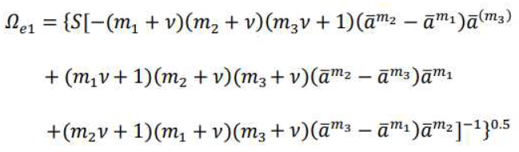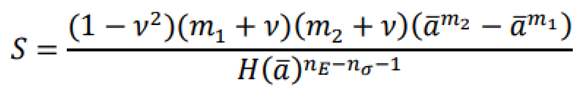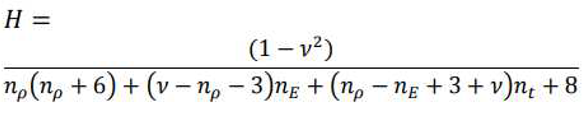1. Introduccian

2. Equations of Motion

there is a hollow disk made of functionally graded materials, which is sufficiently thin and large, with inner radius a and outer radius b, rotating at an angular velocity $\omega$. Considering the geometry of the problem, the formulation and analysis are performed in cylindrical coordinates $(z,\theta ,r)$. The thickness of the disk section, elastic modulus, density, and yield stress are assumed to be power functions (1) of the radial coordinate:

(1)

In order,$h_0$ the values of thickness, Young’s modulus $E_0$ are given by equations (1). ${\rho }_0$density, and ${\sigma }_{Y_0}$ yield stress at the outer radius $(r=b)$ are also provided. The parameters $n_t$,$n_E$,$n_{\rho }$ and $n_{\sigma }$ represent the geometric and material properties and are defined as per equations (2).

(2)

The equation of motion for the rotating disk, considering the effect of thickness, is expressed as equation (3).

(3)

The components of radial and hoop stresses, ${\sigma }_r$ and ${\sigma }_{\theta }$, in equation (3) are represented. It should be noted that the volumetric force due to weight ($\rho g$) has been neglected. Now, the radial and hoop displacements, u and v, are considered. Due to axial symmetry, there is no hoop displacement, and in other words, $v=0$. Therefore, the stress equations in cylindrical coordinates are as follows:

(4)

Using Hooke’s law for the state of plane stress and displacement, strain equations (4) are employed, and the stress-displacement relationship is obtained in the form of equations (5).

(5)

By substituting the stress components into equation (3), the equation of motion the disk is transformed into the form of equation (6).

(6)

The analytical solution of the second-order differential equation (6) has a general solution in the form of equation (7):

(7)

In which $C_1$ and $C_2$ are integration constants. Also, the constant parameters in equation (7) are defined as equations (8).

(8)

By substituting the displacement equation (7) into the strain equations (5), the radial and hoop stresses are obtained in terms of the constants $C_1$ and $C_2$ as equations (9).

(9)

The constants $C_1$ and $C_2$ are obtained. For a hollow disk, the radial stress at the inner boundaries ${\left({\sigma }_r\right)}_{r=a}$ and the exterior ${\left({\sigma }_r\right)}_{r=b}$ is zero. Therefore, by applying the boundary conditions for the disk, the constants $C_1$ and $C_2$ are obtained in equation (10).

(10)

In which R is a constant parameter defined in equation (10) as follows:

(11)

In order to obtain general solutions, the derived equations are made dimensionless using equations (12).

(12)

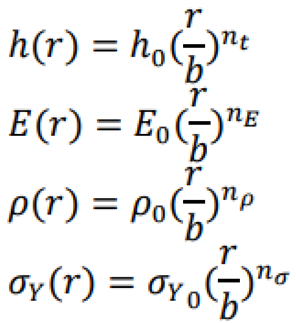
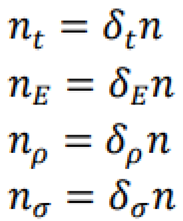
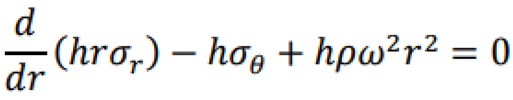
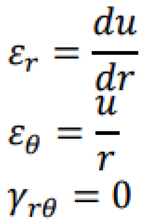
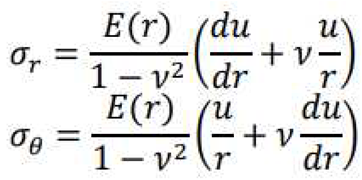
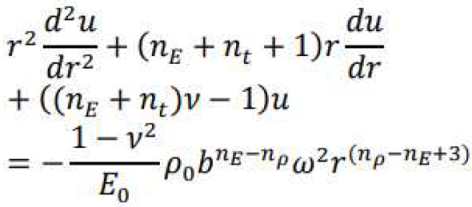
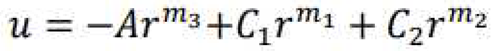
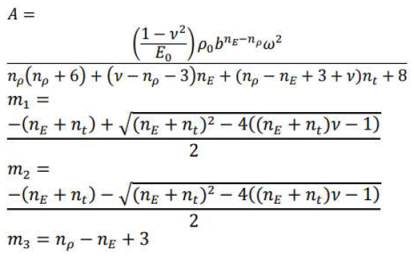
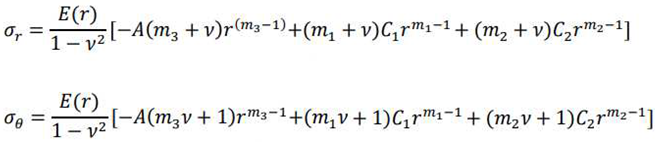
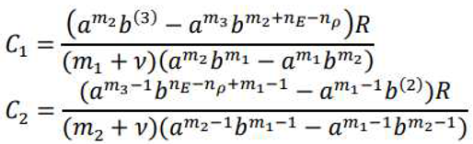
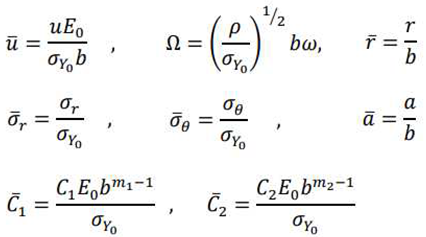
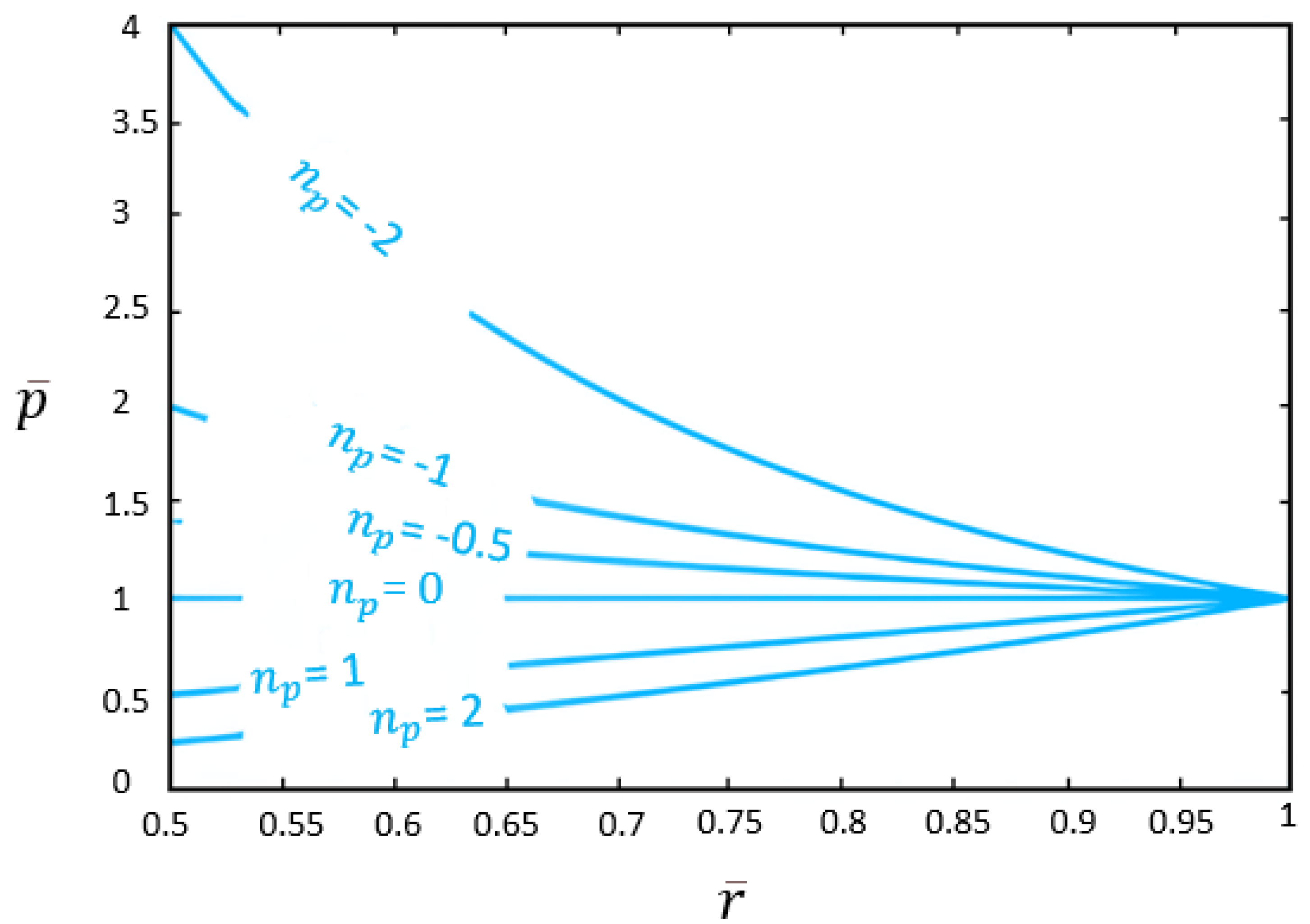
3. Analyze yielding state

In order to determine the angular velocities corresponding to the yielding threshold and examine the yielding conditions, the Tresca yielding criterion has been employed. The utilization of the Tresca yielding criterion necessitates establishing the order of principal stresses ${\sigma }_r$ and ${\sigma }_{\theta }$. On the other hand, the order of principal stresses is dependent on the numerical values of the power parameters ($n_t$, $n_p$,$n_E$ and $n_{\sigma }$) and the ratio of radii $(r/b)$. Therefore, for monitoring the initiation of yielding, a dimensionless variable $\Psi$ based on the Tresca criterion is utilized. This variable is defined by the equation (13).

(13)

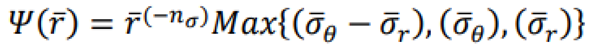
3.1. State 1: Initiating yielding from the inner radius

Yielding occurs when $\Psi \left(\overline{a}\right)=1$ and the function $\Psi$ has its maximum absolute value at the inner radius. By utilizing the stress equations (9) and applying the boundary condition ${\left({\overline{\sigma }}_r\right)}_{\overline{r}=\overline{a}=0}$, the dimensionless terminal rotational velocity ${\Omega }_{e1}$ can be defined as per the equation (14):

(14)

The constant S is defined as equation (15).

(15)

Where H is expressed as equation (16).

(16)

3.2. State 2: Initiating yielding from the outer radius

In this case, yielding occurs when $\Psi \left(1\right)=1$ and the function $\Psi$ has its maximum absolute value at the outer radius. By using the stress equations (9) and applying the boundary condition ${\left({\overline{\sigma }}_r\right)}_{\overline{r}=\overline{b}}=0$, the dimensionless terminal rotational velocity ${\omega }_{e_2}$ is defined as an equation (17):

(17)

In which the constant $S_b$ is defined as equation (18):

(18)

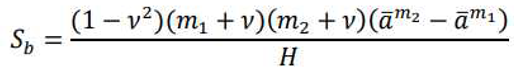
3.3. State 3: Simultaneous yielding initiation from both inner and outer radii.

In this case, yielding commences simultaneously from the inner and outer radii when both $\Psi \left(\overline{a}\right)=1$ and $\Psi \left(1\right)=1$ are satisfied, and the function $\Psi$ must have maximum absolute values at both the inner and outer radii. Considering the boundary conditions of the disc and using equations (14) and(17), the critical dimensionless angular velocity ${\omega }_{c_r}$ and critical power parameter $n_{c_r}$ can be obtained by solving the system of equations (19).

(19)

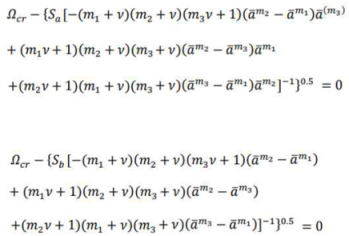
3.4. State 4: Yielding initiation from a radius between the inner and outer radii.

To initiate yielding from a radius between the inner and outer radii, the dimensionless function $\Psi$ at the yielding initiation point $r_{ep}$ must be equal to 1 and have the maximum absolute value at this point. For this reason, equation (20) must hold true to initiate yielding from the boundary between the inner and outer radii.

(20)

Equation (20) is used to calculate the required terminal rotational velocity for initiating plastic flow and the location of yielding initiation point ${\overline{r}}_{ep}$ for a specific power parameter n.

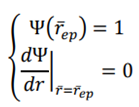
4. Conclusions

References

1. Tajdari, F.; Roncoli, C. Online set-point estimation for feedback-based traffic control applications. IEEE Transactions on Intelligent Transportation Systems 2023. [Google Scholar] [CrossRef]
2. Tajdari, F.; Ramezanian, H.; Paydarfar, S.; Lashgari, A.; Maghrebi, S. Flow metering and lane-changing optimal control with ramp-metering saturation. 2022 CPSSI 4th International Symposium on Real-Time and Embedded Systems and Technologies (RTEST). IEEE, 2022, pp. 1–6. [CrossRef]
3. Rad, N.F.; Yousefi-Koma, A.; Tajdari, F.; Ayati, M. Design of a novel three degrees of freedom ankle prosthesis inspired by human anatomy. 2016 4th International Conference on Robotics and Mechatronics (ICROM). IEEE, 2016, pp. 428–432. [CrossRef]
4. Rad, N.F.; Ayati, M.; Basaeri, H.; Yousefi-Koma, A.; Tajdari, F.; Jokar, M. Hysteresis modeling for a shape memory alloy actuator using adaptive neuro-fuzzy inference system. 2015 3Rd RSI international conference on robotics and mechatronics (ICROM). IEEE, 2015, pp. 320–324. [CrossRef]
5. Tajdari, F.; Huysmans, T.; Song, Y. Non-rigid registration via intelligent adaptive feedback control. IEEE transactions on visualization and computer graphics 2023. [Google Scholar] [CrossRef]
6. Tajdari, M.; Tajdari, F.; Pawar, A.; Zhang, J.; Liu, W.K. 2d to 3d volumetric reconstruction of human spine for diagnosis and prognosis of spinal deformities. Conference: 16th US national congress on computational mechanics, 2021.
7. Tajdari, M.; Pawar, A.; Li, H.; Tajdari, F.; Maqsood, A.; Cleary, E.; Saha, S.; Zhang, Y.J.; Sarwark, J.F.; Liu, W.K. Image-based modelling for adolescent idiopathic scoliosis: mechanistic machine learning analysis and prediction. Computer methods in applied mechanics and engineering 2021, 374, 113590. [Google Scholar] [CrossRef]
8. Tajdari, F.; Roncoli, C.; Papageorgiou, M. Feedback-based ramp metering and lane-changing control with connected and automated vehicles. IEEE Transactions on Intelligent Transportation Systems 2020, 23, 939–951. [Google Scholar] [CrossRef]
9. Tajdari, F.; Roncoli, C.; Bekiaris-Liberis, N.; Papageorgiou, M. Integrated ramp metering and lane-changing feedback control at motorway bottlenecks. 2019 18th European Control Conference (ECC). IEEE, 2019, pp. 3179–3184. [CrossRef]
10. Ghaffari, A.; Khodayari, A.; Kamali, A.; Tajdari, F.; Hosseinkhani, N. New fuzzy solution for determining anticipation and evaluation behavior during car-following maneuvers. Proceedings of the Institution of Mechanical Engineers, Part D: Journal of automobile engineering 2018, 232, 936–945. [Google Scholar] [CrossRef]
11. Khodayari, A.; Ghaffari, A.; Kamali, A.; Tajdari, F. A new model of car following behavior based on lane change effects using anticipation and evaluation idea. Iranian Journal of Mechanical Engineering Transactions of the ISME 2015, 16, 26–38. [Google Scholar]
12. Tajdari, F.; Roncoli, C. Adaptive traffic control at motorway bottlenecks with time-varying fundamental diagram. IFAC-PapersOnLine 2021, 54, 271–277. [Google Scholar] [CrossRef]
13. Tajdari, F.; Toulkani, N.E.; Zhilakzadeh, N. Intelligent optimal feed-back torque control of a 6dof surgical rotary robot. 2020 11th Power Electronics, Drive Systems, and Technologies Conference (PEDSTC). IEEE, 2020, pp. 1–6. [CrossRef]
14. Tajdari, F.; Kabganian, M.; Rad, N.F.; Khodabakhshi, E. Robust control of a 3-dof parallel cable robot using an adaptive neuro-fuzzy inference system. 2017 Artificial Intelligence and Robotics (IRANOPEN). IEEE, 2017, pp. 97–101. [CrossRef]
15. Tajdari, F.; Kabganian, M.; Khodabakhshi, E.; Golgouneh, A. Design, implementation and control of a two-link fully-actuated robot capable of online identification of unknown dynamical parameters using adaptive sliding mode controller. 2017 Artificial Intelligence and Robotics (IRANOPEN). IEEE, 2017, pp. 91–96. [CrossRef]
16. Saleh, B.; Jiang, J.; Fathi, R.; Al-hababi, T.; Xu, Q.; Wang, L.; Song, D.; Ma, A. 30 Years of functionally graded materials: An overview of manufacturing methods, Applications and Future Challenges. Composites Part B: Engineering 2020, 201, 108376. [Google Scholar] [CrossRef]
17. Tajdari, F.; Toulkani, N.E.; Zhilakzadeh, N. Semi-real evaluation, and adaptive control of a 6dof surgical robot. 2020 11th Power Electronics, Drive Systems, and Technologies Conference (PEDSTC). IEEE, 2020, pp. 1–6. [CrossRef]
18. Tajdari, F.; Tajdari, M.; Rezaei, A. Discrete time delay feedback control of stewart platform with intelligent optimizer weight tuner. 2021 IEEE International Conference on Robotics and Automation (ICRA). IEEE, 2021, pp. 12701–12707. [CrossRef]
19. Tajdari, F.; Ebrahimi Toulkani, N. Implementation and intelligent gain tuning feedback–based optimal torque control of a rotary parallel robot. Journal of Vibration and Control 2022, 28, 2678–2695. [Google Scholar] [CrossRef]
20. Tajdari, F. Adaptive time-delay estimation and control of optimized stewart robot. Journal of Vibration and Control 2023, 29, 5511–5531. [Google Scholar] [CrossRef]
21. Tajdari, F.a. Advancing non-rigid 3D/4D human mesh registration for ultra-personalization 2023.
22. Tajdari, F.; Khodabakhshi, E.; Kabganian, M.; Golgouneh, A. Switching controller design to swing-up a two-link underactuated robot. 2017 IEEE 4th International Conference on Knowledge-Based Engineering and Innovation (KBEI). IEEE, 2017, pp. 0595–0599. [CrossRef]
23. Tajdari, F.; Huysmans, T.; Yang, Y.; Song, Y. Feature preserving non-rigid iterative weighted closest point and semi-curvature registration. IEEE Transactions on Image Processing 2022, 31, 1841–1856. [Google Scholar] [CrossRef] [PubMed]
24. Tajdari, F.; Ghaffari, A.; Khodayari, A.; Kamali, A.; Zhilakzadeh, N.; Ebrahimi, N. Fuzzy control of anticipation and evaluation behaviour in real traffic flow. 2019 7th International Conference on Robotics and Mechatronics (ICRoM). IEEE, 2019, pp. 248–253. [CrossRef]
25. Yang, Y.; Yuan, T.; Huysmans, T.; Elkhuizen, W.S.; Tajdari, F.; Song, Y. Posture-invariant three dimensional human hand statistical shape model. Journal of Computing and Information Science in Engineering 2021, 21, 031006. [Google Scholar] [CrossRef]
26. Tajdari, F.; Kwa, F.; Versteegh, C.; Huysmans, T.; Song, Y. Dynamic 3d mesh reconstruction based on nonrigid iterative closest-farthest points registration. International design engineering technical conferences and computers and information in engineering conference. American Society of Mechanical Engineers, 2022, Vol. 86212, p. V002T02A051. [CrossRef]
27. Tajdari, F.; Golgouneh, A.; Ghaffari, A.; Khodayari, A.; Kamali, A.; Hosseinkhani, N. Simultaneous intelligent anticipation and control of follower vehicle observing exiting lane changer. IEEE Transactions on Vehicular Technology 2021, 70, 8567–8577. [Google Scholar] [CrossRef]
28. Tajdari, F.; Eijck, C.; Kwa, F.; Versteegh, C.; Huysmans, T.; Song, Y. Optimal position of cameras design in a 4d foot scanner. International design engineering technical conferences and computers and information in engineering conference. American Society of Mechanical Engineers, 2022, Vol. 86212, p. V002T02A044. [CrossRef]
29. Tajdari, M.; Tajdari, F.; Shirzadian, P.; Pawar, A.; Wardak, M.; Saha, S.; Park, C.; Huysmans, T.; Song, Y.; Zhang, Y.J.; others. Next-generation prognosis framework for pediatric spinal deformities using bio-informed deep learning networks. Engineering with Computers 2022, 38, 4061–4084. [Google Scholar] [CrossRef]
30. Tajdari, F.; Huysmans, T.; Yao, X.; Xu, J.; Song, Y. 4D Feet: Registering Walking Foot Shapes Using Attention Enhanced Dynamic-Synchronized Graph Convolutional LSTM Network. arXiv preprint arXiv:2307.12377, arXiv:2307.12377 2023.
31. Tajdari, F. ; others. Optimal and adaptive controller design for motorway traffic with connected and automated vehicles 2023. [Google Scholar] [CrossRef]
32. Tarvirdizadeh, B.; Golgouneh, A.; Khodabakhshi, E.; Tajdari, F. An assessment of a similarity between the right and left hand photoplethysmography signals, using time and frequency features of heart-rate-variability signal. 2017 IEEE 4th international conference on knowledge-based engineering and innovation (KBEI). IEEE, 2017, pp. 0588–0594. [CrossRef]
33. Tarvirdizadeh, B.; Golgouneh, A.; Tajdari, F.; Khodabakhshi, E. A novel online method for identifying motion artifact and photoplethysmography signal reconstruction using artificial neural networks and adaptive neuro-fuzzy inference system. Neural Computing and Applications 2020, 32, 3549–3566. [Google Scholar] [CrossRef]
34. Golgouneh, A.; Bamshad, A.; Tarvirdizadeh, B.; Tajdari, F. Design of a new, light and portable mechanism for knee CPM machine with a user-friendly interface. 2016 Artificial Intelligence and Robotics (IRANOPEN). IEEE, 2016, pp. 103–108. [CrossRef]
35. Minnoye, A.L.; Tajdari, F.; Doubrovski, E.L.; Wu, J.; Kwa, F.; Elkhuizen, W.S.; Huysmans, T.; Song, Y. Personalized product design through digital fabrication. International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. American Society of Mechanical Engineers, 2022, Vol. 86212, p. V002T02A054. [CrossRef]
36. Timoshenko, S.; Goodier, J. Theory of Elasticity, modulus, 1969.
37. Gamer, U.; Lance, R.H. Stress distribution in a rotating elastic-plastic tube. Acta Mechanica 1983, 50, 1–8. [Google Scholar] [CrossRef]
38. Gamer, U.a. The elastic-plastic stress-distribution in the rotating annulus and in the annulus under external-pressure. ZAMM 1984, 64, T126–T128. [Google Scholar]
39. Gamer, U. Elastic-plastic deformation of the rotating solid disk. Archive of Applied Mechanics 1984, 54, 345–354. [Google Scholar] [CrossRef]
40. Gamer, U.a. Stress distribution in the rotating elastic-plastic disk. Zamm 1985, 65, 136–137. [Google Scholar]
41. Güven, U. Elastic-plastic stresses in a rotating annular disk of variable thickness and variable density. International Journal of Mechanical Sciences 1992, 34, 133–138. [Google Scholar] [CrossRef]
42. Guven, U. On the stresses in an elastic-plastic annular disk of variable thickness under external pressure. International Journal of Solids and Structures 1993, 30, 651–658. [Google Scholar] [CrossRef]
43. Eraslan, A.N.; Argeso, H. Limit angular velocities of variable thickness rotating disks. International Journal of Solids and Structures 2002, 39, 3109–3130. [Google Scholar] [CrossRef]
44. Akis, T.; Eraslan, A.N. The stress response and onset of yield of rotating FGM hollow shafts. Acta Mechanica 2006, 187, 169–187. [Google Scholar] [CrossRef]
45. Argeso, H.; Eraslan, A.N. A computational study on functionally graded rotating solid shafts. International Journal for Computational Methods in Engineering Science and Mechanics 2007, 8, 391–399. [Google Scholar] [CrossRef]
46. Birman, V.; Byrd, L.W. Modeling and analysis of functionally graded materials and structures 2007. [CrossRef]
47. Akis, T.; Eraslan, A.N. Exact solution of rotating FGM shaft problem in the elastoplastic state of stress. Archive of Applied Mechanics 2007, 77, 745–765. [Google Scholar] [CrossRef]
48. Bayat, M.; Saleem, M.; Sahari, B.; Hamouda, A.; Mahdi, E. Analysis of functionally graded rotating disks with variable thickness. Mechanics Research Communications 2008, 35, 283–309. [Google Scholar] [CrossRef]
49. Madan, R.; Saha, K.; Bhowmick, S. Limit speeds and stresses in power law functionally graded rotating disks. Advances in materials Research 2020, 9, 115–131. [Google Scholar] [CrossRef]
50. Dai, T.; Dai, H.L. Investigation of mechanical behavior for a rotating FGM circular disk with a variable angular speed. Journal of Mechanical Science and Technology 2015, 29, 3779–3787. [Google Scholar] [CrossRef]
51. Ma, G.; Hao, H.; Miyamoto, Y. Limit angular velocity of rotating disc with unified yield criterion. International journal of mechanical sciences 2001, 43, 1137–1153. [Google Scholar] [CrossRef]
52. Peng, X.L.; Li, X.F. Effects of gradient on stress distribution in rotating functionally graded solid disks. Journal of Mechanical Science and Technology 2012, 26, 1483–1492. [Google Scholar] [CrossRef]
53. Lomakin, E.; Alexandrov, S.; Jeng, Y.R. Stress and strain fields in rotating elastic/plastic annular discs. Archive of Applied Mechanics 2016, 86, 235–244. [Google Scholar] [CrossRef]