Randomized Nonuniform Sampling for Random Signals Bandlimited in the Special Aﬃne Fourier Transform Domain

Preprint

Article

Randomized Nonuniform Sampling for Random Signals Bandlimited in the Special Aﬃne Fourier Transform Domain

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

12 January 2024

Posted:

12 January 2024

You are already at the latest version

Alerts

Abstract

The special aﬃne Fourier transform (SAFT) is a useful and powerful analyzing tool in signal processing, optics and communications. In this paper, we mainly discuss the randomized nonuniform sampling and reconstruction for random signals bandlimited in the SAFT domain. First, we show that the nonuniform sampling is identical to the uniform sampling after a pre-ﬁlter in the sense of second order statistic characters. Then, we propose an approximate reconstruction based on sinc interpolation for the nonuniform sampling of random signals bandlimited in the SAFT domain. Finally, we give the mean square error estimate for the proposed approximate recovery approach.

Keywords:

Subject: Computer Science and Mathematics - Analysis

MSC: 46E22; 94A20

1. Introduction

The special affine Fourier transform (SAFT) was firstly proposed in [1] to model optical systems. It offers a unified viewpoint of known signal processing transforms, such as Fourier transform (FT), fractional Fourier transform (FrFT), linear canonical transform (LCT), Laplace transform (LT) and so on. It can also include some optical operations on light waves, such as rotation, magnification, hyperbolic transformation, free space propagation, Lens transformation and so on. The SAFT is a six-parameters linear integral transform which is defined by offsetting two extra parameters on the basis of the LCT, so SAFT is also known as the offset linear canonical transform (OLCT). It has been proved that the SAFT is a useful tool for signal processing, communications, quantum mechanics and optics [12,16,23,26]. Many classical results such as Zak transform, Poisson summation formula and convolution theorems are established in the SAFT domain [6,24,33].

Let

A = [\begin{matrix} a & b & u_{0} \\ c & d & ω_{0} \end{matrix}]

be a matrix with six real parameters satisfying

a d - b c = 1

. The continuous-time SAFT associated with the parameter matrix A of a signal

f (t)

is defined as in [1],

F_{A} (u) = S A F T [f] (u) = \{\begin{matrix} \int_{- \infty}^{+ \infty} f (t) K_{A} (t, u) d t, b \neq 0, \\ \sqrt{d} e \frac{j c d {(u - u_{0})}^{2}}{2} + j w_{0} u f [d (u - u_{0})], b = 0, \end{matrix}

(1.1)

where the kernel function

K_{A} (t, u)

is given by

K_{A} (t, u) = \sqrt{\frac{1}{2 π j b}} e^{\frac{j d u_{0}^{2}}{2 b}} e^{\frac{j}{2 b} [a t^{2} + 2 t (u_{0} - u) - 2 u (d u_{0} - b w_{0}) + d u^{2}]} .

(1.2)

It is noted that when

b = 0

, the SAFT of a signal is essentially a chirp multiplication. Therefore, we shall confine our attention to the case of

b \neq 0

. The inverse SAFT is expressed as

f (t) = C \int_{- \infty}^{+ \infty} F_{A} (u) K_{A^{- 1}} (u, t) d u,

(1.3)

where

C = e^{\frac{j}{2} (c d u_{0}^{2} - 2 a d u_{0} w_{0} + a b w_{0}^{2})}

and

A^{- 1} : = [\begin{matrix} d & - b & b ω_{0} - d u_{0} \\ - c & a & c u_{0} - a ω_{0} \end{matrix}] .

Sampling is one of the most fundamental process in digital signal processing which provides a bridge between the continuous physical signals and the discrete digital signals. Beginning with the Shannon’s sampling theorem of bandlimited signals [15], various sampling such as nonuniform sampling, average sampling, dynamic sampling, random sampling, mobile sampling, timing sampling and multi-channel sampling have been generally studied for signals bandlimited in the FT domain [2,3,5,9]. With the appearance and developments of the more general transforms, the corresponding sampling theories are extended to the signals bandlimited in the FrFT, LCT and SAFT domains [6,12,14,18,19,21,22,23,25,26,27,30,32].

Signals in the real world often presents random characteristics and sampling for random signals bandlimited in the FT domain has been generally studied [5,7,8,17]. In recent years, there have existed many researches for sampling of random signals bandlimited in the FrFT and LCT domains [10,11,20,28,31]. The uniform sampling theorems in [10] was extended to the SAFT domain as in [29]. Nonuniform sampling is a more realistic sampling scheme due to the limitations of data acquisition and processing ability. In fact, the nonuniform sampling theories including the periodic nonuniform sampling model, N-order recurrent nonuniform sampling model, nonuniform sampling due to migration of a finite number of uniform samples and the general nonuniform sampling have been given for signals bandlimited in the LCT domain [31] and signals bandlimited in the SAFT domain [4,30], respectively. In particular, the nonuniform sampling problem was also considered in [11] for random signals bandlimited in the LCT domain, where a randomized nonuniform sampling method and a class of approximate recovery approaches by using sinc interpolation functions were studied. In this paper, we will further study the randomized nonuniform sampling for random signals bandlimited in the SAFT domain and also give an approximate recovery method based on the sinc interpolation.

The paper is organized as follows. In section 2, we give the definition of the power spectral density in the SAFT domain. In section 3, we study the nonuniform sampling scheme and propose an approximate recovery approach. In section 4, the mean square error estimate for the proposed approximate recovery method is demonstrated.

2. Power Spectral Density in the SAFT Domain

Given a probability space

(Ω, F, p),

a stochastic process

x (t)

is said to be wide sense stationary if it has zero mean and its auto-correlation function

R_{x x} (t + τ, t) = E [x (t + τ) x^{*} (t)]

(2.1)

is independent of

t \in R

, i.e.,

R_{x x} (t + τ, t) = R_{x x} (τ)

, where

E [\cdot]

denotes mathematical expectation and the superscript * stands for the complex conjugate. Two stochastic processes

x (t)

and

y (t)

are said to be jointly stationary, if

x (t)

and

y (t)

are both stationary and their cross-correlation function

R_{x y} (t + τ, t) = E [x (t + τ) y^{*} (t)]

(2.2)

is independent of

t \in R

, i.e.,

R_{x y} (t + τ, t) = R_{x y} (τ)

We next introduce the SAFT auto-correlation function, the SAFT cross-correlation function, the SAFT auto-power spectral density and the SAFT cross-power spectral density as in [29]. For two random signals

x (t)

and

y (t)

, the SAFT auto-correlation function of

x (t)

is defined as

R_{x x}^{A} (τ) = lim_{T \to + \infty} \frac{1}{2 T} \int_{- T}^{T} R_{x x} (t + τ, t) e^{j \frac{a}{b} t τ} d t .

(2.3)

Similarly, the SAFT cross-correlation function of

x (t)

and

y (t)

is defined as

R_{x y}^{A} (τ) = lim_{T \to + \infty} \frac{1}{2 T} \int_{- T}^{T} R_{x y} (t + τ, t) e^{j \frac{a}{b} t τ} d t .

(2.4)

Remark 2.1.If the random signal

\tilde{x} (t) = x (t) e^{j \frac{a}{2 b} t^{2}}

is stationary, then

x_{1} (t) = \tilde{x} (t) e^{j \frac{u_{0}}{b} t}

is also stationary. In fact,

R_{x_{1} x_{1}} (t + τ, t) = e^{\frac{j u_{0} τ}{b}} R_{\tilde{x} \tilde{x}} (t + τ, t) .

Moreover, one has

\begin{matrix} R_{\tilde{x} \tilde{x}} (t + τ, t) & = E [\tilde{x} (t + τ) {\tilde{x}}^{*} (t)] \\ = E [x (t + τ) e^{j \frac{a}{2 b} {(t + τ)}^{2}} x^{*} (t) e^{- j \frac{a}{2 b} t^{2}}] \\ = E [x (t + τ) x^{*} (t) e^{j \frac{a}{2 b} τ^{2}} e^{j \frac{a t τ}{b}}] \\ = R_{x x} (t + τ, t) e^{j \frac{a t τ}{b}} e^{j \frac{a}{2 b} τ^{2}} . \end{matrix}

Therefore,

R_{x x} (t + τ, t) e^{\frac{j a t τ}{b}}

must be independent of t. In such case, we have

R_{x x}^{A} (τ) = R_{x_{1} x_{1}} (τ) e^{- j \frac{a}{2 b} τ^{2}} e^{- j \frac{u_{0}}{b} τ} .

(2.5)

Define the SAFT auto-power spectral density of the random signal

x (t)

P_{x x}^{A} (u) = \sqrt{\frac{1}{- j 2 π b}} e^{- j \frac{d}{2 b} u^{2}} e^{- j \frac{d u_{0}^{2}}{2 b}} e^{j \frac{u}{b} (d u_{0} - b w_{0})} F_{A} \{R_{x x}^{A} (τ)\} (u)

(2.6)

and the SAFT cross-power spectral density of the random signals

x (t)

and

y (t)

P_{x y}^{A} (u) = \sqrt{\frac{1}{- j 2 π b}} e^{- j \frac{d}{2 b} u^{2}} e^{- j \frac{d u_{0}^{2}}{2 b}} e^{j \frac{u}{b} (d u_{0} - b w_{0})} F_{A} \{R_{x y}^{A} (τ)\} (u) .

(2.7)

It follows from (1.1) and (2.6) that

\begin{matrix} R_{x x}^{A} (τ) & = C \cdot \int_{- \infty}^{+ \infty} P_{x x}^{A} (u) 1 / \sqrt{\frac{1}{- j 2 π b}} e^{j \frac{d}{2 b} u^{2}} e^{j \frac{d}{2 b} u_{0}^{2}} e^{- j \frac{u}{b} (d u_{0} - b w_{0})} \sqrt{\frac{1}{- j 2 π b}} \\ \times e^{- j \frac{a}{2 b} {(b w_{0} - d u_{0})}^{2}} e^{- j \frac{d}{2 b} u^{2}} e^{- j \frac{u}{b} (b w_{0} - d u_{0} - τ)} e^{- j \frac{u_{0}}{b} τ} e^{^{- j \frac{a}{2 b} τ^{2}}} d u \\ = C \cdot \int_{- \infty}^{+ \infty} P_{x x}^{A} (u) e^{j \frac{d}{2 b} u_{0}^{2}} e^{- j \frac{a}{2 b} {(b w_{0} - d u_{0})}^{2}} e^{j \frac{u}{b} τ} e^{- j \frac{u_{0}}{b} τ} e^{^{- j \frac{a}{2 b} τ^{2}}} d u \\ = e^{\frac{j}{2} (c d u_{0}^{2} - 2 a d u_{0} w_{0} + a b w_{0}^{2})} \int_{- \infty}^{+ \infty} P_{x x}^{A} (u) e^{j \frac{d}{2 b} u_{0}^{2}} e^{- j \frac{a}{2 b} {(b w_{0} - d u_{0})}^{2}} e^{j \frac{u}{b} τ} e^{- j \frac{u_{0}}{b} τ} e^{- j \frac{a}{2 b} τ^{2}} d u \\ = \int_{- \infty}^{+ \infty} P_{x x}^{A} (u) e^{- j \frac{a}{2 b} τ^{2}} e^{j \frac{1}{b} (u - u_{0}) τ} d u . \end{matrix}

(2.8)

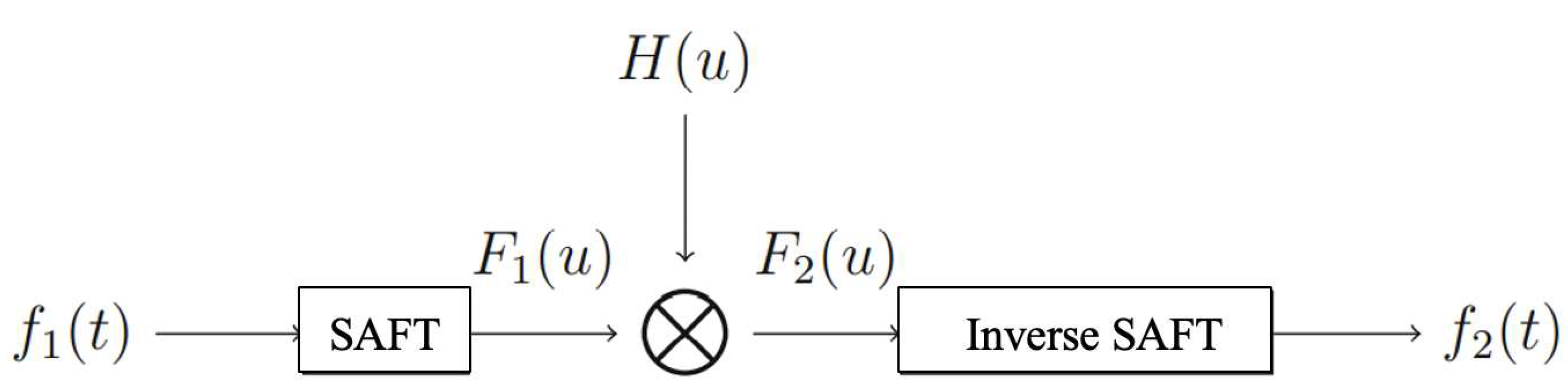
Multiplicative filtering in the SAFT domain is showed in Figure 1, which has been introduced in [29]. More specifically, we first obtain the SAFT of the input signal

f_{1} (t)

and apply the multiplicative filter

H (u)

in the SAFT domain. Then the output signal

f_{2} (t)

in the time domain is obtained by the inverse SAFT. Mathematically, the output

f_{2} (t)

is given by

f_{2} (t) = F_{A}^{- 1} \{F_{2} (u)\} (t) = F_{A}^{- 1} \{F_{1} (u) H (u)\} (t),

(2.9)

where

F_{1} (u) = F_{A} \{f_{1} (t)\} (u)

and

F_{2} (u) = F_{1} (u) H (u)

Define normalized convolution

(f Θ g) (t) = \frac{1}{\sqrt{2 π}} \int_{R} f (x) g (t - x) e^{- j \frac{a}{2 b} (t^{2} - x^{2})} d x

(2.10)

for

f, g \in L^{2} (R)

[23]. Then we have the following conclusion.

Proposition 2.2.

Let

H (u) = \frac{1}{\sqrt{2 π}} \int_{- \infty}^{+ \infty} h (t) e^{- j \frac{(u - u_{0})}{b} t} d t .

(2.11)

Then the multiplicative filter in Figure 1 is equivalent to

f_{2} (t) = (f_{1} Θ h) (t) .

(2.12)

Proof we only need to prove

F_{A} \{(f_{1} Θ h) (t)\} (u) = F_{1} (u) H (u) .

It follows from the definition of the SAFT that

\begin{matrix} F_{A} \{(f_{1} Θ h) (t)\} (u) \\ = \int_{R} (f_{1} Θ h) (t) \sqrt{\frac{1}{2 π j b}} e^{\frac{j d u_{0}^{2}}{2 b}} e^{\frac{j}{2 b} [a t^{2} + 2 t (u_{0} - u) - 2 u (d u_{0} - b w_{0}) + d u^{2}]} d t \\ = \frac{1}{\sqrt{2 π}} \int_{R} \int_{R} f_{1} (x) h (t - x) e^{- j \frac{a}{2 b} (t^{2} - x^{2})} \sqrt{\frac{1}{2 π j b}} e^{\frac{j d u_{0}^{2}}{2 b}} e^{\frac{j}{2 b} [a t^{2} + 2 t (u_{0} - u) - 2 u (d u_{0} - b w_{0}) + d u^{2}]} d x d t \\ = \int_{R} f_{1} (x) \sqrt{\frac{1}{2 π j b}} e^{\frac{j d u_{0}^{2}}{2 b}} e^{\frac{j}{2 b} [a x^{2} + 2 x (u_{0} - u) - 2 u (d u_{0} - b w_{0}) + d u^{2}]} d x \frac{1}{\sqrt{2 π}} \int_{R} h (t - x) e^{\frac{j}{b} t (u_{0} - u)} e^{- \frac{j}{2 b} [2 x (u_{0} - u)]} d t \\ = \int_{R} f_{1} (x) \sqrt{\frac{1}{2 π j b}} e^{\frac{j d u_{0}^{2}}{2 b}} e^{\frac{j}{2 b} [a x^{2} + 2 x (u_{0} - u) - 2 u (d u_{0} - b w_{0}) + d u^{2}]} d x \frac{1}{\sqrt{2 π}} \int_{R} h (t) e^{- j \frac{(u - u_{0})}{b} t} d t \\ = F_{1} (u) H (u) . \end{matrix}

Lemma 2.3.

[29] Suppose that the random signals

x (t)

and

y (t)

are the input and the output in Figure 1, then

P_{x y}^{A} (u) = H (u) P_{x x}^{A} (u)

(2.13)

and

P_{y y}^{A} (u) = {| H (u) |}^{2} P_{x x}^{A} (u) .

(2.14)

3. Nonuniform Sampling and Approximate Recovery

In this section, we will study the nonuniform sampling and reconstruction of random signals which are bandlimited in the SAFT domain.

Definition 3.1.

[29] We say that a random signal

x (t)

is bandlimited in the SAFT domain if its SAFT power spectral density

P_{x x}^{A} (u)

satisfies

P_{x x}^{A} (u) = 0, | u | > u_{r},

(3.1)

where

u_{r}

is called the bandwidth of the random signal

x (t)

in the SAFT domain.

Lemma 3.2.

Assume that a random signal

x (t)

is bandlimited in the SAFT domain with bandwidth

u_{r}

and

\tilde{x} (t) = x (t) e^{j \frac{a}{2 b} t^{2}}

is stationary. Then

x_{1} (t)

is bandlimited in the FT domain with bandwidth

\frac{u_{r}}{b}

and the power spectral density satisfies supp

{P_{x_{1} x_{1}} (u)} \subseteq [- \frac{u_{r}}{b}, \frac{u_{r}}{b}]

Proof Since

x_{1} (t)

is stationary, it follows from (2.5) and (2.6) that

\begin{matrix} P_{x x}^{A} (u) & = \sqrt{\frac{1}{- j 2 π b}} e^{- j \frac{d}{2 b} u^{2}} e^{^{- j \frac{d}{2 b} u_{0}^{2}}} e^{j \frac{u}{b} (d u_{0} - b w_{0})} F_{A} \{R_{x x}^{A} (τ)\} (u) \\ = \sqrt{\frac{1}{- j 2 π b}} e^{- j \frac{d}{2 b} u^{2}} e^{^{- j \frac{d}{2 b} u_{0}^{2}}} e^{j \frac{u}{b} (d u_{0} - b w_{0})} F_{A} \{R_{x_{1} x_{1}} (τ) e^{- j \frac{a}{2 b} τ^{2}} e^{- j \frac{u_{0}}{b} τ}\} (u) \\ = \sqrt{\frac{1}{- j 2 π b}} e^{- j \frac{d}{2 b} (u^{2} + u_{0}^{2})} e^{j \frac{u}{b} (d u_{0} - b w_{0})} \int_{- \infty}^{+ \infty} R_{x_{1} x_{1}} (τ) e^{- j \frac{a}{2 b} τ^{2}} e^{- j \frac{u_{0}}{b} τ} \\ \times \sqrt{\frac{1}{2 π j b}} e^{\frac{j d u_{0}^{2}}{2 b}} e^{\frac{j}{2 b} [a τ^{2} + 2 τ (u_{0} - u) - 2 u (d u_{0} - b w_{0}) + d u^{2}]} d τ \\ = \frac{1}{2 π b} \int_{- \infty}^{+ \infty} R_{x_{1} x_{1}} (τ) e^{- j \frac{u}{b} τ} d τ \end{matrix}

\begin{matrix} = \frac{1}{2 π b} P_{x_{1} x_{1}} (\frac{u}{b}) . \end{matrix}

(3.2)

Note that

P_{x x}^{A} (u) = 0, | u | > u_{r} .

Then the desired result is proved. First, we will show that the nonuniform sampling is identical to uniform sampling after a pre-filter in the sense of second order statistic characters.

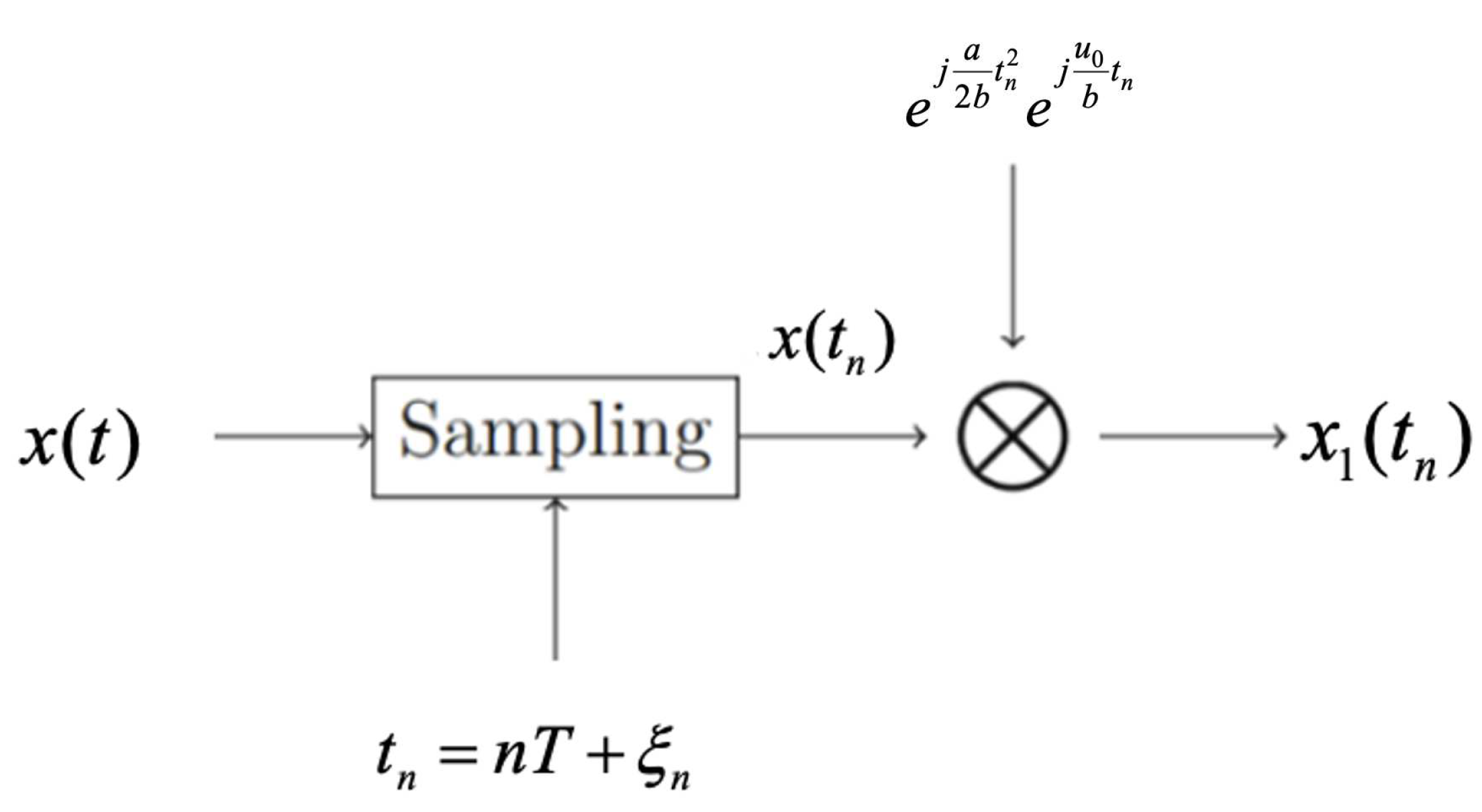
Theorem 3.3.

Suppose that the random signal

x (t)

is bandlimited in the SAFT domain with bandwidth

u_{r}

and

\tilde{x} (t) = x (t) e^{j \frac{a}{2 b} t^{2}}

is stationary. Then in the sense of second order statistic characters, the nonuniform sampling of

x (t)

at the sampling points

t_{n} = n T + ξ_{n}

(Figure 2 ) is identical to the uniform sampling after a SAFT filter

h_{1} (t)

as in Figure 3, where

T \leq T_{N} = \frac{π b}{u_{r}}

, {

ξ_{n}

} is a sequence of independent identically distributed random variables with zero mean in the interval

(- T / 2, T / 2)

. Moreover,

H_{1} (u) = ϕ_{ξ} (\frac{u}{b}) = \frac{1}{\sqrt{2 π}} \int_{- \infty}^{+ \infty} h_{1} (t) e^{- j \frac{(u - u_{0})}{b} t} d t

and

ϕ_{ξ} (u)

denotes the characteristic function of

ξ_{n}

Proof Note that

y (t) = (x Θ h_{1}) (t)

. Then it follows from Lemma 2.2 that

P_{y y}^{A} (u) = {|H_{1} (u)|}^{2} P_{x x}^{A} (u) .

(3.3)

Moreover, one has

\begin{matrix} y_{1} (t) & = y (t) e^{j \frac{a}{2 b} t^{2}} e^{j \frac{u_{0}}{b} t} \\ = \frac{1}{\sqrt{2 π}} e^{j \frac{u_{0}}{b} t} \int_{R} x (s) h_{1} (t - s) e^{j \frac{a}{2 b} s^{2}} d s \\ = \frac{1}{\sqrt{2 π}} e^{j \frac{u_{0}}{b} t} \int_{R} \tilde{x} (s) h_{1} (t - s) d s . \end{matrix}

(3.4)

Hence, we have

R_{y_{1} y_{1}} (t + τ, t) = \frac{1}{2 π} e^{j \frac{u_{0}}{b} τ} \int_{R} \int_{R} h_{1}^{*} (s) R_{\tilde{x} \tilde{x}} (τ - s^{'} + s) h_{1} (s^{'}) d s^{'} d s,

which is independent of t and

y_{1} (t)

is stationary. It follows from (2.8) and (3.3) that

\begin{matrix} R_{y y}^{A} (k T) & = \int_{- u_{r}}^{u_{r}} P_{y y}^{A} (u) e^{- j \frac{a}{2 b} {(k T)}^{2} + j \frac{1}{b} (u - u_{0}) k T} d u \\ = \int_{- u_{r}}^{u_{r}} {|H_{1} (u)|}^{2} P_{x x}^{A} (u) e^{- j \frac{a}{2 b} {(k T)}^{2} + j \frac{1}{b} (u - u_{0}) k T} d u . \end{matrix}

(3.5)

This together with (2.5) obtains

\begin{matrix} R_{y_{1} y_{1}} (n T, (n - k) T) & = R_{y_{1} y_{1}} (k T) \\ = R_{y y}^{A} (k T) e^{j \frac{a}{2 b} {(k T)}^{2}} e^{j \frac{u_{0}}{b} k T} \\ = e^{j \frac{a}{2 b} {(k T)}^{2}} e^{j \frac{u_{0}}{b} (k T)} \int_{- u_{r}}^{u_{r}} {|H_{1} (u)|}^{2} P_{x x}^{A} (u) e^{- j \frac{a}{2 b} {(k T)}^{2} + j \frac{1}{b} (u - u_{0}) k T} d u \\ = \int_{- u_{r}}^{u_{r}} {|H_{1} (u)|}^{2} P_{x x}^{A} (u) e^{j \frac{u}{b} k T} d u . \end{matrix}

(3.6)

Combining (2.5) and (2.8), we have

\begin{matrix} E [R_{x_{1} x_{1}} (k T + ξ_{n} - ξ_{n - k})] \\ = E [R_{x x}^{A} (k T + ξ_{n} - ξ_{n - k}) e^{j \frac{a}{2 b} {(k T + ξ_{n} - ξ_{n - k})}^{2}} e^{j \frac{u_{0}}{b} (k T + ξ_{n} - ξ_{n - k})}] \\ = E [\int_{- u_{r}}^{u_{r}} P_{x x}^{A} (u) e^{- j \frac{a}{2 b} {(k T + ξ_{n} - ξ_{n - k})}^{2} + j \frac{1}{b} (u - u_{0}) (k T + ξ_{n} - ξ_{n - k})} d u \cdot e^{j \frac{a}{2 b} {(k T + ξ_{n} - ξ_{n - k})}^{2}} e^{j \frac{u_{0}}{b} (k T + ξ_{n} - ξ_{n - k})}] \\ = E [\int_{- u_{r}}^{u_{r}} P_{x x}^{A} (u) e^{j \frac{u}{b} (k T + ξ_{n} - ξ_{n - k})} d u] \\ = \int_{- u_{r}}^{u_{r}} P_{x x}^{A} (u) e^{j \frac{u}{b} k T} E [e^{j \frac{u}{b} (ξ_{n} - ξ_{n - k})}] d u . \end{matrix}

(3.7)

Let

Z = ξ_{n} - ξ_{n - k}

and

f_{Z} (η)

be the probability density function of Z. Note that

ξ_{n}

and

ξ_{n - k}

are independent and have identical distributions. Let

f_{ξ} (η)

be their common probability density function. Then we have

f_{Z} (η) = [f_{ξ} (\cdot) * f_{ξ} (- \cdot)] (η),

(3.8)

where * denotes the convolution operator. Moreover, one has

\begin{matrix} E [e^{j \frac{u}{b} (ξ_{n} - ξ_{n - k})}] & = \int_{- \infty}^{+ \infty} f_{Z} (η) e^{j \frac{u}{b} η} d η \\ = \int_{- \infty}^{+ \infty} [f_{ξ} (\cdot) * f_{ξ} (- \cdot)] (η) e^{j \frac{u}{b} η} d η \\ = \int_{- \infty}^{+ \infty} f_{ξ} (η) e^{j \frac{u}{b} η} d η \cdot \int_{- \infty}^{+ \infty} f_{ξ} (- η) e^{j \frac{u}{b} η} d η \\ = {|ϕ_{ξ} (\frac{u}{b})|}^{2}, \end{matrix}

(3.9)

where

ϕ_{ξ} (u) = \int_{- \infty}^{+ \infty} f_{ξ} (η) e^{j u η} d η .

Substituting (3.9) into (3.7) obtains

\begin{matrix} E [R_{x_{1} x_{1}} (k T + ξ_{n} - ξ_{n - k})] = \int_{- u_{r}}^{u_{r}} {|ϕ_{ξ} (\frac{u}{b})|}^{2} P_{x x}^{A} (u) e^{j \frac{u}{b} k T} d u . \end{matrix}

(3.10)

This together with

H_{1} (u) = ϕ_{ξ} (\frac{u}{b})

and (3.6) proves the desired result.

In the following, we will give an approximate recovery method for bandlimited signals in the SAFT domain based on randomized nonuniform samples.

Lemma 3.4.

[13] Suppose that the random signal

x (t)

is bandlimited in the Fourier transform domain with bandwidth

\frac{u_{r}}{b}

, {

ξ_{n}

} and {

ζ_{n}

} are two sequences of independent identically distributed random variables with zero mean. Then an approximate recovery formula of nonuniform sampling for the random signal

x (t)

can be represented by

x^{''} (t) = \frac{T}{T_{N}} \sum_{n = - \infty}^{+ \infty} x (t_{n}) h_{2} (t - {\tilde{t}}_{n}),

(3.11)

where

h_{2} (t) = s i n c (\frac{u_{r} t}{b})

s i n c (x) ≜ \frac{sin x}{x}

t_{n} = n T + ξ_{n}

and

{\tilde{t}}_{n} = n T + ζ_{n}

Theorem 3.5.

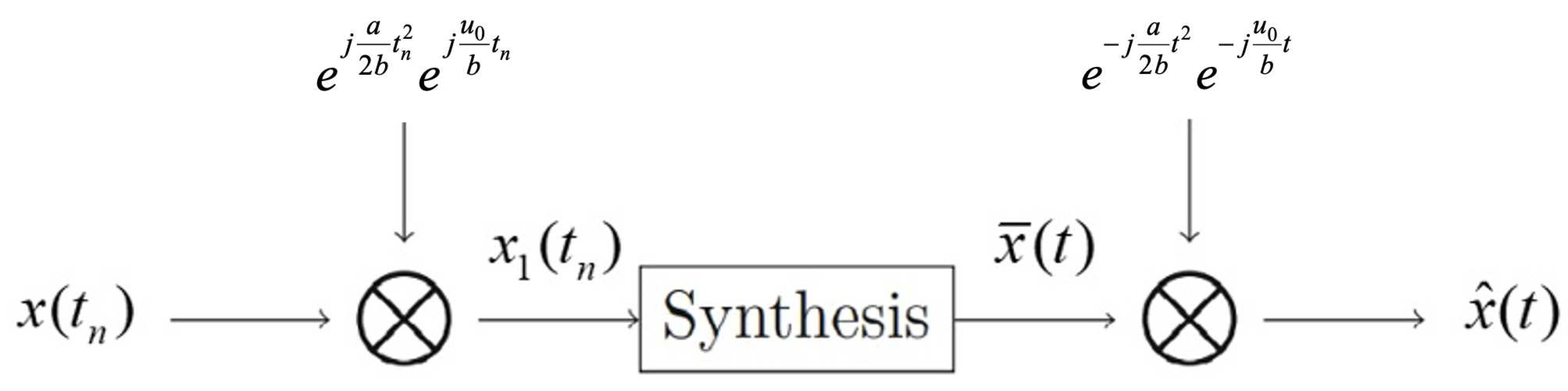
Suppose that the random signal

x (t)

is bandlimited in the SAFT domain with bandwidth

u_{r}

and

\tilde{x} (t) = x (t) e^{j \frac{a}{2 b} t^{2}}

is stationary. Then

x (t)

can be approximated from its nonuniform samples by utilizing the sinc interpolation function as

\hat{x} (t) = \frac{T}{T_{N}} e^{- j \frac{u_{0}}{b} t} e^{- j \frac{a}{2 b} t^{2}} \sum_{n = - \infty}^{+ \infty} x (t_{n}) e^{j \frac{a}{2 b} t_{n}^{2}} e^{j \frac{u_{0}}{b} t_{n}} h_{2} (t - {\tilde{t}}_{n}),

(3.12)

where

t_{n}

and

{\tilde{t}}_{n}

are as in Lemma 3.4.

Proof It follows from Lemma 3.2 that

x_{1} (t)

is bandlimited in the FT domain with bandwidth

\frac{u_{r}}{b}

. By (3.11), we know that

x_{1}^{''} (t) = \frac{T}{T_{N}} \sum_{n = - \infty}^{+ \infty} x_{1} (t_{n}) h_{2} (t - {\tilde{t}}_{n}) = \frac{T}{T_{N}} \sum_{n = - \infty}^{+ \infty} x (t_{n}) e^{j \frac{a}{2 b} t_{n}^{2}} e^{j \frac{u_{0}}{b} t_{n}} h_{2} (t - {\tilde{t}}_{n})

(3.13)

is an approximation of

x_{1} (t)

. Note that

x (t) = e^{- j \frac{u_{0}}{b} t} e^{- j \frac{a}{2 b} t^{2}} x_{1} (t)

. Then

\hat{x} (t)

in (3.12) is an approximate recovery approach of

x (t)

and the proof is completed.

From Theorem 3.5, one can see that the approximate recovery approach using the sinc interpolation for a random signal that is bandlimited in the SAFT domain can be expressed in Figure 4.

4. Error estimate for Nonuniform Sampling

Since the reconstruction with randomized sinc interpolation is an approximate method, we will estimate the approximation error in this section.

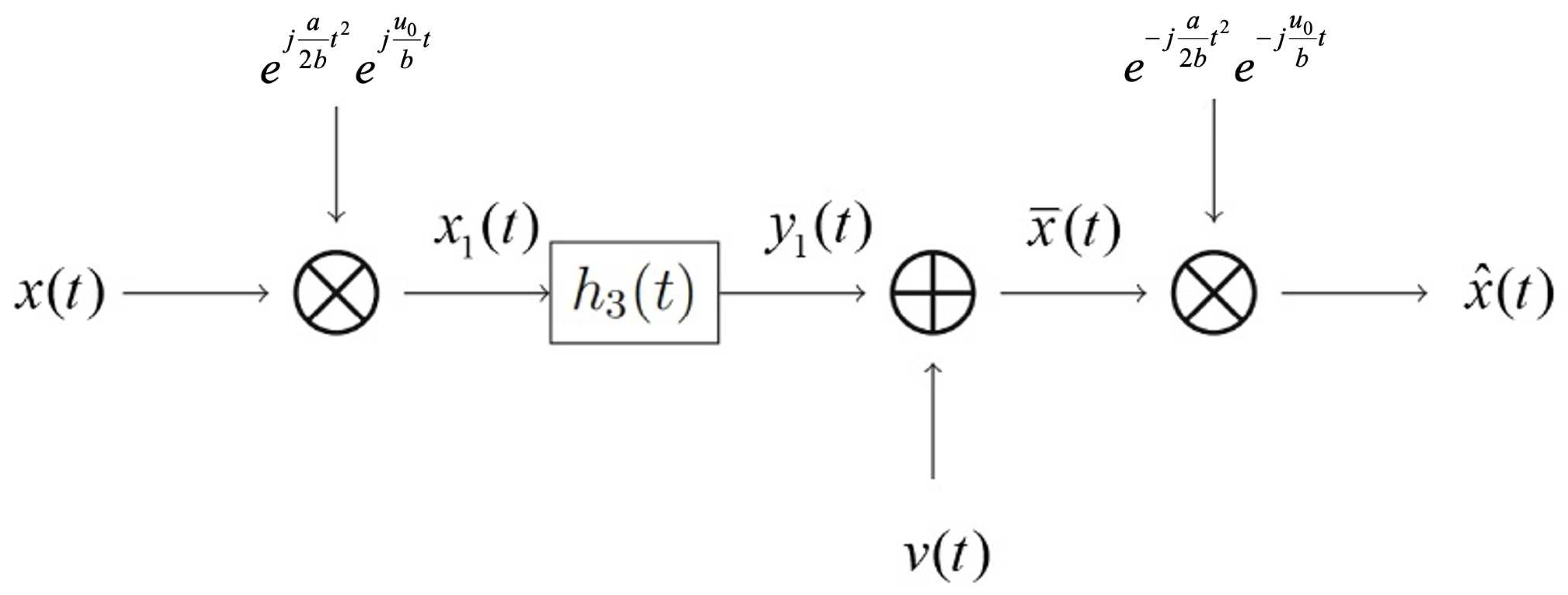
Lemma 4.1.

Let random signals

x_{1} (t)

and

y_{1} (t)

be the input and output of the FT multiplicative filter as in Figure 5. Then

P_{y_{1} y_{1}} (u) = {|{\hat{h}}_{3} (u)|}^{2} P_{x_{1} x_{1}} (u),

where

{\hat{h}}_{3} (u)

is the FT of

h_{3} (t)

, that is,

{\hat{h}}_{3} (u) = \int_{R} h_{3} (t) e^{- j u t} d t .

Proof Note that

y_{1} (t) = \int_{- \infty}^{+ \infty} x_{1} (t - u) h_{3} (u) d u .

Then

R_{y_{1} x_{1}} (t + τ, t) = E [y_{1} (t + τ) x_{1}^{*} (t)] = \int_{- \infty}^{+ \infty} R_{x_{1} x_{1}} (τ - u) h_{3} (u) d u,

(4.1)

which is independent of t. Moreover, one has

R_{y_{1} y_{1}} (t + τ, t) = E [y_{1} (t + τ) y_{1}^{*} (t)] = \int_{- \infty}^{+ \infty} R_{y_{1} x_{1}} (τ + u) h_{3}^{*} (u) d u .

(4.2)

Taking FT on both sides of (4.1) and (4.2) obtains

P_{y_{1} x_{1}} (u) = {\hat{h}}_{3} (u) P_{x_{1} x_{1}} (u)

(4.3)

and

P_{y_{1} y_{1}} (u) = {\hat{h}}_{3}^{*} (u) P_{y_{1} x_{1}} (u) .

(4.4)

Combining (4.3) and (4.4) gives

P_{y_{1} y_{1}} (u) = {|{\hat{h}}_{3} (u)|}^{2} P_{x_{1} x_{1}} (u) .

Theorem 4.2.

Suppose that the random signal

x (t)

is bandlimited in the SAFT domain with bandwidth

u_{r}

and

\tilde{x} (t) = x (t) e^{j \frac{a}{2 b} t^{2}}

is stationary. Let

v (t)

be an additive noise with zero mean, which is stationary, uncorrelated with

x (t)

and has the power spectral density

P_{v v} (u) = T \int_{- u_{r}}^{u_{r}} P_{x x}^{A} (u_{1}) [1 - {|ϕ_{ξ ζ} (\frac{u_{1}}{b}, - u)|}^{2}] d u_{1}, | u | \leq \frac{u_{r}}{b},

(4.5)

where

ϕ_{ξ ζ} (s, t)

is the joint characteristic function of the random variables

ξ_{n}

and

ζ_{n}

. If

ϕ_{ξ ζ} (u, - u)

is the frequency response of the filter

h_{3} (t)

, then the model described in Figure 5 is identical to the procedure represented in Figure 4 in the sense of second order statistic characters. Moreover, we have

\begin{matrix} E [{|\hat{x} (t) - x (t)|}^{2}] & = \int_{- u_{r}}^{u_{r}} P_{x x}^{A} (u) {|1 - ϕ_{ξ ζ} (\frac{u}{b}, - \frac{u}{b})|}^{2} d u \\ + \frac{T}{2 π b} \int_{- u_{r}}^{u_{r}} P_{x x}^{A} (u) \int_{- u_{r}}^{u_{r}} [1 - {|ϕ_{ξ ζ} (\frac{u}{b}, - \frac{u_{1}}{b})|}^{2}] d u_{1} d u . \end{matrix}

Proof It follows from Theorem 3.5 that

\bar{x} (t) = \hat{x} (t) e^{j \frac{u_{0}}{b} t} e^{j \frac{a}{2 b} t^{2}} = \frac{T}{T_{N}} \sum_{n = - \infty}^{+ \infty} x (t_{n}) e^{j \frac{a}{2 b} t_{n}^{2}} e^{\frac{j u_{0} t_{n}}{b}} h_{2} (t - {\tilde{t}}_{n}) .

(4.6)

Then one has

\begin{matrix} R_{\bar{x} \bar{x}} (t, t - τ) & = {(\frac{T}{T_{N}})}^{2} E [(\sum_{n = - \infty}^{+ \infty} x (n T + ξ_{n}) e^{j \frac{a}{2 b} {(n T + ξ_{n})}^{2}} e^{\frac{j u_{0} (n T + ξ_{n})}{b}} h_{2} (t - n T - ζ_{n})) \cdot \\ (\sum_{k = - \infty}^{+ \infty} x^{*} (k T + ξ_{k}) e^{- j \frac{a}{2 b} {(k T + ξ_{k})}^{2}} e^{\frac{- j u_{0} (k T + ξ_{k})}{b}} h_{2}^{*} (t - τ - k T - ζ_{k}))] \\ = {(\frac{T}{T_{N}})}^{2} \sum_{n = - \infty}^{+ \infty} \sum_{k = - \infty}^{+ \infty} E [R_{x_{1} x_{1}} (n T - k T + ξ_{n} - ξ_{k}) h_{2} (t - n T - ζ_{n}) h_{2}^{*} (t - τ - k T - ζ_{k})] . \end{matrix}

Moreover, it can be represented by two terms as

\begin{matrix} R_{\bar{x} \bar{x}} (t, t - τ) & = {(\frac{T}{T_{N}})}^{2} R_{x_{1} x_{1}} (0) \sum_{n = - \infty}^{+ \infty} E [h_{2} (t - n T - ζ_{n}) h_{2}^{*} (t - τ - n T - ζ_{n})] \\ + {(\frac{T}{T_{N}})}^{2} \sum_{n \neq k}^{} E [R_{x_{1} x_{1}} (n T - k T + ξ_{n} - ξ_{k}) h_{2} (t - n T - ζ_{n}) h_{2}^{*} (t - τ - k T - ζ_{k})] \\ \overset{Δ}{=} I + I I . \end{matrix}

(4.7)

Note that

\sum_{n} e^{j (u_{2} - u_{1}) n T} = 2 π \sum_{k} δ ((u_{2} - u_{1}) T - 2 π k)

and

h_{2} (t) = \frac{1}{\sqrt{2 π}} \int_{R} H_{2} (u) e^{j \frac{u}{b} t} d u = \frac{b}{\sqrt{2 π}} \int_{R} H_{2} (u b) e^{j u t} d u .

(4.8)

These together with the fact that

H_{2} (u) = \frac{π}{\sqrt{2 π} u_{r}} χ_{[- u_{r}, u_{r}]} (u)

show that

\begin{matrix} I & = \frac{1}{2 π} {(\frac{T b}{T_{N}})}^{2} R_{x_{1} x_{1}} (0) \int_{R} \int_{R} H_{2} (b u_{1}) H_{2}^{*} (b u_{2}) e^{j (u_{1} - u_{2}) t} e^{j u_{2} τ} \sum_{n = - \infty}^{+ \infty} e^{j (u_{2} - u_{1}) n T} E [e^{j (u_{2} - u_{1}) ζ_{n}}] d u_{1} d u_{2} \\ = {(\frac{T b}{T_{N}})}^{2} R_{x_{1} x_{1}} (0) \int_{- \frac{u_{r}}{b}}^{\frac{u_{r}}{b}} \frac{1}{T} {|H_{2} (b u)|}^{2} e^{j u τ} d u \\ = T {(\frac{b}{T_{N}})}^{2} \frac{1}{2 π} [\int_{- \frac{u_{r}}{b}}^{\frac{u_{r}}{b}} P_{x_{1} x_{1}} (u_{1}) d u_{1}] \int_{- \frac{u_{r}}{b}}^{\frac{u_{r}}{b}} {|H_{2} (b u)|}^{2} e^{j u τ} d u \\ = \frac{T}{4 π^{2}} \int_{- \frac{u_{r}}{b}}^{\frac{u_{r}}{b}} e^{j u τ} [\int_{- \frac{u_{r}}{b}}^{\frac{u_{r}}{b}} P_{x_{1} x_{1}} (u_{1}) d u_{1}] d u . \end{matrix}

(4.9)

Moreover, we have

\begin{matrix} I I & = {(\frac{b T}{2 π T_{N}})}^{2} \sum_{n \neq k}^{} E [\int_{- \frac{u_{r}}{b}}^{\frac{u_{r}}{b}} P_{x_{1} x_{1}} (u) e^{j u (n T - k T + ξ_{n} - ξ_{k})} d u \int_{R} H_{2} (b u_{1}) e^{j u_{1} (t - n T - ζ_{n})} d u_{1} \cdot \\ \int_{R} H_{2}^{*} (b u_{2}) e^{- j u_{2} (t - τ - k T - ζ_{k})} d u_{2}] \\ = {(\frac{b T}{2 π T_{N}})}^{2} \sum_{n \neq k}^{} \int_{- \frac{u_{r}}{b}}^{\frac{u_{r}}{b}} \int_{R} \int_{R} P_{x_{1} x_{1}} (u) H_{2} (b u_{1}) H_{2}^{*} (b u_{2}) e^{j u_{2} τ} e^{j (u_{1} - u_{2}) t} e^{j (u - u_{1}) n T} e^{- j (u - u_{2}) k T} \\ \cdot E [e^{j u ξ_{n}} e^{- j u ξ_{k}} e^{- j u_{1} ζ_{n}} e^{j u_{2} ζ_{k}}] d u_{1} d u_{2} d u \\ = {(\frac{b T}{2 π T_{N}})}^{2} \int_{- \frac{u_{r}}{b}}^{\frac{u_{r}}{b}} \int_{R} \int_{R} P_{x_{1} x_{1}} (u) H_{2} (b u_{1}) H_{2}^{*} (b u_{2}) ϕ_{ξ ζ} (u, - u_{1}) ϕ_{ξ ζ}^{*} (u, - u_{2}) e^{j u_{2} τ} e^{j (u_{1} - u_{2}) t} \\ \cdot (\sum_{n} e^{j (u - u_{1}) n T}) (\sum_{k} e^{- j (u - u_{2}) k T}) d u_{1} d u_{2} d u - {(\frac{b T}{2 π T_{N}})}^{2} \int_{- \frac{u_{r}}{b}}^{\frac{u_{r}}{b}} \int_{R} \int_{R} P_{x_{1} x_{1}} (u) H_{2} (b u_{1}) H_{2}^{*} (b u_{2}) \\ \cdot ϕ_{ξ ζ} (u, - u_{1}) ϕ_{ξ ζ}^{*} (u, - u_{2}) e^{j u_{2} τ} e^{j (u_{1} - u_{2}) t} (\sum_{n} e^{j (u_{2} - u_{1}) n T}) d u_{1} d u_{2} d u \\ = {(\frac{b}{T_{N}})}^{2} \int_{- \frac{u_{r}}{b}}^{\frac{u_{r}}{b}} {P_{x_{1} x_{1}} (u) |ϕ_{ξ ζ} (u, - u)|}^{2} {|H_{2} (b u)|}^{2} e^{j u τ} d u - \\ \frac{T}{2 π} {(\frac{b}{T_{N}})}^{2} \int_{- \frac{u_{r}}{b}}^{\frac{u_{r}}{b}} \int_{- \frac{u_{r}}{b}}^{\frac{u_{r}}{b}} P_{x_{1} x_{1}} (u_{1}) {|ϕ_{ξ ζ} (u_{1}, - u)|}^{2} {|H_{2} (b u)|}^{2} e^{j u τ} d u_{1} d u \\ = {(\frac{b}{T_{N}})}^{2} \int_{- \frac{u_{r}}{b}}^{\frac{u_{r}}{b}} {|H_{2} (b u)|}^{2} e^{j u τ} [P_{x_{1} x_{1}} (u) {|ϕ_{ξ ζ} (u, - u)|}^{2} - \frac{T}{2 π} \int_{- \frac{u_{r}}{b}}^{\frac{u_{r}}{b}} P_{x_{1} x_{1}} (u_{1}) {|ϕ_{ξ ζ} (u_{1}, - u)|}^{2} d u_{1}] du \\ = \frac{1}{2 π} \int_{- \frac{u_{r}}{b}}^{\frac{u_{r}}{b}} e^{j u τ} [P_{x_{1} x_{1}} (u) {|ϕ_{ξ ζ} (u, - u)|}^{2} - \frac{T}{2 π} \int_{- \frac{u_{r}}{b}}^{\frac{u_{r}}{b}} P_{x_{1} x_{1}} (u_{1}) {|ϕ_{ξ ζ} (u_{1}, - u)|}^{2} d u_{1}] d u . \end{matrix}

(4.10)

Substituting (4.9) and (4.10) into (4.7) obtains

\begin{matrix} R_{\bar{x} \bar{x}} (t, t - τ) & = \frac{T}{4 π^{2}} \int_{- \frac{u_{r}}{b}}^{\frac{u_{r}}{b}} (\int_{- \frac{u_{r}}{b}}^{\frac{u_{r}}{b}} P_{x_{1} x_{1}} (u_{1}) [1 - {|ϕ_{ξ ζ} (u_{1}, - u)|}^{2}] d u_{1}) e^{j u τ} d u \\ + \frac{1}{2 π} \int_{- \frac{u_{r}}{b}}^{\frac{u_{r}}{b}} {e^{j u τ} P_{x_{1} x_{1}} (u) |ϕ_{ξ ζ} (u, - u)|}^{2} d u . \end{matrix}

(4.11)

Similarly, we can obtain

R_{\bar{x} x_{1}} (t, t - τ) = \frac{1}{2 π} \int_{- \frac{u_{r}}{b}}^{\frac{u_{r}}{b}} P_{x_{1} x_{1}} (u) e^{j u τ} ϕ_{ξ ζ} (u, - u) d u .

(4.12)

Therefore, we have

P_{\bar{x} \bar{x}} (u) = P_{x_{1} x_{1}} (u) {|ϕ_{ξ ζ} (u, - u)|}^{2} + \frac{T}{2 π} \int_{- \frac{u_{r}}{b}}^{\frac{u_{r}}{b}} P_{x_{1} x_{1}} (u_{1}) [1 - {|ϕ_{ξ ζ} (u_{1}, - u)|}^{2}] d u_{1}

(4.13)

and

P_{\bar{x} x_{1}} (u) = P_{x_{1} x_{1}} (u) ϕ_{ξ ζ} (u, - u) .

(4.14)

It follows from Lemma 4.1 that the first term

P_{x_{1} x_{1}} (u) {|ϕ_{ξ ζ} (u, - u)|}^{2}

in (4.13) is the FT power spectral density of

y_{1} (t)

in Figure 5. Furthermore, since

\bar{x} (t) = y_{1} (t) + v (t)

and

v (t)

is uncorrelated with

x (t)

, then

\begin{matrix} R_{\bar{x} \bar{x}} (t + τ, t) & = E [(y_{1} (t + τ) + v (t + τ)) {(y_{1} (t) + v (t))}^{*}] \\ = R_{y_{1} y_{1}} (t + τ, t) + R_{y_{1} v} (t + τ, t) + R_{v y_{1}} (t + τ, t) + R_{v v} (t + τ, t) \\ = R_{y_{1} y_{1}} (t + τ, t) + R_{v v} (t + τ, t) . \end{matrix}

Moreover, one has

P_{\bar{x} \bar{x}} (u) = P_{y_{1} y_{1}} (u) + P_{v v} (u),

which shows that the second term in (4.13) is just the power spectral density of

v (t)

, that is,

\begin{matrix} P_{v v} (u) & = \frac{T}{2 π} \int_{- \frac{u_{r}}{b}}^{\frac{u_{r}}{b}} P_{x_{1} x_{1}} (u_{1}) [1 - {|ϕ_{ξ ζ} (u_{1}, - u)|}^{2}] d u_{1} \\ = T \int_{- u_{r}}^{u_{r}} P_{x x}^{A} (u_{1}) [1 - {|ϕ_{ξ ζ} (\frac{u_{1}}{b}, - u)|}^{2}] d u_{1}, | u | \leq \frac{u_{r}}{b} . \end{matrix}

Therefore, the model described in Figure 5 is identical to the procedure represented in Figure 4 in the sense of second order statistic characters.

Next, we will estimate the error

E [{|\hat{x} (t) - x (t)|}^{2}]

. Let

ε (t) = \hat{x} (t) - x (t)

. Combining (3.2) and (4.13), we get

\begin{matrix} P_{\hat{x} \hat{x}}^{A} (u) & = \frac{1}{2 π b} P_{\bar{x} \bar{x}}^{} (\frac{u}{b}) \\ = \frac{1}{2 π b} P_{x_{1} x_{1}} (\frac{u}{b}) {|ϕ_{ξ ζ} (\frac{u}{b}, - \frac{u}{b})|}^{2} + \frac{T}{4 π^{2} b} \int_{- \frac{u_{r}}{b}}^{\frac{u_{r}}{b}} P_{x_{1} x_{1}} (u_{1}) [1 - {|ϕ_{ξ ζ} (u_{1}, - \frac{u}{b})|}^{2}] d u_{1} \\ = P_{x x}^{A} (u) {|ϕ_{ξ ζ} (\frac{u}{b}, - \frac{u}{b})|}^{2} + \frac{T}{2 π b} \int_{- u_{r}}^{u_{r}} P_{x x}^{A} (u_{1}) [1 - {|ϕ_{ξ ζ} (\frac{u_{1}}{b}, - \frac{u}{b})|}^{2}] d u_{1} . \end{matrix}

(4.15)

Similarly, we can obtain

P_{\hat{x} x}^{A} (u) = P_{x x}^{A} (u) ϕ_{ξ ζ} (\frac{u}{b}, - \frac{u}{b}) .

(4.16)

In fact, it is easy to see that

\begin{matrix} R_{\bar{x} x_{1}} (t + τ, t) & = E [\hat{x} (t + τ) e^{j \frac{u_{0}}{b} (t + τ)} e^{j \frac{a}{2 b} {(t + τ)}^{2}} x^{*} (t) e^{- j \frac{u_{0}}{b} t} e^{- j \frac{a}{2 b} t^{2}}] \\ = R_{\hat{x} x} (t + τ, t) e^{j \frac{u_{0}}{b} τ} e^{j \frac{a}{b} t τ} e^{j \frac{a}{2 b} τ^{2}} . \end{matrix}

Therefore,

R_{\hat{x} x} (t + τ, t) e^{j \frac{a}{b} t τ}

is independent of t due to (4.12). Then

\begin{matrix} R_{\hat{x} x}^{A} (τ) = & R_{\hat{x} x} (t + τ, t) e^{j \frac{a}{b} t τ} \\ = & R_{\bar{x} x_{1}} (t + τ, t) e^{- j \frac{u_{0}}{b} τ} e^{- j \frac{a}{2 b} τ^{2}} . \end{matrix}

Moreover, it follows from (2.7) that

\begin{matrix} P_{\hat{x} x}^{A} (u) & = \sqrt{\frac{1}{- j 2 π b}} e^{- j \frac{d}{2 b} u^{2}} e^{^{- j \frac{d}{2 b} u_{0}^{2}}} e^{j \frac{u}{b} (d u_{0} - b w_{0})} F_{A} \{R_{\bar{x} x_{1}} (τ) e^{- j \frac{u_{0}}{b} τ} e^{- j \frac{a}{2 b} τ^{2}}\} (u) \\ = \sqrt{\frac{1}{- j 2 π b}} e^{- j \frac{d}{2 b} (u^{2} + u_{0}^{2})} e^{j \frac{u}{b} (d u_{0} - b w_{0})} \int_{- \infty}^{+ \infty} R_{\bar{x} x_{1}} (τ) e^{- j \frac{u_{0}}{b} τ} e^{- j \frac{a}{2 b} τ^{2}} \sqrt{\frac{1}{2 π j b}} e^{\frac{j d u_{0}^{2}}{2 b}} \\ \cdot e^{\frac{j}{2 b} [a τ^{2} + 2 τ (u_{0} - u) - 2 u (d u_{0} - b w_{0}) + d u^{2}]} d τ \\ = \frac{1}{2 π b} \int_{- \infty}^{+ \infty} R_{\bar{x} x_{1}} (τ) e^{- j \frac{u}{b} τ} d τ \\ = \frac{1}{2 π b} P_{\bar{x} x_{1}} (\frac{u}{b}) \\ = \frac{1}{2 π b} P_{x_{1} x_{1}} (\frac{u}{b}) ϕ_{ξ ζ} (\frac{u}{b}, - \frac{u}{b}) \\ = P_{x x}^{A} (u) ϕ_{ξ ζ} (\frac{u}{b}, - \frac{u}{b}) . \end{matrix}

(4.17)

Hence, the SAFT auto-power spectral density of the reconstruction error

ε (t)

\begin{matrix} P_{ε ε}^{A} (u) & = P_{\hat{x} \hat{x}}^{A} (u) - P_{\hat{x} x}^{A} (u) - P_{x \hat{x}}^{A} (u) + P_{x x}^{A} (u) \\ = P_{x x}^{A} (u) {|ϕ_{ξ ζ} (\frac{u}{b}, - \frac{u}{b})|}^{2} + \frac{T}{2 π b} \int_{- u_{r}}^{u_{r}} P_{x x}^{A} (u_{1}) [1 - {|ϕ_{ξ ζ} (\frac{u_{1}}{b}, - \frac{u}{b})|}^{2}] d u_{1} \\ - P_{x x}^{A} (u) ϕ_{ξ ζ} (\frac{u}{b}, - \frac{u}{b}) - {[P_{x x}^{A} (u) ϕ_{ξ ζ} (\frac{u}{b}, - \frac{u}{b})]}^{*} + P_{x x}^{A} (u) \\ = P_{x x}^{A} (u) {|1 - ϕ_{ξ ζ} (\frac{u}{b}, - \frac{u}{b})|}^{2} + \frac{T}{2 π b} \int_{- u_{r}}^{u_{r}} P_{x x}^{A} (u_{1}) [1 - {|ϕ_{ξ ζ} (\frac{u_{1}}{b}, - \frac{u}{b})|}^{2}] d u_{1}, \end{matrix}

(4.18)

where we have used the fact that

P_{x x}^{A} (u)

is real due to (3.2). Note that

ε_{1} (t) = ε (t) e^{j \frac{u_{0}}{b} t} e^{j \frac{a}{2 b} t^{2}} = (\hat{x} (t) - x (t)) e^{j \frac{u_{0}}{b} t} e^{j \frac{a}{2 b} t^{2}} = \bar{x} (t) - x_{1} (t) .

Then

ε_{1} (t)

is stationary. Moreover, it follows from (2.5) and (2.8) that

\begin{matrix} E [{|ε (t)|}^{2}] = R_{ε_{1} ε_{1}} (0) = R_{ε ε}^{A} (0) = \int_{- u_{r}}^{u_{r}} P_{ε ε}^{A} (u) d u \\ = \int_{- u_{r}}^{u_{r}} P_{x x}^{A} (u) {|1 - ϕ_{ξ ζ} (\frac{u}{b}, - \frac{u}{b})|}^{2} d u + \frac{T}{2 π b} \int_{- u_{r}}^{u_{r}} P_{x x}^{A} (u) \int_{- u_{r}}^{u_{r}} [1 - {|ϕ_{ξ ζ} (\frac{u}{b}, - \frac{u_{1}}{b})|}^{2}] d u_{1} d u . \end{matrix}

This completes the proof.

()f

ξ_{n}

and

ζ_{n}

equal to zero, then the nonuniform sampling studied in this paper reduces to the uniform sampling. In such case,

ϕ_{ξ ζ} (s, t) \equiv 1

. Then it follows from Theorem 4.2 that

\begin{matrix} E [| \hat{x} {(t) - x (t) |}^{2}] & = \int_{- u_{r}}^{u_{r}} P_{x x}^{A} (u) {|1 - ϕ_{ξ ζ} (\frac{u}{b}, - \frac{u}{b})|}^{2} d u \\ + \frac{T}{2 π b} \int_{- u_{r}}^{u_{r}} P_{x x}^{A} (u) \int_{- u_{r}}^{u_{r}} [1 - {|ϕ_{ξ ζ} (\frac{u}{b}, - \frac{u_{1}}{b})|}^{2}] d u_{1} d u \\ = 0 . \end{matrix}

That is to say,

x (t)

is equal to its approximation

\hat{x} (t)

in the mean square sense. From Theorem 3.5, one can see that for

T = T_{N} = \frac{π b}{u_{r}}

, the approximation of

x (t)

obtained in (3.12) becomes

\begin{matrix} \hat{x} (t) = e^{- j \frac{a}{2 b} t^{2}} \sum_{n = - \infty}^{+ \infty} x (n T) e^{j \frac{a}{2 b} {(n T)}^{2}} e^{j \frac{u_{0}}{b} (n T - t)} s i n c (\frac{u_{r} (t - n T)}{b}), \end{matrix}

(4.19)

which coincides with Theorem 3 in [29]. Therefore, the result of uniform sampling proposed in [29] is a special case of Theorems 3.5 and 4.2 in this paper.

Acknowledgments

The project is partially supported by the National Natural Science Foundation of China (No.12261025), Center for Applied Mathematics of Guangxi (No. AD23023002), Guangxi Colleges and Universities Key Laboratory of Data Analysis and Computation.

Conflicts of Interest

The authors declare that they have no competing interests.

References

S. Abe, J. T. Sheridan. Optical operations on wave functions as the Abelian subgroups of the special affine Fourier transformation. Optics Letters, 1994, 19: 1801–1803.
K. Adam, A. Scholefield, M. Vetterli. Sampling and reconstruction of bandlimited signals with multi-channel time encoding. IEEE Transactions on Signal Processing, 2020, 69: 1105-1119.
A. Aldroubi, J. Davis, I. Krishtal. Dynamic sampling: Time-space trade-off. Appl. Comput. Harmon. Anal., 2013, 34: 495–503.
Y. Bao, Y. Zhang, Y. Song, B. Li, P. Dang. Nonuniform sampling theorems for random signals in the offset linear canonical transform domain. Proceedings of APSIPA Annual Summit and Conference, 2017, Kuala Lumpur, Malaysia, 94–99.
R. F. Bass, K. Gröchenig. Random sampling of bandlimited functions. Isral J. Math., 2010, 177(1): 1-28.
A. Bhandari, A. I. Zayed. Shift-invariant and sampling spaces associated with the special affine Fourier transform. Applied and Computational Harmonic Analysis, 2019, 47: 30–52.
H. Boche, U. J. Mönich. Approximation of wide-sense stationary stochastic processes by Shannon sampling series. IEEE Transactions on Information Theory, 2010, 56(12): 6459–6469.
F. Gilles, K. Sinuk. Average sampling of band-limited stochastic processes. Applied and Computational Harmonic Analysis, 2013, 35(3): 527–534.
K. Gröchenig, J. L. Romero, J. Unnikrishnan, M. Vetterli. On minimal trajectories for mobile sampling of bandlimited fields. Appl. Comput. Harmon. Anal., 2015, 39: 487–510.
H. Huo, W. Sun. Sampling theorems and error estimates for random signals in the linear canonical transform domain. Signal Processing, 2015, 111: 31–38.
H. Huo, W. Sun. Nonuniform sampling for random signals bandlimited in the linear canonical transform domain. Multidimensional Systems and Signal Processing, 2020, 31: 927–950.
X. Liu, J. Shi, W. Xiang, Q. Zhang, N. Zhang. Sampling expansion for irregularly sampled signals in fractional Fourier transform domain. Digital Signal Processing, 2014, 34: 74–81.
S. Maymon, A. V. Oppenheim. Sinc interpolation of nonuniform samples. IEEE Trans. Signal Process., 2011, 59 (10): 4745–4758.
F. Oktem, H. Ozaktas. Exact relation between continuous and discrete linear canonical transforms. IEEE Signal Processing Letters, 2009, 16(8): 727–730.
C. E. Shannon. Communication in the presence of noise. Proc. IRE, 1949, 37: 10–12.
K. Sharma, S. Joshi. Signal separation using linear canonical and fractional Fourier transforms. Optics Communications, 2006, 265(2): 454–460.
Z. Song, W. Sun, X. Zhou, Z. Hou. An average sampling theorem for bandlimited stochastic processes. IEEE Transactions on Information Theory, 2007, 53(12): 4798–4800.
A. Stern. Sampling of compact signals in the offset linear canonical transform domains. Signal, Image and Video Processing, 2007, 1(4): 359–367.
R. Tao, B. Li, Y. Wang, G. Aggrey. On sampling of band-limited signals associated with the linear canonical transform. IEEE Transactions on Signal Processing, 2008, 56(11): 5454–5464.
R. Tao, F. Zhang, Y. Wang. Sampling random signals in a fractional Fourier domain. Signal Processing, 2011, 91(6): 1394–1400.
D. Wei, Q. Ran, Y. Li. Multichannel sampling and reconstruction of bandlimited signals in the linear canonical transform domain. IET Signal Processing, 2011, 5(8): 717–727.
H. Zhao, R. Wang, D. Song. Recovery of bandlimited signals in linear canonical transform domain from noisy samples. Circuits Systems and Signal Processing, 2014, 33(6): 1997–2008.
H. Zhao, R. Wang, D. Song, T. Zhang, D. Wu. Extrapolation of discrete bandlimited signals in linear canonical transform domain. Signal Processing, 2014, 94: 212–218.
Q. Xiang, K. Qin. Convolution, correlation, and sampling theorems for the offset linear canonical transform. Signal, Image and Video Processing, 2014, 8(3): 433–442.
Q. Xiang, K. Qin, Q. Huang. Multichannel sampling of signals band-limited in offset linear canonical transform domains. Circuits Systems and Signal Processing, 2013, 32(5): 2385–2406.
S. Xu, Y. Chai, Y. Hu. Spectral analysis of sampled band-limited signals in the offset linear canonical transform domain. Circuits Systems and Signal Processing, 2015, 34(12): 3979–3997.
S. Xu, Y. Chai, Y. Hu, C. Jiang, Y. Li. Reconstruction of digital spectrum from periodic nonuniformly sampled signals in offset linear canonical transform domain. Optics Communications, 2015, 348: 59–65.
S. Xu, L. Feng, Y. Chai, Y. He. Analysis of A-stationary random signals in the linear canonical transform domain. Signal Processing, 2018, 146: 126–132.
S. Xu, L. Feng, Y. Chai, Y. Hu, L. Huang. Sampling theorems for bandlimited random signals in the offset linear canonical transform domain. AEU-International Journal of Electronics and Communications, 2017, 81: 114–119.
S. Xu, L. Huang, Y. Chai, Y. He. Nonuniform sampling theorems for bandlimited signals in the offset linear canonical transform. Circuits Systems and Signal Processing, 2018, 37: 3227–3244.
S. Xu, C. Jiang, Y. Chai, Y. Hu, L. Huang. Nonuniform sampling theorems for random signals in the linear canonical transform domain. International Journal of Electronics, 2018, 105(6): 1051–1062.
L. Xu, F. Zhang, R. Tao. Randomized nonuniform sampling and reconstruction in fractional Fourier domain. Signal Processing, 2016, 120: 311–322.
X. Zhi, D. Wei, W. Zhang. A generalized convolution theorem for the special affine Fourier transform and its application to filtering. Optik, 2016, 127: 2613–2616.

Figure 1. Multiplicative filtering in the SAFT

Figure 2. The nonuniform sampling process

Figure 3. The equivalent system of the nonuniform sampling, where the filtering through filter

h_{1} (t)

means that

\tilde{y} (t) = \frac{1}{\sqrt{2 π}} \int_{R} \tilde{x} (s) h_{1} (t - s) d s

Figure 3. The equivalent system of the nonuniform sampling, where the filtering through filter

h_{1} (t)

means that

\tilde{y} (t) = \frac{1}{\sqrt{2 π}} \int_{R} \tilde{x} (s) h_{1} (t - s) d s

Figure 4. The approximate reconstruction with sinc interpolation function, where

\bar{x} (t) = \frac{T}{T_{N}} \sum_{n = - \infty}^{+ \infty} x_{1} (t_{n}) h_{2} (t - {\tilde{t}}_{n})

Figure 4. The approximate reconstruction with sinc interpolation function, where

\bar{x} (t) = \frac{T}{T_{N}} \sum_{n = - \infty}^{+ \infty} x_{1} (t_{n}) h_{2} (t - {\tilde{t}}_{n})

Figure 5. An equivalent nonuniform sampling and reconstruction system to Figure 4, where

v (t)

is an additive noise with zero mean which is uncorrelated with

x (t)

and has power spectral density as (4.5).

Figure 5. An equivalent nonuniform sampling and reconstruction system to Figure 4, where

v (t)

is an additive noise with zero mean which is uncorrelated with

x (t)

and has power spectral density as (4.5).

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Randomized Nonuniform Sampling for Random Signals Bandlimited in the Special Aﬃne Fourier Transform Domain

Abstract

1. Introduction

2. Power Spectral Density in the SAFT Domain

3. Nonuniform Sampling and Approximate Recovery

4. Error estimate for Nonuniform Sampling

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe