Water Supply Network Renewal Strategic Planning Utilizing the VIKOR Method

Water networks are critical infrastructure components, ensuring the continuous supply of high-quality drinking water to consumers. To secure such water supply, regular maintenance, including the replacement of deteriorating pipelines, is essential. In this study, a methodology has been developed for determining optimal pipeline replacement solutions in water supply systems at water utilities with limited data availability. Hydraulic analysis has been conducted on the segment of 25 km of the water supply network using the free software EPANET. Applying water network optimization, eight pipeline replacement projects according to 13 pre-defined criteria have been identified and evaluated. The paper outlines the methods for evaluating the criteria, including defining specific quantitative limits. The Analytical Hierarchical Process (AHP) method was used in the paper to determine the weights of the criteria. The reason for applying this method refers to problems that involve a set of criteria with a mixed structure, including both quantitative and qualitative aspects. Also, the paper describes the steps of the multi-criteria optimization method VIKOR, used to select the optimal project. This paper, considered as case studie, describes a method, i.e. application of a new principles and an innovative way to solve a problem for developing countries.

Keywords:

Subject: Engineering - Other

1. Introduction

Water networks represent the most significant infrastructure objects of the water supply system, providing optimal and reliable water supply [1,2,3]. This implies that the fundamental purpose of a water supply network is to foster social and economic prosperity while safeguarding public health [4].

In addition to the global issue of water scarcity [5], water supply system management faces significant challenges, notably the reduction of water losses within distribution networks [6]. These challenges are particularly acute in less developed countries, as they result in reduced revenue for water utilities (when water losses imply water supply reductions, for limited water availability), compromise water quality, and escalate operational and maintenance costs [5]. Water consumers expect uninterrupted access to water of appropriate quality and pressure, 24/7, 365 days a year [7]. To meet these demands, various types of maintenance (corrective and preventive maintenance) are essential for water supply networks [8]. Properly managing a water supply network requires not only the continuous operation of water supply facilities but also the restoration of their technical characteristics through defect repairs and the replacement of aging water pipes [7,9]. Furthermore, maintenance encompasses the replacement of infrastructure once it exceeds its expected lifespan. Typically, the estimated lifespan of water supply infrastructure is 50 years, necessitating an annual replacement rate of approximately 2%. In this regard, to ensure the longevity and efficiency of the water network, the management structure of water companies must develop plans for infrastructure restoration [10].

Pipeline replacement serves as a critical strategy to uphold the service standards provided to consumers, primarily driven by the need to enhance water quality, maintain health and safety standards, address inadequate permeability, or respond to external factors impacting pipeline integrity. It’s important to note that pipeline replacement isn’t exclusively undertaken to reduce water losses; however, it plays a substantial role in mitigating water loss and can serve as an additional justification for pipeline replacement.

Technical solutions for water supply systems in Bosnia and Herzegovina and neighboring Western Balkan countries were primarily developed during the early and mid-20^th century, when most of the present infrastructure was constructed. At that time, the primary objective of these systems was to meet the water demands of the population, as well as various sectors such as industry and the military. These systems were designed based on data available during that era. Subsequent expansions of water supply systems were carried out without a comprehensive and planned approach, often leading to inefficiencies. Many of these systems are characterized by overcapacity, inadequate maintenance, and continuous construction of new water abstraction facilities. This inefficiency results in high operational costs, making them economically unsustainable. Moreover, the pricing of water is typically a subject of political negotiation and doesn’t accurately reflect the actual costs incurred by water companies. This practice further exacerbates the challenge of maintaining these water systems regularly. Typically, interventions occur only in response to major issues, with each successive problem being more extensive than the previous one.

Recently water supply systems in Bosnia and Herzegovina and the Western Balkan have been shifting their focus away from constant expansion and the construction of new water supply catchment facilities. Instead, there is a growing emphasis on renovating older infrastructure, reducing water losses, and implementing initiatives aimed at raising consumer awareness about the value of water and the importance of its efficient use. Notably, thanks to funding and donations from EU programs in Bosnia and Herzegovina, there has been a discernible trend towards improving the situation regarding water loss reduction in water supply systems [11]. However, it’s worth mentioning that there is relatively less attention paid to the strategic planning of replacing the aging water supply network, despite its importance in addressing the challenges faced by these systems.

In Bosnia and Herzegovina, local communities own and are responsible for managing the water supply network, with the primary obligation of overseeing its maintenance. Water companies, funded by LGs, are entrusted with the vital task of ensuring a consistent water supply to the population. To sustain optimal water supply conditions [1], it becomes imperative to develop strategies for renovation of the water supply network through a combination of repair and replacement efforts [4].

For the pipeline replacement decision-making and prioritization process greatly benefits from the application of multi-criteria optimization (MCO) methods. The relevance of MCO methods becomes evident when considering that pipeline replacement should not be pursued as an isolated objective but rather evaluated from a multifaceted perspective [12,13]. This entails the utilization of relevant criteria to determine priorities when making decisions about replacing segments of the water supply network [14].

Research in water resources management has demonstrated the extensive utility of MCO methods, primarily in the domains of strategic planning and infrastructure management. These methods have been identified as instrumental across eight distinct applications [12] encompassing watershed management, groundwater management, infrastructure selection, project evaluation, water allocation, water supply policy and planning, water quality management, and the management of protected marine areas. Commonly employed methods in these applications include compromise programming, AHP (Analytic Hierarchy Process), ELECTRE (ELimination Et Choice Translating REality), and PROMETHEE (Preference Ranking Organization METHod for Enrichment Evaluation). A recent analysis by [15] categorized the application of VKO methods in water supply issues from 2000 to 2019 into several problem domains: water shortage-based problems, water use management-based problems, water quality-based problems, water environmental/ecosystem-based problems, flood-based problems, and combined water problems, such as those involving water shortage and water quality or water shortage and flood.

The aim of this paper is to contribute to the intricate decision-making process surrounding pipeline replacement within water systems. This contribution is achieved through the development of a methodology that is applicable in the context of water systems in less developed countries, particularly when faced with limited data availability.

2. Materials and Methods

The main objective of this study is to efficiently plan the replacement of pipelines in water supply systems, especially in countries with limited data availability on their water supply networks. In this context, the study identifies the criteria for which data are typically accessible to the majority of water supply companies in less developed countries. Two methods were applied to the problem of choosing the optimal project for the rehabilitation of the pipeline system: the VIKOR method for the process of choosing the optimal project and the AHP method for the process of determining the weights of the criteria. Real data for calculating the criteria for the repair of the pipeline system were taken for the Vojkovići water supply system located in Bosnia and Herzegovina.

2.1. Choice of Criteria for Replacement of the Water Supply Network

Presently prevailing approach in the water supply systems of less developed countries has often relied on the intuition of management, typically focusing on a single, usually financial criterion. However, relying solely on a single criterion and adopting an "ad hoc" approach to tackle intricate problems, such as those associated with water supply systems, can result in unpredictable consequences. Hence, it is imperative to address and analyze these issues from a multi-criteria perspective.

Criteria represent standards, rules, or tests on which decisions are based, that is, they represent a tool for evaluating and comparing potential alternatives. Each criterion should be measurable and not dependent on another criterion, i.e. the criteria should be: operational, applicable for measurements of alternatives, complete but not too many [16].

The criteria can only be defined based on the determination of the goals that the appropriate water system should reach. Through a review of studies, numerous objectives of efficient management of the water supply system were identified (e.g. economic, public health, social, technical, sustainability, operational, financial, infrastructural, etc.) [17,18,19,20,21,22].

Since most papers only consider a subset of the criteria required for effective water supply management Salehi et al. (2017) [23] aggregated all pertinent criteria, categorizing them into technical and non-technical categories. In total, there are 42 parameters for analysis that encompass both technical and non-technical criteria.

Subsequently Salehi et al. (2020) [24] further classified these technical and non-technical criteria into eight distinct categories: Mechanical Criteria, Operational Criteria, Environmental Criteria, Economic Criteria, Hydraulic Criteria, Social Criteria, Physical Criteria, and Qualitative Criteria. This categorization resulted in a total of 48 criteria.

It was evident that comprehensive data necessary for all initially suggested criteria are often lacking in water supply companies in less developed countries. As a result, the criteria for which the majority of water supply companies in Bosnia and Herzegovina and the Western Balkans countries have precise data were singled out, as detailed in Table 1. Consideration was carefully given to the selection of criteria that are really significant for addressing specific problems and for which exact data are readily available. Furthermore, to simplify calculations and avoid redundancy, certain individual criteria were consolidated into a single criterion (for example, criteria color, taste, residual chlorine, the smell of water, and so on are comprised into one criterion, i.e. water quality) [25]. In addition to the 12 adopted criteria, an additional criterion was introduced, namely, ’flat-rate connection,’ representing consumers whose water consumption is not metered. This scenario is frequent in water supply companies throughout Bosnia and Herzegovina and the other Western Balkans countries.

It is important to emphasize that, for each criterion defined in Table 1, data can be obtained in most water companies in less developed countries.

2.2. Evaluation of Criteria

The evaluation of criteria and their evaluation method is presented in Table 1. Quantitative criteria are those criteria characterized by numerical values that distinctly demonstrate variations in the value of each criterion. This group of criteria encompasses parameters such as average pressure, flow rate, pipe age, pipe length, pipe diameter, number of connections, number of flat connections, failure rate, and total investment.

In contrast to quantitative criteria, qualitative criteria cannot be quantified in the initial stage. This category of criteria comprises factors such as the ease of soil excavation around the pipe, water quality, and population density. The general descriptive treatment of qualitative criteria is as follows: H - high; M - medium and L - low. These labels, namely H - high, M – medium and L - low, serve to indicate the impact of an individual alternative on the qualitative criterion. Despite their lack of measurably, it is imperative that the evaluation criteria maintain logical consistency. To achieve such logical grading, each grade should possess clear definitions, that is, the boundaries of the constraints for each grade should be established. Each of the descriptive grades in the second stage can be assigned a numerical value, specifically: H – 1; M – 3 and L - 5.

The qualitative criterion of the ease of excavating the soil around the pipe implies the way of carrying out the works depending on the configuration of the terrain (the impossibility of carrying out the works with machines or the possibility of using modern technologies for the execution of the works), the type and installation of materials (the weight of the terrain for the installation of the materials, digging or under-drilling of roads, the existence of other installation on the route, etc.) and it is possible to evaluate the same in the design service and maintenance service of the water supply company (this criterion is always maximized). Limits for this criterion can be defined as follows:

H - High impact on the performance of works implies impassibility or the impossibility of performing works with machines, i.e. implies inaccessible and impassable terrain.
M – Medium impact implies moderate terrain pass-ability where less techniques can be used. A soil composed of crumbly and soft rocks can also be considered as having a medium impact. On some sections, interventions such as drilling the road, moving installations, etc. are needed.
L - Low impact on the execution of works implies that the route is accessible and passable, and modern equipment can be used on each section, that is, no additional interventions are needed on the section.

The qualitative criterion of water quality is an evaluation of the quality of water (this criterion is minimized) and can be characterized through three descriptive scales:

H - Signifying a high impact on the consumer, this corresponds to low-quality drinking water (which may exhibit impaired taste, smell, and color).
M - Denoting a medium impact on the consumer, this implies that the quality of drinking water is conditionally satisfactory (making it suitable for use as technical water), and
L - Representing a low impact on the consumer, this implies that the quality of drinking water conforms to the standards set out in the Rulebook on the hygienic correctness of drinking water.

Population density, as a qualitative criterion, encompasses factors related to the location of pipeline replacement, distinguishing between urban and rural areas. It takes into account variables such as population density, traffic volume, street congestion, the feasibility of diverting traffic, and more (this criterion is maximized). This criterion can be characterized through three descriptive scales:

H - Signifying an urban area with high population density, frequent traffic, the necessity of prolonged traffic stoppages, presence in tourist zones, and significant disruption to everyday life. Extensive preparations are required for work execution in this zone.
M - Denoting a medium impact, this indicates that population density is not particularly high, and there may be occasional short-term disruptions in traffic. Nevertheless, these disruptions do not significantly affect the daily lives of citizens.
L - Representing a rural area with minimal traffic, no need for traffic stoppages, and no significant disruption to daily life. This zone typically requires fewer logistical preparations for work execution.

2.3. VIKOR Method

The VIKOR method, which stands for Multi-Criteria Compromise Ranking (Serbian language – VIšekriterijumsko KOmpromisno Rangiranje), is employed in this work to determine the optimal solution when faced with multiple criteria. This method was developed based on the idea of presenting a solution to decision-makers that strikes a compromise between their desires and the constraints, or represents a kind of compromise of the diverse interests of decision-making participants [26].

As noted by Thakkr et al. (2021) [27], the VIKOR method is a powerful tool applicable to a range of strategic decision-making scenarios across various domains, including social, technical, economic, and environmental contexts. The approach within the VIKOR method involves several steps: identifying different potential solutions for a given problem, establishing priorities among these solutions, ranking them in ascending order, and ultimately selecting the best solution [27,28,29]. Consequently, the VIKOR method is well-suited for optimizing complex systems with multiple criteria that may be in conflict with each other. It aids in the selection of the most favorable solution from a set of available alternatives by taking into account these conflicting criteria and finding a compromise that aligns with the decision-makers’ objectives and constraints.

2.3.1. Steps of the VIKOR Method

The VIKOR method is typically carried out through a series of steps to evaluate and select the optimal solution when dealing with conflicting criteria and multiple alternatives. Here are the six steps of the VIKOR method [30,31,32]:

STEP 1: The initial step in the optimization process involves gathering information about all the criterion functions for each potential alternative. This requires knowing the values associated with each criterion for all possible alternatives. The problem is then formulated into an evaluation matrix, often in tabular format (Table 2). In the Table 2, the variable "(

a_{1}

a_{2}

, ...,

a_{i}

, ..., a)" represents a finite set of possible alternatives and

f_{1}

(.),

f_{2}

(.), ...,

f_{j}

(.), ...,

f_{k}

(.), a set of evaluation criteria. The VIKOR method assumes that all criteria should be maximized. However, there are situations where certain criteria need to be minimized. To align these minimized criteria with the VIKOR method’s requirement, they are adjusted by multiplying them by -1.

STEP 2: In the second step, the best

f_{i}^{*}

and the worst

f_{i}^{*}

value of all criteria i = 1, 2,... n are determined. When the evaluation matrix is formed, the maximum and minimum values are requested for each criterion:

\begin{matrix} f_{i}^{*} & = max_{j} f_{i j} & f_{i}^{-} & = min_{j} f_{i j} \end{matrix}

(1)

STEP 3: In the third step, the values of

S_{j}

and

R_{j}

, where j = 1, 2, ..., J, corresponding to the norms

L_{1}

and L∞, respectively, are calculated as follows:

S_{j} = \sum_{i = 1}^{n} \frac{w_{i} (f_{i}^{*} - f_{i j})}{(f_{i}^{*} - f_{i}^{-})}

(2)

\begin{matrix} R^{*} = min_{\begin{matrix} j \end{matrix}} & R_{j} R^{-} = max_{\begin{matrix} j \end{matrix}} R_{j} \end{matrix}

(3)

Where the weights of the criteria, represented by

w_{i}

, express their relative importance and reflect the decision maker’s preference.

STEP 4: The values of the compromise solution

Q_{j}

, where j = 1, 2, ..., J, are calculated as follows:

\begin{matrix} Q_{j} & = \frac{v (s_{j} - s^{*})}{(s^{-} - s^{*})} + \frac{(1 - v) (R_{j} - R^{*})}{(R^{-} - R^{*})} \end{matrix}

(4)

the factors in the equation are as follows

\begin{matrix} S^{*} & = min_{j} S_{j} & S^{-} & = max_{j} S_{j} \end{matrix}

(5)

\begin{matrix} R^{*} & = min_{j} R_{j} & R^{-} & = max_{j} R_{j} \end{matrix}

(6)

STEP 5: In the fifth step, the alternatives are ranked by sorting the values of S, R, and Q in ascending order because the best alternative is the one with the lowest value. The ranking is determined by sorting the alternatives based on the measures QS, QR, and finally Q. The best alternative is the one with the minimum value in the measure and has the top position in the ranking list.

STEP 6: In the sixth step, a compromise solution (

a^{'}

) is proposed, which ranks best according to the Q measure if two conditions are met, namely

Acceptable advantage

Q (a^{''}) - Q (a^{'}) \geq Δ Q

where:

a^{''}

is the second-placed alternative in the ranking list Q;

Advantage Threshold DQ = 1/(M - 1);

D Q = 1 / (M - 1)

where M is number of alternatives.

Acceptable stability: Alternative

a^{'}

should also be the best-ranked S and/or R rank.

The VIKOR method is a six-step approach used to calculate compromise values and establish a ranking list of alternatives. It is known for its simplicity in application and versatility, making it suitable for a wide range of criteria and alternatives. What distinguishes the VIKOR method from others are the two essential conditions that a solution must satisfy: acceptable advantage and solution stability. In essence, the obtained result is considered valid only if it meets these two crucial conditions.

3. Case Study East Sarajevo

3.1. Analysis of the Water Supply Area

In the subsequent sections of this study, the analysis is focused on the district metering area (DMA) of the water supply system in Vojkovići, which is managed by the Communal Company "Vodovod i Kanalizacija" a.d. in East Sarajevo. DMA Vojkovići, as informed by data obtained from the municipality of East Ilidza, supplies with water approximately 4,300 inhabitants. This region is predominantly composed of individual residential buildings and is situated in the rural part of the city of East Sarajevo. The precise number of connections to the water supply network is 1257.

Water supply companies, to varying degrees, utilize free software such as EPANET 2.0 or EPANET 2.2 for hydraulic analysis and optimization of their water supply networks [33,34,35,36]. For the purpose of creating the hydraulic model of the Vojkovići water supply system within the EPANET 2.2 software, data concerning the existing types and materials of pipelines were gathered. It was determined that the water supply network in the Vojkovići DMA spans 25 kilometers, featuring pipe diameters ranging from DN 50 to DN 400 mm. Various pipeline materials are in use, including polyethylene, cast iron, and asbestos cement pipelines. Upon analyzing the materials in use, it can be inferred that the water supply network includes pipelines that are over 40 years old, installed using the technology and knowledge available at that time. The expansion of the pipeline network occurred without a comprehensive planning approach and a holistic assessment of the system’s deficiencies.

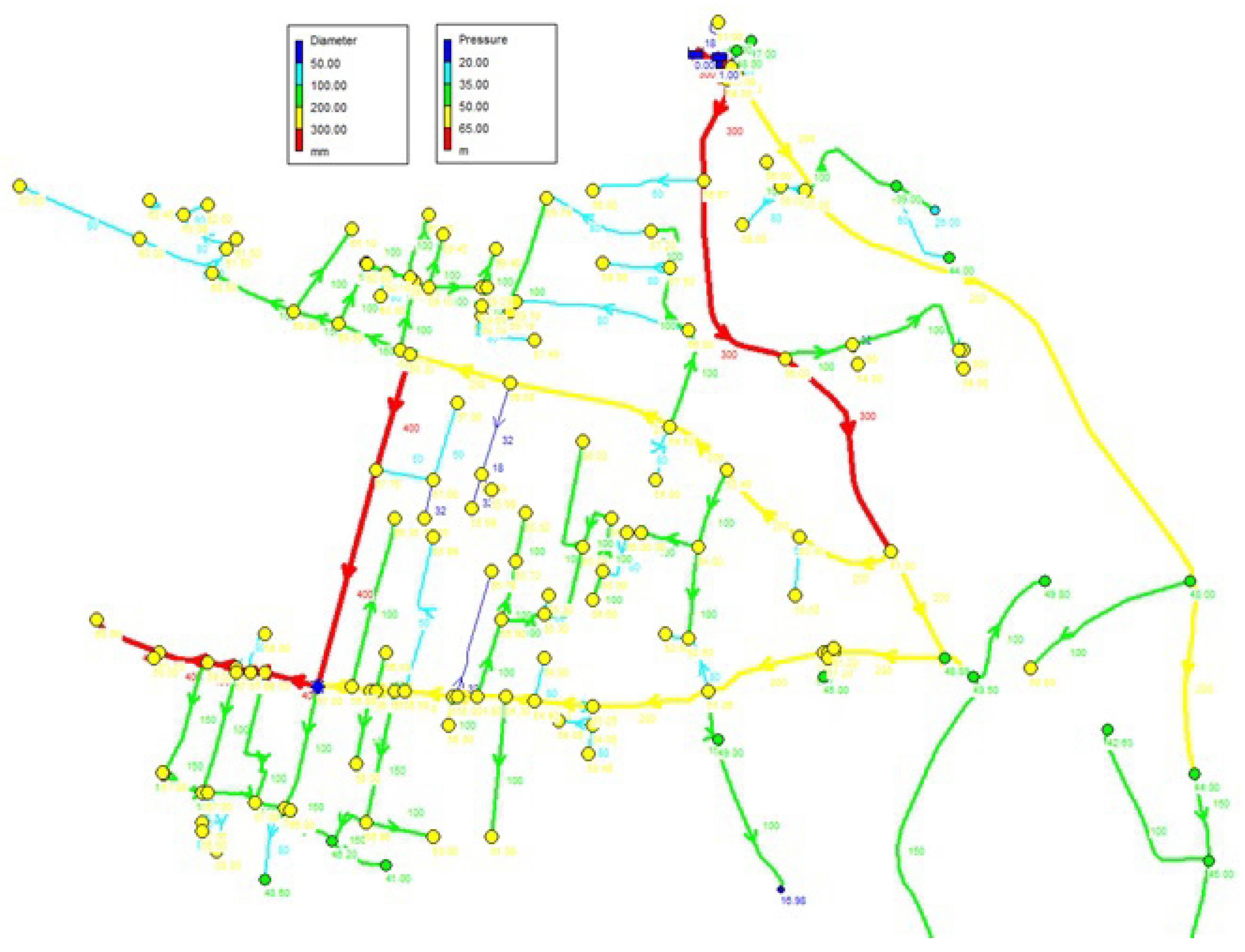
By developing a hydraulic model for the water supply network illustrated in Figure 1, presuming no leaks in the water supply network, it was determined that certain sections of the pipeline have exceptionally low water flow rates and flows, indicating that these segments are oversized for the current and future water demands of the local population. The red line shows pipelines having a diameter higher than 300 mm, and the yellow line shows pipeline diameters from 200 to 300 mm. The age of these pipelines is over 40 years. The pressures in the junctions are largely satisfactory from the point of view of the hydraulic model, however, for the purposes of applying the pipeline replacement methodology, they were checked in the field. It was found that in some places pressure is significantly lower compared to the calculated pressures within the hydraulic model. This observation suggests the presence of leaks or losses within the water supply network. Also, it was established that the need for water in DMA is on average about 14 l/s, and at the inflow to the system this amount is significantly higher and ranges to 35 l/s. Measured high water input amounts indicate water losses in the pipes. The flow rate in the pipeline, according to the hydraulic model without losses, is low even at the time of maximum consumption, which indicates that the pipeline, in addition to its age, is oversized and that it is necessary to replace it with pipelines of the appropriate diameter.

An assessment of the failures that occurred over the past 5 years was conducted, revealing a total of 507 work orders issued for interventions on the water supply network within the Vojkovići measuring area. Following a comprehensive analysis and optimization of the water supply network using the hydraulic model developed in the EPANET software, 8 projects for the replacement of the primary pipelines were identified. These project selections also took into account plans for the construction of new residences and potential commercial entities. Table 3 highlights that the chosen projects consist of substantially oversized pipelines designed to meet both current and anticipated future water demands within the studied region.

3.2. Results and Discussion

The aim of the paper is to present and test the methodology for choosing the optimal solution for the restoration of the water supply network. As outlined in the paper, a list of pertinent criteria has been established as the basis for the analysis and evaluation of all planned projects, with each project being assessed against these criteria. The criteria are classified into categories (Table 1) and the data required for their evaluation are provided as follows:

Hydraulic criteria, for instance, are assessed quantitatively. The mean pressure within the pipeline (C1) was computed using the average values derived from the known pressure at various nodes within the hydraulic model. Furthermore, a comparison between the pressures obtained from the hydraulic model and the actual field pressures was conducted to determine any disparities. The pipeline (C2) water flow velocity was determined through the hydraulic model. Additionally, a query was conducted regarding flow rate velocity, and the flow rate velocity for each segment of the water system was shown. Furthermore, utilizing EPANET software, the water flow through the pipeline (C3) was ascertained based on the flow query conducted. It is necessary to emphasize that the values of the criteria were considered during the time of the highest consumption.

The mechanical criteria category is evaluated quantitatively and is taken from the EPANET software. In order to make the hydraulic model correctly, data on the age of the pipe (C4), length (C5), and diameter of the pipe (C6) are entered into the software.

The category operational criteria, number of connections (C7), and number of fixed connections (C8) are information that is available in the billing service of the water company. The operational criterion of the failure rate (C9) can also be classified in the environmental category because network failures cause water loss in the water supply system. Data on the rate of failures were taken from the maintenance service based on work orders, that is, repairs of failures on certain sections of the water supply system. Criteria that fall into the category of operational criteria are determined quantitatively.

The category of physical criterion - ease of soil excavation (10) implies the method of carrying out the works depending on the configuration of the terrain (the impossibility of carrying out the works with machines or the possibility of using modern technologies for the execution of the works), the type and installation of materials (the complexity of the terrain for material installation, excavation, or under-drilling of roads, as well as the presence of other structures along the route, all contribute to the challenges faced during construction) and the same was assessed by the maintenance department of the water company. It is necessary to emphasize that potential obstacles in soil excavation contribute to a higher investment price. The physical criterion is determined qualitatively.

Water quality (C11), which is part of the qualitative criteria, implies the quality of water for consumers. Depending on the retention of water in the tank, pipeline, or at the ends of the network, the quality of the water changes. Data on water quality was taken from the drinking water control department.

The total cost of the investment (C12) belongs to the group of the economic category, so the data on the investment for the individual alternative is provided by the development department of the water company. In addition to the cost of the investment, attention is also focused on the value of the pipeline that is being changed (eg steel, cast iron, etc.). Criteria from the economic category are determined quantitatively.

The social category of criteria includes population density (C13) and this is the data that was analyzed in the development department of the water company. The social category of criteria is determined qualitatively.

Table 4 illustrates the evaluations of criteria for each of the individual projects. Table 4. show that there isn’t a single project that excels in all criteria values. Furthermore, it’s evident that criteria C2, C11, and C12 should be minimized, while criteria C1, C3, C4, C5, C6, C7, C8, C9, C10, and C13 should be maximized. To achieve this consistency, a simple transformation of the criteria that need minimization (by multiplying by -1) is applied, resulting in all criterion functions being reformulated to maximize them. Since, depending on the criteria category, there are different units of measure, and also no project is the best according to all criteria, the values of the criteria are normalized. The normalization of criteria values is presented in Table 5.

After normalizing the values, weight coefficients must be assigned to all criteria. Determining the weight of each criterion is one of the key problems that occurs in multi-criteria optimization models. There is no unique way of determining the weights of the criteria and they are usually determined subjectively. Since the weights of the criteria can significantly affect the result, it is necessary to pay attention to the objectivity of the weights of the criteria. For problems that involve a set of criteria with a mixed structure, including both quantitative and qualitative aspects, the authors have opted for the Analytical Hierarchical Process (AHP) method. This method, initially formulated by Saaty and further detailed in works such as [37,38,39,40,41], facilitates the systematic evaluation of criteria one by one.

The application of the AHP method for determining the weights of the criteria can be observed through four basic steps [38]:

Step 1: Develop a hierarchical model with the objective at the top, the criteria at a lower level, and the alternatives at the bottom of the model for precise comparison.

Step 2: Using Saaty’s scale (scoring 1, 3, 5, 7, and 9 or Equally Important, Moderate Dominance, Strong Dominance, Demonstrated Dominance, and Absolute Dominance respectively) the criteria are compared in pairs.

Step 3: Based on the assessment of the relative importance of the comparative criteria, the weights of the criteria are calculated.

Step 4: An analysis of the degree of (in)consistency is carried out - the tolerance limit is 0.1.

In the process of comparing the ratio of the criteria, a significant problem arose, which is reflected in the high range of values obtained. Namely, the following participated in the analysis of criteria evaluation: technicians from the water supply company, directors of utility companies, employee of the Ministry of Foreign Trade and Economic Relations of BiH (belongs to the Department for water resources and Environmental Protection), and several consumers, i.e. users who do not belong to any of the listed categories. The rating range for the relationship between the two criteria ranged from 1/3 to 7, which means that the relationships are not consistent and that this type of decision-making is new in Bosnia and Herzegovina. Therefore, it lead to the conclusion that professional help is necessary to draw usable conclusions from the answers offered. In this regard, the authors, based on their experience, proposed consistent criterion ratios and again discussed the proposed ratios with the participants. Based on the proposed evaluation of the ratio of the criteria, consistent ratios were established (degree of consistency is 0.1). The criteria comparison matrix is shown in Table 6.

Through pairwise comparisons of criteria and assessing the consistency of the results obtained, Table 7 displays the weight values assigned to each criterion.

After evaluating the projects according to the criteria and determining the weight coefficients, the values of S, R and Q are calculated, which are shown in the steps of the VIKOR method. A ranking list of projects is obtained for the weight of the strategy, which is v=0.5. The ranking of the projects is shown in Table 8.

The ranking list indicates that the top-ranked project for pipeline replacement is Project P6, followed by Project P5 in the second position. Once the ranking of projects has been determined, it is essential to establish the criteria for acceptable advantage and acceptable stability.

The difference between the rankings of the first and second projects is 0.163, while the DQ (DQ is often used to denote the difference between the maximum and minimum values in VIKOR) is 0.143, indicating that the condition of acceptable advantage has been met. Additionally, Project P6 ranks highest in the R ranking, satisfying the condition of acceptable stability.

As the VIKOR method typically considers the best alternative to be the one with the lowest value, which is not always welcome by real decision makers, alternative is to normalize the values within the range of 0 to 100 so that the best alternative receives the highest value, and the worst receives the lowest. The normalization of the ranked alternatives is achieved using the following expression:

\begin{matrix} R_{i j} = \frac{(A_{i j} - A_{imax})}{(A_{imin} - A_{imax})} \times 100 \end{matrix}

(7)

where is

A_{i j}

the value of the individual project rank shown in the Table 8.,

A_{i m i n}

– the minimal value of the projects rank shown in Table 8,

A_{i m a x}

– maximal value of the projects rank shown in Table 8. By following this approach, the best alternative will be assigned a value of 100, while the worst alternative will have a value of 0. The final ranking list is depicted in Table 9.

Through an analysis of the obtained results, it is evident that, considering the actual conditions in the water supply system, both Project 5 and Project 6 are top priorities for replacement. These pipelines are characterized by being oversized, resulting in water stagnation and very low flow rates, which in turn lead to frequent consumer complaints about water quality and the need for frequent pipeline desalting. While there may be some pressure drop in these pipelines, it is not significantly pronounced compared to other projects, and the number of flat-rate connections is also relatively low.

4. Sensitive analysis

Sensitivity analysis is often used to determine the sensitivity of the decision model, i.e., changes in the ranks of projects with changes in weighting coefficients [42,43,44], There are various ways of changing weighting coefficients. In this study, for one scenario, the same importance was assigned to each criterion, and for the other scenarios, 0.3 values were given to one criterion [43]. Table 10 presents 14 analyzed scenarios with changes in weighting coefficients, and Figure 2 shows the obtained results.

Spearman’s rank correlation coefficient [44] was used to analyze the sensitivity of the results of ranked projects:

\begin{matrix} S = 1 - \frac{6 \sum_{i = 1}^{N} d_{i}^{2}}{N (N^{2} - 1)} \end{matrix}

(8)

\begin{matrix} d_{i} = R (0) - R (i) \end{matrix}

(9)

Where N is number of projects, d is difference between starting (zero) project and i – th project, R rank of the observed project.

Applying Spearman’s rank correlation coefficient, coefficient values from (0.333 to 1) were obtained, which indicates that there are deviations in correlation in different scenarios. Pronounced deviations in correlation occurred in scenarios 4, 6, 7, 8 and 9. In scenarios 1, 2, 3, 5, 10, 11, 12, 13 and 14, the results show a trend towards a positive correlation. It is necessary to emphasize that the deviations are expressed in those scenarios where the priority of 30% of the value was given to the criterion that had low initial weight values. In this regard, the high valuation of coefficients that initially had low values has negative influence on the model, changing ranking of alternatives i.e. projects.

The results obtained by the VIKOR method were compared with the TOPSIS method (Technique for Order Preference by Similarity to Ideal Solution) [31,45], and the results are shown in Figure 3.

The ranking results using the VIKOR and TOPSIS methods indicate that the order of the first three projects is the same for both methods and are 1st - P5, 2nd - P6 and 3rd - P4. During the sensitivity analysis by changing the value of the weighting coefficients, project P5 was in first place among the ranked projects in 12 scenarios, project P6 in second place in 10 scenarios, and project P4 in third place in 8 scenarios.

5. Conclusions:

In less developed countries, water supply systems often find themselves dealing with limited data compared to their counterparts in developed countries. Criteria and a method for their evaluation, complete with clearly established boundaries, were defined based on the available data in these water supply systems. In this paper, a methodology was developed with the aim of determining optimal solutions for pipeline replacement in water supply systems constrained by limited data. The research has demonstrated that the application of the VIKOR method for multi-criteria optimization can significantly assist in making informed decisions regarding pipeline replacement in water supply systems. The VIKOR method stands out for its simplicity in application and its capacity to handle a substantial number of criteria and alternatives. What distinguishes the VIKOR method from other approaches are the two crucial conditions that must be met for a solution to be deemed valid: the requirement of an acceptable advantage and the need for solution stability. The result obtained through the VIKOR method is considered valid only if it satisfies these two conditions. In summary, it can be concluded that the VIKOR method serves as a valuable tool for decision-makers, providing them with a realistic perspective on the situation and aiding in making informed decisions when planning the replacement of pipelines in the water supply system.

The AHP method for multi-criteria optimization was employed to determine the weights of individual criteria. Notably, criteria such as water quality, investment value, frequency of failures, and pipe flow velocity were found to carry greater weight compared to other criteria. These criteria encompassed both the regularity of water supply and the quality of water for consumers, as well as the financial aspect of project implementation. However, it is possible for individual water supply systems to omit certain criteria they deem less important, adjust the model according to system specifics, assign different weights to individual criteria when selecting the appropriate project, or even allocate the same weight to each criterion.

The results obtained in this research can be of value not only to water supply companies but also to technical professionals involved in determining the necessary parameters for pipeline replacement. During this study, other challenges faced by water supply companies were also observed, including pressure drops among consumers, reduced flow, and network leaks. In the future, one potential research direction for hydraulic models of water supply systems could involve the development of an algorithm for predicting potential leaks in the water supply network.

Author Contributions

All authors conceived, designed, and performed the experiments, and all authors analyzed the data. All authors contributed to writing the paper. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Conflicts of Interest

The authors declare no conflict of interest.

References

Da Silva, W.; Souza, M. A decision support model to Baid the management of crises in urban water supply systems (the uwc-model). Urban Water J. 2017, 14, 612–620. [CrossRef]
Kabir, G.; Tesfamariam, S.; Francisque, A.; Sadiq, R. Evaluating risk of water mains failure using a Bayesian belief network model. Eur. J. Oper. Res. 2015, 240, 220–234. [CrossRef]
Loucks, D.; Van Beek, E. Water Resource Systems Planning and Management, An Introduction to Methods, Models, and Applications. Springer 2017, pp. 527–565. [CrossRef]
Nunes, R.; Arraut, E.; Pimente, M. Risk Assessment Model for the Renewal of Water Distribution Networks: A Practical Approach. Water 2023, 15, 3947–3969. [CrossRef]
Kadenge, M.; Masanja, V.G.; Mkandawile, M. Optimisation of Water Loss Management Strategies: Multi-Criteria Decision Analysis Approaches. J. Math. Inform. 2020, 1. [CrossRef]
Aschilean, I.; Giurca, I. Choosing a Water Distribution Pipe Rehabilitation Solution Using the Analytical Network Process Method. Water 2018, 484, 305–318. [CrossRef]
Romaniuk, M. Optimization of maintenance costs of a pipeline for a V-shaped hazard rate of malfunction intensities. Eksploatacja i Niezawodnosc – Maintenance and Reliability 2018 2018, 20, 46–56. [CrossRef]
Romaniuk, M.; Hryniewicz, O. Estimation of maintenance costs of a pipeline for a U-shaped hazard rate function in the imprecise setting. Eksploatacja i Niezawodnosc – Maintenance and Reliability 2020 2020, 22, 352–362. [CrossRef]
Piegdoń, I.; Tchórzewska-Cieślak, B.; Eid, M. Managing the risk of failure of the water supply network using the mass service system. Eksploatacja i Niezawodnosc – Maintenance and Reliability 2018 2018, 20, 284–291. [CrossRef]
Soldi, D.; Candelieri, A.; Archetti, F. Resilience and vulnerability in urban water distribution networks through network theory and hydraulic simulation. Procedia Eng. 2015 2015, 17, 1259–1268. [CrossRef]
Serdarevic, A.; Hadziahmetovic, A.; Dzubur, A.; Hotic, K. Improvements to the water supply system - case study reconstruction of the water supply network of the city of Visoko (Unapređenja sistema za vodosnabdijevanje – case study rekonstrukcija vodovodne mreže grada Visoko). VODOPRIVREDA 0350-0519 2020, 17, 249–258.
Hajkowicz, S.; Collins, K. A review of multiple criteria analysis for water recource planning and management. Water Resour. Manage. 2007, 21, 1553–1566. [CrossRef]
Lade, O.; Oloke, D.; Chinyio, E.; Fullen, M. Use of Multi-criteria Decision Analysis Methods for Water Supply Problems: A Framework for Improved Rainwater Harvesting. J. Environ. Sci. Eng. A1 2012, pp. 909–917. [CrossRef]
Morais, D.; Almeida, A. Water supply system decision making using multicriteria analysis. Water SA 2006, 32, 229 – 236. [CrossRef]
Gebre, S.; Cattrysse, D.; Van Orshoven, J. Multi-Criteria Decision-Making Methods to Address Water Allocation Problems: A Systematic Review. Water 2021, 13, 612–620. [CrossRef]
Baker, D.; Bridges, D.; Hunter, R.; Johnson, G.; Krupa, J.; Murphy, J.; Sorenson, K. Guidebook to decision-making methods. US Department of Energy 2001.
Abrishamchi, A.; Ebranimimian, A.; Tajrishi, M.; Marino, M.; Asce.H.M.. Case Study: Application of Multicriteria Decision Making to Urban Water Supply. J. Water Resour. Plan. Manage. 2005, 131, 326–335. [CrossRef]
Afshar, A.; Marino, M.; Saadatpour, M.; .; Afshar, A. Fuzzy TOPSIS Multicriteria Decision Analysis Applied to Karun reservoir System. Water Resour. Manage. 2011, 25, 545–563. [CrossRef]
Al-Barqawi, H.; Zayed, T. Infrastructure Management: Integrated AHP/ANN Model to Evaluate Municipal Water Mains’ Performance. J. Infrastruct. Syst. 2008, pp. 305–318. [CrossRef]
Mutikanga, H.; Sharma, S.; Vairavamoorthy, K. Multi-criteria decision analysis: A Strategic Planning Tool for Water Loss Management. Water Resour. Manage. 2011, 25, 3947–3969. [CrossRef]
Okeola, O.; Sule, B. Evaluation of management alternatives for urban water supply system using Multicriteria decision Analysis. J. King Saud University – Eng. Sci. 2023, 24, 9–24. [CrossRef]
Orasanin, G.; Vucijak, B. Multi-criteria optimization in planning water supply (Visekriterijumska optimizacija u planiranju vodosnabdijevanja). TEHNIKA 2013, 68, 768–774.
Salehi, S.; Ghazizadeh, M.; Tabesh, M. A comprehensive criteria-based multi-attribute decision-making model for rehabilitation of water distribution systems. Struct. Infrastruct. Eng. 2017, 14, 1–23. [CrossRef]
Salehi, S.; Ghazizadeh, M.; Tabesh, M.; Valadi, S.; S.P.S., N. A risk component-based model to determine pipes renewal strategies in water distribution networks. Struct. Infrastruct. Eng. 2020, 17, 1338–1359. [CrossRef]
Orasanin, G.; Simic, S.; Blagojevic, J.; Milic, D. Analysis of effective criteria and the method of their evaluation in the water network renewal planning (Analiza efektivnih kriterijuma i nacin njihovog vrednovanja u planiranju obnove vodovodne mreze). 44. International conference Water supply and sewerage (44. Medjunardna konferencija Vodovod i kanalizacija) 2023, p. 98–106.
Opricovic, S. Multicriteria optimization of systems in construction (Višekriterijumska optimizacija sistema u građevinarstvu); Faculty of Civil Engineering, University of Belgrade (Građevinski fakultet Univerziteta u Beogradu): Belgrade, 1998.
Thakkar, J. VIseKriterijumska Optimizacija I Kompromisno Resenje (VIKOR). In: Multi-Criteria Decision Making. Studies in Systems, Decision and Control, 2021, Springer 2021, 336. [CrossRef]
Kabir, G.; Sadiq, R.; Tesfamariam, S. A review of multi-criteria decision-making methods for infrastructure management. Struct. Infrastruct. Eng. 2013, 10, 1176–1210. [CrossRef]
Opricovic, S. Compromise in cooperative game and the VIKOR method. Yug.. J. Oper. Res. 19 2009, 2, 225–238. [CrossRef]
Kang, D.; Park, Y. Review-based measurement of customer satisfaction in mobile service: Sentiment analysis and VIKOR approach. Exp. Syst. with Appl. 2013, 41, 1041–1050. [CrossRef]
Opricovic, S.; Tzeng, G. Compromise solution by MCDM methods: A comparative analysis of VIKOR and TOPSIS. Eur. J. Oper. Res. 156 2004, pp. 445–455. [CrossRef]
Opricovic, S.; Tzeng, G. Extended VIKOR method in comparision with outranking methods. Eur. J. Oper. Res. 178 2007, pp. 514–529. [CrossRef]
Gheibi, M.; Emrani, N.; Eftekhari, M.; Behzadian, K.; Mohtasham, M.; Abdollahi, J. Assessing the failures in water distribution networks using a combination of Geographic Information System, EPANET 2, and descriptive statistical analysis: a case study. Sustain. Water Resour. Manage. 2022, 8, 612–620. [CrossRef]
Gorev, N.; 2013., K.I. Noniterative Implementation of Pressure-Dependent Demands Using the Hydraulic Analysis Engine of EPANET 2. Water Resour. Manage. 2022, 27, 3623–3630. [CrossRef]
Košarac, A.; Romić, D.; Orašanin, G.; Blagojević, J. Optimization of Water Supply System Using Software EPANET 2.0. In: Karabegovic, I. (eds) New Technologies, Development and Application. NT 2018. Lecture Notes in Networks and Systems. 2019. [CrossRef]
Widiarti, W.; Wahyuni, S.; Wiyono, R.; Hidayah, E.; Halik, G.; Sisinggih, D. Evaluation of pipe network distribution system using EPANET 2.0 (a case study of the city of Jember). IOP Conf. Series: Earth and Environmental Science 437 2020. [CrossRef]
Saaty, T. The Analytic Hierarchy Process—what it is and how it is used. Mathematical Modelling 1987, 9, 161–176. [CrossRef]
Saaty, T. How to make a decision: The Analytic Hierarchy Process. Eur. J. Oper. Res. 1990, 48, 9 – 26. [CrossRef]
Salo, A.; Hamalainen, R. On the Measurement of Preferences in the Analytic Hierarchy Process. J. MCDA 6 1997, pp. 309–319. [CrossRef]
Saaty, T. Basic theory of the Analytic Hierarchy Process: How to make a decision. Rev. R. Acad. Cienc. Exact. Fis. Nat. (Esp) 1999, 93, 395–423.
Saaty, T. Decision making with the Analytic Hierarchy Process. Int. J. Services Sci. 1 2008, p. 83 – 98.
Bozanic, D.; Milic, A.; Tesic, D.; Sałabun, W.; Pamucar, D. D numbers – fucom – fuzzy rafsi model for selecting the group of construction machines for enabling mobility. Facta Universitatis, Series: Mechanical Engineering 2021, 19, 447–471. [CrossRef]
Radovanovic, M.; Bozanic, D.; Tešic, D.; Puška, A.; Hezam, I.M.; Jana, C. Application of hybrid dibr-fucom-lmaw-bonferroni-grey-edas model in multicriteria decision-making. Facta Universitatis, Series: Mechanical Engineering 2023, 21, 387–403. [CrossRef]
Djukic, D.; Petrovic, I.; Bozanic, D.; Delibašic, B. Selection of Unemployed Aircraft for Training of Small-Range Aircraft Defense System AHP – TOPSIS Optimization Methods. Yugoslav Journal of Operations Research 2022, 32, 389–406. [CrossRef]
Hwang, C.L.; Yoon, K. Multiple Attribute Decision Making: Methods and Applications. New York: Springer-Verlag 1981.

Figure 1. Hydraulic model of DMA Vojkovići.

Figure 2. Changes in ranked projects with changes in the value of criteria weights

Figure 3. Ranked projects by VIKOR and TOPSIS methods

Table 1. Effective criteria for pipeline replacement planning

Number	Criterion	Category	Evaluation method
1	Average pipe pressure	Hydraulic	Quantitative
2	Flow velocity in the pipe	Hydraulic	Quantitative
3	Water flow through the pipeline	Hydraulic (social)	Quantitative
4	Pipe age	Mechanically	Quantitative
5	Pipe length	Mechanically	Quantitative
6	Pipe diameter	Mechanically	Quantitative
7	Number of connections	Operational	Quantitative
8	Number of flat connections	Operational	Quantitative
9	Failure rate	Operational (Environmental)	Quantitative
10	Ease of excavating the soil around the pipe	Physically	Qualitative
11	Water quality	Quality	Qualitative
12	Total investment cost	Economically	Quantitative
13	Population density, urban area or rural	Social	Qualitative

Table 2. Multi-criteria evaluation matrix

	$a_{1}$	$a_{2}$	...	$a_{j}$	...	$a_{n}$
$f_{1}$ (.)	$f_{1} (a_{1})$	$f_{1} (a_{2})$	...	$f_{1} (a_{j})$	...	$f_{1} (a_{n})$
$f_{2}$ (.)	$f_{2} (a_{1})$	$f_{2} (a_{2})$	...	$f_{2} (a_{j})$	...	$f_{2} (a_{n})$
...	...	...	...	...	...	...
$f_{j}$ (.)	$f_{j} (a_{1})$	$f_{j} (a_{2})$	...	$f_{j} (a_{j})$	...	$f_{j} (a_{n})$
...	...	...	...	...	...	...
$f_{k}$ (.)	$f_{k} (a_{1})$	$f_{k} (a_{2})$	...	$f_{k} (a_{j})$	...	$f_{k} (a_{n})$

Table 3. Pipeline replacement projects in the analyzed area

Project	Length (m)	Material Type	Diameter (mm)	Required Diameter (mm)
Project 1	703	Cast Iron, Polyethylene	300, 355	250
Project 2	471	Cast Iron	300	250
Project 3	562	Cast Iron	200	200
Project 4	562	Cast Iron	200	150
Project 5	713	Cast Iron	400	150
Project 6	583	Cast Iron	400	150
Project 7	834	Cast Iron	200	200
Project 8	819	Cast Iron	200	200

Table 4. Evaluation (initial) matrix

	P1	P2	P3	P4	P5	P6	P7	P8	Max/min
C1	1.23	1.30	1.37	1.36	1.52	1.50	1.38	1.58	max
C2	0.15	0.14	0.15	0.085	0.01	0.003	0.14	0.03	min
C3	10.86	10.08	4.76	2.71	0.86	0.44	3.67	0.96	max
C4	43	43	43	43	45	45	43	43	max
C5	703	471	562	562	713	583	834	819	max
C6	300	300	200	200	400	400	200	200	max
C7	57	36	37	43	55	16	39	41	max
C8	1	1	5	5	1	0	0	0	max
C9	17	18	18	37	28	24	34	44	max
C10	1(H)	3(M)	3(M)	3(M)	5(L)	5(L)	3(M)	3(M)	max
C11	5(L)	5(L)	5(L)	3(M)	1(H)	1(H)	3(M)	5(L)	min
C12	134902	90196	87560	59130	61817	50546	129937	127600	min
C13	1(H)	1(H)	3(M)	3(M)	5(L)	3(M)	3(M)	3(M)	max

Table 5. Normalized criteria values

	P1	P2	P3	P4	P5	P6	P7	P8
C1	1.0000	0.8000	0.6000	0.6286	0.1714	0.2286	0.5714	0.0000
C2	1.0000	0.9320	1.0000	0.5578	0.0476	0.0000	0.9320	0.1837
C3	0.0000	0.0749	0.5854	0.7821	0.9597	1.0000	0.6900	0.9501
C4	1.0000	1.0000	1.0000	1.0000	0.0000	0.0000	1.0000	1.0000
C5	0.3609	1.0000	0.7493	0.7493	0.3333	0.6915	0.0000	0.0413
C6	0.5000	0.5000	1.0000	1.0000	0.0000	0.0000	1.0000	1.0000
C7	0.0000	0.5122	0.4878	0.3415	0.0488	1.0000	0.4390	0.3902
C8	0.8000	0.8000	0.0000	0.0000	0.8000	1.0000	1.0000	1.0000
C9	1.0000	0.9630	0.9630	0.2593	0.5926	0.7407	0.3704	0.0000
C10	1.0000	0.5000	0.5000	0.5000	0.0000	0.0000	0.5000	0.5000
C11	1.0000	1.0000	1.0000	0.5000	0.0000	0.0000	0.5000	1.0000
C12	1.0000	0.4700	0.4388	0.1018	0.1336	0.0000	0.9411	0.9134
C13	1.0000	1.0000	0.5000	0.5000	0.0000	0.5000	0.5000	0.5000

Table 6. Initial pairwise comparison matrix

	C1	C2	C3	C4	C5	C6	C7	C8	C9	C10	C11	C12	C13
C1	1	1/3	1	1	1	1	1	1/3	1	1/3	1/5	1/3	1
C2	3	1	1	3	3	3	3	3	1/3	3	1	1/3	3
C3	1	1	1	3	3	3	1	3	1/3	3	1/3	1/3	1/3
C4	1	1/3	1/3	1	1	1	1	3	1	1	1/3	1/3	1/3
C5	1	1/3	1/3	1	1	1	1/3	3	1/3	1/3	1/3	1/3	1/3
C6	1	1/3	1/3	1	1	1	1/3	3	1/3	1/3	1/3	1/3	3
C7	1	1/3	1	1	3	3	1	1	1/3	1	1/3	1/3	1
C8	3	1/3	1/3	1/3	1/3	1/3	1	1	1/3	1	1/5	1/5	1/3
C9	1	3	3	1	3	3	3	3	1	3	1/3	1	3
C10	3	1/3	1/3	1	3	3	1	1	1/3	1	1/5	1/3	1
C11	5	1	3	3	3	3	3	5	3	5	1	3	3
C12	3	3	3	3	3	3	3	5	1	3	1/3	1	3
C13	1	1/3	3	3	3	1/3	1	3	1/3	1	1/3	1/3	1

Table 7. Criteria weights

C1	C2	C3	C4	C5	C6	C7	C8	C9	C10	C11	C12	C13
0.0423	0.1079	0.0741	0.0471	0.0369	0.0470	0.0541	0.0341	0.1185	0.0554	0.1801	0.1361	0.0662

Table 8. Ranking of projects

P5	P6	P4	P7	P8	P3	P2	P1
0	0.1631	0.3076	0.6228	0.8248	0.9352	0.9477	1.0000

Table 9. Final ranking of projects

P5	P6	P4	P7	P8	P3	P2	P1
100	83.69	69.24	37.72	17.52	6.478	5.23	0

Table 10. Initial pairwise comparison matrix

	C1	C2	C3	C4	C5	C6	C7	C8	C9	C10	C11	C12	C13
S0	0.0450	0.1153	0.0752	0.0475	0.0374	0.0475	0.0545	0.0352	0.1216	0.0497	0.1803	0.1241	0.0666
S1	0.0769	0.0769	0.0769	0.0769	0.0769	0.0769	0.0769	0.0769	0.0769	0.0769	0.0769	0.0769	0.0769
S2	0.304	0.058	0.058	0.058	0.058	0.058	0.058	0.058	0.058	0.058	0.058	0.058	0.058
S3	0.058	0.304	0.058	0.058	0.058	0.058	0.058	0.058	0.058	0.058	0.058	0.058	0.058
S4	0.058	0.058	0.304	0.058	0.058	0.058	0.058	0.058	0.058	0.058	0.058	0.058	0.058
S5	0.058	0.058	0.058	0.304	0.058	0.058	0.058	0.058	0.058	0.058	0.058	0.058	0.058
S6	0.058	0.058	0.058	0.058	0.304	0.058	0.058	0.058	0.058	0.058	0.058	0.058	0.058
S7	0.058	0.058	0.058	0.058	0.058	0.304	0.058	0.058	0.058	0.058	0.058	0.058	0.058
S8	0.058	0.058	0.058	0.058	0.058	0.058	0.304	0.058	0.058	0.058	0.058	0.058	0.058
S9	0.058	0.058	0.058	0.058	0.058	0.058	0.058	0.304	0.058	0.058	0.058	0.058	0.058
S10	0.058	0.058	0.058	0.058	0.058	0.058	0.058	0.058	0.304	0.058	0.058	0.058	0.058
S11	0.058	0.058	0.058	0.058	0.058	0.058	0.058	0.058	0.058	0.304	0.058	0.058	0.058
S12	0.058	0.058	0.058	0.058	0.058	0.058	0.058	0.058	0.058	0.058	0.304	0.058	0.058
S13	0.058	0.058	0.058	0.058	0.058	0.058	0.058	0.058	0.058	0.058	0.058	0.304	0.058
S14	0.058	0.058	0.058	0.058	0.058	0.058	0.058	0.058	0.058	0.058	0.058	0.058	0.304

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

	C1	C2	C3	C4	C5	C6	C7	C8	C9	C10	C11	C12	C13
C1	1	1/3	1	1	1	1	1	1/3	1	1/3	1/5	1/3	1
C2	3	1	1	3	3	3	3	3	1/3	3	1	1/3	3
C3	1	1	1	3	3	3	1	3	1/3	3	1/3	1/3	1/3
C4	1	1/3	1/3	1	1	1	1	3	1	1	1/3	1/3	1/3
C5	1	1/3	1/3	1	1	1	1/3	3	1/3	1/3	1/3	1/3	1/3
C6	1	1/3	1/3	1	1	1	1/3	3	1/3	1/3	1/3	1/3	3
C7	1	1/3	1	1	3	3	1	1	1/3	1	1/3	1/3	1
C8	3	1/3	1/3	1/3	1/3	1/3	1	1	1/3	1	1/5	1/5	1/3
C9	1	3	3	1	3	3	3	3	1	3	1/3	1	3
C10	3	1/3	1/3	1	3	3	1	1	1/3	1	1/5	1/3	1
C11	5	1	3	3	3	3	3	5	3	5	1	3	3
C12	3	3	3	3	3	3	3	5	1	3	1/3	1	3
C13	1	1/3	3	3	3	1/3	1	3	1/3	1	1/3	1/3	1

	C1	C2	C3	C4	C5	C6	C7	C8	C9	C10	C11	C12	C13
C1	1	1/3	1	1	1	1	1	1/3	1	1/3	1/5	1/3	1
C2	3	1	1	3	3	3	3	3	1/3	3	1	1/3	3
C3	1	1	1	3	3	3	1	3	1/3	3	1/3	1/3	1/3
C4	1	1/3	1/3	1	1	1	1	3	1	1	1/3	1/3	1/3
C5	1	1/3	1/3	1	1	1	1/3	3	1/3	1/3	1/3	1/3	1/3
C6	1	1/3	1/3	1	1	1	1/3	3	1/3	1/3	1/3	1/3	3
C7	1	1/3	1	1	3	3	1	1	1/3	1	1/3	1/3	1
C8	3	1/3	1/3	1/3	1/3	1/3	1	1	1/3	1	1/5	1/5	1/3
C9	1	3	3	1	3	3	3	3	1	3	1/3	1	3
C10	3	1/3	1/3	1	3	3	1	1	1/3	1	1/5	1/3	1
C11	5	1	3	3	3	3	3	5	3	5	1	3	3
C12	3	3	3	3	3	3	3	5	1	3	1/3	1	3
C13	1	1/3	3	3	3	1/3	1	3	1/3	1	1/3	1/3	1