1. Introduction
The United States relies on a diverse array of energy sources, broadly categorized into primary sources, including fossil fuels, nuclear, and renewables, and secondary sources, represented by electricity generated from primary sources [
1]. Measurement units vary across energy types, with liquid fuels quantified in barrels or gallons, natural gas in cubic feet, coal in short tons, and electricity in kilowatts and kilowatt-hours [
2]. British thermal units (Btu) serve as a standard for energy comparison, revealing that total U.S. primary energy consumption reached 100.41 quadrillion Btu in 2022 [
3,
4]. In the realm of electricity generation, the United States employs a spectrum of sources and technologies that have evolved over time. The three principal categories encompass fossil fuels (coal, natural gas, and petroleum), nuclear energy, and renewables. Predominantly, steam turbines, drawn from fossil fuels, nuclear, biomass, geothermal, and solar thermal energy, stand as the dominant force in electricity generation.
Other technologies contributing to this landscape include gas turbines, hydro turbines, wind turbines, and solar photovoltaics [
5]. Notably, within the domain of fossil fuels, natural gas emerges as the predominant player, contributing approximately 40% to U.S. electricity generation in 2022 [
6]. Coal, occupying the third-largest share at around 18%, predominantly fuels steam turbines, with certain facilities converting coal to gas for utilization in gas turbines. Petroleum’s contribution is nominal, constituting less than 1%, where residual fuel oil and petroleum coke find application in steam turbines, and distillate fuel oil powers diesel-engine generators [
6]. Nuclear energy commands a substantial portion, accounting for nearly one-fifth of U.S. electricity, generated through steam turbines and nuclear fission. Renewable energy sources, constituting approximately 22% of total U.S. electricity generation in 2022, have witnessed substantial growth since 1990, when their contribution to utility-scale electricity generation was approximately 12%. This discernible shift underscores the escalating significance of renewables in shaping the U.S. energy landscape [
3,
6]. In-depth analysis and insights from reputable sources further verify these trends and dynamics.
Navigating the undulating landscape of fuel consumption in electricity generation, as strictly narrated by the U.S. Energy Information Administration, presents a remarkable challenge. The inconsistent nature of these consumption patterns highlights a critical need for precise predictive models, as their absence impedes informed decision-making, leaving us grappling with the dynamic shifts in energy demands. This urgency compels a call to action for establishing research aimed at the development of advanced forecasting techniques, pivotal for strategic planning in the sphere of future electricity generation. Accurate predictions of fuel consumption not only facilitate efficient resource allocation and guide infrastructure development but also serve as the bedrock for informed energy policies [
7]. Beyond the realms of numbers and projections, these forecasts wield a profound impact on investment decisions, environmental planning, grid management, cost optimization, and market strategies. They emerge as indispensable tools for emergency preparedness and play a pivotal role in orchestrating a seamless transition to renewable energy, ultimately forging a path toward a stable, sustainable, and resilient energy sector. As we investigate into the statistics of this fluctuation, the intricate jump of fuel consumption in electricity generation unveils itself, highlighting the pressing need for foresight in steering the future of our energy landscape [
7].
This study mainly focuses to construct a robust forecasting model for fuel consumption in U.S. electricity generation, utilizing comprehensive data spanning the years 2015 to 2022. The method involves systematic analysis of seasonal and trend patterns, rigorous autocorrelation analysis, and refinement by eliminating biases from historical trends. Leveraging actual consumption data, the approach includes model validation and fine-tuning through a detailed comparison of forecasted and real consumption figures. Employing data from the U.S. Energy Information Administration, this eight-year analysis aims to explain the primary trend of fuel consumption for electricity generation across the entire United States, mitigating potential uncertainties associated with regional variations. The forecasting process integrates diverse benchmark methods, including STL, ETS, and ARIMA, facilitating a robust comparison to identify the most accurate model. Evaluation metrics, such as Mean Error (ME), Mean Percentage Error (MPE), Mean Absolute Error (MAE), Root Mean Squared Error (RMSE), and Mean Absolute Percentage Error (MAPE), guide the selection of the optimal model. Once identified, this model will be deployed to predict future fuel consumption trends, offering valuable insights for strategic energy planning. The combination of a comprehensive approach, diverse forecasting models, specific fuel analysis, and a focus on policy impact distinguishes this work from previous studies in the field of fuel consumption forecasting for electricity generation. This research is crucial for informing stakeholders and decision-makers, enabling them to make well-informed decisions on resource allocation, energy planning, and sector-specific strategies, with the main goal of contributing to the formulation of sustainable energy policies for a stable and reliable national energy supply [
8,
9,
10].
1.1. Overall Trend Analysis of Fuel Consumption
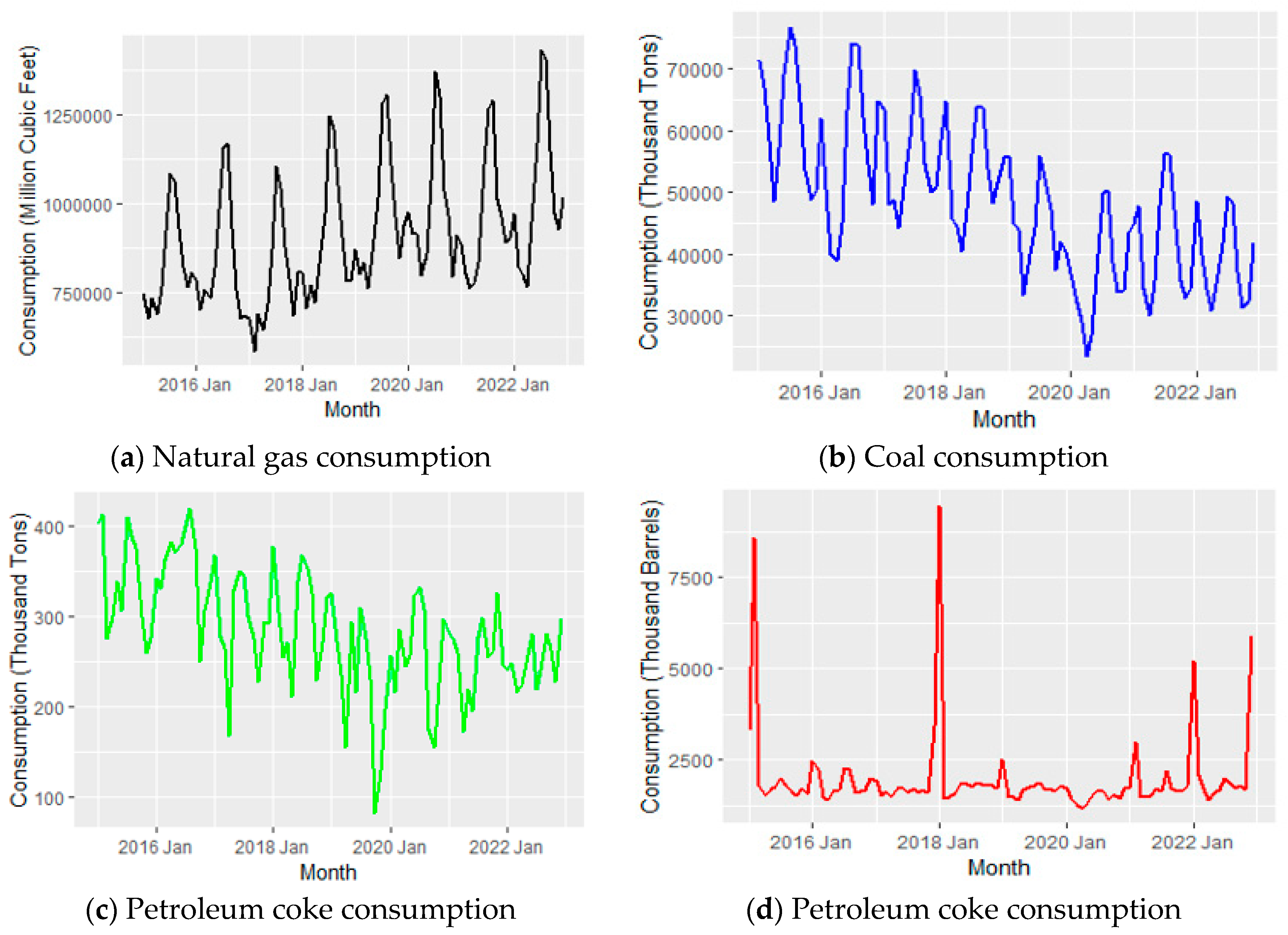
The trends observed in fuel consumption over time, as depicted in
Figure 1 shows the dynamics of various fuel types utilized in U.S. electricity generation. Natural gas consumption exhibits a consistent upward trajectory from January 2016 to January 2022, with occasional fluctuations [
6,
11]. This notable increase, supported by statistical evidence [
11] is attributed to several factors, including the growing preference for natural gas as a cleaner alternative, increased efficiency in gas-powered plants, and a shift towards renewables in the energy mix. In contrast, coal consumption displays a fluctuating trend with distinct periods of growth and decline, reaching a significant trough in January 2020.
This decline aligns with a broader global trend of decreasing reliance on coal, driven by environmental concerns, regulatory shifts, and the pursuit of cleaner energy sources. Notably, the drop in January 2020 coincides with the onset of the COVID-19 pandemic, which induced a temporary reduction in industrial activities and energy demand, contributing to the observed drop in coal consumption. Similarly, petroleum coke usage exhibits variability, experiencing peaks at specific times. The visible drop in January 2020, concurrent with the pandemic’s onset, can be attributed to a combination of reduced industrial activities, altered production patterns, and an overall decline in energy demand during the initial phases of the pandemic. Petroleum liquids demonstrate a diverse trend with notable spikes, particularly in early 2018. This increase can be linked to a confluence of factors, including economic conditions, geopolitical events, and shifts in energy policies. For instance, the spike in early 2018 may be associated with increased demand driven by economic growth and geopolitical factors affecting oil prices.
In summary, the observed trends emphasize the comprehensive nature of fuel consumption patterns, influenced by a complex interplay of economic, environmental, and technological factors. The distinct fluctuations and notable changes, especially during the COVID-19 pandemic, highlight the importance of considering external influences when analyzing fuel consumption dynamics for strategic energy planning and policy formulation.
3. Result and Discussion
3.1. Analysis of forecasting trends for different energy streams
3.1.1. Overall Trend of NG Consumption
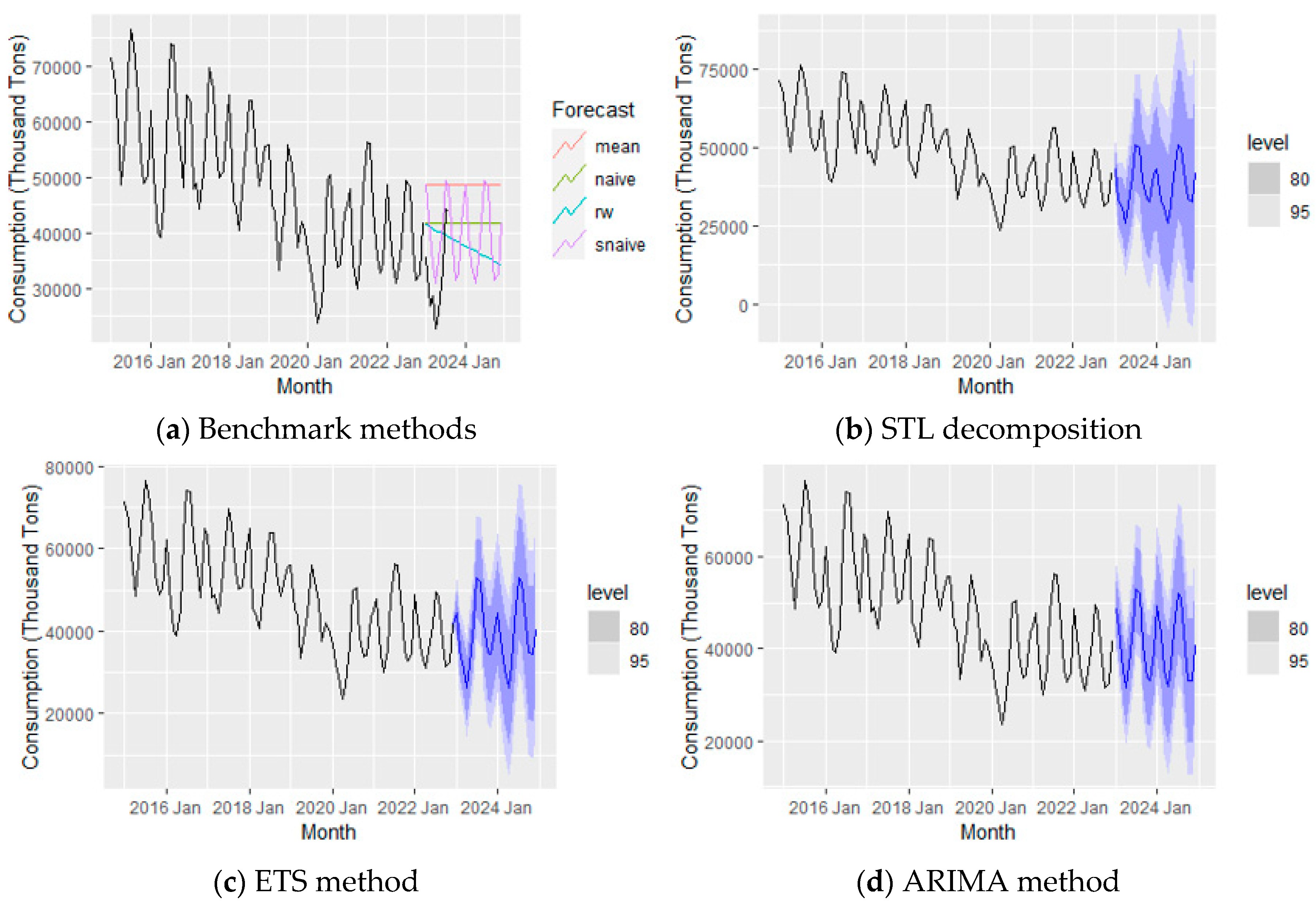
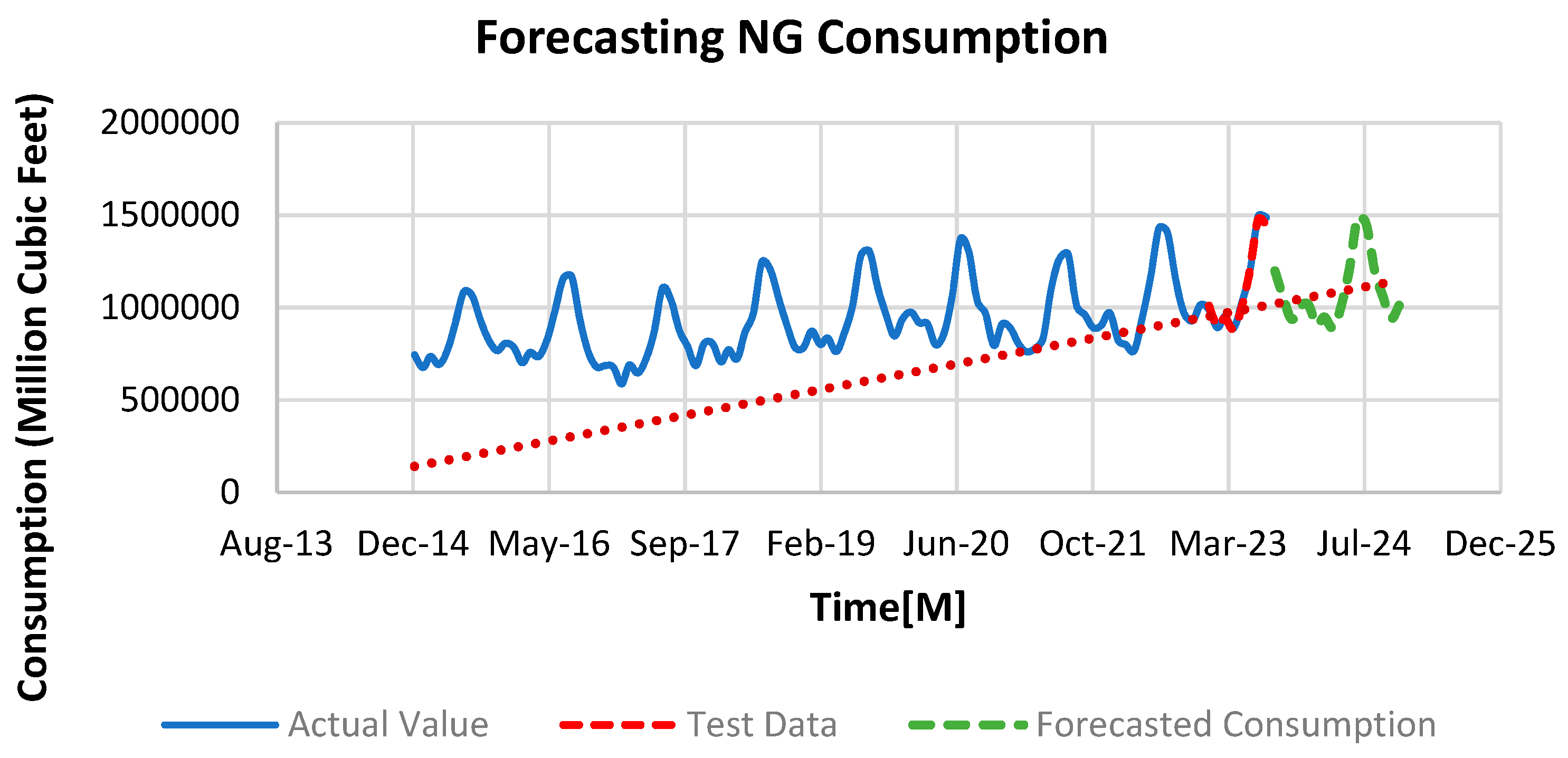
As shown in
Figure 19, the use of Natural Gas (NG) is still increasing, especially during the summer months. This is because natural gas is a versatile and efficient energy source, commonly used for generating electricity. It is considered better for the environment compared to other fuels, and its affordability and reliability make it a popular choice. During hot summer days, when people use more electricity for things like air conditioning, natural gas becomes a preferred option. Overall, because its environmentally friendly, cost-effective, and used in various ways, the demand for natural gas continues to rise.
3.1.2. Overall Trend of Coal Consumption
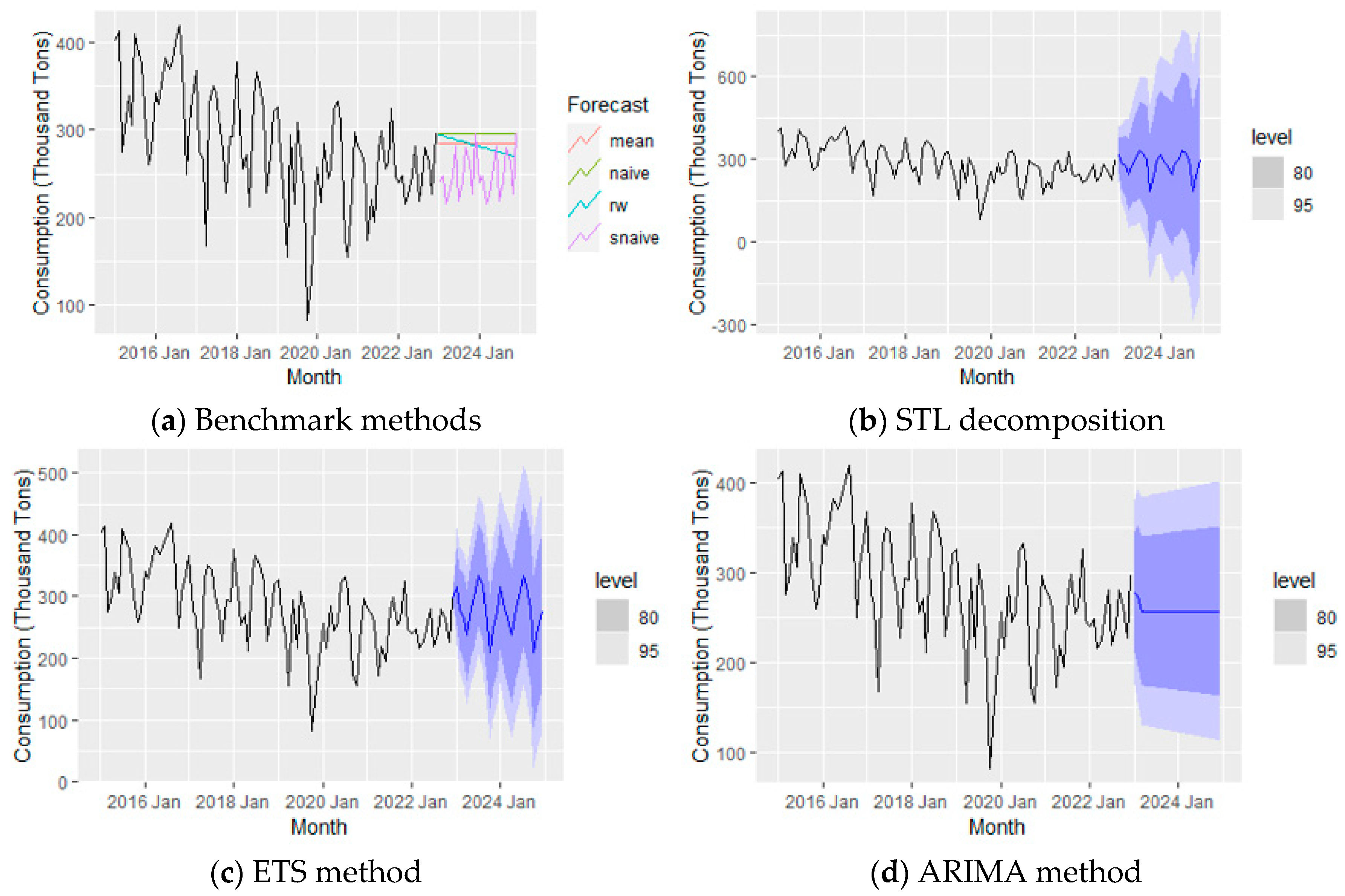
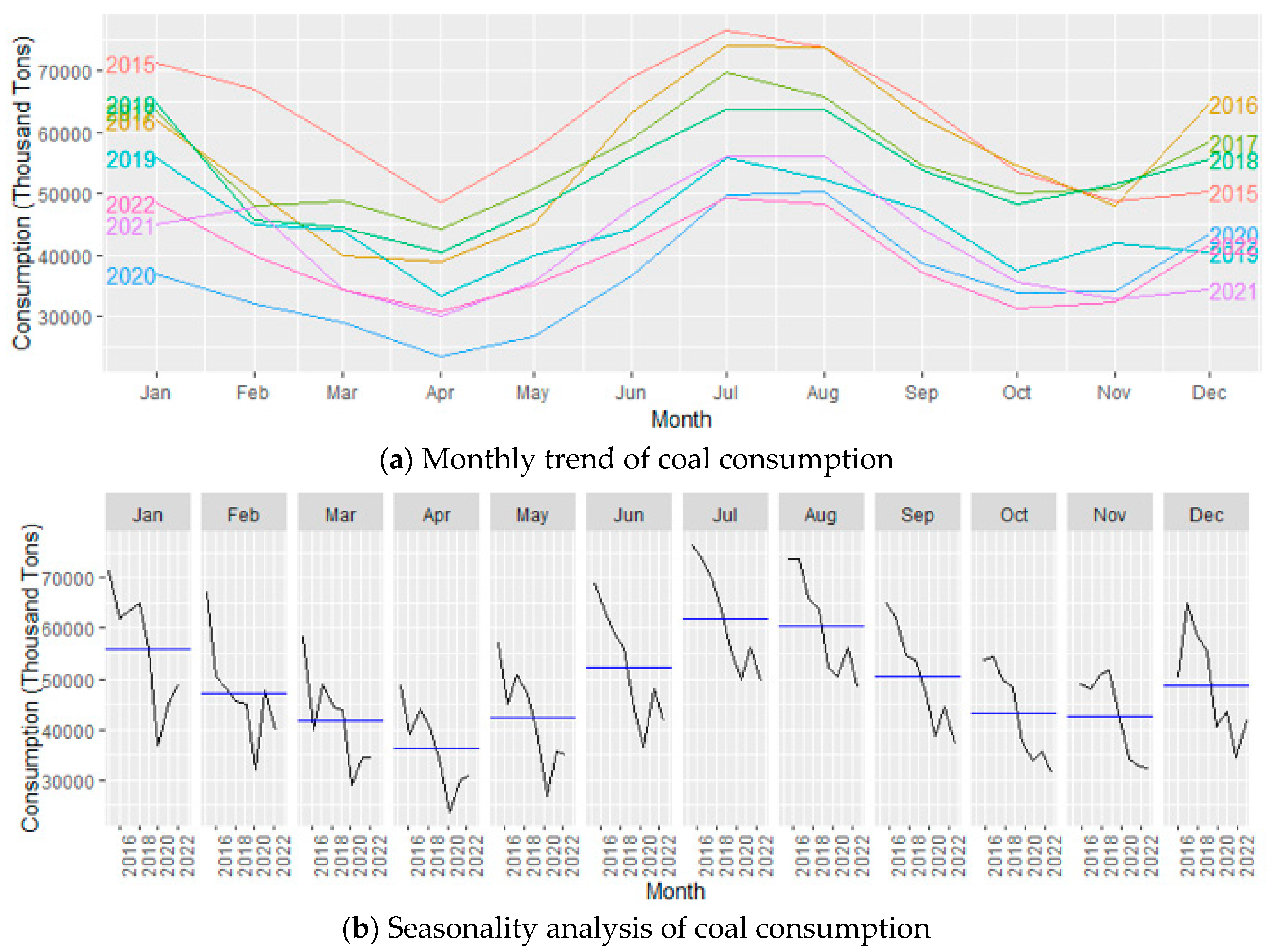
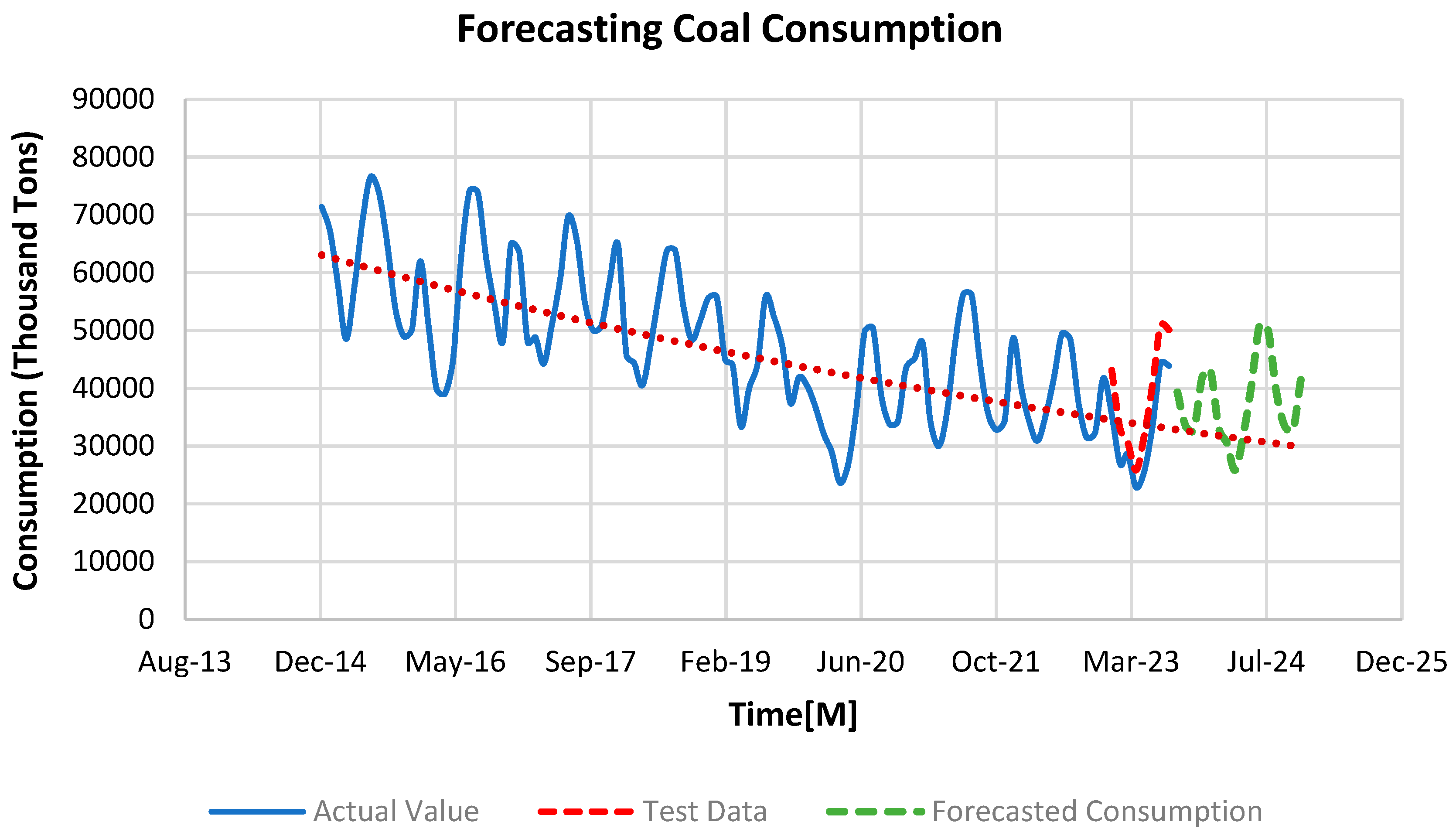
The forecast for coal consumption indicates a decreasing trend, raising questions about the underlying reasons. Analyzing the historical trend from 2015 to 2022, as shown in
Figure 3, reveals a clear seasonality pattern. There is a noticeable peak in coal consumption during the summer months of July and August, followed by a gradual decline in September and October. Consumption reaches a low point in November and then starts to rise again in December. This cyclic pattern suggests a seasonal influence on coal consumption, with similar patterns observed in the forecasted coal consumption (
Figure 20). The decreasing trend in coal consumption can be attributed to several factors. Firstly, there is a global shift towards cleaner and more sustainable energy sources, driven by environmental concerns and efforts to reduce carbon emissions. Governments and industries are increasingly adopting renewable energy sources and natural gas, which are considered more environmentally friendly alternatives to coal.
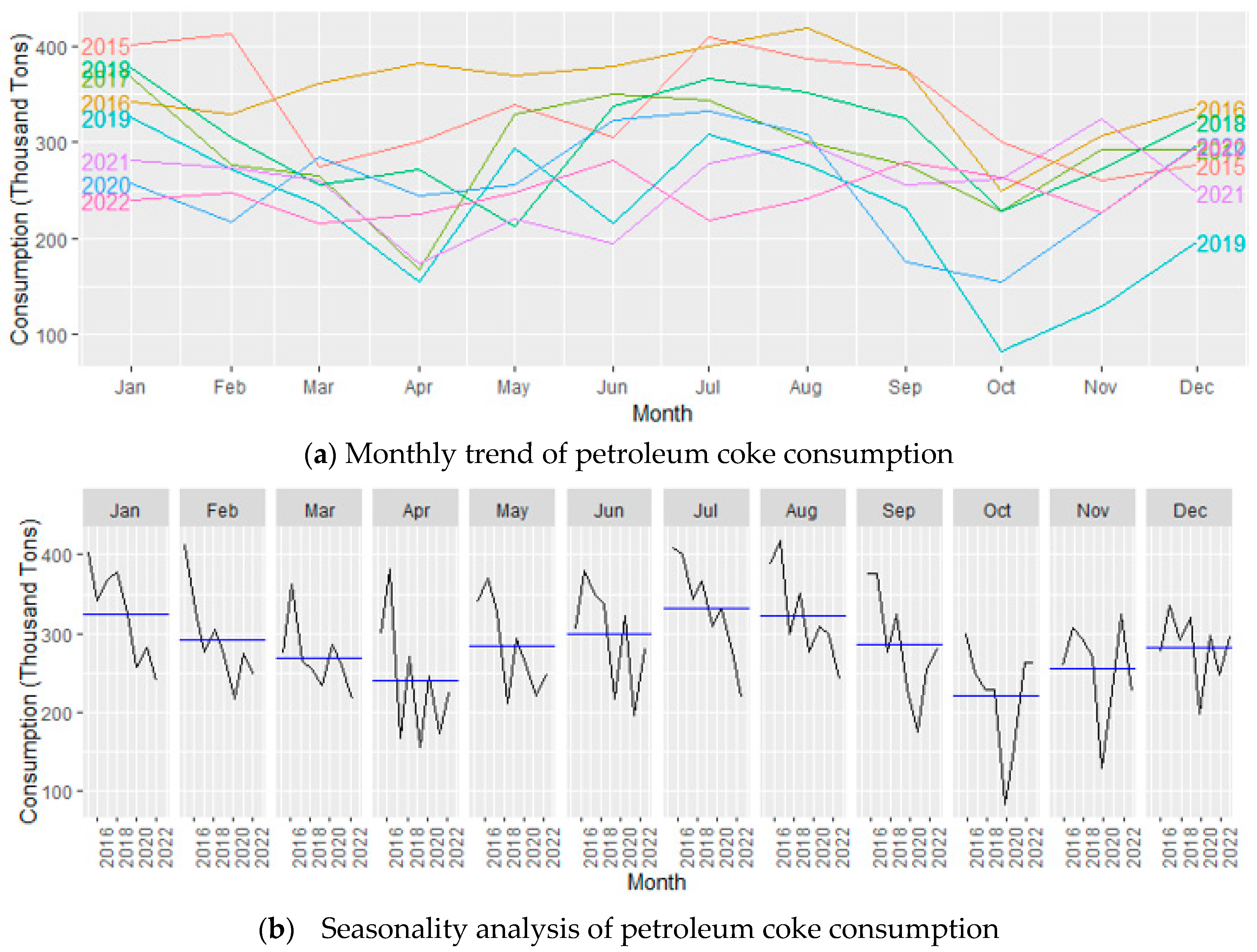
3.1.3. Overall Trend of Petroleum Coke Consumption
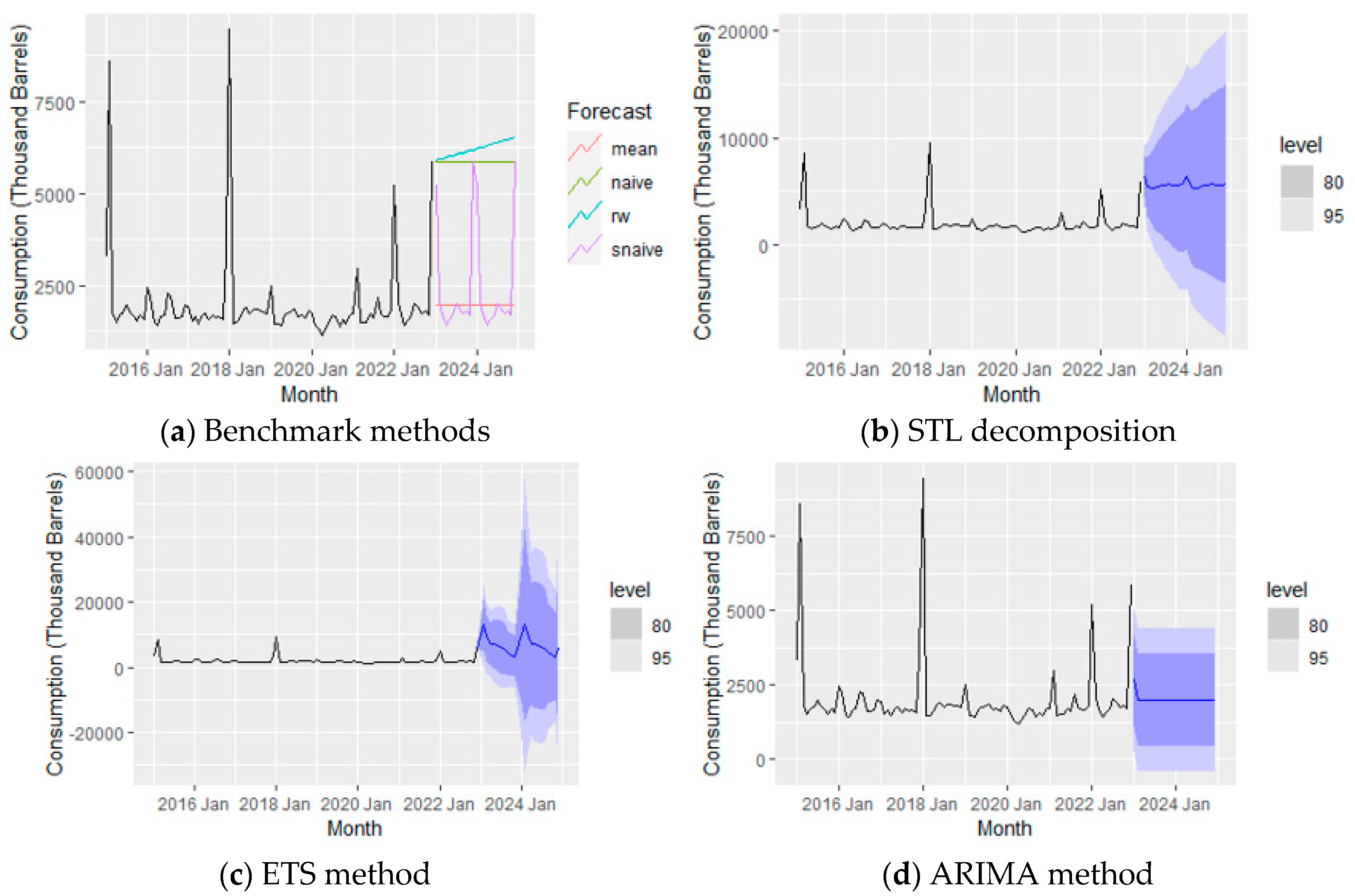
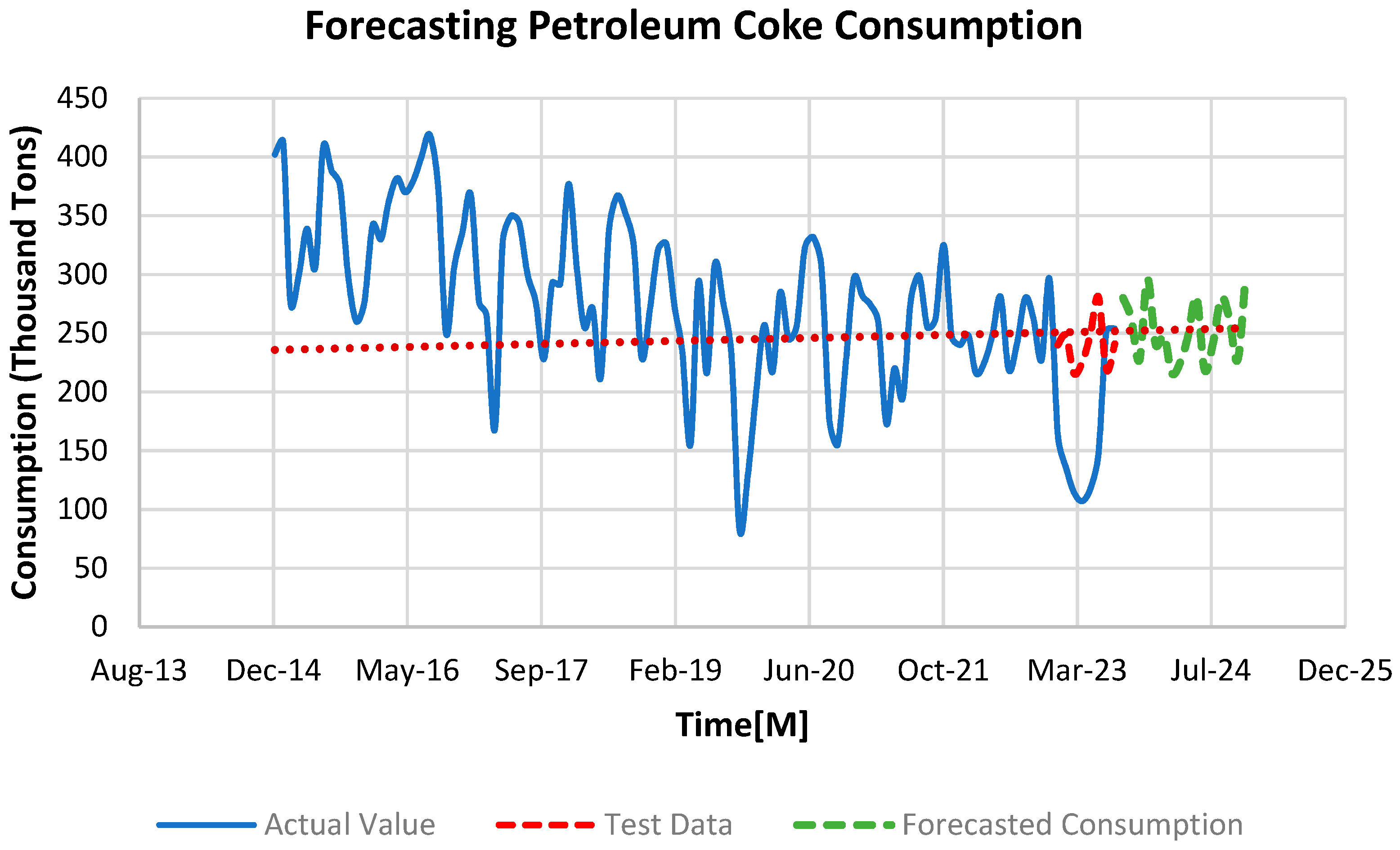
The data shows that petroleum coke use goes up a bit, especially in July and August, and then it goes down in October. This has happened not only in the past but is also expected in the future (
Figure 21). Petroleum coke comes from refining oil and is used in different industries, like making cement and producing power. The small increase might be because some industries need more of it, or it could be happening where economies are growing. The ups and downs in different months might be connected to specific activities in those months. Additionally, changes in how oil is refined globally can affect how much petroleum coke is available and how much people want.
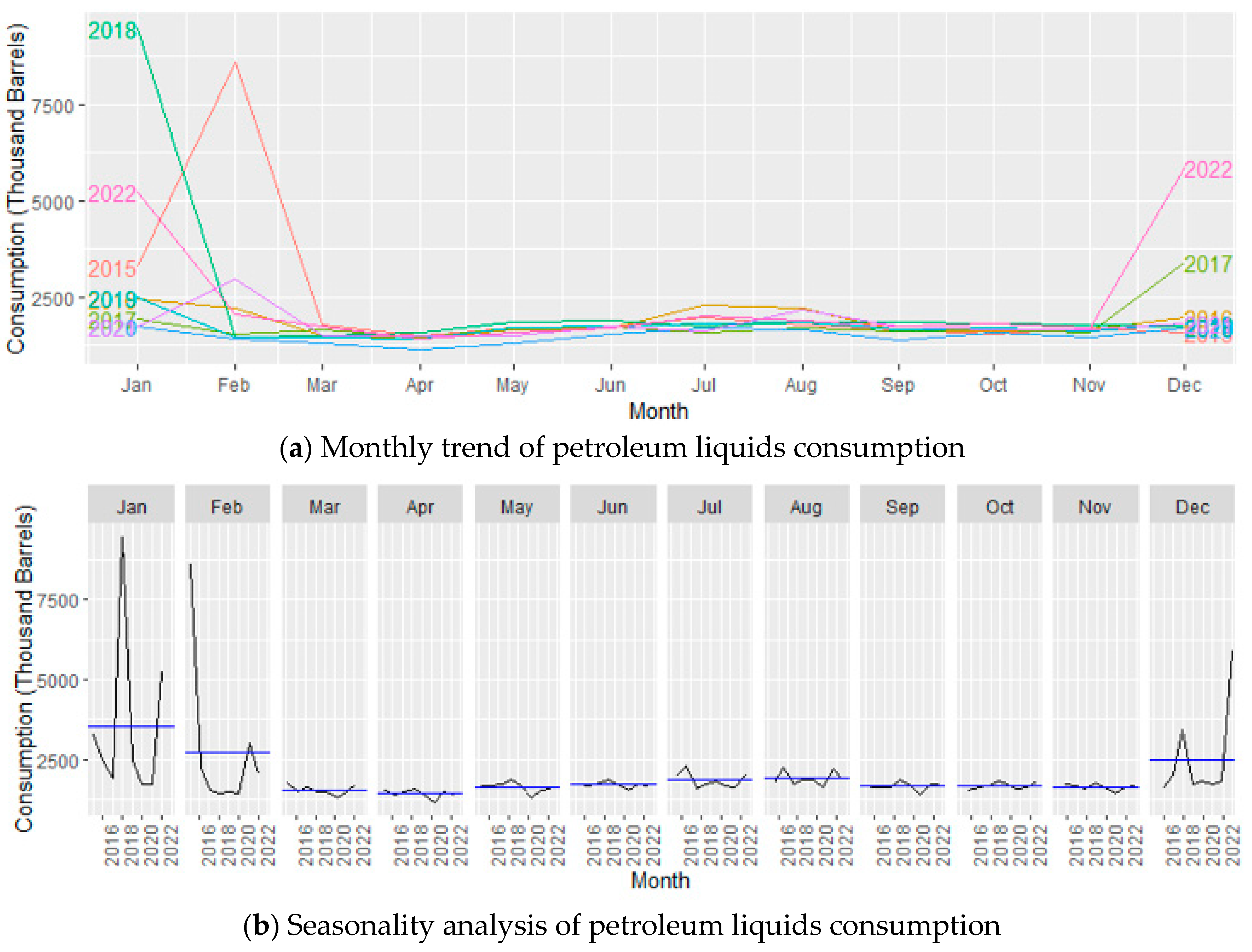
3.1.4. Overall Trend of Petroleum Liquid Consumption
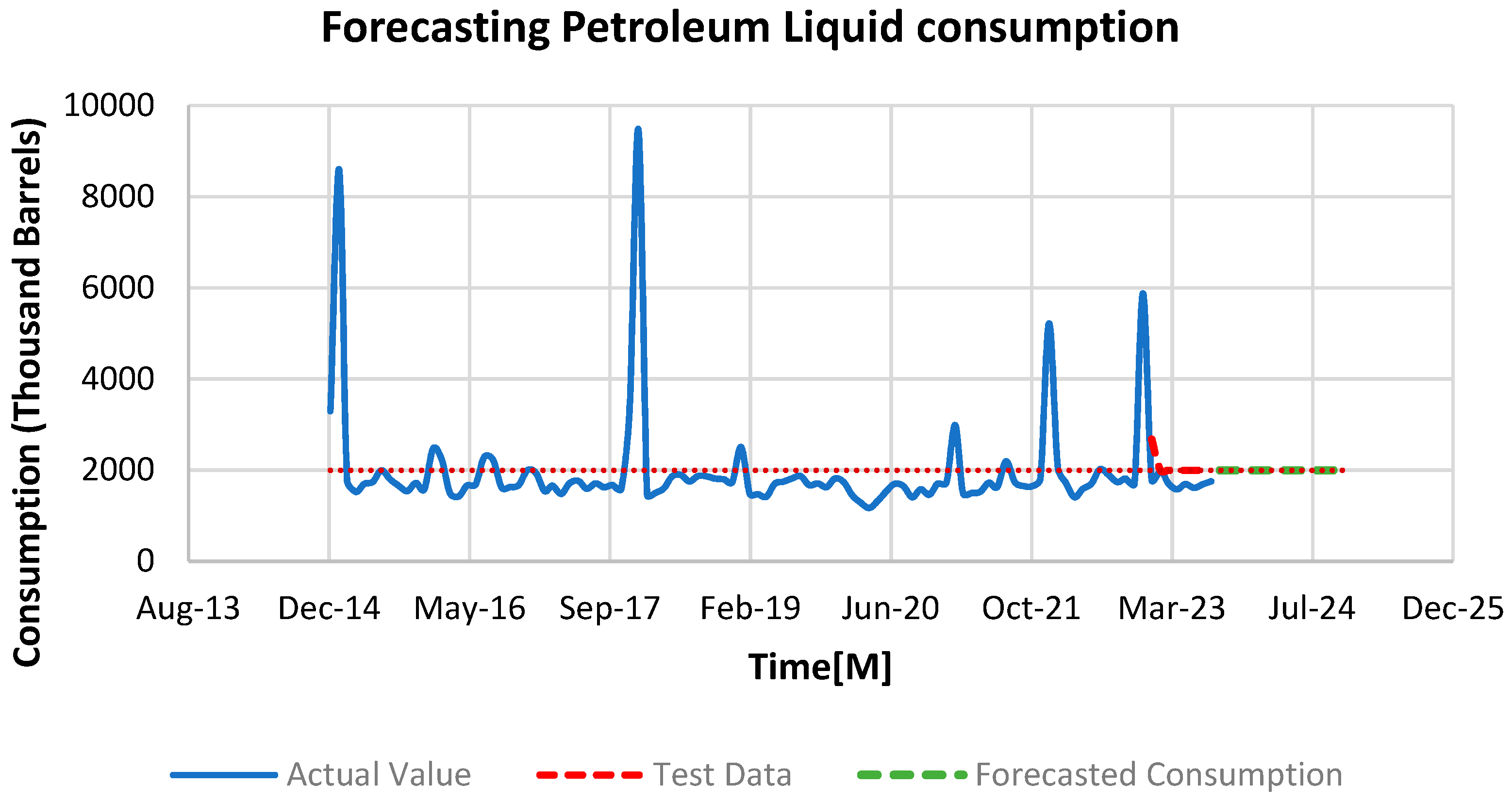
The monthly patterns and seasonality analysis of petroleum liquid consumption between 2015 and 2022 reveal spikes in February 2015, January 2018, January 2022, and December 2022. However, in the forecasted data, there are no unusual spikes. Instead, the forecast predicts consistent and steady consumption (
Figure 22). This lack of anomalies in the forecast suggests that improved forecasting models have been employed. These models take into account historical irregularities but anticipate a more stable trend for the future.
3.2. Comparing the forecasted trends of different energy streams in electricity generation
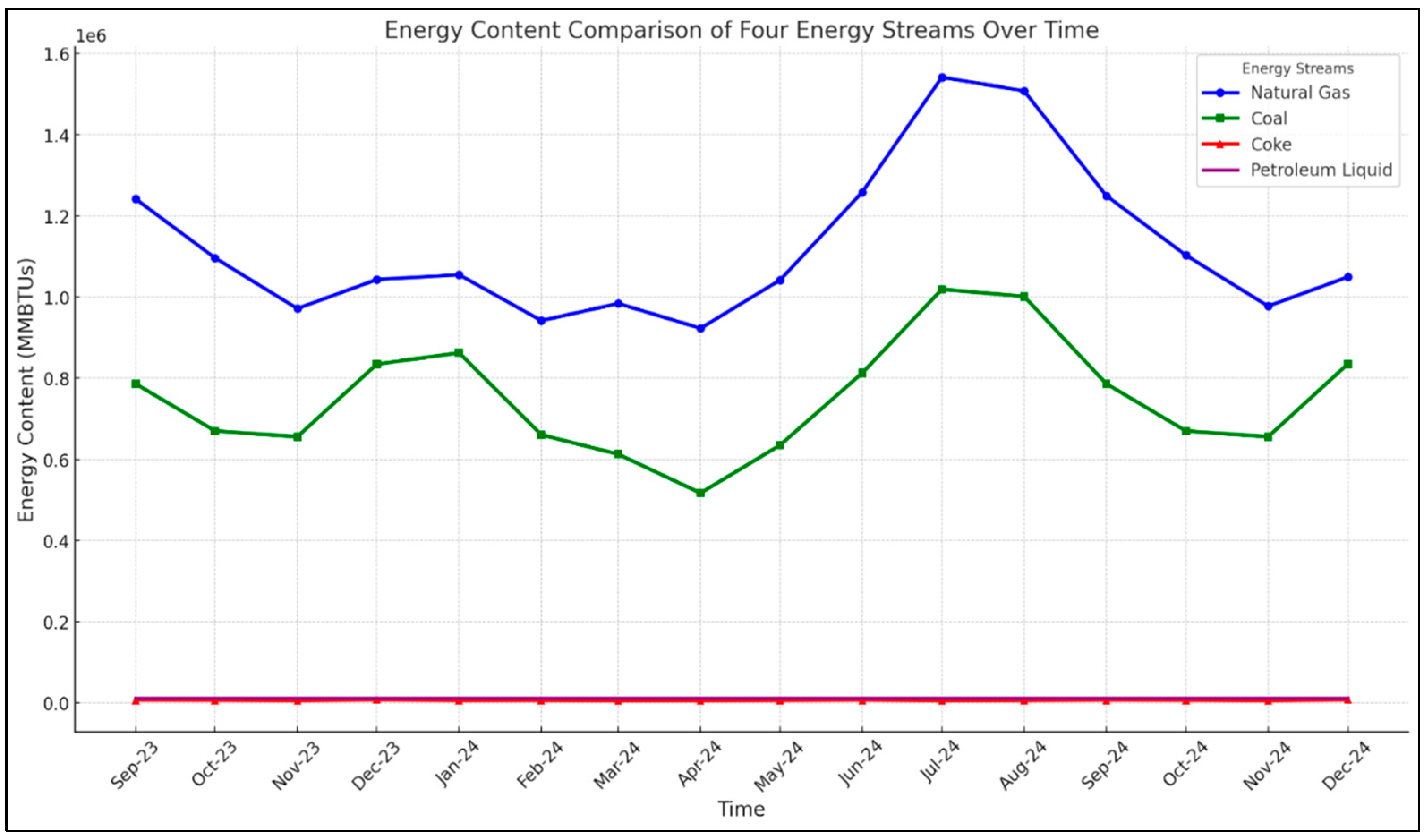
The graph as shown in
Figure 23, explains the projected consumption patterns for four key energy streams used in electricity generation in the USA, spanning from September 2023 to December 2024. Over this period, natural gas consumption fluctuates, with notable peaks in July and August 2024 at approximately 1,542,143 MMBTUs and 1,508,448 MMBTUs, respectively. These surges are likely a response to heightened electricity demand for cooling during the hotter months, a recurring trend that emphasizes the influence of seasonal temperature variations on energy utilization.
Coal consumption, while demonstrating less volatility than natural gas, shows minor variations that could be linked to industrial demand cycles, regulatory impacts, and market pricing. For instance, coal consumption rises to 835,000 MMBTUs in December 2023, which may reflect an increase in energy needs during the winter season. Meanwhile, coke, used primarily in industrial processes like steel manufacturing, maintains a relatively flat demand, with a minor peak at 7,400 MMBTUs in December 2023, suggesting a consistent industrial requirement with little seasonal impact.
Petroleum liquids display an unwavering consumption value of approximately 11,575.176 MMBTUs throughout the forecasted period. This consistency indicates that petroleum liquids may have a set role in the energy mix for electricity generation, potentially due to established supply chains and a stable market for petroleum products.
The forecast result suggests that while natural gas and coal exhibit seasonality and potential sensitivity to external market and policy conditions, coke and petroleum liquids’ demand appears more stable and possibly insulated from such factors. This stability could be due to long-term contracts, stockpiling strategies, or their specific usage domains within the industry, which might be less susceptible to short-term changes. Having said that, the natural gas will be still likely the dominating factor to generate electricity to near future as well for United States. To ensure the reliability of these projections and facilitate strategic energy planning, it is essential to corroborate this data with external literature, including market analyses, industry reports, and regulatory policy documents. This approach would provide a robust foundation for understanding the complex dynamics at play and for preparing the energy sector to meet future demand effectively and sustainably.
4. Conclusion
In this paper, our objective is to provide precise predictions for fuel consumption in electricity generation using time series forecasting models, making a substantial contribution to strategic planning and decision-making processes within the energy sector. Developing accurate predictive models is geared towards forecasting future fuel consumption, equipping stakeholders with valuable insights for well-informed decisions regarding resource allocation and sector-specific strategies.
Our analysis aims to identify sectors undergoing declining or increasing trends in fuel usage, enabling targeted interventions where necessary. This project seeks to deepen our understanding of energy market dynamics, facilitating proactive measures to efficiently meet future fuel demands. The insights derived from this work are poised to significantly impact the formulation of sustainable energy policies and strategies, ensuring a stable and reliable energy supply for the nation. The accurate forecasting of fuel consumption for electricity generation, as indicated by the forecasts for NG, coal, petroleum coke, and petroleum liquids, holds paramount importance for policymakers. These forecasted trends provide valuable insights that guide strategic decision-making in the ever-evolving landscape of the energy sector.
The expected rise in NG consumption suggests a need for increased infrastructure investment to support its growing demand, aligning with environmental goals. Conversely, the anticipated decline in coal usage allows policymakers to plan for a transition to cleaner alternatives, supporting affected communities. A slight increase in petroleum coke usage signals specific industrial needs, prompting policymakers to create supportive regulations. With a steady forecast for petroleum liquids, policymakers can plan infrastructure development to match stable energy needs. These forecasts empower policymakers to encourage sustainable energy practices, support economic growth, and ensure energy security, fostering a resilient and cleaner future.
Author Contributions
Conceptualization, M.M.H.B.; methodology, M.M.H.B.; software, M.M.H.B.; validation, M.M.H.B. and T.R.; formal analysis, M.M.H.B.; investigation, M.M.H.B.; resources, M.M.H.B.; writing—original draft preparation, M.M.H.B. and A.N.S.; writing—review and editing, T.R., S.I.A. and A.N.S.; visualization, supervision, T.R. and M.M.H.B.; project administration, A.N.S. and M.M.H.B. All authors have read and agreed to the published version of the manuscript.
Figure 1.
Trend analysis of different fuel consumption for US electricity generation over time.
Figure 1.
Trend analysis of different fuel consumption for US electricity generation over time.
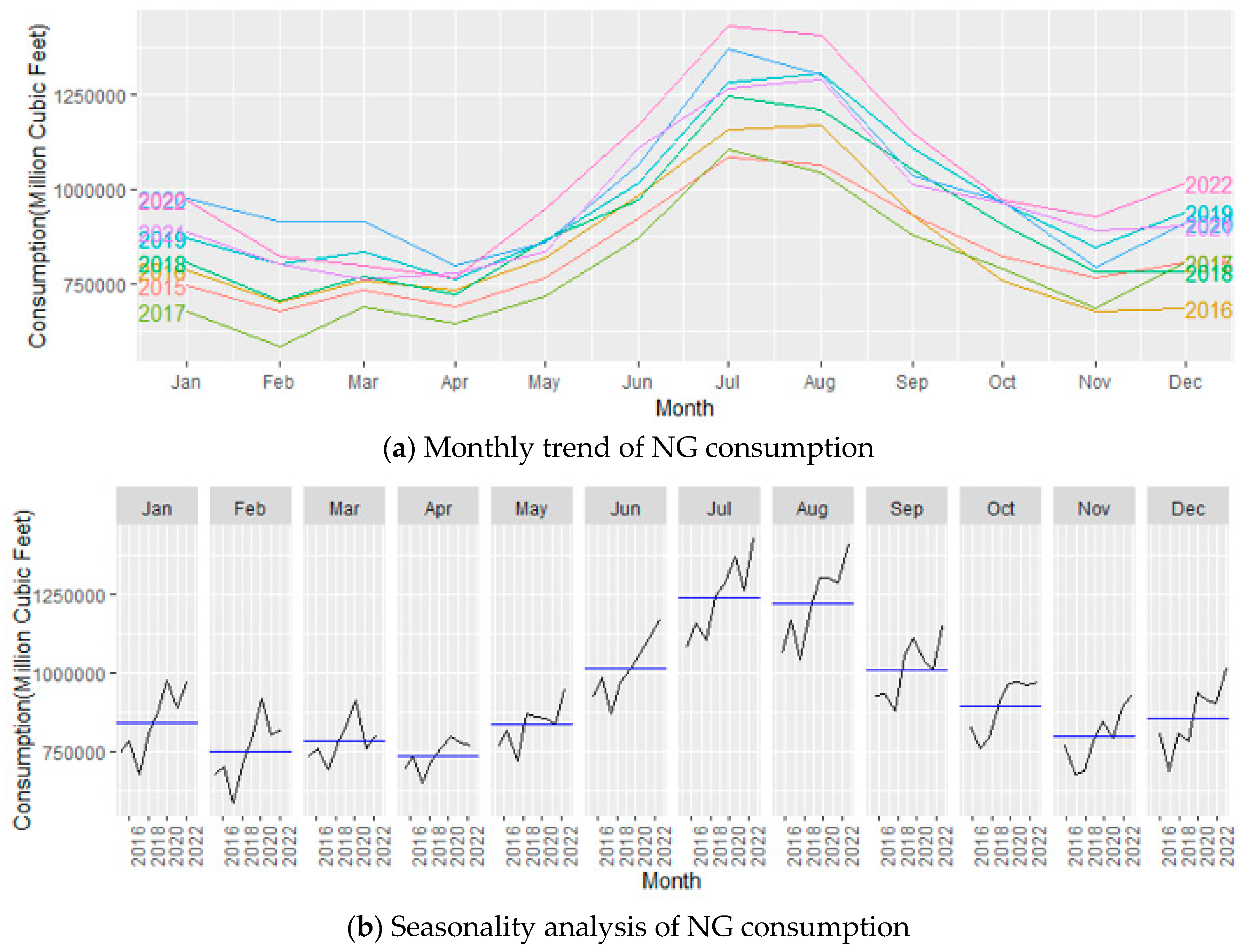
Figure 2.
Monthly consumption and seasonality analysis of NG from the year 2015 to 2022.
Figure 2.
Monthly consumption and seasonality analysis of NG from the year 2015 to 2022.
Figure 3.
Monthly consumption and seasonality analysis of coal from the year 2015 to 2022.
Figure 3.
Monthly consumption and seasonality analysis of coal from the year 2015 to 2022.
Figure 4.
Monthly consumption and seasonality analysis of petroleum coke from the year 2015 to 2022.
Figure 4.
Monthly consumption and seasonality analysis of petroleum coke from the year 2015 to 2022.
Figure 5.
Monthly consumption and seasonality analysis of petroleum liquids from the year 2015 to 2022.
Figure 5.
Monthly consumption and seasonality analysis of petroleum liquids from the year 2015 to 2022.
Figure 6.
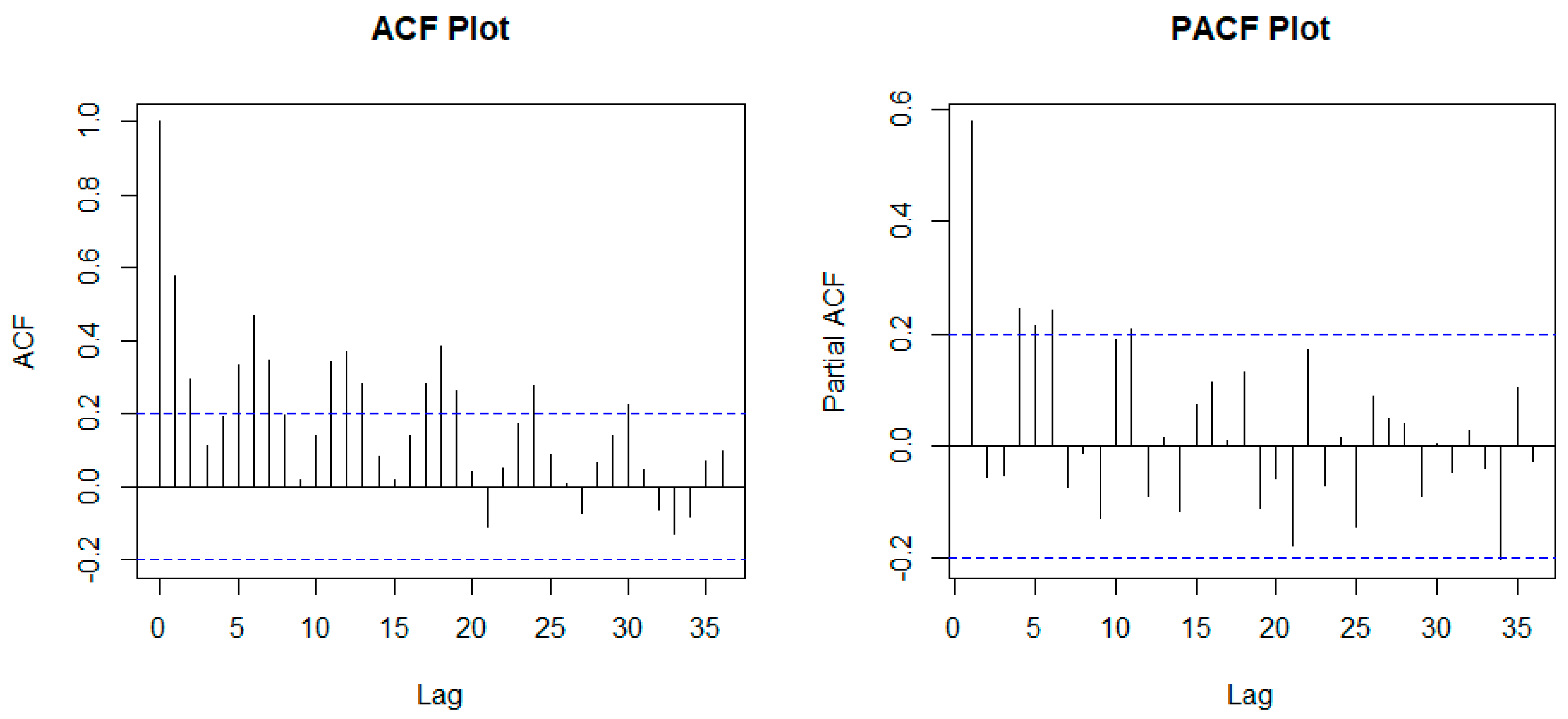
Autocorrelation analysis of NG consumption using ACF and PACF plot.
Figure 6.
Autocorrelation analysis of NG consumption using ACF and PACF plot.
Figure 7.
Autocorrelation analysis of coal consumption using ACF and PACF plot.
Figure 7.
Autocorrelation analysis of coal consumption using ACF and PACF plot.
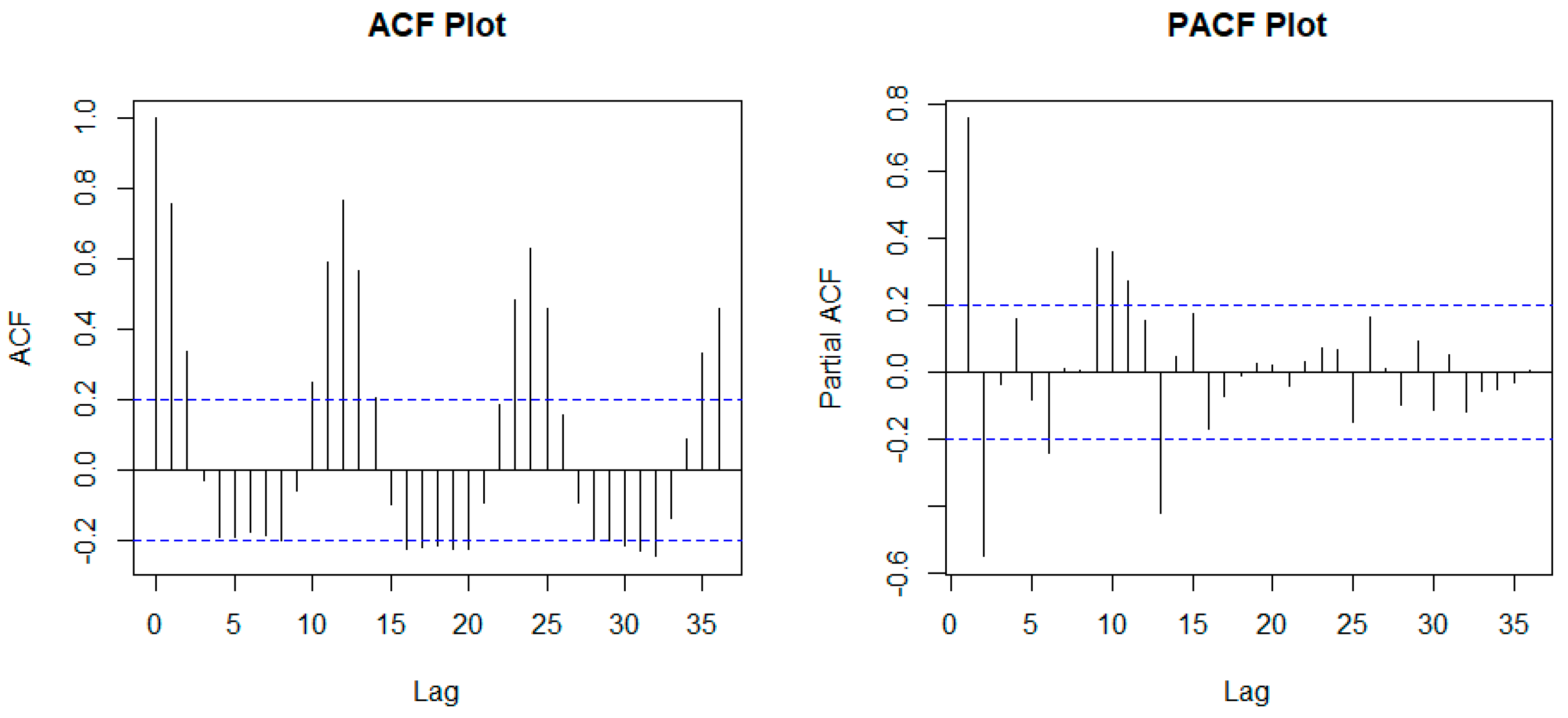
Figure 8.
Autocorrelation analysis of petroleum coke consumption using ACF and PACF plot.
Figure 8.
Autocorrelation analysis of petroleum coke consumption using ACF and PACF plot.
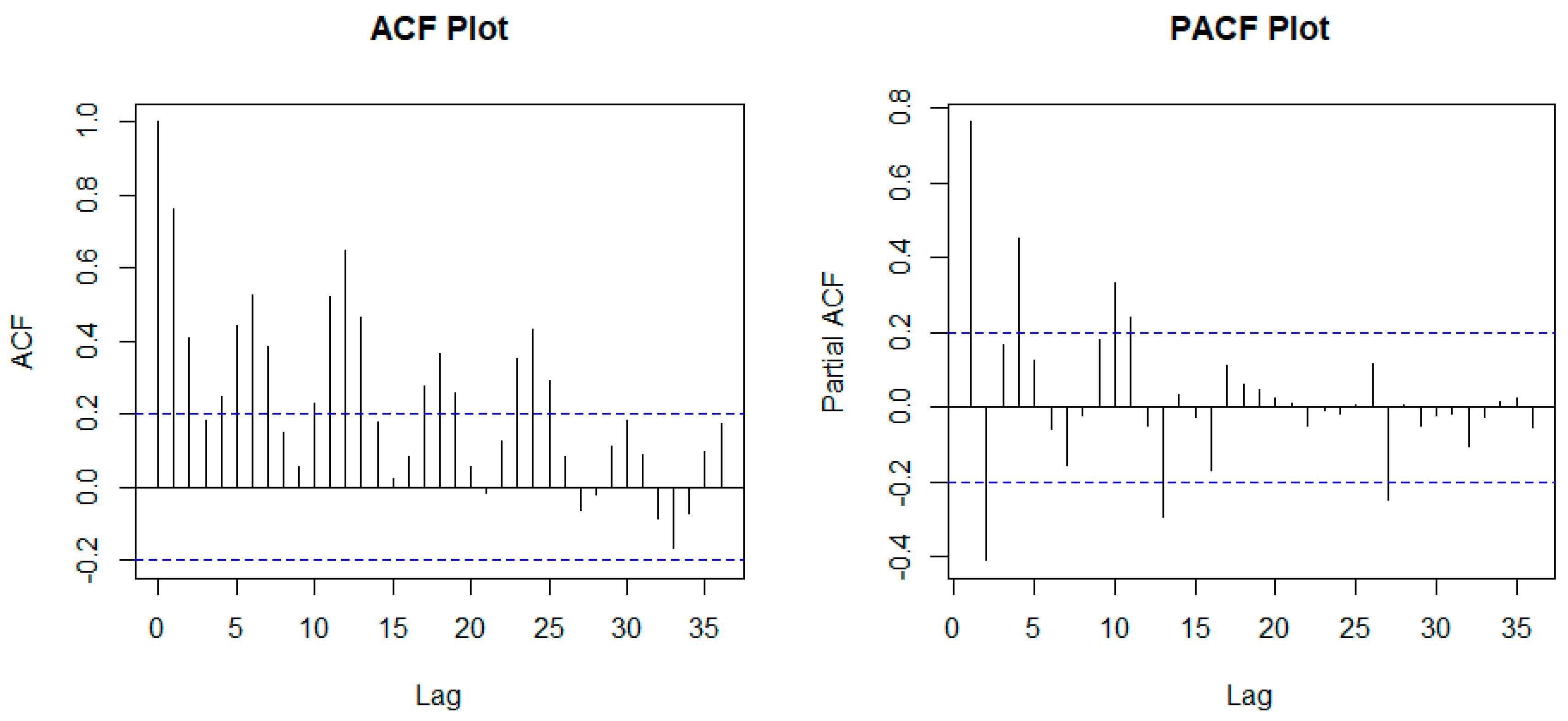
Figure 9.
Autocorrelation analysis of NG consumption using ACF and PACF plot.
Figure 9.
Autocorrelation analysis of NG consumption using ACF and PACF plot.
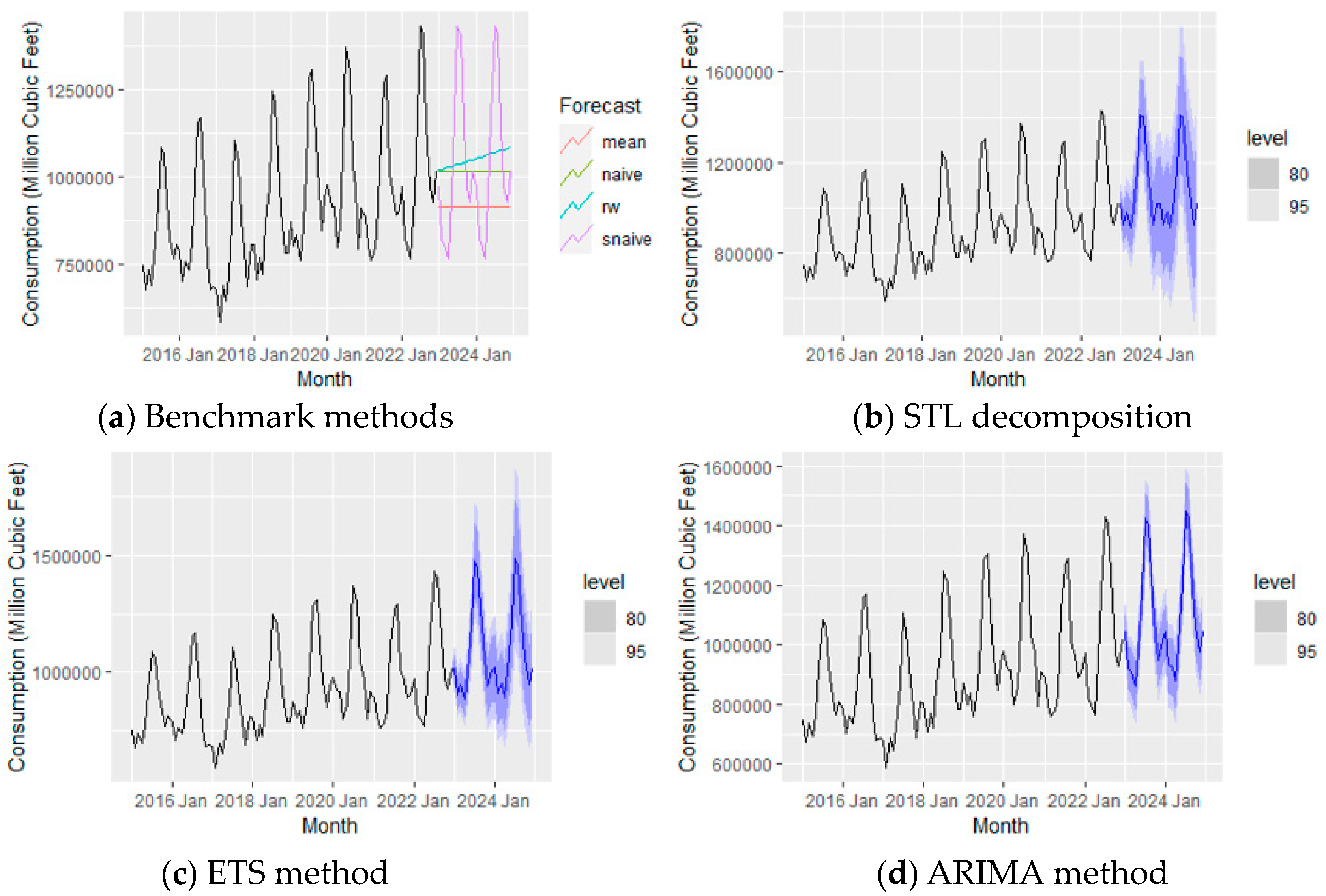
Figure 10.
Forecasting NG consumption for the year 2023 and 2024 using different forecasting methods.
Figure 10.
Forecasting NG consumption for the year 2023 and 2024 using different forecasting methods.
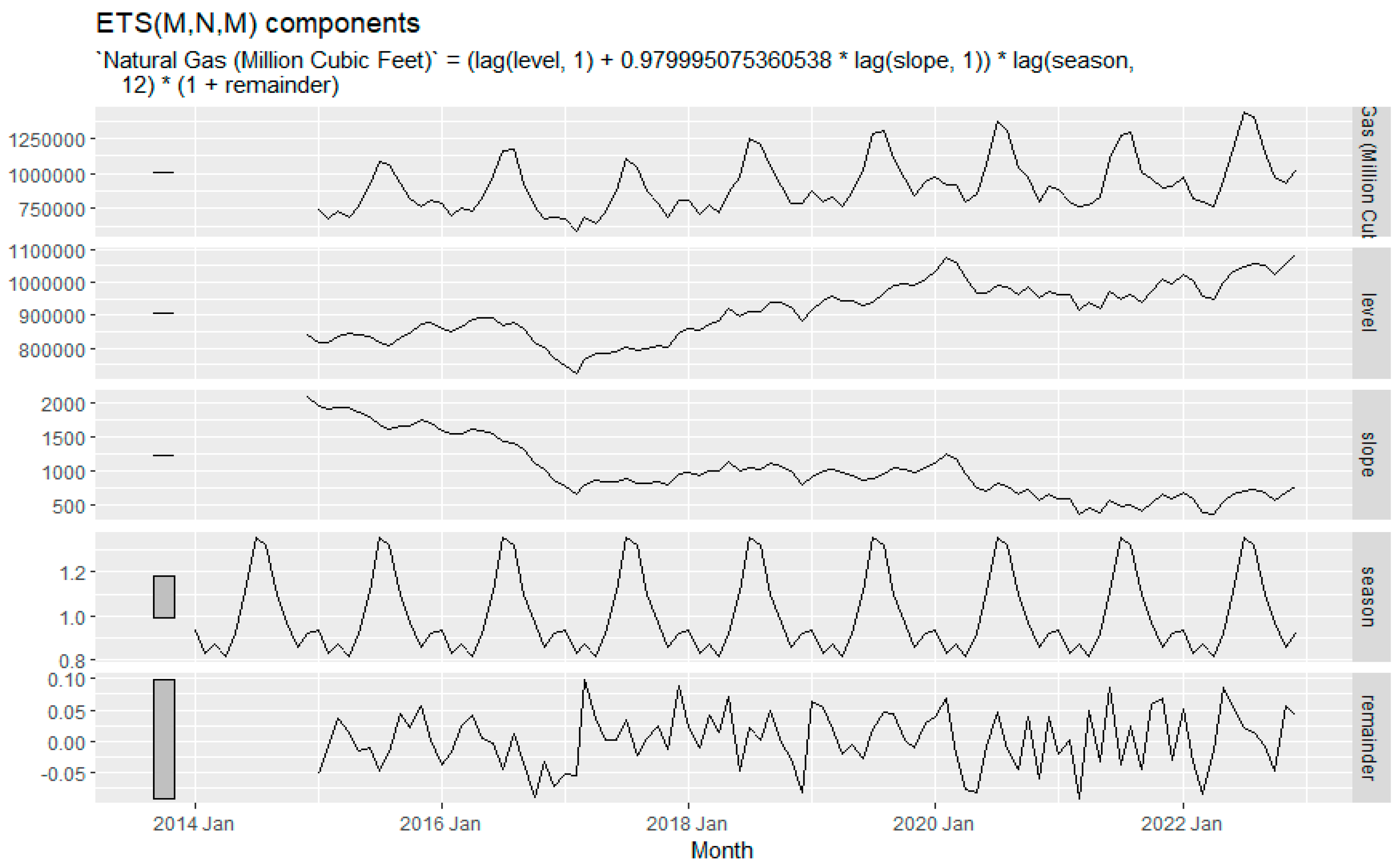
Figure 11.
ETS (M, N, M) decomposition plot of NG consumption.
Figure 11.
ETS (M, N, M) decomposition plot of NG consumption.
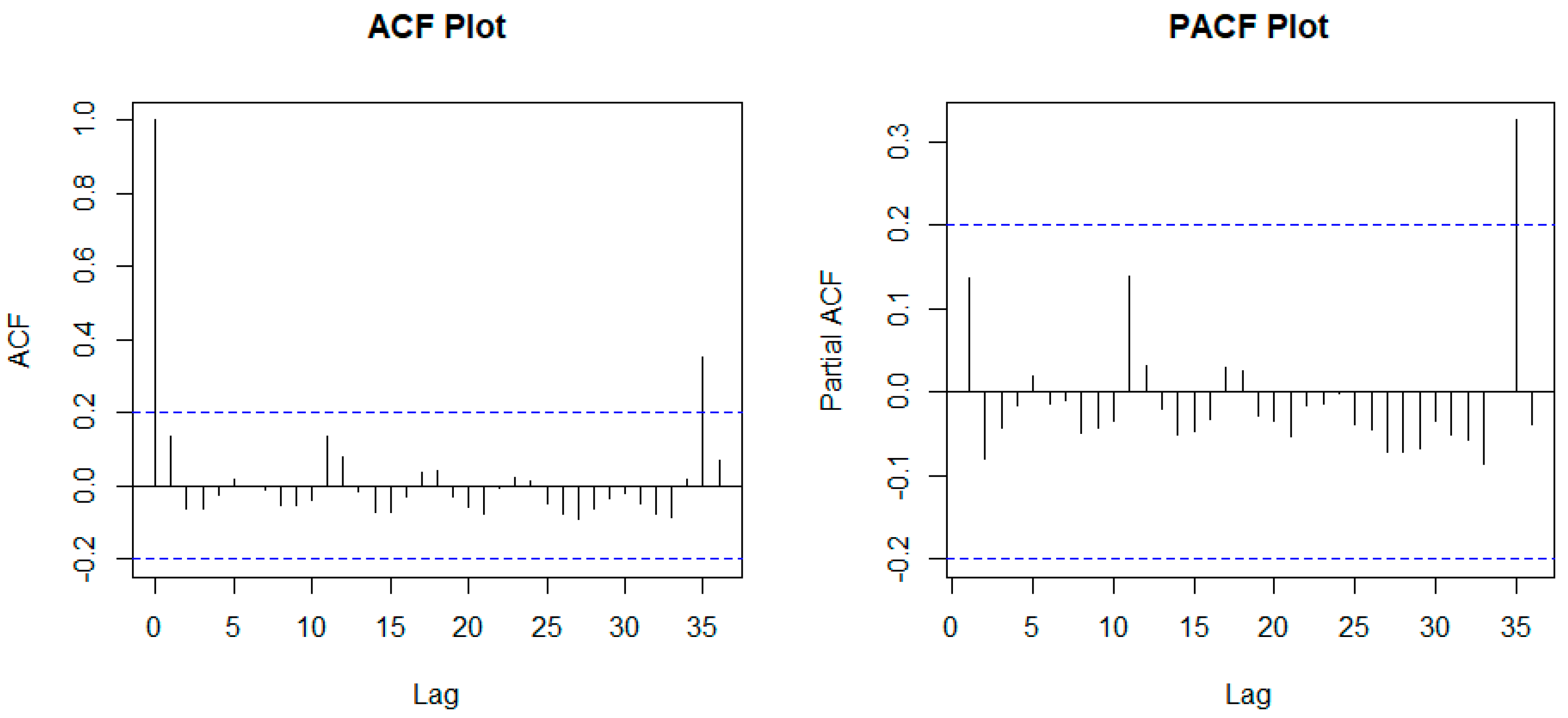
Figure 16.
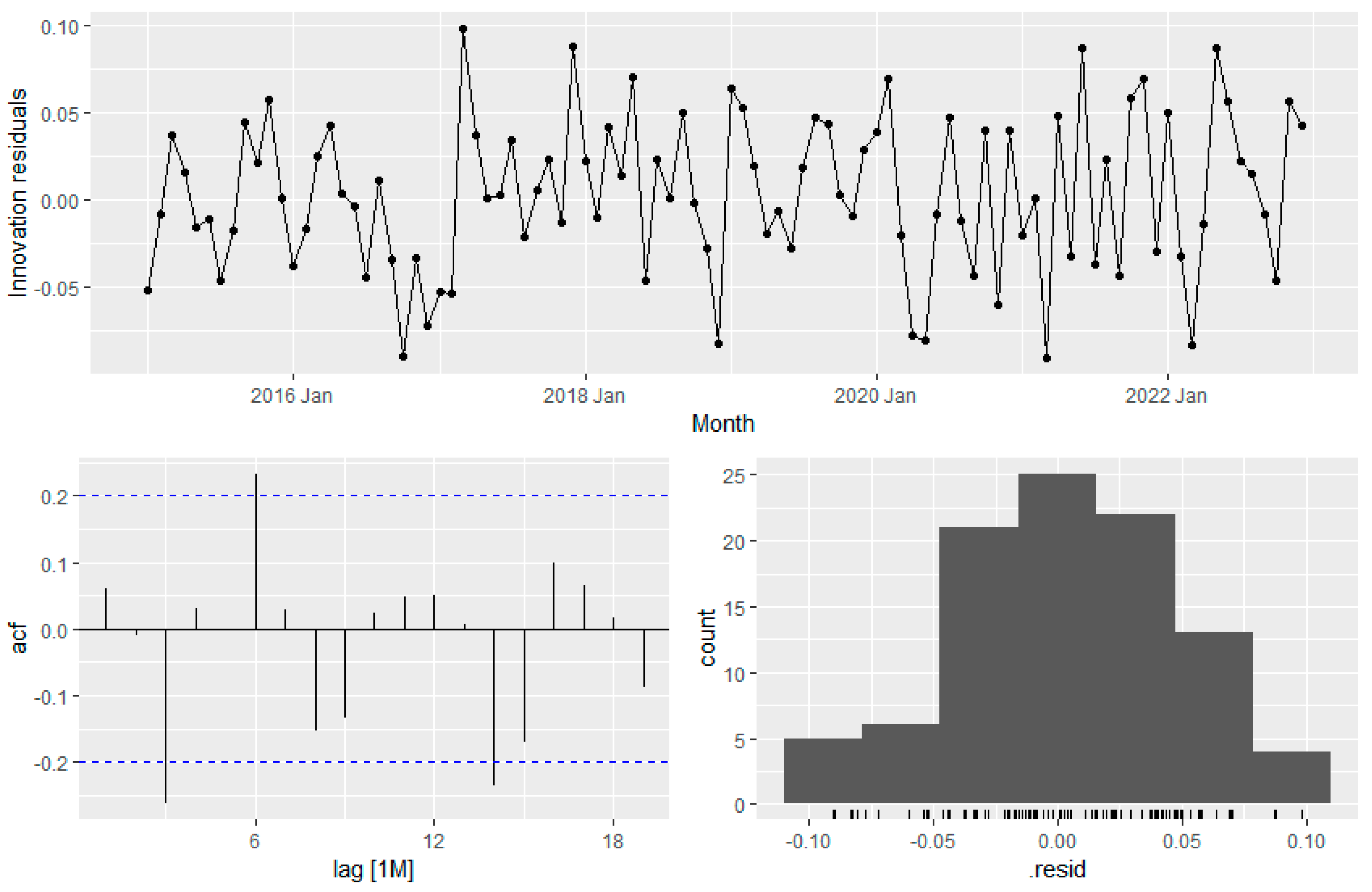
Residual analysis of SNAÏVE forecasting method.
Figure 16.
Residual analysis of SNAÏVE forecasting method.
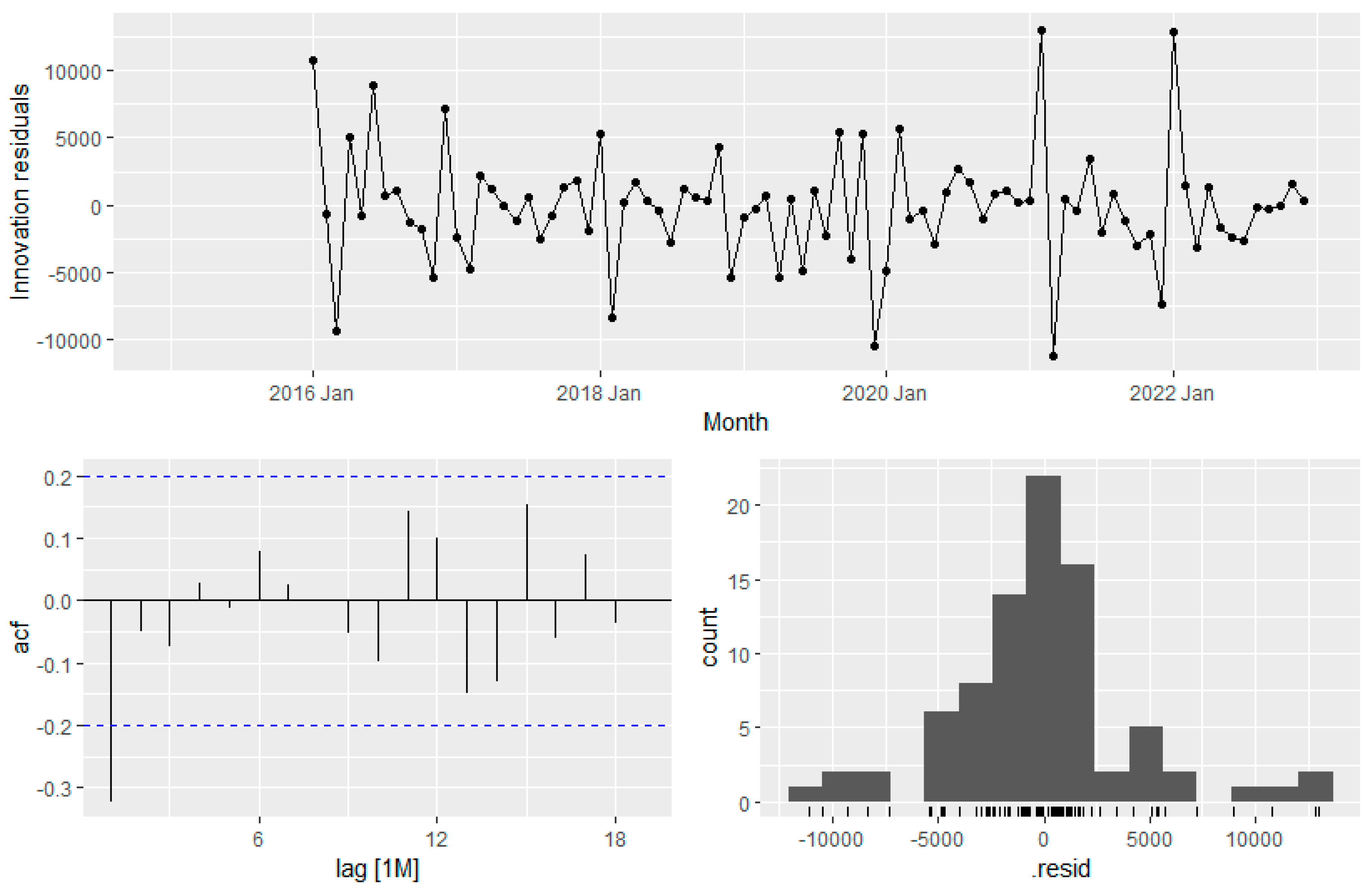
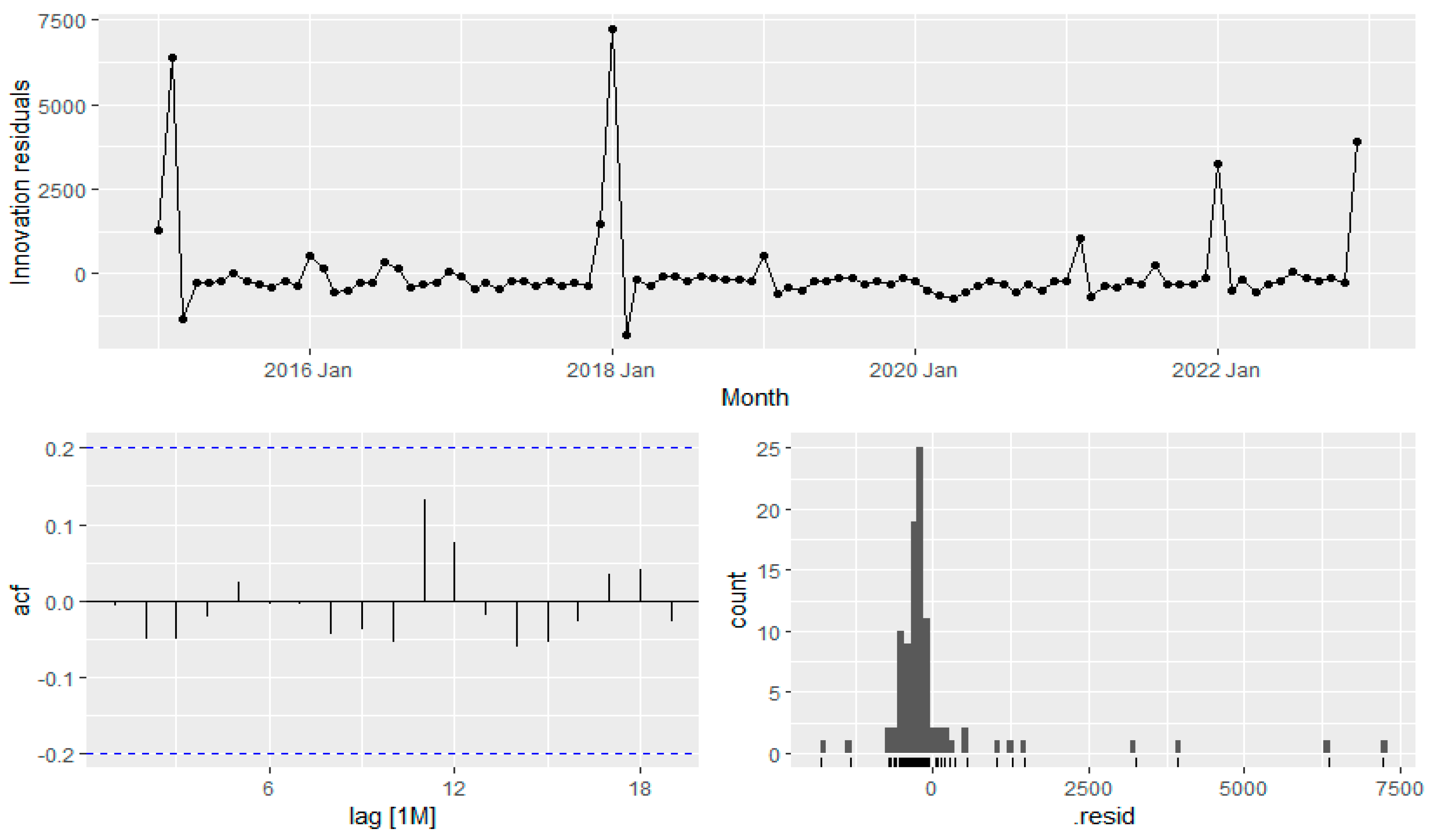
Figure 18.
Residual analysis of ARIMA forecasting method.
Figure 18.
Residual analysis of ARIMA forecasting method.
Figure 19.
Overall trend analysis of NG consumption for US electricity generation.
Figure 19.
Overall trend analysis of NG consumption for US electricity generation.
Figure 20.
Overall Trend Analysis of Coal consumption for US electricity generation.
Figure 20.
Overall Trend Analysis of Coal consumption for US electricity generation.
Figure 21.
Overall Trend Analysis of Petroleum Coke consumption for US electricity generation.
Figure 21.
Overall Trend Analysis of Petroleum Coke consumption for US electricity generation.
Figure 22.
Overall Trend Analysis of Petroleum Liquid consumption for US electricity generation.
Figure 22.
Overall Trend Analysis of Petroleum Liquid consumption for US electricity generation.
Figure 23.
Forecasted trend of all four components for fuel consumption to generate electricity.
Figure 23.
Forecasted trend of all four components for fuel consumption to generate electricity.
Table 1.
Model comparison in terms of errors for the train dataset.
Table 1.
Model comparison in terms of errors for the train dataset.
| Train Data |
Model |
ME |
RMSE |
MAE |
MPE |
MAPE |
ACF1 |
| STLF |
2485.022 |
46311.86 |
37269.12 |
0.19733 |
4.054975 |
-0.31132 |
| ARIMA |
-1003.74 |
42482.11 |
34075.3 |
-0.43476 |
3.772431 |
0.028523 |
| ETS |
2776.487 |
39237.5 |
32580.19 |
0.124194 |
3.633987 |
0.029872 |
| MEAN |
-3.88E-11 |
187831.5 |
150235 |
-3.91587 |
16.47926 |
0.758566 |
| NAÏVE |
2849.021 |
129627.5 |
104644.3 |
-0.54117 |
11.12082 |
0.372243 |
| SNAÏVE |
28184.8 |
85297.44 |
72281.51 |
2.45759 |
8.001223 |
0.716488 |
| RW-DRIFT |
2.94E-11 |
129596.2 |
104914.3 |
-0.86377 |
11.16892 |
0.372243 |
Table 2.
Model comparison in terms of Errors for the Test Data set.
Table 2.
Model comparison in terms of Errors for the Test Data set.
| Test Data |
Model |
ME |
RMSE |
MAE |
MPE |
MAPE |
ACF1 |
| STLF |
14741.56 |
50661.2 |
44064.48 |
0.566659 |
3.729218 |
0.648806 |
| ARIMA |
25348.86 |
51424.27 |
46082.33 |
1.857718 |
4.030831 |
0.341779 |
| ETS |
7600.542 |
20687.46 |
17204.31 |
0.513017 |
1.477106 |
0.117672 |
| MEAN |
199798.9 |
308728.4 |
212774.1 |
14.57299 |
16.03116 |
0.650277 |
| NAÏVE |
99858.38 |
255666.4 |
185054.6 |
5.251944 |
14.63274 |
0.650277 |
| SNAÏVE |
75924.13 |
86594.7 |
75924.13 |
7.302419 |
7.302419 |
0.271527 |
| RW-DRIFT |
87037.78 |
245731.8 |
181637.9 |
4.152805 |
14.53365 |
0.647994 |
Table 3.
Model comparison in terms of Errors for the Train Data set.
Table 3.
Model comparison in terms of Errors for the Train Data set.
| Train Data |
Model |
ME |
RMSE |
MAE |
MPE |
MAPE |
ACF1 |
| STLF |
-96.8973 |
4234.149 |
2884.178 |
-0.74241 |
6.481808 |
-0.32284 |
| ARIMA |
-399.02 |
4385.426 |
3269.713 |
-1.15739 |
7.247969 |
0.012544 |
| ETS |
-334.795 |
3831.801 |
2944.868 |
-1.1289 |
6.287089 |
0.036044 |
| MEAN |
2.43E-12 |
12092.34 |
9731.963 |
-6.69494 |
21.85658 |
0.762233 |
| NAÏVE |
-311.937 |
8018.467 |
6701.453 |
-1.98137 |
14.30493 |
0.269363 |
| SNAÏVE |
-3190.68 |
7797.248 |
6340.655 |
-8.10497 |
14.95868 |
0.679204 |
| RW-DRIFT |
9.19E-13 |
8012.397 |
6687.139 |
-1.29341 |
14.23191 |
0.269363 |
Table 4.
Model comparison in terms of Errors for the Test Data set.
Table 4.
Model comparison in terms of Errors for the Test Data set.
| Test Data |
Model |
ME |
RMSE |
MAE |
MPE |
MAPE |
ACF1 |
| STLF |
-5630.45 |
5936.203 |
5630.449 |
-17.4302 |
17.4302 |
0.35842 |
| ARIMA |
-10728.1 |
11186.03 |
10728.1 |
-35.0688 |
35.06884 |
0.030943 |
| ETS |
-6864.8 |
7288.344 |
6864.795 |
-21.1329 |
21.13289 |
0.338486 |
| MEAN |
-15923.6 |
17662.76 |
15923.57 |
-56.8521 |
56.85209 |
0.536813 |
| NAÏVE |
-9111 |
11892.15 |
10296 |
-34.8482 |
37.53244 |
0.536813 |
| SNAÏVE |
-8444.63 |
9014.585 |
8444.625 |
-28.1565 |
28.15649 |
0.300924 |
| RW-DRIFT |
-7707.28 |
11166.73 |
10062.05 |
-30.5693 |
35.90604 |
0.560167 |
Table 5.
Model comparison in terms of Errors for the Train Data set.
Table 5.
Model comparison in terms of Errors for the Train Data set.
| Train Data |
Model |
ME |
RMSE |
MAE |
MPE |
MAPE |
ACF1 |
| STLF |
0.072135 |
50.30918 |
38.44801 |
-1.7798 |
15.68808 |
-0.31094 |
| ARIMA |
-7.79429 |
50.97813 |
39.21442 |
-6.92597 |
16.82244 |
-0.04866 |
| ETS |
-2.2064 |
44.60708 |
35.05145 |
-3.58674 |
14.38404 |
0.147046 |
| MEAN |
0 |
66.17165 |
52.33333 |
-7.38547 |
21.85282 |
0.57797 |
| NAÏVE |
-1.11579 |
59.88902 |
47.55789 |
-3.72212 |
19.53299 |
-0.17484 |
| SNAÏVE |
-12.619 |
71.87241 |
60.09524 |
-9.37567 |
25.92356 |
0.360049 |
| RW-DRIFT |
1.08E-14 |
59.87863 |
47.54859 |
-3.2987 |
19.48854 |
-0.17484 |
Table 6.
Model comparison in terms of Errors for the Test Data set.
Table 6.
Model comparison in terms of Errors for the Test Data set.
| Test Data |
Model |
ME |
RMSE |
MAE |
MPE |
MAPE |
ACF1 |
| STLF |
-134.524 |
139.2002 |
134.5243 |
-97.8964 |
97.89637 |
0.392624 |
| ARIMA |
-100.747 |
115.8635 |
100.7467 |
-79.5287 |
79.52873 |
0.571681 |
| ETS |
-130.006 |
134.3647 |
130.0063 |
-94.2535 |
94.25347 |
0.375933 |
| MEAN |
-122.75 |
134.7748 |
122.75 |
-94.6778 |
94.67779 |
0.558346 |
| NAÏVE |
-134.75 |
145.7884 |
134.75 |
-102.904 |
102.9036 |
0.558346 |
| SNAIVE |
-78.5 |
99.49749 |
90 |
-64.2448 |
68.79813 |
0.355008 |
| RW-DRIFT |
-129.729 |
141.8381 |
129.7289 |
-99.7341 |
99.73414 |
0.565986 |
Table 7.
Model comparison in terms of Errors for the Train Data set.
Table 7.
Model comparison in terms of Errors for the Train Data set.
| Train Data |
Model |
ME |
RMSE |
MAE |
MPE |
MAPE |
ACF1 |
| STLF |
51.27077 |
1206.734 |
469.8335 |
-5.79073 |
20.42126 |
-0.351 |
| ARIMA |
-0.39939 |
1199.579 |
556.5674 |
-12.6417 |
22.80608 |
-0.00636 |
| ETS |
-72.5277 |
1522.814 |
687.7297 |
-11.0457 |
34.25543 |
-0.26354 |
| MEAN |
0 |
1214.503 |
563.3268 |
-12.923 |
23.11294 |
0.136773 |
| NAÏVE |
27.18947 |
1548.012 |
604.3474 |
-9.65595 |
25.94808 |
-0.37293 |
| SNAÏVE |
-1.96429 |
1494.727 |
578.4881 |
-6.82803 |
22.23511 |
0.142605 |
| RW-DRIFT |
-1.82E-13 |
1547.773 |
604.41 |
-11.2077 |
26.08228 |
-0.37293 |
Table 8.
Model comparison in terms of Errors for the Test Data set.
Table 8.
Model comparison in terms of Errors for the Test Data set.
| Test Data |
Model |
ME |
RMSE |
MAE |
MPE |
MAPE |
ACF1 |
| STLF |
-3879.82 |
3893.528 |
3879.82 |
-225.717 |
225.7167 |
-0.24153 |
| ARIMA |
-353.011 |
424.909 |
354.831 |
-20.8028 |
20.8937 |
-0.39078 |
| ETS |
-6402.64 |
6769.273 |
6402.639 |
-365.768 |
365.7678 |
0.550292 |
| MEAN |
-260.063 |
287.3403 |
263.7344 |
-15.588 |
15.77136 |
0.232705 |
| NAÏVE |
-4147.75 |
4149.55 |
4147.75 |
-241.594 |
241.5938 |
0.232705 |
| SNAÏVE |
-475.75 |
1221.797 |
544.5 |
-26.5977 |
30.84144 |
-0.00337 |
| RW-DRIFT |
-4270.1 |
4273.105 |
4270.103 |
-248.811 |
248.8107 |
0.476336 |