Submitted:
17 January 2024
Posted:
17 January 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Materials and Methods
2.1. The CYGNSS Observatory
2.2. The Bottoms-up Correlated Error Model
2.2.1. Model Assumptions
2.2.1. The Full Correlated Error Model
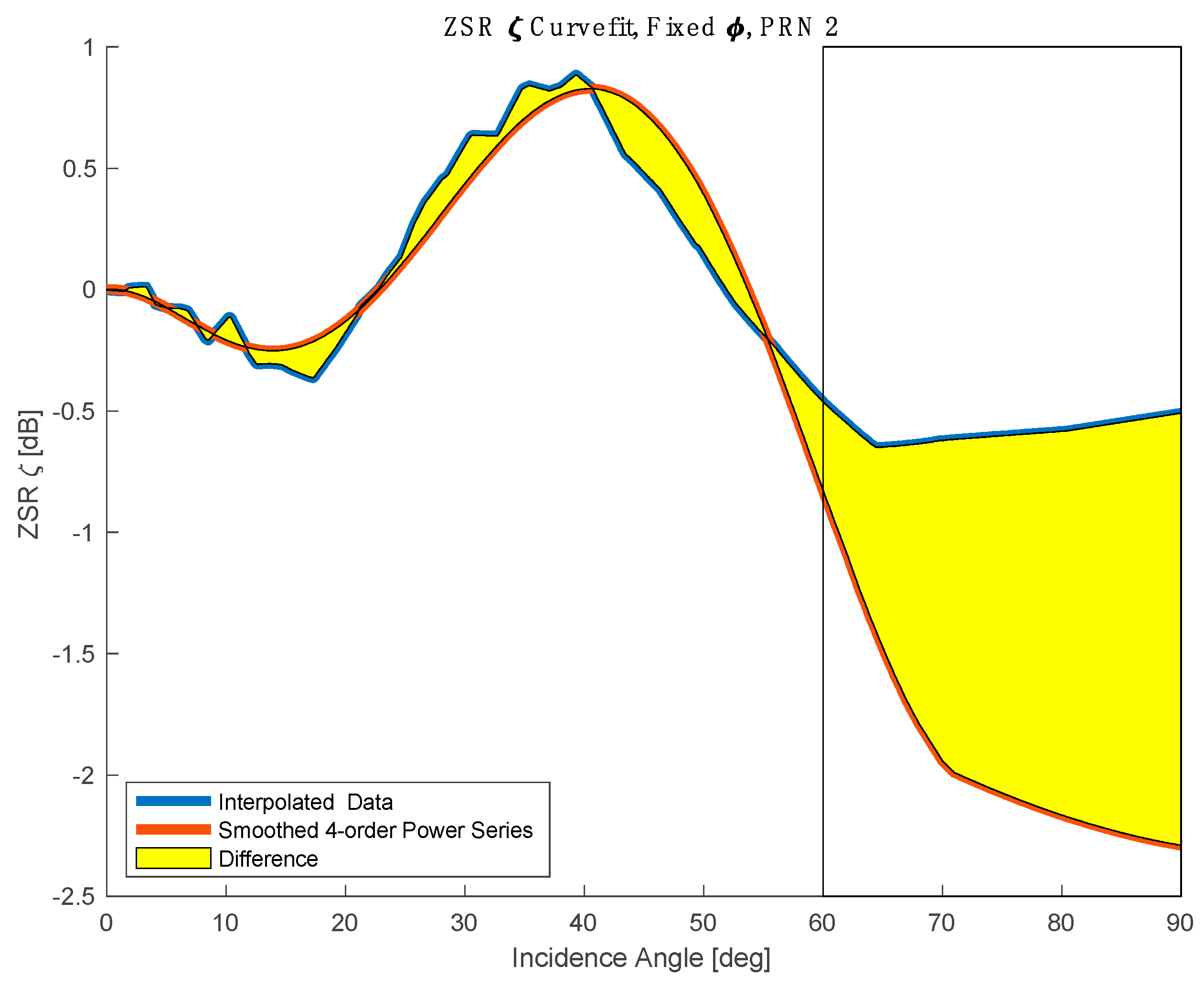
2.3. Verification Techniques
2.3.1. Curating Matchup Observations
- Matched tracks must both have greater than 300 samples;
- Individual sample matchups are valid if samples are within 0.5 degrees (great circle distance);
- Individual samples are screened to ensure no quality control flags apply;
- The matched track is only valid if 60% of the data remains after all other matchup criteria applies.
2.3.2. Generating Model NBRCS
2.3.3. Estimating Total Correlated Error
2.3.4. Model Tuning
- represents the relative magnitude of the white noise component of the error, which decorrelates at ;
- represents the relative magnitude long-decay pedestal, or any residual correlated errors at the edge of our timescales of interest;
- represents the relative magnitude of the correlated caused by terms and , which exhibit smooth decay as samples spread apart when projected through the nadir and zenith antenna coordinates, respectively [see Appendix D for an in-depth discussion]; and
- represents the relative decorrelation roll-off in terms and .
3. Results
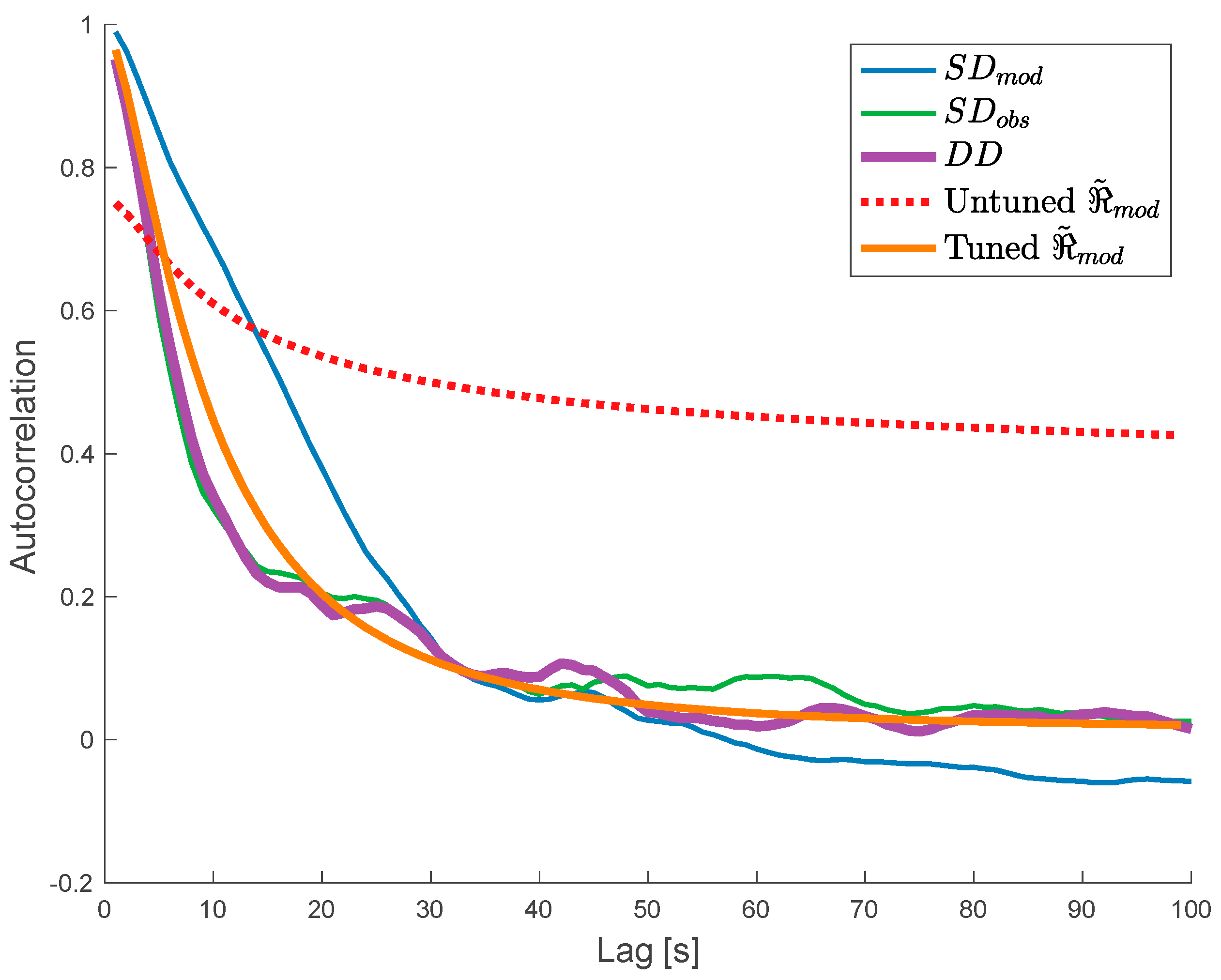
3.1. Bulk Behavior
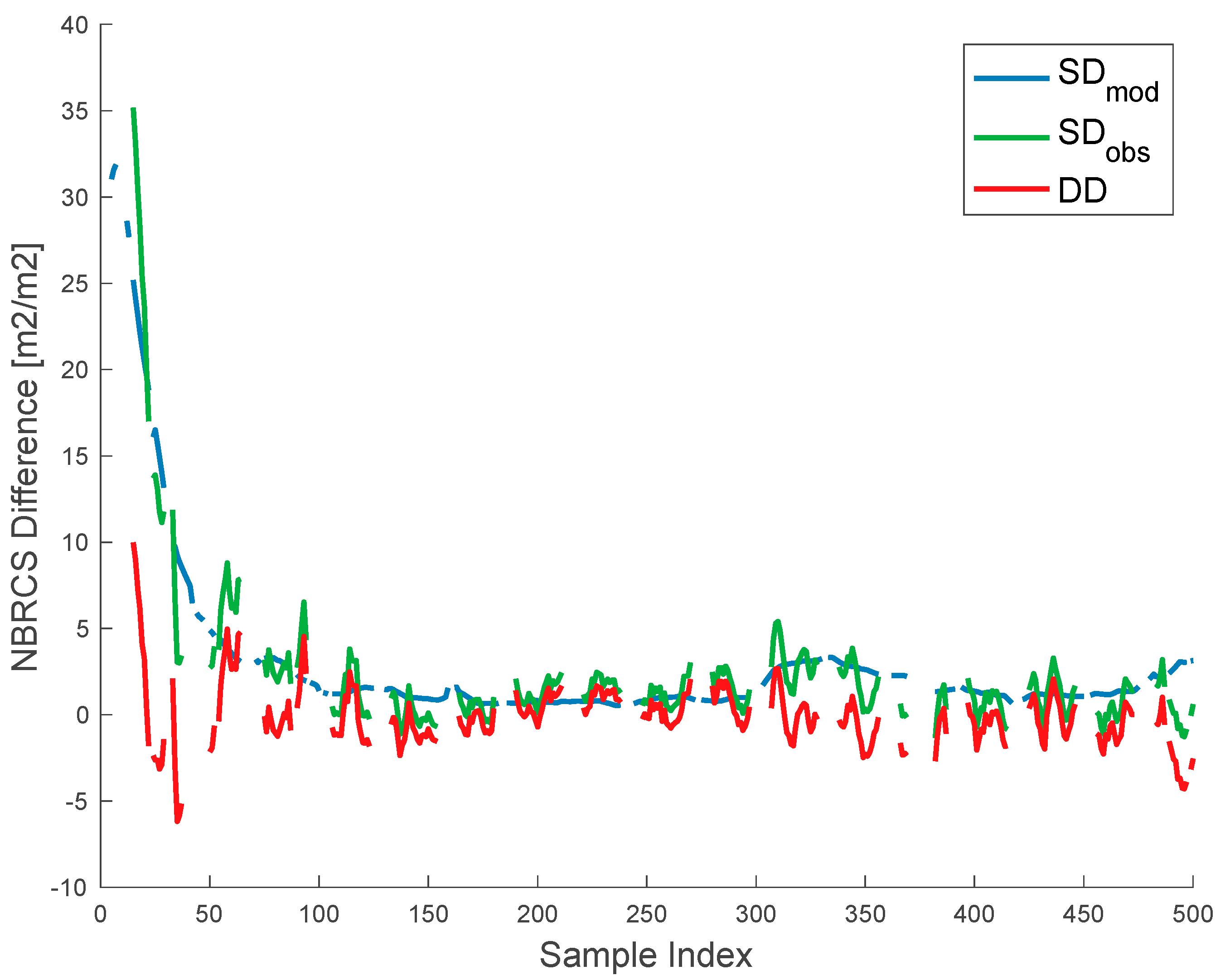
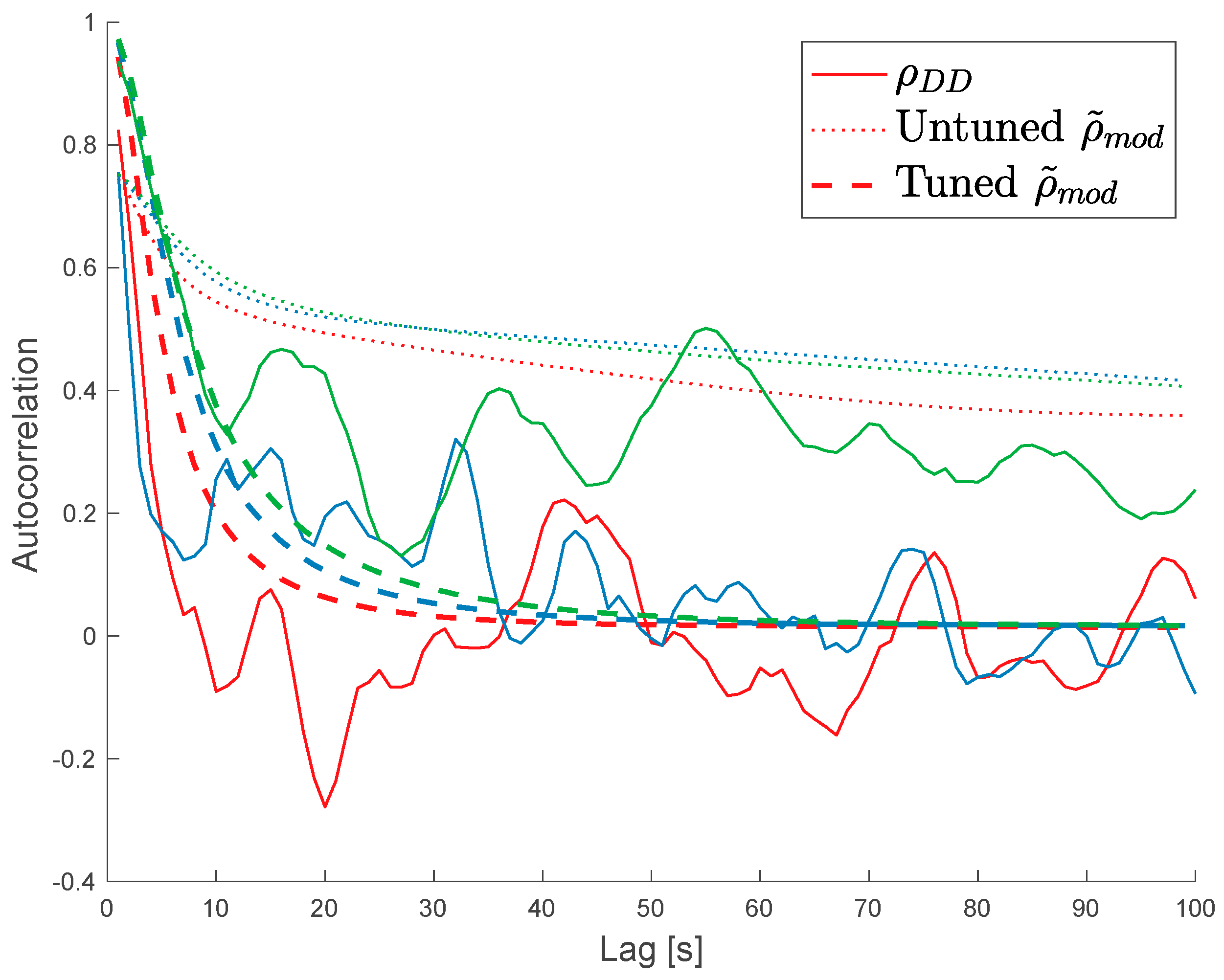
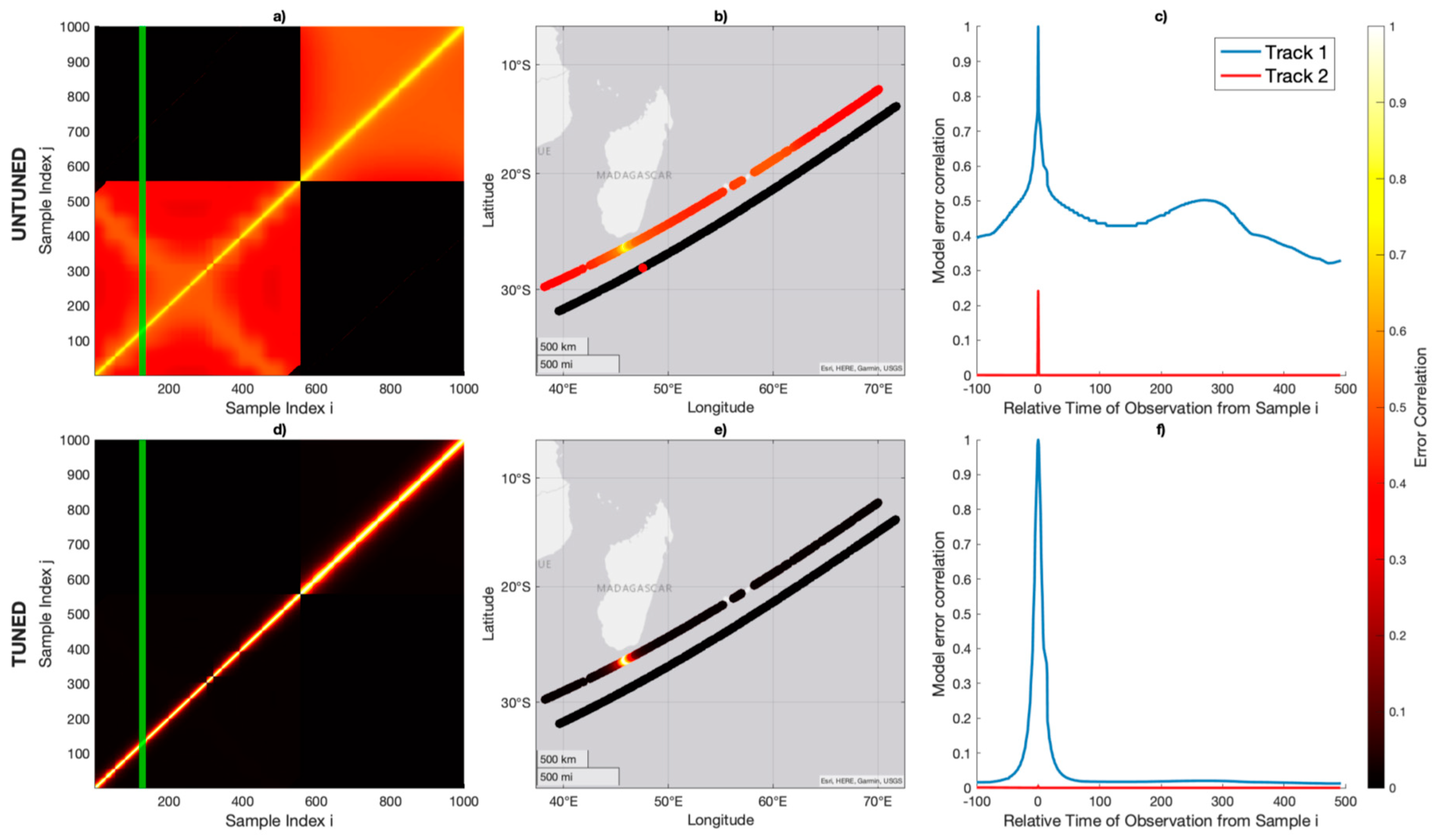
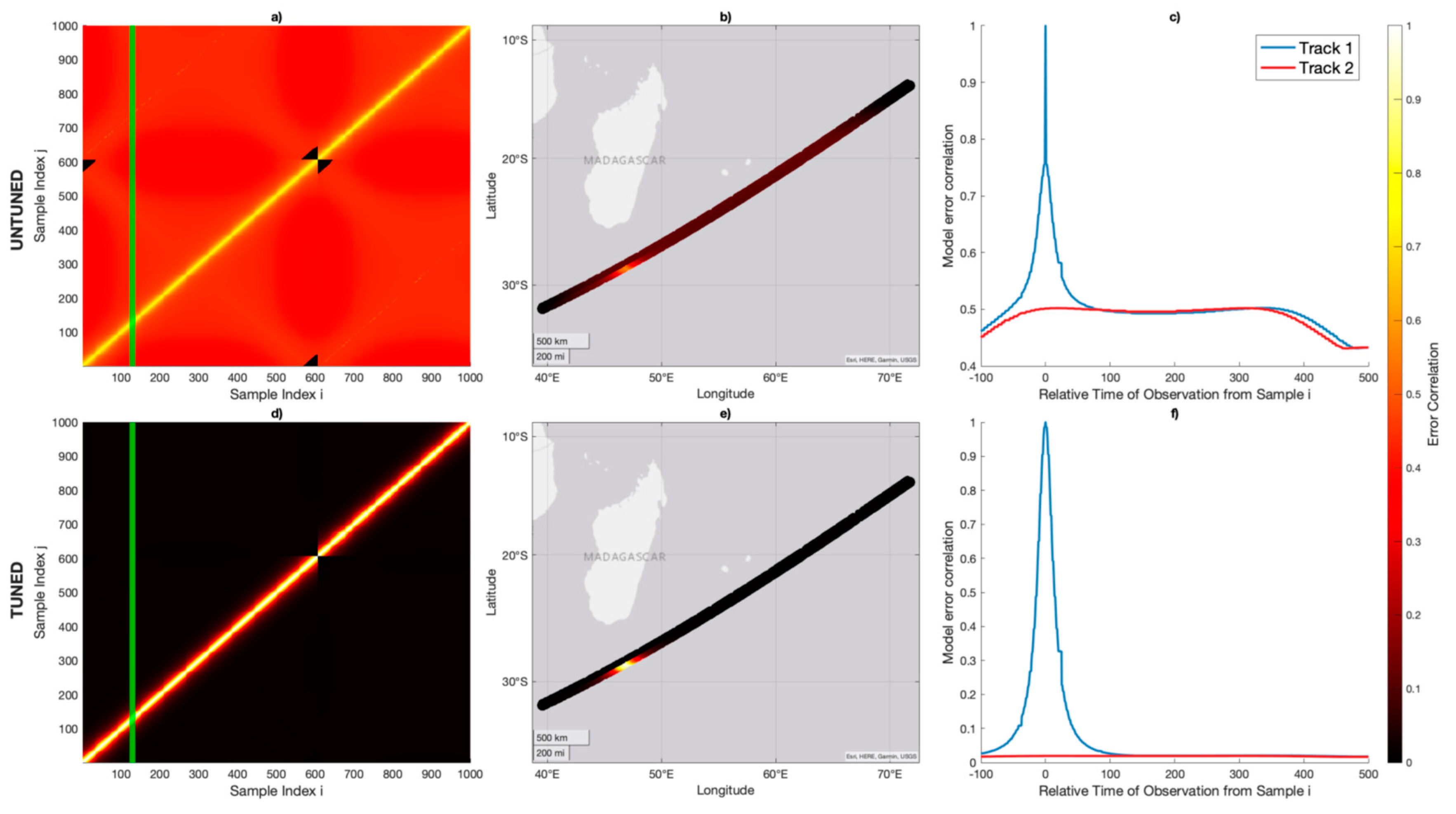
3.2. Single-Track Comparisons
3.3. Dynamic Correlated Error Estimation and Impact of Tuning
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
- The terms as described in Appendix B, Appendix C, Appendix D and Appendix E are not constructed from random variables, but rather through analytic specification to emulate the expected correlated behavior. We generally have insufficient knowledge to measure or estimate the cross correlation between error components. Instead, this model simply estimates the cross-correlation of error within individual components, which then add independently.
- Any residual cross-correlation between error components can be tuned per our tuning parameters.
Appendix B
| Error Term | Error Magnitude [dB] |
|---|---|
| 0.14 [36] | |
| 0.14 [36] | |
| 0.10 [36] | |
| 0.07 [35] | |
| ~0.04 [36] |
Appendix C
Appendix D
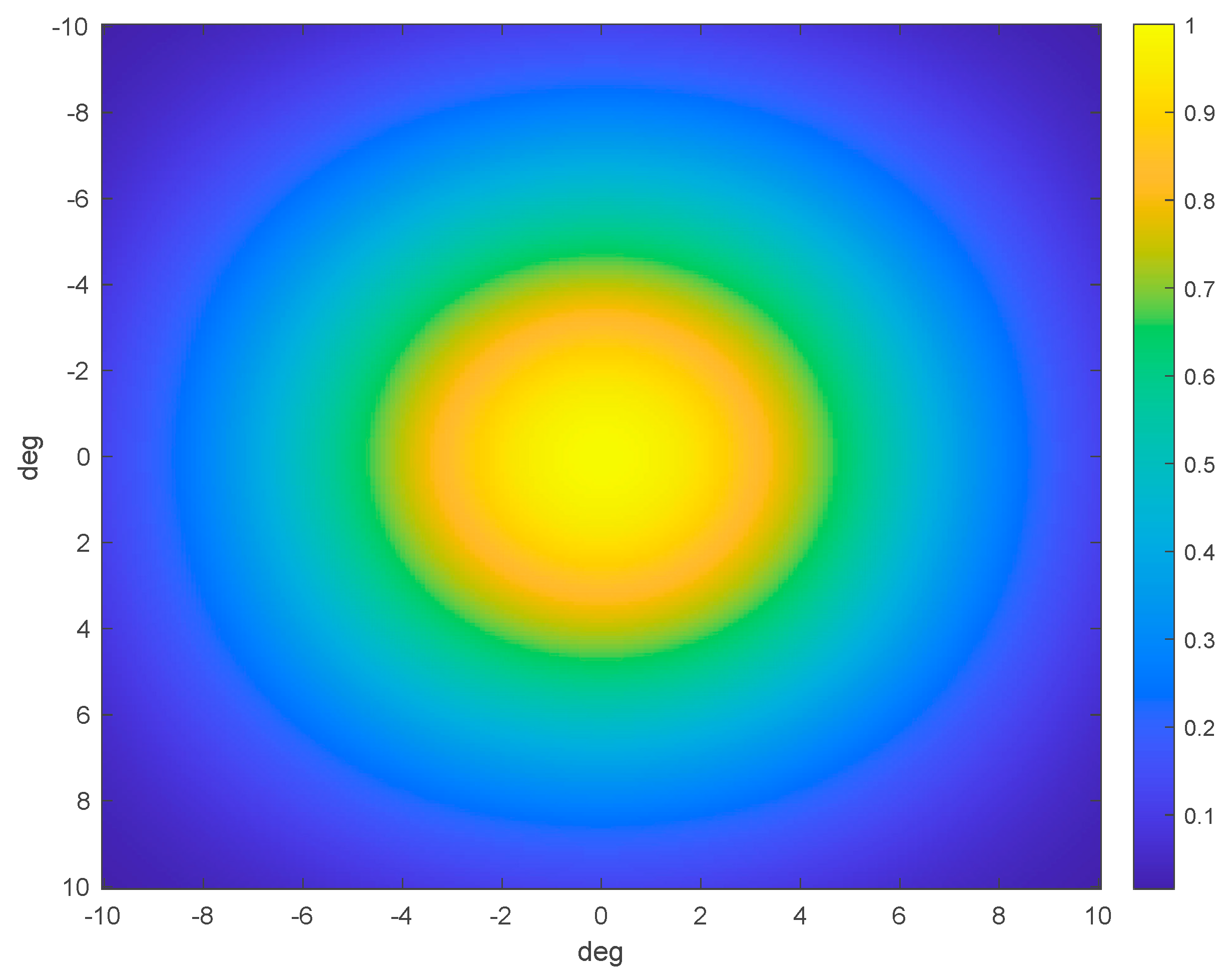
Appendix E
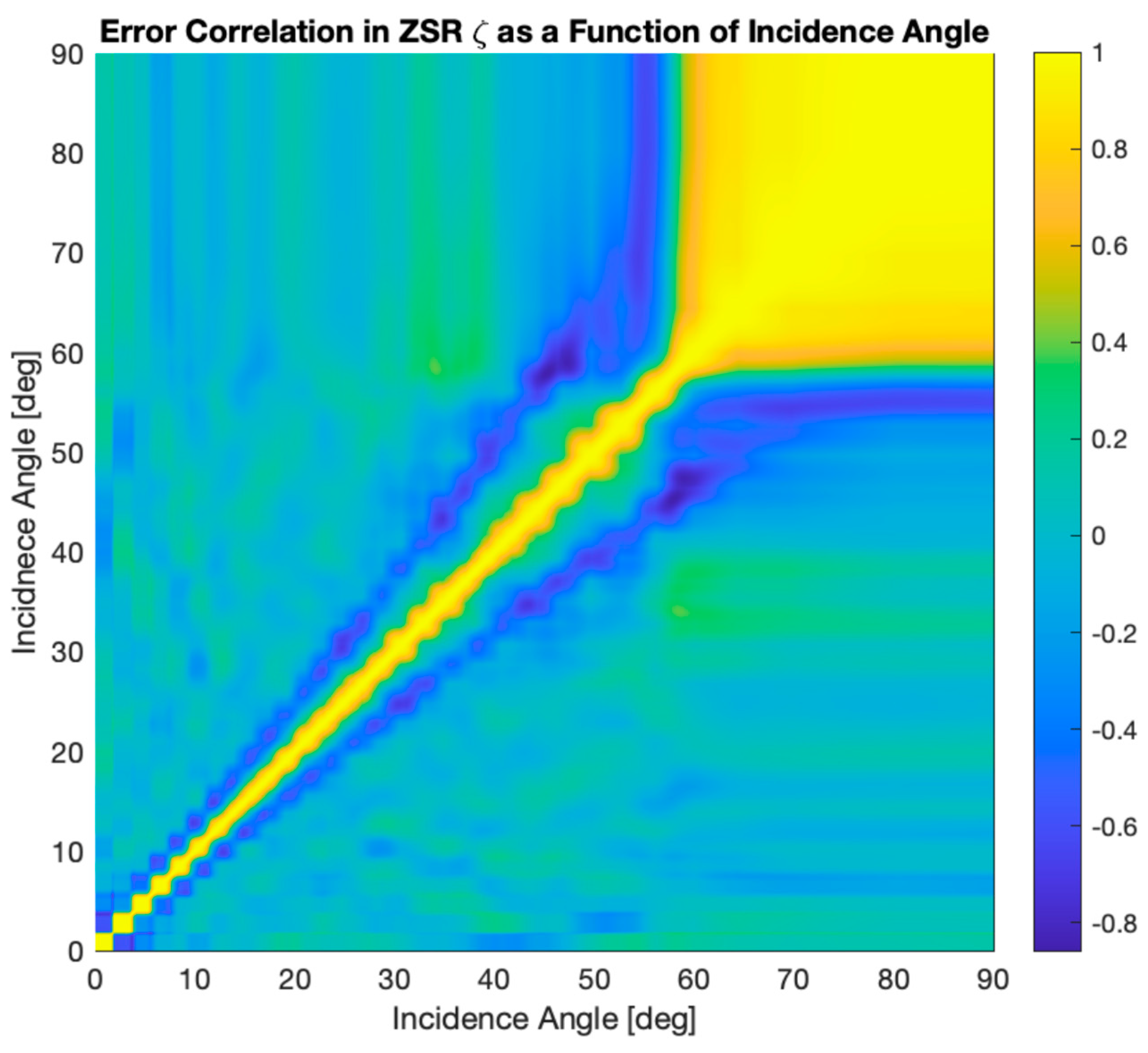
References
- Ruf, C.S.; Chew, C.; Lang, T.; Morris, M.G.; Nave, K.; Ridley, A.; Balasubramaniam, R. A New Paradigm in Earth Environmental Monitoring with the CYGNSS Small Satellite Constellation. Scientific Reports 2018, 8. [Google Scholar] [CrossRef]
- Lorenc, A.C.; Ballard, S.P.; Bell, R.S.; Ingleby, N.B.; Andrews, P.L.F.; Barker, D.M.; Bray, J.R.; Clayton, A.M.; Dalby, T.; Li, D.; et al. The Met. Office Global Three-dimensional Variational Data Assimilation Scheme. Quart J Royal Meteoro Soc 2000, 126, 2991–3012. [Google Scholar] [CrossRef]
- Bannister, R.N. A Review of Forecast Error Covariance Statistics in Atmospheric Variational Data Assimilation. I: Characteristics and Measurements of Forecast Error Covariances. Quart J Royal Meteoro Soc 2008, 134, 1951–1970. [Google Scholar] [CrossRef]
- Bannister, R.N. A Review of Forecast Error Covariance Statistics in Atmospheric Variational Data Assimilation. II: Modelling the Forecast Error Covariance Statistics. Quart J Royal Meteoro Soc 2008, 134, 1971–1996. [Google Scholar] [CrossRef]
- Morss, R.E.; Emanuel, K.A. Influence of Added Observations on Analysis and Forecast Errors: Results from Idealized Systems. Quart J Royal Meteoro Soc 2002, 128, 285–321. [Google Scholar] [CrossRef]
- Stewart, L.M.; Dance, S.L.; Nichols, N.K. Data Assimilation with Correlated Observation Errors: Experiments with a 1-D Shallow Water Model. Tellus A: Dynamic Meteorology and Oceanography 2013, 65, 19546. [Google Scholar] [CrossRef]
- Fowler, A.M.; Dance, S.L.; Waller, J.A. On the Interaction of Observation and Prior Error Correlations in Data Assimilation. Quarterly Journal of the Royal Meteorological Society 2018, 144, 48–62. [Google Scholar] [CrossRef]
- Liu, Z.Q.; Rabier, F. The Interaction between Model Resolution, Observation Resolution and Observation Density in Data Assimilation: A One-Dimensional Study. Quarterly Journal of the Royal Meteorological Society 2002, 128, 1367–1386. [Google Scholar] [CrossRef]
- Stewart, L.M.; Dance, S.L.; Nichols, N.K.; Eyre, J.R.; Cameron, J. Estimating Interchannel Observation-error Correlations for IASI Radiance Data in the Met Office System. Quart J Royal Meteoro Soc 2014, 140, 1236–1244. [Google Scholar] [CrossRef]
- Bormann, N.; Bonavita, M.; Dragani, R.; Eresmaa, R.; Matricardi, M.; McNally, A. Enhancing the Impact of IASI Observations through an Updated Observation-error Covariance Matrix. Quart J Royal Meteoro Soc 2016, 142, 1767–1780. [Google Scholar] [CrossRef]
- Bormann, N.; Bauer, P. Estimates of Spatial and Interchannel Observation-Error Characteristics for Current Sounder Radiances for Numerical Weather Prediction. I: Methods and Application to ATOVS Data. Q.J.R. Meteorol. Soc. 2010, 136, 1036–1050. [Google Scholar] [CrossRef]
- Liu, Y.-A.; Li, Z.; Huang, M. Towards a Data-Derived Observation Error Covariance Matrix for Satellite Measurements. Remote Sensing 2019, 11, 1770. [Google Scholar] [CrossRef]
- Simonin, D.; Waller, J.A.; Ballard, S.P.; Dance, S.L.; Nichols, N.K. A Pragmatic Strategy for Implementing Spatially Correlated Observation Errors in an Operational System: An Application to Doppler Radial Winds. Quart J Royal Meteoro Soc 2019, 145, 2772–2790. [Google Scholar] [CrossRef]
- Waller, J.A.; Dance, S.L.; Nichols, N.K. On Diagnosing Observation-error Statistics with Local Ensemble Data Assimilation. Quart J Royal Meteoro Soc 2017, 143, 2677–2686. [Google Scholar] [CrossRef]
- Yang, J.X.; You, Y.; Blackwell, W.; Da, C.; Kalnay, E.; Grassotti, C.; Liu, Q. (Mark); Ferraro, R.; Meng, H.; Zou, C.-Z.; et al. SatERR: A Community Error Inventory for Satellite Microwave Observation Error Representation and Uncertainty Quantification. Bulletin of the American Meteorological Society 2023. [CrossRef]
- Bauer, P.; Buizza, R.; Cardinali, C.; Noël Thépaut, J. Impact of Singular-Vector-Based Satellite Data Thinning on NWP. Quarterly Journal of the Royal Meteorological Society 2011, 137, 286–302. [Google Scholar] [CrossRef]
- Gao, Y.; Xiao, H.; Jiang, D.; Wan, Q.; Chan, P.W.; Hon, K.K.; Deng, G. Impacts of Thinning Aircraft Observations on Data Assimilation and Its Prediction during Typhoon Nida (2016). Atmosphere 2019, 10, 754. [Google Scholar] [CrossRef]
- Hoffman, R.N. The Effect of Thinning and Superobservations in a Simple One-Dimensional Data Analysis with Mischaracterized Error. Monthly Weather Review 2018, 146, 1181–1195. [Google Scholar] [CrossRef]
- Rainwater, S.; Bishop, C.H.; Campbell, W.F. The Benefits of Correlated Observation Errors for Small Scales. Quart J Royal Meteoro Soc 2015, 141, 3439–3445. [Google Scholar] [CrossRef]
- Stewart, L.M.; Dance, S.L.; Nichols, N.K. Correlated Observation Errors in Data Assimilation. Numerical Methods in Fluids 2008, 56, 1521–1527. [Google Scholar] [CrossRef]
- Daley, R. The Effect of Serially Correlated Observation and Model Error on Atmospheric Data Assimilation. Mon. Wea. Rev. 1992, 120, 164–177. [Google Scholar] [CrossRef]
- Waller, J.A.; Dance, S.L.; Nichols, N.K. Theoretical Insight into Diagnosing Observation Error Correlations Using Observation-minus-background and Observation-minus-analysis Statistics. Quart J Royal Meteoro Soc 2016, 142, 418–431. [Google Scholar] [CrossRef]
- Dee, D.P.; Da Silva, A.M. Maximum-Likelihood Estimation of Forecast and Observation Error Covariance Parameters. Part I: Methodology. Mon. Wea. Rev. 1999, 127, 1822–1834. [Google Scholar] [CrossRef]
- Desroziers, G.; Berre, L.; Chapnik, B.; Poli, P. Diagnosis of Observation, Background and Analysis-error Statistics in Observation Space. Quart J Royal Meteoro Soc 2005, 131, 3385–3396. [Google Scholar] [CrossRef]
- Ruf, C.; McKague, D.; Posselt, D.J.; Gleason, S.; Clarizia, M.P.; Zavorotny, V.U.; Butler, T.; Redfern, J.; Wells, W.; Morris, M.; et al. CYGNSS Handbook; 2nd ed.; Michigan Publishing Services, 2022; ISBN 978-1-60785-787-7.
- Clarizia, M.P.; Ruf, C.S. Wind Speed Retrieval Algorithm for the Cyclone Global Navigation Satellite System (CYGNSS) Mission. IEEE Transactions on Geoscience and Remote Sensing 2016, 54, 4419–4432. [Google Scholar] [CrossRef]
- Ruf, C.S.; Balasubramaniam, R. Development of the CYGNSS Geophysical Model Function for Wind Speed. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing 2019, 12, 66–77. [Google Scholar] [CrossRef]
- Gleason, S.; Ruf, C.S.; Orbrien, A.J.; McKague, D.S. The CYGNSS Level 1 Calibration Algorithm and Error Analysis Based on On-Orbit Measurements. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing 2019, 12, 37–49. [Google Scholar] [CrossRef]
- Wang, T.; Ruf, C.; McKague, D.; Russel, A.; O’Brien, A.; Gleason, S. The Important Role of Antenna Pattern Characterization in the Absolute Calibration of GNSS-R Measurements. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS; IEEE: Brussels, Belgium, July 11 2021; pp. 144–146.
- Wang, T.; Ruf, C.; Gleason, S.; McKague, D.; O’Brien, A.; Block, B. Monitoring GPS Eirp for Cygnss Level 1 Calibration. In Proceedings of the IGARSS 2020 - 2020 IEEE International Geoscience and Remote Sensing Symposium; IEEE: Waikoloa, HI, USA, September 26 2020; pp. 6293–6296.
- Steigenberger, P.; Thölert, S.; Montenbruck, O. Flex Power on GPS Block IIR-M and IIF. GPS Solutions 2019, 23, 1–12. [Google Scholar] [CrossRef]
- Marquis, W.A.; Reigh, D.L. The GPS Block IIR and IIR-M Broadcast L-Band Antenna Panel: Its Pattern and Performance: GPS Block IIR and IIR-M L-Band Antenna Panel Pattern. J Inst Navig 2015, 62, 329–347. [Google Scholar] [CrossRef]
- Wang, T.; Ruf, C.S.; Gleason, S.; O’Brien, A.J.; McKague, D.S.; Block, B.P.; Russel, A. Dynamic Calibration of GPS Effective Isotropic Radiated Power for GNSS-Reflectometry Earth Remote Sensing. IEEE Transactions on Geoscience and Remote Sensing 2021, 1–12. [Google Scholar] [CrossRef]
- Gleason, S. Level 1B DDM Calibration Algorithm Theoritical Basis Document (Rev. 3); University of Michigan, 2020;
- Powell, C.E.; Ruf, C.S.; Russel, A. An Improved Blackbody Calibration Cadence for CYGNSS. IEEE Trans. Geosci. Remote Sensing 2022, 60, 1–7. [Google Scholar] [CrossRef]
- Gleason, S. Level 1A DDM Calibration Algorithm Theoretical Basis Document (Rev. 2); University of Michigan, 2018;
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 Global Reanalysis. Quarterly Journal of the Royal Meteorological Society 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Wang, T.; Zavorotny, V.U.; Johnson, J.; Yi, Y.; Ruf, C. Integration of Cygnss Wind and Wave Observations with the Wavewatch III Numerical Model. In Proceedings of the IGARSS 2019 - 2019 IEEE International Geoscience and Remote Sensing Symposium; IEEE, July 2019; pp. 8350–8353. [Google Scholar]
- Berg, W.; Brown, S.T.; Lim, B.H.; Reising, S.C.; Goncharenko, Y.; Kummerow, C.D.; Gaier, T.C.; Padmanabhan, S. Calibration and Validation of the TEMPEST-D CubeSat Radiometer. IEEE Trans. Geosci. Remote Sensing 2021, 59, 4904–4914. [Google Scholar] [CrossRef]
- Kroodsma, R.A.; McKague, D.S.; Ruf, C.S. Inter-Calibration of Microwave Radiometers Using the Vicarious Cold Calibration Double Difference Method. IEEE J. Sel. Top. Appl. Earth Observations Remote Sensing 2012, 5, 1006–1013. [Google Scholar] [CrossRef]
- Zec, J.; Jones, W.; Alsabah, R.; Al-Sabbagh, A. RapidScat Cross-Calibration Using the Double Difference Technique. Remote Sensing 2017, 9, 1160. [Google Scholar] [CrossRef]
- Powell, C.E.; Ruf, C.S.; Gleason, S.; Rafkin, S.C.R. Sampled Together: Assessing the Value of Simultaneous Co-Located Measurements for Optimal Satellite Configurations. Bull. Amer. Meteor. Soc. [Accepted, Publication Pending]. [CrossRef]
- CYGNSS CYGNSS Level 1 Science Data Record Version 3. 1 2021.
- Hersbach, H.; Bell, B.; Berrisford, P.; Biavati, G.; Horányi, A.; Muñoz Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Razum, I.; et al. ERA5 Hourly Data on Single Levels from 1940 to Present 2023.
- Taylor, J.R. An Introduction to Error Analysis: The Study of Uncertainties in Physical Measurements; 2nd ed.; University Science Books: Sausalito, Calif, 1997; ISBN 978-0-935702-42-2.
- Wang, T.; Ruf, C.S.; Gleason, S.; O’Brien, A.J.; McKague, D.S.; Block, B.P.; Russel, A. Dynamic Calibration of GPS Effective Isotropic Radiated Power for GNSS-Reflectometry Earth Remote Sensing. IEEE Transactions on Geoscience and Remote Sensing 2021, 1–12. [Google Scholar] [CrossRef]

| Error Term | Error Magnitude [dB] |
|---|---|
| 0.43 [25] | |
| 0.23 [35] | |
| 0.20 [33] | |
| 0.18 [33] | |
| 0.15 [33] | |
| 0.05 [34] | |
| 0.04 [34] | |
| <0.01 [34] | |
| <0.01 (assumed ~ ) |
| Tuning Parameter | Magnitude | Function |
|---|---|---|
| 0.005 | Relative magnitude of uncorrelated error | |
| 0.01 | Relative magnitude of endpoint correlated error | |
| 1 | Relative magnitude of nearby roll-off | |
| 1 | Steepness of roll-off component |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





