Prerpints.org logo
Preprint
Article

Weighted Similarity-Confidence Laplacian Synthesis for High-Resolution Art Painting Completion

Altmetrics

Downloads

122

Views

46

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

25 February 2024

Posted:

26 February 2024

You are already at the latest version

Alerts
Abstract
Artistic image completion is fundamental for the preservation and restoration of invaluable art paintings and it has experienced significant progress through the implementation of deep learning methodologies. Despite these advancements, challenges persist, even with sophisticated approaches like Generative Adversarial Networks (GANs), particularly in achieving optimal results for high-resolution paintings. Small-scale texture synthesis and the inference of missing information from distant contexts present persistent issues, leading to distortions in lines and unnatural colors, especially in art paintings with complicated structures and textures. Concurrently, patch-based image synthesis has evolved by incorporating global optimization on the image pyramid to enhance structural coherence and details. However, methods relying on gradient-based synthesis encounter obstacles related to directionality, inconsistency, and the heavy computational burdens associated with solving the Poisson equation in non-integrable gradient fields. This paper introduces a groundbreaking approach, integrating Weighted Similarity-Confidence Laplacian Synthesis, to comprehensively address these challenges and advance the field of artistic image completion. This proposal addresses challenges not only in high-resolution artistic image completion but also makes a significant contribution to the broader field of patch-based synthesis by utilizing the Laplacian pyramid for enhanced edge-aware correspondence search. Experimental result confirms the effectiveness of our approach, offering promising outcomes for the preservation and restoration of art paintings with complicated details and irregular missing regions.
Keywords: 
Subject: Computer Science and Mathematics  -   Computer Vision and Graphics

1. Introduction

The integration of image completion in the realm of art painting restoration is a central focus in contemporary academic exploration within computer vision and image processing. Image completion, or inpainting, a method aimed at restoring missing or damaged segments in an image, serves as a fundamental element in mitigating the impacts of physical deterioration experienced by art paintings in museums, encompassing issues like scratches, tears, and various forms of degradation. In situations where manual completion methods encounter limitations, the digitization of art paintings into high-resolution images has emerged as a viable alternative. When applied to digital images or paintings, high resolution implies an increased number of pixels per unit of area, resulting in a more refined and detailed representation of artistic elements. In the proposed algorithm for art painting completion, achieving high resolution means ensuring that the completed art painting conserves and reproduces complicated details, nuanced textures, and subtle artistic expressions with remarkable fidelity to the original. Moreover, the shift from physical to digital preservation introduces unique challenges, often compounded by the constraints inherent in established completion methods. Standard approaches, reliant on manual techniques and color matching, encounter difficulties in capturing the complicated details of artistic compositions. This challenge becomes evident in potential distortions, unnatural colorations, and a diminished preservation of the original aesthetic essence when compared to the capabilities offered by advanced inpainting techniques. Furthermore, when dealing with high-resolution images, a common necessity in the completion of art paintings, the intricacies of small-scale texture synthesis and the precise inference of missing information from distant contexts become particularly pronounced. The demand for increased precision and fidelity in the inpainting process for high-resolution art paintings adds an additional layer of complexity to the completion endeavor. Consequently, the ongoing exploration of effective inpainting methodologies for high-resolution art paintings underscores the critical necessity for advancements in computer vision and image processing. This is imperative for addressing the distinctive challenges posed by the elaborate textures and structures inherent in artistic masterpieces. Such research endeavors are essential for ensuring the comprehensive digital completion and preservation of art paintings, surpassing the limitations of physical completion within museum contexts.
In the field of art painting completion, traditional image inpainting methods have significantly contributed to the completion of damaged or missing regions. Patch-based methods, exemplified by Criminisi et al. [1] and Efros et al. [2], have proven effective but face challenges in faithfully replicating complicated artistic structures, such as brush strokes and fine textures. The drawbacks include potential distortions and a loss of aesthetic fidelity when applied to varied textures in art paintings. Moreover, Darabi et al. [3] faced challenges in merging art paintings with diverse styles or complex compositions. Recognizing these drawbacks underscored the imperative for tailored advancements in inpainting methods to address the unique intricacies of art painting completion.
In enhancing art painting completion through deep learning, several approaches have been explored, each with distinctive advantages and inherent challenges. Yu et al. [4] effectively captured complicated textures and structures, yet faced difficulties when inpainting areas with highly complicated artistic details, potentially resulting in less accurate replication. However, its application might be limited when faced with irregular structures or unconventional color schemes in diverse art paintings. Yue et al. [5] integrated style transfer techniques, aligning inpainting results more closely with the artistic characteristics of the original painting. Nevertheless, challenges may emerge when transferring highly specific or impressionist artistic styles, demanding careful consideration for optimal performance. These considerations collectively emphasize the dynamic landscape of deep learning methods in art painting completion, highlighting the ongoing need for refinement to address the subtle complexities of diverse artistic compositions. The challenges are particularly pronounced when dealing with impressionist artistic styles, including complicated structures and textures. These intricacies become more apparent in high-resolution images, where the details of brushstrokes are crucial. Our method addresses this challenge by utilizing a pyramid restoration approach that involves the Gaussian pyramid for analyzing base structures and the Laplacian pyramid to enhance edge awareness. This tailored strategy ensures a more effective handling of intricate details in art paintings with impressionist styles, showcasing the adaptability and precision of our approach in diverse contexts.
In advancing beyond persistent challenges, our innovative methodology contributes to the field by presenting a comprehensive solution to rectify damages in high-resolution art painting completion, with a specific emphasis on addressing torn and worn-out areas featuring holes. The introduction of the Weighted Similarity-Confidence Laplacian Synthesis algorithm significantly enhances the generation of consistent structure and texture during the reconstruction of missing regions. This forward-looking approach not only yields satisfactory results with a single input image but also ensures the comprehensive digital completion and preservation of art paintings in high resolution. Importantly, this methodology effectively surpasses the limitations associated with physical completion within the confines of museum contexts. The distinct contributions of our work can be summarized as follows:
  • Integrated Solution for Damaged Areas: Our methodology provides a comprehensive solution for repairing damages in high-resolution art painting completion, particularly addressing torn and worn-out areas with holes.
  • Weighted Similarity-Confidence Laplacian Synthesis: The introduction of this algorithm contributes significantly to the generation of consistent structure and texture, enhancing the reconstruction process for missing regions.
  • Digital Completion and Preservation: Our forward-looking approach ensures not only satisfying results with a single input image but also guarantees the comprehensive digital completion and preservation of art paintings in high resolution.
  • Surpassing Physical Limitations: Importantly, our methodology surpasses the limitations associated with physical completion within museum contexts, offering a more versatile and effective solution for art restoration and preservation.
The subsequent sections of this paper are structured as follows. We commence with a discussion on related works in Section 2. Following that, we introduce our proposed method in Section 3. The experimental results are showcased in Section 4, and we delve into the implementation details in Section 5. Finally, we provide a comprehensive conclusion and outline potential future works in Section 6.

2. Related Work

In recent years, advancements in image completion techniques have been driven by a dual reliance on both deep learning and traditional methods. Researchers have navigated challenges common to both, necessitating robust generalization capabilities for effective image completion. A spectrum of techniques has been explored, from deep neural networks [6,7,8,9,10,11,12,13] to traditional methods [14,15,16,17,18,19,20,21,22,23,24,25,26].
Deep learning methods, particularly those utilizing Generative Adversarial Networks (GANs), have shown promise in producing credible completions for complex images. Liu et al. [13] employed partial convolutions, but challenges included blurriness in repairing large missing regions and limited effectiveness for images with simple structures. Masaoka et al. [27] and Nazeri et al. [28] introduced GAN-based methods emphasizing the importance of vanishing points and adversarial training, respectively, in capturing structural edges during the inpainting process. However, these approaches raised concerns about extended running times, necessitating further optimization for deep learning-based inpainting methodologies.
Traditional methods, such as exemplar-based image inpainting [29] and structure propagation [30], have emerged as efficient alternatives for restoring single damaged images. Despite their efficacy, these methods faced challenges in handling complex structures and textures, sensitivity to patch size, and vulnerabilities to variations in illumination. Irawati et al. [19] and Horikawa et al. [20] presented distinct image inpainting techniques, each with unique weaknesses related to computational constraints, distortions in perspective, and struggles with detailed scenes and fine elements.
Several researchers have explored synergies between deep learning and traditional approaches for art painting completion. Chen et al. [31] combined deep learning with manual sliding windows, facing challenges with detailed textures and unique artistic expressions. Wang et al. [32] introduced user line drawings for inpainting guidance, excelling in simpler paintings but proving time-consuming for complex art paintings. Building upon these insights, this paper proposes the Weighted Similarity-Confidence Laplacian Synthesis algorithm, addressing challenges in structural and textural completion in high resolution for various paintings, even in irregularly missing areas encountered in the painting process.

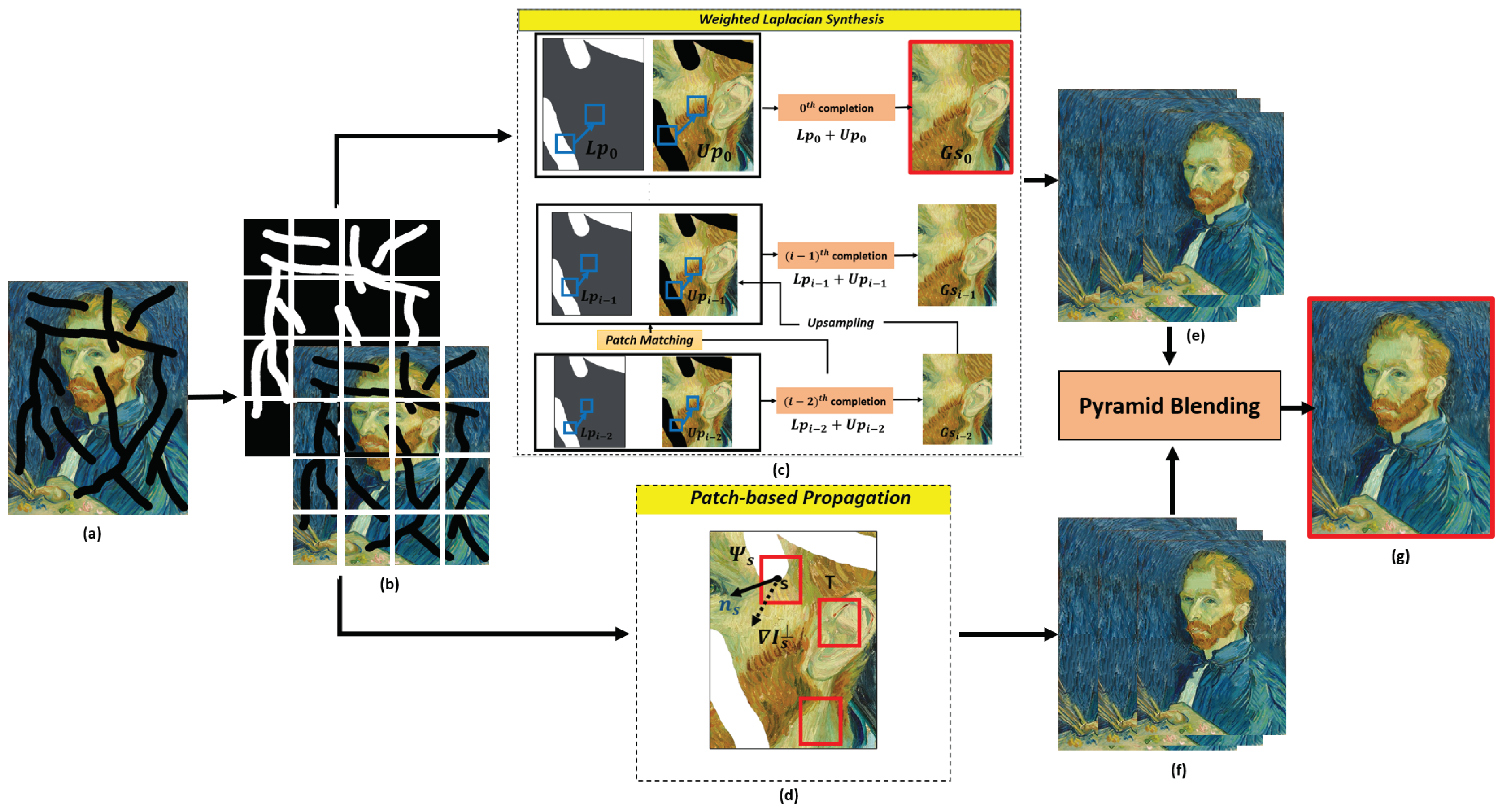
3. Methodology

As previously discussed regarding recent image completion algorithms, the challenge lies in addressing blurriness and artifacts when restoring missing regions. Despite extensive efforts to train deep learning models on various datasets, which are known for their reliability, achieving optimal outcomes remains an ongoing challenge. There is a need for more effective methods to overcome existing limitations, particularly in reducing color discrepancies and speeding up the completion process. In this context, traditional inpainting methods, often overlooked by some researchers, emerge as potential enhancements to completion techniques. They offer a quick and straightforward approach, aligning with the proposed method in this paper. Our method is designed to restore arbitrary missing regions in damaged art paintings. The Weighted Similarity-Confidence Laplacian Synthesis systematically addresses missing regions by considering important components of art paintings in high resolution. The Multi-Region Completion combines the Weighted Laplacian synthesis and patch-based propagation into a unified framework, creating authentic paintings that align with the artist’s original intent. This section explains the key aspects of our approach, focusing on Weighted Similarity-Confidence Laplacian Synthesis.

3.1. Weighted Similarity-Confidence Laplacian Synthesis

Addressing a missing region characterized by complicated structures and textures, as commonly encountered in damaged art paintings, presents a formidable challenge in the realm of image completion. Numerous recent research endeavors have endeavored to tackle this complicated issue [33,34]. However, the persistent issues of blurriness and color discrepancies have proven to be substantial impediments. Moreover, when the missing region lies arbitrarily within the boundary of objects, it intensifies the challenge, leading to the generation of unsatisfactory results marked by significant color divergences, especially in the context of complex structures and textures at high resolutions. In response to these challenges, our proposed approach advocates a proficient problem-solving strategy, involving a consistent collaboration on multi-regions of weighted Laplacian synthesis and patch-based completion.
The detailed explanation of our approach is depicted in Figure 1. Commencing the process, we utilize a high-resolution painting with a size of around 1600×2136 pixels, denoted as I i n in Figure 1(a), featuring damaged holes. Subsequently, we perform segmentation on I i n and its corresponding mask images, M i n , dividing them into 16 multi-regions through the separation of pixels into distinct patches (Figure 1(b)). Each region encompasses approximately 400×400 pixels, resembling the standard size of compressed images but exhibiting more homogeneity in pixels. This approach facilitates a more specific and precise completion of the missing regions within the local area.
Initially, the exploitation of a Laplacian pyramid completion technique proves effective for high-resolution paintings, utilizing the abundance of pixels to make consistent completion decisions across various resolutions. Inspired by Lee et al. [35], we integrate Laplacian ( L p ) and upsampled Gaussian ( U p ) pyramids to progressively enhance completion quality from the coarsest to the finest layer, as exemplified in Figure 1(c). Furthermore, to address the challenge of structure diffusion involving the segmentation of a non-homogeneous missing region along the object boundary into smaller, homogeneous regions, we employ texture synthesis. This process aims to generate a high-quality surface with similar intensities through the estimation of the Laplacian of a Gaussian (LoG). According to [35], the computation of LoG is costly due to its complicated function. However, the Laplacian of a Gaussian operates similarly to the Difference of Gaussian (DoG), which is integral for considering edge structures in the convolution process. Consequently, our choice is to apply the Laplacian of a Gaussian pyramid at different levels, ensuring consistent performance in edge awareness and base textures with more manageable computations. In the texture synthesis process, the initial step entails constructing a Gaussian pyramid ( G s ) to extract pixel intensities at each level for analyzing the base structure. Following this, the construction establishes the Laplacian pyramid to enhance edge awareness:
G s i − 1 = d o w n s a m p l e ( G s i ) U p i − 1 = u p s a m p l e ( G s i − 2 ) L p i = G s i − U p i
Where i is the current level of pyramid. G s i − 1 represents a downsampled Gaussian of G s i , while U p i − 1 denotes an upsampled Gaussian of G s i − 2 . L p i is then transformed into a Laplacian image using G s i and U p i as a basis, following the approach outlined in [35].
Following the construction of Laplacian and Gaussian pyramids, the next step involves identifying matching patches at each level. This is accomplished by improving a nearest neighbor search algorithm that approximates the most similar areas between the source S and target T, denoted as E i T , S . The basis for this approximation relies on the minimum normalized distance. In the subsequent phase, the algorithm refines the search for the most similar patches between the S and T at different levels. This process aims to achieve a more accurate matching of areas, ensuring a robust foundation for subsequent completion efforts:
E i T , S = ∑ q ∈ T m i n p ∈ S w q D ( U p i , p , U p i , q ) + w q D ( L p i , p , L p i , q )
Where U p i , p and L p i , p represent patches of the U p and L p pyramids at level i and location S, while U p i , q and L p i , q exhibit patches of the U p and L p pyramids at level i and location T. The variable D represents a maximum distance metric between two pixels, p and q.
The pursuit of determining the optimal pixel value for completing a missing region was a critical aspect influencing the overall performance of image completion. The approach proposed by Lee et al. [35] involved a weighted blending of scales between the upsampled Gaussian U p i and Laplacian image L p i , aiming to establish the most effective similarity between the target and source areas. However, this method introduced a voting system sensitive to detecting similarity, assuming that all pixels located outside the current target area at the given level would be considered. Unfortunately, this could lead to challenges, as the current target region might not have been fully propagated from the nearest neighbor of the most recently restored area, resulting in a color discrepancy that failed to blend seamlessly with adjacent patches. In response to this challenge, our method innovates the voting similarity function, enhancing its capabilities by considering the potential overlap of nearest neighbor pixels in color, even across different levels. This improvement is achieved by incorporating the advanced weighted average vote c q , which not only provides a measure of similarity but also introduces a confidence weight, denoted as w q . This combined approach leads to a more refined and accurate estimation of optimal pixel values:
w q = Ψ ( p , q , i ) Λ ( q ) , Ψ ( p , q , i ) = e − D ( p , q , i ) 2 σ 2
c q = ∑ q ˜ ϵ Q w q ˜ E i T , S ∑ q ˜ ϵ Q m a x q ˜
Where Ψ ( p , q , i ) and D ( p , q , i ) are instrumental in characterizing the similarity and distance between the source pixel p and target pixel q at level i. E i T , S is a nearest neighbor search algorithm based on Equation 2. Additionally, σ serves as a determinant of the sensitivity for detecting similarity. Further refining the process, Λ ( q ) introduces a confidence weight at target pixel q, strategically designed to alleviate boundary errors. This confidence weight assigns a higher value to target points closer to the completion boundary, ensuring more robust performance. The culmination of these factors is encapsulated in the weight w q at the target pixel q. Moreover, the variable q ˜ denotes the overlapping colors from its nearest neighbor field, while Q represents the total number of q ˜ . These components contribute to a comprehensive assessment of similarity and confidence, laying the foundation for precise and accurate weighting at the target pixel level.
Algorithm 1:Weighted Similarity-Confidence Laplacian Synthesis
Preprints 99806 i001
Completing high-resolution paintings that encompass complicated structures and textures can introduce errors, particularly in the form of ambiguity within the restored pixels. This ambiguity may manifest as color discrepancies and blurriness in the final restored image. To address this challenge, we seamlessly integrate patch-based propagation, employing a locally applied isophote-driven technique to synthesize the complicated details of art painting elements (Figure 1(d)). The core principle involves ensuring that the matched patches Ψ s align along the boundary of a hole situated between two distinct colored regions. The optimal-matched patch from the source area is then replicated into the target area, taking into account both the confidence C ( s ) and data terms D ( s ) . The highest priority is accorded to the best match P ( s ) [1].
P ( s ) = C ( s ) · D ( s )
C ( s ) = ∑ t ϵ Ψ s ∩ ( I − T ) C ( t ) | Ψ s | , D ( s ) = | ▽ I s ⊥ · n s | γ
Where Ψ s represents the current patch, while | Ψ s | delineates the pixel region of Ψ s . The unit vector orthogonal to point s is denoted as n s , with the operator ⊥ signifying the perpendicular operation. The normalization factor, γ , is set to a value of 255. The propagation unfolds systematically, guided by the priority P ( s ) across every pixel along the unknown boundary border, employing a clockwise filling approach.
In the quest for optimal patches, we employ a fused approach that integrates the outcomes of Weighted Laplacian Synthesis and Patch-based Propagation through Pyramid blending [36]. Pyramid blending distinguishes itself among blending methods for its capacity to effectively handle scale differences between images, operating at multiple scales and considering both coarse and fine details. This characteristic ensures a comprehensive blending process that results in smoother transitions between images (Figure 1(e)(f)). The efficacy of pyramid blending extends to its proficiency in managing abrupt changes or discontinuities within images. The hierarchical structure of pyramids facilitates a seamless transition across different levels, preventing artifacts or noticeable seams in the blended result. This proves advantageous, particularly when merging images with diverse content or structures. Moreover, pyramid blending demonstrates computational efficiency. By operating at various levels of resolution, the algorithm can focus on essential details without imposing excessive computational demands, making it suitable for real-time applications or large-scale image blending tasks.

3.2. Our Proposed Algorithm

In addressing the challenging task of completing missing regions in damaged art paintings, our proposed approach stands out as a proficient problem-solving strategy. The method seamlessly integrates weighted Laplacian synthesis and patch-based completion, collaborating consistently across multi-regions. Illustrated in Figure 1(a), the process begins with the utilization of a high-resolution painting, denoted as I i n . Through segmentation of I i n and its corresponding mask images M i n (Figure 1(b)), our approach ensures a more precise and specific completion of missing regions within the local area.
The exploitation of Laplacian pyramid completion proves effective for high-resolution paintings, employing the abundance of pixels for consistent completion decisions across various resolutions. Inspired by Lee et al. [35], Laplacian and upsampled Gaussian pyramids are combined, progressively enhancing completion quality from the coarsest to the finest layer. To address structure diffusion challenges, texture synthesis is introduced, employing Laplacian of a Gaussian pyramid at different levels. The process involves constructing a Gaussian pyramid to analyze base structure intensities and subsequently establishing a Laplacian pyramid for enhanced edge awareness (Figure 1(c)). Matching patches at different levels is achieved through an improved nearest neighbor search algorithm, ensuring a more accurate matching of areas for robust completion. The pursuit of determining the optimal pixel value for completing a missing region involves innovating the voting similarity function. Our method enhances this function by considering potential overlap of nearest neighbor pixels in color, even across different levels, resulting in a refined and accurate estimation of optimal pixel values.
To address errors introduced by ambiguity in restored pixels, patch-based propagation is seamlessly integrated, applying an isophote-driven technique locally (Figure 1(d)). The propagation process ensures that matched patches align along the boundary of a hole between two distinct colored regions, with the best-matched patch duplicated into the target area based on confidence and data terms.
In the quest for optimal patches, our approach employs a fused reaction that integrates the outcomes of weighted Laplacian synthesis and patch-based propagation through Pyramid blending (Figure 1(e)(f)). Pyramid blending emerges as a standout blending method, effectively handling scale differences between images and ensuring smoother transitions. Its hierarchical structure prevents noticeable seams in blended results, particularly advantageous when merging images with diverse content or structures. The computational efficiency of pyramid blending makes it suitable for real-time applications or large-scale image blending tasks.
The proposed algorithm 1 guides the entire process, beginning with segmentation and progressing through weighted Laplacian synthesis, patch-based propagation, and Pyramid blending until multi-regions are empty. This comprehensive approach, applied to a high-resolution art painting with missing regions sized 1600×2136 pixels, results in the completion of visually pleasing and artifact-free art paintings.

4. Experimental Results

In evaluating our proposed approach within the domain of art paintings, especially those distinguished by complicated structures and textures, we conducted experiments utilizing a dataset sourced from https://useum.org/. This dataset is notable for its incorporation of a diverse array of genre paintings, prominently featuring impressionist landscapes and portraits. The integration of such a varied selection enables a nuanced understanding of how effectively our proposed approach navigates the intricacies inherent in diverse artistic styles and subjects. Our methodology is specifically applied to address randomly irregular missing regions, simulating common damages found in paintings.
Two scenarios were considered for experimentation: high-resolution paintings with dimensions around 1600×2136 pixels and low-resolution counterparts with sizes of approximately 400×400 pixels. To establish a comprehensive evaluation, we benchmarked our approach against two comparison methods: EdgeConnect, representing a deep learning approach [28], and a traditional method denoted as Criminisi et al. [1] and Laplacian [35]. Through this comparative framework, our aim is to measure the effectiveness and performance of our proposed method in restoring art paintings with varying complexities and resolutions.
For the experimental setting, specific parameters were applied: the width size of the hole represents 10-20% of the original painting, with irregular shapes simulating frequent damage observed in art paintings within museum contexts due to wear or tear. The number of layers in the pyramid is set at 5, and the patch-based propagation uses a patch size of 15×15 pixels.

4.1. Qualitative Comparison

In examining the fidelity of our results in accordance with human visual perception, we utilize a qualitative comparison to scrutinize the complicated details of structures and textures. Particular emphasis is placed on Figure 2 and Figure 3, pertaining to the genre art painting of impressionist landscapes (Image Scenery) and impressionist portraits (Image Girl, Man, and Woman). This comparative analysis is designed to clarify the noticeable differences and advancements realized through our approach in contrast to earlier methodologies.
In Figure 2, the limitations of the Criminisi method [1] become apparent, revealing evident color discrepancies in the texture area. This issue persists even in the completion of low-resolution damaged images, as highlighted in Figure 3. The root cause of this problem lies in the drawbacks of the patch-based synthesis following the construction of structure propagation. The method heavily relies on image isophotes, significantly impacting the prioritization of filling and resulting in suboptimal color consistency in the final results.
Meanwhile, the Laplacian approach [35] proposes a strategy involving the construction of a Laplacian pyramid to address the unknown area. This method systematically examines consistent patch similarity at each level and resolves the issue through a weighted vote of scales. However, a notable limitation arises from its exclusive focus on the target area of the current level for filling the missing region. This singular approach contributes to significant color inconsistencies and blurriness, as observed in all images depicted in Figure 2 and Figure 3.
In contrast, the deep learning method EdgeConnect [28] takes a distinct approach by utilizing edge-map guidance to predict a model for recovering missing regions. However, despite its innovative strategy, limitations become apparent in the form of bright colors resulting from miscalculations and opaqueness across all presented results in Figure 2 and Figure 3. These issues appear from long-term memorization and an insufficient model derived from a less extensive dataset of painting images.
Furthermore, our proposed method excels over other approaches based on several key aspects of the proposed methodologies. Firstly, the integration of weighted Laplacian synthesis and patch-based completion across multi-regions allows our method to provide more precise and targeted completion. This approach ensures a focused completion process, addressing specific regions with a higher level of accuracy. Secondly, the comparison with existing methods, such as Criminisi method [1], Laplacian approach [35], and EdgeConnect [28] highlights the superiority of our approach in terms of artifact reduction and minimizing blurriness. While these existing methods struggle with color discrepancies, particularly in texture areas, our method exhibits a notable improvement in maintaining color consistency and sharpness.
In addition, our method employs the advantages of pyramid blending, offering a more effective strategy for combining or blending images. The hierarchical structure of pyramids ensures smoother transitions, preventing noticeable seams and artifacts in the blended results. This is an advantage when dealing with images featuring diverse content or structures.

4.2. Quantitative Comparison

The evaluation of our results incorporates two distinct perceptual metrics: Learned Perceptual Image Patch Similarity (LPIPS) [39] and Deep Image Structure and Texture Similarity (DISTS) [40]. In contrast to commonly used metrics like Structural Similarity Index Measure (SSIM) [37] and Peak Signal to Noise Ratio (PSNR) [38], we opt for LPIPS, a metric rooted in deep feature networks that employs human perceptual similarity judgments. This metric involves the learning of linear weights for perceptual calibration, tuning configuration, and Gaussian weights:
d ( x , x 0 ) = ∑ l 1 H l W l ∑ h , w w t l ⊙ ( y ^ h , w l − y ^ 0 h , w l ) 2 2
In this equation, d ( x , x 0 ) represents the distance between the ground truth x and the restored images x 0 . The terms y ^ h , w l and y ^ 0 h , w l ϵ R H l × W l × C l denote feature stacks from l layers, each unit-normalized in the channel dimension. Here, H, W, and C respectively indicate the number of height h, weight w, and channel dimension c of layers, while w t l ϵ R C l serves as an activation channel-wise.
Moreover, our evaluation includes the utilization of Deep Image Structure and Texture Similarity (DISTS) [37]. This approach, anchored in a Conventional Neural Network (CNN), seamlessly integrates spatial texture averages and feature structure maps to generate diverse texture patterns. Within this model, quality assessments are harmonized between convolution layers of texture, as expressed by global means l x ˜ j i , y ˜ j i , and structure, represented by global correlations s x ˜ j i , y ˜ j i . The integration is accomplished through the computation of the weighted sum of different convolution layers, denoted as D ( x , y ; α , β ) :
l ( x ˜ j i , y ˜ j i ) = 2 μ x ˜ j i μ y ˜ j i + c 1 μ x ˜ j i 2 + μ y ˜ j i 2 + c 1
s ( x ˜ j i , y ˜ j i ) = 2 σ x ˜ j i y ˜ j i + c 2 σ x ˜ j i 2 + σ y ˜ j i 2 + c 2
D ( x , y ; α , β ) = 1 − ∑ i = 0 m ∑ j = 1 n i α i j l x ˜ j i , y ˜ j i + β i j s x ˜ j i , y ˜ j i
Where i and j refer to the convolution layers of the ground truth image x and the restored images y, respectively. The variables x ˜ j i and y ˜ j i represent the convolution channels of x and y. The terms m and n i represent the number of convolution layers for x and y in the i-th layer, respectively. The weights α and β are learned weights, satisfying the condition ∑ i = 0 m ∑ j = 1 n i α i j + β i j = 1 . Additionally, μ x ˜ j i , μ y ˜ j i , σ x ˜ j i 2 , σ y ˜ j i 2 denote the global means and variances of x ˜ j i and y ˜ j i , while σ x ˜ j i y ˜ j i represents the global covariance between x ˜ j i and y ˜ j i . Constants c 1 and c 2 are introduced for numerical stability.
Furthermore, our method stands out as a superior choice for high and low-resolution art painting completions due to several key factors that address and surpass the limitations of alternative approaches. Firstly, in the case of high-resolution art paintings, our method excels in handling complicated structures and complicated textures. The integration of weighted Laplacian synthesis and patch-based completion across multi-regions ensures a more precise and specific completion of missing regions within the local area. The proposed algorithm guides the entire process, from segmentation to weighted Laplacian synthesis, patch-based propagation, and Pyramid blending. This comprehensive approach results in visually pleasing and artifact-free art painting, as demonstrated in Figure 1.
Moreover, our method employs the abundance of pixels in high-resolution paintings to make consistent completion decisions across various resolutions. Inspired by Lee et al. [35], the use of Laplacian and upsampled Gaussian pyramids progressively enhances completion quality from the coarsest to the finest layer. Texture synthesis, employing Laplacian of a Gaussian pyramid at different levels, addresses structure diffusion challenges, ensuring enhanced edge awareness. The improved nearest neighbor search algorithm, employed for matching patches at different levels, ensures accurate matching of areas for robust completion. Our method innovates the voting similarity function by considering potential overlap of nearest neighbor pixels in color, even across different levels. This refinement results in a more accurate estimation of optimal pixel values for completing missing regions. To address errors introduced by ambiguity in restored pixels, patch-based propagation is seamlessly integrated, applying an isophote-driven technique locally. This ensures that matched patches align along the boundary of a hole between two distinct colored regions, with the best-matched patch duplicated into the target area based on confidence and data terms.
In the context of low-resolution art paintings, our method demonstrates its versatility by handling randomly irregular missing regions effectively. The comparison with deep learning (EdgeConnect [28]) and traditional (Criminisi [1] and Laplacian [35]) methods showcases the robustness of our approach across different resolutions.

5. Discussion

Qualitatively assessing the fidelity of our results in accordance with human visual perception is fundamental. Figure 2 and Figure 3 showcase the visual comparisons between different methods, providing insights into their strengths and limitations. The Criminisi method [1] exhibits evident color discrepancies in texture areas, even in the completion of low-resolution damaged images. This limitation stems from the drawbacks of the patch-based synthesis, affecting color consistency. The Laplacian approach [35] addresses the unknown area using a Laplacian pyramid but falls short in color consistency and results in blurriness. EdgeConnect [28], while innovative, exhibits issues such as bright colors from miscalculations and opaqueness. Our proposed method excels in several aspects. The integration of weighted Laplacian synthesis and patch-based completion across multi-regions ensures precise and targeted completion, outperforming existing methods. The comparison highlights our method’s superiority in artifact reduction and minimizing blurriness, addressing challenges in color discrepancies observed in texture areas. Additionally, the incorporation of pyramid blending proves advantageous, ensuring smoother transitions and preventing noticeable seams or artifacts in blended results.
Quantitative evaluation is performed using two perceptual metrics: Learned Perceptual Image Patch Similarity (LPIPS) [39] and Deep Image Structure and Texture Similarity (DISTS) [40]. Table 1 and Table 2 present the accuracy of these metrics for different methods and scenarios. Our method consistently outperforms Criminisi [1], Laplacian [35], and EdgeConnect [28] across both high and low resolutions. In terms of LPIPS, our method achieves significantly higher accuracy, indicating better perceptual similarity with ground truth images. The DISTS metric further supports our method’s superiority, emphasizing its ability to synthesize diverse texture patterns and maintain structural quality.
Moreover, our proposed method applies advanced techniques to address challenges in both high and low-resolution scenarios. In high-resolution paintings, the integration of Laplacian and upsampled Gaussian pyramids progressively enhances completion quality. Texture synthesis employing Laplacian of a Gaussian pyramid at different levels ensures improved edge awareness. The nearest neighbor search algorithm is enhanced to consider potential overlap in color, contributing to more accurate completion decisions. In low-resolution paintings, our method showcases versatility in handling randomly irregular missing regions. The comprehensive approach, from weighted Laplacian synthesis to patch-based completion and Pyramid blending, demonstrates the robustness of our method across different resolutions.
Furthermore, our methodology demonstrates a versatile capability, efficiently handling an array of source media types. This inclusivity spans photography, digitized images, and media featuring intricate textures and structures commonly encountered in art paintings. The algorithm’s adaptability stands out as a significant strength, guaranteeing its effectiveness across a wide spectrum of applications. Its consistent efficiency in managing diverse source media not only streamlines workflows but also heightens its utility in digitization and restoration processes. This adaptability underscores the algorithm’s potential to make a substantial impact on the comprehensive preservation and restoration of visual content across various mediums.
In response to these observations, our approach serves as a valuable guide for curators and artists alike. The insights gleaned from the algorithm’s performance highlight the importance of thoughtful decision-making in the creation of art paintings. For instance, the guidance provided can inform choices related to color selection, brushstrokes, and various other elements of the artistic process. By considering these factors during the creation phase, artists and curators can optimize the digitization and subsequent restoration process, particularly when faced with the intricacies of physically restoring damaged original art paintings. This approach not only streamlines the restoration process but also contributes to the preservation and enhancement of the digital representations of these unique and often intricate works of art.

6. Conclusion

In conclusion, our proposed methodology, anchored in weighted Laplacian synthesis and patch-based completion across multi-regions, emerges as a robust solution for the complicated task of restoring art paintings with irregularly damaged regions. Through a comprehensive evaluation, including qualitative and quantitative comparisons, our approach showcased its superiority over existing methods. Notably, the integration of hierarchical pyramid blending and advanced nearest neighbor search algorithms contributed to artifact reduction, minimized blurriness, and ensured visually pleasing outcomes in both high and low-resolution art paintings. The comprehensive calibration of perceptual similarity, as demonstrated by the Learned Perceptual Image Patch Similarity (LPIPS) metric, and the synthesis of diverse texture patterns through Deep Image Structure and Texture Similarity (DISTS) further validated the efficacy of our method. Our proposed approach not only addresses the limitations observed in current methodologies but also establishes a new standard for art completion algorithms, particularly in handling complex structures and textures.
While our current methodology stands as a significant advancement, future work could explore the incorporation of depth considerations in art paintings. This involves a more detailed examination of damaged areas within complicated structures and textures, taking into account the intricacies of brushstrokes and other artistic elements. By enhancing our algorithm to analyze the depth of art paintings, we aim to provide a more nuanced and detailed approach to restoring damaged regions, offering a higher level of precision. This depth-aware analysis can contribute to a more accurate understanding of the damaged areas, especially in complicated art styles where brushstrokes contribute significantly. By delving into the third dimension of art, our algorithm could discern variations in depth, leading to improved restoration outcomes. This approach not only adds an extra layer of sophistication to the algorithm but also aligns with the intricacies of artistic expression. Furthermore, exploring the integration of machine learning techniques to adaptively adjust parameters based on variations in image content can significantly enhance the algorithm’s flexibility and adaptability. Collaborations with art conservationists and experts will be instrumental in gaining insights into the specific nuances of diverse art styles, guiding the refinement of the algorithm for more specialized applications. Continuous refinement and validation across a broader range of art datasets, incorporating depth information, will be crucial for establishing the broader applicability and robustness of our proposed method in the field of digital art completion. This future direction not only addresses the challenges posed by complex structures and textures but also ensures that our methodology evolves to meet the dynamic demands of the digital art landscape and potrait.

References

  1. Criminisi, A.; Pérez, P.;Toyama, K. Object removal by exemplar-based inpainting. In Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 2004.
  2. Efros, A. A.; Leung, T. K. Texture synthesis by non-parametric sampling. In Proceedings of the Seventh IEEE International Conference on Computer Vision, pp: 1033-1038, 1999.
  3. Darabi, S.; Shechtman, E.; Barnes, C.; Goldman, D. B. Image melding: Combining inconsistent images using patch-based synthesis. ACM Transactions on Graphics (TOG), 31(4), 82, 2012.
  4. Yu, J.; Lin, Z.; Yang, J.; Shen, X.; Lu, X.; Huang, T. S. Generative Image Inpainting with Contextual Attention. In IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2018.
  5. Yue, Z.; Zheng, Y. Artistic Style Transfer for Image Inpainting. IEEE Transactions on Image Processing, Volume 29, pp: 5142-5157, 2020.
  6. Zeng, Y.; Lin, Z.; Yang, J.; Zhang, J.; Shechtman, E.; Lu, H. High-resolution image inpainting with iterative confidence feedback and guided upsampling. European Conference on Computer Vision, pp. 1-17, 2020.
  7. Song, Y.; Yang, C.; Shen, Y.; Wang, P.; Huang, Q; Kuo, C. C. J. Spg-net: segmentation prediction and guidance network for image inpainting, arXiv:1805.03356, 2018.
  8. Yu, J.; Lin, Z.; Yang, J. ; Shen, X.; Lu, X.; Huang, T. S. Generative image inpainting with contextual attention. In Proceedings of the IEEE conference on computer vision and pattern recognition, pp. 5505–5514, 2018.
  9. Yi, Z.; Tang, Q.; Azizi, S.; Jang, D.; Xu, Z. Contextual residual aggregation for ultra high-resolution image inpainting. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2020; pp. 7508–7517. [Google Scholar]
  10. Iizuka, S.; Simo-Serra, E.; Ishikawa, H. Globally and locally consistent image completion. ACM Transactions on Graphics (ToG), 36(4):1–14, 2017.
  11. Ma, Y.; Liu, X.; Bai, S.; Wang, L.; Liu, A.; Tao, D.; Hancock, E. Region-wise generative adversarial image inpainting for large missing areas. arXiv:1909.12507, 2019.
  12. Li, J.; Wang, N.; Zhang, L.; Du, B.; Tao, D. Recurrent feature reasoning for image inpainting. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2020; pp. 7760–7768. [Google Scholar]
  13. Liu, G.; Reda, F. A.; Shih, K. J.; Wang, T. C.; Tao, A.; Catanzaro, B. Image inpainting for irregular holes using partial convolutions. In Proceedings of the European Conference on Computer Vision (ECCV), 2018; pp. 85–100. [Google Scholar]
  14. Telea, A. An image inpainting technique based on the fast marching method. J. Graph. Tools, vol. 9, no. 1, pp. 23–34, Jan. 2004.
  15. Zuo, W.; Lin, Z. A generalized accelerated proximal gradient approach for total-variation-based image restoration. IEEE Trans. Image Processing, vol. 20, no. 10, pp. 2748–2759, Oct. 2011.
  16. Dahl, J.; Hansen, P. C.; Jensen, S. H.; Jensen, T. L. Algorithms and software for total variation image reconstruction via first-order methods. Numerical Algorithms, vol. 53, no. 1, pp. 67–92, Jan. 2010.
  17. Chan, T. F.; Shen, J. Nontexture inpainting by curvature-driven diffusions. Journal of Visual Communication and Image Representation, vol. 12, no. 4, pp. 436–449, Dec. 2001.
  18. Chan, T. F.; Kang, S. H.; Shen, J. Total variation denoising and enhancement of color images based on the CB and HSV color models. Journal of Visual Communication and Image Representation, vol. 12, no. 4, pp. 422–435, Dec. 2001.
  19. Irawati, N. S.; Urano, Y.; Du, W. Image inpainting using orthogonal viewpoints and structure consistency in Manhattan World. In the 8th International Virtual Conference on Applied Computing and Information Technology (ACIT), 2021.
  20. Horikawa, E.; Irawati, N. S.; Du, W. Image inpainting using clustered planar structure guidance. In the 8th International Virtual Conference on Applied Computing and Information Technology (ACIT), 2021.
  21. Irawati, N. S.; Horikawa, E.; Du, W. Interactive image inpainting of large-scale missing region. IEEE Access, pp(99):1-1, 2021.
  22. Irawati, N.S.; Du, W. Structure-texture consistent painting completion for artworks. IEEE Access (11), pp. 27369-27381, 2023.
  23. Urano, Y.; Sari, I.N.; Du, W. Image inpainting using automatic structure propagation with auxiliary line construction. 23rd ACIS International Summer Virtual Conference on Software Engineering, Artificial Intelligence, Networking and Parallel/Distributed Computing (SNPD Summer), IEEE, pp. 107-112, Kyoto, Japan, 2022.
  24. Takarabe, J.; Sari, I.N.; Du, W. Depth map estimation of single-view image using smartphone camera for a 3 dimension image generation in augmented reality. Sixth International Symposium on Computer, Consumer and Control (IS3C), IEEE, pp. 167-170, Taichung, Taiwan, 2023.
  25. Masaoka, K.; Sari, I.N.; Du, W. Vanishing points detection with line segments of gaussian sphere. Sixth International Symposium on Computer, Consumer and Control (IS3C), IEEE, pp. 48-51, Taichung, Taiwan, 2023.
  26. Sari, I.N.; Masaoka, K.; Takarabe, J.; Du, W. High-resolution art painting completion using multi-region laplacian fusion. Sixth International Symposium on Computer, Consumer and Control (IS3C), IEEE, pp. 48-51, Taichung, Taiwan, 2023.
  27. Masaoka, K.; Sari, I. N.; Du, W. Edge-enhanced GAN with vanishing points for image inpainting. IEEE/ACIS International Summer Virtual Conference on Software Engineering, Artificial Intelligence, Networking and Parallel/Distributed Computing, 2022.
  28. Nazeri, K.; Joseph, E. Ng, T.; Qureshi, F. Z.; Ebrahimi, M. Edgeconnect: generative image inpainting with adversarial edge learning, arXiv:1901.00212, 2019.
  29. Criminisi, A.; Perez, P.; Toyama, K. Region filling and object removal by exemplar-based image inpainting. IEEE Trans. Image Processing, vol. 13, no. 9, pp. 1200–1212, Sep. 2004.
  30. Sun, J.; Yuan, L.; Jia, J. Image completion with structure propagation. ACMTransactions on Graphic, 2005.
  31. Chen, M.; Zhao, X.; Xu, D. Image inpainting for digital dunhuang murals using partial convolutions and sliding window method. Journal of Physics Conference Series, 1302(3):032040, 2019.
  32. Wang, H.; Li, Q.; Zou, Q. Inpainting of dunhuang durals by sparsely modeling the texture similarity and structure continuity. Journal on Computing and Cultural Heritage, 2018.
  33. Chen, M.; Zhao, X.; Xu, D. Image inpainting for digital dunhuang murals using partial convolutions and sliding window method. Journal of Physics Conference Series, 1302(3):032040, 2019.
  34. Wang, H.; Li, Q.; Zou, Q. Inpainting of dunhuang durals by sparsely modeling the texture similarity and structure continuity. Journal on Computing and Cultural Heritage, 2018.
  35. Lee, J. H.; Choi, I.; Kim, M. H. Laplacian patch-based image synthesis. IEEE Conference on Computer Vision and Pattern Recognition, 2016.
  36. Anmol, B.; Green, R. K. S.; Sachin, D. L. Spatially variant laplacian pyramids for multi-frame exposure fusion. Computer Vision and Image Processing, (pp.73-81), 2020.
  37. Wang, Z.; Bovik, A. C.; Lu, L. Why is image quality assessment so difficult. Proc. IEEE Int. Conf. Acoust. Speech Signal Processing,pp. 3313–3316, vol. 4, 2002.
  38. Qureshi, M. A.; Deriche, M.; Beghdadi, A.; Amin, A. A critical survey of state-of-the-art image inpainting quality assessment metric. Journal of Visual Communication and Image Representation, vol. 49, pp. 177–191, 2017.
  39. Zhang, R.; Isola, P.; Efros, A. A.; Shechtman, E.; Wang, O. The unreasonable effectiveness of deep features as a perceptual metric. IEEE International Conference Computer Vision and Pattern Recognition (CVPR), 2018.
  40. Ding, K.; Ma, K., Wang, S.; Simoncell, E. E. Image quality assessment: unifying structure and texture similarity. IEEE International Conference Computer Vision and Pattern Recognition (CVPR), 2020.
Preprints 99806 g001
Figure 1. Weighted Similarity-Confidence Laplacian Synthesis. (a) Input: An art painting with missing regions, (b) Multi-region input and its mask, (c) Weighted Laplacian Synthesis, (d) Patch-based Propagation, (e) Result of Weighted Laplacian Synthesis, (f) Result of Patch-based Propagation, and (g) Output: A restored art painting.
Figure 1. Weighted Similarity-Confidence Laplacian Synthesis. (a) Input: An art painting with missing regions, (b) Multi-region input and its mask, (c) Weighted Laplacian Synthesis, (d) Patch-based Propagation, (e) Result of Weighted Laplacian Synthesis, (f) Result of Patch-based Propagation, and (g) Output: A restored art painting.
Preprints 99806 g001
Preprints 99806 g002
Figure 2. High-resolution art painting completion with a size of around 1600×2136 pixels. The order of image names, from top to bottom, follows a structured sequence: Girl, Man, Scenery, and Woman. (a) Input, (b) Criminisi et al. [1], (c) Laplacian [35], and (d) EdgeConnect [28], (e) Ours, and (f) Ground Truth.
Figure 2. High-resolution art painting completion with a size of around 1600×2136 pixels. The order of image names, from top to bottom, follows a structured sequence: Girl, Man, Scenery, and Woman. (a) Input, (b) Criminisi et al. [1], (c) Laplacian [35], and (d) EdgeConnect [28], (e) Ours, and (f) Ground Truth.
Preprints 99806 g002
Preprints 99806 g003
Figure 3. Low-resolution art painting completion with a size of around 400×400 pixels. The order of image names, from top to bottom, follows a structured sequence: Girl, Man, Scenery, and Woman. (a) Input, (b) Criminisi et al. [1], (c) Laplacian [35], and (d) EdgeConnect [28], (e) Ours, and (f) Ground Truth.
Figure 3. Low-resolution art painting completion with a size of around 400×400 pixels. The order of image names, from top to bottom, follows a structured sequence: Girl, Man, Scenery, and Woman. (a) Input, (b) Criminisi et al. [1], (c) Laplacian [35], and (d) EdgeConnect [28], (e) Ours, and (f) Ground Truth.
Preprints 99806 g003
Table 1. Accuracy of Learned Perceptual Image Patch Similarity (LPIPS)
Table 1. Accuracy of Learned Perceptual Image Patch Similarity (LPIPS)
Name Criminisi [1] Laplacian [35] EdgeConnect [28] Ours
High Low High Low High Low High Low
Girl 0.631 0.443 0.701 0.562 0.702 0.344 0.846 0.812
Man 0.642 0.531 0.719 0.407 0.745 0.307 0.897 0.808
Scenery 0.611 0.472 0.754 0.592 0.762 0.412 0.853 0.781
Woman 0.714 0.523 0.758 0.575 0.781 0.635 0.892 0.852
Table 2. Accuracy of Deep Image Structure and Texture Similarity (DISTS)
Table 2. Accuracy of Deep Image Structure and Texture Similarity (DISTS)
Name Criminisi [1] Laplacian [35] EdgeConnect [28] Ours
High Low High Low High Low High Low
Girl 0.721 0.543 0.899 0.661 0.895 0.618 0.951 0.786
Man 0.792 0.601 0.872 0.644 0.834 0.562 0.932 0.888
Scenery 0.710 0.592 0.888 0.691 0.842 0.512 0.921 0.834
Woman 0.812 0.611 0.878 0.655 0.852 0.615 0.932 0.891
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated