Prerpints.org logo
Preprint
Article

Nuclear Matter Properties and Neutron Star Phenomenology Using the Finite Range Simple Effective Interaction

Altmetrics

Downloads

107

Views

36

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

16 January 2024

Posted:

17 January 2024

You are already at the latest version

Alerts
Abstract
The saturation properties of symmetric and asymmetric nuclear matter have been computed using the finite range simple effective interaction having Yukawa form-factor. The results of higher order derivatives of the energy per particle and the symmetry energy computed at saturation, namely, Q0, Ksym, Kτ, Qsym, are compared with the corresponding range of values extracted from studies involving theory, experiment and astrophysical observations. The ability of the equations of state computed with this simple effective interaction in predicting the threshold mass for prompt collapse in binary neutron star merger and gravitational redshift have been examined in terms of the compactness of the neutron star and the incompressibility at the central density of the maximum mass star. The correlations existing between neutron star properties with the nuclear matter saturation properties have been analyzed and compared with the predictions of other model calculations.
Keywords: 
Subject: Physical Sciences  -   Nuclear and High Energy Physics

1. Introduction

The empirical properties of infinite nuclear matter (NM) at saturation are key features in the study of any phenomenon resulting from the nucleon-nucleon (NN) interactions in a many-body system. Ideally, the solution of the many body problem with the NN interaction would be the way to determine the NM properties. But in absence of a comprehensive knowledge of NN interaction, microscopic many body models, such as, Dirac-Brueckner-Hartree-Fock (DBHF) and its non relativistic counterpart BHF [1,2], variational methods [3,4], chiral effective field theory [5,6], etc, uses realistic potentials whose parameters are fitted to phase shift data in different partial wave channels and properties of few-body systems (deuteron and triton). The inadequacy of our understanding of the in-medium NN interaction is reflected from the fact that in the aforementioned many-body calculations, the saturation density ρ 0 of symmetric nuclear matter (SNM) is over predicted. This could be brought within the empirical range by incorporating the three-body and higher order many-body effects in an ad hoc phenomenological manner. The consensus range for the value of saturation density ρ 0 = 0.17 ± 0.03 f m   − 3 has been estimated from the studies of various kinds, which includes different variants of liquid drop model, optical model of NN scattering, muonic atoms, and Hartree-Fock (HF) calculations of nuclear density distributions [7]. The values of energy per nucleon at saturation density e ( ρ 0 ) has been extracted to be ∼ -16 MeV from the mass analysis over the periodic table. An alternate method, adopted in contrast to the microscopic realistic calculations to handle the many-body problem, is to use phenomenological effective interactions. Though less fundamental compared to the microscopic calculations, its ability in the analytical calculations of nuclear properties make it highly popular. Skyrme [8], Gogny [9], and M3Y effective forces [10] are some of those successful forces. The basic idea to build up these interactions is to parameterize the effects of the microscopic NN interaction upon averaging over the spin, parity and isospin of the interacting nucleons and constrain the parameters from the ground state properties of finite nuclei and nuclear matter. A drawback of this approach is that the parameters set is not unique, and higher order nuclear matter properties at saturation cannot be unambiguously predicted. Moreover, many parameters of the effective force gets strongly correlated in course of their fixation. Of late another effective force, the so-called finite range simple effective interaction (SEI) [11], which has similar predicting ability, as that of Skyrme and Gogny in the NM and finite nuclei domain, came to picture. The parameter fitting protocol adopted in case of SEI makes it different form other effective forces minimizing the correlation effects. The SEI parameters are systematically fitted in SNM and pure neutron matter (PNM), which allows to study both, SNM and asymmetric nuclear matter (ANM). Moreover, the parameters responsible for the momentum dependence of the mean field are fixed from the experimental/empirical constraints exclusively, so that each of the two aspects of the mean field, the density dependence and the momentum dependence, can could be studied independently without altering the predictions of the other one [12]. Further, in the determination of nine parameter combinations of the eleven SEI parameters required for the study of ANM, one requires to assume only three standard values of saturation properties, namely, ρ 0 , e ( ρ 0 ) and symmetry energy E s y m ( ρ 0 ) . Within this parameter fixation protocol, we shall use the SEI to compute higher order derivatives of the energy per particle and the symmetry energy at saturation density and compare these values with the results extracted from various different studies. The stability conditions in terms of Landau parameters of the interacting Fermi liquid model serves as an acid test for the reliability of an effective force for its applicability in the different channels of spin and isospin. We shall check to which extent the observance of the Landau stability conditions is fulfilled by our SEI.
In section II we have given a brief account of SEI and its parameter fitting protocol. In section III, we have obtained first different properties of SNM at saturation, which are re-evaluated in the framework of interacting Fermi liquid model by computing the Landau parameters using SEI. In the same section, the high-order derivatives of the energy per particle and the symmetry energy are calculated and compared with the empirical range of values extracted from theory, experiment and astrophysical observations. In Section IV we explore the predictive power of the SEI EoSs in the domain of high density neutron rich matter pertaining to the recent NS phenomenology associated with binary neutron star merger (BNSM) and gravitational redshift. Finally, Section V contains the summary and outlook.

2. Formalism

The SEI in this work was initially proposed by Behera et al., [11] and has the following explicit expression if a form-factor of Yukawa type is used.
V e f f = t 0 ( 1 + x 0 P σ ) δ ( r → ) + t 3 6 ( 1 + x 3 P σ ) ρ ( R ) 1 + b ρ ( R ) γ δ ( r → ) + ( W + B P σ − H P τ − M P σ P τ ) e − r / α r / α + Spin - orbit part
We denote this force as SEI-Y thereafter. The SEI-Y in Eq.(1) has 12 parameters in total, namely, α , γ , b , x 0 , x 3 , t 0 , t 3 , W , B , H , and M plus the spin-orbit strength parameter W 0 , which enters in the description of finite nuclei. The energy density in isospin asymmetric nuclear matter for the SEI-Y interaction in Eq.(1) is given by,
H Y ( ρ n , ρ p ) = 3 ℏ 2 10 m ( k n 2 ρ n + k p 2 ρ p ) + ε 0 l 2 ρ 0 ( ρ n 2 + ρ p 2 ) + ε 0 u l ρ 0 ρ n ρ p + ε γ l 2 ρ 0 γ + 1 ( ρ n 2 + ρ p 2 ) + ε γ u l ρ 0 γ + 1 ρ n ρ p ρ ( R ) 1 + b ρ ( R ) γ + ε e x l 2 ρ 0 { ρ n 2 3 Λ 6 32 k n 6 + 9 Λ 4 8 k n 4 ln 1 + 4 k n 2 Λ 2 − 3 Λ 4 8 k n 4 + 9 Λ 2 4 k n 2 − 3 Λ 3 k n 3 tan − 1 2 k n Λ + ρ p 2 3 Λ 6 32 k p 6 + 9 Λ 4 8 k p 4 ln 1 + 4 k p 2 Λ 2 − 3 Λ 4 8 k p 4 + 9 Λ 2 4 k p 2 − 3 Λ 3 k p 3 tan − 1 2 k p Λ } + ε e x u l ρ 0 ρ n ρ p { 3 32 Λ 6 k n 3 k p 3 + 6 Λ 4 k n k p 3 + 6 Λ 4 k n 3 k p − 3 Λ 2 ( k p 2 − k n 2 ) 2 k n 3 k p 3 ln Λ 2 + ( k n + k p ) 2 Λ 2 + ( k p − k n ) 2 + 3 2 Λ 3 k n 3 − Λ 3 k p 3 tan − 1 k p − k n Λ − 3 2 Λ 3 k p 3 + Λ 3 k n 3 tan − 1 k n + k p Λ + 9 8 Λ 2 k p 2 + Λ 2 k n 2 − 3 8 Λ 4 k n 2 k p 2 }
where, ρ n , ρ p are neutron (n) and proton (p) densities, ρ = ρ n + ρ p is the total NM density, Λ ( = 1 / α ) is the inverse of the range of the Yukawa form-factor, and k i = ( 3 π 2 ρ i ) 1 / 3 (i=n,p) is the respective Fermi momentum. The study of ANM involves altogether nine parameters, γ , b, α , ε 0 l , ε 0 u l , ε γ l , ε γ u l , ε e x l , ε e x u l . The connection of these new parameters to the interaction parameters of Eq.(1), which was derived in Ref. [13], is also reported in Appendix A. Here the index l and u l denotes the interaction between like and unlike pairs of nucleons, respectively.

The fitting procedure of SEI

The formulation of NM and PNM using SEI and the parameter fixation protocol has been discussed at length in Refs. [13,14]. We briefly outline it in the following. The SNM requires only the following three combinations of the strength parameters,
ε 0 l + ε 0 u l 2 = ε 0 , ε γ l + ε γ u l 2 = ε γ , ε e x l + ε e x u l 2 = ε e x ,
which together with γ , b and α are the six parameters needed to determine completely the SNM. For a given value of the exponent γ , which characterizes the stiffness parameter and determines the incompressibility K in SNM, the remaining five parameters ε 0 , ε γ , ε e x , b and α of SNM are determined as follows assuming the standard values of the nucleon mass (mc2=939 MeV), the saturation density ρ 0 and the energy per particle at saturation e ( ρ 0 ) . The range α and the exchange strength ε e x are determined simultaneously by adopting an optimization procedure [11], using the condition that the nuclear mean field in SNM at saturation density vanishes for a kinetic energy of the nucleon of 300 MeV, a result extracted from optical model analysis of nucleon-nucleus scattering data [15,16,17,18]. The parameter b is determined to avoid supra-luminous behaviour [19]. The two remaining parameters, namely ε γ and ε 0 , are obtained from the saturation conditions, T f 0 = ℏ 2 k f 0 2 2 m =37MeV, which allow to obtain k f 0 and therefore the saturation density ρ 0 , and e ( ρ 0 ) =-16 MeV. The stiffness parameter γ , kept as a free parameter, is chosen from the range of values for which the pressure-density relation in SNM lies within the region extracted from the analysis of flow data in heavy-ion collision experiments at intermediate energies [20]. It is verified that γ =1 is the upper limit for which the pressure-density relation is obeyed, which corresponds to the nuclear matter incompressibility K ( ρ 0 ) =269 MeV for the SEI-Y model. Therefore, we can study the nuclear matter properties by assuming different values of γ up to a limiting value γ =1. In this work we will use three EoS corresponding to γ = 1 / 3 , 1 / 2 , and 2 / 3 . In order to study ANM we need to know how the strength parameters ε e x , ε γ and ε 0 of Eq. (3) split into the like and unlike components. The splitting of ε e x into ε e x l and ε e x u l is decided to be ε e x l = 2 ε e x / 3 [21] using the condition that the entropy in PNM does not exceed that of the SNM [21]. The splittings of the remaining two strength parameters, ε γ and ε 0 , are decided from the values of the symmetry energy parameter E s y m ( ρ 0 ) and its derivative E s y m ′ ( ρ 0 ) = ρ 0 d E s y m ( ρ 0 ) d ρ 0 at saturation density ρ 0 . For a given E s y m ( ρ 0 ) within its empirical range [22], we can produce different density dependence of symmetry energy E s y m ( ρ ) by assigning arbitrary values to E s y m ′ ( ρ 0 ) . The slope parameter in each case will be L ( ρ 0 ) = 3 E s y m ′ ( ρ 0 ) . In the study where the variation of L ( ρ 0 ) is not an explicit requirement, the value of E s y m ′ ( ρ 0 ) is fixed from the condition that the asymmetric contribution of the nucleonic part of the energy density in charge neutral β -equilibrated neutron star n + p + e + μ matter (NSM), i.e., S N S M ( ρ ) = [ H ( ρ , Y p ) − H ( ρ , Y p = 1 / 2 ) ] is maximum, where Y p is the equilibrium proton fraction. The characteristic E s y m ′ ( ρ 0 ) value thus obtained predicts a density dependence of the symmetry energy which is neither stiff nor very soft [23]. With the parameters determined in this way, the SEI is able to reproduce the trends of the EoS and the properties of the momentum dependence of the mean field with similar quality as predicted by microscopic calculations [3,21,24,25,26]. As a consequence of this fitting procedure, one can also vary the n and p effective mass splitting, which only depend on the ε e x l and ε e x u l parameters, while the density dependence of E s y m ( ρ ) , i.e. the slope parameter L, which depends on the splitting of ε γ and ε 0 , remains invariant and the vice-versa [21,26]. We have now three open parameters that we have chosen as t 0 , x 0 and W 0 . However, to describe ANM the explicit value of the t 0 and x 0 parameters is not necessary because they enter as specific combinations that can be determined from the ε 0 l and ε 0 u l [14]. In our work [13], we further constrained x 0 by using the DBHF predictions on the effective mass splitting between spin-up and spin-down neutrons in spin polarized neutron matter. It was found that the SEI predictions agree well with the DBHF ones [29] for ε e x l , l = ε e x l / 3 , where the superscript ("l,l") (and its counterpart ("l,ul")) symbolizes the exchange strength for parallel (and anti-parallel) spin orientations in polarized neutron matter. This consideration allows to determine x 0 in a unique way as [13], x 0 = 1 − 2 ε 0 l − ε e x l ρ 0 t 0 , if t 0 is known. The two remaining free parameters, t 0 and W 0 , have to be fitted to finite nuclei data as explained in detail in Refs. [14] and [27] in the case of a SEI with a Gaussian form-factor. For the sake of completeness the twelve numbers of parameters of the SEI-Y EoSs corresponding to γ =1/3, 1/2 and 2/3 are given in Table 1. The inputs corresponding to the saturation density, energy per particle in SNM, and symmetry energy needed to obtain these parameters are given in Table 2.

3. Symmetric and Asymmetric Nuclear Matter Properties

The Equation of state of ANM can be expressed as a power series in the isospin asymmetry δ = ( ρ n − ρ p ) / ρ , as given by,
e ( ρ , δ ) = e 0 ( ρ ) + E s y m ( ρ ) . δ 2 + O ( δ 4 )
where, e 0 ( ρ ) is the energy per nucleon in SNM while E s y m ( ρ ) is the symmetry energy. The energy per nucleon in SNM can also be Taylor expanded around the saturation density as:
e 0 ( ρ ) = e 0 ( ρ 0 ) + K 0 2 ! χ 2 + Q 0 3 ! χ 3 + O ( χ 4 ) ,
where χ = ρ − ρ 0 3 ρ 0 and K 0 = 9 ρ 0 2 ∂ 2 e 0 ( ρ ) ∂ ρ 2 | ρ = ρ 0 and Q 0 = 27 ρ 0 3 ∂ 3 e 0 ( ρ ) ∂ ρ 3 | ρ = ρ 0 are the incompressibility and skewness parameter, respectively, in SNM. Notice that the first derivative does not appear in this expansion due to the saturation condition.
The symmetry energy is the energy cost to convert SNM in PNM [30,31,32]. It is defined as
E s y m ( ρ ) = 1 2 ! ∂ 2 e ( ρ , δ ) ∂ δ 2 | δ = 0
The odd-order terms in δ will not appear in Eq.(4) due to the isospin invariance of nuclear force in nuclear matter when one neglects the Coulomb interaction. The nuclear symmetry energy E s y m ( ρ ) corresponds to the lowest order coefficient in the expansion of the energy per particle in ANM in terms of the isospin asymmetry. The contribution from higher order terms δ n , n≥4 is very small and has been estimated to be less than 1 MeV in microscopic many-body as well as effective model calculations [32]. Keeping up to δ 2 -term in Eq.(4) refers to as parabolic approximation (PA) of EoS of ANM. The density dependence of e 0 ( ρ ) is much better understood than that of E s y m ( ρ ) , which is still elusive, even more in the supra saturation regime that makes the study of ANM as an important area of contemporary nuclear research. The analysis of the density dependence of E s y m ( ρ ) is performed in terms of the various coefficients in its Taylor expansion about normal NM density ρ 0 , given by,
E s y m ( ρ ) = E s y m ( ρ 0 ) + L χ + K s y m 2 ! χ 2 + Q s y m 3 ! χ 3 + O ( χ 4 )
where χ has been defined before. The coefficients
L = 3 ρ 0 ∂ E s y m ( ρ ) ∂ ρ | ρ = ρ 0 , K s y m = 9 ρ 0 2 ∂ 2 E s y m ( ρ ) ∂ ρ 2 | ρ = ρ 0 , and Q s y m = 27 ρ 0 3 ∂ 3 E s y m ( ρ ) ∂ ρ 3 | ρ = ρ 0
are the slope parameter, curvature parameter and skew symmetry parameter, respectively, and characterizes the density dependence of the nuclear symmetry energy around the normal nuclear density ρ 0 , and thus carry important information on the properties of nuclear symmetry energy at both high and low densities region. The incompressibility of ANM, which also depends on the density and isospin asymmetry is given by
K ( ρ , δ ) = 9 ∂ P ( ρ , δ ) ∂ ρ = 18 ρ ∂ e ( ρ , δ ) ∂ ρ + 9 ρ 2 ∂ 2 e ( ρ , δ ) ∂ ρ 2 = 18 P ( ρ , δ ) ρ + 9 ρ 2 ∂ 2 e ( ρ , δ ) ∂ ρ 2 ,
where P ( ρ , δ ) = ρ 2 ∂ e ( ρ , δ ) ∂ ρ is the pressure in ANM and e ( ρ , δ ) is given in Eq.(4). At saturation density ρ s a t ( δ ) of ANM the pressure P ( ρ s a t , δ ) =0 and the incompressibility in Eq.(8) becomes a function of δ only, K s a t ( δ ) = 9 ρ s a t 2 ∂ 2 e ( ρ , δ ) ∂ ρ 2 | ρ = ρ s a t , and refers to as isobaric incompressibility coefficient. The saturation density in ANM, ρ s a t ( δ ) is a function of isospin asymmetry and differs from normal NM density ρ 0 . The corrections to ρ 0 on account of the isospin asymmetry δ has been worked out in Ref.[32] in terms of expansion in even powers of δ . For the lowest order correction ρ s a t ( δ ) = ρ 0 + ρ s a t , 2 δ 2 = ρ 0 − 3 L K 0 ρ 0 δ 2 . Under the PA of EoS of ANM, the isobaric incompressibility coefficient reads K s a t ( δ ) = K 0 + K τ ( ρ 0 ) δ 2 , where, K 0 is the incompressibility of SNM at saturation density and K τ = K s y m − 6 L − Q 0 K 0 L is the isospin part of K s a t ( δ ) [32,33]. The value of the nuclear matter saturation properties such as isoscalar effective mass ( m s * / m ), isovector effective mass ( m v * / m ), energy per particle in PNM ( e P N M ), neutron matter incompressibility ( K P N M = K 0 + K s y m ), neutron matter skewness ( Q P N M = Q 0 + Q s y m ), etc. for the SEI-Y( γ =1/3, 1/2, and 2/3) EoSs at saturation density are given in Table 2. The incompressibility of SNM at saturation density K 0 ( ρ 0 ) is mainly obtained from the analysis of experimental data of the giant monopole resonance (GMR) in open and closed-shell nuclei. Theoretical studies using non-relativistic and relativistic mean field models and the analysis of PREX-II and CREX data, also provide useful information about K 0 ( ρ 0 ) . Relevant works using these techniques, which predict different values of K 0 ( ρ 0 ), are collected in Table 3. The K 0 ( ρ 0 ) values predicted by the SEI-Y models, which are given in Table 2, lie in the range 220-253 MeV within the limiting values extracted from the analysis of the experimental GMR [34,35] and PREX-II and CREX [41] data as well from the compilation of the predictions of a large set of relativistic and non-relativistic mean-field models [22,40]

Landau parameters

In the framework of the Landau theory of normal Fermi liquids [42,43], the bulk properties of nuclear matter can be written in terms of a two-body interaction expressed as a functional of the second derivative of the energy per particle with respect to the occupation numbers at the Fermi surface. The interaction energy has the following form, [44,45]
〈 k 1 k 2 | V | k 1 k 2 〉 = N 0 − 1 { F ( θ ) + F ′ ( θ ) τ 1 . τ 2 + G ( θ ) σ 1 . σ 2 + G ′ ( θ ) σ 1 . σ 2 τ 1 . τ 2 } ,
where N 0 − 1 = ℏ 2 π 2 2 k F m s * is the inverse of the level density at the Fermi surface. The quantity m * is the effective mass associated with the interaction, and σ and τ are the Pauli matrices in spin and isospin space, respectively. Since both particles are on the Fermi surface, F, F ′ , G, and G ′ are functions of θ , the angle between k 1 and k 2 , which are expanded in terms of Legendre polynomials [46] as,
F = ∑ l F l P l ( c o s θ )
and likewise for F ′ , G, and G ′ . For a spherical Fermi surface to be stable against any deformation, the parameters must satisfy the relations
F l > − ( 2 l + 1 )
F l ′ > − ( 2 l + 1 )
G l > − ( 2 l + 1 )
G l ′ > − ( 2 l + 1 ) .
We have calculated the Landau parameters for the SEI-Y interaction. The corresponding analytical expressions for F l , F l ′ , G l , and G l ′ with l=0, 1 and 2 are given in the Appendix B. Landau parameters at ρ 0 predicted by the SEI-Y ( γ = 1 / 3 , 1 / 2 , and 2 / 3 ) EoSs together with the results of different Skyrme, Gogny, chiral effective interactions are shown in Figure 1. The density dependence of different Landau parameter is shown for the SEI-Y ( γ = 1 / 2 ) parameter set in Figure 2. All the Landau parameters satisfy the condition given in Eq.(12)-Eq.(14) at all densities, except F 0 , which violates the condition Eq.(12) for densities less than 0.09 f m − 3 .
The values of the Landau parameters at saturation for the three SEI-Y sets for ( γ = 1 / 3 , 1 / 2 , and 2 / 3 ) are given in Table 4.
These dimensionless parameters F l , F l ′ , G l , and G l ′ are directly related to quantities describing SNM and ANM properties, such as effective mass, incompressibility, symmetry energy, the speed of sound, etc. through relationships [59,60],
Incompressibility , K = 3 ℏ 2 k F 2 m s * ( 1 + F 0 )
Isoscalar Effective Mass , m s * m = 1 + F 1 3 ,
Isoscalar / Isovector Effective Mass Ratio [ 60 ] m s * m v * = 1 + F 1 ′ 3 ,
Symmetry Energy , E s y m = ℏ 2 k F 2 6 m s * ( 1 + F 0 ′ )
Spin Asymmetry Coefficient , E σ = ℏ 2 k F 2 6 m s * ( 1 + G 0 )
Spin - Isospin Asymmetry Coefficient , E σ τ = ℏ 2 k F 2 6 m s * ( 1 + G 0 ′ )
The sound velocity is directly related to the compression modulus K ( ρ ) , which can be expressed in terms of the Landau parameters F 0 and F 1 :
m v s 2 = ℏ 2 k F 2 3 m s * ( 1 + F 0 ) = 1 9 K = ℏ 2 k F 2 3 m 1 + F 0 1 + F 1 3 .
The values of these NM properties at saturation are listed in Table 5 for the three EoSs of SEI-Y corresponding to γ = 1 / 3 , 1 / 2 , and 2 / 3 . These results are in agreement with the saturation properties predicted under the parameter fitting protocol given in Table 2.

High-order Derivatives of the Energy per Particle in Asymmetric Nuclear Matter

The symmetry energy is an important quantity in nuclear physics, which rules many properties in the isovector sector of the energy density and has a relevant impact in nuclear astrophysics. The symmetry energy parameter, E s y m ( ρ 0 ) , is constrained somewhat less rigorously as compared to the energy per particle, e ( ρ 0 ) , of SNM. It is determined from the analysis of the predictions of a large set of mean-field models [22] and from data of astrophysical observations [61,62,63], but also using experimental nuclear data such as charged pion spectra at high transverse momenta [64]or charge exchange and elastic nuclear reactions [65]. The values of E s y m ( ρ 0 ) extracted from these works are reported in the upper panel of Table 6. The symmetry energy values used in the SEI-Y models lies between 34.5-35.5 MeV (see Table 2), which are within the ranges predicted by the almost all the analysis displayed in Table 6. Heavy-ion collision (HIC) studies have provided relevant constraints on the EoS of SNM at supra-saturation densities, which allow to predict e 0 ( ρ ) up to about 4.6 times the normal nuclear matter density [20]. In the recent work of Ref.[70] the value for e 0 ( 4 ρ 0 ) is constrained in the range 63.3 − 6.6 + 19.7 at 68% confidence level. However, the EoS of high-density neutron-rich matter is still highly uncertain due to the limited progress on the analysis of isospin sensitive observables of HIC experiments. It also remains as an open question whether the symmetry energy is stiffer or super-soft at supra-saturation densities. In Table 6, the available data found in the literature on nuclear symmetry energy at twice times the saturation density, E s y m ( 2 ρ 0 ) , together with the corresponding predictions provided by the SEI-Y ( γ = 1 / 3 , 1 / 2 , and 2 / 3 ) EoSs, are given. These results are based on theoretical analysis of data from laboratory experiments, such ASY-EoS experiment at GSI [66] and HIC [67,68], astrophysical data of different types, as outlined in Refs. [69,70,71,74,75,76,77,78], theoretical calculations within chiral ETF [72,73] and effective mean-field models [79]. From this Table we see that the SEI-Y predictions are in good agreement with the available data reported in Table 6, in particular with the predictions of Refs.[67,69,71,74,75,76,77] obtained using different techniques. The symmetry pressure at twice saturation density predicted by the SEI-Y( γ = 1 / 3 , 1 / 2 , and 2 / 3 ) EoSs are 10.659, 10.572, and, 10.488 MeVfm−3 respectively, which lies within the range P s y m ( 2 ρ 0 ) = ( 35 ± 32 ) MeV fm−3 extracted from the experimentally derived density functional [81]. The nuclear symmetry energy at three times the saturation density, E s y m ( 3 ρ 0 ) , for SEI-Y( γ = 1 / 3 , 1 / 2 , and 2 / 3 ) EoS are 69.64, 69.38, and 69 MeV respectively. These SEI-Y values are consistent with the results extracted from the GW170817 data ( 76.91 − 25.96 + 25.96 MeV) [74], but are slightly higher than the predictions of Dutra et al., 2012, which range from 33.65 to 60.92 MeV [22].
The parameters associated to higher-order derivatives of the energy per particle and symmetry energy at saturation, specifically, Q 0 , L, K s y m , and Q s y m remain poorly constrained and present challenges for experimental measurements. Among these parameters, the slope of the symmetry energy L is of particular relevance, as far as this quantity is nicely correlated with some finite nuclei properties, for example the neutron skin thickness in heavy neutron rich nuclei as 208Pb. This parameter has been estimated using information extracted from the analysis of terrestrial nuclear experiments and astrophysical observations [61,62,70,77,80], the analysis of the PREX-II data [63], from results of charge exchange and elastic scattering involving isobaric analog states [65], charged pion spectra [64] and isospin diffusion [82], and, very recently, from the charge radii difference in mirror nuclei [28]. The range of the values of the slope parameter L is relatively large and covers from about 40 MeV till 120 MeV depending on the inputs used in the different analysis carried out, as it can be seen in the upper panel of Table 7. The L value predicted by the SEI-Y models are about 75 MeV, which lie, roughly, in the middle of the range of the different considered estimates. The incompressibility parameter in ANM, K s y m , has been estimated from astrophysical inputs provided by astrophysical observations [83,84,85,86], from nuclear and neutron matter calculations using chiral effective field theory [87,88,89], from terrestrial experiments [90] and from the analysis of mean-field predictions [91,92,93]. This parameter is, in general, negative and of the order of few hundreds of MeV. The SEI-Y predictions, given in Table 2, are in line with the estimates obtained from terrestrial experiments and astrophysical observations reported in the middle panel of Table 7.
In Ref.[93], a correlation between the K s y m and 3 E s y m − L parameters is obtained from the analysis of 500 Skyrme and RMF models. However, in the case of SEI-Y, K s y m is also strongly correlated with L in addition to the 3 E s y m − L correlation. In particular, in the case of SEI-Y ( γ = 1 / 2 ) , we find the linear relation K s y m = 4.1165 L − 408.98 . The isovector incompressibility parameter K τ is mainly extracted from experimental data of the isoscalar giant monopole resonances [36,94,95], from theoretical mean-field model calculations for different MDI interactions [32,96] and from information extracted from measurements of neutron skins across the mass table [97]. These estimates have, roughly, an average value about -500 MeV but with large error bars, as it can be seen in lower panel of Table 7. The values predicted by the SEI-Y models, given in Table 2, are in agreement with the values extracted using different techniques given in the lower panel of Table 7.
Experimental constraints on the skewness parameter in both, symmetric and asymmetric nuclear matter, Q 0 and Q s y m , respectively, are currently lacking in precision. Based on the analysis of different experimental and observational data [91,98,99,100,101], it is found that the skewness in SNM is negative and its range covers a range roughly between ≃ -1200 and 400 MeV. The situation is similar for the skewness parameter of the symmetry energy, where different estimates constraint its value within the range between -200 and 800 MeV [69,91,92,93]. The values of Q 0 in SNM predicted by SEI-Y ( γ = 1 / 3 , 1 / 2 , and 2 / 3 ) EoSs are listed in Table 2 and lie consistent with the values extracted from other different analysis. In the same Table 2, we display the skewness parameter of the symmetry energy computed with the SEI-Y models, which are in the range 234-273 MeV that is in good agreement with the value of Q s y m = 296.8 ± 73.6 MeV suggested in Ref. [93]. With the SEY-Y model we also find a strong anti-correlation between the Q s y m & L parameters, which in the case of SEI-Y( γ = 1 / 2 ) EoS reads Q s y m = − 8.805 L + 910.26 .

4. Neutron Star Phenomenology

The Radius of Neutron Stars and the Slope of the Isoscalar Incompressibility

The density derivative of the isoscalar incompressibility of symmetric nuclear matter, which is defined as K ′ ( ρ ) = 3 ρ d K ( ρ ) d ρ , can be written at saturation density as a combination of the skewness and the incompressibility of SNM as K 0 ′ ( ρ 0 ) = Q 0 + 12 K 0 [102]. The value of this parameter, estimated from a large set of non-relativistic and relativistic mean-field models, lies in the range K 0 ′ = 1800 − 2400 [103]. A relatively wider range, 1556 ≤ K 0 ′ ≤ 4971 MeV, is extracted from analysis of the tidal deformability measurement in the BNSM event GW170817 [85]. In Ref. [103] combinations of of the slopes of the nuclear matter incompressibility and the symmetry energy coefficients at saturation, which is almost independent of the NS mass in the range 0.6 M0-1.8 M0, is shown. Here we explore, using the SEI-Y EoSs with ( γ = 1 / 3 , 1/2, and 2/3), the possible correlations between the NS radius and the slope of the incompressibility at saturation for NS of 1.4 M 0 and 1.6 M 0 . To get the radii predicted by these EoSs, we solve the Tolman-Oppenheimer-Volkoff (TOV) equation, where the BPS-BBP EoS [104,105] is used upto 0.07468 fm−3 (the crust-core transition density for SEI) and our EoS thereafter. The values of the radii of these 1.4 M 0 and 1.6 M 0 NSs, R 1.4 and R 1.6 , are shown as a function of the slope of the incompressibility parameter K 0 ′ in Figs. Figure 3 and Figure 4, respectively, for the three aforementioned SEI EoSs. The vertical shaded region in brown in the Figures correspond to the K 0 ′ values predicted in Refs. [103,106]. The data for NS radii, obtained from various recent studies are taken from Refs. [63,84,107,108,109,110,111,112] (for R 1.4 ) and [113,114] (for R 1.6 ) and displayed by different color areas in Figure 3 and Figure 4, respectively. The LIGO-Virgo measurement leads to an upper limit of R 1.4 as 13.6 km [115] and that from the BNSM ascertained to be R 1.4 < 13.76 km [116]. The minimum limit for R 1.6 radius of non rotating NS, constrained from GW170817 data by Bauswein et al., is 10.68 − 0.04 + 0.15 km [117]. This value is shown as orange band in Figs. Figure 4. R 1.4 , R 1.6 and K 0 ′ values predicted by 44-EoSs of Skyrme, RMF and microscopic interactions, which are taken from Table I of the Supplemental Material given in Alam et al., 2016 [103], are also shown in the two Figures by green squares.
Using these 44-EoSs data, a moderate linear correlation between the NS radii and K 0 ′ is obtained, as it was also pointed out by Alam et al., in Ref. [103], whereas a rather strong correlation over the mass range 0.8 M0-1.8 M0 was obtained with a linear combination of K 0 ′ and L 0 , as we mentioned before. However, our three SEI-Y EoSs with γ parameter equal 1/3, 1/2 and 2/3 show, a strong correlation between the radii and the slope of the incompressibility alone for both NS masses, namely, 1.4 M 0 and 1.6 M 0 . We have also verified that another strong linear correlation exists between R 1.4 and R 1.6 and the linear combination of K 0 ′ and L 0 in agreement with the previous findings in [103].

Neutron Star Merger and Incompressibility of Asymmetric Nuclear Matter

The incompressibility of ANM in Eq.(8) depends on both density and isospin asymmetry, and it is found to have important implications in BNSM studies [118,119]. The threshold mass M t h for prompt collapse (PC) to form a black hole (BH) in BNSM is scaled in terms of maximum mass M m a x of the non-rotating NS as, M t h = κ M m a x , where the scaling parameter κ is EoS dependent [120,121]. Bauswein et al. [118], from a simulation study of the BNSM for symmetric binary NS have found, using temperature dependent nuclear EoSs, a strong correlation of κ with the compactness C m a x = G M m a x c 2 R m a x of the TOV configuration ( M m a x , R m a x ) of the NS, where c, and G are the speed of light and gravitational constant, respectively. An universal ansatz proposed by Bauswein et al., (2013) is that
κ = a C m a x + b ,
which is independent of the EoS. Such a linear ansatz does represent a reasonable first approximation to the data, but it is not the most general one [122]. Using weighted averaged values of the linear-fit constants a and b of different works, given in Table II of Ref.[123], we have computed the threshold mass M t h predicted by the three EoSs of SEI-Y ( γ =1/3, 1/2, and 2/3), which are reported in Table 8. In case of a delayed/no collapse, the estimated total binary mass of GW170817 provides a lower bound on the threshold mass for direct BH formation, M t h > M t o t G W 170817 = 2.74 − 0.01 + 0.04 [117]. SEI-Y predictions of M t h for the three sets of values of a and b in Table 8 closely conforms to this limiting value.
In a recent work, Perego et al. [119] have performed a colorred BNSM simulation study taking asymmetric masses in the NS binary. These authors have shown that the nuclear incompressibility at the central density ρ c of M m a x , K m a x = K ( ρ c m a x , δ ) , contains information on M t h for PC in BNS merger. Consequently, if M t h is known, then K m a x can be potentially predicted, which is not possible nowadays in any laboratory experiment. In this Ref.[119] the authors have examined the correlation between K m a x and compactness C m a x of maximum mass NS considering a large sample of EoSs, comprising of nucleonic and also containing hyperons and transition to quark phase as well. A strong power law correlation has been obtained amongst these data. We have computed the density dependence of K ( ρ , δ ) for the three SEI-Y EoSs, where δ for each ρ is obtained by solving the charge neutral β -equilibrated NSM, and the results are shown as a function of the density in panel (a) of Figure 5. The values of the K m a x computed at the central density of M m a x predicted by the SEI-Y EoSs are shown as a function of the compactness C m a x in panel (b) together with the data of the 66-EoSs taken from Supplementary material of Ref.[119]. The values of the C m a x , shown in panel (b) of Figure 5 for different EoSs, lie below the empirical limit of compactness allowed by general relativity, C=4/9 [124], and the Tolman VII analytical solution of the TOV equation, C=0.3428. These limiting values are the universal upper bounds for compactness, as corroborated by the incorporation of realistic EoS [125,126]. The three SEI data lies in the tighter threshold region of K m a x ≈ 12 GeV of Perego et al., 2022 (Fig.4 of [119]). They have also suggested that the information of M t h at different mass asymmetry q of the two NSs in the binary can provide constraint on velocity of sound v s close to the central density ρ c of M m a x .

Sound Speed in Neutron Star Matter

The adiabatic speed of sound in ANM evaluated at constant entropy is given by [89,127,128]
v s 2 c 2 = ∂ P ∂ H s = K ( ρ , δ ) 9 ( m c 2 + e ( ρ , δ ) + P ( ρ , δ ) / ρ )
where, H is the energy density given by Eq. (2) and m is the average nucleon mass.
The square of the speed of the sound v s in NSM, where δ for each ρ in Eq.(23) is the equilibrium value obtained from the β -stability condition, predicted by the three SEI-Y EoSs γ = 1 / 3 , 1 / 2 , and 2 / 3 is displayed as a function of density in panel(a) of Figure 6. From this Figure we can see that the square of the speed of sound increases with the density without exceeding the causality limit and also that increases linearly with the incompressibility of nuclear matter, as predicted by Eq. (23). The magenta line in panel (a) of Figure 6 represents the conformal limit ( v s c ≤ 1 3 ) [129]. More recently, Margaritis et al., (2019) claim that the sound speed likely exceeds the conformal limit by studying maximally rotating neutron stars [130,131].
In panel (b) of Figure 6, we display the speed of sound in NSM as a function of nucleonic pressure at density 1.85 ρ 0 computed with the SEI-Y( γ = 1 / 2 and 2 / 3 ) EoSs with different slope of the symmetry energy L in the range 60-110 MeV together with the results of the EoSs from Bauswein et al., 2012 [114]. The SEI-Y predictions show a nice linear behaviour between the speed of the sound and the pressure with a correlation coefficient, r=0.998 for both EoSs. This linear behaviour is, however, weaker with the set of EoSs selected by Bauswein et al.[114], probably due to the different origin and fitting protocols of these EoSs.
Panels (c), (d) and (e) of Figure 6 show, as a function of the NS radius, the square of the speed of sound, v s 2 , computed at the central densities, ρ c , of the 1.8 M⊙, 1.6 M⊙ and 1.4 M⊙ NSs obtained colorred solving the TOV equations using the SEI-Y ( γ = 1 / 2 and 2 / 3 ) EoSs with different values of the slope parameter L in the range 70-110 MeV. For the three considered masses, the square of the speed of the sound shows an inverse linear relationship with radius of NS, with correlation coefficients close to unity, which show a moderate decreasing trend as the NS mass decreases. The inverse linear relationship in each given mass NS is due to the following. When the slope of the symmetry energy L increases in an EoS of given γ , the M R ratio decreases owing to the growing of the radius R, and therefore the compactness also decreases, which implies a reduction of the incompressibility K ( ρ , δ ) .

Gravitational redshift

The gravitational redshift of a signal from the star surface can be written as,
Z s u r f = 1 − 2 G M c 2 R − 1 / 2 − 1 .
Measurements of the gravitational redshift of spectral lines can provide direct insights into the stellar compactness parameter and, as a result, can constrain the EoS for dense matter. The Z s u r f calculated using the SEI-Y ( γ = 1 / 2 ) and SEI-Y ( γ = 2 / 3 ) EoSs as a function of gravitational mass is shown in Figure 7. From this Figure we can see that
Z s u r f increases as the mass of the NS rises for both considered EoSs. In the lower mass range, the Z s u r f values for both EoS models are almost the same, but they diverge notably in the higher mass range. EoS having higher value of incompressibility predicts lower value of Z s u r f . The magenta horizontal line in the Figure 7 corresponds to Z s u r f =0.35. This value was obtained by Cottam et al. from the X-ray bursts source in the low-mass X-ray binary EXO 07482-676 [132]. The gravitational redshift of RBS 1223, RX J0720.4-3125, and RX J1856.5-3754, which are members of the so-called “The Magnificent Seven”, are 0.16 − 0.02 + 0.03 [green shaded region], 0.205 − 0.003 + 0.006 [orange shaded region], and 0.22 − 0.12 + 0.06 [maroon shaded region] [133,134] with masses 1.08 − 0.11 + 0.2 M 0 , 1.23 − 0.05 + 0.10 M 0 , and 1.24 − 0.29 + 0.29 M 0 , respectively, at 68% confidence level [135]. These observational data, which are also displayed in Figure 7, are well reproduced by our theoretical calculation using the SEI-Y EoSs, which pass well through the shaded areas representing the uncertainties in the respective observed data. The gravitational redshift Z s u r f in different mass NSs, namely, (a) 1.8 M 0 , (b) 1.6 M 0 , and (c) 1.4 M 0 are shown as a function of the auxiliary parameter η = ( K 0 L 2 ) 1 / 3 in Figure 8 for the SEI-Y ( γ = 1 / 2 ) and SEI-Y ( γ = 2 / 3 ) EoSs. The auxiliary parameter η , which was proposed in Refs.[136,137], is a combination of incompressibility in SNM, K 0 , and the slope of the symmetry energy, L. The values of L and K 0 extracted from different nuclear experiments and observations, constrains the value of η in the range between 60.8 ≤ η ≤ 174.5 MeV from S π RIT, RCNP and PREX-II data, as it can be seen in Figure 8. From this Figure we can also observe a strong anti-correlation between Z s u r f and η predicted by the two considered SEI-Y EoSs for the three NS masses, namely 1.8 M 0 , 1.6 M 0 , and 1.4 M 0 , analyzed. The correlation coefficients resulting for the two EoSs are displayed in the respective panels, which predict a relatively strong correlation coefficient for the stiffer EoS. The Z s u r f values as a function of η predicted by the 44 EoSs of Skyrme, RMF and microscopic interactions used by Alam et al., [103] have been computed for the same masses and shown in the respective panels of Figure 8 as green diamonds. The inverse relation between Z s u r f and η is also observed for these EoSs although much weaker, which can be assigned due to the different origin of the EoSs considered in [103].

Neutron star mass, radius and gravitational redshift at different central densities

The correlations between the mass M, radius R, and gravitational redshift Z s u r f of NSs with central densities of ρ 0 , 2 ρ 0 , 3 ρ 0 , 4 ρ 0 , and 6 ρ 0 are studied as a function of the slope L in the range 60-110 MeV using the SEI EoS ( γ =2/3). The corresponding results are shown, in the three panels of Figure 9, which from the left to the right correspond to masses, radii and gravitational redshift, respectively.
A linear correlation has been observed between L and mass M for the NSs at all central densities ρ 0 , 2 ρ 0 , 3 ρ 0 , 4 ρ 0 , and 6 ρ 0 . The correlation coefficients are r=0.999, 0.993, 0.966, 0.926, and 0.858, respectively. The correlation becomes weaker as the density increases, a trend similar to the one found in the work of Ref.[138], which reflects the role of other empirical parameters governing the density dependence of the EoS [138]. For NSs having central densities 2 ρ 0 , 3 ρ 0 , 4 ρ 0 , and 6 ρ 0 , a strong linear correlation between the NSs radii and L is also found. However, for a central density ρ c = ρ 0 , the radius decreases as the slope of the symmetry energy L increases. The reason for this behavior is given in Ref.[138]. A higher value of L, implies a softer EoS for densities below ρ 0 , which explains the anti-correlation observed in the central panel of Figure 9 for NSs having a central density ρ 0 . In contrast, at higher densities, a larger value of the slope parameter L results in a stiffer EoS above ρ 0 and, consequently, the radius, which is correlated with L in this region, shows an increasing trend. In the right panel of Figure 9 we also found a strong linear correlation between the Z s u r f and L for NSs having central densities ρ 0 , 2 ρ 0 , 3 ρ 0 , 4 ρ 0 , and 6 ρ 0 , which gradually degrades as the central density increases, a feature similar to the correlation between mass M and L displayed in left panel of Figure 9.

5. Summary and Outlook

We have used the so-called finite-range simple effective interaction with a Yukawa form-factor to study some non-standard properties of symmetric and asymmetric nuclear matter, such as the Landau parameters associated to this interaction and the high-order derivatives of the energy per particle in symmetric matter and the symmetry energy at saturation density, on the one hand, and to explore the predictive power of SEI-Y in the high-density neutron-rich domain in describing recent neutron star phenomenology associated to binary neutron star merger and gravitational redshift, on the other hand. SEI-Y is a phenomenological effective interaction whose parameters, except one fitted to finite nuclei data, are systematically fitted under very generic considerations to experimental or empirical data of symmetric nuclear matter and pure neutron matter, which give satisfactory account of the nuclear matter properties. An important characteristics of SEI-Y is the fact that the parameters that determine the momentum dependence of the mean-field are decoupled from the ones that fix its density dependence, in such a way that each part in the isovector sector can be studied independently of the other without affecting the isoscalar predictions.
We have computed the Landau parameters for the SEI-Y EoSs that give an overall satisfactory account of the nuclear matter saturation properties as well as the sum rules. The properties of the higher order derivatives of the energy per particle e 0 ( ρ ) and the symmetry energy E s y m ( ρ ) in nuclear matter at saturation density, namely, Q 0 , L, K s y m and Q s y m , have remained unconstrained and their extraction from theoretical calculations, various terrestrial laboratory experiments and astrophysical observations, predict values with largely differing uncertainties, as it can be seen in Table 2, Table 3, Table 6 and Table 7. The results obtained with the SEI-Y EoSs for Q 0 , L, K s y m K τ and Q s y m are found to satisfy the different constraints extracted from different theoretical and experimental analyses. However, the main aim of this study is to discuss some recent phenomenology of neutron stars related to the binary neutron star merger and gravitational redshift. The compactness C m a x of the maximum mass of a neutron star predicted by the three SEI-Y EoSs, which cover, approximately, the range of incompressibilities between 220 and 260 MeV, predict the threshold mass M t h for prompt collapse that satisfies the minimum threshold mass constraint assessed from the binary masses in GW170817 event. The C m a x of these SEI-Y EoSs lies in the tighter threshold region of K m a x ≈12 GeV of Perego et al., 2022 analysis using 34-EoSs of different types. The velocity of sound, v s , computed with the SEI-Y model EoSs is also found to remain causal in neutron star matter and does not exceed the velocity of light. Using SEI-Y EoSs with given symmetry stiffness (given γ ) but different slope parameter L in a given neutron star, we find an antilinear relationship between its radius, R, and the square of its sound speed, v s 2 , computed at its central density. These results are shown in panels (c), (d) and (e) of Figure 6 for neutron stars with masses 1.8 M⊙, 1.6 M⊙ and 1.4 M⊙. We have also used the SEI-Y EoSs to study the gravitational redshift at the surface of a neutron star, Z s u r f , which is intrinsically connected to the compactness parameter, as a function the mass of the neutron star. The SEI-Y predictions of Z s u r f conform to the values constrained from the astrophysical observations on the three neutron stars, namely, RBS 1223, RX J0720.4-3125, and RX J1856.5-3754 in the X-ray binary shown in Figure 7. In a neutron star of given mass the redshift parameter Z s u r f shows a decreasing trend if the slope parameter, L, increases when the incompressibility modulus, K 0 , is kept fix. This implies that for a neutron star of given mass, when the slope parameter L increases, the compactness, C, decreases. This behaviour is also verified using the 44 EoSs of Skyrme, RMF and microscopic type given in the work of Alam et al. shown in Figure 8. On the other hand, Z s u r f in a neutron star also grows with increasing central density, which in turn increases the compactness parameter that is a relevant parameter in order to understand the EoS of dense neutron-rich matter. Our immediate objective is to use SEI-Y to study the neutron star phenomenology at finite temperature, and finite nuclei properties taking deformation into account.

Acknowledgments

P.B. acknowledges support from MANF Fellowship of UGC, India. X.V. acknowledges partial support from Grants No. PID2020-118758GB-I00 and No. CEX2019-000918-M (through the “Unit of Excellence María de Maeztu 2020-2023” award to ICCUB) from the Spanish MCIN/AEI/10.13039/501100011033. Useful discussions with M. Centelles are also warmly acknowledged. T.R.R. offers sincere thanks to B. Behera for useful discussions.

Appendix A. Relations between the six strength parameters and the interaction parameters

The relationships between the six strength parameters in Eq.(2) and the interaction parameters in Eq.(1) are as follows:
ε 0 l = ρ 0 t 0 2 ( 1 − x 0 ) + W + B 2 − H − M 2 ( 4 π α 3 )
ε 0 u l = ρ 0 t 0 2 ( 2 + x 0 ) + W + B 2 ( 4 π α 3 )
ε γ l = t 3 12 ρ 0 γ + 1 ( 1 − x 3 )
ε γ u l = t 3 12 ρ 0 γ + 1 ( 2 + x 3 )
ε e x l = ρ 0 M + H 2 − B − W 2 ( 4 π α 3 )
ε e x u l = ρ 0 M + H 2 ( 4 π α 3 )
where, the superscript indices l and u l denote the contributions resulting from the nucleon interactions between a like-pair and an unlike-pair. By inverting this set of equations and replacing the strength parameters by their values given in Table 1, one obtains the interaction parameters that are reported in Table A1
Table A1. The twelve parameters for the SEI-Y EoSs corresponding to γ =1/3, 1/2, and 2/3.
Table A1. The twelve parameters for the SEI-Y EoSs corresponding to γ =1/3, 1/2, and 2/3.
γ b [ f m 3 ] α [fm] x 3 t 3 [MeVfm3(γ+1)] W [MeV]
1/3 0.4161 0.4232 -0.0630 9536.129 -1380.539
1/2 0.5880 0.4242 -0.112 9277.281 -1321.847
2/3 0.7796 0.4250 -0.153 10228.257 -1214.475
B [MeV] H [MeV] M [MeV] t 0 [ M e V f m 3 ] x 0 W 0 [MeV]
128.0918 -630.968 -808.871 333.5 1.151 119.3
100.950 -575.215 -832.339 566.7 0.664 118.4
49.094 -470.284 -881.144 647.4 0.520 118.2

Appendix B. Landau Parameters

The expression of Landau parameters for SEI-Y EoS are given as follows:
F 0 = N 0 { 3 4 t 0 + t 3 16 ρ 1 + b ρ γ ( γ + 1 ) ( γ + 2 ) − 2 γ ( γ + 2 ) b ρ 1 + b ρ + γ ( γ + 1 ) b ρ 1 + b ρ 2 + 4 π α 3 W + B 2 − H 2 − M 4 + π α k F 2 M + H 2 − B 2 − W 4 ln ( 1 + 4 α 2 k F 2 ) }
F 1 = N 0 3 π α k F 2 M + H 2 − B 2 − W 4 1 + 1 2 α 2 k F 2 ln ( 1 + 4 α 2 k F 2 ) − 2
F 2 = N 0 5 π α 2 k F 2 M + H 2 − B 2 − W 4 { 3 1 + 1 2 α 2 k F 2 2 − 1 ln ( 1 + 4 α 2 k F 2 ) − 6 1 + 1 2 α 2 k F 2 }
F 0 ′ = N 0 { − t 0 4 ( 1 + 2 x 0 ) − t 3 24 ( 1 + 2 x 3 ) ρ 1 + b ρ γ − 4 π α 3 H 2 + M 4 − π α k F 2 B 2 + W 4 ln ( 1 + 4 α 2 k F 2 ) }
F 1 ′ = N 0 − 3 π α k F 2 B 2 + W 4 1 + 1 2 α 2 k F 2 ln ( 1 + 4 α 2 k F 2 ) − 2
F 2 ′ = N 0 − 5 π α 2 k F 2 B 2 + W 4 3 1 + 1 2 α 2 k F 2 2 − 1 ln ( 1 + 4 α 2 k F 2 ) − 6 1 + 1 2 α 2 k F 2
G 0 = N 0 { − t 0 4 ( 1 − 2 x 0 ) − t 3 24 ( 1 − 2 x 3 ) ρ 1 + b ρ γ + 4 π α 3 B 2 − M 4 + π α k F 2 H 2 − W 4 ln ( 1 + 4 α 2 k F 2 ) }
G 1 = N 0 3 π α k F 2 H 2 − W 4 1 + 1 2 α 2 k F 2 ln ( 1 + 4 α 2 k F 2 ) − 2
G 2 = N 0 5 π α 2 k F 2 H 2 − W 4 3 1 + 1 2 α 2 k F 2 2 − 1 ln ( 1 + 4 α 2 k F 2 ) − 6 1 + 1 2 α 2 k F 2
G 0 ′ = N 0 − t 0 4 − t 3 24 ρ 1 + b ρ γ − 4 π α 3 M 4 − π α k F 2 W 4 ln ( 1 + 4 α 2 k F 2 )
G 1 ′ = N 0 − 3 π α k F 2 W 4 1 + 1 2 α 2 k F 2 ln ( 1 + 4 α 2 k F 2 ) − 2
G 2 ′ = N 0 − 5 π α 2 k F 2 W 4 3 1 + 1 2 α 2 k F 2 2 − 1 ln ( 1 + 4 α 2 k F 2 ) − 6 1 + 1 2 α 2 k F 2 ,
where the normalization constant N 0 = 2 k F m s * ℏ 2 π 2 is the level density at the Fermi surface. The numerical values of the Landau parameters reported in Table 4 are obtained with the help of the interaction parameters given in Table A1 and the effective mass and Fermi momentum at saturation taken from Table. Table 2.

References

  1. Haar, B. T.; and Malfliet, R. Nucleons, mesons and deltas in nuclear matter a relativistic Dirac-Brueckner approach. Phys. Rep. 1987, 149, 207. [https://doi.org/10.1016/0370-1573(87)90085-8]; Van Dalen, E. N. E.; Fuchs, C.; and Faessler, A. The relativistic Dirac–Brueckner approach to asymmetric nuclear matter. Nucl. Phys. A 2004, 744, 227-248. [https://doi.org/10.1016/j.nuclphysa.2004.08.019]; Jong, F. de.; and Lenske, H. Asymmetric nuclear matter in the relativistic Brueckner-Hartree-Fock approach. Phys. Rev. C 1998, 57, 3099. [https://doi.org/10.1103/PhysRevC.57.3099]. [CrossRef]
  2. Cugnon, J.; Deneye, P.; and Lejeune, A. Z. Neutron matter properties in an extended Brueckner approach Physik A - Atomic Nuclei 1987 328, 409-415. [https://doi.org/10.1007/BF01289626] ; Zuo, W.; Lejeune A.; Lombardo, U.; and Mathiot, J. F. Microscopic three-body force for asymmetric nuclear matter. Eur. Phys. J. A 2002, 14, 469-475. [https://doi.org/10.1140/epja/i2002-10031-y]; Bombaci, I.; and Lombardo, U.; Asymmetric nuclear matter equation of state. Phys. Rev. C 1991, 44, 1892. [https://doi.org/10.1103/PhysRevC.44.1892]; Day, B. D.; and Wiringa, R. B. Brueckner-Bethe and variational calculations of nuclear matter. Phys. Rev. C 1985, 32, 1057. [https://doi.org/10.1103/PhysRevC.32.1057]; Baldo, M.; Burgio, G. F.; and Schulze, H.-J. Hyperon stars in the Brueckner-Bethe-Goldstone theory. Phys. Rev. C 2000, 61, 055801 [https://doi.org/10.1103/PhysRevC.61.055801]; Vidaña, I.; Polls, A.; Ramos, A.; Engvik, L.; and Hjorth-Jensen, M. Hyperon-hyperon interactions and properties of neutron star matter. Phys. Rev. C 2000, 62, 035801. [https://doi.org/10.1103/PhysRevC.62.035801]. [CrossRef]
  3. Akmal, A.; Pandharipande, V. R.; and Ravenhall, D. G. Equation of state of nucleon matter and neutron star structure. Phys. Rev. C 1998, 58, 1804. [CrossRef]
  4. Mukherjee, A.; and Pandharipande, V. R. Variational theory of hot nucleon matter. Phys. Rev. C 2007, 75, 035802. [CrossRef]
  5. Hebeler, K.; and Schwenk, A. Chiral three-nucleon forces and neutron matter. Phys. Rev. C 2010, 82, 014314. [CrossRef]
  6. Hebeler, K.; Lattimer, J. M.; Pethick, C. J.; and Schwenk, A. Constraints on Neutron Star Radii Based on Chiral Effective Field Theory Interactions. Phys. Rev. Lett. 2010, 105, 161102. [CrossRef]
  7. Haensel, P.; Kutschera, M.; and Prószyński, M. Uncertainty in the saturation density of nuclear matter and neutron star models. Astron. Astrophys. 1981, 102, 299-302. [http://adsabs.harvard.edu/abs/1981A%26A...102..299H].
  8. Skyrme, T. H. R. CVII. The Nuclear Surface. Phil. Mag. (1956) 1, 1043. [CrossRef]
  9. Decharge, J; and Gogny, D. Hartree-Fock-Bogolyubov calculations with the D1 effective interaction on spherical nuclei. Phys. Rev. C 1980, 21, 1568. [CrossRef]
  10. Bertsch, G.; Borysowicz, J.; McManus, H.; and Love, W.G. Interactions for inelastic scattering derived from realistic potentials. Nucl. Phys. A 1977, 284, 399-419. [CrossRef]
  11. Behera, B; Routray, T R; and Satpathy, R K . Momentum and density dependence of the mean field in nuclear matter. J. Phys. G: Nucl. Part. Phys. 1998, 24, 2073. [CrossRef]
  12. Behera, B.; Routray, T. R.; et al. Momentum and density dependence of the isospin part of nuclear mean field and equation of state of asymmetric nuclear matter. Nuclear Physics A 2005, 753, 367-386. [CrossRef]
  13. Behera, B; Vin˜as, X.; Routray, T. R.; Centelles, M.. Study of spin polarized nuclear matter and finite nuclei with finite range simple effective interaction. J. Phys G: Nucl. Part. Phys. 2015, 42, 045103. http://iopscience.iop.org/0954-3899/42/4/045103.
  14. Behera, B; Vi n˜as, X; Bhuyan, M; Routray, T. R.; Sharma, B. K.; and Patra, S. K. Simple effective interaction: infinite nuclear matter and finite nuclei. J. Phys G: Nucl. Part. Phys. 2013, 40, 095105. [http://iopscience.iop.org/0954-3899/40/9/095105].
  15. Bertsch, G. F.; and Das Gupta, S. A guide to microscopic models for intermediate energy heavy ion collisions. Phys. Rep. 1988, 160 189. [CrossRef]
  16. Gale, C; Bertsch, G. F.; and Das Gupta, S. Heavy-ion collision theory with momentum-dependent interactions. Phys. Rev. C, 1987, 35, 1666. [CrossRef]
  17. Gale, C; Welke, G. M.; Prakash, M; Lee, S. J.; and Das Gupta, S. Transverse momenta, nuclear equation of state, and momentum-dependent interactions in heavy-ion collisions. Phys. Rev. C 1990, 41, 1545. [CrossRef]
  18. Csernai, L. P.; Fai, G; Gale, C; and Osnes, E. Nuclear equation of state with momentum-dependent interactions. Phys. Rev. C 1992, 46, 736. [CrossRef]
  19. Behera, B; Routray, T. R.; and Satpathy, R. K. Causal violation of the speed of sound and the equation of state of nuclear matter. J. Phys. G 1997, 23, 445. [http://iopscience.iop.org/0954-3899/23/4/005].
  20. Danielewicz, P.; Lacey, R.; and Lynch, W. G. Determination of the Equation of State of Dense Matter. Science 2002, 298, 1592. [CrossRef]
  21. Behera, B.; Routray, T. R.; and Tripathy, S. K. Neutron–proton effective mass splitting and thermal evolution in neutron-rich matter. J. Phys. G: Nucl. Part. Phys. 2011, 38, 115104. [http://iopscience.iop.org/0954-3899/38/11/115104)].
  22. Dutra, M.; Lourenço, O.; et al. Skyrme interaction and nuclear matter constraints. Phys. Rev. C 2012, 85, 035201. [CrossRef]
  23. Behera, B.; Routray, T. R.; Pradhan, A.; Patra, S. K.; and Sahu, P. K.; Nuclear mean field and equation of state of asymmetric nuclear matterNucl. Phys. A 2007, 794, 132-148. [CrossRef]
  24. Wiringa, R. B. Single-particle potential in dense nuclear matter. Phys. Rev. C 1988, 38, 2967. [CrossRef]
  25. Sammarruca, F. The Microscopic Approach to Nuclear Matter and Neutron Star Matter. Int. J. Mod. Phys. E 2010, 19, 1259-1313. [CrossRef]
  26. Behera, B.; Routray, T. R.; and Tripathy, S. K. Temperature dependence of the nuclear symmetry energy and equation of state of charge neutral n + p + e + μ matter in beta equilibrium. J. Phys. G: Nucl. Part. Phys. 2009, 36, 125105. [CrossRef]
  27. Behera, B.; Viñas, X.; Routray, T. R.; Robledo, L. M.; Centelles, M.; and Pattnaik, S. P. Deformation properties with a finite-range simple effective interaction. J. Phys. G: Nucl. Part. Phys. 2016, 43, 045115. [http://iopscience.iop.org/0954-3899/43/4/045115].
  28. Bano, P; Pattnaik, S. P.; Centelles, M.; Viñas X.; and Routray, T. R. Correlations between charge radii differences of mirror nuclei and stellar observables. Phys. Rev. C 2023, 108, 015802. [CrossRef]
  29. Sammarruca, F.; and Krastev, P. G. Spin polarized neutron matter within the Dirac-Brueckner-Hartree-Fock approach. Phys. Rev. C 2007, 75, 034315. [CrossRef]
  30. Bombaci, I.; and Lombardo, U.; Asymmetric nuclear matter equation of state. Phys. Rev. C 1991, 44, 1892. [CrossRef]
  31. Li, B. A.; Ramos, À.; Verde, G.; Vidaña I. Eur. Phys. J. A 2014, 50, 9. [CrossRef]
  32. Chen, L.W.; Cai, B.J.; Ko, C.M.; Li, B. A.; Shen, C.; and Xu, J. Higher-order effects on the incompressibility of isospin asymmetric nuclear matter. Phys. Rev. C 2009, 80, 014322. [CrossRef]
  33. Prakash, M.; and Bedell, K. S. Incompressibility of neutron-rich nuclear matter. Phys. Rev. C 1985, 32, 1118(R). [CrossRef]
  34. Shlomo, S.; Kolomietz, V.M.; and G, Colò. Deducing the nuclear-matter incompressibility coefficient from data on isoscalar compression modes. Eur. Phys. J. A 2006, 30, 23-30. [CrossRef]
  35. Garg, U and G, Colò. The compression-mode giant resonances and nuclear incompressibility. Prog. Part. Nucl. Phys. 2018, 101, 55. [CrossRef]
  36. Stone, J. R.; Stone, N. J.; and Moszkowski, S. A. Incompressibility in finite nuclei and nuclear matter. Phys. Rev. C, 2014, 89, 044316. [CrossRef]
  37. Avogadro, P.; and Bertulani, C. A.; Role of pairing in the description of giant monopole resonances. Phys. Rev. C, 2013, 88, 044319. [CrossRef]
  38. Khan, E.; Margueron, J.; and Vidaña, I. Constraining the Nuclear Equation of State at Subsaturation Densities . Phys. Rev. Lett. 2012, 109, 092501. [CrossRef]
  39. Vretenar, D.; Nikšić, T. and Ring, P. A microscopic estimate of the nuclear matter compressibility and symmetry energy in relativistic mean-field models. Phys. Rev. C 2003, 68, 024310. [CrossRef]
  40. Dutra, M.; Lourenço, O.; et al. Relativistic mean-field hadronic models under nuclear matter constraints. Phys. Rev. C 2014, 90, 055203. [CrossRef]
  41. Tagami, S.; Wakasa, T.; and Yahiro, M. Slope parameters determined from CREX and PREX2. Results in Physics 2022, 43, 106037. [CrossRef]
  42. Landau, L. D. The Theory of a Fermi Liquid. JETP 1957 3, 920. [http://jetp.ras.ru/cgi-bin/e/index/e/3/6/p920?a=list]; Landau, L. D. Oscillations in a Fermi Liquid. JETP 1957, 5, 101. [http://jetp.ras.ru/cgi-bin/e/index/e/5/1/p101?a=list]; Landau, L. D. On the theory of the Fermi liquid. JETP 1959, 8, 70. [http://jetp.ras.ru/cgi-bin/dn/e_008_01_0070.pdf].
  43. Vautherin, D.; and Brink, D. M. Hartree-Fock calculations with Skyrme’s interaction. I. Spherical nuclei. Phys. Rev. C 1972, 5, 626. [CrossRef]
  44. Bäckman, S. O.; Källman, C. G.; and Sjöberg, O. Calculation of Landau’s fermi-liquid parameters in pure neutron matter. Phys. Lett. B 1973, 43, 263-266. [CrossRef]
  45. Bäckman, S. O.; Jackson, A. D.; and Speth, J. Landau parameters for nuclear matter using the Skyrme interaction. Phys. Lett. B 1975, 56, 209-211. [CrossRef]
  46. Cao, Li-Gang.; G Colò; and Sagawa, H. Spin and spin-isospin instabilities and Landau parameters of Skyrme interactions with tensor correlations. Phys. Rev. C 2010, 81, 044302. [CrossRef]
  47. Chabanat, E.; Bonche, P.; et al. A Skyrme parametrization from subnuclear to neutron star densities Part II. Nuclei far from stabilities. Nuclear Physics A 1998, 635 231-256. [CrossRef]
  48. Chabanat, E.; Bonche, P.; et al. A Skyrme parametrization from subnuclear to neutron star densities. Nuclear Physics A 1997, 627, 710-746. [CrossRef]
  49. Taqi, A. H.; and Khidher, E. G. Nuclear multipole excitations in the framework of self-consistent Hartree–Fock random phase approximation for Skyrme forces. Pramana -J. Phys., 2019, 93, 60. [CrossRef]
  50. Goriely, S.; Tondeur, F.; and Pearson, J. M. A Hartree-Fock nuclear mass table. Atomic Data and Nuclear Data Tables 2001, 77, 311-381. [CrossRef]
  51. Tselyaev, V.; Lyutorovich, N.; et al. Low-energy M1 excitations in 208Pb and the spin channel of the Skyrme energy-density functional. Phys. Rev. C 2019, 99, 064329. [CrossRef]
  52. Agrawal, B. K.; Shlomo, S.; and Kim Au, V. Determination of the parameters of a Skyrme type effective interaction using the simulated annealing approach. Phys. Rev. C, 2005, 72, 014310. [CrossRef]
  53. Lahiri, J.; Atta, D.; and Basu, D. N. Properties of glitching pulsars in the Skyrme-Hartree-Fock framework. arXiv:2207.13384v3 [nucl-th]. [CrossRef]
  54. Keh-Fei. L.; Hongde, L.; Ma, Z.; Shen, Q; and Moszkowski S. A. Skyrme-Landau parameterization of effective interactions (I). Hartree-Fock ground states. Nuclear Physics A 1991, 534, 1-24. [CrossRef]
  55. Vuong, Au Kim. New Skyrme nucleon-nucleon interaction for the mean-field approximation. Doctoral Dissertation, Texas A & M University, 2003. [http://hdl.handle.net/1969.1/5996].
  56. Dutra, M.; Lourenço O.; and Delfino, A. Consistent Skyrme parametrization and its critical parameter values. J. Phys.: Conf. Ser. 2019, 1291, 012040. [https://iopscience.iop.org/article/10.1088/1742-6596/1291/1/012040/meta].
  57. Nakada, H. Hartree-Fock approach to nuclear matter and finite nuclei with M3Y-type nucleon-nucleon interactions. Phys. Rev. C 2003, 68, 014316. [CrossRef]
  58. Idini, A.; Bennaceur, K.; and Dobaczewski, J. Landau parameters for energy density functionals generated by local finite-range pseudopotentials. J. Phys. G: Nucl. Part. Phys. 2017, 44, 064004 (10pp). [CrossRef]
  59. Margueron, J.; Navarro, J.; and Van Giai N. Phys. Rev. C 2002, 66, 014303. [CrossRef]
  60. Goriely, S.; Chamel, N.; and Pearson, J. M. Further explorations of Skyrme-Hartree-Fock-Bogoliubov mass formulas. XII. Stiffness and stability of neutron-star matter. Phys. Rev. C 2010, 82, 035804. [CrossRef]
  61. Li, B. A.; and Han, X.; Constraining the neutron–proton effective mass splitting using empirical constraints on the density dependence of nuclear symmetry energy around normal density. Physics Letters B 2013, 727, 276-281. [CrossRef]
  62. Oertel, M.; Hempel, M.; Klähn, T.; and Typel, S. Equations of state for supernovae and compact stars. Rev. Mod. Phys., 2017, 89, 1. [CrossRef]
  63. Reed, B. T.; Fattoyev, F. J.; Horowitz C. J.; and Piekarewicz, J. Phys. Rev. Lett. 2021, 126, 172503. [CrossRef]
  64. Estee, J.; Lynch, W. G.; et al. Probing the Symmetry Energy with the Spectral Pion Ratio. Phys. Rev. Lett. 2021, 126, 162701. [CrossRef]
  65. Danielewicz, P.; Singh, P.; and Lee, J. Symmetry energy III: Isovector skins. Nucl. Phys. A 2017, 958, 147. [CrossRef]
  66. Russotto P.; et al.; Results of the ASY-EOS experiment at GSI: The symmetry energy at suprasaturation density. Phys. Rev. C 2016, 94, 034608. [CrossRef]
  67. Senger, P. Probing Dense Nuclear Matter in the Laboratory: Experiments at FAIR and NICA. Universe 2021, 7, 171. [CrossRef]
  68. Zhang, Y.; Liu, M.; Xia C. J.; Li, Z.; and Biswal, S. K.; Constraints on the symmetry energy and its associated parameters from nuclei to neutron stars. Phys. Rev. C 2020, 101, 034303. [CrossRef]
  69. Zhang, N. B.; and Li, B. A. Extracting nuclear symmetry energies at high densities from observations of neutron stars and gravitational waves. Eur. Phys. J. A 2019, 55, 39. [CrossRef]
  70. Xie, W.-J.; and Li, B.-A. Bayesian Inference of High-density Nuclear Symmetry Energy from Radii of Canonical Neutron Stars. The Astrophysical Journal 2019, 883:174 (21pp). [CrossRef]
  71. Tong, H.;, Zhao, P.; and Meng J. Symmetry energy at supra-saturation densities via the gravitational waves from GW170817. Phys. Rev C 2020, 101, 035802. [CrossRef]
  72. Drischler, C.; Furnstahl, R. J.; Melendez, J. A.; & Phillips, D. R. How Well Do We Know the Neutron-Matter Equation of State at the Densities Inside Neutron Stars? A Bayesian Approach with Correlated Uncertainties. Phys. rev. Lett. 2020, 125, 202702. [CrossRef]
  73. Lonardoni, D.; Tews, I.; Gandolfi, S.; & Carlson, J. Nuclear and neutron-star matter from local chiral interactions. Phys. Rev. Research, 2020, 2, 022033(R). [CrossRef]
  74. Li, B.-A.; Cai, B.-J.; Xie, W.-J.; Zhang, N.-B. Progress in Constraining Nuclear Symmetry Energy Using Neutron Star Observables Since GW170817 Universe 2021, 7, 182. [CrossRef]
  75. Nakazato, K.;and Suzuki H. Cooling Timescale for Protoneutron Stars and Properties of Nuclear Matter: Effective Mass and Symmetry Energy at High Densities. The Astrophysical Journal 2019, 878:25 (11pp). [CrossRef]
  76. Yue T.-G.; Chen L.-W.;, Zhang, Z.; and Zhou, Y. Constraints on the symmetry energy from PREX-II in the multimessenger era. Phys. Rev. Research 2022, 4, L022054. [CrossRef]
  77. Xie, W. J.; and Li, B. A. Bayesian Inference of the Symmetry Energy of Superdense Neutron-rich Matter from Future Radius Measurements of Massive Neutron Stars. Astrophys. J. 2020, 899, 4. [CrossRef]
  78. Zhou, Y.; Chen, L.-W.; and Zhang, Z. Equation of state of dense matter in the multimessenger era. Phys. Rev. D 2019, 99, 121301(R). [CrossRef]
  79. Chen, L.-W. Symmetry energy systematics and its high density behavior. EPJ Web of Conferences 2015, 88, 00017. [CrossRef]
  80. Lattimer, J. M.; & Lim, Y. Constraining the symmetry parameters of the nuclear interaction. The Astrophysical Journal 2013, 771:51, 14pp. [CrossRef]
  81. Lynch, W. G.; & Tsang, M. B. Decoding the density dependence of the nuclear symmetry energy. Physics Letters B 2022, 830, 137098. [CrossRef]
  82. Chen, L. W.; Ko, C. M.; and Li, B. A. Nuclear matter symmetry energy and the neutron skin thickness of heavy nuclei. Phys. Rev. C 2005, 72, 064309. [CrossRef]
  83. Li B.-A.; and Magno, M. Curvature-slope correlation of nuclear symmetry energy and its imprints on the crust-core transition, radius, and tidal deformability of canonical neutron stars. Phy. Rev. C 2020, 102, 045807. [CrossRef]
  84. d’Etivaux, N. B.; Guillot, S.; Margueron, J.; et al.New Constraints on the Nuclear Equation of State from the Thermal Emission of Neutron Stars in Quiescent Low-mass X-Ray Binaries. The Astrophysical Journal 2019, 887:48, 16pp. [CrossRef]
  85. Carson, Z.; Steiner, A. W.; and Yagi, K. Constraining nuclear matter parameters with GW170817. [CrossRef]
  86. Choi, S.; Miyatsu, T.; Cheoun, M.; and Saito, K. Constraints on Nuclear Saturation Properties from Terrestrial Experiments and Astrophysical Observations of Neutron Stars The Astrophysical Journal 2021, 909:156, 9pp. [CrossRef]
  87. Drischler, C.; Hebeler, K.; & Schwenk, A. Asymmetric nuclear matter based on chiral two- and three-nucleon interactions. Phys. Rev. C 2016, 93, 054314. [CrossRef]
  88. Newton, W. G.; & Crocombe, G. Nuclear symmetry energy from neutron skins and pure neutron matter in a Bayesian framework. Phy Rev C 2021, 103, 064323. [CrossRef]
  89. Grams, G.; Somasundaram, R.; Margueron, J.; and Khan, E. Nuclear incompressibility and speed of sound in uniform matter and finite nuclei. Phys. Rev. C 2022, 106, 044305. [CrossRef]
  90. Sagawa, H.; Yoshida, S.; and Cao, L.-G. Sagawa H, Yoshida S and Cao Li-Gang, EoS from terrestrial experiments: Static and dynamic polarizations of nuclear density .AIP Conference Proceedings 2019, 2127, 020002. [CrossRef]
  91. Tews, I.; Lattimer, J. M.; Ohnishi, A.; & Kolomeitsev, E. E. Symmetry Parameter Constraints from a Lower Bound on Neutron-matter Energy. The Astrophysical Journal 2017, 848, 105. [CrossRef]
  92. Zhang, N. B.; Cai, B. J.; Li, B. A.; Newton, W. G.; & Xu, J. How tightly is the nuclear symmetry energy constrained by a unitary Fermi gas?. Nucl. Sci. Tech. 2017, 28, 181. [CrossRef]
  93. Mondal, C.; Agrawal, B. K.; De, J. N., et al. Interdependence of different symmetry energy elements. Phy. Rev C 2017, 96, 021302(R). [CrossRef]
  94. Sagawa, H.; Yoshida, S.; et al. Isospin dependence of incompressibility in relativistic and nonrelativistic mean field calculations. Phys. Rev. C 2007, 76, 034327; 2008 77, 049902(E). [CrossRef]
  95. Li, T.; et al. Isotopic Dependence of the Giant Monopole Resonance in the Even-A 112-124Sn Isotopes and the Asymmetry Term in Nuclear Incompressibility. 2007 99, 162503. [https://doi.org/10.1103/PhysRevLett.99.162503]; Li, T.; et al. Isoscalar giant resonances in the Sn nuclei and implications for the asymmetry term in the nuclear-matter incompressibility. Phys. Rev. Lett. Phys. Rev. C 2010, 81, 034309. [https://doi.org/10.1103/PhysRevC.81.034309]. [CrossRef]
  96. Cozma, M. D. Feasibility of constraining the curvature parameter of the symmetry energy using elliptic flow data. Eur. Phys. J. A 2018, 54, 40. [CrossRef]
  97. Centelles, M.; Roca-Maza, X.; Viñas, X.; Warda, M. Nuclear Symmetry Energy Probed by Neutron Skin Thickness of Nuclei. Phys. Rev. Lett. 2009, 102, 122502. [CrossRef]
  98. Cai, B. J.; & Chen, L. W. Constraints on the skewness coefficient of symmetric nuclear matter within the nonlinear relativistic mean field model. Nucl Sci Tech 2017, 28, 185. [CrossRef]
  99. Farine, M.; Pearson, J. M.; & Tondeur, F. Nuclear-matter incompressibility from fits of generalized Skyrme force to breathing-mode energies. Nucl. Phy A 1997, 615, 135. [CrossRef]
  100. Xie, W-J.; and Li B-A. Bayesian inference of the incompressibility, skewness and kurtosis of nuclear matter from empirical pressures in relativistic heavy-ion collisions. J. Phys. G: Nucl. Part. Phys. 2021, 48, 025110. [CrossRef]
  101. Steiner, A. W.; Lattimer; J. M.; Brown, E. F. The Equation of State from Observed Masses and Radii of Neutron Stars. Astrophys. J. 2010, 722, 33-54. [CrossRef]
  102. Alam, N.; Agrawal, B. K.; De, J. N.; Samaddar, S. K. and Colò G. Phys. Rev. C 2014, 90, 054317. [CrossRef]
  103. Alam, N.; Agrawal, B. K.; et al. Strong correlations of neutron star radii with the slopes of nuclear matter incompressibility and symmetry energy at saturation. Phys. Rev. C 2016, 94, 052801(R). [CrossRef]
  104. Baym. G.; Bethe, H. A. and Pethick, C. J. Neutron star matter. Nucl. Phys. A 1971, 175, 225-271. [CrossRef]
  105. Baym, G.; Pethick, C. J.; and Sutherland P. The Ground State of Matter at High Densities: Equation of State and Stellar Models . Astrophys. J 1971, 170, 299-317. [CrossRef]
  106. De, J. N.; Samaddar, S. K.; and Agrawal, B. K. Reassessing nuclear matter incompressibility and its density dependence. Phys. Rev. C 2015, 92, 014304. [CrossRef]
  107. Capano, C.; Tews, I.; et al. Stringent constraints on neutron-star radii from multimessenger observations and nuclear theory. Nat Astron 2020, 4, 625-632. [CrossRef]
  108. Raaijmakers, G.; Greif, S. K.; et al. Constraints on the Dense Matter Equation of State and Neutron Star Properties from NICER’s Mass–Radius Estimate of PSR J0740 + 6620 and Multimessenger Observations The Astrophysical Journal Letters 2021, 918:L29, 13pp. [CrossRef]
  109. Miller, M. C.; Lamb, F. K.; et al. The Radius of PSR J0740+6620 from NICER and XMM-Newton Data. The Astrophysical Journal Letters, 918:L28 (31pp), 2021. [CrossRef]
  110. Pang P. T. H.; Tews. I. et al. Nuclear Physics Multimessenger Astrophysics Constraints on the Neutron Star Equation of State: Adding NICER’s PSR J0740 + 6620 Measurement. The Astrophysical Journal, 2021, 922:14, 9pp. [CrossRef]
  111. Jiang J.-L.; Tang S.-P.; et al. The Equation of State and Some Key Parameters of Neutron Stars: Constraints from GW170817, the Nuclear Data, and the Low-mass X-Ray Binary Data. The Astrophysical Journal 2019, 885:39, 10pp. [CrossRef]
  112. Abbott, R.; Abbott, T. D. et al. GW190814: Gravitational Waves from the Coalescence of a 23 Solar Mass Black Hole with a 2.6 Solar Mass Compact Object. (LIGO Scientific Collaboration and Virgo Collaboration), Astrophys. J. 2020, 896, L44. [CrossRef]
  113. Bauswein, A.; Blacker, S. et al. Systematics of prompt black-hole formation in neutron star mergers. Phys. Rev. D 2021, 103, 123004. [CrossRef]
  114. Bauswein, A.; Janka, H.-T. Hebeler, K.; and Schwenk A.; Equation-of-state dependence of the gravitational-wave signal from the ring-down phase of neutron-star mergers. Phys. Rev. D 2012, 86, 063001. [CrossRef]
  115. Annala, E.; Gorda, T.; Kurkela, A.; & Vuorinen, A.; Phys. Rev. Lett. 2018, 120, 172703. [CrossRef]
  116. Fattoyev, F. J.; Piekarewicz, J.; and Horowitz, C. J. Neutron Skins and Neutron Stars in the Multimessenger Era. Phys. Rev. Lett. 2018, 120, 172702. [CrossRef]
  117. Bauswein, A.; Just, O.; et al. Neutron-star Radius Constraints from GW170817 and Future Detections. The Astrophysical Journal Letters, 2017, 850:L34 (5pp). [CrossRef]
  118. Bauswein, A.; Baumgarte, T. W,; and Janka, H. T.; Prompt Merger Collapse and the Maximum Mass of Neutron Stars. Phys. Rev. Lett. 2013, 111, 131101. [CrossRef]
  119. Perego, A.; Logoteta, D.; et al. Probing the Incompressibility of Nuclear Matter at Ultrahigh Density through the Prompt Collapse of Asymmetric Neutron Star Binaries. Phys. Rev. Lett. 2022, 129, 032701. [CrossRef]
  120. Shibata, M.; Taniguchi, K; and Uryū, K. Merger of binary neutron stars with realistic equations of state in full general relativity. Phys. Rev. D 2005, 71, 084021. [CrossRef]
  121. Hotokezaka, k.;, Kyutoku K., Okawa, H.; Shibata M.; and Kiuchi K. Binary neutron star mergers: Dependence on the nuclear equation of state. Phys. Rev. D 2011, 83, 124008. [CrossRef]
  122. Köppel, S.; Bovard, L.; and Rezzolla, L. A General-relativistic Determination of the Threshold Mass to Prompt Collapse in Binary Neutron Star Mergers. The Astrophysical Journal Letters, 2019 872:L16, 5pp. [CrossRef]
  123. Kashyap, R.; Das, A.; et al. Numerical relativity simulations of prompt collapse mergers: Threshold mass and phenomenological constraints on neutron star properties after GW170817. Phys. Rev. D 2022, 105, 103022. [CrossRef]
  124. Glendenning, N. K.; Compact Stars: Nuclear Physics, Particle Physics, and General Relativity (Springer, Berlin, 2000). [CrossRef]
  125. Margaritis, Ch.; Koliogiannis, P. S.; and Moustakidis, Ch. C. Speed of sound constraints on maximally rotating neutron stars. Phys. Rev. D 2020, 101, 043023. [CrossRef]
  126. Koliogiannis, P. S.; and Moustakidis, C. C. Constraints on the equation of state from the stability condition of neutron stars. Astrophys. Space Sci. 2019, 364, 52. [CrossRef]
  127. Blaizot, J. P. Nuclear compressibilities Phys. Rep. 1980, 64, 171-248. [CrossRef]
  128. Zhang, N. B.; and Li, B. A. Impact of symmetry energy on sound speed and spinodal decomposition in dense neutron-rich matter. Eur. Phys. J. A 2023, 59, 86. [CrossRef]
  129. Hartle, J. B. Bounds on the mass and moment of inertia of non-rotating neutron stars. Phys. Rep. 1978, 46, 201-247. [CrossRef]
  130. Margaritis, C.; Koliogiannis, P. S.; and Moustakidis, C. C. Speed of sound constraints on maximally rotating neutron stars. Phys. Rev. D 2020, 101, 043023. [CrossRef]
  131. Reed, B. and Horowitz, C. J. Large sound speed in dense matter and the deformability of neutron stars. Phys. Rev. C 2020, 101, 045803.
  132. Cottam, J.; Paerels, F. & Mendez, M. Gravitationally redshifted absorption lines in the X-ray burst spectra of a neutron star. Nature 2002, 420, 51-54. [CrossRef]
  133. Hambaryan, V.; Neuhäuser, R.; Suleimanov, V.; and Werner, K. J. Phys.: Conf. Ser. 2014, 496, 012015. [CrossRef]
  134. Hambaryan, V.; Suleimanov, V.; Haberl, F. et al., The compactness of the isolated neutron star RXJ0720.4-3125. Astronomy & Astrophysics 2017, 601, A108. [CrossRef]
  135. Tang, S. P.; Jiang, J. L.; et al. The Masses of Isolated Neutron Stars Inferred from the Gravitational Redshift Measurements. The Astrophysical Journal 2020, 888, 45. [CrossRef]
  136. Sotani, H.; Iida, K.; Oyamatsu, K.; and Ohnishi, A. Mass and radius formulas for low-mass neutron stars. Prog. Theor. Exp. Phys. 2014, 5, 051E01. [CrossRef]
  137. Sotani, H.; Nishimura, N.; and Naito, T. New constraints on the neutron-star mass and radius relation from terrestrial nuclear experiments. Prog. Theor. Exp. Phys. 2022, 4, 041D01. [CrossRef]
  138. Carlson, B. V.; Dutra, M; Lourenço, O.; and Margueron, J. Low-energy nuclear physics and global neutron star properties. Phys. Rev. C 2023, 107, 035805. [CrossRef]
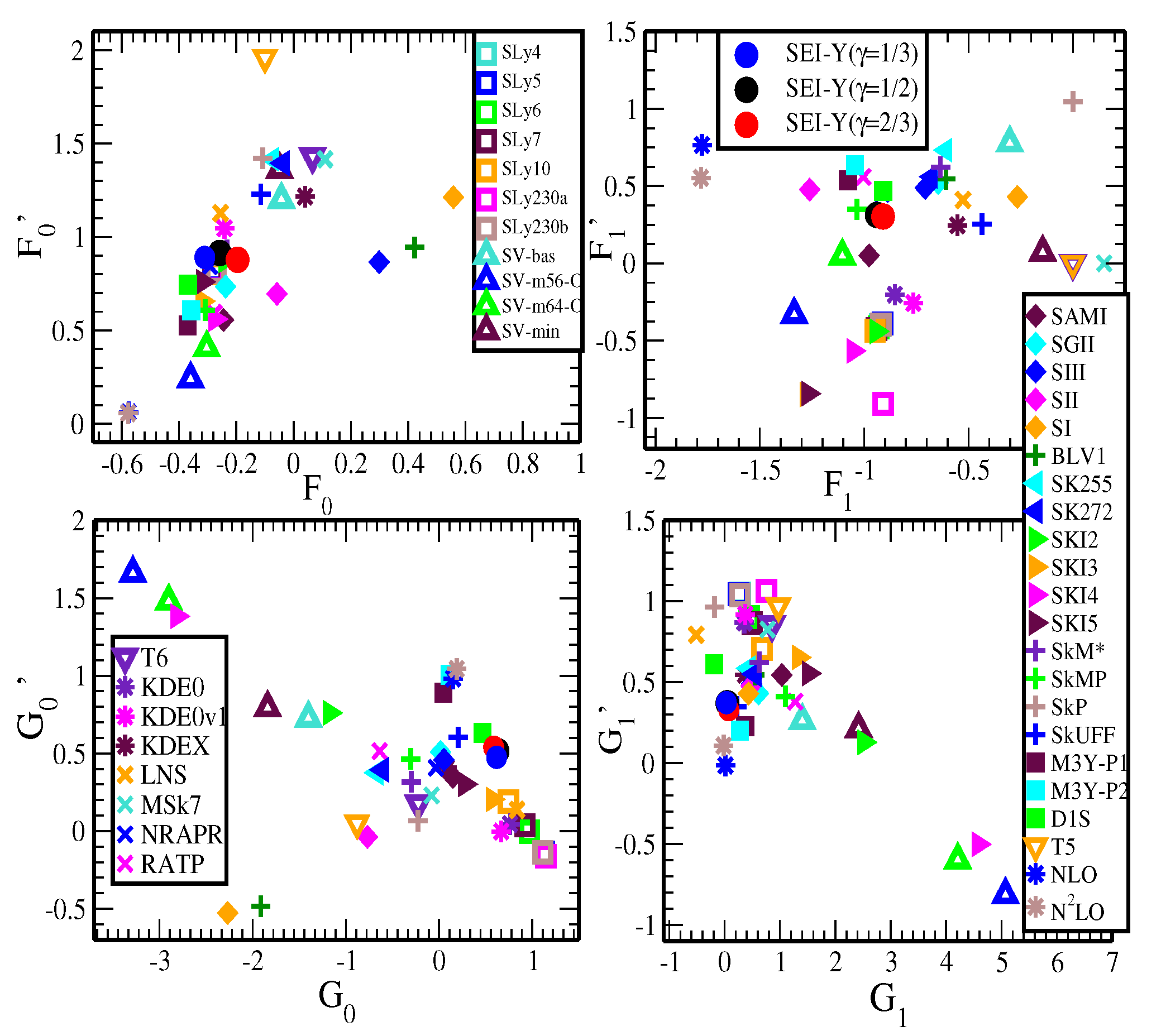
Preprints 96527 g001
Figure 1. Landau parameters for SEI-Y( γ = 1 / 2 ) parameter sets compared with different Skyrme sets (SLy4, SLy5, SLy6, SLy7, SLy10, SLy230a, SLy230b, SI, SII, SIII, BLV1, SGII, SkM*, RATP, SkP, T6, KDE0, KDE0v1, SK255, SKI2, SKI3, SKI4, SKI5, SkMP, LNS, SV-bas, SV-m56-O, SV-m64-O, SV-min, MSk7, T5, KDEX, NRAPR, SAMi, SK272, SkUFF [47,48,49,50,51,52,53,54,55,56]), Gogny interaction (M3Y-P1, M3Y-P2, D1S [57]), and Chiral effective interactions [58].
Figure 1. Landau parameters for SEI-Y( γ = 1 / 2 ) parameter sets compared with different Skyrme sets (SLy4, SLy5, SLy6, SLy7, SLy10, SLy230a, SLy230b, SI, SII, SIII, BLV1, SGII, SkM*, RATP, SkP, T6, KDE0, KDE0v1, SK255, SKI2, SKI3, SKI4, SKI5, SkMP, LNS, SV-bas, SV-m56-O, SV-m64-O, SV-min, MSk7, T5, KDEX, NRAPR, SAMi, SK272, SkUFF [47,48,49,50,51,52,53,54,55,56]), Gogny interaction (M3Y-P1, M3Y-P2, D1S [57]), and Chiral effective interactions [58].
Preprints 96527 g001
Preprints 96527 g002
Figure 2. Landau parameters as a function of density using SEI-Y( γ = 1 / 2 ) set. Saturation density ρ 0 =0.158 f m − 3 is denoted by a grey dashed vertical line.
Figure 2. Landau parameters as a function of density using SEI-Y( γ = 1 / 2 ) set. Saturation density ρ 0 =0.158 f m − 3 is denoted by a grey dashed vertical line.
Preprints 96527 g002
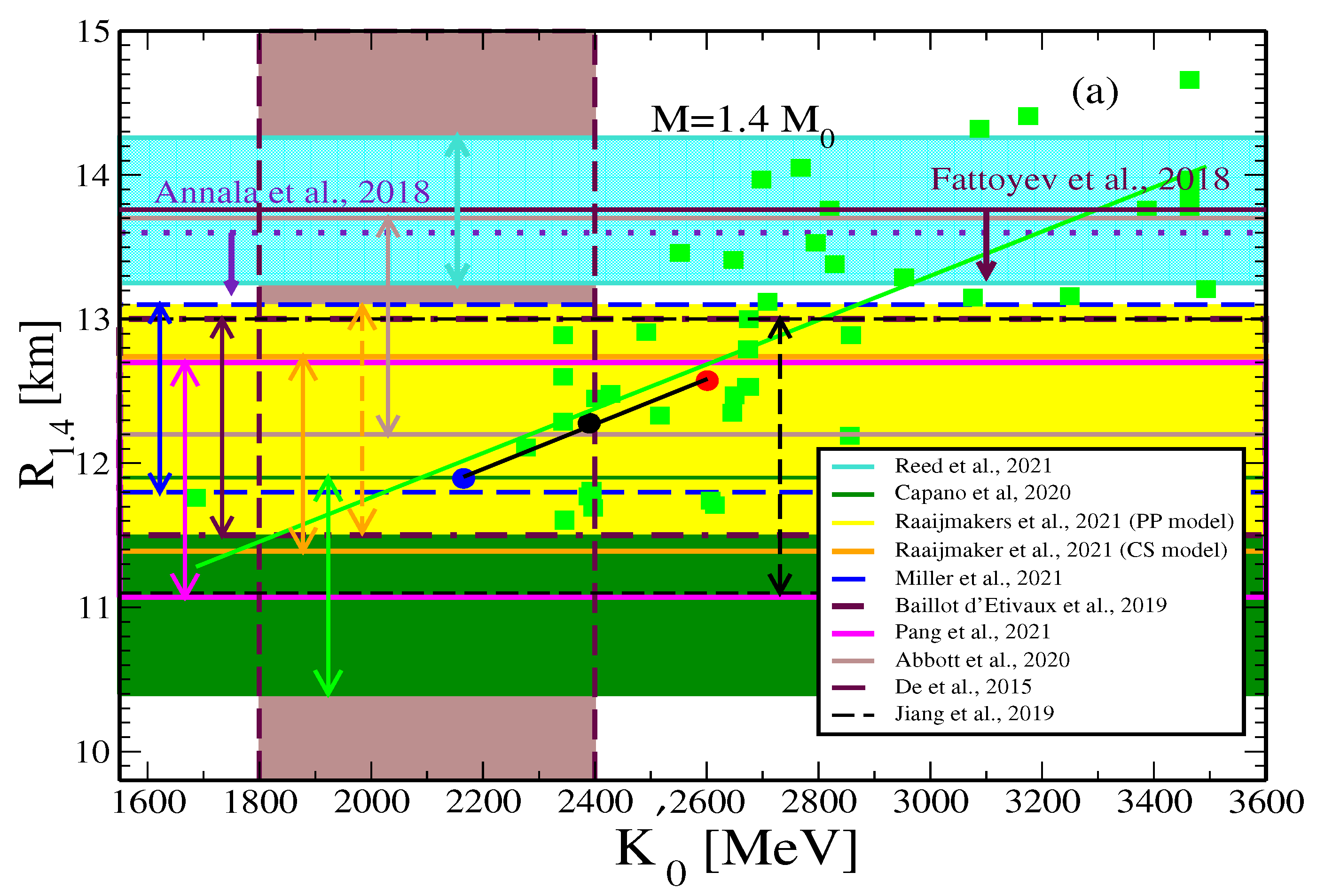
Preprints 96527 g003
Figure 3. R 1.4 of 1.4 M 0 neutron stars versus the slope of the incompressibility obtained using different EoS of SEI-Y having γ =1/3, 1/2, and 2/3. The shaded region data of R 1.4 are taken from: cyan [Reed et al., 2021 [63], dark green [Capano et al, 2020 [107], yellow and orange [Raaijmakers et al., 2021 (PP model & CS model) respectively [108], blue [Miller et al., 2021 [109], maroon [Baillot d’ Etivaux et al., 2019 [84], magenta [Pang et al., 2021 [110], black dashed [Jiang et al., 2019 [111] and brown [Abbott et al., 2020 [112].
Figure 3. R 1.4 of 1.4 M 0 neutron stars versus the slope of the incompressibility obtained using different EoS of SEI-Y having γ =1/3, 1/2, and 2/3. The shaded region data of R 1.4 are taken from: cyan [Reed et al., 2021 [63], dark green [Capano et al, 2020 [107], yellow and orange [Raaijmakers et al., 2021 (PP model & CS model) respectively [108], blue [Miller et al., 2021 [109], maroon [Baillot d’ Etivaux et al., 2019 [84], magenta [Pang et al., 2021 [110], black dashed [Jiang et al., 2019 [111] and brown [Abbott et al., 2020 [112].
Preprints 96527 g003
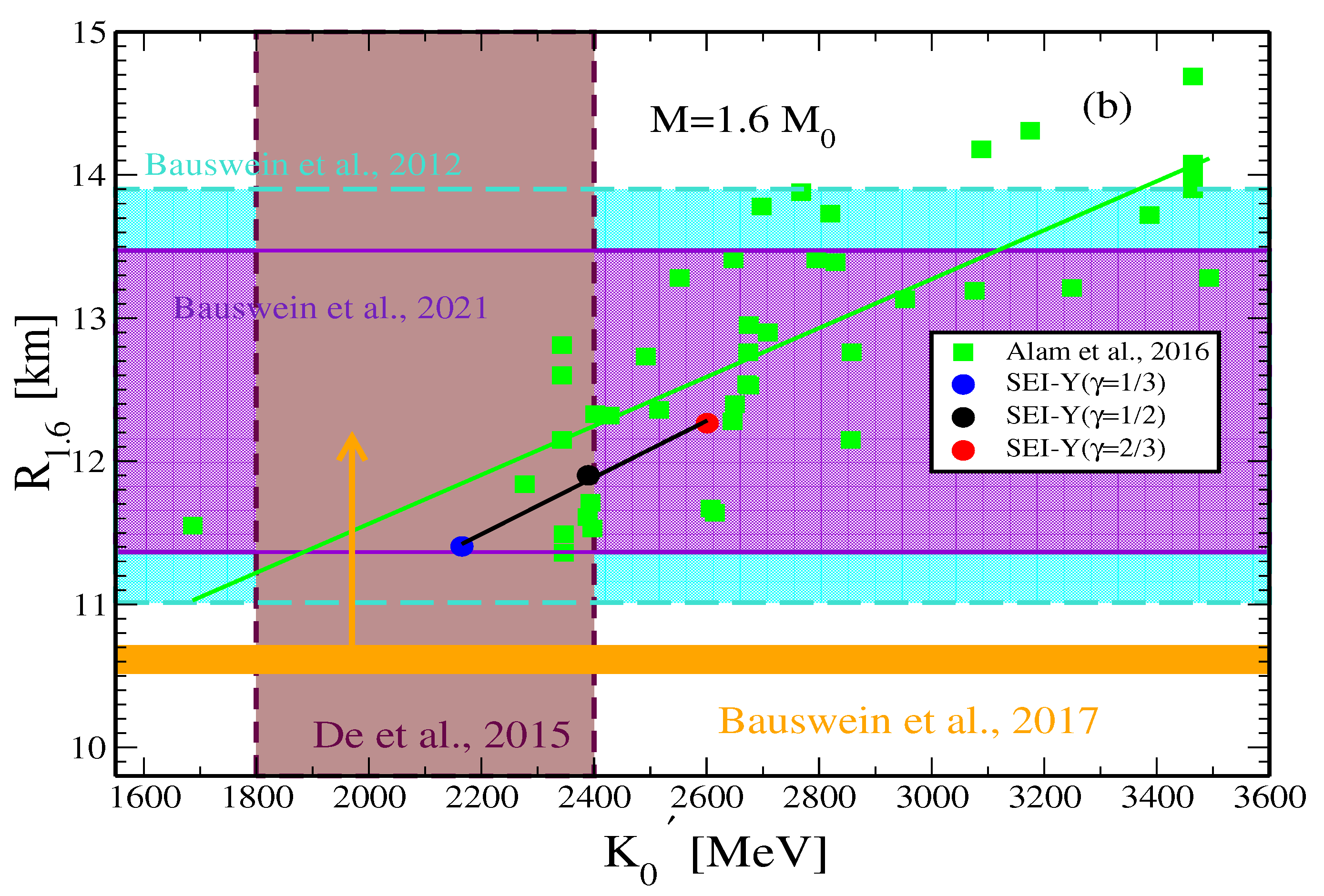
Preprints 96527 g004
Figure 4. R 1.6 of 1.6 M 0 neutron stars versus the slope of the incompressibility obtained using different EoS of SEI-Y having γ =1/3, 1/2, and 2/3. The violet and cyan shaded region data of R 1.6 are calculated from Table IX of [113] and Table I of [114].
Figure 4. R 1.6 of 1.6 M 0 neutron stars versus the slope of the incompressibility obtained using different EoS of SEI-Y having γ =1/3, 1/2, and 2/3. The violet and cyan shaded region data of R 1.6 are calculated from Table IX of [113] and Table I of [114].
Preprints 96527 g004
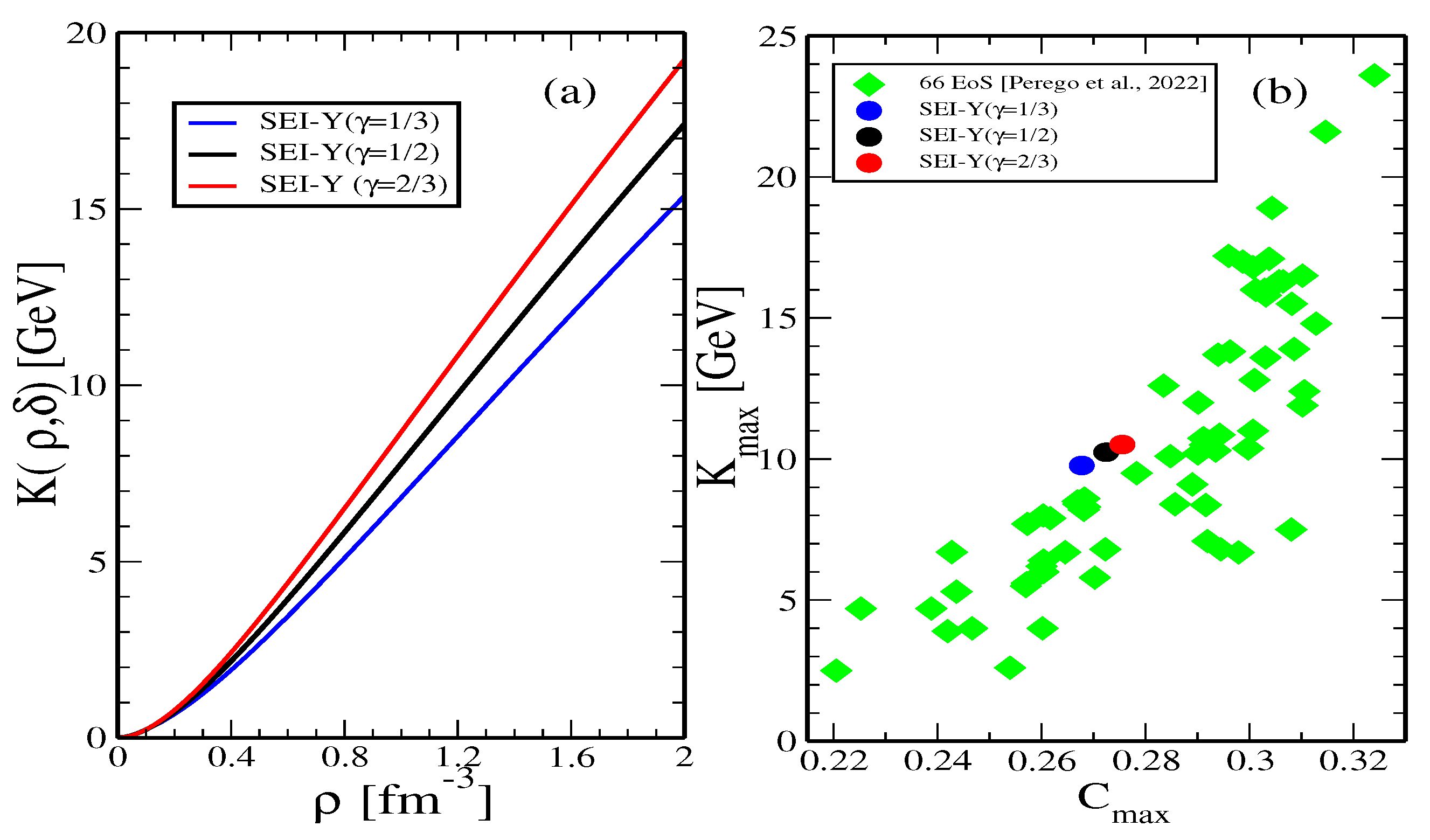
Preprints 96527 g005
Figure 5. (a) K( ρ , δ ) as a function of density in NSM for the SEI-Y( γ = 1 / 3 ), SEI-Y( γ = 1 / 2 ), and SEI-Y( γ = 2 / 3 ) EoS, (b) K m a x as a function of the compactness of the heaviest NS for the three EoS of SEI-Y. Green diamonds are the 66 EoS results taken from [119].
Figure 5. (a) K( ρ , δ ) as a function of density in NSM for the SEI-Y( γ = 1 / 3 ), SEI-Y( γ = 1 / 2 ), and SEI-Y( γ = 2 / 3 ) EoS, (b) K m a x as a function of the compactness of the heaviest NS for the three EoS of SEI-Y. Green diamonds are the 66 EoS results taken from [119].
Preprints 96527 g005
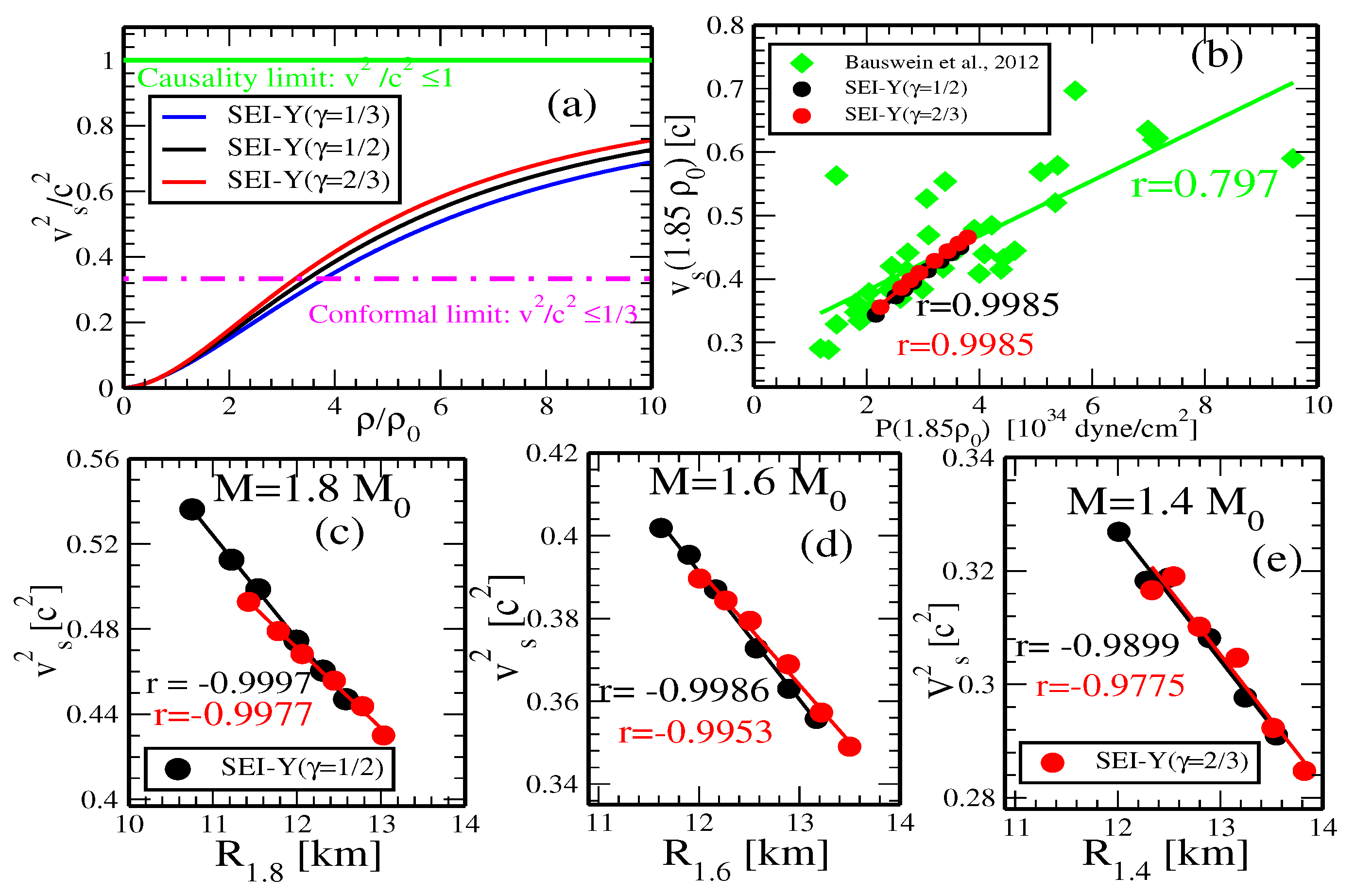
Preprints 96527 g006
Figure 6. (a) Speed of sound in NSM as a function density, where δ for each ρ is the β -equilibrium value, obtained for the three EoS corresponding to γ = 1 / 3 , 1 / 2 , and 2 / 3 of SEI-Y. The magenta and green line is the conformal and Casual limit respectively. (b) Speed of sound as a function of pressure at density (1.85 ρ 0 ) in NSM for SEI-Y ( 1 / 2 and 2 / 3 ) EoS compared with the results of Bauswein et al., 2012 [114]. The square speed of sound at the central densities of 1.8 M ⊙ , 1.6 M ⊙ and 1.4 M ⊙ NSs as a function of radius R1.8, R1.6 and R1.4 for the SEI ( 1 / 2 and 2 / 3 ) EoSs corresponding to different values of L in the range 70-110 MeV shown in panels (c), (d) and (e), respectively.
Figure 6. (a) Speed of sound in NSM as a function density, where δ for each ρ is the β -equilibrium value, obtained for the three EoS corresponding to γ = 1 / 3 , 1 / 2 , and 2 / 3 of SEI-Y. The magenta and green line is the conformal and Casual limit respectively. (b) Speed of sound as a function of pressure at density (1.85 ρ 0 ) in NSM for SEI-Y ( 1 / 2 and 2 / 3 ) EoS compared with the results of Bauswein et al., 2012 [114]. The square speed of sound at the central densities of 1.8 M ⊙ , 1.6 M ⊙ and 1.4 M ⊙ NSs as a function of radius R1.8, R1.6 and R1.4 for the SEI ( 1 / 2 and 2 / 3 ) EoSs corresponding to different values of L in the range 70-110 MeV shown in panels (c), (d) and (e), respectively.
Preprints 96527 g006
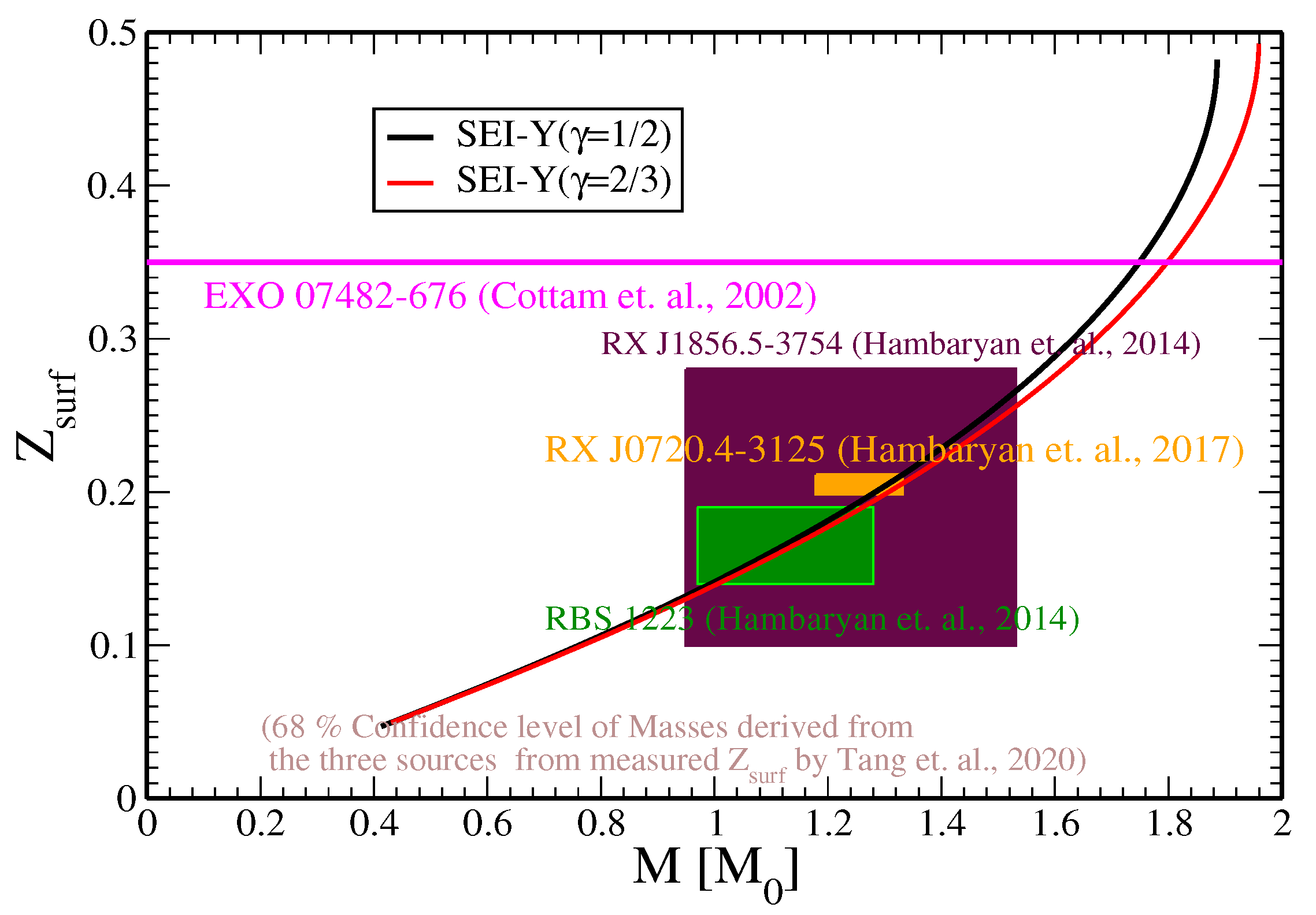
Preprints 96527 g007
Figure 7. Gravitational redshift at the neutron star surface as a function of the stellar gravitational mass for the SEI-Y ( γ = 1 / 2 ) and SEI-Y ( γ = 2 / 3 ) EoSs. The extracted ranges for the three NSs, RBS 1223, RX J0720.4-3125, and RX J1856.5-3754 are shown in different shades.
Figure 7. Gravitational redshift at the neutron star surface as a function of the stellar gravitational mass for the SEI-Y ( γ = 1 / 2 ) and SEI-Y ( γ = 2 / 3 ) EoSs. The extracted ranges for the three NSs, RBS 1223, RX J0720.4-3125, and RX J1856.5-3754 are shown in different shades.
Preprints 96527 g007
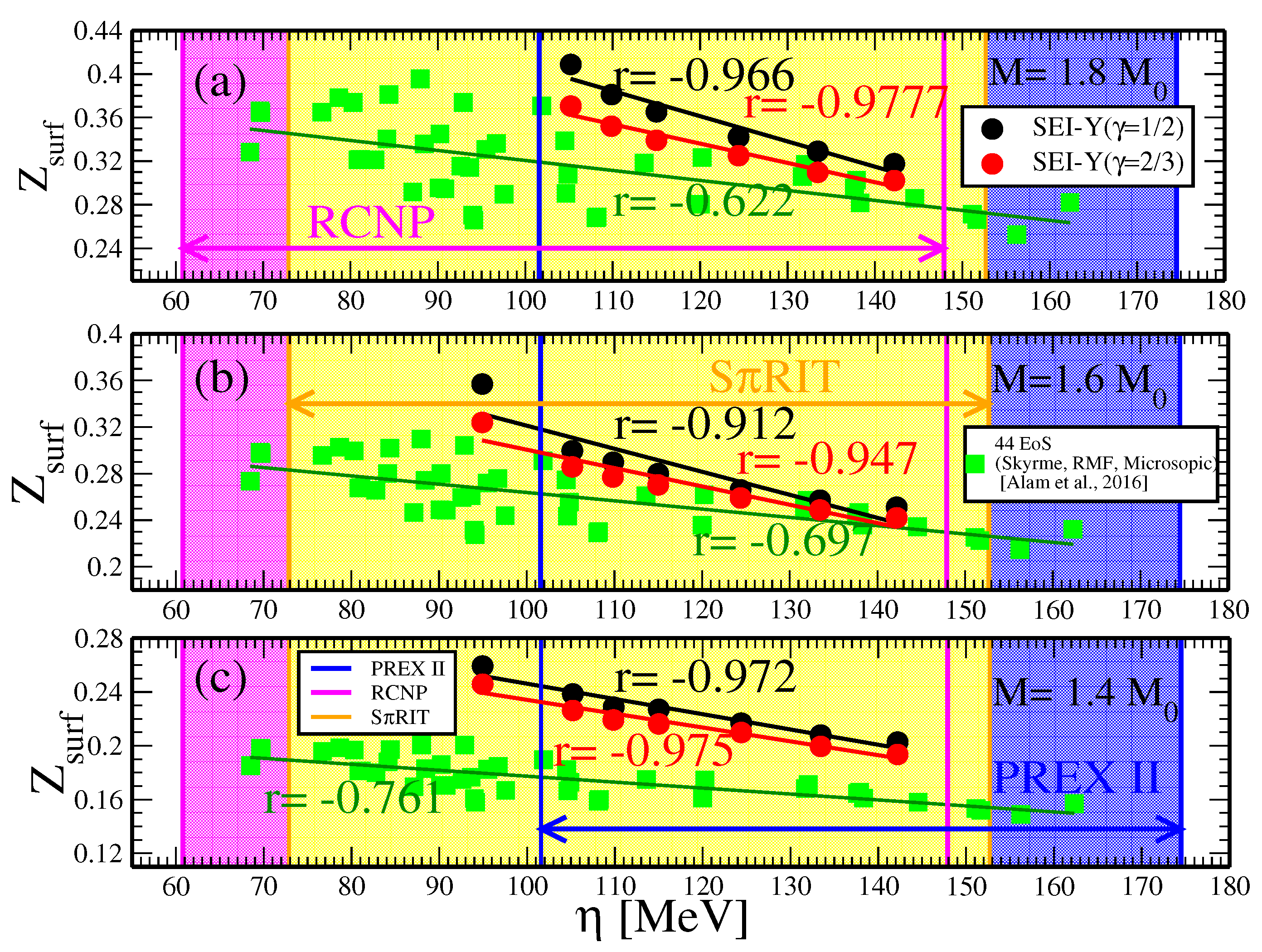
Preprints 96527 g008
Figure 8. Z s u r f as a function of η for 1.8 M 0 , 1.6 M 0 , and 1.4 M 0 NS for SEI-Y ( γ = 1 / 2 ) and SEI-Y ( γ = 2 / 3 ) EoSs. Shaded region is the constrained value of η for PREX II [Blue], RCNP [magenta], and S π RIT [yellow] [137]. The green diamonds are the data for the 44-EoSs of Ref.[103].
Figure 8. Z s u r f as a function of η for 1.8 M 0 , 1.6 M 0 , and 1.4 M 0 NS for SEI-Y ( γ = 1 / 2 ) and SEI-Y ( γ = 2 / 3 ) EoSs. Shaded region is the constrained value of η for PREX II [Blue], RCNP [magenta], and S π RIT [yellow] [137]. The green diamonds are the data for the 44-EoSs of Ref.[103].
Preprints 96527 g008
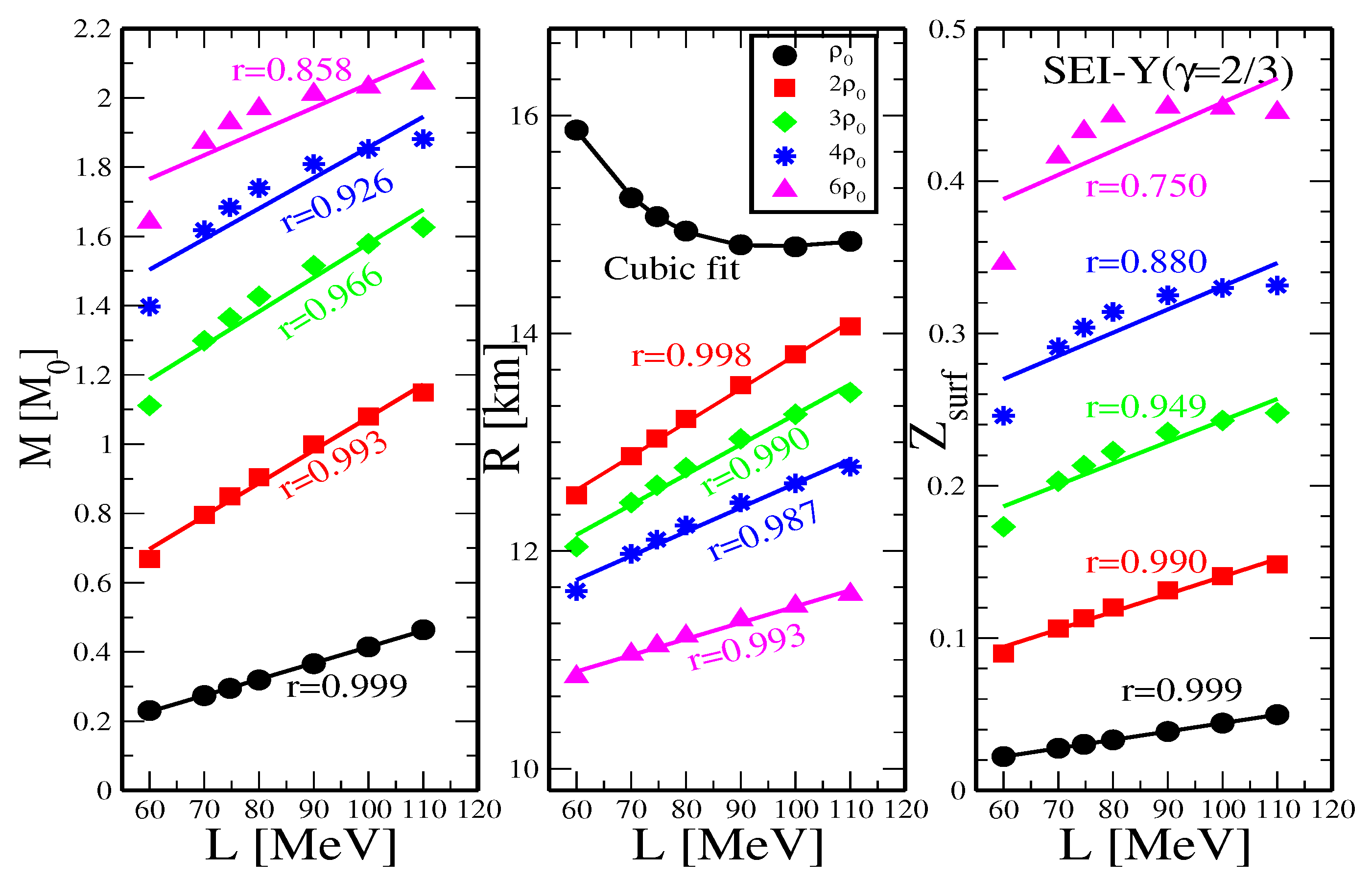
Preprints 96527 g009
Figure 9. (a) Neutron star masses, (b) Neutron star radius (c) Z s u r f corresponding to central densities of ρ 0 , 2 ρ 0 , 3 ρ 0 , 4 ρ 0 , and 6 ρ 0 as a function of L.
Figure 9. (a) Neutron star masses, (b) Neutron star radius (c) Z s u r f corresponding to central densities of ρ 0 , 2 ρ 0 , 3 ρ 0 , 4 ρ 0 , and 6 ρ 0 as a function of L.
Preprints 96527 g009
Table 1. The twelve parameters for the SEI-Y EoSs corresponding to γ =1/3, 1/2 and 2/3.
Table 1. The twelve parameters for the SEI-Y EoSs corresponding to γ =1/3, 1/2 and 2/3.
γ b [ f m 3 ] α [fm] ε e x [MeV] ε e x l [MeV] ε 0 [MeV]
1/3 0.4161 0.4232 -129.344 -86.229 -82.245
1/2 0.5880 0.4242 -127.707 -85.138 -50.600
2/3 0.7796 0.4250 -126.390 -84.260 -34.904
ε 0 l [MeV] ε γ [MeV] ε γ l [MeV] t 0 [ M e V f m 3 ] x 0 W 0 [ M e V f m 5 ]
-47.189 104.428 74.006 333.5 1.151 119.3
-27.509 73.124 54.250 566.7 0.664 118.4
-17.859 58.095 44.690 647.4 0.520 118.2
Table 2. Nuclear matter properties at saturation density ρ 0 for three EoSs SEI-Y( γ = 1 / 3 ), SEI-Y( γ = 1 / 2 ) & SEI-Y( γ = 2 / 3 ).
Table 2. Nuclear matter properties at saturation density ρ 0 for three EoSs SEI-Y( γ = 1 / 3 ), SEI-Y( γ = 1 / 2 ) & SEI-Y( γ = 2 / 3 ).
SEI-Y( γ = 1 / 3 ) SEI-Y( γ = 1 / 2 ) SEI-Y( γ = 2 / 3 )
ρ 0 [ f m − 3 ] 0.161 0.158 0.156
e 0 [MeV] -16.04 -16 -16
( m s * / m ) 0.664 0.686 0.666
( m v * / m ) 0.685 0.621 0.622
K 0 [MeV] 220.346 237.643 253.219
Q 0 [MeV] -478.763 -461.807 -437.529
ρ s a t , 2 [ f m − 3 ] -0.163 -0.149 -0.138
E s y m [MeV] 35.5 35 34.5
L [MeV] 74.4 74.7 74.7
K s y m [MeV] -103.487 -101.471 -99.252
Q s y m [MeV] 273.008 252.462 234.0525
K τ [MeV] -388.232 -404.509 -418.381
e P N M [MeV] 19.46 19 18.5
K P N M [MeV] 116.858 136.172 153.966
Q P N M [MeV] -205.754 -209.345 -203.476
Table 3. Symmetric Nuclear Matter incompressibility
Table 3. Symmetric Nuclear Matter incompressibility
Expt./Theory K 0 [MeV]
Analysis of experimental data of the GMR
S. Shlomo et al., (2006) [34] 240 ± 20
U. Garg et al., (2018) [35] 240 ± 20
J.R. Stone et al., 2014 [36] 250-315
P. Avogadro & C.A. Bertulani, 2013 [37] 200
Relativistic and non-relativistic mean-field calculations of the GMR
E. Khan et al., 2012 [38] 230 ± 40
D. Vretenar et al.,2003 [39] 250-270
M. Dutra et al., 2012 [22] 246±41
M. Dutra et al., 2014 [40] 271±86
Analysis of PREX-II and CREX data
S. Tagami et al., 2022 [41] 210-275
Table 4. Landau parameters at the saturation density for SEI-Y( γ = 1 / 3 ), SEI-Y( γ = 1 / 2 ), and SEI-Y( γ = 2 / 3 ) EoS.
Table 4. Landau parameters at the saturation density for SEI-Y( γ = 1 / 3 ), SEI-Y( γ = 1 / 2 ), and SEI-Y( γ = 2 / 3 ) EoS.
EoS F 0 F 1 F 2 F 0 ′ F 1 ′ F 2 ′
SEI-Y( γ = 1 / 3 ) -0.31 -0.913 -0.247 0.89 0.304 0.0826
SEI-Y( γ = 1 / 2 ) -0.257 -0.939 -0.253 0.914 0.313 0.0845
SEI-Y( γ = 2 / 3 ) -0.195 -0.9091 -0.2447 0.8771 0.303 0.0816
EoS G 0 G 1 G 2 G 0 ′ G 1 ′ G 2 ′
SEI-Y( γ = 1 / 3 ) 0.617 0.0321 0.0087 0.474 0.3739 0.1013
SEI-Y( γ = 1 / 2 ) 0.627 0.0479 0.0129 0.514 0.3690 0.0998
SEI-Y( γ = 2 / 3 ) 0.584 0.0744 0.02001 0.5401 0.3297 0.0887
Table 5. Nuclear matter properties predicted using Landau parameter at saturation density for SEI-Y( γ = 1 / 3 ), SEI-Y( γ = 1 / 2 ), and SEI-Y( γ = 2 / 3 ) sets.
Table 5. Nuclear matter properties predicted using Landau parameter at saturation density for SEI-Y( γ = 1 / 3 ), SEI-Y( γ = 1 / 2 ), and SEI-Y( γ = 2 / 3 ) sets.
SEI-Y( γ ) ρ 0 K 0 m s * m m s * m v * E s y m E σ E σ τ m v s 2
( γ ) [ f m − 3 ] [MeV] [MeV] [MeV] [MeV] [MeV]
( 1 / 3 ) 0.161 230.59 0.695 1.101 35.10 30.02 27.38 24.47
( 1 / 2 ) 0.158 237.74 0.686 1.104 34.048 28.95 26.94 26.38
( 2 / 3 ) 0.156 263.14 0.696 1.101 34.10 28.79 27.97 27.94
Table 6. Symmetry energy at several densities
Table 6. Symmetry energy at several densities
Expt/Observation/Theory E s y m ( ρ 0 ) [MeV]
Mean-field calculations and Astrophysical Observations
Dutra et al.,2012 [22] 27-36
B A Li and Han, 2013 [61] 31.6±0.92
Oertel et al., 2017 [62] 31.7 ± 3.2
PREX II Experiment Reed et al., 2021 [63] 38.1±4.7
Charged Pion Spectra at high momenta Estee et al., 2021 [64] 32.5-38.1
Charge exchange and elastic scattering data Danielewicz et al., 2017 [65] 33.5-36.4
Expt/Observation/Theory E s y m ( 2 ρ 0 ) [MeV]
SEI-Y( γ = 1 / 3 ) 55.74
SEI-Y( γ = 1 / 2 ) 55.38
SEI-Y( γ = 2 / 3 ) 54.93
HIC and Transport Calculations
ASY-EoS experiment at GSI [66] 46-54
UrQMD transport calculation [67] 55±5
Zhang et al., 2020 [68] 35-55
Gravitational Waves Zhang & Li (2019) [69] 46.9 ± 10.1
Xie & Li (2019) [70] 39.2 − 8.2 + 12.1
Tong et al., 2020[71] 60.7±10.9
Chiral Effective Field Theory
Drischler et al., 2020 [72] 45±3
Lonardoni et al.,2020 [73] 45±5
Neutron Star Observables B A Li et al., 2021 [74] 51±13
Nakazato & Suzuki 2019 [75] 40-60
Yue et al., 2022 [76] 62.8±15.9
Xie and Li 2020 [77] 47 − 22 + 23
Zhou et al., 2019[78] [ 39.4 + 7.5 − 6.4 , 54.5 + 3.1 − 3.2 ]
Mean-Field Calculations Chen et al., 2015 [79] 40.2±12.8
Table 7. L, K s y m and K τ at saturation density from different experimental and theoretical analysis along with the results of SEI-Y( γ = 1 / 3 , 1/2, and 2/3) EoS.
Table 7. L, K s y m and K τ at saturation density from different experimental and theoretical analysis along with the results of SEI-Y( γ = 1 / 3 , 1/2, and 2/3) EoS.
Expt/Observation/Theory L[MeV]
Terrestrial Experiments and Astrophysical Observations
Li and Han, 2013 [61] 58.9 ± 16.5
Oertel et al., 2017 [62] 58.7 ± 28.1
Lattimer and Lim, 2013 [80] 40.5-61.9
Xie et al. 2019, 2020 [70,77] 66 − 20 + 12
PREX-II Experiment
Reed et al., 2021 [63] 106±37
Charge exchange and elastic scattering data Danielewicz et al., 2017 [65] 70-101
Charged Pion Spectra at high momenta Estee et al., 2021 [64] 42-117
Isospin Diffusion Data Chen et al., 2005 [82] 63-113
Charge radii difference in mirror pairs
Bano et al. 2023, [28] 70-100
Expt./Observation/Theory K s y m [MeV]
Analysis of Different Neutron Star Observables Li et al., 2020 [83] − 120 − 100 + 80
d’Etivaux et al., 2019 [84] − 85 − 70 + 82
Carson et al., 2019 [85] − 259 − 32
Choi et al., 2021 [86] -128 to -33
Chiral Effective Field Theory
Drischler et al., 2016 [87] -240 to -70
Newton & Crocombe, 2021[88] − 209 − 182 + 270
Grams et. al., 2022 [89] − 200 − 50
Terrestrial Nuclear Experiments and Mean-Field Predictions
Sagawa et al., 2019 [90] − 120 ± 40
Tews et al., 2017 [91], Zhang et al., 2017 [92] -400 to -100
Mondal et al., 2017 [93] − 118.8 ± 71.3
Expt./Theory K τ [MeV]
Experimental data of Isoscalar Giant Monopole Resonances
Sagawa et al., 2008 [94] − 500 ± 50
Li et al., 2010 [95] − 550 ± 100
Stone et al., 2014 [36] -840 to -350
Theoretical calculations of GMR with MDI interactions Chen et al., 2009 [32] − 370 ± 120
Cozma, 2018 [96] − 354 ± 228
Neutron skin sizes across the mass table
Centelles et al., 2009 [97] − 500 − 100 + 125
Table 8. Threshold mass M t h for the three EoSs of SEI-Y( γ =1/3, 1/2, and 2/3) using the values of constants a and b from literature, given in Table II of Ref. [123].
Table 8. Threshold mass M t h for the three EoSs of SEI-Y( γ =1/3, 1/2, and 2/3) using the values of constants a and b from literature, given in Table II of Ref. [123].
SEI-Y( γ = 2 / 3 )
Ref a b R m a x T O V C m a x T O V k M t h
[118] -3.342 2.42 10.523 0.275 1.499 2.937
[117] -3.38 2.43 10.523 0.275 1.498 2.936
[123] − 3.36 − 0.20 + 0.20 2.35 − 0.06 + 0.06 10.523 0.275 1.424 − 0.115 + 0.115 2.790 − 0.225 + 0.225
SEI-Y( γ = 1 / 2 )
Ref a b R m a x T O V C m a x T O V k M t h
[118] -3.342 2.42 10.243 0.272 1.5095 2.846
[117] -3.38 2.43 10.243 0.272 1.5091 2.845
[123] − 3.36 − 0.20 + 0.20 2.35 − 0.06 + 0.06 10.243 0.272 1.434 − 0.114 + 0.114 2.705 − 0.215 + 0.215
SEI-Y( γ = 1 / 3 )
Ref a b R m a x T O V C m a x T O V k M t h
[118] -3.342 2.42 9.943 0.267 1.5252 2.7437
[117] -3.38 2.43 9.943 0.267 1.5250 2.7434
[123] − 3.36 − 0.20 + 0.20 2.35 − 0.06 + 0.06 9.943 0.267 1.45 − 0.113 + 0.113 2.609 − 0.204 + 0.204
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated