Prerpints.org logo
Preprint
Article

Flat Horizon D-Dimensional Black Holes in the Cubic Form of f(Q) Theory

Altmetrics

Downloads

82

Views

20

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

10 January 2024

Posted:

17 January 2024

You are already at the latest version

Alerts
Abstract
Given the AdS/CFT relationship, the study of higher-dimensional AdS black holes is extremely important. Furthermore, since the restriction derived from $f(Q)$'s field equations which prevents it from deriving spherically symmetric black hole solutions, the result is either $Q'=0$ or $f_{QQ}=0$. We derive static anti-de-Sitter black holes in $D$-dimensions using the cylindrical coordinate in the framework of the cubic form of $f(Q)$ gravity, where the coincident gauge condition is imposed \cite{Heisenberg:2023lru,Maurya:2023muz}. Within this study we are going to use the power-law ansatz which is the most viable according to observations where $f(Q)=Q+\frac{1}2\gamma Q^2+\frac{1}3\gamma Q^3-2\Lambda$, and the condition $D \geq 4$ is satisfied. Since these solutions lack a general relativity limit, they belong to a brand-new solution class, the characteristics of which are derived only from the non-metricity $Q$ modification. We investigate the singularities of the solutions by computing the values of different curvature and non-metricity invariants. We discover that the solutions indeed have a central singularity, but because of the f(Q) impact, it is softer than in the typical general relativity case. In conclusion, we compute thermodynamic parameters such as Gibbs free energy, Hawking temperature, and entropy. These thermodynamic calculations confirm that our model is stable.
Keywords: 
Subject: Physical Sciences  -   Astronomy and Astrophysics

1. Introduction

One notable and worrisome observation from the last 20 years is the universe’s acceleration caused by Dark Energy (DE). This cosmological event is confirmed by recent developments in observational cosmology: Cosmic Microwave Background Radiation[3], type Ia supernovae [4,5,6], the Lyman-forest power spectrum from the Sloan Digital Sky Survey[7], large-scale structure observations [8,9,10], and the investigation of high-energy DE models with weak lensing data [11]. However, GR is unable to account for observations of massive pulsars [12,13] and white dwarfs [14,15,16] with masses higher than the Chandrasekhar mass limit, or 1.44 M ⊚ , which is the customary maximum limit. Moreover, GR is contradicted by the strong gravitational field and fresh findings [17,18,19]. Consequently, scientists search for appropriate modifications to the GR, such as gravitation f ( R ) [20,21,22,23,24,25,26], f ( R , G ) , where the Gauss-Bonnet and Ricci scalar expressions are denoted by R and G, respectively [27], f ( T ) gravity, with the torsion scalar T[28,29,30], f ( G ) gravity [31,32,33], Brans-Dicke (BD) gravity [34,35], and so on. The concept of higher-order curvature, or more precisely f ( R ) gravity, is the most successful adaptation of GR, which uses data to refute the theory of gravity and explain the existence of dark matter[36]. Recently, f ( Q ) gravity, a well-motivated theory of gravity, was put forth by Jim’enez et al. [37]. Lagrangian density, on which it is based, produces a general function of the non-metricity scalar Q. Non-metricity drives the gravitational interaction in space-time in this theory. The modified theory of f ( Q ) gravity leads to intriguing cosmic phenomenology at the background level [38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57].
Moreover, it has effectively been tested against diverse observational data related to background and perturbations, Type Ia Supernovae (SNIa), including the Cosmic Microwave Background (CMB), Redshift Space Distortion (RSD), growth data, Baryonic Acoustic Oscillations (BAO), and similar datasets [58,59,60,61,62,63,64]. Ultimately, the constraints of Big Bang Nucleosynthesis (BBN) are simply transcended by f ( Q ) gravity[65]. Different yet comparable theories of gravity are produced depending on T (torsion) or Q (nonmetricity). These are known as the teleparallel equivalent of GR, or ( T E G R ) [66,67] and symmetric teleparallel GR (STGR) [68,69,70]. Instead of curvature and torsion, nonmetricity underpins the concept of gravity in STGR. Inspired by the interesting qualities of f ( Q ) gravity, we are going to derive D − d i m e n s i o n s flat horizons black hole using the cubic form of f ( Q ) , i.e., f ( Q ) = Q + 1 / 2 γ Q 2 + 1 / 3 γ 1 Q 3 − 2 Λ , where γ and γ 1 are two dimensional constants of l e n g t h 2 l e n g t h 3 and Λ . Λ in this study represents the cosmological constant.
The structure of this investigation is outlined as follows: Section 2, deals with the examination of the field equations and a brief summary of the non-mitricity formalism. Subsequently, we present the equation of motion for gravity within the framework of f ( Q ) . The ansatz of the metric with a flat horizon in D-dimensions is utilized to the equations of motion of f ( Q ) gravity in Section 3. Applying this approach leads to deriving a new solution in D-dimensions. The asymptotic behavior of the solution corresponds to Anti-de-Sitter (AdS) space. The relevant physical properties of these solutions are discussed in Section 4. We explore the black holes thermodynamics in Section 5. Finally, Section 6 has closing comments.

2. The theory of f ( Q )

This section covers some of the generic characteristics of f ( Q ) -gravity. We will restrict the scope of this explanation to components (the reader can turn to Ref. [71,72,73] for a more rigorous derivation in terms of forms).
For a parallelizable and differentiable manifold, the affine connection can be written in the form:
Γ μ ν σ = Γ ˜ μ ν σ + K μ ν σ + L μ ν σ ,
where the Levi-Civita connection is represented by Γ ˜ μ ν σ which has the following definition:
Γ ˜ μ ν σ = 1 2 g σ ρ ∂ μ g ρ ν + ∂ ν g ρ μ − ∂ ρ g μ ν .
Also, the contortion K σ μ ν is defined as:
K μ ν σ = 1 2 T μ ν σ + T ( μ ν ) σ ,
with the torsion tensor T μ ν σ = 2 Γ [ μ ν ] σ . Lastly, the deformation is L μ ν σ , which reads,
L μ ν σ = 1 2 Q μ ν σ − Q ( μ ν ) σ ,
where the non-metricity tensor, Q μ ν σ , is provided by
Q σ μ ν = ∇ σ g μ ν = ∂ σ g μ ν − Γ σ μ ρ g ν ρ − Γ σ ν ρ g μ ρ .
Consequently, the scalar of non-metricity is
Q = g μ ν ( L β ν α L μ α β − L α β β L ) μ ν α ≡ Q σ μ ν P σ μ ν ,
where P σ μ ν , the conjugate of non-metricity, is given by
P μ ν σ = 1 4 − Q μ ν σ + 2 Q ( μ ν ) σ + Q σ g μ ν − Q ˜ σ g μ ν − δ ( μ σ Q ν ) ,
where Q σ = Q σ μ μ , and Q ˜ σ = Q σ μ μ .
In the absence of torsion and non-metricity, the connection takes on the same form as the metrically compatible Levi-Civita connection. Curvature and torsion are both zero in STG, non-metricity is contingent on the interaction between the metric and the connection.
In Ref. [37] authors introduced modified symmetric teleparallel gravity, with the action reading,
I = − 1 2 κ 2 ∫ M f ( Q ) − g d 4 x + ∫ M L m − g d 4 x ,
where g is the determinant of the metric tensor g μ ν , M is the space-time manifold, L m is the Lagrangian density of matter contents, and f ( Q ) is a generic function of the non-metricity scalar Q.
One applies to Eq. (8) independent variations with respect to both the metric and the connection in order to obtain the field equations of the theory, having so
ξ ≡ 2 − g ∇ α − g f Q P μ ν α + 1 2 g μ ν f + f Q P μ α β Q ν α β − 2 P α β μ Q ν α β = κ 2 T μ ν ,
∇ μ ∇ ν − g f Q P μ ν α = 0 ,
where T μ ν , as is traditional, represents the energy-momentum tensor of matter
T μ ν = − 2 − g δ ( − g L m ) δ g μ ν .
The above expression has two parts: f Q = d f ( Q ) d Q and f ≡ f ( Q ) . We observe that there is no hyper-momentum because the Lagrangian density of matter is calculated without consideration of the connection. Furthermore, it is well known that by presenting f ( Q ) = Q , the Lagrangian density L = − Q 2 κ 2 + L m may be produced, yielding the results of GR (in the STEGR framework).

3. Static anti-de-Sitter black hole solution

We investigate the cylindrical D-dimensional spacetime using the field equations of f ( Q ) gravity, given by Eq. (9). The line element that emerges from this analysis is shown in cylindrical coordinates (t, r, ζ 1 , ζ 2 ,⋯, ζ D − 2 ), as elaborated in [74]:
d s 2 = μ ( r ) d t 2 − d r 2 ν ( r ) − r 2 ∑ i = 1 D − 2 d ζ i 2 .
In this context, μ ( r ) and ν 1 ( r ) denote two variables that depend on the radial coordinate. Additionally, the form of non-mitricity, Q, given by Eq. (12), yields the following form in D-dimension:
Q = − ( D − 2 ) ν [ ( D − 3 ) μ + μ ′ ] r 2 μ .
By applying Eq. (12) to the equations of motion (9), we derive the following non-zero components:
ξ t t ≡ 1 2 r 2 μ 2 2 ( D − 2 ) 2 ν 2 r 2 f Q Q [ μ ′ 2 − μ μ ′ ′ ] + ( D − 2 ) r μ ν μ ′ [ 2 ( D − 2 ) f Q Q { ν − r μ 1 ′ } + r 2 f Q ] + μ ( D − 2 ) r μ μ 1 ′ r 2 f Q − 2 ( D − 3 ) ( D − 2 ) f Q Q ν + μ ( r 4 f ( Q ) + 2 ( D − 2 ) ( D − 3 ) r 2 ν f Q + 4 ( D − 3 ) ( N − 2 ) 2 ν 2 f Q Q ) = 0 , ξ r r ≡ f ( Q ) r 2 μ + 2 ( D − 2 ) r f Q ν μ ′ + 2 ( D − 2 ) ( D − 3 ) f Q μ ν 2 r 2 μ = 0 , ξ ζ 1 ζ 1 = ξ ζ 2 ζ 2 = ⋯ ⋯ = ξ ζ D − 2 ζ D − 2 ≡ 1 4 r 4 μ 3 2 r 2 ν μ μ ′ ′ [ μ ( r 2 f Q − 2 ( D − 2 ) ( D − 3 ) f Q Q ν ) − ( D − 2 ) r ν μ ′ f Q Q ] + 2 ( D − 2 ) f Q Q r 3 ν 2 μ ′ 3 − r 2 μ ν μ ′ 2 [ r 2 f Q + 2 f Q Q ( D − 2 ) ( r μ 1 ′ − ( 2 D − 5 ) ν ) ] + r μ 2 μ ′ r μ 1 ′ ( r 2 f Q − 6 ( D − 2 ) ( D − 3 ) f Q Q ν ) + 2 ( 2 D − 5 ) r 2 f Q ν + 8 ( D − 2 ) ( D − 3 ) f Q Q ν 2 + 2 μ 2 ( D − 3 ) r μ μ 1 ′ ( r 2 f Q − 2 ( D − 2 ) ( D − 3 ) ν f Q Q ) + μ r 4 f ( Q ) + 2 ( D − 3 ) 2 r 2 ν f Q + 4 ( D − 2 ) ( D − 3 ) 2 f Q Q ν 2 = 0 .
Following that, we will find a complete solution to Eqs. (14) by using a specific expression for f ( Q ) , namely:
f ( Q ) = Q + 1 2 γ Q 2 + 1 3 γ 1 Q 3 − 2 Λ ,
where γ and γ 1 are dimensional constants that have the unites of l e n g t h 2 , l e n g t h 3 , Λ is the cosmological constant. Given this specific f ( Q ) configuration, the following results are obtained from Eqs. (13):
ξ t t ≡ 1 2 r 2 μ 2 2 ( N − 2 ) 2 ν 2 r 2 [ γ + 2 γ 1 Q ] [ μ ′ 2 − μ μ ′ ′ ] + ( N − 2 ) r μ ν μ ′ [ 2 ( N − 2 ) [ γ + 2 γ 1 Q ] { ν − r μ 1 ′ } + r 2 ( 1 + γ Q + γ 1 Q 2 ) ] + μ ( N − 2 ) r μ μ 1 ′ r 2 [ 1 + γ Q + γ 1 Q 2 ] − 2 ( N − 3 ) ( N − 2 ) [ γ + 2 γ 1 Q ] ν + μ r 4 [ Q + 1 2 γ Q 2 + 1 3 γ 1 Q 3 − 2 Λ ] + 2 ( N − 2 ) ( N − 3 ) r 2 ν [ 1 + γ Q + γ 1 Q 2 ] + 4 ( N − 3 ) ( N − 2 ) 2 ν 2 [ γ + 2 γ 1 Q ] = 0 , ξ r r ≡ [ Q + 1 2 γ Q 2 + 1 3 γ 1 Q 3 − 2 Λ ] r 2 μ + 2 ( N − 2 ) r [ 1 + γ Q + γ 1 Q 2 ] ν μ ′ + 2 ( N − 2 ) ( N − 3 ) [ 1 + γ Q + γ 1 Q 2 ] μ ν 2 r 2 μ = 0 , ξ ζ 1 ζ 1 = ξ ζ 2 ζ 2 = ⋯ ⋯ = ξ ζ D − 2 ζ D − 2 ≡ 1 4 r 4 μ 3 2 r 2 ν μ μ ′ ′ μ r 2 [ 1 + γ Q + γ 1 Q 2 ] − 2 ( N − 2 ) ( N − 3 ) [ γ + 2 γ 1 Q ] ν − ( D − 2 ) r ν μ ′ ( γ + γ 1 Q ) + 2 ( D − 2 ) [ γ + 2 γ 1 Q ] r 3 ν 2 μ ′ 3 − r 2 μ ν μ ′ 2 r 2 [ 1 + γ Q + γ 1 Q 2 ] + 2 [ γ + 2 γ 1 Q ] [ r μ 1 ′ − ( 2 D − 5 ) ν ] × ( N − 2 ) + r μ 2 μ ′ r μ 1 ′ ( r 2 [ 1 + γ Q + γ 1 Q 2 ] − 6 ( N − 2 ) ( N − 3 ) [ γ + γ 1 Q ] ν ) + 2 ( 2 D − 5 ) r 2 [ 1 + γ Q + γ 1 Q 2 ] ν + 8 ( D − 2 ) ( D − 3 ) [ γ + γ 1 Q ] ν 2 + 2 μ 2 ( N − 3 ) r μ μ 1 ′ ( r 2 [ 1 + γ Q + γ 1 Q 2 ] − 2 ( D − 2 ) ( D − 3 ) ν [ γ + 2 γ 1 Q ] ) + μ r 4 [ Q + 1 2 γ Q 2 + 1 3 γ 1 Q 3 − 2 Λ ] + 2 ( N − 3 ) 2 r 2 ν [ 1 + γ Q + γ 1 Q 2 ] + 4 ( D − 2 ) ( D − 3 ) 2 [ γ + 2 γ 1 Q ] ν 2 = 0 .
For Eq. (16), a general D-dimensional case solution is:
μ ( r ) = ν ( r ) = 1 3 1 20 600 γ 1 2 Λ − 90 γ 1 α + 27 γ 3 + 10 80 γ 1 − 27 γ 2 − 1080 α 1 γ Λ + 3600 γ 1 2 Λ 2 + 324 Λ γ 3 γ 1 3 γ 1 + r 2 20 9 γ 2 − 20 γ 1 γ 1 600 γ 1 2 Λ − 90 γ 1 γ + 27 γ 3 + 10 80 γ 1 − 27 γ 2 − 1080 γ 1 γ Λ + 3600 γ 1 2 Λ 2 + 324 Λ γ 3 γ 1 3 + 3 20 γ γ 1 + c 1 r .
The general behavior of the above solution shows that μ and ν behave generally as anti-de-Sitter(AdS) or de-Sitter (dS) spacetime. Here, c 1 stands for a dimensional integration constant.In an effort to streamline the computations, we shall assume that
Λ = 1 12 γ , α 1 = 2 γ 2 5 .
This presumption results in a special solution that has the following form:
μ ( r ) = ν ( r ) = r 2 ( D − 1 ) ( D − 2 ) α + c 1 r N − 3 .
It is evident from Eq. (19) that in the case of cubic form, the higher order of f ( Q ) serves as a cosmological constant.

4. The fundamental features of the black hole solutions (19)

Let’s investigate now certain relevant facets of the solution discussed in the previous section. The formulation of the solution’s line element (19) is as follows:
d s 2 = r 2 Λ 1 − 2 M r D − 3 d t 2 − d r 2 r 2 Λ 1 − 2 M r D − 3 − r 2 ∑ i = 1 D − 2 d ζ i 2 ,
with Λ 1 being the cosmological constant that related to the theory of f ( Q ) and is defined as Λ 1 = 1 ( D − 1 ) ( D − 2 ) γ and c 1 = − 2 M . Equation (19) clearly signifies that the line element of the solution approaches AdS geometry. It’s important to highlight that there is no counterpart for the non-metricity solution in its linear form as we approach the limit of γ → 0 .
Singularity:
Physical singularities in this framework are identified by assessing all possible invariants within the domain of f ( Q ) theory. The ansatz μ ( r ) might exhibit roots, represented as r h . Consequently, one must investigate the invariant behavior around these roots. Following the evaluation from the different invariants, we get:
Q = − 1 γ , R μ ν λ ρ R μ ν λ ρ = 2 N ( N − 1 ) ( N − 2 ) 2 γ 2 + ( D − 1 ) ( D − 2 ) 2 ( D − 3 ) M 2 r 2 ( D − 1 ) , R μ ν R μ ν = D ( D − 2 ) 2 γ 2 , R = D ( D − 2 ) γ , Q μ ν ρ Q μ ν ρ ≈ − ( D − 3 ) 2 ( D − 1 ) α + 10 ( D − 3 ) M r D − 1 + O r D − 1 , Q μ Q μ = 4 ( D − 2 ) ( D − 1 ) γ + 4 ( D − 2 ) 2 r ( D − 1 ) ,
where R μ ν λ ρ R μ ν λ ρ , R μ ν Q μ ν , Q, Q μ ν λ Q μ ν λ , Q μ Q μ , Q ˜ μ Q ˜ μ , and Q represent all the conceivable invariants that can be formulated within this theory1 which demonstrates the singularity of the invariants at r = 0 , which is described as a singularity in curvature.

5. The black holes thermodynamic properties as expressed by Eq. (19)

Using the recently found solution given in Eq. (20), we explored the thermodynamic properties by introducing the concept of the Hawking temperature [75,76] as:
T h = μ ′ ( r h ) 4 π .
The notation ′ in this scenario signifies a derivative in relation to the event horizon, r h , which represents the most significant positive root of ν ( r h ) = 0 , while ensuring that ν ′ ( r h ) is not equal to zero. The f ( Q ) theory’s Bekenstein-Hawking entropy is expressed as [77,78]2:
S ( r h ) = 1 4 A f Q ( r h ) .
The event horizon’s surface area in this frame is denoted by A. As per the heat capacity indicator C h , the black hole will be thermodynamically stable; if C h > 0 , it will be stable, and if C h < 0 , it will not be stable. In the next study, we determine if these black hole solutions are thermally stable by looking at how each of their distinct heat capacity behaves.[79,80]
H h = d E 1 d T h = ∂ M ∂ r h ∂ T ∂ r h − 1 .
In this frame, E 1 describes the quasilocal energy. Within the framework of four dimensions and in relation to the solution given in Eq. (20), the horizons are derived as follows:
r h = 12 M γ 3 .
Furthermore, we can obtain the following mass equation from Eq. (20):
M = r h 3 12 γ .
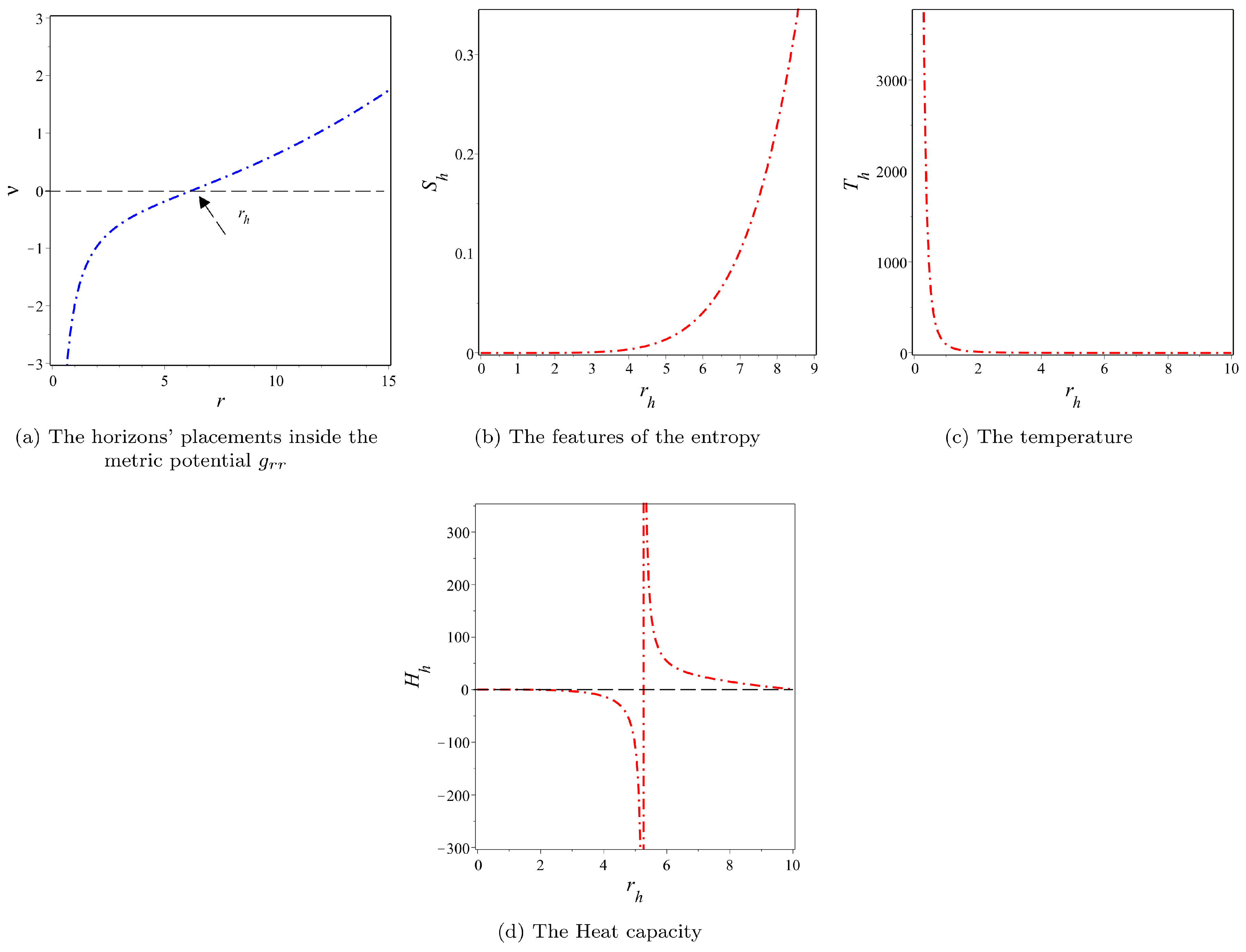
The black hole’s total mass is influenced by the horizon, as demonstrated by equation (26). Figure 1(a) illustrates the relationship between ν ( r ) and r, illustrating the potential horizons.
The entropy of solution (20) takes the following manner:
S h = 2 π r 1 2 5 .
The patterns of entropy are depicted in Figure 1 (b), revealing a consistent behavior of the entropy.
The following formula is used to get the Hawking temperature of Eq. (20):
T h = r h 3 + 6 M γ 2 π r h ( 12 M γ − r h 3 ) .
where, T h represents the Hawking temperature. The Fig. (c), shows the temperature revealing that it is always positive.
Equations (26) and (28) are substituted into (24) to yield:
H h = π r h 4 ( r h 3 − 12 M γ ) 2 2 γ ( r h 6 + 48 r h 3 M γ − 72 M 2 γ 2 ) .
Figure 1(d) shows the patterns of the heat capacity for solution (20) for several values of the model parameters. The heat capacity is consistently positive as long as r > h h , suggesting higher global stability, as seen in Figure 1(d).

6. Conclusions and discussion

In this study, we delved into the intricate realm of the cubic form of the f ( Q ) gravity theory, aiming to unravel its implications and characteristics. The cubic form, encapsulated by the function f ( Q ) where Q represents the non-metricity, introduces a compelling dimension to our understanding of gravitational dynamics. Throughout our investigation, we scrutinized various aspects, including the solutions to the field equations, the behavior of invariants, and the implications for spacetime geometry.
One of the pivotal findings of our study pertains to the reality that the dimensional quantities relate to the quadratic and cubic higher-order theories, i.e., γ and γ 1 are finally unify to show behavior of cosmological constant. This sheds light on the nuanced interplay between the cubic form of f ( Q ) gravity and the fundamental aspects of gravitational physics which indeed ensure that f ( Q ) will generally do not different from the first-order approximation of f ( Q ) in the case of static geometry.
It’s crucial to acknowledge the limitations of our study, such as the charged geometry. This aspect warrant further investigation and refinement in future research endeavors.
In conclusion, our study on the cubic form of f ( Q ) gravity theory represents a step forward in comprehending the complexities of alternative gravitational theories. The intriguing patterns and phenomena uncovered in this exploration pave the way for continued research and offer valuable contributions to the broader landscape of gravitational physics.

References

  1. L. Heisenberg (2023), 2309.15958.
  2. S. K. Maurya, K. N. Singh, M. Govender, G. Mustafa, and S. Ray. Astrophys. J. Suppl. 2023, 269, 35.
  3. D. N. Spergel et al. (WMAP), Astrophys. J. Suppl. 148, 175 (2003), astro-ph/0302209.
  4. S. Perlmutter et al. (Supernova Cosmology Project), Astrophys. J. 517, 565 (1999), astro-ph/9812133.
  5. A. G. Riess et al. (Supernova Search Team), Astrophys. J. 607, 665 (2004), astro-ph/0402512.
  6. A. V. Filippenko and A. G. Riess, Phys. Rept. 307, 31 (1998), astro-ph/9807008.
  7. P. McDonald et al. (SDSS), Astrophys. J. Suppl. 163, 80 (2006), astro-ph/0405013.
  8. T. Koivisto and D. F. Mota, Phys. Rev. D 73, 083502 (2006), astro-ph/0512135.
  9. S. F. Daniel, R. R. S. F. Daniel, R. R. Caldwell, A. Cooray, and A. Melchiorri, Phys. Rev. D 77, 103513 (2008), 0802.1068.
  10. S. Nadathur, W. J. S. Nadathur, W. J. Percival, F. Beutler, and H. Winther, Phys. Rev. Lett. 124, 221301 (2020), 2001.11044.
  11. C. Schimd, I. C. Schimd, I. Tereno, J.-P. Uzan, Y. Mellier, L. van Waerbeke, E. Semboloni, H. Hoekstra, L. Fu, and A. Riazuelo, Astron. Astrophys. 463, 405 (2007), astro-ph/0603158.
  12. P. Demorest, T. P. Demorest, T. Pennucci, S. Ransom, M. Roberts, and J. Hessels, Nature 467, 1081 (2010), 1010.5788.
  13. J. Antoniadis et al., Science 340, 6131 (2013), 1304.6875.
  14. D. A. Howell et al. (SNLS), Nature 443, 308 (2006), astro-ph/0609616.
  15. S. O. Kepler, S. J. S. O. Kepler, S. J. Kleinman, A. Nitta, D. Koester, B. G. Castanheira, O. Giovannini, A. F. M. Costa, and L. Althaus, Mon. Not. Roy. Astron. Soc. 375, 1315 (2007), astro-ph/0612277.
  16. R. A. Scalzo et al., Astrophys. J. 713, 1073 (2010), 1003.2217.
  17. E. Hawkins et al., Mon. Not. Roy. Astron. Soc. 346, 78 (2003), astro-ph/0212375.
  18. D. N. Spergel et al. (WMAP), Astrophys. J. Suppl. 170, 377 (2007), astro-ph/0603449.
  19. S. H. Shekh and V. R. Chirde, Gen. Rel. Grav. 51, 87 (2019).
  20. S. M. Carroll, V. S. M. Carroll, V. Duvvuri, M. Trodden, and M. S. Turner, Phys. Rev. D 70, 043528 (2004), astro-ph/0306438.
  21. G. Allemandi, A. G. Allemandi, A. Borowiec, M. Francaviglia, and S. D. Odintsov, Phys. Rev. D 72, 063505 (2005), gr-qc/0504057.
  22. S. Nojiri and S. D. Odintsov, Phys. Rept. 505, 59 (2011), 1011.0544.
  23. S. Nojiri and S. D. Odintsov, eConf C0602061, 06 (2006), hep-th/0601213.
  24. O. Bertolami, C. G. O. Bertolami, C. G. Boehmer, T. Harko, and F. S. N. Lobo, Phys. Rev. D 75, 104016 (2007), 0704.1733.
  25. S. Nojiri, S. D. S. Nojiri, S. D. Odintsov, and V. K. Oikonomou, Phys. Rept. 692, 1 (2017), 1705.11098.
  26. A. De Felice and S. Tsujikawa, Living Reviews in Relativity 13, 1 (2010).
  27. S. Nojiri and S. D. Odintsov, Phys. Lett. B 631, 1 (2005), hep-th/0508049.
  28. G. R. Bengochea and R. Ferraro, Phys. Rev. D 79, 124019 (2009), 0812.1205.
  29. E. V. Linder, Phys. Rev. D 81, 127301 (2010), [Erratum: Phys.Rev.D 82, 109902 (2010)], 1005.3039.
  30. C. G. Boehmer, A. C. G. Boehmer, A. Mussa, and N. Tamanini, Class. Quant. Grav. 28, 245020 (2011), 1107.4455.
  31. K. Bamba, C.-Q. K. Bamba, C.-Q. Geng, S. Nojiri, and S. D. Odintsov, EPL 89, 50003 (2010a), 0909.4397.
  32. K. Bamba, S. D. K. Bamba, S. D. Odintsov, L. Sebastiani, and S. Zerbini, Eur. Phys. J. C 67, 295 (2010b), 0911.4390.
  33. M. E. Rodrigues, M. J. S. M. E. Rodrigues, M. J. S. Houndjo, D. Momeni, and R. Myrzakulov, Can. J. Phys. 92, 173 (2014), 1212.4488.
  34. A. Avilez and C. Skordis, Phys. Rev. Lett. 113, 011101 (2014), 1303.4330.
  35. S. Bhattacharya, K. F. S. Bhattacharya, K. F. Dialektopoulos, A. E. Romano, and T. N. Tomaras, Phys. Rev. Lett. 115, 181104 (2015), 1505.02375.
  36. K. Bamba, S. K. Bamba, S. Capozziello, S. Nojiri, and S. D. Odintsov, Astrophys. Space Sci. 342, 155 (2012), 1205.3421.
  37. J. Beltrán Jiménez, L. J. Beltrán Jiménez, L. Heisenberg, and T. Koivisto, Phys. Rev. D 98, 044048 (2018), 1710.03116.
  38. J. Beltrán Jiménez, L. J. Beltrán Jiménez, L. Heisenberg, T. S. Koivisto, and S. Pekar, Phys. Rev. D 101, 103507 (2020), 1906.10027.
  39. K. F. Dialektopoulos, T. S. K. F. Dialektopoulos, T. S. Koivisto, and S. Capozziello, Eur. Phys. J. C 79, 606 (2019), 1905.09019.
  40. F. Bajardi, D. F. Bajardi, D. Vernieri, and S. Capozziello, Eur. Phys. J. Plus 135, 912 (2020), 2011.01248.
  41. K. Flathmann and M. Hohmann, Phys. Rev. D 103, 044030 (2021), 2012.12875.
  42. F. D’Ambrosio, M. F. D’Ambrosio, M. Garg, and L. Heisenberg, Phys. Lett. B 811, 135970 (2020), 2004.00888.
  43. S. Mandal, P. K. S. Mandal, P. K. Sahoo, and J. R. L. Santos, Phys. Rev. D 102, 024057 (2020), 2008.01563.
  44. N. Dimakis, A. N. Dimakis, A. Paliathanasis, and T. Christodoulakis, Class. Quant. Grav. 38, 225003 (2021), 2108.01970.
  45. Y. Nakayama, Class. Quant. Grav. 39, 145006 (2022), 2108.10465.
  46. W. Khyllep, A. W. Khyllep, A. Paliathanasis, and J. Dutta, Phys. Rev. D 103, 103521 (2021), 2103.08372.
  47. M. Hohmann, Phys. Rev. D 104, 124077 (2021), 2109.01525.
  48. W. Wang, H. W. Wang, H. Chen, and T. Katsuragawa, Phys. Rev. D 105, 024060 (2022), 2110.13565.
  49. I. Quiros, Phys. Rev. D 105, 104060 (2022), 2111.05490.
  50. J. Ferreira, T. J. Ferreira, T. Barreiro, J. Mimoso, and N. J. Nunes, Phys. Rev. D 105, 123531 (2022), 2203.13788.
  51. R. Solanki, A. R. Solanki, A. De, and P. K. Sahoo, Phys. Dark Univ. 36, 100996 (2022), 2203.03370.
  52. A. De, S. A. De, S. Mandal, J. T. Beh, T.-H. Loo, and P. K. Sahoo, Eur. Phys. J. C 82, 72 (2022), 2201.05036.
  53. R. Solanki, S. K. J. R. Solanki, S. K. J. Pacif, A. Parida, and P. K. Sahoo, Phys. Dark Univ. 32, 100820 (2021), 2105.00876.
  54. S. Capozziello and R. D’Agostino, Phys. Lett. B 832, 137229 (2022), 2204.01015.
  55. N. Dimakis, A. N. Dimakis, A. Paliathanasis, M. Roumeliotis, and T. Christodoulakis, Phys. Rev. D 106, 043509 (2022), 2205.04680.
  56. I. S. Albuquerque and N. Frusciante, Phys. Dark Univ. 35, 100980 (2022), 2202.04637.
  57. S. Arora and P. K. Sahoo, Annalen Phys. 534, 2200233 (2022), 2206.05110.
  58. I. Soudi, G. I. Soudi, G. Farrugia, V. Gakis, J. Levi Said, and E. N. Saridakis, Phys. Rev. D 100, 044008 (2019), 1810.08220.
  59. R. Lazkoz, F. S. N. R. Lazkoz, F. S. N. Lobo, M. Ortiz-Baños, and V. Salzano, Phys. Rev. D 100, 104027 (2019), 1907.13219.
  60. B. J. Barros, T. B. J. Barros, T. Barreiro, T. Koivisto, and N. J. Nunes, Phys. Dark Univ. 30, 100616 (2020), 2004.07867.
  61. I. Ayuso, R. I. Ayuso, R. Lazkoz, and V. Salzano, Phys. Rev. D 103, 063505 (2021), 2012.00046.
  62. S. Mandal and P. K. Sahoo, Phys. Lett. B 823, 136786 (2021), 2111.10511.
  63. L. Atayde and N. Frusciante, Phys. Rev. D 104, 064052 (2021), 2108.10832.
  64. N. Frusciante, Phys. Rev. D 103, 044021 (2021), 2101.09242.
  65. F. K. Anagnostopoulos, V. F. K. Anagnostopoulos, V. Gakis, E. N. Saridakis, and S. Basilakos, Eur. Phys. J. C 83, 58 (2023), 2205.11445.
  66. K. Hayashi and T. Shirafuji, Phys. Rev. D 19, 3524 (1979), [Addendum: Phys.Rev.D 24, 3312–3314 (1982)].
  67. J. W. Maluf, Annalen Phys. 525, 339 (2013), 1303.3897.
  68. M. Adak and O. Sert, Turk. J. Phys. 29, 1 (2005), gr-qc/0412007.
  69. M. Adak, M. M. Adak, M. Kalay, and O. Sert, Int. J. Mod. Phys. D 15, 619 (2006), gr-qc/0505025.
  70. M. Adak, O. M. Adak, O. Sert, M. Kalay, and M. Sari, Int. J. Mod. Phys. A 28, 1350167 (2013), 0810.2388.
  71. R. Aldrovandi and J. G. Pereira, Teleparallel Gravity: An Introduction (Springer, 2013), ISBN 978-94-007-5142-2, 978-94-007-5143-9.
  72. S. Capozziello, V. S. Capozziello, V. De Falco, and C. Ferrara, Eur. Phys. J. C 82, 865 (2022), 2208.03011.
  73. M. Nakahara, Geometry, topology and physics (2003).
  74. A. M. Awad, S. A. M. Awad, S. Capozziello, and G. G. L. Nashed, JHEP 07, 136 (2017), 1706.01773.
  75. G. G. L. Nashed and S. Nojiri, Phys. Rev. D 107, 064069 (2023), 2303.07349.
  76. S. H. Mazharimousavi, Eur. Phys. J. C 83, 406 (2023), [Erratum: Eur.Phys.J.C 83, 597 (2023)], 2304.12935.
  77. G. Cognola, O. G. Cognola, O. Gorbunova, L. Sebastiani, and S. Zerbini, Phys. Rev. D 84, 023515 (2011), 1104.2814.
  78. Y. Zheng and R.-J. Yang, Eur. Phys. J. C 78, 682 (2018), 1806.09858.
  79. K. Nouicer, Class. Quant. Grav. 24, 5917 (2007), [Erratum: Class.Quant.Grav. 24, 6435 (2007)], 0706.2749.
  80. A. Chamblin, R. A. Chamblin, R. Emparan, C. V. Johnson, and R. C. Myers, Phys. Rev. D 60, 064018 (1999), hep-th/9902170.
1
The invariants we used in this study are defined as: R μ ν λ ρ R μ ν λ ρ , R μ ν Q μ ν , Q, Q μ ν λ Q μ ν λ Q μ Q μ , Q ˜ μ Q ˜ μ and Q, which are known as the Kretschmann scalar, the square of the Ricci tensor, the Ricci scalar, the square of the non-metricity tensor, the vectors of the non-metricity square, and the non-metricity, respectively.
2
Remember that the way entropy is framed in f ( Q ) geocentric theory is not the same as it is presented in linear non-metricity theory. We shall be aware of the non-metricity hypothesis when f ( Q ) = Q .
Preprints 96027 g001
Figure 1. (a) The overall trend of g r r is depicted in Figure 1; (b) highlights the entropy behavior; (c) depicts changes in the temperature, while (d) shows the heat capacity behavior. The model parameters are consistently set to γ = 100 and M = 1 .
Figure 1. (a) The overall trend of g r r is depicted in Figure 1; (b) highlights the entropy behavior; (c) depicts changes in the temperature, while (d) shows the heat capacity behavior. The model parameters are consistently set to γ = 100 and M = 1 .
Preprints 96027 g001
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated