Analysis of Blade Aspect Ratio Influence on High-Speed Axial Compressor Performance

The ratio between blade height and chord, named aspect ratio (AR), plays an important role in compressor aerodynamic design. Once selected, it influences stage performance, blade losses, and the stage stability margin. The choice of the design AR involves both aerodynamic and mechanical considerations, and a reasonable aim is frequently to achieve a desired operating range while maximizing efficiency. For a fixed set of aerodynamic and geometric parameters there will be an optimal choice in AR that achieves a maximum efficiency. However, for a state-of-the-art aero-engine design optimality means multi-objective optimality, that is reaching the highest possible efficiency for a number of operating points while achieving a sufficient stability margin. To this end, the influence of the AR on the performance of the first rotor row of a multistage multi-objective high-speed compressor design is analyzed. A careful setup of the high-speed aerodynamic design problem allows the effect of the AR to be isolated. Close to the optimal AR, only a modest efficiency variation is observed, but a considerable change in compressor stability margin (SM) is noted. Decreasing the AR allows for an increasing efficiency, but at the expense of a reduced surge margin. This allows the designer to trade efficiency for stability. Increasing the AR, however, is shown to reduce both surge margin and efficiency, hence a distinct optimality in stability is observed for the analyzed rotor blade row. In this work, the optimality in surge margin with respect to AR is observed whereas a close to optimal efficiency. The predicted range from AR=1.10 to AR=1.64, is only indicative, considering that the definition of a multi-objective optimality requires balancing efficiency and surge margin and that the choice of balancing these two criteria requires making a design choice along a pareto optimal front.

Keywords:

Subject: Engineering - Aerospace Engineering

1. Introduction

In gas turbine industry, the compressor designer usually aims to achieve a high work output per stage while retaining a good efficiency [1]. However, increasing the stage load affects the compressor aerodynamics through increased diffusion and reduced efficiency hence posing a conflicting requirement for the designer [2], sometimes demanding the search for optimization methodologies [3]. For high-speed compressors, which usually present difficulties related to cooling system [4], an increase in diffusion may also result in shock-induced boundary layer separation, drastically lowering efficiency. Still, a highly loaded stage is a possible solution to reduce the number of stages, and consequently to decrease compressor weight, size and cost. Historically, the choice of aspect ratio (AR) has always involved the simultaneous consideration of a number of key design parameters such as work output per stage, diffusion, efficiency, surge margin and mechanical integrity. This discussion is related to changing compressor load by means of geometric changes, although recent research also indicates the possibility to change the machine load based on air extraction [5].

Early work studying the influence of AR focused on high AR blading attempting to make compressors more compact and to reduce secondary flow is reported in [6]. Ultimately, low surge margin and greater risk for forced response drove the designers away from high AR compressors [7,8]. Important work highlighting the limitations of high AR blades was reported by Koch [9], showing that with a lowering of the AR, the surge margin could be increased. Early experimental work relating efficiency and AR noted that efficiency may both increase and decrease with lower AR depending on the stage loading [10]. Wang et al. report on how flow instabilities evolve into rotating stall as related to relative blade clearance [11], and the losses generated by these tip clearances can be reduced through pulsed suction methods [12]. Although the historical reasons to apply low AR designs are valid, new design features such as intentional mistuning [13] and blade design methods to reduce clearance sensitivity [14], could potentially re-open the field for high AR compressor design. The efficiency of gas turbines engines, depending on the turbomachine’s performances (compressors [15] and turbines), including engines with rotating detonation [16] and pulse detonation combustion [17].

Alfredsson [18] studied the use of the Skoch parameter to evaluate the losses as well as predicting the optimum AR range during the compressor design stage. However, as a conclusion the Skoch parameter proved to be ineffective on both accounts. Peters et al. [19] studied a uniform increase in the AR of all stages in a multistage compressor, noting a disproportional decrease in secondary flow loss, as compared to a change in a single stage. To and Miller [20] have addressed the problem of optimum AR for maximum efficiency in a low-speed compressor having repeating stages. For such flows the optimum efficiency is found at relatively low ARs, typically between 1.0 and 1.5. The optimum occurs at the point where the rate of increase in profile loss is equal to the rate of decrease in endwall loss [20]. Since the optimum AR is set by the balance between profile and endwall loss, it is understood that the prediction of optimum AR poses a challenging aerodynamic problem.

The geometry of the high-speed 3.5 stage compressor studied herein [21] is publicly available for download [22]. This design has been subject to extensive multi-objective optimization, balancing stage load, efficiency, and stability. It is believed that the studied geometry represents a state-of-the-art high speed aero engine compressor and that conclusions drawn from the current study on optimal AR, may have relevance for a wider range of modern high-speed compressor design work and not just be applicable to this particular machine. A contribution of this work is the successful isolation of the basic trends of performance with varying AR, as applicable to a multi-objective high speed aero engine compressor.

2. Compressor Specification Description

The test case under consideration is the VINK compressor (Virtual Integrated Compressor), a compressor designed as part of a collaboration project with partners from Swedish universities and industry (Chalmers University of Technology, KTH Royal Institute of Technology, Lund University, GKN Aerospace Sweden AB and Swerea). The VINK compressor is a 3.5 stage high-speed, low AR low shock loss design [21].

For this study only the Inlet Guide Vane (IGV) and the first rotor blade row are considered. Table 1 summarizes the performance of the first stage of the VINK compressor as reported in [21] and Table 2 gives additional geometrical parameters. Together with the boundary conditions defined below, the two tables define the nominal condition which we use to compare with to establish the AR trends. Notice that as AR is parametrically varied from AR=0.57 to AR=2.08, each case has a reference condition defined below, from which the surge margin is quantified.

The design process for the VINK compressor is outlined in [21], starting from aircraft and engine thrust requirements, and ending with 3D models of the blade rows which were made publicly available. The detailed design of the first stage, which is the geometric starting point in the present paper, was the result of a multi-objective optimization with respect to stall margin and efficiency.

This work aims to systematically vary the AR of the first rotor of VINK compressor around its nominal condition to study the variation in key performance variables such as efficiency and surge margin.

Blade and endwall parametrization

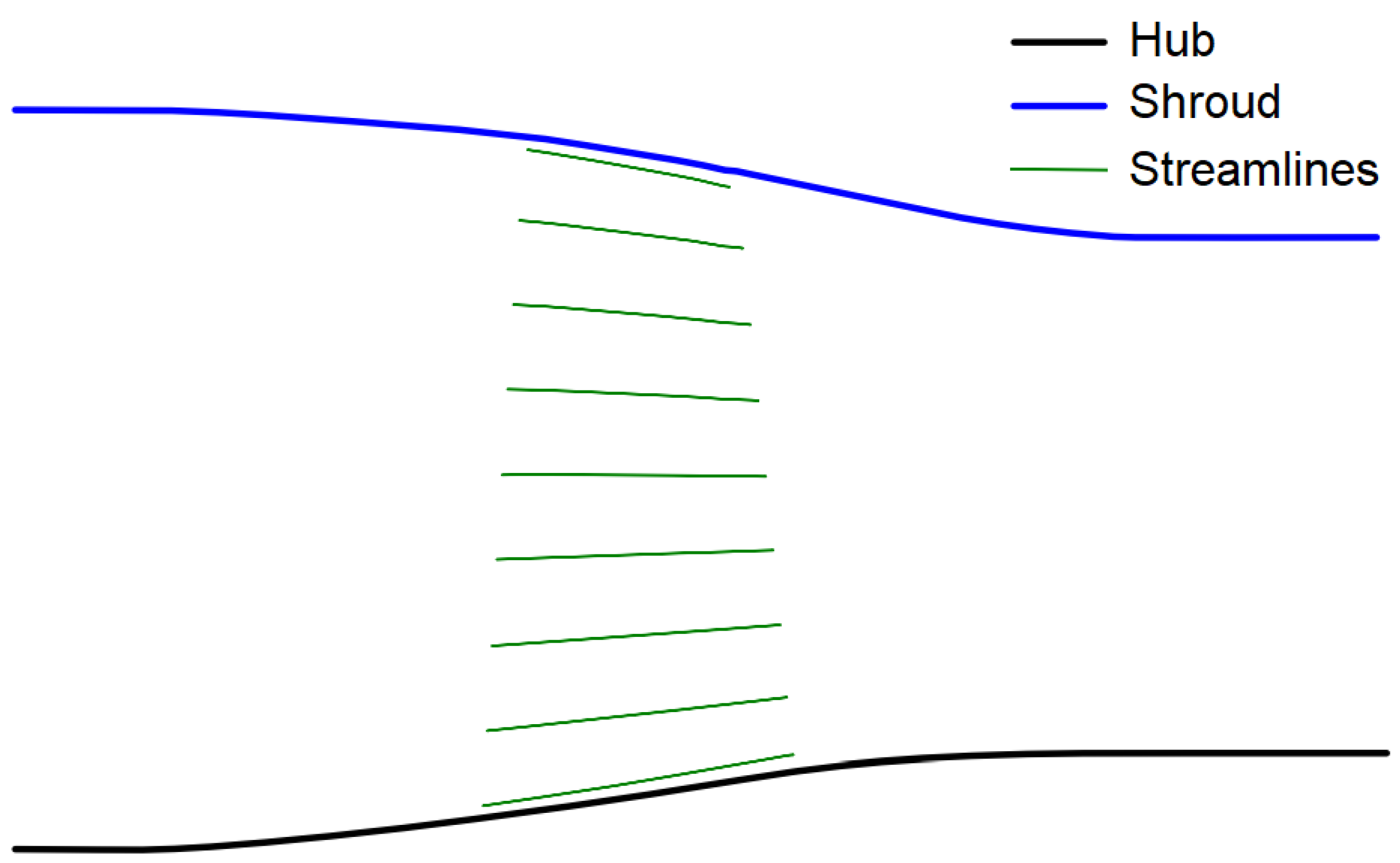
The commercial throughflow tool SC90C [23] was used to perform the preliminary design of the VINK compressor, generating both aerodynamic and geometric data. The resulting streamlines are indicated in Figure 1. Thereafter, the rotor row geometry was introduced into the Chalmers University in-house Python code for 3D blade parametrization. Using the code for 3D blade parametrization, the hub and shroud curves were calculated using cubic spline interpolation. The leading edge is placed at the origin and the location of the trailing edge is calculated with help of the stagger angle and the axial chord length. Then, the axial chord length together with the leading edge and trailing edge thickness are used to calculate the normalized edge thickness. The normalized thickness is used to generate the endpoints for two Bezier curves that describe the suction and pressure side respectively. More details about the 3D blade parametrization can be found in [24].

A high order polynomial curve is used to generate the leading edge and trailing edge radius; however, the physical values of the leading and trailing edge radii were kept constant to achieve flow similarity. Also, the leading-edge axial position was fixed, and the position of the trailing edge varies with the chord length. The leading-edge design is particularly important in compressor blade rows since the initial development of the boundary layer at the leading edge influences the boundary layer over the rest of the blade surface [25], and as a consequence it also has a direct impact on profile loss. The profiles have been created and stacked on streamlines specified by a Bezier curve to create the final blade geometry keeping the lean and sweep constant. Having developed the rotor blade parametrization, the AR can now be varied by changing the blade chord length, still keeping a constant thickness to chord ratio.

The blade parametrization and also the geometry scaling technique is important to achieve an aerodynamic performance similarity. Zhang et al. [26] state that by keeping the similarity of blade solidity, blade angles and thickness to chord distribution, the similarity of key aerodynamic parameters such as loss coefficient and aerodynamic blockage, and thus of overall aerodynamic performance can generally be guaranteed. Although this has generally been achieved herein, as discussed in association with Figure 5, it should be added that the AR scaling process is also quite sensitive to the rotor exit endwall contouring. While varying AR, upstream effects of the endwall may easily corrupt the similarity. To minimize the influence of the exit endwall contouring on the upstream flow through the rotor, constant curvature transition curves were constructed maintaining an inflection point located at the axial middle point between the rotor exit and the domain exit, see Figure 4. As the AR of the rotor is varied, the radial derivative with axial position at the rotor exit and domain exit are kept fixed together with the rotor exit and domain exit radial coordinates.

3. Numerical Methodology

3.1. Approach

The efficiency (η) of a compressor is not only a function of the AR, but also dependent on a number of nondimensional design parameters: such as the flow coefficient (ϕ), the work coefficient (ψ), the degree of reaction (Λ), the diffusion factor (DF), the thickness to chord ratio (t/c), the Mach number (M), the tip-to-chord ratio (s/c), the tip clearance-to-chord ratio (ε/c) and the Reynolds number (Re_c) based on chord and casing configuration (config.). Thus,

η = ƒ (ϕ, ψ, Λ, M, DF, AR, s/c, t/c, ε/c, Re_c, config.)

(1)

to isolate the influence of the AR the design Mach number triangle and DF were fixed, thus ϕ, ψ and Λ are also constant. Thus,

η = ƒ (AR, s/c, t/c, ε/c, Re_c, config)

(2)

the blade profile and pitch-to-chord ratio was fixed throughout this work. Thus, the number of the blades had to be varied accordingly keeping solidity constant.

To isolate the effect of AR on the high-speed compressor stage studied herein, it was decided to exclude the effect of tip-clearance from the study. Tip clearance is known to have a substantial impact on compressor flows and losses [27,28]. More specifically, the choice of tip clearance may alter both the radial distribution of blade loading and contribute to influencing the breakdown of the flow in the tip region [29,30,31]. Hence, for the present study, the use of tip-clearance would introduce substantial additional difficulties for interpreting the flow, since tip clearance leakage vortices play a decisive role in the origin of rotating instabilities and stall inception [32]. Furthermore, the optimization of the VINK compressor [33], was performed for zero tip clearance and hence including a tip clearance would effectively mean studying a non-optimal compressor. In turn this would likely mean that the results observed would provide little general value. In addition, relating our results with the key work by To and Miller [20], would become more difficult since this study assumed zero tip-clearance.

3.2. Mesh study

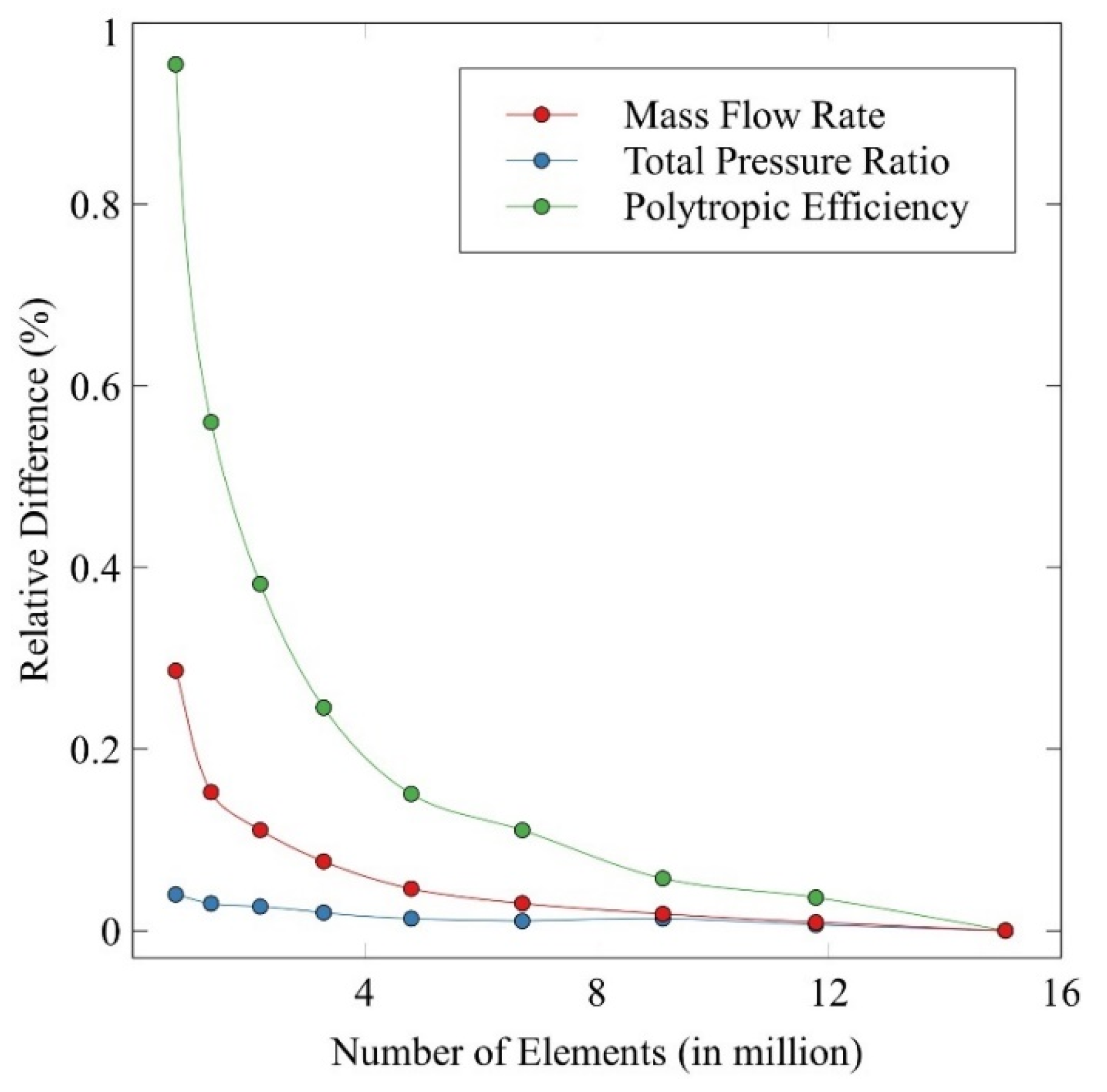
The mesh study is based on the nominal case (AR=1.37 and 51 rotor blades) and the meshes were generated using the commercial software ANSYS®TurboGrid v. 19.1 [34]. Several meshes with different sizes, but always with average y plus less than 1.0, were generated to show mesh independence. The comparison is done based on the relative difference (in %) of each mesh in comparison with the finest one, as shown in Figure 2.

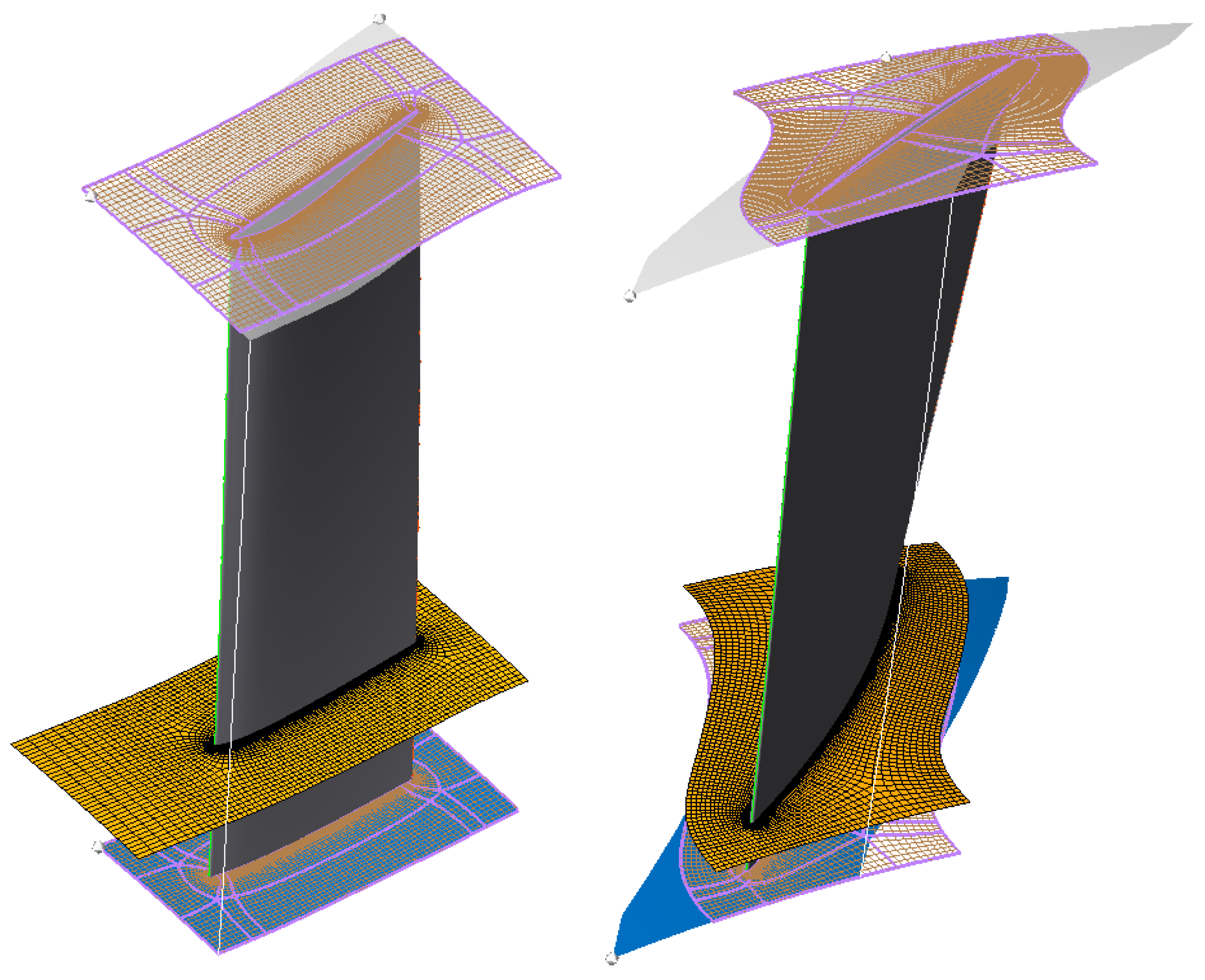
The results showed that the relative difference (in %) of the parameters (mass flow rate, total pressure ratio and polytropic efficiency) varied with less than 1.0% between the coarsest and finest meshes. Therefore, the results were considered independent of mesh, in relation to the spatial discretization and with asymptotic tendency in relation to the number of elements. The mesh with the lowest number of elements presenting a relative difference smaller than 0.1% was chosen for the studies performed in this paper. It has 9.14 million of elements (approximately 5.77 million elements for IGV and 3.37 million elements for rotor) and is shown in Figure 3.

3.3. Numerical settings

The computational fluid dynamics (CFD) calculations were performed using the commercial software ANSYS®CFX v. 19.1 [35]. It is a high-performance software for CFD calculations, that delivers reliable and accurate solutions quickly and robustly. It is a density-based and finite volume discretization technique to solve the partial differential equations, the Reynolds Averaged Navier-Stokes (RANS).

For flows with adverse pressure gradients the two-equation eddy viscosity turbulence model named Shear Stress Transport (SST) Model, as developed by Menter [36], is a standard choice for turbomachine applications. Other works, such as that by Yan et al. [37], show the suitability of the SST model for simulating transonic compressors, including aspects of numerical stability. Wall boundaries have been treated as adiabatic, and an integration to the wall have been used to resolve the boundary layers. All simulation results presented herein have been run assuming steady state flow.

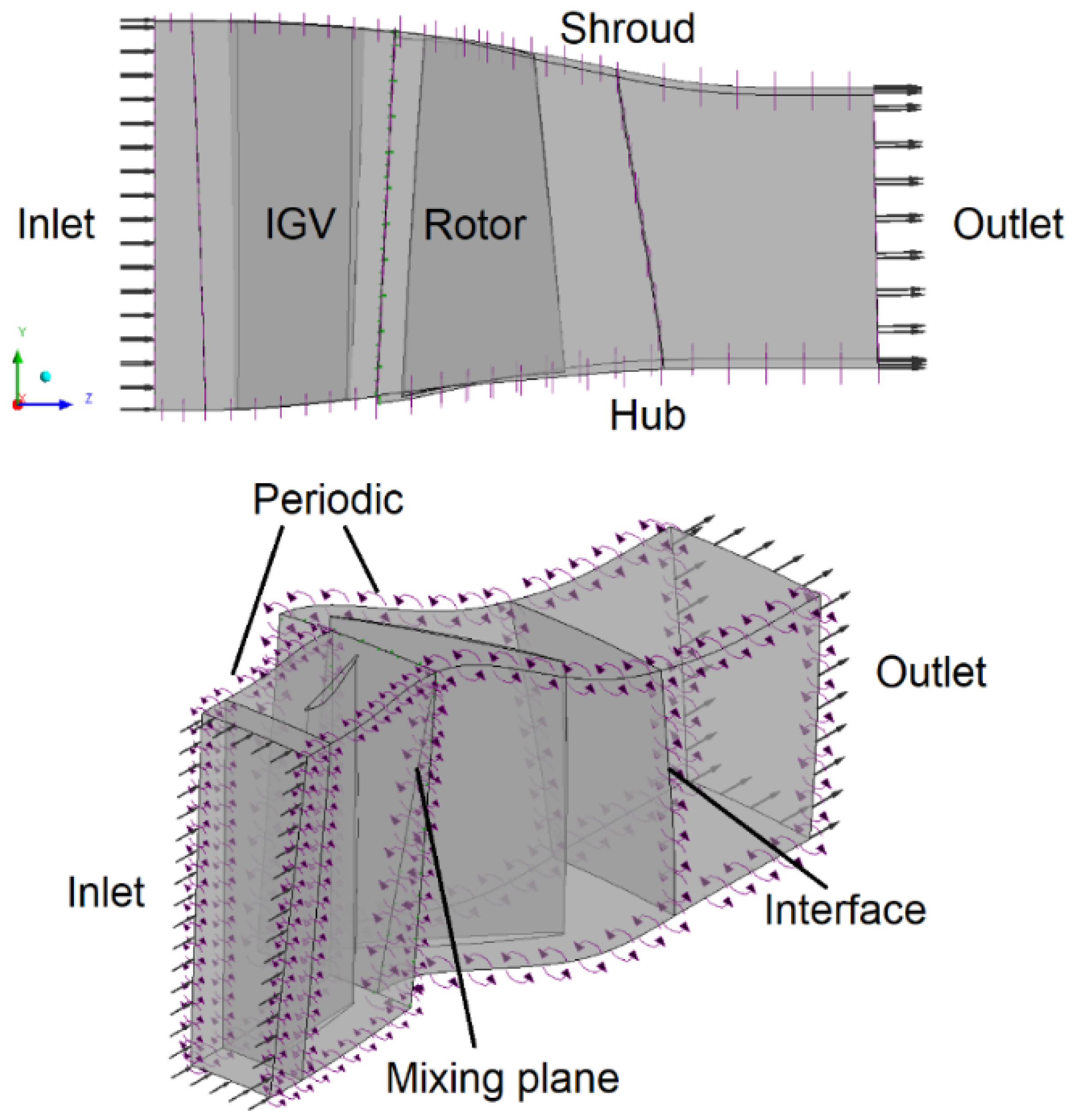
The computational domain investigated in this study consists of one blade-to-blade passage of the axial compressor assuming the flow between two adjacent blades to be periodic in the rotating direction. No boundary layer profile on the hub or shroud is specified for the inlet boundary condition. The outlet boundary is specified using averaged properties. The boundary conditions applied to the blade-to-blade passage are stated below and illustrated in Figure 4.

Inlet: total pressure P₀ = 47.9 kPa (in relation to the static reference frame - stator), total temperature T₀ = 282.4 K (also in relation to the static reference frame - stator), turbulence intensity = 5% and the turbulent length scale = 1 mm;
Outlet: Average static pressure outlet (static reference frame);
Mixing plane: interface between rotating and stationary planes. In this interface type, circumferential averages of the flow properties are calculated at various sections along the blade span. These averages are then communicated to the inlet of the downstream domain;
Periodic: were applied periodic boundary conditions;
Adiabatic wall: non-slip wall condition and the wall velocity is zero for all walls (relative to the walls themselves) and counter rotating for rotor shroud, also no shroud tip clearance for rotor;
Interface: General Grid Interface (GGI) method is used for the connection between the interfaces.

The flow was assumed to be axial at the inlet and the z-axis was taken as the rotation axis. The working fluid is considered as an ideal gas, but the dynamic viscosity varies to keep the Reynolds number constant. The Reynolds number based on the true chord (Re_c) is fixed in 1.022×10⁶, and the true blade chord varies between 67% to 243% relative to the chord-length of the nominal case blade.

The simulations were performed using resources of the Swedish National Infrastructure for Computing (SNIC), using the Tetralith cluster. Each server has two Intel Xeon Gold 6130 processors, providing 32 cores per server.

3.4. Aerodynamic parameters

The rotor blade loading distribution affects the compressor stability, mainly in near-stall points [38]. Thus, to analyze the blade loading [39], the pressure coefficient (

C_{p}

), can be determined along the blade chord by:

C_{p} = \frac{(p - p_{i n l e t})}{(p_{0, r e l, i n l e t} - p_{i n l e t})}

(3)

where the variable p denotes the local static pressure around the blade surface. The variable p_inlet and p_0,rel,inlet respectively denote the static and relative total pressure at the same upstream spanwise position. Based on

C_{p}

it is possible to evaluate the load distribution on the rotor blade comparing suction and pressure side pressure distributions for varying ARs along the blade span.

In a compressor performance map, the distance between the operating line and the surge line is measured using the surge margin (SM), here defined by [40]:

S M = (\frac{{P R}_{T T, l i m i t} \times ṁ_{r e f}}{{P R}_{T T, r e f} {\times ṁ}_{l i m i t}} - 1) \times 100

(4)

for a given rotational speed, the last stable operating point is taken as the operating point with the highest total-to-total pressure ratio for which the numerical solution would converge. This criterion was used to define the performance parameters for last stable operating point (or operating point at the surge line), total-to-total pressure ratio at limit or at surge (PR_TT,limit) and mass flow rate at surge (ṁ_limit). The index ref, the reference condition, refers to the particular point under study as evaluated at a fixed rotational speed maintaining the same outlet static pressure. We emphasize that there is then one reference condition per AR value, but only a single nominal condition which is the reference condition for which also AR = 1.37.

According to Wang et al. [11], along a compressor speed line the flow instability evolution experiences three stages: stable state, rotating instability and rotating stall. As stall develops its hysteresis is then influenced by the relation of the shut-off head to the shape of the compressor characteristic [41]. At any rate, the surge margin should be selected to be sufficient for the compressor to operate safely with respect to variations in the incoming flow field for different rotational speeds and during transient operation [33].

Understanding that the surge phenomenon is inherently a transient 3D phenomenon involving the entire blade row circumference, we adopt the simplistic view that surge is predicted by the last stable operating point for which convergence is possible. Notice that the use of the surge margin herein is not to predict the onset of surge but to establish a measure for the distance to surge supporting the analysis of AR around an optimal compressor design. We believe that the measure is sufficient to rank the compressors with respect to stability and emphasize that our key results are obtained safely away from surge. In addition, the established scaling method is inherently unable to handle unsteady effects such as rotor-stator interaction [42,43], since the reduced frequency would change as the number of blades as well as the rotor blade passage length are changed to maintain pitch chord. The effect rotor-stator interaction is limited herein by the fact that the rotor flow is not entering into a downstream blade row, but obviously the wakes from the upstream IGV will be influenced by the rotor variation in rotor blades numbers and passage length. The change in reduced frequency is limited by that as the number of blades increase the chord lengths decrease proportionally.

4. Results and Discussion

4.1. Design parameter independence of aspect ratio

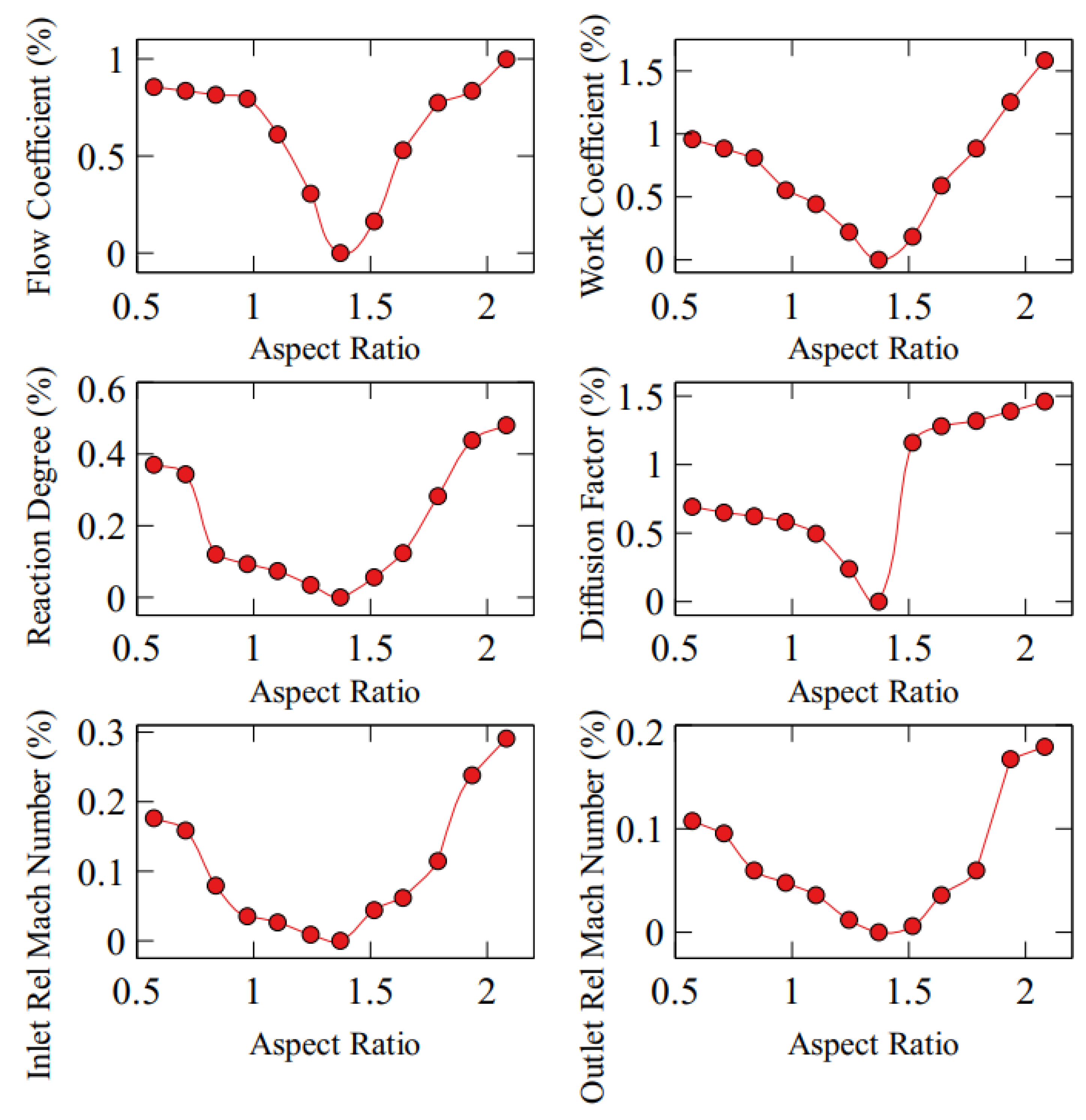
To validate that the key parameters of Equation 1 remain fixed during the AR variation, we plot flow coefficient (ϕ), work coefficient (ψ), degree of reaction (Λ), DF and relative Mach number at inlet and outlet of the domain in Figure 5.

As seen, the variation is quite modest, no larger than 1.6% variation, for an AR variation ranging from 0.57 to 2.08. Notice that all of the points in the curves of Figure 5 are generated in the reference condition and it is only the dependence of different parameters with AR that is assessed.

4.2. Influence of aspect ratio

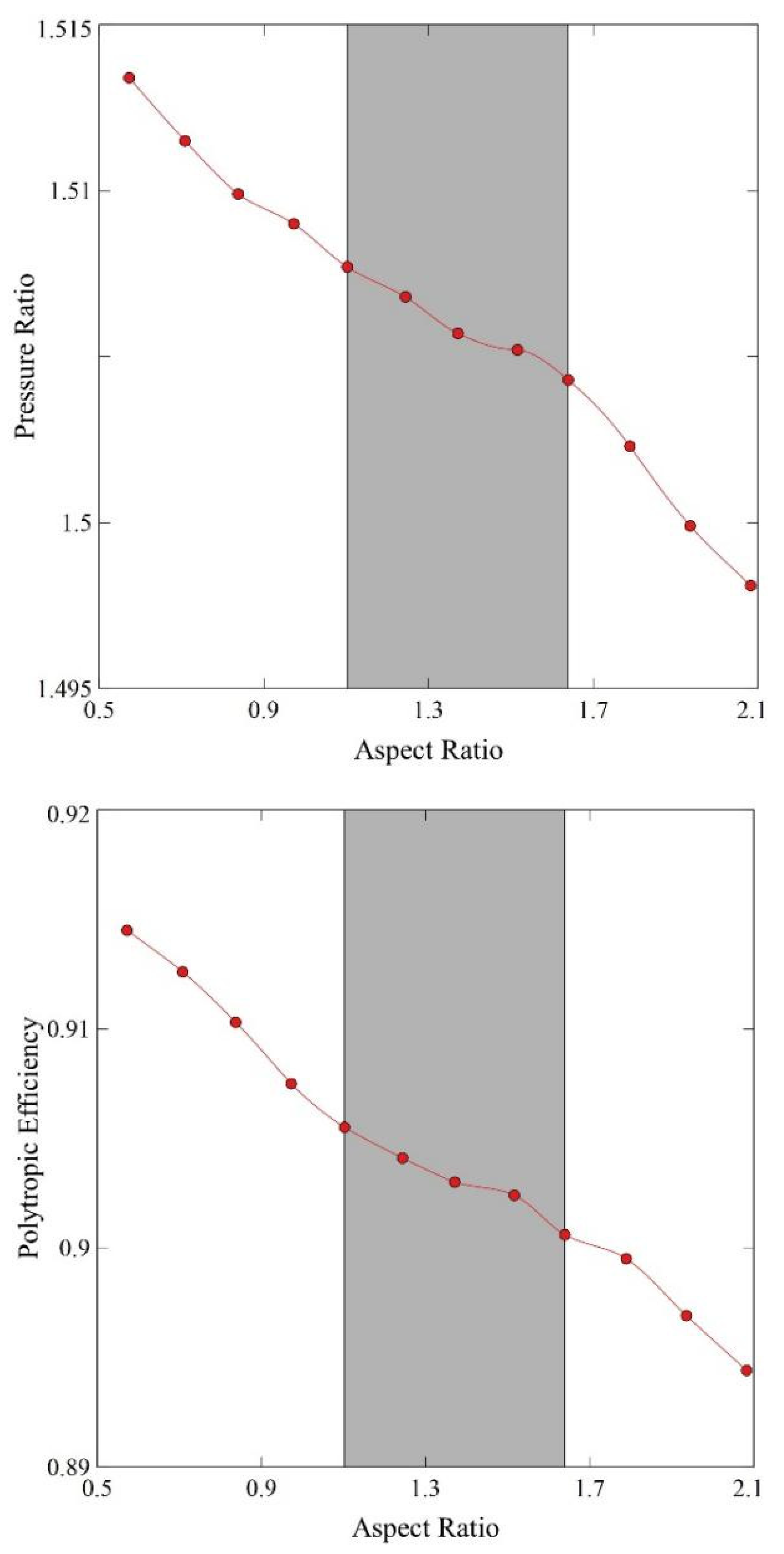
The results collected in Figure 6 show the influence of AR on total-to-total pressure ratio and polytropic efficiency for a high-speed compressor, all simulated in the reference condition defined above. Here we do not see an optimum in efficiency within the AR range from 1.0 to 1.5, as suggested for low-speed compressors [20]. Instead, the two figures show that there is a close to optimal range were the performance changes more slowly, indicated by the grey region (AR=1.10, 1.24, 1.37, 1.52, 1.64), and when deviating from this range larger variations are observed.

Multi-objective optimality is established when both compressor stability and efficiency is considered, as will be outlined more closely below. To analyze the finer details of the flow a range of ± 20% around the nominal case AR was selected for further study. This set of data is comprised of the five points (AR=1.10, 1.24, 1.37, 1.52, 1.64) indicated by the grey area shown in Figure 6.

The increase in AR is accompanied by an increase in the number of blades in order to maintain constant solidity. Thus, while the endwall losses are lower at the hub and shroud for higher AR values, the profile losses become even higher, resulting in lower efficiencies. Conversely, when the AR is decreased, the number of blades also decreases. Thus, higher endwall losses at the hub and shroud are offset by even lower profile losses, resulting in increased efficiency.

4.3. Aspect ratio variation and blade-to-blade flow

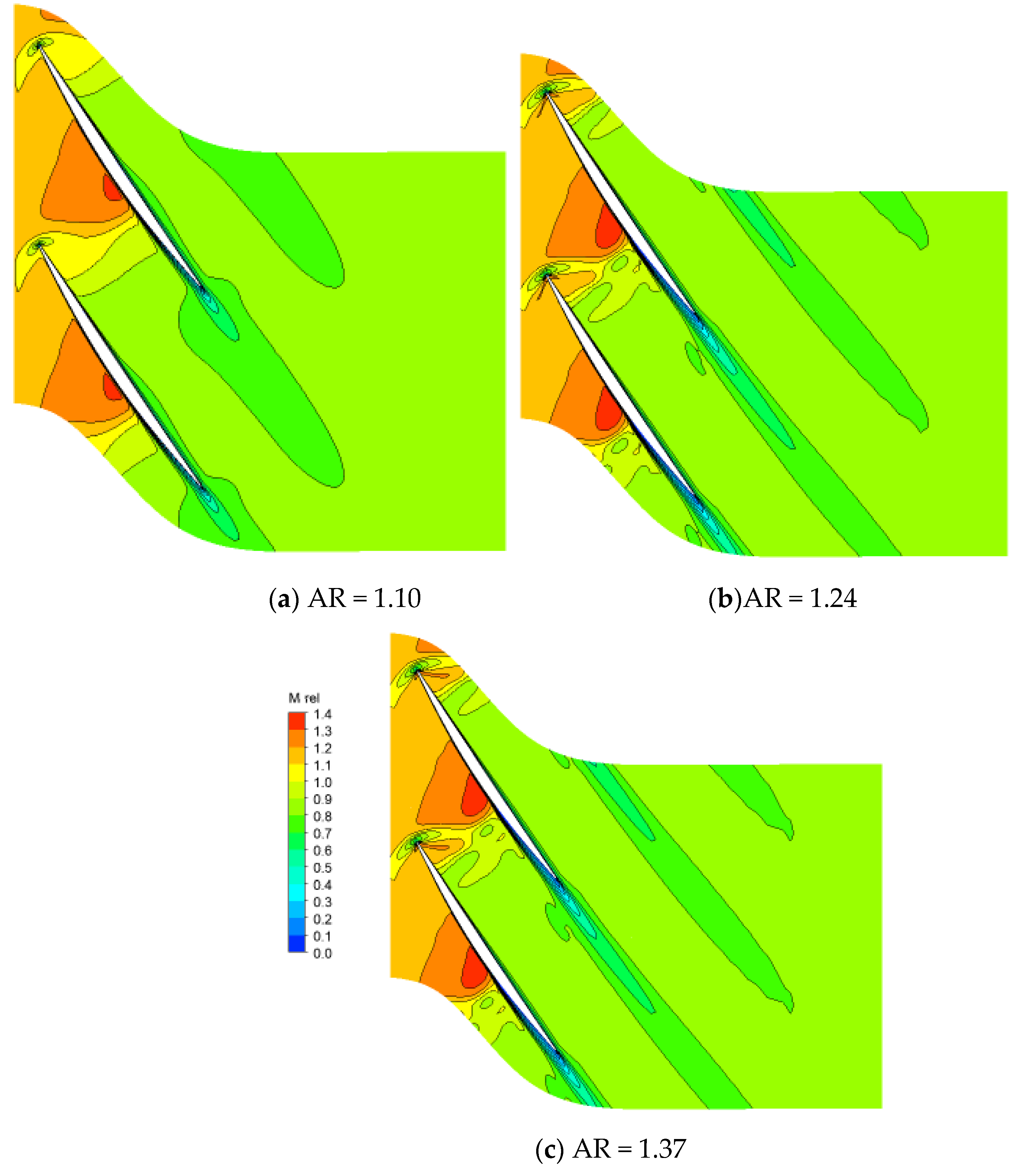
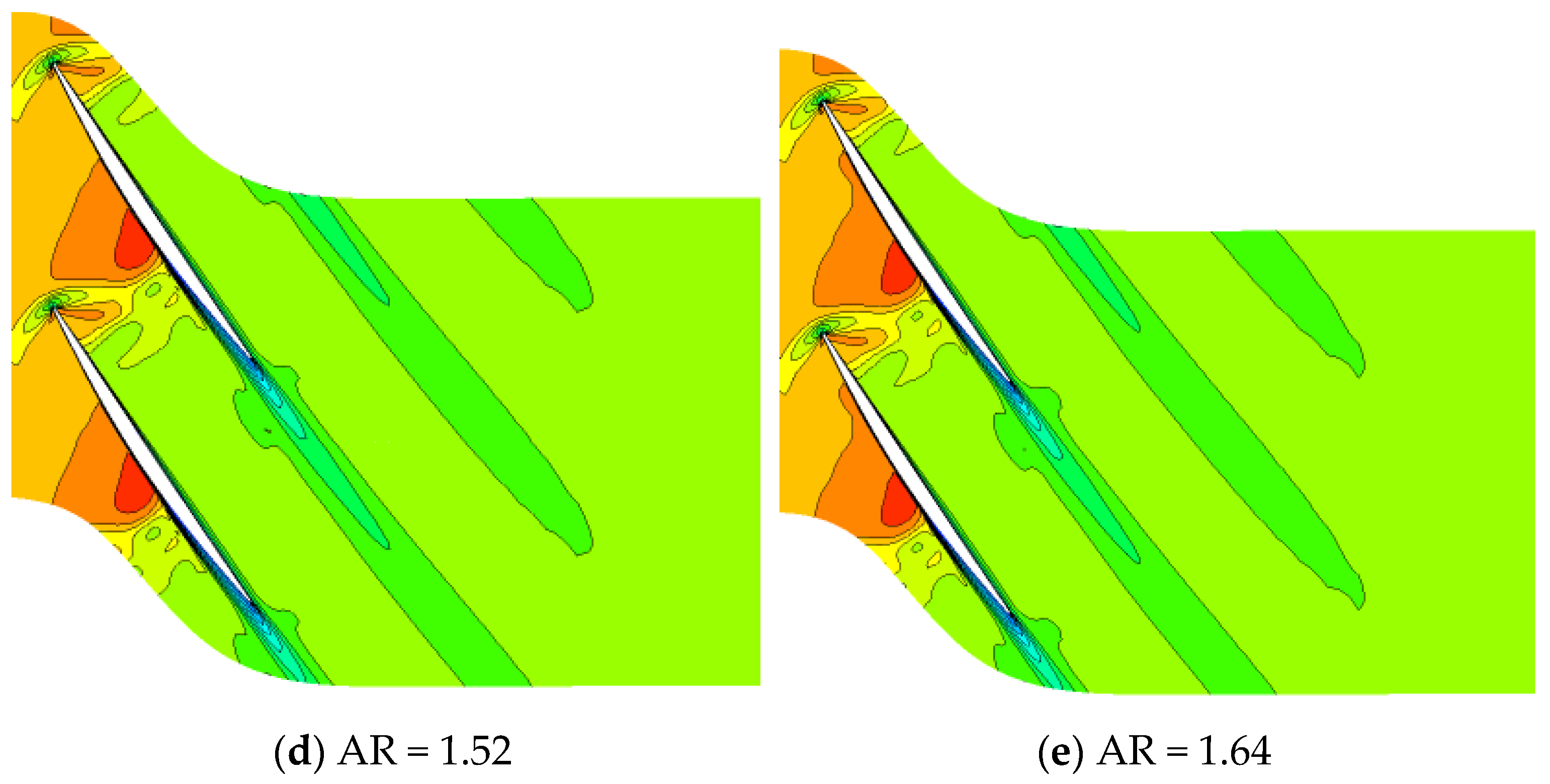
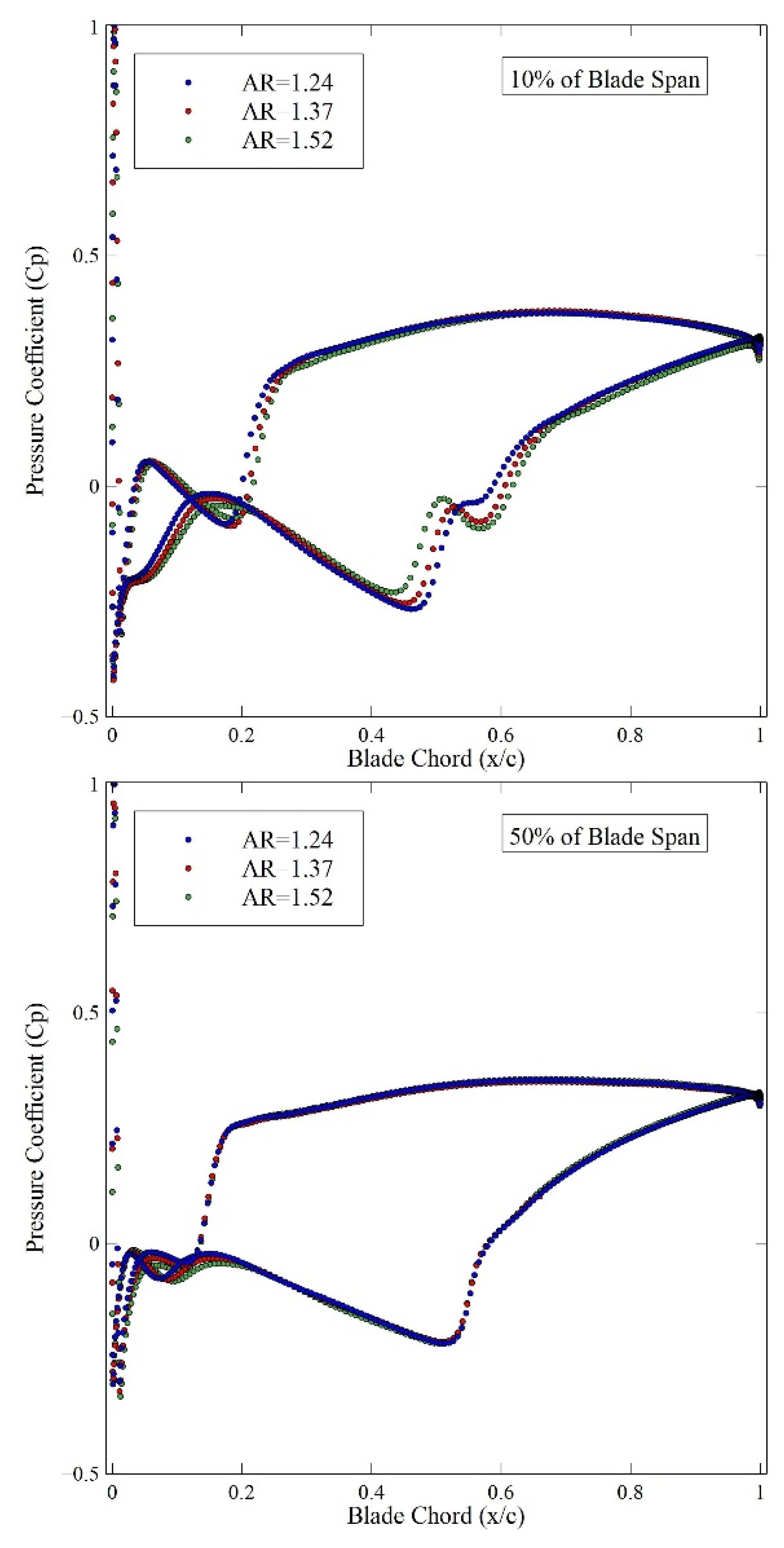
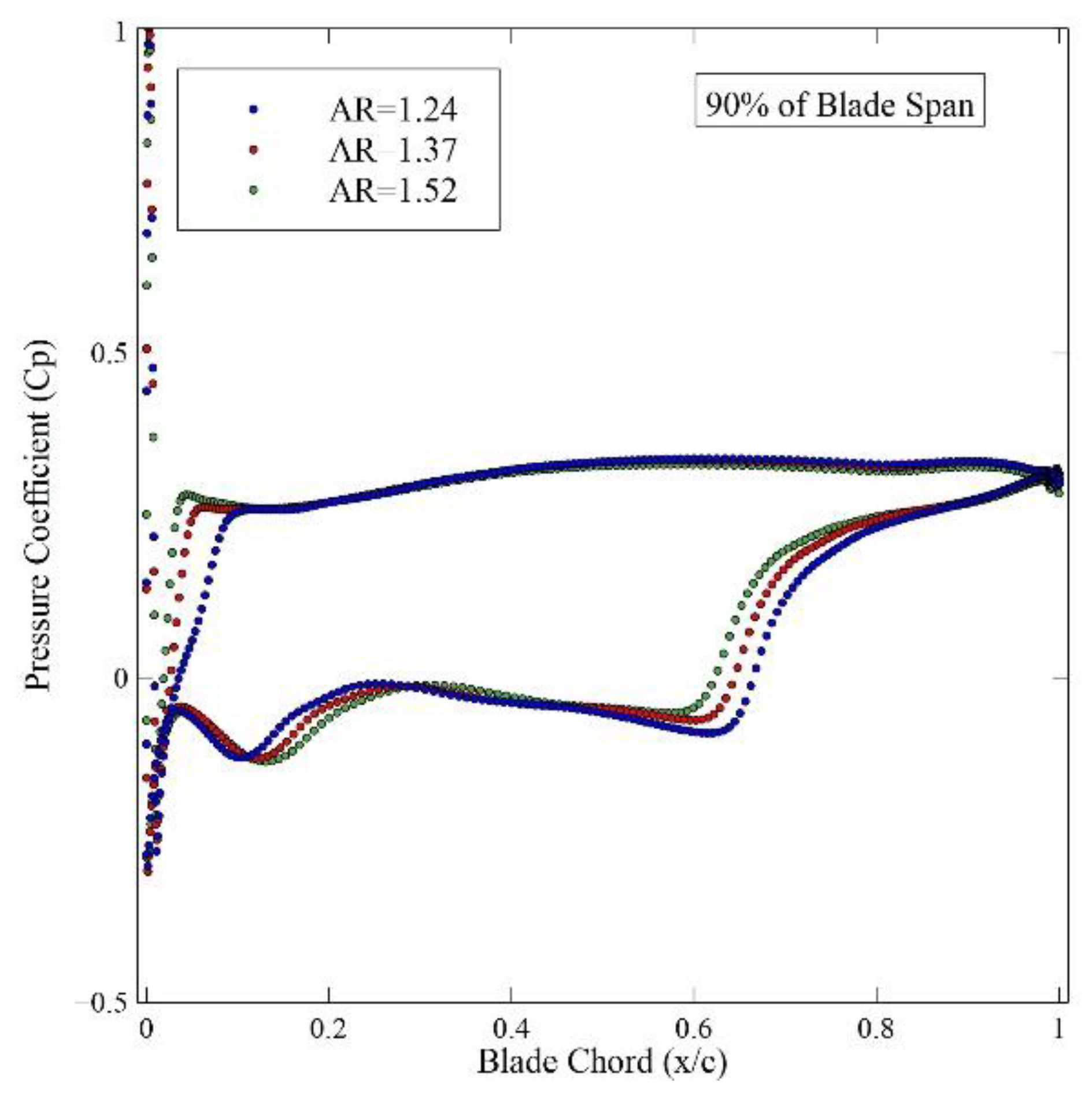
In high-speed compressor flows shocks frequently occur. They are characterized by the static pressure and static temperature of the flowing medium changing abruptly, accompanied with an associated step change in flow velocity and properties of the fluid. The shocks significantly affect the efficiency of the turbomachine and may also change the direction of the flow. Here, however, great care has been taken to isolate the effect of the AR. This necessitates that the position and strength of the shock remains relatively unchanged while the AR is varied. Only small differences in the leading-edge shock wave are observed as the AR is changed. This invariance is mostly attributed to the scaling procedure and the choice of keeping the leading-edge radii fixed. The very modest variation in Mach number is shown in Figure 7, displaying the relative Mach number distribution at mid span for an AR of 1.10, 1.24, 1.37, 1.52 and 1.64 in the reference condition. The computed flow fields indicate that the position of the shock does not show a marked change although a slight increase in shock strength is observed with increasing AR between AR=1.10 and 1.24.

To quantify further on the blade-to-blade flow the

C_{p}

variation is computed around the blade profile. The results are plotted in Figure 8 showing the variation for the nominal case (AR=1.37) and for the two AR values closest to 1.37, that is AR=1.24 and AR=1.52. Here we can see that that differences from the nominal case are more pronounced close to the shroud (90% blade height) and hub (10% blade height). Thus, close to the nominal condition, it seems that it is primarily the end-wall variation that establishes the change in efficiency. Farther away from the nominal condition stronger variation is seen at the mid span but the hub and shroud variation increase even further still dominating the loss variation. It is noteworthy that these end-wall regions are fundamental for understanding internal flow field in compressors, although they are regions that are difficult to instrument for measurements [44].

4.4. Aspect ratio and multi-objective optimality for high-speed compressors

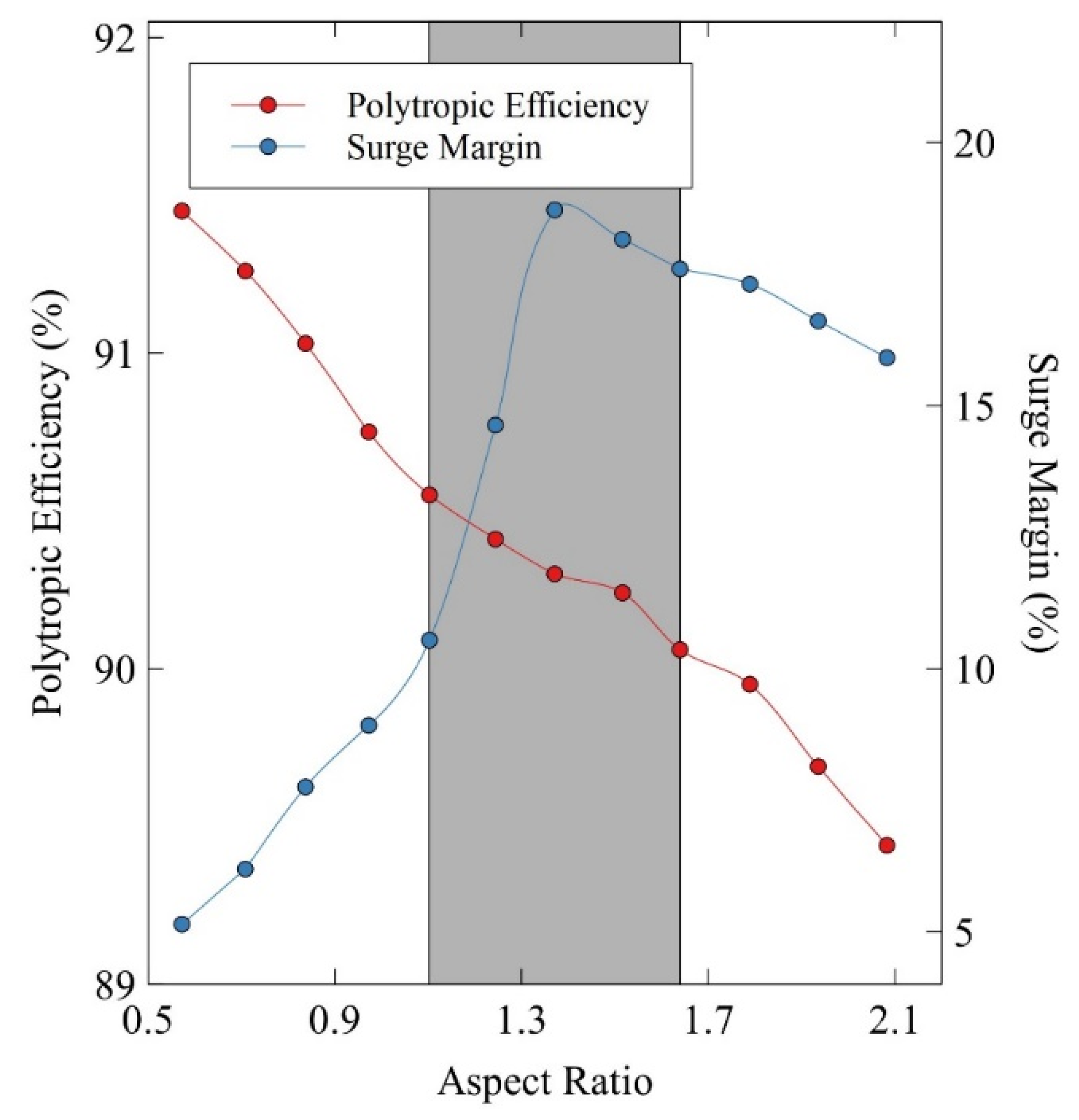
Analyzing the effect of AR around the multi-objective optimum of the VINK compressor, that is around AR=1.37, requires the simultaneous analysis of surge margin and efficiency. As seen from Figure 9 a decreasing trend in the SM is observed for AR lower than AR=1.37 with AR=0.57 being very close to surge. This is noteworthy, being in contrast to the well-known trend of increasing surge margin with decreasing AR [7,10]. The existence of an optimum in SM for the nominal AR is attributed to the multi-objective optimality, that is that both SM and efficiency is considered when choosing the optimal configuration. As explained earlier, we do not include the effect of tip-clearance in fear of compromising the ability to maintain constant values on the other key design variables and hence fail to isolate the effect of AR. Admittedly, inclusion of tip-leakage may have further key effects on the observed flow.

Interestingly enough, for AR higher than 1.37 the SM also decreases however not at the same rapid pace reaching SM=15.9% at AR=2.08. The nominal design, AR=1.37, reaches peak surge margin with SM=18.7%, illustrating the trade between efficiency and surge margin. Here, optimal thus corresponds to a peak in surge margin but the efficiency shows a monotonous increase with reduction in AR. Hence, the designer can trade surge margin with increase in efficiency to a point where stability is no longer possible for the compressor operating range.

Comparing with the fundamental low speed analysis carried out by To and Miller [20] we see a slightly higher range for the multi-objective optimality. To and Miller [20] propose a range between 1.0 and 1.5, with an optimum of 1.16 when the thickness to chord ratio was fixed to 5.4%. The current work suggests a close to optimal range within AR = 1.10 and 1.64, with the lower range from 1.10 to 1.37 being more favorable since a slight efficiency benefit is observed for lower AR. This is achieved at the expense of a relatively large drop in surge margin. The upper range, from 1.37 to 1.64, results in both an efficiency drop and a drop in surge margin but at a much lower rate of surge margin decrease. Although the efficiency varies only slowly around the AR=1.37 case, no distinct optimum in efficiency is noted. It is believed that in general the designer has to choose to maximize surge margin or efficiency and that in general both parameters cannot be simultaneously maximized. Worsk in the literature show passive techniques for improving stability, such as the use of foam metal casing treatment [45].

Although it was decided to keep Re-number constant going across the AR parameter range, by varying the fluid viscosity, it was decided to test the general behavior also for a varying Re-number. For this reason, the simulations for AR=0.57, 0.84, 1.10, 1.37, 1.64 and 2.08 were repeated. The efficiency variation remained almost identical to the one shown in Figure 9, with the slope of the curve somewhat increased. This is because the low AR points now correspond to a higher Reynolds number and thus result in a higher efficiency whereas the opposite holds for the high AR points. For AR=0.57 the efficiency increased by about 0.35% whereas for the AR=2.08 about a reduction of about 0.25% was observed.

Finally, it should also be emphasized that the prediction of the absolute level of surge margin is notoriously difficult, not the least using a simpler two-equation turbulence model such as the SST model used herein. Validation of the predictive capability of our simulations have recently been reported in [38,46], even that the impact of tip clearance and endwall blockage in compressor performance are still not completely understood [47].

Our ambition is to predict consistent trends and rank proximity to surge, not to establish absolute surge prediction. Also, the key observations made in this work are done predominantly well away from surge. Note that the comparison of different ARs are carried out in the reference condition for each AR, hence we are changing the length of the rotor blades but keeping aerodynamic load as well as other key aerodynamic parameters constant.

5. Conclusions

In this work, the first rotor of a high-speed multistage axial compressor [21] was used to analyze the AR influence on compressor performance. Great care was taken to allow the isolated study of the AR on the compressor performance, around its nominal design value of AR=1.37. The isolation of the effect of the AR was achieved using a constant pitch-chord scaling procedure allowing other key design parameters to remain relatively unaffected over a large AR range. The efficiency trend presented around the optimum was quite robust to Re-number variation with only a slightly amplified efficiency increase for the lower AR and a further decrease for the higher AR.

The nominal design of AR=1.37 represents a typical high-speed state-of-the-art aero engine compressor design, for which a multi-objective criterion was used. The optimum was achieved by balancing the surge margin against peak efficiency. Herein, optimality in surge margin with respect to AR is observed whereas a close to optimal efficiency is observed in the range from AR=1.10 to AR=1.64. This is only slightly higher than the AR=1.0-1.5 range suggested for low-speed compressors [20]. Clearly, our predicted range is only indicative, considering that the definition of a multi-objective optimality requires balancing efficiency and surge margin and that the choice of balancing these two criteria requires making a design choice along a pareto optimal front.

Supplementary Materials

The following supporting information can be downloaded at: https://github.com/nikander/VINK.

Author Contributions

Conceptualization, Lucilene Silva, Tomas Grönstedt, Carlos Xisto and Luiz Whitacker; Data curation, Lucilene Silva and Luiz Whitacker; Formal analysis, Lucilene Silva, Tomas Grönstedt, Carlos Xisto, Luiz Whitacker, Cleverson Bringhenti and Marcus Lejon; Funding acquisition, Tomas Grönstedt and Cleverson Bringhenti; Investigation, Lucilene Silva, Tomas Grönstedt, Carlos Xisto and Luiz Whitacker; Methodology, Lucilene Silva, Tomas Grönstedt, Carlos Xisto and Luiz Whitacker; Project administration, Tomas Grönstedt and Cleverson Bringhenti; Resources, Tomas Grönstedt and Cleverson Bringhenti; Software, Lucilene Silva, Tomas Grönstedt, Carlos Xisto and Luiz Whitacker; Supervision, Tomas Grönstedt, Carlos Xisto and Cleverson Bringhenti; Validation, Lucilene Silva, Tomas Grönstedt, Carlos Xisto, Luiz Whitacker and Marcus Lejon; Visualization, Lucilene Silva and Luiz Whitacker; Writing – original draft, Lucilene Silva and Luiz Whitacker; Writing – review & editing, Lucilene Silva, Tomas Grönstedt and Luiz Whitacker.

Funding

This work is financially supported by SAAB AB under the project Jet Engine Design and Testing - Gripen Brazil Offset.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors on request.

Acknowledgments

The authors are grateful to Chalmers University of Technology, Aeronautics Institute of Technology (ITA), the Swedish National Infrastructure for Computing (SNIC) and the Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) to support this project. The authors are also grateful to PCA Engineers (England) for the academic license of the SC90C software.

Conflicts of Interest

The authors declare no conflicts of interest.

References

T. Dickens and I. Day. The Design of Highly Loaded Axial Compressors. Journal of Turbomachinery, 2011; 133, 031007-1–31007-10. [CrossRef]
S. Lieblein. Aerodynamic Design of Axial-Flow Compressors. VI-Experimental Flow in Two-Dimensional Cascades. Re-printed NASA SP-36: Aerodynamic Design of Axial Compressors, 1965; 83–226.
Zhou, S.; Zhao, S.; Zhou, C.; Wu, Y.; Yuan, H.; Lu, X. Optimal Design and Analysis of a High-Load Supersonic Compressor Based on a Surrogate Model. Aerospace 2023, 10, 364. [Google Scholar] [CrossRef]
L. Olmedo, W. Liu, K. Gjika and J. Schiffmann. Thermal management for gas lubricated, high-speed turbomachinery. Applied Thermal Engineering 2023, 218, 119229. [Google Scholar] [CrossRef]
Szymanski, U. Igie, K. Abudu e R. Hamilton. Aerodynamic limits of gas turbine compressor during high air offtakes for minimum load extension. Applied Thermal Engineering 2021, 189, 116697. [Google Scholar] [CrossRef]
J. Wennerstrom. Highly Loaded Axial Flow Compressors: History and Current Development. Journal of Turbomachinery 1990, 112, 567–578. [Google Scholar] [CrossRef]
J. Wennerstrom. Low Aspect Ratio Axial Flow Compressors: Why and What It Means. Journal of Turbomachinery 1989, 111, 357–365. [Google Scholar] [CrossRef]
L. H. Smith. Axial compressor Aerodesign Evolution at General Electric. Journal of Turbomachinery 2002, 124, 321–330. [Google Scholar] [CrossRef]
C. Koch. Stalling Pressure Rise Capability of Axial Flow Compressors. Journal of Engineering for Power, 1981, 103, 645–656. [Google Scholar] [CrossRef]
W. Britsch, W. Osborn and M. Laessig. Effects of Diffusion Factor, Aspect Ratio, and Solidity on Overall Performance of 14 Compressor Middle Stages. Technical Paper 1523, NASA, 1979. [Google Scholar]
H. Wang, Y. Wu, Y. Wang and S. Deng.. Evolution of the flow instabilities in an axial compressor rotor with large tip clearance: An experimental and URANS study. Aerospace Science and Technology 2020, 96, 13. [Google Scholar] [CrossRef]
S. Chen, Y. Gong e C. Zeng. Pulsed suction towards unsteady active flow control in an axial compressor cascade including clearance leakage effects", Applied Thermal Engineering 2023, 219, 119654. [CrossRef]
H. Schönenborn, M. Junge and U. Retze. Contribution to Free and Forced Vibation Analysis of an Intentionally Mistuned Blisk. in Proceedings of ASME Turbo Expo, 2012, Copenhagen, Denmark, 2012. [CrossRef]
T. Schmidt, M. Peters, P. Jeschke, R. Matzgeller and S. J. Hiller. High aspect ratio blading in an axial compressor stage. in Proceedings of ASME Turbo Expo 2017: Turbomachinery Technical Conference & Exposition, 2017. [CrossRef]
Zhong, L.; Liu, R.; Miao, X.; Chen, Y.; Li, S.; Ji, H. Compressor Performance Prediction Based on the Interpolation Method and Support Vector Machine. Aerospace 2023, 10, 558. [Google Scholar] [CrossRef]
Z. Wang, L. Qi, S. Liu, W. Hong e S. Wang. The influence of component parameters on cycle characteristic in rotating detonation gas turbine. Applied Thermal Engineering 2023, 220, 119716. [Google Scholar] [CrossRef]
N. Neumann, M. Asli, N. Garan, D. Peitsch e P. Stathopoulos. A fast approach for unsteady compressor performance simulation under boundary condition caused by pressure gain combustion. Applied Thermal Engineering 2021, 196, 117223. [Google Scholar] [CrossRef]
N. D. Alfredsson. The Impact of the Blade Aspect Ratio on Axial Compressor Efficiency and Stability and its Correlation to the Skoch Parameter. Master Dissertation, Department of Energy Sciences, Lund University, Lund, Sweden, 2018.
M. Peters, T. Schmidt and P. Jeschke. Influence of Blade Aspect Ratio on Axial Compressor Efficiency. Journal of the Global Power and Propulsion Society, 2019; 14. [Google Scholar] [CrossRef]
H. O. To and R. J. Miller. The Effect Aspect Ratio on Compressor Performance. Journal of Turbomachinery 2019, 141, 081011. [Google Scholar] [CrossRef]
M. Lejon, T. Grönstedt, N. Glodic, P. Petrie-Repar, M. Genrup and A. Mann. Multidisciplinary Design of a Three Stage High Speed Booster. in Proceedings of the ASME Turbo Expo 2017: Turbomachinery Technical Conference, Charlotte, North Carolina, USA, 2017. [CrossRef]
N. Andersson. GitHub Repository for VINK. 19 9 2017. [Online]. Available: https://github.com/nikander/VINK. [Accessed 12 10 2019].
PCA Engineers. SC90C a stream line curvature. 2014.
H. Skärnell. Parameterization and Design of Transonic Compressor Blades. Master’s thesis in Engineering Mathematics and Computational Science. Department of Applied Mechanics, Chalmers University of Technology., Gothenburg, Sweden, 2013.
M. N. Goodhand and R. J. Miller. Compressor Leading Edge Spikes: A New Performance Criterion. Journal of Turbomachinery 2011, 133, 021006. [Google Scholar] [CrossRef]
X. Zhang, Y. Ju and C. Zhang. Geometry scaling technique and application to aerodynamic redesign of multi-stage transonic axial-flow compressors. Aerospace Science and Technology 2022, 121, 17. [Google Scholar] [CrossRef]
L. M. Silva, J. T. Tomita and J. R. Barbosa. A study of the influence of the tip-clearance on the tip-leakage flow using CFD techniques. in Brazilian Congress of Mechanical Engineering – COBEM, Natal, RN, Brazil, 2011.
M. Lejon. Simulation and Optimization of an Axial Compressor Considering Tip Clearance Flow. Thesis for the degree of Licentiate of Engineering, Chalmers University of Technology, Gothenburg, Sweden. 2016.
M. Lejon, T. Grönstedt, N. Andersson, E. Ellbrant and H. Mårtensson. On Improving the Surge Margin of a Tip-Critical Axial Compressor Rotor. in Proceedings of the ASME Turbo Expo 2017: Turbomachinery Technical Conference and Exposition, Charlotte, North Caroline, USA, 2017. [CrossRef]
T. Pan, W. Wu and Q. Li. Effect of casing treatment to switch the type of instability inception in a high-speed axial compressor. Aerospace Science and Technology 2021, 115, 11. [Google Scholar] [CrossRef]
Y. J. Jung, H. Jeon, Y. Jung, K. J. Lee and M. Choi. Effects of recessed blade tips on stall margin in a transonic axial compressor. Aerospace Science of Technology 2016, 54, 41–48. [Google Scholar] [CrossRef]
H. Li, Q. Zheng, Z. Chen, Y. Duan, B. Jiang and E. Benini. The role of radial secondary flow in the process of rotating stall for a 1.5-stage axial compressor. Aerospace Science and Technology 2021, 115, 24. [Google Scholar] [CrossRef]
M. Lejon. Aerodynamic design framework for low-pressure compression systems.. Thesis for the Degree of Doctor of Philosophy in Thermo and Fluid Dynamics, Gothenburg, Sweden, 2018.
ANSYS, Writer, ANSYS TurboGrid Tutorial. Release 15.0. [Performance]. ANSYS, Inc., 2018.
ANSYS, Writer, CFX-Pre User's Guide. Release 19.1. [Performance]. ANSYS, Inc., 2018.
F. R. Menter. Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications. AIAA Journal 1994, 32, 1595–1605. [Google Scholar] [CrossRef]
Yan, W.; Sun, Z.; Zhou, J.; Zhang, K.; Wang, J.; Tian, X.; Tian, J. Numerical Simulation of Transonic Compressors with Different Turbulence Models. Aerospace 2023, 10, 784. [Google Scholar] [CrossRef]
R. B. Díaz. Circumferential grooves passive wall treatment in a transonic axial compressor. Thesis for the Degree of Master of Science in Aeronautics and Mechanical engineering, Aeronautics Institute of Technology, São José dos Campos, Brazil, 2018.
Xu, X. Dong, C. Zhou, D. Sun, X. Gui and X. Sun. Effect of rotor axial blade loading distribution on compressor stability. Aerospace Science and Technology 2021, 119, 18. [Google Scholar] [CrossRef]
L. Reid and R. D. Moore. Performance of a single-stage axial-flow transonic compressor with rotor and stator aspect ratios of 1.19 and 1.26, respectively, and with design pressure ratio of 1.82. NASA Technical Paper 1338, 1978.
Z. Li, P. Zhang, D. Yang and J. Zhang.. Numerical investigations on the key contributing factor and flow features of compressor stall hysteresis. Aerospace Science of Technology 2022, 121, 9. [Google Scholar] [CrossRef]
Wang and, X. Huang. A complete rotor–stator coupling method for frequency domain analysis of turbomachinery unsteady flow. Aerospace Science and Technology 2017, 70, 367–377. [Google Scholar] [CrossRef]
Liu, Y. Ju and C. Zhang. Parallel rotor/stator interaction methods and steady/unsteady flow simulations of multi-row axial compressors. Aerospace Science and Technology, 2021; 106859. [Google Scholar] [CrossRef]
Ma, S.; Hu, J.; Wang, X.; Ji, J. The Application of a Laser-Printed Miniature Five-Hole Probe in the End-Wall Flow Measurement of a Multistage Axial Compressor. Aerospace 2023, 10, 1020. [Google Scholar] [CrossRef]
Li, J.; Dong, X.; Sun, D.; Wang, Y.; Geng, C.; Sun, X. Stability Enhancement and Noise Reduction of an Axial Compressor with Foam Metal Casing Treatment. Aerospace 2022, 9, 628. [Google Scholar] [CrossRef]
L. M. da Silva, T. Grönstedt, L. H. L. Whitaker, J. T. A. M. Tomita and V. A. C. Martins. Comparison of Different CFD Unsteady Methods for the Performance Analysis of a Transonic Axial Compressor. in ISABE-2022-255-255, Ottawa, Canada, 2022.
L. H. Smith. Casing Boundary Layers in Multistage Axial Flow Compressors. Flow Research on Blading 1970, 106, 635–647. [Google Scholar]

Figure 1. Hub, shroud and blade passage streamline location.

Figure 2. Comparison of the relative difference (in %) in mass flow rate, total pressure ratio and polytropic efficiency for different mesh sizes.

Figure 3. IGV (left) and rotor (right) using the mesh chosen from the mesh independence study.

Figure 4. Boundary conditions applied in the compuational fluid dynamics (CFD) domain.

Figure 5. Key parameter variation (in %) for the parameters ϕ, ψ, Λ, DF and relative Mach number at inlet and outlet domain, for different ARs.

Figure 6. Polytropic efficiency and total-to-total pressure ratio versus rotor AR.

Figure 7. Relative Mach number distribution for blade-to-blade passage at mid span for different AR: (a) 1.10, (b) 1.24, (c) 1.37, (d) 1.52 and (e) 1.64, at the reference condition.

Figure 8. Pressure coefficient distribution of rotor blade for AR= 1.24, AR=1.37 and AR=1.52 and for 10%, 50% and 90% of the blade span, respectively from top to bottom.

Figure 9. Comparison of polytropic efficiency and surge margin variations versus several rotor aspect ratio.

Table 1. Virtual Integrated Compressor (VINK) first stage specification in nominal condition.

Parameter	Value
Design rotational speed	6242 rpm
Design point pressure ratio	1.51
Design point corrected mass flow	89.5 kg/s
Design point polytropic efficiency	91.0 %
Surge margin at design point¹	19.1 %
De Haller Number	0.74 and 0.92 (stator)

¹Calculated according to the stall margin definition in Equation 4 in the present paper.

Table 2. Additional geometrical VINK compressor data.

Parameter	Inlet Guide Vane (IGV)	Rotor
Blade count	76	51
Chord at mean radius	50.4 mm	98.3 mm
Axial chord at mean radius	49.8 mm	54.7 mm
Rotor AR	-	1.37

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer