Prerpints.org logo
Preprint
Article

Active Distribution Grid Exceeding Testing and Risk Planning Based on Carbon Capture and Multi-Source Data of Power Internet of Things

Altmetrics

Downloads

62

Views

28

Comments

0

Submitted:

17 January 2024

Posted:

18 January 2024

You are already at the latest version

Alerts
Abstract
In order to achieve its carbon peak and neutrality targets, a high proportion of distributed power sources are connected to the distribution network in China, which greatly increases the risk of distribution network operation. Aiming at the above problems, this paper proposes an active distribution network risk planning model based on multi-source data from carbon capture and power internet of things, and conducts exceeding testing of distribution network based on the stochastic load flow algorithm with semi-invariant and level expansion, calculates the semi-invariant of each order of node state vectors and branch current vectors, and then utilizes the Gram-Charlier level expansion to obtain the exceeding probability density function and probability distribution function of the node voltages and line powers of the distribution network. The probability density function and probability distribution function of the exceeding are obtained using the Gram-Charlier series expansion. Combined with multi-source data, the active distribution network with integrated energy system considering carbon capture is modeled. According to the risk scenario of the distribution network, the nonconvex constraints in the model are simplified by the second-order cone relaxation, and the optimal planning scheme of the distribution network is solved by combining the gurobi solver with the risk index as the first-level objective and the economic benefit as the second-level objective. The simulation results of a coupled network consisting of a 39-node distribution network and an 11-node transportation network verify the effectiveness of the proposed model.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

The distribution network is directly facing the power users and is responsible for the important function of power distribution, which plays a key role in improving the economy and security stability of the power grid and promoting the integration of distributed equipment into the grid. With the access of integrated energy systems, the traditional power data acquisition platform has fewer monitorable points, a single type of monitoring data, and a lack of multivariate data processing functions, so it is increasingly difficult for the existing distribution network risk planning technology to adapt to the special requirements of smart distribution networks as well as transparent distribution networks. Power IoT is applied under the condition of multiple monitoring nodes [1] , which has the characteristics of multiple connected nodes and multiple data types, and by virtue of the numerous monitoring nodes, the same data can be characterized from multiple dimensions, which enhances the accuracy and real-time nature of distribution network modeling [2], and realizes the ubiquitous IoT. In order to improve the distribution network operation security system, combined with the electric power IoT related technology, under the premise of multiple source load access to the new electric power system, it is necessary to carry out the risk planning research of the active distribution network containing integrated energy system on the basis of quantitative calculation of the exceeding risk of the distribution network.
The traditional deterministic power flow calculation method [3] needs to be simulated several times to be able to analyze the distribution network operation risk in a certain quantitative way, and the reference [4,5,6,7,8] introduces a variety of probabilistic power flow algorithms that are mainly applied at present. Reference [9,10] analyzed the accuracy of Monte Carlo methods based on specific scenarios. Reference [11,12] considered the correlation that exists between wind farms that are close in spatial distance when analyzing the probabilistic power flow operating characteristics of power systems. Reference [13] illustrated that the semi-invariant method can effectively solve the probability distribution of different state quantities. Reference [14] utilizes linear relationships for probabilistic power flow calculations of distribution networks containing integrated energy sources, and combines them with level expansion to quickly obtain the probability distribution functions of various state quantities.
At present, integrated energy systems emphasizing multi-energy coupling are increasingly connected to distribution grids, which create a close connection between integrated energy systems and distribution grids around the supply, conversion and demand of energy. Reference [15,16,17] explains the role of integrated energy systems and carbon capture technologies in reducing grid carbon emissions and improving the operational stability of distribution grids. Reference [18] proposed the introduction of carbon trading mechanism in distribution grids containing integrated energy sources, and guided the distribution grids to reduce carbon emissions through stepped carbon pricing. Reference [19] introduced the power-to-gas (P2G) device into the integrated energy system, and fixedly participated the CO2 emitted from the gas unit into the methane synthesis reaction through carbon capture to improve the system economy. Reference [20] points out that the nature of active distribution network planning belongs to the category of distribution network optimal power flow, and optimal power flow is currently the main research focused on the direction of AC optimal power flow [21]. AC optimal current belongs to nonlinear planning because of the nonlinear characteristics in its constraints. The earliest validation of its effectiveness in distribution network optimal power flow is mainly evolutionary algorithms, such as genetic algorithm, particle swarm algorithm [22] and so on. However, evolutionary algorithms also have obvious defects such as the inability to guarantee global optimization when solving nonlinear models. To address this need, literature [23] systematically establishes a branch flow model to solve the optimal flow model framework. Meanwhile, reference [24,25] also gives relaxation accuracy proofs. The second-order cone programming is mainly used to obtain the global optimal solution as well as a good solution speed by transforming the original model into a convex programming form.
The current distribution network risk planning research also exists on the strong correlation of random variables less consideration and distribution network improvement planning program randomness is too high. Therefore, to address the above problems, this paper adopts the Gram-Charlier series expansion to obtain the exceeding probability density function and probability distribution function of the distribution network node voltage and line power, establishes a two-layer planning model, and solves the optimal planning scheme of the distribution network through the second-order cone relaxation combined with the gurobi solver under the premise of ensuring that the risk probability of the distribution network is controllable.
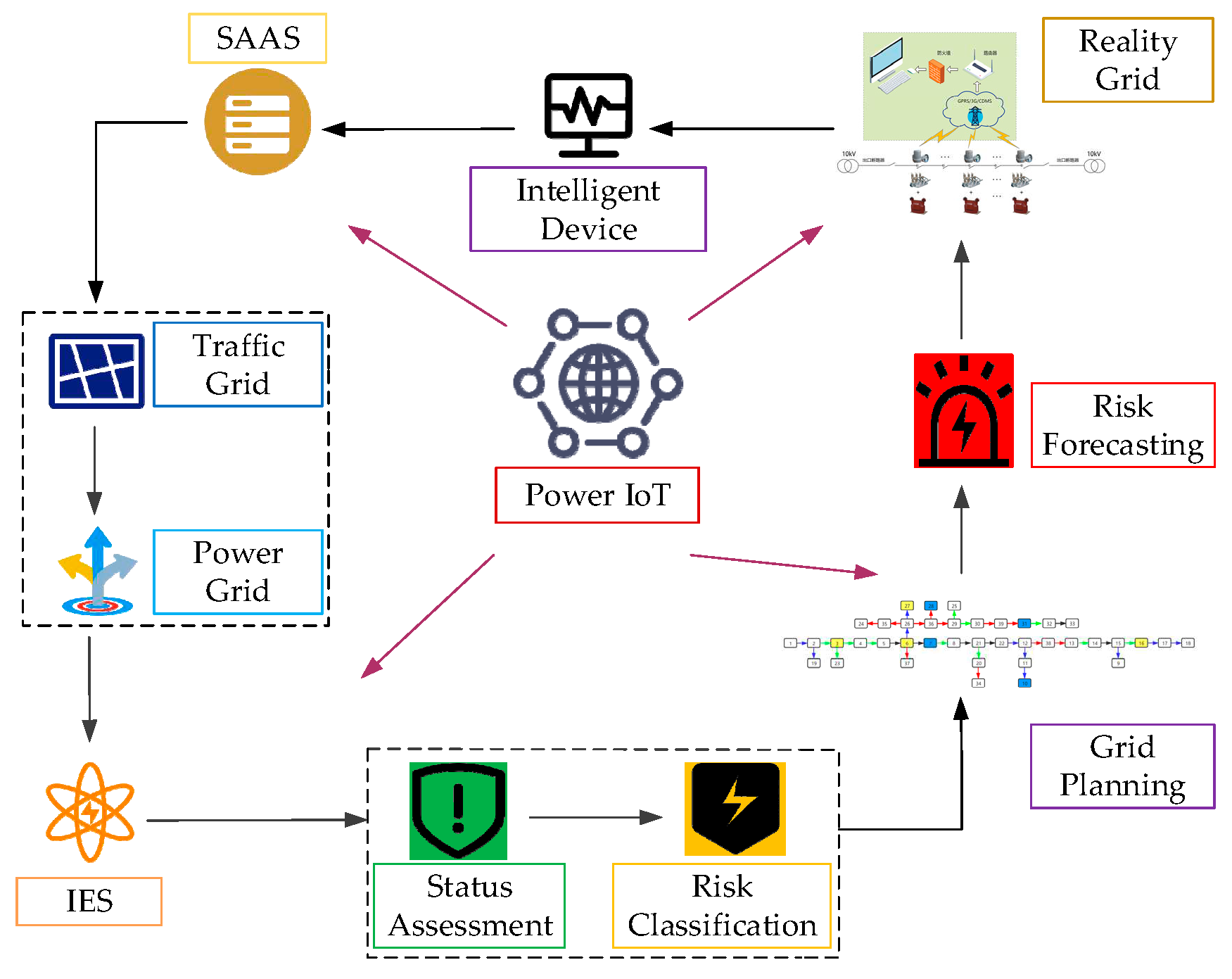
In Figure 1, this paper uses historical data to carry out the status quo twinning, to ensure that its behavior and development law and physical twin with virtual and real accurate mapping relationship, based on the second-order cone planning method to adjust the existing distribution network frame structure and test its characteristic index, using the main characteristics of the data structure to build up the distribution network risk characteristics evaluation system, in the virtual space to make support for the physical entity life cycle of the risk of each prediction.

2. Model Principle Analysis

2.1. Semi-invariant Based Risk Prediction Model for Distribution Networks

Semi-invariance is an important numerical characteristic of a random variable, obtained by applying certain mathematical transformations to the characteristic function of the distribution function F(x). The expression for the characteristic function is:
φ ( t ) = E ( e i t x ) = ∫ − ∞ + ∞ e i t x f ( x ) d x
Taking the natural logarithm of the above equation and expanding it according to the McLaughlin series formula, we have the following equation:
ln φ ( t ) = ∑ r = 1 s y r r ! ( i t ) r + o ( t s )
where the coefficient yr is an r-order semi-invariant, s denotes the number of terms in the expanded expression, and o(ts) denotes the remaining terms.
For normally distributed load power, the first order semi-invariant is the mathematical expectation, the second order semi-invariant is equal to the variance, and the third and higher order semi-invariant has a value of zero.
γ 1 = μ γ 2 = σ 2 γ 3 = γ 4 = ⋯ = 0
For a discretely distributed load power, first find its center moments of each order according to the following equation.
Gram-Charlier Grade Expanded according to the orthogonal properties of Hermite polynomials, hence the name orthogonal expansion. According to the Gram-Charlier series expansion, the cumulative distribution function of a random variable can be expressed as:
F G ( x ) = ϕ ( x s ) + φ ( x s ) [ f 3 3 ! H 2 ( x s ) + f 4 4 ! H 3 ( x s ) + f 5 5 ! H 4 ( x s ) + ... f 6 + 10 f 3   2 6 ! H 5 ( x s ) ]
where xs is the specified random quantity, φ(xs) and ϕ (xs) are the probability density function and the cumulative distribution function of a standard normally distributed random variable, respectively, fr is the r-order specified semi-invariant, and hi(xs) is the i-order Hermite polynomial.
When polar coordinates are used to represent the nodal voltages, the current equation of the power system can be expressed as:
P F = V F ∑ T = 1 n V T ( G F T cos θ F T + B F T sin θ F T ) Q F = V F ∑ T = 1 n V T ( G F T sin θ F T − B F T cos θ F T )
where PF, QF are the active and reactive power of node F, VF, VT are the voltage amplitude between the two nodes, θFT is the phase difference between the two nodes, and GFT, BFT are the real and imaginary parts of the node admittance matrix YFT, respectively.
Each order semi-invariant of the node injected power ∆Sr can be expressed as the algebraic sum of each order semi-invariant of the point load injected power Δ S l o a d r and each order semi-invariant of the distributed power injected power Δ S w i n d r .
Δ S r = Δ S w i n d r ⊕ Δ S l o a d r
Based on the linearized power flow equations and using the properties of semi-invariants instead of convolution calculations, r-order semi-invariants ∆Xr and ∆Zr can be found for the node voltages and branch currents of the variables to be solved.

2.2. Second-order Cone-based Active Distribution Network Planning Model with Integrated Energy Sources

Under the background of "carbon peak and neutrality targets" and the development of distributed smart grid, the supply side and demand side of the distribution network have changed greatly. In addition to the original basic elements, distributed devices and electric vehicles are gradually applied to the distribution network, which makes the optimization method of the distribution network need to be further studied. Distribution network improvement planning is a kind of distribution network optimization measures, through the line optimization and upgrading, to optimize the distribution network operation indexes, such as stability, economy and so on, under the premise of ensuring the stability of the distribution network grid topology.

2.2.1. Queuing Model for Fast Charging Stations

If each fast charging station is simplified as a queuing system, and the driving routes of EVs are simulated by Monte Carlo method, when the battery SOC of EVs, buses and cabs that are in the driving state is lower than the user's threshold, the user will select the optimal charging station for fast replenishment based on the charging station decision-making model. In addition, the electric private cars and cabs are connected to the charging piles in their residential areas for slow replenishment immediately after finishing their respective trips. Assuming that electric vehicles generate charging demand as soon as they drive into the planning area, the sum of the time spent in searching for and arriving at the fast charging station and the queuing time is the waiting cost. The simplification for the actual situation is as follows: establish the road section impedance model according to the road saturation, establish the traffic node impedance model according to the signal cycle, green letter ratio, and road section vehicle arrival rate, and then simulate the dynamic traffic network. The distribution network improvement planning can reduce the problem of increasing network loss caused by large-scale EV and wind power access.
The roadway impedance is modeled as:
L v i j ( t ) = t 0 1 + a ( H ) b , 0 < H ≤ 1.0 t 0 1 + a ( 2 − H ) b , 1.0 < H ≤ 2
Where: a and b are roadway impedance impact factors, t0 is the zero-flow travel time, and H is the roadway saturation.
The transportation node impedance model is:
K v i ( t ) = 9 10 c ( 1 − α ) 2 2 ( 1 − α H ) + H 2 2 q ( 1 − H ) , 0 < H ≤ 0.6 c ( 1 − α ) 2 2 ( 1 − α H ) + 1.5 ( H − 0.6 ) 1 − H H , 0.6 ≤ H
Where: q is the vehicle arrival rate, α is the green signal ratio, c is the traffic signal cycle, Eq. (7) and Eq. (8) can be merged to obtain the actual impedance model of the road.
Electric vehicles arrive at a frequency of:
λ j = ∑ i ω i y i j / t c
Where: λj is the arrival rate of users to fast charging station at point j, tc is the segment duration, and ωi is the charging demand at point i.
The probability that a charging post in a fast charging station is empty is:
λ j = ∑ i ω i y i j / t c
Where: mj is the number of fast charging piles in the fast charging station at point j, pj is the service intensity of the fast charging station at point j, and Pj0 is the probability that the charging pile in the fast charging station at point j is idle.
User queue time expectation is:
W j q = p j 0 p j   m j + 1 m j ! m j ( 1 − p j m j ) 2 λ j
Where: Wjq is the user queuing time expectation of fast charging station at point j. According to the charging pile idle probability and user queuing time expectation in the fast charging station, the electric vehicle charging scenario model can be obtained.

2.2.2. Integrated Energy Station Planning Model with Carbon Capture Consideration

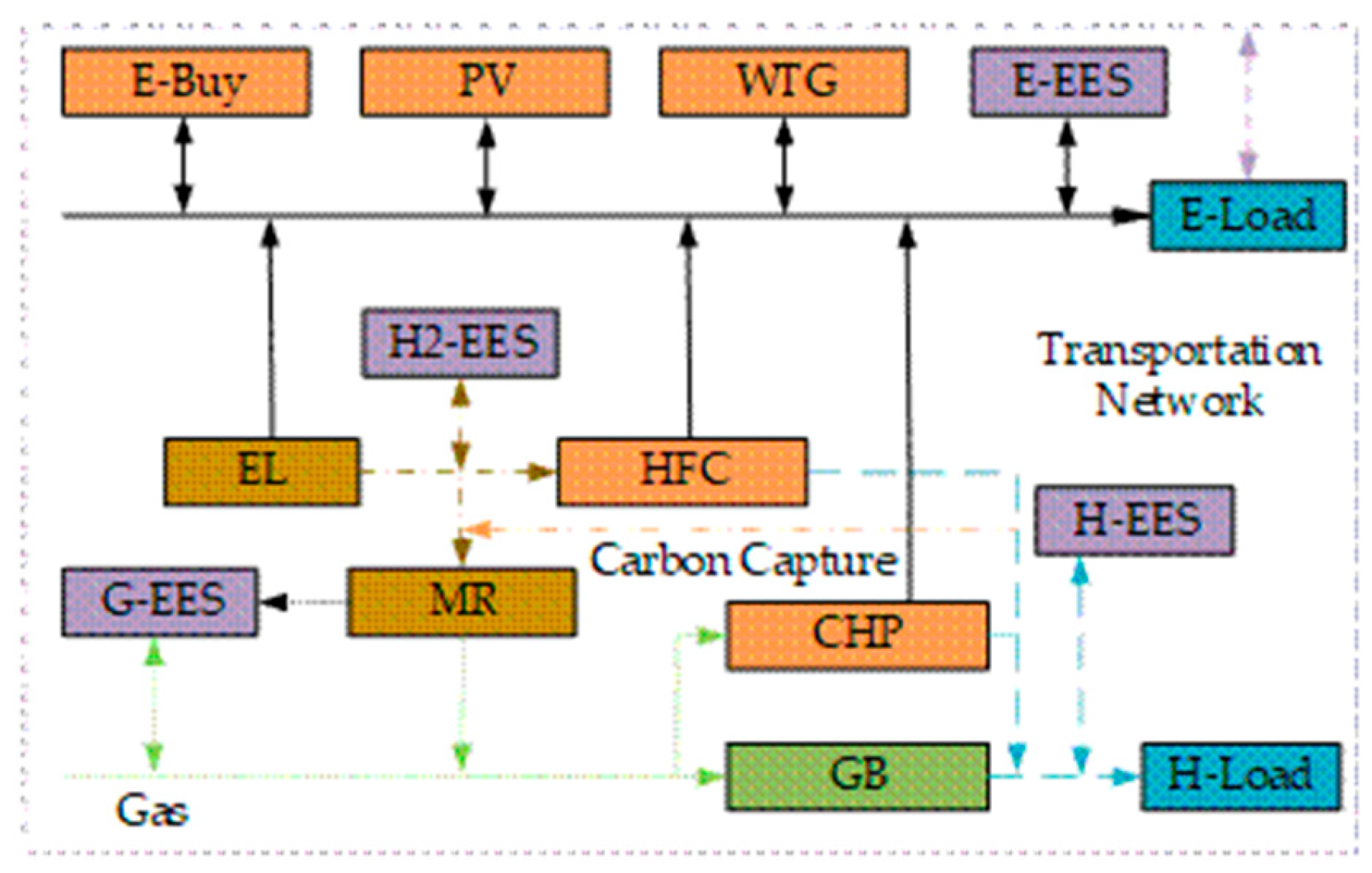
In this paper, the carbon capture device, P2G, hydrogen fuel cell and gas unit are aggregated into a carbon capture-power-to-gas-hydrogen fuel cell(HFC)-gas unit system, in which fixing and feeding CO2 from gas boilers(GB) into methane synthesizer(MR). The part of hydrogen generated by electrolyzer(EL) is utilized to generate natural gas together with CO2 fixed in the carbon capture device to be supplied to the gas unit, and the difference between the amount of natural gas generated and the natural gas demand of the gas unit is involved in the natural gas market, while another part of hydrogen is involved in the reaction of fuel cell to supply power in synergy. The difference between the amount of natural gas generated and the natural gas demand of the gas unit participates in the natural gas market, while another portion of hydrogen participates in the reaction of the fuel cell to synergize the power supply. The system improves the system economy and balances the energy flow through electrical energy storage(EES), gas energy storage(G-EES), heat energy storage(H-EES) and hydrogen energy storage(H2-EES) devices with photovoltaic(PV) and wind turbine generators(WTG). Its specific way of interconversion of each energy is shown in Figure 2.
The cogeneration unit works modeled as:
P C H P e ( t ) = R C H P e P C H P g ( t ) P C H P h ( t ) = R C H P h P C H P g ( t ) P C H P g , min ⩽ P C H P g ( t ) ⩽ P C H P g , max Δ P C H P g , min ⩽ P C H P g ( t + 1 ) − P C H P g ( t ) ⩽ Δ P C H P g , max
Where: P C H P e (t), P C H P h (t) are the electrical and thermal energy output from the CHP unit in time period t, R C H P e , R C H P h are the energy conversion rate of electrical and thermal energy from the CHP unit, P C H P g (t) is the natural gas power input to the CHP unit in time period t, ∆ P g , m a x C H P , ∆ P g , m i n C H P are the upper and lower limits of the CHP unit climbing. The P2G unit operating model is:
P E L H 2 ( t ) = R E L P E L e ( t ) P M R g ( t ) = R M R P M R H 2 ( t ) P E L e , min ⩽ P E L e ( t ) ⩽ P E L e , max P M R H 2 , min ⩽ P M R H 2 ( t ) ⩽ P M R H 2 , max Δ P E L e , min ⩽ P E L e ( t + 1 ) − P E L e ( t ) ⩽ Δ P E L e , max Δ P M R H 2 , min ⩽ P M R H 2 ( t + 1 ) − P E L e ( t ) ⩽ Δ P M R H 2 , max
Where: P E L e (t) is the electrical energy input to the electrolyzer in time period t, P H 2 M R (t) is the hydrogen energy input to the methane synthesis unit in time period t, P M R g (t) is the natural gas power output from the methane synthesis unit in time period t, P H 2 E L (t) is the hydrogen energy output from the electrolyzer in time period t, R E L , R M R are the energy conversion ratio between the electrolyzer and the methane synthesis unit, P e , m a x E L , P e , m i n E L are the upper and lower limits of the electrical energy input to the electrolyzer, ∆ P e , m a x E L , ∆ P e , m i n E L are the upper and lower limits of the electrolyzer climb, P H 2 M R   , m a x , P H 2 M R   , m i n are the upper and lower limits of the hydrogen energy input to the methane synthesis unit, ∆ P H 2 M R   , m a x , ∆ P H 2 M R   , m i n are the upper and lower limits of the methane synthesis unit climb.
Hydrogen fuel cells are modeled to work as:
P H F C e ( t ) = R H F C e P H F C H 2 ( t ) P H F C h ( t ) = R H F C h P H F C H 2 ( t ) P H F C H 2 , min ⩽ P H F C H 2 ( t ) ⩽ P H F C H 2 , max Δ P H F C H 2 , min ⩽ P H F C H 2 ( t + 1 ) − P H F C H 2 ( t ) ⩽ Δ P H F C H 2 , max
Where: P H 2 H F C (t) is the hydrogen energy inputted into the hydrogen fuel cell in time period t, P H F C e (t), P H F C h (t) are the electric and thermal energy outputted from the hydrogen fuel cell in time period t, R H F C e , R H F C h are the conversion rates of the two types of energies of electricity and heat for the hydrogen fuel cell , P H 2 H F C     , m a x , P H 2 H F C     , m i n are the upper and lower limits of the hydrogen energy inputted into the hydrogen fuel cell, ∆ P H 2 H F C     , m a x , ∆ P H 2 H F C     , m i n are the upper and lower limits of the climb of the hydrogen fuel cell.
The gas boiler working model is:
P G B h ( t ) = R G B h P G B g ( t ) P G B g , min ⩽ P G B g ( t ) ⩽ P G B g , max Δ P G B g , min ⩽ P G B g ( t + 1 ) − P G B g ( t ) ⩽ Δ P G B g , max
Where: P G B g (t) is the natural gas power input to the gas boiler in time period t, P G B h (t) is the thermal energy output from the gas boiler in time period t, R G B h is the thermal energy conversion rate of the gas boiler, P g , m a x G B , P g , m i n G B are the upper and lower limits of the natural gas power input to the gas boiler, and ∆ P g , m a x G B , ∆ P g , m i n G B are the upper and lower limits of the creep of the gas boiler.
The working model of the energy storage device is:
0 ⩽ P E S c ( t ) ⩽ B E S c P E S max ( t ) 0 ⩽ P E S d ( t ) ⩽ B E S d P E S max ( t ) P E S ( t ) = P E S c ( t ) R E S c − P E S d ( t ) / R E S d   B E S c + B E S d = 1 S n ( t ) = S n ( t − 1 ) + P E S ( t )
Where: P E S c (t) is the charging power of electric, heat, gas and hydrogen energy storage devices in time period t, P E S d (t) is the output power of the four types of energy storage devices in time period t, B E S c and B E S d are the state parameters of the energy storage devices, PES(t) is the final output power of the four types of energy storage devices in time period t, and Sn(t) is the capacity of the four types of energy storage devices in time period t.

3. Model Constraints

In order to consider economy and security, the distribution network exceeding risk is the main objective and economy is the sub-objective. The objective function expression is:
Min ( φ 0 ∑ | U a v − U | + φ 1 ∑ ( P − P m a x ) ) Max min ( φ 2 ∑ I 2 R + φ 3 ∑ C w d S w d + φ 4 ∑ C E S , e S E S , e + φ 5 ∑ C x j S x j + ... + φ 6 ∑ C p v S p v + φ 7 C I E S + C b u y + C c c s )
where: φ0 is the distribution network voltage exceeding coefficient, φ1 is the distribution network power exceeding coefficient, φ2 is the distribution network loss coefficient, φ3 is the annualized coefficient of investment in wind power, φ4 is the annualized coefficient of investment in charging stations, φ5 is the annualized coefficient of investment in new lines, φ6 is the annualized coefficient of investment in photovoltaic, φ7 is the annualized coefficient of investment in integrated energy stations, Uav is the reference voltage, and Pmax is the maximum risky capacity of the lines. Cwd , Cpv , CES , Cxj, CIES are the construction costs of wind power, photovoltaic, charging piles, lines and integrated energy stations per unit, Cbuy , Cccs are the costs of purchasing electricity from the distribution grid and carbon capture. Swd , Spv , SES , Sxj are the number of wind power, photovoltaic, charging piles and lines per unit.
The optimal power flow constraints for the branch circuit power flow model are:
U F , t 2 − U T , t 2 − 2 R F T P F T , t − 2 X F T Q F T , t + 2 I F T , t 2 ( R F T 2 + X F T 2 ) = = 0 ∀ t ∈ A , ∀ F T ∈ B
P F T , t 2 + Q F T , t 2 U F , t 2 = I F T , t 2 ， ∀ t ∈ A , ∀ F T ∈ B
p T , t = ∑ k ∈ δ ( T ) P T k , t − ∑ F ∈ π ( T ) P F T , t − I F T , t 2 R F T + g T U T , t 2 + P g , t + P w d , t + P p v , t − P E S , t ∀ T ∈ C q T , t = ∑ k ∈ δ ( T ) Q T k , t − ∑ F ∈ π ( T ) Q F T , t − I F T , t 2 X F T + b T U T , t 2 + Q g , t + Q w d , t + Q p v , t − Q E S , t ∀ T ∈ C
U min < = U i , t < = U max I min < = I j , t < = I max P g min < = P g , t < = P g max Q g min < = Q g , t < = Q g max ∀ i ∈ C , ∀ j ∈ B
S j , w d min < = S j , w d < = S j , w d max S j , c d min < = S j , c d < = S j , c d max       ∀ j ∈ C
Where: UF,t , UT,t are the node voltage of the line inflow node and outflow node at the moment t, RFT , XFT are the impedance of the line between the two nodes, PFT,t , QFT,t are the active and reactive power on the line at the moment t, IFT,t is the current on the line at the moment t, Umin , Umax are the lower and upper limit of the node voltage, Imin , Imax are the upper and lower limit of the line current, Pgmin , Pgmax are the upper and lower limit of the active power output from the transformer in the distribution network, Qgmin , Qgmax are the upper and lower limit of the output from the transformer in the distribution network. Sj,wdmin , Sj,wdmax are the upper and lower limits on the number of node turbine accesses, Sj,cdmin , Sj,cdmax are the upper and lower limits on the number of node accesses to charging piles, δ(T) is the ensemble of line outflow nodes with node T as the inflow end and π(T) is the ensemble of line inflow nodes with node T as the outflow end, and A is the collection of time series; B is the collection of line inflow and outflow nodes in the distribution grid, and B is the collection of line inflow and outflow nodes in the distribution grid, and C is the set of all nodes in the distribution network.
The electrical power balance constraints in the integrated energy station are:
P b u y e ( t ) = P L o a d e ( t ) + P E L e ( t ) + P E S , e e ( t ) − P D G ( t ) − P P V ( t ) − P C H P e ( t ) − P H F C e ( t ) 0 ⩽ P b u y e ( t ) ⩽ P b u y e , max
Where: P b u y e (t) is the electrical energy purchased from the grid by the integrated energy station in time period t, P L o a d e (t) is the load of the node where the integrated energy station is located in time period t, PDG(t), PPV(t) are the wind turbine output and photovoltaic output in the integrated energy station in time period t, P e , m a x b u y (t) is the limit of the electrical energy purchased from the grid by the integrated energy station in time period t, and P e E S , e (t) is the amount of electricity charged to the energy storage device in the integrated energy station in time period t.
The hydrogen energy balance and heat energy balance constraints in the integrated energy station are:
P E L H 2 ( t ) = P M R H 2 ( t ) + P H F C H 2 ( t ) + P E S , H 2 H 2 ( t ) P H F C h ( t ) + P G B h ( t ) + P C H P h ( t ) = P L o a d h ( t ) + P E S , h h ( t )
Where: P L o a d h (t) is the heat load of the node where the integrated energy station is located in time period t, P G B h (t) is the heat energy provided by the gas boiler in the integrated energy station in time period t, P h E S , h (t) is the heat energy charged to the thermal storage device in the integrated energy station in time period t, P H 2 H       2             E S , (t) is the hydrogen energy charged to the hydrogen storage device in the integrated energy station in time period t.
The natural gas balance constraints in the integrated energy station are:
P b u y g ( t ) = P L o a d g ( t ) + P G B g ( t ) + P E S , g g ( t ) + P C H P g ( t ) − P M R g ( t ) 0 ⩽ P b u y g ( t ) ⩽ P b u y g , max
Where: P g b u y (t) is the natural gas purchased at the integrated energy station in time period t, P g L o a d (t) is the natural gas load at the node where the integrated energy station is located in time period t, P g , m a x b u y (t) is the limit of the natural gas purchased at the integrated energy station in time period t, and P g E S , g (t) is the gas energy charged to the natural gas energy storage device in the integrated energy station in time period t.
The stepped carbon trading mechanism model mainly contains carbon emission right quota model, actual carbon emission model and stepped carbon emission trading model. For the quota certification of carbon emission right, this paper obtains the carbon emission quota by weighting the power purchased from the superior grid and the energy output from the gas boiler and cogeneration unit. When calculating the actual carbon emission model, the absorption of CO2 by carbon capture devices needs to be taken into account, and the difference between the two is used to obtain the actual carbon trading quota.
The polarized AC power flow constraint introduces nonlinearity and nonconvexity in the distribution network planning model, which makes the solution more difficult. The introduction of intermediate variables transforms the power flow equation into a second-order conic form, which becomes a nonlinear convex planning problem, and the global optimal solution can be obtained according to the theory of convex planning, so that Eq. (17) can be transformed into:
2 P F T , t 2 Q F T , t I F T , t 2 − U F , t 2 2 < = I F T , t 2 + U F , t 2 ， ∀ F T ∈ B
U min 2 < = U − j , t < = U max 2 I min 2 < = I − j , t < = I max 2 ∀ t ∈ A , ∀ j ∈ C

4. Case Study

4.1. Distribution Network exceeding Testing Based on Semi-invariant Approach

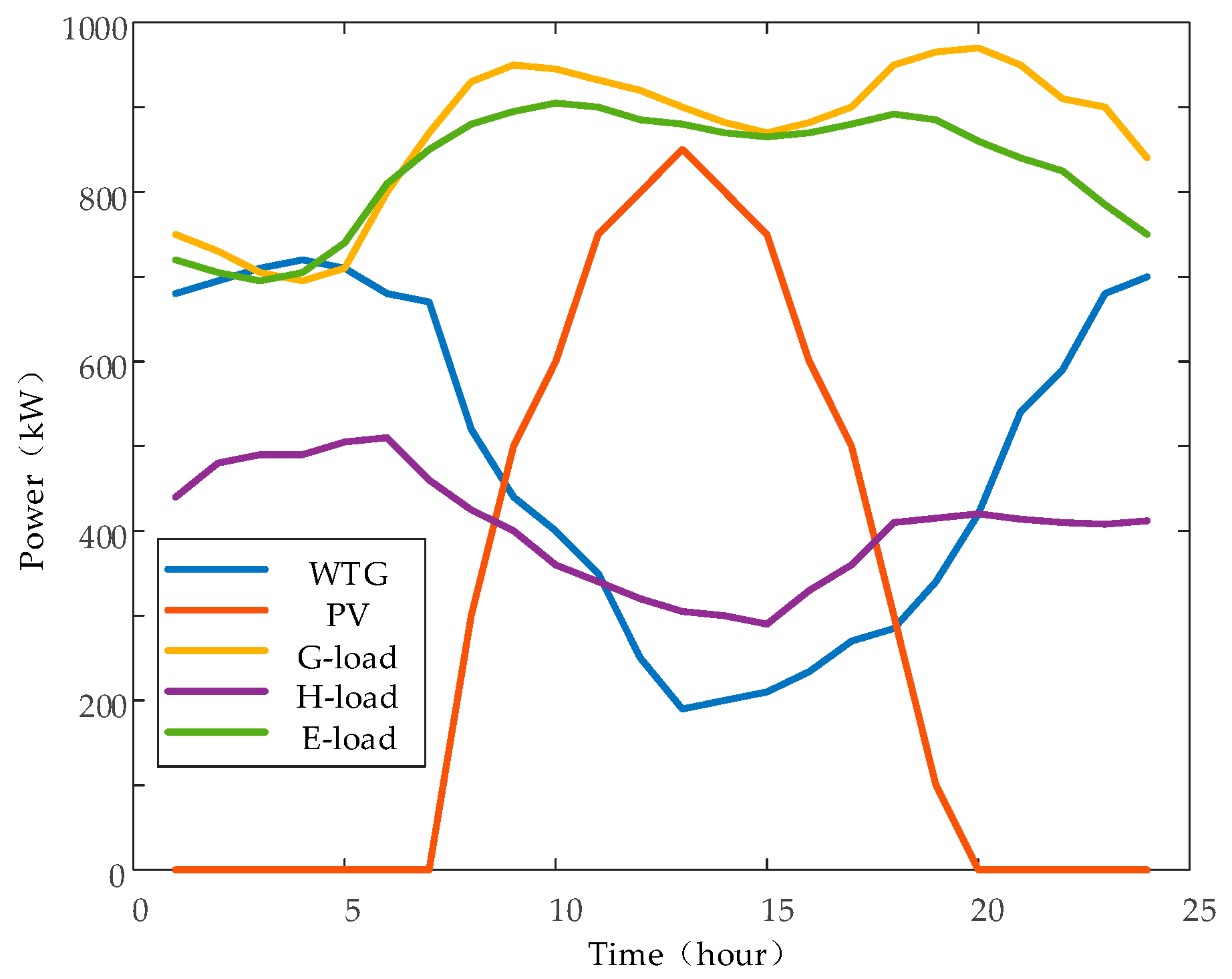
The aggregated multiple load data collected and summarized through the power IoT is input into the probabilistic power flow method based on the semi-invariant method for the calculation of the probability of risk in the state distribution network, and the aggregated source-load data of the integrated energy system is shown in Figure 3:
The IEEE 33-node distribution network model is used for validation. The distribution network has 33 nodes and 32 branches with a total load of 5.57 MW. The nodes that are connected to the wind turbines are: 12 and 19. The capacity of both nodes wind turbines in this system is 300 kW.
The steps for solving the risk prediction model are as follows: Multiple types of load data are imported into the arithmetic example, and semi-invariants of each order are found based on the probability distribution of the injected power at each node. The probability distribution of state variables and branch currents are obtained through the level expansion equation. Using the original node data of the distribution network and related constraints, the improved planning model of AC power distribution network based on mixed integer second-order conic planning is established, and the distribution network risk value is compared with that of the distribution network before the improved planning to determine the distribution network planning scheme.
The list of distribution network risk probabilities is shown in Table 1, and the probability of power exceeding risk for each line is shown in Table 2.
From the Gram-Charlier series expansion to find the distribution network node voltage exceeding and line power exceeding probability density function and probability distribution function, after calculating the example of node voltage exceeding probability as shown in Table 1. In the distribution network, nodes 13-18 have varying degrees of probability of voltage exceeding the lower limit. Nodes 14-16 have a probability of voltage exceeding the limit of more than 1%, indicating a high risk level. Nodes 17 and 18 have a probability of voltage exceeding the limit of more than 10%, indicating a serious risk level. In the calculation example, the probability of power exceeding the limit of the line is shown in Table 2. Lines 6, 22, and 23 all have the possibility of power exceeding the limit. Among them, the probability of power exceeding the limit of lines 6 and 22 exceeds 1%, indicating a higher risk level.
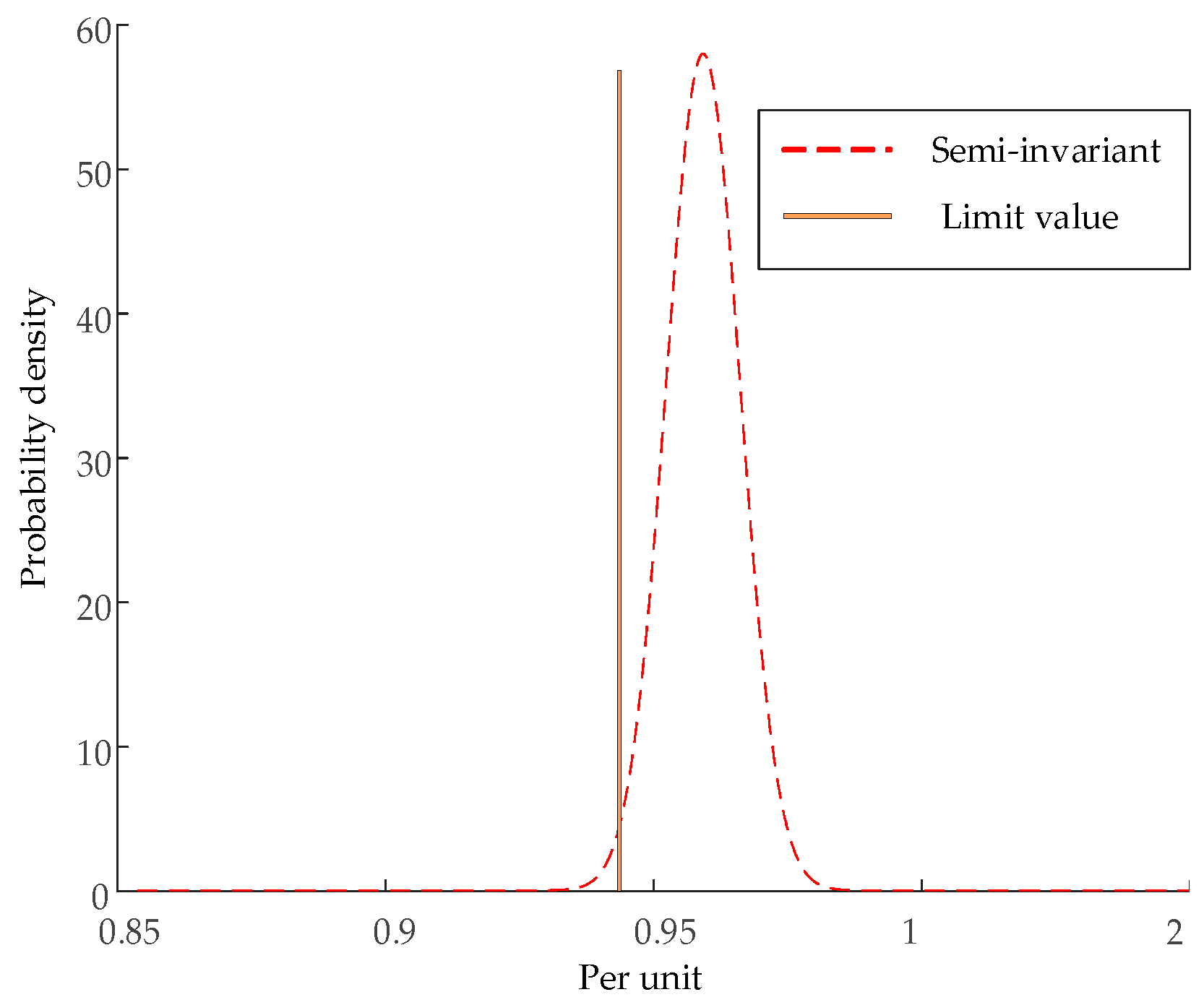
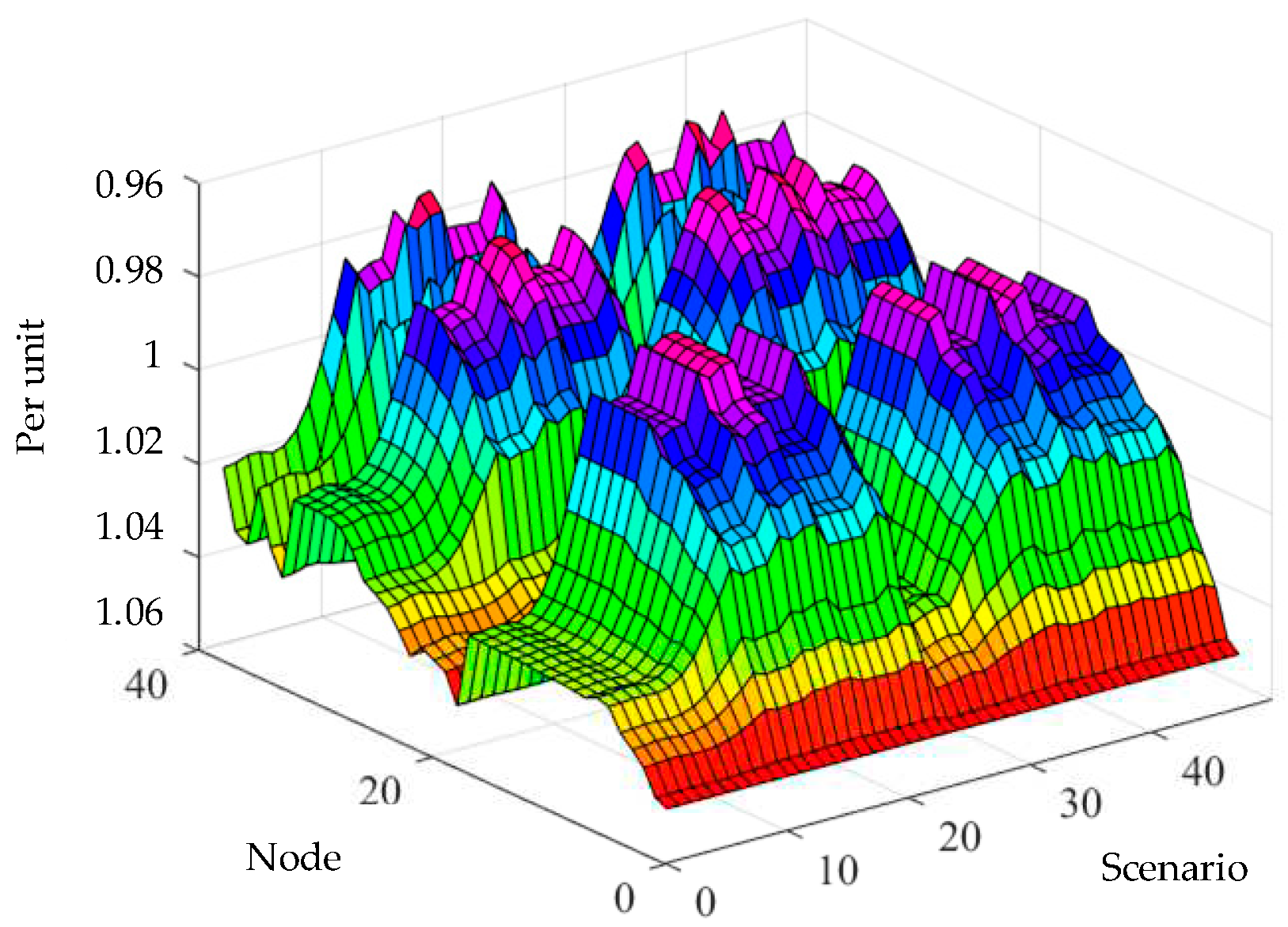
After the calculation of the method described in Chapter 1, the results of the voltage test at the 14th node of the distribution network are shown in Figure 4.

4.2. Validation of a Two-tier Planning Model Based on Second-order Cones for Integrated Energy-containing Distribution Networks

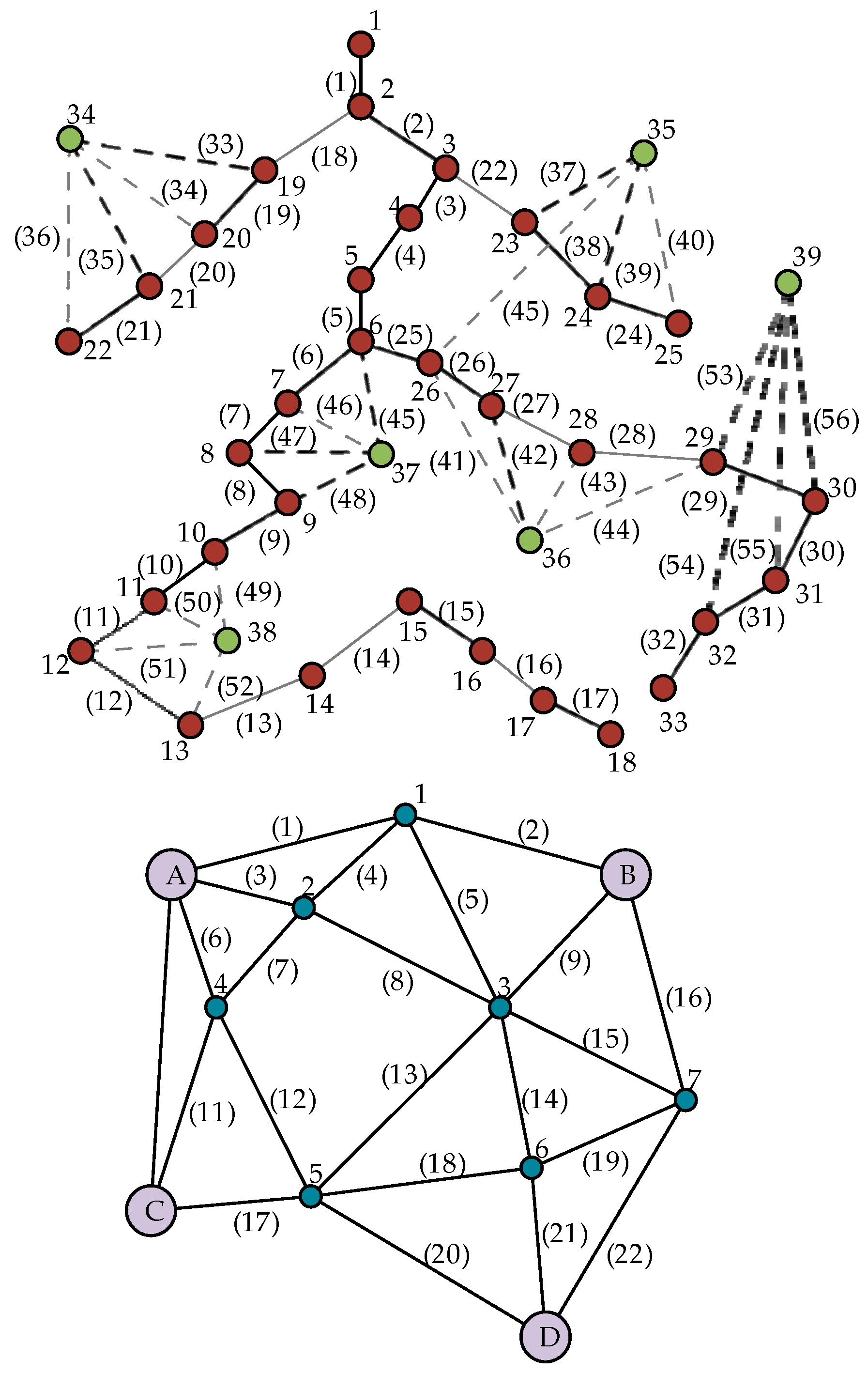
The historical load data is imported into the improved IEEE-33 node, whose topology is shown in Figure 5, and the distribution network has 39 nodes and 56 branch roads and the transportation network has 22 traffic lines. The last six green nodes are new nodes and the last 24 routes are planned to be constructed, with a total load of 6.47 MW. The nodes that are planned to be connected to PV generators are 12, 19, 23, 35, 36, 37, 38, and 39.The capacity of a single wind generator in the system is 50 kW, and its maximum allowable penetration rate is 40%. In this case, the charging demand exists for 4,200 EVs during the service hours, and each EV charging post can provide 48 kW of charging power. The transportation network mainly considers four vehicle source points, A to D. It is planned to select three of the seven EV fast charging station site locations to connect to the new nodes 37-39.
In order to validate the impact of carbon capture and integrated energy systems on the security and economy of distribution network planning, four schemes are designed for validation in this paper:
Scheme 1: Only wind turbines are considered in the integrated energy system;
Scheme2: Only PV units are considered in the integrated energy system;
Scheme 3: Only wind and PV are considered in the integrated energy system, without carbon capture;
Scheme 4: Integrated energy system considering both wind and PV and carbon capture.
From the results of the above four planning schemes, the improvement of the distribution network needs to access both PV and wind turbines, otherwise there is a great risk of crossing the lower limit of the distribution network node voltage, and at the same time there is a certain risk of crossing the upper limit of the line, and the consideration of the carbon capture technology in the improvement of the network can improve the overall energy utilization efficiency of the system, which not only fixes a part of carbon dioxide emitted by the gas turbine, but also through the conversion and energy storage to reduce the impact of integrated energy nodes on the entire network, although carbon capture devices increase the planning economic costs, but combined with the security and environmental protection point of view of the comprehensive consideration, we can choose scheme 4 as the goal of the planning program.
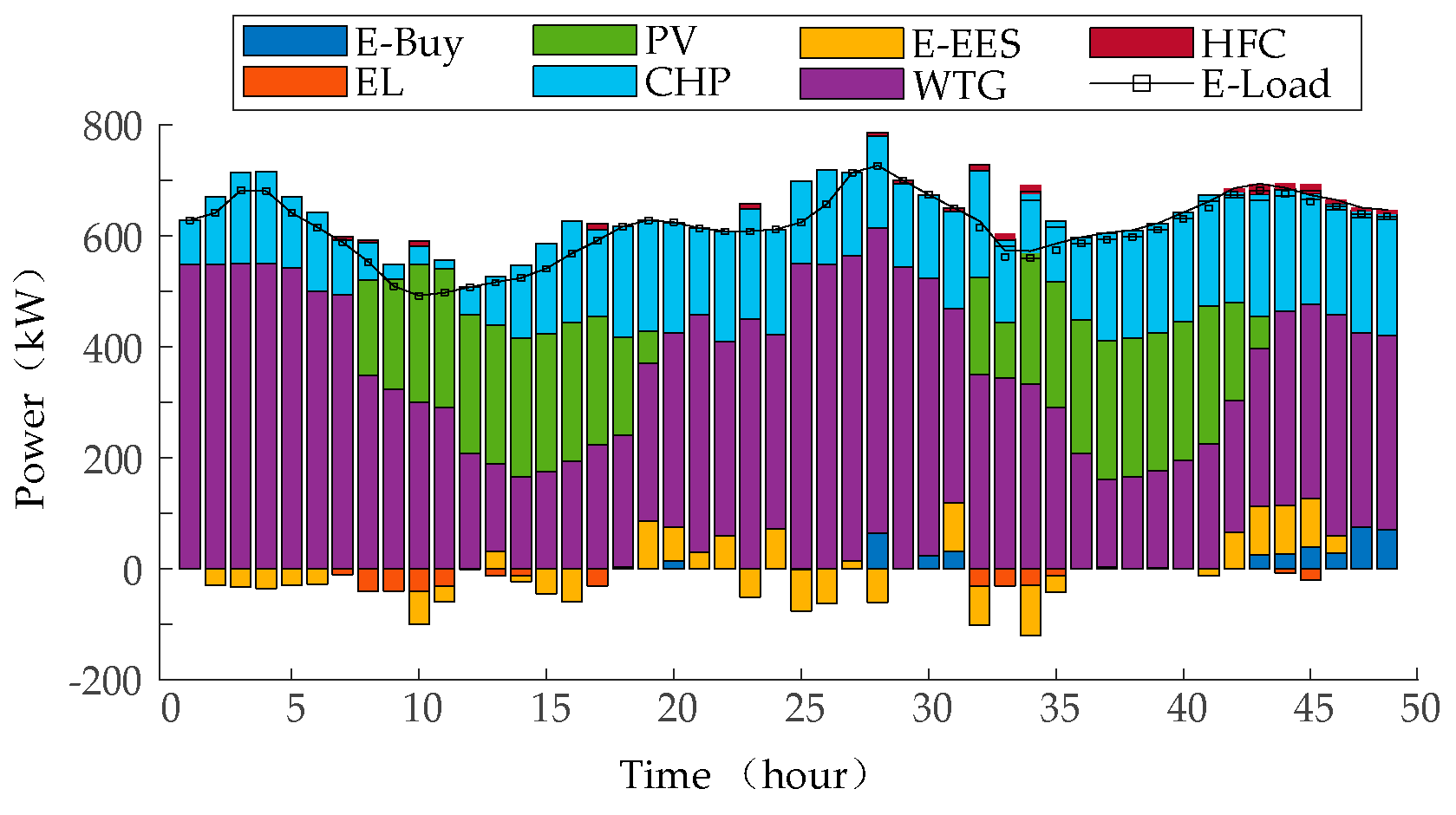
The calculated electric power balance of the integrated energy system in the distribution network is shown in Figure 6:
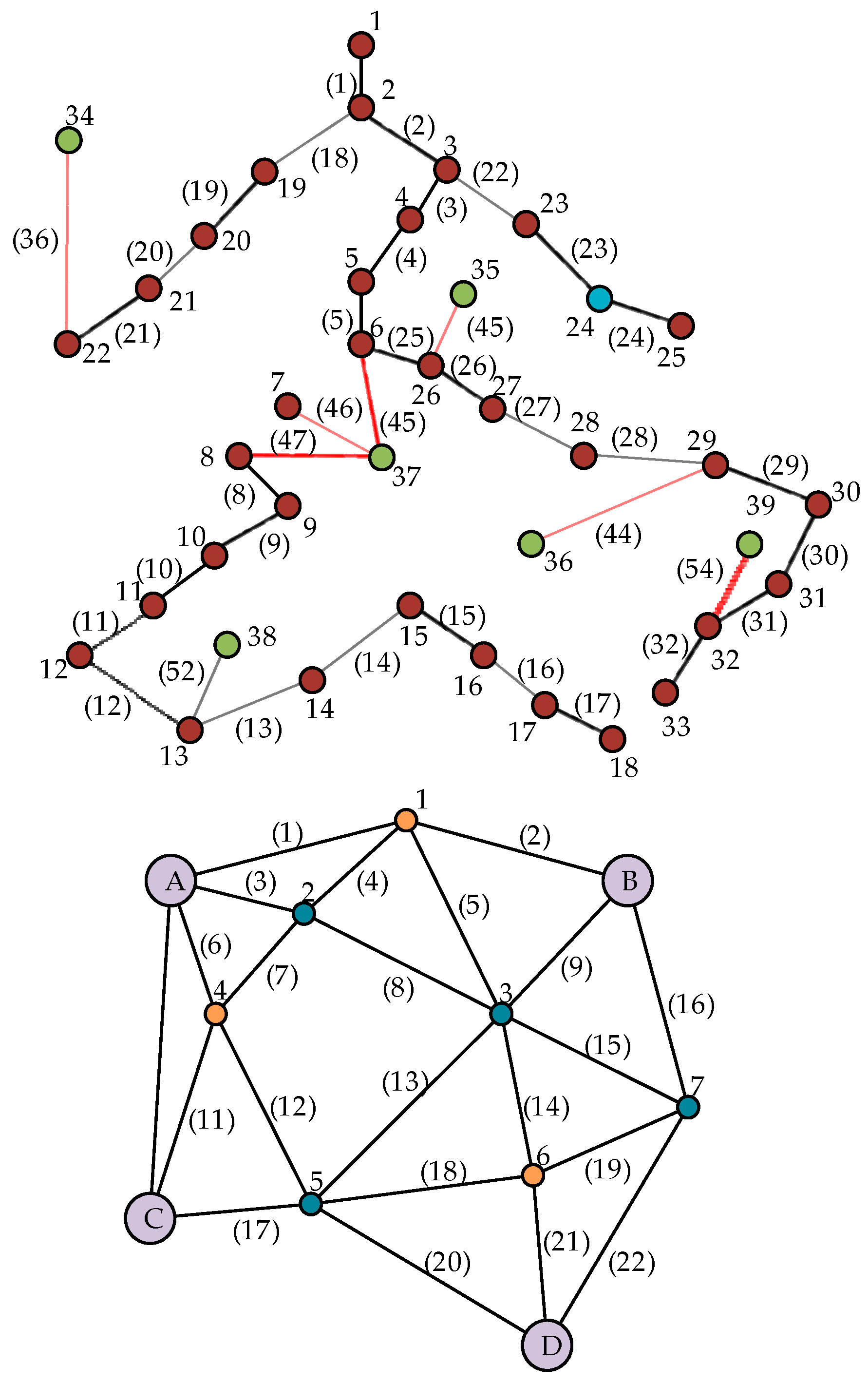
After the improved planning, the resulting 39-node distribution network topology is shown in Figure 7, where the new lines are the red lines in the figure and the integrated energy station access node is the 24th node.
The tested node voltage exceeding probability in the example is shown in Figure 8, and the existence of voltage exceeding probability at each node in the distribution network is negligible. The probability of line power exceeding in the example is shown in Table 5, and there is no risk of power exceeding in each line in the distribution network. The planning scheme of wind turbines in the example is shown in Table 4, in which the planned capacities of nodes 19, 23, 35, and 37 are 0.50, 0.50, 0.35, and 0.50 MW. The planning scheme of EV fast charging stations in the example is shown in Table 6, which is combined with the charging demand and the queuing algorithm, and the corresponding EV fast charging station site numbers of nodes 37-39 are 1, 4, and 6 respectively, and the 50 EV fast charging station site numbers planned at nodes 37, 38, and 39 are 1, 4, and 6 respectively. The number of 50kW charging piles planned are 14, 16, and 15 respectively.

5. Conclusions

This paper utilizes power Internet of Things multi-source data, by comprehensively considering the influencing factors leading to distribution network voltage exceeding and power exceeding combined with mixed access of multiple loads, rising penetration rate of electric vehicles, massive access of distributed equipment such as wind power generation, as well as integrated energy stations and laddering carbon trading mechanism, By analyzing the mechanistic pattern of distribution network fault problem generation, and simulating the actual situation through scenario modeling to provide data for the risk planning afterward. Support.
The distribution network risk test is carried out for the distribution network frame structure and multi-source load data, based on the expectation value and sensitivity matrix of the node voltage and branch currents, the loads and the conventional generators, wind turbine outputs, and the semi-invariants of each order of the injected power at each node are calculated, and the probability density function and the probability distribution function are obtained through the level expansion, and the probabilistic distribution network risk model is constructed, which provides a test and calibration methodology for the subsequent planning of the risk improvement of the distribution network. Provide test calibration methods for the subsequent planning of distribution network risk improvement. After considering economic and social factors such as distribution network source and load allocation, integrated energy system access, electric vehicles, and load types, and taking the distribution network voltage and power exceeding probability as the first level objective function and economic benefit as the second level objective function, the original distribution network improvement planning scheme is calculated by a commercial solver to realize risk localization prejudgement and quantification, and finally, the planning scheme is brought into the distribution network risk prejudgement model to test the feasibility of the method. feasibility of the method. Through the calculation example analysis. The following conclusions are obtained in this paper:
  • The distribution network voltage exceeding and power exceeding test utilizes the probabilistic power flow method, which can effectively calculate the risk of the node voltage and line power of the active distribution network containing integrated energy sources, and compared with the original deterministic test method, the risk probability of the nodes and lines of the distribution network is visually displayed after the expansion of the Gram-Charlier level, so as to realize the quantitative analysis of the risk of the distribution network.
  • Distribution networks need to be rearranged for risk planning after coupling with transportation networks, distributed generation equipment and integrated energy systems. The deep application of power IoT can tap multi-dimensional data to increase the reliability of planning, and changing the network structure, rational planning of distributed generation equipment, fast charging stations and energy storage devices can effectively reduce the probability of risks of distribution networks.
  • The two-layer planning model can take into account the security and economy of the distribution network. The integrated energy system improves the efficiency of energy utilization through the interconversion of multiple energy sources, and the carbon capture combined with the ladder carbon trading mechanism collects CO2 emitted from gas turbines to participate in the reaction of methane synthesis, which improves the economy and security of the system.

Author Contributions

The authors confirm their contributions to the paper as follows: J.W. proposed the idea, performed the experiments, analyzed the data and wrote the paper; K.W., T.W., and S.M. provided example data; H.G. and Q.G. organized example data; Z.H. provided useful advice, revised the manuscript and approved the final version of the manuscript. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Key Research and Development Program of China, grant number 2020YFB0905905.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. G.L.; G.W.; C.W.; X.G.; H.W.; Q.X.; L.L. Operational Risk Prediction of Power IoT with Information-Physical Society Data Fusion Processing. Proceedings of the CSU-EPSA:1-14.
  2. L.C.; H.Z.; Z.T.; G.R. Comprehensive Evaluation of Key Technologies in Power Internet of Things Based on Comprehensive Similarity of Cloud Model. Journal of Shanghai Jiaotong University:1-24. [CrossRef]
  3. Z.B.; X.Q. Solving Probabilistic Optimal Power Flow Problem Using Quasi Monte Carlo Method and Ninth-Order Polynomial Normal Transformation. The IEEE Transactions on Power Systems 2014, 29, 300–306. [CrossRef]
  4. M.D.; S.L.; K.H. Probabilistic Load Flow Analysis Based on Monte-Carlo Simulation. Power System Technology 2001, 25, 10–14.
  5. Y.Y.; J.Z.; P.J. Probabilistic Load Flow Computation of a Power System Containing Wind Farms Using the Method of Combined Cumulants And Gram- Charlier Expansion. IET Renewable Power Generation 2011, 5, 448–454. [CrossRef]
  6. K. T.; S. S.; N. S. Combined Cumulants and Laplace Transform Method for Probabilistic Load Flow Analysis. IET Generation Transmission Distribution 2017, 11, 3548–3556. [CrossRef]
  7. X.L.; J.C.; D.D. Two-point Estimate Method for Probabilistic Optimal Power Flow Computation Including Wind Farms with Correlated Parameters. Intelligent Computing for Sustainable Energy and Environment 2013, 355, 417–423.
  8. H.Y.; L.H.; B.Z. Unified Probabilistic Gas and Power Flow. Modern Power System and Clean Enemy 2017, 5, 400–411. [CrossRef]
  9. Y.C.; J.W.; S.C. Probabilistic Load Flow Method Based on Nataf Transformation and Latin Hypercube Sampling. IEEE Transactions on Sustainable Energy 2013, 4, 294–301. [CrossRef]
  10. B.R.; M.M.; G.B. Application of RBF Neural Networks and Unscented Transformation in Probabilistic Power-Flow of Microgrids Including Correlated Wind/PV Units and Plug-in Hybrid Electric Vehicles. Simulation Modelling Practice and Theory 2017, 72, 51–68. [CrossRef]
  11. K.Y.; J.C.; X.C. Dynamic Probabilistic Power Flow Calculation for Regional Power Grids Containing Distributed Power Sources. Proceedings of the CSEE 2011, 31, 20–25.
  12. K.Y.; J.Z.; Y.Z. A Generalized Computationally Efficient Copula-Polynomial Chaos Framework for Probabilistic Power Flow Considering Nonlinear Correlations of PV Injections. International Journal of Electrical Power & Energy Systems 2022, 136, 107727. [CrossRef]
  13. T.R.; S.H.; S.R. Stochastic Optimal Power Flow in Hybrid Power System Using Reduced-Discrete Point Estimation Method and Latin Hypercube Sampling. IEEE Canadian Journal of Electrical and Computer Engineering 2021, 45, 63–6. [CrossRef]
  14. S.V.; M.T.; J.D. Probabilistic Load Flow for Wind Integrated Power System Considering Node Power Uncertainties and Random Branch Outages. IEEE Transactions on Sustainable Energy 2022, 14, 482–489. [CrossRef]
  15. Y.L.; C.L.; L.Z. A Partition Optimization Design Method for a Regional Integrated Energy System Based on a Clustering Algorithm. Energy 2021, 219, 119562. [CrossRef]
  16. Z.Z.; J.Z.; Z.Z. Development and Modelling of a Novel Electricity-Hydrogen Energy System Based on Reversible Solid Oxide Cells and Power to Gas Technology. International Journal of Hydrogen Energy 2019, 44, 28305–28315. [CrossRef]
  17. S.L.; Y.W. Evaluation of Integrated Energy System Planning Scheme for Industrial Parks Based on Improved Cloud Object-Element Model. Power System Protection and Control 2023, 51, 165–176.
  18. Y.C.; N.Z.; B.Z. Low-Carbon Operation of Multiple Energy Systems Based on Energy-Carbon Integrated Prices. IEEE Transactions on Smart Grid 2020, 11, 1307–1318. [CrossRef]
  19. M.Y.; Y.C.; D.H. Multi-Time-Scale Coordinated Optimal Scheduling of Integrated Energy System Considering Frequency out-of-limit Interval. International Journal of Electrical Power & Energy Systems. 2022, 141, 0142–0615. [CrossRef]
  20. H.G.; J.L.; X.S.; R.X. Research on Optimal Power Flow of Active Distribution Network and Its Application Examples. Chinese Journal of Electrical Engineering 2017, 37, 1634–1645.
  21. H.S.; P.L.; P.A. Multistage Model for Distribution Expansion Planning with Distributed Generation-Part II: Numerical Results. IEEE Transactions on Power Delivery 2008, 23, 924–929. [CrossRef]
  22. Y.L.; D.W.; H.J. Multi-stage stochastic planning of regional integrated energy system based on scenario tree path optimization under long-term multiple uncertainties. Applied Energy 2021, 300, 117224. [CrossRef]
  23. F.D.; B.M.; B.N. Comparison of Mixed-Integer Programming and Genetic Algorithm Methods for Distributed Generation Planning. IEEE Transactions on Power Systems 2013, 29, 833–843. [CrossRef]
  24. Z.R.; R.J.; F.E. Optimal Dispatch of Battery Energy Storage System Using Convex Relaxations in Unbalanced Distribution Grids. IEEE Transactions on Industrial Informatics 2020, 16, 97–108. [CrossRef]
  25. W.G.; O.M.; L.G. Economic Dispatch of Renewable Generators and BESS in DC Microgrids Using Second-Order Cone Optimization. Energies 2020, 13, 1703. [CrossRef]
Preprints 96669 g001
Figure 1. Risk planning model for distribution networks based on the Internet of things for electricity.
Figure 1. Risk planning model for distribution networks based on the Internet of things for electricity.
Preprints 96669 g001
Preprints 96669 g002
Figure 2. Energy flow modeling for integrated energy systems.
Figure 2. Energy flow modeling for integrated energy systems.
Preprints 96669 g002
Preprints 96669 g003
Figure 3. Integrated energy system source and load data.
Figure 3. Integrated energy system source and load data.
Preprints 96669 g003
Preprints 96669 g004
Figure 4. Node 14 voltage probability distribution.
Figure 4. Node 14 voltage probability distribution.
Preprints 96669 g004
Preprints 96669 g005
Figure 5. Topology of improved IEEE-33 distribution and transportation networks.
Figure 5. Topology of improved IEEE-33 distribution and transportation networks.
Preprints 96669 g005
Preprints 96669 g006
Figure 6. Electrical power balance for integrated energy systems.
Figure 6. Electrical power balance for integrated energy systems.
Preprints 96669 g006
Preprints 96669 g007
Figure 7. Distribution and transportation network topology after improved planning.
Figure 7. Distribution and transportation network topology after improved planning.
Preprints 96669 g007
Preprints 96669 g008
Figure 8. The per-unit value of voltage at each node of the distribution network in each scenario.
Figure 8. The per-unit value of voltage at each node of the distribution network in each scenario.
Preprints 96669 g008
Table 1. Probability of distribution network voltage exceeding risk.
Table 1. Probability of distribution network voltage exceeding risk.
Node number Exceeding lower limit probability Node number Exceeding lower limit probability Node number Exceeding lower limit probability
1 -- 12 0 23 0
2 0 13 0.24% 24 0
3 0 14 1.33% 25 0
4 0 15 3.46% 26 0
5 0 16 7.51% 27 0
6 0 17 17.76% 28 0
7 0 18 20.36% 29 0
8 0 19 0 30 0
9 0 20 0 31 0
10 0 21 0 32 0
11 0 22 0 33 0
Table 2. Probability of power exceeding risk in the distribution network.
Table 2. Probability of power exceeding risk in the distribution network.
Line
number		 Exceeding probability Line
number		 Exceeding probability Line
number		 Exceeding probability
1 0 12 0 23 0.37%
2 0 13 0 24 0
3 0 14 0 25 0
4 0 15 0 26 0
5 0 16 0 27 0
6 1.96% 17 0 28 0
7 0 18 0 29 0
8 0 19 0 30 0
9 0 20 0 31 0
10 0 21 0 32 0
11 0 22 1.72%
Table 3. Distribution Network Improvement Planning Program.
Table 3. Distribution Network Improvement Planning Program.
Scheme Voltage exceeding probability Power exceeding probability Investment cost ($ million) Carbon fixation (kg)
1 12.21% 0.35% 3002.03 0
2 24.13% 1.51% 3086.40 0
3 8.42% 0.11% 2923.80 0
4 0.05% 0 2977.31 461.5
Table 4. Distribution network wind turbine planning program.
Table 4. Distribution network wind turbine planning program.
Installation node position Installed capacity (MW) Installation node position Installed capacity (MW)
12 0 36 0
19 0.5 37 0.5
23 0.5 38 0
35 0.35 39 0
Table 5. The probability of power exceeding risk in the distribution network after improved planning.
Table 5. The probability of power exceeding risk in the distribution network after improved planning.
Line
number		 Exceeding
probability		 Line
number		 exceeding probability Line
number		 Exceeding
probability
1 0 14 0 27 0
2 0 15 0 28 0
3 0 16 0 29 0
4 0 17 0 30 0
5 0 18 0 31 0
6 0 19 0 32 0
7 0 20 0 33 0
8 0 21 0 34 0
9 0 22 0 35 0
10 0 23 0 36 0
11 0 24 0 37 0
12 0 25 0 38 0
13 0 26 0
Table 6. Electric vehicle fast charging station planning scheme for distribution grids.
Table 6. Electric vehicle fast charging station planning scheme for distribution grids.
Access node location Number of charging piles
1 14
4 16
6 15
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated