1. Introduction

2. Background

2.1. Move-To-Front Transform

Move-To-Front (MTF) is one of the self-organising list strategies [21,25,26,27] used in caching algorithms [28] and data compression [29,30]. Let $X=\langle x_i\rangle$, $0\le i<n-1$, represent the input sequence of n elements $x_i$ from an alphabet ${\Sigma }_X$, where ${\Sigma }_X$ consists of m elements. MTF reads the elements $x_i\in X$ sequentially, and maps them to the domain of natural numbers, including 0, to obtain the output sequence $Y=\langle y_i\rangle$, $0\le i<n$, $y_i\in {\Sigma }_Y=\{0,1,2,\cdots ,m-1\}$. The list L is employed in this mapping process and it is populated with all the elements from ${\Sigma }_X$ initially. The algorithm finds the position l, $0\le l<m-1$, in L, where $x_i=L_l$ and sends l to Y. After that, the positions of all the elements $L_e$ in L between $0\le e<l$ are increased, while $x_i$ is placed in front of L. The pseudocode for the MTF transform is shown in Algorithm 1. The main loop contains only three functions. The first one, on Line 7, iterates through the elements in L and stops when $L_l=x_i$. It is expected that $x_i$ is found in the constant time $O\left(1\right)$, since MTF is a self-organising list. The function in Line 8 terminates in $O\left(1\right)$, as it just writes l to an array representing Y. The most time-consuming task is performed by the last function in Line 9, which needs to replace the first $l-1$ values in L. It can be realised in various ways. Four different implementations were proposed and analysed in [31].

MTF is used most frequently in data compression [26,27,29], as it reduces the information entropy of X when X contains local correlations. For example, a sequence of the same elements is converted into a sequence of zeros; a sequence of alternating elements gives a sequence of ones; a sequence of alternating triples results in a sequence of twos, and so on. This is the reason why MTF is used typically after BWT, which tends to group the same elements close together [19,20].

Algorithm 1 Pseudocode of MTF transform

2.2. Move with Interleaving

The Burrows-Wheeler transform, (BWT) should be used before MTF to enhance the local correlations of X, as mentioned in the previous Subsection. BWT was introduced in 1994 [18], and is a well-studied transform [22]. Unfortunately, it has $O(n^{2}log\left(n\right))$ time complexity, which is why X should be split into small blocks to achieve a fast enough response [18]. A direct correlation between suffix array and the BWT was determined later [19]. Straightforward implementation of the suffix array also works, unfortunately, in $O(n^{2}log\left(n\right))$ [32,33]. Fortunately, more algorithms were developed for constructing a suffix array of X in $O\left(n\right)$ [34,35,36]. This also enables obtaining the BWT in linear time. However, the implementation of these algorithms is relatively demanding. This is why it would be desirable to replace the pipeline of the three algorithms – an algorithm for constructing the suffix array, an algorithm to generate BWT from the suffix array, and the MTF algorithm – with only one compact algorithm. It was shown recently that, at least for the domain of Raster Images, this can be done by the transform named Move with Interleaving (MwI) [15]. Pixels from a continuous-tone image are arranged into a sequence X at first. Pixels in the close neighbourhood of the considered pixel are, in the majority of cases, similar, but not completely the same. However, this similarity is sufficient for MTF to produce small indices $y_i$. But, when a region of different pixel values is encountered, MTF has to generate many large indices $y_i$ before bringing enough values from this region close to the front of L. This has, unfortunately, a negative effect on the reduction of the information entropy, and this is why BWT should be applied before MTF. Because of this, MwI monitors the value $y_i=MTF\left(x_i\right)$, and reacts when $y_i$ exceeds the given threshold t. MwI assumes that an area with different values is found and that the values similar to $x_i$ will follow. Because of this, it inserts, in addition to $x_i$, $2t$ interleaved values around $x_i$ in front of L, i.e., the values from a generated auxiliary sequence $A=\langle x_i,x_i+1,x_i-1,x_i+2,x_i-2,\cdots ,x_i+t,x_i-t\rangle$.

The MwI pseudocode is shown in Algorithm 2. The algorithm first populates the list L in Line 5. It uses the first element from X and interleaves it with $2t$ values. These values are inserted in front of L, and the remaining values from ${\Sigma }_X$ are filled in alphabetical order. The first element $x_0$ is stored immediately in the output Y in Line 6, as the decoder should perform the same initialisation of L. The algorithm then enters the main loop and processes $X=\langle x_i\rangle$, $1\le i<n$, sequentially. The position l of $x_i$ is determined in L (Line 8). It checks after that whether l is within the given threshold t. If so, the MTF procedure is performed in Lines 11 and 12; otherwise, the algorithm fills the auxiliary sequence A with interleaved elements around $x_i$ in Line 14. The elements from A are then inserted in L in the MTF-style within Lines 16 and 17.

Algorithm 2 Pseudocode of MwI transform

Finally, let us analyse the MwI time complexity. $l>t$ in each iteration for the worst-case scenario. Therefore, for each $x_i$, $1\le i<n$, the algorithm fills A in time $T_A=2t+1$, and then performs the MTF $2t+1$ times. MTF has the expected time complexity $O\left(n\right)$, and, as a result, the expected execution time of MwI is $T_{MwI}=(2t+1)O\left(n\right)$. Since $t\le m<<n$, it can be concluded that MwI’s time complexity is the same as MTF, i.e., $O\left(n\right)$.

3. Materials and Methods

3.1. Implementation I-1

List L is represented as the standard C++ vector in this implementation. Algorithm 3 shows the function that initialises L. This initialisation assumes that the alphabet represents the numbers from the range $[lBound,uBound]$. The last parameter N in function InitL_I controls the number of elements to be inserted. It is set to $uBound-lBound+1$ initially. Variables u and l hold the incremental interleaving values around FirstEl.

Algorithm 3 Implementation I-1: initialization of L

The main function of implementation I-1 is shown in Algorithm 4. The position l of each $x_i$ in L is determined in Line 9 and then stored in Line 10. After that, l is tested (Line 11): if it is smaller than t, the MTF is executed in Lines 12-14; otherwise, more elements interleaved around $x_i$ should be moved-to-front of L. The auxiliary vector A is filled with at most $1+2t$ interleaved values by calling the function InitL_I in Line 17. In Algorithm 3, this time the parameter N gets the value 2t. After that, the content of L is updated in Line 18.

Algorithm 4 Implementation I-1: MwI main function

Algorithm 5 Implementation I-1: L update function

Finally, let us explain the updating procedure for L, when more elements should be moved to the front (see Algorithm 5). In Line 4, $1+2t$ interleaved values from vector A are first copied to a temporary vector Temp. The remaining values of L are added incrementally within the Lines 6– 17 to Temp if they have not yet been added in Line 4. When the for-loop terminates, vector Temp contains the updated status of L, which is then returned in Line 18 for use in the next iteration of Algorithm 4.

3.2. Implementation I-2

In implementation I-2, the data structure used to store L is once again a standard vector. Consequently, the initialisation process remains identical to that given in Algorithm 3. The primary drawback of implementation I-1 is in the update function outlined in Algorithm 5, which contains two nested loops. The first loop iterates through all the elements of L. The nested while loop scans the auxiliary vector A to verify whether the element L[i] also exists in A. If not, the element is added to the temporary vector Temp. Although the UpdateL function is not called for each element being transformed, and the length of the vector A is expected to be small, $1+2t<<m$, it opens up room for an improvement. Namely, the nested while loop can be omitted by introducing a lookup table $LUT$. Its purpose is similar to the lookup table in the Counting-sort algorithm [39]. In our case, $LUT$ consists of m flags set to FALSE initially. The flags in $LUT$ are set during the creation of the auxiliary array A, i.e. each flag is raised at the position $LU{T}_{A_i}$. During the updating of L, for each element in L it checks the status of the flag at the location $LU{T}_{L_i}$. The element is added into the temporary vector if the flag is FALSE. Details, including the construction of vector A and the updating of L, are presented in Algorithm 6.

Algorithm 6 Implementation I-2: MwI with LUT

An array of flags LUT is allocated in Line 5. It consists of m elements, i.e. the size of the alphabet ${\Sigma }_X$. In this implementation it is assumed that the alphabet $\Sigma$ contains elements from the interval $[0,m-1]$. If this is not the case, a simple mapping of the alphabet’s element into this interval should be done before calling the function MwIwithLUT. When the position l of the considered element $x_i>t$, all flags in LUT are set to FALSE in Line 19. The flag belonging to l is set to TRUE after that in Line 20. The same is applied for all the remaining interleaved values in Lines 26 and 30. The update of L is started in Line 34 after A has been prepared. The for loop operates for all elements of ${\Sigma }_X$. For each element of L, it is checked whether its flag in LUT is set (Line 35). If it is not, the considered element is inserted into A. Finally, A is copied into the new L in Line 37.

3.3. Implementation I-3

Implementation I-3 utilises a dynamically linked list of records to represent L. Each record has only two components: el, containing the value, and a pointer next that points to the subsequent record. Concerning MTF, it seems that this data structure could offer benefits, as there is no requirement to move the elements at positions 0 through $l-1$.

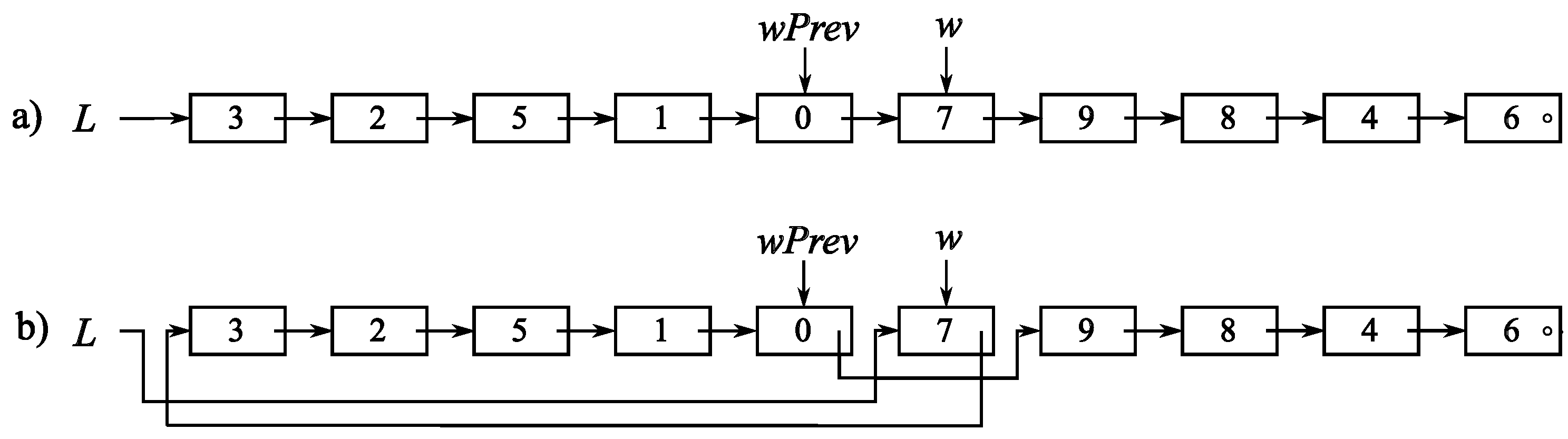
Let us consider an example of L shown in Figure 1a, containing 10 elements. Suppose the element that should be moved to the front of L has the value 7. The record containing this value has already been found and is pointed to by pointer w; its preceding pointer is denoted as wPrev. The new status of L is established in constant time by repointing just three pointers, as illustrated in Figure 1b. The details are provided in Algorithm 7.

Algorithm 7 Implementation I-3: MTF

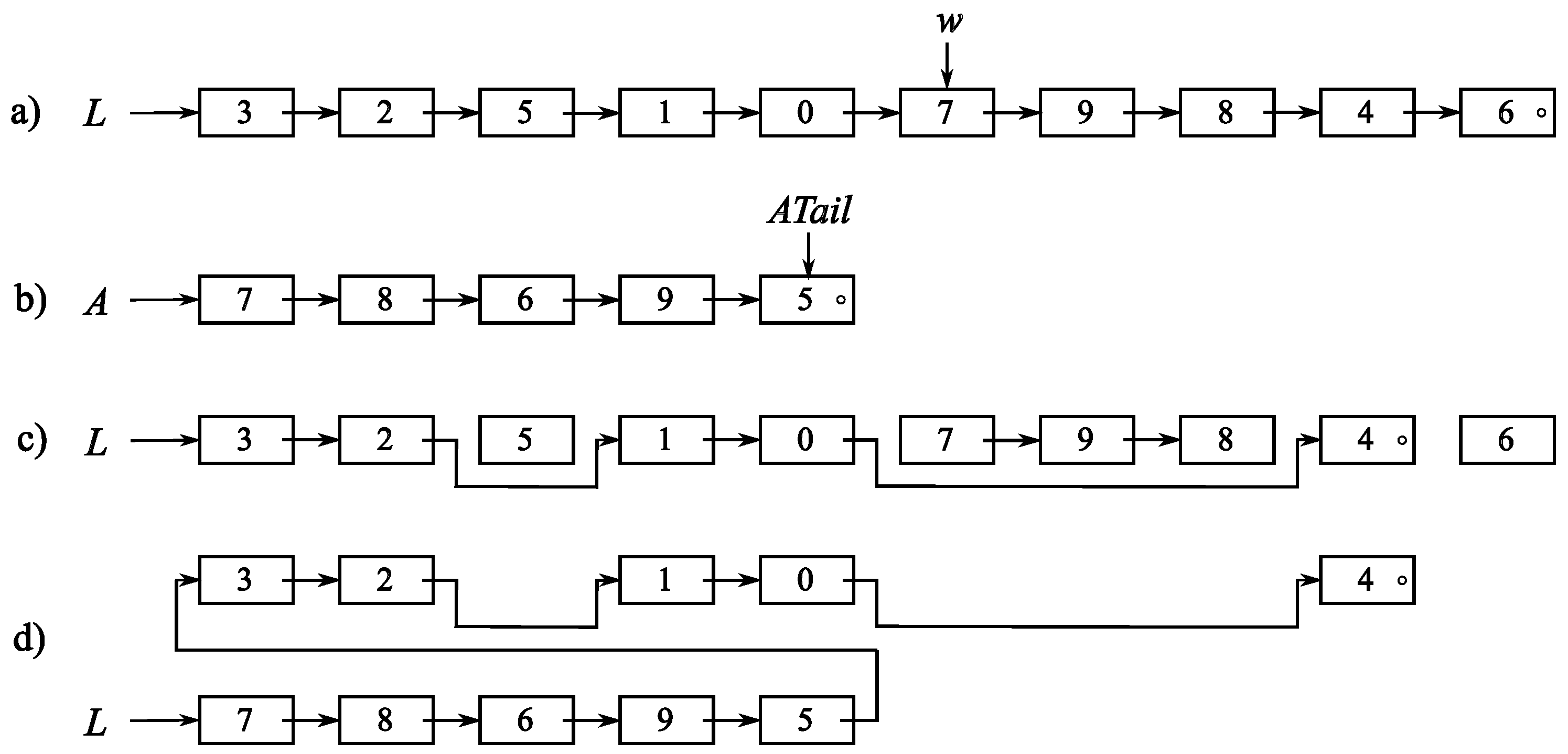
The concept of how the MwI transformation can be realised using a dynamic linked list is shown in Figure 2. Let us suppose that $x_i=7$ is again the considered value in L, which is shown in Figure 2a. In addition, let us suppose that $t=2$. The position of $x_i=7$ is at $l=5$, and as $l>t$, the auxiliary list A of $1+2t$ values should be appended in front of L. The auxiliary list A is shown in Figure 2b. L is inspected, and all its records holding values within the range $[x_i-t,x_i+t]$ are omitted (see Figure 2c). Finally, L and A are linked together using the pointer $ATail$; the result is shown in Figure 2d. We can observe that $1+2t$ new records have been created, and an equal number of them have been deleted. Memory allocation and release are, unfortunately, computationally expensive operations, and should be avoided whenever possible [38]. Therefore, records that should be released, are placed in a stack named Pool in the continuation. Whenever a new record is needed during the process of constructing A, it is taken from the Pool. Details of the implementation can be found in Algorithm 8. In Line 8, the function PreparePool inserts $1+2t$ dynamically allocated records into the stack pointed to by Pool. Function GetPosition (Line 10) performs the same tasks as the programming code in Lines 8 to 14 of Algorithm 7. After that, the records containing the values from the interval $[x_i-t,x_i+t]$ are inserted into Pool by the function in Line 14. The function ConstructA (Line 15) constructs list A with interleaved values around the value $x_i$ using the records from the Pool. It returns pointers A and $ATail$. In Lines  16 and 17, lists L and A are merged into a new list L. In Lines 20, 21, and 22, the record is moved in front as explained earlier.

All implementations are accessible at [40].

Algorithm 8 Implementation I-3: MwI

4. Experiments

5. Conclusion

References

1. Clark, B.G. An efficient implementation of the algorithm "CLEAN". Atron Astrophy. 1980, 89(3), 377–378. [Google Scholar]
2. Hadjiconstantinou, E.; Christofides, N. An efficient implementation of an algorithm for finding K shortest simple paths. Int J Networks. 1999, 34(2), 88–101. [Google Scholar]
3. Goldberg, A. V. An Efficient Implementation of a Scaling Minimum-Cost Flow Algorithm. J Algorithm. 1997, 22(1), 1–29. [Google Scholar] [CrossRef]
4. Lippert, R.A.; Mobarry, C.M.; Walenz, B.P. A Space-Efficient Construction of the Burrows–Wheeler Transform for Genomic Data. J Comput Biol. 2005, 12(7), 943–951. [Google Scholar] [CrossRef] [PubMed]
5. Devkota, S.; Aschwanden, P.; Kunen, A.; Legendre, M.; Isaacs, K. E. CcNav: Understanding Compiler Optimizations in Binary Code. IEEE T Vis Comput Gr. 2021, 27(2), 667–677. [Google Scholar] [CrossRef] [PubMed]
6. Chattopadhyay, S. Compiler design, 2nd ed.; PHI Learning: New Delhi, India, 2022. [Google Scholar]
7. Basford, P.J.; Johnston, S.J.; Perkins, C.S.; Garnock-Jones, T.; Tso, F.P.; Pezaros, D.; Mullins, R.D.; Yoneki, E.; Singer, J.; Cox, S.J. Performance analysis of single board computer clusters. Future Gener Comp Sy. 2020, 102, 278–291. [Google Scholar] [CrossRef]
8. Khan, N.; Yaqoob, I.; Hashem, I.A.T.; Inayat, Z.; Ali, W.K.M.; Alam, M.; Shiraz, M.; Gani, A. Big Data: Survey, Technologies, Opportunities, and Challenges. Sci World J. 2014, 2014, 712826. [Google Scholar] [CrossRef] [PubMed]
9. Stunkel, C.B.; Graham, R.L.; Shainer, G.; Kagan, M.; Sharkawi, S.S.; Rosenburg, B.; Chochoia, G.A. The high-speed networks of the Summit and Sierra supercomputers. IBM J Res Dev. 2020, 64(3/4), 3:1–3:10. [Google Scholar] [CrossRef]
10. Iserte, S.; Prades, J.; Reaño, C.; Silla, F. Improving the management efficiency of GPU workloads in data centres through GPU virtualization. Concurr Comp-Pract E. 2019, 22(2), e5275. [Google Scholar]
11. Khriji, S.; Benbelgacem, Y.; Chéour, R.; El Houssaini, D.; Kanoun, O. Design and implementation of a cloud-based event-driven architecture for real-time data processing in wireless sensor networks. J Supercomput. 2022, 78, 3374–3401. [Google Scholar] [CrossRef]
12. Žlaus, D.; Mongus, D. Efficient method for parallel computation of geodesic transformation on CPU. IEEE T Parall Distr. 2020, 31(4), 935–947. [Google Scholar] [CrossRef]
13. Qiu, M.; Ming, Z.; Li, J.; Gai, K.; Zong, Z. Phase-Change Memory Optimization for Green Cloud with Genetic Algorithm. IEEE T Comput. 2015, 64(12), 3528–3540. [Google Scholar] [CrossRef]
14. Albers, S. Energy-efficient algorithms. Communications of the ACM 2010, 53(6), 86–96. [Google Scholar] [CrossRef]
15. Žalik, B.; Strnad, D.; Podgorelec, D.; Kolingerová; Lukač, L.; Lukač, N.; Kolmanič, S.; Rizman Žalik, K.; Kohek, Š. A New Transformation Technique for Reducing Information Entropy: A Case Study on Greyscale Raster Images. Entropy 2023, 25(12), 1591. [Google Scholar] [CrossRef] [PubMed]
16. Shannon, C.E. A Mathematical Theory of Communication. AT&T Tech J. 1948, 27(3), 379–423. [Google Scholar]
17. Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; Wiley: Hoboken, USA, 2006. [Google Scholar]
18. Burrows, M.; Wheeler, D.J. A block-sorting lossless data compression algorithm. Technical report No. 124, Digital Systems Research Center, 1994.
19. Adjeroh, D.; Bell, T.; Mukherjee, A. The Burrows-Wheeler Transform: Data Compression, Suffix Arrays, and Pattern Matching, 2nd ed.; Springer Science + Business Media: New York, USA, 2008. [Google Scholar]
20. Abel., J. Post BWT stages of the Burrows-Wheeler compression Algorithm. Software Pract Exper. 2010, 40(9), 751–777. [Google Scholar] [CrossRef]
21. Ryabko, B. Y. Data compression by means of a ’book stack’. Probl Inf Transm. 1980, 16(4), 265–269. [Google Scholar]
22. Salomon, D.; Motta, G. Handbook of Data Compression, 5th ed.; Springer: London, U.K, 2010. [Google Scholar]
23. Arnavut, Z.; Magliveras, S. S. Block sorting and compression. In Proceedings of the IEEE Data Compression Conference, DCC’97, Snowbird, Utah, USA, 25-27 Mar 1997; Storer, J. A., Cohn, M., Eds.; IEEE Computer Society Press: USA, 1997; pp. 181–190. [Google Scholar]
24. Sayood, K. Introduction to Data Compression, 4th ed.; Morgan Kaufman, Elsevier: Waltham, USA, 2012. [Google Scholar]
25. Rivest, R. On self-organizing sequential search heuristics. Comm of ACM. 1976, 19(2), 63–67. [Google Scholar] [CrossRef]
26. Bentley, J. L.; Sleator, D. D.; Tarjan, R. E.; Wei, V. K. A Locally Adaptive Data Compression Scheme. Commun ACM. 1986, 29(4), 320–330. [Google Scholar] [CrossRef]
27. Dorrigiv, R.; López-Ortiz, A.; Munro, J. I. An Application of Self-organizing Data Structures to Compression. In Experimental Algorithms, Proceedings of the 8^th International Symposium on Experimental Algorithms, SEA 2009, Dortmund, Germany, 3-6 Jun 2009; Vahrenhold, J., Ed.; Lecture Notes in Computer Science 5526; Springer: Berlin, Germany, 2009; pp. 137–148. [Google Scholar]
28. Jelenković, P.J.; Radovanović, A. Least-recently-used caching with dependent request. Theor Comput Sci. 2004, 2004 326, 293–327. [Google Scholar] [CrossRef]
29. Žalik, B.; Lukač, N. Chain code lossless compression using Move-To-Front transform and adaptive Run-Length Encoding. Signal Process Image Commun. 2014, 29(1), 96–106. [Google Scholar] [CrossRef]
30. Arnavut, Z. Move-To-Front and Inversion Coding. In Proceedings of the IEEE Data Compression Conference, DCC’2000, Snowbird, Utah, USA, 28-30 Mar 2000; Cohn, M., Storer, J. A., Eds.; IEEE Computer Society Press: USA, USA; pp. 193–202. [Google Scholar]
31. Žalik, B.; Žalik, M.; Lipuš, B. On Move-To-Front Implementation. Proceedings on 27^th International Conference on Circuits, Systems, Communications and Computers (CSCC), Rhodes Island, Greece, 19-22 July, 2023. IEEE Computer Society, Los Alamitos (CA), 2023; 43–47.
32. Manber, U.; Myers, G. Suffix arrays: a new method for on-line string search. Proceedings of the first annual ACM-SIAM symposium on Discrete algorithms (SODA ’90), San Francisco (CA), USA, 22-24 Jan, 1990, Society for Industrial and Applied Mathematics, Philadelphia (PA); 319–327.
33. Manber, U.; Myers, G. Suffix arrays: a new method for on-line string search. SIAM J Comput. 1993, 22(5), 935–948. [Google Scholar] [CrossRef]
34. Nong, G.; Zhang, S.; Chan, W. H. Two efficient algorithms for linear time suffix array construction. IEEE T. Comput. 2011, 60(10), 1471–1484. [Google Scholar] [CrossRef]
35. Kärkkäinen, J.; Sanders, P.; Burkhardt, S. Linear work suffix array construction. J. ACM. 2017, 53(6), 918–936. [Google Scholar] [CrossRef]
36. Li, Z; Li, J.; Huo, H. Optimal In-Place Suffix Sorting. In String Processing and Information Retrieval, 25^th International Symposium, SPIRE 2018, Lima, Peru, 9-11 Oct 2018; Gagie, T., Moffat, A., Navaro, G., Cuadros-Vargas, E., Eds.; Lecture Notes in Computer Science 11147; Springer: Cham, Germany, 2018; pp. 268–284. [Google Scholar]
37. Stroustrup, B. The C++ Programming Language, 4th ed.; Addison-Wesley: Upper Saddle River, NJ, USA, 2013. [Google Scholar]
38. What every programmer should know about memory. Available online: https://people.freebsd.org/~lstewart/articles/cpumemory.pdf (accessed on 30. 12. 2023).
39. Cormen, T.H.; Leiserson, C.E.; Rivest, R.L.; Stein, C. Introduction to algorithms, 3th ed.; Massachusetts Institute of Technology: Cambridge, MA, USA, 2009. [Google Scholar]
40. Repnik, B.; Žalik, B. Six implementations of MwI transform. Available online: https://gemma.feri.um.si/projects/slovene-national-research-projects/j2-4458-data-compression-paradigm-based-on-omitting-self-evident-information/software/ (accessed on 15. 01. 2024).