Noise Differentiation and Atom Number Measurement in Optical Lattice Clocks by Analyzing Clock Stabilities with Various Parameters

We propose a method that enables precise determination of the number of atoms in a Dick-noise-free optical lattice clock, by effectively addressing quantum projection noise. Our approach relies on conducting stability measurements at three distinct parameter sets, allowing us to differentiate between quantum projection noise, photon shot noise, and technical noise. Importantly, our method enables accurate extraction of the atom number, even in the presence of photon shot noise and technical noise. To validate the effectiveness of our approach, we employ numerical simulations and optimize the modulation parameters to achieve the smallest uncertainty possible. The numerical simulations show the validity of our method and demonstrate a measurement uncertainty in the atom number that is below 4% across a wide range of atom numbers, provided that the standard deviation of atom number fluctuation is kept below 0.23 times the average atom number.

Keywords:

Subject: Physical Sciences - Applied Physics

1. Introduction

Ultra-cold atoms confined within an optical lattice have played a pivotal role in the development of modern atomic clocks [1,2,3,4], the advancement of quantum techniques [5,6,7,8,9], and the exploration of fundamental physics [10,11,12,13]. Accurate determination of the atom number in the lattice is crucial to fully harness the potential of these applications. For instance, precise knowledge of the atom number is essential for studying many-body interactions [14], thereby reducing systematic uncertainties in optical lattice clocks (OLCs) [1,2,3,4].

Commonly employed methods for atom number measurement include fluorescence detection and absorption imaging [15,16,17]. However, the fluorescence detection method is typically limited by uncertainties arising from the effective solid angle and probe light intensity, resulting in a measurement uncertainty greater than 15% [15]. On the other hand, the absorption imaging technique offers a lower measurement uncertainty below 10%, relying on knowledge of the atomic sample shape and technical noise levels [16]. Recently, advancements in synchronized frequency comparison based on in situ measurements have effectively canceled out interrogation laser noise, improving measurement stability [18,19]. The comparison stability is constrained by atomic detection noises, including quantum projection noise (QPN), photon shot noise, and technical noise [20,21]. This progress has spurred the development of a new method to measure the atom number based on QPN. The previous method of measuring atom numbers from atomic detection noise required the neglect of technical noise [22]. This prerequisite prevented the utilization of atom number measurement based on the QPN.

In this paper, we present a method to distinguish the QPN noise, photon shot noise and technical noise in a Dick-noise-free OLC [18,19,23,24,25]. By conducting three separate stability measurements with modulations of the atom number (N₀) or the photon count (γ₀) detected per atom by the photoelectric detector, it becomes possible to extract the contributions of each noise responsible for clock stability. This method allows us to accurately determine the value of N₀ by differentiating QPN from other sources of noise. To further enhance precision, we use numerical simulations to investigate how modulation parameters influence the measurement uncertainty of N₀ and how measurement precision evolves as N₀ increases.

2. Methods

Assuming a transition probability of 0.5 and disregarding the detection laser noise, which is typically much less significant than other factors in an OLC [21],the clock stability σ_a at τ=1 can be represented by [23,26]

σ_{a}^{2} = σ_{QPN}^{2} + σ_{Shot}^{2} + σ_{Det}^{2} .

(1)

In Eq. (1),

σ_{QPN}^{2} = T_{0} / 4 S_{0}^{2} N_{0}

corresponds to the variance contributed by the QPN, with T₀ representing the clock cycle time and S₀ denoting the frequency-sensitive slope of the spectrum at half-height points.

σ_{Shot}^{2} = T_{0} / 4 S_{0}^{2} N_{0} γ_{0}

refers to the variance originating from the photon shot noise, while

σ_{Det}^{2} = T_{0} δ_{N}^{2} / 2 S_{0}^{2} N_{0}^{2}

represents the contribution of the technical noise. Here, δ_N stands for the rms fluctuation of atoms detected by the photoelectric detector. As the three types of noise exhibit distinct dependencies on N₀ and γ₀, it becomes possible to differentiate them effectively by modulating N₀ and γ₀.

By controlling the detection laser intensity or its duration (T_det), γ₀ can be manipulated. Specifically, by adjusting T_det to T_det /α while keeping other parameters constant as defined in Eq. (1), the value of γ₀ will change to γ₀/α. Consequently, the overall clock stability can be represented as

σ_{b}^{2} = σ_{Q P N}^{2} + α σ_{S h o t}^{2} + σ_{D e t}^{2} .

(2)

In the same manner, by changing N₀ to N₀/β, we can separate the technical noise from other noises, and the overall clock stability is denoted by

σ_{c}^{2} = β (σ_{Q P N}^{2} + σ_{S h o t}^{2}) + β^{2} σ_{D e t}^{2} .

(3)

Combining Eqs. (1)~(3), the contributions of different noise sources can be determined by solving

[\begin{array}{l} 1 & 1 & 1 \\ 1 & α & 1 \\ β & β & β^{2} \end{array}] [\begin{array}{l} σ_{Q P N}^{2} \\ σ_{S h o t}^{2} \\ σ_{D e t}^{2} \end{array}] = [\begin{array}{l} σ_{a}^{2} \\ σ_{b}^{2} \\ σ_{c}^{2} \end{array}] .

(4)

Once the value of σ_QPN is obtained using Eq. (4), it becomes possible to determine the absolute atom number in an OLC.

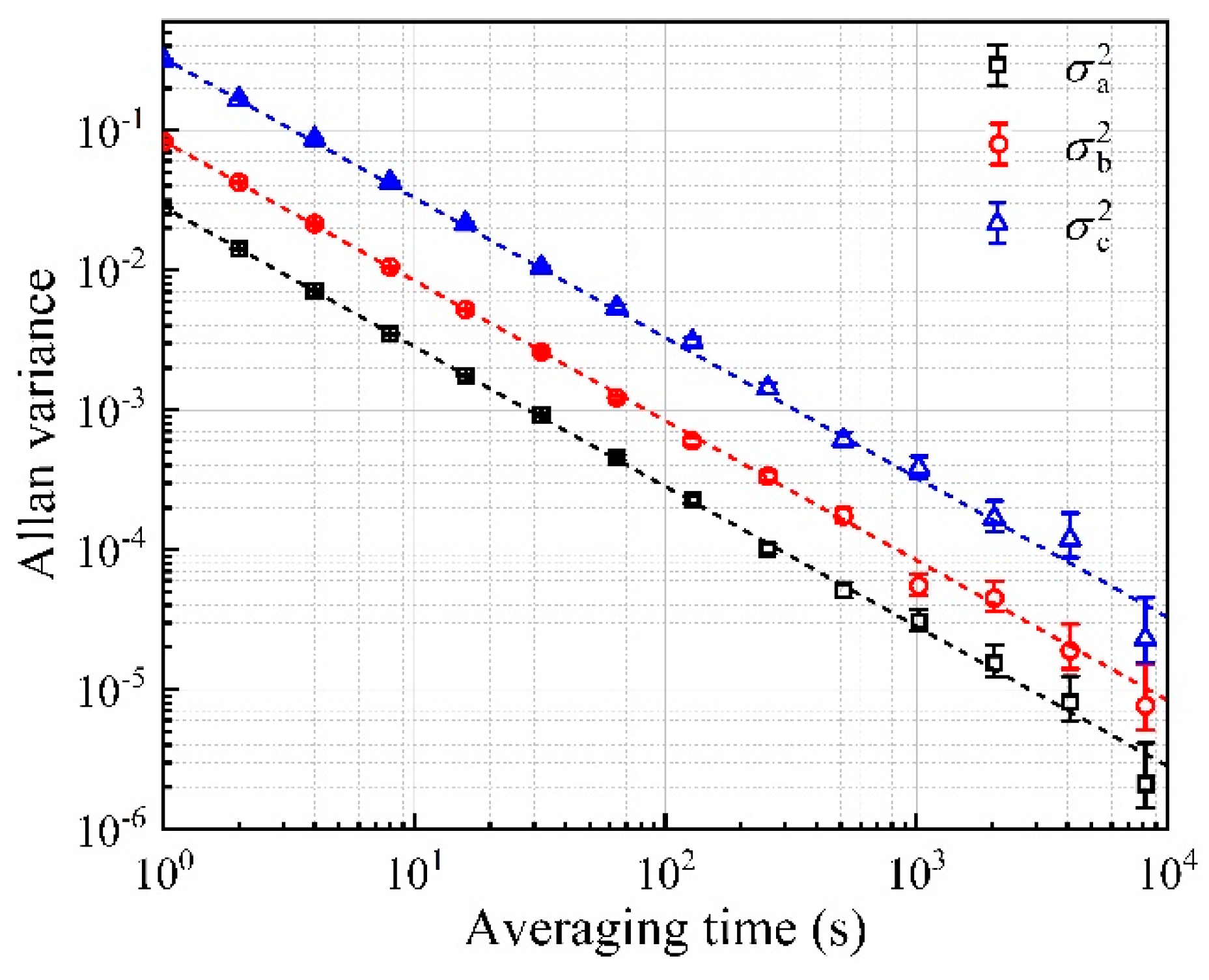
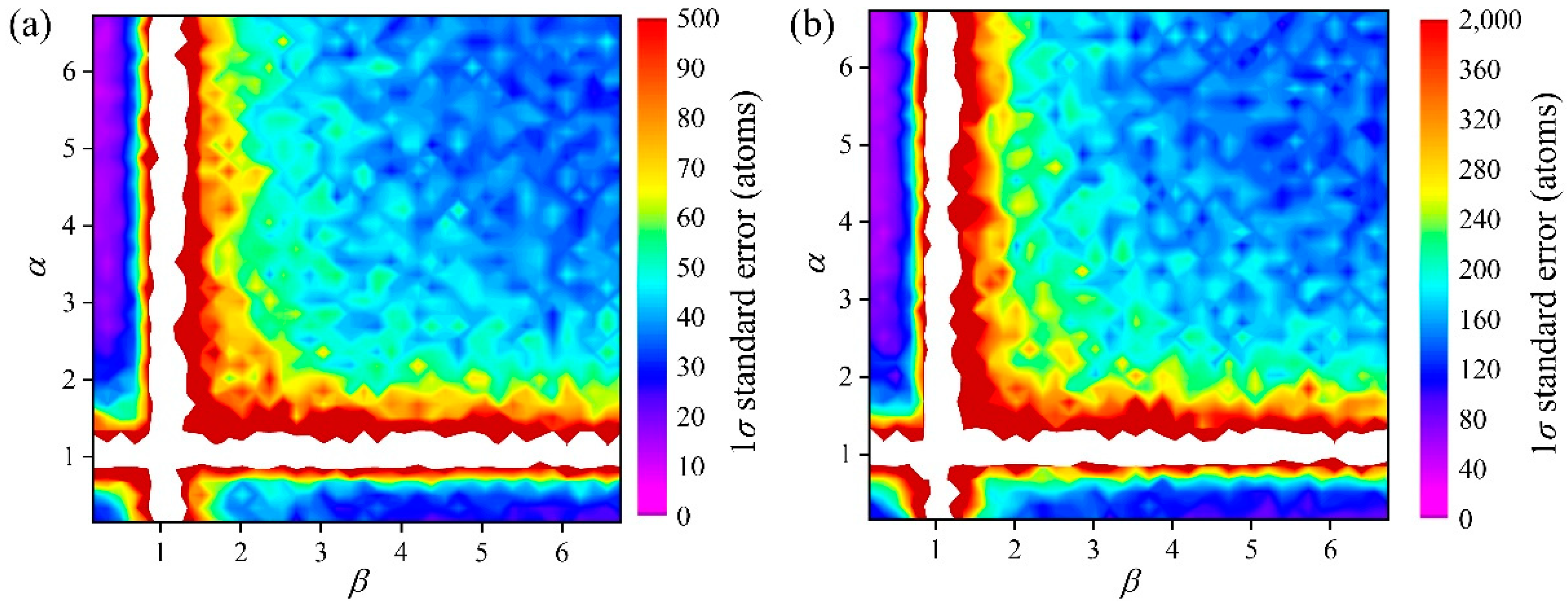
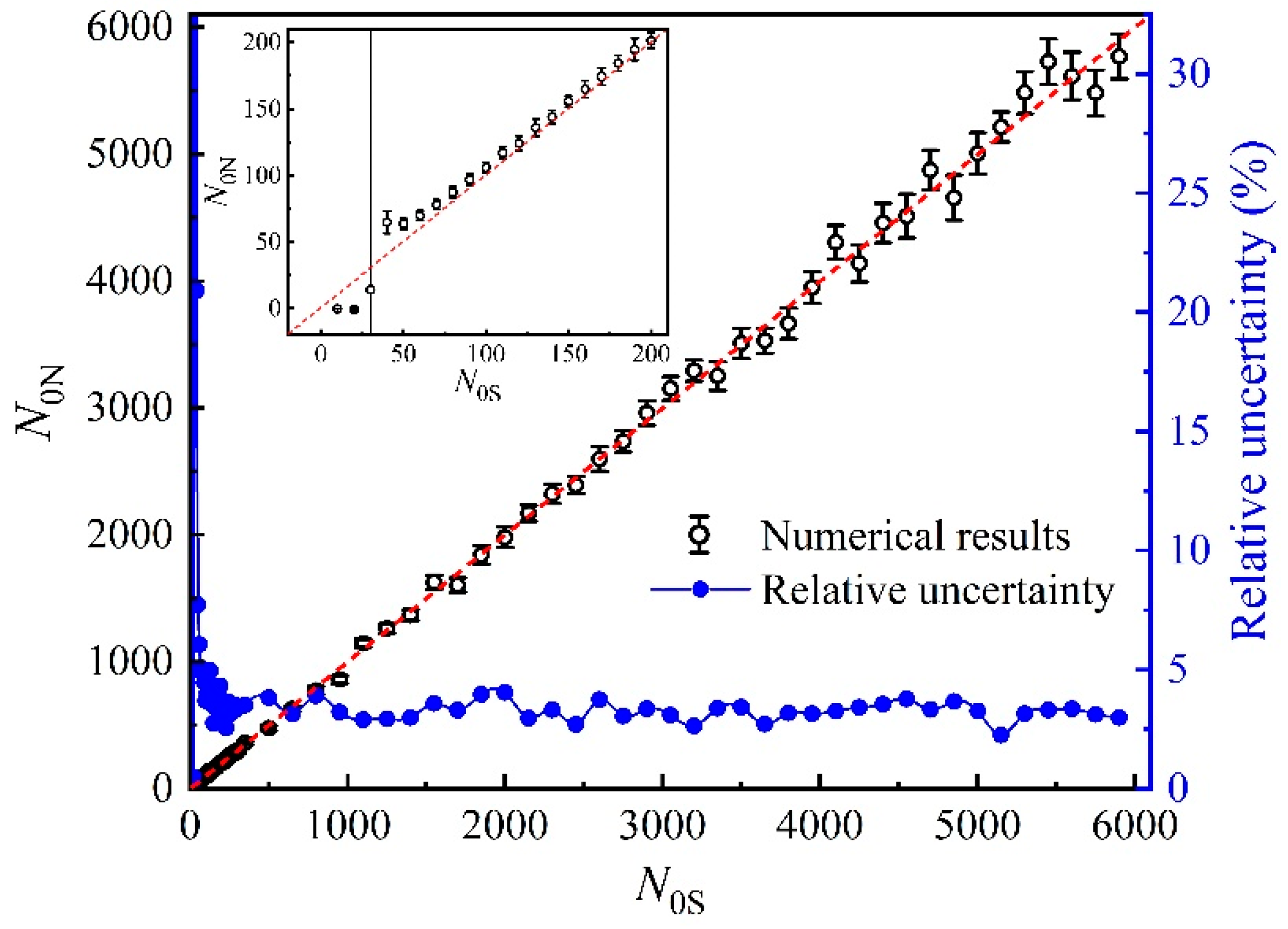
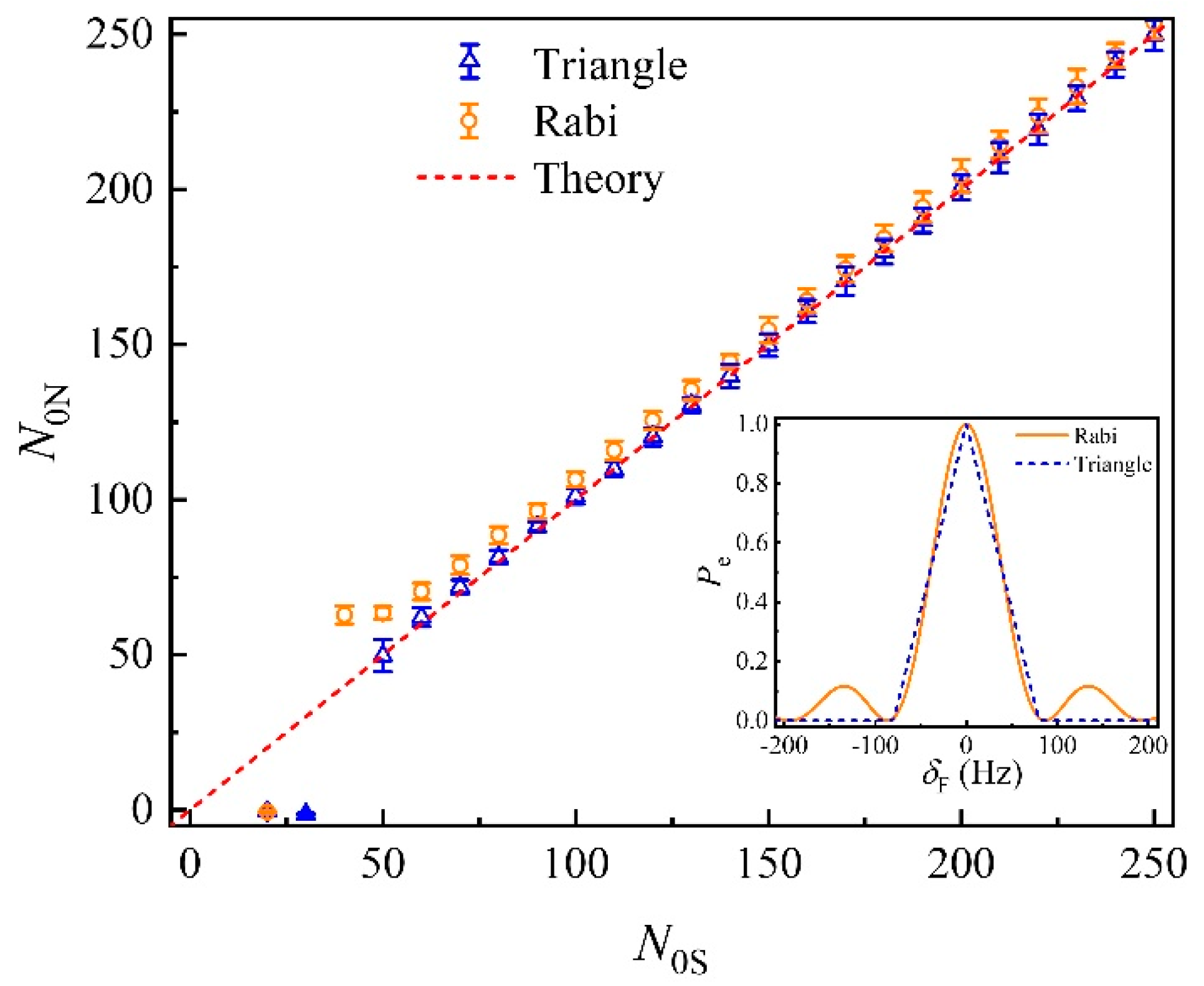
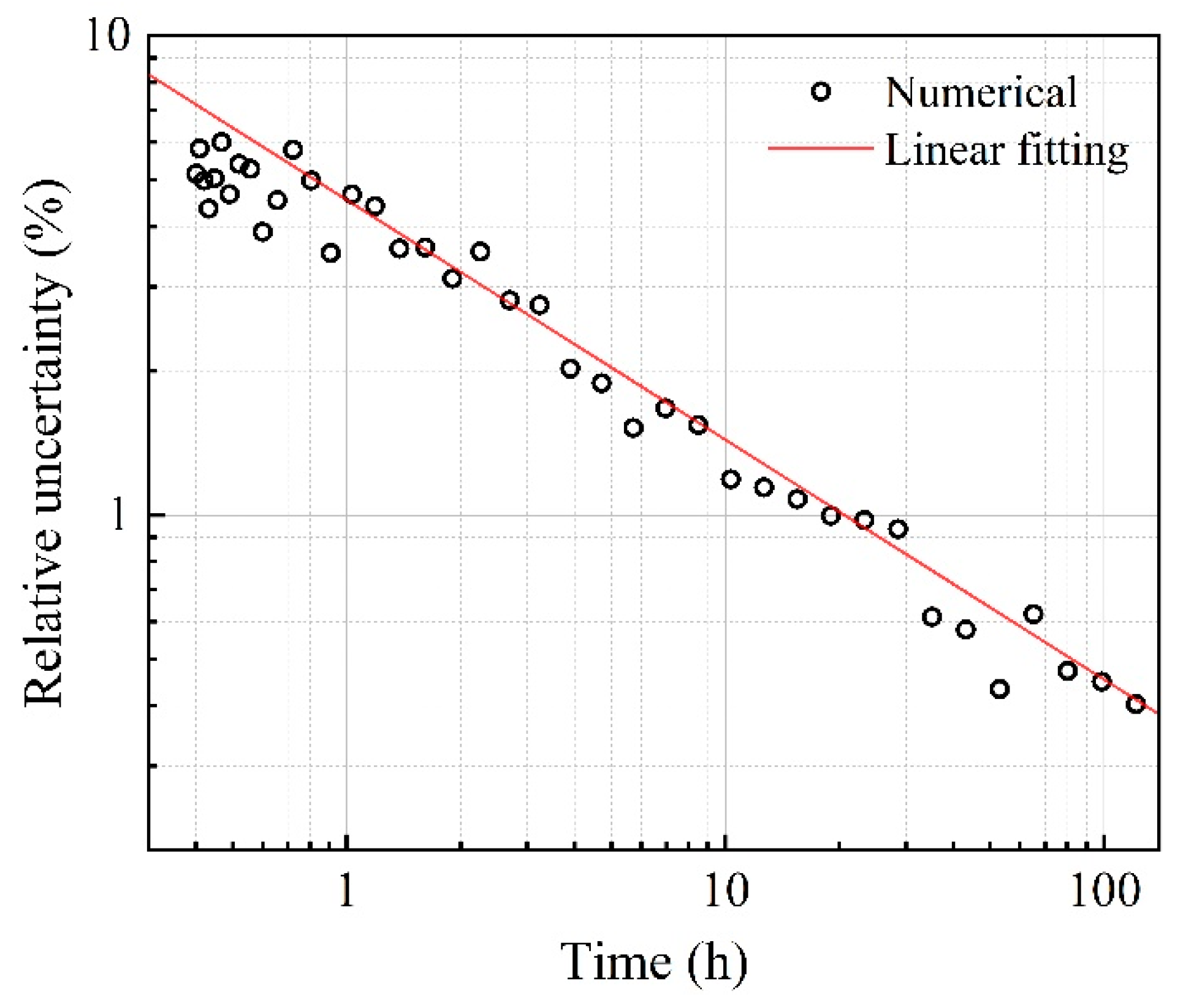
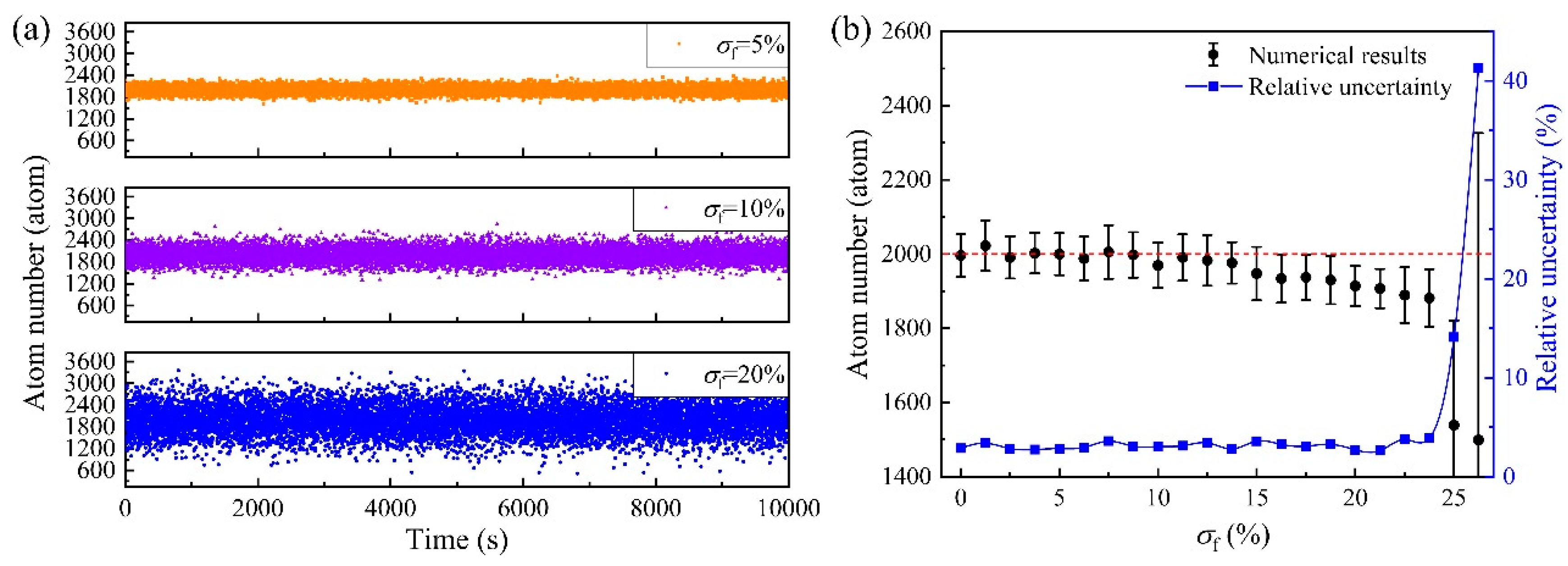
3. Results and Discussion

To validate our approach and identify the optimal modulation parameters (α and β) for minimizing measurement uncertainty, we employ numerical simulations. This simulation involves three main steps. In step 1, all the required parameters are initialized and the values of σ_a~σ_c are calculated. In step 2, the clock comparison process between two clocks is executed with a total measurement time of approximately 2.2 hours, where the Dick effect is cancelled by setting the clock laser noise to be zero [27]. The cancellation of the Dick effect is realized in experiment by synchronous frequency comparison between two clocks [23,28] or using the in situ imaging technique to compare two regions of cold ensembles in a clock [18,19,22,25]. Three cases with noise amplitudes of σ_a, σ_b, and σ_c are simultaneously simulated. The noise-induced frequency fluctuation is generated by multiplying σ_a ~σ_c with normally distributed random numbers. During the frequency correction, the noise is added to the measured frequency errors. Consequently, the comparison stability can be obtained for the Allan variance of the frequency difference between the two clocks. The Allan variance of a single clock should divide the comparison stability by 2 [28]. In this work, we utilize Rabi detection with an interrogation time of T_p =0.1 s, which can be easily implemented in the experiment. It should be noted that the specific choice of T_p has minimal impact on the numerical results obtained. The frequency correction can be expressed as (P_eR- P_eL)/2S₀, where P_eR and P_eL represent the excitation fractions on the right and left sides of the spectrum, respectively. In step 3, the stabilities are calculated and the parameters of σ_QPN, σ_Shot and σ_Det are extracted. Subsequently, the value of N₀ is determined by

T_{0} / 4 S_{0}^{2} σ_{Q P N}^{2}

To verify the accuracy of our numerical calculation code, we compare the stabilities obtained from numerical simulations at three sets of parameters to the theoretical results shown in Figure 1. The parameters used for this comparison are T₀=1 s, N₀=500, γ₀=1, δ_N=3 [23], α=0.2, β=0.1. The excellent agreement observed in Figure 1 between the numerical and theoretical results confirms the correctness of our code and the validity of our method.

To investigate the influence of α and β on the measurement uncertainty of N₀, we study the standard deviation of 50 independent simulations at different combinations of α and β, as shown in Figure 2(a) for N₀=500 and Figure 2(b) for N₀=2000. Similar uncertainty distributions are observed for both cases. The smallest uncertainty is achieved at α=5.71 and β=0.1 for N₀=500, and α=3.84 and β=0.27 for N₀=2000.

We also found that the maximum difference in measurement uncertainty within the ranges of α=0.1~0.44 and β=1.97~6.73 is below 4% at the current total measurement time of 6.7 h. Therefore, we choose the parameters of α=3.84 and β=0.27 to numerically simulate the measurements of N₀ using our approach. Figure 3 demonstrates good agreement between numerical and theoretical results as N₀ exceeds about 200. However, it should be noted that larger measurement uncertainties are observed when N₀ is lower than 200 due to larger noise and reduced stability. The larger noise can correspond to stronger excitation fraction fluctuation, which may cause deviations in the half-height points of the Rabi spectrum more frequently. Although the frequency-sensitivity slope S₀ is not constant for the Rabi spectrum, we use a constant S₀ to infer N₀, leading to deviations for small N₀.

We verify our inference by conducting a comparison of N₀ measurement results using the Rabi and triangular spectra (shown in Figure 4), respectively. Benefitting from the frequency-detuning independent S₀, the triangular spectrum will not be affected by the excitation fraction fluctuations. Figure 4 demonstrates good agreement between theory and numerical result as the triangular spectrum is used, which is the powerful evidence of our hypothesis. Nevertheless, to achieve the triangular spectrum is challenging, this phenomenon suggests that our method can effectively function when N₀ exceeds about 200.

Exploring the relationship between total time consumption and measurement uncertainty using our approach presents an intriguing avenue for further study, given their crucial role in experiments. Figure 5 shows the relationship between relative uncertainty and total measurement time. It is evident that as the time increases, the uncertainties decrease following a slope of -0.5. This observation aligns with the fact that clock-comparison instability also decreases at the same slope of -0.5 with increasing averaging time. Through linear regression analysis, we determined that achieving a 1% uncertainty (one order of smaller than the typical uncertainty of absorption imaging [15,16,17]), requires a measurement time of approximately 20 hours.

In the real world, the number of atoms trapped in the lattice may vary from shot-to-shot clock cycles, making it important to study the relationship between the fluctuation amplitude of atom number and measurement uncertainty using our method. Both factors are critical in experiments. To induce atom number fluctuations, we added discrete random integers to the set value of N₀ in every clock cycle, where the added noise followed a normal distribution N~(2000, 2000σ_f), where σ_f represents the fractional fluctuation of the atom number and can be ranged from 0 to 1. Figure 6(a) shows the atom number as a function of measurement time, while Figure 6(b) presents the numerical results of the extracted averaging atom number and corresponding relative uncertainty as a function of σ_f. Surprisingly, we found that the measurement uncertainty is almost independent of σ_f when the value of σ_f is smaller than about 14%. However, for larger values of σ_f, the measurement uncertainty rapidly increases, and the determined atom number deviates from the theoretical value of 2000. Figure 6(b) indicates that our method is effective, as long as the standard deviation of atom number fluctuation is controlled below 0.14 times the averaging atom number.

4. Conclusions

In conclusion, our proposed method provides a valuable tool for accurately measuring the atom number in an OLC system where clock stability is limited by quantum projection noise, photon shot noise, and technical noise. The numerical results indicate that our approach can achieve a measurement uncertainty below 4% across a wide range of atom numbers with a total measurement time of 6.7 h, and this uncertainty can be further reduced by increasing the measurement time. We also investigated how the fluctuation of atom number affects the measurement results. The numerical results indicate that the standard deviation of atom number fluctuation should be controlled to be below 0.14 times the average atom number. This work can advance research in many-body interaction [14,19], nondestructive detection [29], and entanglement of atoms [30], as the precise measurement of atom number enables more precise control and manipulation of atomic systems.

Author Contributions

writing-original draft preparation, G.Z. and F.G.; software, G.Z., F.G., and X.L.; writing-review and editing, X.L. and H.C.; supervision, H.C. All authors have read and agreed to the published version of the manuscript.

Funding

This work is supported by the National Natural Science Foundation of China (Grant No. 12203057), and the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDB35010202).

Conflicts of Interest

The authors declare no conflict of interest.

References

Bothwell1, T.; Kedar, D.; Oelker, E.; Robinson, J.M.; Bromley, S.L.; Tew, W.L.; Ye, J.; Kennedy, C.J. JILA SrI optical lattice clock with uncertainty of 2.0×10^-18. Metrologia 2019, 56, 065004. [CrossRef]
McGrew, W.F.; Zhang, X.R.; Fasano, J.S.; Schäffer, A.; Beloy, K.; Nicolodi, D.; Brown, R.C.; Hinkley, N.; Milani, G.; Schioppo, M.; Yoon, T.H.; Ludlow, A.D. Atomic clock performance enabling geodesy below the centimetre level. Nature 2018, 564, 87. [CrossRef]
Brewer, S.M.; Chen, J.S.; Hankin, A.M.; Clements, E.R.; Chou, C.W.; Wineland, D.J.; Hume, D.B.; Leibrandt, D.R. ²⁷Al⁺ quantum-logic clock with a systematic uncertainty below 10^-18. Phys. Rev. Lett. 2019, 123, 033201.
Lu, X.T.; Guo, F.; Wang, Y.B.; Xu, Q.F.; Zhou, C.H.; Xia, J.J.; Wu, W.J.; Chang, H. Absolute frequency measurement of the ⁸⁷Sr optical lattice clock at NTSC using international atomic time. Metrologia 2023, 60, 015008. [CrossRef]
Gross, C.; Bloch, I. Quantum simulations with ultracold atoms in optical lattices. Science 2017, 357, 995. [CrossRef]
Nunn, J.; Dorner, U.; Michelberger, P.K.; Lee, C.; Langford, N.K.; Walmsley, I.A.; Jaksch, D. Quantum memory in an optical lattice. Phys. Rev. A 2010, 82, 022327. [CrossRef]
Daley, A.J.; Boyd, M.M.; Ye, J.; Zoller, P. Quantum computing with Alkaline-earth-metal atoms. Phys. Rev. Lett. 2008, 101, 170504. [CrossRef]
Yin, M.J.; Lu, X.T.; Li, T.; Xia, J.J.; Wang, T.; Zhang, X.F.; Chang, H. Floquet engineering Hz-level Rabi spectra in shallow optical lattice clock. Phys. Rev. Lett. 2022, 128, 073603. [CrossRef]
Lu, X.T.; Wang, T.; Li, T.; Zhou, C.H.; Yin, M.J.; Wang, Y.B.; Zhang, X.F.; Chang, H. Doubly modulated optical lattice clock: interference and topology. Phys. Rev. Lett. 2021, 127, 033601. [CrossRef]
Schwarz, R.; Dörscher, S.; Al-Masoudi, A.; Benkler, E.; Legero, T.; Sterr, U.; Weyers, S.; Rahm, J.; Lipphardt, B.; Lisdat, C. Long term measurement of the ⁸⁷Sr clock frequency at the limit of primary Cs clocks. Phys. Rev. Res. 2020, 2, 033242. [CrossRef]
Takamoto, M.; Ushijima, I.; Ohmae, N.; Yahagi, T.; Kokado, K.; Shinkai, H.; Katori, H. Test of general relativity by a pair of transportable optical lattice clocks. Nat. Photon. 2020, 14, 411. [CrossRef]
Miyake, H.; Pisenti, N.C.; Elgee, P.K.; Sitaram, A.; Campbell, G.K. Isotope-shift spectroscopy of the ¹S₀→³P₁ and ¹S₀→³P₀ transitions in strontium. Phys. Rev. Res. 2019, 1, 033113. [CrossRef]
Kennedy, C.J.; Oelker, E.J.; Robinson, M.; Bothwell, T.; Kedar, D.; Milner, W.R.; Marti, G.E.; Derevianko, A.; Ye, J. Precision metrology meets cosmology: Improved constraints on ultralight dark matter from atom-cavity frequency comparisons. Phys. Rev. Lett. 2020, 125, 201302. [CrossRef]
Rey, A.M.; A. Gorshkov, V.C.; Kraus, V.M.; Martin, J.; Bishof, M.; Swallows, M.D.; Zhang, X.; Benko, C.; Ye, J.; Lemke, N.D.; Ludlow, A.D. Probing many-body interactions in an optical lattice clock. Ann. Phys. 2014, 340, 311. [CrossRef]
Gregor, O.K.; Melina, P.; Gustav, W.; Mark, B.; Olivier, M.; Wolf, K. Atom number calibration in absorption imaging at very small atom numbers. Cent. Eur. J. Phys. 2012, 10, 1054. [CrossRef]
Reinaudi, G.; Lahaye, T.; Wang, Z.; Guery-Odelin, D. Strong saturation absorption imaging of dense clouds of ultracold atoms. Opt. Lett. 2007, 32, 3143. [CrossRef]
Hueck, K.; Luick, N.; Sobirey, L.; Siegl, J.; Lompe, T.; Moritz, H.; Clark, L.W.; Chin, C. Calibrating high intensity absorption imaging of ultracold atoms. Opt. Express 2017, 25, 8670. [CrossRef]
Bothwell, T.; Kennedy, C.J.; Aeppli, A.; Robinson, J.M.; Oelker, E.; Staron, A. Ye, J. Resolving the gravitational redshift across a millimetre-scale atomic sample. Nature 2022, 602, 420. [CrossRef]
Aeppli, A.; Chu, A.J.; Bothwell, T.; Kennedy, C.J.; Kedar, D.; He, P.; Rey, A.M.; Ye, J. Hamiltonian engineering of spin-orbit-coupled fermions in a Wannier-Stark optical lattice clock. Sci. Adv. 2022, 8, eadc9242. [CrossRef]
Santarelli, G.; Laurent, Ph.; Lemonde, P.; Clairon, A.; Mann, A.G.; Chang, S.; Luiten, A.N.; Salomon, C. Quantum projection noise in an atomic fountain: a high stability cesium frequency standard. Phys. Rev. Lett. 1999, 82, 4619. [CrossRef]
Al-Masoudi, A.; Dörscher, S.; Häfner, S.; Sterr, U.; Lisdat, C. Noise and instability of an optical lattice clock. Phys. Rev. A 2015, 92, 063814. [CrossRef]
Lu, X.T.; Xia, J.J.; Lu, B.Q.; Wang, Y.B.; Wang, T.; Chang, H. Determining the atom number from detection noise in a one-dimensional optical lattice clock. Appl. Phys. Lett. 2022, 120, 151104. [CrossRef]
Takamoto, M.; Takano, T.; Katori, H. Frequency comparison of optical lattice clocks beyond the Dick limit. Nat. Photon. 2011, 5, 288. [CrossRef]
Lu, X.T.; Zhou, C.H.; Li, T.; Wang, Y.B.; Chang, H. Synchronous frequency comparison beyond the Dick limit based on dual-excitation spectrum in an optical lattice clock. Appl. Phys. Lett. 2020, 117, 231101. [CrossRef]
Campbell, S.L.; Hutson, R.B.; Marti, G.E.; Goban, A.; Darkwah Oppong, N.; McNally, R.L.; Sonderhouse, L.; Robinson, J.M.; Zhang, W.; Bloom, B.J.; Ye, J. A Fermi-degenerate three-dimensional optical lattice clock. Science 2017, 358, 90. [CrossRef]
Lemonde, P.; Laurent, P.; Santarelli, G.; Abgrall, M.; Sortais, Y.; Bize, S.; Nicolas, C.; Zhang, S.; Clairon, A.; Dimarcq, N.; Petit, P.; Mann, A.G.; Luiten, A.N.; Chang, S.; Salomon, C. 2001 Frequency Measurement and Control: Advanced Techniques and Future Trends (Vol. 79) (Berlin: Springer, Berlin, Heidelberg) pp.131-153. [CrossRef]
Dick, G.J. in Proceedings of 19th Annual Precise Time and Time Interval Meeting, Redendo Beach, 1987 (US Naval Observatory, Washington, DC, 1988), pp. 133-147.
Nicholson, T.L.; Martin, M.J.; Williams, J.R.; Bloom, B.J.; Bishof, M.M.; Swallows, D.; Campbell, S.L.; Ye, J. Comparison of two independent Sr optical clocks with 1×10^-17 stability at 10³ s. Phys. Rev. Lett. 2012, 109, 230801.
Orenes, D.B.; Sewell, R.J.; Lodewyck, J.; Mitchell, M.W. Improving short-term stability in optical lattice clocks by quantum nondemolition measurement. Phys. Rev. Lett. 2020, 128, 153201. [CrossRef]
Pedrozo-Peñafie, E.; Colombo, S.; Shu, C.; Adiyatullin, A.F.; Li, Z.Y.; Mendez, E.; Braverman, B.; Kawasaki, A.; Akamatsu, D.; Xiao, Y.H.; Vuletić, V. Entanglement on an optical atomic-clock transition. Nature 2020, 588, 414. [CrossRef]

Figure 1. Comparisons of numerical and theoretical results of stabilities. The Allan variances of frequency fluctuations at three-group parameters. The points represent the numerical results and dotted lines indicate the corresponding theoretical results. All error bars represent the 1σ standard error.

Figure 2. Numerical results of measurement uncertainties at different modulation parameters of α and β. (a) The standard deviation of 50 independent simulations at N₀=500. (b) The case of N₀=2000. The white regions indicate errors larger than 500 for figure (a) and 2000 for figure (b), which occurs when α or β approaches 1. In such cases, the modulation amplitudes of the parameters become close to zero, indicating that the different noises cannot be distinguished.

Figure 3. Numerical results of the determined atom number (N_0N) as a function of set value (N_0S). Points are the results of single simulation, and the relative uncertainties are calculated by dividing corresponding error bars (the standard deviation of 50 numerical simulations) by N_0S. The inset provides a more detailed view of the results when N_0S is smaller than 200. As the N_0S is smaller than 40, strong excitation fraction fluctuation leads to lock-lose, indicating the importance of maintaining a sufficiently high atom number to ensure stable and accurate measurements.

Figure 4. Numerical results of the determined atom number (N_0N) as a function of set value (N_0S) using the Rabi spectrum (circles) and triangular spectrum (triangles), respectively. Points are the results of single simulation, and the error bars indicate the standard deviation of 50 numerical simulations. The inset shows the spectra of Rabi (solid line) and triangular spectrum (dotted line), respectively, wherein δ_F denotes frequency detuning and P_e represents excitation fraction.

Figure 5. Relative uncertainty of the atom number measurement as a function of time consumption. The relative uncertainty is obtained by dividing the standard deviation of 50 numerical simulations by the atom number set at 2000. The red solid lines indicate the linear fitting with a fixed slope of -0.5.

Figure 6. The atom number fluctuation and measurement uncertainty as a function of σ_f. (a) The fluctuation of atom number at σ_f = 5%, 10% and 20%, respectively. (b) Measurements of the atom number (averaging value of 50 simulations) and corresponding relative uncertainty (the standard deviation of 50 simulations) as a function of σ_f. The dotted line shows the set averaging number of atom of 2000.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer