Fractional-Order Load Frequency Control of an Interconnected Power System with Hydrogen Energy-Storage Unit

Modern power systems are confronted with a spread concern on the frequency stability issue due to the widespread integration of randomly fluctuating renewable resources. To address the above concern, this work introduces a load frequency control (LFC) scheme based on a hydrogen based energy-storage unit and a parameter tuning strategy for fractional-order proportional-integral-derivative (FOPID) controller. Firstly, a two-area interconnected power system (IPS) model, including thermal, hydro, solar, wind, gas power generator, and hydrogen based energy-storage unit, is established. Then, a FOPID controller is designed for this IPS model, and an improved gradient-based optimizer (IGBO) is developed to adaptively regulate the parameters of the FOPID controllers. Finally, the effectiveness of the offered LFC scheme are tested through load disturbance and renewable energy fluctuations test scenarios, and provides comparison and robustness analysis among different schemes. The test results validated that the offered LFC scheme can effectively suppress the frequency fluctuations of IPS and has excellent robustness.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

1. Introduction

Development and application of renewable energy generation technology could be one critical enabler of the global transition to low-carbon emissions economies [1]. Nevertheless, solar energy, wind energy, tidal energy and other renewable energies have random and fluctuating characteristics, and renewable energy generators have almost no inertia contribution to power grids since these generators are isolated to the grids by power electronic converters [2,3]. As a result, the IPSs with a substantial integration of renewable energy generators always face the frequency stability issue, and a suitable design of LFC method is commonly required for these power systems.

Over the past few years, various intelligent control technologies such as model predictive control [4], sliding mode control [5], reinforcement learning [6], active disturbance rejection control [7], fuzzy logic control [8] have been utilized in the design of load frequency control (LFC). The LFC scheme developed by the above technologies are usually effective in different test scenarios, but the major challenge of employing these methods is their heavy reliance on model accuracy and engineering feasibility. While traditional proportional-integral-derivative (PID) controller based LFC design, in fact, remains the most extensively used approach in practice [9,10]. However, the interconnected structure and complicated module expressions of modern IPSs make the empirical parameter tuning methods become time consuming and ineffective when using PID controller based LFC scheme. Besides, by using traditional PID controller based LFC design and empirical parameter tuning methods, the robustness and dynamic properties of the system may also get worse in highly volatile renewable energy power generation facilities and highly flexible loads.

To address the above concerns, various parameter tuning and optimization techniques were developed for optimizing PID controller based LFC. These techniques include whale optimization algorithm (WOA) [11], fuzzy rule (FL) [12], articial neural network (ANN) [13], and gray wolf optimizer (GWO) [14]. According to these works, one can find that by introducing optimization strategies to regulate the parameters, the frequency stability of IPSs can be improved significantly. Nonetheless, traditional PID controllers only have three adjustable parameters, their parameter settings are limited, and their performance deteriorate with system nonlinearities and uncertainties. Therefore, FOPID controller is proposed. In comparison to PID controllers, the FOPID controller enhances the adjustable dimensionality of controller parameters by incorporating fractional differential and integral orders. Consequently, it exhibits superior robustness and anti-interference performance in response to variations in the controlled system parameters [15,16,17]. Recently, such controllers have also been used for LFC design. For example, in literature [18], a FOPID controller is used to mitigate the frequency fluctuation of a two-area IPS, and a gases brownian motion optimization (GBMO) is exploited to regulate the parameters of the controller. Literature [19] use a modified FOPID controller-based LFC scheme to enhance frequency regulation performance and the controller parameters are subsequently tuned using Jellyfish Search Optimizer (JSO). In literature [20], a FOPID controller based LFC scheme for IPS with renewable energy power plants is proposed and movable damped wave algorithm (MDWA) is employed to tune the FOPID controller parameters. Besides, the method based on an improved particle swarm optimization (IPSO) and a hybrid artificial gorilla troops optimizer and equilibrium optimizer (AGTOEO) for tuning FOPID controller parameters has also been used in LFC design, as those introduced in reference [21] and [22]. The findings from these studies validate that FOPID controllers demonstrate superior dynamic performance compared to traditional PID controllers in LFC applications.

In addition to designing control strategies, the integration of energy storage facilities has emerged as a prevalent supplementary method to enhance the frequency characteristics of IPSs with renewable resources [23,24]. Among various energy storage technologies such as pumped storage, flywheel energy storage and electrochemical energy storage, hydrogen energy storage exhibits significant advantages in energy storage capacity and economic feasibility [25,26,27]. Over the last decade, significant efforts have been devoted to the development and application of hydrogen energy-based techniques. Various research groups have explored the utilization of hydrogen energy storage units in contributing to the frequency regulation of conventional power systems primarily powered by thermal power plants [28,29]. Through an analysis of existing studies focused on enhancing system structures through the integration of energy storage units, it can be inferred that the incorporation of hydrogen-based energy storage units into integrated energy systems enables power systems to exhibit greater flexibility in responding to energy fluctuations and enhances the utilization of renewable energy sources.

In recent years, the gradient-based optimizer (GBO) has emerged as a promising solution for addressing optimization problems across diverse fields, primarily due to its simple yet powerful structure, ease of implementation, robust exploration capability, and ability to effectively evade local optima [30]. However, the GBO has some limitations when tackling large-scale and complex engineering problems, such as slow convergence speed and low precision in the later stages of the algorithm [31]. To address these challenges, this study proposes an improved GBO (IGBO) for obtaining optimal parameters for the FOPID controller in LFC issues within a two-area IPS integrated with hydrogen energy storage. Firstly, a FOPID controller-based LFC scheme is designed using the Oustaloup approximation algorithm. Subsequently, the IGBO algorithm is developed to adaptively regulate the FOPID controller parameters. Finally, a series of test scenarios are presented to test the effectiveness and superiority of the offered LFC method, along with an analysis of system robustness.

2. LFC model of a two-area IPS

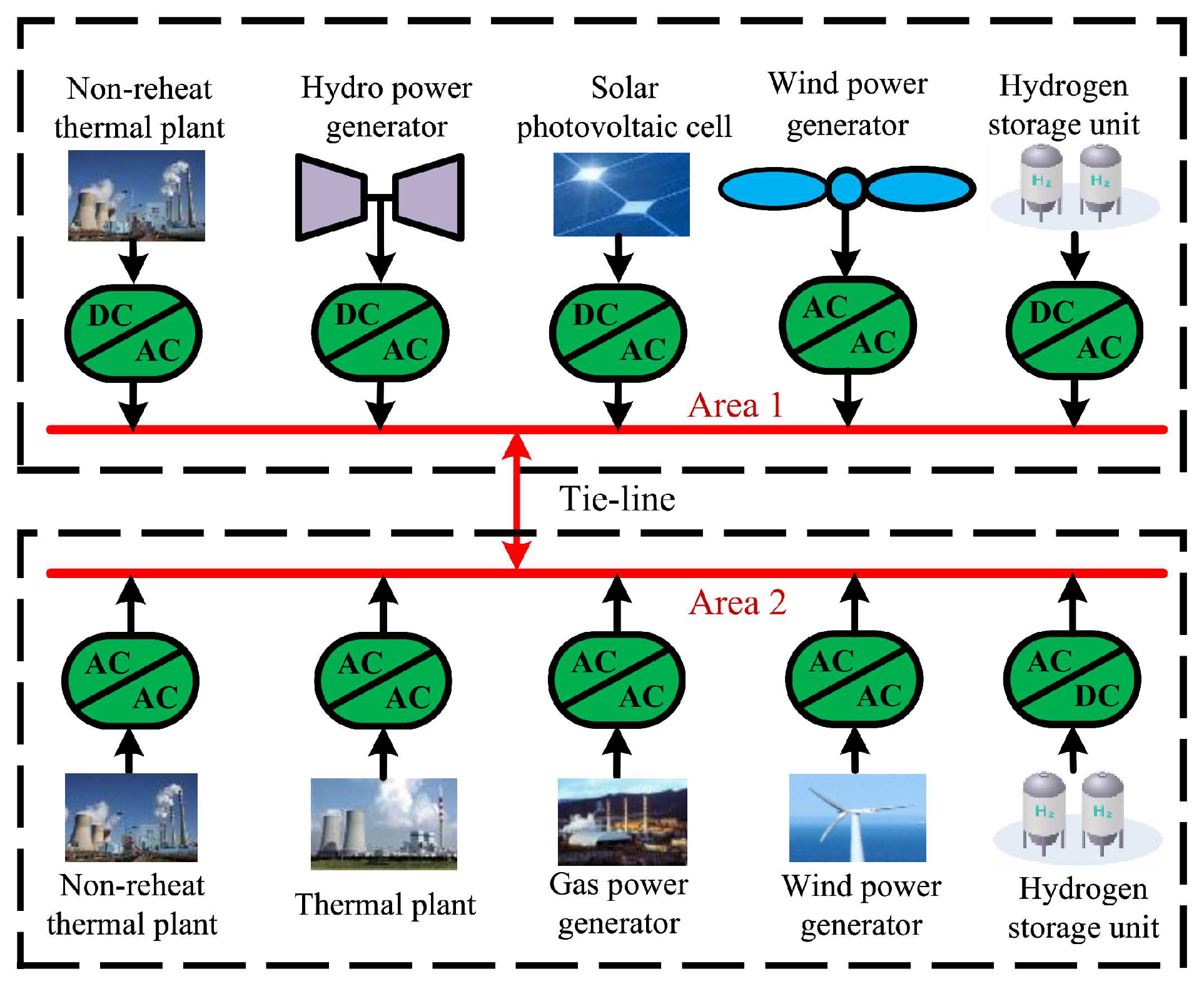
In general, modern power systems are formed by multiple interconnecting areas, with each area consisting of a variety of different types of power sources and load units. In this study, we focus on an IPS model consisting of two areas, which is depicted in Figure 1.

In the two-area IPS, Area 1 comprises a non-reheat thermal plant, hydro power generator, solar photovoltaic cell, wind power generator, while Area 2 consists of a thermal plant, non-reheat thermal plant, gas power generator, and wind power generator. Furthermore, hydrogen storage units are incorporated in both areas to enhance system performance. The mathematical models for each unit can be described as follows:

2.1. Mathematical model of thermal power plant

In a thermal power plant, the primary components are a speed governor and a steam turbine. The transfer function for the governor and steam turbine can be governed as

G_{G} = \frac{1}{1 + s T_{G}}

(1)

G_{T} = \frac{1}{1 + s T_{T}}

(2)

where

T_{G}

and

T_{T}

denote the time constants of the governor and turbine, respectively.

The transfer function of a reheater can be governed by

G_{T} = \frac{1 + s K_{r} T_{r}}{1 + s T_{r}}

(3)

where

K_{r}

and

T_{r}

are the gain and time constants of the reheater, respectively.

2.2. Mathematical model of hydro power generator

The hydro power generator comprises a hydraulic turbine and a hydraulic governor, with its transfer function can be represented as

G_{HT} = \frac{1 - s T_{W}}{1 + 0.5 s T_{W}}

(4)

G_{HG} = \frac{1 + s T_{R}}{(1 + s T_{GH}) (1 + s (R_{T} / R) T_{R})}

(5)

where

T_{W}

and

T_{GH}

represent the time constants of the turbine and the governor, respectively.

T_{R}

represent the reset time constant, R denotes the adjustment coefficient of hydro power generator, and

R_{T}

is the transient fall rate.

2.3. Mathematical model of solar photovoltaic cell

The power output of a solar photovoltaic cell is [21]

P_{PV} = η S Φ \{1 - 0.005 (T_{a} + 25)\}

(6)

where the coefficient

η

represents the conversion efficiency of the photovoltaic unit. The coefficient S represents the surface area of the photovoltaic array,

Φ

denotes the solar radiation on the photovoltaic array, and

T_{a}

denotes the working temperature. The mathematical model of photovoltaic system is

G_{PV} = \frac{K_{PV}}{1 + s T_{PV}}

(7)

where

K_{PV}

and

T_{PV}

are the gain and time constants of the photovoltaic unit, respectively.

2.4. Mathematical model of wind power generator

The modeling of wind power generators consists of two parts: a nonlinear model and a transfer function model. The former, as described in [21], does not contribute to frequency regulation. The power output of a wind power generator is

P_{WTG} = \frac{1}{2} ρ A_{r} C_{p} V_{W}^{3}

(8)

where the coefficient

ρ

refers to air density, and

A_{r}

represents the swept area of blades. The coefficient

C_{p}

denotes the power coefficient,

V_{W}

denotes wind speed. The dynamic model of wind power generator is

G_{W} = \frac{K_{WTG}}{1 + s T_{WTG}}

(9)

where

K_{WTG}

and

T_{WTG}

represent the gain and time constants of the wind power generator, respectively.

The transfer function model focuses on the active standby of wind turbines and takes wind power as an active resource for frequency modulation [5], which can be mathematically expressed as

G_{wind} = \frac{1}{1 + s T_{pw 2}} \frac{K_{pw 1} (1 + s T_{pw 1})}{1 + s} \frac{K_{pw 2}}{1 + s}

(10)

where

T_{pw 1}

T_{pw 2}

K_{pw 1}

, and

K_{pw 2}

denote the time and gain constants of the wind power governor, respectively.

2.5. Mathematical model of gas power generator

The mathematical model of gas power generator can be stated as [32]

G_{GT} = \frac{1}{c_{g} + s b_{g}} \frac{1 + s X_{c}}{1 + s Y_{c}} \frac{1 + s T_{cr}}{1 + s T_{f}} \frac{1}{1 + s T_{cd}}

(11)

where

c_{g}

and

b_{g}

represent the gain and time constants of the gas turbine, respectively.

X_{c}

and

Y_{c}

are complex parameters that reflect the impact of the gas turbine on the phase and amplitude of the input signal,

T_{cr}

T_{f}

and

T_{cd}

are the time constants of the cooling system, fuel injection and entire gas power generator, respectively.

2.6. Mathematical model of hydrogen storage unit

The hydrogen storage system comprises an electrolyzer, a storage tank, and a hydrogen fuel cell. When surplus power is generated by the new energy generators within the system, the electrolyzer produces hydrogen, which is subsequently compressed and stored in the hydrogen storage tanks. During periods of heightened load demand and electricity scarcity, the hydrogen fuel cell converts the chemical energy into electrical power to meet the system’s load requirements. The mathematical model of the electrolyzer and the hydrogen fuel cell in the system can be represented as [28]

G_{HAE} = \frac{K_{HAE}}{1 + s T_{HAE}}

(12)

G_{FC} = \frac{K_{FC}}{1 + s T_{FC}}

(13)

where

K_{HAE}

and

K_{FC}

are the gain constants of the electrolyzer and the hydrogen fuel cell, respectively.

T_{HAE}

and

T_{FC}

represent the time constants of the electrolyzer and the hydrogen fuel cell, respectively.

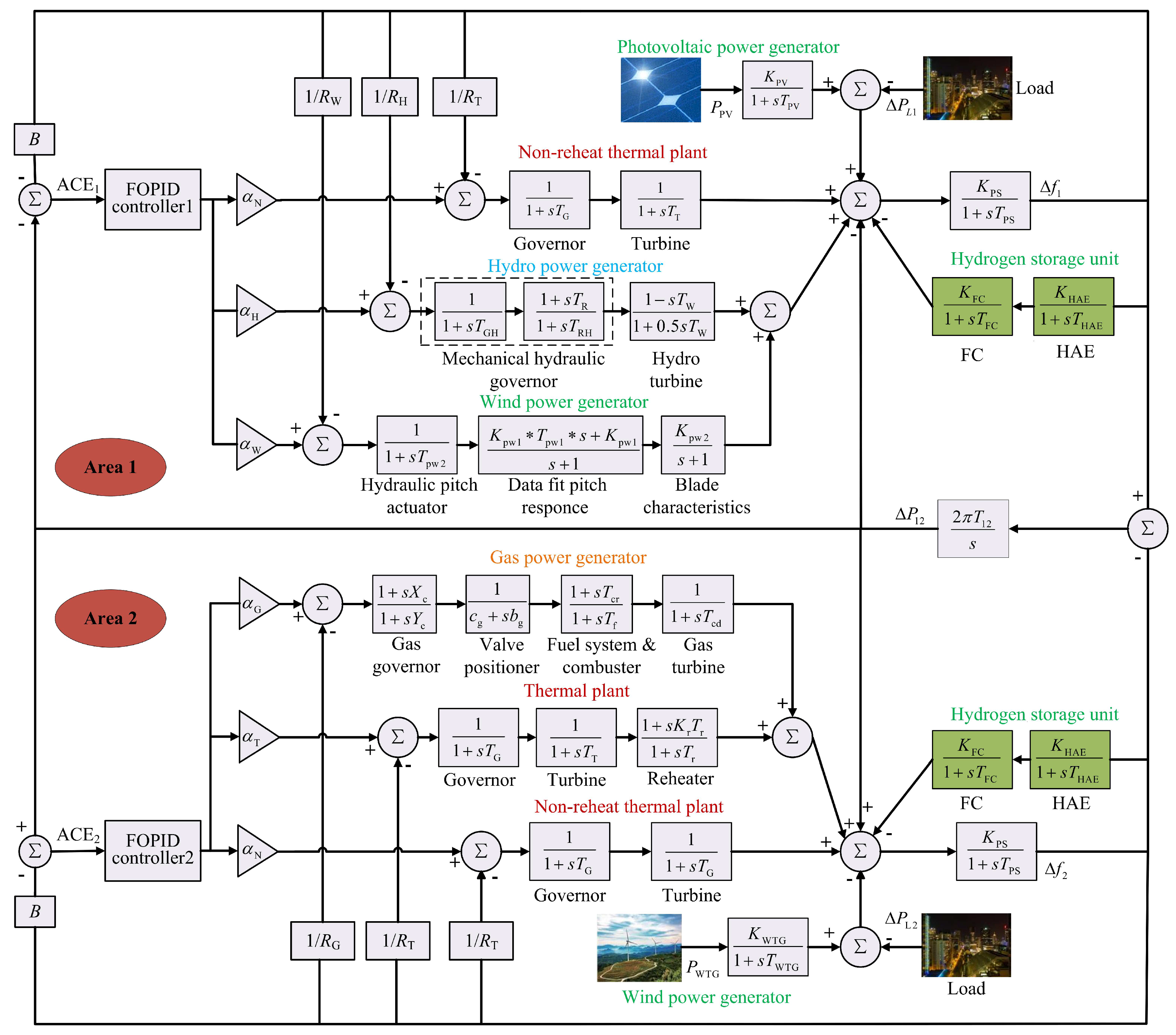
Based on the mathematical models of each unit, as well as the hydrogen storage unit, an LFC model is constructed for the IPS consisting of two areas, as depicted in Figure 2.

In Figure 2, the term B is the frequency offset coefficient,

{ACE}_{1}

and

{ACE}_{2}

represent the area control errors (ACE) for area 1 and area 2, respectively,

R_{T}

and

R_{H}

represent the governor constants of the thermal plants and the hydro power generator, respectively.

R_{G}

and

R_{W}

represent the governor parameters of gas power generator and wind power generator, respectively.

α_{G}

α_{T}

α_{N}

α_{W}

and

α_{H}

represent the power distribution ratio of gas, thermal, non-reheat thermal, wind power and hydro power generators, respectively,

Δ P_{L 1}

and

Δ P_{L 2}

represent load disturbances in area 1 and area 2, respectively.

K_{PS}

and

T_{PS}

denote the gain and time constants of the IPS, respectively.

T_{12}

denotes the synchronization coefficient of the tie line,

Δ f_{1}

and

Δ f_{2}

represent the frequency deviation of the area 1 and area 2, respectively.

Δ P_{12}

denotes the power flow of tie line.

3. Design of FOPID controller based LFC

The LFC scheme in this study is based on a FOPID controller, which is two more parameters compared to the traditional PID controller. Basically, the transfer function of FOPID controller can be expressed by

G_{C} (s) = K_{P} + \frac{K_{I}}{s^{λ}} + K_{D} s^{μ}

(14)

where

K_{P}

K_{I}

and

K_{D}

represent the proportional coefficient, integral coefficient and differential coefficient, respectively. Additionally,

1 / s^{λ}

and

s^{μ}

denote the fractional integral operator and fractional differential operator, respectively. These ideal fractional-order operators cannot be implemented directly by integer order rational fractions. This study adopts an improved Oustaloup’s approximation algorithm [33] to approximate the fractional-order operator within a predetermined frequency range by constructing a transfer function in the form of zeros and poles as follows:

G (s) = {(\frac{d ω_{b}}{b})}^{α} \frac{d s^{2} + b ω_{h} s}{d (1 - α) s^{2} + b ω_{h} s + d α} \prod_{k = - N_{f}}^{N_{f}} \frac{s + ω_{k}^{'}}{s + ω_{k}}

(15)

ω_{k}^{'} = ω_{b} {(\sqrt{\frac{ω_{h}}{ω_{b}}})}^{\frac{k + N_{f} + 0.5 (1 - α)}{2 N_{f} + 1}}

(16)

ω_{k} = ω_{b} {(\sqrt{\frac{ω_{h}}{ω_{b}}})}^{\frac{k + N_{f} + 0.5 (1 + α)}{2 N_{f} + 1}}

(17)

where

α

represents the order of the fractional-order operator, and the coefficients b and d are preset coefficients with values of 9 and 10, respectively.

N_{f}

represents the order of the filter, which we set to 5 in this study.

ω_{b}

and

ω_{h}

represent the lower and upper limits of the predetermined frequency range, with values of 0.001 and 1000, respectively.

ω_{k}^{'}

and

ω_{k}

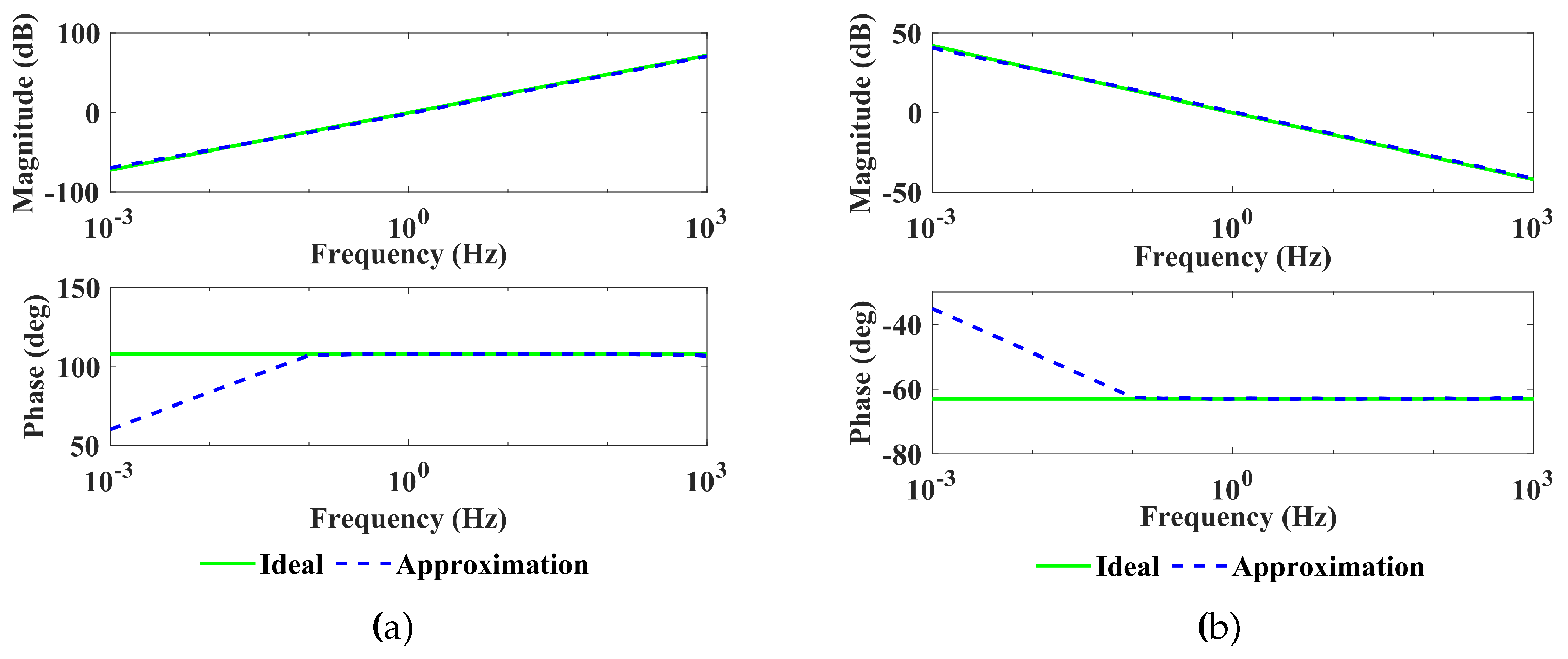
represent the constructed zeros and poles of the transfer function, respectively. The comparison between the ideal fractional-order operators and approximate fractional-order operators is shown in Figure 3.

As depicted in Figure 3, it can be observed that within the predetermined frequency range, the amplitude-frequency characteristic curves of the approximate fractional-order operator and the ideal fractional-order operator coincide with each other. Additionally, the phase-frequency characteristic curves of both operators fall within the preset phase error range throughout the predetermined frequency range. The results of comparison confirm that the approximate fractional-order operators can be applied.

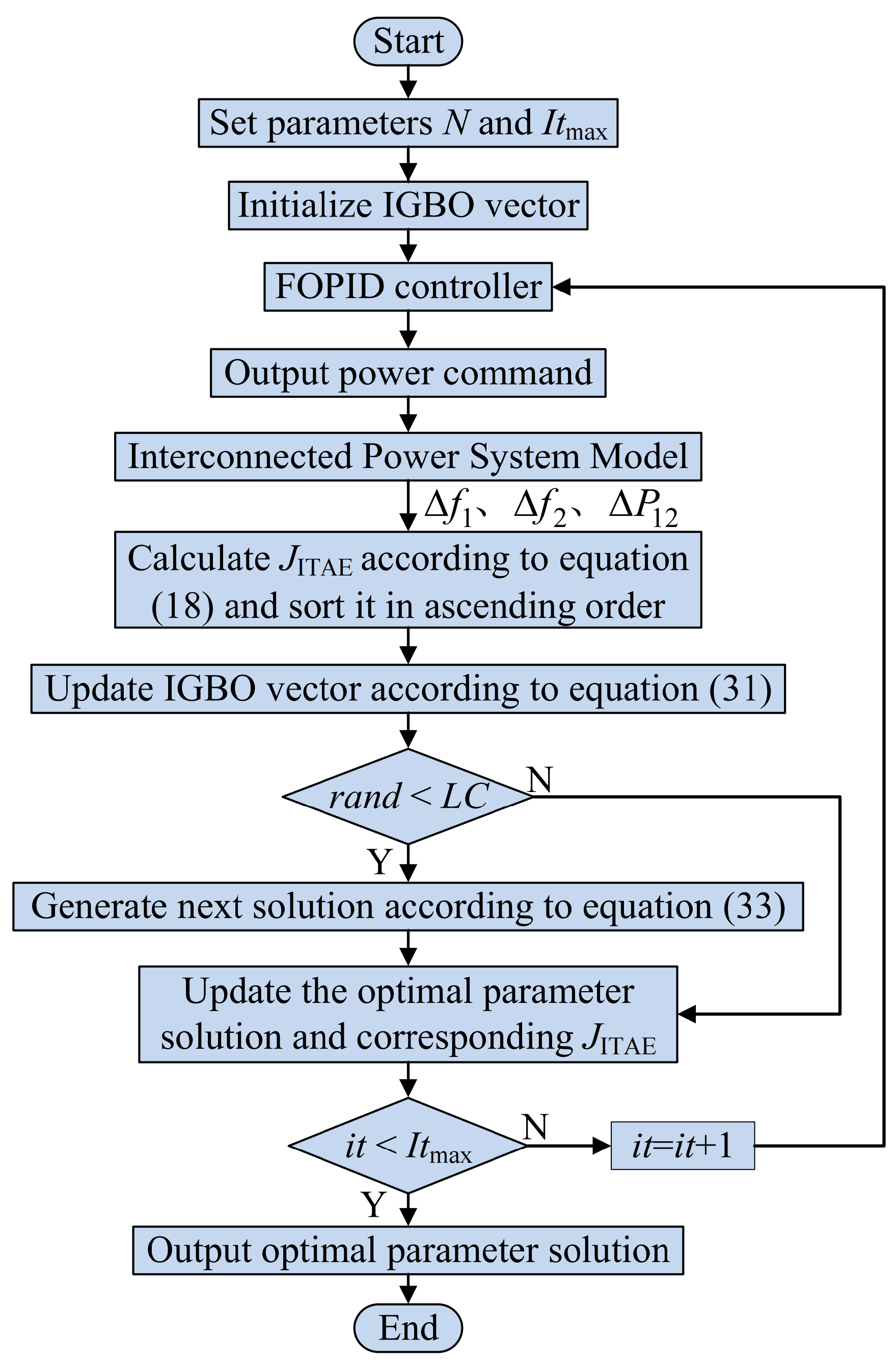
4. Parameter tuning process based on IGBO

To ensure the two-area IPS in Figure 2 can swiftly recover frequency stability under load or renewable resources fluctuations, this paper proposes a parameter tuning strategy by an IGBO algorithm, which uses a combination of the gradient search mechanism (GSM) based on a sorting algorithm and the improved local escape operators (ILEO) based on chaotic mapping in the optimization process [34]. The objective fitness function is formulated using the integral of time multiplied absolute error (ITAE) criterion based on the ACE, which can be as

m i n J_{ITAE} = \int_{0}^{T_{sim}} t (|Δ f_{1}| + |Δ f_{2}| + |Δ P_{12}|) d t

(18)

where

T_{sim}

is the total duration of the optimization process. With the objective of minimizing

J_{ITAE}

, the IGBO algorithm is utilized to tune the parameters of the FOPID-based LFC controllers in the IPS. The specific update method for IGBO is as follows:

4.1. Initialization

The IGBO algorithm initializes the parameters of the FOPID controller based on

X_{n} = L o w + r a n d \times (U p - L o w)

(19)

where

n = 1, 2, . . ., N

, N corresponds to the total number of IGBO vectors.

L o w

and

U p

denote the lower and upper bounds of the parameter space.

r a n d

denotes a randomly generated number within the range 0 to 1.

4.2. Parameter update method based on GSM

GSM is used for global search in the parameter space, and its definition is as

GSM = r a n d n \times ρ_{1} \times \frac{2 Δ X \times X_{n}}{y p_{n} - y q_{n} + ε}

(20)

where

r a n d n

represents a random number that follows a normal distribution, and

ε

represents a small number in the range of 0 to 0.1.

ρ_{1}

is a crucial parameter that determines the global exploration ability of the IGBO algorithm. To obtain a better solution for the FOPID controller parameters, a sorting algorithm is proposed to update the parameter

ρ_{1}

, which can be represented as

ρ_{1} = \{\begin{matrix} \begin{matrix} r 1 / N + 0.15 \times r a n d n & i f r a n d < 0.5 \\ n / N + 0.15 \times r a n d n & e l s e \end{matrix} \end{matrix}

(21)

where

r 1

is a integer randomly selected from 1 to N. Furthermore, the GSM definition is represented by Equation (22) for

Δ X

, and

y p_{n}

and

y q_{n}

are represented by Equation (25) and Equation (26) respectively.

Δ X = r a n d (1 : D) \times |s t e p|

(22)

s t e p = \frac{(X_{best} - X_{r 1}^{i t}) + δ}{2}

(23)

δ = 2 \times r a n d \times (|\frac{X_{r 1}^{i t} + X_{r 2}^{i t} + X_{r 3}^{i t} + X_{r 4}^{i t}}{4} - X_{n}^{i t}|)

(24)

where

r a n d (1 : D)

is a D-dimensional random vector, D corresponds to the number of parameters of the FOPID controller to be optimized.

s t e p

is determined by the optimal solution (

X_{best}

) and the random selection vector (

X_{r 1}^{i t}

) in the iterations.

i t

is the current number of iteration within the range 1 to

I t_{\max}

I t_{\max}

represents the maximum number of iterations. The variables

r 2

r 3

, and

r 4

represent distinct integers are randomly selected from 1 to N.

y p_{n} = r a n d \times (\frac{[Z_{n + 1} + X_{n}]}{2} + r a n d \times Δ X)

(25)

y q_{n} = r a n d \times (\frac{[Z_{n + 1} + X_{n}]}{2} - r a n d \times Δ X)

(26)

Z_{n + 1} = X_{n} - r a n d n \times \frac{2 Δ X \times X_{n}}{X_{worst} - X_{best} + ε} + D M

(27)

D M = r a n d \times ρ_{2} \times (X_{best} - X_{n}^{i t})

(28)

where

X_{worst}

represents the worst vector during the iterations.

D M

is the direction of movement, guiding the individual vector towards a more optimal solution. The update method for parameter

ρ_{2}

is the same as

ρ_{1}

According to GSM, the IGBO generates two solutions with different capabilities using Equation (29) and Equation (30) respectively.

X 1_{n}^{i t} = X_{n}^{i t} - r a n d n \times ρ_{1} \times \frac{2 Δ X \times X_{n}^{i t}}{y p_{n} - y q_{n} + ε} + r a n d \times ρ_{2} \times (X_{best} - X_{n}^{i t})

(29)

X 2_{n}^{i t} = X_{best} - r a n d n \times ρ_{1} \times \frac{2 Δ X \times X_{n}^{i t}}{y p_{n} - y q_{n} + ε} + r a n d \times ρ_{2} \times (X_{r 1}^{i t} - X_{r 2}^{i t})

(30)

where Equation (29) is beneficial for global search and Equation (30) is beneficial for local exploitation. Therefore, based on the solutions

X 1_{n}^{i t}

and

X 2_{n}^{i t}

, the IGBO generates the next solution (

X_{n}^{i t + 1}

) is defined as

X_{n, j}^{i t + 1} = \{\begin{matrix} \{\begin{matrix} X 1_{n, j}^{i t} i f r a n d_{2} < 0.5 \\ X 2_{n, j}^{i t} i f r a n d_{2} \geq 0.5 \end{matrix} i f r a n d_{1} < P_{c r} \\ X_{n, j}^{i t} i f r a n d_{1} \geq P_{c r} \end{matrix} j = 1 t o D

(31)

where

r a n d_{1}

and

r a n d_{2}

are two different random numbers,

P_{c r}

is the crossover probability, and its update method is the same as

ρ_{1}

4.3. ILEO

The ILEO is used in IGBO to avoid algorithms falling into local optimality. The generation method of ILEO vector solution can be expressed as

X_{ILEO}^{i t + 1} = \{\begin{matrix} X_{n}^{i t + 1} + ρ_{1} (X_{best 2} + X_{k}^{i t}) + ρ_{2} (X_{r 1}^{i t} - X_{r 2}^{i t}) i f r a n d < \frac{(1 - i t) / I t_{m a x}}{2} \\ X_{best} + ρ_{1} (X_{best 2} + X_{k}^{i t}) + ρ_{2} (X_{r 1}^{i t} - X_{r 2}^{i t}) e l s e \end{matrix}

(32)

where

X_{best 2}

is the second best solution.

X_{k}^{i t}

represents a solution that is randomly selected from 1 to N. Therefore, the next generation solutions generated by the IGBO can be represented as

X_{n}^{i t + 1} = \{\begin{matrix} X_{I L E O}^{i t + 1} i f r a n d < L C \\ X_{n}^{i t + 1} e l s e \end{matrix}

(33)

where the term

L C

denotes a chaotic logistic map, and its update method is

L C = 4 L C (1 - L C)

, and the initial LC is 0.67. The IGBO optimizes the parameters of two FOPID controllers in the following parameter space.

\{\begin{matrix} K_{P i}^{L o w} \leq K_{P i} \leq K_{P i}^{U p} \\ K_{I i}^{L o w} \leq K_{I i} \leq K_{I i}^{U p} \\ K_{D i}^{L o w} \leq K_{D i} \leq K_{D i}^{U p} \\ λ_{i}^{L o w} \leq λ_{i} \leq λ_{i}^{U p} \\ μ_{i}^{L o w} \leq μ_{i} \leq μ_{i}^{U p} \end{matrix}

(34)

where

i = 1, 2

indicates area 1 and area 2, respectively. The parameter tuning process based on IGBO is depicted in Figure 4.

5. Validation and comparison

In this section, a two-area IPS LFC model is constructed according to Figure 2, and the system parameter settings are depicted in Appendix A. The proposed LFC scheme is initially tested using step load disturbance scenarios. Subsequently, its performance is validated under scenarios involving random fluctuations of photovoltaic and wind power. Furthermore, the robustness of the IPS is evaluated by varying the inertia constant. To test the effectiveness of the offered LFC scheme (IGBO-FOPID) in this study, its control performance is compared with existing LFC methods, including the FOPID controller regulated through WOA (WOA-FOPID), MDWA (MDWA-FOPID), PSO (PSO-FOPID), and GBO tuned PID/FOPID controllers (GBO-PID/FOPID). The maximum number of iterations,

I t_{\max}

, for each control scheme algorithm is set to 30, and N is set to 50. Table 1 lists the controller parameters obtained by different LFC schemes.

5.1. Step load disturbance test scenarios

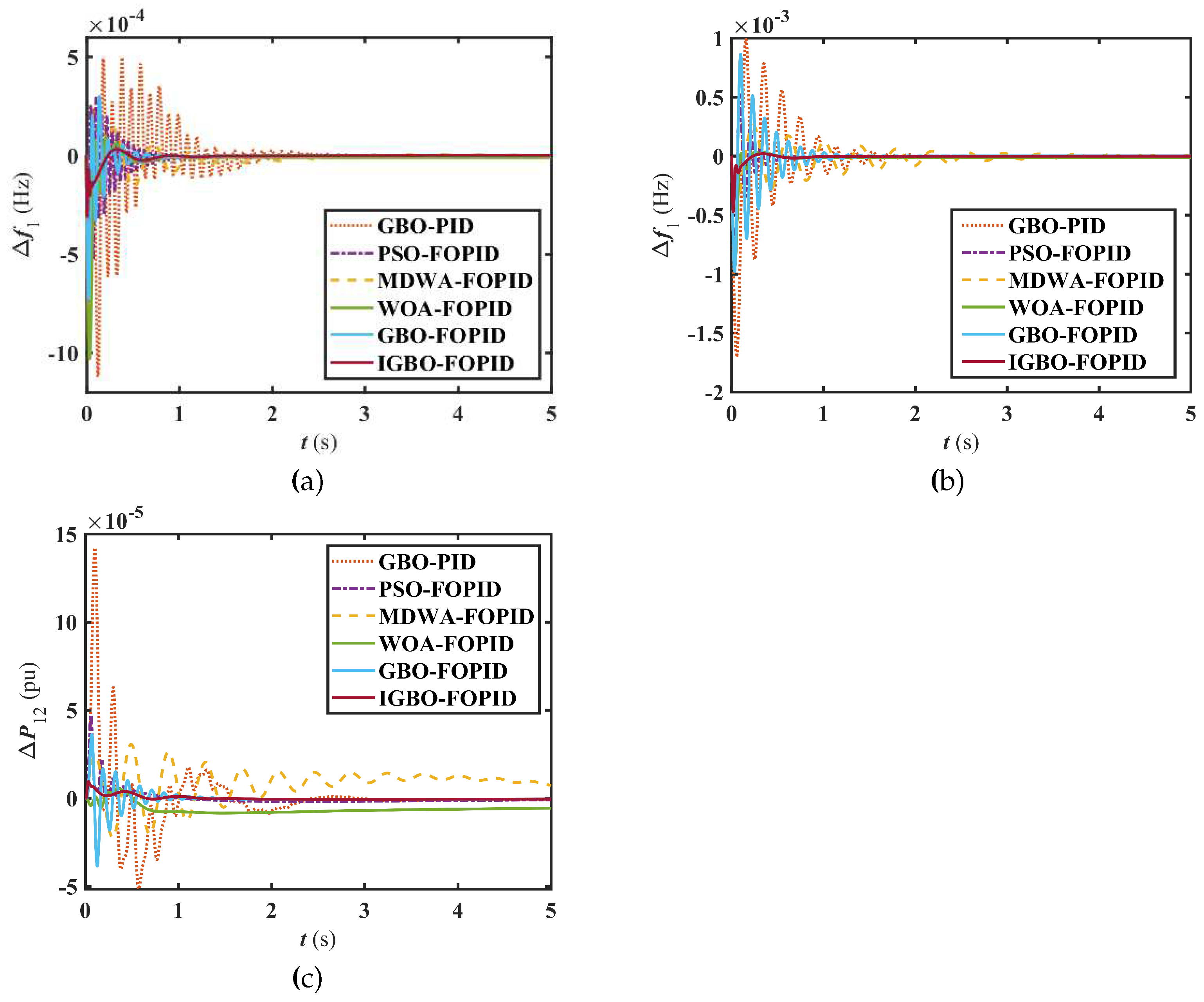
In this scenario, the output of renewable energy units is not considered. At 0s, 0.01 pu step disturbance signals are introduced to area 1 and area 2 at the same time. In simulation, the performances of six different LFC schemes are compared, in which GBO-PID, PSO-FOPID, MDWA-FOPID, WOA-FOPID, GBO-FOPID and IGBO-FOPID based LFC are used. The response of the IPS under step load disturbance with different LFC schemes are depicted in Figure 5.

The results presented in Figure 5 demonstrate the superiority of the FOPID controller-based LFC scheme over the PID controller-based LFC scheme. Implementation of the FOPID controller leads to a considerable enhancement in system frequency modulation performance. Specifically, the FOPID controller-based LFC scheme effectively reduces the frequency deviation overshoot and minimizes frequency fluctuation range within the system. Furthermore, the proposed IGBO-optimized FOPID controller outperforms FOPID controllers optimized using PSO, MDWA, WOA, and GBO algorithms. Notably, the IGBO-FOPID controller-based LFC scheme yields lower overshoot, as well as shorter settling time to achieve system stability. These outcomes affirm that the IGBO-FOPID controller-based LFC scheme significantly enhances the frequency response capability of the IPS.

To further evaluate the superiority of the proposed LFC scheme, Table 2 lists some key performance indicators of the IPS with different LFC schemes, such as maximum undershoot (US), maximum overshoot (OS), integral squared error (ISE), integral time multiplied squared error (ITSE), integral absolute error (IAE), and ITAE of

Δ f_{1}

Δ f_{2}

Δ P_{tie 12}

The comparison in Table 2 showcases that the IGBO-optimized FOPID controller achieves superior values of maximum US, maximum OS, ISE, ITSE, IAE, and ITAE compared to other LFC schemes. This further illustrate that the offered controller outperforms those based on PSO, MDWA, WOA, and GBO optimized PID/FOPID controllers.

5.2. Photovoltaic and wind power random fluctuation test scenarios

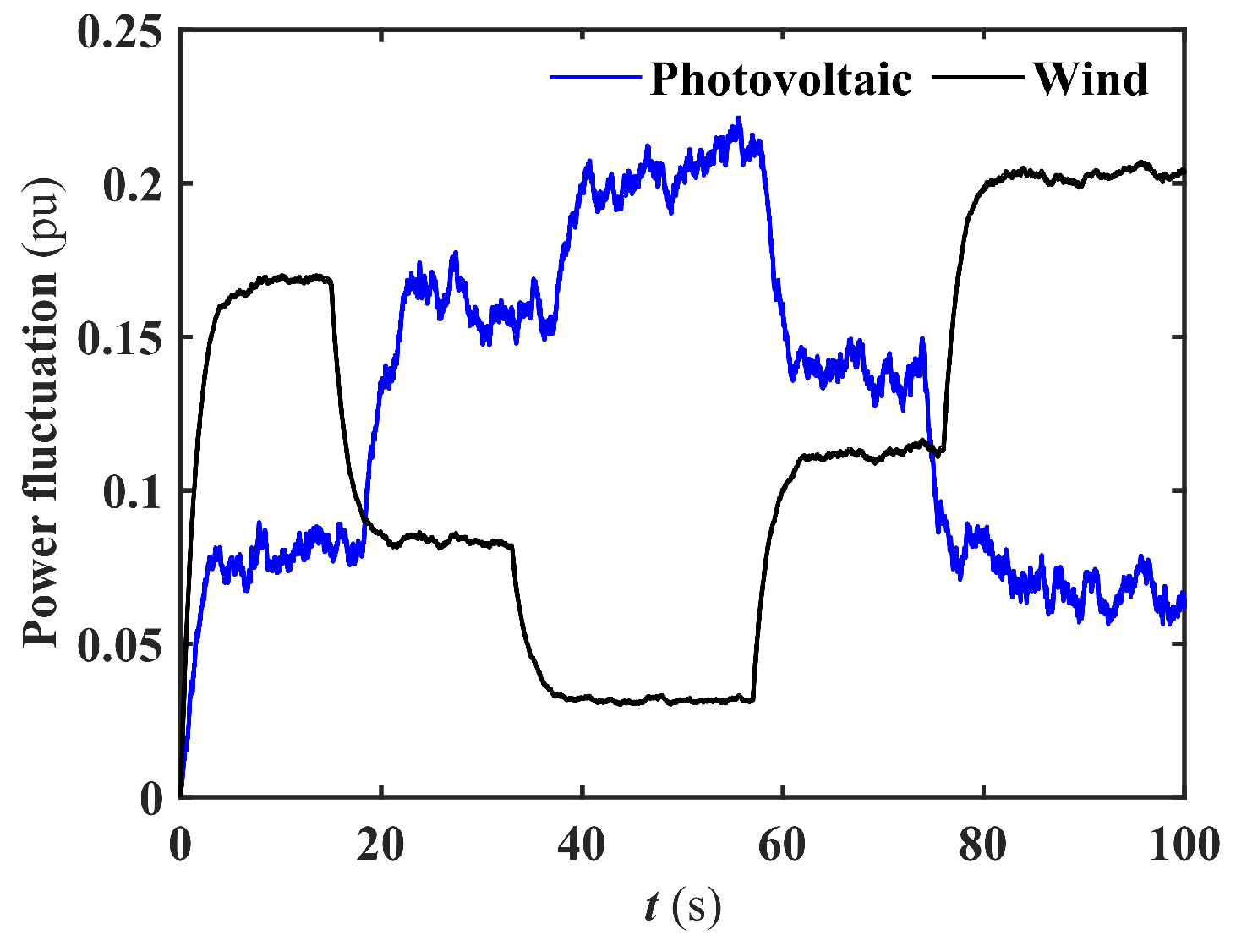
The effectiveness of the IGBO-FOPID based LFC scheme is verified under the scenario of random power output from renewable energy sources. The output fluctuations of photovoltaic power and wind power, as described in literature [21], are utilized in this section. The fluctuations are visualized in Figure 6.

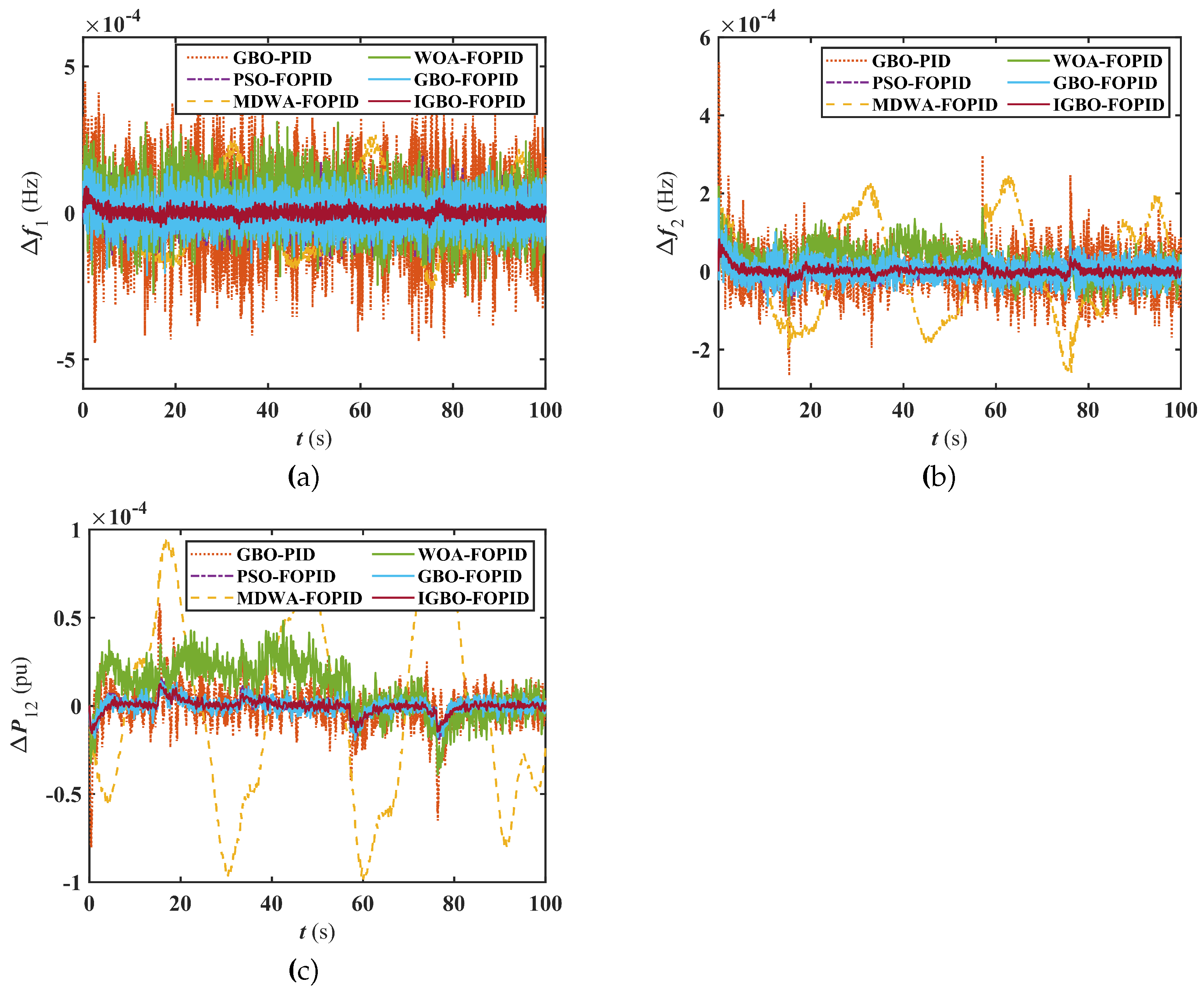
Keep the control parameters in Table 1 unchanged and use different LFC scheme for simulation. The response of IPS under random fluctuations in photovoltaic and wind power using different LFC schemes are shown in Figure 7. The maximum US/maximum OS/ISE/ITSE/IAE/ITAE of

Δ f_{1}

Δ f_{2}

Δ P_{tie 12}

results are displayed in Table 3.

In Figure 7, one can find that the effectiveness of the offered IGBO-FOPID-based LFC scheme in regulating the IPS under scenarios involving random fluctuations in photovoltaic and wind power. Notably, the system incorporating the IGBO-FOPID-based LFC scheme exhibits smaller frequency fluctuations in two areas when compared to other LFC schemes. Additionally, the comparison presented in Table 3 reveals that the IPS performance with the IGBO-FOPID-based LFC scheme outperforms that of other LFC schemes in terms of maximum US, maximum OS, and various performance indicators. These findings highlight the superior anti-jamming capabilities of the proposed LFC scheme compared to other control methods. Thus, the proposed scheme is highly suitable for multi-source IPS applications incorporating renewable energy sources.

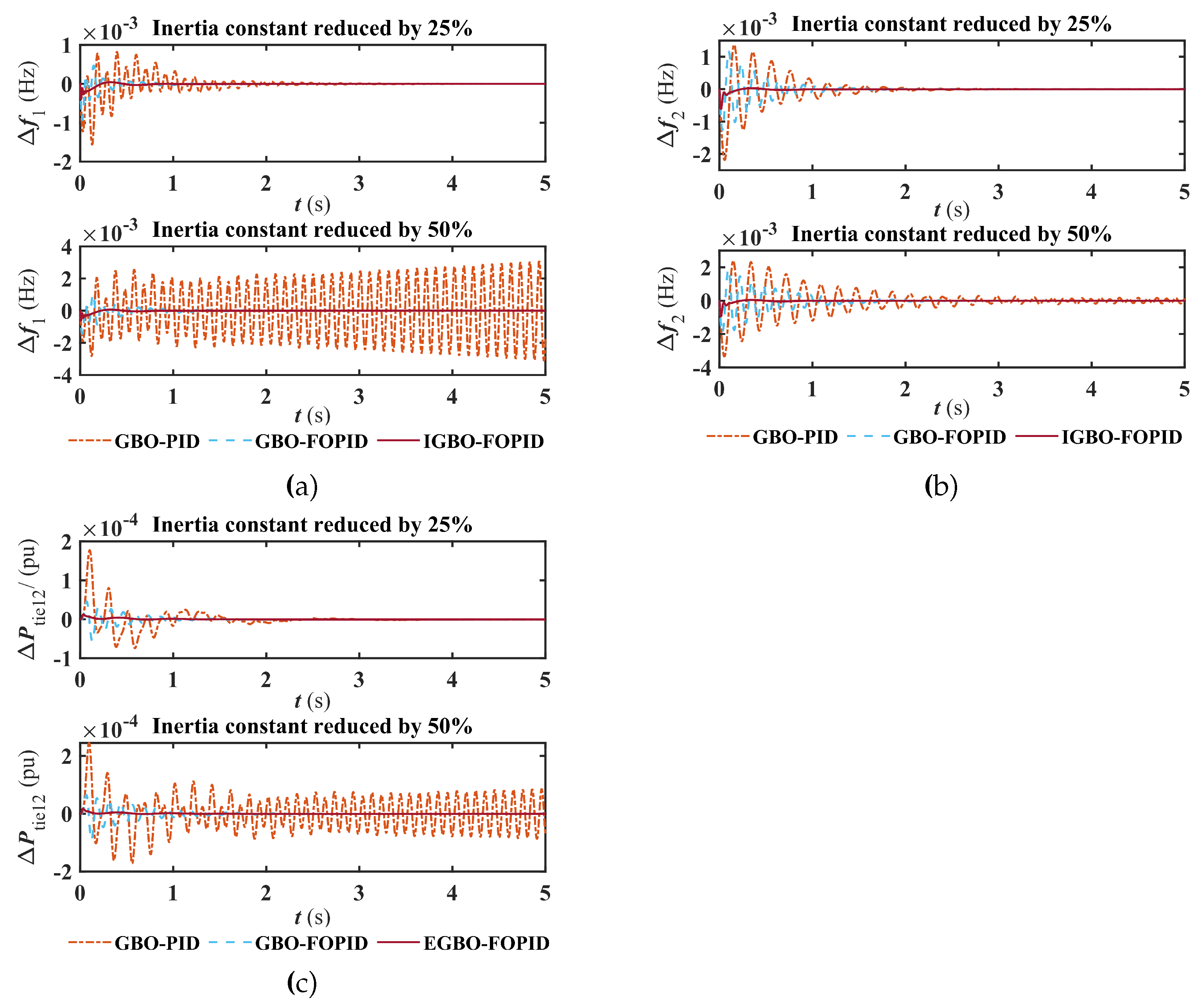
5.3. Robustness analysis

To evaluate the robustness of the IPS with an IGBO optimized FOPID controller, this section tests the dynamic responsiveness of the system when the system’s own inertia constant is reduced by 25% and 50%. System parameters are shown in the Appendix B. Leave the controller parameters in Table 1 remained unchanged, GBO-PID, GBO-FOPID and IGBO-FOPID based LFC schemes were tested, with the results presented in Figure 8.

In Figure 8, one can find that when the inertia constant of the IPS changes, the IPS with the proposed LFC scheme has the best frequency stability compared with those with the traditional GBO-PID based LFC scheme and the GBO-FOPID based LFC scheme, which further confirms that by using the proposed control scheme, the robustness and rapidness of the IPS can be improved.

6. Conclusion

This paper presents an LFC scheme based on optimal parameter optimization and tuning of FOPID controllers to address frequency fluctuation issues in an IPS involving renewable energy generation units. The introduction of FOPID controller increases the adjustable dimension of the system’s load frequency controlloer parameters, allowing for greater flexibility. By utilizing an IGBO algorithm to tune the FOPID controller parameters, lower system frequency deviation performance indicators can be obtained. The proposed LFC scheme can effectively mitigate system frequency fluctuations, reduce the frequency fluctuation range, and exhibit excellent robustness.

Author Contributions

Data curation, writing—original draft preparation, validation, P.W.; conceptualization, writing—review and editing, X. C.; formal analysis, Y. Z.; supervision, L. Z.; project administration, Y. H. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by by Hubei Provincial Natural Science Foundation, China, grant number 2020CFB248.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A. Data of the two-area IPS.

Thermal power plant:

T_{G}

=0.08(s),

T_{T}

=0.3(s),

R_{T}

=2(Hz/pu),

T_{r}

=10(s),

K_{r}

=0.5.

Photovoltaic power generator:

K_{PV}

=1(Hz/pu),

T_{PV}

=1.8(s).

Hydro power generator:

T_{R}

=5(s),

T_{RH}

=0.513(s),

T_{GH}

=48.7(s),

T_{W}

=0.5(s),

R_{H}

=2.4(Hz/pu).

Wind power generator:

K_{WTG}

=1(Hz/pu),

T_{WTG}

=1.5(s).

T_{pw 2}

=0.041(s),

T_{pw 1}

=6(s),

K_{pw 1}

=1(Hz/pu),

K_{pw 2}

=1.75(Hz/pu),

R_{W}

=2(Hz/pu).

Gas power generator:

c_{g}

=1(s),

b_{g}

=0.049(s),

X_{c}

=0.6(s),

Y_{c}

=1.1(s),

R_{G}

=2.4(Hz/pu),

T_{cr}

=0.01(s),

T_{f}

=0.239(s),

T_{cd}

=0.2(s).

Hydrogen storage unit:

K_{HAE}

=0.002(Hz/pu),

T_{HAE}

=0.5(s),

K_{FC}

=0.01(Hz/pu),

T_{FC}

=4(s).

IPS: B=0.425(pu/Hz),

T_{12}

=0.087(pu/rad),

T_{PS}

=20(s),

K_{PS}

=100(Hz/pu).

Appendix B. Data of the two-area IPS when the inertia changes.

Inertia reduced by 25%: B=0.319(pu/Hz),

T_{PS}

=16(s),

R_{W}

=2.5(Hz/pu),

R_{T}

=2.5(Hz/pu),

R_{N}

=2.5(Hz/pu),

R_{G}

=2.5(Hz/pu),

R_{H}

=3(Hz/pu).

Inertia reduced by 50%: B=0.213(pu/Hz),

T_{PS}

=10(s),

R_{W}

=3(Hz/pu),

R_{T}

=3(Hz/pu),

R_{N}

=3(Hz/pu),

R_{G}

=3(Hz/pu),

R_{H}

=3.6(Hz/pu).

References

Dar, A.A.; Hameed, J. Huo, C. Sarfraz, M.; Albasher, G.; Wang, C.Y.; Nawaz, A. Recent optimization and panelizing measures for green energy projects; insights into CO₂ emission influencing to circular economy. Fuel: A journal of fuel science 2022, 314. [Google Scholar] [CrossRef]
Kim, Y.S.; Kim, E. S; Moon, S.I. Frequency and Voltage Control Strategy of Standalone Microgrids With High Penetration of Intermittent Renewable Generation Systems. IEEE Transactions on Power Systems 2015, 31, 718–728. [Google Scholar] [CrossRef]
Ye, Y.D.; Qiao, Y.; Lu, Z.X. Revolution of frequency regulation in the converter-dominated power system. Renewable & Sustainable Energy Reviews 2019, 111, 145–156. [Google Scholar]
Ersdal, A.M.; Imsland, L.; Uhlen, K. Model Predictive Load-Frequency Control. IEEE Transactions on Power Systems 2016, 31, 777–785. [Google Scholar] [CrossRef]
Yang, F.; Shao, X.; Muyeen, S.M.; Li, D.D.; Lin, S.F.; Fang, C. Disturbance Observer Based Fractional-Order Integral Sliding Mode Frequency Control Strategy for Interconnected Power System. Transactions on Power Systems 2021, 36, 5922–5932. [Google Scholar] [CrossRef]
Xi, L.; Yu, L.; Xu, Y.C.; Wang, S.X.; Chen, X. A Novel Multi-Agent DDQN-AD Method-Based Distributed Strategy for Automatic Generation Control of Integrated Energy Systems. IEEE Transactions on Sustainable Energy 2020, 11, 2417–2426. [Google Scholar] [CrossRef]
Liu, F.; Li, Y.; Cao, Y.J.; She, J.H.; Wu, M. A Two-Layer Active Disturbance Rejection Controller Design for Load Frequency Control of Interconnected Power System. IEEE Transactions on Power Systems 2016, 31, 3320–3321. [Google Scholar] [CrossRef]
Shangguan, X.C.; He, Y.; Zhang, C.K.; Jiang, L.; Wu, M. Adjustable Event-Triggered Load Frequency Control of Power Systems Using Control-Performance-Standard-Based Fuzzy Logic. IEEE Transactions on Fuzzy Systems 2022, 30, 3297–3311. [Google Scholar] [CrossRef]
Zuo, J.; Xie, P.P.; Li, Y.H.; Duan, X.Z. Intelligent Optimization Algorithm Based Load Frequency Controller Design and Its Control Performance Assessment in Interconnected Power Grids. Transactions Of China Electrotechnical Society 2018, 33, 478–489. [Google Scholar] [CrossRef]
Chen, Z.H.; Yuan, Y.B.; Yuan, X.H.; Huang, Y.H.; Li, X.S.; Li, W.W. Application of multi-objective controller to optimal tuning of PID gains for a hydraulic turbine regulating system using adaptive grid particle swam optimization. ISA Transactions 2015, 56, 173–187. [Google Scholar] [CrossRef]
Kumar, R.; Sharma, V.K. Whale Optimization Controller for Load Frequency Control of a Two-Area Multi-source Deregulated Power System. International Journal of Fuzzy Systems 2019, 22, 122–137. [Google Scholar] [CrossRef]
Fathy, A.; Kassem, A.M.; Abdelaziz, A.Y. Optimal design of fuzzy PID controller for deregulated LFC of multi-area power system via mine blast algorithm. Neural Computing & Applications 2020, 32, 4531–4551. [Google Scholar] [CrossRef]
Debnath, M.K.; Agrawal, R.; Tripathy, S.R.; Choudhury, S. Artificial neural network tuned PID controller for LFC investigation including distributed generation. International Journal of Numerical Modelling-Electronic Networks Devices and Fields 2020, 33. [Google Scholar] [CrossRef]
Guha, D.; Roy, P.K.; Banerjee, S. Load frequency control of interconnected power system using grey wolf optimization. Swarm and Evolutionary Computation 2016, 27, 97–115. [Google Scholar] [CrossRef]
Shah, P.; Agashe, S. Review of fractional PID controller. Mechatronics 2016, 38, 29–41. [Google Scholar] [CrossRef]
Monje, C.A.; Vinagre, B.M.; Feliu, V.; Chen, Y.Q. Tuning and auto-tuning of fractional order controllers for industry applications. Control Engineering Practice 2008, 16, 798–812. [Google Scholar] [CrossRef]
Sondhi, S.; Hote, Y.V. Fractional order PID controller for load frequency control. Energy Conversion and Management 2014, 85, 343–353. [Google Scholar] [CrossRef]
Zamani, A.; Barakati, S.M.; Yousofi-Darmian, S. Design of a fractional order PID controller using GBMO algorithm for load-frequency control with governor saturation consideration. ISA Trans 2016, 64, 56–66. [Google Scholar] [CrossRef]
Daraz, A.; Malik, S.A.; Basit, A.; Aslam, S.; Zhang, G.Q. Modified FOPID Controller for Frequency Regulation of a Hybrid Interconnected System of Conventional and Renewable Energy Sources. Fractal Fract 2023, 7. [Google Scholar] [CrossRef]
Fathy, A.; Alharbi, A.G. Recent Approach Based Movable Damped Wave Algorithm for Designing Fractional-Order PID Load Frequency Control Installed in Multi-Interconnected Plants With Renewable Energy. IEEE Access 2021, 9, 71072–71089. [Google Scholar] [CrossRef]
Pan, I.; Das, S. Fractional Order AGC for Distributed Energy Resources Using Robust Optimization. IEEE Transactions on Smart Grid 2016, 7, 2175–2186. [Google Scholar] [CrossRef]
Ahmed, N.M.; Ebeed, M.; Magdy, G.; Sayed, K.; Gamoura, S.C.; Metwally, A.S.M.; Mahmoud, A.A. A New Optimized FOPIDA-FOIDN Controller for the Frequency Regulation of Hybrid Multi-Area Interconnected Microgrids. Fractal Fract 2023, 7. [Google Scholar] [CrossRef]
Joshi, A.; Suresh, A.; Kamalasadan, S. Grid Frequency Regulation Based on Point of Common Coupling Angle Deviation Control of Distributed Energy Resources With Fully Active Hybrid Energy Storage System. IEEE Transactions on Industry Applications 2021, 57, 4473–4458. [Google Scholar] [CrossRef]
Fang, J.C.; Wang, Y.F.; Lei, Z.; Xu, Q.S. Control Strategy and Performance Analysis of Electrochemical Energy Storage Station Participating in Power System Frequency Regulation: A Case Study of the Jiangsu Power Grid. Sustainability 2022, 14. [Google Scholar] [CrossRef]
Calero, F.; Cañizares, C.A.; Bhattacharya, K. A Review of Modeling and Applications of Energy Storage Systems in Power Grids. Proceedings of the IEEE 2023, 111, 806–831. [Google Scholar] [CrossRef]
Dong, W.J.; Shao, C.C.; Feng, C.J.; Zhou, Q.; Bie, Z.H.; Wang, X.F. Cooperative Operation of Power and Hydrogen Energy Systems With HFCV Demand Response. IEEE Transactions on Industry Applications 2022, 58, 2630–2639. [Google Scholar] [CrossRef]
Tan, K.M.; Babu, T.S.; Ramachandaramurthy, V.K.; Kasinathan, P.; Solanki, S.G.; Raveendran, S.K. Empowering Smart Grid: A Comprehensive Review of Energy Storage Technology and Application With Renewable Energy Integration. Journal of Energy Storage 2021, 39. [Google Scholar] [CrossRef]
Arya, Y. Impact of Hydrogen Aqua Electrolyzer-Fuel Cell Units on Automatic Generation Control of Power Systems With a New Optimal Fuzzy TIDF-II Controller. Renewable Energy 2019, 139, 468–482. [Google Scholar] [CrossRef]
Yildiz, S.; Gunduz, H.; Yildirim, B.; Özdemir, M.T. An Islanded Microgrid Energy System With an Innovative Frequency Controller Integrating Hydrogen-Fuel Cell. Fuel 2022, 326. [Google Scholar] [CrossRef]
Ahmadianfar, I.; Bozorg-Haddad, O.; Chu, X. Gradient-Based Optimizer: A New Metaheuristic Optimization Algorithm. Information Sciences 2020, 540, 131–159. [Google Scholar] [CrossRef]
Daoud, M.S.; Shehab, M.; Al-Mimi, H.M.; Abualigah, L.; Zitar, R.A.; Shambour, M.K.Y. Gradient-Based Optimizer (GBO): A Review, Theory, Variants, and Applications. Archives of Computational Methods in Engineering 2023. [Google Scholar] [CrossRef]
Arya, Y.; Dahiya, P.; Çelik, E.; Sharma, G.; Gözde, H.; Nasiruddin, I. AGC performance amelioration in multi-area interconnected thermal and thermal-hydro-gas power systems using a novel controller. Engineering Science and Technology, an International Journal 2021, 24, 384–396. [Google Scholar] [CrossRef]
Xiang, L.J.; Chen, H.; Guo, X.H.; Yang, Y.F. Secondary Frequency Control of Multi-Energy Microgrid With Electric Vehicles Based on Fuzzy Fractional-Order PID. Electric Power Automation Equipment 2021, 41, 74–80. [Google Scholar] [CrossRef]
Ahmadianfar, I.; Gong, W.Y.; Heidari, A.A.; Golilarz, N.A.; Samadi-Koucheksaraee, A.; Chen, H.L. Gradient-based optimization with ranking mechanisms for parameter identification of photovoltaic systems. Energy Reports 2021, 7, 3979–3997. [Google Scholar] [CrossRef]

Figure 1. Structure of a two-area IPS.

Figure 2. LFC model of a two-area IPS.

Figure 3. Comparison of ideal fractional-order operators and approximate fractional-order operators: (a) Derivative of order 1.2. (b) Integral of order 0.7.

Figure 4. Parameter tuning process based on IGBO algorithm.

Figure 5. Response curves of the IPS under step load disturbance scenarios: (a) frequency deviation in area 1, (b) frequency deviation in area 2, (c) tie line power.

Figure 6. Photovoltaic and wind power fluctuation curves.

Figure 7. Response curves of the IPS under photovoltaic and wind power random fluctuation scenarios: (a) frequency deviation in area 1, (b) frequency deviation in area 2, (c) tie line power.

Figure 8. Response curves of the IPS for different inertia constants: (a) frequency deviation in area 1, (b) frequency deviation in area 2, (c) tie line power.

Table 1. Parameters of two FOPID controllers obtained by different LFC schemes.

LFC scheme	$K_{P 1}$	$K_{I 1}$	$K_{D 1}$	$λ_{1}$	$μ_{1}$	$K_{P 2}$	$K_{I 2}$	$K_{D 2}$	$λ_{2}$	$μ_{2}$
GBO-PID	68.22	385.33	25.42	-	-	61.77	430.56	16.58	-	-
WOA-FOPID	54.38	308.42	10.66	0.41	1.19	305.22	525.31	12.62	1.17	1.32
MDWA-FOPID	516.76	327.85	4.89	2	1.81	622.30	25.11	3.43	2	1.89
PSO-FOPID	583.84	513.51	31.38	0.97	1.19	461.51	512.46	22.13	1.15	1.21
GBO-FOPID	385.42	519.77	15.98	1.09	1.23	695.18	683.66	16.16	1.12	1.24
IGBO-FOPID	545.39	642.31	11.48	1.02	1.62	697.38	698.66	22.18	1.04	1.47

Table 2. Maximum US/Maximum OS/ ISE/ITSE/IAE/ITAE of system response under step load disturbance scenarios.

LFC scheme	Maximum US			Maximum OS			ISE	ITSE	IAE	ITAE
LFC scheme	$Δ f_{1}$	$Δ f_{2}$	$Δ P_{tie 12}$	$Δ f_{1}$	$Δ f_{2}$	$Δ P_{tie 12}$	ISE	ITSE	IAE	ITAE
GBO-PID	-1.10e-3	-1.70e-3	-5.15e-5	4.97e-4	9.94e-4	1.42e-4	4.86e-7	1.10e-7	8.54e-4	4.27e-4
WOA-FOPID	-1e-2	-9.55e-4	-8.37e-6	9.34e-5	3.45e-5	5.91e-6	7.79e-8	7.75e-9	2.82e-4	4.12e-4
MDWA-FOPID	-3.71e-4	-4.86e-4	-2.22e-5	1.34e-4	2.64e-4	3.07e-5	4.80e-8	2.08e-8	4.02e-4	4.47e-4
PSO-FOPID	-5.62e-4	-9.19e-4	-1.89e-5	2.95e-4	5.23e-4	4.74e-5	6.86e-8	7.33e-9	2.31e-4	8.28e-5
GBO-FOPID	-7.24e-4	-9.76e-4	-3.85e-5	2.98e-4	8.64e-4	3.60e-5	1.20e-7	1.66e-8	3.05e-4	9.93e-5
IGBO-FOPID	-3.09e-4	-4.72e-4	-6.21e-7	3.21e-5	2.06e-5	9.51e-6	9.79e-9	6.87e-10	8.76e-5	4.89e-5

Table 3. Maximum US/Maximum OS/ ISE/ITSE/IAE/ITAE of system response under photovoltaic and wind power random fluctuation scenarios.

LFC scheme	Maximum US			Maximum OS			ISE	ITSE	IAE	ITAE
LFC scheme	$Δ f_{1}$	$Δ f_{2}$	$Δ P_{tie 12}$	$Δ f_{1}$	$Δ f_{2}$	$Δ P_{tie 12}$	ISE	ITSE	IAE	ITAE
GBO-PID	-4.45e-4	-2.67e-4	-8.04e-5	4.49e-4	5.36e-4	5.84e-5	2.14e-6	9.95e-5	1.58e-2	0.77
PSO-FOPID	-1.83e-4	-7.30e-5	-2.45e-5	1.96e-4	1.68e-4	1.63e-5	3.90e-7	1.88e-5	6.58e-3	0.32
MDWA-FOPID	-2.61e-4	-2.59e-4	-9.84e-5	2.67e-4	2.49e-4	9.43e-5	3.35e-6	1.68e-4	2.62e-2	1.31
WOA-FOPID	-2.81e-4	-1.12e-4	-3.91e-5	3.11e-4	2.17e-4	4.82e-5	1.45e-6	5.87e-5	1.51e-2	0.69
GBO-FOPID	-2.13e-4	-8.77e-5	-1.94e-5	1.81e-4	1.87e-4	1.39e-5	4.99e-7	2.36e-5	8.12e-3	0.39
IGBO-FOPID	-5.27e-5	-4.07e-5	-1.55e-5	8.96e-5	8.25e-5	1.25e-5	5.25e-8	1.91e-6	2.55e-3	0.11

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Fractional-Order Load Frequency Control of an Interconnected Power System with Hydrogen Energy-Storage Unit

Abstract

1. Introduction

2. LFC model of a two-area IPS

2.1. Mathematical model of thermal power plant

2.2. Mathematical model of hydro power generator

2.3. Mathematical model of solar photovoltaic cell

2.4. Mathematical model of wind power generator

2.5. Mathematical model of gas power generator

2.6. Mathematical model of hydrogen storage unit

3. Design of FOPID controller based LFC

4. Parameter tuning process based on IGBO

4.1. Initialization

4.2. Parameter update method based on GSM

4.3. ILEO

5. Validation and comparison

5.1. Step load disturbance test scenarios

5.2. Photovoltaic and wind power random fluctuation test scenarios

5.3. Robustness analysis

6. Conclusion

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

Appendix A. Data of the two-area IPS.

Appendix B. Data of the two-area IPS when the inertia changes.

References

MDPI Initiatives

Important Links

Subscribe