Prerpints.org logo
Preprint
Article

Transient Response of an Infinite Isotropic Magneto-Electro-Elastic Material with Multiple Axisymmetric Planar Cracks

Altmetrics

Downloads

65

Views

28

Comments

0

Submitted:

26 January 2024

Posted:

29 January 2024

You are already at the latest version

Alerts
Abstract
Dynamic behavior of coaxial axisymmetric planar cracks in the transversely isotropic magneto-electro-elastic (MEE) material in transient in-plane magneto-electro-mechanical loading is studied. Magneto-electrically impermeable as well as permeable cracks are assumed for crack surface. In the first step, considering prismatic and radial dynamic dislocations, electric and magnetic jumps are obtained through Laplace and Hankel transforms. These solutions are utilized to derive singular integral equations in the Laplace domain for the axisymmetric penny-shaped and annular cracks. Derived Cauchy singular type integral equations are solved to obtain the density of dislocation on the crack surfaces. Dislocation densities are utilized in computation of the dynamic stress intensity factors, electric displacement and magnetic induction in the vicinity tips of crack tips. Finally, some numerical case studies of a single and multiple cracks are presented. The effect of system parameters on the results is then discussed.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

A magneto-electro-elastic medium generally consists of a combination of piezoelectric and piezomagnetic components. These components can be reinforced with layers or fibers. Such structures have the ability to convert electrical energy, magnetism and elasticity into each other. This is a unique property that is not present in a simple piezoelectric material. In special cases, the magnetic-electrical effect of MEE is far greater than that of single-phase magnetic-electric material, even with a significant magneto-electro coefficient [1]. Because of these unique properties, MEEmaterials have a wide range of applications in intelligent structures such as magnetic field probes, medical imaging systems, transducers, sensors and actuators. [2,3,4,5]. Recently, many studies have been conducted by researchers to investigate the cracks in MEE structures. However, most of these studies have been mainly concerned with static loading [6,7,8,9,10,11,12,13]. MEE materials experience dynamic loads in their functional cycle. Therefore, the analysis of the failure mechanism due to crack growth in such structures is one of the important design considerations and many researchers have focused on this issue. In the following, the studies conducted in this regard will be reviewed. Li presented the dynamic analysis of a crack in an MEE medium subjected to mechanical, electrical and magnetic impulse [14]. Hu and Li presented an analytical approach to study the effect of a moving crack with permeable crack-face in an infinite MEE solid excited by shear loading [15]. Zhou et al. [16] addressed the dynamic behavior of collinear cracks between two dissimilar MEE material half planes under the harmonic anti-plane shear waves loading. Zhang et al. [17] studied the dynamic behavior of two collinear interface cracks between two dissimilar functionally graded MEE material layers. Su et al. [18] investigated the transient analysis of interface cracks between different MEE strips in the case of out-of-plane mechanical loading as well as magnetoelectrical impacts. Feng and Pan studied the dynamic fracture of anti-plane interfacial cracks under the influence of simultaneous mechanical and magnetoelectrical loadings in different boundary conditions [19]. Liang examined the dynamic behavior of parallel symmetric cracks in a functionally graded MEE material excited by harmonic shear waves [20]. Sladek et al. utilized Galerkin’ method to study cracks under transient loading in 2D and 3D axisymmetric piezoelectric/piezomagnetic medium [21]. Feng et al. [22] studied the dynamic response of surface cracks between two different MEE materials under simultaneous excitation of magnetic, electrical and mechanical shock. Zhong and Zhang [23] and Zhong et al. [24] investigated the dynamic analysis of an MEE material with a penny-shaped crack subjected to magneto-electro-mechanical impact loading. For the problems of a cracked MEE body under in-plane impacts, Feng et al. [25] studied the dynamic behavior of an MEE penny-shaped cracked layer. Zhong et al. [26] investigated the response of a MEE solid assumed to have a Griffith crack. Wang et al. [27] examined the effect of electric and magnetic boundary conditions of crack-face on the dynamic response of an MEE structure. Li and Lee [28] attempted to address the issue of collinear dissimilar cracks in MEE materials in mode I loadings through simulating dislocations. Wunsche et al. [29] performed boundary element analysis to obtain dynamic response of linear an-isotropic MEE materials. Athanasius and Ang presented a semi-analytic approach using Laplace transform to obtain the dynamic response of a full space MEE with arbitrary number of arbitrarily oriented planar cracks [30]. Li et al. [31] studied the dynamic response of a ring-shaped interface crack between distinct magnetoelectroelastic materials. A ring-shaped crack between magnetoelectroelastic thin film and elastic substrate layers under mechanical, electrical and magnetic stress was reported by Li et al. [32]. Lei et al. [33] analyzed the transient response of an interface crack in MEE bi-materials subjected to magneto-electromechanical loads. The mode III fracture problem of a weakened MEE medium by an alternating array of cracks and rigid inclusions subjected to coupling of anti-plane mechanical and in-plane electrical and magnetic stress was studied by Xiao et al. [34]. As far as the authors’ knowledge, there is no promising research on the transient response of multiple axisymmetric planar cracks in the transversely isotropic MEE material under in-plane magneto-electromechanical load. Among the techniques for solving such problems, the dislocation method [35] is a useful tool for the analysis of multiple cracks. Therefore, this paper aims to specify the generalized dynamic intensity factors for multiple axisymmetric planar cracks in a transversely isotropic MEE medium. Laplace and Hankel transformations are utilized to simplify the problems to Cauchy-type singular integral equations. Then, a numerical Laplace transformation inversion method, presented by Stehfest [36], utilized to formulate the generalized dynamic intensity factors of crack tips. The dislocation densities are determined to construct the multiple axisymmetric planar cracks in the transversely isotropic MEE medium. The influences of the time variation, the applied magnetoelectric impact loadings, boundary conditions of the crack surface and crack type as well as interactions between cracks on the dynamic characteristics of the crack are presented.

2. Derivation of Governing Equations

The problem under study is an infinite transversely isotropic MEE medium with generalized dynamic dislocations. For a transversely isotropic MEE medium with the plane of isotropy perpendicular to the z-axis, the electrical and magnetic poling are assumed parallel to z axis. Assuming planar deformation, the linear constitutive equations for axisymmetric medium, can be stated as follow, ( u θ = 0 )
σ r r r , z , t σ θ θ r , z , t σ z z r , z , t D z r , z , t B z r , z , t = c 11 c 12 c 13 e 31 α 31 c 12 c 11 c 13 e 31 α 31 c 13 c 13 c 33 e 33 α 33 e 31 e 31 e 33 − d 33 − β 33 α 31 α 31 α 33 − β 33 − γ 33 u r , r r , z , t u r r , z , t / r u z , z r , z , t ψ , z r , z , t ϕ , z r , z , t σ r z r , z , t D r r , z , t B r r , z , t = c 44 c 44 e 15 α 15 e 15 e 15 − d 11 − β 11 α 15 α 15 − β 11 − γ 11 u r , z r , z , t u z , r r , z , t ψ , r r , z , t ϕ , r r , z , t ,
The comma states partial differentiation with respect to the suffix space variable and σ i j , D i and B i are stress components, electric displacements and magnetic inductions, respectively; while e i j , α i j and β i j are the piezoelectric, piezomagnetic, and magnetoelectric coupling constants; c i j , d i j and γ i j are elastic stiffnesses, dielectric permittivities, and the magnetic permeabilities, respectively; u r and u z are the radial and axial displacement components; ψ and ϕ are electric and magnetic potential, respectively. The equilibrium equations of transversely isotropic MEE media, considering zero body force, free electric charge and current, are given by
σ r r , r + σ r z , z + ( σ r r − σ θ θ ) / r = ρ u r , t t σ r z , r + σ z z , z + σ r z / r = ρ u z , t t D r , r + D z , z + D r / r = 0 B r , r + B z , z + B r / r = 0
where ρ is the mass density. Electric potential, magnetic potential and elastic displacements, satisfy the basic equations as follows:
c 11 L 1 + c 44 D 2 u r + c 13 + c 44 D u z , r + e 31 + e 15 D ψ , r + α 31 + α 15 D ϕ , r = ρ F 2 u r c 44 L 0 + c 33 D 2 u z + c 13 + c 44 D r u r , r / r + e 15 L 0 + e 33 D 2 ψ + α 15 L 0 + α 33 D 2 ϕ = ρ F 2 u z e 15 + e 31 D r u r , r / r + c 15 L 0 + e 33 D 2 u z − d 11 L 0 + d 33 D 2 ψ − β 11 L 0 + β 33 D 2 ϕ = 0 α 15 + α 31 D r u r , r / r + α 15 L 0 + α 33 D 2 u z − β 11 L 0 + β 33 D 2 ψ − γ 11 L 0 + γ 33 D 2 ϕ = 0
In which the differential operators are introduced as
L k = ∂ 2 ∂ r 2 + 1 r ∂ ∂ r − k r 2 ,         k = 0,1 D = ∂ ∂ z D 2 = ∂ 2 ∂ z 2 F 2 = ∂ 2 ∂ t 2
Applying the standard Laplace transform and letting
f * r , z , p = ∫ 0 ∞ f r , z , t e − p t d t
Eq. (3) can be converted into
c 11 L 1 + c 44 D 2 − ρ p 2 u r * + c 13 + c 44 D u z , r * + e 31 + e 15 D ψ , r * + α 31 + α 15 D ϕ , r * = 0 c 44 L 0 + c 33 D 2 − ρ p 2 u z * + c 13 + c 44 D r u r * , r / r + e 15 L 0 + e 33 D 2 ψ * + α 15 L 0 + α 33 D 2 ϕ * = 0 e 15 + e 31 D r u r * , r / r + c 15 L 0 + e 33 D 2 u z * − d 11 L 0 + d 33 D 2 ψ * − β 11 L 0 + β 33 D 2 ϕ * = 0 α 15 + α 31 D r u r * , r / r + α 15 L 0 + α 33 D 2 u z * − β 11 L 0 + β 33 D 2 ψ * − γ 11 L 0 + γ 33 D 2 ϕ * = 0
Moreover, the Hankel transformation with respect to r is further used to express the solution of the elastic displacements, the electric potential and the magnetic potential in Eq. (6) as follows
u r * r , z , p = ∑ n = 1 4 ∫ 0 ∞ A n η , p     e − η ϱ n η , p z J 1 η r d η u z * r , z , p = ∑ n = 1 4 ∫ 0 ∞ A n η , p   λ 1 n η , p   e − η ϱ n η , p z J 0 η r d η ψ * r , z , p = ∑ n = 1 4 ∫ 0 ∞ A n η , p   λ 2 n η , p   e − η ϱ n η , p z J 0 η r d η ϕ * r , z , p = ∑ n = 1 4 ∫ 0 ∞ A n η , p   λ 3 n η , p   e − η ϱ n η , p z J 0 η r d η
where λ 1 n η , p , λ 2 n η , p , λ 3 n η , p and ϱ n η , p n = 1,2 , 3,4 are known function of the Laplace variable p , Hankel variable η (see Appendix A), and the parameters A n η , p ( n = 1,2 , 3,4 ) are yet unknown. Applying the Laplace transform to the constitutive Eq. (1), one can extract the components of stresses, electric displacements and magnetic inductions in the Laplace domain from (7). For instance
σ r r * r , z , p = ∑ n = 1 4 ∫ 0 ∞ A n η , p   e − η ϱ n η , p z ϑ 1 n η , p η J 0 r η + 1 r c 12 − c 11 J 1 r η d η σ z z * r , z , p = ∑ n = 1 4 ∫ 0 ∞ ϑ 2 n η , p A n η , p η   e − η ϱ n η , p z J 0 η r d η σ r z * r , z , p = − ∑ n = 1 4 ∫ 0 ∞ ϑ 3 n η , p A n η , p η   e − η ϱ n η , p z J 1 η r d η D z * r , z , p = ∑ n = 1 4 ∫ 0 ∞ ϑ 4 n η , p A n η , p η   e − η ϱ n η , p z J 0 η r d η B z * r , z , p = ∑ n = 1 4 ∫ 0 ∞ ϑ 5 n η , p A n η , p η   e − η ϱ n η , p z J 0 η r d η
where ϑ m n η , p ( m = 1,2 , … , 5   a n d   n = 1,2 , 3,4 ) are shown in “Appendix B”. For the present problem, two types of magnetoelectrical boundary conditions [37] are assumed by extending the concept of the electrically impermeable and permeable cracks embedded in piezoelectric medium [38]. They are electrically and magnetically impermeable and electrically and magnetically permeable, respectively, which; the first case is called type-a and the second case is called type-b solution, respectively. Without loss of generality, the type-a solution is considered. The type-b solution can be obtained by reducing the type-a solution. Let the transversely isotropic MEE medium weakened by a Volterra-type dynamic prismatic ring and Somigliana-type dynamic radial ring dislocations with Burgers vectors b z ( t ) and b r ( t ) , respectively, which are located at r = a and z = 0 , wherein the radial cut of dislocations are circular area. The above dislocations conditions can be expressed as [39]
u z r , 0 + , t − u z r , 0 − , t = b z ( t ) H a − r u r r , 0 + , t − u r r , 0 − , t = b r ( t ) H a − r σ z z r , 0 + , t = σ z z r , 0 − , t σ r z r , 0 + , t = σ r z r , 0 − , t
where H . is the Heaviside step-function. The conditions indicating the dynamic electric and magnetic dislocations can be written as
ψ r , 0 + , t − ψ r , 0 − , t = b ψ ( t ) H a − r ϕ r , 0 + , t − ϕ r , 0 − , t = b ϕ ( t ) H a − r
Although the electric and magnetic potential jumps are not of dislocation type, they are known here as dynamic electric and magnetic dislocations with Berger vectors. b ψ ( t ) and b ϕ ( t ) , respectively. Furthermore, the continuity of electric displacement and magnetic induction in the dislocation line requires that
D z r , 0 + , t = D z r , 0 − , t B z r , 0 + , t = B z r , 0 − , t
For prismatic electric and magnetic dislocations, the problem is symmetric with respect to the z=0 plane, and it is antisymmetric for radial dislocations. Therefore, it is convenient to analyze two problems separately and solve them for a half interval. The region z>0 is considered for the rest of the problem. For the symmetric problem, the boundary conditions reduce to the following
u z r , 0 + , t = b z ( t ) 2 H a − r ψ r , 0 + , t = b ψ ( t ) 2 H a − r ϕ r , 0 + , t = b ϕ ( t ) 2 H a − r σ r z r , 0 + , t = 0
for anti-symmetric case, we have
u r r , 0 + , t = b r ( t ) 2 H a − r σ z z r , 0 + , t = 0 D z r , 0 + , t = 0 B z r , 0 + , t = 0
Zero order and first order Hankel transform of the Heaviside step-function H . can be expressed as
H a − r = ∫ 0 ∞ a J 1 ( a η ) J 0 ( r η ) d η H a − r = ∫ 0 ∞ 1 6 a 3 η 2   1 F 2 ⁡ ( 3 2 ; 2 , 5 2 ; − 1 4 a 2 η 2 ) J 1 ( r η ) d η
In the above relation,   1 F 2 a ; b , c ; x = ∑ n = 0 ∞ ( a ) n n ! ( b ) n ( c ) n x n is the Hypergeometric function and the symbol ( a ) n = Γ n + a Γ a is the Pochhammer symbol inwhich Γ . is the Gamma function. Applying the Laplace transform to boundary conditions (12) and (13) and imposing the resultant to Eqs. (7) and (8) and by using Eq. (14), we have
∑ n = 1 4 λ 1 n η , p A n η , p = a   b z * ( p ) 2 J 1 ( a η ) ∑ n = 1 4 λ 2 n η , p   A n η , p   = a   b ψ * ( p ) 2 J 1 ( a η ) ∑ n = 1 4 λ 3 n   η , p A n η , p   = a   b ϕ * ( p ) 2 J 1 ( a η ) ∑ n = 1 4 ϑ 3 n η , p A n η , p = 0
for symmetric problem and
∑ n = 1 4 A n η , p = a 3 η 2 b r * ( p ) 12   1 F 2 ⁡ ( 3 2 ; 2 , 5 2 ; − 1 4 a 2 η 2 ) ∑ n = 1 4 ϑ 2 n η , p A n η , p = 0 ∑ n = 1 4 ϑ 4 n η , p A n η , p = 0 ∑ n = 1 4 ϑ 5 n η , p A n η , p = 0
for anti-symmetric problem. Solving Eqs. (10) and (16) gives the coefficients A n η , p (See appendix C). By substituting A n η , p into Eq. (8), the outcome becomes
σ r r * r , z , p = a 2 ∑ n = 1 4 ∫ 0 ∞ 1 ∆ η , p ∆ 1 n η , p b z * ( p ) + ∆ 2 n η , p b ψ * ( p ) + ∆ 3 n η , p b ϕ * ( p ) J 1 a η + a 2 b r * ( p ) 6 Λ η , p Λ n η , p η 2   1 F 2 ⁡ 3 2 ; 2 , 5 2 ; − 1 4 a 2 η 2 ϑ 1 n η , p η J 0 r η + 1 r c 12 − c 11 J 1 r η e − η ϱ n η , p z d η , σ z z * r , z , p = a 2 ∑ n = 1 4 ∫ 0 ∞ ϑ 2 n η , p 1 ∆ η , p ∆ 1 n η , p b z * ( p ) + ∆ 2 n η , p b ψ * ( p ) + ∆ 3 n η , p b ϕ * ( p ) J 1 a η + a 2 b r * ( p ) 6 Λ η , p Λ n η , p η 2   1 F 2 ⁡ 3 2 ; 2 , 5 2 ; − 1 4 a 2 η 2 η   J 0 η r e − η ϱ n η , p z d η , σ r z * r , z , p = − a 2 ∑ n = 1 4 ∫ 0 ∞ ϑ 3 n η , p 1 ∆ η , p ∆ 1 n η , p b z * p + ∆ 2 n η , p b ψ * p + ∆ 3 n η , p b ϕ * p J 1 a η + a 2 b r * p 6 Λ η , p Λ n η , p η 2   1 F 2 ⁡ 3 2 ; 2 , 5 2 ; − 1 4 a 2 η 2 η   J 1 η r e − η ϱ n η , p z d η , D z * r , z , p = a 2 ∑ n = 1 4 ∫ 0 ∞ ϑ 4 n η , p 1 ∆ η , p ∆ 1 n η , p b z * ( p ) + ∆ 2 n η , p b ψ * ( p ) + ∆ 3 n η , p b ϕ * ( p ) J 1 a η + a 2 b r * ( p ) 6 Λ η , p Λ n η , p η 2   1 F 2 ⁡ 3 2 ; 2 , 5 2 ; − 1 4 a 2 η 2 η   J 0 η r e − η ϱ n η , p z d η , B z * r , z , p = a 2 ∑ n = 1 4 ∫ 0 ∞ ϑ 5 n η , p 1 ∆ η , p ∆ 1 n η , p b z * ( p ) + ∆ 2 n η , p b ψ * ( p ) + ∆ 3 n η , p b ϕ * ( p )   J 1 a η + a 2 b r * ( p ) 6 Λ η , p Λ n   η , p η 2   1 F 2 ⁡ 3 2 ; 2 , 5 2 ; − 1 4 a 2 η 2 e − η ϱ n η , p z η   J 0 η r d η .
In order to study the singularity of the stress components, electric displacement and magnetic inductions in the poling direction, σ z z * , σ r z * , D z * and B z * , at the dislocation, z = 0 is set in the related equation in Eq. (17), therefore
σ z z * r , 0 , p = a 2 ∑ n = 1 4 ∫ 0 ∞ ϑ 2 n η , p 1 ∆ η , p ∆ 1 n η , p b z * ( p ) + ∆ 2 n η , p b ψ * ( p ) + ∆ 3 n η , p b ϕ * ( p ) J 1 a η + a 2 b r * ( p ) 6 Λ η , p Λ n η , p η 2   1 F 2 ⁡ 3 2 ; 2 , 5 2 ; − 1 4 a 2 η 2 η   J 0 η r d η , σ r z * r , 0 , p = − a 2 ∑ n = 1 4 ∫ 0 ∞ ϑ 3 n η , p 1 ∆ η , p ∆ 1 n η , p b z * p + ∆ 2 n η , p b ψ * p + ∆ 3 n η , p b ϕ * p J 1 a η + a 2 b r * p 6 Λ η , p Λ n η , p η 2   1 F 2 ⁡ 3 2 ; 2 , 5 2 ; − 1 4 a 2 η 2 η   J 1 η r d η , D z * r , 0 , p = a 2 ∑ n = 1 4 ∫ 0 ∞ ϑ 4 n η , p 1 ∆ η , p ∆ 1 n η , p b z * ( p ) + ∆ 2 n η , p b ψ * ( p ) + ∆ 3 n η , p b ϕ * ( p ) J 1 a η + a 2 b r * ( p ) 6 Λ η , p Λ n η , p η 2   1 F 2 ⁡ 3 2 ; 2 , 5 2 ; − 1 4 a 2 η 2 η   J 0 η r d η , B z * r , 0 , p = a 2 ∑ n = 1 4 ∫ 0 ∞ ϑ 5 n η , p 1 ∆ η , p ∆ 1 n η , p b z * ( p ) + ∆ 2 n η , p b ψ * ( p ) + ∆ 3 n η , p b ϕ * ( p )   J 1 a η + a 2 b r * ( p ) 6 Λ η , p Λ n   η , p η 2   1 F 2 ⁡ 3 2 ; 2 , 5 2 ; − 1 4 a 2 η 2 η   J 0 η r d η .
Since the integrands in Eq. (18) are continuous functions of η and finite at η = 0 , the singularity occurs while η tends to infinity. Utilizing the formula presented in the “Appendix D”, and after a lengthy analysis, the asymptotic part of the stress components, electric displacement and magnetic induction are obtained as
σ z z * , ∞ r , 0 , p = 1 π r ∑ n = 1 4 ϑ 2 n ∞ ∆ ∞ ∆ 1 n ∞ b z * ( p ) + ∆ 2 n ∞ b ψ * ( p ) + ∆ 3 n ∞ b ϕ * ( p ) K ⁡ a r + r 2 a 2 − r 2 E ⁡ a r           r > a a r a 2 − r 2   E ⁡ r a                                               r < a , σ r z * , ∞ r , 0 , p = − 1 π r ∑ n = 1 4 ϑ 3 n ∞ Λ ∞ Λ n ∞ b r * p a r K ⁡ a r + a r a 2 − r 2 E ⁡ a r                                                                                                       r > a a 2 a 2 − r 2 E ⁡ r a ,                                                                                                                                             r < a , D z * , ∞ r , 0 , p = 1 π r ∑ n = 1 4 ϑ 4 n ∞ ∆ ∞ ∆ 1 n ∞ b z * ( p ) + ∆ 2 n ∞ b ψ * ( p ) + ∆ 3 n ∞ b ϕ * ( p ) K ⁡ a r + r 2 a 2 − r 2 E ⁡ a r         r > a a r a 2 − r 2   E ⁡ r a                                             r < a , B z * , ∞ r , 0 , p = 1 π r ∑ n = 1 4 ϑ 5 n ∞ ∆ ∞ ∆ 1 n ∞ b z * ( p ) + ∆ 2 n ∞ b ψ * ( p ) + ∆ 3 n ∞ b ϕ * ( p ) K ⁡ a r + r 2 a 2 − r 2 E ⁡ a r             r > a a r a 2 − r 2   E ⁡ r a                                             r < a .
where the superscript ( ∞ ) stands for the asymptotic expansion as η → ∞ and K k = ∫ 0 π / 2 d x / 1 − k 2 s i n 2 x and E k = ∫ 0 π / 2 1 − k 2 s i n 2 x d x are the complete elliptic integrals of the first and second type, respectively. In the end, the stress components, electric displacement and magnetic induction at the dislocation site can be obtained by addition and subtraction of the asymptotic terms of the stress components, electric displacement and magnetic induction
σ z z * r , 0 , p = σ z z * , ∞ r , 0 , p + a 2 ∑ n = 1 4 ∫ 0 ∞ ϑ 2 n η , p ∆ η , p ∆ 1 n η , p − ϑ 2 n ∞ ∆ ∞ ∆ 1 n ∞ b z * p + ϑ 2 n η , p ∆ η , p ∆ 2 n η , p − ϑ 2 n ∞ ∆ ∞ ∆ 2 n ∞ b ψ * p + ϑ 2 n η , p ∆ η , p ∆ 3 n η , p − ϑ 2 n ∞ ∆ ∞ ∆ 3 n ∞ b ϕ * p η J 1 a η   J 0 η r d η + a 3 b r * ( p ) 12 ∑ n = 1 4 ∫ 0 ∞ ϑ 2 n η , p Λ η , p Λ n η , p η 3   1 F 2 ⁡ 3 2 ; 2 , 5 2 ; − 1 4 a 2 η 2 J 0 η r d η , σ r z * r , 0 , p = σ r z * , ∞ r , 0 , p − a 2 ∑ n = 1 4 ∫ 0 ∞ ϑ 3 n η , p ∆ η , p ∆ 1 n η , p b z * p + ∆ 2 n η , p b ψ * p + ∆ 3 n η , p b ϕ * p η J 1 a η   J 1 η r d η − a 3 12 ∑ n = 1 4 ∫ 0 ∞ ϑ 3 n η , p Λ η , p Λ n η , p − ϑ 3 n ∞ Λ ∞ Λ n ∞ b r * p η 3   1 F 2 ⁡ 3 2 ; 2 , 5 2 ; − 1 4 a 2 η 2 J 1 η r d η , D z * r , 0 , p = D z * , ∞ r , 0 , p + a 2 ∑ n = 1 4 ∫ 0 ∞ ϑ 4 n η , p ∆ η , p ∆ 1 n η , p − ϑ 4 n ∞ ∆ ∞ ∆ 1 n ∞ b z * ( p ) + ϑ 4 n η , p ∆ η , p ∆ 2 n η , p − ϑ 4 n ∞ ∆ ∞ ∆ 2 n ∞ b ψ * ( p ) + ϑ 4 n η , p ∆ η , p ∆ 3 n η , p − ϑ 4 n ∞ ∆ ∞ ∆ 3 n ∞ b ϕ * ( p ) η J 1 a η   J 0 η r d η + a 3 b r * ( p ) 12 ∑ n = 1 4 ∫ 0 ∞ ϑ 4 n η , p Λ η , p Λ n η , p η 3   1 F 2 ⁡ 3 2 ; 2 , 5 2 ; − 1 4 a 2 η 2 J 0 η r d η , B z * r , 0 , p = B z * , ∞ r , 0 , p + a 2 ∑ n = 1 4 ∫ 0 ∞ ϑ 5 n η , p ∆ η , p ∆ 1 n η , p − ϑ 5 n ∞ ∆ ∞ ∆ 1 n ∞ b z * ( p ) + ϑ 5 n η , p ∆ η , p ∆ 2 n η , p − ϑ 5 n ∞ ∆ ∞ ∆ 2 n ∞ b ψ * ( p ) + ϑ 5 n η , p ∆ η , p ∆ 3 n η , p − ϑ 5 n ∞ ∆ ∞ ∆ 3 n ∞ b ϕ * ( p ) η J 1 a η   J 0 η r d η + a 3 b r * ( p ) 12 ∑ n = 1 4 ∫ 0 ∞ ϑ 5 n η , p Λ η , p Λ n η , p η 3   1 F 2 ⁡ 3 2 ; 2 , 5 2 ; − 1 4 a 2 η 2 J 0 η r d η .
From Eq. (20), we may observe that the stress components, electric displacement and magnetic induction exhibit the Cauchy-type singularity at dislocation locations, i.e. σ z z * , ∞ r , 0 , p ~ 1 r − a , σ r z * , ∞ r , 0 , p ~ 1 r − a , D z * , ∞ r , 0 , p ~ 1 r − a and B z * , ∞ r , 0 , p ~ 1 r − a a s r → a . Existence of the Cauchy singularity in the dislocation for an infinite transversely isotropic cylinder with prismatic and radial dislocations has also been reported by Pourseifi et al. [40,41,42].

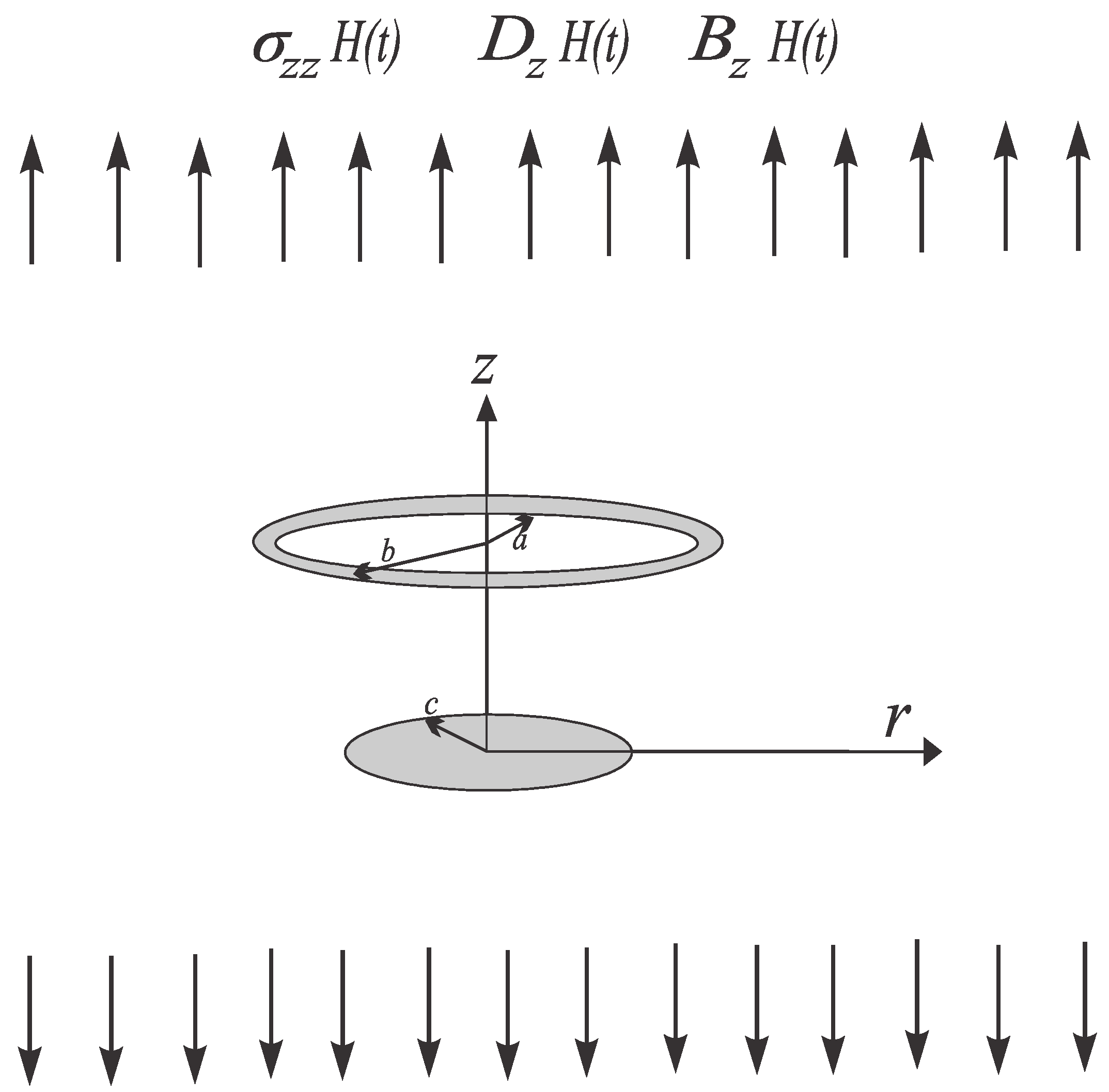
3. Axisymmetric Planar Crack Formulation

The distributed dislocation method was utilized by some researchers for the analysis of cracked bodies subjected to mechanical loading, see e.g.,Weertman and Weertman [43]. The dislocation solutions carried out in the previous section may be used to analyze transversely isotropic MEE medium weakened by multiple axisymmetric planar cracks subjected to transient in-plane loading. Consider a transversely isotropic MEE medium weakened by N 1 annular cracks and N − N 1 penny shaped cracks, while N denotes the number of coaxial located defects. The inner and outer radiuses of the annular cracks are assumed a j and b j , j = 1,2 , … , N 1 .   c j , j = N 1 + 1 , N 1 + 2 , … , N is radii of the j-th penny-shaped crack. Equation (21) represents such axisymmetric planar cracks in the parametric form:
r j s = L j s + 0.5 b j + a j , − 1 ≤ s ≤ 1                                                           f o r   a n n u l a r   c r a c k s r j s = L j 1 − s , − 1 ≤ s ≤ 1                                                                       f o r   p e n n y   s h a p e d   c r a c k s
Noting that,
L j = 0.5 b j − a j                                                                               f o r   a n n u l a r   c r a c k s     j = 1,2 , … , N 1 c j                                 f o r   p e n n y   s h a p e d   c r a c k s     j = N 1 + 1 , … , N 1 + N 2
Suppose the prismatic, radial, electric and magnetic dynamic dislocations with unknown densities of b z * q , p , b r * q , p , b ψ * q , p and b ϕ * q , p , respectively, are distributed on the infinitesimal segment at the surfaces of the j-th concentric crack located at z = z j . Applying the principle of superposition, the components of in-plane traction, electric and magnetic potentials at a point with coordinates r i s , z i , where − 1 ≤ s ≤ 1 , on the surface of all cracks yields
σ z z * r i s , z i , p = ∑ j = 1 N ∫ − 1 1 L j K i j 11 s , q , p b z j * q , p + K i j 12 s , q , p b r j * q , p + K i j 13 s , q , p b ψ j * q , p + K i j 14 s , q , p b ϕ j * q , p d q ,   i = 1,2 , … , N σ r z * r i s , z i , p = ∑ j = 1 N ∫ − 1 1 L j K i j 21 s , q , p b z j * q , p + K i j 22 s , q , p b r j * q , p + K i j 23 s , q , p b ψ j * q , p + K i j 24 s , q , p b ϕ j * q , p d q ,   i = 1,2 , … , N D z * r i s , z i , p = ∑ j = 1 N ∫ − 1 1 L j K i j 31 s , q , p b z j * q , p + K i j 32 s , q , p b r j * q , p + K i j 33 s , q , p b ψ j * q , p + K i j 34 s , q , p b ϕ j * q , p d q ,   i = 1,2 , … , N B z * r i s , z i , p = ∑ j = 1 N ∫ − 1 1 L j K i j 41 s , q , p b z j * q , p + K i j 42 s , q , p b r j * q , p + K i j 43 s , q , p b ψ j * q , p + K i j 44 s , q , p b ϕ j * q , p d q ,   i = 1,2 , … , N
The kernels of the integrals in eq.23 are presented in “Appendix E”. Based on the Buckner’s principle [35] the problem simplifies to one of characterizing the distribution of generalized dynamic dislocations which generates in-plane tractions along the crack-line, equal and opposite to those produced by the applied loads, so that the crack faces remain traction-free. The equations for the crack opening displacement and the electric and magnetic potentials across the j-th axisymmetric planar crack are as follows
u z j * , + s , p − u z j * , − s , p = ∫ − 1 s   L j   b z j * q , p d q                                                   u r j * , + s , p − u r j * , − s , p = ∫ − 1 s   L j   b r j * q , p d q                                               ψ j * , + s , p − ψ j * , − s , p = ∫ − 1 s L j   b ψ j * q , p d q                                               ϕ j * , + s , p − ϕ j * , − s , p = ∫ − 1 s L j   b ϕ j * q , p d q ,                   j = 1,2 , … , N                                            
The closure requirement must be satisfied to ensure the field is single-valued. Accordingly, eq.25 describes these requirements for j-th annular crack
∫ − 1 1   L j   b z j * q , p d q = 0                                                   ∫ − 1 1   L j   b r j * q , p d q = 0                                               ∫ − 1 1   L j   b ψ j * q , p d q = 0                                               ∫ − 1 1 L j   b ϕ j * q , p d q = 0 ,                                                                                         j = 1,2 , … , N                                            
To calculate the dislocation densities on a crack face, the equations (23) and Eq. (25) should be solved simultaneously. The numerical inversion of the Laplace transform is accomplished through Stehfest’s technique [36]. This approach was utilized by several researchers to analyze dynamic crack problems. A time dependent function f ( t ) is approximated as
f ( t ) ≈ l n 2 t ∑ n = 1 M v n   F ( l n 2 t n )
Where, F . denotes the Laplace transform of f ( t ) , M is an even number, and the coefficients are expressed as
v n = ( − 1 ) M 2 + n ∑ j = [ n + 1 2 ] min ( M 2 , n ) j M 2 ( 2 j ) ! ( M 2 − j ) ! j ! ( j − 1 ) ! ( n − j ) ! ( 2 j − n ) !
[.] indicates the integer part of the quantity. Considering Eq. (27) the evaluation of f t at the specific time instant t requires the calculations of F s at M points p = l n 2 t n , n ∈ 1 , 2 , . . . , M . According to the relationships (23) and (25) one can write
σ z z * r i s , z i , l n 2 t n = ∑ j = 1 N ∫ − 1 1 L j K i j 11 s , q , l n 2 t n b z j * q , l n 2 t n + K i j 12 s , q , l n 2 t n b r j * q , l n 2 t n + K i j 13 s , q , l n 2 t n b ψ j * q , l n 2 t n + K i j 14 s , q , l n 2 t n b ϕ j * q , l n 2 t n d q ,   i = 1,2 , … , N σ r z * r i s , z i , l n 2 t n = ∑ j = 1 N ∫ − 1 1 L j K i j 21 s , q , l n 2 t n b z j * q , l n 2 t n + K i j 22 s , q , l n 2 t n b r j * q , l n 2 t n + K i j 23 s , q , l n 2 t n b ψ j * q , l n 2 t n + K i j 24 s , q , l n 2 t n b ϕ j * q , l n 2 t n d q ,   i = 1,2 , … , N D z * r i s , z i , l n 2 t n = ∑ j = 1 N ∫ − 1 1 L j K i j 31 s , q , l n 2 t n b z j * q , l n 2 t n + K i j 32 s , q , l n 2 t n b r j * q , l n 2 t n + K i j 33 s , q , l n 2 t n b ψ j * q , l n 2 t n + K i j 34 s , q , l n 2 t n b ϕ j * q , l n 2 t n d q ,   i = 1,2 , … , N B z * r i s , z i , l n 2 t n = ∑ j = 1 N ∫ − 1 1 L j K i j 41 s , q , l n 2 t n b z j * q , l n 2 t n + K i j 42 s , q , l n 2 t n b r j * q , l n 2 t n + K i j 43 s , q , l n 2 t n b ψ j * q , l n 2 t n + K i j 44 s , q , l n 2 t n b ϕ j * q , l n 2 t n d q ,   i = 1,2 , … , N ∫ − 1 1   L j   b z j * q , l n 2 t n d q = 0                                                   ∫ − 1 1   L j   b r j * q , l n 2 t n d q = 0                                               ∫ − 1 1   L j   b ψ j * q , l n 2 t n d q = 0                                               ∫ − 1 1 L j   b ϕ j * q , l n 2 t n d q = 0 ,    
In the transversely isotropic MEE media, the boundary conditions of the stress field and the electric and magnetic displacement at crack tip behave like 1 / r , where r is the distance from the crack tips. Therefore, by choosing that the embedded crack tips to be singular at q = − 1 , the dislocation densities for each type of crack are classified as [44]
b k j * q , l n 2 t n = G k j * q , l n 2 t n 1 − q 2                                                 f o r   a n n u l a r   c r a c k s b k j * q , l n 2 t n = G k j * q , l n 2 t n 1 − q 1 + q     f o r   p e n n y − s h a p e d   c r a c k , k = z , r , ψ   a n d   ϕ                
Substituting Eq. (29) into Eq. (28) and application of the numerical approach of singular integral equations with Cauchy-type kernel developed by Faal et al. [45] results in G k j * q , l n 2 t n . Using Eq. (26), the inverse Laplace transform of dislocation densities can be expressed as
g k i ( q , t ) = l n 2 t ∑ n = 1 M v n G k i * ( q , l n 2 t n ) ,       − 1 ≤ q ≤ 1 ,       i = 1 , 2 , … N ,   k = z , r , ψ   ​ a n d   ϕ
Finally, the modes I and II dynamic stress intensity factors (DSIFs), dynamic electric displacement intensity factors (DEIFs) and dynamic magnetic induction intensity factors (DMIFs) for annular crack are [46]
K I L j ( t ) K I I L j ( t ) K D L j ( t ) K B L j ( t ) = π L j 2 1 ∆ ∞ ∑ n = 1 4 ϑ 2 n ∞ ∆ 1 n ∞ g z j ( − 1 , t ) + ∆ 2 n ∞ g ψ j ( − 1 , t ) + ∆ 3 n ∞ g ϕ j ( − 1 , t ) − 1 Λ ∞ ∑ n = 1 4 ϑ 3 n ∞ Λ n ∞ g r j ( − 1 , t ) 1 ∆ ∞ ∑ n = 1 4 ϑ 4 n ∞ ∆ 1 n ∞ g z j ( − 1 , t ) + ∆ 2 n ∞ g ψ j ( − 1 , t ) + ∆ 3 n ∞ g ϕ j ( − 1 , t ) 1 ∆ ∞ ∑ n = 1 4 ϑ 5 n ∞ ∆ 1 n ∞ g z j ( − 1 , t ) + ∆ 2 n ∞ g ψ j ( − 1 , t ) + ∆ 3 n ∞ g ϕ j ( − 1 , t ) K I R j ( t ) K I I R j ( t ) K D R j ( t ) K B R j ( t ) = − π L j 2 1 ∆ ∞ ∑ n = 1 4 ϑ 2 n ∞ ∆ 1 n ∞ g z j ( 1 , t ) + ∆ 2 n ∞ g ψ j ( 1 , t ) + ∆ 3 n ∞ g ϕ j ( 1 , t ) − 1 Λ ∞ ∑ n = 1 4 ϑ 3 n ∞ Λ n ∞ g r j ( 1 , t ) 1 ∆ ∞ ∑ n = 1 4 ϑ 4 n ∞ ∆ 1 n ∞ g z j ( 1 , t ) + ∆ 2 n ∞ g ψ j ( 1 , t ) + ∆ 3 n ∞ g ϕ j ( 1 , t ) 1 ∆ ∞ ∑ n = 1 4 ϑ 5 n ∞ ∆ 1 n ∞ g z j ( 1 , t ) + ∆ 2 n ∞ g ψ j ( 1 , t ) + ∆ 3 n ∞ g ϕ j ( 1 , t )
Where L and R in Eq. (31) indicate inner and outer tips of annular crack, respectively. Moreover, DSIFs, DEIFs and DMIFs for a penny-shaped crack are
K I j ( t ) K I I j ( t ) K D j ( t ) K B j ( t ) = π L j 1 ∆ ∞ ∑ n = 1 4 ϑ 2 n ∞ ∆ 1 n ∞ g z j ( − 1 , t ) + ∆ 2 n ∞ g ψ j ( − 1 , t ) + ∆ 3 n ∞ g ϕ j ( − 1 , t ) − 1 Λ ∞ ∑ n = 1 4 ϑ 3 n ∞ Λ n ∞ g r j ( − 1 , t ) 1 ∆ ∞ ∑ n = 1 4 ϑ 4 n ∞ ∆ 1 n ∞ g z j ( − 1 , t ) + ∆ 2 n ∞ g ψ j ( − 1 , t ) + ∆ 3 n ∞ g ϕ j ( − 1 , t ) 1 ∆ ∞ ∑ n = 1 4 ϑ 5 n ∞ ∆ 1 n ∞ g z j ( − 1 , t ) + ∆ 2 n ∞ g ψ j ( − 1 , t ) + ∆ 3 n ∞ g ϕ j ( − 1 , t )
In the case of a crack problem with permeable condition (type-b solution), the electric and magnetic potentials are continuous in the crack positions. Therefore, it is enough to let the jump in electric and magnetic potential be zero, i.e. b ϕ and b ϕ in the boundary conditions (12) and (13). The same process as for impermeable cracks is followed to achieve permeable cracks
K I L j ( t ) K I I L j t K I R j ( t ) K I I R j ( t ) = π L j 2 1 ∆ ∞ ∑ n = 1 4 ϑ 2 n ∞ ∆ 1 n ∞ g z j ( − 1 , t ) − 1 Λ ∞ ∑ n = 1 4 ϑ 3 n ∞ Λ n ∞ g r j − 1 , t − 1 ∆ ∞ ∑ n = 1 4 ϑ 2 n ∞ ∆ 1 n ∞ g z j ( 1 , t ) 1 Λ ∞ ∑ n = 1 4 ϑ 3 n ∞ Λ n ∞ g r j ( 1 , t )
for the DSIFs of annular cracks and
K I j ( t ) K I I j ( t ) = π L j 1 ∆ ∞ ∑ n = 1 4 ϑ 2 n ∞ ∆ 1 n ∞ g z j ( − 1 , t ) − 1 Λ ∞ ∑ n = 1 4 ϑ 3 n ∞ Λ n ∞ g r j ( − 1 , t )
for penny-shaped cracks. Additionally, the DEIFs and DMIFs are related to the DSIFs through
K D j ( t ) K B j ( t ) = ∑ n = 1 4 ϑ 4 n ∞ ∆ 1 n ∞ ∑ n = 1 4 ϑ 2 n ∞ ∆ 1 n ∞ K I j t ∑ n = 1 4 ϑ 5 n ∞ ∆ 1 n ∞ ∑ n = 1 4 ϑ 2 n ∞ ∆ 1 n ∞ K I j ( t )
It is observed that for the permeable condition case, the DSIFs, DEIFs and DMIFs of a collection of multiple cracks do not depend on the electric and magnetic loadings. This property of generalized intensity coefficients for permeable cracks in transversely isotropic MEE materials has been reported in the literature for a single crack [47] as well as for three parallel asymmetric cracks [48].

4. Numerical Examples

The methodology introduced in the preceding section based on generalized distributed dislocation technique, allowed the consideration of a transversely isotropic MEE medium weakened by multiple axisymmetric planar cracks under transient in-plane magneto-electromechanical loading. The analysis covers both penny-shaped and annular cracks, as shown in Figure 1. The BaTiO3–CoFe2O4 composite material is used in numerical calculations. The piezoelectric and piezomagnetic characteristics of bimaterial composite are taken from the reference [49] and presented in Table 1. In all cases, the medium is subjected to far-field uniform dynamic traction σ z z = σ 0 ∞ H ( t ) , dynamic axial electric displacement D z = D 0 ∞ H ( t ) and dynamic axial magnetic induction B z = B 0 ∞ H ( t ) , in which σ 0 ∞ , D 0 ∞ and , B 0 ∞ are the amplitudes of the normal stress, electric displacement and magnetic induction exerted on crack surfaces, respectively, and H ( . ) the Heaviside unit step function. The electro-mechanical and magneto-mechanical coupling factors are defined by λ D = D 0 ∞ e 15 / σ 0 ∞ d 11 and λ B = B 0 ∞ α 15 / σ 0 ∞ γ 11 to integrate the normal traction σ 0 ∞ , electric D 0 ∞ and magnet B 0 ∞ loading. In the following examples, for penny-shaped cracks the modes I and II DSIFs, DEIFs and DMIFs are normalized by K I 0 = 2 σ 0 ∞ l / π , K I I 0 = 2 σ 0 ∞ l / π , K D 0 = K I 0 d 11 / e 15 and K B 0 = K I 0 γ 11 / α 15 ; respectively. Additionally, for annular cracks the generalized dynamic intensity factors are normalized by dividing to K I 0 = σ 0 ∞ π l , K I I 0 = σ 0 ∞ π l , K D 0 = K I 0 d 11 / e 15 and K B 0 = K I 0 γ 11 / α 15 , where l is crack length. The results are presented according to normalized time C T t / l , where C T = μ 0 / ρ 0 with μ 0 = c 44 + d 11 α 15 2 − 2 e 15 α 15 β 11 + γ 11 e 15 2 γ 11 d 11 − β 11 2 being the “extended” shear wave velocity in the transversely isotropic MEE medium.

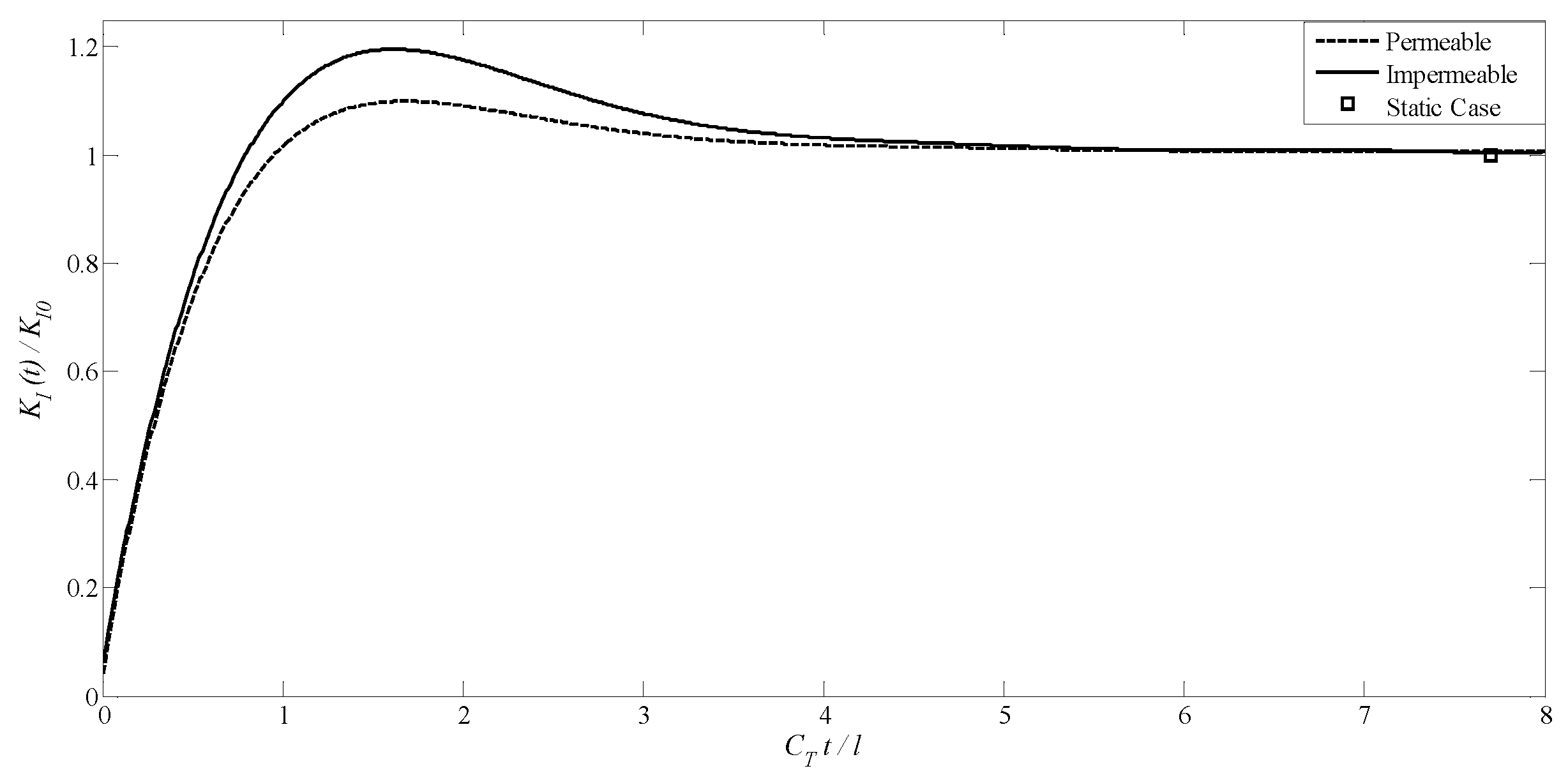
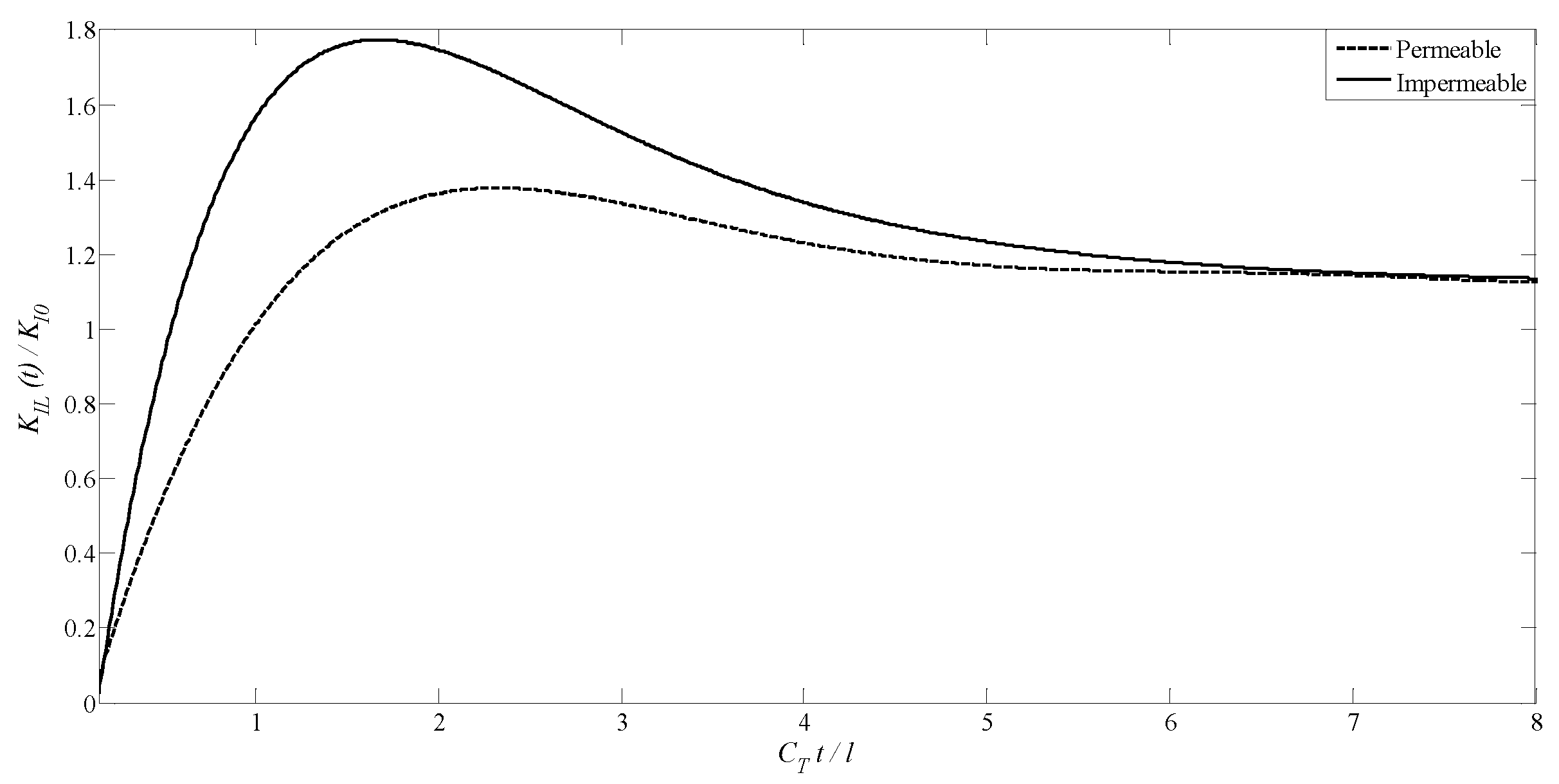
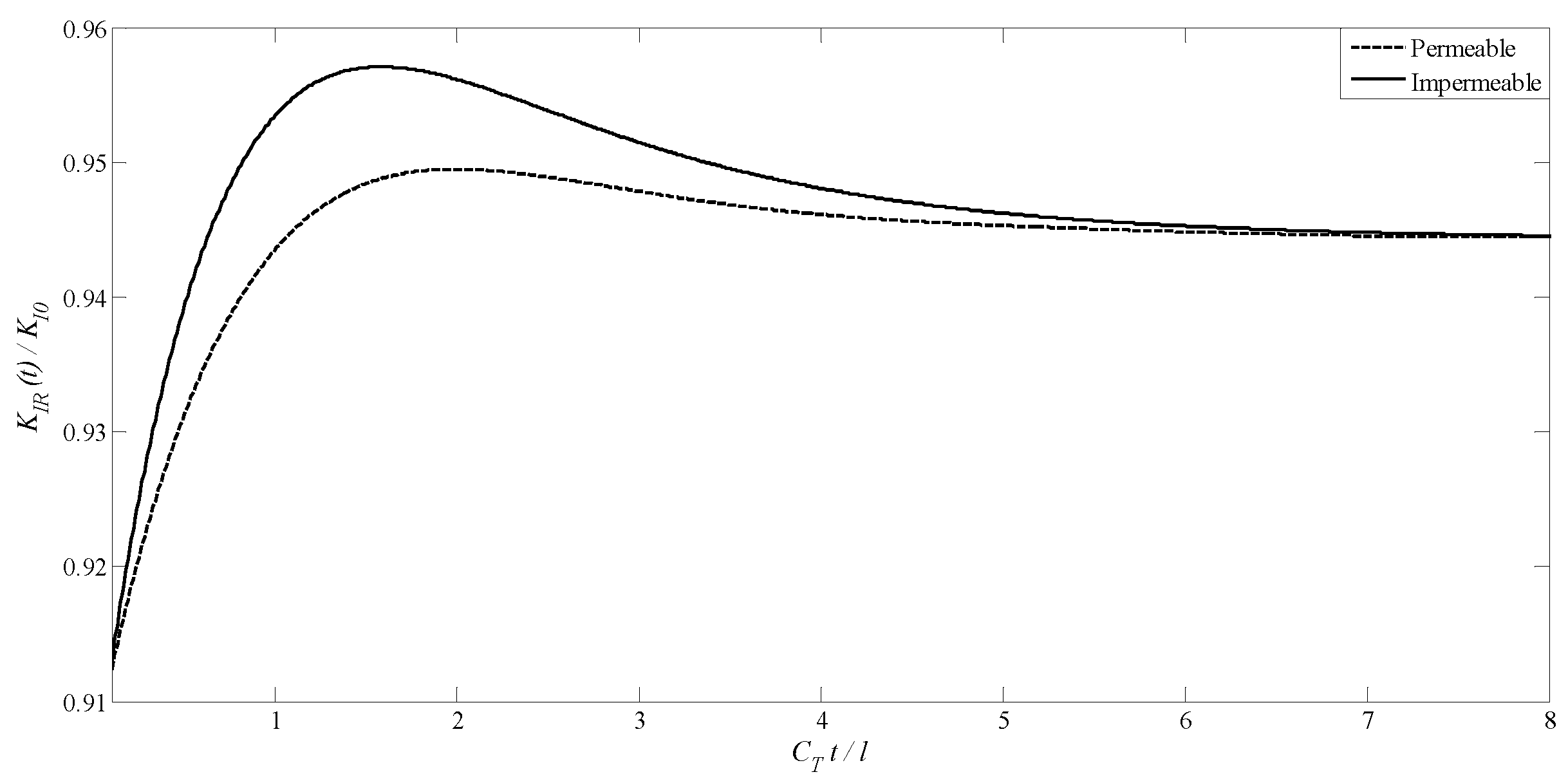
4.1. A Transversely Isotropic MEE Medium with a Penny-Shaped Crack

For first example, the problem of a transversely isotropic MEE medium including a penny-shaped crack with radius l = c 1 is investigated. It is assumed that the crack is located at z = 0 . The variations of normalized mode I DSIFs versus C T t / l for magnetoelectrically impermeable and permeable penny-shaped crack with loading combination parameters λ D = 1 and λ B = 1 , are depicted in Figure 2. This figure indicates that, regardless of magnetoelectrically impermeable and permeable boundary conditions of the crack surface, by increase of C T t / l the normalized DSIFs first increase to high values and then asymptotically tend to static value. However, the maximum values related to the electromagnetically impermeable crack surface are higher than the values related to the permeable crack. Furthermore, the occurring time the peak values of mode I DSIFs for two types of the impermeable and permeable penny-shaped cracks is similar and appears about at the normalized time C T t / l ≅ 1.65 .
Figure 3, Figure 4 and Figure 5 display the variations of normalized generalized dynamic intensity factors versus normalized time for magnetoelectrically impermeable penny-shaped crack under different values of combined magneto-electro-mechanical coupling factors. As it might be observed from Figure 3, the both magnetic and electrical loadings significantly affects the DSIFs of mode-I, so that the magnitudes of DSIFs of the crack increase with increasing values of λ D and λ B . Moreover, Figure 4 and Figure 5, indicate that both the DEIFs and DMIFs are almost constant over the normalized time, and that electrical loadings do not have considerable effects on the DMIFs, and that magnetic loadings do not have considerable effects on the DEIFs as well.

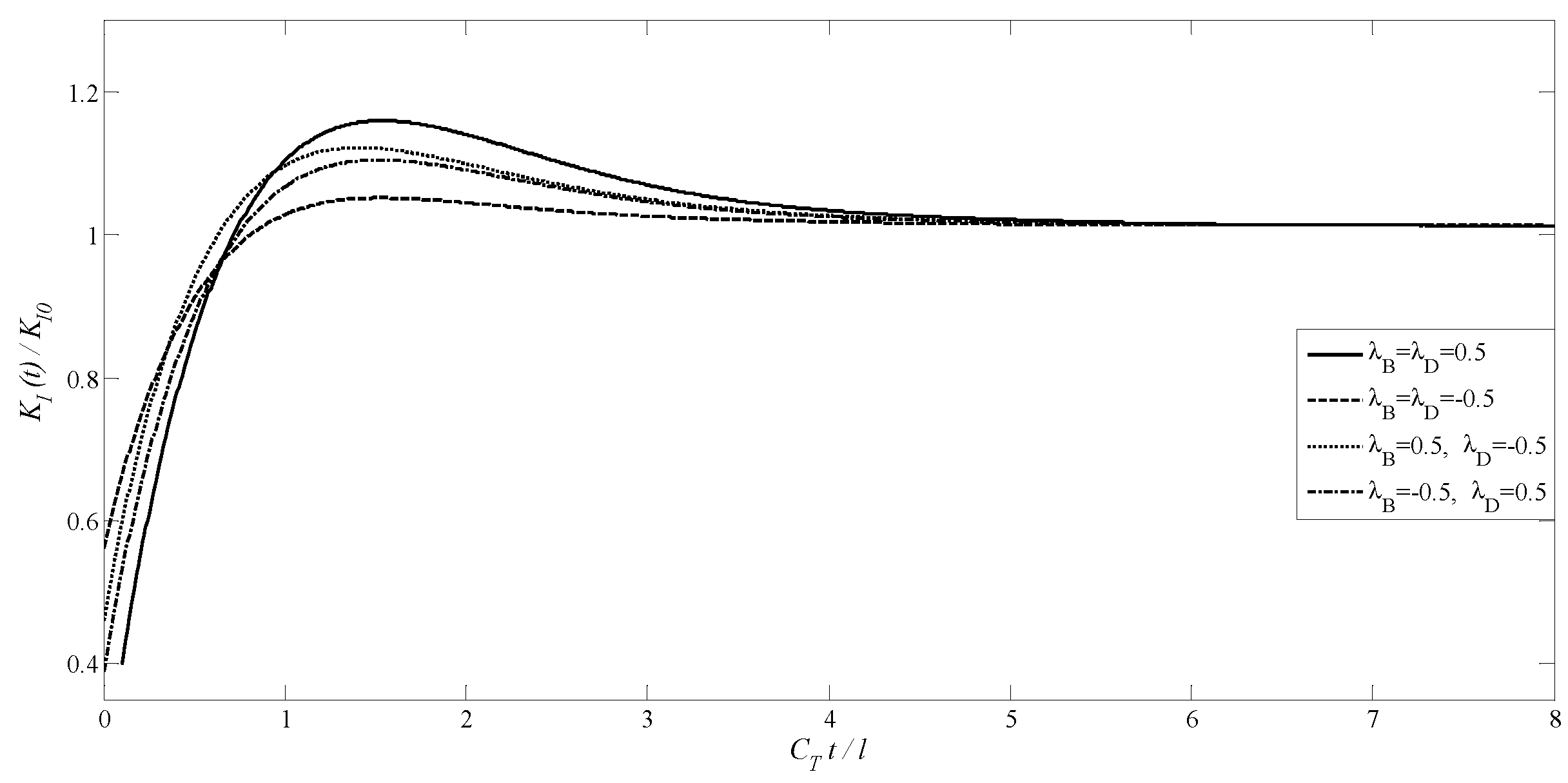
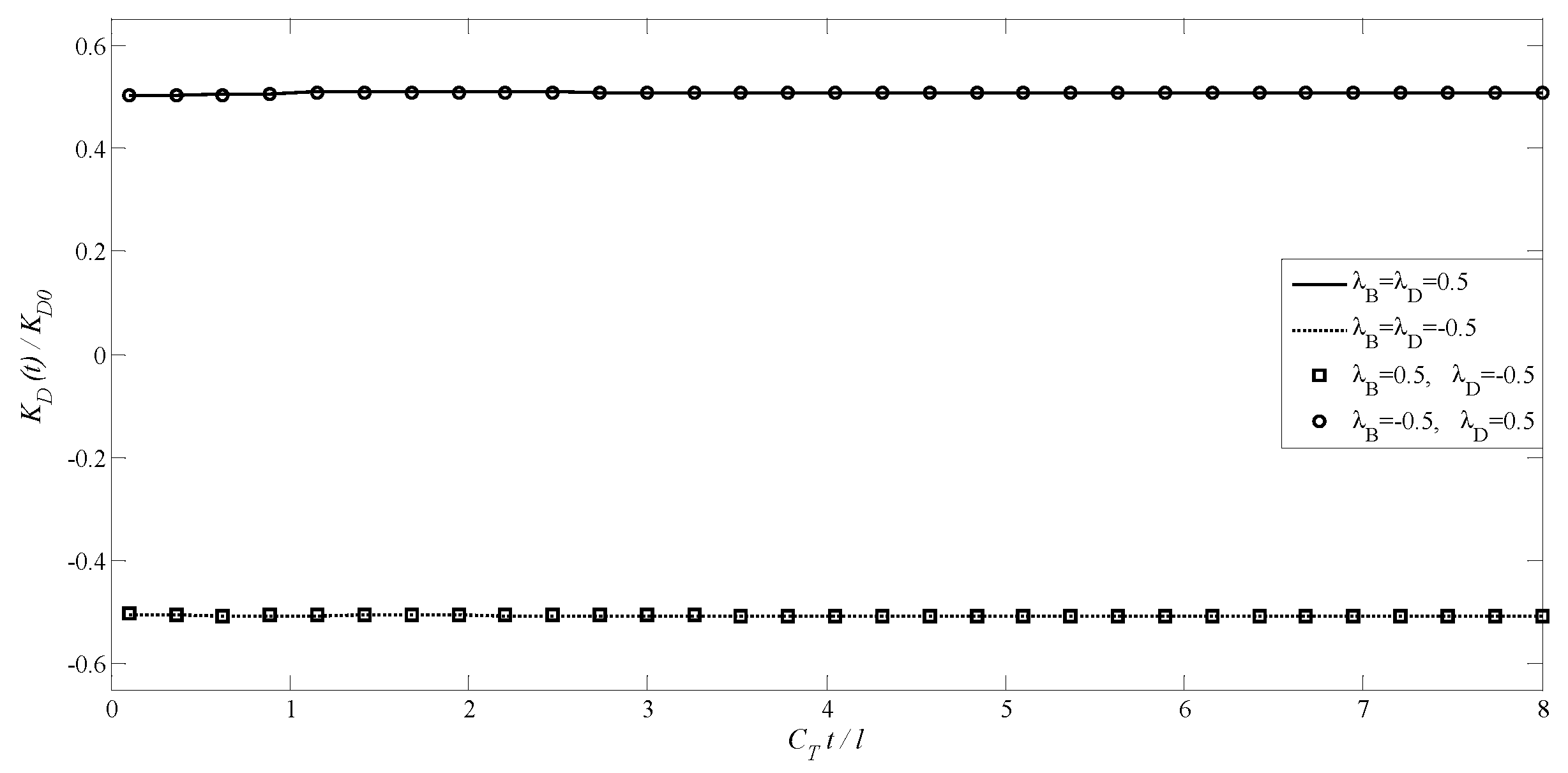
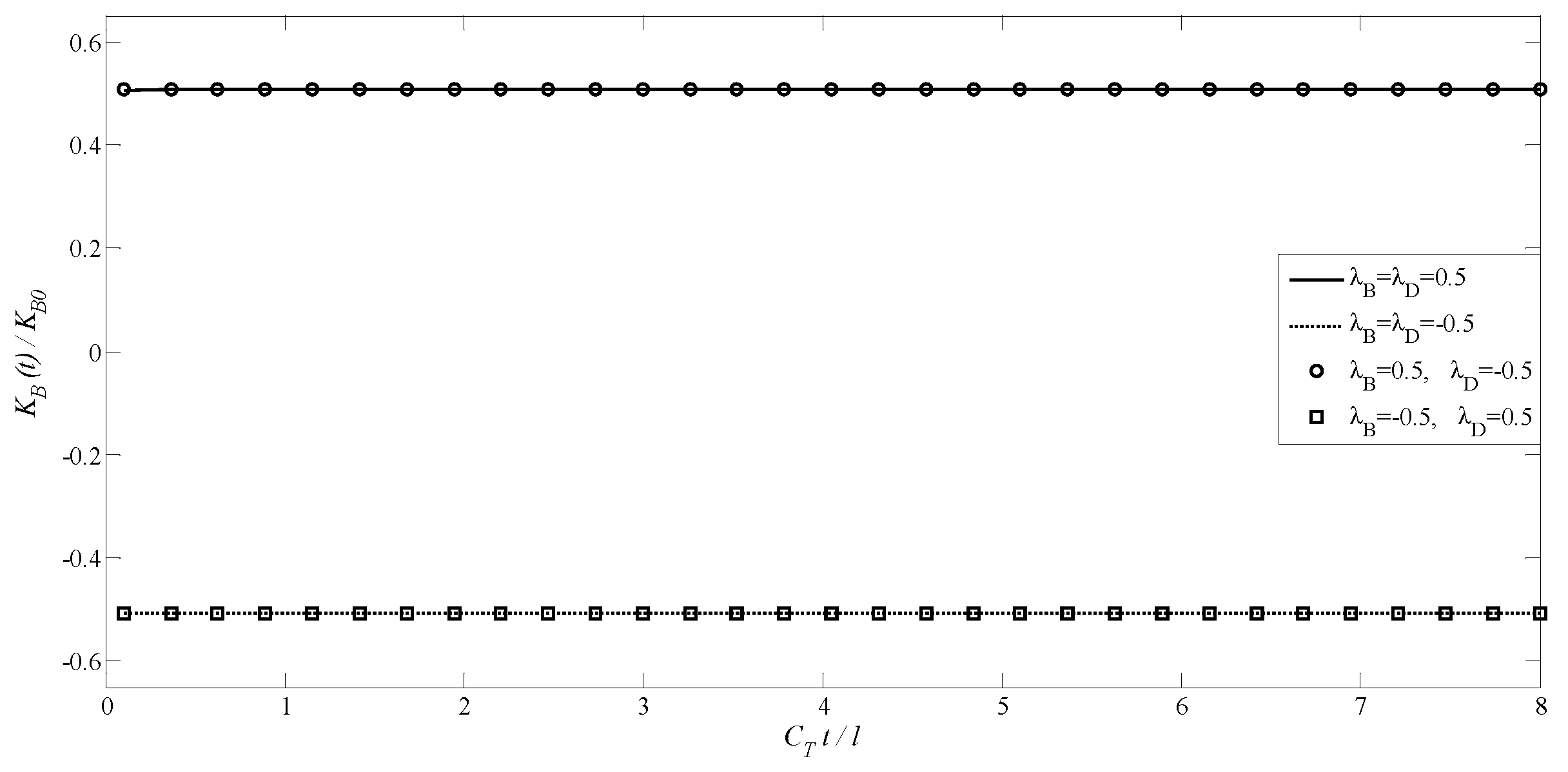
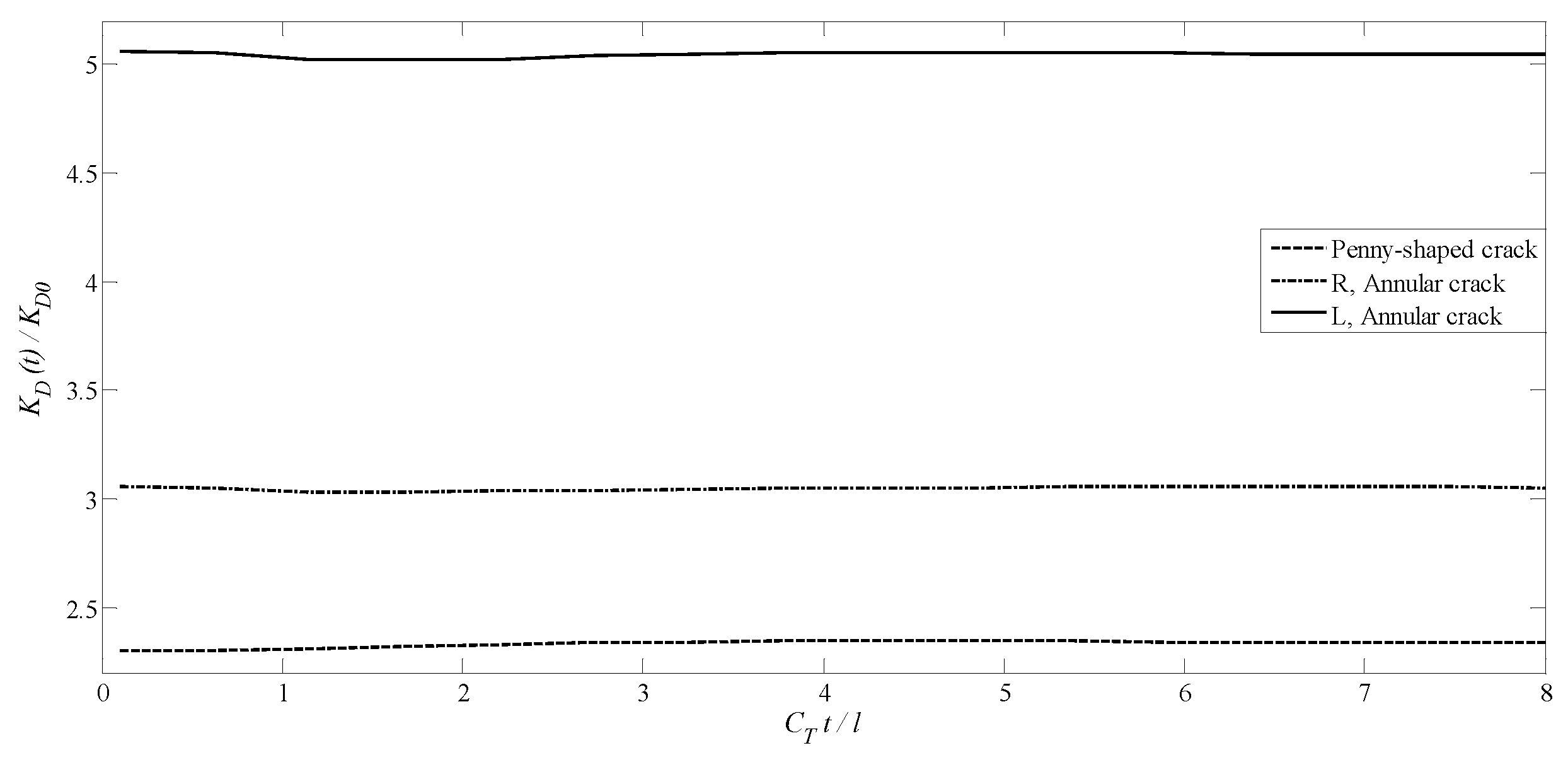
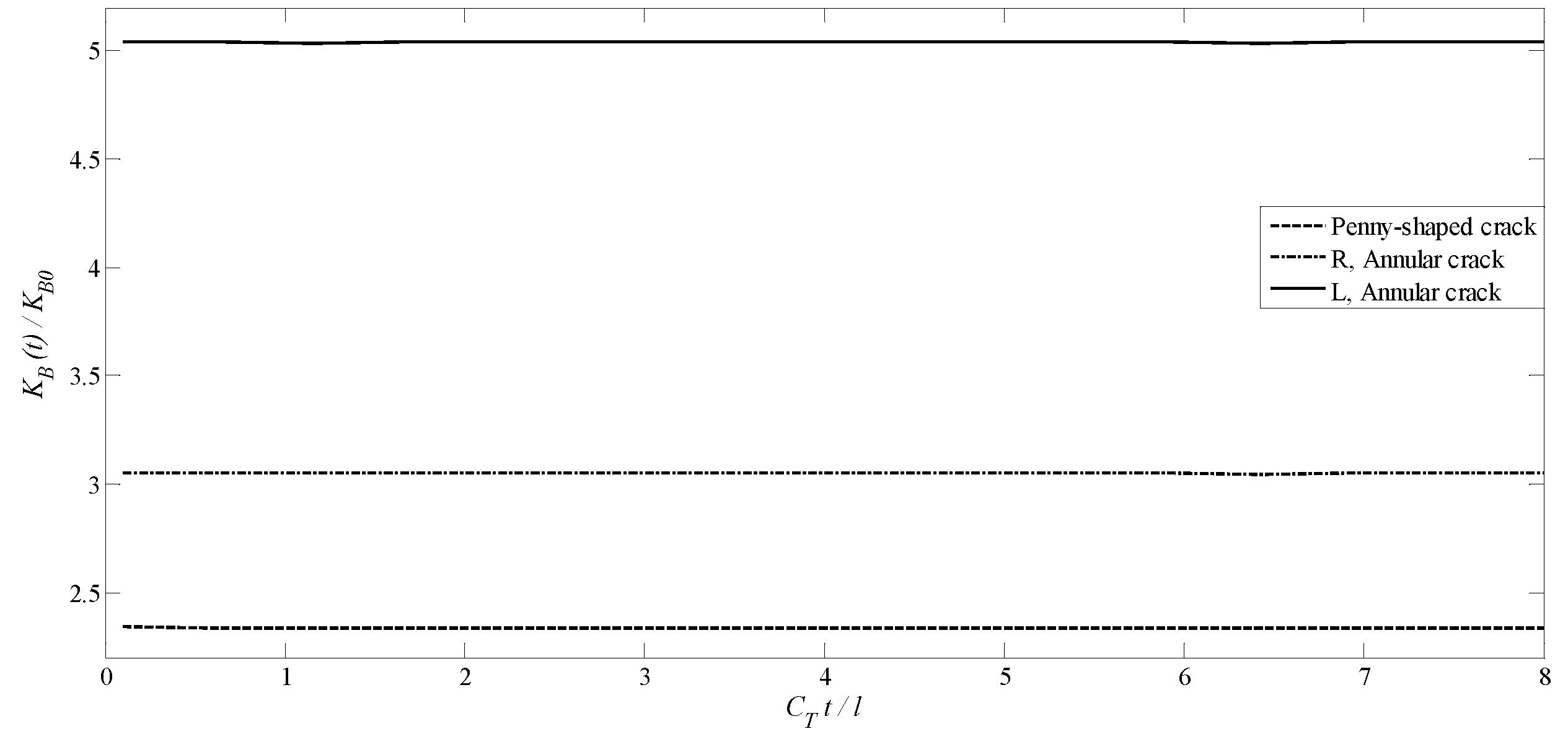
4.2. A Transversely Isotropic MEE Medium with an Annular Crack

In this example, a transversely isotropic MEE medium weakened by an annular crack with length 2 l = b 1 − a 1 is considered. a 1 and b 1 are the inner and outer radii of the annular crack. The crack is assumed to be on the plane z = 0 . For λ D = 1 and λ B = 1 , the non-dimensionalized mode I DSIFs for electrically and magnetically impermeable annular crack are compared with the corresponding DSIFs for electrically and magnetically permeable annular crack in Figure 6 and Figure 7. As expected, regardless of permeability of the crack, the curves of K I L ( t ) / K I 0 and K I R ( t ) / K I 0 exhibit the transient characteristic. So that, for inner and outer tips of annular crack, the DSIFs had a main peak value at about C T t / l = 1.65 for impermeable condition and C T t / l = 2.1 for permeable condition. Afterwards, those values decline gradually to the static values. Moreover, for the annular crack similar to the penny-shaped crack, when t → ∞ , the curves of modes I DSIFs around both the inner and outer crack tip tend to two constant values, respectively. It reveals that, permeability has no significant effect on the stress intensity factors in the static state. Additionally, the modes I DSIFs for inner tips are larger than the outer tips in the case of annular crack,.
Figure 6 and Figure 7 depict the effect of the dimensionless time on the behavior of the annular crack tips for different values of electromechanical and magnetomechanical coupling factors. It is easily seen from figures, that the magneto-electromechanical coupling factors have considerable effect on the DSIFs of mode I. So that, the peak value of DSIFs for greater magneto-electromechanical coupling factors is much more than the small value. While, like to the penny-shaped crack, the DEIFs and DMIFs for tips of annular crack are almost independent of the normalized time, and do not depend on magnetic and electrical loadings, respectively.
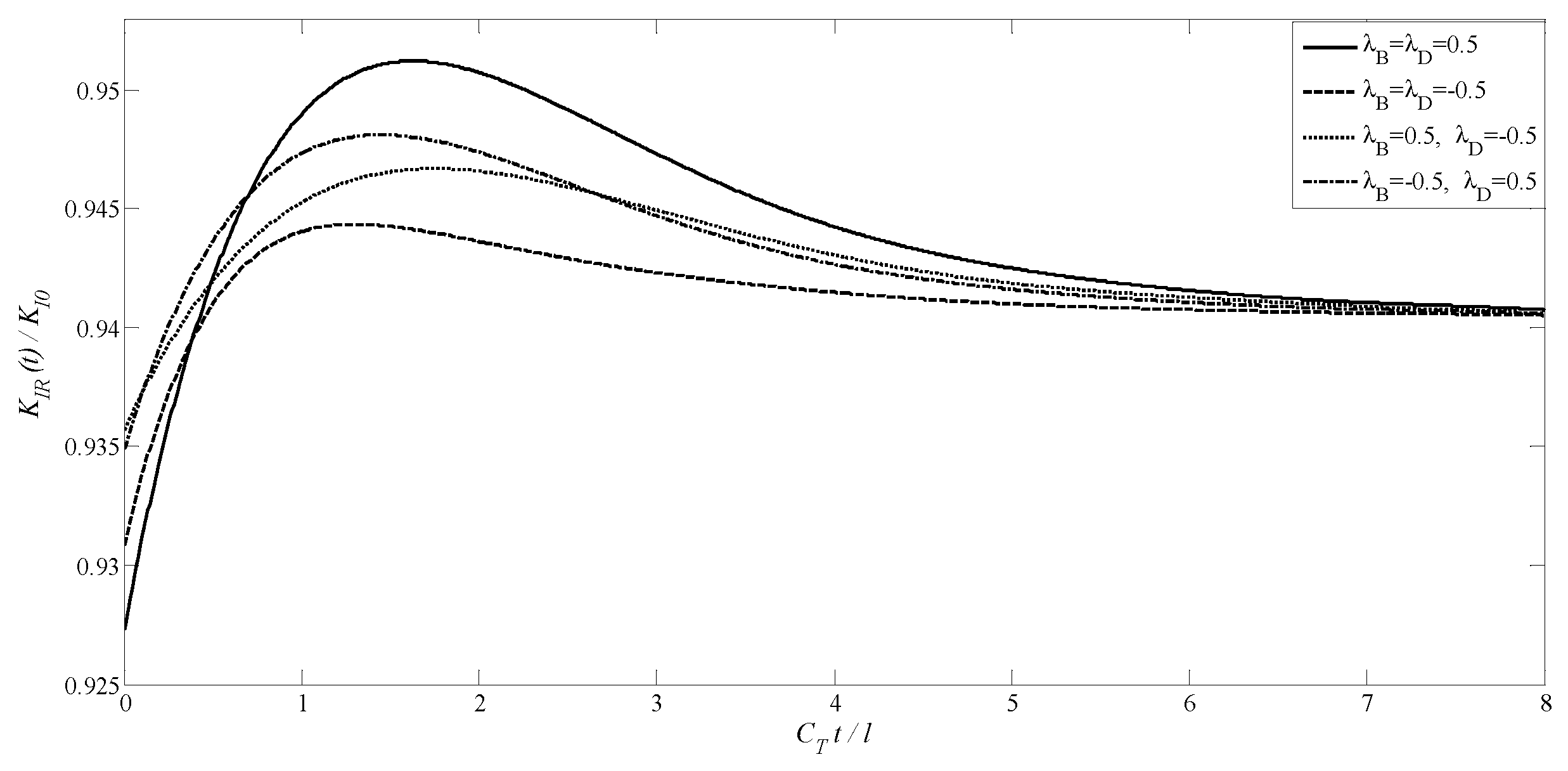
Preprints 97457 g009
Figure 9. Variation of K I R ( t ) / K I 0 versus C T t / l for magnetoelectrically impermeable annular crack under different magneto-electro-mechanical coupling factors.
Figure 9. Variation of K I R ( t ) / K I 0 versus C T t / l for magnetoelectrically impermeable annular crack under different magneto-electro-mechanical coupling factors.
Preprints 97457 g009
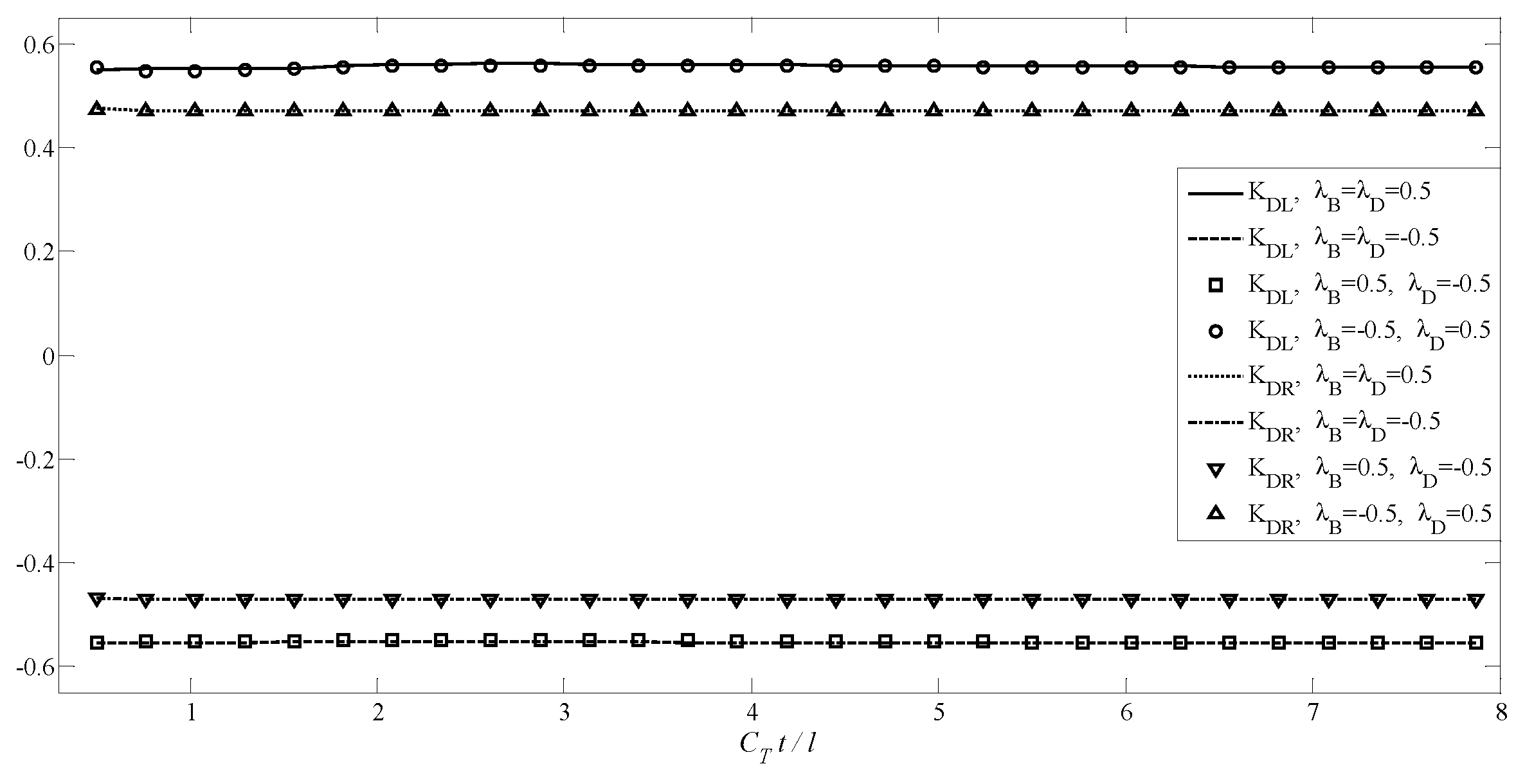
Preprints 97457 g010
Figure 10. Variation of K D ( t ) / K D 0 versus C T t / l for magnetoelectrically impermeable annular crack under different magneto-electro-mechanical coupling factors.
Figure 10. Variation of K D ( t ) / K D 0 versus C T t / l for magnetoelectrically impermeable annular crack under different magneto-electro-mechanical coupling factors.
Preprints 97457 g010
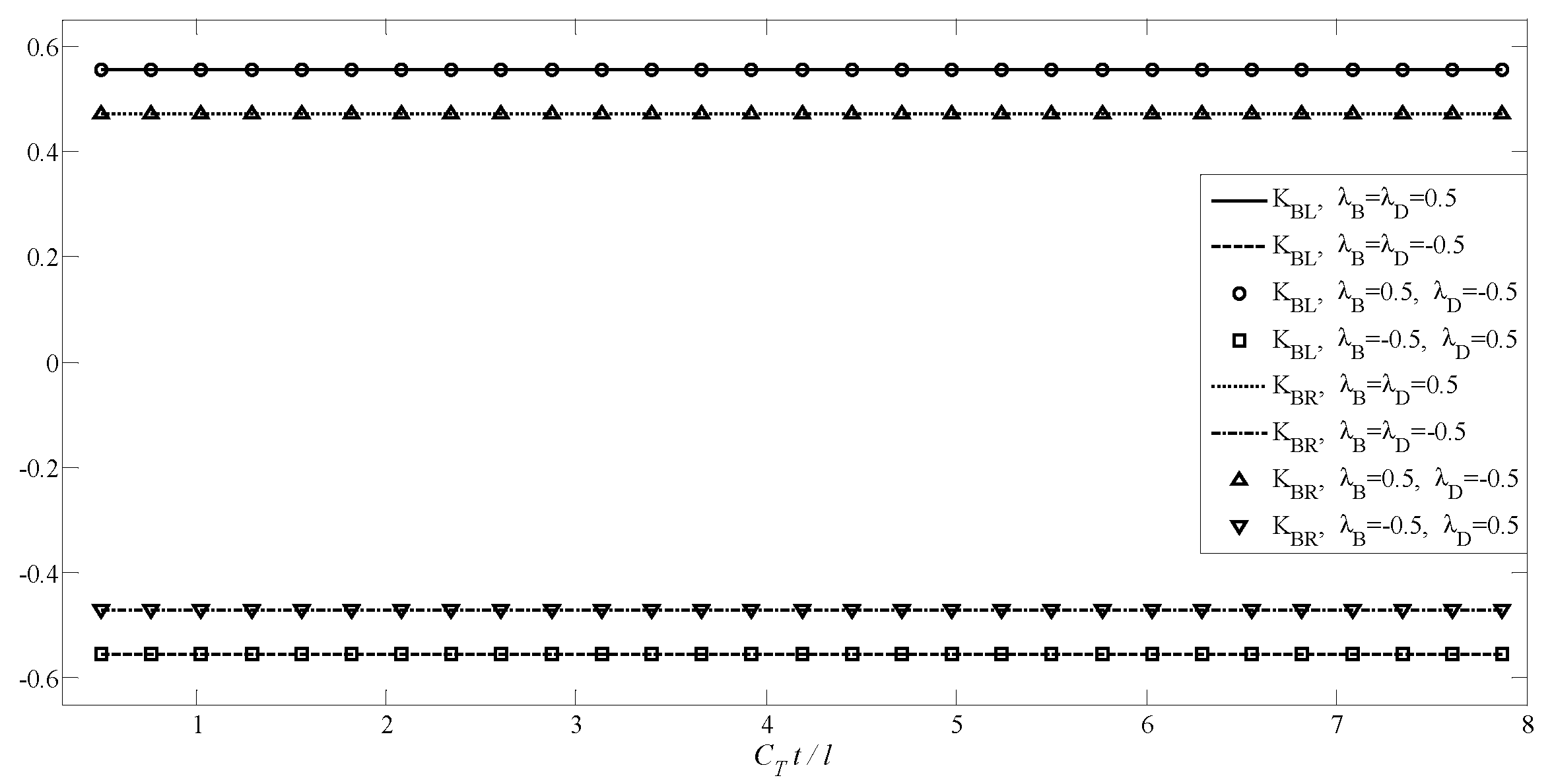
Preprints 97457 g011
Figure 11. Variation of K B ( t ) / K B 0 versus C T t / l for magnetoelectrically impermeable annular crack under different magneto-electro-mechanical coupling factors.
Figure 11. Variation of K B ( t ) / K B 0 versus C T t / l for magnetoelectrically impermeable annular crack under different magneto-electro-mechanical coupling factors.
Preprints 97457 g011

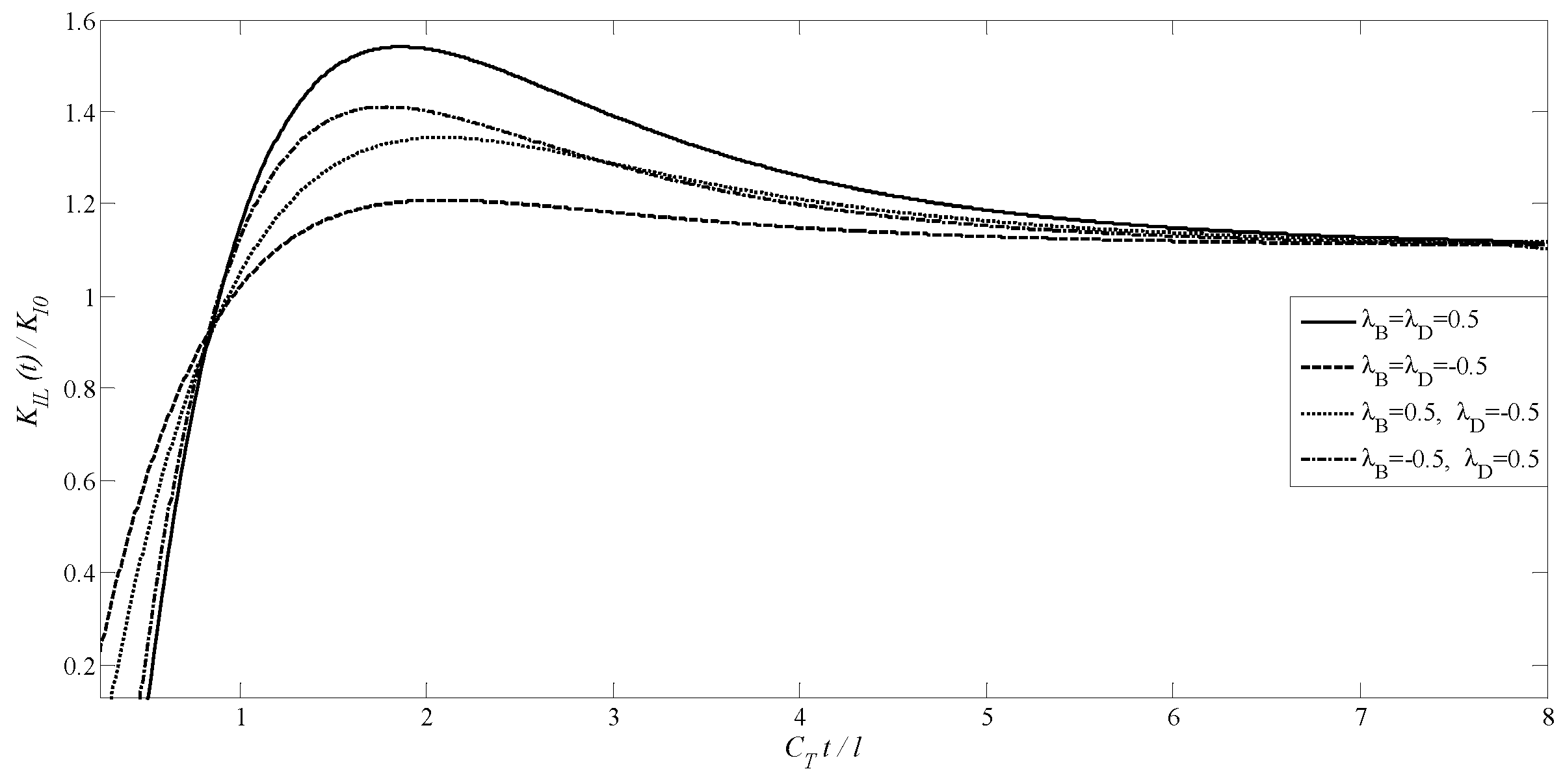
4.3. A Transversely Isotropic MEE Medium with Two Non-Planar Penny-Shaped Cracks

In the third example, a transversely isotropic MEE medium containing two parallel concentric interacting equal-length penny-shaped cracks under impermeable condition is analyzed. The radii of cracks are c 1 and c 2 and the crack length for both of them is l 1 = l 2 = l . The penny-shaped cracks were symmetrically located relative to the z = 0 , where the centers of cracks lie on a vertical line of length h . The graphs of modes I and II DSIFs, DEIFs and DMIFs against the dimensionless time with λ D = 1 and λ B = 1 are shown in Figure 12, Figure 13, Figure 14 and Figure 15, respectively. Figure 12, Figure 13, Figure 14 and Figure 15 demonstrate the effect of the interaction between cracks for h / l = 1,5 and 10 . In Figure 12, for a given h / l , the mode I DSIFs increases to a maximum value and then gradually reduce and tend to the static value. By increasing h / l , both the static and the peak values increase in magnitude. Nevertheless, Figure 13 indicates that, as the distance between two cracks, i.e. h / l , decreases, the magnitude of mode II DSIFs increases. This observation can be interpreted by the well-known phenomenon of Poisson effect. Due to the Poisson effect, the compressive stresses created on the opposite sides of the crack are unequal, as a result, shear stresses are created on each of the cracks. From Figure 14 and Figure 15, it is observed that, by increasing the distance between cracks, the DEIF and DMIF increase. Furthermore, from Figure 12, Figure 13, Figure 14 and Figure 15, it can be seen that as h / l approaches to infinity, the values of generalized intensity factor get close to the values of a penny-shaped crack.

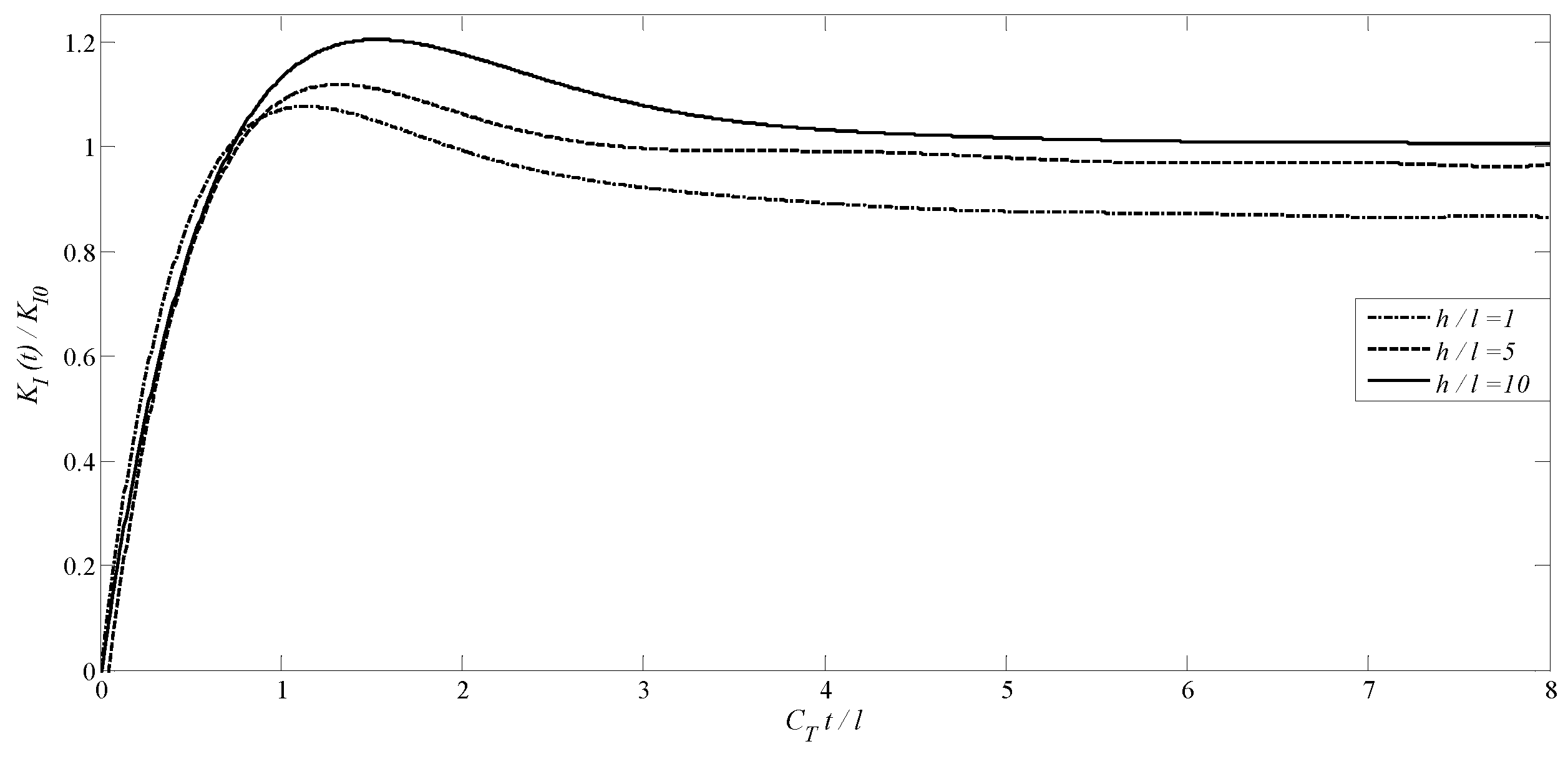
4.4. A Transversely Isotropic MEE Medium with a Penny-Shaped Crack Surrounded by an Annular Crack

The final example describes the interaction between two coplanar concentric axisymmetric cracks. The two axisymmetric interacting cracks are an annular crack (number 1) and a penny-shaped crack (number 2). The cracks are located at z 1 = z 2 = 0 and have radii a 1 ,   b 1 and c 2 , respectively. The annular crack length is 2 l = b 1 − a 1 and the length of penny-shaped crack is l = c 2 . The distance between the tip of penny-shaped crack tip and the inner tip of annular crack is 2 d . In this example, is assumed that d = 0.1 l , and the values of magneto-electro-mechanical coupling factors are λ D = 1 and λ B = 1 . The normalized mode I DSIFs, DEIFs and DMIFs have been computed and plotted graphically in Figure 16, Figure 17 and Figure 18. In comparison with the previous examples (single crack problem), it is revealed that the interaction between cracks enhanced the generalized intensity factors of the crack tips. Both the max and steady-state value of generalized intensity factors increase while increasing the crack tip interaction. Also, these figure state that the magnitudes of the DSIFs, DEIFs and DMIFs for the annular crack are higher compared to the penny-shaped crack.

5. Concluding Remarks

The transient response of a piezo-electro-magneto-elastic material weakened by multiple axisymmetric planar cracks based on the distributed dislocation method is investigated. The system is subjected to sudden in-plane magneto-electro-mechanical impacts. Two kinds of electromagnetic crack-face conditions are considered. Applying the Hankel and Laplace transform methods, the associated boundary value problem is reduced to a singular integral problem with Cauchy kernel. These integral equations were solved through a numerical method and the DSIFs, DEIFs and DMIFs are calculated at the crack tips. According to the numerical results, the most important results obtained are as follows:
1) The DSIFs for magnetoelectrically impermeable and permeable axisymmetric planar cracks rise quickly to a peak. All curves settle down to the static value over time.
2) For two types of the axisymmetric planar crack, the peak values corresponding to the magnetoelectrically impermeable crack surface are greater compared to those of permeable case.
3) For two types of the axisymmetric planar crack, the DSIFs for static value ( t → ∞ ) are independent of the crack-face electric and magnetic boundary condition.
4) For two types of the axisymmetric planar crack, the DSIFs are significantly affected by the magneto-electro-mechanical coupling factor, which the DSIFs at the crack tips increase as the magneto-electro-mechanical coupling parameter increases.
5) For two types of the axisymmetric planar crack, the DEIFs and DMIFs for tips of cracks are almost independent of time, and do not depend on magnetic and electrical loadings, respectively.
6) For the single annular crack, inner tips have larger generalized dynamic intensity compared to the outer tips.
7) For two non-planar penny-shaped cracks, by increasing distance between two cracks, the mode-I DSIF, DEIF and DMIF magnitude increase whereas the magnitudes of mode-II DSIF decrease.
8) The interaction between cracks has a significant effect on generalized intensity factor of crack tips.

Author Contributions

Conceptualization, A.V. and M.S.; methodology, A.V. and M.S.; software, A.V., M.S. and A.G.; validation, M.V. and J.J.F.; formal analysis, A.V.; investigation, A.V. and M.S.; resources, M.V. and J.J.F.; data curation, A.G.; writing—original draft preparation, A.V.; writing—review and editing, M.S.; visualization, A.G., M.V. and J.J.F.; supervision, M.S;; All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

Data are contained within the article.

Conflicts of Interest

The authors declare no conflict of interest.

Declaration of conflicting interests

The authors declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.

Appendix A

ϱ n η , p ( n = 1,2 , … 8 ) in Eq. (7) are the roots of the following characteristic equation
D e t Δ η , p = 0
where the matrix Δ η , p is given by
Δ η , p = c 11 − c 44 ϱ n 2 + ρ p 2 η 2 − c 13 + c 44 ϱ n − e 31 + e 15 ϱ n − α 31 + α 15 ϱ n − c 13 + c 44 ϱ n c 33 ϱ n 2 − c 44 − ρ p 2 η 2 e 33 ϱ n 2 − e 15 α 33 ϱ n 2 − α 15 − e 31 + e 15 ϱ n e 33 ϱ n 2 − e 15 d 11 − d 33 ϱ n 2 β 11 − β 33 ϱ n 2 − α 31 + α 15 ϱ n α 33 ϱ n 2 − α 15 β 11 − β 33 ϱ n 2 γ 11 − γ 33 ϱ n 2
and the λ 1 n η , p , λ 2 n η , p and λ 3 n η , p in Eq. (7) can be achieved by
λ 1 n η , p = − c 11 − c 44 ϱ n 2 + ρ p 2 η 2 − ( e 31 + e 15 ) ϱ n − ( α 31 + α 15 ) ϱ n ( c 13 + c 44 ) ϱ n e 33 ϱ n 2 − e 15 α 33 ϱ n 2 − α 15 ( e 31 + e 15 ) ϱ n d 11 − d 33 ϱ n 2 β 11 − β 33 ϱ n 2 − ( c 13 + c 44 ) ϱ n − ( e 31 + e 15 ) ϱ n − ( α 31 + α 15 ) ϱ n c 33 ϱ n 2 − c 44 − ρ p 2 η 2 e 33 ϱ n 2 − e 15 α 33 ϱ n 2 − α 15 e 33 ϱ n 2 − e 15 d 11 − d 33 ϱ n 2 β 11 − β 33 ϱ n 2 λ 2 n η , p = − ( c 13 + c 44 ) ϱ n − c 11 − c 44 ϱ n 2 + ρ p 2 η 2 − ( α 31 + α 15 ) ϱ n c 33 ϱ n 2 − c 44 ( c 13 + c 44 ) ϱ n α 33 ϱ n 2 − α 15 e 33 ϱ n 2 − e 15 ( e 31 + e 15 ) ϱ n β 11 − β 33 ϱ n 2 − ( c 13 + c 44 ) ϱ n − ( e 31 + e 15 ) ϱ n − ( α 31 + α 15 ) ϱ n c 33 ϱ n 2 − c 44 − ρ p 2 η 2 e 33 ϱ n 2 − e 15 α 33 ϱ n 2 − α 15 e 33 ϱ n 2 − e 15 d 11 − d 33 ϱ n 2 β 11 − β 33 ϱ n 2 λ 3 n η , p = − ( c 13 + c 44 ) ϱ n − ( e 31 + e 15 ) ϱ n − c 11 − c 44 ϱ n 2 + ρ p 2 η 2 c 33 ϱ n 2 − c 44 e 33 ϱ n 2 − e 15 ( c 13 + c 44 ) ϱ n e 33 ϱ n 2 − e 15 d 11 − d 33 ϱ n 2 ( e 31 + e 15 ) ϱ n − ( c 13 + c 44 ) ϱ n − ( e 31 + e 15 ) ϱ n − ( α 31 + α 15 ) ϱ n c 33 ϱ n 2 − c 44 − ρ p 2 η 2 e 33 ϱ n 2 − e 15 α 33 ϱ n 2 − α 15 e 33 ϱ n 2 − e 15 d 11 − d 33 ϱ n 2 β 11 − β 33 ϱ n 2

Appendix B

Coefficients in Eq. (8) are
ϑ 1 n η , p = c 11 − ϱ n η , p α 31 λ 3 n η , p + c 13 λ 1 n η , p + e 31 λ 2 n η , p ϑ 2 n η , p = c 13 − ϱ n η , p c 33 λ 1 n η , p + e 33 λ 2 n η , p + α 33 λ 3 n η , p ϑ 3 n η , p = c 44 ϱ n η , p + λ 1 n η , p + e 15 λ 2 n η , p + α 15 λ 3 n η , p ϑ 4 n η , p = e 31 − ϱ n η , p e 33 λ 1 n η , p − d 33 λ 2 n η , p − β 33 λ 3 n η , p ϑ 5 n η , p = α 31 − ϱ n η , p α 33 λ 1 n η , p − β 33 λ 2 n η , p − γ 33 λ 3 n η , p

Appendix C

For symmetric problem the unknown functions A n η , p n = 1,2 , 3,4 in Eq. (15) are
A 1 η , p = a 2 ∆ η , p ∆ 11 η , p b z * ( p ) + ∆ 21 η , p b ψ * ( p ) + ∆ 31 η , p b ϕ * ( p ) J 1 a η A 2 η , p = a 2 ∆ η , p ∆ 12 η , p b z * ( p ) + ∆ 22 η , p b ψ * ( p ) + ∆ 32 η , p b ϕ * ( p ) J 1 a η A 3 η , p = a 2 ∆ η , p ∆ 13 η , p b z * ( p ) + ∆ 23 η , p b ψ * ( p ) + ∆ 33 η , p b ϕ * ( p ) J 1 a η A 4 η , p = a 2 ∆ η , p ∆ 14 η , p b z * ( p ) + ∆ 24 η , p b ψ * ( p ) + ∆ 31 η , p b ϕ * ( p ) J 1 a η
where
∆ η , p = λ 33 λ 14 λ 22 − λ 12 λ 24 + λ 32 λ 13 λ 24 − λ 14 λ 23 + λ 34 λ 12 λ 23 − λ 13 λ 22 ϑ 11                               + λ 33 λ 11 λ 24 − λ 14 λ 21 + λ 31 λ 14 λ 23 − λ 13 λ 24 + λ 34 λ 13 λ 21 − λ 11 λ 23 ϑ 12                             + λ 14 λ 21 λ 32 − λ 22 λ 31 + λ 24 λ 12 λ 31 − λ 11 λ 32 + λ 34 λ 11 λ 22 − λ 12 λ 21 ϑ 13                             + λ 23 λ 11 λ 32 − λ 12 λ 31 + λ 13 λ 22 λ 31 − λ 21 λ 32 + λ 33 λ 12 λ 21 − λ 11 λ 22 ϑ 14
∆ 11 η , p = λ 23 λ 32 − λ 22 λ 33 ϑ 14 + λ 22 λ 34 − λ 24 λ 32 ϑ 13 + λ 24 λ 33 − λ 23 λ 34 ϑ 12
∆ 21 η , p = ( λ 12 λ 33 − λ 13 λ 32 ) ϑ 14 + ( λ 14 λ 32 − λ 12 λ 34 ) ϑ 13 + ( λ 13 λ 34 − λ 14 λ 33 ) ϑ 12
∆ 31 η , p = ( λ 13 λ 22 − λ 12 λ 23 ) ϑ 14 + ( λ 12 λ 24 − λ 14 λ 22 ) ϑ 13 + ( λ 14 λ 23 − λ 13 λ 24 ) ϑ 12
∆ 12 η , p = ( λ 21 λ 33 − λ 23 λ 31 ) ϑ 14 + ( λ 24 λ 31 − λ 21 λ 34 ) ϑ 13 + ( λ 23 λ 34 − λ 24 λ 33 ) ϑ 11
∆ 22 η , p = ( λ 13 λ 31 − λ 11 λ 33 ) ϑ 14 + ( λ 11 λ 34 − λ 14 λ 31 ) ϑ 13 + ( λ 14 λ 33 − λ 13 λ 34 ) ϑ 11
∆ 32 η , p = ( λ 11 λ 23 − λ 13 λ 21 ) ϑ 14 + ( λ 14 λ 21 − λ 11 λ 24 ) ϑ 13 + ( λ 13 λ 24 − λ 14 λ 23 ) ϑ 11
∆ 13 η , p = ( λ 22 λ 31 − λ 21 λ 32 ) ϑ 14 + ( λ 21 λ 34 − λ 24 λ 31 ) ϑ 12 + ( λ 24 λ 32 − λ 22 λ 34 ) ϑ 11
∆ 23 η , p = ( λ 11 λ 32 − λ 12 λ 31 ) ϑ 14 + ( λ 14 λ 31 − λ 11 λ 34 ) ϑ 12 + ( λ 12 λ 34 − λ 14 λ 32 ) ϑ 11
∆ 33 η , p = ( λ 12 λ 21 − λ 11 λ 22 ) ϑ 14 + ( λ 11 λ 24 − λ 14 λ 21 ) ϑ 12 + ( λ 14 λ 22 − λ 12 λ 24 ) ϑ 11
∆ 14 η , p = ( λ 21 λ 32 − λ 22 λ 31 ) ϑ 13 + ( λ 22 λ 33 − λ 23 λ 32 ) ϑ 11 + ( λ 23 λ 31 − λ 21 λ 33 ) ϑ 12
∆ 24 η , p = ( λ 12 λ 31 − λ 11 λ 32 ) ϑ 13 + ( λ 13 λ 32 − λ 12 λ 33 ) ϑ 11 + ( λ 11 λ 33 − λ 13 λ 31 ) ϑ 12
∆ 34 η , p = ( λ 11 λ 22 − λ 12 λ 21 ) ϑ 13 + ( λ 12 λ 23 − λ 13 λ 22 ) ϑ 11 + ( λ 13 λ 21 − λ 11 λ 23 ) ϑ 12 Moreover, for anti-symmetric problem the unknown functions A n η , p n = 1,2 , 3,4 in Eq. (16) are
A 1 η , p = 1 12 Λ η , p a 3 η 2 Λ 1 η , p b r * ( p )   1 F 2 ⁡ 3 2 ; 2 , 5 2 ; − 1 4 a 2 η 2 A 2 η , p = 1 12 Λ η , p a 3 η 2 Λ 2 η , p b r * ( p )   1 F 2 ⁡ 3 2 ; 2 , 5 2 ; − 1 4 a 2 η 2 A 3 η , p = 1 12 Λ η , p a 3 η 2 Λ 3 η , p b r * ( p )   1 F 2 ⁡ 3 2 ; 2 , 5 2 ; − 1 4 a 2 η 2 A 4 η , p = 1 12 Λ η , p a 3 η 2 Λ 4 η , p b r * ( p )   1 F 2 ⁡ 3 2 ; 2 , 5 2 ; − 1 4 a 2 η 2
where
Λ η , p = ϑ 31 − ϑ 34 ϑ 22 + ϑ 34 − ϑ 32 ϑ 21 ϑ 43                                                                                                                                                                                   + ϑ 41 − ϑ 42 ϑ 33 + ϑ 42 − ϑ 43 ϑ 31 + ϑ 43 − ϑ 41 ϑ 32 ϑ 24                                                                                                           + ϑ 42 − ϑ 41 ϑ 34 + ϑ 41 − ϑ 44 ϑ 32 + ϑ 44 − ϑ 42 ϑ 31 ϑ 23                                                                                                         + ϑ 32 − ϑ 33 ϑ 21 + ϑ 33 − ϑ 31 ϑ 22 ϑ 44 + ϑ 34 − ϑ 33 ϑ 22 ϑ 41 − ϑ 21 ϑ 42                
Λ 1 η , p = ϑ 24 ( ϑ 32 ϑ 43 − ϑ 33 ϑ 42 ) + ϑ 22 ( ϑ 33 ϑ 44 − ϑ 34 ϑ 43 ) + ϑ 23 ( ϑ 34 ϑ 42 − ϑ 32 ϑ 44 )
Λ 2 η , p = ϑ 24 ( ϑ 33 ϑ 41 − ϑ 31 ϑ 43 ) + ϑ 23 ( ϑ 31 ϑ 44 − ϑ 34 ϑ 41 ) + ϑ 21 ( ϑ 34 ϑ 43 − ϑ 33 ϑ 44 )
Λ 3 η , p = ϑ 24 ( ϑ 31 ϑ 42 − ϑ 32 ϑ 41 ) + ϑ 21 ( ϑ 32 ϑ 44 − ϑ 34 ϑ 42 ) + ϑ 22 ( ϑ 34 ϑ 41 − ϑ 31 ϑ 44 )
Λ 4 η , p = ϑ 23 ( ϑ 32 ϑ 41 − ϑ 31 ϑ 42 ) + ϑ 22 ( ϑ 31 ϑ 43 − ϑ 33 ϑ 41 ) + ϑ 21 ( ϑ 33 ϑ 42 − ϑ 32 ϑ 43 )

Appendix D

Mathematical formula
∫ 0 a x J 1 ( b x ) d x = 1 6 a 3 b 1 F 2 ( 3 2 ; 2 , 5 2 ; − 1 4 a 2 b 2 ) , ∫ 0 ∞ x J 1 ( a x ) J 0 ( b x ) d x = 2 π { 1 a b [ K ( a 2 b 2 ) + b 2 a 2 − b 2 E ( a 2 b 2 ) ] ,     b > a 1 a 2 − b 2 E ( b 2 a 2 ) ,     b < a ∫ 0 ∞ 1 F 2 ( 3 2 ; 2 , 5 2 ; − 1 4 a 2 x 2 ) x 3 J 1 ( b x ) d x = 12 π a { 1 a [ 1 b 2 K ( a 2 b 2 ) + 1 a 2 − b 2 E ( a 2 b 2 ) ] ,                 b > a 1 b ( a 2 − b 2 ) E ( b 2 a 2 ) ,                                                             b < a

Appendix F

The kernels of integrals in Eq. (23) are
K i j 11 s , q , p = r j 2 ∑ n = 1 4 ∫ 0 ∞ ∆ 1 n η , p ∆ η , p ϑ 2 n η , p η J 1 r j η J 0 r i η e − η ϱ n η , p z i − z j d η , K i j 12 s , q , p = r j 3 s g n ( z i − z j ) 12 ∑ n = 1 4 ∫ 0 ∞ Λ n η , p Λ η , p ϑ 2 n η , p η 3   1 F 2 ⁡ 3 2 ; 2 , 5 2 ; − 1 4 r j 2 η 2 J 0 r i η e − η ϱ n η , p z i − z j d η , K i j 13 s , q , p = r j 2 ∑ n = 1 4 ∫ 0 ∞ ∆ 2 n η , p ∆ η , p ϑ 2 n η , p η J 1 r j η J 0 r i η e − η ϱ n η , p z i − z j d η , K i j 14 s , q , p = r j 2 ∑ n = 1 4 ∫ 0 ∞ ∆ 3 n η , p ∆ η , p ϑ 2 n η , p η J 1 r j η J 0 r i η e − η ϱ n η , p z i − z j d η , K i j 21 s , q , p = − r j s g n z i − z j 2 ∑ n = 1 4 ∫ 0 ∞ ∆ 1 n η , p ∆ η , p ϑ 3 n η , p e − η ϱ n η , p z i − z j η J 1 r i η J 1 r j η d η , K i j 22 s , q , p = − r j 3 12 ∑ n = 1 4 ∫ 0 ∞ Λ n η , p Λ η , p ϑ 3 n η , p e − η ϱ n η , p z i − z j η 3 J 1 r i η   1 F 2 ⁡ 3 2 ; 2 , 5 2 ; − 1 4 r j 2 η 2 d η , K i j 23 s , q , p = − r j s g n z i − z j 2 ∆ ∑ n = 1 4 ∫ 0 ∞ ∆ 2 n η , p ∆ η , p ϑ 3 n η , p e − η ϱ n η , p z i − z j η J 1 r i η J 1 r j η d η , K i j 24 s , q , p = − r j s g n z i − z j 2 ∆ ∑ n = 1 4 ∫ 0 ∞ ∆ 3 n η , p ∆ η , p ϑ 3 n η , p e − η ϱ n η , p z i − z j η J 1 r i η J 1 r j η d η , K i j 31 s , q , p = r j 2 ∑ n = 1 4 ∫ 0 ∞ ∆ 1 n η , p ∆ η , p ϑ 4 n η , p e − η ϱ n η , p z i − z j η J 0 r i η J 1 r j η d η , K i j 32 s , q , p = r j 3 s g n ( z i − z j ) 12 ∑ n = 1 4 ∫ 0 ∞ Λ n η , p Λ η , p ϑ 4 n η , p e − η ϱ n z i − z j η 3 J 0 r i η   1 F 2 ⁡ 3 2 ; 2 , 5 2 ; − 1 4 r j 2 η 2 d η , K i j 33 s , q , p = r j 2 ∑ n = 1 4 ∫ 0 ∞ ∆ 2 n η , p ∆ η , p ϑ 4 n η , p e − η ϱ n η , p z i − z j η J 0 r i η J 1 r j η d η , K i j 34 s , q , p = r j 2 ∑ n = 1 4 ∫ 0 ∞ ∆ 3 n η , p ∆ η , p ϑ 4 n η , p e − η ϱ n η , p z i − z j η J 0 r i η J 1 r j η d η , K i j 41 s , q , p = r j 2 ∑ n = 1 4 ∫ 0 ∞ ∆ 1 n η , p ∆ η , p ϑ 5 n η , p e − η ϱ n η , p z i − z j η J 0 r i η J 1 r j η d η , K i j 42 s , q , p = r j 3 s g n ( z i − z j ) 12 ∑ n = 1 4 ∫ 0 ∞ Λ n η , p Λ η , p ϑ 5 n η , p e − η ϱ n z i − z j η 3 J 0 r i η   1 F 2 ⁡ 3 2 ; 2 , 5 2 ; − 1 4 r j 2 η 2 d η , K i j 43 s , q , p = r j 2 ∑ n = 1 4 ∫ 0 ∞ ∆ 2 n η , p ∆ η , p ϑ 5 n η , p e − η ϱ n η , p z i − z j η J 0 r i η J 1 r j η d η , K i j 44 s , q , p = r j 2 ∑ n = 1 4 ∫ 0 ∞ ∆ 3 n η , p ∆ η , p ϑ 5 n η , p e − η ϱ n η , p z i − z j η J 0 r i η J 1 r j η d η .

References

  1. Van Run AM, J.G.; Terrell, D.R.; Scholing, J.H. An in situ grown eutectic magnetoelectric composite material. Journal of Materials Science 1974, 9, 1710–1714. [Google Scholar] [CrossRef]
  2. Van den Boomgaard, J.; Terrell, D.R.; Born RA, J.; Giller HF, J.I. An in situ grown eutectic magnetoelectric composite material. Journal of Materials Science 1974, 9, 1705–1709. [Google Scholar] [CrossRef]
  3. Avellaneda, M.; Harshé, G. Magnetoelectric effect in piezoelectric/magnetostrictive multilayer (2-2) composites. Journal of Intelligent Material Systems and Structures 1994, 5, 501–513. [Google Scholar] [CrossRef]
  4. Achenbach, J.D. Quantitative nondestructive evaluation. International Journal of Solids and Structures 2000, 37, 13–27. [Google Scholar] [CrossRef]
  5. Priya, S.; Islam, R.; Dong, S.; Viehland, D. Recent advancements in magnetoelectric particulate and laminate composites. Journal of Electroceramics 2007, 19, 149–166. [Google Scholar] [CrossRef]
  6. Wang, B.L.; Sun, Y.G.; Zhang, H.Y. Analysis of a penny-shaped crack in magnetoelectroelastic materials. Journal of Applied Physics 2008, 103, 083530. [Google Scholar] [CrossRef]
  7. Zhao, M.; Fan, C.; Yang, F.; Liu, T. Analysis method of planar cracks of arbitrary shape in the isotropic plane of a three-dimensional transversely isotropic magnetoelectroelastic medium. International Journal of Solids and Structures 2007, 44, 4505–4523. [Google Scholar] [CrossRef]
  8. Zhong, X.C.; Li, X.F. Magnetoelectroelastic analysis for an opening crack in a piezoelectromagnetic solid. European Journal of Mechanics-A/Solids 2007, 26, 405–417. [Google Scholar] [CrossRef]
  9. Hu, K.Q.; Li, G.Q. Electro-magneto-elastic analysis of a piezoelectromagnetic strip with a finite crack under longitudinal shear. Mechanics of Materials 2005, 37, 925–934. [Google Scholar] [CrossRef]
  10. Tian, W.Y.; Rajapakse, R.K.N.D. Fracture analysis of magnetoelectroelastic solids by using path independent integrals. International Journal of Fracture 2005, 131, 311–335. [Google Scholar] [CrossRef]
  11. Gao, C.F.; Tong, P.; Zhang, T.Y. Fracture mechanics for a mode III crack in a magnetoelectroelastic solid. International Journal of Solids and Structures 2004, 41, 6613–6629. [Google Scholar] [CrossRef]
  12. Sih, G.C.; Jones, R.; Song, Z.F. Piezomagnetic and piezoelectric poling effects on mode I and II crack initiation behavior of magnetoelectroelastic materials. Theoretical and Applied Fracture Mechanics 2003, 40, 161–186. [Google Scholar] [CrossRef]
  13. Jinxi, L.; Xianglin, L.; Yongbin, Z. Green's functions for anisotropic magnetoelectroelastic solids with an elliptical cavity or a crack. International Journal of Engineering Science 2001, 39, 1405–1418. [Google Scholar] [CrossRef]
  14. Li, X.F. Dynamic analysis of a cracked magnetoelectroelastic medium under antiplane mechanical and inplane electric and magnetic impacts. International Journal of Solids and Structures 2005, 42, 3185–3205. [Google Scholar] [CrossRef]
  15. Hu, K.; Li, G. Constant moving crack in a magnetoelectroelastic material under anti-plane shear loading. International Journal of Solids and Structures 2005, 42, 2823–2835. [Google Scholar] [CrossRef]
  16. Zhou, Z.G.; Wu, L.Z.; Wang, B. The dynamic behavior of two collinear interface cracks in magneto-electro-elastic materials. European Journal of Mechanics-A/Solids 2005, 24, 253–262. [Google Scholar] [CrossRef]
  17. Zhang, P.W.; Zhou, Z.G.; Wang, B. Dynamic behavior of two collinear interface cracks between two dissimilar functionally graded piezoelectric/piezomagnetic material strips. Applied Mathematics and Mechanics 2007, 28, 615–625. [Google Scholar] [CrossRef]
  18. Su RK, L.; Feng, W.J.; Liu, J. Transient response of interface cracks between dissimilar magneto-electro-elastic strips under out-of-plane mechanical and in-plane magneto-electrical impact loads. Composite structures 2007, 78, 119–128. [Google Scholar]
  19. Feng, W.J.; Pan, E. Dynamic fracture behavior of an internal interfacial crack between two dissimilar magneto-electro-elastic plates. Engineering Fracture Mechanics 2008, 75, 1468–1487. [Google Scholar] [CrossRef]
  20. Liang, J. The dynamic behavior of two parallel symmetric cracks in functionally graded piezoelectric/piezomagnetic materials. Archive of Applied Mechanics 2008, 78, 443–464. [Google Scholar] [CrossRef]
  21. Sladek, J.; Sladek, V.; Solek, P.; Pan, E. Fracture analysis of cracks in magneto-electro-elastic solids by the MLPG. Computational Mechanics 2008, 42, 697–714. [Google Scholar] [CrossRef]
  22. Feng, W.J.; Li, Y.S.; Xu, Z.H. Transient response of an interfacial crack between dissimilar magnetoelectroelastic layers under magnetoelectromechanical impact loadings: mode-I problem. International Journal of Solids and Structures 2009, 46, 3346–3356. [Google Scholar] [CrossRef]
  23. Zhong, X.C.; Zhang, K.S. Dynamic analysis of a penny-shaped dielectric crack in a magnetoelectroelastic solid under impacts. European Journal of Mechanics-A/Solids 2010, 29, 242–252. [Google Scholar] [CrossRef]
  24. Zhong, X.C.; Liu, F.; Li, X.F. Transient response of a magnetoelectroelastic solid with two collinear dielectric cracks under impacts. International Journal of Solids and Structures 2009, 46, 2950–2958. [Google Scholar] [CrossRef]
  25. Feng, W.J.; Pan, E.; Wang, X. Dynamic fracture analysis of a penny-shaped crack in a magnetoelectroelastic layer. International Journal of Solids and Structures 2007, 44, 7955–7974. [Google Scholar] [CrossRef]
  26. Zhong, X.C.; Li, X.F.; Lee, K.Y. Transient response of a cracked magnetoelectric material under the action of in-plane sudden impacts. Computational Materials Science 2009, 45, 905–911. [Google Scholar] [CrossRef]
  27. Wang, B.L.; Han, J.C.; Du, S.Y. Transient fracture of a layered magnetoelectroelastic medium. Mechanics of Materials 2010, 42, 354–364. [Google Scholar] [CrossRef]
  28. Li, Y.D.; Lee, K.Y. Collinear unequal crack series in magnetoelectroelastic materials: mode I case solved via new real fundamental solutions. Engineering Fracture Mechanics 2010, 77, 2772–2790. [Google Scholar] [CrossRef]
  29. Wünsche, M.; Sáez, A.; García-Sánchez, F.; Zhang, C. Transient dynamic crack analysis in linear magnetoelectroelastic solids by a hypersingular time-domain BEM. European Journal of Mechanics-A/Solids 2012, 32, 118–130. [Google Scholar] [CrossRef]
  30. Athanasius, L.; Ang, W.T. Magnetoelectroelastodynamic interaction of multiple arbitrarily oriented planar cracks. Applied Mathematical Modelling 2013, 37, 6979–6993. [Google Scholar] [CrossRef]
  31. Li, Y.S.; Ren, J.H.; Feng, W.J.; Wang, W. Dynamic fracture analysis of an annular interfacial crack between dissimilar magnetoelectroelastic layers. Archive of Applied Mechanics 2013, 83, 151–170. [Google Scholar] [CrossRef]
  32. Li, Y.S.; Liu, L.B.; Meng, W.Q.; Cai, Z.Y. Interfacial penny-shaped crack between magnetoelectroelastic thin film and elastic substrate. International Journal of Applied Electromagnetics and Mechanics 2013, 42, 501–517. [Google Scholar] [CrossRef]
  33. Lei, J.; Zhang, C.; Bui, T.Q. Transient dynamic interface crack analysis in magnetoelectroelastic bi-materials by a time-domain BEM. European Journal of Mechanics-A/Solids 2015, 49, 146–157. [Google Scholar] [CrossRef]
  34. Xiao, J.; Xu, Y.; Zhang, F. Fracture analysis of magnetoelectroelastic solid weakened by periodic cracks and line inclusions. Engineering Fracture Mechanics 2019, 205, 70–80. [Google Scholar] [CrossRef]
  35. Hills, D.A.; Kelly, P.A.; Dai, D.N.; Korsunsky, A.M. Solution of crack problems: the distributed dislocation technique; Springer Science & Business Media, 2013; Volume 44. [Google Scholar]
  36. Stehfest, H. Algorithm 368: Numerical inversion of Laplace transforms [D5]. Communications of the ACM 1970, 13, 47–49. [Google Scholar] [CrossRef]
  37. Wang, B.L.; Mai, Y.W. Applicability of the crack-face electromagnetic boundary conditions for fracture of magnetoelectroelastic materials. International journal of solids and structures 2007, 44, 387–398. [Google Scholar] [CrossRef]
  38. Zhang, T.Y.; Zhao, M.; Tong, P. Fracture of piezoelectric ceramics. In Advances in applied mechanics; Elsevier, 2002; Volume 38, pp. 289. [Google Scholar]
  39. Pourseifi, M.; Faal, R.T.; Asadi, E. Axisymmetric planar cracks in finite hollow cylinders of transversely isotropic material: part I—dislocation solution for infinite cylinders. Journal of Applied Mathematics and Physics 2017, 68, 74. [Google Scholar] [CrossRef]
  40. Pourseifi, M.; Faal, R.T. Tension analysis of infinite solid circular cylinders with arbitrary located axisymmetric cracks. Theoretical and Applied Fracture Mechanics 2015, 80, 182–192. [Google Scholar] [CrossRef]
  41. Pourseifi, M.; Faal, R.T.; Asadi, E. Axisymmetric planar cracks in finite hollow cylinders of transversely isotropic material: part I—dislocation solution for infinite cylinders. Zeitschrift für angewandte Mathematik und Physik 2017, 68. [Google Scholar] [CrossRef]
  42. Pourseifi, M.; Faal, R.T.; Asadi, E. Axisymmetric planar cracks in finite hollow cylinders of transversely isotropic material: Part II—cutting method for finite cylinders. Zeitschrift für angewandte Mathematik und Physik 2017, 68. [Google Scholar] [CrossRef]
  43. Weertman, J. Dislocation based fracture mechanics; World Scientific Publishing Company, 1996. [Google Scholar]
  44. Monfared, M.M.; Pourseifi, M.; Bagheri, R. Computation of mixed mode stress intensity factors for multiple axisymmetric cracks in an FGM medium under transient loading. International Journal of Solids and Structures 2019, 158, 220–231. [Google Scholar] [CrossRef]
  45. Faal, R.T.; Fariborz, S.J.; Daghyani, H.R. Antiplane deformation of orthotropic strips with multiple defects. Journal of Mechanics of Materials and Structures 2006, 1, 1097–1114. [Google Scholar] [CrossRef]
  46. Vahdati, A.; Salehi, M.; Vahabi, M.; Fesharaki, J.J.; Ghassemi, A. Fracture analysis of piezoelectromagnetic medium with axisymmetric cracks. Theoretical and Applied Fracture Mechanics 2019, 104, 102337. [Google Scholar] [CrossRef]
  47. Zhou, Z.G.; Wu, L.Z.; Wang, B. A closed form solution of a crack in magneto-electro-elastic composites under anti-plane shear stress loading. JSME International Journal Series A Solid Mechanics and Material Engineering 2005, 48, 151–154. [Google Scholar] [CrossRef]
  48. Zhang, P.W.; Zhou, Z.G.; Wu, L.Z. Coupled field state around three parallel non-symmetric cracks in a piezoelectric/piezomagnetic material plane. Archive of Applied Mechanics 2009, 79, 965–979. [Google Scholar] [CrossRef]
  49. Zhong, X.C.; Li, X.F. Magnetoelectroelastic analysis for an opening crack in a piezoelectromagnetic solid. European Journal of Mechanics-A/Solids 2007, 26, 405–417. [Google Scholar] [CrossRef]
Preprints 97457 g001
Figure 1. A transversely isotropic piezoelectromagnetic medium with axisymmetric planar cracks (penny-shaped crack and annular crack) subjected to transient in-plane magneto-electro-mechanical loading.
Figure 1. A transversely isotropic piezoelectromagnetic medium with axisymmetric planar cracks (penny-shaped crack and annular crack) subjected to transient in-plane magneto-electro-mechanical loading.
Preprints 97457 g001
Preprints 97457 g002
Figure 2. Variation of K I ( t ) / K I 0 versus C T t / l for magnetoelectrically impermeable and permeable penny-shaped crack with λ D = 1 and λ B = 1 .
Figure 2. Variation of K I ( t ) / K I 0 versus C T t / l for magnetoelectrically impermeable and permeable penny-shaped crack with λ D = 1 and λ B = 1 .
Preprints 97457 g002
Preprints 97457 g003
Figure 3. Variation of K I ( t ) / K I 0 versus C T t / l for magnetoelectrically impermeable penny-shaped crack under different magneto-electro-mechanical coupling factors.
Figure 3. Variation of K I ( t ) / K I 0 versus C T t / l for magnetoelectrically impermeable penny-shaped crack under different magneto-electro-mechanical coupling factors.
Preprints 97457 g003
Preprints 97457 g004
Figure 4. Variation of K D ( t ) / K D 0 versus C T t / l for magnetoelectrically impermeable penny-shaped crack under different magneto-electro-mechanical coupling factors.
Figure 4. Variation of K D ( t ) / K D 0 versus C T t / l for magnetoelectrically impermeable penny-shaped crack under different magneto-electro-mechanical coupling factors.
Preprints 97457 g004
Preprints 97457 g005
Figure 5. Variation of K B ( t ) / K B 0 versus C T t / l for magnetoelectrically impermeable penny-shaped crack under different magneto-electro-mechanical coupling factors.
Figure 5. Variation of K B ( t ) / K B 0 versus C T t / l for magnetoelectrically impermeable penny-shaped crack under different magneto-electro-mechanical coupling factors.
Preprints 97457 g005
Preprints 97457 g006
Figure 6. Variation of K I L ( t ) / K I 0 versus C T t / l for magnetoelectrically impermeable and permeable annular crack with λ D = 1 and λ B = 1 .
Figure 6. Variation of K I L ( t ) / K I 0 versus C T t / l for magnetoelectrically impermeable and permeable annular crack with λ D = 1 and λ B = 1 .
Preprints 97457 g006
Preprints 97457 g007
Figure 7. Variation of K I R ( t ) / K I 0 versus C T t / l for magnetoelectrically impermeable and permeable annular crack with λ D = 1 and λ B = 1 .
Figure 7. Variation of K I R ( t ) / K I 0 versus C T t / l for magnetoelectrically impermeable and permeable annular crack with λ D = 1 and λ B = 1 .
Preprints 97457 g007
Preprints 97457 g008
Figure 8. Variation of K I L ( t ) / K I 0 versus C T t / l for magnetoelectrically impermeable annular crack under different magneto-electro-mechanical coupling factors.
Figure 8. Variation of K I L ( t ) / K I 0 versus C T t / l for magnetoelectrically impermeable annular crack under different magneto-electro-mechanical coupling factors.
Preprints 97457 g008
Preprints 97457 g012
Figure 12. Variation of K I ( t ) / K I 0 versus C T t / l for magnetoelectrically impermeable two non-planar identical penny-shaped cracks with λ D = 1 and λ B = 1 .
Figure 12. Variation of K I ( t ) / K I 0 versus C T t / l for magnetoelectrically impermeable two non-planar identical penny-shaped cracks with λ D = 1 and λ B = 1 .
Preprints 97457 g012
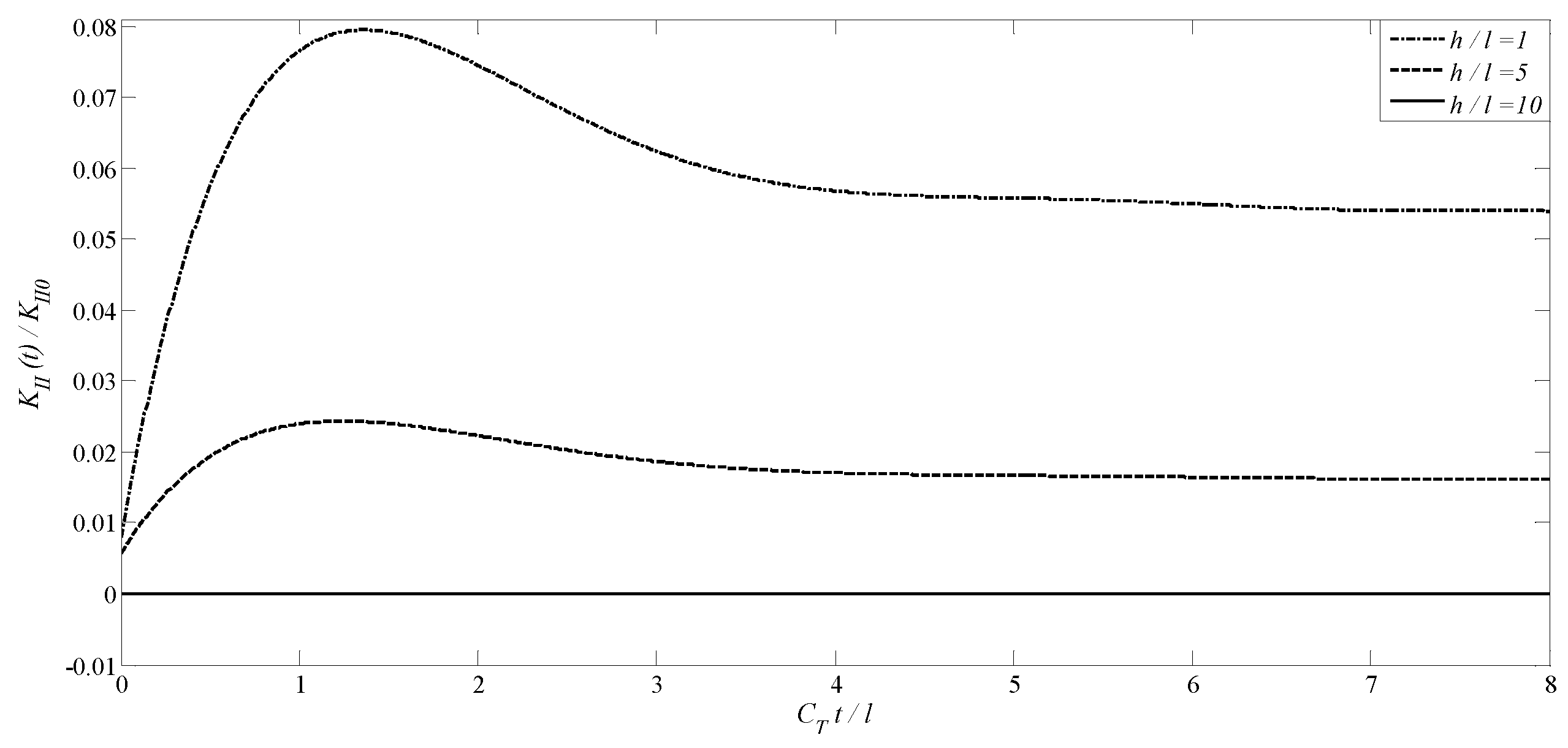
Preprints 97457 g013
Figure 13. Variation of K I I ( t ) / K I I 0 versus C T t / l for magnetoelectrically impermeable two non-planar identical penny-shaped cracks with λ D = 1 and λ B = 1 .
Figure 13. Variation of K I I ( t ) / K I I 0 versus C T t / l for magnetoelectrically impermeable two non-planar identical penny-shaped cracks with λ D = 1 and λ B = 1 .
Preprints 97457 g013
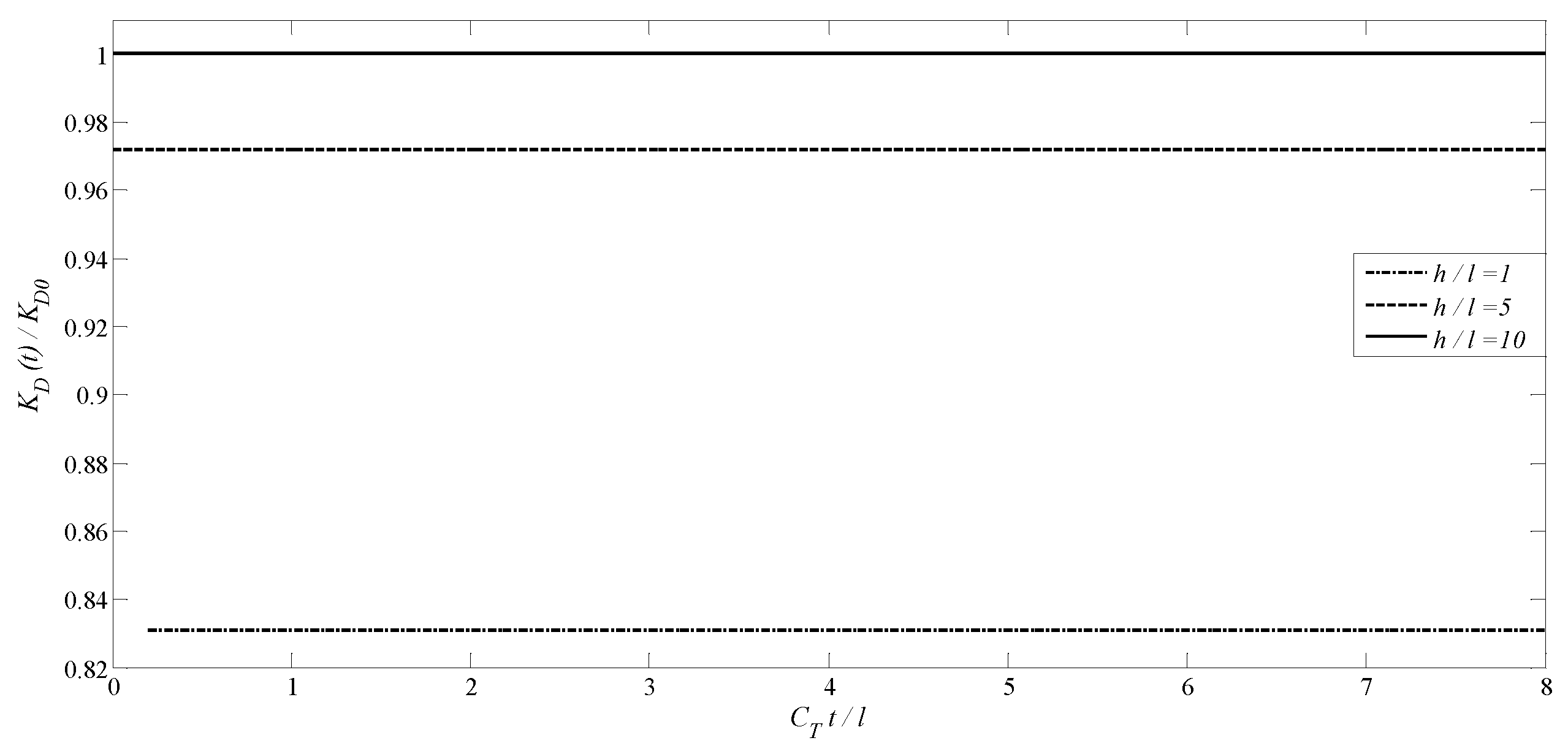
Preprints 97457 g014
Figure 14. Variation of K D ( t ) / K D 0 versus C T t / l for magnetoelectrically impermeable two non-planar identical penny-shaped cracks with λ D = 1 and λ B = 1 .
Figure 14. Variation of K D ( t ) / K D 0 versus C T t / l for magnetoelectrically impermeable two non-planar identical penny-shaped cracks with λ D = 1 and λ B = 1 .
Preprints 97457 g014
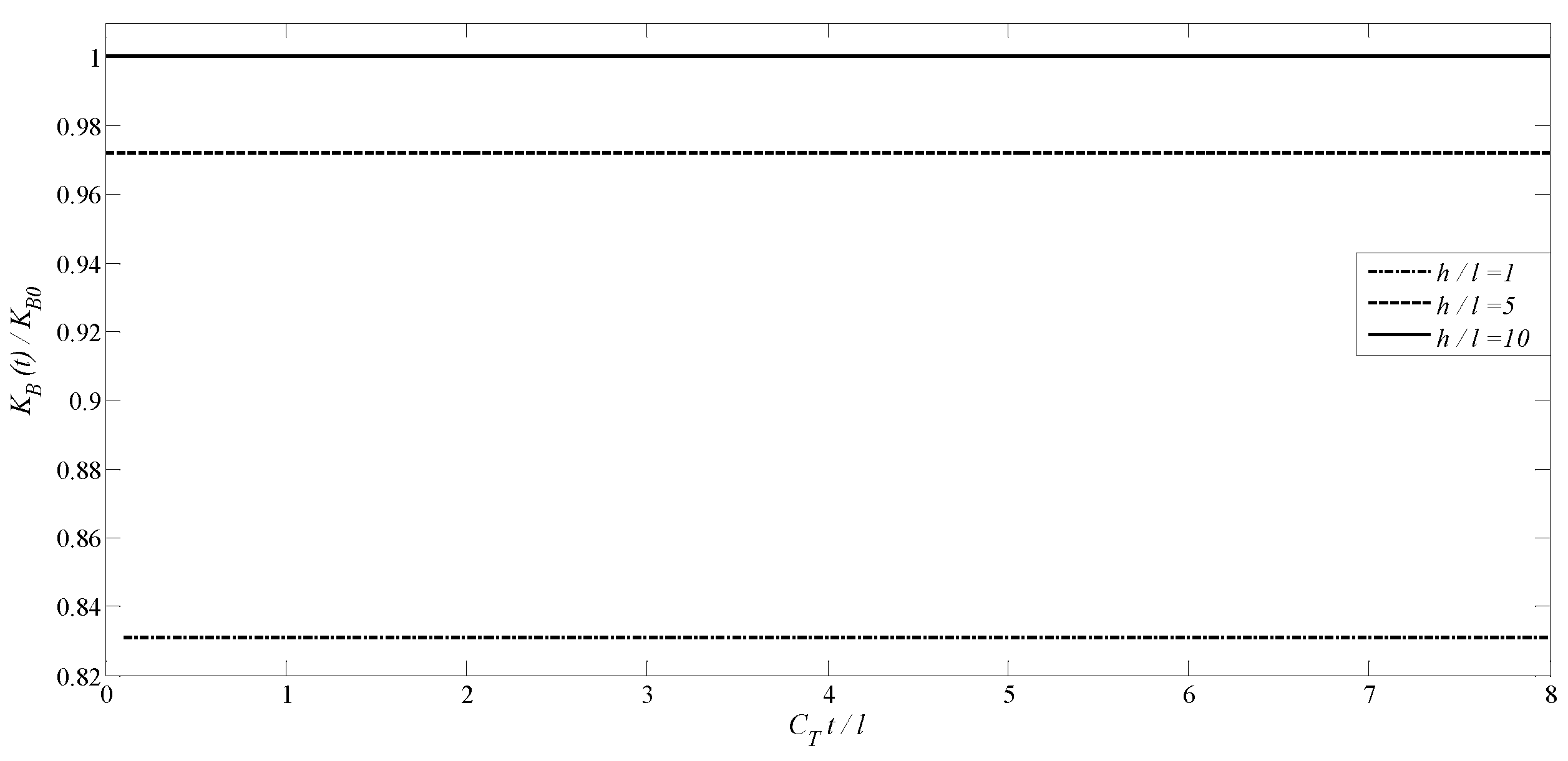
Preprints 97457 g015
Figure 15. Variation of K B ( t ) / K B 0 versus C T t / l for magnetoelectrically impermeable two non-planar identical penny-shaped cracks with λ D = 1 and λ B = 1 .
Figure 15. Variation of K B ( t ) / K B 0 versus C T t / l for magnetoelectrically impermeable two non-planar identical penny-shaped cracks with λ D = 1 and λ B = 1 .
Preprints 97457 g015
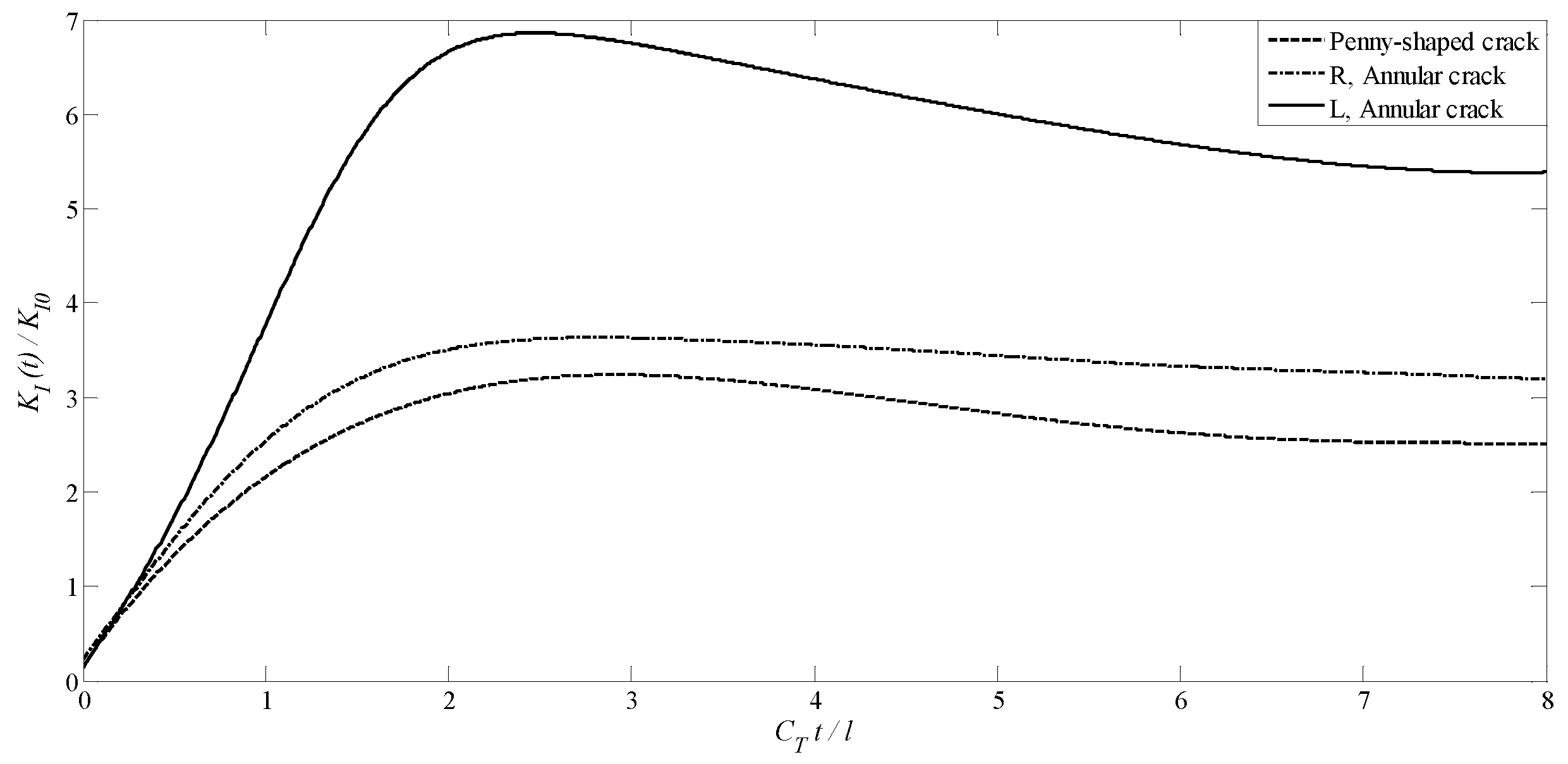
Preprints 97457 g016
Figure 16. Variation of K I ( t ) / K I 0 versus C T t / l for magnetoelectrically impermeable a penny-shaped crack engulfed by an annular crack with λ D = 1 and λ B = 1 .
Figure 16. Variation of K I ( t ) / K I 0 versus C T t / l for magnetoelectrically impermeable a penny-shaped crack engulfed by an annular crack with λ D = 1 and λ B = 1 .
Preprints 97457 g016
Preprints 97457 g017
Figure 17. Variation of K D ( t ) / K D 0 versus C T t / l for magnetoelectrically impermeable a penny-shaped crack engulfed by an annular crack with λ D = 1 and λ B = 1 .
Figure 17. Variation of K D ( t ) / K D 0 versus C T t / l for magnetoelectrically impermeable a penny-shaped crack engulfed by an annular crack with λ D = 1 and λ B = 1 .
Preprints 97457 g017
Preprints 97457 g018
Figure 18. Variation of K B ( t ) / K B 0 versus C T t / l for magnetoelectrically impermeable a penny-shaped crack engulfed by an annular crack with λ D = 1 and λ B = 1 .
Figure 18. Variation of K B ( t ) / K B 0 versus C T t / l for magnetoelectrically impermeable a penny-shaped crack engulfed by an annular crack with λ D = 1 and λ B = 1 .
Preprints 97457 g018
Table 1. Material properties of BaTiO3–CoFe2O4 based on [47].
Table 1. Material properties of BaTiO3–CoFe2O4 based on [47].
c 11 = 22.6 E 10 N m − 2 ,         c 13 = 12.4 E 10 N m − 2 ,         c 33 = 21.6 E 10 N m − 2 ,         c 44 = 4.4 E 10 N m − 2 ,
d 11 = 5.64 E − 9 C 2 N − 1 m − 2 ,   d 33 = 6.35 E − 9 C 2 N − 1 m − 2 ,
γ 11 = 297 E − 6 N s 2 C − 2 ,   γ 33 = 83.5 E − 6 N s 2 C − 2 ,
e 31 = − 2.2 C m − 2 ,   e 33 = 9.3 C m − 2 ,   e 15 = 5.8 C m − 2 ,
α 31 = 290.2 N A − 1 m − 1 ,   α 33 = 350 N A − 1 m − 1 ,   α 15 = 275 N A − 1 m − 1 ,
β 11 = 5.367 E − 12 N s V − 1 C − 1 ,   β 33 = 2737.5 E − 12 N s V − 1 C − 1 .
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated