Information Geometric Analysis of the Dynamics of M/M/∞ Transient Queue Manifold

Dr Ismail A Mageed

doi:10.20944/preprints202401.1994.v1

Preprint

Article

This version is not peer-reviewed.

Dr Ismail A Mageed^*

This version is not peer-reviewed.

Altmetrics

Downloads

100

Views

Comments

Submitted:

27 January 2024

Posted:

29 January 2024

You are already at the latest version

Abstract

From a differential geometric perspective, information geometry (IG) aims to characterise the structure of statistical geodesic models. The research done for this paper offers a novel method for modelling the information geometry of a queuing system. From the perspective of IG, the manifold of the transient M/M/infinity queue is described in this context. The Fisher Information matrix (FIM) as well as the inverse of (FIM), (IFIM) of transient M/M/infinity QM are devised. In addition to that, new results that uncovered the significant impact of stability of QM on the existence of (IFIM) are obtained. Moreover, the Geodesic equations of motion of the coordinates of the underlying transient are obtained. Also, it is revealed that stable QM is developable (i.e., has a zero Gaussian curvature) and has a non-zero Ricci Curvature Tensor (RCT). Novel stability dynamics of transient M/M/iInfinity queue manifold is revealed by discovering the mutual dual impact between the behaviour of (RCT) and the stability(instability) phases of M/M/Infinity QM. Furthermore, a new discovery that presents the significant impact of stability of queue manifold and the continuity of the unique representation between M/G/1 queue manifold and Ricci Curvature Tensor (RCT). The information matrix exponential (IME) is devised. Also, it is shown that stability of the devised (IME) enforces the instability of M/M/ Infinity QM. More interestingly, novel relativistic info-geometric queueing theoretic links are revealed .

Keywords:

Subject:

Computer Science and Mathematics - Probability and Statistics

1. Introduction

Numerous study areas, including statistical inference, stochastic control, and neural networks, have extensively used IG (c.f., Mageed et al, 2023). In other words, the goal of IG is to use statistics to apply the methods of differential geometry (DG).

A manifold (c.f., Mageed and Kouvatsos, 2021) is a topological finite dimensional Cartesian space,

R^{n}

, where one has an infinite-dimensional manifold. In Figure 1, the parameter inference

\hat{θ}

of a model from data can be interpreted as a decision-making problem(c.f., Nielsen, 2020).In (Mageed et al, 2023; Mageed and Zhang 2022), the exponential distribution families were investigated with many variations.

In this paper, a study is undertaken of the geometric structure of the stable

M / G / 1

queue manifold (QM). To our knowledge, there is only one research paper (c.f., Nakagawa, 2002), which studied the IG of a stable M/D/1 queues, where a geometric structure was introduced on the set of

M / D / 1

queues by employing the properties of queue length paths. This point of view motivated the novel track of the research of this paper linking IG with information matrix theories towards a new re-interpretation of the transient M/M/

\infty

queue.As far as we are aware, just one study paper (cf. Nakagawa, 2002) has looked at the IG of stable

M / D / 1

queues and added a geometric structure to the collection of these queues by utilising the features of queue length pathways. This point of view served as the motivation for the original research strategy in this study, which connected information matrix theories with IG to create a novel understanding of the transient

M / M / \infty

queue.

In the context of this paper, Ricci curvature (c.f., Nielsen, 2020) evaluates the deviation of the Riemannian metric (RM) from the standard Euclidean metric (EM), and scalar curvature measures the deviation for the volume of a geodesic ball from the volume of a Euclidean ball of the same radius (c.f., Figure 2).

2. Main Definitions

2.1. Main Definition on IG

Definition 2.1.

Statistical Manifold (SM)

We call

M = {p (x; θ) | θ = (θ^{1}, θ^{2}, \dots, θ^{n}) ϵ R^{n}}

a manifold(c.f., Mageed et al 2023) of n-dimensional distribution with coordinate system

(θ^{1}, θ^{2}, \dots, θ^{n})

Definition 2.2.

Potential Function

The potential function

, Ψ (θ)

(c.f., Mageed et al 2023) is the distinguished negative function of the coordinates alone of (

L (x; θ) = l n (p (x; θ))

). Fundamentally,

Ψ (θ)

is the part of

(- L (x; θ))

which only contains

(θ^{1}, θ^{2}, \dots, θ^{n}) .

Definition 2.3.

FIM

FIM (namely, [

g_{i j}

])is given by the Hessian matrix i.e.,

[g_{i j}] = [\frac{\partial^{2}}{\partial θ^{i} \partial θ^{j}} (Ψ (θ))], i, j \in [1,2, 3, \dots, n\}

(2.1)

Definition 2.4.

IFIM

IFIM(namely, [

g^{i j}

]) reads as(Dodson, 2005)

[g^{i j}] = {([g_{i j}]))}^{- 1} = \frac{a d j [g_{i j}]}{∆}, ∆ = \det [g_{i j}]

(2.2)

The corresponding arc length function is:

{(d s)}^{2} = \sum_{i, j = 1}^{n} g_{i j} {(d θ}^{i}) {(d θ}^{j})

(2.3)

Definition 2.5.

α

-Connection

For each

α ϵ R,

the

α

(or

\nabla^{(α)}

)-connection (c.f., Dodson, 2005) is the torsion-free affine connection with components:

Γ_{i j, k}^{(α)} = (\frac{1 - α}{2}) (\partial_{i} \partial_{j} \partial_{k} (Ψ (θ)))

(2.4)

where

Ψ (θ)

is the potential function and

\partial_{i}

\frac{\partial}{\partial θ_{i}}

Definition 2.7.

(1): The geodesic equations of manifold M with coordinate system $θ = (θ_{1}, θ_{2}, . ., θ_{n})$ are defined by (c.f.,Mageed et al 2023)

$\frac{d^{2} θ^{k}}{d t^{2}} + Γ_{i j}^{k (0)} (\frac{d θ^{i}}{d t}) (\frac{d θ^{j}}{d t}) = 0, i, j = 1,2, \dots, n, Γ_{i j}^{k (α)} = Γ_{i j, s}^{(α)} g^{s k}$

(2.5)
(2): The geodesic equations(c.f., Lecture Notes, 2005) that characterize the curves that minimize the length/energy between two arbitrary points on a smooth manifold M.
(3): The total energy (c.f., Malham, 2016) of a path $θ$ = $θ (t)$ , between $t = a$ and $t = b$ , can be defined in terms of a Lagrangian function $L = L (θ, \frac{d θ}{d t}),$ as follows

$E (θ) = \int_{t_{1}}^{t_{2}} L (θ (t), θ^{.} (t)) d t$

(2.6)

The path $θ = θ (t)$ that minimizes the total energy $E = E (θ)$ necessarily satisfies the Euler–Lagrange equations. Here these take the form of Lagrange’s equations of motion:

$\frac{d}{d t} (\frac{\partial^{2} L}{\partial (\frac{d θ_{j}}{d t})}) - \frac{\partial}{\partial θ_{j}} = 0$

(2.7)

for each $j = 1,2, \dots, n .$ In the following, we use $g^{i j}$ (the inverse Fisher Information Matrix, FIM) to denote symmetric positive matrix $g_{i j}$ (Fisher Information Matrix FIM) (where $i, j = 1,2, . ., n$ ) so that:

$\sum_{k = 1}^{n} g^{i k} g_{k j} = δ_{i j} = f (x) = \{\begin{matrix} 1, i = j \\ 0, o t h e r w i s e \end{matrix}$

(2.8)
(4): Lemma (2.7.4)(Geodesic equations). Lagrange’s equations (c.f., Malham, 2016) of motion for the Lagrangian

Lemma 5 (Geodesic equations).

Lagrange’s equations of motion for the Lagrangian

L = L (θ, \frac{d θ}{d t})

(2.9)

are given in local coordinates by the system of ordinary differential equations:

\frac{d^{2} θ_{i}}{d t^{2}} + \sum_{j, k = 1}^{n} Γ_{j, k}^{i} (\frac{d θ_{j}}{d t}) (\frac{d θ_{k}}{d t}) = 0

(2.10)

where the quantities

Γ_{j, k}^{i}

are known as the Christoffel symbols and for

i, j, k = 1,2, . ., n

By the above definition, it is clear that the geodesic equations are interpreted physically as the information geometric equations of motion , shortly (IGEMs), or the relativitstic equations of motion (REMs) , or the Riemannian equations of motion. At this stage, it is important to note that this report is the first time ever which sets ground breaking discovery of the IG analysis of transient queueuing systems in comparison to that of non-time dependent queueing systems, namely IG analysis of stable queueues (c.f., Mageed and Kouvatsos, 2019,2021).

Definition 2.8.

1.Under the

θ

coordinate system, the

α - c u r v a t u r e R i e m a n n i a n

Tensors,

R_{i j k l}^{(α)}

(c.f.,Li, Sun, Tao, and Jiu, 2007) are defined by

R_{i j k l}^{(α)} = [(\partial_{j} Γ_{i k}^{s (α)} - \partial_{i} Γ_{j k}^{s (α)}) g_{s l} + (Γ_{j β, l}^{(α)} Γ_{i k}^{β (α)} - Γ_{i β, l}^{(α)} Γ_{j k}^{β (α)})], i, j, k, l, s, β = 1,2, 3, \dots ., n

(2.11)

where

Γ_{i j}^{k (α)} = Γ_{i j, s}^{(α)} g^{s k}

2. The

α - R i c c i

curvatures (Ricci Tensors)

R_{i k}^{(α)}

are determined by (c.f., Mageed et al 2023)

R_{i k}^{(α)} = R_{i j k l}^{(α)} g^{j l}

(2.12)

3. The

α - s e c t i o n a l c u r v a t u r e s K_{i j i j}^{(α)}

are defined by (c.f., Mageed et al 2023)

K_{i j i j}^{(α)} = \frac{R_{i j i j}^{(α)}}{(g_{i i}) (g_{j j}) - {(g_{i j})}^{2}}, i, j = 1,2, \dots, n

(2.13)

Specifically, if

n = 2,

the

α - s e c t i o n a l c u r v a t u r e K_{1212}^{(α)}

K^{(α)}

is called

α - G a u s s i a n c u r v a t u r e

and is given by(c.f., Mageed et al 2023)

K^{(α)} = \frac{R_{1212}^{(α)}}{d e t (g_{i j})}

(2.14)

4. The Ricci Tensor (c.f., Loveridge, 2016) is simply a contraction of the Riemannian Tensor (c.f.,Mageed et al 2023).

5.The Ricci curvature Tensor (RCT)(c.f., Rudelius, 2012) of an oriented Riemannian Manifold M means the extent to which the volume of a geodesic ball on the surface differs from the volume of a geodesic ball in Euclidean space.

6. The Ricci curvature (RCT) (c.f., Ollivier, 2010) contracts the evolution of volumes under the geodesic flow. When Ricci curvature is positive, then according to the Bonnet Myers theorem (c.f., Ollivier, 2010) the Riemannian manifold is more positively curved than a sphere and the diameter of the manifold is smaller.

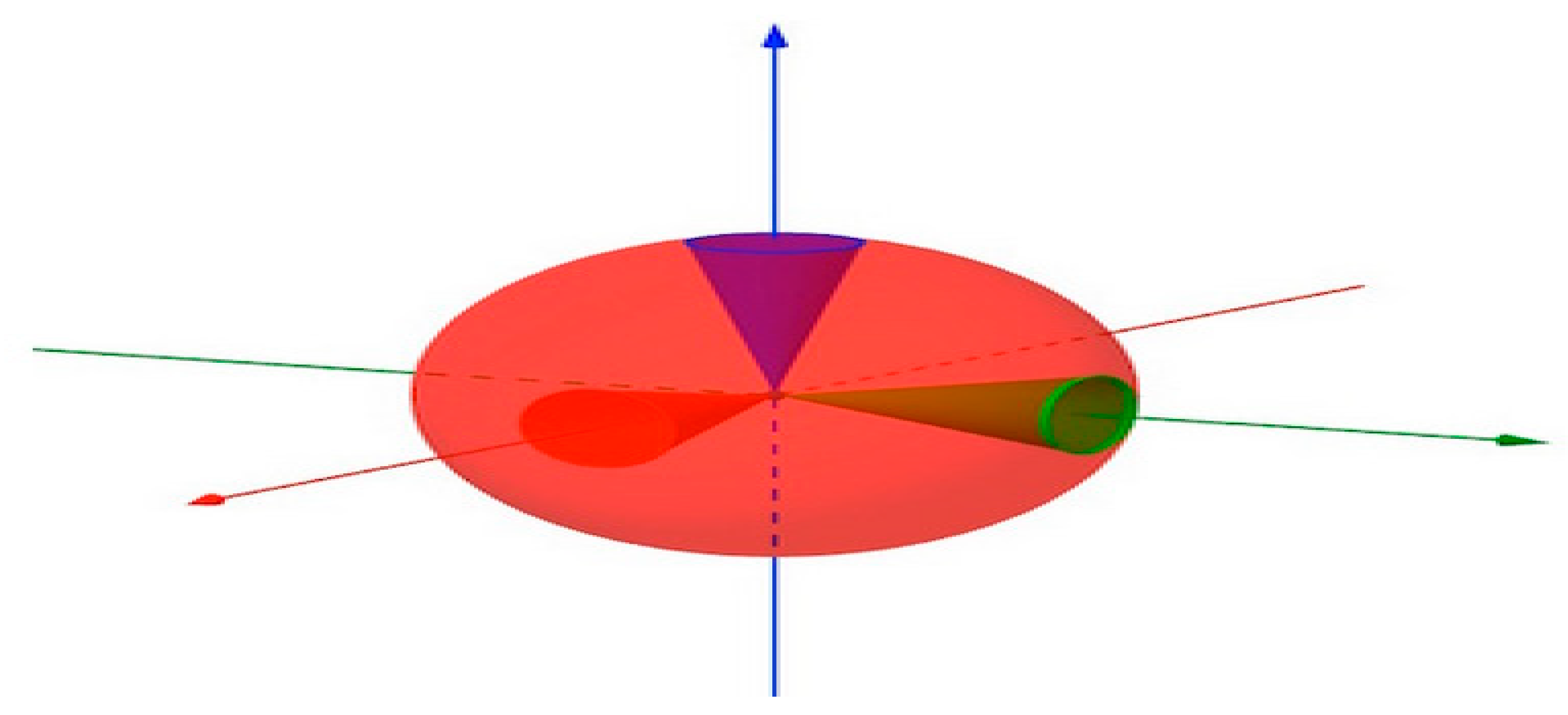
Figure 3. (RCT) describes how conical regions in the manifold differ in volume from the equivalent conical regions in Euclidean space (c.f., Thomas, 2015).

Definition 2.10.

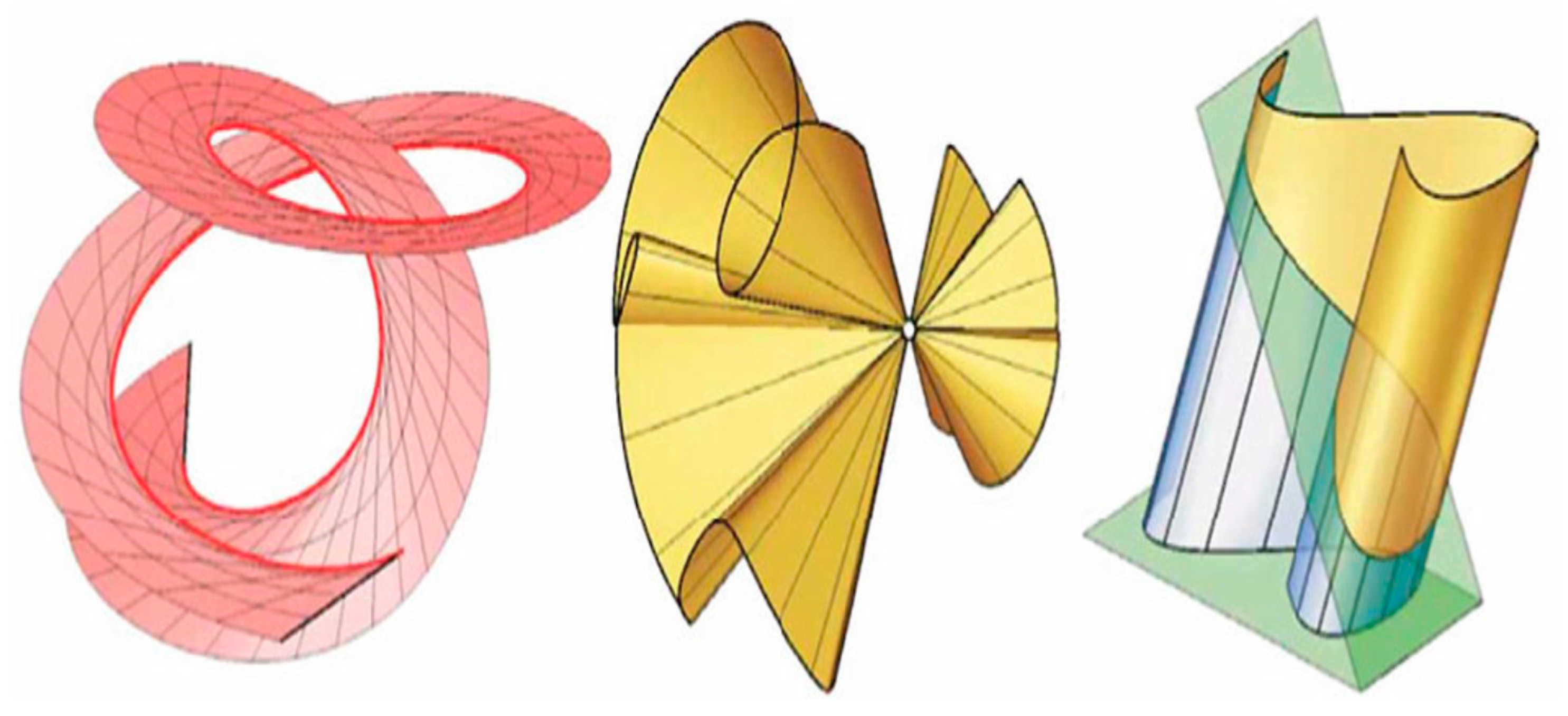
(i) A certain category of ruled surfaces called developable surfaces can be mapped onto a plane surface without causing any deformation to the curves; each curve drawn from such a surface onto the flat plane retains its original shape (c.f., Snezana, 2011).

Figure 4. Three kinds of developable surfaces: Tangential on Figure 5a (on the left), Conical on Figure 5b (on the centre) and Figure 5c (on the right), Cylindrical. Note that curves in bold are directrix or base curves and straight lines in bold are directors or generating lines (curves) (c.f., Snezana, 2011).

Definition 2.12 (c.f., Weisstein, 2013).

1.A function is well-defined if it gives the same result when the representation of the input is changed without changing the value of the input.

Definition 2.13 (c.f., Sankaranarayanan, 2014).

1. function f is said to be one-to-one, or injective, if and only if

f (x) = f (y)

implies

x = y

for all x, y in the domain of

f

. A function is said to be an injection if it is one-to-one. Alternative: A function is one-to-one if and only if

f (x) \neq f (y)

, whenever x ≠ y. This is the contrapositive of the definition.

2.Afunction f from A to B is called onto, or surjective, if and only if for every

b B

there is an element

a A

such that

f (a) = b

. Alternative: all co-domain elements are covered.

3. Afunction f is called a bijection if it is both one-to-one (injection) and onto (surjection).

Preliminary Theorem(PT) 2.15 (Horan and Lavelle, 2005).

Let fbe a function that is defined and differentiable on an open interval (c,d).

(1) If

f^{'} (x) > 0

for all

x \in (c, d)

,then f is increasing on

(c, d) .

(2.15)

(2) If

f^{'} (x) < 0

for all

x \in (c, d)

, then f is decreasing on

(c, d) .

(2.16)

Taylor expansions (c.f., Shaw, 2015) are widely used to approximate functions by expansions. We have for all

x

around zero,

\ln (1 + x) = \sum_{n = 1}^{\infty} {(- 1)}^{n + 1} \frac{x^{n}}{n}

(2.17)

\frac{1}{1 + x} = \sum_{n = 0}^{\infty} {(- 1)}^{n} x^{n}

(2.18)

2.4. Important Inequalities (c.f., Kozma, 2020)

1. Chebyshev inequality

\frac{x}{1 + x} \leq \ln (1 + x) \leq x f o r x \geq - 1

(2.19)

(2.35)can be rewritten as

1 - \frac{1}{x} \leq \ln (x) \leq x - 1 f o r x \geq - 1

(2.20)

2. Lehmer inequality

\frac{x^{n}}{n!} < \frac{x^{n}}{n!} + 1 \leq e^{x} for all x, n > 0

(2.21)

3. The FIM and ITS Inverse for the Transient $M / M / \infty$ QM

In queueing theory, a discipline within the mathematical theory of probability, the

M / M / \infty

queue (c., f., Harrison et al, 1993) is a multi-server queueing model where every arrival experience immediate service and does not wait.

The transient probability of the

M / M / \infty

queueuing system with

P o i s s s o n a r r i v a l r a t e ξ

(c.f., Kumar et al, 2014) and exponentially distributed service time with mean

\frac{1}{ξ}

and arrival rate

λ

is given by:

p_{n} (t) = \frac{{[\frac{λ}{ξ} (1 - e^{- ξ t})]}^{n}}{n!} e x p {- \frac{λ}{ξ} (1 - e^{- ξ t})\}, n = 0,1, 2, \dots .

(3.1)

It has been pointed out by Conolly and Langaris (1993) that one of the best-known Bessel function forms for the time- dependent state probabilities in M/M/1/

\infty q u e u e u i n g

system is given by:

Q_{n} (t) = \frac{e^{- (λ + μ) (t)}}{μ t} {(\frac{λ}{μ})}^{n} \sum_{m = n + 1}^{\infty} m β^{- m} I_{m} (ω t)

(3.2)

Theorem 3.1.

For the transient formalism of M/M/

\infty

queueuing system, we have

(i)

[g_{i j}]

(c.f., (2.1)) reads as

[g_{i j}] = [\begin{matrix} 0 & a & b \\ a & d_{1} & g \\ l & h & r \end{matrix}]

(3.3)

where

a = \frac{1}{ξ^{2}} ([1 + t ξ] e^{- t ξ} - 1)

(3.4)

b = \frac{1}{ξ^{2}} (- ξ^{.} + {ξ e}^{- t ξ} [t ξ^{.} + ξ + ξ^{.}])

(3.5)

d_{1} = \frac{λ}{ξ^{3}} (2 - [1 + t ξ] [t ξ + 2] e^{- t ξ})

(3.6)

g = \frac{1}{ξ^{3}} ([λ^{.} ξ - 2 λ ξ^{.}] + e^{- t ξ} [λ^{.} ξ - 2 λ t ξ ξ^{.} + λ t ξ^{2} - 2 λ {ξ - λ ξ^{2} t^{2} ξ}^{.} - λ t ξ^{3}])

(3.7)

l = \frac{1}{ξ^{2}} (- ξ^{.} + {ξ e}^{- t ξ} [t ξ^{.} + ξ])

(3.8)

h = \frac{(λ^{.} ξ - 2 λ ξ^{.})}{ξ^{3}} [(1 + ξ t) e^{- t ξ} - 1]

(3.9)

r = \frac{1}{ξ^{3}} ((λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 2 λ^{.} ξ ξ^{.} + 2 λ ξ^{. 2}) + e^{- t ξ} [ξ (λ t ξ ξ^{.} + λ t ξ^{. 2} + λ t ξ ξ^{. .} + 3 λ ξ t ξ^{.} + λ^{.} ξ^{2} + λ ξ^{. .} - λ^{. .} ξ) - (ξ [{t ξ}^{.} + ξ] - 2 ξ^{.}) (λ ξ t ξ^{.} + λ ξ^{2} + λ ξ^{.} - λ^{.} ξ)]])

(3.10)

Provided that, . refers to the temporal derivative

\frac{d}{d t}

(iii) IFIM reads as

[g^{i j}] = \frac{a d j [g_{i j}]}{∆} = [\begin{matrix} A & B & L \\ D_{1} & E & F \\ G & H & I \end{matrix}], Δ = d e t ([g_{i j}]) = (- a (l g - a r) + b (a h - l d_{1}))

(3.12)

where

A = \frac{(r d_{1} - g h)}{∆}

(3.13)

B = \frac{(h b - a r)}{∆}

(3.14)

L = \frac{(a g - b d_{1})}{∆}

(3.15)

D_{1} = \frac{(l g - a r)}{∆}

(3.16)

E = \frac{(- l b)}{∆}

(3.17)

F = \frac{(a b)}{∆}

(3.18)

G = \frac{(a h - l d_{1})}{∆}

(3.19)

H = \frac{(l a)}{∆}

(3.20)

I = \frac{(- a^{2})}{∆}

(3.21)

Proof.

(i)Following (3.1), we have:

L (x; θ) = l n (p_{n} (x; θ)) = l n (\frac{{[\frac{λ}{ξ} (1 - e^{- ξ t})]}^{n}}{n!} e x p {- \frac{λ}{ξ} (1 - e^{- ξ t}\}) = l n (\frac{{[\frac{λ}{ξ} (1 - e^{- ξ t})]}^{n}}{n!}) - {\frac{λ}{ξ} (1 - e^{- ξ t}\} θ = {(θ}_{1}, θ_{2}, θ_{3}) = (λ, ξ, t)

(3.22)

Hence, we have

Ψ (θ) = \frac{λ}{ξ} (1 - e^{- ξ t})

(3.23)

Thus,

\partial_{1} = \frac{\partial Ψ}{\partial λ} = \frac{1}{ξ} (1 - e^{- ξ t}), \partial_{2} = \frac{\partial Ψ}{\partial ξ} = \frac{λ}{ξ^{2}} ((1 + ξ t) e^{- ξ t} - 1), \partial_{3} = \frac{\partial Ψ}{\partial t} = \frac{1}{ξ^{2}} ((λ^{.} ξ - λ ξ^{.}) + (λ ξ ξ^{.} t + λ ξ^{2} - λ^{.} ξ + λ ξ^{.}) e^{- ξ t})

(3.24)

\partial_{1} \partial_{1} = 0

(3.25)

\partial_{1} \partial_{2} = \partial_{2} \partial_{1} = \frac{1}{ξ^{2}} ([1 + t ξ] e^{- t ξ} - 1)

(3.26)

\partial_{2} \partial_{2} = \frac{λ}{ξ^{3}} (2 - [1 + t ξ] [t ξ + 2] e^{- t ξ})

(3.27)

\partial_{2} \partial_{3} = \frac{1}{ξ^{3}} ([2 λ ξ^{.} - λ^{.} ξ] + e^{- t ξ} [λ^{.} t ξ^{2} - 2 λ t ξ ξ^{.} + λ t ξ^{2} - λ {ξ - λ ξ^{2} t^{2} ξ}^{.} - λ t ξ^{3} + 2 λ^{.} ξ - 2 λ ξ^{.}])

(3.28)

\partial_{3} \partial_{2} = \frac{(λ^{.} ξ - 2 λ ξ^{.})}{ξ^{3}} [(1 + ξ t) e^{- t ξ} - 1] \neq \partial_{2} \partial_{3}

(3.29)

\partial_{1} \partial_{3} = \frac{1}{ξ^{2}} (- ξ^{.} + {ξ e}^{- t ξ} [t ξ^{.} + ξ + ξ^{.}])

(3.30)

\partial_{3} \partial_{1} = \frac{1}{ξ^{2}} (- ξ^{.} + {ξ e}^{- t ξ} [t ξ^{.} + ξ]) \neq \partial_{1} \partial_{3}

(3.31)

\partial_{3} \partial_{3} = \frac{1}{ξ^{3}} ((λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 2 λ^{.} ξ ξ^{.} + 2 λ ξ^{. 2}) + e^{- t ξ} [ξ (λ t ξ ξ^{.} + λ t ξ^{. 2} + λ t ξ ξ^{. .} + 3 λ ξ t ξ^{.} + λ^{.} ξ^{2} + λ ξ^{. .} - λ^{. .} ξ) - (ξ [{t ξ}^{.} + ξ] - 2 ξ^{.}) (λ ξ t ξ^{.} + λ ξ^{2} + λ ξ^{.} - λ^{.} ξ)]])

(3.32)

Therefore, the Fisher Information Matrix, FIM, is obtained (c.f., (3.3)).

We write IFIM as

[g^{i j}] {= [g_{i j}]}^{- 1} = \frac{a d j [g_{i j}]}{∆} = \frac{T r a n s p o s e (C o v [g_{i j}])}{∆} = \frac{1}{∆} t r a n s p o s e (C o v [\begin{matrix} 0 & a & b \\ a & d_{1} & g \\ l & h & r \end{matrix}])

(3.33)

(C o v [\begin{matrix} 0 & a & b \\ a & d_{1} & g \\ l & h & r \end{matrix}]) = [\begin{matrix} (r d_{1} - g h) & (l g - a r) & (a h - l d_{1}) \\ (h b - a r) & (- l b) & (l a) \\ (a g - {b d}_{1}) & (a b) & (- a^{2}) \end{matrix}]

(3.34)

Thus,

[g^{i j}] = \frac{1}{∆} t r a n s p o s e (C o v [\begin{matrix} (r d_{1} - g h) & (l g - a r) & (a h - l d_{1}) \\ (h b - a r) & (- l b) & (l a) \\ (a g - {b d}_{1}) & (a b) & (- a^{2}) \end{matrix}]) = [\begin{matrix} A & B & L \\ D_{1} & E & F \\ G & H & I \end{matrix}]

(c.f., (3.12)-(3.18))

Notably, the symmetry requirement should hold for FIM. Meanwhile, it is observed that FIM (c.f., (3.3) of Theorem 3.1) is not symmetric, since

\partial_{2} \partial_{3} \neq \partial_{3} \partial_{2}

and

\partial_{1} \partial_{3} \neq \partial_{3} \partial_{1}

. This raises many open problems on such novel phenomenon and shows the significant impact of time as a coordinate in the potential function (c.f., (3.23). it is inevitable to investigate under what conditions will FIM be symmetric. The following theorem answers this question.

Theorem 3.2.

For the transient formalism of M/M/

\infty

queueuing system, as time approaches infinity, FIM (c.f., (3.3) of Theorem 3.1) is symmetric. The converse statement is not always true.

Proof.

It is sufficient to prove that if

t \to \infty

\partial_{2} \partial_{3} = \partial_{3} \partial_{2} and \partial_{1} \partial_{3} = \partial_{3} \partial_{1}

(3.35)

C l e a r l y i f t \to \infty

, it holds that

{l i m}_{t \to \infty} \partial_{2} \partial_{3} = {l i m}_{t \to \infty} \partial_{3} \partial_{2} = \frac{(λ^{.} ξ - 2 λ ξ^{.})}{ξ^{3}} {l i m}_{t \to \infty} \partial_{1} \partial_{3} = {l i m}_{t \to \infty} \partial_{3} \partial_{1} = - \frac{ξ^{.}}{ξ^{2}}

Consequently, the corresponding FIM given by

{[g_{i j}]}_{t \to \infty} = [\begin{matrix} 0 & - \frac{1}{ξ^{2}} & - \frac{ξ^{.}}{ξ^{2}} \\ - \frac{1}{ξ^{2}} & \frac{λ}{ξ^{3}} & \frac{1}{ξ^{3}} (2 λ ξ^{.} - λ^{.} ξ) \\ - \frac{ξ^{.}}{ξ^{2}} & \frac{1}{ξ^{3}} (2 λ ξ^{.} - λ^{.} ξ) & \frac{1}{ξ^{3}} ((λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 2 λ^{.} ξ ξ^{.} + 2 λ ξ^{. 2}) \end{matrix}]

(3.36)

which is symmetric.

To investigate the necessity requirement:

Let

\partial_{2} \partial_{3} = \partial_{3} \partial_{2}

and

\partial_{1} \partial_{3} = \partial_{3} \partial_{1}

. This generates the following two sets of equations:

\frac{1}{ξ^{3}} ([2 λ ξ^{.} - λ^{.} ξ] + e^{- t ξ} [λ^{.} t ξ^{2} - 2 λ t ξ ξ^{.} + λ t ξ^{2} - λ {ξ - λ ξ^{2} t^{2} ξ}^{.} - λ t ξ^{3} + 2 λ^{.} ξ - 2 λ ξ^{.}]) = \frac{(λ^{.} ξ - 2 λ ξ^{.})}{ξ^{3}} [(1 + ξ t) e^{- t ξ} - 1]

(3.37)

and

\frac{1}{ξ^{2}} (- ξ^{.} + {ξ e}^{- t ξ} [t ξ^{.} + ξ + ξ^{.}]) = \frac{1}{ξ^{2}} (- ξ^{.} + {ξ e}^{- t ξ} [t ξ^{.} + ξ])

(3.38)

(3.37) reduces to:

\frac{e^{- t ξ}}{ξ^{3}} [λ^{.} t ξ^{2} - 2 λ t ξ ξ^{.} + λ t ξ^{2} - λ {ξ - λ ξ^{2} t^{2} ξ}^{.} - λ t ξ^{3} + 2 λ^{.} ξ - 2 λ ξ^{.}] = \frac{(λ^{.} ξ - 2 λ ξ^{.})}{ξ^{3}} [(1 + ξ t) e^{- t ξ}]

(3.39)

This implies:

\frac{e^{- t ξ}}{ξ^{3}} = 0

(3.40)

[λ^{.} t ξ^{2} - 2 λ t ξ ξ^{.} + λ t ξ^{2} - λ {ξ - λ ξ^{2} t^{2} ξ}^{.} - λ t ξ^{3} + 2 λ^{.} ξ - 2 λ ξ^{.}] = (λ^{.} ξ - 2 λ ξ^{.})) (1 + ξ t)

(3.41)

Similarly, (3.38) reduces to (3.40) and

ξ [t ξ^{.} + ξ + ξ^{.}] = ξ [t ξ^{.} + ξ]

(3.42)

Clearly, it follows from (3.40),

E i t h e r t \to \infty o r ξ \to \infty

(3.43)

(3.41) generates the following differential equation:

[λ^{.} t ξ^{2} - 2 λ t ξ ξ^{.} + λ t ξ^{2} - λ {ξ - λ ξ^{2} t^{2} ξ}^{.} - λ t ξ^{3} + 2 λ^{.} ξ - 2 λ ξ^{.}] - (λ^{.} ξ - 2 λ ξ^{.})) (1 + ξ t) = 0

(3.44)

It could be verified that

λ = 0

and

ξ = 0

are two solutions of (3.44).

The reader can check that (3.42) reduces to

ξ [t ξ^{.} + ξ + ξ^{.}] = ξ [t ξ^{.} + ξ], o r ξ ξ^{.} = 0

(3.45)

It could be verified that

ξ = c o n s t a n t

is the closed form solution of (3.45). Proof completed.

Theorem 3.2.

For the transient formalism of M/M/

\infty

queueuing system, as time approaches infinity,

{[g^{i j}]}_{t \to \infty}

(c.f., (3.12) of Theorem 3.1) does not exist if and only if one of following requirements is satisfied:

ξ \to \infty

(3.46)

or whenever

λ, ξ

are solutions of the following differential equation:

[λ ξ ξ^{. .} + 2 λ ξ^{. 2} - λ^{. .} ξ^{2}] = 0

(3.47)

Proof.

Following Matrix Algebra,

{[g^{i j}]}_{t \to \infty}

does not exist if and only if

{Δ [g_{i j}]}_{t \to \infty} = 0, {[g_{i j}]}_{t \to \infty} (c . f ., (3.36)) .

Therefore,

{[g^{i j}]}_{t \to \infty}

will never exist if and only if

\frac{1}{ξ^{2}}

[

\frac{1}{ξ^{3}} ((λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 2 λ^{.} ξ ξ^{.} + 2 λ ξ^{. 2}) (- \frac{1}{ξ^{2}}) + \frac{1}{ξ^{3}} (2 λ ξ^{.} - λ^{.} ξ) (\frac{ξ^{.}}{ξ^{2}})] - \frac{ξ^{.}}{ξ^{2}} [\frac{λ}{ξ^{3}} (\frac{ξ^{.}}{ξ^{2}}) - \frac{1}{ξ^{3}} (2 λ ξ^{.} - λ^{.} ξ) (\frac{1}{ξ^{2}})]

=0, equivalently

\frac{1}{ξ^{7}} [λ ξ ξ^{. .} + 2 λ ξ^{. 2} - λ^{. .} ξ^{2}] = 0

(3.48)

H e n c e, {Δ [g_{i j}]}_{t \to \infty} = 0

if and only if

\frac{1}{ξ^{7}} = 0

(3.49)

[λ ξ ξ^{. .} + 2 λ ξ^{. 2} - λ^{. .} ξ^{2}] = 0

(c.f., (3.47))

Clearly, (3.49) implies

ξ \to \infty

(c.f., (3.46)).

It could be verified that

λ = 0

and

ξ = 0

are two solutions of (3.47).Moreover

ξ = 1

in (3.47) implies

λ^{. .} = 0, w h i c h h a s t h e c l o s e d f o r m s o l u t i o n, λ = c_{1} + c_{2} t

, a family of families of temporal straight lines. As time reaches infinity, the arrival rate in this case becomes infinite. This completes the proof.

In the following section, the components of

α

(or

\nabla^{(α)}

)- connection are obtained and it will be shown that the algebraic structure of this connection is no longer symmetric as in the non-time dependent case. This unexpected phenomenon is justified by strong impact of the time coordinate relating to the time-dependency. Also, it is shown that for sufficiently large temporal values(i.e.,

t \to \infty

), the generated special case of

α

(or

\nabla^{(α)}

)- connection is symmetric. All these genuine contributions are new to the knowledge to both information geometry and queueing theorists. These calculated expressions are needed to obtain the corresponding Geodesic Equations (GEs) of the parametric coordinates of

M / M / \infty

QM.

4. Theα(. OR $\nabla^{(α)}$ )-Connection of the Transient $M / M / \infty$ QM

4.1. The obtained $Γ_{i j, k}^{(α)}$ expressions (c.f., definition (2.5)) of the transient $M / M / \infty$ QM

By definition (2.5), the reader can check that:

Γ_{11,1}^{(α)} = 0 = Γ_{11,2}^{(α)} = Γ_{12,1}^{(α)} = Γ_{21,1}^{(α)} = Γ_{31,1}^{(α)}

(4.1)

Γ_{11,3}^{(α)} = 0

(4.2)

Γ_{13,1}^{(α)} = 0 = Γ_{11,3}^{(α)}

(4.3)

Γ_{13,2}^{(α)} = \frac{(1 - α) ξ^{.}}{ξ^{3}} [1 - (1 + ξ t) e^{- t ξ}]

(4.4)

Γ_{12,3}^{(α)} = \frac{(1 - α)}{2 ξ^{3}} (ξ^{.} + e^{- t ξ} [t ξ^{2} - 2 t ξ ξ^{.} - {ξ - ξ^{2} t^{2} ξ}^{.} - t ξ^{3} - 2 ξ^{.}]) \neq Γ_{13,2}^{(α)}

(4.5)

Γ_{12,2}^{(α)} = \frac{(1 - α)}{2 ξ^{3}} (2 - [1 + t ξ] [t ξ + 2] e^{- t ξ})

(4.6)

Γ_{13,3}^{(α)} = \frac{(1 - α)}{2 ξ^{3}} ((2 ξ^{. 2} - ξ ξ^{. .}) + e^{- t ξ} [ξ (t ξ ξ^{.} + t ξ^{. 2} + t ξ ξ^{. .} + 3 ξ t ξ^{.} + ξ^{. .}) - (ξ [{t ξ}^{.} + ξ] - 2 ξ^{.}) (ξ t ξ^{.} + ξ^{2} + ξ^{.})]])

(4.7)

Γ_{21,2}^{(α)} = Γ_{22,1}^{(α)} = \frac{(1 - α)}{2 ξ^{3}} (2 - e^{- t ξ} (t^{2} ξ^{2} + 2 (1 + t ξ))

(4.8)

Engaging the same approach, the remaining

Γ_{i j, k}^{(α)}

expressions can be obtained.

5. $T H E α (O R \nabla^{(α)}) - C O N N E C T I O N$ OF THE TRANSIENT $M / M / \infty$ QM WHEN TIME IS INFINITE

5.1. Geometry of $M / M / \infty$ QM as $t \to \infty$

Now, we are in a situation to reveal the significant temporal impact on the overall IG analysis of the underlying M/M/

\infty

QM. This would be clear as time approaches infinity and in this phase; the FIM will be symmetric which not the case was before as time was not infinite. This also reflects upon the paths of motion of the corresponding geodesic equations of motion for each coordinate of the underlying

M / M / \infty

QM.

Setting

t \to \infty

in (3.4)-(3.10), we have

a = - \frac{1}{ξ^{2}}

(5.1)

b = - \frac{ξ^{.}}{ξ^{2}}

(5.2)

d_{1} = \frac{2 λ}{ξ^{3}}

(5.3)

g = \frac{[λ^{.} ξ - 2 λ ξ^{.}]}{ξ^{3}}

(5.5)

l = - \frac{ξ^{.}}{ξ^{2}}

(5.6)

h = \frac{(2 λ ξ^{.} - λ^{.} ξ)}{ξ^{3}}

(5.7)

r = \frac{(λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 2 λ^{.} ξ ξ^{.} + 2 λ ξ^{. 2})}{ξ^{3}}

(5.8)

with

A = \frac{(r d_{1} - g h)}{∆}

(5.9)

B = \frac{(h b - a r)}{∆}

(5.10)

L = \frac{(a g - b d_{1})}{∆}

(5.12)

D_{1} = \frac{(l g - a r)}{∆}

(5.13)

E = \frac{(- l b)}{∆}

(5.14)

F = \frac{(a b)}{∆}

(5.15)

G = \frac{(a h - l d_{1})}{∆}

(5.16)

H = \frac{(l a)}{∆}

(5.17)

I = \frac{(- a^{2})}{∆}, Δ = d e t ([g_{i j}]) = (- a (l g - a r) + b (a h - l d_{1}))

(5.18)

5.2. The $Γ_{i j}^{k (α)}$ expressions of the $a r r i v a l r a t e$ coordinate, $λ$ of the transient $M / M / \infty$ QM corresponding to infinite temporal values

Γ_{11}^{1 (α)} = 0

(5.19)

Γ_{12}^{1 (α)} = \frac{(1 - α)}{2 ξ^{3}} (2 D_{1} + ξ^{.} G)

(5.20)

Γ_{21}^{1 (α)} = \frac{(1 - α)}{2 ξ^{3}} (2 D_{1} + {2 G ξ}^{.})

(5.21)

Γ_{13}^{1 (α)} = \frac{(1 - α)}{2 ξ^{3}} (2 D_{1} + (2 ξ^{. 2} - ξ ξ^{. .}) G)

(5.22)

Hence, Γ_{13}^{1 (0)} = \frac{1}{2 ξ^{3}} (2 D_{1} + (2 ξ^{. 2} - ξ ξ^{. .}) G))

(5.23)

Γ_{31}^{1 (α)} = \frac{(1 - α)}{2 ξ^{3}} (2 ξ^{.} D_{1} + (2 ξ^{. 2} - ξ ξ^{. .}) G)

(5.24)

Γ_{22}^{1 (α)} = \frac{(1 - α)}{2 ξ^{4}} ((2 A ξ - 6 λ D_{1} + (2 λ^{.} ξ - 6 λ ξ^{.}) G)

(5.25)

Γ_{23}^{1 (α)} = \frac{(1 - α)}{{2 ξ}^{4}} ({2 A ξ}^{.} + (2 λ^{.} ξ - 6 λ ξ^{.}) D_{1} + [(ξ ({2 ξ λ}^{. .} - λ ξ^{. .} - 2 λ^{.} ξ^{.}) - 3 (λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 2 λ^{.} ξ ξ^{.} + 2 λ ξ^{. 2})] G)

(5.26)

Γ_{32}^{1 (α)} = \frac{(1 - α)}{2 ξ^{4}} (2 A ξ ξ^{.} - 6 ξ^{.} D_{1} + (ξ [2 λ ξ^{. .} + λ^{.} ξ^{.} - λ^{. .} ξ] - 3 ξ^{.} [2 λ ξ^{.} - λ^{.} ξ]) G)

(5.27)

Γ_{33}^{1 (α)} = \frac{(1 - α)}{2 ξ^{4}} (ξ A (2 ξ^{. 2} - ξ ξ^{. .}) + ((- λ^{. .} ξ + 2 λ ξ^{. .} + λ^{.} ξ^{.}) ξ + 3 (λ^{.} ξ - 2 λ ξ^{.}) ξ^{.}) D_{1} + (ξ (λ^{. . .} ξ^{2} - λ ξ ξ^{\dots} - 3 λ^{.} ξ ξ^{. .} + 3 λ ξ^{.} ξ^{. .}) - 3 ξ^{.} (λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 2 λ^{.} ξ ξ^{.} + 2 λ ξ^{. 2})) G)

(5.28)

Similarly, the remaining components at infinite temporal can be obtained.

6. The IMES of the Coordinates THE Transient $M / M / \infty$ QM WHEN TIME IS INFINITE

6.1. The $I M E s$ of the $a r r i v a l r a t e$ coordinate, $λ$ of the transient M/M/∞ QM

The IMEs (c.f.,(2.7)) corresponding to the

a r r i v a l r a t e

coordinate,

λ

of the transient M/M/∞ QM are

\frac{d^{2} θ^{1}}{d t^{2}} + Γ_{i j}^{1 (0)} (\frac{d θ^{i}}{d t}) (\frac{d θ^{j}}{d t}) = 0

i, j = 1,2, 3

Now, we are in a situation of trying to find the path of motion of family of families of IMEs corresponding to the arrival rate coordinate,

λ .

[\frac{d^{2} λ}{d t^{2}} + (\frac{1}{2 ξ^{3}} (2 D_{1} + ξ^{.} G) + \frac{1}{2 ξ^{3}} (2 D_{1} + {2 G ξ}^{.})) (\frac{d λ}{d t}) (\frac{d ξ}{d t}) + [\frac{1}{2 ξ^{3}} (2 D_{1} + (2 ξ^{. 2} - ξ ξ^{. .}) G)) \frac{1}{2 ξ^{3}} (2 D_{1} + (2 ξ^{. 2} - ξ ξ^{. .}) G))] (\frac{d λ}{d t}) (\frac{d t}{d t}) + \frac{1}{{2 ξ}^{4}} [((2 A ξ - 6 λ D_{1} + (2 λ^{.} ξ - 6 λ ξ^{.}) G)] {(\frac{d ξ}{d t})}^{2} + [\frac{1}{{2 ξ}^{4}} ({2 A ξ}^{.} + (2 λ^{.} ξ - 6 λ ξ^{.}) D_{1} + [(ξ ({2 ξ λ}^{. .} - λ ξ^{. .} - 2 λ^{.} ξ^{.}) - 3 (λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 2 λ^{.} ξ ξ^{.} + 2 λ ξ^{. 2})] G) + \frac{1}{2 ξ^{4}} (2 A ξ ξ^{.} - 6 ξ^{.} D_{1} + (ξ [2 λ ξ^{. .} + λ^{.} ξ^{.} - λ^{. .} ξ] - 3 ξ^{.} [2 λ ξ^{.} - λ^{.} ξ]) G)] (\frac{d ξ}{d t}) (\frac{d t}{d t}) + (\frac{1}{2 ξ^{4}} (ξ A (2 ξ^{. 2} - ξ ξ^{. .}) + ((- λ^{. .} ξ + 2 λ ξ^{. .} + λ^{.} ξ^{.}) ξ + 3 (λ^{.} ξ - 2 λ ξ^{.}) ξ^{.}) D_{1} + (ξ (λ^{. . .} ξ^{2} - λ ξ ξ^{\dots} - 3 λ^{.} ξ ξ^{. .} + 3 λ ξ^{.} ξ^{. .}) - 3 ξ^{.} (λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 2 λ^{.} ξ ξ^{.} + 2 λ ξ^{. 2})) G) {(\frac{d t}{d t})}^{2}] = 0

(6.1)

Without any loss of generality, let

ξ = 1

, so (6.1) reduces to

[λ^{. . .} G + {(1 - D}_{1}) λ^{. .} + 2 λ^{.} D_{1}] = 0

(6.2)

ξ = 1,

(5.1)-(5.8) reduce to

a = - 1

(6.3)

b = 0

(6.4)

d_{1} = 2 λ

(6.5)

g = λ^{.}

(6.6)

l = 0

(6.7)

h = - λ^{.}

(6.8)

r = λ^{. .}

(6.9)

This implies that (5.13) and (5.16) reduce to

D_{1} = \frac{(l g - a r)}{∆} = \frac{λ^{. .}}{λ^{. .}} = 1

(6.10)

G = \frac{(a h - l d_{1})}{∆} = \frac{λ^{.}}{λ^{. .}}

(6.11)

∆ = λ^{. .}

(6.12)

Consequently,

λ^{. . .} (\frac{λ^{.}}{λ^{. .}}) + 2 λ^{.} = 0 = λ^{.} (λ^{. . .} + 2 λ^{. .}) = 0

(6.13)

(6.13) implies

λ^{.} = 0

, with a closed form solution

λ = c o n s t a n t

.This explains that

λ = c o n s t a n t

characterize the path of motion of the arrival rate coordinate of

M / M / \infty

QM. By (6.13),

(λ^{. . .} + 2 λ^{. .}) = 0

. Let

λ = κ e^{Υ t},

Υ^{3} + 2 Υ^{2} = 0 = Υ^{2} (2 + Υ) = 0

implying

Υ_{1,2, 3} = 0,0, - 2

. Therefore, we have the closed form solutions represented by the family of families,

λ = κ_{1} + κ_{2} t + κ_{2} e^{- 2 t}

(6.14)

This supports a strong evidence that the corresponding paths of motion of the arrival rate for the Poisson arrival rate

ξ = 1

are devised by family of families

λ = c o n s t a n t

.This explains that

λ = c o n s t a n t

λ = κ_{1} + κ_{2} t + κ_{2} e^{- 2 t} .

6.2. The $I M E s$ of the $P o i s s o n a r r i v a l r a t e$ coordinate, $ξ$ of the transient M/M/∞ QM

The IMEs (c.f.,(2.7)) corresponding to the

P o i s s o n a r r i v a l r a t e

coordinate,

ξ

of the transient

M / M / \infty

QM are:

\frac{d^{2} θ^{2}}{d t^{2}} + Γ_{i j}^{1 (0)} (\frac{d θ^{i}}{d t}) (\frac{d θ^{j}}{d t}) = 0

i, j = 1,2, 3

Now, we are in a situation of trying to find the path of motion of family of families of IMEs corresponding to the Poisson arrival rate coordinate,

ξ .

t \to \infty

, we have:

Γ_{11}^{2 (α)} = 0

(6.15)

Γ_{12}^{2 (α)} = \frac{(1 - α)}{2 ξ^{3}} (2 E + ξ^{.} H)

(6.16)

Γ_{21}^{2 (α)} = \frac{(1 - α)}{2 ξ^{3}} (2 E + {2 H ξ}^{.})

(6.17)

Γ_{13}^{2 (α)} = \frac{(1 - α)}{2 ξ^{3}} (2 E + (2 ξ^{. 2} - ξ ξ^{. .}) H)

(6.18)

Γ_{31}^{2 (α)} = \frac{(1 - α)}{2 ξ^{3}} (2 ξ^{.} E + (2 ξ^{. 2} - ξ ξ^{. .}) H)

(6.19)

Γ_{22}^{2 (α)} = \frac{(1 - α)}{2 ξ^{4}} ((2 B ξ - 6 λ E + (2 λ^{.} ξ - 6 λ ξ^{.}) H)

(6.20)

Γ_{23}^{2 (α)} = \frac{(1 - α)}{{2 ξ}^{4}} ({2 B ξ}^{.} + (2 λ^{.} ξ - 6 λ ξ^{.}) E + [(ξ ({2 ξ λ}^{. .} - λ ξ^{. .} - 2 λ^{.} ξ^{.}) - 3 (λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 2 λ^{.} ξ ξ^{.} + 2 λ ξ^{. 2})] H)

(6.21)

Γ_{32}^{2 (α)} = \frac{(1 - α)}{2 ξ^{4}} (2 B ξ ξ^{.} - 6 ξ^{.} E + (ξ [2 λ ξ^{. .} + λ^{.} ξ^{.} - λ^{. .} ξ] - 3 ξ^{.} [2 λ ξ^{.} - λ^{.} ξ]) H)

(6.22)

Γ_{33}^{2 (α)} = \frac{(1 - α)}{2 ξ^{4}} (ξ B (2 ξ^{. 2} - ξ ξ^{. .}) + ((- λ^{. .} ξ + 2 λ ξ^{. .} + λ^{.} ξ^{.}) ξ + 3 (λ^{.} ξ - 2 λ ξ^{.}) ξ^{.}) E + (ξ (λ^{. . .} ξ^{2} - λ ξ ξ^{\dots} - 3 λ^{.} ξ ξ^{. .} + 3 λ ξ^{.} ξ^{. .}) - 3 ξ^{.} (λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 2 λ^{.} ξ ξ^{.} + 2 λ ξ^{. 2})) H)

(6.23)

Setting

λ = 1

, we have

a = \frac{- 1}{ξ^{2}}

(6.24)

b = - \frac{ξ^{.}}{ξ^{2}}

(6.25)

d_{1} = \frac{2}{ξ^{3}}

(6.26)

g = \frac{- 2 ξ^{.}}{ξ^{3}}

(6.27)

l = - \frac{ξ^{.}}{ξ^{2}}

(6.28)

h = \frac{2 ξ^{.}}{ξ^{3}}

(6.29)

r = \frac{(- ξ ξ^{. .} + 2 ξ^{. 2})}{ξ^{3}}, Δ = d e t ([g_{i j}] = \frac{- ξ^{. .}}{ξ^{6}}

(6.30)

Γ_{11}^{2 (0)} = 0

(6.31)

Γ_{12}^{2 (0)} = \frac{1}{2 ξ^{3}} (2 E + ξ^{.} H)

(6.32)

Γ_{21}^{2 (0)} = \frac{1}{2 ξ^{3}} (2 E + {2 H ξ}^{.})

(6.33)

Γ_{13}^{2 (0)} = \frac{1}{2 ξ^{3}} (2 E + (2 ξ^{. 2} - ξ ξ^{. .}) H)

(6.34)

Γ_{31}^{2 (0)} = \frac{1}{2 ξ^{3}} (2 ξ^{.} E + (2 ξ^{. 2} - ξ ξ^{. .}) H)

(6.35)

Γ_{22}^{2 (0)} = \frac{1}{ξ^{4}} ((B ξ - 3 E + (- 3 ξ^{.}) H)

(6.36)

Γ_{23}^{2 (0)} = \frac{1}{{2 ξ}^{4}} ({2 B ξ}^{.} + (- 6 ξ^{.}) E + [(ξ (- ξ^{. .}) - 3 (ξ^{2} - ξ ξ^{. .} + 2 ξ^{. 2})] H)

(6.37)

Γ_{32}^{2 (0)} = \frac{1}{2 ξ^{4}} (2 B ξ ξ^{.} - 6 ξ^{.} E + (ξ [2 ξ^{. .}] - 3 ξ^{.} [2 ξ^{.}]) H)

(6.38)

Γ_{33}^{2 (0)} = \frac{1}{2 ξ^{4}} (ξ B (2 ξ^{. 2} - ξ ξ^{. .}) + ((2 ξ^{. .}) ξ + 3 (- 2 ξ^{.}) ξ^{.}) E + (ξ (- ξ ξ^{\dots}) - 3 ξ^{.} (- ξ ξ^{. .} + 2 ξ^{. 2})) H)

(6.39)

B = \frac{(h b - a r)}{∆} = \frac{((\frac{2 ξ^{.}}{ξ^{3}}) (- \frac{ξ^{.}}{ξ^{2}}) + (\frac{(- ξ ξ^{. .} + 2 ξ^{. 2})}{ξ^{5}}))}{\frac{- ξ^{. .}}{ξ^{6}}} = ξ^{2}

(6.40)

E = \frac{(- l b)}{∆} = - \frac{\frac{ξ^{. 2}}{ξ^{4}}}{\frac{- ξ^{. .}}{ξ^{6}}} = \frac{{ξ^{2} ξ}^{. 2}}{ξ^{. .}}

(6.41)

H = \frac{(l a)}{∆} = \frac{\frac{ξ^{.}}{ξ^{4}}}{\frac{- ξ^{. .}}{ξ^{6}}} = - \frac{{ξ^{2} ξ}^{.}}{ξ^{. .}}

(6.42)

The resulting IMEs corresponding to

λ = 1

is represented by family of families of paths of motions given by

[\frac{d^{2} ξ}{d t^{2}} + (\frac{1}{ξ^{4}} ((B ξ - 3 E + (- 3 ξ^{.}) H)) {(\frac{d ξ}{d t})}^{2} + [\frac{1}{{2 ξ}^{4}} ({2 B ξ}^{.} + (- 6 ξ^{.}) E + [(ξ (- ξ^{. .}) - 3 (ξ^{2} - ξ ξ^{. .} + 2 ξ^{. 2})] H) + \frac{1}{2 ξ^{4}} (2 B ξ ξ^{.} - 6 ξ^{.} E + (ξ [2 ξ^{. .}] - 3 ξ^{.} [2 ξ^{.}]) H)] (\frac{d ξ}{d t}) + [\frac{1}{2 ξ^{4}} (ξ B (2 ξ^{. 2} - ξ ξ^{. .}) + ((2 ξ^{. .}) ξ + 3 (- 2 ξ^{.}) ξ^{.}) E + (ξ (- ξ ξ^{\dots}) - 3 ξ^{.} (- ξ ξ^{. .} + 2 ξ^{. 2})) H) = 0]

(6.43)

By (6.40)-(6.42), we have (6.43) in the form:

[\frac{d^{2} ξ}{d t^{2}} + (\frac{1}{ξ^{4}} ((ξ^{3} - 3 (\frac{{ξ^{2} ξ}^{. 2}}{ξ^{. .}}) + (- 3 ξ^{.}) (- \frac{{ξ^{2} ξ}^{.}}{ξ^{. .}}))) {(\frac{d ξ}{d t})}^{2} + [\frac{1}{{2 ξ}^{4}} ({2 ξ^{2} ξ}^{.} + (- 6 ξ^{.}) (\frac{{ξ^{2} ξ}^{. 2}}{ξ^{. .}}) + [(ξ (- ξ^{. .}) - 3 (ξ^{2} - ξ ξ^{. .} + 2 ξ^{. 2})] (- \frac{{ξ^{2} ξ}^{.}}{ξ^{. .}})) + \frac{1}{2 ξ^{4}} (2 ξ^{3} ξ^{.} - 6 ξ^{.} (\frac{{ξ^{2} ξ}^{. 2}}{ξ^{. .}}) + (ξ [2 ξ^{. .}] - 3 ξ^{.} [2 ξ^{.}]) (- \frac{{ξ^{2} ξ}^{.}}{ξ^{. .}}))] (\frac{d ξ}{d t}) + [\frac{1}{2 ξ^{4}} (ξ^{3} (2 ξ^{. 2} - ξ ξ^{. .}) + ((2 ξ^{. .}) ξ + 3 (- 2 ξ^{.}) ξ^{.}) (\frac{{ξ^{2} ξ}^{. 2}}{ξ^{. .}}) + (ξ (- ξ ξ^{\dots}) - 3 ξ^{.} (- ξ ξ^{. .} + 2 ξ^{. 2})) (- \frac{{ξ^{2} ξ}^{.}}{ξ^{. .}}))] = 0

(6.44)

The complicated equation (6.44) can be rewritten in the form:

[\frac{d^{2} ξ}{d t^{2}} + \frac{1}{ξ} {(\frac{d ξ}{d t})}^{2} + \frac{1}{{2 ξ}^{2}} [({2 ξ}^{.} + (- 6 ξ^{.}) (\frac{ξ^{. 2}}{ξ^{. .}}) + [2 ξ ξ^{. .} - ξ^{2} - 6 ξ^{. 2}] (- \frac{ξ^{.}}{ξ^{. .}})) + (2 ξ ξ^{.} - 6 (\frac{ξ^{. 3}}{ξ^{. .}}) + (2 ξ ξ^{. .} - 6 ξ^{. 2}) (- \frac{ξ^{.}}{ξ^{. .}}))] (\frac{d ξ}{d t}) + \frac{1}{2 ξ^{2}} [(ξ (2 ξ^{. 2} - ξ ξ^{. .}) + (2 ξ ξ^{. .} - 6 ξ^{. 2}) (\frac{ξ^{. 2}}{ξ^{. .}}) + (3 ξ ξ^{.} ξ^{. .} - ξ^{2} ξ^{\dots} - 6 ξ^{. 3}) (- \frac{ξ^{.}}{ξ^{. .}}))] = 0

(6.45)

We can put (6.45) into the more compact form:

[2 ξ^{2} ξ^{. . 2} + 2 ξ ξ^{. .} ξ^{. 2} + [({2 ξ}^{.} ξ^{. .} + (- 6 ξ^{.}) (ξ^{. 2}) + [2 ξ ξ^{. .} - ξ^{2} - 6 ξ^{. 2}] (- ξ^{.})) + (2 ξ {ξ^{. .} ξ}^{.} - 6 (ξ^{. 3}) + (2 ξ ξ^{. .} - 6 ξ^{. 2}) (- ξ))] (ξ^{.}) + [(ξ ξ^{. .} (2 ξ^{. 2} - ξ ξ^{. .}) + (2 ξ ξ^{. .} - 6 ξ^{. 2}) (ξ^{. 2}) + (3 ξ ξ^{.} ξ^{. .} - ξ^{2} ξ^{\dots} - 6 ξ^{. 3}) (- ξ^{.}))] = 0

(6.45)

The family of families of constant paths of motion of the Poisson arrival rate given b y,

ξ = c o n s t a n t

provide a closed form solution of (6.45)

6.3. The $I M E s$ of the $t e m p o r a l$ coordinate, $t$ of the transient $M / M / \infty$ QM

The IMEs (c.f.,(2.7)) corresponding to the

t i m e

coordinate,

t

of the transient

M / M / \infty

QM are:

\frac{d^{2} θ^{3}}{d t^{2}} + Γ_{i j}^{1 (0)} (\frac{d θ^{i}}{d t}) (\frac{d θ^{j}}{d t}) = 0

i, j = 1,2, 3

Setting

λ = 1, ξ = η + ς t

η a n d ς a r e a n y r e a l n u m b e r s

a = \frac{- 1}{ξ^{2}}

(6.46)

b = - \frac{ς}{ξ^{2}}

(6.47)

d_{1} = \frac{2}{ξ^{3}}

(6.48)

g = - \frac{2 ς}{ξ^{3}}

(6.49)

l = - \frac{ς}{ξ^{2}}

(6.50)

h = \frac{2 ς}{ξ^{3}}

(6.51)

r = \frac{2 ς^{2}}{ξ^{3}}

(6.52)

with

L = \frac{(a g - b d_{1})}{∆} = \frac{(\frac{- 1}{ξ^{2}}) (- \frac{2 ς}{ξ^{3}}) - (- \frac{ς}{ξ^{2}}) (\frac{2}{ξ^{3}})}{∆} = \frac{4 ς}{∆ ξ^{5}}

(6.53)

F = \frac{(a b)}{∆} = \frac{ς}{∆ ξ^{4}}

(6.54)

I = \frac{(- a^{2})}{∆} = - \frac{1}{∆ ξ^{4}},

(6.55)

Γ_{22}^{3 (0)} = \frac{ξ L - 3 F - 3 ς I}{ξ^{4}}

(6.56)

Γ_{23}^{3 (α)} = \frac{ς}{ξ^{4}} (L - 3 F - 3 ς I)

(6.57)

Γ_{32}^{3 (α)} = \frac{ς}{ξ^{4}} (L ξ - 3 F - 3 ς I)

(6.58)

Γ_{33}^{3 (α)} = \frac{ς^{2}}{ξ^{4}} (ξ L - 3 F - 3 ς I)

(6.59)

The IMEs of time, for

λ = 1, ξ = η + ς t

are given by

\frac{d^{2} t}{d t^{2}} + Γ_{22}^{3 (0)} {(\frac{d ξ}{d t})}^{2} + Γ_{33}^{3 (0)} {(\frac{d t}{d t})}^{2} + (Γ_{23}^{3 (0)} + Γ_{32}^{3 (0)}) (\frac{d ξ}{d t}) (\frac{d t}{d t})

= 0

Γ_{22}^{3 (0)} {(\frac{d ξ}{d t})}^{2} + Γ_{33}^{3 (0)} + (Γ_{23}^{3 (0)} + Γ_{32}^{3 (0)}) (\frac{d ξ}{d t})

= 0, implying either

ς = 0, o r ξ = η = c o n s t a n t

(6.60)

Γ_{22}^{3 (0)} (\frac{d ξ}{d t}) + Γ_{33}^{3 (0)} + Γ_{23}^{3 (0)} + Γ_{32}^{3 (0)} = 0, or η = (\frac{d ξ}{d t}) = - \frac{(Γ_{33}^{3 (0)} + Γ_{23}^{3 (0)} + Γ_{32}^{3 (0)})}{Γ_{22}^{3 (0)}} = - \frac{(Γ_{33}^{3 (0)} + Γ_{23}^{3 (0)} + Γ_{32}^{3 (0)})}{Γ_{22}^{3 (0)}} = - \frac{\frac{ς}{ξ^{4}} (L - 3 F - 3 ς I) + \frac{ς}{ξ^{4}} (L ξ - 3 F - 3 ς I) + \frac{ς^{2}}{ξ^{4}} (ξ L - 3 F - 3 ς I)}{\frac{ξ L - 3 F - 3 ς I}{ξ^{4}}} = - \frac{ς (L - 3 F - 3 ς I) + ς (L ξ - 3 F - 3 ς I) + ς^{2} (ξ L - 3 F - 3 ς I)}{ξ L - 3 F - 3 ς I} = - ς \frac{(L - 3 F - 3 ς I) + (L ξ - 3 F - 3 ς I) + ς (ξ L - 3 F - 3 ς I)}{ξ L - 3 F - 3 ς I}

(6.61)

This implies :

ς = 0, o r ξ = η = c o n s t a n t

(c.f., 6.60)

1 + \frac{(L - 3 F - 3 ς I) + (L ξ - 3 F - 3 ς I) + ς (ξ L - 3 F - 3 ς I)}{ξ L - 3 F - 3 ς I} = 0

(6.62)

Following (6.62), we have

(L - 3 F - 3 ς I) + (L ξ - 3 F - 3 ς I) + ς (ξ L - 3 F - 3 ς I) + ξ L - 3 F - 3 ς I = 0

(6.63)

Consequently, it follows that:

\frac{2 ς}{∆ ξ^{5}} [2 - ς ξ + 2 ξ] = 0

(6.64)

(6.64) holds if and only if

ς = 0, o r ξ = η = c o n s t a n t

(6.65)

\frac{1}{∆ ξ^{5}} = 0, e q u i v a l e n t l y ξ \to \infty, w h i c h i s e q u i v a l e n t t o \frac{1}{∆} = 0

(6.67)

[2 - ς ξ + 2 ξ] = 0

(6.68)

By (6.68), we have

\frac{ξ d ξ}{1 + ξ} = 2 d t

(6.69)

It could be verified that (6.69) has a closed form solution devised by

(ξ + 1) e^{ξ} = ζ e^{- 2 t}, for some constant ζ

(6.70)

The obtained result in (6.70) is quite new and interesting as it shows that for sufficiently large temporal values, this generates two unexpected values of the Poisson arrival rate, namely ,

ξ = - 1

ξ \to - \infty

At this stage, we need to provide more analysis of the obtained result:

\frac{1}{∆} = 0

((c.f., 6.67))

We have by (6.46)-(6.52) and (5.18),

Δ = d e t ([g_{i j}]) = - 4 \frac{ς^{2}}{ξ^{7}}

(6.71)

Combining (6.67) and (6.71), implies either

ξ = 0 o r ς = \frac{d ξ}{d t} \to \infty

. This means that within the obtaind phase of (6.67), either the Poisson arrival rate vanishes, or we will be in a situation where the corresponding velocity of the Poissonian arrival rate is infinite.

7. The Threshold Theorems for the Potential function (c.f., (3.23) of Theorem 3.1) of the Underlying transient M/M/∞ QM

7.1. The Threshold Theorem for the Potential Function, TTPF (c.f., (3.23) of Theorem 3.1)

Based on the Preliminary Theorem (PT) , the threshold theorem for the potential function, (c.f., (3.23) of Theorem 3.1) corresponding to each coordinate is devised.

Theorem 7.1.

For the obtained potential function

Ψ (θ)

(c.f., (3.23) of Theorem 3.1), the following holds

Ψ (θ)

is forever increasing in

λ .

ii)

Ψ (θ)

is never increasing in

λ .

iii)

Ψ (θ)

is never decreasing in

ξ .

iv)

Ψ (θ)

is forever decreasing in

ξ

for all

λ, ξ, t > 0

Ψ (θ)

is forever increasing in

t

if and only if

ξ > 0

and temporal values satisfying:

(λ^{.} ξ - λ ξ^{.}) e^{ξ t} > (- λ ξ ξ^{.} t - λ ξ^{2} + λ^{.} ξ - λ ξ^{.})

(7.1)

vi)

Ψ (θ)

is never decreasing in

t .

Proof.

i)We have

\partial_{1} = \frac{\partial Ψ}{\partial λ} = \frac{1}{ξ} (1 - e^{- ξ t}), \partial_{2} = \frac{\partial Ψ}{\partial ξ} = \frac{λ}{ξ^{2}} ((1 + ξ t) e^{- ξ t} - 1), \partial_{3} = \frac{\partial Ψ}{\partial t} = \frac{1}{ξ^{2}} ((λ^{.} ξ - λ ξ^{.}) + (λ ξ ξ^{.} + λ ξ^{2} + λ^{.} ξ - λ ξ^{.}) e^{- ξ t})

(c.f.,(3.24))

It holds that

\partial_{1} > 0

if and only if one of the following statements is true:

(1) \frac{1}{ξ} > 0 and (1 - e^{- ξ t}) > 0

(7.2)

(2) \frac{1}{ξ} < 0 and (1 - e^{- ξ t}) < 0

(7.3)

The second statement is impossible since it contradicts the fact

ξ

is positive. So, we have to accept the first statement, (7.2) implies

e^{ξ t} > 1

, which is always true for all

ξ, t > 0

. This proves i).

As for ii),

\partial_{1} < 0

if and only if one of the following statements is true:

(1) \frac{1}{ξ} > 0 and (1 - e^{- ξ t}) < 0

(7.4)

(2) \frac{1}{ξ} < 0 and (1 - e^{- ξ t}) > 0

(7.5)

The second statement is impossible since it contradicts the fact

ξ

is positive. So, we have to accept the first statement, (7.5) implies

e^{ξ t} < 1

, which is never true for all

ξ, t > 0

. This proves ii).

iii)

\partial_{2} > 0

if and only if one of the following statements is true:

(1) \frac{λ}{ξ^{2}} > 0 and ((1 + ξ t) e^{- ξ t} - 1) > 0

(7.6)

(2) \frac{λ}{ξ^{2}} < 0 and ((1 + ξ t) e^{- ξ t} - 1) < 0

(7.7)

The first statement is impossible since it contradicts the fact

ξ

is positive. Since, (7.6) implies

((1 + ξ t) e^{- ξ t} - 1) > 0

, implying

(1 + ξ t) > e^{ξ t}

, a contradiction always true for all

ξ, t > 0

. Moreover, we have to reject the second statement, since

\frac{λ}{ξ^{2}} < 0

is never permissible. This proves iii).

To show iv),

\partial_{2} < 0

if and only if one of the following statements is true:

(1) \frac{λ}{ξ^{2}} > 0 and ((1 + ξ t) e^{- ξ t} - 1) < 0

(7.8)

(2) \frac{λ}{ξ^{2}} < 0 and ((1 + ξ t) e^{- ξ t} - 1) > 0

(7.9)

The second statement is impossible since it contradicts the fact

t h a t λ, ξ > 0

. So, we have to reject (7.9). The first statement, (7.9) implies

((1 + ξ t) e^{- ξ t} - 1) < 0

, implying

(1 + ξ t) > e^{ξ t}

, which is always true for all

ξ, t > 0

. Also,

\frac{λ}{ξ^{2}} > 0

holds for all

λ, ξ > 0

. This proves iv).

v)We have

\partial_{3} = \frac{\partial Ψ}{\partial t} = \frac{1}{ξ^{2}} ((λ^{.} ξ - λ ξ^{.}) + (λ ξ ξ^{.} t + λ ξ^{2} - λ^{.} ξ + λ ξ^{.}) e^{- ξ t})

. So,

\partial_{3} > 0

if and only if one of the following statements is true:

(1) \frac{1}{ξ^{2}} > 0 and ((λ^{.} ξ - λ ξ^{.}) + (λ ξ ξ^{.} t + λ ξ^{2} - λ^{.} ξ + λ ξ^{.}) e^{- ξ t}) > 0

(7.10)

(2) \frac{1}{ξ^{2}} < 0 and ((λ^{.} ξ - λ ξ^{.}) + (λ ξ ξ^{.} t + λ ξ^{2} - λ^{.} ξ + λ ξ^{.}) e^{- ξ t}) < 0

(7.11)

We have to reject (7.11) since

\frac{1}{ξ^{2}} < 0

is non- permissible. As for (7.10),

\frac{1}{ξ^{2}} > 0

holds. Furthermore,

((λ^{.} ξ - λ ξ^{.}) + (λ ξ ξ^{.} t + λ ξ^{2} - λ^{.} ξ + λ ξ^{.}) e^{- ξ t}) > 0

implies

(λ^{.} ξ - λ ξ^{.}) e^{ξ t} = (λ^{.} ξ - λ ξ^{.}) (1 + ξ t + \frac{{(ξ t)}^{2}}{2} + \dots \dots . .) = (λ^{.} ξ - λ ξ^{.} - λ ξ^{.} ξ t + \dots .) > (- λ ξ ξ^{.} t - λ ξ^{2} + λ^{.} ξ - λ ξ^{.})

(7.12)

Hence,

(λ^{.} ξ - λ ξ^{.}) e^{ξ t} > (- λ ξ ξ^{.} t - λ ξ^{2} + λ^{.} ξ - λ ξ^{.})

holds. This proves v).

vi)We have

\partial_{3} = \frac{\partial Ψ}{\partial t} = \frac{1}{ξ^{2}} ((λ^{.} ξ - λ ξ^{.}) + (λ ξ ξ^{.} t + λ ξ^{2} - λ^{.} ξ + λ ξ^{.}) e^{- ξ t})

. So,

\partial_{3} < 0

if and only if one of the following statement is true:

(1) \frac{1}{ξ^{2}} > 0 and ((λ^{.} ξ - λ ξ^{.}) + (λ ξ ξ^{.} t + λ ξ^{2} - λ^{.} ξ + λ ξ^{.}) e^{- ξ t}) < 0

(7.13)

(2) \frac{1}{ξ^{2}} < 0 and ((λ^{.} ξ - λ ξ^{.}) + (λ ξ ξ^{.} t + λ ξ^{2} - λ^{.} ξ + λ ξ^{.}) e^{- ξ t}) > 0

(7.14)

We must reject (7.14). (7.13) is true since

\frac{1}{ξ^{2}} > 0

holds for all

ξ > 0

. Moreover, we have

((λ^{.} ξ - λ ξ^{.}) + (λ ξ ξ^{.} t + λ ξ^{2} - λ^{.} ξ + λ ξ^{.}) e^{- ξ t}) < 0

(7.15)

L e t ξ = 1 = λ, t = 0 .

This provides a counter example generating the inequality,

1 < 0

(7.16)

A contradiction. Therefore, vi) holds.

In what follows,

P A R = ξ = P o i s s o p n A r r i v a l R a t e, A R = λ = A r r i v a l R a t e

P F = P o t e n t i a l F u n c t i o n = Ψ (θ)

7.2.1. Numerical Experiment One

Ψ (θ) = λ (1 - e^{- 1})

The numerical observation in Figure 5 matches the analytic result (c.f., i) of Theorem 7.1).

Figure 5.

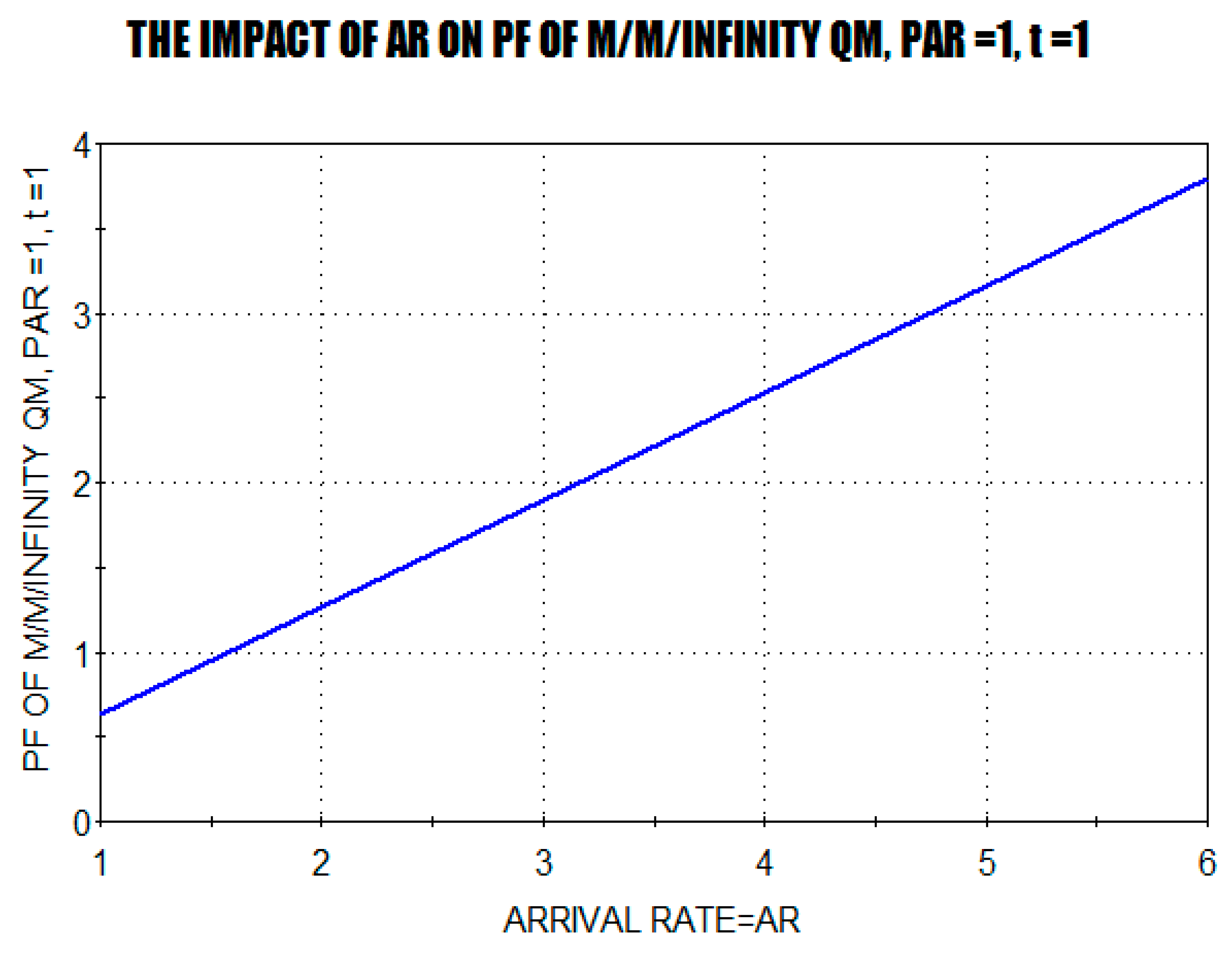
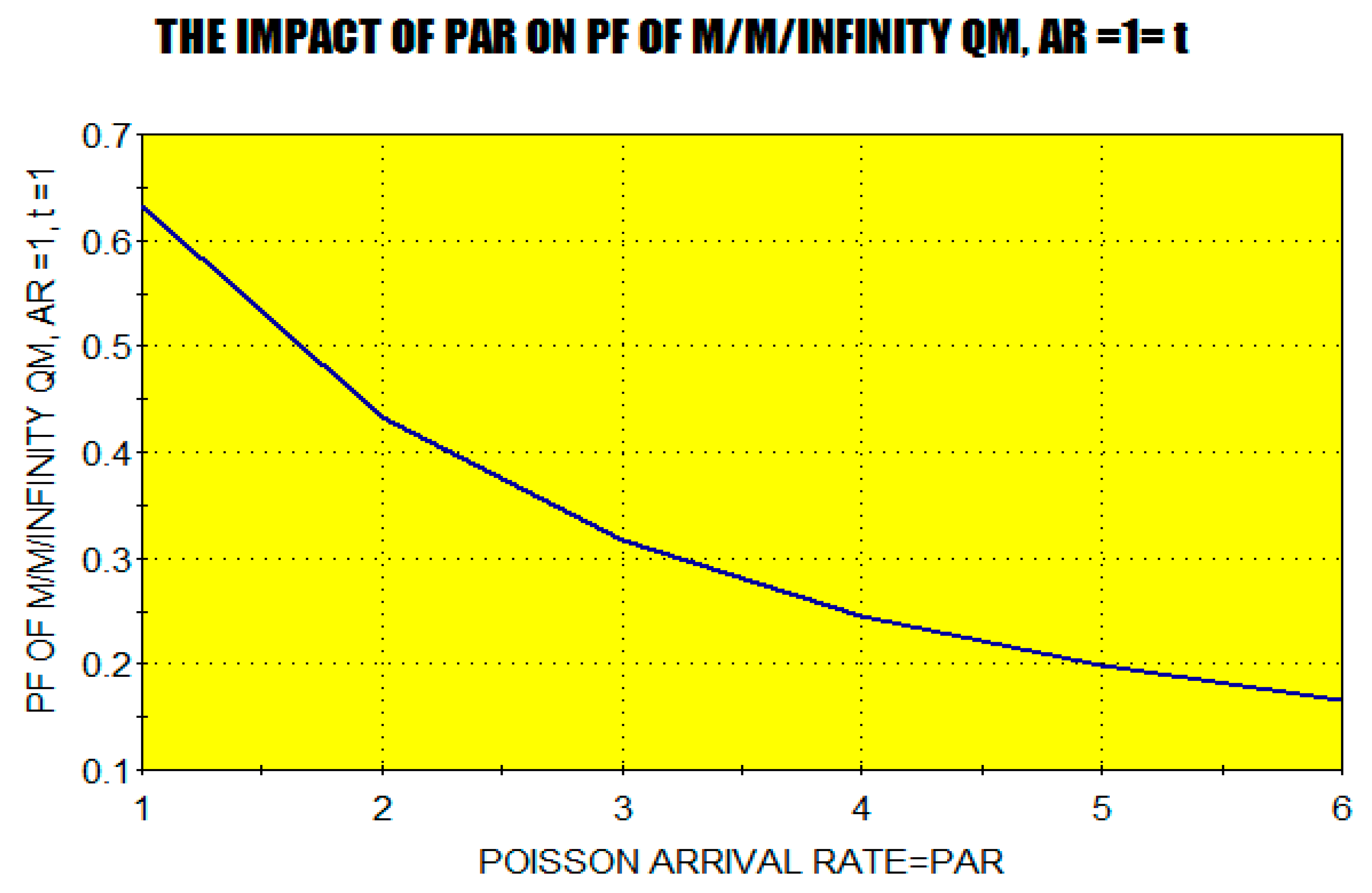
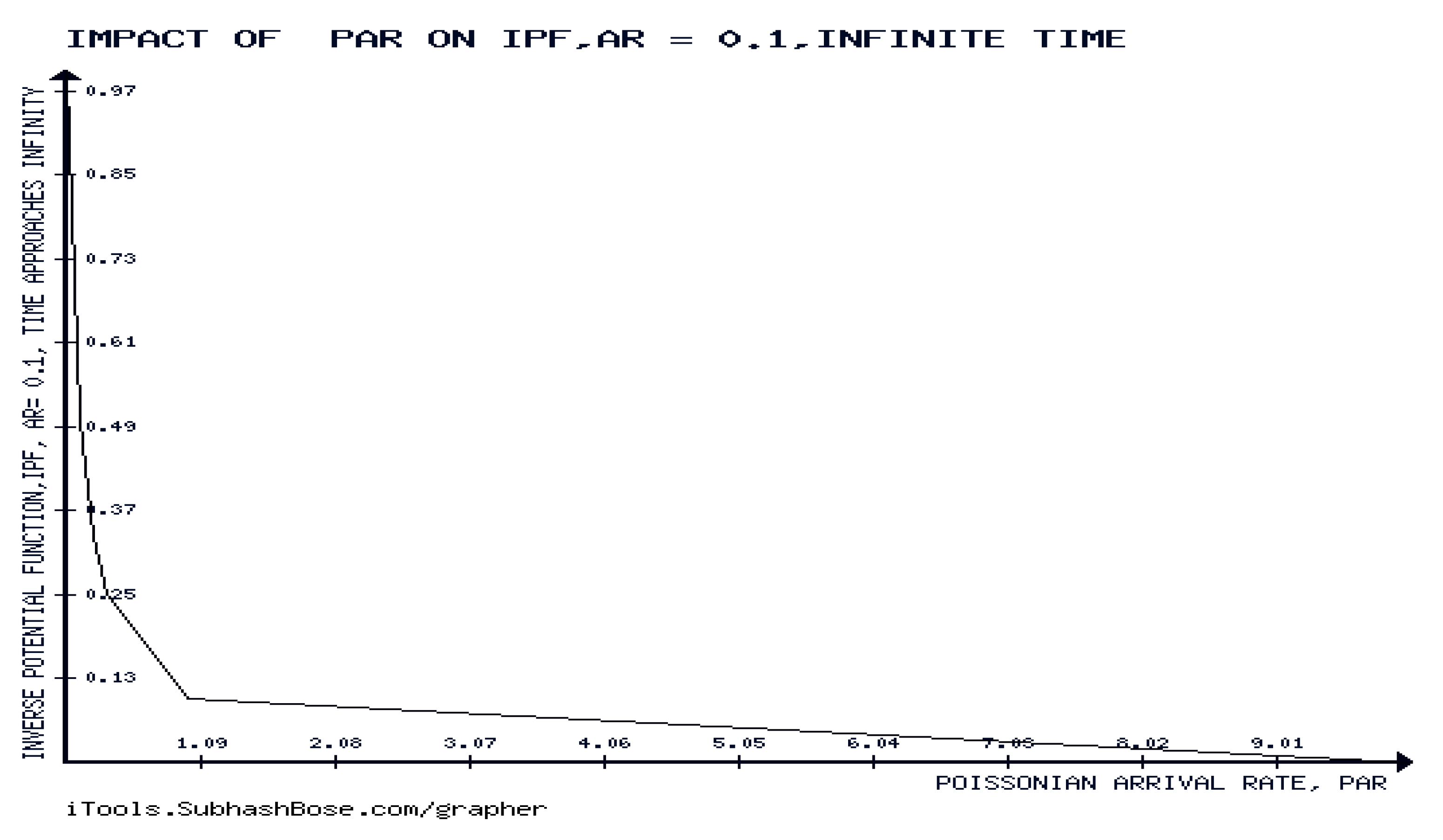
Figure 6 provides an evidence of the forever decreasability phase of the PF in the Poisson Arrival Rate, which agrees with the analytic findings of TTPF.

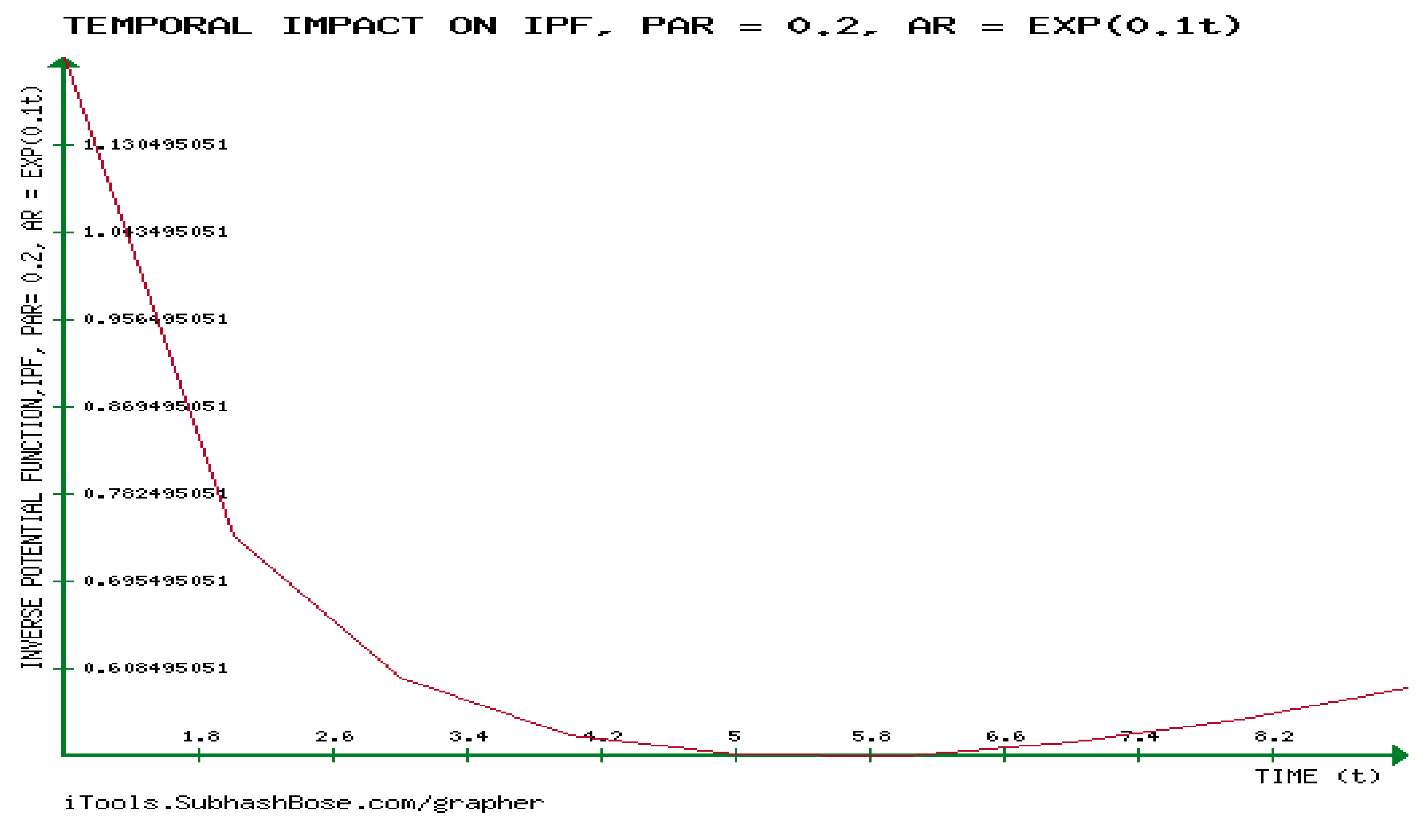
As observed from Figure 7, the potential function, PF is forever increasing in time, which agrees with the analytic results.

8. Some Algebraic Properties of the Potential Function, $Ψ (θ) = \frac{λ}{ξ} (1 - e^{- ξ t})$ (c.f., (3.23))

Theorem 8.1.

The three-dimensional potential function

Ψ (θ) = \frac{λ}{ξ} (1 - e^{- ξ t})

(c.f., (3.23)) is generally not well-defined.

Proof.

Let

λ_{i}, ξ_{i}, t_{i}

i = 1,2

be such that

λ_{1} \neq λ_{2},

ξ_{1} \neq ξ_{2}, t_{1} \neq t_{2} .

Let

Ψ (λ_{1}, ξ_{1}, t_{1}) = Ψ (λ_{2}, ξ_{2}, t_{2}) . T h i s i m p l i e s

\frac{λ_{1}}{ξ_{1}} (1 - e^{- ξ_{1} t_{1}}) = \frac{λ_{2}}{ξ_{2}} (1 - e^{- ξ_{2} t_{2}})

(8.1)

(8.1)

directly implies:

[\frac{λ_{1}}{ξ_{1}} - \frac{λ_{2}}{ξ_{2}}] + [\frac{λ_{2}}{ξ_{2}} e^{- ξ_{2} t_{2}} - \frac{λ_{1}}{ξ_{1}} e^{- ξ_{1} t_{1}}] = 0

(8.2)

So, (8.2) holds if and only if:

\frac{λ_{2}}{ξ_{2}} \sum_{m = 1}^{\infty} \frac{{(- ξ_{2} t_{2})}^{m}}{m!} - \frac{λ_{1}}{ξ_{1}} \sum_{m = 1}^{\infty} \frac{{(- ξ_{1} t_{1})}^{m}}{m!} = 0

(8.3)

Clearly (8.3) is satisfied if and only if:

\frac{{(- 1)}^{m}}{m!} [λ_{2} {(ξ_{2})}^{m - 1} {(t_{2})}^{m} - λ_{1} {(ξ_{1})}^{m - 1} {(t_{1})}^{m}], m = 1,2, \dots .

(8.4)

It can be verified that (8.4) will generate the following sets of equations:

m = 1 ⟹ λ_{2} t_{2} = λ_{1} t_{1}

(8.5)

m = 2 ⟹ {[λ}_{2} {ξ_{2} (t}_{2})^{2} - λ_{1} {ξ_{1} (t}_{1})^{2}] = 0

(8.6)

E n g a g i n g (8.5) a n d (8.6)

yields

λ_{1} t_{1} ({ξ_{2} t}_{2} - {ξ_{1} t}_{1}) = 0 ⟹

λ_{1} t_{1} = 0

(which implies

λ_{1} t_{1} = 0, o r λ_{1} = 0 (c o n t r a d i c t i o n), o r t_{1} = 0) . I f t_{1} = 0, t h e n t h i s i m p l i e s b y (8.5) t h a t e i t h e r λ_{2} = 0 o r t_{2} = 0)

I n b r i e f, t h i s i m p l i e s t h a t e i t h e r a l l t h e t e m p o r a l v a l u e s a r e s e t t o z e r o, w h i c h

is a contradiction. Moreover, the other possibility is to allow the

a r r i v a l r a t e v a l u e s t o b e z e r o, a n o t h e r c o n t r a d i c t i o n . T o t h i s e n d, w e h a v e

{ξ_{2} t}_{2} = {ξ_{1} t}_{1}

(8.7)

The reader can check that after some manipulation,

m = 3 ⟹ {ξ_{2} t}_{2} = {ξ_{1} t}_{1} o r {ξ_{2} t}_{2} + {ξ_{1} t}_{1} = 0 (c o n t r a d i c t i o n)

(8.8)

Based on the analytic results, we can have

λ_{1} \neq λ_{2},

ξ_{1} \neq ξ_{2}, t_{1} \neq t_{2} a n d Ψ (λ_{1}, ξ_{1}, t_{1}) = Ψ (λ_{2}, ξ_{2}, t_{2})

will hold. This means that

Ψ

is not well-defined.

Several emerging important special cases of Theorem 8.1 are obtained in the following theorems.

Theorem 8.2.

For constant values of

λ, ξ

, the three-dimensional potential function

Ψ (θ) = \frac{λ}{ξ} (1 - e^{- ξ t})

(c.f., (3.23)) satisfies the following:

(1)

Ψ

is well-defined.

(2)

Ψ i s

onto

(3)

Ψ i s O n e - t o - O n e

(4)

Ψ h a s a u n i q u e i n v e r s e, Ψ^{- 1}

given by

Ψ^{- 1} (λ, ξ, t) = - \frac{1}{ξ} l n (1 - \frac{t ξ}{λ})

(8.9)

Proof.

(1) For constant values of

λ, ξ, d e f i n e t_{i}, i = 1,2

be such that

t_{1} \neq t_{2} .

Thus,

Ψ (λ, ξ, t_{1}) = Ψ (λ, ξ, t_{2})

implies:

\frac{λ}{ξ} (1 - e^{- ξ t_{1}}) = \frac{λ}{ξ} (1 - e^{- ξ t_{2}})

(8.10)

Hence, it follows that

\frac{λ}{ξ} (e^{- ξ t_{1}} - e^{- ξ t_{2}}) = 0 \Leftrightarrow \frac{λ}{ξ} (c o n t r a d i c t i o n) o r e^{- ξ t_{1}} = e^{- ξ t_{2}}, e q u i v a l e n t l y t_{1} = t_{2} .

(8.11)

This proves (1).

(2) For every arbitrary

\frac{λ}{ξ} (1 - e^{- ξ t})

, for constant values of

λ, ξ

there exist a unique triple

(λ, ξ, t)

such that the that the representation

Ψ (θ) = \frac{λ}{ξ} (1 - e^{- ξ t})

exists. Therefore,

Ψ i s

onto.

(3) It suffices to show that for constant values of

λ, ξ

, it holds that:

Ψ (λ, ξ, t_{1}) = Ψ (λ, ξ, t_{2}) ⟺ t_{1} = t_{2}

(8.12)

⟹ :

follows by (1).

⟸ :

t_{1} = t_{2} i m p l i e s Ψ (λ, ξ, t_{1}) = Ψ (λ, ξ, t_{2})

. The proof is immediate.

Combining (2) and (3),

Ψ

is bijective with a unique inverse, namely

Ψ^{- 1}

. To obtain

Ψ^{- 1},

let

Ψ (θ) = \frac{λ}{ξ} (1 - e^{- ξ t}) = y

(8.13)

H e n c e, i t f o l l o w s t h a t

(1 - e^{- ξ t}) = \frac{ξ y}{λ} ⟹ e^{- ξ t} = 1 - \frac{ξ y}{λ}, e q u i v a l e n t l y, t = - \frac{1}{ξ} l n (1 - \frac{ξ y}{λ})

(8.14)

Following (8.14), we get

Ψ^{- 1} (t) = - \frac{1}{ξ} l n (1 - \frac{ξ t}{λ})

(c.f., (8.9))

Theorem 8.3.

For constant

ξ

t \to \infty

the potential function

Ψ_{\infty, λ} (θ) = \frac{λ}{ξ} (

c.f., (3.23)) satisfies the following:

(1) Ψ_{\infty, λ} (θ)

is well-defined.

(2) Ψ_{\infty, λ} (θ) i s

onto

(3) Ψ_{\infty, λ} (θ) i s O n e - t o - O n e

(4)

Ψ_{\infty, λ} (θ) h a s a u n i q u e i n v e r s e, Ψ_{\infty, λ}^{- 1}

given by

Ψ_{\infty, λ}^{- 1} (λ) = λ ξ

(8.15)

Proof.

Following a similar approach as in Theorem 8.2, the proofs are straightforward.

Theorem 8.4.

For constant

λ

t \to \infty

the potential function

Ψ_{\infty, ξ} (θ) = \frac{λ}{ξ} (

c.f., (3.23)) satisfies the following:

(1) Ψ_{\infty, ξ}

is well-defined.

(2) Ψ_{\infty, ξ} i s

onto.

(3) Ψ_{\infty, ξ} i s O n e - t o - O n e .

(4)

Ψ_{\infty, ξ} h a s a u n i q u e i n v e r s e, Ψ_{\infty, ξ}^{- 1}

given by

Ψ_{\infty, ξ}^{- 1} (ξ) = \frac{λ}{ξ}

(8.16)

Proof.

Following a similar approach as in Theorem 8.2, the proofs are straightforward.

Theorem 8.5.

For constant

λ

, the potential function

Ψ_{ξ, t} (θ) = \frac{λ}{ξ} (1 - e^{- ξ t})

(c.f., (3.23)) satisfies the following:

(1) Ψ_{ξ, t} (θ)

is well-defined if and only if the temporal values are constant.

(2) Ψ_{ξ, t} (θ) i s

onto.

(3) Ψ_{ξ, t} (θ) i s n o t i n g e n e r a l O n e - t o - O n e .

(4)

Ψ_{ξ, t} (θ) h a s a f a m i l y o f f a m i l i e s o f i n v e r s e s, Ψ_{ξ, t}^{- 1}

and they are existing uniquely if and only if the temporal values are constant. In this case,

Ψ_{ξ, t}^{- 1} (ξ) = ξ

Such that,

ξ

satisfies:

λ [\sum_{m = 1}^{\infty} \frac{{(- ξ)}^{m - 2} {(t)}^{m - 1}}{m!}] - 1 = 0

(8.17)

Proof.

(1) Let

ξ_{i}, t_{i}

i = 1,2

be such that

ξ_{1} \neq ξ_{2}, t_{1} \neq t_{2} .

Let

Ψ (λ, ξ_{1}, t_{1}) = Ψ (λ, ξ_{2}, t_{2}) . T h i s i m p l i e s

\frac{λ}{ξ_{1}} (1 - e^{- ξ_{1} t_{1}}) = \frac{λ}{ξ_{2}} (1 - e^{- ξ_{2} t_{2}})

(8.18)

(8.18)

directly implies:

λ ([\frac{1}{ξ_{1}} - \frac{1}{ξ_{2}}] + [\frac{1}{ξ_{2}} e^{- ξ_{2} t_{2}} - \frac{1}{ξ_{1}} e^{- ξ_{1} t_{1}}]) = 0

(8.19)

For the Necessity, if the temporal values are constant, then

t_{1} = t_{2}

holds, which implies by (8.19), that

ξ_{1} = ξ_{2}

, since

λ = 0 i s n o n p e r m i s s i b l e b y t h e h y p o t h e s i s .

Therefore,

Ψ_{ξ, t} (θ)

is well-defined. For the sufficiency, let

Ψ_{ξ, t} (θ)

be well-defined, then it is never permissible that:

ξ_{1} \neq ξ_{2}, t_{1} \neq t_{2} to imply Ψ (λ, ξ_{1}, t_{1}) = Ψ (λ, ξ_{2}, t_{2})

(8.20)

S o, t_{1} = t_{2}

and

ξ_{1} = ξ_{2}

hold. Assume that there is some

t_{m}

such that

ξ_{1} \neq ξ_{2}, t_{1} \neq t_{m}

to imply

Ψ (λ, ξ_{1}, t_{1}) = Ψ (λ, ξ_{2}, t_{m})

. Then, we get a contradiction to the hypothesis of well-defindness of

Ψ_{ξ, t} (θ) . T h u s, ξ_{1} = ξ_{2}, t_{1} = t_{m}

t_{2}

. Therefore, the temporal values should be constant. This completes the proof of (1).

The proof of (2) is straightforward.

It suffices to show that for constant values of

λ, w e h a v e f o r a n y a r b i t r a r y ξ_{1}, ξ_{2}

t_{1}, t_{2}

Ψ (λ, ξ, t_{1}) = Ψ (λ, ξ, t_{2}) ⟺ {ξ_{1} = ξ_{2} a n d t}_{1} = t_{2}

(8.21)

Following the proof of (1), the necessity condition holds if the temporal values are constant. Furthermore, the sufficiency condition implies that

Ψ (λ, ξ, t_{1}) = Ψ (λ, ξ, t_{2}) ⟹ ξ_{1} = ξ_{2}

, which holds if and only if

t_{1} = t_{2} .

Repeating implies the same procedure iteratively would imply

t_{1} = t_{2} = t_{3} = t_{4} = \dots .

This provides an evidence that all the temporal values are constant.

The first part of the proof of (4) is clear. Now, assume that all the temporal values are constant. Then, of course, there should be a uniquely defined and determined inverse, namely,

Ψ_{ξ, t}^{- 1} . L e t

Ψ_{ξ, t} (θ) = \frac{λ}{ξ} (1 - e^{- ξ t})

= z, then it holds that

z = \frac{λ}{ξ} (1 - [\sum_{m = 0}^{\infty} \frac{{(- t ξ)}^{m}}{m!}]) ⟹ \frac{z}{λ} = [\sum_{m = 1}^{\infty} \frac{{(- 1)}^{m - 2} {(ξ)}^{m - 1} {(t)}^{m - 1}}{m!}]

(8.22)

Therefore, the inverse potential function,

Ψ_{ξ, t}^{- 1}

is devised by:

Ψ_{ξ, t}^{- 1} = t h e r o o t s o f t h e e q u a t i o n λ [\sum_{m = 1}^{\infty} \frac{{(- ξ)}^{m - 2} {(t)}^{m - 1}}{m!}] - 1 = 0

(c.f., (8.17))

Theorem 8.6.

For constant

ξ

, the potential function

Ψ_{λ, t} (θ) = \frac{λ}{ξ} (1 - e^{- ξ t})

(c.f., (3.23)) satisfies the following:

(1) Ψ_{λ, t} (θ)

is well-defined if and only if the temporal values are constant.

(2) Ψ_{λ, t} (θ) i s

onto

(3) Ψ_{λ, t} (θ) i s n o t i n g e n e r a l O n e - t o - O n e

(4)

Ψ_{λ, t} (θ) h a s a f a m i l y o f f a m i l i e s o f i n v e r s e s, Ψ_{λ, t}^{- 1}

and it is existing uniquely if and only if the temporal values are constant. In this case,

Ψ_{λ, t}^{- 1} (λ) = \frac{λ ξ}{(1 - e^{- ξ t})}

(8.23)

Proof.

Following the same technique as in Theorem 8.5, the proofs can be easily done.

The following section provides the Threshold Theorems of the derived inverse of the potential functions (c.f.,(8.9), (8.15),(8.16),(8.23)).

9. The Threshold Theorems of the Derived Inverses of Poten-Tial Function, IPFs

Theorem 9.1.

{F o r t h e d e r i v e d i n v e r s e, Ψ}^{- 1} (t) = - \frac{1}{ξ} l n (1 - \frac{ξ t}{λ})

(c.f., (8.9)), we have

Ψ^{- 1} (t)

is forever increasing in

t

if and only if:

t < \frac{λ}{ξ}

(9.1)

ii)

Ψ^{- 1} (t)

is never decreasing in

t

(9.2)

Proof.

i) We have

\frac{{\partial Ψ}^{- 1} (t)}{\partial t} = \frac{- \frac{1}{ξ} (\frac{ξ}{λ})}{(1 - \frac{ξ t}{λ})} = \frac{\frac{1}{λ}}{(1 - \frac{ξ t}{λ})} = \frac{1}{(λ - ξ t)}

(9.3)

B y t h e p r e l i m i n a r y t h e o r e m (P T) (c . f ., (2.15)), Ψ^{- 1}

is forever increasing if and if

\frac{{\partial Ψ}^{- 1} (t)}{\partial t} > 0

. Following (9.3), this holds if and only if

(λ - ξ t) > 0

. Surely, it is implied that i) holds. Engaging the same approach,

\frac{{\partial Ψ}^{- 1} (t)}{\partial t} < 0

if and only if

> \frac{λ}{ξ}

, but this implies

\frac{ξ t}{λ} > 1

, which violates the continuity of

Ψ^{- 1} (t) . H e n c e, i i) f o l l o w s .

Theorem 9.2.

F o r t h e o b t a i n e d i n v e r s e, Ψ_{\infty, λ}^{- 1} (λ) = λ ξ

(c.f., (8.15)), we have

Ψ_{\infty, λ}^{- 1} (λ)

is forever increasing in

λ

ii)

Ψ_{\infty, λ}^{- 1} (λ)

is never decreasing in

λ

Proof.

i) We have

\frac{{\partial Ψ}_{\infty, λ}^{- 1} (λ)}{\partial λ} = ξ

(9.4)

B y t h e p r e l i m i n a r y t h e o r e m (P T) (c . f ., (2.15)), Ψ_{\infty, λ}^{- 1} (λ)

is forever increasing if and if

\frac{{\partial Ψ}_{\infty, λ}^{- 1} (λ)}{\partial λ} > 0

. By (9.4), this is satisfied generally since

ξ

is always positive.

The proof of ii) follows since

ξ

is never negative.

Theorem 9.3.

F o r t h e o b t a i n e d i n v e r s e, Ψ_{\infty, ξ}^{- 1} (ξ) = \frac{λ}{ξ}

(c.f., (8.16)), we have

Ψ_{\infty, ξ}^{- 1} (ξ)

is never increasing in

ξ

ii)

Ψ_{\infty, ξ}^{- 1} (ξ)

is forever decreasing in

ξ

Proof.

i) We have

\frac{{\partial Ψ}_{\infty, ξ}^{- 1} (ξ)}{\partial ξ} = - \frac{λ}{ξ^{2}}

(9.5)

B y t h e p r e l i m i n a r y t h e o r e m (P T) (c . f ., (2.15)), Ψ_{\infty, ξ}^{- 1} (ξ)

is forever increasing if and if

\frac{{\partial Ψ}_{\infty, ξ}^{- 1} (ξ)}{\partial ξ} > 0

. Following (9.5), this never holds since

ξ a n d λ

are always positive. This proves i).

The proof of ii) is immediate.

Theorem 9.4.

F o r t h e o b t a i n e d i n v e r s e, Ψ_{λ, t}^{- 1} (λ) = \frac{λ ξ}{(1 - e^{- ξ t})}

(c.f., (8.23)), we have

Ψ_{λ, t}^{- 1} (λ)

is never increasing in

λ

ii)

Ψ_{λ, t}^{- 1} (λ)

is never decreasing in

λ

iii)

Ψ_{λ, t}^{- 1} (λ)

is forever increasing in

t

if and only if

t > \frac{1}{ξ} l n (1 + \frac{λ ξ}{λ^{.}})

(9.6)

iv)

Ψ_{λ, t}^{- 1} (λ)

is forever decreasing in

t

if and only if

t < \frac{1}{ξ} l n (1 + \frac{λ ξ}{λ^{.}})

(9.7)

Proof.

i) We have

\frac{{\partial Ψ}_{λ, t}^{- 1} (λ)}{\partial λ} = \frac{ξ}{(1 - e^{- ξ t})} = \frac{ξ e^{ξ t}}{(e^{ξ t} - 1)} > 0 (s i n c e ξ i s a l w a y s p a o s i v e, t > 0)

(9.8)

B y t h e p r e l i m i n a r y t h e o r e m (P T) (c . f ., (2.15)), {(9.8), i t f o l l o w s t h a t Ψ}_{λ, t}^{- 1} (λ)

is forever increasing in

λ

.This proves i).

The proof of ii) is immediate.

\frac{{\partial Ψ}_{λ, t}^{- 1} (λ)}{\partial t} = \frac{ξ (λ^{.} (1 - e^{- ξ t}) + λ {ξ e}^{- ξ t})}{{(1 - e^{- ξ t})}^{2}}

(9.9)

B y t h e p r e l i m i n a r y t h e o r e m (P T) (c . f ., (2.15)), {(9.9), i t f o l l o w s t h a t Ψ}_{λ, t}^{- 1} (λ)

is forever increasing in

t

if and only if:

λ^{.} (1 - e^{- ξ t}) + λ e^{- ξ t} (ξ) > 0, equivalently, λ^{.} > λ \frac{ξ e^{- ξ t}}{(1 - e^{- ξ t})} = λ \frac{ξ}{(e^{ξ t} - 1)}

(9.10)

(9.10) could be re-written in the form:

(e^{ξ t} - 1) > \frac{λ ξ}{λ^{.}}, equivalently, t > \frac{1}{ξ} l n (1 + \frac{λ ξ}{λ^{.}})

(c.f., (9.6))

Hence, iii) is done.

As for iv)

f o l l o w i n g t h e p r e l i m i n a r y t h e o r e m (P T) (c . f ., (2.15)), {(9.9), i t f o l l o w s t h a t Ψ}_{λ, t}^{- 1} (λ)

is forever decreasing in

t

if and only if

λ^{.} (1 - e^{- ξ t}) + λ e^{- ξ t} (ξ) < 0, equivalently, λ^{.} < λ \frac{ξ e^{- ξ t}}{(1 - e^{- ξ t})} = λ \frac{ξ}{(e^{ξ t} - 1)}

(9.11)

(9.11) could be re-written in the form:

(e^{ξ t} - 1) < \frac{λ ξ}{λ^{.}}, equivalently, t < \frac{1}{ξ} l n (1 + \frac{λ ξ}{λ^{.}})

(c.f., (9.7))

10. Numerical Experiments on the Threshold Theorems of the Derived Inverses of Potential Function

10.1. Numerical Experiment on Theorem 9.1

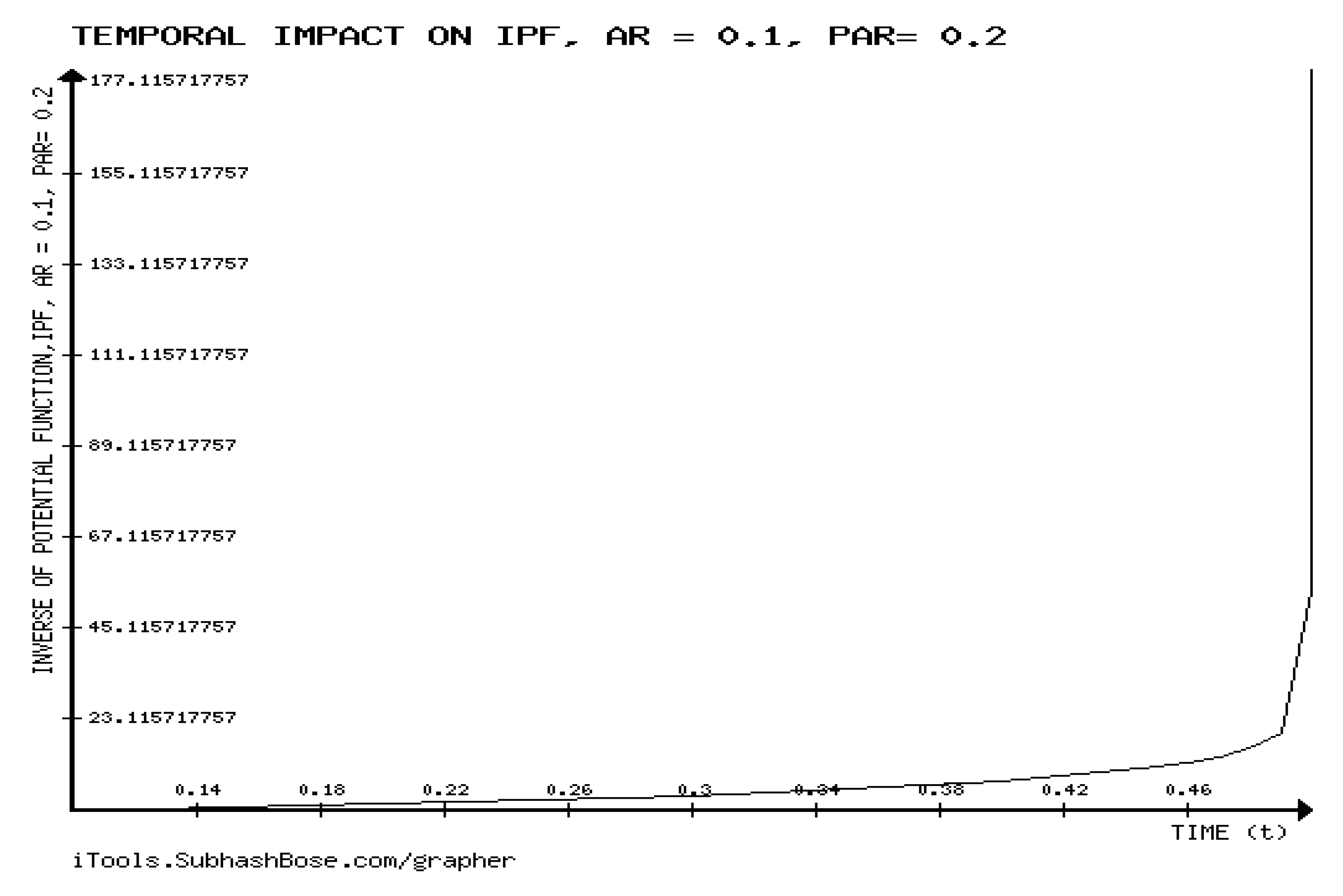
We have, the inverse of the potential function, IPF =

Ψ^{- 1} (t) = - \frac{1}{ξ} l n (1 - \frac{ξ t}{λ})

(c.f., (8.9)). Let the arrival rate, AR=

λ = 0.1, t h e P o i s s o n i a n a r r i v a l r a t e = P A R = ξ = 0.2, t h e n \frac{λ}{ξ} = 0.2

. If

\frac{ξ t}{λ} > 1

,or equivalently,

t > 0.5

, then

Ψ^{- 1} (t) \to \infty

As we can see from Figure 8 that the inverse of potential function, IPF is forever increasing for all the temporal values less than the threshold =

\frac{λ}{ξ}

, where both

λ, ξ

are constants. These experimental results agree with the analytic findings of Theorem 9.1

12.2. Numerical Experiment on Theorem 9.2

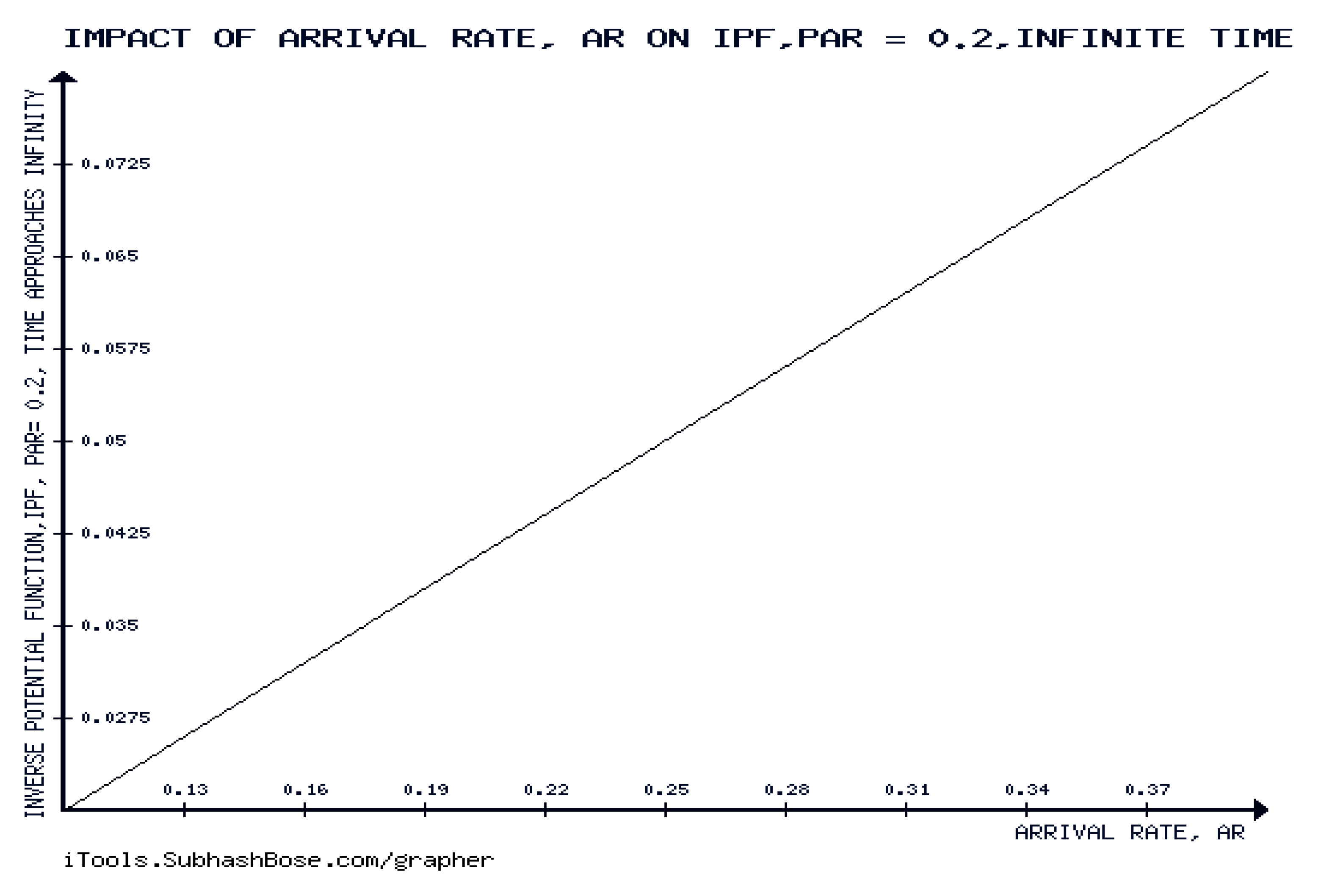
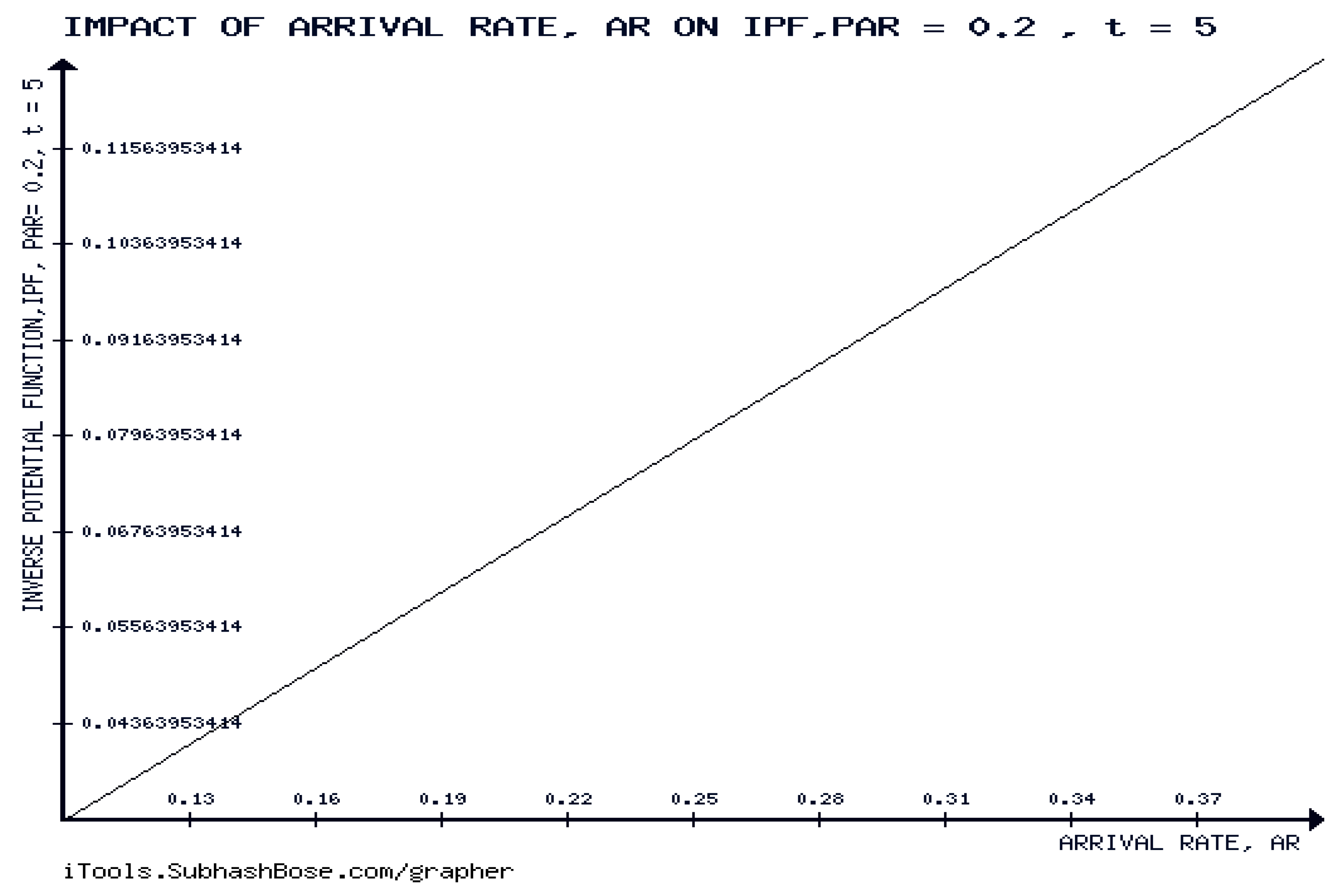
We have, the inverse of the potential function, IPF =

Ψ_{\infty, λ}^{- 1} (λ) = λ ξ

(c.f., (8.15)).

P A R = ξ = 0.2

Figure 9 shows that the inverse of potential function, IPF is forever increasing with respect to the arrival rate, for infinite time and constant Poissonian arrival rate. This agrees with the analytic results of Theorem 10.2.

10.3. Numerical Experiment on Theorem 9.3

We have, the inverse of the potential function, IPF =

Ψ_{\infty, ξ}^{- 1} (ξ) = \frac{λ}{ξ}

(c.f., (8.16)).

A R = λ = 0.1

Figure 10 shows that IPF is forever decreasing in PAR = Poissonian arrival rate, for constant arrival rate and infinite time. This agrees with the analytic findings of theorem 10.3. It is also clear that ,

Ψ_{\infty, ξ}^{- 1} (ξ) = \frac{λ}{ξ} \to 0 a s ξ \to \infty

10.4. Numerical Experiment on Theorem 9.4

We have, the inverse of the potential function, IPF =

Ψ_{λ, t}^{- 1} (λ) = \frac{λ ξ}{(1 - e^{- ξ t})}

(c.f., (8.23)).

P A R = ξ = 0.2

Part One: Let

t = 5

As observed from Figure 11,

Ψ_{λ, t}^{- 1} (λ)

is forever increasing in

λ .

This shows that both analytic and numerical results match .

Part Two:

l e t ξ = 0.2, λ = e^{(0.1) t}

, we have the threshold to be:

\frac{1}{ξ} l n (1 + \frac{λ ξ}{λ^{.}}) = \frac{1}{0.2} l n (1 + \frac{0.2 e^{(0.1) t}}{{0.1 e}^{(0.1) t}}) = \frac{1}{0.2} l n (1 + \frac{0.2 e^{(0.1) t}}{{0.1 e}^{(0.1) t}}) = \frac{1}{0.2} l n (3) = 5.493061443

(10.1)

As observed from Figure 12,

Ψ_{λ, t}^{- 1} (λ) = \frac{λ ξ}{(1 - e^{- ξ t})}

is forever decreasing whenever time is less than the threshold and it starts to increase when time is greater than the threshold.

11. The $α -$ Gaussian Curvature, $K_{\infty}^{(α)}$ of (2.14) as Time Approaches Infinity

Theorem 11.1.

The

α -

Gaussian Curvature,

K_{\infty}^{(α)}

as time approaches infinity is devised by:

K_{\infty}^{(α)} = [(\frac{(1 - α) {λ^{.} ξ^{.} ξ}^{4} (2 λ ξ^{.} - λ^{.} ξ + 2 λ - ξ) (4 ξ^{. 2} - ξ ξ^{. .})}{{(λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 4 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2})}^{3}})]

(11.1)

Proof.

We have

{\begin{matrix} R \end{matrix}}_{i j k l}^{(α)} = [(\partial_{j} Γ_{i k}^{s (α)} - \partial_{i} Γ_{j k}^{s (α)}) g_{s l} + (Γ_{j β, l}^{(α)} Γ_{i k}^{β (α)} - Γ_{i β, l}^{(α)} Γ_{j k}^{β (α)})]

(2.11)

where

Γ_{i j}^{k (α)} = Γ_{i j, s}^{(α)} g^{s k}

Therefore,

R_{1212}^{(α)} = [(\partial_{2} Γ_{11}^{s (α)} - \partial_{1} Γ_{21}^{s (α)}) g_{s l} + (Γ_{j β, l}^{(α)} Γ_{11}^{β (α)} - Γ_{i β, l}^{(α)} Γ_{21}^{β (α)})] = [\begin{matrix} (\frac{\partial}{\partial ξ} {[Γ}_{11}^{1 (α)} + Γ_{11}^{2 (α)} + Γ_{11}^{3 (α)}] - \frac{\partial}{\partial λ} {[Γ}_{21}^{1 (α)} + Γ_{21}^{2 (α)} + Γ_{21}^{3 (α)}]) {(g}_{12} + g_{22} + g_{32}) \\ + ([Γ_{21,2}^{(α)} Γ_{11}^{1 (α)} + Γ_{22,2}^{(α)} Γ_{11}^{2 (α)} + Γ_{23,2}^{(α)} Γ_{11}^{3 (α)}] - {[Γ}_{11,2}^{(α)} Γ_{21}^{1 (α)} + Γ_{12,2}^{(α)} Γ_{21}^{2 (α)} + Γ_{13,2}^{(α)} Γ_{21}^{3 (α)}]) \end{matrix}]

(11.2)

= [\begin{matrix} (- \frac{(1 - α)}{{2 ξ}^{3}} \frac{\partial}{\partial λ} [(2 D_{1} + {2 G ξ}^{.}) + (2 E + {2 H ξ}^{.}) + (F + {I ξ}^{.})]) (a + d_{1} + h) \\ - \frac{(1 - α)}{2 ξ^{3}} ([(2 - [1 + t ξ] [t ξ + 2] e^{- t ξ}) \frac{(1 - α)}{2 ξ^{3}} (2 E + {2 H ξ}^{.}) + \frac{2 (1 - α) ξ^{.}}{ξ^{3}} [1 - (1 + ξ t) e^{- t ξ}] (F + {I ξ}^{.})]) \end{matrix}]

(11.3)

t \to \infty

a = - \frac{1}{ξ^{2}}

(11.4)

b = \frac{- ξ^{.}}{ξ^{2}}

(11.5)

d_{1} = \frac{2 λ}{ξ^{3}}

(11.6)

g = \frac{[λ^{.} ξ - 2 λ ξ^{.}]}{ξ^{3}}

(11.7)

l = \frac{- ξ^{.}}{ξ^{2}} = b

(11.8)

h = \frac{(2 λ ξ^{.} - λ^{.} ξ)}{ξ^{3}}

(11.9)

r = \frac{(λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 2 λ^{.} ξ ξ^{.} + 2 λ ξ^{. 2})}{ξ^{3}}

(11.10)

Δ_{\infty} = (- a (l g - a r) + b (a h - l d_{1}))) = \frac{λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 4 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2}}{ξ^{7}}

(11.11)

R_{1212, t \to \infty}^{(α)} = [\begin{matrix} (- \frac{(1 - α)}{{2 ξ}^{3}} \frac{\partial}{\partial λ} [(2 D_{1} + {2 G ξ}^{.}) + (2 E + {2 H ξ}^{.}) + (F + {I ξ}^{.})]) (a + d_{1} + h) \\ - \frac{(1 - α)}{2 ξ^{3}} ([\frac{(1 - α)}{ξ^{3}} (2 E + {2 H ξ}^{.}) + \frac{2 (1 - α) ξ^{.}}{ξ^{3}} (F + {I ξ}^{.})]) \end{matrix}]

(11.12)

We have

(a + d_{1} + h) = (\frac{2 λ}{ξ^{3}} - \frac{1}{ξ^{2}} + \frac{(2 λ ξ^{.} - λ^{.} ξ)}{ξ^{3}}) = \frac{(2 λ ξ^{.} - λ^{.} ξ + 2 λ - ξ)}{ξ^{3}}

(11.13)

Recall that:

D_{1} = \frac{(l g - a r)}{∆}, E = \frac{(- l b)}{∆}, F = \frac{(a b)}{∆}, G = \frac{(a h - l d_{1})}{∆}, H = \frac{(l a)}{∆} I = (2 D_{1} + {2 G ξ}^{.}) = \frac{(l g - a r) + (a h - l d_{1}) ξ^{.}}{∆_{\infty}} = \frac{ξ^{2} (λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 2 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2})}{λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 4 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2}}

(11.14)

(2 E + {2 H ξ}^{.}) = \frac{2 l [a ξ^{.} - b]}{∆_{\infty}} = \frac{- {2 ξ}^{.}}{ξ^{2}} \frac{[- \frac{1}{ξ^{2}} ξ^{.} + \frac{ξ^{.}}{ξ^{2}}]}{∆_{\infty}} = 0

(11.15)

(F + {I ξ}^{.}) = \frac{a (b - a ξ^{.})}{∆_{\infty}} = \frac{- \frac{1}{ξ^{2}} (- \frac{1}{ξ^{2}} ξ^{.} + \frac{1}{ξ^{2}} ξ^{.})}{∆_{\infty}} = 0

(11.16)

Combining (11.12), (3.14)-(3.16), we have

R_{1212, t \to \infty}^{(α)} = [(- \frac{(1 - α) (2 λ ξ^{.} - λ^{.} ξ + 2 λ - ξ)}{2 ξ^{4}} \frac{\partial}{\partial λ} [\frac{(λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 2 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2})}{λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 4 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2}}])] = [(- \frac{(1 - α) (2 λ ξ^{.} - λ^{.} ξ + 2 λ - ξ) (4 ξ^{. 2} - ξ ξ^{. .})}{2 ξ^{4}} [\frac{(λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 4 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2}) - (λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 2 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2})}{{(λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 4 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2})}^{2}}])] = [(\frac{(1 - α) (2 λ ξ^{.} - λ^{.} ξ + 2 λ - ξ) λ^{.} ξ^{.} (4 ξ^{. 2} - ξ ξ^{. .})}{ξ^{3} {(λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 4 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2})}^{2}})]

(11.17)

B a s e d o n o u r c a l c u l a t i o n s

, the

α -

Gaussian Curvature,

K_{\infty}^{(α)}

as time approaches infinity is devised by:

K_{\infty}^{(α)} = \frac{R_{1212, t \to \infty}^{(α)}}{∆_{\infty}} = \frac{[(\frac{(1 - α) (2 λ ξ^{.} - λ^{.} ξ + 2 λ - ξ) λ^{.} ξ^{.} (4 ξ^{. 2} - ξ ξ^{. .})}{ξ^{3} {(λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 4 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2})}^{2}})]}{\frac{λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 4 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2}}{ξ^{7}}} = [(\frac{(1 - α) {λ^{.} ξ^{.} ξ}^{4} (2 λ ξ^{.} - λ^{.} ξ + 2 λ - ξ) (4 ξ^{. 2} - ξ ξ^{. .})}{{(λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 4 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2})}^{3}})]

(c.f., (11.1))

In the following theorem, the zeros of the

α -

Gaussian Curvature

K_{\infty}^{(α)}

are determined. Based on this, the paths of motion of the coordinates at which the underlying QM is looked at as a developable surface are obtained. The following theorem presents a novel approach which unifies Information Geometry with Riemannian Geometry, the theory of developable surfaces and the theory of time -dependent queueing systems.

Theorem 11.2.

The

u n d e r l y i n g

M/M/

\infty

QM is developable on the following trajectories:

α = 1

, or

λ = c o n s t a n t

ξ = c o n s t a n t

λ = ξ = 0

ξ = ϑ_{2} e^{4 ϑ_{1} t}

λ = a_{1}, (ξ - 2 a_{1}) = a_{2} e^{\frac{t}{2 a_{1}}}

ξ = a_{3}, (2 λ - a_{3}) = a_{4} e^{- \frac{2 t}{a_{3}}}

for any arbitrary non - zero real constants ϑ_{1}, ϑ_{2}, a_{1}, a_{2} a n d a_{3}, a_{4 .}

(11.18)

Proof.

K_{\infty}^{(α)} = 0 i f a n d o n l y i f

(1 - α) {λ^{.} ξ^{.} ξ}^{4} (4 ξ^{. 2} - ξ ξ^{. .}) (2 λ ξ^{.} - λ^{.} ξ + 2 λ - ξ) = 0

(11.19)

If and only if one of the following equations holds:

(i) (1 - α) = 0 ⟹ α = 1

(11.20)

(ii) λ^{.} = 0 ⟹ λ = c o n s t a n t

(11.21)

(iii) ξ^{.} = 0 ⟹ ξ = c o n s t a n t

(11.22)

(iv) ξ^{4} = 0 ⟹ ξ = 0

(11.23)

(4 ξ^{. 2} - ξ ξ^{. .}) = 0 ⟹

(v) 4 \frac{ξ^{.}}{ξ} = \frac{ξ^{. .}}{ξ^{.}}

(11.24)

(13.24) w h i c h h a s a c l o s e d f o r m s o l u t i o n

4 ϑ_{1} ξ = ξ^{.}

(11.25)

w h e r e ϑ_{1} i s a n a r b i t r a r y c o n s t a n t

(11.25) has the closed form solution:

ξ = ϑ_{2} e^{4 ϑ_{1} t}

(11.26)

w h e r e ϑ_{2} i s a n a r b i t r a r y c o n s t a n t

(vi) (2 λ ξ^{.} - λ^{.} ξ + 2 λ - ξ) = 0

(11.27)

It is clear that

λ = 0

and

ξ = 0

are two closed form solutions of (11.26). We can try another closed form solutions of (11.27), for example,

l e t λ = a_{1}

for any arbitrary non-zero real constant

a_{1}

. This implies:

(2 a_{1} ξ^{.} + 2 a_{1} - ξ) = 0

⟹

{2 a_{1} ξ}^{.} = ξ - 2 a_{1} ⟹ \frac{d ξ}{ξ - 2 a_{1}} = \frac{d t}{2 a_{1}}

⟹ l n (ξ - 2 a_{1}) = \frac{t}{2 a_{1}} + l n a_{2}

for some arbitrary non-zero real constant

a_{2}

. Therefore, we have the closed form solutions of (11.27) to be given by

λ = a_{1}, (ξ - 2 a_{1}) = a_{2} e^{\frac{t}{2 a_{1}}}

(11.28)

Moreover, we can deduce more closed form solutions of (11.27), for example,

l e t ξ = a_{3}

for any arbitrary non-zero real constant

a_{3}

. This implies :

(- λ^{.} a_{3} + 2 λ - a_{3}) = 0

⟹

λ^{.} a_{3} = - (2 λ - a_{3}) ⟹ \frac{d λ}{(2 λ - a_{3})} = - \frac{2 d t}{a_{3}}

⟹ l n (2 λ - a_{3}) = - \frac{2 t}{a_{3}} + l n a_{4}

for some arbitrary non-zero real constant

a_{4}

. Therefore, we have the closed form solutions of (11.27) to be given by

ξ = a_{3}, (2 λ - a_{3}) = a_{4} e^{- \frac{2 t}{a_{3}}}

(11.29)

12. Ricci Curvature TENSOR , ${(R C T)}_{\infty}^{\to}$ and the $α - S e c t i o n a l$ Gaussian Curvatures of M/M/∞ QM F M/M/ $\infty$

QM as Time Approaches Infinity

In this section, the Ricci Curvature Tensor, (RCT) of M/M/

\infty

is obtained. These calculations are needed in the following sections.

{(R C T)}_{\infty}^{\to} = [\begin{matrix} R_{11, \infty}^{(α)} & R_{12, \infty}^{(α)} & R_{13, \infty}^{(α)} \\ R_{21, \infty}^{(α)} & R_{22, \infty}^{(α)} & R_{23, \infty}^{(α)} \\ R_{31, \infty}^{(α)} & R_{32, \infty}^{(α)} & R_{33, \infty}^{(α)} \end{matrix}]

Which is a nine-dimensional tensor.

12.1. The First Component, $R_{11, \infty}^{(α)}$

Theorem 12.1.

for the underlying M/M/

\infty

QM, the first component of the Ricci Curvature Tensor as time reaches infinity,

R_{11, \infty}^{(α)} .

R_{11, \infty}^{(α)} = \frac{(1 - α) (4 ξ^{. 2} - ξ ξ^{. .}) ξ^{.} λ^{.}}{{(λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 4 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2})}^{3}} ([- ξ^{. 2} (2 λ ξ^{.} - λ^{.} ξ + 2 λ - ξ)] - [2 λ^{.} ξ ({1 + ξ}^{.})] + [2 (ξ^{.} + 1) (λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 3 λ^{.} ξ ξ^{.} + 2 λ ξ^{. 2})] - [ξ^{. 2} ξ^{4}] + [2 ξ^{.} (- 2 λ ξ^{.} + λ^{.} ξ - 2 λ + ξ)] + [ξ^{.} ξ^{3}])

Proof.

Recalling from (11.4)-(11.10), that

a = - \frac{1}{ξ^{2}}, b = \frac{- ξ^{.}}{ξ^{2}}, d_{1} = \frac{2 λ}{ξ^{3}}, g = \frac{[λ^{.} ξ - 2 λ ξ^{.}]}{ξ^{3}}, l = \frac{- ξ^{.}}{ξ^{2}} = b, h = \frac{(2 λ ξ^{.} - λ^{.} ξ)}{ξ^{3}}, r = \frac{(λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 2 λ^{.} ξ ξ^{.} + 2 λ ξ^{. 2})}{ξ^{3}} Δ_{\infty} = (- a (l g - a r) + b (a h - l d_{1}))) = \frac{λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 4 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2}}{ξ^{7}},

We have

(a + d_{1} + h) = (\frac{2 λ}{ξ^{3}} - \frac{1}{ξ^{2}} + \frac{(2 λ ξ^{.} - λ^{.} ξ)}{ξ^{3}}) = \frac{(2 λ ξ^{.} - λ^{.} ξ + 2 λ - ξ)}{ξ^{3}}

(12.1)

R_{11, \infty}^{(α)} = R_{1111, \infty}^{(α)} g^{11, \infty} + R_{1211, \infty}^{(α)} g^{21, \infty} + R_{1311, \infty}^{(α)} g^{31, \infty} + R_{1112, \infty}^{(α)} g^{12, \infty} + R_{1113}^{(α)} g^{13, \infty} + R_{1212, \infty}^{(α)} g^{22, \infty} + R_{1213, \infty}^{(α)} g^{23, \infty} + R_{1312, \infty}^{(α)} g^{32, \infty} + R_{1313, \infty}^{(α)} g^{33, \infty}

(12.2)

We have

R_{i j k l}^{(α)} = [(\partial_{j} Γ_{i k}^{s (α)} - \partial_{i} Γ_{j k}^{s (α)}) g_{s l} + (Γ_{j β, l}^{(α)} Γ_{i k}^{β (α)} - Γ_{i β, l}^{(α)} Γ_{j k}^{β (α)})]

(2.11)

where

Γ_{i j}^{k (α)} = Γ_{i j, s}^{(α)} g^{s k}

, i,j,k,s = 1,2,...,n

R_{1111, t \to \infty}^{(α)} = [(\partial_{1} Γ_{11}^{s (α)} - \partial_{1} Γ_{11}^{s (α)}) g_{s 1} + (Γ_{1 β, 1}^{(α)} Γ_{11}^{β (α)} - Γ_{1 β, 1}^{(α)} Γ_{11}^{β (α)})] = 0

(12.3)

R_{1113, t \to \infty}^{(α)} = [(\partial_{1} Γ_{11}^{s (α)} - \partial_{1} Γ_{11}^{s (α)}) g_{s 3} + (Γ_{1 β, 3}^{(α)} Γ_{11}^{β (α)} - Γ_{1 β, 3}^{(α)} Γ_{11}^{β (α)})] = 0 = R_{1112, \infty}^{(α)}

(12.4)

R_{1211, t \to \infty}^{(α)} = [(\partial_{2} Γ_{11}^{s (α)} - \partial_{1} Γ_{21}^{s (α)}) g_{s 1} + (Γ_{2 β, l}^{(α)} Γ_{11}^{β (α)} - Γ_{1 β, l}^{(α)} Γ_{21}^{β (α)})] = [(\frac{\partial}{\partial ξ} {(Γ}_{11}^{1 (α)} + Γ_{11}^{2 (α)} + Γ_{11}^{3 (α)}) - \frac{\partial}{\partial λ} {(Γ}_{21}^{1 (α)} + Γ_{21}^{2 (α)} + Γ_{21}^{3 (α)})) + (Γ_{2 β, 1}^{(α)} Γ_{11}^{β (α)} - Γ_{1 β, 1}^{(α)} Γ_{21}^{β (α)})] = [(\frac{\partial}{\partial ξ} (0) - \frac{\partial}{\partial λ} (\frac{(1 - α)}{2 ξ^{3}} (2 D_{1} + {2 G ξ}^{.}) + \frac{(1 - α)}{2 ξ^{3}} (2 E + {2 H ξ}^{.}) + \frac{(1 - α)}{2 ξ^{3}} (2 F + {2 I ξ}^{.})) - (0)] = \frac{(α - 1)}{ξ^{3}} [(\frac{\partial}{\partial λ} (D_{1} + E + F + (H + {G + I) ξ}^{.}))]

(12.5)

(D_{1} + E + F + (H + {G + I) ξ}^{.}) = [\frac{(l g - a r) - l b + a b + {(l a - a^{2} + (a h - l d_{1})) ξ}^{.}}{∆_{\infty}}] = [\frac{(\frac{- ξ^{.}}{ξ^{2}} \frac{[λ^{.} ξ - 2 λ ξ^{.}]}{ξ^{3}} + \frac{1}{ξ^{2}} \frac{(λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 2 λ^{.} ξ ξ^{.} + 2 λ ξ^{. 2})}{ξ^{3}}) - \frac{- ξ^{.}}{ξ^{2}} \frac{- ξ^{.}}{ξ^{2}} + \frac{- 1}{ξ^{2}} \frac{- ξ^{.}}{ξ^{2}} + {(\frac{- 1}{ξ^{2}} \frac{- ξ^{.}}{ξ^{2}} - \frac{1}{ξ^{4}} + (\frac{- 1}{ξ^{2}} \frac{(2 λ ξ^{.} - λ^{.} ξ)}{ξ^{3}} - \frac{- ξ^{.}}{ξ^{2}} \frac{2 λ}{ξ^{3}})) ξ}^{.}}{\frac{λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 4 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2}}{ξ^{7}}}] = [\frac{(\frac{(λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 2 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2})}{ξ^{5}})}{\frac{λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 4 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2}}{ξ^{7}}}] = [\frac{ξ^{2} (λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 2 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2})}{λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 4 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2}}]

(12.6)

[(\frac{\partial}{\partial λ} (D_{1} + E + F + (H + {G + I) ξ}^{.}))] = ξ^{2} \frac{\partial}{\partial λ} [\frac{(λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 2 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2})}{λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 4 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2}}] = [\frac{2 λ^{.} ξ^{.} (ξ ξ^{. .} - 4 ξ^{. 2}) ξ^{3}}{{{(λ}^{. .} ξ^{2} - λ ξ ξ^{. .} - 4 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2})}^{2}}]

(12.7)

Hence,

R_{1211, t \to \infty}^{(α)} = [\frac{2 {(1 - α) λ}^{.} ξ^{.} (ξ ξ^{. .} - 4 ξ^{. 2}) (ξ^{.} + 1)}{{ξ^{2} {(λ}^{. .} ξ^{2} - λ ξ ξ^{. .} - 4 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2})}^{2}}]

(12.8)

R_{1311, t \to \infty}^{(α)} = [(\partial_{3} Γ_{11}^{s (α)} - \partial_{1} Γ_{21}^{s (α)}) g_{s 1} + (Γ_{3 β, 1}^{(α)} Γ_{11}^{β (α)} - Γ_{1 β, 1}^{(α)} Γ_{21}^{β (α)})] = [\frac{2 {(1 - α) λ}^{.} ξ^{.} (ξ ξ^{. .} - 4 ξ^{. 2}) ({1 + ξ}^{.})}{{ξ^{2} {(λ}^{. .} ξ^{2} - λ ξ ξ^{. .} - 4 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2})}^{2}}]

(12.9)

R_{1312, t \to \infty}^{(α)} = \frac{2 (1 - α)}{ξ^{3}} [\frac{λ^{.} ξ^{.} (ξ ξ^{. .} - 4 ξ^{. 2}) (2 λ ξ^{.} - λ^{.} ξ + 2 λ - ξ)}{{{(λ}^{. .} ξ^{2} - λ ξ ξ^{. .} - 4 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2})}^{2}}]

(12.10)

R_{1213, t \to \infty}^{(α)} = \frac{(1 - α)}{ξ^{2}} [\frac{λ^{.} ξ^{. 2} (ξ ξ^{. .} - 4 ξ^{. 2}) ξ^{3}}{{{(λ}^{. .} ξ^{2} - λ ξ ξ^{. .} - 4 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2})}^{2}}]

(12.11)

R_{1313, t \to \infty}^{(α)} = \frac{(1 - α)}{ξ^{2}} [\frac{λ^{.} ξ^{. 2} (ξ ξ^{. .} - 4 ξ^{. 2}) ξ^{3}}{{{(λ}^{. .} ξ^{2} - λ ξ ξ^{. .} - 4 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2})}^{2}}]

(12.12)

Therefore,

R_{11, \infty}^{(α)} = R_{1211, \infty}^{(α)} D_{1} + R_{1311, \infty}^{(α)} G + R_{1212, \infty}^{(α)} E + R_{1213, \infty}^{(α)} F + R_{1312, \infty}^{(α)} H + R_{1313, \infty}^{(α)} I

R_{11, \infty}^{(α)} = ([(\frac{(1 - α) (2 λ ξ^{.} - λ^{.} ξ + 2 λ - ξ) λ^{.} ξ^{.} (4 ξ^{. 2} - ξ ξ^{. .})}{ξ^{3} {(λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 4 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2})}^{2}})] E + [\frac{2 {(1 - α) λ}^{.} ξ^{.} (ξ ξ^{. .} - 4 ξ^{. 2}) ({1 + ξ}^{.})}{{ξ^{2} {(λ}^{. .} ξ^{2} - λ ξ ξ^{. .} - 4 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2})}^{2}}] G + [\frac{2 {(1 - α) λ}^{.} ξ^{.} (ξ ξ^{. .} - 4 ξ^{. 2}) (ξ^{.} + 1)}{{ξ^{2} {(λ}^{. .} ξ^{2} - λ ξ ξ^{. .} - 4 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2})}^{2}}] D_{1} + \frac{(1 - α)}{ξ^{2}} [\frac{λ^{.} ξ^{. 2} (ξ ξ^{. .} - 4 ξ^{. 2}) ξ^{3}}{{{(λ}^{. .} ξ^{2} - λ ξ ξ^{. .} - 4 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2})}^{2}}] F + \frac{2 (1 - α)}{ξ^{3}} [\frac{λ^{.} ξ^{.} (ξ ξ^{. .} - 4 ξ^{. 2}) (2 λ ξ^{.} - λ^{.} ξ + 2 λ - ξ)}{{{(λ}^{. .} ξ^{2} - λ ξ ξ^{. .} - 4 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2})}^{2}}] H + \frac{(1 - α)}{ξ^{2}} [\frac{λ^{.} ξ^{. 2} (ξ ξ^{. .} - 4 ξ^{. 2}) ξ^{3}}{{{(λ}^{. .} ξ^{2} - λ ξ ξ^{. .} - 4 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2})}^{2}}] I)

(12.13)

E = \frac{(- l b)}{∆_{\infty}} = \frac{- {ξ^{3} ξ}^{. 2}}{λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 4 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2}}

(12.14)

G = \frac{(a h - l d_{1})}{∆_{\infty}} = \frac{λ^{.} ξ^{3}}{λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 4 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2}}

(12.15)

D_{1} = \frac{(l g - a r)}{∆_{\infty}} = \frac{(λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 3 λ^{.} ξ ξ^{.} + 2 λ ξ^{. 2}) ξ^{2}}{λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 4 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2}}

(12.16)

F = \frac{(a b)}{∆_{\infty}} = \frac{ξ^{3} ξ^{.}}{λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 4 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2}}

(12.17)

H = \frac{(l a)}{∆_{\infty}} = \frac{ξ^{3} ξ^{.}}{λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 4 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2}}

(12.18)

I = \frac{(- a^{2})}{∆_{\infty}} = - \frac{ξ^{3}}{λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 4 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2}}

(12.19)

Based on the above complicated calculations, we have

R_{11, \infty}^{(α)} = ([(\frac{(1 - α) (2 λ ξ^{.} - λ^{.} ξ + 2 λ - ξ) λ^{.} ξ^{.} (4 ξ^{. 2} - ξ ξ^{. .})}{{(λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 4 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2})}^{2}})] [\frac{- ξ^{. 2}}{λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 4 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2}}] + [\frac{2 {(1 - α) λ}^{.} ξ^{.} (ξ ξ^{. .} - 4 ξ^{. 2}) ({1 + ξ}^{.})}{{{(λ}^{. .} ξ^{2} - λ ξ ξ^{. .} - 4 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2})}^{2}}] [\frac{λ^{.} ξ}{λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 4 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2}}] + [\frac{2 {(1 - α) λ}^{.} ξ^{.} (ξ ξ^{. .} - 4 ξ^{. 2}) (ξ^{.} + 1)}{{{(λ}^{. .} ξ^{2} - λ ξ ξ^{. .} - 4 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2})}^{2}}] [\frac{(λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 3 λ^{.} ξ ξ^{.} + 2 λ ξ^{. 2})}{λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 4 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2}}] + (1 - α) [\frac{λ^{.} ξ^{. 2} (ξ ξ^{. .} - 4 ξ^{. 2}) ξ^{4}}{{{(λ}^{. .} ξ^{2} - λ ξ ξ^{. .} - 4 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2})}^{2}}] [\frac{ξ^{.}}{λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 4 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2}}] + 2 (1 - α) [\frac{λ^{.} ξ^{.} (ξ ξ^{. .} - 4 ξ^{. 2}) (2 λ ξ^{.} - λ^{.} ξ + 2 λ - ξ)}{{{(λ}^{. .} ξ^{2} - λ ξ ξ^{. .} - 4 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2})}^{2}}] [\frac{ξ^{.}}{λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 4 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2}}] + (1 - α) [\frac{λ^{.} ξ^{. 2} (ξ ξ^{. .} - 4 ξ^{. 2}) ξ^{3}}{{{(λ}^{. .} ξ^{2} - λ ξ ξ^{. .} - 4 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2})}^{2}}] [- \frac{1}{λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 4 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2}}]) = \frac{(1 - α)}{{(λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 4 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2})}^{3}} ([- ξ^{. 2} (2 λ ξ^{.} - λ^{.} ξ + 2 λ - ξ) λ^{.} ξ^{.} (4 ξ^{. 2} - ξ ξ^{. .})] + [2 λ^{. 2} {ξ ξ}^{.} (ξ ξ^{. .} - 4 ξ^{. 2}) ({1 + ξ}^{.})] + [2 λ^{.} ξ^{.} (ξ ξ^{. .} - 4 ξ^{. 2}) (ξ^{.} + 1) (λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 3 λ^{.} ξ ξ^{.} + 2 λ ξ^{. 2})] + [λ^{.} ξ^{. 3} (ξ ξ^{. .} - 4 ξ^{. 2}) ξ^{4}] + [{2 λ}^{.} ξ^{. 2} (ξ ξ^{. .} - 4 ξ^{. 2}) (2 λ ξ^{.} - λ^{.} ξ + 2 λ - ξ)] - [λ^{.} ξ^{. 2} (ξ ξ^{. .} - 4 ξ^{. 2}) ξ^{3}])

(12.20)

= \frac{(1 - α) (4 ξ^{. 2} - ξ ξ^{. .}) ξ^{.} λ^{.}}{{(λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 4 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2})}^{3}} ([- ξ^{. 2} (2 λ ξ^{.} - λ^{.} ξ + 2 λ - ξ)] - [2 λ^{.} ξ ({1 + ξ}^{.})] + [2 (ξ^{.} + 1) (λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 3 λ^{.} ξ ξ^{.} + 2 λ ξ^{. 2})] - [ξ^{. 2} ξ^{4}] + [2 ξ^{.} (- 2 λ ξ^{.} + λ^{.} ξ - 2 λ + ξ)] + [ξ^{.} ξ^{3}])

(12.21)

T h i s c o m p l e t e s t h e p r o o f o f o u r t h e o r e m .

Recall that whenever Ricci curvature is positive, then according to the Bonnet Myers theorem (c.f., Ollivier, 2010) the Riemannian manifold is more positively curved than a sphere and the diameter of the manifold is smaller.

Based on this, we are going to open a new thinking framework which designs a decision procedure on when the underlying QM is more positively curved than a sphere and the diameter of the manifold is smaller. This could be obtained by calculating the zeros of the first component of the Ricci Curvature tensor as time approaches infinity,

{(R C T)}_{\infty}^{\to}

, namely,

R_{11, \infty}^{(α)}

. In other words, the following theorem answers this open question.

Theorem 12.2.

{T h e z e r o s o f R}_{11, \infty}^{(α)} (c . f ., (12.21))

is one of the following:

α = 1, i n o t h e r w o r d s, w h e n e v e r t h e c u r v a t u r e p a r a m e t e r i s s e t t o u n i t y .

t h e e q u a t i o n o f m o t i o n o f t h e P o i s s o n i a n a r r i v a l r a t e, ξ i s g o v e r n e d b y t h e t e m p o r a l p a t h

ξ = ϑ_{2} e^{4 ϑ_{1} t}

(c.f., (11.26))

ξ = c o n s t a n t

λ = c o n s t a n t

T h e d y n a m i c s o f b o t h o f a r r i v a l r a t e a n d t h e P o i s s o n i a n a r r i v a l r a t e i s g o v e r n e d b y t h e e q u a t i o n

λ = c_{1} ξ e^{\frac{t}{ξ}} + c_{2}, ξ = c o n s t a n t, c_{1} a n d c_{2} a r e a n y t w o n o n - z e r o r e a l a r b i t r a r y c o n s t a n t s

(12.22)

T h e d y n a m i c s o f b o t h o f a r r i v a l r a t e a n d t h e P o i s s o n i a n a r r i v a l r a t e i s g o v e r n e d b y t h e e q u a t i o n]

ξ = t a n [\frac{(t - \frac{ξ^{2}}{2} + c_{3}) \sqrt{2}}{5}], λ = z e r o a n d c_{3} i s a n y n o n - z e r o r e a l a r b i r a r y constant

(12.23)

Proof.

We have

R_{11, \infty}^{(α)} = \frac{(1 - α) (4 ξ^{. 2} - ξ ξ^{. .}) ξ^{.} λ^{.}}{{(λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 4 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2})}^{3}} ([- ξ^{. 2} (2 λ ξ^{.} - λ^{.} ξ + 2 λ - ξ)] - [2 λ^{.} ξ ({1 + ξ}^{.})] + [2 (ξ^{.} + 1) (λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 3 λ^{.} ξ ξ^{.} + 2 λ ξ^{. 2})] - [ξ^{. 2} ξ^{4}] + [2 ξ^{.} (- 2 λ ξ^{.} + λ^{.} ξ - 2 λ + ξ)] + [ξ^{.} ξ^{3}])

(c.f., (11.21))

Clearly,

R_{11, \infty}^{(α)}

= 0 if and only if one of the following statements holds:

(1 - α) = 0

(12.24)

(4 ξ^{. 2} - ξ ξ^{. .}) = 0

(12.25)

ξ^{.} = 0

(12.26)

λ^{.} = 0

(12.27)

([- ξ^{. 2} (2 λ ξ^{.} - λ^{.} ξ + 2 λ - ξ)] - [2 λ^{.} ξ ({1 + ξ}^{.})] + [2 (ξ^{.} + 1) (λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 3 λ^{.} ξ ξ^{.} + 2 λ ξ^{. 2})] - [ξ^{. 2} ξ^{4}] + [2 ξ^{.} (- 2 λ ξ^{.} + λ^{.} ξ - 2 λ + ξ)] + [ξ^{.} ξ^{3}]) = 0

(12.28)

C l e a r l y (11.24) i m p l i e s 1) .

It has been proven that the exact solution of differential equation (11.25) is determined by

ξ = ϑ_{2} e^{4 ϑ_{1} t}

(c.f., (11.26))

This proves 2).

The proofs of 3) and 4) are straightforward.

Following

([- ξ^{. 2} (2 λ ξ^{.} - λ^{.} ξ + 2 λ - ξ)] - [2 λ^{.} ξ ({1 + ξ}^{.})] + [2 (ξ^{.} + 1) (λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 3 λ^{.} ξ ξ^{.} + 2 λ ξ^{. 2})] - [ξ^{. 2} ξ^{4}] + [2 ξ^{.} (- 2 λ ξ^{.} + λ^{.} ξ - 2 λ + ξ)] + [ξ^{.} ξ^{3}]) = 0

(c.f., (11.28))

Let

ξ = c o n s t a n t

. This reduces (11.28) to

2 ξ (λ^{. .} ξ - λ^{.}) = 0

(12.29)

which implies

ξ = 0

λ^{. .} ξ = λ^{.}

(12.30)

(equivalently,

\frac{d λ^{.}}{λ^{.}}

\frac{d t}{ξ}

). These yields

λ^{.} = c_{1} e^{\frac{t}{ξ}}

, which has a closed form solution:

λ = c_{1} ξ e^{\frac{t}{ξ}} + c_{2}

(c.f., (12.22))

w i t h n o n - z e r o r e a l c o n s t a n t s c_{1}, c_{2}

This proves 5).

Moreover, plugging

λ = 0 i n (11.28)

yields

0 = [(- 5 ξ ξ^{. 2}) - ξ^{. 2} ξ^{4} + 2 ξ ξ^{.} + ξ^{.} ξ^{3}] = {ξ ξ}^{.} [(- 5 ξ ξ^{.}) - ξ^{.} ξ^{4} + 2 ξ + ξ^{3}]

(12.31)

It can be easily seen that (11.31) generates

ξ = 0

ξ = c o n s t a n t

[(- 5 ξ^{.}) - ξ^{.} ξ^{3}

2

ξ^{2}] = 0

, implying

ξ^{.} = \frac{2 + ξ^{2}}{5 + ξ^{3}} ⟹ (\frac{\frac{5}{2} d ξ}{1 + ({\frac{ξ}{\sqrt 2})}^{2}} - 2 \frac{d ξ}{2 + ξ^{2}}) + ξ d ξ = d t

(12.32)

I n t e g r a t i n g b o t h s i d e s o f (11.32), w e h a v e t h e e x a c t s o l u t i o n o f o f t h e f o r m

\frac{5}{\sqrt{2}} {t a n}^{- 1} (\frac{ξ}{\sqrt{2}}) + \frac{ξ^{2}}{2} = (t + c_{3}) \frac{5}{\sqrt{2}} {t a n}^{- 1} (\frac{ξ}{\sqrt{2}}) = (t - \frac{ξ^{2}}{2} + c_{3}), c_{3} i s a n y n o n - z e r o real constant

(12.33)

T h i s r e w r i t e s (11.33) t o t h e c o m p a c t f o r m

ξ = t a n [\frac{(t - \frac{ξ^{2}}{2} + c_{3}) \sqrt{2}}{5}]

(c.f., (12.23))

This proves 6).

11.3. ${T h e α - S e c t i o n a l c u r v a t u r e s, K}_{i j i j}^{(α)} = \frac{R_{i j i j}^{(α)}}{(g_{i i}) (g_{j j}) - {(g_{i j})}^{2}}, i, j = 1,2, \dots, n$ , (c.f., (2.13))

T h e α - S e c t i o n a l C u r v a t u r e s a s t i m e a p p r o a c h e s i n f i n i t y a r e g i v e n b y

K_{i j i j, \infty}^{(α)} = \frac{R_{i j i j, \infty}^{(α)}}{Δ_{\infty}}

(12.34)

T h e r e a d e r c a n e a s i l y c h e c k t h a t

K_{1111, \infty}^{(α)} = 0 = K_{1112, \infty}^{(α)} = K_{1113, \infty}^{(α)}

(12.35)

Δ_{\infty} = (- a (l g - a r) + b (a h - l d_{1}))) = \frac{λ^{. .} ξ^{2} - λ ξ ξ^{. .} - 4 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2}}{ξ^{7}} K_{1211, \infty}^{(α)} = \frac{R_{1211, \infty}^{(α)}}{Δ_{\infty}} = [\frac{2 {(1 - α) λ}^{.} ξ^{.} (ξ ξ^{. .} - 4 ξ^{. 2}) (ξ^{.} + 1) ξ^{5}}{{{(λ}^{. .} ξ^{2} - λ ξ ξ^{. .} - 4 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2})}^{3}}]

(12.36)

K_{1311, \infty}^{(α)} = \frac{R_{1311, \infty}^{(α)}}{Δ_{\infty}} = [\frac{2 {(1 - α) λ}^{.} ξ^{.} (ξ ξ^{. .} - 4 ξ^{. 2}) ({1 + ξ}^{.}) ξ^{5}}{{{(λ}^{. .} ξ^{2} - λ ξ ξ^{. .} - 4 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2})}^{2}}]

(12.37)

K_{1312, \infty}^{(α)} = \frac{R_{1312, \infty}^{(α)}}{Δ_{\infty}} = [\frac{{2 (1 - α) λ}^{.} ξ^{.} (ξ ξ^{. .} - 4 ξ^{. 2}) (2 λ ξ^{.} - λ^{.} ξ + 2 λ - ξ) ξ^{4}}{{{(λ}^{. .} ξ^{2} - λ ξ ξ^{. .} - 4 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2})}^{2}}]

(12.38)

K_{1311, \infty}^{(α)} = \frac{R_{1311, \infty}^{(α)}}{Δ_{\infty}} = [\frac{2 {(1 - α) λ}^{.} ξ^{.} (ξ ξ^{. .} - 4 ξ^{. 2}) ({1 + ξ}^{.}) ξ^{5}}{{{(λ}^{. .} ξ^{2} - λ ξ ξ^{. .} - 4 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2})}^{2}}]

(12.39)

K_{1213, \infty}^{(α)} = \frac{R_{1213, \infty}^{(α)}}{Δ_{\infty}} = [\frac{(1 - α) λ^{.} ξ^{. 2} (ξ ξ^{. .} - 4 ξ^{. 2}) ξ^{8}}{{{(λ}^{. .} ξ^{2} - λ ξ ξ^{. .} - 4 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2})}^{2}}]

(12.40)

K_{1313, \infty}^{(α)} = \frac{R_{1313, \infty}^{(α)}}{Δ_{\infty}} = [\frac{(1 - α) λ^{.} ξ^{. 2} (ξ ξ^{. .} - 4 ξ^{. 2}) ξ^{3}}{{{(λ}^{. .} ξ^{2} - λ ξ ξ^{. .} - 4 λ^{.} ξ ξ^{.} + 4 λ ξ^{. 2})}^{2}}]

(12.41)

The remaining 72

α - S e c t i o n a l C u r v a t u r e s

can be obtained by following the same procedure.

13. Conclusion and Future Work

The research done for this paper offers a fresh method for modelling the information geometry of a queuing system. From the perspective of IG, the manifold of the temporary

M / M / \infty

queue is described in this context.

FIM and IFIM of transient M/M/

\infty

queue manifold is devised. In addition to that, new results that uncovered the significant impact of stability of M/M/

\infty

queue manifold on the existence of (IFIM) are devised. Moreover, the Geodesic equations of motion of the coordinates of the underlying transient

M / M / \infty

are obtained. Also, it is revealed that stable

M / M / \infty

QM is developable (i.e., has a zero Gaussian curvature) and has a non-zero Ricci Curvature Tensor (RCT). Novel stability dynamics of transient M/M/

\infty

queue manifold is revealed by discovering the mutual dual impact between the behaviour of (RCT) and the stability and the instability phases of the underlying

M / M / \infty

queue manifold. Furthermore, a new discovery that presents the significant impact of stability of

M / M / \infty

queue manifold and the continuity of the unique representation between M/G/1 queue manifold and Ricci Curvature Tensor (RCT). The information matrix exponential (IME) is devised. Also, it is shown that stability of the devised (IME) enforces the instability of

M / M / \infty

queue manifold. Unifying IG with Queueing Theory enables the study of dynamics of transient queueing systems from a novel Riemannian Geometric (RG) point of view, leading to the analysis of the transient

M / M / \infty

queue, based on the Theory of Relativity (TR). Full analytic study of the obtained potential function together is provided. Additionally, provision of a novel link between Ricci Curvature (RCT) and the stability analysis of the transient

M / M / \infty

QM combined with a full investigation of the newly introduced QT-IG unifiers together with the impact of stability/ instability of the underlying transient

M / M / \infty

on them. More interestingly, full investigation of the newly introduced (QIGU) unifiers together with the impact of stability/ instability of the underlying transient

M / M / \infty

QM on them is given. There are several avenues of future work. To start with, we are going to extend this novel approach to many existing transient queueing systems. Also, another interesting path is to investigate the Information geometric analysis of the overall dynamic of time dependent distributions in Physics and Quantum Mechanics.

References

I. A. Mageed, et al, "Towards a Revolutionary Info-Geometric Control Theory with Potential Applications of Fokker Planck Kolmogorov(FPK) Equation to System Control, Modelling and Simulation," 2023 28th International Conference on Automation and Computing (ICAC), Birmingham, United Kingdom, 2023, pp. 1-6,. [CrossRef]
Mageed, I. A., & Kouvatsos, D. D. (2021, February). The Impact of Information Geometry on the Analysis of the Stable M/G/1 Queue Manifold. In ICORES (pp. 153-160).
Nielsen, F., 2020, An Elementary Intrduction to Information Geometry, Sony Computer Science Laboratories Inc, Japan, MDPI Journal.
Mageed, I. A., & Zhang, Q. (2022, October). An Information Theoretic Unified Global Theory For a Stable M/G/1 Queue With Potential Maximum Entropy Applications to Energy Works. In 2022 IEEE Global Energy Conference (GEC) (pp. 300-305).
Nakagawa, K., 2002, The geometry of M/D/1 queues on Large Deviation, International Transactions of Operational Research, Volume 9, Issue 2.
Norton, J.D., 2020, Non-Euclidean geometry and curved spaces, department of history and philosophy of science, University of Pittsburgh, available online at.
https://www.pitt.edu/~jdnorton/teaching/HPS_0410/chapters/non_Euclid_curved/index.htm.
Mageed, I. A, et al. (2023). Towards a Revolutionary Info-Geometric Control Theory with Potential Applications of Fokker Planck Kolmogorov (FPK) Equation to System Control, Modelling and Simulation. In 2023 28^th IEEE International Conference on Automation and Computing (ICAC) pp. 1-6.
Dodson, C.T.J., 2005, Topics in Information Geometry, University of Manchester. Available online on.
http://eprints.maths.manchester.ac.uk/131/1/InfoGeom.pdf.
Regli, JB., Silva, R, 2018, Alpha-Beta Divergence For Variational Inference - arXiv preprint arXiv:1805.01045, - arxiv.org. Available online at [1805.01045] Alpha-Beta Divergence For Variational Inference (arxiv.org).
Turner, Richard E and Sahani, Maneesh, 2011, Two problems with variational expectation maximisation for time series models. Bayesian Time series models, pp. 115–137.
Amari, S.,2012, Differential-geometrical methods in statistics, volume 27. Springer Science & Business Media.
Minka, T., 2005, Divergence measures and message passing. Technical report, technical report, Microsoft Research.
Hern´andez-Lobato, Jos´e Miguel, Li, Yingzhen, Rowland, Mark, Hern´andez-Lobato, Daniel, Bui, Thang, D., and Turner, Richard E, 2016, Black-box αdivergence minimization.
Rényi, A., et al., 1961 On measures of entropy and information. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Volume 1: Contributions to the Theory of Statistics. The Regents of the University of California.
Ghosh, Abhik, Harris, Ian R, Maji, Avijit, Basu, Ayanendranath, Pardo, Leandro, et al., 2017, A generalized divergence for statistical inference. Bernoulli, 23 (4A):2746–2783.
Basu, Ayanendranath, Harris, Ian R, Hjort, Nils L, and Jones, MC. , 1998, Robust and efficient estimation by minimising a density power divergence. Biometrika, 85(3):549–559.
Ghosh, Abhik and Basu, Ayanendranath, 2016, Robust bayes estimation using the density power divergence. Annals of the Institute of Statistical Mathematics, 68 (2):413–437.
Cichocki, Andrzej, Cruces, Sergio, and Amari,S., 2011, Generalized alpha-beta divergences and their application to robust nonnegative matrix factorization. Entropy, 13(1):134–170.
Cilingir, K., Manzelli, R., Kulis,B., 2020, Deep Divergence Learning. Online available at: arXiv:2005.02612v1.
Cai, L., Chen, Y., Cai, N., Cheng, W., 2020, Utilizing Amari-Alpha divergence to stabilize the training of generative adversarial networks, Entropy.
Chernoff, H, A measure of Asymptotic efficiency for tests of a hypothesis based on the sum of observations. Ann. Math. Statist.1952,23, 493–507.
Lecture Notes, October 2005: Information Theory and Statistics. Berkeley [Online]. Available on https://www.stat.berkeley.edu/~binyu/summer08/L1P1.pdf.
Malham, S.J.A.,August 23, 2016,An introduction to Lagrangian and Hamiltonian mechanics.[Online] Available on file:///E:/BALKING%20BREAKTHROUGHS/Paper%20Eight/attachments/mechanics.pdf.
Mageed, I. A, and Kouvatsos, D. (2021). The Impact of Information Geometry on the Analysis of the Stable M/G/1 Queue Manifold. In Proceedings of the 10th International Conference on Operations Research and Enterprise Systems - Volume 1: ICORES, ISBN 978-989-758-485-5, pages 153-160.
Mageed, I. A., Kouvatsos, D.D., 2019, Information Geometric Structure of Stable M/G/1 Queue Manifold and its Matrix Exponential, Proceedings of the 35th UK Performance Engineering Workshop, School of Computing, University of Leeds, Edited by Karim Djemame, 16^th of Dec.2019, p.123-135. [Online] at:.
https://sites.google.com/view/ukpew2019/home.
Loveridge, L.C., 7 September 2016, Physical and Geometric interpretations of the Riemannian Tensor, Ricci Tensor and.
Scalar Curvature, [Online] Available on https://arxiv.org/pdf/gr-qc/0401099.pdf.
Shaw, S., 2015, Sequences, Series and Taylor Approximation. Available online on:.
http://www.brunel.ac.uk/~icsrsss/teaching/ma2730/lec/ma2730.pdf.
Rudelius, T., 2012, A Geometric Understanding of Ricci Curvature in the context of Pseudo-Riemannian Manifold, Bachelor of Arts, Cornell University.
Ollivier,Y., 201, A visual interpretation to Riemannian Curvatures and Some Discrete Generalizations. [Online].
www.yann-ollivier.org/rech/publs/visualcurvature.pdf.
Thomas, R., 2015, Kissing the curve – manifolds in many dimensions, online at:.
https://plus.maths.org/content/kissing-curve-manifolds-many-dimensions.
Snezana, L., 2011, Developable Surfaces: Their History and Application, Nexus Network Journal Vol. 13, No. 3.
Weisstein, Eric W., 2021, Well-Defined, From MathWorld- A A Wolfram Web Resource. Available Online at:.
https://mathworld.wolfram.com/Well-Defined.html.
Sankaranarayanan, S., 2014, lecture 18, One-to-One and Onto functions, an online source.https://home.cs.colorado.edu/~srirams/courses/csci2824-spr14/functionTypes-17.html.
Smith,J.T.,2013, Cubic and Quartic Formulas, San Francisco State University. [Online] Available on.
http://Cubic&Quartic.pdf.
Horan, R., Lavelle, M., 2005, Maxima and Minima. Available online at:.
https://www.plymouth.ac.uk/uploads/production/document/path/3/3731/PlymouthUniversity_MathsandStats_maxima.
Roussel, M., R., April 2019, Stability Analysis for ODEs, Morgan & Claypool Publishers.
Kozma, L., 2020, Useful inequalities, online source, available at.
http://www.Lkozma.net/inequalities_cheat_sheet.
Harrison, P.; Patel, Naresh M. 1992, Performance Modelling of Communication Networks and Computer Architectures. Addison–Wesley. p. 173. Online available at:.
https://dblp.org/rec/books/daglib/0072384.bib.
Kumar, B.K, Anantha Lakshmi, S.R., and Anbarasu, S.,2014, Transient and steady-state analysis of queueing systems with catastrophes and impatient customers, Int. J. Mathematics in Operational Research, Vol. 6, No. 5.
Conolly, B.W. and Langaris, C. 1993, On a new formula for the transient state probabilities for M/M/1 queues and computational implications, J. Appl. Prob., Vol. 30, No. 1, pp.237–246.
MIT Open Course Ware,208. Online available at:.
https://ocw.mit.edu/courses/mathematics/18-02sc-multivariable-calculus-fall-2010/4.-triple-integrals-and-surface-integrals-in-3-space/part-b-flux-and-the-divergence-theorem/session-84-divergence-theorem/MIT18_02SC_MNotes_v8.1.pdf.
Kouvatsos, D.D.,1988 A Maximum Entropy Analysis of the G/G/1 Queue at Equilibrium. J. Opl. Res. Soc., 39(2),183- 200.
Amari, S., 2001, Information Geometry on Hierarchy of Probability Distributions, IEEE Transactions on Information Theory.
Hamasha, M.M, Elsaadi,E., Hassonah, Y., Magrabi L., and Alamudi, H., ,2016, Analysis of Service Delivery System Using Markov Chain Approach and M/G/1 Queuing Systems, Asian Journal of Industrial Engineering. [Online] Available at:.
67518-AJIE-KR (docsdrive.com).
Rachev, S.T., 1989, The problem of stability in queueing theory. Queueing Syst 4, 287–317 (1989). https://doi.org/8.1007/BF01159470.
Jefferson,J. 2018, Information Geometry. [Online] available at: https://rojefferson.blog/page/2/.
Lee, J.M., 1950, Riemannian Manifolds: An Introduction to Curvature, Graduate Texts in Mathematics, 176. Springer-Verlag New York, Inc.

Figure 1.

Figure 2. Geometric representation of geodesics on curved surfaces (c.f., Norton, 2020).

Figure 6.

Figure 7.

Figure 8.

Figure 9.

Figure 10.

Figure 11.

Figure 12.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Alerts

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Information Geometric Analysis of the Dynamics of M/M/∞ Transient Queue Manifold

Abstract

Keywords:

Subject:

1. Introduction

2. Main Definitions

2.1. Main Definition on IG

2.4. Important Inequalities (c.f., Kozma, 2020)

3. The FIM and ITS Inverse for the Transient M / M / ∞ QM

4. Theα(. OR ∇ ( α ) )-Connection of the Transient M / M / ∞ QM

4.1. The obtained Γ i j , k ( α ) expressions (c.f., definition (2.5)) of the transient M / M / ∞ QM

5. T H E α ( O R ∇ ( α ) ) − C O N N E C T I O N OF THE TRANSIENT M / M / ∞ QM WHEN TIME IS INFINITE

5.1. Geometry of M / M / ∞ QM as t → ∞

5.2. The Γ i j k α expressions of the a r r i v a l r a t e coordinate, λ of the transient M / M / ∞ QM corresponding to infinite temporal values

6. The IMES of the Coordinates THE Transient M / M / ∞ QM WHEN TIME IS INFINITE

6.1. The I M E s of the a r r i v a l r a t e coordinate, λ of the transient M/M/∞ QM

6.2. The I M E s of the P o i s s o n a r r i v a l r a t e coordinate, ξ of the transient M/M/∞ QM

6.3. The I M E s of the t e m p o r a l coordinate, t of the transient M / M / ∞ QM

7. The Threshold Theorems for the Potential function (c.f., (3.23) of Theorem 3.1) of the Underlying transient M/M/∞ QM

7.1. The Threshold Theorem for the Potential Function, TTPF (c.f., (3.23) of Theorem 3.1)

7.2.1. Numerical Experiment One

8. Some Algebraic Properties of the Potential Function, Ψ θ = λ ξ ( 1 − e − ξ t ) (c.f., (3.23))

9. The Threshold Theorems of the Derived Inverses of Poten-Tial Function, IPFs

10. Numerical Experiments on the Threshold Theorems of the Derived Inverses of Potential Function

10.1. Numerical Experiment on Theorem 9.1

12.2. Numerical Experiment on Theorem 9.2

10.3. Numerical Experiment on Theorem 9.3

10.4. Numerical Experiment on Theorem 9.4

11. The α − Gaussian Curvature, K ∞ ( α ) of (2.14) as Time Approaches Infinity

12. Ricci Curvature TENSOR , ( R C T ) ∞ → and the α − S e c t i o n a l Gaussian Curvatures of M/M/∞ QM F M/M/ ∞

QM as Time Approaches Infinity

12.1. The First Component, R 11 , ∞ ( α )

11.3. T h e α − S e c t i o n a l c u r v a t u r e s , K i j i j ( α ) = R i j i j ( α ) g i i g j j − ( g i j ) 2 , i , j = 1,2 , … , n , (c.f., (2.13))

13. Conclusion and Future Work

References

MDPI Initiatives

Important Links

Subscribe

3. The FIM and ITS Inverse for the Transient $M / M / \infty$ QM

4. Theα(. OR $\nabla^{(α)}$ )-Connection of the Transient $M / M / \infty$ QM

4.1. The obtained $Γ_{i j, k}^{(α)}$ expressions (c.f., definition (2.5)) of the transient $M / M / \infty$ QM

5. $T H E α (O R \nabla^{(α)}) - C O N N E C T I O N$ OF THE TRANSIENT $M / M / \infty$ QM WHEN TIME IS INFINITE

5.1. Geometry of $M / M / \infty$ QM as $t \to \infty$

5.2. The $Γ_{i j}^{k (α)}$ expressions of the $a r r i v a l r a t e$ coordinate, $λ$ of the transient $M / M / \infty$ QM corresponding to infinite temporal values

6. The IMES of the Coordinates THE Transient $M / M / \infty$ QM WHEN TIME IS INFINITE

6.1. The $I M E s$ of the $a r r i v a l r a t e$ coordinate, $λ$ of the transient M/M/∞ QM

6.2. The $I M E s$ of the $P o i s s o n a r r i v a l r a t e$ coordinate, $ξ$ of the transient M/M/∞ QM

6.3. The $I M E s$ of the $t e m p o r a l$ coordinate, $t$ of the transient $M / M / \infty$ QM

8. Some Algebraic Properties of the Potential Function, $Ψ (θ) = \frac{λ}{ξ} (1 - e^{- ξ t})$ (c.f., (3.23))

11. The $α -$ Gaussian Curvature, $K_{\infty}^{(α)}$ of (2.14) as Time Approaches Infinity

12. Ricci Curvature TENSOR , ${(R C T)}_{\infty}^{\to}$ and the $α - S e c t i o n a l$ Gaussian Curvatures of M/M/∞ QM F M/M/ $\infty$

12.1. The First Component, $R_{11, \infty}^{(α)}$

11.3. ${T h e α - S e c t i o n a l c u r v a t u r e s, K}_{i j i j}^{(α)} = \frac{R_{i j i j}^{(α)}}{(g_{i i}) (g_{j j}) - {(g_{i j})}^{2}}, i, j = 1,2, \dots, n$ , (c.f., (2.13))