1. Introduction

1.1. 𝑴/𝑴/∞. Queueing System and the Computation of the Common Average Time for Unsaturated Site Visitors Flows Beneath Double-Parking Situations

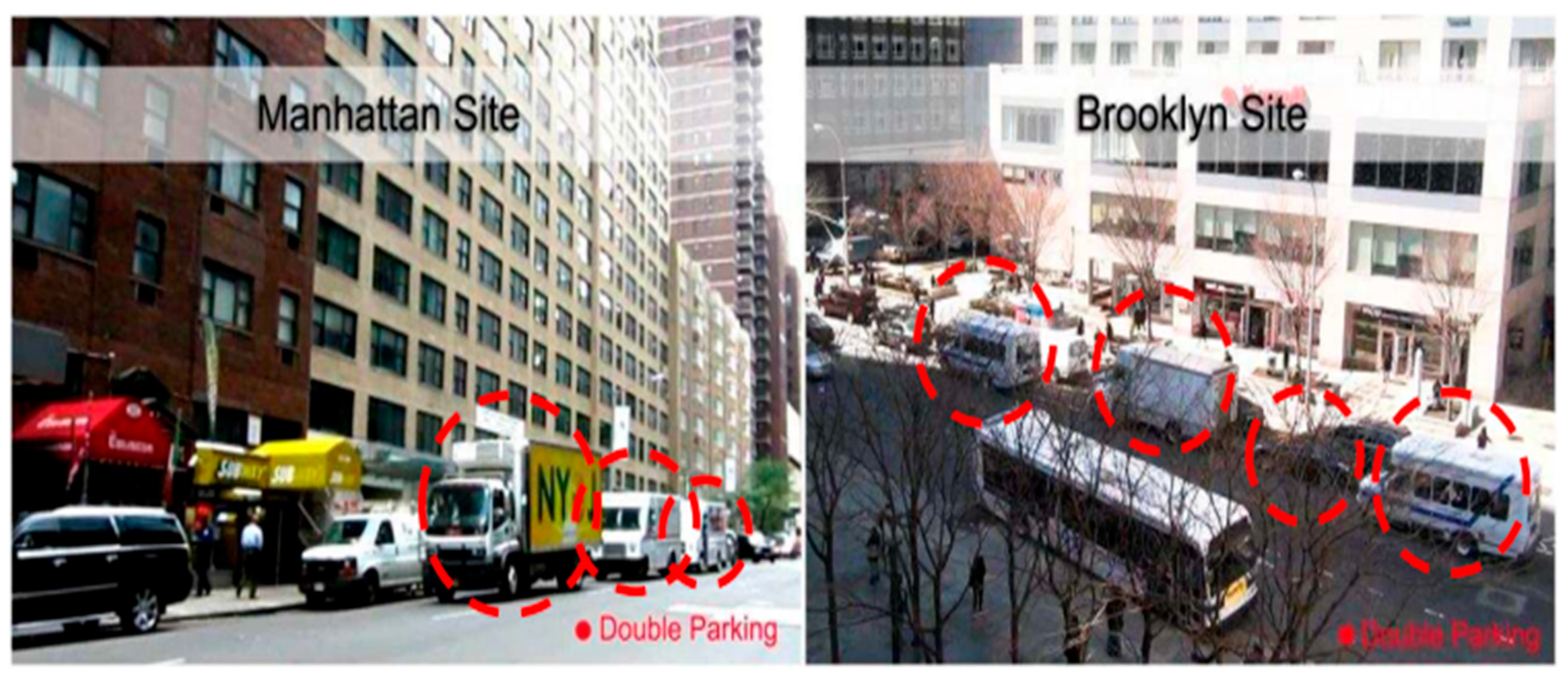
Double parking (DP) violations of industrial trucks whilst they load and dump at transport places with inadequate curb side area may have huge poor effect on site visitors. Motivated by the need to examine such effect on urban streets, [4] make use of parking violation facts for New York City in conjunction with discipline facts accrued the usage of video recording and adopts a complete modelling technique that mixes to be had facts with varieties of fashions. Another implied approach was the micro-simulation version [4] advanced and calibrated to examine personal and mixed outcomes of diverse explanatory variables. The research [4] employed a macroscopic $M/M/\infty$ queueing version and micro-simulation for estimating common tour time with inside the presence of double-parking activities.

Under uncongested site visitors` situations without downstream blocking off, making use of the $M/M/\infty$ queueing version produced an amazing match with the sphere facts. Overall, the $M/M/\infty$ queueing version is a powerful technique to compute the common average time for unsaturated site visitors flows beneath double-parking situations. Micro-simulation is a greater effective device than the $M/M/\infty$ queueing version for comparing such congested situations and may be used to study person and mixed outcomes of diverse explanatory variables.

Figure 1. How DP occurs in the sites under investigation [4].

Figure 1. How DP occurs in the sites under investigation [4].

1.2. Application of $\mathit{M}/\mathit{M}/\infty$ Birth–Death Process to Quantitively Interpret the Wavelet Dynamics in Atrial Fibrillation and Phase Singularity

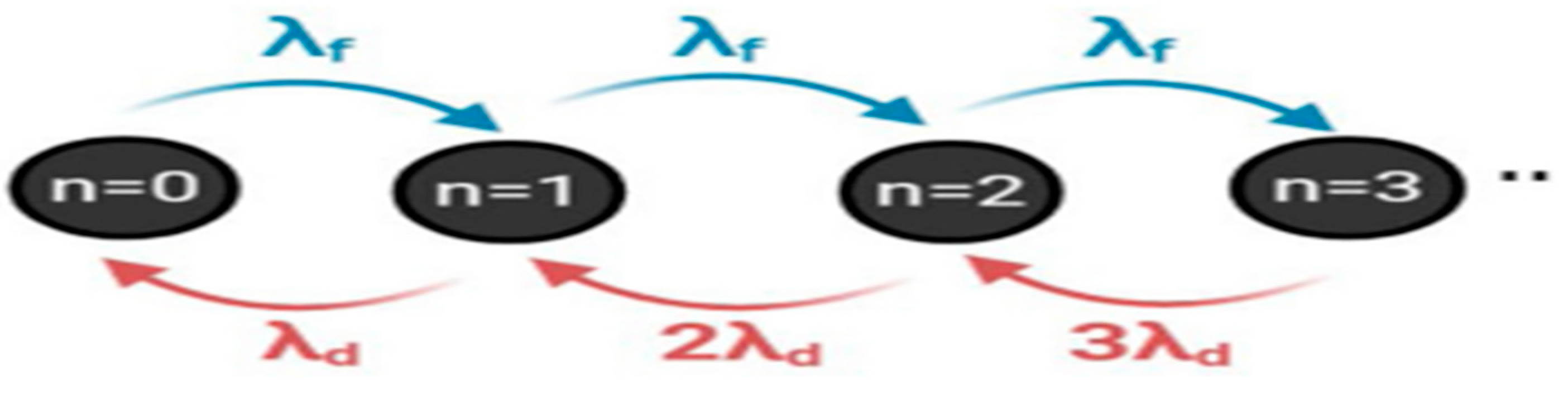
It has been hypothesized that the determined range of PS or wavelets in Atrial Fibrillation (AF) might be ruled with the aid of using a not unusual set of renewal rate constants ${\lambda }_f$ (for PS or wavelet formation) and ${\lambda }_d$ (PS or wavelet destruction), with steady-state population dynamics modelled as an M/M/∞ birth–death manner. It has been demonstrated [5]:

(1) that ${\lambda }_f$ and ${\lambda }_d$ may be blended in a Markov $M/M/\infty$ manner to as it should be a version of the determined common range and population distribution of PS and wavelets in all structures at unique scales of mapping; and

(2) that slowing of the constants denoting rates, namely ${\lambda }_f$ and ${\lambda }_d$ is related to slower mixing rates of the $M/M/\infty$birth–death matrix, presenting an interpretation of spontaneous AF termination.

Figure 2. The birth-death process of a transient $M/M/\infty$ queueing system [5].

Figure 2. The birth-death process of a transient $M/M/\infty$ queueing system [5].

It is worth mentioning that ${\lambda }_f$ and ${\lambda }_d$(PS rates of formation and destruction respectively) are related by the following steady-state equation of the $M/M/\infty$ birth–death [6]

$$N=\frac{{\lambda }_f}{{\lambda }_d}$$

(1)

provided that $N$ serves as the average number of PS and wavelets. Additionally, the PS and wavelet population distribution is characterized by the steady state probability $p_n$ [6] of getting a wavelet population or a phase singularity with size $n$ is determined by:

$$p_n= \frac{{(\frac{{\lambda }_f}{{\lambda }_d})}^n{e}^{-\frac{{\lambda }_f}{{\lambda }_d}}}{n!}$$

(2)

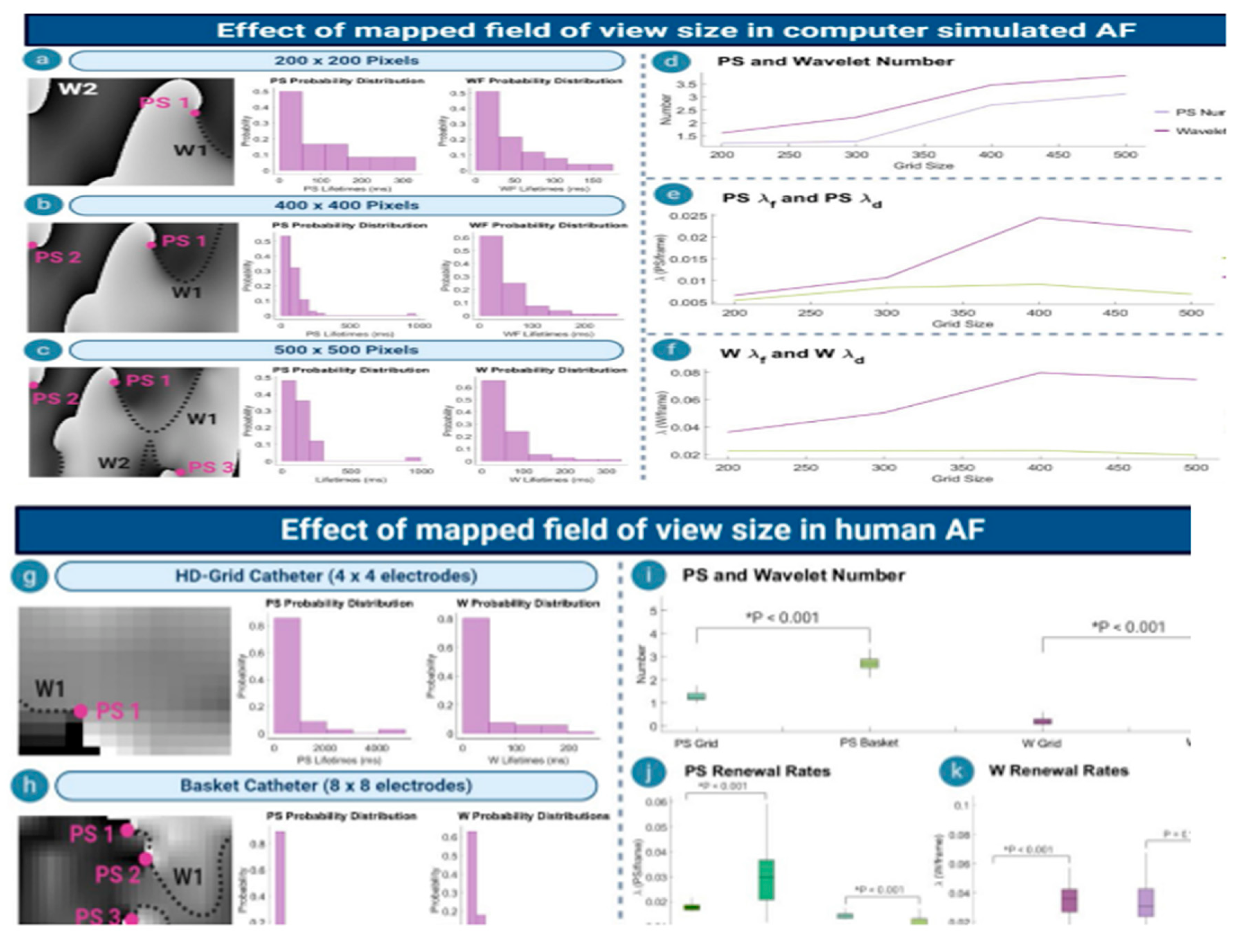
Figure 3. How a mapped field impacts view size [8].

Figure 3. How a mapped field impacts view size [8].

It has been conjectured by [5] that both Equations (1) and (2) provide a strong characterization of the overall dynamics of PS and wavelet population.

To understand and identify PS and wavelet population dynamics in AF, $M/M/\infty$ birth–death approaches provide a unique quantitatively expressive architecture. There are opportunities for scientific application because this conceptual paradigm [7] has been demonstrated to work in a variety of AF studies at unique scales and mapping densities.

1.4. IL as a Concept

Mathematically speaking, if $x$ serves as a nth- order stochastic variable and $p(x,t)$ is a time-dependent PDF of $x$, then the Information Length $\mathcal{L}\left(t\right)$ corresponding to its evolution from the initial time $t_0=0$ to the final time $t_F=t$ is devised by:

$$\mathcal{L}\left(t\right)={\int }_0^t\frac{d{t}_1}{\tau \left(t_1\right)}={\int }_0^t\surd \left(\epsilon \right(t_1\left)\right)d{t}_1$$

(3)

$$\epsilon \left(t_1\right)={\int }_{{\mathbb{R}}^n}\left(\frac{1}{p(x,t_1)}{\left[\frac{\mathsf{\partial }p(x,t_1)}{\mathsf{\partial }{t}_1}\right]}^2\right)dx$$

(4)

provided that $\surd \left(\epsilon \right(t)$ serves as the root-mean- squared fluctuating energy rate.

Having a closer look at (3), it is essential to note that $\tau \left(t\right)$ serves as a dynamic temporal unit which provides the correlation time over which the changes of $p\left(x,t\right)$ take place [16]. Furthermore , $\tau \left(t\right)$ defines the statistical space’s time unit. Having said that, $\surd (\epsilon \left(t\right)=\frac{1}{\tau \left(t\right)}$, quantifies the information velocity [18].

It is preferable to compute the underlying value of the mathematical model of the related physical process to comprehend the meaning of $\mathcal{L}$. Taking the Langevin equation-described first-order stochastic process into consideration:

$$\frac{dx}{dt}=-\gamma \left(t\right)\left(x-f\left(t\right)\right)+\xi$$

(5)

$x$ serves as a random variable, $f$ defines a deterministic force, $\xi$represents a short-correlated random force satisfying that:

$$<\xi \left(t\right)\xi \left(t_1\right)>=2D\delta \left(t-t_1\right)\mathrm{a}\mathrm{n}\mathrm{d}<\xi \left(t\right)>=0$$

(6)

where $D$serves as the amplitude (temperature) of the deterministic force$(\mathrm{s}\mathrm{t}\mathrm{o}\mathrm{c}\mathrm{h}\mathrm{a}\mathrm{s}\mathrm{t}\mathrm{i}\mathrm{c} \mathrm{n}\mathrm{o}\mathrm{s}\mathrm{e}) \xi$

It is to be noted that Equation (6) is so popular to be used as a descriptor of the motion of a particle under a harmonic potential in the form:

$$V\left(x\right)= \frac{1}{2}\gamma {(x-f(t\left)\right)}^2$$

(7)

Following [23,24], it is found that:

$$\epsilon \left(t\right)=\frac{{\left(\frac{d\beta }{dt}\right)}^2}{2{\beta }^2}+2\beta {\left(\frac{dy}{dt}\right)}^2$$

(8)

$$p\left(x,t\right)=\sqrt{\frac{\beta }{\pi }}{e}^{-\left(\beta \right(x-y{\left)\right)}^2},y\left(t\right)=<x>=x\left(0\right)e^{-G\left(t\right)}+F(t)$$

$$\frac{1}{2\beta \left(t\right)}=<(x\left(t\right)-y\left(t\right){)}^2>={\int }_0^{t}2D{e}^{-2\left(G\left(t\right)-G\left(t_1\right)\right)}d{t}_1,$$

$$F\left(t\right)={\int }_0^t e^{-\left(G\left(t\right)-G\left(t_1\right)\right)}\gamma \left(t_1\right)f\left(t_1\right)d{t}_1,$$

(9)

provided that $G\left(t\right)={\int }_0^{t}2D\gamma (t^{\mathrm{\text{'}}})d{t}^{\mathrm{\text{'}}}.$

Considering Equation (4), it is clear that $\epsilon \left(t\right)$ is dependent on the changes in both mean and variance defined by the corresponding dynamics of Equation (3), portraying $p\left(x,t\right)$ three-dimensional space variations, namely $(t,x,p\left(x,t\right))$ as in Figure 4, where the variation of the information velocity, $\surd (\epsilon \left(t\right)$ would occur along the path starting initially from the state probability density function $p(x,t_0)$ to the final state at $p(x,t_F)$ as a descriptor of the speed limit from the statistical deviations of the observables [16].

Figure 4. A graph depicting the evolution of $p(x,t)$ over time $t$. $\mathcal{L}\left(t\right)$ computes the total amount of statistical changes on $p(x, t)$ from $t_0$ to $t_F$ [8].

Figure 4. A graph depicting the evolution of $p(x,t)$ over time $t$. $\mathcal{L}\left(t\right)$ computes the total amount of statistical changes on $p(x, t)$ from $t_0$ to $t_F$ [8].

Fundamentally, employing differential entropy [12], may not enable us to observe the occurring temporal statistical variations. This is a direct implication of the locality’s deficiency since differential entropy is mainly for the quantification of the differences between any two given PDFs disregarding any intermediate states [17]. In a different symbolism, it only notifies us of the differences that have an influence on the underlying system's general development. IL $\mathcal{L}\left(t\right)$, on the other hand, measures any localised changes that occur along the system's course [14,17]. More crucially, IL has been touted as a cutting-edge technique for depicting an attractor structure and as a potent metric that can unite geometry and stochasticity [20,21]. From the point of stable equilibrium, the equivalent value of ${lim}_{t\to \infty }\mathcal{L}\left(t\right)$ would grow linearly depending on where the starting state's mean PDF $p(x,0)$ is located [15,24]. Notably, this strongly underlines that IL preserves the underlying Gaussian process' linear geometry by utilising Equation (6). More importantly, this particular property is lost when employing any other information metric [17,20]. By using definition, this emphasises that IL is a one-dimensional, model-free measure (3). Since IL is independent of data type, it may be devised by calculating the time series’ time-variant PDF [8].

The road of this current paper reads: A spotlight introduction is presented in Section 1. The key findings are established in Section 2. Some challenging open problems, conclusion, and future research work are given in Section 3.

2. The Upper and Lower Bounds of The Data Information Length of Transient $\mathit{M}/\mathit{M}/\mathit{\infty }$ Queuing System

2.2. The Transient $\mathit{M}/\mathit{M}/\infty$ Queue and IL

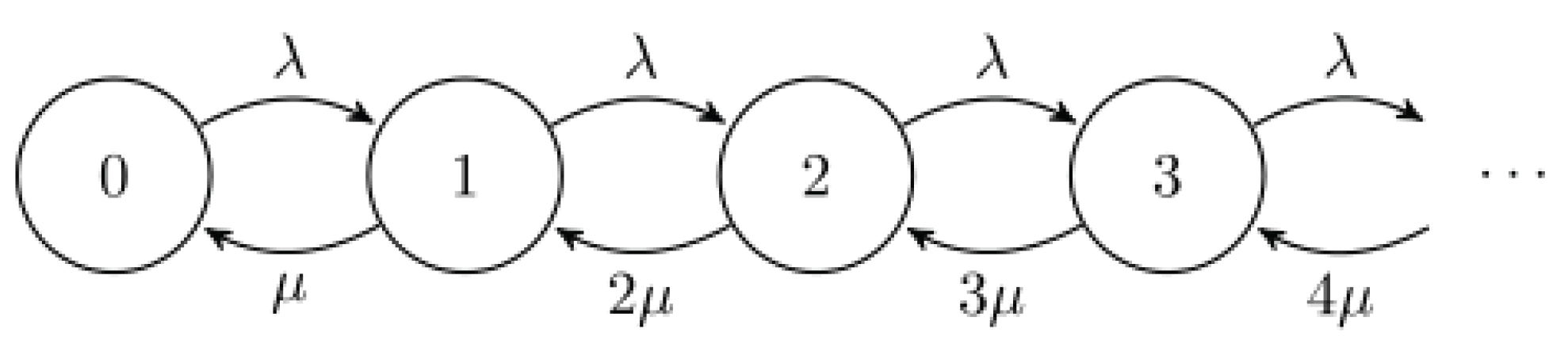
The $M/M/\infty$ queue (c., f., [26]) is a multi-server queueing model used in queueing theory, an emerging applied probabilistic discipline, with instant service-no wait arrival, as demonstrated by Figure 5. According to [27,28], the Poisson distributed service time with mean $\mu$and mean arrival rate i$s \lambda$ in the $M/M/\infty$queueing system's transient probability is given by:

$$p_n\left(t\right)=\frac{{\left[\frac{\lambda }{\mu }\right(1-e^{-\mu t}\left)\right]}^n}{n!}\mathrm{e}\mathrm{x}\mathrm{p}\{-\frac{\lambda }{\mu }\left(1-e^{-\mu t})\right\},n=\mathrm{0,1},2,\dots .$$

(16)

Notably, as $t\to \infty ,$ $p_n\left(t\right)$ of Equation (16) converges to

$$p_n=\frac{{\rho }^n}{n!}{e}^{-\rho },n=\mathrm{0,1},2,\dots .$$

(17)

$\rho$ serves as the server utilization of the underlying queue.

Figure 5. The state space diagram for the $M/M/\infty$ chain.

Figure 5. The state space diagram for the $M/M/\infty$ chain.

$\mathrm{R}\mathrm{e}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{g} \mathrm{t}\mathrm{h}\mathrm{a}\mathrm{t}$the information length (IL) is defined to be:

$$\mathcal{L}\left(t\right)={\int }_0^t\frac{d{t}_1}{\tau \left(t_1\right)}={\int }_0^t\surd \left(\epsilon \right(t_1\left)\right)d{t}_1$$

(c.f., (3))

$$\epsilon \left(t_1\right)={\int }_{{\mathbb{R}}^n}\left(\frac{1}{p(x,t_1)}{[\frac{\mathsf{\partial }p(x,t_1)}{\mathsf{\partial }{t}_1}]}^2\right)dx$$

(c.f., (4))

If ${\mathcal{L}}_{M/M/\infty } \mathrm{s}\mathrm{e}\mathrm{r}\mathrm{v}\mathrm{e}\mathrm{s} \mathrm{a}\mathrm{s} \mathrm{t}\mathrm{h}\mathrm{e}$ IL of the transient $M/M/\infty$queuing system, then the following theorems are devoted to the derivation of the lower and upper bounds of ${\mathcal{L}}_{M/M/\infty },$namely ($LB\left(n,t\right),UB\left(n,t\right)\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{p}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{e}\mathrm{l}\mathrm{y}).$

Theorem 1.

The IL of the transient $M/M/\infty$,  queuing system, ${\mathcal{L}}_{M/M/\infty }$ satisfies the following inequality:

$${ \frac{2(n+1){\left(\rho \right(t\left)\right)}^{\frac{3}{2}}}{3\surd n!}>\mathcal{L}}_{M/M/\infty } (t)> \left(\frac{\sigma {\mu }^n}{2^{n}n!}\right)\underset{0}{\overset{t}{\int }}{t^{n}e}^{-\rho \left(t\right)}{{\rho }^{.}\left(t\right)\left(\rho \left(t\right)\right) }^{n}dt$$

(18)

Proof 

 

We have

$$p_n\left(x,t\right)=\frac{{[\frac{\lambda }{\mu }(1-e^{-\mu t})]}^n}{n!}\mathrm{e}\mathrm{x}\mathrm{p}\{-\frac{\lambda }{\mu }\left(1-e^{-\mu t})\right\}$$

(c.f., (16))

$$=\frac{x^n}{n!}{e}^{-x},x\left(t\right)=\frac{\lambda }{\mu }\left(1-e^{-\mu t}\right)=\rho \left(t\right)\left(1-e^{-\mu t}\right)\left(since\rho \left(t\right)=\frac{\lambda \left(t\right)}{\mu }\right)$$

(19)

By the definition, we have $\mu >0, \mathrm{w}\mathrm{h}\mathrm{i}\mathrm{c}\mathrm{h} \mathrm{i}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{i}\mathrm{e}\mathrm{s} \mathrm{t}\mathrm{h}\mathrm{a}\mathrm{t} e^{-\mu t}<1.\mathrm{H}\mathrm{e}\mathrm{n}\mathrm{c}\mathrm{e},x\left(t\right)<\rho \left(t\right)$ follows. Then, we have the real number $\sigma \in$(0,1) satisfying:

$$x\left(t\right)=\sigma \rho \left(t\right)$$

(20)

Consequently,

$$\frac{\mathsf{\partial }{p}_n\left(t\right)}{\mathsf{\partial }t}=\frac{{\sigma x}^{n-1}{\rho }^{.}\left(t\right)}{n!}{e}^{-x}\left(n-x\right)$$

(21)

$$\frac{{\left[\frac{\mathsf{\partial }{p}_n\left(x,t\right)}{\mathsf{\partial }t}\right]}^2}{p_n\left(x,t\right)}=\frac{{\left(\frac{{\sigma x}^{n-1}{\rho }^{.}\left(t\right)}{n!}{e}^{-x}\left(n-x\right)\right)}^2}{\frac{x^n}{n!}{e}^{-x}}$$

$$=\frac{{{\sigma }^{2}x}^{n-2}{\rho }^{.2}\left(t\right)}{n!}{e}^{-x}{\left(n-x\right)}^2$$

$$=\frac{{{\sigma }^{2}x}^{n-2}{\rho }^{.2}\left(t\right)}{n!}{e}^{-x}\left(n^2-2nx+x^2\right)$$

$$\le (\frac{{\sigma }^2{\rho }^{.2}\left(t\right)}{n!})(n^2+1)(\mathrm{S}\mathrm{i}\mathrm{n}\mathrm{c}\mathrm{e} e^{-x}\le 1,x\in (\mathrm{0,1}))$$

$$<(\frac{{\rho }^{.2}\left(t\right)}{n!})(n^2+1)(\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{c}\mathrm{e} \sigma \in (\mathrm{0,1}))$$

(22)

Hence, it follows that:

$$\begin{gathered} {\mathcal{L}}_{M/M/\mathrm{\infty }}<\underset{0}{\overset{t}{\int }}\surd (\int \frac{{\left(n+1\right)}^2{\rho }^{.2}\left(t\right)}{n!}dx)dt \\ =\frac{(n+1)}{\surd n!}\underset{0}{\overset{t}{\int }}(\surd \int dx]){\rho }^{.}(t)dt \\ =\frac{(n+1)}{\surd n!}\underset{0}{\overset{t}{\int }}(\surd x)){\rho }^{.}(t)dt \\ = \frac{\left(n+1\right)}{\sqrt{n!}}\underset{0}{\overset{t}{\int }}\sqrt{\frac{\lambda }{\xi }\left(1-e^{-\mu t}\right)}{\rho }^{.}\left(t\right)dt \end{gathered}$$

$$< \frac{(n+1)}{\surd n!} \underset{0}{\overset{t}{\int }}\surd (\rho \left(t\right){\rho }^{.}(t)dt{(\mathrm{S}\mathrm{i}\mathrm{n}\mathrm{c}\mathrm{e} e}^{-\mu t}\in (\mathrm{0,1}) = \frac{2(n+1){(\rho (t))}^{\frac{3}{2}}}{3\surd n!}$$

(23)

On the other hand, $\mathrm{b}\mathrm{y} x<\rho \left(t\right)and x<1$, we have

$$\begin{gathered} \frac{{\left[\frac{\mathsf{\partial }{p}_n\left(x,t\right)}{\mathsf{\partial }t}\right]}^2}{p_n\left(x,t\right)}=\frac{{{\sigma }^{2}x}^{n-2}{\rho }^{.2}\left(t\right)}{n!}{e}^{-x}{\left(n-x\right)}^2 \\ >e^{-2x}\left(\frac{{{\sigma }^{2}x}^{n-2}{\rho }^{.2}\left(t\right)}{n!}\right){\left(n-1\right)}^2 \\ >e^{-2\rho \left(t\right)}\left(\frac{{{\sigma }^{2}x}^{2n-1}{\rho }^{.2}\left(t\right)}{n!}\right){\left(n-1\right)}^2 \\ >{\sigma }^2{e}^{-2\rho \left(t\right) }{\rho }^{.2}(t)\left(\frac{x^{2n-1}}{{(n!)}^2}\right){\left(n-1\right)}^2 \end{gathered}$$

(24)

Thus, it follows that:

$$(\surd \int \frac{{\left[\frac{\mathsf{\partial }{p}_n\left(x,t\right)}{\mathsf{\partial }t}\right]}^2}{p_n\left(x,t\right)}dx) >[\int {\sigma }^2{e}^{-2\rho \left(t\right)}{\rho }^{.2}(t)\left(\frac{x^{2n-1}}{{\left(n!\right)}^2}\right){\left(n-1\right)}^2]dx>\sigma {\rho }^{.}(t)e^{-\rho \left(t\right)}\left(\frac{x^n}{n!}\right)$$

(25)

Hence,

$${\mathcal{L}}_{M/M/\mathrm{\infty }}(t)>\left(\frac{\sigma }{n!}\right)\underset{0}{\overset{t}{\int }}{\rho }^{.}\left(t\right)e^{-\rho \left(t\right)}{\left(\rho \left(t\right)\left(1-e^{-\mu t}\right)\right)}^{n}dt$$

$$>\left(\frac{\sigma }{n!}\right)\underset{0}{\overset{t}{\int }}{e}^{-\rho \left(t\right)}(\mathrm{S}\mathrm{i}\mathrm{n}\mathrm{c}\mathrm{e},\left(1-e^{-\mu t}\right)>\frac{\mu t}{2} (\mathrm{c}.\mathrm{f}.,\left[29\right])$$

$$= \left(\frac{\sigma {\mu }^n}{2^{n}n!}\right)\underset{0}{\overset{t}{\int }}{t^{n}e}^{-\rho \left(t\right)}{{\rho }^{.}\left(t\right)\left(\rho \left(t\right)\right) }^{n}dt$$

(26)

Therefore,

$${\frac{2(n+1){(\rho (t))}^{\frac{3}{2}}}{3\surd n!}>\mathcal{L}}_{M/M/\mathrm{\infty }}(t)>\left(\frac{\sigma {\mu }^n}{2^{n}n!}\right)\underset{0}{\overset{t}{\int }}{t^{n}e}^{-\rho \left(t\right)}{{\rho }^{.}(t)\left(\rho (t)\right)}^{n}dt$$

(c.f., (18))

In what follows, an illustration of the temporal impact as well as the potential impact of $n$ on the behaviour of both $LB\left(n,t\right)\mathrm{a}\mathrm{n}\mathrm{d} UB(n,t)$,

$$UB\left(n,t\right)=\frac{2(n+1){(\rho (t))}^{\frac{3}{2}}}{3\surd n!} \mathrm{a}\mathrm{n}\mathrm{d} LB\left(n,t\right)=\left(\frac{\sigma {\mu }^n}{2^{n}n!}\right)\underset{0}{\overset{t}{\int }}{t^{n}e}^{-\rho \left(t\right)}{{\rho }^{.}(t)\left(\rho (t)\right)}^{n}dt$$

(19)

2.3. Numerical Experiments

By choosing $\sigma$= $\frac{1}{2},\rho \left(t\right)= \frac{1}{t}, \mu$ = 2, it can be easily verified that these proposed choices,$UB\left(n,t\right)$ and $LB\left(n,t\right)$ will read:

$$UB\left(n,t\right)=\frac{2(n+1)}{3{\left(t\right)}^{\frac{3}{2}}\surd (n!)} \mathrm{a}\mathrm{n}\mathrm{d} LB\left(n,t\right)=\left(-\frac{1}{2(n!)}\right)\underset{0}{\overset{t}{\int }}{e}^{-\frac{1}{t}}\frac{1}{t^2}dt=\left(-\frac{e^{-\frac{1}{t}}}{2(n!)}\right)$$

(20)

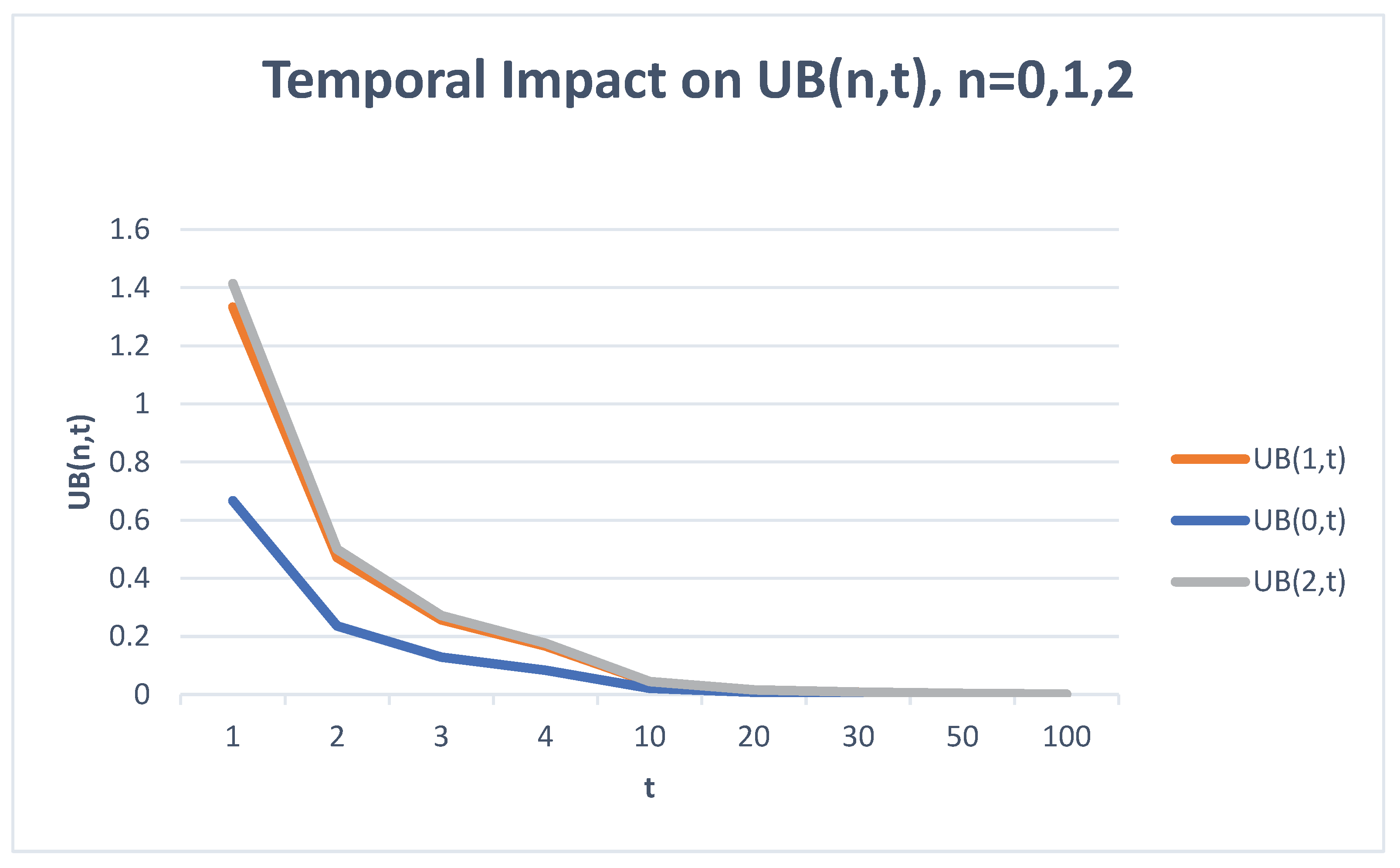
It is clear from Figure 6, that because of the progressive increase of time, $UB\left(n,t\right), n=\mathrm{0,1},2$ are decreasing functions in time. Moreover, for each recorded value of time, by increasing the value of $n,$ $UB\left(n,t\right), n=\mathrm{0,1},2$ are increasing functions. More interestingly, this reveals that $UB\left(n,t\right)$ acts as decreasing function in time and an increasing function with respect to $n.$ Fundamentally, the increase of time and $n$impacts $UB\left(n,t\right)$ to depict longer heavy tails. This translates to seeing the longest heavy tails for $UB\left(2,t\right)$, and these tails become shorter for $UB\left(1,t\right)$ and the shortest would be for $UB\left(0,t\right)$.

Figure 6. Significant Impact of time and $n$ on $UB(n,t)$.

Figure 6. Significant Impact of time and $n$ on $UB(n,t)$.

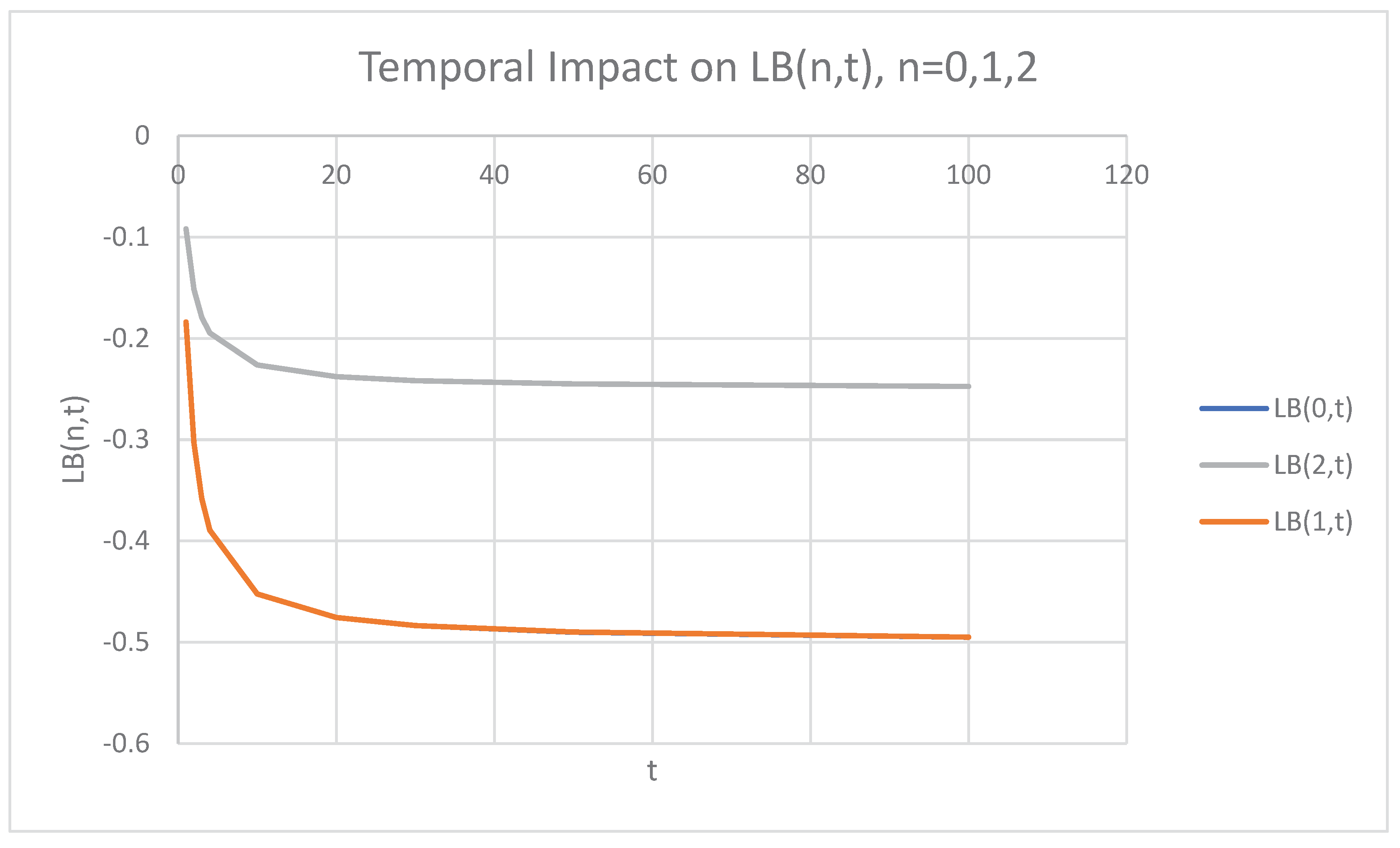
Reading Figure 7, $LB(n,t)$is decreasing in time and increasing as $n$ increases. More potentially, the graph representation of $LB(n,t)$ produces shorter heavy tails by the increase of time and $n.$ This shows a complete converse scenario in comparison to the recorded heavy tails phenomena in $UB(n,t)$.

Figure 7. Significant Impact of time and $n$ on $LB(n,t)$.

Figure 7. Significant Impact of time and $n$ on $LB(n,t)$.

In mathematical terms, as time becomes sufficiently large( $t\to \infty )$, it follows that

$$\begin{gathered} {lim}_{t\to \mathrm{\infty }}UB\left(n,t\right)={lim}_{t\to \mathrm{\infty }}\frac{2\left(n+1\right)}{3{\left(t\right)}^{\frac{3}{2}}\sqrt{n!}}=0={lim}_{t\to \mathrm{\infty }}\left(-\frac{e^{-\frac{1}{t}}}{2\left(n!\right)}\right)={lim}_{t\to \mathrm{\infty }}\left(-\frac{1}{2\left(n!\right)}\right)\underset{0}{\overset{t}{\int }}{e}^{-\frac{1}{t}}\frac{1}{t^2}dt \\ {=lim}_{t\to \infty }LB\left(n,t\right) \end{gathered}$$

(21)

Engaging the findings of Equations (18) and (21), it holds that as time reaches infinity, $n=\mathrm{0,1},2$

$${ {lim}_{t\to \infty }\mathcal{L}}_{M/M/\infty } \left(t\right)=0$$

(22)

Notably, it is shown that for $M/M/\infty$ transient queueing system [27,28] as $t\to \infty$, the correspondent steady state probability density function, $p_n$ is devised by:

$$p_n=\frac{{\rho }^n}{n!}{e}^{-\rho },n=\mathrm{0,1},2,\dots .$$

(c.f., (17))

Since $p_n$(c.f., (17)) does not depend on time, then we have by the definition of IL, (c.f., (2), (3)), that the corresponding stability phase of $M/M/\infty$ queueing system has an underlying zero information length, that is:

$${{lim}_{t\to \mathrm{\infty }}\mathcal{L}}_{M/M/\mathrm{\infty }}\left(t\right)=0,n=\mathrm{0,1},2, M/M/\mathrm{\infty }\mathrm{is}\mathrm{stable}$$

(23)

Clearly, Equations (22) and (23) are equivalent. This provides a strong validation of both obtained mathematical and numerical results. The strategy of the proof can be extended to the remaining values of $n=\mathrm{3,4},5,\dots .$., which will show that $UB\left(n,t\right)$ will start to decrease in both $\left(n,t\right)$, i.e, the behavioural trend will reverse in terms of the Increasability phase in $n$. More interestingly, it can be verified that $LB\left(n,t\right)$ will never change its behavioural trend in $\left(n,t\right)$ by being temporarily decreasing and increasing with the respective increase of $n.$

In a more detailed account, communicating [30], it could be analytically demonstrated that $UB\left(n,t\right)$and $LB\left(n,t\right)$ (c.f., (20)) are both (increasing in$t$)(decreasing in $n$) by showing that:

$$\mathrm{I}) \frac{ \mathsf{\partial }UB\left(n,t\right)}{\mathsf{\partial }t}<0, \frac{\mathsf{\partial }UB\left(n,t\right)}{\mathsf{\partial }n>0}$$

(24)

$$\mathrm{II}) \frac{\mathsf{\partial }LB\left(n,t\right)}{\mathsf{\partial }t}<0, \frac{\mathsf{\partial }LB\left(n,t\right)}{\mathsf{\partial }n>0}$$

(25)

We have

$$\frac{\mathsf{\partial }UB\left(n,t\right)}{\mathsf{\partial }t}=\frac{\mathsf{\partial }}{\mathsf{\partial }t}\left(\frac{2(n+1)}{3{\left(t\right)}^{\frac{3}{2}}\surd (n!)}\right)=-\frac{\left(n+1\right)}{{\left(t\right)}^{\frac{5}{2}}\sqrt{n!}}<0 \mathrm{f}\mathrm{o}\mathrm{r} \mathrm{a}\mathrm{l}\mathrm{l} t>0$$

(26)

Additionally, engaging [31], the Stirling formula to compute $n!$ is written as

$$n!\sim \surd \left(2\pi n\right){\left(\frac{n}{e}\right)}^n,n=\mathrm{3,4},\dots$$

(27)

$$\begin{gathered} \frac{\mathsf{\partial }UB\left(n,t\right)}{\mathsf{\partial }n}\sim \frac{2}{3{\left(t\right)}^{\frac{3}{2}}{\left(2\pi \right)}^{\frac{1}{4}}}\frac{\mathsf{\partial }}{\mathsf{\partial }n}\left(\frac{(n+1)}{{\left(\frac{n}{e}\right)}^{\frac{n}{2}}{n}^{\frac{1}{2}}}\right)=\frac{2}{3{\left(t\right)}^{\frac{3}{2}}{\left(2\pi \right)}^{\frac{1}{4}}}\frac{\mathsf{\partial }}{\mathsf{\partial }n}\left((n^{\frac{1}{2}}+n^{-\frac{1}{2}}){\left(\frac{n}{e}\right)}^{-\frac{n}{2}}\right) \\ =\frac{2}{3{\left(t\right)}^{\frac{3}{2}}{\left(2\pi \right)}^{\frac{1}{4}}}\left(\left({\frac{1}{2}n}^{-\frac{1}{2}}-\frac{1}{2}{n}^{-\frac{3}{2}}\right){\left(\frac{n}{e}\right)}^{-\frac{n}{2}}+(n^{\frac{1}{2}}+n^{-\frac{1}{2}})\left(-\frac{1}{2}(\mathit{lnn}-1)-\frac{1}{2}\right)\left({\left(\frac{n}{e}\right)}^{-\frac{n}{2}}\right)\right) \\ =\frac{{\left(\frac{n}{e}\right)}^{-\frac{n}{2}}}{3{\left(t\right)}^{\frac{3}{2}}{\left(2\pi \right)}^{\frac{1}{4}}}\left(\left(n^{-\frac{1}{2}}(1-lnn)-n^{-\frac{3}{2}}\right)-\left(n^{\frac{1}{2}}\right)lnn\right)<0,n=\mathrm{3,4},\dots \end{gathered}$$

(28)

This proves (I).

Additionally,

$$\frac{\mathsf{\partial }LB\left(n,t\right)}{\mathsf{\partial }t}=\frac{\mathsf{\partial }}{\mathsf{\partial }t}\left(-\frac{e^{-\frac{1}{t}}}{2(n!)}\right)=-\left(\frac{e^{-\frac{1}{t}}}{2(n!)t^2}\right)<0 \mathrm{for} \mathrm{all} t>0,n=\mathrm{3,4},\dots$$

(29)

Additionally,

$$\begin{gathered} \frac{\mathsf{\partial }LB\left(n,t\right)}{\mathsf{\partial }n}\sim \left(-\frac{e^{-\frac{1}{t}}}{2\sqrt{\left(2\pi \right)}}\right)\frac{\mathsf{\partial }}{\mathsf{\partial }n}\left({n^{-\frac{1}{2}}\left(\frac{n}{e}\right)}^{-n}\right) \\ =\left(-\frac{e^{-\frac{1}{t}}{\left(\frac{n}{e}\right)}^{-\frac{n}{2}}}{2\surd \left(2\pi \right)}\right)\left(-\frac{1}{2}{n}^{-\frac{3}{2}}-n^{-\frac{1}{2}}lnn\right) \\ =\left(\frac{e^{-\frac{1}{t}}{n}^{-\frac{3}{2}}{\left(\frac{n}{e}\right)}^{-\frac{n}{2}}}{4\surd \left(2\pi \right)}\right)\left(1+2nlnn\right)>0 \mathrm{for} \mathrm{all} t>0,n=\mathrm{3,4},\dots \end{gathered}$$

(30)

Hence, (II) follows.

Fundamentally, we have demonstrated with strong supporting mathematical evidence that the undertaken experiments agree with the analytic proofs.

3. Concluding Remarks, Open Problems, and Future Research

• Open Problem Two

• Open Problem Three

References

1. [Green, L.V. (2003). “How many hospital beds? Inquiry.”, 39: 400-412.
2. Green, L.V.,et al.(2005). “ Using queueing theory to increase the effectiveness of physician staffing in the emergency department.” Academic Emergency Medicine. [CrossRef]
3. Green, L.V., and Nguyen, V.(2001). “ Strategies for cutting hospital beds: The impact on patient service.” Health Services Research,36: 421-442.
4. Gao, J. and K.Ozbay. (2016). “Modeling double parking impacts on urban street.” In Transportation Research Board 95^th Annual Mesting. Vol 12.
5. Dharmaprani, D; et al.(2021). “M/M/Infinity birth-death process- A quantitative representational framework to summarize and explain phase singularity and wavelet dynamics in atrial fibrillation.” Frontiers in physiology 11:616866. [CrossRef]
6. Mageed, I. A. (2023, July). Where the mighty trio meet: Information Theory (IT), Pathway Model Theory (PMT) and Queueing Theory (QT). In 39^th Annual UK Performance Engineering Workshop (p. 8).
7. Quah, J; et al.(2020). “Prospective cross-sectional study using Poisson renewal theory to study phase singularity formation and destruction rates in atrial fibrillation (RENEWAL-AF): Study design.” Journal of Arrhythmia 36(4):660-7. [CrossRef]
8. Chamorro, HR; et al. (2020). “ Information Length Quantification and Forecasting of Power Systems Kinetic Energy.” IEEE Transactions on Power Systems.
9. Mageed, I. A., Yin, X., Liu, Y., & Zhang, Q. (2023, August). ℤ_(a,b) of the Stable Five-Dimensional $ M/G/1$ Queue Manifold Formalism's Info-Geometric Structure with Potential Info-Geometric Applications to Human Computer Collaborations and Digital Twins. In 2023 28th International Conference on Automation and Computing (ICAC) (pp. 1-6). IEEE.
10. Mageed, I. A., Zhang, Q., Akinci, T. C., Yilmaz, M., & Sidhu, M. S. (2022, October). Towards Abel Prize: The Generalized Brownian Motion Manifold's Fisher Information Matrix With Info-Geometric Applications to Energy Works. In 2022 Global Energy Conference (GEC) (pp. 379-384). IEEE.
11. Mageed, I. A., Zhou, Y., Liu, Y., & Zhang, Q. (2023, August). Towards a Revolutionary Info-Geometric Control Theory with Potential Applications of Fokker Planck Kolmogorov (FPK) Equation to System Control, Modelling and Simulation. In 2023 28th International Conference on Automation and Computing (ICAC) (pp. 1-6). IEEE.
12. Mageed, I. A., & Kouvatsos, D. D. (2021, February). The Impact of Information Geometry on the Analysis of the Stable M/G/1 Queue Manifold. In ICORES (pp. 153-160).
13. Van Erven, T. and Harremos, P. (2014). “Rényi divergence and Kullback-Leibler divergence.” IEEE Transactions on Information Theory 60(7), 3797-3820. [CrossRef]
14. Mageed, I.A. "A Unified Information Data Length (IDL) Theoretic Approach to Information- Theoretic Pathway Model Queueing Theory (QT) with Rényi entropic applications to Fuzzy Logic," 2023 International Conference on Computer and Applications (ICCA), Cairo, Egypt, 2023, pp. 1-6, doi: 10.1109/ICCA59364.2023.10401761.
15. Kim,E. and R. Hollerbach.(2017). “Signature of nonlinear damping in geometric structure of a nonequilibrium process.” Physical Review E vol. 95, no. 2, p. 022137. [CrossRef]
16. Nicholson, S,B. et al.(2020) “Time–information uncertainty relations in thermodynamics.” Nature Physics16.12 : 1211-1215. [CrossRef]
17. Heseltine, J., and E. Kim.(2019). “Comparing information metrics for a coupled- Ornstein–Uhlenbeck process.” Entropy 21(8):775. [CrossRef]
18. Kim, E.(2021). “Information geometry and non-equilibrium thermodynamic relations in the over-damped stochastic processes.” Journal of Statistical Mechanics: Theory and Experiment vol. 2021, no. 9, p. 093406. [CrossRef]
19. Kim,E. and A.-J. Guel-Cortez. (2021). “Causal information rate.” Entropy vol. 23, no. 8, p. 1087. [CrossRef]
20. Guel-Cortez, A.-J. And E. Kim. (2020). “Information length analysis of linear autonomous stochastic processes.” Entropy 22(11). [CrossRef]
21. Guel-Cortez, A.-J. and E. Kim. (2021). “Information geometric theory in the prediction of abrupt changes in system dynamics.” Entropy vol. 23, no. 6, p. 694. [CrossRef]
22. Heseltine, J. and E. Kim.(2016). “Novel mapping in non-equilibrium stochastic processes.”Journal of Physics A: Mathematical and Theoretical vol. 49, no. 17, p. 175002. [CrossRef]
23. Kim,E.(2016). “Geometric structure and geodesic in a solvable model of non-equilibrium process.” Physical Review E vol. 93, no. 6, p. 062127.Entropy vol. 20, no. 8, p. 550. [CrossRef]
24. Hollerbach,R; et al.(2018). “Information geometry of nonlinear stochastic systems.” Entropy: 20(8):550. [CrossRef]
25. Pishro-Nik, H. (2014). “Introduction to probability, statistics, and random processes.”, available at: https://wwww.probnabilitycourse.com, Kappa Research LLC.
26. Harrison P.G. and N.M.Patel.(1992). “Performance modelling of communication networks and computer architectures.” International Computer S. Addison-Wesley Longman Publishing Co., Inc.
27. Kumar, B.K; et al.(2014). “Transient and steady-state analysis of queueing systems with catastrophes and impatient customers.” Int. J. Mathematics in Operational Research Vol. 6, No. 5. [CrossRef]
28. Kulkarni, V.G.(2016). “Modelling and analysis of stochastic systems.” Chapman and Hall/CRC.
29. Ovler, F.W; et al.(2010). “ Digital Library of Mathematical Functions.” National Institute of Standards and Technology from https://dlmf.nist.gov (release date 01-07-2011, Washington, DC. 2010).
30. Guichard, D. (2017). “Single and multivariable calculus: Early transcendentals.” Available online at: https://www.whitman.edu/mathematics/multivariable/.
31. Peng, J., 2020. Shape of Numbers and Calculation Formula of Stirling Numbers. Open Access Library Journal, 7(3), pp.1-11. [CrossRef]
32. P. R. Parthasarathy, “A transient solution to an M /M /1 queue: A simple approach, ”Adv. Appl. Prob., vol. 19, 1987, p. 997-998. [CrossRef]