Prerpints.org logo
Preprint
Article

Characterizing Water Composition with an Autonomous Robotic Team Employing Comprehensive In-Situ Sensing, Hyperspectral Imaging, Machine Learning, and Conformal Prediction

Altmetrics

Downloads

127

Views

131

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

29 January 2024

Posted:

29 January 2024

You are already at the latest version

Alerts
Abstract
Inland waters pose a unique challenge for water quality monitoring by remote sensing techniques due to their complicated spectral features and small-scale variability. At the same time, collecting the high-quality reference data needed to calibrate remote sensing data products is both time consuming and expensive. In this study, we present the further development of a robotic team composed of an uncrewed surface vessel (USV) providing in situ reference measurements and an unmanned aerial vehicle (UAV) equipped with a hyperspectral imager. Together, this team is able to address the limitations of existing approaches by enabling the simultaneous collection of comprehensive in situ data together with high-resolution hyperspectral imagery. We showcase the capabilities of this team using data collected in a north Texas pond during three collections in the fall of 2020. Machine learning models for 13 variables are trained using the data set of paired in situ measurements and coincident reflectance spectra. These models can successfully estimate physical variables, including temperature, conductivity, pH, and turbidity, as well as the concentrations of blue-green algae, colored dissolved organic matter (CDOM), chlorophyll-a, crude oil, optical brighteners and the ions Ca2+, Cl−, and Na+. We extend the training procedure to utilize conformal prediction to estimate 90% confidence intervals for the output of each trained model. The maps generated by applying each trained model to the collected images reveal the small-scale spatial variability within the pond. Additionally, the permutation importance computed for each feature of the trained models highlights the spectral features relevant to each water quality variable.
Keywords: 
Subject: Environmental and Earth Sciences  -   Remote Sensing

1. Introduction

For decades, remote sensing imagery has been used for environmental monitoring with applications ranging from resource mapping, land type classification, and urban growth assessment to wildfire tracking, natural disaster tracking, and many more [1,2,3,4,5]. Among these applications, the retrieval of water quality variables from remote sensing imagery remains challenging due to the difficulty of obtaining in situ reference data that coincide with available satellite imagery. Many studies have shown success modeling relevant water quality variables such as colored dissolved organic matter (CDOM), cholorophyll-a, and total suspended sediment concentrations by using combinations of spectral bands from terrestrial remote sensing satellites. However, the in situ reference data used in these studies typically require the time-consuming collection of individual samples for lab analysis or continuous monitoring at fixed sites [6,7,8,9,10,11].
Much effort has recently been spent on the curation of comprehensive datasets that combine water quality records with decades of satellite imagery to enable the development of new methods for monitoring water quality. For example, Aurin et al. curated over 30 years of oceanographic field campaign data with associated coincident satellite imagery [12]. Similarly, Ross et al. have combined more than 600,000 records of dissolved organic carbon, chlorophyll-a and other variables of water quality together with Landsat historical reflectance data for the period 1984–2019 [13]. With a sufficient quantity of data, machine learning methods can augment traditional approaches using reflectance band ratios to enable estimation of water quality metrics and perform water quality classification [14,15,16,17,18]. However, the low spatial and spectral resolution of available multiband remote sensing satellites makes it difficult to analyze inland waters with small spatial features and complicated spectral signatures. Furthermore, the long return times of these satellites limit their use for real-time monitoring, for example, during oil spills [19].
Advances in multispectral and hyperspectral imaging technology have considerably reduced their size, making it possible to incorporate these cameras into the payload of autonomous aerial vehicles (UAVs) such as quadcopters, hexacopters, and other drones [20]. By controlling altitude during flight, UAVs can produce imagery with pixels at the centimeter scale and limit the need for complicated atmospheric corrections to account for scattering by atmospheric aerosols and gases [21,22]. Already, UAVs equipped with multispectral and hyperspectral imagers are being used in a variety of domains to great effect, including biomass estimation, forest management, precision agriculture, and now water quality monitoring [21,23,24,25,26,27].
Despite the increased spectral and spatial resolution afforded by UAV platforms, these improvements alone cannot address the limited spatial resolution of in situ reference data. To address this gap and enable comprehensive real-time water quality detection, we have developed a robotic team composed of an autonomous uncrewed surface vessel (USV) equipped with a collection of reference grade instruments together with a UAV carrying a hyperspectral imager [28]. By incorporating these reference instruments on a maneuverable USV platform, we are able to rapidly collect large volumes of water quality data for a variety of physical, biochemical, and chemical variables. Critically, the USV enables the collection of reference data with significantly improved spatial resolution compared to other approaches. These in situ measurements then provide the ground-truth data used to train machine learning models which map reflectance spectra captured by the hyperspectral imager to the desired water quality variables.
In this study, we expand on our previous work by demonstrating the capabilities of this coordinated robot team using data collected at a pond in North Texas over three separate days in the fall of 2020. Specifically, we show the ability to accurately predict physical variables such as temperature, conductivity, pH, and turbidity, as well as biochemical constituents, including blue-green algae pigments, CDOM, and chlorophyll-a, in addition to concentrations of crude oils, optical brighteners, and a variety of ions. In addition, the considerable size of the collected data set allows us to quantify the uncertainty in the resulting machine learning models by using conformal prediction techniques. This methodology addresses the shortcomings of existing approaches by facilitating rapid, real-time data collection coupled with on-board hyperspectral image processing and machine learning model deployment with uncertainty quantification. The resulting models are small enough to be deployed on board the UAV to enable real-time streaming of data products to the ground. This approach drastically reduces the time from data collection to insight.

2. Materials and Methods

The robotic team employed in this study consists of two key sensing sentinels: An uncrewed surface vessel (USV) used to collect in situ reference measurements, and an unmanned aerial vehicle (UAV) for performing rapid, wide-area surveys to gather remote sensing data products. Both platforms are coordinated using open source QGroundControl software for flight control and mission planning and are equipped with high-accuracy GPS and INS such that all data points collected are uniquely geolocated and time-stamped [29]. Both the USV and UAV include long-range Ubiquiti 5 GHz LiteBeam airMAX WiFi to enable streaming of data products to a ground station with network attached storage providing redundancy.

2.1. USV: In-Situ Measurements

The USV employed in the robot team is a Maritime Robotics Otter which features a modular design and 20 hour battery life. The USV is equipped with an in situ sensing payload consisting of a combination of Eureka Manta-40 multiprobes including fluorometers, ion selective electrodes, and other physical sensors that together enable the collection of comprehensive near-surface measurements including Colored Dissolved Organic Matter (CDOM), Crude Oil, Blue-Green Algae (phycoerythrin and phycocyanin), Chlorophyll A, Na + , Ca 2 + , Cl − , Temperature, Conductivity, and many others. The full list of measurements utilized in this study is given in Table 1 and is categorized into four distinct types: physical measurements, ion measurements, biochemical measurements, and chemical measurements. Additionally, the USV is equipped with an ultrasonic weather monitoring sensor for measuring air speed and direction, as well as a BioSonics MX Aquatic Habitat Echosounder sonar, which are not explored in this study.
As shown in Table 1, the physical measurements and ion sensors are largely based on different electrode configurations, while the chemical and biochemical measurements are all optically significant in UV and visible light, enabling their determination by fluorometry. The pigments phycoerythrin and phycocyanin are used to determine the blue-green algae content, which together with chlorophyll-a enable us to assess the distribution of photosynthetic life in the pond. In addition, we also measured the concentration of colored dissolved organic matter (CDOM), which impacts light penetration and serves as a primary source of bioavailable carbon. Crude oil (natural petroleum) and optical brightener concentrations are also measured with fluorometers and are relevant for identifying sources of industrial contamination or natural seepage.

2.2. UAV: Hyperspectral Data Cubes

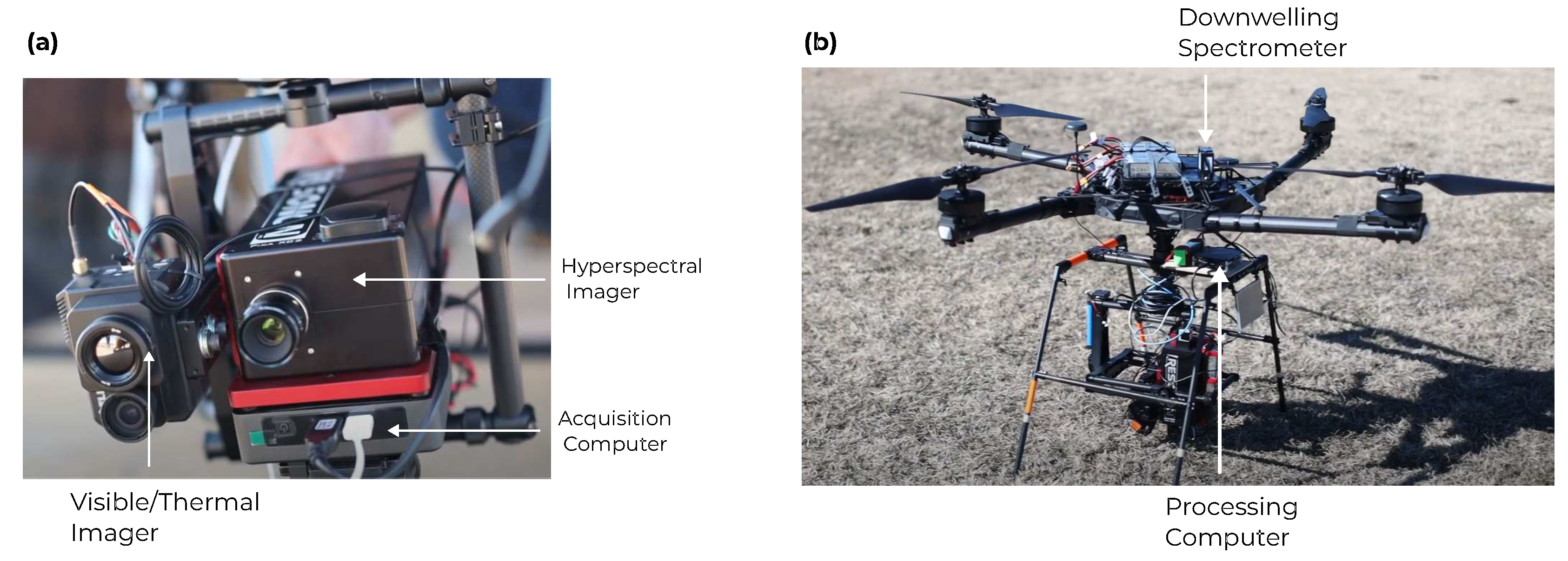
A Freefly Alta-X autonomous quadcopter was used as a UAV platform for the robotic team. The Alta-X is specifically designed to carry cameras that have a payload of up to 35 lbs. We have equipped the UAV with a Resonon Pika XC2 Visible+Near-Infrared (VNIR) hyperspectral imager. For each image pixel, this camera samples 462 wavelengths ranging from 391 to 1,011 nm. Additionally, the UAV includes an upward facing Ocean Optics UV-Vis-NIR spectrometer with a cosine corrector to capture the incident downwelling irradiance spectrum. Data collection by the hyperspectral imager is controlled by an attached Intel NUC small-form factor computer. A second processing NUC is also included for onboard georectification and generation of data products. The collected hyperspectral images (HSIs) are stored locally on a solid state drive which is simultaneously mounted by the processing computer. The configuration of the drone is shown in Figure 1.
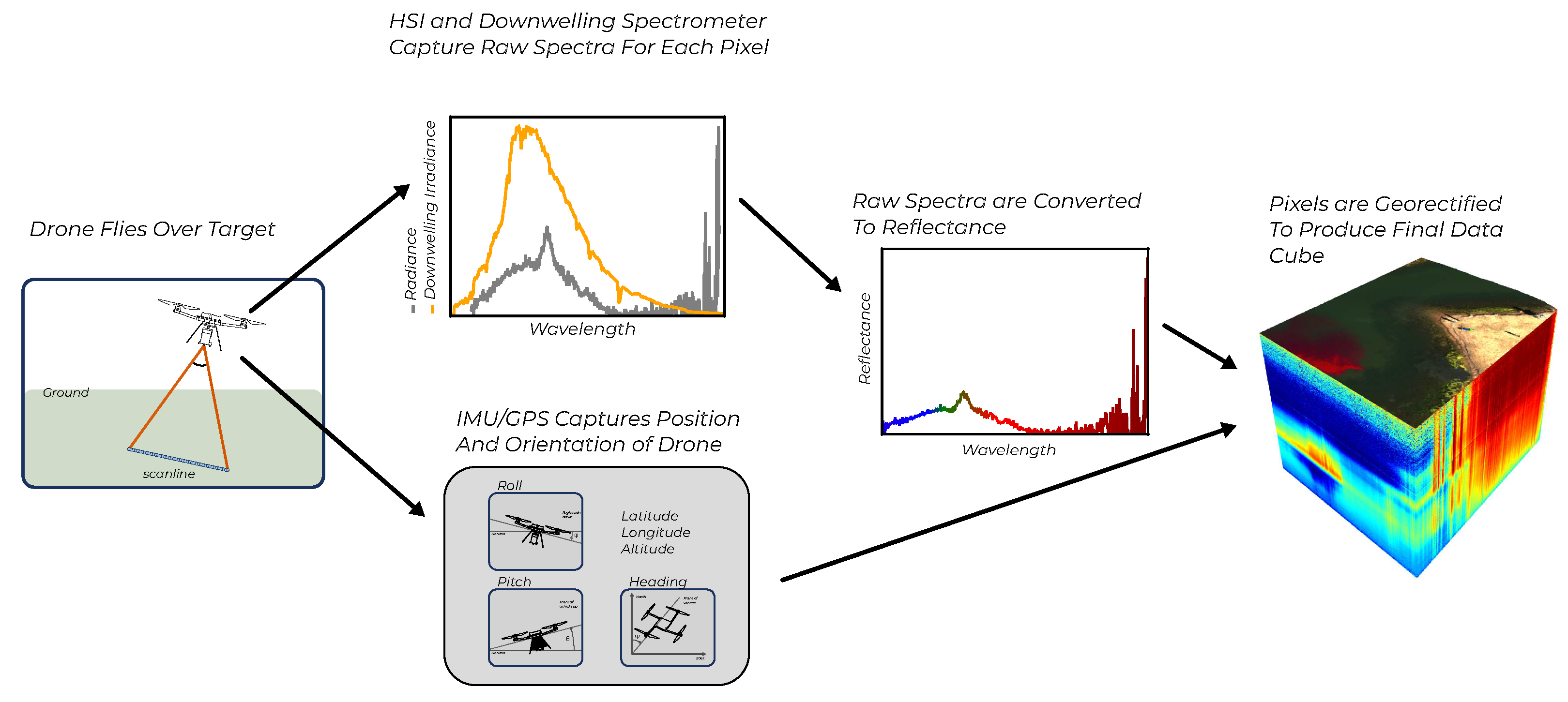
To effectively utilize the spectra collected by our UAV, we must account for the variability of the incident light that illuminates the water and transform the raw hyperspectral data cubes from their native imaging reference frame to a chosen coordinate system compatible with the data collected by the USV. This procedure is illustrated in Figure 2.
The hyperspectral imager utilized in our robot team is in a so-called pushbroom configuration, that is, each image captured by the drone is formed one scan line at a time as the UAV flies. Each scan line consists of 1600 pixels for which incoming light is diffracted into 462 wavelength bins. In the collection software, a regular cutoff of 1000 lines is chosen so that each resulting image forms a array of size 462×1600×1000 called a hyperspectral data cube. Initially, the captured spectra are in units of spectral radiance (measured in microflicks); however, this does not account for the variability of incident light illuminating the water. To this end, we convert the hyperspectral data cubes into units of reflectance utilizing the skyward-facing downwelling irradiance spectrometer (see Figure 1). When the camera is normal to the water surface, the reflectance is given by
R ( λ ) = π L ( λ ) / E d ( λ )
where L is the spectral radiance, E d is the downwelling irradiance, and a factor of π steradians results from assuming the water surface is Lambertian (diffuse) [30].
Having converted the hyperspectral data cube to units of reflectance, we must also georeference each pixel into a geographic coordinate system so that each image pixel can be assigned a latitude and longitude corresponding to the location on the ground from which it was sampled. During our three surveys, the UAV was flown at an altitude of 50 m above the water. At this scale, the surface is essentially flat, so that the hyperspectral data cube can be reliably georectified without the need for an on-board digital elevation map (DEM). We adopt the approach outlined in [31,32,33] whereby each scan line is georeferenced using the known field of view (30.8 deg) together with the position and orientation of the UAV as provided by the on-board GPS/INS. After a sequence of coordinate transformations, the pixel coordinates are obtained in the relevant UTM zone (in meters). The resulting image is then re-sampled to a final output resolution. For these collections, a resolution of 10 cm was utilized, however, this can be adjusted to optimize the processing time and final resolution for real-time applications. Finally, the UTM pixel coordinates obtained are transformed to latitude and longitude for easy comparison with in situ data collected by the USV. The final result is a georectified hyperspectral reflectance data cube. 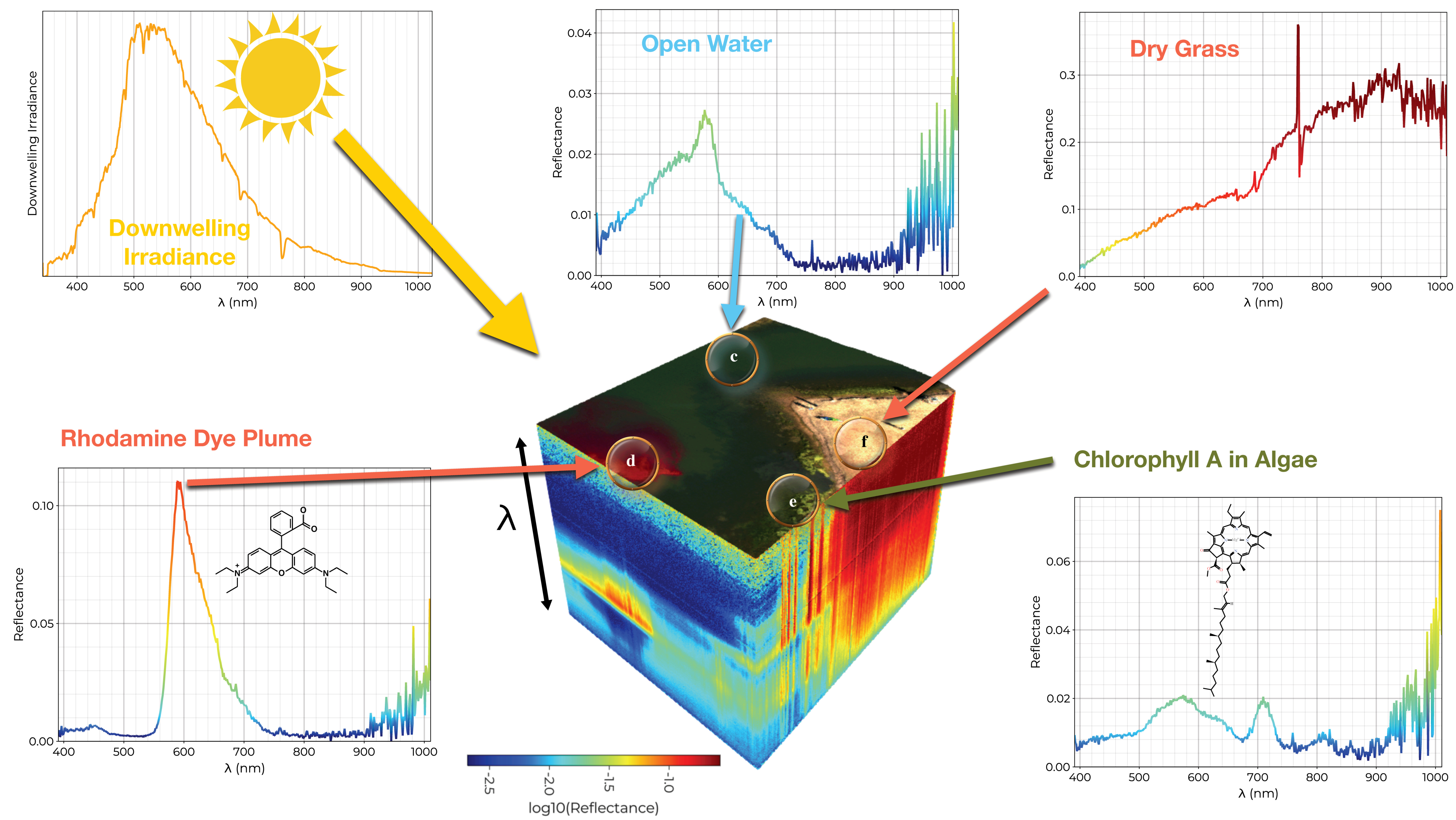In Figure 3 we visualize one of such data cubes, highlighting a selection of exemplar pixel spectra as well as the incident downward irradiance spectrum. A pseudo-color image is generated (plotted on the top of the data cube) to illustrate the scene.
The above processing pipeline was implemented using the Julia programming language, a just-in-time compiled language with native multi-theading support [34]. By running this pipeline on the on board computer, we are able to process the collected hyperspectral data cubes in near real time. This feature is critical for time-sensitive applications where we need to quickly assess if an area is safe and can not afford to wait to download and post-process collected imagery after a flight.

2.3. Data Collection

Data were collected using the robot team at a site in North Texas during three observation periods in the fall of 2020. For each collection period, the UAV first completed a broad survey of the pond, capturing multiple hyperspectral data cubes. Subsequently, the USV sampled across the pond, collecting in situ reference measurements. Each of these reference measurements was then collocated with individual pixel spectra, where the USV track overlapped with UAV pixels. To account for any time lag in the values measured by the in situ instruments and to account for the USV size in comparison to the data cube’s spatial resolution, each in-situ measurement is associated with a 3×3 grid of HSI pixels, that is, a 30 cm × 30 cm square. These combined data form the tabular data set on which we train regression models; pixel spectra form input features, and each separate USV sensor forms a distinct target variable.
Each collection was performed near solar noon to maximize the amount of incident sunlight illuminating the water; however, to account for any potential variation in lighting conditions between data cubes, we augment the training set with additional features including the drone viewing geometry (roll, pitch, heading) and solar illumination geometry (solar azimuth, solar elevation, solar zenith) as well as the total at-pixel intensity before reflectance conversion, the total downwelling intensity, and the drone altitude. Further feature engineering is performed to add additional spectral indices that utilize combinations of specific wavelength bands such as the normalized difference vegetation index (NDVI), normalized difference water index (NDWI), simple ratio (SR), photochemical reflectance index (PRI) and more, as outlined in [35,36,37,38]. A comprehensive list of these added features is provided in Supplementary Table S1. The final dataset includes a total of 526 features (462 reflectance bands plus 64 additional features) with over 120,000 records.

2.4. Machine Learning Methods

For each of the 13 target variables listed in Table 1, the data was randomly partitioned into a 90:10 training/testing split. Using the MLJ machine learning framework, a variety of machine learning models compatible with the regression task were identified [39]. This selection of models included linear regression (and it’s variations), Gaussian process regression, shallow neural networks, and decision tree-based models. Out of this set, the Random Forest Regressor (RFR) model from [40] was selected for its relatively quick training and inference times. Random forests are an ensembling technique based on bagged predictions of individual decision tree regressors trained using the CART algorithm with each individual tree trained on a random subset of features and a random subset of training records [40,41].
As reflectance values in adjacent wavelength bins tend to correlate with each other and, therefore, may not necessarily contribute additional information content to the final model, it is desirable to evaluate the relative importance of each feature to the final predictions of our trained models. This is useful both for identifying the most relevant features and for performing feature selection to reduce the final model size and optimize the inference time. By default, tree-based methods, such as the RFR allow for an impurity-based ranking as described in [41,42]. However, these methods have been shown to be biased towards high cardinality and correlated features [43]. Therefore, we choose to use the model-agnostic permutation importance as described by [44]. To do this, we further partition the training data set, resulting in an 80:10:10 split with 80% of points used for model training, 10% of points used for validation and determination of feature importance, and the final 10% held out as an independent test data set. The importance of the j th feature is then computed as
Imp j = R 2 ( f ( X val ) , y val ) − R 2 ( f ( X val ( j ) ) , y val )
where ( X val , y val ) is the validation set, f ( · ) is the trained model, R 2 ( · , · ) is the coefficient of determination, and X val ( j ) is validation feature set with the j t h column randomly permuted. The permutation importance is therefore understood as the decrease in model performance when the j t h feature is replaced by random values from the validation set.
To assess the uncertainty of the final model’s predictions, we employ Inductive Conformal Prediction as described in [45,46,47,48]. To do this, we compute a set of nonconformity scores of the trained model on the validation set using an uncertainty heuristic, in this case, the absolute error
s i = s ( X i , y i ) = | f ( X i ) − y i | = | y ^ i − y i |
where f ( X i ) = y ^ i denotes the trained ML model applied to the i t h calibration record. These n-many scores are sorted, and the half width of the interval d is calculated as the ⌈ ( 1 − α ) ( n + 1 ) ⌉ n quantile of this set in order to achieve a coverage of 1 − α on the calibration set. Prediction intervals for new data are then formed as f ( X ) ± d . For this study, we have chosen α = 0.1 for a coverage corresponding to a 90% confidence interval.
Using these tools, the training procedure for each model is as follows: First, the model is trained using six-fold cross-validation on the training set with default hyperparameter values. Feature importances for the trained model are then computed, and the top 25 features are identified. A second model is then trained using the same 6-fold cross-validation scheme with only these 25 most important features together with hyperparameter optimization using a random parameter search over the number of trees and sampling fraction. Model performance is evaluated by computing out-of-fold values for the coefficient of determination, as well as the
RMSE = ∑ i = 1 N ( y ^ i − y i ) 2 N ,
MAE = ∑ i = 1 N | y ^ i − y i | N ,
where RMSE is the root-mean-square error, and MAE is the mean absolute error between true values y i and predictions y ^ i .
Having identified the model with the best out-of-fold performance, we proceed to train the final hyperparameter optimized model on the full training set with associated uncertainty estimated using conformal prediction. Then each final model is evaluated on the previously untouched testing set. We visualize model performance across the distribution of testing data with a scatter diagram and quantile-quantile plot for which successful model predictions should lie close to a 1:1 line.
These trained models can then easily be deployed on the on-board processing computer so that during subsequent surveys, target concentrations can be inferred as imagery are collected and processed. The application of each model to the collected hyperspectral data cubes results in a map of the distribution of each water quality variable across the pond.

3. Results

The final data set that combined observations from each of the three separate collections contains more than 120,000 individual records. The collection on 11-23-2020 covered the largest spatial extent across the pond, however, due to flight time constraints resulting from the payload size, imagery from adjacent flight tracks did not overlap, resulting in slight gaps. The collections on 12-09-2020 and 12-10-2020 were adjusted to reduce this gap, resulting in a more uniform coverage over a smaller spatial extent.
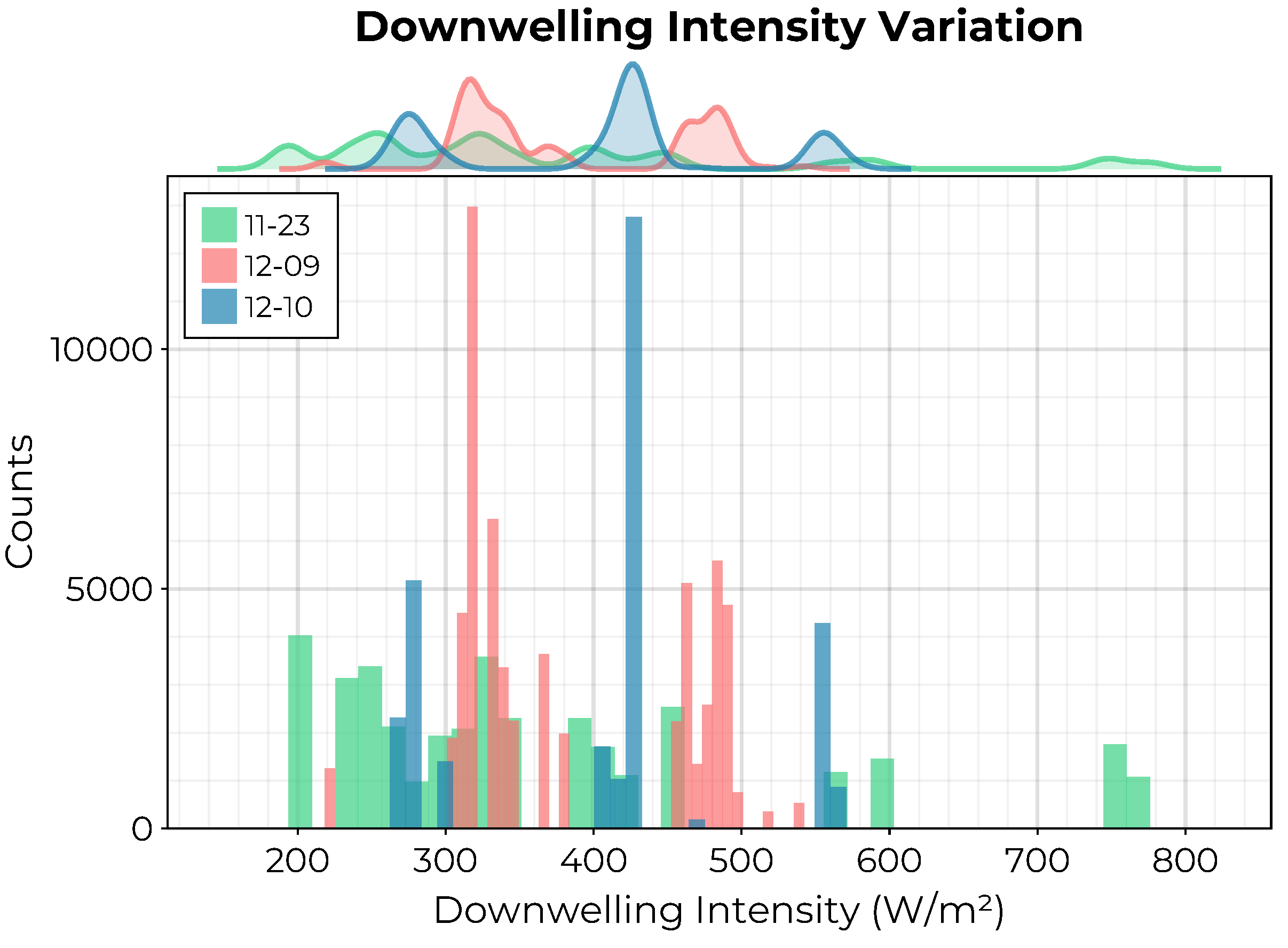
The variability of incident lighting conditions for each collection is visualized in Figure 4 where the distribution of the total downwelling intensity measured by the downwelling irradiance spectrometer across all hyperspectral data cubes is visualized. Despite performing all UAV flights near solar noon, there was a difference in minimum solar zenith angle between collections due to the time of year. Additionally, there was some slight cloudiness during the 12-09 and 12-10 collections.
The results of the model training procedure are presented in Table 2. The performance of the model is identified by the R 2 , RMSE, and MAE out-of-fold estimates (mean ± standard deviation) of the final hyperparameter optimized model in the training set with the target variables ranked in descending order by the R 2 value and separated by sensor type (physical variables, ions, biochemical variables, and chemical variables). The small variation in values across folds confirms that the reported performance is independent of how the training set was sampled. Furthermore, we report the interval width that yields a 90% confidence interval on the holdout validation set determined by the conformal prediction procedure. We then evaluate how the estimated uncertainty generalizes by computing the emprical coverage on the holdout testing set, that is, we compute the percentage of predictions in the test set that actually fall within the estimated 90% confidence interval.
From Table 2, we see that the empirical coverage achieved by the inferred confidence interval evaluated in the independent test set is within 1% of our desired coverage for each target modeled. This indicates that the uncertainties obtained by the conformal prediction procedure are reliable, at least within the bounds of the collected data set. We also note that in all cases, the inferred model uncertainties are larger than the resolution of the in-situ sensors. This lends further credence to the inferred uncertainty estimates as we should not expect to be able to have lower uncertainty than the smallest resolvable difference in reference sensor measurements.
To further examine the differences in model performance between the target variables, we can consider the difference between the RMSE and MAE scores. The MAE is less sensitive to outlier impacts than the RMSE, and, as a consequence, any large difference between the two is indicative of impacts due to the distribution of target values. Indeed, this is the case for turbidity, for which almost all measurements were below 10 FNU with only a small fraction of observations from a small area near the shore. The rest of the models all show a mean perfold RMSE value with size comparable to the mean per-fold MAE.
In the remainder of this section, we compare the models within each target category.

3.1. Physical Variables

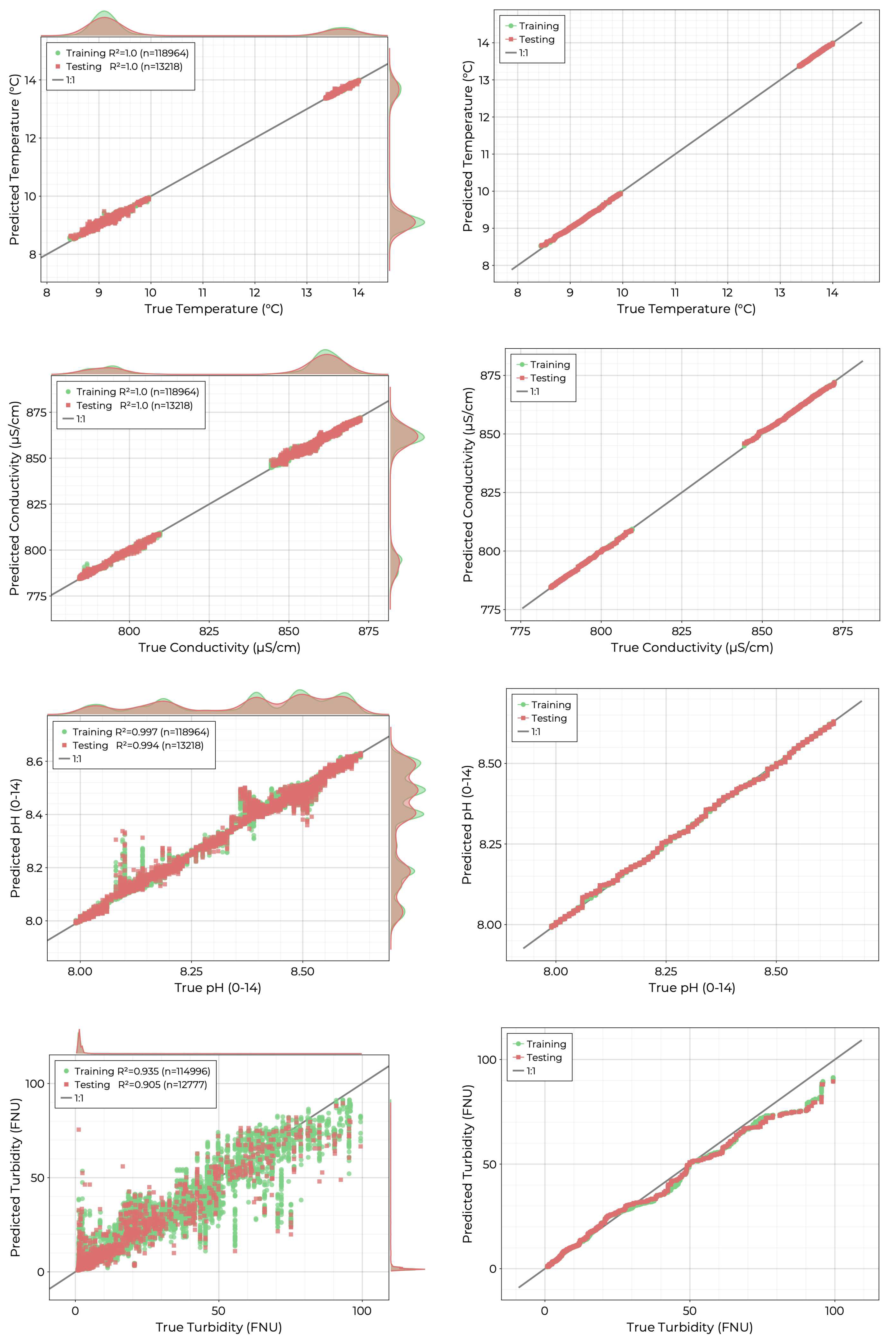
Physical variables included temperature, conductivity, pH, and turbidity. In the combined dataset, the distributions for temperature and conductivity had two distinct, nonoverlapping regions corresponding to the measurements from 11-23 and the measurements from 12-09 and 12-10, respectively. The pH value of the pond was slightly alkaline, showing a multimodal spatial distribution with values ranging from 8.0 to 8.6. As mentioned above, the pond water was very clear for each observation period, with most turbidity values ranging between 1 and 3 FNU and very few above 10.
The results of the hyperparameter optimized RFR fits are shown in Figure 5. Temperature and conductivity show the best performance in the independent training set with R 2 values of 1.0 (to 3 decimal places). Similarly, the pH model achieves an excellent fit, with most predictions falling close to the 1:1 line. Quantile-quantile plots for these three models further confirm that the distributions of true and predicted values match. The turbidity model also achieves a strong fit with a R 2 value of 0.905. The scatter diagram and quantile-quantile plot for this target show that the model performance degrades with larger values where deviation in the predicted distribution is apparent past 25 FNU.
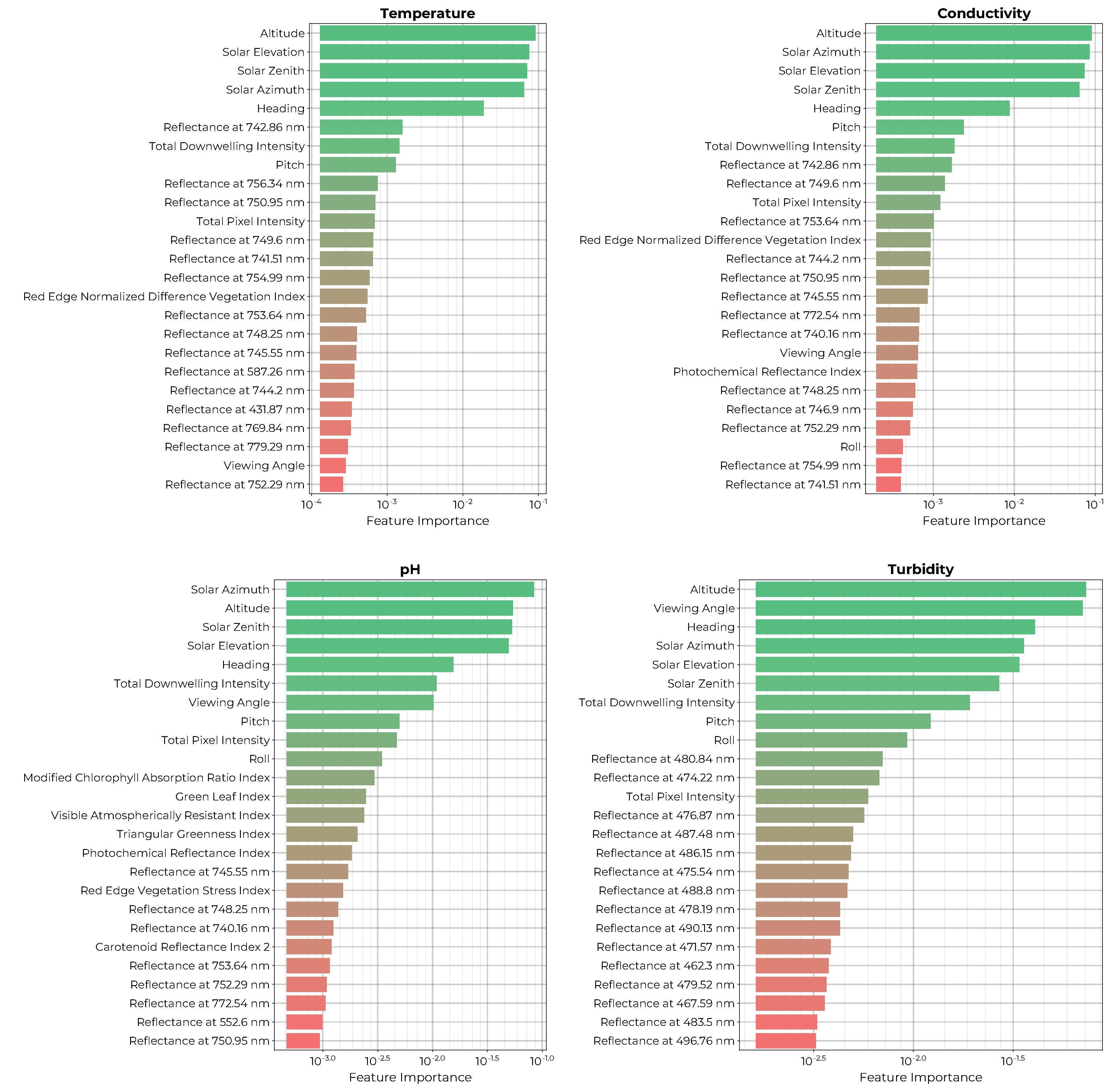
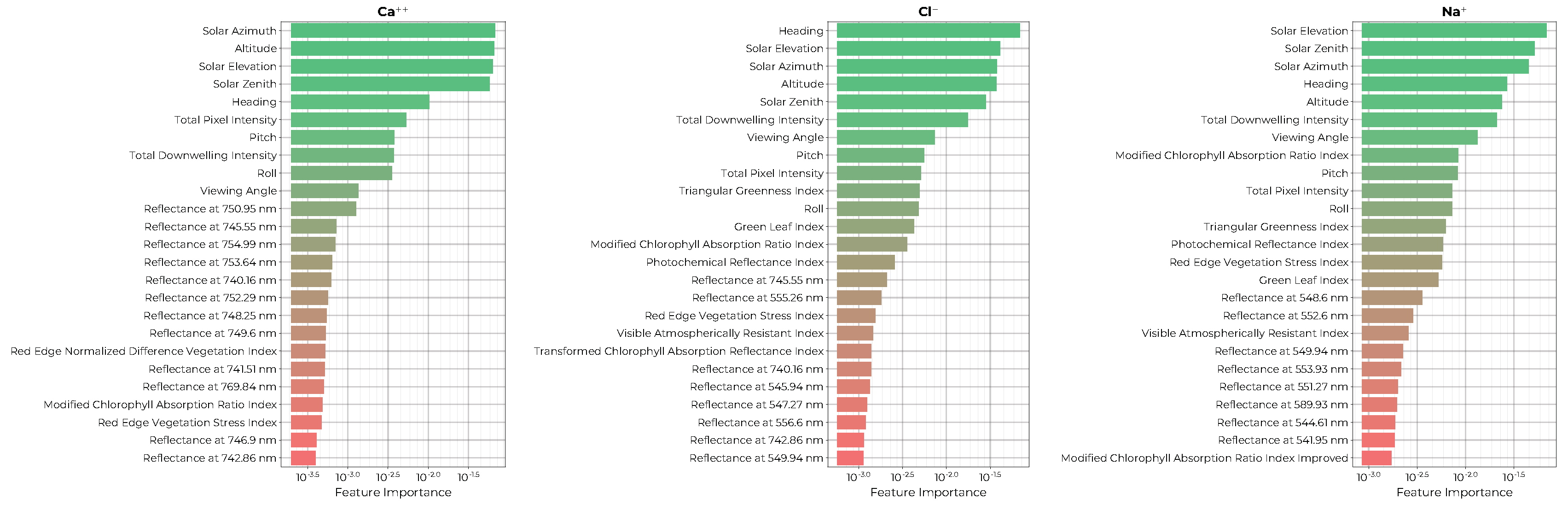
The permutation importance of the top 25 features for each of the models of the physical variables is shown in Figure 6. All four models show a strong dependence on the solar illumination geometry (solar azimuth, elevation, solar zenith) as well as the viewing geometry (pitch, altitude, heading, etc.). All four models also include the total downwelling intensity and the total pixel intensity as highly important features. The temperature, conductivity, and pH models all include red-to-infrared reflectance bins and a combination of spectral indices within their most important features. Finally, the turbidity model relies mainly on blue wavelengths from 462 to 496 nm and did not include any spectral indices amongst the 25 most important features.
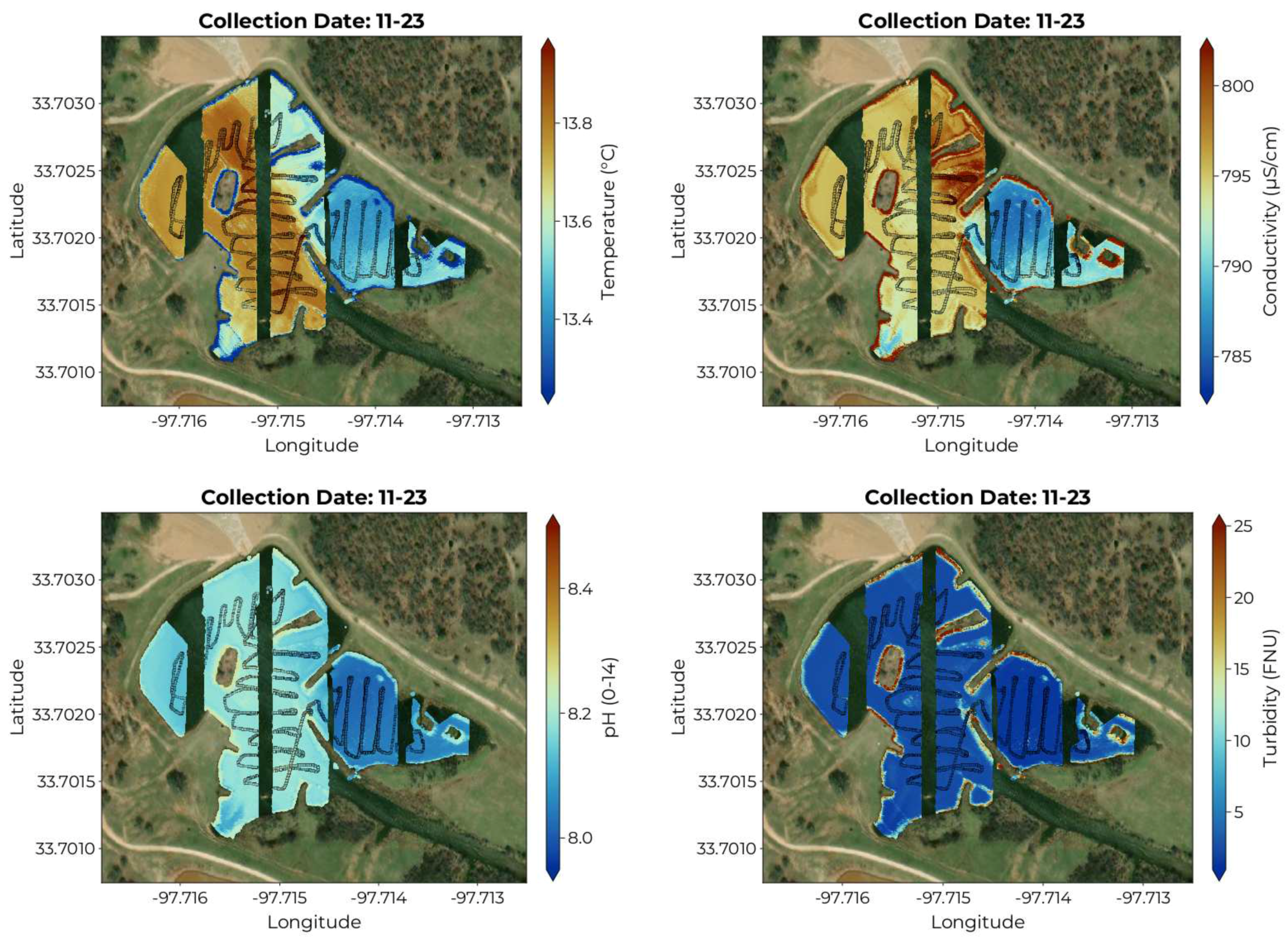
By applying the trained models to the full hyperspectral data cubes, we can produce maps of the distribution of the target variables as in Figure 7. Here we have chosen to show the map produced from the imagery collected during the 11-23 collection period, as they showcase the largest spatial extent. The temperature map shows lower values near the shore, which is to be expected as the air temperature was below the water temperature. The temperature, conductivity, and pH maps all show a distinction between the main body of water and the alcove to the east, which receives little flow from the main body. The turbidity map confirms that the water is largely clear, with elevated levels near the shore.

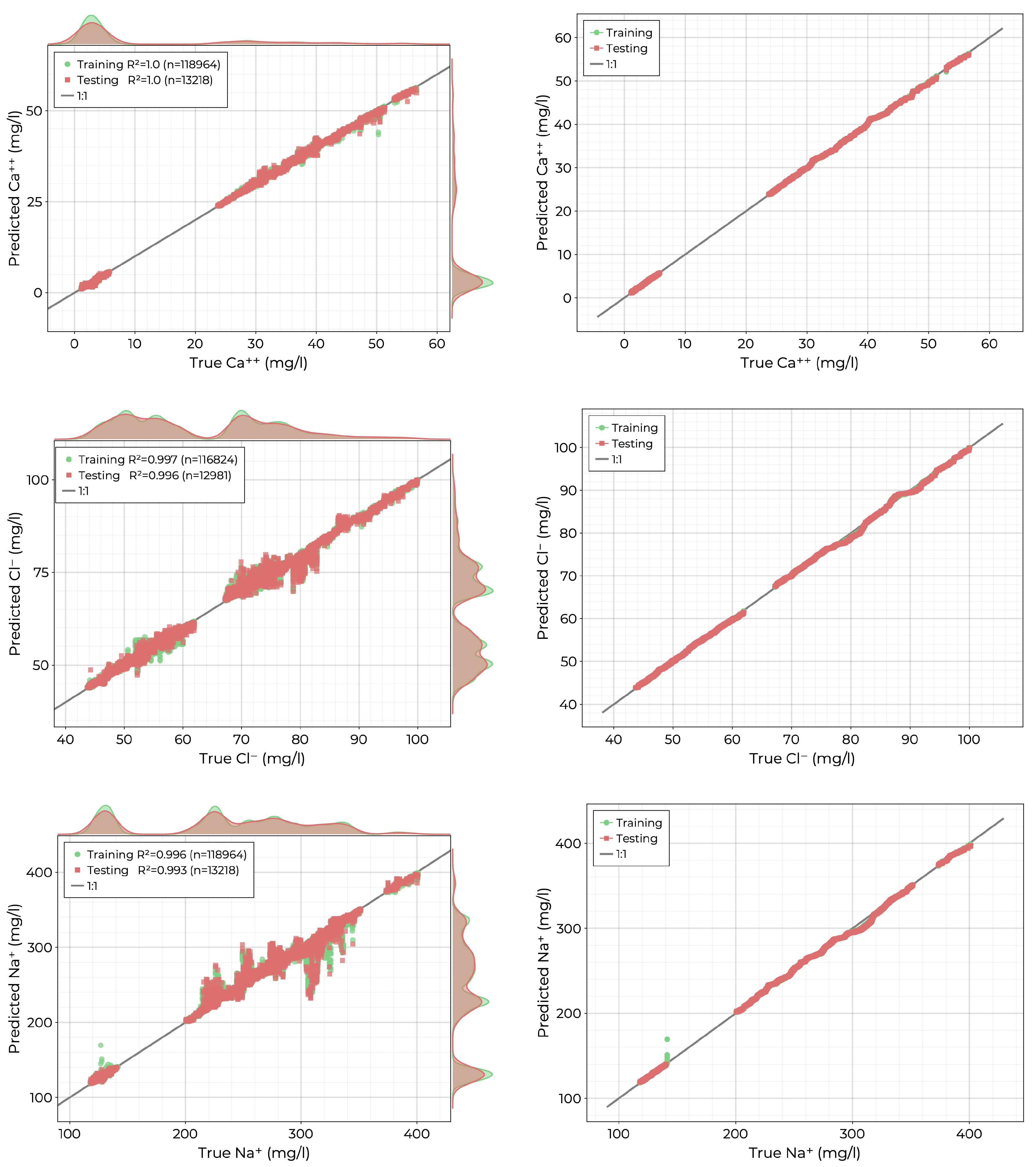
3.2. Ions

The measured ions include Ca 2 + , Cl − , and Na + . All three measurements showed multimodal spatial distributions throughout the pond on each of the three collections. The scatter diagrams and quantile-quantile graphs for the resulting fits are shown in Figure 8. All three models achieved excellent fits with R 2 values of 1.0, 0.996, and 0.993 on the independent testing set, respectively. Furthermore, there is no clear decrease in model performance for low or high concentrations; rather, for Cl − and Na + , the models have the most difficulty in the middle of the target distributions.
The permutation importance ranking for the top 25 features of each of the ion models is shown in Figure 9. Here, we see that all three models depend on the solar illumination and viewing geometries as well as the total downwelling intensity and the total pixel intensity measured at the hyperspectral imager. All three models utilize a combination of spectral indices that combine green, red, and infrared reflectance bins. The Ca + and Cl − models depend on specific red wavelengths of 740 to 769 nm. Cl − and Na + also depend on green and yellow reflectance bins of 541 to 589 nanometers.
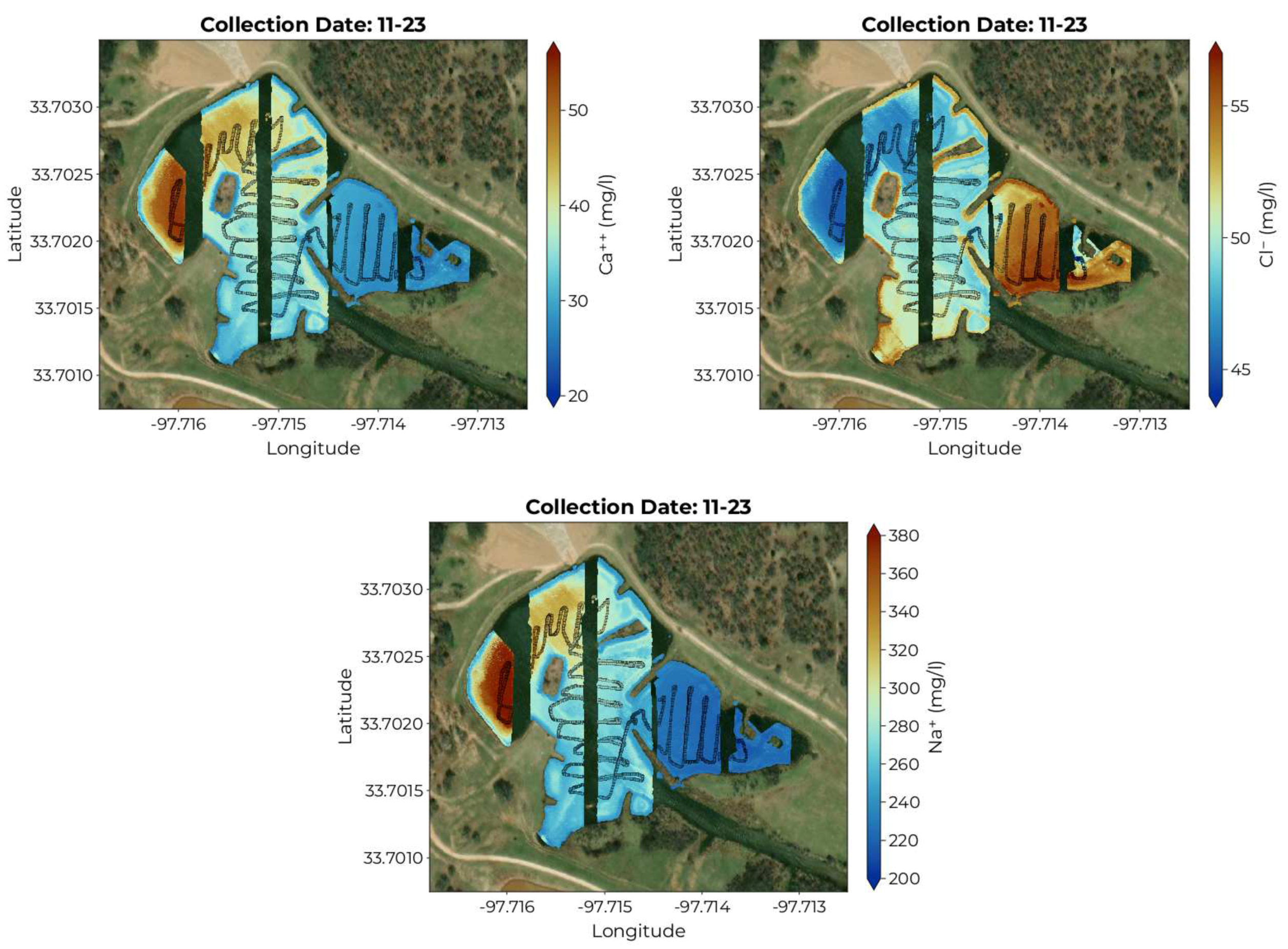
The maps produced by applying the fitted models to the hyperspectral data cubes for 11-23 are shown in Figure 10. Both positive ions Ca 2 + and Na + show high concentrations in the northwest portion of the pond with lower values in the alcove on the eastern side. Positive ion concentrations also appear to decrease near the shore. The negative ion Cl − shows the opposite distribution with larger values in the alcove to the east and lowest values on the western side of the pond. The Cl − ion concentration also appears to increase near the shore.

3.3. Biochemical Variables

The measured biochemical variables include the pigments phycoerythrin, phycocyanin, and chlorophyll-a, as well as CDOM. Phycoerythrin and phycocyanin are both present in blue-green algae, and chlorophyll-a is found in all photosynthetic organisms except bacteria. In the combined dataset, the three pigments showed multimodal distributions separated by collection day with little spatial variation within the individual collection. CDOM showed a variable spatial distribution throughout the pond between the main water body and the eastern alcove on 11-23.
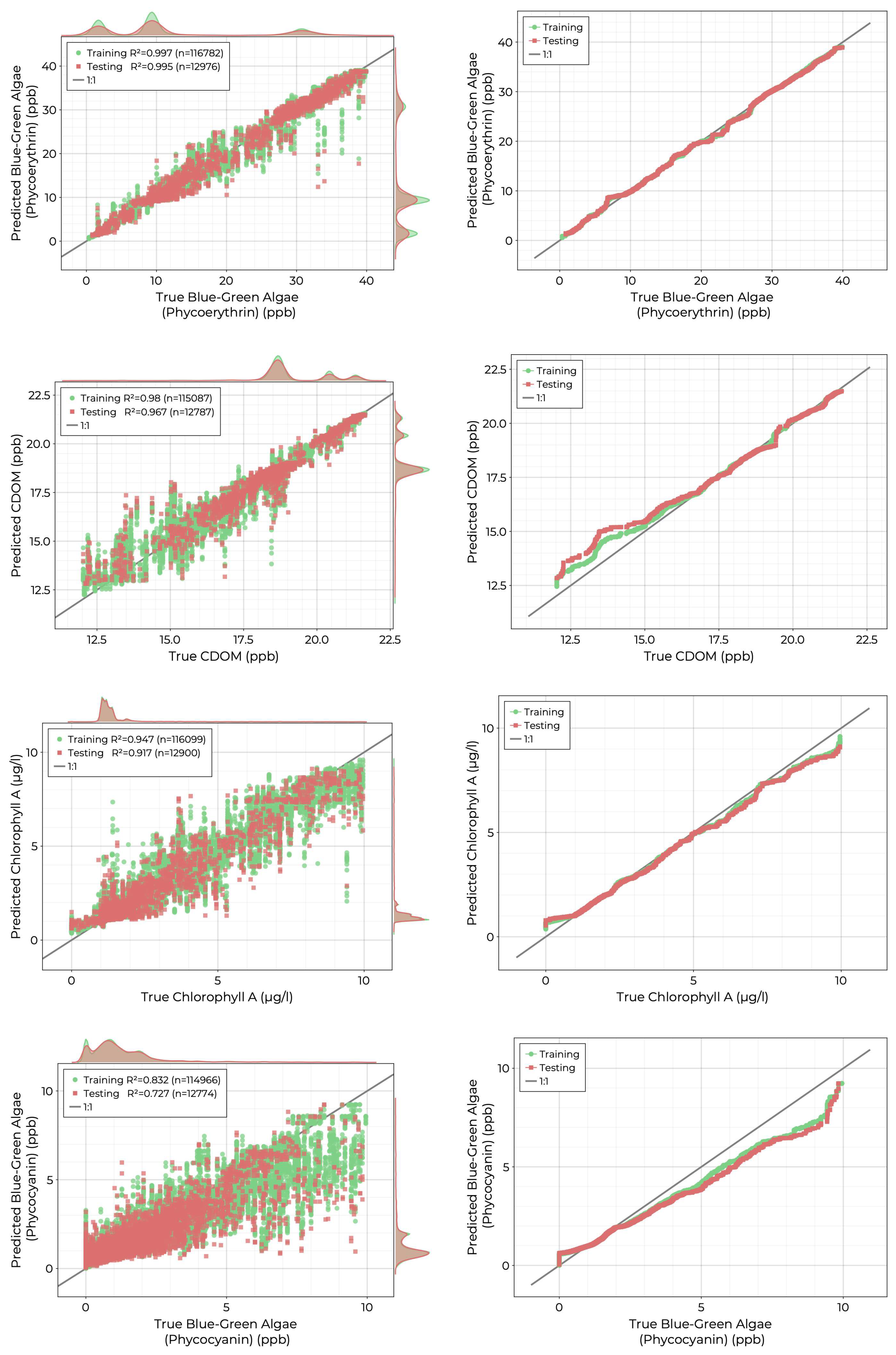
The results of the RFR fits for the biochemical variables are shown in Figure 11. Phycoerythrin showed the best model performance with an R 2 value of 0.995 in the training set. Both CDOM and chlorophyll-a achieved good performance with R 2 values of 0.967 and 0.917 in the training set. Quantile-quantile plots indicate that the CDOM model degrades for values below 16 ppb, where data is sparse. The chlrophyll-a model shows the opposite trend with poorer performance for concentrations above 5 ppb for which there are very few records. The phycocyanin model had the lowest performance of biochemical sensors with a R 2 value of 0.727 and the model predictions rapidly decreased in quality for concentrations greater than 3 ppb.
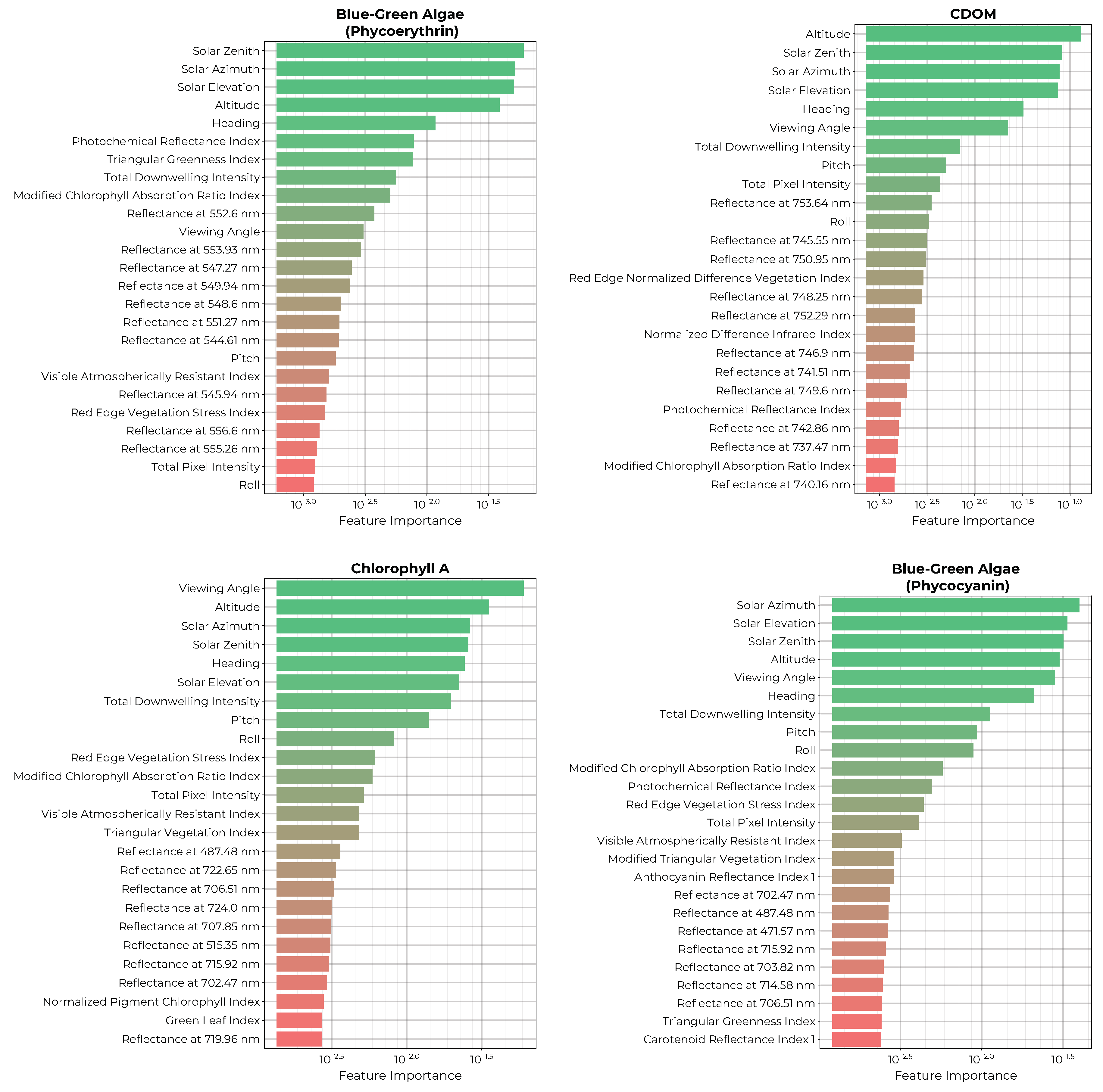
The permutation importance ranking of the top 25 features of each biochemical model is shown in Figure 12. Again, all four models include the solar illumination and viewing geometries amongst their most important features as well as the total downwelling intensity and total pixel intensity at the imager. Additionally, all four models include some vegetation indices amongst the top features, which utilize combinations of blue, green, yellow, red, and infrared reflectance bands. The phycoerythrin model shows a preference for green reflectance bins from 544 to 556 nm while the phycocyanin model prefers blue and red reflectance bins. The CDOM model uses mainly red reflectance values, whereas the chlorophyll-a model includes red, green, and blue reflectance bins.
The maps generated for the 11-23 collection by applying trained biochemical models are shown in Figure 13. The three pigments show low concentrations in the body of water with elevated levels near the shore. The CDOM distribution shows spatial variability with higher values in the eastern alcove similar to the separation seen in the maps for temperature, conductivity, Ca 2 + , Cl − , and Na + .

3.4. Chemical Variables

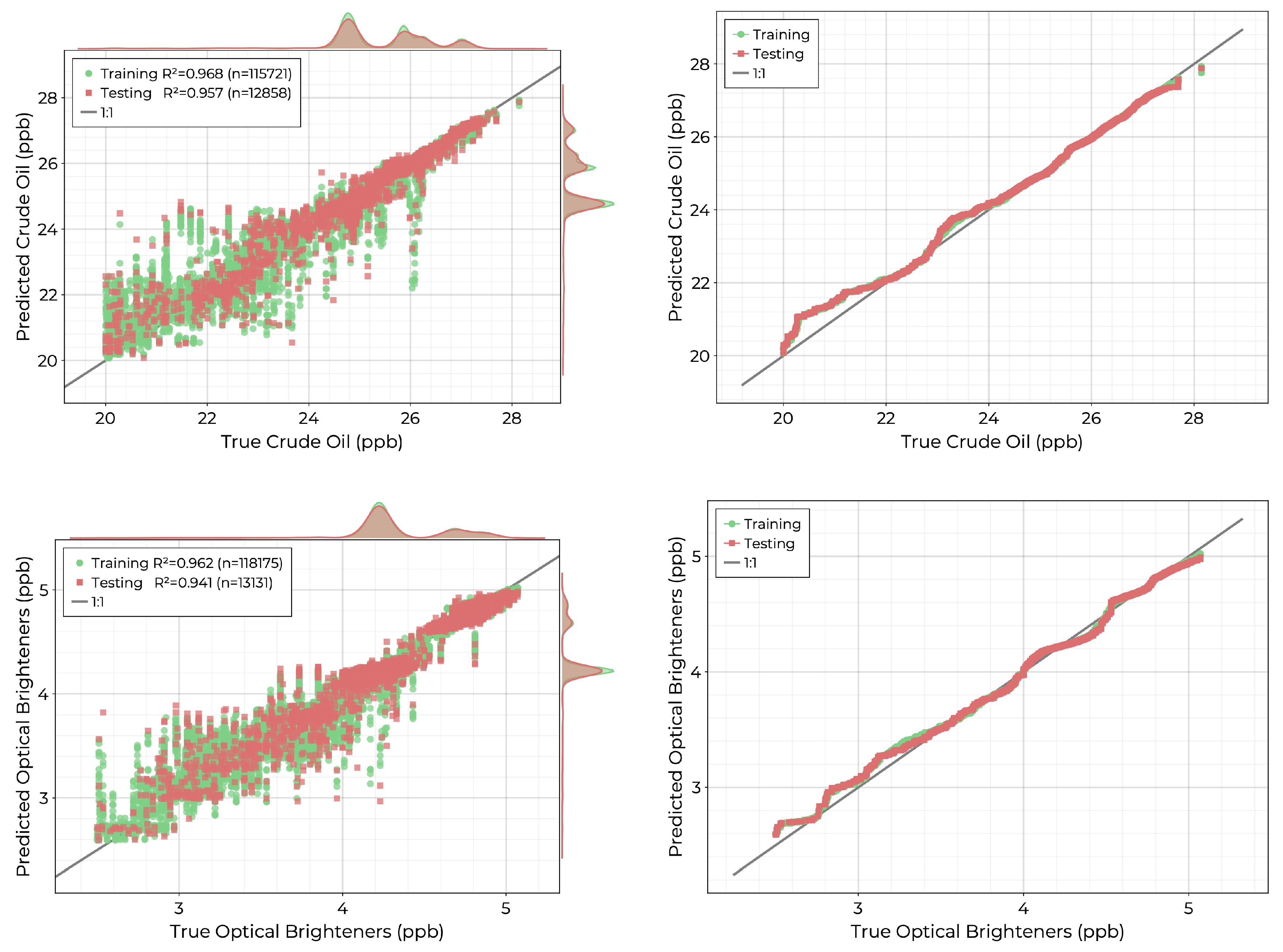
The final two models to consider are for the measured chemical concentrations of crude oil (CO) and optical brighteners (OB). The crude oil measurement includes natural unprocessed petroleum, whereas optical brighteners consist of whitening agents that are often added to products such as soaps, detergents, and cleaning agents. Both the crude oil and optical brightener measurements show multi-modal spatial distributions across each collection period. Scatter diagrams and quantile-quantile plots for the fitted models are shown in Figure 14. Both models achieve good performance with R 2 values of 0.957 and 0.941 for CO and OB on the holdout test set. The performance of the CO model degrades for concentrations below 24 ppb for which there are few records. Similarly, the OB model shows worse performance for concentrations below roughly 3.5 ppb.
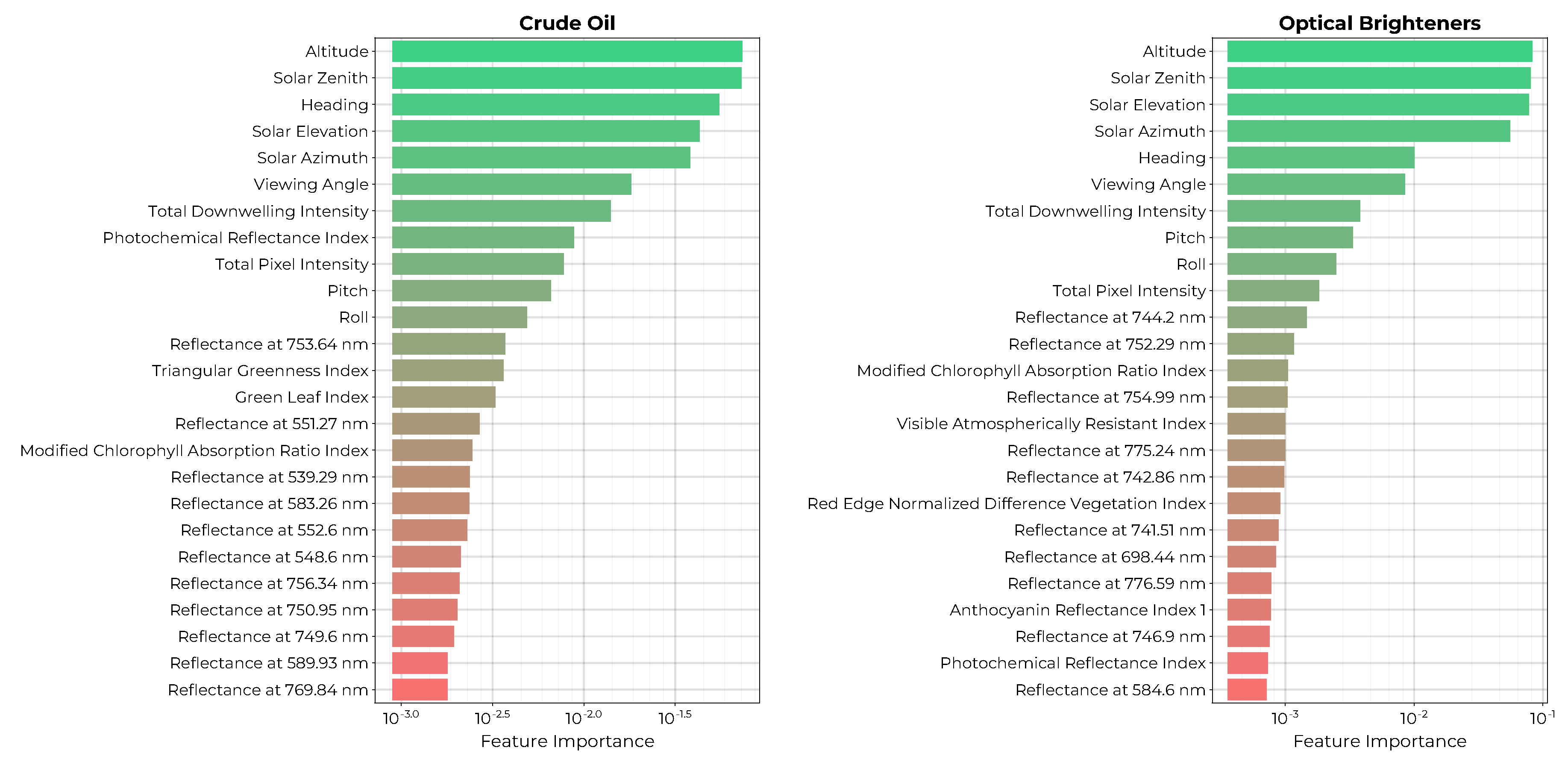
The ranked permutation importances of the top 25 features for each model are shown in Figure 15. Both models rank the solar illumination and viewing geometries together with the total downwelling intensity and total pixel intensities amongst the top features. Both models include a combination of spectral indices using blue, green, yellow, red, and infrared reflectance bins. Additionally, the CO model includes green-yellow reflectances from 539 to 589 nm as well as red reflectances from 749 to 769 nm. The OB model includes a yellow reflectance at 584.6 nm and red reflectance bins.
The maps generated by applying the CO and OB models to the 11-23 data cubes are shown in Figure 16. Both models show a distinct spatial distribution with elevated values in the eastern alcove of the pond similar to the CDOM distribution in Figure 13

4. Discussion

In this paper, we have validated the methodology introduced in our previous work [28]. Specifically, we demonstrate that by using an autonomous team of sensing sentinels, we can
  • Rapidly acquire large volumes in in-situ reference data points for a variety of relevant water quality variables including physical measurements such as temperature, pH, and conductivity as well as ion concentrations, chemicals such as crude oil, and relevant biochemical variables such as blue-green algae pigments, chlorophyll-a, and CDOM.
  • Simultaneously collect hyperspectral remote sensing imagery using an UAV.
  • Rapidly process captured imagery into georectified reflectance data cubes.
  • Train machine learning models to map captured reflectance spectra to water quality variables measured by reference sensors.
  • Apply trained models to rapidly map large bodies of water and identify areas of interest.
Additionally, we have demonstrated that we can extend this methodology in two new ways. First, we have shown that it is possible to combine data sets from separate collection periods and successfully train models using all of the records despite variability in incident lighting conditions that affects the assumptions made in the reflectance conversion of captured hyperspectral data cubes. Second, we have shown that by leveraging the large amount of data collected, we can simultaneously train machine learning models and quantify their prediction uncertainties by utilizing conformal prediction.
As Figure 4 indicates, there is variation in the total downwelling intensity between images collected on the same day and between each separate collection period despite acquiring the imagery consistently near solar noon. These within-collection variations are due to a combination of the stability of the UAV (on which the upward facing downwelling irradiance spectrometer is mounted) together with the occasional interference of clouds. Moreover, the assumption that the water’s surface can be treated as Lambertian is clearly violated when the water is not perfectly still. Despite the potential impact of these limitations on the quality of the resulting reflectance data cubes, the smoothness of the maps generated by our models suggests that we have provided sufficient context by including the relevant solar illumination and viewing geometries as additional features in the final data set. This fact is reinforced by the position of these variables as the most important features for each of the estimated water quality variables. As long as we are primarily interested in these values and not the reflectances themselves, we are able to successfully account for these lighting effects.
With respect to the real-time deployment of these models in the field, we note that training a reduced feature model without further hyperparameter optimization takes roughly 1 minute per target variable of interest using the processing computer included on the UAV. This means that in principle the necessary training data can be collected by the USV, hyperspectral imagery can be acquired and processed into reflectance data cubes by the UAV, the resulting data sets can be combined to identify coincindent records, and this collection can then be used to train machine learning models and generate maps as in Figure 13 all while the investigators are still in the field. Analyzing these resulting maps enables areas of interest to be readily pinpointed, as demonstrated by the identification of elevated crude oil, optical brighteners, and CDOM in the eastern alcove of the pond on 11-23. Having identified a region of interest, the USV can then be sent to collect additional reference data and confirm the presence of any spill, bloom, or other source.
Beyond the potential applications of this robot team for direct water quality monitoring, the combination of reference instruments together with easily co-located hyperspectral imagery provides fertile ground for the development of new spectral indices targeted towards specific water quality variables. In this paper, we have shown how permutation importance ranking for trained machine learning models enables a straightforward interpretation of the relative value of each reflectance bin to the final model predictions. In future work, we plan to utilize this information to construct new combinations of spectral bands which can be readily transferred to remote sensing platforms equipped with hyperspectral imagers such as the German EnMAP mission.

5. Conclusions

In this study, we address the two key limitations of current remote sensing approaches to characterizing water quality, namely the limited spatial, spectral, and temporal resolution provided by existing satellite platforms and the lack of comprehensive, highly resolved in-situ data needed to validate remote sensing data products. By equipping an autonomous USV with a suite of reference sensors, we can collect significantly more data than existing approaches that rely on the collection of individual samples for lab analysis or are constrained to continuous sensing at fixed sites. Utilizing an autonomous UAV equipped with a hyperspectral imager in tandem with the USV allows us to rapidly generate aligned datasets which can be used to train machine learning models which map measured reflectance spectra to the desired water quality variables of interest. Furthermore, by virtue of collecting large training datasets, we are able to simultaneously estimate the uncertainty of our trained models using conformal prediction. This addresses the lack of uncertainty quantification in traditional machine learning approaches. Finally, the rapid hyperspectral data cube processing pipeline employed on board the UAV makes it possible to deploy these trained models in order to rapidly generate maps of the desired target variables across entire bodies of water. The rapid turnaround time from data collection to model deployment is critical for real-time water quality assessment and threat identification.

Supplementary Materials

The following supporting information can be downloaded at: www.mdpi.com/xxx/s1, Table S1: Hyperspectral Reflectance Indices.

Author Contributions

Conceptualization, D.J.L.; methodology, J.L.W. and D.J.L; software, J.L.W; field deployment and preparation, J.L.W, A.A., L.O.H.W., S.T. B.F., P.H., M.I., M.L., D.S., and D.J.L.; validation, J.L.W.; formal analysis, J.L.W.; investigation J.L.W.; resources, D.J.L.; data curation, J.L.W., A.A., L.O.H.W., and D.J.L; writing—original draft preparation, J.L.W.; writing—review and editing, J.L.W. and D.J.L; visualization, J.L.W; supervision, D.J.L; project administration, D.J.L; funding acquisition, D.J.L.; All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the following grants: The Texas National Security Network Excellence Fund award for Environmental Sensing Security Sentinels. SOFWERX award for Machine Learning for Robotic Team and NSF Award OAC-2115094. Support from the University of Texas at Dallas Office of Sponsored Programs, Dean of Natural Sciences and Mathematics, and Chair of the Physics Department is gratefully acknowledged. TRECIS CC* Cyberteam (NSF #2019135), NSF OAC-2115094 Award, and EPA P3 grant number 84057001-0.

Institutional Review Board Statement

Not applicable

Informed Consent Statement

Not applicable

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors on request.

Acknowledgments

Don MacLaughlin, Scotty MacLaughlin and the City of Plano, TX, are gratefully acknowledged for allowing us to deploy the autonomous robot team on their property. Dr. Christopher Simmons is gratefully acknowledged for his computational support. We thank Dr. Antonio Mannino for his advice in selecting the robotic boat sensing suite. Annette Rogers is gratefully acknowledged for support in arranging insurance coverage. Steven Lyles is gratefully acknowledged for support in arranging a secure place for the robot team. The authors acknowledge the OIT-Cyberinfrastructure Research Computing group at the University of Texas at Dallas and the TRECIS CC* Cyberteam (NSF #2019135) for providing HPC resources that contributed to this research, NSF OAC-2115094 Award, and EPA P3 grant number 84057001-0.

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:
GPS Global Positioning System
INS Inertial Navigation System
UTM Universal Transverse Mercator
UV Ultraviolet
ML Machine Learning
USV Uncrewed Surface Vessel
UAV Unmanned Aerial Vehicle
CDOM Colored Dissolved Organic Matter
CO Crude Oil
OB Optical Brighteners
FNU Formazin Nephelometric Unit
RFR Random Forest Regressor
RMSE Root mean square error
MAE Mean absolute error
RENDVI Red-edge normalized difference vegetation index

References

  1. Cohen, W.B.; Goward, S.N. Landsat’s role in ecological applications of remote sensing. Bioscience 2004, 54, 535–545. [Google Scholar] [CrossRef]
  2. Melesse, A.M.; Weng, Q.; Thenkabail, P.S.; Senay, G.B. Remote sensing sensors and applications in environmental resources mapping and modelling. Sensors 2007, 7, 3209–3241. [Google Scholar] [CrossRef] [PubMed]
  3. Allison, R.S.; Johnston, J.M.; Craig, G.; Jennings, S. Airborne optical and thermal remote sensing for wildfire detection and monitoring. Sensors 2016, 16, 1310. [Google Scholar] [CrossRef]
  4. Joyce, K.E.; Belliss, S.E.; Samsonov, S.V.; McNeill, S.J.; Glassey, P.J. A review of the status of satellite remote sensing and image processing techniques for mapping natural hazards and disasters. Progress in physical geography 2009, 33, 183–207. [Google Scholar] [CrossRef]
  5. Robert, E.; Kergoat, L.; Soumaguel, N.; Merlet, S.; Martinez, J.M.; Diawara, M.; Grippa, M. Analysis of suspended particulate matter and its drivers in Sahelian ponds and lakes by remote sensing (Landsat and MODIS): Gourma region, Mali. Remote Sensing 2017, 9, 1272. [Google Scholar] [CrossRef]
  6. Brezonik, P.; Menken, K.D.; Bauer, M. Landsat-based remote sensing of lake water quality characteristics, including chlorophyll and colored dissolved organic matter (CDOM). Lake and Reservoir Management 2005, 21, 373–382. [Google Scholar] [CrossRef]
  7. Paavel, B.; Arst, H.; Metsamaa, L.; Toming, K.; Reinart, A. Optical investigations of CDOM-rich coastal waters in Pärnu Bay. Estonian Journal of Earth Sciences 2011, 60, 102. [Google Scholar] [CrossRef]
  8. Gürsoy, Ö.; Atun, R. Investigating surface water pollution by integrated remotely sensed and field spectral measurement data: A case study. Polish Journal of Environmental Studies 2019, 28. [Google Scholar] [CrossRef]
  9. Bonansea, M.; Ledesma, M.; Rodriguez, C.; Pinotti, L. Using new remote sensing satellites for assessing water quality in a reservoir. Hydrological sciences journal 2019, 64, 34–44. [Google Scholar] [CrossRef]
  10. Sagan, V.; Peterson, K.T.; Maimaitijiang, M.; Sidike, P.; Sloan, J.; Greeling, B.A.; Maalouf, S.; Adams, C. Monitoring inland water quality using remote sensing: Potential and limitations of spectral indices, bio-optical simulations, machine learning, and cloud computing. Earth-Science Reviews 2020, 205, 103187. [Google Scholar] [CrossRef]
  11. Koponen, S.; Attila, J.; Pulliainen, J.; Kallio, K.; Pyhälahti, T.; Lindfors, A.; Rasmus, K.; Hallikainen, M. A case study of airborne and satellite remote sensing of a spring bloom event in the Gulf of Finland. Continental Shelf Research 2007, 27, 228–244. [Google Scholar] [CrossRef]
  12. Aurin, D.; Mannino, A.; Lary, D.J. Remote sensing of CDOM, CDOM spectral slope, and dissolved organic carbon in the global ocean. Applied Sciences 2018, 8, 2687. [Google Scholar] [CrossRef]
  13. Ross, M.R.; Topp, S.N.; Appling, A.P.; Yang, X.; Kuhn, C.; Butman, D.; Simard, M.; Pavelsky, T.M. AquaSat: A data set to enable remote sensing of water quality for inland waters. Water Resources Research 2019, 55, 10012–10025. [Google Scholar] [CrossRef]
  14. Schiller, H.; Doerffer, R. Neural network for emulation of an inverse model operational derivation of Case II water properties from MERIS data. International journal of remote sensing 1999, 20, 1735–1746. [Google Scholar] [CrossRef]
  15. Brown, M.E.; Lary, D.J.; Vrieling, A.; Stathakis, D.; Mussa, H. Neural networks as a tool for constructing continuous NDVI time series from AVHRR and MODIS. International Journal of Remote Sensing 2008, 29, 7141–7158. [Google Scholar] [CrossRef]
  16. Lary, D.J. Artificial intelligence in geoscience and remote sensing. In Geoscience and Remote Sensing New Achievements; IntechOpen, 2010. [Google Scholar]
  17. Feng, Q.; Liu, J.; Gong, J. Urban flood mapping based on unmanned aerial vehicle remote sensing and random forest classifier—A case of Yuyao, China. Water 2015, 7, 1437–1455. [Google Scholar] [CrossRef]
  18. Belgiu, M.; Drăguţ, L. Random forest in remote sensing: A review of applications and future directions. ISPRS journal of photogrammetry and remote sensing 2016, 114, 24–31. [Google Scholar] [CrossRef]
  19. Fingas, M.; Brown, C.E. A review of oil spill remote sensing. sensors 2017, 18, 91. [Google Scholar] [CrossRef]
  20. Hruska, R.; Mitchell, J.; Anderson, M.; Glenn, N.F. Radiometric and geometric analysis of hyperspectral imagery acquired from an unmanned aerial vehicle. Remote Sensing 2012, 4, 2736–2752. [Google Scholar] [CrossRef]
  21. Adão, T.; Hruška, J.; Pádua, L.; Bessa, J.; Peres, E.; Morais, R.; Sousa, J.J. Hyperspectral imaging: A review on UAV-based sensors, data processing and applications for agriculture and forestry. Remote sensing 2017, 9, 1110. [Google Scholar] [CrossRef]
  22. Banerjee, B.P.; Raval, S.; Cullen, P. UAV-hyperspectral imaging of spectrally complex environments. International Journal of Remote Sensing 2020, 41, 4136–4159. [Google Scholar] [CrossRef]
  23. Pádua, L.; Vanko, J.; Hruška, J.; Adão, T.; Sousa, J.J.; Peres, E.; Morais, R. UAS, sensors, and data processing in agroforestry: A review towards practical applications. International journal of remote sensing 2017, 38, 2349–2391. [Google Scholar] [CrossRef]
  24. Arroyo-Mora, J.P.; Kalacska, M.; Inamdar, D.; Soffer, R.; Lucanus, O.; Gorman, J.; Naprstek, T.; Schaaf, E.S.; Ifimov, G.; Elmer, K.; et al. Implementation of a UAV–hyperspectral pushbroom imager for ecological monitoring. Drones 2019, 3, 12. [Google Scholar] [CrossRef]
  25. Kurihara, J.; Ishida, T.; Takahashi, Y. Unmanned Aerial Vehicle (UAV)-based hyperspectral imaging system for precision agriculture and forest management. Unmanned Aerial Vehicle: Applications in Agriculture and Environment 2020, 25–38. [Google Scholar]
  26. Ehmann, K.; Kelleher, C.; Condon, L.E. Monitoring turbidity from above: Deploying small unoccupied aerial vehicles to image in-stream turbidity. Hydrological Processes 2019, 33, 1013–1021. [Google Scholar] [CrossRef]
  27. Lu, Q.; Si, W.; Wei, L.; Li, Z.; Xia, Z.; Ye, S.; Xia, Y. Retrieval of water quality from UAV-borne hyperspectral imagery: A comparative study of machine learning algorithms. Remote Sensing 2021, 13, 3928. [Google Scholar] [CrossRef]
  28. Lary, D.J.; Schaefer, D.; Waczak, J.; Aker, A.; Barbosa, A.; Wijeratne, L.O.H.; Talebi, S.; Fernando, B.; Sadler, J.Z.; Lary, T.; et al. Autonomous Learning of New Environments with a Robotic Team Employing Hyper-Spectral Remote Sensing, Comprehensive In-Situ Sensing and Machine Learning. Sensors (Basel, Switzerland) 2021, 21. [Google Scholar] [CrossRef]
  29. Meier, L.; QGroundControl. MAVLink Micro Air Vehicle Communication Protocol. 2010. Available online: http://qgroundcontrol. org/mavlink/start (accessed on 30 January 2019).
  30. Ruddick, K.G.; Voss, K.; Banks, A.C.; Boss, E.; Castagna, A.; Frouin, R.; Hieronymi, M.; Jamet, C.; Johnson, B.C.; Kuusk, J.; et al. A review of protocols for fiducial reference measurements of downwelling irradiance for the validation of satellite remote sensing data over water. Remote Sensing 2019, 11, 1742. [Google Scholar] [CrossRef]
  31. Müller, R.; Lehner, M.; Muller, R.; Reinartz, P.; Schroeder, M.; Vollmer, B. A program for direct georeferencing of airborne and spaceborne line scanner images. 2002.
  32. Bäumker, M.; Heimes, F. New calibration and computing method for direct georeferencing of image and scanner data using the position and angular data of an hybrid inertial navigation system. In Proceedings of the OEEPE Workshop, Integrated Sensor Orientation; 2001; pp. 1–17. [Google Scholar]
  33. Mostafa, M.M.R.; Schwarz, K.P. A Multi-Sensor System for Airborne Image Capture and Georeferencing. Photogrammetric Engineering and Remote Sensing 2000, 66, 1417–1424. [Google Scholar]
  34. Bezanson, J.; Karpinski, S.; Shah, V.B.; Edelman, A. Julia: A fast dynamic language for technical computing. arXiv 2012, arXiv:1209.5145. [Google Scholar]
  35. Vegetation Indices Background, 2023. https://www.nv5geospatialsoftware.com/docs/backgroundvegetationindices.html, Last accessed on 2024-01-03.
  36. Thenkabail, P.S.; Lyon, J.G.; Huete, A. Hyperspectral indices and image classifications for agriculture and vegetation; CRC press, 2018. [Google Scholar]
  37. Kaufman, Y.J.; Tanre, D. Atmospherically resistant vegetation index (ARVI) for EOS-MODIS. IEEE transactions on Geoscience and Remote Sensing 1992, 30, 261–270. [Google Scholar] [CrossRef]
  38. Zheng, Q.; Huang, W.; Cui, X.; Shi, Y.; Liu, L. New Spectral Index for Detecting Wheat Yellow Rust Using Sentinel-2 Multispectral Imagery. Sensors (Basel, Switzerland) 2018, 18. [Google Scholar] [CrossRef]
  39. Blaom, A.D.; Kiraly, F.; Lienart, T.; Simillides, Y.; Arenas, D.; Vollmer, S.J. MLJ: A Julia package for composable machine learning. Journal of Open Source Software 2020, 5, 2704. [Google Scholar] [CrossRef]
  40. Breiman, L. Classification and regression trees; Routledge, 2017. [Google Scholar]
  41. Breiman, L. Random forests. Machine learning 2001, 45, 5–32. [Google Scholar] [CrossRef]
  42. Louppe, G.; Wehenkel, L.; Sutera, A.; Geurts, P. Understanding variable importances in forests of randomized trees. Advances in neural information processing systems 2013, 26. [Google Scholar]
  43. Strobl, C.; Boulesteix, A.L.; Kneib, T.; Augustin, T.; Zeileis, A. Conditional variable importance for random forests. BMC bioinformatics 2008, 9, 1–11. [Google Scholar] [CrossRef] [PubMed]
  44. Parr, T.; Turgutlu, K.; Csiszar, C.; Howard, J. Beware default random forest importances. March 2018, 26, 2018. [Google Scholar]
  45. Shafer, G.; Vovk, V. A Tutorial on Conformal Prediction. Journal of Machine Learning Research 2008, 9. [Google Scholar]
  46. Angelopoulos, A.N.; Bates, S. A gentle introduction to conformal prediction and distribution-free uncertainty quantification. arXiv 2021, arXiv:2107.07511 2021. [Google Scholar]
  47. Fontana, M.; Zeni, G.; Vantini, S. Conformal prediction: a unified review of theory and new challenges. Bernoulli 2023, 29, 1–23. [Google Scholar] [CrossRef]
  48. Papadopoulos, H. Inductive conformal prediction: Theory and application to neural networks. In Tools in artificial intelligence; Citeseer, 2008. [Google Scholar]
Preprints 97522 g001
Figure 1. Configuration of the UAV: (a) the hyperspectral imager and acquisition computer. (b) the assembled UAV with secondary processing computer and (upward facing) downwelling irradiance spectrometer.
Figure 1. Configuration of the UAV: (a) the hyperspectral imager and acquisition computer. (b) the assembled UAV with secondary processing computer and (upward facing) downwelling irradiance spectrometer.
Preprints 97522 g001
Preprints 97522 g002
Figure 2. Hyperspectral Image Processing: Hyperspectral data cubes are collected one scan-line at a time (left). By utilizing downwelling irradiance spectra we convert each pixel from spectral radiance to reflectance. By using orientation and position data from the on-board GPS and INS, we georeference each pixel to assign it a latitude and longitude on the ground. The final data product is a georectified hyperspectral reflectance data cube visualized at the right.
Figure 2. Hyperspectral Image Processing: Hyperspectral data cubes are collected one scan-line at a time (left). By utilizing downwelling irradiance spectra we convert each pixel from spectral radiance to reflectance. By using orientation and position data from the on-board GPS and INS, we georeference each pixel to assign it a latitude and longitude on the ground. The final data product is a georectified hyperspectral reflectance data cube visualized at the right.
Preprints 97522 g002
Preprints 97522 g003
Figure 3. A georectified reflectance data cube is visualized (center) with the log 10 -reflectance along the z axis and a pseudo-color image on the top. In the top left we visualize the downwelling irradiance spectrum (the incident light). The surrounding plots showcase exemplar pixel reflectance spectra for open water, dry grass, algae, and a rhodamine dye plume used to test the system.
Figure 3. A georectified reflectance data cube is visualized (center) with the log 10 -reflectance along the z axis and a pseudo-color image on the top. In the top left we visualize the downwelling irradiance spectrum (the incident light). The surrounding plots showcase exemplar pixel reflectance spectra for open water, dry grass, algae, and a rhodamine dye plume used to test the system.
Preprints 97522 g003
Preprints 97522 g004
Figure 4. Distribution of total downwelling intensity during each of the three HSI collection flights. The multi-modal nature of these distributions reflects the impact of the relative orientation of the drone to the sun as well as potential occlusion due to the presence of clouds.
Figure 4. Distribution of total downwelling intensity during each of the three HSI collection flights. The multi-modal nature of these distributions reflects the impact of the relative orientation of the drone to the sun as well as potential occlusion due to the presence of clouds.
Preprints 97522 g004
Preprints 97522 g005
Figure 5. Scatter diagrams (left) and quantile-quantile plots (right) for the hyperparameter optimized RFR models for the physical variables measured by the USV.
Figure 5. Scatter diagrams (left) and quantile-quantile plots (right) for the hyperparameter optimized RFR models for the physical variables measured by the USV.
Preprints 97522 g005
Preprints 97522 g006
Figure 6. Ranked permutation importance for each feature in the physical variable models. Permutation importance measured the decrease in model R 2 value after replacing each feature in the prediction set with a random permutation of its values.
Figure 6. Ranked permutation importance for each feature in the physical variable models. Permutation importance measured the decrease in model R 2 value after replacing each feature in the prediction set with a random permutation of its values.
Preprints 97522 g006
Preprints 97522 g007
Figure 7. Maps generated by applying each of the physical variable models to the hyperspectral data cubes collected on 11-23. Overlaid over the predictions are color-filled squares showing the associated in-situ reference data for the same collection period. The size of the squares has been exaggerated for the visualization. We note that there is good agreement between the model predictions and the reference data.
Figure 7. Maps generated by applying each of the physical variable models to the hyperspectral data cubes collected on 11-23. Overlaid over the predictions are color-filled squares showing the associated in-situ reference data for the same collection period. The size of the squares has been exaggerated for the visualization. We note that there is good agreement between the model predictions and the reference data.
Preprints 97522 g007
Preprints 97522 g008
Figure 8. Scatter diagrams (left) and quantile-quantile plots (right) for the hyperparameter optimized RFR models for the ion measurements made by the USV.
Figure 8. Scatter diagrams (left) and quantile-quantile plots (right) for the hyperparameter optimized RFR models for the ion measurements made by the USV.
Preprints 97522 g008
Preprints 97522 g009
Figure 9. Ranked permutation importance for the top 25 features of the ion models. The permutation importance measures the decrease in model R 2 value when each feature is replaced by a random permutation of its values.
Figure 9. Ranked permutation importance for the top 25 features of the ion models. The permutation importance measures the decrease in model R 2 value when each feature is replaced by a random permutation of its values.
Preprints 97522 g009
Preprints 97522 g010
Figure 10. Maps generated by applying the trained ion models to the data cubes collected on 11-23. Overlaid on the maps are the in-situ reference measurements for the same collection period. The size of the squares has been exaggerated for the visualization. We note that there is good agreement between the generated map and the reference data.
Figure 10. Maps generated by applying the trained ion models to the data cubes collected on 11-23. Overlaid on the maps are the in-situ reference measurements for the same collection period. The size of the squares has been exaggerated for the visualization. We note that there is good agreement between the generated map and the reference data.
Preprints 97522 g010
Preprints 97522 g011
Figure 11. Scatter plots (left) and quantile-quantile plots (right) for the final hyperparameter optimized models for the biochemical targets blue-green algae (phycoerythrin), CDOM, chlorophyll-a, and blue-green algae (phycocyanin).
Figure 11. Scatter plots (left) and quantile-quantile plots (right) for the final hyperparameter optimized models for the biochemical targets blue-green algae (phycoerythrin), CDOM, chlorophyll-a, and blue-green algae (phycocyanin).
Preprints 97522 g011
Preprints 97522 g012
Figure 12. Ranked permutation importance for each feature in the trained biochemical models. The permutation importance measures the decrease in model R 2 value after replacing each feature with a random permutation of its values.
Figure 12. Ranked permutation importance for each feature in the trained biochemical models. The permutation importance measures the decrease in model R 2 value after replacing each feature with a random permutation of its values.
Preprints 97522 g012
Preprints 97522 g013
Figure 13. Maps generated by applying the trained biochemical models to the data cubes collected on 11-23. Overlaid are the in-situ reference data for the same collection period. The size of the squares has been exaggerated for the visualization. We note there is good agreement between the predicted map and the reference data.
Figure 13. Maps generated by applying the trained biochemical models to the data cubes collected on 11-23. Overlaid are the in-situ reference data for the same collection period. The size of the squares has been exaggerated for the visualization. We note there is good agreement between the predicted map and the reference data.
Preprints 97522 g013
Preprints 97522 g014
Figure 14. Scatter diagrams (left) and quantile-quantile plots (right) for the hyperparameter optimized RFR models for the chemical variables measured by the USV.
Figure 14. Scatter diagrams (left) and quantile-quantile plots (right) for the hyperparameter optimized RFR models for the chemical variables measured by the USV.
Preprints 97522 g014
Preprints 97522 g015
Figure 15. Ranked permutation importance for for the top 25 features of the chemical models. The permutation importance measures the deacrease in model R 2 value after replacing each feature in the prediction set with a random permutation of its values.
Figure 15. Ranked permutation importance for for the top 25 features of the chemical models. The permutation importance measures the deacrease in model R 2 value after replacing each feature in the prediction set with a random permutation of its values.
Preprints 97522 g015
Preprints 97522 g016
Figure 16. Maps generated by applying the trained chemical variable models to the hyperspectral data cubes collected on 11-23. Overlaid are color-filled squares showing the in-situ reference data for the same collection period. The size of the squares is exaggerated for the visualization. We note that there is good agreement between the model predictions and reference data.
Figure 16. Maps generated by applying the trained chemical variable models to the hyperspectral data cubes collected on 11-23. Overlaid are color-filled squares showing the in-situ reference data for the same collection period. The size of the squares is exaggerated for the visualization. We note that there is good agreement between the model predictions and reference data.
Preprints 97522 g016
Table 1. In-situ reference sensors modelled in this study.
Table 1. In-situ reference sensors modelled in this study.
Sensor Units Resolution Sensor Type Target Category
Temperature °C 0.01 Thermistor Physical
Conductivity μ S/cm 0.01 Four-Electrode Graphite Sensor Physical
pH logarithmic (0-14) 0.01 Flowing-junction Reference Electrode Physical
Turbidity FNU 0.01 Ion-Selective Electrode Physical
Ca 2 + mg/l 0.1 Ion-Selective Electrode Ions
Cl − mg/l 0.1 Ion-Selective Electrode Ions
Na + mg/l 0.1 Ion-Selective Electrode Ions
Blue-Green Algae (phycoerythrin) ppb 0.01 Fluorometer Biochemical
Blue-Green Algae (phycocyanin) ppb 0.01 Fluorometer Biochemical
CDOM ppb 0.01 Fluorometer Biochemical
Chlorophyll A ppb 0.01 Fluorometer Biochemical
Optical Brighteners ppb 0.01 Fluorometer Chemical
Crude Oil ppb 0.01 Fluorometer Chemical
Table 2. Summary of fitting statistics for each target measurement. Models were evaluated using 6-fold cross validation on the training set. The estimated uncertainty is evaluated so that a prediction y ^ ± Δ y achieves 90% coverage on the calibration holdout set. The empirical coverage is the percentage of predictions in the testing set that fall within the inferred confidence interval.
Table 2. Summary of fitting statistics for each target measurement. Models were evaluated using 6-fold cross validation on the training set. The estimated uncertainty is evaluated so that a prediction y ^ ± Δ y achieves 90% coverage on the calibration holdout set. The empirical coverage is the percentage of predictions in the testing set that fall within the inferred confidence interval.
Target Units R 2 RMSE MAE Estimated Uncertainty Empirical Coverage (%)
Temperature °C 1.0 ± 6.04e-6 0.0289 ± 0.000466 0.0162 ± 0.00016 ± 0.039 90.3
Conductivity μ S/cm 1.0 ± 1.54e-5 0.574 ± 0.0128 0.322 ± 0.00579 ± 0.76 90.6
pH 0-14 0.994 ± 0.000288 0.0145 ± 0.000304 0.00739 ± 9.49e-5 ± 0.017 89.5
Turbidity FNU 0.897 ± 0.00611 3.13 ± 0.084 0.736 ± 0.0156 ± 1.1 89.8
Ca 2 + mg/l 1.0 ± 1.06e-5 0.285 ± 0.00357 0.137 ± 0.00224 ± 0.33 89.8
Cl − mg/l 0.995 ± 0.000196 0.895 ± 0.0202 0.516 ± 0.00759 ± 1.2 90.1
Na + mg/l 0.993 ± 0.000229 6.16 ± 0.102 2.83 ± 0.0303 ± 7.3 90.0
Blue-Green Algae (Phycoerythrin) ppb 0.995 ± 0.000601 0.783 ± 0.0489 0.287 ± 0.00959 ± 0.73 89.3
CDOM ppb 0.965 ± 0.00352 0.248 ± 0.0142 0.0921 ± 0.0024 ± 0.15 89.9
Chlorophyll A ppb 0.908 ± 0.00664 0.37 ± 0.00934 0.131 ± 0.00228 ± 0.27 89.2
Blue-Green Algae (Phycocyanin) ppb 0.708 ± 0.00689 0.749 ± 0.0129 0.446 ± 0.00405 ± 0.93 89.8
Crude Oil ppb 0.949 ± 0.00267 0.247 ± 0.00597 0.0935 ± 0.00114 ± 0.17 89.8
Optical Brighteners ppb 0.943 ± 0.00122 0.0806 ± 0.0014 0.0481 ± 0.000416 ± 0.095 89.8
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
An Evaluation of Sun-Glint Correction Methods for UAV-Derived Secchi Depth Estimations in Inland Water Bodies

Edvinas Tiškus

et al.

,

2023

Estimation Method of Chlorophyll Concentration Distribution Based on UAV Aerial Images considering Turbid Water Distribution in a Reservoir

Mitsuteru Irie

et al.

,

2024

Retrieval of Non-Optically Active Parameters for Small Scale Urban Waterbodies by a Machine Learning-Based Strategy

Jinhui Jeanne Huang

et al.

,

2020

Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated