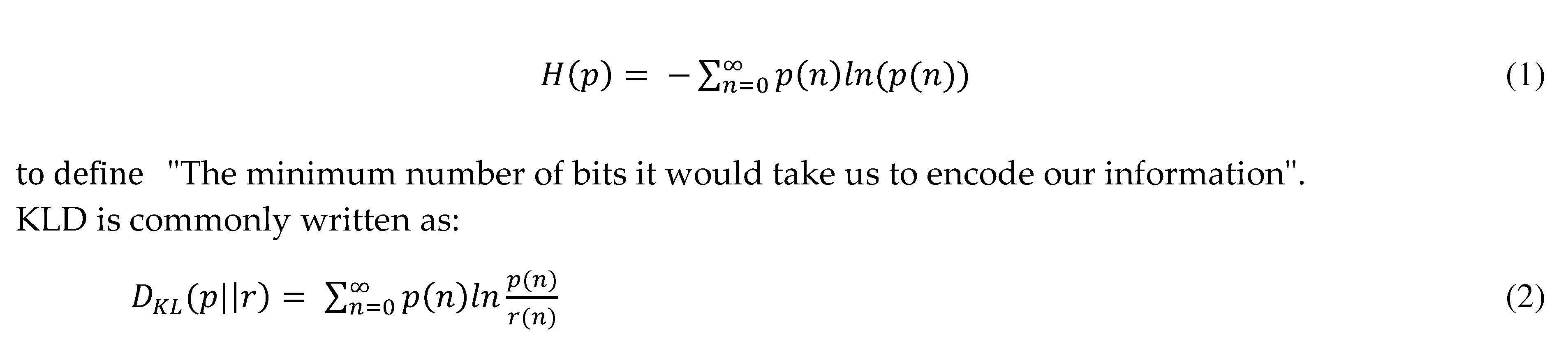Submitted:
29 January 2024
Posted:
31 January 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
1.1. Early Dawn of Minimum Relative Entropy(MRE)
1.2. Information geometry(IG)
2. Main Definitions in Information Geometry
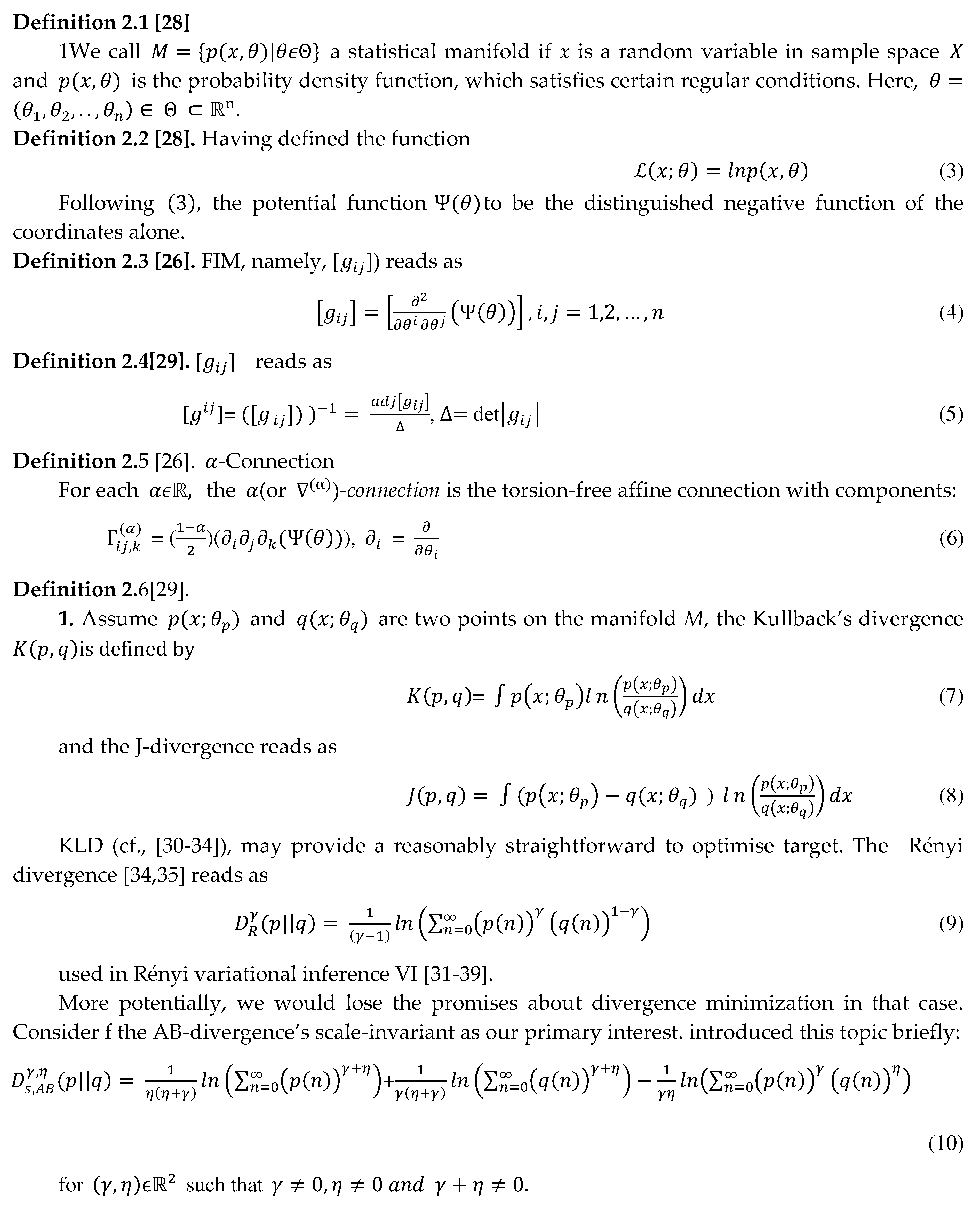
2.7. Well Defined Functions and Bijective Functions

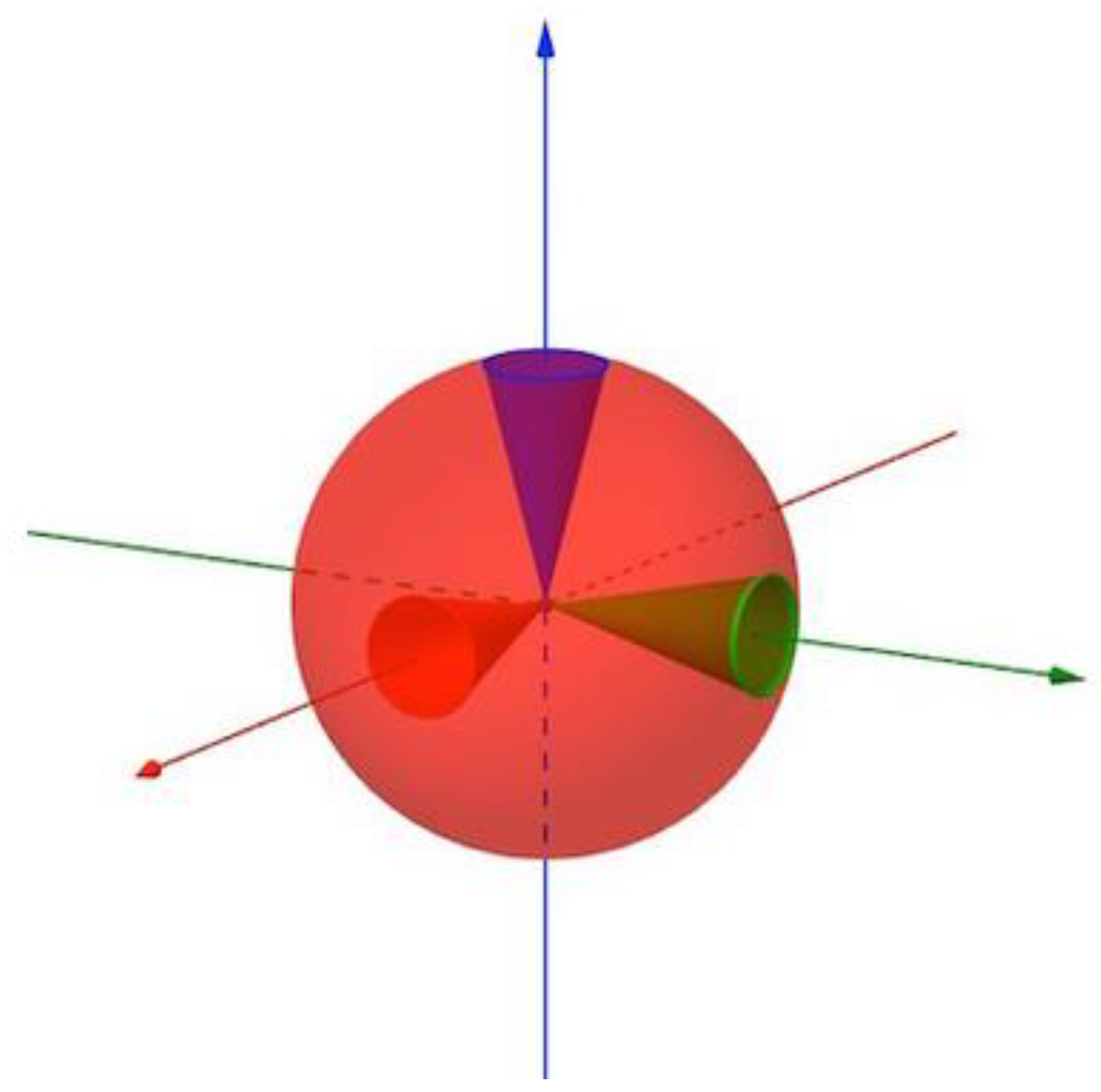

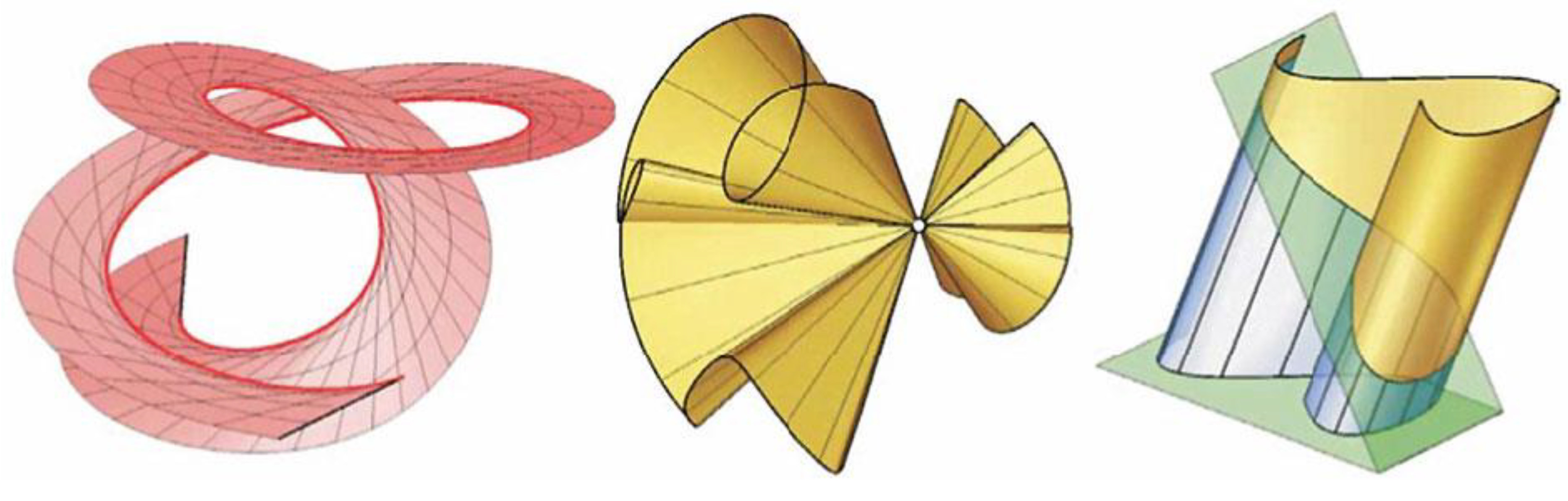

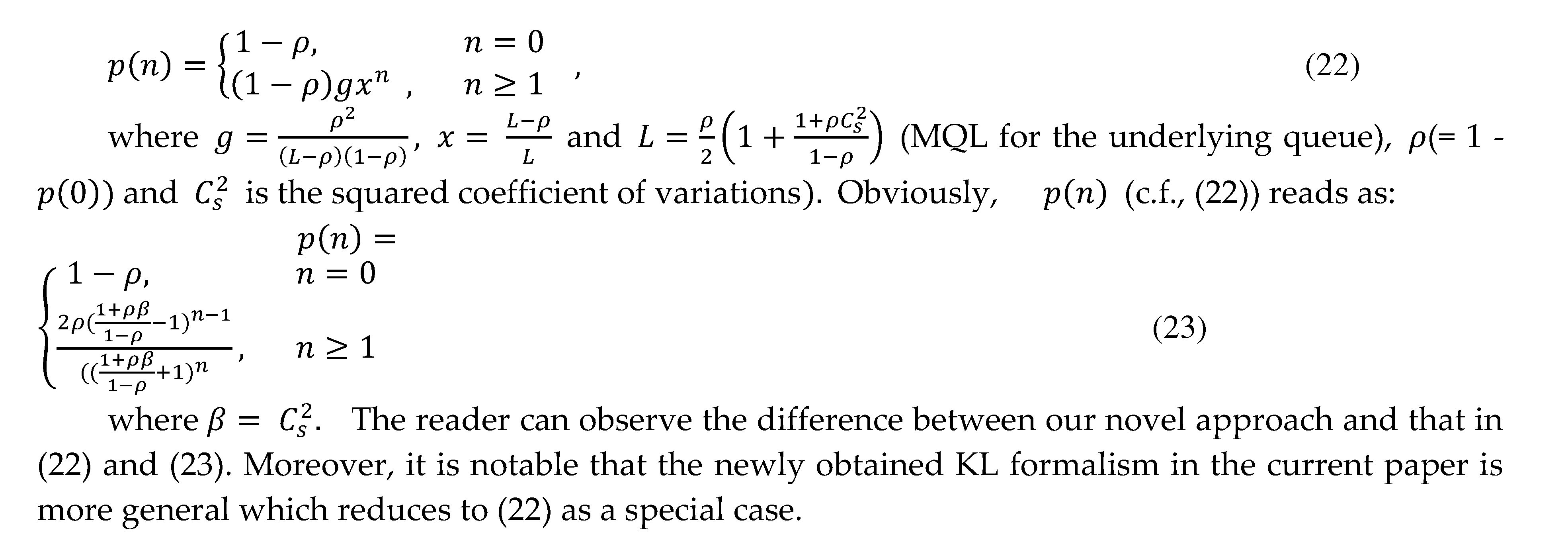
2.11. Scalar Curvature(Ricci Scalar), and Einestein Tensor,

3.1. NME Formalisms and EME Consistency Axioms
3.2. A Stable M/G/1 Queue with Long-Range Interactions
3.3. Background:Shannon’s EME State Probability of a Stable M/G/1 Queue

3.4. KLDF
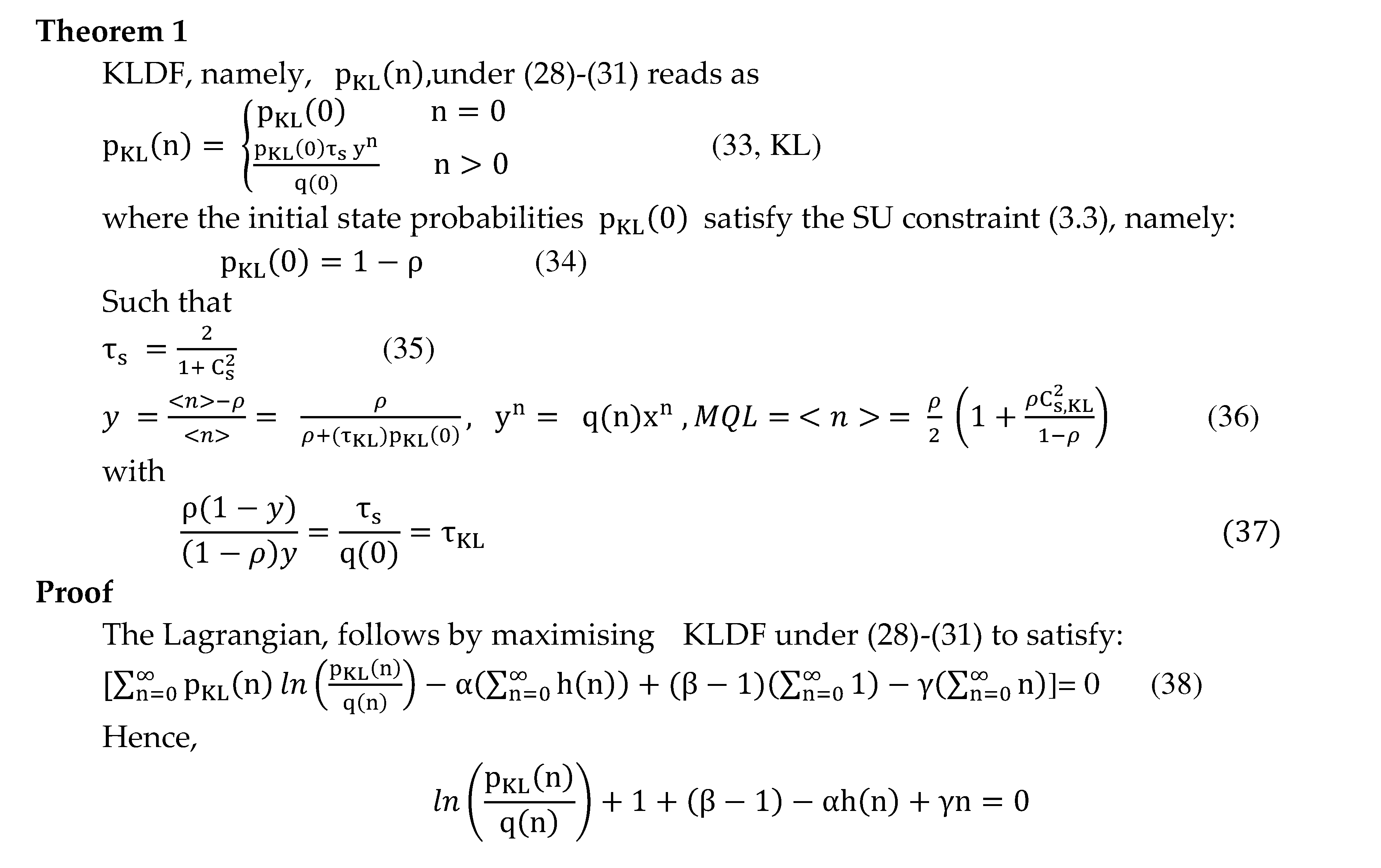

3.5. Exact KL NME State Probabilities with Distinct GEKL-type Service Time Distributions


4. THE THRESHOLD THEOREMS OF KL FORMALISM, and FOR THE UNDERLYING MANIFOLD

4.1. The Threshold Theorem of KL Formalism of The Stable MG1 Queueing System
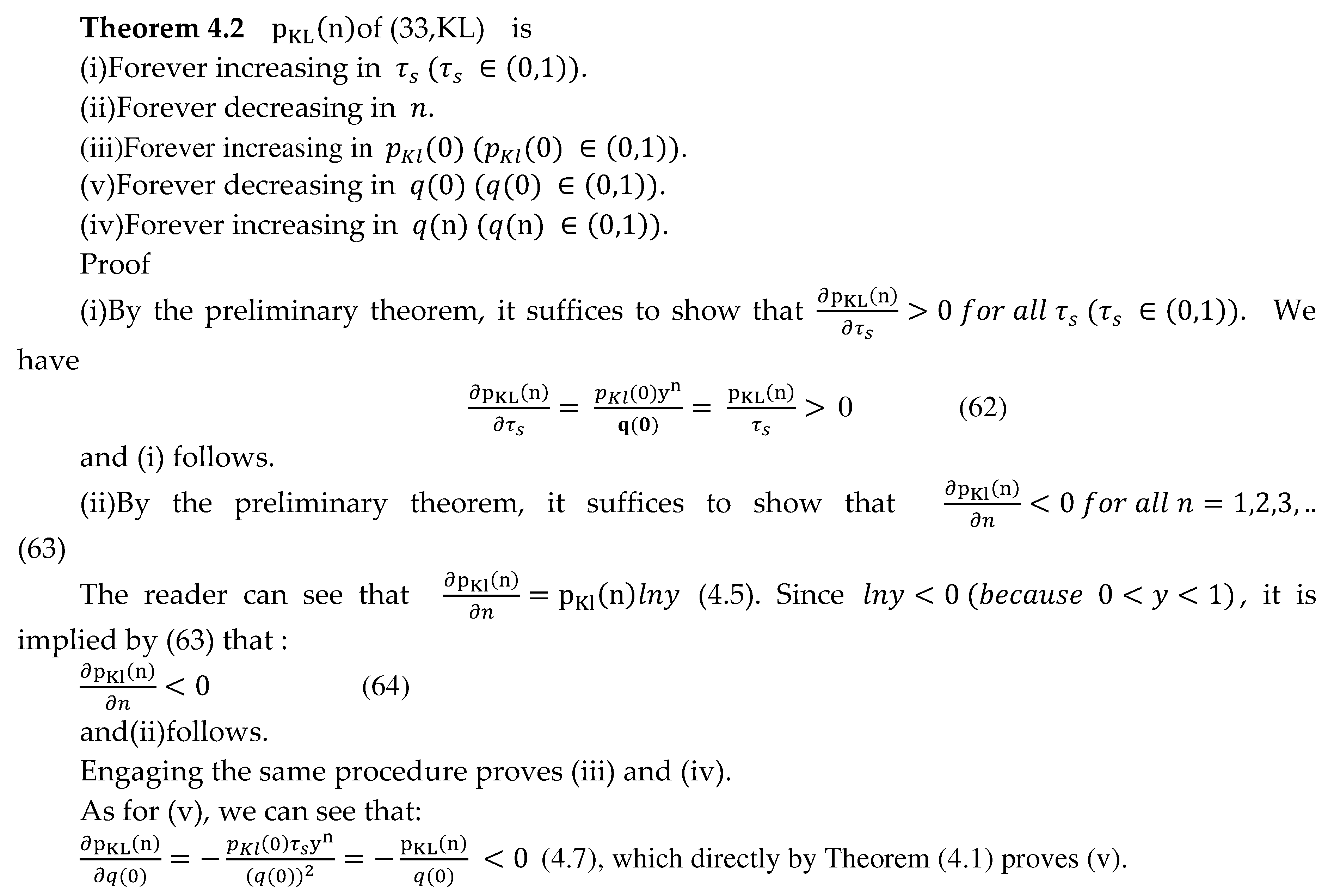
4.2. The Threshold Theorem of of The Stable MG1 Queueing System

4.2. The Threshold Theorem of of The Stable MG1 Queueing System
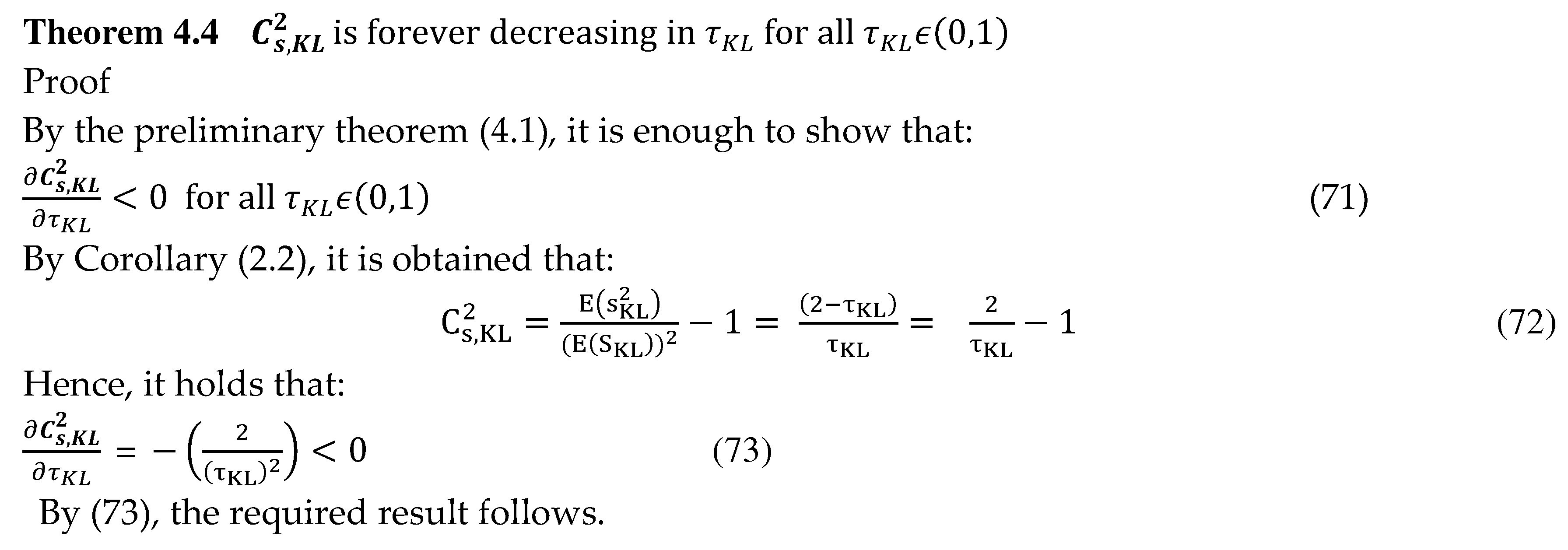
5. FIM and IFIM for KLDF manifold

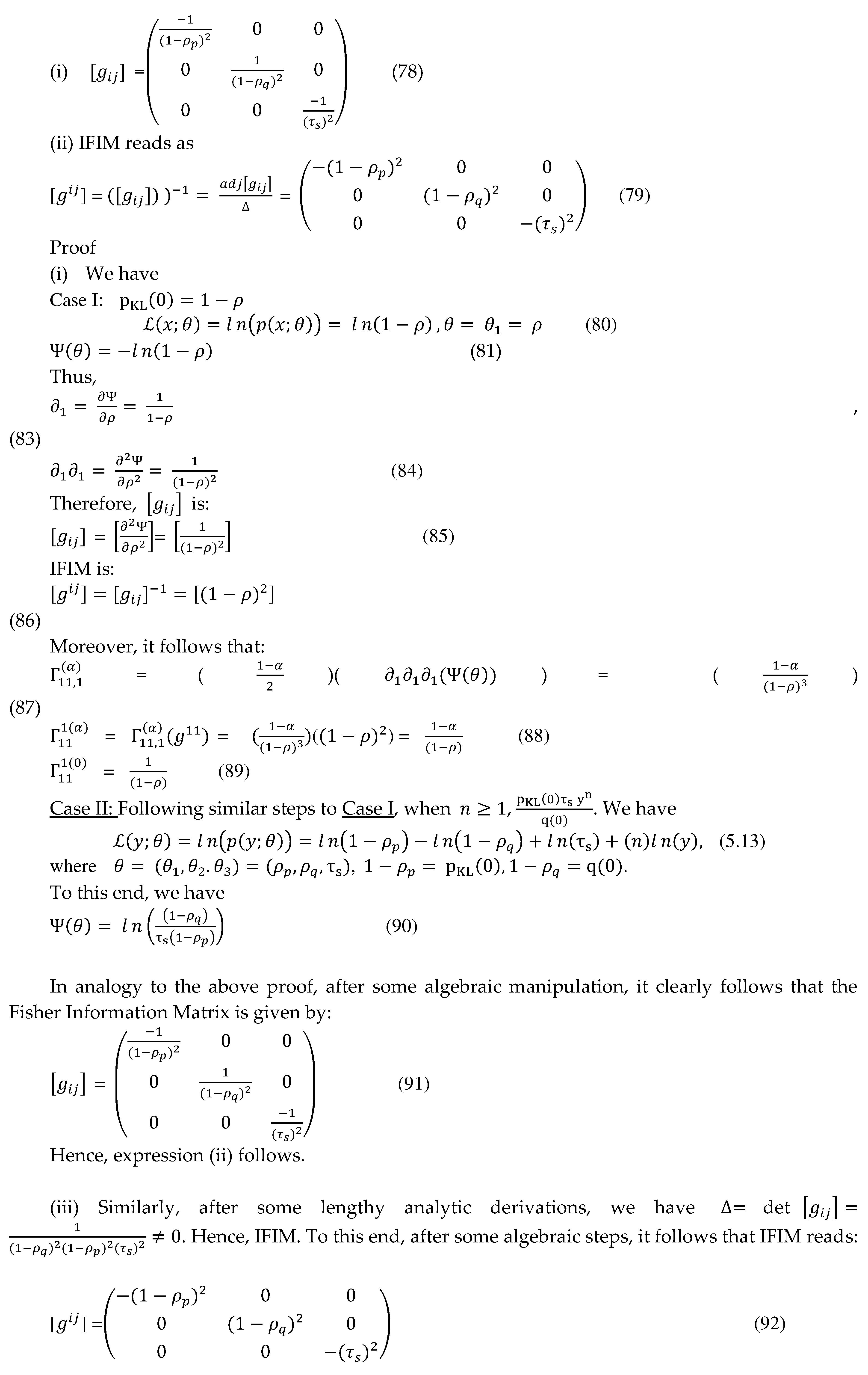
6. The α-connection of the KLDF manifold

7. The Compressibility ( Non-Solonoidability ) of KL Formalism of the Stable M/G/1 QM
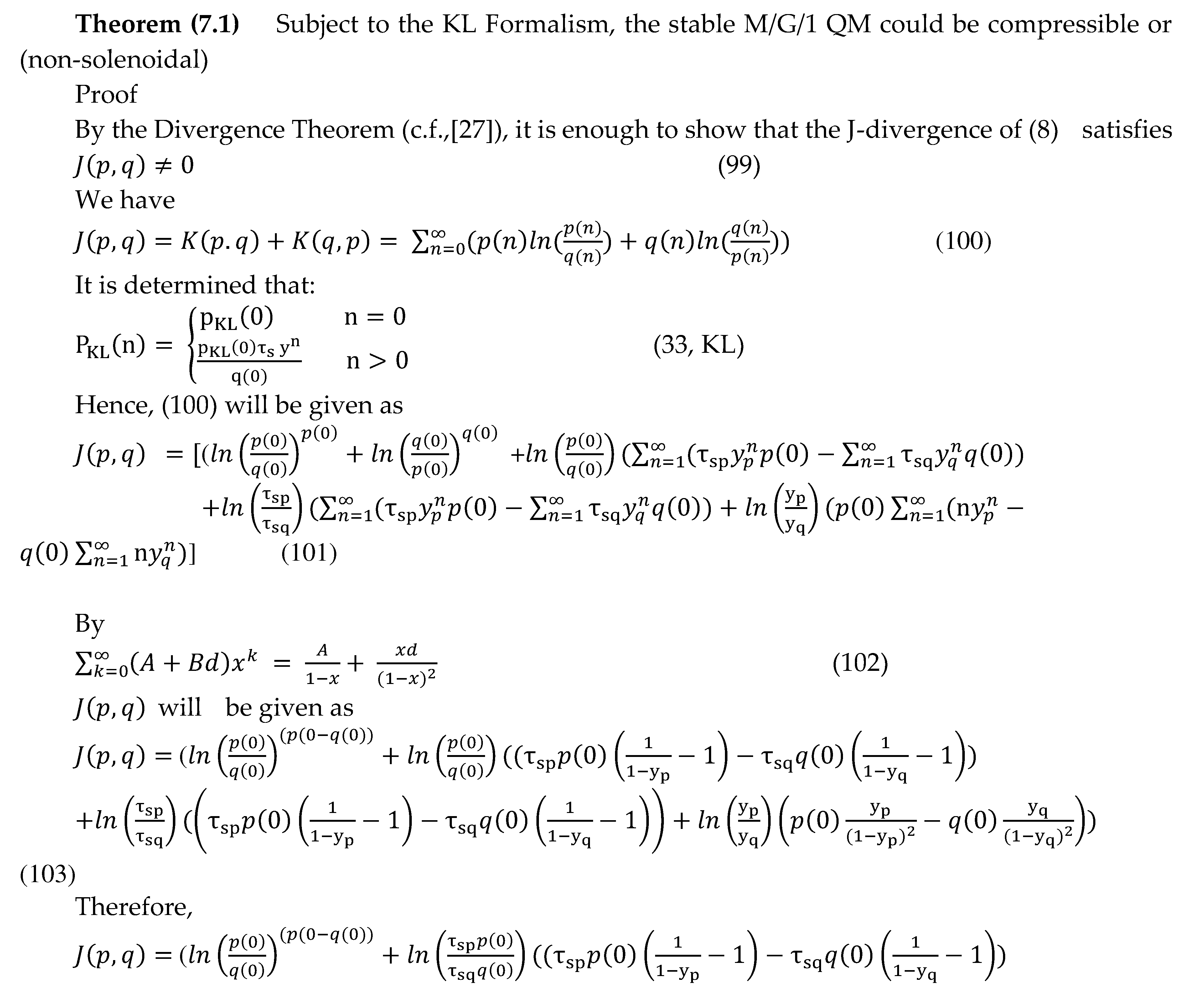
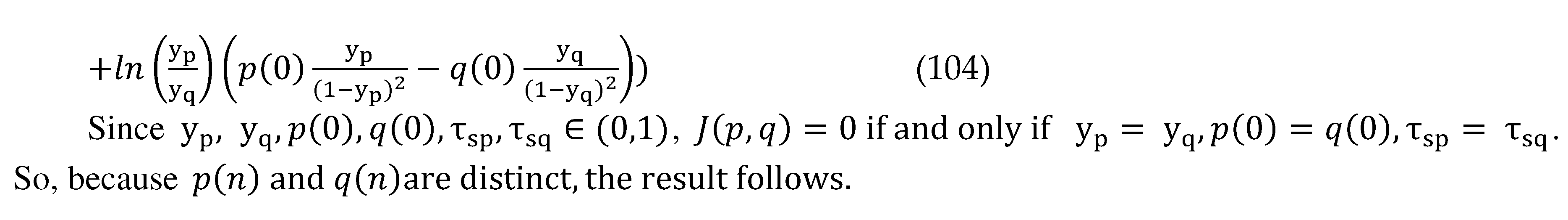
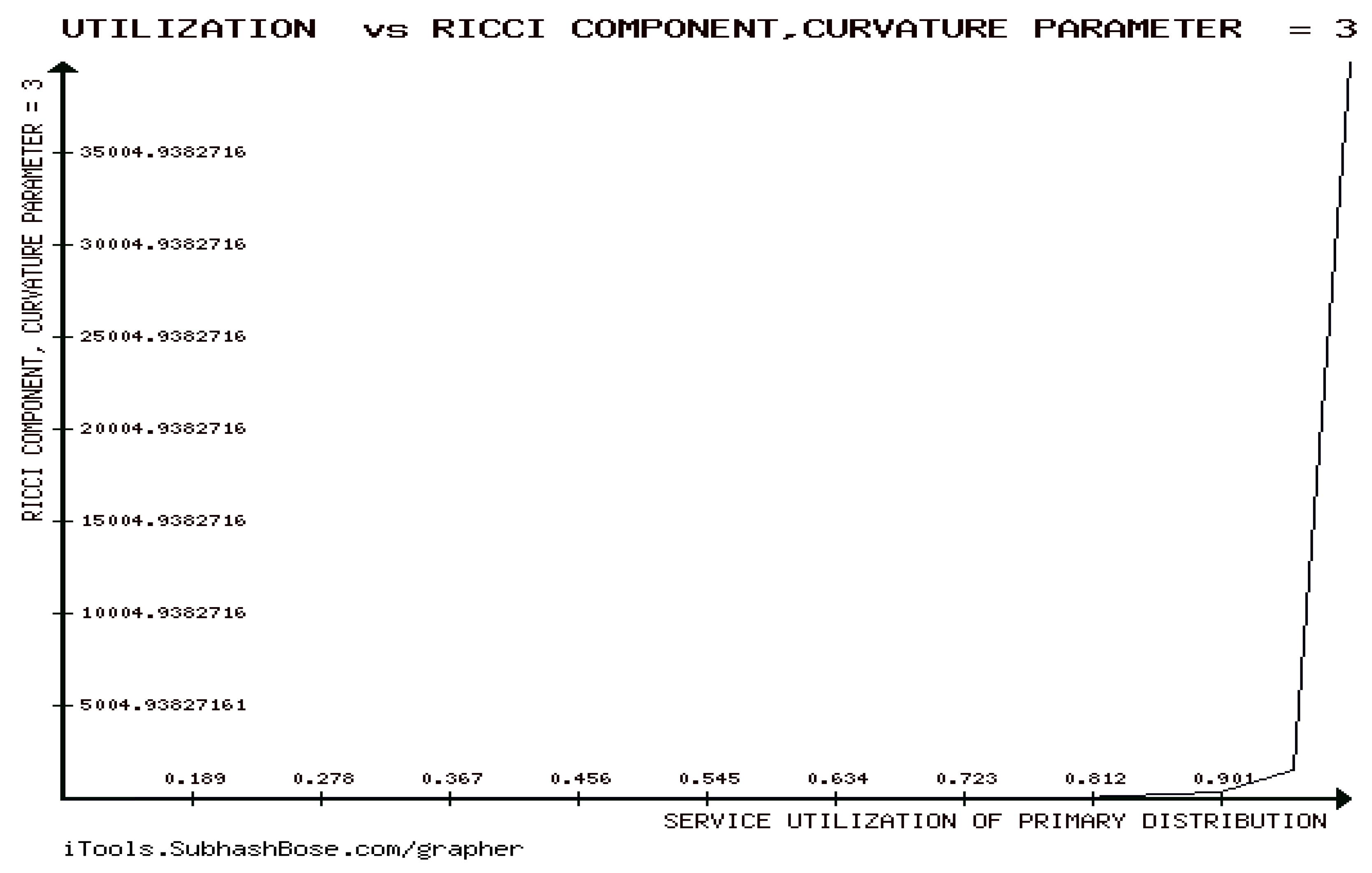
8. The Developability of the Stable M/G/1 QM, the Positivity of Its Ricci Curvature Tensor and The Threshold Theorem of Ricci Curvature Tensor


9. eA of the underlying manifold
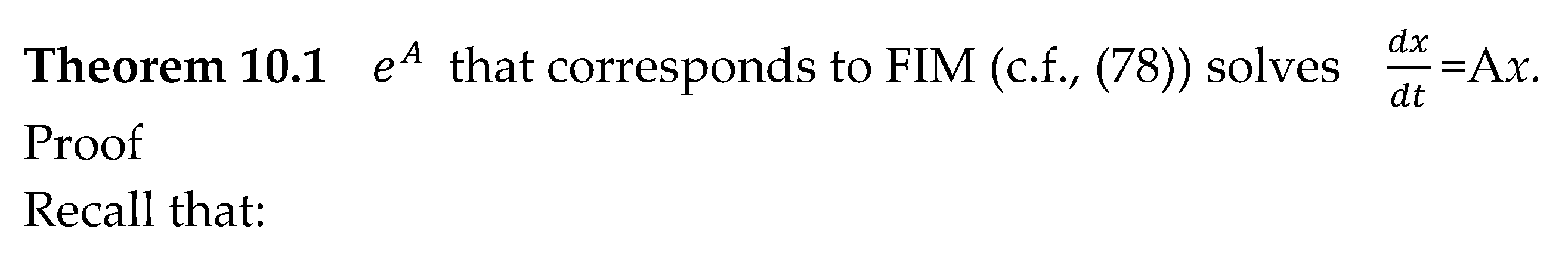

10. Scalar Curvature(Ricci Scalar), and Einestein Tensor, and the stress-energy tensor, of the KLF manifold


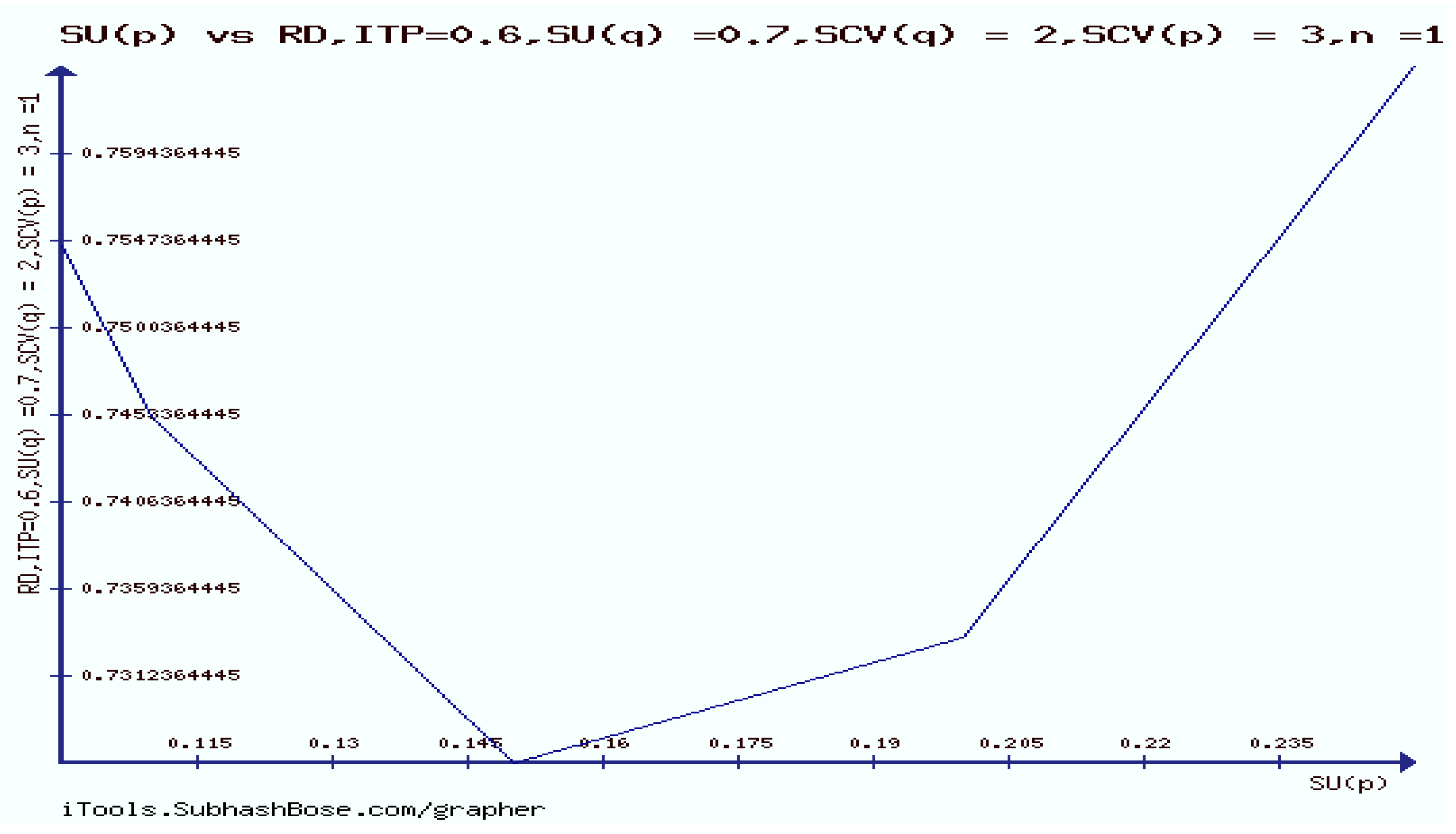
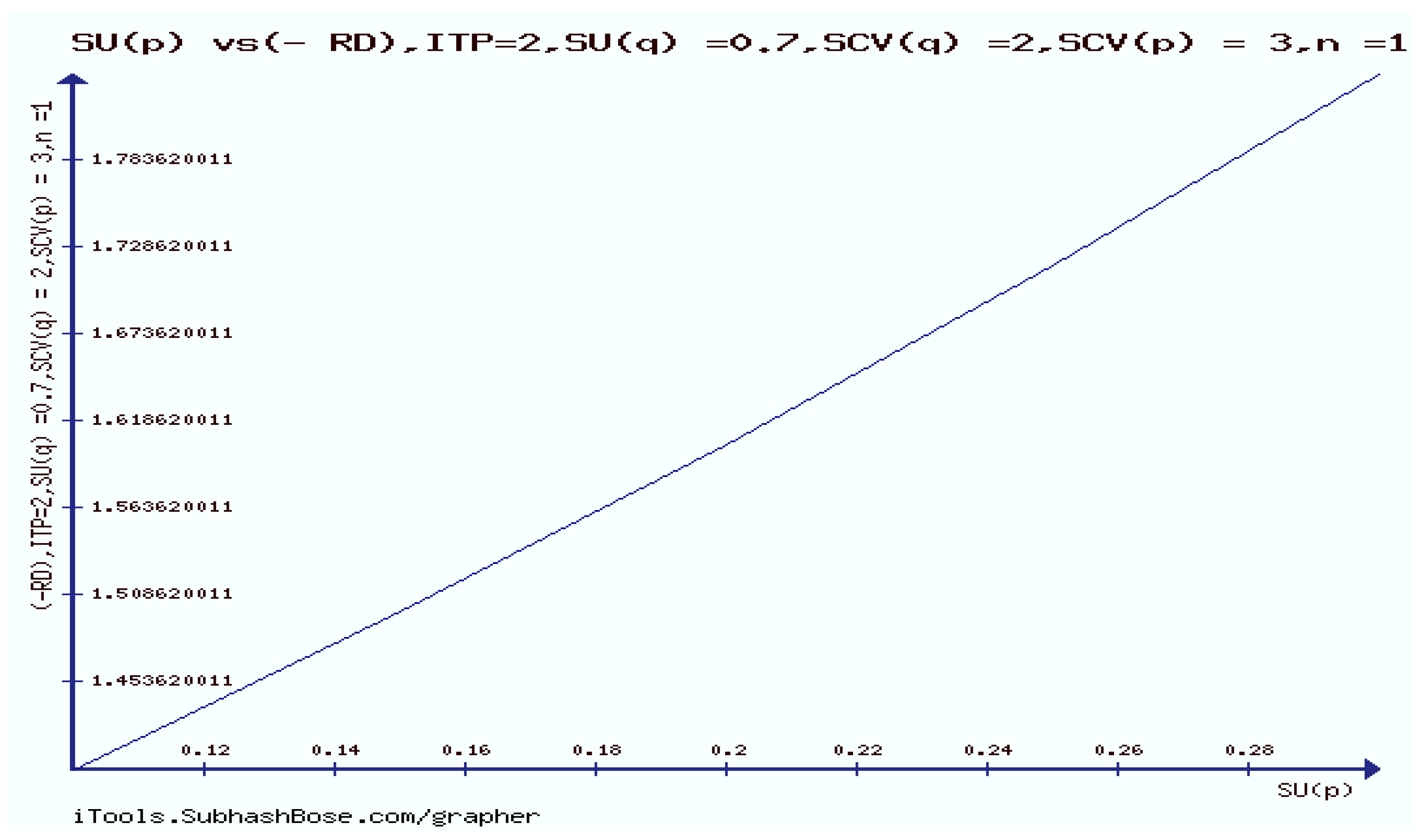
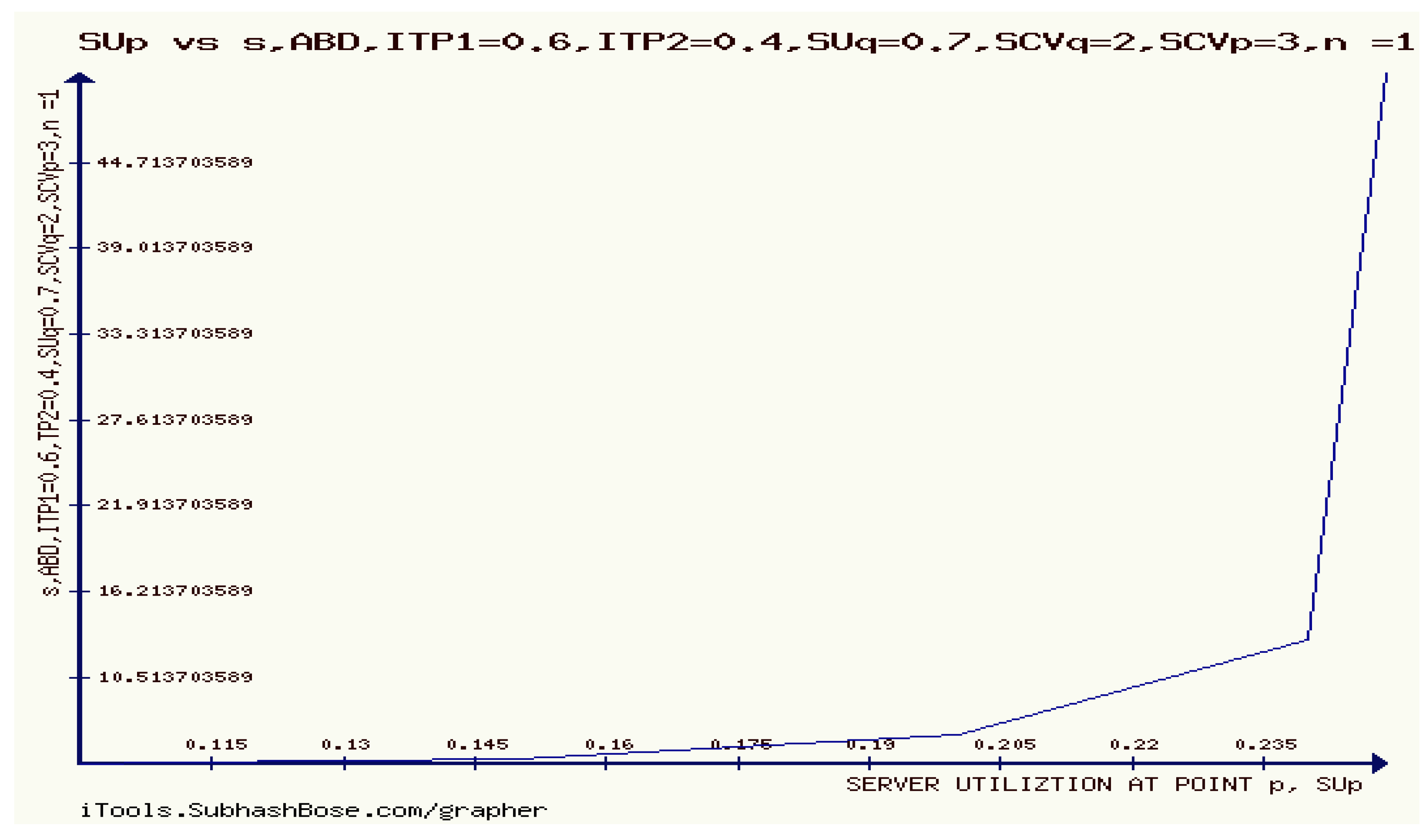
11. The Rényi divergence (RD), and the S, AB-divergence, of the KLF manifold
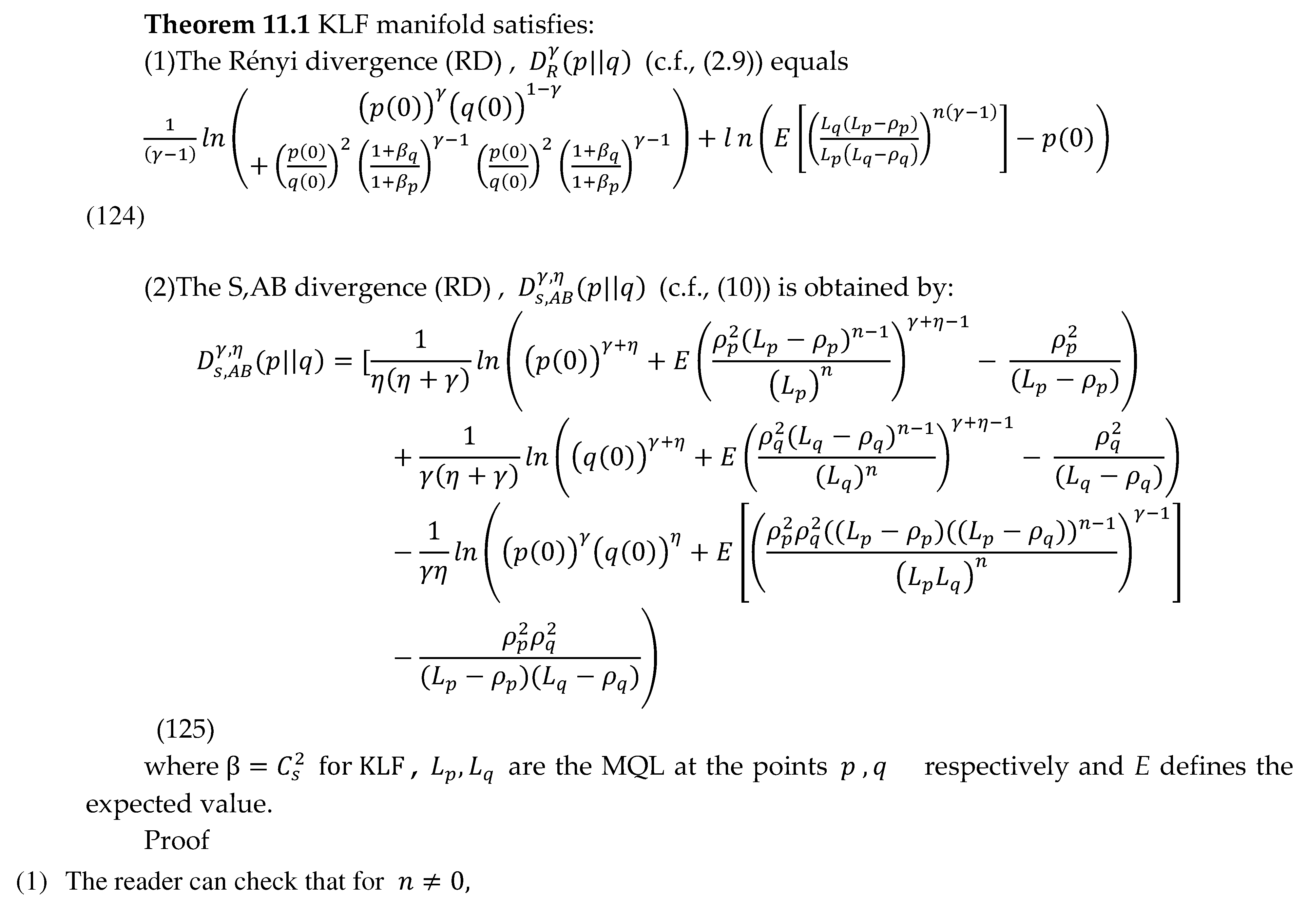

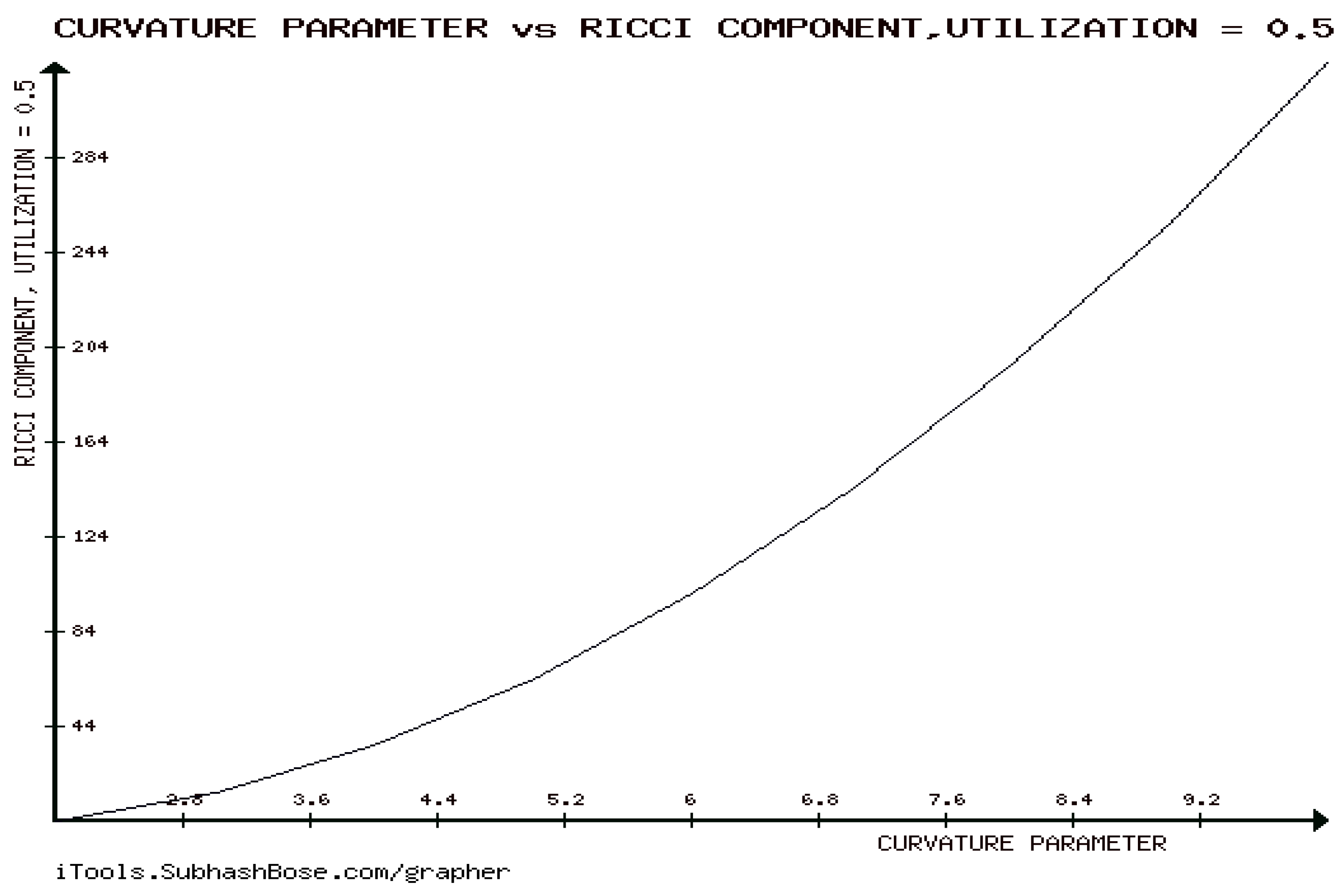
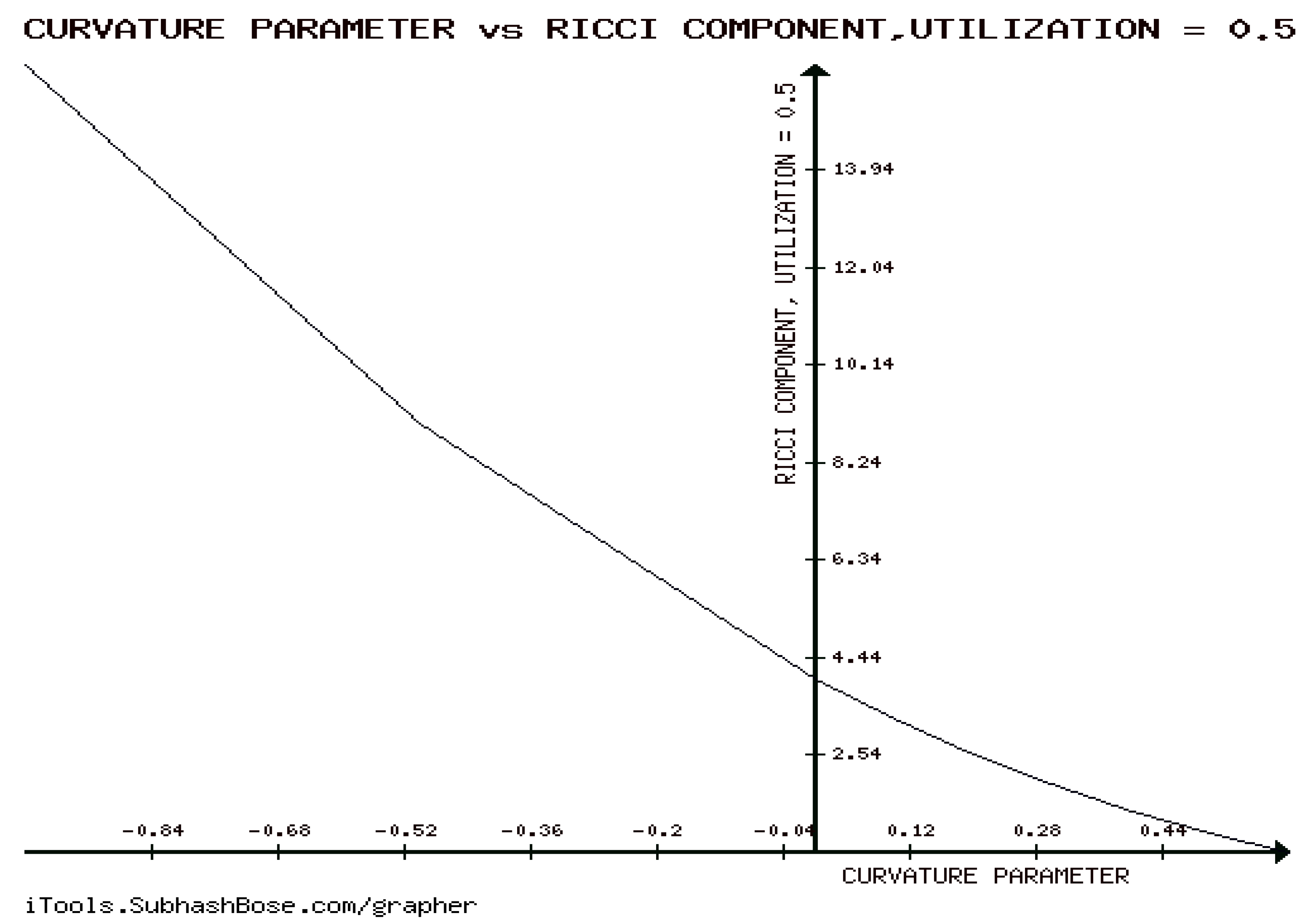
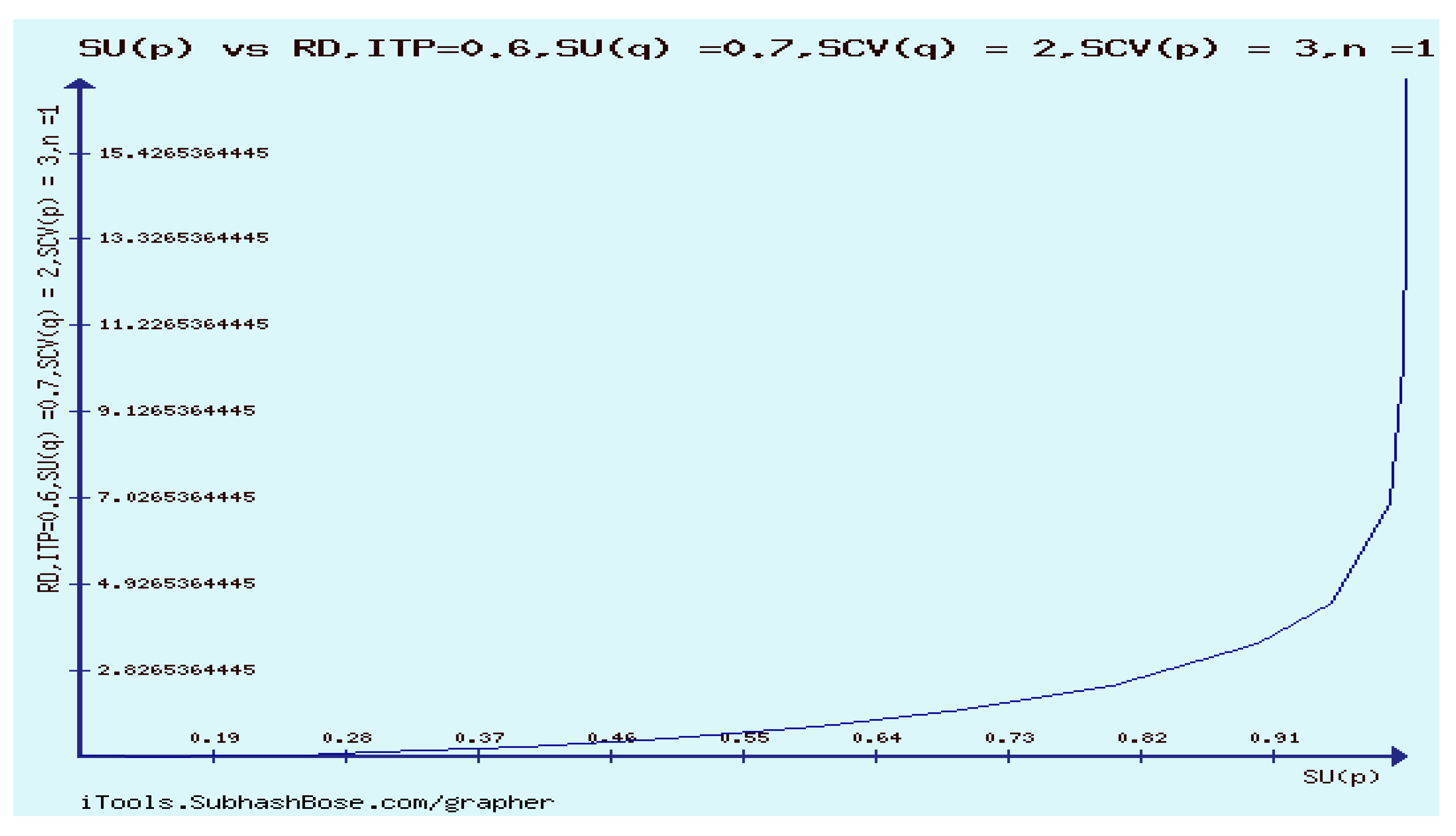
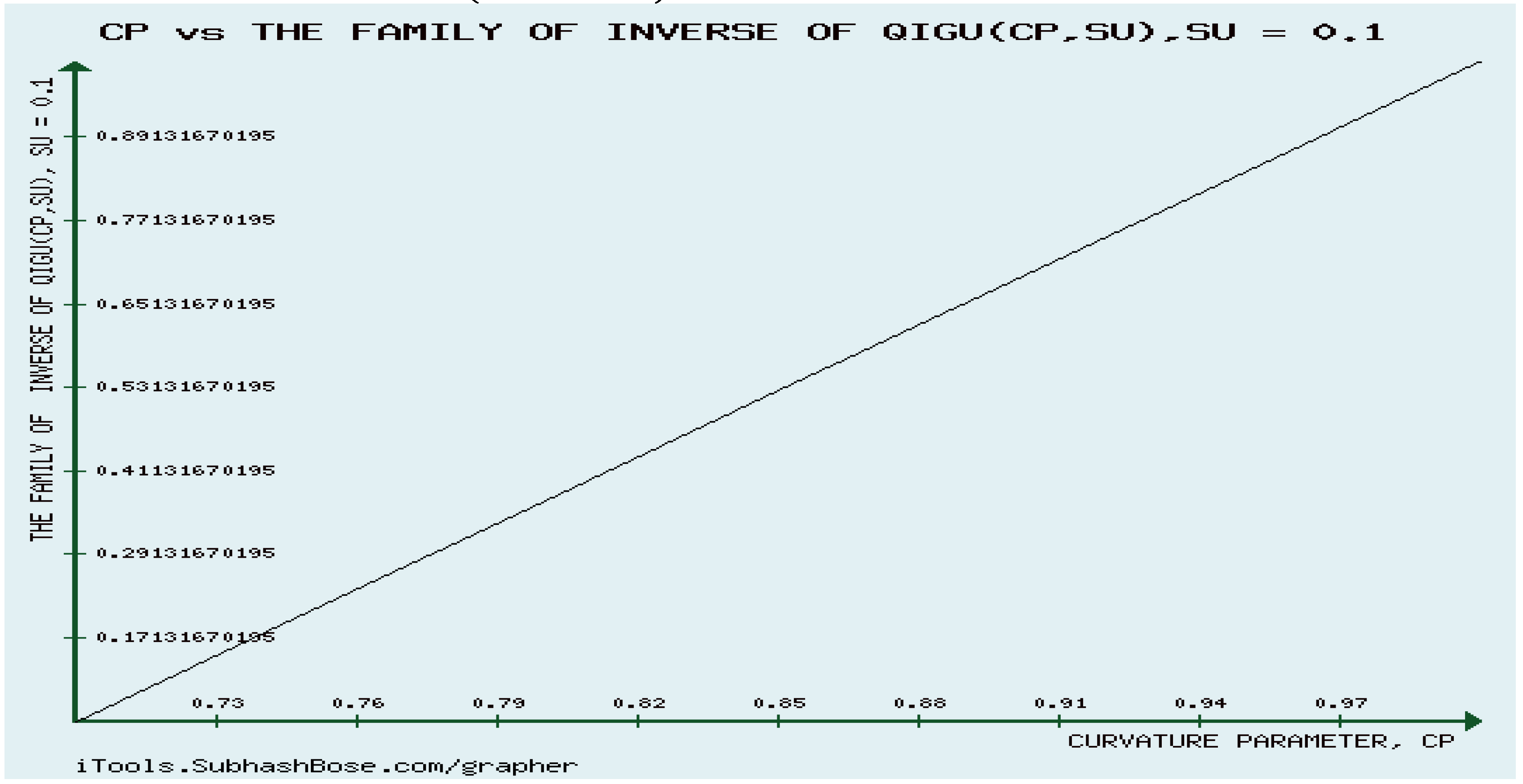
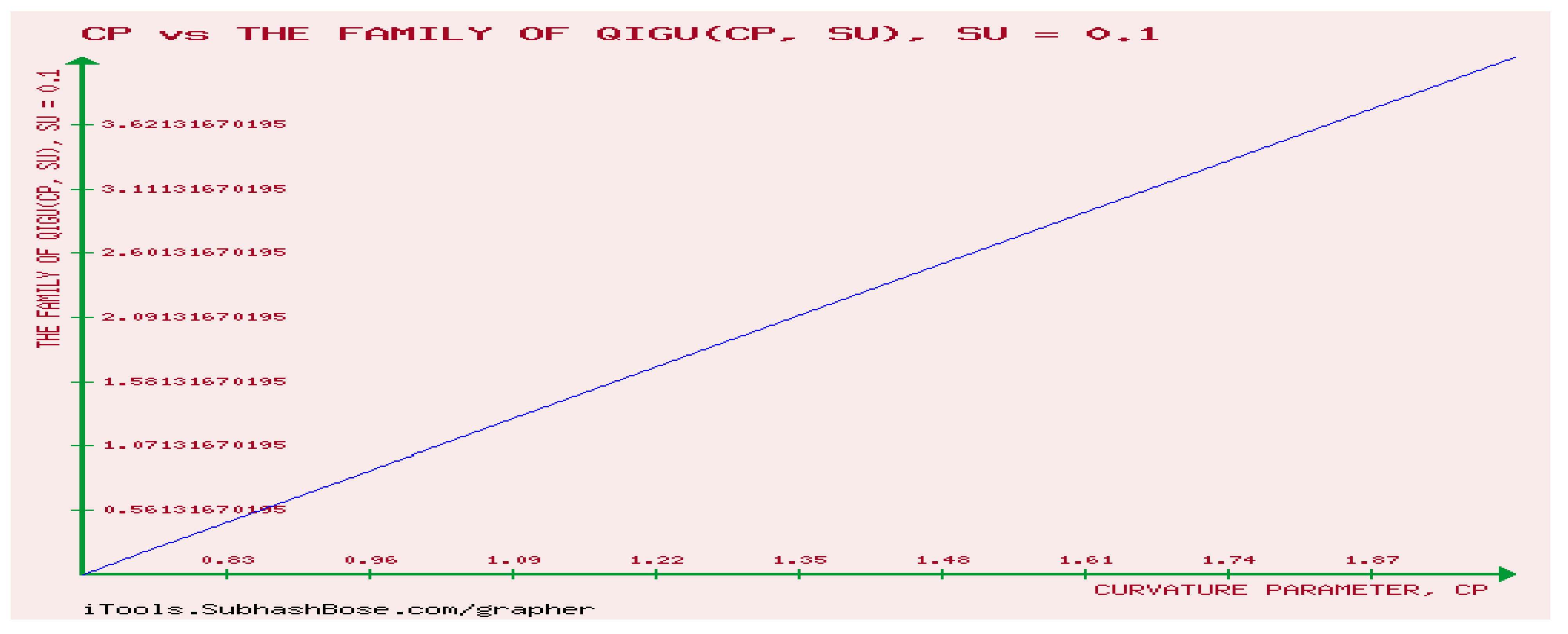
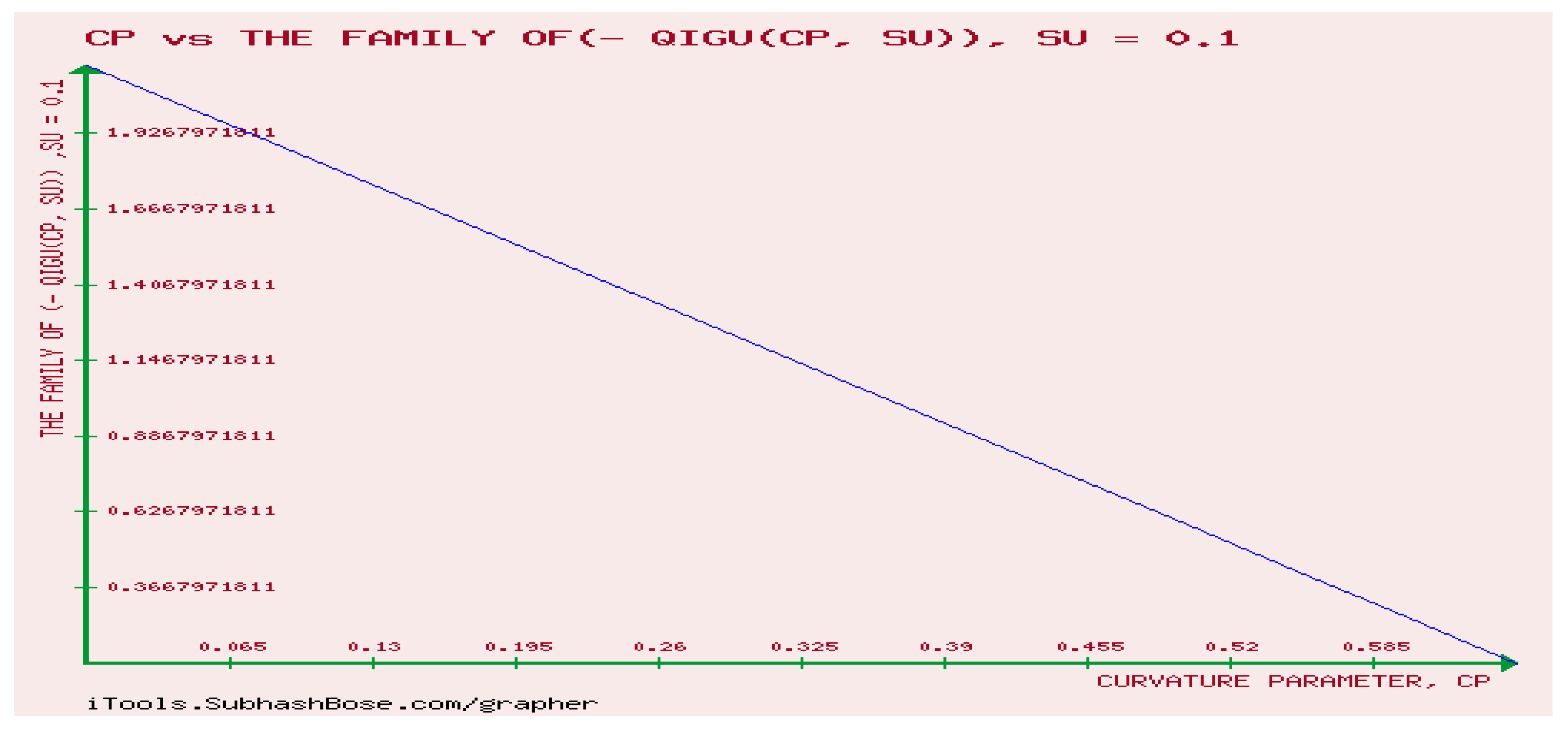
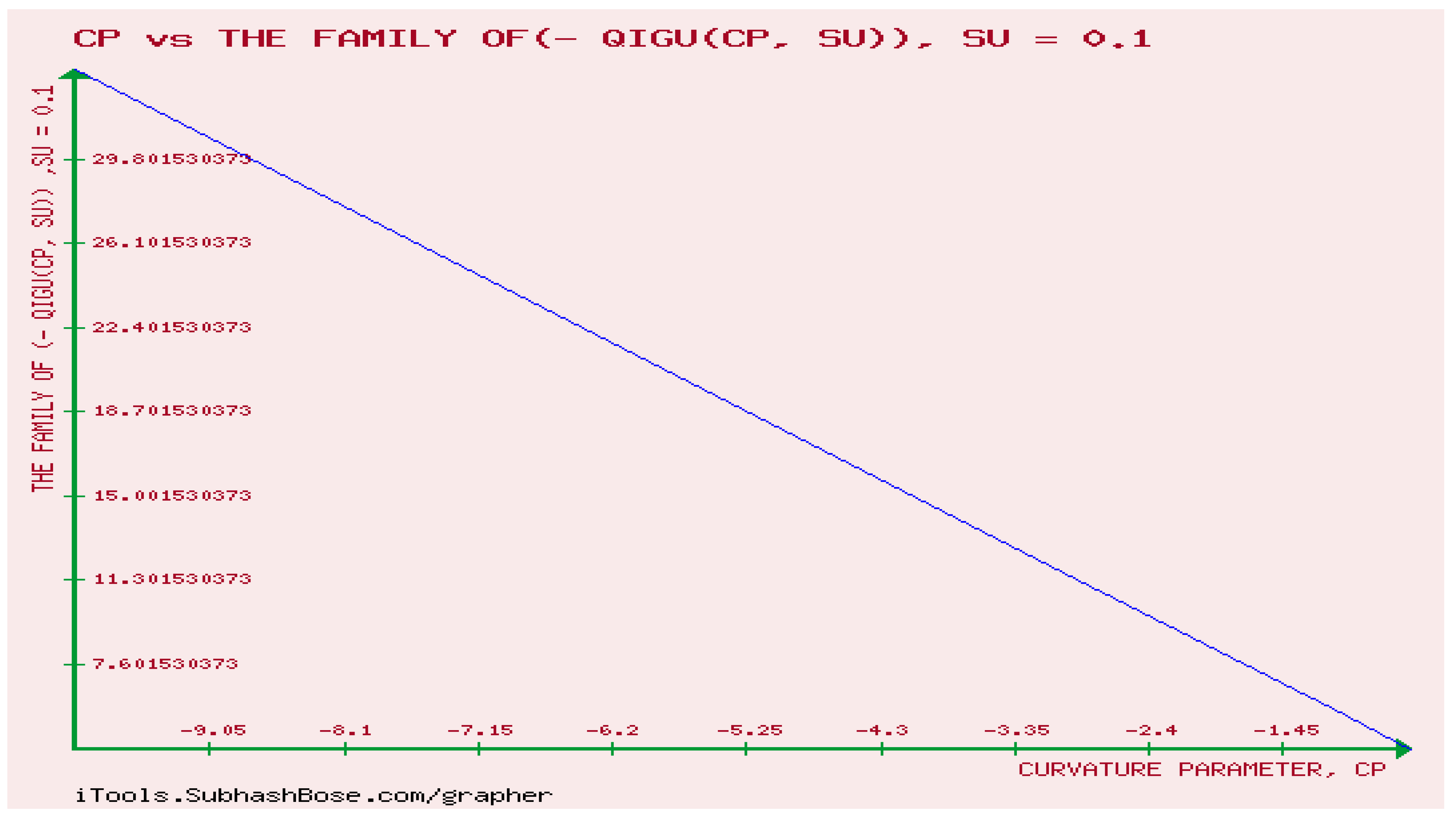
12. Numerical Experiments on The Rényi divergence (RD), and the S, AB-divergence, of the KLF of stable M/G/ 1 QM
13. Unification of Queueing Systems and KLF of stable M/G/ 1 QM
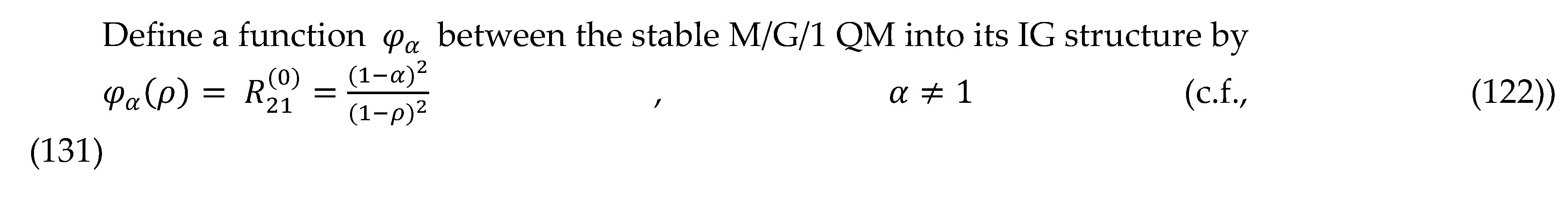

14. Statistical Queueing functionals (SQFs)of KLF of stable M/G/ 1 QM
14.1. The first representation


14.2. The second representation

14.3. The third representation

14.4. The fourth representation

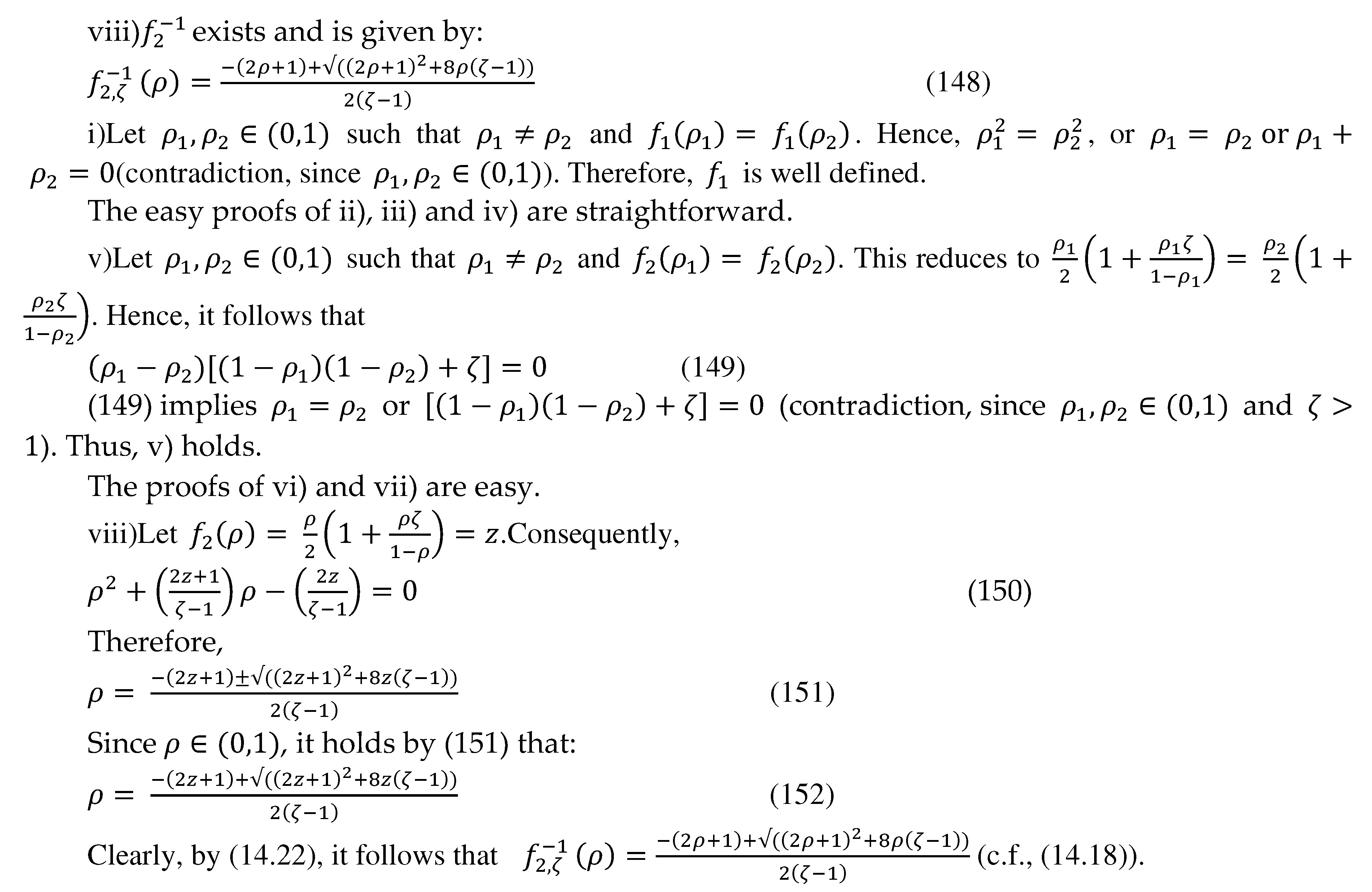
14.5. The fifth representation

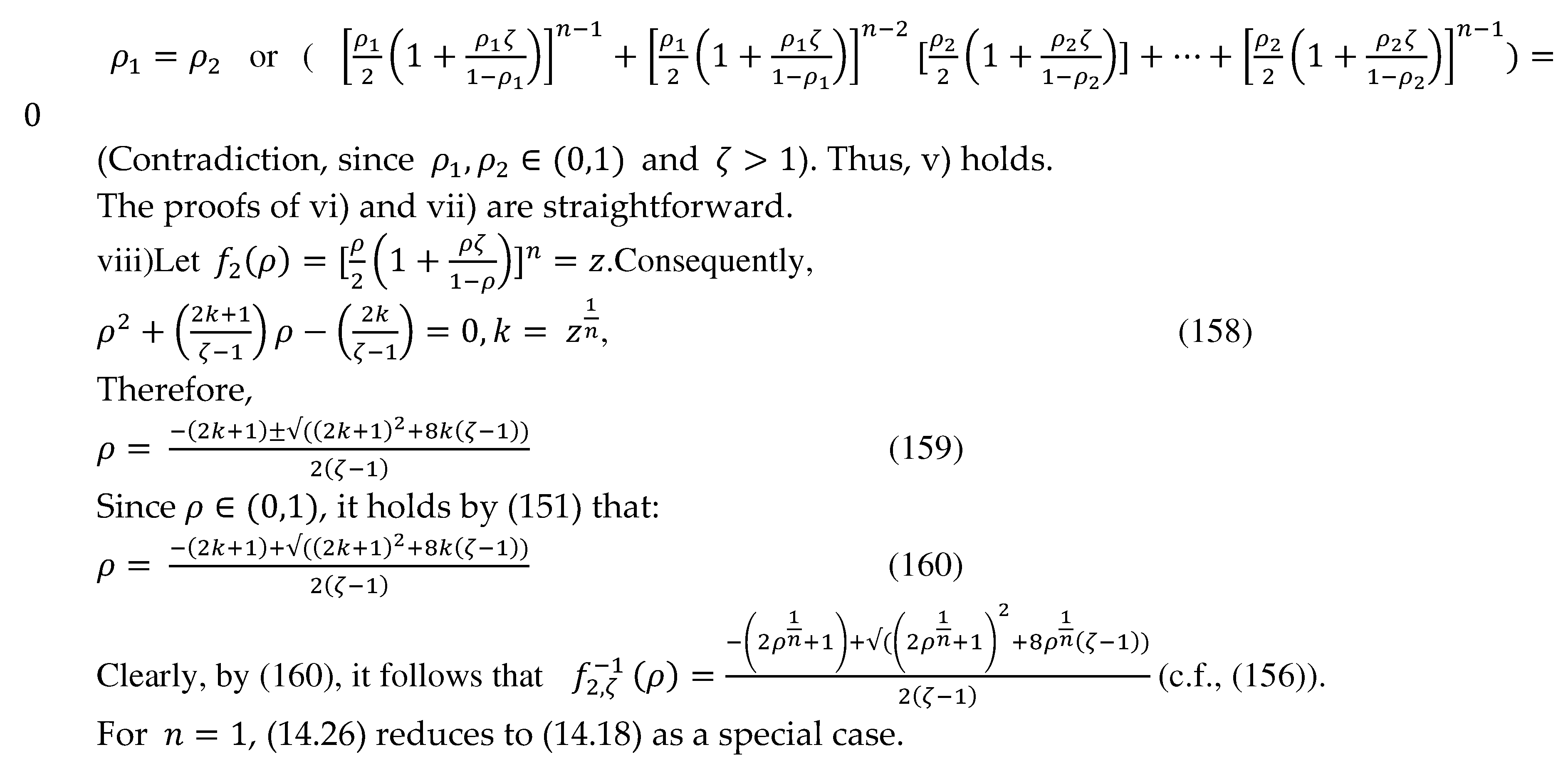
15. Closing remarks and next phase of research
Appendix A: KL Formalism vs. EME Consistency Axioms
1. Uniqueness

2. Invariance
3. System Independence

4. Subset Independence(SI)

References
- Mageed, I. A. (2023). The Entropian Threshold Theorems for the Steady State Probabilities of the Stable M/G/1 Queue with Heavy Tails with Applications of Probability Density Functions to 6G Networks. electronic Journal of Computer Science and Information Technology, 9(1), 24-30.
- Mageed, I. A. (2023, July). Rényi’s Maximum Entropy Formalism of Heavy-Tailed Queues with Hurst Exponent Heuristic Mean Queue Length Combined With Potential Applications of Hurst Exponent to Engineering. In 39th Annual UK Performance Engineering Workshop (p. 21).
- I.A. Mageed, and D.D. Kouvatsos, “Extended Properties of the Class of Rényi Generalized Entropies in the Discrete Time Domain”, 11-13 July 2011, IEEE International Conference on Computer Networks and Information Technology, Abbottabad, Pakistan, pp. 1-7. Available online: https://ieeexplore.ieee.org/document/6020894. [CrossRef]
- D.D. Kouvatsos, and I.A. Mageed (a), “Non-Extensive Maximum Entropy Formalisms and Inductive Inferences of Stable M/G/1 Queue with Heavy Tails”, in “Advanced Trends in Queueing Theory”, March 2021, Vol. 2, Vladimir Anisimov and Nikolaos Limnios (eds.), Books in ‘Mathematics and Statistics’, Sciences by ISTE & J. Wiley, London, UK.
- Mageed and Q. Zhang, "An Information Theoretic Unified Global Theory For a Stable M/G/1 Queue With Potential Maximum Entropy Applications to Energy Works," 2022 Global Energy Conference (GEC), Batman, Turkey, 2022, pp. 300-305. [CrossRef]
- Mageed, I. A. (2023, July). The Threshold Theorems of Generalized Z-entropy (GZE) fractal dimension (FD) Combined with Influential Applications of FD to Biotechnology Engineering. In 39th Annual UK Performance Engineering Workshop (p. 26).
- Kullback, S., 1958. Information Theory And Statistics, John Wiley, New York. USA.
- Mageed, I. A. (2023, July). Where the mighty trio meet: Information Theory (IT), Pathway Model Theory (PMT) and Queueing Theory (QT). In 39th Annual UK Performance Engineering Workshop (p. 8).
- Mageed, I. A., Zhang, Q., & Modu, B. (2023). The Linearity Theorem of Rényian and Tsallisian Maximum Entropy Solutions of The Heavy-Tailed Stable M/G/1 Queueing System entailed with Potential Queueing-Theoretic Applications to Cloud Computing and IoT. electronic Journal of Computer Science and Information Technology, 9(1), 15-23.
- Bhat, A. H., Siddiqui, N. A., Mageed, I. A., Alkhazaleh, S., Das, V. R., & Baig, M. A. K. (2023). Generalization of Renyi’s Entropy and its Application in Source Coding. Appl. Math, 17(5), 941-948.
- ageed, "The Consistency Axioms of The Stable M/G/1 Queue’s Z(a,b) Non-Extensive Maximum Entropy Formalism with M/G/1 Theory Applications to 6G Networks and Multimedia Applications," 2023 International Conference on Computer and Applications (ICCA), Cairo, Egypt, 2023, pp. 1-6,. [CrossRef]
- I.A.Mageed and Q. Zhang (a), “An Introductory Survey of Entropy Applications to Information Theory, Queueing Theory, Engineering, Computer Science and Statistical Mechanics”, Proceedings of 27th IEEE International Conference on Automation and Computing(ICAC), University of the West of England, Bristol, 1-3 September 2022.
- Mageed, I. A., & Zhang, Q. (2023). Threshold Theorems for the Tsallisian and Rényian (TR) Cumulative Distribution Functions (CDFs) of the Heavy-Tailed Stable M/G/1 Queue with Tsallisian and Rényian Entropic Applications to Satellite Images (SIs). electronic Journal of Computer Science and Information Technology, 9(1), 41-47.
- I.A. Mageed and Q. Zhang(b), “Inductive Inferences of Z-Entropy Formalism (ZEF) Stable M/G/1 Queue with Heavy Tails”, Proceedings of the 27th IEEE International Conference on Automation and Computing (ICAC), University of the West of England, Bristol, 1-3 September 2022.
- D.D. Kouvatsos, et I.A.Mageed(b), “Formalismes de maximum d’entropie non extensive et inférence inductive d’une file d’attente M/G/1 stable à queues Lourdes”, “Théorie des files d’attente 2”, Mars 2021, Théorie et Practique, Sous la direction de Vladimir Anisimov et Nikolaos Limnios, Mathématique, Sciences by ISTE & J. Wiley, Londres, Royaume-Uni.
- Count Baysie, May 2017. Available online: https://www.countbayesie.com/blog/2017/5/9/kullback-leibler-divergence-explained.
- E. Shannon, A mathematical theory of communication, Bell system technical journal 27 (3) (1948) 379{423 (1948).
- I.A. Mageed, and D.D. Kouvatsos, “The Impact of Information Geometry on the Analysis of the Stable M/G/1 Queue Manifold”, Major extension of paper [3], 4-6 February 2021, In Proceedings of the 10th International Conference on Operations Research and Enterprise Systems - Volume 1: ICORES, ISBN 978-989-758-485-5, pages 153-160. [CrossRef]
- Mageed IA, Yuyang Zhou, Y, Liu, Y, and Zhang Q, “ Towards a Revolutionary Info-Geometric Control Theory with Potential Applications of Fokker Planck Kolmogorov(FPK) Equation to System Control, Modelling and Simulation”,In2023 28th International Conference on Automation and Computing (ICAC) 2023, 30th Aug- Sep 1. IEEE.
- Mageed IA, Yuyang Zhou, Y, Liu, Y, and Zhang Q, “Za,b -of the Stable Five-Dimensional M/G/1 Queue Manifold Formalism’s Info- Geometric Structure with Potential Info-Geometric Applications to Human Computer Collaborations and Digital Twins”,In2023 28th International Conference on Automation and Computing (ICAC) 2023, 30th Aug- Sep 1. IEEE.
- A Mageed, I. Info-Geometric Analysis of Human-Trust Based Feedback Control (HTBFC) Five-Dimensional Manifold with HTBFC Applications to Robotics. Preprints 2024, 2024012040. [CrossRef]
- B.C. Hall, The Matrix Exponential. In: Lie Groups, Lie Algebras, and Representations. Graduate Texts in Mathematics, vol 222. Springer, Cham, 2015.
- K.Nakagawa, The geometry of M/D/1 queues and Large Deviation, International Transactions of Operational Research, Volume 9, Issue 2, 2002.
- R.Kondor, S.Trivedi, On the Generalization of Equivariance and Convolution in Neural Networks to the action of Compact Groups, Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, PMLR 80, 2018.
- A Mageed, D.I. Info- Geometric Analysis of the Stable G/G/1 Queue Manifold Dynamics With G/G/1 Queue Applications to E-health. Preprints 2024, 2024011813. [CrossRef]
- Mageed, and D.D. Kouvatsos, “Information Geometric Structure of Stable M/G/1 Queue Manifold and its Matrix Exponential”, Proceedings of the 35th UK Performance Engineering Workshop, 16 December 2019,School of Computing, University of Leeds, Edited by Karim Djemame, p.123-135. Available online: https://sites.google.com/view/ukpew2019/home.
- MIT Open Course Ware,2010. Online available at:https://ocw.mit.edu/courses/mathematics/18-02sc-multivariable-calculus-fall-2010/4.-triple-integrals-and-surface-integrals-in-3-space/part-b-flux-and-the-divergence-theorem/session-84-divergence-theorem/MIT18_02SC_MNotes_v10.1.
- A Mageed, D.I. Information Geometric Analysis of the Dynamics of M/M/∞ Transient Queue Manifold. Preprints 2024, 2024011994. [CrossRef]
- Mageed, I. A., & Zhang, K. Q. (2022). Information Geometry? Exercises de Styles. electronic Journal of Computer Science and Information Technology, 8(1), 9-14.
- Regli, JB., Silva, R, 2018, Alpha-Beta Divergence for Variational Inference - arXiv preprint arXiv:1805.01045, - arxiv.org. . arxiv:1805.01045, - arxiv.org. Available online at [1805.01045] Alpha-Beta Divergence For Variational Inference (arxiv.
- Turner, Richard E and Sahani, Maneesh, 2011, Two problems with variational expectation maximisation for time series models. Bayesian Time series models, pp. 115–138.
- A Mageed, I. Info-Geometric Analysis of the Dynamics of Parthasarathian Transient Solution of M/M/1 Queue Manifold with Info-Geometric Applications to Machine Learning. Preprints 2024, 2024012008. [CrossRef]
- Minka, T., 2005, Divergence measures and message passing. Technical report, Technical report, Microsoft Research.
- Hern´andez-Lobato, Jos´e Miguel, Li, Yingzhen, Rowland, Mark, Hern´andez-Lobato, Daniel, Bui, Thang, D., and Turner, Richard E, 2016, Black-box αdivergence minimization.
- Mageed, I. A., & Zhang, Q. (2023). Formalism of the Rényian Maximum Entropy (RMF) of the Stable M/G/1 queue with Geometric Mean (GeoM) and Shifted Geometric Mean (SGeoM) Constraints with Potential GeoM Applications to Wireless Sensor Networks (WSNs). electronic Journal of Computer Science and Information Technology, 9(1), 31-40.
- Ghosh, Abhik, Harris, Ian R, Maji, Avijit, Basu, Ayanendranath, Pardo, Leandro, et al., 2017, A generalized divergence for statistical inference. Bernoulli, 23 (4A):2746–2783.
- Basu, Ayanendranath, Harris, Ian R, Hjort, Nils L, and Jones, MC., 1998, Robust and efficient estimation by minimising a density power divergence. Biometrika, 85(3):549–558.
- Ghosh, Abhik and Basu, Ayanendranath, 2016, Robust bayes estimation using the density power divergence. Annals of the Institute of Statistical Mathematics, 68 (2):413–437.
- Cichocki, Andrzej, Cruces, Sergio, and Amari,S., 2011, Generalized alpha-beta divergences and their application to robust nonnegative matrix factorization. Entropy, 13(1):134–170.
- Cilingir, K., Manzelli, R., Kulis,B., 2020, Deep Divergence Learning. Online available at; arXiv:2005.02612v1.
- Weisstein, E. W., 2021, Well-Defined, From MathWorld- A A Wolfram Web Resource.:. Available online: https://mathworld.wolfram.com/Well-Defined.html.
- Sankaranarayanan, S., 2014, lecture 18, One-to-One and Onto functions, an online source. Available online: https://home.cs.colorado.edu/~srirams/courses/csci2824-spr14/functionTypes-18.html.
- Loveridge, L.C., 7 September 2016, Physical and Geometric interpretations of the Riemannian Tensor, Ricci Tensor and Scalar Curvature, [Online]. Available online: https://arxiv.org/pdf/gr-qc/0401098.pdf.
- A Mageed, D.I. A Theory of Everything: When Information Geometry Meets the Generalized Brownian Motion and the Einsteinian Relativity. Preprints 2024, 2024011827. [CrossRef]
- Ollivier,Y. A visual interpretation to Riemannian Curvatures and Some Discrete Generalizations. 2010 [Online] www.yann-ollivier.org/rech/publs/visualcurvature.
- Thomas, R., Kissing the curve – manifolds in many dimensions. 2015. online at:https://plus.maths.org/content/kissing-curve-manifolds-many-dimensions.
- G.Gunawardena, Matrix Algebra for Beginners, part III, Department of Systems Biology, Harvard Medical school, MA02115, USA.
- L.Snezana, Developable Surfaces: Their History and Application, Nexus Network JournalVol. 13, No. 3, 2011.
- Mageed, I. A., & Bhat, A. H. (2022). Generalized Z-Entropy (Gze) and Fractal Dimensions. Appl. Math, 16(5), 829-834.
- I. A. Mageed, "Fractal Dimension(Df) Theory of Ismail’s Second Entropy(Hiq) with Potential Fractal Applications to ChatGPT, Distributed Ledger Technologies(DLTs) and Image Processing(IP)," 2023 International Conference on Computer and Applications (ICCA), Cairo, Egypt, 2023, pp. 1-6. [CrossRef]
- Mageed, I. A. (2023, July). Rényi’s Maximum Entropy Formalism of Heavy-Tailed Queues with Hurst Exponent Heuristic Mean Queue Length Combined With Potential Applications of Hurst Exponent to Engineering. In 39th Annual UK Performance Engineering Workshop (p. 21).
- I. A. Mageed, Q. Zhang, D. D. Kouvatsos and N. Shah, "M/G/1 queue with Balking Shannonian Maximum Entropy Closed Form Expression with Some Potential Queueing Applications to Energy," 2022 Global Energy Conference (GEC), Batman, Turkey, 2022, pp. 105-110,. [CrossRef]
- Mageed, I. A., & Zhang, Q. (2023). Formalism of the Rényian Maximum Entropy (RMF) of the Stable M/G/1 queue with Geometric Mean (GeoM) and Shifted Geometric Mean (SGeoM) Constraints with Potential GeoM Applications to Wireless Sensor Networks (WSNs). electronic Journal of Computer Science and Information Technology, 9(1), 31-40.
- Mageed, I. A. (2023). The Entropian Threshold Theorems for the Steady State Probabilities of the Stable M/G/1 Queue with Heavy Tails with Applications of Probability Density Functions to 6G Networks. electronic Journal of Computer Science and Information Technology, 9(1), 24-30.
- Garett, P., Calculus Refresher, 1978-2008. Available online: http://wwwusers. math.umn.edu/~garrett/calculus/first_year/notes.pdf.
- Shibuya, N., ,Demystifying KL Divergence, 2018. Available online: https://medium.com/activatingrobotic- minds/demystifying-kl-divergence-7ebe4317ee68.
- Mageed, I. A. Cosistency Axioms of Choice for Ismail’s Entropy Formalism (IEF) Combined with Information-Theoretic (IT) Applications to advance 6G Networks. European Journal of Technique (EJT), 2023, 13(2), 207-213.
- Statistics, T. (2007). http://www.cscs.umich.edu/ Statistical mechanics for non-extensive systems and longrange interactions. notebooks. Available online: http://www.cscs.umich.edu.


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).