A Certificateless Verifiable Bilinear Pair Free Conjunctive Keyword Search Encryption Scheme for IoMT

Preprint

Article

A Certificateless Verifiable Bilinear Pair Free Conjunctive Keyword Search Encryption Scheme for IoMT

Altmetrics

Downloads

100

Views

Comments

A peer-reviewed article of this preprint also exists.

Weifeng Long^*

Jiwen Zeng,Yaying Wu,Yan Gao,Hui Zhang

Weifeng Long^*

Jiwen Zeng,Yaying Wu,Yan Gao,Hui Zhang

This version is not peer-reviewed

Submitted:

30 January 2024

Posted:

31 January 2024

You are already at the latest version

Alerts

Abstract

The Internet of Medical Things(IoMT) has powerful cloud computing ability and efficient data collection ability, which can improve the accuracy and convenience of medical work. As most communications are over open networks, data should encrypted before uploading to ensure the confidentiality of sensitive user data. Searching for encrypted data has become a challenging problem. Public key Encryption with Keyword Search (PEKS) supports the search of encrypted data and provides data privacy protection. PEKS has become a trendy technology, but PEKS still has the following problems: 1. The cloud server, as a semi-honest but curious third party, is likely to return some wrong search results to save computing and bandwidth resources. 2. The single keyword search inevitably produces irrelevant results, wasting computing and bandwidth resources. 3. Most PEKS schemes use bilinear pairing, so the computational efficiency is relatively low. 4. PEKS schemes based on Public Key Infrastructure (PKI) or identity-based cryptography inevitably face problems with certificate management or key escrow. 5. Most PEKS schemes face serious security threats such as Keyword Guessing Attacks (KGA) and File Injection Attacks (FIA). To solve the above problems, we propose a new certificateless verifiable bilinear pair-free conjunctive keyword search encryption scheme(CLVPFCKS) for IoMT using multi-signature.

Keywords:

Subject: Computer Science and Mathematics - Other

0.Introduction

Internet of Things is a network that connects any item to the Internet and uses information sensing devices such as radio frequency identification, infrared sensors, global positioning systems, and laser scanners to exchange and communicate information according to agreed protocols, achieving intelligent identification, positioning, tracking, monitoring, and management [1,2]. The Internet of Medical Things (IoMT) conveniently connects communication technology, medical staff, patients, various medical devices, and intelligent facilities, thus completing brilliant medical care and innovative item management. The Internet of Medical Things system can achieve real-time feedback on the health status of patients, improve medical response speed, provide 24-hour medical care, significantly reduce the work pressure of medical personnel, improve the accuracy and convenience of medical work, improve clinical medical quality, control costs, reduce efficiency, and save lives.

Electronic Medical Record (EMR) is crucial in IoMT systems. It electronically manages personal health status and healthcare information involving patient information collection, storage, transmission, processing, and utilization.The volume of medical data will inevitably surge as medical data is collected through various channels digitally. How to effectively store and manage the increasing number of electronic medical records has become an unprecedented challenge. In response to this problem, cloud computing can be a supplementary tool. With cloud computing, hospitals, and medical organizations outsource EMR to cloud servers for storage to save local data management and system maintenance costs while also achieving resource sharing with data recipients. Figure 1 shows a typical architecture of IoMT for medical IoT.

EHRs involve patients’ privacy, and are often encrypted to protect patients’ privacy and security. However, this causes great inconvenience for users to search for EMRs containing specific keywords. A simple solution to this problem is for users to download all ciphertext data fully, decrypt it, and further search locally. However, this leads to high computational and communication costs, making them impractical. To solve this problem, researchers have proposed searchable encryption (SE) [7] technology. It is an encryption primitive that enables users to search for keywords on ciphertext in a privacy-protected manner. In 2004, Boneh et al. [8] proposed the concept of public key encryption with keyword search (PEKS) to solve the problem of searching data encrypted using public key cryptosystems.

1. Related work

The initial PEKS scheme had many areas for improvement regarding efficiency and safety. Firstly, review the efforts made by numerous researchers in improving the efficiency of PEKS. Baek [9] pointed out the inefficiency of the PEKS [8] scheme due to the use of secure channels. To eliminate the requirement for security channels, Baek et al. proposed the concept of secure channel-free PEKS (SCF-PEKS), also known as PEKS, with designated servers/testers (dPEKS) [10]. The efficiency of SCF-PEKS is improved. However, the PEKS (SCF-PEKS) schemes are built based on PKI or identity-based cryptosystem and encounter certificate management issues and key escrow issues in system deployment. To avoid the problems associated with certificate and key escrow, Peng et al. [11] proposed a certificateless keyword searchable encryption scheme (CLKS) without secure channels. Subsequently, much literature has studied certificateless searchable encryption schemes with keywords, such as [12–15]. Most PEKS schemes focus on searching for a single keyword, but single keyword search inevitably produces many irrelevant results, leading to bandwidth and computational resource waste. Golle et al. [16] proposed the first conjunctive keyword searchable encryption scheme to avoid resource waste. After this, many searchable encryption schemes, such as [17–19], support conjunctive keyword search.

Because the computational complexity of bilinear pairs is much higher than that of scalar multiplication on elliptic curve groups, designing searchable encryption schemes without bilinear pair operations can significantly improve the scheme’s efficiency. However, currently, there are not many searchable encryption schemes without bilinear [11,15,20–27], and they are not perfect enough. In 2019, Lu et al. [28] proposed a pairing-free certificateless searchable public key encryption scheme, proving that this scheme achieves indistinguishability of keyword ciphertext against adaptive keyword selection attacks under the complexity assumption of computing Diffie-Hellman problems in a random oracle model. However, Ma et al. [30] found that the scheme proposed in [28] is not secure against user simulation attacks and offered a new cloud-based IIoT pairing-free dual server CLPEKS scheme. Recently, [25], [26], and [27] respectively proposed secure and effective pairing-free CLPEKS schemes, but they are all single keyword searches.

Cryptography researchers place a high value on security. Next, let’s look at what researchers have done to improve the security of PEKS. The existing SCF-PEKS scheme is susceptible to keyword guessing attacks (KGA) [28] and file injection attacks (FIA) [29]. To avoid keyword guessing attacks and file injection attacks, Hwang et al. [30] embedded random keys in the keyword ciphertext of the PKSE scheme and claim that the scheme can resist the above attacks. However Yang [40] proved Hwang et al.’s SCF-PEKS scheme [30] is insecure under external online keyword attacks. The main reason for being vulnerable to external online keyword attacks is that opponents can generate legitimate ciphertext for the keyword. In addition to being attacked by external attackers, the PEKS scheme is also vulnerable to attacks from internal attackers (usually referring to malicious cloud servers). Jeong et al. [41] demonstrated that the PEKS framework is susceptible to offline keyword attacks (i.e., internal offline keyword attacks) by malicious data storage servers. Later, Shao and Yang [37] proposed a universal attack demonstrating the inability to construct an SCF-PEKS scheme to defend against malicious internal servers. They pointed out that because malicious servers can run keyword encryption and testing algorithms, SCF-PEKS is inherently vulnerable to offline keyword-guessing attacks from malicious insider servers.

In addition, a cloud server is a semi-honest but curious third party that may perform only a small portion of search operations and return a small amount of incorrect search results to save its computing and bandwidth resources. Therefore, the PEKS scheme should be equipped with a verification mechanism to ensure the correctness of search results without decrypting the ciphertext. Reference [31] proposed the first symmetric and verifiable encryption scheme for keyword search. Subsequently, many literature studies have investigated verifiable keyword searchable encryption schemes [32–35]. In reference [34], a verifiable conjunctive keyword search scheme (VCKSM) over mobile e-health cloud in shared multi-owner settings was proposed, and it was secure against keyword guessing attacks under the standard model; In reference [35], an identity-based certificateless verifiable conjunctive keyword searchable encryption scheme (VMKS) was constructed, which avoids certificate management or key escrow restrictions and achieves indistinguishability of ciphertext and unforgeability of signatures.

1.1. Our contribution

We construct a certificateless verifiable bilinear pair-free conjunctive keyword search encryption scheme (CLVPFCKS), and it has been proven under the standard model that it can resist keyword guessing attacks (KGA), file injection attacks (FIA), and choose keyword attacks (CKA). Specifically, the main contributions are as follows:

Search results validation: The scheme allows the signature to be attached to each file to verify the accuracy of the search results.
No bilinear pairing: The calculation of bilinear pairing needs more time, and the scheme’s efficiency will significantly improve without bilinear pairing.
We prove that the new scheme can resist offline keyword guessing attacks, file injection attacks, and choose keyword attacks (CKA) under the standard model.

1.2. Organization

The following is the framework for the rest of this article. We summarize some related work in section 1. We discuss preparatory knowledge in section 2. We give the scheme’s construction and security analysis (including the security model and proof) in section 3. We show the details of the CLVPFCKS scheme in section 4. We discuss the security of the CLVPFCKS scheme in section 5. We analyze the effectiveness of CLVPFCKS in section 6. Finally, we summarize this paper in section 7.

2. Preliminaries

Let

q > 3

be a large prime,

F_{q}

be a prime field, and the elliptic curve E over the field

F_{q}

must satisfy the equation

y^{2} m o d q = (x^{3} + a x + b) m o d q,

Which

a, b, x, y \in F_{q}

and

(4 a^{3} + 27 b^{2}) m o d q \neq 0

. All points on E and the infinite point O form a cyclic group. ECC (elliptic curve cryptosystem) has the following difficulties:

Elliptic curve discrete logarithm problem (ECDLP): given $P, Q \in G_{q}$ , where P is the generator of the group, and Q is the element in $G_{q}$ . It is difficult to calculate the integer k such that $Q = k P$ , where $k \in Z_{q^{*}}$ .
Elliptic curve Computational Diffie-Hellman problem (ECDCHP): for any given $a, b$ in $Z_{q^{*}}$ , it is difficult to calculate $a b P$ , where $(P, a P, b P) \in G_{q}$ .
Elliptic curve Decisional Diffie-Hellman problem (ECDDDH): Given $a P, b P \in G$ where $a, b$ unknown. The DDH (Decisional Diffie-Hellman) problem is to decide whether X equals $a b P$ or a random element in G.

3. The System Model and Attack Model of CLVPFCKS

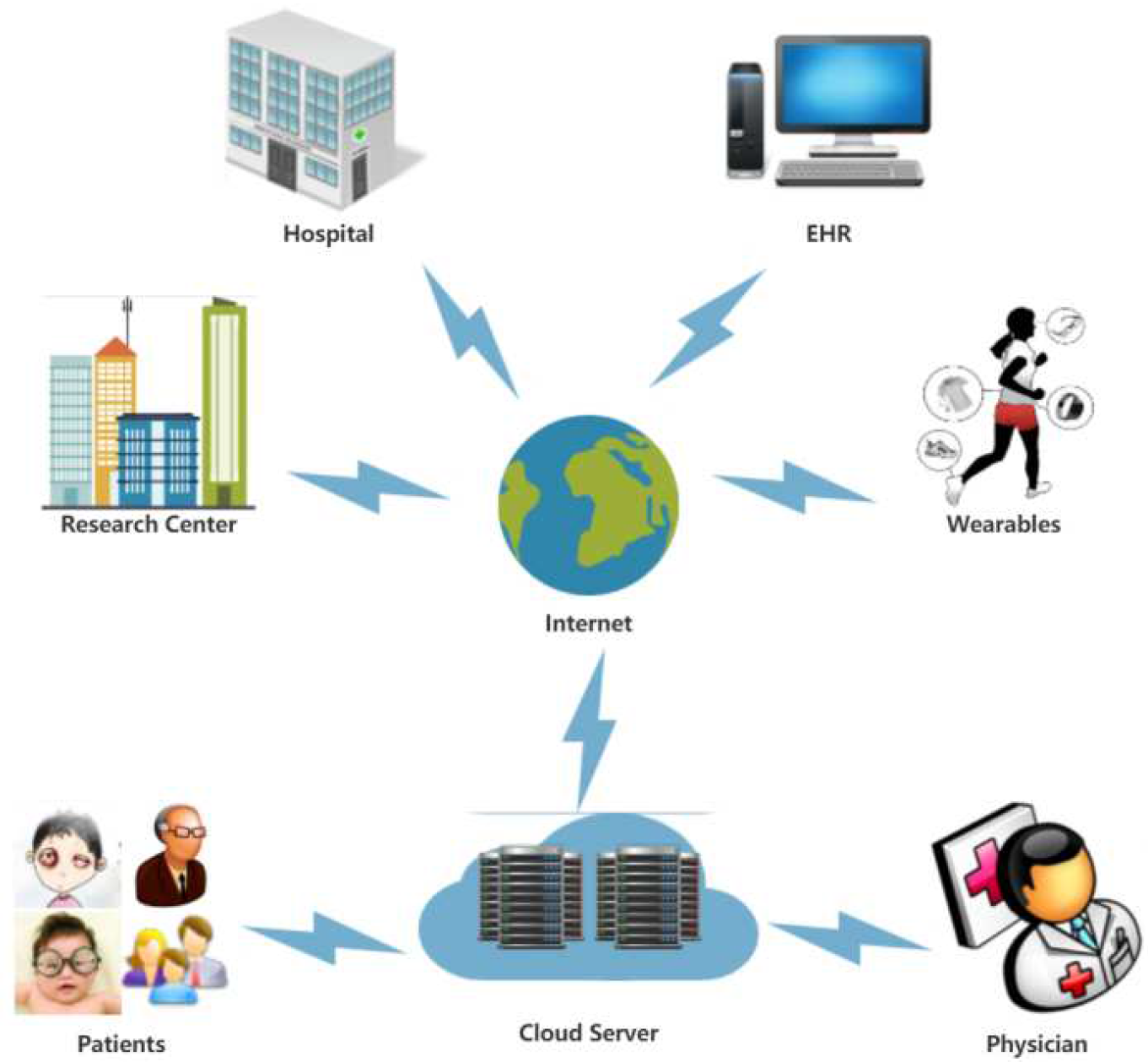
3.1. System model

There exist five entities in the proposed CLVPFCKS scheme for KGC: multiple data owners (patient and his doctors), Cloud Service Provider (CSP), data user (other authorized doctors or healthcare center), and Private Audit Server (PAS), as shown in Figure 2.

KGC: It is a trusted third party, and it is responsible for generating system parameters and producing data owners, Cloud Service Providers (CSP), and data user’s partial private keys.

Multiple data owners: In reality, the cloud search system supports more shared scenarios of multiple data owners, especially in the electronic medical system. For example, one patient and several hospital staff (i.e., surgeons, physicians, etc.) share an electronic medical record jointly, and each staff member is responsible for the content of a specific part (i.e., block). If each block is an independent record, it will inevitably encounter multiple indexes, thus greatly expanding the computational and spatial overhead. Otherwise, the many data owners must have the same random elements, which is not feasible in practice. On the contrary, the scheme designed for shared multi-owner settings only requires a single index of the entire record, saving considerable time and space.

For each EHR jointly owned by the patient and its doctor, each data owner generates a signature on this record. All data users entrust user

O_{j}

to establish an index based on the keywords of each EHR, and then the index and signature are sent to CSP. Note that the detailed algorithm for encrypting each EHR is beyond the discussion, and any public key encryption algorithm can be applied.

CSP: It is a semi-trusted entity. It has professional knowledge and can provide data storage and retrieval services for authorized cloud clients. After receiving a trapdoor from the data user, it returns the corresponding documents. But CSP is a semi-honest but curious third party, which many only perform a small part of the search operation and provide a small portion of the wrong search results to save its computing and bandwidth resources.

Data users: Data users obtain a partial private key from KGC generate the trapdoor of a keyword they wish to search, and then send it to the cloud server.

PAS: This fully trusted server is responsible for verifying the correctness of search results.

The CSP is assumed to be semi-honest but curious. It performs a fraction of search operations honestly but is interested in spying out the sensitive information valuable for the CSP. Furthermore, it may return false search results to save computing resources. On the other hand, the PAS is fully trusted and can guarantee the correctness of search results. Besides, the authorized data user can issue search queries without leaking valuable information to CSP.

3.2. Design Goals

We plan to achieve the following goals:

Multiple keyword search :The proposed scheme allows specific data users to send multiple keyword searches without increasing the trapdoor size and ciphertext search size, which improves the user search experience.

Search results validation: The scheme verifies the accuracy of search results by attaching a signature to each file.

Certificateless: The scheme is based on the certificateless cryptosystem to eliminate the limitations of certificate management and key escrow in existing searchable encryption schemes.

Pairing free: It takes more time to compute bilinear pairing. The efficiency will improve if it does not use bilinear pairing operations.

Free secure channel: It is necessary to eliminate the security channel in practice to reduce the costs of the system.

Supporting safe goals: We have demonstrated under the standard model that our scheme can resist keyword guessing attacks (KGA), file injection attacks (FIA), and chosen keyword attacks (CKA).

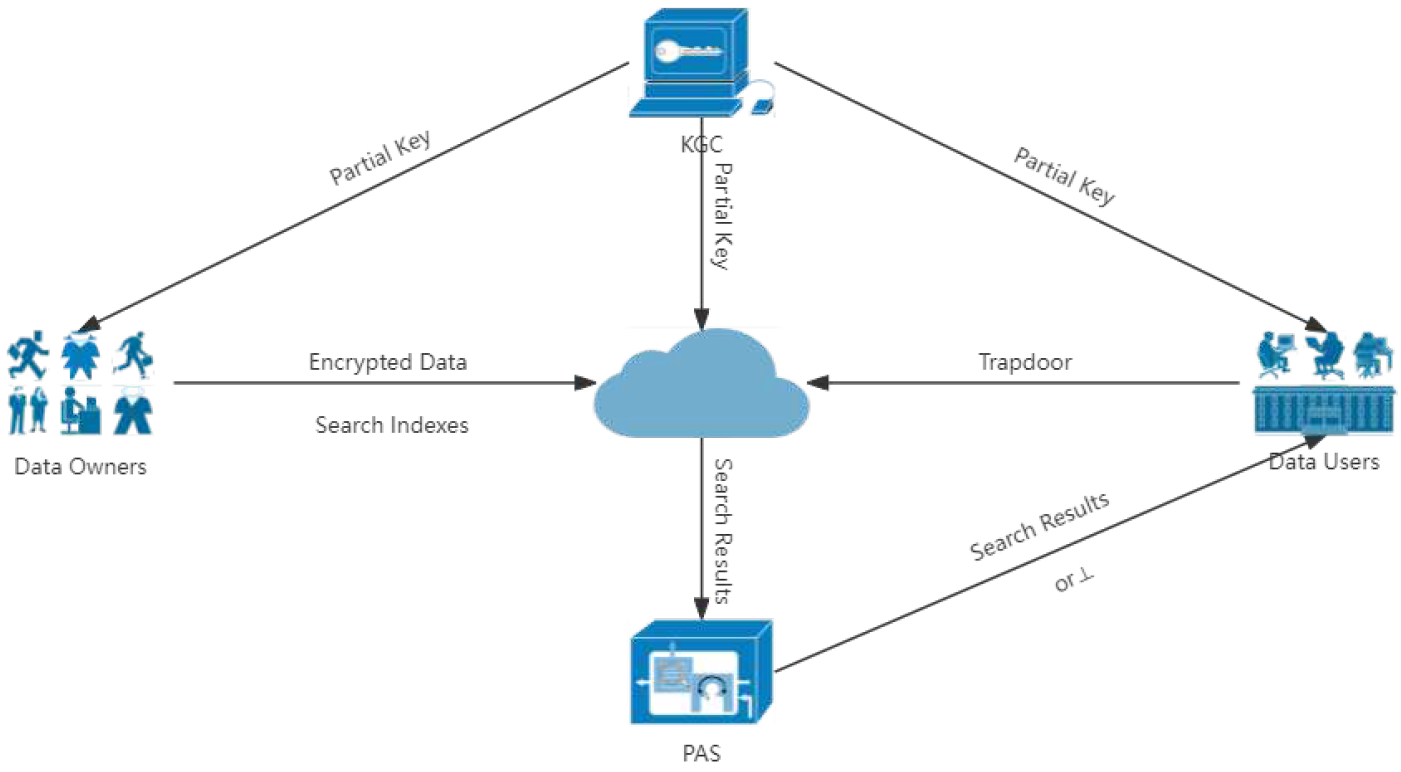
3.3. Solution Framework

Set integer k as security level,

(F, W)

as EHR file and keyword set. Definition1 (Our proposed CLVPFCKS scheme) Our scheme is a tuple of six algorithms, as follows:

(1)SetUp(

1^{k}

):Given the security parameter k, KGC outputs the public parameters

Ω

and the public/secret key pair

(P K, S K)

for the traditional public key algorithm.

(2)KeyGen

(Ω, O, U, C)

:For the data owner set O , data user set U and cloud server, KGC generates the public/secret key pairs {

P K_{i}, S K_{i}

}

(1 \leq i \leq d)

, {

P K_{u}, S K_{u}

} and {

P K_{C}, S K_{C}

}, respectively .

a)Set-Secret-Value:After inputting the public parameters

Ω

, this probabilistic algorithm outputs Data owners, Data users, and CSP’s Secret-Value.

b)Partial-Private-Key-Extract:The KGC executes this algorithm, which accepts the identity of the data owner, data user, and CSP, then uses them in combination with the master key to generate a partial private key for the data owner, data user, and CSP.

c)Set-private-Key:Set the full secret keys of the data owner, data user, and CSP.

d)Set-Public-Key:Set the full public keys of the data owner, data user, and CSP.

(3)

E n c (Ω, F, W, {I D_{i}}, I D, {S K_{i}}, {P K_{i}})

:Data owners first conduct this probabilistic algorithm to generate the ciphertext set C for the set F. Then data owners generate multiple signatures Sig and index set I for ciphertext C. Then he sends the tuple

(C, I, S i g)

to CSP.

(4)

T r a G e n (Ω, S K_{u}, W^{'})

:Given the keyword

W^{'}

, the data user runs this algorithm to output trapdoor

T_{W^{'}}

(5)

T e s t (Ω, T_{W^{'}}, I)

:Using the trapdoor

T_{W^{'}}

as an input, the CSP matches it with the index set I, then returns the relevant ciphertext

C^{'} \subseteq C

and signature

S i g^{'}

set to PAS.

(6)

V e r i f y (Ω, S i g, C_{W'}, P K_{O_{i}})

:PAS runs this algorithm by initiating interaction with CSP to check the correctness of the search result

C_{W'}

. If

C_{W'}

passes the result validation, PAS will return it to the data user. Otherwise, it will abort the algorithm.

3.4. Security Model

To protect the security and privacy of the scheme, we must satisfy the following requirements:

(1)Keyword ciphertext indistinguishability: When encrypted data is stored in CSP, it will attach the corresponding keywords

{w_{i 1}, w_{i 2}, \dots, w_{i m}}

. Even if keyword ciphertext is captured during transmission, no adversary can obtain keywords embedded in the ciphertext.

(2)Indistinguishability of trapdoor:Any adversary shall not obtain any information from the trapdoor.

Our scheme proves that trapdoors are indistinguishable and the keywords ciphertext are indistinguishable in the standard model. They are defined as follows:

ciphertext indistinguishability against chosen keyword ciphertext attack: We will define the definition of ciphertext indistinguishability against chosen keyword and ciphertext attack (CKCA-CIND). There are two types of adversaries: external adversaries (receivers) and internal adversaries (servers).

A_{1}

and

A_{2}

represent these two adversaries, and their attack methods are as follows:

$A_{1}$ :

A_{1}

doesn’t know the master key, but

A_{1}

can replace any user’s public key.

$A_{2}$ :

A_{2}

knows the master key, but

A_{2}

cannot replace any user’s public key.

Call them the adversary of type-1 and the adversary of type-2. There are two games to discuss the security of CKCA-CIND.

Game I.

A_{1}

simulates malicious users and B is the challenger. B and

A_{1}

play this game together.

Setup:B running SetUp(

1^{k}

) program to get public parameters

Ω

and the public/secret key pair

(P K, S K)

.B sends the public key

P K

A_{1}

and keeps the master private key

S K

. Then B sets the key pair of

O_{i}

(i \in {1, 2, \dots, d})

and CSP, i.e.,

(P K_{O_{i}}, S K_{O_{i}})

(i \in {1, 2, \dots, d})

and

(P K_{c}, S K_{c})

.B sends the public key

P K_{O_{i}}

(i \in {1, 2, \dots, d})

and

P K_{c}

A_{1}

, while

S K_{O_{i}}

and

S K_{c}

are unknown to

A_{1}

Phase 1.

A_{1}

executes the User-Public-Key query using date user’s identity

I D_{u}

first and then executes other queries using the identity

I D_{u}

. Set up lists to store the above queries and answers. All lists are initially empty.

A_{1}

makes the queries to the challenger B as following:

(1)User-Public-key query:When

A_{1}

inputs the identity

I D_{u}

, B outputs the user’s public key

P K_{u}

(2)Replace - Public - Key query:

A_{1}

inputs

(I D_{j}, P K_{j}^{'})

,B replaces

P K_{j}

with

P K_{j}^{'}

(3)Secret-Value query:When

A_{1}

inputs the identity

I D_{j}

, B returns the secret value corresponding to the

I D_{j}

. If

P K_{j}

is replaced, B refuses to answer.

(4)Partial-Private-Key-Extract query:When

A_{1}

enters the

I D_{j}

, if

I D_{j} = I D_{u}^{◊}

(

I D_{u}^{◊}

is the challenge identity), B fails and stops. Otherwise, B returns the corresponding Partial Private Key.

(5)Keyword Ciphertext Query:

A_{1}

asks B for the ciphertext of any keyword W it cares about. B runs the

E n c (Ω, F, W, {I D_{i}}, I D, {S K_{i}}, {P K_{i}})

algorithm to answer W’s ciphertext

C_{W}

(6)Keyword Trapdoor Query:

A_{1}

sends a keyword

W^{'}

to B. B runs the

T r a p G e n (Ω, S K_{u}, W^{'})

algorithm to answer

W^{'}

’s trapdoor

T_{W^{'}}

(7)Test Query:

A_{1}

selects and sends the ciphertext

C_{W}

and trapdoor

T_{W^{'}}

to B. B executes the

T e s t (Ω, T_{W^{'}}, I)

algorithm to return the test result of whether the ciphertext and the trapdoor match.

Challenge:

A_{1}

submits a tuple

(W_{0}, W_{1}, {I D_{U}}^{*}, {P K_{U}}^{*})

to B, where

W_{0}

and

W_{1}

are challenging keywords not asked in the previous trapdoor and ciphertext query. If

I D_{u}^{*} \neq I D_{u}^{◊}

, B aborts. Otherwise, B picks

ξ \in {0, 1}

randomly computes keyword trapdoor

C_{W_{ξ}}

, and returns the challenge ciphertexts

C_{W_{ξ}}

A_{1}

Phase 2.

A_{1}

can perform many queries like Phase 1, but

A_{1}

cannot query the ciphertext and trapdoor of

W_{0}

and

W_{1}

Guess:

A_{1}

outputs

ξ^{'} \in {0, 1}

A_{1}

wins if

ξ^{'} = ξ

. Otherwise, it fails.

Game 2.

A_{2}

simulates the malicious server, and B is a challenger. B and

A_{2}

play this game together.

Setup:It differs from Setup of Game 1 only in the following steps. B send spublic key

P K_{O_{i}}

(i \in {1, 2, \dots, d})

and public/secret key pair

(P K, S K)

A_{2}

, and

S K_{O_{i}}

are unknown to

A_{2}

Phase 1.The steps are the same as phase 1 of Game 1, except for Secret Value and Partial Key query. The changes in them are as follows:

Secret-Value query :When

A_{2}

enters the

I D_{j}

, if

I D_{j} = I D_{u}^{◊}

(

I D_{u}^{◊}

is the challenge identity), B fails and stops. Otherwise, B returns the secret value corresponding to

I D_{j}

Partial-Private-Key-Extract query: When

A_{2}

inputs the identity

I D_{j}

, B returns the partial private key corresponding to the

I D_{j}

.If

P K_{j}

is replaced, B refuses to answer.

Phase 2 :Same as Phase 2 of Game 1.

Definition 1(Security of CKCA-CIND) : If the probability that any adversary will win the above two games in polynomial time is negligible, then we state that the CLVPFCKS scheme is CKCA-CIND safe.

Indistinguishability of trapdoor (IND-KGA):No adversary can obtain valuable information from trapdoors. A sufficient condition for ensuring security against offline key-guessing attacks is that the trapdoors are indistinguishable. In the following, we define the concept of indiscernibility of CLVPFCKS against keyword guessing attacks. Specifically, IND-KGA ensures that adversaries (servers or the receivers) cannot observe the connection between the trapdoors and any keywords.

Game 3.

A_{1}

simulates malicious users and B is the challenger. B and

A_{1}

play this game together.

Setup:

A_{1}

B running SetUp(

1^{k}

) program to get public parameters

Ω

and the public/secret key pair

(P K, S K)

. B sends the public key PK to

A_{1}

and keeps the master private key SK. Then B sets the key pair of date user and CSP, i.e.,

(P K_{u}, S K_{u})

and

(P K_{c}, S K_{c})

.The challenger B sends the public key

P K_{u}

and

P K_{c}

A_{1}

, while

S K_{u}

and

S K_{c}

are unknown to

A_{1}

Phase 1.

A_{1}

executes the User-Public-Key query using data owner’s identity

I D_{i}

first and then executes other queries using the identity

I D_{i}

. Set up lists to store the above queries and answers. All lists are initially empty.

A_{1}

makes the queries to the challenger B as following:

(1)User-Public-key query:When

A_{1}

inputs the identity

I D_{j}

, B outputs the user’s public key

P K_{j}

(2)Replace-Public-Key query: same as that in Game 1.

(3)Secret-Value query:same as that in Game 1.

(4)Partial-Private-Key-Extract query:When

A_{1}

enters the

I D_{j}

, if

I D_{j} = I D_{i}^{◊}

(

I D_{i}^{◊}

is the challenge identity), B fails and stops. Otherwise, B returns the corresponding Partial Private Key.

(5)Keyword Ciphertext Query:same as that in Game 1.

(6)Keyword Trapdoor Query:same as that in Game 1.

(7)Test Query: same as that in Game 1.

Challenge :

A_{1}

submits a tuple

(W_{0}, W_{1}, {I D_{i}}^{*}, {P K_{i}}^{*})

to B, where

W_{0}

and

W_{1}

are challenging keywords not asked in the previous trapdoor and ciphertext query. If

I D_{i}^{◊} \notin {I {D_{i}}^{*}}

(i \in {1, 2, \dots d})

, B aborts. Otherwise, B picks

ξ \in {0, 1}

randomly computes keyword trapdoor

T_{W_{ξ}}

, and returns the challenge ciphertexts

T_{W_{ξ}}

to the adversary

A_{1}

Phase 2.

A_{1}

can perform many queries like Phase 1, but

A_{1}

cannot query the ciphertext and trapdoor of

W_{0}

and

W_{1}

Guess:

A_{1}

outputs

ξ^{'} \in {0, 1}

. Adversary

A_{1}

wins if

ξ^{'} = ξ

. Otherwise, it fails.

Game 4.

A_{2}

simulates the malicious server, and B is a challenger. B and

A_{2}

play this game together.

Setup:It differs from Setup of Game 3 only in the following steps. B send spublic key

P K_{u}

and public/secret key pair

(P K, S K)

A_{2}

, and

S K_{u}

are unknown to

A_{2}

Phase 1. The steps are the same as phase 1 of Game 3, except for Secret Value and Partial Key query. The changes in them are as follows:

Secret-Value query: When

A_{2}

enters the

I D_{j}

, if

I D_{j} = I D_{i}^{◊}

(

I D_{i}^{◊}

is the challenge identity), B fails and stops. Otherwise, B returns the secret value corresponding to

I D_{j}

Partial-Private-Key-Extract query: same as that in Game 2.

Phase 2. Same as Phase 2 of Game 3.

Definition 2 (Security of IND-KGA):If the probability that any adversary will win the above two games in polynomial time is negligible, then we state that the CLVPFCKS scheme is IND-KGA safe.

4. the proposed CLVPFCKS

To better understand about our proposed scheme, we explain the pre-defined notations used throughout this paper in Table 1.

Table 1. Notation descriptions

Notations	DESCRIPTIONS
x	Master key
$P_{p u b}$	system public key
$O = {O_{1}, O_{2}, \dots, O_{d}}$	Data Owner Collection
$I D_{i} \in {0, 1}^{*} (1 \leq i \leq d)$	identity set for data owner $O_{i}$
$I D_{C}$	identity set for CSP
$I D_{u}$	identity set for data user
$(P K_{C}, S K_{C})$	Public/secret key pair for CSP
$(P K_{O_{i}}, S K_{O_{i}})$	Public/secret key pair for data owner $O_{i}$
$(P K_{u}, S K_{u})$	Public/secret key pair for data user
$F = {f_{1}, f_{2}, \dots, f_{n}}$	File set F
$C = {c_{1}, c_{2}, \dots, c_{n}}$	ciphertext set
$I D = {i d_{1}, i d_{2}, \dots, i d_{n}}$	identity set for F
$W_{i} = {w_{i 1}, w_{i 2}, \dots, w_{i m}}$	Collection of keywords
$s i g_{i, t}$	Data owner $O_{i} ’$ signature for $c_{t}$
$s i g_{t}$	Data owners’ multi-signatures for $c_{t}$
$S i g = {s i g_{1}, s i g_{2}, \dots, s i g_{n}}$	F’s multi-signature
$I_{i}$	Index of $f_{i}$
$I = {I_{1}, I_{2}, \dots, I_{n}}$	Index set for F
$W^{'} = {w_{1}^{'}, w_{2}^{'}, \dots, w_{l}^{'}}$	Search keyword set
$T_{W^{'}}$	The trapdoor of $W^{'}$
$C^{'} = {c_{k_{1}}, c_{k_{2}}, \dots, c_{k_{s}}}$	Search results
$I D^{'} = {i d_{k_{1}}, i d_{k_{2}}, \dots, i d_{k_{s}}}$	Identity set for $C^{'}$

4.1. Specific construction of CLVPFCKS

This system uses traditional public key encryption algorithm to encrypt files, which we will not discuss. Therefore, the following algorithms focus on indexing and signature.

SetUp $(1^{k})$ :Given a security parameter k, this deterministic algorithm outputs the global public parameters

Ω

and PKG’s master private key (MSK). Given k, PKG performs in the following way:

(1)Chooses a k bits prime number q and determine the tuple

{F_{q}, E / F_{q}, G_{q}, P}

, where the point P is the generator of

G_{q}

(2) Chooses the master key

x \in_{R} Z_{q}^{*}

and computes the system public key

P_{p u b} = x P

. Let

(P K, S K) = (P_{p u b}, x)

(3) Selects five hash functions

H_{0}

H_{1}

H_{2} :

{0, 1}^{*} \times G \times G \to Z_{q}^{*}

h_{1} : {0, 1}^{*} \to Z_{q}^{*}

h_{2} : G_{q} \to Z_{q}^{*}

(4) Let

Ω = {F_{q}, E / F_{q}, G_{q}, P, H_{0}, H_{1}, H_{2}, h_{1}, h_{2}, P_{p u b}}

KeyGen $(Ω, O, U, C S P)$ :Each EHR has a fixed number of data owners

O = {O_{1}, O_{2}, \dots, O_{d}}

, then PKG generates the public/secret key pairs for CSP, data owner set O and data user U, respectively.

(1)Set-Secret-Value: The Participant with

I D_{i} (i = 1, 2, \dots, d, C, u)

selects an element

x_{i} \in_{R} Z_{q}^{*} (i = 1, 2, \dots, d, C, u)

and generates the corresponding public key

P_{i} = x_{i} P (i = 1, 2, \dots, d, C, u)

(2))Extract-Partial-Private-Key: To get the partial private key, the user

I D_{i}

sends

(I D_{i}, P_{i})

to the PKG and then the PKG executes the following steps.

(a)Taking the participant’s

I D_{i} (i = 1, 2, \dots, d, C, u)

as input, KGC selects a random number

r_{i} \in Z_{q}^{*} (i = 1, 2, \dots, d, C, u)

and calculates

R_{i} = r_{i} P (i = 1, 2, \dots, d, C, u)

(b)PKG computes

e_{i} = r_{i} + x H_{0} (I D_{i}, R_{i}, P_{i}) m o d q (i = 1, 2, \dots, d, C, u)

. The partial private key of the participant with

I D_{i} (i = 1, 2, \dots, d, C, u)

e_{i}

. The participant with

I D_{i} (i = 1, 2, \dots, d, C, u)

can verify his partial private key by checking whether the equation

Q_{i} = e_{i} P = R_{i} + l_{i} P_{p u b}

holds, where

l_{i} = H_{0} (I D_{i}, R_{i}, P_{i})

. If the above equation is true, then the private key

I D_{i}

will accepted.

(3)Set-Private-Key: The partial private key of the participant with

I D_{i} (i = 1, 2, \dots, d, C, u)

takes the pair

S K_{i} = (x_{i}, e_{i})

as his full private key.

(4)Set-Public-Key: The participant with

I D_{i} (i = 1, 2, \dots, d, C, u)

takes

P K_{i} = (P_{i}, R_{i})

as his full public key.

Enc $(Ω, F, W, {I D_{i}}, I D, {S K_{i}}, {P K_{i}}} :$

Step 1: Given the EHR set

F = {f_{1}, f_{2}, \dots, f_{n}}

with corresponding identities

I D = {i d_{1}, i d_{2}, \dots, i d_{n}}

, it will be encrypted as the ciphertext set

C = {c_{1}, c_{2}, \dots, c_{n}}

through the traditional public key encryption algorithm. To generate the multi-signature on the encrypted file

c_{t} \in C (1 \leq t \leq n)

, each signer

O_{i} (1 \leq i \leq d)

does the following:

(1)

O_{i}

chooses a number

y_{i, t} \in_{R} Z_{q}^{*}

and computes

Y_{i, t} = y_{i, t} P

(2)

O_{i}

broadcasts

Y_{i, t}

to other members

O_{k} (1 \leq k \leq d, k \neq i)

of the group.

(3)computes

Y_{0, t} = \sum_{i = 1}^{d} Y_{i, t}

P_{0} = \sum_{i = 1}^{d} P_{i}

Q_{0} = \sum_{i = 1}^{d} Q_{i}

(4)computes

h_{t} = H_{1} (c_{t}, i d_{t}, Y_{0, t}, P_{0})

and

h_{t}^{'} = H_{1} (c_{t}, i d_{t}, Y_{0, t}, Q_{0})

(5)

O_{i}

computes

V_{i, t} = y_{i, t} + h_{t} x_{i} + h_{t}^{'} e_{i}

, generates a signature

s i g_{i, t} = (Y_{i, t}, V_{i, t})

for

c_{t}

, and then sends

V_{i, t}

to the designated clerk

O_{z}

(6)Upon receiving

V_{i, t}

O_{z}

computes

V_{0, t} = \sum_{i = 1}^{d} V_{i, t}

and outputs the signature

s i g_{t} = {Y_{0, t}, V_{0, t}}

. Let

s i g = {s i g_{1}, \dots, s i g_{n}}

, where

V_{0, t} P = Y_{0, t} + h_{t} P_{0} + h_{t}^{'} Q_{0}

Step 2: All users specify a user to encrypt files, for example,

O_{j}

O_{j}

runs this algorithm to generate the index of file set F. Given the keyword set W,

O_{j}

builds an index for each file

f_{i} \in F

. The index for each

f_{i}

is generated based on the keyword field

W = {w_{i 1}, w_{i 2}, \dots, w_{i m}}

, where m is a fixed integer.

O_{j}

randomly selects

ξ \in Z_{q}^{*}

and calculates

ξ + x_{j}

O_{1}

through public key encryption.

O_{1}

computes

ξ + x_{j} + x_{1}

and sends it to

O_{2}

through public key encryption.

O_{2}

computes

ξ + x_{j} + x_{1} + x_{2}

and sends it to

O_{3}

through public key encryption. ⋯,

O_{d}

computes

ξ + x_{j} + x_{1} + \dots x_{j - 1} + x_{j + 1} + \dots + x_{d}

and sends it to

O_{j}

through public key encryption.

O_{j}

calculates

x_{0} = ξ + x_{j} + x_{1} + \dots x_{j - 1} + x_{j + 1} + \dots + x_{d} - ξ = x_{1} + x_{2} + \dots + x_{d}

. Calculates

e_{0} = e_{1} + e_{2} + \dots + e_{d}

in the same way as

O_{j}

Let

R_{0} = \sum_{t = 1}^{d} R_{t}

l_{0} = \sum_{t = 1}^{d} l_{t}

, Construct an m-degree polynomial by the following equation:

F (x) = b_{i, m} x^{m} + b_{i, m - 1} x^{m - 1} + \dots + b_{i, 1} x + b_{i, 0}

h_{2} (t) h_{1} (w_{i, 1}), \dots, h_{2} (t) h_{1} (w_{i, m})

is the root of equation

F (x) = 1

, where

t = (x_{0} + e_{0}) P_{u} + x_{0} R_{u} + x_{0} l_{u} P_{p u b}

Then

O_{j}

selects

λ_{i}, μ_{i} \in_{R} {Z_{q}}^{*}

and computes

M_{i} = λ_{i} Q_{c}

, set

I_{i, 1} = M_{i} - μ_{i} P

I_{i, 2} = λ_{i} P

$V_{i, j} = μ_{i} b_{i, j} (0 \leq j \leq m)$ , and the index set is $I = {I_{1}, \dots, I_{n}}$ , where $I_{i} = {I_{i, 1}, I_{i, 2}, V_{i, 0}, V_{i, 1},$ $\dots, V_{i, m}}$ . Finally $O_{j}$ send I to CSP.

TrapGen $(Ω, S K_{u}, W^{'})$ :

The Data user calculates the value of

P_{0}, R_{0}, l_{0}

as follows

P_{0} = \sum_{i = 1}^{d} P_{i}

R_{0} = \sum_{i = 1}^{d} R_{i}

l_{0} = \sum_{i = 1}^{d} l_{i}

. Given the queried keywords set

W^{'} = {w_{1}^{'}, w_{2}^{'}, \dots, w_{l}^{'}}

, the data user U first selects an elements

η \in_{R} Z_{q}^{*}

and sets

T_{{W^{'}}_{m + 1}} = η P

T_{{W^{'}}_{j}} = l^{- 1} h_{2} {(t)}^{j} \sum_{r = 1}^{l} h_{1} {({w^{'}}_{r})}^{j} P + η P_{C}

, where

0 \leq j \leq m

t = (x_{u} + e_{u}) P_{0} + x_{u} R_{0} + x_{u} l_{0} P_{p u b}

. Finally, he sent

T_{w^{'}} = {T_{{w^{'}}_{0}}, T_{{w^{'}}_{1}}, \dots, T_{{w^{'}}_{m}}, T_{{w^{'}}_{m + 1}}}

to CSP.

test $(Ω, T_{W^{'}}, I, C)$ : After gaining the search token

T_{W^{'}}

, the CSP first computes

M_{i} = λ_{i} Q_{C}

, and verifies whether Eq.(1) holds.

I_{i, 1} + \sum_{j = 0}^{m} V_{i, j} (T_{{w^{'}}_{j}} - x_{C} T_{{w^{'}}_{m + 1}}) = M_{i}

(1)

If Eq (1) holds, the CSP returns the relevant ciphertext set

C^{'} = {c_{k_{1}}, c_{k_{2}}, \dots, c_{k_{s}}}

and its corresponding identity set

I D^{'} = {i d_{k_{1}}, i d_{k_{2}}, \dots, i d_{k_{s}}}

to PAS. Otherwise, it returns ⊥. The specific test process is shown in the Algorithm 1.

Algorithm 1 Search over encrypted data

Input: Trapdoor

T_{W^{'}}

, indexes I, ciphertexts C, secret key

S K_{C}

and public parameters

Ω

Output: Search results

C^{'}

and corresponding identity set

I D^{'}

or ⊥.

(1)

T_{w^{'}} = {T_{w_{0}^{'}}, T_{w_{1}^{'}}, \dots, T_{w_{m}^{'}}, T_{w_{m + 1}^{'}}}

(2)

I = {I_{1}, I_{2}, \dots, I_{n}}

I_{i} = {I_{i, 1}, I_{i, 2}, V_{i, 0}, V_{i, 1}, \dots, V_{i, m}}

(3)

M_{i} = e_{C} I_{i, 2}

(4)

f o r 0 \leq i \leq n d o

I_{i, 1} + \sum_{j = 0}^{m} V_{i, j} (T_{{w^{'}}_{j}} - x_{C} T_{{w^{'}}_{m + 1}}) = M_{i}

(5) If Eq.(1) holds, CSP returns the ciphertext

c_{k_{t}}

; otherwise, it returns ⊥;

(6)end for

(7)CSP returns the relevant results

C^{'}

and corresponding identity set

I D^{'}

or ⊥ to PAS.

Verify $(Ω, C^{'}, I D^{'}, s i g)$ :After receiving the search results

C^{'}

, CSP computes the proof information

(ϕ_{1}, ϕ_{2})

through Eq.(2) and sends it to PAS. Finally, PAS verifies whether Eq.(3) holds.

Algorithm 2 results verification

Input: Search results

C^{'}

with corresponding identity set

I D^{'}

, public keys

{P K_{i}}

, signature

s i g = {s i g_{1}, \dots, s i g_{n}}

and public parameters

Ω

, where

s i g_{t} = {Y_{0, t}, V_{0, t}}

Output: "Accept" or "Reject"

()1

C^{'} = {c_{k_{1}}, c_{k_{2}}, \dots, c_{k_{s}}},

I D^{'} = {i d_{k_{1}}, i d_{k_{2}}, \dots, i d_{k_{s}}}

;

(2)

{P K_{1}, P K_{2}, \dots, P K_{d}}

;

(3)

s i g = {s i g_{1}, \dots, s i g_{n}}

s i g_{t} = {Y_{0, t}, V_{0, t}}

;

(4)compute

P_{0} = \sum_{t = 1}^{d} P_{t}

Q_{0} = \sum_{t = 1}^{d} Q_{t}

;

(5)compute

ϕ_{1} = \sum_{τ = 1}^{s} H_{1} (c_{k_{τ}}, i d_{k_{τ}}, Y_{0, k_{τ}}, P_{0})

ϕ_{2} = \sum_{τ = 1}^{s} H_{2} (c_{k_{τ}}, i d_{k_{τ}}, Y_{0, k_{τ}}, Q_{0}),

σ = \sum_{τ = 1}^{s} V_{0, k_{τ}};

(2)

(6)Check

σ P = \sum_{τ = 1}^{s} Y_{{o, k}_{τ}} + ϕ_{1} P_{0} + ϕ_{2} Q_{0}

(3)

(7)If Eq.(3) holds, output "Accept" and send

C^{'}

to data user; otherwise, output "Reject".

5. Security of scheme

In this section, we will analyze the security and correctness of this scheme.

5.1. Correctness

Theorem 1. Our CLVPFCKS scheme is computationally consistent.

Proof: For the correctness of Our CLVPFCKS scheme, we do two things. First, We show that CSP can correctly test whether the index of ciphertext matches the trapdoor when the keyword set

W^{'} \subseteq W

, where

W^{'}

is a set of keywords searched by a specific user and W is the keyword set of ciphertext. Secondly, we will show that if the search results pass the result verification mechanism, data users can guarantee the correctness of the search results.

In the test phase, CSP obtains the index

I = {I_{1}, I_{2}, \dots, I_{n}}

and trapdoor

T_{W^{'}} = {T_{{W^{'}}_{0}} T_{{W^{'}}_{1}}, \dots, T_{W_{m}^{'}}, T_{W_{m}^{'} + 1}}

. The CSP first computes

e_{C} I_{i, 2} = (r_{C} + x l_{C}) λ_{i} P = λ_{i} Q_{C} = M_{i}

I_{i, 1} + \sum_{j = 0}^{m} V_{i, j} (T_{{w^{'}}_{j}} - x_{C} T_{{w^{'}}_{m + 1}})

= M_{i} - μ_{i} P + \sum_{j = 0}^{m} μ_{i} b_{i j} [l^{- 1} h_{2} {(t)}^{j} \sum_{r = 1}^{l} h_{1} {(w_{r}^{'})}^{j} P + η P_{C} - x_{C} η P]

= M_{i} - μ_{i} P + \sum_{j = 0}^{m} μ_{i} b_{i j} (l^{- 1} h_{2} {(t)}^{j} \sum_{r = 1}^{l} h_{1} (w_{r}^{'}) P)

= M_{i} - μ_{i} P + l^{- 1} μ_{i} \sum_{j = 0}^{m} b_{i j} h_{2} {(t)}^{j} \sum_{r = 1}^{l} h_{1} {(w_{r}^{'})}^{j} P

= M_{i} - μ_{i} P + l^{- 1} μ_{i} [\sum_{j = 0}^{m} b_{i j} h_{2} {(t)}^{j} h_{1} {({w^{'}}_{1})}^{j} + \dots + \sum_{j = 0}^{m} b_{i j} h_{2} {(t)}^{j} h_{1} {({w^{'}}_{l})}^{j}] P

W^{'} \subseteq W

, then

h_{2} (t) h_{1} (w_{1}), \dots, h_{2} (t) h_{1} (w_{l})

are the root of the equation

F (x) = 1

, where

F (x) {= b}_{i, m} x^{m} {+ b}_{i, m - 1} x^{m - 1} {+ \dots + b}_{i, 1} x + b_{i, 0}

. Thus

I_{i, 1} + \sum_{j = 0}^{m} V_{i, j} (T_{{w^{'}}_{j}} - x_{C} T_{{w^{'}}_{m + 1}})

= M_{i} - μ_{i} P + l^{- 1} μ_{i} [\sum_{j = 0}^{m} b_{i j} h_{2} {(t)}^{j} h_{1} {({w^{'}}_{1})}^{j} + \dots + \sum_{j = 0}^{m} b_{i j} h_{2} {(t)}^{j} h_{1} {({w^{'}}_{l})}^{j}] P

= M_{i} - μ_{i} P + l^{- 1} μ_{i} (1 + 1 + \dots + 1) P

= M_{i} - μ_{i} P + μ_{i} P

= M_{i}

Equation (1) holds so CSP can correctly test whether the index of ciphertext matches the trapdoor.

In the test phase, PAS obtains signature

s i g = {s i g_{1}, s i g_{2}, \dots, s i g_{n}}

and ciphertext

C^{'} = {c_{k_{1}}, c_{k_{2}}, \dots, c_{k_{s}}}

, computing

ϕ_{1} = \sum_{τ = 1}^{s} H_{1} (c_{k_{τ}}, i d_{k_{τ}}, Y_{0, k_{τ}}, P_{0}),

ϕ_{2} = \sum_{τ = 1}^{s} H_{2} (c_{k_{τ}}, i d_{k_{τ}}, Y_{0, k_{τ}}, Q_{0})

getting the proof information

(ϕ_{1}, ϕ_{2})

, and then continuing to calculate

σ P = \sum_{τ = 1}^{s} V_{0, k_{τ}} P = \sum_{τ = 1}^{s} (Y_{0, k_{τ}} + h_{k_{τ}} P_{0} + h_{k_{τ}}^{'} Q_{0})

= \sum_{τ = 1}^{s} Y_{0, k_{τ}} + \sum_{τ = 1}^{s} h_{k_{τ}} P_{0} + \sum_{τ = 1}^{s} {h^{'}}_{k_{τ}} Q_{0}

= \sum_{τ = 1}^{s} Y_{0, k_{τ}} + \sum_{τ = 1}^{s} H_{1} (c_{k_{τ}}, i d_{k_{τ}}, Y_{0, k_{τ}}, P_{0}) P_{0} + \sum_{τ = 1}^{s} H_{1} (c_{k_{τ}}, i d_{k_{τ}}, Y_{0, k_{τ}}, Q_{0}) Q_{0}

If $C^{'} \subseteq C$ , then

ϕ_{1} = \sum_{τ = 1}^{s} H_{1} (c_{k_{τ}}, i d_{k_{τ}}, Y_{0, k_{τ}}, P_{t0}) = \sum_{τ = 1}^{s} H_{1} (c_{ρ (τ)}, i d_{ρ (τ)}, Y_{0, ρ (τ)}, P_{0})

ϕ_{2} = \sum_{τ = 1}^{s} H_{1} (c_{k_{τ}}, i d_{k_{τ}}, Y_{0, k_{τ}}, Q_{0}) = \sum_{τ = 1}^{s} H_{1} (c_{ρ (τ)}, i d_{ρ (τ)}, Y_{0, ρ (τ)}, Q_{0})

Where

ρ (τ) \in [1, n]

. So we have

σ P = \sum_{τ = 1}^{s} Y_{{o, k}_{τ}} + ϕ_{1} P_{0} + ϕ_{2} Q_{0}

. Eq. (3) in program 2 holds. We can also make sure that the ciphertext can not modified.

5.2. Security

Lemma 1. Assuming the adversary

A_{1}

can win Game 1, then an algorithm B can be constructed to solve the ECDDDH problem.

Proof: Suppose that the tuple

(P, a P, b P, X)

is an example of ECDDDH problem. To determine whether

X = a b P

, B will play the part of the challenger.

Set up : B runs the setup

(1^{k})

program to get public parameters

Ω = {F_{q}, E / F_{q}, G_{q}, P, G, H_{0}, H_{1}, H_{2}, P_{p u b}}

, where master private key

S K = x

and the public key

P K = P_{p u b} = x P

. Then B sends parameter

Ω

A_{1}

, and the master private key SK is kept secret. B selects

x_{i} \in Z_{q}^{*} (i \in {2, \dots, d, C})

r_{i} \in Z_{q}^{*} (i \in {1, 2, \dots, d, C})

randomly and set

P_{i} = x_{i} P

(i \in {2, \dots, d, C})

P_{1} = a P

R_{i} = r_{i} P

(i \in {1, 2, \dots, d, C})

e_{i} = r_{i} + x H_{0} (I D_{i}, R_{i}, P_{i}) mod q

(i \in {1, 2, \dots, d, C})

B sends the public key

P K_{O_{i}}

(i \in {1, 2, \dots, d})

and

P K_{C}

A_{1}

, but

S K_{O_{i}}

(i \in {1, 2, \dots, d})

and

S K_{C}

are unknown to

A_{1}

Phase 1: Executed the user’s public key query before other queries using the identity

I D_{u}

. Set up multiple lists to store the queries and answers. All lists are initially empty.

User public key query: B keeps a list

L_{u}

of the tuple

(I D_{u}, x_{u} P, r_{u} P, r_{u})

and upon receiving an identity

I D_{u}

, performs the following steps.

Case1.

I D_{u} = I D_{u}^{◊}

. B picks at randomly

x_{u}^{◊} \in Z_{q}^{*}

, setting

P K_{u}^{◊} = (x_{u}^{◊} P, b P)

, and adds the tuple

(I D_{u}^{◊}, x_{u}^{◊} P, x_{u}^{◊}, b P, ◊)

to the list

L_{u}

, Where ◊ represents a null value.

Case2.

I D_{u} \neq I D_{u}^{◊}

. B picks at randomly

x_{u}, r_{u} \in Z_{q}^{*}

, setting

P K_{u} = (x_{u} P, r_{u} P)

, and adds the tuple

(I D_{u}, x_{u} P, r_{u} P, r_{u})

to the list

L_{u}

Replace-Public-Key query: B maintains a list

L_{R}

of tuple

(I D_{j}, P K_{j}, P {K_{j}}^{'})

. When

A_{1}

inputs

(I D_{j}, P {K_{j}}^{'})

, B replaces

P K_{j}

with

P {K_{j}}^{'}

, and adds

(I D_{j}, P K_{j}, P {K_{j}}^{'})

to the list

L_{R}

Secret-Value query: When

A_{1}

asks the secret value for

I D_{j}

, B finds

(I D_{j}, x_{j} P, r_{j} P, r_{j})

in the list

L_{u}

and returns

x_{j}

.If

P K_{j}

is replaced, B refuses to answer.

Partial-Private-Key query: B establishes a list

L_{e}

of tuple

(I D_{j}, e_{j})

when

A_{1}

asks the partial private key of

I D_{j}

. If

I D_{j} = I D_{u}^{◊}

, B fails and stops. Otherwise, B finds

(I D_{j}, x_{j} P, r_{j} P, r_{j})

in the list

L_{u}

, running the Extract-Partial-Private-Key algorithm generating

e_{j}

. B output

e_{j}

and adds

(I D_{j}, e_{j})

to the list

L_{e}

Keyword Ciphertext Query: When

A_{1}

asks

W = {w_{i, 1}, w_{i, 2}, \dots, w_{i, m}}

for the ciphertext, B operates the

E n c (Ω, F, W, {I D_{i}}, I D, {S K_{i}}, {P K_{i}}}

algorithm to generate ciphertext

C_{W} = {I_{i, 1}, I_{i, 2}, V_{i, 0}, V_{i, 1}, \dots, V_{i, m}}

Keyword Trapdoor Query: When

A_{1}

asks

W^{'} = {w_{1}^{'}, w_{2}^{'}, \dots, w_{l}^{'}}

for the trapdoor, B operates the

T r a p G e n {Ω, S K_{u}, W^{'}}

algorithm to generate trapdoor

T_{w^{'}} = {T_{{w^{'}}_{0}}, T_{{w^{'}}_{1}}, \dots, T_{{w^{'}}_{m}}, T_{{w^{'}}_{m + 1}}}

Test Query:

A_{1}

gives keyword ciphertext

{C_{W}}_{i} = {I_{i, 1}, I_{i, 2}, V_{i, 0}, V_{i, 1}, \dots, V_{i, m}}

and keyword trapdoor

T_{w^{'}} = {T_{{w^{'}}_{0}}, T_{{w^{'}}_{1}}, \dots, T_{{w^{'}}_{m}}, T_{{w^{'}}_{m + 1}}}

, and B compares them using Algorithm 1.

Challenge:

A_{1}

submits a tuple

(W_{0}, W_{1}, I {D_{u}}^{*}, P K_{u}^{*})

, where

W_{0} = {w_{0, 1}, w_{0, 2}, \dots, w_{0, m}}

and

W_{1} = {w_{1, 1}, w_{1, 2}, \dots, w_{1, m}}

are challenging keywords not requested in the previous trapdoor and ciphertext query. If

I D_{u}^{*} \neq I D_{u}^{◊}

, B aborts. Otherwise

I D_{u}^{*} = I D_{u}^{◊}

, B calculates

{l_{u}}^{◊} = H_{0} (I D_{u}^{◊}, R_{u}^{◊}, P_{u}^{◊})

and picks

ξ \in {0, 1}

randomly. B computes

t = (\sum_{k = 2}^{d} x_{k} + \sum_{k = 1}^{d} e_{k}) P_{u}^{◊} + \sum_{k = 2}^{d} x_{k} R_{u}^{◊} + \sum_{k = 2}^{d} x_{k} l_{u}^{◊} P_{p u b} + x_{u}^{◊} a P + l_{u}^{◊} x a P + X

Let

F (x) = (x - h_{2} (t) h_{1} (w_{ξ, 1})) (x - h_{2} (t) h_{1} (w_{ξ, 2})) \dots (x - h_{2} (t) h_{1} (w_{ξ, m})) - 1

, which can get

F (x) = b_{ξ, m} x^{m} + b_{ξ, m - 1} x^{m - 1} + \dots + b_{ξ, 1} x + b_{ξ, 0}

by combining similar terms. Then B selects

λ_{ξ}, μ_{ξ} \in_{R} {Z_{q}}^{*}

and computes

M_{ξ} = λ_{ξ} Q_{c}

. Set

I_{ξ, 1} = M_{ξ} - μ_{ξ} P, I_{ξ, 2} = λ_{ξ} P

V_{ξ, j} = μ_{ξ} b_{ξ, j} (0 \leq j \leq m)

. Thus, the corresponding ciphertext of

W_{ξ} = {w_{ξ, 1}, w_{ξ, 2}, \dots, w_{ξ, m}}

{C_{W}}_{ξ} = {I_{ξ, 1}, I_{ξ, 2}, V_{ξ, 0}, V_{ξ, 1}, \dots, V_{ξ, m}}

. B returns the challenge ciphertexts

C_{W_{ξ}}

to the adversary

A_{1}

Phase 2:

A_{1}

can continue to execute various queries, but there is a limitation that

A_{1}

is not allowed to query the keyword ciphertext or trapdoor of

W_{0}

W_{1}

Guess:

A_{1}

returns

ξ^{'}

Solve CDH problem: If

ξ^{'} = ξ

, B returns 1, otherwise 0. If

X = a b P

, then

t = (\sum_{k = 2}^{d} x_{k} + \sum_{k = 1}^{d} e_{k}) P_{u}^{◊} + \sum_{k = 2}^{d} x_{k} R_{u}^{◊} + \sum_{k = 2}^{d} x_{k} l_{u}^{◊} P_{p u b} + x_{u}^{◊} a P + l_{u}^{◊} x a P + X

= (x_{0} + e_{0}) P_{u}^{◊} + \sum_{k = 2}^{d} x_{k} R_{u}^{◊} + x_{0} l_{u}^{◊} P_{p u b} + a b P

= (x_{0} + e_{0}) P_{u}^{◊} + x_{0} R_{u}^{◊} + x_{0} l_{u}^{◊} P_{p u b}

Therefore,

{C_{W}}_{ξ}

is a valid ciphertext. Suppose that the advantage of

A_{1}

wins in the above game is

ε

. So

Pr [ξ^{'} = ξ |X = a b P] = \frac{1}{2} + ε

X \neq a b P

, then

C_{W_{ξ}}

is an invalid ciphertext.

A_{1}

has no advantage in distinguishing

ξ = 0

from

ξ = 1

. Hence

Pr [ξ^{'} = ξ |X = a b P] = \frac{1}{2}

Probability: Let

q_{u}

q_{r}

and

q_{e}

be the number of the User public key query, Replace-Public-Key query, and Partial-Private-Key query, respectively. The two events are as follows:

π_{1}

A_{1}

did not replace of

I D_{u}^{◊}

’s public key

R_{u}^{◊}

and query the partial-private-key for

I D_{u}^{◊}

π_{2}

I D_{u}^{*} = I D_{u}^{◊}

It’s not hard to get the following results.

Pr [π_{1}] = \frac{q_{u} - q_{r} - q_{e}}{q_{u}}

Pr [π_{2} |π_{1}] = \frac{1}{q_{u} - q_{r} - q_{e}}

Pr [B

s u c c e s s] = Pr [π_{1} \land π_{2}] = \frac{1}{q_{u}}

A_{1}

win Game 1 with an advantage of

ε

, then B has a probability greater than

\frac{ε}{q_{u}}

to determine whether

X = a b P

Lemma 2. Assuming the adversary

A_{2}

can win Game 2, an algorithm B can constructed to solve the ECDDDH problem by exploiting the adversary’s ability.

Proof: Suppose that the tuple

(P, a P, b P, X)

is an example of an ECDDDH problem. To determine whether

X = a b P

, B will play the part of the challenger.

Set up: B runs the setup

(1^{k})

program to get public parameters

Ω = {F_{q}, E / F_{q}, G_{q}, P, G, H_{0}, H_{1}, H_{2}, P_{p u b}}

, where master private key

S K = x

and the public key

P K = P_{p u b} = x P

. B selects

x_{i} \in Z_{q}^{*} (i \in {1, 2, \dots, d, C})

r_{i} \in Z_{q}^{*} (i \in {2, \dots, d, C})

randomly and set

P_{i} = x_{i} P

(i \in {1, 2, \dots, d, C})

R_{1} = a P

R_{i} = r_{i} P

(i \in {2, \dots, d, C})

e_{1} = a + x H_{0} (I D_{1}, R_{1}, P_{1}) mod q

e_{i} = r_{i} + x H_{0} (I D_{i}, R_{i}, P_{i}) mod q

(i \in {2, \dots, d, C})

B sends the public parameters

Ω

, the public key

P K_{O_{i}}

(i \in {1, 2, \dots, d})

and the public/secret key pair

(P K, S K)

A_{2}

, while

S K_{O_{i}}

(i \in {1, 2, \dots, d})

are unknown to

A_{2}

Phase 1: Executed the user’s public key query before other queries using the identity

I D_{u}

. Set up multiple lists to store the queries and answers. All lists are initially empty.

User public key query: B maintains a list

L_{u}

containing the tuple

(I D_{u}, x_{u} P, r_{u} P, r_{u})

and takes the following actions when receiving an identity

I D_{u}

Case1.

I D_{u} = I D_{u}^{◊}

. B chooses a number

r_{u}^{◊} \in Z_{q}^{*}

at random, sets

P K_{u}^{◊} = (b P, r_{u}^{◊} P)

, and adds the tuple

(I D_{u}^{◊}, b P, ◊, r_{u}^{◊} P, r_{u}^{◊})

to the list

L_{u}

, Where ◊ represents a null value.

Case2.

I D_{u} \neq I D_{u}^{◊}

. B chooses

x_{u}, r_{u} \in Z_{q}^{*}

at random, sets

P K_{u} = (x_{u} P, r_{u} P)

, and adds the tuple

(I D_{u}, x_{u} P, r_{u} P, r_{u})

to the list

L_{u}

Replace-Public-Key query: same as that in Lemma 1

Secret-Value query: B established a list

L_{s}

of tuple

(I D_{j}, x_{j})

. When

A_{2}

asks the secret value for

I D_{j}

. If

I D_{j} = I D_{u}^{◊}

, B fails and stops. Otherwise, B finds

(I D_{j}, x_{j} P, r_{j} P, r_{j})

in list

L_{u}

, returns

x_{j}

Partial-Private-Key query: When

A_{2}

asks the partial private key of

I D_{j}

, B finds

(I D_{j}, x_{j} P, r_{j} P, r_{j})

in list

L_{u}

, running the Extract-Partial-Private-Key algorithm and returning

e_{j}

.If

P K_{j}

is replaced, B refuses to answer.

Keyword Ciphertext Query: same as that in Lemma 1.

Keyword Trapdoor Query: same as that in Lemma 1.

Test Query: same as that in Lemma 1.

Challenge:

A_{2}

submits a tuple

(W_{0}, W_{1}, I D_{u}^{*}, P K_{u}^{*})

that meets the requirements of Game 2, where

W_{0} = {w_{0, 1}, w_{0, 2}, \dots, w_{0, m}}

and

W_{1} = {w_{1, 1}, w_{1, 2}, \dots, w_{1, m}}

are challenging keywords not asked in the previous trapdoor query and ciphertext query. If

I D_{u} \neq I D_{u}^{◊}

, B aborts. Otherwise

I D_{u}^{*} = I D_{u}^{◊}

, B computes

l_{u}^{◊} = H_{0} (I D_{u}^{◊}, R_{u}^{◊}, P_{u}^{◊})

l_{1} = H_{0} (I D_{1}, R_{1}, P_{1})

and picks

ξ \in {0, 1}

randomly. B computes

t = (\sum_{k = 1}^{d} x_{k} + x l_{1} + \sum_{k = 2}^{d} e_{k}) P_{u}^{◊} + \sum_{k = 1}^{d} x_{k} R_{u}^{◊} + \sum_{k = 1}^{d} x_{k} l_{u}^{◊} P_{p u b} + X

Let

F (x) = (x - h_{2} (t) h_{1} (w_{ξ, 1})) (x - h_{2} (t) h_{1} (w_{ξ, 2})) \dots (x - h_{2} (t) h_{1} (w_{ξ, m})) - 1

, which can get

F (x) = b_{ξ, m} x^{m} + b_{ξ, m - 1} x^{m - 1} + \dots + b_{ξ, 1} x + b_{ξ, 0}

by combining similar terms. Then select

λ_{ξ}, μ_{ξ} \in_{R} {Z_{q}}^{*}

at random and compute

M_{ξ} = λ_{ξ} Q_{c}

. Set

I_{ξ, 1} = M_{ξ} - μ_{ξ} P, I_{ξ, 2} = λ_{ξ} P

V_{ξ, j} = μ_{ξ} b_{ξ, j} (0 \leq j \leq m)

, and thus

W_{ξ} = {w_{ξ, 1}, w_{ξ, 2}, \dots, w_{ξ, m}}

’s ciphertext is

C_{W_{ξ}} = {I_{ξ, 1}, I_{ξ, 2}, V_{ξ, 0}, V_{ξ, 1}, \dots, V_{ξ, m}}

. B returns the challenge ciphertexts

C_{W_{ξ}}

to the adversary

A_{2}

Phase 2:The attacker

A_{2}

can continue to execute various queries, but there is a limitation that the attacker

A_{2}

is not allowed to query the keyword ciphertext or trap of

W_{0}

W_{1}

Guess:

A_{2}

returns

ξ^{'}

Solve the ECDDDH problem. If

ξ^{'} = ξ

, B returns 1. Otherwise 0. If

X = a b P

, then

t = (\sum_{k = 2}^{d} x_{k} + \sum_{k = 1}^{d} e_{k}) P_{u}^{◊} + \sum_{k = 2}^{d} x_{k} R_{u}^{◊} + \sum_{k = 2}^{d} x_{k} l_{u}^{◊} P_{p u b} + r_{u}^{◊} a P + l_{u}^{◊} x a P + X

= (\sum_{k = 2}^{d} x_{k} + e_{0}) P_{u}^{◊} + x_{0} R_{u}^{◊} + x_{0} l_{u}^{◊} P_{p u b} + a b P

= (x_{0} + e_{0}) P_{u}^{◊} + x_{0} R_{u}^{◊} + x_{0} l_{u}^{◊} P_{p u b}

Therefore,

C_{W_{ξ}}

is a valid ciphertext. Suppose that the advantage of

A_{2}

wins in the above game is

ε

, so

Pr [ξ^{'} = ξ |X = a b P] = \frac{1}{2} + ε

X \neq a b P

, then

C_{W_{ξ}}

is an invalid ciphertext.

A_{2}

has no advantage in distinguishing

ξ = 0

from

ξ = 1

. Hence

Pr [ξ^{'} = ξ |X = a b P] = \frac{1}{2}

Probability. Let

q_{u}

q_{r}

q_{s}

be the number of User public key query, Replace-Public-Key query, and Secret-Value query, respectively. The two events are as follows:

π_{1}

A_{2}

did not replace of

I D_{u}^{◊}

’s public key

P_{u}^{◊}

nor perform the Secret-Value query for

I D_{u}^{◊}

π_{2}

I D_{u}^{*} = I D_{u}^{◊}

It’s not hard to get the following results.

Pr [π_{1}] = \frac{q_{u} - q_{r} - q_{s}}{q_{u}}

Pr [π_{2} |π_{1}] = \frac{1}{q_{u} - q_{r} - q_{s}}

Pr [B

s u c c e s s] = Pr [π_{1} \land π_{2}] = \frac{1}{q_{u}}

A_{2}

has an

ε

advantage to win Game, then B has a probability greater than

\frac{ε}{q_{u}}

to determine whether

X = a b P

Theorem 2. Our CLVPFCKS scheme is CKCA-CIND secure in standard model if the ECDDDH problem is hard.

Proof: Theorem 2 holds from Lemma 1 and Lemma 2.

Lemma 3. Assuming the adversary

A_{1}

can win Game 3, then an algorithm B can be constructed to solve the ECDDDH problem.

Proof: Suppose that the tuple

(P, a P, b P, X)

is an example of ECDDDH problem. To determine whether

X = a b P

, B will play the part of the challenger.

Set up: B runs the setup

(1^{k})

program to obtain the public parameters

Ω = {F_{q}, E / F_{q}, G_{q}, P, G, H_{0}, H_{1}, H_{2}, P_{p u b}}

, where master private key

S K = x

P K = P_{p u b} = x P

, then randomly selects

r_{u}, x_{C}, r_{C} \in Z_{q}^{*}

,and set

P_{u} = a P

R_{u} = r_{u} P

P_{C} = x_{C} P

R_{C} = r_{C} P

e_{C} = r_{C} + x H_{0} (I D_{C}, R_{C}, P_{C}) mod q

e_{u} = r_{u} + x H_{0} (I D_{u}, R_{u}, P_{u}) mod q

B sends the public key

P K_{u}

and

P K_{C}

A_{1}

, but

S K_{u}

and

S K_{C}

are unknown to

A_{1}

Phase 1: Executed the user’s public key query before other queries using the identity

I D_{i}

. Set up multiple lists to store the queries and answers. All lists are initially empty.

User public key query: B keeps a list

L_{o}

of the tuple

(I D_{i}, x_{i} P, r_{i} P, r_{i})

and upon receiving an identity

I D_{i}

, performs the following steps.

Case1.

I D_{i} = I D_{i}^{◊}

, B picks at randomly

x_{i}^{◊} \in Z_{q}^{*}

, setting

P K_{i}^{◊} = (x_{i}^{◊} P, b P)

, and adds the tuple

(I D_{i}^{◊}, x_{i}^{◊} P, x_{i}^{◊}, b P, ◊)

to the list

L_{o}

,Where ◊ represents a null value.

Case2.

I D_{i} \neq I D_{i}^{◊}

, B picks at randomly

x_{i}, r_{i} \in Z_{q}^{*}

, setting

P K_{i} = (x_{i} P, r_{i} P)

, and adds the tuple

(I D_{i}, x_{i} P, r_{i} P, r_{i})

to the list

L_{o}

Replace-Public-Key query: same as that in Lemma 1.

Secret-Value query:same as that in Lemma 1.

Partial-Private-Key query: B establishes a list

L_{e}

of tuple

(I D_{j}, e_{j})

when

A_{1}

asks the partial private key of

I D_{j}

. If

I D_{j} = I D_{i}^{◊}

, B fails and stops. Otherwise, B finds

(I D_{j}, x_{j} P, r_{j} P, r_{j})

in the list

L_{o}

, running the Extract-Partial-Private-Key algorithm generating

e_{j}

. B output

e_{j}

and adds

(I D_{j}, e_{j})

to the list

L_{e}

Keyword Ciphertext Query: same as that in Lemma 1.

Keyword Trapdoor Query: same as that in Lemma 1.

Test Query: same as that in Lemma 1.

Challenge:

A_{1}

submits a tuple

(W_{0}^{'}, W_{1}^{'}, {I {D_{1}}^{*}, \dots, I {D_{d}}^{*}}, {P {K_{1}}^{*}, \dots, P {K_{d}}^{*}})

, where

W_{0}^{'} = {w_{0, 1}^{'}, w_{0, 2}^{'}, \dots, w_{0, l}^{'}}

and

W_{1}^{'} = {w_{1, 1}^{'}, w_{1, 2}^{'}, \dots, w_{1, l}^{'}}

are challenging keywords not requested in the previous trapdoor and ciphertext query. If

I D_{i}^{◊} \notin {I {D_{1}}^{*}, I {D_{2}}^{*}, \dots, I {D_{d}}^{*}}

, B aborts. Otherwise,without losing generality, it is better to set

I D_{1}^{*}

I D_{i}^{◊}

. B calculates

{l_{0}}^{*} = \sum_{i = 1}^{d} H_{0} (I D_{i}^{*}, R_{i}^{*}, P_{i}^{*})

. B picks

ξ \in {0, 1}

randomly, and computes

t = e_{u} \sum_{i = 1}^{d} {P_{i}}^{*} + \sum_{i = 2}^{d} {x_{i}}^{*} a P + \sum_{i = 1}^{d} {r_{i}}^{*} a P + {l_{0}}^{*} x a P + X

B selects an elements

η_{ξ} \in_{R} Z_{q}^{*}

and sets

T_{{W^{'}}_{ξ, m + 1}} = η_{ξ} P

T_{{W^{'}}_{ξ, j}} = l^{- 1} h_{2} {(t)}^{j} \sum_{r = 1}^{l} h_{1} {({w^{'}}_{ξ, j})}^{j} P + η_{ξ} P_{C}

, where

0 \leq j \leq m

. Finally, B sent

T_{W_{ξ}^{'}} = {T_{{w^{'}}_{ξ}, 0}, T_{{w^{'}}_{ξ}, 1}, \dots, T_{{w^{'}}_{ξ}, m}, T_{{w^{'}}_{ξ, m + 1}}}

to the adversary

A_{1}

Phase 2: The attacker

A_{1}

can continue to execute various queries, but there is a limitation that the attacker

A_{1}

is not allowed to query the keyword ciphertext or trapdoor of

W_{0}

W_{1}

Guess:

A_{1}

returns

ξ^{'}

Solve CDH problem: If

ξ^{'} = ξ

, B returns 1, otherwise 0. If

X = a b P

, then

t = e_{u} \sum_{i = 1}^{d} {P_{i}}^{*} + \sum_{i = 1}^{d} {x_{i}}^{*} a P + \sum_{i = 2}^{d} {r_{i}}^{*} a P + {l_{0}}^{*} x a P + X

= (x_{u} + e_{u}) P_{0}^{*} + \sum_{i = 2}^{d} {r_{i}}^{*} a P + x_{u} l_{0}^{*} P_{p u b} + a b P

= (x_{u} + e_{u}) P_{0}^{*} + x_{u} R_{0}^{*} + x_{u} l_{0}^{*} P_{p u b}

Therefore,

T_{W_{ξ}^{'}}

is a valid ciphertext. Suppose that the advantage of

A_{1}

wins in the above game is

ε

. So

Pr [ξ^{'} = ξ |X = a b P] = \frac{1}{2} + ε

X \neq a b P

, then

T_{W_{ξ}^{'}}

is an invalid ciphertext.

A_{1}

has no advantage in distinguishing

ξ = 0

from

ξ = 1

. Hence

Pr [ξ^{'} = ξ |X = a b P] = \frac{1}{2}

Probability: Let

q_{o}

q_{r}

and

q_{e}

be the number of the User public key query, Replace-Public-Key query, and Partial-Private-Key query, respectively. The two events are as follows:

π_{1}

A_{1}

did not replace of

I D_{i}^{◊}

’s public key

R_{i}^{◊}

and query the partial-private-key for

I D_{i}^{◊}

π_{2}

I D_{1}^{*} = I D_{i}^{◊}

It’s not hard to get the following results.

Pr [π_{1}] = \frac{q_{o} - q_{r} - q_{e}}{q_{o}}

Pr [π_{2} |π_{1}] = \frac{1}{q_{o} - q_{r} - q_{e}}

Pr [B

s u c c e s s] = Pr [π_{1} \land π_{2}] = \frac{1}{q_{u}}

A_{1}

win Game 1 with an advantage of

ε

, then B has a probability greater than

\frac{ε}{q_{o}}

to determine whether

X = a b P

Lemma 4. Assuming the adversary

A_{2}

can win Game 4, then an algorithm B can be constructed to solve the ECDDDH problem.

Proof: Suppose that the tuple

(P, a P, b P, X)

is an example of ECDDDH problem. To determine whether

X = a b P

, B will play the part of the challenger.

Set up : B runs the setup

(1^{k})

program to obtain the public parameters

Ω = {F_{q}, E / F_{q}, G_{q}, P, G, H_{0}, H_{1}, H_{2}, P_{p u b}}

, where master private key

S K = x

P K = P_{p u b} = x P

, then randomly selects

x_{u}, x_{C}, r_{C} \in Z_{q}^{*}

, and set

P_{u} = x_{u} P

R_{u} = a P

P_{C} = x_{C} P

R_{C} = r_{C} P

e_{C} = r_{C} + x H_{0} (I D_{C}, R_{C}, P_{C}) mod q

e_{u} = a + x H_{0} (I D_{u}, R_{u}, P_{u}) mod q

B sends the public parameters

Ω

, the public key

P K_{u}

, and the public/secret key pair

(P K, S K)

A_{2}

, while

S K_{u}

are unknown to

A_{2}

Phase 1: Executed the user’s public key query before other queries using the identity

I D_{i}

. Set up multiple lists to store the queries and answers. All lists are initially empty.

User public key query: user public key query: B keeps a list

L_{o}

of the tuple

(I D_{i}, x_{i} P, r_{i} P, r_{i})

and upon receiving an identity

I D_{i}

, performs the following steps.

Case1.

I D_{i} = I D_{i}^{◊}

, B picks at randomly

r_{i}^{◊} \in Z_{q}^{*}

, setting

P K_{i}^{◊} = (b P, r_{i}^{◊} P)

, and adds the tuple

(I D_{i}^{◊}, b P, ◊, r_{i}^{◊} P, r_{i}^{◊})

to the list

L_{o}

, Where ◊ represents a null value. .

Case2.

I D_{i} \neq I D_{i}^{◊}

, B picks at randomly

x_{i}, r_{i} \in Z_{q}^{*}

, setting

P K_{i} = (x_{i} P, r_{i} P)

, and adds the tuple

(I D_{i}, x_{i} P, r_{i} P, r_{i})

to the list

L_{o}

Replace-Public-Key query: same as that in Lemma 1.

Secret-Value query:B established a list

L_{s}

of tuple

(I D_{j}, x_{j})

. When

A_{2}

asks the secret value for

I D_{j}

. If

I D_{j} = I D_{i}^{◊}

, B fails and stops. Otherwise, B finds

(I D_{j}, x_{j} P, r_{j} P, r_{j})

in list

L_{o}

, returns

x_{j}

Partial-Private-Key query: same as that in Lemma 2.

Keyword Ciphertext Query: same as that in Lemma 1.

Keyword Trapdoor Query: same as that in Lemma 1.

Test Query: same as that in Lemma 1.

Challenge:

A_{2}

submits a tuple

(W_{0}^{'}, W_{1}^{'}, {I {D_{1}}^{*}, \dots, I {D_{d}}^{*}},

{P {K_{1}}^{*}, \dots, P {K_{d}}^{*}})

, where

W_{0}^{'} = {w_{0, 1}^{'}, w_{0, 2}^{'}, \dots, w_{0, l}^{'}}

and

W_{1}^{'} = {w_{1, 1}^{'}, w_{1, 2}^{'}, \dots, w_{1, l}^{'}}

are challenging keywords not requested in the previous trapdoor and ciphertext query. If

I D_{i}^{◊} \notin {I {D_{1}}^{*}, I {D_{2}}^{*}, \dots, I {D_{d}}^{*}}

, B aborts. Otherwise, without losing generality, it is better to set

I D_{1}^{*}

I D_{i}^{◊}

. B calculates

{l_{0}}^{*} = \sum_{i = 1}^{d} H_{0} (I D_{i}^{*}, R_{i}^{*}, P_{i}^{*})

. B picks

ξ \in {0, 1}

randomly, and computes

t = x_{u} \sum_{i = 1}^{d} {P_{i}}^{*} + \sum_{i = 2}^{d} {x_{i}}^{*} a P + l_{u} x \sum_{i = 1}^{d} {P_{i}}^{*} + \sum_{i = 1}^{d} {r_{i}}^{*} a p + x_{u} {l_{0}}^{*} P_{p u b} + X

B selects an elements

η_{ξ} \in_{R} Z_{q}^{*}

and sets

T_{{W^{'}}_{ξ, m + 1}} = η_{ξ} P

T_{{W^{'}}_{ξ, j}} = l^{- 1} h_{2} {(t)}^{j} \sum_{r = 1}^{l} h_{1} {({w^{'}}_{ξ, j})}^{j} P + η_{ξ} P_{C}

, where

0 \leq j \leq m

. Finally, B sent

T_{W_{ξ}^{'}} = {T_{{w^{'}}_{ξ}, 0}, T_{{w^{'}}_{ξ}, 1}, \dots, T_{{w^{'}}_{ξ}, m}, T_{{w^{'}}_{ξ, m + 1}}}

to the adversary

A_{2}

Phase 2: The attacker

A_{2}

can continue to execute various queries, but there is a limitation that the attacker

A_{2}

is not allowed to query the keyword ciphertext or trapdoor of

W_{0}

W_{1}

Guess:

A_{2}

returns

ξ^{'}

Solve CDH problem: If

ξ^{'} = ξ

, B returns 1, otherwise 0. If

X = a b P

, then

t = x_{u} \sum_{i = 1}^{d} {P_{i}}^{*} + \sum_{i = 2}^{d} {x_{i}}^{*} a P + l_{u} x \sum_{i = 1}^{d} {P_{i}}^{*} + \sum_{i = 1}^{d} {r_{i}}^{*} a P + x_{u} {l_{0}}^{*} P_{p u b} + X

= x_{u} P_{0}^{*} + \sum_{i = 2}^{d} {x_{i}}^{*} a P + l_{u} x \sum_{i = 1}^{d} {P_{i}}^{*} + x_{u} R_{0}^{*} + x_{u} l_{0}^{*} P_{p u b} + a b P

= x_{u} P_{0}^{*} + \sum_{i = 1}^{d} {x_{i}}^{*} a P + l_{u} x \sum_{i = 1}^{d} {P_{i}}^{*} + x_{u} R_{0}^{*} + x_{u} l_{0}^{*} P_{p u b}

= x_{u} P_{0}^{*} + (a + l_{u} x) \sum_{i = 1}^{d} {P_{i}}^{*} + x_{u} R_{0}^{*} + x_{u} l_{0}^{*} P_{p u b}

= (x_{u} + e_{u}) P_{0}^{*} + x_{u} R_{0}^{*} + x_{u} l_{0}^{*} P_{p u b}

Therefore,

T_{W_{ξ}^{'}}

is a valid ciphertext. Suppose that the advantage of

A_{2}

wins in the above game is

ε

. So

Pr [ξ^{'} = ξ |X = a b P] = \frac{1}{2} + ε

X \neq a b P

, then

T_{W_{ξ}^{'}}

is an invalid ciphertext.

A_{2}

has no advantage in distinguishing

ξ = 0

from

ξ = 1

. Hence

Pr [ξ^{'} = ξ |X = a b P] = \frac{1}{2}

Probability: Let

q_{o}

q_{r}

and

q_{s}

be the number of User public key query, Replace-Public-Key query, and Secret-Value query, respectively. The two events are as follows:

π_{1}

A_{2}

did not replace of

I D_{i}^{◊}

’s public key

P_{i}^{◊}

and query the secret value for

I D_{i}^{◊}

π_{2}

I D_{1}^{*} = I D_{i}^{◊}

It’s not hard to get the following results.

Pr [π_{1}] = \frac{q_{o} - q_{r} - q_{e}}{q_{u}}

Pr [π_{2} |π_{1}] = \frac{1}{q_{o} - q_{r} - q_{e}}

Pr [B

s u c c e s s] = Pr [π_{1} \land π_{2}] = \frac{1}{q_{u}}

A_{2}

win Game 4 with an advantage of

ε

, then B has a probability greater than

\frac{ε}{q_{o}}

to determine whether

X = a b P

Theorem 3. Our CLVPFCKS scheme is IND-KGA safe in the standard model if the ECDDDH problem is hard. Proof: Theorem 3 holds from Lemma 3 and Lemma 4.

Theorem 4. Under the ECDLP assumption, it is not computationally feasible for the CSP to forge valid proof information through the result verification mechanism.

Proof: The malicious CSP can’t forge a valid multi-signature on each returned record and pass the verification. Since it does not have the key of multiple data owners, it is computationally infeasible to forge a valid multi-signature. Therefore, the malicious CSP can only win the next security game by directly generating valid proof information according to the wrong search result

C^{*}

instead of wining the next security game by forging multiple signatures. But after the following analysis, this is also impossible.

Assume that the correct ciphertext and its identity is

C = {c_{1}, c_{2}, \dots, c_{n}}

and

s i g = {s i g_{1}, \dots, s i g_{n}}

, where

s i g_{t} = {Y_{0, t}, V_{0, t}}

. The malicious CSP may forge wrong proof information

(ϕ_{1}^{*}, ϕ_{2}^{*})

on false search results

C^{*} = {c_{k_{1}}^{*}, c_{k_{2}}^{*}, \dots, c_{k_{s}}^{*}}

, where

{ϕ_{1}}^{*} = \sum_{τ = 1}^{s} H_{1} (c_{k_{τ}}^{*}, i d_{k_{τ}}^{*}, Y_{0, k_{τ}}, P_{0}),

{ϕ_{2}}^{*} = \sum_{τ = 1}^{s} H_{1} (c_{k_{τ}}^{*}, i d_{k_{τ}}^{*}, Y_{0, k_{τ}}, Q_{0}) .

If the forged proof information

(ϕ_{1}^{*}, ϕ_{2}^{*})

can successfully pass the result verification mechanism, the malicious CSP will win the security game; Otherwise, it will fail. Suppose a malicious CSP wins the game. We then know that

{ϕ_{1}}^{*} = \sum_{τ = 1}^{s} H_{1} (c_{k_{τ}}^{*}, i d_{k_{τ}}^{*}, Y_{0, k_{τ}}, P_{0}),

{ϕ_{2}}^{*} = \sum_{τ = 1}^{s} H_{1} (c_{k_{τ}}^{*}, i d_{k_{τ}}^{*}, Y_{0, k_{τ}}, Q_{0})

(4)

where

σ = \sum_{τ = 1}^{s} V_{0, k_{τ}}

. The proof information of correct ciphertext C is

(ϕ_{1}, ϕ_{2})

, where

ϕ_{1} = \sum_{τ = 1}^{s} H_{1} (c_{k_{τ}}, i d_{k_{τ}}, Y_{0, k_{τ}}, P_{0}),

ϕ_{2} = \sum_{τ = 1}^{s} H_{2} (c_{k_{τ}}, i d_{k_{τ}}, Y_{0, k_{τ}}, Q_{0}) .

The signature of the correct ciphertext can pass the verification mechanism, so we have

σ P = \sum_{τ = 1}^{s} Y_{o, k_{τ}} + ϕ_{1} P_{0} + ϕ_{2} Q_{0}

(5)

Subtract Formula (4) from Formula (5) to get

(ϕ_{1} - {ϕ_{1}}^{*}) P_{0} = ({ϕ_{2}}^{*} - ϕ_{2}) Q_{0}

(6)

Because

(ϕ_{1}, ϕ_{2})

is not equal to

(ϕ_{1}^{*}, ϕ_{2}^{*})

, so

ϕ_{1} \neq ϕ_{1}^{*}

ϕ_{2} \neq ϕ_{2}^{*}

. Set

Δ ϕ_{1} = ϕ_{1} - {ϕ_{1}}^{*}

Δ ϕ_{2} = ϕ_{2} - {ϕ_{2}}^{*}

, then

Δ ϕ_{1} \neq 0

Δ ϕ_{2} \neq 0

. Suppose

Δ ϕ_{1}

is not zero, then

P_{0} = \frac{Δ ϕ_{2}}{Δ ϕ_{1}} Q_{0}

. If the probability of

Δ ϕ_{1} = 0

\frac{1}{q}

, then the probability that we can break the ECDLP problem is

1 - \frac{1}{q}

, where q is the length of

G_{q}

. This means that if the malicious CSP can pass the verification, we can break the ECDLP problem.

6. Performance analysis

In this section, we compare our scheme with other certificateless or verifiable search schemes in terms of computational complexity, storage overhead and security.

First, let’s talk about security. Table 2 compares the security of the current scheme with other schemes. The CKCA-CIND, the IND-KGA, the insider KGA, the FIA, the SCF, and the VER are used to measure the scheme’s security. The CKCA-CIND means that the scheme is in differentiability of ciphertext for selected keyword ciphertext attacks, the IND-KGA means the indistinguishability of indiscernibility of trapdoors, the insider-KGA denotes that the scheme is secure against keyword-guessing attacks launched by malicious server, the FIA denotes that the scheme is resistant to file injection attack, the SCF means that the scheme has no secure channel, and the VER indicates that the scheme can prevent malicious CSP from returning wrong search results.

Table 2. COMPARISON OF SAFETY

scheme	CKCA-CIND	IND-KGA	insider-KGA	FIA	SCF	VER
VCKSM[18]	No proof	yes	no	no	yes	yes
VMKS[46]	yes	yes	No proof	No proof	yes	yes
VMKDO[33]	yes	yes	no	no	yes	yes
VCSE[46]	yes	No proof	no	no	yes	yes
CLPAEKS[12]	No proof	No proof	yes	yes	yes	No proof
CL-dPAEKS[11]	No proof	No proof	yes	yes	yes	No proof
our	yes	yes	yes	yes	yes	yes

It is worth noting that no solution can simultaneously achieve result validation, conjunctive keyword search, and certificateless and bilinear pairings, as shown in Table 2. Our proposed solution can simultaneously perform four functions and is proven secure under the standard model.

Next, we compare the computational complexity. To compare the computational complexity, we use the operation time of He et al.’s scheme[47] as the benchmark. He et al. tested the time required for the relevant operations in the experimental environment of Samsung Galaxy S5 based on the Android 4.4.2 operating system, quad-core 2.45G processor, and 2G byte memory. Table 4 shows the exact running time and symbols of the various operations. The mapping

e : G_{1} \times G_{1} \to G_{2}

is a bilinear pair where

G_{1}

is an additive group of singular elliptic curves of order p defined on a finite field

F_{q}

. The lengths of p and q are 512 bits and 160 bits, respectively. G is an additive group of non-sigular elliptic curve of order q defined on the prime finite field

F_{q}

. The length of p and q is 160.

Table 3. Symbol definition

symbols	Definition
$T_{b p}$	Running time required for a bilinear pairing operation, $T_{b p} \approx 32.713 m s$
$T_{h t p}$	Running time required for a hash-to-operation, $T_{h t p} \approx 33.582 m s$
$T_{s m}$	Running time required for a scalar multiplication operation in $G_{1}, T_{s m} \approx 13.405 m s$
$T_{exp}$	Running time required for an exponentiation operation in $G_{2}, T_{exp} \approx 2.249 m s$
$T^{'} s m$	Running time required for a scalar multiplication operation in $G, T_{s m} \approx 3.335 m s$
u	Number of data users
d	Number of data owners
m	Number of keywords in ciphertext
n	Number of ciphertext
s	Number of search keywords

Table 4 shows the comparison results of the running time of the verifiable conjunctive keyword search encryption scheme. To be more intuitive and specific, we taking n=1000, m=100, d=100, u=50, s=50. Table 5 shows the calculation time of the three schemes. Except for the search algorithm, our scheme takes less time than the other two schemes, especially for the verification algorithm. Therefore, our scheme is the most efficient.

Table 4. Comparison of running time of various schemes

scheme	keyGen	Enc	Trap	search	verify
VCKSM[18]	$(u + d + 1) T_{s m}$	[2nd + n(m + 2)] $\begin{matrix} T_{s m} \\ + 2 n T_{exp} + 2 n T_{b p} \\ {+ n T}_{h t p} \end{matrix}$	$(m + 3) T_{s m}$	$\begin{matrix} (n + 3) T_{s m} \\ + [n (m + 1) + 1] T_{b p} \end{matrix}$	$\begin{matrix} (2 s + 1) T_{s m} \\ + s T_{h t p} + 2 T_{b p} \end{matrix}$
VMKS[46]	$(4 u + 4 d) T_{s m}$	$\begin{matrix} n T_{h t p} + \\ (6 n + m n) T_{s m} \end{matrix}$	$(l + 5) T_{s m}$	$4 T_{b p}$	$\begin{matrix} (s + 2) T_{s m} \\ + s T_{h t p} + 3 T_{b p} \end{matrix}$
our	$(2 d + 5) T^{'} sm$	$[n d + n (m + 4)] T^{'} s m$	$(m + 6) T^{'} s m$	$2 + n (m + 1)] T^{'} s m$	$3 T^{'} s m$

Table 5. Comparison of running time of various schemes

scheme	keyGen(ms)	Enc(ms)	Trap(ms)	search(ms)	verify(ms)	Total
VCKSM[18]	2024.155	4151817	1380.715	3305426.428	3098.481	7463746.779
VMKS[46]	8043	1382126	737.275	130.852	2474.349	1393511.476
our	683.675	680340	353.51	336838.335	6.67	1018222.19

Let

|G_{1}|

|G_{2}|

|G|

and

|{Z^{*}}_{q}|

denote the size of an element in

G_{1}

G_{2}

, G and

{Z^{*}}_{q}

, respectively. For more intuitive comparison of communication costs. Table 6 uses n=100, m=10 and s=10. As shown in Figure 3, our solution has the lowest storage cost.

Table 6. Communication Comparison Of Various Schemes

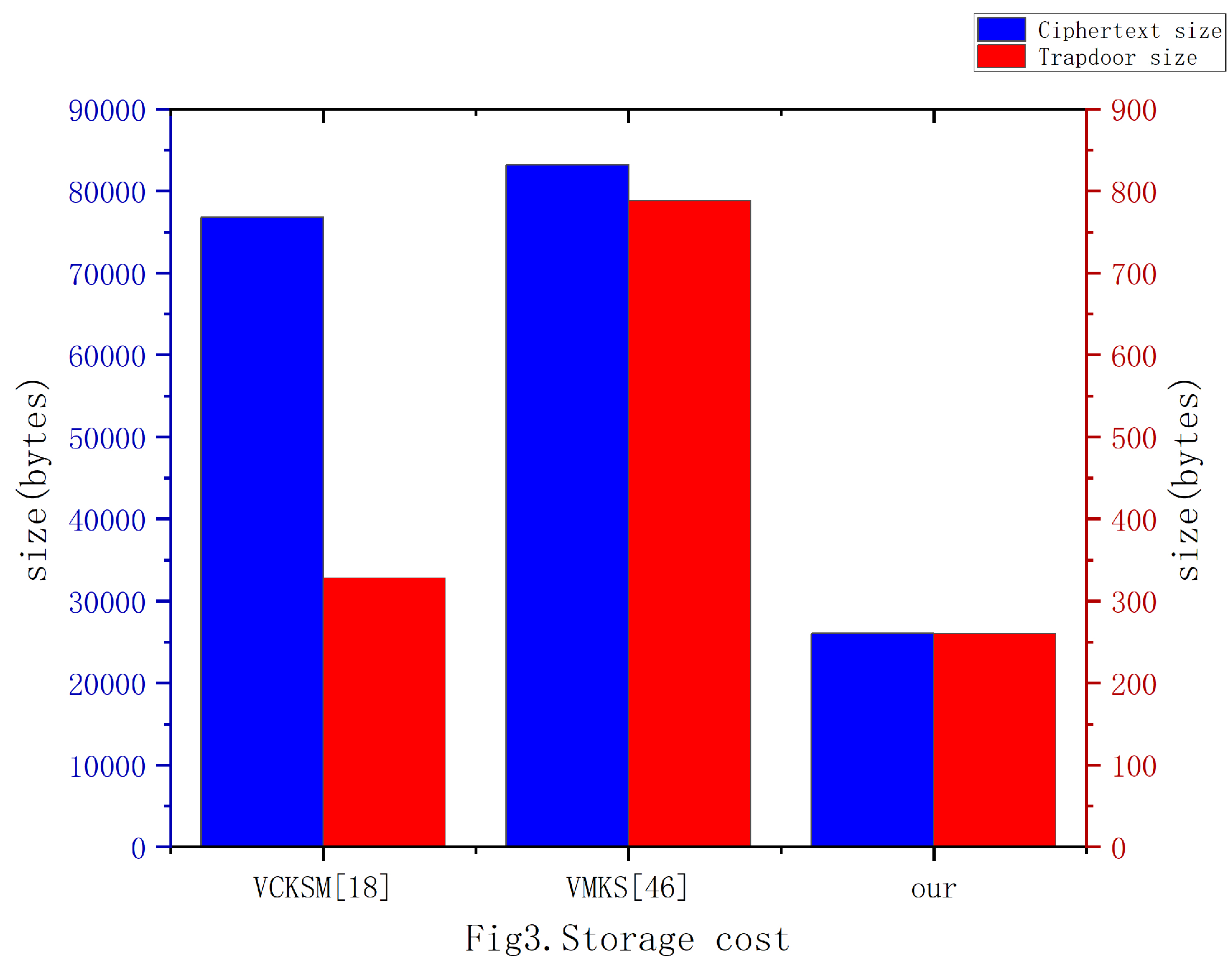
scheme	Ciphertext size(bytes)	Trapdoor size(bytes)
VCKSM[18]	$n (m + 2) \|G_{2}\| = 1200 \times 512 / 8 = 76800$	$\|G_{1}\| + \|G_{2}\| + s \|Z_{q}^{*}\| = (512 + 512 + 10 \times 160) / 8 = 328$
VMKS[46]	$\begin{matrix} n (\|G_{2}\| + (m + 2) \|G_{1}\|) \\ = 100 \times (512 + 12 \times 512) / 8 \\ = 83200 \end{matrix}$	$(m + 2) \|G_{1}\| + \|Z_{q}^{*}\| = (12 \times 512 + 160) / 8 = 788$
our	$n (m + 3) \|G\| = (1300 \times 160) / 8 = 26000$	$(m + 2) \|G\| = 12 \times 160 / 8 = 240$

As stated in the summary, our scheme is more efficient than others in computing and communication costs. And it is also the best in security.

7. Conclusion

Searchable encryption is an essential technology for medical Internet of Things. We have constructed a certificateless verifiable bilinear pair-free conjunctive keyword search encryption scheme (CLVPFCKS) for the Internet of Medical. The performance analysis shows that the CLVPFCKS scheme proposed in this paper performs better than the verifiable conjunctive keyword searchable encryption scheme using bilinear pairing. We prove the new system can resist keyword guessing attacks, choose keyword attacks (CKA), and file injection attacks under the standard model.

References

L. AtzoriA. Iera and G. Morabito, "The Internet of Things: A survey," Comput. Netw., vol. 54, no. 15, pp. 2787-2805, 2010. [CrossRef]
A. Zanella, N. Bui, A. Castellani, L. Vangelista and M. Zorzi, "Internet of Things for Smart Cities," Ieee Internet of Things Journal, vol. 1, no. 1, pp. 22-32, 2014. [CrossRef]
P. Bellavista, G. Cardone, A. Corradi and L. Foschini, "Convergence of MANET and WSN in IoT Urban Scenarios," Ieee Sens. J., vol. 13, no. 10, pp. 3558-3567, 2013. [CrossRef]
V. Jagadeeswari, V. Subramaniyaswamy, R. Logesh and V. Vijayakumar, "A study on medical Internet of Things and Big Data in personalized healthcare system," Health Information Science and Systems, vol. 6, no. 1, 2018. [CrossRef]
D.J. He, R. Ye, S. Chan, M. Guizani and Y.P. Xu, "Privacy in the Internet of Things for Smart Healthcare," Ieee Commun. Mag., vol. 56, no. 4, pp. 38-44, 2018. [CrossRef]
Y.Y. ChenJ.C. Lu and J.K. Jan, "A Secure EHR System Based on Hybrid Clouds," J. Med. Syst., vol. 36, no. 5, pp. 3375-3384, 2012. [CrossRef]
D.X. SongD. Wagner and A. Perrig, Practical Techniques for Searches on Encrypted Data, Proc. IEEE Symposium on Security & Privacy, 2002, pp. 44-55.
D. Boneh, G.D. Crescenzo, R. Ostrovsky and G. Persiano, "Public Key Encryption with Keyword Search," Eurocrypt 2004, pp. 506-522, 2004. [CrossRef]
J. BaekR. Safiavinaini and W. Susilo, Public Key Encryption with Keyword Search Revisited, Proc. International Conference on Computational Science and Its Applications (ICCSA 2008), 2008, pp. 1249-1259. [CrossRef]
H.S. Rhee, J.H. Park, W. Susilo and D.H. Lee, Improved searchable public key encryption with designated tester, Proc. International Symposium on Information, 2009, pp. 376. [CrossRef]
L. Wu, Y. Zhang, M. Ma, N. Kumar and D. He, "Certificateless searchable public key authenticated encryption with designated tester for cloud-assisted medical Internet of Things," Ann. Telecommun., vol. 74, no. 7-8, pp. 423-434, 2019. [CrossRef]
D. He, M. Ma, S. Zeadall, N. Kumar and K. Liang, "Certificateless Public Key Authenticated Encryption with Keyword Search for Industrial Internet of Things," Ieee T. Ind. Inform., pp. 1, 2017. [CrossRef]
M.M. A, D.H.B. C, M.K.K. D and J.C. A, "Certificateless searchable public key encryption scheme for mobile healthcare system," Comput. Electr. Eng., vol. 65, pp. 413-424, 2018. [CrossRef]
M. Ma, D. He, S. Fan and D. Feng, "Certificateless searchable public key encryption scheme secure against keyword guessing attacks for smart healthcare," Journal of Information Security and Applications, vol. 50, 2020. [CrossRef]
Y. Lu and J. Li, "Constructing pairing-free certificateless public key encryption with keyword search," Frontiers of Information Technology & Electronic Engineering, vol. 20, no. 8, pp. 1049-1060, 2019. [CrossRef]
P. GolleJ. Stadon and B. Waters, Secure conjunctive keyword search over encrypted data,3089, M. Jakobsson, et al., eds., 2004, pp. 31-45. [CrossRef]
Y.H. Hwang and P.J. Lee, Public key encryption with conjunctive keyword search and its extension to a multi-user system, Book Public key encryption with conjunctive keyword search and its extension to a multi-user system, Series Public key encryption with conjunctive keyword search and its extension to a multi-user system 4575,ed., Editor ed., 2007, pp. 2. [CrossRef]
Y.B. Miao, et al., "VCKSM: Verifiable conjunctive keyword search over mobile e-health cloud in shared multi-owner settings," Pervasive Mob. Comput., vol. 40, pp. 205-219, 2017. [CrossRef]
Y. Yang and M.D. Ma, "Conjunctive Keyword Search With Designated Tester and Timing Enabled Proxy Re-Encryption Function for E-Health Clouds," Ieee T. Inf. Foren. Sec., vol. 11, no. 4, pp. 746-759, 2016. [CrossRef]
S.H. Heng and K. Kurosawa, k-resilient identity-based encryption in the standard model,2964, T. Okamoto, ed., 2004, pp. 67-80. [CrossRef]
D. Khader, Public key encryption with keyword search based on K-resilient IBE,3982, M. Gavrilova, et al., eds., 2006, pp. 298-308.
H.M. YangC.X. Xu and H.T. Zhao, An Efficient Public Key Encryption with Keyword Scheme Not Using Pairing, Proc. First International Conference on Instrumentation, 2011.
T.F. Vallent and H. Kim, A Pairing-Free Public Key Encryption with Keyword Searching for Cloud Storage Services, Book A Pairing-Free Public Key Encryption with Keyword Searching for Cloud Storage Services, Series A Pairing-Free Public Key Encryption with Keyword Searching for Cloud Storage Services 135,ed., Editor ed., 2014, pp. 70.
N.B. YangS.M. Xu and Z. Quan, "An Efficient Public Key Searchable Encryption Scheme for Mobile Smart Terminal," Ieee Access, vol. 8, pp. 77940-77950, 2020. [CrossRef]
M. Ma, M. Luo, S. Fan and D. Feng, "An Efficient Pairing-Free Certificateless Searchable Public Key Encryption for Cloud-Based IIoT," Wirel. Commun. Mob. Com., vol. 2020, 2020. [CrossRef]
M.R. Senouci, I. Benkhaddra, A. Senouci and F.G. Li, "A provably secure free-pairing certificateless searchable encryption scheme," Telecommun. Syst., vol. 80, no. 3, pp. 383-395, 2022. [CrossRef]
Z.Y. Hu, L.Z. Deng, Y.Y. Wu, H.Y. Shi and Y. Gao, "Secure and Efficient Certificateless Searchable Authenticated Encryption Scheme Without Random Oracle for Industrial Internet of Things," Ieee Syst. J., vol. 17, no. 1, pp. 1304-1315, 2023. [CrossRef]
J.W. Byun, H.S. Rhee, H.A. Park and D.H. Lee, Off-line keyword guessing attacks on recent keyword search schemes over encrypted data,4165, W. Jonker and M. Petkovic, eds., 2006, pp. 75-83.
Y. LuG. Wang and J.G. Li, "Keyword guessing attacks on a public key encryption with keyword search scheme without random oracle and its improvement," Inform. Sciences, vol. 479, pp. 270-276, 2019. [CrossRef]
M.S. HwangS.T. Hsu and C.C. Lee, "A New Public Key Encryption with Conjunctive Field Keyword Search Scheme," Inf. Technol. Control, vol. 43, no. 3, pp. 277-288, 2014. [CrossRef]
Q. Chai and G. Gong, Verifiable symmetric searchable encryption for semi-honest-but-curious cloud servers, Proc. IEEE International Conference on Communications, 2012.
W. Sun, X. Liu, W. Lou, Y.T. Hou and H. Li, Catch You If You Lie to Me: Efficient Verifiable Conjunctive Keyword Search over Large Dynamic Encrypted Cloud Data, Proc. 34th IEEE Conference on Computer Communications (INFOCOM), 2015.
Y. Miao, J. Ma, X. Liu, Z. Liu and F. Wei, "VMKDO: Verifiable multi-keyword search over encrypted cloud data for dynamic data-owner," Peer Peer Netw. Appl., vol. 11, no. 2, pp. 287-297, 2018. [CrossRef]
Y. Miao, J. Weng, X. Liu, K. Raymond Choo, Z. Liu and H. Li, "Enabling verifiable multiple keywords search over encrypted cloud data," Inform. Sciences, vol. 465, pp. 21-37, 2018. [CrossRef]
L. Fang, W. Susilo, C. Ge and J. Wang, "Public key encryption with keyword search secure against keyword guessing attacks without random oracle," Inform. Sciences, vol. 238, pp. 221-241, 2013. [CrossRef]
Z.Y. Shao and B. Yang, "On security against the server in designated tester public key encryption with keyword search," Inform. Process. Lett., vol. 115, no. 12, pp. 957-961, 2015. [CrossRef]
C. Hu and P. Liu, "An Enhanced Searchable Public Key Encryption Scheme with a Designated Tester and Its Extensions," Journal of Computers, vol. 7, no. 3, 2012. [CrossRef]
H.S. Rhee, J.H. Park, W. Susilo and D.H. Lee, "Trapdoor security in a searchable public-key encryption scheme with a designated tester," J. Syst. Software, vol. 83, no. 5, pp. 763-771, 2010. [CrossRef]
Y. LuG. Wang and J. Li, "On Security of a Secure Channel Free Public Key Encryption with Conjunctive Field Keyword Search Scheme," Inf. Technol. Control, vol. 47, no. 1, pp. 56-62, 2018. [CrossRef]
I.R. Jeong, J.O. Kwon, D. Hong and D.H. Lee, "Constructing PEKS schemes secure against keyword guessing attacks is possible?" Computer Communications, vol. 32, no. 2, pp. 394-396, 2009. [CrossRef]
P. Xu, H. Jin, Q. Wu and W. Wang, "Public-Key Encryption with Fuzzy Keyword Search: A Provably Secure Scheme under Keyword Guessing Attack," Ieee T. Comput., vol. 62, no. 11, pp. 2266-2277, 2013. [CrossRef]
X.J. Lin, L. Sun, H.P. Qu and D.X. Liu, "On the Security of Secure Server-Designation Public Key Encryption with Keyword Search," Comput. J., vol. 61, no. 12, pp. 1791-1793, 2018. [CrossRef]
Q. Huang and H.B. Li, "An efficient public-key searchable encryption scheme secure against inside keyword guessing attacks," Inform. Sciences, vol. 403, pp. 1-14, 2017. [CrossRef]
L. Wu, B. Chen, S. Zeadally and D. He, "An efficient and secure searchable public key encryption scheme with privacy protection for cloud storage," Soft Comput., vol. 22, no. 23, pp. 7685-7696, 2018. [CrossRef]
S.S. Al-Riyami and K.G. Paterson, Certificateless public key cryptography,2894, C. S. Laih, ed., 2003, pp. 452-473.
Y.M.J.W. Miao, "VCSE: Verifiable conjunctive keywords search over encrypted data without secure-channel," Peer-to-Peer Netw, pp. 995-1007, 2017.
D.B. He, H.Q. Wang, L.N. Wang, J. Shen and X.Z. Yang, "Efficient certificateless anonymous multi-receiver encryption scheme for mobile devices," Soft Comput., vol. 21, no. 22, pp. 6801-6810, 2017. [CrossRef]

Figure 1. Architecture of IoMT.

Figure 2. System model of CLVPFCKS

Figure 3. System model of CLVPFCKS

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A Certificateless Verifiable Bilinear Pair Free Conjunctive Keyword Search Encryption Scheme for IoMT

Abstract

0.Introduction

1. Related work

1.1. Our contribution

1.2. Organization

2. Preliminaries

3. The System Model and Attack Model of CLVPFCKS

3.1. System model

3.2. Design Goals

3.3. Solution Framework

3.4. Security Model

4. the proposed CLVPFCKS

4.1. Specific construction of CLVPFCKS

5. Security of scheme

5.1. Correctness

5.2. Security

6. Performance analysis

7. Conclusion

References

MDPI Initiatives

Important Links

Subscribe