Binding versus Catalysis in De Novo Enzyme Design

Preprint

Technical Note

Binding versus Catalysis in De Novo Enzyme Design

Altmetrics

Downloads

168

Views

936

Comments

Jose Sanchez-Ruiz^*

This version is not peer-reviewed

Submitted:

30 January 2024

Posted:

31 January 2024

You are already at the latest version

Alerts

Abstract

The catalytic parameters describing enzyme catalysis are discussed in the context of the design of de novo enzymes. It is shown that high values of the catalytic efficiency may in some cases reflect tight substrate binding and lead to an immediate levelling-off of rates to reach a low plateau, an undesirable scenario for many industrial applications. It is argued that increasing the catalytic rate constant should be a main target in de novo enzyme engineering.

Keywords:

Subject: Biology and Life Sciences - Biology and Biotechnology

Enzymes catalyse chemical reactions in all known living organisms. Modern natural enzymes are the result of ~4 billion years of evolution and achieve in many cases huge enhancements in reaction rate thus making life as we know it possible. In an attempt to replicate Nature, protein engineers have strived for many years to design non-natural enzymes with high catalytic power. The design of de novo enzymes is in fact a fundamental goal in protein engineering with important biotechnological implications, as well as with implications for our understanding of the basis of enzyme action and for our understanding of the origin of life. It is also a highly challenging goal with only a handful of success stories having been reported in the literature. Furthermore, in most cases the generated de novo activities were very low [1] and extensive laboratory evolution was required to reach enzyme activity levels comparable to those of modern natural enzymes [2,3]. Against this backdrop, it is relevant that Yeh et al. [4] have recently reported the preparation of de novo luciferases using a combination of rational design, deep learning and variant screening. The work of Yeh et al. [4] successfully addresses a number of major bottlenecks in the biotechnological and biomedical applications of luciferases. More generally, it points to general methodologies for the routine generation of highly-active de novo enzymes. Regarding this possibility, however, it is essential that the reported levels of de novo catalysis are critically examined.

Yeh et al. [4] use the catalytic efficiency as a metric of enzyme activity. Catalytic efficiencies for modern natural enzymes span about seven orders of magnitude [5], from ~10² M^-1s^-1 to ~10⁹ M^-1s^-1, with the maximum of the distribution at ~10⁵ M^-1s^-1. Therefore, the catalytic efficiency values of ~10⁶ M^-1s^-1 reported by Yeh et al. [4] emerge as comparatively high. They are, in fact, only about two orders of magnitude below the range (above 10⁸ M^-1s^-1) usually associated to the diffusion limit [5] (i.e., to the so-called “perfect” enzymes). However, catalytic efficiency is not a simple parameter, but the ratio (k_cat/K_M) of two fundamentally different parameters in the Michaelis-Menten equation [6] almost universally used to describe experimental enzyme kinetics:

\frac{v_{0}}{{[E]}_{0}} = \frac{k_{c a t} [S]}{K_{M} + [S]} = \frac{(\frac{k_{c a t}}{K_{m}}) [S]}{1 + (\frac{[S]}{K_{M}})}

where v₀ is the initial reaction rate, [E]₀ is the total enzyme concentration and [S] is the substrate concentration.

K_M is the so-called Michaelis constant which, in the simple pre-equilibrium interpretation of enzyme kinetics, is the equilibrium constant for substrate binding to the enzyme. [A somewhat more complex interpretation of K_M arises in the Briggs-Haldane mechanism, but this does not affect the main conclusions reported here]. K_M is actually defined as a dissociation constant. Therefore, the tighter the binding, the lower the K_M value.

k_cat, called the turnover number or the catalytic rate constant, is the rate constant for the conversion of the bound substrate to product. Its value immediately reflects the fundamental principle of enzyme catalysis, transition state stabilization, as proposed by Pauling many years ago [7]. A high k_cat value means that the enzyme can effectively “distinguish” between the bound substrate and the transition state of the chemical reaction, preferentially stabilizing the latter.

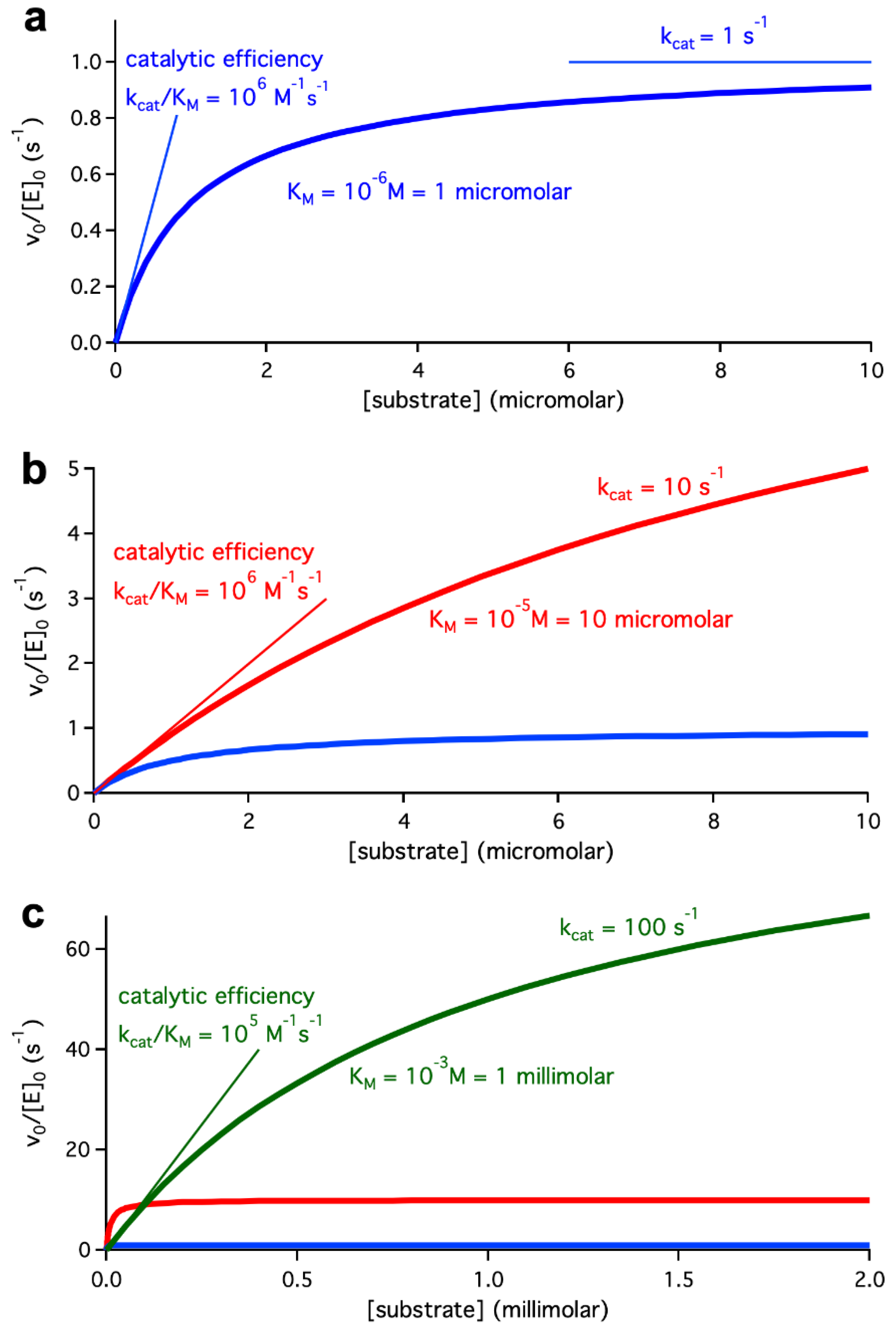
At a more basic level, k_cat defines the rate when the enzyme active site is fully occupied by substrate, which is the rate level approached at sufficiently high substrate concentrations (see Figure 1a). This clearly follows from the fact that, for [S]>>K_M, the Michaelis-Menten equation reduces to v₀/[E]=k_cat. On the other hand, when the substrate concentration is very low ([S]<<K_M), the Michaelis-Menten equation reduces to v₀/[E]=(k_cat/K_M)[S]. The ratio k_cat/K_M is known as catalytic efficiency and obviously describes the initial slope of the plot of rate versus substrate concentration (see Figure 1a).

Since it is defined as k_cat/K_M, it is clear that a high value for the catalytic efficiency may result from a high value of k_cat (enhanced catalysis, reflecting preferential stabilization of the transition state with respect to the bound substrate), but also from a low K_M value (tight substrate binding). K_M values for modern natural enzymes span about eight orders of magnitude [5], from ~10^-8 M to ~1 M, with the maximum of the distribution at ~10^-4 M, i.e., ~100 micromolar. Yeh et al. [4] report substrate binding in the low-micromolar concentration range, which implies K_M~1 micromolar=10^-6M and, therefore, a comparatively tight substrate binding to the de novo luciferases. More importantly, a K_M value of ~10^-6 M combined with a catalytic efficiency k_cat/K_M~10⁶ M^-1s^-1 implies a k_cat for the de novo luciferases on the order 1 s^-1, which is a moderate-low value. Thus, k_cat values for modern natural enzymes span about seven orders of magnitude [5], from ~10^-2 s^-1 to ~10⁵ s^-1, with the maximum of the distribution at ~10 s^-1. Overall, it appears that the high catalytic efficiency reported by Yeh et al. [4], ~10⁶ M^-1s^-1, reflects tight substrate binding to a substantial extent.

It may perhaps seem that the point being made here is of a rather philosophical nature. After all, if a high catalytic efficiency is reached, why should we care whether it has been achieved through a high k_cat value or through a low K_M value? Actually, we should care, in particular if we expect de novo enzymes to be used for common biotechnological applications in a foreseeable future. High catalytic efficiency linked to tight binding and low k_cat value means that there is sharp increase in rate at low substrate concentrations but also that the rate immediately levels off to reach a comparatively low plateau. This is clearly shown in the Michaelis-Menten simulation shown in blue in the several panels of Figure 1, which corresponds to a catalytic efficiency k_cat/K_M=10⁶ M^-1s^-1 achieved with a low k_cat=1 s^-1 and a tight micromolar substrate binding, K_M=10^-6 M.

Of course, changing the relative binding versus catalysis contributions to catalytic efficiency, leads to different results. The Michaelis-Menten simulation shown in red in Figure 1b corresponds to the same catalytic efficiency of k_cat/K_M=10⁶ M^-1s^-1 but, in this case, it is achieved on the basis of a less tight binding (K_M=10^-5 M) and an enhanced catalytic rate constant (k_cat=10 s^-1). The new simulation (red) leads to rates essentially identical to the first one (blue) at very low substrate concentrations, as was to be expected from the fact that the catalytic efficiency value (the same for the two simulations) determines the initial slope of the plot of rate versus concentration. However, at higher substrate concentrations the rates for the new simulation become substantially higher, reflecting that the k_cat value has been increased by one order of magnitude.

The pattern illustrated in Figure 1b emerges as particularly relevant when considering potential biotechnological applications. Certainly, some applications, such as, for instance, the breakdown of contaminants present at very low levels in the environment, may involve very low substrate concentrations. However, in many biotechnological applications (industrial applications, for instance), it is of interest to achieve a high product yield and, therefore, substrate concentrations as high as reasonably possible are likely to be employed. In this scenario, even a comparatively low catalytic efficiency may be acceptable, provided that k_cat is high and that significant binding to the enzyme occurs at the desired (presumably high) substrate concentration. To illustrate this point, we show in Figure 1c (green colour) a Michaelis-Menten simulation in which a high k_cat value of 100 s^-1 is combined with a weak millimolar binding, K_M= 1 mM =10^-3 M. These values imply a catalytic efficiency of 10⁵ M^-1s^-1, which is one order of magnitude below the value of the previous simulations (blue and red in Figure 1C). Yet, the simulation reveals a much-enhanced rate of catalysis at millimolar concentrations.

A diversity of parameters can be used to quantitatively describe enzyme catalysis levels. Besides k_cat and k_cat/K_M, we may mention the ratio of the catalytic rate constant to the uncatalyzed rate constant, k_cat/k_uncat, and the ratio of the catalytic efficiency to the uncatalyzed rate constant, k_cat/(K_M·k_uncat), called catalytic proficiency [9]. All these metrics are useful in specific contexts. However, increasing the catalytic rate constant, k_cat, should be a main target in de novo enzyme engineering. The value of k_cat reflects the fundamental capacity of enzymes to “distinguish” between the transition state of the chemical reaction and the bound substrate. Furthermore, the value of k_cat largely determines the rate at the high substrate concentrations likely to be used in many biotechnological applications. Certainly, improving k_cat has traditionally been a difficult goal. However, recent directed evolution work [9] supports that achieving high k_cat values for de novo enzymes is feasible.

Acknowledgments

Work supported by Spanish Ministry of Science and Innovation/FEDER Funds grant PID2021-124534OB-100.

References

Korendovych, I.V. & DeGrado, W.F. Catalytic efficiency of designed catalytic proteins. Curr. Opin. Struct. Biol. 27, 113-131 (2014). [CrossRef]
Blomberg, R., Kries, H., Pinkas, D.M., Mittl, P.R.E., Grutter, M.G., Privett, H.K., Mayo, S.L. & Hilvert, D. Precision is essential for efficient catalysis in an evolved Kemp eliminase. Nature 503, 418-421 (2013). [CrossRef]
Studer, J., Hansen, D. A., Pianowski Z. L., Mittl, P.R.E., Debon, A., Guffy, S.L., Der, B.S., Kuhlman, B., Hilvert, D. Evolution of a highly active and enantiospecific metalloenzyme from short peptides. Science 362, 1285-1288 (2018). [CrossRef]
Yeh, A.H., Norm, C., Kipnis, Y., Tischer, D., Pellock, S.J., Evans, D., Ma, P., Lee, G.R., Zhang, J.Z., Anishchenko, I., Coventry, B., Cao, L., Dauparas, J., Halabiya, S., DeWitt, M., Carter, L., Houk, K.N. & Baker, D. De novo design of luciferases using deep learning. Nature 614, 774-780 (2023). [CrossRef]
Bar-Even, A., Noor, E., Savir, Y., Liebermeister, W., Davidi, D., Tawfik, D.S. & Milo, R. The moderately efficient enzyme: evolutionary and physicochemical trends shaping enzyme parameters. Biochemistry 50, 4402-4410 (2011). [CrossRef]
Michaelis, L. & Menten, M. L. Die kinetik der invertinwirkung. Biochem. Z. 49, 333-369 (1913).
Pauling, L. Molecular architecture and biological reactions. Chem. Eng. News. 24, 1375-1377 (1946).
Miller, B.G. & Wolfenden, R. Catalytic proficiency: the unusual case of OMP decarboxylase. Annu. Rev. Biochem. 71, 847-885 (2002). [CrossRef]
Bhattacharya, S., Margheritis, E.G., Takahashi, K., Kulesha, A., D’Souza, A., Kim, I., Yoon, J.H. Tame, J.R.H., Volkov, A.N., Makhlynets, O., Korendovych, I.V. NMR-guided directed evolution. Nature 610, 389-393 (2022). [CrossRef]

Figure 1. Effect of changing binding and catalysis parameters on enzyme rates, as shown by Michaelis-Menten simulations. a, profile of rate versus substrate concentration corresponding to comparatively high a catalytic efficiency achieved with a low k_cat and a tight micromolar substrate binding. The interpretations of catalytic efficiency as the initial slope of the profile and that of k_cat as the rate level approached at high substrate concentration, are illustrated. b, profile of rate versus substrate concentration corresponding to same catalytic efficiency as the simulation in panel a, but achieved with a higher k_cat value and a less tight substrate binding (red). For comparison, the simulation in panel a is also shown in blue. Note that increasing the relative contribution the catalytic rate constant (k_cat) to the catalytic efficiency enhances the rate in the whole substrate concentration range. c, profile of rate versus substrate concentration corresponding to a catalytic efficiency value one order of magnitude below that for the simulations in a and b. It has been achieved using a high value of k_cat and a weak millimolar binding. The rates predicted by this new simulation (green) are lower than those for the previous simulations (shown for comparison in blue and red) at the lower substrate concentrations, but they become substantially higher at millimolar substrate concentrations.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Binding versus Catalysis in De Novo Enzyme Design

Abstract

Acknowledgments

References

MDPI Initiatives

Important Links

Subscribe