Prerpints.org logo
Preprint
Communication

Design of Impedance Matching Network for Low-power, Ultra-wideband Applications

Altmetrics

Downloads

132

Views

30

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

30 January 2024

Posted:

31 January 2024

You are already at the latest version

Alerts
Abstract
This paper reviews several techniques, including analytical theories and real frequency techniques, to design ultra-wideband impedance matching networks for low-power applications. The comparison of solutions obtained using the simplified real frequency technique to the published solution using Chebyshev filter theory is demonstrated.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

Ultra-wideband (UWB) technology is characterized by exceptional features, such as high data rate, low power spectral density, enhanced target recognition, and precise localization and ranging capabilities [1]. These qualities make UWB a desirable choice for a wide variety of applications, including wireless communication, radar, and imaging. In these applications, the primary focus is ensuring the optimal transmission and reception of signals within the operational bandwidth. Hence, the design of broadband impedance matching networks (IMN) has emerged as a significant area of interest for engineers [2].
To match a source impedance ZS to an arbitrary load impedance ZL, as illustrated in Figure 1, various theories and techniques have been developed. To meet this objective, Fano [3] and Youla [4] invoked the gain-bandwidth limitation theory and utilized the Darlington representation, where the ZL is represented by a lossless two-port terminated in a unit resistor. Analytical models for determining the IMN are also used, but they require an analytical model of the load impedance [5] and often result in suboptimal solutions in terms of circuit performance metrics and network complexity [6].
Another approach to the design of passive IMNs relies on filter theory [7,8,9,10]. The approach employs either a cascaded L-section topology consisting of high-pass and low-pass filters [7,8] or a bandpass filter [9,10]. These fixed topologies, however, may not necessarily provide a minimum number of elements in the IMN for a specific load [6]. A related approach employs series or tank resonators, and it is based on manipulations of the resonant frequency positions [11,12]. When resonant frequencies can be strategically spaced apart while maintaining an acceptable gain variation, it is possible to attain a broadband IMN. However, it may not prove effective for high fractional bandwidth (FBW) requirements, where many resonators are required.
Design approaches for IMNs with no prior assumption about the network topology, no need for analytical load modelling, and leading to minimum element count have always been desired. To fulfill this need, Carlin [5] developed the so-called real frequency technique (RFT) utilizing the real frequency (e.g., experimental) load impedance data along with numerical optimization. The initial version of the RFT technique was to solve a single matching problem, i.e., a complex load terminating a source of unit internal resistor [5]. The subsequently developed RFTs can be classified into four distinct categories, namely, the line segment technique (RFT-LST), the direct computational technique (DCT), the parametric approach, and the simplified real frequency technique (SRFT) [2]. The line segment technique, direct computational technique, and parametric approach formulate the objective function utilizing the unknown input immittance (driving point admittance or impedance) across the entire angular real frequency ω axis. The procedure starts with the real part of the input immittance, as the imaginary part would be found with the Hilbert transformation or the Gewertz procedure. A lossless two-port IMN can be synthesized by finding an optimized input immittance. The line segment technique formulates the real part of the input immittance as a linear combination of straight lines R i n = ∑ k = 1 N a k ( ω ) R k [5]. On the other hand, the direct computational technique defines the real part of a positive real minimum immittance as a rational even function R i n ( ω ) = E v { Z i n ( s ) } | s = j ω = N ( ω 2 ) D ( ω 2 ) [13]. The parametric approach represents this rational function in a parametric form Z i n ( s ) = ∑ k = 1 N A k s + s k and takes the even function of Zin as the real part of the Zin [14]. Finally, the simplified real frequency technique simplifies the task by defining the two-port scattering parameters of an IMN in rational functions [15], which helps handle the double-matching problems [13,16] and streamline the computation process [17].
In this paper, we present the simplified real frequency technique in detail in Section 2 and apply this technique to the design of the IMN for low-power applications in Section 3, followed by the conclusions.

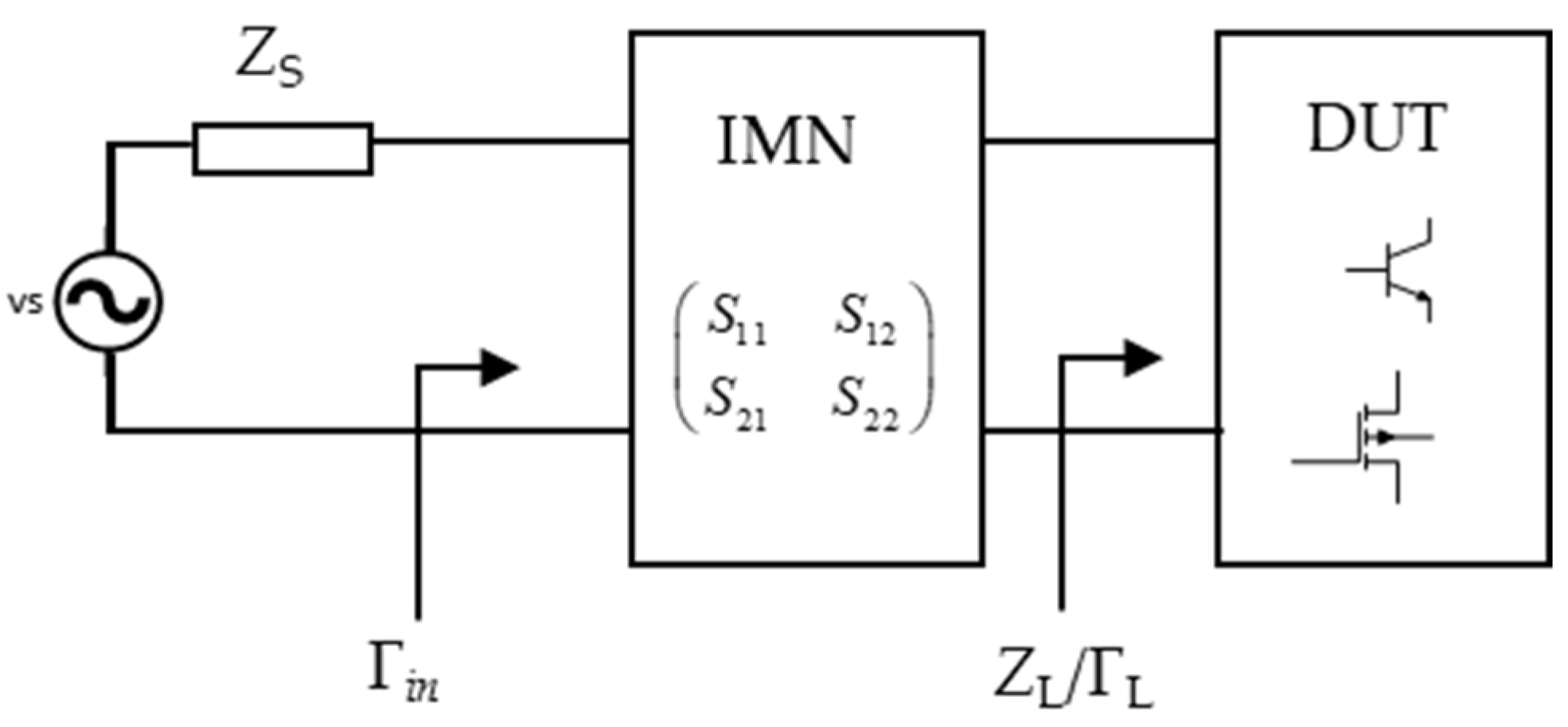
2. Simplified Real Frequency Technique (SRFT)

The SRFT starts with defining the scattering parameters, SIMN, of an IMN containing lossless and reciprocal passive elements based on three polynomials: h, g, and f. Because the IMN should satisfy the paraunitary requirement, i.e., S I M N ⋅ S I M N = I [17,18,19], SIMN is expressed as
S I M N = [ S 11 = h ( s ) g ( s ) S 12 = f ( s ) g ( s ) S 21 = f ( s ) g ( s ) S 22 = − ( − 1 ) k ⋅ h ( − s ) g ( s ) ]
where the polynomial g(s) is strictly Hurwitz, which has all poles on the left-hand side of the complex plane to avoid impractical or unrealizable solutions, and the polynomial f(s) provides the information about the transmission zeros of the IMN. Transmission zeroes are defined as the frequencies at which the output port is completely cut off. In consideration of a transmittance function S21 that may possess finite zeros at ±jωi, zeros at infinity, or zeros at the origin, its general form is expressed as
f ( s ) = s k ∏ i = 1 m ( s 2 + ω i 2 )
Such form implies that f(s) can be either an odd function or an even function. The presence of finite zeros, such as in modified Chebyshev [20], often increases the number of elements and complicated synthesis [21]. Therefore, it is preferable for f(s) to be in the s k form. The parameter k may assume a value of zero in low-pass scenarios and a value greater than one in bandpass and high-pass cases [22].
The lossless condition introduces a relationship among the polynomials f, g, and h. Knowing f(s) allows for expressing g(s) as a function of h(s) as
g ( s ) g ( − s ) = h ( s ) h ( − s ) + f ( s ) ( − s )
The objective in designing the IMN for a known load can be achieved by either maximizing the transductor power gain GT, ideally approaching unity, or minimizing the reflection coefficient Γin, as follows from the relationships as
G T = | S 21 | ( 1 − | Γ L | 2 ) | 1 − S 22 Γ L | 2
and
Γ i n = S 11 + S 21 S 12 Γ L 1 − S 22 Γ L
The SRFT utilizes optimization techniques to determine the optimal polynomial h(s) and, consequently, the corresponding polynomial g(s). Optimization aims to minimize the error function based on the objective function (4) or (5) for load impedance data.

3. Results and Discussion

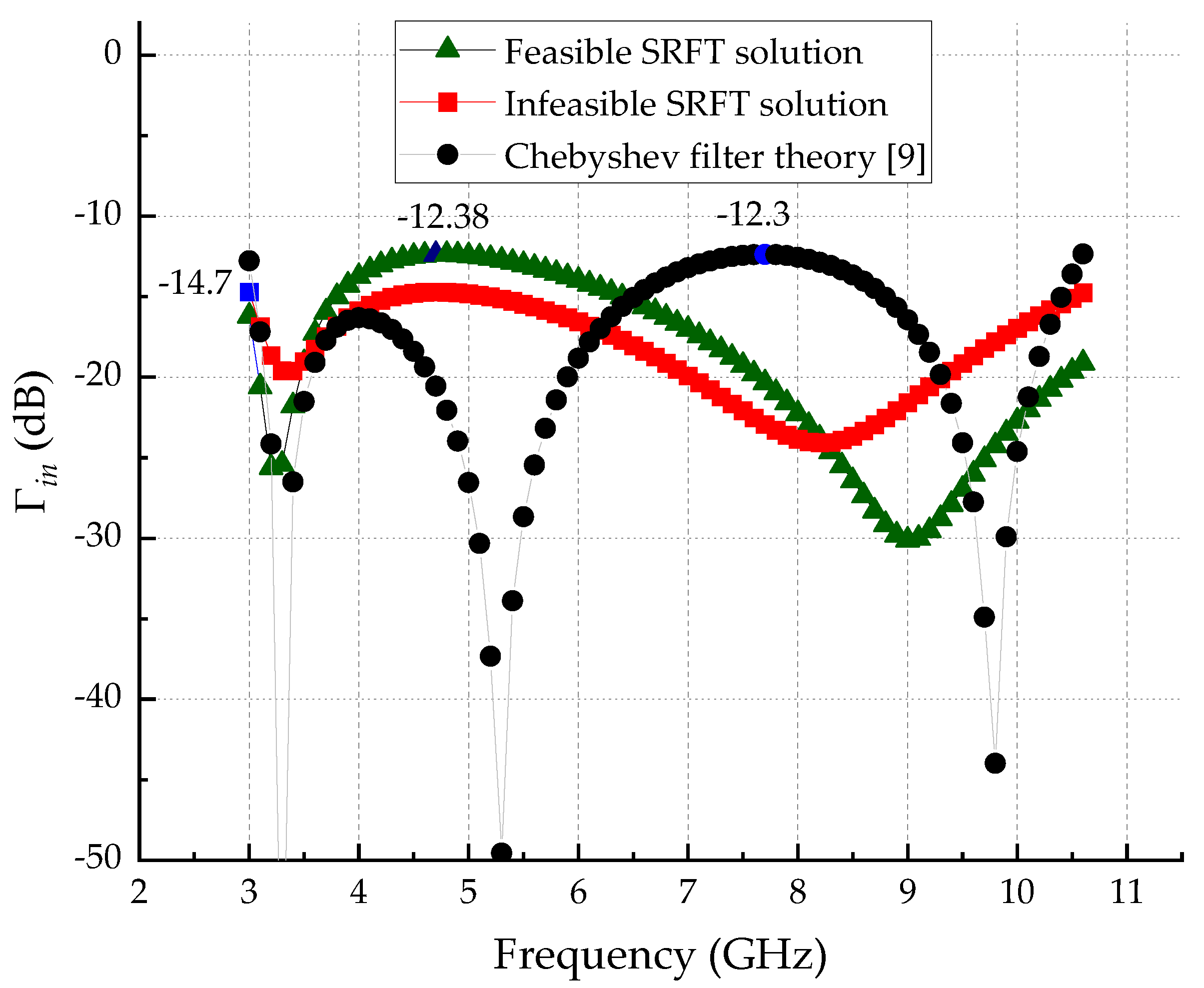
3.1. Comparing SRFT and Chebyshev Filter-Based Solutions

Among filter types, the Chebyshev filter is known to offer the lowest maximum reflection coefficient within the prescribed filter bandwidth. Considering the challenge of achieving a reflection coefficient below −10 dB in the UWB applications, the Chebyshev filter theory is deemed more suitable for meeting this criterion. In [9], a UWB Chebyshev filter theory is used to design the IMN for a load modelled by a 50 Ω resistor in series with a 650 fF capacitor. The IMN comprises five components, with their values in [9] and depicted in Figure 2. The reflection coefficient resulting from this design is illustrated in Figure 4, obtained by simulating the circuit in Figure 2 using the Cadence Virtuoso Spectre circuit simulator with ideal elements from the analog library.
On the other hand, when designing a UWB IMN using SRFT, optimization methods play a significant role in obtaining a solution with better performance. Most reported RFT and SRFT techniques use Levenberg-Marquart optimization [15,17,23]. The Levenberg-Marquardt optimization is a local optimization algorithm that aims to find the minimum of a function in the vicinity of an initial guess. Thus, it is best suited for problems where a solution is expected to be found in the proximity of the initial guess [24]. Selecting a good initial guess in such a highly nonlinear optimization process is critical, and it substantially impacts the ability to reach the optimal IMN [15,22,25].
To see if we can obtain a better solution than the Chebyshev filter approach, we applied the SRFT to the same load as in [9]. It is observed that the SRFT may yield solutions that can not be synthesized by LC elements, even if they demonstrate superior matching performance. We characterize them as infeasible solutions. One such solution is shown by the red line in Figure 4. However, after an exhausting search with various initial guesses and using the Levenberg-Marquardt optimization method, a solution with a maximum reflection coefficient of −12.38 dB in the whole UWB spectrum was found, as shown by the green-line curve in Figure 4. This solution is slightly better than the solution obtained using the Chebyshev filter theory, which features a maximum reflection coefficient of −12.3 dB. However, the solution obtained using the SRFT requires only four elements, as demonstrated in Figure 3, as opposed to the five elements required by the Chebyshev design. This is beneficial, particularly in this example, saving space since an inductor is eliminated.
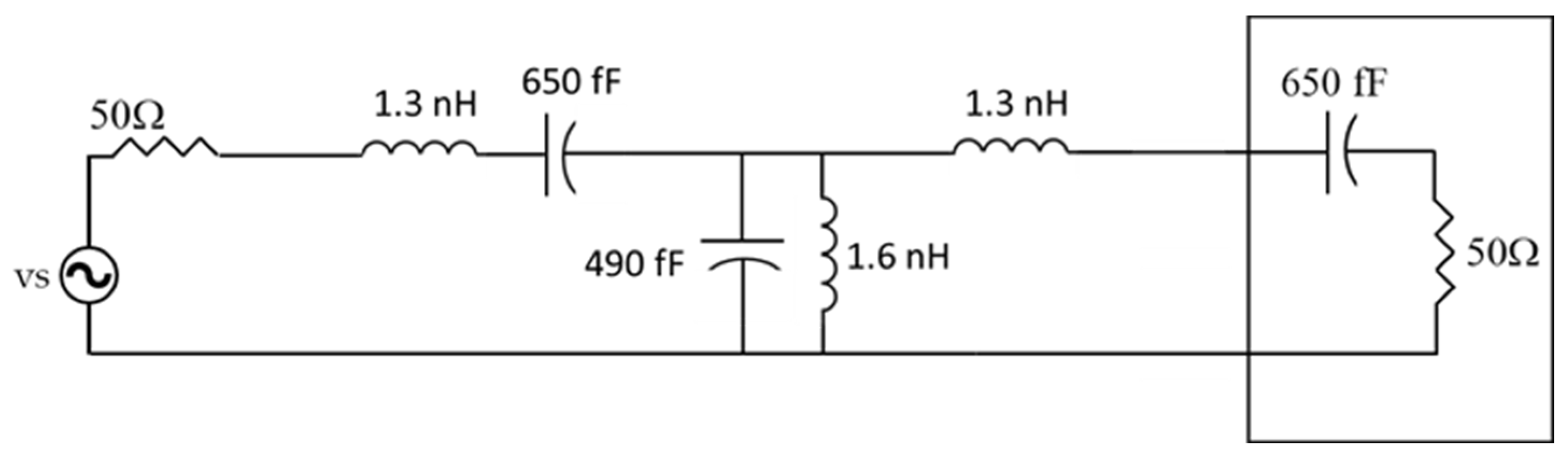
Preprints 97715 g002
Figure 2. UWB IMN based on Chebyshev filter theory in [9].
Figure 2. UWB IMN based on Chebyshev filter theory in [9].
Preprints 97715 g002
Preprints 97715 g003
Figure 3. UWB IMN based on SRFT.
Figure 3. UWB IMN based on SRFT.
Preprints 97715 g003
As an alternative, one may consider utilizing global optimization techniques. These methods can offer the lowest possible reflection coefficient at the expense of significantly longer computations. RFT-based techniques predominantly employ local minimum optimization methods, yielding a solution quickly. As exemplified above, SRFT may result in an infeasible solution, in which case another search must be initiated. With a global optimization method, e.g., the genetic algorithm (GA), the algorithm may bypass a feasible solution and converge to an infeasible solution due to its inclination towards achieving the lowest minimax objective. Indeed, [26] reports an approach using the GA; however, impractical responses are sometimes obtained.
It is clear that synthesizing a feasible solution for a UWB IMN (topology and component values) is problematic. While the optimization may indicate the existence of a solution, it may be difficult or even impossible to synthesize a practical network, particularly in scenarios involving intricate configurations and components like transformers. As shown in [27], some preassumption is required to find the right synthesis.
Preprints 97715 g004
Figure 4. Reflection coefficient of Chebyshev filter, SRFT-based feasible solution and SRFT-based infeasible solution.
Figure 4. Reflection coefficient of Chebyshev filter, SRFT-based feasible solution and SRFT-based infeasible solution.
Preprints 97715 g004

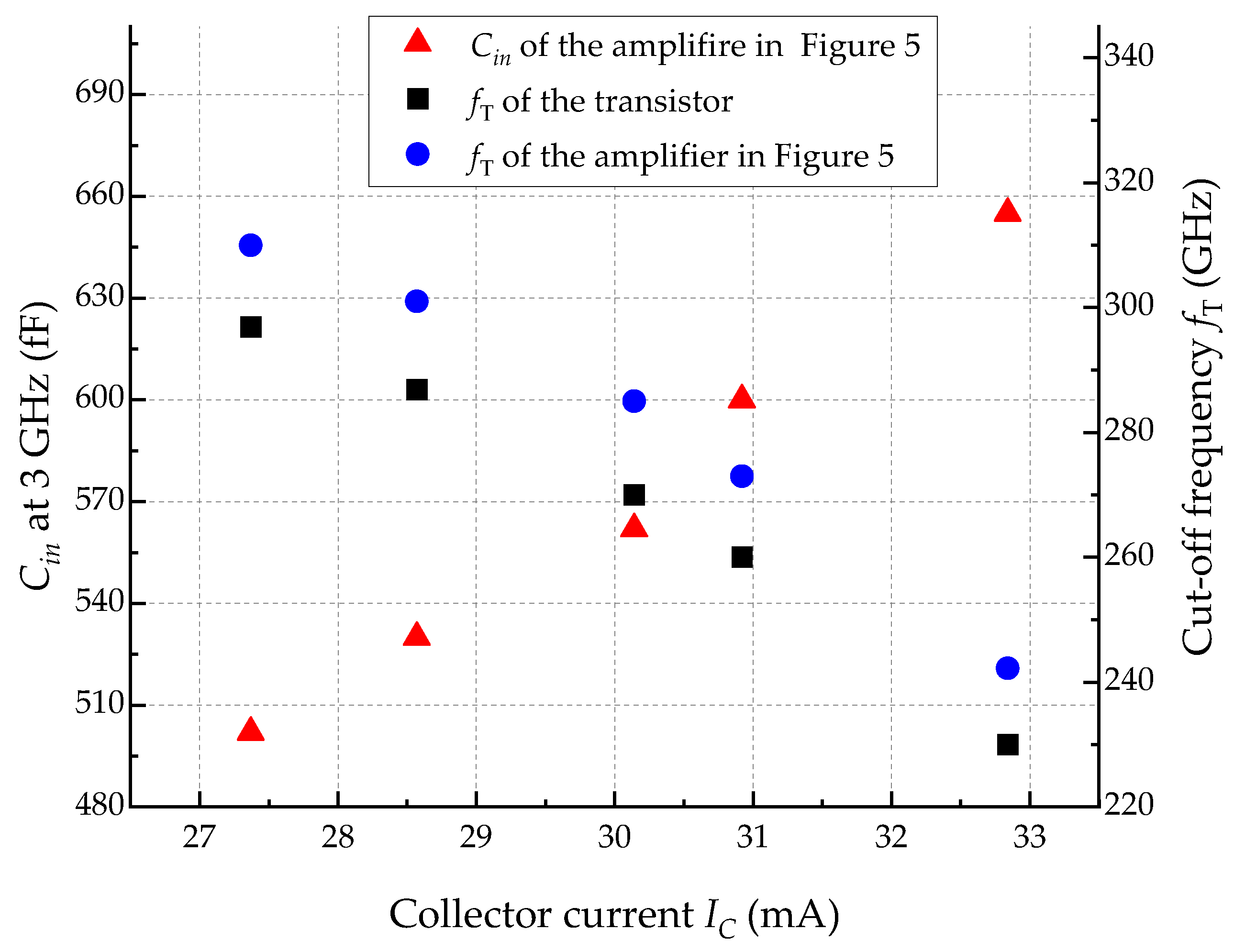
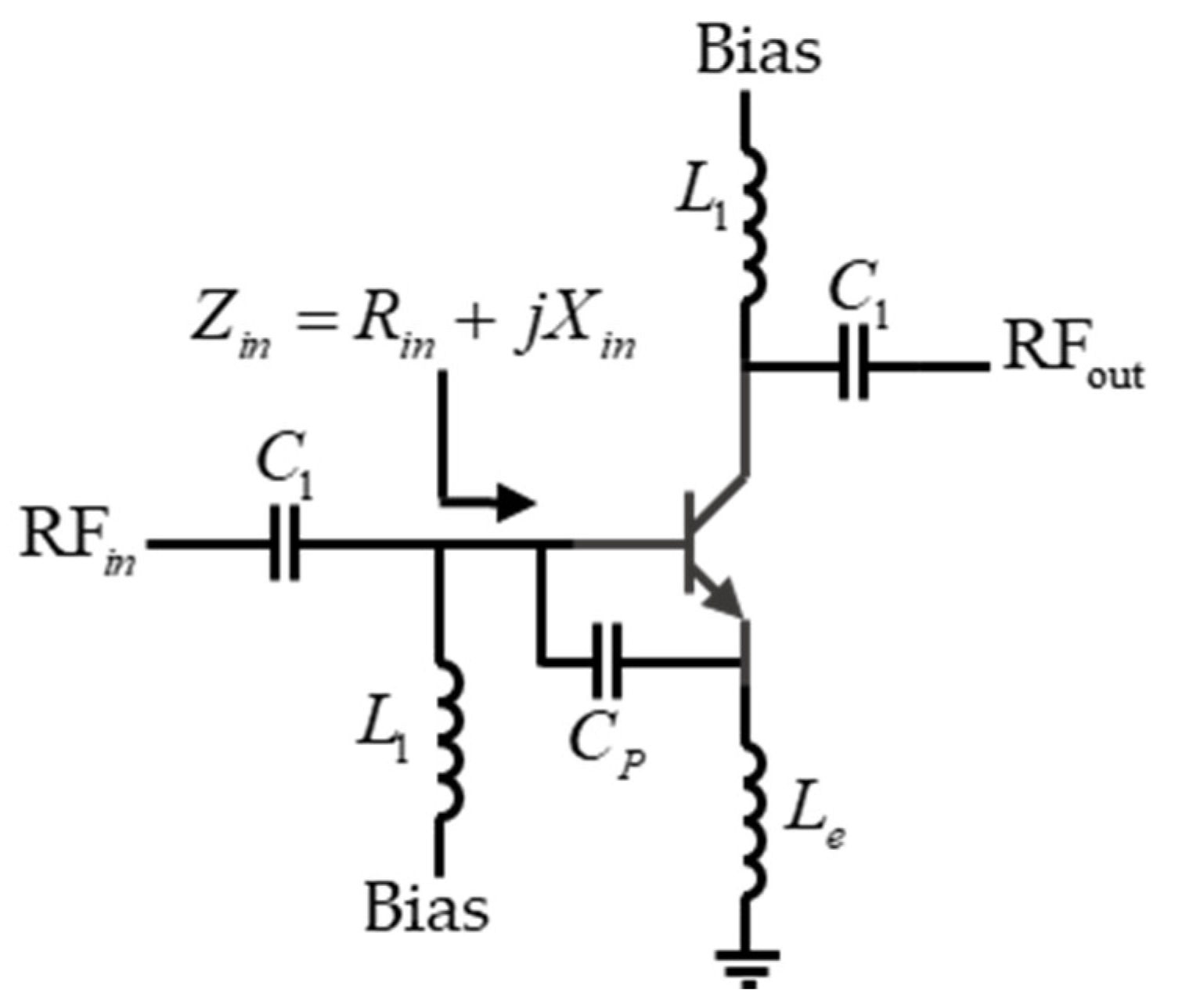
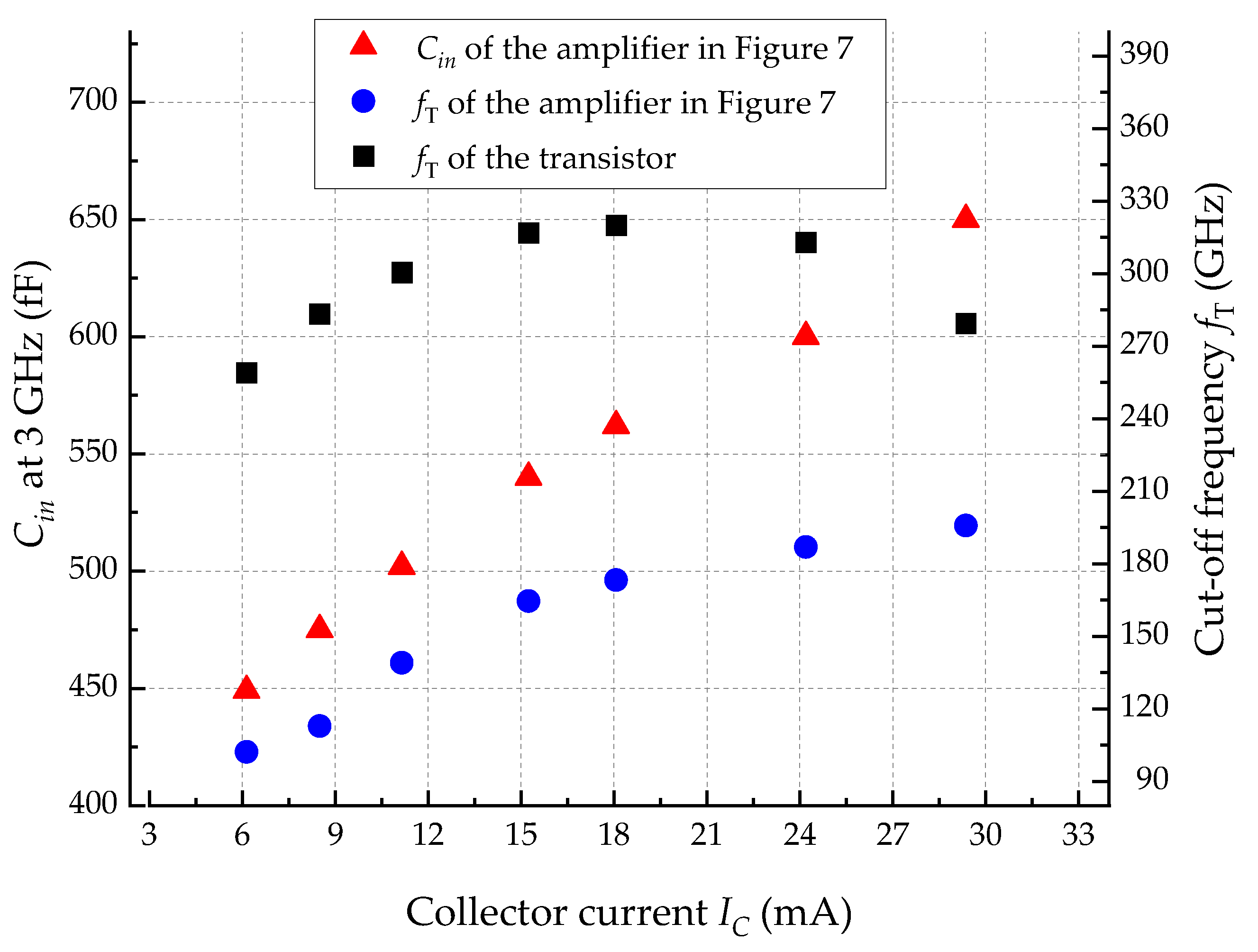
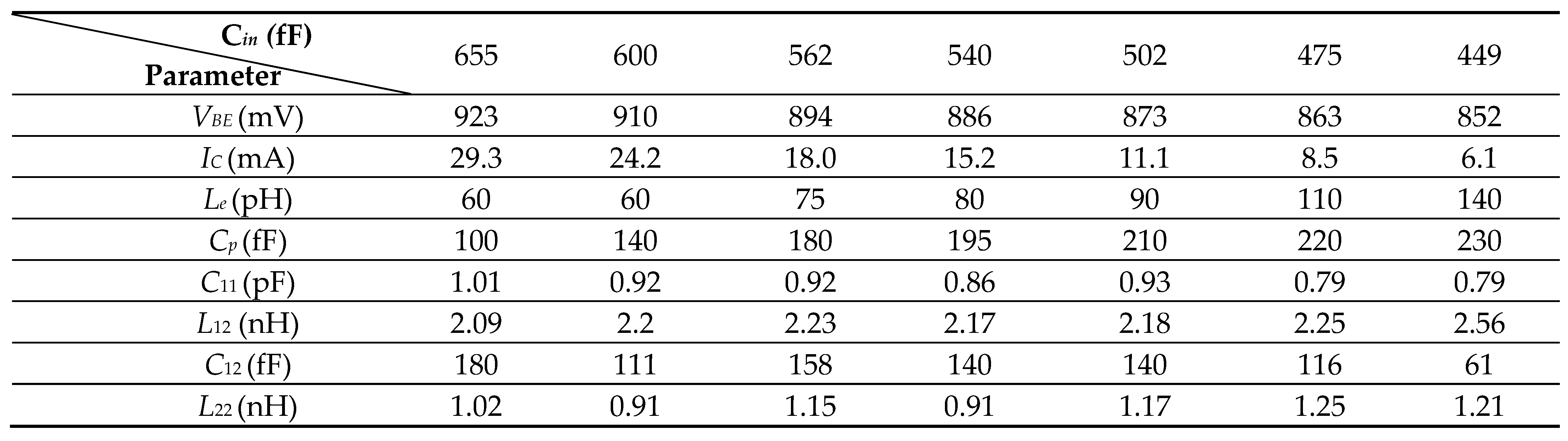
3.2. IMN for Low-Power Applications

In any UWB receiver, the amplifier connected to the antenna should present an input impedance close to 50 Ω across the entire frequency band for a maximum power transfer. The inductor-degenerated topology is a commonly used technique [28] for amplifiers using bipolar junction transistors (BJT) [29] and field-effect transistors (FET) [30]. Figure 5 shows the frequently used common emitter amplifier with a degeneration inductor Le to obtain the required input resistance for narrowband [29] and wideband matching [10]. Here, C1 serves as a DC blocking capacitor, and L1 is an RF choke to isolate the biasing circuit from the RF port. We demonstrate the designs of the input matching networks based on SRFT for different bias conditions and circuit topologies using GlobalFoundries 90nm BiCMOS technology.
For low-power applications, the circuit's input reactance sets the lower power consumption limit. When we reduce the power consumption by decreasing the base-to-emitter voltage applied to the BJT, the base-emitter junction capacitor (Cbe) becomes smaller, resulting in a smaller Cin (or a bigger absolute value of input reactance) and making it more challenging to find an IMN solution at the input. As demonstrated by Bode [31] and Fano [3], there is a physical limitation on broadband impedance matching of a load. Matthaei et al. expounded on the limitation and applied it to an input impedance Zin modelled by a parallel RC network [32]. The limitation indicates that, in order to attain a viable IMN solution within a defined bandwidth, a boundary exists on both the input Zin, resistance and reactance components, and the minimum achievable reflection coefficient Γ i n . In this circuit, when Cbe is smaller than the lower limit, we can no longer find a feasible IMN solution.
To examine the lowest power consumption for the inductive degeneration topology shown in Figure 5 and ensure the circuit has sufficiently high cut-off frequency fT to cover the 3.1 – 10.6 GHz band, Figure 6 shows the equivalent Cin at 3 GHz, the fT of the transistor, and the fT of the amplifier (with Le in the range of 30 – 40 pH) at different collector currents IC. The transistor used in the simulation has a length and width of 90 nm and 10 μm, respectively, and its collector is biased at 1.0 V. To ensure that we can obtain a feasible IMN solution, providing Γ i n below −10 dB over 3.1 – 10.6 GHz, we start with the collector current IC = 32.8 mA, at which Cin is about 650 fF, as suggested in [9]. As expected, the reduction in the collector current decreases the equivalent input capacitance Cin at 3 GHz due to the reduction of Cbe. The lowest collector current for a feasible IMN solution is at IC = 27.4 mA. Further reducing Cin is restricted by the physical limitation mentioned by Bode [31] and Fano [3]. The Rin of this circuit exhibits frequency-dependent variations due to the inherent characteristics of the BJT transistor in this technology. The intrinsic base resistance varies from approximately 50 Ω to 17 Ω across the frequency band of interest. The adjustment of this variation around 50 Ω with the assistance of Le poses an additional challenge in the quest for an IMN compared to a circuit that provides a constant 50 Ω over the bandwidth. In addition, comparing the circuit's cut-off frequency (fT) and the transistor's fT at these bias points indicates that the emitter degeneration inductor Le enhances the fT of the circuit slightly and follows the fT of the transistor.
To further reduce the power consumption, Cin is to be established by adding a capacitor Cp in parallel at the amplifier input, as shown in Figure 7. Incorporating a Cp mitigates variations in Rin with respect to frequency as it places in parallel with the intrinsic impedance of the transistor. This arrangement brings Rin into closer proximity to 50 Ω. When reducing the collector current IC, we adhere to essential criteria: (1) ensuring the IMN remains below −10 dB across the bandwidth and (2) maintaining the circuit's fT above 100 GHz to ensure having the bandwidth up to 10.6 GHz. Cp and Le were adjusted to address Rin and fT carefully to meet this requirement. Figure 8 shows the equivalent Cin at 3 GHz, the cut-off frequencies fT of the transistor and the amplifier (with Le in the range of 60 – 140 pH) at different collector currents IC. It is observed that, although adding Cp decreases the fT of the amplifier, we can further reduce the collector current IC to 6.1 mA, which is an 81.3% reduction from the initial IC = 32.8 mA while maintaining the fT at around 100 GHz. More decrease in collector current IC would yield a circuit with a reduced fT or a Γ i n surpassing −10 dB. Table 1 shows the component values of the IMN, Cp and Le for the bias conditions of the base-to-emitter voltage VBE and the collector current IC in Figure 8.

4. Conclusions

We demonstrated that the simplified real frequency technique SRFT is a highly efficient design method for UWB impedance matching networks (IMNs), which provides solutions with the minimum component count in the IMN. On the other hand, we also show that not all optimal reflection-coefficient responses obtained with the SRFT can be assured to be feasible or synthesizable. The choice of the optimization method and the initial guess are essential for uncovering solutions in RFT-based methodologies. With local optimization, which is usually employed by the RFT methods, an improper initial point can result in a solution that is optimal in a mathematical sense but is physically infeasible with components such as capacitors and inductors. On the other hand, local optimization methods converge fast, thus allowing for exhaustive search with various initial points. Such searches are not feasible with global optimization methods, which are slower and more difficult to steer through an initial guess. Nonetheless, there exists an opportunity for further investigation to rigorously define the underlying SRFT model features leading to infeasible solutions, thereby providing guidelines for the selection of the initial guess as well as the formulation of constraints to steer the optimization away from such solutions. Finally, we have also demonstrated that the SRFT provides a powerful tool to design feasible IMN for low-power applications. This paper demonstrates a UWB IMN solution with an 81.3% power reduction and an amplifier fT at around 100 GHz.

References

  1. Fontana, R.J. Recent system applications of short-pulse ultra-wideband (UWB) technology. IEEE Trans. Microwave Theory Tech. 2004, 52, 2087–2104. [Google Scholar] [CrossRef]
  2. Yarman, B.S. Real frequency techniques a historical review. In Design of Ultra Wideband Antenna Matching Networks, Yarman, B. S. Ed.; Publisher: Springer Science+Business Media B. V., 2008; pp. 1–8. [Google Scholar]
  3. Fano, F.M. Theoretical limitations on the broadband matching of arbitrary impedances. J. Franklin Inst. 1950, 249, 57–83. [Google Scholar] [CrossRef]
  4. Youla, D.C. A new theory of broadband matching. IEEE Trans. Circuit Theory 1964, CT-l 1, 30–50. [Google Scholar] [CrossRef]
  5. Carlin, H.J. A new approach to gain-bandwidth problems. IEEE Trans. Circuits Syst. 1977, CAS-24, 170–175. [Google Scholar] [CrossRef]
  6. Carlin, H.J.; Amstutz, P. On optimum broadband matching. IEEE Trans. Circuits Syst. 1981, CAS-28, 401–405. [Google Scholar] [CrossRef]
  7. Breed, G. Improving the bandwidth of simple matching networks. Summit Technical Media, LLC. 2008, 56–60. [Google Scholar]
  8. Yang, H.; Kim, K. Ultra-wideband impedance matching technique for resistively loaded vee dipole antenna. IEEE Trans. Antennas Propagat. 2013, 66, 5788–5792. [Google Scholar] [CrossRef]
  9. Bevilacqua, A.; Niknejad, A. M. An ultrawideband CMOS low-noise amplifier for 3.1–10.6-GHz wireless receivers. IEEE J. Solid-State Circuits 2004, 39, 2259–2268. [Google Scholar] [CrossRef]
  10. Ismail, A.; Abidi, A.A. A 3–10-GHz low-noise amplifier with wideband LC-ladder matching network. IEEE J. Solid-State Circuits 2004, 39, 2269–2277. [Google Scholar] [CrossRef]
  11. Zhao, C.; Duan, D.; Xiong, Y.; Liu, H.; Yu, Y.; Wu, Y.; Kang, K. A K-/Ka-band broadband low-noise amplifier based on the multiple resonant frequency technique. IEEE Trans. Circuits Syst. I 2022, 69, 3202–3211. [Google Scholar] [CrossRef]
  12. Zailer, E.; Belostotski, L.; Plume, R. Wideband LNA noise matching. IEEE J. Solid-State Circuits Lett. 2020, 3, 62–65. [Google Scholar] [CrossRef]
  13. Carlin, H.J.; Yarman, B.S. The double matching problem: Analytic and real frequency solutions. IEEE Trans. Circuits Syst. 1983, 30, 15–28. [Google Scholar] [CrossRef]
  14. Fettweis, A. Parametric representation of Brune functions. Int. J. Circuit Theory and Appl. 1979, 7, 113–119. [Google Scholar] [CrossRef]
  15. Yarman, B.S.; Carlin, H.J. A simplified "real frequency" technique applied to broad-band multistage microwave amplifiers. IEEE Trans. Microw. Theory Tech. 1982, 30, 2216–2222. [Google Scholar] [CrossRef]
  16. Carlin, H.J.; Civalleri, P. On flat gain with frequency-dependent terminations. IEEE Trans. Circuits Syst. 1985, 32, 827–839. [Google Scholar] [CrossRef]
  17. Jarry, P.; Beneat, J.N. Microwave Amplifier and Active Circuit Design Using the Real Frequency Technique; Publisher: John Wiley & Sons, Inc: Hoboken, New Jersey, 2016. [Google Scholar]
  18. Wu, D.Y.-T.; Mkadem, F.; Boumaiza, S. Design of a Broadband and Highly Efficient 45W GaN Power Amplifier via Simplified Real Frequency Technique. In Proceedings of the IEEE MTT-S International Microwave Symposium; 2010. [Google Scholar]
  19. Carlin, H.J. The scattering matrix in network theory. IRE Trans. Circuit Theory, 1956, 88–97. [Google Scholar] [CrossRef]
  20. Limand, J.S.; Park, D.C. A modified Chebyshev bandpass filter with attenuation poles in the stopband. IEEE Trans. Microw. Theory Tech. 1997, 45, 898–904. [Google Scholar]
  21. Yeung, L.K.; Wu, K.-L. A compact second-order LTCC bandpass filter with two finite transmission zeros. IEEE Trans. Microw. Theory Tech. 2003, 51, 337–341. [Google Scholar] [CrossRef]
  22. Yarman, B.S.; Fettweis, A. Computer-aided double matching via parametric representation of Brune functions. IEEE Trans. CAS 1990, 37, 212–222. [Google Scholar] [CrossRef]
  23. Dai, Z.; He, S.; You, F.; Peng, J.; Chen, P.; Dong, L. A new distributed parameter broadband matching method for power amplifier via real frequency technique. IEEE Trans. Microw. Theory Tech. 2015, 63, 449–458. [Google Scholar] [CrossRef]
  24. Lera, G.; Pinzolas, M. Neighborhood based Levenberg–Marquardt algorithm for neural network training. IEEE Trans. Neural Networks. 2002, 13, 1200–1203. [Google Scholar] [CrossRef] [PubMed]
  25. Sengül, M. Design of practical broadband matching networks with lumped elements. IEEE Trans. Circuits Syst.—II 2013, 60, 552–556. [Google Scholar] [CrossRef]
  26. Yegin, K.; Martin, A.Q. On the design of broadband loaded wire antennas using the simplified real frequency technique and a genetic algorithm. IEEE Trans. Antennas Propagat. 2003, 51, 220–228. [Google Scholar] [CrossRef]
  27. Gerkis, A.N. Broadband impedance matching using the real frequency network synthesis technique. Applied Microwave and Wireless. 1998, 26–36. [Google Scholar]
  28. Bellomo, A.F. Gain and noise considerations in RF feedback amplifier. IEEE J. Solid-State Circuits 1968, SSC-3, 290–294. [Google Scholar] [CrossRef]
  29. Meyer, R.G.; Mack, W.D. A 1-GHz BiCMOS RF front-end IC. IEEE J. Solid-State Circuits 1994, 29, 350–355. [Google Scholar] [CrossRef]
  30. Shaeffer, D.K.; Lee, T.H. A 1.5-V, 1.5-GHz CMOS low noise amplifier. IEEE J. Solid-State Circuits 1997, 32, 745–759. [Google Scholar] [CrossRef]
  31. Bode, H.W. Network Analysis and Feedback Amplifier Design; Publisher: D. Van Nostrand Co.: New York, N.Y., 1945; pp. 350–371. [Google Scholar]
  32. Matthaei, G.; Young, L.; Jones, E.M.T. Microwaves Filters, Impedance-Matching Networks, and Coupling Structures; Publisher: McGraw-Hill: New York, 1985. [Google Scholar]
Preprints 97715 g001
Figure 1. Matching an arbitrary load impedance ZL to a source impedance ZS.
Figure 1. Matching an arbitrary load impedance ZL to a source impedance ZS.
Preprints 97715 g001
Preprints 97715 g005
Figure 5. Inductively degenerated common-emitter amplifier.
Figure 5. Inductively degenerated common-emitter amplifier.
Preprints 97715 g005
Preprints 97715 g006
Figure 6. The equivalent input capacitance Cin (▲) at 3 GHz and the fT (●) of the inductive degeneration common-emitter amplifier in Figure 5 with Le in the range of 30 – 40 pH and the fT (■) of the transistor at different collector currents IC. The transistor used in the simulation has a length and width of 90 nm and 10 μm, respectively, and its collector is biased at 1.0 V.
Figure 6. The equivalent input capacitance Cin (▲) at 3 GHz and the fT (●) of the inductive degeneration common-emitter amplifier in Figure 5 with Le in the range of 30 – 40 pH and the fT (■) of the transistor at different collector currents IC. The transistor used in the simulation has a length and width of 90 nm and 10 μm, respectively, and its collector is biased at 1.0 V.
Preprints 97715 g006
Preprints 97715 g007
Figure 7. An inductively degenerated common-emitter amplifier with a capacitor Cp connected in parallel to the input of the amplifier.
Figure 7. An inductively degenerated common-emitter amplifier with a capacitor Cp connected in parallel to the input of the amplifier.
Preprints 97715 g007
Preprints 97715 g008
Figure 8. The equivalent input capacitance Cin (▲) at 3 GHz and the fT (●) of the inductive degeneration common-emitter amplifier with CP and Le in Figure 7 and the fT (■) of the transistor at different collector currents IC. The transistor used in the simulation has a length and width of 90 nm and 10 μm, respectively, and its collector is biased at 1.0 V.
Figure 8. The equivalent input capacitance Cin (▲) at 3 GHz and the fT (●) of the inductive degeneration common-emitter amplifier with CP and Le in Figure 7 and the fT (■) of the transistor at different collector currents IC. The transistor used in the simulation has a length and width of 90 nm and 10 μm, respectively, and its collector is biased at 1.0 V.
Preprints 97715 g008
Table 1. Component values of the IMN, Le, and Cp for the bias conditions in Figure 8.
Table 1. Component values of the IMN, Le, and Cp for the bias conditions in Figure 8.
Preprints 97715 i001
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated