Numerical Investigation and Efficiency Analysis of Engine-Airframe Integration High speed Vehicle based on Fragment Computation

The performance analysis of the internal/external flows around a high speed vehicle in near-space is fundamental and critical to the configuration and structure design for high speed aircraft. In this paper, the two-dimensional coupled implicit Reynolds Average Navier-Stokes (RANS) solver and RNG k–ε turbulence model is employed to numerically simulate the flow field of an integrated high speed vehicle. The flow field are divided three parts to solve separately and compared with that solved by integrated simulation. The flow field are decomposed to save computer storage and simulation time. The first part is inlet/isolator, the second part is combustion chamber and the third is nozzle. In the computation process, the outlet condition of isolator is endowed to the inlet boundary of combustion chamber and the outlet boundary of combustion chamber is endowed to the inlet boundary of nozzle, then the whole flow field of integrated high speed vehicle is solved. Aerodynamic characteristic of fragment-computation and integration-computation is comparatively analyzed at different angles of attack, the results show that the maximum deviation of lift coefficient obtained by fragment-computation is less than 3% compared with that by integration, the maximum deviation of drag coefficient fragment-computation is less than 5% compared with that by integration, while pitching moment coefficient deviation less than 12%. However, for simulation time-consumption, the time used by fragment-computation reduces 45% compared with integration-computation. Meanwhile, by components force analysis, it can be concluded that the aerodynamic property of inlet/isolator can been obtained separately and hardly effected by other parts.

Keywords:

Subject: Engineering - Aerospace Engineering

1. Introduction

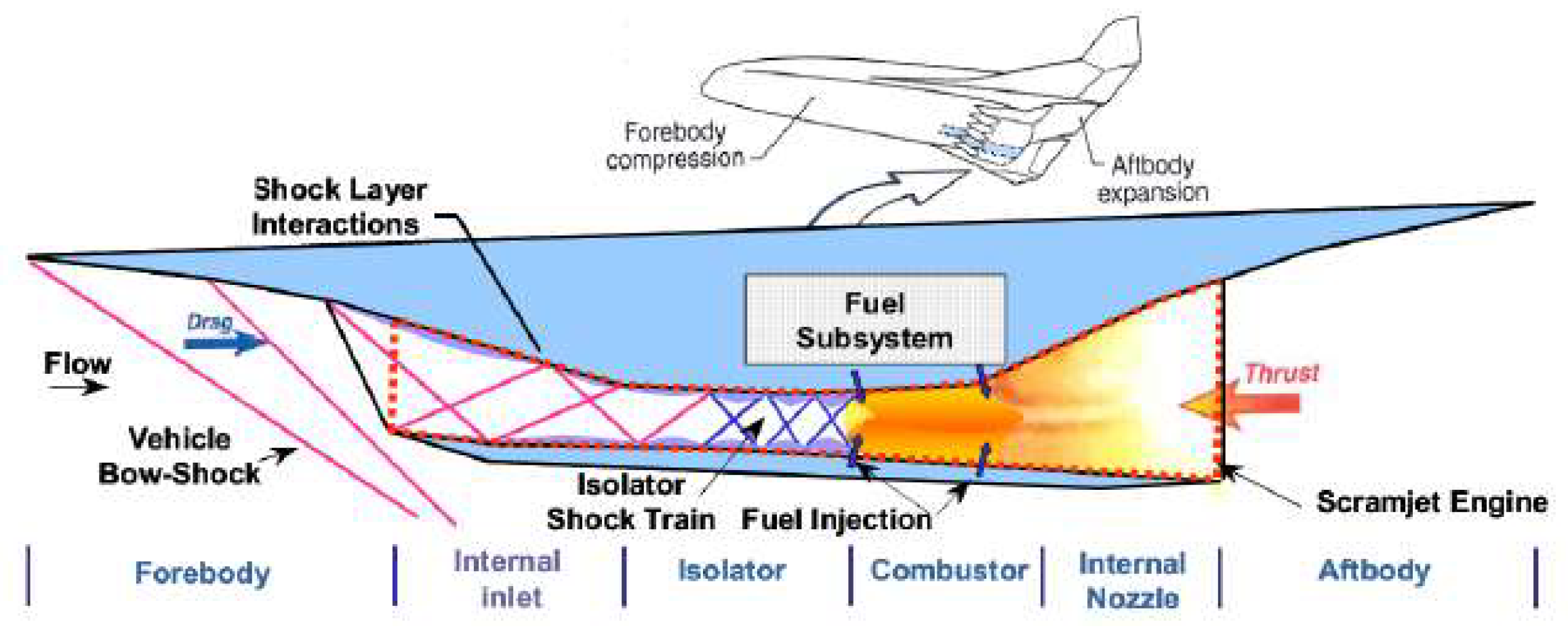
High speed vehicles are rapidly developing in the aeronautical and astronautical realm. The successful flight tests of X-43A[1] and X-51A[2] have attracted widespread attention in high speed airframe/engine integration vehicle. Figure 1 demonstrates the schematic of the typical integrated high speed vehicle[3]. Denman et al[4] implement a series of shock tunnel experiments with a rectangular to elliptical throat transition engine, and achieve the ignition and combustion of hydrocarbon fuels at a high Mach number. To evaluate the effects of trips on oscillatory flows, GAO et al[5] conducted an experimental investigation on axisymmetric high speed inlet, the results indicate that trips exert substantial effects on oscillatory flows of high speed inlet, especially for unstart flows. These researches involve experimental facilities, models, fuels etc, which is complex, costly and time-consuming. Although the experimental tests have a relative high reliability, ground experimental facilities has costly expense and cannot simulate the real flight environment, it is necessary to employ computational fluid dynamic (CFD) method to gain important aerodynamic values and enhance research efficiency.

In recent years, CFD method becomes more and more widespread in high speed aerodynamic and can gain satisfactory values[6, 7]. Brad K.K[8] introduces a new approach to integrated vehicle design known as the top-down design methodology. Daniel Oliden[9] investigates the parametric effect of a high speed inlet using computational fluid dynamics. Han J. L[10] compares the performance of several eddy-viscosity turbulence models in computing supersonic nozzle exhaust flows using ANSYS Fluent. Huang et al[11] studies the effect of cavity location on combustion flow field for integrated high speed vehicle and analyzes the whole flow field characteristic using CFD method. Torrez[12] gives the design and evaluation methods in highly-integrated high speed vehicles, compares the numerical solutions and experimental data. To improve the compression efficiency and aerodynamic performance of inlet, Wang et al[13] use multistage optimization to design the shape morphing high speed inward-turning inlet based CFD, the numerical results demonstrate obvious decrease in flow non-uniformity and the total pressure loss. To achieve successful ignition and stable combustion in an ethylene-fueled scramjet, Shi et al[14] apply the hydrogen as the pilot fuel to ignite ethylene at low flight Mach numbers and investigate the flow characteristics, flame propagation characteristics and combustion stability by various strategies of fuel injections.

However, CFD method requires enough computer storage and long simulation time, how to effectively maintain accuracy and reduce simulation is still an imperative challenge. With super-computer emerging and developing, large-scale numerical simulation becomes feasible, nevertheless, computation resource is finite and expense is difficult to bear, so other method is in demand to explore to improve computation efficiency. Wang et al[15] propose a novel airframe/propulsion integration design method of high speed cruise aircraft, in order to evaluate the performance, the CFD method is used to perform numerical calculation on the design point, the results show a high level of compression efficiency and flow uniformity for the inlet, which enhances the design efficiency of high speed vehicle. Jiao et al[16] perform an unsteady viscous numerical simulation to study the starting process of a high speed nozzle coupled with a simplified inlet model, the impact of the initial backpressure on the pulse-starting characteristics of high speed nozzle-inlet is studied. The results present the intuitional flow phenomenon including separation bubbles, induced shock waves and shock train, specifically the wall pressure distribution, which can help us improve starting characteristics by optimization. To improve inlet performance, a fluidic method to control the high speed inlet external shock based on forebody secondary flow recirculation is proposed and verified by both experimental and numerical methods[17]. The obtained performances by CFD agree well with that by experiments. The predicted ramp shock basically overlaps the numerically obtained one, meanwhile, the numerical approach also provides additional information of the flowfield. Shape optimization is an effective way to upgrade the performance of high speed vehicles, more and more aerodynamic configurations are improved by CFD method because of its high efficiency and low cost[18]. A high speed inlet is optimized by using gradient-based searches informed by an adjoint flow solution, the results show that an undesirable shock is removed in the optimized inlet compared with the original geometry[19]. A parametric numerical study of aftbody design of airbreathing high speed vehicle is conducted using three-dimensional Euler simulation, the results show that large variation in the thrust-to-drag ratio highlights the criticality of the aftbody[20]. Reardon et al[21] apply computational fluid dynamics method to study the unstart problem in variable-geometry inlet, it was found that the quasi-steady CFD was able to correctly predict the started or unstarted operating mode for the different cowl angles considered.

From the public literature, the existing researches mainly focus on the forebody-inlet, combustor and nozzle, independently. Considering the flow and combustion calculation workload of integrated model is large and difficult and the divergence is prone to occur. The main reason is that the problem of shock wave interference for forebody-inlet is more prominent, the iterative period for solving the shock wave is long. For the combustor, the combustion process not only involves the chemical reactions, but also embodies complex flow problems such as shock interference, fuel evaporation and multiphase, which makes the numerical simulation of combustion camber more complicated and difficult. The nozzle mainly expands at a supersonic speed, as a result, the calculation is relatively easy. How to improve the calculation efficiency has become a difficult point while considering the entire integrated high speed vehicle in the full-state numerical simulation.

Based on the above discussion, a multiple fragment computation method is proposed in regimes of high speed airframe/engine integration vehicle. Considering the high speed flow trait, physical variables are extrapolated from the internal flow, therefore, the high speed flow field can be divided three parts, shockwave-solving need more simulation time for inlet and combustor, and expansion wave can be solved rapidly for nozzle. The outlet parameters of the isolator section from inlet are endowed to the inlet boundary conditions of combustion chamber, the condition of the exit of combustor serves as the inlet of nozzle. By the method, it can not only ensure the accuracy of the calculation, but also can classify and study the calculation according to characteristics of the internal flow and improve the efficiency by the distributed calculation of each component.

2. Governing Equations

The flow solver is a Reynolds Averaged Navier-Stokes (RANS) solver that utilizes finite volume approach. The governing equations are the compressible Navier-Stokes equations as follows,

\frac{\partial U}{\partial t} + \frac{\partial (E_{i} - E_{v})}{\partial x} + \frac{\partial (F_{i} - F_{v})}{\partial y} + \frac{\partial (G_{i} - G_{v})}{\partial z} = 0

(1)

Where, U is conservation scalar quantity,

E_{i}, F_{i}, G_{i}

represent the flux quantity at x, y and z direction, respectively. The subscript i represents inviscid flux vector and v is viscid flux vector.

U = {[ρ, ρ u, ρ v, ρ w, ρ e]}^{T} E_{i} = [\begin{matrix} ρ u \\ ρ u^{2} + p \\ ρ u v \\ ρ u w \\ (ρ e_{t} + p) u \end{matrix}], F_{i} = [\begin{matrix} ρ v \\ ρ u v \\ ρ v^{2} + p \\ ρ v w \\ (ρ e_{t} + p) v \end{matrix}], G_{i} = [\begin{matrix} ρ w \\ ρ u w \\ ρ v w \\ ρ w^{2} + p \\ (ρ e_{t} + p) w \end{matrix}] E_{v} = [\begin{matrix} 0 \\ τ_{x x} \\ τ_{x y} \\ τ_{x z} \\ u τ_{x x} + v τ_{x y} + w τ_{x z} + q_{x} \end{matrix}], F_{v} = [\begin{matrix} 0 \\ τ_{x y} \\ τ_{y y} \\ τ_{y z} \\ u τ_{y x} + v τ_{y y} + w τ_{y z} + q_{y} \end{matrix}], G_{v} = [\begin{matrix} 0 \\ τ_{x z} \\ τ_{y z} \\ τ_{z z} \\ u τ_{z x} + v τ_{z y} + w τ_{z z} + q_{z} \end{matrix}]

Where,

τ_{x x} = 2 μ \frac{\partial u}{\partial x} - \frac{2}{3} μ \nabla \cdot V, τ_{y y} = 2 μ \frac{\partial v}{\partial y} - \frac{2}{3} μ \nabla \cdot V, τ_{z z} = 2 μ \frac{\partial w}{\partial z} - \frac{2}{3} μ \nabla \cdot V, \begin{array}{l} τ_{x y} = τ_{y x} = μ (\frac{\partial u}{\partial y} + \frac{\partial v}{\partial x}), τ_{z x} = τ_{x z} = μ (\frac{\partial u}{\partial z} + \frac{\partial w}{\partial x}), τ_{y z} = τ_{z y} = μ (\frac{\partial v}{\partial z} + \frac{\partial w}{\partial y}), \\ q_{x} = k \frac{\partial T}{\partial x}, q_{y} = k \frac{\partial T}{\partial y}, q_{z} = k \frac{\partial T}{\partial z}, e_{t} = \frac{p}{(γ + 1) ρ} + \frac{1}{2} (u^{2} + v^{2} + w^{2}) . \end{array}

Specific heat ratio is set as piecewise-polynomial. Sutherland formula is selected to calculate viscosity as follows,

c_{p} (T) = {\begin{cases} A_{1} + A_{2} T + A_{3} T^{2} + \dots T_{\min, 1} \leq T \leq T_{\max, 1} \\ B_{1} + B_{2} T + B_{3} T^{2} + \dots T_{\min, 2} \leq T \leq T_{\max, 2} \end{cases}

(2)

μ = μ_{0} {(\frac{T}{273.11})}^{1.5} \frac{273.11 + C}{T + C}

(3)

Supposing that ideal gas equation is established,

p = ρ R T

(4)

The governing equations are discretized and numerically integrated based on a finite-volume approach. The RNG k–ε turbulence model is employed to simulate the internal/external flow fields of the two-dimensional high speed vehicle. The second order spatially accurate upwind scheme with the advection upstream splitting method (AUSM) flux vector splitting is utilized and the standard wall functions are introduced to solve the near-wall region flow. The inlet and outlet boundary for the first part is assigned as “far-field” and pressure-outlet boundary condition, the inlet and outlet boundary of combustion chamber and nozzle are assigned as pressure-inlet and pressure-outlet condition, and the no-slip adiabatic conditions are assumed for the walls. Eddy-Dissipation turbulence-chemistry interaction model is applied to compute combustion process in this paper, and the hydrogen(H2) is selected as fuel in the simulation.

3. Physical Geometry and Grid Generation

A. Geometry Description

An airframe/engine integration high speed vehicle is designed in this paper, the external section of inlet has three compression wedge angles and the internal section has two. The upper shape of vehicle is parallel to the freestream at angle of attack

0^{\circ}

. The isolator is a constant-area section that is used to prevent the high pressure in the combustor from pushing forward into the high speed inlet. The engine adopts fractional combustion mode, the first and second stage combustors, see Figure 2. Four cavity flame holders are installed on the walls of the first and second stage combustors to simulate real engine configuration.

To obtain concrete design parameters, some hypotheses are put forward as:

(1)

M a_{\infty} = 6

, H=30km;

(2)

θ_{1} = 6^{\circ}

，

θ_{2} = 11^{\circ}

，

θ_{2} = 15^{\circ}

;

(3)

θ_{c o w l} = 7^{\circ}

;

Once the freestream condition and design requirement are given, the isentropy relations and oblique shock wave method is used to design the basic configuration of inlet. The oblique shock wave angle

β_{1}

meets the following relations,

t a n θ_{1} = \frac{M a_{\infty}^{2} {s i n}^{2} β_{1} - 1}{t a n β_{1} [\frac{γ + 1}{2} M a_{\infty}^{2} - (M a_{\infty}^{2} {s i n}^{2} β_{1} - 1)]}

(5)

\frac{p_{2}}{p_{1}} = 1 + \frac{2 γ}{γ + 1} (M a_{\infty}^{2} {s i n}^{2} β_{1} - 1)

(6)

M a_{1}^{2} = \frac{M a_{\infty}^{2} + \frac{2}{γ - 1}}{\frac{2 γ}{γ - 1} M a_{\infty}^{2} {s i n}^{2} β_{1} - 1} + \frac{M a_{\infty}^{2} - M a_{\infty}^{2} {s i n}^{2} β_{1}}{\frac{γ - 1}{2} M a_{\infty}^{2} {s i n}^{2} β_{1} + 1}

(7)

Where

θ_{1}, β_{1}

is turn angle and wave angle respectively at the first compression surface.

p_{1}, p_{2}

is the upward and downward pressure of oblique shock wave.

M a_{\infty}

is the freestream Mach number,

M a_{1}

is the Mach number that passes through the first oblique shock wave. Other oblique wave parameters can be solved by using the above method. Table 1 gives the main design parameters of the high speed integrated vehicle.

B.Grid Generation

A structured mesh is used for the configuration and generated by commercial software Gambit, the height of the first layer cell is 0.01mm to ensure the accuracy of the turbulent flow solution with the y+ less than 1 based on unit Reynolds number. The total mesh scale is 479,400, including 328,800 cells of inlet/isolator, 77000 cells of combustor, 73600 cells of nozzle as shown in Figure 2. The adjacent faces are defined as interface between different parts. The interfaces would be coupled by matching method to ensure the flow continuity.

Figure 3. Computational domain and grid detail for high speed vehicle.

4. Code Validation

In this section, the inlet/isolator model is numerically investigated and compared with experiment[22, 23]. The investigated subscale inlet model is a two-dimensional configuration with a width-to-height ratio of 3.5. The freestream Mach is 2.41, the unit Reynolds number is

5.07 \times 10^{7}

, the total pressure is 540 Kpa, the total temperature is 305 K, the given angle of attack of the freestream

α =

-10 deg. In this paper, the isolator is set at 79.3mm.

Figure 4. Main dimensions of the model.

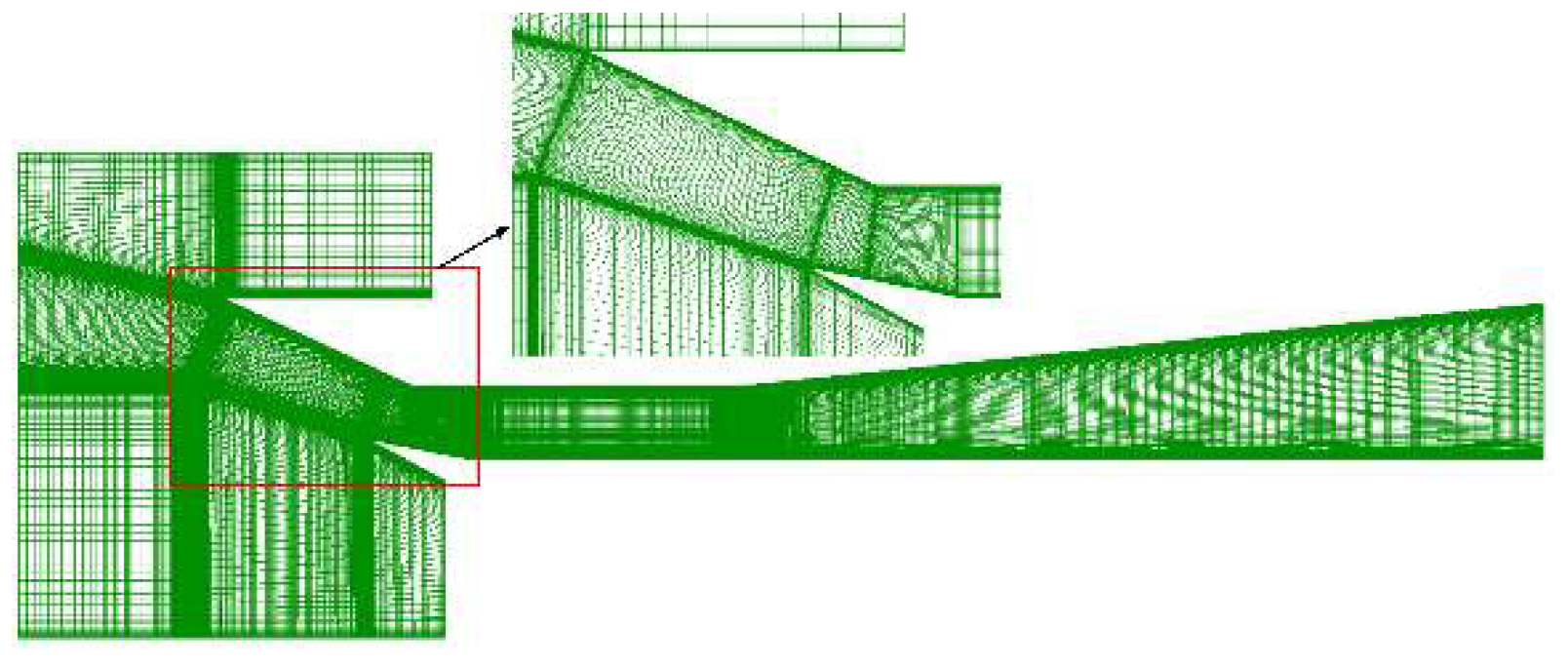
Figure 5. Computational grid.

A sort of structured grid is generated, in order to study the sensitivity analysis of grid on high speed inlet/isolator flow, four sets of grids are generated based on different height of first cell, the overall grid scale is

1150 \times 150

. The grids G1, G2, G3 and G4 are distinguished with

Δ y_{m i n}

(first layer cell height)

1 \times 10^{- 4} m

1 \times 10^{- 5} m

1 \times 10^{- 6} m

and

1 \times 10^{- 7} m

, respectively, the grid description is showed in Table 2.

Here, grid cell Reynolds number is computed as follows,

R e_{c e l l} = \frac{ρ_{\infty} u_{\infty} Δ y_{m i n}}{μ_{\infty}}

(8)

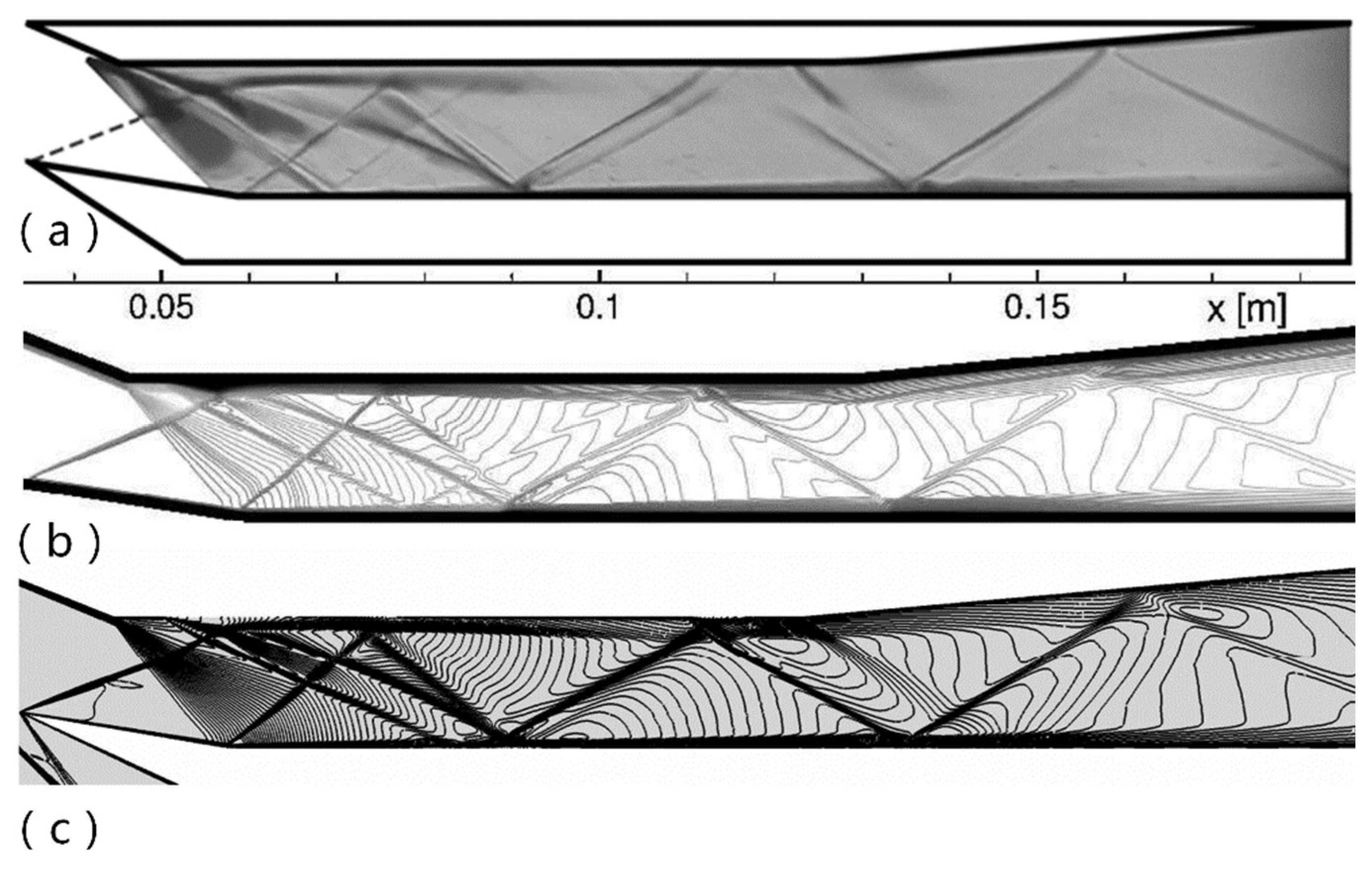
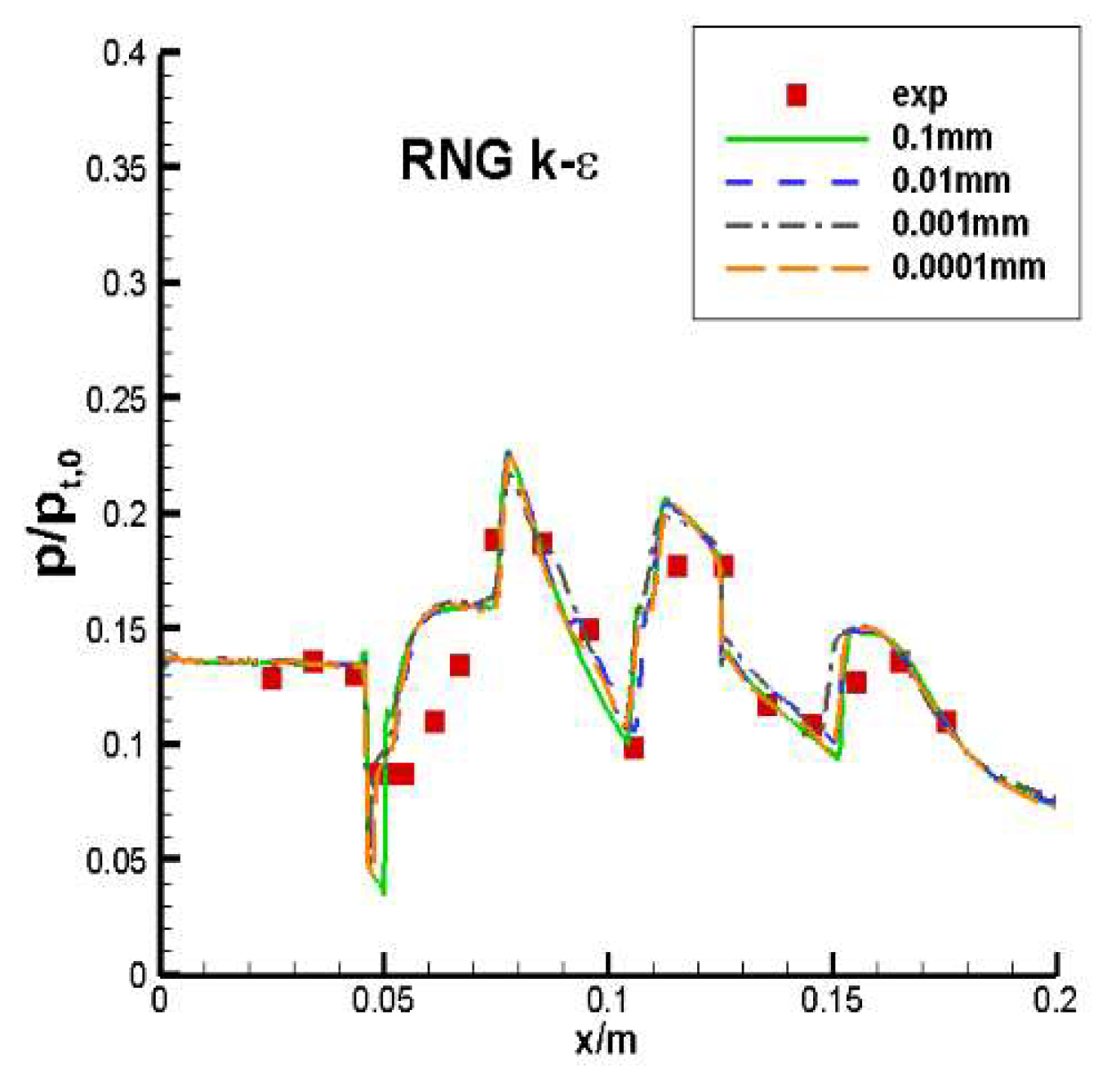
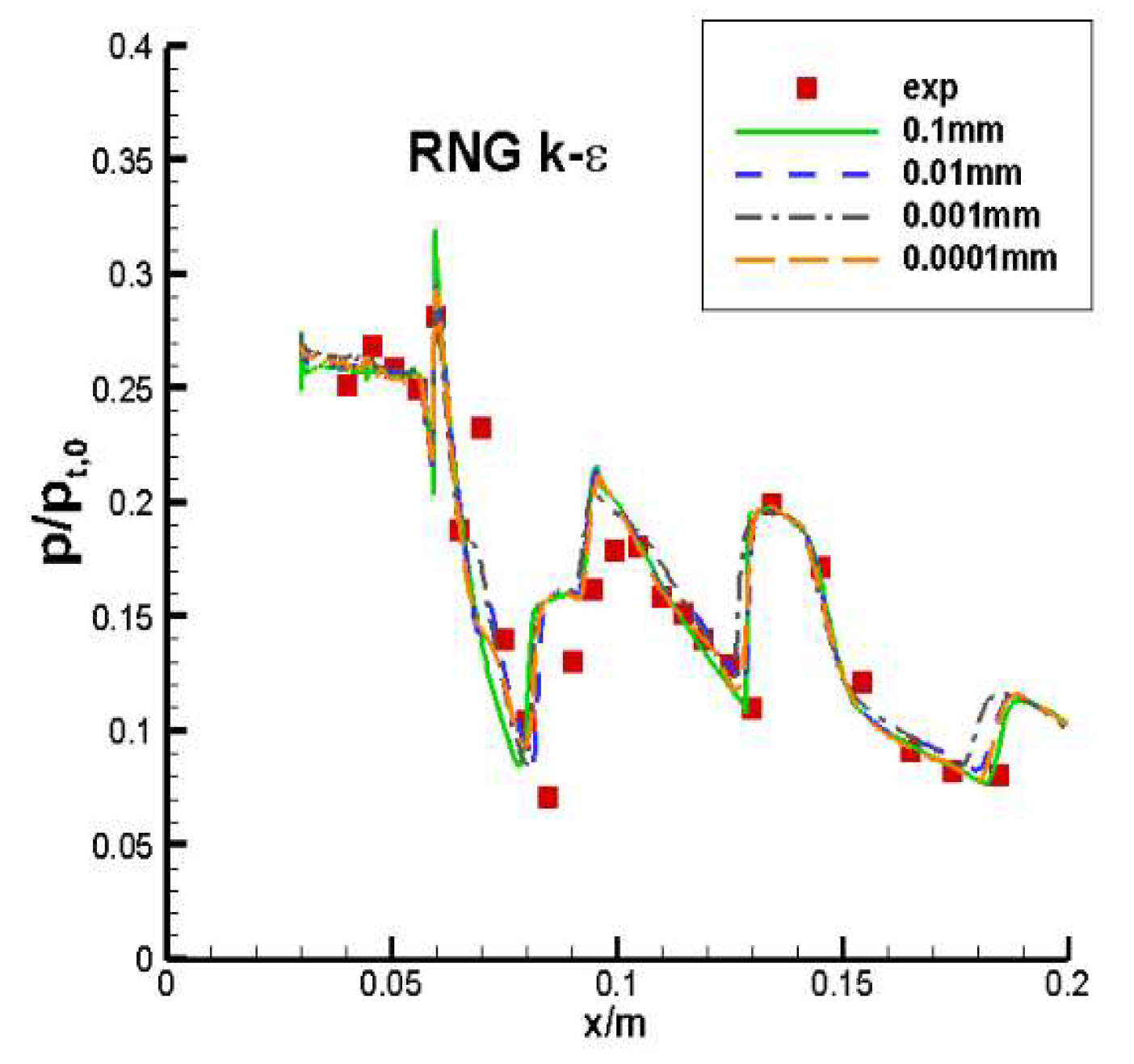
Figure 6 demonstrates the comparison of the experimental schlieren picture and numerical contour from literature and this paper. From the comparison, it illustrates that numerical method in this paper can get credible result close to experiment. Figure 7 presents the wall pressure distributions obtained by numerical simulation and wind tunnel experiments, where p/pt, 0 indicates the ratio of static pressure along the wall and the freestream total pressure. The results show the numerical data match well with measured values.

5. Result and Discussion

A. Time Conclusion

Numerical simulation is executed in the following hardware device: 8 cores intel-i7-4770@3.40-GHz. In this study, it is found that 8 cores parallel does not makes the computer compute efficiency to the utmost and 6 cores parallel can get higher computation efficiency, so 6 cores parallel computation, not 8 cores, is selected in this paper to complete computation and compare the simulation efficiency. In this paper, inviscid flow field also is solved for reference.

Table 3. Simulation time contrast of different computation method.

Cases	model	Courant number	Simulation time
Case1	Inviscid	0.5	450min
Case2	RNG k–ε-through	0.5	684min
Case3	RNG k–ε-fragment-through	0.5	376min
Case4	Reaction-through	0.5	~2950min
Case5	Reaction-fragment-through	0.5	~880min

Integration simulation need more storage and considerable simulation time, for ordinary personal computer, it is difficult to complete the integration flow field computation at large-scale grid because of its inadequate storage. However, if the computational domain is divided multiple fragments and each section is computed independently, it will occupy less storage, which can enhance efficiency and reduce the requirement of computation resource. In the simulation process, the lift coefficient and drag coefficient are plotted to monitor convergence. The courant number is kept 0.5 constantly. As is known, the convergence is determined by the flow feature for each section, for example, it need more iteration steps for shock wave solving and less steps for expansion wave. Through analysis, when it reaches 20000 iterations, the inlet/isolator domain achieves steady and the computation is finished and costs 233 minutes. The combustion chamber domain need 30000 iteration steps with 127 minutes and the nozzle only need 4000 iterations with 16 minutes. The simulation time of whole flow field based on fragment is 376 minutes. The simulation time reaches 684 minutes for integration computation with 40000 iterations. Therefore, it is cheerfully found that it will reduce 45% time by using fragment method.

B. Aerodynamic Characteristic

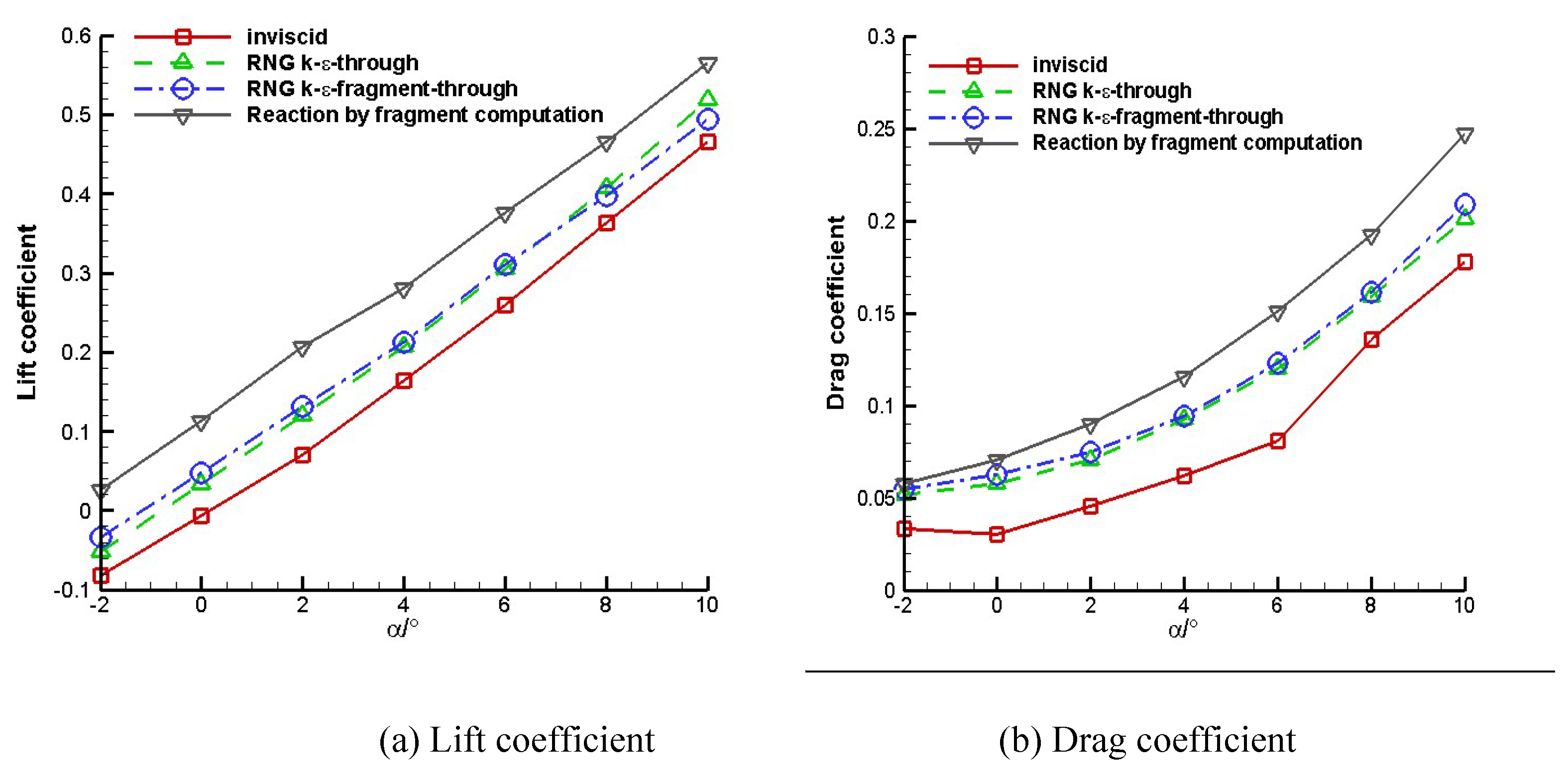
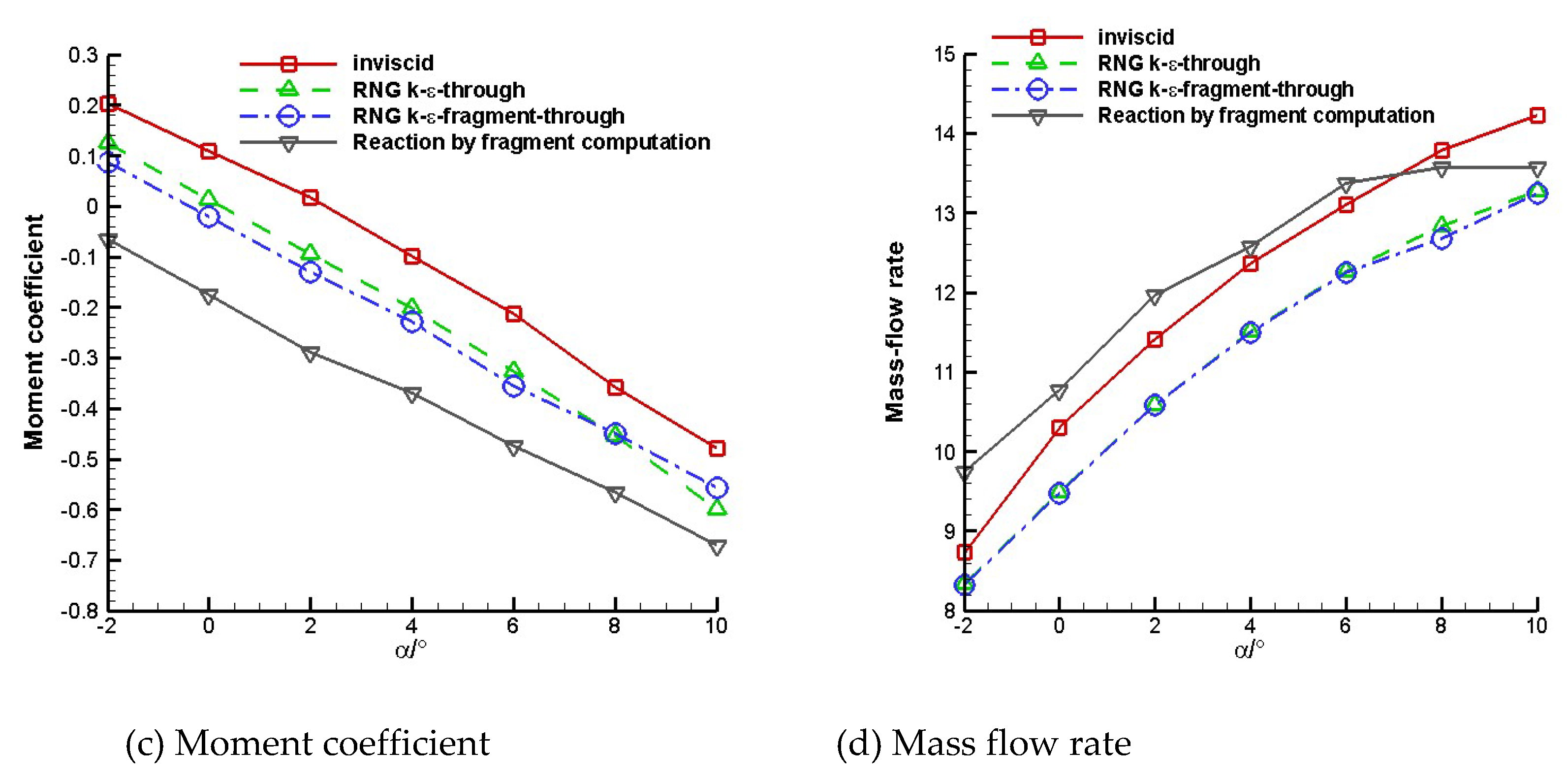
In order to systematically investigate the discrepancy of fragment computation and integration computation of the integrated high speed vehicle. The flow is analyzed at different angles of attack from -2° to 10° at 2-degree intervals. Figure 9(a)~Figure 9(d) present the comparisons of lift coefficient, drag coefficient, pitching moment coefficient and mass flow rate at different computation method, respectively. It is observed that the lift and drag coefficient curves obtained by fragment computation shows reasonably good agreement with the integration computation data, so, the fragment method can be used to solve the flow field of high speed vehicle commendably. The maximum error of lift coefficient by fragment computation is about 3% compared with that by integration computation and drag coefficient error is about 5%. Figure 9(c) shows that the moment coefficient has an obvious deviation but the maximum error is still less than 12%, which is reasonable for numerical simulation. By comparison, we can also find that viscosity has an important effect on aerodynamic characteristic of high speed vehicle, which makes the lift coefficient reduce about 20% and drag coefficient reduce 33%. Figure 9(c) shows that pitching moment coefficient obtained with viscosity decreases 50% than inviscid result. Meanwhile, viscosity makes the mass flow rate reduce, see in Figure 9(d), the reason is that viscosity increases the boundary layer thickness and diminishes the flow effective area.

C. Pressure distribution

1) Without reaction

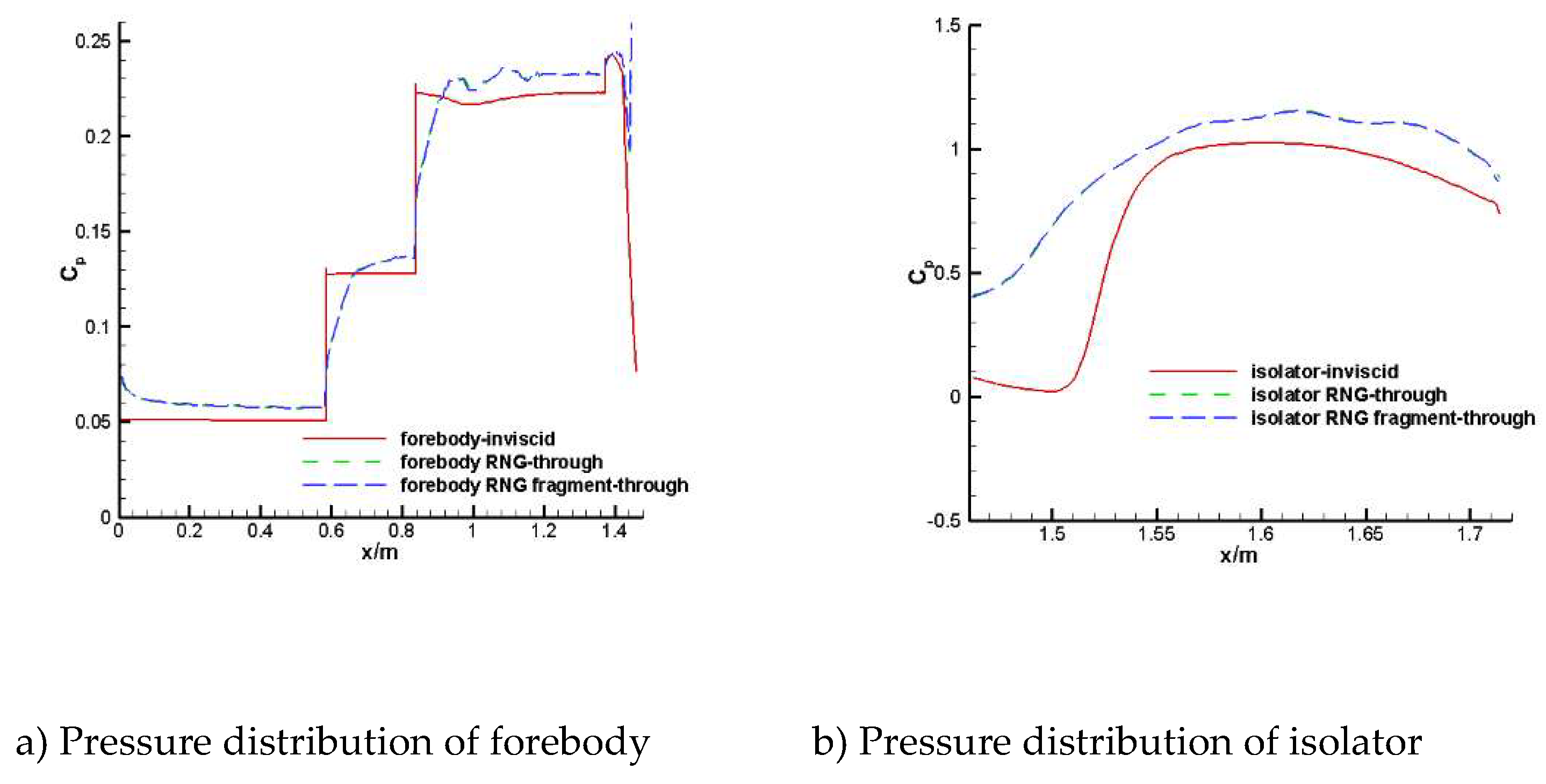
Figure 10 compares the pressure coefficient distribution of the upper surface of the aircraft from head to tail without considering combustion. It can be seen that the calculation results of inviscid and viscous are quite different. For the viscous results, the pressure distribution calculated by through is in good agreement with that calculated by fragment, and the main difference lies in the inlet of combustion chamber and the outlet of nozzle, which is mainly caused by the difference of inlet boundary conditions. From the lift-to-drag characteristics given in Figure 9, the influence on the overall aerodynamic force is very small.

Figure 11 gives a comparison of the pressure coefficient distribution from head to tail on the down-wall of the aircraft without considering combustion conditions. Similar to the pressure distribution on the upper surface, the inviscid and viscous calculation results present obvious distinction. The difference of viscosity calculation results is mainly near the inlet of combustion chamber and the outlet of nozzle, which is mainly caused by the difference of inlet boundary conditions. As a whole, it has little influence on the aerodynamic force of the whole aircraft, which proves the feasibility of using fragment calculation to obtain the aerodynamic performance and flow field distribution of the aircraft without combustion.

2)With reaction

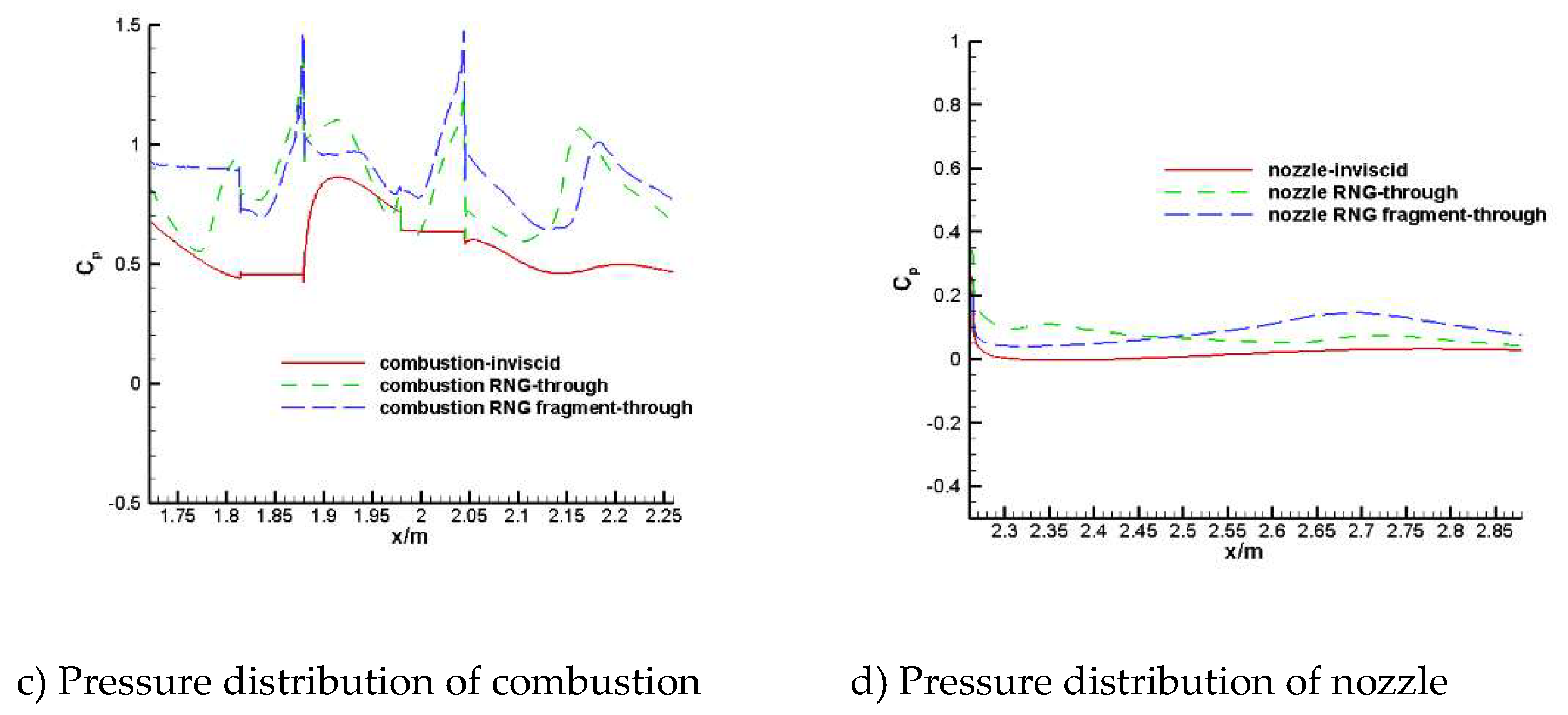
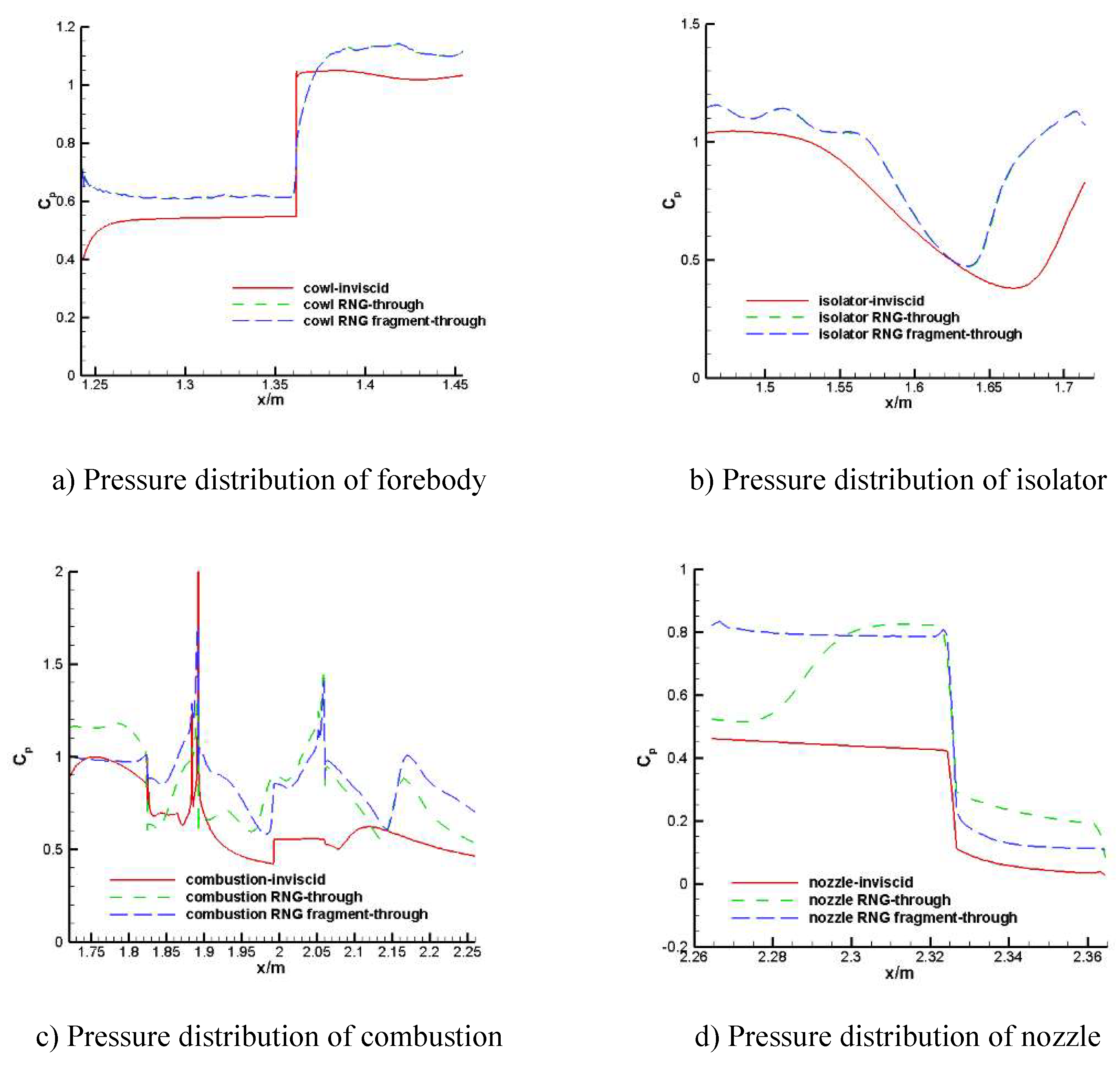
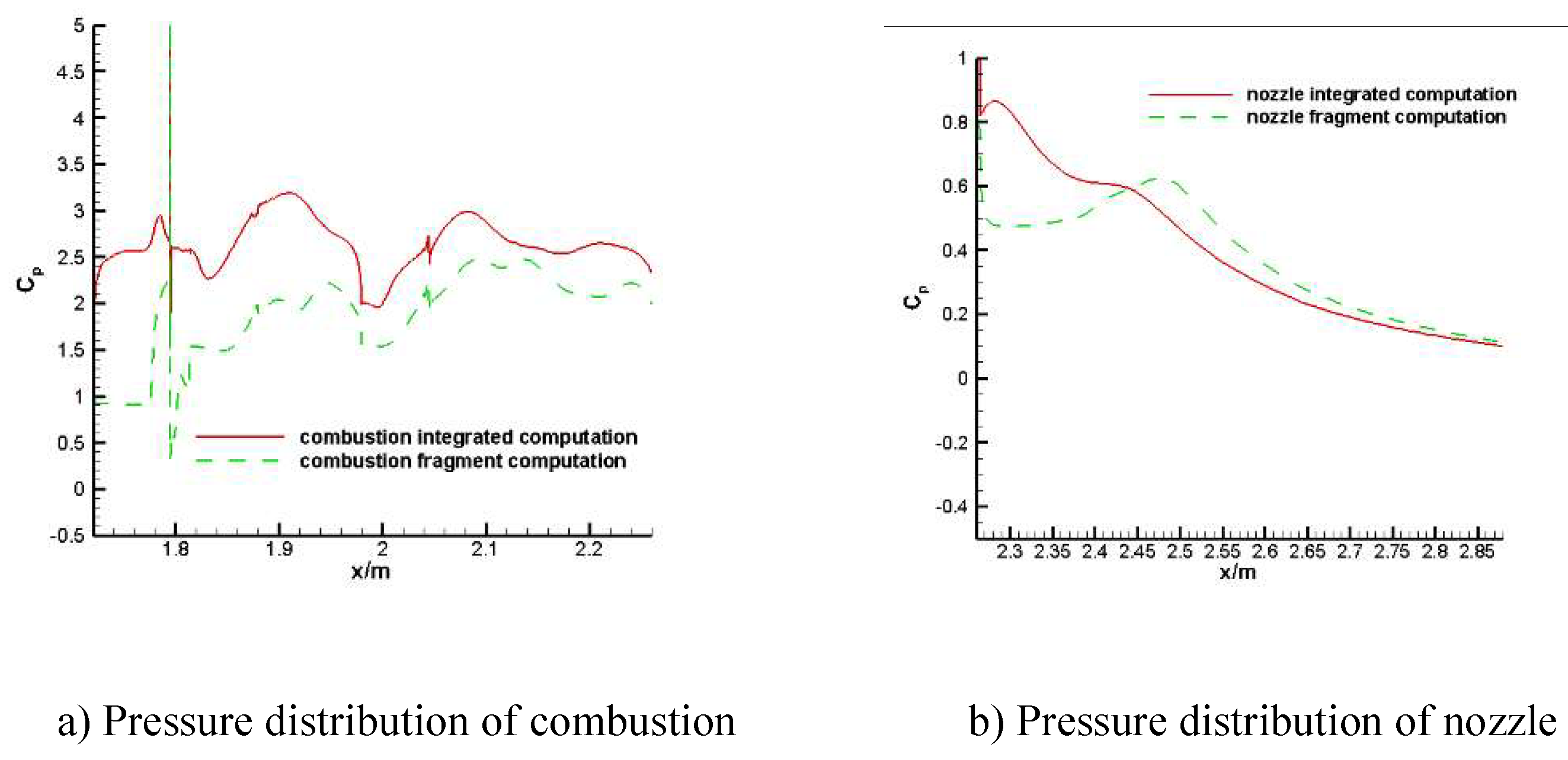
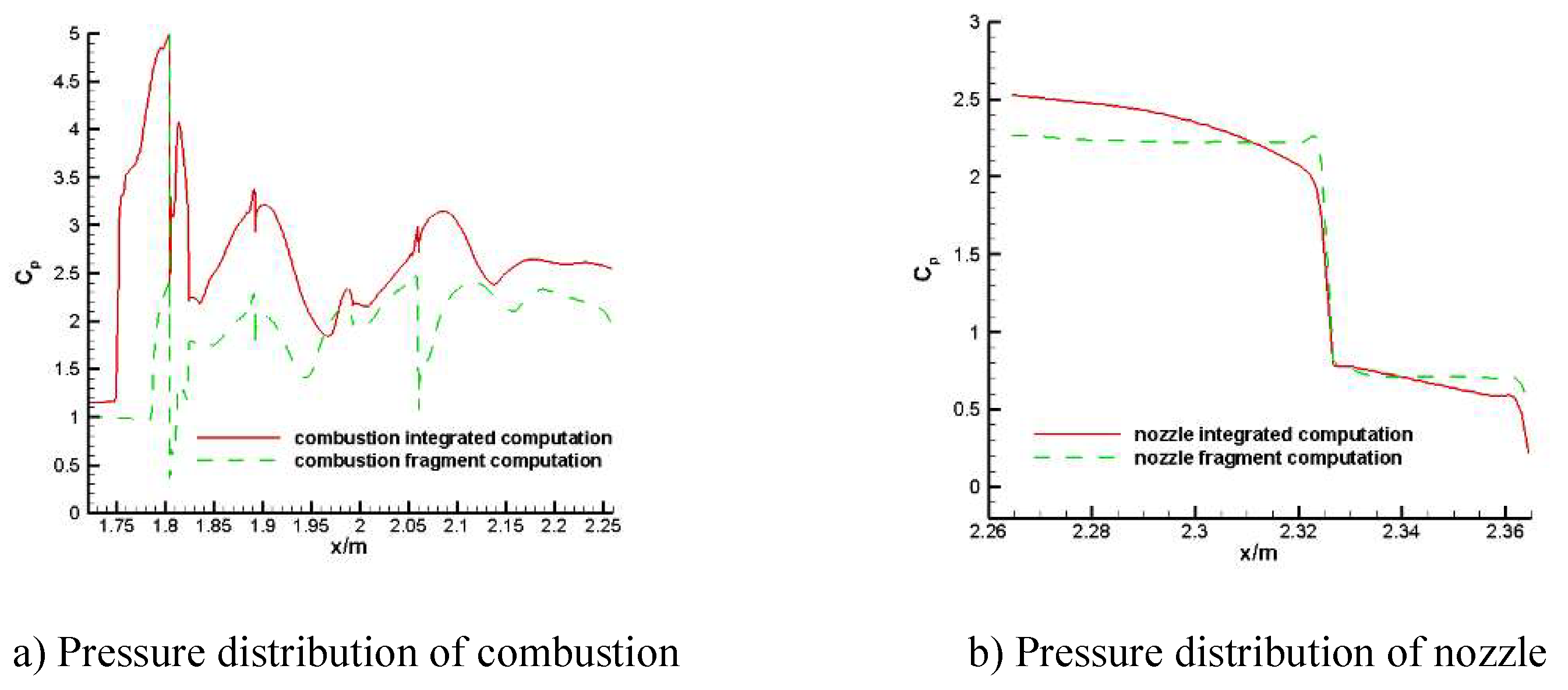
According to the aforemention results, as there is no combustion flow field in the inlet and isolation section, the pressure distribution is basically the same as that in Figure 10 and Figure 11, it is not listed separately here, only the calculation results of the combustion chamber and isolation section are given. Figure 12 shows the pressure distribution on the upper surface of the combustion chamber and nozzle under combustion conditions. As shown in Figure 12(a), the pressure difference at the inlet of the combustion chamber is relatively large, and the pressure value calculated by fragment is smaller than that calculated by through, which show a translation phenomenon as a whole, but the pressure distribution is similar. As shown in Figure 12(b), the pressure difference at the inlet of nozzle is obvious, but the results by the two methods tend to be consistent with the distance becoming larger. Generally speaking, the pressure distribution obtained by fragment calculation is in good agreement with the results by through calculation.

Figure 13 shows the pressure distribution on the lower surface of the combustion chamber and nozzle under combustion conditions. The calculated results are similar to those of the upper surface. There is a big difference in the combustion chamber, and it presents a translation phenomenon as the whole, which may be related to the uniform boundary conditions given by the inlet. There is little difference in the nozzle, but there is a certain pressure deviation at the nozzle inlet. According to the comparison, the fragment calculation can reflect a certain law of engine internal flow.

D. Flow Field Analysis

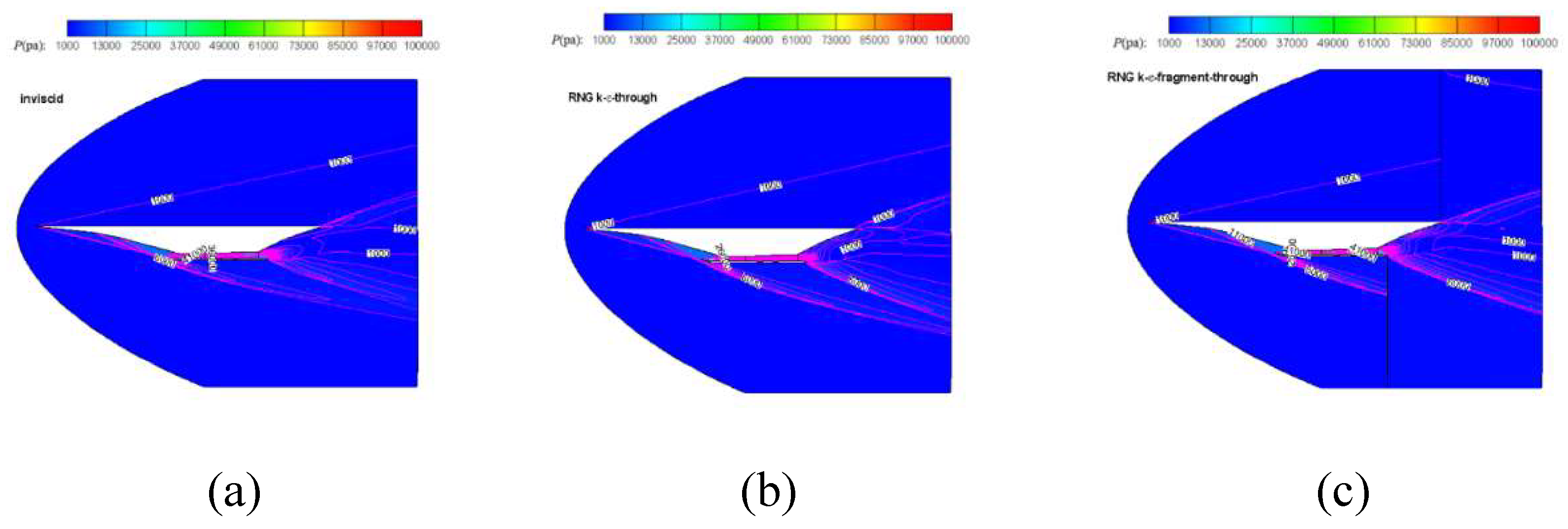
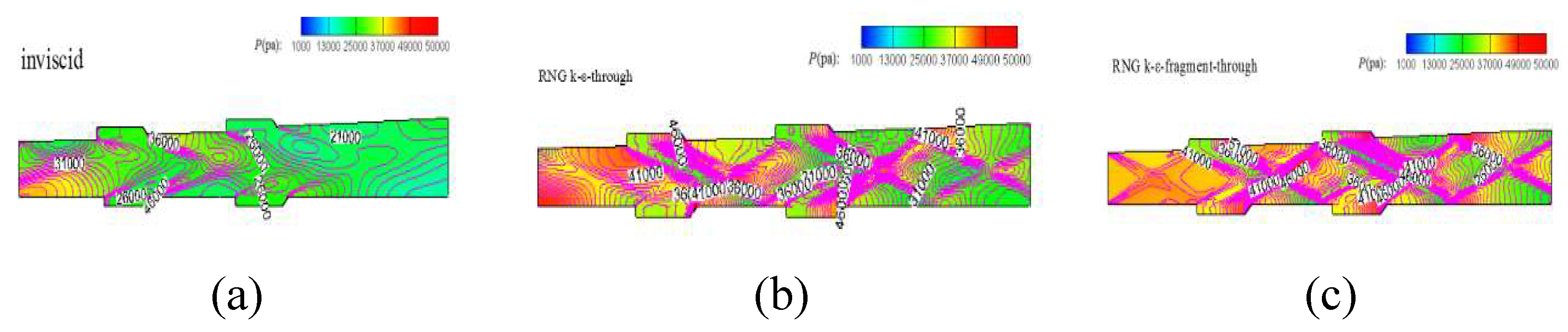
a).Flowfield without reaction

Figure 14 gives the pressure contour of inviscid, RNG k-

ε

through and RNG k-

ε

fragment through when the angle of attack is 4 degrees, respectively. The flow field show similarity in profile. The Mach contour is displayed in Figure 15, which shows that the Mach distribution is similar at the section of inlet and a little different at the nozzle. The detail difference will be further analyzed in the following section.

The inlet/isolator pressure contour is exhibited in Figure 16. Figure 16(a) shows that the oblique shock waves cluster at the lip of cowl. However, Figure 16(b) and Figure 16(c) shows the clustered oblique shock waves have a deflection from the lip, because the inlet is designed based on inviscid flow. when the flow field is solved by viscous method, the existence of boundary layer pushes the shock wave shift a little angle, then the clustered shock would not nestle at the lip of cowl at design condition. As shown in Figure 16(b) and Figure 16(c), the flow field calculated by integration and by fragment is displayed in detail and it presents little difference between two computation method. Therefore, we can conclude that inlet/isolator can be solved separately and obtains corresponding aerodynamic performance.

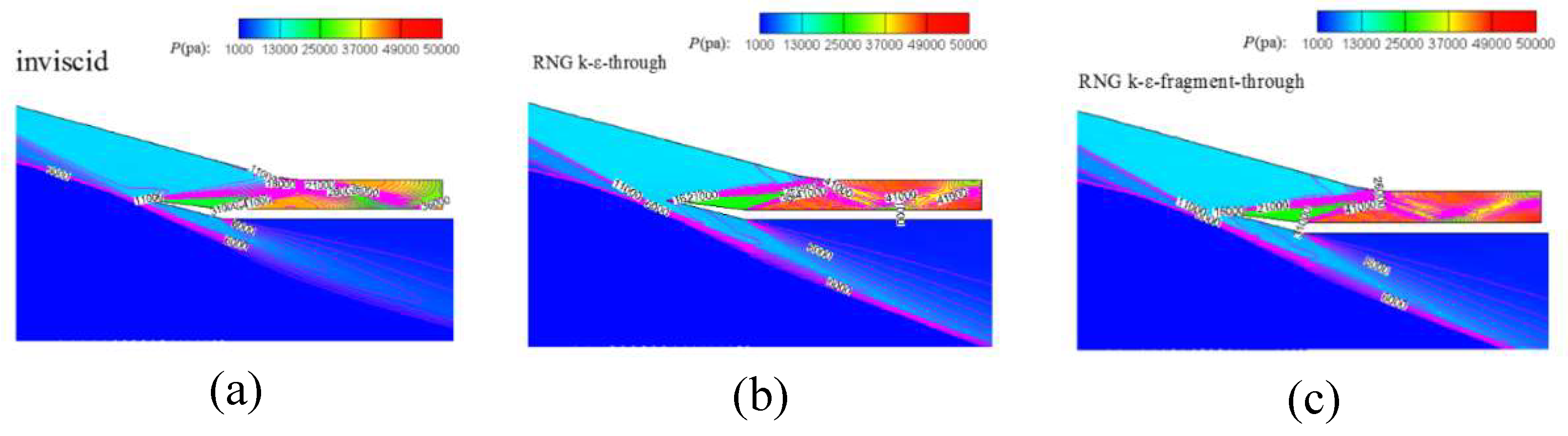
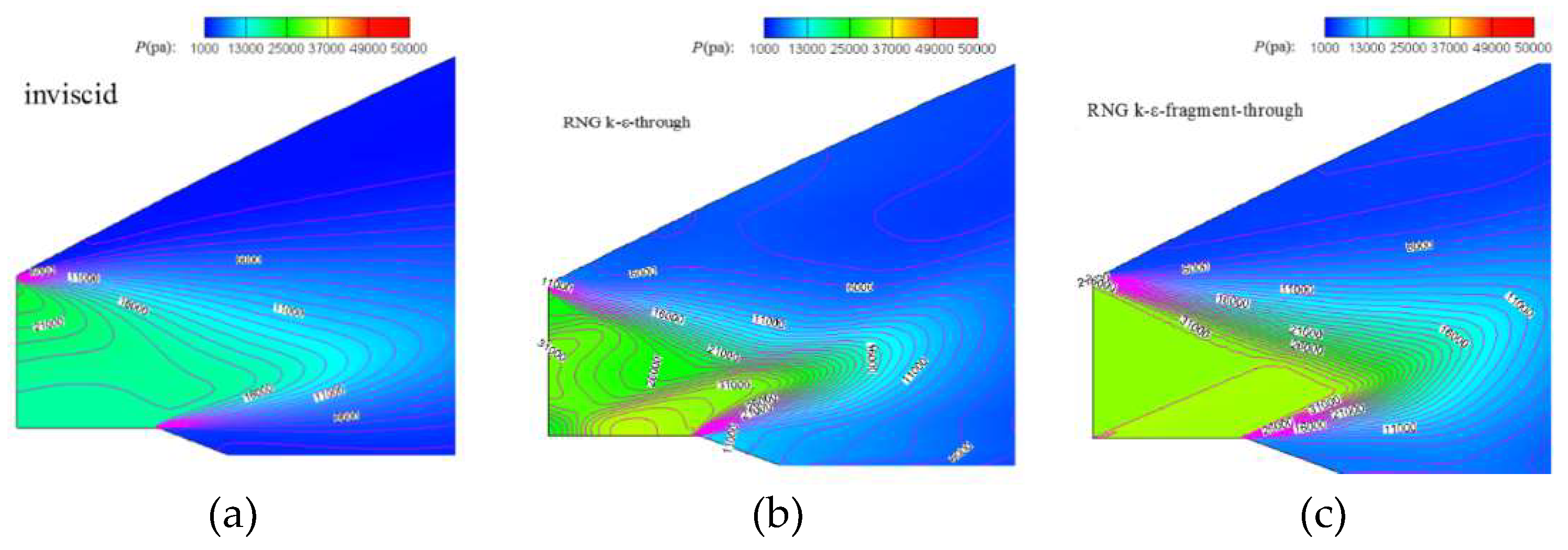
For combustion chamber, the inlet boundary condition is endowed by the outlet condition of isolator in fragment method. While the inlet/isolator is solved completely, the average static pressure, average total pressure and average total temperature are extracted and exerted on the inlet boundary with pressure-in type. As shown in Figure 17, in the vicinity of inlet of combustor, the pressure contour presents a little difference, with the flow field extrapolating, the pressure distribution becomes similar.

Figure 18 demonstrates the pressure contour of nozzle section at different computation method. The flow field appears glossy due to inviscid solution, see in Figure 18(a). Though the inlet boundary is different in the nozzle, the outlines show high resemblance, especially in the region away from inlet, which can be seen in Figure 18(b) and Figure 18(c). Figure 18(b) stems from integration computation with RNG k-

ε

turbulent model, its flow filed is continuous from inlet/isolator to nozzle. Figure 18(c) is from fragment computation with RNG k-

ε

turbulent model, its inlet boundary is endowed by the outlet boundary of combustion chamber with average static pressure, average total pressure and average total temperature. The main distinction behaves in the entrance region, the pressure is uniform along vertical direction in the inlet boundary. Flow developing gradually abates the discrepancy and flow field tends to become coincident.

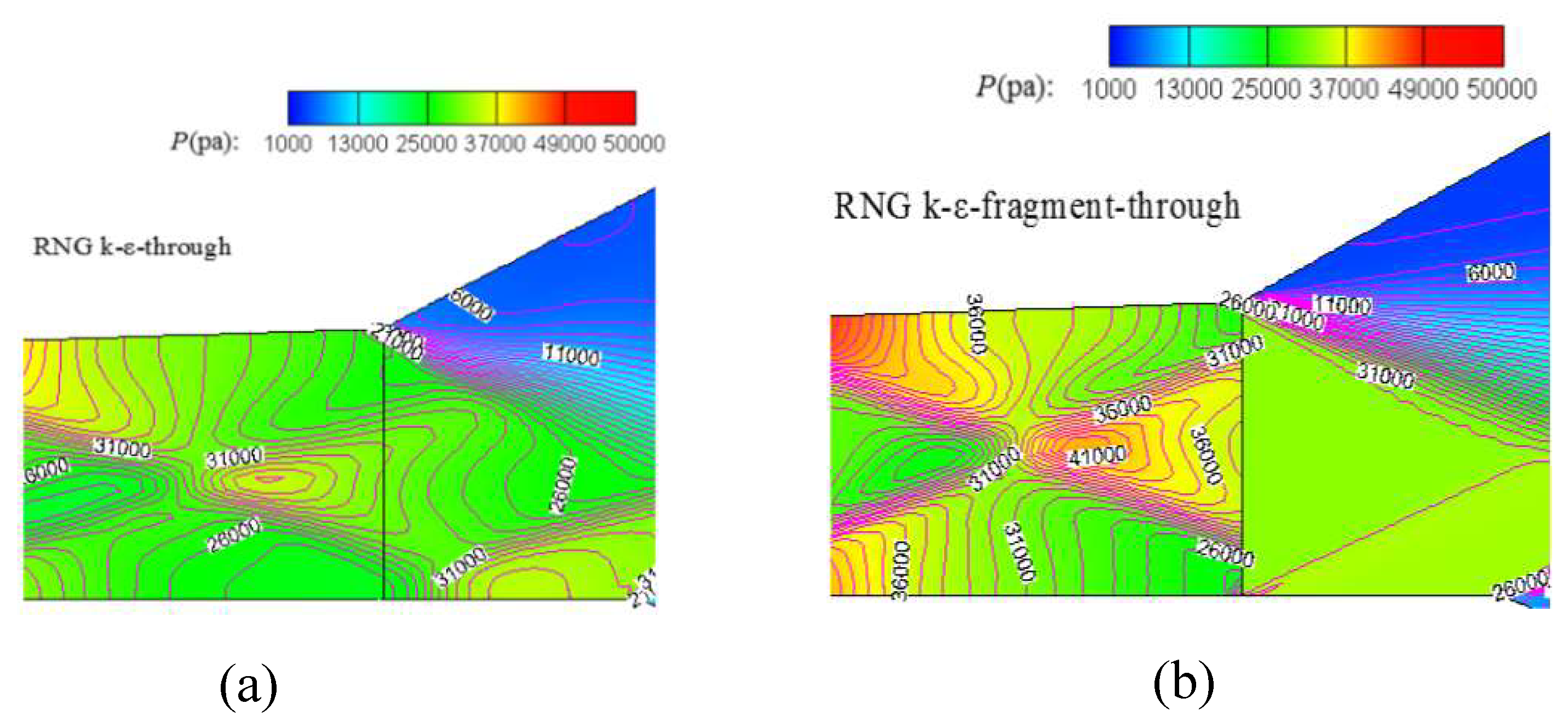
As is shown in Figure 19, the detail description at the interface between isolator and combustion chamber is displayed, because of the boundary condition effect by fragment computation, the flow presents obvious discontinuity at the interface. However, by comparing the section aerodynamic, the discontinuity will bring in subtle error. Additionally, owing to the small fractional contribution to lift coefficient and drag coefficient by combustor, consequently, the effect on the aerodynamic of whole vehicle by the discontinuity commonly can be ignored in the preliminary design.

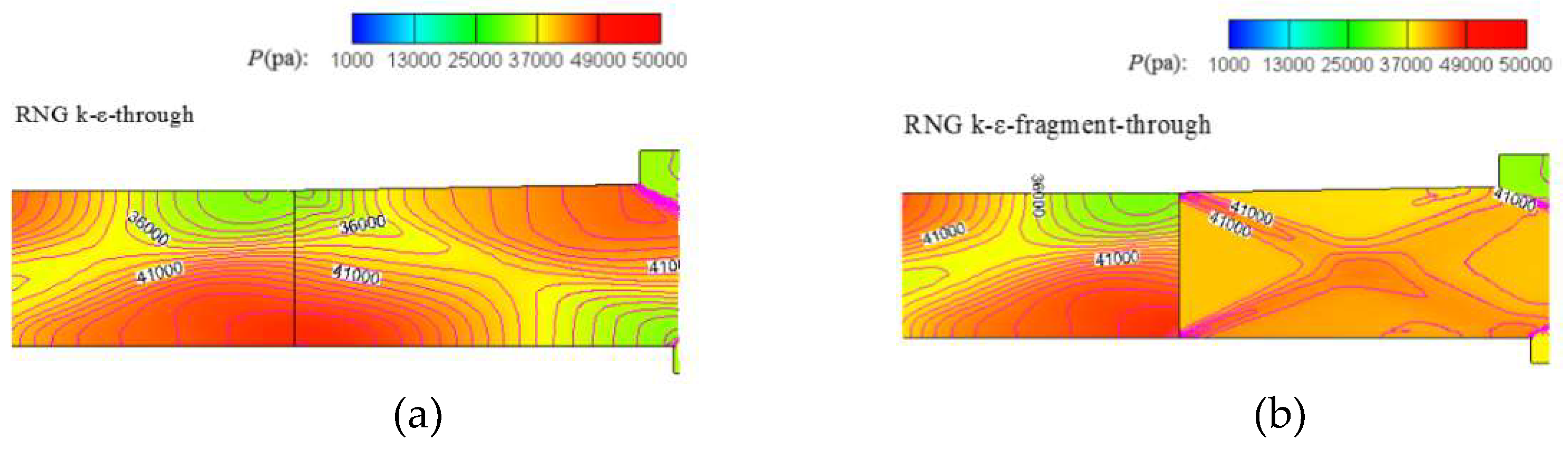
Figure 20 illustrates the pressure contour comparison at the interface of combustor and nozzle. In Figure 20(a), the pressure distribution is continuous and uninterrupted, while the pressure shows discontinuity in Figure 20(b). It is easily understood that the inlet of nozzle is given by uniform pressure boundary in fragment computation that results in the pressure discrepancy. In spite of the obvious existence of pressure difference, once the flow departs from the inlet of nozzle in fragment computation, the pressure distribution gradually approaches result by integration computation under the action of viscosity, especially in the upper face of nozzle. As a result, the aerodynamic force obtained by fragment computation is nearly equivalent to that by integration computation, which can be verified in Figure 9.

From above discussion, we can conclude that the fragment computation method used in high speed vehicle is reasonable and has conspicuous advantage in computation efficiency compared with integration computation.

b) Flowfield with reaction

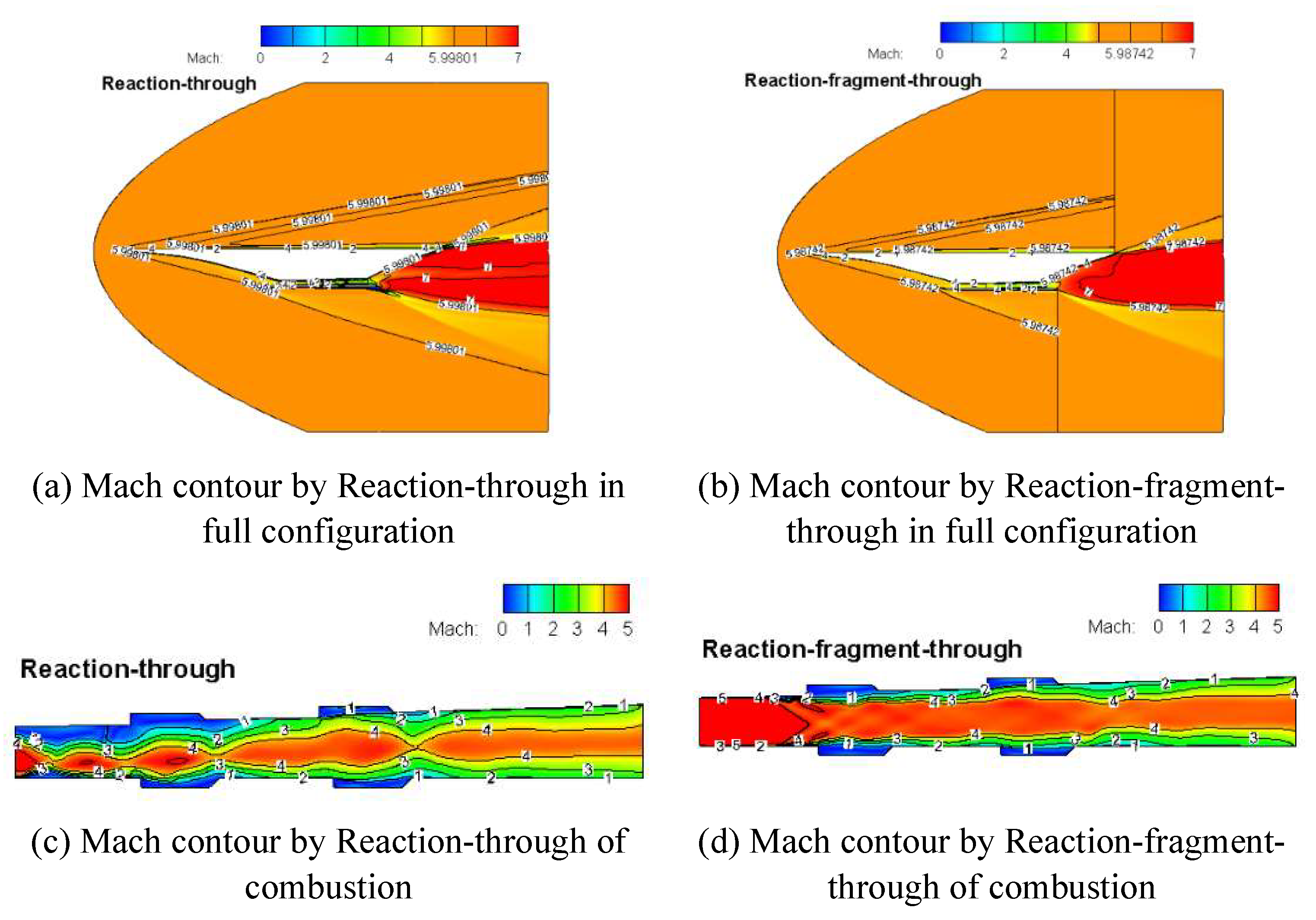
Figure 21 illustrates the Mach contour comparison of reaction-through and reaction-fragment-through in full configuration. In Figure 21(a), the Mach distribution is continuous and uninterrupted, while the Mach shows discontinuity in Figure 21(b). However, it can be seen that the Mach outline close to the wall show a high similarity for the two method. 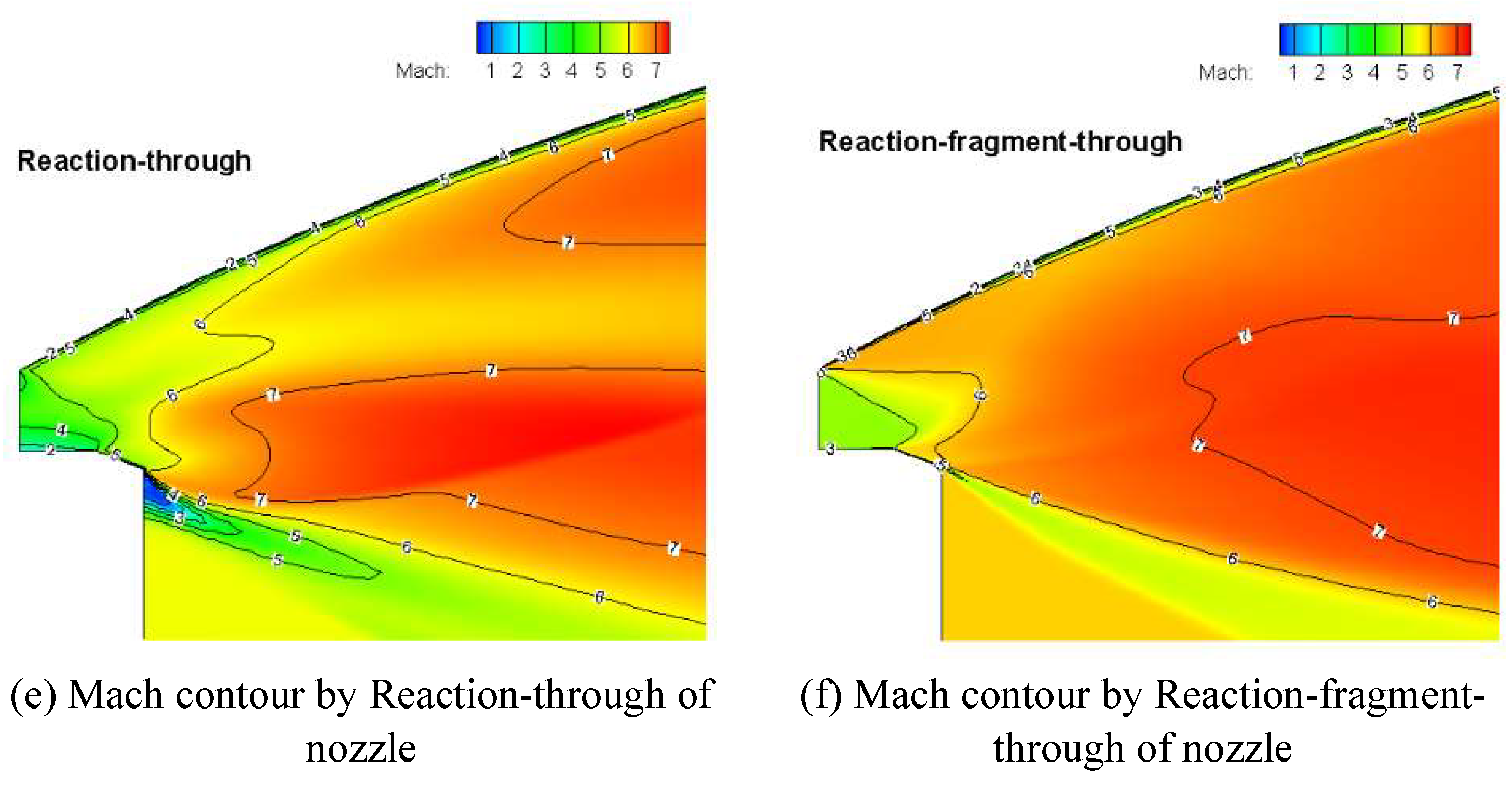The same results can be discovered in the combustion (see Figure 21(c)~ Figure 21(d)) and nozzle (see Figure 21(e)~ Figure 21(f)).

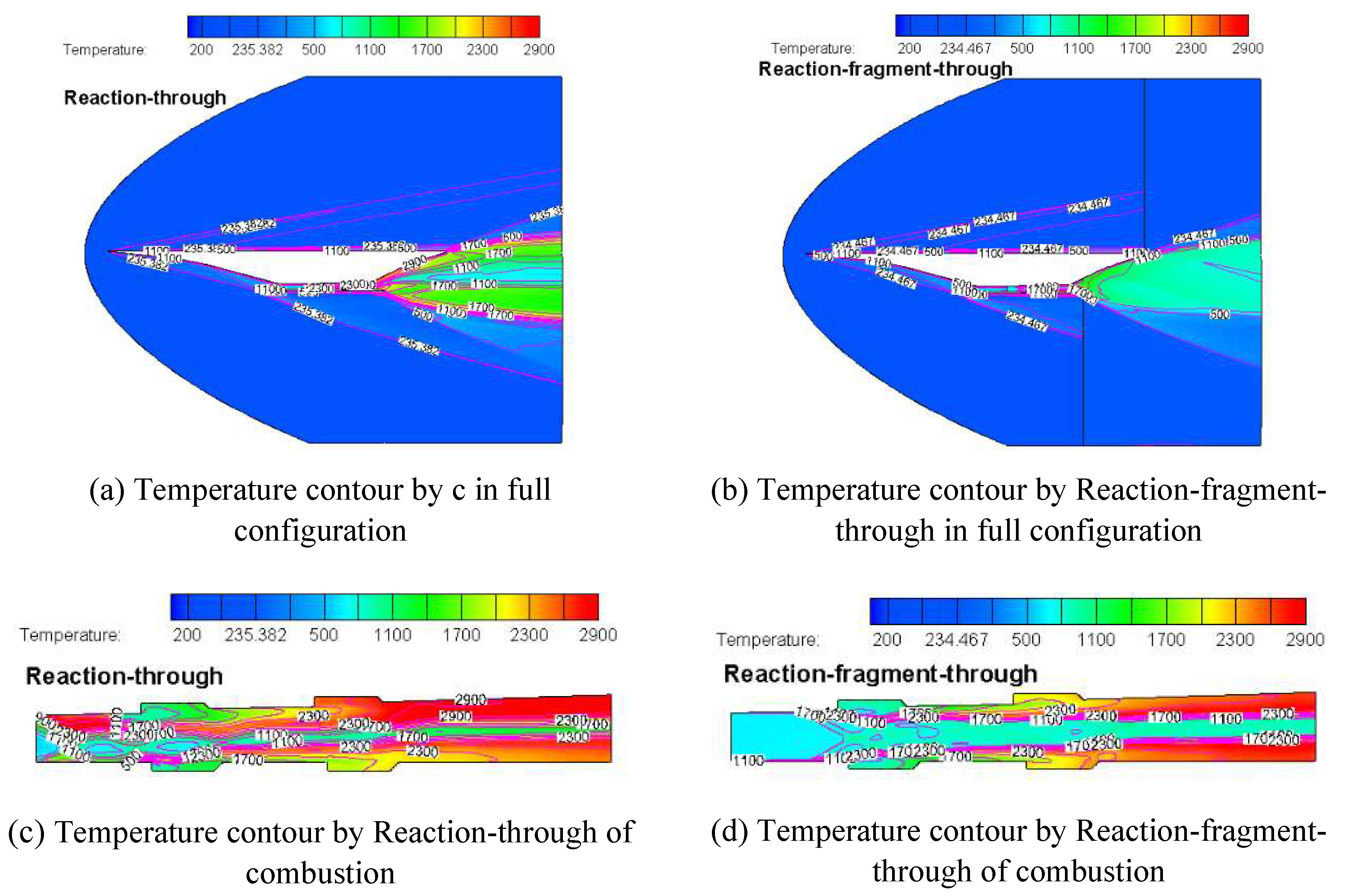
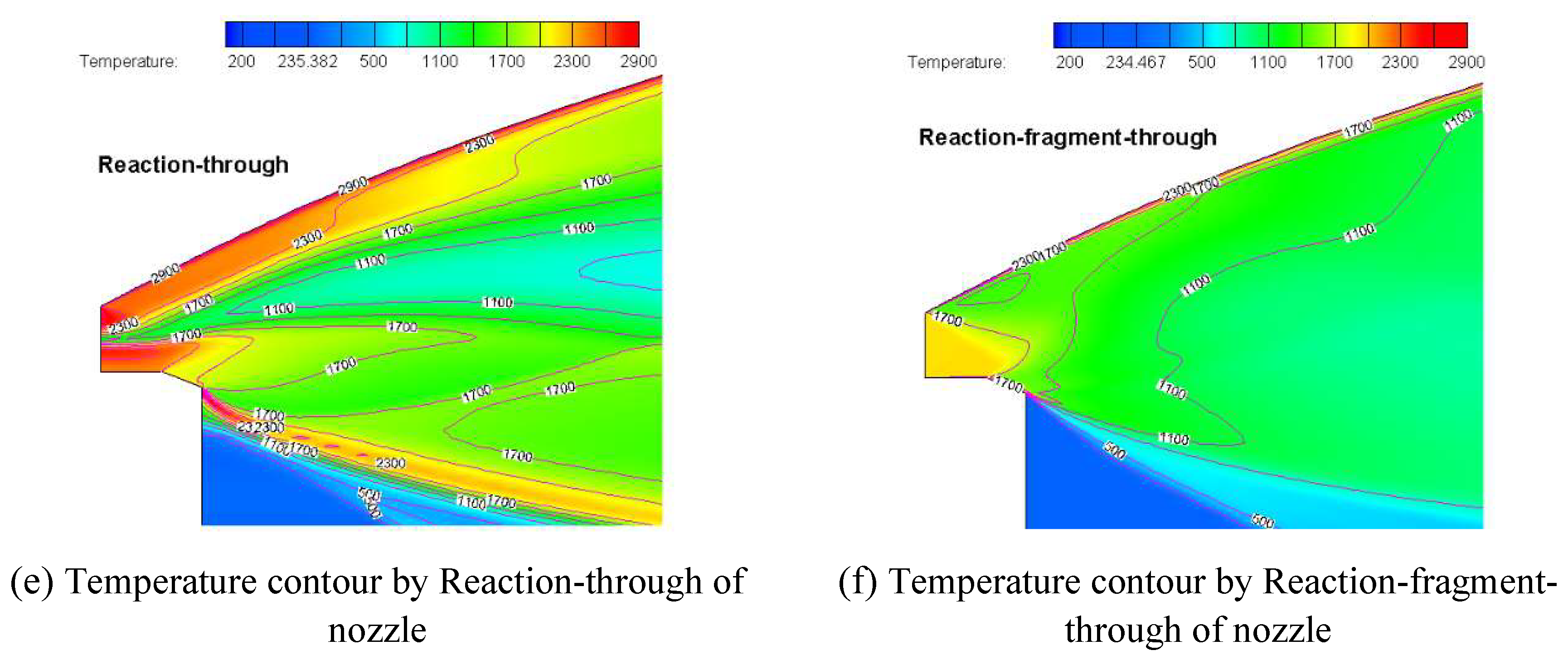
As is shown in Figure 22, the temperature contour comparison corresponding to the two calculation method is displayed. It can be seen from Figure 22(a) and Figure 22(b) that the temperature distribution by Reaction-through show discontinuity. Especially at the outlet of the nozzle, there are certain differences. According to the results from Reaction-through, the temperature shows a slow expansion at the outlet, while the temperature gradient change is not significant from the Reaction-fragment-through calculation, which can be seen in Figure 22(e) and Figure 22(f). In the combustion, the temperature distribution is unlike because the entrance is given a unitary boundary condition. However, as the combustion progresses, the outlet exhibits a high similarity in the temperature distribution. Therefore, the reaction by fragment computation can achieve the expected calculation results.

6. Conclusion

The multiple fragment computation method for high speed airframe/engine integration vehicle is presented and analyzed in this paper. Firstly, through comparing the simulation efficiency, it is found that the fragment computation has a prominent advantage, especially in flowfield-solving with reaction. The simulation time can reduce 45% and 70% for high speed flowfield-solving of without reaction and with reaction by using fragment computation method, respectively. Moreover, fragment computation can gain results close to that by integrated computation for both flowfield. By contrast, we can conclude that fragment computation method is an excellent choice to solve high speed flow of integration vehicle to boost analysis efficiency and shorten research period in the preliminary design phase.

In this paper, the combustion chamber inlet condition is given using the average flow rate of the outlet from the isolator section, which is different from the real inlet conditions, involved parameters such as Mach number and velocity direction etc. A more accurate flowfield distribution at the entrance of the combustion chamber can further improves the research efficiency of the method, the self-defining functions that can express real values would be added in the process to achieve better results.

Nomenclature

CFD	=computational fluid dynamics
P	=pressure
T	=temperature
$μ$	=dynamic viscosity
$ρ$	=gas density
RANS	=Reynolds Averaged Navier-Stokes
R	=Universal gas constant
cp	=Specific heat at constant pressure
$\begin{array}{l} γ \end{array}$	=Specific heat ratio
Re	=Reynolds number
$L_{r a m p}$	=Length of inlet compression ramp
$L_{i s o}$	=Height of isolator
$L_{c o m b}$	=Length of combustion chamber
$L_{n o z z l e}$	=Length of nozzle
$\begin{array}{l} H_{i s o} \end{array}$	=Height of isolator
$T_{c o w l}$	=Thickness of cowl
$β$	=Oblique shock wave angle
Ma	=Mach number
AOA	=Angle of attack
y+	=non-dimensional wall distance for wall-bounded viscous flows

References

Voland, R.T.; Huebner, L.D.; Mcclinton, C.R. X-43A high speed vehicle technology development. Acta Astronautica 2006, 59, 181–191. [Google Scholar] [CrossRef]
Hank, J.M.; Murphy, J.S.; Mutzman, R.C. The X-51A Scramjet Engine Flight Demonstration Program. In Proceedings of the 15th AIAA International Space Planes and High speed Systems and Technologies Conference, F; 2008. [Google Scholar]
Andreadis, D. Scramjet Engines Enabling the Seamless Integration of Air & Space Operations. Industrial Physicist 2004. [Google Scholar]
Denman, Z.J.; Wheatley, V.; Smart, M.K.; et al. Supersonic combustion of hydrocarbons in a shape-transitioning high speed engine. Proc. Combust. Inst. 2017, 36, 2883–2891. [Google Scholar] [CrossRef]
Gao, W.; Li, Z.; Yang, J.; et al. Effects of trips on the oscillatory flow of an axisymmetric high speed inlet with downstream throttle. Chinese Journal of Aeronautics 2018, 31, 225–236. [Google Scholar] [CrossRef]
Knight, D.; Chazot, O.; Austin, J.; et al. Assessment of predictive capabilities for aerodynamic heating in high speed flow. Progress in Aerospace Sciences 2017, 90, 39–53. [Google Scholar] [CrossRef]
Hirt, S.M.; Tacina, K.M.; Conners, T.R.; et al. CFD Results for an Axisymmetric Isentropic Relaxed Compression Inlet. In 46th AIAA Aerospace Sciences Meeting and Exhibit; 2008. [Google Scholar]
Kirkpatrick, B.K. Propulsion integration of high speed air-breathing vehicles utilizing a top-down design methodology. Iowa State University, Ames, IA, USA, 2014. [Google Scholar]
Oliden, D. Parametric Analysis of a High speed Inlet using Computational Fluid Dynamics. Arizona State University, 2013. [Google Scholar]
Lee, H.J.; Wray, T.J.; Agarwal3, R.K. CFD Performance of Turbulence Models for Flow from Supersonic Nozzle Exhausts. In 34th AIAA Applied Aerodynamics Conference; 2016. [Google Scholar]
Huang, W.; Liu, J.; Wang, Z.G.; et al. Effect of cavity location on combustion flow field of integrated high speed vehicle in near space. The Visualization Society of Japan 2011, 14, 339–351. [Google Scholar] [CrossRef]
Torrez, S.M. Design Refinement and Modeling Methods for Highly-Integrated High speed Vehicles. University of Michigan, 2012. [Google Scholar]
Wang, J.; Cai, J.; Duan, Y.; et al. Design of shape morphing high speed inward-turning inlet using multistage optimization. Aerospace Science and Technology 2017, 66, 44–58. [Google Scholar] [CrossRef]
Shi, W.; Tian, Y.; Guo, M.; et al. Investigation of flow characteristics and flame stabilization in an ethylene-fueled scramjet combustor. Chinese Journal of Theoretical and Applied Mechanics 2022, 54, 612–621. [Google Scholar]
Wang, J.; Cai, J.; Liu, C.; et al. Aerodynamic configuration integration design of high speed cruise aircraft with inward-turning inlets. Chinese Journal of Aeronautics 2017, 30, 1349–1362. [Google Scholar] [CrossRef]
Jiao, X.; Chang, J.; Wang, Z.; et al. Numerical study on high speed nozzle-inlet starting characteristics in a shock tunnel. Acta Astronautica 2017, 130, 167–179. [Google Scholar] [CrossRef]
Zhang, Y.; Tan, H.-J.; Chen, H.; et al. Shock Control Method for High speed Inlets Based on Forebody Secondary Flow Recirculation. AIAA Journal 2018, 56, 2124–2130. [Google Scholar] [CrossRef]
Brahmachary, S.; Ogawa, H. Multipoint Design Optimization of Busemann-Based Intakes for Scramjet-Powered Ascent Flight. Journal of Propulsion and Power 2021, 37, 850–867. [Google Scholar] [CrossRef]
Damm, K.A.; Gollan, R.J.; Jacobs, P.A.; et al. Discrete Adjoint Optimization of a High speed Inlet. AIAA Journal 2020, 58, 2621–2634. [Google Scholar] [CrossRef]
Ward AD, T.; Smart, M.K. Parametric Study of the Aftbody Design of an Airbreathing High speed Accelerator. Journal of Spacecraft and Rockets 2021, 58, 1361–1373. [Google Scholar] [CrossRef]
Reardon, J.P.; Schetz, J.A.; Lowe, K.T. Computational Analysis of Unstart in Variable-Geometry Inlet. Journal of Propulsion and Power 2021, 37, 564–576. [Google Scholar] [CrossRef]
Reinartz, B.U.; Herrmann, C.D.; Ballmann, J.; et al. Aerodynamic performance analysis of a high speed inlet isolator using computation and experiment. Journal of Propulsion and Power 2003, 19, 868–875. [Google Scholar] [CrossRef]
Herrmann, C.; Koschel, W. Experimental investigation of the internal compression of a high speed intake. In 38th AIAA/ASMESAE/ASEE Joint Propulsion Conference & Exhibit; 2002. [Google Scholar]

Figure 1. Schematic diagram of the typical integrated high speed vehicle[3].

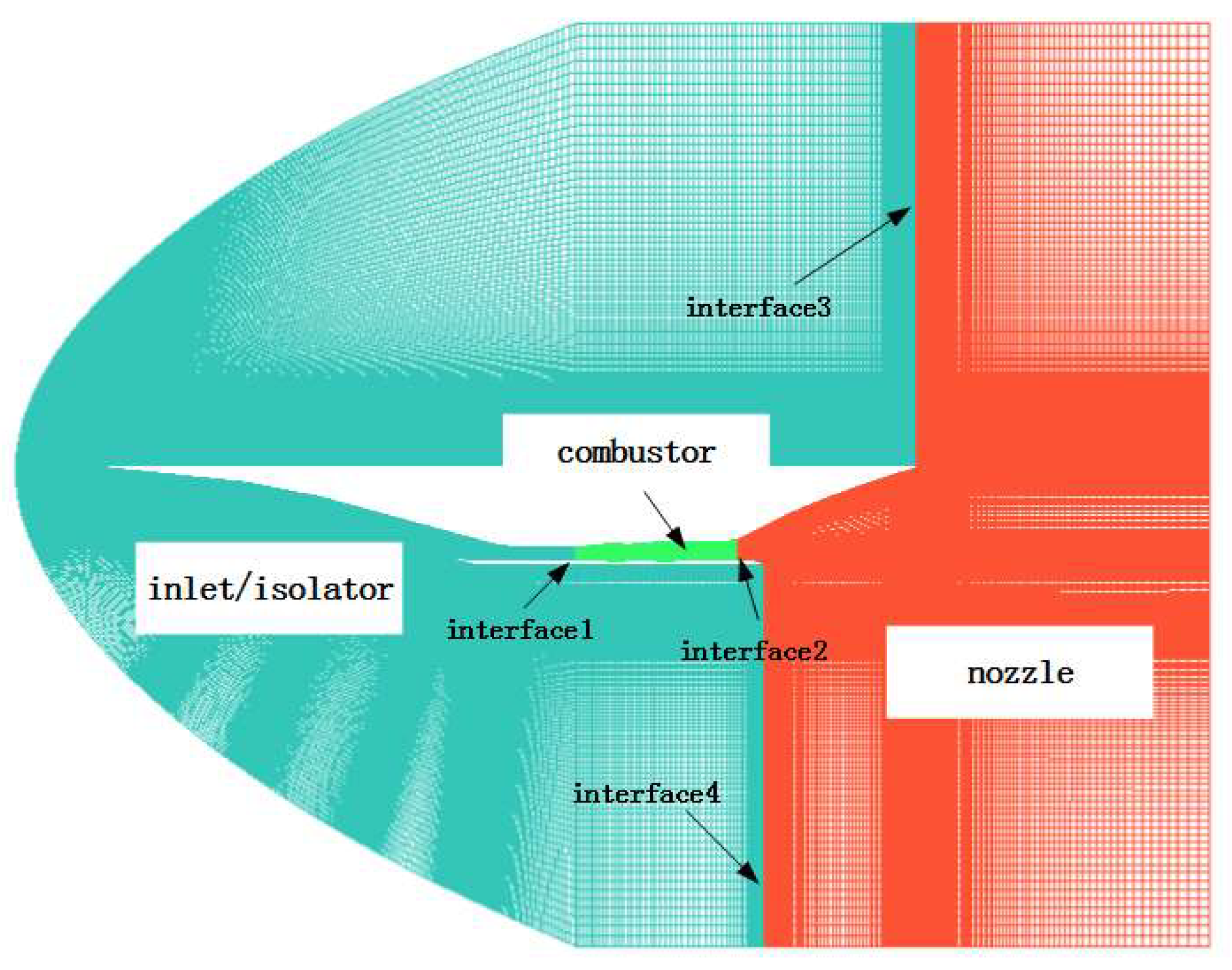
Figure 2. Schematic diagram of the integrated high speed vehicle.

Figure 6. Comparison of schlieren picture (a), numerical contour by literature(b), and numerical results by this paper(c).

Figure 7. Pressure distribution contrast of cowl(top-wall of inlet)

Figure 8. Pressure distribution contrast of compression ramp(down-wall of inlet)

Figure 9. Aerodynamic characteristic comparison of high speed integrated vehicle.

Figure 10. Upper-wall pressure coefficient distribution without reaction at AOA=0°.

Figure 11. Down-wall pressure coefficient distribution without reaction at AOA=0°.

Figure 12. Upper-wall pressure coefficient distribution with reaction at AOA=0°.

Figure 13. Down-wall pressure coefficient distribution with reaction at AOA=0°.

Figure 14. Pressure contour contrast of high speed vehicle at AOA=4°.

Figure 15. Mach contour contrast of high speed vehicle at AOA=4°.

Figure 16. Pressure contour contrast of inlet/isolator at AOA=4°.

Figure 17. Pressure contour contrast of combustion chamber at AOA=4°.

Figure 18. Pressure contour contrast of nozzle at AOA=4°.

Figure 19. Pressure contour at the interface of isolator and combustor at AOA=4°.

Figure 20. Pressure contour at the interface of combustor and nozzle at AOA=4°.

Figure 21. Mach contour comparison at AOA=0°.

Figure 22. Temperature contour comparison at AOA=0°.

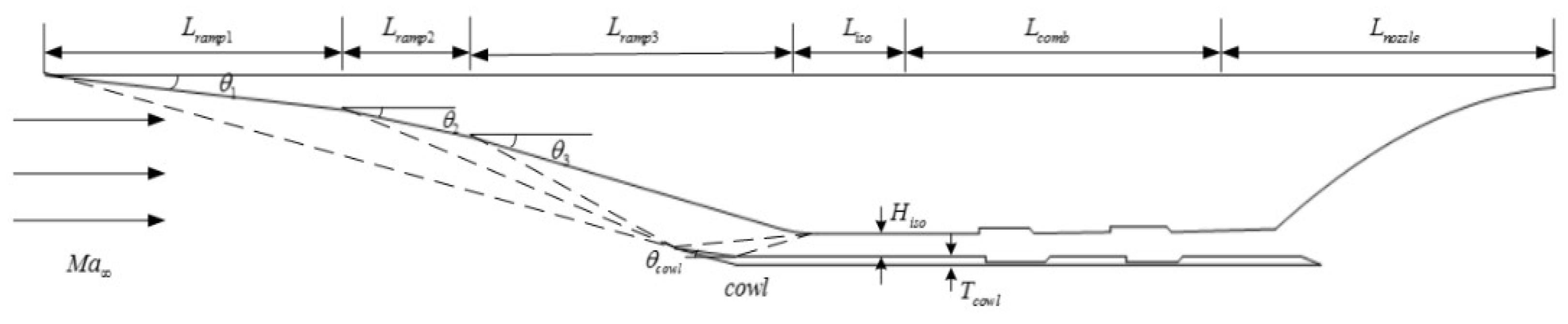
Table 1. Main Parameters of the integrated high speed vehicle.

parameter	Value(mm)	parameter	Value(mm)	parameter	Value(mm)
$L_{r a m p 1}$	585.2	L_iso	252.8	H_iso	45.25
$L_{r a m p 2}$	253.3	L_comb	550.5	$T_{c o w l}$	15
$L_{r a m p 3}$	623.1	L_nozzle	620	L_total	2884.9

Table 2. Grid Description of different Grid Levels.

Grid	Scale	$Δ y_{\min}$ /mm	y+
G1	$1150 \times 150$	0.1	160
G2	$1150 \times 150$	0.01	16
G3	$1150 \times 150$	0.001	1.6
G4	$1150 \times 150$	0.0001	0.16

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer