Meeting at Both Ends Information – Theoretic Semi-group Theory of Uncertain Reasoning

Preprint

Article

Meeting at Both Ends Information – Theoretic Semi-group Theory of Uncertain Reasoning

Altmetrics

Downloads

Views

Comments

Ismail A. Mageed^*

This version is not peer-reviewed

Submitted:

31 January 2024

Posted:

01 February 2024

You are already at the latest version

Alerts

Abstract

This paper provides a first-time ever unification of information theory, semi-group theory with the theory of uncertain reasoning, through functional perspective. Fundamentally, the threshold theorems for the inference functional were devised. Furthermore, numerical experiments are illustrated. The complex proofs in our paper are original results which emphasizes the credibility of the class of Rényi Generalized Entropies as measures of information, and that the field is open to extend an enhanced methodology regarding queuing networks with heavy tails.

Keywords:

Subject: Computer Science and Mathematics - Algebra and Number Theory

Introduction

The current work supplies a complementary part of the research conducted in [1]. As the authors now feel that the task is finish off and demonstrated with both analytic expressions as well as illustrative data to interpret the newly devised research results.

The current paper is a substantial extension of an accepted paper [1]:

The main contributions of [1] are:

Providing the full detailed proofs of the limit theorem as well as the full proofs of RGEs Extended Properties and finding the Discrete Time Domain PV-updates.
Providing these extended properties physical interpretations.

This letter has the following major contributions:

Novel Characterization of for $q > - 1, q \neq 0,$ inference process $U_{q}^{L} (K)$ by a functional equation is devised.
First time unification of the inference process $U_{q}^{L} (K)$ for $q > - 1, q \neq 0$ with group theory is obtained.
Showing the significant information theoretic parameter $r$ on the overall behaviour of inference process functional for both extensive and non-extensive values of the parameter $q .$

2. Definitions

1.: The Belief Function

The Belief (Bel) function is defined by assuming that it satisfies the axioms of probability. Specifically, fix a finite propositional language L and let SL be the set of sentences for this language. In this context,

Bel: SL

\to

[0,1] is a probability function on SL if for all θ, ϕ ϵ SL.

1.If

⊢ (θ \leftrightarrow \emptyset

) , then Bel(

θ) = B e l (\emptyset)

2.If

⊢ θ, t h e n

Bel(

θ) = 1, a n d B e l (\neg θ) = 0

3.I

f ⊢ (θ ⋀ \emptyset)

is false, then Bel (

θ ⋁ \emptyset) = B e l (θ) + B e l (\emptyset

)

2.: Definition of the set Vectors V^L(K) [1]

Let us define the set

V^{L} (K), V^{L} (K) = {x^{\to} \in R^{J}

x^{\to} A_{K = b_{k}^{\to}}, x^{\to} \geq 0}

2.3.: The ME Inference Process, M $E^{L}$ [1]

E^{L}

reads as

{M E}^{L} (K) = x^{\to}, w h i c h m a x i m i z e s t h e S h a n n o n i a n e n t r o p y

The formula for the maximum entropy inference process MEL, which maximizes Shannonian entropy

(- \sum_{i = 1}^{J} x_{i} l o g x_{i}), w i t h t h e c o n v e n t i o n

x l o g x = 0

when

x = 0

3.: $U_{q}^{L} (K)$

We write

U_{q}^{L} (K)

U_{q}^{L} (K) =

that

x^{\to} \in V^{L} (K) f o r w h i c h {(\sum_{i = 1}^{J} x_{i}^{q + 1})}^{- 1 / q}

is maximal.

4 A functional equation is one that has an undefined function. Functional equations can be used to characterise the fundamental functions as one of their many uses. An illustration of a functional equation is the Fibonacci number sequence [2].

5.: Semigroups [3]

A binary operation

\circ

on a set S is a map

\circ : S \times S \to S

If for all elements

x, y, z \in S

x \circ (y \circ z) = (x \circ y) \circ z

, then this operation is associative. A non-empty set having an associative binary operation is known as a semigroup. As a result, semigroups are among the most fundamental types of algebraic structures.

A semigroup, according to some definitions, is a set equipped binary operation “Empty semigroup” that may or may not be empty. That is, the ‘empty semigroup’ is formed by the empty set. From the perspective of category theory, this is advantageous. But keep in mind that if a semigroup might be empty, other definitions must be changed.

Many algebraists are drawn to the theory of semigroups because of its applicability to formal languages, network analogy, automata theory, and other fields. We examined various contexts in which semigroups are applied in section 2. We found some instances of regular, E-inversive, and inverse semigroup structures in biology, sociology, and other fields.

3. Novel Characterization of The Inference Process $U_{q}^{L} (K)$ for $q > - 1, q \neq 0$ By a Functional Equation

This section provides a breakthrough in information theory as it characterizes RGEs through the characterization of the inference functional by a functional equation.

Theorem 3.1

The inference functional (IF),

f (x) = x^{q + 1}

q

- 1

q

\neq 0

is well defined. Moreover, if

Χ

is any arbitrary enumeration set, then (IF) is characterized by the functional equation:

f (x y) = f (x) f (y)

for all

x, y \in Χ

Proof

To start with, we must prove that (IF) is well defined. To obtain that, it suffices to show that it is impossible that for any

x, y \in Χ

with

x \neq y

f (x) = f (y) .

Let

f (x) = f (y) .

Hence,

x^{q + 1} = y^{q + 1}

, equivalently

(q + 1) l o g (\frac{x}{y})

= 0. Therefore,

(q + 1) = 0 o r l o g (\frac{x}{y})

= 0. The statement

(q + 1) = 0 y i e l d s a c o n t r a d i c t i o n .

This implies

l o g (\frac{x}{y})

= 0, or

x = y

, proving the well-definiteness of IF.

Sufficiency: For all

x, y \in Χ,

f (x) = x^{q + 1}, q

- 1

q

\neq 0,

we have

f (x y) =

{(x y)}^{q + 1} = x^{q + 1} y^{q + 1} =

f (x) f (y)

(1)

Necessity: If the suggested functional equation

f (x y) = f (x) f (y)

for all

x, y \in Χ

holds (2)

Differentiating (2),

y \frac{\partial f (x y)}{\partial x} = \frac{d f (x)}{d x} f (y)

(3)

Setting

f (1) = q + 1

. Now putting

x = 1

in (3), implies

y \frac{\partial f (y)}{\partial x} = \frac{d f (1)}{d x} f (y)

(4)

Equation (4) with

x \to y

imply

y \frac{d f (y)}{d y} = (q + 1) f (y)

(5)

It follows by (5) that:

y^{q + 1} \frac{d f (y)}{d y} = (q + 1) y^{q} f (y)

(6)

It can be verified that (6) implies that:

\frac{y^{q + 1} \frac{d f (y)}{d y} - (r + 1) y^{q} f (y)}{{(y^{q + 1})}^{2}} = 0

(7)

Therefore,

\frac{d}{d y} (\frac{f (y)}{y^{q + 1}})

= 0. Consequently,

f (y) = c y^{q + 1}

. Letting

f (1) = 1

. Hence,

c = 1

, implying

f (y) = y^{q + 1}

. The proof is done.

In what follows, let

Φ

denote the set of inference functionals by

Φ = {f (x) : f (x) = x^{q + 1}, \sum_{x \in Χ} f (x) i s m i n i m a l, q

- 1

q

\neq 0

Χ

is any arbitrary enumeration set,

f (x y) = f (x) f (y)} .

4. Unification of The Inference Process $U_{q}^{L} (K)$ for $q > - 1, q \neq 0$ with Semi-Group Theory

Theorem 4.1 The above defined set

Φ

is an abelian(commutative) semi-group, with no identity element.

Proof

To prove the closure of the binary operation, let

f (x) \in Φ

, for all

x \in (0,1),

then it holds that

i s m i n i m a l

. For

q > - 1, q \neq 0

, we have

x^{2 (q + 1)}

<

x^{q + 1}

, which directly implies

\sum_{x \in Χ} x^{2 (q + 1)} < \sum_{x \in Χ} x^{q + 1}

(8)

The above inequality is also satisfied for all the non-extensive values of the parameter

q .

By the definition,

f (x^{2})

{(f (x))}^{2}

. Then showing the minimality of

\sum_{x \in Χ} x^{2 (q + 1)}

, which clearly follows from (8).

The binary operation is associative. To see this, we have for all

f (x), f (y), f (z) \in Φ

. Consequently,

\sum_{x \in Χ} x^{q + 1}, \sum_{y \in Χ} y^{q + 1} a n d \sum_{z \in Χ} z^{q + 1}

are minimal for

q > - 1, q \neq 0 .

By the definition,

f (x y z) = f (x) f (y) f (z)

(9)

We must prove the minimality of

\sum_{x, y, z \in Χ} {(x y z)}^{q + 1}

, equivalently by (9),

(

\sum_{x \in Χ} x^{q + 1}) (\sum_{y \in Χ} y^{q + 1}) (\sum_{z \in Χ} z^{q + 1})

is minimal. This is immediate from the definition.

As for the identity element, let the contradiction be true, that is an identity element

f (e) \in Φ

satisfying that:

f (x e) = f (x) f (e) = f (x)

(10)

This implies

f (e) = 1,

which is only possible if

f (e) = x^{(- 1) + 1}

.This applies whenever

q = - 1

(contradiction)

This completes the proof.

5. The Threshold Theorems for The Inference Functional

In what follows, a new theorem is devised, the threshold theorem of the inference functional (TTIF). We need the following important well-known theorem in mathematical analysis [4] as it is necessary to prove our newly devised results in Theorem 3.

The following theorem outlines a straightforward method for identifying where

f

is increasing or decreasing for differentiable functions.

Preliminary Theorem [4]

Let f be a function that is defined and differentiable on an open interval (c, d).

(1) If

f^{’} (x) > (< 0)

for all

x \in (c, d)

,then f is increasing(decreasing) on

(c, d)

(11)

Recalling,

U_{q}^{L} (K)

to be

U_{q}^{L} (K) =

x \in Χ w h i c h m i n i m i z e s \sum_{x \in Χ} f (x)

,with

U_{q}^{L} (K)

x \in Χ

that minimizes

\sum_{x \in Χ} x^{q + 1}

q

-

q

\neq 0

Χ

is any arbitrary enumeration set.

T h e o r e m 5.1

For

f (x) = x^{q + 1}

q

> - 1

q

\neq 0

Χ

is any arbitrary enumeration set, it holds that:

(i)

f (x)

is well-defined.

(i i) f (x)

is forever decreasing in x if and only if

q

- 1

q

\neq 0

(i i i) f (x)

is forever increasing in x if and only if

q < - 1

(i v) f (x)

is forever decreasing in q if and only if

x \in (0,1) .

(v) f (x)

is forever increasing in q if and only if

x \in (1, \infty) .

Proof

(i)Assume that

f (x) = f (y)

x \neq y f o r q > - 1

q

≠ 0. Thus,

(q + 1) l n (\frac{x}{y}) = 0

. Since

q + 1 \neq 0,

then

l n (\frac{x}{y}) =

0. Hence,

x = y

(contradiction). Therefore,

f

is well-defined.

(ii)We have

\frac{\partial f}{\partial x}

(q + 1) x^{q}

. By the preliminary theorem, (i) holds if and only if

(q + 1) x^{q} > 0 .

Since

x^{q}

is forever positive.

Following the same argument proves (iii).

As for (iv),

\frac{\partial f}{\partial q}

(l n x) x^{q + 1}

. According to the preliminary theorem, (iii) holds if and only if

l n x < 0

, which holds if and only

x \in (0,1) .

The proof of (iv) is like (v).

6. Numerical Experiments

In this section, numerical experiments are determined for the family of families characterized by the inference functional

, f (x) = x^{q + 1}

q

> -1,

q

≠ 0,

Χ

is any arbitrary enumeration set.

6.1. Extensive Information Theoretic Parameter r

For the extensive values of the parameter

q

q \in (- \infty, 1] ⨆ (1, \infty)

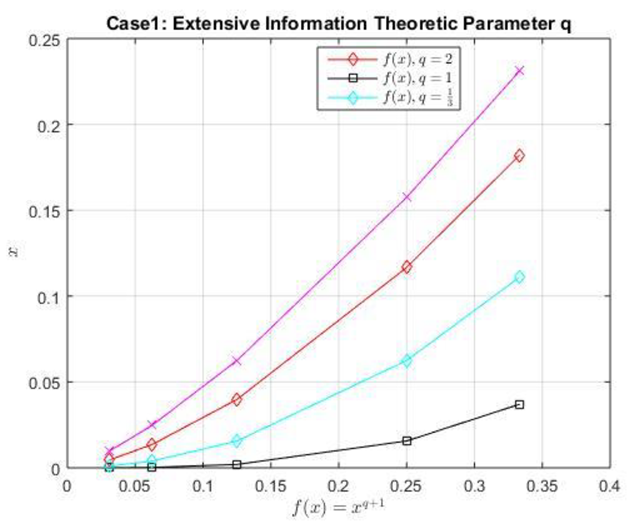
The above graph presents strong evidence of the significant impact of the extensive theoretic parameter on the overall behaviour of the inference functional

, f (x) = x^{q + 1}

. For

q = - 1,

the inference functional is a straight line. As r increases, the inference functional starts to take the curve shape until

q = 2,

it starts to be linear.

6.2. Non - Extensive Information Theoretic Parameter $q$

For the non-extensive values of the parameter

q

q \in (0.5,1)

The above graph shows the strong impact of the non-extensive information theoretic parameter

q (0.5 < q < 1)

. The inference functional decreases for

x = \frac{1}{3}

q (0.5 < q < 1)

. As x decreases the curve starts to be linear, for positive x. Fig.11 shows the increasability of the inference functional in x for all the non-extensive information theoretic parameter q. It is also observed that this numerical experiment agrees with the findings of theorem (11.1), as the graph decreases in r for all x satisfying

0 < x < 1

. This provides an evidence of the information theoretic impact on the inference functional.

7. Conclusions and Future Work

This study is innovative because it makes significant contributions to the theory of uncertain reasoning and investigates inference procedures based on RGES. Novel Characterization for

q > - 1, q \neq 0,

inference process

U_{q}^{L} (K)

by a functional equation is devised. First time unification of the inference process

U_{q}^{L} (K)

for

q > - 1, q \neq 0

with semi- group theory is obtained. Also, the threshold theorems for the inference functional were devised. Furthermore, numerical experiments are illustrated. The complex proofs in our paper are original results which emphasizes the credibility of the class of RGEs as measures of information, and that the field is open to extend an enhanced methodology regarding queuing networks with heavy tails.

There are several avenues for future work. One possibility is to investigate these information theoretic properties for other entropies such as Tsallis [5] and other higher order generalized such as Generalized Z-entropy, which is a generalization to many entropy functionals such as Tsallis and Rényi [6-13].

References

I.A. Mageed, and D.D. Kouvatsos, “Extended Properties of the Class of Rényi Generalized Entropies in the Discrete Time Domain”, Extended version of paper [1], 11-13 July 2011, IEEE International Conference on Computer Networks and Information Technology, Abbottabad, Pakistan, pp. 1-7, doi: 1109/ICCNIT.2011.6020894. Online available at https://ieeexplore.ieee.org/document/6020894.
Z.Lu, “Functional Equations’’, Lecture notes for the Math Circle, Irvine. Partially supported by the NSF grant DMS-1510232, 2017. Available online: https://www.math.uci.edu/~mathcircle/materials/M6L2.pdf.
A. J. Cain, “Nine Chapters on the Semigroup Art’’, Lecture notes for a tour through semigroups, Porto & Lisbon, 2020. Online available at file:///D:/down%20loads/c_semigroups_a4_greyscale.
Mageed, I. A., & Zhang, Q. (2023). Threshold Theorems for the Tsallisian and Rényian (TR) Cumulative Distribution Functions (CDFs) of the Heavy-Tailed Stable M/G/1 Queue with Tsallisian and Rényian Entropic Applications to Satellite Images (SIs). electronic Journal of Computer Science and Information Technology, 9(1), 41-47.
Mageed, I. A. (2023, July). Where the mighty trio meet: Information Theory (IT), Pathway Model Theory (PMT) and Queueing Theory (QT). In 39th Annual UK Performance Engineering Workshop (p. 8).
Mageed, I. A. (2023). The Entropian Threshold Theorems for the Steady State Probabilities of the Stable M/G/1 Queue with Heavy Tails with Applications of Probability Density Functions to 6G Networks. electronic Journal of Computer Science and Information Technology, 9(1), 24-30.
Mageed, I. A., & Bhat, A. H. (2022). Generalized Z-Entropy (Gze) and Fractal Dimensions. Appl. Math, 16(5), 829-834.
Mageed, I. A., & Zhang, Q. (2023). The Rényian-Tsallisian Formalisms of the Stable M/G/1 Queue with Heavy Tails Entropian Threshold Theorems for the Squared Coefficient of Variation. electronic Journal of Computer Science and Information Technology, 9(1), 7-14.
Mageed, I. A., & Zhang, Q. (2023). Formalism of the Rényian Maximum Entropy (RMF) of the Stable M/G/1 queue with Geometric Mean (GeoM) and Shifted Geometric Mean (SGeoM) Constraints with Potential GeoM Applications to Wireless Sensor Networks (WSNs). electronic Journal of Computer Science and Information Technology, 9(1), 31-40.
Bhat, A. H., Siddiqui, N. A., Mageed, I. A., Alkhazaleh, S., Das, V. R., & Baig, M. A. K. (2023). Generalization of Renyi’s Entropy and its Application in Source Coding. Appl. Math, 17(5), 941-948.
Mageed, I. A., Zhang, Q., & Modu, B. (2023). The Linearity Theorem of Rényian and Tsallisian Maximum Entropy Solutions of The Heavy-Tailed Stable M/G/1 Queueing System entailed with Potential Queueing-Theoretic Applications to Cloud Computing and IoT. electronic Journal of Computer Science and Information Technology, 9(1), 15-23.
Mageed, I. A. (2023, July). Rényi’s Maximum Entropy Formalism of Heavy-Tailed Queues with Hurst Exponent Heuristic Mean Queue Length Combined With Potential Applications of Hurst Exponent to Engineering. In 39^th Annual UK Performance Engineering Workshop (p. 21).

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Meeting at Both Ends Information – Theoretic Semi-group Theory of Uncertain Reasoning

Abstract

Introduction

2. Definitions

3. Novel Characterization of The Inference Process U q L K for q > − 1 , q ≠ 0 By a Functional Equation

4. Unification of The Inference Process U q L K for q > − 1 , q ≠ 0 with Semi-Group Theory

5. The Threshold Theorems for The Inference Functional

6. Numerical Experiments

6.1. Extensive Information Theoretic Parameter r

6.2. Non - Extensive Information Theoretic Parameter q

7. Conclusions and Future Work

References

MDPI Initiatives

Important Links

Subscribe

3. Novel Characterization of The Inference Process $U_{q}^{L} (K)$ for $q > - 1, q \neq 0$ By a Functional Equation

4. Unification of The Inference Process $U_{q}^{L} (K)$ for $q > - 1, q \neq 0$ with Semi-Group Theory

6.2. Non - Extensive Information Theoretic Parameter $q$