Preprint

Article

Performance Assessment of Repair and Reinforcement of Concrete Cable-Stayed Bridges in Service Based on Time-Dependent Reliability under Environmental Sustainability Development

Altmetrics

Downloads

113

Views

Comments

This version is not peer-reviewed

Submitted:

04 February 2024

Posted:

05 February 2024

You are already at the latest version

Alerts

Abstract

The reliability of concrete cable-stayed bridge structure is time variant. This is due to strength deterioration and time-variant mechanical and environmental loadings. Demands for keeping concrete cable-stayed bridge structure in functional and reliable states require maintenance interventions. Limited financial resources require optimal maintenance strategies. These strategies have to consider the effects of uncertainties not only on the structural reliability deterioration but also on the maintenance interventions. By analyzing variation of concrete cable-stayed concrete cable-stayed bridge liabilities and benefit expectation through different maintenance programs, on the condition of satisfying the concrete cable-stayed bridge performance, with the maximum expected benefit as the target to discuss repair and reinforcement strategies for the concrete cable-stayed bridges in service. The method takes into account the present performance and future expected benefit, optimizing the performance of the concrete cable-stayed bridge and the expected benefit through determination policies of concrete cable-stayed concrete cable-stayed bridge maintenance program. The proposed method also includes an advanced cost model which takes into account the interaction between costs of maintenance interventions and their effect on reliability. Examples are presented demonstrating the application of the proposed method to a stock of existing deteriorating concrete cable-stayed bridges under various maintenance scenarios.

Keywords:

Subject: Engineering - Civil Engineering

1. Introduction

The design and construction of new structure of civil engineering especially bridges was a dominant trend in the 1960’s and 1970’s. During this period, maintenance based on component replacement was the main solution in terms of management of bridges. Today, many of these bridges are getting old and a very large existing stock of bridge structures is in need of maintenance, rehabilitation, or replacement. In the early stages of implementation of management of structural systems, solutions based on the replacement theory and simple mathematical models such as survival functions were used. These approaches do not include the effects of preventive maintenance interventions and, therefore, are not practical for modern bridge structure management systems. These interventions introduce additional uncertainties in the lifetime performance of structures. The uncertainties associated with maintenance interventions can be taken into account by using different approaches based on probability, reliability, and fuzzy set theory.

Modern bridge management systems include time-variant conditions of bridge elements based on Markov process. Current condition states of bridge elements are investigated and Markov transition probabilities between different condition states are used to evaluate and predict future performance of deteriorating systems. However, currently predominant Markov based management systems have several important limitations. For instance, most of these systems are based on subjective condition assessment associated with visual inspection and empirical probability models to predict future condition states. As a result, objectivity and consistency in treating different condition states, failure modes of elements, and overall system condition and safety cannot be achieved.

Structural management systems should be developed based not only on structural deterioration but also on time-varying loads. In general, uncertainties associated with structural deterioration processes and loads increase over time. In traditional computations, time-varying resistance and loads are considered separately. There are distinct advantages in considering both resistance and loads simultaneously by using a time integrated approach. This can be achieved by using a reliability index profile approach by simultaneously considering time-varying effects of both loads and resistance deterioration.

During the service period, the structural resistance will deteriorate with time due to environmental factors, load factors and their own design and construction factors. At the same time, the reliability of the bridge will decrease with the increasing of the load level during the service period. When the structural reliability is reduced to a certain level, it is necessary to repair and reinforce the bridge structure. However, each maintenance method has a certain scope of application, and will incur corresponding costs. Therefore, it is necessary to allocate the limited maintenance funds reasonably in order to make the concrete bridge structure meet the required service life and the specified service performance. The optimization of concrete bridges maintenance strategy is to solve the problem of when and how to use maintenance methods to achieve the highest efficiency of maintenance costs, that is, the maximum expected value of revenue.

As a built structure, the concrete cable-stayed bridge in service is quite different from the bridge to be built. Firstly, the existing concrete cable-stayed bridge is an objective entity with measurable structural material strength and section size; secondly, the service life of the existing bridge is different from the design reference period of the concrete cable-stayed bridge to be built, which can be shortened or extended according to the specific conditions, purpose and requirements of the structure; thirdly, the existing concrete cable-stayed bridge has successfully withstood traffic load and has accumulated some information for reliability assessment.

In this paper, the time-dependent resistance model and time-dependent load model are revised to calculate time-dependent reliability by considering the durability and the change of load with time during assessment base period of components in various environments. Taking time-dependent reliability as a decision variable, life-cycle as a time parameter, and profit expectation in life-cycle as an objective, maintenance schemes are selected.

The structure of this paper is organized as follows. The conception of time-dependent reliability was firstly introduced. And then a decision-making of maintenance scheme was developed. Latterly, an example was used to demonstrate the application of the proposed method. Finally, the significant conclusion was summarized.

2. Time-dependent symmetry reliability

2.1. Durability analysis in general atmospheric environment

In general, atmospheric environment, for the durability of concrete, this paper considers that the carbonation of concrete leads to the decline of concrete durability. The calculation model of concrete carbonation depth established in Ref. [1] is used to predict the change of concrete carbonation depth with time:

x_{c} (t) = k_{e l} k_{e i} k_{t} (\frac{24.48}{\sqrt{f_{c u k}}} - 2.74) \sqrt{t}

(1)

where,

x_{c} (t)

is carbonation depth of concrete (mm);

f_{c u k}

is standard value of cubic compressive strength of concrete;

k_{e l}

is the regional influence coefficient, 1.0 in the north and 0.5-0.8 in the South and coastal areas;

k_{e i}

is the indoor and outdoor influence coefficient, 1.0 in the outdoor and 1.87 in the indoor;

k_{t}

is the maintenance time influence coefficient, and 1.50 in the general construction situation.

The model takes the standard value

f_{c u k}

of cubic compressive strength of concrete as the main parameter, and it is an effective and practical method for predicting the carbonation depth of concrete. In addition, Ref. [2] gives a more comprehensive and detailed model for predicting the depth of concrete carbonation considering factors, and the two models are comparatively close.

x_{c} (t) = {2.56 k}_{j} k_{{c o}_{2}} k_{p} k_{s} \sqrt[4]{T} (1 - R H) R H (\frac{57.94}{f_{c u k}} - 0.76) \sqrt{t}

(2)

where,

k_{j}

is the corner correction factor,

k_{c o 2}

is the influence factor of CO₂concentration,

k_{p}

is the correction factor of pouring surface,

k_{s}

is the influence coefficient of working stress; T is ambient temperature (°C) and RH is ambient relative humidity (%).

The cracking time of concrete is predicted by the depth of carbonation model:

x_{c} (t) + x_{h c} = d

(3)

where, d is the thickness of concrete cover (mm);

x_{h c}

is the length of partial carbonization zone (mm).

In the process of concrete carbonization, the strength of concrete will deteriorate continuously. At the same time, steel bar begins to corrode along with concrete carbonization and cracking, which reduces the area and the strength of steel bar. The cracking of concrete and the corrosion of steel bar cause the bond between concrete and steel bar changes, as a result, the coefficients of cooperative work between concrete and steel bars are constantly changing. Finally, it leads to the reduction of component resistance.

In Ref. [3], Niu presented a time-dependent model of concrete strength in general atmospheric environment. The model was established through a large number of actual test data and test results, but because the model was obtained through concrete cable-stayed bridge detection in Japan, it needed to be revised in practical application by introducing correction coefficient according to actual environmental conditions. In Ref. [4,5], a model of corrosion depth of steel bars before and after cracking of concrete protective layer in atmospheric environment is given, and the relationship between corrosion depth and corrosion rate of steel bars is also given:

η_{s} (t) \approx \frac{4 δ_{e} (t)}{D}

(4)

where,

η_{s} (t)

is the corrosion rate of reinforcing bars,

δ_{e} (t)

is the corrosion depth of reinforcing bars (mm) and D is the diameter of reinforcing bars (mm).

The calculation model of strength reduction coefficient of corroded steel bars is given in Ref. [6], the calculation model of the cooperative working coefficient of corroded steel bar and concrete is given in in Ref. [7].

2.2. Durability analysis in chloride environment

The durability of concrete members is mainly affected by chloride ions when the concrete cable-stayed bridge structure is in the marine environment or in the environment with more chloride ions. Fick's second diffusion law is used to simulate chloride diffusion in concrete:

C (x, t) = C_{s} (1 - \erf (\frac{x}{2 \sqrt{D_{c} t}}))

(5)

where,

C (x, t)

is the chloride ion concentration (%) a time t from x (mm) of concrete surface;

C_{s}

is the chloride ion concentration (%) in concrete surface environment;

D_{c}

is the concrete diffusion coefficient (mm²/a); erf () is the error function.

In Eq. (4), let

x = d

C (x, t) = C_{c r} - C_{i}

then the initial corrosion time

t_{i}

of reinforcing bars under chloride ion environment can be calculated; d is the thickness of concrete cover (mm);

C_{c r}

is the critical chloride ion concentration (%) for reinforcing bars to start corrosion; and

C_{i}

is the initial chloride ion concentration (%) in concrete.

Similarly, under the chloride ion environment, the strength of concrete will continue to deteriorate. At the same time, the steel bar will also corrode with chloride ion, which will reduce the area of steel bar and the strength of steel bar. Due to cracking of concrete and the corrosion of steel bar, the bond between concrete and steel bar changes, which leads to the constant change of the cooperative working coefficient between concrete and steel bar and reduce component resistance.

A time-dependent model of concrete strength in marine environment is given in Ref. [8]. In Ref. [9], the diameter of t-moment of corroded steel bar in chloride ion environment is given as follows:

D (t) = D_{0} - 0.0232 \int_{0}^{t - t_{i}} i_{c o r r} (t) d t

(6)

In the formula,

D (t)

is the diameter of corroded steel bar at time t (mm);

D_{0}

is the diameter of non-corroded steel bar (mm);

i_{c o r r} (t)

is the current density at time t (

μ A / {c m}^{2}

) after the beginning of corrosion, which is measured on site or calculated according to the formula below.

i_{c o r r} (t) = 32.13 \frac{{(1 - \frac{W}{C})}^{- 1.64}}{d} t^{- 0.29}

(7)

Corrosion rate of reinforcing bar is:

η_{s} (t) = [D_{0}^{2} - D^{2} (t)] / D_{0}^{2}

(8)

2.3. Time-dependent resistance

Referring to Specifications for design of highway reinforced concrete and prestressed concrete cable-stayed bridges and culverts (JTGD62-2015) and considering the change of durability parameters with time, the probability model of resistance attenuation of existing concrete cable-stayed bridge members can be expressed as follows:

R (t) = K_{T F} (t) K_{p} R_{p} [f_{c i} (t), a_{i} (t), k_{b i} (t)]

(9)

where,

R (t)

is a stochastic process of component resistance;

K_{T F} (t)

is a stochastic process taking into account the influence of resistance parameter testing and prediction, and the subscripts T and F represent the test and prediction respectively;

K_{p}

is an uncertain random variable of resistance calculation model, as shown in Table 1;

R_{p}

is a resistance function;

f_{c i} (t)

a_{i} (t)

are the predicted value of performance and geometric parameters of the type material based on test;

k_{b i} (t)

is the predicted value of the cooperative working coefficient of the ith reinforcing bar. It should be pointed out that the time zero of the prediction model is the current moment, and the resistance parameters of the current moment are measured. The resistance parameters of the prediction model are based on the predicted values of the current moment test.

2.4. Time-varying characteristics of Cable

Once the structural system of the concrete cable-stayed bridge is determined, the stress state of the completed bridge is mainly determined by cable force. However, due to the influence of its own relaxation effect, the cable force will change with time. At this time, the relaxation effect of the cable will affect the stress and strain of the whole bridge. The variation law of the relaxation rate of the cable of this bridge over time is as follows:

μ = 0.6233 + 0.3357 \lg t

(10)

2.5. Time-dependent loading

The dead load belongs to the permanent load, which changes slightly with time. It can be approximated that the stochastic variable probability model can be used to describe the dead load, which keeps a constant value during its continued use period. It is generally believed that the dead load of structures obeys normal distribution. When evaluating the reliability of old concrete cable-stayed bridges, the standard values can be used for statistic parameters of dead load (Ref. [11]).

For a long time, there are two opinions about the variable load value of service structure in engineering circles: the first is that when the trial period of service structure does not exceed the original design reference period T, the working state of the structure in [

t_{0}, T

] is still in the design reference period, and its load is the same as that of the design structure; the second is that the load of the service structure should be in accordance with the available one. The continuation life of reliability analysis is re-estimated. At present, in the load estimation of serving structures, a more consistent view is that if the load of serving structures is still taken according to the design reference period, it is unreasonable to estimate the load according to the continuing service period of serving structures. The evaluation reference period refers to the time parameter used to determine the evaluation load. Ref. [12] gives the calculation method of evaluation reference period based on equal transcendence probability criterion.

As the basic variable load of concrete cable-stayed bridge structure, vehicle load plays an important role in the load of concrete cable-stayed bridge. For the vehicle load, because of its strong randomness, the stochastic process model can be used to describe it. In order to simplify the analysis, the full-pavement stationary binomial stochastic process is often used in the stochastic process of vehicle load, as shown in Figure 1.

Considering the influence of evaluation reference period and concrete cable-stayed bridge overload, the probabilistic model of vehicle load effect of existing concrete cable-stayed bridges is established:

S_{q} (T_{1}) = K_{S_{q}} (T_{1}) ξ_{q} S_{q k}

(11)

where,

S_{q} (T_{1})

is assessment value for vehicle load effect;

K_{S_{q}} (T_{1})

is a random variable considering the ratio of vehicle load effect to Sqk in the evaluation reference period T₁,

K_{S_{q}} (T_{1})

obeys the extreme value I distribution,

ξ_{q}

is the correction factor of live load effect, and

S_{q k}

is the correction factor of live load effect. In order to standardize the effect value of standard automobile load calculation, highway-class II standard load is used in general operation state and highway-class I standard load is used in intensive operation state.

With the same vehicle load, the crowd load of highway concrete cable-stayed bridges can be described by a stationary binomial stochastic process with full pavement. The hypothesis test shows that the distribution of load section obeys the extreme value I distribution. For the convenience of reliability analysis, the process of crowd load shorthand should be converted into random variables.

Considering the influence of the evaluation reference period, the probability model of crowd load effectiveness of existing concrete cable-stayed bridges is as follows:

S_{r} (T_{1}) = K_{S_{r}} (T_{1}) S_{r k}

(12)

where,

S_{r} (T_{1})

is the evaluation value of crowd load effect;

K_{S_{r}} (T_{1})

is the random variable considering the ratio of crowd load effect to Srk in the evaluation reference period T₁;

K_{S_{r}} (T_{1})

obeys the extreme value I distribution;

S_{r k}

is the effect value of standard vehicle load calculation.

2.6. Time-dependent symmetry reliability assessment of concrete cable-stayed bridges in service

The time-dependent reliability of bridge components is defined as the ability of a bridge structure to complete its intended functions within a specified period of service, under normal service and maintenance conditions, taking into account factors such as environment and component resistance attenuation. Measured by reliability [13]:

P_{r} (t) = P \{Z (t) > 0\}, t \in [t_{0}, T_{s}]

(13)

Z (t) = R (t) - S_{G} - S_{q} (T_{1}) - φ_{c} S_{r} (T_{1})

(14)

where,

R (t)

is a component resistance prediction based on current resistance value;

S_{G}

is the component dead load effect;

S_{q} (T_{1})

is the vehicle load effect considering the evaluation reference period;

S_{r} (T_{1})

is the crowd load effect considering the evaluation reference period;

φ_{c}

is effect combination coefficient taken as 0.8 according to literature [14]; T₁ is the evaluation reference period.

The resistance random process

R (t)

is divided into m random variables

R_{i}

. The size of

R_{i}

is taken as the median value of resistance in the ith period. The equivalent resistance, which reflects the process of resistance change in the subsequent service period, can be expressed as:

R = - \frac{1}{α_{T}} \ln [\frac{1}{m} \sum_{i = 1}^{m} e x p (- α_{T} R_{i})]

(15)

where,

α_{T}

is a parameter in the probability distribution function of the maximum vehicle load effect S_QT in the design reference period (0, T_s). See Ref. [11].

3. Decision-making of maintenance scheme

3.1. Minimum reliability index

The reliability of serving concrete cable-stayed bridges decreases due to various reasons. When the reliability decreases to the lowest allowable reliability index, the concrete cable-stayed bridges need to be repaired and strengthened. Therefore, in the decision-making of concrete cable-stayed bridge maintenance scheme, the lowest reliability index of components should be determined first.

In Ref. [11], the target reliability index of the code is calculated according to the maximum value calibration method of load effect in the design reference period, and the corresponding time region is the design reference period. For serving concrete cable-stayed bridges, the corresponding time zone is the evaluation reference period, so the lowest reliability index of serving concrete cable-stayed bridges should be adjusted. In this paper, the lowest reliability index is 0.85

β_{T}

(Ref. [15]), and

β_{T}

is the target reliability index in the design reference period.

3.2. Revenue expectation

Because the structural cost and reliability index have the following exponential relationship roughly:

p_{r} (C) = 1 - (1 - p_{r}) e^{- C_{g}}

(16)

Increasing reliability must come at the expense of greater costs. Therefore, it is necessary to carry out economic optimization analysis of concrete cable-stayed bridge maintenance and reinforcement.

Bridge life expectancy mainly includes bridge life-cycle cost-initial cost

C_{0}

, periodic inspection cost

C_{I N S}

, maintenance and reinforcement cost

C_{R N S}

, bridge operation benefit-economic benefit I of bridge in normal service life, which is a time-dependent parameter with the change of traffic volume and national economy, bridge failure loss-bridge damage to national property. The loss S caused by personal safety and transportation is related to the traffic volume and the flow of people, and it changes with time.

When calculating concrete cable-stayed bridge operation benefit and failure loss, the influence of risk rate should be considered. The risk rate is the conditional probability that an event does not occur until t, but occurs in the subsequent

d_{t}

period.

h (t)

is used to express the risk rate of concrete cable-stayed bridge structure at time t (Ref. [16]), then:

h (t) = \frac{1}{1 - p_{f} (t)} \frac{d p_{f} (t)}{d t}

(17)

Because different maintenance schemes have different effects on structural reliability, the operation time and annual failure risk of the strengthened bridge are also different. In addition, in theory, several maintenance and reinforcement optimization designs can be carried out for a concrete cable-stayed bridge, but after one maintenance and reinforcement, it can be operated for many years, so the maintenance and reinforcement after many years still needs to be maintained according to the actual situation at that time. Optimal analysis of repair and reinforcement. Therefore, the calculation method of the expected return of maintenance plan is as follows:

E = \sum_{t = t_{0}}^{t_{i}} [\frac{I_{t} (1 - h (t))}{{(1 + r_{t})}^{(t - t_{0})}} - \frac{S_{t} h (t)}{{(1 + r_{t})}^{(t - t_{0})}}] - C_{R E S} - \sum_{t = t_{0}}^{t_{i}} \frac{C_{I N S}}{{(1 + r_{t})}^{(t - t_{0})}}

(18)

where,

I_{t}

is the normal operation benefit of the concrete cable-stayed bridge in the t year; h (t) is the failure risk of the concrete cable-stayed bridge after T-Year normal operation;

r_{t}

is the first T-year the discount rate of funds;

S_{t}

is the loss caused by the failure in the t year;

C_{I N S}

is the cost for the periodic inspection of concrete cable-stayed bridges; and

C_{R E S}

is the cost for the maintenance and reinforcement of concrete cable-stayed bridges using this scheme.

The impact of various maintenance schemes on structural reliability indicators are shown in Table 2.

3.3. Optimal analysis of maintenance scheme

The optimization model of concrete cable-stayed bridge maintenance scheme is as follows:

\{\begin{matrix} m a x E \\ s . t . E \geq 0 \\ β_{t} \geq β_{m} \\ C_{R E S} \leq C_{R E S M} \end{matrix}

(19)

where,

β_{t}

is the reliable index in the remaining service life,

β_{m}

is the lowest reliable index, and

C_{R E S M}

is the allowable maintenance and reinforcement cost.

In order to solve the constraint equation (18), the optimization algorithms named decomposition techniques was used in this paper. More details about the algorithms of decomposition techniques can be found in the Reference [17].

4. Probabilistic analsysis method

The relationship between the load wind effect

S

and the basic random vector

X

(such as flutter derivatives, aerodynamic coefficients, wind resistance safety factor, etc.) can be expressed as

S = S (X)

(20)

when applying the finite element first-order reliability method to an implicit function such as that regarding wind resistance of flutter or aerostatic instability of cable-supported bridges, the limit state function is

g [s (x), x] = G (u)

(21)

In order to solve the Equations (19), we can use the symmetry reliability method [18]. The equation

β (X, d, r) = β^{T}

can be rewritten as a general nonlinear equation

f = β (X, d, r) - β^{T}

(22)

Using the Taylor expansion,

β_{T}

at point

β^{j}

can be expressed as

β_{T} = β^{j} + {\frac{\partial β}{\partial θ}|}_{θ^{j}} (θ^{j + 1} - θ^{j})

(23)

where

θ

is the design parameter and j is the number of iterations.

The solution of the equation of assessment parameter can be obtained as:

θ = θ^{*} + \frac{β^{T} - β (X, θ^{*})}{{\frac{\partial β (X, θ)}{\partial θ}|}_{θ^{*}}}

(24)

5. Example

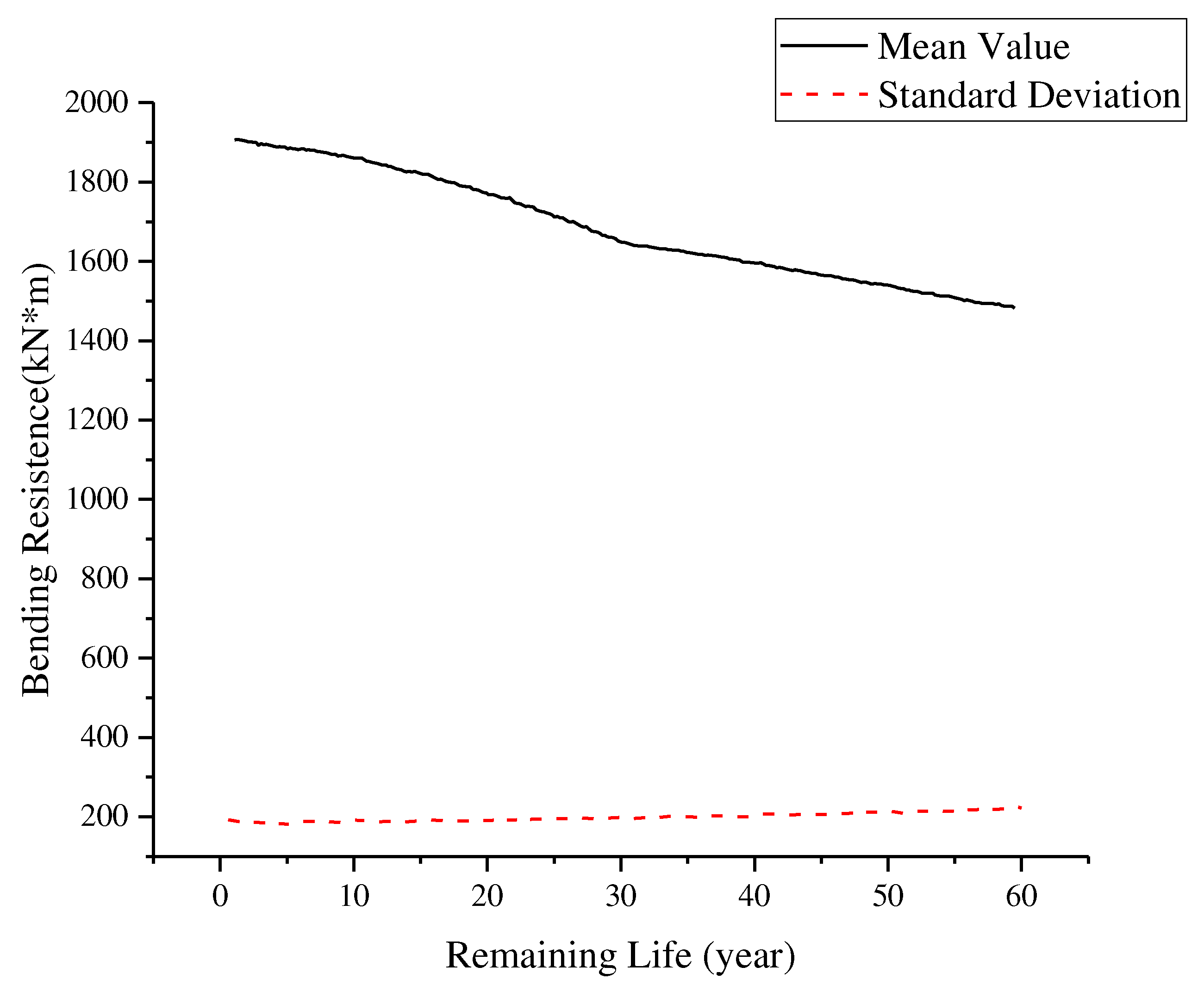
A reinforced concrete cable-stayed bridge near 40 years of service has a main span with 180m. Based on the test data and the calculation model, the strength correction coefficient

k_{c}

of beam concrete, the cross-section corrosion rate

η_{s}

of main reinforcements, the cooperative working coefficient

k_{b s}

of main reinforcement and concrete, and yield strength reduction coefficient

k_{y s}

with time for corroded main bars are obtained, and the variation law of mean and standard deviation of bending resistance with time is obtained, as shown in Figure 2. The rule of reliability varying with time under maintenance and reinforcement can be obtained. Considering concrete cable-stayed bridge maintenance cost, operation benefit, service life and expert opinions, the following maintenance options and related costs are obtained.

Scheme 1: glass fiber + epoxy resin injection.

Scheme 2: adding measurement + epoxy resin injection.

Scheme 3: two steel plates are pasted.

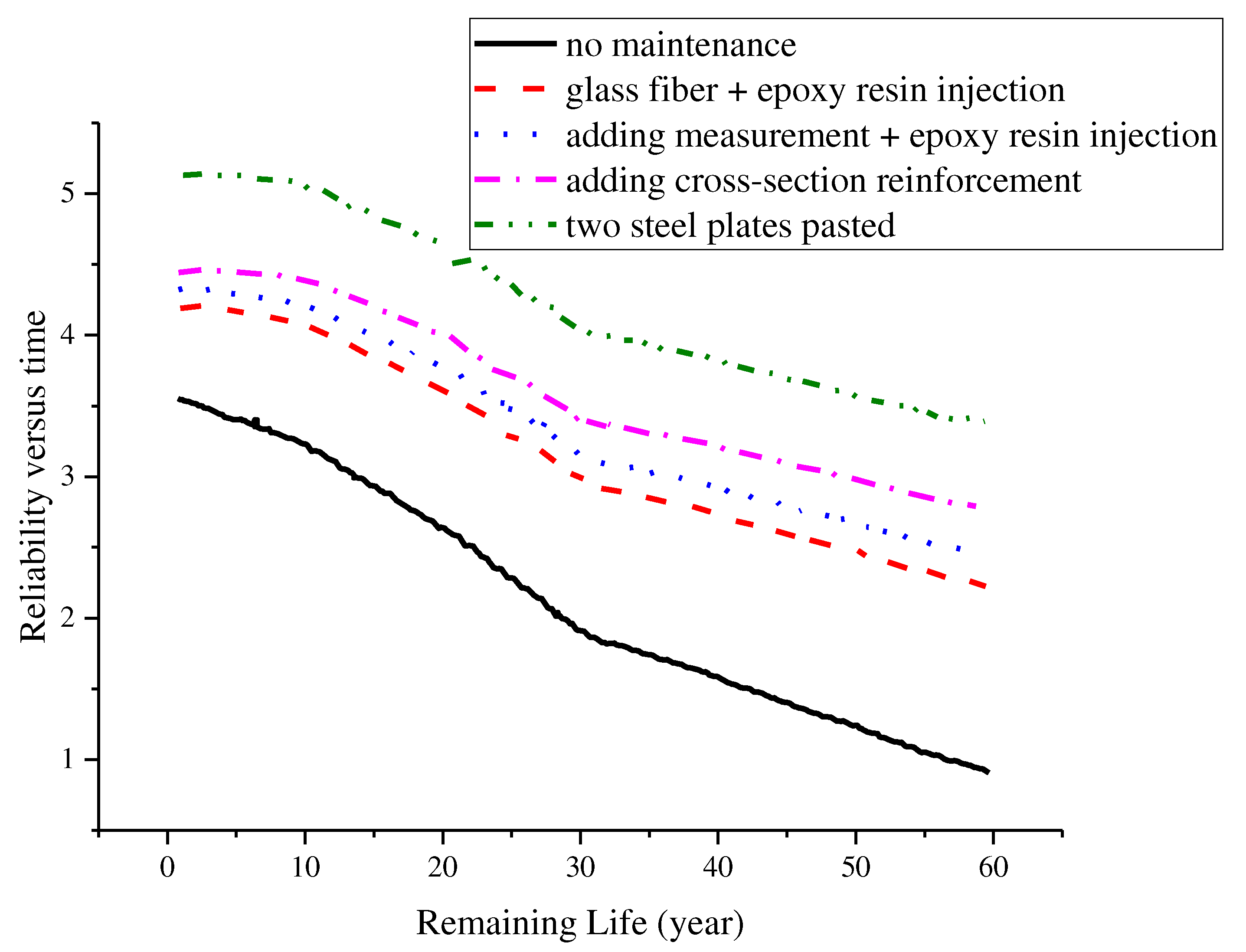
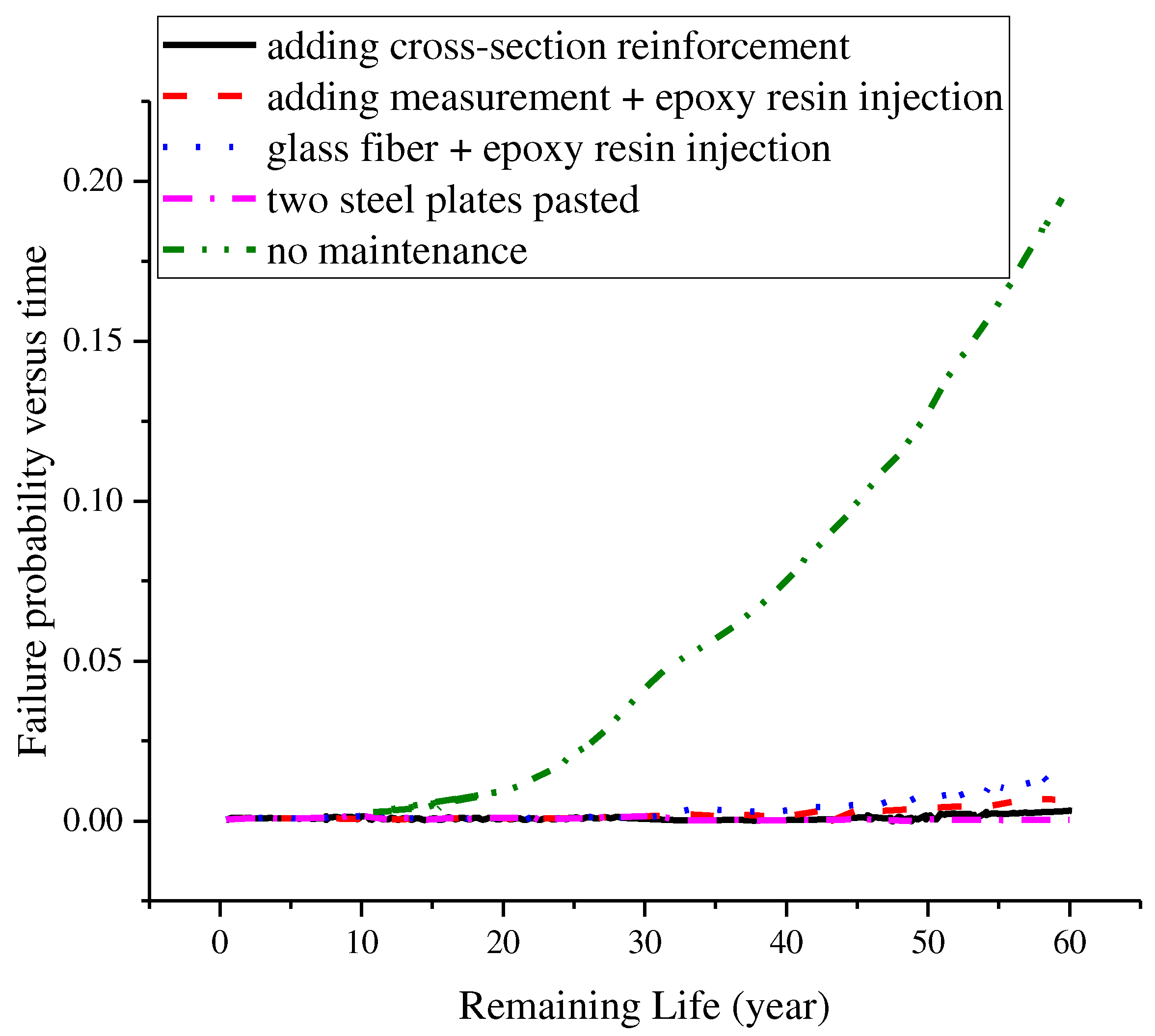
Scheme 4: adding cross-section reinforcement cost. Considering the influence of maintenance on reliability, comparing the reliability of unmaintained reinforcement, the variation law of reliability with time after maintenance and reinforcement is shown in Figure 3, and the variation law of failure probability with time is shown in Figure 4. By calculating the earnings expectation of each scheme, the expected earnings of each scheme can be obtained as shown in Table 3.

The studies above indicate that shrinkage and creep have strong influence on the stiffening girder; it is therefore necessary to take the long-term effects of shrinkage and creep in the operation into consideration when determining the reasonable bridge state. The reduction of the hanger force has the greatest impact on the mechanical properties of stiffening girders during operation; thus, increasing the hanger force of the initial completed bridge state by an appropriate percentage can lead to good results. The increase of the hanger force (usually less than 5% of the devised hanger force) will alleviate the impacts of shrinkage and creep on the hanger force and ensure the reasonableness of the final completed bridge state in 60 years.

After increasing by 2.5~5% of the devised hanger force, the stress in corresponding sections is shown in Table 3.

From the above results with Table 3 and Figure 2, Figure 3 and Figure 4, it can be seem that the failure probability with time was increase quickly because it has no maintenance measure. Through the comparison of various schemes, it can be seen that scheme 3 - sticking two steel plates is the best scheme. In practical bridge engineering, the measure of two steel plates pasted can be recommended to strengthen the bridge structure both considering the reliability and cost.

The probability parameter that affects the safety performance of large-span cable supported bridges is mainly the coefficient of variation, and the magnitude of variation has a significant impact on the structural reliability index and probability safety factor of maximum cable stress results. In order to quantitatively study the impact of the magnitude of variability on the structural reliability indicators and cable probability safety factors of structure, parameter sensitivity analysis was only conducted on the structural reliability indicators and cable probability safety factors for 10, 20, and 30 years. The coefficient of variation is taken as 0.5, 1, and 2 times the original value, respectively. The specific results are shown in Table 4.

Through the analysis of Table 4, it can be found that the structural reliability index decreases with the increase of parameter variability. The reason is that the coefficient of variation reflects the discreteness of structural parameters and is located in the denominator term of the reliability index calculation expression. Therefore, the calculation result of the reliability index is inversely proportional to the magnitude of parameter variability. Similarly, through the analysis of Table 4, it can be found that the probability safety factor of cable with maximum stress decreases with the increase of parameter variability. The reason is that the coefficient of variation reflects the discreteness of structural parameters, and the greater the variability, the smaller the safety reserve of the structure. Therefore, the calculation result of the probability safety factor is inversely proportional to the magnitude of parameter variability.

6. Conclusions

In this paper, the time-dependent resistance of concrete cable-stayed bridges is obtained based on the durability changes of concrete cable-stayed bridges in various environments, and the time-dependent reliability of concrete cable-stayed bridges is obtained by considering the load changes during assessment base period. By taking time-dependent reliability as a decision variable and taking the expected value of benefit in the whole life cycle of concrete cable-stayed bridge as a decision objective, the decision-making of concrete cable-stayed bridge maintenance and reinforcement is carried out. Through the analysis of an example concrete cable-stayed bridge application, the following conclusions can be drawn.

(1): A computational tool that can be used to predict the lifecycle reliability performance, cost, and optimal maintenance interventions of deteriorating concrete cable-stayed bridge structures was described. This tool uses random variables to describe reliability index profiles and cost functions of individual or groups of deteriorating bridge structures.
(2): For the loads on concrete cable-stayed bridge structures, the loads in the design base period should be calibrated, and the assessment base period should be taken as the time variable. And the resistance of concrete cable-stayed bridge structures should also consider the effect of time variable. Based on the time-dependent of resistance and load in performance function, the results of cost and reliability index can be calculated reasonably.
(3): The economic evaluation of maintenance and reinforcement should consider not only the cost of maintenance and reinforcement, but also the benefits of various maintenance and reinforcement schemes, so as to prevent the situation of low cost but low benefit.
(4): In the decision-making process of maintenance and reinforcement, reliability and benefit expectation should be considered comprehensively to avoid excessive one-time investment and unnecessary safety reserve. The decomposition technique was recommended to solve the maintenance scheme.
(5): The variability of parameters has a significant impact on the reliability index and probability safety coefficient of the structure. In the operation process of cable-stayed bridges, it is necessary to focus on observing the discreteness of the main parameters that affect the safety performance of the structure, and develop targeted measures to ensure the safety of the structure.

Data Availability Statement

The data used in the manuscript can be replicated through calculation method as described in the manuscript. The data supporting the conclusions of the study can be obtained in the manuscript.

Acknowledgments

The authors wish to express their sincere to the Natural Science Foundation of Jiangsu Province (Grant No. BK20200793).

Conflicts of Interest

The authors declare that there is no conflict of interest regarding the publication of this paper.

References

Niu D.T. and Chen Y.Q., “Analysis of carbonation mode and carbonation life of concrete structures,” Journal of Xi'an University of Architectural Science and Technology, 27(4):365-269,1995.
Niu D.T., “The prediction of durability and life of concrete structures,” Beijing: Science Press, 2003.
Niu D.T. and Wang Q.L., “time-dependent model of concrete strength in general atmospheric environment,” Industrial Buildings, 25(6): 36-38,1995.
Jiang L.X. and Zhang Y., “Analysis and Calculation of the Length of Partial Carbonation Zone of Concrete,” Industrial Buildings, 29(1): 4-7,1999.
Niu, D.T. , “The prediction of durability and life of concrete structures,” Beijing: Science Press, 2003.
Hui Y.L., Lin Z.S., and Li R., “Experimental Study and Analysis on the Properties of Corroded Reinforcement Bars,” Industrial Buildings, 27(6): 10-13,1997.
Niu D.T., “time-dependent model of concrete strength in marine environment,” Journal of Xi'an University of Architectural Science and Technology, 27(1):49-52,1995.
Wu J. and Wu S.X., “Reliability evaluation of corroded reinforced concrete structures,” Engineering mechanics, 22(1): 118-122,2005.
JTG D62-2004 Specifications for design of highway reinforced concrete and prestressed concrete bridges and culverts.
GB/T 5283-1999 Unified standard for reliability design of highway engineering structures.
Ou J.P., Liu X.D., and Wang G.Y., “Study on Environmental Load Standard for Safety Assessment of Active Structures,” Industrial Buildings, 25(8): 11-16,1995.
Specification for testing and assessment of bearing capacity of highway bridges, 2005.
Nowak A.S. Szerszen M.M., “Structural reliability as applied to highway bridges,” Progress in Structural Engineering & Materials, 2(2):218-224, 2015. [CrossRef]
Zhao G.F., “Reliability theory and application of engineering structures, ”Dalian: Dalian Polytechnic University Press, 1996.
Wang G.Y., “Soft theory of engineering design,” Beijing: Science Press, 1982.
Ayaho Miyamoto, Kei Kawamura, hideaki Nakamura, “Development of a bridges management system for existing bridges,”Advances in Engineering software, 32: 821-833,2001. [CrossRef]
Minguez R., Castillo E., Hadi A. S., “Solving the inverse reliability problem using decomposition techniques,” Structural Safety, 27(1):1-23, 2005. [CrossRef]
Dong F., Gao J., Hao A., Wei Y., Huang X., Shi F., Zheng K. A New Approach to Symmetry Reliability: Combination of Forward and Inverse Reliability Principle and Its Application to Frame Structures and Bamboo Bridges, Symmetry,2022, 14(2), 318. [CrossRef]

Figure 1. Full paved stationary binomial random processes.

Figure 2. Time-dependent variation of mean and standard deviation of flexural resistance.

Figure 3. The curve of reliability versus time.

Figure 4. The curve of failure probability versus time.

Table 1. Statistical parameters of basic concrete cable-stayed bridge components Kp.

Stress state		Mean value μ	Standard deviation σ	Coefficient of variation ν
Axial compression (short column)		1.0105	0.0709	0.0702
Axial tension		1.0000	0.0400	0.0400
Bending of normal section		1.0980	0.0780	0.0710
Oblique section sheared	Rectangular cross section	1.4861	0.4209	0.2832
Oblique section sheared	T shaped section	2.0152	0.1781	0.0884
Eccentric stub column	Rectangular cross section (large eccentricity)	1.0650	0.0937	0.0880
	Rectangular cross section (small eccentricity)	1.0700	0.1017	0.0950
	Circular section	0.9480	0.1062	0.1120

Table 2. Effects of various maintenance schemes on structural reliability indices and costs.

Maintenance activities	Number	Reliability index increment	Degradation rate	Effect duration/year
Epoxy resin injection + section repair	R1	0.50	0.055	3
Glass fiber + epoxy resin injection	R2	0.60	0.06	5
Adding Beam + Epoxy Resin Injection	R3	0.70	0.1	3
Stick 2 steel plates	R4	1.50	0.08	5
Stick 4 steel plates	R5	2.10	0.075	5
Reinforcement by adding section	R6	0.80	0.09	9

Table 3. Solution options and revenue expectations.

Scheme	Scheme 1	Scheme2	Scheme3	Scheme4
Remaining service life/year	24	27	57	30
Expectations of earnings/ten thousand yuan	87	143	152	105

Table 4. The effect of variability on reliability index and safety factor of concrete cable-stayed bridge.

Time (Year)	Structural reliability index			Safety factor of cable with maximum stress
Time (Year)	0.5	1	2	0.5	1	2
10	11.5132	10.9171	9.6221	8.1824	7.6543	6.6471
20	10.7215	9.9533	8.8187	7.6276	6.6431	5.2232
30	19.1157	8.2152	6.8319	6.7391	5.9887	4.5265

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Performance Assessment of Repair and Reinforcement of Concrete Cable-Stayed Bridges in Service Based on Time-Dependent Reliability under Environmental Sustainability Development

Abstract

1. Introduction

2. Time-dependent symmetry reliability

2.1. Durability analysis in general atmospheric environment

2.2. Durability analysis in chloride environment

2.3. Time-dependent resistance

2.4. Time-varying characteristics of Cable

2.5. Time-dependent loading

2.6. Time-dependent symmetry reliability assessment of concrete cable-stayed bridges in service

3. Decision-making of maintenance scheme

3.1. Minimum reliability index

3.2. Revenue expectation

3.3. Optimal analysis of maintenance scheme

4. Probabilistic analsysis method

5. Example

6. Conclusions

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe