Magnetic Black Hole Thermodynamics in an Extended Phase Space with Nonlinear Electrodynamics

Preprint

Article

Magnetic Black Hole Thermodynamics in an Extended Phase Space with Nonlinear Electrodynamics

Altmetrics

Downloads

128

Views

Comments

A peer-reviewed article of this preprint also exists.

Sergey Il'ich Kruglov^*

This version is not peer-reviewed

Submitted:

07 February 2024

Posted:

08 February 2024

Read the latest preprint version here

Alerts

Abstract

We study Einstein's gravity coupled to nonlinear electrodynamics with two parameters in Anti-de Sitter spacetime. Magnetically charged black holes in an extended phase space is investigated. We obtain the mass and metric functions, their asymptotic and corrections to the Reissner--Nordstr\"{o}m metric function. The first law of black hole thermodynamics in extended phase space is formulated and the magnetic potential and the thermodynamic conjugate to the coupling are obtained. We proved the generalized Smarr relation. The heat capacity and the Gibbs free energy are computed and phase transitions are studied. It was shown that the electric field of charged objects at the origin and electrostatic self-energy are finite within the nonlinear electrodynamics proposed.

Keywords:

Subject: Physical Sciences - Astronomy and Astrophysics

1. Introduction

That black holes being the thermodynamic systems possess the entropy and temperature connected with the black hole area and surface gravity, correspondingly [1,2,3,4,5]. Gravity in Anti-de Sitter (AdS) spacetime has applications in condensed matter physics which is of the holographic principle [6]. Firstly black hole phase transitions in Schwarzschild-AdS spacetime were studied in Ref. [7]. The negative cosmological constant, in an extended phase space black hole thermodynamics, is linked with a thermodynamic pressure conjugated to the volume [8,9,10,11]. The first law of black hole thermodynamics can be formulated within Einstein gravity in AdS spacetime. In this paper, we study Einstein-AdS gravity coupled to nonlinear electrodynamics (NED) with two parameters, proposed here, that allows us to smooth out singularities. First NED was Born–Infeld electrodynamics [12] without singularities of point-like particles possessing the electric self-energy finite and at weak-field limit it is converted into Maxwell’s theory. Our NED model has similar behaviour. We will study magnetic black holes and their thermodynamics in the Einstein-AdS gravity in the extended phase space.

The structure of the paper is as follows. In section 2 we find the mass and metric functions and their asymptotic. Corrections to the Reissner–Nordström metric function are obtained. We proof the first law of black hole thermodynamics in extended phase space and obtain the magnetic potential and the thermodynamic conjugate to the coupling. The generalized Smarr formula is proved. The Gibbs free energy is calculated and depicted for some parameters and phase transitions are studied in section 3. In Appendix A we obtain the electric field of charged objects and corrections to Coulomb law. We show that the electrostatic self-energy of charged particles is finite in Appendix B. Section 4 is a discussion of results obtained.

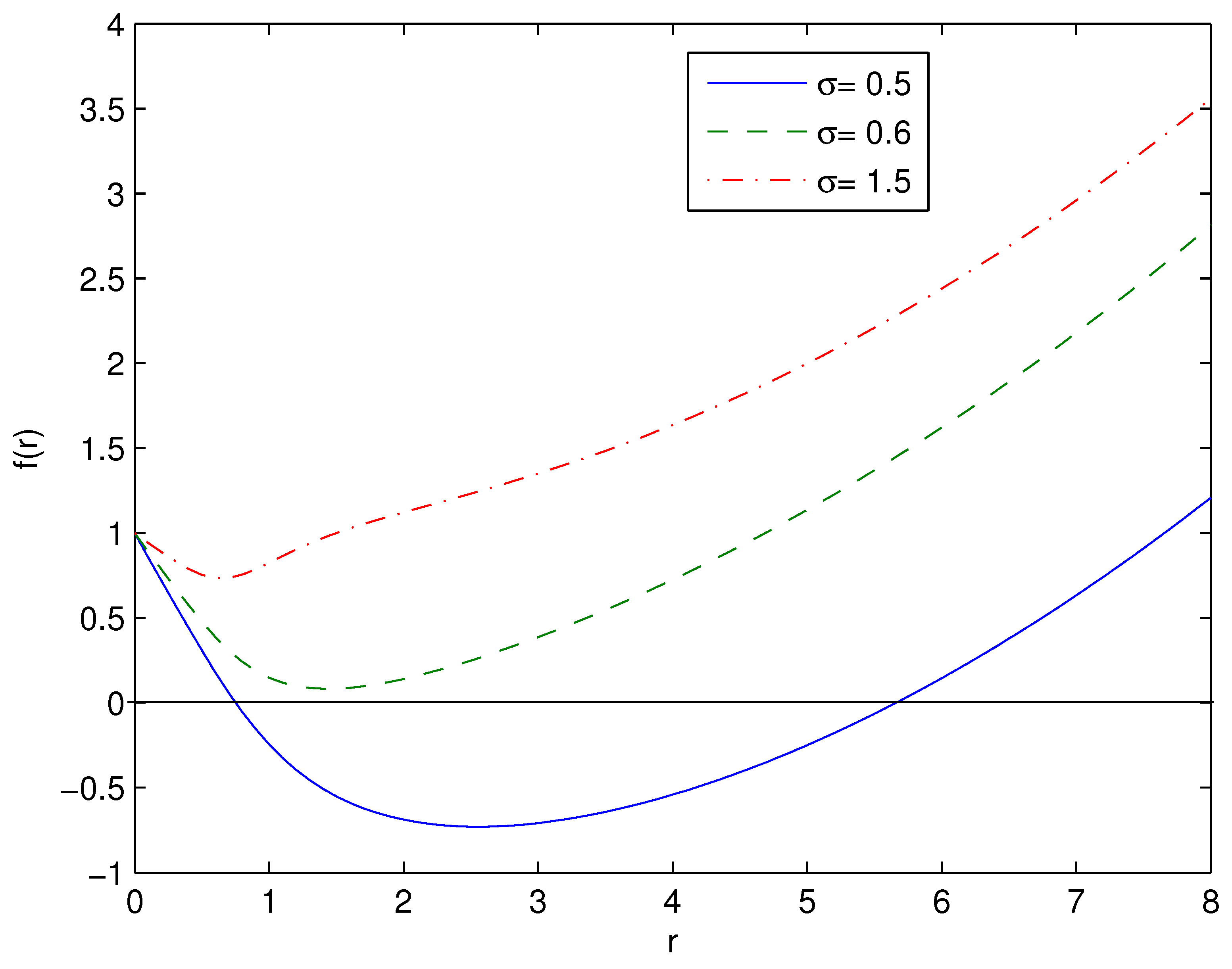
2. Einstein-AdS black hole solution

The action of Einstein’s gravity in AdS spacetime is given by

I = \int d^{4} x \sqrt{- g} (\frac{R - 2 Λ}{16 π G} + L (F)),

(1)

where G is the gravitation constant,

Λ = - 3 / l^{2}

is the negative cosmological constant and l is the AdS radius. We propose the NED Lagrangian as follows:

L (F) = - \frac{F}{4 π {(1 + 2 β F)}^{σ}},

(2)

where

F = F^{μ ν} F_{μ ν} / 4 = (B^{2} - E^{2}) / 2

is the Lorenz invariant and E and B are the electric and magnetic fields, correspondingly. The coupling

β > 0

has the dimension

[L] = 4

, and the dimensionless parameter

γ > 0

. The weak-field limit of Lagrangian (2) is the Maxwell’s Lagrangian. The Lagrangian (2) at

σ = 1

becomes the rational NED Lagrangian [13]. The NED Lagrangian (2) for some values of

σ

was used in the inflation scenario [14,15,16,17]. From action (1) one finds the Einstein and field equations

R_{μ ν} - \frac{1}{2} g_{μ ν} R + Λ g_{μ ν} = 8 π G T_{μ ν},

(3)

\partial_{μ} (\sqrt{- g} L_{F} F^{μ ν}) = 0,

(4)

where

L_{F} = \partial L (F) / \partial F

. The energy-stress tensor reads

T_{μ ν} = F_{μ ρ} F_{ν}^{ρ} L_{F} + g_{μ ν} L (F) .

(5)

We consider here spherical symmetry with the line element

d s^{2} = - f (r) d t^{2} + \frac{1}{f (r)} d r^{2} + r^{2} (d θ^{2} + {sin}^{2} (θ) d ϕ^{2}) .

(6)

The magnetic black holes possess the magnetic field

B = q / r^{2}

where q is the magnetic charge. The metric function is given by [18]

f (r) = 1 - \frac{2 m (r) G_{N}}{r},

(7)

with the mass function

m (r) = m_{0} + 4 π \int ρ (r) r^{2} d r,

(8)

where

m_{0}

is an integration constant (the Schwarzschild mass) and

ρ

being the energy density. We obtain the energy density

ρ = ρ_{M} - \frac{3}{8 π G l^{2}},

(9)

where the magnetic energy density found from Eq. (5) is

ρ_{M} = \frac{q^{2} r^{4 (σ - 1)}}{8 π {[r^{4} + q^{2} β]}^{σ}} .

Making use of Eqs. (8) and (9) we obtain the mass function

m (r) = m_{0} + \frac{q^{2} r^{4 σ - 1}}{2 (4 σ - 1) {(q^{2} β)}^{σ}} F (σ - \frac{1}{4}, σ; σ + \frac{3}{4}; - \frac{r^{4}}{q^{2} β}) - \frac{r^{3}}{2 G l^{2}},

(10)

where

F (a, b; c; z)

is the hypergeometric function. The magnetic energy is given by

m_{M} = 4 π \int_{0}^{\infty} ρ_{M} (r) r^{2} d r = \frac{q^{3 / 2} Γ (σ - 1 / 4) Γ (5 / 4)}{2 β^{1 / 4} Γ (σ)},

(11)

where

Γ (x)

is Gamma-function. From Eqs. (7) and (10) one finds the metric function

f (r) = 1 - \frac{2 m_{0} G_{N}}{r} - \frac{q^{2} G r^{4 σ - 2}}{(4 σ - 1) {(q^{2} β)}^{σ}} F (σ - \frac{1}{4}, σ; σ + \frac{3}{4}; - \frac{r^{4}}{q^{2} β}) + \frac{r^{2}}{l^{2}} .

(12)

We use the relation [19]

F (a, b; c; z) = 1 + \frac{a b}{c} z + \frac{a (a + 1) b (b + 1)}{c (c + 1)} z^{2} + . . . .,

(13)

for

| z | < 1

, which will be used to obtain the asymptotic of the metric function as

r \to 0

. When the Schwarzschild mass is zero (

m_{0} = 0

) and as

r \to 0

, the asymptotic is

f (r) = 1 + \frac{r^{2}}{l^{2}} - \frac{G q^{2} r^{4 σ - 2}}{{(q^{2} β)}^{σ} (4 σ - 1)} + \frac{G σ r^{4 σ + 2}}{β^{σ + 1} q^{2 σ} (4 σ + 3)} + O (r^{4 σ + 6}) .

(14)

We imply that

σ \geq 1 / 2

. Then from Eq. (14) we find

f (0) = 1

that is a necessary condition to have the spacetime regular. We explore the transformation [19]

F (a, b; c; z) = \frac{Γ (c) Γ (b - a)}{Γ (b) Γ (c - a)} {(- z)}^{- a} F (a, 1 - c + a; 1 - b + a; \frac{1}{z})

+ \frac{Γ (c) Γ (a - b)}{Γ (a) Γ (c - b)} {(- z)}^{- b} F (b, 1 - c + b; 1 - a + b; \frac{1}{z}),

(15)

to obtain the asymptotic of the metric function as

r \to \infty

. By virtue of Eqs. (13) and (15) we find

f (r) = 1 - \frac{2 (m_{0} + m_{M}) G}{r} + \frac{q^{2} G}{r^{2}} F (σ, \frac{1}{4}; \frac{5}{4}; - \frac{q^{2} β}{r^{4}}) + \frac{r^{2}}{l^{2}},

(16)

where the relation

Γ (1 + z) = z Γ (z)

and

F (a, 0; c; z) = 1

were used. Making use of Eqs. (13) and (16) as

r \to \infty

when the cosmological constant vanishes (

l \to \infty

) we find

f (r) = 1 - \frac{2 M G}{r} + \frac{q^{2} G}{r^{2}} - \frac{q^{4} β σ G}{5 r^{6}} + O (r^{- 10}),

(17)

where

M = m_{0} + m_{M}

is the ADM mass (the total black hole mass as

r \to \infty

). It follows from Eq. (17) that corrections to the Reissner–Nordström solution are

O (r^{- 6})

. When

β \to 0

the metric function (17) is converted into the Reissner–Nordström metric function. The plot of metric function (12) is given in Figure 1 with

m_{0} = 0

G = q = 1

β = 0.5

l = 5

In accordance with Figure 1, if parameter

σ

increases the event horizon radius

r_{+}

decreases. Figure 1 shows that black holes can have one or two horizons.

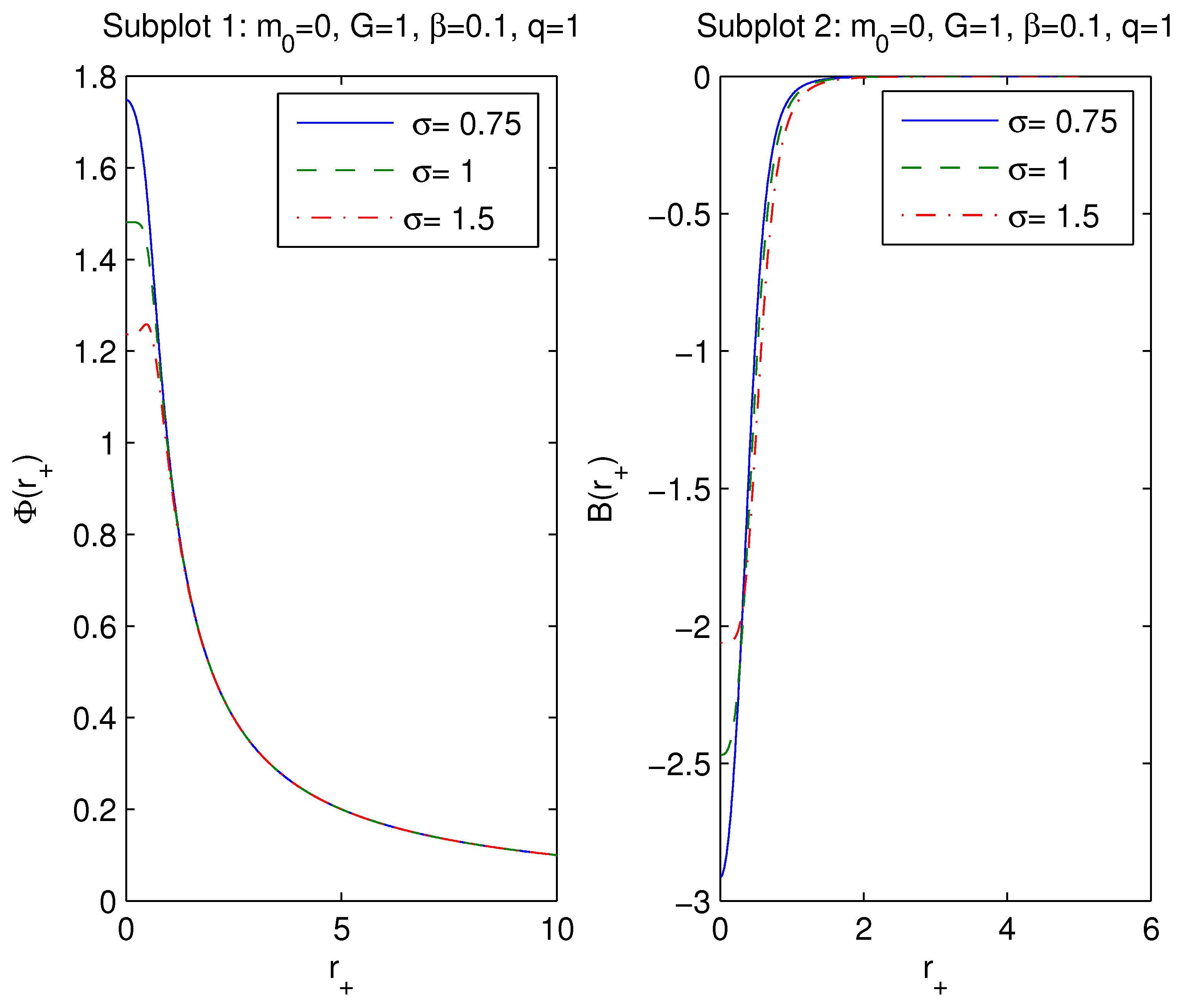
3. First law of black hole thermodynamics

The pressure, in extended phase space thermodynamics, is defined as

P = - Λ / (8 π)

[20,21,22,23,24]. The coupling

β

is treated as the thermodynamic value and the mass M is a chemical enthalpy so that

M = U + P V

and U being the internal energy. By using the Euler’s dimensional analysis with

G = 1

[20,25], we have dimensions

[M] = L

[S] = L^{2}

[P] = L^{- 2}

[J] = L^{2}

[q] = L

[β] = L^{2}

and

M = 2 S \frac{\partial M}{\partial S} - 2 P \frac{\partial M}{\partial P} + 2 J \frac{\partial M}{\partial J} + q \frac{\partial M}{\partial q} + 2 β \frac{\partial M}{\partial β},

(18)

where J is the black hole angular momentum. In the following we consider non-rotating black holes and, therefore,

J = 0

. The thermodynamic conjugate to coupling

β

B = \partial M / \partial β

(so-called vacuum polarization) [10]. The black hole volume V, entropy S, and pressure P are defined as

V = \frac{4}{3} π r_{+}^{3},, S = π r_{+}^{2}, P = - \frac{Λ}{8 π} = \frac{3}{8 π l^{2}} .

(19)

From Eq. (16), and equation

f (r_{+}) = 0

, where

r_{+}

is the event horizon radius, one finds

M (r_{+}) = \frac{r_{+}}{2} + \frac{q^{2}}{2 r_{+}} F (σ, \frac{1}{4}; \frac{5}{4}; - \frac{q^{2} β}{r^{4}}) + \frac{r^{3}}{2 l^{2}} .

(20)

Making use of Eq. (20), we obtain

d M (r_{+}) = [\frac{1}{2} + \frac{3 r_{+}^{2}}{2 l^{2}} - \frac{q^{2}}{2 r_{+}^{2}} F (σ, \frac{1}{4}; \frac{5}{4}; - \frac{q^{2} β}{r^{4}})

+ \frac{2 σ q^{4} β}{5 r_{+}^{6}} F (σ + 1, \frac{5}{4}; \frac{9}{4}; - \frac{q^{2} β}{r^{4}})] d r_{+} - \frac{r_{+}^{3}}{l^{3}} d l

+ [\frac{q}{r_{+}} F (σ, \frac{1}{4}; \frac{5}{4}; - \frac{q^{2} β}{r^{4}}) - \frac{q^{3} β σ}{5 r_{+}^{5}} F (σ + 1, \frac{5}{4}; \frac{9}{4}; - \frac{q^{2} β}{r^{4}})] d q

- \frac{q^{4} σ}{10 r_{+}^{5}} F (σ + 1, \frac{5}{4}; \frac{9}{4}; - \frac{q^{2} β}{r^{4}}) d β .

(21)

Here, we have used the relation [19]

\frac{d F (a, b; c; z)}{d z} = \frac{a b}{c} F (a + 1, b + 1; c + 1; z) .

(22)

Defining the Hawking temperature

T = \frac{f^{'} {(r) |}_{r = r_{+}}}{4 π},

(23)

where

f^{'} (r) = \partial f (r) / \partial r

, and by virtue of Eqs. (16) and (23), we obtain

T = \frac{1}{4 π} [\frac{1}{r_{+}} + \frac{3 r_{+}}{l^{2}} - \frac{q^{2}}{r_{+}^{3}} F (σ, \frac{1}{4}; \frac{5}{4}; - \frac{q^{2} β}{r^{4}}) + \frac{4 σ q^{4} β}{5 r_{+}^{7}} F (σ + 1, \frac{5}{4}; \frac{9}{4}; - \frac{q^{2} β}{r^{4}})] .

(24)

β = 0

in Eq. (24), one finds the Maxwell-AdS black hole Hawking temperature. The first law of black hole thermodynamics follows from Eqs. (19), (20) and (24),

d M = T d S + V d P + Φ d q + B d β .

(25)

From Eqs. (21) and (25) we obtain the magnetic potential

Φ

and the thermodynamic conjugate to coupling

β

(vacuum polarization)

B

Φ = \frac{q}{r_{+}} F (σ, \frac{1}{4}; \frac{5}{4}; - \frac{q^{2} β}{r^{4}}) - \frac{q^{3} β σ}{5 r_{+}^{5}} F (σ + 1, \frac{5}{4}; \frac{9}{4}; - \frac{q^{2} β}{r^{4}}),

B = - \frac{q^{4} σ}{10 r_{+}^{5}} F (σ + 1, \frac{5}{4}; \frac{9}{4}; - \frac{q^{2} β}{r^{4}}) .

(26)

The plots of

Φ

and

B

versus

r_{+}

are depicted in Figure 2.

Figure 2, in the left panel, shows that as

r_{+} \to \infty

the magnetic potential vanishes (

Φ (\infty) = 0

), and at

r_{+} = 0

Φ

is finite. If the parameter

σ

increases,

Φ (0)

decreases. According to the right panel of Figure 2 at

r_{+} = 0

the vacuum polarization is finite and as

r_{+} \to \infty

B

vanishes (

B (\infty) = 0

). When the parameter

σ

increases,

B (0)

also increases. With the aid of Eqs. (19), (24) and (26) we find the generalized Smarr relation

M = 2 S T - 2 P V + q Φ + 2 β B .

(27)

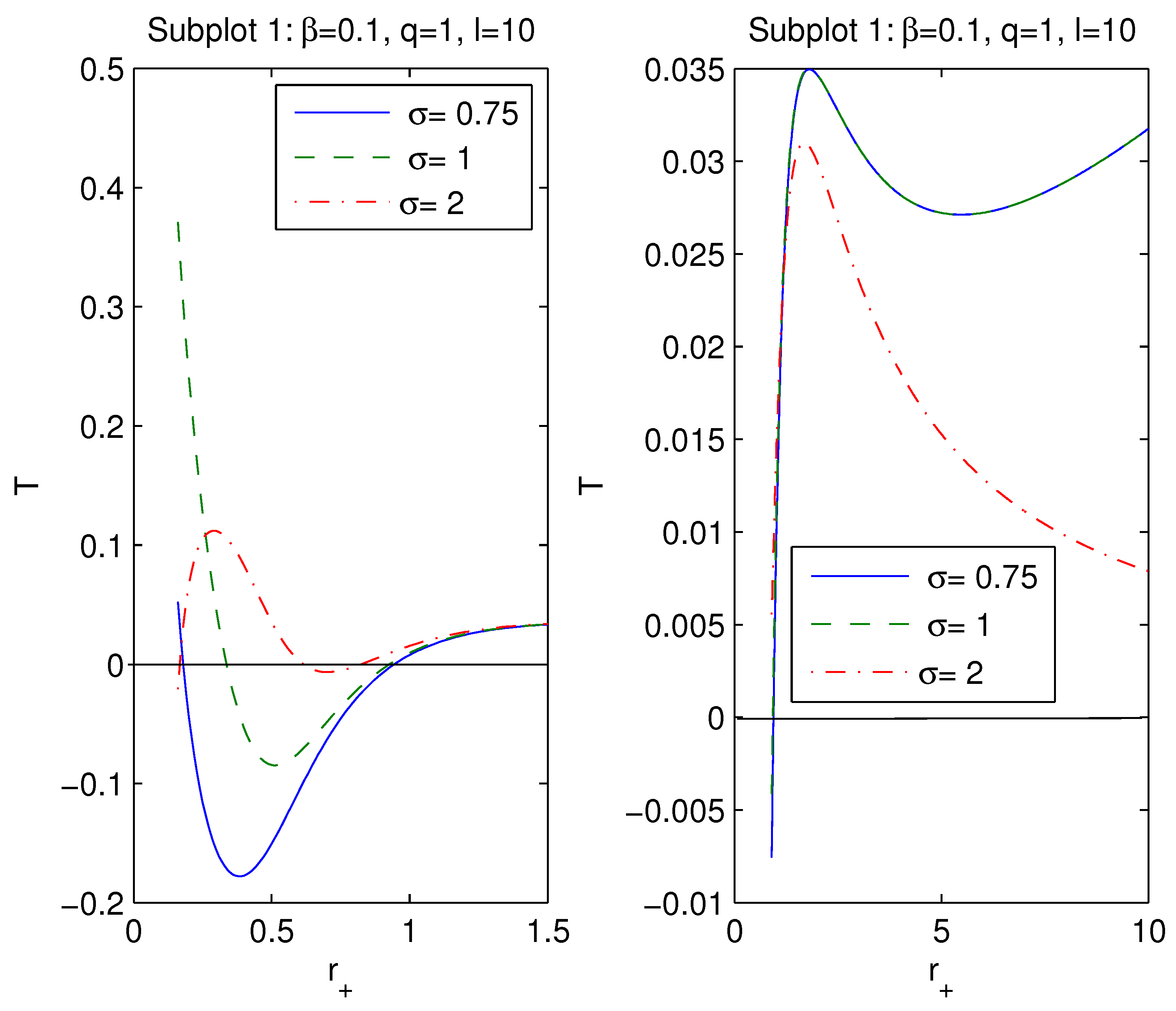
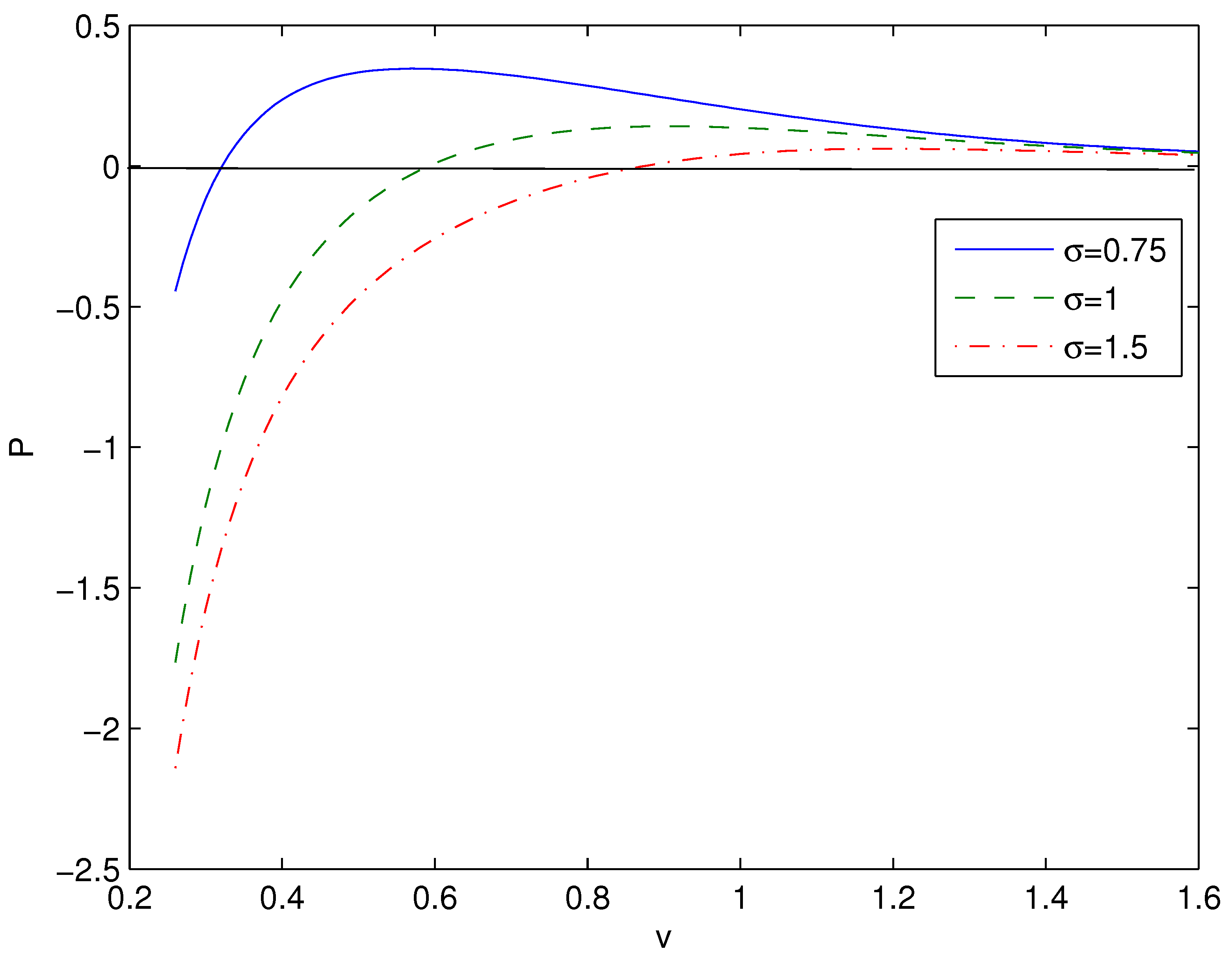
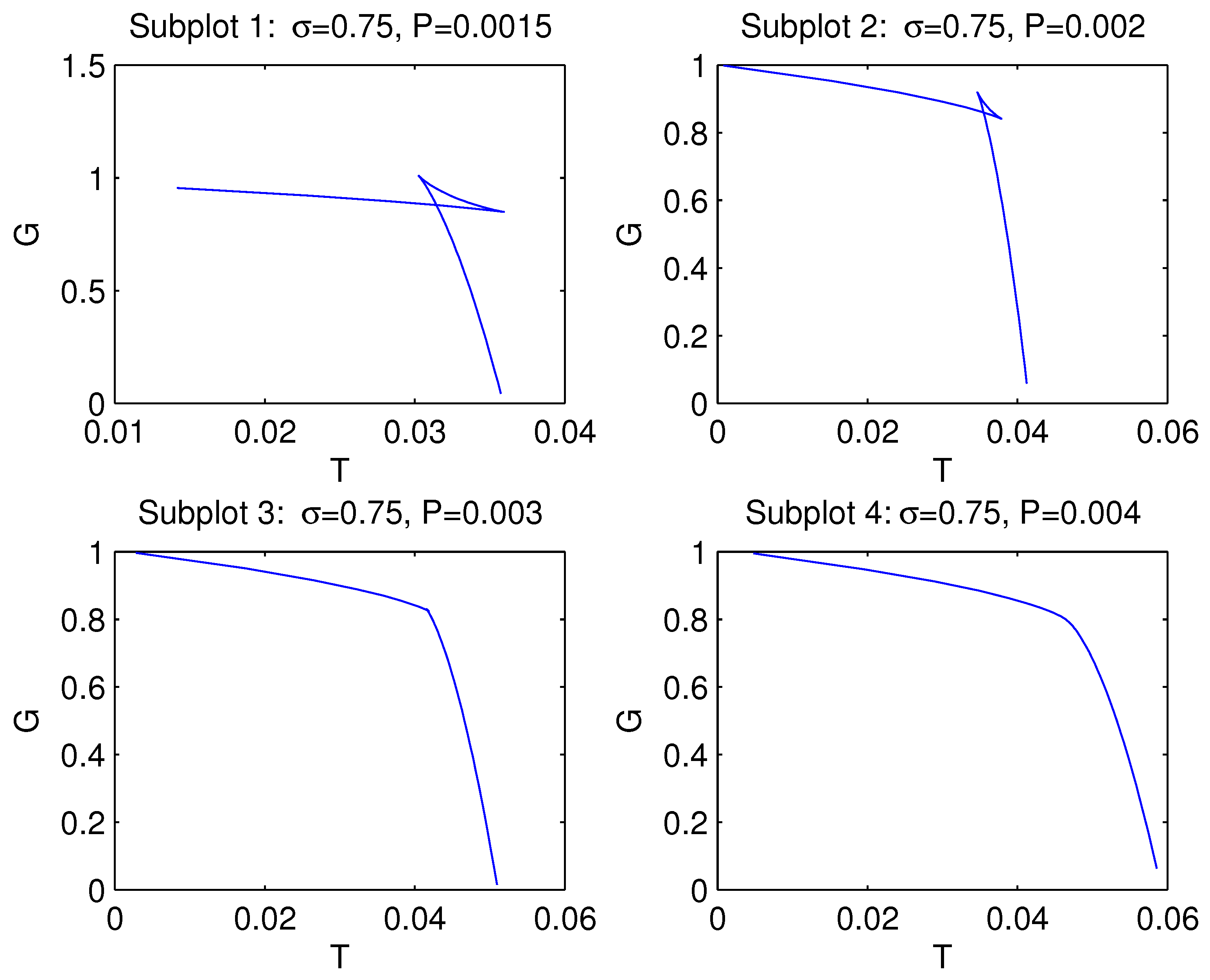
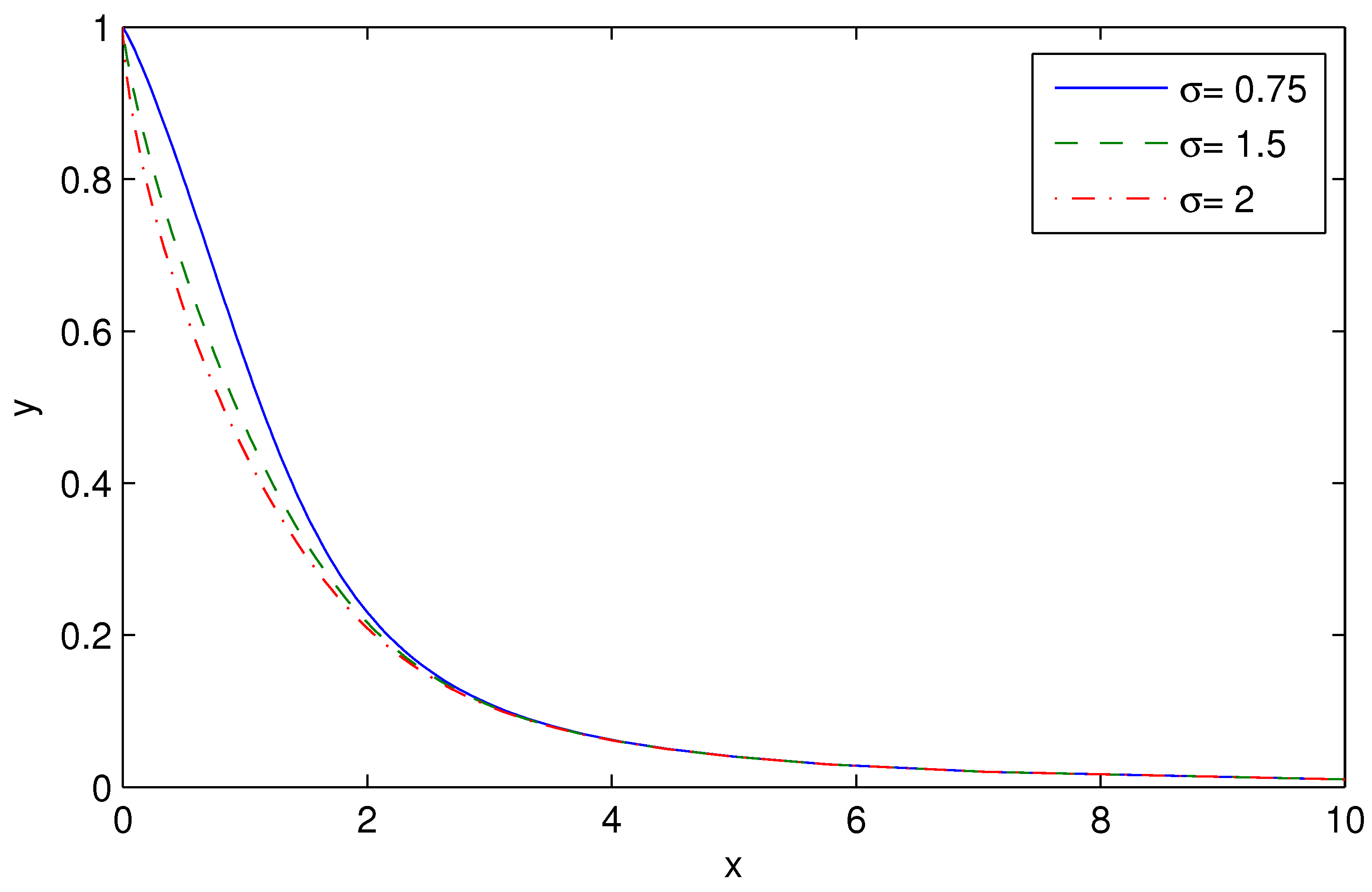
4. Thermodynamics of black holes

To study the local stability of black holes one can analyze the heat capacity

C_{q} = T {(\frac{\partial S}{\partial T})}_{q} = \frac{T \partial S / \partial r_{+}}{\partial T / \partial r_{+}} = \frac{2 π r_{+} T}{\partial T / \partial r_{+}} .

(28)

Equation (28) shows that when the Hawking temperature has an extremum the heat capacity possesses the singularity and the black hole phase transition occurs. With the help of Eq. (24) we depicted in Figure 3 the Hawking temperature as a function of the event horizon radius.

For the case

σ = 1

the analysis of black holes local stability was performed in [26]. The behavior of T and

C_{q}

depends on many parameters. By virtue of Eq. (24) we obtain

\frac{\partial T}{\partial r_{+}} = \frac{1}{4 π} [- \frac{1}{r_{+}^{2}} + \frac{3}{l^{2}} + \frac{3 q^{2}}{r_{+}^{4}} F (σ, \frac{1}{4}; \frac{5}{4}; - \frac{q^{2} β}{r^{4}}) - \frac{32 σ q^{4} β}{5 r_{+}^{8}} F (σ + 1, \frac{5}{4}; \frac{9}{4}; - \frac{q^{2} β}{r^{4}})

+ \frac{16 q^{6} β^{2} σ (4 σ + 1)}{9 r_{+}^{12}} F (σ + 2, \frac{9}{4}; \frac{13}{4}; - \frac{q^{2} β}{r^{4}})] .

(29)

Equations (24) and (29) define the heat capacity (28). Making use of Eqs. (24), (28) and (29), one can study the heat capacity and the black hole phase transition for different parameters

β

σ

, q and l.

With the help of Eq. (24) we obtain the black hole equation of state (EoS)

P = \frac{T}{2 r_{+}} - \frac{1}{8 π r_{+}^{2}} + \frac{q^{2}}{8 π r_{+}^{4}} [F (σ, \frac{1}{4}; \frac{5}{4}; - \frac{q^{2} β}{r^{4}})

- \frac{4 q^{2} β σ}{5 r_{+}^{4}} F (σ + 1, \frac{5}{4}; \frac{9}{4}; - \frac{q^{2} β}{r^{4}})] .

(30)

β = 0

, Eq. (30) gives EoS for charged Maxwell-AdS black hole [23]. The specific volume is given by

v = 2 l_{P} r_{+}

(

l_{P} = \sqrt{G} = 1

) [23]. Equation (30) is similar to EoS of the Van der Waals liquid. Putting

v = 2 r_{+}

into Eq. (30) we obtain

P = \frac{T}{v} - \frac{1}{2 π v^{2}} + \frac{2 q^{2}}{π v^{4}} [F (σ, \frac{1}{4}; \frac{5}{4}; - \frac{16 q^{2} β}{v^{4}})

- \frac{64 q^{2} β σ}{5 v^{4}} F (σ + 1, \frac{5}{4}; \frac{9}{4}; - \frac{16 q^{2} β}{v^{4}})] .

(31)

The plot of P vs. v is given in Figure 4.

The critical points (inflection points) are defined by equations

\partial P / \partial v = 0

\partial^{2} P / \partial v^{2} = 0

which look cumbersome, so that we will not present them here. The analytical solutions for critical points do not exist. The

P - v

diagrams at the critical values are similar to Van der Waals liquid diagrams having inflection points.

Because M is treated as a chemical enthalpy the Gibbs free energy reads

G = M - T S .

(32)

Making use of Eqs. (19), (20),(24) and (32) we obtain

G = \frac{r_{+}}{4} - \frac{2 π r_{+}^{3} P}{3} + \frac{3 q^{2}}{4 r_{+}} F (σ, \frac{1}{4}; \frac{5}{4}; - \frac{q^{2} β}{r^{4}})

- \frac{q^{4} β σ}{5 r_{+}^{5}} F (σ + 1, \frac{5}{4}; \frac{9}{4}; - \frac{q^{2} β}{r^{4}}) .

(33)

The plot of G versus T is given in Figure 5 for

β = 0.1

1 = 1

σ = 0.75

The critical points and phase transitions of black holes for

σ = 1

were studied in [26]. One can investigate black holes phase transitions in our model for arbitrary

σ

with the help of Gibbs’s free energy (33).

Appendix A

Making use of Eq. (4) the Euler–Lagrange equation gives

\nabla_{μ} (L_{F} F^{μ ν}) = 0, (A 1)

where

L_{F} = \frac{\partial L}{\partial F} = \frac{2 β (σ - 1) F - 1}{4 π {(1 + 2 β F)}^{σ + 1}} . (A 2)

The electric field, with spherical symmetry and Eq. (A1), becomes (

F = - E^{2} (r) / 2

))

\frac{1}{r} \frac{d (r^{2} E (r) L_{F})}{d r} = 0 . (A 3)

By virtue of Eq. (A2) and integrating Eq. (A3), we obtain

\frac{E (r) (1 + β (σ - 1) E {(r)}^{2})}{(1 - {(β E {(r)}^{2})}^{σ + 1}} = \frac{Q}{r^{2}}, (A 4)

where Q is the electric charge (the integration constant). At

β = 0

, Eq. (A4) gives the Coulomb’s electric field

E_{C} (r) = Q / r^{2}

. It is convenient to define unitless variables

x = \frac{r}{β^{1 / 4} \sqrt{Q}}, y = \sqrt{β} E . (A 5)

Then Eq. (A4) becomes

\frac{y (1 + (σ - 1) y^{2})}{{(1 - y^{2})}^{σ + 1}} = \frac{1}{x^{2}} . (A 6)

From Eq. (A6), we obtain for small x (and small r)

y = 1 + O (x) . (A 7)

Fromf Eqs. (A5) and (A7) one finds as

r \to 0

E (r) = \frac{1}{\sqrt{β}} + O (r) . (A 8)

As a result, we have the finite value of the electric field at the origin

E (0) = 1 / \sqrt{β}

that is the maximum of the electric field. The plot of y versus x is depicted in Figure 6 for

σ = 0.75, 1.5, 2

We obtain from Eq. (A4) as

r \to \infty

E (r) = \frac{Q}{r^{2}} + O (r^{- 4}) . (A 9)

Equation (A9) shows that corrections to Coulomb’s law are in the order of

O (r^{- 4})

. According to Figure 6 the electric field is finite at the origin,

y = 1

, at

r = 0

, and becomes zero as

r \to \infty

Appendix B

By virtue of Eq. (5) we obtain the electric energy density

ρ = T_{0}^{0} = - E^{2} L_{F} - L = \frac{E^{2} + β E^{4} (2 σ - 1)}{8 π {(1 - β E^{2})}^{σ + 1}} . (B 1)

Making use of dimensionless variables (A5) one finds the electric energy density

ρ = \frac{y^{2} + y^{4} (2 σ - 1)}{8 π β {(1 - y^{2})}^{σ + 1}} . (B 2)

The total electric energy becomes

E = \int_{0}^{\infty} ρ (r) r^{2} d r = \frac{Q^{3 / 2}}{β^{1 / 4}}

\times \int_{0}^{1} \frac{{(1 - y^{2})}^{(σ - 1) / 2} [1 + y^{2} (2 σ - 1)] [(2 σ^{2} - 3 σ + 1) y^{4} + (5 σ - 2) y^{2} + 1] d y}{{[1 + (σ - 1) y^{2}]}^{2} \sqrt{y [y^{2} (σ - 1) + 1]}}, (B 3)

where we have used Eq. (A6). By numerical calculations of integral (B3) we obtain dimensionless variables

\bar{E} \equiv E β^{1 / 4} / Q^{3 / 2}

which are presented in Table 1.

Table 1. Approximate values of

\bar{E} \equiv E β^{1 / 4} / Q^{3 / 2}

Table 1. Approximate values of

\bar{E} \equiv E β^{1 / 4} / Q^{3 / 2}

$σ$	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1
$\bar{E}$	1.272	1.233	1.202	1.176	1.153	1.132	1.108	1.097	1.081	1.067

As a result, in our NED model the electrostatic energy of charged objects is finite. According to the Abraham and Lorentz idea, the electron mass may be identified with the electromagnetic energy [12,27,28]. Then one can obtain the parameters

β^{1 / 4}

and

σ

to have the electron mass

m_{e} = E \approx 0.51

MeV. Dirac also considered that the electron can be the classical charged object [29].

5. Summary

We have obtained magnetic black hole solutions in Einstein-AdS gravity coupled to NED with two parameters which we propose here. The metric and mass functions and their asymptotic with corrections to the Reissner–Nordström solution have been found. The total black hole mass includes the Schwarzschild mass and the magnetic mass that is finite. We have plotted the metric function showing that black holes may have one or two horizons. When parameter

σ

increases the event horizon radius

r_{+}

decreases. The black holes thermodynamics in an extended phase space was studied. We formulated the first law of black hole thermodynamics where the pressure is connected with the negative cosmological constant (AdS spacetime). The thermodynamic potential conjugated to magnetic charge and the thermodynamic quantity conjugated to coupling

β

(so called vacuum polarization), were computed and plotted. It was proofed that the generalized Smarr relation holds for any parameter

σ

. We calculated the Hawking temperature, the heat capacity and the Gibbs free energy. The analyses of first-order and second-order phase transitions for arbitrary

σ

were performed for some parameters. The Gibbs free energy has shown the critical ’swallowtail’ behavior that is similar to the Van der Waals liquid–gas behavior. It was shown within the NED proposed that the electric field of charged objects at the origin and electrostatic self-energy are finite.

References

J. D. Bekenstein. Black holes and entropy, Phys. Rev. D 7 (1973), 2333-2346. [CrossRef]
S. W. Hawking. Particle Creation by Black Holes, Commun. Math. Phys. 43 (1975), 199-220. [CrossRef]
J. M. Bardeen, B. Carter and S. W. Hawking. The four laws of black hole mechanics, Commun. Math. Phys. 31 (1973), 161-170. [CrossRef]
T. Jacobson. Thermodynamics of space-time: The Einstein equation of state, Phys. Rev. Lett. 75 (1995), 1260-1263. [CrossRef]
T. Padmanabhan. Thermodynamical Aspects of Gravity: New insights, Rept. Prog. Phys. 73 (2010), 046901. [CrossRef]
J. M. Maldacena. The Large N limit of superconformal field theories and supergravity, Int. J. Theor. Phys. 38 (1999), 1113-1133. [CrossRef]
S. W. Hawking and D. N. Page. Thermodynamics of Black Holes in anti-de Sitter Space, Commun. Math. Phys. 87 (1983), 577. [CrossRef]
B. P. Dolan. Black holes and Boyle’s law? The thermodynamics of the cosmological constant, Mod. Phys. Lett. A 30 (2015), 1540002. [CrossRef]
D. Kubiznak and R. B. Mann. Black hole chemistry, Can. J. Phys. 93 (2015), 999-1002. [CrossRef]
D. Kubiznak, R. B. Mann and M. Teo. Black hole chemistry: thermodynamics with Lambda, Class. Quant. Grav. 34 (2017), 063001. [CrossRef]
S. Gunasekaran, R. B. Mann and D. Kubiznak. Extended phase space thermodynamics for charged and rotating black holes and Born–-Infeld vacuum polarization, JHEP 1211 (2012), 110. [CrossRef]
M. Born and L. Infeld. Foundations of the new field theory, Nature 132 (1933), 1004; Proc. Royal Soc. (London) 144 (1934), 425-451. [CrossRef]
S. I. Kruglov. A model of nonlinear electrodynamics, Ann. Phys. 353 (2014), 299-306. [CrossRef]
S. I. Kruglov. Rational nonlinear electrodynamics causes the inflation of the universe, Int. J. Mod.Phys. A 35 (2020), 2050168. [CrossRef]
S.I. Kruglov, Universe inflation based on nonlinear electrodynamics, Eur. Phys. J. Plus 135 (2020), 370. [CrossRef]
S.I. Kruglov. Inflation of universe due to nonlinear electrodynamics, Int. J. Mod. Phys. A 32 (2017), 1750071. [CrossRef]
S.I. Kruglov, Universe acceleration and nonlinear electrodynamics, Phys. Rev. D 92 (2015), 123523. [CrossRef]
K. A. Bronnikov. Regular magnetic black holes and monopoles from nonlinear electrodynamics, Phys. Rev. D 63 (2001), 044005. [CrossRef]
Handbook of Mathematical Functions with Formulas, Graphs and Mathematical Tables, Edit by M. Abramowitz and I. Stegun. National Bureau of Standarts, Applied Mathematics Series 55 (1972).
D. Kastor, S. Ray and J. Traschen. Enthalpy and the Mechanics of AdS Black Holes, Class. Quant. Grav. 26 (2009), 195011. [CrossRef]
B. P. Dolan. The cosmological constant and the black hole equation of state, Class. Quant. Grav. 28 (2011), 125020.
M. Cvetic, G. W. Gibbons, D. Kubiznak and C. N. Pope. Black Hole Enthalpy and an Entropy Inequality for the Thermodynamic Volume, Phys. Rev. D 84 (2011), 024037. [CrossRef]
D. Kubiznak and R. B. Mann. P-V criticality of charged AdS black holes, JHEP 07 (2012), 033. [CrossRef]
Wan Cong, D. Kubiznak, R. B. Mann and M. Visser. Holographic CFT Phase Transitions and Criticality for Charged AdS Black Holes, JHEP 08 (2022), 174. [CrossRef]
L. Smarr. Mass Formula for Kerr Black Holes, Phys. Rev. Lett. 30 (1973), 71-73; Erratum Phys. Rev. Lett. 30 (1973), 521. [CrossRef]
S. I. Kruglov. Rational non-linear electrodynamics of AdS black holes and extended phase space thermodynamics, Eur. Phys. J. C 82 (2022), 292. [CrossRef]
F. Rohrlich, Classical Charged Particles, Addison Wesley, Redwood City, CA (1990).
H. Spohn, Dynamics of Charged Particles and Their Radiation Field, Cambridge University Press, Cambridge (2004).
P. A. M. Dirac. An extensible model of the electron, Proc. Royal Soc. (London) A 268 (1962), 57-67. [CrossRef]

Figure 1. The function

f (r)

m_{0} = 0

G = 1

q = 1

β = 0.5

l = 5

. Figure 1 shows that black holes may have one or two horizons. When

σ

increases the event horizon radius

r_{+}

decreases.

Figure 1. The function

f (r)

m_{0} = 0

G = 1

q = 1

β = 0.5

l = 5

. Figure 1 shows that black holes may have one or two horizons. When

σ

increases the event horizon radius

r_{+}

decreases.

Figure 2. The functions

Φ

and

B

vs.

r_{+}

q = 1

β = 0.1

. The solid curve in subplot 1 is for

σ = 0.75

, the dashed curve is for

σ = 1

, and the dashed-doted curve is for

σ = 1.5

. It follows that the magnetic potential

Φ

is finite at

r_{+} = 0

and becomes zero as

r_{+} \to \infty

. The function

B

, in subplot 2, vanishes as

r_{+} \to \infty

and is finite at

r_{+} = 0

Figure 2. The functions

Φ

and

B

vs.

r_{+}

q = 1

β = 0.1

. The solid curve in subplot 1 is for

σ = 0.75

, the dashed curve is for

σ = 1

, and the dashed-doted curve is for

σ = 1.5

. It follows that the magnetic potential

Φ

is finite at

r_{+} = 0

and becomes zero as

r_{+} \to \infty

. The function

B

, in subplot 2, vanishes as

r_{+} \to \infty

and is finite at

r_{+} = 0

Figure 3. The functions T vs.

r_{+}

q = 1

β = 0.1

l = 25

. The solid curve in left panel is for

σ = 0.75

, the dashed curve is for

σ = 1

, and the dashed-doted curve is for

σ = 2

. In some interval of

r_{+}

the Hawking temperature is negative and, therefore, black holes do not exist at these parameters. There are extrema of the Hawking temperature T where the black hole phase transitions occur.

Figure 3. The functions T vs.

r_{+}

q = 1

β = 0.1

l = 25

. The solid curve in left panel is for

σ = 0.75

, the dashed curve is for

σ = 1

, and the dashed-doted curve is for

σ = 2

. In some interval of

r_{+}

the Hawking temperature is negative and, therefore, black holes do not exist at these parameters. There are extrema of the Hawking temperature T where the black hole phase transitions occur.

Figure 4. The functions P vs. v at

q = 1

β = 0.1

T = 0.05

. The solid line is for

σ = 0.75

, the dashed curve is for

σ = 1

, and the dashed-doted curve is for

σ = 1.5

Figure 4. The functions P vs. v at

q = 1

β = 0.1

T = 0.05

. The solid line is for

σ = 0.75

, the dashed curve is for

σ = 1

, and the dashed-doted curve is for

σ = 1.5

Figure 5. The functions G vs. T at

q = 1

1 = 1

β = 0.1

σ = 0.75

for

P = 0.0015

P = 0.002

P = 0.003

and

P = 0.004

. Subplots 1 and 2 show the critical ’swallowtail’ behavior with first-order phase transitions between small and large black holes. Subplots 3 corresponds to the case of critical point where second-order phase transition occurs (

P_{c} \approx 0.003

). Subplots 4 shows non-critical behavior of the Gibbs free energy.

Figure 5. The functions G vs. T at

q = 1

1 = 1

β = 0.1

σ = 0.75

for

P = 0.0015

P = 0.002

P = 0.003

and

P = 0.004

P_{c} \approx 0.003

). Subplots 4 shows non-critical behavior of the Gibbs free energy.

Figure 6. The function y vs. x at

σ = 0.75, 1.5, 2

Figure 6. The function y vs. x at

σ = 0.75, 1.5, 2

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Magnetic Black Hole Thermodynamics in an Extended Phase Space with Nonlinear Electrodynamics

Abstract

1. Introduction

2. Einstein-AdS black hole solution

3. First law of black hole thermodynamics

4. Thermodynamics of black holes

5. Summary

References

MDPI Initiatives

Important Links

Subscribe