Submitted:
08 February 2024
Posted:
08 February 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Preliminary
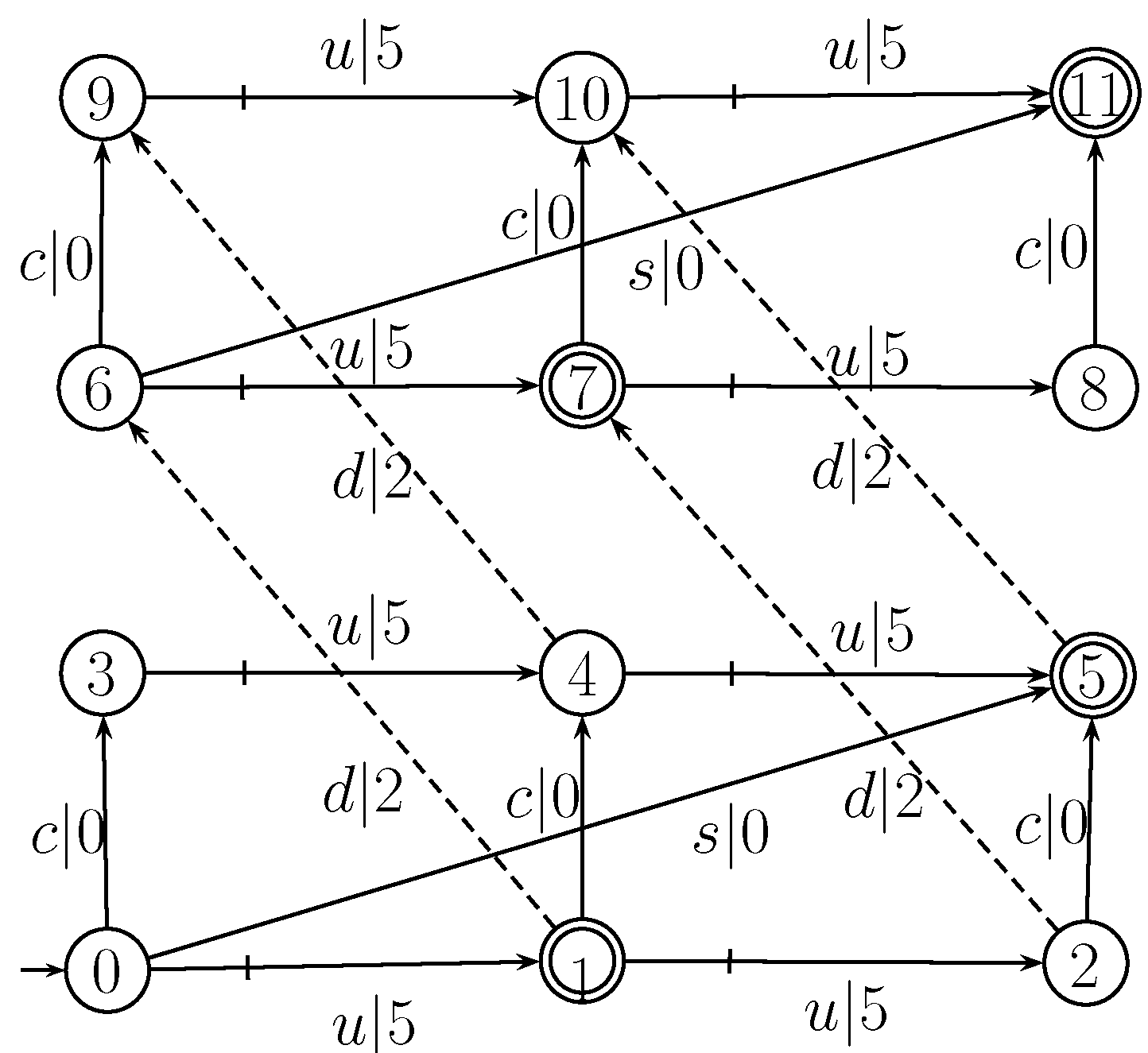
2.1. Supervisory Control Theory
- ;
- .
2.2. Supervisory Control for Opacity
2.3. The Definition of Choosing Cost
3. Optimal Supervisory Control Model on Opacity

- 1.
- K is opaque with respect to and ;
- 2.
- Secret K permitted by supervisor f is "the largest it can be";
- 3.
- For the closed-loop behavior , the discount total choosing cost is minimal.
4. Solution of Optimal Model on Choosing Cost
- Assumption *
- If and , then we have .
- Scenario 1
- Secret K is opaque w.r.t. and .
- Scenario 2
- Secret K is not opaque w.r.t. and .
4.1. Scenario 1: Secret K is opaque w.r.t. and .
4.1.1. Case 1: .
4.1.2. Case 2: and such that .
- If is not controllable w.r.t. , we can find a controllable and closed superlanguage of . Obviously, the superlanguage not only ensures the opacity of K(in Theorem A1 of Appendix), but also maximizes the secret K. So, the feasible region of model (2) is not empty.

4.1.3. Case 3: and such that




- 1.
-
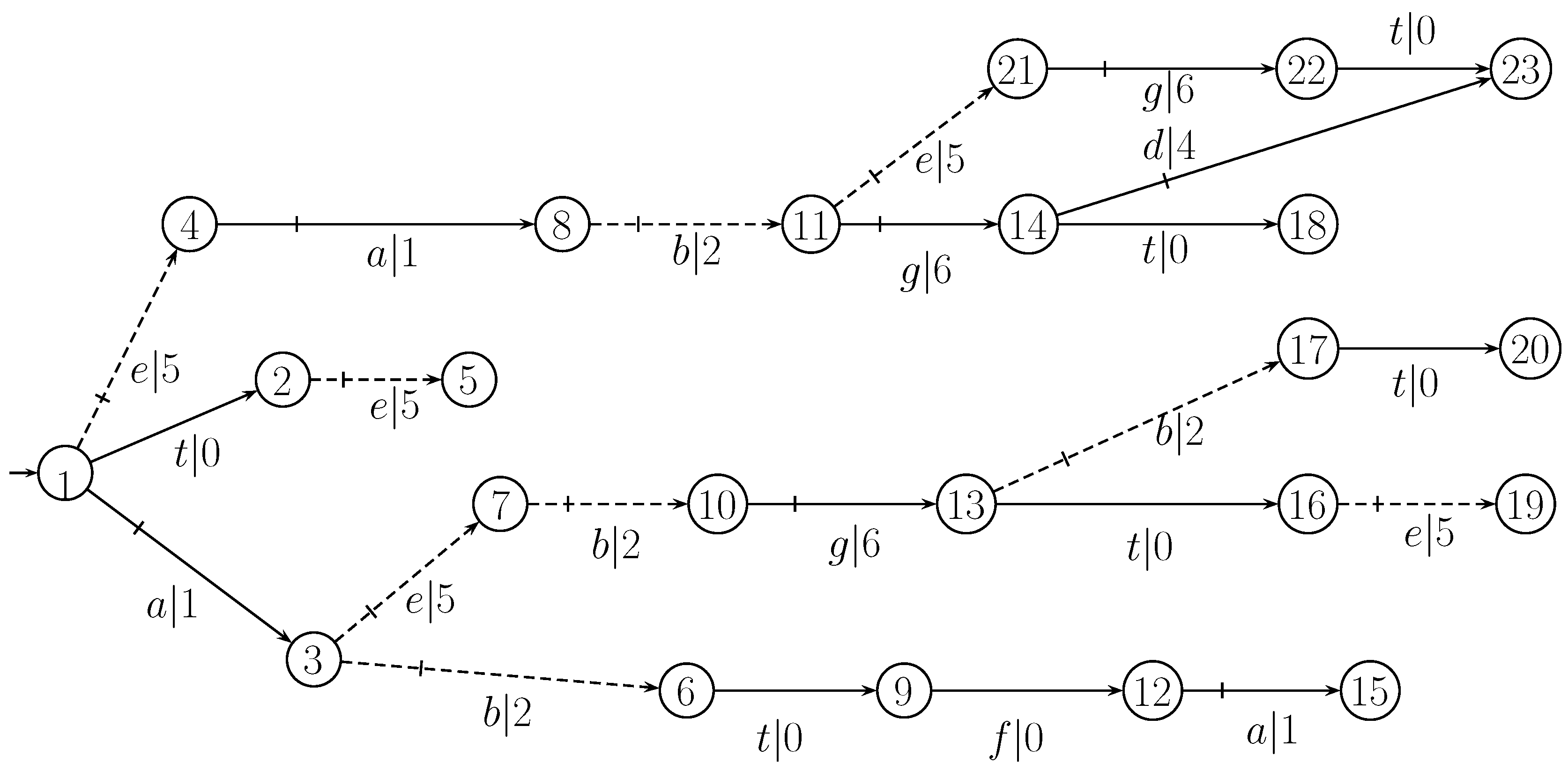
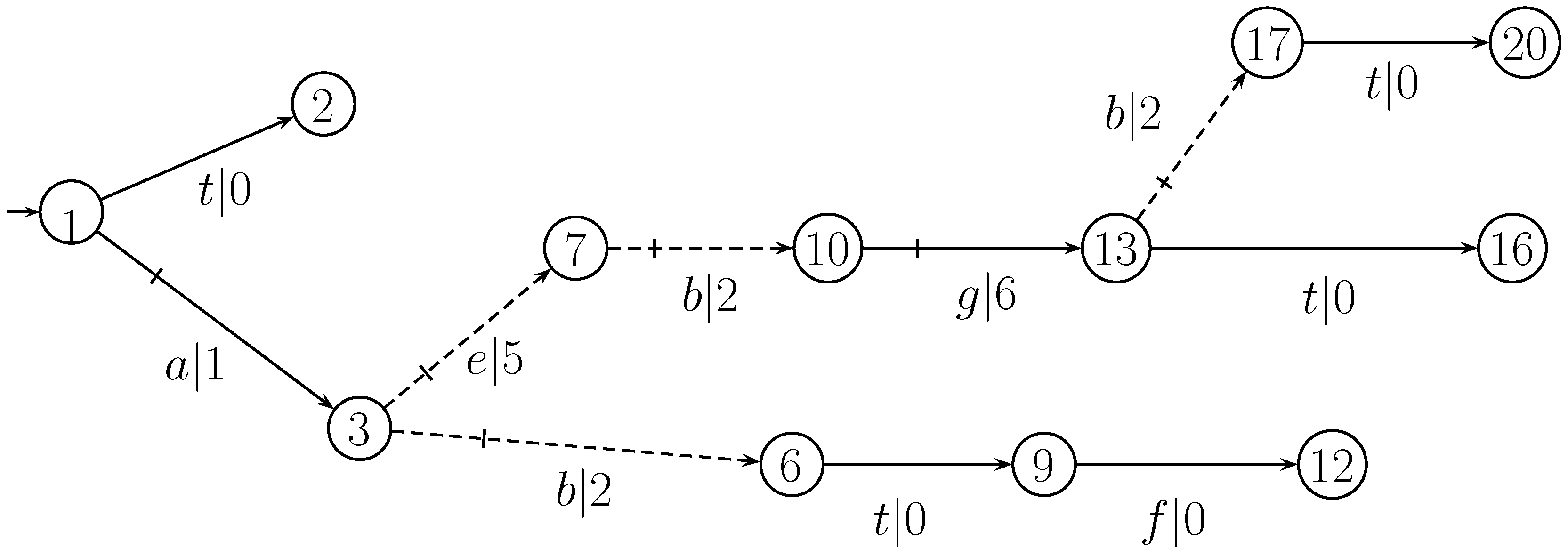
To prove the opacity (the first constraint condition).As shown in case 3, the secret of can be confused by the non-secret strings of . For , all the non-secret in which can not be distinguished with the secret in are in of Line 12. At Lines 14 and 15, the string is from , where . At Lines 15 and 16, we have and . So, the closed-loop behavior produced in Algorithm 3 can ensure the opacity of secret K.
- 2.
- To prove the secret remained in the closed-loop system is maximal (the second constraint condition).
4.2. Scenario 2: secret K is not opaque w.r.t. and .

- 1.
-
To show the opacity of .At Lines 3-5, it is obvious that is opaque w.r.t. and . At Lines 6-14, by Theorems 4, 5 and 6, it holds that is opaque w.r.t. and , which implies that . According to Lines 4, 5 and 15, we have . Since , we have . So, holds, which means is true. Therefore, K is opaque w.r.t. and .
- 2.
-
To show that the closed-loop behavior can preserve the maximal secret information.For system and secret , at Lines 4-14, it is obvious that is a feasible solution of model (2), which implies that . Since at line 5 and at Line 15, it holds that , which implies that . Since holds, it is true that . So, we have . Therefore, we have .
- Case 1
-
If , we will discuss the relation between and .
- 1.1
- If , it holds that at Lines 6-7, which contracts with the assumption that .
- 1.2
- If , it holds that by Theorem 5 and 6 at Lines 9-13, which contracts with the assumption that .
- Case 2
-
If , it is true that for any because of the formulas and , which implies that s is out of . Then, we will discuss the relation between and again.
- 2.1
- If , there exists such that for any , which means that all the secret string in can be confused by the non-secret string in . By Corollary 2, it holds that . At Lines 9-10, it is true that . So, it holds that , which contracts with assumption that .
- 2.2
-
If , we will discuss the following two sub-cases.
- 2.2.1
- If there exists such that for any , it is obvious that by Corollary 2. At Lines 9, 10 and 15 of Algorithm 7, it holds that . So, it is true that , which contracts with assumption that .
- 2.2.2
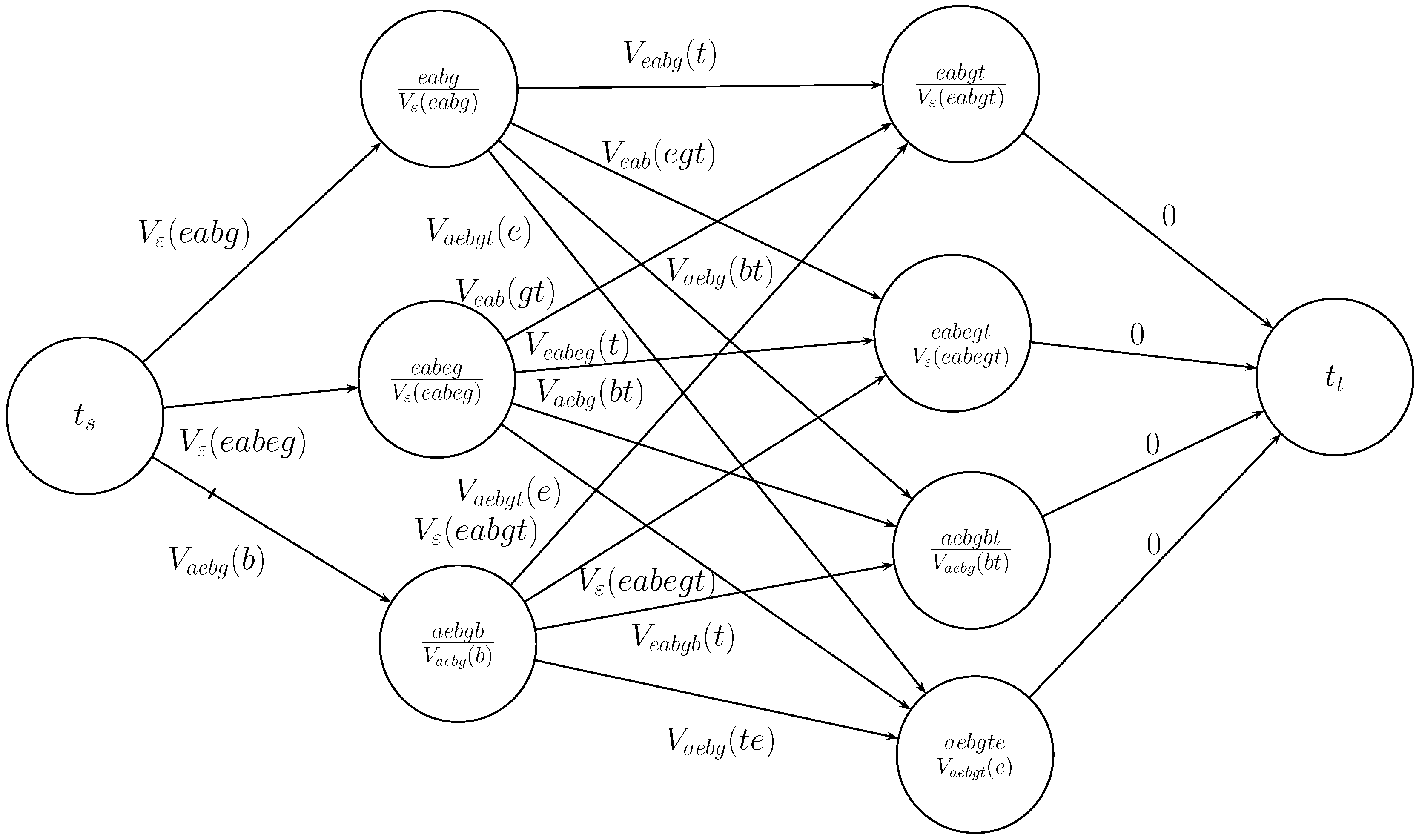
- If there exists such that for any , we have the following formulas.Owing to the definition of feasible solution, we have and . So, it holds that . For the remaining part of formulas (4) and (5), we construct two weight directed diagrams and T, where (or T) is produced in Algorithm 5 (e.g. Line 14 of Algorithm 3 if ( or ) is inputed in Algorithm 3. By the constructions of L and H in Algorithm 3, it is obvious that (i.e. is a sub-diagram of T) and that , where (and ) is the weight of arc in diagram (and T respectively). So, the sum of weight of shortest path of T is less than that of , which implies that . According to the formulas (4) and (5), we have that , which contracts with assumption that .
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A.
References
- Dubreil, J.; Darondeau, P.; Marchand, H. Supervisory control for opacity. IEEE Transactions on Automatic Control 2010, 55, 1089–1100. [Google Scholar] [CrossRef]
- Takai, S.; Oka, Y. A formula for the supremal controllable and opaque sublanguage arising in supervisory control. SICE Journal of Control, Measurement, and System Integration 2008, 1, 307–311. [Google Scholar] [CrossRef]
- Takai, S.; Watanabe, Y. Modular synthesis of maximally permissive opacity-enforcing supervisors for discrete event systems. IEICE Transactions on Fundamentals of Electronics Communications and Computer Sciences 2011, E94A, 1041–1044. [Google Scholar] [CrossRef]
- Moulton, R.; Hamgini, B.; Khouzani, Z.; Meira-Goes, R.; Wang, F.; Rudie, K. Using subobservers to synthesize opacity enforcing supervisors. Discrete Event Dynamic Systems 2022, 32, 611–640. [Google Scholar] [CrossRef]
- Mazare, L. Using unification for opacity properties. Proceedings of Workshop on Information Technology& Systems, 2004, pp. 165–176.
- Bryans, J.W.; Koutny, M.; Ryan, P.Y. Modelling opacity using petri nets. Electronic Notes in Theoretical Computer Science 2005, 121, 101–115. [Google Scholar] [CrossRef]
- Lin, F. Opacity of discrete event systems and its applications. Automatica 2011, 47, 496–503. [Google Scholar] [CrossRef]
- Ben-Kalefa, M.; Lin, F. Opaque superlanguages and sublanguages in discrete event systems. Cybernetics and Systems 2016, 47, 392–426. [Google Scholar] [CrossRef]
- Saboori, A.; Hadjicostis, C.N. Notions of security and opacity in discrete event systems. IEEE Conference on Decision and Control, 2008, pp. 5056–5061.
- Saboori, A.; Hadjicostis, C.N. Verification of k-step opacity and analysis of its complexity. IEEE Transactions on Automation Science and Engineering 2011, 8, 549–559. [Google Scholar] [CrossRef]
- Falcone, Y.; Marchand, H. Enforcement and validation (at runtime) of various notions of opacity. Discrete Event Dynamic Systems 2015, 25, 531–570. [Google Scholar] [CrossRef]
- Saboori, A.; Hadjicostis, C.N. Verification of infinite-step opacity and analysis of its complexity. IFAC Workshop on Dependable Control of Discrete Systems;, 2009; pp. 46–51.
- Wu, Y.C.; Lafortune, S. Comparative analysis of related notions of opacity in centralized and coordinated architectures. Discrete Event Dynamic Systems 2013, 23, 307–339. [Google Scholar] [CrossRef]
- Saboori, A.; Hadjicostis, C.N. Verification of initial-state opacity in security applications of DES. International Workshop on Discrete Event Systems, 2008, pp. 328–333.
- Balun, J.; Masopust, T. Comparing the notions of opacity for discrete-event systems. Discrete Event Dynamic Systems 2021, 31, 553–582. [Google Scholar] [CrossRef]
- Wintenberg, A.; Blischke, M.; Lafortune, S.; Ozay, N. A general language-based framework for specifying and verifying notions of opacity. Discrete Event Dynamic Systems 2022, 32, 253–289. [Google Scholar] [CrossRef]
- Ma, Z.; Yin, X.; Li, Z. Verification and enforcement of strong infinite- and k-step opacity using state recognizers. Automatica 2021, 133. [Google Scholar] [CrossRef]
- Liu, R.; Lu, J. Enforcement for infinite-step opacity and K-step opacity via insertion mechanism. Automatica 2022, 140. [Google Scholar] [CrossRef]
- Ji, Y.; Wu, Y.C.; Lafortune, S. Enforcement of opacity by public and private insertion functions. Automatica 2018, 93, 369–378. [Google Scholar] [CrossRef]
- Ji, Y.; Yin, X.; Lafortune, S. Enforcing opacity by insertion functions under multiple energy constraints. Automatica 2019, 108. [Google Scholar] [CrossRef]
- Ji, Y.; Yin, X.; Lafortune, S. Opacity enforcement using nondeterministic publicly-known edit functions. IEEE Transactions on Automatic Control 2019, 64, 4369–4376. [Google Scholar] [CrossRef]
- Zhou, Y.; Chen, Z.; Liu, Z.X. Verification and enforcement of current-state opacity based on a state space approach. European Journal of Control 2023, 71. [Google Scholar] [CrossRef]
- Wu, Y.C.; Lafortune, S. Synthesis of insertion functions for enforcement of opacity security properties. Automatica 2014, 50, 1336–1348. [Google Scholar] [CrossRef]
- Zhang, B.; Shu, S.L.; Lin, F. Maximum information release while ensuring opacity in discrete event systems. IEEE Transactions on Automation Science and Engineering 2015, 12, 1067–1079. [Google Scholar] [CrossRef]
- Behinaein, B.; Lin, F.; Rudie, K. Optimal information release for mixed opacity in discrete-event systems. IEEE Transactions on Automation Science and Engineering 2019, 16, 1960–1970. [Google Scholar] [CrossRef]
- Khouzani, Z.A. Optimal payoff to ensure opacity in discrete-event systems; Queen’s University, 2019.
- Hou, J.; Yin, X.; Li, S. A framework for current-state opacity under dynamic information release mechanism. Automatica 2022. [Google Scholar] [CrossRef]
- Sengupta, R.; Lafortune, S. An optimal control theory for discrete event systems. SIAM Journal on Control and Optimization 1998, 36, 488–541. [Google Scholar] [CrossRef]
- Pruekprasert, S.; Ushio, T. Optimal stabilizing supervisor of quantitative discrete event systems under partial observation. IEICE Transactions on Fundamentals of Electronics Communications and Computer Sciences 2016, 99, 475–482. [Google Scholar] [CrossRef]
- Ji, X.; Lafortune, S. Optimal supervisory control with mean payoff objectives and under partial observation. Automatica 2021, 123. [Google Scholar] [CrossRef]
- Hu, Q.; Yue, W. Two new optimal models for controlling discrete event systems. Journal of Industrial and Management Optimization 2017, 1, 65–80. [Google Scholar] [CrossRef]
- Yue, W.; Hu, Q. Optimal control for discrete event systems with arbitrary control pattern. Discrete and Continuous Dynamical Systems - Series B (DCDS-B) 2012, 6, 535–558. [Google Scholar]
- Cassandras, C.; Lafortune, S. Introduction to discrete event systems; Springer, 2008.
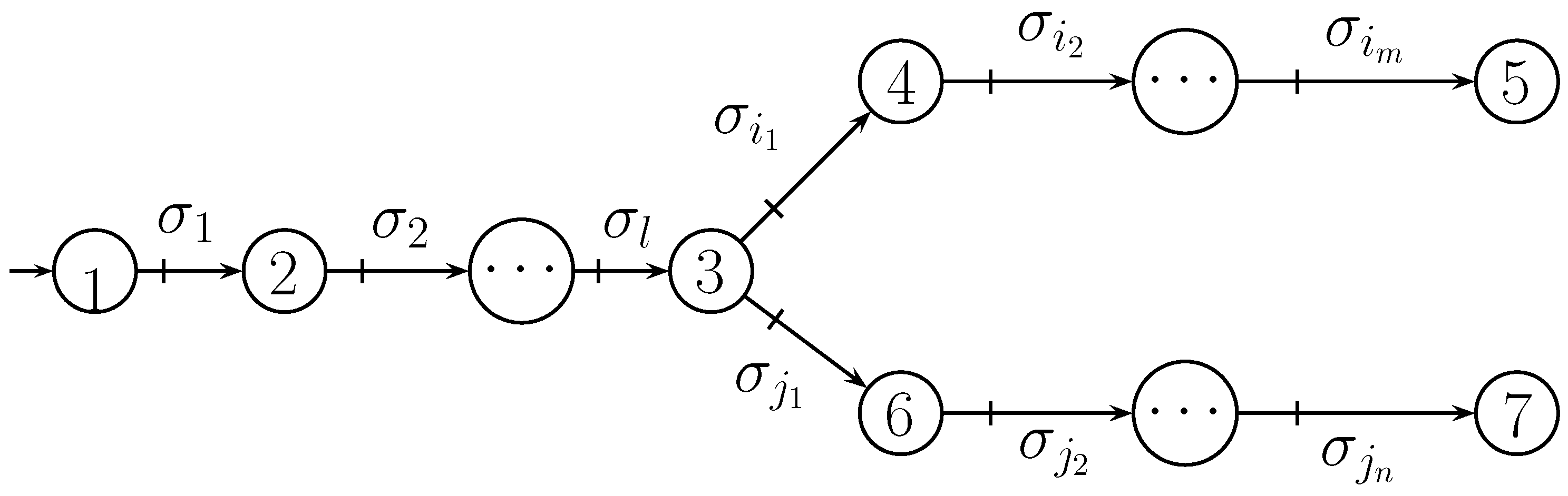
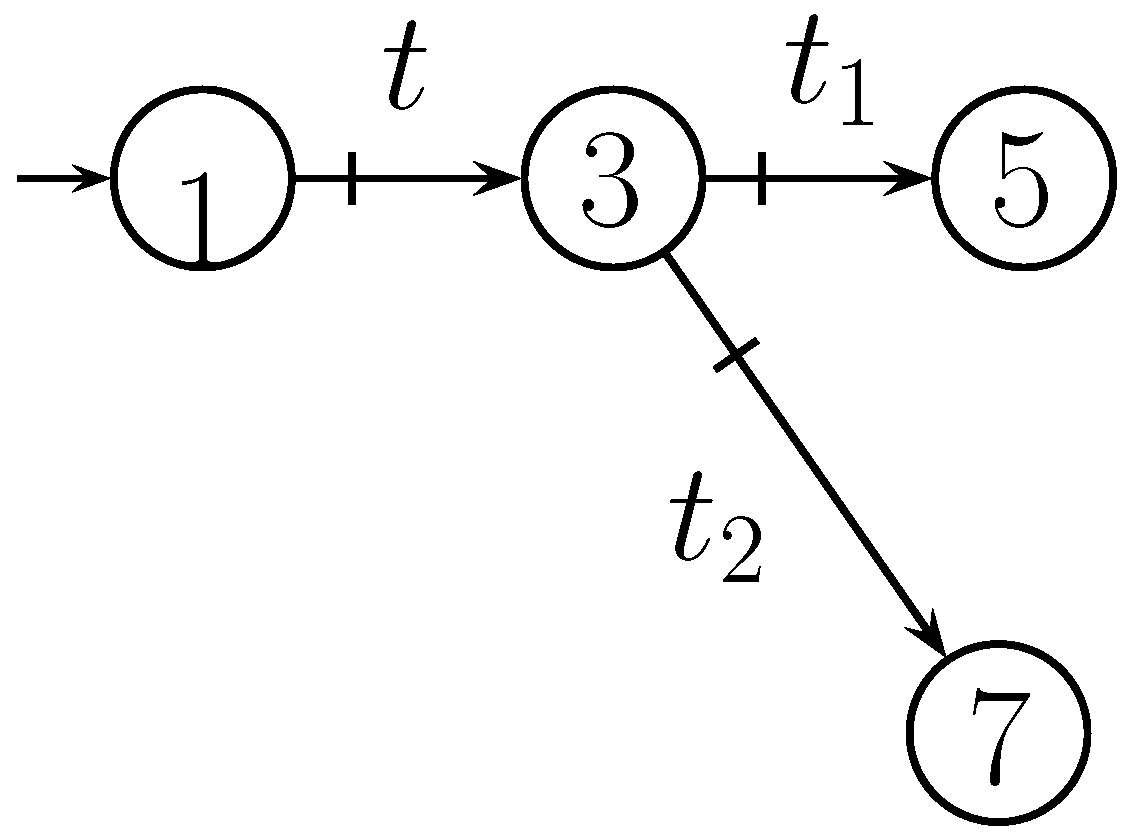
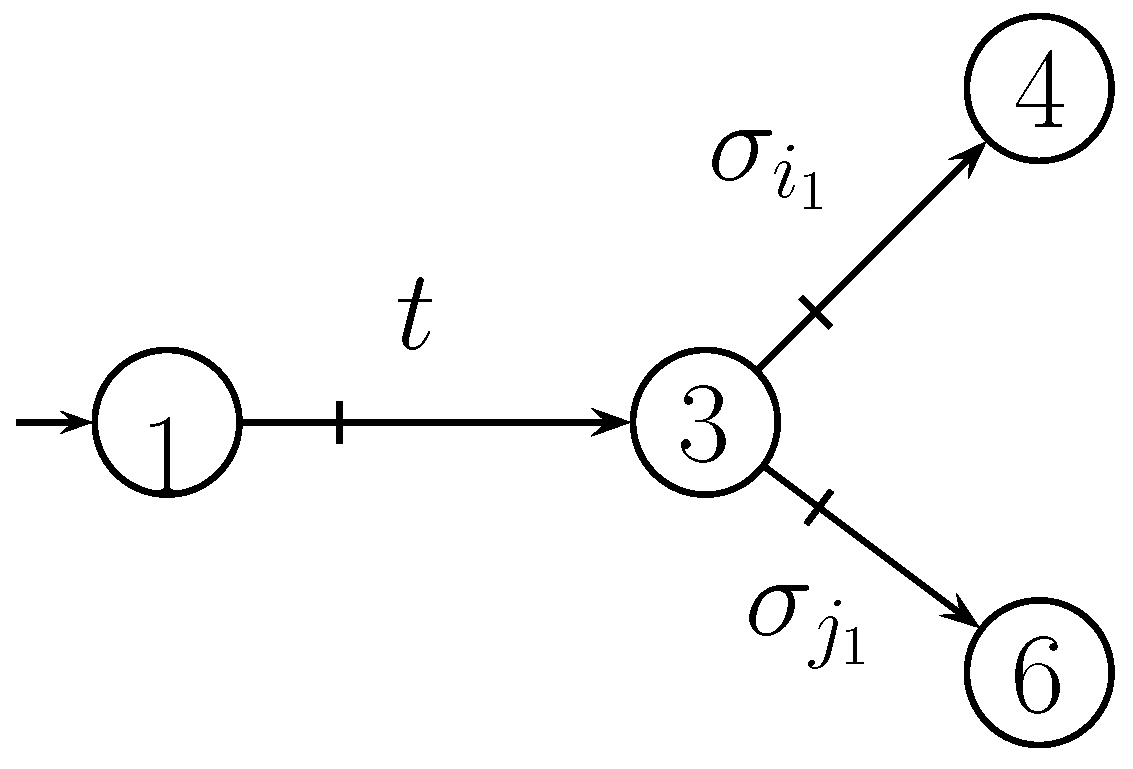
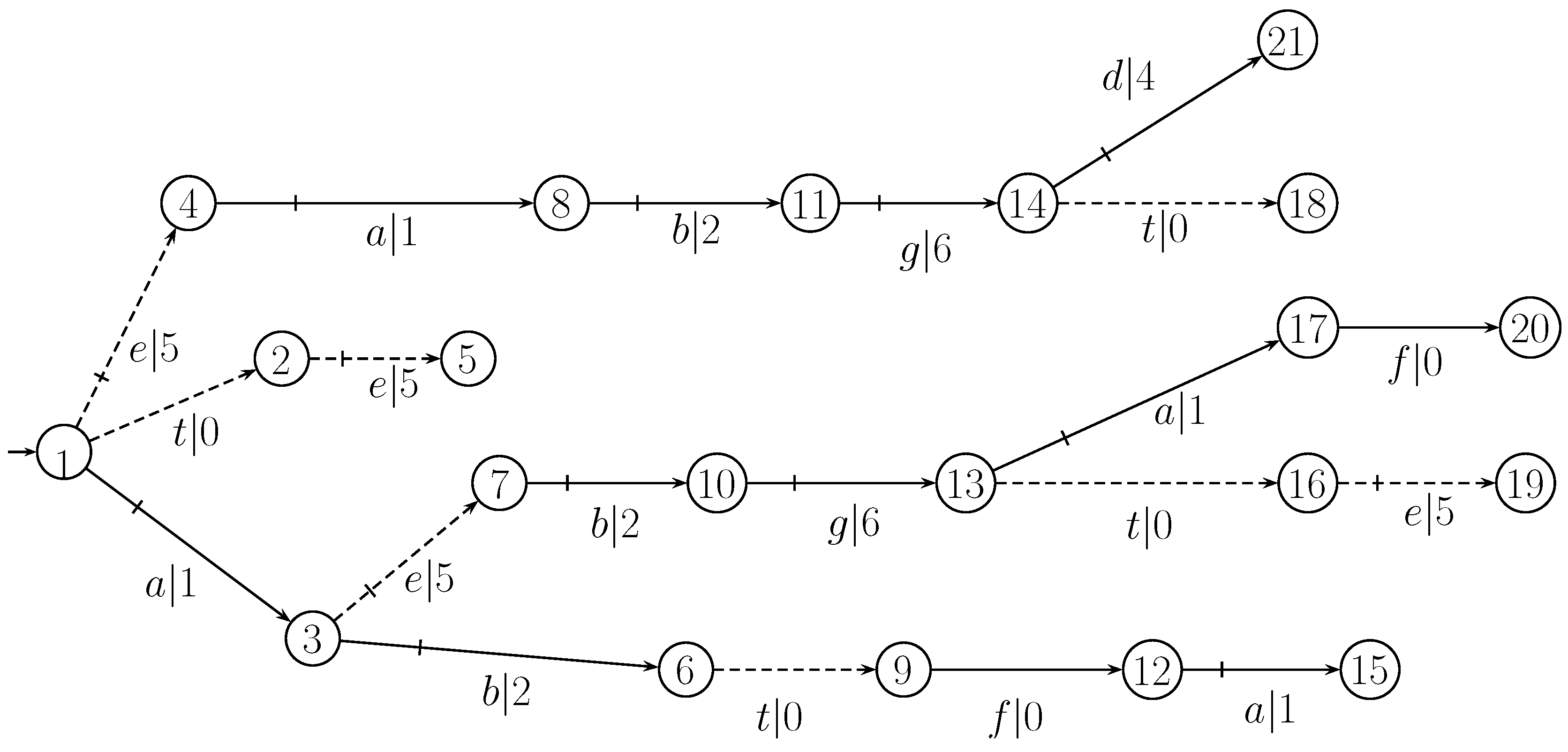

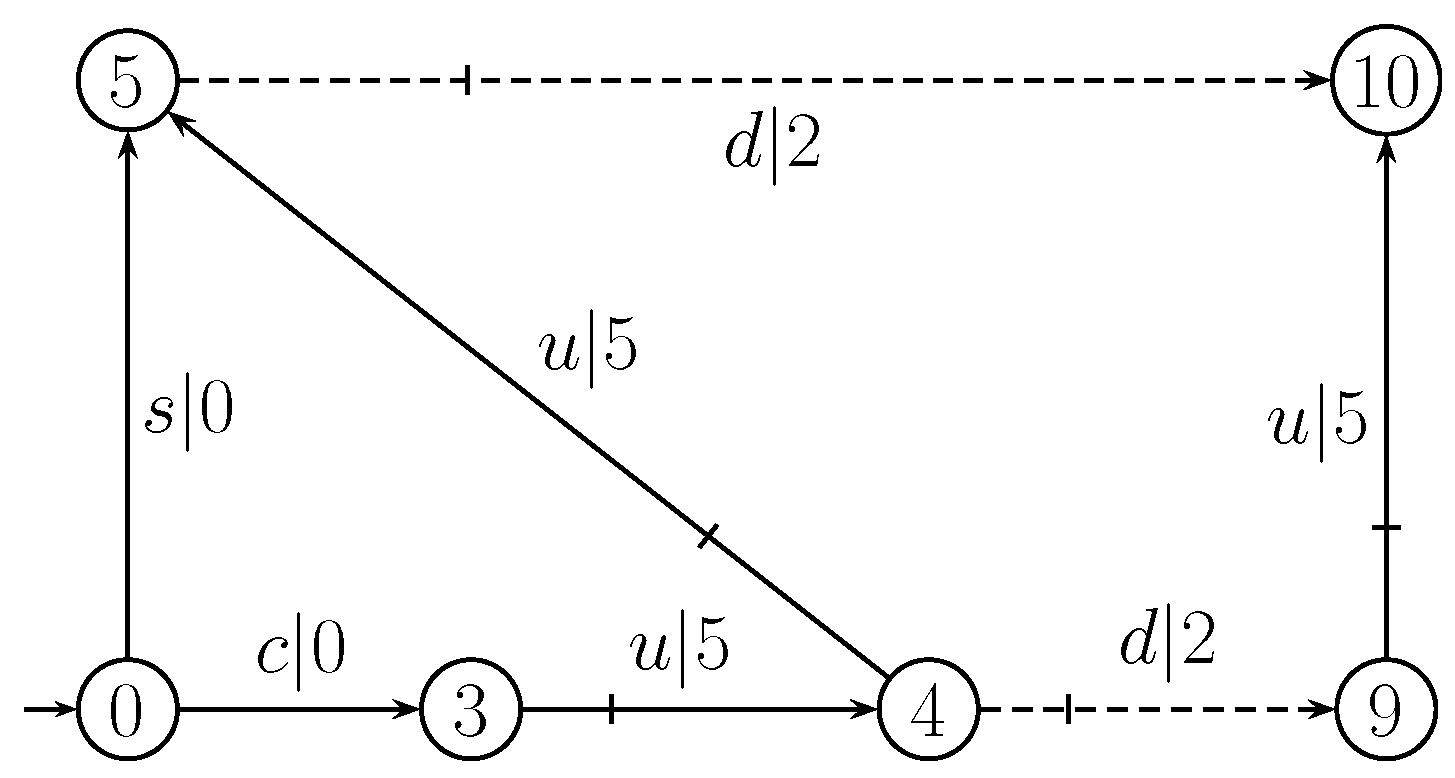
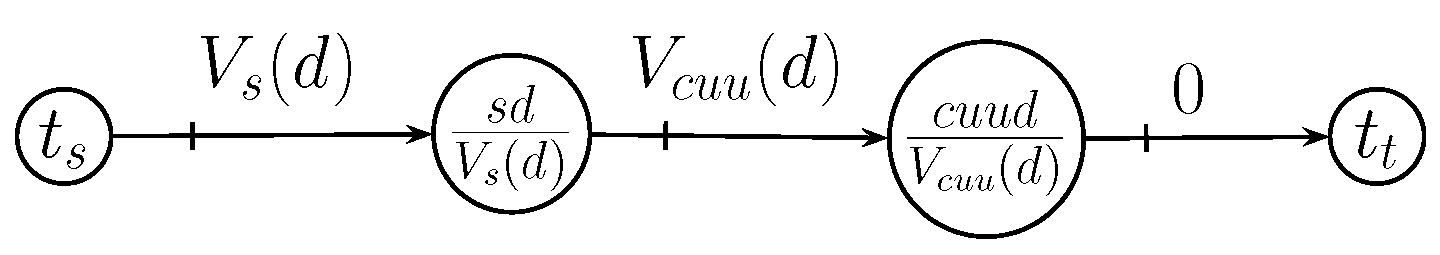
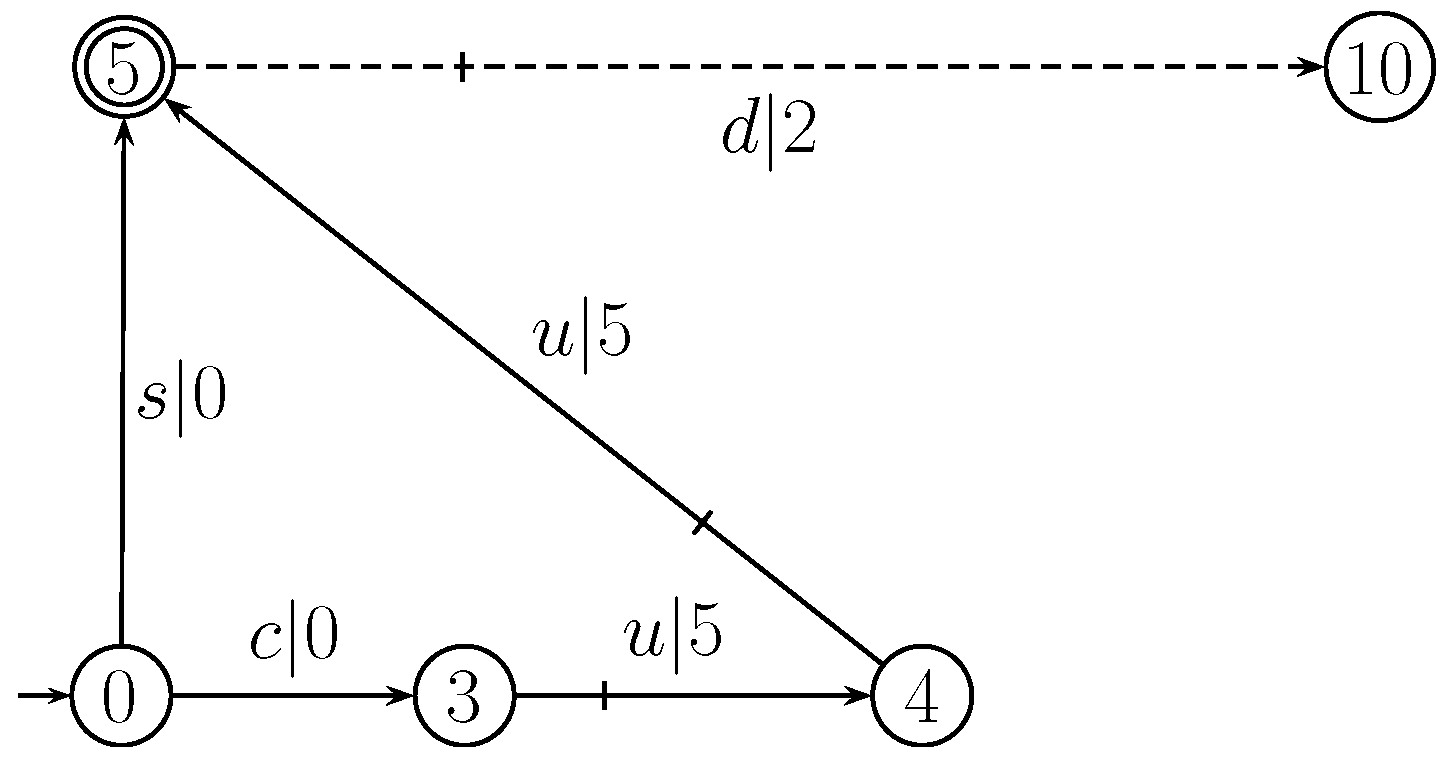
| s | |||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





