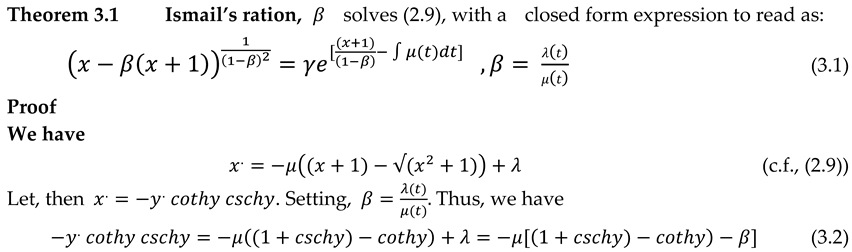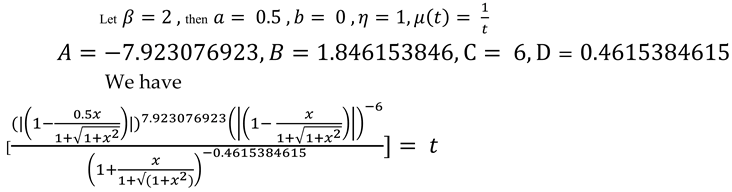Ismail’s Ratio Conquers New Horizons the Non-stationary M/D/1 Queue’s State Variable Closed Form Expression

Preprint

Article

Ismail’s Ratio Conquers New Horizons the Non-stationary M/D/1 Queue’s State Variable Closed Form Expression

Altmetrics

Downloads

125

Views

Comments

Dr Ismail A Mageed^*

This version is not peer-reviewed

Submitted:

07 February 2024

Posted:

12 February 2024

You are already at the latest version

Alerts

Abstract

This paper investigates the search for an exact analytic solution to a temporal first-order differential equation that represents the number of customers in a non-stationary or time-varying

Keywords:

Subject: Computer Science and Mathematics - Probability and Statistics

1. Introduction

The field of transient/non-stationary analysis has limited literature, which can be categorized into simulation, transient analysis, analysis, and applications techniques. These categories encompass various approaches to studying systems that change over time, including simulations, analysing transient behaviour, and exploring non-stationary phenomena. In certain cases, mathematical transformations can be used to obtain a closed form expression for analysing non-stationary queueing systems. However, evaluating these expressions can be computationally complex. As a result, there has been a focus on numerically determining the transient behaviour of such systems instead of deriving closed form expressions.

The current exposition contributes to solving for first time ever, the longstanding unsolved problem of obtaining the state variable of the time varying 𝑀/𝐷/1 queueing system.

The following flowchart shows how this paper is organized.

2. PSFFA

Let

f_{i n} (t)

and

f_{o u t} (t)

serve as the temporal flow in, and fow out

,

respectively. Therefore,

\frac{d x (t)}{d t} = x^{.} (t) = - f_{o u t} (t) + f_{i n} (t), x (t) a s t h e s t a t e v a r i a b l e

(2.1)

f_{o u t} (t)

links server utilization,

ρ (t)

and the time-dependent mean service rate,

μ (t)

by:

f_{o u t} (t) = μ (t) ρ (t)

(2.2)

For an infite queue waiting space:

f_{i n} (t) = M e a n a r r i v a l r a t e = λ (t)

(2.3)

Thus (2.1) rewrites to:

x^{.} (t) = - μ (t) ρ (t) + λ (t), 1 > ρ (t) = \frac{λ (t)}{μ (t)} > 0

(2.4)

The stable subcase of (2.4) (i.e.,

x^{.} (t) =

0), implies:

x = G_{1} (ρ)

(2.5)

The numerical invertibility of

G_{1} (ρ)

, yields

ρ = G_{1}^{- 1} (x)

(2.6)

Hence,

x^{.} (t) = - μ (t) (G_{1}^{- 1} (x (t))) + λ (t)

(2.7)

The

M / D / 1

queueing system is made of Poisson arrival, one exponential (Poisson) server, FIFO (First-In-First-Out). Thus,

M / D / 1

queueing system’s -

G_{1}

(c.f., [1]) reads:

G_{1} (x) = \frac{x}{x + 1}

(2.8)

Therefore, the time varying

M / D / 1

queueing system’s -PSFFA model reads:

x^{.} = - μ ((x + 1) - \sqrt (x^{2} + 1)) + λ

(2.9)

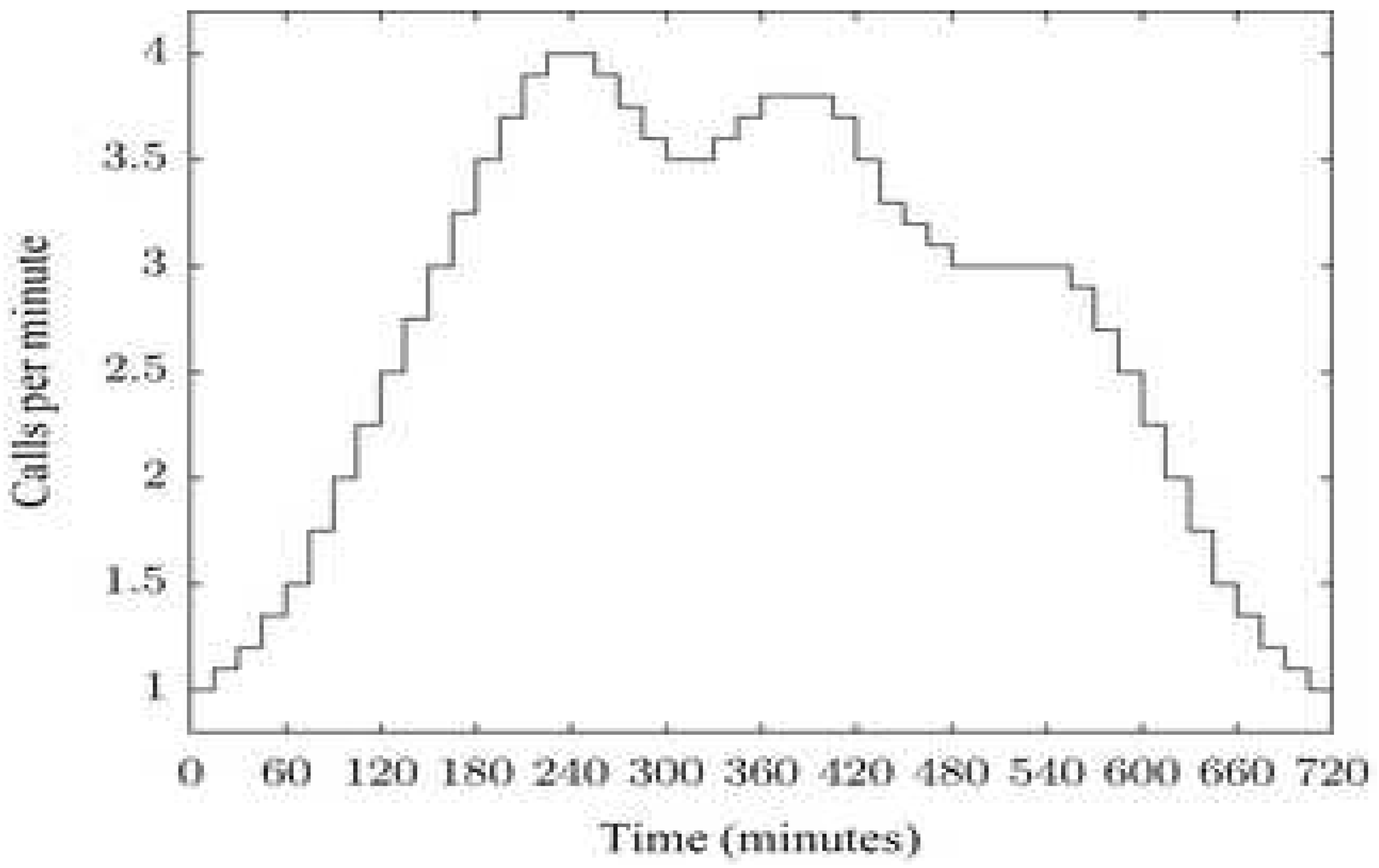
TVQSs’ life example [6] is depicted by Figure1.

Figure 1.

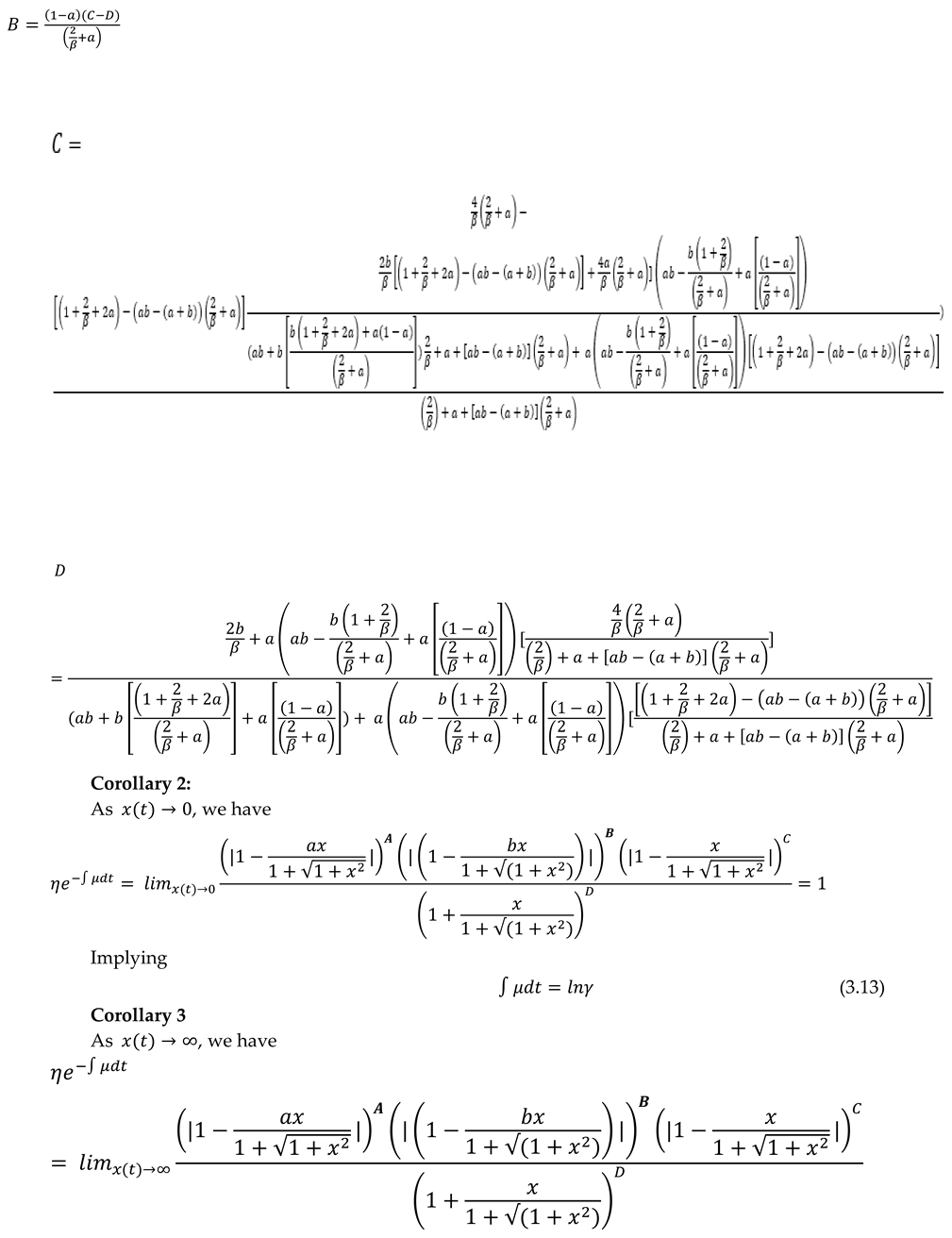
3. Solving the Non-Stationary M/D/1 queueing System’s PSFFA (c,f., (2.9))

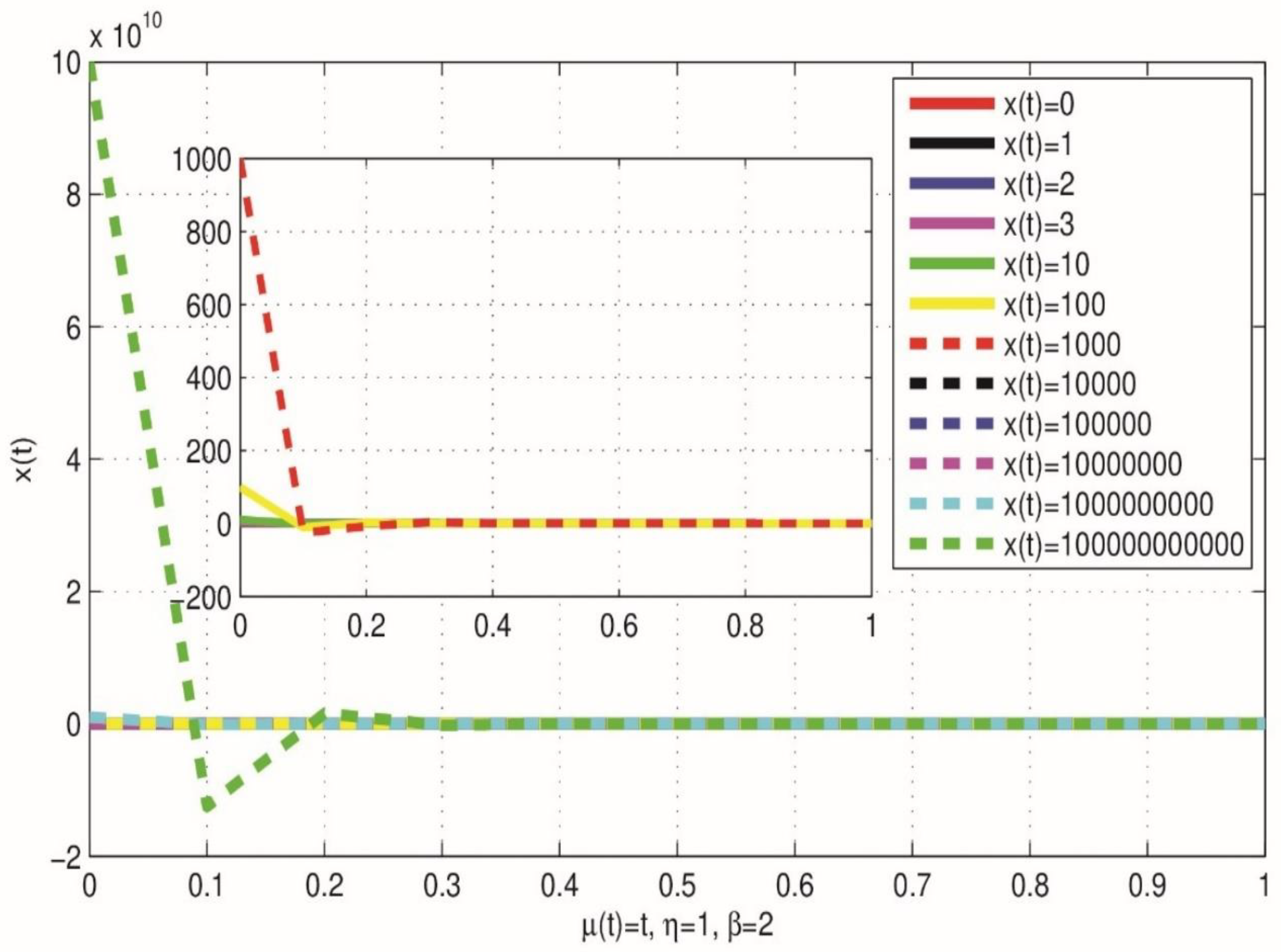
Figure 2 shows a new phenomenon to queuing theorist. The possibility that time will converge to a certain value for sufficiently large number in the time varying

M / D / 1

queuing system. This is for an increasing temporal mean service rate.

This shows that as the time varying

M / D / 1

queuing system’s state variable becomes sufficiently large, time vanishes.

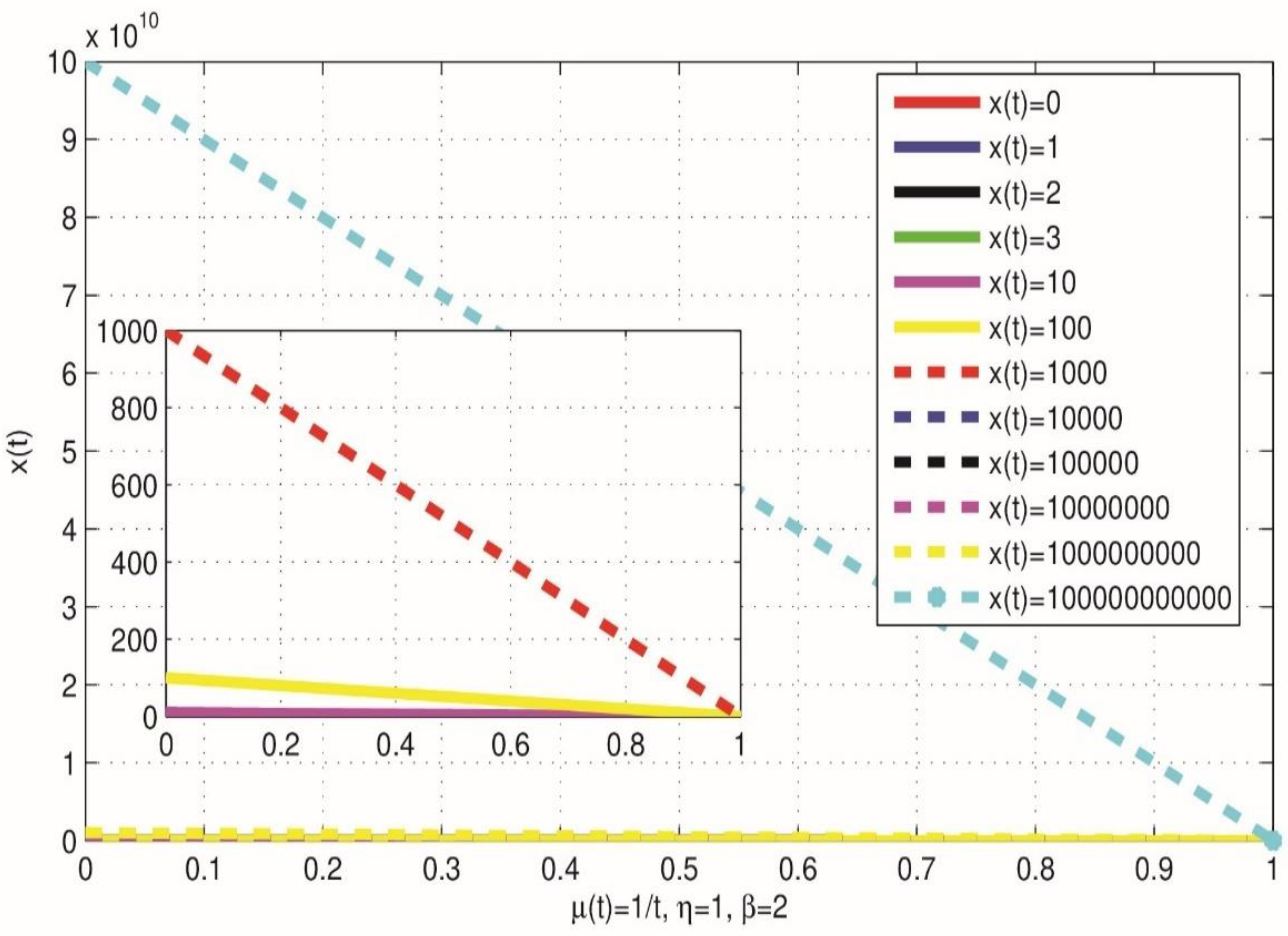
Numerical experiment Two

Figure 3 visualizes a new phenomenon to queuing theorist. The possibility that time will converge to a certain value for sufficiently large number in the time varying

M / D / 1

queuing system. This is for a decreasing temporal mean service rate.

4. Closing Remarks with Next Phase of Research

In this work, a challenging topic in queueing theory is examined; more precisely, the underlying queue’s state variable is determined. The article offers a solution to this issue by utilizing a pointwise stationary fluid flow approximation (PSFFA) technique to formulate the non-stationary

M / D / 1

queueing system. Future work will concentrate on resolving open research issues and investigating applications of non-stationary queues in other scientific areas. The study also examines the effects of time, combined with and queueing parameters on the underlying queue’s stability dynamics.

References

Zhao, X.; Wang, Y.; Li, L.; Delahaye, D. A queuing network model of a multi-airport system based on point-wise stationary approximation. Aerospace 2022, 9, 390. [Google Scholar] [CrossRef]
Iversen, V.B. ITU Teletraffic Engineering Handbook; Technical University of Denmark: Kongens Lyngby, Denmark, 2021. [Google Scholar]
Mageed, I.A.; Zhang, Q. Solving the open problem for GI/M/1 pointwise stationary fluid flow approximation model (PSFFA) of the non-stationary D/M/1 queueing system. Electron. J. Comput. Sci. Inf. Technol. 2023, 1, 1–6. [Google Scholar]
A Mageed, D.I. Upper and Lower Bounds of the State Variable of M/G/1 PSFFA Model of the Non-Stationary M/E_k/1 Queueing System. Preprints 2024, 2024012243. [Google Scholar] [CrossRef]
Hu, L.; Zhao, B.; Zhu, J.; Jiang, Y. Two time-varying and state-dependent fluid queuing models for traffic circulation systems. Eur. J. Oper. Res. 2019, 275, 997–1019. [Google Scholar] [CrossRef]
Roubos, A.; Bhulai, S.; Koole, G. Flexible staffing for call centers with non-stationary arrival rates. Markov Decis. Process. Pract. 2017, 487–503. [Google Scholar]

Figure 2.

Figure 3.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Ismail’s Ratio Conquers New Horizons the Non-stationary M/D/1 Queue’s State Variable Closed Form Expression

Abstract

1. Introduction

2. PSFFA

3. Solving the Non-Stationary M/D/1 queueing System’s PSFFA (c,f., (2.9))

4. Closing Remarks with Next Phase of Research

References

MDPI Initiatives

Important Links

Subscribe