Prerpints.org logo
Preprint
Article

Molecular Dynamics Simulation Properties Study of Ferroelectric Polymer Thin Films and Composites Based on Polyvinylidene Fluoride and Graphene Layers

Altmetrics

Downloads

142

Views

52

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

07 February 2024

Posted:

09 February 2024

You are already at the latest version

Alerts
Abstract
This work is devoted to consideration and analysis of the application of molecular dynamics simulation (MDS) methods to the study of nanosized polymer polyvinylidene fluoride (PVDF) thin ferroelectric films (two-dimensional ferroelectrics) and their composites with graphene layers: 1) to study and calculations of the polarization switching time depending on the electric field and PVDF film thickness; 2) to study and calculations of the polarization switching time depending changes of the PVDF on PVDF-TrFE film; 3) to study the polarization switching time in PVDF under influence of graphene layers. All calculations at each MDS step were carried out using quantum semi-empirical methods PM3. A comparison and analysis of the results of these calculations and the kinetics of polarization switching within the framework of the Landau-Ginzburg-Devonshire theory for homogeneous switching in ferroelectric polymer films is carried out. The study of the composite heterostructures of the “graphene-PVDF” type and calculations of their polarization switching times were presented too. It is shown that replacing PVDF with PVDF-TrFE significantly changes the polarization switching times in these thin polymer films, and that introducing various graphene layers into the PVDF layered structure leads to both an increase and a decrease in the polarization switching time. Here everything also depends on the position and displacement of the ferroelectric coercive field depending on the system damping parameters.
Keywords: 
Subject: Physical Sciences  -   Condensed Matter Physics

1. Introduction

Polymer ferroelectrics Polyvinylidene fluoride (PVDF) and its copolymer with Trifluoroethylene (PVDF-TrFE) are well-known materials with excellent piezoelectric properties, mechanical and thermal stability, and constantly growing areas of application [1,2]: in energy harvesting devices, in sensor and actuator materials mechanisms, in various biomedical and other devices, in the field of flexible organic electronics/nanoelectronics as layers and coatings for various heterostructures. Due to their flexibility, thin films of these ferroelectric polymers make it possible to create piezoelectric composite materials based on them for use in flexible piezoelectric nanogenerators [3]. These include piezoelectric sensors integrated into clothing, which represents great potential for future wearable electronics, and an approach for fabricating flexible piezoelectric sensors based on PVDF/graphene composite coating on commercially available fabrics is also reported [4]. Moreover, various modifications of graphene (G), graphene oxide (GO), reduced graphene oxide (rGO)and the use of these materials to create nanocomposites with various polymer matrices are being studied.
Based on polystyrene graphene foam (PSGF) on a PVDF substrate, their composition has been proposed as an efficient current collector and for lithium metal anodes to improve their lithium battery performance [5].
Another direction of application of thin ferroelectric layers based on PVDF and P(VDF-TrFE) films is the production of metal-ferroelectric-semiconductor field-effect transistors (MFSFETs) [6]. The characteristics of such MFSFETs made from thin PVDF and P(VDF-TrFE) films have been shown very good ferroelectric hysteresis curves with a counterclockwise loop, the same as other ferroelectric materials.
In recent years, due to the rapid development of nanoelectronics, new organic devices based on PVDF and PVDF-TrFE thin films have attracted intense research interest. Here, along with experimental studies, theoretical approaches are widely used, including the use of computer modeling and calculations using various numerical methods. For the theoretical study of such thin ferroelectric nanofilms and modeling of polarization switching processes in them, modern methods of molecular dynamics (MD) [7,8,9] in combination with the use of computer molecular modeling and quantum chemical calculations are very well suited here. Molecular dynamics simulation (MDS) is a rigorous theoretical tool that, when used effectively, can provide reliable answers to many questions related to structural-functional relationships, interaction mechanisms and properties of the studied atomic-molecular structures in molecular biology and pharmacology, biophysics and physics of nanomaterials [7,8,9,10].
This paper discusses computer modeling methods and especially the application of the MDS method to study the properties of nanomaterials that are promising for many applications, such as nanoscale ferroelectrics [10,11,12,13,14,15,16]. And these are, first of all, nanomaterials based on polymer structures (PVDF) and its copolymers P(VDF-TrFE) [17,18,19,20,21,22], as well as their composites with graphene (G) [23,24,25,26]. It is important that these theoretical studies were carried out in close combination with their experimental studies.
The point is that these ferroelectrics demonstrate a striking finite size effect [11]. The switching time and coercive field increase with decreasing film thickness, while the polarization and phase transition temperature decrease with decreasing thickness [10,11,12,13]. This is important for applications that require operation at low voltage, for example in devices such as non-volatile memory, where ferroelectric films must be quite thin.
The discovery of Langmuir-Blodgett (LB) ferroelectric polymer films [18] led here to new studies of ferroelectric properties at the nanoscale (one to two monolayers thick (ML, 0.5 - 1.0 nm)) [11,12,13,14,15,16,17,18,19,20]. This has opened the way for studying the finite size effect at the nanoscale, which is also important in many technical applications. The results obtained on P(VDF-TrFE) LB films open new directions and in the fundamental physics: the existence of two-dimensional ferroelectrics [12,21] and the transition from domain to homogeneous polarization switching in the context of the Landau-Ginzburg-Devonshire (LGD) mean field theory for thicknesses less than 15-20 nm [11,12,13,14,15,16,17,18,19,20,21,22]. However, there is still considerable debate about the theoretical models used to explain the experiments.
Therefore, here it is extremely important for the development of further practical applications of such ferroelectric thin layers and coatings based on PVDF and PVDF-TrFE (including their composites with graphene and graphene-like layers [23,24,25,26,27,28]) to clarify the theoretical basis of the physical processes in these thin ferroelectric layers, the processes of polarization switching, which are important for nanoelectronics.
To study the properties of such ferroelectric nanomaterials and nanocomposites, to elucidate the effect of changes in compositions on these properties, in addition to traditional experimental methods, various methods of computer simulation and numerical quantum-chemical studies are also used [29,30,31,32]. They save the cost of full-scale experiments and materials, and also make it possible to predict composite compositions of new nanomaterials with desired and required properties. One of the important modern numerical methods for studying the properties of various complex atomic and molecular structures is precisely the method of molecular dynamics simulation (MDS) [7,8,9,10]. The MDS method consists in solving Newton’s equation of motion for an atomic-molecular system, with a certain time step, by repeatedly calculating the forces acting on each atom, and then using those forces to update the position and velocity of each atom in the next step.
In this work, we applied the MDS methods, in which the calculations of the interaction of the atomic-molecular system of the nanomaterials are carried out on the basis of semi-empirical quantum-mechanical (QM) calculations at each step of the MDS run, using methods such as AM1, PM3, etc., [10,33,34,35,36,37,38] in restricted Hartree-Fock (RHF) approximations, presented in the HyperChem software [38]. We have already carried out these calculations for such polymer ferroelectircs PVDF and P(VDF–TrFE) [39,40,41,42,43,44]. These QM methods during MDS runs were used to calculate the following properties in the aforementioned nanomaterials at each step: 1) polarization switching time depending on the magnitude of the electric field [10,12,13,14,15]; 2) pyroelectric coefficients depending on the temperature range [23].
At present, the creation of new composite materials based on PVDF, PVDF-TrFE and graphene with their improved characteristics is of great interest [12,13,14,15,45,46]. MDS methods here can help and significantly improve and clarify our understanding of the interaction between graphene layers and polymer ferroelectric layers.
This work also examines in more detail the study, beyond of PVDF and PVDF-G, also PVDF-TrFE and composite structures of the “PVDF-TrFE-G”, "G-PVDF-TrFE-G" type, calculations of the polarization switching times in them, performed by MDS methods using semi-empirical quantum calculations at each step of the MDS run [47,48,49,50].
This article is devoted to a discussion and analysis of such recent computed results on PVDF, PVDF-TrFE with various G layers composites heterostructures, both in experiment and in simulation, as well as further prospects for studying their properties by these methods.

2. Basic models and methods

First, we consider the main experimental data and models of PVDF and P(VDF-TrFE) ferroelectrics and thin ferroelectric films, as well as the theoretical foundations and estimates of the polarization switching times in them. Then we will also consider calculations of the polarization switching time in them using the methods of the molecular MDS runs.

2.1. Nanoscale two-dimensional and polymer ferroelectric thin films

Ferroelectric single-crystal thin films based on PVDF/P(VDF-TrFE) were obtained for the first time in the early and mid-1990s using the LB technique [17,18,19,20,21,22], based on the transfer of chains and layers (monolayers - ML) of the polymer formed on the surface of the water, from this water surface to the substrate carrying the electrodes.
Figure 1a-d shows the models of PVDF polymer chains in polar (ferroelectric) and non-polar (paraelectric) phases and the corresponding cells of their crystal structure (in sections across the polymer axis). These model images were built using HyperChem [38] and are wide used in our works [12,13,14,15,23,24,25,26,42,43,44,47,48,49,50]. Figure 1e, f shows a transferring scheme of LB PVDF layers and chain’s patterns of 1 ML observed in a tunnelling microscope (Figure 1g).
Langmuir ferroelectric films obtained by this method in [17,18,19,20] turned out to be record thin. These nanosized two-dimensional ferroelectrics with a thickness of 0.5–1.0 nm, consisting of a single monolayer, were obtained in [17] for with the polarization at the order of P ~ 0.1 C/m2 [17,18,19,20,21]. The thickness of these Langmuir polymer films (two-dimensional ferroelectrics) was controlled by ellipsometry and atomic force spectroscopy [17,18,19,20,21,22,51]. The thickness of one monolayer (1 ML) was L = 0.5 nm = 5Å, i.e., much less than the theoretical estimate of the size of the ferroelectric critical domain nucleus x0 ~ 10...20 nm (L << x0) known from the literature [11,13,52]. Thus, nanoscale two-dimensional ferroelectrics with a thickness of 0.5–1.0 nm, consisting of a single monolayer, were obtained in [17], and the existence of ferroelectricity at the nanoscale was proved. The discovery of the nanosized two-dimensional polymer ferroelectrics [17,18,19,20,21,22,53] led to a new stage of the ferroelectric properties, including the study of switching in the ultrathin films, using the MDS method [10]. The LGD theory is well suited for describing ferroelectric phenomena in such nanosized polymer ferroelectrics [11,12,13,14,15,16,21].
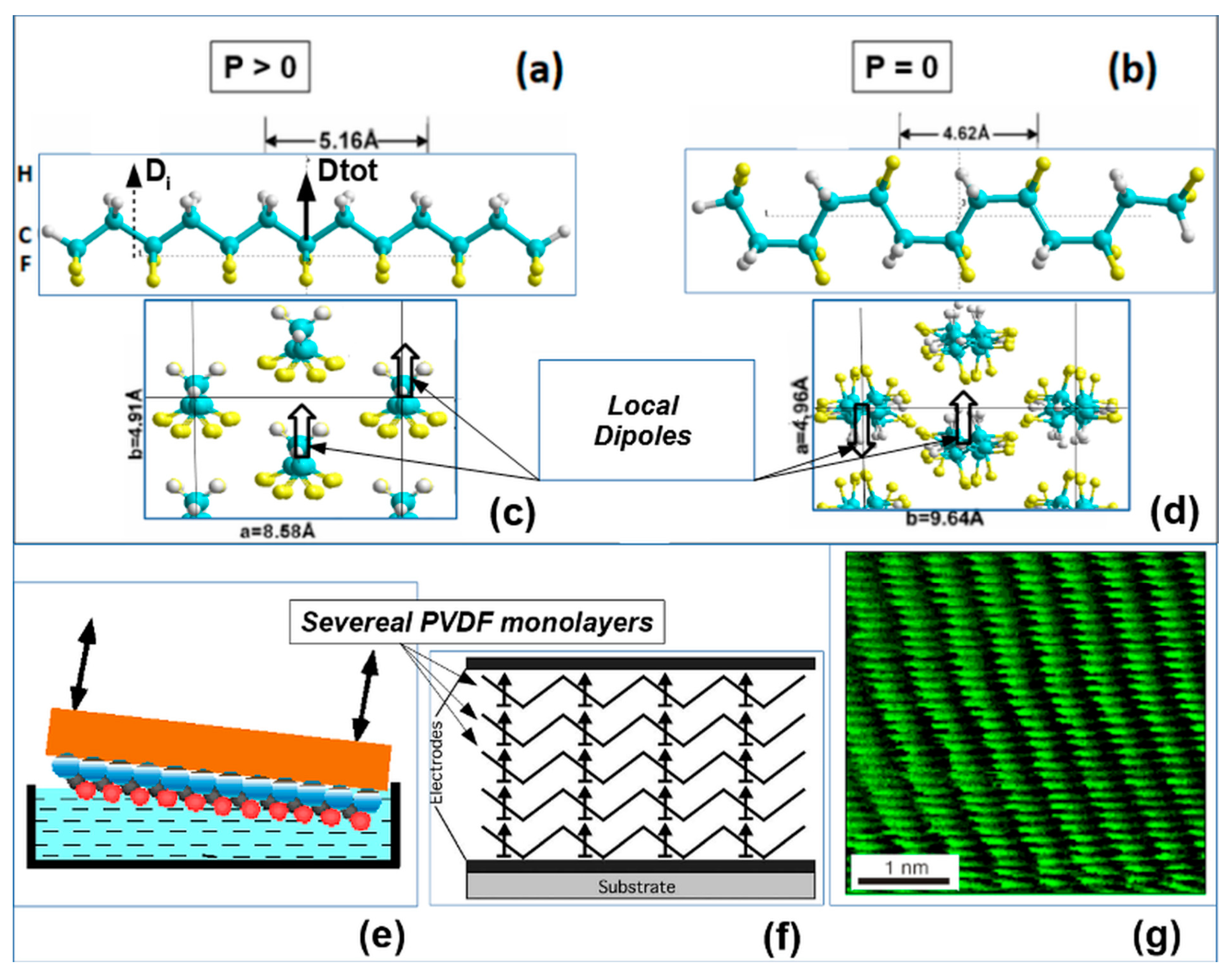
Preprints 98410 g001
Figure 1. Ferroelectric polymer polyvinylidene fluoride (PVDF): (a) and (c) PVDF in polar Trans conformation and total polarization P > 0; (b) and (d) PVDF in a nonpolar Gauche conformation with total polarization P = 0 [52]. (e) The formation of the PVDF Langmuir-Blodgett (LB) film on the surface of the water [21]. (d) Transferring several mono-layers (ML) of LB PVDF film onto a substrate with an electrode [22]. (e) Image of the 1 M LB film of polyvinylidene fluoride-trifluoroethylene P(VDF-TrFE) by scanning tunneling microscopy [11,17]. (Reprinted with permission from [13]).
Figure 1. Ferroelectric polymer polyvinylidene fluoride (PVDF): (a) and (c) PVDF in polar Trans conformation and total polarization P > 0; (b) and (d) PVDF in a nonpolar Gauche conformation with total polarization P = 0 [52]. (e) The formation of the PVDF Langmuir-Blodgett (LB) film on the surface of the water [21]. (d) Transferring several mono-layers (ML) of LB PVDF film onto a substrate with an electrode [22]. (e) Image of the 1 M LB film of polyvinylidene fluoride-trifluoroethylene P(VDF-TrFE) by scanning tunneling microscopy [11,17]. (Reprinted with permission from [13]).
Preprints 98410 g001

2.2. Main Theoretical Approach

2.2.1. Main Features of the LGD Theory for Nanoscale Ferroelectrics

The theoretical description of ferroelectrics was developed by Ginzburg [54,55], and then by Devonshire, based on Landau’s theory of phase transitions [56]. This phenomenological LGD thermodynamic theory was the main basis for the development of the physics of ferroelectrics [11,16]. The LGD theory explained all the basic properties of ferroelectrics, including polarization switching in an external electric field and the hysteresis loop. But it turned out that it does not describe all the switching phenomena of a ferroelectric, since it predicts the magnitude of the coercive field, which is 2-3 orders of magnitude larger than the experimental one. The large coercive fields predicted by the LGD theory will here be called intrinsic (or proper), while their experimental values are extrinsic (or improper). It is significant here that the LGD theory considered the ferroelectric crystal as a homogeneous infinite medium. The study of nanosized two-dimensional ferroelectrics based on PVDF, and then on the basis of other other materials, showed that in these nanomaterials ferroelectricity exists even at sizes much smaller than x0 ~ 10...20 nm (at least in the thickness of one monolayers of such materials), as in a continuous homogeneous media. In this case, it is precisely homogeneous domainless switching of polarization that occurs here immediately in the entire volume of such a nanosized ferroelectric in full accordance with the LGD theory. Thus, within size L ≤ x0, the system is homogeneous. And then the theory of LGD turns out to be quite applicable and completely valid to it. This has been convincingly demonstrated in recent works [12,13,14,15] on the analysis of the switching phenomena in such nanosized two-dimensional ferroelectrics. Therefore, here we justifiably rely on this LGD theory when considering ferroelectric phenomena in thin polymeric materials based on PVDF/P(VDF-TrFE).

2.2.2. Main theoretical approach description

1) Main mathematical relations of LGD theory.
Let’s take a quick introduction to LGD theory. In ferroelectrics, polarization is the main order parameter (or ordering) of the system. Therefore, according to the Landau theory [56], and its development in the LGD theory [54,55], the behavior of a system (ferroelectric) in the vicinity of a phase transition (PT) between the paraelectric and ferroelectric phases can be described by expanding the thermodynamic potential F (or Gibbs free energy density) in the even degrees of the spontaneous polarization P (in the simple uni-axial case) [11,16]:
F = F 0 + α 2 P 2 + β 4 P 4 + γ 6 P 6 − E P ,
with known from LGD theory by expansion coefficients α, β, γ (which have in general temperature and pressure dependence), E is an external electric field and F0 is the thermodynamic potential of the paraelectric phase (when E = 0). The equilibrium conditions correspond to the minimum of the thermodynamic potential, where
∂ F ∂ P = 0 ,   ∂ 2 F ∂ P 2 > 0 ,
In the LGD theory of first-order ferro-electric phase transitions (PT1), the expansion coefficients have the values
α = 1 ε 0 C T − T 0 , β < 0 ,   γ > 0 ,
where T0 > 0 is the Curie temperature, C > 0 is the Curie–Weiss constant, and ε0 is the permittivity of free space. The phase transition temperature TC is
T C = T 0 + 3 ε 0 16 β 2 C γ ,
2) The intrinsic coercive field.
The electric field is calculated from thermodynamic potential (1) and Eq. (2) [11,53]:
E = ∂ F ∂ P = α P + β P 3 + γ P 5 ,
The intrinsic coercive field is determined from the extreme of Eq. (5) [11,53]:
E C = P 0 χ 0 f t ,
f t = 3 25 3 5 1 − 25 24 t ,
where t is the reduced temperature, P 0 = P S 0 2 is the value of the spontaneous polarization and χ 0 = χ T = T 0 = γ / 2 β 2 is the ferroelectric contribution to the dielectric susceptibility, both evaluated at t = 0 (T = T0). For estimates, it can be assumed approximately EC ~ P/χ0 ~ P/εε0, where ε is the relative permittivity and ε0 is the dielectric constant of the vacuum.
3) Polarization switching kinetics.
The polarization switching kinetics of two-dimensional polymer ferroelectrics was described by Landau – Khalatnikov equation [11] and its solution for first-order phase transitions in two-dimenstional ferroelectrics were considered in [57,58,59]:
ξ d P d t = − ∂ F ∂ P = − α P − β P 3 − γ P 5 + E ,
where ξ is the damping coefficient. In the general case, the gradient term can be taken into account. An investigation of the solution of this equation showed that in the vicinity of the coercive field EC (when E → EC and E > EC) the switching time t increases abruptly and its dependence from E can be expressed [58,59]:
1 τ s 2 = 1 τ 0 2 E − E C E C ,
where
τ 0 = 6.3 ξ γ β − 2 .
In this case, EC is the proper (intrinsic) coercive field of the ferroelectrics. This relation (12) shows directly linear behaviour of τ-2 along E in the vicinity of EC. This relation is more suitable for comparison with experimentally measured data and used in [60,61,62]. Also, this relationship turned out to be convenient for analyzing the results of theoretical calculations when modeling the polarization switching processes in polymer ferroelectrics and allow us to perform this investigation by MDS methods [10,12,13,14,15,44].

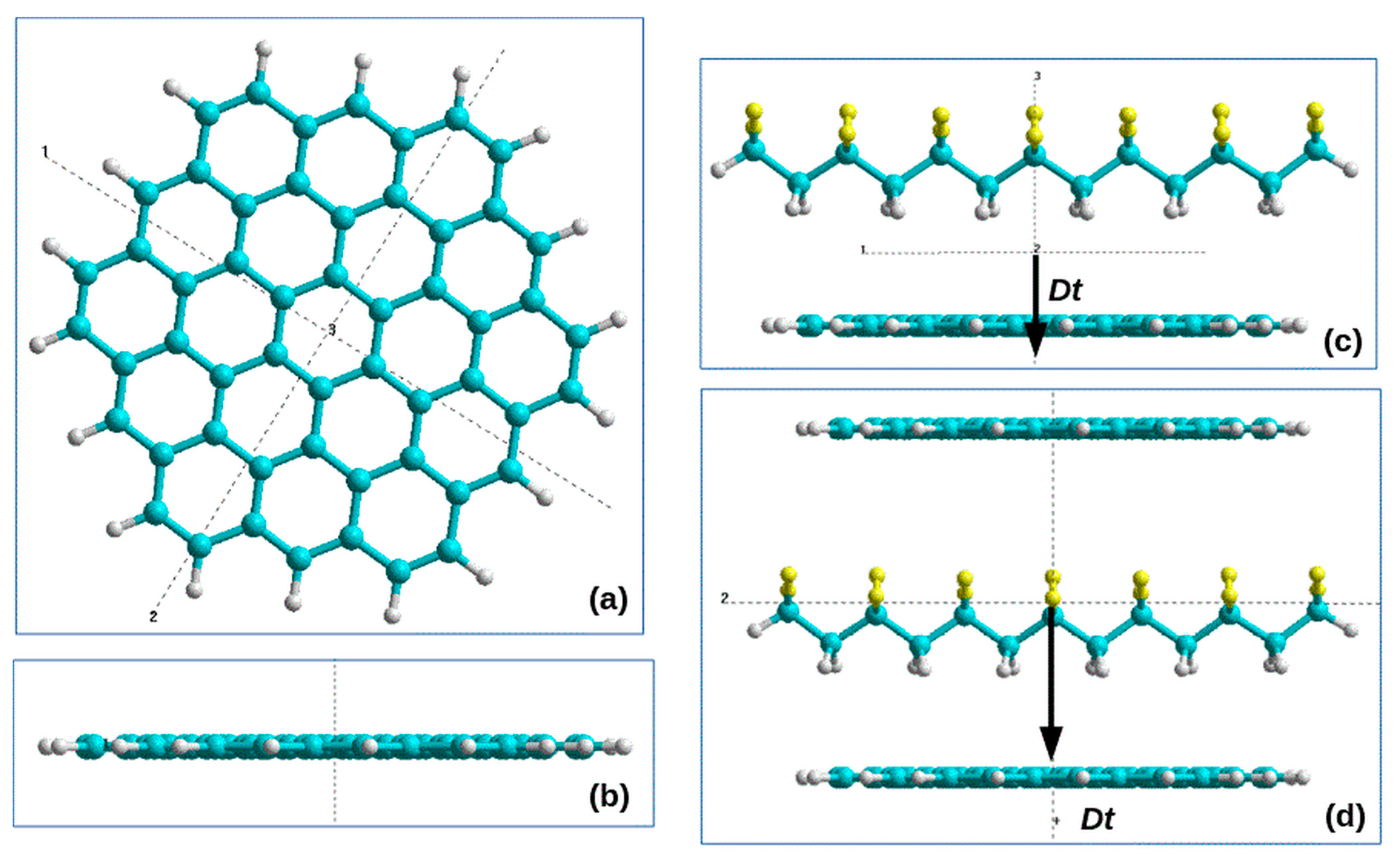
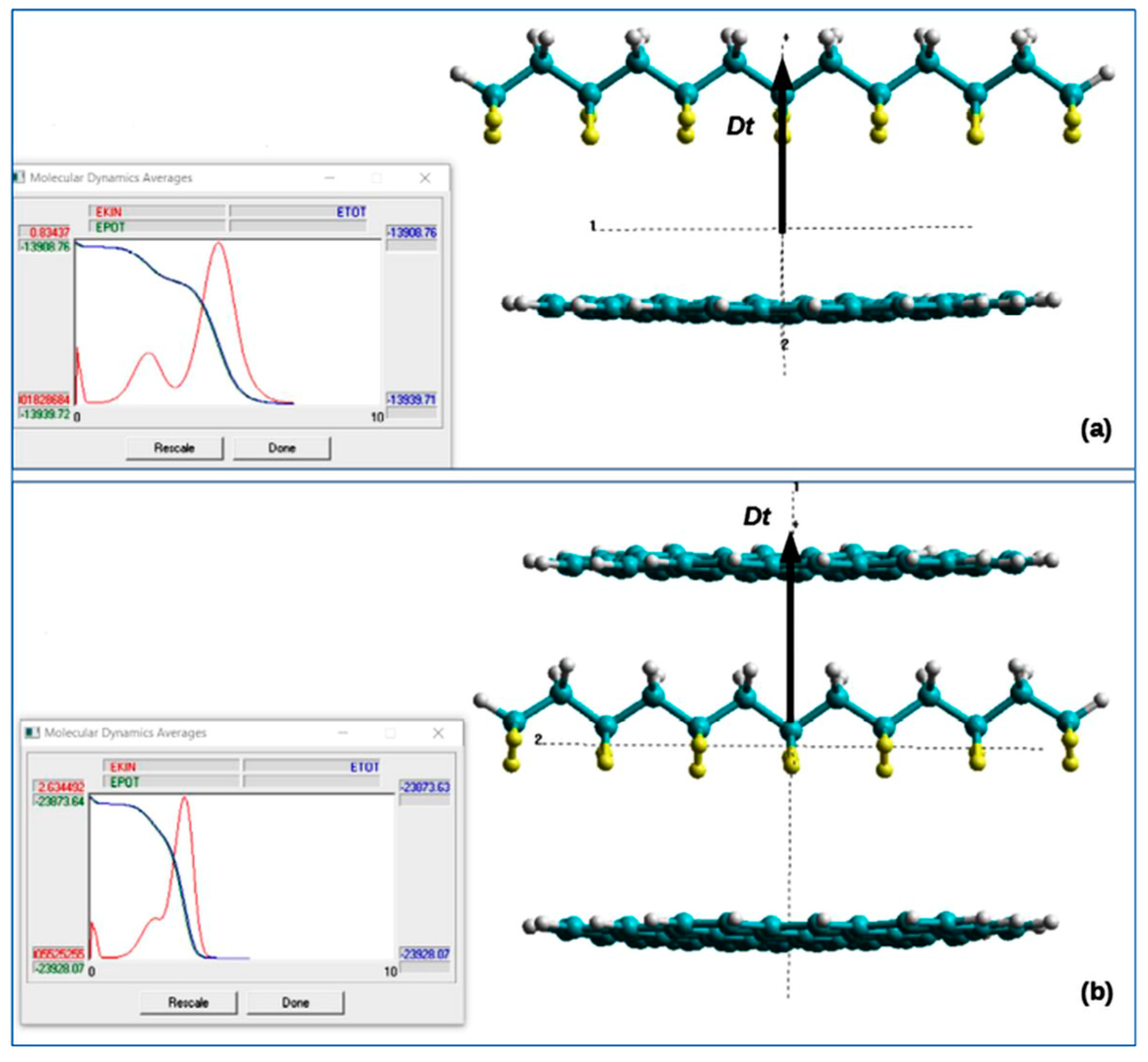
2.3. Main models, methods and computational details for thin polymer ferroelectric films

Polymer ferroelectric films based on PVDF and P(VDF-TrE) were also known before [11,16]. These were the bulk ferroelectric spun films formed by solvent techniques, they were usually made by spin-coating method [63,64,65]. They possessed the main ferroelectric properties similar as the thin LB films [11,16,17,18,19,20,21,22], but unlike the thin two-dimensional LB films they were thicker and volumetric (three-dimensional bulk). Besides, these spun ferroelectric polymer films were not (and could not be) so well structurally ordered as LB films, and they had many of their structural inhomogeneities, deposits of amorphous phases and polycrystals and had completely different (domain) polarization switching mechanisms [52].
Nevertheless, in its main polar b-phase, they have been similar to LB films in their chemical composition and organizations. In its β-phase, PVDF has a spontaneous polarization P of about 0.08–0.1 C∙m−2 [11,16]. Similar properties can be obtained in thin polymer films fabricated by the LB technique - in b-phase structure this LB film with the dipoles of all PVDF chains is high-ordered aligned in a structure with maximum polarization P ~ 0.13 C∙m-2 [11,17,18,19,20,21,22].
It is important to note that ferroelectric polymers based on PVDF and P(VDF-TRFE) turned out to be a convenient object for molecular modeling: they had a sufficiently clear structure of the polymer chains consisting of periodically repeated C2H2F2 units having their dipole moment (Figure 2). For quantum-mechanical calculations, a semi-empirical method of molecular orbitals with a self-consistent field [31,32,33,34,35,36,37,38] was applied here in the PM3 parameterization in the Hartree-Fock approximation, similar to AM1 [38]. The approach was developed in detail and tested by Stewart [34,35,36,37] and it was also shown the effectiveness of its use on systems of similar organic polymers. In [10,12,13,14,15], the Hyperchem software package [38] was used, containing all the above-mentioned necessary methods. In addition, this package contains the necessary means of optimizing the system - to search for a minimum of the system energy, the method of conjugate gradients (Polak-Ribiere) is used [38]. The HyperChem package has implemented special software for molecular dynamics and the ability to perform MDS calculations (runs) using different calculation methods at each step of the MD run and allows you to simulate the application of an external electric field.
The main motive of the PVDF ferroelectric polymer structure in the polar b-phase is a linear fluorinated hydrocarbon with a repeat unit (CH2–CF2) of spacing c = 2.58 Å (Figure 1a and Figure 2a - these chains, like other images of the structures of the ferroelectric polymers, easy and convenient receive on the basis of their simulation in the Hyperchem [38] program).
Each CH2-CF2 unit has its own Di dipole moment, directed from electronegative fluorine F to electropoitive hydrogen H, producing a net dipole moment nearly perpendicular to the polymer chain. and the entire chain of PVDF as a whole has a total dipole moment Dt (Figure 1a and Figure 2a). In the low-temperature polar phase, the structure has a conformation (TTTT), organized in the form of strictly oriented dipoles. These chains can crystallize in the form of a quasi-hexagonal dense packaging (Figure 1a,c), the crystallographic parameters of which a = 8.58 Å, b = 4.91 Å, c = 2.58 Å [11,16,17,18,19,20,21,22]. This is the b-phase structure in which dipoles of all chains are aligned into a highly ordered structure with the maximum value polarization P = 0.13 Cm-2 [11]. Polarization and switching are performed by applying a electric field E, perpendicular to the circuits, to change the direction of polarization P.
In the high-temperature phase, the polymer structure changes to the alternating trans-gosh (TGTG) configuration having a non-polar phase consisting of oppositely directed dipoles of an antipolar arrangement of trans-gosh chains (Figure 1b,d). Copolymers PVDF-TrFE also have a slightly large elementary unit cell volume, and the period along the chains doubles c = 4.62 Å ~ 2 · 2.58 Å = 5.16 Å due to the change in the chain structure (Figure 1b) [11,16,17,18,19,20,21,22]. However, the temperature of the paraelectric-ferroelectric phase transition in PVDF is above its melting temperature point [11]. This is not suitable for many practical applications. Therefore, most experimental studies of ferroelectric properties were carried out on the copolymers P(VDF-TrFE), statistical random copolymers of polyvinylidenefluoride monomers and trifluoroethylene monomers with the structure (CH2-CF2)n-(CHF-CF2)m.
The copolymers with the content of 50% TrFE or less are ferroelectric. Although with reduced polarization and the temperature of the transition, because some of the hydrogen atoms are replaced with fluorine, reducing the pure dipole moment polymer chains [11,16]. Examples of the formation of such individual chains with different concentrations are shown on the models of Figure 2b–d. In polymer LB films with different composition of copolymers, ferroelectric switching is observed, depending on the electric field and film thickness [11,12,13,14,15]. All these models were used in modeling and calculations of the properties of ferroelectric copolymers at the different electric fields and thicknesses [12,13,14,15,39,40,41,42,43].
In this article, it is primarily interested in the results of the use of MDS method for modeling the polarization switching. The main features of the behavior of ferroelectric thin films in the electric field can be well demonstrated can be well demonstrated using a simpler PVDF model containing 6 monomer C2H2F2 units. More precisely, for reasons of symmetry, 6.5 monomer units are used here. This model is shown below in Figure 3.
Testing of the PVDF models with different numbers of monomer units [40,42,43,44] showed that PVDF model with 6 units is quite comparable to a PVDF chain with 10 monomers.
Preprints 98410 g002
Figure 2. Molecular models of polymer chains in the initial equilibrium optimized state in the absence of an electric field (Dt - the total total dipole moment of the chain, Di is a selected individual moment of one element C2H2F2): a) the PVDF chain out of 10 (and a half) elements C2H2F2, with shown selected individual dipole moment Di of one element C2H2F2; b) polymer chain of 10 elements with replacement of 2 hydrogen atoms by 2 fluorine atom (80:20); c) polymer chain of 10 elements with a replacement of 3 hydrogen atoms by 3 fluorine atom (70:30); d) Polymer chain of 10 elements with a replacement of 4 hydrogen atoms by 4 fluorine atom (60:40). Original models made using HyperChem [38].
Figure 2. Molecular models of polymer chains in the initial equilibrium optimized state in the absence of an electric field (Dt - the total total dipole moment of the chain, Di is a selected individual moment of one element C2H2F2): a) the PVDF chain out of 10 (and a half) elements C2H2F2, with shown selected individual dipole moment Di of one element C2H2F2; b) polymer chain of 10 elements with replacement of 2 hydrogen atoms by 2 fluorine atom (80:20); c) polymer chain of 10 elements with a replacement of 3 hydrogen atoms by 3 fluorine atom (70:30); d) Polymer chain of 10 elements with a replacement of 4 hydrogen atoms by 4 fluorine atom (60:40). Original models made using HyperChem [38].
Preprints 98410 g002
Preprints 98410 g003
Figure 3. Schematic of the MD run process for one “PVDF-6” chains model using PM3 RHF method calculations by HyperChem software at the each MD run’s step: (a) initial state; (b) final state after MD run with rotated (switched) on the opposite direction dipole moment Dt orientation in electric field E. Inset (c) show the energies changes during MDS run with the time (in ps). (Adapted with permission from ref. [10]; Elsevier, 2014).
Figure 3. Schematic of the MD run process for one “PVDF-6” chains model using PM3 RHF method calculations by HyperChem software at the each MD run’s step: (a) initial state; (b) final state after MD run with rotated (switched) on the opposite direction dipole moment Dt orientation in electric field E. Inset (c) show the energies changes during MDS run with the time (in ps). (Adapted with permission from ref. [10]; Elsevier, 2014).
Preprints 98410 g003
Adding TrFE to PVDF for its copolymers P(VDF-TrFE) shifts a phase transition point and slightly changes polarization parameters. We are interested in the main characteristics of polarization switching precisely in the low-temperature polar phase, where the PVDF model chain is quite valid. Nevertheless, we will also consider here a similar simple model of a copolymer.

3. Results

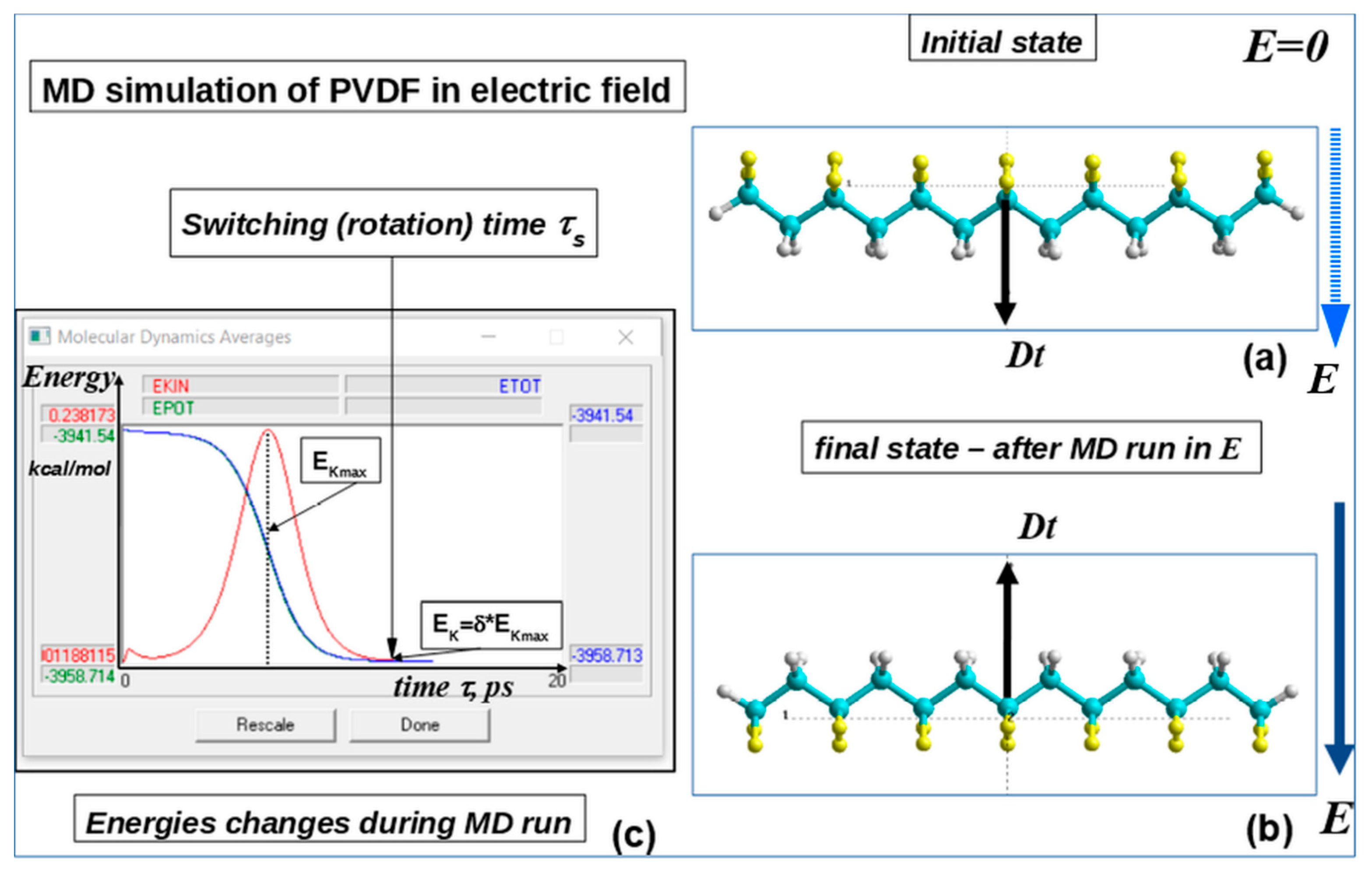
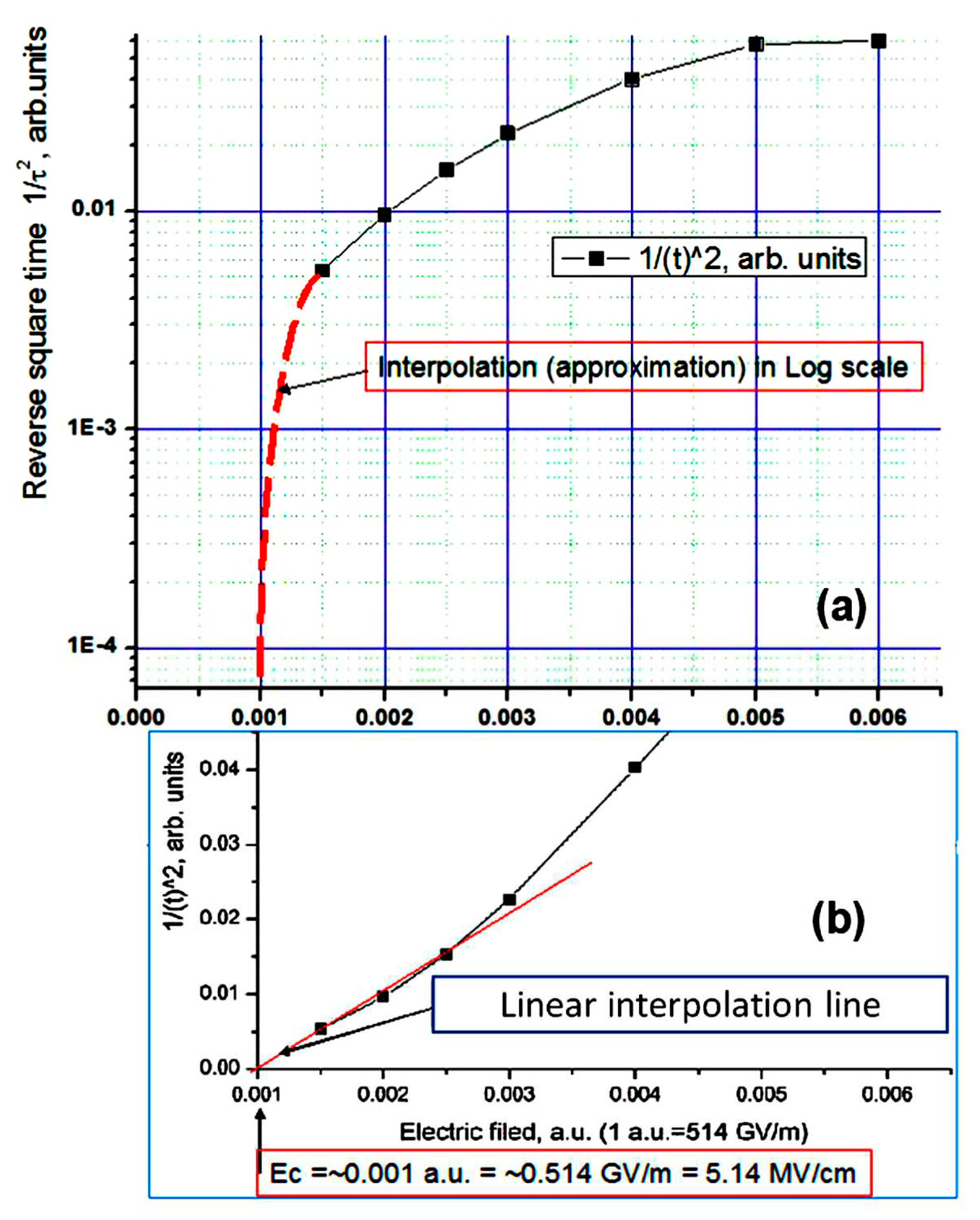
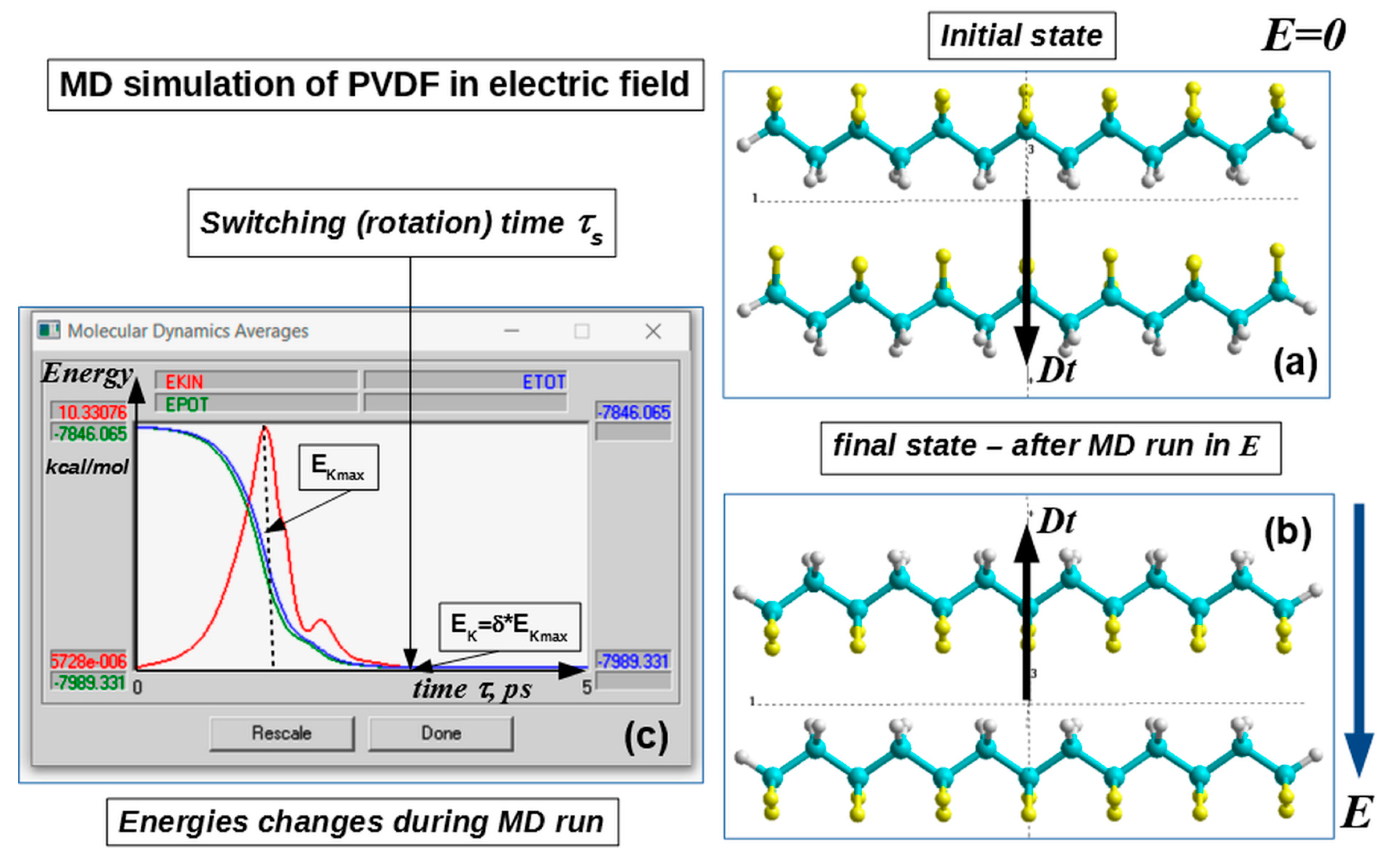
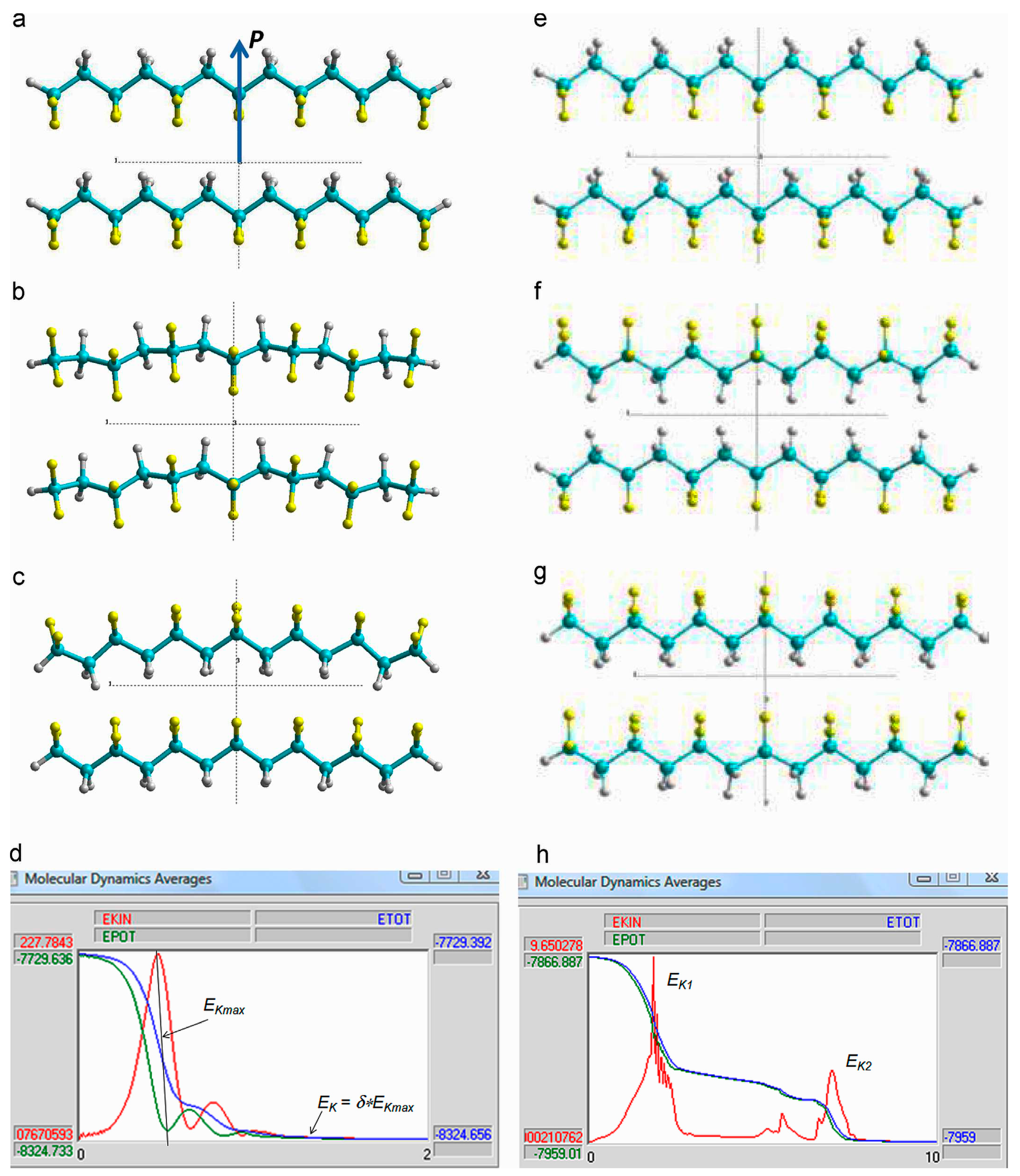
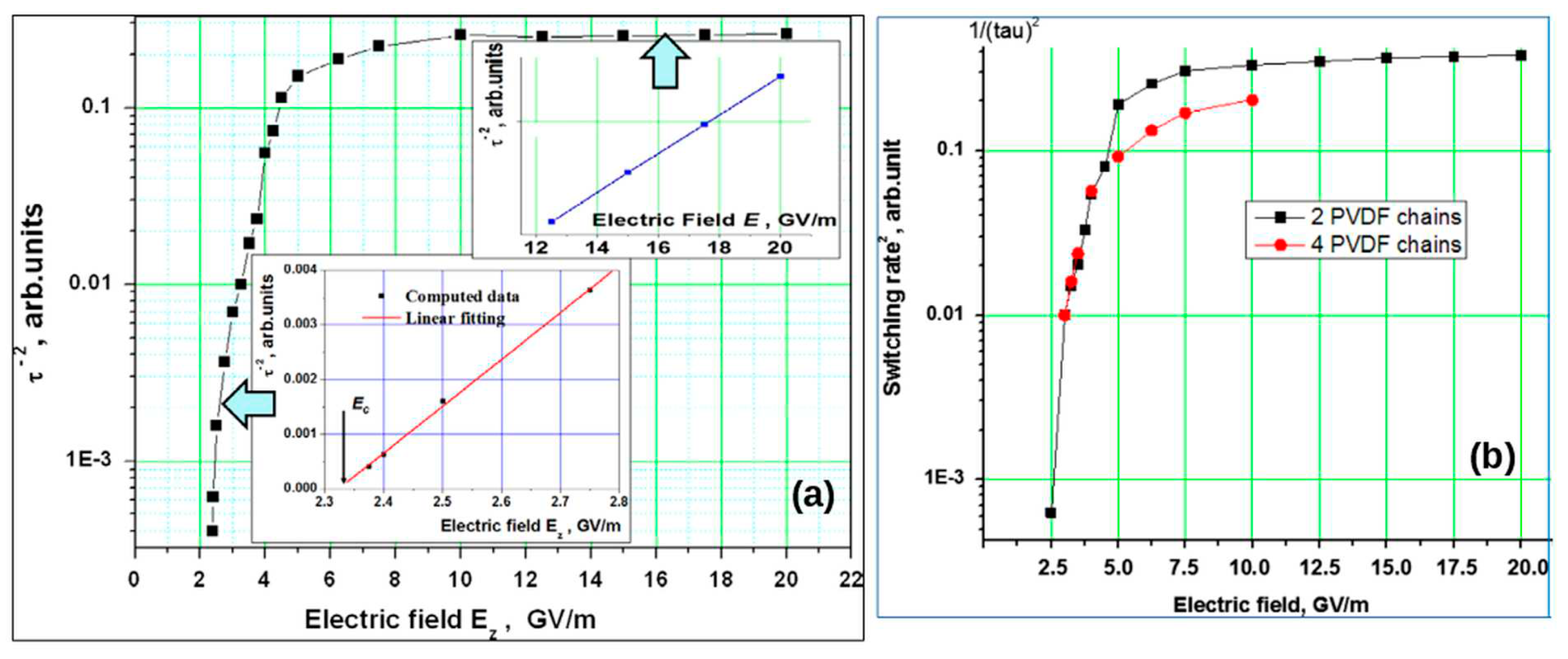
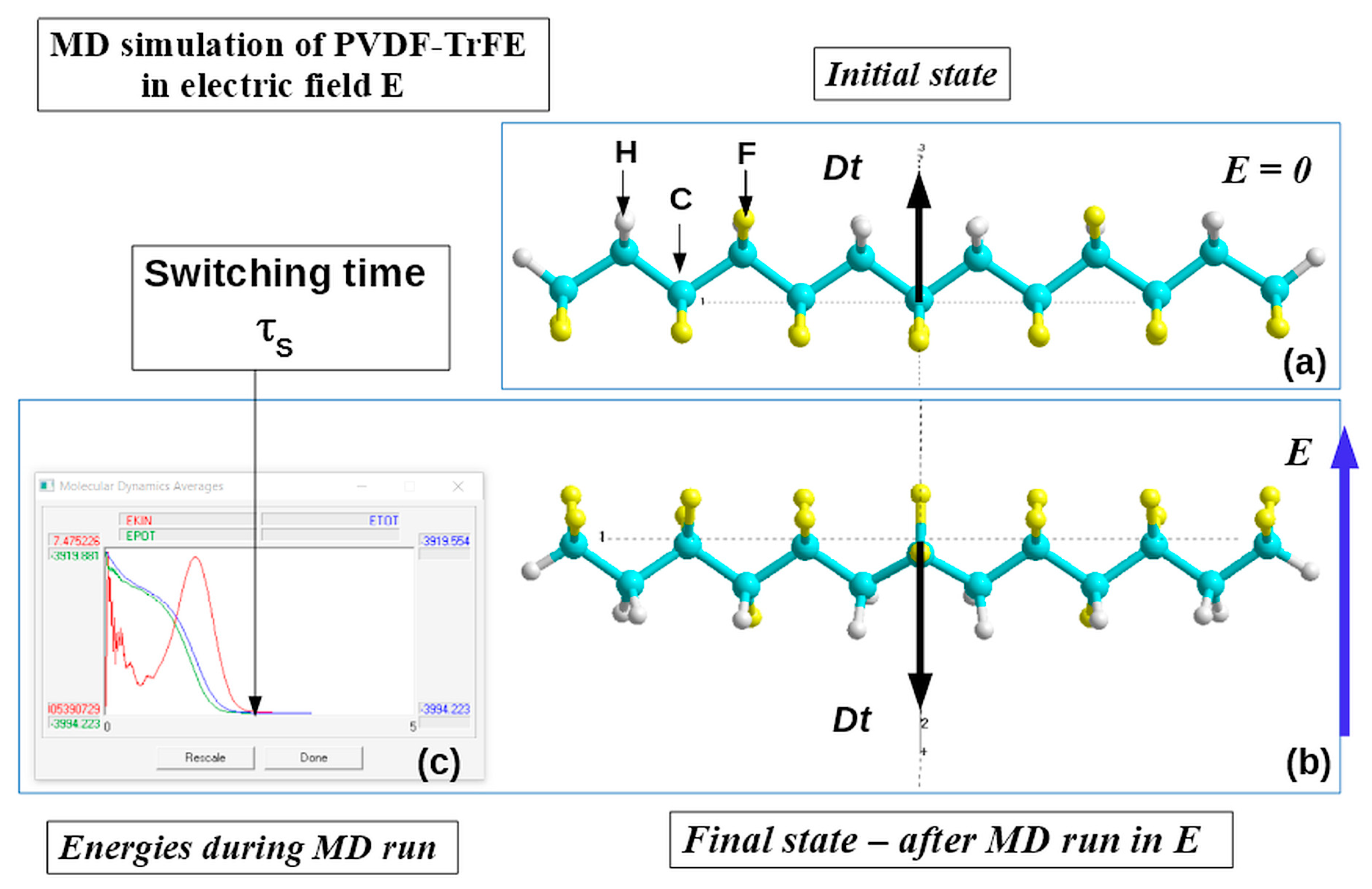
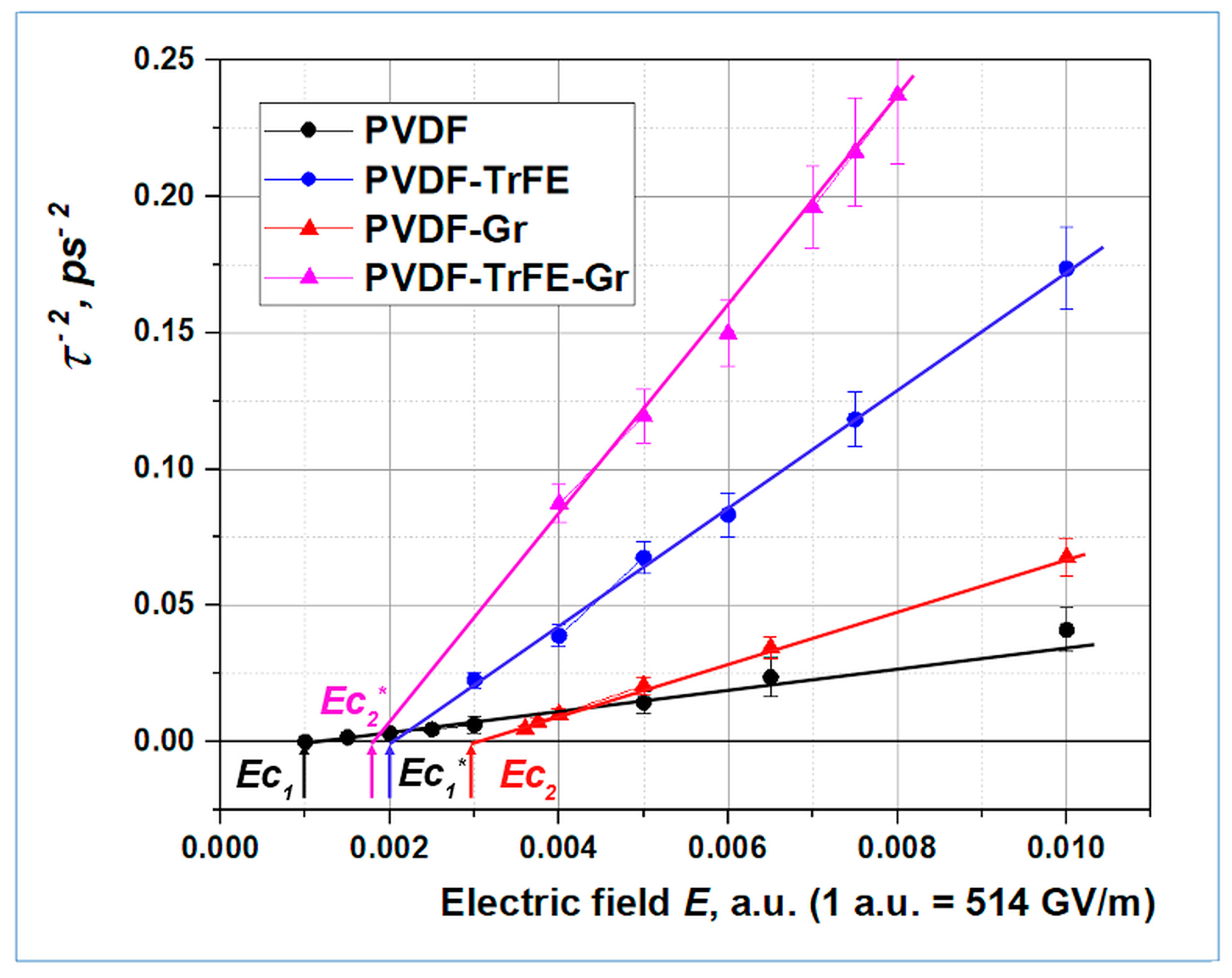
3.1. Homogeneous polarization switching in polymer ferroelectrics by MDS method

The main approach used in this work is MDS run and changes of the modelled structures under applied electric field E action with its various values using HyperChem software [38], firstly proposed and performed in our work [10] for one PVDF chain (Figure 3).
In our case, we are interested in the change in the structure of the entire system under the influence of the applied electric field E. Figure 3 shows the case of the simplest model of the PVDF chain of the 6 main CH2-CF2 units (“PVDF-6” model), which is rotated in the applied electric field E. Here it is shown how occurs the switching of the direction of the general moment of the dipole moment Dt (and the corresponding polarization vector P) from the initial direction to the opposite under the influence of an external electric field.
Performing of such MDS calculations and MD runs requires specifying a certain set of parameters, which are indicated in the special Molecular Dynamics Options of the HyperChem program [38]. The main initial parameters for considered PVDF model and other related models are following: 1) MD calculations perform here at the constant temperature (for each used electric field value) in vacuum, 2) with parameter of the "bath relaxation" time = 0.05 ps; 3) with the MD run parameter “run time” = 5 – 20 ps (depending of necessary time interval, in which switching process observed for various applied electric field value) and 4) with time step or “step size” Dt = 0.0005 – 0.001 ps, which varied depending of the applied electric field and the rate of the PVDF molecular chain rotation (polarization switching). These calculations were performed when the electric field E changed in the range of order ~ (0.001 – 0.010) a.u. ~ (0.514 - 5.14) GV/m.
In this work the main calculations were carried out by the PM3 quantum method in a restricted Hartree-Fock approximation (RHF) [38] at the each step of the MDS run. All calculation results are collected in special numerical files and displayed in the form of trajectories on a special window for MD run data in the HyperChem workspace (Figure 1c). The final time (switching time τS) is estimated from these MD energy trajectories (see Figure 1c) using the criteria [10]: δ = EK/EKmax <10–3, where EK is the kinetic energy at the end point, and EKmax is the kinetic energy at the maximum point EKIN of chain rotation (as shown by red line in Figure 1c). In fact, this corresponds to the achievement of the rest point of the rotating PVDF chains, when EK ~ 0, and its position with an opposite orientation of the total dipole vector Dt in relation to the initial one and the corresponding polarization vector P. These data of times tS - polarization switching times obtained in MD runs at the different values of the applied field E are then used to plot the t(E) and t-2(E) dependencies according to Eq.( 9).
It is characteristic that the results obtained in the time calculations of the switching time t with different values of the electric field E is even on such a simple model showed the validity of the polarization switching homogeneous kinetics in accordance with the LGD theory and of Landau-Khalatnikov Eq. (8) - the linear behavior of the reverse square of the switching time t-2 from electric field E in Eq. (9) for the E seeking to the critical point of the EC (when E → EC and E > EC), where EC is the boundary value of the coercive field (Figure 4).
It is notables that the behavior of this dependence of the t-2 from E (by MD run) in a logarithmic scale, shown on Figure 4a, it turned out to be qualitatively close to experimentally observed t-2(E) dependencies on the thin ferroelectric LB films with various thickness in the works [10,60,61] (Figure 5), especially for the most thin case.
As further example of the MD run calculations, sample 2 PVDF chains affected by an external electric filed E (Figure 6).
This model corresponds to a sample of two PVDF monolayers. Figure 6 shows a diagram of the MD in an electric field E for a model already consisting of two PVDF chains and a change in the orientation of their dipole moment Dt with a change in the electric field E at the point of the coercive field EC.
It is important that this approach of MD runs allows one to directly determine the switching time τS (flip or overturn of a chain, and a group of chains) depending on the value of the applied external electric field E and thereby directly determine this dependence τ(E) from the numerical MDS experiment.
It is noteworthy that the switching times tS and the very nature of the behavior of the PVDF chains during the switching process are very different in strong and weak electric fields E (Figure 7).
Figure 8 shows the behavior of τ−2(E) on a logarithmic scale, which again qualitatively coincides with the experimentally established behavior [60,61] (Figure 5). In the region of weak fields E (close to the coercive field and E > EC), the plotted plots of the t-2(E) dependence had the same explicit linear dependence (9) and made it possible to determine the value of the coercive field EC at the point of intersection of the line graph with OX axis.
On this basis, further calculations were carried out for PVDF and P(VDF-TrFE) chains of different tyes and the case of a different number of chains - as a model of the LB films with different numbers of the monolayers (ML) and thicknesses. Thus, calculations were performed for four, six, ten and more parallel chains at different electric field values. In all this case, the simulated number of chains corresponds to the number of the ML in the experimental LB PVDF and/or P(VDF-TrFE) thin films.
Insert in Figure 8 shows the linear dependence (9) τ−2(E) on E near EC, with approximation to the point of intersection with the horizontal axis, which determines the value of the coercive field EC ~ 2.4 GV/m for 2-4 chains (ML - monolayers). Taking into account that the field E is external and that for thin polymer layers representing monomolecular layers, the dielectric constant is ε ~ 2.4 [12,13,40,42] (while ε = 5 is for thick films), we obtain the limiting maximum value ECmax ~ EC /ε ≅ 1 GV/m, which is a proper coercive field corresponds to known experimental data and LGD theory [11,12,13,14,15].
Similarly, hysteresis loops were also calculated using this technique for PVDF and P(VDF-TrFE) chains of different types and the case of a different number of chains (as models of ferroelectric LB films with different numbers of monolayers ML and thicknesses). These data also made it possible to determine the critical value of the electric field required to switch the polarization - the intrinsic coercive field Ec for these films of different thicknesses (or different numbers of monolayers ML). All these data (obtained both by the MDS method and from the hysteresis loops calculations [43,44]) were subsequently used to calculate the dependence of the coercive field EC on the thickness of the ferroelectric film (depending on the number of its monolayers). Experimentally, such a dependence of the behavior of polarization switching in PVDF and P(VDF-TrFE) on the thickness of the films in different electric fields were studied in works [51] and in more details [62] (Figure 9).
The detailed experimental study of the P(VDF-TrFE) LB films of the different thicknesses was carried out in [62] (Figure 9). It was shown that for small thicknesses of 2–6 nm, the coercive field EC is proper and practically unchanged, and in the region of thicknesses greater than 8 nm, a transition region arises, and for thicknesses greater than 10–12 nm, the proper coercive field EC becomes improper and is determined by the domain mechanism.
Another method for obtaining a coercive field is calculation of hysteresis loops P(E) [43]. Calculations performed for different number of chains and film thickness using both these methods showed that the dependence of the coercive field obtained [10,12,13,14,15,44] is in good agreement with the experimentally established dependence of the coercive field EC on the film thickness [62], as well as with our calculations based on MDS run in various electric field (Figure 10).
This dependence can be conditionally divided into 3 regions: the region of purely homogeneous LGD switching (up to 8 nm), the transition region (8-12 nm), where a kind of domain precursor is noted, and the region above 12-16 nm and further, where the domain switching mechanism predominates (the coercive field remains almost unchanged and is kept at a low level of ~ 0.07–0.05 GV/m) [10,11,12,13,14,15,43,44]. Thus, these switching calculations of ultrathin polymer ferroelectrics confirm that two-dimensional ferroelectrics can consist, in principle, of several monolayers or several unit cells. These data are also in good agreement with the results for thin BaTiO3 films, in which a homogeneous switching has recently been found at the scale level up 10 nm, and with a further increase in thickness they already correspond to thick films [11,12,66].

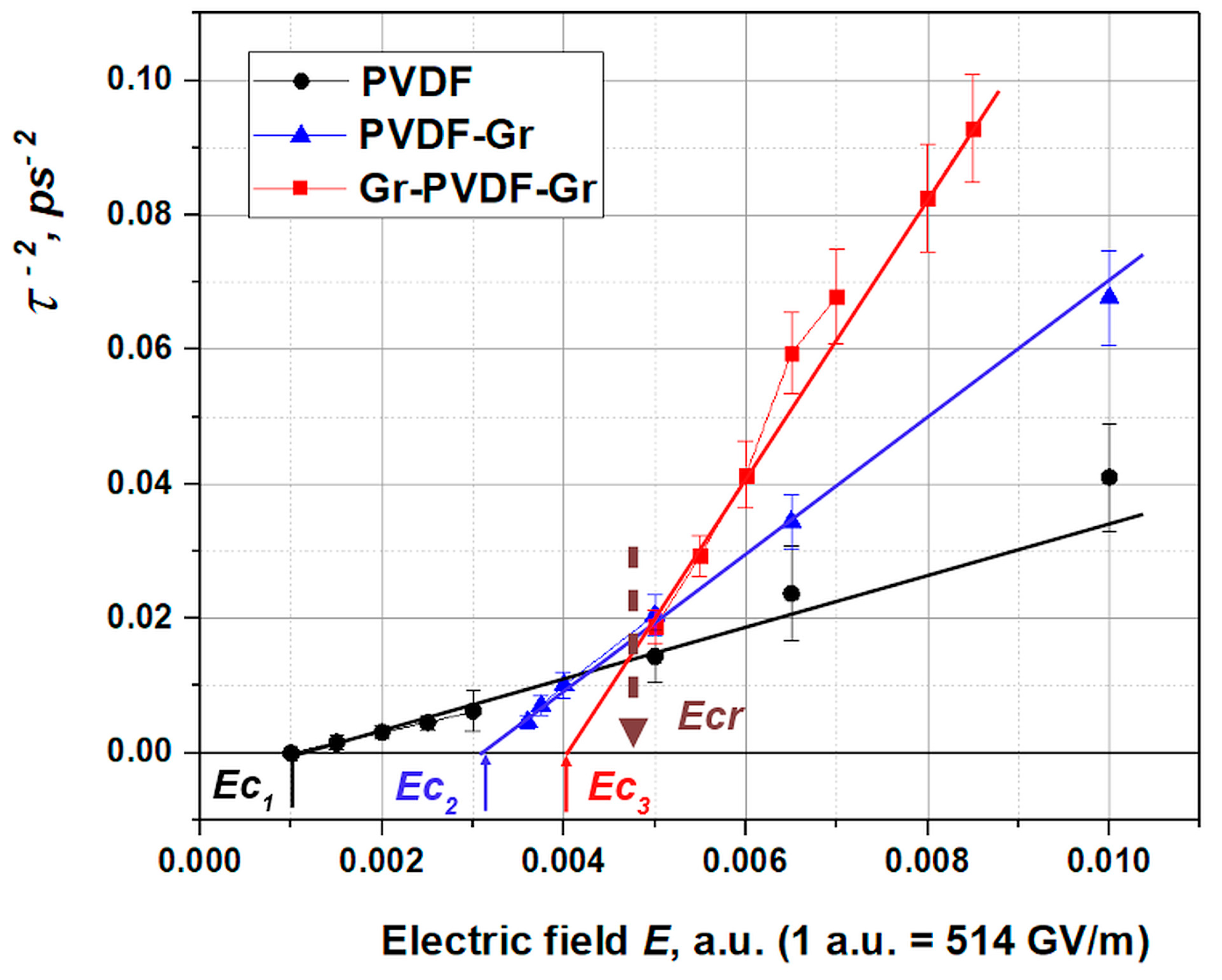
3.2. Polarization switching in a heterostructure consisting of PVDF and graphene layers

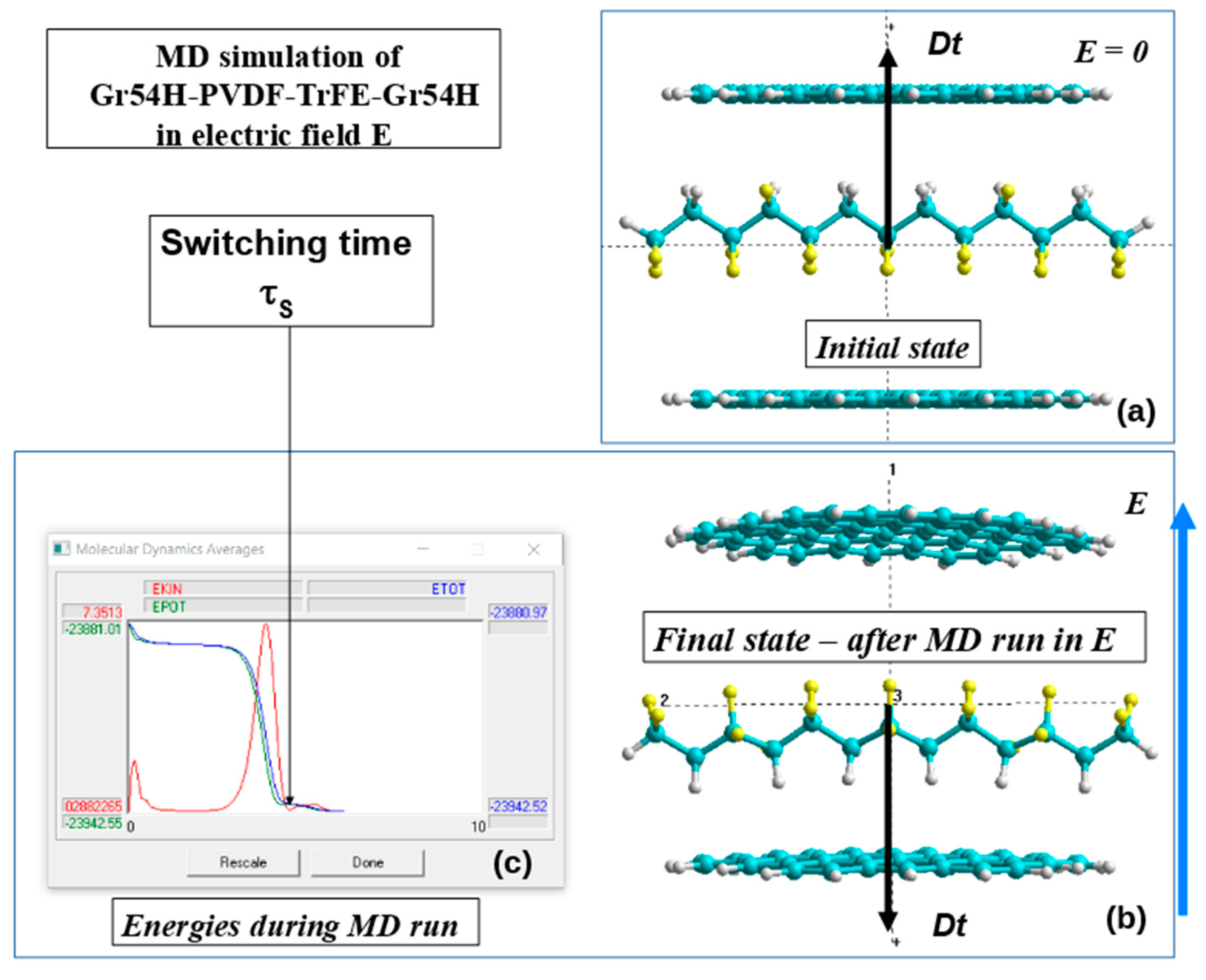
3.2.1. Main details

In this part of the work, we examined the influence of graphene layers on important properties of PVDF polymer films, such as polarization switching. The main approaches and models were developed earlier in [10,12,13,14,15,23,24,25,26,44,47,48,49,50,51,52] and are used here. To assess the influence of graphene on the polarization switching times in a heterostructure, consisting of a polymer ferroelectric PVDF and graphene, the above-considered model of PVDF as a chain of n = 6 basic elementary units (C2H2F2)n (“PVDF6”) and molecular dynamics methods are used here [10,12,13,14,15], discussed above in section 3.1.
To model graphene layers, molecular models from [24,25,26,47,48], consisting of 54 carbon atoms C surrounded at the edge by hydrogen atoms H [47,48] (Figure 11a,b - “Gr54H” model) are used.
Two types of models are considered here as models of the main composite heterostructures of a ferroelectric polymer with graphene:
1) one-sided model of a PVDF chain and a graphene layer “PVDF6+G54H_H-C”, where the PVDF chain (or layer) is oriented towards the graphene layer by hydrogen atoms H (Figure 11c);
2) a double-sided model (or sandwich model), consisting of a PVDF chain enclosed between two layers of graphene “G54H+PVDF6+G54H” (Figure 11d).
The construction of models of ferroelectric polymer and graphene heterostructures presented here is similar to the models that we used to calculate the piezoelectric coefficients of PVDF and graphene composite structures [47,48]. Further, all such calculations and runs of MDS with quantum semi-empirical PM3 method under conditions of a simulated applied constant electric field were carried out similarly to those described above in section 3.1 with the necessary set of parameters indicated there in special MDS options of the HyperChem program [38].

3.2.2. Results

Let us now consider the results of these calculations in more detail.
Similarly to the procedures of MDS runs with models of pure PVDF chains, MDS runs of composite models of PVDF with Graphene, presented in the initial states in Figure 11, were carried out. As a result, all initial models of the system (shown both in Figure 3a and Figure 11c,d) undergo various structural changes under the action of applied electric fields E of various magnitudes - here the PVDF dipole structure rotates, which occurs at different speeds depending on the magnitude of the applied electric field.
Examples of the final states of these various considered composite models of a PVDF chain with graphene layers after such a rotation or flip (switch) are shown in Figure 12a,b (final state). And here it is clearly seen their inverted (switched) state relative to the initial states shown in Figure 11c,d (initial state). In this case, the flip occurs only with PVDF, while the graphene layers remain in the same form (they are only slightly distorted and shifted). The estimations of the distances between the components of the heterostructure and their change upon switching polarization were considered in [50].
Corresponding changes of all mean MDS run energies with time were shown earlier in Figure 3c and Figure 6c for pure PVDF and now in Figure 12 for both heterostructures of PVDF with graphene layers. The final rotation time of the PVDF chain (switching time τS ) was estimated similarly to that written above for these MD energy trajectories under the criteria δ ~ EK/EKmax ≤ 0.01 – 0.001, where EK is the kinetic energy at the final point and EKmax is the kinetic energy at the chain rotation maximum. The calculated data and performed MD runs in various electric fields E allow one to obtain a linear critical behaviour of the t-2 at an electric field E ~ EC at the lower limit values of this electric field for the case, when E → EC (for E > EC), that also fully corresponds to equation (9) from LGD theory (as described above in section 2.2.2).
The results of changing the switching time τS and t-2, obtained from the calculations of MDS runs for various values of the electric field E, for both heterostructure’s type, are shown below in Figure 13. The scatter of the obtained data and estimates of the error in values when determining the final switching time (rotation of the total dipole vector Dt of the entire PVDF chain) in the electric field E, determined in the MD process by the relation δ ~ EK/EKmax, were analyzed previously in [50].
In this work, new calculations were carried out and basic average data were obtained, taking into account errors. Figure 13 here presents the final improved new data (compared to [50]) taking into account new error analysis of MD runs and switching time calculations.
The data obtained is very interesting and we consider here their further analysis.
First, the behavior of only one PVDF chain is presented here - the black line in Figure 13. This compares well with previous calculations of PVDF chain (Figure 3c,d) and considered in [10,12,13,14,15], which showed linear behavior according to Eq. (9) with a coercive field Ec1 ~ 0.001 a.u. ~ 0.5 GV/m.
Second, the behaviour of one-side heterostructure “PVDF6+G54H_H-C” model was investigated (initial state on Figure 11c, dependence of the switching time is marked by blue line in Figure 13). The result showed that the rotation (switching) time τS became shorter, that is, the rotation is faster under the influence of the graphene layer at the same electric field value E. However, at this case the coercive field is increased up to the value Ec2 ~ 0.003 a.u. ~ 1.5 GV/m.
This leads to the fact that near Ec2 the switching time τS begins to increase more significantly than in the 1st case near Ec1. That is, the deceleration of the rotation of the PVDF chain occurs here in the immediate vicinity of the coercive field Ec2, which is more noticeable than in case 1 at the same field value. Such a change in the behavior of the switching time occurs at the field values E in the surrounding area less then value of E = Ecr ~ 0.0045 a.u. ~ 2.3 GV/m. It is shown as the intersection area at the E = Ecr in Figure 13, marked with a dashed brown arrow.
Third, the behaviour of the sandwich “Gr54H+PVDF6+Gr54H” heterostructure shows even shorter switching times τS (see on Figure 3d, and red line in Figure 13) and increasing of coercive field up to Ec3 ~ 2 GV/m. In this case, too, the same characteristic change in the switching time τS occurs with a critical point in the field value of E = Ecr, but more sharply expressed.
In all these cases the graphene layer itself does not turn over, but basically retains its previous position - it is in free, uncharged and unrestricted positions, may be only a little relaxed, moved and shifted (while maintaining the general center of mass or center of inertia of the entire simulated heterostructure system). Only the PVDF chain was rotating in the applied electric field - it had a dipole moment.
Thus, the calculations performed by the quantum MD simulation method show that, under the influence of graphene layers, the switching times tS in the ferroelectric "PVDF-graphene" composite heterostructure decrease for the same field values E, but in the area above Ecr (E > Ecr), with an increase in the number of the inserted graphene layers. While up to this point Ecr (below this point) the inserted graphene layers increase these times tS for any model. At the same time the coercive field EС increase, that lead to sharpest rise of the switching time tS in the very close vicinity of the changed EC values.

3.2.3. The possible reasons for the graphene layers influence on switching times

Comparison and correlation of the obtained results with known experimental data can only be carried out based on the relative changes in these parameters (switching times) in these switching processes, since the immediate time scales of the simulated structures and experimental samples are very different. However, you can use some experimental results from [58]. Such an analysis was recently carried out in [50].
Analysis of the kinetics of the polarization switching within the framework of the LGD theory showed that such a changes in the switching time this is possible due to decrease of the damping coefficient ξ value, describing switching time, in the Landau-Khalatnikov kinetic equations (8) - (10).
Thus, it was found that the introduction of first one layer of graphene, and then two layers of graphene, leads to a decrease in the damping coefficient ξ compared to the initial case of a pure single layer of PVDF when it is rotated (switched) in an electric field E - these values of ξ decrease successively:
ξ = ξ 1 = 3.61 10 10 m s V C − 1 ,
ξ 2 = ξ 1 / 3 = 1.2 10 10 m s V C − 1 ,
ξ 3 = ξ 1 / 4.47 = 0.81 10 10 m s V C − 1 .
As a result, we conclude that the introduction of graphene layers into a PVDF film of a thin polymer ferroelectrics changes its switching time (this switching time decrease, in the area, when E > Ecr, where Ecr is intersection point of the dependences 1/(tS2) with change of E and tS(E) for different considered cases (i = 1, 2, 3) of the embedded graphene layers) and at the same time increases the value of the coercive field Eci. As shown our analysis, probably, these changes are due to a decrease in the damping coefficient (as it follows to relations obtained from the Landau-Khalatnikov equation and the LGD theory). Wherein, in the nearest neighbourhood of the coercive filed (for different values of the coercive fields Eci < Ecr, below the intersection point Ecr), the switching times increase more sharply under the influence of the embedded graphene layers. This result can be very important for practical applications and, of course, it should be verified experimentally.

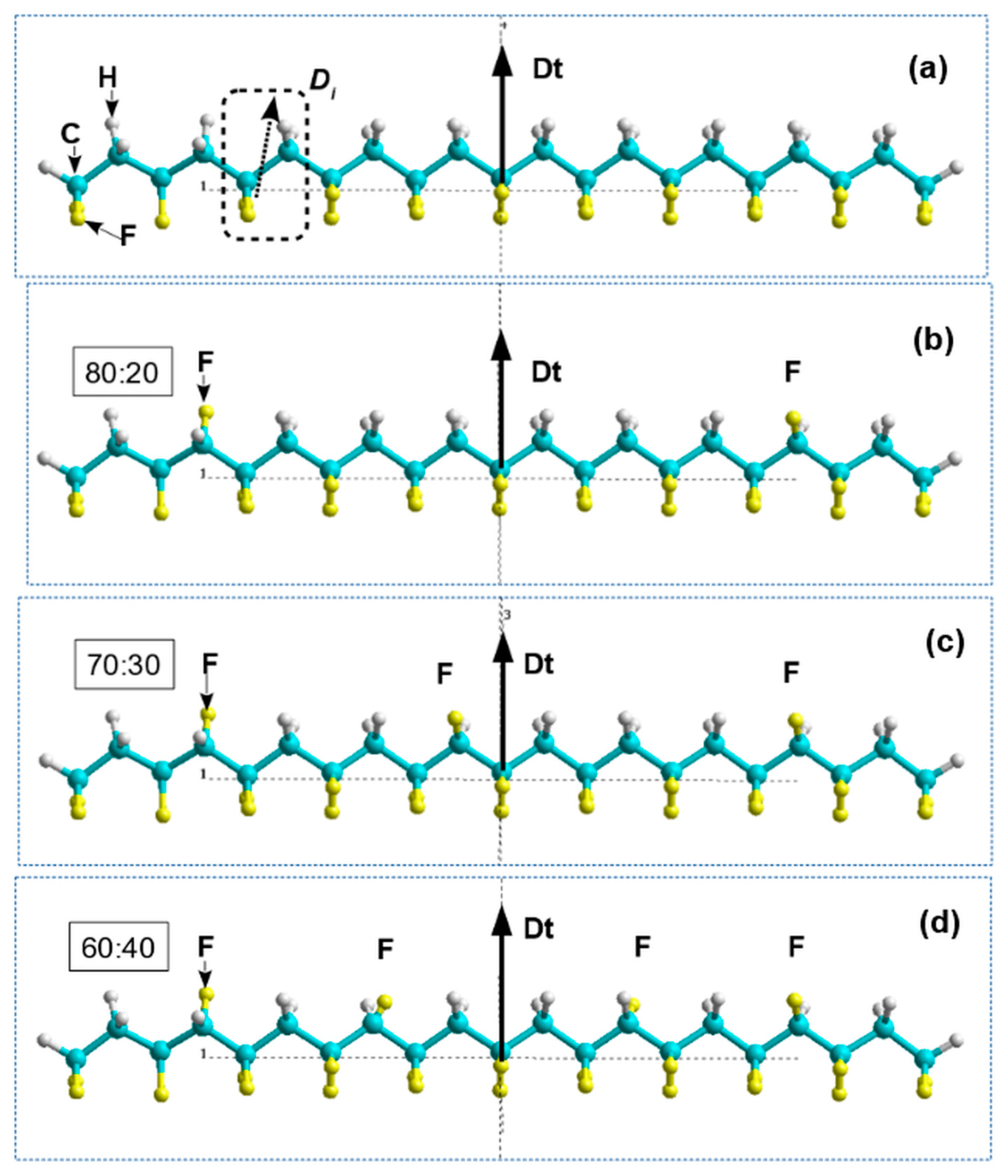
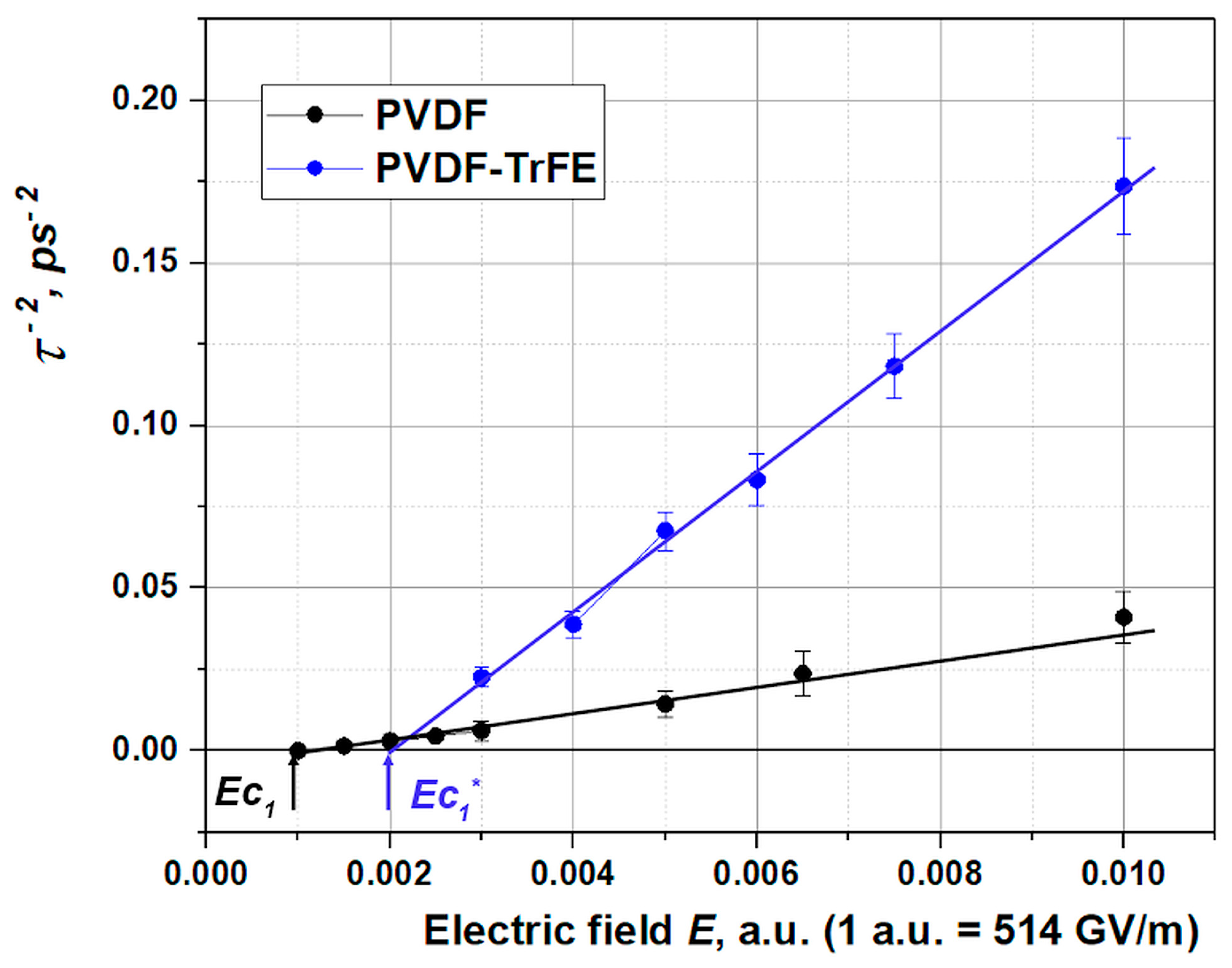
3.3. Polarization switching in PVDF-TrFE

3.3.1. Main details

To carry out similar MDS runs with polymer ferroelectrics based on PVDF-TrFE copolymers, we also chose here a simpler model of 6 main units of the polymer chain, rather than 10 (shown earlier in Figure 2). The fact is that longer chains, when turning in strong electric fields, often “get entangled” and cannot reach an equilibrium final state for a long time. This distorts the results of determining the switching time.
In addition, the correctly chosen initial symmetry of the model structure is important here, since the rotation of the chain occurs under conditions of “free suspension” in space while maintaining the general center of mass or the value of inertia of the entire system. If the initial configuration is poorly chosen, the mutually consistent motion of all atoms of the system can lead to noticeable distortions in the final configuration of the structure.
In this case, we chose a symmetrical initial arrangement at the positions of fluorine atoms, which replace hydrogen atoms in the copolymer structure (Figure 14a). This made it possible to carry out fairly adequate MDS runs at various applied electric field values and obtain symmetrical rotation of the copolymer chain to the final state ( ).
It should be noted that this model is quite close to experimental structures with ratios of hydrogen and fluorine atoms at the level of (70:30) and (60:40), which is close to the modeled structures shown in Figure 2d.

3.3.2. Results

MDS runs at the different applied values of the external electric field E, performed similarly and according to the method described above (section 3.1), made it possible to obtain the polarization switching times tS depending on the field E.
On this basis, similar graphs of the dependence of the square of the reverse switching time tS-2were constructed on the magnitude of the electric field E, which also turned out to be linear (especially near the values of the corresponding coercive field Ec) in full accordance with equation (9). Figure 15 presents these results, from which the linear law of behavior tS-2on E is clearly visible, and the position and value of the coercive field Ec1* = ~ 0.002 a.u. ~ 1.028 GV/m for PVDF-TrFE is easily determined.
The results obtained clearly show that the switching times tS in PVDF-TrFE become shorter compared to pure PVDF, while the coercive field Ec1* becomes larger in comparison with Ec1 for PVDF and its values correspond to both experimental data [11] and previously calculated values [43,44] by various methods.

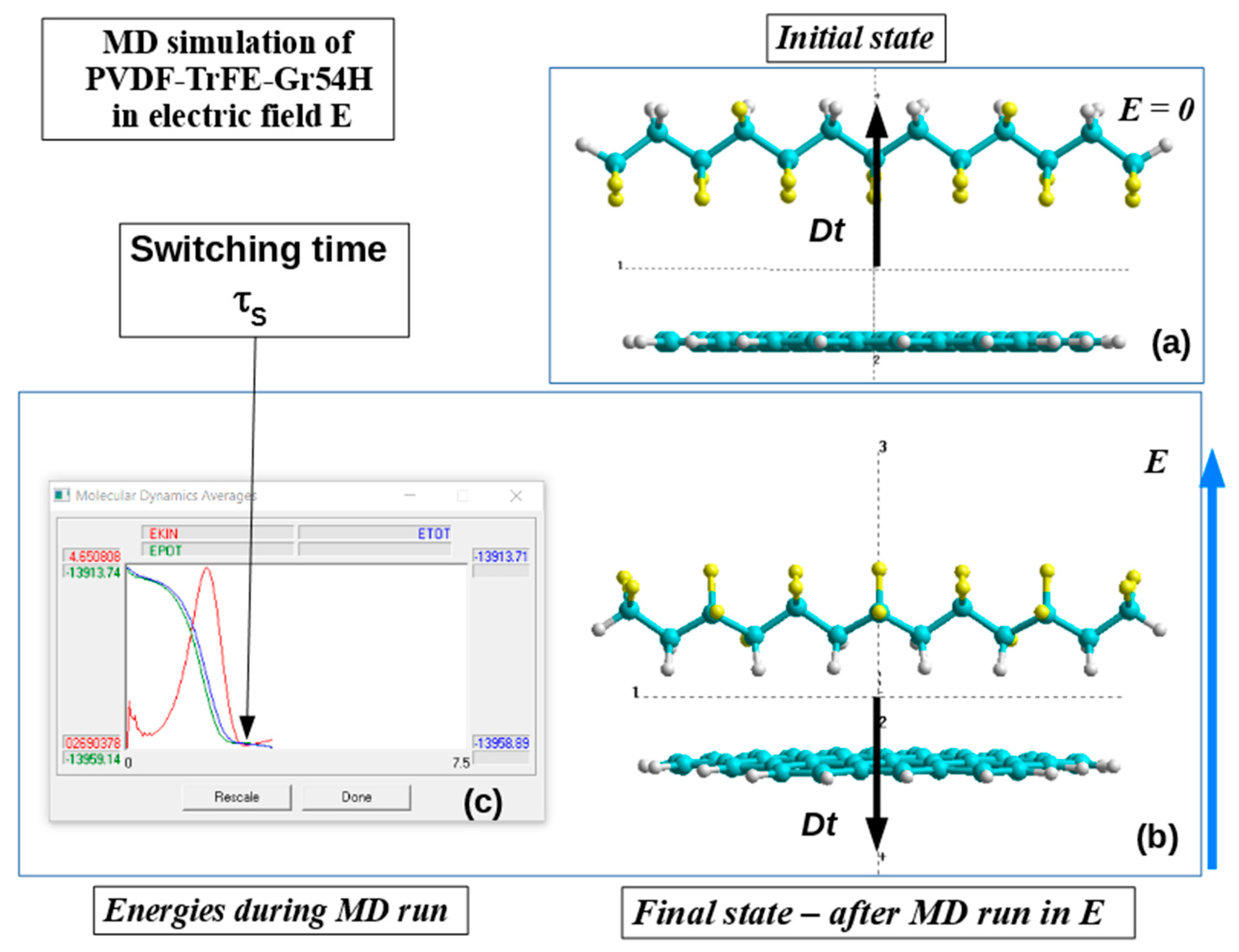
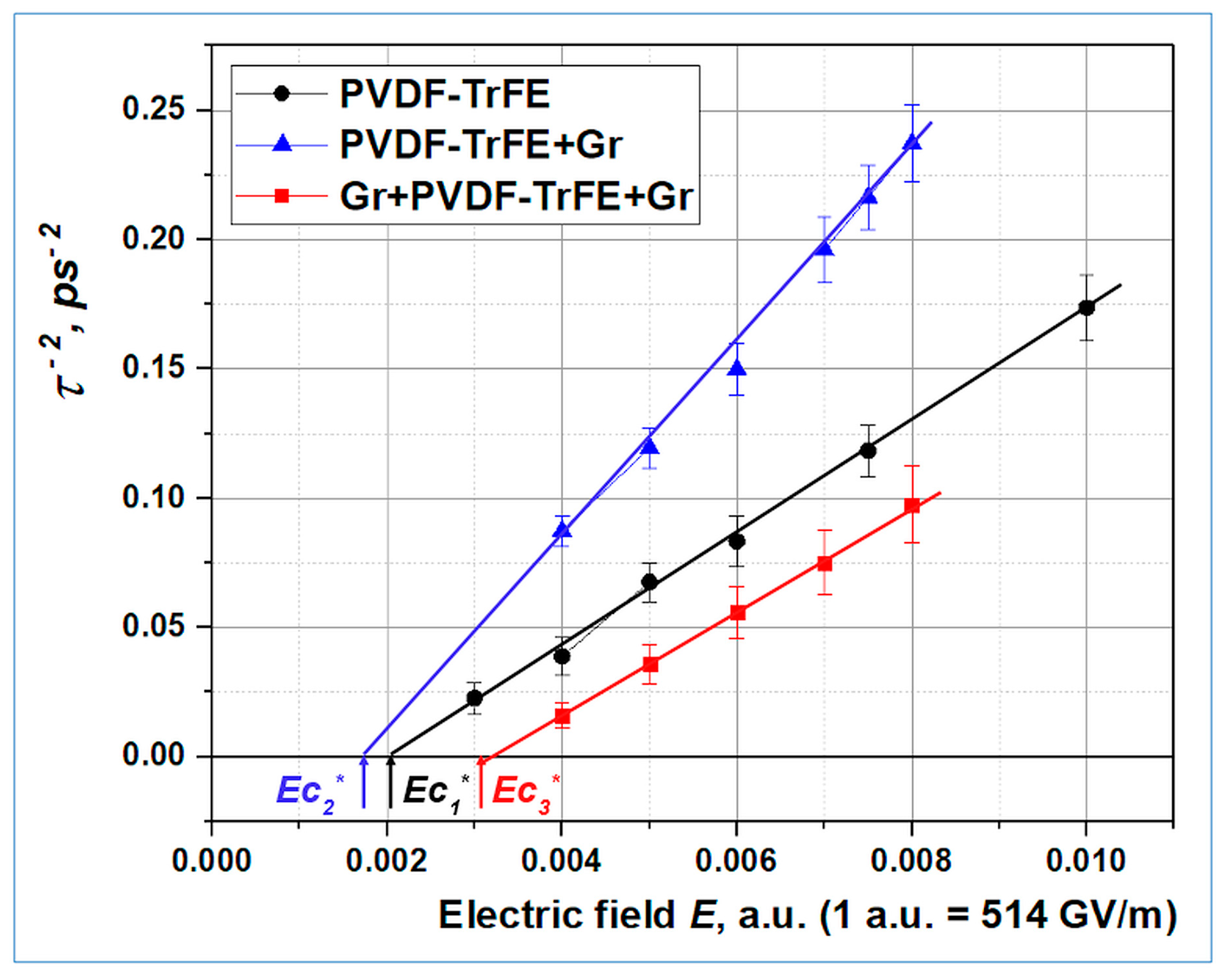
3.4. Polarization switching in a heterostructure consisting of PVDF-TrFE and graphene layers

3.4.1. Main details

MDS runs for cases of PVDF-TrFE heterostructures with both types of graphene (one-sided model and two-sided sandwich model) are considered here in the same way as described above as in cases with PVDF.
The initial states of both heterostructure models are shown in Figure 16 and Figure 17.

3.4.2. Results

The main results obtained or these models are shown on Figure 18 and Figure 19.
Analysis of the obtained results of calculations of the polarization switching time on the applied electric field for models of heterostructures based on polymer ferroelectrics and graphene layers, presented in Figure 18 and Figure 19, allows us to draw the following conclusions: 1) in all cases, for all considered models of both the initial polymer ferroelectrics PVDF and PVDF-TrFE copolymer, and for their heterostructures with graphene layers, good agreement is demonstrated with the linear behavior of the square of the reciprocal switching time t-2 from the magnitude of the applied electric field E at field values greater than the coercive field E > Ec and in the immediate vicinity of Ec, which is quite consistent with expression (9) obtained from the Landau-Khalatniklva equation (8) and corresponds to the LGD theory for such thin homogeneous layers of ferroelectrics; 2) the influence of graphene layers, in the case of a one-sided model, leads to an increase in t-2 values depending on E and, accordingly, to a decrease in the switching times tS, both in the cases of pure PVDF and its PVDF-TrFE copolymer; in this case, the values of the coercive field are shifted: in the case of changes in PVDF to PVDF-Gr, the value of Ec1 ~ 0.001 a.u. ~ 0.5 GV/m increases to Ec1* ~ 0.002 a.u. ~ 1 GV/m, whereas in the case of changing PVDF-TrFE to PVDF-TrFE-Gr, the coercive field decreases from Ec2 ~ 0.003 a.u. ~ 1.54 GV/m to Ec2* ~ 0.0018 a.u. ~ 0.92 GV/m; 3) the influence of graphene layers in the case of a two-sided (sandwich) model is more complex: if initially, when pure PVDF was included between 2 layers of graphene, there was a further increase in t-2 depending on E (and, accordingly, a decrease in switching time tS) with increasing coercive field to values of Eс3 ~ 0.004 a.u. ~ 2.06 GV/m, then in the case of the PVPD-TrFE copolymer these changes occur differently: after increasing the t-2 values depending on E for the one-sided PVDF-TrFE-Gr model, for the sandwich model Gr-PVDF-TrFE-Gr there is a noticeable decrease in this dependence so that the t-2 values on E become even smaller than in the case one PVDF-TrFE (that is, the switching times tS themselves increase) and the coercive field increases to values of Ec3* = 0.0032 = 1.65 GV/m.
The obtained values of switching times and coercive fields for the copolymer correspond well to the known experimental values, but for models with graphene they were obtained here for the first time and these calculated and predicted values can serve as a good guide for new experimental studies in this area when creating such promising heterostructures based on thin polymers layers of ferroelectrics and graphene.

4. Conclusions

Modeling and computer study of a composite nanostructure containing a ferroelectric PVDF polymer and graphene layers were carried out in this work by molecular modeling and molecular dynamics (MD) simulation with semi-empirical quantum PM3 method in the Hartree-Fock approximation (RHF) using the HyperChem software. The calculations and MD simulations presented in this article unambiguously show that the coercive field increases and the polarization switching time mainly decreases under the influence of graphene layers in thin layers of polymer ferroelectrics. But, in the very closest vicinity of the coercive fields Eci < Ecr, below the intersection point Ecr of the dependences tS(E), the behaviour of the switching times is reversed and they increase here more sharply under the influence of the embedded graphene layers.
The obtained results of modeling PVDF-TrFE copolymers and MDS runs on these models showed that they have switching times shorter than pure PVDF. This is important for practical applications. In addition, it has been shown that the introduction of a single graphene layer further reduces the switching time in such a heterostructure.
At the same time, in the case of a double-sided (sandwich) model with 2 layers of graphene around a PVDF-TrFE layer, switching times increase. This is also an undoubtedly important result that must be taken into account when creating practical heterostructures based on graphene and polymer ferroelectrics.
As a result of the MDS calculations performed, it is unambiguously shown that for all considered thin ferroelectric heterostructures based on polymer ferroelectrics and graphene, the LGD theory is completely valid, which well describes the linear law of the behavior of the square of the inverse polarization switching time in the immediate vicinity of the coercive field, that is, homogeneous switching in thin ferroelectric structures. Analysis of the kinetics of the polarization switching within the framework of the LGD theory showed that this is possible due to decrease of the damping coefficient value, describing switching time, in the Landau-Khalatnikov kinetic equations.
These results of modeling and calculations, of course, require experimental verification. This can be done directly by production of samples of the type of PVDF layers deposited by the LB method on graphene layers or similar hetero-structures (of different thicknesses and / or different numbers of layers - similar, for example, to the work [13]). Following measurements of the switching times and hysteresis loops (similar to the works of the [12,13,14,15,16]) of these samples could be done for the proceeded experimental verification of obtained in this work results. The results of performed investigation are undoubtedly important and relevant, since they demonstrate the direction of the necessary structural modifications of newly produced nanomaterials with predetermined and desired properties. Based on the calculated results, new heterostructures and nanomaterials with adjustable polarization switching times and coercive fields can be constructed and fabricated using polymer ferroelectrics and graphene/graphene oxide layers and similar two-dimensional hybrid heterostructures. This opens up new possibilities for creating such new generation of the devices and sensors (for example, memory devices or switching sensors).

Author Contributions

E.P. and V.B. wrote the manuscript. V.F. supervised and supported this study and critically revised the manuscript. X.M., H.S., T.L. and J.W. - experiments and data analysis contribution. All authors have read and agreed to the published version of the manuscript.

Funding

No funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Acknowledgments

Prof. Xiang-Jian Meng expresses his gratitude to the National Natural Science Foundation of China (NNSFC) for grant # 61574151 and Prof. Hong Shen for grant # 62011530043. The authors are grateful for the opportunity to perform calculations using the computing and information resources of the IMPB RAS.

Conflicts of Interest

We declare no potential conflict of interest in this article.

References

  1. Mohammadpourfazeli, S.; Arash, S.; Ansari, A.; Yang, S.; Mallick, K.; Bagherzaden, R. Future prospects and recent developments of polyvinylidene fluoride (PVDF) piezoelectric polymer; fabrication methods, structure, and electro-mechanical properties. RSC Advances 2023, 13, 370–387. [Google Scholar] [CrossRef]
  2. Mai, M.; Ke, S.; Lin, P.; Zeng, X. Ferroelectric Polymer Thin Films for Organic Electronics. J. of Nanomaterials 2015, 2015, 812538. [Google Scholar] [CrossRef]
  3. Yan, M.; Liu, S.; Liu, Y.; Xiao, Z.; Yuan, X.; Zhai, D.; Zhou, K.; Wang, Q.; Zhang, D.; Bowen, C.; Zhang, Y. Flexible PVDF-TrFE Nanocomposites with Ag-decorated BCZT Heterostructures for Piezoelectric Nanogenerator Applications. ACS Appl Mater Interfaces. 2022, 14, 53261–53273. [Google Scholar] [CrossRef]
  4. Huang, T.; Yang, S.; He, P.; Sun, J.; Zhang, S.; Li, D.; Meng, Y.; Zhou, J.; Tang, H.; Liang, J.; Ding, G.; Xie, X. Phase-Separation-Induced PVDF/Graphene Coating on Fabrics toward Flexible Piezoelectric Sensors. ACS Applied Materials & Interfaces. 2018, 10. [Google Scholar] [CrossRef]
  5. Shi, L.; Hu, Z.; Hong, Y. PVDF-supported graphene foam as a robust current collector for lithium metal anodes. RSC Adv. 2020, 10, 20915–20920. [Google Scholar] [CrossRef]
  6. Park, B.E. Non-volatile Ferroelectric Memory Transistors Using PVDF and P(VDF-TrFE) Thin Films. In Ferroelectric-Gate Field Effect Transistor Memories. Topics in Applied Physics; Park, BE., Ishiwara, H., Okuyama, M., Sakai, S., Yoon, SM., Eds.; Springer: Dordrecht, Netherlands, 2016; Volume 131. [Google Scholar] [CrossRef]
  7. Kamberaj, H. Molecular Dynamics Simulations in Statistical Physics: Theory and Applications; Springer Nature Switzerland AG: Cham, Switzerland, 2020. [Google Scholar]
  8. Hollingsworth, S.A.; Dror, R.O. Molecular dynamics Simulation for All. Neuron 2018, 99, 1129–1143. [Google Scholar] [CrossRef]
  9. Grigoriev, F.V.; Sulimov, V.B.; Tikhonravov, A.V. Molecular Dynamics Simulation of Laser Induced Heating of Silicon Dioxide Thin Films. Nanomaterials 2021, 11, 2986. [Google Scholar] [CrossRef] [PubMed]
  10. Bystrov, V.S. Molecular modeling and molecular dynamic simulation of the polarization switching phenomena in the ferroelectric polymers PVDF at the nanoscale. Physica B: Condensed Matter 2014, 432, 21–25. [Google Scholar] [CrossRef]
  11. Fridkin, V.M.; Ducharme, S. Ferroelectricity at the Nanoscale. Basic and Applications, 1st ed.; Springer: New York, NY, USA, 2014. [Google Scholar]
  12. Bystrov, V.S.; Fridkin, V.M. Two-dimensional ferroelectrics and homogeneous switching. To the 75th anniversary of the Landau—Ginzburg theory of ferroelectricity. Phys. Usp. 2020, 63, 417–439. [Google Scholar] [CrossRef]
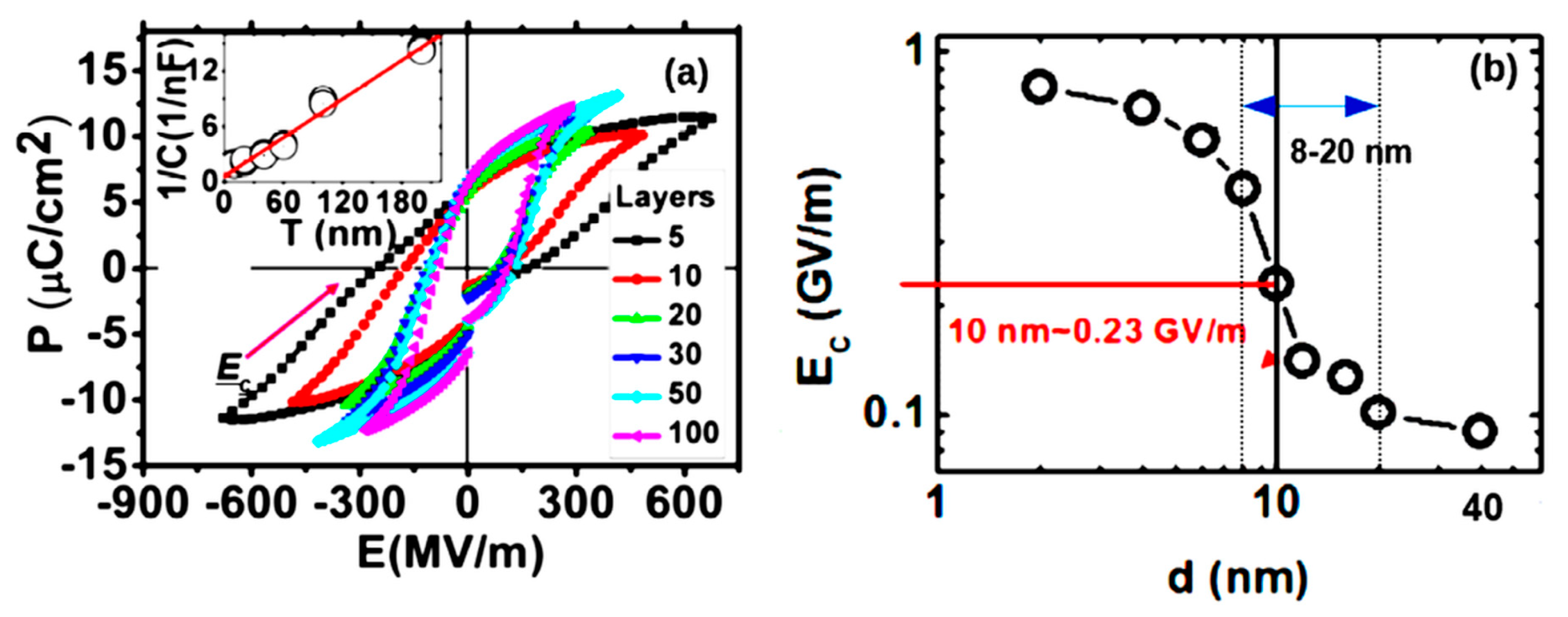
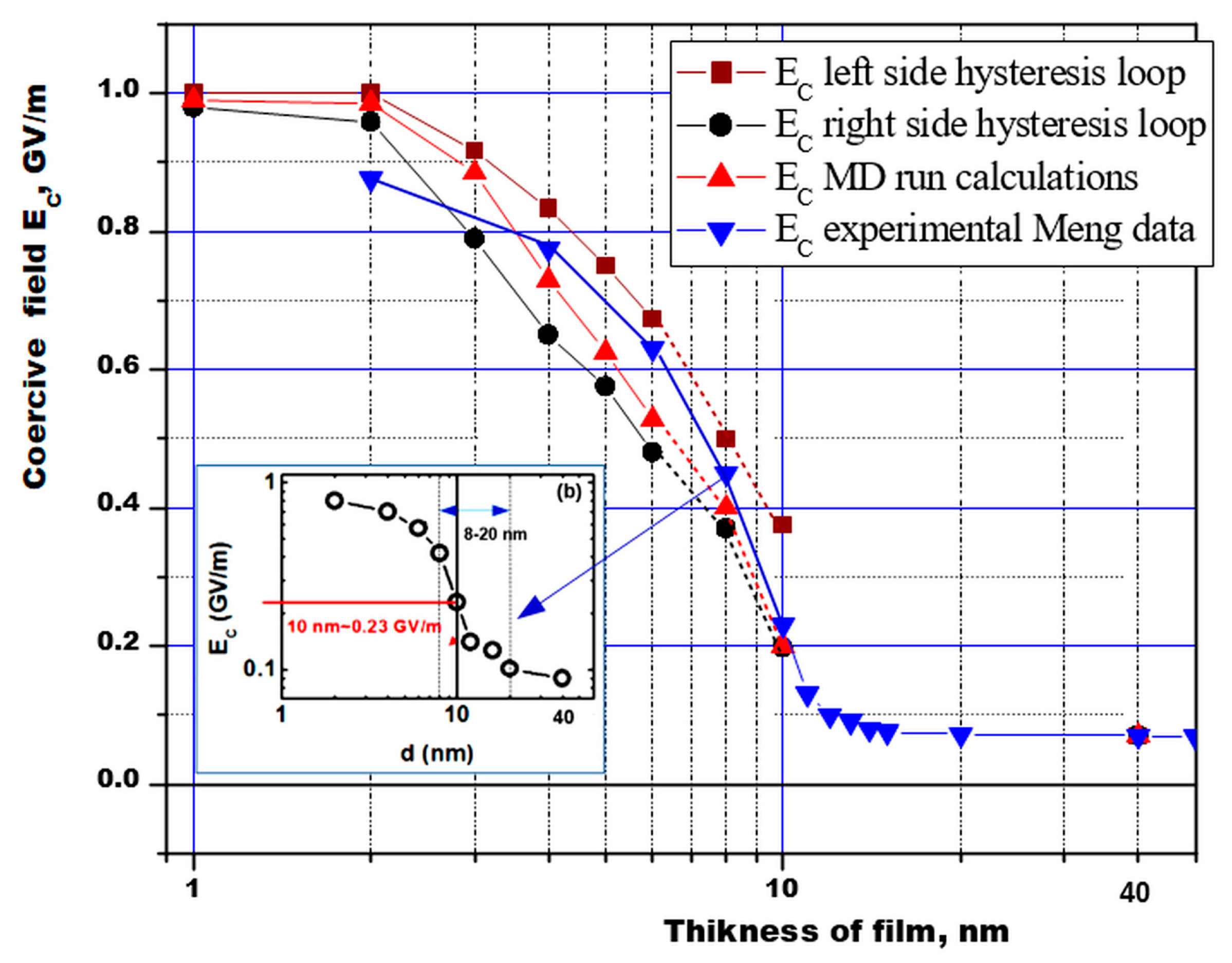
  13. Paramonova, E.V.; Bystrov, V.S.; Meng, X.; Shen, H.; Wang, J.; Fridkin, V.M. Polarization Switching in 2D Nanoscale Ferroelectrics: Computer Simulation and Experimental Data Analysis. Nanomaterials 2020, 10, 1841. [Google Scholar] [CrossRef]
  14. Paramonova, E.V.; Bystrov, V.S.; Meng, X.; Shen, H.; Wang, J.; Fridkin, V.M. Polarization switching in nanoscale ferroelectrics. Ferroelectrics 2021, 575, 103–116. [Google Scholar] [CrossRef]
  15. Bystrov, V.S.; Fridkin, V.M. Domain and homogeneous switching in ferroelectrics. On the 75th anniversary of the Landau–Ginzburg theory of ferroelectricity. Ferroelectrics 2020, 569, 164–181. [Google Scholar] [CrossRef]
  16. Lines, M.E.; Glass, A.M. Principles and applications of ferroelectrics and related materials; Clarendon Press: Oxford, USA, 1977. [Google Scholar]
  17. Bune, A.V.; Fridkin, V.M.; Ducharme, S.; Blinov, L.M.; Palto, S.P.; Sorokin, A.V.; Yudin, S.G.; Zlatkin, A. Two-dimensional ferroelectric films. Nature 1998, 391, 874–877. [Google Scholar] [CrossRef]
  18. Palto, S.; Blinov, L.; Bune, A.; Dubovik, E.; Fridkin, V.; Petukhova, N.; Verkhovskaya, K.; Yudin, S. Ferroelectric Langmuir-Blodgett films. Ferroelectr. Lett. 1995, 19, 65–68. [Google Scholar] [CrossRef]
  19. Bune, A.; Ducharme, S.; Fridkin, V.; Blinov, L.; Palto, S.; Petukhova, N.; Yudin, S. Novel switching phenomena in ferroelectric Langmuir–Blodgett films. Appl. Phys. Lett. 1995, 67, 3975. [Google Scholar] [CrossRef]
  20. Palto, S.; Blinov, L.; Bune, A.; Dubovik, E.; Fridkin, V.; Petukhova, N.; Verkhovskaya, K.; Yudin, S. Ferroelectric Langmuir-Blodgett films. Ferroelectrics 1996, 184, 127–129. [Google Scholar] [CrossRef]
  21. Blinov, L.M.; Fridkin, V.M.; Palto, S.P.; Bune, A.V.; Dowben, P.A.; Ducharme, S. Two-dimensional ferroelectrics. Phys. Usp. 2000, 43, 243–257. [Google Scholar] [CrossRef]
  22. Fridkin, V.M.; Ducharme, S. Ferroelectricity at the nanoscale. Phys. Usp. 2014, 57, 597–603. [Google Scholar] [CrossRef]
  23. Bystrov, V.; Bdikin, I.; Silibin, M.; Meng, X.; Tian, B.; Wang, J.; Karpysky, D.; Bystrova, A.; Paramonova, E. Ferroelectric PVDF Films and Graphene-based Composites. Journal of Physics: Conference Series 2018, 1053, 012043. [Google Scholar] [CrossRef]
  24. Bystrov, V.S.; Bdikin, I.K.; Silibin, M.V.; Karpinsky, D.V.; Kopyl, S.; Goncalves, G.; Sapronova, A.V.; Kuznetsova, T.; Bystrova, V.V. Graphene/graphene oxide and polyvinylidene fluoride polymer ferroelectric composites for multifunctional applications. Ferroelectrics 2017, 509, 124–142. [Google Scholar] [CrossRef]
  25. Silibin, M.V.; Bystrov, V.S.; Karpinsky, D.V.; et al. Local mechanical and electromechanical properties of the P(VDF-TrFE)-graphene oxide thin films. Applied Surface Science 2017, 421 Part A, 42–51. [Google Scholar] [CrossRef]
  26. Silibin, M.; Karpinsky, D.; Bystrov, V.; et al. Preparation, Stability and Local Piezoelectrical Properties of P(VDF-TrFE)/Graphene Oxide Composite Fibers. C - Journal of Carbon Research 2019, 5, 48. [Google Scholar] [CrossRef]
  27. Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; et al. Electric Field Effect in Atomically Thin Carbon Films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed]
  28. Geim, A.K. Graphene: status and prospects. Science 2009, 324, 1530–1534. [Google Scholar] [CrossRef] [PubMed]
  29. Winsberg, E. Computer Simulations in Science. The Stanford Encyclopedia of Philosophy (Spring 2019 Edition). Edward, N.Z., Ed.; Available online: https://plato.stanford.edu/archives/spr2019/entries/simulations-science/.
  30. Ramachandran, K.I.; Deepa, G.; Namboori, K. Computational chemistry and molecular modeling: Principles and applications; Springer-Verlag: Berlin/Heidelberg, Germany, 2008. [Google Scholar] [CrossRef]
  31. Szabo, A.; Ostlund, N. Modern Quantum Chemistry; Macmillan: New York, NY, USA, 1985. [Google Scholar]
  32. Clark, T.A. Handbook of Computational Chemistry; John Wiley and Sons: New York, NY, USA, 1985. [Google Scholar]
  33. Pople, J.A.; Beveridge, D.L. Approximate Molecular Orbital Theory; McGraw-Hill, 1970. [Google Scholar]
  34. Stewart, J.J.P. Optimization of Parameters for Semiempirical Methods. I. Method. J. Comput. Chem. 1989, 10, 209–220. [Google Scholar] [CrossRef] [PubMed]
  35. Stewart, J.J.P. Optimization of parameters for semiempirical methods II. Applications. J. Comput. Chem. 1989, 10, 221–264. [Google Scholar] [CrossRef]
  36. Stewart, J.J.P. Optimization of parameters for semiempirical methods V: modification of NDDO approximations and application to 70 elements. J. Mol. Mod. 2007, 13, 1173–1213. [Google Scholar] [CrossRef] [PubMed]
  37. Rezac, J.; Hobza, P. Advanced Corrections of Hydrogen Bonding and Dispersion for Semiempirical Quantum Mechanical Methods. J. Chem. Theory Comput. 2012, 8, 141–151. [Google Scholar] [CrossRef] [PubMed]
  38. HyperChem, Versions 8.0/01, Tools for Molecular Modeling. Professional Edition For Windows AC Release 8.0 USB (on CD); Hypercube. Inc.: Gainesville, FL, USA, 2011; p. 32601.
  39. Bystrov, V.; Bystrova, N.; Paramonova, E.; Sapronova, A. Computational nanostructures and physical properties of the ultra-thin ferroelectric Langmuir-Blodgett films. Ferroelectric Letters 2006, 33, 153–162. [Google Scholar] [CrossRef]
  40. Bystrov, V.S.; Bystrova, N.K.; Paramonova, E.V.; Vizdrik, G.; Sapronova, A.V.; Kuehn, M.; Kliem, H.; Kholkin, A.L. First principle calculations of molecular polarization switching in P(VDF–TrFE) ferroelectric thin Langmuir–Blodgett films. J. Phys: Condens. Matter. 2007, 19, 456210. [Google Scholar] [CrossRef]
  41. Bystrov, V.S.; Bdikin, I.K.; Kiselev, D.A.; Yudin, S.G.; Fridkin, V.M.; Kholkin, A.L. Nanoscale polarization patterning of ferroelectric Langmuir-Blodgett P(VDF-TrFE) films. J. Phys. D: Appl. Phys. 2007, 40, 4571–4577. [Google Scholar] [CrossRef]
  42. Bystrov, V.S.; Dekhtyar, Yu.; Paramonova, E.; Pullar, R.; Katashev, A.; et al. Polarization of PVDF and P(VDF- TrFE) thin films revealed by emission spectroscopy with computational simulation during phase transition. J. Appl. Phys. 2012, 111, 104113. [Google Scholar] [CrossRef]
  43. Gevorkyan, V.E.; Paramonova, E.V.; Avakyan, L.A.; Bystrov, V.S. Computer modeling and molecular dynamics of polarization switching in the ferroelectric films PVDF and P(VDF-TrFE) on nanoscale. Mathematical Biology and Bioinformatics 2015, 10, 131–153. [Google Scholar] [CrossRef]
  44. Paramonova, E.V.; Filippov, S.V.; Gevorkyan, V.E.; Avakyan, L.A.; Meng, X.J.; Tian, B.B.; Wang, J.L.; Bystrov, V.S. Polarization switching in ultrathin polyvinylidene fluoride homopolymer ferroelectric films. Ferroelectrics 2017, 509, 143–157. [Google Scholar] [CrossRef]
  45. Haghighi, S.; Ansari, R.; Ajori, S. A molecular dynamics study on the interfacial properties of carbone-functionalized graphene/polymer nanocomposites. Int. J. Mech. Mater. Des. 2020, 16, 387–400. [Google Scholar] [CrossRef]
  46. Safina, L.R.; Baimova, J.A.; Krylova, K.A.; Murzaev, R.T.; Mulyukov, R.R. Simulation of metal-graphene composites by molecular dynamics: a review. Lett. Mater. 2020, 10, 351–360. [Google Scholar] [CrossRef]
  47. Bystrov, V.S.; Paramonova, E.V.; Bdikin, I.K.; et al. Molecular modelling of the piezoelectric effect in the ferroelectric polymer poly(vinylidene fluoride) (PVDF). J. Mol. Mod. 2013, 19, 3591–3602. [Google Scholar] [CrossRef] [PubMed]
  48. Bystrov, V.S.; Bdikin, I.K.; Silibin, M.; et al. Molecular modeling of the piezoelectric properties of ferroelectric composites containing polyvinylidene fluoride (PVDF) and either graphene or graphene oxide. J. Mol. Mod. 2017, 23, 128. [Google Scholar] [CrossRef]
  49. Bystrov, V.S.; Bdikin, I.K.; Silibin, M.V.; Meng, X.J.; Lin, T.; Wang, J.L.; et al. Pyroelectric properties of the ferroelectric composites based on the polyvinylidene fluoride (PVDF) with graphene and graphene oxide. Ferroelectrics 2019, 541, 17–24. [Google Scholar] [CrossRef]
  50. Bystrov, V.S.; Paramonova, E.V.; Meng, X.; Shen, H.; Wang, J.; Fridkin, V.M. Polarization switching in nanoscale ferroelectric composites containing PVDF polymer film and graphene layers. Ferroelectrics 2022, 590, 27–40. [Google Scholar] [CrossRef]
  51. Kliem, H.; Tadros-Morgane, R. Extrinsic versus intrinsic ferroelectric switching: Experimental investigations using ultra-thin PVDF Langmuir–Blodgett films. J. Phys. D: Appl. Phys. 2005, 38, 1860–1868. [Google Scholar] [CrossRef]
  52. Tagantsev, A.K.; Cross, L.E.; Fousek, J. Domains in Ferroelectric Crystals and Thin Films; Springer: New York, NY, USA, 2010. [Google Scholar]
  53. Ducharme, S.; Fridkin, V.M.; Bune, A.V.; Palto, S.P.; Blinov, L.M.; Petukhova, N.N.; Yudin, S.G. Intrinsic Ferroelectric Coercive Field. Phys. Rev. Lett. 2000, 84, 175. [Google Scholar] [CrossRef] [PubMed]
  54. Ginzburg, V.L. On the dielectric properties of ferroelectric (seignetteelectric) crystals and barium titanate. Zh. Eksp. Teor. Fiz. 1945, 15, 739–750. [Google Scholar]
  55. Ginzburg, V.L. On polarization and piezoelectric effect of barium titanate near the point of ferroelectric transition. Zh. Eksp. Teor. Fiz. 1949, 19, 36–41. [Google Scholar]
  56. Landau, L.D. On the theory of phase transitions. [Phys. Z. Sowjet. 1937, 11, 545.]. Nature 1936, 138, 840–841. [Google Scholar]
  57. Landau, L.D.; Khalatnikov, I.M. On the anomalous absorption of sound near a second-order phase transition point. Dokl. Akad. Nauk SSSR 1954, 96, 469. [Google Scholar]
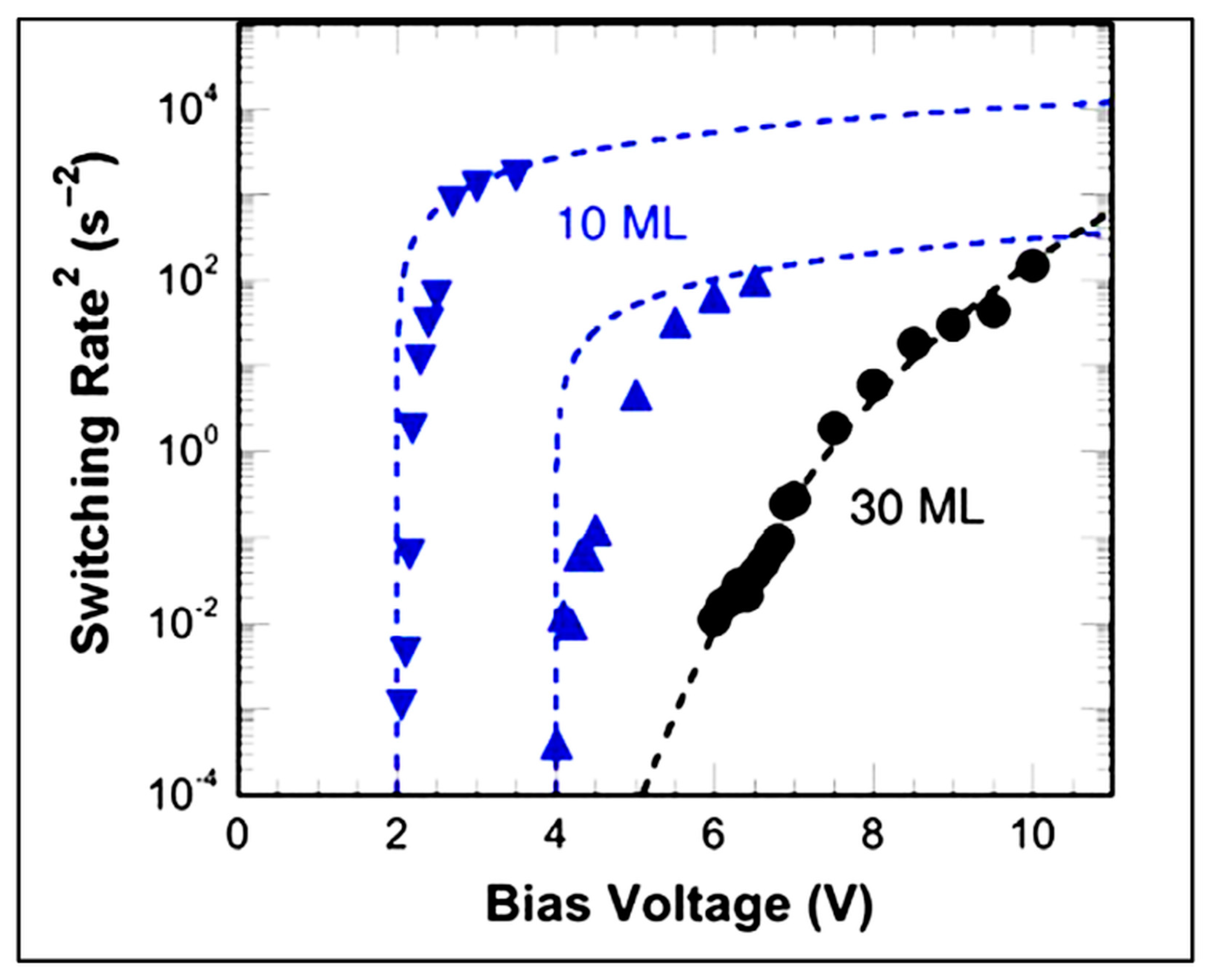
  58. Vizdrik, G.; Ducharme, S.; Fridkin, V.M.; Yudin, S.G. Kinetic of ferroelectric switching in ultrathin films. Phys. Rev. B 2003, 68, 094113. [Google Scholar] [CrossRef]
  59. Ievlev, A.; Verkhovskaya, K.; Fridkin, V. Landau-Khalatnikov switching kinetics in the ferroelectric copolymers nanostructures. Ferroelectr. Lett. 2006, 33, 147–152. [Google Scholar] [CrossRef]
  60. Gaynutdinov, R.V.; Mitko, S.; Yudin, S.G.; Fridkin, V.M.; Ducharme, S. Polarization switching at the nanoscale in ferroelectric copolymer thin films. Appl. Phys. Lett. 2011, 99, 142904. [Google Scholar] [CrossRef]
  61. Gaynutdinov, R.; Yudin, S.; Ducharme, S.; Fridkin, V. Homogeneous switching in ultrathin ferroelectric films. J Phys: Condens Matter. 2012, 24, 015902. [Google Scholar] [CrossRef]
  62. Wang, J.L.; Liu, B.L.; Zhao, X.L.; Tian, B.B.; Zou, Y.H.; Sun, S.; Shen, H.; Sun, J.L.; Meng, X.J. and Chu, J.H. Transition of the polarization switching from extrinsic to intrinsic in the ultrathin polyvinylidene fluoride homopolymer films. Appl. Phys. Lett. 2014, 104, 182907. [Google Scholar] [CrossRef]
  63. Yin, Z.; Tian, B.; Zhu, Q.; Duan, C. Characterization and Application of PVDF and Its Copolymer Films Prepared by Spin-Coating and Langmuir–Blodgett Method. Polymers 2019, 11, 2033. [Google Scholar] [CrossRef]
  64. Cardoso, V.F.; Costa, C.M.; Minas, G.; Lanceros-Mendez, S. Improving the optical and electroactive response of poly(vinylidene fluoride-trifluoroethylene) spin-coated films for sensor and actuator applications. Smart Mater. Struct. 2012, 21, 085020. [Google Scholar] [CrossRef]
  65. Dawson, N.M.; Atencio, P.M.; Malloy, K.J. Facile deposition of high quality ferroelectric poly(vinylidene fluoride) thin films by thermally modulated spin coating. J. Polym. Sci. Part B Polym. Phys. 2017, 55, 221–227. [Google Scholar] [CrossRef]
  66. Gaynutdinov, R.; Minnekaev, M.; Mitko, S.; Tolstikhina, A.; Zenkevich, A.; Ducharme, S.; Fridkin, V. Polarization switching kinetics in ultrathin ferroelectric barium titanate film. Physica B: Condensed Matter 2013, 424, 8–12. [Google Scholar] [CrossRef]
Preprints 98410 g004
Figure 4. Dependence of the switching time t (overturn of the total dipole moment Dt) of the PVDF chain of 6 monomer units (“PVDF-6”) on the magnitude of the electric field E (see on Figure 3): a) t-2(E) dependence over the entire range; b) t-2(E) dependence in the region at the low field values E (E → EC and E > EC), corresponding to the linear dependence according to Eq. (9) (red line), for homogeneous switching according to the LGD theory and Landau-Khalatnikov Eq. (8). .
Figure 4. Dependence of the switching time t (overturn of the total dipole moment Dt) of the PVDF chain of 6 monomer units (“PVDF-6”) on the magnitude of the electric field E (see on Figure 3): a) t-2(E) dependence over the entire range; b) t-2(E) dependence in the region at the low field values E (E → EC and E > EC), corresponding to the linear dependence according to Eq. (9) (red line), for homogeneous switching according to the LGD theory and Landau-Khalatnikov Eq. (8). .
Preprints 98410 g004
Preprints 98410 g005
Figure 5. Dependence of t-2 on voltage V for a P(VDF-TrFE) LB film measured by the pulsed-probe method. For a sample with 30 ML, the dots correspond to experimental data and the dashed curve indicates correspondence with the exponential dependence. For samples with 10 ML, the triangles show the experimental data, while the dashed curves indicate correspondence to equation (12) of the data on the sample [60,61].(Reproduced with permission from [60]; AIP Publishing, 2011).
Figure 5. Dependence of t-2 on voltage V for a P(VDF-TrFE) LB film measured by the pulsed-probe method. For a sample with 30 ML, the dots correspond to experimental data and the dashed curve indicates correspondence with the exponential dependence. For samples with 10 ML, the triangles show the experimental data, while the dashed curves indicate correspondence to equation (12) of the data on the sample [60,61].(Reproduced with permission from [60]; AIP Publishing, 2011).
Preprints 98410 g005
Preprints 98410 g006
Figure 6. MD run process for 2 PVDF-6 chains model with PM3 RHF calculations at each MD run step: (a) initial state; (b) final state after MD run with rotated (switched) on the opposite dipole moment Dt orientation in electric field E. Inset show the energies changes and determinate the switching time τS for this PVDF system. (Adapted with permission from ref. [10]; Elsevier, 2014).
Figure 6. MD run process for 2 PVDF-6 chains model with PM3 RHF calculations at each MD run step: (a) initial state; (b) final state after MD run with rotated (switched) on the opposite dipole moment Dt orientation in electric field E. Inset show the energies changes and determinate the switching time τS for this PVDF system. (Adapted with permission from ref. [10]; Elsevier, 2014).
Preprints 98410 g006
Preprints 98410 g007
Figure 7. Molecular model of two PVDF chains and consequence of its rotation steps under applied electrical field, calculated by PM3 UHF MD run: (a)–(c) chains rotation in high electric field Ez ~ 0.04a.u. ~ 20 GV/m; (e)–(g) chains rotation in the low electric field Ez ~ 0.0065a.u. ~ 3 GV/m (1a.u. ~ 500 GV/m);(d) and (h) present corresponding data of MD averages energies during MD simulation run for both types of PVDF chains rotation. (Reproduced with permission from ref. [10]; Elsevier, 2014).
Figure 7. Molecular model of two PVDF chains and consequence of its rotation steps under applied electrical field, calculated by PM3 UHF MD run: (a)–(c) chains rotation in high electric field Ez ~ 0.04a.u. ~ 20 GV/m; (e)–(g) chains rotation in the low electric field Ez ~ 0.0065a.u. ~ 3 GV/m (1a.u. ~ 500 GV/m);(d) and (h) present corresponding data of MD averages energies during MD simulation run for both types of PVDF chains rotation. (Reproduced with permission from ref. [10]; Elsevier, 2014).
Preprints 98410 g007
Preprints 98410 g008
Figure 8. Dependence of τ-2 on external electric field E (τ is switching time, is presenting in natural logarithmic scale along OY axis): a) for two PVDF chains; b) for two and four PVDF chains. Insert: (down) show the behavior of τ-2 in the vicinity of critical field E ~ EC ~ 2.3 GV/m; squares are computational data, solid line coincides with Eq. (9); (upper) shows the behavior of ln(τ-2) on high value of external electric field E, corresponding to exponential decay with. (Reproduced with permission from ref. [10]; Elsevier, 2014).
Figure 8. Dependence of τ-2 on external electric field E (τ is switching time, is presenting in natural logarithmic scale along OY axis): a) for two PVDF chains; b) for two and four PVDF chains. Insert: (down) show the behavior of τ-2 in the vicinity of critical field E ~ EC ~ 2.3 GV/m; squares are computational data, solid line coincides with Eq. (9); (upper) shows the behavior of ln(τ-2) on high value of external electric field E, corresponding to exponential decay with. (Reproduced with permission from ref. [10]; Elsevier, 2014).
Preprints 98410 g008
Preprints 98410 g009
Figure 9. Hysteresis loops of the LB PVDF film [16]: (a) with a different number of monolayers with 5, 10, 20, 30, 50 and 100 (the insert shows the linearity of the reciprocal capacity depending on the thickness); (b) EC as a function of the LB thickness of the PVDF film (at 8–20 nm, the transition region). Adopted with permission from ref. [62]. (Reprinted with permission from [62]; AIP Publishing, 2014).
Figure 9. Hysteresis loops of the LB PVDF film [16]: (a) with a different number of monolayers with 5, 10, 20, 30, 50 and 100 (the insert shows the linearity of the reciprocal capacity depending on the thickness); (b) EC as a function of the LB thickness of the PVDF film (at 8–20 nm, the transition region). Adopted with permission from ref. [62]. (Reprinted with permission from [62]; AIP Publishing, 2014).
Preprints 98410 g009
Preprints 98410 g010
Figure 10. The dependence of the coercive field of the ferroelectric polymer PVDF on the film thickness according to the results of calculations by different methods (from hysteresis loops and MD runs) in comparison with experimental data [62], taking into account the dielectric constant of an ultrathin molecular film ε = 2.4. (Reprinted with permission from [13]).
Figure 10. The dependence of the coercive field of the ferroelectric polymer PVDF on the film thickness according to the results of calculations by different methods (from hysteresis loops and MD runs) in comparison with experimental data [62], taking into account the dielectric constant of an ultrathin molecular film ε = 2.4. (Reprinted with permission from [13]).
Preprints 98410 g010
Preprints 98410 g011
Figure 11. Models of initial states for Graphene layers and PVDF6 chain: a) one PVDF chain and one graphene layer model Gr54H with 54 carbon atoms C (Cyan), arranged round by the hydrogen atoms H (Gray), in Z-plane; b) the same in Y-projection plane; c) “PVDF6+G54H_H-C” model in the initial state of PVDF6 chain and Gr54H with “H-C” positions; c) one PVDF chain and two graphene layers - the sandwich structure “Gr54H+PVDF6+Gr54H” model in the initial state. Initial dipole moment Dt orientation is shown by vector – black arrow. (Reprinted with permission from [50]; Taylor & Francis 2022).
Figure 11. Models of initial states for Graphene layers and PVDF6 chain: a) one PVDF chain and one graphene layer model Gr54H with 54 carbon atoms C (Cyan), arranged round by the hydrogen atoms H (Gray), in Z-plane; b) the same in Y-projection plane; c) “PVDF6+G54H_H-C” model in the initial state of PVDF6 chain and Gr54H with “H-C” positions; c) one PVDF chain and two graphene layers - the sandwich structure “Gr54H+PVDF6+Gr54H” model in the initial state. Initial dipole moment Dt orientation is shown by vector – black arrow. (Reprinted with permission from [50]; Taylor & Francis 2022).
Preprints 98410 g011
Preprints 98410 g012
Figure 12. Final states of the heterostructure “PVDF+Gr54H” models after PVDF chain and total dipole Dt rotation (switching) in the applied electric field E: a) one-side “PVDF6+G54H_H-C” model with switched opposite orientation of the total dipole moment Dt in comparison with initial state on Figure 11c; b) sandwich “G54H+PVDF6+G54H” model with the same opposite switched Dt in comparison with initial state on Figure 11d. On right side shown the MD energies trajectory over time during the MD run. (Reprinted with permission from [50]; Taylor & Francis 2022).
Figure 12. Final states of the heterostructure “PVDF+Gr54H” models after PVDF chain and total dipole Dt rotation (switching) in the applied electric field E: a) one-side “PVDF6+G54H_H-C” model with switched opposite orientation of the total dipole moment Dt in comparison with initial state on Figure 11c; b) sandwich “G54H+PVDF6+G54H” model with the same opposite switched Dt in comparison with initial state on Figure 11d. On right side shown the MD energies trajectory over time during the MD run. (Reprinted with permission from [50]; Taylor & Francis 2022).
Preprints 98410 g012
Preprints 98410 g013
Figure 13. Values of the inverse square τS-2 of the switching time τS (9) as a linear function of the electric field E in the vicinity of coercive field EC for different models. The main lines are followings: black line – the PVDF6 chain model of PVDF without graphene component; blue line – the model “PVDF6+G54H_H-C” with one-side graphene layer; red line – the sandwich model “Gr54H+PVDF6+Gr54H” with 2 graphene layers. Intersection area for all lines is at the E ~ Ecr.
Figure 13. Values of the inverse square τS-2 of the switching time τS (9) as a linear function of the electric field E in the vicinity of coercive field EC for different models. The main lines are followings: black line – the PVDF6 chain model of PVDF without graphene component; blue line – the model “PVDF6+G54H_H-C” with one-side graphene layer; red line – the sandwich model “Gr54H+PVDF6+Gr54H” with 2 graphene layers. Intersection area for all lines is at the E ~ Ecr.
Preprints 98410 g013
Preprints 98410 g014
Figure 14. Schematic of the MD run process in applied electric field E for one copolymer PVDF-TrFE chain (“PVDF6-TrFE” model) using PM3 RHF method calculations by HyperChem software at the each MD run’s step: (a) initial state; (b) final state after MD run with rotated (switched) on the opposite direction total dipole moment Dt orientation in electric field E. Inset (c) show the energies changes during MDS run with the time (in ps).
Figure 14. Schematic of the MD run process in applied electric field E for one copolymer PVDF-TrFE chain (“PVDF6-TrFE” model) using PM3 RHF method calculations by HyperChem software at the each MD run’s step: (a) initial state; (b) final state after MD run with rotated (switched) on the opposite direction total dipole moment Dt orientation in electric field E. Inset (c) show the energies changes during MDS run with the time (in ps).
Preprints 98410 g014
Preprints 98410 g015
Figure 15. Values of the inverse square τS-2 of the switching time τS (9) as a linear function of the electric field E in the vicinity of coercive field EC for PVDF-TrFE in compare with PVDF models. The main lines are followings: black line – the “PVDF6” chain model of PVDF; blue line – the model “PVDF6-TrFE” model.
Figure 15. Values of the inverse square τS-2 of the switching time τS (9) as a linear function of the electric field E in the vicinity of coercive field EC for PVDF-TrFE in compare with PVDF models. The main lines are followings: black line – the “PVDF6” chain model of PVDF; blue line – the model “PVDF6-TrFE” model.
Preprints 98410 g015
Preprints 98410 g016
Figure 16. Models of Graphene layers and PVDF-TrFE chain: a) initial states for “PVDF6-TrFE” model chain and one graphene layer “Gr54H” model with 54 carbon atoms C, arranged round by the hydrogen atoms H; b) final state of “PVDF6+G54H_H-C” model after rotation in electric field E during MD run; c) energies trajectories. Dipole moment Dt orientation shown by black arrow.
Figure 16. Models of Graphene layers and PVDF-TrFE chain: a) initial states for “PVDF6-TrFE” model chain and one graphene layer “Gr54H” model with 54 carbon atoms C, arranged round by the hydrogen atoms H; b) final state of “PVDF6+G54H_H-C” model after rotation in electric field E during MD run; c) energies trajectories. Dipole moment Dt orientation shown by black arrow.
Preprints 98410 g016
Preprints 98410 g017
Figure 17. Models of 2 Graphene layers and PVDF-TrFE chain: a) initial states for “PVDF6-TrFE” model chain and 2 graphene layer “Gr54H” model with 54 carbon atoms C, arranged round by the hydrogen atoms H; b) final state of “Gr54H-PVDF6+G54H” model after rotation in electric field E during MD run; c) energies trajectories. Dipole moment Dt orientation shown by black arrow.
Figure 17. Models of 2 Graphene layers and PVDF-TrFE chain: a) initial states for “PVDF6-TrFE” model chain and 2 graphene layer “Gr54H” model with 54 carbon atoms C, arranged round by the hydrogen atoms H; b) final state of “Gr54H-PVDF6+G54H” model after rotation in electric field E during MD run; c) energies trajectories. Dipole moment Dt orientation shown by black arrow.
Preprints 98410 g017
Preprints 98410 g018
Figure 18. Values of the inverse square τS-2 as a linear function of the electric field E for PVDF and PVDF-TrFE in compare with PVDF-Gr and PVDF-TrFE-Gr models. Lines are: black – “PVDF6”; blue – “PVDF6-TrFE”; magenta - “PVDF6-Gr54H”; red line - “PVDF6-TrFE-Gr54H”.
Figure 18. Values of the inverse square τS-2 as a linear function of the electric field E for PVDF and PVDF-TrFE in compare with PVDF-Gr and PVDF-TrFE-Gr models. Lines are: black – “PVDF6”; blue – “PVDF6-TrFE”; magenta - “PVDF6-Gr54H”; red line - “PVDF6-TrFE-Gr54H”.
Preprints 98410 g018
Preprints 98410 g019
Figure 19. Values of the inverse square τS-2 as a linear function of the electric field E for PVDF-TrFE and PVDF-TrFE-Gr in compare with sandwich Gr-PVDF-TrFE-Gr models. Lines are: black – “PVDF6-TrFE”; blue – “PVDF6-TrFE-Gr54H”; red line - “Gr54H-PVDF6-TrFE-Gr54H”.
Figure 19. Values of the inverse square τS-2 as a linear function of the electric field E for PVDF-TrFE and PVDF-TrFE-Gr in compare with sandwich Gr-PVDF-TrFE-Gr models. Lines are: black – “PVDF6-TrFE”; blue – “PVDF6-TrFE-Gr54H”; red line - “Gr54H-PVDF6-TrFE-Gr54H”.
Preprints 98410 g019
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated