Quality Assessment of GNSS, SLR, VLBI, and Doris Inputs for ITRF2014 and ITRF2020 Using Trf Stacking Methods

Preprint

Technical Note

Quality Assessment of GNSS, SLR, VLBI, and Doris Inputs for ITRF2014 and ITRF2020 Using Trf Stacking Methods

This version is not peer-reviewed.

Jin Zhang

Chengli Huang^*

Lizhen Lian,Simeng Zhang

Jin Zhang

Chengli Huang^*

Lizhen Lian,Simeng Zhang

This version is not peer-reviewed.

Altmetrics

Downloads

164

Views

103

Comments

Submitted:

09 February 2024

Posted:

12 February 2024

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract

ITRF input data which are integrated by GNSS, SLR, VLBI, DORIS combination centers are considered to be relatively high-quality and accurate solutions. However, when utilizing these inputs, one still needs to identify outliers, rescale inaccurate covariance matrix and evaluate the precision of the observed datum information. To achieve the above-mentioned objectives, we propose a terrestrial reference frame (TRF) stacking approach to establish the single technical reference frameworks for the ITRF2014 and ITRF2020 datasets of all four technologies. As a result, roughly 0.5% or less of the SLR observations are identified as outliers, while the ratio of DORIS, GNSS, and VLBI observations are below 1%, around 2%, and ranging from 1% to 1.2%, respectively. The post-rescaling covariance scale factors are 25.07, 27.25, 18.84, 6.98 for GNSS, SLR, VLBI, and DORIS in ITRF2014 datasets, and 8.95, 14.9, 16.8, 7.78 in ITRF2020 datasets, respectively. It is shown that the consistency between the SLR scale and ITRF has improved, increasing from around -5mm in ITRF2014 datasets to approximately -1mm in ITRF2020 datasets. The scale velocity derived from fitting the VLBI scale parameter series with all epochs in ITRF2020 datasets differs by approximately 0.21mm/year from the velocity obtained by fitting the data up to 2013.75 because of the scale drift of VLBI at around 2013. The decreasing standard deviations of the Polar motion parameter (XPO, YPO) offsets between Stacking TRFs and 14C04 (20C04) indicating an improvement in the precision of polar motion observations for all of the four techniques. From the perspective of the Weighted Root Mean Square in station coordinates, the measurement precision of GNSS, SLR, and DORIS techniques has improved, while VLBI shows no significant change.

Keywords:

Subject:

Environmental and Earth Sciences - Space and Planetary Science

1. Introduction

A unique standard terrestrial reference frame (TRF) is the fundamental to ensure inter-operability and consistency of geodetic products and to adequately exploit various measurements collected by ground-based sensors, or via artificial satellites for Earth science and geodesy applications [1,2,3], including plate tectonics [4,5], co-seismic and post-seismic deformations [6,7], global geophysical fluid dynamics [8,9], ice melting [10], accurately determine point positions, and the rate of sea level rise [11,12], etc. Generally, the most widely utilized reference framework is the International Terrestrial Reference Frame (ITRF) series [13], which has a history spanning four decades. Since its inception in 1988, the ITRF has undergone 14 versions, namely ITRF 88, 89, 90, 91, 92, 93, 94, 96, 97, 00, 05, 08, 14, and 20.

The current ITRF2020 encompasses the positions, velocities, and annual and semi-annual signals of globally distributed reference stations, integrating the strengths of the four Space Geodesy technologies: GNSS, SLR, VLBI, and DORIS [2]. Typically, analysis centers (AC) for GNSS, SLR, VLBI, and DORIS reprocess historical observations employing the latest optimal computation strategies and models. Then, the results from these centers are combined by the combination centers (CC) for the four technologies, IGS, IVS, ILRS, and IDS. These integrated outcomes are considered to be relatively high-quality and accurate solutions because of the latest processing strategies and models, and the correction of system errors of different analysis centers, and submitted as the input data for establishing and updating ITRF.

However, when utilizing these high-quality solutions, one must still consider outliers, inaccurate covariance, and datum precision evaluation. While SLR employs a loosely constrained solution, VLBI utilizes a normal equation, and DORIS derives a technical solution from internal constraints. Consequently, the solutions of these three technologies are not aligned to a fixed frame and traditional time series analysis methods prove insufficient in assessing the quality of these solutions. Additionally, traditional time series analysis methods cannot assess the datum information for all of the four techniques either. Therefore, we propose a TRF stacking approach following Altamimi, et al. [14] to achieve the previously mentioned objectives. TRF stacking accumulates epoch solutions to long-term TRF expressed by coordinates and velocities in a specific epoch, enabling us to evaluate observational qualities and the datum precision. Furthermore, to establish 2014 and 2020 ITRF, solutions of each Space Geodesy technique incorporated new strategies and models, we can investigate the impact of these strategies at the stacking TRF level.

In general, the solutions for each technique in 2020 exhibit significant improvements compared to the previous versions. For GNSS, the new IERS secular pole model was adopted in Repro3, replacing the previous mean pole model used in Repro2 from the original IERS 2010 Conventions. Consequently, Repro3 and IGS14 exhibit systematic biases, making alignment impractical. Therefore, a special reference frame, IGSR3, was utilized, aligning with the new IERS secular pole model, the igsR3.atx satellite PCOs, and the igsR3.atx ground antenna calibrations [15].

For SLR, a series of improvement measures were implemented to address its systematic biases [16], like enhancements to the satellite center of mass model corrections [17]. A comprehensive investigation into the site-specific systematic errors in the data collected since 1983 was conducted [18]. Regardless of reported issues or configuration changes at the sites, both the coordinates and systematic biases were simultaneously estimated for all of the 7 ACs and CCs (ASI, BKG, DGFI, ESA, GFZ, JCET, NSGF) [19].

For VLBI, some new and improved models for the IVS analysis have been applied like a constant drift of 5.8 µas/year on Galactic aberration. Additionally, mid-session-epoch solutions are calculated to present the best performance of VLBI, but they are transformed to 12-hour to ensure the consistency with the epochs of other techniques which are submitted for establishing the ITRF. [20,21].

When combining results from various analysis centers, IDS avoids introducing external reference frames and employs internal constraints during technical within-group combinations [22]. Consequently, the geocenter and scale results from DORIS observations directly reflect its precision in determining geocenter and scale. Compared to 2014, DORIS 2020 solution has undergone some new improvements: the application of new phase center variations for Alcatel DORIS ground antennas and the gradual replacement of Alcatel with Starec antennas over time; better modeling of the surface forces on the satellites [22,23].

The remaining sections of this paper are organized as follows: Section 2 presents the methods employed in this study, Section 3 introduces the input data and the results, finally, Section 4 provides the conclusions.

2. Methods

2.1. Stacking Model

A significant application of space geodetic observations is the continuous determination of ground station coordinates [24]. Using four technologies, GNSS, SLR, VLBI, and DORIS, coordinates sets and their internally consistent Earth Orientation Parameters (EOP) can be estimated based on observations collected at each measurement interval, daily and weekly [25]. Due to the complex surface deformation characteristics of the Earth, the coordinates of individual epochs not only include Earth’s crustal movements, terrain variations, and surface loads as geophysical signals but also involve various random errors. Consequently, in order to mitigate the influence of random factors and better apply physical signals, it is common to stacking observations from individual epochs over a certain time span to coordinates, velocities, and other modelable parameters (such as periodic signals) at a specific reference epoch. This process yields a reference framework through the stacking of observations, and we call it TRF Stacking method.

The transformation relationship between TRFs is typically represented using the Helmert similarity transformation model. For a station i of technique s, located in a specific epoch

t_{s}^{i}

, the coordinates

X_{s}^{i}

in the epoch reference frame are related to the stacking reference frame coordinates

X_{c k}^{i}

at the reference epoch

t_{0}

, as well as the Earth Orientation Parameters (EOP) in the two reference frames, according to the following transformation:

X_{s}^{i} = X_{c k}^{i} + (t_{s}^{i} - t_{0}) {\dot{X}}_{c k}^{i} + T_{s} + D_{s} X_{c k}^{i} + {R_{s} X}_{c k}^{i}

(2.1)

\{\begin{matrix} x_{s}^{p} = x_{c}^{p} + {R 2}_{s} \\ y_{s}^{p} = y_{c}^{p} + {R 1}_{s} \\ \begin{matrix} {U T}_{s} = {U T}_{c} - \frac{1}{f} {R 3}_{s} \\ {\dot{x}}_{s}^{p} = {\dot{x}}_{c}^{p} \\ \begin{matrix} {\dot{y}}_{s}^{p} = {\dot{y}}_{c}^{p} \\ {L O D}_{s} = {L O D}_{c} \end{matrix} \end{matrix} \end{matrix}

(2.2)

where

f =

1.002737909350795,

T_{s}

represents the three translation parameters,

D_{s}

denotes scale parameters,

R_{s}

signifies rotation parameters and

R_{s} = [\begin{matrix} 0 & - {R 3}_{s} & {R 2}_{s} \\ {R 3}_{s} & 0 & - {R 1}_{s} \\ - {R 2}_{s} & {R 1}_{s} & 0 \end{matrix}]

. If there is a need to model additional signals such as periodic terms for the stations, further model optimization can be performed in Equation 2.1. Corresponding adjustments should be made in the subsequent datum definition part [2]. However, the primary objective of using single- technique TRF stacking in this paper is not to analyze nonlinear features. Therefore, only linear terms are included.

2.2. Datum Definition

According to Eq. 2.1, the introduction of transformation parameters and the estimation of velocity terms result in a rank deficiency in the normal equations, with a rank deficiency of 14 [26]. It can also be considered as the datum for the stacking TRF,

X_{c k}^{i}

and

{\dot{X}}_{c k}^{i}

, is undefined. The rank deficiency can to be addressed by datum defining.

According to the definition by the International Earth Rotation and Reference Systems Service (IERS), the datum for the International Terrestrial Reference System (ITRS) includes the origin, scale, orientation, and their variations over time [27].

Due to the distinct characteristics of various space geodetic techniques, such as SLR, GNSS, DORIS, which are sensitive to the Earth’s center of mass, the TRF origin (CM) can be defined [28,29,30].

The scale, by definition, should be the scale of a local TRF in the sense of general relativity. All of the four techniques are sensitive to the scale, and in practical applications, physical parameters (such as Earth’s gravitational constant GM and the speed of light c) and a certain relativistic correction model are employed to determine it. If different techniques use distinct physical parameter values and models, their scales may differ. However, adopting recommended values from the IERS specifications in data processing tends to minimize scale differences determined by various techniques.

The orientation of the current ITRS has evolved from the orientation defined by BIH1984.0, and new versions of ITRS maintain consistency with the previous version’s orientation by conforming to the no-net-rotation (NNR) condition, which ensures horizontal motion relative to the Earth’s surface [31].

In mathematics, the definition of a datum is typically realized through the imposition of constraints. Generally, two constraint methods are employed: when defining the datum using a set of external reference coordinates and their velocities, denoted as

X_{R}

and

{\dot{X}}_{R}

, the minimum constraint approach is utilized; when preserving the intrinsic physical parameter information associated with

X_{c}

, the minimum constraint is applied.

Minimum constraint means the minimization of Helmert transformation parameters between external reference frames,

X_{R}

{\dot{X}}_{R}

, and the Stacking TRF,

X_{c}

{\dot{X}}_{c}

[32]. The relationship of

X_{R}

{\dot{X}}_{R}

and

X_{c}

{\dot{X}}_{c}

can be defined as

[\begin{matrix} X_{R} \\ {\dot{X}}_{R} \end{matrix}] - [\begin{matrix} X_{c} \\ {\dot{X}}_{c} \end{matrix}] = [\begin{matrix} \begin{matrix} A & 0 \end{matrix} \\ \begin{matrix} 0 & A \end{matrix} \end{matrix}] [\begin{matrix} θ \\ \dot{θ} \end{matrix}]

(2.3)

[\begin{matrix} θ \\ \dot{θ} \end{matrix}]

encompasses the seven transformation parameters and their rates, the matrix A includes the partial derivatives of the transformation parameters, and the design matrix A is defined as

A = [\begin{matrix} 1 & 0 & 0 & x_{c}^{i} & 0 & z_{c}^{i} & - y_{c}^{i} \\ 0 & 1 & 0 & y_{c}^{i} & - z_{c}^{i} & 0 & x_{c}^{i} \\ 0 & 0 & 1 & z_{c}^{i} & y_{c}^{i} & - x_{c}^{i} & 0 \end{matrix}]

(2.4)

Expressing Equation 2.3 as

X_{1} - X_{0} = G ϑ

, where

ϑ

is the least squares solution and given by

ϑ = {(G^{T} G)}^{- 1} G^{T} (X_{1} - X_{0})

(2.5)

Letting

{(G^{T} G)}^{- 1} G^{T} = B

, considering

ϑ

as the observed quantity with a weight

P_{ϑ} = {(Q_{ϑ})}^{- 1}

, and treating

X_{0}

as the parameter, the minimization condition

ϑ = 0

leads to the normal equation for Equation 2.5:

B^{T} P_{ϑ} B δ {\hat{X}}_{0} = B^{T} P_{ϑ} B (X_{1} - X_{0}^{(0)})

(2.6)

δ {\hat{X}}_{0}

represents the correction to the parameters

X_{0}

Internal constraint signifies that for all transformation parameters within the span, they are set to zero at the reference epoch

t_{0}

, including both the values and velocities.

\{\begin{matrix} θ_{k} (t_{0}) = 0 \\ {\dot{θ}}_{k} = 0 \end{matrix}

(2.7)

Following the derivation, we obtain:

\{\begin{matrix} \sum_{k \in K} θ_{k} = 0 \\ \sum_{k \in K} \frac{θ_{k}}{{(t_{k} - t_{0})}^{- 1}} = 0 \end{matrix}

(2.8)

2.3. Outliers and Variance Component Estimation

Based on the posterior residuals

v_{s}

, the posterior variance factor can be computed by

σ_{s}^{2} = \frac{v_{s}^{T} P_{s} v_{s}}{f_{s}}

(2.9)

where

P_{s}

is the weight matrix of the observations (obtained by taking the inverse of the covariance matrix), and

f_{s}

f_{s} = 6 n_{s} - t r (A_{s} N^{- 1} A_{s}^{T} P_{s})

(2.10)

This approach can also be referred to Davies and Blewitt [33]. It can serve as a residual-based posterior weighting method until

σ_{s}^{2}

approaches unity. Observations with normalized residuals (residual divide standard deviation) exceeding 4 are considered outliers and are subsequently removed during this rescale process.

Weighted Root Mean Square (WRMS) is computed by

W R M S = \frac{v_{s}^{T} P_{s} v_{s}}{t r a c e (P_{s})}

(2.11)

3. Results and Analysis

3.1. Data Introduction and Preprocessing

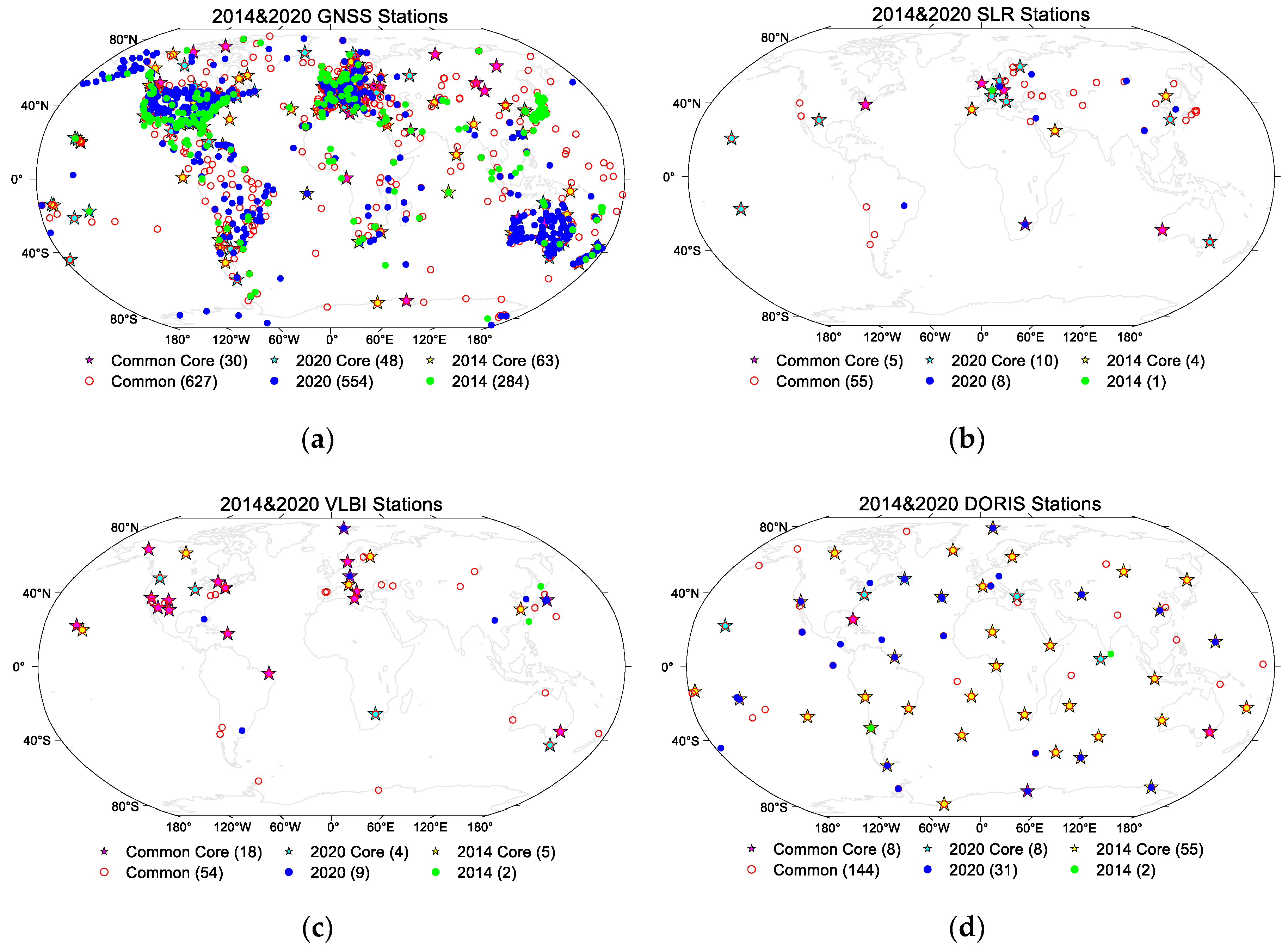
The selected data for this study is presented in the Table 1. To ensure a stable estimation of velocities and prevent situations where only one observation exists in a segment, making velocity unsolvable, stations with an observation count greater than 50 are chosen. For VLBI, we opted to use data from a minimum of three stations per session, starting from the 600th GPS week onwards. In 2014, 2887 sessions are chosen, with 20 sessions excluded due to abnormal transformation parameters. In 2020, 4433 sessions are selected, and 11 sessions with abnormal transformation parameters were excluded. Mid-session epoch solutions are used rather than 12-hour epoch solutions. Regarding SLR, the 2014 solutions had fixed weekly solutions from the 678th GPS week onwards, so both the 2020 and 2014 SLR datasets are selected from weeks beyond the 678th GPS week. For GNSS, weekly solutions rather than daily solutions are utilized here. All weekly solutions of IDS-09 for 2014 and IDS-16 for 2020 are selected for DORIS. Core stations are selected referred to ITRF2014 and ITRF2020 core-networks, for DORIS 2014 we select more core stations, because there are only two DORIS stations in ITRF2014 core-network.

When conducting datum definition or orientation, the external reference frame coordinates of a set of core stations from each technique are employed, station and core station distributions are illustrated in Figure 1. Generally, the utilized station numbers of GNSS, SLR, VLBI, DORIS are 911, 56, 56, 146 (1656, 33, 30, 57) for 2014 and 1181, 63, 63, 175 (2773, 34, 25, 80) for 2020, where the numbers in parentheses indicate the count of segments due to discontinuities. We can observe that there is an abundance of GNSS stations, mainly concentrated in terrestrial regions, VLBI and SLR have a relatively limited number of stations, and the north-south distribution is uneven for all three techniques. DORIS stations, on the other hand, exhibit a more uniform north-south distribution, and often exists multiple stations within one site.

SLR inputs consist of solutions with loose constraints, and the substantial formal errors documented in the SINEX files result from the relaxed positional constraints implemented during laser range data reductions. These errors are indicative of rotational noise associated with the reference frame. To mitigate this effect, the covariance matrices of the solutions are adjusted by imposing the no-net-rotation (NNR) condition. No no-net-scale (NNS) condition or no-net-translation (NNT) is applied to preserve the intrinsic SLR origin and scale [34,35,36].

The NEQs for each VLBI session are inverted by incorporating NNT and NNR conditions into the a priori station position coordinates provided in the input SINEX files. To maintain the inherent scale of VLBI, no NNS condition is applied during the inversion of the NEQs.

The post-seismic deformations for all four techniques are initially subtracted based on the analysis results from the ITRF. The segmentation of the time series is also referred to the results obtained from the ITRF. Corresponding file download links can be accessed at the following address: https://itrf.ign.fr/.

3.2. Stacking Results

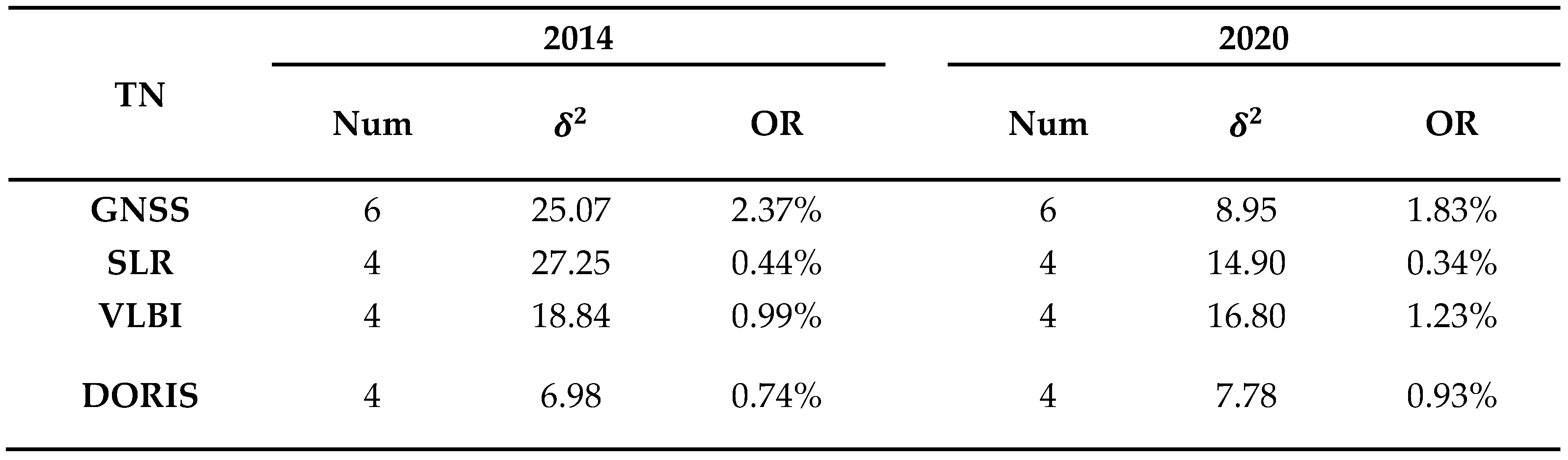
We perform outlier removal of the coordinate observations and posterior scaling of the covariance matrix through iterative Space Geodesy TRF stacking. Observations with normalized residuals exceeding 4 are considered outliers and are subsequently removed. This iterative process continues until no outliers can be detected and the variance scale factor approaches 1. The iteration results are tabulated in Table 2.

Two datum definition strategies are utilized for TRF stacking. Initially, to understand the characteristics of the origin and scale determination for GNSS, SLR, and DORIS technologies, we applied internal constraints to their translation and scale parameters to retain their internally determined origin and scale information. Since the results from GNSS are already fixed to ITRF2014 and IGSR3 for Repro2 and Repro3, the origin and scale information represents the observed origin and scale measured in the corresponding reference frame. Additionally, to study the frame characteristics of each technique relative to ITRF, we defined the translation and scale parameters through the ITRF core stations using minimum constraints. Both orientation schemes align with either ITRF2014 or ITRF2020. As VLBI is not sensitive to the origin, when solving with an internal constraint scheme, only scale parameters are constrained, and other reference datum information is still defined by ITRF.

Table 3 illustrates the 14 transformation parameters between the Stacking Space Geodesy TRFs of single technique and the ITRF2014 (ITRF2020). The transformation parameters are computed based on the core station networks. When the origin and scale are aligned with the ITRF, the 14 transformation parameters between the Stacking Space Geodesy TRF and ITRF generally approach zero. However, when the origin and scale of the Space Geodesy TRFs are defined using internal constraints, the transformation parameters then reflect the differences between the techniques and the ITRF.

3.3. Analysis of Translation and Scale Time Series

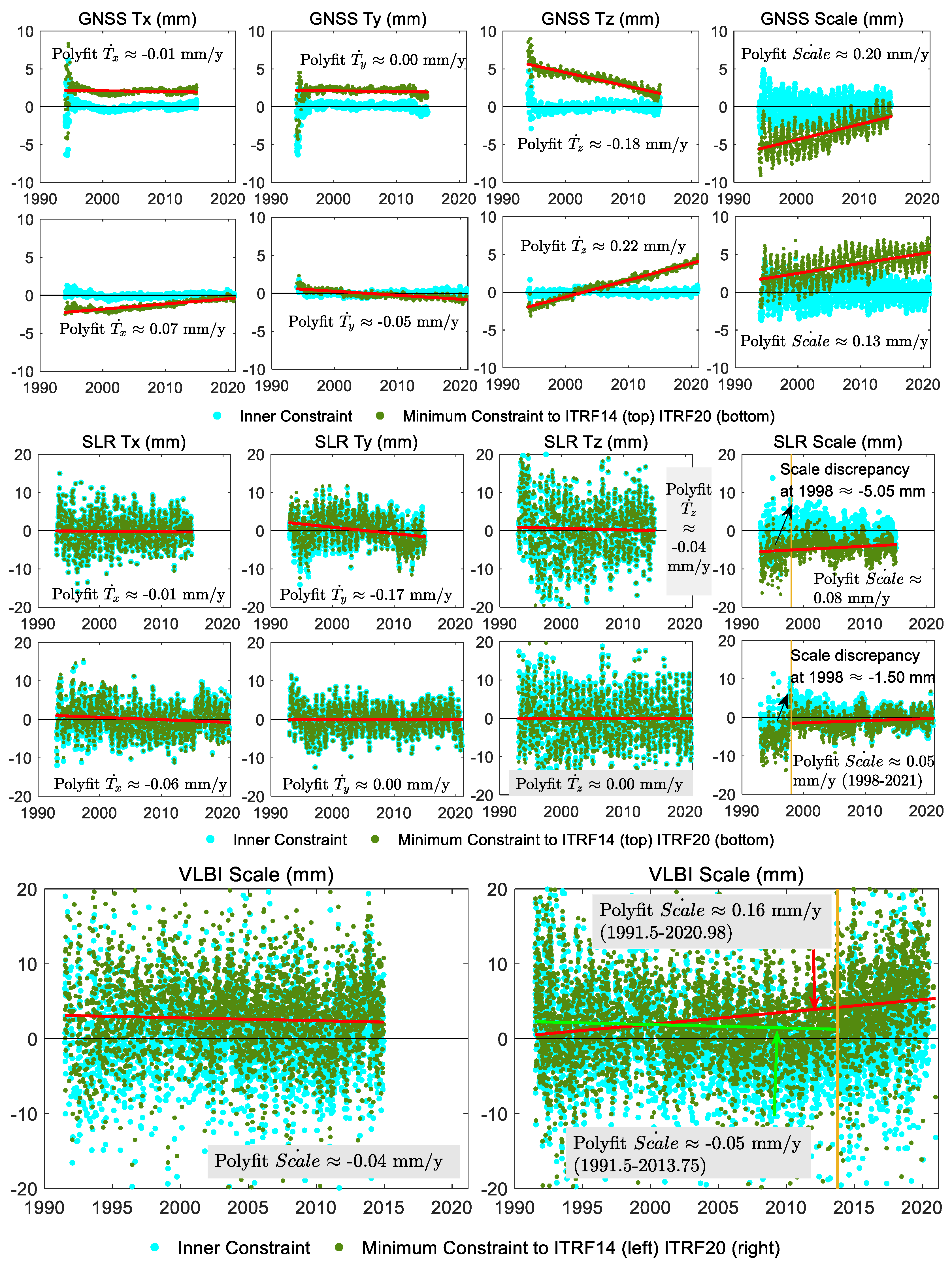
Figure 2 presents the series of translation and scale parameters between the observations and the Stacking Space Geodesy TRFs under two types of constraints: internal constraints and minimum constraints.

When internal constraints are applied, the translation and scale parameters of GNSS characterize the observational datum precision of GNSS in its aligned reference framework, specifically ITRF2008 and IGSR3. In the GNSS 2014 Stacking TRF, under the minimum constraint definition, the translation parameter Tx and Ty are approximately 2mm, with their velocities essentially close to zero. The 2014 GNSS input data reference frame is fixed to ITRF2008, after stacking and defining the reference frame to ITRF2014, the calculated Tx and Ty values reflect the differences between ITRF2008 and ITRF2014. The drift of the translation parameter in the Z direction and the scale parameter is primarily influenced by the technical characteristics of GNSS [37,38]. In 2020, GNSS adopted a secular polar motion model during the data processing, resulting in non-zero translation velocities for both Tx and Ty where

{\dot{T}}_{X} = 0.07 m m / y

and

{\dot{T}}_{y} = - 0.05 m m / y

(by linear fit). In general, although GNSS provides numerous stations and high precision in positioning, its datum observation lacks stability, especially in the Z component and scale [39]. The GNSS coordinate calculations exhibit a significant dependence on the reference framework. Consequently, notable differences exist between the outcomes obtained under the two types of datum definitions.

From Figure 2, it is evident that the translational parameter series of SLR exhibit excellent consistency between internal and minimum constraints. This is attributed to the stability in determining the origin by the SLR. The translation velocity of

{\dot{T}}_{y}

in SLR 2014 is due to the drift at around 2010, which can be also found in ITRF2014 results. From the scale parameter time series, it is noticeable that there is a drift in the SLR scale around 1998. Therefore, for defining the scale in ITRF2020, only SLR data from after 1997.75 is chosen [2]. The consistency of scale between SLR and ITRF has improved, increasing from around -5mm in 2014 to approximately -1mm in 2020.

The determination of scale parameters in VLBI exhibits a significant level of noise, with a consistency of 3mm with ITRF2014 and 2mm with ITRF2020. A noticeable drift in VLBI scale occurred around 2013, prompting ITRF2020 to only incorporate data before 2013.75 when defining the scale using VLBI. Consequently, the scale velocity derived from fitting the VLBI scale parameter series with all epochs in 2020 differs by approximately 0.21mm/year from the velocity obtained by fitting the data up to 2013.75.

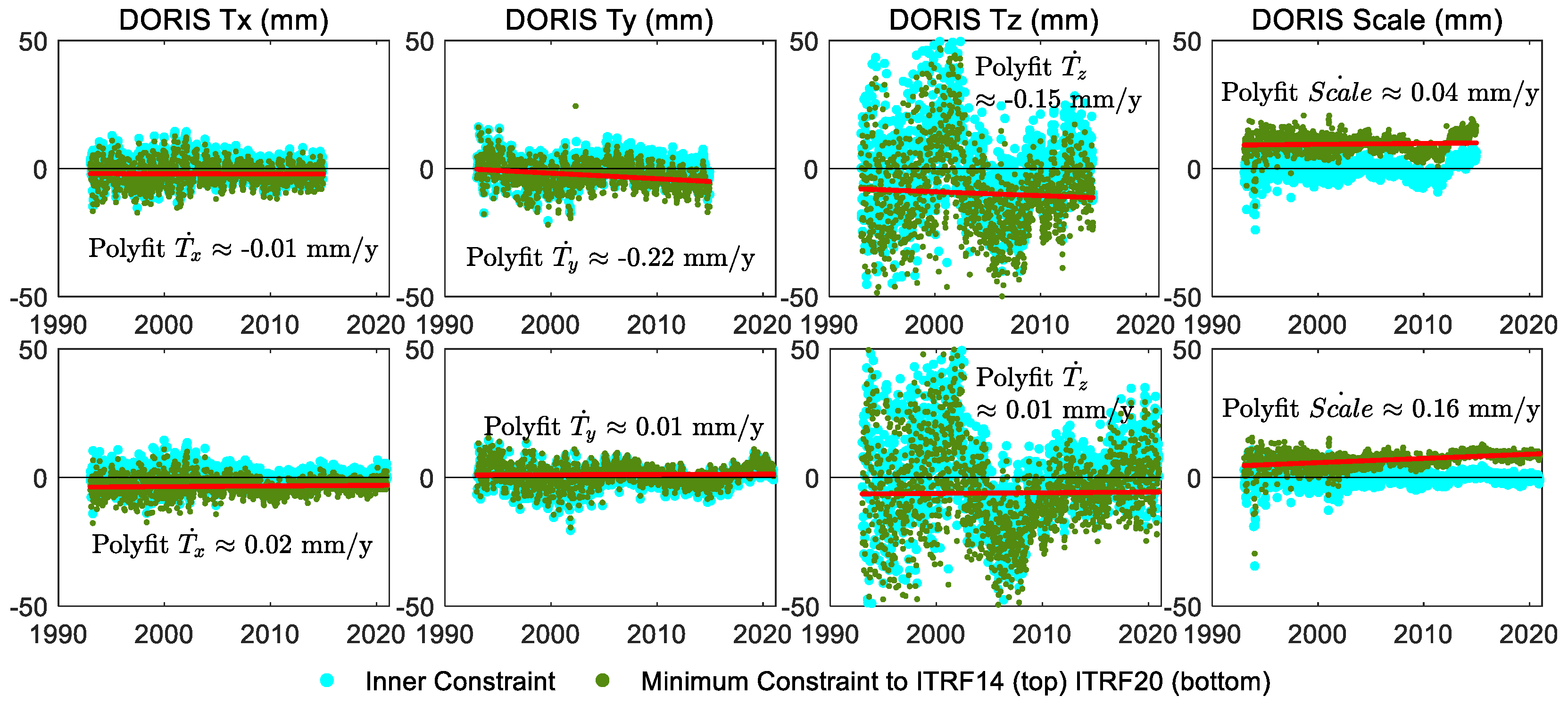
The origin determinations in the X and Y directions from DORIS demonstrate accuracy comparable to SLR. However, there is notable variability in the Z direction. The translation velocity of

{\dot{T}}_{y}

in DORIS 2014 may be caused by the selected core station network. The consistency in scale between DORIS and ITRF is approximately within the range of 5-10 mm, and not stable enough compared to SLR and VLBI.

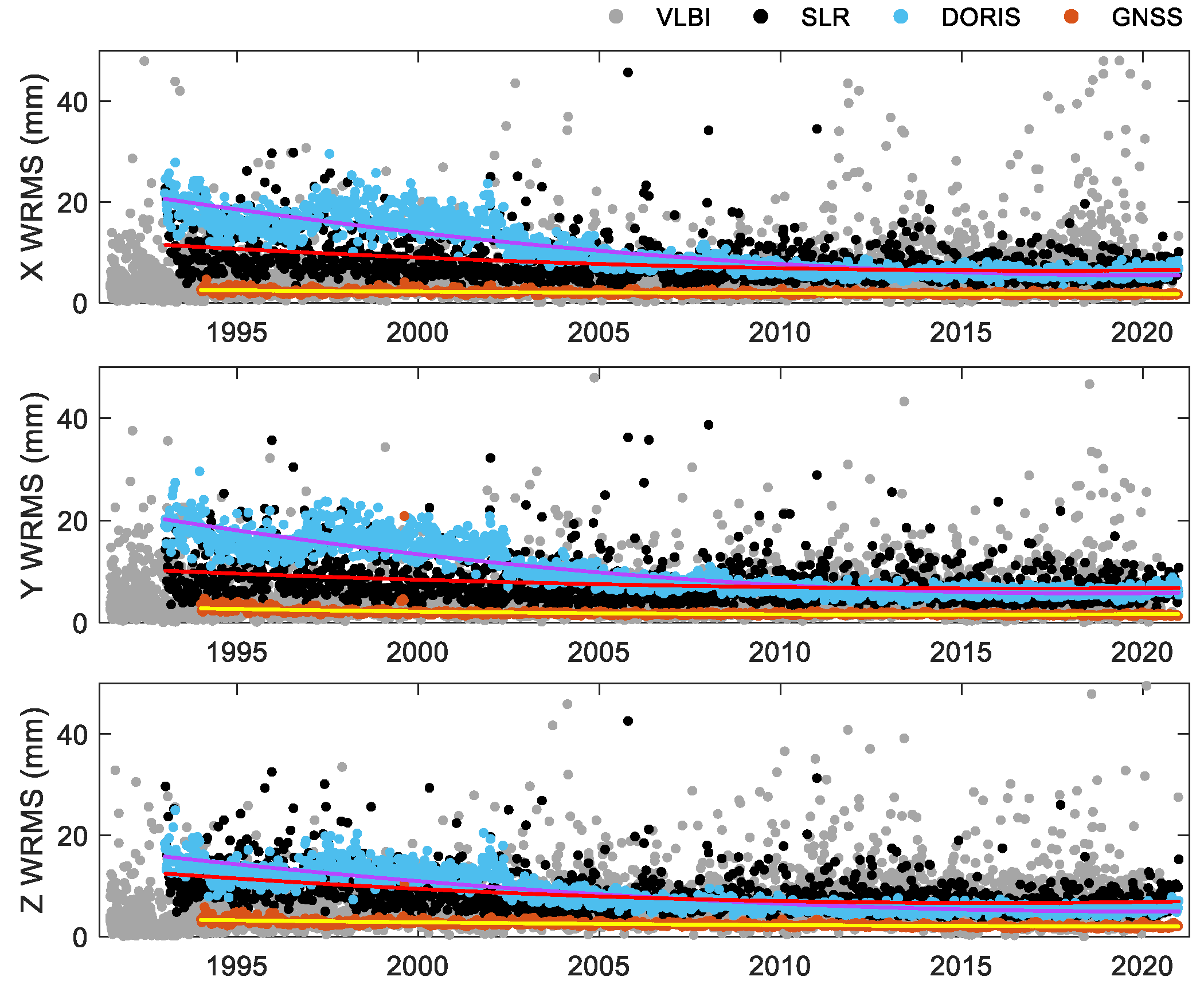
3.4. Analysis of Coordinate Residuals

Figure 3 illustrates the WRMS of the station coordinate residuals for each technique across their time span. Since the WRMS of the 2014 datasets are similar to those for the 2020 datasets during the same period, only 2020 WRMS are presented. It is evident that the accuracy of DORIS, SLR, and GNSS techniques gradually improve over time. The WRMS for the DORIS in the X and Y directions decreased from 30mm to 5mm, while the Z direction WRMS decreased from 25mm to 5mm. For SLR, the WRMS in the X, Y, and Z directions decreased from 20mm to better than 10mm. In the case of GNSS, the WRMS in the X and Y directions decreased from 4mm to 1.5mm, while the Z direction WRMS decreased from 5mm to 2mm. The station coordinates’ precision of DORIS surpasses SLR slightly after 2015, with GNSS exhibiting the highest coordinate precision. The variation in DORIS station coordinate precision is closely linked to changes in the DORIS satellite constellation [22,23]. VLBI shows significant variability in position precision within individual sessions and exhibit no significant change over time.

Furthermore, Table 4 displays the average WRMS for each technique that calculated separately for each stations. The precision of stations for GNSS, SLR, and DORIS in the 2020 version is improved compared to that in 2014.

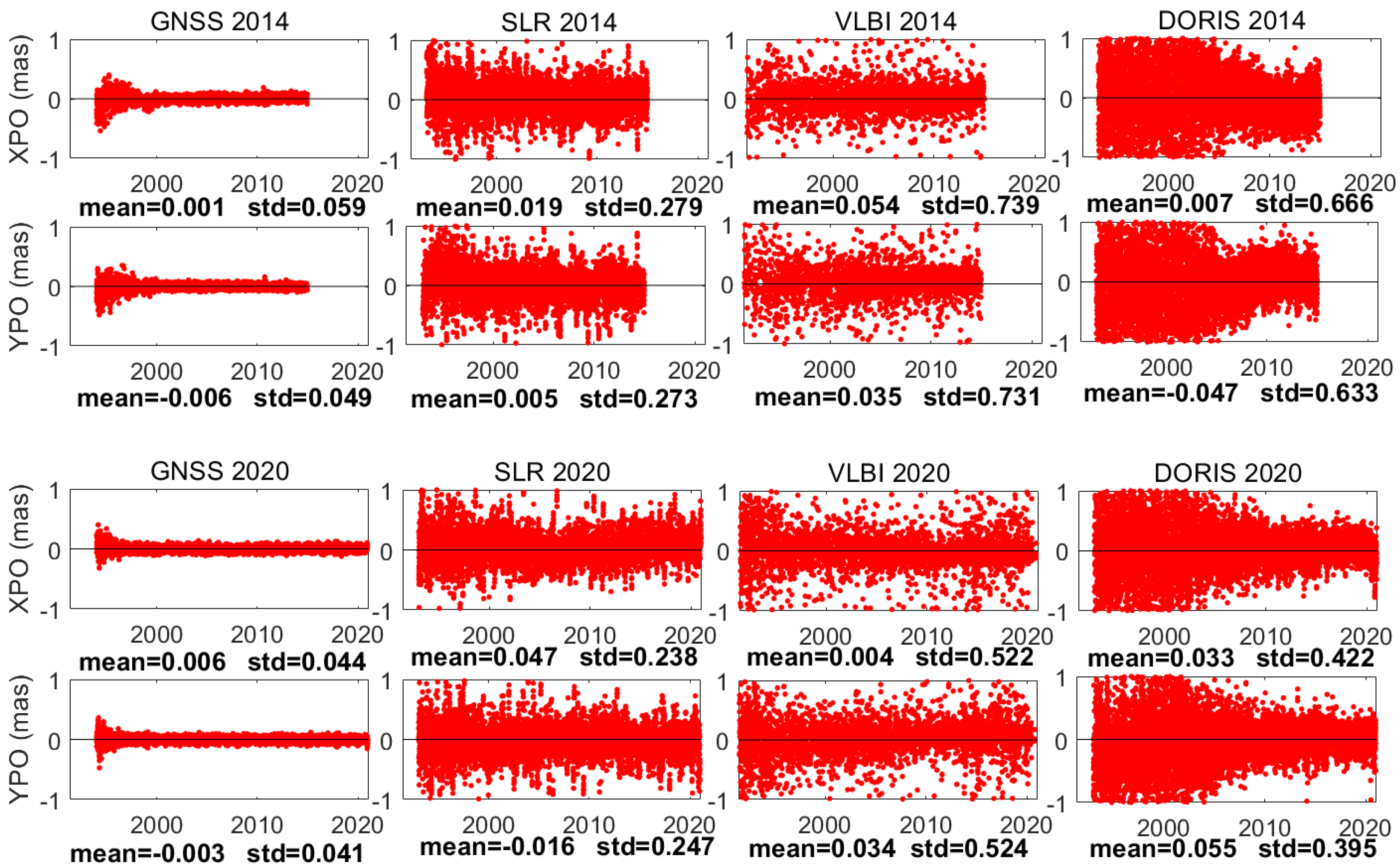
3.5. XPO and YPO Residuals Compared to 14C04 and 20C04

As depicted in Figure 4, a comparison is made between the stacking polar motion parameters (XPO, YPO) and the corresponding C04 series, namely 14C04 and 20C04. Mean residuals and standard deviations are then calculated to characterize the observational precision of polar motion parameters for each technique. The results indicate that GNSS has the highest precision in polar motion measurement, with a difference standard deviationof approximately 0.05mas compared to C04. VLBI exhibits relatively large noise in polar motion observations. The polar motion observations of SLR show differences with C04 within 0.3mas. The precision of DORIS polar motion observations gradually improves, with differences from C04 within 0.2mas after the year 2015.

4. Conclusions

In this study, we employed the TRF stacking method to assess the precision of inputs from four techniques, GNSS, SLR, VLBI, and DORIS, in ITRF2014 and ITRF2020. The evaluation encompassed outlier removal, post-rescaling of covariance matrices, datum analysis, coordinate precision analysis, and polar motion precision analysis.

Roughly 0.5% or less of the SLR observations are identified as outliers, while the ratio of DORIS, GNSS, and VLBI observations are below 1%, around 2%, and ranging from 1% to 1.2%, respectively. In 2014, the post-rescaling covariance scale factors are 25.07, 27.25, 18.84, 6.98 for GNSS, SLR, VLBI, and DORIS, respectively. The results for JTRF2014 were 32.49, 27.04, 34.81, 7.29, respectively, while ITRF2014 yielded 5.29, 25.20, 23.04, 6.86, respectively. In 2020, the post-rescaling covariance scale factors are 8.95, 14.9, 16.8, 7.78, respectively, with ITRF2020 results being 6.76, 15.44, 133.63, 8.53, respectively. It is important to note that ITRF uses daily solutions for GNSS data instead of weekly solutions, and the epoch spans for VLBI and SLR selected by us differ from those in JTRF and ITRF. Furthermore, ITRF2020 uses 12-hour epoch solutions for VLBI data, whereas our analysis utilizes mid-session epoch solutions. These are the primary reasons for the differences in covariance matrix rescale factors.

Based on the datum analysis results, it is shown than the data processing strategy for SLR has improved the consistency of SLR scale with ITRF from -5mm in ITRF2014 datasets to -1mm in ITRF2020 datasets. VLBI exhibits a drift in scale around 2013, resulting in an approximate scale difference of 0.21mm/year. Therefore, when using VLBI for scale definition, this drift needs to be taken into consideration. The stability of DORIS origin observations has been enhanced, with the scale consistency with ITRF falling within the range of 5-10mm. The datum accuracy of DORIS significantly improves with the progression of time. The rates of X and Y translation components between GNSS 2020 input data and ITRF2020 indicate

{\dot{T}}_{X} = 0.07 m m / y

and

{\dot{T}}_{y} = - 0.05 m m / y

The decreasing standard deviations of the Polar motion parameter (XPO, YPO) discrepancies between Stacking TRFs and 14C04 (20C04) indicating an improvement in the precision of polar motion observations for all of the four techniques. The standard deviations of (XPO, YPO) offsets from 2014 to 2020 are: (0.059, 0.049) to (0.044, 0.041) for GNSS, (0.279, 0.273) to (0.238, 0.247) for SLR, (0.739, 0.731) to (0.522, 0.524) for VLBI and (0.666, 0.633) to (0.422, 0.395) for DORIS in miliarcseconds.

From the perspective of the WRMS in station coordinates, Since the inception of the technique, the station coordinate WRMS of DORIS decreased from 30mm to 5mm for X and Y components, and 25mm to 5mm for Z component; SLR WRMS decreased from 20mm to better than 10mm (X, Y and Z); GNSS WRMS decreased from 4mm to 1.5mm (X and Y) and 5mm to 2mm (Z); while VLBI shows no significant change.

Author Contributions

Jin Zhang did conceptualization, methodology, software, writing original draft. Chengli Huang and Lizhen Lian designed this research, did review and editing. All authors reviewed the manuscript.

Funding

This Study is supported by National Nature Science Foundation of China (Grants 12233010, 11903065).

Data Availability Statement

Space Geodesy solutions can be found at: ftp://gdc.cddis.eosdis.nasa.gov.

Acknowledgments

We appreciate the IGS, ILRS, IVS and IDS for providing the Space Geodesy solutions. We also thanks to ITRF for the post-seismic deformation results and discontinuity detection results. Especial thank goes to Manuela Seitz for sending us the 12-hour 2020 VLBI solutions.

Conflicts of Interest

The authors declare that they have no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:

AC	Analysis Center
CC	Combination Center
CM	Center of Mass
DORIS	Doppler Orbitography and Radiopositioning integrated by Satellite
EOP	Earth Orientation Parameters
GNSS	Global Navigation Satellite System
ITRF	International Terrestrial Reference Frame
NNR	no-net-rotation
NNT	no-net-translation
NNS	no-net-scale
PCO	antenna phase center offset
SLR	Satellite Laser Ranging
TRF	Terrestrial Reference Frame
VLBI	Very Long Baseline Interferometry

References

Altamimi, Z.; Rebischung, P.; Metivier, L.; Collilieux, X. ITRF2014: A new release of the International Terrestrial Reference Frame modeling nonlinear station motions. Journal of Geophysical Research-Solid Earth 2016, 121, 6109–6131. [Google Scholar] [CrossRef]
Altamimi, Z.; Rebischung, P.; Collilieux, X.; Métivier, L.; Chanard, K. ITRF2020: an augmented reference frame refining the modeling of nonlinear station motions. Journal of Geodesy 2023, 97. [Google Scholar] [CrossRef]
Lian, L.-Z.; Wang, J.-X.; Huang, C.-L.; Xu, M.-H. Weekly inter-technique combination of SLR, VLBI, GPS and DORIS at the solution level. Research in Astronomy and Astrophysics 2018, 18. [Google Scholar] [CrossRef]
Altamimi, Z.; Métivier, L.; Rebischung, P.; Collilieux, X.; Chanard, K.; Barnéoud, J. ITRF2020 Plate Motion Model. Geophysical Research Letters 2023, 50. [Google Scholar] [CrossRef]
Argus, D.F.; Heflin, M.B. Plate motion and crustal deformation estimated with geodetic data from the Global Positioning System. Geophysical Research Letters 2012, 22, 1973–1976. [Google Scholar] [CrossRef]
Gomez, D.D.; Pinon, D.A.; Smalley, R.; Bevis, M.; Cimbaro, S.R.; Lenzano, L.E.; Baron, J. Reference frame access under the effects of great earthquakes: a least squares collocation approach for non-secular post-seismic evolution. Journal of Geodesy 2016, 90, 263–273. [Google Scholar] [CrossRef]
Xu, C.Y.; Chao, B.F. Seismological versus geodetic reference frames for seismic dislocation: consistency under momentum conservations. Geophysical Journal International 2015, 200, 998–1002. [Google Scholar] [CrossRef]
Fu, Y.; Argus, D.F.; Landerer, F.W. GPS as an independent measurement to estimate terrestrial water storage variations in Washington and Oregon. Journal of Geophysical Research: Solid Earth 2015, 120, 552–566. [Google Scholar] [CrossRef]
Borsa, A.A.; Agnew, D.C.; Cayan, D.R. Remote Hydrology. Ongoing drought-induced uplift in the western United States. Science 2014, 345, 1587–1590. [Google Scholar] [CrossRef]
Argus, D.F.; Peltier, W.R.; Watkins, M.M. Glacial isostatic adjustment observed using very long baseline interferometry and satellite laser ranging geodesy. Journal of Geophysical Research: Solid Earth 1999, 104, 29077–29093. [Google Scholar] [CrossRef]
Collilieux, X.; Wöppelmann, G. Global sea-level rise and its relation to the terrestrial reference frame. Journal of Geodesy 2010, 85, 9–22. [Google Scholar] [CrossRef]
Wöppelmann, G.; Marcos, M. Vertical land motion as a key to understanding sea level change and variability. Rev Geophys 2016, 54, 64–92. [Google Scholar] [CrossRef]
Liu, J.; Chen, J.; Liu, P.; Tan, W.; Dong, D.; Qu, W. Comparison and Assessment of Three ITRS Realizations. Remote Sensing 2021, 13. [Google Scholar] [CrossRef]
Altamimi, Z.; Collilieux, X.; Legrand, J.; Garayt, B.; Boucher, C. ITRF2005: A new release of the International Terrestrial Reference Frame based on time series of station positions and earth orientation parameters. Journal of Geophysical Research-Solid Earth 2007, 112, 19. [Google Scholar] [CrossRef]
Rebischung, P.; Altamimi, Z.; Ray, J.; Garayt, B. The IGS contribution to ITRF2014. Journal of Geodesy 2016, 90, 611–630. [Google Scholar] [CrossRef]
Luceri, V.; Pirri, M.; Rodríguez, J.; Appleby, G.; Pavlis, E.C.; Müller, H. Systematic errors in SLR data and their impact on the ILRS products. Journal of Geodesy 2019, 93, 2357–2366. [Google Scholar] [CrossRef]
Rodríguez, J.; Appleby, G.; Otsubo, T. Upgraded modelling for the determination of centre of mass corrections of geodetic SLR satellites: impact on key parameters of the terrestrial reference frame. Journal of Geodesy 2019, 93, 2553–2568. [Google Scholar] [CrossRef]
Appleby, G.; Rodriguez, J.; Altamimi, Z. Assessment of the accuracy of global geodetic satellite laser ranging observations and estimated impact on ITRF scale: estimation of systematic errors in LAGEOS observations 1993-2014. Journal of Geodesy 2016, 90, 1371–1388. [Google Scholar] [CrossRef]
Pavlis, E.; Luceri, V.; Basoni, A.; Sarrocco, D.; Kuzmicz-Cieslak, M.; Evans, K.; Bianco, G. ITRF2020: The ILRS Contribution and Operational Implementation. 2023. [Google Scholar] [CrossRef]
Hellmers, H.; Modiri, S.; Bachmann, S.; Thaller, D.; Bloßfeld, M.; Seitz, M.; Gipson, J. Combined IVS Contribution to the ITRF2020. Cham, 2023; pp. 3-13.
Bachmann, S.; Thaller, D.; Roggenbuck, O.; Lösler, M.; Messerschmitt, L. IVS contribution to ITRF2014. Journal of Geodesy 2016, 90, 631–654. [Google Scholar] [CrossRef]
Moreaux, G.; Lemoine, F.G.; Capdeville, H.; Otten, M.; Štěpánek, P.; Saunier, J.; Ferrage, P. The international DORIS service contribution to ITRF2020. Advances in Space Research 2023, 72, 65–91. [Google Scholar] [CrossRef]
Moreaux, G.; Lemoine, F.G.; Capdeville, H.; Kuzin, S.; Otten, M.; Stepanek, P.; Willis, P.; Ferrage, P. The International DORIS Service contribution to the 2014 realization of the International Terrestrial Reference Frame. Advances in Space Research 2016, 58, 2479–2504. [Google Scholar] [CrossRef]
Metivier, L.; Altamimi, Z.; Rouby, H. Past and present ITRF solutions from geophysical perspectives. Advances in Space Research 2020, 65, 2711–2722. [Google Scholar] [CrossRef]
Belda, S.; Heinkelmann, R.; Ferrandiz, J.M.; Nilsson, T.; Schuh, H. On the consistency of the current conventional EOP series and the celestial and terrestrial reference frames. Journal of Geodesy 2017, 91, 135–149. [Google Scholar] [CrossRef]
Blewitt, G.; Heflin, M.B.; Webb, F.H.; Lindqwister, U.J.; Malla, R.P. GLOBAL COORDINATES WITH CENTIMETER ACCURACY IN THE INTERNATIONAL TERRESTRIAL REFERENCE FRAME USING GPS. Geophysical Research Letters 1992, 19, 853–856. [Google Scholar] [CrossRef]
Petit, G.; Luzum, B. IERS conventions (2010). Tech. Rep. DTIC Document 2010, 36, 180. [Google Scholar]
Dong, D.; Yunck, T.; Heflin, M. Origin of the International Terrestrial Reference Frame. Journal of Geophysical Research: Solid Earth 2003, 108. [Google Scholar] [CrossRef]
Huang, C.; Jin, W.; Xu, H. The terrestrial and lunar reference frame in lunar laser ranging. Journal of Geodesy 1999, 73, 125–129. [Google Scholar] [CrossRef]
Dong, D.; Yunck, T.; Heflin, M. Origin of the international Terrestrial Reference Frame. Journal of Geophysical Research-Solid Earth 2003, 108, 10. [Google Scholar] [CrossRef]
Kwak, Y.; Blossfeld, M.; Schmid, R.; Angermann, D.; Gerstl, M.; Seitz, M. Consistent realization of Celestial and Terrestrial Reference Frames. Journal of Geodesy 2018, 92, 1047–1061. [Google Scholar] [CrossRef]
Kotsakis, C. Reference frame stability and nonlinear distortion in minimum-constrained network adjustment. Journal of Geodesy 2012, 86, 755–774. [Google Scholar] [CrossRef]
Davies, P.; Blewitt, G. Methodology for global geodetic time series estimation: A new tool for geodynamics. Journal of Geophysical Research-Solid Earth 2000, 105, 11083–11100. [Google Scholar] [CrossRef]
Altamimi, Z.; Sillard, P.; Boucher, C. ITRF2000: A new release of the International Terrestrial Reference frame for earth science applications. Journal of Geophysical Research-Solid Earth 2002, 107, 19. [Google Scholar] [CrossRef]
Sillard, P.; Boucher, C. A review of algebraic constraints in terrestrial reference frame datum definition. Journal of Geodesy 2001, 75, 63–73. [Google Scholar] [CrossRef]
Song, S.Z.; Zhang, Z.K.; Wang, G.L. Toward an Optimal Selection of Constraints for Terrestrial Reference Frame (TRF). Remote Sensing 2022, 14, 18. [Google Scholar] [CrossRef]
Altamimi, Z.; Collilieux, X. IGS contribution to the ITRF. Journal of Geodesy 2009, 83, 375–383. [Google Scholar] [CrossRef]
Collilieux, X.; Metivier, L.; Altamimi, Z.; van Dam, T.; Ray, J. Quality assessment of GPS reprocessed terrestrial reference frame. Gps Solutions 2011, 15, 219–231. [Google Scholar] [CrossRef]
Haines, B.J.; Bar-Sever, Y.E.; Bertiger, W.I.; Desai, S.D.; Harvey, N.; Sibois, A.E.; Weiss, J.P. Realizing a terrestrial reference frame using the Global Positioning System. Journal of Geophysical Research-Solid Earth 2015, 120, 5911–5939. [Google Scholar] [CrossRef]

Figure 1. Station and core station distributions of Space Geodesy input data. “Common” and “Common Core” refers to stations and core stations used in both 2014 and 2020. “2020”, “2014”, “2020 Core” and “2014 Core” means stations and core stations used only in 2014 or 2020. The station numbers are counted and labeled within their respective parentheses.

Figure 2. Translation and scale parameter series between the observations and the Stacking Space Geodesy TRFs under two types of constraints: internal (inner) constraints and minimum constraints. The linear fit lines along with their slopes for the results of minimum constraints are also illustrated.

Figure 3. WRMS of posteriori station coordinate residuals between observations and stacked Space Geodesy TRFs. To better identify variations in station accuracy, quadratic polynomial fits were applied to the WRMS series for GNSS, SLR, and DORIS.

Figure 4. Residuals of XPO and YPO from Stacking Space Geodesy TRFs compared to 14C04 and 20C04. The mean and standard deviation statistics for the residual sequences are presented below the respective graphs. “std” refers to standard deviation.

Table 1. This is a table. Tables should be placed in the main text near to the first time they are cited. Space Geodesy Inputs utilized in this work. TN in the first column identifies the technique type. TS in the third column designates the time span. SOL in the third column specifies the kind of SINEX format released by the four corresponding technique centers: VC stands for variance-covariance, NE for normal equations. TR in the fourth column relates to the temporal resolution; CONS in the fifth column is the constraint type; SN in the sixth column is the solution number namely SINEX file numbers for each technique selected here.

TN	TS	SOL	TR	CONS	SN
GNSS	1994.0-2015.1 1994.0-2021.0	VC	Weekly	Minimum	1094 1408
SLR	1993.0-2015.1 1993.0-2021.0	VC	Weekly	Loose	1135 1451
VLBI	1991.5-2105.1 1991.5-2021.0	NE	Session wise	None	2867 4422
DORIS	1993.0-2015.1 1993.0-2021.0	VC	Weekly	Minimum	1140 1456

Table 2. Outlier ratios (OR), covariance scale factor (

δ^{2}

) and number of iterations (Num).

Table 2. Outlier ratios (OR), covariance scale factor (

δ^{2}

) and number of iterations (Num).

Table 3. The 14 transformation parameters between Stacking Space Geodesy TRFs and ITRF2104 (ITRF2020).

Solutions	Tx mm	Ty mm	Tz mm	D ppb	Rx .001”	Ry .001”	Rz .001”	Epoch	Datum Definition
Rates	$\dot{T} x$ mm/y	$\dot{T} y$ mm/y	$\dot{T} z$ mm/y	$\dot{D}$ ppb/y	$\dot{R} x$ .001”/y	$\dot{R} y$ .001”/y	$\dot{R} z$ .001”/y	Epoch	Datum Definition
14 Transformation parameters between GNSS Stacking TRF 2020 (2014) and ITRF2020 (2014)
GNSS2020 rates	0.00 0.00	0.00 0.00	0.00 0.00	0.00 0.00	0.00 0.00	0.00 0.00	0.00 0.00	2015.0	Origin: ITRF Scale: ITRF
GNSS2020 rates	-0.81 0.07	-0.55 -0.05	2.71 0.22	0.70 0.02	0.00 0.00	0.03 0.00	0.00 0.00	2015.0	Origin: Internal Scale: Internal
GNSS2014 rates	0.00 0.00	0.00 0.00	0.00 0.00	0.00 0.00	0.00 0.00	0.00 0.00	0.00 0.00	2010.0	Origin: ITRF Scale: ITRF
GNSS2014 rates	1.89 -0.02	2.17 0.01	2.68 -0.18	-0.37 0.03	0.04 0.00	-0.02 0.00	-0.01 0.00	2010.0	Origin: Internal Scale: Internal
14 Transformation parameters between SLR Stacking TRF 2020 (2014) and ITRF2020 (2014)
SLR2020 rates	0.00 0.00	0.00 0.00	0.00 0.00	0.00 0.00	0.00 0.00	0.00 0.00	0.00 0.00	2015.0	Origin: ITRF Scale: ITRF
SLR2020 rates	-0.38 -0.06	-0.13 0.00	-0.23 0.05	-0.04 0.03	0.00 0.00	0.00 0.00	0.00 0.00	2015.0	Origin: Internal Scale: Internal
SLR2014 rates	0.00 0.00	0.00 0.00	0.00 0.00	0.00 0.00	0.00 0.00	0.00 0.00	0.00 0.00	2010.0	Origin: ITRF Scale: ITRF
SLR2014 rates	-0.29 -0.01	-0.76 -0.17	0.22 -0.04	-0.64 0.01	-0.01 0.00	0.00 0.00	0.00 0.00	2010.0	Origin: Internal Scale: Internal
14 Transformation parameters between VLBI Stacking TRF 2020 (2014) and ITRF2020 (2014)
VLBI2020 rates	0.00 0.00	0.00 0.00	0.00 0.00	0.00 0.00	0.00 0.00	0.00 0.00	0.00 0.00	2015.0	Origin: ITRF Scale: ITRF
VLBI2020 rates	-0.16 -0.01	1.21 0.05	-1.97 -0.07	0.69 0.03	0.00 0.00	0.00 0.00	0.00 0.00	2015.0	Origin: ITRF Scale: Internal
VLBI2014 rates	0.00 0.00	0.00 0.00	0.00 0.00	0.00 0.00	0.00 0.00	0.00 0.00	0.00 0.00	2010.0	Origin: ITRF Scale: ITRF
VLBI2014 rates	-0.13 0.00	0.42 -0.01	-1.36 0.02	0.38 -0.01	0.00 0.00	0.00 0.00	0.00 0.00	2010.0	Origin: ITRF Scale: Internal
14 Transformation parameters between DORIS Stacking TRF 2020 (2014) and ITRF2020 (2014)
DORIS2020 rates	0.00 0.00	0.00 0.00	0.00 0.00	0.00 0.00	0.00 0.00	0.00 0.00	0.00 0.00	2015.0	Origin: ITRF Scale: ITRF
DORIS2020 rates	-3.16 0.02	1.26 0.01	-5.76 0.03	1.30 0.03	0.04 0.00	0.00 0.00	-0.04 0.00	2015.0	Origin: Internal Scale: Internal
DORIS2014 rates	0.00 0.00	-0.02 0.00	0.02 0.00	0.00 0.00	0.01 0.00	-0.01 0.00	0.00 0.00	2010.0	Origin: ITRF Scale: ITRF
DORIS2014 rates	-1.74 0.02	-2.54 -0.10	-10.59 -0.19	1.52 0.00	-0.03 -0.02	0.01 0.02	0.02 0.00	2010.0	Origin: Internal Scale: Internal

Table 4. The average WRMS for the four technologies which is calculated by taking the mean of the WRMS values from each station.

TN	Mean WRMS X (mm)	Mean WRMS Y (mm)	Mean WRMS Z (mm)	Datasets
GNSS	2.51 2.32	2.50 2.37	2.60 2.48	2014 2020
SLR	12.09 11.46	11.57 11.11	12.31 12.68	2014 2020
VLBI	5.28 5.22	5.50 5.60	6.19 6.25	2014 2020
DORIS	14.02 12.00	13.86 11.96	10.64 8.60	2014 2020

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Alerts

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Quality Assessment of GNSS, SLR, VLBI, and Doris Inputs for ITRF2014 and ITRF2020 Using Trf Stacking Methods

Abstract

Keywords:

Subject:

1. Introduction

2. Methods

2.1. Stacking Model

2.2. Datum Definition

2.3. Outliers and Variance Component Estimation

3. Results and Analysis

3.1. Data Introduction and Preprocessing

3.2. Stacking Results

3.3. Analysis of Translation and Scale Time Series

3.4. Analysis of Coordinate Residuals

3.5. XPO and YPO Residuals Compared to 14C04 and 20C04

4. Conclusions

Author Contributions

Funding

Data Availability Statement

Acknowledgments

Conflicts of Interest

Abbreviations

References

MDPI Initiatives

Important Links

Subscribe