Prerpints.org logo
Preprint
Article

Estimation of Environmental Effects and Response Time in Gas Phase Explosives Detection Using Photoluminescence Quenching Method

This version is not peer-reviewed.

Submitted:

12 February 2024

Posted:

12 February 2024

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract
Detecting the presence of explosives is important to protect human lives in military conflicts and peacetime. Gas-phase detection of explosives can make use of the change of material properties, which can be sensitive to environmental conditions such as temperature and humidity. This paper describes a remote-controlled automatic shutter method for environmental impact assessment of photoluminescence (PL) sensors under near-open conditions. Utilizing the remote-sensing method, we obtained environmental effects without being exposed to sensing vapor molecules, and explained how PL intensity was influenced by the temperature, humidity, and exposure time. We also developed a theoretical model including the effect of exciton diffusion for PL quenching, which worked well under limited molecular diffusions. Incomplete recovery of PL intensity, or degradation effect, was considered as an additional factor in the model.
Keywords: 
Subject: 
Chemistry and Materials Science  -   Polymers and Plastics

1. Introduction

Detecting the presence of explosives is important to protect human lives in military conflicts and in peacetime. In the case of landmine detection, the predominant approach is the use of metal detectors to identify metallic components of buried mines. However, this method faces challenges when detecting non-metallic mines, such as wooden mines or plastic explosives. To address this, ground penetrating radar (GPR) has been developed. Nevertheless, GPR has drawbacks such as complex signal processing and high power consumption. On the other hand, since most explosive materials contain nitro compounds such as trinitrotoluene (TNT) and dinitrotoluene (DNT) molecules, direct sensing of these molecules is possible by ion mobility spectrometry, surface-enhanced Raman spectroscopy, and photoluminescence (PL) based methods [1,2,3,4,5,6,7,8,9,10,11]. Among these methods, the PL-based method utilizing the decrease of PL intensity of sensing materials (known as fluorescence quenching) attracted much attention for fast and efficient detection [10]. One of the materials used for this method is conjugated polymers. The electron affinities of these sensing polymers are smaller than those of explosive molecules, and thus photoinduced electron transfer is allowed; this non-radiative recombination pathway by charge transfer, or energy migration, is known to be the essential mechanism of the PL quenching.
For real-time sensing, non-invasive and passive explosives detection in the vapor phase usually offers more advantages. Our motivation for the PL quenching study is utilizing conjugated polymer films for real-time applications. PL quenching experiments have been mostly carried out in solution-phase, probably because of the convenient use of commercially available PL equipment, but it has been reported that PL quenching mechanisms of polymers in solutions and those in films are governed by different factors [10].
Gas-phase detection makes use of the change of material properties including PL intensity, electrical conductivity, and electrochemical reaction rate, which can be sensitive to environmental conditions such as temperature and humidity. Ensuring a low false-positive rate under real environmental conditions has been a challenge in PL quenching-based sensors [12]. In this regard, improving environmental stability of PL intensity is necessary. For example, false positive alarms may be caused by the reduced PL intensity simply due to hot air inside of a building as we try to detect bombs in the building. Thus, to improve the reliability of the PL quenching sensors, there must be extra efforts to fully understand the changes in the PL intensity caused by various environmental conditions. The ultimate goal of our research is to develop an algorithm to compensate for the effects of environmental conditions. One alternative way is to keep the sensing parts at constant temperature and humidity, etc., which would be also difficult due to the continuous flow of the air that needs to be tested.
This paper demonstrated how one can evaluate environmental impacts due to temperature and humidity in explosives detection using PL quenching methods. PL quenching (PQ) efficiencies were measured repeatedly with a short time exposure of the explosive vapors under near-open conditions, while temperature and humidity inside of the PL apparatus were recorded in real time.

2. Experimental set-up for data acquisition

2.1. Materials and Methods

A pentiptycene-containing conjugated polymer (PCC) was used as the sensor material. The polymer samples were spin-coated on quartz substrates and used without additional treatment. The thickness of the film was estimated to be ~20 nm. PL measurements were performed in two different experimental set-ups; a home-made PL system that we reported previously [11] and a detector system developed by PNL Global (Seoul, South Korea). The former was used to measure PL spectra and to separately monitor temperature and humidity effects. The latter was used to detect 2,4-DNT vapor under near-open conditions in a custom-built lab.
Most of the vapor measurements were performed without controlling the room condition except for the air circulation system. However, some measurements were performed with a radiator-type heater (for a room) and a plate-type heater (for a box).

2.2. Automatic shutter control and real-time PL intensity monitoring system

A shutter was installed on an acrylic box (20x20x40 cm3), and the PL intensity of polymer film inside of the equipment placed in front of the shutter was monitored by opening and closing at regular times (Figure 1). Only 0.1 g of 2,4-DNT powders were placed inside of an acrylic box with a shutter that was remotely controlled in another city so that the exposure to the potentially harmful vapors can be minimized.
Data communications between the equipment and a computer were carried out through Bluetooth wireless communication, and the shutter was directly controlled from the computer through wired serial communication. With pre-scheduled experimental plans, measurements (the equipment control, the shutter operation, and data transmission) were started by remotely accessing the control computer (located in Seoul) from another computer (located in Daejeon), and data were typically acquired for several hours.
Figure 1a shows a schematic diagram of a box with an automatic shutter control system as well as an apparatus used for PL quenching measurements. The temporal variation of PL intensity (black) together with that of the shutter angle (red) are shown in Figure 1c. The apparatus contains sensing polymer substrates, an LED, a photo-diode, a fan, and a flow-guiding part to supply air into an optical sensing part as well as to completely block the room light (Figure 1b). In this study, air flow velocity near the polymer sample was ~10 m/s.
As seen in Figure 1c, PL intensity was immediately decreased within 1 sec with shutter opening and started recovering within 2 sec with shutter closing, although the complete recovery of PL intensity may take a few minutes. The details of the response time will be discussed in Section 3.2.
To monitor the PL intensity, an excitation wavelength of 400 nm from a light-emitting diode (LED) was used. For real-time intensity monitoring for gas-phase sensing, a photo-diode was utilized in the PL apparatus and band-pass (BP) optical filters were used to remove the parasitically scattered light from the LED.

2.3. Measurements of photoluminescence spectra

Pentiptycene-containing conjugated (PCC) polymer films coated on quartz substrates were used for explosives gas sensing. Figure 2 shows the PL spectrum of a PCC film. In the set-up, the parasitically scattered light at 400 nm (3 eV) was monitored to ensure the absence of water condensation in the optical components as well as to ensure the stability of the excitation light.

2.4. In-situ measurement of temperature and humidity

Temperature and humidity sensors were positioned close to the polymer substrates inside of the apparatus. Figure 3 shows an example of a data set composed of temperature, humidity, PL intensity, and shutter angle as a function of time. With the decrease of the temperature (blue), relative humidity (magenta) was increased as expected, and the PL (black) quenching was observed for the exposure of DNT vapors as a response to the opening of the shutter in five-minute intervals. It was often observed that the PQ was decreased after 20-30 times of shutter openings, as the vapor molecules repeatedly escaped from the box. On the other hand, the repeated responses demonstrate that the amount of the vapor molecules that escape during 10 sec is considerably lower than the total amount of the DNT vapor molecules inside the box.

3. Results and discussion

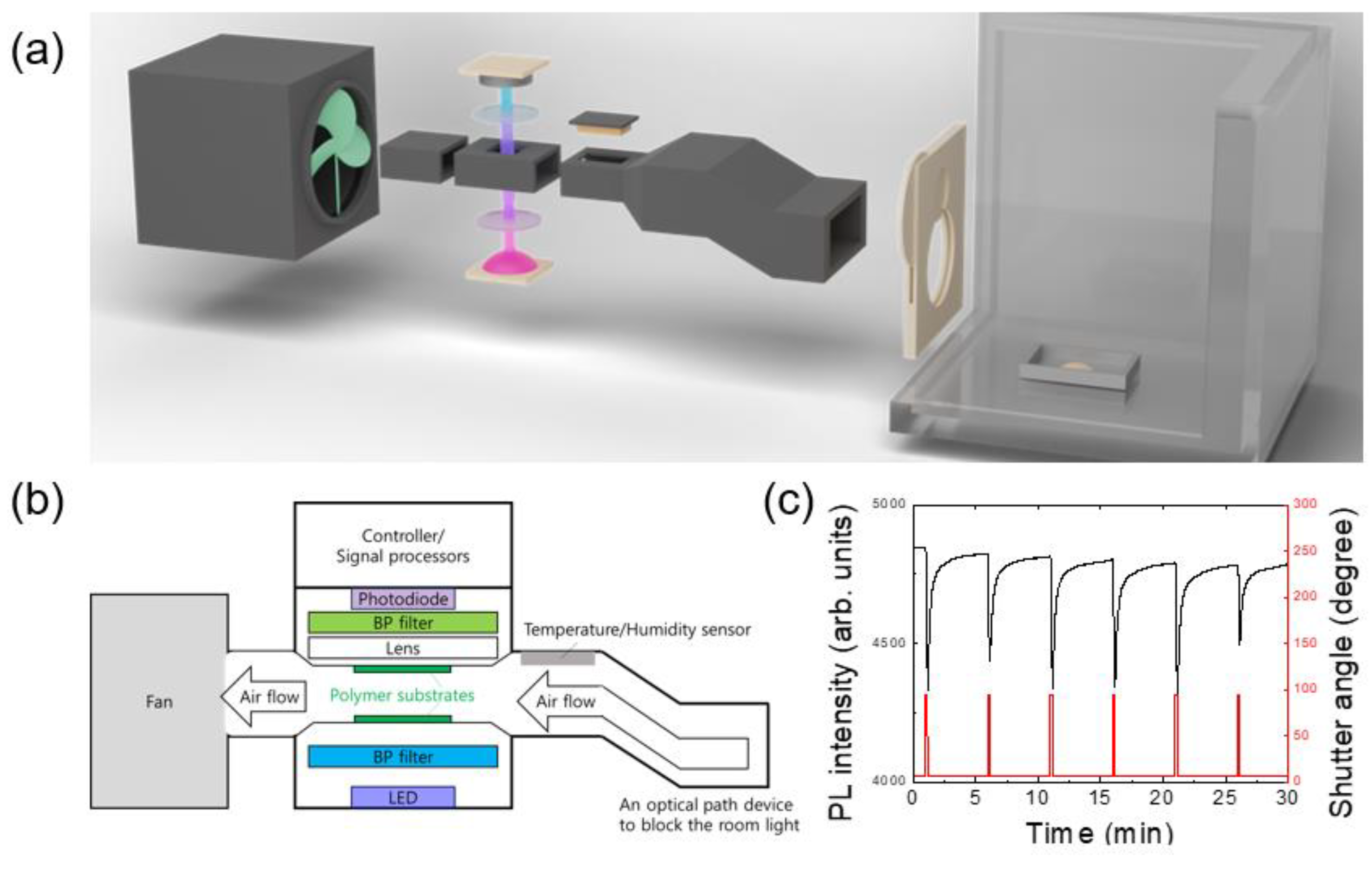
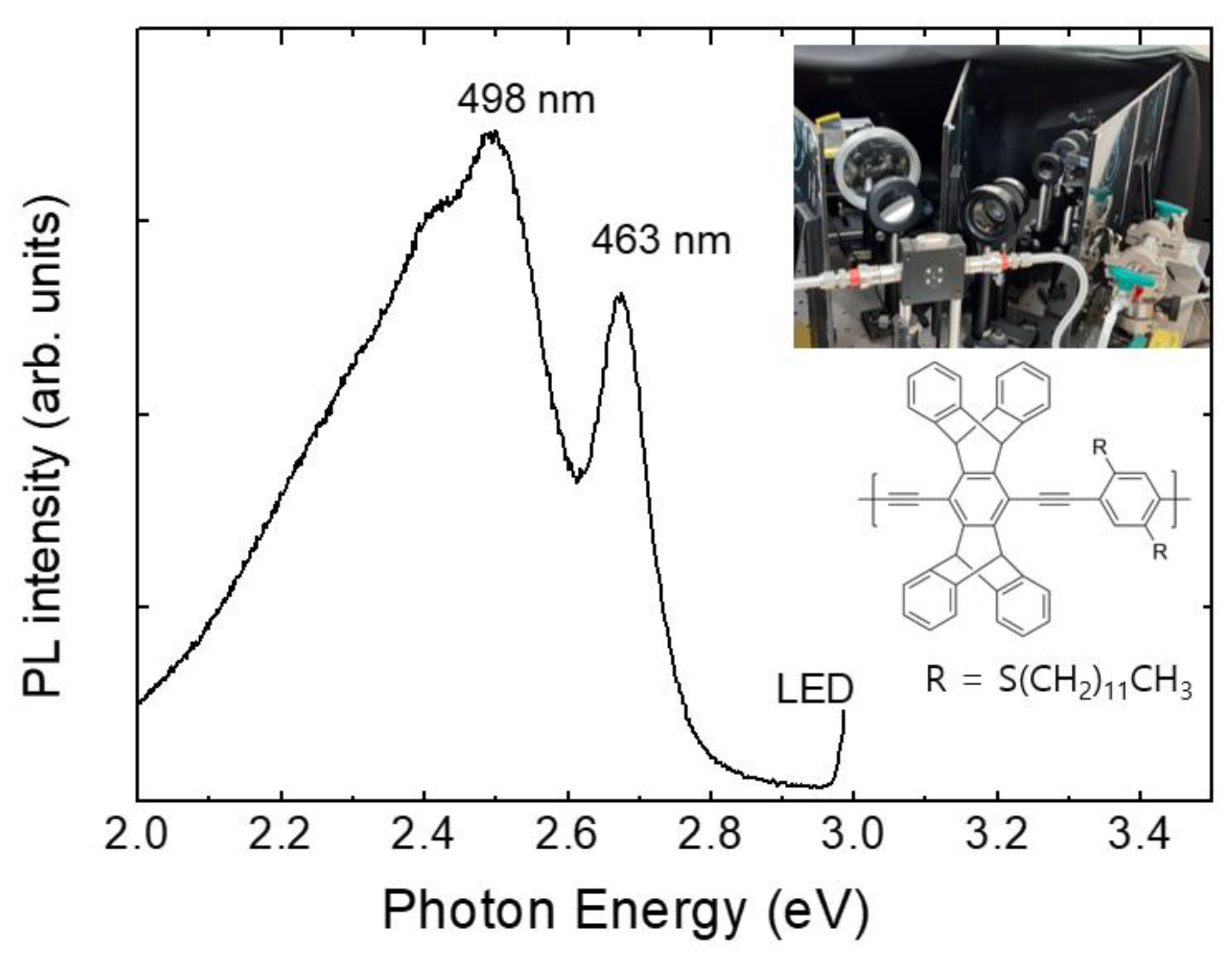
Most measurements were started in the evening and the air of the lab. was ventilated in the next morning by opening the windows. After using a polymer film over one month, the PL intensity gradually decreased, but the sensing performance was not noticeably decreased until the PL intensity became about 1/3 of the initial value. Even when no measurements were carried out for 10 days, the PL intensity was found to be slightly decreased. For this reason, spin-coated polymer films were usually stored in a vacuum-sealed box and were covered with aluminum foil to block the lights.

3.1. Shutter exposure time dependence

PL intensity was decreased whenever a shutter was open, as DNT molecules were adsorbed on the surface of a polymer film, or possibly diffused into the film. Figure 4a shows the integrated PL intensity (black) of a polymer film and shutter angle (red) as a function of time with various opening (exposure) times. The change of the PL intensity every 5 minutes with the shutter opening was apparent in Figure 4a. The exposure time for the DNT vapor was pre-scheduled with random values ranging from 2 seconds to 20 seconds.
The time response of the PL intensity with the opening and closing of the shutters will be discussed in detail in the next section together with a theoretical model.

3.2. Response time analysis

In this section, we discuss the temporal PL behavior during quenching and recovering responses. We started with the classical Langmuir adsorption model for the analyte mass transport and utilized the exciton diffusion model for quenching efficiency calculation.
In some cases, the dynamics of analyte molecules in PL quenching were explained by molecular diffusion into sensing films. After the sensing films were exposed to quencher vapors, swelling and mass increase of the polymer films were reported through neutron scattering and in-situ QCM measurements, which supported a specific diffusion mechanism of analyte molecules, the so-called case 2, or super case 2 [13,14,15,16]. In addition, as a result of these studies, it was argued that molecular diffusion may be more important than exciton diffusion [15], but most of these diffusion studies have been conducted under conditions such as exposure to analyte vapor for several minutes or longer. In our cases with repeated exposure to diluted analyte(2,4-DNT) vapor, it is unclear how much exciton diffusion and analyte diffusion contribute to quenching, respectively, and a cautious approach may be necessary.
Regardless of the molecular diffusion and adsorption mechanism, desorption of adsorbed/absorbed molecules does not ensure complete recovery of PL intensity. We note here that in most polymer/dendrimer PL quenching sensors the PL intensity of a film once exposed to the DNT analytes may not recover to its original value despite the decrease in adsorption/absorption mass [15,16]. This phenomenon is probably related to the binding affinity between the analyte molecules and the polymers as well as the molecular diffusion behavior in the film, and the quenching efficiency may also be affected by the binding affinity [13].
To obtain a sufficient amount of data without significant DNT diffusion into the sensing film, we chose a rather short exposure time (10 s) and a time interval of 5-min. We try to understand the temporal response of PL and environmental effects on PL under such simple conditions first. Then an incomplete recovery of the PL, which was more pronounced for higher DNT vapor pressures and longer DNT exposures, will be discussed in Section 3.4.
We start with the classical Langmuir adsorption model to explain the molecular dynamics of the analyte vapor molecules. In the model, the adsorption and desorption processes can be expressed by the following equations:
Adsorption:
θ 0 = 0 d θ d t =   k a d s o r p t i o n P ( 1 − θ ) −   k d e s o r p t i o n θ θ ( t ) = K e q P 1 + K e q P ( 1 − e − k d e s o r p t i o n ( K e q P + 1 ) t )
Desorption:
d θ d t = − k d e s o r p t i o n θ θ ( t ) = θ q 0 e − k d e s o r p t i o n t ,
where
t : t i m e P : f r a c t i o n a l   p r e s s u r e   o f   t h e   q u e n c h e r   v a p o r   o n   t h e   s u r f a c e   o f   f i l m s θ : s u r f a c e   c o v e r a g e θ q 0 : s u r f a c e   c o v e r a g e   a t   t h e   m o m e n t   w h e n   t h e   s h u t t e r   i s   c l o s e d   ( t = t q ) k a d s o r p t i o n : a d s o r p t i o n   r a t e   c o n s t a n t k d e s o r p t i o n : d e s o r p t i o n   r a t e   c o n s t a n t K e q = k a d s o r p t i o n k d e s o r p t i o n
To relate the surface coverage and the quenching efficiency, we make use of a 1-D exciton diffusion model.
If we consider only the quenching sites at the surface (x=d), the differential equation for the diffusion model will have the form:
f o r   0 < x < d ∂ n ( x ,   t ) ∂ t = D ∂ 2 n ( x ,   t ) ∂ x 2 − 1 τ n ( x ,   t ) + g  
With boundary conditions:
∂ n ( x ,   t ) ∂ x | x = 0 = 0 ∂ n ( x ,   t ) ∂ t | x = d = D ∂ 2 n ( x ,   t ) ∂ x 2 | x = d + k q n ( d ,   t ) [ S ] θ ( t )
At the surface ( x = d ), the amount of exciton diffusion flux is proportional to the rate of the quenching reaction.
Here,
x : t h e   c o o r d i n a t e   w h i c h   i s   n o r m a l   t o   t h e   f i l m   s u r f a c e n : e x c i t o n   d e n s i t y τ : e x c i t o n   l i f e t i m e g : e x c i t o n   g e n e r a t i o n   r a t e D : e x c i t o n   d i f f u s i o n   c o n s t a n t d : f i l m   t h i c k n e s s k q : q u e n c h i n g   r a t e   c o n s t a n t [ S ] : t o t a l   s u r f a c e     s i t e   d e n s i t y   f o r   a d s o r p t i o n   o f   q u e n c h e r   m o l e c u l e s Q : t h e   r a t e   o f   q u e n c h i n g   a t   t h e   s u r f a c e   b y   t h e   a d s o r b e d   q u e n c h e r   m o l e c u l e s
The solution of this differential equation is:
n ( x ,   t ) = τ g ( 1 − cosh ( x L D ) τ k q [ S ] θ ( t ) ( 1 + τ k q [ S ] θ ( t ) ) cosh ( d L D ) ) n ( d ,   t ) = τ g 1 + τ k q [ S ] θ ( t )
where
L D : e x c i t o n   d i f f u s i o n   l e n g t h   ( L D = D τ ) .
Then, PL intensity I(t) becomes:
I ( t ) I 0 = ∫ 0 d n   d x ∫ 0 d n | θ = 0   d x = ∫ 0 d ( 1 − cosh ( x L D ) τ k q [ S ] θ ( t ) ( 1 + τ k q [ S ] θ ( t ) ) cosh ( d L D ) )   d x ∫ 0 d 1   d x = 1 − τ k q [ S ] θ ( t ) 1 + τ k q [ S ] θ ( t ) L D d tan h ( d L D )
If we combine the exciton diffusion model with the Langmuir adsorption model, the PL intensity is
Adsorption:
I ( t ) I 0 = 1 − τ k q [ S ] K e q P 1 + K e q P ( 1 − e − k d e s o r p t i o n ( K e q P + 1 ) t ) 1 + τ k q [ S ] K e q P 1 + K e q P ( 1 − e − k d e s o r p t i o n ( K e q P + 1 ) t ) L D d tan h ( d L D )
Desorption:
I ( t ) I 0 = 1 − τ k q [ S ] θ q 0 e − k d e s o r p t i o n ( t − t q ) 1 + τ k q [ S ] θ q 0 e − k d e s o r p t i o n ( t − t q ) L D d tan h ( d L D ) θ q 0 : s u r f a c e   c o v e r a g e   a t   t = t q t q : e x p o s u r e   t i m e
Then the expression for PQ in adsorption becomes:
P Q = ( 1 − e − k t ) A k + ( 1 − e − k t ) Φ
where
A = 1 τ k q [ S ] k a d s o r p t i o n P k = k d e s o r p t i o n ( K e q P + 1 ) Φ = L D d tan h ( d L D )
The fitting parameter Φ represents the effect of polymer film thickness and exciton diffusion length, which is independent of other parameters. For photovoltaic conversion in organic photovoltaics, exciton diffusion is important since excitons need be collected before the recombination of excitons [17]. In case of PL quenching for sensing applications, PQ will be affected by the exciton diffusion since the photo-electrons which are generated within the diffusion length from the film surface can diffuse to the surface where the sensing molecules are adsorbed.
In this model, we assumed that there is a finite number of binding sites on the surface. In these expressions, some effects were not taken into consideration, such as photo-induced PL enhancement, photo-degradation, and diffusion (out-diffusion) of DNT molecules into (from) the inner part of the polymer films.
To take care of these effects, we modified as follows:
For adsorption:
I ( t ) I 0 =   1 − ( 1 − e − k t ) A k + ( 1 − e − k t ) Φ + b t P Q ( t ) = 1 − I ( t ) I 0 = ( 1 − e − k t ) A k + ( 1 − e − k t ) Φ − b t
For desorption:
I ( t ) I 0 = 1 − a ( 1 − e − k t q ) e − k d e s o r p t i o n ( t − t q ) A k + ( 1 − e − k t q ) e − k d e s o r p t i o n ( t − t q ) Φ − ( 1 − a ) ( 1 − e − k t q ) A k + ( 1 − e − k t q ) Φ + b t = 1 − a ( 1 − e − k t q ) e − k d e s o r p t i o n ( t − t q ) A k + ( 1 − e − k t q ) e − k d e s o r p t i o n ( t − t q ) Φ − ( 1 − a ) ( P Q ( t q ) + b t q ) + b t a ,   b : c o n s t a n t s
Here, the variable ‘a’ represents PL intensity recovered during the refresh period with respect to Io. If PL is completely recovered, a=1. A non-zero value of 1-a means that the DNT molecules are strongly bound at the surface, or the DNT molecules from the inner part of the polymer films do not diffuse out completely. The parameter ‘b’ represents a slow linear term which may be due to other temporal responses including photo-induced PL enhancement and photo-degradation.
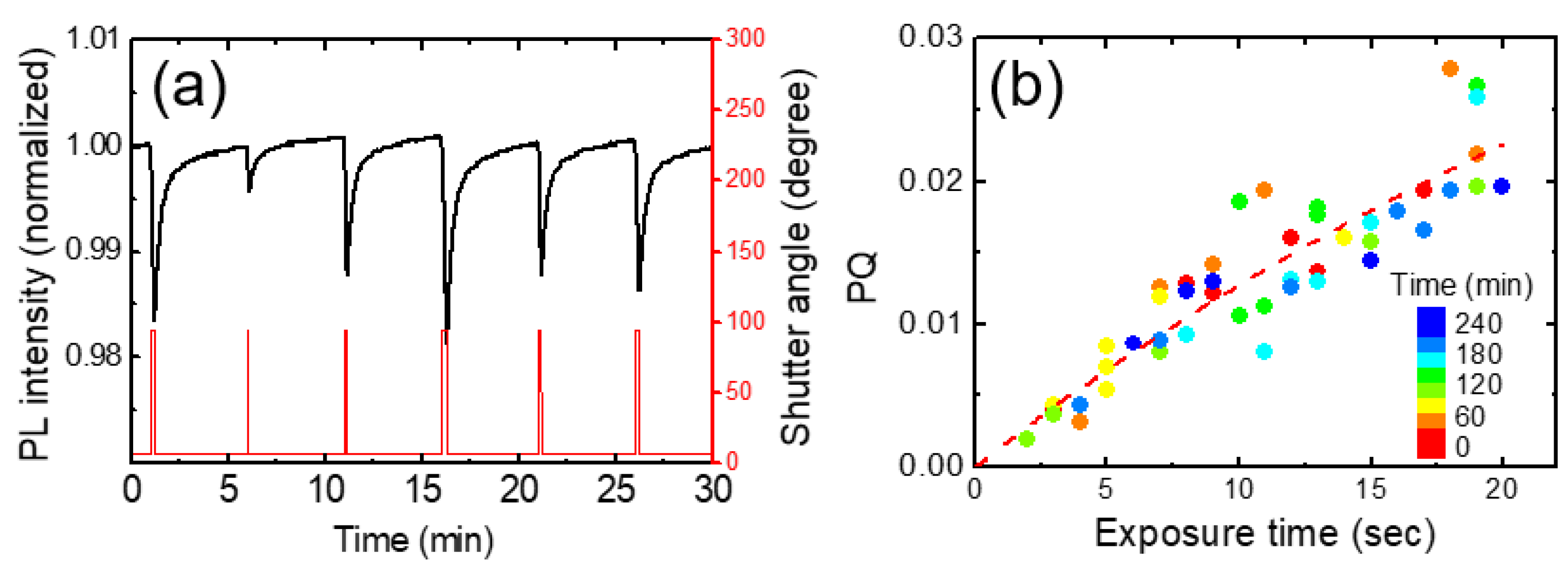
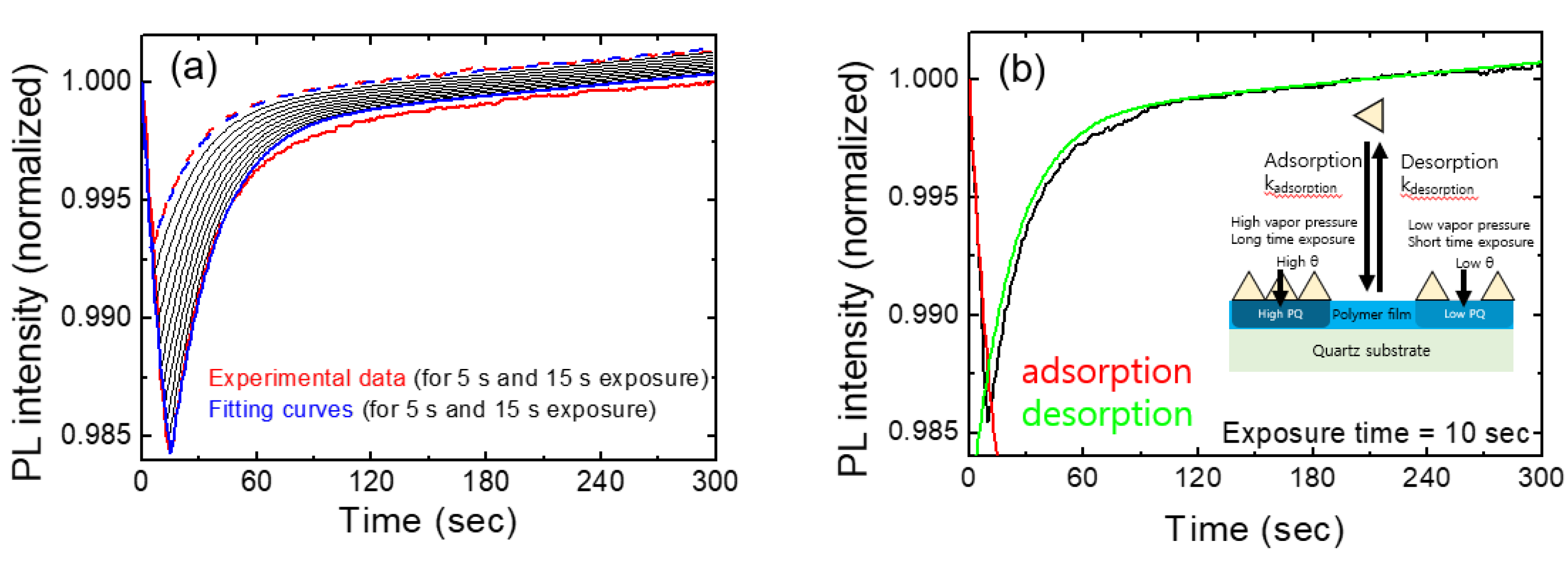
In Figure 5a, we show the temporal behavior of normalized PL intensities for various exposure times. The red curves represent experimental results for exposures of 5 s and 15 s, while the blue curves depict the model-predicted PL intensities for the corresponding exposure times. Additionally, black curves illustrate the expected PL intensities at 1 s intervals, ranging from 6 s to 14 s. These calculations were performed using fitting parameters derived from the 10 s exposure data.
As we checked the value of the linear term of bt in the Table, the linear contribution was significantly smaller than the other two terms, as expected. Despite many assumptions and simplifications, this model seemed to well explain the experimental results at least under the conditions of short exposure times (up to 15 seconds) and for relatively low vapor concentrations.
Table 1 shows the fitting parameters used for Figure 5. Instead of the individual values of ‘kadsorption’, ‘kq’, and dilution factor ‘Pr’, the value of ‘τkq[S]kadsorptionP2,4-DNTPr’ represents the quenching speed. P2,4-DNT is the equilibrium vapor pressure of DNT and the dilation factor ‘Pr’ is to take care of the fact that the vapor pressure of DNT molecules is significantly lower than that of the equilibrium vapor pressure at a given temperature due to the small amount of powders inside of the box; another factor for the dilation of the DNT vapors was due to the mixture of the air from the box and the air in the lab.
As the exposure time and the vapor pressure increase, the degradation of the polymer film may become severe, and hence it will be difficult to describe the temporal behavior of the PL intensity with this simplified model. Swelling and mass increase of polymer thin films exposed to high concentrations of quencher molecules have been reported.
In this study, the surface adsorption by exposure to low vapor pressure for a short time and the desorption of the adsorbed molecules were our main concerns, and the experiment was conducted under the condition that PL intensity was restored by more than 80% after the five-minute refresh time; the effect of molecular diffusion into the thin film was not our primary factor.
To explain the change in PL intensity due to continuous excitation light illumination and the incomplete recovery of the PL intensity in the quenching reaction, a and b parameters were introduced into the equation for the fitting process.

3.3. Effect of temperature and humidity

In this section, we discuss the temperature and humidity dependence of the polymer PL intensity and the real-time variation of the PL intensity, rather than of the quantitative characteristics of quenching behaviors.
It is well-known that PL intensity decreases with increasing temperature since the lattice vibrations, or phonons induce non-radiative recombination of photo-excited electrons. In addition to the PL intensity, other properties such as PL spectra [18], the adsorption of target molecules, and the efficiency of the quenching reaction can also be affected, and thus great efforts are needed to resolve all these issues. Of course, temperature has a great impact on the vapor pressure of target molecules, which will be discussed shortly at the end of this paper.
Although various temperature-dependent properties can affect sensing, PL intensity change with temperature is particularly important and also easy to monitor because the intensity changes even without the presence of analyte vapor. On the other hand, in the case of adsorption or reaction rate change, it is difficult to distinguish whether the effect is due to the vapor pressure or due to the reaction rate, and the temperature dependence of the reaction rate is not considered in this study.
In general, reducing the effect of humidity is an important issue for chemical sensors. In many cases, water molecules can induce oxidation or degradation of materials, and they can cause variations in the PL intensity for many materials including perovskites and polymers [19,20]. To prevent this, an additional hydrophobic protective layer or functionalization can be introduced [21], but the change due to moisture is still an important factor because such a protective layer can affect the sensing characteristics.
The optical properties of polymers are influenced by various factors such as molecular conformations, aggregation, and degree of crystallization [22,23]; the infiltration of water molecules into sensing materials can have a significant impact on those characteristics. One extreme example is a hydrogel, where its structure can be affected by humidity [24]. Not only for hydrophilic polymers but also for hydrophobic polymers, it is important to consider the influence of humidity on PL intensity.
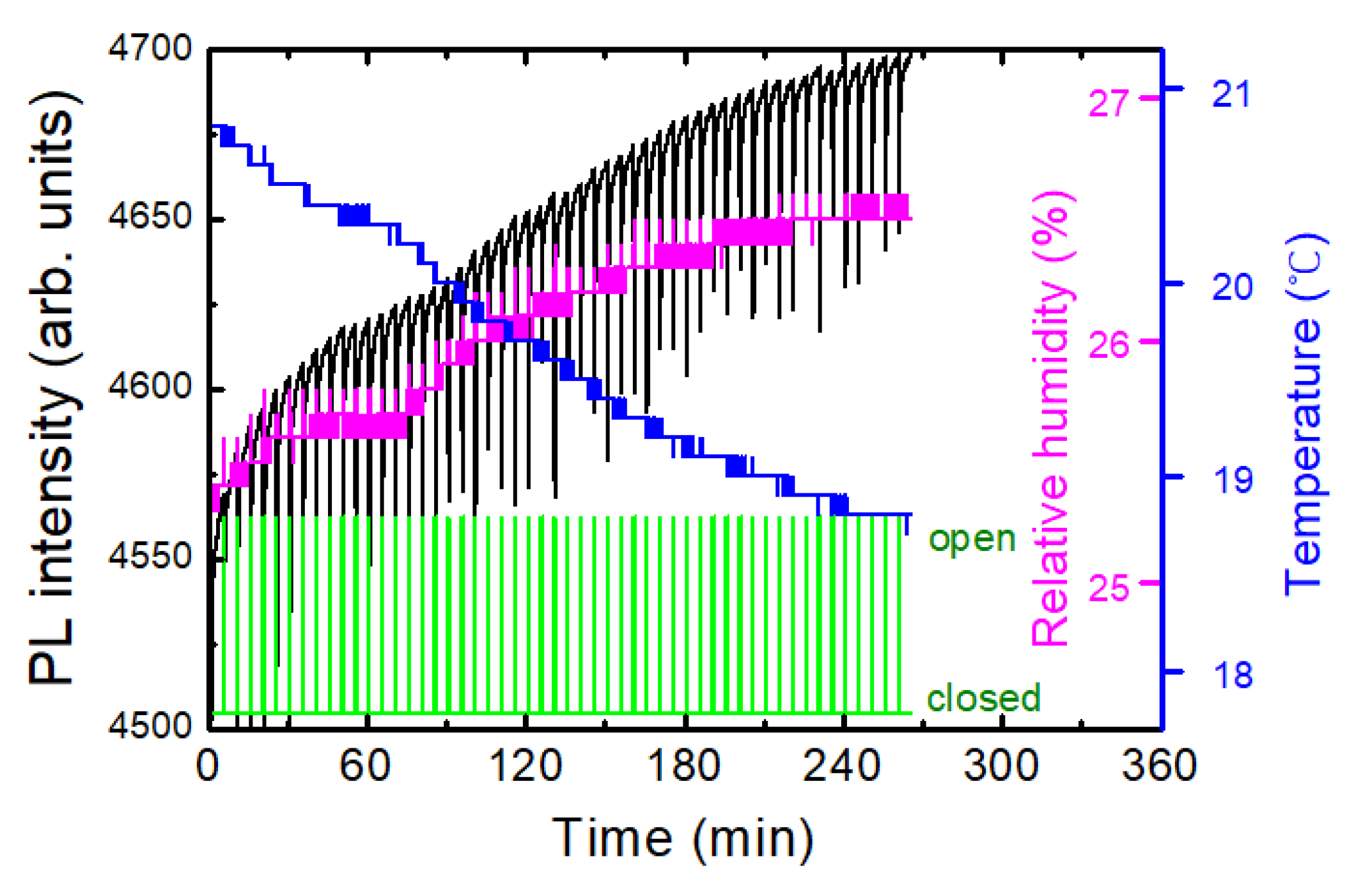
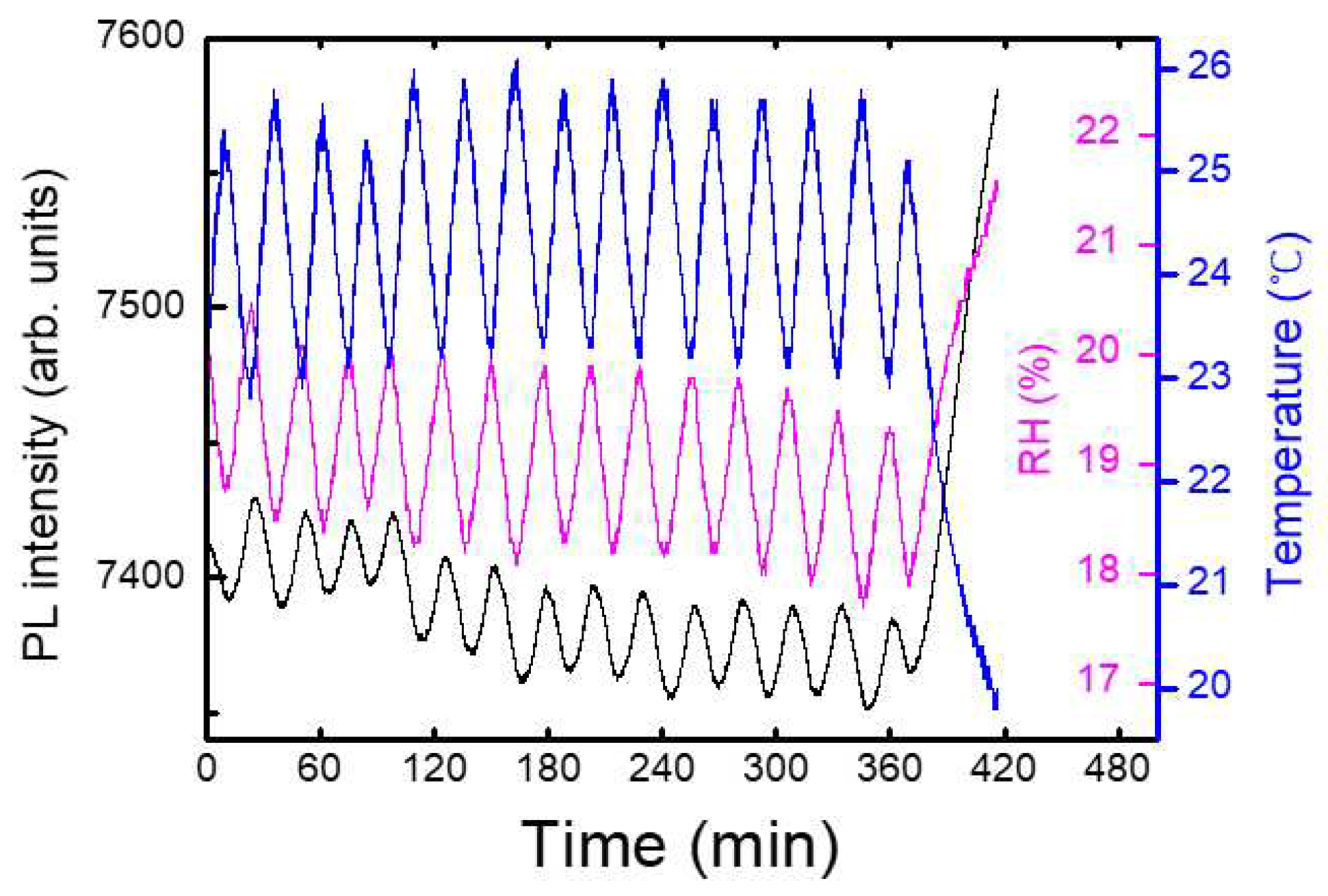
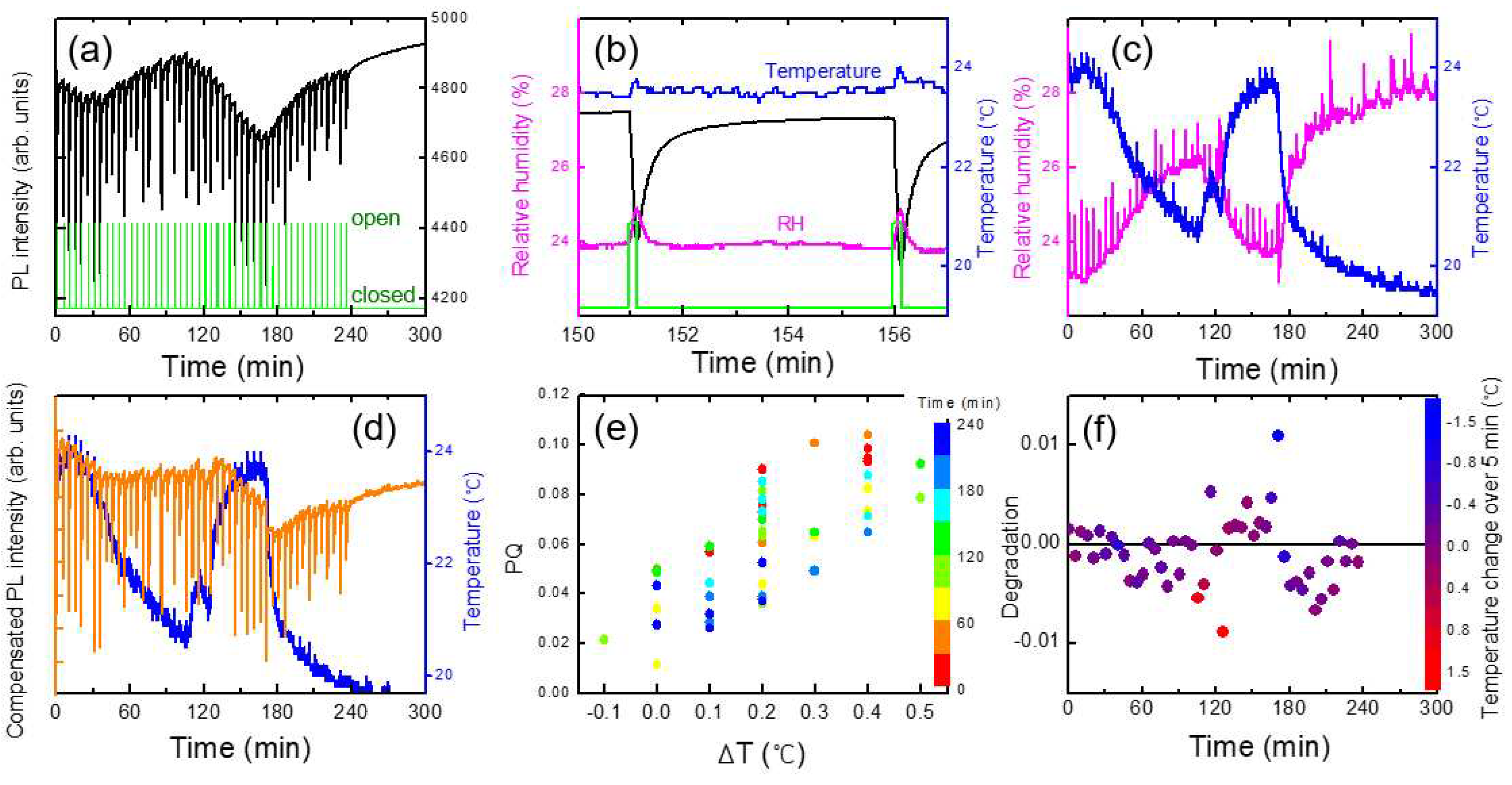
On the contrary to most DNT sensing systems in a lab., our experiments were carried out in a near-open system, where the air from the box was mixed with the air in the lab. Figure 6a shows an example of a temporal behavior of PL intensity (black), temperature (blue), and relative humidity, RH (magenta), where the oscillation of the temperature was due to a heater operation during winter. In this case, the PL apparatus was set at 1 m above the box with the shutter, and no immediate PL response was observed. On the other hand, the variation in the relative humidity as a result of the temperature change can be seen, as expected.
To separately estimate the effect of T and RH on PL intensity, we heated a polymer substrate and measured PL, while the RH inside of the lab. remained constant. In this case, the temperature of the substrate was measured with a thermocouple which was in direct contact with the substrate.
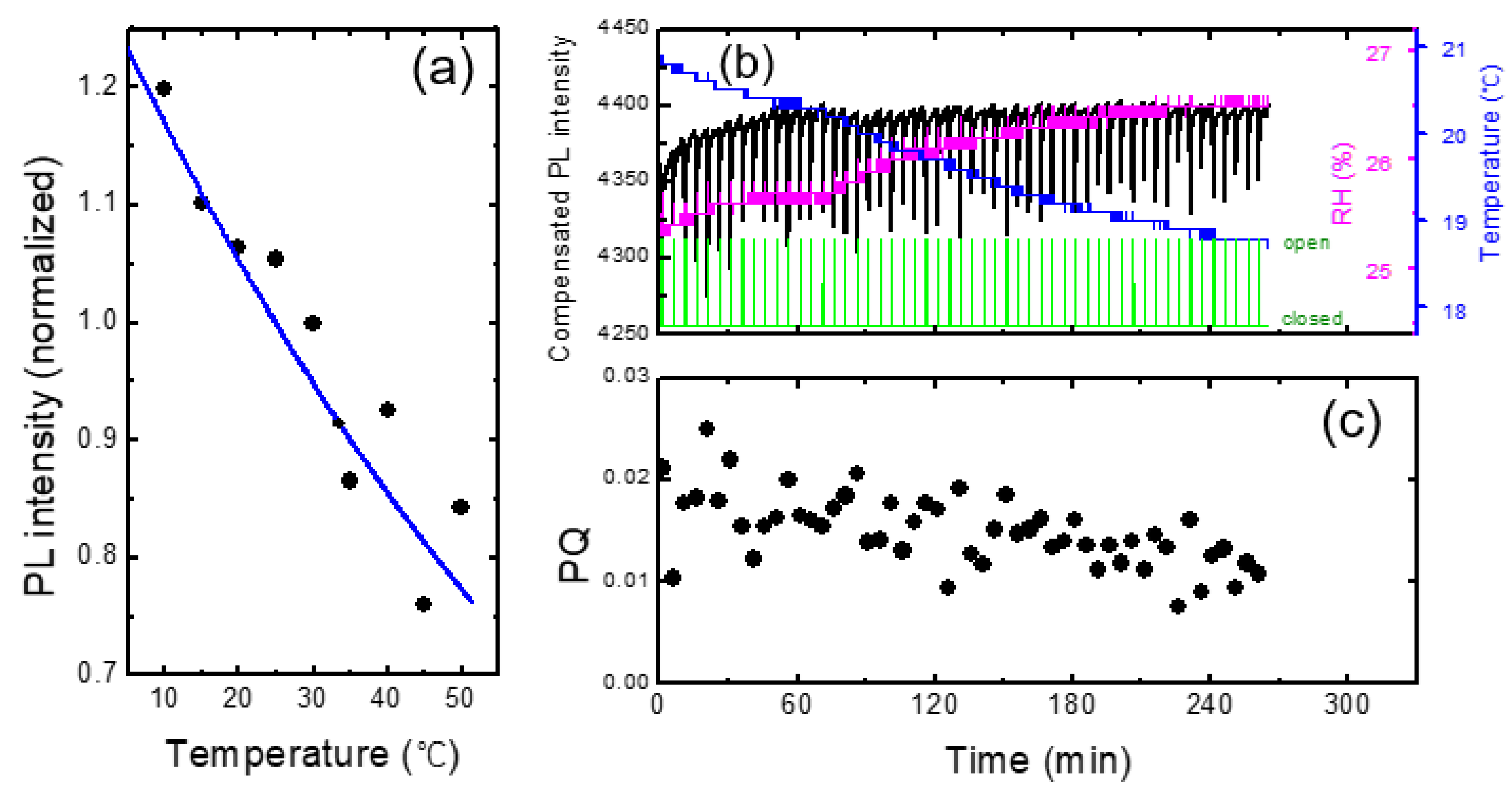
In Figure 7a we show the PL intensity as a function of temperature for a PCC film. Arrhenius equation I0/(1+A*exp(-Ea/kBT)) was used for the fitting curve, where A=265, Ea = 0.131 eV, and kB is the Boltzmann constant. Similar to the result in Figure 6, PL intensity was reduced by about 1 % for the increase of the temperature by 1 degree. This result indicates that when the change of RH was within 2 %, the effect of humidity on PL intensity was less than that of the temperature.
In Figure 7b, we show the PL intensity compensated with temperature variation using the raw data in Figure 3. The PL intensity after 60 minutes of the device operation remained fairly constant after the compensation, whereas the initial PL increase for the first 20 minutes was still clearly observed. The PL enhancement for the first 20 minutes was attributed to the effect of the light exposure, discussed in ref. [11,25,26,27].
The temperature compensation appeared to be very powerful and sufficient for the monotonic and slow change of the temperature. However, for more complicated data, such compensation was not sufficient, as we will discuss in the next section.
As shown in Figure 7c, the PQ value was found to be reduced as a function of time, which was attributed to the decrease of the vapor pressure as the continuous operation of the shutter. On the other hand, even before the vapor pressure inside of the box was not much decreased, or even when the operating time was only half an hour, the variation of PQ was found to be fairly large. As the air containing the DNT vapor was released from the box when the shutter was open, it would take some time to reach the equilibrium vapor pressure outside of the box; when we measured the PQ immediately after opening the shutter, the distribution of the vapor molecules may not be uniform, possibly causing the large variation of PQ values.
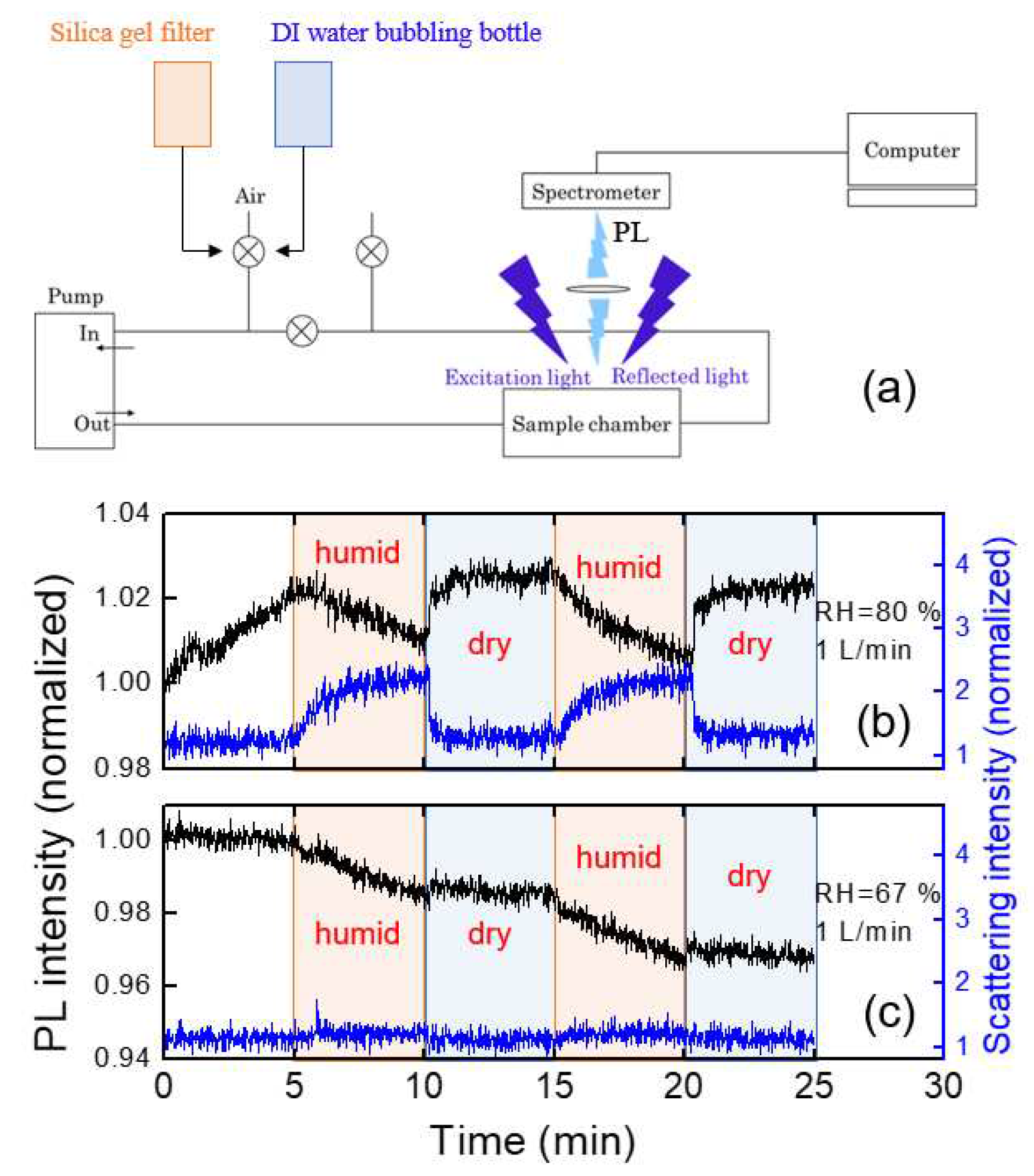
To estimate the humidity effect, we utilized a syringe filter filled with a silica gel and DI water, and the experiments were conducted by alternating filtering and bubbling connected with our home-made PL system. A schematic diagram for the experimental setup is shown in Figure 8a. The values of RH were estimated to be around 20% (filtering) and 90% (bubbling), corresponding to the “dry” and “humid” conditions, respectively. For RH=90%, PL intensity gradually decreased (Figure 8b), which was recovered within a second with dry air with 1 liter/min flow rate.
The humidity dependence of the PL intensity can be somewhat complicated by some additional factors: 1) under very high humid conditions, water molecules may condensate on the optical components reducing the apparent PL intensity 2) scattering of PL in the air may be affected by the water molecules.
It was found that the immediate change of the PL intensity with dry air within tens of seconds was associated with the reduction of the scattering at the interface of the optical component, or at the surface of the polymer film, as shown in Figure 8b. The parasitically scattered light was estimated from the intensity near the LED wavelength of 400 nm in Figure 3. The origin of the increased scattering under such humid air conditions may be due to the water condensation on the surface of optical components as well as from the polymer films. With the injection of the dry air, the PL intensity was quickly recovered.
We also used room air on a humid day (RH=67 %) during the rainy season in July. Figure 8c shows the PL intensity change of the polymer thin film under humid and dry air conditions. In this case, there was no abrupt change in PL intensity unlike Figure 8b, but the PL intensity slowly decreased during the humid period.
In the case of RH=67 %, as in Figure 8c, the parasitically scattered light remained almost constant, indicating the water condensation effect and the scattering by water molecules were minor, whereas the slow decrease of the PL intensity was observed. When polymer films are exposed to humid air, the PL intensity may not be fully recovered even after exposure of dry air due to the semi-permanent degradation of the polymer.
On rainy days, a false positive detection may occur more frequently due to the light scattering of PL associated with the water condensation. In addition, the deterioration of polymer films needs to be considered after a long period of device operation, especially in very humid weather, or after the exposure of highly concentrated DNT vapors.

3.4. Analysis of complicated situations and degradation of polymer films

In some cases, the compensation of temperature and humidity may be sufficient for the compensation of sensing characteristics such as PL and resistivity. However, when environmental factors are complicated, those corrections alone cannot fully explain the data. In particular, in the case of vapor phase measurement, since the vapor collection efficiency is greatly affected by the airflow, care must be taken in data processing and statistical analysis.
It is very challenging to understand the effect of convection wind inside a building especially when we use a heater, or when we open the windows. The distribution of the DNT vapor molecules may constantly vary with convection airflow. We examined how the convection and turbulence caused by the temperature difference affected the PL quenching results, while we heated the box by placing a heater under the acrylic box. Figure 9 shows an example of a data set to demonstrate such complicated effects. With every shutter opening, the change of temperature (ΔT) inside the PL apparatus was monitored (Figure 9b) and compared with PQ efficiencies Figure 9e.
When the shutter was open, not only DNT vapors but also warmer air diffused out and entered the PL apparatus, and an instantaneous increase in temperature (ΔT) was observed, which was a fairly good indicator of airflow. In some cases, the humidity inside the acrylic box was slightly higher than outside the box, possibly due to the speed difference in moisture condensation and drying. In such cases, ΔRH was also clearly observed (Figure 9c), despite the difference in the diffusion coefficients of DNT and water vapors.
In the experimental set-up, the PL apparatus was located slightly higher than the center of the shutter to optimize the PQ efficiency; the greater the upward convection, the greater the amount of DNT vapor flowing into the apparatus. The correlation between ΔT and PQ shown in Figure 9e was likely due to the airflow.
The orange curve in Figure 9d represents the PL intensity compensated for temperature variation. In this case, the value of PQ was 5.4 (± 2.4) %, which was larger due to the heating of the box. For a~1 and b~0, PL intensity would completely recover within 5 min according to the desorption model. After about 130 minutes, however, it was found that the PL intensity was not fully recovered within 5 minutes after the large PL quenching. Although we compensated the PL intensity with the temperature change, PL intensity was decreased with increasing time and with continuous exposure to the high concentration of the DNT molecules. It is worth mentioning that the PL intensity seemed to recover without any shutter operation between 240 and 300 min.
To quantify the incomplete recovery of PL intensity, or the degradation, we plot (Io - I (5min))/Io. Figure 9f shows the degradation as a function of the PQ value after the temperature compensation. As seen in the figure, there were two data points (blue and red) that exhibited significant deviations. We think that these points were associated with the rapid changes in temperature and a slower response of the polymer film.
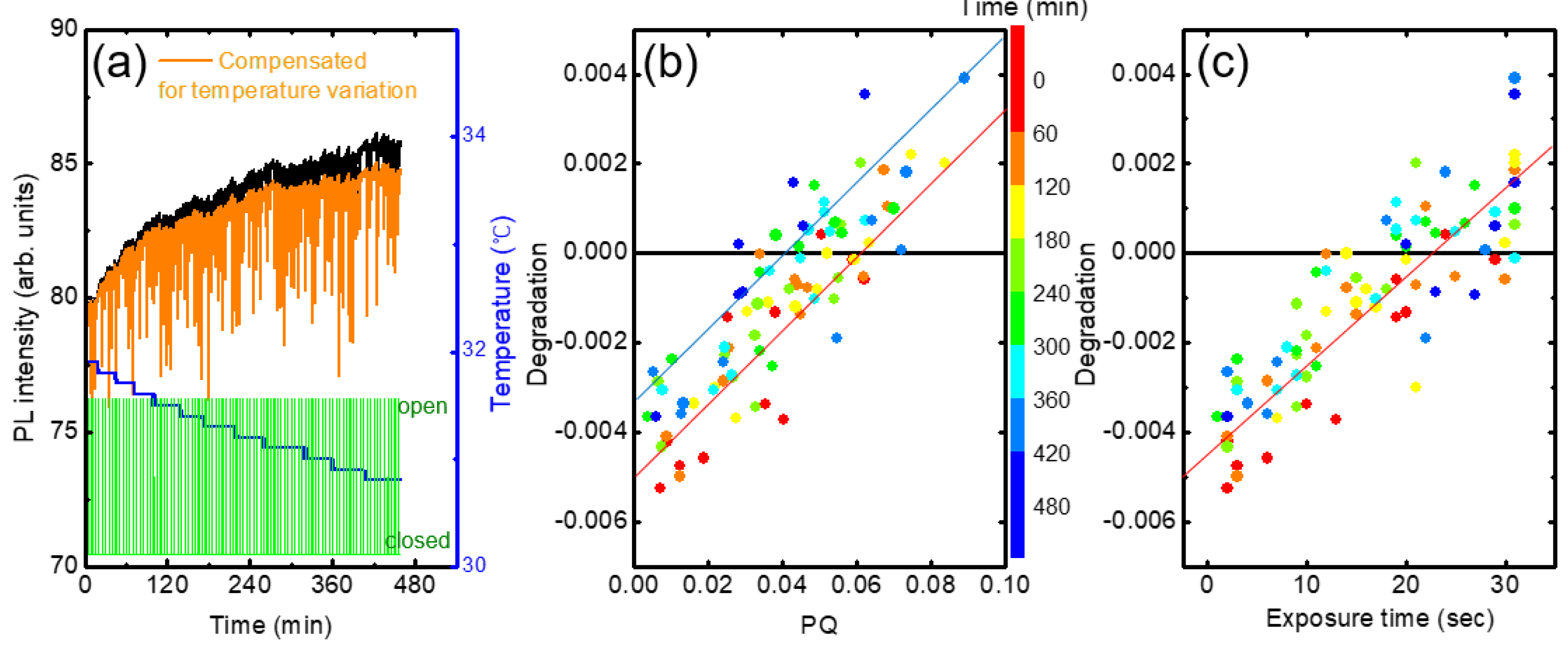
In Figure 10a we show the PL intensity variation of a fresh (as-deposited) film. Even after the temperature compensation, PL intensity was found to be still increased with time (orange). In the modeling in the previous section, we assumed that the incomplete PL recovery is proportional to PQ. In a plot of degradation vs. PQ, the slope and y-intercept are expected to be ‘1-a’ and ‘-b(t-(1-a)tq)’, respectively.
In practice, these parameters depend on several factors such as the condition of the polymer film, elapsed time, and PQ value. For example, the extent of the increase appeared to be larger for as-deposit films, and the y-intercept became more negative in the degradation vs. PQ plot. Figure 10b shows the degradation as a function of PQ obtained from the raw data in Figure 10a. The color indicates elapsed time. The y-intercept was slightly increased from ~-0.005 to ~-0.0035 with the time from ~60 to ~400 min. Similarly, the degradation was also increased with the increase of the exposure time, as seen in Figure 10c.

4. Conclusions

Explosives detection using PL quenching has been studied for a long time, but it is difficult to find literature on a statistical analysis of environmental effects. This is probably because it is difficult to obtain a sufficient amount of environmental data including temperature, humidity, and convection airflow, and it is also difficult to take care of the continuous degradation of sensing films. We implemented a method that allowed the vapor molecules inside a box to diffuse out into the air by remote control of a shutter, while the direct exposure of the pollutant vapors to a human body was prevented via remote sensing.
To obtain a sufficient amount of data without significant degradation of a sensing film, we chose a rather short exposure time (10 seconds) and 5-minute time intervals. We then considered the incomplete recovery of the PL intensity after the refresh time of 5 minutes. The degradation, or the incomplete recovery of the PL, was more evident for higher DNT vapor pressure, longer exposure, and higher humidity.
The degradation includes the effect of vapor molecular diffusion into polymer films, which was thoroughly investigated, and the mass increase of polymer films was manifested [14,15]. There was a study that explained the quenching behavior over time using molecular diffusion and Stern-Volmer relationships. However, those results did not consider exciton diffusion, and, the research focused more on numerical analysis rather than providing analytical solutions [28].
In this study, we analyzed the effects of temperature, humidity, and DNT exposure time, and then considered the degradation effect as an additional factor. Our approach started with short exposure times and relatively low vapor concentrations and provided explanations for the temporal behavior of the PL quenching and refresh. Despite many assumptions and simplifications, our theoretical model seemed to well explain the experimental results at least under limited degradation conditions. Photo-induced PL enhancement, photo-degradation, and diffusion (out-diffusion) of DNT molecules into (from) the inner part of the polymer films were taken into consideration empirically with parameters a and b in the model. Our study may be useful for real-field applications of PL-based chemical gas sensors and for other types of chemical sensors based on semiconductors and polymers.

Author Contributions

Conceptualization, D.N. and E.O.; methodology, D.N. and E.O.; software, D.N.; validation, D.N. and E.O.; formal analysis, D.N. and E.O.; investigation, D.N. and E.O.; data curation, D.N. and E.O.; writing—original draft preparation, D.N. and E.O.; writing—review and editing, D.N. and E.O.; supervision, E.O.; project administration, E.O.

Funding

This research was supported by a Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (NRF- 2020R1A6A1A03047771).

Institutional Review Board Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

We appreciate Mr. Jongman Lee for the help of experiments.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Ewing, R.G.; Atkinson, D.A.; Eiceman, G.A.; Ewing, G.J. A Critical Review of Ion Mobility Spectrometry for the Detection of Explosives and Explosive Related Compounds. Talanta 2001, 54, 515–529. [Google Scholar] [CrossRef] [PubMed]
  2. Moore, D. S. Instrumentation for Trace Detection of High Explosives. Review of Scientific Instruments 2004, 75, 2499–2512. [Google Scholar] [CrossRef]
  3. Adhikari, S.; Ampadu, E. K.; Kim, M.; Noh, D.; Oh, E.; Lee, D. Detection of Explosives by SERS Platform Using Metal Nanogap Substrates. Sensors 2021, 21, 5567. [Google Scholar] [CrossRef]
  4. Caygill, J. S.; Davis, F.; Higson, S. P. J. Current Trends in Explosive Detection Techniques. Talanta 2012, 88, 14–29. [Google Scholar] [CrossRef]
  5. Yang, J.; Aschemeyer, S.; Martinez, H. P.; Trogler, W. C. Hollow Silica Nanospheres Containing a Silafluorene–Fluorene Conjugated Polymer for Aqueous TNT and RDX Detection. Chem. Commun. 2010, 46, 6804. [Google Scholar] [CrossRef] [PubMed]
  6. Mathew, A.; Sajanlal, P. R.; Pradeep, T. Selective Visual Detection of TNT at the Sub-Zeptomole Level. Angew Chem Int Ed 2012, 51, 9596–9600. [Google Scholar] [CrossRef]
  7. Ma, Y.; Huang, S.; Deng, M.; Wang, L. White Upconversion Luminescence Nanocrystals for the Simultaneous and Selective Detection of 2,4,6-Trinitrotoluene and 2,4,6-Trinitrophenol. ACS Appl. Mater. Interfaces 2014, 6, 7790–7796. [Google Scholar] [CrossRef]
  8. Enkin, N.; Sharon, E.; Golub, E.; Willner, I. Ag Nanocluster/DNA Hybrids: Functional Modules for the Detection of Nitroaromatic and RDX Explosives. Nano Lett. 2014, 14, 4918–4922. [Google Scholar] [CrossRef]
  9. Ma, Y.; Wang, L. Upconversion Luminescence Nanosensor for TNT Selective and Label-Free Quantification in the Mixture of Nitroaromatic Explosives. Talanta 2014, 120, 100–105. [Google Scholar] [CrossRef]
  10. Yang, J.-S.; Swager, T. M. Fluorescent Porous Polymer Films as TNT Chemosensors: Electronic and Structural Effects. J. Am. Chem. Soc. 1998, 120, 11864–11873. [Google Scholar] [CrossRef]
  11. Noh, D.; Ampadu, E. K.; Oh, E. Influence of Air Flow on Luminescence Quenching in Polymer Films towards Explosives Detection Using Drones. Polymers 2022, 14, 483. [Google Scholar] [CrossRef] [PubMed]
  12. Geng, Y.; Ali, M. A.; Clulow, A. J.; Fan, S.; Burn, P. L.; Gentle, I. R.; Meredith, P.; Shaw, P. E. Unambiguous Detection of Nitrated Explosive Vapours by Fluorescence Quenching of Dendrimer Films. Nat Commun 2015, 6, 8240. [Google Scholar] [CrossRef]
  13. Shaw, P. E.; Burn, P. L. Real-Time Fluorescence Quenching-Based Detection of Nitro-Containing Explosive Vapours: What Are the Key Processes? Phys. Chem. Chem. Phys. 2017, 19, 29714–29730. [Google Scholar] [CrossRef] [PubMed]
  14. Ali, M. A.; Geng, Y.; Cavaye, H.; Burn, P. L.; Gentle, I. R.; Meredith, P.; Shaw, P. E. Molecular versus Exciton Diffusion in Fluorescence-Based Explosive Vapour Sensors. Chem. Commun. 2015, 51, 17406–17409. [Google Scholar] [CrossRef] [PubMed]
  15. Ali, M. A.; Shoaee, S.; Fan, S.; Burn, P. L.; Gentle, I. R.; Meredith, P.; Shaw, P. E. Detection of Explosive Vapors: The Roles of Exciton and Molecular Diffusion in Real-Time Sensing. ChemPhysChem 2016, 17, 3350–3353. [Google Scholar] [CrossRef]
  16. Cavaye, H.; Shaw, P. E.; Smith, A. R. G.; Burn, P. L.; Gentle, I. R.; James, M.; Lo, S.-C.; Meredith, P. Solid State Dendrimer Sensors: Effect of Dendrimer Dimensionality on Detection and Sequestration of 2,4-Dinitrotoluene. J. Phys. Chem. C 2011, 115, 18366–18371. [Google Scholar] [CrossRef]
  17. Tamai, Y.; Ohkita, H.; Benten, H.; Ito, S. Exciton Diffusion in Conjugated Polymers: From Fundamental Understanding to Improvement in Photovoltaic Conversion Efficiency. J. Phys. Chem. Lett. 2015, 6, 3417–3428. [Google Scholar] [CrossRef]
  18. Rörich, I.; Schönbein, A.-K.; Mangalore, D. K.; Halda Ribeiro, A.; Kasparek, C.; Bauer, C.; Crăciun, N. I.; Blom, P. W. M.; Ramanan, C. Temperature Dependence of the Photo- and Electroluminescence of Poly( p -Phenylene Vinylene) Based Polymers. J. Mater. Chem. C 2018, 6, 10569–10579. [Google Scholar] [CrossRef]
  19. Kawano, K.; Pacios, R.; Poplavskyy, D.; Nelson, J.; Bradley, D. D. C.; Durrant, J. R. Degradation of Organic Solar Cells Due to Air Exposure. Solar Energy Materials and Solar Cells 2006, 90, 3520–3530. [Google Scholar] [CrossRef]
  20. Gao, X.; Xue, D.; Gao, D.; Han, Q.; Ge, Q.; Ma, J.; Ding, J.; Zhang, W.; Zhang, B.; Feng, Y.; Yu, G.; Hu, J. High-Mobility Hydrophobic Conjugated Polymer as Effective Interlayer for Air-Stable Efficient Perovskite Solar Cells. Solar RRL 2019, 3, 1800232. [Google Scholar] [CrossRef]
  21. Chen, Z.; Yu, C.; Bai, W.; Ye, W.; Wang, J.; Wei, J.; Wang, Y.; He, J.; Lu, J. Surface Functionalization of Ion-in-Conjugation Polymer Sensors for Humidity-Independent Gas Detection at Room Temperature. Sensors and Actuators B: Chemical 2022, 372, 132654. [Google Scholar] [CrossRef]
  22. Satrijo, A.; Kooi, S. E.; Swager, T. M. Enhanced Luminescence from Emissive Defects in Aggregated Conjugated Polymers. Macromolecules 2007, 40, 8833–8841. [Google Scholar] [CrossRef] [PubMed]
  23. Eder, T.; Stangl, T.; Gmelch, M.; Remmerssen, K.; Laux, D.; Höger, S.; Lupton, J. M.; Vogelsang, J. Switching between H- and J-Type Electronic Coupling in Single Conjugated Polymer Aggregates. Nat Commun 2017, 8, 1641. [Google Scholar] [CrossRef] [PubMed]
  24. Tian, E.; Wang, J.; Zheng, Y.; Song, Y.; Jiang, L.; Zhu, D. Colorful Humidity Sensitive Photonic Crystal Hydrogel. J. Mater. Chem. 2008, 18, 1116. [Google Scholar] [CrossRef]
  25. Gobato, Y. G.; Marletta, A.; Faria, R. M.; Guimarães, F. E. G.; De Souza, J. M.; Pereira, E. C. Photoinduced Photoluminescence Intensity Enhancement in Poly( p -Phenylene Vinylene) Films. Applied Physics Letters 2002, 81, 942–944. [Google Scholar] [CrossRef]
  26. AlShetwi, Y. A.; Schiefer, D.; Sommer, M.; Reiter, G. Continuous Illumination of a Conjugated Polymer Causes Strong Enhancement of Photoluminescence. J. Phys. Chem. B 2021, 125, 5636–5644. [Google Scholar] [CrossRef]
  27. Wu, C.; Bull, B.; Szymanski, C.; Christensen, K.; McNeill, J. Multicolor Conjugated Polymer Dots for Biological Fluorescence Imaging. ACS Nano 2008, 2, 2415–2423. [Google Scholar] [CrossRef]
  28. Campbell, I. A.; Turnbull, G. A. A Kinetic Model of Thin-Film Fluorescent Sensors for Strategies to Enhance Chemical Selectivity. Phys. Chem. Chem. Phys. 2021, 23, 10791–10798. [Google Scholar] [CrossRef]
Preprints 98760 g001
Figure 1. (a) A schematic picture of the experimental set-up consisting of a box with a shutter and a PL apparatus. 0.1 gram of 2,4-DNT powder was placed in a stainless-steel bowl. (b) A schematic diagram of the PL apparatus. (c) Photoluminescence response by shutter opening and closing. The period was 5 minutes and the shutter opening time was 10 seconds.
Figure 1. (a) A schematic picture of the experimental set-up consisting of a box with a shutter and a PL apparatus. 0.1 gram of 2,4-DNT powder was placed in a stainless-steel bowl. (b) A schematic diagram of the PL apparatus. (c) Photoluminescence response by shutter opening and closing. The period was 5 minutes and the shutter opening time was 10 seconds.
Preprints 98760 g001
Preprints 98760 g002
Figure 2. Photoluminescence (PL) spectra of a PCC polymer film at room temperature. A picture of a home-made PL system is included.
Figure 2. Photoluminescence (PL) spectra of a PCC polymer film at room temperature. A picture of a home-made PL system is included.
Preprints 98760 g002
Preprints 98760 g003
Figure 3. An example of real-time PL intensity (black), temperature (blue), and relative humidity (magenta) monitored inside of a PL quenching apparatus. Also shown is the shutter angle (green). PL responses for the exposure of DNT vapors are observed in every 5 min intervals.
Figure 3. An example of real-time PL intensity (black), temperature (blue), and relative humidity (magenta) monitored inside of a PL quenching apparatus. Also shown is the shutter angle (green). PL responses for the exposure of DNT vapors are observed in every 5 min intervals.
Preprints 98760 g003
Preprints 98760 g004
Figure 4. (a) PL quenching vs. time for PCC polymer film. (b) The corresponding PL quenching (PQ) as a function of the exposure time, which was obtained from the raw data as in (a). The dashed curve is a fitting curve obtained from a theoretical model used for response time analysis.
Figure 4. (a) PL quenching vs. time for PCC polymer film. (b) The corresponding PL quenching (PQ) as a function of the exposure time, which was obtained from the raw data as in (a). The dashed curve is a fitting curve obtained from a theoretical model used for response time analysis.
Preprints 98760 g004
Preprints 98760 g005
Figure 5. (a) PL intensity for various exposure times as a function of time. The shutter opening time is set to zero. The PL values were averaged for each exposure time. Theoretical curves are also shown for comparison. The dash and solid curves represent 5 s and 15 s results, respectively. (b) Fitting curves of the PL intensity using a theoretical model. The fitting parameters are listed in Table 1.
Figure 5. (a) PL intensity for various exposure times as a function of time. The shutter opening time is set to zero. The PL values were averaged for each exposure time. Theoretical curves are also shown for comparison. The dash and solid curves represent 5 s and 15 s results, respectively. (b) Fitting curves of the PL intensity using a theoretical model. The fitting parameters are listed in Table 1.
Preprints 98760 g005
Preprints 98760 g006
Figure 6. As a heater inside the lab. produced oscillations of temperature (blue), relative humidity (magenta) and PL intensity (black) were correspondingly changed.
Figure 6. As a heater inside the lab. produced oscillations of temperature (blue), relative humidity (magenta) and PL intensity (black) were correspondingly changed.
Preprints 98760 g006
Preprints 98760 g007
Figure 7. (a) PL intensity vs. temperature for a PCC film. In contrast to the case of Figure 6, RH remained constant as only the film substrates were heated and cooled. (b) PL intensity compensated for temperature variation (black) as a function of time. Temperature and RH are also shown. (c) PQ as a function of time.
Figure 7. (a) PL intensity vs. temperature for a PCC film. In contrast to the case of Figure 6, RH remained constant as only the film substrates were heated and cooled. (b) PL intensity compensated for temperature variation (black) as a function of time. Temperature and RH are also shown. (c) PQ as a function of time.
Preprints 98760 g007
Preprints 98760 g008
Figure 8. (a) A schematic diagram of an experimental set-up for humidity effects. (b-c) Variation of PL intensity (black) and parasitically scattered light intensity (blue) under dry and humid air conditions.
Figure 8. (a) A schematic diagram of an experimental set-up for humidity effects. (b-c) Variation of PL intensity (black) and parasitically scattered light intensity (blue) under dry and humid air conditions.
Preprints 98760 g008
Preprints 98760 g009
Figure 9. (a) PL intensity variation as a function of time. (b) An enlarged view of temperature T and relative humidity RH to demonstrate the variations under shutter operations. As the box was heated, a slight increase of the temperature ΔT during the DNT exposure time of 10 sec was observed. (c) T and RH as a function of time. (d) PL intensity compensated with temperature variation. (e) PQ vs ΔT during the 10 sec exposure time. The correlation was due to the warm airflow. The colors represent the elapsed time. (f) Degradation, or the incomplete recovery of PL intensity after five minutes. The color bars represent the temperature change in 5 minutes.
Figure 9. (a) PL intensity variation as a function of time. (b) An enlarged view of temperature T and relative humidity RH to demonstrate the variations under shutter operations. As the box was heated, a slight increase of the temperature ΔT during the DNT exposure time of 10 sec was observed. (c) T and RH as a function of time. (d) PL intensity compensated with temperature variation. (e) PQ vs ΔT during the 10 sec exposure time. The correlation was due to the warm airflow. The colors represent the elapsed time. (f) Degradation, or the incomplete recovery of PL intensity after five minutes. The color bars represent the temperature change in 5 minutes.
Preprints 98760 g009
Preprints 98760 g010
Figure 10. (a) PL intensity without (black) and with (orange) temperature compensation. (b) Degradation vs PQ. The color indicates elapsed time. (c) Degradation as a function of exposure time.
Figure 10. (a) PL intensity without (black) and with (orange) temperature compensation. (b) Degradation vs PQ. The color indicates elapsed time. (c) Degradation as a function of exposure time.
Preprints 98760 g010
Table 1. Fitting parameters used for a theoretical model.
Table 1. Fitting parameters used for a theoretical model.
Parameter Value Unit
P2,4-DNT 1.93 x 10-7
kdesorption 4.698 x 10-2 s-1
a 8.755 x 10-1
b 7.820 x 10-6 s-1
1/τkq[S]kadsorptionP2,4-DNTPr 63.61
kadsorptionP2,4-DNTPr + kdesorption 4.701 x 10-2 s-1
(LD/d)tanh(d/LD) 1.094 x 10-1
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated