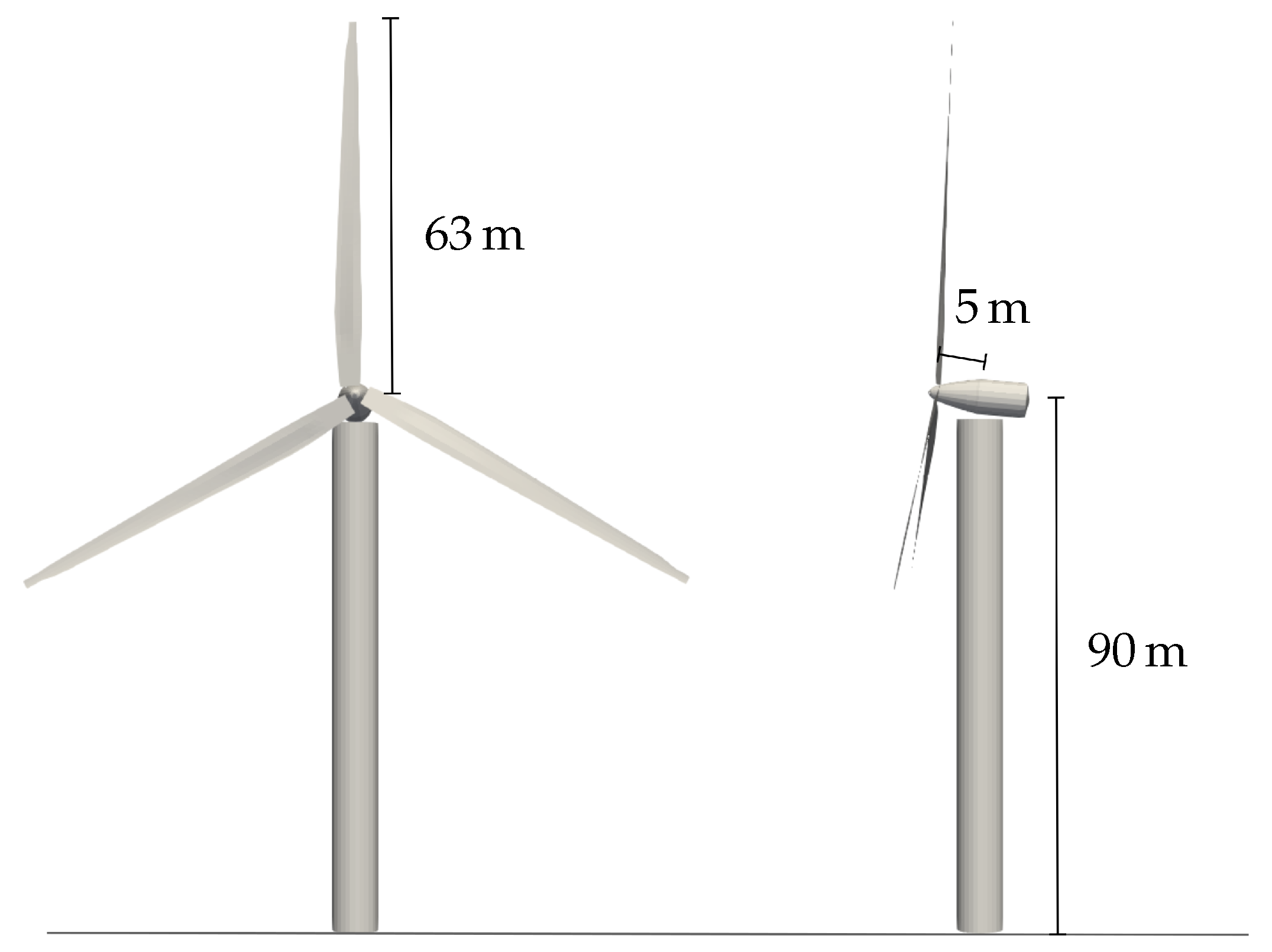
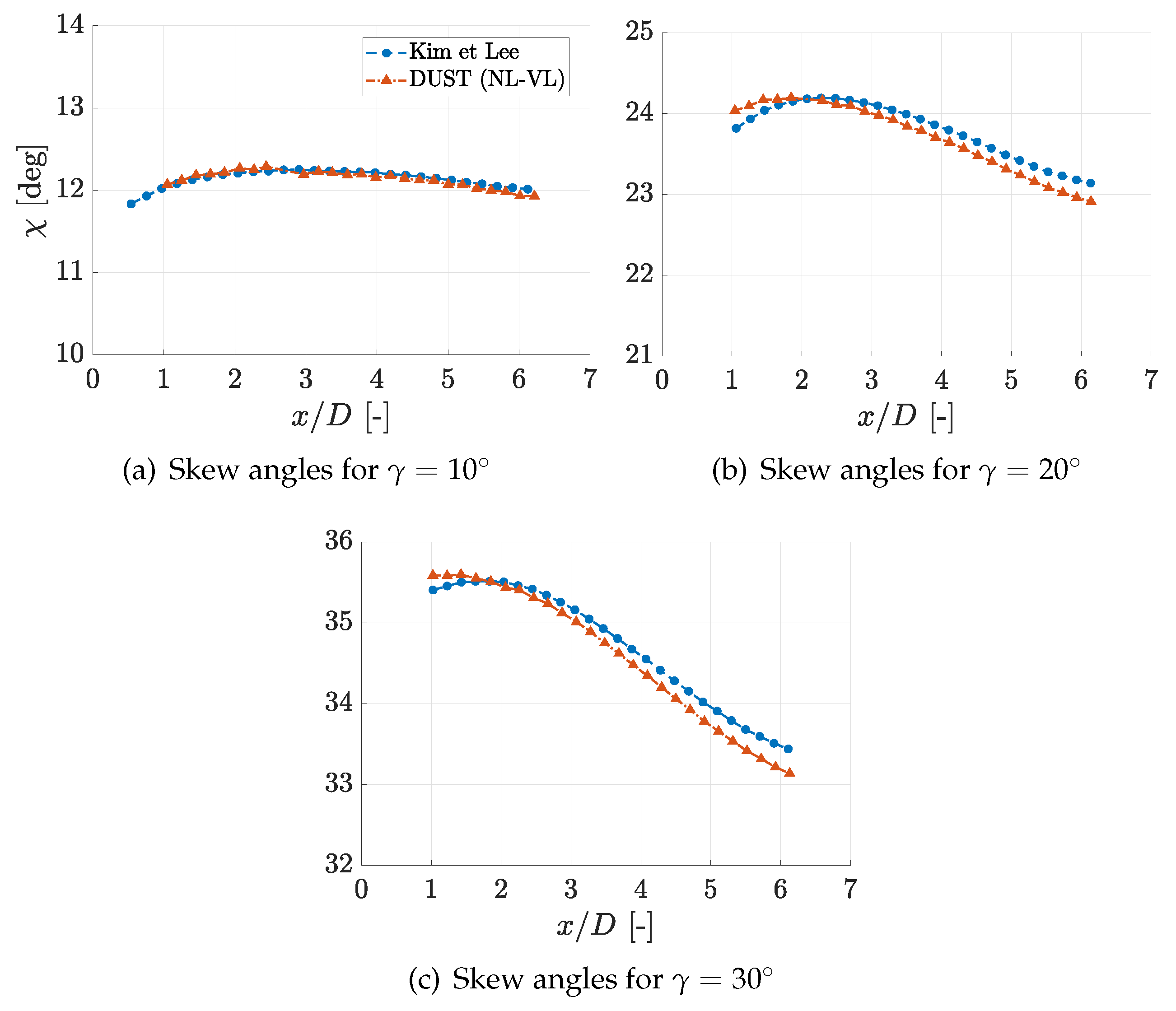4.1. NREL-5
Wind Turbine
The first step of the validation process involves simulating the simplest configuration of the wind turbine C1 at rated conditions, not taking into account neither the shaft tilt angle
nor blade cone angle
. DUST results are compared to the ones obtained with high-fidelity numerical simulation conducted by Dose
et al. [
26] using RANS approach and by Leng
et al. [
44].
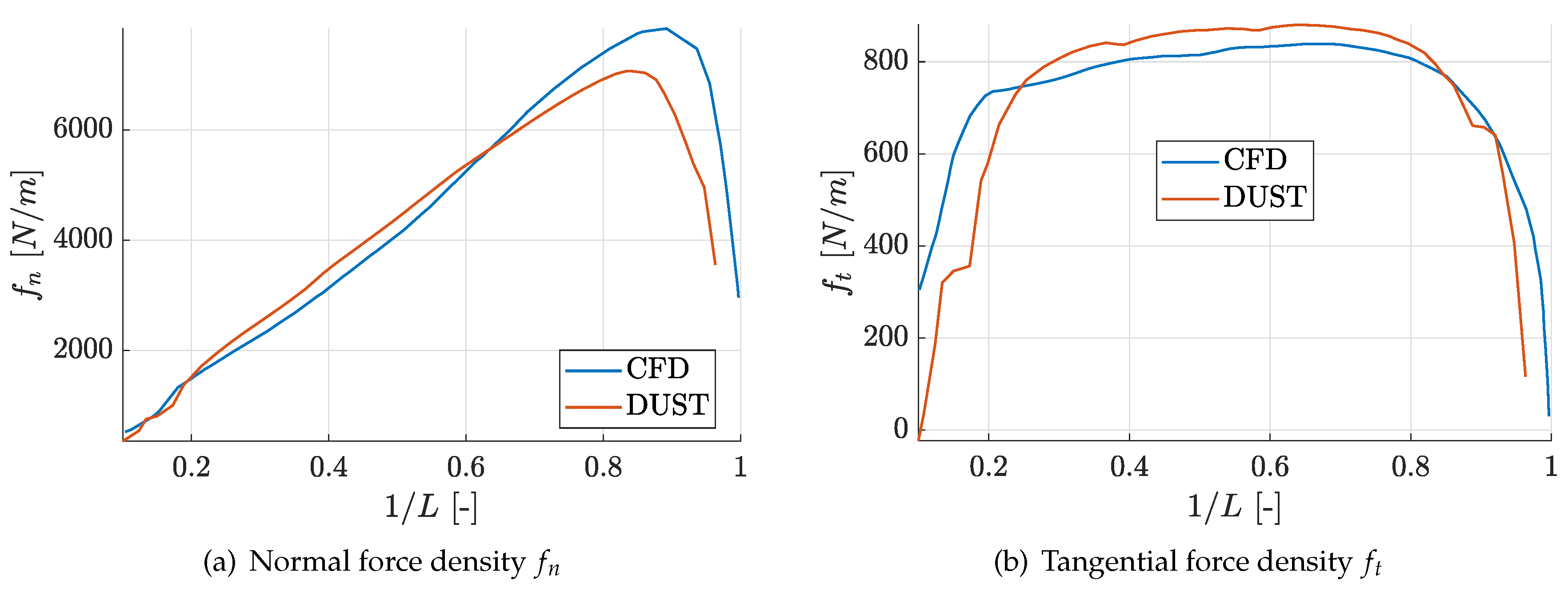
Figure 6 shows the comparison of the normal and tangential sectional forces acting along the normalised spanwise coordinate of the blade computed by DUST NL-VL model and high fidelity CFD simulation by Dose
et al. [
26]. The normal force density comparison illustrated in Figure 6a exhibits a close alignment between DUST and high fidelity CFD data along almost the majority of the blade span. However, near the blade tip DUST slightly underestimate the normal force. This behaviour is expected as wing tip are characterized by a more complex flow regime where three-dimensional phenomena and tip vortices generation typically leads to significant viscous effects and separated flow regions, which can not be accurately captured by DUST mid-fidelity approach. Tangential force density comparison depicted in Figure 6b shows an underestimation of DUST computation before the first 30% of blade span and a slight overestimation in the central spanwise region. High-fidelity CFD model, however, shows a more pronounced decrease in tangential force towards the blade tip with respect to DUST results. Generally speaking, the behaviour of the sectional force comparison confirms the capability of DUST to competently reproduces the general force distribution along the blade span.
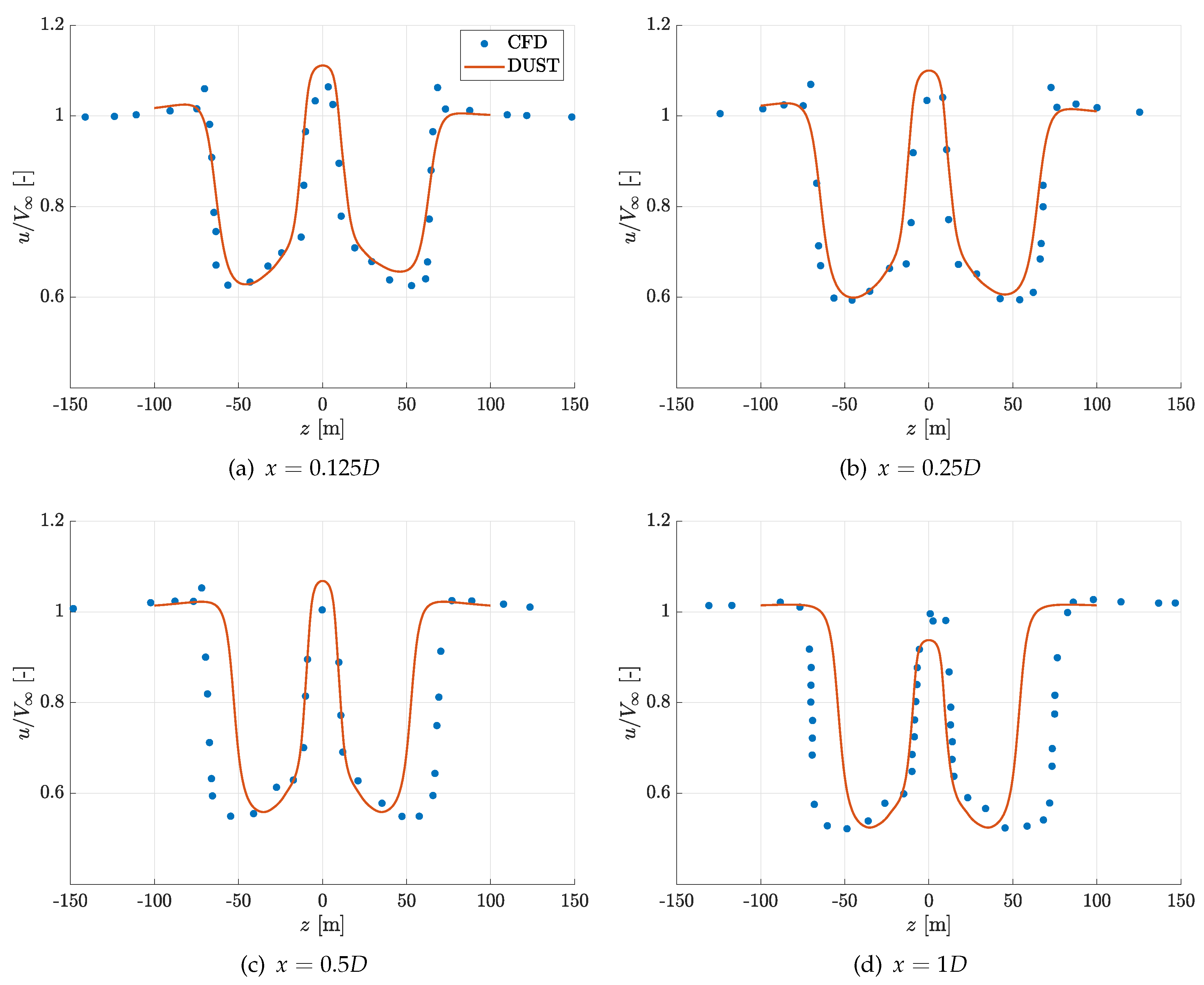
The performance of a wind turbine are significantly affected by the wind turbine wake, then a crucial step for DUST validation is the ability to correctly capture the wake development and its main features in terms of velocity field. Then, the deficit of the axial velocity in the wake calculated by DUST is compared with the high-fidelity simulation by [
45], considering 4 stream wise position located at different distances
x downstream from the rotor plane. Velocity profiles comparison is shown in
Figure 7 as function of
z, representing the distance from the shaft axis parallel to the rotor plane.
A quite good agreement was found between axial velocity profiles in the wake of the wind turbine, particularly near to the rotor disk, i.e.
and
. Some discrepancies were found at higher distances where CFD results show a slightly larger extension of the wake, probably due to numerical diffusion. Generally,
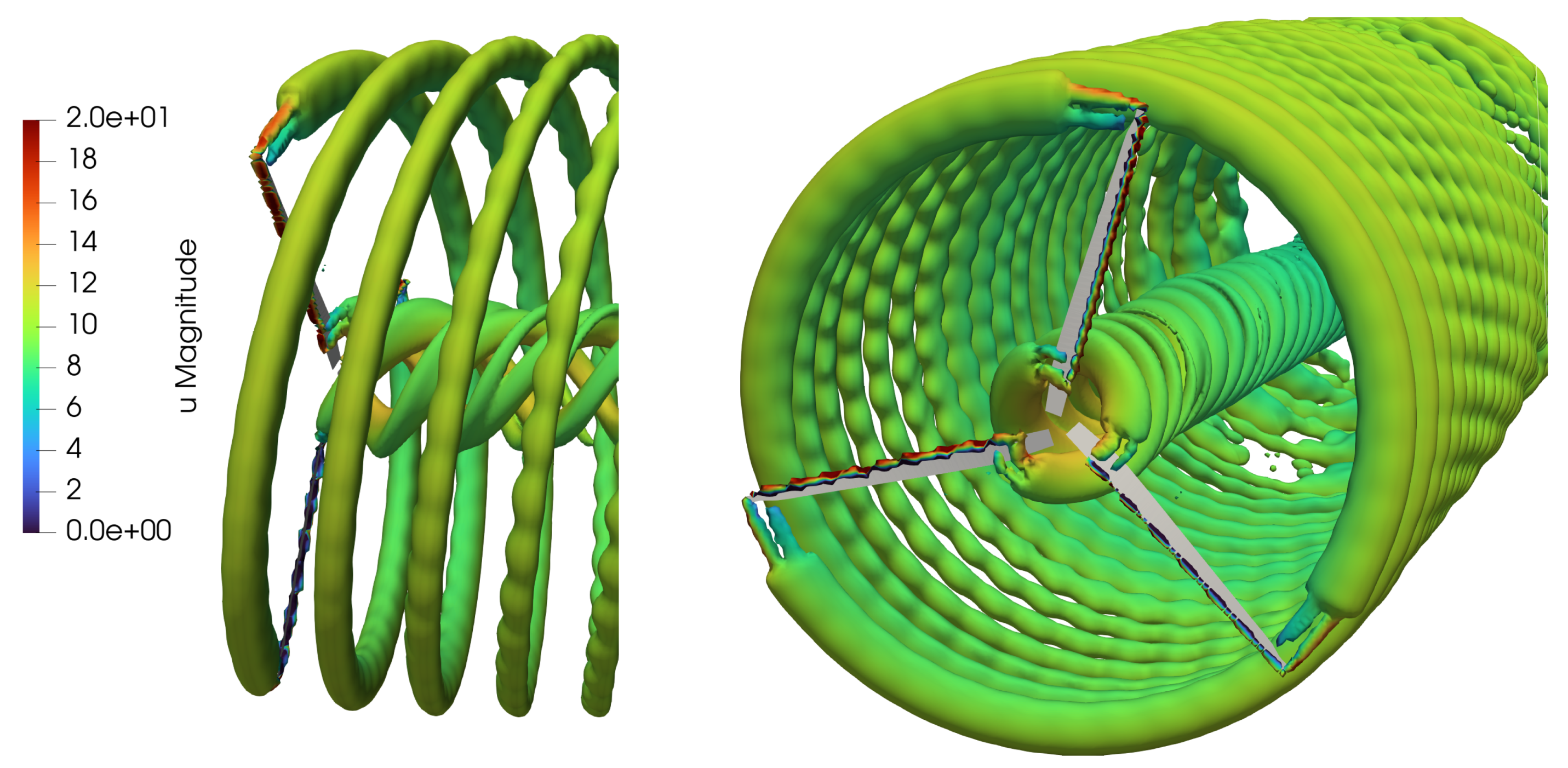
Figure 8 illustrates the wake structure computed by DUST shown as an iso-surface of the vortex Q-criterion. Readers are referred to results reported in [
45] to appreciate DUST capability to capture the behaviour of the wake structure computed by CFD.
The influence of blade cone angle
and shaft tilt angle
on the aerodynamic performance under rated inflow conditions is now explored by comparing results obtained with DUST and high-fidelity CFD by Dose
et al. [
26] over C1, C3 and C4 cases. Generally, the sensitivity of integral loads to cone and tilt angles variations is minimal. Indeed, adding a blade cone angle a slight increase of the rotor power is observed. On the other hand, introducing a shaft tilt slightly reduces rotor power and thrust. In particular, the integral power and thrust on the rotor are compared in
Table 7. Both DUST models provide values quite similar to high-fidelity CFD findings. A difference below 2% is found for power evaluation with both LL and NL-VL elements, while thrust evaluation obtained by DUST with NL-VL is in quite good agreement with CFD. An underestimation of rotor thrust of about 8% is found for LL DUST model with respect to CFD.
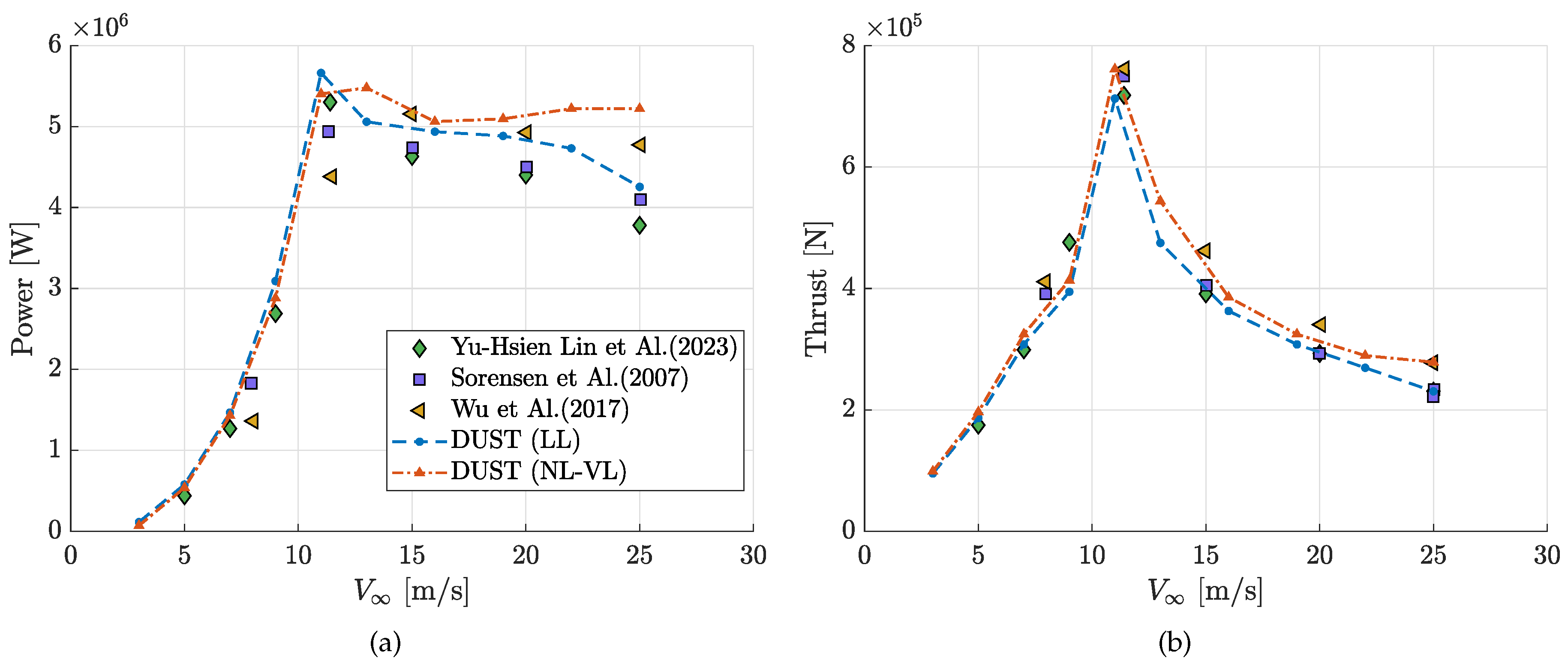
Case C4 enabled to provide an insight of the effects of varying freestream velocity, thanks to high-fidelity CFD results from Sørensen and Johansen [
20], Lin
et al. [
21], Wu and Nguyen [
22].
Figure 9 compares the computed power and thrust as function of wind speeds. Generally, both DUST models capture the behaviour of power and thrust curves evaluated by CFD, thus confirming the capability to model correctly the effects of wind inflow on rotor performance. In particular, LL elements model tends to slightly overestimate power production below the rated wind speed, while NL-VL elements model slightly overestimates rotor power above the rated speed. Now considering thrust evaluation, LL elements model tends to underestimate CFD high-fidelity data along the entire velocity spectrum, while a quite better agreement is obtained with NL-VL elements model.
Different yawed configurations are then investigated. At first, a yaw angle
is considered to assess the integral and the sectional parameters with respect to high fidelity CFD simulation by Dose
et al. [
26]. Then, other two yaw angles configurations are considered, respectively
to be compared with the LES study by yaw [
24].
Table 8 compares the integral rotor power and thrust computed for C2 configuration with
where errors in terms of power and thrust with respect to CFD by Dose
et al. [
26] are below 10% for LL model and below 5% for NL-VL model. Compared to the axial flow condition case, power and thrust outputs decrease in accordance to CFD evaluation by Dose
et al. [
26]. Results by Dose
et al. [
26] are based on blade resolving CFD method, so dynamic stall effects occurring particularly in yawed conditions are implicitly included. On the other hand, no dynamic stall models are considered in DUST formulation.
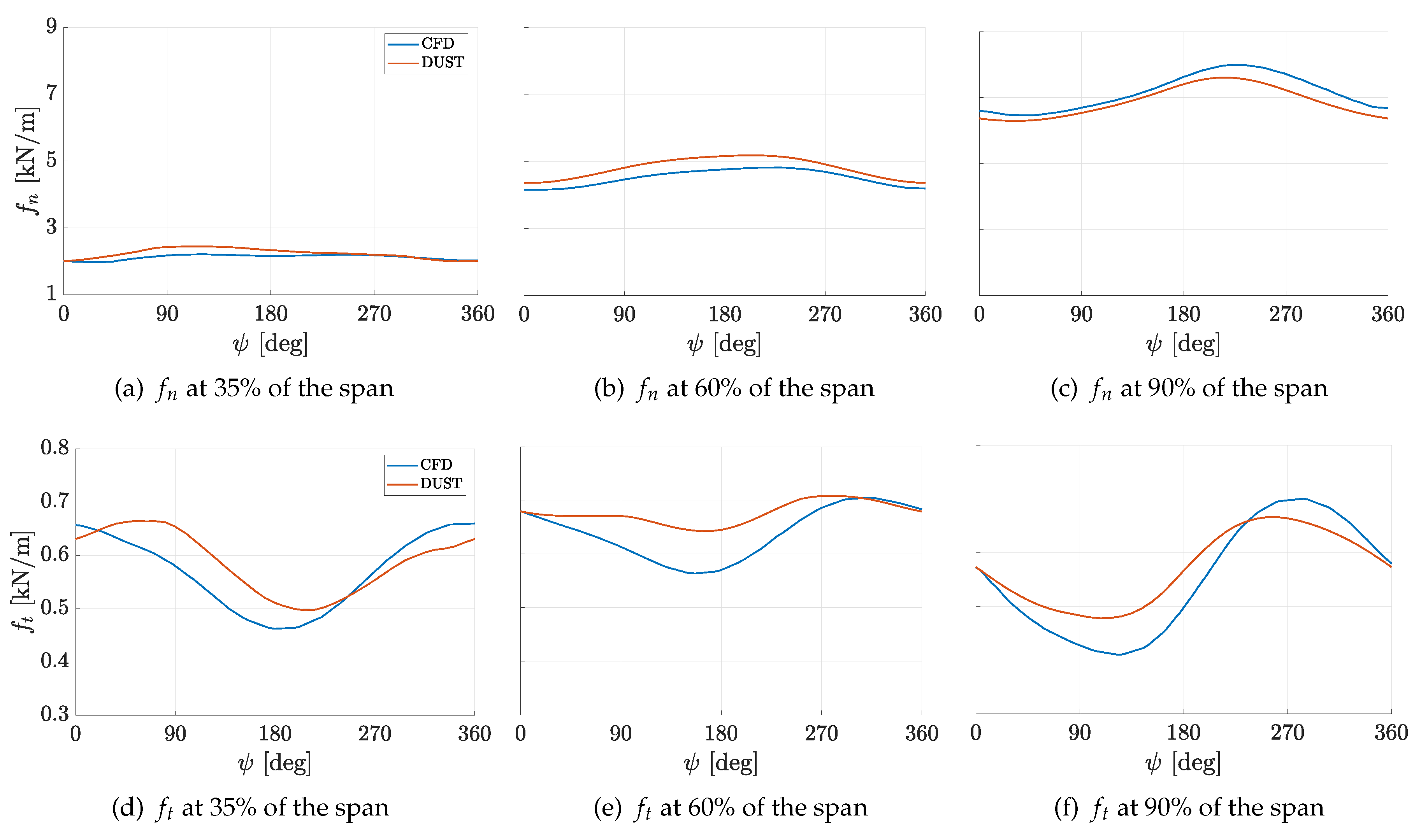
In order to quantify the local effect on blades subjected to yawed inflow, sectional normal and tangential forces are compared at three different spanwise coordinates in
Figure 10 as function of blade azimuthal angle
in the last computed revolution. DUST tends to calculate higher normal and tangential force densities up to 60% of the span coordinate, while a slightly lower normal force density is found near the blade tip compared to the high-fidelity CFD results. Nevertheless, generally the global behaviour of the sectional forces acting on blades are captured by DUST representation also in yawed condition.
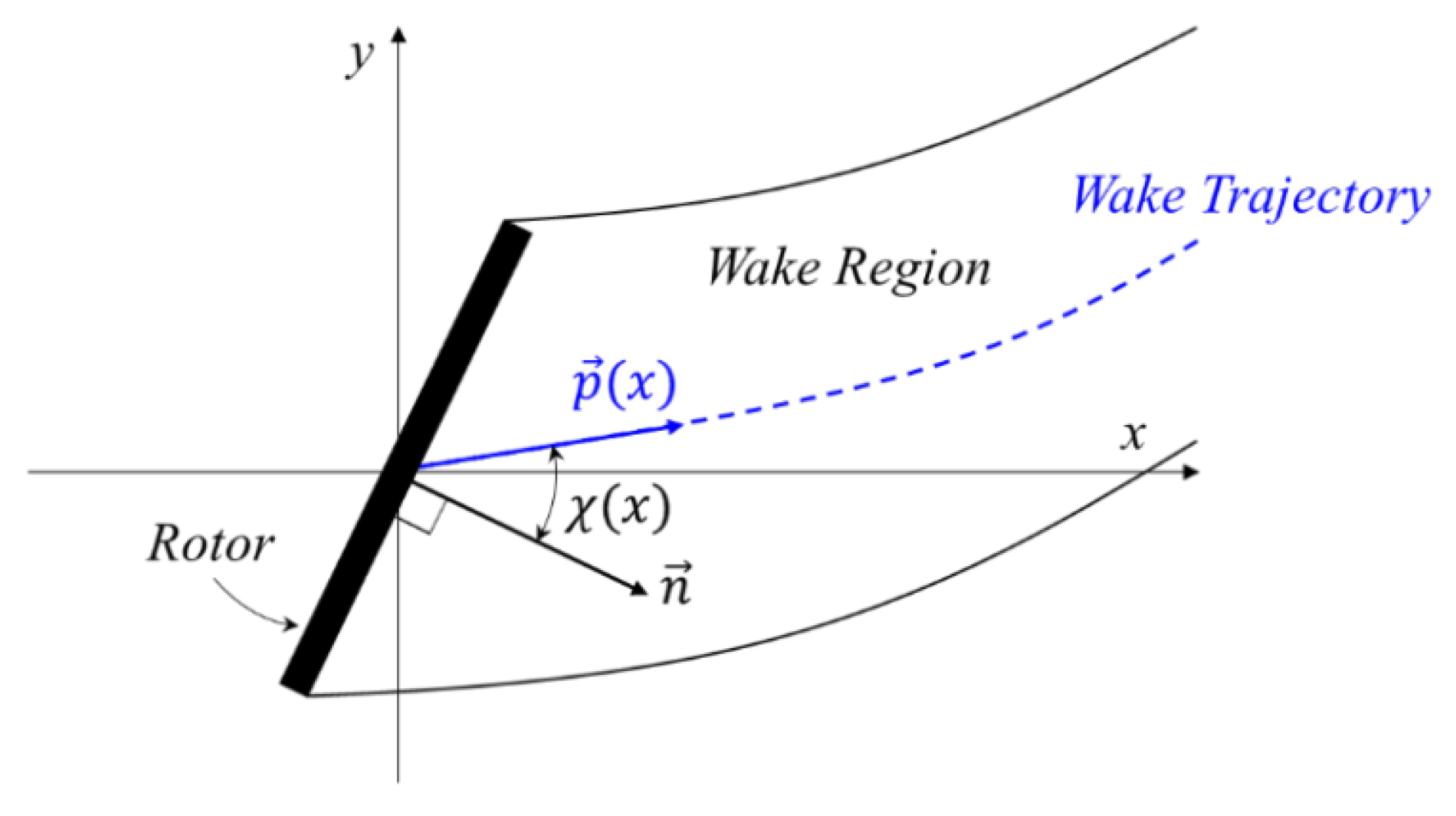
Another important feature to better understand the capability to capture the wind turbine wake behaviour for yawed configuration is the study of the evolution of the wake center-lines and the associated skew angles. The wake center-lines is an imaginary line that runs through the middle of the wake, marking the trajectory of the region with the highest velocity deficit caused by the wind turbine and represents the path that the wake follows downstream the turbine. This line can be calculated as the integral of the velocity deficit on a wake section perpendicular to the flow direction divided by the area of that section [
46]. This method gives an average value that accounts for the different velocities across the entire wake area, providing a singular measure of the wake’s strength. The skew angles, instead, gives a more quantitative analysis of the wake center trajectories. Skew angle
is the angular measure between the position vector
extending from the rotor disk midpoint and the normal vector to the rotor disc, as shown in
Figure 11 and defined in Eq.
1.
Figure 12 shows the skew angles behaviour calculated by DUST compared with LES results by Kim and Lee [
25], for yawed conditions ranging from
to
. The comparison shows how DUST is capable to evaluate correctly the wake center line evolution and the corresponding skew angles that change with respect to yaw angle and show a peak around
.
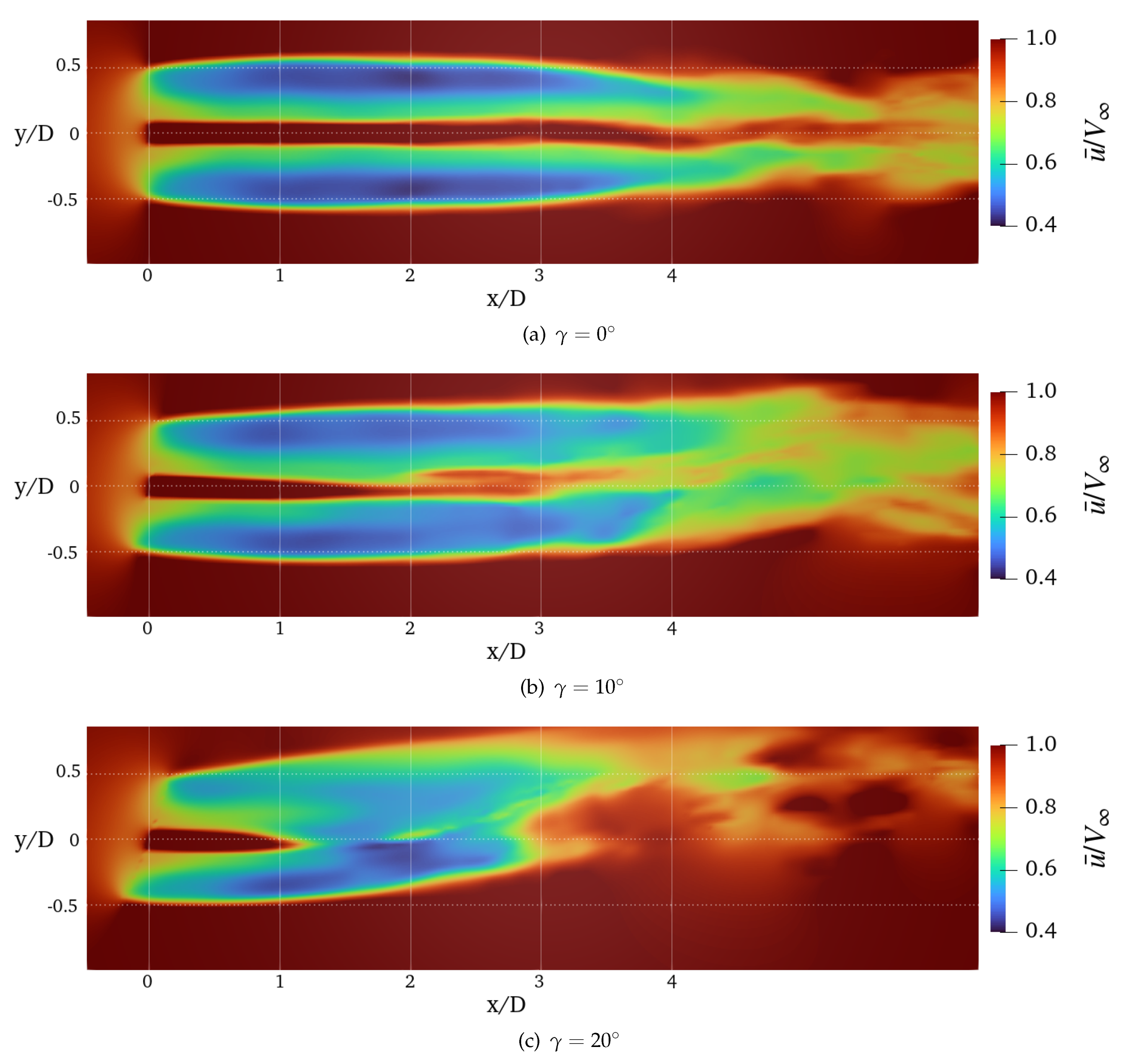
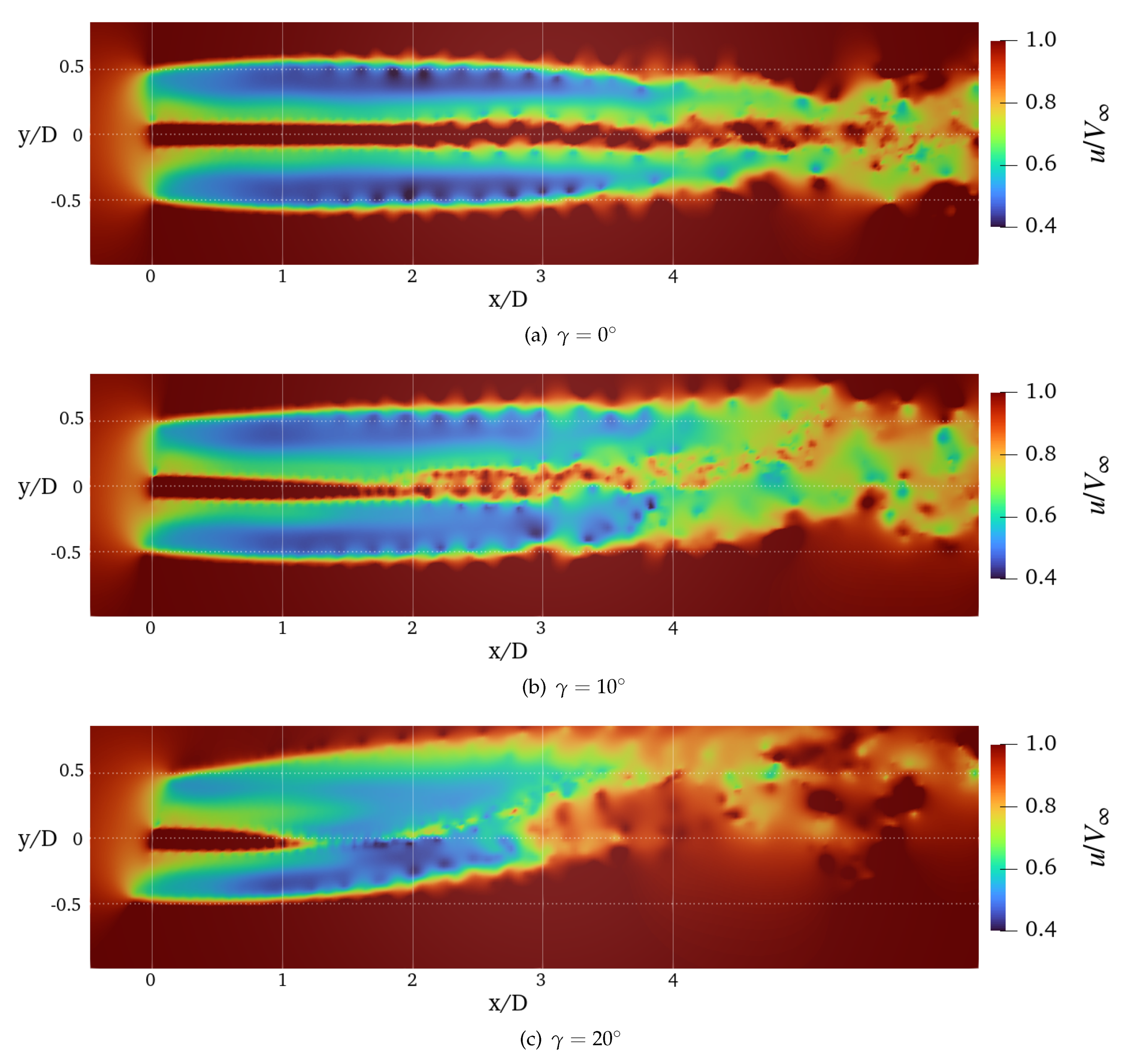
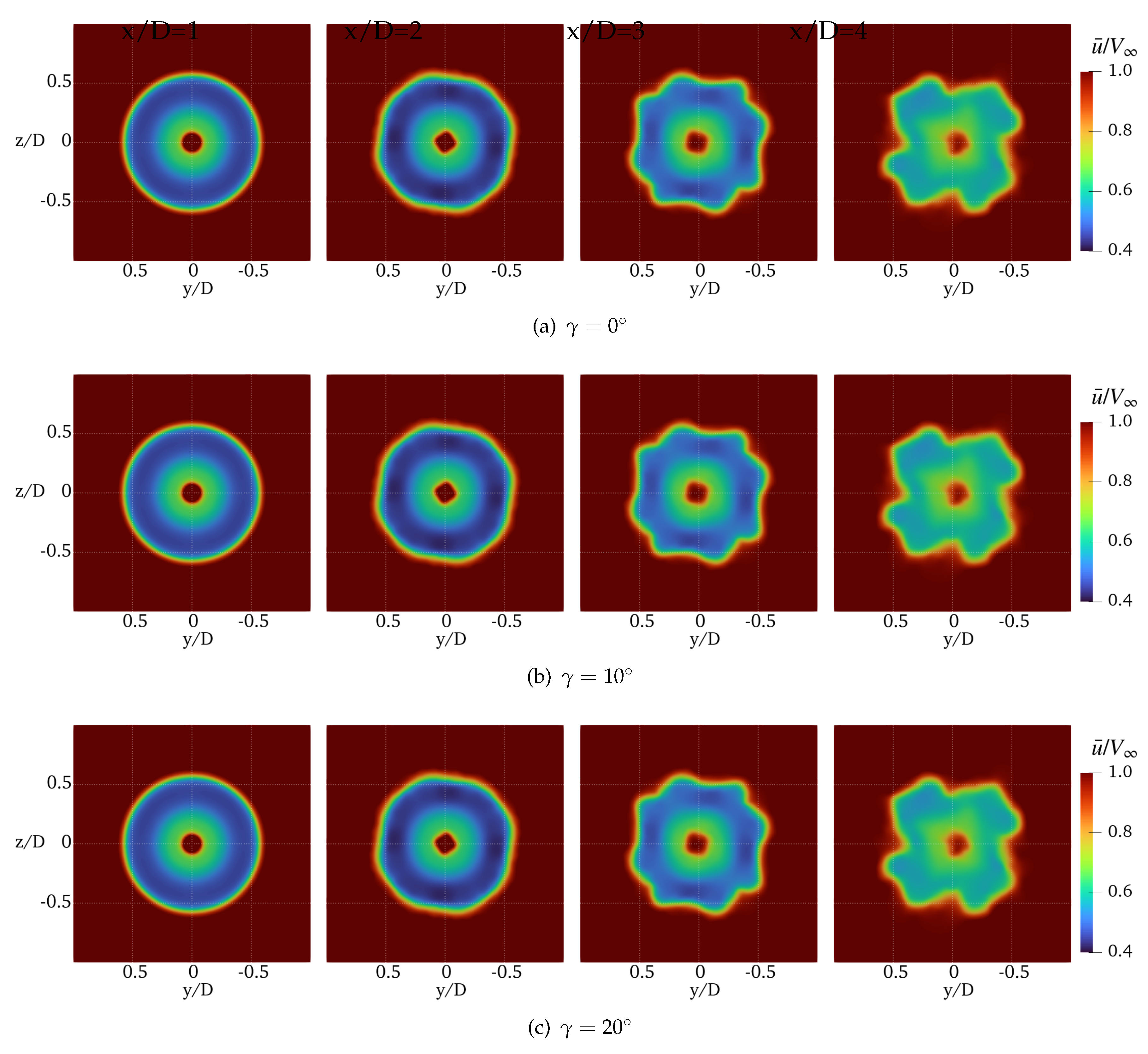
A more general evaluation of DUST capabilities to capture wind turbine wake is provided by the visualization of the flow fields.
Figure 13 and
Figure 14 show the contours of the averaged and instantaneous streamwise velocity computed by DUST (NL-VL) at different yaw angles. This flow field representation highlights the capability of DUST to evaluate the evolution and deflection of the wakes occurring at yawed conditions, as well as the highly unsteady behaviour of the flow fields in these conditions. If compared with LES results by Kim and Lee [
25], the global behaviour of the flow field is captured but the speed of deformation of the sectional shape of the wakes computed by DUST is higher. Indeed, the coherence of the wake shape is lost at a lower distance from the rotor disk with respect to LES computation by Kim and Lee [
25], as shown by the contours of the averaged streamwise velocity on transversal planes shown in
Figure 15.
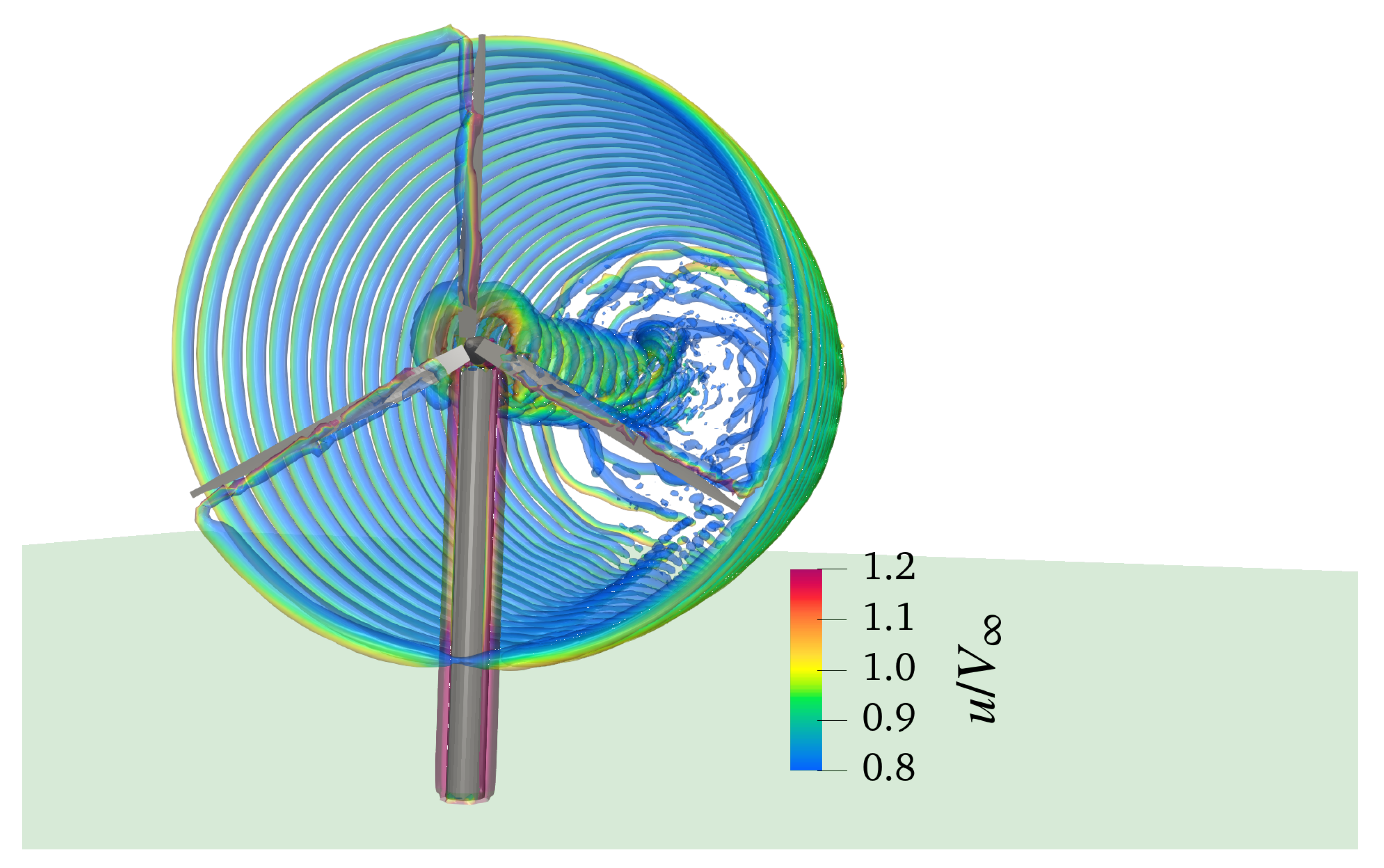
The final configuration considered deals with the complete case equipped with tower and nacelle for C4 rotor condition.
Figure 8 illustrates a visualisation of wake structure computed by DUST for the complete wind turbine shown as an iso-surface of the vortex Q-criterion.
As done before, DUST simulations results using both LL and NL-VL models are compared with the high fidelity CFD calculation by Yu and Kwon [
30] and Lin
et al. [
21]. The results in terms of integral loads comparison are presented in
Table 9 for single rotor and full wind turbine.
The introduction of nacelle and tower provides a reduction of the rotor performance for both power and thrust. This behaviour is captured by DUST simulations, thus showing the capability to reproduce interactional effects between rotor wake and tower, as done by CFD. In particular, NL-VL model shows integral values in quite good agreement with high-fidelity CFD [
21] as evaluated differences are below than 5% for both power and thrust.
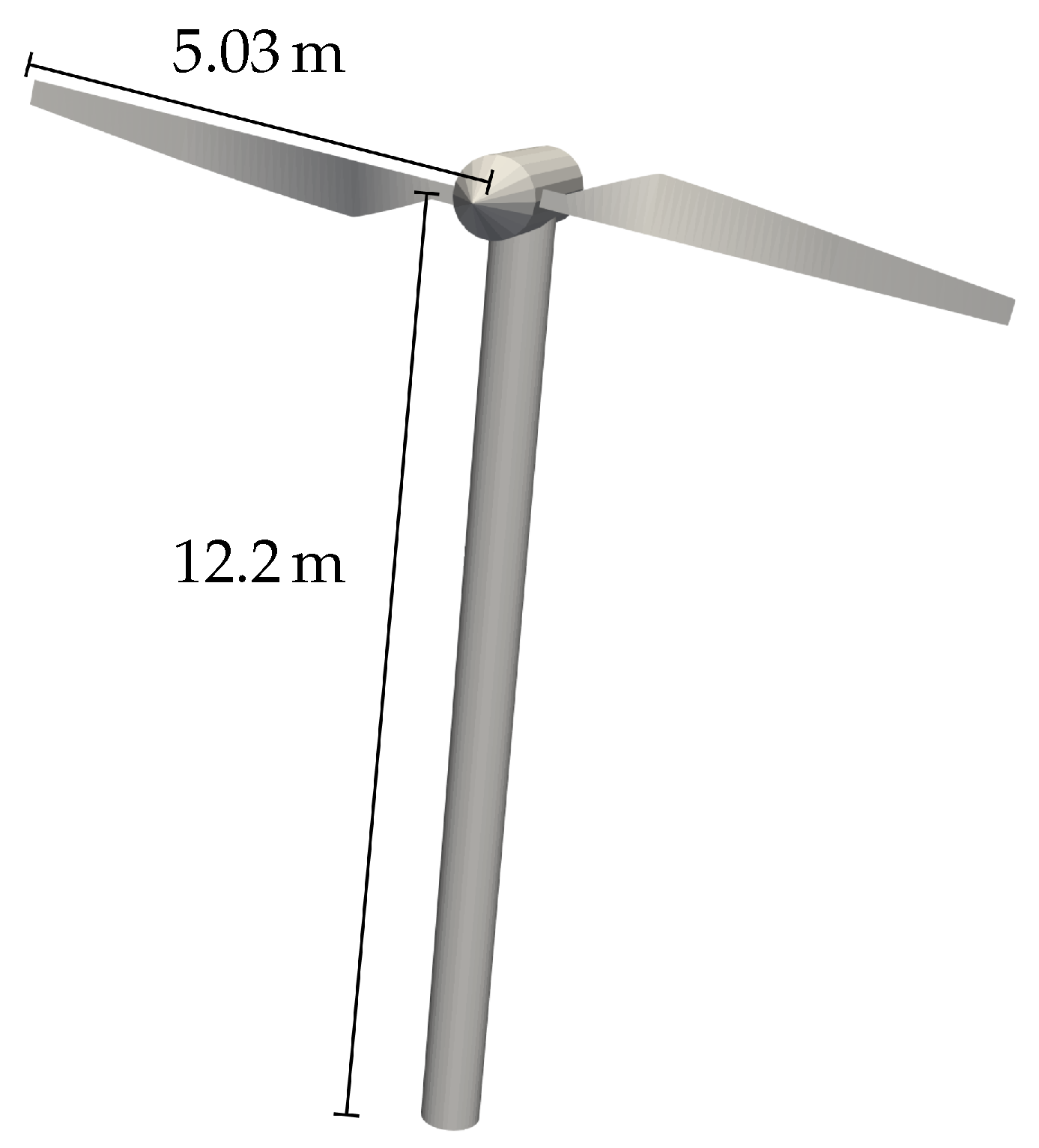
4.2. NREL Phase VI
The second part of the validation deals with the NREL Phase VI wind turbine and was focused in particular of the analysis of highly yawed conditions for 7 m/s freestream velocity. Firstly, an overview of rotor thrust and torque computed by DUST at zero yaw is given in
Table 10 and compared with experiments by Hand
et al. [
1] and high-fidelity CFD data by Länger-Möller
et al. [
32].
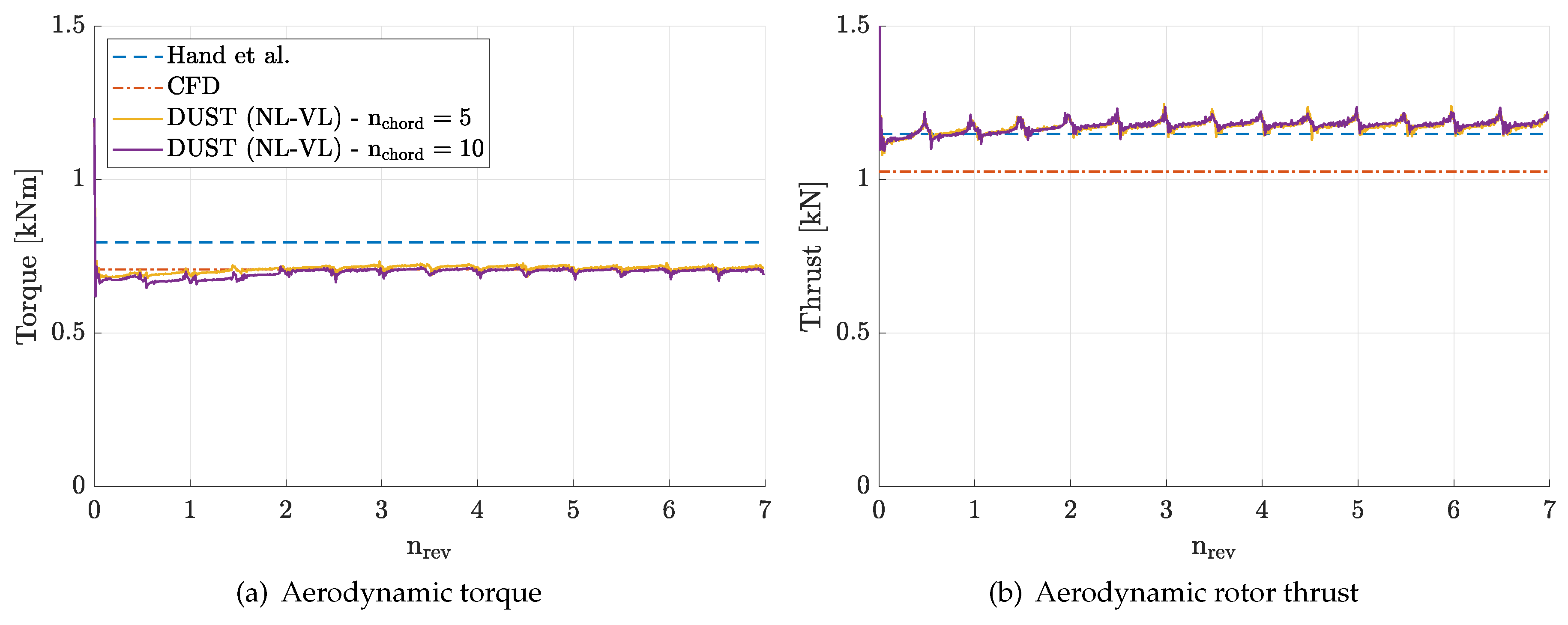
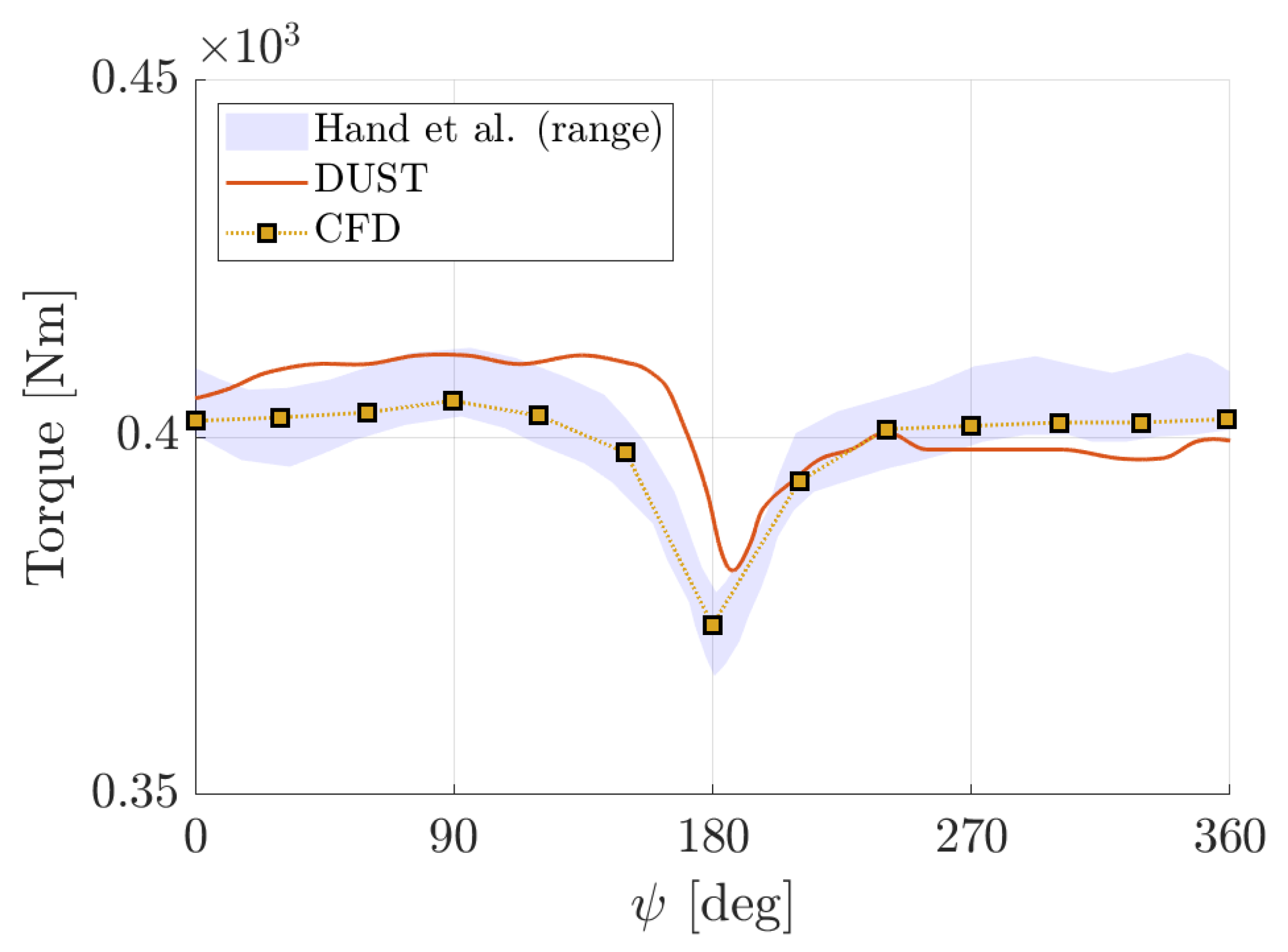
A good agreement of the integral loads values are found for DUST simulations for the complete wind turbine model, as thrust is near to the mean experimental value, while torque is slightly underestimated similarly to CFD. A detailed insight on loads behaviour is provided by the time history of the single blade aerodynamic torque evaluated on the last computed revolution, compared with experiments and CFD [
33] in
Figure 17. Results distinctly illustrate DUST capability to reproduce time evolution of the blade torque observed by experiments and particularly the bump occurring as a blade passes in front of the tower around azimuthal angle of
.
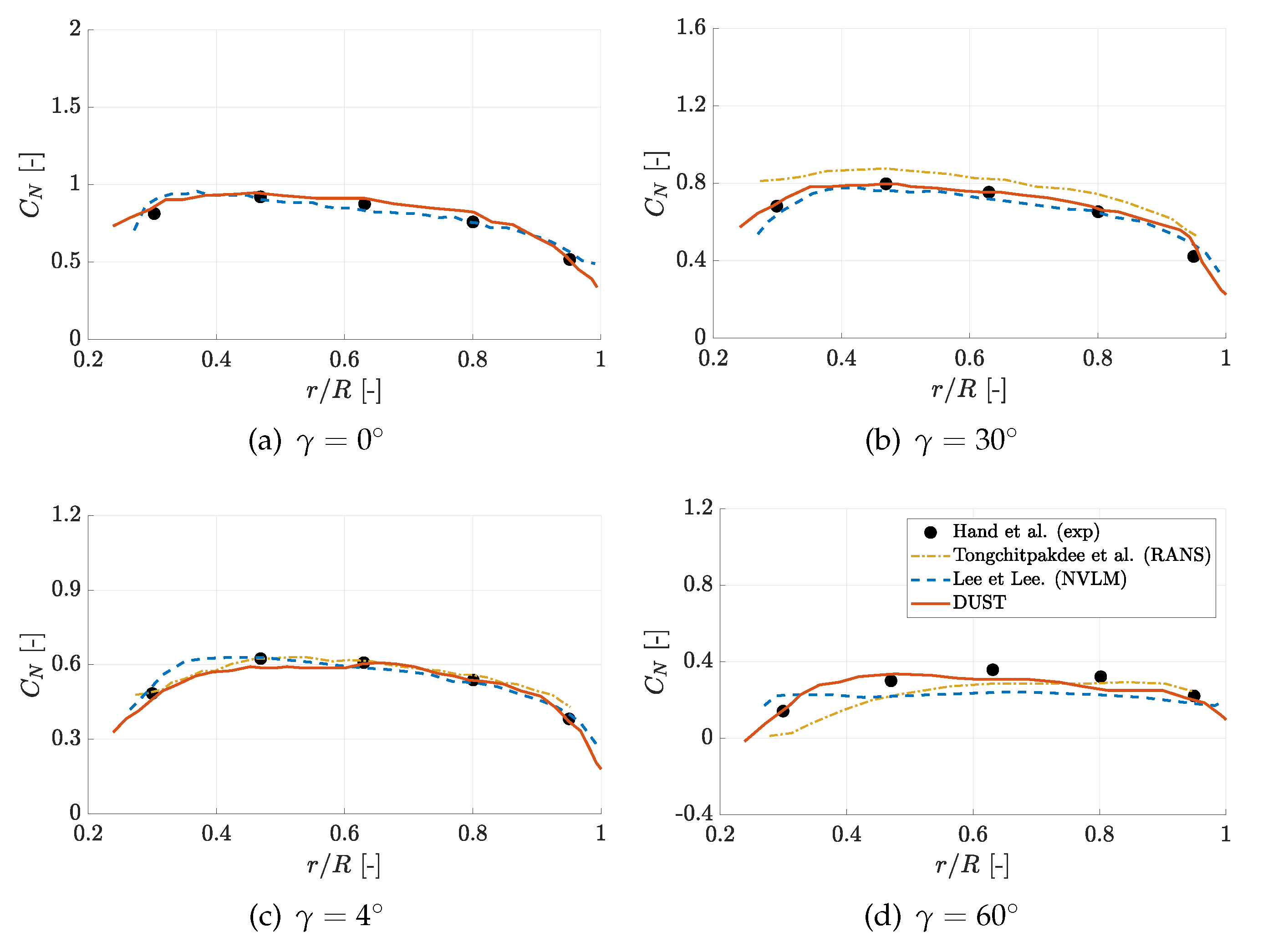
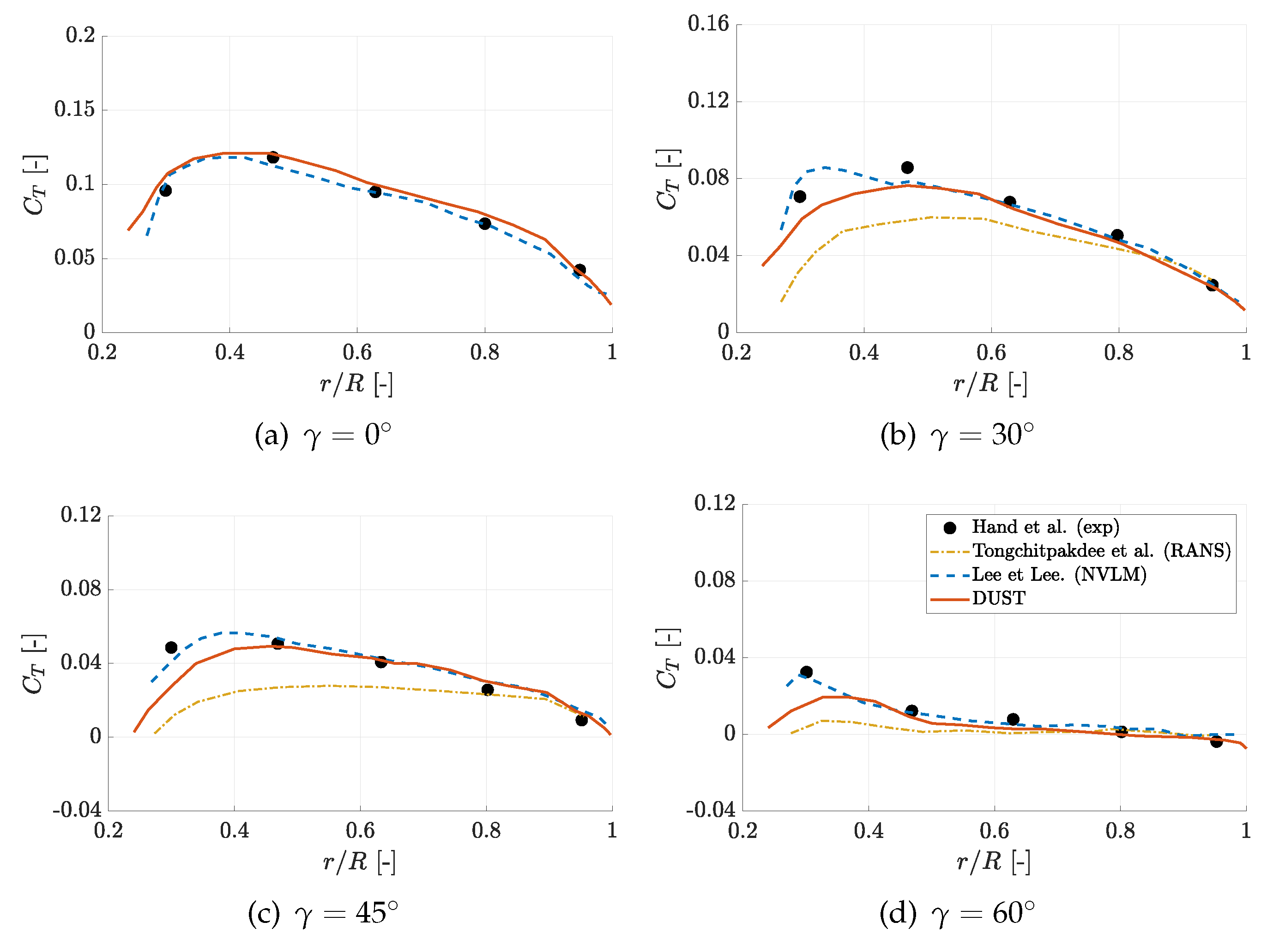
Now, the attention is focused on the evaluation of loads for yawed conditions. Thus, blade sectional normal and tangential force are compared respectively in
Figure 18 and
Figure 19 for different yaw angles. In particular, DUST results are compared with NREL measurements [
1] and with numerical results obtained by RANS simulations [
47] and by a non-linear vortex lattice method NVLM described in [
48].
The trends of the normal sectional forces computed by DUST resembles the experimental data for the considered yawed angles, just showing a slight downward offset with respect to the mean experimental values at
, similarly to what found by both RANS and NVLM approach used as comparison. Concerning tangential force density, a quite good agreement with experiments and NVLM approach results [
47] is obtained particularly at
. Some discrepancies are observed at higher yaw angles in the inner blade region, where also RANS approach shows larger error with respect to experiments. On the other hand, a quite good agreement with both experimental and numerical data are also found for higher yaw angles in the outer half region of the blade. Generally, the sectional loads values obtained by DUST resemble an accuracy comparable with the similar NVLM method used in [
48] and somewhere higher than the one obtained by high-fidelity CFD, thus further confirming the promising capability of DUST mid-fidelity approach for the evaluation of wind turbine aerodynamic performance also under deeply yawed conditions.
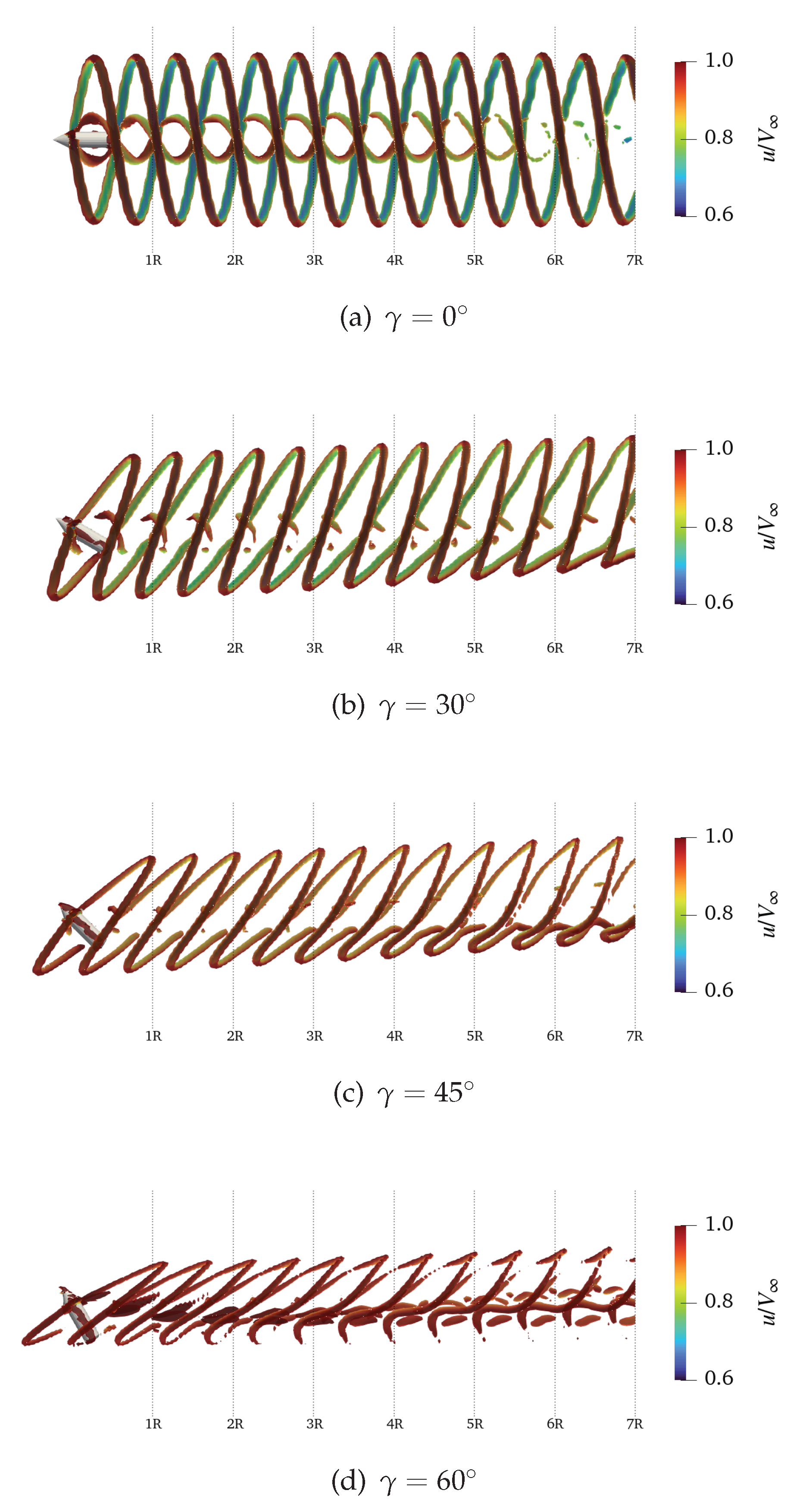
Finally, a representation of the wind turbine wakes under the different considered yawed conditions is shown in
Figure 20 by means of iso-surfaces of Q-criterion coloured by non-dimensional axial velocity component contours. To impose the yaw rotation, the entire turbine was rotated as done during the wind tunnel tests, assuming the flow always directed from left to right. This comparison shows the capability of DUST to evaluate the coherent vortical structure of the wind turbine wake as well as their deflection related to the different yawed conditions.