Prerpints.org logo
Preprint
Article

Creating An Array Of Parallel Vortical Optical Needles

Altmetrics

Downloads

189

Views

70

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

14 February 2024

Posted:

15 February 2024

You are already at the latest version

Alerts
Abstract
We propose a method for creating parallel Bessel-like vortical optical needles with an arbitrary axial intensity distribution via superposition of different cone-angle Bessel vortices. We analyze the interplay between the separation of individual optical vortical needles and their respective lengths and introduce a super-Gaussian function as their axial profile. We also analyze the physical limitations to observe well-separated optic needles, as they are influenced by mutual interference of the individual beams. To verify our theoretical and numerical results, we generate controllable spatial arrays of individual Bessel beams with various numbers and spatial separations by altering the spectrum of the incoming laser beam via the spatial light modulator. We demonstrate experimentally how to implement such beams using a diffractive mask. The presented method facilitates the creation of diverse spatial intensity distributions in three dimensions, potentially finding applications in specific microfabrication tasks or other contexts. These beams may have benefits in laser material processing applications such as nanochannel machining, glass via production, modification of glass refractive indices, and glass dicing.
Keywords: 
Subject: Physical Sciences  -   Optics and Photonics

1. Introduction

Over time, lasers have proven to be a versatile tool across various domains, including manufacturing [1], biomedicine [2,3], telecommunication [4,5], and more. Precise adjustment of laser parameters is crucial for achieving specific applications, with beam shape being a critical factor. The Gaussian beam is the most common due to its ability to be focused to a small volume.
The structure and properties of the electromagnetic field play a vital role in modern optics and its applications [6,7,8,9]. However, non-diffracting beams have recently gained traction due to their capacity to maintain shape over long distances compared to Gaussian beams [8]. One example of structured illumination is non-diffracting beams, such as Bessel beams [10,11], known for their elongated focal line and self-reconstruction capability [12,13]. Laser beams with a long depth of focus and a narrow transverse intensity distribution [14] are useful for laser applications. These beams can be generated by axicons [15,16]. They have shown benefits in laser material processing applications like nanochannel machining [17], glass via production [18], modification of glass refractive indices [19], and glass dicing [20,21,22]. In other fields, they have been used successfully for THz imaging [23], particle manipulation [24], and microscopy [25].
They have a fixed bell-shaped axial intensity distribution in the Bessel zone [26]. However, this distribution may not be optimal for some applications, such as laser micro-machining [17,27,28,29,30] and optical tweezers [31]. For some applications, such as surface patterning, Bessel beams can provide a less sensitive process to surface height variations [32,33,34], but shaping the focal region could improve stability even further. Several methods to create non-diffractive beams with a flat longitudinal intensity distribution were suggested, for example, the implementation of a logarithmic axicon [35,36], modulating the spatial spectrum of the Bessel beam [37,38] or using diffractive optical elements [29,39].
Similar characteristics are exhibited by other types of structured light without diffraction, such as Mathieu-Gaussian [40] and parabolic-Gaussian (Weber-Gaussian) beams [41,42]. Another well-known non-diffracting beam is the Airy beam [43], notable for its main lobe propagating along a parabolic trajectory in the longitudinal plane [44]. Airy beams have been used for particle trapping, optical manipulation [45,46,47], machining curved structures along the beam path [48], multiphoton polymerization [49], and imaging around obstacles in the THz wavelength [50].
In some applications, additional engineering of the focal zone is desirable. The axial behavior of the laser beam, another aspect of beam shaping, has been rapidly evolving [12,51,52] since the introduction of non-diffracting Bessel beams [11], which have a large ratio between transverse and longitudinal widths of the focal line [10]. The discovery of axial engineering has further stimulated research on focal line engineering, leading to the development of optical needles [38,53,54,55].
Another degree of freedom is associated with the azimuthal phase dependence of higher-order non-diffracting Bessel beams J m , expressed as exp ( i m ϕ ) , where m is a topological charge. This dependence results in a phase singularity, also known as an optical vortex [56,57,58], which presents as a helical wavefront with m nested screw dislocations [59,60]. Optical vortices, commonly observed in electromagnetics, carry orbital angular momentum [61]. The first instance of optical engineering using cylindrical beams was reported in Ref. [62], where a coherent superposition of the Bessel and Neumann beams was considered, despite the Neumann beam having an amplitude singularity on the axis. By implying the periodicity of the transverse beam pattern in the infinite sum of Bessel eigenmodes, rotating patterns were realized using binary diffractive elements [63,64]. An alternative approach to generating rotating scale-invariant fields was presented in [65].
A single vortex is a dark spot of light with a phase singularity at its core. Consequently, its three-dimensional trajectory can be considered as a unified entity, especially considering that time reversal would change the signs of single vortices in the beam. Therefore, a negatively charged optical vortex can be interpreted as a positively charged vortex propagating backwards, and the creation and annihilation of positive and negative vortices in pairs under diffraction can be viewed as a dark knot of light [66,67,68]. This interpretation of the intricate evolution of vortical structures with various topologies has led to the emergence of terminology such as knots, braids, and bundles of dark light [69].
Multispot beam splitting is another attractive topic in the field. Various techniques are used to create an array of Gaussian beams, for instance, direct laser interference [70,71], beam shaping by free-form surface lens array [72], by SLM and phase mask created by iterative algorithms [73], or by diffractive optical elements [74,75]. A generation of Bessel beam array has also been reported in the literature. The superposition of multiple shifted axicon holograms in SLM [76] or the illumination of the axicon with a phase modulated beam [77] can lead to the formation of multiple Bessel beams. A particular microstructure array can also be used for this purpose [78]. Furthermore, when using these elaborate intensity distributions, aberrations can have positive effects on these beams [79] or can suffer negative aberrations when they pass through a planar dielectric material interface (e.g., air-bulk material) [38,55,80], which affects their performance and efficiency and requires correction [81].
In this work, we propose a method for creating parallel Bessel-like optical needles with adjustable individual axial intensity patterns and individual topological charges. We used a superposition of vortical Bessel beams with specific axicon angles and complex amplitudes, as suggested in Refs. [37,38,82,83,84,85]. We also demonstrate experimentally how to implement such beams using a spatial light modulator. We study the interaction of the topological charge and transverse displacements of individual vortical Bessel-like needles of different topological charges. This investigation is important for practical applications, as it improves the laser energy deposition and the axial intensity distribution of the optical needles [84,86].

2. Axial Intensity Control in an Vortical Optical Needle and Translation of Optical Needles

In this section, we outline the theoretical foundation for generating arrays of parallel Bessel-like vortical optical needle beams characterized by a controlled axial intensity pattern. Our approach involves employing ideal Bessel vortices as fundamental basis functions, derived from an angular spectrum described by Dirac’s delta function [87]. These non-diffracting beams serve as sufficiently accurate approximations of intensity distributions experimentally observed in the vicinity of the Fourier lens’s focal point.

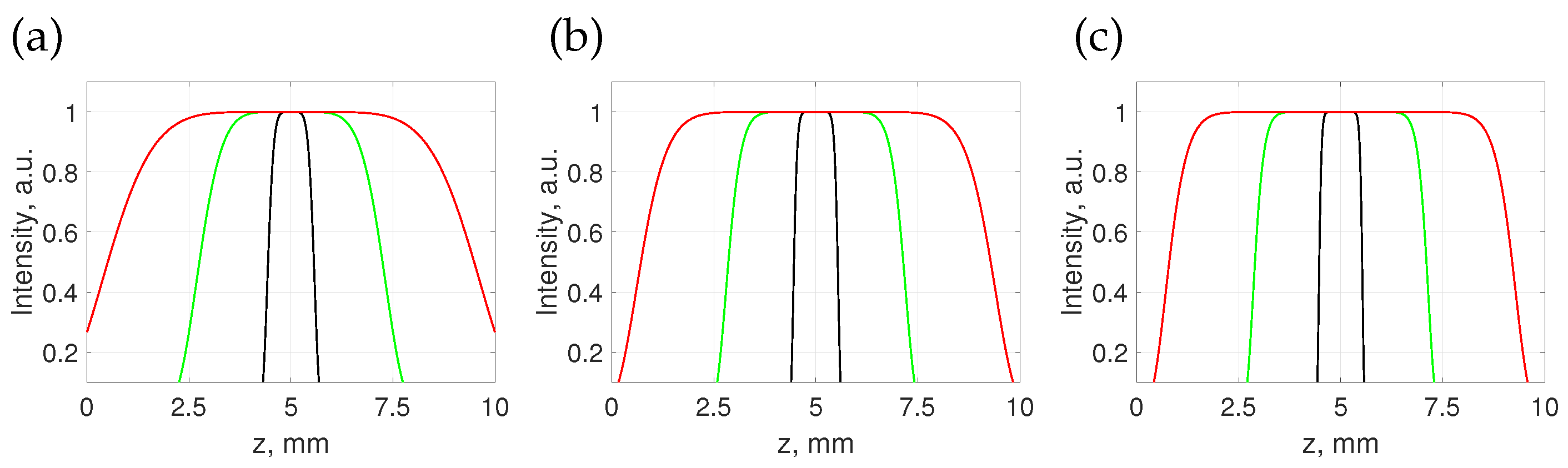
2.1. Axial Intensity Control in an Optical Needle

A non-diffracting Bessel vortex is a solution of the scalar Helmholtz equation in the cylindrical coordinates
ψ ( ρ , φ , z ) = J m k ρ ρ exp i m φ + i z k z ,
where ψ is electric field, J m is the m-th order Bessel function, ρ , φ , z are cylindrical coordinates, m is the topological charge and k ρ , k z are radial and longitudinal components of the wavevector k = ( k ρ , 0 , k z ) . The components of the independent wave vectors are defined through the cone angle θ of the Bessel beam as k ρ = k sin θ and k z = k cos θ [87].
Every solution to the scalar Helmholtz equation can be expressed through a 3D integral comprising plane waves with distinct wave vectors. This integral can be simplified to a 2D form when dealing with axisymmetric fields, as outlined by Stratton [87]. This two-dimensional representation is based on a Fourier-Bessel transform and can be modified for our specific needs by adjusting the integration variables from k ρ to k z . The axial component of the wave vector becomes the coordinate of the Fourier transform within the integral expression.
A comprehensive discussion on this method for designing axial profiles can be found in extensive detail in [37,38,82]. When the radial coordinate ρ is zero, the expression of the combined electric field becomes a Fourier series with respect to the axial coordinate z, achieved through the superposition of the Bessel beams, see Equation (1). In this context, a Fourier integral is explicitly defined as
Ψ ( r ) = ∫ − ∞ ∞ A K z + k z 0 ψ r ; K z d K z
where k z = k z 0 + K z , where k z 0 is a carrier wave vector and A k z is a spatial spectral amplitude of the combined beam. The carrier wave vector k z 0 restricts K z to forward propagating waves only by shifting the spectral coordinates k z to positive values. A specific case of m = 0 was discussed in Ref. [55], here, we investigate the general case. Near the optical axis ρ ≈ 0 , we can rewrite Equation (1) as
ψ ( ρ , φ , z ) = 1 m ! k ρ ρ 2 m exp i m φ + i z k z ,
so, using Equation (3) in Equation (2) results in
Ψ ( r ) = 1 m ! k ρ ρ 2 m exp i m φ + i z k z 0 ∫ − ∞ ∞ A K z + k z 0 exp i z K z d K z
Thus, finally, we arrive at the expression
Ψ ( r ) = 1 m ! k ρ ρ 2 m exp i m φ + i z k z 0 f ( z ) ,
where f ( z ) is the axial distribution of the combined vortical beam with engineered axial profile, this profile is expressed as
f ( z ) = ∫ − ∞ ∞ A K z + k z 0 exp i z K z d K z .
Alternatively, knowing the axial profile f ( z ) of the vortical optical needle we can arrive at the spatial spectra A ( k z ) as
A k z = 1 2 π ∫ − ∞ + ∞ f ( z ) e − i K z z d z .
Therefore, the continuous superposition of Bessel beams Ψ ( r ) , as defined in Equation (2) with a spatial spectrum (3), is capable of axial intensity properties resembling those defined by a function f ( z ) .
An optical needle (or an optical bottle) is created when the axial profile f ( z ) is a constant step function. The step function with abrupt start and ending points will cause undesired effects due to the Gibbs phenomenon. Therefore, our aim is to mimic this desired profile by selecting the function f ( z ) to be a super-Gaussian function
f ( z ) = exp − z − z 0 z 0 2 N
where z 0 = L / 2 log 2 / 2 1 / 2 N is a some control parameter of the profile at the full width at half maximum (FWHM), N is the order of a super-Gaussian beam, L is the length at the FWHM. This choice enables smoother axial intensity profiles, see Figure 1.

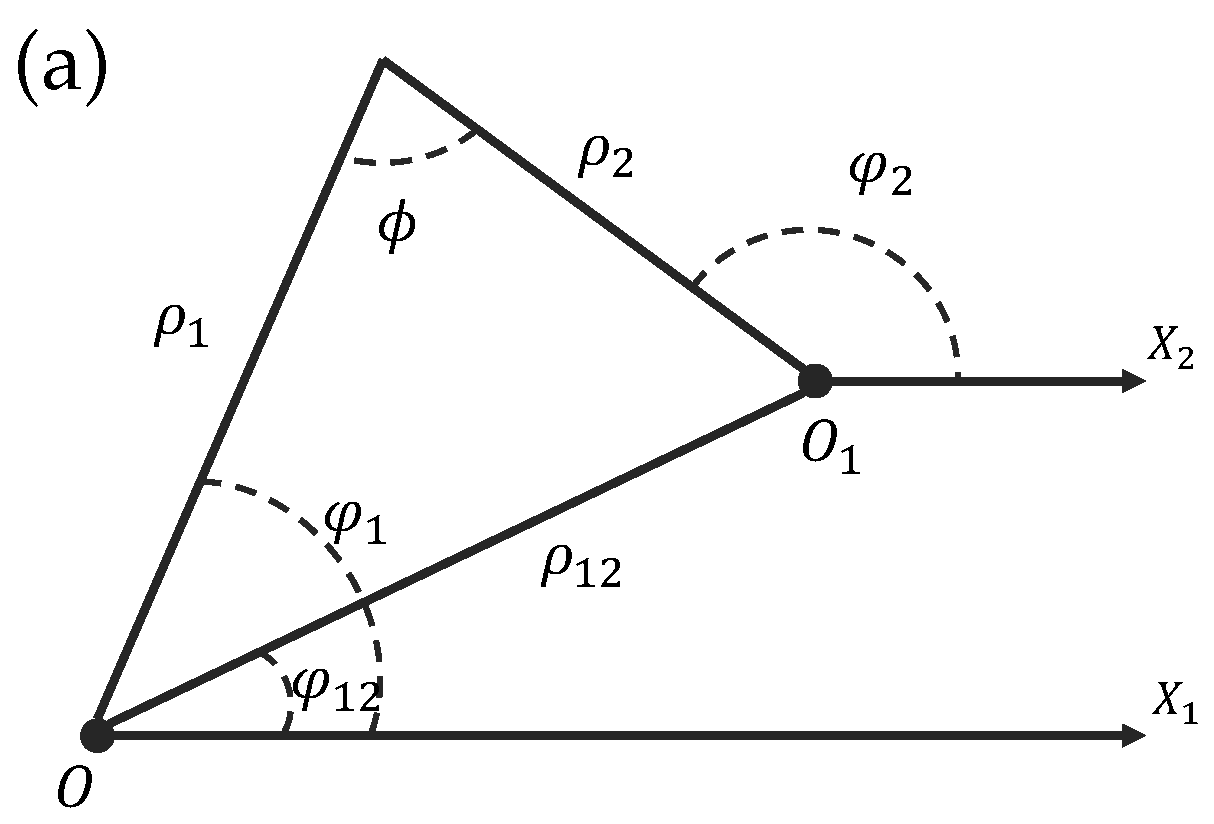
2.2. Translation of the Vortical Optical Needle

The control of the transverse position of an optical needle can be performed with the help of the addition theorem of Bessel beams [87]
J n k ρ ρ 2 e i n φ 2 = ∑ m = − ∞ ∞ J m k ρ ρ 12 J n + m k ρ ρ 1 e i m φ 1 − φ 12 .
Here, the indices 1 and 2 indicate the coordinates of the first and second cylindrical coordinate systems, n is an index, and ρ 12 and φ 12 are the coordinates of the translated origin O 1 with respect to the untranslated origin O, see Figure 2 (a). The spatial spectrum of individual Bessel beam, see Equation (1) is the Dirac delta function multiplied by the azimuthal phase term, therefore the shifted coordinates it becomes
ψ ^ k ρ , φ k = ∑ m = − ∞ ∞ J m k ρ ρ 12 e − i m φ 12 i m e i m φ k δ k sin θ − k ρ k ρ ,
where φ k is the azimuth of the spatial spectral coordinates. In this way, the Bessel beam with origin at the shifted point is expressed as a superposition of Bessel beams in the non-shifted origin, see Figure 2 (a).
Our intention here is to have a number p = 1 , 2 , ⋯ , P of independent parallel vortical needles, each with its own axial profile f p ( z ) and individual position x p , y p in the transverse plane. According to the superposition principle, the resulting spatial spectrum of the combined beam is
Ψ ^ k x , k y = ∑ p ∫ − ∞ ∞ A p K z + k z 0 ψ ^ p k x , k y d K z .
where
A p k z = 1 2 π ∫ − ∞ + ∞ f p ( z ) e − i K z z d z .
and ψ ^ p is given in Equation (10) for translation to the coordinate center located at x p , y p .

3. Experimental Results

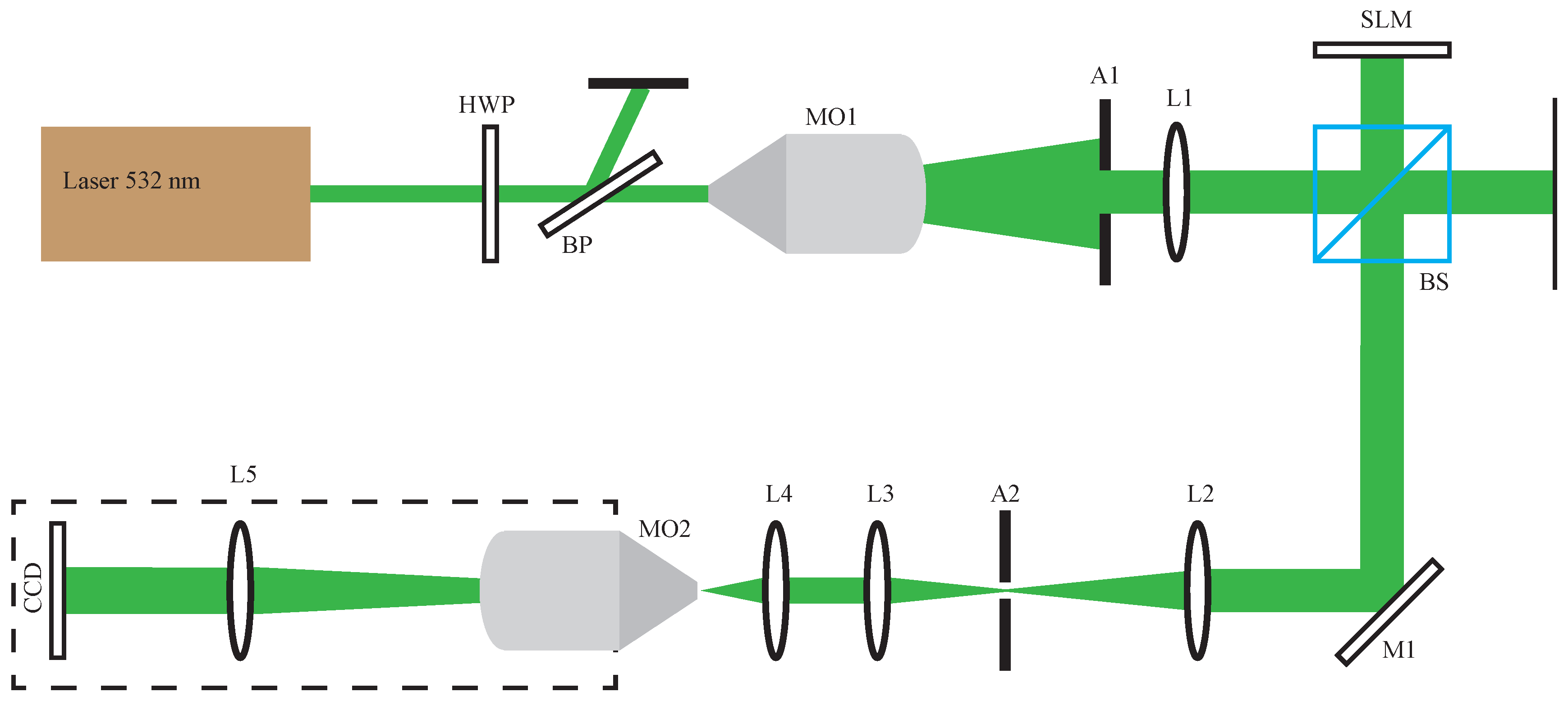
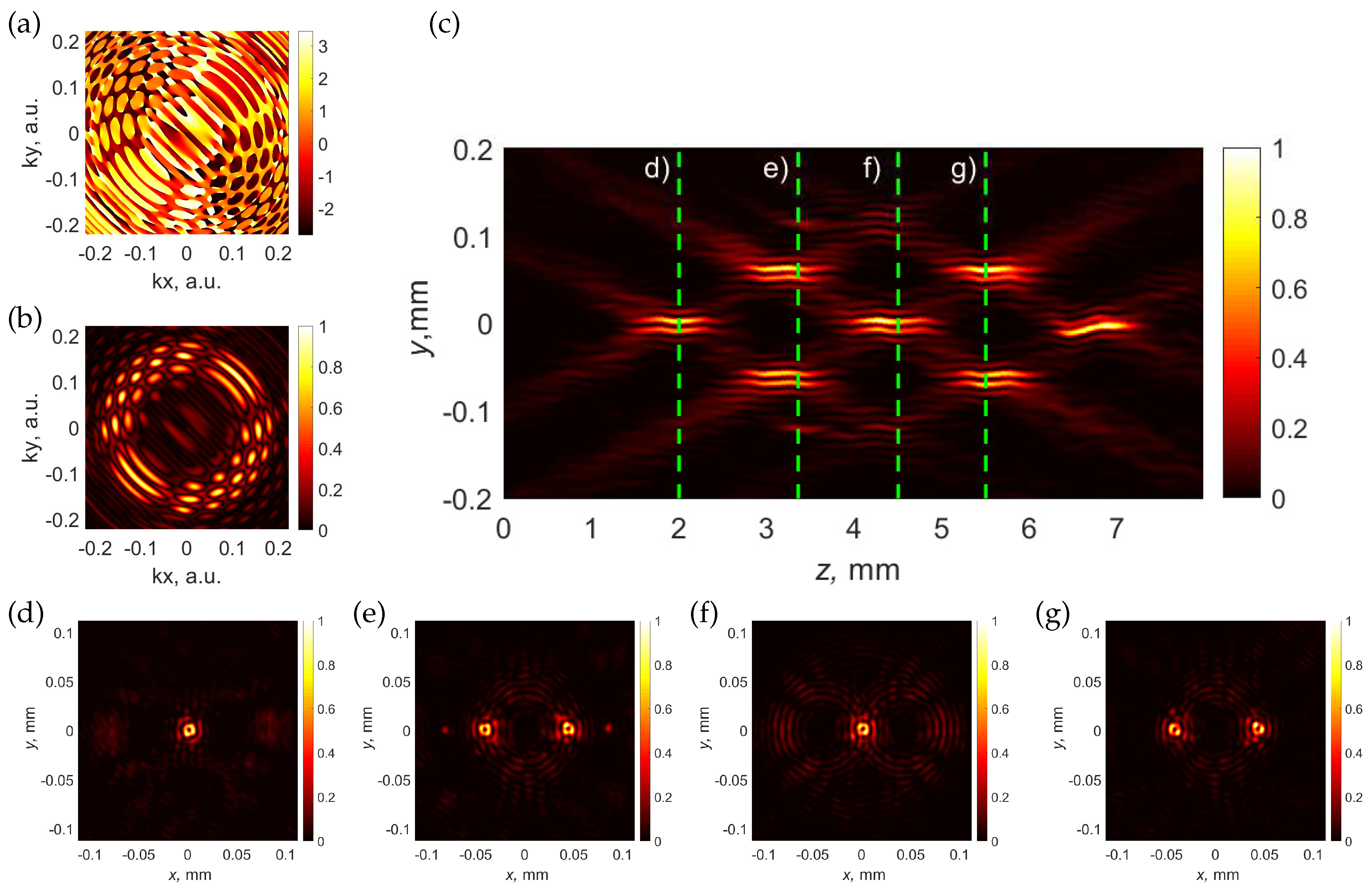
3.1. Optical Setup

Optical setup used throughout the experiment is displayed in Figure 3. A λ = 532 nm DPSS laser beam is attenuated by a half-waveplate (HWP) and a Brewster’s polarizer (BP) and then expanded by 40x, N A = 0.65 microscope objective (MO1) and the beam is collimated by the lens L1 ( f = 125 mm). The beam is then directed to a spatial light modulator (SLM) (PLUTOVIS-006-A, HOLOEYE Photonics AG, 8 bit, 1920x1080 pixels, 8 µm pitch) by means of a non-polarizing beam splitter (BS) at 0 deg angle. The correct polarization direction is set by the polarizer (BP). The size of the beam (~ 8.5 mm diameter) is selected by an aperture (A1) to fill the SLM screen ( 8.64 mm). The SLM shapes the beam spectrum, which is directed to a 3x demagnifying optical setup 4 f comprised of lenses L2 ( f = 150 mm) and L3 ( f = 50 mm). This demagnifies the transverse coordinates three times and the longitudinal coordinates nine times. In the focal plane of lens L2, additional diffraction maxima created by the checkerboard mask are filtered out by aperture A2. Lastly, the spectrum is focused by a Fourier lens L4 ( f = 25.4 mm). Dimensions of the central lobe would be too small to register directly by a camera, therefore, the beam is captured by an optical imaging setup assembled on a motorized stage. This setup contains a 10x microscope objective (MO2), a collimating lens L5 ( f = 200 mm), and a CCD camera. The entire beam is scanned using 0.05 mm steps.

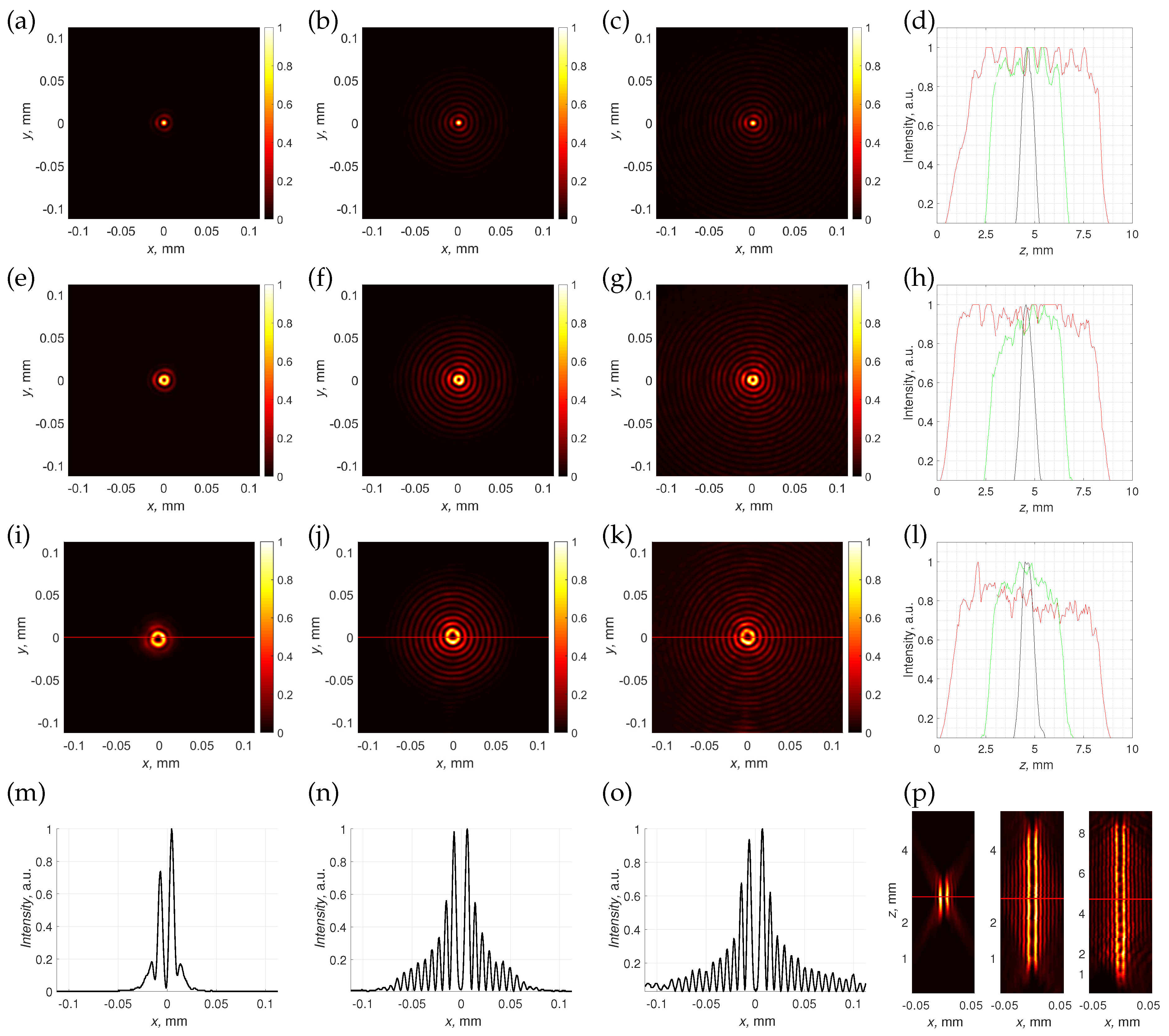
3.2. Creation of Single Vortical Needles

The optical setup used in this work is a bit different from that used in our previous research [38,55]. This time a different set of lenses is used for magnification. Therefore, we begin with experiments to verify the concept of single vortical needles with controllable axial profiles f ( z ) , described in the Equation (8). The spatial spectra of the engineered beams are found using Equation (7) and encoded in a phase-only mask using a checkerboard method [88]. The parameters for the axial profiles f ( z ) used in the experiments are the same as in the theoretical section, see Figure 1.
Our intention here is to reproduce optical needles without topological charge (i.e. m = 0 ) to ensure smooth operation of the optical setup before proceeding to the masks with topological charges. For this purpose, we selected three different lengths of optical needles L = 1 mm, L = 4 mm, and L = 8 mm and experimentally verified their creation (see Figure 4). We performed experiments with various orders N of the super-Gaussian function, but our experimentation identified the number N = 7 as optimal, which is in line with previous work [38,55].
The optical needle with the shortest length L = 1 m m has a central spike that is ~7.3 µm in diameter (at the intensity level 1 / e 2 ) and two detectable rings in the transverse intensity pattern, see Figure 4 (a). This is an expected outcome given its small longitudinal dimension. As the length L decreases, the properties of the optical needle are not similar to the properties of a Bessel beam but are more like those of a Gaussian beam. Moving on to the four-time longer optical needle with L = 4 mm, we observe the appearance of additional rings (seven in total) around the central spike. The size of the central spike did remain the same within experimental tolerance, and the transverse profile largely resembles a Bessel-Gaussian beam with a significant number of concentric rings surrounding the center of the beam. Lastly, we do increase the length of the optical needle twice more to L = 8 mm, see Figure 4 (c). The system of concentric rings becomes more pronounced, and the central lobe is not significantly affected. We have verified the propagation of these optical needles by measuring the intensity of the central lobes for various positions of z coordinate, see Figure 4 (d). In general, the behavior was detected to be as expected from numerical simulations, with no sharp oscillations on edges; the intensity drop is smooth as desired. However, we did observe some axial oscillations, which might be caused by inaccuracies in the positioning of the translation stage and some possible misalignment in the optical system.
Having verified that the optical setup acts at an intended level of performance, we now introduce nonzero topological charges m = 1 and m = 2 , see Figure 4. Starting with the shortest vortical needle with a length of L = 1 mm, we observe similarities with the previous case; compare Figure 4 (e) and (i) to Figure 4 (a). We observe two pronounced rings, the first ring with the vortical core inside and the second one surrounding it. The third ring is weak in both cases. In the expected manner, the radii of the first rings are different: the higher topological charge results in a larger central ring; compare Figure 4(e) to Figure 4(i). In the case of the topological charge m = 1 , the size of a dark spot inside a first ring is ~5.6 µm measured at ( 1 − 1 / e 2 ) intensity level. Setting the length of the axial profile to four times larger values L = 4 mm immediately results in the appearance of a good pronounced concentric structure with nine rings in it for both topological charges. The sizes of the central rings surrounding the vortex cores with topological charges m = 1 (Figure 4(f)) and m = 2 (Figure 4(j)) do not change significantly. Lastly, setting the length of the super-Gaussian axial profile to L = 8 mm gives us the transverse intensity patterns depicted in Figure 4(g) and (k). In a similar fashion to the non-vortical optical needle, see Figure 4(c), the ring-like structure of the field becomes more pronounced. We verify the intended action of the phase mask by measuring the intensity on the first ring while performing a z scan, see Figure 4(h,l). In both cases, the axial profile of the vortical beams with the shortest length L = 1 mm resembles our expectation well; see the black curves in Figure 4(h,l). Longer axial profiles have expected lengths but are somehow distorted; see the green curves in Figure 4(h,l). This might happen due to the azimuthal intensity fluctuations on the first ring, compare to Figure 4(f,j) - we might have used a non-optimal detection method or some misalignment are present in the optical setup. The situation improves for axial profiles designed with length L = 8 mm; see the red curves in Figure 4(h,l). For the topological charge m = 1 , we were able to measure the intended axial profile. The axial profile of the topological charge m = 2 is flat enough, but some spikes appear. As we do not integrate azimuths into a ring but measure them at a single azimuthal angle, this might occur due to the coherent addition of a small background, which causes splitting of the central vortex and the appearance of single charged vortices [89,90]. Figure 4 (m, n, o) show the cross sections of the m = 2 beams marked by a red line in Figures (i, j, k), respectively. As stated above, the main ring is intensity dominant for the shortest optical needle. The first side ring is less than 20% of the maximum (Fig. Figure 4). Side rings appear with increasing length of the optical needle. For the case of L = 4 mm, the first side ring is 55% while for the case of L = 8 mm it is 65%. Both of these values are higher compared to the second ring intensity of the ideal 2nd order Bessel beam which would be 42% of the maximum. The size of the dark central spot is ~11.2 µm, which is twice as large compared to the intensity minima of the vortical optical needle of topological charge m = 1 . Lastly, in Figure 4 (p) we present x z distributions of optical needles of lengths L = 1 , L = 4 and L = 8 mm and with topological charge m = 2 . Smooth intensity distributions are generated for optical needles with L = 1 mm and L = 4 mm. In the case of L = 8 mm axial modulation is present that might occur due to splitting of the central vortex into single charged vortices [89,90] as mentioned before.

3.3. Creation of an Array of Optical Needles

Having ensured ourselves that single vortical Bessel-like beams with controllable axial profile can be created similarly as optical vortices, we proceed to the experimental verification of the creation of an array of independent optical needles using Equation (11). In our previous study, we have already investigated this question, see Ref. [55], but as the optical setup differs from that used in those studies, we will briefly verify that those results are still valid under different conditions.
For this purpose, we create four different phase masks for a set of three optical needles with topological charges m = 0 , angles φ 12 = − π / 4 , and φ 13 = 3 π / 4 having four distinct values of ρ 12 = ρ 13 , see Figure 5. In the first case, we wish to create an array where two adjacent optical needles are separated by ρ 12 = 20 λ , see Figure 5 (a). We observe a homogeneous rod-shaped structure, which appears in the combined beam, with a transverse length similar to the combined distance ρ 12 + ρ 13 = 40 λ . However, the side lobes in the direction perpendicular to the axis of the array are comparatively strong, making the spatial lobe of the combined beam complex. This is an expected outcome, as we estimate f / ≈ 9 . This implies a classical diffraction limit of approximately 11.5 µm or approximately 22.1 λ , so the individual objects are not resolvable in Figure 5 (a). Moving on to the next case, when ρ 12 = ρ 13 = 40 λ , see Figure 5 (b), we observe a separation of the rod-shaped structure in the center of the array into three distinct lobes, located in the engineered positions, and separated by less intense rod-shaped intensity patters. This is a minimal separation distance that we have detected to have a distinct three-spike pattern. A further increase in the separation parameter to ρ 12 = ρ 13 = 60 λ results in visibly enhanced central lobes of individual optical needles and reduces the intensity of the side lobes; see Figure 5 (c). Most notably, though individual objects had only one-two intense rings in the transverse plane, see Figure 4 (a), the structure of the side lobe appears to be spatially larger than that of a single needle. Moving on to even larger spatial separation ρ 12 = ρ 13 = 80 λ results in a clearly pronounced array of three optical needles with additional interference patterns; see Figure 5 (d).
Thus, we have confirmed that the optical setup in use acts as intended.

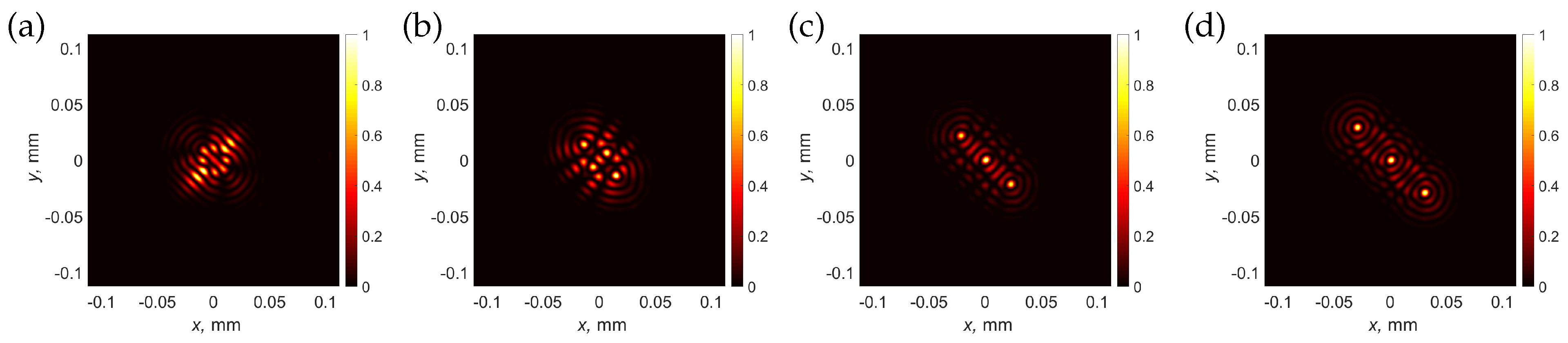
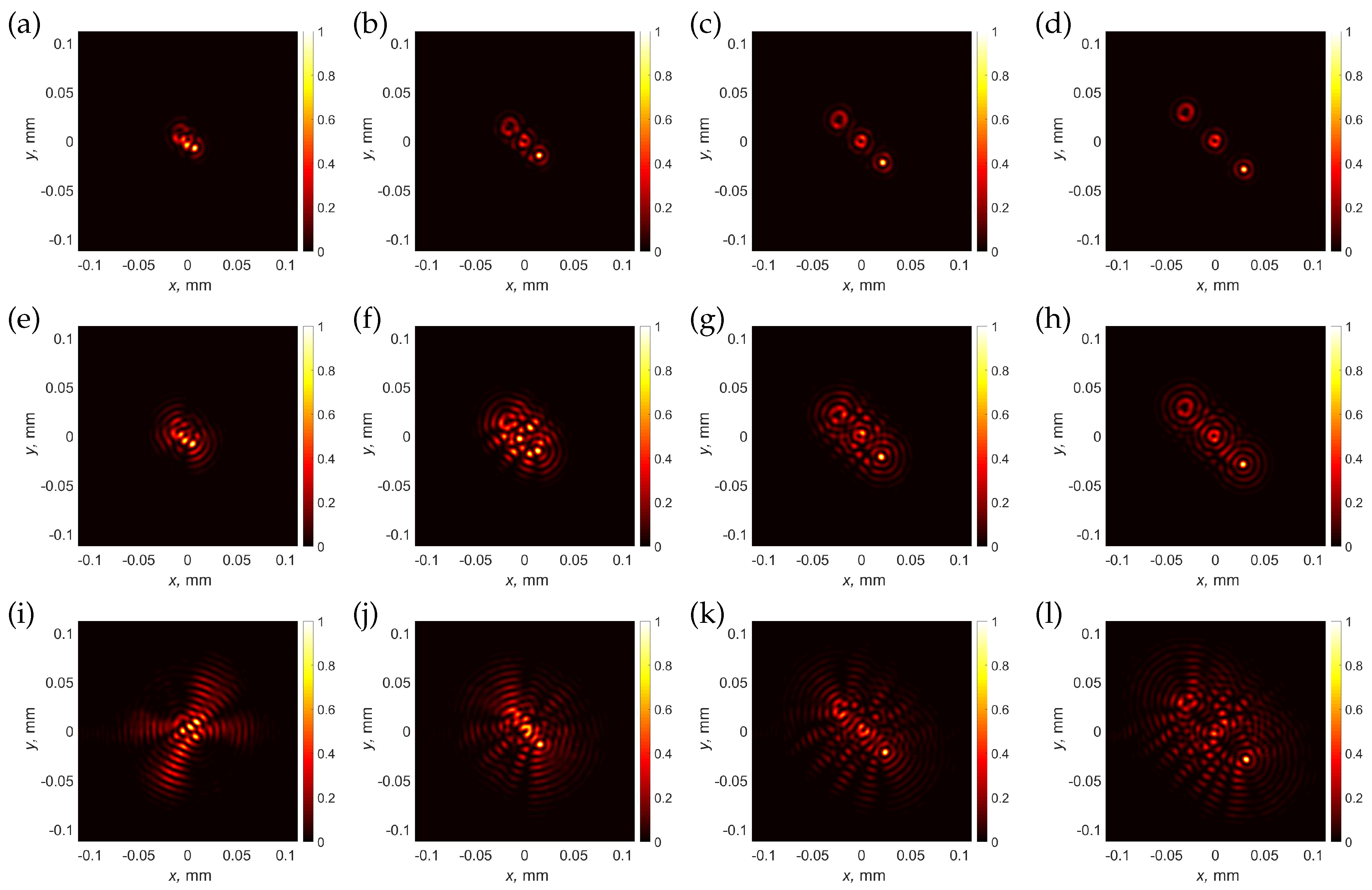
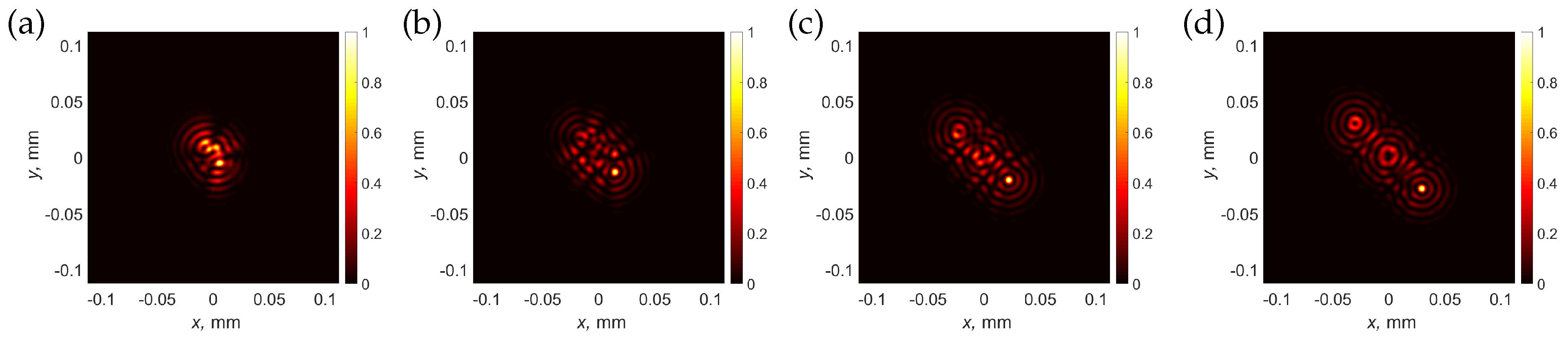
3.4. Creation of an Array of Vortical Needles with Individual Topological Charges

In this Section we introduce into array individual topological charges m. We start with a particular example of three optical vortical needles with topological charges m 1 = 1 , m 2 = 2 , m 3 = 0 . We investigate how the lengths L of individual super-Gaussian axial profiles together with separation distances ρ 12 and ρ 13 influence the resulting intensity profile of the combined beam, see Figure 6.
The first case, which we study, is the case where the azimuthal locations of adjacent vortical structures are given by angles φ 12 = − π / 4 and φ 13 = 3 π / 4 . Separation distances are ρ 12 = ρ 13 in all cases. We note that the interference pattern of overlapping Laguerre-Gaussian vortices was studied in Ref. [91], so in the case of coaxial Bessel vortices, we should expect some similar effects. In the first case, we wish to create an array where two adjacent optical needles are separated by ρ 12 = 20 λ , see Figure 6 (a,e,i). In general, we see that for all axial profile lengths L the introduction of vorticity has resulted in a largely skewed and distorted profile, although needles with charges m 3 = 0 and m 2 = 2 can be recognized in the profile of the combined beam for the smallest length L = 1 mm. Longer structures are unrecognizable; see Figure 6 (e,i).
As a next step, we increase the separation lengths ρ 12 = ρ 13 to 40 λ , see Figure 6 (b,f,j). For the case with the shortest lengths L = 1 mm, we observe an almost complete separation of individual profiles, see Figure 6 (b). The increase in the length of the optical vortical needle distorts the combined beam; see Figure 6 (f,j). A further increase in the separation of individual optical beams to ρ 12 = ρ 13 = 60 λ is shown in Figure 6 (c,g,k). We see that for L = 1 mm, the individual transverse profiles are now fully separated; see Figure 6 (c). A twofold increase in the length of individual objects is induced as multiple interference patterns between adjacent to the individual center rings, but the structure is recognizable and looks as expected, see Figure 6 (g). A further twofold increase in the length of the optical needles induces stronger interference distortions, see Figure 6 (k), and, as expected, the central optical needle is the most distorted. Lastly, we further increase the separation distance to ρ 12 = ρ 13 = 80 λ , see Figure 6 (d,h,l). The first two cases are distinctly pronounced, see Figure 6 (d, h), while the array of three longest needles shows the main destroyed features of the central and upper structure in the transverse plane, see Figure 6 (l).
Lastly, we are curious whether the order of topological charges in the combined array has any influence on the quality of the combined beam, see Figure 7. For this investigation, we chose an intermediate length of an individual structure L = 2 mm, and the individual topological charges are now m 1 = 2 , m 2 = 1 , m 3 = 0 . The general idea behind this experiment is that the spatial extent of the higher order vortex is larger, so the change in the spatial position of the vortex with topological charge m = 2 will have an immediate effect on the intensity pattern of the combined beam.
As expected, spatial separation ρ 12 = ρ 13 = 20 λ does not show improvement; see Figure 7 (a). The slight increase of ρ 12 = ρ 13 to 40 λ , see Figure 7 (b) demonstrates that only the non-vortical spike is recognized. However, most notably, when ρ 12 = ρ 13 = 60 λ , see Figure 7 (c), we observe that the topological charge needle m = 2 being central affects adjacent beams more than in the previous case, compared to Figure 6 (g). This means that the choice of the optimal separation distance depends not only on individual topological charges, but also on the local position of that structure within an array. Lastly, we select ρ 12 = ρ 13 = 80 λ , see Figure 6 (d). When comparing this combined beam with the previous case, see Figure 6 (h), we observe that due to the larger spatial extent, the vortical needle with topological charge m = 2 is now more distorted due to the presence of two adjacent optical needles.

3.5. Creation of an Array of Vortical Needles with Complex Positions and Axial Profiles

Lastly, given we found an optimal separation distance of ρ 12 = 80 λ , we aim to create a more complex array of vortical Bessel-like needles with individual positions in the space around the focal point; see Figure 8.
In this case, we create a structure of seven independent vortical needle-like structures. For convenience, we did select their lengths to be the same, that is, L = 1 mm and topological charges m = 1 , however, the positions of those individual vortex needles were different.
The amplitude and phase distribution of the mask are shown in Figure 8 (a,b). The longitudinal intensity profile is shown in Figure 8 (c). We observe the intended propagation of the combined beam, although the vortical cores with topological charges m = 1 are not optimally resolved. This effect is caused by the fact that the resolution of the SLM in use is somehow pushed to the limit, and the z scan quality, blur, appears due to scan inhomogeneities and some inevitable inaccuracies. The signal-to-noise ratio in this case was estimated from Figure 8 (e) comparing the minimal value in the center to the maximum value, and it was S N R = 200 .
Inspection of the array at four individual positions z is presented in Figure 8 (d-g). We do observe some side-lobes in parts peripheral to vortex cores, but the main vortical pairs of vortical needles seem to be intact though slightly distorted.

4. Discussion and Conclusions

We have discussed the creation of complex structures consisting of a number of individual vortical optical needles with individual topological charges.
We have introduced a versatile method that empowers the controlled creation of arrays of parallel optical vortical needles with independent axial intensity profiles and topological charges. Our analysis delves into the interplay between the separation of individual optical vortical needles and their respective lengths. We observe that destructive interference between adjacent needles is less pronounced when they vary in length. Preliminary findings suggest that this phenomenon arises from the distinct spatial modulation in Fourier space associated with optical needles of different lengths. The distortion between neighboring optical needles is the result of spatial overlap, emphasizing the importance of minimizing such overlap for optimal results. However, this technique imposes limitations on the smallest separation between the beams, the length of the needle, the topological charge, or the width of the beam.
Additionally, we have introduced a step-like axial intensity profile described using a super-Gaussian function. This choice mitigates issues related to the Gibbs phenomenon, ensuring a smooth varying profile and sharp edges. Our experimentation has identified the optimal parameter for the super-Gaussian function as N = 7 .
In conclusion, the presented method facilitates the creation of diverse spatial intensity distributions in three dimensions, potentially finding applications in specific microfabrication tasks or other contexts.

Author Contributions

“Conceptualization, S.O.; methodology, S.O.; software, S.O. and P.Š.; validation, P.Š; formal analysis, S.O.; investigation, P.Š.; resources, S.O.; data curation, P.Š.; writing—original draft preparation, S.O.; writing—review and editing, S.O. and P.Š.; visualization, P.Š.; supervision, S.O.; project administration, S.O.; funding acquisition, S.O. All authors have read and agreed to the published version of the manuscript.”

Funding

This research has received funding from the Research Council of Lithuania (LMTLT) via agreement No [S-MIP-23-71].

Data Availability Statement

Data will be made available on request

Conflicts of Interest

“The authors declare no conflict of interest.”

Abbreviations

The following abbreviations are used in this manuscript:
SLM Spatial Light Modulator
FWHM Full Width at Half Maximum
CCD Charge-Coupled Device
LD Linear dichroism

References

  1. Orazi, L.; Romoli, L.; Schmidt, M.; Li, L. Ultrafast laser manufacturing: From physics to industrial applications. CIRP Ann. 2021, 70, 543–566. [Google Scholar] [CrossRef]
  2. Sibbett, W.; Lagatsky, A.A.; Brown, C.T.A. The development and application of femtosecond laser systems. Opt. Express 2012, 20, 6989–7001. [Google Scholar] [CrossRef]
  3. Sussulini, A.; Becker, J.S.; Becker, J.S. Laser ablation ICP-MS: Application in biomedical research. Mass Spectrom. Rev. 2017, 36, 47–57. [Google Scholar] [CrossRef]
  4. Knox, W. Ultrafast technology in telecommunications. IEEE J. Sel. Top. Quantum Electron. 2000, 6, 1273–1278. [Google Scholar] [CrossRef]
  5. Weng, Y.; Ip, E.; Pan, Z.; Wang, T. Advanced Spatial-Division Multiplexed Measurement Systems Propositions—From Telecommunication to Sensing Applications: A Review. Sensors 2016, 16. [Google Scholar] [CrossRef]
  6. Rubinsztein-Dunlop, H.; Forbes, A.; Berry, M.V.; Dennis, M.R.; Andrews, D.L.; Mansuripur, M.; Denz, C.; Alpmann, C.; Banzer, P.; Bauer, T.; et al. Roadmap on structured light. J. Opt. 2016, 19, 013001. [Google Scholar] [CrossRef]
  7. Angelsky, O.V.; Bekshaev, A.Y.; Hanson, S.G.; Zenkova, C.Y.; Mokhun, I.I.; Jun, Z. Structured light: Ideas and concepts. Front. Phys. 2020, 8, 114. [Google Scholar] [CrossRef]
  8. Courvoisier, F. Nonstandard Light for Ultrafast Laser Microstructuring and Nanostructuring. In Ultrafast Laser Nanostructuring: The Pursuit of Extreme Scales; 2023; pp. 581–621. [Google Scholar]
  9. Porfirev, A.; Khonina, S.; Kuchmizhak, A. Light–matter interaction empowered by orbital angular momentum: Control of matter at the micro-and nanoscale. Progress in Quantum Electronics 2023, 100459. [Google Scholar] [CrossRef]
  10. Durnin, J. Exact solutions for nondiffracting beams. I. The scalar theory. JOSA A 1987, 4, 651–654. [Google Scholar] [CrossRef]
  11. Durnin, J.; Miceli Jr, J.; Eberly, J.H. Diffraction-free beams. Phys. Rev. Lett. 1987, 58, 1499. [Google Scholar] [CrossRef]
  12. Khonina, S.N.; Kazanskiy, N.L.; Karpeev, S.V.; Butt, M.A. Bessel Beam: Significance and Applications—A Progressive Review. Micromachines 2020, 11, 997. [Google Scholar] [CrossRef]
  13. Grunwald, R.; Bock, M. Needle beams: A review. Adv. Physics: X 2020, 5, 1736950. [Google Scholar] [CrossRef]
  14. Misawa, H.; Juodkazis, S. 3D laser microfabrication: Principles and applications; John Wiley & Sons, 2006. [Google Scholar]
  15. Jarutis, V.; Paškauskas, R.; Stabinis, A. Focusing of Laguerre–Gaussian beams by axicon. Opt. Commun. 2000, 184, 105–112. [Google Scholar] [CrossRef]
  16. Khonina, S.N.; Kazanskiy, N.L.; Khorin, P.A.; Butt, M.A. Modern types of axicons: New functions and applications. Sensors 2021, 21, 6690. [Google Scholar] [CrossRef]
  17. Bhuyan, M.K.; Courvoisier, F.; Lacourt, P.A.; Jacquot, M.; Salut, R.; Furfaro, L.; Dudley, J.M. High aspect ratio nanochannel machining using single shot femtosecond Bessel beams. Appl. Phys. Lett. 2010, 97, 081102. [Google Scholar] [CrossRef]
  18. Chen, L.; Yu, D. Investigation of low-cost through glass vias formation on borosilicate glass by picosecond laser-induced selective etching. J. Mater. Sci. Mater. Electron. 2021, 32, 16481–16493. [Google Scholar] [CrossRef]
  19. Mikutis, M.; Kudrius, T.; Šlekys, G.; Paipulas, D.; Juodkazis, S. High 90% efficiency Bragg gratings formed in fused silica by femtosecond Gauss-Bessel laser beams. Opt. Mater. Express 2013, 3, 1862–1871. [Google Scholar] [CrossRef]
  20. Meyer, R.; Froehly, L.; Giust, R.; Del Hoyo, J.; Furfaro, L.; Billet, C.; Courvoisier, F. Extremely high-aspect-ratio ultrafast Bessel beam generation and stealth dicing of multi-millimeter thick glass. Appl. Phys. Lett. 2019, 114, 201105. [Google Scholar] [CrossRef]
  21. Rapp, L.; Meyer, R.; Furfaro, L.; Billet, C.; Giust, R.; Courvoisier, F. High speed cleaving of crystals with ultrafast Bessel beams. Opt. Express 2017, 25, 9312–9317. [Google Scholar] [CrossRef]
  22. Feuer, A.; Thomas, J.U.; Freitag, C.; Weber, R.; Graf, T. Single-pass laser separation of 8 mm thick glass with a millijoule picosecond pulsed Gaussian–Bessel beam. Appl. Phys. A 2019, 125, 332. [Google Scholar] [CrossRef]
  23. Minkevičius, L.; Jokubauskis, D.; Kašalynas, I.; Orlov, S.; Urbas, A.; Valušis, G. Bessel terahertz imaging with enhanced contrast realized by silicon multi-phase diffractive optics. Opt. Express 2019, 27, 36358–36367. [Google Scholar] [CrossRef]
  24. McGloin, D.; Garcés-Chávez, V.; Dholakia, K. Interfering Bessel beams for optical micromanipulation. Opt. Lett. 2003, 28, 657–659. [Google Scholar] [CrossRef]
  25. Gao, L.; Shao, L.; Chen, B.C.; Betzig, E. 3D live fluorescence imaging of cellular dynamics using Bessel beam plane illumination microscopy. Nat. Protoc. 2014, 9, 1083–1101. [Google Scholar] [CrossRef]
  26. Zhu, M.; Cao, Q.; Gao, H. Creation of a 50,000 λ long needle-like field with 0.36 λ width. JOSA A 2014, 31, 500–504. [Google Scholar] [CrossRef]
  27. Lightman, S.; Gvishi, R.; Hurvitz, G.; Arie, A. Shaping of light beams by 3D direct laser writing on facets of nonlinear crystals. Opt. Lett. 2015, 40, 4460–4463. [Google Scholar] [CrossRef]
  28. Courvoisier, F.; Zhang, J.; Bhuyan, M.; Jacquot, M.; Dudley, J.M. Applications of femtosecond Bessel beams to laser ablation. Appl. Phys. A 2013, 112, 29–34. [Google Scholar] [CrossRef]
  29. Gotovski, P.; Šlevas, P.; Orlov, S.; Ulčinas, O.; Urbas, A. Generation of an optical needle beam with a laser inscribed Pancharatnam-Berry phase element under imperfect conditions. Opt. Express 2021, 29, 33331–33345. [Google Scholar] [CrossRef]
  30. Šlevas, P.; Mundrys, K.; Ulčinas, O.; Orlov, S. An optical needle with elongated transversal profile created using Airy beams for laser processing of glasses. Opt. Laser Technol. 2024, 174, 110558. [Google Scholar] [CrossRef]
  31. Orlov, S.; Stabinis, A. Propagation of superpositions of coaxial optical Bessel beams carrying vortices. J. Opt. A: Pure Appl. Opt. 2004, 6, S259. [Google Scholar] [CrossRef]
  32. Doan, D.H.; Iida, R.; Kim, B.; Satoh, I.; Fushinobu, K. Bessel beam laser-scribing of thin film silicon solar cells by ns pulsed laser. J. Therm. Sci. Technol. 2016, 11, JTST0011–JTST0011. [Google Scholar] [CrossRef]
  33. Wetzel, B.; Xie, C.; Lacourt, P.A.; Dudley, J.M.; Courvoisier, F. Femtosecond laser fabrication of micro and nano-disks in single layer graphene using vortex Bessel beams. Appl. Phys. Lett. 2013, 103. [Google Scholar] [CrossRef]
  34. Li, X.; Xu, Z.; Jiang, L.; Shi, Y.; Wang, A.; Huang, L.; Wei, Q. Creating a three-dimensional surface with antireflective properties by using femtosecond-laser Bessel-beam-assisted thermal oxidation. Opt. Lett. 2020, 45, 2989–2992. [Google Scholar] [CrossRef]
  35. Jaroszewicz, Z.; Sochacki, J.; Kołodziejczyk, A.; Staronski, L.R. Apodized annular-aperture logarithmic axicon: Smoothness and uniformity of intensity distributions. Opt. Lett. 1993, 18, 1893–1895. [Google Scholar] [CrossRef]
  36. Golub, I.; Chebbi, B.; Shaw, D.; Nowacki, D. Characterization of a refractive logarithmic axicon. Opt. Lett. 2010, 35, 2828–2830. [Google Scholar] [CrossRef]
  37. Čižmár, T.; Dholakia, K. Tunable Bessel light modes: Engineering the axial propagation. Opt. Express 2009, 17, 15558–15570. [Google Scholar] [CrossRef]
  38. Orlov, S.; Juršėnas, A.; Nacius, E. Optical Bessel-like beams with engineered axial phase and intensity distribution. J. Laser Micro Nanoeng. 2018, 13, 244–248. [Google Scholar]
  39. Dharmavarapu, R.; Bhattacharya, S.; Juodkazis, S. Diffractive optics for axial intensity shaping of Bessel beams. J. Opt. 2018, 20, 085606. [Google Scholar] [CrossRef]
  40. Gutiérrez-Vega, J.C.; Iturbe-Castillo, M.; Chávez-Cerda, S. Alternative formulation for invariant optical fields: Mathieu beams. Opt. Lett. 2000, 25, 1493–1495. [Google Scholar] [CrossRef]
  41. Bandres, M.A.; Rodríguez-Lara, B. Nondiffracting accelerating waves: Weber waves and parabolic momentum. New J. Phys. 2013, 15, 013054. [Google Scholar] [CrossRef]
  42. Orlov, S.; Vosylius, V.; Gotovski, P.; Grabusovas, A.; Baltrukonis, J.; Gertus, T. Vector beams with parabolic and elliptic cross-sections for laser material processing applications. J. Laser Micro Nanoeng. 2018, 13, 280–286. [Google Scholar]
  43. Berry, M.V.; Balazs, N.L. Nonspreading wave packets. Am. J. Phys. 1979, 47, 264–267. [Google Scholar] [CrossRef]
  44. Siviloglou, G.A.; Broky, J.; Dogariu, A.; Christodoulides, D.N. Observation of Accelerating Airy Beams. Phys. Rev. Lett. 2007, 99, 213901. [Google Scholar] [CrossRef]
  45. Baumgartl, J.; Mazilu, M.; Dholakia, K. Optically mediated particle clearing using Airy wavepackets. Nat. Photonics 2008, 2, 675–678. [Google Scholar] [CrossRef]
  46. Cheng, H.; Zang, W.; Zhou, W.; Tian, J. Analysis of optical trapping and propulsion of Rayleigh particles using Airy beam. Opt. Express 2010, 18, 20384–20394. [Google Scholar] [CrossRef] [PubMed]
  47. Zheng, Z.; Zhang, B.F.; Chen, H.; Ding, J.; Wang, H.T. Optical trapping with focused Airy beams. Appl. Opt. 2011, 50, 43–49. [Google Scholar] [CrossRef]
  48. Mathis, A.; Courvoisier, F.; Froehly, L.; Furfaro, L.; Jacquot, M.; Lacourt, P.A.; Dudley, J.M. Micromachining along a curve: Femtosecond laser micromachining of curved profiles in diamond and silicon using accelerating beams. Appl. Phys. Lett. 2012, 101, 071110. [Google Scholar] [CrossRef]
  49. Manousidaki, M.; Papazoglou, D.G.; Farsari, M.; Tzortzakis, S. Abruptly autofocusing beams enable advanced multiscale photo-polymerization. Optica 2016, 3, 525–530. [Google Scholar] [CrossRef]
  50. Ivaškevičiūtė-Povilauskienė, R.; Kizevičius, P.; Nacius, E.; Jokubauskis, D.; Ikamas, K.; Lisauskas, A.; Alexeeva, N.; Matulaitienė, I.; Jukna, V.; Orlov, S.; et al. Terahertz structured light: Nonparaxial Airy imaging using silicon diffractive optics. Light. Sci. & Appl. 2022, 11, 326. [Google Scholar] [CrossRef]
  51. Duocastella, M.; Arnold, C.B. Bessel and annular beams for materials processing. Laser Photonics Rev. 2012, 6, 607–621. [Google Scholar] [CrossRef]
  52. Stoian, R.; Bhuyan, M.K.; Zhang, G.; Cheng, G.; Meyer, R.; Courvoisier, F. Ultrafast Bessel beams: Advanced tools for laser materials processing. Adv. Opt. Technol. 2018, 7, 165–174. [Google Scholar] [CrossRef]
  53. Wang, J.; Chen, W.; Zhan, Q. Engineering of high purity ultra-long optical needle field through reversing the electric dipole array radiation. Opt. Express 2010, 18, 21965–21972. [Google Scholar] [CrossRef]
  54. Rogers, E.T.; Savo, S.; Lindberg, J.; Roy, T.; Dennis, M.R.; Zheludev, N.I. Super-oscillatory optical needle. Appl. Phys. Lett. 2013, 102. [Google Scholar] [CrossRef]
  55. Orlov, S.; Juršėnas, A.; Baltrukonis, J.; Jukna, V. Controllable spatial array of Bessel-like beams with independent axial intensity distributions for laser microprocessing. J. Laser Micro Nanoeng. 2018, 13, 324–329. [Google Scholar]
  56. Coullet, P.; Gil, L.; Rocca, F. Optical vortices. Opt. Commun. 1989, 73, 403–408. [Google Scholar] [CrossRef]
  57. Gahagan, K.; Swartzlander, G.J. Optical vortex trapping of particles. Opt. Lett. 1996, 21, 827–829. [Google Scholar] [CrossRef]
  58. Molina-Terriza, G.; Torres, J.P.; Torner, L. Twisted photons. Nat. Phys. 2007, 3, 305–310. [Google Scholar] [CrossRef]
  59. Shen, Y.; Wang, X.; Xie, Z.; Min, C.; Fu, X.; Liu, Q.; Gong, M.; Yuan, X. Optical vortices 30 years on: OAM manipulation from topological charge to multiple singularities. Light. Sci. Appl. 2019, 8, 1–29. [Google Scholar] [CrossRef]
  60. Porfirev, A.P.; Kuchmizhak, A.A.; Gurbatov, S.O.; Juodkazis, S.; Khonina, S.N.; Kulchin, Y.N. Phase singularities and optical vortices in photonics. Phys. Usp. 2022, 65, 789–811. [Google Scholar] [CrossRef]
  61. Allen, L.; Beijersbergen, M.W.; Spreeuw, R.J.C.; Woerdman, J.P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 1992, 45, 8185–8189. [Google Scholar] [CrossRef]
  62. Chávez-Cerda, S.; McDonald, G.; New, G. Nondiffracting beams: Travelling, standing, rotating and spiral waves. Opt. Commun. 1996, 123, 225–233. [Google Scholar] [CrossRef]
  63. Kotlyar, V.; Soifer, V.; Khonina, S. An algorithm for the generation of laser beams with longitudinal periodicity: Rotating images. J. Mod. Opt. 1997, 44, 1409–1416. [Google Scholar] [CrossRef]
  64. Khonina, S.; Kotlyar, V.; Soifer, V.; Lautanen, J.; Honkanen, M.; Turunen, J. Generating a couple of rotating nondiffracting beams using a binary-phase DOE. Opt.-Int. J. Light Electron Opt. 1999, 110, 137–144. [Google Scholar]
  65. Tervo, J.; Turunen, J. Rotating scale-invariant electromagnetic fields. Opt. Express 2001, 9, 9–15. [Google Scholar] [CrossRef] [PubMed]
  66. Leach, J.; Dennis, M.R.; Courtial, J.; Padgett, M.J. Knotted threads of darkness. Nature 2004, 432, 165–165. [Google Scholar] [CrossRef] [PubMed]
  67. Dennis, M.R.; King, R.P.; Jack, B.; O’holleran, K.; Padgett, M.J. Isolated optical vortex knots. Nat. Phys. 2010, 6, 118–121. [Google Scholar] [CrossRef]
  68. Sugic, D.; Dennis, M.R. Singular knot bundle in light. JOSA A 2018, 35, 1987–1999. [Google Scholar] [CrossRef] [PubMed]
  69. Bode, B.; Dennis, M.R.; Foster, D.; King, R.P. Knotted fields and explicit fibrations for lemniscate knots. Proc. R. Soc. A: Math. Phys. Eng. Sci. 2017, 473, 20160829. [Google Scholar] [CrossRef] [PubMed]
  70. Lasagni, A.F.; Gachot, C.; Trinh, K.E.; Hans, M.; Rosenkranz, A.; Roch, T.; Eckhardt, S.; Kunze, T.; Bieda, M.; Günther, D.; et al. Direct laser interference patterning, 20 years of development: From the basics to industrial applications. In Proceedings of the Laser-based micro-and nanoprocessing XI; SPIE, 2017; Volume 10092, pp. 186–196. [Google Scholar]
  71. Zabila, Y.; Perzanowski, M.; Dobrowolska, A.; Kąc, M.; Polit, A.; Marszałek, M. Direct laser interference patterning: Theory and application. Acta Phys. Pol. A 2009, 115, 591–593. [Google Scholar] [CrossRef]
  72. Si, J.; Feng, Z.; Cheng, D.; Wang, Y. Freeform beam splitting system design for generating an array of identical sub-beams. Opt. Express 2021, 29, 29918–29935. [Google Scholar] [CrossRef]
  73. Kahle, M.; Nodop, D.; Rücker, J. Beam shaping and splitting for high-power USP-lasers. Procedia CIRP 2020, 94, 807–811. [Google Scholar] [CrossRef]
  74. Katz, S.; Kaplan, N.; Grossinger, I. Using Diffractive Optical Elements: DOEs for beam shaping–fundamentals and applications. Opt. Photonik 2018, 13, 83–86. [Google Scholar] [CrossRef]
  75. Brodsky, A.; Kaplan, N. Laser surface texturing using a single diffractive optical element as an alternative for direct laser interference patterning. J. Laser Appl. 2020, 32. [Google Scholar] [CrossRef]
  76. Bowman, R.; Muller, N.; Zambrana-Puyalto, X.; Jedrkiewicz, O.; Di Trapani, P.; Padgett, M. Efficient generation of Bessel beam arrays by means of an SLM. Eur. Phys. J. Spec. Top. 2011, 199, 159–166. [Google Scholar] [CrossRef]
  77. Lutz, C.; Schwarz, S.; Marx, J.; Esen, C.; Hellmann, R. Multi-Bessel Beams Generated by an Axicon and a Spatial Light Modulator for Drilling Applications. Photonics 2023, 10. [Google Scholar] [CrossRef]
  78. Stankevicius, E.; Garliauskas, M.; Raciukaitis, G. Bessel-like beam array generation using round-tip microstructures and their use in the material treatment. J. Laser Micro Nanoeng. 2016, 11, 352. [Google Scholar]
  79. Dudutis, J.; Stonys, R.; Račiukaitis, G.; Gečys, P. Aberration-controlled Bessel beam processing of glass. Opt. Express 2018, 26, 3627–3637. [Google Scholar] [CrossRef]
  80. Novotny, L.; Hecht, B. Principles of nano-optics; Cambridge university press, 2012. [Google Scholar]
  81. Jenne, M.; Flamm, D.; Ouaj, T.; Hellstern, J.; Kleiner, J.; Grossmann, D.; Koschig, M.; Kaiser, M.; Kumkar, M.; Nolte, S. High-quality tailored-edge cleaving using aberration-corrected Bessel-like beams. Opt. Lett. 2018, 43, 3164–3167. [Google Scholar] [CrossRef]
  82. Zamboni-Rached, M.; Recami, E.; Hernández-Figueroa, H.E. Theory of “frozen waves”: Modeling the shape of stationary wave fields. JOSA A 2005, 22, 2465–2475. [Google Scholar] [CrossRef]
  83. Yan, W.; Gao, Y.; Yuan, Z.; Wang, Z.; Ren, Z.C.; Wang, X.L.; Ding, J.; Wang, H.T. Non-diffracting and self-accelerating Bessel beams with on-demand tailored intensity profiles along arbitrary trajectories. Opt. Lett. 2021, 46, 1494–1497. [Google Scholar] [CrossRef]
  84. Lutz, C.; Schwarz, S.; Marx, J.; Esen, C.; Hellmann, R. Multi-Bessel Beams Generated by an Axicon and a Spatial Light Modulator for Drilling Applications. Photonics 2023, 10, 413. [Google Scholar] [CrossRef]
  85. Zeng, Y.; Yu, Y.; Wu, P.; Chen, M.; Zheng, S.; Pan, M.; Zhan, Q. Generation of a linear array of focal spots with prescribed characteristic using the radiation pattern from a tapered line source antenna. Opt. Commun. 2023, 534, 129329. [Google Scholar] [CrossRef]
  86. Lutz, C.; Schwarz, S.; Rung, S.; Marx, J.; Esen, C.; Hellmann, R. Optical system for multi Bessel beam high power ultrashort pulsed laser processing using a spatial light modulator. In Proceedings of the Lasers in Manufacturing-LiM 2021; 2021. [Google Scholar]
  87. Stratton, J.A. Electromagnetic theory; John Wiley & Sons, 2007; Volume 33. [Google Scholar]
  88. Wang, Y.; Potoček, V.; Barnett, S.M.; Feng, X. Programmable holographic technique for implementing unitary and nonunitary transformations. Phys. Rev. A 2017, 95, 033827. [Google Scholar] [CrossRef]
  89. Orlov, S.; Regelskis, K.; Smilgevičius, V.; Stabinis, A. Propagation of Bessel beams carrying optical vortices. Opt. Commun. 2002, 209, 155–165. [Google Scholar] [CrossRef]
  90. Orlov, S.; Stabinis, A. Free-space propagation of light field created by Bessel–Gauss and Laguerre–Gauss singular beams. Opt. Commun. 2003, 226, 97–105. [Google Scholar] [CrossRef]
  91. Pyragaite, V.; Stabinis, A. Free-space propagation of overlapping light vortex beams. Opt. Commun. 2002, 213, 187–191. [Google Scholar] [CrossRef]
Preprints 98938 g001
Figure 1. Examples of axial profiles used for both numerical simulations and experimental measurements, the order of the super-Gaussian function is N = 3 , 5 , 7 in (a), (b), and (c), respectively. The lengths L of the axial profile function f ( z ) are 1 mm (black), 4 mm (green), 8 mm (red).
Figure 1. Examples of axial profiles used for both numerical simulations and experimental measurements, the order of the super-Gaussian function is N = 3 , 5 , 7 in (a), (b), and (c), respectively. The lengths L of the axial profile function f ( z ) are 1 mm (black), 4 mm (green), 8 mm (red).
Preprints 98938 g001
Preprints 98938 g002
Figure 2. Depiction of the original and translated cylindrical coordinates. O is the original coordinate ( x 1 , ρ 1 , φ 1 ), O 1 is the center of the translated coordinate ( x 2 , ρ 2 , φ 2 ).
Figure 2. Depiction of the original and translated cylindrical coordinates. O is the original coordinate ( x 1 , ρ 1 , φ 1 ), O 1 is the center of the translated coordinate ( x 2 , ρ 2 , φ 2 ).
Preprints 98938 g002
Preprints 98938 g003
Figure 3. Optical setup of the experiments. HWP is the half-wave plate, BP is Brewster polarizer, MO1, MO2 are microscope objectives, L1, L2, L3, L4 and L5 are lenses, A1 and A2 are apertures, SLM is a spatial light modulator, BS is a beam splitter, M1 is a mirror, CCD is charge-coupled device camera.
Figure 3. Optical setup of the experiments. HWP is the half-wave plate, BP is Brewster polarizer, MO1, MO2 are microscope objectives, L1, L2, L3, L4 and L5 are lenses, A1 and A2 are apertures, SLM is a spatial light modulator, BS is a beam splitter, M1 is a mirror, CCD is charge-coupled device camera.
Preprints 98938 g003
Preprints 98938 g004
Figure 4. Transverse intensity distributions for vortical needles with topological charges m = 0 (a-c), m = 1 (e-g) and m = 2 (i-k) and lengths of the axial super-Gaussian profile L = 1 mm (a,e,i), L = 4 mm (b,f,j), L = 8 mm (c,g,k). Longitudinal axial profiles of vortical optical needles, measured in the brightest ring (or central lobe) for topological charges m = 0 (d), m = 1 (h) and m = 2 (l) and different lengths L = 8 mm (red), L = 4 mm (green) and L = 1 mm (black). Intensity distributions (m, n, o) of cross sections marked by a red line in (i, j, k), respectively. Longitudinal intensity distributions for optical needles with topological charge m = 2 (p).
Figure 4. Transverse intensity distributions for vortical needles with topological charges m = 0 (a-c), m = 1 (e-g) and m = 2 (i-k) and lengths of the axial super-Gaussian profile L = 1 mm (a,e,i), L = 4 mm (b,f,j), L = 8 mm (c,g,k). Longitudinal axial profiles of vortical optical needles, measured in the brightest ring (or central lobe) for topological charges m = 0 (d), m = 1 (h) and m = 2 (l) and different lengths L = 8 mm (red), L = 4 mm (green) and L = 1 mm (black). Intensity distributions (m, n, o) of cross sections marked by a red line in (i, j, k), respectively. Longitudinal intensity distributions for optical needles with topological charge m = 2 (p).
Preprints 98938 g004
Preprints 98938 g005
Figure 5. Transverse intensity distributions for an array of three optical needles with topological charges m = 0 and length of the axial super-Gaussian profile L = 1 mm. The spatial separation of the individual optical needles is ρ 12 = 20 λ (a), ρ 12 = 40 λ (b), ρ 12 = 60 λ (c), ρ 12 = 80 λ (d).
Figure 5. Transverse intensity distributions for an array of three optical needles with topological charges m = 0 and length of the axial super-Gaussian profile L = 1 mm. The spatial separation of the individual optical needles is ρ 12 = 20 λ (a), ρ 12 = 40 λ (b), ρ 12 = 60 λ (c), ρ 12 = 80 λ (d).
Preprints 98938 g005
Preprints 98938 g006
Figure 6. Transverse intensity distributions for an array of three optical needles with topological charges m 1 = 1 , m 2 = 2 , m 3 = 0 and length of axial super-Gaussian profile L = 1 mm (a-d), L = 2 mm (e-h) and L = 4 mm (i-l). The spatial separation of individual optical needles is ρ 12 = 20 λ (a,e,i), ρ 12 = 40 λ (b,f,j), ρ 12 = 60 λ (c,g,k), ρ 12 = 80 λ (d,h,l).
Figure 6. Transverse intensity distributions for an array of three optical needles with topological charges m 1 = 1 , m 2 = 2 , m 3 = 0 and length of axial super-Gaussian profile L = 1 mm (a-d), L = 2 mm (e-h) and L = 4 mm (i-l). The spatial separation of individual optical needles is ρ 12 = 20 λ (a,e,i), ρ 12 = 40 λ (b,f,j), ρ 12 = 60 λ (c,g,k), ρ 12 = 80 λ (d,h,l).
Preprints 98938 g006
Preprints 98938 g007
Figure 7. Transverse intensity distributions for an array of three optical needles with topological charges m 1 = 2 , m 2 = 1 , m 3 = 0 and length of the axial super-Gaussian profile L = 2 mm. The spatial separation of individual optical needles is ρ 12 = 20 λ (a), ρ 12 = 40 λ (b), ρ 12 = 60 λ (c), ρ 12 = 80 λ (d).
Figure 7. Transverse intensity distributions for an array of three optical needles with topological charges m 1 = 2 , m 2 = 1 , m 3 = 0 and length of the axial super-Gaussian profile L = 2 mm. The spatial separation of individual optical needles is ρ 12 = 20 λ (a), ρ 12 = 40 λ (b), ρ 12 = 60 λ (c), ρ 12 = 80 λ (d).
Preprints 98938 g007
Preprints 98938 g008
Figure 8. Phase (a) and amplitude (b) of the spatial spectra of a complex array of vortical needles. Longitudinal intensity distribution of an array of seven vortical optical needles with individual positions and topological charges (c). Transverse intensity distributions of an array and the particular positions in (c), marked green; see (d-g).
Figure 8. Phase (a) and amplitude (b) of the spatial spectra of a complex array of vortical needles. Longitudinal intensity distribution of an array of seven vortical optical needles with individual positions and topological charges (c). Transverse intensity distributions of an array and the particular positions in (c), marked green; see (d-g).
Preprints 98938 g008
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated